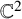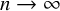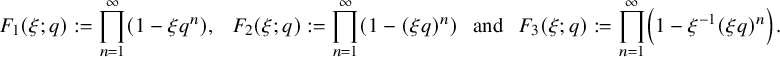1 Introduction and statement of results
A partition of a nonnegative integer n, denoted
![]() $\lambda \vdash n$
, is any nonincreasing sequence of positive integers, say
$\lambda \vdash n$
, is any nonincreasing sequence of positive integers, say
![]() $\lambda =(\lambda _1, \lambda _2, \dots , \lambda _m)$
, that satisfies
$\lambda =(\lambda _1, \lambda _2, \dots , \lambda _m)$
, that satisfies
![]() $|\lambda |:=\lambda _1+\dots +\lambda _m= n$
. As usual, we let
$|\lambda |:=\lambda _1+\dots +\lambda _m= n$
. As usual, we let
![]() $p(n)$
denote the number of such partitions. One hundred years ago, Hardy and Ramanujan [Reference Hardy and Ramanujan16] proved their striking asymptotic formula
$p(n)$
denote the number of such partitions. One hundred years ago, Hardy and Ramanujan [Reference Hardy and Ramanujan16] proved their striking asymptotic formula
 $$ \begin{align} p(n)\sim \frac{1}{4\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}{3}}}, \end{align} $$
$$ \begin{align} p(n)\sim \frac{1}{4\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}{3}}}, \end{align} $$
as
![]() $n\rightarrow \infty $
. This work marked the birth of the so-called Circle Method.
$n\rightarrow \infty $
. This work marked the birth of the so-called Circle Method.
Partitions appear in many areas of mathematics. We consider recently discovered structures that arise at the interface of algebraic combinatorics, algebraic geometry, number theory and topology, where the size n partitions play a prominent role in defining various integer-valued invariants. These invariants can be sorted by congruence conditions, resulting in identities of the form
where
![]() $C(a,b;n)$
counts those partitions whose invariant is in the congruence class
$C(a,b;n)$
counts those partitions whose invariant is in the congruence class
![]() $a\,\,(\mathrm {mod}\,\,{b})$
. In the spirit of Dirichlet’s Theorem on primes, where primes are equidistributed over admissible congruence classes, one may ask how the partitions are distributed, as
$a\,\,(\mathrm {mod}\,\,{b})$
. In the spirit of Dirichlet’s Theorem on primes, where primes are equidistributed over admissible congruence classes, one may ask how the partitions are distributed, as
![]() $n\to \infty $
, over the arithmetic progressions modulo
$n\to \infty $
, over the arithmetic progressions modulo
![]() $b.$
We answer these questions for t-hooks, which arise in work of Han [Reference Han14] that refined the Nekrasov–Okounkov hook product formula and for Betti numbers of various Hilbert schemes on n points in
$b.$
We answer these questions for t-hooks, which arise in work of Han [Reference Han14] that refined the Nekrasov–Okounkov hook product formula and for Betti numbers of various Hilbert schemes on n points in
![]() ${\mathbb {C}}^2$
, as established by Göttsche [Reference Göttsche10, Reference Göttsche11] and Buryak, Feigin and Nakajima [Reference Buryak, Feigin and Nakajima4, Reference Göttsche10, Reference Göttsche11].
${\mathbb {C}}^2$
, as established by Göttsche [Reference Göttsche10, Reference Göttsche11] and Buryak, Feigin and Nakajima [Reference Buryak, Feigin and Nakajima4, Reference Göttsche10, Reference Göttsche11].
We first consider the distribution of t-hooks. Each partition has a Ferrers–Young diagram
 $$ \begin{align*}\begin{matrix} \bullet & \bullet & \bullet & \dots & \bullet & \leftarrow & \lambda_1 \text{ many nodes}\\ \bullet & \bullet & \dots & \bullet & & \leftarrow & \lambda_2 \text{ many nodes}\\ \vdots & \vdots & \vdots & & & \\ \bullet & \dots & \bullet & & & \leftarrow & \lambda_m \text{ many nodes}, \end{matrix} \end{align*} $$
$$ \begin{align*}\begin{matrix} \bullet & \bullet & \bullet & \dots & \bullet & \leftarrow & \lambda_1 \text{ many nodes}\\ \bullet & \bullet & \dots & \bullet & & \leftarrow & \lambda_2 \text{ many nodes}\\ \vdots & \vdots & \vdots & & & \\ \bullet & \dots & \bullet & & & \leftarrow & \lambda_m \text{ many nodes}, \end{matrix} \end{align*} $$
and each node has a hook length. The node in row k and column j has hook length
![]() $h(k,j):=(\lambda _k-k)+(\lambda ^{\prime }_j-j)+1$
, where
$h(k,j):=(\lambda _k-k)+(\lambda ^{\prime }_j-j)+1$
, where
![]() $\lambda ^{\prime }_j$
is the number of nodes in column j. These numbers play many significant roles in combinatorics, number theory and representation theory (for example, see [Reference James and Kerber17, Reference Rains and Warnaar26]).
$\lambda ^{\prime }_j$
is the number of nodes in column j. These numbers play many significant roles in combinatorics, number theory and representation theory (for example, see [Reference James and Kerber17, Reference Rains and Warnaar26]).
We investigate those hook lengths that are multiples of a fixed positive integer t, the so-called t-hooks. We let
![]() $\mathcal {H}_t(\lambda )$
denote the multiset of t-hooks of a partition
$\mathcal {H}_t(\lambda )$
denote the multiset of t-hooks of a partition
![]() $\lambda $
. In recent work, the second author and Pun [Reference Craig and Pun7] analysed the t-hook partition functions
$\lambda $
. In recent work, the second author and Pun [Reference Craig and Pun7] analysed the t-hook partition functions
which divide the partitions of n into two subsets: those with an even (respectively, odd) number of t-hooks. For even t, they proved that partitions are equidistributed between these subsets as
![]() $n\rightarrow \infty $
. Namely, they showed that
$n\rightarrow \infty $
. Namely, they showed that
However, for odd t, they found that the partitions are not equidistributed. More precisely, if
![]() $a\in \{0, 1\}$
, then they proved thatFootnote 1
$a\in \{0, 1\}$
, then they proved thatFootnote 1
 $$ \begin{align*} \lim_{n\rightarrow \infty} \frac{p_t^e(2n+a)}{p(2n+a)}= \frac{1}{2}+\frac{(-1)^a}{2^{\frac{1}{2}(t+1)}}. \end{align*} $$
$$ \begin{align*} \lim_{n\rightarrow \infty} \frac{p_t^e(2n+a)}{p(2n+a)}= \frac{1}{2}+\frac{(-1)^a}{2^{\frac{1}{2}(t+1)}}. \end{align*} $$
In view of this unexpected result, it is natural to consider the more general t-hook partition functions
The
![]() $p_t(a,b;n)$
are clear generalisations of
$p_t(a,b;n)$
are clear generalisations of
![]() $p_t^e(n)$
and
$p_t^e(n)$
and
![]() $p_t^o(n)$
. In this setting, (1.2) is
$p_t^o(n)$
. In this setting, (1.2) is
For odd primes b, we determine the distribution of these decompositions as
![]() $n\rightarrow \infty $
, and in many situations they turn out to be nonuniform. To this end, we first obtain asymptotic formulas for
$n\rightarrow \infty $
, and in many situations they turn out to be nonuniform. To this end, we first obtain asymptotic formulas for
![]() $p_t(a,b;n)$
. For this, we define a modified indicator function
$p_t(a,b;n)$
. For this, we define a modified indicator function
![]() $\mathbb {I}$
by
$\mathbb {I}$
by
 $$ \begin{align} \mathbb{I}(a,b,t,n):= \begin{cases} b-1 & \text{if } \frac{1}{24} \left(1-t^2\right)\left(1-b^2\right) + at - n \equiv 0 \,\,(\mathrm{mod}\,\,{b}), \\ -1 & \text{otherwise}, \end{cases} \end{align} $$
$$ \begin{align} \mathbb{I}(a,b,t,n):= \begin{cases} b-1 & \text{if } \frac{1}{24} \left(1-t^2\right)\left(1-b^2\right) + at - n \equiv 0 \,\,(\mathrm{mod}\,\,{b}), \\ -1 & \text{otherwise}, \end{cases} \end{align} $$
and a distribution function

where
![]() $(\frac {\bullet }{b})$
is the Legendre symbol and
$(\frac {\bullet }{b})$
is the Legendre symbol and
![]() $\varepsilon _d:=1$
if
$\varepsilon _d:=1$
if
![]() $d\equiv 1 \,\,(\mathrm {mod}\,\,{4})$
and
$d\equiv 1 \,\,(\mathrm {mod}\,\,{4})$
and
![]() $\varepsilon _d:=i$
if
$\varepsilon _d:=i$
if
![]() $d\equiv 3 \,\,(\mathrm {mod}\,\,{4})$
. This function exactly characterises the distribution properties of the
$d\equiv 3 \,\,(\mathrm {mod}\,\,{4})$
. This function exactly characterises the distribution properties of the
![]() $p_t(a,b;n)$
. In particular, the second summand in equation (1.4) represents the obstruction to equidistribution.
$p_t(a,b;n)$
. In particular, the second summand in equation (1.4) represents the obstruction to equidistribution.
We prove the following asymptotic formulae for
![]() $p_t(a,b;n)$
.
$p_t(a,b;n)$
.
Theorem 1.1. If
![]() $t>1$
, b is an odd prime and
$t>1$
, b is an odd prime and
![]() $0\leq a<b $
, then as
$0\leq a<b $
, then as
![]() $n\rightarrow \infty $
, we have
$n\rightarrow \infty $
, we have
 $$ \begin{align*}p_t(a,b;n)\sim \frac{c_t(a,b;n)}{4\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}}. \end{align*} $$
$$ \begin{align*}p_t(a,b;n)\sim \frac{c_t(a,b;n)}{4\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}}. \end{align*} $$
Remark. Thanks to equation (3.7) in the proof of Theorem 1.1, we actually obtain an exact formula for
![]() $p_t(a,b;n)$
as a complicated convergent infinite sum.
$p_t(a,b;n)$
as a complicated convergent infinite sum.
As a corollary, we obtain the following limiting distributions.
Corollary 1.2. Assuming the hypotheses in Theorem 1.1, if
![]() $0\leq a_1<b$
and
$0\leq a_1<b$
and
![]() $0\leq a_2 <b$
, then
$0\leq a_2 <b$
, then
Example. For
![]() $4$
-hooks with
$4$
-hooks with
![]() $b=3$
, the collection of values
$b=3$
, the collection of values
![]() $c_4(a_1,3;a_2)$
in Corollary 1.2 implies that
$c_4(a_1,3;a_2)$
in Corollary 1.2 implies that
 $$ \begin{align*}\lim_{n\rightarrow \infty} \frac{p_4(a,3;3n)}{p(3n)}=\begin{cases} \frac49 \ \ \ \ \ &{\text{if }a=0,}\\ \frac13 \ \ \ \ \ &{\text{if }a=1,}\\ \frac29 \ \ \ \ \ &{\text{if }a=2.} \end{cases} \end{align*} $$
$$ \begin{align*}\lim_{n\rightarrow \infty} \frac{p_4(a,3;3n)}{p(3n)}=\begin{cases} \frac49 \ \ \ \ \ &{\text{if }a=0,}\\ \frac13 \ \ \ \ \ &{\text{if }a=1,}\\ \frac29 \ \ \ \ \ &{\text{if }a=2.} \end{cases} \end{align*} $$
Further examples are offered in Section 5.
The cases where
![]() $t\in \{2, 3\}$
are particularly striking. In addition to many instances of nonuniform distribution, there are situations where certain counts are identically zero.
$t\in \{2, 3\}$
are particularly striking. In addition to many instances of nonuniform distribution, there are situations where certain counts are identically zero.
Theorem 1.3. The following are true.
-
(1) If
 $\ell $
is an odd prime and
$\ell $
is an odd prime and
 $0\leq a_1, a_2<\ell $
satisfy
$0\leq a_1, a_2<\ell $
satisfy
 $(\frac {-16a_1+8a_2+1}{\ell })=-1$
, then for every nonnegative integer n, we have
$(\frac {-16a_1+8a_2+1}{\ell })=-1$
, then for every nonnegative integer n, we have  $$ \begin{align*}p_2(a_1,\ell;\ell n+a_2)=0. \end{align*} $$
$$ \begin{align*}p_2(a_1,\ell;\ell n+a_2)=0. \end{align*} $$
-
(2) If
 $\ell \equiv 2\,\,(\mathrm {mod}\,\,{3})$
is prime and
$\ell \equiv 2\,\,(\mathrm {mod}\,\,{3})$
is prime and
 $0\leq a_1, a_2<\ell ^2$
have the property that
$0\leq a_1, a_2<\ell ^2$
have the property that
 ${\mathrm {ord}}_{\ell }(-9a_1+3a_2+1)=1$
, then for every nonnegative integer n, we have
${\mathrm {ord}}_{\ell }(-9a_1+3a_2+1)=1$
, then for every nonnegative integer n, we have  $$ \begin{align*}p_3\left(a_1,\ell^2;\ell^2 n+a_2\right)=0. \end{align*} $$
$$ \begin{align*}p_3\left(a_1,\ell^2;\ell^2 n+a_2\right)=0. \end{align*} $$
Example. For
![]() $\ell =3$
, Theorem 1.3 (1) implies that
$\ell =3$
, Theorem 1.3 (1) implies that
More generally, for every odd prime
![]() $\ell $
and each
$\ell $
and each
![]() $0\leq a_1<\ell $
, there are
$0\leq a_1<\ell $
, there are
![]() $\frac {1}{2}(\ell -1)$
choices of
$\frac {1}{2}(\ell -1)$
choices of
![]() $0\leq a_2<\ell $
satisfying the given hypotheses. In particular, there are
$0\leq a_2<\ell $
satisfying the given hypotheses. In particular, there are
![]() $\frac {1}{2}(\ell ^2-\ell )$
many pairs of
$\frac {1}{2}(\ell ^2-\ell )$
many pairs of
![]() $a_1$
and
$a_1$
and
![]() $a_2$
giving rise to vanishing arithmetic progressions for
$a_2$
giving rise to vanishing arithmetic progressions for
![]() $2$
-hooks.
$2$
-hooks.
Example. For
![]() $\ell =2$
, Theorem 1.3 (2) gives
$\ell =2$
, Theorem 1.3 (2) gives
Moreover, for each
![]() $\ell $
and each
$\ell $
and each
![]() $0\leq a_1<\ell ^2$
, there are
$0\leq a_1<\ell ^2$
, there are
![]() $\ell -1$
choices for
$\ell -1$
choices for
![]() $a_2$
.
$a_2$
.
Remark. Theorem 1.3 depends on the paucity of
![]() $2$
-core and
$2$
-core and
![]() $3$
-core partitions. Recall that a partition
$3$
-core partitions. Recall that a partition
![]() $\lambda $
is a t-core if
$\lambda $
is a t-core if
![]() $\mathcal {H}_{t}(\lambda )=\emptyset $
. There are no such vanishing results for
$\mathcal {H}_{t}(\lambda )=\emptyset $
. There are no such vanishing results for
![]() $t\geq 4$
. This follows from the proof of the t-core conjecture by Granville and the fourth author [Reference Granville and Ono12]. McSpirit and Scheckelhoff [Reference McSpirit and Scheckelhoff18] have found a beautiful combinatorial proof of Theorem 1.3 that makes use of the theory of abaci, t-cores and t-quotients.
$t\geq 4$
. This follows from the proof of the t-core conjecture by Granville and the fourth author [Reference Granville and Ono12]. McSpirit and Scheckelhoff [Reference McSpirit and Scheckelhoff18] have found a beautiful combinatorial proof of Theorem 1.3 that makes use of the theory of abaci, t-cores and t-quotients.
We now turn to applications of partitions in algebraic geometry and topology. The fundamental goal of topology is to determine whether two spaces have the same topological, differentiable or complex analytic structure. One seeks invariants that distinguish dissimilar spaces. For complex manifolds, the Hodge numbers are one class of invariants. For any n-dimensional complex manifold M and any
![]() $0 \leq s,t,\leq n$
, the Hodge number
$0 \leq s,t,\leq n$
, the Hodge number
![]() $h^{s,t}(M)$
gives the dimension of a certain vector space of differential forms on M. For the manifolds we consider, the Betti numbers arise as linear combinations of the Hodge numbers (for example, see [Reference Wells29]). We shall determine the asymptotics and modular distribution properties of certain Betti numbers.
$h^{s,t}(M)$
gives the dimension of a certain vector space of differential forms on M. For the manifolds we consider, the Betti numbers arise as linear combinations of the Hodge numbers (for example, see [Reference Wells29]). We shall determine the asymptotics and modular distribution properties of certain Betti numbers.
We consider examples occurring in the algebraic geometry of Hilbert schemes (for example, see [Reference Nakajima20]). The nth Hilbert scheme of a projective variety S is a projective variety
![]() $\mathrm {Hilb}^n(S)$
that is a ‘smoothed’ version of the nth symmetric product of S (for example, see [Reference Göttsche11, Reference Nakajima20]). The nth symmetric product of a manifold M admits a simple combinatorial interpretation: outside of a negligible subset, the symmetric product is the collection of subsets of M of size n assembled as a manifold on its own. Rather nicely, the Hodge numbers of a complex projective surface S determine the Hodge numbers of
$\mathrm {Hilb}^n(S)$
that is a ‘smoothed’ version of the nth symmetric product of S (for example, see [Reference Göttsche11, Reference Nakajima20]). The nth symmetric product of a manifold M admits a simple combinatorial interpretation: outside of a negligible subset, the symmetric product is the collection of subsets of M of size n assembled as a manifold on its own. Rather nicely, the Hodge numbers of a complex projective surface S determine the Hodge numbers of
![]() $\mathrm {Hilb}^n(S)$
in a beautiful combinatorial way. This is captured by the pleasing formula of Göttsche [Reference Göttsche10, Reference Göttsche11]
$\mathrm {Hilb}^n(S)$
in a beautiful combinatorial way. This is captured by the pleasing formula of Göttsche [Reference Göttsche10, Reference Göttsche11]
 $$ \begin{align*} \sum_{n,s,t}(-1)^{s+t}h^{s,t}(\mathrm{Hilb}^n(S))x^{s-n}y^{t-n}q^n =\prod_{n =1}^\infty \frac{\prod_{s +t \mathrm{\ odd}} \left(1- x^{s-1}y^{t-1}q^n\right)^{h^{s,t}(S)}}{\prod_{s +t \mathrm{\ even}} \left(1- x^{s-1}y^{t-1}q^n\right)^{h^{s,t}(S)}}. \end{align*} $$
$$ \begin{align*} \sum_{n,s,t}(-1)^{s+t}h^{s,t}(\mathrm{Hilb}^n(S))x^{s-n}y^{t-n}q^n =\prod_{n =1}^\infty \frac{\prod_{s +t \mathrm{\ odd}} \left(1- x^{s-1}y^{t-1}q^n\right)^{h^{s,t}(S)}}{\prod_{s +t \mathrm{\ even}} \left(1- x^{s-1}y^{t-1}q^n\right)^{h^{s,t}(S)}}. \end{align*} $$
These q-infinite products often essentially specialise to modular forms, which then leads to asymptotics and distribution results via a standard application of the Circle Method. Indeed, the fourth author and his collaborators carried this out in [Reference Gillman, Gonzalez, Ono and Rolen9]. Here we consider a prominent situation involving partitions, where modular forms do not arise, a fact that complicates the computation of asymptotics and distributions. Namely, we investigate the Hilbert schemes that arise from n points on
![]() ${\mathbb {C}}^2$
that have been considered recently by Göttsche [Reference Göttsche10, Reference Göttsche11] and Buryak, Feigin and Nakajima [Reference Buryak and Feigin3, Reference Buryak, Feigin and Nakajima4].
${\mathbb {C}}^2$
that have been considered recently by Göttsche [Reference Göttsche10, Reference Göttsche11] and Buryak, Feigin and Nakajima [Reference Buryak and Feigin3, Reference Buryak, Feigin and Nakajima4].
We denote the Hilbert scheme of n points of
![]() ${\mathbb {C}}^2$
by
${\mathbb {C}}^2$
by
![]() $({\mathbb {C}}^2)^{[n]}$
. For
$({\mathbb {C}}^2)^{[n]}$
. For
![]() $0\leq a<b$
, we consider the modular sums of Betti numbers
$0\leq a<b$
, we consider the modular sums of Betti numbers
 $$ \begin{align*} B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right):=\sum_{j\equiv a\,\,(\mathrm{mod}\,\,{b})} b_j\left(\left({\mathbb{C}}^2\right)^{[n]}\right)= \sum_{j\equiv a\,\,(\mathrm{mod}\,\,{b})} \dim \left(H_j\left(\left({\mathbb{C}}^2\right)^{[n]},{\mathbb{Q}}\right)\right). \end{align*} $$
$$ \begin{align*} B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right):=\sum_{j\equiv a\,\,(\mathrm{mod}\,\,{b})} b_j\left(\left({\mathbb{C}}^2\right)^{[n]}\right)= \sum_{j\equiv a\,\,(\mathrm{mod}\,\,{b})} \dim \left(H_j\left(\left({\mathbb{C}}^2\right)^{[n]},{\mathbb{Q}}\right)\right). \end{align*} $$
We also consider their quasihomogeneous versions. To define them, we use the torus
![]() $({\mathbb {C}}^{\times })^2$
-action on
$({\mathbb {C}}^{\times })^2$
-action on
![]() ${\mathbb {C}}^2$
defined by scalar multiplication (i.e.,
${\mathbb {C}}^2$
defined by scalar multiplication (i.e.,
![]() $(t_1, t_2)\cdot (x,y):=(t_1x, t_2 y)$
). This action lifts to
$(t_1, t_2)\cdot (x,y):=(t_1x, t_2 y)$
). This action lifts to
![]() $({\mathbb {C}}^2)^{[n]}$
. For relatively prime
$({\mathbb {C}}^2)^{[n]}$
. For relatively prime
![]() $\alpha , \beta \in {\mathbb {N}}$
, we let
$\alpha , \beta \in {\mathbb {N}}$
, we let
![]() $T_{\alpha ,\beta }:=\{(t^{\alpha }, t^{\beta }) \ : \ t\in {\mathbb {C}}^{\times }\}$
, a one-dimensional subtorus. The quasihomogeneous Hilbert scheme
$T_{\alpha ,\beta }:=\{(t^{\alpha }, t^{\beta }) \ : \ t\in {\mathbb {C}}^{\times }\}$
, a one-dimensional subtorus. The quasihomogeneous Hilbert scheme
![]() $(({\mathbb {C}}^2)^{[n]})^{T_{\alpha ,\beta }}$
is the fixed point set of
$(({\mathbb {C}}^2)^{[n]})^{T_{\alpha ,\beta }}$
is the fixed point set of
![]() $({\mathbb {C}}^2)^{[n]}$
. We consider their modular sums of Betti numbers
$({\mathbb {C}}^2)^{[n]}$
. We consider their modular sums of Betti numbers

Remark. The odd index Betti numbers for these Hilbert schemes are always zero. In fact, for a odd and b even, simple calculations using Corollary 4.3 reveal that both
![]() $B(a,b; ({\mathbb {C}}^2)^{[n]})$
and
$B(a,b; ({\mathbb {C}}^2)^{[n]})$
and
![]() $B(a,b;(({\mathbb {C}}^2)^{[n]})^{T_{\alpha ,\beta }})$
identically vanish. Moreover, in accord with (1.2), we have the homology decompositions for
$B(a,b;(({\mathbb {C}}^2)^{[n]})^{T_{\alpha ,\beta }})$
identically vanish. Moreover, in accord with (1.2), we have the homology decompositions for
![]() $p(n)$
$p(n)$
 $$ \begin{align} p(n)=\sum_{a=0}^{b-1} B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right) =\sum_{a=0}^{b-1} B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right). \end{align} $$
$$ \begin{align} p(n)=\sum_{a=0}^{b-1} B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right) =\sum_{a=0}^{b-1} B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right). \end{align} $$
These results require the rational numbers
 $$ \begin{align} d(a,b):=\begin{cases} \frac{1}{b} \ \ \ \ \ &{\text{if }b \text{ is odd,}}\\ \frac{2}{b} \ \ \ \ \ &{\text{if }a \text{ and }b \text{ are even,}}\\ 0 \ \ \ \ \ &{\text{if }a \text{ is odd and }b \text{ is even.}} \end{cases} \end{align} $$
$$ \begin{align} d(a,b):=\begin{cases} \frac{1}{b} \ \ \ \ \ &{\text{if }b \text{ is odd,}}\\ \frac{2}{b} \ \ \ \ \ &{\text{if }a \text{ and }b \text{ are even,}}\\ 0 \ \ \ \ \ &{\text{if }a \text{ is odd and }b \text{ is even.}} \end{cases} \end{align} $$
Theorem 1.4. Assuming the notation above, the following are true.
-
(1) As
 $n\rightarrow \infty $
, we have
$n\rightarrow \infty $
, we have  $$ \begin{align*} B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right)\sim \frac{d(a,b)}{4\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}}.\\[-17pt] \end{align*} $$
$$ \begin{align*} B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right)\sim \frac{d(a,b)}{4\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}}.\\[-17pt] \end{align*} $$
-
(2) If
 $\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then as
$\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then as
 $n\rightarrow \infty $
, we have
$n\rightarrow \infty $
, we have  $$ \begin{align*} B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)\sim \frac{d(a,b)}{4\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}{3}}}.\\[-17pt] \end{align*} $$
$$ \begin{align*} B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)\sim \frac{d(a,b)}{4\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}{3}}}.\\[-17pt] \end{align*} $$
As a consequence of Theorem 1.4, we obtain distributions (i.e., see (1.5)) for the proportions
 $$ \begin{align*} \delta(a,b;n):= \frac{B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right)}{p(n)}\ \ \ \ {\text{and}}\ \ \ \ \delta_{\alpha,\beta}(a,b;n):=\frac{B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)}{p(n)}.\\[-17pt] \end{align*} $$
$$ \begin{align*} \delta(a,b;n):= \frac{B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right)}{p(n)}\ \ \ \ {\text{and}}\ \ \ \ \delta_{\alpha,\beta}(a,b;n):=\frac{B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)}{p(n)}.\\[-17pt] \end{align*} $$
Corollary 1.5. If
![]() $0\leq a<b$
, then the following are true.
$0\leq a<b$
, then the following are true.
-
(1) We have that
 $$ \begin{align*} \lim_{n\rightarrow \infty} \delta(a,b;n)=d(a,b).\\[-17pt] \end{align*} $$
$$ \begin{align*} \lim_{n\rightarrow \infty} \delta(a,b;n)=d(a,b).\\[-17pt] \end{align*} $$
-
(2) If
 $\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then we have
$\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then we have  $$ \begin{align*} \lim_{n\rightarrow \infty} \delta_{\alpha,\beta}(a,b;n)=d(a,b).\\[-17pt] \end{align*} $$
$$ \begin{align*} \lim_{n\rightarrow \infty} \delta_{\alpha,\beta}(a,b;n)=d(a,b).\\[-17pt] \end{align*} $$
This paper is organised as follows. In Section 2, we state and prove a general theorem (see Theorem 2.1) on the asymptotic properties (near roots of unity) of the three infinite products given in the abstract, a result that is of independent interest. The proof is obtained by suitably adapting the method of Euler–Maclaurin summation in two cases and via modularity in the other. In Section 3, we recall recent work of Han extending the Nekrasov–Okounkov partition formula, and we prove Theorems 1.1 and 1.3. To show Theorem 1.1 and Corollary 1.2, we employ Theorem 2.1 (2) and results of Zuckerman pertaining to exact formulas for Fourier coefficients of modular forms. In Section 4, we recall the work of Göttsche and Buryak, Feigin and Nakajima on homogeneous and quasihomogeneous Hilbert schemes for n points, which we then employ to prove Theorem 1.4 and Corollary 1.5 using Theorem 2.1 (1) and (3) and results of Ngo–Rhoades using Wright’s Circle Method. Finally, in Section 5, we offer numerical examples of these results.
2 Asymptotics for special q-infinite products
The Hardy–Ramanujan asymptotic formula given in equation (1.1) marked the birth of the Circle Method. Its proof relied on the modular transformation properties of Dedekind’s eta-function
![]() $\eta (\tau ):= q^{\frac {1}{24}} \prod _{n=1}^{\infty }(1-q^n)$
, where
$\eta (\tau ):= q^{\frac {1}{24}} \prod _{n=1}^{\infty }(1-q^n)$
, where
![]() $q:=e^{2\pi i \tau }$
(for example, see Chapter 1 of [Reference Ono23]). Their work has been thoroughly developed in the theory of modular forms and harmonic Maass forms (for example, see Chapter 15 of [Reference Bringmann, Folsom, Ono and Rolen1]) and has been generalised beyond this setting in papers by Grosswald, Meinardus, Richmond, Roth and Szekeres [Reference Grosswald13, Reference Meinardus19, Reference Richmond27, Reference Roth and Szekeres28], to name a few.
$q:=e^{2\pi i \tau }$
(for example, see Chapter 1 of [Reference Ono23]). Their work has been thoroughly developed in the theory of modular forms and harmonic Maass forms (for example, see Chapter 15 of [Reference Bringmann, Folsom, Ono and Rolen1]) and has been generalised beyond this setting in papers by Grosswald, Meinardus, Richmond, Roth and Szekeres [Reference Grosswald13, Reference Meinardus19, Reference Richmond27, Reference Roth and Szekeres28], to name a few.
2.1 Statement of the results
Generalising the infinite product that defines
![]() $\eta $
, we consider the ubiquitous q-infinite products
$\eta $
, we consider the ubiquitous q-infinite products
 $$ \begin{align*} F_1(\xi; q):=\prod_{n=1}^{\infty}\left(1-\xi q^n\right),\ \ \ F_2(\xi; q):=\prod_{n=1}^{\infty}\left(1-(\xi q)^n\right), \ \ \ {\text {and}}\ \ \ F_3(\xi;q):=\prod_{n=1}^{\infty} \left(1-\xi^{-1}(\xi q)^n\right). \end{align*} $$
$$ \begin{align*} F_1(\xi; q):=\prod_{n=1}^{\infty}\left(1-\xi q^n\right),\ \ \ F_2(\xi; q):=\prod_{n=1}^{\infty}\left(1-(\xi q)^n\right), \ \ \ {\text {and}}\ \ \ F_3(\xi;q):=\prod_{n=1}^{\infty} \left(1-\xi^{-1}(\xi q)^n\right). \end{align*} $$
These infinite products are common as factors of generating functions in combinatorics, number theory and representation theory. We obtain the asymptotic properties for
![]() $F_1(\xi ;q), F_2(\xi ;q)$
and
$F_1(\xi ;q), F_2(\xi ;q)$
and
![]() $F_3(\xi ;q)$
, where
$F_3(\xi ;q)$
, where
![]() $\xi $
is a root of unity, which are generally required for implementing the Circle Method to such generating functions. This result is of independent interest.
$\xi $
is a root of unity, which are generally required for implementing the Circle Method to such generating functions. This result is of independent interest.
To make this precise, we recall Lerch’s transcendent
 $$ \begin{align*} \Phi(z,s,a):=\sum_{n=0}^\infty \frac{z^n}{(n+a)^s}. \end{align*} $$
$$ \begin{align*} \Phi(z,s,a):=\sum_{n=0}^\infty \frac{z^n}{(n+a)^s}. \end{align*} $$
Moreover, for coprime
![]() $h,k\in {\mathbb {N}}$
, we define
$h,k\in {\mathbb {N}}$
, we define
using the Dedekind sum
 $$ \begin{align*} s(h,k):=\sum_{\mu \,\,(\mathrm{mod}\,\,{k})} \left(\left(\frac{\mu}{k}\right)\right)\left(\left(\frac{h\mu}{k}\right)\right). \end{align*} $$
$$ \begin{align*} s(h,k):=\sum_{\mu \,\,(\mathrm{mod}\,\,{k})} \left(\left(\frac{\mu}{k}\right)\right)\left(\left(\frac{h\mu}{k}\right)\right). \end{align*} $$
Here we use the standard notation
 $$ \begin{align*} ((x)):=\begin{cases} x-\lfloor x \rfloor-\frac{1}{2} & \text{if} \ x\in \mathbb R \setminus \mathbb Z, \\ 0 & \text{if} \ x \in \mathbb Z. \end{cases} \end{align*} $$
$$ \begin{align*} ((x)):=\begin{cases} x-\lfloor x \rfloor-\frac{1}{2} & \text{if} \ x\in \mathbb R \setminus \mathbb Z, \\ 0 & \text{if} \ x \in \mathbb Z. \end{cases} \end{align*} $$
For arbitrary positive integers m and n, we define
![]() $\omega _{m,n} := \omega _{\frac {m}{\gcd (m,n)}, \frac {n}{\gcd (m,n)}}$
. Note that
$\omega _{m,n} := \omega _{\frac {m}{\gcd (m,n)}, \frac {n}{\gcd (m,n)}}$
. Note that
![]() $s(h,k)$
only depends on
$s(h,k)$
only depends on
![]() $h\,\,(\mathrm {mod}\,\,{k})$
and that
$h\,\,(\mathrm {mod}\,\,{k})$
and that
![]() $s(0,1)=0$
. Moreover, we let
$s(0,1)=0$
. Moreover, we let

For
![]() $0\leq \theta < \frac {\pi }{2}$
, we define the domain
$0\leq \theta < \frac {\pi }{2}$
, we define the domain
Theorem 2.1. Assume the notation above. For
![]() $b>0$
, let
$b>0$
, let
![]() $\xi $
be a primitive bth root of unity; then the following are true.
$\xi $
be a primitive bth root of unity; then the following are true.
-
(1) As
 $z \to 0$
in
$z \to 0$
in
 $D_\theta $
, we have
$D_\theta $
, we have  $$ \begin{align*} F_{1}\left(\xi;e^{-z}\right) =\frac{1}{\sqrt{1-\xi}} \, e^{-\frac{\xi\Phi(\xi,2,1)}{z}}\left( 1+O\left(|z|\right) \right). \end{align*} $$
$$ \begin{align*} F_{1}\left(\xi;e^{-z}\right) =\frac{1}{\sqrt{1-\xi}} \, e^{-\frac{\xi\Phi(\xi,2,1)}{z}}\left( 1+O\left(|z|\right) \right). \end{align*} $$
-
(2) Suppose that b is an odd prime, and let
 $\xi = e^{\frac {2\pi i a}{b}}$
,
$\xi = e^{\frac {2\pi i a}{b}}$
,
 $t \in {\mathbb {N}}$
,
$t \in {\mathbb {N}}$
,
 $q = e^{\frac {2\pi i}{k}(h + iz)}$
for
$q = e^{\frac {2\pi i}{k}(h + iz)}$
for
 $0 \leq h < k$
with
$0 \leq h < k$
with
 $\gcd (h,k) = 1$
and
$\gcd (h,k) = 1$
and
 $z \in {\mathbb {C}}$
with
$z \in {\mathbb {C}}$
with
 $\mathrm {Re}(z)> 0$
. Then as
$\mathrm {Re}(z)> 0$
. Then as
 $z \to 0$
, we have
$z \to 0$
, we have  $$ \begin{align*}F_2\left(\xi;q^t\right) \sim \omega_{\frac{hbt+ak}{\lambda_{t,a,b,h,k}}, \frac{kb}{\lambda_{t,a,b,h,k}}}^{-1} \left(\frac{\lambda_{t,a,b,h,k}}{tbz}\right)^{\frac 12} e^{-\frac{\pi \lambda_{t,a,b,h,k}^2}{12 b^2 ktz}}.\end{align*} $$
$$ \begin{align*}F_2\left(\xi;q^t\right) \sim \omega_{\frac{hbt+ak}{\lambda_{t,a,b,h,k}}, \frac{kb}{\lambda_{t,a,b,h,k}}}^{-1} \left(\frac{\lambda_{t,a,b,h,k}}{tbz}\right)^{\frac 12} e^{-\frac{\pi \lambda_{t,a,b,h,k}^2}{12 b^2 ktz}}.\end{align*} $$
-
(3) As
 $z\to 0$
in
$z\to 0$
in
 $D_\theta $
, we have
$D_\theta $
, we have  $$ \begin{align*} F_3\left(\xi;e^{-z}\right)= \frac{\sqrt{2\pi} \left(b^2z\right)^{\frac 12-\frac 1b}}{\Gamma\left(\frac{1}{b}\right)} \prod_{j=1}^{b-1}\frac{1}{(1-\xi^j)^{\frac jb}} e^{-\frac{\pi^2}{6b^2z}}\left( 1+ O\left(|z|\right) \right). \end{align*} $$
$$ \begin{align*} F_3\left(\xi;e^{-z}\right)= \frac{\sqrt{2\pi} \left(b^2z\right)^{\frac 12-\frac 1b}}{\Gamma\left(\frac{1}{b}\right)} \prod_{j=1}^{b-1}\frac{1}{(1-\xi^j)^{\frac jb}} e^{-\frac{\pi^2}{6b^2z}}\left( 1+ O\left(|z|\right) \right). \end{align*} $$
Remark. If
![]() $\xi =1$
and
$\xi =1$
and
![]() $q=e^{2\pi i \tau }$
, then we have
$q=e^{2\pi i \tau }$
, then we have
Asymptotic properties in this case are well-known consequences of the modularity of
![]() $\eta (\tau )$
.
$\eta (\tau )$
.
2.2 The Euler–Maclaurin summation formula
We require the following generalisation of the Euler–Maclaurin summation formula. To state it, we need some notation. For
![]() $s,z\in {\mathbb {C}}$
with
$s,z\in {\mathbb {C}}$
with
![]() $\operatorname {Re}(s)>1, \operatorname {Re}(z)>0$
, we recall the Hurwitz zeta function
$\operatorname {Re}(s)>1, \operatorname {Re}(z)>0$
, we recall the Hurwitz zeta function
![]() $\zeta (s,z):=\sum _{n=0}^\infty \frac {1}{(n+z)^s}$
, the digamma function
$\zeta (s,z):=\sum _{n=0}^\infty \frac {1}{(n+z)^s}$
, the digamma function
![]() $\psi (x):=\frac {\Gamma '(x)}{\Gamma (x)}$
and the Euler–Mascheroni constant
$\psi (x):=\frac {\Gamma '(x)}{\Gamma (x)}$
and the Euler–Mascheroni constant
![]() $\gamma $
. Furthermore, we let
$\gamma $
. Furthermore, we let
![]() $B_n(x)$
denote the nth Bernoulli polynomial defined via its generating function
$B_n(x)$
denote the nth Bernoulli polynomial defined via its generating function
![]() $\frac {te^{xt}}{e^t-1}=\sum _{n=0}^\infty B_n(x)\frac {t^n}{n!}$
. The consequence of the Euler–Maclaurin summation formula required is described by the following lemma. A function f on a domain in
$\frac {te^{xt}}{e^t-1}=\sum _{n=0}^\infty B_n(x)\frac {t^n}{n!}$
. The consequence of the Euler–Maclaurin summation formula required is described by the following lemma. A function f on a domain in
![]() ${\mathbb {C}}$
is of sufficient decay if there exists
${\mathbb {C}}$
is of sufficient decay if there exists
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $f(w) \ll w^{-1-\varepsilon }$
as
$f(w) \ll w^{-1-\varepsilon }$
as
![]() $|w| \rightarrow \infty $
in the domain. Throughout, we say that
$|w| \rightarrow \infty $
in the domain. Throughout, we say that
 $$\begin{align*}f(z) \sim \sum_{n=0}^\infty a_nz^n \end{align*}$$
$$\begin{align*}f(z) \sim \sum_{n=0}^\infty a_nz^n \end{align*}$$
if for any
![]() $N\in {\mathbb {N}}_0$
,
$N\in {\mathbb {N}}_0$
,
![]() $f(z)=\sum _{n=0}^N a_nz^n+O(|z|^{N+1})$
.
$f(z)=\sum _{n=0}^N a_nz^n+O(|z|^{N+1})$
.
Lemma 2.2. Let
![]() $0 < a \leq 1$
and
$0 < a \leq 1$
and
![]() $A \in {\mathbb {R}}^+$
, and let
$A \in {\mathbb {R}}^+$
, and let
![]() $D_{\theta }$
be defined by equation (2.3). Assume that
$D_{\theta }$
be defined by equation (2.3). Assume that
![]() $f(z) \sim \sum _{n=n_0}^{\infty } c_n z^n \ (n_0\in {\mathbb {Z}})$
as
$f(z) \sim \sum _{n=n_0}^{\infty } c_n z^n \ (n_0\in {\mathbb {Z}})$
as
![]() $z \rightarrow 0$
in
$z \rightarrow 0$
in
![]() $D_\theta $
. Furthermore, assume that f and all of its derivatives are of sufficient decay in
$D_\theta $
. Furthermore, assume that f and all of its derivatives are of sufficient decay in
![]() $D_\theta $
in the above sense. Then we have that
$D_\theta $
in the above sense. Then we have that
 $$ \begin{align*} \sum_{n=0}^\infty f((n+a)z)\sim \sum_{n=n_0}^{-2} c_{n} \zeta(-n,a)z^{n}+ \frac{I_{f,A}^*}{z}-\frac{c_{-1}}{z} \left( \operatorname{\mathrm{Log}} \left(Az \right) +\psi(a)+\gamma \right)-\sum_{n=0}^\infty c_n \frac{B_{n+1}(a)}{n+1} z^n, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty f((n+a)z)\sim \sum_{n=n_0}^{-2} c_{n} \zeta(-n,a)z^{n}+ \frac{I_{f,A}^*}{z}-\frac{c_{-1}}{z} \left( \operatorname{\mathrm{Log}} \left(Az \right) +\psi(a)+\gamma \right)-\sum_{n=0}^\infty c_n \frac{B_{n+1}(a)}{n+1} z^n, \end{align*} $$
as
![]() $z \rightarrow 0$
uniformly in
$z \rightarrow 0$
uniformly in
![]() $D_\theta $
, where
$D_\theta $
, where
 $$ \begin{align*} I_{f,A}^*:=\int_{0}^{\infty} \left(f(u)-\sum_{n=n_0}^{-2}c_{n}u^n-\frac{c_{-1}e^{-Au}}{u}\right)du. \end{align*} $$
$$ \begin{align*} I_{f,A}^*:=\int_{0}^{\infty} \left(f(u)-\sum_{n=n_0}^{-2}c_{n}u^n-\frac{c_{-1}e^{-Au}}{u}\right)du. \end{align*} $$
Remark. Note that for
![]() $a=1$
, we have that
$a=1$
, we have that
![]() $\psi (a)+\gamma =0$
.
$\psi (a)+\gamma =0$
.
Proof of Lemma 2.2
A generalisation of an observation of Zagier [Reference Zagier32, Proposition 3] is that of [Reference Bringmann, Jennings-Shaffer and Mahlburg2, Theorem 1.2], which states the following. Let h be a holomorphic function on a domain containing
![]() $D_\theta $
so that in particular h is holomorphic at the origin, such that h and all of its derivatives have sufficient decay and
$D_\theta $
so that in particular h is holomorphic at the origin, such that h and all of its derivatives have sufficient decay and
![]() $h(z) \sim \sum _{n=0}^{\infty } c_n z^n$
as
$h(z) \sim \sum _{n=0}^{\infty } c_n z^n$
as
![]() $z \rightarrow 0$
in
$z \rightarrow 0$
in
![]() $D_\theta $
. Furthermore, let
$D_\theta $
. Furthermore, let
![]() . Then we have for
. Then we have for
![]() $a\in {\mathbb {R}}$
$a\in {\mathbb {R}}$
 $$ \begin{align} \sum_{n=0}^\infty h((n+a)z)\sim\frac{I_h}{z}-\sum_{n=0}^\infty c_n \frac{ B_{n+1}(a)}{n+1}z^n, \end{align} $$
$$ \begin{align} \sum_{n=0}^\infty h((n+a)z)\sim\frac{I_h}{z}-\sum_{n=0}^\infty c_n \frac{ B_{n+1}(a)}{n+1}z^n, \end{align} $$
as
![]() $z \rightarrow 0$
in
$z \rightarrow 0$
in
![]() $D_\theta $
. For the given A, write
$D_\theta $
. For the given A, write
 $$ \begin{align} f(z) = g(z) + \frac{c_{-1}e^{-Az}}{z} + \sum_{n=n_0}^{-2} c_nz^n, \end{align} $$
$$ \begin{align} f(z) = g(z) + \frac{c_{-1}e^{-Az}}{z} + \sum_{n=n_0}^{-2} c_nz^n, \end{align} $$
which means that
 $$ \begin{align*} g(z) = f(z) - \frac{c_{-1}e^{-Az}}{z} - \sum_{n=n_0}^{-2} c_nz^n. \end{align*} $$
$$ \begin{align*} g(z) = f(z) - \frac{c_{-1}e^{-Az}}{z} - \sum_{n=n_0}^{-2} c_nz^n. \end{align*} $$
The final term in equation (2.5) yields the first term in the right-hand side of the lemma. Since g has no pole, equation (2.4) gives that
 $$ \begin{align*} \sum_{n=0}^\infty g((n+a)z)\sim\frac{I_g}{z}- \sum_{n=0}^\infty c_n(g) \frac{ B_{n+1}(a)}{n+1}z^n, \end{align*} $$
$$ \begin{align*} \sum_{n=0}^\infty g((n+a)z)\sim\frac{I_g}{z}- \sum_{n=0}^\infty c_n(g) \frac{ B_{n+1}(a)}{n+1}z^n, \end{align*} $$
where
![]() $c_n(g)$
are the coefficients of g. Note that
$c_n(g)$
are the coefficients of g. Note that
![]() $I_g = I_{f,A}^*$
. We compute that
$I_g = I_{f,A}^*$
. We compute that
 $$ \begin{align*} - \sum_{n=0}^\infty c_n(g) \frac{ B_{n+1}(a)}{n+1}z^n = - \sum_{n=0}^\infty \left(c_n - \frac{(-A)^{n+1} c_{-1}}{(n+1)!}\right) \frac{ B_{n+1}(a)}{n+1}z^n. \end{align*} $$
$$ \begin{align*} - \sum_{n=0}^\infty c_n(g) \frac{ B_{n+1}(a)}{n+1}z^n = - \sum_{n=0}^\infty \left(c_n - \frac{(-A)^{n+1} c_{-1}}{(n+1)!}\right) \frac{ B_{n+1}(a)}{n+1}z^n. \end{align*} $$
Combining the contribution from the second term with the contribution from the second term from equation (2.5), we obtain
 $$ \begin{align*} \frac{c_{-1}}{z} \left( \sum_{n =0}^{\infty} \frac{e^{-A(n+a)z}}{n+a} + \sum_{n=1}^{\infty} \frac{B_n(a)}{n \cdot n!} (-Az)^n \right). \end{align*} $$
$$ \begin{align*} \frac{c_{-1}}{z} \left( \sum_{n =0}^{\infty} \frac{e^{-A(n+a)z}}{n+a} + \sum_{n=1}^{\infty} \frac{B_n(a)}{n \cdot n!} (-Az)^n \right). \end{align*} $$
Using [Reference Bringmann, Jennings-Shaffer and Mahlburg2, equation (5.10)], the term in the parentheses is equal to
![]() $-(\operatorname {\mathrm {Log}}(Az)+\psi (a)+\gamma )$
. Combining the contributions yields the statement of the lemma.
$-(\operatorname {\mathrm {Log}}(Az)+\psi (a)+\gamma )$
. Combining the contributions yields the statement of the lemma.
2.3 An integral evaluation
We require the following integral evaluation.
Lemma 2.3. We have for
![]() $N\in {\mathbb {R}}^+$
$N\in {\mathbb {R}}^+$
 $$ \begin{align*} \int_0^\infty&\left(\frac{e^{-x}}{x\left(1-e^{Nx}\right)}-\frac{1}{Nx^2}+\left(\frac 1N-\frac 12\right)\frac{e^{-x}}{x} \right)dx\\ &\phantom{\frac{e^{-x}}{x\left(1-e^{Nx}\right)}-\frac{1}{Nx^2}+\left(\frac 1N-\frac 12\right)}=\log\left(\Gamma\left(\frac 1N\right) \right) +\left(\frac 12-\frac 1N\right) \log\left(\frac 1N\right)-\frac 12\log(2\pi). \end{align*} $$
$$ \begin{align*} \int_0^\infty&\left(\frac{e^{-x}}{x\left(1-e^{Nx}\right)}-\frac{1}{Nx^2}+\left(\frac 1N-\frac 12\right)\frac{e^{-x}}{x} \right)dx\\ &\phantom{\frac{e^{-x}}{x\left(1-e^{Nx}\right)}-\frac{1}{Nx^2}+\left(\frac 1N-\frac 12\right)}=\log\left(\Gamma\left(\frac 1N\right) \right) +\left(\frac 12-\frac 1N\right) \log\left(\frac 1N\right)-\frac 12\log(2\pi). \end{align*} $$
Proof. Making the change of variables
![]() $x\mapsto \frac xN$
, the left-hand side equals
$x\mapsto \frac xN$
, the left-hand side equals
 $$ \begin{align*} \int_0^\infty\left(\frac{e^{-\frac{x}{N}}}{x\left(1-e^{-x}\right)} - \frac{1}{x^2} +\left(\frac 1N-\frac 12\right)\frac{e^{-\frac {1}N}}{x} \right) dx. \end{align*} $$
$$ \begin{align*} \int_0^\infty\left(\frac{e^{-\frac{x}{N}}}{x\left(1-e^{-x}\right)} - \frac{1}{x^2} +\left(\frac 1N-\frac 12\right)\frac{e^{-\frac {1}N}}{x} \right) dx. \end{align*} $$
Now write
Thus the integral becomes
 $$ \begin{align*} \int_0^\infty\left(\frac{1}{e^x-1}+\frac 12-\frac 1x\right)\frac{e^{-\frac{x}{N}}}{x}dx +\int_0^\infty\left(\frac{e^{-\frac{x}{N}}}{x} - \frac{1}{x^2} +\left(\frac 1N-\frac 12\right)\frac{e^{-\frac {x}N}}{x} -\frac{e^{-\frac{x}{N}}}{2x}+\frac{e^{-\frac{x}{N}}}{x^2}\right) dx.\\[-15pt] \end{align*} $$
$$ \begin{align*} \int_0^\infty\left(\frac{1}{e^x-1}+\frac 12-\frac 1x\right)\frac{e^{-\frac{x}{N}}}{x}dx +\int_0^\infty\left(\frac{e^{-\frac{x}{N}}}{x} - \frac{1}{x^2} +\left(\frac 1N-\frac 12\right)\frac{e^{-\frac {x}N}}{x} -\frac{e^{-\frac{x}{N}}}{2x}+\frac{e^{-\frac{x}{N}}}{x^2}\right) dx.\\[-15pt] \end{align*} $$
We evaluate the second integral as
![]() $-\frac {1}{N}$
. The claim now follows, using Binet’s first integral formula (see 12.31 of [Reference Whittaker and Watson31]).
$-\frac {1}{N}$
. The claim now follows, using Binet’s first integral formula (see 12.31 of [Reference Whittaker and Watson31]).
2.4 Proof of Theorem 2.1
We employ the generalised Euler–Maclaurin summation formula to prove Theorem 2.1 (1) and (3); for part (2), we use modularity.
2.4.1 Proof of Theorem 2.1 (1)
Let
![]() $|z|<1$
. Taking logarithms, we have
$|z|<1$
. Taking logarithms, we have
 $$ \begin{align*} G_{\xi}\left(e^{-z}\right)&:=\operatorname{Log} \left(F_{1}\left(\xi;e^{-z}\right) \right) =-z\sum_{j=1}^b \xi^j \sum_{m=0}^{\infty}f\left(\left(m+\frac j b\right)bz\right),\\[-15pt] \end{align*} $$
$$ \begin{align*} G_{\xi}\left(e^{-z}\right)&:=\operatorname{Log} \left(F_{1}\left(\xi;e^{-z}\right) \right) =-z\sum_{j=1}^b \xi^j \sum_{m=0}^{\infty}f\left(\left(m+\frac j b\right)bz\right),\\[-15pt] \end{align*} $$
where
 $$ \begin{align*} f(z):=\frac{e^{-z}}{z\left(1-e^{-z}\right)}=\frac{1}{z^2}-\frac{1}{2z} +\sum_{n=0}^\infty \frac{B_{n+2}}{(n+2)!}z^n.\\[-15pt] \end{align*} $$
$$ \begin{align*} f(z):=\frac{e^{-z}}{z\left(1-e^{-z}\right)}=\frac{1}{z^2}-\frac{1}{2z} +\sum_{n=0}^\infty \frac{B_{n+2}}{(n+2)!}z^n.\\[-15pt] \end{align*} $$
By Lemma 2.2, it follows that
 $$ \begin{align*} \sum_{m=0}^\infty f \left( \left( m+\frac{j}{b} \right)bz\right) =\frac{\zeta\left(2,\frac j b\right)}{b^2z^2}+\frac{I_{f,1}^*}{bz} +{\frac{1}{2bz}}\left(\operatorname{\mathrm{Log}} \left( {bz}\right) +\psi \left(\frac{j}{b}\right)+\gamma \right) +O(1).\\[-15pt] \end{align*} $$
$$ \begin{align*} \sum_{m=0}^\infty f \left( \left( m+\frac{j}{b} \right)bz\right) =\frac{\zeta\left(2,\frac j b\right)}{b^2z^2}+\frac{I_{f,1}^*}{bz} +{\frac{1}{2bz}}\left(\operatorname{\mathrm{Log}} \left( {bz}\right) +\psi \left(\frac{j}{b}\right)+\gamma \right) +O(1).\\[-15pt] \end{align*} $$
Therefore, we find that
 $$\begin{align*}G_{\xi} \left(e^{-z}\right) = -\frac{1}{b^2z} \sum_{j=1}^b \xi^j \zeta\left(2,\frac jb\right) -\frac{I_{f,1}^*}{b} \sum_{j=1}^b \xi^{j}-\frac{1}{2b} \sum_{j=1}^b \xi^j \left(\operatorname{\mathrm{Log}}\left(bz\right) +\psi\left(\frac jb\right)+\gamma\right) +O(|z|).\\[-15pt] \end{align*}$$
$$\begin{align*}G_{\xi} \left(e^{-z}\right) = -\frac{1}{b^2z} \sum_{j=1}^b \xi^j \zeta\left(2,\frac jb\right) -\frac{I_{f,1}^*}{b} \sum_{j=1}^b \xi^{j}-\frac{1}{2b} \sum_{j=1}^b \xi^j \left(\operatorname{\mathrm{Log}}\left(bz\right) +\psi\left(\frac jb\right)+\gamma\right) +O(|z|).\\[-15pt] \end{align*}$$
Now note that
![]() $\sum _{j=1}^b \xi ^{j}=0$
. Moreover, we require the identity [Reference Campbell5, p. 39] (correcting a minus sign and erroneous k on the right-hand side)
$\sum _{j=1}^b \xi ^{j}=0$
. Moreover, we require the identity [Reference Campbell5, p. 39] (correcting a minus sign and erroneous k on the right-hand side)
 $$ \begin{align} \sum_{j=1}^b \psi \left( \frac{j}{b} \right) \xi^{j}=b\operatorname{Log }\left( 1-\xi \right).\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \sum_{j=1}^b \psi \left( \frac{j}{b} \right) \xi^{j}=b\operatorname{Log }\left( 1-\xi \right).\\[-15pt]\nonumber \end{align} $$
Combining these observations, we obtain
 $$ \begin{align*} G_{\xi}\left( e^{-z} \right)=-\frac{1}{b^2z} \sum_{j=1}^b \xi^{j} \zeta\left( 2,\frac{j}{b} \right)-\frac{1}{2} \operatorname{Log }(1-\xi) + O\left(|z|\right).\\[-15pt] \end{align*} $$
$$ \begin{align*} G_{\xi}\left( e^{-z} \right)=-\frac{1}{b^2z} \sum_{j=1}^b \xi^{j} \zeta\left( 2,\frac{j}{b} \right)-\frac{1}{2} \operatorname{Log }(1-\xi) + O\left(|z|\right).\\[-15pt] \end{align*} $$
After noting that
 $$ \begin{align*} \sum_{j=1}^b \xi^{j} \zeta \left(2,\frac{j}{b} \right)&=b^2 \xi\Phi(\xi,2,1),\\[-15pt] \end{align*} $$
$$ \begin{align*} \sum_{j=1}^b \xi^{j} \zeta \left(2,\frac{j}{b} \right)&=b^2 \xi\Phi(\xi,2,1),\\[-15pt] \end{align*} $$
the claim follows by exponentiation.
![]() $\Box $
$\Box $
2.4.2 Proof of Theorem 2.1 (2)
Note that
where
![]() $(q;q)_\infty := \prod _{j=1}^\infty (1 - q^j)$
. The classical modular transformation law for the Dedekind
$(q;q)_\infty := \prod _{j=1}^\infty (1 - q^j)$
. The classical modular transformation law for the Dedekind
![]() $\eta $
-function (see 5.8.1 of [Reference Cohen and Stromberg6]) along with the identity
$\eta $
-function (see 5.8.1 of [Reference Cohen and Stromberg6]) along with the identity
![]() $\eta (\tau ) = q^{ \frac {1}{24}} (q;q)_\infty $
implies that
$\eta (\tau ) = q^{ \frac {1}{24}} (q;q)_\infty $
implies that
where
![]() $q_1 := e^{\frac {2\pi i}{k}( h' + \frac {i}{z})}$
, where
$q_1 := e^{\frac {2\pi i}{k}( h' + \frac {i}{z})}$
, where
![]() $0 \leq h' < k$
is defined by
$0 \leq h' < k$
is defined by
![]() $h h' \equiv -1 \,\,(\mathrm {mod}\,\,{k})$
and
$h h' \equiv -1 \,\,(\mathrm {mod}\,\,{k})$
and
![]() $\omega _{h,k}$
is defined as in equation (2.1). In particular, this implies that
$\omega _{h,k}$
is defined as in equation (2.1). In particular, this implies that
as
![]() $z\rightarrow 0$
with
$z\rightarrow 0$
with
![]() ${\text {Re}\left ({z}\right )}>0$
. Now, by using the definitions of
${\text {Re}\left ({z}\right )}>0$
. Now, by using the definitions of
![]() $\xi , q$
given in the statement of Theorem 2.1 (2), we have
$\xi , q$
given in the statement of Theorem 2.1 (2), we have
We claim that
![]() $\lambda _{t,a,b,h,k}$
as defined in equation (2.2) satisfies
$\lambda _{t,a,b,h,k}$
as defined in equation (2.2) satisfies
![]() $\lambda _{t,a,b,h,k} = \gcd (kb, hbt + ak)$
. If
$\lambda _{t,a,b,h,k} = \gcd (kb, hbt + ak)$
. If
![]() $k=1$
, then the claim is clear, so we assume that
$k=1$
, then the claim is clear, so we assume that
![]() $k> 1$
. Write
$k> 1$
. Write
![]() $k = \gcd (k,t) k_1$
and
$k = \gcd (k,t) k_1$
and
![]() $t = \gcd (k,t) t_1$
. Then we have
$t = \gcd (k,t) t_1$
. Then we have
Noting that
![]() $\gcd (k_1,b)$
divides each of
$\gcd (k_1,b)$
divides each of
![]() $k_1b, hbt_1$
and
$k_1b, hbt_1$
and
![]() $ak_1$
, it follows that
$ak_1$
, it follows that
 $$\begin{align*}\gcd(kb, hbt + ak) = \gcd(k,t) \gcd(k_1, b) \gcd\left( \frac{k_1 b}{\gcd(k_1, b)}, \frac{hbt_1}{\gcd(k_1, b)} + a\frac{k_1}{\gcd(k_1,b)} \right). \end{align*}$$
$$\begin{align*}\gcd(kb, hbt + ak) = \gcd(k,t) \gcd(k_1, b) \gcd\left( \frac{k_1 b}{\gcd(k_1, b)}, \frac{hbt_1}{\gcd(k_1, b)} + a\frac{k_1}{\gcd(k_1,b)} \right). \end{align*}$$
Note that since b is prime,
![]() $\gcd (k_1, b) \in \{ 1, b \}$
. If
$\gcd (k_1, b) \in \{ 1, b \}$
. If
![]() $\gcd (k_1,b) = 1$
, then
$\gcd (k_1,b) = 1$
, then
If, on the other hand
![]() $\gcd (k_1,b) = b$
, then write
$\gcd (k_1,b) = b$
, then write
![]() $k_1 = b^\kappa k_2$
with
$k_1 = b^\kappa k_2$
with
![]() $\gcd (k_2, b) = 1$
. Then
$\gcd (k_2, b) = 1$
. Then
 $$ \begin{align*} \gcd\left(k_1, ht_1 + a\frac{k_1}{b}\right) &= \gcd\left(b^\kappa k_2, ht_1 + a k_2 b^{\kappa-1}\right) = \gcd\left(b^\kappa, ht_1 + ak_2 b^{\kappa-1}\right) \gcd(k_2, ht_1)\\ &= \gcd\left(b^\kappa, ht_1 + a k_2 b^{\kappa-1}\right). \end{align*} $$
$$ \begin{align*} \gcd\left(k_1, ht_1 + a\frac{k_1}{b}\right) &= \gcd\left(b^\kappa k_2, ht_1 + a k_2 b^{\kappa-1}\right) = \gcd\left(b^\kappa, ht_1 + ak_2 b^{\kappa-1}\right) \gcd(k_2, ht_1)\\ &= \gcd\left(b^\kappa, ht_1 + a k_2 b^{\kappa-1}\right). \end{align*} $$
If
![]() $\kappa> 1$
, then
$\kappa> 1$
, then
![]() $\gcd (b^\kappa , ht_1 + ak_2 b^{\kappa -1}) = 1$
since
$\gcd (b^\kappa , ht_1 + ak_2 b^{\kappa -1}) = 1$
since
![]() $\gcd (b, ht_1) = 1$
. If
$\gcd (b, ht_1) = 1$
. If
![]() $\kappa = 1$
, then we are left with
$\kappa = 1$
, then we are left with
![]() $\gcd (b, ht_1 + ak_2)$
. Therefore, we obtain
$\gcd (b, ht_1 + ak_2)$
. Therefore, we obtain

which is equal to
![]() $\lambda _{t,a,b,h,k}$
.
$\lambda _{t,a,b,h,k}$
.
It follows that
![]() $\gcd (\frac {kb}{\lambda _{t,a,b,h,k}},\frac {hbt+ak}{\lambda _{t,a,b,h,k}}) = 1$
. Therefore, by making the replacements
$\gcd (\frac {kb}{\lambda _{t,a,b,h,k}},\frac {hbt+ak}{\lambda _{t,a,b,h,k}}) = 1$
. Therefore, by making the replacements
![]() $h \mapsto \frac {hbt+ak}{\lambda _{t,a,b,h,k}}$
,
$h \mapsto \frac {hbt+ak}{\lambda _{t,a,b,h,k}}$
,
![]() $k \mapsto \frac {kb}{\lambda _{t,a,b,h,k}}$
and
$k \mapsto \frac {kb}{\lambda _{t,a,b,h,k}}$
and
![]() $z \mapsto \frac {tbz}{\lambda _{t,a,b,h,k}}$
in equation (2.8), the result follows.
$z \mapsto \frac {tbz}{\lambda _{t,a,b,h,k}}$
in equation (2.8), the result follows.
![]() $\Box $
$\Box $
2.4.3 Proof of Theorem 2.1 (3)
Again assume that
![]() $|z|<1$
. Writing
$|z|<1$
. Writing
 $$ \begin{align*} F_3(\xi;q)=\prod_{j=1}^b\prod_{n=0}^{\infty}\left(1-\xi^{j-1}q^{bn+j}\right),\\[-15pt] \end{align*} $$
$$ \begin{align*} F_3(\xi;q)=\prod_{j=1}^b\prod_{n=0}^{\infty}\left(1-\xi^{j-1}q^{bn+j}\right),\\[-15pt] \end{align*} $$
we compute
 $$ \begin{align*} \operatorname{Log}\left(F_3\left(\xi;e^{-z}\right)\right)=-z\sum_{1\leq j,r \leq b} \xi^{(j-1)r}\sum_{m=0}^\infty f_j\left(\left( m+\frac{r}{b}\right) bz\right),\\[-15pt] \end{align*} $$
$$ \begin{align*} \operatorname{Log}\left(F_3\left(\xi;e^{-z}\right)\right)=-z\sum_{1\leq j,r \leq b} \xi^{(j-1)r}\sum_{m=0}^\infty f_j\left(\left( m+\frac{r}{b}\right) bz\right),\\[-15pt] \end{align*} $$
where
![]() $f_j(z):=\frac {e^{-jz}}{z(1-e^{-bz})}$
. By Lemma 2.2, we obtain
$f_j(z):=\frac {e^{-jz}}{z(1-e^{-bz})}$
. By Lemma 2.2, we obtain
 $$ \begin{align*} \sum_{m=0}^{\infty}f_j\left(\left(m+\frac r b\right)bz \right) \sim \frac{\zeta\left(2,\frac r b\right)}{b^3z^2}+ \frac{I_{f_{j,1}}^*}{bz}+\frac{B_1\left(\frac{j}{b}\right)}{bz}\left(\operatorname{\mathrm{Log}}\left({bz}\right)+\psi \left(\frac{r}{b}\right)+\gamma\right)+O(1).\\[-15pt] \end{align*} $$
$$ \begin{align*} \sum_{m=0}^{\infty}f_j\left(\left(m+\frac r b\right)bz \right) \sim \frac{\zeta\left(2,\frac r b\right)}{b^3z^2}+ \frac{I_{f_{j,1}}^*}{bz}+\frac{B_1\left(\frac{j}{b}\right)}{bz}\left(\operatorname{\mathrm{Log}}\left({bz}\right)+\psi \left(\frac{r}{b}\right)+\gamma\right)+O(1).\\[-15pt] \end{align*} $$
The first term contributes
![]() $-\frac {\pi ^2}{6b^2z}$
. By Lemma 2.3, the second term contributes
$-\frac {\pi ^2}{6b^2z}$
. By Lemma 2.3, the second term contributes
 $$ \begin{align*} -\frac 1b \sum_{j=1}^{b}I_{f_{j,1}}^*\sum_{r=1}^{b}\xi^{(j-1)r}& =-I_{f_{1,1}}^* =-\log\left(\Gamma\left(\frac{1}{b}\right)\right) - \left(\frac{1}{2}-\frac{1}{b}\right)\log\left(\frac{1}{b}\right)+\frac 12\log(2\pi) \\ &= \log\left( \frac{b^{\frac{1}{2} -\frac{1}{b}} (2\pi)^{\frac{1}{2}} }{\Gamma\left(\frac{1}{b}\right)} \right).\\[-15pt] \end{align*} $$
$$ \begin{align*} -\frac 1b \sum_{j=1}^{b}I_{f_{j,1}}^*\sum_{r=1}^{b}\xi^{(j-1)r}& =-I_{f_{1,1}}^* =-\log\left(\Gamma\left(\frac{1}{b}\right)\right) - \left(\frac{1}{2}-\frac{1}{b}\right)\log\left(\frac{1}{b}\right)+\frac 12\log(2\pi) \\ &= \log\left( \frac{b^{\frac{1}{2} -\frac{1}{b}} (2\pi)^{\frac{1}{2}} }{\Gamma\left(\frac{1}{b}\right)} \right).\\[-15pt] \end{align*} $$
Next we evaluate
 $$ \begin{align*} -\frac{1}{b}\left(\operatorname{\mathrm{Log}}\left({bz}\right)+\gamma\right)\sum_{1\leq j\leq b}B_1\left(\frac{j}{b}\right) \sum_{1\leq r\leq b} \xi^{(j-1)r}=-B_1\left(\frac{1}{b}\right)\left(\operatorname{\mathrm{Log}}\left({bz}\right)+\gamma\right).\\[-15pt] \end{align*} $$
$$ \begin{align*} -\frac{1}{b}\left(\operatorname{\mathrm{Log}}\left({bz}\right)+\gamma\right)\sum_{1\leq j\leq b}B_1\left(\frac{j}{b}\right) \sum_{1\leq r\leq b} \xi^{(j-1)r}=-B_1\left(\frac{1}{b}\right)\left(\operatorname{\mathrm{Log}}\left({bz}\right)+\gamma\right).\\[-15pt] \end{align*} $$
Finally we are left to compute
 $$ \begin{align*} -\frac{1}{b}\sum_{1\leq j,r \leq b} \xi^{(j-1)r} \left(\frac{j}{b}-\frac{1}{2}\right)\psi\left(\frac{r}{b}\right)=-\frac{1}{b}\sum_{\substack{0\leq j\leq b-1 \\ 1\leq r \leq b}} \xi^{jr}\left(\frac{j}{b}+\frac{1}{b}-\frac{1}{2}\right)\psi\left(\frac{r}{b}\right).\\[-15pt] \end{align*} $$
$$ \begin{align*} -\frac{1}{b}\sum_{1\leq j,r \leq b} \xi^{(j-1)r} \left(\frac{j}{b}-\frac{1}{2}\right)\psi\left(\frac{r}{b}\right)=-\frac{1}{b}\sum_{\substack{0\leq j\leq b-1 \\ 1\leq r \leq b}} \xi^{jr}\left(\frac{j}{b}+\frac{1}{b}-\frac{1}{2}\right)\psi\left(\frac{r}{b}\right).\\[-15pt] \end{align*} $$
The
![]() $(\frac {1}{b}-\frac {1}{2})$
-term yields
$(\frac {1}{b}-\frac {1}{2})$
-term yields
![]() $\gamma (\frac {1}{b}-\frac {1}{2})$
. Thanks to equation (2.6), the
$\gamma (\frac {1}{b}-\frac {1}{2})$
. Thanks to equation (2.6), the
![]() $\frac {j}{b}$
term contributes
$\frac {j}{b}$
term contributes
 $$ \begin{align*} -\frac{1}{b^2} \sum_{0\leq j\leq b-1} j \sum_{1\leq r \leq b} \psi \left(\frac{r}{b}\right) \xi^{jr}=-\frac{1}{b}\sum_{1\leq j\leq b-1}j\operatorname{Log }\left(1-\xi^j\right).\\[-15pt] \end{align*} $$
$$ \begin{align*} -\frac{1}{b^2} \sum_{0\leq j\leq b-1} j \sum_{1\leq r \leq b} \psi \left(\frac{r}{b}\right) \xi^{jr}=-\frac{1}{b}\sum_{1\leq j\leq b-1}j\operatorname{Log }\left(1-\xi^j\right).\\[-15pt] \end{align*} $$
Combining these observations yields that
 $$ \begin{align*} \operatorname{Log}\left(F_3\left(\xi;e^{-z}\right)\right) &= \log\left( \frac{b^{\frac{1}{2} -\frac{1}{b}} (2\pi)^{\frac{1}{2}} }{\Gamma\left(\frac{1}{b}\right)} \right) -\frac{\pi^2}{6b^2z} -B_1\left(\frac{1}{b}\right)\operatorname{\mathrm{Log}}\left({bz}\right) \\ &\quad - \sum_{1\leq j\leq b-1} \frac{j}{b} \operatorname{Log }\left(1-\xi^j\right) + O\left(|z|\right).\\[-15pt] \end{align*} $$
$$ \begin{align*} \operatorname{Log}\left(F_3\left(\xi;e^{-z}\right)\right) &= \log\left( \frac{b^{\frac{1}{2} -\frac{1}{b}} (2\pi)^{\frac{1}{2}} }{\Gamma\left(\frac{1}{b}\right)} \right) -\frac{\pi^2}{6b^2z} -B_1\left(\frac{1}{b}\right)\operatorname{\mathrm{Log}}\left({bz}\right) \\ &\quad - \sum_{1\leq j\leq b-1} \frac{j}{b} \operatorname{Log }\left(1-\xi^j\right) + O\left(|z|\right).\\[-15pt] \end{align*} $$
Exponentiating gives the desired claim.
![]() $\Box $
$\Box $
3 Proof of Theorem 1.1, Corollary 1.2 and Theorem 1.3
Here we recall a beautiful q-series identity of Han, who offered the generating functions we require for Theorems 1.1 and 1.3 and Corollary 1.2. Apart from factors that naturally correspond to quotients of Dedekind’s eta-function, these generating functions have factors of the form
![]() $F_2(\xi ;q^t)^{-t}$
. The proof of Theorem 1.3 follows directly from this fact along with known identities for the
$F_2(\xi ;q^t)^{-t}$
. The proof of Theorem 1.3 follows directly from this fact along with known identities for the
![]() $2$
-core and
$2$
-core and
![]() $3$
-core generating functions. To prove Theorem 1.1, we apply Zuckerman’s exact formulas to these functions, making strong use of Theorem 2.1 (2).
$3$
-core generating functions. To prove Theorem 1.1, we apply Zuckerman’s exact formulas to these functions, making strong use of Theorem 2.1 (2).
3.1 Work of Han
Here we derive the generating functions for the modular t-hook functions
![]() $p_t(a,b;n)$
. To this end, we recall the following beautiful formula of Han that he derived in his work on extensions of the celebrated Nekrasov–Okounkov formulaFootnote 2 (see (6.12) of [Reference Nekrasov and Okounkov22]) with
$p_t(a,b;n)$
. To this end, we recall the following beautiful formula of Han that he derived in his work on extensions of the celebrated Nekrasov–Okounkov formulaFootnote 2 (see (6.12) of [Reference Nekrasov and Okounkov22]) with
![]() $w \in {\mathbb {C}}$
:
$w \in {\mathbb {C}}$
:
 $$ \begin{align*}\sum_{\lambda \in \mathcal{P}} q^{|\lambda|} \prod_{h\in \mathcal{H}(\lambda)} \left(1-\frac{w}{h^2}\right) =\prod_{n=1}^{\infty}\left(1-q^n\right)^{w-1}.\\[-17pt] \end{align*} $$
$$ \begin{align*}\sum_{\lambda \in \mathcal{P}} q^{|\lambda|} \prod_{h\in \mathcal{H}(\lambda)} \left(1-\frac{w}{h^2}\right) =\prod_{n=1}^{\infty}\left(1-q^n\right)^{w-1}.\\[-17pt] \end{align*} $$
Here
![]() $\mathcal {P}$
denotes the set of all integer partitions, including the empty partition, and
$\mathcal {P}$
denotes the set of all integer partitions, including the empty partition, and
![]() $\mathcal {H}(\lambda )$
denotes the multiset of hook lengths for
$\mathcal {H}(\lambda )$
denotes the multiset of hook lengths for
![]() $\lambda $
. Han [Reference Han14] proved the following beautiful identity for the generating function for t-hooks in partitions
$\lambda $
. Han [Reference Han14] proved the following beautiful identity for the generating function for t-hooks in partitions
Theorem 3.1 Corollary 5.1 of [Reference Han14]
As formal power series, we have
 $$ \begin{align*}H_t(\xi;q)=\frac{1}{F_2(\xi;q^t)^t}\prod_{n=1}^{\infty} \frac{\left(1-q^{tn}\right)^t}{1-q^n}.\\[-17pt] \end{align*} $$
$$ \begin{align*}H_t(\xi;q)=\frac{1}{F_2(\xi;q^t)^t}\prod_{n=1}^{\infty} \frac{\left(1-q^{tn}\right)^t}{1-q^n}.\\[-17pt] \end{align*} $$
As a corollary, we obtain the following generating function for
![]() $p_t(a,b;n)$
.
$p_t(a,b;n)$
.
Corollary 3.2. If
![]() $t>1$
and
$t>1$
and
![]() $0\leq a<b$
, then as formal power series we have
$0\leq a<b$
, then as formal power series we have
 $$ \begin{align*} H_t(a,b;q):=\sum_{n=0}^{\infty}p_t(a,b;n)q^n=\frac{1}{b} \sum_{r=0}^{b-1} \zeta_b^{-ar}H_t\left(\zeta_b^r;q\right),\\[-17pt] \end{align*} $$
$$ \begin{align*} H_t(a,b;q):=\sum_{n=0}^{\infty}p_t(a,b;n)q^n=\frac{1}{b} \sum_{r=0}^{b-1} \zeta_b^{-ar}H_t\left(\zeta_b^r;q\right),\\[-17pt] \end{align*} $$
where
![]() $\zeta _b:=e^{\frac {2\pi i}b}$
.
$\zeta _b:=e^{\frac {2\pi i}b}$
.
Proof. We have that
 $$ \begin{align*} \begin{aligned} \frac{1}{b} \sum_{r=0}^{b-1} \zeta_b^{-ar} H_t(\zeta_b^r;q)&= \frac{1}{b} \sum_{\lambda \in \mathcal{P}}q^{|\lambda|} \sum_{r=0}^{b-1}\zeta_b^{\left(\#\mathcal{H}_t(\lambda)-a\right)r}=H_t(a,b;q). \end{aligned}\\[-46pt] \end{align*} $$
$$ \begin{align*} \begin{aligned} \frac{1}{b} \sum_{r=0}^{b-1} \zeta_b^{-ar} H_t(\zeta_b^r;q)&= \frac{1}{b} \sum_{\lambda \in \mathcal{P}}q^{|\lambda|} \sum_{r=0}^{b-1}\zeta_b^{\left(\#\mathcal{H}_t(\lambda)-a\right)r}=H_t(a,b;q). \end{aligned}\\[-46pt] \end{align*} $$
The dependence of
![]() $H_t(\xi ;q)$
on
$H_t(\xi ;q)$
on
![]() $F_2(\xi ;q^t)$
enables us to compute asymptotic behavior of
$F_2(\xi ;q^t)$
enables us to compute asymptotic behavior of
![]() $H_t(\xi ;q)$
using Theorem 2.1 (2) and, by Corollary 3.2, the asymptotic behavior of
$H_t(\xi ;q)$
using Theorem 2.1 (2) and, by Corollary 3.2, the asymptotic behavior of
![]() $H_t(a,b;q)$
.
$H_t(a,b;q)$
.
3.2 Proof of Theorem 1.3
Here we prove Theorem 1.3. We first consider the case (1), where
![]() $\ell $
is an odd prime. We consider the generating function, using Corollary 3.2
$\ell $
is an odd prime. We consider the generating function, using Corollary 3.2
 $$ \begin{align*}H_2(a_1,\ell ;q)=\sum_{n=0}^{\infty}p_2(a_1,\ell;n)q^n=\frac{1}{\ell} \sum_{r_1=0}^{\ell-1} \zeta_\ell^{-a_1 r_1}H_2\left(\zeta_\ell^{r_1};q\right). \end{align*} $$
$$ \begin{align*}H_2(a_1,\ell ;q)=\sum_{n=0}^{\infty}p_2(a_1,\ell;n)q^n=\frac{1}{\ell} \sum_{r_1=0}^{\ell-1} \zeta_\ell^{-a_1 r_1}H_2\left(\zeta_\ell^{r_1};q\right). \end{align*} $$
Applying again orthogonality of roots of unity, keeping only those terms
![]() $a_2\,\,(\mathrm {mod}\,\,{\ell })$
, where
$a_2\,\,(\mathrm {mod}\,\,{\ell })$
, where
![]() $a_2\in \{0, 1,\dots , \ell -1\}$
, we find that
$a_2\in \{0, 1,\dots , \ell -1\}$
, we find that
 $$ \begin{align*}\sum_{n=0}^{\infty} p_2(a_1,\ell;\ell n+a_2)q^{\ell n +a_2}= \frac{1}{\ell^2}\sum_{r_1, r_2\,\,(\mathrm{mod}\,\,{\ell})}\zeta_{\ell}^{-a_1 r_1 -a_2 r_2} H_2\left(\zeta_{\ell}^{r_1};\zeta_{\ell}^{r_2}q\right). \end{align*} $$
$$ \begin{align*}\sum_{n=0}^{\infty} p_2(a_1,\ell;\ell n+a_2)q^{\ell n +a_2}= \frac{1}{\ell^2}\sum_{r_1, r_2\,\,(\mathrm{mod}\,\,{\ell})}\zeta_{\ell}^{-a_1 r_1 -a_2 r_2} H_2\left(\zeta_{\ell}^{r_1};\zeta_{\ell}^{r_2}q\right). \end{align*} $$
Making use of the definition of
![]() $H_t(\xi ;q)$
, if we define
$H_t(\xi ;q)$
, if we define
![]() $\mathcal {B}_2(q)$
and
$\mathcal {B}_2(q)$
and
![]() $\mathcal {C}_2(q)$
by
$\mathcal {C}_2(q)$
by
 $$ \begin{align} \mathcal{B}_2(q)=\sum_{n=0}^{\infty}b_2(n)q^n:=\prod_{n=1}^{\infty}\frac{1}{\left(1-q^n\right)^2} \ \ \ \ {\text{and}}\ \ \ \ \mathcal{C}_2(q):=\prod_{n=1}^{\infty}\frac{\left(1-q^{2n}\right)^2}{1-q^n}, \end{align} $$
$$ \begin{align} \mathcal{B}_2(q)=\sum_{n=0}^{\infty}b_2(n)q^n:=\prod_{n=1}^{\infty}\frac{1}{\left(1-q^n\right)^2} \ \ \ \ {\text{and}}\ \ \ \ \mathcal{C}_2(q):=\prod_{n=1}^{\infty}\frac{\left(1-q^{2n}\right)^2}{1-q^n}, \end{align} $$
then we have
 $$ \begin{align*}\sum_{\substack{n\geq 0 \\n\equiv a_2\,\,(\mathrm{mod}\,\,{\ell})}}p_2(a_1,\ell;n)q^n= \frac{1}{\ell^2}\sum_{r_1, r_2\,\,(\mathrm{mod}\,\,{\ell})}\zeta_{\ell}^{-a_1 r_1 -a_2 r_2} \mathcal{B}_2\left(\zeta_{\ell}^{r_1+2r_2}q^2\right) \mathcal{C}_2\left(\zeta_{\ell}^{r_2} q\right). \end{align*} $$
$$ \begin{align*}\sum_{\substack{n\geq 0 \\n\equiv a_2\,\,(\mathrm{mod}\,\,{\ell})}}p_2(a_1,\ell;n)q^n= \frac{1}{\ell^2}\sum_{r_1, r_2\,\,(\mathrm{mod}\,\,{\ell})}\zeta_{\ell}^{-a_1 r_1 -a_2 r_2} \mathcal{B}_2\left(\zeta_{\ell}^{r_1+2r_2}q^2\right) \mathcal{C}_2\left(\zeta_{\ell}^{r_2} q\right). \end{align*} $$
Thanks to the classical identity of Jacobi
 $$ \begin{align*} \mathcal{C}_2(q)=\sum_{k=0}^{\infty}q^{\frac{k(k+1)}{2}}, \end{align*} $$
$$ \begin{align*} \mathcal{C}_2(q)=\sum_{k=0}^{\infty}q^{\frac{k(k+1)}{2}}, \end{align*} $$
for
![]() $N\equiv a_2\,\,(\mathrm {mod}\,\,{\ell })$
, we find that
$N\equiv a_2\,\,(\mathrm {mod}\,\,{\ell })$
, we find that
 $$ \begin{align} p_2(a_1,\ell;N)&=\frac{1}{\ell^2}\sum_{r_1, r_2\,\,(\mathrm{mod}\,\,{\ell})}\zeta_{\ell}^{-a_1 r_1-a_2 r_2} \sum_{\substack{k,m\geq 0\\ 2m+\frac{k(k+1)}{2}=N}} b_2(m)\zeta_{\ell}^{(r_1+2r_2)m+r_2\frac{k(k+1)}{2}} \nonumber \\ &=\sum_{\substack{m\equiv a_1\,\,(\mathrm{mod}\,\,{\ell})\\ 2m+\frac{k(k+1)}{2}=N}} b_2(m), \end{align} $$
$$ \begin{align} p_2(a_1,\ell;N)&=\frac{1}{\ell^2}\sum_{r_1, r_2\,\,(\mathrm{mod}\,\,{\ell})}\zeta_{\ell}^{-a_1 r_1-a_2 r_2} \sum_{\substack{k,m\geq 0\\ 2m+\frac{k(k+1)}{2}=N}} b_2(m)\zeta_{\ell}^{(r_1+2r_2)m+r_2\frac{k(k+1)}{2}} \nonumber \\ &=\sum_{\substack{m\equiv a_1\,\,(\mathrm{mod}\,\,{\ell})\\ 2m+\frac{k(k+1)}{2}=N}} b_2(m), \end{align} $$
by making the linear change of variables
![]() $r_1\mapsto r_1-2r_2$
and again using orthogonality of roots of unity. This then requires the solvability of the congruence
$r_1\mapsto r_1-2r_2$
and again using orthogonality of roots of unity. This then requires the solvability of the congruence
![]() $a_2-2a_1\equiv \frac {k(k+1)}{2}\,\,(\mathrm {mod}\,\,{\ell })$
. Completing the square produces the quadratic residue condition that prohibits this solvability and hence completes the proof of (1).
$a_2-2a_1\equiv \frac {k(k+1)}{2}\,\,(\mathrm {mod}\,\,{\ell })$
. Completing the square produces the quadratic residue condition that prohibits this solvability and hence completes the proof of (1).
The proof of (2) follows similarly, with
![]() $\ell $
replaced by
$\ell $
replaced by
![]() $\ell ^2$
for primes
$\ell ^2$
for primes
![]() $\ell \equiv 2\,\,(\mathrm {mod}\,\,{3})$
. The functions in (3.1) are replaced with
$\ell \equiv 2\,\,(\mathrm {mod}\,\,{3})$
. The functions in (3.1) are replaced with
 $$ \begin{align*}\mathcal{B}_3(q)=\sum_{n=0}^{\infty}b_3(n)q^n:=\prod_{n=1}^{\infty}\frac{1}{\left(1-q^n\right)^3} \ \ \ \ {\text {and}}\ \ \ \ \mathcal{C}_3(q):=\prod_{n=1}^{\infty}\frac{\left(1-q^{3n}\right)^3}{1-q^n}. \end{align*} $$
$$ \begin{align*}\mathcal{B}_3(q)=\sum_{n=0}^{\infty}b_3(n)q^n:=\prod_{n=1}^{\infty}\frac{1}{\left(1-q^n\right)^3} \ \ \ \ {\text {and}}\ \ \ \ \mathcal{C}_3(q):=\prod_{n=1}^{\infty}\frac{\left(1-q^{3n}\right)^3}{1-q^n}. \end{align*} $$
It is well-known that (for example, see Section 3 of [Reference Granville and Ono12] or [Reference Han and Ono15, Lemma 2.5]),
 $$ \begin{align*}\mathcal{C}_3(q)=:\sum_{n=0}^{\infty}c_3(n)q^n=\sum_{n=0}^{\infty}\sum_{d\mid (3n+1)} \left(\frac{d}{3}\right) q^n. \end{align*} $$
$$ \begin{align*}\mathcal{C}_3(q)=:\sum_{n=0}^{\infty}c_3(n)q^n=\sum_{n=0}^{\infty}\sum_{d\mid (3n+1)} \left(\frac{d}{3}\right) q^n. \end{align*} $$
For primes
![]() $\ell \equiv 2\,\,(\mathrm {mod}\,\,{3})$
, this implies that
$\ell \equiv 2\,\,(\mathrm {mod}\,\,{3})$
, this implies that
![]() $c_3(\ell ^2 n+a)=0$
for every positive integer n, whenever
$c_3(\ell ^2 n+a)=0$
for every positive integer n, whenever
![]() ${\mathrm {ord}}_{\ell }(3a+1)=1$
. For example, this means that
${\mathrm {ord}}_{\ell }(3a+1)=1$
. For example, this means that
![]() $c_3(4n+3)=0$
if
$c_3(4n+3)=0$
if
![]() $\ell =2$
.
$\ell =2$
.
Let
![]() $0\leq a_1, a_2<\ell ^2$
. In direct analogue with (3.2), a calculation reveals that nonvanishing for
$0\leq a_1, a_2<\ell ^2$
. In direct analogue with (3.2), a calculation reveals that nonvanishing for
![]() $N\equiv a_2\,\,(\mathrm {mod}\,\,{\ell ^2})$
relies on sums of the form
$N\equiv a_2\,\,(\mathrm {mod}\,\,{\ell ^2})$
relies on sums of the form
 $$ \begin{align*}\sum_{\substack{m\equiv a_1\,\,(\mathrm{mod}\,\,{\ell^2})\\ 3m+k=N}} b_3(m)c_3(k). \end{align*} $$
$$ \begin{align*}\sum_{\substack{m\equiv a_1\,\,(\mathrm{mod}\,\,{\ell^2})\\ 3m+k=N}} b_3(m)c_3(k). \end{align*} $$
If
![]() ${\mathrm {ord}}_{\ell }(3a+1)=1$
and
${\mathrm {ord}}_{\ell }(3a+1)=1$
and
![]() $a_2-3a_1\equiv a\,\,(\mathrm {mod}\,\,{\ell ^2})$
, then
$a_2-3a_1\equiv a\,\,(\mathrm {mod}\,\,{\ell ^2})$
, then
![]() $p_3(a_1,\ell ^2; \ell ^2+a)=0$
. This is claim (2).
$p_3(a_1,\ell ^2; \ell ^2+a)=0$
. This is claim (2).
3.3 Evaluating certain Kloosterman sums
The proof of Theorem 1.1 relies on the arithmetic of the Kloosterman sums
 $$ \begin{align*} K(a,b,t;n) := \sum_{h=1}^{b-1} \frac{\omega_{h,b}}{\omega_{th,b}^t} \zeta_b^{(at-n)h}, \end{align*} $$
$$ \begin{align*} K(a,b,t;n) := \sum_{h=1}^{b-1} \frac{\omega_{h,b}}{\omega_{th,b}^t} \zeta_b^{(at-n)h}, \end{align*} $$
where b is an odd prime and
![]() $s \geq 1$
,
$s \geq 1$
,
![]() $t> 1$
are integers. We evaluate this sum if t is coprime to b. We start by computing
$t> 1$
are integers. We evaluate this sum if t is coprime to b. We start by computing
![]() $\omega _{h,b} \omega _{th,b}^{-t}$
.
$\omega _{h,b} \omega _{th,b}^{-t}$
.
Proposition 3.3. Let b be an odd prime, h, t integers coprime to b, and let
![]() $\omega _{h,k}$
be defined by equation (2.1). Then we have
$\omega _{h,k}$
be defined by equation (2.1). Then we have
 $$ \begin{align*} \frac{\omega_{h,b}}{\omega_{th,b}^t} = \left( \frac{h}{b} \right) \left( \frac{th}{b} \right)^t e^{\pi i \frac{(1-t)(b-1)}{4}} e^{\frac{2\pi i}{b} \frac{1}{24} \left(1-t^2\right)\left(1-b^2\right)h}. \end{align*} $$
$$ \begin{align*} \frac{\omega_{h,b}}{\omega_{th,b}^t} = \left( \frac{h}{b} \right) \left( \frac{th}{b} \right)^t e^{\pi i \frac{(1-t)(b-1)}{4}} e^{\frac{2\pi i}{b} \frac{1}{24} \left(1-t^2\right)\left(1-b^2\right)h}. \end{align*} $$
Proof. The proof of this proposition uses the
![]() $\eta $
-multiplier, which we label
$\eta $
-multiplier, which we label
![]() $\psi $
. Theorem 5.8.1 of [Reference Cohen and Stromberg6] yields that for
$\psi $
. Theorem 5.8.1 of [Reference Cohen and Stromberg6] yields that for
![]() $\left ( \begin {smallmatrix} \alpha & \beta \\ \gamma & \delta \end {smallmatrix} \right ) \in \text {SL}_2({\mathbb {Z}})$
with
$\left ( \begin {smallmatrix} \alpha & \beta \\ \gamma & \delta \end {smallmatrix} \right ) \in \text {SL}_2({\mathbb {Z}})$
with
![]() $\gamma> 0$
odd, we have
$\gamma> 0$
odd, we have
 $$ \begin{align*}\psi \begin{pmatrix} \alpha & \beta \\ \gamma & \delta \end{pmatrix} = \left( \frac{\delta }{\gamma } \right) e^{\frac{\pi i}{12} \left( (\alpha +\delta )\gamma - \beta \delta \left(\gamma ^2-1\right) - 3\gamma \right)}.\end{align*} $$
$$ \begin{align*}\psi \begin{pmatrix} \alpha & \beta \\ \gamma & \delta \end{pmatrix} = \left( \frac{\delta }{\gamma } \right) e^{\frac{\pi i}{12} \left( (\alpha +\delta )\gamma - \beta \delta \left(\gamma ^2-1\right) - 3\gamma \right)}.\end{align*} $$
We also have from formula (57b) of [Reference Rademacher and Grosswald25] that for
![]() $\left (\begin {smallmatrix} \alpha & \beta \\ \gamma & \delta \end {smallmatrix}\right ) \in \text {SL}_2({\mathbb {Z}})$
$\left (\begin {smallmatrix} \alpha & \beta \\ \gamma & \delta \end {smallmatrix}\right ) \in \text {SL}_2({\mathbb {Z}})$
 $$ \begin{align*}\psi \begin{pmatrix} \alpha & \beta \\ \gamma & \delta \end{pmatrix} = e^{\pi i \left( \frac{\alpha+\delta }{12\gamma } - \frac{1}{4} \right)}\omega_{\delta,\gamma}^{-1}. \end{align*} $$
$$ \begin{align*}\psi \begin{pmatrix} \alpha & \beta \\ \gamma & \delta \end{pmatrix} = e^{\pi i \left( \frac{\alpha+\delta }{12\gamma } - \frac{1}{4} \right)}\omega_{\delta,\gamma}^{-1}. \end{align*} $$
By letting
![]() $\delta = h$
,
$\delta = h$
,
![]() $\gamma = b$
, we obtain
$\gamma = b$
, we obtain
 $$ \begin{align*} \omega_{h,b} = \left( \frac{h}{b} \right) e^{\pi i \left( \frac{1}{12b}(\alpha+h - \beta hb)\left(1-b^2\right) + \frac{b-1}{4} \right)}, \end{align*} $$
$$ \begin{align*} \omega_{h,b} = \left( \frac{h}{b} \right) e^{\pi i \left( \frac{1}{12b}(\alpha+h - \beta hb)\left(1-b^2\right) + \frac{b-1}{4} \right)}, \end{align*} $$
where
![]() $\alpha ,\beta $
satisfy
$\alpha ,\beta $
satisfy
![]() $\alpha h-\beta b=1$
. We therefore may conclude that
$\alpha h-\beta b=1$
. We therefore may conclude that
 $$ \begin{align*} \frac{\omega_{h,b}}{\omega_{th,b}^t} = \left( \frac{h}{b} \right) \left( \frac{th}{b} \right)^t e^{\pi i \frac{(1-t)(b-1)}{4}} e^{\frac{\pi i}{12b} \left( (\alpha - tA )\left(1-b^2\right) + h\left(1 - \beta b - t^2\left(1-B b\right)\right)\left(1-b^2\right) \right)}, \end{align*} $$
$$ \begin{align*} \frac{\omega_{h,b}}{\omega_{th,b}^t} = \left( \frac{h}{b} \right) \left( \frac{th}{b} \right)^t e^{\pi i \frac{(1-t)(b-1)}{4}} e^{\frac{\pi i}{12b} \left( (\alpha - tA )\left(1-b^2\right) + h\left(1 - \beta b - t^2\left(1-B b\right)\right)\left(1-b^2\right) \right)}, \end{align*} $$
where
![]() $\alpha h - \beta b = A th - B b = 1$
. A straightforward calculation then gives the claim.
$\alpha h - \beta b = A th - B b = 1$
. A straightforward calculation then gives the claim.
We now turn to evaluating the Kloosterman sum
![]() $K(a,b,t;n)$
.
$K(a,b,t;n)$
.
Proposition 3.4. Suppose that b is an odd prime,
![]() $a, n$
are integers, and
$a, n$
are integers, and
![]() $t> 1$
is an integer coprime to b. Then we have
$t> 1$
is an integer coprime to b. Then we have
 $$\begin{align*}K(a,b,t;n) = \begin{cases} \mathbb{I}(a,b,t,n) (-1)^{\frac{(1-t)(b-1)}{4}} \left( \frac{t}{b} \right) & \text{ if } t \text{ is odd}, \\ (-1)^{\frac{(1-t)(b-1)}{4}}\varepsilon_b \left( \frac{\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right) + at - n}{b} \right) \sqrt{b} & \text{ if } t \text{ is even,} \end{cases} \end{align*}$$
$$\begin{align*}K(a,b,t;n) = \begin{cases} \mathbb{I}(a,b,t,n) (-1)^{\frac{(1-t)(b-1)}{4}} \left( \frac{t}{b} \right) & \text{ if } t \text{ is odd}, \\ (-1)^{\frac{(1-t)(b-1)}{4}}\varepsilon_b \left( \frac{\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right) + at - n}{b} \right) \sqrt{b} & \text{ if } t \text{ is even,} \end{cases} \end{align*}$$
where
![]() $\mathbb {I}(a,b,t,n)$
is defined by equation (1.3).
$\mathbb {I}(a,b,t,n)$
is defined by equation (1.3).
Proof. By Proposition 3.3, we have
 $$ \begin{align*} K(a,b,t;n) &= e^{\frac{\pi i}{4}(1-t)(b-1)} \sum_{h=1}^{b-1} \left(\frac hb\right) \left(\frac{th}{b}\right)^t \zeta_b^{(at-n)h+\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)h}. \end{align*} $$
$$ \begin{align*} K(a,b,t;n) &= e^{\frac{\pi i}{4}(1-t)(b-1)} \sum_{h=1}^{b-1} \left(\frac hb\right) \left(\frac{th}{b}\right)^t \zeta_b^{(at-n)h+\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)h}. \end{align*} $$
The multiplicativity of the Legendre symbol implies
 $$ \begin{align*} \left( \frac{h}{b} \right) \left( \frac{th}{b} \right)^t = \left( \frac{h}{b} \right)^{t+1} \left( \frac{t}{b} \right)^t = \begin{cases} \left( \frac{t}{b} \right) & \text{ if } t \text{ is odd}, \\ \left( \frac{h}{b} \right) & \text{ if } t \text{ is even}. \end{cases} \end{align*} $$
$$ \begin{align*} \left( \frac{h}{b} \right) \left( \frac{th}{b} \right)^t = \left( \frac{h}{b} \right)^{t+1} \left( \frac{t}{b} \right)^t = \begin{cases} \left( \frac{t}{b} \right) & \text{ if } t \text{ is odd}, \\ \left( \frac{h}{b} \right) & \text{ if } t \text{ is even}. \end{cases} \end{align*} $$
We proceed to distinguish the parity of t. Suppose first that t is odd. Then since b is odd,
![]() $\frac 14 (1-t)(b-1)$
is an integer, and the claim directly follows.
$\frac 14 (1-t)(b-1)$
is an integer, and the claim directly follows.
Suppose next that t is even. Then we have
 $$ \begin{align*} K(a,b,t;n) = e^{\pi i\frac{(1-t)(b-1)}{4}} \sum_{h=1}^{b-1} \left(\frac hb\right) \zeta_b^{h\left(\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)+at-n\right)}. \end{align*} $$
$$ \begin{align*} K(a,b,t;n) = e^{\pi i\frac{(1-t)(b-1)}{4}} \sum_{h=1}^{b-1} \left(\frac hb\right) \zeta_b^{h\left(\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)+at-n\right)}. \end{align*} $$
Using the classical evaluation of the Gauss sum (see for example pages 12-13 of [Reference Davenport8]), we obtain
 $$\begin{align*}\sum_{h=1}^{b-1} \left(\frac hb\right) \zeta_b^{\left(\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)+at-n\right)h} = \left(\frac{\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)+at-n}{b}\right) \varepsilon_b \sqrt{b}. \\[-46pt]\end{align*}$$
$$\begin{align*}\sum_{h=1}^{b-1} \left(\frac hb\right) \zeta_b^{\left(\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)+at-n\right)h} = \left(\frac{\frac{1}{24}\left(1-t^2\right)\left(1-b^2\right)+at-n}{b}\right) \varepsilon_b \sqrt{b}. \\[-46pt]\end{align*}$$
3.4 An exact formula of Zuckerman
Here we recall a result of Zuckerman [Reference Zuckerman33], building on work of Rademacher [Reference Rademacher24]. Using the Circle Method, Zuckerman computed exact formulae for Fourier coefficients for weakly holomorphic modular forms of arbitrary nonpositive weight on finite index subgroups of
![]() ${\operatorname {SL}}_2({\mathbb {Z}})$
in terms of the cusps of the underlying subgroup and the principal parts of the form at each cusp. Let F be a weakly holomorphic modular form of weight
${\operatorname {SL}}_2({\mathbb {Z}})$
in terms of the cusps of the underlying subgroup and the principal parts of the form at each cusp. Let F be a weakly holomorphic modular form of weight
![]() $\kappa \leq 0$
with transformation law
$\kappa \leq 0$
with transformation law
for all
![]() $\gamma = \left ( \begin {smallmatrix} a & b \\ c & d \end {smallmatrix} \right )$
in some finite index subgroup of
$\gamma = \left ( \begin {smallmatrix} a & b \\ c & d \end {smallmatrix} \right )$
in some finite index subgroup of
![]() ${\operatorname {SL}}_2({\mathbb {Z}})$
. The transformation law can be viewed alternatively in terms of the cusp
${\operatorname {SL}}_2({\mathbb {Z}})$
. The transformation law can be viewed alternatively in terms of the cusp
![]() $\frac {h}{k} \in {\mathbb {Q}}$
. Let
$\frac {h}{k} \in {\mathbb {Q}}$
. Let
![]() $h'$
be defined through the congruence
$h'$
be defined through the congruence
![]() $hh' \equiv -1 \,\,(\mathrm {mod}\,\,{k})$
. Taking
$hh' \equiv -1 \,\,(\mathrm {mod}\,\,{k})$
. Taking
![]() $\tau = \frac {h'}{k} + \frac {i}{kz}$
and choosing
$\tau = \frac {h'}{k} + \frac {i}{kz}$
and choosing
![]() $\gamma =\gamma _{h,k} := \left ( \begin {smallmatrix} h & \beta \\ k & -h' \end {smallmatrix} \right ) \in \mathrm {SL}_2(\mathbb {Z})$
, we obtain the equivalent transformation law
$\gamma =\gamma _{h,k} := \left ( \begin {smallmatrix} h & \beta \\ k & -h' \end {smallmatrix} \right ) \in \mathrm {SL}_2(\mathbb {Z})$
, we obtain the equivalent transformation law
 $$ \begin{align*}F\left( \frac{h}{k}+\frac{iz}{k} \right) = \chi(\gamma_{h,k})(-iz)^{-\kappa} F\left( \frac{h'}{k}+\frac{i}{kz} \right). \end{align*} $$
$$ \begin{align*}F\left( \frac{h}{k}+\frac{iz}{k} \right) = \chi(\gamma_{h,k})(-iz)^{-\kappa} F\left( \frac{h'}{k}+\frac{i}{kz} \right). \end{align*} $$
Let F have the Fourier expansion at
![]() $i\infty $
given by
$i\infty $
given by
and Fourier expansions at each rational number
![]() $0 \leq \frac {h}{k} < 1$
given by
$0 \leq \frac {h}{k} < 1$
given by
 $$ \begin{align*} F|_{\kappa}\gamma_{h,k}(\tau) = \sum_{n \gg -\infty} a_{h,k}(n) q^{\frac{n + \alpha_{h,k}}{c_{k}}}. \end{align*} $$
$$ \begin{align*} F|_{\kappa}\gamma_{h,k}(\tau) = \sum_{n \gg -\infty} a_{h,k}(n) q^{\frac{n + \alpha_{h,k}}{c_{k}}}. \end{align*} $$
Furthermore, let
![]() $I_\alpha $
denote the usual I-Bessel function. In this framework, the relevant theorem of Zuckerman [Reference Zuckerman33, Theorem 1] may be stated as follows.
$I_\alpha $
denote the usual I-Bessel function. In this framework, the relevant theorem of Zuckerman [Reference Zuckerman33, Theorem 1] may be stated as follows.
Theorem 3.5. Assume the notation and hypotheses above. If
![]() $n + \alpha> 0$
, then we have
$n + \alpha> 0$
, then we have
 $$ \begin{align*} &a(n) = 2\pi (n+\alpha)^{\frac{\kappa-1}{2}} \sum_{k=1}^\infty \dfrac{1}{k} \sum_{\substack{0 \leq h < k \\ \gcd(h,k) = 1}}\chi(\gamma_{h,k}) e^{- \frac{2\pi i (n+\alpha) h}{k}} \\ &\ \times \sum_{m+\alpha_{h,k} \leq 0} a_{h,k}(m) e^{ \frac{2\pi i}{k c_{k}} (m + \alpha_{h,k}) h' } \left( \dfrac{\lvert m +\alpha_{h,k} \rvert }{c_{k}} \right)^{ \frac{1 - \kappa}{2}} I_{-\kappa+1}\left( \dfrac{4\pi}{k} \sqrt{\dfrac{(n + \alpha)\lvert m +\alpha_{h,k} \rvert}{c_{k}}} \right). \end{align*} $$
$$ \begin{align*} &a(n) = 2\pi (n+\alpha)^{\frac{\kappa-1}{2}} \sum_{k=1}^\infty \dfrac{1}{k} \sum_{\substack{0 \leq h < k \\ \gcd(h,k) = 1}}\chi(\gamma_{h,k}) e^{- \frac{2\pi i (n+\alpha) h}{k}} \\ &\ \times \sum_{m+\alpha_{h,k} \leq 0} a_{h,k}(m) e^{ \frac{2\pi i}{k c_{k}} (m + \alpha_{h,k}) h' } \left( \dfrac{\lvert m +\alpha_{h,k} \rvert }{c_{k}} \right)^{ \frac{1 - \kappa}{2}} I_{-\kappa+1}\left( \dfrac{4\pi}{k} \sqrt{\dfrac{(n + \alpha)\lvert m +\alpha_{h,k} \rvert}{c_{k}}} \right). \end{align*} $$
3.5 Proof of Theorem 1.1 and Corollary 1.2
We next provide proofs of both Theorem 1.1 and Corollary 1.2. Our main tool is the powerful theorem of Zuckerman described in Section 3.4.
Proof of Theorem 1.1
Using Corollary 3.2, we have
 $$ \begin{align} H_t(a,b;q) = \frac{1}{b(q;q)_\infty} + \sum_{r=1}^{b-1} \zeta_b^{-ar}H_t\left(\zeta_b^r;q\right). \end{align} $$
$$ \begin{align} H_t(a,b;q) = \frac{1}{b(q;q)_\infty} + \sum_{r=1}^{b-1} \zeta_b^{-ar}H_t\left(\zeta_b^r;q\right). \end{align} $$
From Theorem 3.1, we conclude
 $$ \begin{align*} H_t\left(\zeta_b^r;q \right) = \frac{\left(q^t;q^t\right)^t_\infty}{\left(\zeta_b^rq^t; \zeta_b^rq^t\right)^t_\infty \left(q;q\right)_\infty}. \end{align*} $$
$$ \begin{align*} H_t\left(\zeta_b^r;q \right) = \frac{\left(q^t;q^t\right)^t_\infty}{\left(\zeta_b^rq^t; \zeta_b^rq^t\right)^t_\infty \left(q;q\right)_\infty}. \end{align*} $$
To obtain the transformation formula for
![]() $H_t(\zeta _b^r;q)$
at the cusp
$H_t(\zeta _b^r;q)$
at the cusp
![]() $\frac hk$
, we write
$\frac hk$
, we write
where we note that
![]() $\gcd (h\frac {t}{\gcd (k,t)}, \frac {k}{\gcd (k,t)}) = 1$
. Thus we may use equation (2.7) with
$\gcd (h\frac {t}{\gcd (k,t)}, \frac {k}{\gcd (k,t)}) = 1$
. Thus we may use equation (2.7) with
![]() $k \mapsto \frac {k}{\gcd (k,t)}, h \mapsto h \frac {t}{\gcd (k,t)}, z \mapsto \frac {t}{\gcd (k,t)}z$
to obtain
$k \mapsto \frac {k}{\gcd (k,t)}, h \mapsto h \frac {t}{\gcd (k,t)}, z \mapsto \frac {t}{\gcd (k,t)}z$
to obtain
 $$ \begin{align} \left(q^t;q^t\right)_\infty = \omega_{h \frac{t}{\gcd(k,t)},\frac{k}{\gcd(k,t)}}^{-1} &\left(\frac{t}{\gcd(k,t)}z\right)^{-\frac{1}{2}} e^{\frac{\pi \gcd(k,t)}{12k} \left( \frac{t}{\gcd(k,t)}z -\frac{\gcd(k,t)}{t z} \right)} \nonumber\\ &\quad\times \left(e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }; e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }\right)_\infty, \end{align} $$
$$ \begin{align} \left(q^t;q^t\right)_\infty = \omega_{h \frac{t}{\gcd(k,t)},\frac{k}{\gcd(k,t)}}^{-1} &\left(\frac{t}{\gcd(k,t)}z\right)^{-\frac{1}{2}} e^{\frac{\pi \gcd(k,t)}{12k} \left( \frac{t}{\gcd(k,t)}z -\frac{\gcd(k,t)}{t z} \right)} \nonumber\\ &\quad\times \left(e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }; e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }\right)_\infty, \end{align} $$
where
![]() $0 \leq h_{k,t} < \frac {k}{\gcd (k,t)}$
is defined by
$0 \leq h_{k,t} < \frac {k}{\gcd (k,t)}$
is defined by
![]() $ h \frac {t}{\gcd (k,t)} h_{k,t} \equiv -1 \,\,(\mathrm {mod}\,\,{\frac {k}{\gcd (k,t)}})$
.
$ h \frac {t}{\gcd (k,t)} h_{k,t} \equiv -1 \,\,(\mathrm {mod}\,\,{\frac {k}{\gcd (k,t)}})$
.
Similarly, for
![]() $\left (\zeta _b^rq^t;\zeta _b^rq^t\right )_\infty $
the proof of Theorem 2.1 (2) implies that we may use equation (2.7) with
$\left (\zeta _b^rq^t;\zeta _b^rq^t\right )_\infty $
the proof of Theorem 2.1 (2) implies that we may use equation (2.7) with
![]() $h \mapsto \frac {hbt+rk}{\lambda _{t,r,b,h,k}}, k \mapsto \frac {kb}{\lambda _{t,r,b,h,k}}, z \mapsto \frac {tbz}{\lambda _{t,r,b,h,k}}$
and obtain
$h \mapsto \frac {hbt+rk}{\lambda _{t,r,b,h,k}}, k \mapsto \frac {kb}{\lambda _{t,r,b,h,k}}, z \mapsto \frac {tbz}{\lambda _{t,r,b,h,k}}$
and obtain
 $$ \begin{align} \left(\zeta_b^rq^t;\zeta_b^rq^t\right)_\infty &= \omega_{\frac{hbt+rk}{\lambda_{t,r,b,h,k}}, \frac{kb}{\lambda_{t,r,b,h,k}}}^{-1} \left(\frac{tbz}{\lambda_{t,r,b,h,k}}\right)^{-\frac{1}{2}} e^{\frac{\pi \lambda_{t,r,b,h,k}}{12kb} \left( \frac{tbz}{\lambda_{t,r,b,h,k}} - \frac{\lambda_{t,r,b,h,k}}{tbz} \right) } \nonumber\\ &\quad\times \left( e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb} \left( h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \right)}; e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb} \left( h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \right)} \right)_\infty, \end{align} $$
$$ \begin{align} \left(\zeta_b^rq^t;\zeta_b^rq^t\right)_\infty &= \omega_{\frac{hbt+rk}{\lambda_{t,r,b,h,k}}, \frac{kb}{\lambda_{t,r,b,h,k}}}^{-1} \left(\frac{tbz}{\lambda_{t,r,b,h,k}}\right)^{-\frac{1}{2}} e^{\frac{\pi \lambda_{t,r,b,h,k}}{12kb} \left( \frac{tbz}{\lambda_{t,r,b,h,k}} - \frac{\lambda_{t,r,b,h,k}}{tbz} \right) } \nonumber\\ &\quad\times \left( e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb} \left( h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \right)}; e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb} \left( h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \right)} \right)_\infty, \end{align} $$
where
![]() $0 \leq h_{k,t,b,r} < \frac {kb}{\lambda _{t,r,b,h,k}}$
is defined by
$0 \leq h_{k,t,b,r} < \frac {kb}{\lambda _{t,r,b,h,k}}$
is defined by
![]() $ \frac {hbt+rk}{\lambda _{t,r,b,h,k}} h_{k,t,b,r} \equiv -1 \,\,(\mathrm {mod}\,\,{\frac {kb}{\lambda _{t,r,b,h,k}}})$
.
$ \frac {hbt+rk}{\lambda _{t,r,b,h,k}} h_{k,t,b,r} \equiv -1 \,\,(\mathrm {mod}\,\,{\frac {kb}{\lambda _{t,r,b,h,k}}})$
.
Combining equation (2.7), equation (3.4), and equation (3.5) yields
 $$ \begin{align} H_t\left(\zeta_b^r;q\right) &= \Omega_{b,t}(r;h,k) \left( \frac{\gcd(k,t)b}{\lambda_{t,r,b,h,k}}\right)^{\frac{t}{2}} z^{\frac{1}{2}} e^{\frac{\pi}{12k} \left(-z + \left(1-\gcd(k,t)^2 + \frac{\lambda_{t,r,b,h,k}^2}{b^2} \right) \frac{1}{z}\right) } \nonumber\\ &\quad\times \frac{ \left(e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }; e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }\right)_\infty^t }{ \left(\! e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb}\! \left(\! h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \!\right)}; e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb} \!\left( h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \!\right)} \!\right)_\infty^t \!\left(\! e^{\frac{2\pi i}{k}\!\left(\! h'+\frac iz \!\right)}; e^{\frac{2\pi i}{k}\left(\! h'+\frac{i}{z} \!\right)} \!\right)_\infty}, \end{align} $$
$$ \begin{align} H_t\left(\zeta_b^r;q\right) &= \Omega_{b,t}(r;h,k) \left( \frac{\gcd(k,t)b}{\lambda_{t,r,b,h,k}}\right)^{\frac{t}{2}} z^{\frac{1}{2}} e^{\frac{\pi}{12k} \left(-z + \left(1-\gcd(k,t)^2 + \frac{\lambda_{t,r,b,h,k}^2}{b^2} \right) \frac{1}{z}\right) } \nonumber\\ &\quad\times \frac{ \left(e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }; e^{\frac{2\pi i \gcd(k,t)}{k} \left(h_{k,t} + i\frac{\gcd(k,t)}{tz}\right) }\right)_\infty^t }{ \left(\! e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb}\! \left(\! h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \!\right)}; e^{\frac{2\pi i \lambda_{t,r,b,h,k}}{kb} \!\left( h_{k,t,b,r} + i\frac{\lambda_{t,r,b,h,k}}{tbz} \!\right)} \!\right)_\infty^t \!\left(\! e^{\frac{2\pi i}{k}\!\left(\! h'+\frac iz \!\right)}; e^{\frac{2\pi i}{k}\left(\! h'+\frac{i}{z} \!\right)} \!\right)_\infty}, \end{align} $$
where

As usual, we define
![]() $P_t(q):=(q;q)_\infty ^t=:\sum _{n=0}^\infty q_t(n)q^n$
and
$P_t(q):=(q;q)_\infty ^t=:\sum _{n=0}^\infty q_t(n)q^n$
and
![]() $P(q)^t=:\sum _{n=0}^\infty p_t(n)q^n$
. Then we see that the principal part of equation (3.6) is governed by the sum
$P(q)^t=:\sum _{n=0}^\infty p_t(n)q^n$
. Then we see that the principal part of equation (3.6) is governed by the sum
 $$ \begin{align*} \sum_{\substack{n_1,n_2,n_3 \geq 0 \\ r_{k,h,t,b}(n_1,n_2,n_3)\geq 0}} q_t(n_1) p_t(n_2) p(n_3) \zeta_{kb}^{\gcd(k,t)b h_{k,t} n_1 + \lambda_{t,r,b,h,k} h_{k,t,b,r} n_2 + bh'n_3} e^{\frac{\pi}{12 kz} r_{k,h,t,b}(n_1,n_2,n_3) }, \end{align*} $$
$$ \begin{align*} \sum_{\substack{n_1,n_2,n_3 \geq 0 \\ r_{k,h,t,b}(n_1,n_2,n_3)\geq 0}} q_t(n_1) p_t(n_2) p(n_3) \zeta_{kb}^{\gcd(k,t)b h_{k,t} n_1 + \lambda_{t,r,b,h,k} h_{k,t,b,r} n_2 + bh'n_3} e^{\frac{\pi}{12 kz} r_{k,h,t,b}(n_1,n_2,n_3) }, \end{align*} $$
where

We denote the Fourier coefficients of
![]() $H_t(\zeta _b^r;q)$
by
$H_t(\zeta _b^r;q)$
by
![]() $c_{t,b,r}(n)$
. Using Theorem 3.5, we conclude that
$c_{t,b,r}(n)$
. Using Theorem 3.5, we conclude that
 $$ \begin{align} &c_{t,b,r}(n) = \nonumber\\ &\frac{2\pi}{n^{\frac{3}{4}}} b^{\frac{t}{2}} \sum_{k = 1}^\infty \frac{\gcd(k,t)^{\frac{t}{2}}}{k} \sum_{\substack{0 \leq h < k \\ \gcd(h,k)=1}} \Omega_{b,t}(r; h,k) e^{- \frac{2\pi i n h}{k}} \lambda_{t,r,b,h,k}^{-\frac{t}{2}} \sum_{\substack{n_1,n_2,n_3 \geq 0 \\ r_{k,h,t,b}(n_1,n_2,n_3) \geq 0}} q_t(n_1) p_t(n_2) p(n_3) \nonumber\\ &\times \zeta_{kb}^{\gcd(k,t)b h_{k,t} n_1 + \lambda_{t,r,b,h,k} h_{k,t,b,r} n_2 + bh'n_3} \left(\frac{r_{k,h,t,b}(n_1,n_2,n_3)}{24}\right)^{\frac34} I_{\frac{3}{2}} \left(\frac{\pi}{k}\sqrt{\frac{2nr_{k,h,t,b}(n_1,n_2,n_3)}{3}} \right). \end{align} $$
$$ \begin{align} &c_{t,b,r}(n) = \nonumber\\ &\frac{2\pi}{n^{\frac{3}{4}}} b^{\frac{t}{2}} \sum_{k = 1}^\infty \frac{\gcd(k,t)^{\frac{t}{2}}}{k} \sum_{\substack{0 \leq h < k \\ \gcd(h,k)=1}} \Omega_{b,t}(r; h,k) e^{- \frac{2\pi i n h}{k}} \lambda_{t,r,b,h,k}^{-\frac{t}{2}} \sum_{\substack{n_1,n_2,n_3 \geq 0 \\ r_{k,h,t,b}(n_1,n_2,n_3) \geq 0}} q_t(n_1) p_t(n_2) p(n_3) \nonumber\\ &\times \zeta_{kb}^{\gcd(k,t)b h_{k,t} n_1 + \lambda_{t,r,b,h,k} h_{k,t,b,r} n_2 + bh'n_3} \left(\frac{r_{k,h,t,b}(n_1,n_2,n_3)}{24}\right)^{\frac34} I_{\frac{3}{2}} \left(\frac{\pi}{k}\sqrt{\frac{2nr_{k,h,t,b}(n_1,n_2,n_3)}{3}} \right). \end{align} $$
Since
![]() $x^\alpha I_{\alpha }(x)$
is monotonically increasing as
$x^\alpha I_{\alpha }(x)$
is monotonically increasing as
![]() $x \rightarrow \infty $
for any fixed
$x \rightarrow \infty $
for any fixed
![]() $\alpha $
, the terms that dominate asymptotically are those which have the largest possible value of
$\alpha $
, the terms that dominate asymptotically are those which have the largest possible value of
![]() $\frac 1k \sqrt {r_{k,h,t,b}(n_1, n_2, n_3)}$
. In particular for this we require
$\frac 1k \sqrt {r_{k,h,t,b}(n_1, n_2, n_3)}$
. In particular for this we require
![]() $n_1 = n_2 = n_3 = 0$
. Note that we have
$n_1 = n_2 = n_3 = 0$
. Note that we have
![]() $q_t(0) = p_t(0) = p(0) = 1$
. Since the expression in question is positive, we can maximise its square: that is, we maximise
$q_t(0) = p_t(0) = p(0) = 1$
. Since the expression in question is positive, we can maximise its square: that is, we maximise
 $$ \begin{align*} \dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1}{k^2} \left( 1 - \gcd(k,t)^2 + \dfrac{\lambda_{t,r,b,h,k}^2}{b^2} \right). \end{align*} $$
$$ \begin{align*} \dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1}{k^2} \left( 1 - \gcd(k,t)^2 + \dfrac{\lambda_{t,r,b,h,k}^2}{b^2} \right). \end{align*} $$
We consider the three possible values of
![]() $\lambda _{t,r,b,h,k}$
. If
$\lambda _{t,r,b,h,k}$
. If
![]() $\lambda _{t,r,b,h,k} = \gcd (k,t)$
; then
$\lambda _{t,r,b,h,k} = \gcd (k,t)$
; then
 $$ \begin{align*}\dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1}{k^2} \left( 1 + \left( \dfrac{1}{b^2} - 1 \right) \gcd(k,t)^2 \right) \leq \left(1+ \left(\frac{1}{9}-1\right)\right) < 1.\end{align*} $$
$$ \begin{align*}\dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1}{k^2} \left( 1 + \left( \dfrac{1}{b^2} - 1 \right) \gcd(k,t)^2 \right) \leq \left(1+ \left(\frac{1}{9}-1\right)\right) < 1.\end{align*} $$
If
![]() $\lambda _{t,r,b,h,k} = b \gcd (k,t)$
, then (noting that in this case
$\lambda _{t,r,b,h,k} = b \gcd (k,t)$
, then (noting that in this case
![]() $k>1$
)
$k>1$
)
Finally, if
![]() $\lambda _{t,r,b,h,k} = b^2 \gcd (k,t)$
, then we have
$\lambda _{t,r,b,h,k} = b^2 \gcd (k,t)$
, then we have
Since
![]() $b \mid \mid \dfrac {k}{\gcd (k,t)}$
in this case, we may write
$b \mid \mid \dfrac {k}{\gcd (k,t)}$
in this case, we may write
![]() $\gcd (k,t) = b^\varrho d$
, where
$\gcd (k,t) = b^\varrho d$
, where
![]() $\gcd (b,d) = 1$
,
$\gcd (b,d) = 1$
,
![]() $b^\varrho \mid \mid t$
and
$b^\varrho \mid \mid t$
and
![]() $k = b^{\varrho + 1} d k_0$
for
$k = b^{\varrho + 1} d k_0$
for
![]() $\gcd (k_0, \frac {t}{\gcd (k,t)}) = \gcd (k_0,b) = 1$
. Therefore,
$\gcd (k_0, \frac {t}{\gcd (k,t)}) = \gcd (k_0,b) = 1$
. Therefore,
 $$ \begin{align*}\dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1 + \left(b^2-1\right) b^{2\varrho} d^2}{b^{2\varrho + 2} d^2 k_0^2},\end{align*} $$
$$ \begin{align*}\dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1 + \left(b^2-1\right) b^{2\varrho} d^2}{b^{2\varrho + 2} d^2 k_0^2},\end{align*} $$
which is maximised if
![]() $k_0 = 1$
. In this case, we have
$k_0 = 1$
. In this case, we have
![]() $k = b \gcd (k,t)$
, and therefore we may write
$k = b \gcd (k,t)$
, and therefore we may write
 $$ \begin{align*}\dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1 + \left(b^2 - 1\right) \gcd(k,t)^2}{b^2 \gcd(k,t)^2} = \dfrac{b^2-1}{b^2}+\dfrac{1}{b^2 \gcd(k,t)^2}.\end{align*} $$
$$ \begin{align*}\dfrac{r_{k,h,t,b}(0,0,0)}{k^2} = \dfrac{1 + \left(b^2 - 1\right) \gcd(k,t)^2}{b^2 \gcd(k,t)^2} = \dfrac{b^2-1}{b^2}+\dfrac{1}{b^2 \gcd(k,t)^2}.\end{align*} $$
To maximise this, we need to minimise
![]() $\gcd (k,t)$
, which is
$\gcd (k,t)$
, which is
![]() $\gcd (k,t) = 1$
. Note that in this case
$\gcd (k,t) = 1$
. Note that in this case
Since
![]() $ht+r \equiv 0 \,\,(\mathrm {mod}\,\,{b})$
, we have
$ht+r \equiv 0 \,\,(\mathrm {mod}\,\,{b})$
, we have
 $$ \begin{align*} \Omega_{b,t}(r;h,b) = \dfrac{\omega_{\frac{ht+r}{b}, 1}^{t} \omega_{h,b}}{\omega_{ht,b}^{t}} = \dfrac{\omega_{-r\bar{t},b}}{\omega_{-r,b}^{t}}, \end{align*} $$
$$ \begin{align*} \Omega_{b,t}(r;h,b) = \dfrac{\omega_{\frac{ht+r}{b}, 1}^{t} \omega_{h,b}}{\omega_{ht,b}^{t}} = \dfrac{\omega_{-r\bar{t},b}}{\omega_{-r,b}^{t}}, \end{align*} $$
where
![]() $\bar {t}$
denotes the inverse of
$\bar {t}$
denotes the inverse of
![]() $t \,\,(\mathrm {mod}\,\,{b})$
. Then by equation (3.7), we have
$t \,\,(\mathrm {mod}\,\,{b})$
. Then by equation (3.7), we have
 $$ \begin{align*} c_{t,b,r}(n) &\sim \dfrac{2\pi b^{\frac t2} \omega_{-r\bar{t},b} e^{\frac{2\pi i n r\bar{t}}{b}}}{(24n)^{\frac 34} \omega_{-r,b}^{t} b^{t+1}} I_{\frac 32} \left( \pi \sqrt{\frac{2n}{3}} \right) \sim \dfrac{e^{\pi\sqrt{\frac{2n}{3}}}}{4\sqrt{3} n b^{\frac{t}{2}+1}} \dfrac{\omega_{-r\bar{t},b}}{ \omega_{-r,b}^{t}} e^{\frac{2\pi i n r\bar{t}}{b}} , \end{align*} $$
$$ \begin{align*} c_{t,b,r}(n) &\sim \dfrac{2\pi b^{\frac t2} \omega_{-r\bar{t},b} e^{\frac{2\pi i n r\bar{t}}{b}}}{(24n)^{\frac 34} \omega_{-r,b}^{t} b^{t+1}} I_{\frac 32} \left( \pi \sqrt{\frac{2n}{3}} \right) \sim \dfrac{e^{\pi\sqrt{\frac{2n}{3}}}}{4\sqrt{3} n b^{\frac{t}{2}+1}} \dfrac{\omega_{-r\bar{t},b}}{ \omega_{-r,b}^{t}} e^{\frac{2\pi i n r\bar{t}}{b}} , \end{align*} $$
as
![]() $n \to \infty $
, where we use that
$n \to \infty $
, where we use that
![]() $I_\alpha (x) \sim \frac {e^x}{\sqrt {2\pi x}}$
as
$I_\alpha (x) \sim \frac {e^x}{\sqrt {2\pi x}}$
as
![]() $x \rightarrow \infty $
. Using equation (1.1), we obtain
$x \rightarrow \infty $
. Using equation (1.1), we obtain

By equation (3.3), we have
 $$ \begin{align*} p_t(a,b;n) = \dfrac{1}{b}p(n) + \dfrac{1}{b} \sum_{r = 1}^{b-1} \zeta_b^{-ar} c_{t,b,r}(n), \end{align*} $$
$$ \begin{align*} p_t(a,b;n) = \dfrac{1}{b}p(n) + \dfrac{1}{b} \sum_{r = 1}^{b-1} \zeta_b^{-ar} c_{t,b,r}(n), \end{align*} $$
and so dividing through by
![]() $p(n)$
yields
$p(n)$
yields

as
![]() $n \to \infty $
. This completes the proof in the case where
$n \to \infty $
. This completes the proof in the case where
![]() $b | t$
. Otherwise, setting
$b | t$
. Otherwise, setting
![]() $h = -r\bar {t}$
shows
$h = -r\bar {t}$
shows
 $$ \begin{align*} \dfrac{p_t(a,b;n)}{p(n)} \sim \dfrac{1}{b} + \dfrac{1}{b^{\frac{t}{2} + 2}} \sum_{h=1}^{b-1} \dfrac{\omega_{h,b}}{\omega^t_{th,b}}\zeta_b^{(at-n)h} = \dfrac{1}{b} \left( 1 + \dfrac{K(a,b,t;n)}{b^{\frac{t}{2} + 1}} \right) \end{align*} $$
$$ \begin{align*} \dfrac{p_t(a,b;n)}{p(n)} \sim \dfrac{1}{b} + \dfrac{1}{b^{\frac{t}{2} + 2}} \sum_{h=1}^{b-1} \dfrac{\omega_{h,b}}{\omega^t_{th,b}}\zeta_b^{(at-n)h} = \dfrac{1}{b} \left( 1 + \dfrac{K(a,b,t;n)}{b^{\frac{t}{2} + 1}} \right) \end{align*} $$
as
![]() $n \to \infty $
. The evaluation of
$n \to \infty $
. The evaluation of
![]() $K(a,b,t;n)$
in Proposition 3.4 then completes the proof.
$K(a,b,t;n)$
in Proposition 3.4 then completes the proof.
4 Proof of Theorem 1.4 and Corollary 1.5
Here we recall the relevant generating functions for the Poincaré polynomials of the Hilbert schemes that pertain to Theorem 1.4.
4.1 Work of Göttsche and Buryak, Feigin and Nakajima
For convenience, we let
![]() $P(X;T)$
be the usual Poincaré polynomial
$P(X;T)$
be the usual Poincaré polynomial
which is the generating function for the Betti numbers of X. For the various Hilbert schemes on n points we consider, the work of Göttsche and Buryak, Feigin and Nakajima [Reference Buryak and Feigin3, Reference Buryak, Feigin and Nakajima4, Reference Göttsche10, Reference Göttsche11] offers the generating function of these Poincaré polynomials as a formal power series in q. Namely, we have the following.
Theorem 4.1 Göttsche
We have that
 $$ \begin{align*}G(T;q):=\sum_{n=0}^{\infty} P\left(\left({\mathbb{C}}^2\right)^{[n]};T \right)q^n=\prod_{m=1}^{\infty}\frac{1}{1-T^{2m-2}q^m}=\frac{1}{ F_3(T^2; q)}. \end{align*} $$
$$ \begin{align*}G(T;q):=\sum_{n=0}^{\infty} P\left(\left({\mathbb{C}}^2\right)^{[n]};T \right)q^n=\prod_{m=1}^{\infty}\frac{1}{1-T^{2m-2}q^m}=\frac{1}{ F_3(T^2; q)}. \end{align*} $$
Theorem 4.2 Buryak and Feigin
If
![]() $\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then we have that
$\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then we have that
 $$ \begin{align*}G_{\alpha,\beta}(T;q):=\sum_{n=0}^{\infty} P\left(\left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}};T\right)q^n= \frac{1}{F_1(T^2;q^{\alpha+\beta})} \prod_{m=1}^{\infty}\frac{1-q^{(\alpha+\beta)m}}{1-q^m}. \end{align*} $$
$$ \begin{align*}G_{\alpha,\beta}(T;q):=\sum_{n=0}^{\infty} P\left(\left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}};T\right)q^n= \frac{1}{F_1(T^2;q^{\alpha+\beta})} \prod_{m=1}^{\infty}\frac{1-q^{(\alpha+\beta)m}}{1-q^m}. \end{align*} $$
Remark. The Poincaré polynomials in these cases only have even degree terms. The odd index Betti numbers are always zero. Moreover, letting
![]() $T=1$
in these generating functions give Euler’s generating function for
$T=1$
in these generating functions give Euler’s generating function for
![]() $p(n)$
. Therefore, we directly see that
$p(n)$
. Therefore, we directly see that
 $$ \begin{align*}p(n)=P\left(\left({\mathbb{C}}^2\right)^{[n]};1 \right)=P\left(\left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}};1\right), \end{align*} $$
$$ \begin{align*}p(n)=P\left(\left({\mathbb{C}}^2\right)^{[n]};1 \right)=P\left(\left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}};1\right), \end{align*} $$
confirming (1.5). Of course, the proofs of these theorems begin with partitions of size n.
Arguing as in the proof of Corollary 3.2, we obtain the following generating functions for the modular sums of Betti numbers.
Corollary 4.3. For
![]() $0\leq a<b$
, the following are true.
$0\leq a<b$
, the following are true.
(1) We have that
 $$ \begin{align*}\sum_{n=0}^{\infty}B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right)q^n=\frac{1}{b}\sum_{r=0}^{b-1}\zeta_b^{-ar}G(\zeta_b^r;q). \end{align*} $$
$$ \begin{align*}\sum_{n=0}^{\infty}B\left(a,b; \left({\mathbb{C}}^2\right)^{[n]}\right)q^n=\frac{1}{b}\sum_{r=0}^{b-1}\zeta_b^{-ar}G(\zeta_b^r;q). \end{align*} $$
(2) If
![]() $\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then we have
$\alpha , \beta \in {\mathbb {N}}$
are relatively prime, then we have
 $$ \begin{align*}\sum_{n=0}^{\infty}B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)q^n=\frac{1}{b}\sum_{r=0}^{b-1}\zeta_b^{-ar}G_{\alpha,\beta}(\zeta_b^r;q). \end{align*} $$
$$ \begin{align*}\sum_{n=0}^{\infty}B\left(a,b; \left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)q^n=\frac{1}{b}\sum_{r=0}^{b-1}\zeta_b^{-ar}G_{\alpha,\beta}(\zeta_b^r;q). \end{align*} $$
4.2 Wright’s variant of the Circle Method
The classical Circle Method, as utilised by Hardy–Ramanujan and many others, derives asymptotic or exact formulas for the Fourier coefficients of q-series by leveraging modular properties of the generating functions. More recently, a variation of the Circle Method due to Wright has grown increasingly important in number theory. For the proof of Theorem 1.4 and Corollary 1.5, we use Wright’s variation, which obtains asymptotic formulas for generating functions carrying suitable analytic properties.
Remark. Ngo and Rhoades [Reference Ngo and Rhoades21] proved a more restricted versionFootnote 3 of the following proposition where the generating function F split as two functions. Our purposes do not require such a splitting, so we state the proposition in terms of a single function F.
Proposition 4.4. Suppose that
![]() $F(q)$
is analytic for
$F(q)$
is analytic for
![]() $q = e^{-z}$
, where
$q = e^{-z}$
, where
![]() $z=x+iy \in {\mathbb {C}}$
satisfies
$z=x+iy \in {\mathbb {C}}$
satisfies
![]() $x> 0$
and
$x> 0$
and
![]() $|y| < \pi $
, and suppose that
$|y| < \pi $
, and suppose that
![]() $F(q)$
has an expansion
$F(q)$
has an expansion
![]() $F(q) = \sum _{n=0}^\infty c(n) q^n$
near 1. Let
$F(q) = \sum _{n=0}^\infty c(n) q^n$
near 1. Let
![]() $c,N,M>0$
be fixed constants. Consider the following hypotheses:
$c,N,M>0$
be fixed constants. Consider the following hypotheses:
-
(1) As
 $z\to 0$
in the bounded cone
$z\to 0$
in the bounded cone
 $|y|\le Mx$
(major arc), we have where
$|y|\le Mx$
(major arc), we have where $$ \begin{align*} F(e^{-z}) = z^{B} e^{\frac{A}{z}} \left( \sum_{j=0}^{N-1} \alpha_j z^j + O_\delta\left(|z|^N\right) \right), \end{align*} $$
$$ \begin{align*} F(e^{-z}) = z^{B} e^{\frac{A}{z}} \left( \sum_{j=0}^{N-1} \alpha_j z^j + O_\delta\left(|z|^N\right) \right), \end{align*} $$
 $\alpha _s \in {\mathbb {C}}$
,
$\alpha _s \in {\mathbb {C}}$
,
 $A\in {\mathbb {R}}^+$
and
$A\in {\mathbb {R}}^+$
and
 $B \in {\mathbb {R}}$
.
$B \in {\mathbb {R}}$
.
-
(2) As
 $z\to 0$
in the bounded cone
$z\to 0$
in the bounded cone
 $Mx\le |y| < \pi $
(minor arc), we have for some
$Mx\le |y| < \pi $
(minor arc), we have for some $$ \begin{align*} \lvert F(e^{-z}) \rvert \ll_\delta e^{\frac{1}{\mathrm{Re}(z)}(A - \kappa)}. \end{align*} $$
$$ \begin{align*} \lvert F(e^{-z}) \rvert \ll_\delta e^{\frac{1}{\mathrm{Re}(z)}(A - \kappa)}. \end{align*} $$
 $\kappa \in {\mathbb {R}}^+$
.
$\kappa \in {\mathbb {R}}^+$
.
If (1) and (2) hold, then as
![]() $n \to \infty $
, we have for any
$n \to \infty $
, we have for any
![]() $N\in {\mathbb {R}}^+$
$N\in {\mathbb {R}}^+$
 $$ \begin{align*} c(n) = n^{\frac{1}{4}(- 2B -3)}e^{2\sqrt{An}} \left( \sum\limits_{r=0}^{N-1} p_r n^{-\frac{r}{2}} + O\left(n^{-\frac N2}\right) \right), \end{align*} $$
$$ \begin{align*} c(n) = n^{\frac{1}{4}(- 2B -3)}e^{2\sqrt{An}} \left( \sum\limits_{r=0}^{N-1} p_r n^{-\frac{r}{2}} + O\left(n^{-\frac N2}\right) \right), \end{align*} $$
where
![]() $p_r := \sum \limits _{j=0}^r \alpha _j c_{j,r-j}$
and
$p_r := \sum \limits _{j=0}^r \alpha _j c_{j,r-j}$
and
 $c_{j,r} := \dfrac {(-\frac {1}{4\sqrt {A}})^r \sqrt {A}^{j + B + \frac 12}}{2\sqrt {\pi }} \dfrac {\Gamma (j + B + \frac 32 + r)}{r! \Gamma (j + B + \frac 32 - r)}$
.
$c_{j,r} := \dfrac {(-\frac {1}{4\sqrt {A}})^r \sqrt {A}^{j + B + \frac 12}}{2\sqrt {\pi }} \dfrac {\Gamma (j + B + \frac 32 + r)}{r! \Gamma (j + B + \frac 32 - r)}$
.
Proof. By Cauchy’s Theorem, we have
where
![]() $\mathcal {C}$
is a circle centred at the origin inside the unit circle surrounding zero exactly once counterclockwise. We choose
$\mathcal {C}$
is a circle centred at the origin inside the unit circle surrounding zero exactly once counterclockwise. We choose
![]() $|q|=e^{-\lambda }$
with
$|q|=e^{-\lambda }$
with
![]() $\lambda :=\sqrt {\frac {A}{n}}$
. Set
$\lambda :=\sqrt {\frac {A}{n}}$
. Set
 $$ \begin{align*} A_j(n):= \frac{1}{2\pi i} \int_{\mathcal{C}_1} \frac{z^{B+j} e^{\frac Az}}{q^{n+1}}dq, \end{align*} $$
$$ \begin{align*} A_j(n):= \frac{1}{2\pi i} \int_{\mathcal{C}_1} \frac{z^{B+j} e^{\frac Az}}{q^{n+1}}dq, \end{align*} $$
where
![]() $\mathcal {C}_1$
is the major arc. We claim that
$\mathcal {C}_1$
is the major arc. We claim that
 $$ \begin{align} c(n)= \sum_{j=0}^{N-1} \alpha_j A_j(n) + O\left( n^{\frac12 (-B-N-1)} e^{2\sqrt{An}} \right). \end{align} $$
$$ \begin{align} c(n)= \sum_{j=0}^{N-1} \alpha_j A_j(n) + O\left( n^{\frac12 (-B-N-1)} e^{2\sqrt{An}} \right). \end{align} $$
For this, write
 $$ \begin{align*} c(n)-\sum_{j=0}^{N-1} \alpha_j A_j(n)=\mathcal{E}_1(n) + \mathcal{E}_2(n), \end{align*} $$
$$ \begin{align*} c(n)-\sum_{j=0}^{N-1} \alpha_j A_j(n)=\mathcal{E}_1(n) + \mathcal{E}_2(n), \end{align*} $$
where
 $$ \begin{align*} \mathcal{E}_1(n):=\frac{1}{2\pi i} \int_{\mathcal{C}_2} \frac{F(q)}{q^{n+1}} dq, \quad \mathcal{E}_2(n):=\frac{1}{2\pi i} \int_{\mathcal{C}_1} \left( F(q)z^{-B} e^{-\frac Az} - \sum_{j=0}^{N-1} \alpha_jz^j\right) z^{B} e^{\frac Az} q^{-n-1}dq, \end{align*} $$
$$ \begin{align*} \mathcal{E}_1(n):=\frac{1}{2\pi i} \int_{\mathcal{C}_2} \frac{F(q)}{q^{n+1}} dq, \quad \mathcal{E}_2(n):=\frac{1}{2\pi i} \int_{\mathcal{C}_1} \left( F(q)z^{-B} e^{-\frac Az} - \sum_{j=0}^{N-1} \alpha_jz^j\right) z^{B} e^{\frac Az} q^{-n-1}dq, \end{align*} $$
where
![]() $\mathcal {C}_2$
is the minor arc.
$\mathcal {C}_2$
is the minor arc.
We next bound
![]() $\mathcal {E}_1(n)$
and
$\mathcal {E}_1(n)$
and
![]() $\mathcal {E}_2(n)$
. For
$\mathcal {E}_2(n)$
. For
![]() $\mathcal {E}_2(n)$
, we have, by condition (1)
$\mathcal {E}_2(n)$
, we have, by condition (1)
 $$ \begin{align*} \left| F\left( e^{-z}\right) z^{-B}e^{-\frac Az}-\sum_{j=0}^{N-1}\alpha_j z^j \right| \ll_\delta |z|^N. \end{align*} $$
$$ \begin{align*} \left| F\left( e^{-z}\right) z^{-B}e^{-\frac Az}-\sum_{j=0}^{N-1}\alpha_j z^j \right| \ll_\delta |z|^N. \end{align*} $$
Note that on
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
![]() $x=\lambda $
and that
$x=\lambda $
and that
 $$ \begin{align*} \left| \exp \left( \frac Az+nz \right)\right| \leq \exp\left( 2 \sqrt{An}\right). \end{align*} $$
$$ \begin{align*} \left| \exp \left( \frac Az+nz \right)\right| \leq \exp\left( 2 \sqrt{An}\right). \end{align*} $$
Since the length of
![]() $\mathcal {C}_1$
is
$\mathcal {C}_1$
is
![]() $\approx \lambda $
, we obtain
$\approx \lambda $
, we obtain
On
![]() $\mathcal {C}_1$
, we have
$\mathcal {C}_1$
, we have
![]() $y \ll \lambda $
, implying
$y \ll \lambda $
, implying
![]() $|z|\sim \frac {1}{\sqrt {n}}$
. This gives
$|z|\sim \frac {1}{\sqrt {n}}$
. This gives
![]() $\mathcal {E}_1(n)$
satisfies the bound required in equation (4.1).
$\mathcal {E}_1(n)$
satisfies the bound required in equation (4.1).
On
![]() $\mathcal {C}_2$
, we estimate
$\mathcal {C}_2$
, we estimate
Therefore,
The required bound equation (4.1) follows. Using Lemma 3.7 of [Reference Ngo and Rhoades21] to estimate the integrals
![]() $A_j(n)$
now gives the claim.
$A_j(n)$
now gives the claim.
4.3 Proof of Theorem 1.4 and Corollary 1.5
We now apply the Circle Method to the generating functions in Theorems 4.1 and 4.2.
Proof of Theorem 1.4
Using first Corollary 4.3 (1) and then Theorem 4.1, we obtain
 $$\begin{align*}H_{a,b}(q) := \sum_{n=0}^\infty B\left(a,b;\left({\mathbb{C}}^2\right)^{[n]}\right)q^n = \frac1b\left(1+\delta_{2\mid b}\right) \frac{1}{(q;q)_\infty} + \frac1b \sum_{\substack{1\le r\le b-1\\r\ne\frac b2}} \zeta_b^{-ar} \frac{1}{F_3\left(\zeta_b^{2r};q\right)}. \end{align*}$$
$$\begin{align*}H_{a,b}(q) := \sum_{n=0}^\infty B\left(a,b;\left({\mathbb{C}}^2\right)^{[n]}\right)q^n = \frac1b\left(1+\delta_{2\mid b}\right) \frac{1}{(q;q)_\infty} + \frac1b \sum_{\substack{1\le r\le b-1\\r\ne\frac b2}} \zeta_b^{-ar} \frac{1}{F_3\left(\zeta_b^{2r};q\right)}. \end{align*}$$
We want to apply Proposition 4.4. For this, we first show (
![]() $M>0$
arbitrary) that we have as
$M>0$
arbitrary) that we have as
![]() $z\to 0$
on the major arc
$z\to 0$
on the major arc
![]() $|y|\le Mx$
$|y|\le Mx$
 $$ \begin{align} H_{a,b}\left(e^{-z}\right) = \frac1b\left(1+\delta_{2\mid b}\right) \sqrt{\frac{z}{2\pi}} e^{\frac{\pi^2}{6z}} (1+O(|z|)). \end{align} $$
$$ \begin{align} H_{a,b}\left(e^{-z}\right) = \frac1b\left(1+\delta_{2\mid b}\right) \sqrt{\frac{z}{2\pi}} e^{\frac{\pi^2}{6z}} (1+O(|z|)). \end{align} $$
Recall that we have
![]() $P(q):=\sum _{n=0}^\infty p(n)q^n=(q;q)_\infty ^{-1}$
. First we note the well-known bound (for
$P(q):=\sum _{n=0}^\infty p(n)q^n=(q;q)_\infty ^{-1}$
. First we note the well-known bound (for
![]() $|y|\le Mx$
, as
$|y|\le Mx$
, as
![]() $z\to 0$
)
$z\to 0$
)
 $$\begin{align*}P\left(e^{-z}\right) = \sqrt{\frac{z}{2\pi}} e^{\frac{\pi^2}{6z}} (1+O(|z|)). \end{align*}$$
$$\begin{align*}P\left(e^{-z}\right) = \sqrt{\frac{z}{2\pi}} e^{\frac{\pi^2}{6z}} (1+O(|z|)). \end{align*}$$
Next we consider
![]() $\frac {1}{F_3(\zeta _b^{2r};q)}$
for
$\frac {1}{F_3(\zeta _b^{2r};q)}$
for
![]() $\zeta _b^{2r}\ne 1$
on the major arc. By Theorem 2.1 (3)
$\zeta _b^{2r}\ne 1$
on the major arc. By Theorem 2.1 (3)
 $$\begin{align*}\frac{1}{F_3\left(\zeta_b^{2r};e^{-z}\right)} = \frac{\left(b^2z\right)^{\frac1b-\frac12}\Gamma\left(\frac1b\right)}{\sqrt{2\pi}} \prod_{j=1}^{b-1} \left(1-\zeta_b^{2rj}\right)^{\frac jb} e^{\frac{\pi^2}{6b^2z}}(1+O(|z|)) \ll |z|^{-N} e^{\frac{\pi^2}{6z}} \end{align*}$$
$$\begin{align*}\frac{1}{F_3\left(\zeta_b^{2r};e^{-z}\right)} = \frac{\left(b^2z\right)^{\frac1b-\frac12}\Gamma\left(\frac1b\right)}{\sqrt{2\pi}} \prod_{j=1}^{b-1} \left(1-\zeta_b^{2rj}\right)^{\frac jb} e^{\frac{\pi^2}{6b^2z}}(1+O(|z|)) \ll |z|^{-N} e^{\frac{\pi^2}{6z}} \end{align*}$$
for any
![]() $N\in {\mathbb {N}}$
. This gives equation (4.2).
$N\in {\mathbb {N}}$
. This gives equation (4.2).
Next we show that we have as
![]() $z\to 0$
on the minor arc
$z\to 0$
on the minor arc
![]() $|y|\ge Mx$
$|y|\ge Mx$
It is well-known (and follows by logarithmic differentiation) that for some
![]() $\mathcal {C}>0$
$\mathcal {C}>0$
We are left to bound
![]() $\frac {1}{F_3(\zeta _b^{2r};q)}$
on the minor arc. For this, we write
$\frac {1}{F_3(\zeta _b^{2r};q)}$
on the minor arc. For this, we write
 $$\begin{align*}\operatorname{\mathrm{Log}}\left(\frac{1}{F_3\left(\zeta_b^{2r};q\right)}\right) = \sum_{m=1}^\infty \frac{q^m}{m\left(1-\zeta_b^{2rm}q^m\right)}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Log}}\left(\frac{1}{F_3\left(\zeta_b^{2r};q\right)}\right) = \sum_{m=1}^\infty \frac{q^m}{m\left(1-\zeta_b^{2rm}q^m\right)}. \end{align*}$$
Noting that
![]() $|1-\zeta _b^{2rm}q^m|\ge 1-|q|^m$
, we obtain
$|1-\zeta _b^{2rm}q^m|\ge 1-|q|^m$
, we obtain
 $$\begin{align*}\left|\mathrm{Log}\left(\frac{1}{F_3\left(\zeta_b^{2r};q\right)}\right)\right| \le \left|\frac{q}{1-\zeta_b^{2r}q}\right|-\frac{|q|}{1-|q|}+\log(P|q|) \end{align*}$$
$$\begin{align*}\left|\mathrm{Log}\left(\frac{1}{F_3\left(\zeta_b^{2r};q\right)}\right)\right| \le \left|\frac{q}{1-\zeta_b^{2r}q}\right|-\frac{|q|}{1-|q|}+\log(P|q|) \end{align*}$$
so we are done once we show that
 $$\begin{align*}\left|\frac{q}{1-\zeta_b^{2r}q}\right| - \frac{|q|}{1-|q|} < -\frac{\mathcal{C}}{x} \end{align*}$$
$$\begin{align*}\left|\frac{q}{1-\zeta_b^{2r}q}\right| - \frac{|q|}{1-|q|} < -\frac{\mathcal{C}}{x} \end{align*}$$
for some
![]() $\mathcal {C}>0$
. Note that
$\mathcal {C}>0$
. Note that
 $$\begin{align*}\frac{1}{1-\zeta_b^{2r}q} = O_{b,r}(1) \end{align*}$$
$$\begin{align*}\frac{1}{1-\zeta_b^{2r}q} = O_{b,r}(1) \end{align*}$$
and thus
 $$\begin{align*}\left|\frac{q}{1-\zeta_b^{2r}q}\right| - \frac{|q|}{1-|q|} = -\frac1x+O_{b,r}(1), \end{align*}$$
$$\begin{align*}\left|\frac{q}{1-\zeta_b^{2r}q}\right| - \frac{|q|}{1-|q|} = -\frac1x+O_{b,r}(1), \end{align*}$$
giving equation (4.3). The claim of (1) now follows by Proposition 4.4.
(2) By Corollary 4.3 (2) and Theorem 4.2, we have

We show the same bounds as in (1) with the only additional condition that
 $$ \begin{align} M < \frac{2\pi^2}{b^2} \min_{1\le r<\frac b2} \frac{r(b-2r)}{\left|\sum_{n=1}^\infty \frac{\sin\left(\frac{4\pi r}{b}\right)}{n^2}\right|}. \end{align} $$
$$ \begin{align} M < \frac{2\pi^2}{b^2} \min_{1\le r<\frac b2} \frac{r(b-2r)}{\left|\sum_{n=1}^\infty \frac{\sin\left(\frac{4\pi r}{b}\right)}{n^2}\right|}. \end{align} $$
We only need to prove the bounds for
 $$\begin{align*}\mathcal{H}_{\alpha,\beta}(q) := \frac{\left(q^{\alpha+\beta};q^{\alpha+\beta}\right)_\infty}{F_1\left(\zeta_b^{2r};q^{\alpha+\beta}\right)(q;q)_\infty} \end{align*}$$
$$\begin{align*}\mathcal{H}_{\alpha,\beta}(q) := \frac{\left(q^{\alpha+\beta};q^{\alpha+\beta}\right)_\infty}{F_1\left(\zeta_b^{2r};q^{\alpha+\beta}\right)(q;q)_\infty} \end{align*}$$
for
![]() $\zeta _b^{2r}\ne 1$
. We may assume without loss of generality that
$\zeta _b^{2r}\ne 1$
. We may assume without loss of generality that
![]() $1\le 2r<b$
. We start by showing the major arc bound. By Theorem 2.1 (1) and equation (2.8), we have, for z on the major arc
$1\le 2r<b$
. We start by showing the major arc bound. By Theorem 2.1 (1) and equation (2.8), we have, for z on the major arc
 $$\begin{align*}\mathcal{H}_{\alpha,\beta}(q) \ll \left|e^{\frac{\pi^2}{6z}-\frac{\pi^2}{6(\alpha+\beta)z}+\frac{\zeta_b^{2r}\phi\left(\zeta_b^{2r},2,1\right)}{(\alpha+\beta)z}}\right|. \end{align*}$$
$$\begin{align*}\mathcal{H}_{\alpha,\beta}(q) \ll \left|e^{\frac{\pi^2}{6z}-\frac{\pi^2}{6(\alpha+\beta)z}+\frac{\zeta_b^{2r}\phi\left(\zeta_b^{2r},2,1\right)}{(\alpha+\beta)z}}\right|. \end{align*}$$
So to prove the major arc bound, we need to show that for some
![]() $\varepsilon>0$
$\varepsilon>0$
 $$\begin{align*}\left(\frac{\pi^2}{6}-\varepsilon\right) \mathrm{Re}\left(\frac1z\right) - \mathrm{Re}\left(\frac{\zeta_b^{2r}\phi\left(\zeta_b^{2r},2,1\right)}{z}\right)> 0. \end{align*}$$
$$\begin{align*}\left(\frac{\pi^2}{6}-\varepsilon\right) \mathrm{Re}\left(\frac1z\right) - \mathrm{Re}\left(\frac{\zeta_b^{2r}\phi\left(\zeta_b^{2r},2,1\right)}{z}\right)> 0. \end{align*}$$
We first rewrite
 $$\begin{align*}\zeta_b^{2r} \phi\left(\zeta_b^{2r},2,1\right) = \sum_{n=1}^\infty \frac{\cos\left(\frac{4\pi rn}{b}\right)+i\sin\left(\frac{4\pi rn}{b}\right)}{n^2}. \end{align*}$$
$$\begin{align*}\zeta_b^{2r} \phi\left(\zeta_b^{2r},2,1\right) = \sum_{n=1}^\infty \frac{\cos\left(\frac{4\pi rn}{b}\right)+i\sin\left(\frac{4\pi rn}{b}\right)}{n^2}. \end{align*}$$
Now note the evaluation for
![]() $0\le \theta \le 2\pi $
(see, for example, [Reference Zagier32])
$0\le \theta \le 2\pi $
(see, for example, [Reference Zagier32])
 $$\begin{align*}\sum_{n=1}^\infty \frac{\cos(n\theta)}{n^2} = \frac{\pi^2}{6}-\frac{\theta(2\pi-\theta)}{4}. \end{align*}$$
$$\begin{align*}\sum_{n=1}^\infty \frac{\cos(n\theta)}{n^2} = \frac{\pi^2}{6}-\frac{\theta(2\pi-\theta)}{4}. \end{align*}$$
Thus we are left to show
 $$\begin{align*}\frac{2\pi^2r}{b^2}(b-2r)x \ge \left|\sum_{n=1}^\infty \frac{\sin\left(\frac{4\pi rn}{b}\right)}{n^2}\right|y. \end{align*}$$
$$\begin{align*}\frac{2\pi^2r}{b^2}(b-2r)x \ge \left|\sum_{n=1}^\infty \frac{\sin\left(\frac{4\pi rn}{b}\right)}{n^2}\right|y. \end{align*}$$
This follows by the definition of M given in equation (4.4).
5 Examples
This section includes examples of the main results in this paper.
5.1 Examples of Theorem 1.1 and Corollary 1.2
This subsection pertains to Han’s t-hook generating functions. For convenience, we define the proportion functions
Example. In the case of
![]() $t=3$
, we find that
$t=3$
, we find that
 $$ \begin{align*} H_3(\xi;q)=1+q+2q^2+3\xi q^3+(2+3\xi)q^4+(1+6\xi)q^5+\left(2+9\xi^2\right)q^6+\left(6\xi+9\xi^2\right)q^7\\ +\left(1+3\xi+18\xi^2\right)q^8+\dots. \end{align*} $$
$$ \begin{align*} H_3(\xi;q)=1+q+2q^2+3\xi q^3+(2+3\xi)q^4+(1+6\xi)q^5+\left(2+9\xi^2\right)q^6+\left(6\xi+9\xi^2\right)q^7\\ +\left(1+3\xi+18\xi^2\right)q^8+\dots. \end{align*} $$
and the three generating functions
![]() $H_3(a,3;q)$
begin with the terms
$H_3(a,3;q)$
begin with the terms
 $$ \begin{align*} \begin{aligned} H_3(0,3;q)&=1+q+2q^2+2q^4+q^5+2q^6+q^8+\dots,\\ H_3(1,3;q)&=3q^3+3q^4+6q^5+6q^7+3q^8+\dots,\\ H_3(2,3;q)&=9q^6+9q^7+18q^8+\dots. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} H_3(0,3;q)&=1+q+2q^2+2q^4+q^5+2q^6+q^8+\dots,\\ H_3(1,3;q)&=3q^3+3q^4+6q^5+6q^7+3q^8+\dots,\\ H_3(2,3;q)&=9q^6+9q^7+18q^8+\dots. \end{aligned} \end{align*} $$
Theorem 1.1 implies (independently of a) that
 $$ \begin{align*}p_3(a,3;n)\sim \frac{1}{12\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}3}} \sim \frac{1}{3}\cdot p(n). \end{align*} $$
$$ \begin{align*}p_3(a,3;n)\sim \frac{1}{12\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}3}} \sim \frac{1}{3}\cdot p(n). \end{align*} $$
The next table illustrates the conclusion of Corollary 1.2, that the proportions
![]() $\Psi _3(a,b;n) \to \frac 13$
.
$\Psi _3(a,b;n) \to \frac 13$
.

Example. We consider a typical case where the modular sums of t-hook functions are not equidistributed. We consider
![]() $t=2$
, where we have
$t=2$
, where we have
 $$ \begin{align*} H_2(\xi;q)=1+q+2\xi q^2+(1+2\xi)q^3+5\xi^2 q^4 +\left(2\xi+5\xi^2\right)q^5+\left(1+10\xi^3\right)q^6+\left(5\xi^2+10\xi^3\right)q^7\\ +\left(2\xi +20\xi^4\right)q^8+\dots. \end{align*} $$
$$ \begin{align*} H_2(\xi;q)=1+q+2\xi q^2+(1+2\xi)q^3+5\xi^2 q^4 +\left(2\xi+5\xi^2\right)q^5+\left(1+10\xi^3\right)q^6+\left(5\xi^2+10\xi^3\right)q^7\\ +\left(2\xi +20\xi^4\right)q^8+\dots. \end{align*} $$
The three generating functions
![]() $H_2(a,3;q)$
begin with the terms
$H_2(a,3;q)$
begin with the terms
 $$ \begin{align*} \begin{aligned} H_2(0,3;q)&=1+q+q^3+11q^6+10q^7+\dots,\\ H_2(1,3;q)&=2q^2+2q^3+2q^5+22q^8+\dots,\\ H_2(2,3;q)&=5q^4+5q^5+5q^7+\dots. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} H_2(0,3;q)&=1+q+q^3+11q^6+10q^7+\dots,\\ H_2(1,3;q)&=2q^2+2q^3+2q^5+22q^8+\dots,\\ H_2(2,3;q)&=5q^4+5q^5+5q^7+\dots. \end{aligned} \end{align*} $$
Theorem 1.1 implies that
 $$ \begin{align*}p_2(a,3;n)\sim \frac{A(a,n)}{12\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}} \sim \frac{A(a,n)}{3} \cdot p(n), \end{align*} $$
$$ \begin{align*}p_2(a,3;n)\sim \frac{A(a,n)}{12\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}} \sim \frac{A(a,n)}{3} \cdot p(n), \end{align*} $$
where
![]() $A(a,n)\in \{0, 1, 2\}$
satisfies the congruence
$A(a,n)\in \{0, 1, 2\}$
satisfies the congruence
![]() $A(a,n)\equiv 2-a-n\,\,(\mathrm {mod}\,\,{3})$
. This explains the uneven distribution established by Corollary 1.2 in this case. In particular, we have that
$A(a,n)\equiv 2-a-n\,\,(\mathrm {mod}\,\,{3})$
. This explains the uneven distribution established by Corollary 1.2 in this case. In particular, we have that
Of course, this zero distribution is weaker than the vanishing obtained in Theorem 1.3.
The next table illustrates the uneven asymptotics for
![]() $n\equiv 0\,\,(\mathrm {mod}\,\,{3})$
.
$n\equiv 0\,\,(\mathrm {mod}\,\,{3})$
.

Example. We consider another typical case where the modular sums of t-hook functions are not equidistributed. We consider
![]() $t=4$
, where we have
$t=4$
, where we have
 $$ \begin{align*}H_4(\xi;q)&=1+q+2q^2+3q^3+(1+4\xi)q^4+(3+4\xi)q^5+(3+8\xi)q^6+(3+12\xi)q^7\\ &\quad +\left(4+4\xi+14\xi^2\right)q^8+\dots. \end{align*} $$
$$ \begin{align*}H_4(\xi;q)&=1+q+2q^2+3q^3+(1+4\xi)q^4+(3+4\xi)q^5+(3+8\xi)q^6+(3+12\xi)q^7\\ &\quad +\left(4+4\xi+14\xi^2\right)q^8+\dots. \end{align*} $$
The three generating functions
![]() $H_4(a,3;q)$
begin with the terms
$H_4(a,3;q)$
begin with the terms
 $$ \begin{align*} \begin{aligned} H_4(0,3;q)&=1+q+2q^2+3q^3+q^4+3q^5+3q^6+3q^7+4q^8+\dots,\\ H_4(1,3;q)&=4q^4+4q^5+8q^6+12q^7+4q^8+\dots,\\ H_4(2,3;q)&=14q^8+\dots. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} H_4(0,3;q)&=1+q+2q^2+3q^3+q^4+3q^5+3q^6+3q^7+4q^8+\dots,\\ H_4(1,3;q)&=4q^4+4q^5+8q^6+12q^7+4q^8+\dots,\\ H_4(2,3;q)&=14q^8+\dots. \end{aligned} \end{align*} $$
Theorem 1.1, restricted to partitions of integers that are multiples of 12, gives
 $$ \begin{align*}p_4(a,3;12n)\sim \begin{cases} \frac{4}{9}\cdot p(12n)\ \ \ \ \ &{\text{if }a=0,}\\ \frac{1}{3}\cdot p(12n) \ \ \ \ \ &{\text{if }a=1,}\\ \frac{2}{9}\cdot p(12n) \ \ \ \ \ &{\text{if }a=2.} \end{cases} \end{align*} $$
$$ \begin{align*}p_4(a,3;12n)\sim \begin{cases} \frac{4}{9}\cdot p(12n)\ \ \ \ \ &{\text{if }a=0,}\\ \frac{1}{3}\cdot p(12n) \ \ \ \ \ &{\text{if }a=1,}\\ \frac{2}{9}\cdot p(12n) \ \ \ \ \ &{\text{if }a=2.} \end{cases} \end{align*} $$
The next table illustrates these asymptotics.

5.2 Examples of Theorem 1.4 and Corollary 1.5
Finally, we consider examples of the asymptotics and distributions in the setting of Hilbert schemes on n points.
Example. By Göttsche’s Theorem (i.e., Theorem 4.1), we have
 $$ \begin{align*} \begin{aligned} G(T;q)&:=\sum_{n=0}^{\infty} P\left(\left({\mathbb{C}}^2\right)^{[n]};T \right)q^n=\prod_{m=1}^{\infty}\frac{1}{1-T^{2m-2}q^m}=\frac{1}{F_3(T^{-2}; T^2q)}\\[6pt] &=1+q+\left(1+T^2\right)q^2+\left(1+T^2+T^4\right)q^3+\left(1+T^2+2T^4+T^6\right)q^4+\dots. \\ \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} G(T;q)&:=\sum_{n=0}^{\infty} P\left(\left({\mathbb{C}}^2\right)^{[n]};T \right)q^n=\prod_{m=1}^{\infty}\frac{1}{1-T^{2m-2}q^m}=\frac{1}{F_3(T^{-2}; T^2q)}\\[6pt] &=1+q+\left(1+T^2\right)q^2+\left(1+T^2+T^4\right)q^3+\left(1+T^2+2T^4+T^6\right)q^4+\dots. \\ \end{aligned} \end{align*} $$
Theorem 1.4 (1) implies that
 $$ \begin{align*}B\left(a,3; \left({\mathbb{C}}^2\right)^{[n]}\right) \sim \frac{1}{12\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}}, \end{align*} $$
$$ \begin{align*}B\left(a,3; \left({\mathbb{C}}^2\right)^{[n]}\right) \sim \frac{1}{12\sqrt{3}n}\cdot e^{\pi \sqrt{\frac{2n}{3}}}, \end{align*} $$
and so Corollary 1.5 implies that
![]() $\delta (a,3;n)\to \frac 13$
. The next table illustrates this phenomenon.
$\delta (a,3;n)\to \frac 13$
. The next table illustrates this phenomenon.

Example. By Theorem 4.2, for
![]() $\alpha =2$
and
$\alpha =2$
and
![]() $\beta =3$
, we have
$\beta =3$
, we have
 $$ \begin{align*} \begin{aligned} G_{2,3}(T;q)&:=\sum_{n=0}^{\infty} P\left(\left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{2,3}};T\right)q^n= \frac{1}{F_1(T^2;q^{5})} \prod_{m=1}^{\infty}\frac{\left(1-q^{5m}\right)}{1-q^m}\\[6pt] &=1+q+2q^2+\dots+\left(6+T^2\right)q^5+\left(10+T^2\right)q^6+\left(13+2T^2\right)q^7+\dots. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} G_{2,3}(T;q)&:=\sum_{n=0}^{\infty} P\left(\left(\left({\mathbb{C}}^2\right)^{[n]}\right)^{T_{2,3}};T\right)q^n= \frac{1}{F_1(T^2;q^{5})} \prod_{m=1}^{\infty}\frac{\left(1-q^{5m}\right)}{1-q^m}\\[6pt] &=1+q+2q^2+\dots+\left(6+T^2\right)q^5+\left(10+T^2\right)q^6+\left(13+2T^2\right)q^7+\dots. \end{aligned} \end{align*} $$
Theorem 1.4 (2) implies that
 $$ \begin{align*} B\left(a,3; \left(\left ({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)\sim \frac{1}{12\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}{3}}}, \end{align*} $$
$$ \begin{align*} B\left(a,3; \left(\left ({\mathbb{C}}^2\right)^{[n]}\right)^{T_{\alpha,\beta}}\right)\sim \frac{1}{12\sqrt{3}n} \cdot e^{\pi \sqrt{\frac{2n}{3}}}, \end{align*} $$
so Corollary 1.5 yields that
![]() $\delta _{2,3}(a,3;n)\to \frac 13$
. The next table illustrates this phenomenon.
$\delta _{2,3}(a,3;n)\to \frac 13$
. The next table illustrates this phenomenon.

Acknowledgements
The authors thank George Andrews, Walter Bridges, Giulia Cesana, Johann Franke, Jack Morava and Ole Warnaar for helpful discussions related to the results in this paper. Moreover, we thank the referees for helpful comments.
Conflicts of Interest
None.
Financial support
The first author has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 101001179). The research of the third author conducted for this paper is supported by the Pacific Institute for the Mathematical Sciences (PIMS). The research and findings may not reflect those of the Institute. The fourth author thanks the support of the Thomas Jefferson Fund and the NSF (DMS-1601306 and DMS-2055118) and the Kavli Institute grant NSF PHY-1748958.