1 Introduction
Residual intersections have a long history in algebraic geometry which goes back to Cayley–Bacharach theory, or at least in the middle of the nineteenth century to Chasles [Reference ChaslesCha64] who counted the number of conics tangent to a given conic (see Eisenbud’s talk [Reference EisenbudEis18] or Kleiman [Reference KleimanKle80] for the historical introduction).
In intersection theory, the concept of ‘residual schemes’ and ‘residual intersections’ are the base of the residual intersection formula of Fulton, Kleiman, Laksov, and MacPherson (or others such as [Reference WuWu94]) which describes a decomposition of the refined intersection product [Reference FultonFul98, Corollary 9.2.3]. The theory became part of commutative algebra in the work of Artin and Nagata [Reference Artin and NagataAN72] wherein Artin and Nagata defined ‘Algebraic Residual Intersections’ to study the ‘double point locus’ of maps between schemes of finite type over a field. Although Fulton’s definition [Reference FultonFul98, Definition 9.2.2] is not the same as the following definition of the algebraic residual intersection, there is a tight relation between them in the affine case (see the introduction of [Reference Hassanzadeh and NaelitonHN16]).
From the commutative algebra point of view, the theory of residual intersections is a vast generalization of the ‘Linkage theory’ of Peskine and Szpiro [Reference Peskine and SzpiroPS74]. The family of
$s$
-residual intersections contains determinantal ideals and, obviously, complete intersections of codimension
$s$
. Precisely, if
$R$
is a commutative Noetherian ring,
$I$
an ideal of grade
$g$
and
$s\geqslant g$
an integer, then the following hold.
∙ An (algebraic)
$s$
-residual intersection of
$I$
is a proper ideal
$J$
of
$R$
such that
$\operatorname{ht}(J)\geqslant s$
and
$J=(\mathfrak{a}:_{R}I)$
for some ideal
$\mathfrak{a}\subset I$
which is generated by
$s$
elements.∙ A geometric
$s$
-residual intersection of
$I$
is an algebraic
$s$
-residual intersection
$J$
of
$I$
such that
$\operatorname{ht}(I+J)\geqslant s+1$
.∙ An arithmetic
$s$
-residual intersection of
$I$
is an algebraic
$s$
-residual intersection such that
$\unicode[STIX]{x1D707}_{R_{\mathfrak{p}}}((I/\mathfrak{a})_{\mathfrak{p}})\leqslant 1$
for all prime ideal
$\mathfrak{p}\supseteq (I+J)$
with
$\operatorname{ht}(\mathfrak{p})\leqslant s$
(
$\unicode[STIX]{x1D707}$
denotes the minimum number of generators).
Since 1983, after the work of Huneke [Reference HunekeHun83], the theory became stronger and stronger due to a series of works of Huneke, Ulrich, Kustin, Chardin, Eisenbud, and others. Due to the ubiquity of residual intersections, the theory has attained more attention in the recent years (e.g. [Reference Chardin, Eisenbud and UlrichCEU01, Reference Chardin, Eisenbud and UlrichCEU15, Reference Chardin, Naeliton and TranCNT19, Reference Eisenbud and UlrichEU18, Reference EisenbudEis18] and [Reference Hartshorne, Huneke and UlrichHHU12]). However, there are still many basic and mysterious properties of
$s$
-residual intersections which are not established. One of the very basic tasks is to determine the generators of an
$s$
-residual intersection.
Even from the computational point of view, calculating the generators of
$J=\mathfrak{a}:I$
using elimination, is expensive. Theoretically, there are few cases for which the set of generators of
$J$
can be described, namely:
∙ if
$R$
is Gorenstein
$I$
is perfect and
$s=g$
, [Reference Peskine and SzpiroPS74];∙ if
$R$
is Gorenstein and
$I$
is a complete intersection, [Reference Bruns, Kustin and MillerBKM90, Theorem 4.8] and [Reference Huneke and UlrichHU88, Theorem 5.9(i)];∙ if
$R$
is Cohen–Macaulay(CM) and
$I$
is a perfect ideal of height 2, [Reference HunekeHun83, Reference Kustin and UlrichKU92] and [Reference Chardin, Eisenbud and UlrichCEU01, Theorem 1.1];∙ if
$R$
is Gorenstein and
$I$
is perfect Gorenstein ideal of height 3, [Reference Kustin and UlrichKU92, §10];∙ if
$R$
is Gorenstein,
$I$
is Gorenstein licci, generically a complete intersection ideal and
$s=g+1$
, [Reference Kustin, Miller and UlrichKMU92, Corollary 2.18].
In this paper, we describe the generators of residual intersections if
$s\leqslant g+1$
, or if the ideal
$I$
satisfies the sliding depth condition
$\operatorname{SD}_{1}$
, Definition 4.3. This wide range contains all of the above cases. The turning point is that, instead of looking at the module structure of Koszul homologies of
$I$
, we study the differential graded algebra structure of
$H_{\bullet }(I)$
. There is a new ideal which comes into being. We call this ideal the Koszul–Fitting ideal associated to
$I$
and
$\mathfrak{a}$
, and we denote it by
$\operatorname{Kitt}(\mathfrak{a},I)$
.Footnote
1
The ideal
$\operatorname{Kitt}(\mathfrak{a},I)$
is defined as follows.
Let
$R$
be a commutative Noetherian ring,
$I=(f_{1},\ldots ,f_{r})\subseteq R$
an ideal,
$\mathfrak{a}=(a_{1},\ldots ,a_{s})\subseteq I$
. Let
$\unicode[STIX]{x1D6F7}=(c_{ij})$
be an
$r\times s$
matrix in
$R$
such that
$(a_{1},\ldots ,a_{s})=(f_{1},\ldots ,f_{r})\cdot \unicode[STIX]{x1D6F7}$
. Let
$K_{\bullet }=R\langle e_{1},\ldots ,e_{r};\unicode[STIX]{x2202}(e_{i})=f_{i}\rangle$
be the Koszul complex equipped with the structure of the differential graded algebra. Let
$\unicode[STIX]{x1D701}_{j}=\sum _{i=1}^{r}c_{ij}e_{i},1\leqslant j\leqslant s$
,
$\unicode[STIX]{x1D6E4}_{\bullet }=R\langle \unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{s}\rangle$
the algebra generated by the
$\unicode[STIX]{x1D701}$
values, and
$Z_{\bullet }$
be the algebra of Koszul cycles. Then we look at the elements of degree
$r$
in the sub-algebra of
$K_{\bullet }$
generated by
$\unicode[STIX]{x1D6E4}_{\bullet }$
and
$Z_{\bullet }$
and define
$$\begin{eqnarray}\operatorname{Kitt}(\mathfrak{a},I):=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}\subseteq K_{r}=R.\end{eqnarray}$$
We summarize some of our results in the following theorem.
Theorem 1.1. With the above notation, we have the following.
(1) The ideal
$\operatorname{Kitt}(\mathfrak{a},I)$
depends only on the ideals
$\mathfrak{a}$
and
$I$
and not on the generators or representative matrix.(2) The ideal
$\operatorname{Kitt}(\mathfrak{a},I)$
is, indeed, the disguised residual intersection introduced in [Reference Hassanzadeh and NaelitonHN16]; hence
$\operatorname{Kitt}(\mathfrak{a},I)\subseteq \mathfrak{a}:_{R}I$
, they have the same radical and
$\operatorname{Kitt}(\mathfrak{a},I)=\mathfrak{a}:_{R}I$
if
$\unicode[STIX]{x1D707}(I/\mathfrak{a})\leqslant 1$
.(3) The ideal
$\operatorname{Kitt}(\mathfrak{a},I)=\mathfrak{a}+\langle \unicode[STIX]{x1D6E4}_{\bullet }\,\cdot \,\tilde{H}_{\bullet }\rangle _{r}$
where
$\tilde{H}_{\bullet }$
is the sub-algebra of
$K_{\bullet }$
generated by the representatives of Koszul homologies. However
$\operatorname{Kitt}(\mathfrak{a},I)\supseteq \operatorname{Fitt}_{0}(I/\mathfrak{a})$
.(4) If
$R$
is CM,
$J=\mathfrak{a}:_{R}I$
is an
$s$
-residual intersection and
$I$
satisfies
$\operatorname{SD}_{1}$
, then
$\operatorname{Kitt}(\mathfrak{a},I)=J$
and it is a CM ideal.
So not only the Cohen–Macaulayness but also the structure of the residual intersections is determined by the above theorem.
We briefly recall the history behind this theorem. In 1983, Huneke [Reference HunekeHun83] showed that the
$G_{s}$
condition defined by Artin and Nagata [Reference Artin and NagataAN72], in 1972, is not enough to prove the CM-ness of residual intersections in a CM ring (indeed the main theorem in the Artin–Nagata paper was wrong although the applications were not); so Huneke defined Strongly Cohen–Macaulay (SCM) ideals to show that residual intersections of
$\text{SCM}+G_{s}$
ideals are Cohen–Macaulay. The Strongly Cohen–Macaulay condition then relaxed to the sliding depth condition in [Reference Herzog, Vasconcelos and VillarrealHVV85]. In their 1988 landmark paper, [Reference Huneke and UlrichHU88], Huneke and Ulrich asked the question of whether the
$G_{s}$
condition is at all needed to prove that SCM ideals have CM residual intersection? Following earlier work of Chardin and Ulrich [Reference Chardin and UlrichCU02], Hassanzadeh [Reference HassanzadehHas12] answered this question, affirmatively, for arithmetic residual intersections. The answer is based on new construction which is called disguised residual intersection
Footnote
2
in [Reference Hassanzadeh and NaelitonHN16]. Disguised residual intersections are CM under sliding depth conditions and coincide with the algebraic residual intersections in many different cases; so Hassanzadeh and Naeliton in [Reference Hassanzadeh and NaelitonHN16, Conjecture 5.9] conjectured that the disguised residual intersection is the same as the residual intersection for ideals with sliding depth. Cohen–Macaulayness of algebraic residual intersection for ideals with sliding depth was finally proved in [Reference Chardin, Naeliton and TranCNT19] in 2018. Theorem 1.1(4) proves [Reference Hassanzadeh and NaelitonHN16, Conjecture 5.9], in particular.
The whole paper is designed to prove Theorem 5.1 (Theorem 1.1(4)). The idea of the proof is to use reduction modulo regular sequences which reduces the problem to the case where
$I$
has height
$2$
; one then uses the important duality result of [Reference Chardin, Naeliton and TranCNT19] to show that the disguised residual and algebraic residual are the same. The byproduct is that we have already taken off the mask of the disguised residual intersection in Theorem 4.9 (Theorem 1.1(2)); hence we have a description of the generators of the residual intersection.
The paper is divided into five sections. To understand the structure of disguised residual intersections, one needs to explicitly determine the maps in any pages of the Koszul–Čech-
${\mathcal{Z}}_{\bullet }$
spectral sequence. This part is done in the first section where we define
$r$
-liftable elements and determine when an element in any pages of spectral sequences is liftable, Theorems 2.5 and 2.6. This study led us to a rediscovery of the Buchsbaum–Eisenbud family of complexes which in turn contains the Eagon–Northcott and Buchsbaum–Rim complexes. In § 3, we show that the structure of Buchsbaum–Eisenbud family can be simply explained by a Koszul–Čech spectral sequence; so the structure of the complex acyclicity and many other properties are natural consequences of the convergence of the spectral sequence. The crucial point is the connecting maps, Theorem 3.6, which have been determined in § 3. In order not to diverge from the main goal we do not add any corollaries in this section. In § 4, we first recall some of the basic definitions including ‘disguised residual intersection’ and determine the generators of disguised residual intersections in a quite general setting, Theorem 4.9. This is due to the structure of the Eagon–Northcott complex and its coincidence with a strand Koszul–Čech spectral sequence (the fact developed in § 3). Section 4.3 is devoted to showing that the construction of the disguised residual intersection does not depend on the choice of the generators. Theorem 4.23 covers the assertion of Theorem 1.1(3) and provides more details about the number of generators. Another structural result in this section is Theorem 4.27 wherein it is shown that disguised residual intersections specialize. Finally, in § 5 we collect several corollaries and applications, more notably, Theorem 5.1 proves Conjecture [Reference Hassanzadeh and NaelitonHN16, Conjecture 5.9] to a certain extent. We finish the paper by gathering some interesting corollaries of the main theorems.
2 Maps in spectral sequences
To explain the structure of the disguised residual intersection, we need a concrete explanation of the maps in spectral sequences. Unfortunately there does not exist such an explanation in the literature although the facts may be known to the experts. Here we follow the notation in [Reference EisenbudEis95].
More details may be found in the first author’s PhD thesis [Reference BouçaBou19].
Definition 2.1. Let
$R$
be a commutative ring and
$(E^{\bullet ,\bullet },d_{v},d_{h})$
be a first quadrant double complex of
$R$
-modules. The total complex of this bi-complex is a graded module with
$k$
th component
$$\begin{eqnarray}\operatorname{Tot}(E^{\bullet ,\bullet })^{k}=\bigoplus _{p+q=k}E^{p,q}\end{eqnarray}$$
coming with a degree-one differential
$d$
given by
$$\begin{eqnarray}d(m)=(d_{v}(m),d_{h}(m))\in E^{p+1,q}\oplus E^{p,q+1}\quad \text{for all }m\in E^{p,q}.\end{eqnarray}$$
The
$p$
th vertical filtration of
$\operatorname{Tot}(E^{\bullet ,\bullet })$
is defined by
$$\begin{eqnarray}(\text{}_{\text{ver}}\text{Tot}(E^{\bullet ,\bullet })^{p})^{k}=\bigoplus _{i\geqslant p}E^{i,k-i}.\end{eqnarray}$$
Similarly, we can define the
$p$
th horizontal filtration by putting
$$\begin{eqnarray}(\text{}_{\text{hor}}\text{Tot}(E^{\bullet ,\bullet })^{p})^{k}=\bigoplus _{i\geqslant p}E^{k-i,i}.\end{eqnarray}$$
In what follows, we will be working with the totalization of a first quadrant spectral sequence, as in Definition 2.1, filtered by the vertical filtration. Let
$F_{\bullet }=\bigoplus _{p}(\text{}_{\text{ver}}\text{Tot}(E^{\bullet ,\bullet })^{p})$
and
$$\begin{eqnarray}\text{}^{0}E^{\bullet ,\bullet }=\bigoplus _{p}\frac{(\text{}_{\text{ver}}\text{Tot}(E^{\bullet ,\bullet })^{p})}{(\text{}_{\text{ver}}\text{Tot}(E^{\bullet ,\bullet })^{p+1})}\simeq \bigoplus _{p}E^{p,\bullet }.\end{eqnarray}$$
These modules are bi-graded: one degree, given by
$p$
, is given by the filtration, and the other, given by
$k$
, is the grading coming from the complex
$\operatorname{Tot}(E^{\bullet ,\bullet })$
. Let
$q=k-p$
. Consider the exact sequence (we remove the subscript
$ver$
for the rest of this section)
It is clear that
$\text{}^{0}E^{p,q}=E^{p,q}$
. Moreover, if we fix the degree
$p$
, then
$\text{}^{0}E^{p,\bullet }$
, with the induced differential
$d_{0}$
, is just the complex
$E^{p,\bullet }$
with the differential
$d_{v}$
. So, from the above complex, we get the exact couple
$(H(F),H(E),i^{\ast },\unicode[STIX]{x1D70B}^{\ast },\unicode[STIX]{x1D6FF})$
. Both
$H(F),H(E)$
are also bi-graded and defined below. Setting
$k=p+q$
, we have the following.
So, if we put
$F^{(1)}=H(F)$
,
$\text{}^{1}E=H(E)$
and
$d_{1}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D6FF}$
and iterate the process, we get exact couples (
$F^{(r)},\text{}^{r}E,i^{\ast (r)},(\unicode[STIX]{x1D70B})^{(r)},\unicode[STIX]{x1D6FF}^{(r)}$
) with differentials
$d^{r}=(\unicode[STIX]{x1D70B})^{(r)}\,\circ \,\unicode[STIX]{x1D6FF}^{(r)}$
on
$\text{}^{r}E$
. The spectral sequence
$(\text{}^{r}E^{\bullet ,\bullet },d^{r})$
constructed above is the spectral sequence associated to the vertical filtration.
We denote the kernel and the image of
$d^{r}$
by
$\text{}^{r}Z^{\bullet ,\bullet }$
and
$\text{}^{r}B^{\bullet ,\bullet }$
respectively.
The following definition is new to the context.
Definition 2.2. Let
$m\in E^{p,q}$
. We say that
$m$
is an
$r$
-liftable element, for some integer
$r$
, if
$d_{v}(m)=0$
and there is a sequence of elements
$(m,a_{1},\ldots ,a_{r})$
such that:
(1)
$d_{h}(m)=d_{v}(a_{1})$
;(2)
$d_{h}(a_{i})=d_{v}(a_{i+1})$
for every
$0\leqslant i\leqslant r-1$
.
The element
$a_{r}$
is called an
$r$
th lift of
$m$
and the sequence
$(m,a_{1},\ldots ,a_{r})$
is called an
$r$
-lift sequence of
$m$
.
Remark 2.3. Let
$m\in E^{p,q}$
,
$k=p+q$
and
$(m,a_{1},\ldots ,a_{r})$
be an
$r$
-lift sequence with
$d_{h}(a_{r})=0$
. Then the sequence
$(\mathbf{0},m,-a_{1},a_{2},\ldots ,(-1)^{r}a_{r},\mathbf{0})$
gives a cohomology class in
$H^{k}(\operatorname{Tot}(E^{\bullet ,\bullet }))$
. Conversely, if
$(\mathbf{0},m,a_{1},\ldots ,a_{r},\mathbf{0})$
gives a cohomology class in
$H^{k}(\operatorname{Tot}(E^{\bullet ,\bullet }))$
, then
$$\begin{eqnarray}d_{v}(m)=0,d_{v}(a_{1})=-d_{h}(m),d_{v}(a_{i+1})=-d_{h}(a_{i}).\end{eqnarray}$$
Therefore
$(m,-a_{1},a_{2},\ldots ,(-1)^{r}a_{r})$
is an
$r$
-lift sequence for
$m$
.
We now describe the differentials
$d^{r}$
on the
$r$
th page of the spectral sequence.
Proposition 2.4. Let
$m\in E^{p,q}$
be an
$r$
-liftable element, and
$(m,a_{1},a_{2},\ldots ,a_{r})$
an
$r$
-lift sequence. Then
$m\in \text{}^{i}Z^{p,q}$
for all
$0\leqslant i\leqslant r$
and
$d^{r+1}(m)$
is the class of
$d_{h}(a_{r})$
in
$\text{}^{r+1}E^{p+r+1,q-r}$
.
Proof. We need to follow the rules of definition of the spectral sequence by an exact couple. It is easy to see that
$d^{0}=d_{v}$
and
$d^{1}=d_{h}$
.
We start with the case
$r=1$
. Suppose that
$m$
is
$1$
-liftable and let
$(m,a)$
be a
$1$
-lift sequence. Considering the map
$\unicode[STIX]{x1D6FF}$
in (2.1)
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}(m)=(d_{h}(m),0,\ldots ,0)\in H^{k+1}(\operatorname{Tot}(E^{\bullet ,\bullet })).\end{eqnarray}$$
As
$(m,a)$
is a
$1$
-lift sequence, we have
$d_{h}(m)=-d_{v}(a)$
. Moreover,
$(-d_{v}(a),0,\ldots ,0)$
and
$(0,d_{h}(a),\ldots ,0)$
are cohomologous in
$H^{k+1}(\operatorname{Tot}(E^{\bullet ,\bullet }))$
. To calculate
$d^{1}(m)$
, we have to project
$(0,d_{h}(a),\ldots ,0)$
onto the first coordinate. Therefore
$m\in \ker d^{1}$
. To calculate
$d^{2}(m)$
we must calculate
$\unicode[STIX]{x1D70B}^{(1)}(0,d_{h}(a),\ldots ,0)$
. By definition, we must take preimage by
$i^{\ast }$
once and then project onto the first coordinate, as
$$\begin{eqnarray}(i^{\ast })^{-1}((0,d_{h}(a),\ldots ,0))=(d_{h}(a),\ldots ,0),\end{eqnarray}$$
$d^{2}(m)$
is the class of
$d_{h}(a)$
in
$\text{}^{2}E^{p+2,q-1}$
.
Suppose now that
$m$
is
$r$
-liftable and that
$(m,a_{1},\ldots ,a_{r})$
is an
$r$
-lift sequence. Again, applying
$\unicode[STIX]{x1D6FF}$
to
$m$
, we have the same equation as in (2.2). Thence
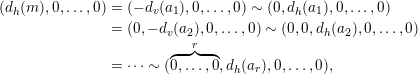$$\begin{eqnarray}\displaystyle (d_{h}(m),0,\ldots ,0) & = & \displaystyle (-d_{v}(a_{1}),0,\ldots ,0)\sim (0,d_{h}(a_{1}),0,\ldots ,0)\nonumber\\ \displaystyle & = & \displaystyle (0,-d_{v}(a_{2}),0,\ldots ,0)\sim (0,0,d_{h}(a_{2}),0,\ldots ,0)\nonumber\\ \displaystyle & = & \displaystyle \cdots \sim (\overbrace{0,\ldots ,0}^{r},d_{h}(a_{r}),0,\ldots ,0),\end{eqnarray}$$
where
${\sim}$
means homologous. To apply
$d^{i}$
, we must take
$(i-1)$
times the preimage by
$i^{\ast }$
and then project onto the first coordinate. Thus, if
$i\leqslant r$
, then
$m\in \ker d^{i}$
. To calculate
$d^{r+1}(m)$
, we must,
$r$
times, take the preimage by
$i^{\ast }$
. As
$$\begin{eqnarray}(i^{\ast })^{r}(\overbrace{0,\ldots ,0}^{r},d_{h}(a_{r}),0,\ldots ,0)=(d_{h}(a_{r}),0,\ldots ,0).\end{eqnarray}$$
Therefore, projecting in the first coordinate yields the result. ◻
We now prove the converse.
Theorem 2.5. Let
$m\in E^{p,q}$
. If
$m\in \text{}^{r}Z^{p,q}$
, then
$m$
is
$r$
-liftable.
Proof. For
$r=1$
the proof is easy:
$d^{1}(m)=d_{h}(m)=0\in \text{}^{1}E^{p+1,q}=H^{q}(M^{p+1.\bullet })$
implies
$d_{h}(m)=d_{v}(a)$
for some
$a\in M^{p+1,q-1}$
.
To illustrate the proof, we do the case
$r=2$
. Let
$m\in \text{}^{2}Z^{p,q}$
. In particular,
$m\in \text{}^{1}Z^{p,q}$
which implies that
$m$
is
$1$
-liftable. Let
$(m,a)$
be a
$1$
-lift sequence. As
$d^{2}(m)\in \text{}^{1}B^{p+2,q-1}$
, there is
$a^{\prime }$
with
$d_{v}(a^{\prime })=0$
such that
$d_{h}(a)=d_{h}(a^{\prime })$
in
$\text{}^{1}E$
. By the case
$r=1$
, there is
$a^{\prime \prime }\in E^{p+2,q-2}$
with
$d_{v}(a^{\prime \prime })=d_{h}(a-a^{\prime })$
. Now,
$(m,a-a^{\prime },a^{\prime \prime })$
is a
$2$
-lift sequence for
$m$
.
For the general case, let
$m\in \text{}^{r}Z^{p,q}$
. Then, by induction,
$m$
is
$(r-1)$
-liftable. Let
$(m,a_{1},\ldots ,a_{r-1})$
be an
$(r-1)$
-lift sequence. Then by Proposition 2.4,
$d_{h}(a_{r-1})=d^{r}(m)=0$
in
$\text{}^{r}E$
. Therefore, there is
$a_{r-1}^{(1)}\in \text{}^{r-1}Z^{p,q}$
such that
$d_{v}(a_{r-1})=0$
and
$d_{h}(a_{r-1})=d^{r-1}(a_{1}^{(1)})$
in
$\text{}^{r-1}E$
. Again by induction
$a_{1}^{(1)}$
is
$(r-2)$
-liftable. Take an
$(r-2)$
-lift sequence
$$\begin{eqnarray}(0,a_{1}^{(1)},a_{2}^{(1)},\ldots ,a_{r-1}^{(1)})\end{eqnarray}$$
such that
$d_{h}(a_{r-1}-a_{r-1}^{(1)})=0$
in
$\text{}^{r-1}E$
. It is immediate to see that
$$\begin{eqnarray}(m,a_{1}-a_{1}^{(1)},a_{2}-a_{2}^{(1)},\ldots ,a_{r-1}-a_{r-1}^{(1)})\end{eqnarray}$$
is an
$(r-1)$
-lift sequence. Now we may construct inductively, for each
$1\leqslant i\leqslant r-1$
,
$(r-1-i)$
-lift sequences
$$\begin{eqnarray}(0,\ldots ,0,a_{i}^{(i)},\ldots ,a_{r-1}^{(i)})\end{eqnarray}$$
such that
$d_{h}(a_{r-1}-a_{1}^{(i)}-\cdots -a_{r-1}^{(i)})=0$
in
$\text{}^{r-i}E$
. If
$i=r-1$
, we have that
$d_{h}(a_{r-1}-\sum _{i=1}^{r-1}a_{r-1}^{(i)})=0$
in
$\text{}^{1}E$
, that is, there is
$a_{r}$
such that
$$\begin{eqnarray}d_{h}\biggl(a_{r-1}-\mathop{\sum }_{i=1}^{r-1}a_{r-1}^{(i)}\biggr)=d_{v}(a_{r}).\end{eqnarray}$$
It follows that
$$\begin{eqnarray}\biggl(m,a_{1}-a_{1}^{(1)},a_{2}-\mathop{\sum }_{i=1}^{2}a_{2}^{(i)},\ldots ,a_{r-1}-\mathop{\sum }_{i=1}^{r-1}a_{r-1}^{(i)},a_{r}\biggr)\end{eqnarray}$$
is an
$r$
-lift sequence.◻
The same method of the proof of Theorem 2.4 gives us the following characterization of
$\text{}^{r}B^{p,q}$
.
Theorem 2.6. Let
$m\in E^{p,q}$
. Then
$m\in \text{}^{r}B^{p,q}$
if and only if there is an
$(r-1)$
-lift sequence
$(a_{1},\ldots ,a_{r-1},m)$
and an element
$a_{r}$
such that
$m=d_{h}(a_{r-1})+d_{v}(a_{r})$
.
Again, considering the vertical filtration of the first quadrant double complex
$E^{\bullet ,\bullet }$
, the inclusions
$$\begin{eqnarray}i:\operatorname{Tot}(E^{\bullet ,\bullet })^{p}\rightarrow \operatorname{Tot}(E^{\bullet ,\bullet })\end{eqnarray}$$
induce a filtration
$$\begin{eqnarray}H^{k}(\operatorname{Tot}(E^{\bullet ,\bullet }))\supset i^{\ast }(H^{k}(\operatorname{Tot}(E^{\bullet ,\bullet })^{1}))\supset i^{\ast }(H^{k}(\operatorname{Tot}(E^{\bullet ,\bullet })^{2}))\supset \cdots \supset i^{\ast }(H^{k}(\operatorname{Tot}(E^{\bullet ,\bullet })^{p}))\supset \cdots \,.\end{eqnarray}$$
The following theorem explicitly explains the convergence of spectral sequences.
Proposition 2.7. Let
$E^{\bullet ,\bullet }$
be a first quadrant bi-complex with the vertical filtration. Then the map
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D711}_{p,q}:i^{\ast }(H^{k}(\operatorname{Tot}(M^{\bullet ,\bullet })^{p}))/i^{\ast }(H^{k}((\operatorname{Tot}(M^{\bullet ,\bullet })^{p+1}))) & \rightarrow & \text{}^{\infty }E^{p,q}\\ (m,a_{p+1},\ldots ,a_{k}) & \mapsto & \bar{m},\end{array}\end{eqnarray}$$
(
$q=k-p$
) is a well-defined isomorphism.
To finish this section, we give some remarks: we have chosen to work with a first-quadrant double complex with differentials increasing the degree for the sake of clarity. All the definitions and arguments can be adapted to double complexes placed in other quadrants or with other configurations for the differentials. For the convergence, the proof of Theorem 2.7 shows that the only thing we need is a complex with finite diagonals.
3 Buchsbaum–Eisenbud complexes are strands of Koszul–Čech spectral sequences
To understand the structure of the disguised residual intersection, we need an explicit expression for a transgression map in a Koszul–Čech spectral sequence. This expression is exactly the same as the connecting map in the Buchsbaum–Eisenbud complexes explained in [Reference EisenbudEis95, § A2.6]. The surprising fact is that the whole family of Buchsbaum–Eisenbud complexes can be explained by the complexes Koszul and Čech. This, we will explain in this section.
3.1 Preliminaries
We explain the new structures as much complete as possible here and refer to [Reference EisenbudEis95, § A2] for the details about the family of complexes
${\mathcal{C}}_{\bullet }^{i}$
; where
${\mathcal{C}}_{\bullet }^{0}$
is the Eagon–Northcott complex and
${\mathcal{C}}_{\bullet }^{1}$
is the Buchsbaum–Rim complex. Besides some basic notation, we will recall some notation and the basic structure of the Buchsbaum–Eisenbud family of complexes. We avoid repeating the whole well-known structures. Instead, we keep the same notation and names as in [Reference EisenbudEis95, § A2.6], for the sake of consistency, and refer the reader to [Reference EisenbudEis95].
Let
$R$
be a commutative ring. For an
$R$
-module
$M$
, we denote by
$M^{\ast }$
the dual
$\operatorname{Hom}_{R}(M,R)$
.
Recall that for
$R$
-module
$G$
and any linear map
$\unicode[STIX]{x1D711}\in G^{\ast }$
one can define a differential
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D711}}:\bigwedge G\rightarrow \bigwedge G$
, called the Koszul differential of the linear map
$\unicode[STIX]{x1D711}$
; see [Reference Bruns and HerzogBH98, Definition 1.6.1]. This defines an action of
$G^{\ast }$
on
$\bigwedge G$
given by
$$\begin{eqnarray}\unicode[STIX]{x1D713}\cdot w=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D713}}(w).\end{eqnarray}$$
Clearly, if
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in G^{\ast }$
, then
$\unicode[STIX]{x1D711}\cdot \unicode[STIX]{x1D713}\cdot w=-\unicode[STIX]{x1D713}\cdot \unicode[STIX]{x1D711}\cdot w$
and this gives a natural action of
$\bigwedge G^{\ast }$
on
$\bigwedge G$
.
Let
$\unicode[STIX]{x1D6F7}:F=R^{f}\rightarrow G=R^{g}$
be a linear map. Then we can construct the generalized Koszul complex
$\mathbb{K}(\unicode[STIX]{x1D6F7})$
, defined in [Reference VasconcelosVas94] as follows. Let
$S(G)$
be the symmetric algebra of
$G$
and
$\unicode[STIX]{x1D719}$
be the composition of the maps
$$\begin{eqnarray}F\otimes _{R}S(G)\xrightarrow[{}]{\unicode[STIX]{x1D6F7}\otimes 1}G\otimes _{R}S(G)\rightarrow S(G),\end{eqnarray}$$
where the last map is just the multiplication on
$S(G)$
. Then we can construct the Koszul differential
$$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}:\bigwedge F\otimes _{R}S(G)\rightarrow \bigwedge F\otimes _{R}S(G).\end{eqnarray}$$
The module
$\bigwedge G^{\ast }$
acts on
$\bigwedge F$
as follows. For any
$\unicode[STIX]{x1D702}\in G^{\ast }$
and any
$v\in \bigwedge F$
,
$$\begin{eqnarray}\unicode[STIX]{x1D702}\cdot v:=\unicode[STIX]{x1D6F7}^{\ast }(\unicode[STIX]{x1D702})\cdot v=(\unicode[STIX]{x1D702}\circ \unicode[STIX]{x1D6F7})\cdot v.\end{eqnarray}$$
Moreover, the module
$G$
acts naturally on
$S(G)$
via the multiplication. Therefore, we have an action of the module
$G^{\ast }\otimes _{R}G$
on
$\bigwedge F\otimes _{R}S(G)$
given by
$$\begin{eqnarray}(\unicode[STIX]{x1D702}\otimes u)\cdot (v\otimes w)=\unicode[STIX]{x1D702}\cdot v\otimes uw.\end{eqnarray}$$
The differential of the complex
$\mathbb{K}(\unicode[STIX]{x1D6F7})$
can be explained via this action: it is just the action of the element
$c$
which is the pullback of
$1$
via the natural evaluation map
$G\otimes G^{\ast }\rightarrow R$
. Moreover for any
$S(G)$
-module
$M$
, one can define the generalized Koszul complex with coefficients in
$M$
given by
$\mathbb{K}(\unicode[STIX]{x1D6F7})\otimes _{S(G)}M$
. Again,
$G^{\ast }\otimes G$
acts on
$\bigwedge F\otimes M$
and the differential of
$\mathbb{K}(\unicode[STIX]{x1D6F7})\otimes _{S(G)}M$
is again given by the action of the element
$c$
.
Definition 3.1. A connecting map of degree
$d$
for the map
$\unicode[STIX]{x1D6F7}$
is a map of the form
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{d}:\bigwedge ^{d+g}F\rightarrow \bigwedge ^{d}F\end{eqnarray}$$
given by the action of a generator
$\unicode[STIX]{x1D6FE}$
of
$\bigwedge ^{g}G^{\ast }$
.
Definition 3.2. Let
$\unicode[STIX]{x1D6F7}:F=R^{f}\rightarrow G=R^{g}$
be a linear map with
$f\geqslant g$
. The complex obtained by joining
$(K(\unicode[STIX]{x1D6F7})_{(f-g-d)})^{\ast }$
and
$K(\unicode[STIX]{x1D6F7})_{(d)}$
via a connecting map
$\unicode[STIX]{x1D700}_{d}$
is denoted by
${\mathcal{C}}^{d}(\unicode[STIX]{x1D6F7})$
.
$\{{\mathcal{C}}^{d}(\unicode[STIX]{x1D6F7})\}_{d\in \mathbb{Z}}$
is the family of Buchsbaum–Eisenbud complexes. The complex
${\mathcal{C}}^{0}(\unicode[STIX]{x1D6F7})$
is called the Eagon–Northcott complex, and the complex
${\mathcal{C}}^{1}(\unicode[STIX]{x1D6F7})$
is the Buchsbaum–Rim complex.
Let
$T_{1},\ldots ,T_{g}$
be a basis of
$G$
. Then
$S(G)\simeq R[T_{1},\ldots ,T_{g}]$
is a polynomial extension and has the standard grading, and the complex
$\mathbb{K}(\unicode[STIX]{x1D6F7})$
is graded as well.
In terms of the basis
$T_{1},\ldots ,T_{g}$
the map
$\unicode[STIX]{x1D6F7}$
has a decomposition
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(w)=\unicode[STIX]{x1D719}_{1}(w)T_{1}+\cdots +\unicode[STIX]{x1D719}_{g}(w)T_{g},\end{eqnarray}$$
where
$\unicode[STIX]{x1D719}_{i}\in F^{\ast }$
for all
$i$
. In this case the differential
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}$
of
$\mathbb{K}(\unicode[STIX]{x1D6F7})$
can be expressed as
$$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}}(w)=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{1}}(w)T_{1}+\cdots +\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{g}}(w)T_{g}.\end{eqnarray}$$
The connecting map
$\unicode[STIX]{x1D700}_{d}$
can also be easily described in terms of the basis
$T_{1},\ldots ,T_{g}$
.
Let
$T_{1}^{\prime },\ldots ,T_{g}^{\prime }$
be the basis of
$G^{\ast }$
which is dual to
$T_{1},\ldots ,T_{g}$
. Then the associated connecting map,
$\unicode[STIX]{x1D700}_{d}$
, associated to the generator
$T_{1}^{\prime }\wedge \cdots \wedge T_{g}^{\prime }$
is given by
$$\begin{eqnarray}w\rightarrow \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{1}}\cdots \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{g}}(w).\end{eqnarray}$$
3.2 The new structure
Let
$R$
be a commutative ring,
$\unicode[STIX]{x1D6F7}:F=R^{f}\rightarrow G=R^{g},f\geqslant g$
a linear map and
$K_{\bullet }=\mathbb{K}(\unicode[STIX]{x1D6F7})$
its generalized Koszul complex. Let
$T_{1},\ldots ,T_{g}$
be a basis for
$G$
and
$\operatorname{Sym}(G)=S=R[T_{1},\ldots ,T_{g}]$
. Moreover, let
${\check{C}}_{\mathfrak{t}}^{\bullet }$
be the Čech complex of
$S$
with respect to the sequence
$\mathfrak{t}=(T_{1},\ldots ,T_{g})$
. Consider then the bi-complex
$K_{\bullet }\otimes _{S}{\check{C}}_{\mathfrak{t}}^{\bullet }$
and write
${\mathcal{D}}_{\bullet }=\operatorname{Tot}(K_{\bullet }\otimes _{S}{\check{C}}_{\mathfrak{t}}^{\bullet })$
. We display
$K_{\bullet }\otimes _{S}{\check{C}}_{\mathfrak{t}}^{\bullet }$
as a third-quadrant bi-complex with
$K_{0}\otimes _{R}C_{\mathfrak{t}}^{0}(S)$
at the origin of the plane.
We begin to explain our construction by looking at the spectral sequence coming from the vertical filtration. As
$H_{\mathfrak{t}}^{i}(S)=0$
for
$i<g$
, the spectral sequence collapses on the
$g$
th row on the complex
Since
$K_{i}=S^{\binom{f}{i}}(-i)$
and
$H_{\mathfrak{t}}^{g}(S)_{(d)}=0$
for
$d>-g$
, we have, for a fixed degree
$d$
,
$$\begin{eqnarray}(\text{}^{1}E_{\text{vert}})_{(d)}^{\ast ,-g}:0\rightarrow H_{\mathfrak{ t}}^{g}(K_{f})_{(d)}\rightarrow H_{\mathfrak{t}}^{g}(K_{f-1})_{(d)}\rightarrow \ldots \rightarrow H_{\mathfrak{t}}^{g}(K_{g+d+1})_{(d)}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{d}}H_{\mathfrak{t}}^{g}(K_{g+d})_{(d)}\rightarrow 0.\end{eqnarray}$$
Then
$$\begin{eqnarray}(\text{}^{2}E_{\text{ver}}^{-d-g,-g})_{(d)}=(\text{}^{\infty }E_{\text{ver}}^{-d-g,-g})_{(d)}\simeq \operatorname{Coker}(\unicode[STIX]{x1D713}_{d}).\end{eqnarray}$$
Now, we look at the spectral sequence coming from the horizontal filtration. The second page of this spectral sequence is given by
$$\begin{eqnarray}(\text{}^{2}E_{\text{hor}}^{-p,-q})_{(d)}=H_{\mathfrak{t}}^{q}(H_{p}(K_{\bullet }))_{(d)}.\end{eqnarray}$$
The
$0$
th row of
$\text{}^{0}E_{\text{hor}}^{\ast ,\ast }$
in degree
$d$
is the complex
$$\begin{eqnarray}0\rightarrow (K_{d})_{(d)}\xrightarrow[{}]{\unicode[STIX]{x1D707}_{d}}\cdots \rightarrow (K_{0})_{(d)}\rightarrow 0;\end{eqnarray}$$
so that
$$\begin{eqnarray}(\text{}^{2}E_{\text{hor}}^{-d,0})_{(d)}\simeq H_{\mathfrak{t}}^{0}(\operatorname{Ker}(\unicode[STIX]{x1D707}_{d}))\subseteq \operatorname{Ker}(\unicode[STIX]{x1D707}_{d}).\end{eqnarray}$$
By the convergence of the spectral sequences, we have
$$\begin{eqnarray}(\text{}^{\infty }E_{\text{ver}}^{-d-g,-g})_{(d)}\simeq H^{d}({\mathcal{D}}_{\bullet })_{(d)}.\end{eqnarray}$$
Moreover, there is a filtration
$$\begin{eqnarray}H^{d}({\mathcal{D}}_{\bullet })_{(d)}={\mathcal{F}}_{d,0}\supseteq {\mathcal{F}}_{d,1}\supseteq \cdots\end{eqnarray}$$
such that
$$\begin{eqnarray}\frac{{\mathcal{F}}_{d,i}}{{\mathcal{F}}_{d,i+1}}\simeq \text{}^{\infty }(E_{\text{hor}}^{-d-i,-i})_{(d)}.\end{eqnarray}$$
We then have a natural surjection
$H^{d}({\mathcal{D}}_{\bullet })_{(d)}\rightarrow (\text{}^{\infty }E_{\text{hor}}^{d,0})_{(d)}$
. Define the map
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{d}:H_{\mathfrak{t}}^{g}(K_{d+g})_{(d)}\rightarrow (K_{d})_{(d)}\end{eqnarray}$$
to be the composition
$$\begin{eqnarray}H_{\mathfrak{t}}^{g}(K_{d+g})_{(d)}\rightarrow \operatorname{Coker}(\unicode[STIX]{x1D713}_{d})\xrightarrow[{}]{{\sim}}H^{d}({\mathcal{D}}_{\bullet })_{(d)}\rightarrow (\text{}^{\infty }E_{\text{hor}}^{-d,0})_{(d)}{\hookrightarrow}(\text{}^{1}E_{\text{hor}}^{-d,0})_{(d)}=\operatorname{Ker}(\unicode[STIX]{x1D707}_{d}){\hookrightarrow}(K_{d})_{(d)}.\end{eqnarray}$$
We define the complex
${\mathcal{K}}_{d}(\unicode[STIX]{x1D6F7})$
to be the complex
$$\begin{eqnarray}0\rightarrow H_{\mathfrak{t}}^{g}(K_{f})_{(d)}\rightarrow \ldots \rightarrow H_{\mathfrak{t}}^{g}(K_{d+g})_{(d)}\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{d}}(K_{d})_{(d)}\rightarrow \ldots \rightarrow (K_{0})_{(d)}\rightarrow 0.\end{eqnarray}$$
The principal theorem of this chapter is the following.
Theorem 3.3. Let
$\unicode[STIX]{x1D6F7}:F=R^{f}\rightarrow G=R^{g}$
be a linear map with
$f\geqslant g$
. Then the complexes
${\mathcal{C}}^{d}(\unicode[STIX]{x1D6F7})$
and
${\mathcal{K}}_{d}(\unicode[STIX]{x1D6F7})$
are isomorphic for
$d\leqslant f-g$
.
Fix
$d\leqslant f-g$
. The complexes
${\mathcal{C}}^{d}(\unicode[STIX]{x1D6F7})$
and
${\mathcal{K}}_{d}(\unicode[STIX]{x1D6F7})$
are isomorphic at the right side of the joining maps
$\unicode[STIX]{x1D70F}_{d}$
and
$\unicode[STIX]{x1D700}_{d}$
as they are both the generalized Koszul complex of
$\unicode[STIX]{x1D6F7}$
. Therefore we must study the left parts and the joining map of both complexes.
Proposition 3.4. The left parts of
${\mathcal{C}}^{d}(\unicode[STIX]{x1D6F7})$
and
${\mathcal{K}}_{d}(\unicode[STIX]{x1D6F7})$
are isomorphic.
Proof. Recall that
$H_{\mathfrak{t}}^{g}(S)$
has an inverse polynomial structure, and
$H_{\mathfrak{t}}^{g}(S)_{(-g)}$
is a free
$R$
-module generated by the monomials
$1/(T_{1}^{\unicode[STIX]{x1D6FC}_{1}}\ldots T_{g}^{\unicode[STIX]{x1D6FC}_{g}})$
with
$\sum _{i=1}^{g}\unicode[STIX]{x1D6FC}_{i}=g,\unicode[STIX]{x1D6FC}_{i}\geqslant 1$
. Thus there is a perfect pairing
$$\begin{eqnarray}S_{(d)}\otimes _{R}H_{\mathfrak{t}}^{g}(S)_{(-d-g)}\longrightarrow H_{\mathfrak{t}}^{g}(S)_{(-g)}\simeq R\end{eqnarray}$$
given by multiplication. The isomorphism
$(S_{(d)})^{\ast }\simeq H_{\mathfrak{t}}^{g}(S)_{(-d-g)}$
induced by this pairing takes the element
$(T_{1}^{\unicode[STIX]{x1D6FC}_{1}}\ldots T_{g}^{\unicode[STIX]{x1D6FC}_{g}})^{\prime }$
to the element
$1/(T_{1}^{\unicode[STIX]{x1D6FC}_{1}+1}\ldots T_{g}^{\unicode[STIX]{x1D6FC}_{g}+1})$
. Using this paring, we have the following isomorphisms:
$$\begin{eqnarray}\displaystyle {\mathcal{K}}_{d}(\unicode[STIX]{x1D6F7})_{d+i} & = & \displaystyle H_{\mathfrak{t}}^{g}(K_{g+d+i-1})_{(d)}\nonumber\\ \displaystyle & \simeq & \displaystyle H_{\mathfrak{t}}^{g}\biggl(\bigwedge ^{d+g+i-1}F\otimes _{R}S(-g-d-i+1)\biggr)_{(d)}\nonumber\\ \displaystyle & \simeq & \displaystyle \bigwedge ^{g+d+i-1}F\otimes _{R}H_{\mathfrak{t}}^{g}(S(-g-d-i+1))_{(d)}\nonumber\\ \displaystyle & \simeq & \displaystyle \bigwedge ^{g+d+i-1}F\otimes _{R}H_{\mathfrak{t}}^{g}(S)_{(-g-i+1)}\nonumber\\ \displaystyle & \simeq & \displaystyle \bigwedge ^{g+d+i-1}F\otimes _{R}(S_{(i-1)})^{\ast }\simeq ({\mathcal{C}}^{d})_{d+i}.\nonumber\end{eqnarray}$$
Hence components of the complexes are isomorphic.
For the differentials, notice that the left part of
${\mathcal{C}}^{d}$
is a strand of the generalized Koszul complex of
$\unicode[STIX]{x1D6F7}$
with coefficients in
$S^{\ast }$
and the left part of
${\mathcal{K}}_{d}(\unicode[STIX]{x1D6F7})$
is a strand of the generalized Koszul complex of
$\unicode[STIX]{x1D6F7}$
with coefficients in
$H_{\mathfrak{t}}^{g}(S)$
. Both differentials are induced by the action of the element
$c\in G^{\ast }\otimes G$
defined earlier in this section, and this action commutes with the isomorphism induced by the above perfect pairing. The proposition is therefore proved.◻
It remains to analyze the joining maps
$\unicode[STIX]{x1D70F}_{d}:H_{\mathfrak{t}}^{g}(K_{g+d})_{(d)}\rightarrow (K_{d})_{(d)}$
defined in (3.7) and
$\unicode[STIX]{x1D700}_{d}$
defined in Definition 3.1.
We use the following notation in what follows.
Notation 3.5.
∙ For any
$L\subset \{1,\ldots ,g\}$
with
$|L|=\ell$
, we define
$\operatorname{sgn}(L)$
to be the sign of the permutation that put the elements of
$L$
on the first
$\ell$
positions.∙ For the set of variables
$T_{1},\ldots ,T_{g}$
and
$L\subset \{1,\ldots ,g\}$
, we define
$T_{L}:=\prod _{j\notin L}T_{j}$
.∙ For a set of maps
$\{\unicode[STIX]{x1D711}_{\ell _{i}}:i=1,\ldots ,m\}$
in
$F^{\ast }$
, we use the notation
$\unicode[STIX]{x2202}_{L}$
to denote the composition
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D711}_{\ell _{1}}}\cdots \unicode[STIX]{x2202}_{\unicode[STIX]{x1D711}_{\ell _{m}}}$
where
$L=\{\ell _{1},\ldots ,\ell _{m}\}$
.
Using the theorems developed in § 2 about the structure of the maps in spectral sequences, we have an explicit description for
$\unicode[STIX]{x1D70F}_{d}$
.
Theorem 3.6. Let
$R$
be a commutative ring,
$\unicode[STIX]{x1D6F7}:F=R^{f}\rightarrow G=R^{g}$
a linear map with
$f\geqslant g$
and
$K_{\bullet }=\mathbb{K}(\unicode[STIX]{x1D6F7})$
the generalized Koszul complex.
Let
$T_{1},\ldots ,T_{g}$
be a basis of
$G$
,
$\unicode[STIX]{x1D6F7}=\sum _{i=1}^{r}\unicode[STIX]{x1D719}_{i}\cdot T_{i}$
and
$S:=S(G)=R[T_{1},\ldots ,T_{g}]$
.
Consider the double complex
$K_{\bullet }\otimes _{S}{\check{C}}_{\mathfrak{t}}^{\bullet }(S)$
and its horizontal and vertical spectral sequences. Then, for each
$0\leqslant d\leqslant f-g$
and
$w\in K_{g+d}$
, the element
$$\begin{eqnarray}m=w\otimes \frac{1}{T_{1}\ldots T_{g}}\in K_{g+d}\otimes {\check{C}}_{\mathfrak{t}}^{g}(S)\end{eqnarray}$$
is
$g$
-liftable. Moreover, the
$i$
th lift of this element is, up to a sign,
$$\begin{eqnarray}\mathop{\sum }_{|L|=i}\unicode[STIX]{x2202}_{L}(w)\otimes \operatorname{sgn}(L)\frac{1}{T_{L}}.\end{eqnarray}$$
In particular,
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{d}(m)=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{1}}\cdots \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{g}}(m).\end{eqnarray}$$
Hence
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D700}_{d}$
.
Proof. In the course of the proof we do all the liftings without concerning the signs coming from the bi-complex, for the sake of clarity. Finally, we stress that the involved signs depends only on
$g$
.
In
$(\text{}^{0}E_{\text{ver}}^{-d-g,-g})_{(d)}$
the differential
$d^{0}=d_{v}$
is zero. By (3.4),
$(\text{}^{1}E_{\text{ver}}^{-d-g+1,-g})_{(d)}=0$
and
$(\text{}^{r}E_{\text{ver}}^{-d-g+r,-g-r+1})_{(d)}=0$
for all
$r\geqslant 2$
. Therefore all differentials
$d^{r}$
are zero in
$(\text{}^{r}E_{\text{ver}}^{-d-g,-g})_{(d)}$
and
$(\text{}^{0}E_{\text{ver}}^{-d-g,-g})_{(d)}=(\text{}^{\infty }Z_{\text{ver}}^{-d-g,-g})_{(d)}$
. Then by Theorem 2.5,
$m$
is
$g$
-liftable.
We now show the formula for the
$i$
th lift by using an induction on
$i$
. The process of lifting is by applying the horizontal map, Koszul differentials, in each step and then taking the pre-image by the vertical maps which are the Čech differentials.
$$\begin{eqnarray}d_{h}(m)=\mathop{\sum }_{i=1}^{g}\unicode[STIX]{x2202}_{i}(w)\otimes \frac{T_{i}}{T_{1}\ldots T_{g}}.\end{eqnarray}$$
It is immediate to see that (3.10) is a Čech boundary, and the 1-lift is given by
$$\begin{eqnarray}\unicode[STIX]{x2202}_{1}(w)\otimes \frac{1}{T_{\{1\}}}-\unicode[STIX]{x2202}_{2}(w)\otimes \frac{1}{T_{\{2\}}}+\cdots +(-1)^{g}\unicode[STIX]{x2202}_{g}(w)\otimes \frac{1}{T_{\{g\}}},\end{eqnarray}$$
as required.
Now suppose that
$i\geqslant 1$
and that the
$i$
th lift of
$m$
is given by
$$\begin{eqnarray}m_{i}=\mathop{\sum }_{|L|=i}\unicode[STIX]{x2202}_{L}(w)\otimes \operatorname{sgn}(L)\frac{1}{T_{L}}.\end{eqnarray}$$
Applying the Koszul differential, we then have
$$\begin{eqnarray}d_{h}(m_{i})=\mathop{\sum }_{|L|=i}\biggl(\mathop{\sum }_{i=1}^{g}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{L}(m)T_{i}\biggr)\otimes \operatorname{sgn}(L)\frac{1}{T_{L}}.\end{eqnarray}$$
Notice that if
$i\in L$
, then
$\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{L}=0$
. This shows that
$d_{h}(m_{i})$
is the image of the Čech map of the element
$$\begin{eqnarray}m_{i+1}=\mathop{\sum }_{|L|=i+1}\unicode[STIX]{x2202}_{L}(w)\otimes \operatorname{sgn}(L)\frac{1}{T_{L}},\end{eqnarray}$$
as desired.
To see that
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D700}_{d}$
, we analyze the construction of
$\unicode[STIX]{x1D70F}_{d}$
given in (3.7). Since
$$\begin{eqnarray}H_{\mathfrak{t}}^{g}\biggl(\bigwedge ^{d+g}(S(-d-g))^{f}\biggr)\simeq \bigwedge ^{d+g}F\otimes H_{\mathfrak{ t}}^{g}(S)_{(-g)},\end{eqnarray}$$
any element of
$\operatorname{Coker}(\unicode[STIX]{x1D711}_{d})$
is presented by an element
$$\begin{eqnarray}m=w\otimes \frac{1}{T_{1}\ldots T_{g}}\in K_{g+d}\otimes {\check{C}}_{\mathfrak{t}}^{g}(S).\end{eqnarray}$$
By Theorem 2.7, the isomorphism
$\operatorname{Coker}(\unicode[STIX]{x1D711}_{d})\simeq H^{d}({\mathcal{D}}_{\bullet })_{(d)}$
sends
$m$
to the cohomology class
$(m,-a_{1},\ldots ,(-1)^{g}a_{g})\in H^{d}({\mathcal{D}}_{\bullet })_{(d)}$
where
$(m,a_{1},\ldots ,a_{g})$
is a
$g$
-lift sequence for
$m$
.
Again by Theorem 2.7, the map
$H^{d}({\mathcal{D}}_{\bullet })_{(d)}\rightarrow \text{}^{\infty }E^{-d,0}$
sends the cohomology class
$(m,-a_{1},\ldots ,(-1)^{g}a_{g})$
to the element
$(-1)^{g}a_{g}$
, as
$a_{g}$
is just the
$g$
-lift of
$m$
calculated above. Comparing with Definition 3.1, we see that
$\unicode[STIX]{x1D70F}_{d}=\unicode[STIX]{x1D700}_{d}$
up to a sign.◻
The proof of Theorem 3.3 now follows from Proposition 3.4 and Theorem 3.6.
4 Generators of residual intersections
In this section, we recall the definition of ‘residual approximation complexes’ and ‘disguised residual intersections’. Based on the materials developed so far, we show how Kitt ideals (defined in the introduction) can approximate a general colon ideal
$(\mathfrak{a}:I)$
. By general colon ideal we mean, in most of the coming results,
$J=\mathfrak{a}:I$
needs not to be a residual intersection. However, it is not true that
$\operatorname{Kitt}(\mathfrak{a},I)=(\mathfrak{a}:I)$
for any colon ideal, see Example 5.9.
4.1 Definitions and known results
Definition 4.1. Let
$R$
be a commutative ring and
$I\subset R$
an ideal of grade
$g$
and
$s\geqslant g$
. We say that an ideal
$J$
is an algebraic
$s$
-residual intersection of
$I$
, if
$J=(\mathfrak{a}:I)$
, with
$\mathfrak{a}=(a_{1},\ldots ,a_{s})\subset I$
, and
$\operatorname{ht}(J)\geqslant s$
. Moreover, we say that:
(1)
$J$
is an arithmetic
$s$
-residual intersection if
$\unicode[STIX]{x1D707}_{R_{\mathfrak{p}}}(I/\mathfrak{a})_{\mathfrak{p}}\leqslant 1$
for all prime ideals
$\mathfrak{p}$
with
$\operatorname{ht}(\mathfrak{p})=s$
;(2)
$J$
is a geometric
$s$
-residual intersection if
$\operatorname{ht}(I+J)\geqslant s+1$
.
In [Reference HassanzadehHas12, Reference Hassanzadeh and NaelitonHN16, Reference Chardin, Naeliton and TranCNT19] the authors tackle the problem of the Cohen–Macaulayness of an
$s$
-residual intersection
$J=(\mathfrak{a}:I)$
without assuming that
$I$
satisfies the
$G_{s}$
-condition.Footnote
3
These works rely upon the construction of a family of complexes, called the residual approximation complexes, that we now describe.
Let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})$
an ideal of
$R$
and
$\mathfrak{a}=(a_{1},\ldots ,a_{s})\subseteq I$
. For each
$1\leqslant j\leqslant s$
, let
$a_{j}=\sum _{i=1}^{r}c_{ij}f_{i}$
for some
$c_{ij}\in R$
. Let
$S=R[T_{1},\ldots ,T_{r}]$
be a standard polynomial extension of
$R$
and
$\unicode[STIX]{x1D6FE}_{j}=\sum _{i=1}^{r}c_{ij}T_{i}\in S_{1}$
. We then consider the
${\mathcal{Z}}$
-complex,
${\mathcal{Z}}_{\bullet }(\mathbf{f};R)$
, of Herzog, Simis and Vasconcelos [Reference Herzog, Simis and VasconcelosHSV83]:
$$\begin{eqnarray}0\rightarrow Z_{r}(\mathbf{f};R)\otimes _{R}S(-r)\rightarrow Z_{r-1}(\mathbf{f};R)\otimes _{R}S(-r+1)\rightarrow \ldots \rightarrow Z_{0}(\mathbf{f};R)\otimes _{R}S\rightarrow 0,\end{eqnarray}$$
where
$Z_{i}(\mathbf{f};R)$
stands for the
$i$
th module of Koszul cycles of the sequence
$\mathbf{f}=(f_{1},\ldots ,f_{r})$
.
Subsequently we consider the bold form
$\mathbf{f},\mathbf{a}$
and
$\boldsymbol{\unicode[STIX]{x1D6FE}}$
for the sequences
$f_{1},\ldots ,f_{r}$
,
$a_{1},\ldots ,a_{s}$
and
$\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s}$
.
Now, consider a new complex, given by
$$\begin{eqnarray}{\mathcal{D}}_{\bullet }=\operatorname{Tot}({\mathcal{Z}}_{\bullet }(\mathbf{f};R)\otimes _{S}K_{\bullet }(\boldsymbol{\unicode[STIX]{x1D6FE}},S)),\end{eqnarray}$$
where
$K_{\bullet }(\boldsymbol{\unicode[STIX]{x1D6FE}},S)$
is the Koszul complex
$K_{\bullet }(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s},S)$
. The
$i$
th component of this complex is given by
$$\begin{eqnarray}{\mathcal{D}}_{i}=\bigoplus _{k=i-s}^{\min \{i,r\}}(Z_{k}(\mathbf{f};R)\otimes _{R}S(-k))\otimes _{S}S^{\binom{s}{i-k}}(-i+k)\simeq \bigoplus _{k=i-s}^{\min \{i,r\}}(Z_{k}(\mathbf{f};R)\otimes _{R}S^{\binom{s}{i-k}})(-i).\end{eqnarray}$$
We then tensor
${\mathcal{D}}_{\bullet }$
to the Čech complex
${\check{C}}_{\mathfrak{t}}^{\bullet }(S)$
, where
$\mathfrak{t}=(T_{1},\ldots ,T_{r})$
, and repeat the same procedure as in § 3.2 to glue the horizontal spectral sequence to the vertical spectral sequence. Thence for each degree
$k$
, we have the complex
$$\begin{eqnarray}\text{}_{k}{\mathcal{Z}}_{\bullet }^{+}:0\rightarrow H_{\mathfrak{ t}}^{r}({\mathcal{D}}_{r+s-1})_{(k)}\rightarrow \ldots \rightarrow H_{\mathfrak{t}}^{r}({\mathcal{D}}_{r+k})_{(k)}\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{k}}({\mathcal{D}}_{k})_{(k)}\rightarrow \ldots \rightarrow ({\mathcal{D}}_{0})_{(k)}\rightarrow 0.\end{eqnarray}$$
Definition 4.2. The complex
$\text{}_{k}{\mathcal{Z}}_{\bullet }^{+}$
constructed above is called the
$k$
th residual approximation complex with respect to the generating sets
$\mathbf{f}$
and
$\mathbf{a}$
of
$I$
and
$\mathfrak{a}$
.
Having these approximation complexes in hand, the first interesting property is their acyclicity. Here is where the Cohen–Macaulayness of the ring
$R$
and sliding depth conditions come into play. We recall the definitions here.
Definition 4.3. Let
$(R,\mathfrak{m})$
be a Noetherian local ring of dimension
$d$
and
$I=(f_{1},\ldots ,f_{r})=(\mathbf{f})$
an ideal. Let
$k$
be an integer. We say that the ideal
$I$
satisfies
$\operatorname{SD}_{k}$
if
$$\begin{eqnarray}\operatorname{depth}(H_{i}(\mathbf{f};R))\geqslant \min \{d-g,d-r+i+k\}\end{eqnarray}$$
for all
$i\geqslant 0$
; also
$\operatorname{SD}$
stands for
$\operatorname{SD}_{0}$
. Similarly, we say that
$I$
satisfies the sliding depth condition on cycles,
$\operatorname{SDC}_{k}$
, at level
$t$
, if
$\operatorname{depth}(Z_{i}(\mathbf{f};R))\geqslant \min \{d-r+i+k,d-g+2,d\}$
for all
$r-g-t\leqslant i\leqslant r-g$
.
The ideal
$I$
is said to be strongly Cohen–Macaulay, SCM, if
$H_{i}(\mathbf{f};R)$
is CM for all
$i$
.
We state an acyclicity criterion.
Theorem 4.4 [Reference Hassanzadeh and NaelitonHN16, Theorem 2.6].
Let
$(R,\mathfrak{m})$
be a CM local ring of dimension
$d$
,
$I=(f_{1},\ldots ,f_{r})$
an ideal with height
$g\geqslant 1$
. Let
$s\geqslant g$
and fix
$0\leqslant k\leqslant s-g+2$
. Suppose that
$I$
satisfies
$\operatorname{SD}$
and that one the following hypotheses holds:
(i)
$r+k\leqslant s$
or;(ii)
$r+k\geqslant s+1$
and
$\operatorname{depth}(Z_{i}(\mathbf{f}))\geqslant \min \{d,d-s+k\}$
for
$0\leqslant i\leqslant k$
.
Then for any
$s$
-residual intersection
$J=(\mathfrak{a}:I)$
, the complex
$\text{}_{k}{\mathcal{Z}}_{\bullet }^{+}$
is acyclic. Furthermore,
$H_{0}(\text{}_{k}{\mathcal{Z}}_{\bullet }^{+})$
is a Cohen–Macaulay
$R$
-module of dimension
$d-s$
.
The last map of the complex
$\text{}_{0}{\mathcal{Z}}_{\bullet }^{+}$
is
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{0}:H_{\mathfrak{t}}^{r}({\mathcal{D}}_{r})_{0}\rightarrow (D_{0})_{0}\simeq R.\end{eqnarray}$$
Hence
$H_{0}(\text{}_{0}{\mathcal{Z}}_{\bullet }^{+})\simeq R/K$
for some ideal
$K\subset R$
ideal. This ideal is called the disguised residual intersection. More specifically, we have the following.
Definition 4.5. Let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})$
and
$\mathfrak{a}=(a_{1},\ldots ,a_{s})\subseteq I$
be ideals of
$R$
and
$\unicode[STIX]{x1D6F7}=(c_{ij})$
be an
$r\times s$
matrix such that
$(\mathbf{a})=(\mathbf{f}).\unicode[STIX]{x1D6F7}$
.
Then the disguised residual intersection of
$I$
with respect to the representation matrix
$\unicode[STIX]{x1D6F7}$
is the image of the map
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{0}:H_{\mathfrak{t}}^{r}({\mathcal{D}}_{r})_{0}\rightarrow R\end{eqnarray}$$
in
$\text{}_{0}{\mathcal{Z}}_{\bullet }^{+}$
-complex; we denote it by
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})$
.
There are some tight relations between the disguised residual intersection and the residual intersection as the following theorems state.
Theorem 4.6. Let
$R$
be a commutative ring and keep the notation in the Definition 4.5. Let
$J=\mathfrak{a}:_{R}I$
and
$K=K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})$
. Then we have the following.
(1)
$K\subseteq J$
, and
$V(K)=V(J)$
[Reference HassanzadehHas12, Theorem 2.11].(2)
$J=K$
if
$\mathbf{f}=(a_{1},\ldots ,a_{s},b)$
[Reference Hassanzadeh and NaelitonHN16, Theorem 4.4].(3) If
$R$
is Cohen–Macaulay local ring,
$I$
is an ideal of height
$g\geqslant 1$
satisfying
$\operatorname{SDC}_{1}$
at level
$\min \{s-g,r-g\}$
and
$J$
is an arithmetic
$s$
-residual intersection, then
$K=J$
and it is Cohen–Macaulay of height
$s$
, [Reference HassanzadehHas12, Theorem 2.11].(4) If
$R$
is Cohen–Macaulay local ring,
$I$
is an ideal of height
$2$
satisfying
$\operatorname{SD}_{1}$
and
$J$
is any algebraic
$s$
-residual intersection, then
$K=J$
, [Reference Chardin, Naeliton and TranCNT19, Theorem 4.5].
In [Reference Chardin, Naeliton and TranCNT19, Theorem 4.5] Chardin, Naeliton and Tran also show that if
$R$
is a Cohen–Macaulay local ring and
$I$
is an ideal of height
$g\geqslant 1$
satisfying
$\operatorname{SD}_{1}$
, then any algebraic
$s$
-residual intersection of
$I$
is Cohen–Macaulay of height
$s$
. This provides an affirmative answer to the question of Huneke and Ulrich [Reference Huneke and UlrichHU88].
Hassanzadeh and Naeliton proposed the following conjecture in [Reference Hassanzadeh and NaelitonHN16].
Conjecture 4.7. If
$R$
is a Cohen–Macaulay local ring and
$I$
an ideal satisfying SD and
$\text{depth}(R/I)\geqslant d-s$
, then any algebraic
$s$
-residual intersection of
$I$
coincides with the disguised residual intersection.
4.2 The structure of disguised residual intersections
An obstruction to generalizing the techniques in [Reference Chardin, Naeliton and TranCNT19, Theorem 4.5] for ideals
$I$
with
$\operatorname{ht}(I)>2$
is that the usual reduction modulo a regular sequence does not work smoothly if one does not know the explicit structure of the disguised residual intersection. This is why in this paper we look for explicit descriptions of the maps in spectral sequences in order to determine the generators of disguised residual intersections.
Since the bi-complex
${\mathcal{D}}_{\bullet }=\operatorname{Tot}(K_{\bullet }(\boldsymbol{\unicode[STIX]{x1D6FE}};S)\otimes _{S}{\mathcal{Z}}_{\bullet }(\mathbf{f};R))$
is a subcomplex of the complex
${\mathcal{F}}_{\bullet }=K_{\bullet }(\boldsymbol{\unicode[STIX]{x1D6FE}},T_{1},\ldots ,T_{r};S)\simeq \operatorname{Tot}(K_{\bullet }(\boldsymbol{\unicode[STIX]{x1D6FE}};S)\,\otimes _{S}\,K_{\bullet }(T_{1},\ldots T_{r};S))$
and
${\check{C}}_{\mathfrak{t}}^{\bullet }$
is a complex of flat modules, the map
$\unicode[STIX]{x1D70F}_{0}$
in (4.4) is just the restriction of the comparison map
$\unicode[STIX]{x1D70F}_{0}$
constructed in § 3.2 for the bi-complex
${\mathcal{F}}_{\bullet }\otimes _{S}{\check{C}}_{\mathfrak{t}}^{\bullet }$
. By Theorem 3.6, this map is just the connecting map in the Eagon–Northcott complex
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}:\bigwedge ^{r}R^{r+s}\rightarrow R,\end{eqnarray}$$
defined in Proposition 3.1, associated to the matrix
$M=(c_{ij}|\operatorname{id}_{(r\times r)})$
.
For the rest of this section, we set
$e_{1}^{\prime },\ldots ,e_{s}^{\prime },e_{1},\ldots ,e_{r}$
for the basis of
$K_{1}(\unicode[STIX]{x1D6FE}_{1},\ldots ,\unicode[STIX]{x1D6FE}_{s},T_{1},\ldots ,T_{r};S)$
as a free
$S$
-module; so
$\unicode[STIX]{x2202}(e_{i}^{\prime })=\unicode[STIX]{x1D6FE}_{i}$
and
$\unicode[STIX]{x2202}(e_{i})=T_{i}$
, in the corresponding Koszul complex. We also denote the columns of the matrix
$M$
with
$C_{1},\ldots ,C_{s},I_{1},\ldots ,I_{r}$
.
Lemma 4.8. Keeping the above notation, let
$L_{1}\subseteq \{1,\ldots ,s\}$
and
$L_{2}\subseteq \{1,\ldots ,r\}=L$
such that
$|L_{1}|+|L_{2}|=r$
. Then
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}(e_{L_{1}}^{\prime }\otimes e_{L_{2}})=\bigwedge _{i\in L_{1}}C_{i}\bigwedge _{j\in L_{2}}I_{j},\end{eqnarray}$$
where
$C_{i}$
and
$I_{j}$
are the columns of
$M$
considered as elements in
$\bigwedge ^{1}R^{r}$
. In other words,
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}(e_{L_{1}}^{\prime }\otimes e_{L_{2}})=\pm \det \unicode[STIX]{x1D6F7}_{L\setminus L_{2}}^{L_{1}},\end{eqnarray}$$
where
$\unicode[STIX]{x1D6F7}_{L\setminus L_{2}}^{L_{1}}$
is the sub-matrix of
$\unicode[STIX]{x1D6F7}=(c_{ij})$
whose rows indexed by
$L\setminus L_{2}$
and columns indexed by
$L_{1}$
.
Proof. The complex
${\mathcal{F}}_{\bullet }$
is just the generalized Koszul complex of the linear map
$\unicode[STIX]{x1D6F9}$
presented by the matrix
$M$
. According to the notation in Definition 3.2, the differential of this complex
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6F9}}$
can be expressed as
$$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6F9}}(w)=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D713}_{1}}(w)T_{1}+\cdots +\unicode[STIX]{x2202}_{\unicode[STIX]{x1D713}_{r}}(w)T_{r},\end{eqnarray}$$
where
$\unicode[STIX]{x1D713}_{i}$
is determined by the
$i$
th row of the matrix
$M$
. Henceforth
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}(w)=\unicode[STIX]{x2202}_{\unicode[STIX]{x1D713}_{1}}\cdots \unicode[STIX]{x2202}_{\unicode[STIX]{x1D713}_{r}}(w).\end{eqnarray}$$
Therefore the equality
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}(e_{L_{1}}^{\prime }\otimes e_{L_{2}})=\bigwedge _{i\in L_{1}}C_{i}\bigwedge _{j\in L_{2}}I_{j}\end{eqnarray}$$
follows from the elementary properties of the exterior product.
For the second expression, one has
$$\begin{eqnarray}\bigwedge _{i\in L_{1}}C_{i}\bigwedge _{j\in L_{2}}I_{j}=\det (\unicode[STIX]{x1D6F7}^{L_{1}}|\operatorname{id}_{(r\times r)}^{L_{2}})=\pm \det \left[\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6F7}_{L\setminus L_{2}}^{L_{1}} & 0\\ \ast & \operatorname{id}_{|L_{2}|\times |L_{2}|}\end{array}\right]=\pm \det \unicode[STIX]{x1D6F7}_{L\setminus L_{2}}^{L_{1}}.\Box\end{eqnarray}$$
The following theorem explains the generators of the disguised residual intersection.
Theorem 4.9. Let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})\subseteq R$
,
$\mathfrak{a}=(a_{1},\ldots ,a_{s})\subseteq I$
ideals and
$\unicode[STIX]{x1D6F7}=(c_{ij})$
a matrix such that
$(\mathbf{a})=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}$
. Consider the differential graded algebra
$K_{\bullet }(\mathbf{f};R)=R\langle e_{1},\ldots ,e_{r};\unicode[STIX]{x2202}(e_{i})=f_{i}\rangle$
. Let
$\unicode[STIX]{x1D701}_{j}=\sum _{i=1}^{r}c_{ij}e_{i},1\leqslant j\leqslant s$
,
$\unicode[STIX]{x1D6E4}_{\bullet }=R\langle \unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{s}\rangle$
be the sub-algebra generated by
$\{\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{s}\}$
, and
$Z_{\bullet }=Z_{\bullet }(\mathbf{f};R)$
be the sub-algebra of Koszul cycles. Then the disguised residual intersection satisfies
$$\begin{eqnarray}K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}.\end{eqnarray}$$
Proof. By Definition 4.5,
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})$
is the image of the map
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{0}:H_{\mathfrak{t}}^{r}({\mathcal{D}}_{r})_{0}\rightarrow R.\end{eqnarray}$$
Since
then
$$\begin{eqnarray}\displaystyle H_{\mathfrak{t}}^{r}({\mathcal{D}}_{r})_{0}=\bigoplus _{k=r-s}^{r}\bigwedge ^{r-k}R^{s}\otimes _{R}Z_{k}(\mathbf{f},R)\otimes _{R}H_{\mathfrak{t}}^{r}(S)_{-r}. & & \displaystyle \nonumber\end{eqnarray}$$
The map
$\unicode[STIX]{x1D70F}_{0}$
above is the restriction of the same named map in Theorem 3.6 which is, up to a sign, equal to the connecting map in the Eagon–Northcott complex,
$\unicode[STIX]{x1D700}_{0}$
. Hence it is enough to determine
$$\begin{eqnarray}\{\unicode[STIX]{x1D700}_{0}(e_{L_{1}}^{\prime }\otimes z_{j}):r-s\leqslant j\leqslant r,|L_{1}|=r-j\text{ and }z_{j}\in Z_{j}(\mathbf{f};R)\}.\end{eqnarray}$$
More explicitly, for a cycle
$z_{j}=\sum _{|L_{2}|=j}\unicode[STIX]{x1D6FC}_{L_{2}}e_{L_{2}}$
, according to the proof of Lemma 4.8,
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}(e_{L_{1}}^{\prime }\otimes z_{j})=\mathop{\sum }_{|L_{2}|=j}\unicode[STIX]{x1D6FC}_{L_{2}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{1}}\cdots \unicode[STIX]{x2202}_{\unicode[STIX]{x1D719}_{r}}(e_{L_{1}}^{\prime }\otimes e_{L_{2}})=\mathop{\sum }_{|L_{2}|=j}\unicode[STIX]{x1D6FC}_{L_{2}}\bigwedge _{i\in L_{1}}C_{i}\bigwedge _{j\in L_{2}}I_{j}.\end{eqnarray}$$
Now, identifying
$C_{i}$
with
$\unicode[STIX]{x1D701}_{i}=\sum _{k=1}^{r}c_{ki}e_{k}\in \bigwedge ^{1}R^{r}$
and
$I_{j}$
with
$e_{j}$
, we get
$$\begin{eqnarray}\unicode[STIX]{x1D700}_{0}(e_{L_{1}}^{\prime }\otimes z_{j})=\mathop{\sum }_{|L_{2}|=j}\unicode[STIX]{x1D6FC}_{L_{2}}\bigwedge _{i\in L_{1}}C_{i}\bigwedge _{j\in L_{2}}I_{j}=\mathop{\sum }_{|L_{2}|=j}\unicode[STIX]{x1D6FC}_{L_{2}}\bigwedge _{i\in L_{1}}\unicode[STIX]{x1D701}_{i}\bigwedge _{j\in L_{2}}e_{j}=\biggl(\bigwedge _{i\in L_{1}}\unicode[STIX]{x1D701}_{i}\biggr)\bigwedge z_{j}.\end{eqnarray}$$
We also notice that
$\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}\subseteq K_{r}(\mathbf{f};R)=\bigwedge ^{r}R^{r}\simeq R$
. Hence
$\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}$
is isomorphic to an ideal of
$R$
.◻
Remark 4.10. As it may be understood from the proof of the above theorem, to construct
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})$
one may only need cycles of order
$j\geqslant r-s$
. However, this fact is implicit in the equation
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}$
. Since
$\unicode[STIX]{x1D6E4}_{\bullet }=R\langle \unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{s}\rangle$
, an element of
$\unicode[STIX]{x1D6E4}_{\bullet }$
has degree at most
$s$
.
We postpone the corollaries of this structural theorem until § 5. We first show that the definition of the disguised residual intersection does not depend on any choices of generators of
$\mathfrak{a}$
and
$I$
and neither on the choices of the matrix
$\unicode[STIX]{x1D6F7}$
.
4.3 Independence from the generating sets
In this subsection let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})$
,
$\mathfrak{a}=(a_{1},\ldots ,a_{s})\subseteq I$
and
$(\mathbf{a})=(\mathbf{f})\unicode[STIX]{x1D6F7}$
for some matrix
$\unicode[STIX]{x1D6F7}=(c_{ij})$
.
Proposition 4.11. The disguised residual intersection does not depend on the presentation matrix.
Proof. Let
$\unicode[STIX]{x1D6F7}=(c_{ij})$
and
$\widetilde{\unicode[STIX]{x1D6F7}}=(\widetilde{c_{ij}})$
be two matrices such that
$(\mathbf{a})=(\mathbf{f})\unicode[STIX]{x1D6F7}=(\mathbf{f})\widetilde{\unicode[STIX]{x1D6F7}}$
. As
$(\mathbf{f})(\unicode[STIX]{x1D6F7}-\widetilde{\unicode[STIX]{x1D6F7}})=(a_{1}-a_{1},\ldots ,a_{s}-a_{s})=\mathbf{0}$
, the columns of the matrix
$\unicode[STIX]{x1D6F7}-\widetilde{\unicode[STIX]{x1D6F7}}$
are syzygies of the sequence
$\mathbf{f}$
. Hence setting
$\unicode[STIX]{x1D701}_{j}=\sum _{i=1}^{r}c_{ij}e_{i}$
,
$\widetilde{\unicode[STIX]{x1D701}_{j}}=\sum _{i=1}^{r}\widetilde{c_{ij}}e_{i}$
,
$\unicode[STIX]{x1D6E4}_{\bullet }=R\langle \unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{s}\rangle$
,
$\widetilde{\unicode[STIX]{x1D6E4}}_{\bullet }=R\langle \widetilde{\unicode[STIX]{x1D701}_{1}},\ldots ,\widetilde{\unicode[STIX]{x1D701}_{s}}\rangle$
, and
$Z_{\bullet }$
the algebra of Koszul cycles of the sequence
$\mathbf{f}$
, we have, by Theorem 4.9,
$$\begin{eqnarray}K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}\end{eqnarray}$$
and
$$\begin{eqnarray}K(\mathbf{a},\mathbf{f},,\widetilde{\unicode[STIX]{x1D6F7}})=\langle \widetilde{\unicode[STIX]{x1D6E4}}_{\bullet }\cdot Z_{\bullet }\rangle _{r}.\end{eqnarray}$$
Since, for all
$j$
,
$\unicode[STIX]{x1D701}_{j}=\widetilde{\unicode[STIX]{x1D701}_{j}}+z_{j}$
for some
$z_{j}\in Z_{1}$
, we have
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E4}}_{i}\subseteq \unicode[STIX]{x1D6E4}_{i}+\unicode[STIX]{x1D6E4}_{i-1}\cdot Z_{1}+\cdots +\unicode[STIX]{x1D6E4}_{1}\cdot Z_{i-1}+Z_{i}.\end{eqnarray}$$
Hence for
$1\leqslant i\leqslant s$
$$\begin{eqnarray}\widetilde{\unicode[STIX]{x1D6E4}}_{i}\cdot Z_{r-i}\subseteq \unicode[STIX]{x1D6E4}_{i}\cdot Z_{r-i}+\unicode[STIX]{x1D6E4}_{i-1}\cdot Z_{r-i+1}+\cdots +\unicode[STIX]{x1D6E4}_{1}\cdot Z_{r-1}+Z_{r}.\end{eqnarray}$$
This proves the inclusion
$$\begin{eqnarray}K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})\supseteq K(\mathbf{a},\mathbf{f},\widetilde{\unicode[STIX]{x1D6F7}}).\end{eqnarray}$$
The opposite inclusion follows similarly. ◻
Proposition 4.12. The disguised residual intersection does not depend on the choice of generators of
$\mathfrak{a}$
.
Proof. Let
$(a_{1},\ldots ,a_{s})=(\mathbf{a})$
,
$(a_{1}^{\prime },\ldots ,a_{s^{\prime }}^{\prime })=(\mathbf{a}^{\prime })$
be two generating sets of the ideal
$\mathfrak{a}$
. There exists an
$s\times s^{\prime }$
matrix
$M$
, and an
$s^{\prime }\times s$
matrix
$M^{\prime }$
such that
$$\begin{eqnarray}\displaystyle (\mathbf{a})\cdot M & = & \displaystyle (\mathbf{a}^{\prime }),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\mathbf{a}^{\prime })\cdot M^{\prime } & = & \displaystyle (\mathbf{a}).\end{eqnarray}$$
Therefore, choosing
$\unicode[STIX]{x1D6F7}$
such that
$(\mathbf{a})=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}$
, we have
$$\begin{eqnarray}(\mathbf{a}^{\prime })=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}\cdot M.\end{eqnarray}$$
Let
$\unicode[STIX]{x1D701}_{j},1\leqslant j\leqslant s$
, be the elements in
$K_{\bullet }(\mathbf{f};R)$
associated to the matrix
$\unicode[STIX]{x1D6F7}$
and let
$\unicode[STIX]{x1D701}_{j}^{\prime },1\leqslant j\leqslant s^{\prime }$
, be the elements in
$K_{\bullet }(\mathbf{f};R)$
associated to the matrix
$\unicode[STIX]{x1D6F7}\cdot M$
. By elementary properties of the wedge product, any wedge product of
$\{\unicode[STIX]{x1D701}_{1}^{\prime },\ldots ,\unicode[STIX]{x1D701}_{s^{\prime }}^{\prime }\}$
is a linear combination of wedge products of
$\{\unicode[STIX]{x1D701}_{1},\ldots ,\unicode[STIX]{x1D701}_{s}\}$
with coefficients some minors of the matrix
$M$
. Hence, by Theorem 4.9,
$$\begin{eqnarray}K(\mathbf{a}^{\prime },f,\unicode[STIX]{x1D6F7}\cdot M)\subseteq K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7}).\end{eqnarray}$$
On the other hand,
$\unicode[STIX]{x1D6F7}\cdot M\cdot M^{\prime }$
is a matrix such that
$(\mathbf{a})=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}\cdot M\cdot M^{\prime }$
. By the same argument as above, we have
$$\begin{eqnarray}K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7}\cdot M\cdot M^{\prime })\subseteq K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7}\cdot M^{\prime })\subseteq K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7}).\end{eqnarray}$$
The result now follows from the independence from the choice of the matrix
$\unicode[STIX]{x1D6F7}$
, Proposition 4.11. ◻
It now remains to prove that the disguised residual intersection does not depend on a choice of generators of
$I$
. For that we need two lemmas.
Lemma 4.13. Let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})$
an ideal,
$1\leqslant i\leqslant r+1$
,
$f_{0}\in \operatorname{Ann}H_{i-1}(\mathbf{f};R)$
and
$K_{\bullet }(f_{0},\mathbf{f};R)=R\langle e_{0},e_{1},\ldots ,e_{r};\unicode[STIX]{x2202}(e_{i})=f_{i}\rangle$
the Koszul DG-Algebra. Then any cycle
$z\in Z_{i}(f_{0},\mathbf{f};R)$
can be uniquely written in the form
$$\begin{eqnarray}z=e_{0}\wedge w+w^{\prime },\end{eqnarray}$$
where
$w\in Z_{i-1}(\mathbf{f};R)$
,
$w^{\prime }\in K_{i}(f_{0},\mathbf{f};R)$
and
$\unicode[STIX]{x2202}(w^{\prime })=-f_{0}w$
. Conversely, for any
$w\in Z_{i-1}(\mathbf{f};R)$
there exists
$w^{\prime }\in K_{i}(f_{0},\mathbf{f};R)$
such that
$e_{0}\wedge w+w^{\prime }\in Z_{i}(f_{0},\mathbf{f};R)$
.
Proof. Every element
$z\in K_{i}(f_{0},\mathbf{f};R)$
can be uniquely written in the form
$z=e_{0}\wedge w+w^{\prime }$
where
$w\in K_{i-1}(\mathbf{f};R)$
and
$w^{\prime }\in K_{i}(f_{0},\mathbf{f};R)$
. If
$z$
is a cycle, then
$$\begin{eqnarray}0=\unicode[STIX]{x2202}(z)=f_{0}.w-e_{0}\wedge \unicode[STIX]{x2202}(w^{\prime })+\unicode[STIX]{x2202}(w).\end{eqnarray}$$
Hence
$\unicode[STIX]{x2202}(w)=0$
and
$\unicode[STIX]{x2202}(w^{\prime })=-f_{0}w$
.
For the converse, suppose that
$w\in Z_{i-1}(\mathbf{f};R)$
. Since
$f_{0}\in \operatorname{Ann}H_{i-1}(\mathbf{f};R)$
,
$-f_{0}w$
is a boundary, that is, there is
$w^{\prime }\in K_{i}(\mathbf{f};R)$
with
$\unicode[STIX]{x2202}(w^{\prime })=-f_{0}w$
. Taking
$z=e_{0}\,\wedge \,w+w^{\prime }\in K_{i}(f_{0},\mathbf{f};R)$
, we have
$$\begin{eqnarray}\unicode[STIX]{x2202}(z)=\unicode[STIX]{x2202}(e_{0}\wedge w+w^{\prime })=f_{0}w+e_{0}\wedge \unicode[STIX]{x2202}(w)+\unicode[STIX]{x2202}(w^{\prime })=0,\end{eqnarray}$$
which proves the lemma. ◻
Lemma 4.14. Let
$f_{0}\in \bigcap _{i=\max \{0,r-s\}}^{r}\operatorname{Ann}H_{i}(\mathbf{f},R)$
and
$K_{\bullet }(f_{0},\mathbf{f};R)=R\langle e_{0},e_{1},\ldots ,e_{r};\unicode[STIX]{x2202}(e_{i})=f_{i}\rangle$
the Koszul DG-Algebra. Then
$$\begin{eqnarray}M=\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \unicode[STIX]{x1D6F7}\end{array}\right]\end{eqnarray}$$
satisfies
$(\mathbf{a})=(f_{0},\mathbf{f})\cdot M$
, and
$$\begin{eqnarray}K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})=K(\mathbf{a},(f_{0},\mathbf{f}),M).\end{eqnarray}$$
Proof. The assertion about the matrix is obvious. Let
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{j}=0.e_{0}+\mathop{\sum }_{i=1}^{r}c_{ij}e_{i},\end{eqnarray}$$
the
$\unicode[STIX]{x1D701}$
values corresponding to the representation matrix
$M$
. These elements can be viewed as the
$\unicode[STIX]{x1D701}$
values corresponding to the matrix
$\unicode[STIX]{x1D6F7}$
. By Theorem 4.9, we have
$K(\mathbf{a},(f_{0},\mathbf{f}),M)=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r+1}$
. Hence, to construct a generator of
$K(\mathbf{a},(f_{0},\mathbf{f}),M)$
, we take
$z\in Z_{j}(f_{0},\mathbf{f};R)$
,
$r+1-s\leqslant j\leqslant r+1$
and
$L_{1}\subseteq \{1,\ldots ,s\}$
with
$|L_{1}|=r+1-j$
. By Lemma 4.13
$z=e_{0}\wedge w+w^{\prime }$
, where
$w\in Z_{j-1}(\mathbf{f};R),w^{\prime }\in K_{j}(\mathbf{f};R)$
. Therefore
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge z=\unicode[STIX]{x1D701}_{L_{1}}\wedge e_{0}\wedge w+\unicode[STIX]{x1D701}_{L_{1}}.\wedge w^{\prime }.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D701}_{L_{1}}\wedge w^{\prime }$
is the wedge product of
$r+1$
elements containing only
$e_{1},\ldots ,e_{r}$
,
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge w^{\prime }=0.\end{eqnarray}$$
The product
$\unicode[STIX]{x1D701}_{L_{1}}\wedge w$
is the product of a cycle of degree
$j-1$
with
$(r+1-j)$
values of
$\unicode[STIX]{x1D701}$
. Hence it gives an element in
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})$
. Therefore
$$\begin{eqnarray}K(\mathbf{a},(f_{0},\mathbf{f}),M)\subseteq K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7}).\end{eqnarray}$$
For the converse, let
$w\in Z_{j}(\mathbf{f};R)$
. By Lemma 4.13, there exists
$w^{\prime }\in K_{j+1}(\mathbf{f};R)$
such that
$$\begin{eqnarray}e_{0}\wedge w+w^{\prime }\in Z_{j+1}(a,(f_{0},\mathbf{f});R).\end{eqnarray}$$
Let
$L_{1}\subseteq \{1,\ldots ,s\}$
with
$|L_{1}|=r-j$
. We have that
$e_{0}\wedge \unicode[STIX]{x1D701}_{L_{1}}\wedge w=\unicode[STIX]{x1D701}_{L_{1}}\wedge (e_{0}\wedge w+w^{\prime })$
. This shows that
$\unicode[STIX]{x1D701}_{L_{1}}\wedge w\in K(\mathbf{a},(f_{0},\mathbf{f}),M)$
.◻
We are now ready to prove the last part of the independence.
Proposition 4.15. The disguised residual intersection does not depend on the choice of generators of
$I$
.
Proof. Let
$(f_{1},\ldots ,f_{r})=(\mathbf{f}),(f_{1}^{\prime },\ldots ,f_{t}^{\prime })=(\mathbf{f}^{\prime })$
be two sets of generators of
$I$
,
$(a_{1},\ldots ,a_{s})=(\mathbf{a})$
a generating set for
$\mathfrak{a}$
,
$\unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D6F7}^{\prime }$
matrices such that
$(\mathbf{a})=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}$
and
$(\mathbf{a}^{\prime })=(\mathbf{f}^{\prime })\cdot \unicode[STIX]{x1D6F7}^{\prime }$
. By using repeatedly Lemma 4.14, we have that
$$\begin{eqnarray}M=\left[\begin{array}{@{}c@{}}\mathbf{0}\\ \unicode[STIX]{x1D6F7}\end{array}\right]\end{eqnarray}$$
satisfies
$(\mathbf{a})=(\mathbf{f}^{\prime },\mathbf{f})\cdot M$
, and
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})=K(\mathbf{a},(\mathbf{f}^{\prime },\mathbf{f}),M)$
. Now, by Proposition 4.11,
$K(\mathbf{a},(\mathbf{f}^{\prime },\mathbf{f}),M)=K(\mathbf{a},(\mathbf{f}^{\prime },\mathbf{f}),M^{\prime })$
where
$$\begin{eqnarray}M^{\prime }=\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D6F7}^{\prime }\\ \mathbf{0}\end{array}\right].\end{eqnarray}$$
Again, repeated applications of Lemma 4.14 gives us
$K(\mathbf{a},(\mathbf{f}^{\prime },\mathbf{f}),M^{\prime })=K(\mathbf{a},\mathbf{f}^{\prime },\unicode[STIX]{x1D6F7}^{\prime })$
.◻
Now that we know the disguised residual intersection does not depend on any choice of generators or matrix
$\unicode[STIX]{x1D6F7}$
, we introduce the following notation.
Definition 4.16. Let
$R$
be a commutative ring and
$\mathfrak{a}\subseteq I$
be two finitely generated ideals. We denote the disguised residual intersection,
$K(\mathbf{a},\mathbf{f},\unicode[STIX]{x1D6F7})$
, defined in Definition 4.5 by
$\operatorname{Kitt}(\mathfrak{a},I)$
.
This notation reminds that the disguised residual intersections are Koszul–Fitting ideals, based on Theorem 4.9.
Lemmas 4.13 and 4.14 provides some unexpected results about the codimension of the colon ideals and at the same time on the structure of the common annihilators of Koszul homologies. Both of these topics were mentioned as desirable in the works [Reference Corso, Huneke, Katz and VasconcelosCHKV06] and [Reference Ulrich, Eisenbud and HunekeUlr92].
Corollary 4.17. Let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})$
an ideal and
$$\begin{eqnarray}\mathfrak{a}=(a_{1},\ldots ,a_{s})\subseteq I.\end{eqnarray}$$
Then
$\operatorname{Kitt}(\mathfrak{a},I)=\operatorname{Kitt}(\mathfrak{a},I^{\prime })$
for any ideal
$I^{\prime }$
satisfying
$$\begin{eqnarray}I\subseteq I^{\prime }\subseteq \mathop{\bigcap }_{\max \{0,r-s\}}^{r}\operatorname{Ann}H_{i}(\mathbf{f};R).\end{eqnarray}$$
In particular, if
$\operatorname{ht}(I)=\operatorname{ht}(I^{\prime })$
(for instance when
$R$
is Cohen–Macaulay), then
$(\mathfrak{a}:I)$
being an
$s$
-residual intersection implies that
$(\mathfrak{a}:I^{\prime })$
is an
$s$
-residual intersection.
Proof. Let
$(f_{1}^{\prime },\ldots ,f_{t}^{\prime })$
be a generating set for
$I^{\prime }$
. The proof of Proposition 4.15 is applicable: it relies on of Lemma 4.14, which works for elements
$f_{0}\in \bigcap _{\max \{0,r-s\}}^{r}\operatorname{Ann}H_{i}(\mathbf{f},R)$
. Therefore
$\operatorname{Kitt}(\mathfrak{a},I)=\operatorname{Kitt}(\mathfrak{a},I^{\prime })$
. The second part of the statement follows from Theorem 4.6, stating that these ideals have the same radical and [Reference HunekeHun85, Remark 1.5].◻
Remark 4.18. Although, in the above propositions, we have shown that the structure of the disguised residual intersection
$K=H_{0}(\text{}_{0}{\mathcal{Z}}_{\bullet }^{+})$
is independent of the choice of generators, the other homologies of
$\text{}_{0}{\mathcal{Z}}_{\bullet }^{+}$
are not independent of the choice of generators in general; see [Reference Hassanzadeh and NaelitonHN16, Theorem 4.4].
4.4 Properties of Kitt ideals
In this section we exhibit some basic properties of the
$\operatorname{Kitt}$
ideals (disguised residual intersections), based on structure Theorem 4.9.
Proposition 4.19. Let
$R$
be a commutative ring and keep the same notation as in Theorem 4.9; we have
$$\begin{eqnarray}\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot \langle Z_{1}(\mathbf{f};R)\rangle \rangle _{r}=\operatorname{Fitt}_{0}(I/\mathfrak{a}).\end{eqnarray}$$
In particular, if the algebra of Koszul cycles of the Koszul complex
$K_{\bullet }(\mathbf{f};R)$
is generated by cycles of degree one, then
$\operatorname{Kitt}(\mathfrak{a},I)=\operatorname{Fitt}_{0}(I/\mathfrak{a})$
.
Proof. Let
$\unicode[STIX]{x1D6F7}$
be an
$r\times s$
matrix for which
$(\mathbf{a})=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}$
and
$\unicode[STIX]{x1D6F9}=(b_{ij})$
be a syzygy matrix for the sequence
$(\mathbf{f})$
which has
$r$
rows. Then
$Z_{1}=Z_{1}(\mathbf{f};R)$
is generated by the elements
$z_{i}=\sum _{i=1}^{r}b_{ij}e_{i}$
. Therefore,
$\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot \langle Z_{1}(\mathbf{f};R)\rangle \rangle _{r}$
is obtained by taking all the products of the form
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge z_{L_{2}},|L_{1}|+|L_{2}|=r.\end{eqnarray}$$
By elementary properties of the wedge product, a product as in (4.24) is an
$r\times r$
minor of the matrix
$(\unicode[STIX]{x1D6F7}|\unicode[STIX]{x1D6F9})$
. This matrix is the representation matrix of
$I/\mathfrak{a}$
as it is obtained by taking the mapping-cone of the following diagram.
Thus
$\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot \langle Z_{1}(\mathbf{f};R)\rangle \rangle _{r}=\text{I}_{r}(\unicode[STIX]{x1D6F7}|\unicode[STIX]{x1D6F9})=\operatorname{Fitt}_{0}(I/\mathfrak{a})$
.◻
In the next theorem, we prove that the structure of
$\operatorname{Kitt}(\mathfrak{a},I)$
is encrypted on the Koszul homology algebra of the ideal
$I$
. The main part of the proof is the following lemma. We fix some notation.
Notation 4.20. Let
$n$
be an integer and
$I=\{i_{1},\ldots ,i_{n}\}$
be an ordered set. For any
$J\subset I$
with
$|J|=j$
, define
$$\begin{eqnarray}\operatorname{sgn}(J\subset I)\end{eqnarray}$$
to be the sign of the permutation that put the elements of
$J$
on the first
$j$
positions.
Notation 4.21. Let
$\unicode[STIX]{x1D6F7}=(c_{ij})$
be a
$r\times s$
matrix.
(1) Let
$I\subset \{1,\ldots ,r\},J\subset \{1,\ldots ,s\}$
be two ordered subsets. Define to be the submatrix with rows indexed by$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{I}^{J}\end{eqnarray}$$
$I$
and columns indexed by
$J$
. If
$I=\{1,\ldots ,r\}$
we suppress the subscript and write We use an analogous notation if$$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{J}.\end{eqnarray}$$
$J=\{1,\ldots ,s\}$
.(2) Let
$I\subset \{1,\ldots ,r\},J_{1},J_{2}\subset \{1,\ldots ,s\}$
be three ordered subsets. Define to be the submatrix with rows indexed by$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{I}^{J_{1},J_{2}}\end{eqnarray}$$
$I$
, the first columns indexed by
$J_{1}$
and the last columns indexed by
$J_{2}$
.
Lemma 4.22. Let
$R$
be a commutative ring and keep the same notation as in Theorem 4.9; let
$B_{\bullet }(\mathbf{f};R)$
be the ideal of Koszul boundaries. Then
$$\begin{eqnarray}\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot B_{\bullet }\rangle _{r}=\mathfrak{a}.\end{eqnarray}$$
Proof. In the Koszul complex
$K_{\bullet }(\mathbf{f};R)$
, the module of boundaries of degree
$k$
is generated by elements of the form
$\unicode[STIX]{x2202}(e_{L_{2}})$
where
$|L_{2}|=k+1$
. For any
$L_{1}\subseteq \{1,\ldots ,s\}$
with
$|L_{1}|=r-k$
, we have
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge \unicode[STIX]{x2202}(e_{L_{2}})=\unicode[STIX]{x1D701}_{L_{1}}\wedge \biggl(\mathop{\sum }_{j\in L_{2}}\operatorname{sgn}(\{j\}\subseteq L_{2})f_{j}e_{L_{2}\setminus \{j\}}\biggr)=\mathop{\sum }_{j\in L_{2}}(\operatorname{sgn}(\{j\}\subseteq L_{2})f_{j}\unicode[STIX]{x1D701}_{L_{1}}\wedge e_{L_{2}\setminus \{j\}}).\end{eqnarray}$$
According to Lemma 4.8, the above equation (4.26) can be written as
$$\begin{eqnarray}\mathop{\sum }_{j\in L_{2}}\operatorname{sgn}(\{j\}\subseteq L_{2})\operatorname{sgn}(L_{2}\setminus \{j\}\subseteq L)\det \unicode[STIX]{x1D6F7}_{L\setminus (L_{2}\setminus \{j\})}^{I}f_{j}.\end{eqnarray}$$
If we rearrange every determinant in a way such that the
$j$
th row becomes the first one, (4.27) becomes
$$\begin{eqnarray}\mathop{\sum }_{j\in L_{2}}\operatorname{sgn}(\{j\}\subseteq L_{2})\operatorname{sgn}(L_{2}\setminus \{j\}\subseteq L)\operatorname{sgn}(\{j\}\subseteq L\setminus (L_{2}\setminus \{j\}))\det \unicode[STIX]{x1D6F7}_{\{j\},L\setminus L_{2}}^{L_{1}}f_{j}.\end{eqnarray}$$
One can verify that
$\operatorname{sgn}(\{j\}\subseteq L_{2})\operatorname{sgn}(L_{2}\setminus \{j\}\subseteq L)\operatorname{sgn}(\{j\}\subseteq L\setminus (L_{2}\setminus \{j\}))$
does not depend on
$j\in L_{2}$
. Thus we can ignore this sign and take
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge \unicode[STIX]{x2202}(e_{L_{2}})=\mathop{\sum }_{j\in L_{2}}\det \unicode[STIX]{x1D6F7}_{\{j\},L\setminus L_{2}}^{L_{1}}f_{j}.\end{eqnarray}$$
If
$j\notin L_{2}$
, then
$\det \unicode[STIX]{x1D6F7}_{\{j\},L\setminus L_{2}}^{L_{1}}=0$
, since
$\unicode[STIX]{x1D6F7}_{\{j\},L\setminus L_{2}}^{L_{1}}$
has a repeated row. Therefore (4.29) is equal to
$$\begin{eqnarray}\mathop{\sum }_{j=1}^{r}\det \unicode[STIX]{x1D6F7}_{\{j\},L\setminus L_{2}}^{L_{1}}f_{j}.\end{eqnarray}$$
Now, we expand every determinant in this sum over the first row. Looking at each summand separately, we have
$$\begin{eqnarray}\det \unicode[STIX]{x1D6F7}_{\{j\},L\setminus L_{2}}^{L_{1}}f_{j}=\mathop{\sum }_{i\in L_{1}}\operatorname{sgn}(\{i\}\subset L_{1})\det \unicode[STIX]{x1D6F7}_{L\setminus L_{2}}^{L_{1}\setminus \{i\}}\,.\,c_{ji}f_{j}.\end{eqnarray}$$
Summing over all
$j$
, we get
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge \unicode[STIX]{x2202}(e_{L_{2}})=\mathop{\sum }_{i\in L_{1}}\operatorname{sgn}(\{i\}\subset L_{1})\det \unicode[STIX]{x1D6F7}_{L\setminus L_{2}}^{L_{1}\setminus \{i\}}a_{i}.\end{eqnarray}$$
This shows that
$\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot B_{\bullet }\rangle _{r}\subseteq \mathfrak{a}$
.
As to the other inclusion, we consider the last boundary given by
$$\begin{eqnarray}\unicode[STIX]{x2202}(e_{1}\wedge \cdots \wedge e_{r})=\mathop{\sum }_{i=1}^{r}(-1)^{i+1}f_{i}e_{1}\wedge \cdots \hat{e_{i}}\cdots \wedge e_{r}=:z.\end{eqnarray}$$
Then, for any
$1\leqslant j\leqslant s$
, we have
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{j}\wedge z=\mathop{\sum }_{i=1}^{r}c_{ij}f_{i}=a_{j}.\end{eqnarray}$$
◻
Theorem 4.23. Let
$R$
be a commutative ring and keep the same notation as in Theorem 4.9 with
$g=\operatorname{grade}(I)$
. Let
$\tilde{H}_{\bullet }$
be the sub-algebra of
$K_{\bullet }(\mathbf{f};R)$
generated by the representatives of Koszul homologies. Then
$$\begin{eqnarray}\operatorname{Kitt}(\mathfrak{a},I)=\mathfrak{a}+\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot \tilde{H}_{\bullet }\rangle _{r}=\mathfrak{a}+\mathop{\sum }_{i=\max \{0,r-s\}}^{r-g}\unicode[STIX]{x1D6E4}_{r-i}\cdot \tilde{H}_{i}.\end{eqnarray}$$
In particular
$\operatorname{Kitt}(\mathfrak{a},I)$
is generated by at most
$s+\sum _{i=\max \{0,r-s\}}^{r-g}\binom{s}{r-i}\unicode[STIX]{x1D707}(H_{i}(\mathbf{f}))$
elements.
Proof. According to Theorem 4.9,
$\operatorname{Kitt}(\mathfrak{a},I)=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}$
. Since
$Z_{\bullet }=B_{\bullet }+\tilde{H}_{\bullet }$
, we have
$\operatorname{Kitt}(\mathfrak{a},I)=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot B_{\bullet }\rangle _{r}+\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot \tilde{H}_{\bullet }\rangle _{r}$
. By Lemma 4.22,
$\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot B_{\bullet }\rangle _{r}=\mathfrak{a}$
which yields the result.◻
Remark 4.24. The fact that
$\mathfrak{a}\subseteq \operatorname{Kitt}(\mathfrak{a},I)$
is not clear from the definition. Hence, concerning the inclusions
$$\begin{eqnarray}\operatorname{Fitt}_{0}(I/\mathfrak{a})\subseteq \operatorname{Kitt}(\mathfrak{a},I)\subseteq (\mathfrak{a}:I),\end{eqnarray}$$
$\operatorname{Kitt}(\mathfrak{a},I)$
is closer to
$(\mathfrak{a}:I)$
than
$\operatorname{Fitt}_{0}(I/\mathfrak{a})$
. Combining Theorem 4.23 with Proposition 4.19, one has that if an ideal
$I=(\mathbf{f})$
in a commutative ring
$R$
is such that the algebra of Koszul cycles of the Koszul complex
$K_{\bullet }(\mathbf{f};R)$
is generated by cycles of degree one, then for any ideal
$\mathfrak{a}\subseteq I$
,
$\mathfrak{a}\subseteq \operatorname{Fitt}_{0}(I/\mathfrak{a})$
.
Another importance of Theorem 4.23 is that it connects the DG-algebra structure of Koszul homologies of
$I$
to any colon ideal
$\mathfrak{a}:I$
. Even in the extremal cases where
$I$
is complete intersection or an almost complete intersection this theorem provides highly non-trivial information about the structure of
$J=\mathfrak{a}:I$
.
Corollary 4.25. Let
$R$
be a commutative ring and
$I=(f_{1},\ldots ,f_{r})=(\mathbf{f})$
be an ideal such that the Koszul homology algebra
$H_{\bullet }(\mathbf{f};R)$
is generated by elements of degree one. Then, for any finitely generated ideal
$\mathfrak{a}\subseteq I$
, one has
$\operatorname{Kitt}(\mathfrak{a},I)=\text{Fitt}_{0}(I/\mathfrak{a})+\mathfrak{a}$
. In particular, this is the case when
$(f_{1},\ldots ,f_{r})$
is an almost regular sequence (grade of
$I$
is
$r-1$
).
If
$(f_{1},\ldots ,f_{r})$
is a regular sequence then
$\operatorname{Kitt}(\mathfrak{a},I)=I_{r}(\unicode[STIX]{x1D6F7})+\mathfrak{a}$
where
$\unicode[STIX]{x1D6F7}$
is an
$r\times s$
matrix satisfying
$\mathbf{a}=\mathbf{f}\cdot \unicode[STIX]{x1D6F7}$
.
Proof. Just notice that in the case of complete intersection,
$\tilde{H}_{\bullet }$
in Theorem 4.23 is concentrated in degree zero, that is
$\tilde{H}_{\bullet }=R$
; hence
$$\begin{eqnarray}\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot \tilde{H}_{\bullet }\rangle _{r}=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot R\rangle _{r}=I_{r}(\unicode[STIX]{x1D6F7}).\Box\end{eqnarray}$$
It is clear that the construction of Kitt ideals commutes with localization. The case of specialization modulo a regular sequence
$\unicode[STIX]{x1D6FC}=(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g})\subset \mathfrak{a}$
is more subtle and will be fixed in the next proposition. The following lemma is necessary for the proof.
Lemma 4.26. Let
$R$
be a commutative ring,
$I=(f_{1},\ldots ,f_{r})=(\mathbf{f})$
. Let
$f_{0}\in I$
be a
$R$
-regular element and consider the Koszul complex
$K_{\bullet }=R\langle e_{0},\ldots ,e_{r}:\unicode[STIX]{x2202}(e_{i})=f_{i}\rangle$
.Then there is an isomorphism
$$\begin{eqnarray}H_{i}(f_{0},\mathbf{f};R)\rightarrow H_{i}(\mathbf{f};R/f_{0})\end{eqnarray}$$
given by the map
$$\begin{eqnarray}e_{0}\wedge w+w^{\prime }\rightarrow \tilde{w}^{\prime },\end{eqnarray}$$
where
$w\in Z_{i-1}(\mathbf{f};R)$
,
$w^{\prime }\in K_{i}(f_{0},\mathbf{f};R)$
and
$\unicode[STIX]{x2202}(w^{\prime })=-f_{0}w$
.
Proof. The proof is essentially the one of Lemma 4.13; see also [Reference Bruns and HerzogBH98, Proposition 1.6.12(c)]. ◻
We now prove the last theorem in this section, showing that the disguised residual intersection specializes modulo a regular sequence contained in
$\mathfrak{a}$
.
Theorem 4.27. Let
$R$
be a commutative ring
$\mathfrak{a}\subseteq I$
finitely generated ideals and
$f_{0}\in \mathfrak{a}$
an
$R$
-regular element. Then
$\operatorname{Kitt}(\mathfrak{a},I)/(f_{0})=\operatorname{Kitt}(\mathfrak{a}/(f_{0}),I/(f_{0}))$
.
Proof. First, we notice that
$f_{0}\in \operatorname{Kitt}(\mathfrak{a},I)$
by Theorem 4.23. Also for an element
$r\in R$
, put
$\widetilde{r}$
to denote the image of
$r$
via the projection homomorphism
$R\rightarrow R/(f_{0})$
.
Fix generators
$(f_{1},\ldots ,f_{r})$
of
$I$
,
$(a_{1},\ldots ,a_{s})$
of
$\mathfrak{a}$
, a matrix
$\unicode[STIX]{x1D6F7}=(c_{ij})$
such that
$(\mathbf{a})=(\mathbf{f})\cdot \unicode[STIX]{x1D6F7}$
, and let
$\unicode[STIX]{x1D701}_{j}=\sum _{i=1}^{r}c_{ij}e_{i}\in K_{1}(f_{1},\ldots ,f_{r};R)$
. It is clear that
$\widetilde{I}=(\widetilde{\mathbf{f}})$
,
$\widetilde{\mathfrak{a}}=(\widetilde{\mathbf{a}})$
and
$\widetilde{\unicode[STIX]{x1D6F7}}$
satisfies
$(\widetilde{\mathbf{a}})=(\widetilde{\mathbf{f}})\cdot \widetilde{\unicode[STIX]{x1D6F7}}$
. Setting
$\widetilde{\unicode[STIX]{x1D701}_{j}}=\sum _{i=1}^{r}\widetilde{c_{ij}}e_{i}$
and
$\widetilde{\unicode[STIX]{x1D6E4}}_{\bullet }=(R/(f_{0}))[\widetilde{\unicode[STIX]{x1D701}_{1}},\ldots ,\widetilde{\unicode[STIX]{x1D701}_{s}}]\subseteq K_{\bullet }(\widetilde{\mathbf{f}};R/(f_{0}))$
, we have, by Theorem 4.9,
$$\begin{eqnarray}\operatorname{Kitt}\biggl(\frac{\mathfrak{a}}{(f_{0})},\frac{I}{(f_{0})}\biggr)=\langle \widetilde{\unicode[STIX]{x1D6E4}}_{\bullet }\cdot Z_{\bullet }(\widetilde{\mathbf{f}};R/(f_{0}))\rangle _{r}.\end{eqnarray}$$
Let
$z\in Z_{j}(\widetilde{\mathbf{f}};R/(f_{0}))$
,
$0\leqslant j\leqslant r$
and
$L_{1}\subseteq \{1,\ldots ,s\}$
such that
$|L_{1}|=r-j$
. We need to prove that
$\widetilde{\unicode[STIX]{x1D701}}_{L_{1}}\wedge z$
is the specialization of some elements in
$\operatorname{Kitt}(\mathfrak{a},I)$
. By Lemma 4.26, there is a cycle
$c=e_{0}\wedge w+w^{\prime }\in Z_{j}(f_{0},\mathbf{f};R)$
such that
$z=\widetilde{w^{\prime }}$
in
$H_{j}(\widetilde{\mathbf{f}};R/(f_{0}))$
.
According to Theorem 4.23, it suffices to prove that
$\unicode[STIX]{x1D701}_{L_{1}}\wedge w^{\prime }$
is an element in
$\operatorname{Kitt}(\mathfrak{a},I)$
. Since
$f_{0}\in \mathfrak{a}$
there exist
$\unicode[STIX]{x1D6FC}_{i}\in R$
such that
$$\begin{eqnarray}f_{0}=\mathop{\sum }_{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}a_{i}.\end{eqnarray}$$
Hence
$e_{0}-\sum _{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\in Z_{1}(f_{0},\mathbf{f};R)$
. Therefore, Theorem 4.9 implies that
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge \biggl(e_{0}-\mathop{\sum }_{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\biggr)\wedge c\in \operatorname{Kitt}(\mathfrak{a},I).\end{eqnarray}$$
On the other hand,
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{L_{1}}\wedge \biggl(e_{0}-\mathop{\sum }_{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\biggr)\wedge c=\unicode[STIX]{x1D701}_{L_{1}}\wedge \biggl(-w^{\prime }\wedge e_{0}-\mathop{\sum }_{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\wedge w\wedge e_{0}-\mathop{\sum }_{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\wedge w^{\prime }\biggr).\end{eqnarray}$$
On the summands on the right side, we have:
∙
$\unicode[STIX]{x1D701}_{L_{1}}\wedge \sum _{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\wedge w^{\prime }$
, which is zero, since it is a wedge product of
$r+1$
elements involving only
$e_{1},\ldots ,e_{r}$
;∙
$\unicode[STIX]{x1D701}_{L_{1}}\wedge \sum _{i=1}^{s}\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D701}_{i}\wedge w$
, which gives us a generator of
$\operatorname{Kitt}(\mathfrak{a},I)$
by Theorem 4.9.
It then follows that
$\unicode[STIX]{x1D701}_{L_{1}}\wedge w^{\prime }$
is an element in
$\operatorname{Kitt}(\mathfrak{a},I)$
as desired.◻
5 Applications and corollaries
For the first applications of the facts developed in the previous sections, we will present the following theorem which proves Conjecture 4.7 to a certain extent.
Theorem 5.1. Let
$R$
be a Cohen–Macaulay local ring and
$I$
be an ideal of height
$g\geqslant 2$
which satisfies the
$\operatorname{SD}_{1}$
condition. Then any algebraic
$s$
-residual intersection
$J=\mathfrak{a}:I$
coincides with the disguised residual intersection.
Proof. According to Theorem 4.6(i),
$K\subseteq J$
. Hence to prove the equality, without loss of generality, we may assume that
$R$
is a complete Cohen–Macaulay local ring and so possesses a canonical module. Moreover
$K=\operatorname{Kitt}(\mathfrak{a},I)$
by the structure theorems in § 4.
Let
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{g-2}\subseteq \mathfrak{a}$
be a regular sequence which is a part of
$s$
generators of
$\mathfrak{a}$
. The
$R/\unicode[STIX]{x1D6FC}$
-ideal
$I/\unicode[STIX]{x1D6FC}$
still satisfies the
$\operatorname{SD}_{1}$
condition [Reference Chardin, Naeliton and TranCNT19, Proposition 4.1] and
$(\mathfrak{a}/\unicode[STIX]{x1D6FC}:I/\unicode[STIX]{x1D6FC})=J/\unicode[STIX]{x1D6FC}$
is an
$(s-g+2)$
-residual intersection. Hence [Reference Chardin, Naeliton and TranCNT19, Theorem 4.5] (Theorem 4.6(4)) implies that
$$\begin{eqnarray}\operatorname{Kitt}\biggl(\frac{\mathfrak{a}}{\unicode[STIX]{x1D6FC}},\frac{I}{\unicode[STIX]{x1D6FC}}\biggr)=\biggl(\frac{\mathfrak{a}}{\unicode[STIX]{x1D6FC}}:\frac{I}{\unicode[STIX]{x1D6FC}}\biggr)=\frac{J}{\unicode[STIX]{x1D6FC}}.\end{eqnarray}$$
Now by Theorem 4.27, we have
$$\begin{eqnarray}\operatorname{Kitt}\biggl(\frac{\mathfrak{a}}{\unicode[STIX]{x1D6FC}},\frac{I}{\unicode[STIX]{x1D6FC}}\biggr)=\frac{\operatorname{Kitt}(\mathfrak{a},I)}{\unicode[STIX]{x1D6FC}}\end{eqnarray}$$
which proves the theorem. ◻
Theorem 5.1 has several consequences. Indeed all of the known properties of disguised residual intersections are the properties of algebraic residual intersections if the ideal
$I$
satisfies the
$\operatorname{SD}_{1}$
condition. Among these, there are the Cohen–Macaulayness, the Castelnuovo–Mumford regularity and the type of algebraic residual intersections.
Corollary 5.2. Let
$R$
be a Cohen–Macaulay local ring and let
$I$
be an ideal of height
$g\geqslant 2$
which satisfies the
$\operatorname{SD}_{1}$
condition. Then any algebraic
$s$
-residual intersection
$J=\mathfrak{a}:I$
is a Cohen–Macaulay ideal of height
$s$
, it is generated by at most
$s+\sum _{i=\max \{0,r-s\}}^{r-g}\binom{s}{r-i}\unicode[STIX]{x1D707}(H_{i}(\mathbf{f}))$
elements, and it is resolved by the complex
$\text{}_{0}{\mathcal{Z}}_{\bullet }^{+}$
.
We also have the following important property about the behaviors of the Hilbert functions.
Corollary 5.3. Let
$R$
be a CM standard graded ring over an Artinian local ring
$R_{0}$
. Suppose that
$I$
satisfies the
$\operatorname{SD}_{1}$
condition. Then for any
$s$
-residual intersection
$J=(\mathfrak{a}:I)$
, the Hilbert function of
$R/J$
depends on the ideal
$I$
and merely on the degrees of the generators of
$\mathfrak{a}$
.
Proof. The fact has been already proved for disguised residual intersections in [Reference Hassanzadeh and NaelitonHN16, Proposition 3.1]. Due to Theorem 5.1 the disguised residual intersection is the same as the algebraic residual intersection for ideals with
$\operatorname{SD}_{1}$
.◻
Besides the coincidence of disguised and algebraic residual intersections, we have the structure of the generators of the disguised residual intersections by Theorem 4.23. This fact leads to some important classification of residual intersections. We mention one immediate corollary here.
Corollary 5.4. Let
$R$
be a Cohen–Macaulay ring and
$I$
be a complete intersection ideal generated by
$\mathbf{f}=f_{1},\ldots ,f_{r}$
. Suppose that
$J=\mathfrak{a}:I$
is an algebraic
$s$
-residual intersection of
$I$
. Then
$J=I_{r}(\unicode[STIX]{x1D6F7})+\mathfrak{a}$
where
$\unicode[STIX]{x1D6F7}$
is an
$r\times s$
matrix satisfying
$\mathbf{a}=\mathbf{f}\cdot \unicode[STIX]{x1D6F7}$
.
Proof. Complete intersections are obviously
$\operatorname{SD}_{1}$
, so we have
$J=\operatorname{Kitt}(\mathfrak{a},I)$
by Theorem 5.1, and one may localize
$R$
as needed. The result now follows from Corollary 4.25.◻
This corollary provides generalizations to [Reference Bruns, Kustin and MillerBKM90, Theorem 4.8] and [Reference Huneke and UlrichHU88, Theorem 5.9(i)]. The former works for geometric residual intersections and the latter needs
$R$
to be a Gorenstein domain; the proof of the latter in turn appeals to a result of Deconcini and Strickland [Reference Deconcini and StricklandDS81] to determine the structure of residual intersection ideal
$J$
.
As far as we know, there is no structural result as above for residual intersections of almost complete intersections. We have the following.
Corollary 5.5. Let
$R$
be a Cohen–Macaulay local ring and let
$I$
be an almost complete intersection ideal which is Cohen–Macaulay. Let
$J=\mathfrak{a}:I$
be an algebraic
$s$
-residual intersection of
$I$
. Then
$J=\operatorname{Fitt}_{0}(I/\mathfrak{a})+\mathfrak{a}$
.
Proof. Since almost complete intersection CM ideals are SCM, this is another consequence of Theorem 5.1 and Corollary 4.25. ◻
The DG-algebra structure of
$I$
has some non-trivial impacts on the structure of residual intersections. For instance we have the following.
Corollary 5.6. Let
$R$
be a Cohen–Macaulay local ring and let
$I$
be a perfect ideal of height
$2$
. Let
$J=\mathfrak{a}:I$
be an algebraic
$s$
-residual intersection of
$I$
. Then
$J=\operatorname{Fitt}_{0}(I/\mathfrak{a})$
.
Proof. A result of Avramov and Herzog [Reference Avramov and HerzogAH80, Proof of Theorem 2.1(e)] shows that for perfect ideals of height
$2$
the algebra of cycles of Koszul is generated in degree one. Hence the result follows from Theorem 5.1 and Proposition 4.19.◻
There are other ways to prove the above result, see for example [Reference HunekeHun83, Reference Kustin and UlrichKU92] or [Reference Chardin, Eisenbud and UlrichCEU01, Theorem 1.1].
We can also study the common annihilator of Koszul homologies using Corollary 4.17 without any presence of sliding depth hypotheses.
Corollary 5.7. Let
$R$
be a Cohen–Macaulay local ring and
$\mathfrak{a}\subseteq I=(f_{1},\ldots ,f_{r})=(\mathbf{f})$
ideals of
$R$
. Let
$J=\mathfrak{a}:I$
be an
$s$
-residual intersection of
$I$
. Suppose in addition that either
$\mathfrak{a}$
is NOT generated by an analytic independent set of generators or else
$\operatorname{ht}(J)\geqslant s+1$
. Then
$$\begin{eqnarray}\mathop{\bigcap }_{\max \{0,r-s\}}^{r}\operatorname{Ann}H_{i}(\mathbf{f};R)\subseteq \bar{\mathfrak{a}}\end{eqnarray}$$
where
$\bar{\mathfrak{a}}$
is the integral closure of
$\mathfrak{a}$
.
Proof. The proof is a consequence of Corollary 4.17 applied to a nice result of Huneke and(or) Ulrich [Reference Ulrich, Eisenbud and HunekeUlr92, Proposition 3]. ◻
Although the
$\operatorname{SD}_{1}$
condition appears in the Theorem 5.1 and hence we need it in all of the corollaries, it is not in an essential way. If one can show that the disguised residual intersection and the algebraic residual intersection coincide for any nice class of ideals of small height, then the techniques above will provide equality
$\operatorname{Kitt}(\mathfrak{a},I)=(\mathfrak{a}:I)$
quite generally. However, sliding depth conditions are necessary if one seeks Cohen–Macaulay residual intersections [Reference UlrichUlr94]. On the other hand, we conjecture that to prove
$\operatorname{Kitt}(\mathfrak{a},I)=(\mathfrak{a}:I)$
one can totally forget it.
Conjecture 5.8. Let
$R$
be a Cohen–Macaulay ring then
$\operatorname{Kitt}(\mathfrak{a},I)=(\mathfrak{a}:I)$
whenever
$J=\mathfrak{a}:I$
is an algebraic
$s$
-residual intersection.
By the way one may not expect that
$\operatorname{Kitt}(\mathfrak{a},I)=(\mathfrak{a}:I)$
for any pair of ideals
$\mathfrak{a}$
and
$I$
.
Example 5.9. Let
$R=\mathbb{Z}_{3}[x,y,z,t]$
,
$I=(x^{2},y^{2},xy,xt-yz)$
and
$\mathfrak{a}=(x^{4},y^{4},x^{2}y^{2})$
. Then
$J=\mathfrak{a}:I$
has height
$2$
so that it is not a
$3$
-residual intersection. One can check that the Koszul homology algebra of
$I$
is generated in degree one; so
$\operatorname{Kitt}(\mathfrak{a},I)=\mathfrak{a}+\operatorname{Fitt}_{0}(I/\mathfrak{a})$
by Corollary 4.25. A Macaulay verification shows that
$\operatorname{Kitt}(\mathfrak{a},I)\neq J$
.
In the following proposition, we prove Conjecture 5.8 in the case where
$s\leqslant g+1$
.
Proposition 5.10. Let
$R$
be a Cohen–Macaulay ring,
$I\subset R$
an ideal with
$\operatorname{ht}(I)=g$
and
$J=\mathfrak{a}:I$
an
$s$
-residual intersection. If
$s\leqslant g+1$
then
$\operatorname{Kitt}(\mathfrak{a}:I)=J$
.
Proof. Let
$a_{1},\ldots ,a_{s}$
be a set of generators of
$\mathfrak{a}$
. By Proposition 4.12, we can suppose that
$a_{1},\ldots ,a_{g}$
is a regular sequence. By Theorem 5.1, we can mod out this regular sequence and hence we may and do suppose that
$g=\operatorname{ht}(I)=0$
. Let
$f_{1},\ldots ,f_{r}$
be a set of generators of
$I$
and let
$K_{\bullet }=R\langle e_{1},\ldots ,e_{r};\unicode[STIX]{x2202}(e_{i})=f_{i}\rangle$
be the Koszul complex of
$\mathbf{f}$
.
If
$s=0$
, then
$\mathfrak{a}=0$
and we must show that
$\operatorname{Kitt}((0),I)=(0:I)$
. In this case,
$\unicode[STIX]{x1D6E4}_{\bullet }=R$
and we have
$$\begin{eqnarray}\operatorname{Kitt}(\mathfrak{a},I)=\unicode[STIX]{x1D6E4}_{0}\cdot Z_{r}(\mathbf{f};R)=R\cdot (0:I)=(0:I)=J.\end{eqnarray}$$
If
$s=1$
, then by Proposition 4.15 we may suppose that
$\mathfrak{a}=(f_{1})$
. In this case,
$\unicode[STIX]{x1D6E4}_{\bullet }=R\oplus R\cdot e_{1}$
and then
$$\begin{eqnarray}\operatorname{Kitt}(\mathfrak{a},I)=\unicode[STIX]{x1D6E4}_{0}\cdot Z_{r}(\mathbf{f};R)+\unicode[STIX]{x1D6E4}_{1}\cdot Z_{r-1}.\end{eqnarray}$$
Write
$\hat{e_{i}}$
for
$e_{1}\wedge \cdots \wedge \hat{e_{i}}\wedge \cdots \wedge e_{r}$
. Then
$c=\sum _{i=1}^{r}a_{i}^{\prime }\hat{e_{i}}\in Z_{r-1}(\mathbf{f};R)$
if and only if
$$\begin{eqnarray}I_{2}\left[\begin{array}{@{}cccc@{}}a_{1}^{\prime } & a_{2}^{\prime } & \cdots \, & a_{r}^{\prime }\\ f_{1} & f_{2} & \cdots \, & f_{r}\end{array}\right]=0.\end{eqnarray}$$
Moreover the element of
$\operatorname{Kitt}(\mathfrak{a},I)$
produced by
$c$
is
$e_{1}\wedge c=a_{1}^{\prime }$
. Let
$\unicode[STIX]{x1D6FC}\in J$
. To show that
$\unicode[STIX]{x1D6FC}\in \operatorname{Kitt}(\mathfrak{a},I)$
, one needs to show that there are
$\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{r}\in R$
such that
$$\begin{eqnarray}I_{2}\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D6FC} & \unicode[STIX]{x1D6FC}_{2} & \cdots \, & \unicode[STIX]{x1D6FC}_{n}\\ f_{1} & f_{2} & \cdots \, & f_{r}\end{array}\right]=0.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D6FC}\in J=(f_{1}):I$
, there are
$\unicode[STIX]{x1D6FC}_{2},\ldots ,\unicode[STIX]{x1D6FC}_{r}$
such that
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}f_{i}=\unicode[STIX]{x1D6FC}_{i}f_{1}.\end{eqnarray}$$
If one shows that
$\unicode[STIX]{x1D6FC}_{i}f_{j}=\unicode[STIX]{x1D6FC}_{j}f_{i}$
for
$i,j\geqslant 2$
, then
$(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{r})$
satisfies (5.1); hence
$\unicode[STIX]{x1D6FC}\in \operatorname{Kitt}(\mathfrak{a},I)$
. If we suppose in addition that
$\unicode[STIX]{x1D6FC}$
is
$R$
-regular. Then the desired equality is equivalent to
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{i}f_{j}\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{j}f_{i}\unicode[STIX]{x1D6FC},\end{eqnarray}$$
which holds, due to (5.2).
Thence any
$R$
-regular element in
$J$
belongs to
$\operatorname{Kitt}(\mathfrak{a},I)$
. Now, let
$\unicode[STIX]{x1D6FD}\in J$
be an arbitrary element. Since
$J$
is a
$1$
-residual intersection,
$\operatorname{ht}(J)\geqslant 1$
. Since
$R$
is Cohen–Macaulay,
$\operatorname{grade}(J)\geqslant 1$
. Therefore there exists
$\unicode[STIX]{x1D6FC}\in J$
which is
$R$
-regular. Let
$\unicode[STIX]{x1D6FC}_{i},2\leqslant i\leqslant r$
satisfy (5.1). Let
$\unicode[STIX]{x1D6FD}_{2},\ldots ,\unicode[STIX]{x1D6FD}_{r}$
be such that
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}f_{i}=\unicode[STIX]{x1D6FD}_{i}f_{1}.\end{eqnarray}$$
The equations (5.2) and (5.4) imply that
$$\begin{eqnarray}(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})f_{i}=f_{1}(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FD}_{i}).\end{eqnarray}$$
By applying (5.1), we have
$$\begin{eqnarray}f_{i}(\unicode[STIX]{x1D6FC}_{j}+\unicode[STIX]{x1D6FD}_{j})-f_{j}(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FD}_{i})=(f_{i}\unicode[STIX]{x1D6FC}_{j}-f_{j}\unicode[STIX]{x1D6FC}_{i})+(f_{i}\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FD}_{j}f_{i})=f_{i}\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FD}_{j}f_{i}.\end{eqnarray}$$
According to (5.5),
$(f_{i}(\unicode[STIX]{x1D6FC}_{j}+\unicode[STIX]{x1D6FD}_{j})-f_{j}(\unicode[STIX]{x1D6FC}_{i}+\unicode[STIX]{x1D6FD}_{i}))(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})=0$
. This in conjunction with (5.6) implies that
$$\begin{eqnarray}(f_{i}\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FD}_{j}f_{i})(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})=0.\end{eqnarray}$$
Equation (5.4) implies that
$$\begin{eqnarray}(f_{i}\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FD}_{j}f_{i})(\unicode[STIX]{x1D6FD})=0.\end{eqnarray}$$
Subtracting the last two equations we get
$$\begin{eqnarray}(f_{i}\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FD}_{j}f_{i})(\unicode[STIX]{x1D6FC})=0,\end{eqnarray}$$
which implies, by the regularity of
$\unicode[STIX]{x1D6FC}$
, that
$$\begin{eqnarray}f_{i}\unicode[STIX]{x1D6FD}_{j}-\unicode[STIX]{x1D6FD}_{j}f_{i}=0.\end{eqnarray}$$
Therefore
$$\begin{eqnarray}I_{2}\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D6FD} & \unicode[STIX]{x1D6FD}_{2} & \cdots \, & \unicode[STIX]{x1D6FD}_{r}\\ f_{1} & f_{2} & \cdots \, & f_{r}\end{array}\right]=0\end{eqnarray}$$
which implies that
$\unicode[STIX]{x1D6FD}\in \operatorname{Kitt}(\mathfrak{a},I)$
.◻
Remark 5.11. One can see from the proof of Proposition 5.10 that the Cohen–Macaulay assumption on
$R$
is only needed to guarantee the existence of a regular sequence in
$J$
. In other words, if one replaces
$\operatorname{ht}(J)\geqslant s$
with
$\operatorname{grade}(J)\geqslant s$
, in the definition of residual intersection, Definition 4.1, the result of Proposition 5.10 holds for any Noetherian ring.
Even the case where
$s=g$
, the above result for
$J=\mathfrak{a}:I$
is more general than the known linkage theory, as here
$R$
is not Gorenstein and
$I$
is not unmixed, necessarily. However, Proposition 5.10 determines the set of generators of
$J=\mathfrak{a}:I$
.
Another important aspect of Conjecture 5.8 or Theorem 5.1 and Proposition 5.10 is that, from the structure of colon ideal,
$J=\mathfrak{a}:I$
, it is not clear that
$J$
can be specialized, particularly from a generic choice of
$\mathfrak{a}$
to a general choice of
$\mathfrak{a}$
. However
$\operatorname{Kitt}(\mathfrak{a},I)=\langle \unicode[STIX]{x1D6E4}_{\bullet }\cdot Z_{\bullet }\rangle _{r}$
specializes naturally.
One can also detect Cohen–Macaulay residual intersections under very slight conditions.
Proposition 5.12. Let
$R$
be a Cohen–Macaulay local ring of dimension
$d$
,
$I\subset R$
an ideal with
$\operatorname{ht}(I)=g$
and
$J=\mathfrak{a}:I$
an
$s$
-residual intersection with
$s\leqslant g+1$
. Then
$_{0}{\mathcal{Z}}_{\bullet }^{+}$
resolves
$R/J$
.
More precisely, let
$I=(f_{1},\ldots ,f_{r})$
,
$Z_{i}=Z_{i}(\mathbf{f},R)$
the Koszul cycles and
$Z_{j}^{+}$
mean a direct sum of copies of Koszul cycles
$Z_{i}$
for
$i\geqslant j$
. Then we have the following.
(1) If
$s=g$
, there exists an exact complex
$0\rightarrow F_{g}\rightarrow \cdots \rightarrow F_{2}\rightarrow Z_{r-g}^{+}\rightarrow R\rightarrow R/J\rightarrow 0$
wherein the
$F_{i}$
are free
$R$
-modules.(2) If
$s=g+1$
, there exists an exact complex
$0\rightarrow F_{g+1}\rightarrow \cdots \rightarrow F_{3}\rightarrow Z_{r-g}^{+}\rightarrow Z_{r-g-1}^{+}\rightarrow R\rightarrow R/J\rightarrow 0$
wherein the
$F_{i}$
are free
$R$
-modules.
In particular we have the following.
∙ If
$s=g$
, then
$R/J$
is Cohen–Macaulay if and only if
$\operatorname{depth}(Z_{r-g})\geqslant d-g+1$
. In this case
$\operatorname{depth}(Z_{r-g})=d-g+1$
.∙ If
$s=g+1$
, then
$R/J$
is Cohen–Macaulay if
$\operatorname{depth}(Z_{r-g})\geqslant d-g+1$
and
$\operatorname{depth}(Z_{r-g-1})\geqslant d-g$
.
Proof. Parts (1) and (2) follow from the construction of
${\mathcal{Z}}_{\bullet }^{\prime }$
complex in [Reference HassanzadehHas12, p. 6375] and [Reference HassanzadehHas12, Corollary 2.9(c)]. The statements about the Cohen–Macaulay property follow from a usual diagram chasing (or spectral sequence) applying to the complexes in the first part. We notice that one cannot deduce these Cohen–Macaulay properties by appealing to the standard sequence
$0\rightarrow B_{r-g}\rightarrow Z_{r-g}\rightarrow H_{r-g}\rightarrow 0$
.◻
Ulrich [Reference UlrichUlr94] defines the Artin–Nagata property,
$\text{AN}_{s}$
, for the ideal
$I$
in a Cohen–Macaulay ring
$R$
, if every
$i$
-residual intersection of
$I$
is Cohen–Macaulay for any
$i\leqslant s$
. As a consequence of Conjecture 4.7, [Reference HassanzadehHas12, Theorem 2.11] implies that
$\text{AN}_{s}$
is equivalent to the
$\operatorname{SDC}_{1}$
condition at level
$\min \{s-g,r-g\}$
, Definition 4.3. Nevertheless, we have the following corollary.
Corollary 5.13. Let
$R$
be a Cohen–Macaulay local ring of dimension
$d$
,
$I\subset R$
an ideal generated by
$r$
elements with
$\operatorname{ht}(I)=g$
and
$g\leqslant s\leqslant g+1$
. Then the following are equivalent:
(i)
$I$
satisfies
$\text{AN}_{s}$
;(ii) for any
$i\leqslant s$
there exists an
$i$
-residual intersection of
$I$
which is Cohen–Macaulay;(iii)
$I$
satisfies the
$\operatorname{SDC}_{1}$
condition at level
$\min \{s-g,r-g\}$
.
Proof. The implication
$\text{(i)}\Rightarrow \text{(ii)}$
holds trivially. The implication
$\text{(iii)}\Rightarrow \text{(ii)}$
also holds, according to Proposition 5.10 and [Reference HassanzadehHas12, Theorem 2.11]. For
$\text{(ii)}\Rightarrow \text{(iii)}$
, we use the resolutions in Proposition 5.12. Since, by hypothesis, a Cohen–Macaulay
$g$
-residual intersection exists, Proposition 5.12(1) implies that
$\operatorname{depth}(Z_{r-g})\geqslant d-g+1$
. Now having
$\operatorname{depth}(Z_{r-g})\geqslant d-g+1$
and
$\operatorname{depth}(R/J)\geqslant d-g-1$
, Proposition 5.12(2) implies that
$\operatorname{depth}(Z_{r-g-1})\geqslant d-g$
.◻
Acknowledgements
The authors would like to thank CAPES and CNPq for their support. They also thank Marc Chardin and Jose Naeliton for useful discussions.
