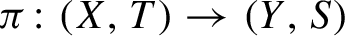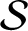1 Introduction
An ordered Bratteli diagram is an infinite directed graph
![]() $B = (V,E,\leq )$
such that the vertex set V and the edge set E are partitioned into levels
$B = (V,E,\leq )$
such that the vertex set V and the edge set E are partitioned into levels
![]() $V= V_0\cup V_1\cup \cdots $
,
$V= V_0\cup V_1\cup \cdots $
,
![]() $E = E_0\cup \cdots $
so that
$E = E_0\cup \cdots $
so that
![]() $E_n$
are edges from
$E_n$
are edges from
![]() $V_{n+1}$
to
$V_{n+1}$
to
![]() $V_n$
,
$V_n$
,
![]() $V_0$
is a singleton, each
$V_0$
is a singleton, each
![]() $V_n$
is finite and
$V_n$
is finite and
![]() $\leq $
is a partial order on E such that two edges are comparable if and only if they start at the same vertex. The order
$\leq $
is a partial order on E such that two edges are comparable if and only if they start at the same vertex. The order
![]() $\leq $
can be extended to the set
$\leq $
can be extended to the set
![]() $X_B$
of all infinite paths in B, and the Vershik action
$X_B$
of all infinite paths in B, and the Vershik action
![]() $V_B$
on
$V_B$
on
![]() $X_B$
is defined when B has unique minimal and maximal infinite paths with respect to
$X_B$
is defined when B has unique minimal and maximal infinite paths with respect to
![]() $\leq $
. We say that
$\leq $
. We say that
![]() $(X_B,V_B)$
is a Bratteli–Vershik (BV) representation of the Cantor system
$(X_B,V_B)$
is a Bratteli–Vershik (BV) representation of the Cantor system
![]() $(X,T)$
if both are conjugate. Bratteli diagrams are a tool coming from
$(X,T)$
if both are conjugate. Bratteli diagrams are a tool coming from
![]() $C^*$
-algebras that, at the beginning of the 1990’s, Herman et al [Reference Herman, Putnam and SkauHPS92] used to study minimal Cantor systems. Their success at characterizing the strong and weak orbit equivalence for systems of this kind marked a milestone in the theory that motivated many posterior works. Some of these works focused on using Bratteli diagrams to study specific classes of systems and, as a consequence, many of the classical minimal systems have been characterized as BV systems with a specific structure. Some examples include odometers as those systems that have a BV representation with one vertex per level, substitutive subshifts as stationary BV (all levels are the same) [Reference Durand, Host and SkauDHS99], certain Toeplitz sequences as ‘equal row-sum’ BV [Reference Gjerde and JohansenGJ00], and (codings of) interval exchanges as BV where the diagram codifies a path in a Rauzy graph [Reference Gjerde and JohansenGJ02]. Now, almost all of these examples share certain coarse dynamical behavior: they have finitely many ergodic measures, are not strongly mixing, have zero entropy, are subshifts, and their BV representations have a bounded number of vertices per level, among many others. It turns out that just having a BV representation with a bounded number of vertices per level (or, from now on, having finite topological rank) implies the previous properties (see, for example, [Reference Bezuglyi, Kwiatkowski, Medynets and SolomyakBKMS13, Reference Downarowicz and MaassDM08]). Hence, the finite topological rank class arises as a possible framework for studying minimal subshifts and proving general theorems.
$C^*$
-algebras that, at the beginning of the 1990’s, Herman et al [Reference Herman, Putnam and SkauHPS92] used to study minimal Cantor systems. Their success at characterizing the strong and weak orbit equivalence for systems of this kind marked a milestone in the theory that motivated many posterior works. Some of these works focused on using Bratteli diagrams to study specific classes of systems and, as a consequence, many of the classical minimal systems have been characterized as BV systems with a specific structure. Some examples include odometers as those systems that have a BV representation with one vertex per level, substitutive subshifts as stationary BV (all levels are the same) [Reference Durand, Host and SkauDHS99], certain Toeplitz sequences as ‘equal row-sum’ BV [Reference Gjerde and JohansenGJ00], and (codings of) interval exchanges as BV where the diagram codifies a path in a Rauzy graph [Reference Gjerde and JohansenGJ02]. Now, almost all of these examples share certain coarse dynamical behavior: they have finitely many ergodic measures, are not strongly mixing, have zero entropy, are subshifts, and their BV representations have a bounded number of vertices per level, among many others. It turns out that just having a BV representation with a bounded number of vertices per level (or, from now on, having finite topological rank) implies the previous properties (see, for example, [Reference Bezuglyi, Kwiatkowski, Medynets and SolomyakBKMS13, Reference Downarowicz and MaassDM08]). Hence, the finite topological rank class arises as a possible framework for studying minimal subshifts and proving general theorems.
This idea has been exploited in many works: Durand et al, in a series of papers (with [Reference Durand, Frank and MaassDFM19] being the last one), developed techniques from the well-known substitutive case and obtained criteria for any BV of finite topological rank to decide if a given complex number is a continuous or measurable eigenvalue; Bezuglyi et al described in [Reference Bezuglyi, Kwiatkowski, Medynets and SolomyakBKMS13] the simplex of invariant measures together with natural conditions for being uniquely ergodic; Giordano et al bounded the rational rank of the dimension group by the topological rank [Reference Herman, Putnam and SkauHPS92, Reference Giordano, Handelman and HosseiniGHH18], among other works. It is important to remark that these works were inspired by or first proved in the substitutive case.
Now, since Bratteli–Vershik systems with finite topological rank at least two are conjugate to a subshift [Reference Downarowicz and MaassDM08], it is interesting to try to define them directly as a subshift. This can be done by codifying the levels of the Bratteli diagram as substitutions and then iterate them to obtain a sequence of symbols defining a subshift conjugate to the initial BV system. This procedure also makes sense for arbitrary nested sequences of substitutions (called directive sequences), independently from the Bratteli diagram and the various additional properties of its codifying substitutions. Subshifts obtained in this way are called
![]() ${\mathcal S}$
-adic (substitution-adic) and may be non-minimal (see, for example, [Reference Berthé, Steiner, Thuswaldner and YassawiBSTY19]).
${\mathcal S}$
-adic (substitution-adic) and may be non-minimal (see, for example, [Reference Berthé, Steiner, Thuswaldner and YassawiBSTY19]).
Although there are some open problems about finite topological rank systems depending directly on the combinatorics of the underlying Bratteli diagrams, others are more naturally stated in the
![]() ${\mathcal S}$
-adic setting (e.g. when dealing with endomorphisms, it is useful to have the Curtisâ–Hedlundâ–Lyndon theorem) and, hence, there exists an interplay between
${\mathcal S}$
-adic setting (e.g. when dealing with endomorphisms, it is useful to have the Curtisâ–Hedlundâ–Lyndon theorem) and, hence, there exists an interplay between
![]() ${\mathcal S}$
-adic subshifts and finite topological rank systems in which theorems and techniques obtained for one of these classes can sometimes be transferred to the other. The question about which is the exact relation between these classes has been recently addressed in [Reference Donoso, Durand, Maass and PetiteDDMP21] and, in particular, the authors proved the following.
${\mathcal S}$
-adic subshifts and finite topological rank systems in which theorems and techniques obtained for one of these classes can sometimes be transferred to the other. The question about which is the exact relation between these classes has been recently addressed in [Reference Donoso, Durand, Maass and PetiteDDMP21] and, in particular, the authors proved the following.
Theorem 1.1. [Reference Donoso, Durand, Maass and PetiteDDMP21]
A minimal subshift
![]() $(X,T)$
has topological rank at most K if and only if it is generated by a proper, primitive, and recognizable
$(X,T)$
has topological rank at most K if and only if it is generated by a proper, primitive, and recognizable
![]() ${\mathcal S}$
-adic sequence of alphabet rank at most K.
${\mathcal S}$
-adic sequence of alphabet rank at most K.
In this context, a fundamental question is the following.
Question 1.2. Are subshift factors of finite topological rank systems of finite topological rank?
Indeed, the topological rank controls various coarse dynamical properties (number of ergodic measures, rational rank of dimension group, among others) which cannot increase after a factor map, and we also know that big subclasses of the finite topological rank class are stable under symbolic factors, such as the linearly recurrent and the non-superlineal complexity classes [Reference Donoso, Durand, Maass and PetiteDDMP21], so it is expected that this question has an affirmative answer. However, when trying to prove this using Theorem 1.1, we realize that the naturally inherited
![]() ${\mathcal S}$
-adic structure of finite alphabet rank that a symbolic factor has is never recognizable. Moreover, this last property is crucial for many of the currently known techniques to handle finite topological rank systems (even in the substitutive case, it is a deep and fundamental theorem of Mossé), so it is not clear why it would be always possible to obtain this property while keeping the alphabet rank bounded or why recognizability is not connected with a dynamical property of the system. Thus, an answer to this question seems to be fundamental to the understanding of the finite topological rank class.
${\mathcal S}$
-adic structure of finite alphabet rank that a symbolic factor has is never recognizable. Moreover, this last property is crucial for many of the currently known techniques to handle finite topological rank systems (even in the substitutive case, it is a deep and fundamental theorem of Mossé), so it is not clear why it would be always possible to obtain this property while keeping the alphabet rank bounded or why recognizability is not connected with a dynamical property of the system. Thus, an answer to this question seems to be fundamental to the understanding of the finite topological rank class.
This question has been recently addressed, first in [Reference EspinozaEsp20] by purely combinatorial methods, and then also in [Reference Golestani and HosseiniGH21] in the BV formulation by using an abstract construction from [Reference Amini, Elliott and GolestaniAEG15]. In this work, we refine both approaches and obtain, as a first consequence, the optimal answer to Question 1.2 in a more general, non-minimal context.
Theorem 1.3. Let
![]() $(X,T)$
be an
$(X,T)$
be an
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing and proper directive sequence of alphabet rank equal to K, and
${\mathcal S}$
-adic subshift generated by an everywhere growing and proper directive sequence of alphabet rank equal to K, and
![]() $\pi \colon (X,T)\to (Y,S)$
be an aperiodic subshift factor. Then,
$\pi \colon (X,T)\to (Y,S)$
be an aperiodic subshift factor. Then,
![]() $(Y,S)$
is an
$(Y,S)$
is an
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing, proper, and recognizable directive sequence of alphabet rank at most K.
${\mathcal S}$
-adic subshift generated by an everywhere growing, proper, and recognizable directive sequence of alphabet rank at most K.
Here, a directive sequence
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
is everywhere growing if
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
is everywhere growing if
![]() $\lim _{n\to \infty }\min _{a\in {\mathcal A}_n}|\sigma _0\ldots \sigma _{n-1}(a)| = \infty $
, and a system
$\lim _{n\to \infty }\min _{a\in {\mathcal A}_n}|\sigma _0\ldots \sigma _{n-1}(a)| = \infty $
, and a system
![]() $(X,T)$
is aperiodic if every orbit
$(X,T)$
is aperiodic if every orbit
![]() $\{T^nx:n\in {\mathbb Z}\}$
is infinite. Theorem 1.3 implies that the topological rank cannot increase after a factor map (Corollary 4.8). Theorem 1.3 implies the following sufficient condition for a system to be of finite topological rank.
$\{T^nx:n\in {\mathbb Z}\}$
is infinite. Theorem 1.3 implies that the topological rank cannot increase after a factor map (Corollary 4.8). Theorem 1.3 implies the following sufficient condition for a system to be of finite topological rank.
Corollary 1.4. Let
![]() $(X,T)$
be an aperiodic minimal
$(X,T)$
be an aperiodic minimal
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing directive sequence of finite alphabet rank. Then, the topological rank of
${\mathcal S}$
-adic subshift generated by an everywhere growing directive sequence of finite alphabet rank. Then, the topological rank of
![]() $(X,T)$
is finite.
$(X,T)$
is finite.
An interesting corollary of the underlying construction of the proof of Theorem 1.3 is the coalescence property for this kind of system, in the following stronger form.
Corollary 1.5. Let
![]() $(X,T)$
be an
$(X,T)$
be an
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing and proper directive sequence of alphabet rank equal to K, and
${\mathcal S}$
-adic subshift generated by an everywhere growing and proper directive sequence of alphabet rank equal to K, and
 $(X,T) \overset {\pi _1}{\to } (X_1,T_1)\overset {\pi _2}{\to }\ldots \overset {\pi _L}{\to }(X_L,T_L)$
be a chain of aperiodic subshift factors. If
$(X,T) \overset {\pi _1}{\to } (X_1,T_1)\overset {\pi _2}{\to }\ldots \overset {\pi _L}{\to }(X_L,T_L)$
be a chain of aperiodic subshift factors. If
![]() $L> \log _2K$
, then at least one
$L> \log _2K$
, then at least one
![]() $\pi _j$
is a conjugacy.
$\pi _j$
is a conjugacy.
One of the results in [Reference DurandDur00] is that factor maps between aperiodic linearly recurrent subshifts are finite-to-one. In particular, they are almost k-to-1 for some finite k. For finite topological rank subshifts, we prove the following.
Theorem 1.6. Let
![]() $\pi \colon (X,T)\to (Y,S)$
be a factor map between aperiodic minimal subshifts. Suppose that
$\pi \colon (X,T)\to (Y,S)$
be a factor map between aperiodic minimal subshifts. Suppose that
![]() $(X,T)$
has topological rank equal to K. Then
$(X,T)$
has topological rank equal to K. Then
![]() $\pi $
is almost k-to-1 for some
$\pi $
is almost k-to-1 for some
![]() $k \leq K$
.
$k \leq K$
.
We use this theorem, in Corollary 4.12, to prove that Cantor factors of finite topological rank subshifts are either odometers or subshifts.
In [Reference DurandDur00], the author proved that linearly recurrent subshifts have finite topological rank, and that this kind of system has finitely many aperiodic subshift factors up to conjugacy. Inspired by this result, we use ideas from the proof of Theorem 1.3 to obtain the following.
Theorem 1.7. Let
![]() $(X,T)$
be a minimal subshift of topological rank K. Then,
$(X,T)$
be a minimal subshift of topological rank K. Then,
![]() $(X,T)$
has at most
$(X,T)$
has at most
![]() $(3K)^{32K}$
aperiodic subshift factors up to conjugacy.
$(3K)^{32K}$
aperiodic subshift factors up to conjugacy.
Altogether, these results give a rough picture of the set of totally disconnected factors of a given finite topological rank system: they are either equicontinuous or subshifts satisfying the properties in Theorems 1.3, 1.5, 1.7, and 1.6. Now, in a topological sense, totally disconnected factors of a given system
![]() $(X,T)$
are ‘maximal,’ so, the natural next step in the study of finite topological rank systems is asking about the connected factors. As we have seen, the finite topological rank condition is a rigidity condition. By this reason, we think that the following question has an affirmative answer.
$(X,T)$
are ‘maximal,’ so, the natural next step in the study of finite topological rank systems is asking about the connected factors. As we have seen, the finite topological rank condition is a rigidity condition. By this reason, we think that the following question has an affirmative answer.
Question 1.8. Let
![]() $(X,T)$
be a minimal system of finite topological rank and
$(X,T)$
be a minimal system of finite topological rank and
![]() $\pi \colon (X,T)\to (Y,S)$
be a factor map. Suppose that Y is connected. Is
$\pi \colon (X,T)\to (Y,S)$
be a factor map. Suppose that Y is connected. Is
![]() $(Y,S)$
an equicontinuous system?
$(Y,S)$
an equicontinuous system?
We remark that the finite topological rank class contains all minimal subshifts of non-superlinear complexity [Reference Donoso, Durand, Maass and PetiteDDMP21], but even for the much smaller class of linear complexity subshifts, the author is not aware of results concerning Question 1.8.
1.1 Organization
In the next section, we give the basic background in topological and symbolic dynamics needed in this article. Section 3 is devoted to prove some combinatorial lemmas. The main results about the topological rank of factors are stated and proved in §4. Next, in §5, we prove Theorem 1.6, which is mainly a consequence of the so-called critical factorization theorem. Finally, in §6, we study the problem about the number of symbolic factors and prove Theorem 1.7.
2 Preliminaries
For us, the set of natural numbers starts with zero, i.e.
![]() ${\mathbb N}=\{0,1,2,\ldots \}$
.
${\mathbb N}=\{0,1,2,\ldots \}$
.
2.1 Basics in topological dynamics
A topological dynamical system (or just a system) is a pair
![]() $(X,T)$
, where X is a compact metric space and
$(X,T)$
, where X is a compact metric space and
![]() $T\colon X \to X$
is a homeomorphism of X. We denote by
$T\colon X \to X$
is a homeomorphism of X. We denote by
![]() $\text {Orb}_T(x)$
the orbit
$\text {Orb}_T(x)$
the orbit
![]() $\{T^nx : n\in {\mathbb Z}\}$
of
$\{T^nx : n\in {\mathbb Z}\}$
of
![]() $x \in X$
. A point
$x \in X$
. A point
![]() $x\in X$
is p-periodic if
$x\in X$
is p-periodic if
![]() $T^px=x$
, periodic if it is p-periodic for some
$T^px=x$
, periodic if it is p-periodic for some
![]() $p\geq 1$
, and aperiodic otherwise. A topological dynamical system is aperiodic if any point
$p\geq 1$
, and aperiodic otherwise. A topological dynamical system is aperiodic if any point
![]() $x\in X$
is aperiodic, is minimal if the orbit of every point is dense in X, and is Cantor if X is a Cantor space (i.e. X is totally disconnected and does not have isolated points). We use the letter T to denote the action of a topological dynamical system independently of the base set X. The hyperspace of
$x\in X$
is aperiodic, is minimal if the orbit of every point is dense in X, and is Cantor if X is a Cantor space (i.e. X is totally disconnected and does not have isolated points). We use the letter T to denote the action of a topological dynamical system independently of the base set X. The hyperspace of
![]() $(X,T)$
is the system
$(X,T)$
is the system
![]() $(2^X,T)$
, where
$(2^X,T)$
, where
![]() $2^X$
is the set of all closed subsets of X with the topology generated by the Hausdorff metric
$2^X$
is the set of all closed subsets of X with the topology generated by the Hausdorff metric
![]() $d_H(A,B) = \max (\sup _{x\in A}d(x,A),\ \sup _{y\in B}d(y,A))$
, and T the action
$d_H(A,B) = \max (\sup _{x\in A}d(x,A),\ \sup _{y\in B}d(y,A))$
, and T the action
![]() $A\mapsto T(A)$
.
$A\mapsto T(A)$
.
A factor between the topological dynamical systems
![]() $(X,T)$
and
$(X,T)$
and
![]() $(Y,T)$
is a continuous function
$(Y,T)$
is a continuous function
![]() $\pi $
from X onto Y such that
$\pi $
from X onto Y such that
![]() $\pi \circ T=T\circ \pi $
. We use the notation
$\pi \circ T=T\circ \pi $
. We use the notation
![]() $\pi \colon (X,T)\to (Y,T)$
to indicate the factor. A factor map
$\pi \colon (X,T)\to (Y,T)$
to indicate the factor. A factor map
![]() $\pi \colon (X,T) \to (Y,T)$
is almost K-to-1 if
$\pi \colon (X,T) \to (Y,T)$
is almost K-to-1 if
![]() $\#\pi ^{-1}(y) = K$
for all y in a residual subset of Y. We say that
$\#\pi ^{-1}(y) = K$
for all y in a residual subset of Y. We say that
![]() $\pi $
is distal if whenever
$\pi $
is distal if whenever
![]() $\pi (x) = \pi (x')$
and
$\pi (x) = \pi (x')$
and
![]() $x\not =x'$
, we have
$x\not =x'$
, we have
![]() $\inf _{k\in {\mathbb Z}}\mathrm {dist}(T^kx,T^kx')> 0$
.
$\inf _{k\in {\mathbb Z}}\mathrm {dist}(T^kx,T^kx')> 0$
.
Given a system
![]() $(X,T)$
, the Ellis semigroup
$(X,T)$
, the Ellis semigroup
![]() $E(X,T)$
associated with
$E(X,T)$
associated with
![]() $(X,T)$
is defined as the closure of
$(X,T)$
is defined as the closure of
![]() $\{x\mapsto T^nx:n\in {\mathbb Z}\} \subseteq X^X$
in the product topology, where the semi-group operation is given by the composition of functions. On X, we may consider the
$\{x\mapsto T^nx:n\in {\mathbb Z}\} \subseteq X^X$
in the product topology, where the semi-group operation is given by the composition of functions. On X, we may consider the
![]() $E(X,T)$
-action given by
$E(X,T)$
-action given by
![]() $x\mapsto ux$
. Then, the closure of the orbit under T of a point
$x\mapsto ux$
. Then, the closure of the orbit under T of a point
![]() $x\in X$
is equal to the orbit of x under
$x\in X$
is equal to the orbit of x under
![]() $E(X,T)$
. If
$E(X,T)$
. If
![]() $\pi \colon (X,T) \to (Y,T)$
is a factor between minimal systems, then
$\pi \colon (X,T) \to (Y,T)$
is a factor between minimal systems, then
![]() $\pi $
induces a surjective map
$\pi $
induces a surjective map
![]() $\pi ^*\colon E(X,T) \to E(Y,T)$
, which is characterized by the formula
$\pi ^*\colon E(X,T) \to E(Y,T)$
, which is characterized by the formula
If the context is clear, we will not distinguish between u and
![]() $\pi ^*(u)$
. When
$\pi ^*(u)$
. When
![]() $u \in E(2^X,T)$
, we write
$u \in E(2^X,T)$
, we write
![]() $u\circ A$
instead of
$u\circ A$
instead of
![]() $uA$
, the last symbol being reserved to mean
$uA$
, the last symbol being reserved to mean
![]() $uA = \{ux : x \in A\}$
. We can describe more explicitly
$uA = \{ux : x \in A\}$
. We can describe more explicitly
![]() $u\circ A$
as follows: it is the set of all
$u\circ A$
as follows: it is the set of all
![]() $x\in X$
for which we can find nets
$x\in X$
for which we can find nets
![]() $x_\unicode{x3bb} \in A$
and
$x_\unicode{x3bb} \in A$
and
![]() $m_\unicode{x3bb} \in {\mathbb Z}$
such that
$m_\unicode{x3bb} \in {\mathbb Z}$
such that
![]() $\lim _\unicode{x3bb} T^{m_\unicode{x3bb} } x_\unicode{x3bb} = x$
and
$\lim _\unicode{x3bb} T^{m_\unicode{x3bb} } x_\unicode{x3bb} = x$
and
![]() $\lim _\unicode{x3bb} T^{m_\unicode{x3bb} } = u$
. Finally, we identify X with
$\lim _\unicode{x3bb} T^{m_\unicode{x3bb} } = u$
. Finally, we identify X with
![]() $\{\{x\} \subseteq 2^X : x\in X\}$
, so that the restriction map
$\{\{x\} \subseteq 2^X : x\in X\}$
, so that the restriction map
![]() $E(2^X,T) \to E(X,T)$
, which sends
$E(2^X,T) \to E(X,T)$
, which sends
![]() $u\in E(2^X,T)$
to the restriction
$u\in E(2^X,T)$
to the restriction
![]() $u|_X\colon X\to X$
, is an onto morphism of semigroups. As above, we will not distinguish between
$u|_X\colon X\to X$
, is an onto morphism of semigroups. As above, we will not distinguish between
![]() $u\in 2^X$
and
$u\in 2^X$
and
![]() $u|_X$
.
$u|_X$
.
2.2 Basics in symbolic dynamics
2.2.1 Words and subshifts
Let
![]() ${\mathcal A}$
be an alphabet i.e. a finite set. Elements in
${\mathcal A}$
be an alphabet i.e. a finite set. Elements in
![]() ${\mathcal A}$
are called letters and concatenations
${\mathcal A}$
are called letters and concatenations
![]() $w = a_1\ldots a_\ell $
of them are called words. The number
$w = a_1\ldots a_\ell $
of them are called words. The number
![]() $\ell $
is the length of w and it is denoted by
$\ell $
is the length of w and it is denoted by
![]() $|w|$
, the set of all words in
$|w|$
, the set of all words in
![]() ${\mathcal A}$
of length
${\mathcal A}$
of length
![]() $\ell $
is
$\ell $
is
![]() ${\mathcal A}^\ell $
, and
${\mathcal A}^\ell $
, and
 ${\mathcal A}^+ = \bigcup _{\ell \geq 1}{\mathcal A}^\ell $
. The word
${\mathcal A}^+ = \bigcup _{\ell \geq 1}{\mathcal A}^\ell $
. The word
![]() $w\in {\mathcal A}^+$
is
$w\in {\mathcal A}^+$
is
![]() $|u|$
-periodic, with
$|u|$
-periodic, with
![]() $u\in {\mathcal A}^+$
, if w occurs in a word of the form
$u\in {\mathcal A}^+$
, if w occurs in a word of the form
![]() $uu\ldots u$
. We define
$uu\ldots u$
. We define
![]() ${\mathrm {per}}(w)$
as the smallest p for which w is p-periodic. We will use notation analogous to that introduced in this paragraph when dealing with infinite words
${\mathrm {per}}(w)$
as the smallest p for which w is p-periodic. We will use notation analogous to that introduced in this paragraph when dealing with infinite words
![]() $x \in {\mathcal A}^{\mathbb N}$
and bi-infinite words
$x \in {\mathcal A}^{\mathbb N}$
and bi-infinite words
![]() $x \in {\mathcal A}^{\mathbb Z}$
. The set
$x \in {\mathcal A}^{\mathbb Z}$
. The set
![]() ${\mathcal A}^+$
equipped with the operation of concatenation can be viewed as the free semigroup on
${\mathcal A}^+$
equipped with the operation of concatenation can be viewed as the free semigroup on
![]() ${\mathcal A}$
. It is convenient to introduce the empty word
${\mathcal A}$
. It is convenient to introduce the empty word
![]() $1$
, which has length
$1$
, which has length
![]() $0$
and is a neutral element for the concatenation. In particular,
$0$
and is a neutral element for the concatenation. In particular,
![]() ${\mathcal A}^+\cup \{1\}$
is the free monoid in
${\mathcal A}^+\cup \{1\}$
is the free monoid in
![]() ${\mathcal A}$
. Finally, for
${\mathcal A}$
. Finally, for
![]() ${\mathcal W}\subseteq {\mathcal A}^+$
, we write
${\mathcal W}\subseteq {\mathcal A}^+$
, we write
![]() $\langle {\mathcal W}\rangle := \min _{w\in {\mathcal W}}|w|$
and
$\langle {\mathcal W}\rangle := \min _{w\in {\mathcal W}}|w|$
and
![]() $|W| := \max _{w\in {\mathcal W}}|w|$
.
$|W| := \max _{w\in {\mathcal W}}|w|$
.
The shift map
![]() $T \colon {\mathcal A}^{\mathbb Z} \to {\mathcal A}^{\mathbb Z}$
is defined by
$T \colon {\mathcal A}^{\mathbb Z} \to {\mathcal A}^{\mathbb Z}$
is defined by
![]() $T ((x_n)_{n\in \mathbb {Z}}) = (x_{n+1})_{n\in \mathbb {Z}}$
. For
$T ((x_n)_{n\in \mathbb {Z}}) = (x_{n+1})_{n\in \mathbb {Z}}$
. For
![]() $x \in {\mathcal A}^{\mathbb Z}$
and integers
$x \in {\mathcal A}^{\mathbb Z}$
and integers
![]() $i < j$
, we denote by
$i < j$
, we denote by
![]() $x_{[i,j)}$
the word
$x_{[i,j)}$
the word
![]() $x_ix_{i+1}\ldots x_j$
. Analogous notation will be used when dealing with intervals of the form
$x_ix_{i+1}\ldots x_j$
. Analogous notation will be used when dealing with intervals of the form
![]() $[i,\infty )$
,
$[i,\infty )$
,
![]() $(i,\infty )$
,
$(i,\infty )$
,
![]() $(-\infty ,i]$
, and
$(-\infty ,i]$
, and
![]() $(-\infty ,i)$
. A subshift is a topological dynamical system
$(-\infty ,i)$
. A subshift is a topological dynamical system
![]() $(X,T)$
, where X is a closed and T-invariant subset of
$(X,T)$
, where X is a closed and T-invariant subset of
![]() ${\mathcal A}^{\mathbb Z}$
(we consider the product topology in
${\mathcal A}^{\mathbb Z}$
(we consider the product topology in
![]() ${\mathcal A}^{\mathbb Z}$
) and T is the shift map. Classically one identifies
${\mathcal A}^{\mathbb Z}$
) and T is the shift map. Classically one identifies
![]() $(X,T)$
with X, so one says that X itself is a subshift. When we say that a sequence in a subshift is periodic (respectively aperiodic), we implicitly mean that this sequence is periodic (respectively aperiodic) for the action of the shift. Therefore, if
$(X,T)$
with X, so one says that X itself is a subshift. When we say that a sequence in a subshift is periodic (respectively aperiodic), we implicitly mean that this sequence is periodic (respectively aperiodic) for the action of the shift. Therefore, if
![]() $x\in {\mathcal A}^{\mathbb Z}$
is periodic, then
$x\in {\mathcal A}^{\mathbb Z}$
is periodic, then
![]() ${\mathrm {per}}(x)$
is equal to the size of the orbit of x. The language of a subshift
${\mathrm {per}}(x)$
is equal to the size of the orbit of x. The language of a subshift
![]() $X\subseteq {\mathcal A}^{\mathbb Z}$
is the set
$X\subseteq {\mathcal A}^{\mathbb Z}$
is the set
![]() ${\mathcal L}(X)$
of all words
${\mathcal L}(X)$
of all words
![]() $w\in {\mathcal A}^+$
that occur in some
$w\in {\mathcal A}^+$
that occur in some
![]() $x\in X$
.
$x\in X$
.
The pair
![]() $(x,\tilde {x}) \in {\mathcal A}^{\mathbb Z}\times {\mathcal A}^{\mathbb Z}$
is right asymptotic if there exist
$(x,\tilde {x}) \in {\mathcal A}^{\mathbb Z}\times {\mathcal A}^{\mathbb Z}$
is right asymptotic if there exist
![]() $k \in {\mathbb Z}$
satisfying
$k \in {\mathbb Z}$
satisfying
![]() $x_{(k,\infty )} = \tilde {x}_{(k,\infty )}$
and
$x_{(k,\infty )} = \tilde {x}_{(k,\infty )}$
and
![]() $x_k\not =\tilde {x}_k$
. If moreover
$x_k\not =\tilde {x}_k$
. If moreover
![]() $k=0$
,
$k=0$
,
![]() $(x,\tilde {x})$
is a centered right asymptotic. A right asymptotic tail is an element
$(x,\tilde {x})$
is a centered right asymptotic. A right asymptotic tail is an element
![]() $x_{(0,\infty )}$
, where
$x_{(0,\infty )}$
, where
![]() $(x,\tilde {x})$
is a centered right asymptotic pair. We make similar definitions for left asymptotic pairs and tails.
$(x,\tilde {x})$
is a centered right asymptotic pair. We make similar definitions for left asymptotic pairs and tails.
2.2.2 Morphisms and substitutions
Let
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() ${\mathcal B}$
be finite alphabets and
${\mathcal B}$
be finite alphabets and
![]() $\tau \colon {\mathcal A}^+ \to {\mathcal B}^+$
be a morphism between the free semigroups that they define. Then,
$\tau \colon {\mathcal A}^+ \to {\mathcal B}^+$
be a morphism between the free semigroups that they define. Then,
![]() $\tau $
extends naturally to maps from
$\tau $
extends naturally to maps from
![]() ${\mathcal A}^{\mathbb {N}}$
to itself and from
${\mathcal A}^{\mathbb {N}}$
to itself and from
![]() ${\mathcal A}^{\mathbb {Z}}$
to itself in the obvious way by concatenation (in the case of a two-sided sequence, we apply
${\mathcal A}^{\mathbb {Z}}$
to itself in the obvious way by concatenation (in the case of a two-sided sequence, we apply
![]() $\tau $
to positive and negative coordinates separately and we concatenate the results at coordinate zero). We say that
$\tau $
to positive and negative coordinates separately and we concatenate the results at coordinate zero). We say that
![]() $\tau $
is positive if for every
$\tau $
is positive if for every
![]() $a\in {\mathcal A}$
, all letters
$a\in {\mathcal A}$
, all letters
![]() $b \in {\mathcal B}$
occur in
$b \in {\mathcal B}$
occur in
![]() $\tau (a)$
, is r-proper, with
$\tau (a)$
, is r-proper, with
![]() $r\geq 1$
, if there exist
$r\geq 1$
, if there exist
![]() $u,v \in {\mathcal B}^r$
such that
$u,v \in {\mathcal B}^r$
such that
![]() $\tau (a)$
starts with u and ends with v for any
$\tau (a)$
starts with u and ends with v for any
![]() $a \in {\mathcal A}$
, is proper when is
$a \in {\mathcal A}$
, is proper when is
![]() $1$
-proper, and is letter-onto if for every
$1$
-proper, and is letter-onto if for every
![]() $b \in {\mathcal B}$
there exists
$b \in {\mathcal B}$
there exists
![]() $a \in {\mathcal A}$
such that b occurs in a. The minimum and maximum lengths of
$a \in {\mathcal A}$
such that b occurs in a. The minimum and maximum lengths of
![]() $\tau $
are respectively the numbers
$\tau $
are respectively the numbers
![]() $\langle \tau \rangle := \langle \tau ({\mathcal A})\rangle = \min _{a\in {\mathcal A}}|\tau (a)|$
and
$\langle \tau \rangle := \langle \tau ({\mathcal A})\rangle = \min _{a\in {\mathcal A}}|\tau (a)|$
and
![]() $|\tau | := |\tau ({\mathcal A})| = \max _{a\in {\mathcal A}}|\tau (a)|$
.
$|\tau | := |\tau ({\mathcal A})| = \max _{a\in {\mathcal A}}|\tau (a)|$
.
We observe that any map
![]() $\tau \colon {\mathcal A}\to {\mathcal B}^+$
can be naturally extended to a morphism (that we also denote by
$\tau \colon {\mathcal A}\to {\mathcal B}^+$
can be naturally extended to a morphism (that we also denote by
![]() $\tau $
) from
$\tau $
) from
![]() ${\mathcal A}^+$
to
${\mathcal A}^+$
to
![]() ${\mathcal B}^+$
by concatenation, and any morphism
${\mathcal B}^+$
by concatenation, and any morphism
![]() $\tau \colon {\mathcal A}^+\to {\mathcal B}^+$
is uniquely determined by its restriction to
$\tau \colon {\mathcal A}^+\to {\mathcal B}^+$
is uniquely determined by its restriction to
![]() ${\mathcal A}$
. From now on, we will use the same notation for denoting a map
${\mathcal A}$
. From now on, we will use the same notation for denoting a map
![]() $\tau \colon {\mathcal A}\to {\mathcal B}^+$
and its extension to a morphism
$\tau \colon {\mathcal A}\to {\mathcal B}^+$
and its extension to a morphism
![]() $\tau \colon {\mathcal A}^+\to {\mathcal B}^+$
.
$\tau \colon {\mathcal A}^+\to {\mathcal B}^+$
.
Definition 2.1. Let
![]() $X\subseteq {\mathcal A}^{\mathbb Z}$
be a subshift and
$X\subseteq {\mathcal A}^{\mathbb Z}$
be a subshift and
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism. We say that
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism. We say that
![]() $(k,x) \in {\mathbb Z}\times X$
is a
$(k,x) \in {\mathbb Z}\times X$
is a
![]() $\sigma $
-factorization of
$\sigma $
-factorization of
![]() $y \in {\mathcal B}^{\mathbb Z}$
in X if
$y \in {\mathcal B}^{\mathbb Z}$
in X if
![]() $y = T^k\sigma (x)$
. If moreover
$y = T^k\sigma (x)$
. If moreover
![]() $k\in [0,|\sigma (x_0)|)$
, then
$k\in [0,|\sigma (x_0)|)$
, then
![]() $(k,x)$
is a centered
$(k,x)$
is a centered
![]() $\sigma $
-factorization in X.
$\sigma $
-factorization in X.
The pair
![]() $(X,\sigma )$
is recognizable if every point
$(X,\sigma )$
is recognizable if every point
![]() $y \in {\mathcal B}^{\mathbb Z} $
has at most one centered
$y \in {\mathcal B}^{\mathbb Z} $
has at most one centered
![]() $\sigma $
-factorization in X, and recognizable with constant
$\sigma $
-factorization in X, and recognizable with constant
![]() $r \in {\mathbb N}$
if whenever
$r \in {\mathbb N}$
if whenever
 $y_{[-r,r]} = y^{\prime }_{[-r,r]}$
and
$y_{[-r,r]} = y^{\prime }_{[-r,r]}$
and
![]() $(k,x)$
,
$(k,x)$
,
![]() $(k',x')$
are centered
$(k',x')$
are centered
![]() $\sigma $
-factorizations of
$\sigma $
-factorizations of
![]() $y, y' \in {\mathcal B}^{\mathbb Z}$
in X, respectively, we have
$y, y' \in {\mathcal B}^{\mathbb Z}$
in X, respectively, we have
![]() $(k,x_0) = (k',x^{\prime }_0)$
.
$(k,x_0) = (k',x^{\prime }_0)$
.
The cuts of
![]() $(k,x)$
are defined by
$(k,x)$
are defined by
 $$ \begin{align*} c_{\sigma,j}(k,x) = \begin{cases} -k + |\sigma(x_{[0,j)})| &\text{if }j \geq 0, \\ -k - |\sigma(x_{[j,0)})| &\text{if }j < 0. \end{cases} \end{align*} $$
$$ \begin{align*} c_{\sigma,j}(k,x) = \begin{cases} -k + |\sigma(x_{[0,j)})| &\text{if }j \geq 0, \\ -k - |\sigma(x_{[j,0)})| &\text{if }j < 0. \end{cases} \end{align*} $$
We write
![]() $C_\sigma (k,x) = \{c_{\sigma ,j}(k,x) : j \in {\mathbb Z}\}$
.
$C_\sigma (k,x) = \{c_{\sigma ,j}(k,x) : j \in {\mathbb Z}\}$
.
Remark 2.2. In the context of the previous definition we have the following.
-
(i) The point
 $y \in {\mathcal B}^{\mathbb Z}$
has a (centered)
$y \in {\mathcal B}^{\mathbb Z}$
has a (centered)
 $\sigma $
-factorization in X if and only if y belongs to the subshift
$\sigma $
-factorization in X if and only if y belongs to the subshift
 $Y := \bigcup _{n\in {\mathbb Z}}T^n\sigma (X)$
. Hence,
$Y := \bigcup _{n\in {\mathbb Z}}T^n\sigma (X)$
. Hence,
 $(X,\sigma )$
is recognizable if and only if every
$(X,\sigma )$
is recognizable if and only if every
 $y\in Y$
has a exactly one centered
$y\in Y$
has a exactly one centered
 $\sigma $
-factorization in X.
$\sigma $
-factorization in X. -
(ii) If
 $(k,x)$
is a
$(k,x)$
is a
 $\sigma $
-factorization of
$\sigma $
-factorization of
 $y \in {\mathcal B}^{\mathbb Z}$
in X, then
$y \in {\mathcal B}^{\mathbb Z}$
in X, then
 $(c_{\sigma ,j}(k,x), T^j x)$
is a
$(c_{\sigma ,j}(k,x), T^j x)$
is a
 $\sigma $
-factorization of y in X for any
$\sigma $
-factorization of y in X for any
 $j \in {\mathbb Z}$
. There is exactly one factorization in this class that is centered.
$j \in {\mathbb Z}$
. There is exactly one factorization in this class that is centered. -
(iii) If
 $(X,\sigma )$
is recognizable, then it is recognizable with constant r for some
$(X,\sigma )$
is recognizable, then it is recognizable with constant r for some
 $r \in {\mathbb N}$
[Reference Donoso, Durand, Maass and PetiteDDMP21].
$r \in {\mathbb N}$
[Reference Donoso, Durand, Maass and PetiteDDMP21].
The behavior of recognizability under composition of morphisms is given by the following lemma.
Lemma 2.3. [Reference Berthé, Steiner, Thuswaldner and YassawiBSTY19, Lemma 3.5]
Let
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
and
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
and
![]() $\tau \colon {\mathcal B}^+\to {\mathcal C}^+$
be morphisms,
$\tau \colon {\mathcal B}^+\to {\mathcal C}^+$
be morphisms,
![]() $X\subseteq {\mathcal A}^{\mathbb Z}$
be a subshift, and
$X\subseteq {\mathcal A}^{\mathbb Z}$
be a subshift, and
 $Y = \bigcup _{k\in {\mathbb Z}}T^k\sigma (X)$
. Then,
$Y = \bigcup _{k\in {\mathbb Z}}T^k\sigma (X)$
. Then,
![]() $(X, \tau \sigma )$
is recognizable if and only if
$(X, \tau \sigma )$
is recognizable if and only if
![]() $(X,\sigma )$
and
$(X,\sigma )$
and
![]() $(Y,\tau )$
are recognizable.
$(Y,\tau )$
are recognizable.
Let
![]() $X \subseteq {\mathcal A}^{\mathbb Z}$
and
$X \subseteq {\mathcal A}^{\mathbb Z}$
and
![]() $Z \subseteq {\mathcal C}^{\mathbb Z}$
be subshifts and
$Z \subseteq {\mathcal C}^{\mathbb Z}$
be subshifts and
![]() $\pi \colon (X,T) \to (Z,T)$
a factor map. The classic Curtisâ–Hedlundâ–Lyndon theorem asserts that
$\pi \colon (X,T) \to (Z,T)$
a factor map. The classic Curtisâ–Hedlundâ–Lyndon theorem asserts that
![]() $\pi $
has a local code, this is, a function
$\pi $
has a local code, this is, a function
![]() $\psi \colon {\mathcal A}^{2r+1}\to {\mathcal C}$
, where
$\psi \colon {\mathcal A}^{2r+1}\to {\mathcal C}$
, where
![]() $r\in {\mathbb N}$
, such that
$r\in {\mathbb N}$
, such that
![]() $\pi (x) = (\psi (x_{[i-r,i+r]}))_{i\in {\mathbb Z}}$
for all
$\pi (x) = (\psi (x_{[i-r,i+r]}))_{i\in {\mathbb Z}}$
for all
![]() $x \in X$
. The integer r is called the a radius of
$x \in X$
. The integer r is called the a radius of
![]() $\pi $
. The following lemma relates the local code of a factor map to proper morphisms.
$\pi $
. The following lemma relates the local code of a factor map to proper morphisms.
Lemma 2.4. Let
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism,
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism,
![]() $X \subseteq {\mathcal A}^{\mathbb Z}$
and
$X \subseteq {\mathcal A}^{\mathbb Z}$
and
![]() $Z\subseteq {\mathcal C}^{\mathbb Z}$
be subshifts, and
$Z\subseteq {\mathcal C}^{\mathbb Z}$
be subshifts, and
 $Y = \bigcup _{k\in {\mathbb Z}}T^k\sigma (X)$
. Suppose that
$Y = \bigcup _{k\in {\mathbb Z}}T^k\sigma (X)$
. Suppose that
![]() $\pi \colon (Y,T)\to (Z,T)$
is a factor map of radius r and that
$\pi \colon (Y,T)\to (Z,T)$
is a factor map of radius r and that
![]() $\sigma $
is r-proper. Then, there exists a proper morphism
$\sigma $
is r-proper. Then, there exists a proper morphism
![]() $\tau \colon {\mathcal A}^+\to {\mathcal C}^+$
such that
$\tau \colon {\mathcal A}^+\to {\mathcal C}^+$
such that
![]() $|\tau (a)| = |\sigma (a)|$
for any
$|\tau (a)| = |\sigma (a)|$
for any
![]() $a \in {\mathcal A}$
,
$a \in {\mathcal A}$
,
 $Z = \bigcup _{k\in {\mathbb Z}}T^k\tau (X)$
and the following diagram commutes:
$Z = \bigcup _{k\in {\mathbb Z}}T^k\tau (X)$
and the following diagram commutes:

Proof. Let
![]() $\psi \colon {\mathcal A}^{2r+1}\to {\mathcal B}$
be a local code of radius r for
$\psi \colon {\mathcal A}^{2r+1}\to {\mathcal B}$
be a local code of radius r for
![]() $\pi $
and
$\pi $
and
![]() $u,v \in {\mathcal B}^r$
be such that
$u,v \in {\mathcal B}^r$
be such that
![]() $\sigma (a)$
starts with u and ends with v for all
$\sigma (a)$
starts with u and ends with v for all
![]() $a \in {\mathcal A}$
. We define
$a \in {\mathcal A}$
. We define
![]() $\tau \colon {\mathcal A}\to {\mathcal C}^+$
by
$\tau \colon {\mathcal A}\to {\mathcal C}^+$
by
![]() $\tau (a) = \psi (v\sigma (a)u)$
. Then, since
$\tau (a) = \psi (v\sigma (a)u)$
. Then, since
![]() $\sigma $
is r-proper,
$\sigma $
is r-proper,
![]() $\tau $
is proper and we have
$\tau $
is proper and we have
![]() $\pi (\sigma (x)) = \tau (x)$
for all
$\pi (\sigma (x)) = \tau (x)$
for all
![]() $x \in X$
(that is, Diagram (1) commutes). In particular,
$x \in X$
(that is, Diagram (1) commutes). In particular,
 $$ \begin{align*} \bigcup_{k\in{\mathbb Z}}T^k\tau(X) = \bigcup_{k\in{\mathbb Z}}T^k\pi(\sigma(X)) = \pi(Y) = Z.\\[-46pt] \end{align*} $$
$$ \begin{align*} \bigcup_{k\in{\mathbb Z}}T^k\tau(X) = \bigcup_{k\in{\mathbb Z}}T^k\pi(\sigma(X)) = \pi(Y) = Z.\\[-46pt] \end{align*} $$
2.2.3
 ${\mathcal S}$
-adic subshifts
${\mathcal S}$
-adic subshifts
We recall the definition of an
![]() ${\mathcal S}$
-adic subshift as stated in [Reference Berthé, Steiner, Thuswaldner and YassawiBSTY19]. A directive sequence
${\mathcal S}$
-adic subshift as stated in [Reference Berthé, Steiner, Thuswaldner and YassawiBSTY19]. A directive sequence
 $\boldsymbol {\sigma } = (\sigma _n \colon \mathcal {A}_{n+1}^+\to \mathcal {A}_n^+)_{n \in {\mathbb N}}$
is a sequence of morphisms. For
$\boldsymbol {\sigma } = (\sigma _n \colon \mathcal {A}_{n+1}^+\to \mathcal {A}_n^+)_{n \in {\mathbb N}}$
is a sequence of morphisms. For
![]() $0\leq n<N$
, we denote by
$0\leq n<N$
, we denote by
![]() $\sigma _{[n,N)}$
the morphism
$\sigma _{[n,N)}$
the morphism
![]() $\sigma _n \circ \sigma _{n+1} \circ \cdots \circ \sigma _{N-1}$
. We say that
$\sigma _n \circ \sigma _{n+1} \circ \cdots \circ \sigma _{N-1}$
. We say that
![]() $\boldsymbol {\sigma }$
is everywhere growing if
$\boldsymbol {\sigma }$
is everywhere growing if
 $$ \begin{align} \lim_{N\to +\infty}\langle\sigma_{[0,N)}\rangle = +\infty, \end{align} $$
$$ \begin{align} \lim_{N\to +\infty}\langle\sigma_{[0,N)}\rangle = +\infty, \end{align} $$
and primitive if for any
![]() $n\in {\mathbb N}$
, there exists
$n\in {\mathbb N}$
, there exists
![]() $N>n$
such that
$N>n$
such that
![]() $\sigma _{[n,N)}$
is positive. We remark that this notion is slightly different from the usual one used in the context of substitutional dynamical systems. Observe that
$\sigma _{[n,N)}$
is positive. We remark that this notion is slightly different from the usual one used in the context of substitutional dynamical systems. Observe that
![]() $\boldsymbol {\sigma }$
is everywhere growing if
$\boldsymbol {\sigma }$
is everywhere growing if
![]() $\boldsymbol {\sigma }$
is primitive. Let
$\boldsymbol {\sigma }$
is primitive. Let
![]() ${\mathcal P}$
be a property for morphisms (e.g. proper, letter-onto, etc). We say that
${\mathcal P}$
be a property for morphisms (e.g. proper, letter-onto, etc). We say that
![]() $\boldsymbol {\sigma }$
has property
$\boldsymbol {\sigma }$
has property
![]() ${\mathcal P}$
if
${\mathcal P}$
if
![]() $\sigma _n$
has property
$\sigma _n$
has property
![]() ${\mathcal P}$
for every
${\mathcal P}$
for every
![]() $n \in {\mathbb N}$
.
$n \in {\mathbb N}$
.
For
![]() $n\in {\mathbb N}$
, we define
$n\in {\mathbb N}$
, we define
 $$ \begin{align*} X^{(n)}_{\boldsymbol{\sigma}} = \{x \in \mathcal{A}_n^{\mathbb Z} :\text{ for all } \ell\in{\mathbb N}, x_{[-\ell,\ell]}\ \text{occurs in}\ \sigma_{[n,N)}(a)\ \text{for some}\ N>n, a \in\mathcal{A}_N\}. \end{align*} $$
$$ \begin{align*} X^{(n)}_{\boldsymbol{\sigma}} = \{x \in \mathcal{A}_n^{\mathbb Z} :\text{ for all } \ell\in{\mathbb N}, x_{[-\ell,\ell]}\ \text{occurs in}\ \sigma_{[n,N)}(a)\ \text{for some}\ N>n, a \in\mathcal{A}_N\}. \end{align*} $$
This set clearly defines a subshift that we call the nth level of the
![]() ${\mathcal S}$
-adic subshift generated by
${\mathcal S}$
-adic subshift generated by
![]() $\boldsymbol {\sigma }$
. We set
$\boldsymbol {\sigma }$
. We set
 $X_{\boldsymbol {\sigma }} = X^{(0)}_{\boldsymbol {\sigma }}$
and simply call it the
$X_{\boldsymbol {\sigma }} = X^{(0)}_{\boldsymbol {\sigma }}$
and simply call it the
![]() ${\mathcal S}$
-adic subshift generated by
${\mathcal S}$
-adic subshift generated by
![]() $\boldsymbol {\sigma }$
. If
$\boldsymbol {\sigma }$
. If
![]() $\boldsymbol {\sigma }$
is everywhere growing, then every
$\boldsymbol {\sigma }$
is everywhere growing, then every
 $X^{(n)}_{\boldsymbol {\sigma }}$
,
$X^{(n)}_{\boldsymbol {\sigma }}$
,
![]() $n\in {\mathbb N}$
, is non-empty; if
$n\in {\mathbb N}$
, is non-empty; if
![]() $\boldsymbol {\sigma }$
is primitive, then
$\boldsymbol {\sigma }$
is primitive, then
 $X^{(n)}_{\boldsymbol {\sigma }}$
is minimal for every
$X^{(n)}_{\boldsymbol {\sigma }}$
is minimal for every
![]() $n\in {\mathbb N}$
. There are non-everywhere growing directive sequences that generate minimal subshifts.
$n\in {\mathbb N}$
. There are non-everywhere growing directive sequences that generate minimal subshifts.
The relation between levels of an
![]() ${\mathcal S}$
-adic subshift is given by the following lemma.
${\mathcal S}$
-adic subshift is given by the following lemma.
Lemma 2.5. [Reference Berthé, Steiner, Thuswaldner and YassawiBSTY19, Lemma 4.2]
Let
 $\boldsymbol {\sigma } = (\sigma _n \colon \mathcal {A}_{n+1}^+\to \mathcal {A}_n^+)_{n \in {\mathbb N}}$
be a directive sequence of morphisms. If
$\boldsymbol {\sigma } = (\sigma _n \colon \mathcal {A}_{n+1}^+\to \mathcal {A}_n^+)_{n \in {\mathbb N}}$
be a directive sequence of morphisms. If
![]() $0\leq n < N$
and
$0\leq n < N$
and
 $x \in X_{\boldsymbol {\sigma }}^{(n)}$
, then there exists a (centered)
$x \in X_{\boldsymbol {\sigma }}^{(n)}$
, then there exists a (centered)
![]() $\sigma _{[n,N)}$
-factorization in
$\sigma _{[n,N)}$
-factorization in
 $X_{\boldsymbol {\sigma }}^{(N)}$
. In particular,
$X_{\boldsymbol {\sigma }}^{(N)}$
. In particular,
 $X_{\boldsymbol {\sigma }}^{(n)} = \bigcup _{k\in {\mathbb Z}}T^k\sigma _{[n,N)}(X_{\boldsymbol {\sigma }}^{(N)})$
.
$X_{\boldsymbol {\sigma }}^{(n)} = \bigcup _{k\in {\mathbb Z}}T^k\sigma _{[n,N)}(X_{\boldsymbol {\sigma }}^{(N)})$
.
The levels
 $X_{\boldsymbol {\sigma }}^{(n)}$
can be described in an alternative way if
$X_{\boldsymbol {\sigma }}^{(n)}$
can be described in an alternative way if
![]() $\boldsymbol {\sigma }$
satisfies the correct hypothesis.
$\boldsymbol {\sigma }$
satisfies the correct hypothesis.
Lemma 2.6. Let
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be an everywhere growing and proper directive sequence. Then, for every
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be an everywhere growing and proper directive sequence. Then, for every
![]() $n \in {\mathbb N}$
,
$n \in {\mathbb N}$
,
 $$ \begin{align} X_{\boldsymbol{\sigma}}^{(n)} = \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\sigma_{[n,N)}({\mathcal A}_N^{\mathbb Z}). \end{align} $$
$$ \begin{align} X_{\boldsymbol{\sigma}}^{(n)} = \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\sigma_{[n,N)}({\mathcal A}_N^{\mathbb Z}). \end{align} $$
Proof. Let Z be the set in the right-hand side of (3). Since, by Lemma 2.5,
 $X_{\boldsymbol {\sigma }}^{(n)} = \bigcup _{k\in {\mathbb Z}}T^k\sigma _{[n,N)}(X_{\boldsymbol {\sigma }}^{(N)})$
for any
$X_{\boldsymbol {\sigma }}^{(n)} = \bigcup _{k\in {\mathbb Z}}T^k\sigma _{[n,N)}(X_{\boldsymbol {\sigma }}^{(N)})$
for any
![]() $N> n$
, we have that
$N> n$
, we have that
 $X_{\boldsymbol {\sigma }}^{(n)}$
included in Z.
$X_{\boldsymbol {\sigma }}^{(n)}$
included in Z.
Conversely, let
![]() $x\in Z$
and
$x\in Z$
and
![]() $\ell \in {\mathbb N}$
. We have to show that
$\ell \in {\mathbb N}$
. We have to show that
![]() $x_{[-\ell ,\ell )}$
occurs in
$x_{[-\ell ,\ell )}$
occurs in
![]() $\sigma _{[n,N)}(a)$
for some
$\sigma _{[n,N)}(a)$
for some
![]() $N>n$
and
$N>n$
and
![]() $a \in {\mathcal A}_N$
. Let
$a \in {\mathcal A}_N$
. Let
![]() $N>n$
be big enough so that
$N>n$
be big enough so that
![]() $\sigma _{[n,N)}$
is
$\sigma _{[n,N)}$
is
![]() $\ell $
-proper. Then, by the definition of Z, there exists
$\ell $
-proper. Then, by the definition of Z, there exists
 $y \in {\mathcal A}_N^{\mathbb Z}$
such that
$y \in {\mathcal A}_N^{\mathbb Z}$
such that
![]() $x_{[-\ell ,\ell )}$
occurs in
$x_{[-\ell ,\ell )}$
occurs in
![]() $\sigma _{[n,N)}(y)$
. Since
$\sigma _{[n,N)}(y)$
. Since
![]() $\langle \sigma _{[n,N)}\rangle \geq \ell $
(as
$\langle \sigma _{[n,N)}\rangle \geq \ell $
(as
![]() $\sigma _{[n,N)}$
is
$\sigma _{[n,N)}$
is
![]() $\ell $
-proper), we deduce that
$\ell $
-proper), we deduce that
Hence, by denoting by u and v the suffix and prefix of length
![]() $\ell $
of
$\ell $
of
![]() $\tau _{[n,N)}(a)$
and
$\tau _{[n,N)}(a)$
and
![]() $\tau _{[n,N)}(b)$
, respectively, we have that
$\tau _{[n,N)}(b)$
, respectively, we have that
![]() $x_{[-\ell ,\ell )}$
occurs in
$x_{[-\ell ,\ell )}$
occurs in
![]() $\sigma _{[n,N)}(a)$
, in
$\sigma _{[n,N)}(a)$
, in
![]() $\tau _{[n,N)}(b)$
, or in
$\tau _{[n,N)}(b)$
, or in
![]() $uv$
. In the first two cases, we are done. In the last case, we observe that since
$uv$
. In the first two cases, we are done. In the last case, we observe that since
![]() $\sigma _{[n,N)}$
is
$\sigma _{[n,N)}$
is
![]() $\ell $
-proper, the following is true: for every
$\ell $
-proper, the following is true: for every
![]() $M>N$
such that
$M>N$
such that
![]() $\langle \sigma _{[N,M)}\rangle \geq 2$
,
$\langle \sigma _{[N,M)}\rangle \geq 2$
,
![]() $vu\sqsubseteq \sigma _{[n,M)}(c)$
for any
$vu\sqsubseteq \sigma _{[n,M)}(c)$
for any
![]() $c \in {\mathcal A}_M$
. In particular,
$c \in {\mathcal A}_M$
. In particular,
![]() $x_{[-\ell ,\ell )}\sqsubseteq \tau _{[n,M)}(c)$
for such M and c. We have proved that
$x_{[-\ell ,\ell )}\sqsubseteq \tau _{[n,M)}(c)$
for such M and c. We have proved that
 $x \in X_{\boldsymbol {\sigma }}^{(n)}$
.
$x \in X_{\boldsymbol {\sigma }}^{(n)}$
.
We define the alphabet rank of a directive sequence
![]() $\boldsymbol {\tau }$
as
$\boldsymbol {\tau }$
as
 $$\begin{align*}AR(\boldsymbol{\tau}) = \liminf_{n\to +\infty} \#{\mathcal A}_n.\end{align*}$$
$$\begin{align*}AR(\boldsymbol{\tau}) = \liminf_{n\to +\infty} \#{\mathcal A}_n.\end{align*}$$
A contraction of
![]() $\boldsymbol {\tau }$
is a sequence
$\boldsymbol {\tau }$
is a sequence
 $\tilde {\boldsymbol {\tau }} = (\tau _{[n_k,n_{k+1})}\colon {\mathcal A}_{n_{k+1}}^+\to {\mathcal A}_{n_k}^+)_{k\in {\mathbb N}}$
, where
$\tilde {\boldsymbol {\tau }} = (\tau _{[n_k,n_{k+1})}\colon {\mathcal A}_{n_{k+1}}^+\to {\mathcal A}_{n_k}^+)_{k\in {\mathbb N}}$
, where
![]() $0 = n_0 < n_1 < n_2 < \ldots $
. Observe that any contraction of
$0 = n_0 < n_1 < n_2 < \ldots $
. Observe that any contraction of
![]() $\boldsymbol {\tau }$
generates the same
$\boldsymbol {\tau }$
generates the same
![]() ${\mathcal S}$
-adic subshift
${\mathcal S}$
-adic subshift
![]() $X_{\boldsymbol {\tau }}$
. When the context is clear, we will use the same notation to refer to
$X_{\boldsymbol {\tau }}$
. When the context is clear, we will use the same notation to refer to
![]() $\boldsymbol {\tau }$
and its contractions. If
$\boldsymbol {\tau }$
and its contractions. If
![]() $\boldsymbol {\tau }$
has finite alphabet rank, then there exists a contraction
$\boldsymbol {\tau }$
has finite alphabet rank, then there exists a contraction
 $\tilde {\boldsymbol {\tau }} = (\tau _{[n_k,n_{k+1})}\colon {\mathcal A}_{n_{k+1}}^+\to {\mathcal A}_{n_k}^+)_{k\in {\mathbb N}}$
of
$\tilde {\boldsymbol {\tau }} = (\tau _{[n_k,n_{k+1})}\colon {\mathcal A}_{n_{k+1}}^+\to {\mathcal A}_{n_k}^+)_{k\in {\mathbb N}}$
of
![]() $\boldsymbol {\tau }$
in which
$\boldsymbol {\tau }$
in which
![]() ${\mathcal A}_{n_k}$
has cardinality
${\mathcal A}_{n_k}$
has cardinality
![]() $AR(\boldsymbol {\tau })$
for every
$AR(\boldsymbol {\tau })$
for every
![]() $k\geq 1$
.
$k\geq 1$
.
Finite alphabet rank
![]() ${\mathcal S}$
-adic subshifts are eventually recognizable.
${\mathcal S}$
-adic subshifts are eventually recognizable.
Theorem 2.7. [Reference Donoso, Durand, Maass and PetiteDDMP21, Theorem 3.7]
Let
![]() $\boldsymbol {\sigma }$
be an everywhere growing directive sequence of alphabet rank equal to K. Suppose that
$\boldsymbol {\sigma }$
be an everywhere growing directive sequence of alphabet rank equal to K. Suppose that
![]() $X_{\boldsymbol {\sigma }}$
is aperiodic. Then, at most
$X_{\boldsymbol {\sigma }}$
is aperiodic. Then, at most
![]() $\log _2 K$
levels
$\log _2 K$
levels
 $(X_{\boldsymbol {\sigma }}^{(n)},\sigma _n)$
are not recognizable.
$(X_{\boldsymbol {\sigma }}^{(n)},\sigma _n)$
are not recognizable.
We will also need the following property.
Theorem 2.8. [Reference Espinoza and MaassEM21, Theorem 3.3]
Let
![]() $(X,T)$
be an
$(X,T)$
be an
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing directive sequence of alphabet rank K. Then, X has at most
${\mathcal S}$
-adic subshift generated by an everywhere growing directive sequence of alphabet rank K. Then, X has at most
![]() $144K^7$
right (respectively left) asymptotic tails.
$144K^7$
right (respectively left) asymptotic tails.
Proof. In the proof of theorem 3.3 in [Reference Espinoza and MaassEM21], the authors show the following: the set consisting of pairs
![]() $(x,y) \in X \times X$
such that
$(x,y) \in X \times X$
such that
![]() $x_{(-\infty ,0)} = y_{(-\infty ,0)}$
and
$x_{(-\infty ,0)} = y_{(-\infty ,0)}$
and
![]() $x_0\not =y_0$
has at most
$x_0\not =y_0$
has at most
![]() $144K^7$
elements. In our language, this is equivalent to saying that X has at most
$144K^7$
elements. In our language, this is equivalent to saying that X has at most
![]() $144K^7$
left asymptotic tails. Since this is valid for any
$144K^7$
left asymptotic tails. Since this is valid for any
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing directive sequence of alphabet rank K,
${\mathcal S}$
-adic subshift generated by an everywhere growing directive sequence of alphabet rank K,
![]() $144K^7$
is also an upper bound for right asymptotic tails.
$144K^7$
is also an upper bound for right asymptotic tails.
3 Combinatorics on words lemmas
In this section, we present several combinatorial lemmas that will be used throughout the article.
3.1 Lowering the rank
Let
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism. Following ideas from [Reference Rozenberg and SalomaaRS97], we define the rank of
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism. Following ideas from [Reference Rozenberg and SalomaaRS97], we define the rank of
![]() $\sigma $
as the least cardinality of a set of words
$\sigma $
as the least cardinality of a set of words
![]() ${\mathcal D} \subseteq {\mathcal B}^+$
such that
${\mathcal D} \subseteq {\mathcal B}^+$
such that
![]() $\sigma ({\mathcal A}^+) \subseteq {\mathcal D}^+$
. Equivalently, the rank is the minimum cardinality of an alphabet
$\sigma ({\mathcal A}^+) \subseteq {\mathcal D}^+$
. Equivalently, the rank is the minimum cardinality of an alphabet
![]() ${\mathcal C}$
in a decomposition into morphisms
${\mathcal C}$
in a decomposition into morphisms
![]() ${\mathcal A}^+ \overset {q}{\longrightarrow } {\mathcal C}^+ \overset {p}{\longrightarrow } {\mathcal B}^+$
such that
${\mathcal A}^+ \overset {q}{\longrightarrow } {\mathcal C}^+ \overset {p}{\longrightarrow } {\mathcal B}^+$
such that
![]() $\sigma = pq$
. In this subsection, we prove Lemma 3.6, which states that in certain technical situations, the rank of the morphism
$\sigma = pq$
. In this subsection, we prove Lemma 3.6, which states that in certain technical situations, the rank of the morphism
![]() $\sigma $
under consideration is small and its decomposition
$\sigma $
under consideration is small and its decomposition
![]() $\sigma = pq$
satisfies additional properties.
$\sigma = pq$
satisfies additional properties.
We start by defining some morphisms that will be used in the proofs of this subsection. If
![]() $a\not =b \in {\mathcal A}$
are different letters and
$a\not =b \in {\mathcal A}$
are different letters and
![]() $\tilde {a}$
is a letter not in
$\tilde {a}$
is a letter not in
![]() ${\mathcal A}$
, then we define
${\mathcal A}$
, then we define
![]() $\phi _{a,b}\colon {\mathcal A}^+\to ({\mathcal A}\setminus \{b\})^+$
,
$\phi _{a,b}\colon {\mathcal A}^+\to ({\mathcal A}\setminus \{b\})^+$
,
![]() $\psi _{a,b}\colon {\mathcal A}^+\to {\mathcal A}^+$
, and
$\psi _{a,b}\colon {\mathcal A}^+\to {\mathcal A}^+$
, and
![]() $\theta _{a, \tilde {a}}\colon {\mathcal A}^+\to ({\mathcal A}\cup \{\tilde {a}\})^+$
by
$\theta _{a, \tilde {a}}\colon {\mathcal A}^+\to ({\mathcal A}\cup \{\tilde {a}\})^+$
by
 $$ \begin{align*} \phi_{a,b}(c) = \begin{cases} c & \text{if}\ c\not=b, \\ a & \text{if}\ c=b. \end{cases} \qquad \psi_{a,b}(c) = \begin{cases} c & \text{if}\ c\not=b, \\ ab & \text{if}\ c=b. \end{cases} \qquad \theta_{a,\tilde{a}}(c) = \begin{cases} c & \text{if}\ c\not=a, \\ \tilde{a}a & \text{if}\ c=a. \end{cases} \end{align*} $$
$$ \begin{align*} \phi_{a,b}(c) = \begin{cases} c & \text{if}\ c\not=b, \\ a & \text{if}\ c=b. \end{cases} \qquad \psi_{a,b}(c) = \begin{cases} c & \text{if}\ c\not=b, \\ ab & \text{if}\ c=b. \end{cases} \qquad \theta_{a,\tilde{a}}(c) = \begin{cases} c & \text{if}\ c\not=a, \\ \tilde{a}a & \text{if}\ c=a. \end{cases} \end{align*} $$
Observe that these morphisms are letter-onto. Before stating the basic properties of these morphisms, we need one more set of definitions.
For a morphism
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
, we define
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
, we define
![]() $|\sigma |_1 = \sum _{a\in {\mathcal A}}|\sigma (a)|$
. When
$|\sigma |_1 = \sum _{a\in {\mathcal A}}|\sigma (a)|$
. When
![]() $u,v,w\in {\mathcal A}^+$
satisfy
$u,v,w\in {\mathcal A}^+$
satisfy
![]() $w = uv$
, we say that u is a prefix of w and that v a suffix of w. Recall that
$w = uv$
, we say that u is a prefix of w and that v a suffix of w. Recall that
![]() $1$
stands for the empty word.
$1$
stands for the empty word.
Lemma 3.1. Let
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism.
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism.
-
(i) If
 $\sigma (a) = \sigma (b)$
for some
$\sigma (a) = \sigma (b)$
for some
 $a\not =b\in {\mathcal A}$
, then
$a\not =b\in {\mathcal A}$
, then
 $\sigma = \sigma '\phi _{a,b}$
, where
$\sigma = \sigma '\phi _{a,b}$
, where
 $\sigma '\colon ({\mathcal A}\setminus \{b\})^+\to {\mathcal B}^+$
is the restriction of
$\sigma '\colon ({\mathcal A}\setminus \{b\})^+\to {\mathcal B}^+$
is the restriction of
 $\sigma $
to
$\sigma $
to
 $({\mathcal A}\setminus \{b\})^+$
.
$({\mathcal A}\setminus \{b\})^+$
. -
(ii) If
 $\sigma (a)$
is a prefix of
$\sigma (a)$
is a prefix of
 $\sigma (b)$
and
$\sigma (b)$
and
 $\sigma (b) = \sigma (a)t$
for some non-empty
$\sigma (b) = \sigma (a)t$
for some non-empty
 $t\in {\mathcal B}^+$
, then
$t\in {\mathcal B}^+$
, then
 $\sigma = \sigma '\psi _{a,b}$
, where
$\sigma = \sigma '\psi _{a,b}$
, where
 $\sigma '\colon {\mathcal A}^+\to {\mathcal B}^+$
is defined by (5)
$\sigma '\colon {\mathcal A}^+\to {\mathcal B}^+$
is defined by (5) $$ \begin{align} \sigma'(c) = \begin{cases} \sigma(c) & \text{if}\ c\not=b, \\ t & \text{if}\ c=b. \end{cases} \end{align} $$
$$ \begin{align} \sigma'(c) = \begin{cases} \sigma(c) & \text{if}\ c\not=b, \\ t & \text{if}\ c=b. \end{cases} \end{align} $$
-
(iii) If
 $\sigma (a) = st$
for some
$\sigma (a) = st$
for some
 $s,t\in {\mathcal B}^+$
and
$s,t\in {\mathcal B}^+$
and
 $a\in {\mathcal A}$
, then
$a\in {\mathcal A}$
, then
 $\sigma = \sigma '\theta _{a,\tilde {a}}$
, where
$\sigma = \sigma '\theta _{a,\tilde {a}}$
, where
 $\sigma '\colon ({\mathcal A}\cup \{\tilde {a}\})^+\to {\mathcal B}^+$
is defined by (6)
$\sigma '\colon ({\mathcal A}\cup \{\tilde {a}\})^+\to {\mathcal B}^+$
is defined by (6) $$ \begin{align} \sigma'(c) = \begin{cases} \sigma(c) & \text{if}\ c\not=a,\tilde{a}, \\ s & \text{if}\ c=\tilde{a}, \\ t & \text{if}\ c=a. \end{cases} \end{align} $$
$$ \begin{align} \sigma'(c) = \begin{cases} \sigma(c) & \text{if}\ c\not=a,\tilde{a}, \\ s & \text{if}\ c=\tilde{a}, \\ t & \text{if}\ c=a. \end{cases} \end{align} $$
Proof. The lemma follows from unraveling the definitions. For instance, in case (ii), we have
![]() $\sigma '(\psi _{a,b}(a)) = \sigma '(a) = \sigma (a)$
,
$\sigma '(\psi _{a,b}(a)) = \sigma '(a) = \sigma (a)$
,
![]() $\sigma '(\psi _{a,b}(b)) = \sigma '(ab) = \sigma (a)t = \sigma (b)$
, and
$\sigma '(\psi _{a,b}(b)) = \sigma '(ab) = \sigma (a)t = \sigma (b)$
, and
![]() $\sigma '(\psi _{a,b}(c)) = \sigma '(c) = \sigma (c)$
for all
$\sigma '(\psi _{a,b}(c)) = \sigma '(c) = \sigma (c)$
for all
![]() $c \not = a,b$
, which shows that
$c \not = a,b$
, which shows that
![]() $\sigma '\psi _{a,b} = \sigma $
.
$\sigma '\psi _{a,b} = \sigma $
.
Lemma 3.2. Let
 $\{\sigma _j\colon {\mathcal A}^+\to {\mathcal B}_j^+\}_{j\in J}$
be a set of morphisms such that
$\{\sigma _j\colon {\mathcal A}^+\to {\mathcal B}_j^+\}_{j\in J}$
be a set of morphisms such that
and
![]() $u,v \in {\mathcal A}^+$
, with u of length at least
$u,v \in {\mathcal A}^+$
, with u of length at least
![]() $\ell := \sum _{a\in {\mathcal A}}\ell _a$
. Assume that u and v start with different letters and that
$\ell := \sum _{a\in {\mathcal A}}\ell _a$
. Assume that u and v start with different letters and that
![]() $\sigma _j(u)$
is a prefix of
$\sigma _j(u)$
is a prefix of
![]() $\sigma _j(v)$
for every
$\sigma _j(v)$
for every
![]() $j \in J$
.
$j \in J$
.
Then, there exists a letter-onto morphism
![]() $q\colon {\mathcal A}^+ \to {\mathcal C}^+$
, with
$q\colon {\mathcal A}^+ \to {\mathcal C}^+$
, with
![]() $\#{\mathcal C} < \#{\mathcal A}$
, and morphisms
$\#{\mathcal C} < \#{\mathcal A}$
, and morphisms
 $\{p_j\colon {\mathcal C}^+\to {\mathcal B}_j^+\}_{j\in J}$
satisfying a condition analogous to (7) and such that
$\{p_j\colon {\mathcal C}^+\to {\mathcal B}_j^+\}_{j\in J}$
satisfying a condition analogous to (7) and such that
![]() $\sigma _j = p_jq$
.
$\sigma _j = p_jq$
.
Remark 3.3. If in the previous lemma we change the last hypothesis to ‘u and v end with different letters and
![]() $\sigma _j(u)$
is a suffix of
$\sigma _j(u)$
is a suffix of
![]() $\sigma _j(v)$
for every
$\sigma _j(v)$
for every
![]() $j \in J$
’, then the same conclusion holds. This observation will be used in the proof of Lemma 6.7.
$j \in J$
’, then the same conclusion holds. This observation will be used in the proof of Lemma 6.7.
Proof of Lemma 3.2
By contradiction, we assume that u, v, and
![]() $\{\sigma _j\}_{j \in J}$
are counterexamples for the lemma. Moreover, we suppose that
$\{\sigma _j\}_{j \in J}$
are counterexamples for the lemma. Moreover, we suppose that
![]() $\ell $
is as small as possible.
$\ell $
is as small as possible.
Let us write
![]() $u = au'$
and
$u = au'$
and
![]() $v=bv'$
, where
$v=bv'$
, where
![]() $a,b \in {\mathcal A}$
. Since
$a,b \in {\mathcal A}$
. Since
![]() $\sigma _j(u)$
is a prefix of
$\sigma _j(u)$
is a prefix of
![]() $\sigma _j(v)$
, we have that for every
$\sigma _j(v)$
, we have that for every
![]() $j \in J$
,
$j \in J$
,
We consider two cases. First, we suppose that
![]() $\ell _a = \ell _b$
. In this case, (8) implies that
$\ell _a = \ell _b$
. In this case, (8) implies that
![]() $\sigma _j(a) = \sigma _j(b)$
for every
$\sigma _j(a) = \sigma _j(b)$
for every
![]() $j\in J$
. Hence, we can use (i) of Lemma 3.1 to decompose each
$j\in J$
. Hence, we can use (i) of Lemma 3.1 to decompose each
![]() $\sigma _j$
as
$\sigma _j$
as
 $\sigma _j'\phi _{a,b}$
, where
$\sigma _j'\phi _{a,b}$
, where
![]() $\sigma ^{\prime }_j$
is the restriction of
$\sigma ^{\prime }_j$
is the restriction of
![]() $\sigma _j$
to
$\sigma _j$
to
![]() $({\mathcal A}\setminus \{b\})^+$
. Since
$({\mathcal A}\setminus \{b\})^+$
. Since
![]() $\phi _{a,b}$
is letter-onto and
$\phi _{a,b}$
is letter-onto and
 $\ell _c = |\sigma ^{\prime }_j(c)|$
for every
$\ell _c = |\sigma ^{\prime }_j(c)|$
for every
![]() $j \in J$
,
$j \in J$
,
![]() $c\in {\mathcal A}\setminus \{b\}$
, the conclusion of the lemma holds, contrary to our assumptions.
$c\in {\mathcal A}\setminus \{b\}$
, the conclusion of the lemma holds, contrary to our assumptions.
This leaves to consider the case in which
![]() $\ell _a \not = \ell _b$
. We only do the case
$\ell _a \not = \ell _b$
. We only do the case
![]() $\ell _a < \ell _b$
as the other is similar. Then, by (8), for every
$\ell _a < \ell _b$
as the other is similar. Then, by (8), for every
![]() $j \in J$
, there exists a non-empty word
$j \in J$
, there exists a non-empty word
 $t_j \in {\mathcal B}_j^{\ell _b-\ell _a}$
of length
$t_j \in {\mathcal B}_j^{\ell _b-\ell _a}$
of length
![]() $\ell _b-\ell _a$
such that
$\ell _b-\ell _a$
such that
![]() $\sigma _j(b) = \sigma _j(a)t_j$
. Thus, we can use (ii) of Lemma 3.1 to write, for any
$\sigma _j(b) = \sigma _j(a)t_j$
. Thus, we can use (ii) of Lemma 3.1 to write, for any
![]() $j \in J$
,
$j \in J$
,
 $\sigma _j = \sigma ^{\prime }_j\psi _{a,b}$
, where
$\sigma _j = \sigma ^{\prime }_j\psi _{a,b}$
, where
![]() $\sigma ^{\prime }_j$
is defined as in (5).
$\sigma ^{\prime }_j$
is defined as in (5).
Let
![]() $\tilde {u} = \psi _{a,b}(u')$
and
$\tilde {u} = \psi _{a,b}(u')$
and
![]() $\tilde {v} = b\psi _{a,b}(v')$
. We want now to prove that
$\tilde {v} = b\psi _{a,b}(v')$
. We want now to prove that
![]() $\tilde {u}$
,
$\tilde {u}$
,
![]() $\tilde {v}$
, and
$\tilde {v}$
, and
 $\{\sigma ^{\prime }_j : j \in J\}$
satisfy the hypothesis of the lemma. First, we observe that for every
$\{\sigma ^{\prime }_j : j \in J\}$
satisfy the hypothesis of the lemma. First, we observe that for every
![]() $j \in J$
,
$j \in J$
,
 $$ \begin{align} \text{if }c\not=b, \text{ then } |\sigma^{\prime}_j(c)| = \ell_c, \text{ and } |\sigma^{\prime}_j(b)| = |t_j| = \ell_b-\ell_a. \end{align} $$
$$ \begin{align} \text{if }c\not=b, \text{ then } |\sigma^{\prime}_j(c)| = \ell_c, \text{ and } |\sigma^{\prime}_j(b)| = |t_j| = \ell_b-\ell_a. \end{align} $$
Therefore,
 $\{\sigma ^{\prime }_j\}_{j\in J}$
satisfy (7). Also, since
$\{\sigma ^{\prime }_j\}_{j\in J}$
satisfy (7). Also, since
![]() $\psi _{a,b}(c)$
never starts with b, we have that
$\psi _{a,b}(c)$
never starts with b, we have that
Furthermore, by using the symbol
![]() $\leq _p$
to denote the prefix relation, we can compute:
$\leq _p$
to denote the prefix relation, we can compute:
 $$ \begin{align*} \sigma_j(a)\sigma^{\prime}_j(\tilde{u}) &= \sigma_j(a)\sigma_j(u') = \sigma_j(u) \leq_p \sigma_j(v) = \sigma^{\prime}_j(\psi_{a,b}(v)) = \sigma^{\prime}_j(a)\sigma^{\prime}_j(\tilde{v}). \end{align*} $$
$$ \begin{align*} \sigma_j(a)\sigma^{\prime}_j(\tilde{u}) &= \sigma_j(a)\sigma_j(u') = \sigma_j(u) \leq_p \sigma_j(v) = \sigma^{\prime}_j(\psi_{a,b}(v)) = \sigma^{\prime}_j(a)\sigma^{\prime}_j(\tilde{v}). \end{align*} $$
This and the fact that
![]() $\sigma _j(a)$
is equal to
$\sigma _j(a)$
is equal to
 $\sigma ^{\prime }_j(a)$
imply that
$\sigma ^{\prime }_j(a)$
imply that
 $$ \begin{align} \sigma^{\prime}_j(\tilde{u}) \text{ is a prefix of } \sigma^{\prime}_j(\tilde{v}) \text{ for every } j \in J. \end{align} $$
$$ \begin{align} \sigma^{\prime}_j(\tilde{u}) \text{ is a prefix of } \sigma^{\prime}_j(\tilde{v}) \text{ for every } j \in J. \end{align} $$
Finally, we note
 $$ \begin{align} |\tilde{u}| \geq |u|-1 \geq \sum_{c\in{\mathcal A}}\ell_c - \ell_a =: \ell'. \end{align} $$
$$ \begin{align} |\tilde{u}| \geq |u|-1 \geq \sum_{c\in{\mathcal A}}\ell_c - \ell_a =: \ell'. \end{align} $$
We conclude from (9), (10), (11), and (12) that
![]() $\tilde {u}$
,
$\tilde {u}$
,
![]() $\tilde {v}$
, and
$\tilde {v}$
, and
 $\{\sigma ^{\prime }_j : j \in J\}$
satisfy the hypothesis of this lemma. Since
$\{\sigma ^{\prime }_j : j \in J\}$
satisfy the hypothesis of this lemma. Since
![]() $\ell ' < \ell $
, the minimality of
$\ell ' < \ell $
, the minimality of
![]() $\ell $
implies that there exist a letter-onto morphism
$\ell $
implies that there exist a letter-onto morphism
![]() $q'\colon {\mathcal A}^+\to {\mathcal C}^+$
, with
$q'\colon {\mathcal A}^+\to {\mathcal C}^+$
, with
![]() $\#{\mathcal C} < \#{\mathcal A}$
, and morphisms
$\#{\mathcal C} < \#{\mathcal A}$
, and morphisms
 $\{p_j\colon {\mathcal C}^+\to {\mathcal B}_j^+\}_{j\in J}$
satisfying
$\{p_j\colon {\mathcal C}^+\to {\mathcal B}_j^+\}_{j\in J}$
satisfying
 $\sigma ^{\prime }_j=p_jq'$
and a property analogous to (7). However, then
$\sigma ^{\prime }_j=p_jq'$
and a property analogous to (7). However, then
![]() $q := q'\psi _{a,b}$
is also letter-onto and the morphisms
$q := q'\psi _{a,b}$
is also letter-onto and the morphisms
![]() $\{p_j\}_{j\in J}$
satisfy
$\{p_j\}_{j\in J}$
satisfy
![]() $\sigma _j = p_jq$
and a property analogous to (7). Thus, the conclusion of the lemma holds for
$\sigma _j = p_jq$
and a property analogous to (7). Thus, the conclusion of the lemma holds for
![]() $\{\sigma _j\}_{j\in J}$
, contrary to our assumptions.
$\{\sigma _j\}_{j\in J}$
, contrary to our assumptions.
Lemma 3.4. Let
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism,
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism,
![]() $u,v \in {\mathcal A}^+$
,
$u,v \in {\mathcal A}^+$
,
![]() $a,b$
be the first letters of
$a,b$
be the first letters of
![]() $u,v$
respectively, and
$u,v$
respectively, and
![]() $\sigma (a) = st$
be a decomposition of
$\sigma (a) = st$
be a decomposition of
![]() $\sigma (a)$
in which t is non-empty. Assume that
$\sigma (a)$
in which t is non-empty. Assume that
![]() $\sigma (u)$
is a prefix of
$\sigma (u)$
is a prefix of
![]() $s\sigma (v)$
,
$s\sigma (v)$
,
![]() $|u| \geq |\sigma |_1+|s|$
, and either that
$|u| \geq |\sigma |_1+|s|$
, and either that
![]() $s = 1$
and
$s = 1$
and
![]() $a\not =b$
or that
$a\not =b$
or that
![]() $s \not = 1$
.
$s \not = 1$
.
Then, there exist morphisms
![]() $q\colon {\mathcal A}^+ \to {\mathcal C}^+$
and
$q\colon {\mathcal A}^+ \to {\mathcal C}^+$
and
![]() $p\colon {\mathcal C}^+\to {\mathcal B}^+$
such that
$p\colon {\mathcal C}^+\to {\mathcal B}^+$
such that
![]() $\#{\mathcal C} \leq \#{\mathcal A}$
, q is letter-onto,
$\#{\mathcal C} \leq \#{\mathcal A}$
, q is letter-onto,
![]() $|p|_1 < |\sigma |_1$
, and
$|p|_1 < |\sigma |_1$
, and
![]() $\sigma = pq$
.
$\sigma = pq$
.
Remark 3.5. As in Lemma 3.2, there are symmetric hypotheses for the previous lemma that involve suffixes instead of prefixes and which give the same conclusion. We will use this in the proof of Lemma 3.6.
Proof of Lemma 3.4
Let us write
![]() $u = au'$
and
$u = au'$
and
![]() $v = bv'$
. We first consider the case in which
$v = bv'$
. We first consider the case in which
![]() $s=1$
. In this situation, u and v start with different letters, so Lemma 3.2 can be applied (with the index set J chosen as a singleton) to obtain a decomposition
$s=1$
. In this situation, u and v start with different letters, so Lemma 3.2 can be applied (with the index set J chosen as a singleton) to obtain a decomposition
![]() ${\mathcal A}^+ \overset {q}{\to } {\mathcal C}^+ \overset {p}{\to } {\mathcal B}^+$
such that q is letter-onto,
${\mathcal A}^+ \overset {q}{\to } {\mathcal C}^+ \overset {p}{\to } {\mathcal B}^+$
such that q is letter-onto,
![]() $\#{\mathcal C} < \#{\mathcal A}$
, and
$\#{\mathcal C} < \#{\mathcal A}$
, and
![]() $\sigma = pq$
. Since
$\sigma = pq$
. Since
![]() ${\mathcal C}$
has strictly fewer elements than
${\mathcal C}$
has strictly fewer elements than
![]() ${\mathcal A}$
, we have
${\mathcal A}$
, we have
![]() $|p|_1 < |\sigma |_1$
. Hence, the conclusion of the lemma holds in this case.
$|p|_1 < |\sigma |_1$
. Hence, the conclusion of the lemma holds in this case.
We now assume that
![]() $s\not =1$
. In this case, t and s are non-empty, so we can use (iii) of Lemma 3.1 to factorize
$s\not =1$
. In this case, t and s are non-empty, so we can use (iii) of Lemma 3.1 to factorize
![]() $\sigma = \sigma '\theta _{a, \tilde {a}}$
, where
$\sigma = \sigma '\theta _{a, \tilde {a}}$
, where
![]() $\tilde {a}$
is a letter not in
$\tilde {a}$
is a letter not in
![]() ${\mathcal A}$
and
${\mathcal A}$
and
![]() $\sigma '$
is defined as in (6). We set
$\sigma '$
is defined as in (6). We set
![]() $\tilde {u} = a\theta _{a,\tilde {a}}(u')$
and
$\tilde {u} = a\theta _{a,\tilde {a}}(u')$
and
![]() $\tilde {v} = \theta _{a,\tilde {a}}(v)$
. Our plan is to use Lemma 3.2 with
$\tilde {v} = \theta _{a,\tilde {a}}(v)$
. Our plan is to use Lemma 3.2 with
![]() $\tilde {u}$
,
$\tilde {u}$
,
![]() $\tilde {v}$
and
$\tilde {v}$
and
![]() $\sigma '$
.
$\sigma '$
.
Observe that
![]() $\theta _{a,\tilde {a}}(c)$
never starts with a, so
$\theta _{a,\tilde {a}}(c)$
never starts with a, so
Also, by using, as in the previous proof, the symbol
![]() $\leq _p$
to denote the prefix relation,
$\leq _p$
to denote the prefix relation,
which implies that
Finally, we use (6) to compute:
We conclude, by (13), (14), and (15) that Lemma 3.2 can be applied with
![]() $\tilde {u}$
,
$\tilde {u}$
,
![]() $\tilde {v}$
, and
$\tilde {v}$
, and
![]() $\sigma '$
(and J as a singleton). Thus, there exist morphisms
$\sigma '$
(and J as a singleton). Thus, there exist morphisms
![]() $q'\colon ({\mathcal A}\cup \{\tilde {a}\})^+\to {\mathcal C}^+$
and
$q'\colon ({\mathcal A}\cup \{\tilde {a}\})^+\to {\mathcal C}^+$
and
![]() $p\colon {\mathcal C}^+\to {\mathcal B}^+$
such that
$p\colon {\mathcal C}^+\to {\mathcal B}^+$
such that
![]() $\#{\mathcal C} < \#({\mathcal A}\cup \{\tilde {a}\})$
,
$\#{\mathcal C} < \#({\mathcal A}\cup \{\tilde {a}\})$
,
![]() $q'$
is letter-onto, and
$q'$
is letter-onto, and
![]() $\sigma '=pq'$
. Then,
$\sigma '=pq'$
. Then,
![]() $\#{\mathcal C} \leq \#{\mathcal A}$
,
$\#{\mathcal C} \leq \#{\mathcal A}$
,
![]() $q := q'\theta _{a, \tilde {a}}$
is letter-onto, and
$q := q'\theta _{a, \tilde {a}}$
is letter-onto, and
![]() $\sigma = p q'\theta _{a, \tilde {a}} = pq$
. Moreover, since
$\sigma = p q'\theta _{a, \tilde {a}} = pq$
. Moreover, since
![]() $\theta _{a, \tilde {a}}$
is not the identity function, we have
$\theta _{a, \tilde {a}}$
is not the identity function, we have
![]() $|p|_1 < |\sigma |_1$
.
$|p|_1 < |\sigma |_1$
.
The next lemma is the main result of this subsection. To state it, we introduce additional notation. For an alphabet
![]() ${\mathcal A}$
, let
${\mathcal A}$
, let
![]() ${\mathcal A}^{++}$
be the set of words
${\mathcal A}^{++}$
be the set of words
![]() $w \in {\mathcal A}^+$
in which all letters occur. Observe that
$w \in {\mathcal A}^+$
in which all letters occur. Observe that
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
is letter-onto if and only if
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
is letter-onto if and only if
![]() $\sigma ({\mathcal A}^{++}) \subseteq {\mathcal B}^{++}$
.
$\sigma ({\mathcal A}^{++}) \subseteq {\mathcal B}^{++}$
.
Lemma 3.6. Let
![]() $\phi \colon {\mathcal A}^+ \to {\mathcal C}^+$
,
$\phi \colon {\mathcal A}^+ \to {\mathcal C}^+$
,
![]() $\tau \colon {\mathcal B}^+\to {\mathcal C}^+$
be morphisms such that
$\tau \colon {\mathcal B}^+\to {\mathcal C}^+$
be morphisms such that
![]() $\tau $
is
$\tau $
is
![]() $\ell $
-proper, with
$\ell $
-proper, with
 $\ell \geq |\phi |_1^4$
, and
$\ell \geq |\phi |_1^4$
, and
![]() $\phi ({\mathcal A}^+) \cap \tau ({\mathcal B}^{++}) \not = \emptyset $
. Then, there exist
$\phi ({\mathcal A}^+) \cap \tau ({\mathcal B}^{++}) \not = \emptyset $
. Then, there exist
![]() ${\mathcal B}^+ \overset {q}{\longrightarrow } {\mathcal D}^+ \overset {p}{\longrightarrow } {\mathcal C}^+$
such that
${\mathcal B}^+ \overset {q}{\longrightarrow } {\mathcal D}^+ \overset {p}{\longrightarrow } {\mathcal C}^+$
such that
Proof. By contradiction, we suppose that the lemma does not hold for
![]() $\phi $
and
$\phi $
and
![]() $\tau $
and, moreover, that
$\tau $
and, moreover, that
![]() $|\phi |_1$
as small as possible.
$|\phi |_1$
as small as possible.
That
![]() $\phi ({\mathcal A})^+ \cap \tau ({\mathcal B}^{++})$
is non-empty means that there exist
$\phi ({\mathcal A})^+ \cap \tau ({\mathcal B}^{++})$
is non-empty means that there exist
![]() $u = u_1\ldots u_n \in {\mathcal A}^+$
and
$u = u_1\ldots u_n \in {\mathcal A}^+$
and
![]() $w = w_1\ldots w_m \in {\mathcal B}^{++}$
with
$w = w_1\ldots w_m \in {\mathcal B}^{++}$
with
![]() $\phi (u) = \tau (w)$
. If
$\phi (u) = \tau (w)$
. If
![]() $m = 1$
, then, since
$m = 1$
, then, since
![]() $w \in {\mathcal B}^{++}$
, we have
$w \in {\mathcal B}^{++}$
, we have
![]() $\#{\mathcal B} = \{v_1\}$
and the conclusion of the lemma trivially holds for
$\#{\mathcal B} = \{v_1\}$
and the conclusion of the lemma trivially holds for
![]() ${\mathcal D} = \{a\in {\mathcal C}:a\ \text {occurs in}\ \tau (w_1)\}$
,
${\mathcal D} = \{a\in {\mathcal C}:a\ \text {occurs in}\ \tau (w_1)\}$
,
![]() $q\colon {\mathcal B}^+\to {\mathcal D}^+$
,
$q\colon {\mathcal B}^+\to {\mathcal D}^+$
,
![]() $w_1\mapsto \tau (w_1)$
, and
$w_1\mapsto \tau (w_1)$
, and
![]() $p\colon {\mathcal D}^+\to {\mathcal C}^+$
the inclusion map, contradicting our initial assumption. Therefore,
$p\colon {\mathcal D}^+\to {\mathcal C}^+$
the inclusion map, contradicting our initial assumption. Therefore,
![]() $m \geq 2$
and
$m \geq 2$
and
![]() $\{1,\ldots ,m-1\}$
is non-empty.
$\{1,\ldots ,m-1\}$
is non-empty.
Let
![]() $k \in \{1,\ldots ,m-1\}$
. We define
$k \in \{1,\ldots ,m-1\}$
. We define
![]() $i_k$
as the smallest number in
$i_k$
as the smallest number in
![]() $\{1,\ldots ,n\}$
for which
$\{1,\ldots ,n\}$
for which
![]() $|\tau (w_1\ldots w_k)| < |\phi (u_1\ldots u_{i_k})|$
holds. Since
$|\tau (w_1\ldots w_k)| < |\phi (u_1\ldots u_{i_k})|$
holds. Since
![]() $|\phi (u_1)| \leq |\phi |_1 \leq \ell \leq |\tau (w_1\ldots w_k)|$
,
$|\phi (u_1)| \leq |\phi |_1 \leq \ell \leq |\tau (w_1\ldots w_k)|$
,
![]() $i_k$
is at least
$i_k$
is at least
![]() $2$
and, thus,
$2$
and, thus,
![]() $|\phi (u_1\ldots u_{i_k-1})| \leq |\tau (w_1\ldots w_k)|$
by minimality of
$|\phi (u_1\ldots u_{i_k-1})| \leq |\tau (w_1\ldots w_k)|$
by minimality of
![]() $i_k$
. Hence, there exists a decomposition
$i_k$
. Hence, there exists a decomposition
![]() $\phi (u_{i_k}) = s_kt_k$
such that
$\phi (u_{i_k}) = s_kt_k$
such that
![]() $t_k$
is non-empty and
$t_k$
is non-empty and
Our next objective is to use Lemma 3.4 to prove that
![]() $s_k$
and
$s_k$
and
![]() $u_k$
have a very particular form.
$u_k$
have a very particular form.
Claim 3.6.1. For every
![]() $k\in \{1,\ldots ,m-1\}$
,
$k\in \{1,\ldots ,m-1\}$
,
![]() $s_k = 1$
and
$s_k = 1$
and
![]() $u_1 = u_{i_k}$
.
$u_1 = u_{i_k}$
.
Proof. To prove this, we suppose that it is not true, that is, there exists
![]() $k\in \{1,\ldots ,m-1\}$
such that
$k\in \{1,\ldots ,m-1\}$
such that
Let
 $\tilde {u} := u_{i_k}\ldots u_{i_k+|\phi |^2_1-1}$
and
$\tilde {u} := u_{i_k}\ldots u_{i_k+|\phi |^2_1-1}$
and
 $\tilde {v} := u_1\ldots u_{|\phi |^3_1}$
. We are going to check the hypothesis of Lemma 3.4 for
$\tilde {v} := u_1\ldots u_{|\phi |^3_1}$
. We are going to check the hypothesis of Lemma 3.4 for
![]() $\tilde {u}$
,
$\tilde {u}$
,
![]() $\tilde {v}$
and
$\tilde {v}$
and
![]() $\phi $
.
$\phi $
.
First, we observe that, since
![]() $\phi (u)=\tau (v)$
, we have that
$\phi (u)=\tau (v)$
, we have that
![]() $\phi (\tilde {v})$
is a prefix of
$\phi (\tilde {v})$
is a prefix of
![]() $\tau (v)$
. Moreover, given that
$\tau (v)$
. Moreover, given that
 $|\phi (\tilde {v})| \leq |\phi |_1^4 \leq \ell $
and that
$|\phi (\tilde {v})| \leq |\phi |_1^4 \leq \ell $
and that
![]() $\tau $
is
$\tau $
is
![]() $\ell $
-proper,
$\ell $
-proper,
![]() $\phi (\tilde {v})$
is a prefix of
$\phi (\tilde {v})$
is a prefix of
![]() $\tau (b)$
for every
$\tau (b)$
for every
![]() $b \in {\mathcal B}$
. In particular,
$b \in {\mathcal B}$
. In particular,
Second, from (16) and the inequalities
 $|t_k\phi (u_{i_k+1}\ldots u_{i_k+|\phi |^2_1-1})| \leq |\phi |_1^3 \leq \ell \leq |\tau (w_k)|$
, we deduce that
$|t_k\phi (u_{i_k+1}\ldots u_{i_k+|\phi |^2_1-1})| \leq |\phi |_1^3 \leq \ell \leq |\tau (w_k)|$
, we deduce that
 $t_k\phi (u_{i_k+1}\ldots u_{i_k+|\phi |^2_1-1})$
is a prefix of
$t_k\phi (u_{i_k+1}\ldots u_{i_k+|\phi |^2_1-1})$
is a prefix of
![]() $\tau (w_k)$
. Therefore,
$\tau (w_k)$
. Therefore,
 $$ \begin{align} \phi(\tilde{u}) = s_kt_k\phi(u_{i_k+1}\ldots u_{i_k+|\phi|^2_1-1})\ \text{is a prefix of}\ s_k\tau(w_k). \end{align} $$
$$ \begin{align} \phi(\tilde{u}) = s_kt_k\phi(u_{i_k+1}\ldots u_{i_k+|\phi|^2_1-1})\ \text{is a prefix of}\ s_k\tau(w_k). \end{align} $$
We conclude from (18), (19), and the inequality
 $|\phi (\tilde {u})| \leq |\phi |_1^3 = |\tilde {v}| \leq |s_k\phi (\tilde {v})|$
that
$|\phi (\tilde {u})| \leq |\phi |_1^3 = |\tilde {v}| \leq |s_k\phi (\tilde {v})|$
that
This, the inequality
![]() $|\tilde {u}| \geq |\phi |_1+|s_k|$
and (17) allow us to use Lemma 3.4 with
$|\tilde {u}| \geq |\phi |_1+|s_k|$
and (17) allow us to use Lemma 3.4 with
![]() $\tilde {u}$
,
$\tilde {u}$
,
![]() $\tilde {v}$
, and
$\tilde {v}$
, and
![]() $\phi $
and obtain morphisms
$\phi $
and obtain morphisms
 ${\mathcal A}^+ \overset {\tilde {q}}{\longrightarrow } \tilde {{\mathcal A}}^+ \overset {\tilde {\phi }}{\longrightarrow } {\mathcal C}^+$
such that
${\mathcal A}^+ \overset {\tilde {q}}{\longrightarrow } \tilde {{\mathcal A}}^+ \overset {\tilde {\phi }}{\longrightarrow } {\mathcal C}^+$
such that
![]() $\#\tilde {{\mathcal A}} \leq \#{\mathcal A}$
,
$\#\tilde {{\mathcal A}} \leq \#{\mathcal A}$
,
![]() $\phi = \tilde {\phi }\tilde {q}$
and
$\phi = \tilde {\phi }\tilde {q}$
and
![]() $|\tilde {\phi }|_1 < |\phi |_1$
. Then,
$|\tilde {\phi }|_1 < |\phi |_1$
. Then,
 $\ell \geq |\phi |_1^4> |\tilde {\phi }|_1^4$
and
$\ell \geq |\phi |_1^4> |\tilde {\phi }|_1^4$
and
 $\tilde {\phi }(\tilde {{\mathcal A}}^+) \cap \tau ({\mathcal B}^{++})$
contains the element
$\tilde {\phi }(\tilde {{\mathcal A}}^+) \cap \tau ({\mathcal B}^{++})$
contains the element
![]() $\tilde {\phi }(\tilde {q}(u)) = \tau (w)$
, and so
$\tilde {\phi }(\tilde {q}(u)) = \tau (w)$
, and so
![]() $\tau $
and
$\tau $
and
![]() $\tilde {\phi }$
satisfy the hypothesis of this lemma. Therefore, by the minimality of
$\tilde {\phi }$
satisfy the hypothesis of this lemma. Therefore, by the minimality of
![]() $|\phi |_1$
, there exists a decomposition
$|\phi |_1$
, there exists a decomposition
![]() ${\mathcal B}^+ \overset {q}{\to } {\mathcal D}^+ \overset {p}{\to } {\mathcal C}^+$
of
${\mathcal B}^+ \overset {q}{\to } {\mathcal D}^+ \overset {p}{\to } {\mathcal C}^+$
of
![]() $\tau $
satisfying conditions (i)–(iii) of this lemma, contrary to our assumptions.
$\tau $
satisfying conditions (i)–(iii) of this lemma, contrary to our assumptions.
An argument similar to the one used in the proof of the previous claim gives us that
We refer the reader to Remark 3.5 for further details.
Now we can finish the proof. First, from (16) and the first part of the claim, we get that
![]() $\tau (w_k) = \phi (u_{i_{k-1}}\ldots u_{i_k-1})$
for
$\tau (w_k) = \phi (u_{i_{k-1}}\ldots u_{i_k-1})$
for
![]() $k \in \{2,\ldots ,m-1\}$
,
$k \in \{2,\ldots ,m-1\}$
,
![]() $\tau (w_1) = \phi (u_1\ldots u_{i_1-1})$
and
$\tau (w_1) = \phi (u_1\ldots u_{i_1-1})$
and
![]() $\tau (w_m) = \phi (u_{i_{m-1}}\ldots u_n)$
. Being
$\tau (w_m) = \phi (u_{i_{m-1}}\ldots u_n)$
. Being
![]() $w \in {\mathcal B}^{++}$
, these equations imply that each
$w \in {\mathcal B}^{++}$
, these equations imply that each
![]() $\tau (b)$
,
$\tau (b)$
,
![]() $b \in {\mathcal B}$
, can be written as a concatenation
$b \in {\mathcal B}$
, can be written as a concatenation
![]() $x_1\ldots x_N$
, with
$x_1\ldots x_N$
, with
![]() $x_j \in \phi ({\mathcal A})$
. Moreover, by the second part of the claim and (20), we can choose this decomposition so that
$x_j \in \phi ({\mathcal A})$
. Moreover, by the second part of the claim and (20), we can choose this decomposition so that
![]() $x_1 = u_1$
and
$x_1 = u_1$
and
![]() $x_N = u_n$
. This defines (maybe non-unique) morphisms
$x_N = u_n$
. This defines (maybe non-unique) morphisms
 ${\mathcal B}^+ \overset {q}{\longrightarrow } {\mathcal D}_1^+ \overset {p_1}{\longrightarrow } {\mathcal C}^+$
such that
${\mathcal B}^+ \overset {q}{\longrightarrow } {\mathcal D}_1^+ \overset {p_1}{\longrightarrow } {\mathcal C}^+$
such that
![]() $\tau = p_1q$
,
$\tau = p_1q$
,
![]() $\#{\mathcal D}_1 \leq \#\{\phi (u_1),\ldots ,\phi (u_n)\} \leq \#{\mathcal A}$
, and q is proper. If we define
$\#{\mathcal D}_1 \leq \#\{\phi (u_1),\ldots ,\phi (u_n)\} \leq \#{\mathcal A}$
, and q is proper. If we define
![]() ${\mathcal D}$
as the set of letters
${\mathcal D}$
as the set of letters
![]() $d \in {\mathcal D}_1$
that occur in some
$d \in {\mathcal D}_1$
that occur in some
![]() $w \in q({\mathcal B})$
, and p as the restriction of
$w \in q({\mathcal B})$
, and p as the restriction of
![]() $p_1$
to
$p_1$
to
![]() ${\mathcal D}$
, then we obtain a decomposition
${\mathcal D}$
, then we obtain a decomposition
![]() ${\mathcal B}^+ \overset {q}{\longrightarrow } {\mathcal D}^+ \overset {p}{\longrightarrow } {\mathcal C}^+$
that still satisfies the previous properties, but in which q is letter-onto. Hence, p and q met conditions (i), (ii), and (iii).
${\mathcal B}^+ \overset {q}{\longrightarrow } {\mathcal D}^+ \overset {p}{\longrightarrow } {\mathcal C}^+$
that still satisfies the previous properties, but in which q is letter-onto. Hence, p and q met conditions (i), (ii), and (iii).
3.2 Periodicity lemmas
We will also need classic results from combinatorics on words. We follow the presentation of [Reference Rozenberg and SalomaaRS97, Ch. 6].
Let
![]() $w\in {\mathcal A}^*$
be a non-empty word. We say that p is a local period of w at the position
$w\in {\mathcal A}^*$
be a non-empty word. We say that p is a local period of w at the position
![]() $|u|$
if
$|u|$
if
![]() $w=uv$
, with
$w=uv$
, with
![]() $u,v\not =1$
, and there exists a word z, with
$u,v\not =1$
, and there exists a word z, with
![]() $|z|=p$
, such that one of the following conditions holds for some words
$|z|=p$
, such that one of the following conditions holds for some words
![]() $u'$
and
$u'$
and
![]() $v'$
:
$v'$
:
 $$ \begin{align} \begin{cases} \mathrm{(i)}\quad & u=u'z \ \text{and}\ v=zv';\\ \mathrm{(ii)}\quad & z =u'u \ \text{and}\ v=zv';\\ \mathrm{(iii)}\quad &u =u'z \ \text{and}\ z=vv';\\ \mathrm{(iv)}\quad & z =u'u = vv'.\end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \mathrm{(i)}\quad & u=u'z \ \text{and}\ v=zv';\\ \mathrm{(ii)}\quad & z =u'u \ \text{and}\ v=zv';\\ \mathrm{(iii)}\quad &u =u'z \ \text{and}\ z=vv';\\ \mathrm{(iv)}\quad & z =u'u = vv'.\end{cases} \end{align} $$
Further, the local period of w at the position
![]() $|u|$
, in symbols
$|u|$
, in symbols
![]() ${\mathrm {per}}(w,u)$
, is defined as the smallest local period of w at the position u (see Fig. 1). It follows directly from (21) that
${\mathrm {per}}(w,u)$
, is defined as the smallest local period of w at the position u (see Fig. 1). It follows directly from (21) that
![]() ${\mathrm {per}}(w,u) \leq {\mathrm {per}}(w)$
.
${\mathrm {per}}(w,u) \leq {\mathrm {per}}(w)$
.

Figure 1 Illustration of a local period.
The following result is known as the critical factorization theorem.
Theorem 3.7. (Theorem 6.2 and Ch. 6, [Reference Rozenberg and SalomaaRS97])
Each non-empty word
![]() $w \in {\mathcal A}^*$
, with
$w \in {\mathcal A}^*$
, with
![]() $|w|\geq 2$
, possesses at least one factorization
$|w|\geq 2$
, possesses at least one factorization
![]() $w = uv$
, with
$w = uv$
, with
![]() $u,v\not =1$
, which is critical, i.e.
$u,v\not =1$
, which is critical, i.e.
![]() ${\mathrm {per}}(w) = {\mathrm {per}}(w,u)$
.
${\mathrm {per}}(w) = {\mathrm {per}}(w,u)$
.
4 Rank of symbolic factors
In this section, we prove Theorem 1.3. We start by introducing the concept of factor between directive sequences and, in Proposition 4.4, its relation with factor maps between
![]() ${\mathcal S}$
-adic subshifts. These ideas are the
${\mathcal S}$
-adic subshifts. These ideas are the
![]() ${\mathcal S}$
-adic analogs of the concept of premorphism between ordered Bratteli diagrams from [Reference Amini, Elliott and GolestaniAEG15] and their proposition 4.6. Although Proposition 4.4 can be deduced from proposition 4.6 in [Reference Amini, Elliott and GolestaniAEG15] by passing from directive sequences to ordered Bratteli diagrams and backwards, we consider this a little bit artificial since it is possible to provide a direct combinatorial proof; this is done in the Appendix. It is interesting to note that our proof is constructive (in contrast of the existential proof in [Reference Amini, Elliott and GolestaniAEG15]) and shows some additional features that are a consequence of the combinatorics on words analysis made.
${\mathcal S}$
-adic analogs of the concept of premorphism between ordered Bratteli diagrams from [Reference Amini, Elliott and GolestaniAEG15] and their proposition 4.6. Although Proposition 4.4 can be deduced from proposition 4.6 in [Reference Amini, Elliott and GolestaniAEG15] by passing from directive sequences to ordered Bratteli diagrams and backwards, we consider this a little bit artificial since it is possible to provide a direct combinatorial proof; this is done in the Appendix. It is interesting to note that our proof is constructive (in contrast of the existential proof in [Reference Amini, Elliott and GolestaniAEG15]) and shows some additional features that are a consequence of the combinatorics on words analysis made.
Next, we use ideas from [Reference EspinozaEsp20, Reference Golestani and HosseiniGH21] to prove Theorem 1.3. In particular, this improves the previous bounds in [Reference EspinozaEsp20, Reference Golestani and HosseiniGH21] to the best possible one. We apply these results, in Corollary 4.8, to answer affirmatively Question 1.2 and, in Theorem 1.5, to prove a strong coalescence property for the class of systems considered in Theorem 1.3. It is worth noting that this last result is only possible due to the bound in Theorem 1.3 being optimal. We end this section by proving that Cantor factors of finite topological rank systems are either subshifts or odometers.
4.1 Rank of factors of directive sequences
The following is the
![]() ${\mathcal S}$
-adic analog of the notion of premorphism between ordered Bratteli diagrams in [Reference Amini, Elliott and GolestaniAEG15].
${\mathcal S}$
-adic analog of the notion of premorphism between ordered Bratteli diagrams in [Reference Amini, Elliott and GolestaniAEG15].
Definition 4.1. Let
 $\boldsymbol {\sigma } = ({\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
,
$\boldsymbol {\sigma } = ({\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
,
 $\boldsymbol {\tau } = ({\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\in {\mathbb N}}$
be directive sequences. A factor
$\boldsymbol {\tau } = ({\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\in {\mathbb N}}$
be directive sequences. A factor
![]() $\boldsymbol {\phi }\colon \boldsymbol {\sigma }\to \boldsymbol {\tau }$
is a sequence of morphisms
$\boldsymbol {\phi }\colon \boldsymbol {\sigma }\to \boldsymbol {\tau }$
is a sequence of morphisms
![]() $\boldsymbol {\phi } = (\phi _n)_{n\in {\mathbb N}}$
, where
$\boldsymbol {\phi } = (\phi _n)_{n\in {\mathbb N}}$
, where
 $\phi _0\colon {\mathcal A}_1^+\to {\mathcal B}_0^+$
and
$\phi _0\colon {\mathcal A}_1^+\to {\mathcal B}_0^+$
and
![]() $\phi _n\colon {\mathcal A}_n^+\to {\mathcal B}_n^+$
for
$\phi _n\colon {\mathcal A}_n^+\to {\mathcal B}_n^+$
for
![]() $n \geq 1$
, such that
$n \geq 1$
, such that
![]() $\phi _0 = \tau _0\phi _1$
and
$\phi _0 = \tau _0\phi _1$
and
![]() $\phi _n\sigma _n = \tau _n\phi _{n+1}$
for every
$\phi _n\sigma _n = \tau _n\phi _{n+1}$
for every
![]() $n \geq 1$
.
$n \geq 1$
.
We say that
![]() $\boldsymbol {\phi }$
is proper (respectively letter-onto) if
$\boldsymbol {\phi }$
is proper (respectively letter-onto) if
![]() $\phi _n$
is proper (respectively letter-onto) for every
$\phi _n$
is proper (respectively letter-onto) for every
![]() $n\in {\mathbb N}$
.
$n\in {\mathbb N}$
.
Remark 4.2. Factors are not affected by contractions. More precisely, if
![]() $0=n_0<n_1<n_2<\ldots $
, then
$0=n_0<n_1<n_2<\ldots $
, then
![]() $\boldsymbol {\phi '} = (\phi _{n_k})_{k\in {\mathbb N}}$
is a factor from
$\boldsymbol {\phi '} = (\phi _{n_k})_{k\in {\mathbb N}}$
is a factor from
![]() $\boldsymbol {\sigma '} = (\sigma _{[n_k,n_{k+1})})_{k\in {\mathbb N}}$
to
$\boldsymbol {\sigma '} = (\sigma _{[n_k,n_{k+1})})_{k\in {\mathbb N}}$
to
![]() $\boldsymbol {\tau '} = (\tau _{[n_k,n_{k+1})})_{k\in {\mathbb N}}$
.
$\boldsymbol {\tau '} = (\tau _{[n_k,n_{k+1})})_{k\in {\mathbb N}}$
.
The next lemma will be needed at the end of this section.
Lemma 4.3. Let
![]() $\boldsymbol {\phi } = (\phi _n)_{n\geq 1}\colon \boldsymbol {\sigma }\to \boldsymbol {\tau }$
be a factor. Assume that
$\boldsymbol {\phi } = (\phi _n)_{n\geq 1}\colon \boldsymbol {\sigma }\to \boldsymbol {\tau }$
be a factor. Assume that
![]() $\boldsymbol {\sigma }$
and
$\boldsymbol {\sigma }$
and
![]() $\boldsymbol {\tau }$
are everywhere growing and proper and that
$\boldsymbol {\tau }$
are everywhere growing and proper and that
![]() $\boldsymbol {\phi }$
is letter-onto. Then,
$\boldsymbol {\phi }$
is letter-onto. Then,
 $X_{\boldsymbol {\tau }} = \bigcup _{k\in {\mathbb Z}}T^k\phi _0(X_{\boldsymbol {\sigma }}^{(1)})$
and
$X_{\boldsymbol {\tau }} = \bigcup _{k\in {\mathbb Z}}T^k\phi _0(X_{\boldsymbol {\sigma }}^{(1)})$
and
 $X_{\boldsymbol {\tau }}^{(n)} = \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n)})$
for every
$X_{\boldsymbol {\tau }}^{(n)} = \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n)})$
for every
![]() $n \geq 1$
.
$n \geq 1$
.
Proof. We start by proving that
 $X_{\boldsymbol {\tau }}^{(n)} \subseteq \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n)})$
. Let
$X_{\boldsymbol {\tau }}^{(n)} \subseteq \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n)})$
. Let
 $y \in X_{\boldsymbol {\tau }}^{(n)}$
and
$y \in X_{\boldsymbol {\tau }}^{(n)}$
and
![]() $\ell \in {\mathbb N}$
. There exist
$\ell \in {\mathbb N}$
. There exist
![]() $N>n$
and
$N>n$
and
![]() $b \in {\mathcal B}_n$
such that
$b \in {\mathcal B}_n$
such that
![]() $y_{[-\ell ,\ell ]}$
occurs in
$y_{[-\ell ,\ell ]}$
occurs in
![]() $\tau _{[n,N)}(b)$
. In addition, since
$\tau _{[n,N)}(b)$
. In addition, since
![]() $\phi _N$
is letter-onto, there exists
$\phi _N$
is letter-onto, there exists
![]() $a \in {\mathcal A}_N$
for which b occurs in
$a \in {\mathcal A}_N$
for which b occurs in
![]() $\phi _N(a)$
. Then,
$\phi _N(a)$
. Then,
![]() $y_{[-\ell ,\ell ]}$
occurs in
$y_{[-\ell ,\ell ]}$
occurs in
![]() $\tau _{[n,N)}\phi _N(b)$
and, consequently, also in
$\tau _{[n,N)}\phi _N(b)$
and, consequently, also in
![]() $\phi _n\sigma _{[n,N)}(b)$
as
$\phi _n\sigma _{[n,N)}(b)$
as
![]() $\tau _{[n,N)}\phi _N = \phi _n\sigma _{[n,N)}$
. Hence, by taking the limit
$\tau _{[n,N)}\phi _N = \phi _n\sigma _{[n,N)}$
. Hence, by taking the limit
![]() $\ell \to \infty $
, we can find
$\ell \to \infty $
, we can find
 $(k',x) \in {\mathbb Z}\times X_{\boldsymbol {\sigma }}^{(n)}$
such that
$(k',x) \in {\mathbb Z}\times X_{\boldsymbol {\sigma }}^{(n)}$
such that
![]() $y = T^{k'}\phi _n(x)$
. Therefore,
$y = T^{k'}\phi _n(x)$
. Therefore,
 $y \in \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n)})$
. To prove the other inclusion, we use Lemma 2.6 to compute:
$y \in \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n)})$
. To prove the other inclusion, we use Lemma 2.6 to compute:
 $$ \begin{align*} \phi_n(X_{\boldsymbol{\sigma}}^{(n)}) &= \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\phi_n\sigma_{[n,N)}({\mathcal A}_N^{\mathbb Z}) = \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\tau_{[n,N)}\phi_N({\mathcal A}_N^{\mathbb Z}) \\&\subseteq \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\tau_{[n,N)}({\mathcal B}_N^{\mathbb Z}) = X_{\boldsymbol{\tau}}^{(n)}.\\[-46pt] \end{align*} $$
$$ \begin{align*} \phi_n(X_{\boldsymbol{\sigma}}^{(n)}) &= \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\phi_n\sigma_{[n,N)}({\mathcal A}_N^{\mathbb Z}) = \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\tau_{[n,N)}\phi_N({\mathcal A}_N^{\mathbb Z}) \\&\subseteq \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\tau_{[n,N)}({\mathcal B}_N^{\mathbb Z}) = X_{\boldsymbol{\tau}}^{(n)}.\\[-46pt] \end{align*} $$
As we mentioned before, the following proposition is a consequence of the main result in [Reference Amini, Elliott and GolestaniAEG15]. We provide a combinatorial proof in the Appendix.
Proposition 4.4. Let
![]() $\boldsymbol {\sigma }$
be a letter-onto, everywhere growing, and proper directive sequence. Suppose that
$\boldsymbol {\sigma }$
be a letter-onto, everywhere growing, and proper directive sequence. Suppose that
![]() $X_{\boldsymbol {\sigma }}$
is aperiodic. Then, there exist a contraction
$X_{\boldsymbol {\sigma }}$
is aperiodic. Then, there exist a contraction
![]() $\boldsymbol {\sigma }' = (\sigma ^{\prime }_n)_{n\in {\mathbb N}}$
, a letter-onto, everywhere growing, proper and recognizable
$\boldsymbol {\sigma }' = (\sigma ^{\prime }_n)_{n\in {\mathbb N}}$
, a letter-onto, everywhere growing, proper and recognizable
![]() $\boldsymbol {\tau } = (\tau _n)_{n\in {\mathbb N}}$
generating
$\boldsymbol {\tau } = (\tau _n)_{n\in {\mathbb N}}$
generating
![]() $X_{\boldsymbol {\sigma }}$
, and a letter-onto factor
$X_{\boldsymbol {\sigma }}$
, and a letter-onto factor
![]() $\boldsymbol {\phi }\colon \boldsymbol {\sigma }' \to \boldsymbol {\tau }$
,
$\boldsymbol {\phi }\colon \boldsymbol {\sigma }' \to \boldsymbol {\tau }$
,
![]() $\boldsymbol {\phi } = (\phi _n)_{n\in {\mathbb N}}$
, such that
$\boldsymbol {\phi } = (\phi _n)_{n\in {\mathbb N}}$
, such that
![]() $\phi _0 = \sigma ^{\prime }_0$
.
$\phi _0 = \sigma ^{\prime }_0$
.
The next proposition is the main technical result of this section. To state it, it is convenient to introduce the following concept. The directive sequences
![]() $\boldsymbol {\sigma }$
and
$\boldsymbol {\sigma }$
and
![]() $\boldsymbol {\tau }$
are equivalent if
$\boldsymbol {\tau }$
are equivalent if
![]() $\boldsymbol {\sigma } = \boldsymbol {\nu }'$
,
$\boldsymbol {\sigma } = \boldsymbol {\nu }'$
,
![]() $\boldsymbol {\tau } = \boldsymbol {\nu }''$
for some contractions
$\boldsymbol {\tau } = \boldsymbol {\nu }''$
for some contractions
![]() $\boldsymbol {\nu }'$
,
$\boldsymbol {\nu }'$
,
![]() $\boldsymbol {\nu }''$
of a directive sequence
$\boldsymbol {\nu }''$
of a directive sequence
![]() $\boldsymbol {\nu }$
. Observe that equivalent directive sequences generate the same
$\boldsymbol {\nu }$
. Observe that equivalent directive sequences generate the same
![]() ${\mathcal S}$
-adic subshift.
${\mathcal S}$
-adic subshift.
Proposition 4.5. Let
![]() $\boldsymbol {\phi }\colon \boldsymbol {\sigma } \to \boldsymbol {\tau }$
be a letter-onto factor between the everywhere growing and proper directive sequences. Then, there exist a letter-onto and proper factor
$\boldsymbol {\phi }\colon \boldsymbol {\sigma } \to \boldsymbol {\tau }$
be a letter-onto factor between the everywhere growing and proper directive sequences. Then, there exist a letter-onto and proper factor
![]() $\boldsymbol {\psi }\colon \boldsymbol {\sigma }'\to \boldsymbol {\nu }$
, where:
$\boldsymbol {\psi }\colon \boldsymbol {\sigma }'\to \boldsymbol {\nu }$
, where:
-
(1)
 $\boldsymbol {\sigma }'$
is a contraction of
$\boldsymbol {\sigma }'$
is a contraction of
 $\boldsymbol {\sigma }$
;
$\boldsymbol {\sigma }$
; -
(2)
 $\boldsymbol {\nu }$
is letter-onto, everywhere growing, proper, equivalent to
$\boldsymbol {\nu }$
is letter-onto, everywhere growing, proper, equivalent to
 $\boldsymbol {\tau }$
,
$\boldsymbol {\tau }$
,
 $\mathrm {AR}(\boldsymbol {\nu }) \leq \mathrm {AR}(\boldsymbol {\sigma })$
, and the first coordinate of
$\mathrm {AR}(\boldsymbol {\nu }) \leq \mathrm {AR}(\boldsymbol {\sigma })$
, and the first coordinate of
 $\boldsymbol {\psi }$
and
$\boldsymbol {\psi }$
and
 $\boldsymbol {\phi }$
coincide;
$\boldsymbol {\phi }$
coincide; -
(3) if
 $\boldsymbol {\tau }$
is recognizable, then
$\boldsymbol {\tau }$
is recognizable, then
 $\boldsymbol {\nu }$
is recognizable.
$\boldsymbol {\nu }$
is recognizable.
Proof. Let us write
 $\boldsymbol {\sigma } = ({\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
and
$\boldsymbol {\sigma } = ({\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
and
 $\boldsymbol {\tau } = ({\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\in {\mathbb N}}$
. Up to contractions, we can suppose that for every
$\boldsymbol {\tau } = ({\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\in {\mathbb N}}$
. Up to contractions, we can suppose that for every
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\#{\mathcal A}_n = \mathrm {AR}(\boldsymbol {\sigma })$
and that
$\#{\mathcal A}_n = \mathrm {AR}(\boldsymbol {\sigma })$
and that
![]() $\tau _n$
is
$\tau _n$
is
 $|\phi _n|^4_1$
-proper (for the last property, we used that
$|\phi _n|^4_1$
-proper (for the last property, we used that
![]() $\boldsymbol {\tau }$
is everywhere growing and proper).
$\boldsymbol {\tau }$
is everywhere growing and proper).
Using that
![]() $\phi _{n+1}$
is letter-onto, we can compute:
$\phi _{n+1}$
is letter-onto, we can compute:
 $$ \begin{align*} \tau_n({\mathcal B}_{n+1}^{++}) \supseteq \tau_n(\phi_{n+1}({\mathcal A}_{n+1}^{++})) = \phi_n(\sigma_n({\mathcal A}_{n+1}^{++})) \subseteq \phi_n({\mathcal A}_n^+), \end{align*} $$
$$ \begin{align*} \tau_n({\mathcal B}_{n+1}^{++}) \supseteq \tau_n(\phi_{n+1}({\mathcal A}_{n+1}^{++})) = \phi_n(\sigma_n({\mathcal A}_{n+1}^{++})) \subseteq \phi_n({\mathcal A}_n^+), \end{align*} $$
where in the middle step, we used the commutativity property of
![]() $\boldsymbol {\phi }$
. We deduce that
$\boldsymbol {\phi }$
. We deduce that
 $$ \begin{align*} \tau_n({\mathcal B}_{n+1}^{++}) \cap \phi_n({\mathcal A}_n^+) \not= \emptyset\quad \text{for every}\ n \in {\mathbb N}. \end{align*} $$
$$ \begin{align*} \tau_n({\mathcal B}_{n+1}^{++}) \cap \phi_n({\mathcal A}_n^+) \not= \emptyset\quad \text{for every}\ n \in {\mathbb N}. \end{align*} $$
This and the fact that
![]() $\tau _n$
is a
$\tau _n$
is a
 $|\phi _n|^4_1$
-proper morphism allow us to use Lemma 3.6 to find morphisms
$|\phi _n|^4_1$
-proper morphism allow us to use Lemma 3.6 to find morphisms
 ${\mathcal B}_{n+1}^+ \overset {q_{n+1}}{\longrightarrow } {\mathcal D}_{n+1}^+ \overset {p_n}{\longrightarrow } {\mathcal B}_n^+$
such that
${\mathcal B}_{n+1}^+ \overset {q_{n+1}}{\longrightarrow } {\mathcal D}_{n+1}^+ \overset {p_n}{\longrightarrow } {\mathcal B}_n^+$
such that
We define
![]() $\nu _0 := p_0$
, the morphisms
$\nu _0 := p_0$
, the morphisms
 $\nu _n := q_np_n \colon {\mathcal D}_{n+1}^+ \to {\mathcal D}_n^+$
and
$\nu _n := q_np_n \colon {\mathcal D}_{n+1}^+ \to {\mathcal D}_n^+$
and
![]() $\psi _n := q_n\phi _n\colon {\mathcal A}_n^+\to {\mathcal D}_n^+$
,
$\psi _n := q_n\phi _n\colon {\mathcal A}_n^+\to {\mathcal D}_n^+$
,
![]() $n \geq 1$
, and the sequences
$n \geq 1$
, and the sequences
![]() $\boldsymbol {\nu } = (\nu _n)_{n\in {\mathbb N}}$
and
$\boldsymbol {\nu } = (\nu _n)_{n\in {\mathbb N}}$
and
![]() $\boldsymbol {\psi } = (\psi _n)_{n\in {\mathbb N}}$
, where
$\boldsymbol {\psi } = (\psi _n)_{n\in {\mathbb N}}$
, where
![]() $\psi _0 := \phi _0$
. We are going to show that these objects satisfy the conclusion of the proposition.
$\psi _0 := \phi _0$
. We are going to show that these objects satisfy the conclusion of the proposition.
We start by observing that it follows from the definitions that the diagram below commutes for all
![]() $n\geq 1$
:
$n\geq 1$
:

In particular,
![]() $\nu _n\nu _{n+1} = q_n\tau _np_{n+1}$
, so
$\nu _n\nu _{n+1} = q_n\tau _np_{n+1}$
, so
![]() $\langle \nu _{[n,n+1]} \rangle \geq \langle \tau _n\rangle $
. Being
$\langle \nu _{[n,n+1]} \rangle \geq \langle \tau _n\rangle $
. Being
![]() $\boldsymbol {\tau }$
everywhere growing, this implies that
$\boldsymbol {\tau }$
everywhere growing, this implies that
![]() $\boldsymbol {\nu }$
has the same property. We also observe that condition (iii) implies that
$\boldsymbol {\nu }$
has the same property. We also observe that condition (iii) implies that
![]() $\nu _n = q_np_n$
is letter-onto and proper. Altogether, these arguments prove that, up to contracting the first levels,
$\nu _n = q_np_n$
is letter-onto and proper. Altogether, these arguments prove that, up to contracting the first levels,
![]() $\boldsymbol {\nu }$
is everywhere growing and proper.
$\boldsymbol {\nu }$
is everywhere growing and proper.
Next, we note that
![]() $\boldsymbol {\nu }$
and
$\boldsymbol {\nu }$
and
![]() $\boldsymbol {\tau }$
are equivalent as both are contractions of
$\boldsymbol {\tau }$
are equivalent as both are contractions of
![]() $(p_0, q_1, p_1, q_2, \ldots )$
. This implies, by Lemma 2.3, that
$(p_0, q_1, p_1, q_2, \ldots )$
. This implies, by Lemma 2.3, that
![]() $\boldsymbol {\nu }$
is recognizable if
$\boldsymbol {\nu }$
is recognizable if
![]() $\boldsymbol {\tau }$
is recognizable. Further, by condition (i),
$\boldsymbol {\tau }$
is recognizable. Further, by condition (i),
![]() $\boldsymbol {\nu }$
has alphabet rank at most
$\boldsymbol {\nu }$
has alphabet rank at most
![]() $\mathrm {AR}(\boldsymbol {\sigma })$
.
$\mathrm {AR}(\boldsymbol {\sigma })$
.
It is only left to prove that
![]() $\boldsymbol {\psi }$
is a letter-onto and proper factor. By unraveling the definitions we can compute:
$\boldsymbol {\psi }$
is a letter-onto and proper factor. By unraveling the definitions we can compute:
and from the diagram, we have
![]() $\sigma _n\psi _n = \psi _{n+1}\tau _n$
for all
$\sigma _n\psi _n = \psi _{n+1}\tau _n$
for all
![]() $n\geq 1$
. Therefore,
$n\geq 1$
. Therefore,
![]() $\boldsymbol {\psi }$
is a factor. Finally, since
$\boldsymbol {\psi }$
is a factor. Finally, since
![]() $q_n$
is letter-onto and proper by condition (iii) and
$q_n$
is letter-onto and proper by condition (iii) and
![]() $\boldsymbol {\phi }$
was assumed to be letter-onto,
$\boldsymbol {\phi }$
was assumed to be letter-onto,
![]() $\psi _n = q_n\phi _n$
is letter-onto and proper.
$\psi _n = q_n\phi _n$
is letter-onto and proper.
4.2 Rank of factors of
 ${\mathcal S}$
-adic subshifts
${\mathcal S}$
-adic subshifts
In this section, we will prove Theorem 1.3 and its consequences. We start with a technical lemma.
The next lemma will allow us to assume without loss of generality that our directive sequences are letter-onto.
Lemma 4.6. Let
 $\boldsymbol {\tau } = (\tau _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be an everywhere growing and proper directive sequence. If
$\boldsymbol {\tau } = (\tau _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be an everywhere growing and proper directive sequence. If
 $\tilde {{\mathcal A}}_n = {\mathcal A}_n \cap {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n)})$
,
$\tilde {{\mathcal A}}_n = {\mathcal A}_n \cap {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n)})$
,
![]() $\tilde {\tau }_n$
is the restriction of
$\tilde {\tau }_n$
is the restriction of
![]() $\tau _n$
to
$\tau _n$
to
![]() $\tilde {{\mathcal A}}_{n+1}$
and
$\tilde {{\mathcal A}}_{n+1}$
and
![]() $\boldsymbol {\tilde {\tau }} = (\tilde {\tau }_0,\tilde {\tau }_1,\ldots )$
, then
$\boldsymbol {\tilde {\tau }} = (\tilde {\tau }_0,\tilde {\tau }_1,\ldots )$
, then
![]() $\boldsymbol {\tilde {\tau }}$
is letter-onto and
$\boldsymbol {\tilde {\tau }}$
is letter-onto and
 $X_{\boldsymbol {\tilde {\tau }}}^{(n)} = X_{\boldsymbol {\tau }}^{(n)}$
for every
$X_{\boldsymbol {\tilde {\tau }}}^{(n)} = X_{\boldsymbol {\tau }}^{(n)}$
for every
![]() $n \in {\mathbb N}$
. Conversely, if
$n \in {\mathbb N}$
. Conversely, if
![]() $\boldsymbol {\tau }$
is letter-onto, then
$\boldsymbol {\tau }$
is letter-onto, then
 ${\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})$
for every
${\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})$
for every
![]() $n \in {\mathbb N}$
.
$n \in {\mathbb N}$
.
Proof. By Lemma 2.5,
![]() $\tilde {\tau }_n$
is letter-onto mapping
$\tilde {\tau }_n$
is letter-onto mapping
 $\tilde {{\mathcal A}}_{n+1}^+$
into
$\tilde {{\mathcal A}}_{n+1}^+$
into
![]() $\tilde {{\mathcal A}}_n$
. Moreover, that lemma also gives that for every
$\tilde {{\mathcal A}}_n$
. Moreover, that lemma also gives that for every
 $x \in X_{\boldsymbol {\tau }}^{(n)}$
and
$x \in X_{\boldsymbol {\tau }}^{(n)}$
and
![]() $N>n$
, there exists a
$N>n$
, there exists a
![]() $\tau _{[n,N)}$
-factorization
$\tau _{[n,N)}$
-factorization
![]() $(k',x')$
of x in
$(k',x')$
of x in
 $X_{\boldsymbol {\tau }}^{(N)}$
. This together with the inclusion
$X_{\boldsymbol {\tau }}^{(N)}$
. This together with the inclusion
 $X_{\boldsymbol {\tau }}^{(N)} \subseteq \tilde {{\mathcal A}}_N^{\mathbb Z}$
imply that
$X_{\boldsymbol {\tau }}^{(N)} \subseteq \tilde {{\mathcal A}}_N^{\mathbb Z}$
imply that
 $$ \begin{align*} Z := \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\tau_{[n,N)}(\tilde{{\mathcal A}}_N^{\mathbb Z}) \supseteq X_{\boldsymbol{\tau}}^{(n)}. \end{align*} $$
$$ \begin{align*} Z := \bigcap_{N>n}\bigcup_{k\in{\mathbb Z}}T^k\tau_{[n,N)}(\tilde{{\mathcal A}}_N^{\mathbb Z}) \supseteq X_{\boldsymbol{\tau}}^{(n)}. \end{align*} $$
Now,
![]() $\boldsymbol {\tilde {\tau }}$
is everywhere growing and proper, so we can apply Lemma 2.6 to obtain that
$\boldsymbol {\tilde {\tau }}$
is everywhere growing and proper, so we can apply Lemma 2.6 to obtain that
 $X_{\boldsymbol {\tilde {\tau }}}^{(n)} = Z \supseteq X_{\boldsymbol {\tau }}^{(n)}$
. Since it is clear that
$X_{\boldsymbol {\tilde {\tau }}}^{(n)} = Z \supseteq X_{\boldsymbol {\tau }}^{(n)}$
. Since it is clear that
 $X_{\boldsymbol {\tilde {\tau }}}^{(n)}\subseteq X_{\boldsymbol {\tau }}^{(n)}$
as
$X_{\boldsymbol {\tilde {\tau }}}^{(n)}\subseteq X_{\boldsymbol {\tau }}^{(n)}$
as
![]() $\tilde {{\mathcal A}}_N \subseteq {\mathcal A}_N$
for every N, we conclude that
$\tilde {{\mathcal A}}_N \subseteq {\mathcal A}_N$
for every N, we conclude that
 $X_{\boldsymbol {\tilde {\tau }}}^{(n)} = X_{\boldsymbol {\tau }}^{(n)}$
.
$X_{\boldsymbol {\tilde {\tau }}}^{(n)} = X_{\boldsymbol {\tau }}^{(n)}$
.
If
![]() $\boldsymbol {\tau }$
is letter-onto, then
$\boldsymbol {\tau }$
is letter-onto, then
 ${\mathcal A}_n \subseteq {\mathcal L}(\bigcup _{k\in {\mathbb Z}}T^k\tau _{[n,N)}({\mathcal A}_N^{\mathbb Z}))$
for every
${\mathcal A}_n \subseteq {\mathcal L}(\bigcup _{k\in {\mathbb Z}}T^k\tau _{[n,N)}({\mathcal A}_N^{\mathbb Z}))$
for every
![]() $N>n$
, and hence, by the formula in Lemma 2.6,
$N>n$
, and hence, by the formula in Lemma 2.6,
 ${\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})$
.
${\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})$
.
Now we are ready to prove Theorem 1.3. We re-state it in a more precise way.
Theorem 1.3. Let
![]() $\pi \colon (X,T) \to (Y,T)$
be a factor map between aperiodic subshifts. Suppose that X is generated by the everywhere growing and proper directive sequence
$\pi \colon (X,T) \to (Y,T)$
be a factor map between aperiodic subshifts. Suppose that X is generated by the everywhere growing and proper directive sequence
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
of alphabet rank K. Then, Y is generated by a letter-onto, everywhere growing, proper, and recognizable directive sequence
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
of alphabet rank K. Then, Y is generated by a letter-onto, everywhere growing, proper, and recognizable directive sequence
![]() $\boldsymbol {\tau }$
of alphabet rank at most K.
$\boldsymbol {\tau }$
of alphabet rank at most K.
Moreover, if
![]() $\boldsymbol {\sigma }$
is letter-onto, then, up to contracting the sequences, there exists a proper factor
$\boldsymbol {\sigma }$
is letter-onto, then, up to contracting the sequences, there exists a proper factor
![]() $\boldsymbol {\phi }\colon \boldsymbol {\sigma }\to \boldsymbol {\tau }$
such that
$\boldsymbol {\phi }\colon \boldsymbol {\sigma }\to \boldsymbol {\tau }$
such that
![]() $\pi (\sigma _0(x)) = \phi _0(x)$
for all
$\pi (\sigma _0(x)) = \phi _0(x)$
for all
 $x \in X_{\boldsymbol {\sigma }}^{(1)}$
and
$x \in X_{\boldsymbol {\sigma }}^{(1)}$
and
![]() $|\sigma _0(a)| = |\phi _0(a)|$
for all
$|\sigma _0(a)| = |\phi _0(a)|$
for all
![]() $a \in {\mathcal A}_{1}$
.
$a \in {\mathcal A}_{1}$
.
Proof. Thanks to Lemma 4.6, we can assume without loss of generality that
![]() $\boldsymbol {\sigma }$
is letter-onto. Moreover, in this case,
$\boldsymbol {\sigma }$
is letter-onto. Moreover, in this case,
 $$ \begin{align} {\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol{\sigma}}^{(n)})\quad \text{for every}\ n \in {\mathbb N}. \end{align} $$
$$ \begin{align} {\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol{\sigma}}^{(n)})\quad \text{for every}\ n \in {\mathbb N}. \end{align} $$
Let us write
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
. By contracting
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
. By contracting
![]() $\boldsymbol {\sigma }$
, we can further assume that
$\boldsymbol {\sigma }$
, we can further assume that
![]() $\sigma _0$
is r-proper and
$\sigma _0$
is r-proper and
![]() $\pi $
has radius r. Then, Lemma 2.4 gives us a proper morphism
$\pi $
has radius r. Then, Lemma 2.4 gives us a proper morphism
 $\tau \colon {\mathcal A}_1^+\to {\mathcal B}^+$
, where
$\tau \colon {\mathcal A}_1^+\to {\mathcal B}^+$
, where
![]() ${\mathcal B}$
is the alphabet of Y, such that
${\mathcal B}$
is the alphabet of Y, such that
 $$ \begin{align} \pi(\sigma_0(x)) = \tau(x)\ \text{for all}\ x \in X_{\boldsymbol{\sigma}}^{(1)}\quad \text{and}\quad |\sigma_0(a)| = |\tau(a)|\ \text{for every}\ a \in {\mathcal A}_1. \end{align} $$
$$ \begin{align} \pi(\sigma_0(x)) = \tau(x)\ \text{for all}\ x \in X_{\boldsymbol{\sigma}}^{(1)}\quad \text{and}\quad |\sigma_0(a)| = |\tau(a)|\ \text{for every}\ a \in {\mathcal A}_1. \end{align} $$
In particular,
![]() $\pi (\sigma _{[0,n)}(x)) = \tau \sigma _{[1,n)}(x)$
and
$\pi (\sigma _{[0,n)}(x)) = \tau \sigma _{[1,n)}(x)$
and
![]() $|\sigma _{[0,n)}(a)| = |\tau \sigma _{[1,n)}(a)|$
for all
$|\sigma _{[0,n)}(a)| = |\tau \sigma _{[1,n)}(a)|$
for all
![]() $n \in {\mathbb N}$
,
$n \in {\mathbb N}$
,
 $x \in X_{\boldsymbol {\sigma }}^{(n)}$
, and
$x \in X_{\boldsymbol {\sigma }}^{(n)}$
, and
![]() $a \in {\mathcal A}_n$
, so (23) holds for any contraction of
$a \in {\mathcal A}_n$
, so (23) holds for any contraction of
![]() $\boldsymbol {\sigma }$
.
$\boldsymbol {\sigma }$
.
We define
![]() $\boldsymbol {\tilde {\sigma }} = (\tau , \sigma _1, \sigma _2, \ldots )$
and observe this is a letter-onto, everywhere growing and proper sequence generating Y. This and that Y is aperiodic allow us to use Proposition 4.4 and obtain, after a contraction, a letter-onto factor
$\boldsymbol {\tilde {\sigma }} = (\tau , \sigma _1, \sigma _2, \ldots )$
and observe this is a letter-onto, everywhere growing and proper sequence generating Y. This and that Y is aperiodic allow us to use Proposition 4.4 and obtain, after a contraction, a letter-onto factor
![]() $\boldsymbol {\tilde {\phi }}\colon \boldsymbol {\tilde {\sigma }}\to \boldsymbol {\tilde {\tau }}$
, where
$\boldsymbol {\tilde {\phi }}\colon \boldsymbol {\tilde {\sigma }}\to \boldsymbol {\tilde {\tau }}$
, where
![]() $\tilde {\phi }_0 = \tilde {\sigma }_0 = \tau $
and
$\tilde {\phi }_0 = \tilde {\sigma }_0 = \tau $
and
![]() $\boldsymbol {\tilde {\tau }}$
is a letter-onto, everywhere growing, proper, and recognizable directive sequence generating Y. The sequence
$\boldsymbol {\tilde {\tau }}$
is a letter-onto, everywhere growing, proper, and recognizable directive sequence generating Y. The sequence
![]() $\boldsymbol {\tilde {\tau }}$
has all the properties required by the theorem but having alphabet rank bounded by K. To overcome this, we use Proposition 4.5 with
$\boldsymbol {\tilde {\tau }}$
has all the properties required by the theorem but having alphabet rank bounded by K. To overcome this, we use Proposition 4.5 with
![]() $\boldsymbol {\tilde {\phi }}$
and do more contractions to obtain a letter-onto and proper factor
$\boldsymbol {\tilde {\phi }}$
and do more contractions to obtain a letter-onto and proper factor
![]() $\boldsymbol {\phi }\colon \boldsymbol {\tilde {\sigma }} \to \boldsymbol {\tau }$
such that
$\boldsymbol {\phi }\colon \boldsymbol {\tilde {\sigma }} \to \boldsymbol {\tau }$
such that
![]() $\phi _0 = \tilde {\phi }_0 = \tau $
and
$\phi _0 = \tilde {\phi }_0 = \tau $
and
![]() $\boldsymbol {\tau }$
is a letter-onto, everywhere growing, proper, and recognizable directive sequence generating Y and satisfying
$\boldsymbol {\tau }$
is a letter-onto, everywhere growing, proper, and recognizable directive sequence generating Y and satisfying
![]() $\mathrm {AR}(\boldsymbol {\tau }) \leq \mathrm {AR}(\tilde {\boldsymbol {\sigma }}) = \mathrm {AR}(\boldsymbol {\sigma })$
.
$\mathrm {AR}(\boldsymbol {\tau }) \leq \mathrm {AR}(\tilde {\boldsymbol {\sigma }}) = \mathrm {AR}(\boldsymbol {\sigma })$
.
It is left to prove the last part of the theorem. Observe that since
![]() $\boldsymbol {\tilde {\sigma }}$
and
$\boldsymbol {\tilde {\sigma }}$
and
![]() $\boldsymbol {\sigma }$
differ only at their first coordinate,
$\boldsymbol {\sigma }$
differ only at their first coordinate,
![]() $\boldsymbol {\phi }$
is also a factor from
$\boldsymbol {\phi }$
is also a factor from
![]() $\boldsymbol {\sigma }$
to
$\boldsymbol {\sigma }$
to
![]() $\boldsymbol {\tau }$
. Further, by (23) and the fact that
$\boldsymbol {\tau }$
. Further, by (23) and the fact that
![]() $\phi _0 = \tau $
, we have
$\phi _0 = \tau $
, we have
![]() $\pi (\sigma _0(x)) = \tau (x) = \phi _0(x)$
and
$\pi (\sigma _0(x)) = \tau (x) = \phi _0(x)$
and
![]() $|\sigma _0(a)| = |\phi _0(a)|$
for every
$|\sigma _0(a)| = |\phi _0(a)|$
for every
 $x \in X_{\boldsymbol {\sigma }}^{(1)}$
and
$x \in X_{\boldsymbol {\sigma }}^{(1)}$
and
![]() $a \in {\mathcal A}_1$
.
$a \in {\mathcal A}_1$
.
Corollary 4.7. Let
![]() $(X,T)$
be an aperiodic minimal subshift generated by an everywhere growing and proper directive sequence of alphabet rank K. Then, the topological rank of X is at most K.
$(X,T)$
be an aperiodic minimal subshift generated by an everywhere growing and proper directive sequence of alphabet rank K. Then, the topological rank of X is at most K.
Proof. We can use Theorem 1.3 to obtain an everywhere growing, proper, and recognizable directive sequence
 $\boldsymbol {\tau } = (\tau _n\colon {\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\in {\mathbb N}}$
generating X and having alphabet rank at most K. Due to Lemma 4.6, we can assume that
$\boldsymbol {\tau } = (\tau _n\colon {\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\in {\mathbb N}}$
generating X and having alphabet rank at most K. Due to Lemma 4.6, we can assume that
![]() $\boldsymbol {\tau }$
is letter-onto. In particular,
$\boldsymbol {\tau }$
is letter-onto. In particular,
 ${\mathcal B}_n \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})$
for every
${\mathcal B}_n \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})$
for every
![]() $n \in {\mathbb N}$
.
$n \in {\mathbb N}$
.
We claim that
 $X_{\boldsymbol {\tau }}^{(n)}$
is minimal. Indeed, if
$X_{\boldsymbol {\tau }}^{(n)}$
is minimal. Indeed, if
 $Y \subseteq X_{\boldsymbol {\tau }}^{(n)}$
is a subshift, then
$Y \subseteq X_{\boldsymbol {\tau }}^{(n)}$
is a subshift, then
![]() $\tau _{[0,n)}(Y)$
is closed (as
$\tau _{[0,n)}(Y)$
is closed (as
 $\tau _{[0,n)}\colon X_{\boldsymbol {\tau }}^{(n)}\to X_{\boldsymbol {\tau }}$
is continuous), so
$\tau _{[0,n)}\colon X_{\boldsymbol {\tau }}^{(n)}\to X_{\boldsymbol {\tau }}$
is continuous), so
 $\bigcup _{k\in {\mathbb Z}}T^k\tau _{[0,n)}(Y) = \bigcup _{|k|\leq |\tau _{[0,n)}|}T^k\tau _{[0,n)}(Y)$
is a subshift in
$\bigcup _{k\in {\mathbb Z}}T^k\tau _{[0,n)}(Y) = \bigcup _{|k|\leq |\tau _{[0,n)}|}T^k\tau _{[0,n)}(Y)$
is a subshift in
![]() $X_{\boldsymbol {\tau }}$
which, by minimality, is equal to it. Thus, any point
$X_{\boldsymbol {\tau }}$
which, by minimality, is equal to it. Thus, any point
 $x \in X_{\boldsymbol {\tau }}^{(n)}$
has a
$x \in X_{\boldsymbol {\tau }}^{(n)}$
has a
![]() $\tau _{[0,n)}$
-factorization
$\tau _{[0,n)}$
-factorization
![]() $(k,z)$
with
$(k,z)$
with
![]() $z \in Y$
. The recognizability property of
$z \in Y$
. The recognizability property of
 $(X_{\boldsymbol {\tau }}^{(n)},\tau _{[0,n)})$
then implies that
$(X_{\boldsymbol {\tau }}^{(n)},\tau _{[0,n)})$
then implies that
 $Y = X_{\boldsymbol {\tau }}^{(n)}$
.
$Y = X_{\boldsymbol {\tau }}^{(n)}$
.
Now, we prove that for any
![]() $n\in {\mathbb N}$
, there exists
$n\in {\mathbb N}$
, there exists
![]() $N>n$
such that
$N>n$
such that
![]() $\tau _{[n,N)}$
is positive. This would imply that the topological rank of X is at most K and hence would complete the proof. Let
$\tau _{[n,N)}$
is positive. This would imply that the topological rank of X is at most K and hence would complete the proof. Let
![]() $n \in {\mathbb N}$
and R be a constant of recognizability for
$n \in {\mathbb N}$
and R be a constant of recognizability for
 $(X_{\boldsymbol {\tau }}^{(n)},\tau _{[0,n)})$
. Since
$(X_{\boldsymbol {\tau }}^{(n)},\tau _{[0,n)})$
. Since
 $X_{\boldsymbol {\tau }}^{(n)}$
is minimal, there exists a constant
$X_{\boldsymbol {\tau }}^{(n)}$
is minimal, there exists a constant
![]() $L\geq 1$
such that two consecutive occurrences of a word
$L\geq 1$
such that two consecutive occurrences of a word
 $w \in {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})\cap {\mathcal B}_n^{2R+1}$
in a point
$w \in {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})\cap {\mathcal B}_n^{2R+1}$
in a point
 $x \in X_{\boldsymbol {\tau }}^{(n)}$
are separated by at most L. Let
$x \in X_{\boldsymbol {\tau }}^{(n)}$
are separated by at most L. Let
![]() $N> n$
be big enough so that
$N> n$
be big enough so that
![]() $\langle \tau _{[0,N)}\rangle \geq L+2R$
. Then, for all
$\langle \tau _{[0,N)}\rangle \geq L+2R$
. Then, for all
 $a \in {\mathcal B}_N \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(N)})$
and
$a \in {\mathcal B}_N \subseteq {\mathcal L}(X_{\boldsymbol {\tau }}^{(N)})$
and
 $w \in {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})\cap {\mathcal B}_n^{2R+1}$
, w occurs at a position
$w \in {\mathcal L}(X_{\boldsymbol {\tau }}^{(n)})\cap {\mathcal B}_n^{2R+1}$
, w occurs at a position
![]() $i \in \{R,R+1,\ldots ,|\tau _{[0,N)}(a)|-R\}$
of
$i \in \{R,R+1,\ldots ,|\tau _{[0,N)}(a)|-R\}$
of
![]() $\tau _{[0,N)}(a)$
. Since R is a recognizability constant for
$\tau _{[0,N)}(a)$
. Since R is a recognizability constant for
 $(X_{\boldsymbol {\tau }}^{(n)},\tau _{[0,n)})$
, we deduce that for all
$(X_{\boldsymbol {\tau }}^{(n)},\tau _{[0,n)})$
, we deduce that for all
![]() $a \in {\mathcal B}_N$
and
$a \in {\mathcal B}_N$
and
![]() $b \in {\mathcal B}_n$
, b occurs in
$b \in {\mathcal B}_n$
, b occurs in
![]() $\tau _{[n,N)}(a)$
. Thus,
$\tau _{[n,N)}(a)$
. Thus,
![]() $\tau _{[n,N)}$
is positive.
$\tau _{[n,N)}$
is positive.
We can now prove Corollary 1.4.
Corollary 1.4. Let
![]() $(X,T)$
be an aperiodic minimal subshift generated by an everywhere growing directive sequence of finite alphabet rank. Then, the topological rank of
$(X,T)$
be an aperiodic minimal subshift generated by an everywhere growing directive sequence of finite alphabet rank. Then, the topological rank of
![]() $(X,T)$
is finite.
$(X,T)$
is finite.
Proof. We are going to prove that X is generated by an everywhere growing and proper directive sequence
![]() $\boldsymbol {\tau }$
of finite alphabet rank. This would imply, by Corollary 4.7, that the topological rank of X is finite. Let
$\boldsymbol {\tau }$
of finite alphabet rank. This would imply, by Corollary 4.7, that the topological rank of X is finite. Let
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be an everywhere growing directive sequence of finite alphabet rank generating X. We contract
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be an everywhere growing directive sequence of finite alphabet rank generating X. We contract
![]() $\boldsymbol {\tau }$
in a way such that
$\boldsymbol {\tau }$
in a way such that
![]() $\#{\mathcal A}_n \leq K$
for every
$\#{\mathcal A}_n \leq K$
for every
![]() $n\geq 1$
.
$n\geq 1$
.
We are going to inductively define subshifts
![]() $X_n$
,
$X_n$
,
![]() $n\in {\mathbb N}$
. We start with
$n\in {\mathbb N}$
. We start with
![]() $X_0 := X$
. We now assume that
$X_0 := X$
. We now assume that
![]() $X_n$
is defined for some
$X_n$
is defined for some
![]() $n \in {\mathbb N}$
. Then the set
$n \in {\mathbb N}$
. Then the set
 $X^{\prime }_{n+1} = \{x \in X_{\boldsymbol {\sigma }}^{(n+1}: \sigma _n(x) \in X_n\}$
is a subshift. We define
$X^{\prime }_{n+1} = \{x \in X_{\boldsymbol {\sigma }}^{(n+1}: \sigma _n(x) \in X_n\}$
is a subshift. We define
![]() $X_{n+1}$
as any minimal subshift contained in
$X_{n+1}$
as any minimal subshift contained in
 $X^{\prime }_{n+1}$
. It follows from the definition of
$X^{\prime }_{n+1}$
. It follows from the definition of
![]() $X_{n+1}$
that
$X_{n+1}$
that
 $\bigcup _{k\in {\mathbb Z}}T^k\sigma _n(X_{n+1}) \subseteq X_n$
. Being
$\bigcup _{k\in {\mathbb Z}}T^k\sigma _n(X_{n+1}) \subseteq X_n$
. Being
![]() $X_n$
minimal,
$X_n$
minimal,
 $$ \begin{align} \bigcup_{k\in{\mathbb Z}}T^k\sigma_n(X_{n+1}) = X_n. \end{align} $$
$$ \begin{align} \bigcup_{k\in{\mathbb Z}}T^k\sigma_n(X_{n+1}) = X_n. \end{align} $$
Let
![]() $\tilde {{\mathcal A}}_n = {\mathcal A}_n \cap {\mathcal L}(X_n)$
. Equation (24) and the fact that
$\tilde {{\mathcal A}}_n = {\mathcal A}_n \cap {\mathcal L}(X_n)$
. Equation (24) and the fact that
![]() $\boldsymbol {\sigma }$
is everywhere growing allow us to assume without loss of generality that, after a contraction of
$\boldsymbol {\sigma }$
is everywhere growing allow us to assume without loss of generality that, after a contraction of
![]() $\boldsymbol {\sigma }$
, the following holds for every
$\boldsymbol {\sigma }$
, the following holds for every
![]() $n\in {\mathbb N}$
:
$n\in {\mathbb N}$
:
Let us fix a word
![]() $w_n = a_nb_nc_b \in {\mathcal L}(X_n)$
of length
$w_n = a_nb_nc_b \in {\mathcal L}(X_n)$
of length
![]() $3$
. Then, by (25), we can decompose
$3$
. Then, by (25), we can decompose
![]() $\sigma _n(a) = u_n(a)v_n(a)$
in a way such that
$\sigma _n(a) = u_n(a)v_n(a)$
in a way such that
To define
![]() $\boldsymbol {\tau }$
, we need to introduce additional notation first. Let
$\boldsymbol {\tau }$
, we need to introduce additional notation first. Let
![]() ${\mathcal B}_n$
be the alphabet consisting of tuples
${\mathcal B}_n$
be the alphabet consisting of tuples
![]() ${a\brack b}$
such that
${a\brack b}$
such that
![]() $ab \in {\mathcal L}(X_n)$
. Also, if
$ab \in {\mathcal L}(X_n)$
. Also, if
![]() $w = w_1\ldots w_{|w|} \in {\mathcal L}(X_n)$
has length
$w = w_1\ldots w_{|w|} \in {\mathcal L}(X_n)$
has length
![]() $|w|\geq 2$
, then
$|w|\geq 2$
, then
 $\chi _n(w) := {w_1\brack w_2} {w_2\brack w_3}\ldots {w_{|w|-1}\brack w_{|w|}} \in {\mathcal B}_n^+$
, and if
$\chi _n(w) := {w_1\brack w_2} {w_2\brack w_3}\ldots {w_{|w|-1}\brack w_{|w|}} \in {\mathcal B}_n^+$
, and if
 $w' = {w_1\brack w_2}\ldots {w_{|w|-1}\brack w_{|w|}} \in {\mathcal B}_0^+$
, then
$w' = {w_1\brack w_2}\ldots {w_{|w|-1}\brack w_{|w|}} \in {\mathcal B}_0^+$
, then
 $\eta (w') := w_1\ldots w_{|w|-1} \in {\mathcal A}_0^+$
. Observe that
$\eta (w') := w_1\ldots w_{|w|-1} \in {\mathcal A}_0^+$
. Observe that
 $\eta \colon {\mathcal B}_0^+\to {\mathcal A}_0^+$
is a morphism.
$\eta \colon {\mathcal B}_0^+\to {\mathcal A}_0^+$
is a morphism.
We now define
![]() $\boldsymbol {\tau }$
. Let
$\boldsymbol {\tau }$
. Let
 $\tau _n\colon {\mathcal B}_{n+1}^+\to {\mathcal B}_n^+$
be the unique morphism such that
$\tau _n\colon {\mathcal B}_{n+1}^+\to {\mathcal B}_n^+$
be the unique morphism such that
 $\tau _n({a\brack b}) = \chi _n(v_n(a)u_n(a)b_n)$
for every
$\tau _n({a\brack b}) = \chi _n(v_n(a)u_n(a)b_n)$
for every
 ${a\brack b} \in {\mathcal B}_{n+1}$
. Observe that since
${a\brack b} \in {\mathcal B}_{n+1}$
. Observe that since
![]() $v_n(a)u_n(a)b_n \in {\mathcal L}(X_n)$
, it is indeed the case that
$v_n(a)u_n(a)b_n \in {\mathcal L}(X_n)$
, it is indeed the case that
 $\tau _n({a\brack b})\in {\mathcal B}_n^+$
. We set
$\tau _n({a\brack b})\in {\mathcal B}_n^+$
. We set
![]() $\boldsymbol {\tau } = (\eta \tau _0,\tau _1,\tau _2,\ldots )$
.
$\boldsymbol {\tau } = (\eta \tau _0,\tau _1,\tau _2,\ldots )$
.
It follows from (26) that for every
![]() $n \in {\mathbb N}$
and
$n \in {\mathbb N}$
and
 ${a\brack b} \in {\mathcal B}_{n+1}$
,
${a\brack b} \in {\mathcal B}_{n+1}$
,
 $\tau _n({a\brack b})$
starts with
$\tau _n({a\brack b})$
starts with
 ${b_n\brack c_n}$
and ends with
${b_n\brack c_n}$
and ends with
 ${a_n \brack b_n}$
. Thus,
${a_n \brack b_n}$
. Thus,
![]() $\boldsymbol {\tau }$
is proper. Moreover, since
$\boldsymbol {\tau }$
is proper. Moreover, since
![]() $|v_n(a)| \geq 2$
, we have
$|v_n(a)| \geq 2$
, we have
![]() $|v_n(a)u_n(a)b_n| \geq 3$
and thus
$|v_n(a)u_n(a)b_n| \geq 3$
and thus
 $|\tau _n({a\brack b})| \geq 2$
. Therefore,
$|\tau _n({a\brack b})| \geq 2$
. Therefore,
![]() $\langle \tau _n\rangle \geq 2$
and
$\langle \tau _n\rangle \geq 2$
and
![]() $\boldsymbol {\tau }$
is everywhere growing. Also,
$\boldsymbol {\tau }$
is everywhere growing. Also,
 $\#{\mathcal B}_n \leq \#{\mathcal A}_n^2 \leq K^2$
for every
$\#{\mathcal B}_n \leq \#{\mathcal A}_n^2 \leq K^2$
for every
![]() $n \in {\mathbb N}$
, so the alphabet rank of
$n \in {\mathbb N}$
, so the alphabet rank of
![]() $\boldsymbol {\tau }$
is finite.
$\boldsymbol {\tau }$
is finite.
It remains to prove that
![]() $X = X_{\boldsymbol {\tau }}$
. By minimality, it is enough to prove that
$X = X_{\boldsymbol {\tau }}$
. By minimality, it is enough to prove that
![]() $X \supseteq X_{\boldsymbol {\tau }}$
. Observe that since
$X \supseteq X_{\boldsymbol {\tau }}$
. Observe that since
![]() $\tau _n\chi _{n+1}(ab) = \chi _n(v_n(a)u_n(b)b_n)$
, the word
$\tau _n\chi _{n+1}(ab) = \chi _n(v_n(a)u_n(b)b_n)$
, the word
![]() $\tau _n\chi _{n+1}(ab)$
occurs in
$\tau _n\chi _{n+1}(ab)$
occurs in
![]() $\chi _n\sigma _n(ab)$
. Moreover, for every
$\chi _n\sigma _n(ab)$
. Moreover, for every
 $w = w_1\ldots w_{|w|} \in {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n)})$
,
$w = w_1\ldots w_{|w|} \in {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n)})$
,
![]() $\tau _n\chi _{n+1}(w)$
occurs in
$\tau _n\chi _{n+1}(w)$
occurs in
![]() $\chi _n\sigma _n(w)$
. Then, by using the symbol
$\chi _n\sigma _n(w)$
. Then, by using the symbol
![]() $\sqsubseteq $
to denote the ‘subword’ relation, we can write for every
$\sqsubseteq $
to denote the ‘subword’ relation, we can write for every
![]() $n \in {\mathbb N}$
and
$n \in {\mathbb N}$
and
 $ab \in {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n)})$
:
$ab \in {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n)})$
:
 $$ \begin{align*} \tau_{[0,n)}\chi_n(ab) &\sqsubseteq \tau_{[0,n-1)}\chi_{n-1}\sigma_{n-1}(ab) \\[3pt] &\sqsubseteq \tau_{[0,n-2)}\chi_{n-2}\sigma_{[n-2,n)}(ab) \sqsubseteq \cdots \sqsubseteq \chi_0\sigma_{[0,n)}(ab). \end{align*} $$
$$ \begin{align*} \tau_{[0,n)}\chi_n(ab) &\sqsubseteq \tau_{[0,n-1)}\chi_{n-1}\sigma_{n-1}(ab) \\[3pt] &\sqsubseteq \tau_{[0,n-2)}\chi_{n-2}\sigma_{[n-2,n)}(ab) \sqsubseteq \cdots \sqsubseteq \chi_0\sigma_{[0,n)}(ab). \end{align*} $$
Hence,
 $\eta \tau _{[0,n)}({a\brack b}) \sqsubseteq \eta \chi _0\sigma _{[0,n)}(ab) \sqsubseteq \sigma _{[0,n)}(ab)$
. We conclude that
$\eta \tau _{[0,n)}({a\brack b}) \sqsubseteq \eta \chi _0\sigma _{[0,n)}(ab) \sqsubseteq \sigma _{[0,n)}(ab)$
. We conclude that
![]() $X_{\boldsymbol {\tau }} \subseteq X_{\boldsymbol {\sigma }} = X$
.
$X_{\boldsymbol {\tau }} \subseteq X_{\boldsymbol {\sigma }} = X$
.
Corollary 4.8. Let
![]() $(X,T)$
be a minimal subshift of topological rank K and
$(X,T)$
be a minimal subshift of topological rank K and
![]() $\pi \colon (X,T)\to (Y,T)$
a factor map, where Y is an aperiodic subshift. Then, the topological rank of Y is at most K.
$\pi \colon (X,T)\to (Y,T)$
a factor map, where Y is an aperiodic subshift. Then, the topological rank of Y is at most K.
Proof. By Theorem 1.1,
![]() $(X,T)$
is generated by a proper and primitive directive sequence
$(X,T)$
is generated by a proper and primitive directive sequence
![]() $\boldsymbol {\sigma }$
of alphabet rank equal to K. In particular,
$\boldsymbol {\sigma }$
of alphabet rank equal to K. In particular,
![]() $\boldsymbol {\sigma }$
is everywhere growing and proper, so we can use Theorem 1.3 to obtain an everywhere growing, proper, and recognizable directive sequence
$\boldsymbol {\sigma }$
is everywhere growing and proper, so we can use Theorem 1.3 to obtain an everywhere growing, proper, and recognizable directive sequence
 $\boldsymbol {\tau } = (\tau _n\colon {\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\geq 0}$
generating
$\boldsymbol {\tau } = (\tau _n\colon {\mathcal B}_{n+1}^+\to {\mathcal B}_n^+)_{n\geq 0}$
generating
![]() $(Y,T)$
and having alphabet rank at most K. Then, the hypothesis of Corollary 4.7 holds for
$(Y,T)$
and having alphabet rank at most K. Then, the hypothesis of Corollary 4.7 holds for
![]() $(Y,T)$
, and thus the topological rank of
$(Y,T)$
, and thus the topological rank of
![]() $(Y,T)$
is at most K.
$(Y,T)$
is at most K.
The following notion will be used in the proof of the theorem below:
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n)_{n\geq 0}$
has exact alphabet rank at most K if
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n)_{n\geq 0}$
has exact alphabet rank at most K if
![]() $\#{\mathcal A}_n\leq K$
for all
$\#{\mathcal A}_n\leq K$
for all
![]() $n\geq 1$
.
$n\geq 1$
.
Corollary 1.5. Let
![]() $(X,T)$
be an
$(X,T)$
be an
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing and proper sequence of alphabet rank K, and
${\mathcal S}$
-adic subshift generated by an everywhere growing and proper sequence of alphabet rank K, and
![]() $\pi _j\colon (X_{j+1},T) \to (X_j,T)$
,
$\pi _j\colon (X_{j+1},T) \to (X_j,T)$
,
![]() $j=0,\ldots ,L$
be a chain of aperiodic symbolic factors, with
$j=0,\ldots ,L$
be a chain of aperiodic symbolic factors, with
![]() $X_L = X$
. Suppose that
$X_L = X$
. Suppose that
![]() $L> \log _2(K)$
. Then
$L> \log _2(K)$
. Then
![]() $\pi _j$
is a conjugacy for some j.
$\pi _j$
is a conjugacy for some j.
Proof. We start by using Theorem 1.3 with the identity function
![]() $\mathrm {id}\colon (X,T)\to (X,T)$
to obtain a letter-onto, everywhere growing, proper, and recognizable directive sequence
$\mathrm {id}\colon (X,T)\to (X,T)$
to obtain a letter-onto, everywhere growing, proper, and recognizable directive sequence
![]() $\boldsymbol {\sigma _L}$
of alphabet rank at most K generating X. By doing a contraction, we can assume that
$\boldsymbol {\sigma _L}$
of alphabet rank at most K generating X. By doing a contraction, we can assume that
![]() $\boldsymbol {\sigma _L}$
has exact alphabet rank at most K.
$\boldsymbol {\sigma _L}$
has exact alphabet rank at most K.
By Theorem 1.3 applied to
![]() $\pi _{L-1}$
and
$\pi _{L-1}$
and
![]() $\boldsymbol {\sigma _L}$
, there exists, after a contraction of
$\boldsymbol {\sigma _L}$
, there exists, after a contraction of
![]() $\boldsymbol {\sigma _L}$
, a letter-onto factor
$\boldsymbol {\sigma _L}$
, a letter-onto factor
![]() $\boldsymbol {\phi _{L-1}}\colon \boldsymbol {\sigma _L}\to \boldsymbol {\sigma _{L-1}}$
, where
$\boldsymbol {\phi _{L-1}}\colon \boldsymbol {\sigma _L}\to \boldsymbol {\sigma _{L-1}}$
, where
![]() $\boldsymbol {\sigma _{L-1}}$
is letter-onto, everywhere growing, proper, recognizable, has alphabet rank at most K, generates
$\boldsymbol {\sigma _{L-1}}$
is letter-onto, everywhere growing, proper, recognizable, has alphabet rank at most K, generates
![]() $X_{L-1}$
, and, if
$X_{L-1}$
, and, if
![]() $\phi _{L-1,0}$
and
$\phi _{L-1,0}$
and
![]() $\sigma _{L,0}$
are the first coordinates of
$\sigma _{L,0}$
are the first coordinates of
![]() $\boldsymbol {\phi _{L-1}}$
and
$\boldsymbol {\phi _{L-1}}$
and
![]() $\boldsymbol {\sigma _{L}}$
, respectively, then
$\boldsymbol {\sigma _{L}}$
, respectively, then
![]() $\pi _{L-1}(\sigma _{L,0}(x)) = \phi _{L-1,0}(x)$
for every
$\pi _{L-1}(\sigma _{L,0}(x)) = \phi _{L-1,0}(x)$
for every
 $x \in X_{\boldsymbol {\sigma _L}}^{(1)}$
and
$x \in X_{\boldsymbol {\sigma _L}}^{(1)}$
and
![]() $|\sigma _{L,0}(a)| = |\phi _{L-1,0}(a)|$
for every letter a in the domain of
$|\sigma _{L,0}(a)| = |\phi _{L-1,0}(a)|$
for every letter a in the domain of
![]() $\sigma _{L,0}$
. By contracting these sequences, we can also suppose that
$\sigma _{L,0}$
. By contracting these sequences, we can also suppose that
![]() $\boldsymbol {\sigma _{L-1}}$
has exact alphabet rank at most K. The same procedure applies to
$\boldsymbol {\sigma _{L-1}}$
has exact alphabet rank at most K. The same procedure applies to
![]() $\pi _{L-2}$
and
$\pi _{L-2}$
and
![]() $\boldsymbol {\sigma _{L-1}}$
. Thus, by continuing in this way, we obtain for every
$\boldsymbol {\sigma _{L-1}}$
. Thus, by continuing in this way, we obtain for every
![]() $j=0,\ldots ,L-1$
a letter-onto factor
$j=0,\ldots ,L-1$
a letter-onto factor
![]() $\boldsymbol {\phi _j}\colon \boldsymbol {\sigma _{j+1}}\to \boldsymbol {\sigma _j}$
such that the following holds.
$\boldsymbol {\phi _j}\colon \boldsymbol {\sigma _{j+1}}\to \boldsymbol {\sigma _j}$
such that the following holds.
-
•
 $\boldsymbol {\sigma _j}$
is letter-onto, everywhere growing, proper, recognizable, has exact alphabet rank at most K, generates
$\boldsymbol {\sigma _j}$
is letter-onto, everywhere growing, proper, recognizable, has exact alphabet rank at most K, generates
 $X_j$
,
$X_j$
,
 $\pi _{j}(\sigma _{j+1,0}(x)) = \phi _{j,0}(x)$
for every
$\pi _{j}(\sigma _{j+1,0}(x)) = \phi _{j,0}(x)$
for every
 $x \in X_{\boldsymbol {\sigma _{j+1}}}^{(1)}$
, and
$x \in X_{\boldsymbol {\sigma _{j+1}}}^{(1)}$
, and
 $|\sigma _{j+1,0}(a)| = |\phi _{j,0}(a)|$
for every
$|\sigma _{j+1,0}(a)| = |\phi _{j,0}(a)|$
for every
 $a \in {\mathcal A}_{j+1,1}$
.
$a \in {\mathcal A}_{j+1,1}$
.
Here, we are using the notation
 $\boldsymbol {\sigma _j} = (\sigma _{j,n}\colon {\mathcal A}_{j,n+1}^+\to {\mathcal A}_{j,n}^+)_{n\in {\mathbb N}}$
,
$\boldsymbol {\sigma _j} = (\sigma _{j,n}\colon {\mathcal A}_{j,n+1}^+\to {\mathcal A}_{j,n}^+)_{n\in {\mathbb N}}$
,
 $\boldsymbol {\phi _j} = (\phi _{j,n}\colon {\mathcal A}_{j+1,n}^+\to {\mathcal A}_{j,n}^+)_{n\in {\mathbb N}}$
and
$\boldsymbol {\phi _j} = (\phi _{j,n}\colon {\mathcal A}_{j+1,n}^+\to {\mathcal A}_{j,n}^+)_{n\in {\mathbb N}}$
and
 $X_j^{(n)} = X_{\boldsymbol {\sigma _j}}^{(n)}$
. We note that:
$X_j^{(n)} = X_{\boldsymbol {\sigma _j}}^{(n)}$
. We note that:
-
(△1 ) for every
 $x \in X_{j+1}^{(1)}$
,
$x \in X_{j+1}^{(1)}$
,
 $\pi _j(\sigma _{j+1,0}(x)) = \phi _{j,0}(x) = \sigma _{j,0}\phi _{j,1}(x)$
since
$\pi _j(\sigma _{j+1,0}(x)) = \phi _{j,0}(x) = \sigma _{j,0}\phi _{j,1}(x)$
since
 $\phi _{j,0} = \sigma _{j,0}\phi _{j,1}$
;
$\phi _{j,0} = \sigma _{j,0}\phi _{j,1}$
; -
(△2 )
 $X_j^{(1)} = \bigcup _{k\in {\mathbb Z}}T^k\phi _{j,1}(X_{j+1}^{(1)})$
by Lemma 4.3.
$X_j^{(1)} = \bigcup _{k\in {\mathbb Z}}T^k\phi _{j,1}(X_{j+1}^{(1)})$
by Lemma 4.3.
Hence, the following diagram commutes:

Claim 4.8.1. If
 $(X_{j+1}^{(1)}, \phi _{j,1})$
is recognizable, then
$(X_{j+1}^{(1)}, \phi _{j,1})$
is recognizable, then
![]() $\pi _j$
is a conjugacy.
$\pi _j$
is a conjugacy.
Proof. Let us assume that
 $(X_{j+1}^{(1)}, \phi _{j,1})$
is recognizable, and let, for
$(X_{j+1}^{(1)}, \phi _{j,1})$
is recognizable, and let, for
![]() $i=0,1$
,
$i=0,1$
,
 $x^i \in X_{j+1}^{(1)}$
such that
$x^i \in X_{j+1}^{(1)}$
such that
 $y = \pi _j(x^0) = \pi _j(x^1)$
. We have to show that
$y = \pi _j(x^0) = \pi _j(x^1)$
. We have to show that
![]() $x^0 = x^1$
. First, we use Lemma 2.5 to find a centered
$x^0 = x^1$
. First, we use Lemma 2.5 to find a centered
![]() $\sigma _{j+1,0}$
-factorization
$\sigma _{j+1,0}$
-factorization
![]() $(k^i,z^i)$
of
$(k^i,z^i)$
of
![]() $x^i$
in
$x^i$
in
 $X_{j+1}^{(1)}$
. Then, equation
$X_{j+1}^{(1)}$
. Then, equation
![]() $\triangle _1$
allows us to compute:
$\triangle _1$
allows us to compute:
 $$ \begin{align*} T^{k^0}\sigma_{j,0}\phi_{j,1}(z^0) = T^{k^0}\pi_j(\sigma_{j+1,0}(z^0)) = \pi_j(x^0) = \pi_j(x^1) = T^{k^1}\sigma_{j,0}\phi_{j,1}(z^1). \end{align*} $$
$$ \begin{align*} T^{k^0}\sigma_{j,0}\phi_{j,1}(z^0) = T^{k^0}\pi_j(\sigma_{j+1,0}(z^0)) = \pi_j(x^0) = \pi_j(x^1) = T^{k^1}\sigma_{j,0}\phi_{j,1}(z^1). \end{align*} $$
This implies that
![]() $(k^i,z^i)$
is a
$(k^i,z^i)$
is a
![]() $\sigma _{j,0}\phi _{j,1}$
-factorization of y in
$\sigma _{j,0}\phi _{j,1}$
-factorization of y in
 $X_{j+1}^{(1)}$
for
$X_{j+1}^{(1)}$
for
![]() $i=0,1$
. Moreover, these are centered factorizations as, by
$i=0,1$
. Moreover, these are centered factorizations as, by
![]() $\bullet $
,
$\bullet $
,
![]() $|\sigma _{j,0}\phi _{j,1}(a)| = |\sigma _{j+1,0}(a)|$
for all
$|\sigma _{j,0}\phi _{j,1}(a)| = |\sigma _{j+1,0}(a)|$
for all
![]() $a \in {\mathcal A}_{j+1,1}$
. Now, being
$a \in {\mathcal A}_{j+1,1}$
. Now, being
 $(X_j^{(1)},\sigma _{0,j})$
and
$(X_j^{(1)},\sigma _{0,j})$
and
 $(X_{j+1}^{(1)}, \phi _{j,1})$
recognizable, Lemma 2.3 gives that
$(X_{j+1}^{(1)}, \phi _{j,1})$
recognizable, Lemma 2.3 gives that
 $(X_{j+1}^{(1)},\sigma _{j,1}\phi _{j,1})$
is recognizable, and thus we have that
$(X_{j+1}^{(1)},\sigma _{j,1}\phi _{j,1})$
is recognizable, and thus we have that
![]() $(k^0,z^0) = (k^1,z^1)$
. Therefore,
$(k^0,z^0) = (k^1,z^1)$
. Therefore,
![]() $x^0 = x^1$
and
$x^0 = x^1$
and
![]() $\pi $
is a conjugacy.
$\pi $
is a conjugacy.
Now we can finish the proof. We assume, by contradiction, that
![]() $\pi _j$
is not a conjugacy for all j. Then, by the claim,
$\pi _j$
is not a conjugacy for all j. Then, by the claim,
 $$ \begin{align} (X_j^{(1)},\phi_{1,j})\ \text{is not recognizable for every}\ j \in \{0,\ldots,L-1\}. \end{align} $$
$$ \begin{align} (X_j^{(1)},\phi_{1,j})\ \text{is not recognizable for every}\ j \in \{0,\ldots,L-1\}. \end{align} $$
Let
The idea is to use Theorem 2.7 with
![]() $\boldsymbol {\nu }$
to obtain a contradiction. To do so, we first note that, since
$\boldsymbol {\nu }$
to obtain a contradiction. To do so, we first note that, since
![]() $\boldsymbol {\nu }$
and
$\boldsymbol {\nu }$
and
![]() $\boldsymbol {\sigma }^{(L)}$
have the same ‘tail’,
$\boldsymbol {\sigma }^{(L)}$
have the same ‘tail’,
 $X_{\boldsymbol {\nu }}^{(m+L)} = X_{L}^{(m+1)}$
for all
$X_{\boldsymbol {\nu }}^{(m+L)} = X_{L}^{(m+1)}$
for all
![]() $m \in {\mathbb N}$
. Moreover,
$m \in {\mathbb N}$
. Moreover,
![]() $\triangle _2$
and the previous relation imply that
$\triangle _2$
and the previous relation imply that
 $$ \begin{align*} X_{\boldsymbol{\nu}}^{(j)} &= \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}(X_{\boldsymbol{\nu}}^{(j+1)}) = \cdots = \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}\ldots\phi_{L-1,1}(X_{\boldsymbol{\nu}}^{(L)}) \\[3pt] &= \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}\ldots\phi_{L-1,1}(X_{L}^{(1)}) = \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}\ldots\phi_{L-2,1}(X_{L-1}^{(1)}) = \cdots = X_j^{(1)}. \end{align*} $$
$$ \begin{align*} X_{\boldsymbol{\nu}}^{(j)} &= \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}(X_{\boldsymbol{\nu}}^{(j+1)}) = \cdots = \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}\ldots\phi_{L-1,1}(X_{\boldsymbol{\nu}}^{(L)}) \\[3pt] &= \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}\ldots\phi_{L-1,1}(X_{L}^{(1)}) = \bigcup_{k\in{\mathbb Z}} T^k\phi_{j,1}\ldots\phi_{L-2,1}(X_{L-1}^{(1)}) = \cdots = X_j^{(1)}. \end{align*} $$
This and (27) imply that for every
![]() $j \in \{1,\ldots ,L-1\}$
, the level
$j \in \{1,\ldots ,L-1\}$
, the level
 $(X_{\boldsymbol {\nu }}^{(j)}, \phi _{j,1})$
of
$(X_{\boldsymbol {\nu }}^{(j)}, \phi _{j,1})$
of
![]() $\boldsymbol {\nu }$
is not recognizable. Being
$\boldsymbol {\nu }$
is not recognizable. Being
![]() $\boldsymbol {\nu }$
everywhere growing as
$\boldsymbol {\nu }$
everywhere growing as
![]() $\boldsymbol {\sigma _L}$
has this property, we conclude that Theorem 2.7 can be applied and, therefore, that
$\boldsymbol {\sigma _L}$
has this property, we conclude that Theorem 2.7 can be applied and, therefore, that
 $X_0^{(1)} = X_{\boldsymbol {\nu }}$
is periodic. However, then
$X_0^{(1)} = X_{\boldsymbol {\nu }}$
is periodic. However, then
 $X_0 = \bigcup _{k\in {\mathbb Z}}T^k\sigma _{0,0}(X_0^{(1)})$
is periodic, contrary to our assumptions.
$X_0 = \bigcup _{k\in {\mathbb Z}}T^k\sigma _{0,0}(X_0^{(1)})$
is periodic, contrary to our assumptions.
A system
![]() $(X,T)$
is coalescent if every endomorphism
$(X,T)$
is coalescent if every endomorphism
![]() $\pi \colon (X,T)\to (X,T)$
is an automorphism. This notion has been relevant in the context of topological dynamics; see for example [Reference DownarowiczDow97].
$\pi \colon (X,T)\to (X,T)$
is an automorphism. This notion has been relevant in the context of topological dynamics; see for example [Reference DownarowiczDow97].
Corollary 4.9. Let
![]() $(X,T)$
be an
$(X,T)$
be an
![]() ${\mathcal S}$
-adic subshift generated by an everywhere growing and proper directive sequence of finite alphabet rank. Then,
${\mathcal S}$
-adic subshift generated by an everywhere growing and proper directive sequence of finite alphabet rank. Then,
![]() $(X,T)$
is coalescent.
$(X,T)$
is coalescent.
Remark 4.10. A linearly recurrent subshift of constant C is generated by a primitive and proper directive sequence of alphabet rank at most
![]() $C(C+1)^2$
[Reference DurandDur00, Proposition 6]. In [Reference Durand, Host and SkauDHS99], the authors proved the following.
$C(C+1)^2$
[Reference DurandDur00, Proposition 6]. In [Reference Durand, Host and SkauDHS99], the authors proved the following.
Theorem 4.11. [Reference Durand, Host and SkauDHS99, Theorem 3]
For a linearly recurrent subshift X of constant C, in any chain of factors
![]() $\pi _j\colon (X_j,T)\to (X_{j+1},T)$
,
$\pi _j\colon (X_j,T)\to (X_{j+1},T)$
,
![]() $j=0,\ldots ,L$
, with
$j=0,\ldots ,L$
, with
![]() $X_0 = X$
and
$X_0 = X$
and
 $L \geq (2C(2C+1)^2)^{4C^3(2C+1)^2}$
, there is at least one
$L \geq (2C(2C+1)^2)^{4C^3(2C+1)^2}$
, there is at least one
![]() $\pi _j$
which is a conjugacy.
$\pi _j$
which is a conjugacy.
Thus, Theorem 1.5 is not only a generalization of this result to a much larger class of systems, but also improves the previous super-exponential constant to a logarithmic one.
In Proposition 28 of [Reference Durand, Host and SkauDHS99], the authors proved that Cantor factors of linearly recurrent systems are either subshifts or odometers. Their proof only uses that this kind of system satisfies the strong coalescence property that we proved in Corollary 4.9 for finite topological rank systems. Therefore, by the same proof, we have the following.
Corollary 4.12. Let
![]() $\pi \colon (X,T) \to (Y,T)$
be a factor map between minimal systems. Assume that
$\pi \colon (X,T) \to (Y,T)$
be a factor map between minimal systems. Assume that
![]() $(X,T)$
has finite topological rank and that
$(X,T)$
has finite topological rank and that
![]() $(Y,T)$
is a Cantor system. Then,
$(Y,T)$
is a Cantor system. Then,
![]() $(Y,T)$
is either a subshift or a odometer.
$(Y,T)$
is either a subshift or a odometer.
Proof. We sketch the proof from [Reference Durand, Host and SkauDHS99] that we mentioned above.
Let
![]() $({\mathcal P}_n)_{n\in {\mathbb N}}$
be a sequence of clopen partitions of Y such that
$({\mathcal P}_n)_{n\in {\mathbb N}}$
be a sequence of clopen partitions of Y such that
![]() ${\mathcal P}_{n+1}$
is finer than
${\mathcal P}_{n+1}$
is finer than
![]() ${\mathcal P}_n$
and their union generates the topology of Y. Also, let
${\mathcal P}_n$
and their union generates the topology of Y. Also, let
![]() $Y_n$
be the subshift obtained by codifying the orbits of
$Y_n$
be the subshift obtained by codifying the orbits of
![]() $(Y,T)$
by using the atoms of
$(Y,T)$
by using the atoms of
![]() ${\mathcal P}_n$
. Then, the fact that
${\mathcal P}_n$
. Then, the fact that
![]() ${\mathcal P}_n$
is a clopen partition induces a factor map
${\mathcal P}_n$
is a clopen partition induces a factor map
![]() $\pi _n\colon (Y,T) \to (Y_n,T)$
. Moreover, since
$\pi _n\colon (Y,T) \to (Y_n,T)$
. Moreover, since
![]() ${\mathcal P}_{n+1}$
is finer than
${\mathcal P}_{n+1}$
is finer than
![]() ${\mathcal P}_n$
, there exists a factor map
${\mathcal P}_n$
, there exists a factor map
![]() $\xi _n\colon (Y_{n+1},T)\to (Y_n,T)$
such that
$\xi _n\colon (Y_{n+1},T)\to (Y_n,T)$
such that
![]() $\xi _n\pi _{n+1} = \pi _n$
. Hence, we have the following chain of factors:
$\xi _n\pi _{n+1} = \pi _n$
. Hence, we have the following chain of factors:
 $$ \begin{align*} (X,T) \overset{\pi}{\longrightarrow} (Y,T) \overset{\pi_n}{\longrightarrow} (Y_n,T) \overset{\xi_{n-1}}{\longrightarrow} (Y_{n-1},T) \overset{\xi_{n-2}}{\longrightarrow} \cdots \overset{\xi_{1}}{\longrightarrow} (Y_0,T). \end{align*} $$
$$ \begin{align*} (X,T) \overset{\pi}{\longrightarrow} (Y,T) \overset{\pi_n}{\longrightarrow} (Y_n,T) \overset{\xi_{n-1}}{\longrightarrow} (Y_{n-1},T) \overset{\xi_{n-2}}{\longrightarrow} \cdots \overset{\xi_{1}}{\longrightarrow} (Y_0,T). \end{align*} $$
We conclude, by also using the fact that the partitions
![]() ${\mathcal P}_n$
generate the topology of Y, that
${\mathcal P}_n$
generate the topology of Y, that
![]() $(Y,T)$
is conjugate to the inverse limit
$(Y,T)$
is conjugate to the inverse limit
 $\overleftarrow {\lim }_{n\to \infty }(Y_n;\xi _n)$
.
$\overleftarrow {\lim }_{n\to \infty }(Y_n;\xi _n)$
.
Now we consider two cases. If
![]() $Y_n$
is periodic for every
$Y_n$
is periodic for every
![]() $n \in {\mathbb N}$
, then Y is the inverse limit of periodic system, and hence an odometer. In the other case, we have, by Corollary 1.5, that
$n \in {\mathbb N}$
, then Y is the inverse limit of periodic system, and hence an odometer. In the other case, we have, by Corollary 1.5, that
![]() $\xi _n$
is a conjugacy for all big enough
$\xi _n$
is a conjugacy for all big enough
![]() $n \in {\mathbb N}$
, and thus that
$n \in {\mathbb N}$
, and thus that
![]() $(Y,T)$
is conjugate to one of the subshifts
$(Y,T)$
is conjugate to one of the subshifts
![]() $Y_n$
.
$Y_n$
.
5 Fibers of symbolic factors
The objective of this section is to prove Theorem 1.6, which states that factor maps
![]() $\pi \colon (X,T)\to (Y,T)$
between
$\pi \colon (X,T)\to (Y,T)$
between
![]() ${\mathcal S}$
-adic subshifts of finite topological rank are always almost k-to-
${\mathcal S}$
-adic subshifts of finite topological rank are always almost k-to-
![]() $1$
for some k bounded by the topological rank of X. We start with some lemmas from topological dynamics.
$1$
for some k bounded by the topological rank of X. We start with some lemmas from topological dynamics.
Lemma 5.1. [Reference AuslanderAus88]
Let
![]() $\pi \colon X \to Y $
be a continuous map between compact metric spaces. Then
$\pi \colon X \to Y $
be a continuous map between compact metric spaces. Then
![]() $\pi ^{-1}\colon Y \to 2^X$
is continuous at every point of a residual subset of Y.
$\pi ^{-1}\colon Y \to 2^X$
is continuous at every point of a residual subset of Y.
The next lemma gives a sufficient condition for a factor map
![]() $\pi $
to be almost k-to-1. Recall that
$\pi $
to be almost k-to-1. Recall that
![]() $E(X,T)$
stands for the Ellis semigroup of
$E(X,T)$
stands for the Ellis semigroup of
![]() $(X,T)$
.
$(X,T)$
.
Lemma 5.2. Let
![]() $\pi \colon (X,T) \to (Y,T)$
be a factor map between topological dynamical systems, with
$\pi \colon (X,T) \to (Y,T)$
be a factor map between topological dynamical systems, with
![]() $(Y,T)$
minimal and
$(Y,T)$
minimal and
![]() $K\geq 1$
an integer. Suppose that for every
$K\geq 1$
an integer. Suppose that for every
![]() $y \in Y$
, there exists
$y \in Y$
, there exists
![]() $u \in E(2^X,T)$
such that
$u \in E(2^X,T)$
such that
![]() $\#u\circ \pi ^{-1}(y) \leq K$
. Then,
$\#u\circ \pi ^{-1}(y) \leq K$
. Then,
![]() $\pi $
is almost k-to-1 for some
$\pi $
is almost k-to-1 for some
![]() $k\leq K$
.
$k\leq K$
.
Proof. First, we observe that by the description of
![]() $u\circ A$
in terms of nets at the end of §2.1, we have
$u\circ A$
in terms of nets at the end of §2.1, we have
Now, by the previous lemma, there exists a residual set
![]() $\tilde {Y} \subseteq Y$
of continuity points for
$\tilde {Y} \subseteq Y$
of continuity points for
![]() $\pi ^{-1}$
. Let
$\pi ^{-1}$
. Let
![]() $y,y'\in \tilde {Y}$
be arbitrary. Since Y is minimal, there exists a sequence
$y,y'\in \tilde {Y}$
be arbitrary. Since Y is minimal, there exists a sequence
![]() $(n_\ell )_\ell $
such that
$(n_\ell )_\ell $
such that
![]() $\lim _\ell T^{n_\ell }y = y'$
. If
$\lim _\ell T^{n_\ell }y = y'$
. If
![]() $w \in E(2^X,T)$
is the limit of a convergent subnet of
$w \in E(2^X,T)$
is the limit of a convergent subnet of
![]() $(T^{n_\ell })_\ell $
, then
$(T^{n_\ell })_\ell $
, then
![]() $wy = y'$
. By the continuity of
$wy = y'$
. By the continuity of
![]() $\pi ^{-1}$
at
$\pi ^{-1}$
at
![]() $y'$
and (28), we have
$y'$
and (28), we have
We deduce, by symmetry, that
![]() $\#\pi ^{-1}(y') = \#\pi ^{-1}(y)$
. Hence,
$\#\pi ^{-1}(y') = \#\pi ^{-1}(y)$
. Hence,
![]() $k:= \pi ^{-1}(y)$
does not depend on the chosen
$k:= \pi ^{-1}(y)$
does not depend on the chosen
![]() $y\in \tilde {Y}$
. To end the proof, we have to show that
$y\in \tilde {Y}$
. To end the proof, we have to show that
![]() $k\leq K$
. We fix
$k\leq K$
. We fix
![]() $y \in \tilde {Y}$
and take, using the hypothesis,
$y \in \tilde {Y}$
and take, using the hypothesis,
![]() $u \in E(2^X,T)$
such that
$u \in E(2^X,T)$
such that
![]() $\#u\circ \pi ^{-1}(y) \leq K$
. As above, by minimality, there exists
$\#u\circ \pi ^{-1}(y) \leq K$
. As above, by minimality, there exists
![]() $v\in E(2^X,T)$
such that
$v\in E(2^X,T)$
such that
![]() $vuy = y$
. Then, by the continuity of
$vuy = y$
. Then, by the continuity of
![]() $\pi ^{-1}$
at y,
$\pi ^{-1}$
at y,
This and (28) imply that
![]() $k = \#\pi ^{-1}(y) \leq \#u\circ \pi ^{-1}(y) \leq K$
.
$k = \#\pi ^{-1}(y) \leq \#u\circ \pi ^{-1}(y) \leq K$
.
Let
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism,
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism,
![]() $(k,x)$
a centered
$(k,x)$
a centered
![]() $\sigma $
-factorization of
$\sigma $
-factorization of
![]() $y \in {\mathcal B}^{\mathbb Z}$
in
$y \in {\mathcal B}^{\mathbb Z}$
in
![]() ${\mathcal A}^{\mathbb Z}$
, and
${\mathcal A}^{\mathbb Z}$
, and
![]() $\ell \in {\mathbb Z}$
. Note that there exists a unique
$\ell \in {\mathbb Z}$
. Note that there exists a unique
![]() $j \in {\mathbb Z}$
such that
$j \in {\mathbb Z}$
such that
![]() $\ell \in [c_{\sigma ,j}(k,x), c_{\sigma ,j+1}(k,x))$
(recall the notion of cut from Definition 2.1). In this context, we say that
$\ell \in [c_{\sigma ,j}(k,x), c_{\sigma ,j+1}(k,x))$
(recall the notion of cut from Definition 2.1). In this context, we say that
![]() $(c_{\sigma ,j}(k,x),x_j)$
is the symbol of
$(c_{\sigma ,j}(k,x),x_j)$
is the symbol of
![]() $(k,x)$
covering position
$(k,x)$
covering position
![]() $\ell $
of y.
$\ell $
of y.
Theorem 1.6. Let
![]() $\pi \colon (X,T) \to (Y,T)$
be a factor between subshifts, with
$\pi \colon (X,T) \to (Y,T)$
be a factor between subshifts, with
![]() $(Y,T)$
minimal and aperiodic. Suppose that X is generated by a proper and everywhere growing directive sequence
$(Y,T)$
minimal and aperiodic. Suppose that X is generated by a proper and everywhere growing directive sequence
![]() $\boldsymbol {\sigma }$
of alphabet rank K. Then,
$\boldsymbol {\sigma }$
of alphabet rank K. Then,
![]() $\pi $
is almost k-to-1 for some
$\pi $
is almost k-to-1 for some
![]() $k\leq K$
.
$k\leq K$
.
Proof. Let
![]() $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}\to {\mathcal A}_n)_{n\geq 0}$
be a proper and everywhere growing directive sequence of alphabet rank at most K generating X. Due the possibility of contracting
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}\to {\mathcal A}_n)_{n\geq 0}$
be a proper and everywhere growing directive sequence of alphabet rank at most K generating X. Due the possibility of contracting
![]() $\boldsymbol {\sigma }$
, we can assume without loss of generality that
$\boldsymbol {\sigma }$
, we can assume without loss of generality that
![]() $\#{\mathcal A}_{n} \leq K$
for every
$\#{\mathcal A}_{n} \leq K$
for every
![]() $n\geq 1$
and that
$n\geq 1$
and that
![]() $\sigma _0$
is r-proper, where r is the radius of
$\sigma _0$
is r-proper, where r is the radius of
![]() $\pi $
. Then, by Lemma 2.4, Y is generated by an everywhere growing directive sequence of the form
$\pi $
. Then, by Lemma 2.4, Y is generated by an everywhere growing directive sequence of the form
![]() $\boldsymbol {\tau } = (\tau ,\sigma _1,\sigma _2,\ldots )$
, where
$\boldsymbol {\tau } = (\tau ,\sigma _1,\sigma _2,\ldots )$
, where
 $\tau \colon {\mathcal A}_1^+\to {\mathcal B}^+$
is such that
$\tau \colon {\mathcal A}_1^+\to {\mathcal B}^+$
is such that
![]() $\tau (x) = \pi (\sigma _0(x))$
for every
$\tau (x) = \pi (\sigma _0(x))$
for every
 $x\in X_{\boldsymbol {\tau }}^{(1)} = X_{\boldsymbol {\sigma }}^{(1)}$
. We will use the notation
$x\in X_{\boldsymbol {\tau }}^{(1)} = X_{\boldsymbol {\sigma }}^{(1)}$
. We will use the notation
![]() $\tau _{[0,n)} = \tau \sigma _{[1,n)}$
. Further, for
$\tau _{[0,n)} = \tau \sigma _{[1,n)}$
. Further, for
![]() $y \in Y$
and
$y \in Y$
and
![]() $n\geq 1$
, we write
$n\geq 1$
, we write
![]() $F_n(y)$
to denote the set of
$F_n(y)$
to denote the set of
![]() $\tau _{[0,n)}$
-factorizations of y in
$\tau _{[0,n)}$
-factorizations of y in
 $Y_{\boldsymbol {\tau }}^{(n)}$
.
$Y_{\boldsymbol {\tau }}^{(n)}$
.
Before continuing, we prove the following claim.
Claim 5.2.1. There exist
![]() $\ell _n\in {\mathbb Z}$
and
$\ell _n\in {\mathbb Z}$
and
![]() $G_n \subseteq {\mathbb Z}\times {\mathcal B}_{n+1}$
with at most K elements such that if
$G_n \subseteq {\mathbb Z}\times {\mathcal B}_{n+1}$
with at most K elements such that if
![]() $(k,x)\in F_n(y)$
, then the symbol of
$(k,x)\in F_n(y)$
, then the symbol of
![]() $(k,x)$
covering position
$(k,x)$
covering position
![]() $\ell _n$
of y is in
$\ell _n$
of y is in
![]() $G_n$
.
$G_n$
.
Proof. First, since Y is aperiodic, there exists
![]() $L \in {\mathbb N}$
such that
$L \in {\mathbb N}$
such that
We assume, by contradiction, that the claim does not hold. In particular, for every
![]() $\ell \in [0,L)$
, there exist
$\ell \in [0,L)$
, there exist
![]() $K+1 \tau _{[0,n)}$
-factorizations
$K+1 \tau _{[0,n)}$
-factorizations
![]() $(x,k)$
of y in
$(x,k)$
of y in
 $Y_{\boldsymbol {\tau }}^{(n)}$
such that their symbols covering position
$Y_{\boldsymbol {\tau }}^{(n)}$
such that their symbols covering position
![]() $\ell $
of y are all different. Now, since
$\ell $
of y are all different. Now, since
![]() $\#\tau _{[0,n)}({\mathcal A}_{n+1}) \leq K$
, we can use the pigeonhole principle to find two of such factorizations, say
$\#\tau _{[0,n)}({\mathcal A}_{n+1}) \leq K$
, we can use the pigeonhole principle to find two of such factorizations, say
![]() $(k,x)$
and
$(k,x)$
and
![]() $(k',x')$
, such that if
$(k',x')$
, such that if
![]() $(c,a)$
and
$(c,a)$
and
![]() $(c',a')$
are their symbols covering position
$(c',a')$
are their symbols covering position
![]() $\ell $
of y, then
$\ell $
of y, then
![]() $a = a'$
and
$a = a'$
and
![]() $c<c'$
. Then,
$c<c'$
. Then,
and, thus,
![]() $y_{(c,c'+|\tau _{[0,n)}(a)|]}$
is
$y_{(c,c'+|\tau _{[0,n)}(a)|]}$
is
![]() $(c'-c)$
-periodic. Being
$(c'-c)$
-periodic. Being
![]() $\ell \in (c',c+|\tau _{[0,n)}(a)|)$
, we deduce that the local period of
$\ell \in (c',c+|\tau _{[0,n)}(a)|)$
, we deduce that the local period of
![]() $y_{[0,L)}$
at
$y_{[0,L)}$
at
![]() $\ell $
is at most
$\ell $
is at most
![]() $c'-c \leq |\tau _{[0,n)}|$
. Since this is true for every
$c'-c \leq |\tau _{[0,n)}|$
. Since this is true for every
![]() $\ell \in [0,L)$
and since, by Theorem 3.7,
$\ell \in [0,L)$
and since, by Theorem 3.7,
![]() ${\mathrm {per}}(y_{[0,L)}) = {\mathrm {per}}(y_{[0,L)}, y_{[0,\ell )})$
for some
${\mathrm {per}}(y_{[0,L)}) = {\mathrm {per}}(y_{[0,L)}, y_{[0,\ell )})$
for some
![]() $\ell \in [0,L)$
, we conclude that
$\ell \in [0,L)$
, we conclude that
![]() ${\mathrm {per}}(y_{[0,L)}) \leq |\tau _{[0,n)}|$
. This contradicts (29) and proves thereby the claim.
${\mathrm {per}}(y_{[0,L)}) \leq |\tau _{[0,n)}|$
. This contradicts (29) and proves thereby the claim.
Now we prove the theorem. It is enough to show that the hypothesis of Lemma 5.2 holds. Let
![]() $y \in Y$
and
$y \in Y$
and
![]() $\tilde {F}_n(y) \subseteq F_n(y)$
be such that
$\tilde {F}_n(y) \subseteq F_n(y)$
be such that
![]() $\#\tilde {F}_n(y) = \#G_n$
and the set consisting of all the symbols of factorizations
$\#\tilde {F}_n(y) = \#G_n$
and the set consisting of all the symbols of factorizations
![]() $(k,x) \in \tilde {F}_n(y)$
covering position
$(k,x) \in \tilde {F}_n(y)$
covering position
![]() $\ell _n$
of y is equal to
$\ell _n$
of y is equal to
![]() $G_n$
. Let
$G_n$
. Let
![]() $z \in \pi ^{-1}(y)$
and
$z \in \pi ^{-1}(y)$
and
![]() $(k,x)$
be a
$(k,x)$
be a
![]() $\sigma _{[0,n)}$
-factorization of z in
$\sigma _{[0,n)}$
-factorization of z in
 $X_{\boldsymbol {\sigma }}^{(n)}$
. Then,
$X_{\boldsymbol {\sigma }}^{(n)}$
. Then,
![]() $T^k\tau _{[0,n)}(x) = T^k\pi (\sigma _{[0,n)}(x)) = \pi (z) = y$
and
$T^k\tau _{[0,n)}(x) = T^k\pi (\sigma _{[0,n)}(x)) = \pi (z) = y$
and
![]() $(k,x)$
is a
$(k,x)$
is a
![]() $\tau _{[0,n)}$
-factorization of y in
$\tau _{[0,n)}$
-factorization of y in
 $Y_{\boldsymbol {\tau }}^{(n)}$
. Thus, we can find
$Y_{\boldsymbol {\tau }}^{(n)}$
. Thus, we can find
![]() $(k',x') \in \tilde {F}_n(y)$
such that the symbols of
$(k',x') \in \tilde {F}_n(y)$
such that the symbols of
![]() $(k,x)$
and
$(k,x)$
and
![]() $(k',x')$
covering position
$(k',x')$
covering position
![]() $\ell _n$
of y are the same; let
$\ell _n$
of y are the same; let
![]() $(m,a)$
be this common symbol. Since
$(m,a)$
be this common symbol. Since
![]() $\boldsymbol {\sigma }$
is proper, we have
$\boldsymbol {\sigma }$
is proper, we have
 $$ \begin{align*} z_{[m-\langle\sigma_{[0,n-1)}\rangle,m+|\sigma_{[0,n)}(a)|+\langle\sigma_{[0,n-1)}\rangle]} = z^{\prime}_{[m-\langle\sigma_{[0,n-1)}\rangle,m+|\sigma_{[0,n)}(a)|+\langle\sigma_{[0,n-1)}\rangle]}, \end{align*} $$
$$ \begin{align*} z_{[m-\langle\sigma_{[0,n-1)}\rangle,m+|\sigma_{[0,n)}(a)|+\langle\sigma_{[0,n-1)}\rangle]} = z^{\prime}_{[m-\langle\sigma_{[0,n-1)}\rangle,m+|\sigma_{[0,n)}(a)|+\langle\sigma_{[0,n-1)}\rangle]}, \end{align*} $$
where
 $z' = T^{k'}\sigma _{[0,n)}(x') \in X$
is the point that
$z' = T^{k'}\sigma _{[0,n)}(x') \in X$
is the point that
![]() $(k',x')$
factorizes in
$(k',x')$
factorizes in
 $(X_{\boldsymbol {\sigma }}^{(n)}, \sigma _{[0,n)})$
. Then, as
$(X_{\boldsymbol {\sigma }}^{(n)}, \sigma _{[0,n)})$
. Then, as
![]() $\ell _n \in (m, m+|\sigma _{[0,n)}(a)|]$
,
$\ell _n \in (m, m+|\sigma _{[0,n)}(a)|]$
,
 $$ \begin{align*} z_{(\ell_n-\langle\sigma_{[0,n-1)}\rangle, \ell_n+\langle\sigma_{[0,n-1)}\rangle]} = z^{\prime}_{(\ell_n-\langle\sigma_{[0,n-1)}\rangle, \ell_n+\langle\sigma_{[0,n-1)}\rangle]}. \end{align*} $$
$$ \begin{align*} z_{(\ell_n-\langle\sigma_{[0,n-1)}\rangle, \ell_n+\langle\sigma_{[0,n-1)}\rangle]} = z^{\prime}_{(\ell_n-\langle\sigma_{[0,n-1)}\rangle, \ell_n+\langle\sigma_{[0,n-1)}\rangle]}. \end{align*} $$
Thus,
![]() $\mathrm {dist}(T^{\ell _n}z, T^{\ell _n}P_n(y)) \leq \exp (-\langle \sigma _{[0,n-1)}\rangle )$
, where
$\mathrm {dist}(T^{\ell _n}z, T^{\ell _n}P_n(y)) \leq \exp (-\langle \sigma _{[0,n-1)}\rangle )$
, where
![]() $P_n(y)\subseteq \pi ^{-1}(y)$
is the set of all points
$P_n(y)\subseteq \pi ^{-1}(y)$
is the set of all points
 $T^{k''}\sigma _{[0,n)}(x'') \in X$
such that
$T^{k''}\sigma _{[0,n)}(x'') \in X$
such that
![]() $(k'',x'') \in \tilde {F}_n(y)$
. Since this holds for every
$(k'',x'') \in \tilde {F}_n(y)$
. Since this holds for every
![]() $n \geq 1$
, we obtain that
$n \geq 1$
, we obtain that
![]() $d_{\mathrm {H}}(T^{\ell _n}\pi ^{-1}(y),T^{\ell _n} P_n(y))$
converges to zero as n goes to infinity (where, we recall,
$d_{\mathrm {H}}(T^{\ell _n}\pi ^{-1}(y),T^{\ell _n} P_n(y))$
converges to zero as n goes to infinity (where, we recall,
![]() $d_{\mathrm {H}}$
is the Hausdorff distance). By taking an appropriate convergent subnet
$d_{\mathrm {H}}$
is the Hausdorff distance). By taking an appropriate convergent subnet
![]() $u \in E(2^X,T)$
of
$u \in E(2^X,T)$
of
![]() $(T^{\ell _n})_{n\in {\mathbb N}}$
, we obtain
$(T^{\ell _n})_{n\in {\mathbb N}}$
, we obtain
![]() $\# u\circ \pi ^{-1}(y) \leq \sup _{n\in {\mathbb N}}\#P_n = \sup _{n\in {\mathbb N}}\#G_n \leq K$
. This proves that the hypothesis of Lemma 5.2 holds. Therefore,
$\# u\circ \pi ^{-1}(y) \leq \sup _{n\in {\mathbb N}}\#P_n = \sup _{n\in {\mathbb N}}\#G_n \leq K$
. This proves that the hypothesis of Lemma 5.2 holds. Therefore,
![]() $\pi $
is almost k-to-1 for some
$\pi $
is almost k-to-1 for some
![]() $k\leq K$
.
$k\leq K$
.
6 Number of symbolic factors
In this section, we prove Theorem 1.7. To do this, we split the proof into three subsections. First, in Lemma 6.3 of §6.1, we deal with the case of Theorem 1.7 in which the factor maps are distal. Next, we show in Lemma 6.7 from §6.2 that in certain technical situation—which will arise when we consider non-distal factor maps—it is possible to reduce the problem to a similar one, but where the alphabet is smaller. Then, we prove Theorem 1.7 in §6.3 by a repeated application of the previous lemmas.
6.1 Distal factor maps
We start with some definitions. If
![]() $(X,T)$
is a system, then we always give
$(X,T)$
is a system, then we always give
![]() $X^k$
the diagonal action
$X^k$
the diagonal action
![]() $T^{[k]} := T\times \cdots \times T$
. If
$T^{[k]} := T\times \cdots \times T$
. If
![]() $\pi \colon (X,T)\to (Y,T)$
is a factor map and
$\pi \colon (X,T)\to (Y,T)$
is a factor map and
![]() $k \geq 1$
, then we define
$k \geq 1$
, then we define
![]() $R_\pi ^k = \{(x^1,\ldots ,x^k)\in X^k : \pi (x^1) = \cdots =\pi (x^k)\}$
. Observe that
$R_\pi ^k = \{(x^1,\ldots ,x^k)\in X^k : \pi (x^1) = \cdots =\pi (x^k)\}$
. Observe that
![]() $R_\pi ^k$
is a closed
$R_\pi ^k$
is a closed
![]() $T^{[k]}$
-invariant subset of
$T^{[k]}$
-invariant subset of
![]() $X^k$
.
$X^k$
.
The next lemma follows from classical ideas from topological dynamics. See, for example, theorem 6 in ch. 10 of [Reference AuslanderAus88].
Lemma 6.1. Let
![]() $\pi \colon (X,T)\to (Y,T)$
be a distal almost k-to-1 factor between minimal systems,
$\pi \colon (X,T)\to (Y,T)$
be a distal almost k-to-1 factor between minimal systems,
![]() $z = (z^1,\ldots ,z^k) \in R_\pi ^k$
and
$z = (z^1,\ldots ,z^k) \in R_\pi ^k$
and
![]() $Z = \overline {\mathrm {orb}}_{T^{[k]}}(z)$
. Then,
$Z = \overline {\mathrm {orb}}_{T^{[k]}}(z)$
. Then,
![]() $\pi $
is k-to-1 and Z is minimal.
$\pi $
is k-to-1 and Z is minimal.
We will also need the following lemma.
Lemma 6.2. [Reference DurandDur00, Lemma 21]
Let
![]() $\pi _i\colon (X,T) \to (Y_i,T)$
,
$\pi _i\colon (X,T) \to (Y_i,T)$
,
![]() $i=0,1$
, be two factors between aperiodic minimal systems. Suppose that
$i=0,1$
, be two factors between aperiodic minimal systems. Suppose that
![]() $\pi _0$
is finite-to-one. If
$\pi _0$
is finite-to-one. If
![]() $x,y\in X$
are such that
$x,y\in X$
are such that
![]() $\pi _0(x) = \pi _0(y)$
and
$\pi _0(x) = \pi _0(y)$
and
![]() $\pi _1(x) = T^p\pi _1(y)$
, then
$\pi _1(x) = T^p\pi _1(y)$
, then
![]() $p=0$
.
$p=0$
.
Lemma 6.3. Let
![]() $(X,T)$
be an infinite minimal subshift of topological rank K and J an index set of cardinality
$(X,T)$
be an infinite minimal subshift of topological rank K and J an index set of cardinality
![]() $\#J> K(144K^7)^K$
. Suppose that for every
$\#J> K(144K^7)^K$
. Suppose that for every
![]() $j \in J$
there exists a distal symbolic factor
$j \in J$
there exists a distal symbolic factor
![]() $\pi _j\colon (X,T)\to (Y_j,T)$
. Then, there are
$\pi _j\colon (X,T)\to (Y_j,T)$
. Then, there are
![]() $i\not =j \in J$
such that
$i\not =j \in J$
such that
![]() $(Y_i,T)$
is conjugate to
$(Y_i,T)$
is conjugate to
![]() $(Y_j,T)$
.
$(Y_j,T)$
.
Proof. We start by introducing the necessary objects for the proof and doing some general observations about them. First, thanks to Theorem 1.6, we know that
![]() $\pi _j$
is almost
$\pi _j$
is almost
![]() $k_j$
-to-1 for some
$k_j$
-to-1 for some
![]() $k_j \leq K$
, so, by the pigeonhole principle, there exist
$k_j \leq K$
, so, by the pigeonhole principle, there exist
![]() $J_1 \subseteq J$
and
$J_1 \subseteq J$
and
![]() $k \leq K$
such that
$k \leq K$
such that
![]() $\#J_1 \geq \#J/K> (144K^7)^K$
and
$\#J_1 \geq \#J/K> (144K^7)^K$
and
![]() $k_j = k$
for every
$k_j = k$
for every
![]() $j \in J_1$
. For
$j \in J_1$
. For
![]() $j \in J_1$
, we fix
$j \in J_1$
, we fix
 $z^j = (z_1^j, \ldots , z_k^j) \in R_{\pi _j}^k$
with
$z^j = (z_1^j, \ldots , z_k^j) \in R_{\pi _j}^k$
with
 $z_n^j \not = z_m^j$
for all
$z_n^j \not = z_m^j$
for all
![]() $n\not =m$
. Let
$n\not =m$
. Let
 $Z_j = \overline {\mathrm {orb}}_{T^{[k]}}(z^j)$
and
$Z_j = \overline {\mathrm {orb}}_{T^{[k]}}(z^j)$
and
![]() $\rho \colon X^k\to X$
be the factor map that projects onto the first coordinate. By Lemma 6.1,
$\rho \colon X^k\to X$
be the factor map that projects onto the first coordinate. By Lemma 6.1,
![]() $\pi _j$
is k-to-1 and
$\pi _j$
is k-to-1 and
![]() $Z_j$
minimal. This implies that if
$Z_j$
minimal. This implies that if
![]() $x = (x_1,\ldots ,x_k) \in Z_j$
, then
$x = (x_1,\ldots ,x_k) \in Z_j$
, then
 $$ \begin{align} \{x_1,\ldots,x_k\} &= \pi_j^{-1}(\pi_j(x_n)) \quad\text{for all}\ n\in \{1,\ldots,k\}, \end{align} $$
$$ \begin{align} \{x_1,\ldots,x_k\} &= \pi_j^{-1}(\pi_j(x_n)) \quad\text{for all}\ n\in \{1,\ldots,k\}, \end{align} $$
Indeed, since
![]() $Z_j$
is minimal,
$Z_j$
is minimal,
![]() $(T^{[k]})^{n_\ell }z \to x$
for some sequence
$(T^{[k]})^{n_\ell }z \to x$
for some sequence
![]() $(n_\ell )_\ell $
, so,
$(n_\ell )_\ell $
, so,
 $$\begin{align*}\inf_{n\not=m}\mathrm{dist}(x_n,x_m) \geq \inf_{n\not=m, l\in{\mathbb Z}}\mathrm{dist}(T^lz_n,T^lz_m)> 0,\end{align*}$$
$$\begin{align*}\inf_{n\not=m}\mathrm{dist}(x_n,x_m) \geq \inf_{n\not=m, l\in{\mathbb Z}}\mathrm{dist}(T^lz_n,T^lz_m)> 0,\end{align*}$$
where in the last step is due to the fact that
![]() $\pi _j$
is distal. This gives (31). For (30), we first note that
$\pi _j$
is distal. This gives (31). For (30), we first note that
 $\{x_1,\ldots ,x_k\} \subseteq \pi _j^{-1}(\pi _j(x_n))$
as
$\{x_1,\ldots ,x_k\} \subseteq \pi _j^{-1}(\pi _j(x_n))$
as
![]() $x \in R_{\pi _j}$
, and then that the equality must hold since
$x \in R_{\pi _j}$
, and then that the equality must hold since
 $\#\pi _j^{-1}(\pi _j(x_n)) = k = \#\{x_1,\ldots ,x_k\}$
by (31).
$\#\pi _j^{-1}(\pi _j(x_n)) = k = \#\{x_1,\ldots ,x_k\}$
by (31).
The next step is to prove that asymptotic pairs in
![]() $Z_j$
are well-behaved.
$Z_j$
are well-behaved.
Claim 6.3.1. Let
![]() $j \in J_1$
and
$j \in J_1$
and
 $(x^j = (x_1^j,\ldots ,x_k^j)$
,
$(x^j = (x_1^j,\ldots ,x_k^j)$
,
 $\tilde {x}^j = (\tilde {x}_1^j,\ldots ,\tilde {x}_k^j))$
be a right asymptotic pair in
$\tilde {x}^j = (\tilde {x}_1^j,\ldots ,\tilde {x}_k^j))$
be a right asymptotic pair in
![]() $Z_j$
, this is,
$Z_j$
, this is,
 $$ \begin{align} \lim_{n\to-\infty}\mathrm{dist}((T^{[k]})^nx^j, T^{[k]}\tilde{x}^j) = 0\quad\text{and}\quad x^j \not= \tilde{x}^j. \end{align} $$
$$ \begin{align} \lim_{n\to-\infty}\mathrm{dist}((T^{[k]})^nx^j, T^{[k]}\tilde{x}^j) = 0\quad\text{and}\quad x^j \not= \tilde{x}^j. \end{align} $$
Then,
 $(x_n^j,\tilde {x}_n^j)$
is right asymptotic for every
$(x_n^j,\tilde {x}_n^j)$
is right asymptotic for every
![]() $n \in \{1,\ldots ,k\}$
.
$n \in \{1,\ldots ,k\}$
.
Proof. Suppose, with the aim to obtain a contradiction, that
 $(x_n^j, \tilde {x}_n^j)$
is not right asymptotic for some
$(x_n^j, \tilde {x}_n^j)$
is not right asymptotic for some
![]() $n \in \{1,\ldots ,k\}$
. Observe that (32) implies that
$n \in \{1,\ldots ,k\}$
. Observe that (32) implies that
 $$ \begin{align} \text{for every}\ m \in \{1,\ldots,k\}, \text{either}\ (x_m^j,\tilde{x}_m^j)\ \text{is right asymptotic or}\ x_n^j = \tilde{x}_n^j. \end{align} $$
$$ \begin{align} \text{for every}\ m \in \{1,\ldots,k\}, \text{either}\ (x_m^j,\tilde{x}_m^j)\ \text{is right asymptotic or}\ x_n^j = \tilde{x}_n^j. \end{align} $$
Therefore,
 $x_n^j = \tilde {x}_n^j$
. Using this and that
$x_n^j = \tilde {x}_n^j$
. Using this and that
 $x^j,\tilde {x}^j \in R_{\pi _j}^k$
, we can compute:
$x^j,\tilde {x}^j \in R_{\pi _j}^k$
, we can compute:
 $$ \begin{align*} \pi_j(x_m^j) = \pi_j(x_n^j) = \pi_j(\tilde{x}_n^j) = \pi_j(\tilde{x}_l^j) \quad\text{for all } m,l\in\{1,\ldots,k\}, \end{align*} $$
$$ \begin{align*} \pi_j(x_m^j) = \pi_j(x_n^j) = \pi_j(\tilde{x}_n^j) = \pi_j(\tilde{x}_l^j) \quad\text{for all } m,l\in\{1,\ldots,k\}, \end{align*} $$
and thus, by (30),
 $$ \begin{align*} \{x_1^j,\ldots,x_k^j\} = \pi_j^{-1}(\pi_j(x_n^j)) = \pi_j^{-1}(\pi_j(\tilde{x}_n^j)) = \{\tilde{x}_1^j,\ldots,\tilde{x}_k^j\}. \end{align*} $$
$$ \begin{align*} \{x_1^j,\ldots,x_k^j\} = \pi_j^{-1}(\pi_j(x_n^j)) = \pi_j^{-1}(\pi_j(\tilde{x}_n^j)) = \{\tilde{x}_1^j,\ldots,\tilde{x}_k^j\}. \end{align*} $$
The last equation, (31), and that
![]() $x^j\not =\tilde {x}^j$
imply that there exist
$x^j\not =\tilde {x}^j$
imply that there exist
![]() $m\not =l \in \{1,\ldots ,k\}$
such that
$m\not =l \in \{1,\ldots ,k\}$
such that
 $\tilde {x}_{l}^j = x_m^j$
. This last equality and (33) tell us that
$\tilde {x}_{l}^j = x_m^j$
. This last equality and (33) tell us that
![]() $x^j_m$
and
$x^j_m$
and
![]() $x^j_l$
are either asymptotic or equal. However, in both cases a contradiction occurs: in the first one with the distality of
$x^j_l$
are either asymptotic or equal. However, in both cases a contradiction occurs: in the first one with the distality of
![]() $\pi $
and in the second one with (31).
$\pi $
and in the second one with (31).
Let
![]() $j \in J_1$
. Since
$j \in J_1$
. Since
![]() $Y_j$
is infinite,
$Y_j$
is infinite,
![]() $Z_j$
is a infinite subshift. It is a well-known fact from symbolic dynamics that this implies that there exists a right asymptotic pair
$Z_j$
is a infinite subshift. It is a well-known fact from symbolic dynamics that this implies that there exists a right asymptotic pair
 $(x^j = (x_1^j,\ldots ,x_k^j)$
,
$(x^j = (x_1^j,\ldots ,x_k^j)$
,
 $\tilde {x}^j = (\tilde {x}_1^j,\ldots ,\tilde {x}_k^j))$
in
$\tilde {x}^j = (\tilde {x}_1^j,\ldots ,\tilde {x}_k^j))$
in
![]() $Z_j$
. We are now going to use Theorem 2.8 to prove the following.
$Z_j$
. We are now going to use Theorem 2.8 to prove the following.
Claim 6.3.2. There exists
![]() $i,j \in J_1$
,
$i,j \in J_1$
,
![]() $i\not =j$
, such that
$i\not =j$
, such that
![]() $Z_i = Z_j$
.
$Z_i = Z_j$
.
Proof. On one hand, by the previous claim,
 $(x_n^j, \tilde {x}_n^j) \in X^2$
is right asymptotic for every
$(x_n^j, \tilde {x}_n^j) \in X^2$
is right asymptotic for every
![]() $n \in \{1,\ldots , k\}$
and
$n \in \{1,\ldots , k\}$
and
![]() $j \in J_1$
. Let
$j \in J_1$
. Let
 $p_n^j \in {\mathbb Z}$
be such that
$p_n^j \in {\mathbb Z}$
be such that
 $(T^{p_n^j}x_n^j, T^{p_n^j}\tilde {x}_n^j)$
is centered right asymptotic. On the other hand, Theorem 2.8 asserts that the set
$(T^{p_n^j}x_n^j, T^{p_n^j}\tilde {x}_n^j)$
is centered right asymptotic. On the other hand, Theorem 2.8 asserts that the set
has at most
![]() $144K^7$
elements. Since
$144K^7$
elements. Since
![]() $\#J_1> (144K^7)^K$
, we conclude, by the pigeonhole principle, that there exist
$\#J_1> (144K^7)^K$
, we conclude, by the pigeonhole principle, that there exist
![]() $i,j \in J_1$
,
$i,j \in J_1$
,
![]() $i\not =j$
, such that
$i\not =j$
, such that
 $$ \begin{align} T^{p_n^i}x_n^i \text{ and } T^{p_n^j}x_n^j \text{ agree on }(0,\infty) \text{ for every }n \in \{1,\ldots,k\}. \end{align} $$
$$ \begin{align} T^{p_n^i}x_n^i \text{ and } T^{p_n^j}x_n^j \text{ agree on }(0,\infty) \text{ for every }n \in \{1,\ldots,k\}. \end{align} $$
We are going to show that
![]() $Z_i = Z_j$
.
$Z_i = Z_j$
.
Using (34), we can find
![]() $u \in E(X,T)$
such that
$u \in E(X,T)$
such that
 $uT^{p_n^i}x_n^i = uT^{p_n^j}x_n^j$
for every n. Then, by putting
$uT^{p_n^i}x_n^i = uT^{p_n^j}x_n^j$
for every n. Then, by putting
![]() $y_n^i = ux_n^i$
,
$y_n^i = ux_n^i$
,
 $y_n^j = ux_n^j$
and
$y_n^j = ux_n^j$
and
 $q_n = p_n^j-p_n^i$
, we have
$q_n = p_n^j-p_n^i$
, we have
 $$ \begin{align*} y^i := (y_1^i,\ldots,y_k^i) \in Z_i, y^j := (y_1^j,\ldots,y_k^j) \in Z_j\text{ and } y_n^i = T^{q_n}y_n^j. \end{align*} $$
$$ \begin{align*} y^i := (y_1^i,\ldots,y_k^i) \in Z_i, y^j := (y_1^j,\ldots,y_k^j) \in Z_j\text{ and } y_n^i = T^{q_n}y_n^j. \end{align*} $$
Hence,
 $\pi (y_n^i) = T^{q_n}\pi (y_n^j)$
and Lemma 6.2 can be applied to deduce that
$\pi (y_n^i) = T^{q_n}\pi (y_n^j)$
and Lemma 6.2 can be applied to deduce that
![]() $q := q_n$
has the same value for every n. We conclude that
$q := q_n$
has the same value for every n. We conclude that
![]() $y^i = T^qy^j \in T^qZ_j = Z_j$
, that
$y^i = T^qy^j \in T^qZ_j = Z_j$
, that
![]() $Z_i \cap Z_j$
is not empty, and, therefore, that
$Z_i \cap Z_j$
is not empty, and, therefore, that
![]() $Z_i = Z_j$
as these are minimal systems.
$Z_i = Z_j$
as these are minimal systems.
We can now finish the proof. Let
![]() $i\not =j\in J_1$
be the elements given by the previous claim, so that
$i\not =j\in J_1$
be the elements given by the previous claim, so that
![]() $Z := Z_i = Z_j$
. Let
$Z := Z_i = Z_j$
. Let
![]() $y \in Y_i$
and
$y \in Y_i$
and
 $x = (x_1,\ldots ,x_k) \in \rho ^{-1}\pi _i^{-1}(y)\cap Z$
. Then, by (30),
$x = (x_1,\ldots ,x_k) \in \rho ^{-1}\pi _i^{-1}(y)\cap Z$
. Then, by (30),
 $\pi _i^{-1}(y) = \{x_1,\ldots ,x_k\} = \pi _j^{-1}(\pi _j(x_1))$
, and so
$\pi _i^{-1}(y) = \{x_1,\ldots ,x_k\} = \pi _j^{-1}(\pi _j(x_1))$
, and so
 $\pi _j\pi _i^{-1}(y)$
contains exactly one element, which is
$\pi _j\pi _i^{-1}(y)$
contains exactly one element, which is
![]() $\pi _j(x_1)$
. We define
$\pi _j(x_1)$
. We define
![]() $\psi \colon Y_i\to Y_j$
by
$\psi \colon Y_i\to Y_j$
by
![]() $\psi (y) = \pi _j(x_1)$
.
$\psi (y) = \pi _j(x_1)$
.
Observe that
 $\pi _i^{-1}\colon Y_i\to 2^X$
is continuous (as
$\pi _i^{-1}\colon Y_i\to 2^X$
is continuous (as
![]() $\pi _i$
is distal and hence open) and commutes with T. Being
$\pi _i$
is distal and hence open) and commutes with T. Being
![]() $\pi _j$
a factor map,
$\pi _j$
a factor map,
![]() $\psi $
is continuous and commutes with T. Therefore,
$\psi $
is continuous and commutes with T. Therefore,
![]() $\psi \colon (Y_i,T)\to (Y_j,T)$
is a factor map. A similar construction gives a factor map
$\psi \colon (Y_i,T)\to (Y_j,T)$
is a factor map. A similar construction gives a factor map
![]() $\phi \colon Y_j\to Y_i$
which is the inverse function of
$\phi \colon Y_j\to Y_i$
which is the inverse function of
![]() $\psi $
. We conclude that
$\psi $
. We conclude that
![]() $\psi $
is a conjugacy and, thus, that
$\psi $
is a conjugacy and, thus, that
![]() $Y_i$
and
$Y_i$
and
![]() $Y_j$
are conjugate.
$Y_j$
are conjugate.
6.2 Non-distal factor maps and asymptotic pairs lying in fibers
To deal with non-factor maps, we study asymptotic pairs belonging to fibers of this kind of factor. The starting point is the following lemma.
Lemma 6.4. Let
![]() $\pi \colon (X,T) \to (Y,T)$
be a factor between minimal subshifts. Then, either
$\pi \colon (X,T) \to (Y,T)$
be a factor between minimal subshifts. Then, either
![]() $\pi $
is distal or there exists a fiber
$\pi $
is distal or there exists a fiber
![]() $\pi ^{-1}(y)$
containing a pair of right or left asymptotic points.
$\pi ^{-1}(y)$
containing a pair of right or left asymptotic points.
Proof. Assume that
![]() $\pi $
is not distal. Then, we can find a fiber
$\pi $
is not distal. Then, we can find a fiber
![]() $\pi ^{-1}(y)$
and proximal points
$\pi ^{-1}(y)$
and proximal points
![]() $x,x' \in \pi ^{-1}(y)$
, with
$x,x' \in \pi ^{-1}(y)$
, with
![]() $x\not =x'$
. This implies that for every
$x\not =x'$
. This implies that for every
![]() $k \in {\mathbb N}$
, there exist a (may be infinite) interval
$k \in {\mathbb N}$
, there exist a (may be infinite) interval
![]() $I_k = (a_k,b_k) \subseteq {\mathbb Z}$
, with
$I_k = (a_k,b_k) \subseteq {\mathbb Z}$
, with
![]() $b_k-a_k\geq k$
, for which x and
$b_k-a_k\geq k$
, for which x and
![]() $x'$
coincide on I, and
$x'$
coincide on I, and
![]() $I_k$
is maximal (with respect to the inclusion) with this property. Since
$I_k$
is maximal (with respect to the inclusion) with this property. Since
![]() $x\not =x'$
, then
$x\not =x'$
, then
![]() $a_k> -\infty $
or
$a_k> -\infty $
or
![]() $b_k < \infty $
. Hence, there exists an infinite set
$b_k < \infty $
. Hence, there exists an infinite set
![]() $E \subseteq {\mathbb N}$
such that
$E \subseteq {\mathbb N}$
such that
![]() $a_k> -\infty $
for every
$a_k> -\infty $
for every
![]() $k \in E$
or
$k \in E$
or
![]() $b_k < \infty $
for every
$b_k < \infty $
for every
![]() $k \in E$
. In the first case, we have that
$k \in E$
. In the first case, we have that
![]() $(T^{b_k}(x,x'))_{k\in E}$
has a left asymptotic pair
$(T^{b_k}(x,x'))_{k\in E}$
has a left asymptotic pair
![]() $(z,z')$
as an accumulation point, while in the second case, it is a right asymptotic pair
$(z,z')$
as an accumulation point, while in the second case, it is a right asymptotic pair
![]() $(z,z')$
which is an accumulation point of
$(z,z')$
which is an accumulation point of
![]() $(T^{a_k}(x,x'))_{k\in E}$
. In both cases we have that
$(T^{a_k}(x,x'))_{k\in E}$
. In both cases we have that
![]() $(z,z') \in R_\pi ^2$
since
$(z,z') \in R_\pi ^2$
since
![]() $(T^{b_k}(x,x'))_{k\in E}$
and
$(T^{b_k}(x,x'))_{k\in E}$
and
![]() $(T^{a_k}(x,x'))_{k\in E}$
are contained in
$(T^{a_k}(x,x'))_{k\in E}$
are contained in
![]() $R_\pi ^2$
and
$R_\pi ^2$
and
![]() $R_\pi ^2$
is closed. Therefore, the fiber
$R_\pi ^2$
is closed. Therefore, the fiber
![]() $\pi ^{-1}(\pi (z))$
contains a pair
$\pi ^{-1}(\pi (z))$
contains a pair
![]() $z,z'$
of asymptotic points.
$z,z'$
of asymptotic points.
The next lemma allows us to pass from morphisms
![]() $\sigma \colon X\to Y$
to factors
$\sigma \colon X\to Y$
to factors
![]() $\pi \colon X'\to Y$
in such a way that
$\pi \colon X'\to Y$
in such a way that
![]() $X'$
is defined on the same alphabet as X and has the ‘same’ asymptotic pairs. We remark that its proof is simple, but tedious.
$X'$
is defined on the same alphabet as X and has the ‘same’ asymptotic pairs. We remark that its proof is simple, but tedious.
Lemma 6.5. Let
![]() $X \subseteq {\mathcal A}^+$
be an aperiodic subshift,
$X \subseteq {\mathcal A}^+$
be an aperiodic subshift,
![]() $\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism, and
$\sigma \colon {\mathcal A}^+\to {\mathcal B}^+$
be a morphism, and
 $Y = \bigcup _{k\in {\mathbb Z}}T^k\sigma (X)$
. Define the morphism
$Y = \bigcup _{k\in {\mathbb Z}}T^k\sigma (X)$
. Define the morphism
![]() $i_\sigma \colon {\mathcal A}^+\to {\mathcal A}^+$
by
$i_\sigma \colon {\mathcal A}^+\to {\mathcal A}^+$
by
![]() $i_\sigma (a) = a^{|\sigma (a)|}$
,
$i_\sigma (a) = a^{|\sigma (a)|}$
,
![]() $a \in {\mathcal A}$
, and
$a \in {\mathcal A}$
, and
 $X' = \bigcup _{k\in {\mathbb Z}}T^ki_\sigma (X)$
. Then, centered asymptotic pairs in
$X' = \bigcup _{k\in {\mathbb Z}}T^ki_\sigma (X)$
. Then, centered asymptotic pairs in
![]() $X'$
are of the form
$X'$
are of the form
![]() $(i_\sigma (x),i_\sigma (\tilde {x}))$
, where
$(i_\sigma (x),i_\sigma (\tilde {x}))$
, where
![]() $(x,\tilde {x})$
is a centered asymptotic pair in X, and there exists a factor map
$(x,\tilde {x})$
is a centered asymptotic pair in X, and there exists a factor map
![]() $\pi \colon (X',T)\to (Y,T)$
such that
$\pi \colon (X',T)\to (Y,T)$
such that
![]() $\pi (i_\sigma (x)) = \tau (x)$
for all
$\pi (i_\sigma (x)) = \tau (x)$
for all
![]() $x \in X$
.
$x \in X$
.
Proof. Our first objective is to prove that
![]() $(X,i_\sigma )$
is recognizable. We start by observing that
$(X,i_\sigma )$
is recognizable. We start by observing that
Indeed, since the factorizations are centered, we have
![]() $x_0 = i_\sigma (x_0)_k = y_0 = i_\sigma (\tilde {x}_0)_{\tilde {k}} = \tilde {x}_0$
.
$x_0 = i_\sigma (x_0)_k = y_0 = i_\sigma (\tilde {x}_0)_{\tilde {k}} = \tilde {x}_0$
.
Let
![]() $\Lambda $
be the set of tuples
$\Lambda $
be the set of tuples
![]() $(k,x,\tilde {k},\tilde {x})$
such that
$(k,x,\tilde {k},\tilde {x})$
such that
![]() $(k,x),(\tilde {k},\tilde {x})$
are centered
$(k,x),(\tilde {k},\tilde {x})$
are centered
![]() $i_\sigma $
-factorizations of the same point. Moreover, for
$i_\sigma $
-factorizations of the same point. Moreover, for
![]() ${\mathcal R} \in \{=,>\}$
, let
${\mathcal R} \in \{=,>\}$
, let
![]() $\Lambda _{\mathcal R}$
be the set of those
$\Lambda _{\mathcal R}$
be the set of those
![]() $(k,x,\tilde {k},\tilde {x}) \in \Lambda $
satisfying
$(k,x,\tilde {k},\tilde {x}) \in \Lambda $
satisfying
![]() $k\ {\mathcal R}\ \tilde {k}$
.
$k\ {\mathcal R}\ \tilde {k}$
.
Claim 6.5.1. If
![]() $(k,x,\tilde {k},\tilde {x}) \in \Lambda _=$
, then
$(k,x,\tilde {k},\tilde {x}) \in \Lambda _=$
, then
![]() $(0,Tx,0,T\tilde {x}) \in \Lambda _=$
, and if
$(0,Tx,0,T\tilde {x}) \in \Lambda _=$
, and if
![]() $(k,x,\tilde {k},\tilde {x}) \in \Lambda _>$
, then
$(k,x,\tilde {k},\tilde {x}) \in \Lambda _>$
, then
![]() $(|i_\sigma (x_0)|-k+\tilde {k},\tilde {x},0,Tx) \in \Lambda _>$
.
$(|i_\sigma (x_0)|-k+\tilde {k},\tilde {x},0,Tx) \in \Lambda _>$
.
Proof. If
![]() $(k,x,\tilde {k},\tilde {x}) \in \Lambda _=$
, then, since
$(k,x,\tilde {k},\tilde {x}) \in \Lambda _=$
, then, since
![]() $x_0 = \tilde {x}_0$
by (35), we can write
$x_0 = \tilde {x}_0$
by (35), we can write
 $i_\sigma (Tx) = T^ki_\sigma (x) = T^{\tilde {k}}i_\sigma (\tilde {x}) = i_\sigma (T\tilde {x})$
. Thus,
$i_\sigma (Tx) = T^ki_\sigma (x) = T^{\tilde {k}}i_\sigma (\tilde {x}) = i_\sigma (T\tilde {x})$
. Thus,
![]() $(0,Tx,0,T\tilde {x}) \in \Lambda _=$
. Let now
$(0,Tx,0,T\tilde {x}) \in \Lambda _=$
. Let now
![]() $(k,x,\tilde {k},\tilde {x}) \in \Lambda _>$
and
$(k,x,\tilde {k},\tilde {x}) \in \Lambda _>$
and
 $y := T^ki_\sigma (x) = T^{\tilde {k}}i_\sigma (\tilde {x})$
. We note that
$y := T^ki_\sigma (x) = T^{\tilde {k}}i_\sigma (\tilde {x})$
. We note that
 $$ \begin{align*} T^{|i_\sigma(x_0)|-k+\tilde{k}}i_\sigma(\tilde{x}) = T^{|i_\sigma(x_0)|-k}y = T^{|i_\sigma(x_0)|}i_\sigma(x) = i_\sigma(Tx), \end{align*} $$
$$ \begin{align*} T^{|i_\sigma(x_0)|-k+\tilde{k}}i_\sigma(\tilde{x}) = T^{|i_\sigma(x_0)|-k}y = T^{|i_\sigma(x_0)|}i_\sigma(x) = i_\sigma(Tx), \end{align*} $$
so
![]() $(|i_\sigma (x_0)|-k+\tilde {k},\tilde {x})$
and
$(|i_\sigma (x_0)|-k+\tilde {k},\tilde {x})$
and
![]() $(0,Tx)$
are
$(0,Tx)$
are
![]() $i_\sigma $
-factorizations of the same point. Now, since
$i_\sigma $
-factorizations of the same point. Now, since
![]() $x_0 = \tilde {x}_0$
(by (35)) and
$x_0 = \tilde {x}_0$
(by (35)) and
![]() $(k,x),(\tilde {k},\tilde {x})$
are centered, we have
$(k,x),(\tilde {k},\tilde {x})$
are centered, we have
![]() $k,\tilde {k}\in [0,|i_\sigma (x_0)|)$
. This and the fact that
$k,\tilde {k}\in [0,|i_\sigma (x_0)|)$
. This and the fact that
![]() $k>\tilde {k}$
imply that
$k>\tilde {k}$
imply that
![]() $k-\tilde {k}\in (0,|i_\sigma (x_0)|)$
. Therefore,
$k-\tilde {k}\in (0,|i_\sigma (x_0)|)$
. Therefore,
![]() $|i_\sigma (x_0)|-k+\tilde {k} \in (0,|i_\sigma (x_0)|)$
and, consequently,
$|i_\sigma (x_0)|-k+\tilde {k} \in (0,|i_\sigma (x_0)|)$
and, consequently,
![]() $(|i_\sigma (x_0)|-k+\tilde {k},\tilde {x},0,Tx) \in \Lambda _>$
.
$(|i_\sigma (x_0)|-k+\tilde {k},\tilde {x},0,Tx) \in \Lambda _>$
.
We prove now that
![]() $(X,i_\sigma )$
is recognizable. Let
$(X,i_\sigma )$
is recognizable. Let
![]() $(k,x,\tilde {k},\tilde {x}) \in \Lambda $
. We have to show that
$(k,x,\tilde {k},\tilde {x}) \in \Lambda $
. We have to show that
![]() $(k,x) = (\tilde {k},\tilde {x})$
. First, we consider the case in which
$(k,x) = (\tilde {k},\tilde {x})$
. First, we consider the case in which
![]() $k = \tilde {k}$
. In this situation, the previous claim implies that
$k = \tilde {k}$
. In this situation, the previous claim implies that
![]() $(0,Tx,0,T\tilde {x}) \in \Lambda _=$
. We use again the claim, but with
$(0,Tx,0,T\tilde {x}) \in \Lambda _=$
. We use again the claim, but with
![]() $(0,Tx,0,T\tilde {x})$
, to obtain that
$(0,Tx,0,T\tilde {x})$
, to obtain that
![]() $(0,T^2x,0,T^2\tilde {x}) \in \Lambda _=$
. By continuing in this way, we get
$(0,T^2x,0,T^2\tilde {x}) \in \Lambda _=$
. By continuing in this way, we get
![]() $(0,T^nx,0,T^n\tilde {x}) \in \Lambda _=$
for any
$(0,T^nx,0,T^n\tilde {x}) \in \Lambda _=$
for any
![]() $n\geq 0$
. Then, (35) implies that
$n\geq 0$
. Then, (35) implies that
![]() $x_n = \tilde {x}_n$
for all
$x_n = \tilde {x}_n$
for all
![]() $n\geq 0$
. A similar argument shows that
$n\geq 0$
. A similar argument shows that
![]() $x_n = \tilde {x}_n$
for any
$x_n = \tilde {x}_n$
for any
![]() $n\leq 0$
, and so
$n\leq 0$
, and so
![]() $(k,x) = (\tilde {k},\tilde {x})$
. We now do the case
$(k,x) = (\tilde {k},\tilde {x})$
. We now do the case
![]() $k> \tilde {k}$
. Another application of the claim gives us
$k> \tilde {k}$
. Another application of the claim gives us
![]() $(p_1,\tilde {x},0,Tx) \in \Lambda _>$
for some
$(p_1,\tilde {x},0,Tx) \in \Lambda _>$
for some
![]() $p_1 \in {\mathbb Z}$
. As before, we iterate this procedure to obtain that
$p_1 \in {\mathbb Z}$
. As before, we iterate this procedure to obtain that
![]() $(p_2,Tx,0,T\tilde {x}) \in \Lambda _>$
,
$(p_2,Tx,0,T\tilde {x}) \in \Lambda _>$
,
![]() $(p_3,T\tilde {x},0,T^2x) \in \Lambda _>$
, and so on. From these relations and (35), we deduce that
$(p_3,T\tilde {x},0,T^2x) \in \Lambda _>$
, and so on. From these relations and (35), we deduce that
![]() $x_0 = \tilde {x}_0$
,
$x_0 = \tilde {x}_0$
,
![]() $\tilde {x}_0 = (Tx)_0 = x_1$
,
$\tilde {x}_0 = (Tx)_0 = x_1$
,
![]() $x_1 = (Tx)_0 = (T\tilde {x})_0 = \tilde {x}_1$
,
$x_1 = (Tx)_0 = (T\tilde {x})_0 = \tilde {x}_1$
,
![]() $\tilde {x}_1 = (T\tilde {x})_0 = (T^2x)_0 = x_2$
, etc. We conclude that
$\tilde {x}_1 = (T\tilde {x})_0 = (T^2x)_0 = x_2$
, etc. We conclude that
![]() $x_n = \tilde {x}_n = x_0$
for any
$x_n = \tilde {x}_n = x_0$
for any
![]() $n \geq 0$
. Then, by compacity, the periodic point
$n \geq 0$
. Then, by compacity, the periodic point
![]() $\cdots x_0.x_0x_0\cdots $
belongs to X, contrary to our aperiodicity hypothesis on X. Thus, the case
$\cdots x_0.x_0x_0\cdots $
belongs to X, contrary to our aperiodicity hypothesis on X. Thus, the case
![]() $k> \tilde {k}$
does not occur. This proves that
$k> \tilde {k}$
does not occur. This proves that
![]() $(X,i_\sigma )$
is recognizable.
$(X,i_\sigma )$
is recognizable.
Using the property we just proved, we can define the factor map
![]() $\pi \colon X'\to Y$
as follows: if
$\pi \colon X'\to Y$
as follows: if
![]() $x' \in X'$
, then we set
$x' \in X'$
, then we set
![]() $\pi (x') = T^k\tau (x) \in Y$
, where
$\pi (x') = T^k\tau (x) \in Y$
, where
![]() $(k,x)$
is the unique centered
$(k,x)$
is the unique centered
![]() $i_\sigma $
-factorization of
$i_\sigma $
-factorization of
![]() $x'$
in X. To show that
$x'$
in X. To show that
![]() $\pi $
is indeed a factor map, we first observe that since
$\pi $
is indeed a factor map, we first observe that since
![]() $\pi $
commutes with T. Moreover, thanks to condition (iii) in Remark 2.2,
$\pi $
commutes with T. Moreover, thanks to condition (iii) in Remark 2.2,
![]() $\pi $
is continuous. Finally, if
$\pi $
is continuous. Finally, if
![]() $y \in Y$
, then by the definition of Y, there exist a centered
$y \in Y$
, then by the definition of Y, there exist a centered
![]() $(k,x) \tau $
-factorization of y in X. Thus, by (36),
$(k,x) \tau $
-factorization of y in X. Thus, by (36),
![]() $(k,x)$
is a centered
$(k,x)$
is a centered
![]() $i_\sigma $
factorization of
$i_\sigma $
factorization of
![]() $x' := T^ki_\sigma (x)$
. Therefore,
$x' := T^ki_\sigma (x)$
. Therefore,
![]() $\pi (x') = y$
and
$\pi (x') = y$
and
![]() $\pi $
is onto. Altogether, these arguments show that
$\pi $
is onto. Altogether, these arguments show that
![]() $\pi $
is a factor map. That
$\pi $
is a factor map. That
![]() $\pi (i_\sigma (x)) = \tau (x)$
for every
$\pi (i_\sigma (x)) = \tau (x)$
for every
![]() $x \in X$
follows directly from the definition of
$x \in X$
follows directly from the definition of
![]() $\pi $
.
$\pi $
.
It is left to prove the property about the asymptotic pairs. We only prove it for left asymptotic pairs since the other case is similar. We will use the following notation: if Z is a subshift, then
![]() $A(Z)$
denotes the set of centered left asymptotic pairs. To start, we observe that
$A(Z)$
denotes the set of centered left asymptotic pairs. To start, we observe that
![]() $(i_\sigma (x),i_\sigma (x')) \in A(X')$
for every
$(i_\sigma (x),i_\sigma (x')) \in A(X')$
for every
![]() $(x,\tilde {x}) \in A(X)$
. Let now
$(x,\tilde {x}) \in A(X)$
. Let now
![]() $(z,\tilde {z}) \in A(X')$
, and
$(z,\tilde {z}) \in A(X')$
, and
![]() $(k,x)$
and
$(k,x)$
and
![]() $(\tilde {k},\tilde {x})$
be the unique centered
$(\tilde {k},\tilde {x})$
be the unique centered
![]() $i_\sigma $
-factorizations of z and
$i_\sigma $
-factorizations of z and
![]() $\tilde {z}$
in X, respectively. We have to show that
$\tilde {z}$
in X, respectively. We have to show that
![]() $k = \tilde {k} = 0$
and that
$k = \tilde {k} = 0$
and that
![]() $(x,\tilde {x}) \in A(X)$
. Due to condition (iii) in Remark 2.2,
$(x,\tilde {x}) \in A(X)$
. Due to condition (iii) in Remark 2.2,
![]() $(X,i_\sigma )$
has a recognizability constant. This and the fact that
$(X,i_\sigma )$
has a recognizability constant. This and the fact that
![]() $(z,\tilde {z})$
is centered left asymptotic imply that
$(z,\tilde {z})$
is centered left asymptotic imply that
![]() $(k,x)$
and
$(k,x)$
and
![]() $(\tilde {k},\tilde {x})$
have a common cut in
$(\tilde {k},\tilde {x})$
have a common cut in
![]() $(-\infty ,0]$
, this is, that there exist
$(-\infty ,0]$
, this is, that there exist
![]() $p,q \leq 0$
such that
$p,q \leq 0$
such that
 $$ \begin{align*} m := -k-|i_\sigma(x_{[p,0)})| = -\tilde{k}-|i_\sigma(\tilde{x}_{[q,0)})| \in (-\infty, 0]. \end{align*} $$
$$ \begin{align*} m := -k-|i_\sigma(x_{[p,0)})| = -\tilde{k}-|i_\sigma(\tilde{x}_{[q,0)})| \in (-\infty, 0]. \end{align*} $$
We take m as big as possible with this property. Then,
![]() $x_p \not = \tilde {x}_q$
. Moreover, being
$x_p \not = \tilde {x}_q$
. Moreover, being
![]() $z_{m} = x_p$
and
$z_{m} = x_p$
and
![]() $\tilde {z}_{m} = \tilde {x}_p$
by the definition of
$\tilde {z}_{m} = \tilde {x}_p$
by the definition of
![]() $i_\sigma $
, we have that
$i_\sigma $
, we have that
![]() $z_m \not = \tilde {z}_m$
and consequently, by also using that
$z_m \not = \tilde {z}_m$
and consequently, by also using that
![]() $(z,\tilde {z})$
is centered left asymptotic, that
$(z,\tilde {z})$
is centered left asymptotic, that
![]() $m \geq 0$
. We conclude that
$m \geq 0$
. We conclude that
![]() $m = 0$
, i.e. that
$m = 0$
, i.e. that
 $k+|i_\sigma (x_{[p,0)})| = \tilde {k}+|i_\sigma (\tilde {x}_{[q,0)})| = 0$
. Hence,
$k+|i_\sigma (x_{[p,0)})| = \tilde {k}+|i_\sigma (\tilde {x}_{[q,0)})| = 0$
. Hence,
![]() $k =\tilde {k}=p=q=0$
. Now, it is clear that
$k =\tilde {k}=p=q=0$
. Now, it is clear that
![]() $x_{(-\infty ,p]} = \tilde {x}_{(-\infty ,q]}$
, so from the last equations, we obtain that
$x_{(-\infty ,p]} = \tilde {x}_{(-\infty ,q]}$
, so from the last equations, we obtain that
![]() $(x,\tilde {x}) \in A(X)$
. This completes the proof.
$(x,\tilde {x}) \in A(X)$
. This completes the proof.
We will also need the following lemma to slightly strengthen Proposition 2.8.
Lemma 6.6. Let
![]() $X \subseteq {\mathcal A}^{\mathbb Z}$
be an aperiodic subshift with L asymptotic tails. Then,
$X \subseteq {\mathcal A}^{\mathbb Z}$
be an aperiodic subshift with L asymptotic tails. Then,
![]() $(X,T)$
has at most
$(X,T)$
has at most
![]() $2L^2\cdot \#{\mathcal A}^2$
centered asymptotic pairs.
$2L^2\cdot \#{\mathcal A}^2$
centered asymptotic pairs.
Proof. Let
![]() ${\mathcal P}_r$
be the set of centered right asymptotic pairs in X and
${\mathcal P}_r$
be the set of centered right asymptotic pairs in X and
 ${\mathcal T}_r = \{x_{(0,\infty )} : (x,\tilde {x}) \in \Lambda \} \subseteq {\mathcal A}^{{\mathbb N}_{\geq 1}}$
be the set of right asymptotic tails, where
${\mathcal T}_r = \{x_{(0,\infty )} : (x,\tilde {x}) \in \Lambda \} \subseteq {\mathcal A}^{{\mathbb N}_{\geq 1}}$
be the set of right asymptotic tails, where
![]() ${\mathbb N}_{\geq 1} = \{1,2,\ldots \}$
. We are going to prove that
${\mathbb N}_{\geq 1} = \{1,2,\ldots \}$
. We are going to prove that
 $$ \begin{align} \#{\mathcal P}_r \leq \#{\mathcal T}_r^2\cdot \#{\mathcal A}^2. \end{align} $$
$$ \begin{align} \#{\mathcal P}_r \leq \#{\mathcal T}_r^2\cdot \#{\mathcal A}^2. \end{align} $$
Once this is done, we will have by symmetry the same relation for the centered left asymptotic pairs
![]() ${\mathcal P}_l$
, and thus we are going to be able to conclude that the number of centered asymptotic pairs in X is at most
${\mathcal P}_l$
, and thus we are going to be able to conclude that the number of centered asymptotic pairs in X is at most
 $(\#{\mathcal T}_r^2+\#{\mathcal T}_l^2)\cdot \#{\mathcal A}^2 \leq 2L^2\cdot \#{\mathcal A}^2$
, completing the proof.
$(\#{\mathcal T}_r^2+\#{\mathcal T}_l^2)\cdot \#{\mathcal A}^2 \leq 2L^2\cdot \#{\mathcal A}^2$
, completing the proof.
Let
![]() $(x,\tilde {x}) \in {\mathcal P}_r$
and
$(x,\tilde {x}) \in {\mathcal P}_r$
and
![]() ${\mathcal R}_x = \{k\leq 0 : x_{(k,\infty )} \in {\mathcal T}_r\}$
. We claim that
${\mathcal R}_x = \{k\leq 0 : x_{(k,\infty )} \in {\mathcal T}_r\}$
. We claim that
![]() $\#{\mathcal R}_x \leq \#{\mathcal T}_r$
. Indeed, if this is not the case, then, by the pigeonhole principle, we can find
$\#{\mathcal R}_x \leq \#{\mathcal T}_r$
. Indeed, if this is not the case, then, by the pigeonhole principle, we can find
![]() $k' < k$
and
$k' < k$
and
![]() $w \in {\mathcal T}_r$
such that
$w \in {\mathcal T}_r$
such that
![]() $w = x_{(k,\infty )} = x_{(k',\infty )}$
. However, this implies that w has period
$w = x_{(k,\infty )} = x_{(k',\infty )}$
. However, this implies that w has period
![]() $k-k'$
, and so X contains a point of period
$k-k'$
, and so X contains a point of period
![]() $k-k'$
, contrary to the aperiodicity hypothesis. Thus,
$k-k'$
, contrary to the aperiodicity hypothesis. Thus,
![]() ${\mathcal R}_x$
is finite and, since
${\mathcal R}_x$
is finite and, since
![]() ${\mathcal R}_x$
is non-empty as it contains
${\mathcal R}_x$
is non-empty as it contains
![]() $x_{(0,\infty )}$
,
$x_{(0,\infty )}$
,
![]() $k_x := \min {\mathcal R}_x$
is a well-defined non-positive integer.
$k_x := \min {\mathcal R}_x$
is a well-defined non-positive integer.
Let now
 $\phi \colon {\mathcal P}_r \to {\mathcal T}_r^2\times {\mathcal A}^2$
be the function defined by
$\phi \colon {\mathcal P}_r \to {\mathcal T}_r^2\times {\mathcal A}^2$
be the function defined by
If
![]() $\phi $
is injective, then (37) follows. Let us then prove that
$\phi $
is injective, then (37) follows. Let us then prove that
![]() $\phi $
is injective.
$\phi $
is injective.
We argue by contradiction and assume that there exist
![]() $(x,\tilde {x})\not =(y,\tilde {y})$
such that
$(x,\tilde {x})\not =(y,\tilde {y})$
such that
![]() $\phi (x,\tilde {x}) = \phi (y,\tilde {y}) = (z,\tilde {z},a,\tilde {a})$
. Without loss of generality, we may assume that
$\phi (x,\tilde {x}) = \phi (y,\tilde {y}) = (z,\tilde {z},a,\tilde {a})$
. Without loss of generality, we may assume that
![]() $x \not = y$
. Then,
$x \not = y$
. Then,
![]() $x_{(k_x,\infty )} = z = y_{(k_y,\infty )}$
and
$x_{(k_x,\infty )} = z = y_{(k_y,\infty )}$
and
![]() $x_{k_x} = a = y_{k_y}$
. Being
$x_{k_x} = a = y_{k_y}$
. Being
![]() $x \not = y$
, this implies that
$x \not = y$
, this implies that
![]() $(x,y)$
is asymptotic. Furthermore, it implies that there exist
$(x,y)$
is asymptotic. Furthermore, it implies that there exist
![]() $p < k$
and
$p < k$
and
![]() $q < \ell $
such that
$q < \ell $
such that
![]() $(T^px, T^qy)$
is centered right asymptotic. In particular,
$(T^px, T^qy)$
is centered right asymptotic. In particular,
![]() $x_{(p,\infty )} \in {\mathcal T}_r$
and
$x_{(p,\infty )} \in {\mathcal T}_r$
and
![]() $p < k_x$
, contrary to the definition of
$p < k_x$
, contrary to the definition of
![]() $k_x$
. We conclude that
$k_x$
. We conclude that
![]() $\phi $
is injective and thereby complete the proof of the lemma.
$\phi $
is injective and thereby complete the proof of the lemma.
Lemma 6.7. Let
![]() $X \subseteq {\mathcal A}^{\mathbb Z}$
be a subshift of topological rank K, J be an index set, and, for
$X \subseteq {\mathcal A}^{\mathbb Z}$
be a subshift of topological rank K, J be an index set, and, for
![]() $j \in J$
, let
$j \in J$
, let
 $\tau _j\colon {\mathcal A}^+\to {\mathcal B}_j^+$
be a morphism. Suppose that for every
$\tau _j\colon {\mathcal A}^+\to {\mathcal B}_j^+$
be a morphism. Suppose that for every
![]() $j \in J$
:
$j \in J$
:
-
(I)
 $Y_j = \bigcup _{k\in {\mathbb Z}}T^k\tau _j(X)$
is aperiodic;
$Y_j = \bigcup _{k\in {\mathbb Z}}T^k\tau _j(X)$
is aperiodic; -
(II) for every fixed
 $a \in {\mathcal A}$
,
$a \in {\mathcal A}$
,
 $|\tau _j(a)|$
is equal to a constant
$|\tau _j(a)|$
is equal to a constant
 $\ell _a$
independent of
$\ell _a$
independent of
 $j \in J$
.
$j \in J$
.
Then, one of the following situations occur.
-
(1) There exist
 $i,j\in J$
,
$i,j\in J$
,
 $i\not =j$
, such that
$i\not =j$
, such that
 $(Y_i,T)$
is conjugate to
$(Y_i,T)$
is conjugate to
 $(Y_j,T)$
.
$(Y_j,T)$
. -
(2) There exist
 $\phi \colon {\mathcal A}^+\to {\mathcal A}_1^+$
with
$\phi \colon {\mathcal A}^+\to {\mathcal A}_1^+$
with
 $\#{\mathcal A}_1 < \#{\mathcal A}$
, a set
$\#{\mathcal A}_1 < \#{\mathcal A}$
, a set
 $J_1 \subseteq J$
having at least
$J_1 \subseteq J$
having at least
 $\#J / 2\#{\mathcal A}^2(144K^7)^2 - K(144K^7)^K$
elements, and morphisms
$\#J / 2\#{\mathcal A}^2(144K^7)^2 - K(144K^7)^K$
elements, and morphisms
 $\tau ^{\prime }_j\colon {\mathcal C}_1^+\to {\mathcal B}_j$
,
$\tau ^{\prime }_j\colon {\mathcal C}_1^+\to {\mathcal B}_j$
,
 $j \in J_1$
, such that
$j \in J_1$
, such that
 $\tau _j = \tau ^{\prime }_j\phi $
. In particular, the hypothesis of this lemma holds for
$\tau _j = \tau ^{\prime }_j\phi $
. In particular, the hypothesis of this lemma holds for
 $X_1 := \bigcup _{k\in {\mathbb Z}}T^k\phi (X)$
and
$X_1 := \bigcup _{k\in {\mathbb Z}}T^k\phi (X)$
and
 $\tau ^{\prime }_j$
,
$\tau ^{\prime }_j$
,
 $j \in J_1$
.
$j \in J_1$
.
Proof. Let
![]() $\mathfrak {i}\colon {\mathcal A}^+\to {\mathcal A}^+$
be the morphism defined by
$\mathfrak {i}\colon {\mathcal A}^+\to {\mathcal A}^+$
be the morphism defined by
![]() $\mathfrak {i}(a) = a^{\ell _a}$
,
$\mathfrak {i}(a) = a^{\ell _a}$
,
![]() $a \in {\mathcal A}$
, and
$a \in {\mathcal A}$
, and
 $X' = \bigcup _{k\in {\mathbb Z}}T^k\mathfrak {i}(X)$
. We use Lemma 6.5 with X and
$X' = \bigcup _{k\in {\mathbb Z}}T^k\mathfrak {i}(X)$
. We use Lemma 6.5 with X and
![]() $\tau _j$
to obtain a factor map
$\tau _j$
to obtain a factor map
![]() $\pi _j\colon (X',T) \to (Y_j,T)$
such that
$\pi _j\colon (X',T) \to (Y_j,T)$
such that
If
![]() $\pi _j$
is distal for
$\pi _j$
is distal for
![]() $K(144K^7)^K+1$
different values of
$K(144K^7)^K+1$
different values of
![]() $j \in J$
, then by Lemma 6.3, we can find
$j \in J$
, then by Lemma 6.3, we can find
![]() $i,j$
such that
$i,j$
such that
![]() $(Y_i,T)$
is conjugate to
$(Y_i,T)$
is conjugate to
![]() $(Y_j,T)$
. Therefore, we can suppose that there exists
$(Y_j,T)$
. Therefore, we can suppose that there exists
![]() $J' \subseteq J$
such that
$J' \subseteq J$
such that
 $$ \begin{align} \#J' \geq \#J-K(144K^7)^K\quad \text{and}\quad\pi_j\ \text{is not distal for every}\ j \in J'. \end{align} $$
$$ \begin{align} \#J' \geq \#J-K(144K^7)^K\quad \text{and}\quad\pi_j\ \text{is not distal for every}\ j \in J'. \end{align} $$
From this and Lemma 6.4, we obtain, for every
![]() $j \in J'$
, a centered asymptotic pair
$j \in J'$
, a centered asymptotic pair
![]() $(x^{(j)},\tilde {x}^{(j)})$
in
$(x^{(j)},\tilde {x}^{(j)})$
in
![]() $X'$
such that
$X'$
such that
 $\pi _j(x^{(j)}) = \pi _j(\tilde {x}^{(j)})$
. This and (38) imply that
$\pi _j(x^{(j)}) = \pi _j(\tilde {x}^{(j)})$
. This and (38) imply that
 $$ \begin{align} \tau_j(x^{(j)}) = \pi_j(x^{(j)}) = \pi_j(\tilde{x}^{(j)}) = \tau_j(\tilde{x}^{(j)}). \end{align} $$
$$ \begin{align} \tau_j(x^{(j)}) = \pi_j(x^{(j)}) = \pi_j(\tilde{x}^{(j)}) = \tau_j(\tilde{x}^{(j)}). \end{align} $$
Now, by Lemma 6.6, X has at most
![]() $2\#{\mathcal A}^2(144K^7)^2$
centered asymptotic pairs and thus, thanks to Lemma 6.5, the same bound holds for
$2\#{\mathcal A}^2(144K^7)^2$
centered asymptotic pairs and thus, thanks to Lemma 6.5, the same bound holds for
![]() $X'$
. Therefore, by the pigeonhole principle, there exist
$X'$
. Therefore, by the pigeonhole principle, there exist
![]() $J_1 \subseteq J$
satisfying
$J_1 \subseteq J$
satisfying
![]() $\#J_1 \geq \#J'/2\#{\mathcal A}^2(144K^7)^2 \geq \#J / 2\#{\mathcal A}^2(144K^7)^2 - K(144K^7)^K$
and a centered asymptotic pair
$\#J_1 \geq \#J'/2\#{\mathcal A}^2(144K^7)^2 \geq \#J / 2\#{\mathcal A}^2(144K^7)^2 - K(144K^7)^K$
and a centered asymptotic pair
![]() $(x,\tilde {x})$
in
$(x,\tilde {x})$
in
![]() $X'$
such that
$X'$
such that
![]() $(x,\tilde {x}) = (x^{(j)},\tilde {x}^{(j)})$
for every
$(x,\tilde {x}) = (x^{(j)},\tilde {x}^{(j)})$
for every
![]() $j \in J_1$
.
$j \in J_1$
.
We assume that
![]() $(x,\tilde {x})$
is right asymptotic as the other case is similar. Then, (40) implies that if
$(x,\tilde {x})$
is right asymptotic as the other case is similar. Then, (40) implies that if
![]() $\ell = \sum _{a\in {\mathcal A}}\ell _a$
, then, for every
$\ell = \sum _{a\in {\mathcal A}}\ell _a$
, then, for every
![]() $j \in J_1$
,
$j \in J_1$
,
This, hypothesis (II), and the fact that, since
![]() $(x,\tilde {x})$
is a centered asymptotic pair,
$(x,\tilde {x})$
is a centered asymptotic pair,
![]() $x_0 \not = \tilde {x}_0$
allows us to use Lemma 3.2 with
$x_0 \not = \tilde {x}_0$
allows us to use Lemma 3.2 with
![]() $u := x_{[0,\ell )}$
,
$u := x_{[0,\ell )}$
,
![]() $v := \tilde {x}_{[0,\ell )}$
,
$v := \tilde {x}_{[0,\ell )}$
,
![]() $J := J_1$
, and
$J := J_1$
, and
![]() $w^j := \tau _j(x_{[0,\infty )})_{[0,\ell )}$
, and obtain morphisms
$w^j := \tau _j(x_{[0,\infty )})_{[0,\ell )}$
, and obtain morphisms
 $\phi \colon {\mathcal A}^+\to {\mathcal A}_1^+$
and
$\phi \colon {\mathcal A}^+\to {\mathcal A}_1^+$
and
 $\tau ^{\prime }_j\colon {\mathcal A}_1^+\to {\mathcal B}_j^+$
,
$\tau ^{\prime }_j\colon {\mathcal A}_1^+\to {\mathcal B}_j^+$
,
![]() $j \in J_1$
, such that
$j \in J_1$
, such that
![]() $\#{\mathcal A}_1 < \#{\mathcal A}$
,
$\#{\mathcal A}_1 < \#{\mathcal A}$
,
 $\tau _j = \tau ^{\prime }_j\phi $
, and
$\tau _j = \tau ^{\prime }_j\phi $
, and
 $$ \begin{align} \text{for every}\ a \in {\mathcal A}_1, \ell^{\prime}_a := |\tau^{\prime}_j(c)|\ \text{does not depend on the chosen}\ j \in J. \end{align} $$
$$ \begin{align} \text{for every}\ a \in {\mathcal A}_1, \ell^{\prime}_a := |\tau^{\prime}_j(c)|\ \text{does not depend on the chosen}\ j \in J. \end{align} $$
Finally, we observe that
![]() $X_1$
and
$X_1$
and
![]() $\tau ^{\prime }_j$
,
$\tau ^{\prime }_j$
,
![]() $j \in J_1$
, satisfy the hypothesis of the lemma: condition (I) holds since, by the relation
$j \in J_1$
, satisfy the hypothesis of the lemma: condition (I) holds since, by the relation
 $\tau _j = \tau ^{\prime }_j\phi $
, the subshift
$\tau _j = \tau ^{\prime }_j\phi $
, the subshift
 $X_1 := \bigcup _{k\in {\mathbb Z}}T^k\phi (X)$
satisfies that
$X_1 := \bigcup _{k\in {\mathbb Z}}T^k\phi (X)$
satisfies that
 $\bigcup _{k\in {\mathbb Z}}T^k\tau ^{\prime }_j(X_1) = Y_j$
is aperiodic; condition (II) is given by (42).
$\bigcup _{k\in {\mathbb Z}}T^k\tau ^{\prime }_j(X_1) = Y_j$
is aperiodic; condition (II) is given by (42).
6.3 Proof of main result
We now prove Theorem 1.7. We restate it for convenience.
Theorem 1.7. Let
![]() $(X,T)$
be an minimal subshift of topological rank K. Then,
$(X,T)$
be an minimal subshift of topological rank K. Then,
![]() $(X,T)$
has at most
$(X,T)$
has at most
![]() $(3K)^{32K}$
aperiodic symbolic factors up to conjugacy.
$(3K)^{32K}$
aperiodic symbolic factors up to conjugacy.
Proof. We set
![]() $R = (3K)^{32K}$
. We prove the theorem by contradiction: assume that there exist
$R = (3K)^{32K}$
. We prove the theorem by contradiction: assume that there exist
![]() $X \subseteq {\mathcal A}^{\mathbb Z}$
of topological rank K and, for
$X \subseteq {\mathcal A}^{\mathbb Z}$
of topological rank K and, for
![]() $j \in \{0,\ldots ,R\}$
, factor maps
$j \in \{0,\ldots ,R\}$
, factor maps
![]() $\pi _j\colon (X,T) \to (Y_j,T)$
such that
$\pi _j\colon (X,T) \to (Y_j,T)$
such that
![]() $(Y_i,T)$
is not conjugate to
$(Y_i,T)$
is not conjugate to
![]() $(Y_j,T)$
for every
$(Y_j,T)$
for every
![]() $i\not =j \in \{0,\ldots ,R\}$
. We remark that X must be infinite as, otherwise, it would not have any aperiodic factor.
$i\not =j \in \{0,\ldots ,R\}$
. We remark that X must be infinite as, otherwise, it would not have any aperiodic factor.
To start, we build
![]() ${\mathcal S}$
-representations for the subshifts X and
${\mathcal S}$
-representations for the subshifts X and
![]() $Y_j$
. Let
$Y_j$
. Let
 $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be the primitive and proper directive sequence of alphabet rank K generating X given by Theorem 1.1. Let
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_{n+1}^+\to {\mathcal A}_n^+)_{n\in {\mathbb N}}$
be the primitive and proper directive sequence of alphabet rank K generating X given by Theorem 1.1. Let
![]() $r \in {\mathbb N}$
be such that every
$r \in {\mathbb N}$
be such that every
![]() $\pi _j$
has a radius r and let
$\pi _j$
has a radius r and let
![]() ${\mathcal B}_j$
be the alphabet of
${\mathcal B}_j$
be the alphabet of
![]() $Y_j$
. By contracting
$Y_j$
. By contracting
![]() $\boldsymbol {\sigma }$
, we can assume that
$\boldsymbol {\sigma }$
, we can assume that
![]() $\sigma _0$
is r-proper and
$\sigma _0$
is r-proper and
![]() $\#{\mathcal A}_n = K$
for all
$\#{\mathcal A}_n = K$
for all
![]() $n\geq 1$
. Then, we can use Lemma 2.4 to find morphisms
$n\geq 1$
. Then, we can use Lemma 2.4 to find morphisms
 $\tau _{j} \colon {\mathcal A}_1^+\to {\mathcal B}_j^+$
such that
$\tau _{j} \colon {\mathcal A}_1^+\to {\mathcal B}_j^+$
such that
 $$ \begin{align} \pi_j(\sigma_1(x)) = \tau_j(x)\quad \text{for all}\ x \in X_{\boldsymbol{\sigma}}^{(1)}\quad \text{and}\quad |\tau_{j}(a)| = |\sigma_0(a)|\quad \text{for all}\ a \in {\mathcal A}_1. \end{align} $$
$$ \begin{align} \pi_j(\sigma_1(x)) = \tau_j(x)\quad \text{for all}\ x \in X_{\boldsymbol{\sigma}}^{(1)}\quad \text{and}\quad |\tau_{j}(a)| = |\sigma_0(a)|\quad \text{for all}\ a \in {\mathcal A}_1. \end{align} $$
Next, we inductively define subshifts
 $X_n \subseteq {\mathcal C}_n^{\mathbb Z}$
and morphisms
$X_n \subseteq {\mathcal C}_n^{\mathbb Z}$
and morphisms
![]() $\{\tau _{n,j}\colon {\mathcal C}_n^+\to {\mathcal B}_j : j\in J_n\}$
such that:
$\{\tau _{n,j}\colon {\mathcal C}_n^+\to {\mathcal B}_j : j\in J_n\}$
such that:
-
(i)
 $X_n$
has topological rank at most K;
$X_n$
has topological rank at most K; -
(ii)
 $Y_j = \bigcup _{k\in {\mathbb Z}} \tau _{n,j}(X_n)$
;
$Y_j = \bigcup _{k\in {\mathbb Z}} \tau _{n,j}(X_n)$
; -
(iii) for every
 $c \in {\mathcal C}_n$
,
$c \in {\mathcal C}_n$
,
 $\ell _{n,a} := |\tau _{n,j}(c)|$
does not depend on the chosen
$\ell _{n,a} := |\tau _{n,j}(c)|$
does not depend on the chosen
 $j \in J_n$
.
$j \in J_n$
.
First, we set
 $X_0 = X_{\boldsymbol {\sigma }}^{(1)}$
,
$X_0 = X_{\boldsymbol {\sigma }}^{(1)}$
,
![]() ${\mathcal C}_0 = {\mathcal A}_1$
,
${\mathcal C}_0 = {\mathcal A}_1$
,
![]() $J_0 = J$
, and, for
$J_0 = J$
, and, for
![]() $j\in J_0$
,
$j\in J_0$
,
![]() $\tau _{0,j} = \tau _{j}$
, and note that by the hypothesis and (43), they satisfy conditions (i), (ii), and (iii). Let now
$\tau _{0,j} = \tau _{j}$
, and note that by the hypothesis and (43), they satisfy conditions (i), (ii), and (iii). Let now
![]() $n \geq 0$
and suppose that
$n \geq 0$
and suppose that
 $X_n \subseteq {\mathcal C}_n^{\mathbb Z}$
and
$X_n \subseteq {\mathcal C}_n^{\mathbb Z}$
and
![]() $\tau _{n,j}$
,
$\tau _{n,j}$
,
![]() $j\in J_n$
, has been defined in a way such that conditions (i), (ii), and (iii) hold. If
$j\in J_n$
, has been defined in a way such that conditions (i), (ii), and (iii) hold. If
![]() $\#J_n / 2\#{\mathcal A}^2(144K^7)^2 - K(144K^7)^K \leq 1$
, then the procedure stops. Otherwise, we define step
$\#J_n / 2\#{\mathcal A}^2(144K^7)^2 - K(144K^7)^K \leq 1$
, then the procedure stops. Otherwise, we define step
![]() $n+1$
as follows. Thanks to conditions (i), (ii), and (iii), we can use Lemma 6.7, and since there are no two conjugate
$n+1$
as follows. Thanks to conditions (i), (ii), and (iii), we can use Lemma 6.7, and since there are no two conjugate
![]() $(Y_i,T)$
, this lemma gives us a morphism
$(Y_i,T)$
, this lemma gives us a morphism
 $\phi \colon {\mathcal C}_n^+\to {\mathcal C}_{n+1}^+$
, a set
$\phi \colon {\mathcal C}_n^+\to {\mathcal C}_{n+1}^+$
, a set
![]() $J_{n+1} \subseteq J_n$
, and morphisms
$J_{n+1} \subseteq J_n$
, and morphisms
 $\{\tau _{n+1,j}\colon {\mathcal C}_{n+1}^+\to {\mathcal B}_j^+ : j\in J_{n+1}\}$
such that
$\{\tau _{n+1,j}\colon {\mathcal C}_{n+1}^+\to {\mathcal B}_j^+ : j\in J_{n+1}\}$
such that
 $$ \begin{align*} \#{\mathcal C}_{n+1} < \#{\mathcal C}_n, \#J_{n+1} \geq \#J_n / 2\#{\mathcal C}_n^2(144K^7)^2 - K(144K^7)^K\quad \text{and}\quad\tau_{n,j} = \tau_{n+1,j}\phi_n. \end{align*} $$
$$ \begin{align*} \#{\mathcal C}_{n+1} < \#{\mathcal C}_n, \#J_{n+1} \geq \#J_n / 2\#{\mathcal C}_n^2(144K^7)^2 - K(144K^7)^K\quad \text{and}\quad\tau_{n,j} = \tau_{n+1,j}\phi_n. \end{align*} $$
Furthermore,
 $X_{n+1} := \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_n)$
and
$X_{n+1} := \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_n)$
and
![]() $\tau _{n+1,j}$
satisfy the hypothesis of that lemma, that is, conditions (ii) and (iii) above. Since
$\tau _{n+1,j}$
satisfy the hypothesis of that lemma, that is, conditions (ii) and (iii) above. Since
![]() $(\phi _n\ldots \phi _0\sigma _1,\sigma _2,\sigma _3,\ldots )$
is a primitive and proper sequence of alphabet rank K generating
$(\phi _n\ldots \phi _0\sigma _1,\sigma _2,\sigma _3,\ldots )$
is a primitive and proper sequence of alphabet rank K generating
![]() $X_{n+1}$
, Theorem 1.3 implies that condition (i) is met as well.
$X_{n+1}$
, Theorem 1.3 implies that condition (i) is met as well.
Since
![]() $\#{\mathcal C}_0> \#{\mathcal C}_1 > \ldots $
, there is a last
$\#{\mathcal C}_0> \#{\mathcal C}_1 > \ldots $
, there is a last
![]() ${\mathcal C}_N$
defined. Our next objective is to prove that
${\mathcal C}_N$
defined. Our next objective is to prove that
![]() $N \geq K$
. Observe that
$N \geq K$
. Observe that
![]() $\#{\mathcal C}_n \leq K$
, so
$\#{\mathcal C}_n \leq K$
, so
Using this recurrence and the inequalities
![]() $\#J_0> (3K)^{32K}$
and
$\#J_0> (3K)^{32K}$
and
![]() $K\geq 2$
, it is routine to verify that the following bound holds for every
$K\geq 2$
, it is routine to verify that the following bound holds for every
![]() $n \in \{0,\ldots ,K-1\}$
such that the nth step is defined:
$n \in \{0,\ldots ,K-1\}$
such that the nth step is defined:
 $$ \begin{align*} \#J_n / 2\#{\mathcal C}_n^2(144K^7)^2 - K(144K^7)^K> 1. \end{align*} $$
$$ \begin{align*} \#J_n / 2\#{\mathcal C}_n^2(144K^7)^2 - K(144K^7)^K> 1. \end{align*} $$
Therefore,
![]() $N \geq K$
. We conclude that
$N \geq K$
. We conclude that
![]() $\#{\mathcal C}_N \leq \#{\mathcal C}_0-K = 0$
, which is a contradiction.
$\#{\mathcal C}_N \leq \#{\mathcal C}_0-K = 0$
, which is a contradiction.
Remark 6.8. In theorem 1 of [Reference DurandDur00], the author proved that linearly recurrent subshifts have finitely many aperiodic symbolic factors up to conjugacy. Since this kind of systems have finite topological rank (see Remark 4.10), Theorem 1.7 generalizes the theorem of [Reference DurandDur00] to the much larger class of minimal finite topological rank subshifts.
Acknowledgements
This research was partially supported by grant ANID-AFB 170001. The first author thanks Doctoral Fellowship CONICYT-PFCHA/Doctorado Nacional/2020-21202229.
A Appendix
To prove Proposition 4.4, we start with some lemmas concerning how to construct recognizable pairs
![]() $(Z,\tau )$
for a fixed subshift
$(Z,\tau )$
for a fixed subshift
 $Y = \bigcup _{k\in {\mathbb Z}}T^k\tau (Z)$
.
$Y = \bigcup _{k\in {\mathbb Z}}T^k\tau (Z)$
.
A.1 Codings of subshifts
If
![]() $Y \subseteq {\mathcal B}^{\mathbb Z}$
is a subshift,
$Y \subseteq {\mathcal B}^{\mathbb Z}$
is a subshift,
![]() $U \subseteq Y$
and
$U \subseteq Y$
and
![]() $y\in Y$
, we denote by
$y\in Y$
, we denote by
![]() ${\mathcal R}_U(y)$
the set of return times of y to U, this is,
${\mathcal R}_U(y)$
the set of return times of y to U, this is,
![]() ${\mathcal R}_U(y) = \{k\in {\mathbb Z} : T^ky \in U\}$
. We recall that the set
${\mathcal R}_U(y) = \{k\in {\mathbb Z} : T^ky \in U\}$
. We recall that the set
![]() $C_\tau (k,z)$
in the lemma below corresponds to the cuts of
$C_\tau (k,z)$
in the lemma below corresponds to the cuts of
![]() $(k,z)$
(see Definition 2.1 for further details).
$(k,z)$
(see Definition 2.1 for further details).
Lemma A.1. Let
![]() $Y \subseteq {\mathcal B}^{\mathbb Z}$
be an aperiodic subshift, with
$Y \subseteq {\mathcal B}^{\mathbb Z}$
be an aperiodic subshift, with
![]() ${\mathcal B} \subseteq {\mathcal L}(Y)$
. Suppose that
${\mathcal B} \subseteq {\mathcal L}(Y)$
. Suppose that
![]() $U \subseteq Y$
is:
$U \subseteq Y$
is:
-
(I) d-syndetic, for every
 $y \in Y$
there exists
$y \in Y$
there exists
 $k \in [0,d-1]$
with
$k \in [0,d-1]$
with
 $T^ky\in U$
;
$T^ky\in U$
; -
(II) of radius r,
 $U \subseteq \bigcup _{u\in {\mathcal A}^r,v\in {\mathcal A}^{r+1}}[u.v]$
;
$U \subseteq \bigcup _{u\in {\mathcal A}^r,v\in {\mathcal A}^{r+1}}[u.v]$
; -
(III)
 $\ell $
-proper,
$\ell $
-proper,
 $U \subseteq [u.v]$
for some
$U \subseteq [u.v]$
for some
 $u,v\in {\mathcal A}^\ell $
;
$u,v\in {\mathcal A}^\ell $
; -
(IV)
 $\rho $
-separated,
$\rho $
-separated,
 $U,TU,\ldots ,T^{\rho -1}U$
are disjoint.
$U,TU,\ldots ,T^{\rho -1}U$
are disjoint.
Then, there exist a letter-onto morphism
![]() $\tau \colon {\mathcal C}^+ \to {\mathcal B}^+$
and a subshift
$\tau \colon {\mathcal C}^+ \to {\mathcal B}^+$
and a subshift
![]() $Z \subseteq {\mathcal C}^{\mathbb Z}$
such that:
$Z \subseteq {\mathcal C}^{\mathbb Z}$
such that:
-
(1)
 $Y = \bigcup _{n\in {\mathbb Z}}T^n\tau (Z)$
and
$Y = \bigcup _{n\in {\mathbb Z}}T^n\tau (Z)$
and
 ${\mathcal C} \subseteq {\mathcal L}(Y)$
;
${\mathcal C} \subseteq {\mathcal L}(Y)$
; -
(2)
 $(Z,\tau )$
is recognizable with constant
$(Z,\tau )$
is recognizable with constant
 $r+d$
;
$r+d$
; -
(3)
 $|\tau | \leq d$
,
$|\tau | \leq d$
,
 $\langle \tau \rangle \geq \rho $
and
$\langle \tau \rangle \geq \rho $
and
 $\tau $
is
$\tau $
is
 $\min (\rho ,\ell )$
-proper;
$\min (\rho ,\ell )$
-proper; -
(4)
 $C_\tau (k,z) = {\mathcal R}_U(y)$
for all
$C_\tau (k,z) = {\mathcal R}_U(y)$
for all
 $y \in Y$
and
$y \in Y$
and
 $\tau $
-factorization
$\tau $
-factorization
 $(k,z)$
of y in Z.
$(k,z)$
of y in Z.
Remark A.2. If
![]() $U \subseteq Y$
satisfies condition (III), then U is
$U \subseteq Y$
satisfies condition (III), then U is
![]() $\rho := \min {\mathrm {per}}({\mathcal L}_{\ell }(Y))$
-separated. Indeed, if
$\rho := \min {\mathrm {per}}({\mathcal L}_{\ell }(Y))$
-separated. Indeed, if
![]() $U\cap T^k U\not =\emptyset $
for some
$U\cap T^k U\not =\emptyset $
for some
![]() $k> 0$
, then
$k> 0$
, then
![]() $[v]\cap T^k[v]\not =\emptyset $
, where
$[v]\cap T^k[v]\not =\emptyset $
, where
![]() $v \in {\mathcal A}^\ell $
is such that
$v \in {\mathcal A}^\ell $
is such that
![]() $U \subseteq [v]$
. Hence, v is k periodic and
$U \subseteq [v]$
. Hence, v is k periodic and
![]() $k \geq \rho $
.
$k \geq \rho $
.
Proof. Let
![]() $y \in Y$
. By condition (I), the sets
$y \in Y$
. By condition (I), the sets
![]() ${\mathcal R}_U(y)\cap [0,\infty )$
,
${\mathcal R}_U(y)\cap [0,\infty )$
,
![]() ${\mathcal R}_U(y)\cap (-\infty ,0]$
are infinite. Thus, we can write
${\mathcal R}_U(y)\cap (-\infty ,0]$
are infinite. Thus, we can write
![]() ${\mathcal R}_U(y) = \{\cdots k_{-1}(y) < k_0(y) < k_1(y) \cdots \}$
, with
${\mathcal R}_U(y) = \{\cdots k_{-1}(y) < k_0(y) < k_1(y) \cdots \}$
, with
![]() $\min \{i\in {\mathbb Z}:k_i(y)> 0\}=1$
. Let
$\min \{i\in {\mathbb Z}:k_i(y)> 0\}=1$
. Let
![]() ${\mathcal W} = \{y_{[k_i(y), k_{i+1}(y))} : y\in Y,\ i\in {\mathbb Z}\} \subseteq {\mathcal B}^+$
. By condition (I),
${\mathcal W} = \{y_{[k_i(y), k_{i+1}(y))} : y\in Y,\ i\in {\mathbb Z}\} \subseteq {\mathcal B}^+$
. By condition (I),
![]() ${\mathcal W}$
is finite, so we can write
${\mathcal W}$
is finite, so we can write
![]() ${\mathcal C} := \{1,\ldots , \#{\mathcal W}\}$
and choose a bijection
${\mathcal C} := \{1,\ldots , \#{\mathcal W}\}$
and choose a bijection
![]() $\phi \colon {\mathcal C} \to {\mathcal W}$
. Then,
$\phi \colon {\mathcal C} \to {\mathcal W}$
. Then,
![]() $\phi $
extends to a morphism
$\phi $
extends to a morphism
![]() $\tau \colon {\mathcal C}^+ \to {\mathcal B}^+$
. As
$\tau \colon {\mathcal C}^+ \to {\mathcal B}^+$
. As
![]() ${\mathcal B} \subseteq {\mathcal L}(Y)$
,
${\mathcal B} \subseteq {\mathcal L}(Y)$
,
![]() $\phi $
is letter-onto. We define
$\phi $
is letter-onto. We define
![]() $\psi \colon Y \to {\mathcal C}^{\mathbb Z}$
by
$\psi \colon Y \to {\mathcal C}^{\mathbb Z}$
by
 $\psi (y) = (\phi ^{-1}(y_{[k_i(y), k_{i+1}(y))}))_{i\in {\mathbb Z}}$
and set
$\psi (y) = (\phi ^{-1}(y_{[k_i(y), k_{i+1}(y))}))_{i\in {\mathbb Z}}$
and set
![]() $Z = \psi (Y)$
. We are going to prove that
$Z = \psi (Y)$
. We are going to prove that
![]() $\tau $
and Z satisfy items (1–4).
$\tau $
and Z satisfy items (1–4).
Claim A.2.1.
-
(i) If
 $y_{[-d-r,d+r]} = y^{\prime }_{[-d-r,d+r]}$
, then
$y_{[-d-r,d+r]} = y^{\prime }_{[-d-r,d+r]}$
, then
 $\psi (y)_0 = \psi (y')_0$
.
$\psi (y)_0 = \psi (y')_0$
. -
(ii)
 $\tau (\psi (y)) = T^{k_0(y)}y$
.
$\tau (\psi (y)) = T^{k_0(y)}y$
. -
(iii)
 $T^j\psi (y) = \psi (T^ky)$
for
$T^j\psi (y) = \psi (T^ky)$
for
 $j\in {\mathbb Z}$
and
$j\in {\mathbb Z}$
and
 $k \in [k_j(y),k_{j+1}(y))$
.
$k \in [k_j(y),k_{j+1}(y))$
.
Proof. Let
![]() $y,y' \in Y$
such that
$y,y' \in Y$
such that
 $y_{[-d-r,d+r]} = y^{\prime }_{[-d-r,d+r]}$
. By condition (I), we have
$y_{[-d-r,d+r]} = y^{\prime }_{[-d-r,d+r]}$
. By condition (I), we have
![]() $k_{i+1}(y)-k_i(y) \leq d$
for all
$k_{i+1}(y)-k_i(y) \leq d$
for all
![]() $i \in {\mathbb Z}$
and, thus,
$i \in {\mathbb Z}$
and, thus,
![]() $|k_0(y)|, |k_1(y)| \leq d$
. Since U has radius r and
$|k_0(y)|, |k_1(y)| \leq d$
. Since U has radius r and
 $y_{[-d-r,d+r]} = y^{\prime }_{[-d-r,d+r]}$
, we deduce that
$y_{[-d-r,d+r]} = y^{\prime }_{[-d-r,d+r]}$
, we deduce that
![]() $k_0(y) = k_0(y')$
and
$k_0(y) = k_0(y')$
and
![]() $k_1(y) = k_0(y')$
. Hence,
$k_1(y) = k_0(y')$
. Hence,
 $\psi (y)_0 = \phi ^{-1}(y_{[k_0(y), k_1(y))}) = \phi ^{-1}(y^{\prime }_{[k_0(y'), k_1(y'))}) =\psi (y')_0$
. To prove claim (ii) we compute:
$\psi (y)_0 = \phi ^{-1}(y_{[k_0(y), k_1(y))}) = \phi ^{-1}(y^{\prime }_{[k_0(y'), k_1(y'))}) =\psi (y')_0$
. To prove claim (ii) we compute:
 $$ \begin{align*} \tau(\psi(y)) &= \tau(\cdots \phi^{-1}(y_{[k_{-1}(y),k_0(y))}).\phi^{-1}(y_{[k_0(y),k_1(y))})\cdots) \\[3pt] &= \cdots y_{[k_{-1}(y),k_0(y))}.y_{[k_0(y),k_1(y))}\cdots = T^{k_0}y. \end{align*} $$
$$ \begin{align*} \tau(\psi(y)) &= \tau(\cdots \phi^{-1}(y_{[k_{-1}(y),k_0(y))}).\phi^{-1}(y_{[k_0(y),k_1(y))})\cdots) \\[3pt] &= \cdots y_{[k_{-1}(y),k_0(y))}.y_{[k_0(y),k_1(y))}\cdots = T^{k_0}y. \end{align*} $$
Finally, for claim (iii) we write, for
![]() $k \in [k_j(y),k_{j+1}(y))$
,
$k \in [k_j(y),k_{j+1}(y))$
,
 $$ \begin{align*} T^j\psi(y) = \cdots \phi^{-1}(y_{[k_{j-1}(y),k_j(y))}).\phi^{-1}(y_{[k_j(y),k_{j+1}(y))})\cdots = \psi(T^ky). \end{align*} $$
$$ \begin{align*} T^j\psi(y) = \cdots \phi^{-1}(y_{[k_{j-1}(y),k_j(y))}).\phi^{-1}(y_{[k_j(y),k_{j+1}(y))})\cdots = \psi(T^ky). \end{align*} $$
Now we prove the desired properties of
![]() $\tau $
and Z.
$\tau $
and Z.
(1) From claim (i), we see that
![]() $\psi $
is continuous and, therefore, Z is closed. By claim (iii), Z is also shift-invariant and, then, a subshift. By claim (ii),
$\psi $
is continuous and, therefore, Z is closed. By claim (iii), Z is also shift-invariant and, then, a subshift. By claim (ii),
![]() $Y = \bigcup _{n\in {\mathbb Z}}T^n\tau (Z)$
. The condition
$Y = \bigcup _{n\in {\mathbb Z}}T^n\tau (Z)$
. The condition
![]() ${\mathcal C} \subseteq {\mathcal L}(Y)$
follows from the definition of
${\mathcal C} \subseteq {\mathcal L}(Y)$
follows from the definition of
![]() ${\mathcal W}$
and
${\mathcal W}$
and
![]() $\tau $
.
$\tau $
.
(2) We claim that the only centered
![]() $\tau $
-interpretation in Z of a point
$\tau $
-interpretation in Z of a point
![]() $y \in Y$
is
$y \in Y$
is
![]() $(-k_0(y), \psi (y))$
. Indeed, this pair is a
$(-k_0(y), \psi (y))$
. Indeed, this pair is a
![]() $\tau $
-interpretation in Z by claim (ii), and it is centered because
$\tau $
-interpretation in Z by claim (ii), and it is centered because
![]() $k_0(y) \leq 0 < k_1(y)$
implies
$k_0(y) \leq 0 < k_1(y)$
implies
![]() $-k_0(y) \in [0, k_1(y)-k_0(y)) = [0, |\psi (y)_0|)$
. Let
$-k_0(y) \in [0, k_1(y)-k_0(y)) = [0, |\psi (y)_0|)$
. Let
![]() $(n,z)$
be another centered
$(n,z)$
be another centered
![]() $\tau $
-interpretation of y in Z. By the definition of Z, there exists
$\tau $
-interpretation of y in Z. By the definition of Z, there exists
![]() $y' \in Y$
with
$y' \in Y$
with
![]() $z = \psi (y')$
. Then, by claim (ii),
$z = \psi (y')$
. Then, by claim (ii),
 $$ \begin{align} T^{n+k_0(y')}y' = T^n\tau(\psi(y')) = T^n\tau(z) = y. \end{align} $$
$$ \begin{align} T^{n+k_0(y')}y' = T^n\tau(\psi(y')) = T^n\tau(z) = y. \end{align} $$
Now, on one hand, we have
![]() $|\tau (z_0)| = |\tau (\psi (y')_0)| = k_1(y')-k_0(y')$
. On the other hand, that
$|\tau (z_0)| = |\tau (\psi (y')_0)| = k_1(y')-k_0(y')$
. On the other hand, that
![]() $(n,\psi (y'))$
is centered gives that
$(n,\psi (y'))$
is centered gives that
![]() $n \in [0,|\tau (z_0)|)$
. Therefore,
$n \in [0,|\tau (z_0)|)$
. Therefore,
![]() $n +k_0(y')\in (k_0(y'),k_1(y')]$
. We conclude from this, claim (iii), and (44) that
$n +k_0(y')\in (k_0(y'),k_1(y')]$
. We conclude from this, claim (iii), and (44) that
![]() $\psi (y') = \psi (y)$
. Hence,
$\psi (y') = \psi (y)$
. Hence,
![]() $y = T^n\tau \psi (y') = T^n\tau \psi (y) = T^{n+k_0(y)}y$
, which implies that
$y = T^n\tau \psi (y') = T^n\tau \psi (y) = T^{n+k_0(y)}y$
, which implies that
![]() $n = -k_0(y)$
as Y is aperiodic. This proves that
$n = -k_0(y)$
as Y is aperiodic. This proves that
![]() $(-k_0(y), \psi (y))$
is the only
$(-k_0(y), \psi (y))$
is the only
![]() $\tau $
-interpretation of y in Z. From this and claim (i), we deduce property (2).
$\tau $
-interpretation of y in Z. From this and claim (i), we deduce property (2).
(3) Since U is d-syndetic,
![]() $|\tau (\psi (y)_i)| = |y_{[k_i(y), k_{i+1}(y))}| = k_{i+1}(y)-k_i(y) \leq d$
for
$|\tau (\psi (y)_i)| = |y_{[k_i(y), k_{i+1}(y))}| = k_{i+1}(y)-k_i(y) \leq d$
for
![]() $y\in Y$
and
$y\in Y$
and
![]() $i\in {\mathbb Z}$
, so
$i\in {\mathbb Z}$
, so
![]() $|\tau | \leq d$
. Similarly, we can obtain
$|\tau | \leq d$
. Similarly, we can obtain
![]() $\langle \tau \rangle \geq \rho $
using that U is
$\langle \tau \rangle \geq \rho $
using that U is
![]() $\rho $
-separated. Let
$\rho $
-separated. Let
![]() $u,v \in {\mathcal B}^\ell $
satisfying
$u,v \in {\mathcal B}^\ell $
satisfying
![]() $U \subseteq [u.v]$
. Since
$U \subseteq [u.v]$
. Since
![]() $k_i, k_{i+1} \in {\mathcal R}_U(y)$
, we have that
$k_i, k_{i+1} \in {\mathcal R}_U(y)$
, we have that
![]() $u = y_{[k_i(y), k_i(y)+|u|)}$
,
$u = y_{[k_i(y), k_i(y)+|u|)}$
,
![]() $v = y_{[k_{i+1}(y)-|v|, k_{i+1}(y))}$
and, thus, that
$v = y_{[k_{i+1}(y)-|v|, k_{i+1}(y))}$
and, thus, that
![]() $\tau $
is
$\tau $
is
![]() $\min (\ell ,\langle \tau \rangle )$
-proper. In particular, it is
$\min (\ell ,\langle \tau \rangle )$
-proper. In particular, it is
![]() $\min (\ell ,\rho )$
-proper.
$\min (\ell ,\rho )$
-proper.
(4) This follows directly from the definition of
![]() $\tau $
and
$\tau $
and
![]() ${\mathcal R}_U(y)$
.
${\mathcal R}_U(y)$
.
Lemma A.3. For
![]() $j\in \{0,1\}$
, let
$j\in \{0,1\}$
, let
 $\sigma _j \colon {\mathcal A}_j^+ \to {\mathcal B}^+$
be a morphism and
$\sigma _j \colon {\mathcal A}_j^+ \to {\mathcal B}^+$
be a morphism and
 $X_j \subseteq {\mathcal A}_j^{\mathbb Z}$
be a subshift such that
$X_j \subseteq {\mathcal A}_j^{\mathbb Z}$
be a subshift such that
![]() $Y := \bigcup _{n\in {\mathbb Z}}T^n\sigma _j(X_j)$
and
$Y := \bigcup _{n\in {\mathbb Z}}T^n\sigma _j(X_j)$
and
![]() ${\mathcal A}_j \subseteq {\mathcal L}(X_j)$
for every
${\mathcal A}_j \subseteq {\mathcal L}(X_j)$
for every
![]() $j \in \{0,1\}$
. Suppose that:
$j \in \{0,1\}$
. Suppose that:
-
(1)
 $(X_0, \sigma _0)$
is recognizable with constant
$(X_0, \sigma _0)$
is recognizable with constant
 $\ell $
;
$\ell $
; -
(2)
 $\sigma _1$
is
$\sigma _1$
is
 $\ell $
-proper;
$\ell $
-proper; -
(3)
 $C_{\sigma _0}(k^0,x^0)(y) \supseteq C_{\sigma _1}(k^1,x^1)(y)$
for all
$C_{\sigma _0}(k^0,x^0)(y) \supseteq C_{\sigma _1}(k^1,x^1)(y)$
for all
 $y \in Y$
and
$y \in Y$
and
 $\sigma _j$
-factorizations
$\sigma _j$
-factorizations
 $(k^j,x^j)$
of y in
$(k^j,x^j)$
of y in
 $X_j$
,
$X_j$
,
 $j=0,1$
.
$j=0,1$
.
Then, there exist a letter-onto and proper morphism
 $\nu \colon {\mathcal A}_1^+\to {\mathcal A}_0^+$
such that
$\nu \colon {\mathcal A}_1^+\to {\mathcal A}_0^+$
such that
![]() $\sigma _1 = \sigma _0\nu $
and
$\sigma _1 = \sigma _0\nu $
and
 $X_0 = \bigcup _{k\in {\mathbb Z}}T^k\nu (X_1)$
.
$X_0 = \bigcup _{k\in {\mathbb Z}}T^k\nu (X_1)$
.
Proof. Since
![]() $\sigma _1$
is
$\sigma _1$
is
![]() $\ell $
-proper, we can find
$\ell $
-proper, we can find
![]() $u,v \in {\mathcal B}^\ell $
such that
$u,v \in {\mathcal B}^\ell $
such that
![]() $\sigma _1(a)$
starts with u and ends with v for every
$\sigma _1(a)$
starts with u and ends with v for every
![]() $a \in {\mathcal A}_1$
. We define
$a \in {\mathcal A}_1$
. We define
![]() $\nu $
as follows. Let
$\nu $
as follows. Let
![]() $a\in {\mathcal A}_1$
and
$a\in {\mathcal A}_1$
and
![]() $x \in X_1$
such that
$x \in X_1$
such that
![]() $a = x_0$
. Since
$a = x_0$
. Since
![]() $\sigma _1$
is
$\sigma _1$
is
![]() $\ell $
-proper, the word
$\ell $
-proper, the word
![]() $v.\sigma _1(a)u$
occurs in
$v.\sigma _1(a)u$
occurs in
![]() $\sigma _1(x) \in Y$
at position
$\sigma _1(x) \in Y$
at position
![]() $0$
. By item (3), we can find
$0$
. By item (3), we can find
![]() $w \in {\mathcal L}(X_0)$
with
$w \in {\mathcal L}(X_0)$
with
![]() $\sigma _1(x_0) = \sigma _0(w)$
. We set
$\sigma _1(x_0) = \sigma _0(w)$
. We set
![]() $\nu (a) = w$
. Since
$\nu (a) = w$
. Since
![]() $(X_0,\sigma _0)$
is recognizable with constant
$(X_0,\sigma _0)$
is recognizable with constant
![]() $\ell $
and
$\ell $
and
![]() $u,v$
have length
$u,v$
have length
![]() $\ell $
, w uniquely determined by
$\ell $
, w uniquely determined by
![]() $v.\sigma _1(a)u$
and, therefore,
$v.\sigma _1(a)u$
and, therefore,
![]() $\nu $
is well defined. Moreover, the recognizability implies that the first letter of
$\nu $
is well defined. Moreover, the recognizability implies that the first letter of
![]() $\nu (a)$
depends only on
$\nu (a)$
depends only on
![]() $v.u$
, so
$v.u$
, so
![]() $\nu $
is left-proper. A symmetric argument shows that
$\nu $
is left-proper. A symmetric argument shows that
![]() $\nu $
is right-proper and, in conclusion, that it is proper. We also note that
$\nu $
is right-proper and, in conclusion, that it is proper. We also note that
![]() $\nu $
is letter-onto as
$\nu $
is letter-onto as
![]() ${\mathcal A}_0 \subseteq {\mathcal L}(X_0)$
. It follows from the definition of
${\mathcal A}_0 \subseteq {\mathcal L}(X_0)$
. It follows from the definition of
![]() $\nu $
that
$\nu $
that
![]() $\sigma _1 = \sigma _0\nu $
. Now, let
$\sigma _1 = \sigma _0\nu $
. Now, let
![]() $x \in X_1$
and
$x \in X_1$
and
![]() $(k,x')$
be a centered
$(k,x')$
be a centered
![]() $\sigma _0$
-factorization of
$\sigma _0$
-factorization of
![]() $\sigma _1(x)$
in
$\sigma _1(x)$
in
![]() $X_0$
. By item (3),
$X_0$
. By item (3),
![]() $k=0$
and
$k=0$
and
 $\sigma _1(x_j) = \sigma _0(x^{\prime }_{[k_j,k_{j+1})})$
for some sequence
$\sigma _1(x_j) = \sigma _0(x^{\prime }_{[k_j,k_{j+1})})$
for some sequence
![]() $\cdots < k_{-1} < k_0 < \cdots $
Hence, by the definition of
$\cdots < k_{-1} < k_0 < \cdots $
Hence, by the definition of
![]() $\nu $
,
$\nu $
,
![]() $\nu (x) = x' \in X_0$
. This argument shows that
$\nu (x) = x' \in X_0$
. This argument shows that
![]() $X^{\prime }_0 := \bigcup _{n\in {\mathbb Z}}T^n\nu (X_1) \subseteq X_0$
. Then,
$X^{\prime }_0 := \bigcup _{n\in {\mathbb Z}}T^n\nu (X_1) \subseteq X_0$
. Then,
![]() $\bigcup _{n\in {\mathbb Z}}T^n\sigma _0(X^{\prime }_0) = \bigcup _{n\in {\mathbb Z}}T^n\sigma _0\nu (X_1) = Y$
, where in the last step, we used that
$\bigcup _{n\in {\mathbb Z}}T^n\sigma _0(X^{\prime }_0) = \bigcup _{n\in {\mathbb Z}}T^n\sigma _0\nu (X_1) = Y$
, where in the last step, we used that
![]() $\sigma _0\nu =\sigma _1$
. Since the points in Y have exactly one
$\sigma _0\nu =\sigma _1$
. Since the points in Y have exactly one
![]() $\sigma _0$
-factorization, we must have
$\sigma _0$
-factorization, we must have
![]() $X^{\prime }_0 = X_0$
. This ends the proof.
$X^{\prime }_0 = X_0$
. This ends the proof.
A.2 Factors of
 ${\mathcal S}$
-adic sequences
${\mathcal S}$
-adic sequences
Now we are ready to prove Proposition 4.4. For convenience, we repeat its statement.
Proposition A.4. Let
![]() $\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_n \to {\mathcal A}_{n-1})_{n\geq 0}$
be a letter-onto, everywhere growing, and proper directive sequence. Suppose that
$\boldsymbol {\sigma } = (\sigma _n\colon {\mathcal A}_n \to {\mathcal A}_{n-1})_{n\geq 0}$
be a letter-onto, everywhere growing, and proper directive sequence. Suppose that
![]() $X_{\boldsymbol {\sigma }}$
is aperiodic. Then, there exists a contraction
$X_{\boldsymbol {\sigma }}$
is aperiodic. Then, there exists a contraction
![]() $\boldsymbol {\sigma }' = (\sigma _{n_k})_{k\in {\mathbb N}}$
and a letter-onto and proper factor
$\boldsymbol {\sigma }' = (\sigma _{n_k})_{k\in {\mathbb N}}$
and a letter-onto and proper factor
![]() $\boldsymbol {\phi }\colon \boldsymbol {\sigma }' \to \boldsymbol {\tau }$
, where
$\boldsymbol {\phi }\colon \boldsymbol {\sigma }' \to \boldsymbol {\tau }$
, where
![]() $\boldsymbol {\tau }$
is letter-onto, everywhere growing, proper, recognizable, and generates
$\boldsymbol {\tau }$
is letter-onto, everywhere growing, proper, recognizable, and generates
![]() $X_{\boldsymbol {\sigma }}$
.
$X_{\boldsymbol {\sigma }}$
.
Proof. We start by observing that from Lemma 4.6, we can get that
 $$ \begin{align} {\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol{\sigma}}^{(n)})\quad \text{for every}\ n\in{\mathbb N}. \end{align} $$
$$ \begin{align} {\mathcal A}_n \subseteq {\mathcal L}(X_{\boldsymbol{\sigma}}^{(n)})\quad \text{for every}\ n\in{\mathbb N}. \end{align} $$
Let
![]() $p_n = \min \{{\mathrm {per}}(\sigma _{[0,n)}(a)) : a \in {\mathcal A}_n\}$
. Since
$p_n = \min \{{\mathrm {per}}(\sigma _{[0,n)}(a)) : a \in {\mathcal A}_n\}$
. Since
![]() $\boldsymbol {\sigma }$
is everywhere growing and
$\boldsymbol {\sigma }$
is everywhere growing and
![]() $X_{\boldsymbol {\sigma }}$
is aperiodic,
$X_{\boldsymbol {\sigma }}$
is aperiodic,
![]() $\lim _{n\to \infty }p_n = \infty $
. Hence, we can contract
$\lim _{n\to \infty }p_n = \infty $
. Hence, we can contract
![]() $\boldsymbol {\sigma }$
in a way such that, for every
$\boldsymbol {\sigma }$
in a way such that, for every
![]() $n\geq 2$
,
$n\geq 2$
,
For
![]() $n\geq 2$
, let
$n\geq 2$
, let
 $U_n = \bigcup _{u,v\in {\mathcal A}_n^2}[\sigma _{[0,n)}(u.v)]$
. Observe that
$U_n = \bigcup _{u,v\in {\mathcal A}_n^2}[\sigma _{[0,n)}(u.v)]$
. Observe that
![]() $U_n$
is
$U_n$
is
![]() $|\sigma _{[0,n)}|$
-syndetic, has radius
$|\sigma _{[0,n)}|$
-syndetic, has radius
![]() $2|\sigma _{[0,n)}|$
, is
$2|\sigma _{[0,n)}|$
, is
![]() $3|\sigma _{[0,n-1)}|$
-proper and, by Remark A.2, is
$3|\sigma _{[0,n-1)}|$
-proper and, by Remark A.2, is
![]() $p_n$
-separated. Thus, by
$p_n$
-separated. Thus, by
![]() $(\mathrm {I}_n)$
, U is
$(\mathrm {I}_n)$
, U is
![]() $3|\sigma _{[0,n-1)}|$
-separated. We can then use Lemma A.1 with
$3|\sigma _{[0,n-1)}|$
-separated. We can then use Lemma A.1 with
 $(X_{\boldsymbol {\sigma }}^{(n)},\sigma _{[0,n)})$
to obtain a letter-onto morphism
$(X_{\boldsymbol {\sigma }}^{(n)},\sigma _{[0,n)})$
to obtain a letter-onto morphism
 $\nu _n\colon {\mathcal B}_n^+ \to {\mathcal A}_0^+$
and a subshift
$\nu _n\colon {\mathcal B}_n^+ \to {\mathcal A}_0^+$
and a subshift
 $Y_n \subseteq {\mathcal B}_n^{\mathbb Z}$
such that:
$Y_n \subseteq {\mathcal B}_n^{\mathbb Z}$
such that:
-
 $(P^1_n)$
$(P^1_n)$
 $X_{\boldsymbol {\sigma }} = \bigcup _{k\in {\mathbb Z}}T^k\nu _n(Y_n)$
and
$X_{\boldsymbol {\sigma }} = \bigcup _{k\in {\mathbb Z}}T^k\nu _n(Y_n)$
and
 ${\mathcal B}_n \subseteq {\mathcal L}(Y_n)$
;
${\mathcal B}_n \subseteq {\mathcal L}(Y_n)$
; -
 $(P^2_n)$
$(P^2_n)$
 $(Y_n,\nu _n)$
is recognizable with constant
$(Y_n,\nu _n)$
is recognizable with constant
 $3|\sigma _{[0,n)}|$
;
$3|\sigma _{[0,n)}|$
; -
 $(P^3_n)$
$(P^3_n)$
 $|\nu _n| \leq |\sigma _{[0,n)}|$
,
$|\nu _n| \leq |\sigma _{[0,n)}|$
,
 $\langle \nu _n\rangle \geq 3|\sigma _{[0,n-1)}|$
, and
$\langle \nu _n\rangle \geq 3|\sigma _{[0,n-1)}|$
, and
 $\nu _n$
is
$\nu _n$
is
 $3|\sigma _{[0,n-1)}|$
-proper;
$3|\sigma _{[0,n-1)}|$
-proper; -
 $(P^4_n)$
$(P^4_n)$
 $C_{\nu _n}(k,y) = {\mathcal R}_{U_n}(x)$
for all
$C_{\nu _n}(k,y) = {\mathcal R}_{U_n}(x)$
for all
 $x \in X_{\boldsymbol {\sigma }}$
and
$x \in X_{\boldsymbol {\sigma }}$
and
 $\nu _n$
-factorization
$\nu _n$
-factorization
 $(k,y)$
of x in
$(k,y)$
of x in
 $Y_n$
.
$Y_n$
.
We write
![]() $C_{\nu _n}(x) := C_{\nu _n}(k,y)$
if
$C_{\nu _n}(x) := C_{\nu _n}(k,y)$
if
![]() $x \in X_{\boldsymbol {\sigma }}$
and
$x \in X_{\boldsymbol {\sigma }}$
and
![]() $(k,y)$
is the unique
$(k,y)$
is the unique
![]() $\nu _n$
-factorization of x in
$\nu _n$
-factorization of x in
![]() $Y_n$
. Observe that
$Y_n$
. Observe that
![]() $U_{n+1} \subseteq U_n$
for
$U_{n+1} \subseteq U_n$
for
![]() $n \geq 2$
. Thus,
$n \geq 2$
. Thus,
![]() $C_{\nu _{n+1}}(x) = {\mathcal R}_{U_{n+1}}(x) \subseteq {\mathcal R}_{U_n}(x) = C_{\nu _n}(x)$
for all
$C_{\nu _{n+1}}(x) = {\mathcal R}_{U_{n+1}}(x) \subseteq {\mathcal R}_{U_n}(x) = C_{\nu _n}(x)$
for all
![]() $x \in X_{\boldsymbol {\sigma }}$
. This,
$x \in X_{\boldsymbol {\sigma }}$
. This,
![]() $(P^2_n)$
and
$(P^2_n)$
and
 $(P^3_{n+1})$
allow us to use Lemma A.3 with
$(P^3_{n+1})$
allow us to use Lemma A.3 with
![]() $(Y_{n+1},\nu _{n+1})$
and
$(Y_{n+1},\nu _{n+1})$
and
![]() $(Y_n,\nu _n)$
and find a letter-onto and proper morphism
$(Y_n,\nu _n)$
and find a letter-onto and proper morphism
 $\tau _n\colon {\mathcal B}_{n+1}^+ \to {\mathcal B}_{n}^+$
such that
$\tau _n\colon {\mathcal B}_{n+1}^+ \to {\mathcal B}_{n}^+$
such that
![]() $\nu _n\tau _n = \nu _{n+1}$
and
$\nu _n\tau _n = \nu _{n+1}$
and
 $Y_{n} = \bigcup _{k\in {\mathbb Z}}T^k\tau _n(Y_{n+1})$
.
$Y_{n} = \bigcup _{k\in {\mathbb Z}}T^k\tau _n(Y_{n+1})$
.
Next, we claim that
![]() $C_{\nu _n}(x) \supseteq C_{\sigma _{[0,n+1)}}(k,z)$
for all
$C_{\nu _n}(x) \supseteq C_{\sigma _{[0,n+1)}}(k,z)$
for all
![]() $x \in X_{\boldsymbol {\sigma }}$
and
$x \in X_{\boldsymbol {\sigma }}$
and
![]() $\sigma _{[0,n+1)}$
-factorization
$\sigma _{[0,n+1)}$
-factorization
![]() $(k,z)$
of x in
$(k,z)$
of x in
 $X_{\boldsymbol {\sigma }}^{(n+1)}$
. Indeed, if
$X_{\boldsymbol {\sigma }}^{(n+1)}$
. Indeed, if
![]() $j \in {\mathbb Z}$
, then
$j \in {\mathbb Z}$
, then
 $T^{c_{\sigma _{[0,n+1)},j}(k,z)}x \in [\sigma _{[0,n+1)}(z_{j-1}.z_jz_{j+1})] \subseteq [\sigma _{[0,n)}(a.bc)] \subseteq U_n$
, where a is the last letter of
$T^{c_{\sigma _{[0,n+1)},j}(k,z)}x \in [\sigma _{[0,n+1)}(z_{j-1}.z_jz_{j+1})] \subseteq [\sigma _{[0,n)}(a.bc)] \subseteq U_n$
, where a is the last letter of
![]() $\sigma _{n}(z_{j-1})$
and
$\sigma _{n}(z_{j-1})$
and
![]() $bc$
the first two letters of
$bc$
the first two letters of
![]() $\sigma _{n}(z_jz_{j+1})$
, so
$\sigma _{n}(z_jz_{j+1})$
, so
![]() $c_{\sigma _{[0,n+1)},j}(k,z) \in {\mathcal R}_{U_n}(x) = C_{\nu _n}(x)$
, as desired.
$c_{\sigma _{[0,n+1)},j}(k,z) \in {\mathcal R}_{U_n}(x) = C_{\nu _n}(x)$
, as desired.
Thanks to the claim,
![]() $(P^2_n)$
,
$(P^2_n)$
,
![]() $(\mathrm {I}_{n+1})$
, and (45), we can use Lemma A.3 with
$(\mathrm {I}_{n+1})$
, and (45), we can use Lemma A.3 with
![]() $(Y_{n}, \nu _{n})$
and
$(Y_{n}, \nu _{n})$
and
 $(X_{\boldsymbol {\sigma }}^{(n+1)},\sigma _{[0,n+1)})$
to obtain a proper morphism
$(X_{\boldsymbol {\sigma }}^{(n+1)},\sigma _{[0,n+1)})$
to obtain a proper morphism
 $\phi _n\colon {\mathcal A}_{n+1}^+\to {\mathcal B}_{n}^+$
such that
$\phi _n\colon {\mathcal A}_{n+1}^+\to {\mathcal B}_{n}^+$
such that
![]() $\sigma _{[0,n+1)} = \nu _n\phi _n$
and
$\sigma _{[0,n+1)} = \nu _n\phi _n$
and
 $Y_{n} = \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n+1)})$
.
$Y_{n} = \bigcup _{k\in {\mathbb Z}}T^k\phi _n(X_{\boldsymbol {\sigma }}^{(n+1)})$
.
Now we can define the morphisms
![]() $\tau _1 := \nu _2$
and
$\tau _1 := \nu _2$
and
![]() $\phi _1 := \nu _2\phi _2$
and the sequence:
$\phi _1 := \nu _2\phi _2$
and the sequence:
We are going to prove that
![]() $\boldsymbol {\phi }$
,
$\boldsymbol {\phi }$
,
![]() $\boldsymbol {\sigma '}$
, and
$\boldsymbol {\sigma '}$
, and
![]() $\boldsymbol {\tau }$
are the objects that satisfy the conclusion of the proposition.
$\boldsymbol {\tau }$
are the objects that satisfy the conclusion of the proposition.
These sequences are letter-onto as each
![]() $\nu _n$
and each
$\nu _n$
and each
![]() $\phi _n$
is letter-onto. Next, we show that
$\phi _n$
is letter-onto. Next, we show that
![]() $\boldsymbol {\phi }$
is a factor. The relation
$\boldsymbol {\phi }$
is a factor. The relation
![]() $\phi _1 = \tau _1\phi _2$
follows from the definitions. To prove the other relations, we observe that from the commutative relations for
$\phi _1 = \tau _1\phi _2$
follows from the definitions. To prove the other relations, we observe that from the commutative relations for
![]() $\tau _n$
and
$\tau _n$
and
![]() $\phi _n$
, we have that
$\phi _n$
, we have that
In particular,
![]() $\nu _{n}\phi _n\sigma _{n+1}(x) = \nu _{n}\tau _n\phi _{n+1}(x)$
for any
$\nu _{n}\phi _n\sigma _{n+1}(x) = \nu _{n}\tau _n\phi _{n+1}(x)$
for any
 $x \in X_{\boldsymbol {\sigma }}^{(n+2)}$
. Since
$x \in X_{\boldsymbol {\sigma }}^{(n+2)}$
. Since
![]() $\phi _n\sigma _{n+1}(x)$
and
$\phi _n\sigma _{n+1}(x)$
and
![]() $\tau _n\phi _{n+1}(x)$
are both elements of
$\tau _n\phi _{n+1}(x)$
are both elements of
![]() $Y_{n}$
and
$Y_{n}$
and
![]() $(Y_{n},\nu _{n})$
is recognizable, we deduce that
$(Y_{n},\nu _{n})$
is recognizable, we deduce that
![]() $\phi _n\sigma _{n+1}(x) = \tau _n\phi _{n+1}(x)$
for any
$\phi _n\sigma _{n+1}(x) = \tau _n\phi _{n+1}(x)$
for any
 $x \in X_{\boldsymbol {\sigma }}^{(n+2)}$
. Thus, one of the words in
$x \in X_{\boldsymbol {\sigma }}^{(n+2)}$
. Thus, one of the words in
![]() $\{\phi _n\sigma _{n+1}(x_0)$
,
$\{\phi _n\sigma _{n+1}(x_0)$
,
![]() $\tau _n\phi _{n+1}(x_0)\}$
is a prefix of the other. Since
$\tau _n\phi _{n+1}(x_0)\}$
is a prefix of the other. Since
 ${\mathcal A}_{n+2} \subseteq {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n+2)})$
, we deduce that, for any
${\mathcal A}_{n+2} \subseteq {\mathcal L}(X_{\boldsymbol {\sigma }}^{(n+2)})$
, we deduce that, for any
![]() $a \in {\mathcal A}_{n+2}$
, one of the words in
$a \in {\mathcal A}_{n+2}$
, one of the words in
![]() $\{\tau _n\phi _{n+1}(a)$
,
$\{\tau _n\phi _{n+1}(a)$
,
![]() $\nu _{n}\phi _n\sigma _{n+1}(a)\}$
is a prefix of the other. However, by (46), the words
$\nu _{n}\phi _n\sigma _{n+1}(a)\}$
is a prefix of the other. However, by (46), the words
![]() $\nu _{n}\tau _n\phi _{n+1}(a)$
and
$\nu _{n}\tau _n\phi _{n+1}(a)$
and
![]() $\nu _{n}\phi _n\sigma _{n+1}(a)$
have the same length, so
$\nu _{n}\phi _n\sigma _{n+1}(a)$
have the same length, so
![]() $\phi _n\sigma _{n+1}(a)$
must be equal to
$\phi _n\sigma _{n+1}(a)$
must be equal to
![]() $\tau _n\phi _{n+1}(a)$
for every
$\tau _n\phi _{n+1}(a)$
for every
![]() $n\geq 2$
. This proves that
$n\geq 2$
. This proves that
![]() $\phi _n\sigma _{n+1} = \tau _n\phi _{n+1}$
for every
$\phi _n\sigma _{n+1} = \tau _n\phi _{n+1}$
for every
![]() $n\geq 2$
and that
$n\geq 2$
and that
![]() $\boldsymbol {\phi }\colon \boldsymbol {\sigma '}\to \boldsymbol {\tau }$
is a factor.
$\boldsymbol {\phi }\colon \boldsymbol {\sigma '}\to \boldsymbol {\tau }$
is a factor.
The following commutative diagram, valid for all
![]() $n\geq 2$
, summarizes the construction so far:
$n\geq 2$
, summarizes the construction so far:

As shown in the diagram, we have that
![]() $\nu _{n}\tau _n = \nu _{n+1}$
for
$\nu _{n}\tau _n = \nu _{n+1}$
for
![]() $n\geq 2$
. Thus,
$n\geq 2$
. Thus,
![]() $\tau _1\tau _2\ldots \tau _n = \nu _{n+1}$
, and hence
$\tau _1\tau _2\ldots \tau _n = \nu _{n+1}$
, and hence
![]() $\langle \tau _1\tau _2\ldots \tau _n \rangle \geq \langle \nu _{n+1} \rangle \geq p_n \to _{n\to \infty } \infty $
. Therefore,
$\langle \tau _1\tau _2\ldots \tau _n \rangle \geq \langle \nu _{n+1} \rangle \geq p_n \to _{n\to \infty } \infty $
. Therefore,
![]() $\boldsymbol {\tau }$
is everywhere growing. Also, by using Lemma 2.3 with
$\boldsymbol {\tau }$
is everywhere growing. Also, by using Lemma 2.3 with
![]() $(Y_{n},\nu _{n}) = (Y_{n},\tau _1\tau _2\ldots \tau _{n-1})$
, we deduce that
$(Y_{n},\nu _{n}) = (Y_{n},\tau _1\tau _2\ldots \tau _{n-1})$
, we deduce that
![]() $(Y_{n},\tau _{n-1})$
is recognizable for every
$(Y_{n},\tau _{n-1})$
is recognizable for every
![]() $n\geq 2$
, which implies that
$n\geq 2$
, which implies that
![]() $\boldsymbol {\tau }$
is recognizable. Finally, as each
$\boldsymbol {\tau }$
is recognizable. Finally, as each
![]() $\tau _n$
is proper,
$\tau _n$
is proper,
![]() $\boldsymbol {\tau }$
is proper.
$\boldsymbol {\tau }$
is proper.