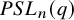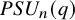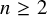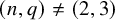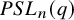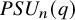1 Introduction
The classification of finite simple groups (CFSG) is one of the greatest achievements in the history of mathematics. Its proof required around 15,000 pages and spreads out over many hundred articles in various journals. Many mathematicians from all over the world were involved in the proof, whose final steps were published in 2004 by Aschbacher and Smith, after it was prematurely announced as finished already in 1983. Because of its extreme length, a simplified and shortened proof of the CFSG would be very valuable. There are three programmes working towards this goal: the Gorenstein–Lyons–Solomon programme (see [Reference Gorenstein, Lyons and Solomon26]), the Meierfrankenfeld–Stellmacher–Stroth programme (see [Reference Meierfrankenfeld, Stellmacher and Stroth43]) and Aschbacher’s programme.
The goal of Aschbacher’s programme is to obtain a new proof of the CFSG by using fusion systems. The standard examples of fusion systems are the fusion categories of finite groups over p-subgroups (p a prime). If G is a finite group and S is a p-subgroup of G for some prime p, then the fusion category of G over S is defined to be the category
![]() $\mathcal {F}_S(G)$
given as follows: The objects of
$\mathcal {F}_S(G)$
given as follows: The objects of
![]() $\mathcal {F}_S(G)$
are precisely the subgroups of S, the morphisms in
$\mathcal {F}_S(G)$
are precisely the subgroups of S, the morphisms in
![]() $\mathcal {F}_S(G)$
are precisely the group homomorphisms between subgroups of S induced by conjugation in G and the composition of morphisms in
$\mathcal {F}_S(G)$
are precisely the group homomorphisms between subgroups of S induced by conjugation in G and the composition of morphisms in
![]() $\mathcal {F}_S(G)$
is the usual composition of group homomorphisms. Abstract fusion systems are a generalization of this concept. A fusion system over a finite p-group S, where p is a prime, is a category whose objects are the subgroups of S and whose morphisms behave as if they are induced by conjugation inside a finite group containing S as a p-subgroup. For the precise definition, we refer to [Reference Aschbacher, Kessar and Oliver10, Part I, Definition 2.1]. A fusion system is called saturated if it satisfies certain axioms motivated by properties of fusion categories of finite groups over Sylow subgroups (see [Reference Aschbacher, Kessar and Oliver10, Part I, Definition 2.2]). If G is a finite group and
$\mathcal {F}_S(G)$
is the usual composition of group homomorphisms. Abstract fusion systems are a generalization of this concept. A fusion system over a finite p-group S, where p is a prime, is a category whose objects are the subgroups of S and whose morphisms behave as if they are induced by conjugation inside a finite group containing S as a p-subgroup. For the precise definition, we refer to [Reference Aschbacher, Kessar and Oliver10, Part I, Definition 2.1]. A fusion system is called saturated if it satisfies certain axioms motivated by properties of fusion categories of finite groups over Sylow subgroups (see [Reference Aschbacher, Kessar and Oliver10, Part I, Definition 2.2]). If G is a finite group and
![]() $S_1, S_2 \in \mathrm {Syl}_p(G)$
for some prime p, then
$S_1, S_2 \in \mathrm {Syl}_p(G)$
for some prime p, then
![]() $\mathcal {F}_{S_1}(G)$
and
$\mathcal {F}_{S_1}(G)$
and
![]() $\mathcal {F}_{S_2}(G)$
are easily seen to be isomorphic (in the sense of [Reference Aschbacher and Oliver11, p. 560]). Given a finite group G, a prime p and a Sylow p-subgroup S of G, we refer to
$\mathcal {F}_{S_2}(G)$
are easily seen to be isomorphic (in the sense of [Reference Aschbacher and Oliver11, p. 560]). Given a finite group G, a prime p and a Sylow p-subgroup S of G, we refer to
![]() $\mathcal {F}_S(G)$
as the p-fusion system of G.
$\mathcal {F}_S(G)$
as the p-fusion system of G.
Originally considered by the representation theorist Puig, fusion systems have become an object of active research in finite group theory, representation theory and algebraic topology. It has always been a problem of great interest in the theory of fusion systems to translate group-theoretic concepts into suitable concepts for fusion systems. For example, there is a notion of normalizers and centralizers of p-subgroups in fusion systems, a notion of the center of a fusion system, a notion of factor systems, a notion of normal subsystems of saturated fusion systems and a notion of simple saturated fusion systems (see [Reference Aschbacher, Kessar and Oliver10, Parts I and II]). Roughly speaking, Aschbacher’s programme consists of the following two steps.
-
1. Classify the simple saturated fusion systems on finite
 $2$
-groups. Use the original proof of the CFSG as a ‘template’.
$2$
-groups. Use the original proof of the CFSG as a ‘template’. -
2. Use the first step to give a new and simplified proof of the CFSG.
There is the hope that several steps of the original proof of the CFSG become easier when working with fusion systems. For example, in the original proof of the CFSG, the study of centralizers of involutions plays an important role. The
![]() $2'$
-cores of the involution centralizers, i.e., their largest normal odd order subgroups, cause serious difficulties and are obstructions to many arguments. Such difficulties are not present in fusion systems since cores do not exist in fusion systems. This is suggested by the well-known fact that the
$2'$
-cores of the involution centralizers, i.e., their largest normal odd order subgroups, cause serious difficulties and are obstructions to many arguments. Such difficulties are not present in fusion systems since cores do not exist in fusion systems. This is suggested by the well-known fact that the
![]() $2$
-fusion system of a finite group G is isomorphic to the
$2$
-fusion system of a finite group G is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $G/O(G)$
, where
$G/O(G)$
, where
![]() $O(G)$
denotes the
$O(G)$
denotes the
![]() $2'$
-core of G. For an outline of and recent progress on Aschbacher’s programme, we refer to [Reference Aschbacher7].
$2'$
-core of G. For an outline of and recent progress on Aschbacher’s programme, we refer to [Reference Aschbacher7].
So far, Aschbacher’s programme has focused mainly on Step 1, while not much has been done on Step 2. An important part of Step 2 is to identify finite simple groups from their
![]() $2$
-fusion systems. The present paper contributes to Step 2 of Aschbacher’s programme by characterizing the finite simple groups
$2$
-fusion systems. The present paper contributes to Step 2 of Aschbacher’s programme by characterizing the finite simple groups
![]() $PSL_n(q)$
and
$PSL_n(q)$
and
![]() $PSU_n(q)$
in terms of their
$PSU_n(q)$
in terms of their
![]() $2$
-fusion systems, where
$2$
-fusion systems, where
![]() $n \ge 2$
and where q is a nontrivial odd prime power with
$n \ge 2$
and where q is a nontrivial odd prime power with
![]() $(n,q) \ne (2,3)$
.
$(n,q) \ne (2,3)$
.
In order to state our results, we introduce some notation and recall some definitions. Let G be a finite group. A component of G is a quasisimple subnormal subgroup of G, and a
![]() $2$
-component of G is a perfect subnormal subgroup L of G such that
$2$
-component of G is a perfect subnormal subgroup L of G such that
![]() $L/O(L)$
is quasisimple. The natural homomorphism
$L/O(L)$
is quasisimple. The natural homomorphism
![]() $G \rightarrow G/O(G)$
induces a one-to-one correspondence between the set of
$G \rightarrow G/O(G)$
induces a one-to-one correspondence between the set of
![]() $2$
-components of G and the set of components of
$2$
-components of G and the set of components of
![]() $G/O(G)$
(see [Reference Gorenstein, Lyons and Solomon27, Proposition 4.7]). We use
$G/O(G)$
(see [Reference Gorenstein, Lyons and Solomon27, Proposition 4.7]). We use
![]() $Z^{*}(G)$
to denote the full preimage of the center
$Z^{*}(G)$
to denote the full preimage of the center
![]() $Z(G/O(G))$
in G. In Step 2 of Aschbacher’s programme, one may assume that a finite group G is a minimal counterexample to the CFSG. Such a group G has the following property.
$Z(G/O(G))$
in G. In Step 2 of Aschbacher’s programme, one may assume that a finite group G is a minimal counterexample to the CFSG. Such a group G has the following property.
 $$ \begin{align} &\mbox{Whenever} \ x\in G \ \mbox{is an involution and} \ J \mbox{is a} \ 2\mbox{-component of} \ C_G(x),\\ &\mbox{then} \ J/Z^*(J) \ \mbox{is a known finite simple group.} \nonumber \end{align} $$
$$ \begin{align} &\mbox{Whenever} \ x\in G \ \mbox{is an involution and} \ J \mbox{is a} \ 2\mbox{-component of} \ C_G(x),\\ &\mbox{then} \ J/Z^*(J) \ \mbox{is a known finite simple group.} \nonumber \end{align} $$
By a known finite simple group, we mean a finite simple group appearing in the statement of the CFSG.
For each integer
![]() $n \ne 0$
, we use
$n \ne 0$
, we use
![]() $n_2$
to denote the
$n_2$
to denote the
![]() $2$
-part of n, i.e., the largest power of
$2$
-part of n, i.e., the largest power of
![]() $2$
dividing n. Given odd integers
$2$
dividing n. Given odd integers
![]() $a, b$
with
$a, b$
with
![]() $|a|, |b|> 1$
, we write
$|a|, |b|> 1$
, we write
![]() $a \sim b$
provided that
$a \sim b$
provided that
![]() $(a-1)_2 = (b-1)_2$
and
$(a-1)_2 = (b-1)_2$
and
![]() $(a+1)_2 = (b+1)_2$
. If q is a nontrivial prime power and if n is a positive integer, then we write
$(a+1)_2 = (b+1)_2$
. If q is a nontrivial prime power and if n is a positive integer, then we write
![]() $PSL_n^{+}(q)$
for
$PSL_n^{+}(q)$
for
![]() $PSL_n(q)$
and
$PSL_n(q)$
and
![]() $PSL_n^{-}(q)$
for
$PSL_n^{-}(q)$
for
![]() $PSU_n(q)$
. With this notation, we can now state our main results.
$PSU_n(q)$
. With this notation, we can now state our main results.
Theorem A. Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number. Let G be a finite simple group. Suppose that G satisfies (𝒞𝒦) if
$n \ge 2$
be a natural number. Let G be a finite simple group. Suppose that G satisfies (𝒞𝒦) if
![]() $n \ge 6$
. Then the
$n \ge 6$
. Then the
![]() $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
if and only if one of the following holds:
$PSL_n(q)$
if and only if one of the following holds:
-
(i)
 $G \cong PSL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$G \cong PSL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
 $q^{*}$
and some
$q^{*}$
and some
 $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
 $\varepsilon q^{*} \sim q$
;
$\varepsilon q^{*} \sim q$
; -
(ii)
 $n = 2$
,
$n = 2$
,
 $\vert PSL_2(q) \vert _2 = 8$
, and
$\vert PSL_2(q) \vert _2 = 8$
, and
 $G \cong A_7$
;
$G \cong A_7$
; -
(iii)
 $n = 3$
,
$n = 3$
,
 $(q+1)_2 = 4$
, and
$(q+1)_2 = 4$
, and
 $G \cong M_{11}$
.
$G \cong M_{11}$
.
Our second main result is an extension of Theorem A. In order to state it, we briefly mention some concepts from the local theory of fusion systems. Let
![]() $\mathcal {F}$
be a saturated fusion system on a finite p-group S for some prime p, and let
$\mathcal {F}$
be a saturated fusion system on a finite p-group S for some prime p, and let
![]() $\mathcal {E}$
be a normal subsystem of
$\mathcal {E}$
be a normal subsystem of
![]() $\mathcal {F}$
. In [Reference Aschbacher6, Chapter 6], Aschbacher introduced a subgroup
$\mathcal {F}$
. In [Reference Aschbacher6, Chapter 6], Aschbacher introduced a subgroup
![]() $C_S(\mathcal {E})$
of S, which plays the role of the centralizer of
$C_S(\mathcal {E})$
of S, which plays the role of the centralizer of
![]() $\mathcal {E}$
in S. In [Reference Aschbacher6, Chapter 9], he defined a normal subsystem
$\mathcal {E}$
in S. In [Reference Aschbacher6, Chapter 9], he defined a normal subsystem
![]() $F^{*}(\mathcal {F})$
of
$F^{*}(\mathcal {F})$
of
![]() $\mathcal {F}$
, called the generalized Fitting subsystem of
$\mathcal {F}$
, called the generalized Fitting subsystem of
![]() $\mathcal {F}$
, and proved that
$\mathcal {F}$
, and proved that
![]() $C_S(F^{*}(\mathcal {F})) = Z(F^{*}(\mathcal {F}))$
, where the latter denotes the center of
$C_S(F^{*}(\mathcal {F})) = Z(F^{*}(\mathcal {F}))$
, where the latter denotes the center of
![]() $F^{*}(\mathcal {F})$
.
$F^{*}(\mathcal {F})$
.
Theorem B. Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number. If
$n \ge 2$
be a natural number. If
![]() $n = 2$
, suppose that
$n = 2$
, suppose that
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \mod 8$
. Let G be a finite simple group, and let S be a Sylow
$7 \mod 8$
. Let G be a finite simple group, and let S be a Sylow
![]() $2$
-subgroup of G. Suppose that
$2$
-subgroup of G. Suppose that
![]() $\mathcal {F}_S(G)$
has a normal subsystem
$\mathcal {F}_S(G)$
has a normal subsystem
![]() $\mathcal {E}$
on a subgroup T of S such that
$\mathcal {E}$
on a subgroup T of S such that
![]() $\mathcal {E}$
is isomorphic to the
$\mathcal {E}$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
and such that
$PSL_n(q)$
and such that
![]() $C_S(\mathcal {E}) = 1$
. Then
$C_S(\mathcal {E}) = 1$
. Then
![]() $\mathcal {F}_S(G)$
is isomorphic to the
$\mathcal {F}_S(G)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
. In particular, if
$PSL_n(q)$
. In particular, if
![]() $n \le 5$
or if G satisfies (𝒞𝒦), then one of the properties (i)–(iii) from Theorem A holds.
$n \le 5$
or if G satisfies (𝒞𝒦), then one of the properties (i)–(iii) from Theorem A holds.
Corollary C. Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number. If
$n \ge 2$
be a natural number. If
![]() $n = 2$
, suppose that
$n = 2$
, suppose that
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \mod 8$
. Let G be a finite simple group, and let S be a Sylow
$7 \mod 8$
. Let G be a finite simple group, and let S be a Sylow
![]() $2$
-subgroup of G. Suppose that
$2$
-subgroup of G. Suppose that
![]() $F^{*}(\mathcal {F}_S(G))$
is isomorphic to the
$F^{*}(\mathcal {F}_S(G))$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
. Then
$PSL_n(q)$
. Then
![]() $\mathcal {F}_S(G)$
is isomorphic to the
$\mathcal {F}_S(G)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
. In particular, if
$PSL_n(q)$
. In particular, if
![]() $n \le 5$
or if G satisfies (𝒞𝒦), then one of the properties (i)–(iii) from Theorem A holds.
$n \le 5$
or if G satisfies (𝒞𝒦), then one of the properties (i)–(iii) from Theorem A holds.
Plan of the Paper
In Sections 2 and 3, we collect several results needed for the proofs of our main results. Preliminary results on abstract finite groups and abstract fusion systems are proved in Section 2. Section 3 presents some results on linear and unitary groups over finite fields, mainly focusing on
![]() $2$
-local properties and on the automorphisms of these groups.
$2$
-local properties and on the automorphisms of these groups.
In Section 4, we will verify Theorem A for the case
![]() $n \le 5$
. Our proofs strongly depend on work of Gorenstein and Walter [Reference Gorenstein and Walter30] (for
$n \le 5$
. Our proofs strongly depend on work of Gorenstein and Walter [Reference Gorenstein and Walter30] (for
![]() $n = 2$
), on work of Alperin, Brauer and Gorenstein [Reference Alperin, Brauer and Gorenstein1], [Reference Alperin, Brauer and Gorenstein2] (for
$n = 2$
), on work of Alperin, Brauer and Gorenstein [Reference Alperin, Brauer and Gorenstein1], [Reference Alperin, Brauer and Gorenstein2] (for
![]() $n = 3$
) and on work of Mason [Reference Mason40], [Reference Mason41], [Reference Mason42] (for
$n = 3$
) and on work of Mason [Reference Mason40], [Reference Mason41], [Reference Mason42] (for
![]() $n = 4$
and
$n = 4$
and
![]() $n = 5$
).
$n = 5$
).
For
![]() $n \ge 6$
, we will prove Theorem A by induction over n. In order to do so, we will consider a finite group G realizing the
$n \ge 6$
, we will prove Theorem A by induction over n. In order to do so, we will consider a finite group G realizing the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
, where q is a nontrivial odd prime power and where
$PSL_n(q)$
, where q is a nontrivial odd prime power and where
![]() $n \ge 6$
is a natural number such that Theorem A is true with m instead of n for any natural number m with
$n \ge 6$
is a natural number such that Theorem A is true with m instead of n for any natural number m with
![]() $6 \le m < n$
. We will also assume that
$6 \le m < n$
. We will also assume that
![]() $O(G) = 1$
and that G satisfies (𝒞𝒦). To prove that Theorem A is satisfied for the natural number n, we will prove the existence of a normal subgroup
$O(G) = 1$
and that G satisfies (𝒞𝒦). To prove that Theorem A is satisfied for the natural number n, we will prove the existence of a normal subgroup
![]() $G_0$
of G such that
$G_0$
of G such that
![]() $G_0$
is isomorphic to a nontrivial quotient of
$G_0$
is isomorphic to a nontrivial quotient of
![]() $SL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$SL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +, - \rbrace $
with
$\varepsilon \in \lbrace +, - \rbrace $
with
![]() $\varepsilon q^{*} \sim q$
. This will happen in Sections 5-8.
$\varepsilon q^{*} \sim q$
. This will happen in Sections 5-8.
In Section 5, we will introduce some notation and prove some preliminary lemmas. Section 6 describes the
![]() $2$
-components of the centralizers of involutions of G. In Section 7, we will use signalizer functor methods to describe the components of the centralizers of certain involutions of G. This will be used in Section 8 to construct the subgroup
$2$
-components of the centralizers of involutions of G. In Section 7, we will use signalizer functor methods to describe the components of the centralizers of certain involutions of G. This will be used in Section 8 to construct the subgroup
![]() $G_0$
of G. One of the main tools here will be a version of the Curtis–Tits theorem [Reference Gorenstein, Lyons and Solomon29, Chapter 13, Theorem 1.4] and a related theorem of Phan reproved by Bennett and Shpectorov in [Reference Bennett and Shpectorov13].
$G_0$
of G. One of the main tools here will be a version of the Curtis–Tits theorem [Reference Gorenstein, Lyons and Solomon29, Chapter 13, Theorem 1.4] and a related theorem of Phan reproved by Bennett and Shpectorov in [Reference Bennett and Shpectorov13].
Finally, in Section 9, we will give a full proof of Theorem A (basically summarizing Sections 4–8), and we will prove Theorem B and Corollary C.
Notation and Terminology
Our notation and terminology are fairly standard. The reader is referred to [Reference Gorenstein23], [Reference Gorenstein, Lyons and Solomon27], [Reference Kurzweil and Stellmacher37] for unfamiliar definitions on groups and to [Reference Aschbacher, Kessar and Oliver10], [Reference Craven18] for unfamiliar definitions on fusion systems.
However, we shall now explain some particularly important notation and definitions (before stating our main results, we already introduced some other important definitions).
Given a map
![]() $\alpha : A \rightarrow B$
and an element or a subset X of A, we write
$\alpha : A \rightarrow B$
and an element or a subset X of A, we write
![]() $X^{\alpha }$
for the image of X under
$X^{\alpha }$
for the image of X under
![]() $\alpha $
. Also, if
$\alpha $
. Also, if
![]() $C \subseteq A$
and
$C \subseteq A$
and
![]() $D \subseteq B$
such that
$D \subseteq B$
such that
![]() $C^{\alpha } \subseteq D$
, we use
$C^{\alpha } \subseteq D$
, we use
![]() $\alpha |_{C,D}$
to denote the map
$\alpha |_{C,D}$
to denote the map
![]() $C \rightarrow D, c \mapsto c^{\alpha }$
. Given two maps
$C \rightarrow D, c \mapsto c^{\alpha }$
. Given two maps
![]() $\alpha : A \rightarrow B$
and
$\alpha : A \rightarrow B$
and
![]() $\beta : B \rightarrow C$
, we write
$\beta : B \rightarrow C$
, we write
![]() $\alpha \beta $
for the map
$\alpha \beta $
for the map
![]() $A \rightarrow C, a \mapsto (a^{\alpha })^{\beta }$
.
$A \rightarrow C, a \mapsto (a^{\alpha })^{\beta }$
.
Sometimes, we will interpret the symbols
![]() $+$
and
$+$
and
![]() $-$
as the integers
$-$
as the integers
![]() $1$
and
$1$
and
![]() $-1$
, respectively. For example, if n is an integer and if
$-1$
, respectively. For example, if n is an integer and if
![]() $\varepsilon $
is assumed to be an element of
$\varepsilon $
is assumed to be an element of
![]() $\lbrace +,- \rbrace $
, then
$\lbrace +,- \rbrace $
, then
![]() $n \equiv \varepsilon \mod 4$
shall express that
$n \equiv \varepsilon \mod 4$
shall express that
![]() $n \equiv 1 \mod 4$
if
$n \equiv 1 \mod 4$
if
![]() $\varepsilon = +$
and that
$\varepsilon = +$
and that
![]() $n \equiv -1 \mod 4$
if
$n \equiv -1 \mod 4$
if
![]() $\varepsilon = -$
.
$\varepsilon = -$
.
Let G be a finite group. We write
![]() $G^{\#}$
for the set of nonidentity elements of G. Given an element g of G and an element or a subset X of G, we write
$G^{\#}$
for the set of nonidentity elements of G. Given an element g of G and an element or a subset X of G, we write
![]() $X^g$
for
$X^g$
for
![]() $g^{-1}Xg$
. The inner automorphism
$g^{-1}Xg$
. The inner automorphism
![]() $G \rightarrow G, x \mapsto x^g$
is denoted by
$G \rightarrow G, x \mapsto x^g$
is denoted by
![]() $c_g$
. For subgroups Q and H of G, we write
$c_g$
. For subgroups Q and H of G, we write
![]() $\mathrm {Aut}_H(Q)$
for the subgroup of
$\mathrm {Aut}_H(Q)$
for the subgroup of
![]() $\mathrm {Aut}(Q)$
consisting of all automorphisms of Q of the form
$\mathrm {Aut}(Q)$
consisting of all automorphisms of Q of the form
![]() $c_h|_{Q,Q}$
, where
$c_h|_{Q,Q}$
, where
![]() $h \in N_H(Q)$
.
$h \in N_H(Q)$
.
We write
![]() $E(G)$
for the subgroup of G generated by the components of G and
$E(G)$
for the subgroup of G generated by the components of G and
![]() $L_{2'}(G)$
for the subgroup of G generated by the
$L_{2'}(G)$
for the subgroup of G generated by the
![]() $2$
-components of G. We say that G is core-free if
$2$
-components of G. We say that G is core-free if
![]() $O(G) = 1$
. If G is core-free and if L is a subnormal subgroup of G, then L is said to be a solvable
$O(G) = 1$
. If G is core-free and if L is a subnormal subgroup of G, then L is said to be a solvable
![]() $2$
-component of G if
$2$
-component of G if
![]() $L \cong SL_2(3)$
or
$L \cong SL_2(3)$
or
![]() $PSL_2(3)$
.
$PSL_2(3)$
.
Let n be a natural number. Then we use
![]() $E_{2^n}$
to denote an elementary abelian
$E_{2^n}$
to denote an elementary abelian
![]() $2$
-group of order
$2$
-group of order
![]() $2^n$
, and we say that n is the rank of
$2^n$
, and we say that n is the rank of
![]() $E_{2^n}$
. The maximal rank of an elementary abelian
$E_{2^n}$
. The maximal rank of an elementary abelian
![]() $2$
-subgroup of a finite
$2$
-subgroup of a finite
![]() $2$
-group S is said to be the rank of S. It is denoted by
$2$
-group S is said to be the rank of S. It is denoted by
![]() $m(S)$
.
$m(S)$
.
Now let p be a prime, and let
![]() $\mathcal {F}$
be a fusion system on a finite p-group S. Then S is said to be the Sylow group of
$\mathcal {F}$
be a fusion system on a finite p-group S. Then S is said to be the Sylow group of
![]() $\mathcal {F}$
, and
$\mathcal {F}$
, and
![]() $\mathcal {F}$
is said to be nilpotent if
$\mathcal {F}$
is said to be nilpotent if
![]() $\mathcal {F} = \mathcal {F}_S(S)$
. Given a fusion system
$\mathcal {F} = \mathcal {F}_S(S)$
. Given a fusion system
![]() $\mathcal {F}_1$
on a finite p-group
$\mathcal {F}_1$
on a finite p-group
![]() $S_1$
, we say that
$S_1$
, we say that
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {F}_1$
are isomorphic if there is a group isomorphism
$\mathcal {F}_1$
are isomorphic if there is a group isomorphism
![]() $\varphi : S \rightarrow S_1$
such that
$\varphi : S \rightarrow S_1$
such that
for all
![]() $Q,R \le S$
. In this case, we say that
$Q,R \le S$
. In this case, we say that
![]() $\varphi $
induces an isomorphism from
$\varphi $
induces an isomorphism from
![]() $\mathcal {F}$
to
$\mathcal {F}$
to
![]() $\mathcal {F}_1$
. Let T be a strongly
$\mathcal {F}_1$
. Let T be a strongly
![]() $\mathcal {F}$
-closed subgroup of S, i.e., for any subgroup P of T and any
$\mathcal {F}$
-closed subgroup of S, i.e., for any subgroup P of T and any
![]() $\alpha \in \mathrm {Hom}_{\mathcal {F}}(P,S)$
, we have
$\alpha \in \mathrm {Hom}_{\mathcal {F}}(P,S)$
, we have
![]() $P^{\alpha } \le T$
. If Q and R are subgroups of S containing T and if
$P^{\alpha } \le T$
. If Q and R are subgroups of S containing T and if
![]() $\alpha : Q \rightarrow R$
is a morphism in
$\alpha : Q \rightarrow R$
is a morphism in
![]() $\mathcal {F}$
, we write
$\mathcal {F}$
, we write
![]() $\alpha /T$
for the group homomorphism
$\alpha /T$
for the group homomorphism
![]() $Q/T \rightarrow R/T$
induced by
$Q/T \rightarrow R/T$
induced by
![]() $\alpha $
. The fusion system
$\alpha $
. The fusion system
![]() $\mathcal {F}/T$
on
$\mathcal {F}/T$
on
![]() $S/T$
with
$S/T$
with
![]() $\mathrm {Hom}_{\mathcal {F}/T}(Q/T,R/T) = \lbrace \alpha /T \ \vert \ \alpha \in \mathrm {Hom}_{\mathcal {F}}(Q,R)\rbrace $
for all
$\mathrm {Hom}_{\mathcal {F}/T}(Q/T,R/T) = \lbrace \alpha /T \ \vert \ \alpha \in \mathrm {Hom}_{\mathcal {F}}(Q,R)\rbrace $
for all
![]() $Q, R \le S$
containing T is said to be the factor system of
$Q, R \le S$
containing T is said to be the factor system of
![]() $\mathcal {F}$
modulo T.
$\mathcal {F}$
modulo T.
Suppose now that
![]() $\mathcal {F}$
is saturated. We write
$\mathcal {F}$
is saturated. We write
![]() $\mathfrak {foc}(\mathcal {F})$
for the focal subgroup of
$\mathfrak {foc}(\mathcal {F})$
for the focal subgroup of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathfrak {hnp}(\mathcal {F})$
for the hyperfocal subgroup of
$\mathfrak {hnp}(\mathcal {F})$
for the hyperfocal subgroup of
![]() $\mathcal {F}$
. We say that
$\mathcal {F}$
. We say that
![]() $\mathcal {F}$
is quasisimple if
$\mathcal {F}$
is quasisimple if
![]() $\mathcal {F}/Z(\mathcal {F})$
is simple and
$\mathcal {F}/Z(\mathcal {F})$
is simple and
![]() $\mathfrak {foc}(\mathcal {F}) = S$
. A component of
$\mathfrak {foc}(\mathcal {F}) = S$
. A component of
![]() $\mathcal {F}$
is a subnormal quasisimple subsystem of
$\mathcal {F}$
is a subnormal quasisimple subsystem of
![]() $\mathcal {F}$
. Given a normal subsystem
$\mathcal {F}$
. Given a normal subsystem
![]() $\mathcal {E}$
of S and a subgroup R of S, we write
$\mathcal {E}$
of S and a subgroup R of S, we write
![]() $\mathcal {E}R$
for the product of
$\mathcal {E}R$
for the product of
![]() $\mathcal {E}$
and R, as defined in [Reference Aschbacher6, Chapter 8].
$\mathcal {E}$
and R, as defined in [Reference Aschbacher6, Chapter 8].
2 Preliminaries on finite groups and fusion systems
In this section, we present some general results on finite groups and fusion systems.
2.1 Preliminaries on finite groups
Lemma 2.1 [Reference Kurzweil and Stellmacher37, 3.2.8]
Let G be a finite group, and let N be a normal
![]() $p'$
-subgroup of G for some prime p. Set
$p'$
-subgroup of G for some prime p. Set
![]() . If R is a p-subgroup of G, then we have
. If R is a p-subgroup of G, then we have
![]() $N_{\overline {G}}(\overline {R}) = \overline {N_G(R)}$
and
$N_{\overline {G}}(\overline {R}) = \overline {N_G(R)}$
and
![]() $C_{\overline {G}}(\overline {R}) = \overline {C_G(R)}$
.
$C_{\overline {G}}(\overline {R}) = \overline {C_G(R)}$
.
Corollary 2.2. Let G be a finite group, and let N be a normal
![]() $p'$
-subgroup of G for some prime p. Set
$p'$
-subgroup of G for some prime p. Set
![]() . If
. If
![]() $x \in G$
has order p, then we have
$x \in G$
has order p, then we have
![]() .
.
Lemma 2.3. Let G be a finite group, and let Z be a cyclic central subgroup of G. Then each
![]() $E_8$
-subgroup of
$E_8$
-subgroup of
![]() $G/Z$
has an involution which is the image of an involution of G.
$G/Z$
has an involution which is the image of an involution of G.
Proof. Let
![]() $Z \le E \le G$
such that
$Z \le E \le G$
such that
![]() $E/Z \cong E_8$
. Let R be a Sylow
$E/Z \cong E_8$
. Let R be a Sylow
![]() $2$
-subgroup of E. Then
$2$
-subgroup of E. Then
![]() $E = RZ$
. It suffices to show that R has an involution not lying in
$E = RZ$
. It suffices to show that R has an involution not lying in
![]() $R \cap Z$
. Assume that any involution of R is an element of
$R \cap Z$
. Assume that any involution of R is an element of
![]() $R \cap Z$
. Then R has a unique involution since Z is cyclic. We have
$R \cap Z$
. Then R has a unique involution since Z is cyclic. We have
![]() $R/(R \cap Z) \cong RZ/Z = E/Z \cong E_8$
, and so R is not cyclic. Applying [Reference Kurzweil and Stellmacher37, 5.3.7], we conclude that R is generalized quaternion. In particular,
$R/(R \cap Z) \cong RZ/Z = E/Z \cong E_8$
, and so R is not cyclic. Applying [Reference Kurzweil and Stellmacher37, 5.3.7], we conclude that R is generalized quaternion. In particular,
![]() $Z(R)$
has order
$Z(R)$
has order
![]() $2$
, and so we have
$2$
, and so we have
![]() $R \cap Z = Z(R)$
. Since R is a generalized quaternion group,
$R \cap Z = Z(R)$
. Since R is a generalized quaternion group,
![]() $R/Z(R)$
is dihedral. In particular,
$R/Z(R)$
is dihedral. In particular,
![]() $E/Z \cong R/(R \cap Z) = R/Z(R) \not \cong E_8$
. This contradiction shows that R has an involution not lying in
$E/Z \cong R/(R \cap Z) = R/Z(R) \not \cong E_8$
. This contradiction shows that R has an involution not lying in
![]() $R \cap Z$
, as required.
$R \cap Z$
, as required.
The following proposition is well-known. We include a proof since we could not find a reference in which it appears in the form given here.
Proposition 2.4. Let G be a finite group, and let N be a normal subgroup of G with odd order. If L is a
![]() $2$
-component of G, then
$2$
-component of G, then
![]() $LN/N$
is a
$LN/N$
is a
![]() $2$
-component of
$2$
-component of
![]() $G/N$
. The map from the set of
$G/N$
. The map from the set of
![]() $2$
-components of G to the set of
$2$
-components of G to the set of
![]() $2$
-components of
$2$
-components of
![]() $G/N$
sending each
$G/N$
sending each
![]() $2$
-component L of G to
$2$
-component L of G to
![]() $LN/N$
is a bijection. Moreover, if
$LN/N$
is a bijection. Moreover, if
![]() $N \le K \le G$
and
$N \le K \le G$
and
![]() $K/N$
is a
$K/N$
is a
![]() $2$
-component of
$2$
-component of
![]() $G/N$
, then
$G/N$
, then
![]() $O^{2'}(K)$
is the associated
$O^{2'}(K)$
is the associated
![]() $2$
-component of G.
$2$
-component of G.
Proof. Let L be a
![]() $2$
-component of G. Hence, L is a perfect subnormal subgroup of G such that
$2$
-component of G. Hence, L is a perfect subnormal subgroup of G such that
![]() $L/O(L)$
is quasisimple. Clearly,
$L/O(L)$
is quasisimple. Clearly,
![]() $LN/N$
is perfect and subnormal in
$LN/N$
is perfect and subnormal in
![]() $G/N$
. Also, we have
$G/N$
. Also, we have
![]() $(LN/N)/O(LN/N) \cong L/O(L)$
, and so
$(LN/N)/O(LN/N) \cong L/O(L)$
, and so
![]() $(LN/N)/O(LN/N)$
is quasisimple. It follows that
$(LN/N)/O(LN/N)$
is quasisimple. It follows that
![]() $LN/N$
is a
$LN/N$
is a
![]() $2$
-component of
$2$
-component of
![]() $G/N$
.
$G/N$
.
Let
![]() $N \le K \le G$
such that
$N \le K \le G$
such that
![]() $K/N$
is a
$K/N$
is a
![]() $2$
-component of
$2$
-component of
![]() $G/N$
. In order to prove the second statement of the proposition, it is enough to show that there is precisely one
$G/N$
. In order to prove the second statement of the proposition, it is enough to show that there is precisely one
![]() $2$
-component L of G such that
$2$
-component L of G such that
![]() $LN/N = K/N$
.
$LN/N = K/N$
.
Since
![]() $K/N$
is subnormal in
$K/N$
is subnormal in
![]() $G/N$
, we have that K is subnormal in G. Therefore,
$G/N$
, we have that K is subnormal in G. Therefore,
![]() $L := O^{2'}(K)$
is subnormal in G. Since
$L := O^{2'}(K)$
is subnormal in G. Since
![]() $O^{2'}(K/N) = K/N$
, we have that
$O^{2'}(K/N) = K/N$
, we have that
![]() $K/N = LN/N$
. Clearly,
$K/N = LN/N$
. Clearly,
![]() $O^{2'}(L) = L$
. We have
$O^{2'}(L) = L$
. We have
![]() $L/O(L) \cong (LN/N)/O(LN/N) = (K/N)/O(K/N)$
, and so
$L/O(L) \cong (LN/N)/O(LN/N) = (K/N)/O(K/N)$
, and so
![]() $L/O(L)$
is quasisimple. Applying [Reference Gorenstein, Lyons and Solomon27, Lemma 4.8], we conclude that L is a
$L/O(L)$
is quasisimple. Applying [Reference Gorenstein, Lyons and Solomon27, Lemma 4.8], we conclude that L is a
![]() $2$
-component of G.
$2$
-component of G.
Now let
![]() $L_0$
be a
$L_0$
be a
![]() $2$
-component of G such that
$2$
-component of G such that
![]() $K/N = L_0 N /N$
. Then
$K/N = L_0 N /N$
. Then
![]() $K = L_0 N$
. In particular,
$K = L_0 N$
. In particular,
![]() $L_0$
is a subgroup of K with odd index in K. Since
$L_0$
is a subgroup of K with odd index in K. Since
![]() $L_0$
is subnormal in G, we have that
$L_0$
is subnormal in G, we have that
![]() $L_0$
is subnormal in K. Applying [Reference Ballester-Bolinches, Esteban-Romero and Asaad12, Lemma 1.1.11], we conclude that
$L_0$
is subnormal in K. Applying [Reference Ballester-Bolinches, Esteban-Romero and Asaad12, Lemma 1.1.11], we conclude that
![]() $L_0 = O^{2'}(L_0) = O^{2'}(K) = L$
. The proof of the second statement of the proposition is now complete. The third statement also follows from the above arguments.
$L_0 = O^{2'}(L_0) = O^{2'}(K) = L$
. The proof of the second statement of the proposition is now complete. The third statement also follows from the above arguments.
Lemma 2.5. Let G be a finite group, and let n be a positive integer. Assume that
![]() $L_1$
, …,
$L_1$
, …,
![]() $L_n$
are the distinct
$L_n$
are the distinct
![]() $2$
-components of G, and assume that
$2$
-components of G, and assume that
![]() $L_i \trianglelefteq G$
for all
$L_i \trianglelefteq G$
for all
![]() $1 \le i \le n$
. Let x be a
$1 \le i \le n$
. Let x be a
![]() $2$
-element of G, and let L be a
$2$
-element of G, and let L be a
![]() $2$
-component of
$2$
-component of
![]() $C_G(x)$
. Then L is a
$C_G(x)$
. Then L is a
![]() $2$
-component of
$2$
-component of
![]() $C_{L_i}(x)$
for some
$C_{L_i}(x)$
for some
![]() $1 \le i \le n$
.
$1 \le i \le n$
.
Proof. For each
![]() $1 \le i \le n$
, let
$1 \le i \le n$
, let
![]() $\mathfrak {L}_i$
denote the set of
$\mathfrak {L}_i$
denote the set of
![]() $2$
-components of
$2$
-components of
![]() $C_{L_i}(x)$
, and let
$C_{L_i}(x)$
, and let
![]() $\mathfrak {L} := \mathfrak {L}_1 \cup \dots \mathfrak {L}_n$
. It suffices to show that
$\mathfrak {L} := \mathfrak {L}_1 \cup \dots \mathfrak {L}_n$
. It suffices to show that
![]() $L \in \mathfrak {L}$
.
$L \in \mathfrak {L}$
.
By [Reference Gorenstein and Walter31, Corollary 3.2], we have
![]() $L_{2'}(C_G(x)) = L_{2'}(C_{L_{2'}(G)}(x))$
, and by [Reference Gorenstein and Walter31, Lemma 2.18 (iii)], we have
$L_{2'}(C_G(x)) = L_{2'}(C_{L_{2'}(G)}(x))$
, and by [Reference Gorenstein and Walter31, Lemma 2.18 (iii)], we have
![]() $L_{2'}(C_{L_{2'}(G)}(x)) = \prod _{i=1}^n L_{2'}(C_{L_i}(x))$
. Thus
$L_{2'}(C_{L_{2'}(G)}(x)) = \prod _{i=1}^n L_{2'}(C_{L_i}(x))$
. Thus
![]() $L_{2'}(C_G(x)) = \langle \mathfrak {L} \rangle $
. Set
$L_{2'}(C_G(x)) = \langle \mathfrak {L} \rangle $
. Set
![]() .
.
Assume that
![]() $L \not \in \mathfrak {L}$
. Let J be an element of
$L \not \in \mathfrak {L}$
. Let J be an element of
![]() $\mathfrak L$
. Since
$\mathfrak L$
. Since
![]() $L \ne J$
and since L and J are
$L \ne J$
and since L and J are
![]() $2$
-components of
$2$
-components of
![]() $C_G(x)$
, we have
$C_G(x)$
, we have
![]() by Proposition 2.4. Also, since
by Proposition 2.4. Also, since
![]() and
and
![]() are components of
are components of
![]() , we have
, we have
![]() by [Reference Kurzweil and Stellmacher37, 6.5.3]. Since
by [Reference Kurzweil and Stellmacher37, 6.5.3]. Since
![]() , it follows that
, it follows that
![]() lies in the center of
lies in the center of
![]() . This is impossible since
. This is impossible since
![]() is nontrivial and perfect. So we have
is nontrivial and perfect. So we have
![]() $L \in \mathfrak {L}$
.
$L \in \mathfrak {L}$
.
The concepts introduced by the following two definitions will play a crucial role in the proof of Theorem A (see [Reference Gorenstein and Walter31] for a detailed study of these concepts).
Definition 2.6. Let G be a finite group, k be a positive integer and A be an elementary abelian
![]() $2$
-subgroup of G.
$2$
-subgroup of G.
-
(i) For each nontrivial elementary abelian
 $2$
-subgroup E of G, we define
$2$
-subgroup E of G, we define  $$ \begin{align*} \Delta_G(E) := \bigcap_{a \in E^{\#}} O(C_G(a)). \end{align*} $$
$$ \begin{align*} \Delta_G(E) := \bigcap_{a \in E^{\#}} O(C_G(a)). \end{align*} $$
-
(ii) We say that G is k-balanced with respect to A if, whenever E is a subgroup of A of rank k and a is a nontrivial element of A, we have
 $$ \begin{align*} \Delta_G(E) \cap C_G(a) \le O(C_G(a)). \end{align*} $$
$$ \begin{align*} \Delta_G(E) \cap C_G(a) \le O(C_G(a)). \end{align*} $$
-
(iii) We say that G is k-balanced if, whenever E is an elementary abelian
 $2$
-subgroup of G of rank k and a is an involution of G centralizing E, we have
$2$
-subgroup of G of rank k and a is an involution of G centralizing E, we have  $$ \begin{align*} \Delta_G(E) \cap C_G(a) \le O(C_G(a)). \end{align*} $$
$$ \begin{align*} \Delta_G(E) \cap C_G(a) \le O(C_G(a)). \end{align*} $$
-
(iv) By saying that G is balanced (respectively, balanced with respect to A), we mean that G is
 $1$
-balanced (respectively,
$1$
-balanced (respectively,
 $1$
-balanced with respect to A).
$1$
-balanced with respect to A).
Definition 2.7. Let G be a finite quasisimple group, and let k be a positive integer. Then G is said to be locally k-balanced if whenever H is a subgroup of
![]() $\mathrm {Aut}(G)$
containing
$\mathrm {Aut}(G)$
containing
![]() $\mathrm {Inn}(G)$
, we have
$\mathrm {Inn}(G)$
, we have
for any elementary abelian
![]() $2$
-subgroup E of H of rank k. We say that G is locally balanced if G is locally
$2$
-subgroup E of H of rank k. We say that G is locally balanced if G is locally
![]() $1$
-balanced.
$1$
-balanced.
We need the following proposition for the proof of Theorem A. It includes [Reference Gorenstein and Walter31, Theorem 6.10] and some additional statements, which should be also known. We include a proof for the convenience of the reader.
Proposition 2.8. Let k be a positive integer, and let G be a finite group. For each elementary abelian
![]() $2$
-subgroup A of G of rank at least
$2$
-subgroup A of G of rank at least
![]() $k+1$
, let
$k+1$
, let
Then, for any elementary abelian
![]() $2$
-subgroup A of G of rank at least
$2$
-subgroup A of G of rank at least
![]() $k+1$
, the following hold:
$k+1$
, the following hold:
-
(i)
 $(W_A)^g = W_{A^g}$
for all
$(W_A)^g = W_{A^g}$
for all
 $g \in G$
.
$g \in G$
. -
(ii) Suppose that A has rank at least
 $k + 2$
and that G is k-balanced with respect to A. Then
$k + 2$
and that G is k-balanced with respect to A. Then
 $W_A$
has odd order. Moreover, if
$W_A$
has odd order. Moreover, if
 $A_0$
is a subgroup of A of rank at least
$A_0$
is a subgroup of A of rank at least
 $k+1$
, then we have
$k+1$
, then we have
 $W_A = W_{A_0}$
and
$W_A = W_{A_0}$
and
 $N_G(A_0) \le N_G(W_A)$
.
$N_G(A_0) \le N_G(W_A)$
.
In order to prove Proposition 2.8, we need the following theorem.
Theorem 2.9 [Reference Gorenstein and Walter31, Theorem 6.9]
Let k be a positive integer, G be a finite group and A be an elementary abelian
![]() $2$
-subgroup of G of rank at least
$2$
-subgroup of G of rank at least
![]() $k+2$
. Suppose that G is k-balanced with respect to A. Then we obtain an A-signalizer functor on G (in the sense of [Reference Gorenstein24, Definition 4.37]) by defining
$k+2$
. Suppose that G is k-balanced with respect to A. Then we obtain an A-signalizer functor on G (in the sense of [Reference Gorenstein24, Definition 4.37]) by defining
for each
![]() $a \in A^{\#}$
.
$a \in A^{\#}$
.
We also need the following lemma.
Lemma 2.10. Let the hypothesis and notation be as in Theorem 2.9. Suppose that
![]() $A_0$
is subgroup of A of rank
$A_0$
is subgroup of A of rank
![]() $k+1$
. Then we have
$k+1$
. Then we have
Proof. To prove this, we follow arguments found on pp. 40–41 of [Reference Mason40].
Since
![]() $\theta $
is an A-signalizer functor on G,
$\theta $
is an A-signalizer functor on G,
![]() $\theta (C_G(a))$
is A-invariant and in particular
$\theta (C_G(a))$
is A-invariant and in particular
![]() $A_0$
-invariant for each
$A_0$
-invariant for each
![]() $a \in A^{\#}$
. Consequently,
$a \in A^{\#}$
. Consequently,
![]() $\theta (G,A)$
is
$\theta (G,A)$
is
![]() $A_0$
-invariant. By the solvable signalizer functor theorem [Reference Kurzweil and Stellmacher37, 11.3.2],
$A_0$
-invariant. By the solvable signalizer functor theorem [Reference Kurzweil and Stellmacher37, 11.3.2],
![]() $\theta $
is complete (in the sense of [Reference Gorenstein24, Definition 4.37]). In particular,
$\theta $
is complete (in the sense of [Reference Gorenstein24, Definition 4.37]). In particular,
![]() $\theta (G,A)$
has odd order. Applying [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we conclude that
$\theta (G,A)$
has odd order. Applying [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we conclude that
Since
![]() $\theta $
is complete, we have
$\theta $
is complete, we have
![]() $C_{\theta (G,A)}(a) = \theta (C_G(a))$
for each
$C_{\theta (G,A)}(a) = \theta (C_G(a))$
for each
![]() $a \in A^{\#}$
. By definition of
$a \in A^{\#}$
. By definition of
![]() $\theta $
and since G is k-balanced with respect to A, we have
$\theta $
and since G is k-balanced with respect to A, we have
![]() $\theta (C_G(a)) \le O(C_G(a))$
for each
$\theta (C_G(a)) \le O(C_G(a))$
for each
![]() $a \in A^{\#}$
. So, if E is a subgroup of
$a \in A^{\#}$
. So, if E is a subgroup of
![]() $A_0$
of rank k, then
$A_0$
of rank k, then
It follows that
![]() $\theta (G,A) \le W_{A_0}$
.
$\theta (G,A) \le W_{A_0}$
.
Let
![]() $E \le A_0$
with
$E \le A_0$
with
![]() $m(E) = k$
. Clearly,
$m(E) = k$
. Clearly,
![]() $\Delta _G(E)$
is A-invariant. As a consequence of [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
$\Delta _G(E)$
is A-invariant. As a consequence of [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
By definition of
![]() $\theta $
, we have
$\theta $
, we have
![]() $\Delta _G(E) \cap C_G(a) \le \theta (C_G(a))$
for each
$\Delta _G(E) \cap C_G(a) \le \theta (C_G(a))$
for each
![]() $a \in A^{\#}$
. It follows that
$a \in A^{\#}$
. It follows that
![]() $\Delta _G(E) \le \theta (G,A)$
. Consequently,
$\Delta _G(E) \le \theta (G,A)$
. Consequently,
![]() $W_{A_0} \le \theta (G,A)$
.
$W_{A_0} \le \theta (G,A)$
.
Proof of Proposition 2.8
It is straightforward to verify (i).
To verify (ii), let A be an elementary abelian
![]() $2$
-subgroup of G of rank at least
$2$
-subgroup of G of rank at least
![]() $k+2$
such that G is k-balanced with respect to A. Let
$k+2$
such that G is k-balanced with respect to A. Let
![]() $\theta $
be the A-signalizer functor on G given by Theorem 2.9, and let
$\theta $
be the A-signalizer functor on G given by Theorem 2.9, and let
![]() $\theta (G,A) := \langle \theta (C_G(a)) \ \vert \ a \in A^{\#} \rangle $
. As a consequence of Lemma 2.10, we have
$\theta (G,A) := \langle \theta (C_G(a)) \ \vert \ a \in A^{\#} \rangle $
. As a consequence of Lemma 2.10, we have
![]() $\theta (G,A) = W_A$
. By the proof of Lemma 2.10,
$\theta (G,A) = W_A$
. By the proof of Lemma 2.10,
![]() $W_A = \theta (G,A)$
has odd order.
$W_A = \theta (G,A)$
has odd order.
Now let
![]() $A_0$
be a subgroup of A of rank at least
$A_0$
be a subgroup of A of rank at least
![]() $k+1$
. By Lemma 2.10,
$k+1$
. By Lemma 2.10,
![]() $W_A = \theta (G,A) \le W_{A_0} \le W_A$
, and so
$W_A = \theta (G,A) \le W_{A_0} \le W_A$
, and so
![]() $W_A = W_{A_0}$
. Finally, if
$W_A = W_{A_0}$
. Finally, if
![]() $g \in N_G(A_0)$
, then
$g \in N_G(A_0)$
, then
![]() $(W_A)^g = (W_{A_0})^g = W_{(A_0)^g} = W_{A_0} = W_A$
, and hence,
$(W_A)^g = (W_{A_0})^g = W_{(A_0)^g} = W_{A_0} = W_A$
, and hence,
![]() $N_G(A_0) \le N_G(W_A)$
.
$N_G(A_0) \le N_G(W_A)$
.
2.2 Preliminaries on fusion systems
Lemma 2.11. Let p be a prime, G be a finite group, N be a normal subgroup of G and
![]() $S \in \mathrm {Syl}_p(G)$
. Then the canonical group isomorphism
$S \in \mathrm {Syl}_p(G)$
. Then the canonical group isomorphism
![]() $S/(S \cap N) \rightarrow SN/N$
induces an isomorphism from
$S/(S \cap N) \rightarrow SN/N$
induces an isomorphism from
![]() $\mathcal {F}_S(G)/(S \cap N)$
to
$\mathcal {F}_S(G)/(S \cap N)$
to
![]() $\mathcal {F}_{SN/N}(G/N)$
.
$\mathcal {F}_{SN/N}(G/N)$
.
Proof. Let
![]() $\varphi $
denote the canonical group isomorphism
$\varphi $
denote the canonical group isomorphism
![]() $S/(S \cap N) \rightarrow SN/N$
. Let P and Q be two subgroups of S such that
$S/(S \cap N) \rightarrow SN/N$
. Let P and Q be two subgroups of S such that
![]() $S \cap N$
is contained in both P and Q. Set
$S \cap N$
is contained in both P and Q. Set
![]() $\widetilde P := P/(S \cap N)$
,
$\widetilde P := P/(S \cap N)$
,
![]() $\widetilde Q := Q/(S \cap N)$
,
$\widetilde Q := Q/(S \cap N)$
,
and
. For any
![]() $g \in G$
, let
$g \in G$
, let
. Moreover, define
![]() $\widetilde {\mathcal {F}} := \mathcal {F}_S(G)/(S \cap N)$
and
$\widetilde {\mathcal {F}} := \mathcal {F}_S(G)/(S \cap N)$
and
. It is enough to show that
Let
![]() $\alpha \in \mathrm {Hom}_{\widetilde {\mathcal {F}}}(\widetilde P, \widetilde Q)$
. Then there exists
$\alpha \in \mathrm {Hom}_{\widetilde {\mathcal {F}}}(\widetilde P, \widetilde Q)$
. Then there exists
![]() $g \in G$
with
$g \in G$
with
![]() $P^g \le Q$
and
$P^g \le Q$
and
![]() $\alpha = (c_g|_{P,Q})/(S \cap N)$
. By a direct calculation,
$\alpha = (c_g|_{P,Q})/(S \cap N)$
. By a direct calculation,
.
Now let
![]() . Then there exists
. Then there exists
![]() $g \in G$
with
$g \in G$
with
![]() and
and
![]() . Clearly,
. Clearly,
![]() $P^g \le QN$
. Since
$P^g \le QN$
. Since
![]() $S \cap N \le Q$
, we have that Q is a Sylow p-subgroup of
$S \cap N \le Q$
, we have that Q is a Sylow p-subgroup of
![]() $QN$
. Since
$QN$
. Since
![]() $P^g$
is a p-subgroup of
$P^g$
is a p-subgroup of
![]() $QN$
, it follows that there exists an element
$QN$
, it follows that there exists an element
![]() $n \in N$
with
$n \in N$
with
![]() $P^{gn} \le Q$
. Set
$P^{gn} \le Q$
. Set
![]() $\alpha := (c_{gn}|_{P,Q})/(S \cap N)$
. Then a direct calculation shows that
$\alpha := (c_{gn}|_{P,Q})/(S \cap N)$
. Then a direct calculation shows that
![]() .
.
Corollary 2.12 [Reference Aschbacher, Kessar and Oliver10, Part II, Exercise 2.1]
Let p be a prime, G be a finite group and
![]() $S \in \mathrm {Syl}_p(G)$
. Then the canonical group isomorphism
$S \in \mathrm {Syl}_p(G)$
. Then the canonical group isomorphism
![]() induces an isomorphism from
induces an isomorphism from
![]() $\mathcal {F}_S(G)$
to
$\mathcal {F}_S(G)$
to
![]() .
.
Lemma 2.13. Let G be a finite group and
![]() $S \in \mathrm {Syl}_2(G)$
. Then
$S \in \mathrm {Syl}_2(G)$
. Then
![]() $Z(\mathcal {F}_S(G)) = S \cap Z^{*}(G)$
. In particular, if
$Z(\mathcal {F}_S(G)) = S \cap Z^{*}(G)$
. In particular, if
![]() $Z^{*}(G)$
is
$Z^{*}(G)$
is
![]() $2$
-closed, then
$2$
-closed, then
![]() $Z(\mathcal {F}_S(G)) = S \cap Z(G)$
.
$Z(\mathcal {F}_S(G)) = S \cap Z(G)$
.
Proof. By Glauberman’s
![]() $Z^{*}$
-Theorem, more precisely by [Reference Glauberman22, Corollary 1], we have
$Z^{*}$
-Theorem, more precisely by [Reference Glauberman22, Corollary 1], we have
![]() $Z(\mathcal {F}_S(G)) = S \cap Z^{*}(G)$
. Assume now that
$Z(\mathcal {F}_S(G)) = S \cap Z^{*}(G)$
. Assume now that
![]() $Z^{*}(G)$
is
$Z^{*}(G)$
is
![]() $2$
-closed, and let
$2$
-closed, and let
![]() $S_0 := S \cap Z^{*}(G)$
. Then
$S_0 := S \cap Z^{*}(G)$
. Then
![]() $S_0 \trianglelefteq G$
and hence
$S_0 \trianglelefteq G$
and hence
![]() $[S_0,G] \le S_0 \cap [Z^{*}(G),G] \le S_0 \cap O(G) = 1$
. Thus,
$[S_0,G] \le S_0 \cap [Z^{*}(G),G] \le S_0 \cap O(G) = 1$
. Thus,
![]() $Z(\mathcal {F}_S(G)) = S_0 = S \cap Z(G)$
.
$Z(\mathcal {F}_S(G)) = S_0 = S \cap Z(G)$
.
Lemma 2.14. Let
![]() $K_1$
and
$K_1$
and
![]() $K_2$
be two quasisimple finite groups. If the
$K_2$
be two quasisimple finite groups. If the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are isomorphic, then the
$K_2$
are isomorphic, then the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $K_1/Z(K_1)$
and
$K_1/Z(K_1)$
and
![]() $K_2/Z(K_2)$
are isomorphic.
$K_2/Z(K_2)$
are isomorphic.
Proof. Suppose that the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are isomorphic. Let
$K_2$
are isomorphic. Let
![]() $S_i$
be a Sylow
$S_i$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $K_i$
and
$K_i$
and
![]() $\mathcal {F}_i := \mathcal {F}_{S_i}(K_i)$
for
$\mathcal {F}_i := \mathcal {F}_{S_i}(K_i)$
for
![]() $i \in \lbrace 1,2 \rbrace $
. Since
$i \in \lbrace 1,2 \rbrace $
. Since
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are quasisimple, we have
$K_2$
are quasisimple, we have
![]() $Z^{*}(K_i) = Z(K_i)$
for
$Z^{*}(K_i) = Z(K_i)$
for
![]() $i \in \lbrace 1,2 \rbrace $
. So, by Lemma 2.13, we have
$i \in \lbrace 1,2 \rbrace $
. So, by Lemma 2.13, we have
![]() $Z(\mathcal {F}_i) = S_i \cap Z(K_i)$
for
$Z(\mathcal {F}_i) = S_i \cap Z(K_i)$
for
![]() $i \in \lbrace 1,2 \rbrace $
. Since
$i \in \lbrace 1,2 \rbrace $
. Since
![]() $\mathcal {F}_1 \cong \mathcal {F}_2$
, it follows that
$\mathcal {F}_1 \cong \mathcal {F}_2$
, it follows that
Applying Lemma 2.11, we may conclude that the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $K_1/Z(K_1)$
is isomorphic to the
$K_1/Z(K_1)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $K_2/Z(K_2)$
.
$K_2/Z(K_2)$
.
Lemma 2.15. Let S be a finite
![]() $2$
-group, and let A and B be normal subgroups of S such that S is the internal direct product of A and B. Suppose that
$2$
-group, and let A and B be normal subgroups of S such that S is the internal direct product of A and B. Suppose that
![]() $A \cong Q_8$
. Let
$A \cong Q_8$
. Let
![]() $\mathcal {F}$
be a (not necessarily saturated) fusion system on S. Assume that A and B are strongly
$\mathcal {F}$
be a (not necessarily saturated) fusion system on S. Assume that A and B are strongly
![]() $\mathcal {F}$
-closed and that there is an automorphism
$\mathcal {F}$
-closed and that there is an automorphism
![]() $\alpha \in \mathrm {Aut}_{\mathcal {F}}(S)$
such that
$\alpha \in \mathrm {Aut}_{\mathcal {F}}(S)$
such that
![]() $\alpha |_{A,A}$
has order
$\alpha |_{A,A}$
has order
![]() $3$
, while
$3$
, while
![]() $\alpha |_{B,B} = \mathrm {id}_B$
. Then each strongly
$\alpha |_{B,B} = \mathrm {id}_B$
. Then each strongly
![]() $\mathcal {F}$
-closed subgroup of S contains or centralizes A.
$\mathcal {F}$
-closed subgroup of S contains or centralizes A.
Proof. Let C be a strongly
![]() $\mathcal {F}$
-closed subgroup of S not containing A. Our task is to show that C centralizes A.
$\mathcal {F}$
-closed subgroup of S not containing A. Our task is to show that C centralizes A.
Since A and C are strongly
![]() $\mathcal {F}$
-closed, we have that
$\mathcal {F}$
-closed, we have that
![]() $A \cap C$
is strongly
$A \cap C$
is strongly
![]() $\mathcal {F}$
-closed. In particular,
$\mathcal {F}$
-closed. In particular,
![]() $\alpha $
normalizes
$\alpha $
normalizes
![]() $A \cap C$
. An automorphism of
$A \cap C$
. An automorphism of
![]() $A \cong Q_8$
of order
$A \cong Q_8$
of order
![]() $3$
is irreducible on
$3$
is irreducible on
![]() $A/\Phi (A)$
. So, as
$A/\Phi (A)$
. So, as
![]() $\alpha |_{A,A}$
has order
$\alpha |_{A,A}$
has order
![]() $3$
and normalizes
$3$
and normalizes
![]() $A \cap C$
, we have that
$A \cap C$
, we have that
![]() $A \cap C$
has order
$A \cap C$
has order
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
By [Reference Kurzweil and Stellmacher37, 8.2.7], we have
By hypothesis
![]() $[S, \alpha ] = A$
, so
$[S, \alpha ] = A$
, so
![]() $[C, \alpha ] \le [S, \alpha ] \cap C = A \cap C$
. As
$[C, \alpha ] \le [S, \alpha ] \cap C = A \cap C$
. As
![]() $|A \cap C| \le 2, [A \cap C, \alpha ] = 1$
, so
$|A \cap C| \le 2, [A \cap C, \alpha ] = 1$
, so
![]() $[C, \alpha ] = [C, \alpha , \alpha ] = [A \cap C, \alpha ] = 1$
. Hence,
$[C, \alpha ] = [C, \alpha , \alpha ] = [A \cap C, \alpha ] = 1$
. Hence,
![]() $C \le C_S (\alpha ) = Z(A)B = C_S(A)$
.
$C \le C_S (\alpha ) = Z(A)B = C_S(A)$
.
We need the following definition in order to state the next proposition.
Definition 2.16. A nonabelian finite simple group G is said to be a Goldschmidt group provided that one of the following holds:
-
(1) G has an abelian Sylow
 $2$
-subgroup.
$2$
-subgroup. -
(2) G is isomorphic to a finite simple group of Lie type in characteristic
 $2$
of Lie rank
$2$
of Lie rank
 $1$
.
$1$
.
Proposition 2.17. Let G be a finite group, and let S be a Sylow
![]() $2$
-subgroup of G. Assume that, for each
$2$
-subgroup of G. Assume that, for each
![]() $2$
-component L of G, the factor group
$2$
-component L of G, the factor group
![]() $L/Z^{*}(L)$
is a known finite simple group. Let
$L/Z^{*}(L)$
is a known finite simple group. Let
![]() $\mathfrak {L}_{2'}$
denote the set of
$\mathfrak {L}_{2'}$
denote the set of
![]() $2$
-components L of G such that
$2$
-components L of G such that
![]() $L/Z^{*}(L)$
is not a Goldschmidt group. Then the following hold:
$L/Z^{*}(L)$
is not a Goldschmidt group. Then the following hold:
-
(i) Let L be a
 $2$
-component of G. Then
$2$
-component of G. Then
 $\mathcal {F}_{S \cap L}(L)$
is a component of
$\mathcal {F}_{S \cap L}(L)$
is a component of
 $\mathcal {F}_S(G)$
if and only if
$\mathcal {F}_S(G)$
if and only if
 $L \in \mathfrak {L}_{2'}$
.
$L \in \mathfrak {L}_{2'}$
. -
(ii) The map from
 $\mathfrak {L}_{2'}$
to the set of components of
$\mathfrak {L}_{2'}$
to the set of components of
 $\mathcal {F}_S(G)$
sending each element L of
$\mathcal {F}_S(G)$
sending each element L of
 $\mathfrak {L}_{2'}$
to
$\mathfrak {L}_{2'}$
to
 $\mathcal {F}_{S \cap L}(L)$
is a bijection.
$\mathcal {F}_{S \cap L}(L)$
is a bijection.
Proof. Let L be a
![]() $2$
-component of G. Set
$2$
-component of G. Set
![]() $\mathcal {G} := \mathcal {F}_{S \cap L}(L)$
. Since L is subnormal in G, we have that
$\mathcal {G} := \mathcal {F}_{S \cap L}(L)$
. Since L is subnormal in G, we have that
![]() $\mathcal {G}$
is subnormal in
$\mathcal {G}$
is subnormal in
![]() $\mathcal {F}_S(G)$
(see [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 6.2]). Therefore,
$\mathcal {F}_S(G)$
(see [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 6.2]). Therefore,
![]() $\mathcal {G}$
is a component of
$\mathcal {G}$
is a component of
![]() $\mathcal {F}_S(G)$
if and only if
$\mathcal {F}_S(G)$
if and only if
![]() $\mathcal {G}$
is quasisimple. We have
$\mathcal {G}$
is quasisimple. We have
![]() $\mathfrak {foc}(\mathcal {G}) = S \cap L' = S \cap L$
by the focal subgroup theorem [Reference Gorenstein23, Chapter 7, Theorem 3.4], and so
$\mathfrak {foc}(\mathcal {G}) = S \cap L' = S \cap L$
by the focal subgroup theorem [Reference Gorenstein23, Chapter 7, Theorem 3.4], and so
![]() $\mathcal {G}$
is quasisimple if and only if
$\mathcal {G}$
is quasisimple if and only if
![]() $\mathcal {G}/Z(\mathcal {G})$
is simple. By Lemma 2.13, we have
$\mathcal {G}/Z(\mathcal {G})$
is simple. By Lemma 2.13, we have
![]() $Z(\mathcal {G}) = S \cap Z^{*}(L)$
. Lemma 2.11 implies that
$Z(\mathcal {G}) = S \cap Z^{*}(L)$
. Lemma 2.11 implies that
![]() $\mathcal {G}/Z(\mathcal {G})$
is isomorphic to the
$\mathcal {G}/Z(\mathcal {G})$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $L/Z^{*}(L)$
. By [Reference Aschbacher9, Theorem 5.6.18], the
$L/Z^{*}(L)$
. By [Reference Aschbacher9, Theorem 5.6.18], the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $L/Z^{*}(L)$
is simple if and only if
$L/Z^{*}(L)$
is simple if and only if
![]() $L \in \mathfrak {L}_{2'}$
. So
$L \in \mathfrak {L}_{2'}$
. So
![]() $\mathcal {G}$
is a component of
$\mathcal {G}$
is a component of
![]() $\mathcal {F}_S(G)$
if and only if
$\mathcal {F}_S(G)$
if and only if
![]() $L \in \mathfrak {L}_{2'}$
, and (i) holds.
$L \in \mathfrak {L}_{2'}$
, and (i) holds.
(ii) follows from [Reference Aschbacher8, (1.8)].
Lemma 2.18. Let G be a finite group with
![]() $O(G) = 1$
, and let S be a Sylow
$O(G) = 1$
, and let S be a Sylow
![]() $2$
-subgroup of G. Let
$2$
-subgroup of G. Let
![]() $n \ge 1$
be a natural number, and let
$n \ge 1$
be a natural number, and let
![]() $L_1, \dots , L_n$
be pairwise distinct subgroups of G such that
$L_1, \dots , L_n$
be pairwise distinct subgroups of G such that
![]() $L_i$
is either a component or a solvable
$L_i$
is either a component or a solvable
![]() $2$
-component of G for each
$2$
-component of G for each
![]() $1 \le i \le n$
. Set
$1 \le i \le n$
. Set
![]() $Q := (S \cap L_1)\cdots (S \cap L_n)$
. Assume that Q is strongly closed in S with respect to
$Q := (S \cap L_1)\cdots (S \cap L_n)$
. Assume that Q is strongly closed in S with respect to
![]() $\mathcal {F}_S(G)$
and that
$\mathcal {F}_S(G)$
and that
![]() $\mathcal {F}_S(G)/Q$
is nilpotent. Then, if
$\mathcal {F}_S(G)/Q$
is nilpotent. Then, if
![]() $L_0$
is a component or a solvable
$L_0$
is a component or a solvable
![]() $2$
-component of G, we have
$2$
-component of G, we have
![]() $L_0 = L_i$
for some
$L_0 = L_i$
for some
![]() $1 \le i \le n$
.
$1 \le i \le n$
.
Proof. Let
![]() $L^s(G)$
denote the subgroup of G generated by the components and the solvable
$L^s(G)$
denote the subgroup of G generated by the components and the solvable
![]() $2$
-components of G. By [Reference Kurzweil and Stellmacher37, 6.5.2] and [Reference Gorenstein, Lyons and Solomon27, Proposition 13.5],
$2$
-components of G. By [Reference Kurzweil and Stellmacher37, 6.5.2] and [Reference Gorenstein, Lyons and Solomon27, Proposition 13.5],
![]() $L^s(G)$
is the central product of the subgroups of G which are components or solvable
$L^s(G)$
is the central product of the subgroups of G which are components or solvable
![]() $2$
-components. Set
$2$
-components. Set
![]() $L := L_1 \cdots L_n \trianglelefteq L^s(G)$
.
$L := L_1 \cdots L_n \trianglelefteq L^s(G)$
.
Let
![]() $\mathcal {G} := \mathcal {F}_{S \cap L^s(G)}(L^s(G))$
. Clearly,
$\mathcal {G} := \mathcal {F}_{S \cap L^s(G)}(L^s(G))$
. Clearly,
![]() $S \cap L = (S \cap L_1) \cdots (S \cap L_n) = Q$
. Lemma 2.11 implies that the
$S \cap L = (S \cap L_1) \cdots (S \cap L_n) = Q$
. Lemma 2.11 implies that the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $L^s(G)/L$
is isomorphic to
$L^s(G)/L$
is isomorphic to
![]() $\mathcal {G}/Q$
. By hypothesis,
$\mathcal {G}/Q$
. By hypothesis,
![]() $\mathcal {F}_S(G)/Q$
is nilpotent, and so
$\mathcal {F}_S(G)/Q$
is nilpotent, and so
![]() $\mathcal {G}/Q$
is nilpotent. So the
$\mathcal {G}/Q$
is nilpotent. So the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $L^s(G)/L$
is nilpotent. Applying [Reference Linckelmann39, Theorem 1.4], we conclude that
$L^s(G)/L$
is nilpotent. Applying [Reference Linckelmann39, Theorem 1.4], we conclude that
![]() $L^s(G)/L$
is
$L^s(G)/L$
is
![]() $2$
-nilpotent.
$2$
-nilpotent.
Suppose
![]() $L_0 \ne L_i$
for any
$L_0 \ne L_i$
for any
![]() $1 \le i \le n$
. Then from paragraph one,
$1 \le i \le n$
. Then from paragraph one,
![]() $L_0$
centralizes L, so
$L_0$
centralizes L, so
![]() $L \cap L_0 \le Z(L_0)$
, and hence,
$L \cap L_0 \le Z(L_0)$
, and hence,
![]() $L_0 L/L \cong L_0 /(L \cap L_0)$
is quasisimple,
$L_0 L/L \cong L_0 /(L \cap L_0)$
is quasisimple,
![]() $A_4$
, or
$A_4$
, or
![]() $SL_2(3)$
. In particular,
$SL_2(3)$
. In particular,
![]() $L_0L/L$
is not
$L_0L/L$
is not
![]() $2$
-nilpotent, a contradiction.
$2$
-nilpotent, a contradiction.
Corollary 2.19. Let G be a finite group, and let S be a Sylow
![]() $2$
-subgroup of G. Let
$2$
-subgroup of G. Let
![]() $n \ge 1$
be a natural number, and let
$n \ge 1$
be a natural number, and let
![]() $L_1, \dots , L_n$
be pairwise distinct
$L_1, \dots , L_n$
be pairwise distinct
![]() $2$
-components of G. Assume that
$2$
-components of G. Assume that
![]() $Q := (S \cap L_1)\cdots (S \cap L_n)$
is strongly closed in S with respect to
$Q := (S \cap L_1)\cdots (S \cap L_n)$
is strongly closed in S with respect to
![]() $\mathcal {F}_S(G)$
and that
$\mathcal {F}_S(G)$
and that
![]() $\mathcal {F}_S(G)/Q$
is nilpotent. Then, if
$\mathcal {F}_S(G)/Q$
is nilpotent. Then, if
![]() $L_0$
is a
$L_0$
is a
![]() $2$
-component of G, we have
$2$
-component of G, we have
![]() $L_0 = L_i$
for some
$L_0 = L_i$
for some
![]() $1 \le i \le n$
.
$1 \le i \le n$
.
Proposition 2.20. Let p be a prime, and let
![]() $\mathcal {E}$
be a simple saturated fusion system on a finite p-group T. Suppose that
$\mathcal {E}$
be a simple saturated fusion system on a finite p-group T. Suppose that
![]() $\mathcal {E}$
is tamely realized (in the sense of [Reference Andersen, Oliver and Ventura3, Section 2.2]) by a nonabelian known finite simple group K such that
$\mathcal {E}$
is tamely realized (in the sense of [Reference Andersen, Oliver and Ventura3, Section 2.2]) by a nonabelian known finite simple group K such that
![]() $\mathrm {Out}(K)$
is p-nilpotent. Assume moreover that G is a nonabelian finite simple group containing a Sylow p-subgroup S of G with
$\mathrm {Out}(K)$
is p-nilpotent. Assume moreover that G is a nonabelian finite simple group containing a Sylow p-subgroup S of G with
![]() $T \le S$
such that
$T \le S$
such that
![]() $\mathcal {E} \trianglelefteq \mathcal {F}_S(G)$
and
$\mathcal {E} \trianglelefteq \mathcal {F}_S(G)$
and
![]() $C_S(\mathcal {E}) = 1$
. Then
$C_S(\mathcal {E}) = 1$
. Then
![]() $\mathcal {F}_S(G)$
is tamely realized by a subgroup L of
$\mathcal {F}_S(G)$
is tamely realized by a subgroup L of
![]() $\mathrm {Aut}(K)$
containing
$\mathrm {Aut}(K)$
containing
![]() $\mathrm {Inn}(K)$
such that the index of
$\mathrm {Inn}(K)$
such that the index of
![]() $\mathrm {Inn}(K)$
in L is coprime to p.
$\mathrm {Inn}(K)$
in L is coprime to p.
Proof. Set
![]() $\mathcal {F} := \mathcal {F}_S(G)$
. By a result of Bob Oliver, namely by [Reference Oliver44, Corollary 2.4],
$\mathcal {F} := \mathcal {F}_S(G)$
. By a result of Bob Oliver, namely by [Reference Oliver44, Corollary 2.4],
![]() $\mathcal {F}$
is tamely realized by a subgroup L of
$\mathcal {F}$
is tamely realized by a subgroup L of
![]() $\mathrm {Aut}(K)$
containing
$\mathrm {Aut}(K)$
containing
![]() $\mathrm {Inn}(K)$
. We are going to show that the index of
$\mathrm {Inn}(K)$
. We are going to show that the index of
![]() $\mathrm {Inn}(K)$
in L is coprime to p.
$\mathrm {Inn}(K)$
in L is coprime to p.
Let
![]() $S_0$
be a Sylow p-subgroup of L. Then
$S_0$
be a Sylow p-subgroup of L. Then
![]() $\mathcal {F} \cong \mathcal {F}_{S_0}(L)$
. We have
$\mathcal {F} \cong \mathcal {F}_{S_0}(L)$
. We have
![]() $O^p(G) = G$
since G is nonabelian simple, and so
$O^p(G) = G$
since G is nonabelian simple, and so
![]() $\mathfrak {hnp}(\mathcal {F}) = S$
by the hyperfocal subgroup theorem [Reference Craven18, Theorem 1.33]. It follows that
$\mathfrak {hnp}(\mathcal {F}) = S$
by the hyperfocal subgroup theorem [Reference Craven18, Theorem 1.33]. It follows that
![]() $\mathfrak {hnp}(\mathcal {F}_{S_0}(L)) = S_0$
.
$\mathfrak {hnp}(\mathcal {F}_{S_0}(L)) = S_0$
.
By the hyperfocal subgroup theorem [Reference Craven18, Theorem 1.33],
![]() $S_0 = \mathfrak {hnp}(\mathcal {F}_{S_0}(L)) = O^p(L) \cap S_0$
. Consequently,
$S_0 = \mathfrak {hnp}(\mathcal {F}_{S_0}(L)) = O^p(L) \cap S_0$
. Consequently,
![]() $O^p(L)$
has
$O^p(L)$
has
![]() $p'$
-index in L, whence
$p'$
-index in L, whence
![]() $O^p(L) = L$
. So we have
$O^p(L) = L$
. So we have
![]() $O^p(L/\mathrm {Inn}(K)) = L/\mathrm {Inn}(K)$
. On the other hand,
$O^p(L/\mathrm {Inn}(K)) = L/\mathrm {Inn}(K)$
. On the other hand,
![]() $L/\mathrm {Inn}(K)$
is p-nilpotent since
$L/\mathrm {Inn}(K)$
is p-nilpotent since
![]() $\mathrm {Out}(K)$
is p-nilpotent. It follows that
$\mathrm {Out}(K)$
is p-nilpotent. It follows that
![]() $L/\mathrm {Inn}(K)$
is a
$L/\mathrm {Inn}(K)$
is a
![]() $p'$
-group, as claimed.
$p'$
-group, as claimed.
3 Auxiliary results on linear and unitary groups
In this section, we collect several results on linear and unitary groups needed for the proofs of our main results. Some of the results stated here are known, while others seem to be new. For the convenience of the reader, we also include proofs of known results when we could not find a reference in which they appear in the form stated here.
3.1 Basic definitions
We begin with some basic definitions. Let q be a nontrivial prime power, and let n be a positive integer. The general linear group
![]() $GL_n(q)$
is the group of all invertible
$GL_n(q)$
is the group of all invertible
![]() $n \times n$
matrices over
$n \times n$
matrices over
![]() $\mathbb {F}_q$
under matrix multiplication. The special linear group
$\mathbb {F}_q$
under matrix multiplication. The special linear group
![]() $SL_n(q)$
is the subgroup of
$SL_n(q)$
is the subgroup of
![]() $GL_n(q)$
consisting of all
$GL_n(q)$
consisting of all
![]() $n \times n$
matrices over
$n \times n$
matrices over
![]() $\mathbb {F}_q$
with determinant
$\mathbb {F}_q$
with determinant
![]() $1$
. The center of
$1$
. The center of
![]() $GL_n(q)$
consists of all scalar matrices
$GL_n(q)$
consists of all scalar matrices
![]() $\lambda I_n$
with
$\lambda I_n$
with
![]() $\lambda \in (\mathbb {F}_q)^{*}$
. We have
$\lambda \in (\mathbb {F}_q)^{*}$
. We have
![]() $Z(SL_n(q)) = SL_n(q) \cap Z(GL_n(q))$
. Set
$Z(SL_n(q)) = SL_n(q) \cap Z(GL_n(q))$
. Set
![]() $PGL_n(q) := GL_n(q)/Z(GL_n(q))$
and
$PGL_n(q) := GL_n(q)/Z(GL_n(q))$
and
![]() $PSL_n(q) := SL_n(q)/Z(SL_n(q))$
. By [Reference Huppert and Endliche Gruppen35, Kapitel II, Satz 6.10] and [Reference Huppert and Endliche Gruppen35, Kapitel II, Hauptsatz 6.13],
$PSL_n(q) := SL_n(q)/Z(SL_n(q))$
. By [Reference Huppert and Endliche Gruppen35, Kapitel II, Satz 6.10] and [Reference Huppert and Endliche Gruppen35, Kapitel II, Hauptsatz 6.13],
![]() $SL_n(q)$
is quasisimple if
$SL_n(q)$
is quasisimple if
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $(n,q) \ne (2,2),(2,3)$
.
$(n,q) \ne (2,2),(2,3)$
.
As in [Reference Huppert and Endliche Gruppen35, Kapitel II, Bemerkung 10.5 (b)], we consider the general unitary group
![]() $GU_n(q)$
as the subgroup of
$GU_n(q)$
as the subgroup of
![]() $GL_n(q^2)$
consisting of all
$GL_n(q^2)$
consisting of all
![]() $(a_{ij}) \in GL_n(q^2)$
satisfying the condition
$(a_{ij}) \in GL_n(q^2)$
satisfying the condition
![]() $((a_{ij})^q)(a_{ij})^t = I_n$
. The special unitary group
$((a_{ij})^q)(a_{ij})^t = I_n$
. The special unitary group
![]() $SU_n(q)$
is the subgroup of
$SU_n(q)$
is the subgroup of
![]() $GU_n(q)$
consisting of all elements of
$GU_n(q)$
consisting of all elements of
![]() $GU_n(q)$
with determinant
$GU_n(q)$
with determinant
![]() $1$
. By [Reference Huppert and Endliche Gruppen35, Kapitel II, Hilfssatz 8.8], we have
$1$
. By [Reference Huppert and Endliche Gruppen35, Kapitel II, Hilfssatz 8.8], we have
![]() $SL_2(q) \cong SU_2(q)$
. The center of
$SL_2(q) \cong SU_2(q)$
. The center of
![]() $GU_n(q)$
consists of all scalar matrices
$GU_n(q)$
consists of all scalar matrices
![]() $\lambda I_n$
, where
$\lambda I_n$
, where
![]() $\lambda \in (\mathbb {F}_{q^2})^{*}$
and
$\lambda \in (\mathbb {F}_{q^2})^{*}$
and
![]() $\lambda ^{q+1} = 1$
. We have
$\lambda ^{q+1} = 1$
. We have
![]() $Z(SU_n(q)) = SU_n(q) \cap Z(GU_n(q))$
. Set
$Z(SU_n(q)) = SU_n(q) \cap Z(GU_n(q))$
. Set
![]() $PGU_n(q) := GU_n(q)/Z(GU_n(q))$
and
$PGU_n(q) := GU_n(q)/Z(GU_n(q))$
and
![]() $PSU_n(q) := SU_n(q)/Z(SU_n(q))$
. By [Reference Grove32, Theorems 11.22 and 11.26],
$PSU_n(q) := SU_n(q)/Z(SU_n(q))$
. By [Reference Grove32, Theorems 11.22 and 11.26],
![]() $SU_n(q)$
is quasisimple if
$SU_n(q)$
is quasisimple if
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $(n,q) \ne (2,2),(2,3),(3,2)$
.
$(n,q) \ne (2,2),(2,3),(3,2)$
.
We write
![]() $(P)GL_n^{+}(q)$
and
$(P)GL_n^{+}(q)$
and
![]() $(P)SL_n^{+}(q)$
for
$(P)SL_n^{+}(q)$
for
![]() $(P)GL_n(q)$
and
$(P)GL_n(q)$
and
![]() $(P)SL_n(q)$
, respectively. Also, we write
$(P)SL_n(q)$
, respectively. Also, we write
![]() $(P)GL_n^{-}(q)$
for
$(P)GL_n^{-}(q)$
for
![]() $(P)GU_n(q)$
and
$(P)GU_n(q)$
and
![]() $(P)SL_n^{-}(q)$
for
$(P)SL_n^{-}(q)$
for
![]() $PSU_n(q)$
.
$PSU_n(q)$
.
3.2 Central extensions of
 $PSL_n(q)$
and
$PSL_n(q)$
and
 $PSU_n(q)$
$PSU_n(q)$
In the proofs of the following two lemmas, we use the terminology of [Reference Aschbacher5, Section 33].
Lemma 3.1. Let
![]() $n \ge 3$
be a natural number, and let q be a nontrivial odd prime power. Let H be a perfect central extension of
$n \ge 3$
be a natural number, and let q be a nontrivial odd prime power. Let H be a perfect central extension of
![]() $PSL_n(q)$
. Then there is a subgroup
$PSL_n(q)$
. Then there is a subgroup
![]() $Z \le Z(SL_n(q))$
such that
$Z \le Z(SL_n(q))$
such that
![]() $H \cong SL_n(q)/Z$
.
$H \cong SL_n(q)/Z$
.
Proof. By [Reference Gorenstein, Lyons and Solomon28, pp. 312-313], the Schur multiplier of
![]() $PSL_n(q)$
is isomorphic to
$PSL_n(q)$
is isomorphic to
![]() $C_{(n,q-1)} \cong Z(SL_n(q))$
. From [Reference Aschbacher5, 33.6], we see that this is just another way to say that
$C_{(n,q-1)} \cong Z(SL_n(q))$
. From [Reference Aschbacher5, 33.6], we see that this is just another way to say that
![]() $SL_n(q)$
is the universal covering group of
$SL_n(q)$
is the universal covering group of
![]() $PSL_n(q)$
. Applying [Reference Aschbacher5, 33.6] again, we conclude that
$PSL_n(q)$
. Applying [Reference Aschbacher5, 33.6] again, we conclude that
![]() $H \cong SL_n(q)/Z$
for some
$H \cong SL_n(q)/Z$
for some
![]() $Z \le Z(SL_n(q))$
.
$Z \le Z(SL_n(q))$
.
Lemma 3.2. Let
![]() $n \ge 3$
be a natural number, and let q be a nontrivial odd prime power. Let H be a perfect central extension of
$n \ge 3$
be a natural number, and let q be a nontrivial odd prime power. Let H be a perfect central extension of
![]() $PSU_n(q)$
. Assume that
$PSU_n(q)$
. Assume that
![]() $(n,q) \ne (4,3)$
or that
$(n,q) \ne (4,3)$
or that
![]() $Z(H)$
is a
$Z(H)$
is a
![]() $2$
-group. Then there is a subgroup
$2$
-group. Then there is a subgroup
![]() $Z \le Z(SU_n(q))$
such that
$Z \le Z(SU_n(q))$
such that
![]() $H \cong SU_n(q)/Z$
.
$H \cong SU_n(q)/Z$
.
Proof. Suppose that
![]() $(n,q) \ne (4,3)$
. By [Reference Gorenstein, Lyons and Solomon28, pp. 312-313], the Schur multiplier of
$(n,q) \ne (4,3)$
. By [Reference Gorenstein, Lyons and Solomon28, pp. 312-313], the Schur multiplier of
![]() $PSU_n(q)$
is isomorphic to
$PSU_n(q)$
is isomorphic to
![]() $C_{(n,q+1)} \cong Z(SU_n(q))$
. As in the proof of Lemma 3.1, we conclude that
$C_{(n,q+1)} \cong Z(SU_n(q))$
. As in the proof of Lemma 3.1, we conclude that
![]() $H \cong SU_n(q)/Z$
for some
$H \cong SU_n(q)/Z$
for some
![]() $Z \le Z(SU_n(q))$
.
$Z \le Z(SU_n(q))$
.
Suppose now that
![]() $(n,q)=(4,3)$
and that
$(n,q)=(4,3)$
and that
![]() $Z(H)$
is a
$Z(H)$
is a
![]() $2$
-group. Let
$2$
-group. Let
![]() $G := PSU_4(3)$
, and let
$G := PSU_4(3)$
, and let
![]() $\widetilde G$
be the universal covering group of G. Then the Schur multiplier of G is isomorphic to
$\widetilde G$
be the universal covering group of G. Then the Schur multiplier of G is isomorphic to
![]() $Z(\widetilde G)$
. By [Reference Gorenstein, Lyons and Solomon28, pp. 312-313], the Schur multiplier of G is isomorphic to
$Z(\widetilde G)$
. By [Reference Gorenstein, Lyons and Solomon28, pp. 312-313], the Schur multiplier of G is isomorphic to
![]() $C_4 \times C_3 \times C_3$
. Thus,
$C_4 \times C_3 \times C_3$
. Thus,
![]() $Z(\widetilde G) \cong C_4 \times C_3 \times C_3$
. Since
$Z(\widetilde G) \cong C_4 \times C_3 \times C_3$
. Since
![]() $\widetilde G$
is quasisimple, we have
$\widetilde G$
is quasisimple, we have
![]() $Z(\widetilde G / Z) = Z(\widetilde G)/Z$
whenever
$Z(\widetilde G / Z) = Z(\widetilde G)/Z$
whenever
![]() $Z \le Z(\widetilde G)$
. Let Q be the unique Sylow
$Z \le Z(\widetilde G)$
. Let Q be the unique Sylow
![]() $3$
-subgroup of
$3$
-subgroup of
![]() $Z(\widetilde G)$
. By [Reference Aschbacher5, 33.6],
$Z(\widetilde G)$
. By [Reference Aschbacher5, 33.6],
![]() $\widetilde G$
is a central extension of
$\widetilde G$
is a central extension of
![]() $SU_4(3)$
and of H. Since
$SU_4(3)$
and of H. Since
![]() $SU_4(3)$
has a center of order
$SU_4(3)$
has a center of order
![]() $4$
, we have
$4$
, we have
![]() $SU_4(3) \cong \widetilde G / Q$
. Let
$SU_4(3) \cong \widetilde G / Q$
. Let
![]() $Z \le Z(\widetilde G)$
with
$Z \le Z(\widetilde G)$
with
![]() $H \cong \widetilde G / Z$
. As
$H \cong \widetilde G / Z$
. As
![]() $Z(H)$
is a
$Z(H)$
is a
![]() $2$
-group, we have
$2$
-group, we have
![]() $Q \le Z$
, whence
$Q \le Z$
, whence
![]() $H \cong \widetilde G / Z \cong (\widetilde G / Q) / (Z/Q)$
is isomorphic to a quotient of
$H \cong \widetilde G / Z \cong (\widetilde G / Q) / (Z/Q)$
is isomorphic to a quotient of
![]() $SU_4(3)$
by a central subgroup.
$SU_4(3)$
by a central subgroup.
3.3 Involutions
In this subsection, we collect several results on the involutions of the groups
![]() $(P)GL_n^{\varepsilon }(q)$
and
$(P)GL_n^{\varepsilon }(q)$
and
![]() $(P)SL_n^{\varepsilon }(q)$
, where q is a nontrivial odd prime power,
$(P)SL_n^{\varepsilon }(q)$
, where q is a nontrivial odd prime power,
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $\varepsilon \in \lbrace +,- \rbrace $
.
$\varepsilon \in \lbrace +,- \rbrace $
.
Lemma 3.3. Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
. Let T be an element of
$n \ge 2$
. Let T be an element of
![]() $GL_n(q)$
such that
$GL_n(q)$
such that
![]() $T^2 = \lambda I_n$
for some
$T^2 = \lambda I_n$
for some
![]() $\lambda \in \mathbb {F}_q^{*}$
. Then one of the following holds:
$\lambda \in \mathbb {F}_q^{*}$
. Then one of the following holds:
-
(i) There is some
 $\mu \in \mathbb {F}_q^{*}$
such that
$\mu \in \mathbb {F}_q^{*}$
such that
 $\lambda = \mu ^2$
, and T is
$\lambda = \mu ^2$
, and T is
 $GL_n(q)$
-conjugate to a diagonal matrix with diagonal entries in
$GL_n(q)$
-conjugate to a diagonal matrix with diagonal entries in
 $\lbrace \mu , -\mu \rbrace $
.
$\lbrace \mu , -\mu \rbrace $
. -
(ii) n is even,
 $\lambda $
is a nonsquare element of
$\lambda $
is a nonsquare element of
 $\mathbb {F}_q^{*}$
, and T is
$\mathbb {F}_q^{*}$
, and T is
 $GL_n(q)$
-conjugate to the matrix Moreover, we have
$GL_n(q)$
-conjugate to the matrix Moreover, we have $$ \begin{align*} \begin{pmatrix} & I_{n/2} \ \\ \lambda I_{n/2} & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} & I_{n/2} \ \\ \lambda I_{n/2} & \end{pmatrix}. \end{align*} $$
 $C_{GL_n(q)}(T) \cong GL_{\frac {n}{2}}(q^2)$
.
$C_{GL_n(q)}(T) \cong GL_{\frac {n}{2}}(q^2)$
.
Proof. We identify the field
![]() $\mathbb {F}_q$
with the subfield of
$\mathbb {F}_q$
with the subfield of
![]() $\mathbb {F}_{q^2}$
consisting of all
$\mathbb {F}_{q^2}$
consisting of all
![]() $x \in \mathbb {F}_{q^2}$
satisfying
$x \in \mathbb {F}_{q^2}$
satisfying
![]() $x^q = x$
. As
$x^q = x$
. As
![]() $q + 1 = (q^2 - 1)/(q - 1)$
is even, any element of
$q + 1 = (q^2 - 1)/(q - 1)$
is even, any element of
![]() $\mathbb {F}_q^{*}$
is the square of an element of
$\mathbb {F}_q^{*}$
is the square of an element of
![]() $\mathbb {F}_{q^2}^{*}$
. Let
$\mathbb {F}_{q^2}^{*}$
. Let
![]() $\mu \in \mathbb {F}_{q^2}^{*}$
with
$\mu \in \mathbb {F}_{q^2}^{*}$
with
![]() $\lambda = \mu ^2$
.
$\lambda = \mu ^2$
.
If
![]() $\mu \in \mathbb {F}_q$
, then the minimal polynomial of T divides
$\mu \in \mathbb {F}_q$
, then the minimal polynomial of T divides
![]() $(x - \mu )(x + \mu )$
, so T is diagonalizable over
$(x - \mu )(x + \mu )$
, so T is diagonalizable over
![]() $\mathbb {F}_q$
, and it follows that (i) holds.
$\mathbb {F}_q$
, and it follows that (i) holds.
Assume now that
![]() $\mu \not \in \mathbb {F}_q$
. Then
$\mu \not \in \mathbb {F}_q$
. Then
![]() $\lambda $
is a nonsquare element of
$\lambda $
is a nonsquare element of
![]() $\mathbb {F}_q^{*}$
. Let V be an n-dimensional vector space over
$\mathbb {F}_q^{*}$
. Let V be an n-dimensional vector space over
![]() $\mathbb {F}_q$
, and let B be an ordered basis of V. Let
$\mathbb {F}_q$
, and let B be an ordered basis of V. Let
![]() $\varphi $
be the element of
$\varphi $
be the element of
![]() $GL(V)$
such that
$GL(V)$
such that
![]() $\varphi $
is represented by T with respect to B. Since
$\varphi $
is represented by T with respect to B. Since
![]() $\mu \not \in \mathbb {F}_q$
, we have that
$\mu \not \in \mathbb {F}_q$
, we have that
![]() $1$
and
$1$
and
![]() $\mu $
are linearly independent; so
$\mu $
are linearly independent; so
![]() $(1,\mu )$
is an
$(1,\mu )$
is an
![]() $\mathbb {F}_q$
-basis of
$\mathbb {F}_q$
-basis of
![]() $\mathbb {F}_{q^2}$
. Using that
$\mathbb {F}_{q^2}$
. Using that
![]() $\varphi ^2 = \lambda \mathrm {id}_V$
, one can check that V becomes a vector space over
$\varphi ^2 = \lambda \mathrm {id}_V$
, one can check that V becomes a vector space over
![]() $\mathbb {F}_{q^2}$
by defining
$\mathbb {F}_{q^2}$
by defining
for all
![]() $x,y \in \mathbb {F}_q$
and
$x,y \in \mathbb {F}_q$
and
![]() $v \in V$
. Let m be the dimension of V over
$v \in V$
. Let m be the dimension of V over
![]() $\mathbb {F}_{q^2}$
, and let
$\mathbb {F}_{q^2}$
, and let
![]() $(v_1,\dots ,v_m)$
be an
$(v_1,\dots ,v_m)$
be an
![]() $\mathbb {F}_{q^2}$
-basis of V. Then
$\mathbb {F}_{q^2}$
-basis of V. Then
![]() $B_0 := (v_1,\dots ,v_m,\mu v_1, \dots , \mu v_m)$
is an
$B_0 := (v_1,\dots ,v_m,\mu v_1, \dots , \mu v_m)$
is an
![]() $\mathbb {F}_q$
-basis of V. In particular,
$\mathbb {F}_q$
-basis of V. In particular,
![]() $n = 2m$
is even. For
$n = 2m$
is even. For
![]() $1 \le i \le m$
, we have
$1 \le i \le m$
, we have
![]() $v_i^{\varphi } = \mu v_i$
and
$v_i^{\varphi } = \mu v_i$
and
![]() $(\mu v_i)^{\varphi } = (v_i)^{\varphi ^2} = \lambda v_i$
. So, with respect to
$(\mu v_i)^{\varphi } = (v_i)^{\varphi ^2} = \lambda v_i$
. So, with respect to
![]() $B_0$
,
$B_0$
,
![]() $\varphi $
is represented by the matrix
$\varphi $
is represented by the matrix
 $$ \begin{align*} M := \begin{pmatrix} & I_{n/2} \ \\ \lambda I_{n/2} & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} M := \begin{pmatrix} & I_{n/2} \ \\ \lambda I_{n/2} & \end{pmatrix}. \end{align*} $$
It follows that T and M are
![]() $GL_n(q)$
-conjugate.
$GL_n(q)$
-conjugate.
Let
![]() $\psi $
be an automorphism of V as an
$\psi $
be an automorphism of V as an
![]() $\mathbb {F}_q$
-vector space centralizing
$\mathbb {F}_q$
-vector space centralizing
![]() $\varphi $
. For
$\varphi $
. For
![]() $x,y \in \mathbb {F}_q$
and
$x,y \in \mathbb {F}_q$
and
![]() $v \in V$
, we have
$v \in V$
, we have
whence
![]() $\psi $
is
$\psi $
is
![]() $\mathbb {F}_{q^2}$
-linear. Conversely, if
$\mathbb {F}_{q^2}$
-linear. Conversely, if
![]() $\psi $
is
$\psi $
is
![]() $\mathbb {F}_{q^2}$
-linear, then
$\mathbb {F}_{q^2}$
-linear, then
and hence
![]() $\psi \varphi = \varphi \psi $
. It follows that the centralizer of
$\psi \varphi = \varphi \psi $
. It follows that the centralizer of
![]() $\varphi $
in the general linear group of V as an
$\varphi $
in the general linear group of V as an
![]() $\mathbb {F}_q$
-vector space is equal to the general linear group of V as an
$\mathbb {F}_q$
-vector space is equal to the general linear group of V as an
![]() $\mathbb {F}_{q^2}$
-vector space. Thus,
$\mathbb {F}_{q^2}$
-vector space. Thus,
![]() $C_{GL_n(q)}(T) \cong GL_{\frac {n}{2}}(q^2)$
. So (ii) holds.
$C_{GL_n(q)}(T) \cong GL_{\frac {n}{2}}(q^2)$
. So (ii) holds.
Lemma 3.4. Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number. Let
$n \ge 2$
be a natural number. Let
![]() $T \in GU_n(q)$
.
$T \in GU_n(q)$
.
-
(i) If
 $T^2 = \lambda I_n$
for some
$T^2 = \lambda I_n$
for some
 $\lambda \in \mathbb {F}_{q^2}^{*}$
, then
$\lambda \in \mathbb {F}_{q^2}^{*}$
, then
 $\lambda $
is a square in
$\lambda $
is a square in
 $\mathbb {F}_{q^2}^{*}$
.
$\mathbb {F}_{q^2}^{*}$
. -
(ii) If
 $T^2 = \rho ^2 I_n$
for some
$T^2 = \rho ^2 I_n$
for some
 $\rho \in \mathbb {F}_{q^2}^{*}$
with
$\rho \in \mathbb {F}_{q^2}^{*}$
with
 $\rho ^{q+1} = 1$
, then T is
$\rho ^{q+1} = 1$
, then T is
 $GU_n(q)$
-conjugate to a diagonal matrix with diagonal entries in
$GU_n(q)$
-conjugate to a diagonal matrix with diagonal entries in
 $\lbrace \rho ,-\rho \rbrace $
.
$\lbrace \rho ,-\rho \rbrace $
. -
(iii) If
 $T^2 = \rho ^2 I_n$
for some
$T^2 = \rho ^2 I_n$
for some
 $\rho \in \mathbb {F}_{q^2}^{*}$
with
$\rho \in \mathbb {F}_{q^2}^{*}$
with
 $\rho ^{q+1} \ne 1$
, then n is even, and we have
$\rho ^{q+1} \ne 1$
, then n is even, and we have
 $C_{GU_n(q)}(T) \cong GL_{\frac {n}{2}}(q^2)$
.
$C_{GU_n(q)}(T) \cong GL_{\frac {n}{2}}(q^2)$
.
Proof. Suppose that
![]() $T^2 = \lambda I_n$
for some
$T^2 = \lambda I_n$
for some
![]() $\lambda \in \mathbb {F}_{q^2}^{*}$
. Since
$\lambda \in \mathbb {F}_{q^2}^{*}$
. Since
![]() $T^2 \in GU_n(q)$
, we have that
$T^2 \in GU_n(q)$
, we have that
![]() $\lambda ^{q+1} = 1$
, so
$\lambda ^{q+1} = 1$
, so
![]() $\lambda $
is a square in
$\lambda $
is a square in
![]() $\mathbb {F}_{q^2}^{*}$
.
$\mathbb {F}_{q^2}^{*}$
.
A proof of (ii) and (iii) can be extracted from [Reference Phan47, pp. 314-315].
Proposition 3.5. Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number. Let
$n \ge 2$
be a natural number. Let
![]() $\rho $
be an element of
$\rho $
be an element of
![]() $\mathbb {F}_q^{*}$
of order
$\mathbb {F}_q^{*}$
of order
![]() $(n,q-1)$
. For each even natural number i with
$(n,q-1)$
. For each even natural number i with
![]() $2 \le i < n$
, let
$2 \le i < n$
, let
 $$ \begin{align*} \widetilde{t_i} := \begin{pmatrix} I_{n-i} & \\ & -I_i \end{pmatrix} \in SL_n(q) \end{align*} $$
$$ \begin{align*} \widetilde{t_i} := \begin{pmatrix} I_{n-i} & \\ & -I_i \end{pmatrix} \in SL_n(q) \end{align*} $$
and let
![]() $t_i$
be the image of
$t_i$
be the image of
![]() $\widetilde {t_i}$
in
$\widetilde {t_i}$
in
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
-
(i) Assume that n is odd. Then each involution of
 $PSL_n(q)$
is
$PSL_n(q)$
is
 $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
 $t_i$
for some even
$t_i$
for some even
 $2 \le i < n$
.
$2 \le i < n$
. -
(ii) Assume that n is even and that there is some
 $\mu \in \mathbb {F}_q^{*}$
with
$\mu \in \mathbb {F}_q^{*}$
with
 $\rho = \mu ^2$
. For each odd natural number i with
$\rho = \mu ^2$
. For each odd natural number i with
 $1 \le i < n$
, the matrix lies in
$1 \le i < n$
, the matrix lies in $$ \begin{align*} \widetilde{t_i} := \begin{pmatrix} \mu I_{n-i} & \\ & -\mu I_i \end{pmatrix} \end{align*} $$
$$ \begin{align*} \widetilde{t_i} := \begin{pmatrix} \mu I_{n-i} & \\ & -\mu I_i \end{pmatrix} \end{align*} $$
 $SL_n(q)$
. Let
$SL_n(q)$
. Let
 $t_i$
denote the image of
$t_i$
denote the image of
 $\widetilde {t_i}$
in
$\widetilde {t_i}$
in
 $PSL_n(q)$
for each odd
$PSL_n(q)$
for each odd
 $1 \le i < n$
. Then each involution of
$1 \le i < n$
. Then each involution of
 $PSL_n(q)$
is
$PSL_n(q)$
is
 $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
 $t_i$
for some (even or odd)
$t_i$
for some (even or odd)
 $1 \le i \le \frac {n}{2}$
.
$1 \le i \le \frac {n}{2}$
.
-
(iii) Assume that n is even and that
 $\rho $
is a nonsquare element of
$\rho $
is a nonsquare element of
 $\mathbb {F}_q$
. Let If
$\mathbb {F}_q$
. Let If $$ \begin{align*} \widetilde w := \begin{pmatrix} & I_{n/2} \ \\ \rho I_{n/2} & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \widetilde w := \begin{pmatrix} & I_{n/2} \ \\ \rho I_{n/2} & \end{pmatrix}. \end{align*} $$
 $\widetilde w \in SL_n(q)$
, then each involution of
$\widetilde w \in SL_n(q)$
, then each involution of
 $PSL_n(q)$
is
$PSL_n(q)$
is
 $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
 $t_i$
for some even
$t_i$
for some even
 $2 \le i \le \frac {n}{2}$
or to
$2 \le i \le \frac {n}{2}$
or to
 $w := \widetilde {w} Z(SL_n(q)) \in PSL_n(q)$
. If
$w := \widetilde {w} Z(SL_n(q)) \in PSL_n(q)$
. If
 $\widetilde w \not \in SL_n(q)$
, then each involution of
$\widetilde w \not \in SL_n(q)$
, then each involution of
 $PSL_n(q)$
is
$PSL_n(q)$
is
 $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
 $t_i$
for some even
$t_i$
for some even
 $2 \le i \le \frac {n}{2}$
.
$2 \le i \le \frac {n}{2}$
.
Proof. We follow arguments found in the proof of [Reference Phan46, Lemma 1.1].
Assume that n is odd. Then
![]() $Z(SL_n(q))$
has odd order, and therefore, any involution of
$Z(SL_n(q))$
has odd order, and therefore, any involution of
![]() $PSL_n(q)$
is the image of an involution of
$PSL_n(q)$
is the image of an involution of
![]() $SL_n(q)$
. As a consequence of Lemma 3.3, each involution of
$SL_n(q)$
. As a consequence of Lemma 3.3, each involution of
![]() $SL_n(q)$
is
$SL_n(q)$
is
![]() $SL_n(q)$
-conjugate to
$SL_n(q)$
-conjugate to
![]() $\widetilde {t_i}$
for some even
$\widetilde {t_i}$
for some even
![]() $2 \le i < n$
. So (i) follows.
$2 \le i < n$
. So (i) follows.
Assume now that n is even and that
![]() $\rho = \mu ^2$
for some
$\rho = \mu ^2$
for some
![]() $\mu \in \mathbb {F}_q^{*}$
. Note that
$\mu \in \mathbb {F}_q^{*}$
. Note that
![]() $Z(SL_n(q))$
equals
$Z(SL_n(q))$
equals
![]() $\langle \rho I_n \rangle $
. We claim that
$\langle \rho I_n \rangle $
. We claim that
![]() $\mu ^n = -1$
. Since
$\mu ^n = -1$
. Since
![]() $\mu ^{2n} = \rho ^n = 1$
, we have that
$\mu ^{2n} = \rho ^n = 1$
, we have that
![]() $\mu ^n = 1$
or
$\mu ^n = 1$
or
![]() $-1$
. If
$-1$
. If
![]() $\mu ^n = 1$
, then
$\mu ^n = 1$
, then
![]() $\mu \in \langle \rho \rangle $
, and so
$\mu \in \langle \rho \rangle $
, and so
![]() $\rho $
is a square in
$\rho $
is a square in
![]() $\langle \rho \rangle $
, which is impossible. So we have
$\langle \rho \rangle $
, which is impossible. So we have
![]() $\mu ^n = -1$
. It follows that
$\mu ^n = -1$
. It follows that
![]() $\widetilde {t_i} \in SL_n(q)$
for each odd
$\widetilde {t_i} \in SL_n(q)$
for each odd
![]() $1 \le i < n$
. Now let
$1 \le i < n$
. Now let
![]() $T \in SL_n(q)$
such that
$T \in SL_n(q)$
such that
![]() $TZ(SL_n(q)) \in PSL_n(q)$
is an involution. Then we have
$TZ(SL_n(q)) \in PSL_n(q)$
is an involution. Then we have
![]() $T^2 = \rho ^{\ell }I_n = \mu ^{2\ell }I_n$
for some
$T^2 = \rho ^{\ell }I_n = \mu ^{2\ell }I_n$
for some
![]() $1 \le \ell \le (n,q-1)$
. Using Lemma 3.3, we conclude that T is
$1 \le \ell \le (n,q-1)$
. Using Lemma 3.3, we conclude that T is
![]() $SL_n(q)$
-conjugate to a diagonal matrix
$SL_n(q)$
-conjugate to a diagonal matrix
![]() $D \in SL_n(q)$
with diagonal entries in
$D \in SL_n(q)$
with diagonal entries in
![]() $\lbrace \mu ^{\ell }, - \mu ^{\ell } \rbrace $
. Let
$\lbrace \mu ^{\ell }, - \mu ^{\ell } \rbrace $
. Let
![]() $1 \le i < n$
such that
$1 \le i < n$
such that
![]() $- \mu ^{\ell }$
occurs precisely i times as a diagonal entry of D. If i is odd, we may assume that
$- \mu ^{\ell }$
occurs precisely i times as a diagonal entry of D. If i is odd, we may assume that
![]() $D = \mu ^{\ell -1} \widetilde {t_i}$
, and if i is even, we may assume that
$D = \mu ^{\ell -1} \widetilde {t_i}$
, and if i is even, we may assume that
![]() $D = \mu ^{\ell } \widetilde {t_i}$
. In either case, the image of D in
$D = \mu ^{\ell } \widetilde {t_i}$
. In either case, the image of D in
![]() $PSL_n(q)$
is
$PSL_n(q)$
is
![]() $t_i$
. Hence,
$t_i$
. Hence,
![]() $TZ(SL_n(q))$
is
$TZ(SL_n(q))$
is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_i$
. Noticing that
$t_i$
. Noticing that
![]() $t_i$
is
$t_i$
is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_{n-i}$
, we conclude that (ii) holds.
$t_{n-i}$
, we conclude that (ii) holds.
Now assume that n is even and that
![]() $\rho $
is a nonsquare element of
$\rho $
is a nonsquare element of
![]() $\mathbb {F}_q$
. Again, let T be an element of
$\mathbb {F}_q$
. Again, let T be an element of
![]() $SL_n(q)$
such that
$SL_n(q)$
such that
![]() $TZ(SL_n(q)) \in PSL_n(q)$
is an involution. We have
$TZ(SL_n(q)) \in PSL_n(q)$
is an involution. We have
![]() $T^2 = \rho ^{\ell }I_n$
for some
$T^2 = \rho ^{\ell }I_n$
for some
![]() $1 \le \ell \le (n,q-1)$
. Assume that
$1 \le \ell \le (n,q-1)$
. Assume that
![]() $\ell $
is even. Then Lemma 3.3 implies that T or
$\ell $
is even. Then Lemma 3.3 implies that T or
![]() $-T$
is
$-T$
is
![]() $SL_n(q)$
-conjugate to
$SL_n(q)$
-conjugate to
![]() $\rho ^{\frac {\ell }{2}}\widetilde {t_i}$
for some even
$\rho ^{\frac {\ell }{2}}\widetilde {t_i}$
for some even
![]() $2 \le i \le \frac {n}{2}$
. It follows that
$2 \le i \le \frac {n}{2}$
. It follows that
![]() $TZ(SL_n(q))$
is
$TZ(SL_n(q))$
is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_i$
for some even
$t_i$
for some even
![]() $2 \le i \le \frac {n}{2}$
. Assume now that
$2 \le i \le \frac {n}{2}$
. Assume now that
![]() $\ell $
is odd. As
$\ell $
is odd. As
![]() $\rho $
is not a square in
$\rho $
is not a square in
![]() $\mathbb {F}_q$
, but
$\mathbb {F}_q$
, but
![]() $\rho ^{\ell -1}$
is a square in
$\rho ^{\ell -1}$
is a square in
![]() $\mathbb {F}_q$
,
$\mathbb {F}_q$
,
![]() $\rho ^{\ell }$
cannot be a square in
$\rho ^{\ell }$
cannot be a square in
![]() $\mathbb {F}_q$
. Using Lemma 3.3, we may conclude that T is
$\mathbb {F}_q$
. Using Lemma 3.3, we may conclude that T is
![]() $GL_n(q)$
-conjugate to the matrix
$GL_n(q)$
-conjugate to the matrix
 $$ \begin{align*} M := \begin{pmatrix} 0 & \rho^{\ell} & & & \\ 1 & 0 & & &\\ & & \ddots & & \\ & & & 0 & \rho^{\ell} \\ & & & 1 & 0 \end{pmatrix} \in SL_n(q). \end{align*} $$
$$ \begin{align*} M := \begin{pmatrix} 0 & \rho^{\ell} & & & \\ 1 & 0 & & &\\ & & \ddots & & \\ & & & 0 & \rho^{\ell} \\ & & & 1 & 0 \end{pmatrix} \in SL_n(q). \end{align*} $$
It is rather easy to see that T and M are even conjugate in
![]() $SL_n(q)$
. Let
$SL_n(q)$
. Let
![]() $k := \frac {\ell -1}{2}$
. It is not hard to show that the matrices
$k := \frac {\ell -1}{2}$
. It is not hard to show that the matrices
 $$ \begin{align*} \begin{pmatrix} 0 & \rho^{\ell} \\ 1 & 0 \end{pmatrix} \ \text{and} \ \begin{pmatrix} 0 & \rho^{k+1} \\ \rho^k & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0 & \rho^{\ell} \\ 1 & 0 \end{pmatrix} \ \text{and} \ \begin{pmatrix} 0 & \rho^{k+1} \\ \rho^k & 0 \end{pmatrix} \end{align*} $$
are
![]() $SL_2(q)$
-conjugate. So it follows that M, and hence, T is
$SL_2(q)$
-conjugate. So it follows that M, and hence, T is
![]() $SL_n(q)$
-conjugate to
$SL_n(q)$
-conjugate to
![]() $\rho ^k M_2$
, where
$\rho ^k M_2$
, where
 $$ \begin{align*} M_2 := \begin{pmatrix} 0 & \rho & & & \\ 1 & 0 & & &\\ & & \ddots & & \\ & & & 0 & \rho \\ & & & 1 & 0 \end{pmatrix} \in SL_n(q). \end{align*} $$
$$ \begin{align*} M_2 := \begin{pmatrix} 0 & \rho & & & \\ 1 & 0 & & &\\ & & \ddots & & \\ & & & 0 & \rho \\ & & & 1 & 0 \end{pmatrix} \in SL_n(q). \end{align*} $$
Consequently, the images of T and
![]() $M_2$
in
$M_2$
in
![]() $PSL_n(q)$
are conjugate. Furthermore, as
$PSL_n(q)$
are conjugate. Furthermore, as
![]() $\mathrm {det}(M_2) = \mathrm {det}(\widetilde w)$
, we see that
$\mathrm {det}(M_2) = \mathrm {det}(\widetilde w)$
, we see that
![]() $\widetilde w \in SL_n(q)$
. Also,
$\widetilde w \in SL_n(q)$
. Also,
![]() $\widetilde w$
is
$\widetilde w$
is
![]() $SL_n(q)$
-conjugate to
$SL_n(q)$
-conjugate to
![]() $M_2$
, and so
$M_2$
, and so
![]() $TZ(SL_n(q))$
is
$TZ(SL_n(q))$
is
![]() $PSL_n(q)$
-conjugate to w.
$PSL_n(q)$
-conjugate to w.
Lemma 3.6. Let q be a nontrivial odd prime power, and let
![]() $n \ge 4$
be an even natural number. Let
$n \ge 4$
be an even natural number. Let
![]() $\rho $
be an element of
$\rho $
be an element of
![]() $\mathbb {F}_q^{*}$
of order
$\mathbb {F}_q^{*}$
of order
![]() $(n,q-1)$
. Suppose that
$(n,q-1)$
. Suppose that
![]() $\rho $
is a nonsquare element of
$\rho $
is a nonsquare element of
![]() $\mathbb {F}_q$
and that
$\mathbb {F}_q$
and that
 $$ \begin{align*} \widetilde w := \begin{pmatrix} & I_{n/2} \\ \rho I_{n/2} & \end{pmatrix} \end{align*} $$
$$ \begin{align*} \widetilde w := \begin{pmatrix} & I_{n/2} \\ \rho I_{n/2} & \end{pmatrix} \end{align*} $$
lies in
![]() $SL_n(q)$
. Denote the image of
$SL_n(q)$
. Denote the image of
![]() $\widetilde w$
in
$\widetilde w$
in
![]() $PSL_n(q)$
by w. Set
$PSL_n(q)$
by w. Set
![]() $C := C_{PSL_n(q)}(w)$
. Let P be a Sylow
$C := C_{PSL_n(q)}(w)$
. Let P be a Sylow
![]() $2$
-subgroup of C. Then the following hold:
$2$
-subgroup of C. Then the following hold:
-
(i) C has a unique
 $2$
-component J, and J is isomorphic to a nontrivial quotient of
$2$
-component J, and J is isomorphic to a nontrivial quotient of
 $SL_{\frac {n}{2}}(q^2)$
.
$SL_{\frac {n}{2}}(q^2)$
. -
(ii)
 $P \cap J$
is strongly closed in P with respect to
$P \cap J$
is strongly closed in P with respect to
 $\mathcal {F}_P(C)$
, and the factor system
$\mathcal {F}_P(C)$
, and the factor system
 $\mathcal {F}_P(C)/(P \cap J)$
is nilpotent.
$\mathcal {F}_P(C)/(P \cap J)$
is nilpotent. -
(iii) If
 $n \ge 6$
, then P has rank at least
$n \ge 6$
, then P has rank at least
 $4$
.
$4$
.
Proof. Set
![]() $C_0 := C_{SL_n(q)}(\widetilde w)/Z(SL_n(q)) \le C$
.
$C_0 := C_{SL_n(q)}(\widetilde w)/Z(SL_n(q)) \le C$
.
Let
![]() $y \in C \setminus C_0$
, and let
$y \in C \setminus C_0$
, and let
![]() $\widetilde y$
be a preimage of y in
$\widetilde y$
be a preimage of y in
![]() $SL_n(q)$
. Then
$SL_n(q)$
. Then
![]() $\widetilde w^{\widetilde y} = \lambda \widetilde w$
for some
$\widetilde w^{\widetilde y} = \lambda \widetilde w$
for some
![]() $1 \ne \lambda \in \langle \rho \rangle $
. The characteristic polynomial of
$1 \ne \lambda \in \langle \rho \rangle $
. The characteristic polynomial of
![]() $\widetilde w$
is
$\widetilde w$
is
![]() $(x^2-\rho )^{\frac {n}{2}}$
, and
$(x^2-\rho )^{\frac {n}{2}}$
, and
![]() $\lambda \widetilde w$
has the characteristic polynomial
$\lambda \widetilde w$
has the characteristic polynomial
![]() $(x^2 - \lambda ^2 \rho )^{\frac {n}{2}}$
. Since
$(x^2 - \lambda ^2 \rho )^{\frac {n}{2}}$
. Since
![]() $\widetilde w^{\widetilde y} = \lambda \widetilde w$
, both polynomials are equal, and so we have
$\widetilde w^{\widetilde y} = \lambda \widetilde w$
, both polynomials are equal, and so we have
![]() $\lambda ^2 = 1$
. Thus,
$\lambda ^2 = 1$
. Thus,
![]() $\lambda = -1$
and hence
$\lambda = -1$
and hence
![]() $\widetilde w^{\widetilde y} = - \widetilde w$
. If z is another element of
$\widetilde w^{\widetilde y} = - \widetilde w$
. If z is another element of
![]() $C \setminus C_0$
and if
$C \setminus C_0$
and if
![]() $\widetilde {z}$
is a preimage of z in
$\widetilde {z}$
is a preimage of z in
![]() $SL_n(q)$
, then we have
$SL_n(q)$
, then we have
![]() $\widetilde w^{\widetilde y} = - \widetilde w = \widetilde w^{\widetilde z}$
, and so
$\widetilde w^{\widetilde y} = - \widetilde w = \widetilde w^{\widetilde z}$
, and so
![]() $\widetilde y \widetilde {z}^{-1}$
centralizes
$\widetilde y \widetilde {z}^{-1}$
centralizes
![]() $\widetilde w$
. This implies that
$\widetilde w$
. This implies that
![]() $y{z}^{-1} \in C_0$
. It follows that
$y{z}^{-1} \in C_0$
. It follows that
![]() $|C : C_0| \le 2$
(and one can show that in fact
$|C : C_0| \le 2$
(and one can show that in fact
![]() $|C : C_0| = 2$
).
$|C : C_0| = 2$
).
By the preceding paragraph,
![]() $C/C_0$
is abelian, and so the
$C/C_0$
is abelian, and so the
![]() $2$
-components of C are precisely the
$2$
-components of C are precisely the
![]() $2$
-components of
$2$
-components of
![]() $C_0$
. One may deduce from Lemma 3.3 that
$C_0$
. One may deduce from Lemma 3.3 that
![]() $C_{SL_n(q)}(\widetilde w)$
has a normal subgroup
$C_{SL_n(q)}(\widetilde w)$
has a normal subgroup
![]() $\widetilde J$
isomorphic to
$\widetilde J$
isomorphic to
![]() $SL_{\frac {n}{2}}(q^2)$
such that the corresponding factor group is cyclic. Let J be the image of
$SL_{\frac {n}{2}}(q^2)$
such that the corresponding factor group is cyclic. Let J be the image of
![]() $\widetilde J$
in
$\widetilde J$
in
![]() $PSL_n(q)$
. Then J is isomorphic to a nontrivial quotient of
$PSL_n(q)$
. Then J is isomorphic to a nontrivial quotient of
![]() $SL_{\frac {n}{2}}(q^2)$
. Moreover,
$SL_{\frac {n}{2}}(q^2)$
. Moreover,
![]() $J \trianglelefteq C_0$
and
$J \trianglelefteq C_0$
and
![]() $C_0/J$
is cyclic. Therefore, J is the only
$C_0/J$
is cyclic. Therefore, J is the only
![]() $2$
-component of
$2$
-component of
![]() $C_0$
and hence the only
$C_0$
and hence the only
![]() $2$
-component of C. Thus, (i) holds.
$2$
-component of C. Thus, (i) holds.
Since
![]() $J \trianglelefteq C$
, we have that
$J \trianglelefteq C$
, we have that
![]() $P \cap J$
is strongly closed in P with respect to
$P \cap J$
is strongly closed in P with respect to
![]() $\mathcal {F}_P(C)$
. By Lemma 2.11, the factor system
$\mathcal {F}_P(C)$
. By Lemma 2.11, the factor system
![]() $\mathcal {F}_P(C)/(P \cap J)$
is isomorphic to the
$\mathcal {F}_P(C)/(P \cap J)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $C/J$
. Since
$C/J$
. Since
![]() $C_0$
has index
$C_0$
has index
![]() $\le 2$
in C and
$\le 2$
in C and
![]() $C_0/J$
is abelian, we have that
$C_0/J$
is abelian, we have that
![]() $C/J$
is
$C/J$
is
![]() $2$
-nilpotent. So
$2$
-nilpotent. So
![]() $C/J$
has a nilpotent
$C/J$
has a nilpotent
![]() $2$
-fusion system, and (ii) follows.
$2$
-fusion system, and (ii) follows.
We now prove (iii). Assume that
![]() $n \ge 6$
. Let u denote the image of
$n \ge 6$
. Let u denote the image of
 $$ \begin{align*} \begin{pmatrix} 0 & \rho & & & \\ 1 & 0 & & & \\ & & \ddots & & \\ & & & 0 & \rho \\ & & & 1 & 0 \end{pmatrix} \in SL_n(q) \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0 & \rho & & & \\ 1 & 0 & & & \\ & & \ddots & & \\ & & & 0 & \rho \\ & & & 1 & 0 \end{pmatrix} \in SL_n(q) \end{align*} $$
in
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
We claim that there exist
![]() $a, b \in \mathbb {F}_q$
with
$a, b \in \mathbb {F}_q$
with
![]() $a^2 \rho - b^2 \rho ^2 = 1$
. The field
$a^2 \rho - b^2 \rho ^2 = 1$
. The field
![]() $\mathbb {F}_q$
has precisely
$\mathbb {F}_q$
has precisely
![]() $\frac {q+1}{2}$
square elements. Therefore, each of the sets
$\frac {q+1}{2}$
square elements. Therefore, each of the sets
![]() $M_1 := \lbrace a^2 \rho \mid a \in \mathbb {F}_q \rbrace $
and
$M_1 := \lbrace a^2 \rho \mid a \in \mathbb {F}_q \rbrace $
and
![]() $M_2 := \lbrace 1 + b^2 \rho ^2 \mid b \in \mathbb {F}_q \rbrace $
has cardinality
$M_2 := \lbrace 1 + b^2 \rho ^2 \mid b \in \mathbb {F}_q \rbrace $
has cardinality
![]() $\frac {q+1}{2}$
. It follows that
$\frac {q+1}{2}$
. It follows that
![]() $M_1 \cap M_2 \ne \emptyset $
. So there exist
$M_1 \cap M_2 \ne \emptyset $
. So there exist
![]() $a, b \in \mathbb {F}_q$
with
$a, b \in \mathbb {F}_q$
with
![]() $a^2 \rho = 1 + b^2 \rho ^2$
, or in other words
$a^2 \rho = 1 + b^2 \rho ^2$
, or in other words
![]() $a^2 \rho - b^2 \rho ^2 = 1$
.
$a^2 \rho - b^2 \rho ^2 = 1$
.
Let s be the image of
 $$ \begin{align*} \begin{pmatrix} -b \rho & a \rho & & & \\ -a & b\rho & & & \\ & & \ddots & & \\ & & & -b \rho & a \rho \\ & & & -a & b \rho \end{pmatrix} \in SL_n(q) \end{align*} $$
$$ \begin{align*} \begin{pmatrix} -b \rho & a \rho & & & \\ -a & b\rho & & & \\ & & \ddots & & \\ & & & -b \rho & a \rho \\ & & & -a & b \rho \end{pmatrix} \in SL_n(q) \end{align*} $$
in
![]() $PSL_n(q)$
. By a direct calculation,
$PSL_n(q)$
. By a direct calculation,
![]() $s \in C_{PSL_n(q)}(u)$
. Another direct calculation shows that s is an involution. Let
$s \in C_{PSL_n(q)}(u)$
. Another direct calculation shows that s is an involution. Let
![]() $z_1$
denote the image of
$z_1$
denote the image of
 $$ \begin{align*} \begin{pmatrix} -I_2 & \\ & I_{n-2}\end{pmatrix} \in SL_n(q) \end{align*} $$
$$ \begin{align*} \begin{pmatrix} -I_2 & \\ & I_{n-2}\end{pmatrix} \in SL_n(q) \end{align*} $$
in
![]() $PSL_n(q)$
, and let
$PSL_n(q)$
, and let
![]() $z_2$
denote the image of
$z_2$
denote the image of
 $$ \begin{align*} \begin{pmatrix} I_2 & & \\ & - I_2 & \\ & & I_{n-4} \end{pmatrix} \in SL_n(q) \end{align*} $$
$$ \begin{align*} \begin{pmatrix} I_2 & & \\ & - I_2 & \\ & & I_{n-4} \end{pmatrix} \in SL_n(q) \end{align*} $$
in
![]() $PSL_n(q)$
. Then one can easily verify that
$PSL_n(q)$
. Then one can easily verify that
![]() $\langle s, u, z_1, z_2 \rangle \le C_{PSL_n(q)}(u)$
is isomorphic to
$\langle s, u, z_1, z_2 \rangle \le C_{PSL_n(q)}(u)$
is isomorphic to
![]() $E_{16}$
. So a Sylow
$E_{16}$
. So a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{PSL_n(q)}(u)$
has rank at least
$C_{PSL_n(q)}(u)$
has rank at least
![]() $4$
. This is also true for P as w and u are conjugate (see Proposition 3.5).
$4$
. This is also true for P as w and u are conjugate (see Proposition 3.5).
Lemma 3.7. Let
![]() $n \ge 2$
be a natural number, and let
$n \ge 2$
be a natural number, and let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Also, let
$\varepsilon \in \lbrace +,- \rbrace $
. Also, let
![]() $T \in GL_n^{\varepsilon }(3) \setminus Z(GL_n^{\varepsilon }(3))$
such that
$T \in GL_n^{\varepsilon }(3) \setminus Z(GL_n^{\varepsilon }(3))$
such that
![]() $T^2 \in Z(GL_n^{\varepsilon }(3))$
. Then
$T^2 \in Z(GL_n^{\varepsilon }(3))$
. Then
![]() $C_{GL_n^{\varepsilon }(3)}(T)$
is core-free.
$C_{GL_n^{\varepsilon }(3)}(T)$
is core-free.
Proof. By Lemmas 3.3 and 3.4, we either have
![]() $C_{GL_n^{\varepsilon }(3)}(T) \cong GL_i^{\varepsilon }(3) \times GL_{n-i}^{\varepsilon }(3)$
for some
$C_{GL_n^{\varepsilon }(3)}(T) \cong GL_i^{\varepsilon }(3) \times GL_{n-i}^{\varepsilon }(3)$
for some
![]() $1 \le i < n$
, or n is even and
$1 \le i < n$
, or n is even and
![]() $C_{GL_n^{\varepsilon }(3)}(T) \cong GL_{n/2}(9)$
. So we have that
$C_{GL_n^{\varepsilon }(3)}(T) \cong GL_{n/2}(9)$
. So we have that
![]() $C_{GL_n^{\varepsilon }(3)}(T)$
is core-free.
$C_{GL_n^{\varepsilon }(3)}(T)$
is core-free.
Noticing that
![]() $GL_n^{\varepsilon }(3)/SL_n^{\varepsilon }(3)$
and
$GL_n^{\varepsilon }(3)/SL_n^{\varepsilon }(3)$
and
![]() $Z(GL_n^{\varepsilon }(3))$
are
$Z(GL_n^{\varepsilon }(3))$
are
![]() $2$
-groups for any
$2$
-groups for any
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $\varepsilon \in \lbrace +,- \rbrace $
, one can deduce the following two corollaries from Lemma 3.7.
$\varepsilon \in \lbrace +,- \rbrace $
, one can deduce the following two corollaries from Lemma 3.7.
Corollary 3.8. Let
![]() $n \ge 2$
be a natural number, and let
$n \ge 2$
be a natural number, and let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Then any involution centralizer in
$\varepsilon \in \lbrace +,- \rbrace $
. Then any involution centralizer in
![]() $SL_n^{\varepsilon }(3)$
is core-free.
$SL_n^{\varepsilon }(3)$
is core-free.
Corollary 3.9. Let
![]() $n \ge 2$
be a natural number, and let
$n \ge 2$
be a natural number, and let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Then any involution centralizer in
$\varepsilon \in \lbrace +,- \rbrace $
. Then any involution centralizer in
![]() $PGL_n^{\varepsilon }(3)$
is core-free.
$PGL_n^{\varepsilon }(3)$
is core-free.
3.4 Sylow
 $2$
-subgroups and
$2$
-subgroups and
 $2$
-fusion systems
$2$
-fusion systems
In this subsection, we consider several properties of Sylow
![]() $2$
-subgroups and
$2$
-subgroups and
![]() $2$
-fusion systems of linear and unitary groups.
$2$
-fusion systems of linear and unitary groups.
Lemma 3.10 [Reference Carter and Fong17, p. 142]
Let q be a nontrivial odd prime power. Let
![]() $k,s \in \mathbb {N}$
such that
$k,s \in \mathbb {N}$
such that
![]() $2^k$
is the
$2^k$
is the
![]() $2$
-part of
$2$
-part of
![]() $q-1$
and that
$q-1$
and that
![]() $2^s$
is the
$2^s$
is the
![]() $2$
-part of
$2$
-part of
![]() $q+1$
. Then:
$q+1$
. Then:
-
(i) Assume that
 $q \equiv 1 \ \mathrm {mod} \ 4$
. Then is a Sylow
$q \equiv 1 \ \mathrm {mod} \ 4$
. Then is a Sylow $$ \begin{align*} \left \lbrace \begin{pmatrix} \lambda & \ \ \\ \ \ & \ \mu \\ \end{pmatrix} \ : \ \lambda, \mu \ \text{are } 2\text{-elements of } \mathbb{F}_{q}^{*} \right \rbrace \cdot \left \langle \begin{pmatrix} 0 \ & \ 1 \\ 1 \ & \ 0 \\ \end{pmatrix} \right \rangle \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} \lambda & \ \ \\ \ \ & \ \mu \\ \end{pmatrix} \ : \ \lambda, \mu \ \text{are } 2\text{-elements of } \mathbb{F}_{q}^{*} \right \rbrace \cdot \left \langle \begin{pmatrix} 0 \ & \ 1 \\ 1 \ & \ 0 \\ \end{pmatrix} \right \rangle \end{align*} $$
 $2$
-subgroup of
$2$
-subgroup of
 $GL_2(q)$
. In particular, the Sylow
$GL_2(q)$
. In particular, the Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $GL_2(q)$
are isomorphic to the wreath product
$GL_2(q)$
are isomorphic to the wreath product
 $C_{2^k} \wr C_2$
.
$C_{2^k} \wr C_2$
.
-
(ii) If
 $q \equiv 3 \ \mathrm {mod} \ 4$
, then the Sylow
$q \equiv 3 \ \mathrm {mod} \ 4$
, then the Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $GL_2(q)$
are semidihedral of order
$GL_2(q)$
are semidihedral of order
 $2^{s+2}$
.
$2^{s+2}$
.
Lemma 3.11 [Reference Carter and Fong17, p. 143]
Let q be a nontrivial odd prime power. Let
![]() $k,s \in \mathbb {N}$
such that
$k,s \in \mathbb {N}$
such that
![]() $2^k$
is the
$2^k$
is the
![]() $2$
-part of
$2$
-part of
![]() $q-1$
and that
$q-1$
and that
![]() $2^s$
is the
$2^s$
is the
![]() $2$
-part of
$2$
-part of
![]() $q+1$
. Then:
$q+1$
. Then:
-
(i) If
 $q \equiv 1 \ \mathrm {mod} \ 4$
, then the Sylow
$q \equiv 1 \ \mathrm {mod} \ 4$
, then the Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $GU_2(q)$
are semidihedral of order
$GU_2(q)$
are semidihedral of order
 $2^{k+2}$
.
$2^{k+2}$
. -
(ii) If
 $q \equiv 3 \ \mathrm {mod} \ 4$
, then the Sylow
$q \equiv 3 \ \mathrm {mod} \ 4$
, then the Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $GU_2(q)$
are isomorphic to the wreath product
$GU_2(q)$
are isomorphic to the wreath product
 $C_{2^s} \wr C_2$
. If
$C_{2^s} \wr C_2$
. If
 $\varepsilon \in \mathbb {F}_{q^2}^{*}$
has order
$\varepsilon \in \mathbb {F}_{q^2}^{*}$
has order
 $2^s$
, then a Sylow
$2^s$
, then a Sylow
 $2$
-subgroup of
$2$
-subgroup of
 $GU_2(q)$
is concretely given by
$GU_2(q)$
is concretely given by  $$ \begin{align*} W := \left \lbrace \begin{pmatrix} \lambda \ & \ \ \\ \ \ & \ \mu \\ \end{pmatrix} \ : \ \lambda, \mu \in \langle \varepsilon \rangle \right \rbrace \cdot \left \langle \begin{pmatrix} 0 \ & \ 1 \\ 1 \ & \ 0 \\ \end{pmatrix} \right \rangle. \end{align*} $$
$$ \begin{align*} W := \left \lbrace \begin{pmatrix} \lambda \ & \ \ \\ \ \ & \ \mu \\ \end{pmatrix} \ : \ \lambda, \mu \in \langle \varepsilon \rangle \right \rbrace \cdot \left \langle \begin{pmatrix} 0 \ & \ 1 \\ 1 \ & \ 0 \\ \end{pmatrix} \right \rangle. \end{align*} $$
Lemma 3.12 [Reference Huppert and Endliche Gruppen35, Kapitel II, Satz 8.10 a)]
If q is a nontrivial odd prime power, then a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_2(q)$
is generalized quaternion of order
$SL_2(q)$
is generalized quaternion of order
![]() $(q^2-1)_2$
.
$(q^2-1)_2$
.
Lemma 3.13 [Reference Huppert and Endliche Gruppen35, Kapitel II, Satz 8.10 b)]
If q is a nontrivial odd prime power, then
![]() $PSL_2(q)$
has dihedral Sylow
$PSL_2(q)$
has dihedral Sylow
![]() $2$
-subgroups of order
$2$
-subgroups of order
![]() $\frac {1}{2}(q^2-1)_2$
.
$\frac {1}{2}(q^2-1)_2$
.
Lemma 3.14 [Reference Carter and Fong17, Lemma 1]
Let q be a nontrivial odd prime power, and let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let r be a positive integer. Let
$\varepsilon \in \lbrace +,- \rbrace $
. Let r be a positive integer. Let
![]() $W_r$
be a Sylow
$W_r$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^r}^{\varepsilon }(q)$
. Then
$GL_{2^r}^{\varepsilon }(q)$
. Then
![]() $W_r \wr C_2$
is isomorphic to a Sylow
$W_r \wr C_2$
is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^{r+1}}^{\varepsilon }(q)$
. A Sylow
$GL_{2^{r+1}}^{\varepsilon }(q)$
. A Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^{r+1}}^{\varepsilon }(q)$
is concretely given by
$GL_{2^{r+1}}^{\varepsilon }(q)$
is concretely given by
 $$ \begin{align*} \left \lbrace \begin{pmatrix} A & \ \\ \ & B \\ \end{pmatrix} \ : \ A, B \in W_r \right \rbrace \cdot \left \langle \begin{pmatrix} \ & I_{2^r} \\ I_{2^r} & \ \\ \end{pmatrix} \right \rangle. \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} A & \ \\ \ & B \\ \end{pmatrix} \ : \ A, B \in W_r \right \rbrace \cdot \left \langle \begin{pmatrix} \ & I_{2^r} \\ I_{2^r} & \ \\ \end{pmatrix} \right \rangle. \end{align*} $$
Lemma 3.15 [Reference Carter and Fong17, Theorem 1]
Let q be a nontrivial odd prime power, and let n be a positive integer. Let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let
$\varepsilon \in \lbrace +,- \rbrace $
. Let
![]() $0 \le r_1 < \dots < r_t$
such that
$0 \le r_1 < \dots < r_t$
such that
![]() $n = 2^{r_1} + \dots + 2^{r_t}$
. Let
$n = 2^{r_1} + \dots + 2^{r_t}$
. Let
![]() $W_i \in \mathrm {Syl}_2(GL_{2^{r_i}}^{\varepsilon }(q))$
for all
$W_i \in \mathrm {Syl}_2(GL_{2^{r_i}}^{\varepsilon }(q))$
for all
![]() $1 \le i \le t$
. Then
$1 \le i \le t$
. Then
![]() $W_1 \times \dots \times W_t$
is isomorphic to a Sylow
$W_1 \times \dots \times W_t$
is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n^{\varepsilon }(q)$
. A Sylow
$GL_n^{\varepsilon }(q)$
. A Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n^{\varepsilon }(q)$
is concretely given by
$GL_n^{\varepsilon }(q)$
is concretely given by
 $$ \begin{align*} \left \lbrace \begin{pmatrix} A_1 & \ & \ \\ \ & \ddots & \ \\ \ & \ & A_t \end{pmatrix} \ : \ A_i \in W_i \right \rbrace. \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} A_1 & \ & \ \\ \ & \ddots & \ \\ \ & \ & A_t \end{pmatrix} \ : \ A_i \in W_i \right \rbrace. \end{align*} $$
Lemma 3.16. Let q be a prime power with
![]() $q \equiv 3 \mod 4$
. Let W be a Sylow
$q \equiv 3 \mod 4$
. Let W be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
, and let
$GL_2(q)$
, and let
![]() $m \in \mathbb {N}$
such that
$m \in \mathbb {N}$
such that
![]() $|W| = 2^m$
. Then:
$|W| = 2^m$
. Then:
-
(i) W is semidihedral. In particular, there are elements
 $a, b \in W$
with
$a, b \in W$
with
 $\mathrm {ord}(a)=2^{m-1}$
and
$\mathrm {ord}(a)=2^{m-1}$
and
 $\mathrm {ord}(b)=2$
such that
$\mathrm {ord}(b)=2$
such that
 $a^b = a^{2^{m-2}-1}$
.
$a^b = a^{2^{m-2}-1}$
. -
(ii) We have
 $W \cap SL_2(q) = \langle a^2 \rangle \langle ab \rangle $
.
$W \cap SL_2(q) = \langle a^2 \rangle \langle ab \rangle $
. -
(iii) Let
 $1 \le \ell \le 2^{m-1}$
. If
$1 \le \ell \le 2^{m-1}$
. If
 $\ell $
is odd, then
$\ell $
is odd, then
 $a^{\ell }$
has determinant
$a^{\ell }$
has determinant
 $-1$
, and
$-1$
, and
 $a^{\ell }b$
has determinant
$a^{\ell }b$
has determinant
 $1$
. If
$1$
. If
 $\ell $
is even, then
$\ell $
is even, then
 $a^{\ell }$
has determinant
$a^{\ell }$
has determinant
 $1$
, and
$1$
, and
 $a^{\ell }b$
has determinant
$a^{\ell }b$
has determinant
 $-1$
.
$-1$
. -
(iv) The involutions of W are precisely the elements
 $a^{2^{m-2}}$
and
$a^{2^{m-2}}$
and
 $a^{\ell }b$
, where
$a^{\ell }b$
, where
 $2 \le \ell \le 2^{m-1}$
is even.
$2 \le \ell \le 2^{m-1}$
is even.
Proof. By Lemma 3.10 (ii), we have (i).
Let
![]() $W_0 := W \cap SL_2(q)$
. By Lemma 3.12,
$W_0 := W \cap SL_2(q)$
. By Lemma 3.12,
![]() $W_0$
is generalized quaternion. Also,
$W_0$
is generalized quaternion. Also,
![]() $W_0$
is a maximal subgroup of W since
$W_0$
is a maximal subgroup of W since
![]() $SL_2(q)$
has index
$SL_2(q)$
has index
![]() $q-1$
in
$q-1$
in
![]() $GL_2(q)$
and
$GL_2(q)$
and
![]() $q \equiv 3 \mod 4$
. By [Reference Gorenstein23, Chapter 5, Theorem 4.3 (ii) (b)], we have
$q \equiv 3 \mod 4$
. By [Reference Gorenstein23, Chapter 5, Theorem 4.3 (ii) (b)], we have
![]() $\Phi (W) = \langle a^2 \rangle $
. So the maximal subgroups of W are precisely the groups
$\Phi (W) = \langle a^2 \rangle $
. So the maximal subgroups of W are precisely the groups
![]() $M_1 := \langle a \rangle $
,
$M_1 := \langle a \rangle $
,
![]() $M_2 :=\langle a^2 \rangle \langle b \rangle $
and
$M_2 :=\langle a^2 \rangle \langle b \rangle $
and
![]() $M_3 := \langle a^2 \rangle \langle ab \rangle $
. One can check that
$M_3 := \langle a^2 \rangle \langle ab \rangle $
. One can check that
![]() $M_1 \cong C_{2^{n-1}}$
,
$M_1 \cong C_{2^{n-1}}$
,
![]() $M_2 \cong D_{2^{n-1}}$
and
$M_2 \cong D_{2^{n-1}}$
and
![]() $M_3 \cong Q_{2^{n-1}}$
. Consequently,
$M_3 \cong Q_{2^{n-1}}$
. Consequently,
![]() $W_0 = \langle a^2 \rangle \langle ab \rangle $
, and (ii) holds.
$W_0 = \langle a^2 \rangle \langle ab \rangle $
, and (ii) holds.
(iii) follows from (ii) since any element of
![]() $W \setminus W_0$
has determinant
$W \setminus W_0$
has determinant
![]() $-1$
.
$-1$
.
The proof of (iv) is an easy exercise.
Lemma 3.17. Let q be a nontrivial odd prime power, n a positive integer and
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let
$\varepsilon \in \lbrace +,- \rbrace $
. Let
![]() $0 \le r_1 < \dots < r_t$
such that
$0 \le r_1 < \dots < r_t$
such that
![]() $n = 2^{r_1} + \dots + 2^{r_t}$
. Then there is a Sylow
$n = 2^{r_1} + \dots + 2^{r_t}$
. Then there is a Sylow
![]() $2$
-subgroup W of
$2$
-subgroup W of
![]() $G := GL_n^{\varepsilon }(q)$
containing all diagonal matrices in G with
$G := GL_n^{\varepsilon }(q)$
containing all diagonal matrices in G with
![]() $2$
-power order such that
$2$
-power order such that
![]() $C_W(W \cap SL_n^{\varepsilon }(q))$
consists precisely of the matrices
$C_W(W \cap SL_n^{\varepsilon }(q))$
consists precisely of the matrices
 $$ \begin{align*} \begin{pmatrix} \lambda_1 I_{2^{r_1}} \ & \ & \ \\ \ & \ddots \ & \ \\ \ & \ & \lambda_t I_{2^{r_t}} \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \lambda_1 I_{2^{r_1}} \ & \ & \ \\ \ & \ddots \ & \ \\ \ & \ & \lambda_t I_{2^{r_t}} \end{pmatrix}, \end{align*} $$
where
![]() $\lambda _1, \dots , \lambda _t$
are
$\lambda _1, \dots , \lambda _t$
are
![]() $2$
-elements of
$2$
-elements of
![]() $\mathbb {F}_q^{*}$
if
$\mathbb {F}_q^{*}$
if
![]() $G = GL_n(q)$
and
$G = GL_n(q)$
and
![]() $2$
-elements of
$2$
-elements of
![]() $\mathbb {F}_{q^2}^{*}$
with
$\mathbb {F}_{q^2}^{*}$
with
![]() $\lambda _i^{q+1}=1$
(for each
$\lambda _i^{q+1}=1$
(for each
![]() $1 \le i \le t$
) if
$1 \le i \le t$
) if
![]() $G=GU_n(q)$
.
$G=GU_n(q)$
.
Proof. Using Lemmas 3.10 and 3.11, one can check that the centralizer of a Sylow 2-subgroup of
![]() $SL_2^{\varepsilon }(q)$
inside a Sylow 2-subgroup of
$SL_2^{\varepsilon }(q)$
inside a Sylow 2-subgroup of
![]() $GL_2^{\varepsilon }(q)$
is the Sylow 2-subgroup of
$GL_2^{\varepsilon }(q)$
is the Sylow 2-subgroup of
![]() $Z(GL_2^{\varepsilon }(q))$
. Applying Lemma 3.14 and arguing by induction, one can see that a similar statement holds for the centralizer of a Sylow 2-subgroup of
$Z(GL_2^{\varepsilon }(q))$
. Applying Lemma 3.14 and arguing by induction, one can see that a similar statement holds for the centralizer of a Sylow 2-subgroup of
![]() $SL_{2^r}^{\varepsilon }(q)$
inside a Sylow 2-subgroup of
$SL_{2^r}^{\varepsilon }(q)$
inside a Sylow 2-subgroup of
![]() $GL_{2^r}^{\varepsilon }(q)$
for all
$GL_{2^r}^{\varepsilon }(q)$
for all
![]() $r \ge 0$
. Now we may apply Lemma 3.15 to obtain a Sylow 2-subgroup of G with the desired properties.
$r \ge 0$
. Now we may apply Lemma 3.15 to obtain a Sylow 2-subgroup of G with the desired properties.
Lemma 3.18. Let q be a nontrivial odd prime power, n a positive integer and
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let
$\varepsilon \in \lbrace +,- \rbrace $
. Let
![]() $G := SL_n^{\varepsilon }(q)$
, and let S be a Sylow
$G := SL_n^{\varepsilon }(q)$
, and let S be a Sylow
![]() $2$
-subgroup of G. Then we have
$2$
-subgroup of G. Then we have
![]() $Z(\mathcal {F}_S(G)) = S \cap Z(G)$
.
$Z(\mathcal {F}_S(G)) = S \cap Z(G)$
.
Proof. This follows from Lemma 2.13.
Proposition 3.19. Let n be a positive integer. Let
![]() $q, q^{*}$
be nontrivial odd prime powers, and let
$q, q^{*}$
be nontrivial odd prime powers, and let
![]() $\varepsilon , \varepsilon ^{*} \in \lbrace +,-\rbrace $
. If
$\varepsilon , \varepsilon ^{*} \in \lbrace +,-\rbrace $
. If
![]() $\varepsilon q \sim \varepsilon ^{*}q^{*}$
, then the
$\varepsilon q \sim \varepsilon ^{*}q^{*}$
, then the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $SL_n^{\varepsilon }(q)$
and
$SL_n^{\varepsilon }(q)$
and
![]() $SL_n^{\varepsilon ^{*}}(q^{*})$
are isomorphic.
$SL_n^{\varepsilon ^{*}}(q^{*})$
are isomorphic.
Proof. Assume that
![]() $\varepsilon \ne \varepsilon ^{*}$
. From
$\varepsilon \ne \varepsilon ^{*}$
. From
![]() $\varepsilon q \sim \varepsilon ^{*}q^{*}$
, it is easy to deduce that
$\varepsilon q \sim \varepsilon ^{*}q^{*}$
, it is easy to deduce that
![]() $\varepsilon q \equiv \varepsilon ^{*} q^{*} \mod 8$
and
$\varepsilon q \equiv \varepsilon ^{*} q^{*} \mod 8$
and
![]() $(q^2-1)_2 = ((q^{*})^2-1)_2$
. So, in view of the remarks at the bottom of p. 11 of [Reference Broto, Møller and Oliver14], we may apply [Reference Broto, Møller and Oliver14, Proposition 3.3 (a)] to conclude that the 2-fusion system of
$(q^2-1)_2 = ((q^{*})^2-1)_2$
. So, in view of the remarks at the bottom of p. 11 of [Reference Broto, Møller and Oliver14], we may apply [Reference Broto, Møller and Oliver14, Proposition 3.3 (a)] to conclude that the 2-fusion system of
![]() $SL_n^{\varepsilon }(q)$
is isomorphic to the 2-fusion system of
$SL_n^{\varepsilon }(q)$
is isomorphic to the 2-fusion system of
![]() $SL_n^{\varepsilon ^{*}}(q^{*})$
.
$SL_n^{\varepsilon ^{*}}(q^{*})$
.
Assume now that
![]() $\varepsilon = \varepsilon ^{*}$
. Using Dirichlet’s theorem [Reference Fine and Rosenberger20, Theorem 3.3.1], one can easily see that there is an odd prime
$\varepsilon = \varepsilon ^{*}$
. Using Dirichlet’s theorem [Reference Fine and Rosenberger20, Theorem 3.3.1], one can easily see that there is an odd prime
![]() $q_0$
with
$q_0$
with
![]() $\varepsilon q \sim \varepsilon q^{*} \sim -\varepsilon q_0$
. By the preceding paragraph, both the 2-fusion system of
$\varepsilon q \sim \varepsilon q^{*} \sim -\varepsilon q_0$
. By the preceding paragraph, both the 2-fusion system of
![]() $SL_n^{\varepsilon }(q)$
and the 2-fusion system of
$SL_n^{\varepsilon }(q)$
and the 2-fusion system of
![]() $SL_n^{\varepsilon }(q^{*})$
are isomorphic to the 2-fusion system of
$SL_n^{\varepsilon }(q^{*})$
are isomorphic to the 2-fusion system of
![]() $SL_n^{-\varepsilon }(q_0)$
. Consequently, the 2-fusion systems of
$SL_n^{-\varepsilon }(q_0)$
. Consequently, the 2-fusion systems of
![]() $SL_n^{\varepsilon }(q)$
and
$SL_n^{\varepsilon }(q)$
and
![]() $SL_n^{\varepsilon ^{*}}(q^{*})$
are isomorphic.
$SL_n^{\varepsilon ^{*}}(q^{*})$
are isomorphic.
Proposition 3.20. Let n be a positive integer. Let
![]() $q, q^{*}$
be nontrivial odd prime powers, and let
$q, q^{*}$
be nontrivial odd prime powers, and let
![]() $\varepsilon , \varepsilon ^{*} \in \lbrace +,-\rbrace $
. If
$\varepsilon , \varepsilon ^{*} \in \lbrace +,-\rbrace $
. If
![]() $\varepsilon q \sim \varepsilon ^{*} q^{*}$
, then the
$\varepsilon q \sim \varepsilon ^{*} q^{*}$
, then the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $PSL_n^{\varepsilon }(q)$
and
$PSL_n^{\varepsilon }(q)$
and
![]() $PSL_n^{\varepsilon ^{*}}(q^{*})$
are isomorphic.
$PSL_n^{\varepsilon ^{*}}(q^{*})$
are isomorphic.
Proof. Let S and
![]() $S^{*}$
be Sylow
$S^{*}$
be Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $G:= SL_n^{\varepsilon }(q)$
and
$G:= SL_n^{\varepsilon }(q)$
and
![]() $G^{*} := SL_n^{\varepsilon ^{*}}(q^{*})$
, respectively. By Proposition 3.19,
$G^{*} := SL_n^{\varepsilon ^{*}}(q^{*})$
, respectively. By Proposition 3.19,
![]() $\mathcal {F} := \mathcal {F}_S(G)$
and
$\mathcal {F} := \mathcal {F}_S(G)$
and
![]() $\mathcal {F}^{*} := \mathcal {F}_{S^{*}}(G^{*})$
are isomorphic. Therefore,
$\mathcal {F}^{*} := \mathcal {F}_{S^{*}}(G^{*})$
are isomorphic. Therefore,
![]() $\mathcal {F}/Z(\mathcal {F})$
and
$\mathcal {F}/Z(\mathcal {F})$
and
![]() $\mathcal {F}^{*}/Z(\mathcal {F}^{*})$
are isomorphic. Lemma 3.18 implies that
$\mathcal {F}^{*}/Z(\mathcal {F}^{*})$
are isomorphic. Lemma 3.18 implies that
![]() $\mathcal {F}/(S \cap Z(G))$
and
$\mathcal {F}/(S \cap Z(G))$
and
![]() $\mathcal {F}^{*}/(S^{*} \cap Z(G^{*}))$
are isomorphic. Now the proposition follows from Lemma 2.11.
$\mathcal {F}^{*}/(S^{*} \cap Z(G^{*}))$
are isomorphic. Now the proposition follows from Lemma 2.11.
The following lemma shows together with [Reference Aschbacher9, Theorem 5.6.18] that the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
is simple whenever q is odd and
$PSL_n(q)$
is simple whenever q is odd and
![]() $n \ge 3$
.
$n \ge 3$
.
Lemma 3.21. Let q be a nontrivial odd prime power and
![]() $n \ge 2$
a natural number such that
$n \ge 2$
a natural number such that
![]() $(n,q) \ne (2,3)$
. Moreover, let
$(n,q) \ne (2,3)$
. Moreover, let
![]() $\varepsilon $
be an element of
$\varepsilon $
be an element of
![]() $\lbrace +,- \rbrace $
. Then
$\lbrace +,- \rbrace $
. Then
![]() $PSL_n^{\varepsilon }(q)$
is a Goldschmidt group if and only if
$PSL_n^{\varepsilon }(q)$
is a Goldschmidt group if and only if
![]() $n = 2$
and
$n = 2$
and
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
.
$5 \ \mathrm {mod} \ 8$
.
Proof. Set
![]() $G := PSL_n^{\varepsilon }(q)$
.
$G := PSL_n^{\varepsilon }(q)$
.
Assume that
![]() $n = 2$
. Then
$n = 2$
. Then
![]() $G \cong PSL_2(q)$
. By Lemma 3.13, G has dihedral Sylow
$G \cong PSL_2(q)$
. By Lemma 3.13, G has dihedral Sylow
![]() $2$
-subgroups of order
$2$
-subgroups of order
![]() $\frac {1}{2}(q-1)_2(q+1)_2$
. So, if
$\frac {1}{2}(q-1)_2(q+1)_2$
. So, if
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
, then G has abelian Sylow
$5 \ \mathrm {mod} \ 8$
, then G has abelian Sylow
![]() $2$
-subgroups and is thus a Goldschmidt group. If
$2$
-subgroups and is thus a Goldschmidt group. If
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
, then the Sylow
$7 \ \mathrm {mod} \ 8$
, then the Sylow
![]() $2$
-subgroups of G are dihedral of order at least
$2$
-subgroups of G are dihedral of order at least
![]() $8$
and hence nonabelian. Moreover, if
$8$
and hence nonabelian. Moreover, if
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
, then [Reference Steinberg49, Theorem 37] shows that G is not isomorphic to a finite simple group of Lie type in characteristic
$7 \ \mathrm {mod} \ 8$
, then [Reference Steinberg49, Theorem 37] shows that G is not isomorphic to a finite simple group of Lie type in characteristic
![]() $2$
of Lie rank
$2$
of Lie rank
![]() $1$
. So G is not a Goldschmidt group if
$1$
. So G is not a Goldschmidt group if
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
.
$7 \ \mathrm {mod} \ 8$
.
Assume now that
![]() $n \ge 3$
. Again, we see from [Reference Steinberg49, Theorem 37] that there is no finite simple group of Lie type in characteristic
$n \ge 3$
. Again, we see from [Reference Steinberg49, Theorem 37] that there is no finite simple group of Lie type in characteristic
![]() $2$
of Lie rank
$2$
of Lie rank
![]() $1$
which is isomorphic to G. Also, G has a subgroup isomorphic to
$1$
which is isomorphic to G. Also, G has a subgroup isomorphic to
![]() $SL_2^{\varepsilon }(q) \cong SL_2(q)$
, and therefore, the Sylow
$SL_2^{\varepsilon }(q) \cong SL_2(q)$
, and therefore, the Sylow
![]() $2$
-subgroups of G are nonabelian. Consequently, G is not a Goldschmidt group.
$2$
-subgroups of G are nonabelian. Consequently, G is not a Goldschmidt group.
Lemma 3.22. Let n be a positive integer, q a nontrivial odd prime power and
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let E be the subgroup of
$\varepsilon \in \lbrace +,- \rbrace $
. Let E be the subgroup of
![]() $SL_n^{\varepsilon }(q)$
consisting of the diagonal matrices in
$SL_n^{\varepsilon }(q)$
consisting of the diagonal matrices in
![]() $SL_n^{\varepsilon }(q)$
with diagonal entries in
$SL_n^{\varepsilon }(q)$
with diagonal entries in
![]() $\lbrace 1,-1 \rbrace $
. Then
$\lbrace 1,-1 \rbrace $
. Then
![]() $\vert E \vert = 2^{n-1}$
. Moreover, any elementary abelian
$\vert E \vert = 2^{n-1}$
. Moreover, any elementary abelian
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_n^{\varepsilon }(q)$
is conjugate to a subgroup of E.
$SL_n^{\varepsilon }(q)$
is conjugate to a subgroup of E.
Proof. It is straightforward to check that
![]() $\vert E \vert = 2^{n-1}$
.
$\vert E \vert = 2^{n-1}$
.
Let
![]() $E_0$
be an elementary abelian
$E_0$
be an elementary abelian
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_n^{\varepsilon }(q)$
. We show that
$SL_n^{\varepsilon }(q)$
. We show that
![]() $E_0$
is conjugate to a subgroup of E. Using Dirichlet’s theorem [Reference Fine and Rosenberger20, Theorem 3.3.1], one can see that there is an odd prime number
$E_0$
is conjugate to a subgroup of E. Using Dirichlet’s theorem [Reference Fine and Rosenberger20, Theorem 3.3.1], one can see that there is an odd prime number
![]() $q^{*}$
with
$q^{*}$
with
![]() $-q \sim q^{*}$
, and Proposition 3.19 shows that the
$-q \sim q^{*}$
, and Proposition 3.19 shows that the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $SU_n(q)$
and
$SU_n(q)$
and
![]() $SL_n(q^{*})$
are isomorphic. Therefore, it is enough to consider the case
$SL_n(q^{*})$
are isomorphic. Therefore, it is enough to consider the case
![]() $\varepsilon = +$
.
$\varepsilon = +$
.
Since
![]() $E_0$
is an elementary abelian
$E_0$
is an elementary abelian
![]() $2$
-group, any two elements of
$2$
-group, any two elements of
![]() $E_0$
commute, and any element of
$E_0$
commute, and any element of
![]() $E_0$
is diagonalizable (see Lemma 3.3). It follows that
$E_0$
is diagonalizable (see Lemma 3.3). It follows that
![]() $E_0$
is simultaneously diagonalizable, and this implies that
$E_0$
is simultaneously diagonalizable, and this implies that
![]() $E_0$
is conjugate to a subgroup of E.
$E_0$
is conjugate to a subgroup of E.
Lemma 3.23. Let the notation be as in Lemma 3.22, and set
![]() $Y := SL_n^{\varepsilon }(q)$
. Moreover, for any
$Y := SL_n^{\varepsilon }(q)$
. Moreover, for any
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
, let
$A \subseteq \lbrace 1, \dots , n \rbrace $
, let
![]() $t_A$
be the matrix
$t_A$
be the matrix
![]() $\mathrm {diag}(d_1,\dots ,d_n)$
, where
$\mathrm {diag}(d_1,\dots ,d_n)$
, where
![]() $d_i = -1$
if
$d_i = -1$
if
![]() $i \in A$
and
$i \in A$
and
![]() $d_i = 1$
if
$d_i = 1$
if
![]() $i \in \lbrace 1, \dots , n \rbrace \setminus A$
. Then the following hold:
$i \in \lbrace 1, \dots , n \rbrace \setminus A$
. Then the following hold:
-
(i) For each
 $\pi \in S_n$
, there is a unique
$\pi \in S_n$
, there is a unique
 $\varphi _{\pi } \in \mathrm {Aut}_Y(E)$
such that for any
$\varphi _{\pi } \in \mathrm {Aut}_Y(E)$
such that for any $$ \begin{align*} (t_A)^{\varphi_{\pi}} = t_{A^{\pi}} \end{align*} $$
$$ \begin{align*} (t_A)^{\varphi_{\pi}} = t_{A^{\pi}} \end{align*} $$
 $A \subseteq \lbrace 1, \dots , n \rbrace $
of even order.
$A \subseteq \lbrace 1, \dots , n \rbrace $
of even order.
-
(ii)
 $\mathrm {Aut}_Y(E) = \lbrace \varphi _{\pi } \mid \pi \in S_n \rbrace $
.
$\mathrm {Aut}_Y(E) = \lbrace \varphi _{\pi } \mid \pi \in S_n \rbrace $
.
Proof. Let V be the defining module for Y. Let
![]() $B = (v_1,\dots ,v_n)$
be a basis for V with B orthonormal if V is unitary. For any
$B = (v_1,\dots ,v_n)$
be a basis for V with B orthonormal if V is unitary. For any
![]() $A \subseteq \lbrace 1,\dots ,n \rbrace $
, let
$A \subseteq \lbrace 1,\dots ,n \rbrace $
, let
![]() $e_A$
be the linear map
$e_A$
be the linear map
![]() $V \rightarrow V$
represented by
$V \rightarrow V$
represented by
![]() $t_A$
with respect to B. Then
$t_A$
with respect to B. Then
![]() $e_A \in GL^{\varepsilon }(V)$
.
$e_A \in GL^{\varepsilon }(V)$
.
Let
![]() $\pi \in S_n$
. To prove (i), it suffices to find some
$\pi \in S_n$
. To prove (i), it suffices to find some
![]() $\alpha _{\pi } \in SL^{\varepsilon }(V)$
such that
$\alpha _{\pi } \in SL^{\varepsilon }(V)$
such that
![]() $(e_A)^{\alpha _{\pi }} = e_{A^{\pi }}$
for any
$(e_A)^{\alpha _{\pi }} = e_{A^{\pi }}$
for any
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
of even order. Let
$A \subseteq \lbrace 1, \dots , n \rbrace $
of even order. Let
![]() $\widetilde {\alpha }_{\pi }$
be the linear map
$\widetilde {\alpha }_{\pi }$
be the linear map
![]() $V \rightarrow V$
sending
$V \rightarrow V$
sending
![]() $v_i$
to
$v_i$
to
![]() $v_{i^{\pi }}$
for each
$v_{i^{\pi }}$
for each
![]() $1 \le i \le n$
. Then
$1 \le i \le n$
. Then
![]() $\mathrm {det}(\widetilde {\alpha }_{\pi }) = \mathrm {sgn}(\pi ) \in \lbrace -1, 1 \rbrace $
. Set
$\mathrm {det}(\widetilde {\alpha }_{\pi }) = \mathrm {sgn}(\pi ) \in \lbrace -1, 1 \rbrace $
. Set
![]() $\alpha _{\pi } := \widetilde {\alpha }_{\pi }$
if
$\alpha _{\pi } := \widetilde {\alpha }_{\pi }$
if
![]() $\mathrm {det}(\widetilde {\alpha }_{\pi }) = 1$
and
$\mathrm {det}(\widetilde {\alpha }_{\pi }) = 1$
and
![]() $\alpha _{\pi } := e_{\lbrace 1 \rbrace } \widetilde {\alpha }_{\pi }$
if
$\alpha _{\pi } := e_{\lbrace 1 \rbrace } \widetilde {\alpha }_{\pi }$
if
![]() $\mathrm {det}(\widetilde {\alpha }_{\pi }) = -1$
. Then
$\mathrm {det}(\widetilde {\alpha }_{\pi }) = -1$
. Then
![]() $\alpha _{\pi } \in SL^{\varepsilon }(V)$
. Also, if
$\alpha _{\pi } \in SL^{\varepsilon }(V)$
. Also, if
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
and
$A \subseteq \lbrace 1, \dots , n \rbrace $
and
![]() $1 \le i \le n$
, then
$1 \le i \le n$
, then
 $$ \begin{align*} (v_i)^{(\alpha_{\pi})^{-1}e_A \alpha_{\pi}} = v_i^{(\widetilde{\alpha}_{\pi})^{-1}e_A\widetilde{\alpha}_{\pi}} = \begin{cases} -v_i & \, \text{if } i \in A^{\pi} \\ v_i & \, \text{if } i \not\in A^{\pi} \end{cases} \end{align*} $$
$$ \begin{align*} (v_i)^{(\alpha_{\pi})^{-1}e_A \alpha_{\pi}} = v_i^{(\widetilde{\alpha}_{\pi})^{-1}e_A\widetilde{\alpha}_{\pi}} = \begin{cases} -v_i & \, \text{if } i \in A^{\pi} \\ v_i & \, \text{if } i \not\in A^{\pi} \end{cases} \end{align*} $$
and hence
![]() $(e_A)^{\alpha _{\pi }} = e_{A^{\pi }}$
. The proof of (i) is now complete.
$(e_A)^{\alpha _{\pi }} = e_{A^{\pi }}$
. The proof of (i) is now complete.
We now prove (ii). If
![]() $n \in \lbrace 1,2 \rbrace $
, then
$n \in \lbrace 1,2 \rbrace $
, then
![]() $\mathrm {Aut}_Y(E) = \lbrace \mathrm {id}_E \rbrace = \lbrace \varphi _{\pi } \mid \pi \in S_n \rbrace $
. Assume now that
$\mathrm {Aut}_Y(E) = \lbrace \mathrm {id}_E \rbrace = \lbrace \varphi _{\pi } \mid \pi \in S_n \rbrace $
. Assume now that
![]() $n \ge 3$
. Let
$n \ge 3$
. Let
![]() $\varphi \in \mathrm {Aut}_Y(E)$
, and let
$\varphi \in \mathrm {Aut}_Y(E)$
, and let
![]() $y \in Y$
with
$y \in Y$
with
![]() $\varphi = c_y|_{E,E}$
. We are going to show that y is a generalized permutation matrix, which implies the desired conclusion that
$\varphi = c_y|_{E,E}$
. We are going to show that y is a generalized permutation matrix, which implies the desired conclusion that
![]() $\varphi = \varphi _{\pi }$
for some
$\varphi = \varphi _{\pi }$
for some
![]() $\pi \in S_n$
. Let
$\pi \in S_n$
. Let
![]() $y_1, \dots , y_n$
denote the columns of y, and let
$y_1, \dots , y_n$
denote the columns of y, and let
![]() $1 \le j \le n$
. To prove that y is a generalized permutation matrix, it suffices to show that
$1 \le j \le n$
. To prove that y is a generalized permutation matrix, it suffices to show that
![]() $y_j$
has precisely one nonzero entry. Let
$y_j$
has precisely one nonzero entry. Let
![]() $1 \le k \ne \ell \le n$
with
$1 \le k \ne \ell \le n$
with
![]() $k \ne j \ne \ell $
. Let
$k \ne j \ne \ell $
. Let
![]() $A := \lbrace j,k \rbrace $
and
$A := \lbrace j,k \rbrace $
and
![]() $C := \lbrace j, \ell \rbrace $
. As y normalizes E, there exist distinct subsets
$C := \lbrace j, \ell \rbrace $
. As y normalizes E, there exist distinct subsets
![]() $A_0, C_0 \subseteq \lbrace 1, \dots , n \rbrace $
with
$A_0, C_0 \subseteq \lbrace 1, \dots , n \rbrace $
with
![]() $|A_0| = 2 = |C_0|$
and
$|A_0| = 2 = |C_0|$
and
![]() $(t_{A_0})^y = t_A$
,
$(t_{A_0})^y = t_A$
,
![]() $(t_{C_0})^y = t_C$
. Hence,
$(t_{C_0})^y = t_C$
. Hence,
![]() $t_{A_0} \cdot y = y \cdot t_A$
and
$t_{A_0} \cdot y = y \cdot t_A$
and
![]() $t_{C_0} \cdot y = y \cdot t_C$
, and so
$t_{C_0} \cdot y = y \cdot t_C$
, and so
![]() $y_j$
is an eigenvector of
$y_j$
is an eigenvector of
![]() $t_{A_0}$
and of
$t_{A_0}$
and of
![]() $t_{C_0}$
with eigenvalue
$t_{C_0}$
with eigenvalue
![]() $-1$
. Together with the fact that
$-1$
. Together with the fact that
![]() $|A_0| = 2 = |C_0|$
and
$|A_0| = 2 = |C_0|$
and
![]() $A_0 \ne C_0$
, it follows that
$A_0 \ne C_0$
, it follows that
![]() $y_j$
has only one nonzero entry, as required.
$y_j$
has only one nonzero entry, as required.
Lemma 3.24. Let q be a nontrivial odd prime power,
![]() $n \ge 3$
a natural number and S a Sylow
$n \ge 3$
a natural number and S a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_n(q)$
. Then
$PSL_n(q)$
. Then
![]() $\mathrm {Aut}_{PSL_n(q)}(S) = \mathrm {Inn}(S)$
.
$\mathrm {Aut}_{PSL_n(q)}(S) = \mathrm {Inn}(S)$
.
Proof. Let
![]() $R \in \mathrm {Syl}_2(SL_n(q))$
such that S is the image of R in
$R \in \mathrm {Syl}_2(SL_n(q))$
such that S is the image of R in
![]() $PSL_n(q)$
. Let T be a Sylow
$PSL_n(q)$
. Let T be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n(q)$
with
$GL_n(q)$
with
![]() $R \le T$
. By [Reference Kondrat’ev36, Theorem 1], we have
$R \le T$
. By [Reference Kondrat’ev36, Theorem 1], we have
![]() $N_{GL_n(q)}(R) = T C_{GL_n(q)}(T)$
. So we have that
$N_{GL_n(q)}(R) = T C_{GL_n(q)}(T)$
. So we have that
![]() $\mathrm {Aut}_{SL_n(q)}(R)$
is a
$\mathrm {Aut}_{SL_n(q)}(R)$
is a
![]() $2$
-group. Since the image of
$2$
-group. Since the image of
![]() $N_{SL_n(q)}(R)$
in
$N_{SL_n(q)}(R)$
in
![]() $PSL_n(q)$
equals
$PSL_n(q)$
equals
![]() $N_{PSL_n(q)}(S)$
(see [Reference Huppert and Endliche Gruppen35, Kapitel I, Hilfssatz 7.7 c)]), it follows that
$N_{PSL_n(q)}(S)$
(see [Reference Huppert and Endliche Gruppen35, Kapitel I, Hilfssatz 7.7 c)]), it follows that
![]() $\mathrm {Aut}_{PSL_n(q)}(S)$
is a
$\mathrm {Aut}_{PSL_n(q)}(S)$
is a
![]() $2$
-group, and this implies
$2$
-group, and this implies
![]() $\mathrm {Aut}_{PSL_n(q)}(S) = \mathrm {Inn}(S)$
.
$\mathrm {Aut}_{PSL_n(q)}(S) = \mathrm {Inn}(S)$
.
3.5 k-connectivity
In this subsection, we prove some connectivity properties of the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $SL_n(q)$
and
$SL_n(q)$
and
![]() $PSL_n(q)$
, where q is a nontrivial odd prime power and
$PSL_n(q)$
, where q is a nontrivial odd prime power and
![]() $n \ge 6$
. We will work with the following definition (see [Reference Gorenstein and Walter31, Section 8]):
$n \ge 6$
. We will work with the following definition (see [Reference Gorenstein and Walter31, Section 8]):
Definition 3.25. Let S be a finite
![]() $2$
-group, and let k be a positive integer. If A and B are elementary abelian subgroups of S of rank at least k, then A and B are said to be k-connected if there is a sequence
$2$
-group, and let k be a positive integer. If A and B are elementary abelian subgroups of S of rank at least k, then A and B are said to be k-connected if there is a sequence
of elementary abelian subgroups
![]() $A_i$
,
$A_i$
,
![]() $1 \le i \le n$
, of S with rank at least k such that
$1 \le i \le n$
, of S with rank at least k such that
for all
![]() $1 \le i \le n-1$
. The group S is said to be k-connected if any two elementary abelian subgroups of S of rank at least k are k-connected.
$1 \le i \le n-1$
. The group S is said to be k-connected if any two elementary abelian subgroups of S of rank at least k are k-connected.
Lemma 3.26 [Reference Gorenstein and Walter31, Lemma 8.4]
Let S be a finite
![]() $2$
-group, and let k be a positive integer. If S has a normal elementary abelian subgroup of rank at least
$2$
-group, and let k be a positive integer. If S has a normal elementary abelian subgroup of rank at least
![]() $2^{k-1}+1$
, then S is k-connected.
$2^{k-1}+1$
, then S is k-connected.
Lemma 3.27. Let q be a nontrivial odd prime power with
![]() $q \equiv 1 \ \mathrm {mod} \ 4$
, and let
$q \equiv 1 \ \mathrm {mod} \ 4$
, and let
![]() $n \ge 6$
be a natural number. Then the Sylow
$n \ge 6$
be a natural number. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_n(q)$
and those of
$PSL_n(q)$
and those of
![]() $SL_n(q)$
are
$SL_n(q)$
are
![]() $3$
-connected.
$3$
-connected.
Proof. Let
![]() $W_0$
be the unique Sylow
$W_0$
be the unique Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_1(q)$
, and let
$GL_1(q)$
, and let
![]() $W_1$
be the Sylow
$W_1$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
given in Lemma 3.10 (i). For each
$GL_2(q)$
given in Lemma 3.10 (i). For each
![]() $r \ge 2$
, let
$r \ge 2$
, let
![]() $W_r$
be the Sylow
$W_r$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^r}(q)$
obtained from
$GL_{2^r}(q)$
obtained from
![]() $W_{r-1}$
by the construction given in the last statement of Lemma 3.14. Let
$W_{r-1}$
by the construction given in the last statement of Lemma 3.14. Let
![]() $0 \le r_1 < \dots < r_t$
such that
$0 \le r_1 < \dots < r_t$
such that
![]() $n = 2^{r_1} + \dots + 2^{r_t}$
, and let W be the Sylow
$n = 2^{r_1} + \dots + 2^{r_t}$
, and let W be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n(q)$
obtained from
$GL_n(q)$
obtained from
![]() $W_{r_1}, \dots , W_{r_t}$
by using the last statement of Lemma 3.15.
$W_{r_1}, \dots , W_{r_t}$
by using the last statement of Lemma 3.15.
For any
![]() $k \ge 1$
, let
$k \ge 1$
, let
![]() $R_k(q)$
denote the subgroup of
$R_k(q)$
denote the subgroup of
![]() $GL_k(q)$
consisting of all diagonal matrices
$GL_k(q)$
consisting of all diagonal matrices
![]() $D \in GL_k(q)$
, where
$D \in GL_k(q)$
, where
![]() $D^2 \in Z(GL_k(q))$
and any diagonal element of D is a
$D^2 \in Z(GL_k(q))$
and any diagonal element of D is a
![]() $2$
-element of
$2$
-element of
![]() $\mathbb {F}_q^{*}$
. Also, let
$\mathbb {F}_q^{*}$
. Also, let
![]() $R := R_6(q)$
. By Lemma 3.14 and induction on r,
$R := R_6(q)$
. By Lemma 3.14 and induction on r,
![]() $R_{2^r}(q) \trianglelefteq W_r$
, using Lemma 3.10 (i) to anchor the induction. Then
$R_{2^r}(q) \trianglelefteq W_r$
, using Lemma 3.10 (i) to anchor the induction. Then
![]() $R = R_{2^{r_1}}(q) \times \dots \times R_{2^{r_t}}(q) \trianglelefteq W$
. Let
$R = R_{2^{r_1}}(q) \times \dots \times R_{2^{r_t}}(q) \trianglelefteq W$
. Let
![]() $R_0 := R \cap SL_n(q)$
and
$R_0 := R \cap SL_n(q)$
and
![]() $E := \Omega _1(R_0)$
. By Lemma 3.22,
$E := \Omega _1(R_0)$
. By Lemma 3.22,
![]() $m(E) = n-1 \ge 5$
, so by Lemma 3.26,
$m(E) = n-1 \ge 5$
, so by Lemma 3.26,
![]() $W_0 := W \cap SL_n(q)$
is
$W_0 := W \cap SL_n(q)$
is
![]() $3$
-connected. Set
$3$
-connected. Set
![]() $W^{*} := W/(W \cap Z(SL_n(q)))$
; then
$W^{*} := W/(W \cap Z(SL_n(q)))$
; then
![]() $m(E^{*}) \ge m(E) - 1 = n - 2$
, so by Lemma 3.26,
$m(E^{*}) \ge m(E) - 1 = n - 2$
, so by Lemma 3.26,
![]() $W_0^{*}$
is
$W_0^{*}$
is
![]() $3$
-connected, unless possibly
$3$
-connected, unless possibly
![]() $n = 6$
. But if
$n = 6$
. But if
![]() $n = 6$
, then
$n = 6$
, then
![]() $F^{*} = R_0^{*}$
is of rank
$F^{*} = R_0^{*}$
is of rank
![]() $5$
, where
$5$
, where
![]() $F = \langle E, iI_6 \cdot r \rangle $
for some reflection
$F = \langle E, iI_6 \cdot r \rangle $
for some reflection
![]() $r \in R$
and some
$r \in R$
and some
![]() $i \in \mathbb {F}_q^{*}$
of order
$i \in \mathbb {F}_q^{*}$
of order
![]() $4$
.
$4$
.
Lemma 3.26 and the proof of Lemma 3.27 show that we also have the following:
Lemma 3.28. Let q be a nontrivial odd prime power with
![]() $q \equiv 1 \ \mathrm {mod} \ 4$
, and let
$q \equiv 1 \ \mathrm {mod} \ 4$
, and let
![]() $n \ge 6$
be a natural number. Then the Sylow
$n \ge 6$
be a natural number. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_n(q)$
and those of
$PSL_n(q)$
and those of
![]() $SL_n(q)$
are
$SL_n(q)$
are
![]() $2$
-connected.
$2$
-connected.
We now study the case
![]() $q \equiv 3 \mod 4$
.
$q \equiv 3 \mod 4$
.
Lemma 3.29. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
, and let
$q \equiv 3 \ \mathrm {mod} \ 4$
, and let
![]() $n \ge 6$
be a natural number. Then the Sylow
$n \ge 6$
be a natural number. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_n(q)$
and those of
$PSL_n(q)$
and those of
![]() $SL_n(q)$
are
$SL_n(q)$
are
![]() $2$
-connected. If
$2$
-connected. If
![]() $n \ge 10$
, then we even have that the Sylow
$n \ge 10$
, then we even have that the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_n(q)$
and those of
$PSL_n(q)$
and those of
![]() $SL_n(q)$
are
$SL_n(q)$
are
![]() $3$
-connected.
$3$
-connected.
Proof. Let
![]() $W_0$
denote the unique Sylow
$W_0$
denote the unique Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_1(q)$
, and let
$GL_1(q)$
, and let
![]() $W_1$
be a Sylow
$W_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
. By Lemma 3.10 (ii),
$GL_2(q)$
. By Lemma 3.10 (ii),
![]() $W_1$
is semidihedral. Let
$W_1$
is semidihedral. Let
![]() $m \in \mathbb {N}$
with
$m \in \mathbb {N}$
with
![]() $|W_1| = 2^m$
. Also, let
$|W_1| = 2^m$
. Also, let
![]() $h,a \in W_1$
such that
$h,a \in W_1$
such that
![]() $\mathrm {ord}(h) = 2^{m-1}$
,
$\mathrm {ord}(h) = 2^{m-1}$
,
![]() $\mathrm {ord}(a) = 2$
and
$\mathrm {ord}(a) = 2$
and
![]() $h^a = h^{2^{m-2}-1}$
. Set
$h^a = h^{2^{m-2}-1}$
. Set
![]() $z := -I_2 = h^{2^{m-2}}$
. For each
$z := -I_2 = h^{2^{m-2}}$
. For each
![]() $r \ge 2$
, let
$r \ge 2$
, let
![]() $W_r$
be the Sylow
$W_r$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^r}(q)$
obtained from
$GL_{2^r}(q)$
obtained from
![]() $W_{r-1}$
by the construction given in the last statement of Lemma 3.14. Let
$W_{r-1}$
by the construction given in the last statement of Lemma 3.14. Let
![]() $0 \le r_1 < \dots < r_t$
such that
$0 \le r_1 < \dots < r_t$
such that
![]() $n = 2^{r_1} + \dots + 2^{r_t}$
, and let W be the Sylow
$n = 2^{r_1} + \dots + 2^{r_t}$
, and let W be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n(q)$
obtained from
$GL_n(q)$
obtained from
![]() $W_{r_1}, \dots , W_{r_t}$
by using the last statement of Lemma 3.15.
$W_{r_1}, \dots , W_{r_t}$
by using the last statement of Lemma 3.15.
Given a natural number
![]() $\ell \ge 1$
and elements
$\ell \ge 1$
and elements
![]() $x_1,\dots ,x_{\ell } \in GL_2(q)$
, we write
$x_1,\dots ,x_{\ell } \in GL_2(q)$
, we write
![]() $\mathrm {diag}(x_1,\dots ,x_{\ell })$
for the block diagonal matrix
$\mathrm {diag}(x_1,\dots ,x_{\ell })$
for the block diagonal matrix
 $$ \begin{align*} \begin{pmatrix} x_1 & & \\ & \ddots & \\ & & x_{\ell} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} x_1 & & \\ & \ddots & \\ & & x_{\ell} \end{pmatrix}. \end{align*} $$
For each natural number
![]() $r \ge 1$
, let
$r \ge 1$
, let
![]() $A_r$
denote the subgroup of
$A_r$
denote the subgroup of
![]() $GL_{2^r}(q)$
consisting of the matrices
$GL_{2^r}(q)$
consisting of the matrices
![]() $\mathrm {diag}(x_1, \dots , x_{2^{r-1}})$
, where either
$\mathrm {diag}(x_1, \dots , x_{2^{r-1}})$
, where either
![]() $x_i \in \langle z \rangle $
for all
$x_i \in \langle z \rangle $
for all
![]() $1 \le i \le 2^{r-1}$
or
$1 \le i \le 2^{r-1}$
or
![]() $x_i$
is an element of
$x_i$
is an element of
![]() $\langle h \rangle $
with order
$\langle h \rangle $
with order
![]() $4$
for all
$4$
for all
![]() $1 \le i \le 2^{r-1}$
. By induction over r, one can see that
$1 \le i \le 2^{r-1}$
. By induction over r, one can see that
![]() $A_r \trianglelefteq W_r$
for all
$A_r \trianglelefteq W_r$
for all
![]() $r \ge 1$
. Also, let
$r \ge 1$
. Also, let
![]() $\widetilde {A_r} := \Omega _1(A_r)$
for all
$\widetilde {A_r} := \Omega _1(A_r)$
for all
![]() $r \ge 1$
. Clearly,
$r \ge 1$
. Clearly,
![]() $\widetilde {A_r} \trianglelefteq W_r$
for all
$\widetilde {A_r} \trianglelefteq W_r$
for all
![]() $r \ge 1$
.
$r \ge 1$
.
We now consider two cases.
Case 1: n is even.
Let E be the subgroup of
![]() $GL_n(q)$
consisting of the matrices
$GL_n(q)$
consisting of the matrices
![]() $\mathrm {diag}(x_1,\dots ,x_{\frac {n}{2}})$
, where either
$\mathrm {diag}(x_1,\dots ,x_{\frac {n}{2}})$
, where either
![]() $x_i \in \langle z \rangle $
for all
$x_i \in \langle z \rangle $
for all
![]() $1 \le i \le \frac {n}{2}$
or
$1 \le i \le \frac {n}{2}$
or
![]() $x_i$
is an element of
$x_i$
is an element of
![]() $\langle h \rangle $
with order
$\langle h \rangle $
with order
![]() $4$
for all
$4$
for all
![]() $1 \le i \le \frac {n}{2}$
. Let
$1 \le i \le \frac {n}{2}$
. Let
![]() $\widetilde {E} := \Omega _1(E)$
. Since
$\widetilde {E} := \Omega _1(E)$
. Since
![]() $A_{r_i} \trianglelefteq W_{r_i}$
for all
$A_{r_i} \trianglelefteq W_{r_i}$
for all
![]() $1 \le i \le t$
, we have that E and
$1 \le i \le t$
, we have that E and
![]() $\widetilde E$
are normal subgroups of W. Lemma 3.16 (iii) shows that
$\widetilde E$
are normal subgroups of W. Lemma 3.16 (iii) shows that
![]() $E \le W \cap SL_n(q)$
.
$E \le W \cap SL_n(q)$
.
As
![]() $\widetilde E$
is elementary abelian of order
$\widetilde E$
is elementary abelian of order
![]() $2^{\frac {n}{2}}$
, Lemma 3.26 implies that
$2^{\frac {n}{2}}$
, Lemma 3.26 implies that
![]() $W \cap SL_n(q)$
is
$W \cap SL_n(q)$
is
![]() $2$
-connected and even
$2$
-connected and even
![]() $3$
-connected if
$3$
-connected if
![]() $n \ge 10$
. Since
$n \ge 10$
. Since
![]() $EZ(SL_n(q))/Z(SL_n(q))$
is a normal elementary abelian subgroup of
$EZ(SL_n(q))/Z(SL_n(q))$
is a normal elementary abelian subgroup of
![]() $(W \cap SL_n(q))Z(SL_n(q))/Z(SL_n(q))$
with order
$(W \cap SL_n(q))Z(SL_n(q))/Z(SL_n(q))$
with order
![]() $2^{\frac {n}{2}}$
, Lemma 3.26 also shows that a Sylow
$2^{\frac {n}{2}}$
, Lemma 3.26 also shows that a Sylow
![]() $2$
-subgroup is
$2$
-subgroup is
![]() $2$
-connected, and even
$2$
-connected, and even
![]() $3$
-connected if
$3$
-connected if
![]() $n \ge 10$
.
$n \ge 10$
.
Case 2: n is odd.
Now let E denote the subgroup of
![]() $GL_n(q)$
consisting of the matrices
$GL_n(q)$
consisting of the matrices
 $$ \begin{align*} \left( \begin{array}{c|cc} 1 & \begin{matrix} & & \end{matrix} \\ \hline \begin{matrix} & \\ & \\ & \end{matrix} & \begin{matrix} x_1 & & \\ & \ddots & \\ & & x_{\frac{n-1}{2}} \end{matrix} \end{array} \right), \end{align*} $$
$$ \begin{align*} \left( \begin{array}{c|cc} 1 & \begin{matrix} & & \end{matrix} \\ \hline \begin{matrix} & \\ & \\ & \end{matrix} & \begin{matrix} x_1 & & \\ & \ddots & \\ & & x_{\frac{n-1}{2}} \end{matrix} \end{array} \right), \end{align*} $$
where
![]() $x_i \in \langle z \rangle $
for all
$x_i \in \langle z \rangle $
for all
![]() $1 \le i \le \frac {n-1}{2}$
. Since
$1 \le i \le \frac {n-1}{2}$
. Since
![]() $\widetilde {A_{r_i}} \trianglelefteq W_{r_i}$
for all
$\widetilde {A_{r_i}} \trianglelefteq W_{r_i}$
for all
![]() $2 \le i \le t$
, we have that E is a normal subgroup of
$2 \le i \le t$
, we have that E is a normal subgroup of
![]() $W \cap SL_n(q)$
. Moreover, E is elementary abelian of order
$W \cap SL_n(q)$
. Moreover, E is elementary abelian of order
![]() $2^{\frac {n-1}{2}}$
. Lemma 3.26 implies that
$2^{\frac {n-1}{2}}$
. Lemma 3.26 implies that
![]() $W \cap SL_n(q)$
is
$W \cap SL_n(q)$
is
![]() $2$
-connected and even
$2$
-connected and even
![]() $3$
-connected if
$3$
-connected if
![]() $n \ge 11$
. There is nothing else to show since the Sylow
$n \ge 11$
. There is nothing else to show since the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_n(q)$
are isomorphic to those of
$PSL_n(q)$
are isomorphic to those of
![]() $SL_n(q)$
(as n is odd).
$SL_n(q)$
(as n is odd).
We show next that the groups
![]() $SL_n(q)$
, where
$SL_n(q)$
, where
![]() $6 \le n \le 9$
and
$6 \le n \le 9$
and
![]() $q \equiv 3 \mod 4$
, and the groups
$q \equiv 3 \mod 4$
, and the groups
![]() $PSL_n(q)$
, where
$PSL_n(q)$
, where
![]() $7 \le n \le 9$
and
$7 \le n \le 9$
and
![]() $q \equiv 3 \mod 4$
, also have
$q \equiv 3 \mod 4$
, also have
![]() $3$
-connected Sylow
$3$
-connected Sylow
![]() $2$
-subgroups.
$2$
-subgroups.
Lemma 3.30. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \mod 4$
. Then the Sylow
$q \equiv 3 \mod 4$
. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $SL_6(q)$
and those of
$SL_6(q)$
and those of
![]() $SL_7(q)$
are
$SL_7(q)$
are
![]() $3$
-connected.
$3$
-connected.
Proof. Let
![]() $W_1$
be a Sylow
$W_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
, let
$GL_2(q)$
, let
![]() $W_2$
be the Sylow
$W_2$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
obtained from
$GL_4(q)$
obtained from
![]() $W_1$
by the construction given in the last statement of Lemma 3.14 and let W be the Sylow
$W_1$
by the construction given in the last statement of Lemma 3.14 and let W be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_6(q)$
obtained from
$GL_6(q)$
obtained from
![]() $W_1$
and
$W_1$
and
![]() $W_2$
by using the last statement of Lemma 3.15.
$W_2$
by using the last statement of Lemma 3.15.
From Lemma 3.15, we see that the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $SL_7(q)$
are isomorphic to those of
$SL_7(q)$
are isomorphic to those of
![]() $GL_6(q)$
. So it is enough to show that W and
$GL_6(q)$
. So it is enough to show that W and
![]() $W \cap SL_6(q)$
are
$W \cap SL_6(q)$
are
![]() $3$
-connected. Given elements
$3$
-connected. Given elements
![]() $x_1,x_2,x_3 \in GL_2(q)$
, we write
$x_1,x_2,x_3 \in GL_2(q)$
, we write
![]() $\mathrm {diag}(x_1,x_2,x_3)$
for the block diagonal matrix
$\mathrm {diag}(x_1,x_2,x_3)$
for the block diagonal matrix
 $$ \begin{align*} \begin{pmatrix} x_1 & & \\ & x_2 & \\ & & x_3 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} x_1 & & \\ & x_2 & \\ & & x_3 \end{pmatrix}. \end{align*} $$
Let A be the subgroup of
![]() $W \cap SL_6(q)$
consisting of the matrices
$W \cap SL_6(q)$
consisting of the matrices
![]() $\mathrm {diag}(x_1,x_2,x_3)$
, where
$\mathrm {diag}(x_1,x_2,x_3)$
, where
![]() $x_i \in \langle -I_2 \rangle $
for
$x_i \in \langle -I_2 \rangle $
for
![]() $1 \le i \le 3$
. Then
$1 \le i \le 3$
. Then
![]() $A \cong E_8$
. We prove the following:
$A \cong E_8$
. We prove the following:
-
(1) If E is an elementary abelian subgroup of W of rank at least
 $3$
, then E is
$3$
, then E is
 $3$
-connected to an elementary abelian subgroup of
$3$
-connected to an elementary abelian subgroup of
 $W \cap SL_6(q)$
of rank at least
$W \cap SL_6(q)$
of rank at least
 $3$
.
$3$
. -
(2) If E is an elementary abelian subgroup of
 $W \cap SL_6(q)$
of rank at least
$W \cap SL_6(q)$
of rank at least
 $3$
, then E is
$3$
, then E is
 $3$
-connected to A in
$3$
-connected to A in
 $W \cap SL_6(q)$
.
$W \cap SL_6(q)$
.
By (1) and (2), any elementary abelian subgroup of W of rank at least
![]() $3$
is
$3$
is
![]() $3$
-connected to A, and so W is
$3$
-connected to A, and so W is
![]() $3$
-connected. Similarly, (2) implies that
$3$
-connected. Similarly, (2) implies that
![]() $W \cap SL_6(q)$
is
$W \cap SL_6(q)$
is
![]() $3$
-connected.
$3$
-connected.
Let
![]() $Z := \langle \mathrm {diag}(-I_2, I_2, I_2), \mathrm {diag}(I_2,-I_2,-I_2) \rangle $
. Since
$Z := \langle \mathrm {diag}(-I_2, I_2, I_2), \mathrm {diag}(I_2,-I_2,-I_2) \rangle $
. Since
![]() $Z \le Z(W)$
, we have that any elementary abelian subgroup of W of rank at least
$Z \le Z(W)$
, we have that any elementary abelian subgroup of W of rank at least
![]() $3$
is
$3$
is
![]() $3$
-connected to an
$3$
-connected to an
![]() $E_8$
-subgroup of W containing Z. Also, any elementary abelian subgroup of
$E_8$
-subgroup of W containing Z. Also, any elementary abelian subgroup of
![]() $W \cap SL_6(q)$
of rank at least
$W \cap SL_6(q)$
of rank at least
![]() $3$
is
$3$
is
![]() $3$
-connected (in
$3$
-connected (in
![]() $W \cap SL_6(q)$
) to an
$W \cap SL_6(q)$
) to an
![]() $E_8$
-subgroup of
$E_8$
-subgroup of
![]() $W \cap SL_6(q)$
containing Z. Therefore, we only need to consider
$W \cap SL_6(q)$
containing Z. Therefore, we only need to consider
![]() $E_8$
-subgroups containing Z in order to prove (1) and (2).
$E_8$
-subgroups containing Z in order to prove (1) and (2).
So let E be an
![]() $E_8$
-subgroup of W with
$E_8$
-subgroup of W with
![]() $Z \le E$
, and let
$Z \le E$
, and let
![]() $s \in E \setminus Z$
. Suppose that
$s \in E \setminus Z$
. Suppose that
![]() $s = \mathrm {diag}(s_1,s_2,s_3)$
, where
$s = \mathrm {diag}(s_1,s_2,s_3)$
, where
![]() $s_1,s_2,s_3 \in W_1$
. Then
$s_1,s_2,s_3 \in W_1$
. Then
![]() $[E,A] = 1$
, and it is easy to deduce that E is
$[E,A] = 1$
, and it is easy to deduce that E is
![]() $3$
-connected to A so that E satisfies (1). Also, if
$3$
-connected to A so that E satisfies (1). Also, if
![]() $E \le W \cap SL_6(q)$
, it is easy to deduce that E satisfies (2).
$E \le W \cap SL_6(q)$
, it is easy to deduce that E satisfies (2).
Suppose now that
 $$ \begin{align*} s = \begin{pmatrix} s_1 & & \\ & & s_2 \\ & s_3 & \end{pmatrix} \end{align*} $$
$$ \begin{align*} s = \begin{pmatrix} s_1 & & \\ & & s_2 \\ & s_3 & \end{pmatrix} \end{align*} $$
for some
![]() $s_1, s_2, s_3 \in W_1$
. Since
$s_1, s_2, s_3 \in W_1$
. Since
![]() $s^2 = I_6$
, we have
$s^2 = I_6$
, we have
![]() $s_2 = s_3^{-1}$
. Let a be an involution of
$s_2 = s_3^{-1}$
. Let a be an involution of
![]() $W_1$
with
$W_1$
with
![]() $a \ne -I_2$
. Set
$a \ne -I_2$
. Set
![]() $s^{*} := \mathrm {diag}(I_2,a,a^{s_2})$
and
$s^{*} := \mathrm {diag}(I_2,a,a^{s_2})$
and
![]() $E^{*} := \langle Z, s^{*} \rangle \cong E_8$
. Clearly,
$E^{*} := \langle Z, s^{*} \rangle \cong E_8$
. Clearly,
![]() $E^{*} \le W \cap SL_6(q)$
. It is easy to check that
$E^{*} \le W \cap SL_6(q)$
. It is easy to check that
![]() $[E,E^{*}] = 1$
, which implies that E is
$[E,E^{*}] = 1$
, which implies that E is
![]() $3$
-connected to
$3$
-connected to
![]() $E^{*}$
. So E satisfies (1). If
$E^{*}$
. So E satisfies (1). If
![]() $E \le W \cap SL_6(q)$
, then E is
$E \le W \cap SL_6(q)$
, then E is
![]() $3$
-connected to
$3$
-connected to
![]() $E^{*}$
in
$E^{*}$
in
![]() $W \cap SL_6(q)$
, and
$W \cap SL_6(q)$
, and
![]() $E^{*}$
is
$E^{*}$
is
![]() $3$
-connected to A in
$3$
-connected to A in
![]() $W \cap SL_6(q)$
since
$W \cap SL_6(q)$
since
![]() $[E^{*},A] = 1$
. Therefore, E satisfies (2) when
$[E^{*},A] = 1$
. Therefore, E satisfies (2) when
![]() $E \le W \cap SL_6(q)$
.
$E \le W \cap SL_6(q)$
.
Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \mod 4$
. A Sylow
$q \equiv 3 \mod 4$
. A Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_7(q)$
is isomorphic to a Sylow
$PSL_7(q)$
is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_7(q)$
. So, by Lemma 3.30, the Sylow
$SL_7(q)$
. So, by Lemma 3.30, the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_7(q)$
are
$PSL_7(q)$
are
![]() $3$
-connected.
$3$
-connected.
We need the following lemma in order to prove that the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $SL_n(q)$
and
$SL_n(q)$
and
![]() $PSL_n(q)$
are
$PSL_n(q)$
are
![]() $3$
-connected when
$3$
-connected when
![]() $n \in \lbrace 8,9 \rbrace $
.
$n \in \lbrace 8,9 \rbrace $
.
Lemma 3.31. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
, and let V be a Sylow
$q \equiv 3 \ \mathrm {mod} \ 4$
, and let V be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
. Let
$GL_4(q)$
. Let
![]() $u \in V$
with
$u \in V$
with
![]() $u^2 = I_4$
or
$u^2 = I_4$
or
![]() $u^2 = -I_4$
. Then there is an involution
$u^2 = -I_4$
. Then there is an involution
![]() $v \in V \setminus \langle u, -I_4 \rangle $
which commutes with u.
$v \in V \setminus \langle u, -I_4 \rangle $
which commutes with u.
Proof. Fix a Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $W_1$
of
$W_1$
of
![]() $GL_2(q)$
, and let
$GL_2(q)$
, and let
![]() $W_2$
be the Sylow
$W_2$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
obtained from
$GL_4(q)$
obtained from
![]() $W_1$
by the construction given in the last statement of Lemma 3.14. By Sylow’s theorem, we may assume that
$W_1$
by the construction given in the last statement of Lemma 3.14. By Sylow’s theorem, we may assume that
![]() $V = W_2$
. Let a be an involution of
$V = W_2$
. Let a be an involution of
![]() $W_1$
with
$W_1$
with
![]() $a \ne -I_2$
.
$a \ne -I_2$
.
First, we consider the case that
 $$ \begin{align*} u = \begin{pmatrix} x & \\ & y \end{pmatrix} \end{align*} $$
$$ \begin{align*} u = \begin{pmatrix} x & \\ & y \end{pmatrix} \end{align*} $$
with elements
![]() $x,y \in W_1$
. If
$x,y \in W_1$
. If
![]() $x \not \in \langle -I_2 \rangle $
or
$x \not \in \langle -I_2 \rangle $
or
![]() $y \not \in \langle -I_2 \rangle $
, then
$y \not \in \langle -I_2 \rangle $
, then
 $$ \begin{align*} \begin{pmatrix} -I_2 & \\ & I_2 \end{pmatrix} \in W_2 \end{align*} $$
$$ \begin{align*} \begin{pmatrix} -I_2 & \\ & I_2 \end{pmatrix} \in W_2 \end{align*} $$
is an involution commuting with u and not lying in
![]() $\langle u, -I_4 \rangle $
. If
$\langle u, -I_4 \rangle $
. If
![]() $x,y \in \langle -I_2 \rangle $
, then we may choose
$x,y \in \langle -I_2 \rangle $
, then we may choose
 $$ \begin{align*} v := \begin{pmatrix} a & \\ & a \end{pmatrix}. \end{align*} $$
$$ \begin{align*} v := \begin{pmatrix} a & \\ & a \end{pmatrix}. \end{align*} $$
Assume now that
 $$ \begin{align*} u = \begin{pmatrix} & x \\ y & \end{pmatrix} \end{align*} $$
$$ \begin{align*} u = \begin{pmatrix} & x \\ y & \end{pmatrix} \end{align*} $$
with elements
![]() $x,y \in W_1$
. Let
$x,y \in W_1$
. Let
 $$ \begin{align*} v := \begin{pmatrix}a & \\ & a^x \end{pmatrix}. \end{align*} $$
$$ \begin{align*} v := \begin{pmatrix}a & \\ & a^x \end{pmatrix}. \end{align*} $$
As a is an involution of
![]() $W_1$
, we have that v is an involution of
$W_1$
, we have that v is an involution of
![]() $W_2$
. By a direct calculation (using that
$W_2$
. By a direct calculation (using that
![]() $xy \in \langle -I_2 \rangle $
), v has the desired properties.
$xy \in \langle -I_2 \rangle $
), v has the desired properties.
Lemma 3.32. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
. Then the Sylow
$q \equiv 3 \ \mathrm {mod} \ 4$
. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $SL_8(q)$
and those of
$SL_8(q)$
and those of
![]() $SL_9(q)$
are
$SL_9(q)$
are
![]() $3$
-connected.
$3$
-connected.
Proof. Fix a Sylow
![]() $2$
-subgroup
$2$
-subgroup
![]() $W_1$
of
$W_1$
of
![]() $GL_2(q)$
, let
$GL_2(q)$
, let
![]() $W_2$
be the Sylow
$W_2$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
obtained from
$GL_4(q)$
obtained from
![]() $W_1$
by the construction given in the last statement of Lemma 3.14 and let W be the Sylow
$W_1$
by the construction given in the last statement of Lemma 3.14 and let W be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_8(q)$
obtained from
$GL_8(q)$
obtained from
![]() $W_2$
by the construction given in the last statement of Lemma 3.14. Set
$W_2$
by the construction given in the last statement of Lemma 3.14. Set
![]() $S := W \cap SL_8(q)$
.
$S := W \cap SL_8(q)$
.
From Lemma 3.15, we see that the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $SL_9(q)$
are isomorphic to those of
$SL_9(q)$
are isomorphic to those of
![]() $GL_8(q)$
. So it is enough to show that W and S are
$GL_8(q)$
. So it is enough to show that W and S are
![]() $3$
-connected.
$3$
-connected.
Given a natural number
![]() $\ell \ge 1$
and
$\ell \ge 1$
and
![]() $x_1, \dots , x_{\ell } \in GL_2(q) \cup GL_4(q)$
, we write
$x_1, \dots , x_{\ell } \in GL_2(q) \cup GL_4(q)$
, we write
![]() $\mathrm {diag}(x_1,\dots ,x_{\ell })$
for the block diagonal matrix
$\mathrm {diag}(x_1,\dots ,x_{\ell })$
for the block diagonal matrix
 $$ \begin{align*} \begin{pmatrix} x_1 & & \\ & \ddots & \\ & & x_{\ell} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} x_1 & & \\ & \ddots & \\ & & x_{\ell} \end{pmatrix}. \end{align*} $$
Set
and
Then
![]() $A \cong E_{16}$
. Since
$A \cong E_{16}$
. Since
![]() $Z \le Z(W)$
, we have that any elementary abelian subgroup of W of rank at least
$Z \le Z(W)$
, we have that any elementary abelian subgroup of W of rank at least
![]() $3$
is
$3$
is
![]() $3$
-connected to an
$3$
-connected to an
![]() $E_8$
-subgroup of W containing Z. Similarly, any elementary abelian subgroup of S of rank at least
$E_8$
-subgroup of W containing Z. Similarly, any elementary abelian subgroup of S of rank at least
![]() $3$
is
$3$
is
![]() $3$
-connected to an
$3$
-connected to an
![]() $E_8$
-subgroup of S containing Z. So it suffices to prove that any
$E_8$
-subgroup of S containing Z. So it suffices to prove that any
![]() $E_8$
-subgroup E of W with
$E_8$
-subgroup E of W with
![]() $Z \le E$
is
$Z \le E$
is
![]() $3$
-connected to A, where E is even
$3$
-connected to A, where E is even
![]() $3$
-connected in S to A if
$3$
-connected in S to A if
![]() $E \le S$
. Thus, let E be an
$E \le S$
. Thus, let E be an
![]() $E_8$
-subgroup of W containing Z, and let
$E_8$
-subgroup of W containing Z, and let
![]() $x,y \in E$
with
$x,y \in E$
with
![]() $E = \langle Z, x, y \rangle $
.
$E = \langle Z, x, y \rangle $
.
We consider a number of cases. Below, a will always denote an involution of
![]() $W_1$
with
$W_1$
with
![]() $a \ne -I_2$
.
$a \ne -I_2$
.
Case 1:
![]() $x = \mathrm {diag}(-I_4,I_4)$
and
$x = \mathrm {diag}(-I_4,I_4)$
and
![]() $y = \mathrm {diag}(b_1,b_2)$
for some
$y = \mathrm {diag}(b_1,b_2)$
for some
![]() $b_1,b_2 \in W_2$
.
$b_1,b_2 \in W_2$
.
We determine an involution
![]() $y_1 \in C_W(E) \setminus \langle Z, x \rangle $
such that
$y_1 \in C_W(E) \setminus \langle Z, x \rangle $
such that
![]() $\langle Z, x, y_1 \rangle \cong E_8$
is
$\langle Z, x, y_1 \rangle \cong E_8$
is
![]() $3$
-connected to A. In the case that
$3$
-connected to A. In the case that
![]() $E \le S$
, we determine
$E \le S$
, we determine
![]() $y_1$
such that
$y_1$
such that
![]() $y_1 \in S$
and such that
$y_1 \in S$
and such that
![]() $\langle Z, x, y_1 \rangle $
is
$\langle Z, x, y_1 \rangle $
is
![]() $3$
-connected to A in S. The existence of such an involution
$3$
-connected to A in S. The existence of such an involution
![]() $y_1$
easily implies that E is
$y_1$
easily implies that E is
![]() $3$
-connected to A and even
$3$
-connected to A and even
![]() $3$
-connected to A in S if
$3$
-connected to A in S if
![]() $E \le S$
. The involution
$E \le S$
. The involution
![]() $y_1$
is given by the following table in dependence of y. In each row,
$y_1$
is given by the following table in dependence of y. In each row,
![]() $r_1, r_2, r_3, r_4$
are assumed to be elements of
$r_1, r_2, r_3, r_4$
are assumed to be elements of
![]() $W_1$
such that y is equal to the matrix given in the column “y” and such that the conditions in the column ‘Conditions’ (if any) are satisfied. The column ‘
$W_1$
such that y is equal to the matrix given in the column “y” and such that the conditions in the column ‘Conditions’ (if any) are satisfied. The column ‘
![]() $y_1$
’ gives the involution
$y_1$
’ gives the involution
![]() $y_1$
with the desired properties. For each row, one can verify the stated properties of
$y_1$
with the desired properties. For each row, one can verify the stated properties of
![]() $y_1$
by a direct calculation or by using the previous rows.
$y_1$
by a direct calculation or by using the previous rows.

Case 2:
![]() $x = \mathrm {diag}(a_1,a_2)$
and
$x = \mathrm {diag}(a_1,a_2)$
and
![]() $y = \mathrm {diag}(b_1,b_2)$
for some
$y = \mathrm {diag}(b_1,b_2)$
for some
![]() $a_1, a_2, b_1, b_2 \in W_2$
.
$a_1, a_2, b_1, b_2 \in W_2$
.
Set
![]() $x_1 := \mathrm {diag}(-I_4,I_4)$
. Since
$x_1 := \mathrm {diag}(-I_4,I_4)$
. Since
![]() $E = \langle Z, x, y \rangle \cong E_8$
, the elements x and y cannot be both contained in
$E = \langle Z, x, y \rangle \cong E_8$
, the elements x and y cannot be both contained in
![]() $\langle Z, x_1 \rangle $
. Without loss of generality, we may assume that
$\langle Z, x_1 \rangle $
. Without loss of generality, we may assume that
![]() $y \not \in \langle Z, x_1 \rangle $
. Then
$y \not \in \langle Z, x_1 \rangle $
. Then
![]() $E_1 := \langle Z, x_1, y \rangle \cong E_8$
. The group
$E_1 := \langle Z, x_1, y \rangle \cong E_8$
. The group
![]() $E_1$
is
$E_1$
is
![]() $3$
-connected to A by Case 1, and it is
$3$
-connected to A by Case 1, and it is
![]() $3$
-connected to E since E and
$3$
-connected to E since E and
![]() $E_1$
commute. Hence, E is
$E_1$
commute. Hence, E is
![]() $3$
-connected to A. Clearly, if
$3$
-connected to A. Clearly, if
![]() $E \le S$
, then E is even
$E \le S$
, then E is even
![]() $3$
-connected in S to A.
$3$
-connected in S to A.
Case 3: There are
![]() $a_1, a_2, b_1, b_2 \in W_2$
with
$a_1, a_2, b_1, b_2 \in W_2$
with
 $$ \begin{align*} \lbrace x, y \rbrace = \left \lbrace \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix}, \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix} \right \rbrace. \end{align*} $$
$$ \begin{align*} \lbrace x, y \rbrace = \left \lbrace \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix}, \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix} \right \rbrace. \end{align*} $$
Without loss of generality, we assume that
 $$ \begin{align*} x = \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix} \ \text{and} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix} \ \text{and} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
Since x and y are commuting involutions, we have
![]() $b_1 = b_2^{-1}$
and
$b_1 = b_2^{-1}$
and
![]() $a_2 = {a_1}^{b_1}$
. By Lemma 3.31, there is an involution
$a_2 = {a_1}^{b_1}$
. By Lemma 3.31, there is an involution
![]() $\widetilde {a_1} \in W_2 \setminus \langle a_1, -I_4 \rangle $
which commutes with
$\widetilde {a_1} \in W_2 \setminus \langle a_1, -I_4 \rangle $
which commutes with
![]() $a_1$
. Set
$a_1$
. Set
 $$ \begin{align*} y_1 := \begin{pmatrix} \widetilde{a_1} & \\ & {\widetilde{a_1}}^{b_1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} y_1 := \begin{pmatrix} \widetilde{a_1} & \\ & {\widetilde{a_1}}^{b_1} \end{pmatrix}. \end{align*} $$
It is easy to see that
![]() $y_1 \in S$
, and
$y_1 \in S$
, and
![]() $y_1$
is an involution since
$y_1$
is an involution since
![]() $\widetilde {a_1}$
is an involution of
$\widetilde {a_1}$
is an involution of
![]() $W_2$
. We have
$W_2$
. We have
![]() $[x,y_1] = 1$
since
$[x,y_1] = 1$
since
![]() $\widetilde {a_1}$
commutes with
$\widetilde {a_1}$
commutes with
![]() $a_1$
and
$a_1$
and
![]() $\widetilde {a_1}^{b_1}$
commutes with
$\widetilde {a_1}^{b_1}$
commutes with
![]() ${a_1}^{b_1} = a_2$
. A direct calculation using that
${a_1}^{b_1} = a_2$
. A direct calculation using that
![]() $b_1 = b_2^{-1}$
shows that we also have
$b_1 = b_2^{-1}$
shows that we also have
![]() $[y,y_1] = 1$
. Thus,
$[y,y_1] = 1$
. Thus,
![]() $E = \langle Z,x,y \rangle $
commutes with
$E = \langle Z,x,y \rangle $
commutes with
![]() $E_1 := \langle Z, x, y_1 \rangle $
. Since
$E_1 := \langle Z, x, y_1 \rangle $
. Since
![]() $\widetilde {a_1} \not \in \langle a_1, -I_4 \rangle $
, we have
$\widetilde {a_1} \not \in \langle a_1, -I_4 \rangle $
, we have
![]() $y_1 \not \in \langle Z,x \rangle $
and hence
$y_1 \not \in \langle Z,x \rangle $
and hence
![]() $E_1 \cong E_8$
. Applying Case 2, it follows that E is
$E_1 \cong E_8$
. Applying Case 2, it follows that E is
![]() $3$
-connected to A (and even
$3$
-connected to A (and even
![]() $3$
-connected in S to A when
$3$
-connected in S to A when
![]() $E \le S$
).
$E \le S$
).
Case 4: There are
![]() $a_1, a_2, b_1, b_2 \in W_2$
with
$a_1, a_2, b_1, b_2 \in W_2$
with
 $$ \begin{align*} x = \begin{pmatrix} & a_1 \\ a_2 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} & a_1 \\ a_2 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
This case can be reduced to Case 3 since
![]() $E = \langle Z, x, y \rangle = \langle Z, x, xy \rangle $
.
$E = \langle Z, x, y \rangle = \langle Z, x, xy \rangle $
.
Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \mod 4$
. A Sylow
$q \equiv 3 \mod 4$
. A Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_9(q)$
is isomorphic to a Sylow
$PSL_9(q)$
is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_9(q)$
. So, by Lemma 3.32, the Sylow
$SL_9(q)$
. So, by Lemma 3.32, the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_9(q)$
are
$PSL_9(q)$
are
![]() $3$
-connected.
$3$
-connected.
Lemma 3.33. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
. Then the Sylow
$q \equiv 3 \ \mathrm {mod} \ 4$
. Then the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_8(q)$
are
$PSL_8(q)$
are
![]() $3$
-connected.
$3$
-connected.
Proof. Let
![]() $W_1$
be a Sylow
$W_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
. Let
$GL_2(q)$
. Let
![]() $W_2$
be the Sylow
$W_2$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
obtained from
$GL_4(q)$
obtained from
![]() $W_1$
by the construction given in the last statement of Lemma 3.14, and let
$W_1$
by the construction given in the last statement of Lemma 3.14, and let
![]() $W_3$
be the Sylow
$W_3$
be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_8(q)$
obtained from
$GL_8(q)$
obtained from
![]() $W_2$
by the construction given in the last statement of Lemma 3.14. Set
$W_2$
by the construction given in the last statement of Lemma 3.14. Set
![]() $S := W_3 \cap SL_8(q)$
. For each subgroup or element X of
$S := W_3 \cap SL_8(q)$
. For each subgroup or element X of
![]() $SL_8(q)$
, let
$SL_8(q)$
, let
![]() denote the image of X in
denote the image of X in
![]() $PSL_8(q)$
. We prove that
$PSL_8(q)$
. We prove that
![]() is
is
![]() $3$
-connected.
$3$
-connected.
Given a natural number
![]() $\ell \ge 1$
and
$\ell \ge 1$
and
![]() $x_1, \dots , x_{\ell } \in GL_2(q) \cup GL_4(q)$
, we write
$x_1, \dots , x_{\ell } \in GL_2(q) \cup GL_4(q)$
, we write
![]() $\mathrm {diag}(x_1,\dots ,x_{\ell })$
for the block diagonal matrix
$\mathrm {diag}(x_1,\dots ,x_{\ell })$
for the block diagonal matrix
 $$ \begin{align*} \begin{pmatrix} x_1 & & \\ & \ddots & \\ & & x_{\ell} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} x_1 & & \\ & \ddots & \\ & & x_{\ell} \end{pmatrix}. \end{align*} $$
Set
We have
![]() .
.
Set
We have
![]() . Using this, it is easy to note that any elementary abelian subgroup of
. Using this, it is easy to note that any elementary abelian subgroup of
![]() of rank at least
of rank at least
![]() $3$
is
$3$
is
![]() $3$
-connected to an
$3$
-connected to an
![]() $E_8$
-subgroup of
$E_8$
-subgroup of
![]() containing
containing
![]() . Hence, it suffices to prove that any
. Hence, it suffices to prove that any
![]() $E_8$
-subgroup of
$E_8$
-subgroup of
![]() containing
containing
![]() is
is
![]() $3$
-connected to
$3$
-connected to
![]() .
.
Let
![]() $x, y \in S$
and
$x, y \in S$
and
![]() . Suppose that
. Suppose that
![]() $B \cong E_8$
. Considering a number of cases, we will prove that B is
$B \cong E_8$
. Considering a number of cases, we will prove that B is
![]() $3$
-connected to
$3$
-connected to
![]() . Below, a will always denote an involution of
. Below, a will always denote an involution of
![]() $W_1$
with
$W_1$
with
![]() $a \ne -I_2$
.
$a \ne -I_2$
.
Case 1:
![]() $x = \mathrm {diag}(r_1,r_2,r_3,r_4)$
and
$x = \mathrm {diag}(r_1,r_2,r_3,r_4)$
and
![]() $y = \mathrm {diag}(m_1,m_2)$
for some
$y = \mathrm {diag}(m_1,m_2)$
for some
![]() $r_1,r_2,r_3,r_4 \in W_1$
and
$r_1,r_2,r_3,r_4 \in W_1$
and
![]() $m_1,m_2 \in W_2$
.
$m_1,m_2 \in W_2$
.
We consider a number of subcases. These subcases are given by the rows of the table below. In each row, we assume that
![]() $s_1, s_2, s_3, s_4$
are elements of
$s_1, s_2, s_3, s_4$
are elements of
![]() $W_1$
such that y is equal to the matrix given in the column “y”. We also assume that the conditions in the column ‘Conditions’ (if any) are satisfied. The column ‘
$W_1$
such that y is equal to the matrix given in the column “y”. We also assume that the conditions in the column ‘Conditions’ (if any) are satisfied. The column ‘
![]() $y_1$
’ gives an element of S such that
$y_1$
’ gives an element of S such that
![]() is an involution in
is an involution in
![]() and such that
and such that
![]() is
is
![]() $3$
-connected to
$3$
-connected to
![]() . The existence of such an element
. The existence of such an element
![]() $y_1$
easily implies that B is
$y_1$
easily implies that B is
![]() $3$
-connected to
$3$
-connected to
![]() .
.

The subcase that y has the form
 $$ \begin{align*} \begin{pmatrix} s_1 & & & \\ & s_2 & & \\ & & & s_3\\ & & s_4 & \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} s_1 & & & \\ & s_2 & & \\ & & & s_3\\ & & s_4 & \end{pmatrix} \end{align*} $$
can be easily reduced to Cases 1.2 and 1.3.
Case 2: There are
![]() $r_1,r_2,r_3,r_4 \in W_1$
and
$r_1,r_2,r_3,r_4 \in W_1$
and
![]() $m_1, m_2 \in W_2$
with
$m_1, m_2 \in W_2$
with
 $$ \begin{align*} x = \begin{pmatrix} & r_1 & & \\ r_2 & & & \\ & & r_3 & \\ & & & r_4 \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} & r_1 & & \\ r_2 & & & \\ & & r_3 & \\ & & & r_4 \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix}. \end{align*} $$
Case 2.1: There are
![]() $s_1,s_2,s_3,s_4 \in W_1$
with
$s_1,s_2,s_3,s_4 \in W_1$
with
 $$ \begin{align*} y = \begin{pmatrix} s_1 & & & \\ & s_2 & & \\ & & s_3 & \\ & & & s_4 \end{pmatrix} \ {\textit{or}} \ y = \begin{pmatrix} & s_1 & & \\ s_2 & & & \\ & & s_3 & \\ & & & s_4 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} y = \begin{pmatrix} s_1 & & & \\ & s_2 & & \\ & & s_3 & \\ & & & s_4 \end{pmatrix} \ {\textit{or}} \ y = \begin{pmatrix} & s_1 & & \\ s_2 & & & \\ & & s_3 & \\ & & & s_4 \end{pmatrix}. \end{align*} $$
Noticing that
![]() , this case can be reduced to Case 1.
, this case can be reduced to Case 1.
Case 2.2: There are
![]() $s_1,s_2,s_3,s_4 \in W_1$
with
$s_1,s_2,s_3,s_4 \in W_1$
with
 $$ \begin{align*} y = \begin{pmatrix} s_1 & & & \\ & s_2 & & \\ & & & s_3 \\ & & s_4 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} y = \begin{pmatrix} s_1 & & & \\ & s_2 & & \\ & & & s_3 \\ & & s_4 & \end{pmatrix}. \end{align*} $$
Since
![]() $B \cong E_8$
, we have
$B \cong E_8$
, we have
![]() $\varepsilon x^y = x$
, where
$\varepsilon x^y = x$
, where
![]() $\varepsilon \in \lbrace +,- \rbrace $
. By a direct calculation, we have
$\varepsilon \in \lbrace +,- \rbrace $
. By a direct calculation, we have
 $$ \begin{align*} x^y = \begin{pmatrix} & s_1^{-1}r_1 s_2 & & \\ s_2^{-1} r_2 s_1 & & & \\ & & r_4^{s_4} & \\ & & & r_3^{s_3} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x^y = \begin{pmatrix} & s_1^{-1}r_1 s_2 & & \\ s_2^{-1} r_2 s_1 & & & \\ & & r_4^{s_4} & \\ & & & r_3^{s_3} \end{pmatrix}. \end{align*} $$
As
![]() $x = \varepsilon x^y$
, we have
$x = \varepsilon x^y$
, we have
![]() $r_1 = \varepsilon s_1^{-1} r_1 s_2$
,
$r_1 = \varepsilon s_1^{-1} r_1 s_2$
,
![]() $r_2 = \varepsilon s_2^{-1}r_2s_1$
,
$r_2 = \varepsilon s_2^{-1}r_2s_1$
,
![]() $r_3 = \varepsilon r_4^{s_4}$
and
$r_3 = \varepsilon r_4^{s_4}$
and
![]() $r_4 = \varepsilon r_3^{s_3}$
. Note that
$r_4 = \varepsilon r_3^{s_3}$
. Note that
![]() $\varepsilon s_1^{r_1} = s_2$
and
$\varepsilon s_1^{r_1} = s_2$
and
![]() $\varepsilon s_2^{r_2}=s_1$
.
$\varepsilon s_2^{r_2}=s_1$
.
We now consider a number of subsubcases. These subsubcases are given by the rows of the table below. The columns ‘Condition 1’ and ‘Condition 2’ describe the subsubcase under consideration. The column ‘
![]() $y_1$
’ gives an element
$y_1$
’ gives an element
![]() $y_1 \in S$
such that
$y_1 \in S$
such that
![]() is an involution in
is an involution in
![]() and such that
and such that
![]() is
is
![]() $3$
-connected to
$3$
-connected to
![]() . In each subsubcase, one can see from the above calculations and from the previous cases that
. In each subsubcase, one can see from the above calculations and from the previous cases that
![]() $y_1$
indeed has the stated properties. The existence of such an element
$y_1$
indeed has the stated properties. The existence of such an element
![]() $y_1$
easily implies that B is
$y_1$
easily implies that B is
![]() $3$
-connected to
$3$
-connected to
![]() in all subsubcases.
in all subsubcases.

The case that
![]() $x^2 = -I_8$
and
$x^2 = -I_8$
and
![]() $y^2 = I_8$
can be easily reduced to Cases 2.2.4 and 2.2.5.
$y^2 = I_8$
can be easily reduced to Cases 2.2.4 and 2.2.5.
Case 2.3: There are
![]() $s_1,s_2,s_3,s_4 \in W_1$
with
$s_1,s_2,s_3,s_4 \in W_1$
with
 $$ \begin{align*} y = \begin{pmatrix} & s_1 & & \\ s_2 & & & \\ & & & s_3 \\ & & s_4 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} y = \begin{pmatrix} & s_1 & & \\ s_2 & & & \\ & & & s_3 \\ & & s_4 & \end{pmatrix}. \end{align*} $$
Since
![]() , this case can be reduced to Case 2.2.
, this case can be reduced to Case 2.2.
Case 3: There are
![]() $r_1,r_2,r_3,r_4 \in W_1$
and
$r_1,r_2,r_3,r_4 \in W_1$
and
![]() $m_1,m_2 \in W_2$
with
$m_1,m_2 \in W_2$
with
 $$ \begin{align*} x = \begin{pmatrix} r_1 & & & \\ & r_2 & & \\ & & & r_3 \\ & & r_4 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} r_1 & & & \\ & r_2 & & \\ & & & r_3 \\ & & r_4 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix}. \end{align*} $$
This case can be reduced to Case 2.
Case 4: There are
![]() $r_1,r_2,r_3,r_4 \in W_1$
and
$r_1,r_2,r_3,r_4 \in W_1$
and
![]() $m_1,m_2 \in W_2$
with
$m_1,m_2 \in W_2$
with
 $$ \begin{align*} x = \begin{pmatrix} & r_1 & & \\ r_2 & & & \\ & & & r_3 \\ & & r_4 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} & r_1 & & \\ r_2 & & & \\ & & & r_3 \\ & & r_4 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix}. \end{align*} $$
In view of Cases 1–3, we may assume that
 $$ \begin{align*} y = \begin{pmatrix} & s_1 & & \\ s_2 & & & \\ & & & s_3 \\ & & s_4 & \end{pmatrix} \end{align*} $$
$$ \begin{align*} y = \begin{pmatrix} & s_1 & & \\ s_2 & & & \\ & & & s_3 \\ & & s_4 & \end{pmatrix} \end{align*} $$
for some
![]() $s_1,s_2,s_3,s_4 \in W_1$
. Since
$s_1,s_2,s_3,s_4 \in W_1$
. Since
![]() , we can now reduce the given case to Case 1.
, we can now reduce the given case to Case 1.
Case 5: There are
![]() $a_1,a_2,b_1,b_2 \in W_2$
with
$a_1,a_2,b_1,b_2 \in W_2$
with
 $$ \begin{align*} \lbrace x,y \rbrace = \left \lbrace \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix}, \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix} \right\rbrace. \end{align*} $$
$$ \begin{align*} \lbrace x,y \rbrace = \left \lbrace \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix}, \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix} \right\rbrace. \end{align*} $$
Without loss of generality, we assume that
 $$ \begin{align*} x = \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix} \ \text{and} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} a_1 & \\ & a_2 \end{pmatrix} \ \text{and} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
We have
![]() $x^2 \in \langle -I_8 \rangle $
since
$x^2 \in \langle -I_8 \rangle $
since
![]() , and hence,
, and hence,
![]() ${a_1}^2 \in \langle -I_4 \rangle $
. So, by Lemma 3.31, there is an involution
${a_1}^2 \in \langle -I_4 \rangle $
. So, by Lemma 3.31, there is an involution
![]() $\widetilde {a_1} \in W_2 \setminus \langle a_1, -I_4 \rangle $
which commutes with
$\widetilde {a_1} \in W_2 \setminus \langle a_1, -I_4 \rangle $
which commutes with
![]() $a_1$
. Set
$a_1$
. Set
 $$ \begin{align*} y_1 := \begin{pmatrix} \widetilde{a_1} & \\ & \widetilde{a_1}^{b_1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} y_1 := \begin{pmatrix} \widetilde{a_1} & \\ & \widetilde{a_1}^{b_1} \end{pmatrix}. \end{align*} $$
Clearly,
![]() is an involution of
is an involution of
![]() . As
. As
![]() $[x,y] \in \langle -I_8 \rangle $
, we have
$[x,y] \in \langle -I_8 \rangle $
, we have
![]() ${a_1}^{b_1} \in \lbrace a_2, -a_2 \rbrace $
. Since
${a_1}^{b_1} \in \lbrace a_2, -a_2 \rbrace $
. Since
![]() $a_1$
and
$a_1$
and
![]() $\widetilde {a_1}$
commute, it follows that
$\widetilde {a_1}$
commute, it follows that
![]() $\widetilde {a_1}^{b_1}$
and
$\widetilde {a_1}^{b_1}$
and
![]() $a_2$
commute. So we have
$a_2$
commute. So we have
![]() $[x,y_1] = 1$
and hence
$[x,y_1] = 1$
and hence
![]() . Using that
. Using that
![]() $y^2 \in \langle -I_8 \rangle $
, one can easily verify that
$y^2 \in \langle -I_8 \rangle $
, one can easily verify that
![]() $[y,y_1] = 1$
and hence
$[y,y_1] = 1$
and hence
![]() . As
. As
![]() $\widetilde {a_1} \not \in \langle a_1, -I_4 \rangle $
, we have
$\widetilde {a_1} \not \in \langle a_1, -I_4 \rangle $
, we have
![]() .
.
Now
![]() is an
is an
![]() $E_8$
-subgroup of
$E_8$
-subgroup of
![]() which commutes with B and which is
which commutes with B and which is
![]() $3$
-connected to
$3$
-connected to
![]() by Cases 1-4. Thus, B is
by Cases 1-4. Thus, B is
![]() $3$
-connected to
$3$
-connected to
![]() .
.
Case 6: There are
![]() $a_1,a_2,b_1,b_2 \in W_2$
with
$a_1,a_2,b_1,b_2 \in W_2$
with
 $$ \begin{align*} x = \begin{pmatrix} & a_1 \\ a_2 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} x = \begin{pmatrix} & a_1 \\ a_2 & \end{pmatrix} \ {\textit{and}} \ y = \begin{pmatrix} & b_1 \\ b_2 & \end{pmatrix}. \end{align*} $$
Noticing that
![]() , we can reduce this case to Case 5.
, we can reduce this case to Case 5.
We summarize the above lemmas in the following corollary.
Corollary 3.34. Let q be a nontrivial odd prime power and
![]() $n \ge 6$
. Then the following hold:
$n \ge 6$
. Then the following hold:
-
(i) The Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $SL_n(q)$
and those of
$SL_n(q)$
and those of
 $PSL_n(q)$
are
$PSL_n(q)$
are
 $2$
-connected.
$2$
-connected. -
(ii) The Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $SL_n(q)$
are
$SL_n(q)$
are
 $3$
-connected.
$3$
-connected. -
(iii) If
 $q \equiv 1 \ \mathrm {mod} \ 4$
or
$q \equiv 1 \ \mathrm {mod} \ 4$
or
 $n \ge 7$
, then the Sylow
$n \ge 7$
, then the Sylow
 $2$
-subgroups of
$2$
-subgroups of
 $PSL_n(q)$
are
$PSL_n(q)$
are
 $3$
-connected.
$3$
-connected.
Unfortunately, the Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $PSL_6(q)$
are not
$PSL_6(q)$
are not
![]() $3$
-connected when
$3$
-connected when
![]() $q \equiv 3 \mod 4$
(this is not terribly difficult to observe).
$q \equiv 3 \mod 4$
(this is not terribly difficult to observe).
Corollary 3.35. Let q be a nontrivial odd prime power and
![]() $n \ge 6$
. Let
$n \ge 6$
. Let
![]() $G = SL_n(q)$
, or
$G = SL_n(q)$
, or
![]() $G = PSL_n(q)$
and
$G = PSL_n(q)$
and
![]() $n \ge 7$
if
$n \ge 7$
if
![]() $q \equiv 3 \mod 4$
. For any Sylow
$q \equiv 3 \mod 4$
. For any Sylow
![]() $2$
-subgroup S of G and any elementary abelian subgroup A of S with
$2$
-subgroup S of G and any elementary abelian subgroup A of S with
![]() $m(A) \le 3$
, there is some elementary abelian subgroup B of S with
$m(A) \le 3$
, there is some elementary abelian subgroup B of S with
![]() $A < B$
and
$A < B$
and
![]() $m(B) = 4$
.
$m(B) = 4$
.
Proof. By Corollary 3.34, S is
![]() $2$
-connected and
$2$
-connected and
![]() $3$
-connected. Applying [Reference Gorenstein and Walter31, Lemma 8.7], the claim follows.
$3$
-connected. Applying [Reference Gorenstein and Walter31, Lemma 8.7], the claim follows.
3.6 Generation
Next, we discuss some generational properties of
![]() $(P)SL_n(q)$
and
$(P)SL_n(q)$
and
![]() $(P)SU_n(q)$
, where
$(P)SU_n(q)$
, where
![]() $n \ge 3$
and q is a nontrivial odd prime power. We need the following definition (see [Reference Gorenstein and Walter31, Section 8]).
$n \ge 3$
and q is a nontrivial odd prime power. We need the following definition (see [Reference Gorenstein and Walter31, Section 8]).
Definition 3.36. Let G be a finite group, let S be a Sylow
![]() $2$
-subgroup of G and let k be a positive integer. We say that G is k-generated if
$2$
-subgroup of G and let k be a positive integer. We say that G is k-generated if
The following two lemmas will later prove to be useful.
Lemma 3.37 (see [Reference Aschbacher4])
Let q be a nontrivial odd prime power. Then the groups
![]() $SL_3(q)$
,
$SL_3(q)$
,
![]() $PSL_3(q)$
,
$PSL_3(q)$
,
![]() $SU_3(q)$
and
$SU_3(q)$
and
![]() $PSU_3(q)$
are
$PSU_3(q)$
are
![]() $2$
-generated.
$2$
-generated.
Lemma 3.38. Let q be a nontrivial odd prime power, and let
![]() $n \ge 4$
be a natural number. Moreover, let
$n \ge 4$
be a natural number. Moreover, let
![]() $\varepsilon \in \lbrace +,- \rbrace $
and
$\varepsilon \in \lbrace +,- \rbrace $
and
![]() $Z \le Z(SL_n^{\varepsilon }(q))$
. Assume that one of the following holds:
$Z \le Z(SL_n^{\varepsilon }(q))$
. Assume that one of the following holds:
-
(i)
 $n \ge 5$
,
$n \ge 5$
, -
(ii)
 $q \equiv \varepsilon \ \mathrm {mod} \ 8$
,
$q \equiv \varepsilon \ \mathrm {mod} \ 8$
, -
(iii)
 $Z = 1$
.
$Z = 1$
.
Then
![]() $SL_n^{\varepsilon }(q)/Z$
is
$SL_n^{\varepsilon }(q)/Z$
is
![]() $3$
-generated.
$3$
-generated.
We need the following lemma in order to prove Lemma 3.38.
Lemma 3.39 (see [Reference Phan45], [Reference Bennett and Shpectorov13])
Let
![]() $q> 2$
be a prime power, and let
$q> 2$
be a prime power, and let
![]() $n \ge 3$
be a natural number. Let
$n \ge 3$
be a natural number. Let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Define
$\varepsilon \in \lbrace +,- \rbrace $
. Define
 $$ \begin{align*} U_1 := \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} U_1 := \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q) \right\rbrace \end{align*} $$
and
 $$ \begin{align*} U_{n-1} := \left\lbrace \begin{pmatrix} I_{n-2} & \\ & A \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q) \right\rbrace. \end{align*} $$
$$ \begin{align*} U_{n-1} := \left\lbrace \begin{pmatrix} I_{n-2} & \\ & A \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q) \right\rbrace. \end{align*} $$
Moreover, for each
![]() $2 \le i \le n-2$
, let
$2 \le i \le n-2$
, let
 $$ \begin{align*} U_i := \left\lbrace \begin{pmatrix} I_{i-1} & & \\ & A & \\ & & I_{n-i-1} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q) \right\rbrace. \end{align*} $$
$$ \begin{align*} U_i := \left\lbrace \begin{pmatrix} I_{i-1} & & \\ & A & \\ & & I_{n-i-1} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q) \right\rbrace. \end{align*} $$
Then the following hold:
-
(i) We have
 $SL_n^{\varepsilon }(q) = \langle U_i \ : \ 1 \le i \le n-1 \rangle $
.
$SL_n^{\varepsilon }(q) = \langle U_i \ : \ 1 \le i \le n-1 \rangle $
. -
(ii) For each
 $1 \le i \le n-2$
, there is a monomial matrix
$1 \le i \le n-2$
, there is a monomial matrix
 $m_i$
in
$m_i$
in
 $SL_n^{\varepsilon }(q)$
with
$SL_n^{\varepsilon }(q)$
with
 $U_i^{m_i} = U_{i+1}$
.
$U_i^{m_i} = U_{i+1}$
.
Proof of Lemma 3.38
Let q be a nontrivial odd prime power,
![]() $n \ge 4$
be a natural number,
$n \ge 4$
be a natural number,
![]() $\varepsilon \in \lbrace +,- \rbrace $
,
$\varepsilon \in \lbrace +,- \rbrace $
,
![]() $L := SL_n^{\varepsilon }(q)$
and
$L := SL_n^{\varepsilon }(q)$
and
![]() $Z \le Z(L)$
. Suppose that one of the conditions
$Z \le Z(L)$
. Suppose that one of the conditions
![]() $n \ge 5$
,
$n \ge 5$
,
![]() $q \equiv \ \varepsilon \ \mathrm {mod} \ 8$
or
$q \equiv \ \varepsilon \ \mathrm {mod} \ 8$
or
![]() $Z = 1$
is satisfied. We have to show that
$Z = 1$
is satisfied. We have to show that
![]() $L/Z$
is
$L/Z$
is
![]() $3$
-generated.
$3$
-generated.
Let
![]() $U_1, \dots , U_{n-1}$
denote the
$U_1, \dots , U_{n-1}$
denote the
![]() $SL_2^{\varepsilon }(q)$
-subgroups of L corresponding to the
$SL_2^{\varepsilon }(q)$
-subgroups of L corresponding to the
![]() $2 \times 2$
blocks along the main diagonal (as in Lemma 3.39). Let E be the subgroup of L consisting of the diagonal matrices in L with diagonal entries in
$2 \times 2$
blocks along the main diagonal (as in Lemma 3.39). Let E be the subgroup of L consisting of the diagonal matrices in L with diagonal entries in
![]() $\lbrace -1,1 \rbrace $
.
$\lbrace -1,1 \rbrace $
.
Assume that
![]() $n \ge 5$
. We claim that there is an
$n \ge 5$
. We claim that there is an
![]() $E_8$
-subgroup
$E_8$
-subgroup
![]() $E_i$
of E with
$E_i$
of E with
![]() $E_i \cap Z(L) = 1$
and
$E_i \cap Z(L) = 1$
and
![]() $[E_i,U_i] = 1$
for each
$[E_i,U_i] = 1$
for each
![]() $i \in \lbrace 1,\dots ,n-1\rbrace $
. Let V be the module defining L. Let
$i \in \lbrace 1,\dots ,n-1\rbrace $
. Let V be the module defining L. Let
![]() $X = \lbrace x_1,\dots ,x_n \rbrace $
be a basis for V, with X orthonormal if V is unitary, and let
$X = \lbrace x_1,\dots ,x_n \rbrace $
be a basis for V, with X orthonormal if V is unitary, and let
![]() $V_i := \langle x_i,x_{i+1} \rangle $
for
$V_i := \langle x_i,x_{i+1} \rangle $
for
![]() $1 \le i < n$
. Then
$1 \le i < n$
. Then
![]() $U_i = SL^{\varepsilon }(V_i)$
. We have
$U_i = SL^{\varepsilon }(V_i)$
. We have
![]() $m(E) = n-1 \ge 4$
. For
$m(E) = n-1 \ge 4$
. For
![]() $1 \le i < n$
let
$1 \le i < n$
let
![]() $e_i \in E$
invert
$e_i \in E$
invert
![]() $V_i$
and centralize
$V_i$
and centralize
![]() $x_j$
for
$x_j$
for
![]() $x_j \not \in V_i$
, and set
$x_j \not \in V_i$
, and set
![]() $F_i := C_E(V_i)\langle e_i \rangle $
. Then
$F_i := C_E(V_i)\langle e_i \rangle $
. Then
![]() $F_i$
is a hyperplane of E centralizing
$F_i$
is a hyperplane of E centralizing
![]() $U_i$
. If n is odd, then
$U_i$
. If n is odd, then
![]() $|Z(L)|$
is odd, so we may choose
$|Z(L)|$
is odd, so we may choose
![]() $E_i \le F_i$
. Thus, we may take n even, so
$E_i \le F_i$
. Thus, we may take n even, so
![]() $n \ge 6$
. Choose a hyperplane
$n \ge 6$
. Choose a hyperplane
![]() $D_i$
of
$D_i$
of
![]() $F_i$
with
$F_i$
with
![]() $D_i \cap Z(L) = 1$
, and take
$D_i \cap Z(L) = 1$
, and take
![]() $E_i \le D_i$
.
$E_i \le D_i$
.
For
![]() $1 \le i < n$
,
$1 \le i < n$
,
![]() $U_iZ/Z$
centralizes
$U_iZ/Z$
centralizes
![]() $E_iZ/Z \cong E_8$
since
$E_iZ/Z \cong E_8$
since
![]() $[E_i,U_i] = 1$
. Now, if S is a Sylow
$[E_i,U_i] = 1$
. Now, if S is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $L/Z$
containing
$L/Z$
containing
![]() $EZ/Z$
, we have
$EZ/Z$
, we have
![]() $U_iZ/Z \le \Gamma _{S,3}(L/Z)$
for each
$U_iZ/Z \le \Gamma _{S,3}(L/Z)$
for each
![]() $i \in \lbrace 1,\dots , n-1 \rbrace $
, and Lemma 3.39 (i) implies that
$i \in \lbrace 1,\dots , n-1 \rbrace $
, and Lemma 3.39 (i) implies that
![]() $L/Z$
is
$L/Z$
is
![]() $3$
-generated.
$3$
-generated.
We now consider the case
![]() $n = 4$
. By hypothesis,
$n = 4$
. By hypothesis,
![]() $Z = 1$
or
$Z = 1$
or
![]() $q \equiv \varepsilon \ \mathrm {mod} \ 8$
. Let
$q \equiv \varepsilon \ \mathrm {mod} \ 8$
. Let
 $$ \begin{align*} U := \left \lbrace \left( \begin{array}{c|c} A & \begin{matrix} 0 \\ 0 \end{matrix} \\ \hline \begin{matrix} 0 & 0 \end{matrix} & 1 \end{array} \right) \ : \ A \in SL_3^{\varepsilon}(q) \right\rbrace. \end{align*} $$
$$ \begin{align*} U := \left \lbrace \left( \begin{array}{c|c} A & \begin{matrix} 0 \\ 0 \end{matrix} \\ \hline \begin{matrix} 0 & 0 \end{matrix} & 1 \end{array} \right) \ : \ A \in SL_3^{\varepsilon}(q) \right\rbrace. \end{align*} $$
If
![]() $Z = 1$
, set
$Z = 1$
, set
![]() $y := -I_4$
. If
$y := -I_4$
. If
![]() $q \equiv \varepsilon \ \mathrm {mod} \ 8$
, let
$q \equiv \varepsilon \ \mathrm {mod} \ 8$
, let
![]() $\lambda $
be an element of
$\lambda $
be an element of
![]() $\mathbb {F}_{q^2}^{*}$
of order
$\mathbb {F}_{q^2}^{*}$
of order
![]() $8$
such that
$8$
such that
![]() $\lambda ^{q-\varepsilon } = 1$
. Note that
$\lambda ^{q-\varepsilon } = 1$
. Note that
![]() $\lambda \in \mathbb {F}_q^{*}$
if
$\lambda \in \mathbb {F}_q^{*}$
if
![]() $\varepsilon = +$
. Also, if
$\varepsilon = +$
. Also, if
![]() $q \equiv \varepsilon \ \mathrm {mod} \ 8$
and
$q \equiv \varepsilon \ \mathrm {mod} \ 8$
and
![]() $\vert Z \vert = 2$
, let
$\vert Z \vert = 2$
, let
![]() $y := \lambda ^2 I_4 \in L$
, and if
$y := \lambda ^2 I_4 \in L$
, and if
![]() $q \equiv \varepsilon \ \mathrm {mod} \ 8$
and
$q \equiv \varepsilon \ \mathrm {mod} \ 8$
and
![]() $\vert Z \vert = 4$
, let
$\vert Z \vert = 4$
, let
![]() $y := \mathrm {diag}(\lambda , \lambda , \lambda , - \lambda ) \in L$
.
$y := \mathrm {diag}(\lambda , \lambda , \lambda , - \lambda ) \in L$
.
Let
![]() $S_0$
be a Sylow
$S_0$
be a Sylow
![]() $2$
-subgroup of U containing
$2$
-subgroup of U containing
![]() $E \cap U$
. Let
$E \cap U$
. Let
![]() $\widetilde S$
be a Sylow
$\widetilde S$
be a Sylow
![]() $2$
-subgroup of L containing
$2$
-subgroup of L containing
![]() $S_0$
and y. Denote the image of
$S_0$
and y. Denote the image of
![]() $\widetilde S$
in
$\widetilde S$
in
![]() $L/Z$
by S. We have
$L/Z$
by S. We have
![]() $S \cap UZ/Z = S_0Z/Z \in \mathrm {Syl}_2(UZ/Z)$
. By Lemma 3.37,
$S \cap UZ/Z = S_0Z/Z \in \mathrm {Syl}_2(UZ/Z)$
. By Lemma 3.37,
![]() $UZ/Z \cong U \cong SL_3^{\varepsilon }(q)$
is
$UZ/Z \cong U \cong SL_3^{\varepsilon }(q)$
is
![]() $2$
-generated. So we have
$2$
-generated. So we have
Let
![]() $T \le S_0 Z/Z$
with
$T \le S_0 Z/Z$
with
![]() $m(T) \ge 2$
and
$m(T) \ge 2$
and
![]() $\widehat T := \langle T, yZ \rangle $
. Clearly,
$\widehat T := \langle T, yZ \rangle $
. Clearly,
![]() $yZ$
is an involution of S not contained in
$yZ$
is an involution of S not contained in
![]() $UZ/Z$
and centralizing
$UZ/Z$
and centralizing
![]() $UZ/Z$
. Therefore, we have that
$UZ/Z$
. Therefore, we have that
![]() $m(\widehat T) \ge 3$
and
$m(\widehat T) \ge 3$
and
![]() $N_{UZ/Z}(T) \le N_{L/Z}(\widehat T)$
. It follows that
$N_{UZ/Z}(T) \le N_{L/Z}(\widehat T)$
. It follows that
![]() $UZ/Z \le \Gamma _{S,3}(L/Z)$
. In particular,
$UZ/Z \le \Gamma _{S,3}(L/Z)$
. In particular,
![]() $U_iZ/Z \le \Gamma _{S,3}(L/Z)$
for
$U_iZ/Z \le \Gamma _{S,3}(L/Z)$
for
![]() $i \in \lbrace 1,2 \rbrace $
.
$i \in \lbrace 1,2 \rbrace $
.
From Lemma 3.39 (ii), we see that there is some
![]() $m \in L$
such that
$m \in L$
such that
![]() ${U_2}^m = U_3$
and such that m normalizes
${U_2}^m = U_3$
and such that m normalizes
![]() $\langle E, y \rangle $
. So
$\langle E, y \rangle $
. So
![]() $mZ$
normalizes
$mZ$
normalizes
![]() $\langle EZ/Z, yZ \rangle $
. It is easy to note that
$\langle EZ/Z, yZ \rangle $
. It is easy to note that
![]() $\langle EZ/Z, yZ \rangle \cong E_8$
, and so we have
$\langle EZ/Z, yZ \rangle \cong E_8$
, and so we have
![]() $mZ \in \Gamma _{S,3}(L/Z)$
. It follows that
$mZ \in \Gamma _{S,3}(L/Z)$
. It follows that
![]() $U_3 Z/Z = (U_2 Z/Z)^{mZ} \le \Gamma _{S,3}(L/Z)$
.
$U_3 Z/Z = (U_2 Z/Z)^{mZ} \le \Gamma _{S,3}(L/Z)$
.
So we have
![]() $U_iZ/Z \le \Gamma _{S,3}(L/Z)$
for
$U_iZ/Z \le \Gamma _{S,3}(L/Z)$
for
![]() $i \in \lbrace 1,2,3 \rbrace $
, and Lemma 3.39 (i) implies that
$i \in \lbrace 1,2,3 \rbrace $
, and Lemma 3.39 (i) implies that
![]() $L/Z$
is
$L/Z$
is
![]() $3$
-generated.
$3$
-generated.
3.7 Automorphisms of
 $(P)SL_n(q)$
$(P)SL_n(q)$
Fix a prime number p, a positive integer f and a natural number
![]() $n \ge 2$
. Set
$n \ge 2$
. Set
![]() $q := p^f$
and
$q := p^f$
and
![]() $T := SL_n(q)$
. We now briefly describe the structure of
$T := SL_n(q)$
. We now briefly describe the structure of
![]() $\mathrm {Aut}(T/Z)$
, where
$\mathrm {Aut}(T/Z)$
, where
![]() $Z \le Z(T)$
, referring to [Reference Dieudonné19] and [Reference Burness and Giudici16, Section 2.1] for further details.
$Z \le Z(T)$
, referring to [Reference Dieudonné19] and [Reference Burness and Giudici16, Section 2.1] for further details.
Let
![]() $\mathrm {Inndiag}(T) := \mathrm {Aut}_{GL_n(q)}(T)$
. Note that
$\mathrm {Inndiag}(T) := \mathrm {Aut}_{GL_n(q)}(T)$
. Note that
The map
is an automorphism of T with order f. One can check that
![]() $\phi $
normalizes
$\phi $
normalizes
![]() $\mathrm {Inndiag}(T)$
. Set
$\mathrm {Inndiag}(T)$
. Set
It is easy to note that
![]() $\langle \phi \rangle \cap \mathrm {Inndiag}(T) = 1$
so that
$\langle \phi \rangle \cap \mathrm {Inndiag}(T) = 1$
so that
![]() $P \Gamma L_n(q)$
is the inner semidirect product of
$P \Gamma L_n(q)$
is the inner semidirect product of
![]() $\mathrm {Inndiag}(T)$
and
$\mathrm {Inndiag}(T)$
and
![]() $\langle \phi \rangle $
.
$\langle \phi \rangle $
.
The map
is an automorphism of T with order
![]() $2$
. If
$2$
. If
![]() $n = 2$
, then
$n = 2$
, then
![]() $\iota $
turns out to be an inner automorphism of T, while we have
$\iota $
turns out to be an inner automorphism of T, while we have
![]() $\iota \not \in P\Gamma L_n(q)$
when
$\iota \not \in P\Gamma L_n(q)$
when
![]() $n \ge 3$
. By a direct calculation,
$n \ge 3$
. By a direct calculation,
![]() $\iota $
normalizes
$\iota $
normalizes
![]() $\mathrm {Inndiag}(T)$
and commutes with
$\mathrm {Inndiag}(T)$
and commutes with
![]() $\phi $
. In particular,
$\phi $
. In particular,
![]() $A := P \Gamma L_n(q) \langle \iota \rangle $
is a subgroup of
$A := P \Gamma L_n(q) \langle \iota \rangle $
is a subgroup of
![]() $\mathrm {Aut}(T)$
, and we have
$\mathrm {Aut}(T)$
, and we have
where
![]() $a = 1$
if
$a = 1$
if
![]() $n = 2$
and
$n = 2$
and
![]() $a = 2$
if
$a = 2$
if
![]() $n \ge 3$
.
$n \ge 3$
.
Now let Z be a central subgroup of T. As
![]() $Z(T)$
is cyclic, Z is characteristic in T. Then as T is perfect,
$Z(T)$
is cyclic, Z is characteristic in T. Then as T is perfect,
![]() $SL_2(2)$
or
$SL_2(2)$
or
![]() $SL_2(3)$
, the natural homomorphism
$SL_2(3)$
, the natural homomorphism
![]() $\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is injective. The image of
$\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is injective. The image of
![]() $\mathrm {Inndiag}(T)$
under this homomorphism will be denoted by
$\mathrm {Inndiag}(T)$
under this homomorphism will be denoted by
![]() $\mathrm {Inndiag}(T/Z)$
. By abuse of notation, we denote the image of
$\mathrm {Inndiag}(T/Z)$
. By abuse of notation, we denote the image of
![]() $P\Gamma L_n(q)$
in
$P\Gamma L_n(q)$
in
![]() $\mathrm {Aut}(T/Z)$
again by
$\mathrm {Aut}(T/Z)$
again by
![]() $P \Gamma L_n(q)$
and the images of
$P \Gamma L_n(q)$
and the images of
![]() $\iota $
and
$\iota $
and
![]() $\phi $
again by
$\phi $
again by
![]() $\iota $
and
$\iota $
and
![]() $\phi $
, respectively.
$\phi $
, respectively.
With this notation, we have
Note that the natural homomorphism
![]() $\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is an isomorphism and that it induces an isomorphism
$\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is an isomorphism and that it induces an isomorphism
![]() $\mathrm {Out}(T) \rightarrow \mathrm {Out}(T/Z)$
.
$\mathrm {Out}(T) \rightarrow \mathrm {Out}(T/Z)$
.
The elements of
![]() $\mathrm {Inndiag}(T/Z) \setminus \mathrm {Inn}(T/Z)$
are said to be the (nontrivial) diagonal automorphisms of
$\mathrm {Inndiag}(T/Z) \setminus \mathrm {Inn}(T/Z)$
are said to be the (nontrivial) diagonal automorphisms of
![]() $T/Z$
. An automorphism of
$T/Z$
. An automorphism of
![]() $T/Z$
is called a field automorphism if it is conjugate to
$T/Z$
is called a field automorphism if it is conjugate to
![]() $\phi ^i$
for some
$\phi ^i$
for some
![]() $1 \le i < f$
. The automorphisms of the form
$1 \le i < f$
. The automorphisms of the form
![]() $\alpha \iota $
, where
$\alpha \iota $
, where
![]() $\alpha \in \mathrm {Inndiag}(T/Z)$
, are said to be the graph automorphisms of
$\alpha \in \mathrm {Inndiag}(T/Z)$
, are said to be the graph automorphisms of
![]() $T/Z$
. An automorphism of
$T/Z$
. An automorphism of
![]() $T/Z$
is said to be a graph-field automorphism if it is conjugate to an automorphism of the form
$T/Z$
is said to be a graph-field automorphism if it is conjugate to an automorphism of the form
![]() $\phi ^i \iota $
for some
$\phi ^i \iota $
for some
![]() $1 \le i < f$
. We remark that these definitions are particular cases of more general definitions; see [Reference Steinberg49, Chapter 10].
$1 \le i < f$
. We remark that these definitions are particular cases of more general definitions; see [Reference Steinberg49, Chapter 10].
Proposition 3.40. Let q be a nontrivial prime power, and let
![]() $n \ge 2$
. Then
$n \ge 2$
. Then
![]() $\mathrm {Out}(PSL_n(q))$
is
$\mathrm {Out}(PSL_n(q))$
is
![]() $2$
-nilpotent.
$2$
-nilpotent.
Proof. By the above remarks,
![]() $\mathrm {Out}(PSL_n(q))$
has a chief series with cyclic factors. Consequently,
$\mathrm {Out}(PSL_n(q))$
has a chief series with cyclic factors. Consequently,
![]() $\mathrm {Out}(PSL_n(q))$
is supersolvable. By [Reference Li, Zhang and Yi38, Lemma 2.4 (4)], any supersolvable finite group is
$\mathrm {Out}(PSL_n(q))$
is supersolvable. By [Reference Li, Zhang and Yi38, Lemma 2.4 (4)], any supersolvable finite group is
![]() $2$
-nilpotent, and so the proposition follows.
$2$
-nilpotent, and so the proposition follows.
The following proposition also follows from the above remarks.
Proposition 3.41. Let
![]() $n \ge 2$
be a natural number. Then
$n \ge 2$
be a natural number. Then
![]() $\mathrm {Out}(SL_n(3))$
is a
$\mathrm {Out}(SL_n(3))$
is a
![]() $2$
-group.
$2$
-group.
3.8 Automorphisms of
 $(P)SU_n(q)$
$(P)SU_n(q)$
Let p be a prime number, f be a positive integer and
![]() $n \ge 3$
be a natural number. Set
$n \ge 3$
be a natural number. Set
![]() $q := p^f$
and
$q := p^f$
and
![]() $T := SU_n(q)$
. We now briefly describe the structure of
$T := SU_n(q)$
. We now briefly describe the structure of
![]() $\mathrm {Aut}(T/Z)$
, where
$\mathrm {Aut}(T/Z)$
, where
![]() $Z \le Z(T)$
, referring to [Reference Dieudonné19] and [Reference Burness and Giudici16, Section 2.3] for further details.
$Z \le Z(T)$
, referring to [Reference Dieudonné19] and [Reference Burness and Giudici16, Section 2.3] for further details.
Let
![]() $\mathrm {Inndiag}(T) := \mathrm {Aut}_{GU_n(q)}(SU_n(q))$
. It is rather easy to note that
$\mathrm {Inndiag}(T) := \mathrm {Aut}_{GU_n(q)}(SU_n(q))$
. It is rather easy to note that
The map
is an automorphism of T with order
![]() $2f$
. One can check that
$2f$
. One can check that
![]() $\phi $
normalizes
$\phi $
normalizes
![]() $\mathrm {Inndiag}(T)$
. Set
$\mathrm {Inndiag}(T)$
. Set
It is rather easy to note that
![]() $\langle \phi \rangle \cap \mathrm {Inndiag}(T) = 1$
so that
$\langle \phi \rangle \cap \mathrm {Inndiag}(T) = 1$
so that
![]() $P\Gamma U_n(q)$
is the inner semidirect product of
$P\Gamma U_n(q)$
is the inner semidirect product of
![]() $\mathrm {Inndiag}(T)$
and
$\mathrm {Inndiag}(T)$
and
![]() $\langle \phi \rangle $
. Note that
$\langle \phi \rangle $
. Note that
Now let Z be a central subgroup of T. As in the case
![]() $T = SL_n(q)$
, the natural homomorphism
$T = SL_n(q)$
, the natural homomorphism
![]() $\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is injective. The image of
$\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is injective. The image of
![]() $\mathrm {Inndiag}(T)$
under this homomorphism will be denoted by
$\mathrm {Inndiag}(T)$
under this homomorphism will be denoted by
![]() $\mathrm {Inndiag}(T/Z)$
. By abuse of notation, we denote the image of
$\mathrm {Inndiag}(T/Z)$
. By abuse of notation, we denote the image of
![]() $P \Gamma U_n(q)$
in
$P \Gamma U_n(q)$
in
![]() $\mathrm {Aut}(T/Z)$
again by
$\mathrm {Aut}(T/Z)$
again by
![]() $P \Gamma U_n(q)$
and the image of
$P \Gamma U_n(q)$
and the image of
![]() $\phi $
again by
$\phi $
again by
![]() $\phi $
.
$\phi $
.
With this notation, we have
Note that the natural homomorphism
![]() $\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is an isomorphism and that it induces an isomorphism
$\mathrm {Aut}(T) \rightarrow \mathrm {Aut}(T/Z)$
is an isomorphism and that it induces an isomorphism
![]() $\mathrm {Out}(T) \rightarrow \mathrm {Out}(T/Z)$
.
$\mathrm {Out}(T) \rightarrow \mathrm {Out}(T/Z)$
.
The elements of
![]() $\mathrm {Inndiag}(T/Z) \setminus \mathrm {Inn}(T/Z)$
are said to be the (nontrivial) diagonal automorphisms of
$\mathrm {Inndiag}(T/Z) \setminus \mathrm {Inn}(T/Z)$
are said to be the (nontrivial) diagonal automorphisms of
![]() $T/Z$
. An automorphism of
$T/Z$
. An automorphism of
![]() $T/Z$
is called a field automorphism if it is conjugate to
$T/Z$
is called a field automorphism if it is conjugate to
![]() $\phi ^i$
for some
$\phi ^i$
for some
![]() $1 \le i < 2f$
such that
$1 \le i < 2f$
such that
![]() $\phi ^i$
has odd order. The automorphisms of the form
$\phi ^i$
has odd order. The automorphisms of the form
![]() $\alpha \phi ^i$
, where
$\alpha \phi ^i$
, where
![]() $\phi ^i$
has even order and
$\phi ^i$
has even order and
![]() $\alpha \in \mathrm {Inndiag}(T/Z)$
, are said to be the graph automorphisms of
$\alpha \in \mathrm {Inndiag}(T/Z)$
, are said to be the graph automorphisms of
![]() $T/Z$
. There are no graph-field automorphisms of
$T/Z$
. There are no graph-field automorphisms of
![]() $T/Z$
.
$T/Z$
.
Proposition 3.42. Let q be a nontrivial prime power, and let
![]() $n \ge 3$
. Then
$n \ge 3$
. Then
![]() $\mathrm {Out}(PSU_n(q))$
is
$\mathrm {Out}(PSU_n(q))$
is
![]() $2$
-nilpotent.
$2$
-nilpotent.
Proof. We see from the above remarks that
![]() $\mathrm {Out}(PSU_n(q))$
is supersolvable. So
$\mathrm {Out}(PSU_n(q))$
is supersolvable. So
![]() $\mathrm {Out}(PSU_n(q))$
is
$\mathrm {Out}(PSU_n(q))$
is
![]() $2$
-nilpotent by [Reference Li, Zhang and Yi38, Lemma 2.4 (4)].
$2$
-nilpotent by [Reference Li, Zhang and Yi38, Lemma 2.4 (4)].
The following proposition also follows from the above remarks.
Proposition 3.43. Let
![]() $n \ge 3$
be a natural number. Then
$n \ge 3$
be a natural number. Then
![]() $\mathrm {Out}(SU_n(3))$
is a
$\mathrm {Out}(SU_n(3))$
is a
![]() $2$
-group.
$2$
-group.
3.9 Some lemmas
We now prove several results on the automorphism groups of
![]() $(P)SL_n(q)$
and
$(P)SL_n(q)$
and
![]() $(P)SU_n(q)$
, where
$(P)SU_n(q)$
, where
![]() $n \ge 2$
and q is a nontrivial odd prime power.
$n \ge 2$
and q is a nontrivial odd prime power.
Lemma 3.44. Let q be a nontrivial odd prime power. Also, let
![]() $T := SL_2(q)$
and
$T := SL_2(q)$
and
![]() $S \in \mathrm {Syl}_2(T)$
. Suppose that
$S \in \mathrm {Syl}_2(T)$
. Suppose that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are
$\beta $
are
![]() $2$
-elements of
$2$
-elements of
![]() $\mathrm {Aut}(T)$
such that
$\mathrm {Aut}(T)$
such that
![]() $S^{\alpha } = S = S^{\beta }$
and
$S^{\alpha } = S = S^{\beta }$
and
![]() $\alpha |_{S,S} = \beta |_{S,S}$
. Then
$\alpha |_{S,S} = \beta |_{S,S}$
. Then
![]() $\alpha = \beta $
.
$\alpha = \beta $
.
Proof. Let
![]() $\gamma := \alpha \beta ^{-1} \in C_{\mathrm {Aut}(T)}(S)$
. We have
$\gamma := \alpha \beta ^{-1} \in C_{\mathrm {Aut}(T)}(S)$
. We have
![]() $C_{\mathrm {Inndiag}(T)}(S) = 1$
by [Reference Gorenstein, Lyons and Solomon28, Lemma 4.10.10]. Therefore, it suffices to show that
$C_{\mathrm {Inndiag}(T)}(S) = 1$
by [Reference Gorenstein, Lyons and Solomon28, Lemma 4.10.10]. Therefore, it suffices to show that
![]() $\gamma \in \mathrm {Inndiag}(T)$
. Clearly, the images of
$\gamma \in \mathrm {Inndiag}(T)$
. Clearly, the images of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta ^{-1}$
in
$\beta ^{-1}$
in
![]() $\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
are
$\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
are
![]() $2$
-elements of
$2$
-elements of
![]() $\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
. Since
$\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
. Since
![]() $\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
is abelian,
$\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
is abelian,
is still a
![]() $2$
-element of
$2$
-element of
![]() $\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
. By [Reference Gorenstein, Lyons and Solomon28, Lemma 4.10.10],
$\mathrm {Aut}(T)/\mathrm {Inndiag}(T)$
. By [Reference Gorenstein, Lyons and Solomon28, Lemma 4.10.10],
![]() $C_{\mathrm {Aut}(T)}(S)$
is a
$C_{\mathrm {Aut}(T)}(S)$
is a
![]() $2'$
-group, and so
$2'$
-group, and so
![]() $\gamma $
has odd order. Therefore,
$\gamma $
has odd order. Therefore,
![]() $\gamma \cdot \mathrm {Inndiag}(T)$
has odd order. It follows that
$\gamma \cdot \mathrm {Inndiag}(T)$
has odd order. It follows that
![]() $\gamma \in \mathrm {Inndiag}(T)$
, as required.
$\gamma \in \mathrm {Inndiag}(T)$
, as required.
Lemma 3.45. Let
![]() $q = p^f$
, where p is an odd prime and f is a positive integer. Let
$q = p^f$
, where p is an odd prime and f is a positive integer. Let
![]() $T := PSL_2(q)$
, and let
$T := PSL_2(q)$
, and let
![]() $\alpha $
be an involution of
$\alpha $
be an involution of
![]() $\mathrm {Aut}(T)$
. Suppose that
$\mathrm {Aut}(T)$
. Suppose that
![]() $C_T(\alpha )$
has a
$C_T(\alpha )$
has a
![]() $2$
-component K. Then we have
$2$
-component K. Then we have
![]() $2 \mid f$
,
$2 \mid f$
,
![]() $(f,p) \ne (2,3)$
and
$(f,p) \ne (2,3)$
and
![]() $K \cong PSL_2(p^{\frac {f}{2}})$
. In particular, K is a component of
$K \cong PSL_2(p^{\frac {f}{2}})$
. In particular, K is a component of
![]() $C_T(\alpha )$
.
$C_T(\alpha )$
.
Proof. Note that
![]() $C_T(\alpha ) \cong C_{\mathrm {Inn}(T)}(\alpha )$
.
$C_T(\alpha ) \cong C_{\mathrm {Inn}(T)}(\alpha )$
.
Assume that
![]() $\alpha \in \mathrm {Inndiag}(T)$
. Noticing that
$\alpha \in \mathrm {Inndiag}(T)$
. Noticing that
![]() $\mathrm {Inndiag}(T) \cong PGL_2(q)$
, we see from Lemma 3.3 that
$\mathrm {Inndiag}(T) \cong PGL_2(q)$
, we see from Lemma 3.3 that
![]() $C_{\mathrm {Inndiag}(T)}(\alpha )$
is solvable. Thus,
$C_{\mathrm {Inndiag}(T)}(\alpha )$
is solvable. Thus,
![]() $C_T(\alpha ) \cong C_{\mathrm {Inn}(T)}(\alpha )$
is solvable, and
$C_T(\alpha ) \cong C_{\mathrm {Inn}(T)}(\alpha )$
is solvable, and
![]() $C_T(\alpha )$
has no
$C_T(\alpha )$
has no
![]() $2$
-components, a contradiction to the choice of
$2$
-components, a contradiction to the choice of
![]() $\alpha $
.
$\alpha $
.
So we have
![]() $\alpha \not \in \mathrm {Inndiag}(T)$
. By the structure of
$\alpha \not \in \mathrm {Inndiag}(T)$
. By the structure of
![]() $\mathrm {Aut}(PSL_2(q))$
and since
$\mathrm {Aut}(PSL_2(q))$
and since
![]() $\alpha $
has order
$\alpha $
has order
![]() $2$
, we can write
$2$
, we can write
![]() $\alpha $
as a product of an inner-diagonal automorphism and a field automorphism of order
$\alpha $
as a product of an inner-diagonal automorphism and a field automorphism of order
![]() $2$
. In particular, f must be even. Consulting [Reference Gorenstein, Lyons and Solomon28, Proposition 4.9.1 (d)], we see that
$2$
. In particular, f must be even. Consulting [Reference Gorenstein, Lyons and Solomon28, Proposition 4.9.1 (d)], we see that
![]() $\alpha $
itself is a field automorphism. So we can apply [Reference Gorenstein, Lyons and Solomon28, Proposition 4.9.1 (b)] to conclude that
$\alpha $
itself is a field automorphism. So we can apply [Reference Gorenstein, Lyons and Solomon28, Proposition 4.9.1 (b)] to conclude that
![]() $C_{\mathrm {Inndiag}(T)}(\alpha ) \cong \mathrm {Inndiag}(PSL_2(p^{\frac {f}{2}})) \cong PGL_2(p^{\frac {f}{2}})$
. Consequently, K is isomorphic to a
$C_{\mathrm {Inndiag}(T)}(\alpha ) \cong \mathrm {Inndiag}(PSL_2(p^{\frac {f}{2}})) \cong PGL_2(p^{\frac {f}{2}})$
. Consequently, K is isomorphic to a
![]() $2$
-component of
$2$
-component of
![]() $PGL_2(p^{\frac {f}{2}})$
. It follows that
$PGL_2(p^{\frac {f}{2}})$
. It follows that
![]() $(f,p) \ne (2,3)$
and
$(f,p) \ne (2,3)$
and
![]() $K \cong PSL_2(p^{\frac {f}{2}})$
.
$K \cong PSL_2(p^{\frac {f}{2}})$
.
Before we state the next lemma, we introduce some notational conventions for adjoint Chevalley groups. Given a nontrivial prime power q, we denote
![]() $A_1(q)$
also by
$A_1(q)$
also by
![]() $B_1(q)$
and by
$B_1(q)$
and by
![]() $C_1(q)$
. Moreover,
$C_1(q)$
. Moreover,
![]() $B_2(q)$
will be also denoted by
$B_2(q)$
will be also denoted by
![]() $C_2(q)$
, and
$C_2(q)$
, and
![]() $A_3(q)$
will be also denoted by
$A_3(q)$
will be also denoted by
![]() $D_3(q)$
. We also set
$D_3(q)$
. We also set
![]() $D_2(q) := A_1(q) \times A_1(q)$
and
$D_2(q) := A_1(q) \times A_1(q)$
and
![]() $^2D_2(q) := A_1(q^2)$
.
$^2D_2(q) := A_1(q^2)$
.
Lemma 3.46. Let
![]() $q = p^f$
, where p is an odd prime and f is a positive integer. Let
$q = p^f$
, where p is an odd prime and f is a positive integer. Let
![]() $n \ge 3$
be a natural number and
$n \ge 3$
be a natural number and
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let
$\varepsilon \in \lbrace +,- \rbrace $
. Let
![]() $T := PSL_n^{\varepsilon }(q)$
, and let
$T := PSL_n^{\varepsilon }(q)$
, and let
![]() $\alpha $
be an involution of
$\alpha $
be an involution of
![]() $\mathrm {Aut}(T)$
. Suppose that
$\mathrm {Aut}(T)$
. Suppose that
![]() $C_T(\alpha )$
has a
$C_T(\alpha )$
has a
![]() $2$
-component K. Then K is in fact a component, and one of the following holds:
$2$
-component K. Then K is in fact a component, and one of the following holds:
-
(i)
 $K \cong SL_i^{\varepsilon }(q)$
for some
$K \cong SL_i^{\varepsilon }(q)$
for some
 $2 \le i < n$
, where
$2 \le i < n$
, where
 $i> 2$
if
$i> 2$
if
 $q = 3$
;
$q = 3$
; -
(ii) n is even, and K is isomorphic to a nontrivial quotient of
 $SL_{\frac {n}{2}}(q^2)$
;
$SL_{\frac {n}{2}}(q^2)$
; -
(iii)
 $\varepsilon = +$
, f is even,
$\varepsilon = +$
, f is even,
 $K \cong PSL_n(p^{\frac {f}{2}})$
or
$K \cong PSL_n(p^{\frac {f}{2}})$
or
 $K \cong PSU_n(p^{\frac {f}{2}})$
;
$K \cong PSU_n(p^{\frac {f}{2}})$
; -
(iv)
 $q \ne 3$
,
$q \ne 3$
,
 $n = 3$
or
$n = 3$
or
 $4$
, and
$4$
, and
 $K \cong PSL_2(q)$
;
$K \cong PSL_2(q)$
; -
(v) n is odd,
 $n \ge 5$
and
$n \ge 5$
and
 $K \cong B_{\frac {n-1}{2}}(q)$
;
$K \cong B_{\frac {n-1}{2}}(q)$
; -
(vi) n is even and
 $K \cong C_{\frac {n}{2}}(q)$
;
$K \cong C_{\frac {n}{2}}(q)$
; -
(vii) n is even,
 $n \ge 6$
and
$n \ge 6$
and
 $K \cong D_{\frac {n}{2}}(q)$
;
$K \cong D_{\frac {n}{2}}(q)$
; -
(viii) n is even,
 $n \ge 6$
and
$n \ge 6$
and
 $K \cong \ {}^2D_{\frac {n}{2}}(q)$
.
$K \cong \ {}^2D_{\frac {n}{2}}(q)$
.
Here, the (twisted) Chevalley groups appearing in (v)–(viii) are adjoint.
Proof. It can be shown that any involution of
![]() $\mathrm {Aut}(T)$
is an inner-diagonal automorphism, a field automorphism, a graph automorphism or a graph-field automorphism (see [Reference Burness and Giudici16, Section 3.1.3] or [Reference Gorenstein, Lyons and Solomon28, Section 4.9]).
$\mathrm {Aut}(T)$
is an inner-diagonal automorphism, a field automorphism, a graph automorphism or a graph-field automorphism (see [Reference Burness and Giudici16, Section 3.1.3] or [Reference Gorenstein, Lyons and Solomon28, Section 4.9]).
Case 1:
![]() $\alpha \in \mathrm {Inndiag}(T)$
, or
$\alpha \in \mathrm {Inndiag}(T)$
, or
![]() $\alpha $
is a graph automorphism.
$\alpha $
is a graph automorphism.
Set
![]() $C^{*} := C_{\mathrm {Inndiag}(T)}(\alpha )$
and
$C^{*} := C_{\mathrm {Inndiag}(T)}(\alpha )$
and
![]() $L^{*} := O^{p'}(C^{*})$
. One can see from [Reference Gorenstein, Lyons and Solomon28, Theorem 4.2.2 and Table 4.5.1] that
$L^{*} := O^{p'}(C^{*})$
. One can see from [Reference Gorenstein, Lyons and Solomon28, Theorem 4.2.2 and Table 4.5.1] that
![]() $C^{*}/L^{*}$
is solvable and that one of the following holds:
$C^{*}/L^{*}$
is solvable and that one of the following holds:
-
(1)
 $L^{*}$
is the central product of two subgroups isomorphic to
$L^{*}$
is the central product of two subgroups isomorphic to
 $SL_i^{\varepsilon }(q)$
and
$SL_i^{\varepsilon }(q)$
and
 $SL_{n-i}^{\varepsilon }(q)$
for some natural number i with
$SL_{n-i}^{\varepsilon }(q)$
for some natural number i with
 $1 \le i \le \frac {n}{2}$
,
$1 \le i \le \frac {n}{2}$
, -
(2) n is even and
 $L^{*}$
is isomorphic to a nontrivial quotient of
$L^{*}$
is isomorphic to a nontrivial quotient of
 $SL_{\frac {n}{2}}(q^2)$
,
$SL_{\frac {n}{2}}(q^2)$
, -
(3) n is odd and
 $L^{*} \cong B_{\frac {n-1}{2}}(q)$
,
$L^{*} \cong B_{\frac {n-1}{2}}(q)$
, -
(4) n is even and
 $L^{*} \cong C_{\frac {n}{2}}(q)$
,
$L^{*} \cong C_{\frac {n}{2}}(q)$
, -
(5) n is even and
 $L^{*} \cong D_{\frac {n}{2}}(q)$
,
$L^{*} \cong D_{\frac {n}{2}}(q)$
, -
(6) n is even and
 $L^{*} \cong \ {}^2D_{\frac {n}{2}}(q)$
,
$L^{*} \cong \ {}^2D_{\frac {n}{2}}(q)$
,
where the (twisted) Chevalley groups appearing in the last four cases are adjoint. Since
![]() $C_T(\alpha )$
is isomorphic to
$C_T(\alpha )$
is isomorphic to
![]() $C_{\mathrm {Inn}(T)}(\alpha ) \trianglelefteq C^{*}$
, we have that K is isomorphic to a
$C_{\mathrm {Inn}(T)}(\alpha ) \trianglelefteq C^{*}$
, we have that K is isomorphic to a
![]() $2$
-component of
$2$
-component of
![]() $C^{*}$
and thus isomorphic to a
$C^{*}$
and thus isomorphic to a
![]() $2$
-component of
$2$
-component of
![]() $L^{*}$
. Therefore, one of the conditions (i)-(viii) is satisfied.
$L^{*}$
. Therefore, one of the conditions (i)-(viii) is satisfied.
Case 2:
![]() $\alpha $
is a field automorphism or a graph-field automorphism.
$\alpha $
is a field automorphism or a graph-field automorphism.
Again, let
![]() $C^{*} := C_{\mathrm {Inndiag}(T)}(\alpha )$
. Since the field automorphisms of
$C^{*} := C_{\mathrm {Inndiag}(T)}(\alpha )$
. Since the field automorphisms of
![]() $PSU_n(q)$
have odd order and
$PSU_n(q)$
have odd order and
![]() $PSU_n(q)$
has no graph-field automorphisms, we have
$PSU_n(q)$
has no graph-field automorphisms, we have
![]() $\varepsilon = +$
. Also, f is even since
$\varepsilon = +$
. Also, f is even since
![]() $\alpha $
is a field automorphism or a graph-field automorphism of order
$\alpha $
is a field automorphism or a graph-field automorphism of order
![]() $2$
. From [Reference Gorenstein, Lyons and Solomon28, Proposition 4.9.1 (a), (b)], we see that
$2$
. From [Reference Gorenstein, Lyons and Solomon28, Proposition 4.9.1 (a), (b)], we see that
![]() $C^{*} \cong PGL_n(p^{\frac {f}{2}})$
if
$C^{*} \cong PGL_n(p^{\frac {f}{2}})$
if
![]() $\alpha $
is a field automorphism and that
$\alpha $
is a field automorphism and that
![]() $C^{*} \cong PGU_n(p^{\frac {f}{2}})$
if
$C^{*} \cong PGU_n(p^{\frac {f}{2}})$
if
![]() $\alpha $
is a graph-field automorphism. Since K is isomorphic to a
$\alpha $
is a graph-field automorphism. Since K is isomorphic to a
![]() $2$
-component of
$2$
-component of
![]() $C^{*}$
, it follows that (iii) is satisfied.
$C^{*}$
, it follows that (iii) is satisfied.
Corollary 3.47. Let
![]() $q = p^f$
, where p is an odd prime and f is a positive integer. Let
$q = p^f$
, where p is an odd prime and f is a positive integer. Let
![]() $n \ge 2$
be a natural number and
$n \ge 2$
be a natural number and
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Let Z be a central subgroup of
$\varepsilon \in \lbrace +,- \rbrace $
. Let Z be a central subgroup of
![]() $SL_n^{\varepsilon }(q)$
, and let
$SL_n^{\varepsilon }(q)$
, and let
![]() $T := SL_n^{\varepsilon }(q)/Z$
. Let
$T := SL_n^{\varepsilon }(q)/Z$
. Let
![]() $\alpha $
be an involution of
$\alpha $
be an involution of
![]() $\mathrm {Aut}(T)$
, and let K be a
$\mathrm {Aut}(T)$
, and let K be a
![]() $2$
-component of
$2$
-component of
![]() $C_T(\alpha )$
. Then the following hold:
$C_T(\alpha )$
. Then the following hold:
-
(i) K is a component of
 $C_T(\alpha )$
, and
$C_T(\alpha )$
, and
 $K/Z(K)$
is a known finite simple group.
$K/Z(K)$
is a known finite simple group. -
(ii)
 $K/Z(K) \not \cong M_{11}$
.
$K/Z(K) \not \cong M_{11}$
. -
(iii) Assume that
 $K/Z(K) \cong PSL_k^{\varepsilon ^{*}}(q^{*})$
for some positive integer
$K/Z(K) \cong PSL_k^{\varepsilon ^{*}}(q^{*})$
for some positive integer
 $2 \le k \le n$
, some nontrivial odd prime power
$2 \le k \le n$
, some nontrivial odd prime power
 $q^{*}$
and some
$q^{*}$
and some
 $\varepsilon ^{*} \in \lbrace +,- \rbrace $
. Then one of the following holds:
$\varepsilon ^{*} \in \lbrace +,- \rbrace $
. Then one of the following holds:-
(a)
 $q^{*} = q$
;
$q^{*} = q$
; -
(b)
 $q^{*} = q^2$
,
$q^{*} = q^2$
,
 $n \ge 4$
is even,
$n \ge 4$
is even,
 $k = \frac {n}{2}$
and
$k = \frac {n}{2}$
and
 $\varepsilon ^{*} = +$
if
$\varepsilon ^{*} = +$
if
 $n \ge 6$
;
$n \ge 6$
; -
(c) f is even,
 $k = n$
,
$k = n$
,
 $q^{*} = p^{\frac {f}{2}}$
.
$q^{*} = p^{\frac {f}{2}}$
.
-
Proof. Set
![]() . Let
. Let
![]() $\overline \alpha $
be the automorphism of
$\overline \alpha $
be the automorphism of
![]() $\overline T$
induced by
$\overline T$
induced by
![]() $\alpha $
.
$\alpha $
.
As
![]() is a
is a
![]() $2$
-component of
$2$
-component of
![]() and
and
![]() , it follows that
, it follows that
![]() is a
is a
![]() $2$
-component of
$2$
-component of
![]() . Lemmas 3.45 and 3.46 imply that
. Lemmas 3.45 and 3.46 imply that
![]() is a component of
is a component of
![]() and that
and that
![]() is a known finite simple group. Applying [Reference Kurzweil and Stellmacher37, 6.5.1], we conclude that
is a known finite simple group. Applying [Reference Kurzweil and Stellmacher37, 6.5.1], we conclude that
![]() $K'$
is a component of
$K'$
is a component of
![]() $C_T(\alpha )$
. We have
$C_T(\alpha )$
. We have
![]() $K = K'$
since K is a
$K = K'$
since K is a
![]() $2$
-component of
$2$
-component of
![]() $C_T(\alpha )$
, and so it follows that K is a component of
$C_T(\alpha )$
, and so it follows that K is a component of
![]() $C_T(\alpha )$
. Also,
$C_T(\alpha )$
. Also,
![]() so that
so that
![]() $K/Z(K)$
is a known finite simple group. Hence, (i) holds.
$K/Z(K)$
is a known finite simple group. Hence, (i) holds.
If
![]() $K/Z(K) \cong M_{11}$
, then
$K/Z(K) \cong M_{11}$
, then
![]() , which is not possible by Lemmas 3.45 and 3.46. So (ii) holds.
, which is not possible by Lemmas 3.45 and 3.46. So (ii) holds.
Suppose that
![]() $K/Z(K) \cong PSL_k^{\varepsilon ^{*}}(q^{*})$
for some positive integer
$K/Z(K) \cong PSL_k^{\varepsilon ^{*}}(q^{*})$
for some positive integer
![]() $2 \le k \le n$
, some nontrivial odd prime power
$2 \le k \le n$
, some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon ^{*} \in \lbrace +,- \rbrace $
. By Lemmas 3.45 and 3.46, one of the following holds:
$\varepsilon ^{*} \in \lbrace +,- \rbrace $
. By Lemmas 3.45 and 3.46, one of the following holds:
-
(1)
 for some
for some
 $2 \le i < n$
;
$2 \le i < n$
; -
(2) n is even, and
 is isomorphic to
is isomorphic to
 $PSL_{\frac {n}{2}}(q^2)$
;
$PSL_{\frac {n}{2}}(q^2)$
; -
(3) f is even,
 or
or
 $PSU_n(p^{\frac {f}{2}})$
;
$PSU_n(p^{\frac {f}{2}})$
; -
(4)
 $q \ne 3$
,
$q \ne 3$
,
 $n = 3$
or
$n = 3$
or
 $4$
,
$4$
,
 ;
; -
(5) n is odd,
 $n \ge 5$
,
$n \ge 5$
,
 ;
; -
(6) n is even,
 $n \ge 4$
,
$n \ge 4$
,
 ;
; -
(7) n is even,
 $n \ge 6$
,
$n \ge 6$
,
 ;
; -
(8) n is even,
 $n \ge 6$
,
$n \ge 6$
,
 .
.
Here, the (twisted) Chevalley groups appearing in (5)–(8) are adjoint. On the other hand, we have
![]() . Now, if (1) holds, then
. Now, if (1) holds, then
![]() $PSL_k^{\varepsilon ^{*}}(q^{*}) \cong PSL_i^{\varepsilon }(q)$
for some
$PSL_k^{\varepsilon ^{*}}(q^{*}) \cong PSL_i^{\varepsilon }(q)$
for some
![]() $2 \le i < n$
, and [Reference Steinberg49, Theorem 37] shows that this is only possible when
$2 \le i < n$
, and [Reference Steinberg49, Theorem 37] shows that this is only possible when
![]() $q^{*} = q$
so that (a) holds. Similarly, if (2) holds, then we have (b). Moreover, (3) implies (c) and (4) implies (a). As Theorem [Reference Steinberg49, Theorem 37] shows, the cases (5) and (6) cannot occur, while (7) and (8) can only occur when
$q^{*} = q$
so that (a) holds. Similarly, if (2) holds, then we have (b). Moreover, (3) implies (c) and (4) implies (a). As Theorem [Reference Steinberg49, Theorem 37] shows, the cases (5) and (6) cannot occur, while (7) and (8) can only occur when
![]() $n = 6$
. As above, one can see that if
$n = 6$
. As above, one can see that if
![]() $n = 6$
and (7) or (8) holds, then we have (a).
$n = 6$
and (7) or (8) holds, then we have (a).
Lemma 3.48. Let
![]() $n \ge 3$
and
$n \ge 3$
and
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Then
$\varepsilon \in \lbrace +,- \rbrace $
. Then
![]() $SL_n^{\varepsilon }(3)$
is locally balanced (in the sense of Definition 2.7).
$SL_n^{\varepsilon }(3)$
is locally balanced (in the sense of Definition 2.7).
Proof. Set
![]() $T := SL_n^{\varepsilon }(3)$
. Let H be a subgroup of
$T := SL_n^{\varepsilon }(3)$
. Let H be a subgroup of
![]() $\mathrm {Aut}(T)$
containing
$\mathrm {Aut}(T)$
containing
![]() $\mathrm {Inn}(T)$
, and let x be an involution of H. It is enough to show that
$\mathrm {Inn}(T)$
, and let x be an involution of H. It is enough to show that
![]() $O(C_H(x)) = 1$
.
$O(C_H(x)) = 1$
.
Assume that
![]() $O(C_H(x)) \ne 1$
. Then
$O(C_H(x)) \ne 1$
. Then
![]() $x \in \mathrm {Inndiag}(T)$
by [Reference Gorenstein, Lyons and Solomon28, Theorem 7.7.1]. By Propositions 3.41 and 3.43,
$x \in \mathrm {Inndiag}(T)$
by [Reference Gorenstein, Lyons and Solomon28, Theorem 7.7.1]. By Propositions 3.41 and 3.43,
![]() $\mathrm {Out}(T)$
is a
$\mathrm {Out}(T)$
is a
![]() $2$
-group. This implies
$2$
-group. This implies
![]() $O(C_H(x)) = O(C_{\mathrm {Inn}(T)}(x)) = O(C_{\mathrm {Inndiag}(T)}(x))$
. Since x is an involution of
$O(C_H(x)) = O(C_{\mathrm {Inn}(T)}(x)) = O(C_{\mathrm {Inndiag}(T)}(x))$
. Since x is an involution of
![]() $\mathrm {Inndiag}(T) \cong PGL_n^{\varepsilon }(3)$
, we have
$\mathrm {Inndiag}(T) \cong PGL_n^{\varepsilon }(3)$
, we have
![]() $O(C_{\mathrm {Inndiag}(T)}(x)) = 1$
by Corollary 3.9. Thus,
$O(C_{\mathrm {Inndiag}(T)}(x)) = 1$
by Corollary 3.9. Thus,
![]() $O(C_H(x)) = 1$
. This contradiction completes the proof.
$O(C_H(x)) = 1$
. This contradiction completes the proof.
Lemma 3.49. Let
![]() $n \ge 3$
be a natural number, let q be a nontrivial odd power, and let
$n \ge 3$
be a natural number, let q be a nontrivial odd power, and let
![]() $\varepsilon \in \lbrace +,- \rbrace $
. Then any nontrivial quotient of
$\varepsilon \in \lbrace +,- \rbrace $
. Then any nontrivial quotient of
![]() $SL_n^{\varepsilon }(q)$
is locally
$SL_n^{\varepsilon }(q)$
is locally
![]() $2$
-balanced (in the sense of Definition 2.7).
$2$
-balanced (in the sense of Definition 2.7).
Proof. By [Reference Gorenstein24, Theorem 4.61] or [Reference Gorenstein, Lyons and Solomon28, Theorem 7.7.4],
![]() $PSL_n^{\varepsilon }(q)$
is locally
$PSL_n^{\varepsilon }(q)$
is locally
![]() $2$
-balanced. Let K be a nontrivial quotient of
$2$
-balanced. Let K be a nontrivial quotient of
![]() $SL_n^{\varepsilon }(q)$
. As we have seen, there is an isomorphism
$SL_n^{\varepsilon }(q)$
. As we have seen, there is an isomorphism
![]() $\mathrm {Aut}(K) \rightarrow \mathrm {Aut}(PSL_n^{\varepsilon }(q))$
mapping
$\mathrm {Aut}(K) \rightarrow \mathrm {Aut}(PSL_n^{\varepsilon }(q))$
mapping
![]() $\mathrm {Inn}(K)$
to
$\mathrm {Inn}(K)$
to
![]() $\mathrm {Inn}(PSL_n^{\varepsilon }(q))$
. So the local
$\mathrm {Inn}(PSL_n^{\varepsilon }(q))$
. So the local
![]() $2$
-balance of K follows from the local
$2$
-balance of K follows from the local
![]() $2$
-balance of
$2$
-balance of
![]() $PSL_n^{\varepsilon }(q)$
.
$PSL_n^{\varepsilon }(q)$
.
Lemma 3.50. Let q be a nontrivial odd prime power and
![]() $n \ge 4$
be a natural number. Let
$n \ge 4$
be a natural number. Let
![]() $Z \le Z(SL_n(q))$
and
$Z \le Z(SL_n(q))$
and
![]() $T := SL_n(q)/Z$
. Let
$T := SL_n(q)/Z$
. Let
![]() $K_1$
be the image of
$K_1$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SL_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SL_2(q) \right\rbrace \end{align*} $$
in T, and let
![]() $K_2$
be the image of
$K_2$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SL_{n-2}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SL_{n-2}(q) \right\rbrace \end{align*} $$
in T. Let
![]() $\alpha $
be an automorphism of T with odd order such that
$\alpha $
be an automorphism of T with odd order such that
![]() $\alpha $
normalizes
$\alpha $
normalizes
![]() $K_1$
and centralizes
$K_1$
and centralizes
![]() $K_2$
. Then
$K_2$
. Then
![]() $\alpha |_{K_1,K_1}$
is an inner automorphism.
$\alpha |_{K_1,K_1}$
is an inner automorphism.
Proof. By hypothesis,
![]() $q = p^f$
for some odd prime number p and some positive integer f. We have
$q = p^f$
for some odd prime number p and some positive integer f. We have
![]() $\alpha \in P \Gamma L_n(q)$
since
$\alpha \in P \Gamma L_n(q)$
since
![]() $\alpha $
has odd order and
$\alpha $
has odd order and
![]() $|\mathrm {Aut}(T)/P \Gamma L_n(q)| = 2$
. So there are some
$|\mathrm {Aut}(T)/P \Gamma L_n(q)| = 2$
. So there are some
![]() $m \in GL_{n}(q)$
and some
$m \in GL_{n}(q)$
and some
![]() $1 \le r \le f$
such that, for each element
$1 \le r \le f$
such that, for each element
![]() $(a_{ij})$
of
$(a_{ij})$
of
![]() $SL_n(q)$
,
$SL_n(q)$
,
![]() $\alpha $
maps
$\alpha $
maps
![]() $(a_{ij})Z$
to
$(a_{ij})Z$
to
![]() $((a_{ij})^{p^r})^mZ$
.
$((a_{ij})^{p^r})^mZ$
.
Let x be the image of
![]() $\mathrm {diag}(-1,-1,1,\dots ,1) \in SL_n(q)$
in T. Then x is the unique involution of
$\mathrm {diag}(-1,-1,1,\dots ,1) \in SL_n(q)$
in T. Then x is the unique involution of
![]() $K_1$
, and so we have
$K_1$
, and so we have
![]() $x^{\alpha } = x$
. This easily implies that
$x^{\alpha } = x$
. This easily implies that
 $$ \begin{align*} m = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} m = \begin{pmatrix} m_1 & \\ & m_2 \end{pmatrix} \end{align*} $$
for some
![]() $m_1 \in GL_2(q)$
and some
$m_1 \in GL_2(q)$
and some
![]() $m_2 \in GL_{n-2}(q)$
.
$m_2 \in GL_{n-2}(q)$
.
Since
![]() $\alpha $
centralizes
$\alpha $
centralizes
![]() $K_2$
, we have
$K_2$
, we have
![]() $((a_{ij})^{p^r})^{m_2} = (a_{ij})$
for all
$((a_{ij})^{p^r})^{m_2} = (a_{ij})$
for all
![]() $(a_{ij}) \in SL_{n-2}(q)$
. Therefore, the automorphism
$(a_{ij}) \in SL_{n-2}(q)$
. Therefore, the automorphism
![]() $SL_{n-2}(q) \rightarrow SL_{n-2}(q), (a_{ij}) \mapsto (a_{ij})^{p^r}$
is an element of
$SL_{n-2}(q) \rightarrow SL_{n-2}(q), (a_{ij}) \mapsto (a_{ij})^{p^r}$
is an element of
![]() $\mathrm {Inndiag}(SL_{n-2}(q))$
. This implies
$\mathrm {Inndiag}(SL_{n-2}(q))$
. This implies
![]() $r = f$
.
$r = f$
.
Thus, under the isomorphism
![]() $\mathrm {Aut}(SL_2(q)) \rightarrow \mathrm {Aut}(K_1)$
induced by the canonical isomorphism
$\mathrm {Aut}(SL_2(q)) \rightarrow \mathrm {Aut}(K_1)$
induced by the canonical isomorphism
![]() $SL_2(q) \rightarrow K_1$
, the automorphism
$SL_2(q) \rightarrow K_1$
, the automorphism
![]() $\alpha |_{K_1,K_1}$
of
$\alpha |_{K_1,K_1}$
of
![]() $K_1$
corresponds to the inner-diagonal automorphism
$K_1$
corresponds to the inner-diagonal automorphism
![]() $\widetilde \alpha : SL_2(q) \rightarrow SL_2(q), a \mapsto a^{m_1}$
, and this automorphism has odd order since
$\widetilde \alpha : SL_2(q) \rightarrow SL_2(q), a \mapsto a^{m_1}$
, and this automorphism has odd order since
![]() $\alpha $
has odd order. The index of
$\alpha $
has odd order. The index of
![]() $\mathrm {Inn}(SL_2(q))$
in
$\mathrm {Inn}(SL_2(q))$
in
![]() $\mathrm {Inndiag}(SL_2(q))$
is
$\mathrm {Inndiag}(SL_2(q))$
is
![]() $2$
, and so it follows that
$2$
, and so it follows that
![]() $\widetilde \alpha \in \mathrm {Inn}(SL_2(q))$
. Consequently,
$\widetilde \alpha \in \mathrm {Inn}(SL_2(q))$
. Consequently,
![]() $\alpha |_{K_1,K_1} \in \mathrm {Inn}(K_1)$
.
$\alpha |_{K_1,K_1} \in \mathrm {Inn}(K_1)$
.
By using similar arguments as in the proof of Lemma 3.50, one can prove the following lemma.
Lemma 3.51. Let q be a nontrivial odd prime power and
![]() $n \ge 4$
be a natural number. Let
$n \ge 4$
be a natural number. Let
![]() $Z \le Z(SU_n(q))$
and
$Z \le Z(SU_n(q))$
and
![]() $T := SU_n(q)/Z$
. Let
$T := SU_n(q)/Z$
. Let
![]() $K_1$
be the image of
$K_1$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SU_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SU_2(q) \right\rbrace \end{align*} $$
in T, and let
![]() $K_2$
be the image of
$K_2$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SU_{n-2}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SU_{n-2}(q) \right\rbrace \end{align*} $$
in T. Let
![]() $\alpha $
be an automorphism of T with odd order such that
$\alpha $
be an automorphism of T with odd order such that
![]() $\alpha $
normalizes
$\alpha $
normalizes
![]() $K_1$
and centralizes
$K_1$
and centralizes
![]() $K_2$
. Then
$K_2$
. Then
![]() $\alpha |_{K_1,K_1}$
is an inner automorphism.
$\alpha |_{K_1,K_1}$
is an inner automorphism.
Our next goal is to prove the following lemma.
Lemma 3.52. Let q and
![]() $q^{*}$
be nontrivial odd prime powers. Let L be a group isomorphic to
$q^{*}$
be nontrivial odd prime powers. Let L be a group isomorphic to
![]() $SL_2(q^{*})$
. Let Q be a Sylow
$SL_2(q^{*})$
. Let Q be a Sylow
![]() $2$
-subgroup of L. Moreover, let V be a Sylow
$2$
-subgroup of L. Moreover, let V be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
and
$GL_2(q)$
and
![]() $V_0 := V \cap SL_2(q)$
. Suppose that there is a group isomorphism
$V_0 := V \cap SL_2(q)$
. Suppose that there is a group isomorphism
![]() $\psi : V_0 \rightarrow Q$
. Let
$\psi : V_0 \rightarrow Q$
. Let
![]() $v_1, v_2, v_3$
be elements of V such that
$v_1, v_2, v_3$
be elements of V such that
![]() $v_3 = v_1v_2$
and such that the square of any element of
$v_3 = v_1v_2$
and such that the square of any element of
![]() $\lbrace v_1,v_2,v_3 \rbrace $
lies in
$\lbrace v_1,v_2,v_3 \rbrace $
lies in
![]() $Z(GL_2(q))$
. For each
$Z(GL_2(q))$
. For each
![]() $i \in \lbrace 1,2,3 \rbrace $
, let
$i \in \lbrace 1,2,3 \rbrace $
, let
![]() $\alpha _i$
be a
$\alpha _i$
be a
![]() $2$
-element of
$2$
-element of
![]() $\mathrm {Aut}(L)$
normalizing Q such that
$\mathrm {Aut}(L)$
normalizing Q such that
Then we have
 $$ \begin{align*} \bigcap_{i=1}^3 O(C_L(\alpha_i)) = 1. \end{align*} $$
$$ \begin{align*} \bigcap_{i=1}^3 O(C_L(\alpha_i)) = 1. \end{align*} $$
To prove Lemma 3.52, we need to prove some other lemmas.
Lemma 3.53. Let q be a nontrivial odd prime power with
![]() $q \equiv 1 \ \mathrm {mod} \ 4$
, and let
$q \equiv 1 \ \mathrm {mod} \ 4$
, and let
![]() $k \in \mathbb {N}$
with
$k \in \mathbb {N}$
with
![]() $(q-1)_2 = 2^k$
. Let G be a group isomorphic to
$(q-1)_2 = 2^k$
. Let G be a group isomorphic to
![]() $SL_2(q)$
and
$SL_2(q)$
and
![]() $Q \in \mathrm {Syl}_2(G)$
. Then the following hold:
$Q \in \mathrm {Syl}_2(G)$
. Then the following hold:
-
(i) There are elements
 $a, b$
generating Q such that
$a, b$
generating Q such that
 $\mathrm {ord}(a) = 2^k$
,
$\mathrm {ord}(a) = 2^k$
,
 $\mathrm {ord}(b) = 4$
,
$\mathrm {ord}(b) = 4$
,
 $a^b = a^{-1}$
and
$a^b = a^{-1}$
and
 $b^2 = a^{2^{k-1}}$
.
$b^2 = a^{2^{k-1}}$
. -
(ii) Let a and b be as in (i). Then there is a group isomorphism
 $\varphi : G \rightarrow SL_2(q)$
such that for some
$\varphi : G \rightarrow SL_2(q)$
such that for some $$ \begin{align*} a^{\varphi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} a^{\varphi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
 $\lambda \in \mathbb {F}_q^{*}$
with order
$\lambda \in \mathbb {F}_q^{*}$
with order
 $2^k$
and
$2^k$
and  $$ \begin{align*} b^{\varphi} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} b^{\varphi} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
Proof. (i) follows from Lemma 3.12.
We now prove (ii). Assume that
![]() $k \ge 3$
. By Lemma 3.10 (i),
$k \ge 3$
. By Lemma 3.10 (i),
 $$ \begin{align*} R = \left\lbrace \begin{pmatrix} \mu & 0 \\ 0 & \mu^{-1} \end{pmatrix} \ : \ \mu \text{ is a } 2\text{-element of } \mathbb{F}_q^{*} \right\rbrace \left\langle \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right\rangle \end{align*} $$
$$ \begin{align*} R = \left\lbrace \begin{pmatrix} \mu & 0 \\ 0 & \mu^{-1} \end{pmatrix} \ : \ \mu \text{ is a } 2\text{-element of } \mathbb{F}_q^{*} \right\rbrace \left\langle \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \right\rangle \end{align*} $$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_2(q)$
. Choose a group isomorphism
$SL_2(q)$
. Choose a group isomorphism
![]() $\psi : G \rightarrow SL_2(q)$
such that
$\psi : G \rightarrow SL_2(q)$
such that
![]() $Q^{\psi } = R$
. Since
$Q^{\psi } = R$
. Since
![]() $k \ge 3$
, Q has only one cyclic subgroup of order
$k \ge 3$
, Q has only one cyclic subgroup of order
![]() $2^k$
. This implies that
$2^k$
. This implies that
 $$ \begin{align*} a^{\psi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} a^{\psi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
for some
![]() $\lambda \in \mathbb {F}_q^{*}$
with order
$\lambda \in \mathbb {F}_q^{*}$
with order
![]() $2^k$
. Since
$2^k$
. Since
![]() $b \not \in \langle a \rangle $
, we have
$b \not \in \langle a \rangle $
, we have
 $$ \begin{align*} b^{\psi} = \begin{pmatrix} 0 & \mu \\ -\mu^{-1} & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} b^{\psi} = \begin{pmatrix} 0 & \mu \\ -\mu^{-1} & 0 \end{pmatrix} \end{align*} $$
for some
![]() $2$
-element
$2$
-element
![]() $\mu $
of
$\mu $
of
![]() $\mathbb {F}_q^{*}$
. Composing
$\mathbb {F}_q^{*}$
. Composing
![]() $\psi $
with the automorphism
$\psi $
with the automorphism
 $$ \begin{align*} SL_2(q) \rightarrow SL_2(q), \ A \mapsto \begin{pmatrix} \mu^{-1} & 0 \\ 0 & 1 \end{pmatrix}A\begin{pmatrix} \mu & 0 \\ 0 & 1 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} SL_2(q) \rightarrow SL_2(q), \ A \mapsto \begin{pmatrix} \mu^{-1} & 0 \\ 0 & 1 \end{pmatrix}A\begin{pmatrix} \mu & 0 \\ 0 & 1 \end{pmatrix}, \end{align*} $$
we get a group isomorphism
![]() $\varphi : G \rightarrow SL_2(q)$
with the desired properties. This completes the proof of (ii) for the case
$\varphi : G \rightarrow SL_2(q)$
with the desired properties. This completes the proof of (ii) for the case
![]() $k \ge 3$
.
$k \ge 3$
.
Assume now that
![]() $k = 2$
. Let
$k = 2$
. Let
![]() $\psi : G \rightarrow SL_2(q)$
be a group isomorphism. We have
$\psi : G \rightarrow SL_2(q)$
be a group isomorphism. We have
![]() $(a^{\psi })^2 = -I_2$
since
$(a^{\psi })^2 = -I_2$
since
![]() $-I_2$
is the only involution of
$-I_2$
is the only involution of
![]() $SL_2(q)$
and
$SL_2(q)$
and
![]() $\mathrm {ord}(a^2) = 2$
. So, by Lemma 3.3, we may assume that
$\mathrm {ord}(a^2) = 2$
. So, by Lemma 3.3, we may assume that
 $$ \begin{align*} a^{\psi} = \begin{pmatrix}\lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} a^{\psi} = \begin{pmatrix}\lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
for some
![]() $\lambda \in \mathbb {F}_q^{*}$
with order
$\lambda \in \mathbb {F}_q^{*}$
with order
![]() $4$
. Since
$4$
. Since
![]() $a^b = a^{-1}$
, we have
$a^b = a^{-1}$
, we have
 $$ \begin{align*} \begin{pmatrix}\lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix}^{b^{\psi}} = \begin{pmatrix}\lambda^{-1} & 0 \\ 0 & \lambda \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix}\lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix}^{b^{\psi}} = \begin{pmatrix}\lambda^{-1} & 0 \\ 0 & \lambda \end{pmatrix}. \end{align*} $$
This implies that
 $$ \begin{align*} b^{\psi} = \begin{pmatrix} 0 & \mu \\ -\mu^{-1} & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} b^{\psi} = \begin{pmatrix} 0 & \mu \\ -\mu^{-1} & 0 \end{pmatrix} \end{align*} $$
for some
![]() $\mu \in \mathbb {F}_q^{*}$
. Again, we may compose
$\mu \in \mathbb {F}_q^{*}$
. Again, we may compose
![]() $\psi $
with a suitable diagonal automorphism of
$\psi $
with a suitable diagonal automorphism of
![]() $SL_2(q)$
to obtain a group isomorphism
$SL_2(q)$
to obtain a group isomorphism
![]() $\varphi : G \rightarrow SL_2(q)$
with the desired properties.
$\varphi : G \rightarrow SL_2(q)$
with the desired properties.
By using similar arguments as in the proof of Lemma 3.53, one can prove the following lemma.
Lemma 3.54. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \mod 4$
, and let
$q \equiv 3 \mod 4$
, and let
![]() $s \in \mathbb N$
with
$s \in \mathbb N$
with
![]() $(q+1)_2 = 2^s$
. Let G be a group isomorphic to
$(q+1)_2 = 2^s$
. Let G be a group isomorphic to
![]() $SU_2(q)$
and
$SU_2(q)$
and
![]() $Q \in \mathrm {Syl}_2(G)$
. Then the following hold:
$Q \in \mathrm {Syl}_2(G)$
. Then the following hold:
-
(i) There are elements
 $a, b \in Q$
such that
$a, b \in Q$
such that
 $\mathrm {ord}(a) = 2^s$
,
$\mathrm {ord}(a) = 2^s$
,
 $\mathrm {ord}(b) = 4$
,
$\mathrm {ord}(b) = 4$
,
 $a^b = a^{-1}$
and
$a^b = a^{-1}$
and
 $b^2 = a^{2^{s-1}}$
.
$b^2 = a^{2^{s-1}}$
. -
(ii) Let a and b be as in (i). Then there is a group isomorphism
 $\varphi : G \rightarrow SU_2(q)$
such that for some
$\varphi : G \rightarrow SU_2(q)$
such that for some $$ \begin{align*} a^{\varphi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} a^{\varphi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
 $\lambda \in \mathbb {F}_{q^2}^{*}$
with order
$\lambda \in \mathbb {F}_{q^2}^{*}$
with order
 $2^s$
and
$2^s$
and  $$ \begin{align*} b^{\varphi} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} b^{\varphi} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
Lemma 3.55. Let q be a nontrivial odd prime power with
![]() $q \equiv 1 \ \mathrm {mod} \ 4$
. Let
$q \equiv 1 \ \mathrm {mod} \ 4$
. Let
![]() $\rho $
be a generating element of the Sylow
$\rho $
be a generating element of the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathbb {F}_q^{*}$
, and let
$\mathbb {F}_q^{*}$
, and let
 $$ \begin{align*} a := \begin{pmatrix} \rho & \\ & \rho^{-1} \end{pmatrix}, \ \ \ \ b := \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} a := \begin{pmatrix} \rho & \\ & \rho^{-1} \end{pmatrix}, \ \ \ \ b := \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
Let V be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
given by Lemma 3.10 (i), and let
$GL_2(q)$
given by Lemma 3.10 (i), and let
![]() $v,w \in V$
such that
$v,w \in V$
such that
![]() $v^2,w^2,(vw)^2 \in Z(GL_2(q))$
. Then one of the following holds:
$v^2,w^2,(vw)^2 \in Z(GL_2(q))$
. Then one of the following holds:
-
(i)
 $\lbrace v,w,vw \rbrace \cap Z(GL_2(q)) \ne \emptyset $
.
$\lbrace v,w,vw \rbrace \cap Z(GL_2(q)) \ne \emptyset $
. -
(ii) There exist
 $r,s \in \lbrace v,w,vw \rbrace $
with
$r,s \in \lbrace v,w,vw \rbrace $
with
 $a^{r} = a$
,
$a^{r} = a$
,
 $b^{r} = b^3$
and
$b^{r} = b^3$
and
 $a^{s} = a^{-1}$
.
$a^{s} = a^{-1}$
.
Proof. It is easy to note that (i) holds if v and w are diagonal matrices.
Suppose now that v or w is not a diagonal matrix. If neither v nor w is a diagonal matrix, then
![]() $vw$
is a diagonal matrix. So there exist
$vw$
is a diagonal matrix. So there exist
![]() $r, s \in \lbrace v,w,vw \rbrace $
such that
$r, s \in \lbrace v,w,vw \rbrace $
such that
 $$ \begin{align*} r = \begin{pmatrix} \lambda_1 & \\ & \lambda_2 \end{pmatrix}, \ \ \ \ s = \begin{pmatrix} & \mu_1 \\ \mu_2 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} r = \begin{pmatrix} \lambda_1 & \\ & \lambda_2 \end{pmatrix}, \ \ \ \ s = \begin{pmatrix} & \mu_1 \\ \mu_2 \end{pmatrix}, \end{align*} $$
where
![]() $\lambda _1$
,
$\lambda _1$
,
![]() $\lambda _2$
,
$\lambda _2$
,
![]() $\mu _1$
and
$\mu _1$
and
![]() $\mu _2$
are
$\mu _2$
are
![]() $2$
-elements of
$2$
-elements of
![]() $\mathbb {F}_q^{*}$
.
$\mathbb {F}_q^{*}$
.
If
![]() $\lambda _1 = \lambda _2$
, then (i) holds. Assume now that
$\lambda _1 = \lambda _2$
, then (i) holds. Assume now that
![]() $\lambda _1 \ne \lambda _2$
. Then
$\lambda _1 \ne \lambda _2$
. Then
![]() $\lambda _2 = - \lambda _1$
since
$\lambda _2 = - \lambda _1$
since
![]() $r^2 \in Z(GL_2(q))$
, and a direct calculation shows that
$r^2 \in Z(GL_2(q))$
, and a direct calculation shows that
![]() $a^{r} = a$
,
$a^{r} = a$
,
![]() $b^{r} = b^3$
and
$b^{r} = b^3$
and
![]() $a^{s} = a^{-1}$
.
$a^{s} = a^{-1}$
.
Lemma 3.56. Let q be a nontrivial odd prime power with
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
, and let
$q \equiv 3 \ \mathrm {mod} \ 4$
, and let
![]() $k \in \mathbb {N}$
with
$k \in \mathbb {N}$
with
![]() $(q+1)_2 = 2^k$
. Let V be a Sylow
$(q+1)_2 = 2^k$
. Let V be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_2(q)$
.
$GL_2(q)$
.
-
(i) There exist
 $x, y \in V$
with
$x, y \in V$
with
 $\mathrm {ord}(x) = 2^{k+1}$
,
$\mathrm {ord}(x) = 2^{k+1}$
,
 $\mathrm {ord}(y) = 2$
and
$\mathrm {ord}(y) = 2$
and
 $x^y = x^{-1+2^k}$
. We have
$x^y = x^{-1+2^k}$
. We have
 $V \cap SL_2(q) = \langle x^2 \rangle \langle xy \rangle $
.
$V \cap SL_2(q) = \langle x^2 \rangle \langle xy \rangle $
. -
(ii) Let x and y be as above, and let
 $a := x^2$
and
$a := x^2$
and
 $b := xy$
. Let
$b := xy$
. Let
 $v, w \in V$
with
$v, w \in V$
with
 $v^2,w^2,(vw)^2 \in Z(GL_2(q))$
. Then one of the following holds:
$v^2,w^2,(vw)^2 \in Z(GL_2(q))$
. Then one of the following holds:-
(a)
 $\lbrace v,w,vw \rbrace \cap Z(GL_2(q)) \ne \emptyset $
.
$\lbrace v,w,vw \rbrace \cap Z(GL_2(q)) \ne \emptyset $
. -
(b) There exist
 $r,s \in \lbrace v,w,vw \rbrace $
such that
$r,s \in \lbrace v,w,vw \rbrace $
such that
 $a^r = a$
,
$a^r = a$
,
 $b^r = b^3$
and
$b^r = b^3$
and
 $a^s = a^{-1}$
.
$a^s = a^{-1}$
.
-
Proof. (i) follows from Lemma 3.16 (i), (ii).
We now prove (ii). We have
![]() $Z(V) = \langle x^{2^k} \rangle $
by Lemma [Reference Gorenstein23, Chapter 5, Theorem 4.3]. Thus,
$Z(V) = \langle x^{2^k} \rangle $
by Lemma [Reference Gorenstein23, Chapter 5, Theorem 4.3]. Thus,
![]() $Z(GL_2(q)) \cap V = \langle x^{2^k} \rangle $
. Clearly,
$Z(GL_2(q)) \cap V = \langle x^{2^k} \rangle $
. Clearly,
![]() $\lbrace v,w,vw \rbrace \cap \langle x \rangle \subseteq \langle x^{2^{k-1}} \rangle $
.
$\lbrace v,w,vw \rbrace \cap \langle x \rangle \subseteq \langle x^{2^{k-1}} \rangle $
.
If
![]() $v,w \in \langle x \rangle $
, then
$v,w \in \langle x \rangle $
, then
![]() $v,w \in \langle x^{2^{k-1}} \rangle $
, and it easily follows that (a) holds.
$v,w \in \langle x^{2^{k-1}} \rangle $
, and it easily follows that (a) holds.
Assume now that
![]() $v \not \in \langle x \rangle $
or
$v \not \in \langle x \rangle $
or
![]() $w \not \in \langle x \rangle $
. If neither v nor w lies in
$w \not \in \langle x \rangle $
. If neither v nor w lies in
![]() $\langle x \rangle $
, then
$\langle x \rangle $
, then
![]() $vw \in \langle x \rangle $
. Consequently,
$vw \in \langle x \rangle $
. Consequently,
![]() $\lbrace v,w,vw \rbrace $
has an element r of the form
$\lbrace v,w,vw \rbrace $
has an element r of the form
![]() $x^{\ell 2^{k-1}}$
for some
$x^{\ell 2^{k-1}}$
for some
![]() $1 \le \ell \le 4$
and an element s of the form
$1 \le \ell \le 4$
and an element s of the form
![]() $x^i y$
for some
$x^i y$
for some
![]() $1 \le i \le 2^{k+1}$
. If
$1 \le i \le 2^{k+1}$
. If
![]() $\ell = 2$
or
$\ell = 2$
or
![]() $4$
, then (a) holds. Assume now that
$4$
, then (a) holds. Assume now that
![]() $\ell = 1$
or
$\ell = 1$
or
![]() $3$
. It is clear that
$3$
. It is clear that
![]() $a^r = a$
. Furthermore, we have
$a^r = a$
. Furthermore, we have
 $$ \begin{align*} b^r &= (xy)^{x^{\ell 2^{k-1}}} \\ &= x y^{x^{\ell 2^{k-1}}} \\ &= x x^{-\ell 2^{k-1}} y x^{\ell 2^{k-1}} y^2 \\ &= x^{1-\ell 2^{k-1}} (x^y)^{\ell 2^{k-1}} y \\ &= x^{1-\ell 2^{k-1}}(x^{-1+2^k})^{\ell 2^{k-1}} y \\ &= x^{1-\ell 2^k+\ell 2^{2k-1}} y \\ &= x^{1-\ell 2^k} y \\ &\stackrel{{\ell}\, \text{odd}}{=} x^{1+2^k}y. \end{align*} $$
$$ \begin{align*} b^r &= (xy)^{x^{\ell 2^{k-1}}} \\ &= x y^{x^{\ell 2^{k-1}}} \\ &= x x^{-\ell 2^{k-1}} y x^{\ell 2^{k-1}} y^2 \\ &= x^{1-\ell 2^{k-1}} (x^y)^{\ell 2^{k-1}} y \\ &= x^{1-\ell 2^{k-1}}(x^{-1+2^k})^{\ell 2^{k-1}} y \\ &= x^{1-\ell 2^k+\ell 2^{2k-1}} y \\ &= x^{1-\ell 2^k} y \\ &\stackrel{{\ell}\, \text{odd}}{=} x^{1+2^k}y. \end{align*} $$
On the other hand, we have
Consequently,
![]() $b^r = b^3$
. Finally, we also have
$b^r = b^3$
. Finally, we also have
Thus, (b) holds.
Proof of Lemma 3.52
If
![]() $\alpha _j|_{Q,Q} = \mathrm {id}_Q$
for some
$\alpha _j|_{Q,Q} = \mathrm {id}_Q$
for some
![]() $j \in \lbrace 1,2,3 \rbrace $
, then
$j \in \lbrace 1,2,3 \rbrace $
, then
![]() $\alpha _j = \mathrm {id}_L$
by Lemma 3.44, which implies that
$\alpha _j = \mathrm {id}_L$
by Lemma 3.44, which implies that
 $$ \begin{align*} \bigcap_{i=1}^3 O(C_L(\alpha_i)) \le O(C_L(\alpha_j)) = O(L) = 1. \end{align*} $$
$$ \begin{align*} \bigcap_{i=1}^3 O(C_L(\alpha_i)) \le O(C_L(\alpha_j)) = O(L) = 1. \end{align*} $$
Suppose now that
![]() $\alpha _i$
acts nontrivially on Q for all
$\alpha _i$
acts nontrivially on Q for all
![]() $i \in \lbrace 1,2,3 \rbrace $
. Let
$i \in \lbrace 1,2,3 \rbrace $
. Let
![]() $m \in \mathbb {N}$
with
$m \in \mathbb {N}$
with
![]() $|Q| = 2^m$
. Using Lemma 3.55 (together with Sylow’s theorem) and Lemma 3.56, we see that there exist
$|Q| = 2^m$
. Using Lemma 3.55 (together with Sylow’s theorem) and Lemma 3.56, we see that there exist
![]() $a,b \in Q$
and
$a,b \in Q$
and
![]() $i,j \in \lbrace 1,2,3 \rbrace $
such that the following hold:
$i,j \in \lbrace 1,2,3 \rbrace $
such that the following hold:
-
(i)
 $\mathrm {ord}(a) = 2^{m-1}$
,
$\mathrm {ord}(a) = 2^{m-1}$
,
 $\mathrm {ord}(b) = 4$
,
$\mathrm {ord}(b) = 4$
,
 $a^b = a^{-1}$
,
$a^b = a^{-1}$
,
 $b^2 = a^{2^{m-2}}$
;
$b^2 = a^{2^{m-2}}$
; -
(ii)
 $a^{\alpha _i} = a$
,
$a^{\alpha _i} = a$
,
 $b^{\alpha _i} = b^3$
,
$b^{\alpha _i} = b^3$
,
 $a^{\alpha _j} = a^{-1}$
.
$a^{\alpha _j} = a^{-1}$
.
Clearly,
![]() $b^{\alpha _j} = a^{\ell }b$
for some
$b^{\alpha _j} = a^{\ell }b$
for some
![]() $1 \le \ell \le 2^{m-1}$
.
$1 \le \ell \le 2^{m-1}$
.
Assume that
![]() $q^{*} \equiv 1 \ \mathrm {mod} \ 4$
. By Lemma 3.53, there is group isomorphism
$q^{*} \equiv 1 \ \mathrm {mod} \ 4$
. By Lemma 3.53, there is group isomorphism
![]() $\varphi : L \rightarrow SL_2(q^{*})$
with
$\varphi : L \rightarrow SL_2(q^{*})$
with
 $$ \begin{align*} a^{\varphi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
$$ \begin{align*} a^{\varphi} = \begin{pmatrix} \lambda & 0 \\ 0 & \lambda^{-1} \end{pmatrix} \end{align*} $$
for some generator
![]() $\lambda $
of the Sylow
$\lambda $
of the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $(\mathbb {F}_{q^{*}})^{*}$
and
$(\mathbb {F}_{q^{*}})^{*}$
and
 $$ \begin{align*} b^{\varphi} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} b^{\varphi} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}. \end{align*} $$
Set
![]() $\beta _k := \varphi ^{-1}\alpha _k \varphi $
for
$\beta _k := \varphi ^{-1}\alpha _k \varphi $
for
![]() $k \in \lbrace 1,2,3 \rbrace $
. Let i and j be as in (ii). Also, let
$k \in \lbrace 1,2,3 \rbrace $
. Let i and j be as in (ii). Also, let
 $$ \begin{align*} m_i := \begin{pmatrix} 1 & \\ & -1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} m_i := \begin{pmatrix} 1 & \\ & -1 \end{pmatrix}. \end{align*} $$
Then
![]() $\beta _i$
and
$\beta _i$
and
![]() $c_{m_i}$
normalize
$c_{m_i}$
normalize
![]() $Q^{\varphi }$
, and we have
$Q^{\varphi }$
, and we have
![]() $\beta _i|_{Q^{\varphi },Q^{\varphi }} = c_{m_i}|_{Q^{\varphi },Q^{\varphi }}$
. Applying Lemma 3.44, we conclude that
$\beta _i|_{Q^{\varphi },Q^{\varphi }} = c_{m_i}|_{Q^{\varphi },Q^{\varphi }}$
. Applying Lemma 3.44, we conclude that
![]() $\beta _i = c_{m_i}$
.
$\beta _i = c_{m_i}$
.
Clearly,
 $$ \begin{align*} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}^{\beta_j} = \begin{pmatrix} 0 & \mu \\ -\mu^{-1} & 0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}^{\beta_j} = \begin{pmatrix} 0 & \mu \\ -\mu^{-1} & 0 \end{pmatrix} \end{align*} $$
for some
![]() $2$
-element
$2$
-element
![]() $\mu $
of
$\mu $
of
![]() $(\mathbb {F}_{q^{*}})^{*}$
. Set
$(\mathbb {F}_{q^{*}})^{*}$
. Set
 $$ \begin{align*} m_j := \begin{pmatrix} 0 & \mu \\ -1 & 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} m_j := \begin{pmatrix} 0 & \mu \\ -1 & 0 \end{pmatrix}. \end{align*} $$
Then
![]() $\beta _j$
and
$\beta _j$
and
![]() $c_{m_j}$
normalize
$c_{m_j}$
normalize
![]() $Q^{\varphi }$
, and we have
$Q^{\varphi }$
, and we have
![]() $\beta _j|_{Q^{\varphi },Q^{\varphi }} = c_{m_j}|_{Q^{\varphi },Q^{\varphi }}$
. Applying Lemma 3.44, we conclude that
$\beta _j|_{Q^{\varphi },Q^{\varphi }} = c_{m_j}|_{Q^{\varphi },Q^{\varphi }}$
. Applying Lemma 3.44, we conclude that
![]() $\beta _j = c_{m_j}$
.
$\beta _j = c_{m_j}$
.
It follows that
![]() $C_{SL_2(q^{*})}(\beta _i) \cap C_{SL_2(q^{*})}(\beta _j) = Z(SL_2(q^{*}))$
. So we have
$C_{SL_2(q^{*})}(\beta _i) \cap C_{SL_2(q^{*})}(\beta _j) = Z(SL_2(q^{*}))$
. So we have
![]() $C_L(\alpha _i) \cap C_L(\alpha _j) = Z(L)$
, and this implies that
$C_L(\alpha _i) \cap C_L(\alpha _j) = Z(L)$
, and this implies that
 $$ \begin{align*} \bigcap_{k=1}^3 O(C_L(\alpha_k)) = 1 \end{align*} $$
$$ \begin{align*} \bigcap_{k=1}^3 O(C_L(\alpha_k)) = 1 \end{align*} $$
since
![]() $|Z(L)| = 2$
.
$|Z(L)| = 2$
.
If
![]() $q^{*} \equiv 3 \mod 4$
, then a very similar argumentation shows that the same conclusion holds. Here, one has to use Lemma 3.54 instead of Lemma 3.53, together with the fact that
$q^{*} \equiv 3 \mod 4$
, then a very similar argumentation shows that the same conclusion holds. Here, one has to use Lemma 3.54 instead of Lemma 3.53, together with the fact that
![]() $SL_2(q^{*}) \cong SU_2(q^{*})$
.
$SL_2(q^{*}) \cong SU_2(q^{*})$
.
We bring this section to a close with a proof of the following lemma, which will play an important role in the proof of Theorem B.
Lemma 3.57. Let q be a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
and
$\varepsilon \in \lbrace +,- \rbrace $
and
![]() $n \ge 2$
a natural number. Set
$n \ge 2$
a natural number. Set
![]() $T := \mathrm {Inn}(PSL_n^{\varepsilon }(q))$
. Let A be a subgroup of
$T := \mathrm {Inn}(PSL_n^{\varepsilon }(q))$
. Let A be a subgroup of
![]() $\mathrm {Aut}(PSL_n^{\varepsilon }(q))$
such that
$\mathrm {Aut}(PSL_n^{\varepsilon }(q))$
such that
![]() $T \le A$
and such that the index of T in A is odd. Let S be a Sylow
$T \le A$
and such that the index of T in A is odd. Let S be a Sylow
![]() $2$
-subgroup of T. Then we have
$2$
-subgroup of T. Then we have
![]() $\mathcal {F}_S(T) = \mathcal {F}_S(A)$
.
$\mathcal {F}_S(T) = \mathcal {F}_S(A)$
.
To prove Lemma 3.57, we need to prove some other lemmas first.
Lemma 3.58. Let q be a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
, and let r be positive integer. Also, let W be a Sylow
$\varepsilon \in \lbrace +,- \rbrace $
, and let r be positive integer. Also, let W be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^r}^{\varepsilon }(q)$
. Then
$GL_{2^r}^{\varepsilon }(q)$
. Then
![]() $\mathrm {Aut}(W)$
is a
$\mathrm {Aut}(W)$
is a
![]() $2$
-group.
$2$
-group.
Proof. We proceed by induction over r.
Suppose that
![]() $r = 1$
. If
$r = 1$
. If
![]() $q \equiv -\varepsilon \mod 4$
, then W is semidihedral by Lemmas 3.10 and 3.11, and so
$q \equiv -\varepsilon \mod 4$
, then W is semidihedral by Lemmas 3.10 and 3.11, and so
![]() $\mathrm {Aut}(W)$
is a
$\mathrm {Aut}(W)$
is a
![]() $2$
-group by [Reference Craven18, Proposition 4.53]. If
$2$
-group by [Reference Craven18, Proposition 4.53]. If
![]() $q \equiv \varepsilon \mod 4$
, then
$q \equiv \varepsilon \mod 4$
, then
![]() $W \cong C_{2^k} \wr C_2$
for some positive integer k by Lemmas 3.10 and 3.11, and so
$W \cong C_{2^k} \wr C_2$
for some positive integer k by Lemmas 3.10 and 3.11, and so
![]() $\mathrm {Aut}(W)$
is a
$\mathrm {Aut}(W)$
is a
![]() $2$
-group as a consequence of [Reference Fumagalli21, Theorem 2].
$2$
-group as a consequence of [Reference Fumagalli21, Theorem 2].
Assume now that
![]() $r> 1$
and that the lemma is true with
$r> 1$
and that the lemma is true with
![]() $r-1$
instead of r. Let
$r-1$
instead of r. Let
![]() $W_0$
be a Sylow
$W_0$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{2^{r-1}}^{\varepsilon }(q)$
. Hence,
$GL_{2^{r-1}}^{\varepsilon }(q)$
. Hence,
![]() $\mathrm {Aut}(W_0)$
is a
$\mathrm {Aut}(W_0)$
is a
![]() $2$
-group. By Lemma 3.14, we have
$2$
-group. By Lemma 3.14, we have
![]() $W \cong W_0 \wr C_2$
. Applying [Reference Fumagalli21, Theorem 2], we conclude that
$W \cong W_0 \wr C_2$
. Applying [Reference Fumagalli21, Theorem 2], we conclude that
![]() $\mathrm {Aut}(W)$
is a
$\mathrm {Aut}(W)$
is a
![]() $2$
-group.
$2$
-group.
Lemma 3.59. Let q be a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
, and let
$\varepsilon \in \lbrace +,- \rbrace $
, and let
![]() $n \ge 3$
be a natural number. Let
$n \ge 3$
be a natural number. Let
![]() $T := SL_n^{\varepsilon }(q)$
, and let S be a Sylow
$T := SL_n^{\varepsilon }(q)$
, and let S be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathrm {Inndiag}(T)$
. Then
$\mathrm {Inndiag}(T)$
. Then
![]() $\mathrm {Aut}_{P\Gamma L_n^{\varepsilon }(q)}(S)$
is a
$\mathrm {Aut}_{P\Gamma L_n^{\varepsilon }(q)}(S)$
is a
![]() $2$
-group.
$2$
-group.
Proof. Let
![]() $\alpha \in N_{P\Gamma L_n^{\varepsilon }(q)}(S)$
. It suffices to show that
$\alpha \in N_{P\Gamma L_n^{\varepsilon }(q)}(S)$
. It suffices to show that
![]() $c_{\alpha }|_{S,S}$
is a
$c_{\alpha }|_{S,S}$
is a
![]() $2$
-automorphism of S.
$2$
-automorphism of S.
Let
![]() $0 \le r_1 < \dots < r_t$
such that
$0 \le r_1 < \dots < r_t$
such that
![]() $n = 2^{r_1} + \dots + 2^{r_t}$
. Let
$n = 2^{r_1} + \dots + 2^{r_t}$
. Let
![]() $W_i \in \mathrm {Syl}_2(GL_{2^{r_i}}^{\varepsilon }(q))$
for all
$W_i \in \mathrm {Syl}_2(GL_{2^{r_i}}^{\varepsilon }(q))$
for all
![]() $1 \le i \le t$
. By Lemma 3.15,
$1 \le i \le t$
. By Lemma 3.15,
 $$ \begin{align*} W = \left \lbrace \begin{pmatrix} A_1 & \ & \ \\ \ & \ddots & \ \\ \ & \ & A_t \end{pmatrix} \ : \ A_i \in W_i \right \rbrace \end{align*} $$
$$ \begin{align*} W = \left \lbrace \begin{pmatrix} A_1 & \ & \ \\ \ & \ddots & \ \\ \ & \ & A_t \end{pmatrix} \ : \ A_i \in W_i \right \rbrace \end{align*} $$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n^{\varepsilon }(q)$
.
$GL_n^{\varepsilon }(q)$
.
We have that
![]() $\lbrace c_w|_{T,T} \ \vert \ w \in W \rbrace $
is a Sylow
$\lbrace c_w|_{T,T} \ \vert \ w \in W \rbrace $
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathrm {Inndiag}(T)$
since it is the image of W under the canonical group epimorphism
$\mathrm {Inndiag}(T)$
since it is the image of W under the canonical group epimorphism
![]() $GL_n^{\varepsilon }(q) \rightarrow \mathrm {Inndiag}(T)$
. Without loss of generality, we assume that
$GL_n^{\varepsilon }(q) \rightarrow \mathrm {Inndiag}(T)$
. Without loss of generality, we assume that
![]() $S = \lbrace c_w|_{T,T} \ \vert \ w \in W \rbrace $
.
$S = \lbrace c_w|_{T,T} \ \vert \ w \in W \rbrace $
.
Let p be the odd prime number and f be the positive integer with
![]() $q = p^f$
. Since
$q = p^f$
. Since
![]() $\alpha \in P \Gamma L_n^{\varepsilon }(q)$
, there exist some
$\alpha \in P \Gamma L_n^{\varepsilon }(q)$
, there exist some
![]() $m \in GL_n^{\varepsilon }(q)$
and some natural number
$m \in GL_n^{\varepsilon }(q)$
and some natural number
![]() $\ell $
, where
$\ell $
, where
![]() $1 \le \ell \le f$
if
$1 \le \ell \le f$
if
![]() $\varepsilon = +$
and
$\varepsilon = +$
and
![]() $1 \le \ell \le 2f$
if
$1 \le \ell \le 2f$
if
![]() $\varepsilon = -$
, such that
$\varepsilon = -$
, such that
for all
![]() $(a_{ij}) \in T$
.
$(a_{ij}) \in T$
.
Let
Observe that
is the product of a field automorphism with an inner automorphism of
![]() $GL_n^{\varepsilon }(q)$
. Using this fact, one can see that
$GL_n^{\varepsilon }(q)$
. Using this fact, one can see that
for all
![]() $w \in W$
.
$w \in W$
.
Let
![]() $w \in W$
. Since
$w \in W$
. Since
![]() $\alpha $
normalizes S, there is some
$\alpha $
normalizes S, there is some
![]() $\widetilde w \in W$
with
$\widetilde w \in W$
with
![]() . It follows that
. It follows that
![]() . This implies
. This implies
![]() since W is the unique Sylow
since W is the unique Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $W Z(GL_n^{\varepsilon }(q))$
. In particular,
$W Z(GL_n^{\varepsilon }(q))$
. In particular,
![]() induces an automorphism of W.
induces an automorphism of W.
Let
 $$ \begin{align*} d_i := \begin{pmatrix} I_{2^{r_1}} & & & & \\ & \ddots & & & \\ & & -I_{2^{r_i}} & & \\ & & & \ddots & \\ & & & & I_{2^{r_t}} \end{pmatrix} \end{align*} $$
$$ \begin{align*} d_i := \begin{pmatrix} I_{2^{r_1}} & & & & \\ & \ddots & & & \\ & & -I_{2^{r_i}} & & \\ & & & \ddots & \\ & & & & I_{2^{r_t}} \end{pmatrix} \end{align*} $$
for each
![]() $1 \le i \le t$
. Then
$1 \le i \le t$
. Then
![]() $d_i$
is a central involution of W for each
$d_i$
is a central involution of W for each
![]() $1 \le i \le t$
and centralized by the field automorphism
$1 \le i \le t$
and centralized by the field automorphism
![]() $(a_{ij}) \mapsto (a_{ij}^p)$
. So we have that
$(a_{ij}) \mapsto (a_{ij}^p)$
. So we have that
![]() is a central involution of W for each
is a central involution of W for each
![]() $1 \le i \le t$
. As we see from Lemma 3.17, this already implies that
$1 \le i \le t$
. As we see from Lemma 3.17, this already implies that
![]() $(d_i)^m = d_i$
for each
$(d_i)^m = d_i$
for each
![]() $1 \le i \le t$
. For
$1 \le i \le t$
. For
![]() $d_i$
is the unique member d of
$d_i$
is the unique member d of
![]() $\langle d_1,\dots ,d_n \rangle $
with
$\langle d_1,\dots ,d_n \rangle $
with
![]() $m([V, d]) = 2^{r_i}$
, where V is the defining module for
$m([V, d]) = 2^{r_i}$
, where V is the defining module for
![]() $GL_n^{\varepsilon }(q)$
. So there is some
$GL_n^{\varepsilon }(q)$
. So there is some
![]() $m_i \in GL_{2^{r_i}}^{\varepsilon }(q)$
for each
$m_i \in GL_{2^{r_i}}^{\varepsilon }(q)$
for each
![]() $1 \le i \le t$
such that
$1 \le i \le t$
such that
 $$ \begin{align*} m = \begin{pmatrix} m_1 & & \\ & \ddots & \\ & & m_t \end{pmatrix}. \end{align*} $$
$$ \begin{align*} m = \begin{pmatrix} m_1 & & \\ & \ddots & \\ & & m_t \end{pmatrix}. \end{align*} $$
Now
is an automorphism of
![]() $W_r$
for each
$W_r$
for each
![]() $1 \le r \le t$
. Applying Lemma 3.58, we conclude that
$1 \le r \le t$
. Applying Lemma 3.58, we conclude that
![]() is a
is a
![]() $2$
-automorphism of W. Since
$2$
-automorphism of W. Since
![]() for all
for all
![]() $w \in W$
, it follows that
$w \in W$
, it follows that
![]() $c_{\alpha }|_{S,S}$
is a
$c_{\alpha }|_{S,S}$
is a
![]() $2$
-automorphism of S, as required.
$2$
-automorphism of S, as required.
Corollary 3.60. Let q be a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
, and let
$\varepsilon \in \lbrace +,- \rbrace $
, and let
![]() $n \ge 3$
be a natural number. Let
$n \ge 3$
be a natural number. Let
![]() $T := PSL_n^{\varepsilon }(q)$
, and let S be a Sylow
$T := PSL_n^{\varepsilon }(q)$
, and let S be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathrm {Inndiag}(T)$
. Then
$\mathrm {Inndiag}(T)$
. Then
![]() $\mathrm {Aut}_{P \Gamma L_n^{\varepsilon }(q)}(S)$
is a
$\mathrm {Aut}_{P \Gamma L_n^{\varepsilon }(q)}(S)$
is a
![]() $2$
-group.
$2$
-group.
Lemma 3.61. Let q be a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
, and
$\varepsilon \in \lbrace +,- \rbrace $
, and
![]() $n \ge 3$
be a natural number. Let S be a Sylow
$n \ge 3$
be a natural number. Let S be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_n^{\varepsilon }(q)$
, and let
$PSL_n^{\varepsilon }(q)$
, and let
![]() $S_1$
be a Sylow
$S_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PGL_n^{\varepsilon }(q)$
containing S. Then
$PGL_n^{\varepsilon }(q)$
containing S. Then
![]() $N_{PGL_n^{\varepsilon }(q)}(S) = N_{PGL_n^{\varepsilon }(q)}(S_1)$
.
$N_{PGL_n^{\varepsilon }(q)}(S) = N_{PGL_n^{\varepsilon }(q)}(S_1)$
.
Proof. Let
![]() $T_1$
be a Sylow
$T_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_n^{\varepsilon }(q))$
such that
$GL_n^{\varepsilon }(q))$
such that
![]() $S_1 = T_1 Z(GL_n^{\varepsilon }(q))/Z(GL_n^{\varepsilon }(q))$
. Let
$S_1 = T_1 Z(GL_n^{\varepsilon }(q))/Z(GL_n^{\varepsilon }(q))$
. Let
![]() $T := T_1 \cap SL_n^{\varepsilon }(q)$
. Then
$T := T_1 \cap SL_n^{\varepsilon }(q)$
. Then
![]() $S = T Z(GL_n^{\varepsilon }(q))/Z(GL_n^{\varepsilon }(q))$
. It is rather easy to show
$S = T Z(GL_n^{\varepsilon }(q))/Z(GL_n^{\varepsilon }(q))$
. It is rather easy to show
![]() $N_{PGL_n^{\varepsilon }(q)}(S) = N_{GL_n^{\varepsilon }(q)}(T)Z(GL_n^{\varepsilon }(q))/Z(GL_n^{\varepsilon }(q))$
. By [Reference Kondrat’ev36, Theorem 1],
$N_{PGL_n^{\varepsilon }(q)}(S) = N_{GL_n^{\varepsilon }(q)}(T)Z(GL_n^{\varepsilon }(q))/Z(GL_n^{\varepsilon }(q))$
. By [Reference Kondrat’ev36, Theorem 1],
![]() $N_{GL_n^{\varepsilon }(q)}(T) = T_1 C_{GL_n^{\varepsilon }(q)}(T_1) \le N_{GL_n^{\varepsilon }(q)}(T_1)$
. It follows that
$N_{GL_n^{\varepsilon }(q)}(T) = T_1 C_{GL_n^{\varepsilon }(q)}(T_1) \le N_{GL_n^{\varepsilon }(q)}(T_1)$
. It follows that
![]() $N_{PGL_n^{\varepsilon }(q)}(S) \le N_{PGL_n^{\varepsilon }(q)}(S_1)$
. It is clear that we also have
$N_{PGL_n^{\varepsilon }(q)}(S) \le N_{PGL_n^{\varepsilon }(q)}(S_1)$
. It is clear that we also have
![]() $N_{PGL_n^{\varepsilon }(q)}(S_1) \le N_{PGL_n^{\varepsilon }(q)}(S)$
.
$N_{PGL_n^{\varepsilon }(q)}(S_1) \le N_{PGL_n^{\varepsilon }(q)}(S)$
.
Corollary 3.62. Let q be a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
, and let
$\varepsilon \in \lbrace +,- \rbrace $
, and let
![]() $n \ge 3$
be a natural number. Let
$n \ge 3$
be a natural number. Let
![]() $T := PSL_n^{\varepsilon }(q)$
, let S be a Sylow
$T := PSL_n^{\varepsilon }(q)$
, let S be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathrm {Inn}(T)$
and let
$\mathrm {Inn}(T)$
and let
![]() $S_1$
be a Sylow
$S_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathrm {Inndiag}(T)$
containing S. Then
$\mathrm {Inndiag}(T)$
containing S. Then
![]() $N_{\mathrm {Inndiag}(T)}(S) = N_{\mathrm {Inndiag}(T)}(S_1)$
.
$N_{\mathrm {Inndiag}(T)}(S) = N_{\mathrm {Inndiag}(T)}(S_1)$
.
We are now ready to prove Lemma 3.57.
Proof of Lemma 3.57
Assume that
![]() $n = 2$
and
$n = 2$
and
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \mod 8$
. Then
$5 \mod 8$
. Then
![]() $S \cong C_2 \times C_2$
by Lemma 3.13. There is only one nonnilpotent fusion system on S. Since T and A are not
$S \cong C_2 \times C_2$
by Lemma 3.13. There is only one nonnilpotent fusion system on S. Since T and A are not
![]() $2$
-nilpotent, we have that
$2$
-nilpotent, we have that
![]() $\mathcal {F}_S(T)$
and
$\mathcal {F}_S(T)$
and
![]() $\mathcal {F}_S(A)$
are not nilpotent (see [Reference Linckelmann39, Theorem 1.4]). It follows that
$\mathcal {F}_S(A)$
are not nilpotent (see [Reference Linckelmann39, Theorem 1.4]). It follows that
![]() $\mathcal {F}_S(T) = \mathcal {F}_S(A)$
.
$\mathcal {F}_S(T) = \mathcal {F}_S(A)$
.
From now on, we assume that either
![]() $n \ge 3$
, or
$n \ge 3$
, or
![]() $n = 2$
and
$n = 2$
and
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \mod 8$
. Let
$7 \mod 8$
. Let
![]() $P, Q \le S$
and
$P, Q \le S$
and
![]() $a \in A$
such that
$a \in A$
such that
![]() $P^a \le Q$
. We are going to show that
$P^a \le Q$
. We are going to show that
![]() $c_a|_{P,Q}$
is a morphism in
$c_a|_{P,Q}$
is a morphism in
![]() $\mathcal {F}_S(T)$
. By the Frattini argument, we have
$\mathcal {F}_S(T)$
. By the Frattini argument, we have
![]() $a = wu$
for some
$a = wu$
for some
![]() $w \in N_A(S)$
and some
$w \in N_A(S)$
and some
![]() $u \in T$
. We prove that
$u \in T$
. We prove that
![]() $c_w|_{S,S} \in \mathrm {Inn}(S)$
so that
$c_w|_{S,S} \in \mathrm {Inn}(S)$
so that
![]() $c_a|_{P,Q}$
is a morphism in
$c_a|_{P,Q}$
is a morphism in
![]() $\mathcal {F}_S(T)$
.
$\mathcal {F}_S(T)$
.
Suppose that
![]() $n = 2$
. Then S is dihedral of order at least
$n = 2$
. Then S is dihedral of order at least
![]() $8$
by Lemma 3.13, and so
$8$
by Lemma 3.13, and so
![]() $\mathrm {Aut}(S)$
is a
$\mathrm {Aut}(S)$
is a
![]() $2$
-group by [Reference Craven18, Proposition 4.53]. This implies that
$2$
-group by [Reference Craven18, Proposition 4.53]. This implies that
![]() $\mathrm {Aut}_A(S) = \mathrm {Inn}(S)$
, whence
$\mathrm {Aut}_A(S) = \mathrm {Inn}(S)$
, whence
![]() $c_w|_{S,S} \in \mathrm {Inn}(S)$
.
$c_w|_{S,S} \in \mathrm {Inn}(S)$
.
Suppose now that
![]() $n \ge 3$
. Let
$n \ge 3$
. Let
![]() $S_1$
be a Sylow
$S_1$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $\mathrm {Inndiag}(PSL_n^{\varepsilon }(q))$
containing S. Since T has odd index in A, we have that
$\mathrm {Inndiag}(PSL_n^{\varepsilon }(q))$
containing S. Since T has odd index in A, we have that
![]() $A \le P \Gamma L_n^{\varepsilon }(q)$
. By the Frattini argument,
$A \le P \Gamma L_n^{\varepsilon }(q)$
. By the Frattini argument,
![]() $w = w_1w_2$
for some
$w = w_1w_2$
for some
![]() $w_1 \in N_{P \Gamma L_n^{\varepsilon } (q)}(S_1)$
and some
$w_1 \in N_{P \Gamma L_n^{\varepsilon } (q)}(S_1)$
and some
![]() $w_2 \in \mathrm {Inndiag}(PSL_n^{\varepsilon }(q))$
. Since
$w_2 \in \mathrm {Inndiag}(PSL_n^{\varepsilon }(q))$
. Since
![]() $w_1$
normalizes both
$w_1$
normalizes both
![]() $S_1$
and T, we have that
$S_1$
and T, we have that
![]() $w_1$
normalizes S. And since
$w_1$
normalizes S. And since
![]() $w = w_1w_2$
normalizes S, we also have that
$w = w_1w_2$
normalizes S, we also have that
![]() $w_2$
normalizes S. So
$w_2$
normalizes S. So
![]() $w_2$
normalizes
$w_2$
normalizes
![]() $S_1$
by Corollary 3.62. Consequently,
$S_1$
by Corollary 3.62. Consequently,
![]() $w = w_1 w_2 \in N_{P \Gamma L_n^{\varepsilon } (q)}(S_1)$
. By Corollary 3.60,
$w = w_1 w_2 \in N_{P \Gamma L_n^{\varepsilon } (q)}(S_1)$
. By Corollary 3.60,
![]() $c_w|_{S_1,S_1}$
is a
$c_w|_{S_1,S_1}$
is a
![]() $2$
-automorphism of
$2$
-automorphism of
![]() $S_1$
. So
$S_1$
. So
![]() $c_w|_{S,S}$
is a
$c_w|_{S,S}$
is a
![]() $2$
-automorphism of S. Since
$2$
-automorphism of S. Since
![]() $S \in \mathrm {Syl}_2(A)$
and
$S \in \mathrm {Syl}_2(A)$
and
![]() $w \in A$
, this implies that
$w \in A$
, this implies that
![]() $c_w|_{S,S} \in \mathrm {Inn}(S)$
, as required.
$c_w|_{S,S} \in \mathrm {Inn}(S)$
, as required.
4 The case
 $n \le 5$
$n \le 5$
In this section, we verify Theorem A for the case
![]() $n \le 5$
.
$n \le 5$
.
Proposition 4.1. Let q be a nontrivial odd prime power, and let G be a finite simple group. Then the following are equivalent:
-
(i) the
 $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $PSL_2(q)$
;
$PSL_2(q)$
; -
(ii) the Sylow
 $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
 $PSL_2(q)$
;
$PSL_2(q)$
; -
(iii)
 $G \cong PSL_2^{\varepsilon }(q^{*})$
for some
$G \cong PSL_2^{\varepsilon }(q^{*})$
for some
 $\varepsilon \in \lbrace +,- \rbrace $
and some odd prime power
$\varepsilon \in \lbrace +,- \rbrace $
and some odd prime power
 $q^{*} \ge 5$
with
$q^{*} \ge 5$
with
 $\varepsilon q^{*} \sim q$
, or
$\varepsilon q^{*} \sim q$
, or
 $\vert PSL_2(q) \vert _2 = 8$
and
$\vert PSL_2(q) \vert _2 = 8$
and
 $G \cong A_7$
.
$G \cong A_7$
.
In particular, Theorem A holds for
![]() $n = 2$
.
$n = 2$
.
Proof. The implication (i)
![]() $\Rightarrow $
(ii) is clear.
$\Rightarrow $
(ii) is clear.
(ii)
![]() $\Rightarrow $
(iii): Assume that the Sylow
$\Rightarrow $
(iii): Assume that the Sylow
![]() $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
![]() $PSL_2(q)$
. Hence, G has dihedral Sylow
$PSL_2(q)$
. Hence, G has dihedral Sylow
![]() $2$
-subgroups of order
$2$
-subgroups of order
![]() $\frac {1}{2}(q-1)_2(q+1)_2$
. Applying a result of Gorenstein and Walter [Reference Gorenstein and Walter30, Theorem 1], we may conclude that
$\frac {1}{2}(q-1)_2(q+1)_2$
. Applying a result of Gorenstein and Walter [Reference Gorenstein and Walter30, Theorem 1], we may conclude that
![]() $G \cong PSL_2(q^{*})$
for some odd prime power
$G \cong PSL_2(q^{*})$
for some odd prime power
![]() $q^{*} \ge 5$
, or
$q^{*} \ge 5$
, or
![]() $G \cong A_7$
. Suppose that the former holds. Then
$G \cong A_7$
. Suppose that the former holds. Then
![]() $(q^{*}-1)_2(q^{*}+1)_2 = 2 \vert G \vert _2 = (q-1)_2(q+1)_2$
, whence either
$(q^{*}-1)_2(q^{*}+1)_2 = 2 \vert G \vert _2 = (q-1)_2(q+1)_2$
, whence either
![]() $q^{*} \sim q$
or
$q^{*} \sim q$
or
![]() $-q^{*} \sim q$
. Since
$-q^{*} \sim q$
. Since
![]() $PSL_2(q^{*}) \cong PSU_2(q^{*})$
, this implies that the first statement in (iii) is satisfied. If
$PSL_2(q^{*}) \cong PSU_2(q^{*})$
, this implies that the first statement in (iii) is satisfied. If
![]() $G \cong A_7$
, then
$G \cong A_7$
, then
![]() $\vert PSL_2(q) \vert _2 = \vert G \vert _2 = 8$
so that the second statement in (iii) is satisfied.
$\vert PSL_2(q) \vert _2 = \vert G \vert _2 = 8$
so that the second statement in (iii) is satisfied.
(iii)
![]() $\Rightarrow $
(i): Assume that (iii) holds. Set
$\Rightarrow $
(i): Assume that (iii) holds. Set
![]() $G_1 := G$
and
$G_1 := G$
and
![]() $G_2 := PSL_2(q)$
. For
$G_2 := PSL_2(q)$
. For
![]() $i \in \lbrace 1,2 \rbrace $
, let
$i \in \lbrace 1,2 \rbrace $
, let
![]() $S_i \in \mathrm {Syl}_2(G_i)$
and
$S_i \in \mathrm {Syl}_2(G_i)$
and
![]() $\mathcal {F}_i := \mathcal {F}_{S_i}(G_i)$
. Clearly,
$\mathcal {F}_i := \mathcal {F}_{S_i}(G_i)$
. Clearly,
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are dihedral groups of the same order. Let
$S_2$
are dihedral groups of the same order. Let
![]() $i \in \lbrace 1,2 \rbrace $
. By [Reference Gorenstein23, Chapter 5, Theorem 4.3], any subgroup of
$i \in \lbrace 1,2 \rbrace $
. By [Reference Gorenstein23, Chapter 5, Theorem 4.3], any subgroup of
![]() $S_i$
is cyclic or dihedral. By [Reference Craven18, Proposition 4.53], a dihedral subgroup of
$S_i$
is cyclic or dihedral. By [Reference Craven18, Proposition 4.53], a dihedral subgroup of
![]() $S_i$
with order greater than
$S_i$
with order greater than
![]() $4$
cannot be
$4$
cannot be
![]() $\mathcal {F}_i$
-essential. Since the automorphism group of a finite cyclic
$\mathcal {F}_i$
-essential. Since the automorphism group of a finite cyclic
![]() $2$
-group is itself a
$2$
-group is itself a
![]() $2$
-group, a cyclic subgroup of
$2$
-group, a cyclic subgroup of
![]() $S_i$
cannot be
$S_i$
cannot be
![]() $\mathcal {F}_i$
-essential either. So we have that any
$\mathcal {F}_i$
-essential either. So we have that any
![]() $\mathcal {F}_i$
-essential subgroup of
$\mathcal {F}_i$
-essential subgroup of
![]() $S_i$
is a Klein four group. Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver10, Part I, Theorem 3.5] implies that
$S_i$
is a Klein four group. Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver10, Part I, Theorem 3.5] implies that
If
![]() $\vert S_i \vert = 4$
, then
$\vert S_i \vert = 4$
, then
![]() $\mathrm {Aut}_{\mathcal {F}_i}(S_i)$
is the unique subgroup of
$\mathrm {Aut}_{\mathcal {F}_i}(S_i)$
is the unique subgroup of
![]() $\mathrm {Aut}(S_i)$
with order
$\mathrm {Aut}(S_i)$
with order
![]() $3$
, because otherwise
$3$
, because otherwise
![]() $\mathrm {Aut}_{\mathcal {F}_i}(S_i) = \mathrm {Inn}(S_i)$
, so that [Reference Linckelmann39, Theorem 1.4] would imply that
$\mathrm {Aut}_{\mathcal {F}_i}(S_i) = \mathrm {Inn}(S_i)$
, so that [Reference Linckelmann39, Theorem 1.4] would imply that
![]() $G_i$
is
$G_i$
is
![]() $2$
-nilpotent. If
$2$
-nilpotent. If
![]() $\vert S_i \vert \ge 8$
, then
$\vert S_i \vert \ge 8$
, then
![]() $\mathrm {Aut}_{\mathcal {F}_i}(S_i) = \mathrm {Inn}(S_i)$
since
$\mathrm {Aut}_{\mathcal {F}_i}(S_i) = \mathrm {Inn}(S_i)$
since
![]() $\mathrm {Aut}(S_i)$
is a
$\mathrm {Aut}(S_i)$
is a
![]() $2$
-group by [Reference Craven18, Proposition 4.53], and for any Klein four subgroup P of
$2$
-group by [Reference Craven18, Proposition 4.53], and for any Klein four subgroup P of
![]() $S_i$
, we have
$S_i$
, we have
![]() $\mathrm {Aut}_{\mathcal {F}_i}(P) = \mathrm {Aut}(P)$
by [Reference Gorenstein23, Chapter 7, Theorem 7.3]. As
$\mathrm {Aut}_{\mathcal {F}_i}(P) = \mathrm {Aut}(P)$
by [Reference Gorenstein23, Chapter 7, Theorem 7.3]. As
![]() $S_1 \cong S_2$
and as the preceding observations do not depend on whether i is
$S_1 \cong S_2$
and as the preceding observations do not depend on whether i is
![]() $1$
or
$1$
or
![]() $2$
, we may conclude that
$2$
, we may conclude that
![]() $\mathcal {F}_1 \cong \mathcal {F}_2$
, as required.
$\mathcal {F}_1 \cong \mathcal {F}_2$
, as required.
Proposition 4.2. Let q be a nontrivial odd prime power, and let G be a finite simple group. Then the following are equivalent:
-
(i) the
 $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $PSL_3(q)$
;
$PSL_3(q)$
; -
(ii) the Sylow
 $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
 $PSL_3(q)$
;
$PSL_3(q)$
; -
(iii)
 $G \cong PSL_3^{\varepsilon }(q^{*})$
for some
$G \cong PSL_3^{\varepsilon }(q^{*})$
for some
 $\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
$\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
 $q^{*}$
with
$q^{*}$
with
 $\varepsilon q^{*} \sim q$
, or
$\varepsilon q^{*} \sim q$
, or
 $(q+1)_2 = 4$
and
$(q+1)_2 = 4$
and
 $G \cong M_{11}$
.
$G \cong M_{11}$
.
In particular, Theorem A holds for
![]() $n = 3$
.
$n = 3$
.
Proof. The implication (i)
![]() $\Rightarrow $
(ii) is clear.
$\Rightarrow $
(ii) is clear.
(ii)
![]() $\Rightarrow $
(iii): Assume that the Sylow
$\Rightarrow $
(iii): Assume that the Sylow
![]() $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
![]() $PSL_3(q)$
. Hence, a Sylow
$PSL_3(q)$
. Hence, a Sylow
![]() $2$
-subgroup of G is wreathed (i.e., isomorphic to
$2$
-subgroup of G is wreathed (i.e., isomorphic to
![]() $C_{2^k} \wr C_2$
for some positive integer k) if
$C_{2^k} \wr C_2$
for some positive integer k) if
![]() $q \equiv 1 \mod 4$
and semidihedral if
$q \equiv 1 \mod 4$
and semidihedral if
![]() $q \equiv 3 \mod 4$
. Applying work of Alperin, Brauer and Gorenstein, namely [Reference Alperin, Brauer and Gorenstein1, Third Main Theorem] and [Reference Alperin, Brauer and Gorenstein2, First Main Theorem], we may conclude that either
$q \equiv 3 \mod 4$
. Applying work of Alperin, Brauer and Gorenstein, namely [Reference Alperin, Brauer and Gorenstein1, Third Main Theorem] and [Reference Alperin, Brauer and Gorenstein2, First Main Theorem], we may conclude that either
![]() $G \cong PSL_3^{\varepsilon }(q^{*})$
for some
$G \cong PSL_3^{\varepsilon }(q^{*})$
for some
![]() $\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
$\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
![]() $q^{*}$
with
$q^{*}$
with
![]() $\varepsilon q^{*} \equiv q \mod 4$
or
$\varepsilon q^{*} \equiv q \mod 4$
or
![]() $q \equiv 3 \mod 4$
and
$q \equiv 3 \mod 4$
and
![]() $G \cong M_{11}$
. If the former holds, then
$G \cong M_{11}$
. If the former holds, then
![]() $((q^{*}-\varepsilon )_2)^2(q^{*}+\varepsilon )_2 = \vert G \vert _2 = ((q-1)_2)^2(q+1)_2$
, and it easily follows that
$((q^{*}-\varepsilon )_2)^2(q^{*}+\varepsilon )_2 = \vert G \vert _2 = ((q-1)_2)^2(q+1)_2$
, and it easily follows that
![]() $\varepsilon q^{*} \sim q$
. If
$\varepsilon q^{*} \sim q$
. If
![]() $G \cong M_{11}$
, then
$G \cong M_{11}$
, then
![]() $16 = \vert G \vert _2 = ((q-1)_2)^2(q+1)_2$
, and hence,
$16 = \vert G \vert _2 = ((q-1)_2)^2(q+1)_2$
, and hence,
![]() $(q+1)_2 = 4$
.
$(q+1)_2 = 4$
.
(iii)
![]() $\Rightarrow $
(i): Assume that (iii) holds. If
$\Rightarrow $
(i): Assume that (iii) holds. If
![]() $q \equiv 1 \mod 4$
, then Proposition 3.20 implies that the
$q \equiv 1 \mod 4$
, then Proposition 3.20 implies that the
![]() $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_3(q)$
. Alternatively, this can be seen from [Reference Craven18, Proposition 5.87]. Now suppose that
$PSL_3(q)$
. Alternatively, this can be seen from [Reference Craven18, Proposition 5.87]. Now suppose that
![]() $q \equiv 3 \mod 4$
. If
$q \equiv 3 \mod 4$
. If
![]() $(q+1)_2 \ne 4$
, then we could apply Proposition 3.20 again, but we are going to argue in a more elementary way. Let
$(q+1)_2 \ne 4$
, then we could apply Proposition 3.20 again, but we are going to argue in a more elementary way. Let
![]() $G_1 := G$
and
$G_1 := G$
and
![]() $G_2 := PSL_3(q)$
. For
$G_2 := PSL_3(q)$
. For
![]() $i \in \lbrace 1,2 \rbrace $
, let
$i \in \lbrace 1,2 \rbrace $
, let
![]() $S_i \in \mathrm {Syl}_2(G_i)$
and
$S_i \in \mathrm {Syl}_2(G_i)$
and
![]() $\mathcal {F}_i := \mathcal {F}_{S_i}(G_i)$
. Clearly,
$\mathcal {F}_i := \mathcal {F}_{S_i}(G_i)$
. Clearly,
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are semidihedral groups of the same order. Let
$S_2$
are semidihedral groups of the same order. Let
![]() $i \in \lbrace 1,2 \rbrace $
. By [Reference Gorenstein23, Chapter 5, Theorem 4.3], any proper subgroup of
$i \in \lbrace 1,2 \rbrace $
. By [Reference Gorenstein23, Chapter 5, Theorem 4.3], any proper subgroup of
![]() $S_i$
is cyclic, dihedral or generalized quaternion. By [Reference Craven18, Proposition 4.53], dihedral subgroups of
$S_i$
is cyclic, dihedral or generalized quaternion. By [Reference Craven18, Proposition 4.53], dihedral subgroups of
![]() $S_i$
with order greater than
$S_i$
with order greater than
![]() $4$
and generalized quaternion subgroups of
$4$
and generalized quaternion subgroups of
![]() $S_i$
with order greater than
$S_i$
with order greater than
![]() $8$
cannot be
$8$
cannot be
![]() $\mathcal {F}_i$
-essential. Since the automorphism group of a finite cyclic
$\mathcal {F}_i$
-essential. Since the automorphism group of a finite cyclic
![]() $2$
-group is itself a
$2$
-group is itself a
![]() $2$
-group, a cyclic subgroup of
$2$
-group, a cyclic subgroup of
![]() $S_i$
cannot be
$S_i$
cannot be
![]() $\mathcal {F}_i$
-essential either. Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver10, Part I, Theorem 3.5] implies that
$\mathcal {F}_i$
-essential either. Alperin’s fusion theorem [Reference Aschbacher, Kessar and Oliver10, Part I, Theorem 3.5] implies that
Since
![]() $\mathrm {Aut}(S_i)$
is a
$\mathrm {Aut}(S_i)$
is a
![]() $2$
-group by [Reference Craven18, Proposition 4.53], we have
$2$
-group by [Reference Craven18, Proposition 4.53], we have
![]() $\mathrm {Aut}_{\mathcal {F}_i}(S_i) = \mathrm {Inn}(S_i)$
. From [Reference Alperin, Brauer and Gorenstein1, pp. 10-11, Proposition 1], one can see that
$\mathrm {Aut}_{\mathcal {F}_i}(S_i) = \mathrm {Inn}(S_i)$
. From [Reference Alperin, Brauer and Gorenstein1, pp. 10-11, Proposition 1], one can see that
![]() $\mathrm {Aut}_{\mathcal {F}_i}(P) = \mathrm {Aut}(P)$
for any subgroup P of
$\mathrm {Aut}_{\mathcal {F}_i}(P) = \mathrm {Aut}(P)$
for any subgroup P of
![]() $S_i$
isomorphic to
$S_i$
isomorphic to
![]() $C_2 \times C_2$
or
$C_2 \times C_2$
or
![]() $Q_8$
. As
$Q_8$
. As
![]() $S_1 \cong S_2$
and as the preceding observations do not depend on whether i is
$S_1 \cong S_2$
and as the preceding observations do not depend on whether i is
![]() $1$
or
$1$
or
![]() $2$
, we may conclude that
$2$
, we may conclude that
![]() $\mathcal {F}_1 \cong \mathcal {F}_2$
, as required.
$\mathcal {F}_1 \cong \mathcal {F}_2$
, as required.
The following lemma is required to verify Theorem A for the case
![]() $n = 4$
.
$n = 4$
.
Lemma 4.3. Let q be a nontrivial odd prime power. Assume that G is
![]() $A_{10},A_{11},M_{22},M_{23}$
or
$A_{10},A_{11},M_{22},M_{23}$
or
![]() $McL$
. Then the
$McL$
. Then the
![]() $2$
-fusion system of G is not isomorphic to the
$2$
-fusion system of G is not isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_4(q)$
.
$PSL_4(q)$
.
Proof. Assume otherwise. Let
![]() $L := PSL_4(q)$
and
$L := PSL_4(q)$
and
![]() $S \in \mathrm {Syl}_2(L)$
. Then
$S \in \mathrm {Syl}_2(L)$
. Then
![]() $|S| = |G|_2 = 2^7$
, so
$|S| = |G|_2 = 2^7$
, so
![]() $q \equiv \pm 3 \mod 8$
. Let
$q \equiv \pm 3 \mod 8$
. Let
![]() $\mathcal {E} := \mathcal {F}_S(L)$
.
$\mathcal {E} := \mathcal {F}_S(L)$
.
Take a Sylow
![]() $2$
-subgroup V of
$2$
-subgroup V of
![]() $GL_2(q)$
, and let W be the Sylow
$GL_2(q)$
, and let W be the Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
obtained from V by the construction given in the last statement of Lemma 3.14. Then
$GL_4(q)$
obtained from V by the construction given in the last statement of Lemma 3.14. Then
![]() $S_0 := W \cap SL_4(q)$
is a Sylow
$S_0 := W \cap SL_4(q)$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_4(q)$
, and we assume without loss of generality that S is the image of
$SL_4(q)$
, and we assume without loss of generality that S is the image of
![]() $S_0$
in L.
$S_0$
in L.
Now
![]() $Z(S) = \langle z \rangle $
, where z is the image of
$Z(S) = \langle z \rangle $
, where z is the image of
![]() $\mathrm {diag}(1,1,-1,-1)$
in L. Let F be the image of
$\mathrm {diag}(1,1,-1,-1)$
in L. Let F be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} : A, B \in SL_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} : A, B \in SL_2(q) \right\rbrace \end{align*} $$
in L, and let Q be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} : A, B \in V_0 \right\rbrace, \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} : A, B \in V_0 \right\rbrace, \end{align*} $$
in L, where
![]() $V_0 := V \cap SL_2(q)$
. Then
$V_0 := V \cap SL_2(q)$
. Then
![]() $F \trianglelefteq C_L(z)$
, and so
$F \trianglelefteq C_L(z)$
, and so
![]() $Q = S \cap F$
is strongly closed in S with respect to
$Q = S \cap F$
is strongly closed in S with respect to
![]() $C_{\mathcal {E}}(z)$
. Also,
$C_{\mathcal {E}}(z)$
. Also,
![]() $Q' = \langle z \rangle $
is strongly closed in S with respect to
$Q' = \langle z \rangle $
is strongly closed in S with respect to
![]() $C_{\mathcal {E}}(z)$
, and we have
$C_{\mathcal {E}}(z)$
, and we have
![]() $[Q,\langle z \rangle ] = 1$
. Applying [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 4.6], we conclude that
$[Q,\langle z \rangle ] = 1$
. Applying [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 4.6], we conclude that
![]() $Q \trianglelefteq C_{\mathcal {E}}(z)$
. Since Q is a self-centralizing subgroup of S, it follows that
$Q \trianglelefteq C_{\mathcal {E}}(z)$
. Since Q is a self-centralizing subgroup of S, it follows that
![]() $C_{\mathcal {E}}(z)$
is constrained. Set
$C_{\mathcal {E}}(z)$
is constrained. Set
![]() $M := N_{C_L(z)}(Q)$
. Then M is the image of
$M := N_{C_L(z)}(Q)$
. Then M is the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} : A,B \in N_{GL_2(q)}(V_0), \mathrm{det}(AB) = 1\right\rbrace\left \langle \begin{pmatrix} 0 & I_2 \\ I_2 & 0 \end{pmatrix} \right \rangle \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} : A,B \in N_{GL_2(q)}(V_0), \mathrm{det}(AB) = 1\right\rbrace\left \langle \begin{pmatrix} 0 & I_2 \\ I_2 & 0 \end{pmatrix} \right \rangle \end{align*} $$
in L. Since
![]() $q \equiv \pm 3 \mod 8$
, we have
$q \equiv \pm 3 \mod 8$
, we have
![]() $N_{SL_2(q)}(V_0) \cong SL_2(3)$
by [Reference Shi48, Proposition 3.1]. Thus,
$N_{SL_2(q)}(V_0) \cong SL_2(3)$
by [Reference Shi48, Proposition 3.1]. Thus,
![]() $|N_{GL_2(q)}(V_0)| = 24(q-1)$
, and it follows that
$|N_{GL_2(q)}(V_0)| = 24(q-1)$
, and it follows that
![]() $|M| = 2^7 \cdot 3^2$
. By [Reference Héthely, Szőke and Zalesski34, Proposition 8.8], M is a model of
$|M| = 2^7 \cdot 3^2$
. By [Reference Héthely, Szőke and Zalesski34, Proposition 8.8], M is a model of
![]() $C_{\mathcal {E}}(z)$
.
$C_{\mathcal {E}}(z)$
.
Now let
![]() $R \in \mathrm {Syl}_2(G)$
and
$R \in \mathrm {Syl}_2(G)$
and
![]() $\mathcal {F} := \mathcal {F}_R(G)$
. Also, let u be the central involution of R. Then
$\mathcal {F} := \mathcal {F}_R(G)$
. Also, let u be the central involution of R. Then
![]() $C_{\mathcal {F}}(u) \cong C_{\mathcal {E}}(z)$
is constrained with M a model
$C_{\mathcal {F}}(u) \cong C_{\mathcal {E}}(z)$
is constrained with M a model
![]() $C_{\mathcal {F}}(u)$
. By [Reference Héthely, Szőke and Zalesski34, Proposition 8.8], there is a core-free section of
$C_{\mathcal {F}}(u)$
. By [Reference Héthely, Szőke and Zalesski34, Proposition 8.8], there is a core-free section of
![]() $C_G(u)$
which is isomorphic to M.
$C_G(u)$
which is isomorphic to M.
If G is
![]() $McL$
, then
$McL$
, then
![]() $C_G(u)/\langle u \rangle \cong A_8$
by [Reference Gorenstein, Lyons and Solomon28, Table 5.3] so that
$C_G(u)/\langle u \rangle \cong A_8$
by [Reference Gorenstein, Lyons and Solomon28, Table 5.3] so that
![]() $C_{\mathcal {F}}(u)/\langle u \rangle $
is nonsolvable. On the other hand,
$C_{\mathcal {F}}(u)/\langle u \rangle $
is nonsolvable. On the other hand,
![]() $C_{\mathcal {E}}(z)/\langle z \rangle \cong C_{\mathcal {F}}(u)/\langle u \rangle $
is solvable. Thus,
$C_{\mathcal {E}}(z)/\langle z \rangle \cong C_{\mathcal {F}}(u)/\langle u \rangle $
is solvable. Thus,
![]() $G \ne McL$
.
$G \ne McL$
.
If G is
![]() $A_{10}, M_{22}$
or
$A_{10}, M_{22}$
or
![]() $M_{23}$
, then
$M_{23}$
, then
![]() $|C_G(u)| = 2^7 \cdot 3$
or
$|C_G(u)| = 2^7 \cdot 3$
or
![]() $2^7 \cdot 21$
so that
$2^7 \cdot 21$
so that
![]() $|M|$
does not divide
$|M|$
does not divide
![]() $|C_G(u)|$
, a contradiction.
$|C_G(u)|$
, a contradiction.
So G must be
![]() $A_{11}$
. Then
$A_{11}$
. Then
![]() $|C_G(u)| = 2^7 \cdot 3^2$
, and
$|C_G(u)| = 2^7 \cdot 3^2$
, and
![]() $C_G(u)$
has a normal subgroup of order
$C_G(u)$
has a normal subgroup of order
![]() $3$
. Therefore, M cannot be isomorphic to a core-free section of
$3$
. Therefore, M cannot be isomorphic to a core-free section of
![]() $C_G(u)$
, which is again a contradiction.
$C_G(u)$
, which is again a contradiction.
The proof is now complete.
Proposition 4.4. Let q be a nontrivial odd prime power, and let G be a finite simple group. Then the following are equivalent:
-
(i) the
 $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $PSL_4(q)$
;
$PSL_4(q)$
; -
(ii)
 $G \cong PSL_4^{\varepsilon }(q^{*})$
for some
$G \cong PSL_4^{\varepsilon }(q^{*})$
for some
 $\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
$\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
 $q^{*}$
with
$q^{*}$
with
 $\varepsilon q^{*} \sim q$
.
$\varepsilon q^{*} \sim q$
.
In particular, Theorem A holds for
![]() $n = 4$
.
$n = 4$
.
Proof. The implication (ii)
![]() $\Rightarrow $
(i) is given by Proposition 3.20.
$\Rightarrow $
(i) is given by Proposition 3.20.
(i)
![]() $\Rightarrow $
(ii): Assume that the
$\Rightarrow $
(ii): Assume that the
![]() $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_4(q)$
. Then the Sylow
$PSL_4(q)$
. Then the Sylow
![]() $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
![]() $PSL_4(q)$
. Applying Mason’s results [Reference Mason41, Theorem 1.1 and Corollary 1.3] and [Reference Mason40, Theorems 1.1 and 3.15], the latter together with [Reference Gorenstein, Lyons and Solomon28, Theorem 4.10.5 (f)], we see that one of the following holds:
$PSL_4(q)$
. Applying Mason’s results [Reference Mason41, Theorem 1.1 and Corollary 1.3] and [Reference Mason40, Theorems 1.1 and 3.15], the latter together with [Reference Gorenstein, Lyons and Solomon28, Theorem 4.10.5 (f)], we see that one of the following holds:
-
(1)
 $G \cong PSL_4^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$G \cong PSL_4^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
 $q^{*}$
and some
$q^{*}$
and some
 $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
 $\varepsilon q^{*} \equiv q \mod 4$
;
$\varepsilon q^{*} \equiv q \mod 4$
; -
(2)
 $G \cong A_{10}$
or
$G \cong A_{10}$
or
 $A_{11}$
;
$A_{11}$
; -
(3)
 $G \cong M_{22}$
,
$G \cong M_{22}$
,
 $M_{23}$
or
$M_{23}$
or
 $McL$
.
$McL$
.
However, we know from Lemma 4.3 that the
![]() $2$
-fusion system of G is not isomorphic to the
$2$
-fusion system of G is not isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_4(q)$
when (2) or (3) holds. Thus, (1) holds.
$PSL_4(q)$
when (2) or (3) holds. Thus, (1) holds.
Let
![]() $q_0$
be a nontrivial odd prime power,
$q_0$
be a nontrivial odd prime power,
![]() $\varepsilon _0 \in \lbrace +,- \rbrace $
, and
$\varepsilon _0 \in \lbrace +,- \rbrace $
, and
![]() $k_0, s_0 \in \mathbb {N}$
such that
$k_0, s_0 \in \mathbb {N}$
such that
![]() $2^{k_0} = (q_0 - \varepsilon _0)_2$
and
$2^{k_0} = (q_0 - \varepsilon _0)_2$
and
![]() $2^{s_0} = (q_0 + \varepsilon _0)_2$
. Then we have
$2^{s_0} = (q_0 + \varepsilon _0)_2$
. Then we have
 $$ \begin{align*} \vert PSL_4^{\varepsilon_0}(q_0) \vert_2 = \frac{\vert GL_4^{\varepsilon_0}(q_0) \vert_2}{2^{k_0}(4,2^{k_0})} = \frac{2 (\vert GL_2^{\varepsilon_0}(q_0) \vert_2)^2}{2^{k_0}(4,2^{k_0})} = \frac{2^{3k_0 + 2s_0 + 1}}{(4,2^{k_0})}. \end{align*} $$
$$ \begin{align*} \vert PSL_4^{\varepsilon_0}(q_0) \vert_2 = \frac{\vert GL_4^{\varepsilon_0}(q_0) \vert_2}{2^{k_0}(4,2^{k_0})} = \frac{2 (\vert GL_2^{\varepsilon_0}(q_0) \vert_2)^2}{2^{k_0}(4,2^{k_0})} = \frac{2^{3k_0 + 2s_0 + 1}}{(4,2^{k_0})}. \end{align*} $$
Let
![]() $k, k^{*}, s, s^{*} \in \mathbb {N}$
such that
$k, k^{*}, s, s^{*} \in \mathbb {N}$
such that
![]() $2^k = (q-1)_2$
,
$2^k = (q-1)_2$
,
![]() $2^{k^{*}} = (q^{*}-\varepsilon )_2$
,
$2^{k^{*}} = (q^{*}-\varepsilon )_2$
,
![]() $2^s = (q+1)_2$
and
$2^s = (q+1)_2$
and
![]() $2^{s^{*}} = (q^{*} + \varepsilon )_2$
. Then we have
$2^{s^{*}} = (q^{*} + \varepsilon )_2$
. Then we have
 $$ \begin{align*} \frac{2^{3k^{*} + 2s^{*} + 1}}{(4,2^{k^{*}})} = \vert G \vert_2 = \frac{2^{3k + 2s + 1}}{(4,2^{k})}. \end{align*} $$
$$ \begin{align*} \frac{2^{3k^{*} + 2s^{*} + 1}}{(4,2^{k^{*}})} = \vert G \vert_2 = \frac{2^{3k + 2s + 1}}{(4,2^{k})}. \end{align*} $$
Since
![]() $\varepsilon q^{*} \equiv q \mod 4$
, it follows that
$\varepsilon q^{*} \equiv q \mod 4$
, it follows that
![]() $\varepsilon q^{*} \sim q$
.
$\varepsilon q^{*} \sim q$
.
Proposition 4.5. Let q be a nontrivial odd prime power, and let G be a finite simple group. Then the following are equivalent:
-
(i) the
 $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $PSL_5(q)$
;
$PSL_5(q)$
; -
(ii) the Sylow
 $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
 $PSL_5(q)$
;
$PSL_5(q)$
; -
(iii)
 $G \cong PSL_5^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$G \cong PSL_5^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
 $q^{*}$
and some
$q^{*}$
and some
 $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
 $\varepsilon q^{*} \sim q$
.
$\varepsilon q^{*} \sim q$
.
In particular, Theorem A holds for
![]() $n = 5$
.
$n = 5$
.
Proof. The implication (i)
![]() $\Rightarrow $
(ii) is clear, and the implication (iii)
$\Rightarrow $
(ii) is clear, and the implication (iii)
![]() $\Rightarrow $
(i) is given by Proposition 3.20.
$\Rightarrow $
(i) is given by Proposition 3.20.
(ii)
![]() $\Rightarrow $
(iii): Assume that the Sylow
$\Rightarrow $
(iii): Assume that the Sylow
![]() $2$
-subgroups of G are isomorphic to those of
$2$
-subgroups of G are isomorphic to those of
![]() $PSL_5(q)$
. Applying work of Mason [Reference Mason42, Theorem 1.1], it follows that
$PSL_5(q)$
. Applying work of Mason [Reference Mason42, Theorem 1.1], it follows that
![]() $G \cong PSL_5^{\varepsilon }(q^{*})$
for some
$G \cong PSL_5^{\varepsilon }(q^{*})$
for some
![]() $\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
$\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
![]() $q^{*}$
. In view of Lemma 3.15, it is easy to see that a Sylow
$q^{*}$
. In view of Lemma 3.15, it is easy to see that a Sylow
![]() $2$
-subgroup of G is isomorphic to a Sylow
$2$
-subgroup of G is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4^{\varepsilon }(q^{*})$
, while a Sylow
$GL_4^{\varepsilon }(q^{*})$
, while a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_5(q)$
is isomorphic to a Sylow
$PSL_5(q)$
is isomorphic to a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_4(q)$
. Now it is easy to deduce from Lemmas 3.10, 3.11 and 3.14 that a Sylow
$GL_4(q)$
. Now it is easy to deduce from Lemmas 3.10, 3.11 and 3.14 that a Sylow
![]() $2$
-subgroup of G has a center of order
$2$
-subgroup of G has a center of order
![]() $(q^{*}-\varepsilon )_2$
, while a Sylow
$(q^{*}-\varepsilon )_2$
, while a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_5(q)$
has a center of order
$PSL_5(q)$
has a center of order
![]() $(q-1)_2$
. It follows that
$(q-1)_2$
. It follows that
![]() $(q^{*}-\varepsilon )_2 = (q-1)_2$
. Let
$(q^{*}-\varepsilon )_2 = (q-1)_2$
. Let
![]() $k,s,k^{*},s^{*} \in \mathbb {N}$
with
$k,s,k^{*},s^{*} \in \mathbb {N}$
with
![]() $2^k = (q-1)_2, 2^s = (q+1)_2, 2^{k^{*}} = (q^{*} - \varepsilon )_2$
and
$2^k = (q-1)_2, 2^s = (q+1)_2, 2^{k^{*}} = (q^{*} - \varepsilon )_2$
and
![]() $2^{s^{*}} = (q^{*} + \varepsilon )_2$
. Then
$2^{s^{*}} = (q^{*} + \varepsilon )_2$
. Then
Since
![]() $2^{k^{*}} = 2^k$
, we thus have
$2^{k^{*}} = 2^k$
, we thus have
![]() $k = k^{*}$
and
$k = k^{*}$
and
![]() $s = s^{*}$
. This implies
$s = s^{*}$
. This implies
![]() $\varepsilon q^{*} \sim q$
.
$\varepsilon q^{*} \sim q$
.
5 The case
 $n \ge 6$
: preliminary discussion and notation
$n \ge 6$
: preliminary discussion and notation
Given a natural number
![]() $k \ge 6$
, we say that
$k \ge 6$
, we say that
![]() $P(k)$
is satisfied if whenever
$P(k)$
is satisfied if whenever
![]() $q_0$
is a nontrivial odd prime power and H is a finite simple group satisfying (𝒞𝒦) and realizing the
$q_0$
is a nontrivial odd prime power and H is a finite simple group satisfying (𝒞𝒦) and realizing the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_k(q_0)$
, we have
$PSL_k(q_0)$
, we have
![]() $H \cong PSL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$H \cong PSL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $\varepsilon q^{*} \sim q_0$
.
$\varepsilon q^{*} \sim q_0$
.
In order to establish Theorem A for
![]() $n \ge 6$
, we are going to prove by induction that
$n \ge 6$
, we are going to prove by induction that
![]() $P(k)$
is satisfied for all
$P(k)$
is satisfied for all
![]() $k \ge 6$
. From now on until the end of Section 8, we will assume the following hypothesis.
$k \ge 6$
. From now on until the end of Section 8, we will assume the following hypothesis.
Hypothesis 5.1. Let
![]() $n \ge 6$
be a natural number such that
$n \ge 6$
be a natural number such that
![]() $P(k)$
is satisfied for all natural numbers k with
$P(k)$
is satisfied for all natural numbers k with
![]() $6 \le k < n$
, and let q be a nontrivial odd prime power. Moreover, let G be a finite group satisfying the following properties:
$6 \le k < n$
, and let q be a nontrivial odd prime power. Moreover, let G be a finite group satisfying the following properties:
-
(i) G realizes the
 $2$
-fusion system of
$2$
-fusion system of
 $PSL_n(q)$
;
$PSL_n(q)$
; -
(ii)
 $O(G) = 1$
;
$O(G) = 1$
; -
(iii) G satisfies (𝒞𝒦).
We will prove the following theorem.
Theorem 5.2. There is a normal subgroup
![]() $G_0$
of G isomorphic to a nontrivial quotient of
$G_0$
of G isomorphic to a nontrivial quotient of
![]() $SL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$SL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +, - \rbrace $
with
$\varepsilon \in \lbrace +, - \rbrace $
with
![]() $\varepsilon q^{*} \sim q$
. In particular,
$\varepsilon q^{*} \sim q$
. In particular,
![]() $P(n)$
is satisfied.
$P(n)$
is satisfied.
The proof of Theorem 5.2 will occupy Sections 5-8. In this section, we introduce some notation and prove some preliminary results needed for the proof.
For each
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
of even order, let
$A \subseteq \lbrace 1, \dots , n \rbrace $
of even order, let
![]() $t_A$
be the image of the diagonal matrix
$t_A$
be the image of the diagonal matrix
![]() $\mathrm {diag}(d_1,\dots ,d_n)$
in
$\mathrm {diag}(d_1,\dots ,d_n)$
in
![]() $PSL_n(q)$
, where
$PSL_n(q)$
, where
 $$ \begin{align*} d_i = \begin{cases} -1 & \, \text{if } i \in A \\ 1 & \, \text{if } i \not\in A \end{cases} \end{align*} $$
$$ \begin{align*} d_i = \begin{cases} -1 & \, \text{if } i \in A \\ 1 & \, \text{if } i \not\in A \end{cases} \end{align*} $$
for each
![]() $1 \le i \le n$
. If i is an even natural number with
$1 \le i \le n$
. If i is an even natural number with
![]() $2 \le i < n$
and
$2 \le i < n$
and
![]() $A = \lbrace n-i+1,\dots ,n \rbrace $
, then we write
$A = \lbrace n-i+1,\dots ,n \rbrace $
, then we write
![]() $t_i$
for
$t_i$
for
![]() $t_A$
. We denote
$t_A$
. We denote
![]() $t_2$
by t, and we write u for
$t_2$
by t, and we write u for
![]() $t_{\lbrace 1,2 \rbrace }$
.
$t_{\lbrace 1,2 \rbrace }$
.
We assume
![]() $\rho $
to be an element of
$\rho $
to be an element of
![]() $\mathbb {F}_q^{*}$
of order
$\mathbb {F}_q^{*}$
of order
![]() $(n,q-1)$
. If
$(n,q-1)$
. If
![]() $\rho $
is a square in
$\rho $
is a square in
![]() $\mathbb {F}_q$
, then we assume
$\mathbb {F}_q$
, then we assume
![]() $\mu $
to be a fixed element of
$\mu $
to be a fixed element of
![]() $\mathbb {F}_q$
with
$\mathbb {F}_q$
with
![]() $\rho = \mu ^2$
.
$\rho = \mu ^2$
.
If n is even,
![]() $\rho $
is a square in
$\rho $
is a square in
![]() $\mathbb {F}_q$
, and i is an odd natural number with
$\mathbb {F}_q$
, and i is an odd natural number with
![]() $1 \le i < n$
, then
$1 \le i < n$
, then
 $$ \begin{align*} \begin{pmatrix} \mu I_{n-i} & \\ & -\mu I_i \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \mu I_{n-i} & \\ & -\mu I_i \end{pmatrix} \end{align*} $$
is an element of
![]() $SL_n(q)$
by Proposition 3.5, and we will denote its image in
$SL_n(q)$
by Proposition 3.5, and we will denote its image in
![]() $PSL_n(q)$
by
$PSL_n(q)$
by
![]() $t_i$
.
$t_i$
.
If n is even and
![]() $\rho $
is a nonsquare element of
$\rho $
is a nonsquare element of
![]() $\mathbb {F}_q$
, then we denote the matrix
$\mathbb {F}_q$
, then we denote the matrix
 $$ \begin{align*} \begin{pmatrix} & I_{n/2} \\ \rho I_{n/2} & \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} & I_{n/2} \\ \rho I_{n/2} & \end{pmatrix} \end{align*} $$
by
![]() $\widetilde w$
, and if
$\widetilde w$
, and if
![]() $\widetilde w \in SL_n(q)$
, then we use w to denote its image in
$\widetilde w \in SL_n(q)$
, then we use w to denote its image in
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
Note that, by Proposition 3.5, any involution of
![]() $PSL_n(q)$
is conjugate to
$PSL_n(q)$
is conjugate to
![]() $t_i$
for some
$t_i$
for some
![]() $1 \le i < n$
such that
$1 \le i < n$
such that
![]() $t_i$
is defined, or to w (if defined).
$t_i$
is defined, or to w (if defined).
Next, we construct a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{PSL_n(q)}(t)$
containing some ‘nice’ elements of
$C_{PSL_n(q)}(t)$
containing some ‘nice’ elements of
![]() $PSL_n(q)$
. Take a Sylow
$PSL_n(q)$
. Take a Sylow
![]() $2$
-subgroup V of
$2$
-subgroup V of
![]() $GL_2(q)$
containing each diagonal matrix in
$GL_2(q)$
containing each diagonal matrix in
![]() $GL_2(q)$
with
$GL_2(q)$
with
![]() $2$
-elements of
$2$
-elements of
![]() $\mathbb {F}_q^{*}$
along the main diagonal. Similarly, we assume
$\mathbb {F}_q^{*}$
along the main diagonal. Similarly, we assume
![]() $V_2$
to be a Sylow
$V_2$
to be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{n-4}(q)$
containing each diagonal matrix in
$GL_{n-4}(q)$
containing each diagonal matrix in
![]() $GL_{n-4}(q)$
with
$GL_{n-4}(q)$
with
![]() $2$
-elements of
$2$
-elements of
![]() $\mathbb {F}_q^{*}$
along the main diagonal. Now let W be a Sylow
$\mathbb {F}_q^{*}$
along the main diagonal. Now let W be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $GL_{n-2}(q)$
containing
$GL_{n-2}(q)$
containing
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in V, B \in V_2 \right\rbrace. \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in V, B \in V_2 \right\rbrace. \end{align*} $$
If
![]() $n = 6$
, then we assume that
$n = 6$
, then we assume that
![]() $V = V_2$
and that W is the Sylow
$V = V_2$
and that W is the Sylow
![]() $2$
-subgroup
$2$
-subgroup
 $$ \begin{align*} \left\lbrace\begin{pmatrix} A & \\ & B \\ \end{pmatrix} \ : \ A, B \in V \right\rbrace \cdot \left\langle \begin{pmatrix} & I_{2} \\ I_{2} & \\ \end{pmatrix} \right\rangle \end{align*} $$
$$ \begin{align*} \left\lbrace\begin{pmatrix} A & \\ & B \\ \end{pmatrix} \ : \ A, B \in V \right\rbrace \cdot \left\langle \begin{pmatrix} & I_{2} \\ I_{2} & \\ \end{pmatrix} \right\rangle \end{align*} $$
of
![]() $GL_4(q)$
.
$GL_4(q)$
.
Let
![]() $\widetilde t := \mathrm {diag}(1,\dots ,1,-1,-1) \in SL_n(q)$
. Then we have
$\widetilde t := \mathrm {diag}(1,\dots ,1,-1,-1) \in SL_n(q)$
. Then we have
 $$ \begin{align*} C_{SL_n(q)}(\widetilde t) = \left \lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in GL_{n-2}(q), B \in GL_2(q), \mathrm{det}(A)\mathrm{det}(B) = 1 \right \rbrace. \end{align*} $$
$$ \begin{align*} C_{SL_n(q)}(\widetilde t) = \left \lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in GL_{n-2}(q), B \in GL_2(q), \mathrm{det}(A)\mathrm{det}(B) = 1 \right \rbrace. \end{align*} $$
It is easy to note that
 $$ \begin{align*} \widetilde T := \left \lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in W, B \in V, \mathrm{det}(A)\mathrm{det}(B) = 1 \right \rbrace \end{align*} $$
$$ \begin{align*} \widetilde T := \left \lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in W, B \in V, \mathrm{det}(A)\mathrm{det}(B) = 1 \right \rbrace \end{align*} $$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{SL_n(q)}(\widetilde t)$
. Let T denote the image of
$C_{SL_n(q)}(\widetilde t)$
. Let T denote the image of
![]() $\widetilde T$
in
$\widetilde T$
in
![]() $PSL_n(q)$
. As the centralizer of t in
$PSL_n(q)$
. As the centralizer of t in
![]() $PSL_n(q)$
is the image of
$PSL_n(q)$
is the image of
![]() $C_{SL_n(q)}(\widetilde t)$
in
$C_{SL_n(q)}(\widetilde t)$
in
![]() $PSL_n(q)$
, we have that T is a Sylow
$PSL_n(q)$
, we have that T is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{PSL_n(q)}(t)$
. We assume S to be a Sylow
$C_{PSL_n(q)}(t)$
. We assume S to be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $PSL_n(q)$
containing T. Since
$PSL_n(q)$
containing T. Since
![]() $C_S(t) = T \in \mathrm {Syl_2}(C_{PSL_n(q)}(t))$
, we have that
$C_S(t) = T \in \mathrm {Syl_2}(C_{PSL_n(q)}(t))$
, we have that
![]() $\langle t \rangle $
is fully
$\langle t \rangle $
is fully
![]() $\mathcal {F}_S(PSL_n(q))$
-centralized.
$\mathcal {F}_S(PSL_n(q))$
-centralized.
Let
![]() $K_1$
be the image of
$K_1$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_2\end{pmatrix} \ : \ A \in SL_{n-2}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_2\end{pmatrix} \ : \ A \in SL_{n-2}(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
, and let
$PSL_n(q)$
, and let
![]() $K_2$
be the image of
$K_2$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_{n-2} & \\ & B\end{pmatrix} \ : \ B \in SL_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_{n-2} & \\ & B\end{pmatrix} \ : \ B \in SL_2(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
. Clearly,
$PSL_n(q)$
. Clearly,
![]() $K_1$
and
$K_1$
and
![]() $K_2$
are normal subgroups of
$K_2$
are normal subgroups of
![]() $C_{PSL_n(q)}(t)$
isomorphic to
$C_{PSL_n(q)}(t)$
isomorphic to
![]() $SL_{n-2}(q)$
and
$SL_{n-2}(q)$
and
![]() $SL_2(q)$
, respectively. Define
$SL_2(q)$
, respectively. Define
![]() $X_1$
to be the image of
$X_1$
to be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_2\end{pmatrix} \ : \ A \in W \cap SL_{n-2}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_2\end{pmatrix} \ : \ A \in W \cap SL_{n-2}(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
, and define
$PSL_n(q)$
, and define
![]() $X_2$
to be the image of
$X_2$
to be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_{n-2} & \\ & B \end{pmatrix} \ : \ B \in V \cap SL_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_{n-2} & \\ & B \end{pmatrix} \ : \ B \in V \cap SL_2(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
Note that
![]() $X_1 = T \cap K_1 \in \mathrm {Syl}_2(K_1)$
and
$X_1 = T \cap K_1 \in \mathrm {Syl}_2(K_1)$
and
![]() $X_2 = T \cap K_2 \in \mathrm {Syl}_2(K_2)$
. Define
$X_2 = T \cap K_2 \in \mathrm {Syl}_2(K_2)$
. Define
for
![]() $i \in \lbrace 1,2 \rbrace $
. By [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 6.2],
$i \in \lbrace 1,2 \rbrace $
. By [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 6.2],
![]() $\mathcal {C}_1$
and
$\mathcal {C}_1$
and
![]() $\mathcal {C}_2$
are normal subsystems of
$\mathcal {C}_2$
are normal subsystems of
![]() $\mathcal {F}_T(C_{PSL_n(q)}(t))$
.
$\mathcal {F}_T(C_{PSL_n(q)}(t))$
.
Lemma 5.3. Let
![]() $\mathcal {F} := \mathcal {F}_S(PSL_n(q))$
. If
$\mathcal {F} := \mathcal {F}_S(PSL_n(q))$
. If
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
, then the components of
$7 \ \mathrm {mod} \ 8$
, then the components of
![]() $C_{\mathcal {F}}(\langle t \rangle )$
are precisely the subsystems
$C_{\mathcal {F}}(\langle t \rangle )$
are precisely the subsystems
![]() $\mathcal {C}_1$
and
$\mathcal {C}_1$
and
![]() $\mathcal {C}_2$
. If
$\mathcal {C}_2$
. If
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
, then
$5 \ \mathrm {mod} \ 8$
, then
![]() $\mathcal {C}_1$
is the only component of
$\mathcal {C}_1$
is the only component of
![]() $C_{\mathcal {F}}(\langle t \rangle )$
.
$C_{\mathcal {F}}(\langle t \rangle )$
.
Proof. Set
![]() $C := C_{PSL_n(q)}(t)$
. Observe that the
$C := C_{PSL_n(q)}(t)$
. Observe that the
![]() $2$
-components of C are precisely the quasisimple members of
$2$
-components of C are precisely the quasisimple members of
![]() $\lbrace K_1, K_2 \rbrace $
. As
$\lbrace K_1, K_2 \rbrace $
. As
![]() $n \ge 6$
and as
$n \ge 6$
and as
![]() $K_1 \cong SL_{n-2}(q)$
and
$K_1 \cong SL_{n-2}(q)$
and
![]() $K_2 \cong SL_2(q)$
, it follows that the
$K_2 \cong SL_2(q)$
, it follows that the
![]() $2$
-components of C are
$2$
-components of C are
![]() $K_1$
and
$K_1$
and
![]() $K_2$
if
$K_2$
if
![]() $q \ne 3$
and that
$q \ne 3$
and that
![]() $K_1$
is the only
$K_1$
is the only
![]() $2$
-component of C if
$2$
-component of C if
![]() $q = 3$
.
$q = 3$
.
By Lemma 3.21,
![]() $K_1/Z(K_1)$
is not a Goldschmidt group. If
$K_1/Z(K_1)$
is not a Goldschmidt group. If
![]() $q \ne 3$
, then the lemma just cited also shows that
$q \ne 3$
, then the lemma just cited also shows that
![]() $K_2/Z(K_2)$
is a Goldschmidt group if and only if
$K_2/Z(K_2)$
is a Goldschmidt group if and only if
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
.
$5 \ \mathrm {mod} \ 8$
.
Now we apply Proposition 2.17 to conclude that
![]() $\mathcal {F}_{T \cap K_1}(K_1)$
and
$\mathcal {F}_{T \cap K_1}(K_1)$
and
![]() $\mathcal {F}_{T \cap K_2}(K_2)$
are precisely the components of
$\mathcal {F}_{T \cap K_2}(K_2)$
are precisely the components of
![]() $\mathcal {F}_T(C)$
if
$\mathcal {F}_T(C)$
if
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
and that
$7 \ \mathrm {mod} \ 8$
and that
![]() $\mathcal {F}_{T \cap K_1}(K_1)$
is the only component of
$\mathcal {F}_{T \cap K_1}(K_1)$
is the only component of
![]() $\mathcal {F}_T(C)$
if
$\mathcal {F}_T(C)$
if
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. This completes the proof because
$5 \ \mathrm {mod} \ 8$
. This completes the proof because
![]() $C_{\mathcal {F}}(\langle t \rangle ) = \mathcal {F}_T(C)$
,
$C_{\mathcal {F}}(\langle t \rangle ) = \mathcal {F}_T(C)$
,
![]() $\mathcal {C}_1 = \mathcal {F}_{T \cap K_1}(K_1)$
and
$\mathcal {C}_1 = \mathcal {F}_{T \cap K_1}(K_1)$
and
![]() $\mathcal {C}_2 = \mathcal {F}_{T \cap K_2}(K_2)$
.
$\mathcal {C}_2 = \mathcal {F}_{T \cap K_2}(K_2)$
.
Lemma 5.4. Let
![]() $\mathcal {F} := \mathcal {F}_S(PSL_n(q))$
. Then the factor system
$\mathcal {F} := \mathcal {F}_S(PSL_n(q))$
. Then the factor system
![]() $C_{\mathcal {F}}(\langle t \rangle )/X_1X_2$
is nilpotent.
$C_{\mathcal {F}}(\langle t \rangle )/X_1X_2$
is nilpotent.
Proof. Set
![]() $C := C_{PSL_n(q)}(t)$
. As
$C := C_{PSL_n(q)}(t)$
. As
![]() $X_i = K_i \cap T$
is Sylow in
$X_i = K_i \cap T$
is Sylow in
![]() $K_i$
,
$K_i$
,
![]() $X_1 X_2 = K_1 K_2 \cap T$
. By Lemma 2.11,
$X_1 X_2 = K_1 K_2 \cap T$
. By Lemma 2.11,
![]() $C_{\mathcal {F}}(\langle t \rangle )/X_1X_2$
is isomorphic to the
$C_{\mathcal {F}}(\langle t \rangle )/X_1X_2$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $C/K_1K_2$
. The factor group
$C/K_1K_2$
. The factor group
![]() $C/K_1K_2$
is
$C/K_1K_2$
is
![]() $2$
-nilpotent by Propositions 3.40 and 3.42, and so the
$2$
-nilpotent by Propositions 3.40 and 3.42, and so the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $C/K_1K_2$
is nilpotent. Hence,
$C/K_1K_2$
is nilpotent. Hence,
![]() $C_{\mathcal {F}}(\langle t \rangle )/X_1X_2$
is nilpotent.
$C_{\mathcal {F}}(\langle t \rangle )/X_1X_2$
is nilpotent.
Lemma 5.5. Let
![]() $A \in W$
and
$A \in W$
and
![]() $B \in V$
such that
$B \in V$
such that
![]() $\mathrm {det}(A)\mathrm {det}(B) = 1$
. Let
$\mathrm {det}(A)\mathrm {det}(B) = 1$
. Let
 $$ \begin{align*} m := \begin{pmatrix}A & \\ & B \end{pmatrix}Z(SL_n(q)) \in T. \end{align*} $$
$$ \begin{align*} m := \begin{pmatrix}A & \\ & B \end{pmatrix}Z(SL_n(q)) \in T. \end{align*} $$
Then we have
![]() $m \in Z(\mathcal {C}_1 \langle m \rangle )$
if and only if
$m \in Z(\mathcal {C}_1 \langle m \rangle )$
if and only if
![]() $A \in Z(GL_{n-2}(q))$
.
$A \in Z(GL_{n-2}(q))$
.
Proof. By [Reference Henke33, Proposition 1], we have
![]() $\mathcal {C}_1 \langle m \rangle = \mathcal {F}_{X_1 \langle m \rangle }(K_1 \langle m \rangle )$
. So, by Lemma 2.13,
$\mathcal {C}_1 \langle m \rangle = \mathcal {F}_{X_1 \langle m \rangle }(K_1 \langle m \rangle )$
. So, by Lemma 2.13,
![]() $m \in Z(\mathcal {C}_1\langle m \rangle )$
if and only if
$m \in Z(\mathcal {C}_1\langle m \rangle )$
if and only if
![]() $m \in Z^{*}(K_1\langle m \rangle )$
. This is the case if and only if
$m \in Z^{*}(K_1\langle m \rangle )$
. This is the case if and only if
![]() $[K_1,\langle m \rangle ] \le O(K_1)$
. If the latter holds, then
$[K_1,\langle m \rangle ] \le O(K_1)$
. If the latter holds, then
![]() $[\langle m \rangle , K_1, K_1] = [K_1,\langle m \rangle , K_1] = 1$
as
$[\langle m \rangle , K_1, K_1] = [K_1,\langle m \rangle , K_1] = 1$
as
![]() $O(K_1) \le Z(K_1)$
, and so
$O(K_1) \le Z(K_1)$
, and so
![]() $[K_1,\langle m \rangle ] = 1$
by the three subgroups lemma. Thus, the condition
$[K_1,\langle m \rangle ] = 1$
by the three subgroups lemma. Thus, the condition
![]() $[K_1,\langle m \rangle ] \le O(K_1)$
is satisfied if and only if
$[K_1,\langle m \rangle ] \le O(K_1)$
is satisfied if and only if
![]() $[K_1,\langle m \rangle ] = 1$
. So we have
$[K_1,\langle m \rangle ] = 1$
. So we have
![]() $m \in Z(\mathcal {C}_1\langle m \rangle )$
if and only if m centralizes
$m \in Z(\mathcal {C}_1\langle m \rangle )$
if and only if m centralizes
![]() $K_1$
, and this is the case if and only if
$K_1$
, and this is the case if and only if
![]() $A \in Z(GL_{n-2}(q))$
.
$A \in Z(GL_{n-2}(q))$
.
Lemma 5.6. Set
![]() $\mathcal {F} := \mathcal {F}_S(PSL_n(q))$
and
$\mathcal {F} := \mathcal {F}_S(PSL_n(q))$
and
![]() $\mathcal {G} := C_{\mathcal {F}}(\langle t \rangle )$
. Then
$\mathcal {G} := C_{\mathcal {F}}(\langle t \rangle )$
. Then
![]() $\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) = X_2$
.
$\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) = X_2$
.
Proof. Set
![]() $C := C_{PSL_n(q)}(t)$
. Note that
$C := C_{PSL_n(q)}(t)$
. Note that
![]() $C' = K_1 K_2$
.
$C' = K_1 K_2$
.
By [Reference Gorenstein23, Chapter 7, Theorem 3.4], we have
![]() $\mathfrak {foc}(C_{\mathcal {G}}(X_1)) = C_T(X_1) \cap C_C(X_1)' \le C_T(X_1) \cap C' = C_T(X_1) \cap X_1X_2 = Z(X_1)X_2$
. As
$\mathfrak {foc}(C_{\mathcal {G}}(X_1)) = C_T(X_1) \cap C_C(X_1)' \le C_T(X_1) \cap C' = C_T(X_1) \cap X_1X_2 = Z(X_1)X_2$
. As
![]() $\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) \le \mathfrak {foc}(C_{\mathcal {G}}(X_1))$
, it follows that
$\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) \le \mathfrak {foc}(C_{\mathcal {G}}(X_1))$
, it follows that
![]() $\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) \le Z(X_1)X_2$
.
$\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) \le Z(X_1)X_2$
.
Let P be a subgroup of
![]() $C_T(X_1)$
, and let
$C_T(X_1)$
, and let
![]() $\varphi $
be a
$\varphi $
be a
![]() $2'$
-element of
$2'$
-element of
![]() $\mathrm {Aut}_{C_C(X_1)}(P)$
. By [Reference Kurzweil and Stellmacher37, 8.2.7], we have
$\mathrm {Aut}_{C_C(X_1)}(P)$
. By [Reference Kurzweil and Stellmacher37, 8.2.7], we have
Since
![]() $\varphi \in \mathrm {Aut}_{C_C(X_1)}(P)$
,
$\varphi \in \mathrm {Aut}_{C_C(X_1)}(P)$
,
![]() $K_2 \trianglelefteq C$
and
$K_2 \trianglelefteq C$
and
![]() $X_2 = T \cap K_2$
, it follows
$X_2 = T \cap K_2$
, it follows
![]() $[P,\langle \varphi \rangle ] \le X_2$
. Consequently,
$[P,\langle \varphi \rangle ] \le X_2$
. Consequently,
![]() $\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) \le X_2$
.
$\mathfrak {hnp}(C_{\mathcal {G}}(X_1)) \le X_2$
.
On the other hand, since
![]() $K_2 \le O^2(C_C(X_1))$
, we have
$K_2 \le O^2(C_C(X_1))$
, we have
![]() $X_2 \le \mathfrak {hnp}(C_{\mathcal {G}}(X_1))$
by [Reference Craven18, Theorem 1.33].
$X_2 \le \mathfrak {hnp}(C_{\mathcal {G}}(X_1))$
by [Reference Craven18, Theorem 1.33].
Lemma 5.7. Set
![]() $C := C_{PSL_n(q)}(t)$
. Then
$C := C_{PSL_n(q)}(t)$
. Then
![]() $\mathrm {Aut}_{C}(X_1)$
is a
$\mathrm {Aut}_{C}(X_1)$
is a
![]() $2$
-group.
$2$
-group.
Proof. Let
![]() $m \in N_C(X_1)$
. We have
$m \in N_C(X_1)$
. We have
 $$ \begin{align*} m = \begin{pmatrix} M_1 & \\ & M_2 \end{pmatrix} Z(SL_n(q)) \end{align*} $$
$$ \begin{align*} m = \begin{pmatrix} M_1 & \\ & M_2 \end{pmatrix} Z(SL_n(q)) \end{align*} $$
for some
![]() $M_1 \in GL_{n-2}(q)$
and some
$M_1 \in GL_{n-2}(q)$
and some
![]() $M_2 \in GL_2(q)$
with
$M_2 \in GL_2(q)$
with
![]() $\mathrm {det}(M_1)\mathrm {det}(M_2) = 1$
. Let
$\mathrm {det}(M_1)\mathrm {det}(M_2) = 1$
. Let
![]() $A \in W \cap SL_{n-2}(q)$
and
$A \in W \cap SL_{n-2}(q)$
and
 $$ \begin{align*} x := \begin{pmatrix} A & \\ & I_2 \end{pmatrix} Z(SL_n(q)) \in X_1. \end{align*} $$
$$ \begin{align*} x := \begin{pmatrix} A & \\ & I_2 \end{pmatrix} Z(SL_n(q)) \in X_1. \end{align*} $$
As m normalizes
![]() $X_1$
, we have
$X_1$
, we have
 $$ \begin{align*} \begin{pmatrix} A^{M_1} & \\ & I_2 \end{pmatrix} Z(SL_n(q)) = x^m \in X_1. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} A^{M_1} & \\ & I_2 \end{pmatrix} Z(SL_n(q)) = x^m \in X_1. \end{align*} $$
This easily implies that
![]() $A^{M_1} \in W \cap SL_{n-2}(q)$
. It follows that
$A^{M_1} \in W \cap SL_{n-2}(q)$
. It follows that
![]() $M_1$
normalizes
$M_1$
normalizes
![]() $W \cap SL_{n-2}(q)$
. By [Reference Kondrat’ev36, Theorem 1], we have
$W \cap SL_{n-2}(q)$
. By [Reference Kondrat’ev36, Theorem 1], we have
![]() $N_{GL_{n-2}(q)}(W \cap SL_{n-2}(q)) = W C_{GL_{n-2}(q)}(W)$
. It follows that
$N_{GL_{n-2}(q)}(W \cap SL_{n-2}(q)) = W C_{GL_{n-2}(q)}(W)$
. It follows that
![]() $c_m|_{X_1,X_1}$
is a
$c_m|_{X_1,X_1}$
is a
![]() $2$
-automorphism.
$2$
-automorphism.
Define
![]() $T_1$
to be the image of
$T_1$
to be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in V \cap SL_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in V \cap SL_2(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
and
$PSL_n(q)$
and
![]() $T_2$
to be the image of
$T_2$
to be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & & \\ & B & \\ & & I_2 \end{pmatrix} \ : \ B \in V_2 \cap SL_{n-4}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & & \\ & B & \\ & & I_2 \end{pmatrix} \ : \ B \in V_2 \cap SL_{n-4}(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
. By the definitions of
$PSL_n(q)$
. By the definitions of
![]() $X_1$
and of W,
$X_1$
and of W,
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are subgroups of
$T_2$
are subgroups of
![]() $X_1$
. Recall that we use u to denote
$X_1$
. Recall that we use u to denote
![]() $t_{\lbrace 1,2 \rbrace } \in X_1$
. The following lemma sheds light on some properties of the centralizer fusion system
$t_{\lbrace 1,2 \rbrace } \in X_1$
. The following lemma sheds light on some properties of the centralizer fusion system
![]() $C_{\mathcal {C}_1}(\langle u \rangle )$
.
$C_{\mathcal {C}_1}(\langle u \rangle )$
.
Lemma 5.8. The following hold.
-
(i) We have
 $C_{X_1}(u) \in \mathrm {Syl}_2(C_{K_1}(u))$
. In particular,
$C_{X_1}(u) \in \mathrm {Syl}_2(C_{K_1}(u))$
. In particular,
 $\langle u \rangle $
is fully
$\langle u \rangle $
is fully
 $\mathcal {C}_1$
-centralized.
$\mathcal {C}_1$
-centralized. -
(ii)
 $\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = T_1 T_2$
.
$\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = T_1 T_2$
. -
(iii) If
 $n = 6$
and
$n = 6$
and
 $q \equiv 3$
or
$q \equiv 3$
or
 $5 \ \mathrm {mod} \ 8$
, then
$5 \ \mathrm {mod} \ 8$
, then
 $T_1$
and
$T_1$
and
 $T_2$
are the only subgroups of
$T_2$
are the only subgroups of
 $\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle ))$
which are isomorphic to
$\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle ))$
which are isomorphic to
 $Q_8$
and strongly closed in
$Q_8$
and strongly closed in
 $C_{\mathcal {C}_1}(\langle u \rangle )$
.
$C_{\mathcal {C}_1}(\langle u \rangle )$
. -
(iv) If
 $n \ge 7$
and
$n \ge 7$
and
 $q \equiv 3$
or
$q \equiv 3$
or
 $5 \ \mathrm {mod} \ 8$
, then
$5 \ \mathrm {mod} \ 8$
, then
 $T_1$
is the only subgroup of the intersection
$T_1$
is the only subgroup of the intersection
 $\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) \cap C_{X_1}(T_2)$
which is isomorphic to
$\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) \cap C_{X_1}(T_2)$
which is isomorphic to
 $Q_8$
and strongly closed in
$Q_8$
and strongly closed in
 $C_{\mathcal {C}_1}(\langle u \rangle )$
.
$C_{\mathcal {C}_1}(\langle u \rangle )$
. -
(v) Let
 $C_1$
be the image of in
$C_1$
be the image of in $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SL_2(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2} \end{pmatrix} \ : \ A \in SL_2(q) \right\rbrace \end{align*} $$
 $PSL_n(q)$
and
$PSL_n(q)$
and
 $C_2$
be the image of in
$C_2$
be the image of in $$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & &\\ & B & \\ & & I_2 \end{pmatrix} \ : \ A \in SL_{n-4}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & &\\ & B & \\ & & I_2 \end{pmatrix} \ : \ A \in SL_{n-4}(q) \right\rbrace \end{align*} $$
 $PSL_n(q)$
. Then any component of
$PSL_n(q)$
. Then any component of
 $C_{\mathcal {C}_1}(\langle u \rangle )$
lies in
$C_{\mathcal {C}_1}(\langle u \rangle )$
lies in
 $\lbrace \mathcal {F}_{T_1}(C_1), \mathcal {F}_{T_2}(C_2) \rbrace $
. Moreover,
$\lbrace \mathcal {F}_{T_1}(C_1), \mathcal {F}_{T_2}(C_2) \rbrace $
. Moreover,
 $\mathcal {F}_{T_1}(C_1)$
is a component if and only if
$\mathcal {F}_{T_1}(C_1)$
is a component if and only if
 $q \equiv 1$
or
$q \equiv 1$
or
 $7 \ \mathrm {mod} \ 8$
, and
$7 \ \mathrm {mod} \ 8$
, and
 $\mathcal {F}_{T_2}(C_2)$
is a component if and only if
$\mathcal {F}_{T_2}(C_2)$
is a component if and only if
 $n \ge 7$
or
$n \ge 7$
or
 $q \equiv 1$
or
$q \equiv 1$
or
 $7 \ \mathrm {mod} \ 8$
.
$7 \ \mathrm {mod} \ 8$
.
Proof. Clearly,
![]() $C_{K_1}(u)$
is the image of
$C_{K_1}(u)$
is the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & & \\ & B & \\ & & I_2 \end{pmatrix} \ : \ A \in GL_2(q), B \in GL_{n-4}(q), \mathrm{det}(A)\mathrm{det}(B) = 1 \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & & \\ & B & \\ & & I_2 \end{pmatrix} \ : \ A \in GL_2(q), B \in GL_{n-4}(q), \mathrm{det}(A)\mathrm{det}(B) = 1 \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
. Let
$PSL_n(q)$
. Let
![]() $\widetilde W$
be the image of
$\widetilde W$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & & \\ & B & \\ & & I_2 \end{pmatrix} \ : \ A \in V, B \in V_2, \mathrm{det}(A) \mathrm{det}(B) = 1 \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & & \\ & B & \\ & & I_2 \end{pmatrix} \ : \ A \in V, B \in V_2, \mathrm{det}(A) \mathrm{det}(B) = 1 \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
. By definition of
$PSL_n(q)$
. By definition of
![]() $X_1$
, we have
$X_1$
, we have
![]() $\widetilde W \le C_{X_1}(u)$
. We have
$\widetilde W \le C_{X_1}(u)$
. We have
![]() $|C_{K_1}(u)| = |GL_2(q)||SL_{n-4}(q)|$
and
$|C_{K_1}(u)| = |GL_2(q)||SL_{n-4}(q)|$
and
![]() $|\widetilde W| = |V||V_2 \cap SL_{n-4}(q)|$
; so
$|\widetilde W| = |V||V_2 \cap SL_{n-4}(q)|$
; so
![]() $\widetilde W$
is a Sylow
$\widetilde W$
is a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{K_1}(u)$
. Thus,
$C_{K_1}(u)$
. Thus,
![]() $C_{X_1}(u) = \widetilde W \in \mathrm {Syl}_2(C_{K_1}(u))$
. Hence, (i) holds.
$C_{X_1}(u) = \widetilde W \in \mathrm {Syl}_2(C_{K_1}(u))$
. Hence, (i) holds.
We have
![]() $C_{\mathcal {C}_1}(\langle u \rangle ) = \mathcal {F}_{C_{X_1}(u)}(C_{K_1}(u)) = \mathcal {F}_{\widetilde W}(C_{K_1}(u))$
. The focal subgroup theorem [Reference Gorenstein23, Chapter 7, Theorem 3.4] implies that
$C_{\mathcal {C}_1}(\langle u \rangle ) = \mathcal {F}_{C_{X_1}(u)}(C_{K_1}(u)) = \mathcal {F}_{\widetilde W}(C_{K_1}(u))$
. The focal subgroup theorem [Reference Gorenstein23, Chapter 7, Theorem 3.4] implies that
![]() $\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = \widetilde W \cap (C_{K_1}(u))'$
. It is easy to see that
$\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = \widetilde W \cap (C_{K_1}(u))'$
. It is easy to see that
![]() $(C_{K_1}(u))' = C_1C_2$
, where
$(C_{K_1}(u))' = C_1C_2$
, where
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are as in (v). We thus have
$C_2$
are as in (v). We thus have
![]() $\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = T_1T_2$
. Hence, (ii) holds.
$\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = T_1T_2$
. Hence, (ii) holds.
Now we turn to the proofs of (iii) and (iv). Assume that
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. Clearly,
$5 \ \mathrm {mod} \ 8$
. Clearly,
![]() $C_1$
and
$C_1$
and
![]() $C_2$
are normal subgroups of
$C_2$
are normal subgroups of
![]() $C_{K_1}(u)$
and we have
$C_{K_1}(u)$
and we have
![]() $T_1 = C_1 \cap \widetilde W$
,
$T_1 = C_1 \cap \widetilde W$
,
![]() $T_2 = C_2 \cap \widetilde W$
. This implies that
$T_2 = C_2 \cap \widetilde W$
. This implies that
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are strongly closed in
$T_2$
are strongly closed in
![]() $C_{\mathcal {C}_1}(\langle u \rangle )$
. By Lemma 3.12, we have
$C_{\mathcal {C}_1}(\langle u \rangle )$
. By Lemma 3.12, we have
![]() $T_1 \cong Q_8$
and, if
$T_1 \cong Q_8$
and, if
![]() $n = 6$
, we also have
$n = 6$
, we also have
![]() $T_2 \cong Q_8$
. Clearly, any strongly
$T_2 \cong Q_8$
. Clearly, any strongly
![]() $C_{\mathcal {C}_1}(\langle u \rangle )$
-closed subgroup of
$C_{\mathcal {C}_1}(\langle u \rangle )$
-closed subgroup of
![]() $\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = T_1T_2$
is strongly closed in
$\mathfrak {foc}(C_{\mathcal {C}_1}(\langle u \rangle )) = T_1T_2$
is strongly closed in
![]() $\mathcal {F}_{T_1T_2}(C_1C_2)$
. Hence, in order to prove (iii), it suffices to show that if
$\mathcal {F}_{T_1T_2}(C_1C_2)$
. Hence, in order to prove (iii), it suffices to show that if
![]() $n = 6$
, then
$n = 6$
, then
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are the only strongly
$T_2$
are the only strongly
![]() $\mathcal {F}_{T_1T_2}(C_1C_2)$
-closed subgroups of
$\mathcal {F}_{T_1T_2}(C_1C_2)$
-closed subgroups of
![]() $T_1T_2$
which are isomorphic to
$T_1T_2$
which are isomorphic to
![]() $Q_8$
. Similarly, in order to prove (iv), it suffices to show that if
$Q_8$
. Similarly, in order to prove (iv), it suffices to show that if
![]() $n \ge 7$
, then
$n \ge 7$
, then
![]() $T_1$
is the only subgroup of
$T_1$
is the only subgroup of
![]() $T_1T_2$
which centralizes
$T_1T_2$
which centralizes
![]() $T_2$
, which is isomorphic to
$T_2$
, which is isomorphic to
![]() $Q_8$
, and which is strongly closed in
$Q_8$
, and which is strongly closed in
![]() $\mathcal {F}_{T_1T_2}(C_1C_2)$
.
$\mathcal {F}_{T_1T_2}(C_1C_2)$
.
Continue to assume that
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. In order to prove the two statements just mentioned, we need some observations. As
$5 \ \mathrm {mod} \ 8$
. In order to prove the two statements just mentioned, we need some observations. As
![]() $C_1 \cong SL_2(q)$
, we have that
$C_1 \cong SL_2(q)$
, we have that
![]() $C_1$
is not
$C_1$
is not
![]() $2$
-nilpotent. So
$2$
-nilpotent. So
![]() $\mathcal {F}_{T_1}(C_1)$
is not nilpotent by [Reference Linckelmann39, Theorem 1.4]. Again, by [Reference Linckelmann39, Theorem 1.4], it follows that
$\mathcal {F}_{T_1}(C_1)$
is not nilpotent by [Reference Linckelmann39, Theorem 1.4]. Again, by [Reference Linckelmann39, Theorem 1.4], it follows that
![]() $\mathrm {Aut}_{C_1}(T_1)$
is not a
$\mathrm {Aut}_{C_1}(T_1)$
is not a
![]() $2$
-group. So
$2$
-group. So
![]() $\mathrm {Aut}_{C_1}(T_1)$
has an element of order
$\mathrm {Aut}_{C_1}(T_1)$
has an element of order
![]() $3$
. Similarly, if
$3$
. Similarly, if
![]() $n = 6$
, then
$n = 6$
, then
![]() $\mathrm {Aut}_{C_2}(T_2)$
has an element of order
$\mathrm {Aut}_{C_2}(T_2)$
has an element of order
![]() $3$
. It follows that there is an element
$3$
. It follows that there is an element
![]() $\alpha \in \mathrm {Aut}_{C_1C_2}(T_1T_2)$
such that
$\alpha \in \mathrm {Aut}_{C_1C_2}(T_1T_2)$
such that
![]() $\alpha |_{T_1,T_1}$
has order
$\alpha |_{T_1,T_1}$
has order
![]() $3$
, while
$3$
, while
![]() $\alpha |_{T_2,T_2} = \mathrm {id}_{T_2}$
. Moreover, if
$\alpha |_{T_2,T_2} = \mathrm {id}_{T_2}$
. Moreover, if
![]() $n = 6$
, then there is an element
$n = 6$
, then there is an element
![]() $\beta \in \mathrm {Aut}_{C_1C_2}(T_1T_2)$
such that
$\beta \in \mathrm {Aut}_{C_1C_2}(T_1T_2)$
such that
![]() $\beta |_{T_1,T_1} = \mathrm {id}_{T_1}$
, while
$\beta |_{T_1,T_1} = \mathrm {id}_{T_1}$
, while
![]() $\beta |_{T_2,T_2}$
has order
$\beta |_{T_2,T_2}$
has order
![]() $3$
.
$3$
.
Continue to assume that
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. If
$5 \ \mathrm {mod} \ 8$
. If
![]() $n = 6$
, then the observations in the preceding two paragraphs show together with Lemma 2.15 that
$n = 6$
, then the observations in the preceding two paragraphs show together with Lemma 2.15 that
![]() $T_1$
and
$T_1$
and
![]() $T_2$
are the only strongly
$T_2$
are the only strongly
![]() $\mathcal {F}_{T_1T_2}(C_1C_2)$
-closed subgroups of
$\mathcal {F}_{T_1T_2}(C_1C_2)$
-closed subgroups of
![]() $T_1T_2$
which are isomorphic to
$T_1T_2$
which are isomorphic to
![]() $Q_8$
. As observed above, this is enough to conclude that (iii) holds. If
$Q_8$
. As observed above, this is enough to conclude that (iii) holds. If
![]() $n \ge 7$
, then we may apply the observations in the preceding two paragraphs together with Lemma 2.15 to conclude that if
$n \ge 7$
, then we may apply the observations in the preceding two paragraphs together with Lemma 2.15 to conclude that if
![]() $T_0$
is a strongly
$T_0$
is a strongly
![]() $\mathcal {F}_{T_1T_2}(C_1C_2)$
-closed subgroup of
$\mathcal {F}_{T_1T_2}(C_1C_2)$
-closed subgroup of
![]() $T_1T_2$
such that
$T_1T_2$
such that
![]() $T_0 \cong Q_8$
and such that
$T_0 \cong Q_8$
and such that
![]() $T_0$
centralizes
$T_0$
centralizes
![]() $T_2$
, then
$T_2$
, then
![]() $T_0 = T_1$
. As observed above, this is enough to conclude that (iv) holds.
$T_0 = T_1$
. As observed above, this is enough to conclude that (iv) holds.
Noticing that the
![]() $2$
-components of
$2$
-components of
![]() $C_{K_1}(u)$
are precisely the quasisimple members of
$C_{K_1}(u)$
are precisely the quasisimple members of
![]() $\lbrace C_1,C_2 \rbrace $
, we obtain (v) from Proposition 2.17 and Lemma 3.21.
$\lbrace C_1,C_2 \rbrace $
, we obtain (v) from Proposition 2.17 and Lemma 3.21.
Let G be as in Hypothesis 5.1. The group G realizes the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
. So, if R is a Sylow
$PSL_n(q)$
. So, if R is a Sylow
![]() $2$
-subgroup of G, then
$2$
-subgroup of G, then
![]() $\mathcal {F}_S(PSL_n(q)) \cong \mathcal {F}_R(G)$
. For the sake of simplicity, we will identify S with a Sylow
$\mathcal {F}_S(PSL_n(q)) \cong \mathcal {F}_R(G)$
. For the sake of simplicity, we will identify S with a Sylow
![]() $2$
-subgroup R of G and
$2$
-subgroup R of G and
![]() $\mathcal {F}_S(PSL_n(q))$
with
$\mathcal {F}_S(PSL_n(q))$
with
![]() $\mathcal {F}_R(G)$
. Hence, we will work under the following hypothesis.
$\mathcal {F}_R(G)$
. Hence, we will work under the following hypothesis.
Hypothesis 5.9. We will treat G as a group with
![]() $S \in \mathrm {Syl}_2(G)$
and
$S \in \mathrm {Syl}_2(G)$
and
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
.
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
.
The following lemma will play a key role in the proof of Theorem 5.2.
Lemma 5.10. Let x be an involution of S such that
![]() $C_S(x) \in \mathrm {Syl}_2(C_G(x))$
. Let
$C_S(x) \in \mathrm {Syl}_2(C_G(x))$
. Let
![]() $\mathcal {C}$
be a component of
$\mathcal {C}$
be a component of
![]() $\mathcal {F}_{C_S(x)}(C_G(x))$
, and let k be a natural number with
$\mathcal {F}_{C_S(x)}(C_G(x))$
, and let k be a natural number with
![]() $3 \le k < n$
. Then the following hold.
$3 \le k < n$
. Then the following hold.
-
(i) There is a unique
 $2$
-component Y of
$2$
-component Y of
 $C_G(x)$
such that
$C_G(x)$
such that
 $\mathcal {C} = \mathcal {F}_{C_S(x) \cap Y}(Y)$
.
$\mathcal {C} = \mathcal {F}_{C_S(x) \cap Y}(Y)$
. -
(ii) If
 $\mathcal {C}$
is isomorphic to the
$\mathcal {C}$
is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $SL_k(q)$
, then we either have that
$SL_k(q)$
, then we either have that
 $Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/O(SL_k^{\varepsilon }(q^{*}))$
for some nontrivial odd prime power
$Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/O(SL_k^{\varepsilon }(q^{*}))$
for some nontrivial odd prime power
 $q^{*}$
and some
$q^{*}$
and some
 $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
 $q \sim \varepsilon q^{*}$
; or
$q \sim \varepsilon q^{*}$
; or
 $k = 3$
,
$k = 3$
,
 $(q+1)_2 = 4$
, and
$(q+1)_2 = 4$
, and
 $Y/Z^{*}(Y) \cong M_{11}$
.
$Y/Z^{*}(Y) \cong M_{11}$
. -
(iii) If
 $\mathcal {C}$
is isomorphic to the
$\mathcal {C}$
is isomorphic to the
 $2$
-fusion system of a nontrivial quotient of
$2$
-fusion system of a nontrivial quotient of
 $SL_k(q^2)$
, then
$SL_k(q^2)$
, then
 $Y/O(Y)$
is isomorphic to a nontrivial quotient of
$Y/O(Y)$
is isomorphic to a nontrivial quotient of
 $SL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$SL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
 $q^{*}$
and some
$q^{*}$
and some
 $\varepsilon \in \lbrace +,-\rbrace $
with
$\varepsilon \in \lbrace +,-\rbrace $
with
 $q^2 \sim \varepsilon q^{*}$
.
$q^2 \sim \varepsilon q^{*}$
.
In order to prove Lemma 5.10, we need the following observation.
Lemma 5.11. Let
![]() $k \ge 6$
be a natural number satisfying
$k \ge 6$
be a natural number satisfying
![]() $P(k)$
. If
$P(k)$
. If
![]() $q_0$
is a nontrivial odd prime power and H is a known finite simple group realizing the
$q_0$
is a nontrivial odd prime power and H is a known finite simple group realizing the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_k(q_0)$
, then
$PSL_k(q_0)$
, then
![]() $H \cong PSL_k^{\varepsilon }(q^{*})$
for some
$H \cong PSL_k^{\varepsilon }(q^{*})$
for some
![]() $\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
$\varepsilon \in \lbrace +,- \rbrace $
and some nontrivial odd prime power
![]() $q^{*}$
with
$q^{*}$
with
![]() $\varepsilon q^{*} \sim q_0$
.
$\varepsilon q^{*} \sim q_0$
.
Proof. It suffices to show that any known finite simple group H satisfies (𝒞𝒦). Without using the CFSG, this is a priori not clear. It can be deduced from [Reference Gorenstein, Lyons and Solomon28, Proposition 5.2.9] if H is alternating, from [Reference Gorenstein, Lyons and Solomon28, Table 4.5.1] if H is a finite simple group of Lie type in odd characteristic, and from [Reference Gorenstein, Lyons and Solomon28, Table 5.3] if H is sporadic. If H is a finite simple group of Lie type in characteristic
![]() $2$
, then H satisfies (𝒞𝒦) since, in this case, no involution centralizer in H has a
$2$
, then H satisfies (𝒞𝒦) since, in this case, no involution centralizer in H has a
![]() $2$
-component (see [Reference Aschbacher5, 47.8 (3)]).
$2$
-component (see [Reference Aschbacher5, 47.8 (3)]).
Proof of Lemma 5.10
Since G satisfies (𝒞𝒦), we have that
![]() $Y/Z^{*}(Y)$
is a known finite simple group for each
$Y/Z^{*}(Y)$
is a known finite simple group for each
![]() $2$
-component Y of
$2$
-component Y of
![]() $C_G(x)$
. Proposition 2.17 implies that there is a unique
$C_G(x)$
. Proposition 2.17 implies that there is a unique
![]() $2$
-component Y of
$2$
-component Y of
![]() $C_G(x)$
with
$C_G(x)$
with
![]() $\mathcal {C} = \mathcal {F}_{C_S(x) \cap Y}(Y)$
. Thus, (i) holds.
$\mathcal {C} = \mathcal {F}_{C_S(x) \cap Y}(Y)$
. Thus, (i) holds.
Suppose that
![]() $\mathcal {C}$
is isomorphic to the
$\mathcal {C}$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_k(q_0)/Z$
, where either
$SL_k(q_0)/Z$
, where either
![]() $q_0 = q$
and
$q_0 = q$
and
![]() $Z = 1$
, or
$Z = 1$
, or
![]() $q_0 = q^2$
and
$q_0 = q^2$
and
![]() $Z \le Z(SL_k(q^2))$
. In order to prove (ii) and (iii), we need the following three claims.
$Z \le Z(SL_k(q^2))$
. In order to prove (ii) and (iii), we need the following three claims.
(1) The
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $Y/Z^{*}(Y)$
and
$Y/Z^{*}(Y)$
and
![]() $PSL_k(q_0)$
are isomorphic.
$PSL_k(q_0)$
are isomorphic.
As
![]() $\mathcal {C} = \mathcal {F}_{C_S(x) \cap Y}(Y)$
, we have that the
$\mathcal {C} = \mathcal {F}_{C_S(x) \cap Y}(Y)$
, we have that the
![]() $2$
-fusion system of Y is isomorphic to the
$2$
-fusion system of Y is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_k(q_0)/Z$
. So, by Corollary 2.12, the
$SL_k(q_0)/Z$
. So, by Corollary 2.12, the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $Y/O(Y)$
is isomorphic to the
$Y/O(Y)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_k(q_0)/Z$
. Lemma 2.14 implies that the
$SL_k(q_0)/Z$
. Lemma 2.14 implies that the
![]() $2$
-fusion systems of
$2$
-fusion systems of
![]() $Y/Z^{*}(Y)$
and
$Y/Z^{*}(Y)$
and
![]() $PSL_k(q_0)$
are isomorphic.
$PSL_k(q_0)$
are isomorphic.
(2) We have
![]() $Y/Z^{*}(Y) \cong PSL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$Y/Z^{*}(Y) \cong PSL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $q_0 \sim \varepsilon q^{*}$
, or
$q_0 \sim \varepsilon q^{*}$
, or
![]() $k = 3$
,
$k = 3$
,
![]() $(q_0+1)_2 = 4$
and
$(q_0+1)_2 = 4$
and
![]() $Y/Z^{*}(Y) \cong M_{11}$
.
$Y/Z^{*}(Y) \cong M_{11}$
.
If
![]() $k = 3$
, then it follows from (1) and Proposition 4.2. If
$k = 3$
, then it follows from (1) and Proposition 4.2. If
![]() $k \in \lbrace 4, 5 \rbrace $
, then it follows from (1) together with Propositions 4.4 and 4.5. Assume now that
$k \in \lbrace 4, 5 \rbrace $
, then it follows from (1) together with Propositions 4.4 and 4.5. Assume now that
![]() $k \ge 6$
. By Hypothesis 5.1 and since
$k \ge 6$
. By Hypothesis 5.1 and since
![]() $k < n$
, we have that k satisfies
$k < n$
, we have that k satisfies
![]() $P(k)$
. Since
$P(k)$
. Since
![]() $Y/Z^{*}(Y)$
is a known finite simple group, the claim follows from (1) and Lemma 5.11.
$Y/Z^{*}(Y)$
is a known finite simple group, the claim follows from (1) and Lemma 5.11.
(3) Suppose that
![]() $Y/Z^{*}(Y) \cong PSL_k^{\varepsilon }(q^{*})$
, where
$Y/Z^{*}(Y) \cong PSL_k^{\varepsilon }(q^{*})$
, where
![]() $q^{*}$
and
$q^{*}$
and
![]() $\varepsilon $
are as in (2). Then we have
$\varepsilon $
are as in (2). Then we have
![]() $Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/U$
, where
$Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/U$
, where
![]() $U \le Z(SL_k^{\varepsilon }(q^{*}))$
and the index of U in
$U \le Z(SL_k^{\varepsilon }(q^{*}))$
and the index of U in
![]() $Z(SL_k^{\varepsilon }(q^{*}))$
is equal to the
$Z(SL_k^{\varepsilon }(q^{*}))$
is equal to the
![]() $2$
-part of
$2$
-part of
![]() $|Z(SL_k(q_0))/Z|$
.
$|Z(SL_k(q_0))/Z|$
.
The group
![]() $Y/O(Y)$
is a perfect central extension of
$Y/O(Y)$
is a perfect central extension of
![]() $PSL_k^{\varepsilon }(q^{*})$
. Since
$PSL_k^{\varepsilon }(q^{*})$
. Since
![]() $Y/O(Y)$
is core-free, the center of
$Y/O(Y)$
is core-free, the center of
![]() $Y/O(Y)$
is a
$Y/O(Y)$
is a
![]() $2$
-group. So, by Lemmas 3.1 and 3.2, there is a central subgroup U of
$2$
-group. So, by Lemmas 3.1 and 3.2, there is a central subgroup U of
![]() $SL_k^{\varepsilon }(q^{*})$
with
$SL_k^{\varepsilon }(q^{*})$
with
![]() $Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/U$
. The claim now follows from
$Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/U$
. The claim now follows from
 $$ \begin{align*} |PSL_k(q_0)|_2|Z(SL_k(q_0))/Z|_2 &= |SL_k(q_0)/Z|_2 \\ &= |Y|_2 \\ &= |Y/Z^{*}(Y)|_2 |Z(Y/O(Y))| \\ &= |PSL_k(q_0)|_2 |Z(SL_k^{\varepsilon}(q^{*}))/U|. \end{align*} $$
$$ \begin{align*} |PSL_k(q_0)|_2|Z(SL_k(q_0))/Z|_2 &= |SL_k(q_0)/Z|_2 \\ &= |Y|_2 \\ &= |Y/Z^{*}(Y)|_2 |Z(Y/O(Y))| \\ &= |PSL_k(q_0)|_2 |Z(SL_k^{\varepsilon}(q^{*}))/U|. \end{align*} $$
Here, the second equality follows from the fact that Y realizes
![]() $\mathcal {C}$
, the third one holds since
$\mathcal {C}$
, the third one holds since
![]() $|Z^{*}(Y)|_2 = |Z^{*}(Y)/O(Y)|_2 = |Z(Y/O(Y))|_2 = |Z(Y/O(Y))|$
, and the fourth one follows from (1).
$|Z^{*}(Y)|_2 = |Z^{*}(Y)/O(Y)|_2 = |Z(Y/O(Y))|_2 = |Z(Y/O(Y))|$
, and the fourth one follows from (1).
Assume that
![]() $q_0 = q$
and
$q_0 = q$
and
![]() $Z = 1$
. By (2) and (3), one of the following holds: either
$Z = 1$
. By (2) and (3), one of the following holds: either
![]() $k=3$
,
$k=3$
,
![]() $(q+1)_2 = 4$
and
$(q+1)_2 = 4$
and
![]() $Y/Z^{*}(Y) \cong M_{11}$
or
$Y/Z^{*}(Y) \cong M_{11}$
or
![]() $Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/U$
, where
$Y/O(Y) \cong SL_k^{\varepsilon }(q^{*})/U$
, where
![]() $q^{*}$
is a nontrivial odd prime power,
$q^{*}$
is a nontrivial odd prime power,
![]() $\varepsilon \in \lbrace +,- \rbrace $
,
$\varepsilon \in \lbrace +,- \rbrace $
,
![]() $q \sim \varepsilon q^{*}$
,
$q \sim \varepsilon q^{*}$
,
![]() $U \le Z(SL_k^{\varepsilon }(q^{*}))$
and the index of U in
$U \le Z(SL_k^{\varepsilon }(q^{*}))$
and the index of U in
![]() $Z(SL_k^{\varepsilon }(q^{*}))$
is equal to the
$Z(SL_k^{\varepsilon }(q^{*}))$
is equal to the
![]() $2$
-part of
$2$
-part of
![]() $|Z(SL_k(q))|$
. Assume that the latter holds. As
$|Z(SL_k(q))|$
. Assume that the latter holds. As
![]() $q \sim \varepsilon q^{*}$
, we have
$q \sim \varepsilon q^{*}$
, we have
![]() $(q-1)_2 = (\varepsilon q^{*} - 1)_2 = (q^{*}-\varepsilon )_2$
. Since
$(q-1)_2 = (\varepsilon q^{*} - 1)_2 = (q^{*}-\varepsilon )_2$
. Since
![]() $|Z(SL_k(q))| = (k,q-1)$
and
$|Z(SL_k(q))| = (k,q-1)$
and
![]() $|Z(SL_k^{\varepsilon }(q^{*}))| = (k,q^{*}-\varepsilon )$
, it follows that the
$|Z(SL_k^{\varepsilon }(q^{*}))| = (k,q^{*}-\varepsilon )$
, it follows that the
![]() $2$
-part of
$2$
-part of
![]() $|Z(SL_k(q))|$
is equal to the
$|Z(SL_k(q))|$
is equal to the
![]() $2$
-part of
$2$
-part of
![]() $|Z(SL_k^{\varepsilon }(q^{*}))|$
. It follows that
$|Z(SL_k^{\varepsilon }(q^{*}))|$
. It follows that
![]() $U=O(Z(SL_k^{\varepsilon }(q^{*}))) = O(SL_k^{\varepsilon }(q^{*}))$
. This completes the proof of (ii).
$U=O(Z(SL_k^{\varepsilon }(q^{*}))) = O(SL_k^{\varepsilon }(q^{*}))$
. This completes the proof of (ii).
Assume now that
![]() $q_0 = q^2$
. Then, since
$q_0 = q^2$
. Then, since
![]() $q^2 \equiv 1 \ \mathrm {mod} \ 4$
, (2) and (3) imply that
$q^2 \equiv 1 \ \mathrm {mod} \ 4$
, (2) and (3) imply that
![]() $Y/O(Y)$
is isomorphic to a nontrivial quotient of
$Y/O(Y)$
is isomorphic to a nontrivial quotient of
![]() $SL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$SL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $q^2 \sim \varepsilon q^{*}$
. Thus, (iii) holds.
$q^2 \sim \varepsilon q^{*}$
. Thus, (iii) holds.
6
 $2$
-components of involution centralizers
$2$
-components of involution centralizers
In this section, we continue to assume Hypotheses 5.1 and 5.9. We will use the notation introduced in the last section without further explanation.
The main goal of this section is to describe the
![]() $2$
-components and the solvable
$2$
-components and the solvable
![]() $2$
-components of the centralizers of involutions of G.
$2$
-components of the centralizers of involutions of G.
6.1 The subgroups K and L of
 $C_G(t)$
$C_G(t)$
We start by considering
![]() $C_G(t)$
. Let
$C_G(t)$
. Let
![]() $\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. Since
$\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. Since
![]() $\langle t \rangle $
is fully
$\langle t \rangle $
is fully
![]() $\mathcal {F}$
-centralized, we have that
$\mathcal {F}$
-centralized, we have that
![]() $T = C_S(t) \in \mathrm {Syl}_2(C_G(t))$
. Also, note that
$T = C_S(t) \in \mathrm {Syl}_2(C_G(t))$
. Also, note that
![]() $\mathcal {F}_T(C_G(t)) = C_{\mathcal {F}}(\langle t \rangle ) = \mathcal {F}_T(C_{PSL_n(q)}(t))$
.
$\mathcal {F}_T(C_G(t)) = C_{\mathcal {F}}(\langle t \rangle ) = \mathcal {F}_T(C_{PSL_n(q)}(t))$
.
Proposition 6.1. There is a unique
![]() $2$
-component K of
$2$
-component K of
![]() $C_G(t)$
such that
$C_G(t)$
such that
![]() $\mathcal {C}_1 = \mathcal {F}_{T \cap K}(K)$
. We have
$\mathcal {C}_1 = \mathcal {F}_{T \cap K}(K)$
. We have
![]() $K/O(K) \cong SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
for some nontrivial odd prime power
$K/O(K) \cong SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $q \sim \varepsilon q^{*}$
. Moreover, K is a normal subgroup of
$q \sim \varepsilon q^{*}$
. Moreover, K is a normal subgroup of
![]() $C_G(t)$
.
$C_G(t)$
.
Proof. Set
![]() $\mathcal {F} := \mathcal {F}_S(G)$
. By Lemma 5.3,
$\mathcal {F} := \mathcal {F}_S(G)$
. By Lemma 5.3,
![]() $\mathcal {C}_1$
is a component of
$\mathcal {C}_1$
is a component of
![]() $C_{\mathcal {F}}(\langle t \rangle )$
. Lemma 5.10 (i) implies that there is a unique
$C_{\mathcal {F}}(\langle t \rangle )$
. Lemma 5.10 (i) implies that there is a unique
![]() $2$
-component K of
$2$
-component K of
![]() $C_G(t)$
such that
$C_G(t)$
such that
![]() $\mathcal {C}_1 = \mathcal {F}_{T \cap K}(K)$
. By definition, the component
$\mathcal {C}_1 = \mathcal {F}_{T \cap K}(K)$
. By definition, the component
![]() $\mathcal {C}_1$
is isomorphic to the
$\mathcal {C}_1$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_{n-2}(q)$
. Lemma 5.10 (ii) implies that
$SL_{n-2}(q)$
. Lemma 5.10 (ii) implies that
![]() $K/O(K) \cong SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
for some nontrivial odd prime power
$K/O(K) \cong SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $q \sim \varepsilon q^{*}$
.
$q \sim \varepsilon q^{*}$
.
It remains to show that K is a normal subgroup of
![]() $C_G(t)$
. Suppose that
$C_G(t)$
. Suppose that
![]() $\widetilde {K}$
is a
$\widetilde {K}$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_G(t)$
such that
$C_G(t)$
such that
![]() $K \cong \widetilde {K}$
. Set
$K \cong \widetilde {K}$
. Set
![]() $\widetilde {\mathcal {C}} := \mathcal {F}_{T \cap \widetilde {K}}(\widetilde {K})$
. Since
$\widetilde {\mathcal {C}} := \mathcal {F}_{T \cap \widetilde {K}}(\widetilde {K})$
. Since
![]() $\widetilde K$
is subnormal in
$\widetilde K$
is subnormal in
![]() $C_G(t)$
, it easily follows from [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 6.2] that
$C_G(t)$
, it easily follows from [Reference Aschbacher, Kessar and Oliver10, Part I, Proposition 6.2] that
![]() $\widetilde {\mathcal {C}}$
is subnormal in
$\widetilde {\mathcal {C}}$
is subnormal in
![]() $C_{\mathcal {F}}(\langle t \rangle )$
. Moreover,
$C_{\mathcal {F}}(\langle t \rangle )$
. Moreover,
![]() $\widetilde {\mathcal {C}} \cong \mathcal {C}_1$
as
$\widetilde {\mathcal {C}} \cong \mathcal {C}_1$
as
![]() $\widetilde {K} \cong K$
. Hence,
$\widetilde {K} \cong K$
. Hence,
![]() $\widetilde {\mathcal {C}}$
is a component of
$\widetilde {\mathcal {C}}$
is a component of
![]() $C_{\mathcal {F}}(\langle t \rangle )$
. But as a consequence of Lemma 5.3, there is no component of
$C_{\mathcal {F}}(\langle t \rangle )$
. But as a consequence of Lemma 5.3, there is no component of
![]() $C_{\mathcal {F}}(\langle t \rangle )$
which is isomorphic to
$C_{\mathcal {F}}(\langle t \rangle )$
which is isomorphic to
![]() $\mathcal {C}_1$
and different from
$\mathcal {C}_1$
and different from
![]() $\mathcal {C}_1$
. So we have
$\mathcal {C}_1$
. So we have
![]() $\mathcal {C}_1 = \widetilde {\mathcal {C}}$
. The uniqueness in the first statement of the proposition implies that
$\mathcal {C}_1 = \widetilde {\mathcal {C}}$
. The uniqueness in the first statement of the proposition implies that
![]() $K = \widetilde {K}$
. Consequently,
$K = \widetilde {K}$
. Consequently,
![]() $C_G(t)$
has no
$C_G(t)$
has no
![]() $2$
-component which is different from K and isomorphic to K. So K is characteristic and hence normal in
$2$
-component which is different from K and isomorphic to K. So K is characteristic and hence normal in
![]() $C_G(t)$
.
$C_G(t)$
.
From now on, K,
![]() $q^{*}$
and
$q^{*}$
and
![]() $\varepsilon $
will always have the meanings given to them by Proposition 6.1.
$\varepsilon $
will always have the meanings given to them by Proposition 6.1.
Our next goal is to prove the existence and uniqueness of a normal subgroup
![]() of
of
![]() such that
such that
![]() and to show that the image
and to show that the image
![]() of K in
of K in
![]() and
and
![]() are the only subgroups of
are the only subgroups of
![]() which are components or solvable
which are components or solvable
![]() $2$
-components of
$2$
-components of
![]() . First, we need to prove some lemmas.
. First, we need to prove some lemmas.
Lemma 6.2. Let
![]() $A \in W$
and
$A \in W$
and
![]() $B \in V$
such that
$B \in V$
such that
![]() $\mathrm {det}(A)\mathrm {det}(B) = 1$
. Let
$\mathrm {det}(A)\mathrm {det}(B) = 1$
. Let
 $$ \begin{align*} m := \begin{pmatrix}A & \\ & B \end{pmatrix} Z(SL_n(q)) \in T. \end{align*} $$
$$ \begin{align*} m := \begin{pmatrix}A & \\ & B \end{pmatrix} Z(SL_n(q)) \in T. \end{align*} $$
Set
![]() . Then
. Then
![]() centralizes
centralizes
![]() if and only if
if and only if
![]() $A \in Z(GL_{n-2}(q))$
.
$A \in Z(GL_{n-2}(q))$
.
Proof. Let
![]() $\overline {\mathcal {C}_1}$
be the subsystem of
$\overline {\mathcal {C}_1}$
be the subsystem of
corresponding to
![]() $\mathcal {C}_1$
under the isomorphism from
$\mathcal {C}_1$
under the isomorphism from
![]() $\mathcal {F}_{T}(C_G(t))$
to
$\mathcal {F}_{T}(C_G(t))$
to
given by Corollary 2.12. By [Reference Henke33, Proposition 1], we have
Since
is a
![]() $2$
-element of
$2$
-element of
, we have
. Applying Lemma 2.13, it follows that the center of the fusion system
is equal to the center of
. In particular,
centralizes
if and only if
. By Lemma 5.5, this is the case if and only if
![]() $A \in Z(GL_{n-2}(q))$
.
$A \in Z(GL_{n-2}(q))$
.
Lemma 6.3. Suppose that
![]() $q^{*} = 3$
. Let
$q^{*} = 3$
. Let
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Then:
. Then:
-
(i) The factor group
 is a
is a
 $2$
-group.
$2$
-group. -
(ii) The centralizer
 is core-free.
is core-free. -
(iii) The factor group
 is core-free.
is core-free.
Proof. Clearly,
![]() is isomorphic to a subgroup of
is isomorphic to a subgroup of
![]() . Since
. Since
![]() $q^{*} = 3$
, we have that
$q^{*} = 3$
, we have that
![]() . By Propositions 3.41 and 3.43,
. By Propositions 3.41 and 3.43,
![]() is a
is a
![]() $2$
-group. So (i) holds.
$2$
-group. So (i) holds.
Set
![]() . As a consequence of (i),
. As a consequence of (i),
![]() is a
is a
![]() $2$
-group. Hence, in order to prove (ii), it suffices to show that
$2$
-group. Hence, in order to prove (ii), it suffices to show that
![]() is core-free. As
is core-free. As
![]() , we have
, we have
![]() . It follows that
. It follows that
![]() . By Corollary 3.8,
. By Corollary 3.8,
![]() is core-free. This easily implies that
is core-free. This easily implies that
![]() is core-free. It follows that
is core-free. It follows that
![]() is core-free. Consequently,
is core-free. Consequently,
![]() . So (ii) follows.
. So (ii) follows.
Finally, (iii) is true since
![]() is a
is a
![]() $2$
-group and
$2$
-group and
![]() is core-free.
is core-free.
Lemma 6.4. Let
![]() . Then there is a unique pair
. Then there is a unique pair
![]() $({A_1}^{+},{A_2}^{+})$
of normal subgroups
$({A_1}^{+},{A_2}^{+})$
of normal subgroups
![]() ${A_1}^{+}$
,
${A_1}^{+}$
,
![]() ${A_2}^{+}$
of
${A_2}^{+}$
of
![]() such that
such that
![]() ,
,
![]() ${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
,
${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
,
![]() ${A_2}^{+} \cong SL_{n-4}^{\varepsilon }(q^{*})$
and
${A_2}^{+} \cong SL_{n-4}^{\varepsilon }(q^{*})$
and
![]() . Moreover, the following hold.
. Moreover, the following hold.
-
(i)
 .
. -
(ii)
 .
. -
(iii) There is a group isomorphism
 under which
under which
 ${A_1}^{+}$
corresponds to the image of in
${A_1}^{+}$
corresponds to the image of in $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-4} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-4} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
 $SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
and under which
$SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
and under which
 ${A_2}^{+}$
corresponds to the image of in
${A_2}^{+}$
corresponds to the image of in $$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SL_{n-4}^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SL_{n-4}^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
 $SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
.
$SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
.
Proof. For each subsystem
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() $\mathcal {F}_T(C_G(t))$
, we use
$\mathcal {F}_T(C_G(t))$
, we use
![]() to denote the subsystem of
to denote the subsystem of
![]() corresponding to
corresponding to
![]() $\mathcal {G}$
under the isomorphism from
$\mathcal {G}$
under the isomorphism from
![]() $\mathcal {F}_T(C_G(t))$
to
$\mathcal {F}_T(C_G(t))$
to
![]() given by Corollary 2.12. Note that
given by Corollary 2.12. Note that
![]() .
.
Set
![]() $H := SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
. For each even natural number i with
$H := SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
. For each even natural number i with
![]() $2 \le i \le n-2$
, let
$2 \le i \le n-2$
, let
![]() $h_i$
be the image of
$h_i$
be the image of
![]() $\widetilde {h_i} := \mathrm {diag}(-1,\dots ,-1,1,\dots ,1) \in SL_{n-2}^{\varepsilon }(q^{*})$
in H, where
$\widetilde {h_i} := \mathrm {diag}(-1,\dots ,-1,1,\dots ,1) \in SL_{n-2}^{\varepsilon }(q^{*})$
in H, where
![]() $-1$
occurs precisely i times as a diagonal entry.
$-1$
occurs precisely i times as a diagonal entry.
We claim that there is a group isomorphism
![]() such that
such that
![]() for some even
for some even
![]() $2 \le i < n-2$
. By Proposition 6.1, we have
$2 \le i < n-2$
. By Proposition 6.1, we have
![]() . As a consequence of Lemmas 3.3 and 3.4, any involution of
. As a consequence of Lemmas 3.3 and 3.4, any involution of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
is conjugate to
$SL_{n-2}^{\varepsilon }(q^{*})$
is conjugate to
![]() $\widetilde {h_i}$
for some even
$\widetilde {h_i}$
for some even
![]() $2 \le i \le n-2$
. Since any involution of H is induced by an involution of
$2 \le i \le n-2$
. Since any involution of H is induced by an involution of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
, it follows that any involution of H is conjugate to
$SL_{n-2}^{\varepsilon }(q^{*})$
, it follows that any involution of H is conjugate to
![]() $h_i$
for some even
$h_i$
for some even
![]() $2 \le i \le n-2$
. As
$2 \le i \le n-2$
. As
![]() is an involution of
is an involution of
![]() , it follows that there is an isomorphism
, it follows that there is an isomorphism
![]() mapping
mapping
![]() to
to
![]() $h_i$
for some even
$h_i$
for some even
![]() $2 \le i \le n-2$
. Assume that
$2 \le i \le n-2$
. Assume that
![]() $i = n-2$
. Then
$i = n-2$
. Then
![]() is central in
is central in
![]() . Thus,
. Thus,
![]() and hence
and hence
![]() $u \in Z(\mathcal {C}_1)$
. This is a contradiction to Lemma 3.18 and the definition of
$u \in Z(\mathcal {C}_1)$
. This is a contradiction to Lemma 3.18 and the definition of
![]() $\mathcal {C}_1$
. So we have
$\mathcal {C}_1$
. So we have
![]() $i < n-2$
.
$i < n-2$
.
Set
![]() . Also, let
. Also, let
![]() $H_1$
be the image of
$H_1$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2-i} \end{pmatrix} \ : \ A \in SL_i^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-2-i} \end{pmatrix} \ : \ A \in SL_i^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
in H, and let
![]() $H_2$
be the image of
$H_2$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_i & \\ & B \end{pmatrix} \ : \ B \in SL_{n-2-i}^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_i & \\ & B \end{pmatrix} \ : \ B \in SL_{n-2-i}^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
in H. For
![]() $j \in \lbrace 1,2 \rbrace $
, let
$j \in \lbrace 1,2 \rbrace $
, let
![]() ${A_j}^{+}$
be the subgroup of
${A_j}^{+}$
be the subgroup of
![]() corresponding to
corresponding to
![]() $H_j$
under
$H_j$
under
![]() $\varphi $
.
$\varphi $
.
We now proceed in a number of steps in order to complete the proof.
(1) We have
![]() ,
,
![]() $[{A_1}^{+},{A_2}^{+}] = 1$
,
$[{A_1}^{+},{A_2}^{+}] = 1$
,
![]() ,
,
![]() and
and
![]() .
.
It is easy to note that
![]() $C_H(h)'$
is the central product of
$C_H(h)'$
is the central product of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
and that
$H_2$
and that
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are normal in
$H_2$
are normal in
![]() $C_H(h)$
. Therefore,
$C_H(h)$
. Therefore,
![]() is the central product of
is the central product of
![]() ${A_1}^{+}$
and
${A_1}^{+}$
and
![]() ${A_2}^{+}$
, and
${A_2}^{+}$
, and
![]() ${A_1}^{+}, {A_2}^{+}$
are normal in
${A_1}^{+}, {A_2}^{+}$
are normal in
![]() . By definition of
. By definition of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
, we have
$H_2$
, we have
![]() $h \in H_1$
and
$h \in H_1$
and
![]() $h \not \in H_2$
. Thus,
$h \not \in H_2$
. Thus,
![]() and
and
![]() .
.
(2) We have
![]() , and
, and
![]() contains every component of
contains every component of
![]() .
.
By Lemma 5.8 (i), we have that
![]() is fully
is fully
![]() $\overline {\mathcal {C}_1}$
-centralized. So we have
$\overline {\mathcal {C}_1}$
-centralized. So we have
![]() .
.
Set
![]() . Noticing that the
. Noticing that the
![]() $2$
-components of
$2$
-components of
![]() $C_H(h)$
are precisely the quasisimple members of
$C_H(h)$
are precisely the quasisimple members of
![]() $\lbrace H_1, H_2 \rbrace $
, we see from Proposition 2.17 that the components of
$\lbrace H_1, H_2 \rbrace $
, we see from Proposition 2.17 that the components of
![]() $\mathcal {F}_P(C_H(h))$
are precisely the quasisimple members of
$\mathcal {F}_P(C_H(h))$
are precisely the quasisimple members of
![]() $\lbrace \mathcal {F}_{P \cap H_1}(H_1), \mathcal {F}_{P \cap H_2}(H_2) \rbrace $
.
$\lbrace \mathcal {F}_{P \cap H_1}(H_1), \mathcal {F}_{P \cap H_2}(H_2) \rbrace $
.
Thus, the components of
![]() are precisely the quasisimple members of
are precisely the quasisimple members of
![]() .
.
(3)
![]() and
and
![]() are subgroups of
are subgroups of
![]() and are strongly closed in
and are strongly closed in
![]() .
.
We have
![]() by the focal subgroup theorem [Reference Gorenstein23, Chapter 7, Theorem 3.4]. So the claim follows from (1).
by the focal subgroup theorem [Reference Gorenstein23, Chapter 7, Theorem 3.4]. So the claim follows from (1).
(4) Suppose that
![]() $n = 6$
and
$n = 6$
and
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. Then we have
$5 \ \mathrm {mod} \ 8$
. Then we have
![]() $i = 2$
and hence
$i = 2$
and hence
![]() ${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*}) \cong {A_2}^{+}$
. Moreover,
${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*}) \cong {A_2}^{+}$
. Moreover,
![]() and
and
![]() .
.
Since
![]() $n = 6$
and
$n = 6$
and
![]() $2 \le i < n-2 = 4$
, we have
$2 \le i < n-2 = 4$
, we have
![]() $i = 2$
. Thus,
$i = 2$
. Thus,
![]() ${A_1}^{+} \cong H_1 \cong SL_2^{\varepsilon }(q^{*}) \cong H_2 \cong {A_2}^{+}$
. By Proposition 6.1, we have
${A_1}^{+} \cong H_1 \cong SL_2^{\varepsilon }(q^{*}) \cong H_2 \cong {A_2}^{+}$
. By Proposition 6.1, we have
![]() $q \sim \varepsilon q^{*}$
, whence
$q \sim \varepsilon q^{*}$
, whence
![]() $q^{*} \equiv 3$
or
$q^{*} \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. Clearly,
$5 \ \mathrm {mod} \ 8$
. Clearly,
![]() and
and
![]() . Lemma 3.12 implies that
. Lemma 3.12 implies that
![]() . By Lemma 5.8 (iii),
. By Lemma 5.8 (iii),
![]() and
and
![]() are the only subgroups of
are the only subgroups of
![]() which are isomorphic to
which are isomorphic to
![]() $Q_8$
and strongly closed in
$Q_8$
and strongly closed in
![]() . So, by (3),
. So, by (3),
![]() . We have
. We have
![]() , and
, and
![]() by (1). It follows that
by (1). It follows that
![]() and
and
![]() .
.
(5) Suppose that
![]() $n = 6$
and
$n = 6$
and
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
or that
$7 \ \mathrm {mod} \ 8$
or that
![]() $n \ge 7$
. Then we have
$n \ge 7$
. Then we have
![]() $i = 2$
, and hence
$i = 2$
, and hence
![]() ${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
and
${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
and
![]() ${A_2}^{+} \cong SL_{n-4}^{\varepsilon }(q^{*})$
. Moreover,
${A_2}^{+} \cong SL_{n-4}^{\varepsilon }(q^{*})$
. Moreover,
![]() and
and
![]() .
.
We begin by proving that
![]() . As a consequence of Lemma 5.8 (v),
. As a consequence of Lemma 5.8 (v),
![]() has a component with Sylow group
has a component with Sylow group
![]() . Applying (2), we may conclude that
. Applying (2), we may conclude that
![]() or
or
![]() . Since
. Since
![]() by (1), but
by (1), but
![]() , we have
, we have
![]() .
.
We show next that
![]() $i = 2$
. Using Proposition 3.19, or using the order formulas for
$i = 2$
. Using Proposition 3.19, or using the order formulas for
![]() $\vert SL_{n-4}(q^{*}) \vert $
and
$\vert SL_{n-4}(q^{*}) \vert $
and
![]() $\vert SU_{n-4}(q^{*}) \vert $
given by [Reference Grove32, Proposition 1.1 and Corollary 11.29], we see that
$\vert SU_{n-4}(q^{*}) \vert $
given by [Reference Grove32, Proposition 1.1 and Corollary 11.29], we see that
Using the order formulas cited above, we may conclude that
![]() $n-2-i = n-4$
, whence
$n-2-i = n-4$
, whence
![]() $i = 2$
. In particular,
$i = 2$
. In particular,
![]() ${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
and
${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
and
![]() ${A_2}^{+} \cong SL_{n-4}^{\varepsilon }(q^{*})$
.
${A_2}^{+} \cong SL_{n-4}^{\varepsilon }(q^{*})$
.
It remains to prove
![]() . If
. If
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \ \mathrm {mod} \ 8$
, then Lemma 5.8 (v) shows that
$7 \ \mathrm {mod} \ 8$
, then Lemma 5.8 (v) shows that
![]() has a component with Sylow group
has a component with Sylow group
![]() . Since
. Since
![]() , but
, but
![]() , we have
, we have
![]() by (2).
by (2).
Now suppose that
![]() $q \equiv 3$
or
$q \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
. Then we have
$5 \ \mathrm {mod} \ 8$
. Then we have
![]() $q^{*} \equiv 3$
or
$q^{*} \equiv 3$
or
![]() $5 \ \mathrm {mod} \ 8$
since
$5 \ \mathrm {mod} \ 8$
since
![]() $q \sim \varepsilon q^{*}$
. So, by Lemma 3.12, a Sylow
$q \sim \varepsilon q^{*}$
. So, by Lemma 3.12, a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() ${A_1}^{+}$
is isomorphic to
${A_1}^{+}$
is isomorphic to
![]() $Q_8$
. In particular,
$Q_8$
. In particular,
![]() . By (3),
. By (3),
![]() is a subgroup of
is a subgroup of
![]() and is strongly closed in
and is strongly closed in
![]() . Moreover, by (1),
. Moreover, by (1),
![]() centralizes
centralizes
![]() . Lemma 5.8 (iv) now implies that
. Lemma 5.8 (iv) now implies that
![]() .
.
(6)
![]() .
.
We have
![]() ${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
by (4) and (5), and
${A_1}^{+} \cong SL_2^{\varepsilon }(q^{*})$
by (4) and (5), and
![]() by (1). It follows that
by (1). It follows that
![]() . By (1),
. By (1),
![]() ${A_1}^{+} \cap {A_2}^{+} \le Z({A_1}^{+})$
and
${A_1}^{+} \cap {A_2}^{+} \le Z({A_1}^{+})$
and
![]() . It follows that
. It follows that
![]() ${A_1}^{+} \cap {A_2}^{+} = 1$
. So (1) implies that
${A_1}^{+} \cap {A_2}^{+} = 1$
. So (1) implies that
![]() .
.
(7) Assume that
![]() ${A_1}^{\circ }$
and
${A_1}^{\circ }$
and
![]() ${A_2}^{\circ }$
are normal subgroups of
${A_2}^{\circ }$
are normal subgroups of
![]() such that
such that
![]() ,
,
![]() ${A_1}^{\circ } \cong SL_2^{\varepsilon }(q^{*})$
,
${A_1}^{\circ } \cong SL_2^{\varepsilon }(q^{*})$
,
![]() ${A_2}^{\circ } \cong SL_{n-4}^{\varepsilon }(q^{*})$
and
${A_2}^{\circ } \cong SL_{n-4}^{\varepsilon }(q^{*})$
and
![]() . Then
. Then
![]() ${A_1}^{\circ } = {A_1}^{+}$
and
${A_1}^{\circ } = {A_1}^{+}$
and
![]() ${A_2}^{\circ } = {A_2}^{+}$
.
${A_2}^{\circ } = {A_2}^{+}$
.
Let
![]() $j \in \lbrace 1,2 \rbrace $
. As a consequence of (4) and (5),
$j \in \lbrace 1,2 \rbrace $
. As a consequence of (4) and (5),
![]() ${A_j}^{+}$
is either quasisimple or isomorphic to
${A_j}^{+}$
is either quasisimple or isomorphic to
![]() $SL_2(3)$
. In either case,
$SL_2(3)$
. In either case,
![]() ${A_j}^{+}$
is indecomposable, i.e.,
${A_j}^{+}$
is indecomposable, i.e.,
![]() ${A_j}^{+}$
cannot be written as an internal direct product of two proper normal subgroups. Moreover,
${A_j}^{+}$
cannot be written as an internal direct product of two proper normal subgroups. Moreover,
![]() $\vert {A_1}^{+}/({A_1}^{+})' \vert $
and
$\vert {A_1}^{+}/({A_1}^{+})' \vert $
and
![]() $\vert Z({A_{2}}^{+}) \vert $
as well as
$\vert Z({A_{2}}^{+}) \vert $
as well as
![]() $\vert {A_2}^{+}/({A_2}^{+})' \vert $
and
$\vert {A_2}^{+}/({A_2}^{+})' \vert $
and
![]() $\vert Z({A_{1}}^{+}) \vert $
are coprime. A consequence of the Krull–Remak–Schmidt theorem, namely [Reference Huppert and Endliche Gruppen35, Kapitel I, Satz 12.6], implies that
$\vert Z({A_{1}}^{+}) \vert $
are coprime. A consequence of the Krull–Remak–Schmidt theorem, namely [Reference Huppert and Endliche Gruppen35, Kapitel I, Satz 12.6], implies that
![]() $\lbrace {A_1}^{+}, {A_2}^{+} \rbrace = \lbrace {A_1}^{\circ }, {A_2}^{\circ } \rbrace $
. Since
$\lbrace {A_1}^{+}, {A_2}^{+} \rbrace = \lbrace {A_1}^{\circ }, {A_2}^{\circ } \rbrace $
. Since
![]() and
and
![]() , we have
, we have
![]() ${A_1}^{+} = {A_1}^{\circ }$
and
${A_1}^{+} = {A_1}^{\circ }$
and
![]() ${A_2}^{+} = {A_2}^{\circ }$
.
${A_2}^{+} = {A_2}^{\circ }$
.
(8) The isomorphism
![]() maps
maps
![]() ${A_1}^{+}$
to the image of
${A_1}^{+}$
to the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-4} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-4} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
in H and
![]() ${A_2}^{+}$
to the image of
${A_2}^{+}$
to the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SL_{n-4}^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_2 & \\ & B \end{pmatrix} \ : \ B \in SL_{n-4}^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
in H.
By (4) and (5), we have
![]() $i = 2$
. So the claim follows from the definitions of
$i = 2$
. So the claim follows from the definitions of
![]() ${A_1}^{+}$
and
${A_1}^{+}$
and
![]() ${A_2}^{+}$
.
${A_2}^{+}$
.
From now on,
![]() ${A_1}^{+}$
and
${A_1}^{+}$
and
![]() ${A_2}^{+}$
will always have the meanings given to them by Lemma 6.4.
${A_2}^{+}$
will always have the meanings given to them by Lemma 6.4.
Lemma 6.5. Let
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Then
. Then
![]() ${A_1}^{+}$
and
${A_1}^{+}$
and
![]() ${A_2}^{+}$
are normal subgroups of
${A_2}^{+}$
are normal subgroups of
![]() .
.
Proof. We have
![]() as
as
![]() . Thus,
. Thus,
![]() . Having this observed, the lemma is immediate from Lemma 6.4.
. Having this observed, the lemma is immediate from Lemma 6.4.
Let
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Next, we introduce certain preimages of
. Next, we introduce certain preimages of
![]() ${A_1}^{+}$
and
${A_1}^{+}$
and
![]() ${A_2}^{+}$
in
${A_2}^{+}$
in
![]() $C_{C}(u)$
. By Corollary 2.2, we have
$C_{C}(u)$
. By Corollary 2.2, we have
![]() . We may see from Proposition 2.4 that there is a bijection from the set of
. We may see from Proposition 2.4 that there is a bijection from the set of
![]() $2$
-components of
$2$
-components of
![]() $C_C(u)$
to the set of
$C_C(u)$
to the set of
![]() $2$
-components of
$2$
-components of
![]() sending each
sending each
![]() $2$
-component A of
$2$
-component A of
![]() $C_C(u)$
to
$C_C(u)$
to
![]() .
.
Suppose that
![]() $q^{*} \ne 3$
. Then
$q^{*} \ne 3$
. Then
![]() ${A_1}^{+}$
is a component and hence a
${A_1}^{+}$
is a component and hence a
![]() $2$
-component of
$2$
-component of
![]() . We use
. We use
![]() $A_1$
to denote the
$A_1$
to denote the
![]() $2$
-component of
$2$
-component of
![]() $C_{C}(u)$
corresponding to
$C_{C}(u)$
corresponding to
![]() ${A_1}^{+}$
under the bijection described above.
${A_1}^{+}$
under the bijection described above.
Suppose that
![]() $q^{*} \ne 3$
or
$q^{*} \ne 3$
or
![]() $n \ge 7$
. Then
$n \ge 7$
. Then
![]() ${A_2}^{+}$
is a component and hence a
${A_2}^{+}$
is a component and hence a
![]() $2$
-component of
$2$
-component of
![]() . We use
. We use
![]() $A_2$
to denote the
$A_2$
to denote the
![]() $2$
-component of
$2$
-component of
![]() $C_{C}(u)$
corresponding to
$C_{C}(u)$
corresponding to
![]() ${A_2}^{+}$
under the bijection described above.
${A_2}^{+}$
under the bijection described above.
Suppose that
![]() $q^{*} = 3$
. By Lemma 6.3 (ii),
$q^{*} = 3$
. By Lemma 6.3 (ii),
![]() . So the factor group
. So the factor group
![]() $C_{C}(u)/(C_{C}(u) \cap O(C))$
is core-free, whence
$C_{C}(u)/(C_{C}(u) \cap O(C))$
is core-free, whence
![]() $O(C_{C}(u)) = C_{C}(u) \cap O(C)$
. Let
$O(C_{C}(u)) = C_{C}(u) \cap O(C)$
. Let
![]() $O(C_{C}(u)) \le A_1 \le C_{C}(u)$
such that
$O(C_{C}(u)) \le A_1 \le C_{C}(u)$
such that
![]() $A_1/O(C_{C}(u))$
corresponds to
$A_1/O(C_{C}(u))$
corresponds to
![]() ${A_1}^{+}$
under the natural group isomorphism
${A_1}^{+}$
under the natural group isomorphism
![]() . Furthermore, if
. Furthermore, if
![]() $n = 6$
, let
$n = 6$
, let
![]() $O(C_{C}(u)) \le A_2 \le C_{C}(u)$
such that
$O(C_{C}(u)) \le A_2 \le C_{C}(u)$
such that
![]() $A_2/O(C_{C}(u))$
corresponds to
$A_2/O(C_{C}(u))$
corresponds to
![]() ${A_2}^{+}$
under the natural group isomorphism
${A_2}^{+}$
under the natural group isomorphism
![]() .
.
Lemma 6.6. We have
![]() $T_1 \le A_1$
and
$T_1 \le A_1$
and
![]() $T_2 \le A_2$
.
$T_2 \le A_2$
.
Proof. Let
![]() $i \in \lbrace 1,2 \rbrace $
. Set
$i \in \lbrace 1,2 \rbrace $
. Set
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() .
.
Let
![]() $C_C(u) \cap O(C) \le \widetilde {A_i} \le C_C(u)$
such that
$C_C(u) \cap O(C) \le \widetilde {A_i} \le C_C(u)$
such that
![]() $\widetilde {A_i}/(C_C(u) \cap O(C))$
corresponds to
$\widetilde {A_i}/(C_C(u) \cap O(C))$
corresponds to
![]() ${A_i}^{+}$
under the natural group isomorphism
${A_i}^{+}$
under the natural group isomorphism
![]() . We have
. We have
![]() $T_i \le C_C(u)$
and, by Lemma 6.4,
$T_i \le C_C(u)$
and, by Lemma 6.4,
![]() . Thus,
. Thus,
![]() $T_i \le \widetilde {A_i}$
. If
$T_i \le \widetilde {A_i}$
. If
![]() ${A_i}^{+} \cong SL_2(3)$
, then we have
${A_i}^{+} \cong SL_2(3)$
, then we have
![]() $A_i = \widetilde {A_i}$
, and thus,
$A_i = \widetilde {A_i}$
, and thus,
![]() $T_i \le A_i$
. Assume now that
$T_i \le A_i$
. Assume now that
![]() ${A_i}^{+}$
is a component of
${A_i}^{+}$
is a component of
![]() . Then
. Then
![]() $A_i$
is the
$A_i$
is the
![]() $2$
-component of
$2$
-component of
![]() $C_C(u)$
associated to the
$C_C(u)$
associated to the
![]() $2$
-component
$2$
-component
![]() $\widetilde {A_i}/(C_C(u) \cap O(C))$
of
$\widetilde {A_i}/(C_C(u) \cap O(C))$
of
![]() $C_C(u)/(C_C(u) \cap O(C))$
. So, by Proposition 2.4,
$C_C(u)/(C_C(u) \cap O(C))$
. So, by Proposition 2.4,
![]() $A_i = O^{2'}(\widetilde {A_i})$
, and hence,
$A_i = O^{2'}(\widetilde {A_i})$
, and hence,
![]() $T_i \le A_i$
.
$T_i \le A_i$
.
Lemma 6.7. There is an element
![]() $g \in G$
such that
$g \in G$
such that
![]() ${T_1}^g = X_2$
and
${T_1}^g = X_2$
and
![]() ${X_2}^g = T_1$
. For each such
${X_2}^g = T_1$
. For each such
![]() $g \in G$
, we have
$g \in G$
, we have
![]() $u^g = t$
and
$u^g = t$
and
![]() $t^g = u$
.
$t^g = u$
.
Proof. The first statement easily follows from
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. By Lemma 3.12, the groups
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. By Lemma 3.12, the groups
![]() $T_1$
and
$T_1$
and
![]() $X_2$
are generalized quaternion. So u is the only involution of
$X_2$
are generalized quaternion. So u is the only involution of
![]() $T_1$
and t is the only involution of
$T_1$
and t is the only involution of
![]() $X_2$
. Thus,
$X_2$
. Thus,
![]() $u^g = t$
and
$u^g = t$
and
![]() $t^g = u$
for any
$t^g = u$
for any
![]() $g \in G$
with
$g \in G$
with
![]() ${T_1}^g = X_2$
and
${T_1}^g = X_2$
and
![]() ${X_2}^g = T_1$
.
${X_2}^g = T_1$
.
With the above lemmas at hand, we can now prove the following proposition.
Proposition 6.8. Take an element
![]() $g \in G$
such that
$g \in G$
such that
![]() ${T_1}^g = X_2$
and
${T_1}^g = X_2$
and
![]() ${X_2}^g = T_1$
. Set
${X_2}^g = T_1$
. Set
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Let
. Let
![]() $L := {A_1}^g$
. Then the following hold.
$L := {A_1}^g$
. Then the following hold.
-
(i)
 $L \le C_C(u)$
.
$L \le C_C(u)$
. -
(ii)
 is subnormal in
is subnormal in
 and
and
 .
. -
(iii) The subgroups
 and
and
 are the only subgroups of
are the only subgroups of
 which are components or solvable
which are components or solvable
 $2$
-components of
$2$
-components of
 . In particular,
. In particular,
 and
and
 are normal subgroups of
are normal subgroups of
 .
.
Proof. By Lemma 6.7, we have
![]() $t^g = u$
and
$t^g = u$
and
![]() $u^g = t$
. Hence,
$u^g = t$
. Hence,
![]() $C_C(u)^g = C_C(u)$
. As
$C_C(u)^g = C_C(u)$
. As
![]() $A_1$
is a subgroup of
$A_1$
is a subgroup of
![]() $C_C(u)$
, we thus have
$C_C(u)$
, we thus have
![]() $L = {A_1}^g \le C_C(u)$
. So (i) holds.
$L = {A_1}^g \le C_C(u)$
. So (i) holds.
Before proving (ii), we show that
![]() is a normal subgroup of
is a normal subgroup of
![]() containing
containing
![]() . Since
. Since
![]() , we have
, we have
![]() . Because of Lemma 6.6, we have
. Because of Lemma 6.6, we have
![]() $X_2 = {T_1}^g \le {A_1}^g = L$
. Thus,
$X_2 = {T_1}^g \le {A_1}^g = L$
. Thus,
![]() . By the definition of
. By the definition of
![]() $X_2$
and by Lemma 6.2, we have
$X_2$
and by Lemma 6.2, we have
![]() . Thus,
. Thus,
![]() .
.
Note that
![]() is generalized quaternion by Lemma 3.12 and in particular nonabelian.
is generalized quaternion by Lemma 3.12 and in particular nonabelian.
We now prove (ii) for the case
![]() $q^{*} \ne 3$
. Then
$q^{*} \ne 3$
. Then
![]() $A_1$
is a
$A_1$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_C(u)$
. As g normalizes
$C_C(u)$
. As g normalizes
![]() $C_C(u)$
and
$C_C(u)$
and
![]() $L = {A_1}^g$
, it follows that L is a
$L = {A_1}^g$
, it follows that L is a
![]() $2$
-component of
$2$
-component of
![]() $C_C(u)$
. So
$C_C(u)$
. So
![]() is a
is a
![]() $2$
-component of
$2$
-component of
![]() . Moreover, we have
. Moreover, we have
![]() $A_1/O(A_1) \cong SL_2(q^{*})$
since
$A_1/O(A_1) \cong SL_2(q^{*})$
since
![]() . Hence,
. Hence,
![]() $L/O(L)$
is isomorphic to
$L/O(L)$
is isomorphic to
![]() $SL_2(q^{*})$
. The group
$SL_2(q^{*})$
. The group
![]() is normal in
is normal in
![]() , and it is nonabelian since
, and it is nonabelian since
![]() . As
. As
![]() is quasisimple, it follows that
is quasisimple, it follows that
![]() . So
. So
![]() has odd index in
has odd index in
![]() . Since
. Since
![]() is a
is a
![]() $2$
-component of
$2$
-component of
![]() , we have
, we have
![]() . It follows that
. It follows that
![]() . Since
. Since
![]() is subnormal in
is subnormal in
![]() and
and
![]() , we have that
, we have that
![]() is subnormal in
is subnormal in
![]() . Hence,
. Hence,
![]() is subnormal in
is subnormal in
![]() . As
. As
![]() is core-free, we have
is core-free, we have
![]() . It follows that
. It follows that
![]() $O(L) = L \cap O(C)$
and hence
$O(L) = L \cap O(C)$
and hence
![]() . So we have proved (ii) for the case
. So we have proved (ii) for the case
![]() $q^{*} \ne 3$
.
$q^{*} \ne 3$
.
Assume now that
![]() $q^{*} = 3$
. Then
$q^{*} = 3$
. Then
![]() $O(C_C(u)) = C_C(u) \cap O(C)$
,
$O(C_C(u)) = C_C(u) \cap O(C)$
,
![]() $O(C_C(u)) \le A_1 \le C_C(u)$
, and
$O(C_C(u)) \le A_1 \le C_C(u)$
, and
![]() $A_1/O(C_C(u))$
corresponds to
$A_1/O(C_C(u))$
corresponds to
![]() ${A_1}^{+} \cong SL_2(3)$
under the natural isomorphism
${A_1}^{+} \cong SL_2(3)$
under the natural isomorphism
![]() . By Lemma 6.5,
. By Lemma 6.5,
![]() ${A_1}^{+}$
is normal in
${A_1}^{+}$
is normal in
![]() . Hence,
. Hence,
![]() $A_1/O(C_C(u))$
is a normal subgroup of
$A_1/O(C_C(u))$
is a normal subgroup of
![]() $C_C(u)/O(C_C(u))$
isomorphic to
$C_C(u)/O(C_C(u))$
isomorphic to
![]() $SL_2(3)$
. Since g normalizes
$SL_2(3)$
. Since g normalizes
![]() $C_C(u)$
and
$C_C(u)$
and
![]() $L = {A_1}^g$
, it follows that
$L = {A_1}^g$
, it follows that
![]() $O(C_C(u)) \le L$
and that
$O(C_C(u)) \le L$
and that
![]() $L/O(C_C(u))$
is a normal subgroup of
$L/O(C_C(u))$
is a normal subgroup of
![]() $C_C(u)/O(C_C(u))$
isomorphic to
$C_C(u)/O(C_C(u))$
isomorphic to
![]() $SL_2(3)$
. Since
$SL_2(3)$
. Since
![]() $L/O(C_C(u))$
corresponds to
$L/O(C_C(u))$
corresponds to
![]() under the natural isomorphism
under the natural isomorphism
![]() , it follows that
, it follows that
![]() is a normal subgroup of
is a normal subgroup of
![]() isomorphic to
isomorphic to
![]() $SL_2(3)$
. Recall that
$SL_2(3)$
. Recall that
![]() . As
. As
![]() has order
has order
![]() $24$
and
$24$
and
![]() has order
has order
![]() $8$
,
$8$
,
![]() either equals
either equals
![]() or has index
or has index
![]() $3$
in
$3$
in
![]() . However, if the latter holds, then
. However, if the latter holds, then
![]() is a normal subgroup of
is a normal subgroup of
![]() of order
of order
![]() $3$
, which is a contradiction to Lemma 6.3 (iii). Thus,
$3$
, which is a contradiction to Lemma 6.3 (iii). Thus,
![]() . As
. As
![]() and
and
![]() , it follows that
, it follows that
![]() is normal in
is normal in
![]() and hence subnormal in
and hence subnormal in
![]() . So we have proved (ii) for the case
. So we have proved (ii) for the case
![]() $q^{*} = 3$
.
$q^{*} = 3$
.
We now prove (iii). We have
![]() since
since
![]() and
and
![]() . Also,
. Also,
![]() since
since
![]() and
and
![]() . As a consequence of Lemma 5.4, the fusion system
. As a consequence of Lemma 5.4, the fusion system
![]() is nilpotent. Applying Lemma 2.18, we may conclude that
is nilpotent. Applying Lemma 2.18, we may conclude that
![]() and
and
![]() are the only subgroups of
are the only subgroups of
![]() which are components or solvable
which are components or solvable
![]() $2$
-components of
$2$
-components of
![]() . As
. As
![]() and
and
![]() are not isomorphic, both are characteristic and hence normal in
are not isomorphic, both are characteristic and hence normal in
![]() .
.
Let
![]() $E = \langle u, t \rangle $
. By construction, g acts on E and
$E = \langle u, t \rangle $
. By construction, g acts on E and
![]() $A_1 \trianglelefteq C_G(E)$
. Hence, the definition of L in Proposition 6.8 is independent of the choice of g. From now on, L will always have the meaning given to it by the above proposition.
$A_1 \trianglelefteq C_G(E)$
. Hence, the definition of L in Proposition 6.8 is independent of the choice of g. From now on, L will always have the meaning given to it by the above proposition.
6.2
 $2$
-components of centralizers of involutions conjugate to
$2$
-components of centralizers of involutions conjugate to
 $t_i$
,
$t_i$
,
 $i \ne 2$
$i \ne 2$
Having described the components and the solvable
![]() $2$
-components of the group
$2$
-components of the group
![]() $C_G(t)/O(C_G(t))$
, we now turn our attention to centralizers of involutions of G not conjugate to t.
$C_G(t)/O(C_G(t))$
, we now turn our attention to centralizers of involutions of G not conjugate to t.
First, we recall some notation from Section 5. Let
![]() $1 \le i < n$
. If i is even, then
$1 \le i < n$
. If i is even, then
![]() $t_i$
denotes the image of
$t_i$
denotes the image of
 $$ \begin{align*} \begin{pmatrix} I_{n-i} & \\ & -I_i \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} I_{n-i} & \\ & -I_i \end{pmatrix} \end{align*} $$
in
![]() $PSL_n(q)$
. We use
$PSL_n(q)$
. We use
![]() $\rho $
to denote an element of
$\rho $
to denote an element of
![]() $\mathbb {F}_q^{*}$
with order
$\mathbb {F}_q^{*}$
with order
![]() $(n,q-1)$
, and if
$(n,q-1)$
, and if
![]() $\rho $
is a square in
$\rho $
is a square in
![]() $\mathbb {F}_q$
, then
$\mathbb {F}_q$
, then
![]() $\mu $
denotes an element of
$\mu $
denotes an element of
![]() $\mathbb {F}_q^{*}$
with
$\mathbb {F}_q^{*}$
with
![]() $\mu ^2 = \rho $
. If n is even,
$\mu ^2 = \rho $
. If n is even,
![]() $\rho $
is a square in
$\rho $
is a square in
![]() $\mathbb {F}_q$
and i is odd, then
$\mathbb {F}_q$
and i is odd, then
![]() $t_i$
is defined to be the image of
$t_i$
is defined to be the image of
 $$ \begin{align*} \begin{pmatrix} \mu I_{n-i} & \\ & -\mu I_i \end{pmatrix} \in SL_n(q) \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \mu I_{n-i} & \\ & -\mu I_i \end{pmatrix} \in SL_n(q) \end{align*} $$
in
![]() $PSL_n(q)$
. It is easy to note that
$PSL_n(q)$
. It is easy to note that
![]() $t_i$
lies in T and hence in S whenever
$t_i$
lies in T and hence in S whenever
![]() $t_i$
is defined.
$t_i$
is defined.
Let
![]() $\mathcal {S}$
denote the set of all subgroups E of
$\mathcal {S}$
denote the set of all subgroups E of
![]() $PSL_n(q)$
such that there is some elementary abelian
$PSL_n(q)$
such that there is some elementary abelian
![]() $2$
-subgroup
$2$
-subgroup
![]() $\widetilde E \le SL_n(q)$
with
$\widetilde E \le SL_n(q)$
with
![]() $E = \widetilde {E} Z(SL_n(q))/Z(SL_n(q))$
. For each
$E = \widetilde {E} Z(SL_n(q))/Z(SL_n(q))$
. For each
![]() $3 \le i \le n$
, we define
$3 \le i \le n$
, we define
![]() $\mathcal {S}_i$
to be the set of all elements E of
$\mathcal {S}_i$
to be the set of all elements E of
![]() $\mathcal {S}$
such that E contains a
$\mathcal {S}$
such that E contains a
![]() $PSL_n(q)$
-conjugate of
$PSL_n(q)$
-conjugate of
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < i$
.
$2 \le j < i$
.
Lemma 6.9. Let
![]() $1 \le i < n$
such that
$1 \le i < n$
such that
![]() $t_i$
is defined. Assume that
$t_i$
is defined. Assume that
![]() $i \ne 2$
and that
$i \ne 2$
and that
![]() $i \le \frac {n}{2}$
if n is even. Let P be a Sylow
$i \le \frac {n}{2}$
if n is even. Let P be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{PSL_n(q)}(t_i)$
and
$C_{PSL_n(q)}(t_i)$
and
![]() $\mathcal {F} := \mathcal {F}_P(C_{PSL_n(q)}(t_i))$
. Then the following hold.
$\mathcal {F} := \mathcal {F}_P(C_{PSL_n(q)}(t_i))$
. Then the following hold.
-
(i) Assume that
 $i \not \in \lbrace 1,n-1 \rbrace $
. Then
$i \not \in \lbrace 1,n-1 \rbrace $
. Then
 $\mathcal {F}$
has precisely two components. Denoting them in a suitable way by
$\mathcal {F}$
has precisely two components. Denoting them in a suitable way by
 $\mathcal {E}_1$
and
$\mathcal {E}_1$
and
 $\mathcal {E}_2$
, the following hold.
$\mathcal {E}_2$
, the following hold.-
(a)
 $\mathcal {E}_1$
is isomorphic to the
$\mathcal {E}_1$
is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $SL_{n-i}(q)$
.
$SL_{n-i}(q)$
. -
(b)
 $\mathcal {E}_2$
is isomorphic to the
$\mathcal {E}_2$
is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $SL_i(q)$
.
$SL_i(q)$
. -
(c) Let
 $Y_1$
be the Sylow group of
$Y_1$
be the Sylow group of
 $\mathcal {E}_1$
, and let
$\mathcal {E}_1$
, and let
 $Y_2$
be the Sylow group of
$Y_2$
be the Sylow group of
 $\mathcal {E}_2$
. Then
$\mathcal {E}_2$
. Then
 $Y_1Y_2$
is strongly
$Y_1Y_2$
is strongly
 $\mathcal {F}$
-closed and
$\mathcal {F}$
-closed and
 $\mathcal {F}/Y_1Y_2$
is nilpotent. The group
$\mathcal {F}/Y_1Y_2$
is nilpotent. The group
 $Y_i$
, where
$Y_i$
, where
 $i \in \lbrace 1,2 \rbrace $
, contains a
$i \in \lbrace 1,2 \rbrace $
, contains a
 $PSL_n(q)$
-conjugate of t. Moreover, any elementary abelian subgroup of
$PSL_n(q)$
-conjugate of t. Moreover, any elementary abelian subgroup of
 $Y_1$
of rank at least
$Y_1$
of rank at least
 $2$
is contained in
$2$
is contained in
 $\mathcal {S}_{n-i}$
, and any elementary abelian subgroup of
$\mathcal {S}_{n-i}$
, and any elementary abelian subgroup of
 $Y_2$
of rank at least
$Y_2$
of rank at least
 $2$
is contained in
$2$
is contained in
 $\mathcal {S}_i$
.
$\mathcal {S}_i$
.
-
-
(ii) Assume that
 $i = 1$
or
$i = 1$
or
 $i = n-1$
. Then
$i = n-1$
. Then
 $\mathcal {F}$
has a unique component. This component is isomorphic to the
$\mathcal {F}$
has a unique component. This component is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $SL_{n-1}(q)$
. If Y is its Sylow group, then Y is strongly
$SL_{n-1}(q)$
. If Y is its Sylow group, then Y is strongly
 $\mathcal {F}$
-closed and
$\mathcal {F}$
-closed and
 $\mathcal {F}/Y$
is nilpotent. Moreover, any elementary abelian subgroup of Y of rank at least
$\mathcal {F}/Y$
is nilpotent. Moreover, any elementary abelian subgroup of Y of rank at least
 $2$
is contained in
$2$
is contained in
 $\mathcal {S}_{n-1}$
.
$\mathcal {S}_{n-1}$
.
Proof. Assume that
![]() $i \not \in \lbrace 1,n-1 \rbrace $
. By hypothesis, we have
$i \not \in \lbrace 1,n-1 \rbrace $
. By hypothesis, we have
![]() $i \ne 2$
, and
$i \ne 2$
, and
![]() $i \le \frac {n}{2}$
if n is even. It follows that
$i \le \frac {n}{2}$
if n is even. It follows that
![]() $i \ge 3$
and
$i \ge 3$
and
![]() $n-i \ge 3$
. Let
$n-i \ge 3$
. Let
![]() $J_1$
be the image of
$J_1$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_i \end{pmatrix} \ : \ A \in SL_{n-i}(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_i \end{pmatrix} \ : \ A \in SL_{n-i}(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
, and let
$PSL_n(q)$
, and let
![]() $J_2$
be the image of
$J_2$
be the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} I_{n-i} & \\ & A \end{pmatrix} \ : \ A \in SL_i(q) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} I_{n-i} & \\ & A \end{pmatrix} \ : \ A \in SL_i(q) \right\rbrace \end{align*} $$
in
![]() $PSL_n(q)$
. Then
$PSL_n(q)$
. Then
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are the only
$J_2$
are the only
![]() $2$
-components of
$2$
-components of
![]() $C_{PSL_n(q)}(t_i)$
. Applying Proposition 2.17 and Lemma 3.21, we may conclude that
$C_{PSL_n(q)}(t_i)$
. Applying Proposition 2.17 and Lemma 3.21, we may conclude that
![]() $\mathcal {E}_1 := \mathcal {F}_{P \cap J_1}(J_1)$
and
$\mathcal {E}_1 := \mathcal {F}_{P \cap J_1}(J_1)$
and
![]() $\mathcal {E}_2 := \mathcal {F}_{P \cap J_2}(J_2)$
are the only components of
$\mathcal {E}_2 := \mathcal {F}_{P \cap J_2}(J_2)$
are the only components of
![]() $\mathcal {F} = \mathcal {F}_P(C_{PSL_n(q)}(t_i))$
. By definition,
$\mathcal {F} = \mathcal {F}_P(C_{PSL_n(q)}(t_i))$
. By definition,
![]() $\mathcal {E}_1$
is isomorphic to the
$\mathcal {E}_1$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_{n-i}(q)$
, while
$SL_{n-i}(q)$
, while
![]() $\mathcal {E}_2$
is isomorphic to the
$\mathcal {E}_2$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_i(q)$
. Set
$SL_i(q)$
. Set
![]() $Y_1 := P \cap J_1$
and
$Y_1 := P \cap J_1$
and
![]() $Y_2 := P \cap J_2$
. Since
$Y_2 := P \cap J_2$
. Since
![]() $Y_1Y_2 \le P \cap J_1J_2$
and since both
$Y_1Y_2 \le P \cap J_1J_2$
and since both
![]() $Y_1Y_2$
and
$Y_1Y_2$
and
![]() $P \cap J_1J_2$
are Sylow
$P \cap J_1J_2$
are Sylow
![]() $2$
-subgroups of
$2$
-subgroups of
![]() $J_1J_2$
, we have
$J_1J_2$
, we have
![]() $Y_1Y_2 = P \cap J_1J_2$
. As
$Y_1Y_2 = P \cap J_1J_2$
. As
![]() $J_1J_2 \trianglelefteq C_{PSL_n(q)}(t_i)$
, we have that
$J_1J_2 \trianglelefteq C_{PSL_n(q)}(t_i)$
, we have that
![]() $Y_1Y_2$
is strongly
$Y_1Y_2$
is strongly
![]() $\mathcal {F}$
-closed. By Lemma 2.11,
$\mathcal {F}$
-closed. By Lemma 2.11,
![]() $\mathcal {F}/Y_1Y_2$
is isomorphic to the
$\mathcal {F}/Y_1Y_2$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $C_{PSL_n(q)}(t_i)/J_1J_2$
. Since
$C_{PSL_n(q)}(t_i)/J_1J_2$
. Since
![]() $C_{PSL_n(q)}(t_i)/J_1J_2$
is
$C_{PSL_n(q)}(t_i)/J_1J_2$
is
![]() $2$
-nilpotent, it follows from [Reference Linckelmann39, Theorem 1.4] that
$2$
-nilpotent, it follows from [Reference Linckelmann39, Theorem 1.4] that
![]() $\mathcal {F}/Y_1Y_2$
is nilpotent. As
$\mathcal {F}/Y_1Y_2$
is nilpotent. As
![]() $i \ge 3 \le n - i$
, both
$i \ge 3 \le n - i$
, both
![]() $J_1$
and
$J_1$
and
![]() $J_2$
contain a
$J_2$
contain a
![]() $PSL_n(q)$
-conjugate of t. Hence,
$PSL_n(q)$
-conjugate of t. Hence,
![]() $Y_k$
has an element which is
$Y_k$
has an element which is
![]() $PSL_n(q)$
-conjugate to t for
$PSL_n(q)$
-conjugate to t for
![]() $k \in \lbrace 1,2 \rbrace $
. For any elementary abelian
$k \in \lbrace 1,2 \rbrace $
. For any elementary abelian
![]() $2$
-subgroup E of
$2$
-subgroup E of
![]() $J_k$
,
$J_k$
,
![]() $k \in \lbrace 1,2 \rbrace $
,
$k \in \lbrace 1,2 \rbrace $
,
![]() $E \cap Z(SL_n(q)) = 1$
, so E lies in
$E \cap Z(SL_n(q)) = 1$
, so E lies in
![]() $\mathcal {S}$
. Moreover, any noncentral involution of
$\mathcal {S}$
. Moreover, any noncentral involution of
![]() $J_1$
is
$J_1$
is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < n-i$
, and any noncentral involution of
$2 \le j < n-i$
, and any noncentral involution of
![]() $J_2$
is
$J_2$
is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < i$
. This implies that any elementary abelian subgroup of
$2 \le j < i$
. This implies that any elementary abelian subgroup of
![]() $Y_1$
of rank at least
$Y_1$
of rank at least
![]() $2$
is contained in
$2$
is contained in
![]() $\mathcal {S}_{n-i}$
and that any elementary abelian subgroup of
$\mathcal {S}_{n-i}$
and that any elementary abelian subgroup of
![]() $Y_2$
of rank at least
$Y_2$
of rank at least
![]() $2$
is contained in
$2$
is contained in
![]() $\mathcal {S}_i$
. This completes the proof of (i).
$\mathcal {S}_i$
. This completes the proof of (i).
We omit the proof of (ii) since it is very similar to the one of (i).
Proposition 6.10. Let
![]() $1 \le i < n$
such that
$1 \le i < n$
such that
![]() $t_i$
is defined. Assume that
$t_i$
is defined. Assume that
![]() $i \not \in \lbrace 1, 2, n-1 \rbrace $
and that
$i \not \in \lbrace 1, 2, n-1 \rbrace $
and that
![]() $i \le \frac {n}{2}$
if n is even. Let x be an involution of S which is G-conjugate to
$i \le \frac {n}{2}$
if n is even. Let x be an involution of S which is G-conjugate to
![]() $t_i$
. Then
$t_i$
. Then
![]() $C_G(x)$
has precisely two
$C_G(x)$
has precisely two
![]() $2$
-components. Denoting them in a suitable way by
$2$
-components. Denoting them in a suitable way by
![]() $J_1$
and
$J_1$
and
![]() $J_2$
, the following hold.
$J_2$
, the following hold.
-
(i)
 $J_1/O(J_1)$
is isomorphic to
$J_1/O(J_1)$
is isomorphic to
 $SL_{n-i}^{\varepsilon }(q^{*})/O(SL_{n-i}^{\varepsilon }(q^{*}))$
, where
$SL_{n-i}^{\varepsilon }(q^{*})/O(SL_{n-i}^{\varepsilon }(q^{*}))$
, where
 $\varepsilon $
and
$\varepsilon $
and
 $q^{*}$
are as in Proposition 6.1.
$q^{*}$
are as in Proposition 6.1. -
(ii)
 $J_2/O(J_2) \cong SL_i^{\varepsilon }(q^{*})/O(SL_i^{\varepsilon }(q^{*}))$
, where
$J_2/O(J_2) \cong SL_i^{\varepsilon }(q^{*})/O(SL_i^{\varepsilon }(q^{*}))$
, where
 $\varepsilon $
and
$\varepsilon $
and
 $q^{*}$
are as in Proposition 6.1.
$q^{*}$
are as in Proposition 6.1. -
(iii) Any elementary abelian
 $2$
-subgroup of
$2$
-subgroup of
 $J_1$
of rank at least
$J_1$
of rank at least
 $2$
is G-conjugate to a subgroup of S lying in
$2$
is G-conjugate to a subgroup of S lying in
 $\mathcal {S}_{n-i}$
, and any elementary abelian
$\mathcal {S}_{n-i}$
, and any elementary abelian
 $2$
-subgroup of
$2$
-subgroup of
 $J_2$
of rank at least
$J_2$
of rank at least
 $2$
is G-conjugate to a subgroup of S lying in
$2$
is G-conjugate to a subgroup of S lying in
 $\mathcal {S}_i$
.
$\mathcal {S}_i$
.
Proof. Let
![]() $\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. It suffices to prove the proposition under the assumption that
$\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. It suffices to prove the proposition under the assumption that
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}$
-centralized, and we will assume that this is the case. So we have
$\mathcal {F}$
-centralized, and we will assume that this is the case. So we have
![]() $C_S(x) \in \mathrm {Syl}_2(C_G(x))$
and
$C_S(x) \in \mathrm {Syl}_2(C_G(x))$
and
![]() $C_S(x) \in \mathrm {Syl}_2(C_{PSL_n(q)}(x))$
. Also,
$C_S(x) \in \mathrm {Syl}_2(C_{PSL_n(q)}(x))$
. Also,
![]() $\mathcal {F}_{C_S(x)}(C_G(x)) = C_{\mathcal {F}}(\langle x \rangle ) = \mathcal {F}_{C_S(x)}(C_{PSL_n(q)}(x))$
.
$\mathcal {F}_{C_S(x)}(C_G(x)) = C_{\mathcal {F}}(\langle x \rangle ) = \mathcal {F}_{C_S(x)}(C_{PSL_n(q)}(x))$
.
As x is G-conjugate to
![]() $t_i$
, we have that x is
$t_i$
, we have that x is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_i$
. So Lemma 6.9 (i) shows together with Lemma 5.10 (i) that there exist two distinct
$t_i$
. So Lemma 6.9 (i) shows together with Lemma 5.10 (i) that there exist two distinct
![]() $2$
-components
$2$
-components
![]() $J_1$
and
$J_1$
and
![]() $J_2$
of
$J_2$
of
![]() $C_G(x)$
satisfying the following conditions, where
$C_G(x)$
satisfying the following conditions, where
![]() $Y_1 := C_S(x) \cap J_1$
and
$Y_1 := C_S(x) \cap J_1$
and
![]() $Y_2 := C_S(x) \cap J_2$
.
$Y_2 := C_S(x) \cap J_2$
.
-
(1)
 $\mathcal {F}_{Y_1}(J_1)$
is isomorphic to the
$\mathcal {F}_{Y_1}(J_1)$
is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $SL_{n-i}(q)$
.
$SL_{n-i}(q)$
. -
(2)
 $\mathcal {F}_{Y_2}(J_2)$
is isomorphic to the
$\mathcal {F}_{Y_2}(J_2)$
is isomorphic to the
 $2$
-fusion system of
$2$
-fusion system of
 $SL_i(q)$
.
$SL_i(q)$
. -
(3)
 $Y_1Y_2$
is strongly closed in
$Y_1Y_2$
is strongly closed in
 $C_S(x)$
with respect to
$C_S(x)$
with respect to
 $C_{\mathcal {F}}(\langle x \rangle )$
, and
$C_{\mathcal {F}}(\langle x \rangle )$
, and
 $C_{\mathcal {F}}(\langle x \rangle )/Y_1Y_2$
is nilpotent.
$C_{\mathcal {F}}(\langle x \rangle )/Y_1Y_2$
is nilpotent. -
(4) For
 $k \in \lbrace 1,2 \rbrace $
,
$k \in \lbrace 1,2 \rbrace $
,
 $Y_k$
contains a G-conjugate of t.
$Y_k$
contains a G-conjugate of t. -
(5) Any elementary abelian subgroup of
 $Y_1$
of rank at least
$Y_1$
of rank at least
 $2$
lies in
$2$
lies in
 $\mathcal {S}_{n-i}$
, and any elementary abelian subgroup of
$\mathcal {S}_{n-i}$
, and any elementary abelian subgroup of
 $Y_2$
of rank at least
$Y_2$
of rank at least
 $2$
lies in
$2$
lies in
 $\mathcal {S}_i$
.
$\mathcal {S}_i$
.
By (3) and Corollary 2.19,
![]() $J_1$
and
$J_1$
and
![]() $J_2$
are the only
$J_2$
are the only
![]() $2$
-components of
$2$
-components of
![]() $C_G(x)$
. It remains to show that
$C_G(x)$
. It remains to show that
![]() $J_1$
and
$J_1$
and
![]() $J_2$
satisfy (i)-(iii). As
$J_2$
satisfy (i)-(iii). As
![]() $Y_k \in \mathrm {Syl}_2(J_k)$
for
$Y_k \in \mathrm {Syl}_2(J_k)$
for
![]() $k \in \lbrace 1,2 \rbrace $
, (5) implies (iii).
$k \in \lbrace 1,2 \rbrace $
, (5) implies (iii).
We now prove (ii). The proof of (i) will be omitted since it is very similar to the proof of (ii).
Let s be an element of
![]() $J_1$
which is G-conjugate to t. Set
$J_1$
which is G-conjugate to t. Set
![]() $C := C_G(s)$
,
$C := C_G(s)$
,
![]() $\widehat C := C/O(C)$
and
$\widehat C := C/O(C)$
and
![]() .
.
Since
![]() and
and
![]() are distinct components of
are distinct components of
![]() , we have
, we have
![]() by [Reference Kurzweil and Stellmacher37, 6.5.3]. As
by [Reference Kurzweil and Stellmacher37, 6.5.3]. As
![]() , it follows that
, it follows that
![]() is a component of
is a component of
![]() . As a consequence of Corollary 2.2 and Proposition 2.4,
. As a consequence of Corollary 2.2 and Proposition 2.4,
![]() $C_G(x) \cap C$
has a
$C_G(x) \cap C$
has a
![]() $2$
-component H with
$2$
-component H with
![]() .
.
By assumption, s is G-conjugate to t. So, by Proposition 6.8,
![]() $\widehat {C}$
has a unique normal subgroup
$\widehat {C}$
has a unique normal subgroup
![]() $K^{+}$
isomorphic to
$K^{+}$
isomorphic to
![]() $SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
and a unique normal subgroup
$SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
and a unique normal subgroup
![]() $L^{+}$
isomorphic to
$L^{+}$
isomorphic to
![]() $SL_2(q^{*})$
. Moreover,
$SL_2(q^{*})$
. Moreover,
![]() $K^{+}$
and
$K^{+}$
and
![]() $L^{+}$
are the only subgroups of
$L^{+}$
are the only subgroups of
![]() $\widehat C$
which are components or solvable
$\widehat C$
which are components or solvable
![]() $2$
-components of
$2$
-components of
![]() $\widehat C$
.
$\widehat C$
.
Clearly,
![]() $\widehat {H}$
is a
$\widehat {H}$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_{\widehat {C}}(\widehat x)$
. Lemma 2.5 implies that
$C_{\widehat {C}}(\widehat x)$
. Lemma 2.5 implies that
![]() $\widehat H$
is a
$\widehat H$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_{K^{+}}(\widehat x)$
or of
$C_{K^{+}}(\widehat x)$
or of
![]() $C_{L^{+}}(\widehat x)$
. By Corollary 3.47 (i), we even have that
$C_{L^{+}}(\widehat x)$
. By Corollary 3.47 (i), we even have that
![]() $\widehat H$
is a component of
$\widehat H$
is a component of
![]() $C_{K^{+}}(\widehat x)$
or
$C_{K^{+}}(\widehat x)$
or
![]() $C_{L^{+}}(\widehat x)$
. It is easy to note that
$C_{L^{+}}(\widehat x)$
. It is easy to note that
![]() . By Corollary 3.47 (ii), we have
. By Corollary 3.47 (ii), we have
![]() $\widehat {H}/Z(\widehat H) \not \cong M_{11}$
, and so
$\widehat {H}/Z(\widehat H) \not \cong M_{11}$
, and so
![]() . Now (2) and Lemma 5.10 (ii) imply that
. Now (2) and Lemma 5.10 (ii) imply that
![]() for some nontrivial odd prime power
for some nontrivial odd prime power
![]() $q_0$
and some
$q_0$
and some
![]() $\varepsilon _0 \in \lbrace +,- \rbrace $
with
$\varepsilon _0 \in \lbrace +,- \rbrace $
with
![]() $q \sim \varepsilon _0 q_0$
. Hence,
$q \sim \varepsilon _0 q_0$
. Hence,
![]() . Note that
. Note that
![]() $\varepsilon q^{*} \sim q \sim \varepsilon _0 q_0$
and in particular
$\varepsilon q^{*} \sim q \sim \varepsilon _0 q_0$
and in particular
![]() $({q^{*}}^2-1)_2 = ({q_0}^2-1)_2$
. Applying Corollary 3.47 (iii), we may conclude that
$({q^{*}}^2-1)_2 = ({q_0}^2-1)_2$
. Applying Corollary 3.47 (iii), we may conclude that
![]() $q_0 = q^{*}$
and
$q_0 = q^{*}$
and
![]() $\varepsilon _0 = \varepsilon $
. Consequently, we have
$\varepsilon _0 = \varepsilon $
. Consequently, we have
![]() $J_2/O(J_2) \cong SL_i^{\varepsilon }(q^{*})/O(SL_i^{\varepsilon }(q^{*}))$
. So we have proved (ii).
$J_2/O(J_2) \cong SL_i^{\varepsilon }(q^{*})/O(SL_i^{\varepsilon }(q^{*}))$
. So we have proved (ii).
The proof of the following proposition runs along the same lines as that of the previous result.
Proposition 6.11. Suppose that n is odd and
![]() $i = n-1$
or that n is even,
$i = n-1$
or that n is even,
![]() $i = 1$
and
$i = 1$
and
![]() $t_1$
is defined. Let x be an involution of S which is G-conjugate to
$t_1$
is defined. Let x be an involution of S which is G-conjugate to
![]() $t_i$
. Then
$t_i$
. Then
![]() $C_G(x)$
has precisely one
$C_G(x)$
has precisely one
![]() $2$
-component J. We have
$2$
-component J. We have
![]() $J/O(J) \cong SL_{n-1}^{\varepsilon }(q^{*})/O(SL_{n-1}^{\varepsilon }(q^{*}))$
, where
$J/O(J) \cong SL_{n-1}^{\varepsilon }(q^{*})/O(SL_{n-1}^{\varepsilon }(q^{*}))$
, where
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $q^{*}$
are as in Proposition 6.1. Moreover, any elementary abelian
$q^{*}$
are as in Proposition 6.1. Moreover, any elementary abelian
![]() $2$
-subgroup of J of rank at least
$2$
-subgroup of J of rank at least
![]() $2$
is G-conjugate to a subgroup of S lying in
$2$
is G-conjugate to a subgroup of S lying in
![]() $\mathcal {S}_{n-1}$
.
$\mathcal {S}_{n-1}$
.
Proof. Let
![]() $\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. It suffices to prove the proposition under the assumption that
$\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. It suffices to prove the proposition under the assumption that
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}$
-centralized, and we will assume that this is the case. So we have
$\mathcal {F}$
-centralized, and we will assume that this is the case. So we have
![]() $C_S(x) \in \mathrm {Syl}_2(C_G(x))$
and
$C_S(x) \in \mathrm {Syl}_2(C_G(x))$
and
![]() $C_S(x) \in \mathrm {Syl}_2(C_{PSL_n(q)}(x))$
. Also,
$C_S(x) \in \mathrm {Syl}_2(C_{PSL_n(q)}(x))$
. Also,
![]() $\mathcal {F}_{C_S(x)}(C_G(x)) = C_{\mathcal {F}}(\langle x \rangle ) = \mathcal {F}_{C_S(x)}(C_{PSL_n(q)}(x))$
.
$\mathcal {F}_{C_S(x)}(C_G(x)) = C_{\mathcal {F}}(\langle x \rangle ) = \mathcal {F}_{C_S(x)}(C_{PSL_n(q)}(x))$
.
As x is G-conjugate to
![]() $t_i$
, we have that x is
$t_i$
, we have that x is
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_i$
. Lemma 6.9 (ii) implies that
$t_i$
. Lemma 6.9 (ii) implies that
![]() $C_{\mathcal {F}}(\langle x \rangle )$
has a unique component
$C_{\mathcal {F}}(\langle x \rangle )$
has a unique component
![]() $\mathcal {E}$
and that
$\mathcal {E}$
and that
![]() $\mathcal {E}$
is isomorphic to the
$\mathcal {E}$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_{n-1}(q)$
. Applying Lemma 5.10 (i), we may conclude that
$SL_{n-1}(q)$
. Applying Lemma 5.10 (i), we may conclude that
![]() $C_G(x)$
has a unique
$C_G(x)$
has a unique
![]() $2$
-component J with
$2$
-component J with
![]() $\mathcal {E} = \mathcal {F}_{C_S(x) \cap J}(J)$
. By Lemma 5.10 (ii),
$\mathcal {E} = \mathcal {F}_{C_S(x) \cap J}(J)$
. By Lemma 5.10 (ii),
![]() $J/O(J) \cong SL_{n-1}^{\varepsilon _0}(q_0)/O(SL_{n-1}^{\varepsilon _0}(q_0))$
for some nontrivial odd prime power
$J/O(J) \cong SL_{n-1}^{\varepsilon _0}(q_0)/O(SL_{n-1}^{\varepsilon _0}(q_0))$
for some nontrivial odd prime power
![]() $q_0$
and some
$q_0$
and some
![]() $\varepsilon _0 \in \lbrace +,- \rbrace $
with
$\varepsilon _0 \in \lbrace +,- \rbrace $
with
![]() $\varepsilon _0 q_0 \sim q$
.
$\varepsilon _0 q_0 \sim q$
.
Set
![]() $Y := C_S(x) \cap J$
. By Lemma 6.9 (ii), Y is strongly closed in
$Y := C_S(x) \cap J$
. By Lemma 6.9 (ii), Y is strongly closed in
![]() $C_S(x)$
with respect to
$C_S(x)$
with respect to
![]() $C_{\mathcal {F}}(\langle x \rangle )$
and
$C_{\mathcal {F}}(\langle x \rangle )$
and
![]() $C_{\mathcal {F}}(\langle x \rangle )/Y$
is nilpotent. Applying Corollary 2.19, we may conclude that J is the only
$C_{\mathcal {F}}(\langle x \rangle )/Y$
is nilpotent. Applying Corollary 2.19, we may conclude that J is the only
![]() $2$
-component of
$2$
-component of
![]() $C_G(x)$
. Using Lemma 6.9 (ii), we see that any elementary abelian subgroup of Y of rank at least
$C_G(x)$
. Using Lemma 6.9 (ii), we see that any elementary abelian subgroup of Y of rank at least
![]() $2$
lies in
$2$
lies in
![]() $\mathcal {S}_{n-1}$
. As
$\mathcal {S}_{n-1}$
. As
![]() $Y \in \mathrm {Syl}_2(J)$
, it follows that any elementary abelian
$Y \in \mathrm {Syl}_2(J)$
, it follows that any elementary abelian
![]() $2$
-subgroup of J of rank at least
$2$
-subgroup of J of rank at least
![]() $2$
is G-conjugate to a subgroup of S lying in
$2$
is G-conjugate to a subgroup of S lying in
![]() $\mathcal {S}_{n-1}$
.
$\mathcal {S}_{n-1}$
.
It remains to show that
![]() $\varepsilon _0 = \varepsilon $
and
$\varepsilon _0 = \varepsilon $
and
![]() $q_0 = q^{*}$
. Define
$q_0 = q^{*}$
. Define
![]() $s := t_i$
if
$s := t_i$
if
![]() $i = 1$
and
$i = 1$
and
![]() $s := t_A$
, where
$s := t_A$
, where
![]() $A := \lbrace 1, \dots , n-1 \rbrace $
, if
$A := \lbrace 1, \dots , n-1 \rbrace $
, if
![]() $i = n-1$
. Then we have
$i = n-1$
. Then we have
![]() $s \in C_G(t)$
, and s is G-conjugate to x. Set
$s \in C_G(t)$
, and s is G-conjugate to x. Set
![]() . Lemma 6.2 shows that
. Lemma 6.2 shows that
![]() centralizes
centralizes
![]() . Hence,
. Hence,
![]() is a component of
is a component of
![]() . As a consequence of Corollary 2.2 and Proposition 2.4,
. As a consequence of Corollary 2.2 and Proposition 2.4,
![]() $C_G(t) \cap C_G(s)$
has a
$C_G(t) \cap C_G(s)$
has a
![]() $2$
-component H with
$2$
-component H with
![]() . Set
. Set
![]() $C := C_G(s)$
and
$C := C_G(s)$
and
![]() $\widehat C := C/O(C)$
. Then
$\widehat C := C/O(C)$
. Then
![]() $\widehat H$
is a
$\widehat H$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_{\widehat C}(\widehat t)$
. Since s is G-conjugate to x,
$C_{\widehat C}(\widehat t)$
. Since s is G-conjugate to x,
![]() $\widehat C$
has precisely one component
$\widehat C$
has precisely one component
![]() $J^{+}$
, and
$J^{+}$
, and
![]() $J^{+}$
is isomorphic to
$J^{+}$
is isomorphic to
![]() $SL_{n-1}^{\varepsilon _0}(q_0)/O(SL_{n-1}^{\varepsilon _0}(q_0))$
. By Lemma 2.5,
$SL_{n-1}^{\varepsilon _0}(q_0)/O(SL_{n-1}^{\varepsilon _0}(q_0))$
. By Lemma 2.5,
![]() $\widehat H$
is a
$\widehat H$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_{J^{+}}(\widehat t)$
. We see from Corollary 3.47 (i) that
$C_{J^{+}}(\widehat t)$
. We see from Corollary 3.47 (i) that
![]() $\widehat H$
is in fact a component of
$\widehat H$
is in fact a component of
![]() $C_{J^{+}}(\widehat t)$
. It is easy to see that
$C_{J^{+}}(\widehat t)$
. It is easy to see that
![]() . Note that
. Note that
![]() $\varepsilon _0 q_0 \sim q \sim \varepsilon q^{*}$
and in particular
$\varepsilon _0 q_0 \sim q \sim \varepsilon q^{*}$
and in particular
![]() $({q_0}^2-1)_2 = ({q^{*}}^2-1)_2$
. Using this, we may deduce from Corollary 3.47 (iii) that
$({q_0}^2-1)_2 = ({q^{*}}^2-1)_2$
. Using this, we may deduce from Corollary 3.47 (iii) that
![]() $q_0 = q^{*}$
and
$q_0 = q^{*}$
and
![]() $\varepsilon _0 = \varepsilon $
.
$\varepsilon _0 = \varepsilon $
.
6.3
 $2$
-components of centralizers of involutions conjugate to w
$2$
-components of centralizers of involutions conjugate to w
Recall that we assume
![]() $\rho $
to be an element of
$\rho $
to be an element of
![]() $\mathbb {F}_q^{*}$
with order
$\mathbb {F}_q^{*}$
with order
![]() $(n,q-1)$
. Recall moreover that if n is even and
$(n,q-1)$
. Recall moreover that if n is even and
![]() $\rho $
is a nonsquare element of
$\rho $
is a nonsquare element of
![]() $\mathbb {F}_q$
, then
$\mathbb {F}_q$
, then
![]() $\widetilde w$
denotes the matrix
$\widetilde w$
denotes the matrix
 $$ \begin{align*} \begin{pmatrix} & I_{n/2} \\ \rho I_{n/2} & \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} & I_{n/2} \\ \rho I_{n/2} & \end{pmatrix} \end{align*} $$
and, if
![]() $\widetilde w \in SL_n(q)$
, then w denotes its image in
$\widetilde w \in SL_n(q)$
, then w denotes its image in
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
Lemma 6.12. Suppose that w is defined. Let P be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_{PSL_n(q)}(w)$
, and let
$C_{PSL_n(q)}(w)$
, and let
![]() $\mathcal {F}$
denote the fusion system
$\mathcal {F}$
denote the fusion system
![]() $\mathcal {F}_P(C_{PSL_n(q)})(w))$
. Then
$\mathcal {F}_P(C_{PSL_n(q)})(w))$
. Then
![]() $\mathcal {F}$
has precisely one component. This component is isomorphic to the
$\mathcal {F}$
has precisely one component. This component is isomorphic to the
![]() $2$
-fusion system of a nontrivial quotient of
$2$
-fusion system of a nontrivial quotient of
![]() $SL_{\frac {n}{2}}(q^2)$
. If Y is its Sylow subgroup, then Y is strongly
$SL_{\frac {n}{2}}(q^2)$
. If Y is its Sylow subgroup, then Y is strongly
![]() $\mathcal {F}$
-closed, and
$\mathcal {F}$
-closed, and
![]() $\mathcal {F}/Y$
is nilpotent.
$\mathcal {F}/Y$
is nilpotent.
Proof. By Lemma 3.6 (i),
![]() $C_{PSL_n(q)}(w)$
has precisely one
$C_{PSL_n(q)}(w)$
has precisely one
![]() $2$
-component J, and J is isomorphic to a nontrivial quotient of
$2$
-component J, and J is isomorphic to a nontrivial quotient of
![]() $SL_{\frac {n}{2}}(q^2)$
. Applying Proposition 2.17 and Lemma 3.21, we may conclude that
$SL_{\frac {n}{2}}(q^2)$
. Applying Proposition 2.17 and Lemma 3.21, we may conclude that
![]() $\mathcal {F}_{P \cap J}(J)$
is the only component of
$\mathcal {F}_{P \cap J}(J)$
is the only component of
![]() $\mathcal {F}$
. The last statement of the lemma is given by Lemma 3.6 (ii).
$\mathcal {F}$
. The last statement of the lemma is given by Lemma 3.6 (ii).
Proposition 6.13. Suppose that w is defined. Let x be an involution of S which is
![]() $PSL_n(q)$
-conjugate to w. Then
$PSL_n(q)$
-conjugate to w. Then
![]() $C_G(x)$
has precisely one
$C_G(x)$
has precisely one
![]() $2$
-component, say J. The group
$2$
-component, say J. The group
![]() $J/O(J)$
is isomorphic to a nontrivial quotient of
$J/O(J)$
is isomorphic to a nontrivial quotient of
![]() $SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
$SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
![]() $q_0$
and some
$q_0$
and some
![]() $\varepsilon _0 \in \lbrace +,-\rbrace $
with
$\varepsilon _0 \in \lbrace +,-\rbrace $
with
![]() $q^2 \sim \varepsilon _0 q_0$
.
$q^2 \sim \varepsilon _0 q_0$
.
Proof. Let
![]() $\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. It suffices to prove the proposition under the assumption that
$\mathcal {F} := \mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
. It suffices to prove the proposition under the assumption that
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}$
-centralized, and we will assume that this is the case. So we have
$\mathcal {F}$
-centralized, and we will assume that this is the case. So we have
![]() $C_S(x) \in \mathrm {Syl}_2(C_G(x))$
and
$C_S(x) \in \mathrm {Syl}_2(C_G(x))$
and
![]() $C_S(x) \in \mathrm {Syl}_2(C_{PSL_n(q)}(x))$
. Also,
$C_S(x) \in \mathrm {Syl}_2(C_{PSL_n(q)}(x))$
. Also,
![]() $\mathcal {F}_{C_S(x)}(C_G(x)) = C_{\mathcal {F}}(\langle x \rangle ) = \mathcal {F}_{C_S(x)}(C_{PSL_n(q)}(x))$
.
$\mathcal {F}_{C_S(x)}(C_G(x)) = C_{\mathcal {F}}(\langle x \rangle ) = \mathcal {F}_{C_S(x)}(C_{PSL_n(q)}(x))$
.
As x is
![]() $PSL_n(q)$
-conjugate to w, Lemma 6.12 implies that
$PSL_n(q)$
-conjugate to w, Lemma 6.12 implies that
![]() $C_{\mathcal {F}}(\langle x \rangle )$
has precisely one component, say
$C_{\mathcal {F}}(\langle x \rangle )$
has precisely one component, say
![]() $\mathcal {E}$
, and that
$\mathcal {E}$
, and that
![]() $\mathcal {E}$
is isomorphic to the
$\mathcal {E}$
is isomorphic to the
![]() $2$
-fusion system of a nontrivial quotient of
$2$
-fusion system of a nontrivial quotient of
![]() $SL_{\frac {n}{2}}(q^2)$
. By Lemma 5.10 (i),
$SL_{\frac {n}{2}}(q^2)$
. By Lemma 5.10 (i),
![]() $C_G(x)$
has a unique
$C_G(x)$
has a unique
![]() $2$
-component J such that
$2$
-component J such that
![]() $\mathcal {E} = \mathcal {F}_{C_S(x) \cap J}(J)$
. Set
$\mathcal {E} = \mathcal {F}_{C_S(x) \cap J}(J)$
. Set
![]() $Y := C_S(x) \cap J$
. As a consequence of Lemma 6.12, Y is strongly closed in
$Y := C_S(x) \cap J$
. As a consequence of Lemma 6.12, Y is strongly closed in
![]() $C_S(x)$
with respect to
$C_S(x)$
with respect to
![]() $C_{\mathcal {F}}(\langle x \rangle )$
, and the factor system
$C_{\mathcal {F}}(\langle x \rangle )$
, and the factor system
![]() $C_{\mathcal {F}}(\langle x \rangle )/Y$
is nilpotent. So, by Corollary 2.19, J is the only
$C_{\mathcal {F}}(\langle x \rangle )/Y$
is nilpotent. So, by Corollary 2.19, J is the only
![]() $2$
-component of
$2$
-component of
![]() $C_G(x)$
. Lemma 5.10 (iii) shows that
$C_G(x)$
. Lemma 5.10 (iii) shows that
![]() $J/O(J)$
is isomorphic to a nontrivial quotient of
$J/O(J)$
is isomorphic to a nontrivial quotient of
![]() $SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
$SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
![]() $q_0$
and some
$q_0$
and some
![]() $\varepsilon _0 \in \lbrace +,- \rbrace $
with
$\varepsilon _0 \in \lbrace +,- \rbrace $
with
![]() $q^2 \sim \varepsilon _0 q_0$
.
$q^2 \sim \varepsilon _0 q_0$
.
7 The components of
 $C_G(t)$
$C_G(t)$
The goal of this section is to determine the isomorphism types of K and L. In order to do so, we will apply the signalizer functor techniques introduced by Gorenstein and Walter in [Reference Gorenstein and Walter31]. In particular, we will see that L is isomorphic to
![]() $SL_2(q^{*})$
. This will enable us in Section 8 to prove that a certain collection of conjugates of L generates a subgroup
$SL_2(q^{*})$
. This will enable us in Section 8 to prove that a certain collection of conjugates of L generates a subgroup
![]() $G_0$
of G which is isomorphic to a nontrivial quotient of
$G_0$
of G which is isomorphic to a nontrivial quotient of
![]() $SL_n^{\varepsilon }(q^{*})$
and normal in G. This will complete the proof of Theorem 5.2.
$SL_n^{\varepsilon }(q^{*})$
and normal in G. This will complete the proof of Theorem 5.2.
7.1
 $3$
-generation of involution centralizers
$3$
-generation of involution centralizers
For each
![]() $3 \le i \le n$
, we define
$3 \le i \le n$
, we define
![]() $\mathcal {U}_i$
to be the set of all subgroups U of
$\mathcal {U}_i$
to be the set of all subgroups U of
![]() $PSL_n(q)$
such that U has a subgroup E with
$PSL_n(q)$
such that U has a subgroup E with
![]() $E \in \mathcal {S}_i$
and
$E \in \mathcal {S}_i$
and
![]() $m(E) \ge 3$
. The following lemma will be important later in this section.
$m(E) \ge 3$
. The following lemma will be important later in this section.
Lemma 7.1. Let
![]() $1 \le i < n$
such that
$1 \le i < n$
such that
![]() $t_i$
is defined. Suppose that
$t_i$
is defined. Suppose that
![]() $i \le \frac {n}{2}$
if n is even. Let x be an involution of S such that x is G-conjugate to
$i \le \frac {n}{2}$
if n is even. Let x be an involution of S such that x is G-conjugate to
![]() $t_i$
and such that
$t_i$
and such that
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}_S(G)$
-centralized. Then
$\mathcal {F}_S(G)$
-centralized. Then
![]() $C_G(x)$
is
$C_G(x)$
is
![]() $3$
-generated in the sense of Definition 3.36. Moreover, if
$3$
-generated in the sense of Definition 3.36. Moreover, if
![]() $i \ge 4$
, then we have
$i \ge 4$
, then we have
If
![]() $i = 2$
, then we have
$i = 2$
, then we have
Proof. Set
![]() $C := C_G(x)$
and
$C := C_G(x)$
and
![]() . Recall that
. Recall that
![]() $L_{2'}(C)$
denotes the subgroup of C generated by the
$L_{2'}(C)$
denotes the subgroup of C generated by the
![]() $2$
-components of C and that
$2$
-components of C and that
![]() denotes the product of all components of
denotes the product of all components of
![]() . As a consequence of Proposition 2.4,
. As a consequence of Proposition 2.4,
![]() .
.
First, we consider the case
![]() $(n,i) \ne (6,3)$
. Then, by Propositions 6.1, 6.10 and 6.11, C has a
$(n,i) \ne (6,3)$
. Then, by Propositions 6.1, 6.10 and 6.11, C has a
![]() $2$
-component J such that
$2$
-component J such that
![]() for some
for some
![]() $k \ge 4$
and such that any elementary abelian subgroup of
$k \ge 4$
and such that any elementary abelian subgroup of
![]() $Y := C_S(x) \cap J$
of rank at least
$Y := C_S(x) \cap J$
of rank at least
![]() $2$
lies in
$2$
lies in
![]() $\mathcal {S}_k$
. If
$\mathcal {S}_k$
. If
![]() $i \ge 4$
, then we may assume that
$i \ge 4$
, then we may assume that
![]() $k = i$
, and if
$k = i$
, and if
![]() $i = 2$
, then
$i = 2$
, then
![]() $k = n-2$
.
$k = n-2$
.
We have
![]() $Y \in \mathrm {Syl}_2(J)$
since
$Y \in \mathrm {Syl}_2(J)$
since
![]() $C_S(x) \in \mathrm {Syl}_2(C)$
and J is subnormal in C. By Lemma 3.38, we have that
$C_S(x) \in \mathrm {Syl}_2(C)$
and J is subnormal in C. By Lemma 3.38, we have that
is
![]() $3$
-generated. So we have
$3$
-generated. So we have
Set
![]() $X := C_S(x) \cap L_{2'}(C)$
. By the Frattini argument,
$X := C_S(x) \cap L_{2'}(C)$
. By the Frattini argument,
and
. It follows that
Lemma 2.1 implies that C is generated by
![]() $O(C)$
together with the normalizers
$O(C)$
together with the normalizers
![]() $N_C(U)$
, where
$N_C(U)$
, where
![]() $U = X$
, or
$U = X$
, or
![]() $U \le Y$
and
$U \le Y$
and
![]() $m(U) \ge 3$
.
$m(U) \ge 3$
.
Let E denote the subgroup of S generated by t,
![]() $t_{\lbrace n-2,n-1 \rbrace }$
,
$t_{\lbrace n-2,n-1 \rbrace }$
,
![]() $t_{\lbrace n-3,n-2 \rbrace }$
and
$t_{\lbrace n-3,n-2 \rbrace }$
and
![]() $t_{\lbrace n-4,n-3 \rbrace }$
. Then
$t_{\lbrace n-4,n-3 \rbrace }$
. Then
![]() $E \cong E_{16}$
. Since x is G-conjugate to
$E \cong E_{16}$
. Since x is G-conjugate to
![]() $t_i$
and
$t_i$
and
![]() $E \le C_G(t_i)$
, there is a subgroup
$E \le C_G(t_i)$
, there is a subgroup
![]() $E_x$
of
$E_x$
of
![]() $C_S(x)$
which is G-conjugate to E. By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
$C_S(x)$
which is G-conjugate to E. By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
As remarked above, any elementary abelian subgroup of Y of rank at least
![]() $2$
lies in
$2$
lies in
![]() $\mathcal {S}_k$
. So, if
$\mathcal {S}_k$
. So, if
![]() $U \le Y$
and
$U \le Y$
and
![]() $m(U) \ge 3$
, then
$m(U) \ge 3$
, then
![]() $U \in \mathcal {U}_k$
. Also,
$U \in \mathcal {U}_k$
. Also,
![]() $X \in \mathcal {U}_k$
. Clearly, any
$X \in \mathcal {U}_k$
. Clearly, any
![]() $E_8$
-subgroup of
$E_8$
-subgroup of
![]() $E_x$
lies in
$E_x$
lies in
![]() $\mathcal {S}_k$
and hence in
$\mathcal {S}_k$
and hence in
![]() $\mathcal {U}_k$
. We therefore have
$\mathcal {U}_k$
. We therefore have
Consequently, C is
![]() $3$
-generated, and the last two statements of the lemma are satisfied.
$3$
-generated, and the last two statements of the lemma are satisfied.
Suppose now that
![]() $(n,i) = (6,3)$
. By Proposition 6.10, C has precisely two
$(n,i) = (6,3)$
. By Proposition 6.10, C has precisely two
![]() $2$
-components
$2$
-components
![]() $J_1$
and
$J_1$
and
![]() $J_2$
, and we have
$J_2$
, and we have
. Set
![]() $Y_1 := C_S(x) \cap J_1$
and
$Y_1 := C_S(x) \cap J_1$
and
![]() $Y_2 := C_S(x) \cap J_2$
. Since
$Y_2 := C_S(x) \cap J_2$
. Since
is
![]() $2$
-generated by Lemma 3.37, we have
$2$
-generated by Lemma 3.37, we have
Let y be an involution of
![]() $Y_2$
. We have
$Y_2$
. We have
by [Reference Kurzweil and Stellmacher37, 6.5.3], and so
centralizes
. As
, we have
. Now let
![]() $U \le Y_1$
with
$U \le Y_1$
with
![]() $m(U) \ge 2$
. Then
$m(U) \ge 2$
. Then
has rank at least
![]() $3$
. Moreover,
$3$
. Moreover,
normalizes
as
centralizes
. Thus,
Interchanging the roles of
![]() $J_1$
and
$J_1$
and
![]() $J_2$
, we also see that
$J_2$
, we also see that
By the Frattini argument,
. Lemma 2.1 implies that C is generated by
![]() $O(C)$
together with the normalizers
$O(C)$
together with the normalizers
![]() $N_C(U)$
, where
$N_C(U)$
, where
![]() $U \le Y_1Y_2$
and
$U \le Y_1Y_2$
and
![]() $m(U) \ge 3$
. For any
$m(U) \ge 3$
. For any
![]() $E_{16}$
-subgroup A of
$E_{16}$
-subgroup A of
![]() $C_S(x)$
, we have
$C_S(x)$
, we have
by [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23]. It follows that C is
![]() $3$
-generated. The proof is now complete.
$3$
-generated. The proof is now complete.
Lemma 7.2. Suppose that w is defined. Let x be an involution of S which is
![]() $PSL_n(q)$
-conjugate to w. Then
$PSL_n(q)$
-conjugate to w. Then
![]() $C_G(x)$
is
$C_G(x)$
is
![]() $3$
-generated.
$3$
-generated.
Proof. Set
![]() $C := C_G(x)$
and
$C := C_G(x)$
and
![]() . By Proposition 6.13, C has a unique
. By Proposition 6.13, C has a unique
![]() $2$
-component J, and
$2$
-component J, and
![]() is isomorphic to a nontrivial quotient of
is isomorphic to a nontrivial quotient of
![]() $SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
$SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
![]() $q_0$
and some
$q_0$
and some
![]() $\varepsilon _0 \in \lbrace +,-\rbrace $
with
$\varepsilon _0 \in \lbrace +,-\rbrace $
with
![]() $q^2 \sim \varepsilon _0 q_0$
. Note that
$q^2 \sim \varepsilon _0 q_0$
. Note that
![]() $q_0 \equiv \varepsilon _0 \mod 8$
.
$q_0 \equiv \varepsilon _0 \mod 8$
.
First, we prove that
![]() is
is
![]() $3$
-generated. Let R be a Sylow
$3$
-generated. Let R be a Sylow
![]() $2$
-subgroup of C and
$2$
-subgroup of C and
![]() $Y := R \cap J$
. We consider two cases.
$Y := R \cap J$
. We consider two cases.
Case 1:
![]() $n \ge 8$
.
$n \ge 8$
.
As
![]() $q_0 \equiv \varepsilon _0 \mod 8$
, by Lemma 3.38,
$q_0 \equiv \varepsilon _0 \mod 8$
, by Lemma 3.38,
is
![]() $3$
-generated. Hence,
$3$
-generated. Hence,
By the Frattini argument,
. So
is
![]() $3$
-generated.
$3$
-generated.
Case 2:
![]() $n = 6$
.
$n = 6$
.
We have
. By Lemma 3.37,
is
![]() $2$
-generated. Applying the Frattini argument, we may conclude that
$2$
-generated. Applying the Frattini argument, we may conclude that
Now let
![]() $U \le Y$
with
$U \le Y$
with
![]() $m(U) \ge 2$
. Since
$m(U) \ge 2$
. Since
is a central involution of
and
is trivial, we have
and hence
. It follows
has rank at least
![]() $3$
. Moreover, as
$3$
. Moreover, as
is central in
, we have
. Clearly,
. It follows that
Hence,
is
![]() $3$
-generated.
$3$
-generated.
Applying Lemma 2.1, we may conclude that C is generated by
![]() $O(C)$
together with the normalizers
$O(C)$
together with the normalizers
![]() $N_C(U)$
, where
$N_C(U)$
, where
![]() $U \le R$
and
$U \le R$
and
![]() $m(U) \ge 3$
. By Lemma 3.6 (iii), R has an elementary abelian
$m(U) \ge 3$
. By Lemma 3.6 (iii), R has an elementary abelian
![]() $2$
-subgroup of rank
$2$
-subgroup of rank
![]() $4$
, say A. By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
$4$
, say A. By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
So C is
![]() $3$
-generated.
$3$
-generated.
Corollary 7.3. Let x be an involution of S. Then
![]() $C_G(x)$
is
$C_G(x)$
is
![]() $3$
-generated.
$3$
-generated.
7.2 The case
 $q^{*} = 3$
$q^{*} = 3$
Recall that our goal is to determine the isomorphism types of K and L. First, we will deal with the case
![]() $q^{*} = 3$
. We will prove that, in this case,
$q^{*} = 3$
. We will prove that, in this case,
![]() $O(C_G(t)) = 1$
.
$O(C_G(t)) = 1$
.
Lemma 7.4. Let x be an involution of S, and let J be a
![]() $2$
-component of
$2$
-component of
![]() $C_G(x)$
. Let
$C_G(x)$
. Let
![]() $1 \le i < n$
such that
$1 \le i < n$
such that
![]() $t_i$
is defined. Suppose that
$t_i$
is defined. Suppose that
![]() $q^{*} = 3$
and that x is G-conjugate to
$q^{*} = 3$
and that x is G-conjugate to
![]() $t_i$
. Then
$t_i$
. Then
![]() $J/O(J)$
is locally balanced.
$J/O(J)$
is locally balanced.
Proof. By Propositions 6.8 (iii), 6.10 and 6.11, we have
![]() $J/O(J) \cong SL_k^{\varepsilon }(3)$
for some
$J/O(J) \cong SL_k^{\varepsilon }(3)$
for some
![]() $3 \le k < n$
. So
$3 \le k < n$
. So
![]() $J/O(J)$
is locally balanced by Lemma 3.48.
$J/O(J)$
is locally balanced by Lemma 3.48.
Lemma 7.5. Let P and Q be subgroups of S.
-
(i) If
 $P \in \mathcal {S}$
and
$P \in \mathcal {S}$
and
 $m(P) \le 2$
, then there is a subgroup
$m(P) \le 2$
, then there is a subgroup
 of S such that
of S such that
 ,
,
 and
and
 .
. -
(ii) If P and Q are elements of
 $\mathcal {S}$
of rank at least
$\mathcal {S}$
of rank at least
 $3$
, then there exist some
$3$
, then there exist some
 $m \ge 1$
and a sequence where
$m \ge 1$
and a sequence where $$ \begin{align*} P = P_1, \dots, P_m = Q, \end{align*} $$
$$ \begin{align*} P = P_1, \dots, P_m = Q, \end{align*} $$
 $P_i$
,
$P_i$
,
 $1 \le i \le m$
, is a subgroup of S of rank at least
$1 \le i \le m$
, is a subgroup of S of rank at least
 $2$
lying in
$2$
lying in
 $\mathcal {S}$
and where for all
$\mathcal {S}$
and where for all $$ \begin{align*} P_i \subseteq P_{i+1} \ \text{or} \ P_{i+1} \subseteq P_i \end{align*} $$
$$ \begin{align*} P_i \subseteq P_{i+1} \ \text{or} \ P_{i+1} \subseteq P_i \end{align*} $$
 $1 \le i < m$
.
$1 \le i < m$
.
Proof. Suppose that
![]() $P \in \mathcal {S}$
and
$P \in \mathcal {S}$
and
![]() $m(P) \le 2$
. Let
$m(P) \le 2$
. Let
![]() $\widetilde S$
be a Sylow
$\widetilde S$
be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $SL_n(q)$
such that S is the image of
$SL_n(q)$
such that S is the image of
![]() $\widetilde S$
in
$\widetilde S$
in
![]() $PSL_n(q)$
. Note that
$PSL_n(q)$
. Note that
![]() $\widetilde S$
is unique. Since P is an element of
$\widetilde S$
is unique. Since P is an element of
![]() $\mathcal {S}$
, there exists some elementary abelian
$\mathcal {S}$
, there exists some elementary abelian
![]() $2$
-subgroup
$2$
-subgroup
![]() $\widetilde P$
of
$\widetilde P$
of
![]() $SL_n(q)$
such that P is the image of
$SL_n(q)$
such that P is the image of
![]() $\widetilde P$
in
$\widetilde P$
in
![]() $PSL_n(q)$
. Clearly,
$PSL_n(q)$
. Clearly,
![]() $\widetilde P \le \widetilde S$
. We have
$\widetilde P \le \widetilde S$
. We have
![]() $m(\widetilde P) \le 3$
as
$m(\widetilde P) \le 3$
as
![]() $m(P) \le 2$
. By Corollary 3.35,
$m(P) \le 2$
. By Corollary 3.35,
![]() $\widetilde P$
is contained in an
$\widetilde P$
is contained in an
![]() $E_{16}$
-subgroup of
$E_{16}$
-subgroup of
![]() $\widetilde S$
. This implies (i).
$\widetilde S$
. This implies (i).
We now prove (ii). Suppose that P and Q are elements of
![]() $\mathcal {S}$
of rank at least
$\mathcal {S}$
of rank at least
![]() $3$
. There are elementary abelian subgroups
$3$
. There are elementary abelian subgroups
![]() $\widetilde P$
and
$\widetilde P$
and
![]() $\widetilde Q$
of
$\widetilde Q$
of
![]() $SL_n(q)$
such that P is the image of
$SL_n(q)$
such that P is the image of
![]() $\widetilde P$
in
$\widetilde P$
in
![]() $PSL_n(q)$
and such that Q is the image of
$PSL_n(q)$
and such that Q is the image of
![]() $\widetilde Q$
in
$\widetilde Q$
in
![]() $PSL_n(q)$
. Clearly,
$PSL_n(q)$
. Clearly,
![]() $\widetilde P, \widetilde Q \le \widetilde S$
. Also,
$\widetilde P, \widetilde Q \le \widetilde S$
. Also,
![]() $m(\widetilde P), m(\widetilde Q) \ge 3$
. Since
$m(\widetilde P), m(\widetilde Q) \ge 3$
. Since
![]() $\widetilde S$
is
$\widetilde S$
is
![]() $3$
-connected by Corollary 3.34, there exist some
$3$
-connected by Corollary 3.34, there exist some
![]() $m \ge 1$
and a sequence
$m \ge 1$
and a sequence
where
![]() $\widetilde {P}_i$
(
$\widetilde {P}_i$
(
![]() $1 \le i \le m$
) is an elementary abelian subgroup of
$1 \le i \le m$
) is an elementary abelian subgroup of
![]() $\widetilde S$
of rank at least
$\widetilde S$
of rank at least
![]() $3$
and where
$3$
and where
for all
![]() $1 \le i < m$
. Let
$1 \le i < m$
. Let
![]() $P_i$
,
$P_i$
,
![]() $1 \le i \le m$
, denote the image of
$1 \le i \le m$
, denote the image of
![]() $\widetilde {P}_i$
in S. Then the sequence
$\widetilde {P}_i$
in S. Then the sequence
has the desired properties.
Lemma 7.6. Suppose that
![]() $q^{*} = 3$
. For each elementary abelian subgroup E of S of rank at least
$q^{*} = 3$
. For each elementary abelian subgroup E of S of rank at least
![]() $2$
, let
$2$
, let
Let P and Q be subgroups of S with
![]() $P, Q \in \mathcal {S}$
and
$P, Q \in \mathcal {S}$
and
![]() $m(P), m(Q) \ge 3$
. Then
$m(P), m(Q) \ge 3$
. Then
![]() $W_P = W_Q$
.
$W_P = W_Q$
.
Proof. By Lemma 7.5 (ii), there exist some
![]() $m \ge 1$
and a sequence
$m \ge 1$
and a sequence
where
![]() $P_i$
,
$P_i$
,
![]() $1 \le i \le m$
, is a subgroup of S of rank at least
$1 \le i \le m$
, is a subgroup of S of rank at least
![]() $2$
lying in
$2$
lying in
![]() $\mathcal {S}$
and where
$\mathcal {S}$
and where
for all
![]() $1 \le i < m$
. By Lemma 7.5 (i), there is a subgroup
$1 \le i < m$
. By Lemma 7.5 (i), there is a subgroup
![]() of S such that
of S such that
![]() ,
,
![]() and
and
![]() for each
for each
![]() $1 \le i \le m$
.
$1 \le i \le m$
.
Let
![]() $1 \le i \le m$
, and let x be an involution of
$1 \le i \le m$
, and let x be an involution of
![]() . Also, let J be a
. Also, let J be a
![]() $2$
-component of
$2$
-component of
![]() $C_G(x)$
. As
$C_G(x)$
. As
![]() , we have that x is G-conjugate to
, we have that x is G-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < n$
. Therefore, by Lemma 7.4,
$2 \le j < n$
. Therefore, by Lemma 7.4,
![]() $J/O(J)$
is locally balanced. Applying [Reference Gorenstein and Walter31, Corollary 5.6], we may conclude that G is balanced with respect to
$J/O(J)$
is locally balanced. Applying [Reference Gorenstein and Walter31, Corollary 5.6], we may conclude that G is balanced with respect to
![]() .
.
Let
![]() $1 \le i < m$
. We have
$1 \le i < m$
. We have
![]() $m(P_i \cap P_{i+1}) \ge 2$
since
$m(P_i \cap P_{i+1}) \ge 2$
since
![]() $P_i \subseteq P_{i+1}$
or
$P_i \subseteq P_{i+1}$
or
![]() $P_{i+1} \subseteq P_i$
and
$P_{i+1} \subseteq P_i$
and
![]() $m(P_i), m(P_{i+1}) \ge 2$
. Hence,
$m(P_i), m(P_{i+1}) \ge 2$
. Hence,
. Proposition 2.8 (ii) implies
Consequently,
![]() $W_P = W_Q$
, as wanted.
$W_P = W_Q$
, as wanted.
Proposition 7.7. Suppose that
![]() $q^{*} = 3$
. Let x be an involution of S which is G-conjugate to
$q^{*} = 3$
. Let x be an involution of S which is G-conjugate to
![]() $t_i$
for some even
$t_i$
for some even
![]() $2 \le i < n$
. Then we have
$2 \le i < n$
. Then we have
![]() $O(C_G(x)) = 1$
. In particular,
$O(C_G(x)) = 1$
. In particular,
![]() $O(C_G(t)) = 1$
.
$O(C_G(t)) = 1$
.
Proof. We follow the pattern of the proof of [Reference Gorenstein and Walter31, Theorem 9.1]. Let E be the subgroup of S consisting of all
![]() $t_A$
, where
$t_A$
, where
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. For each elementary abelian
$A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. For each elementary abelian
![]() $2$
-subgroup A of G of rank at least
$2$
-subgroup A of G of rank at least
![]() $2$
, let
$2$
, let
Set
![]() $W_0 := W_E$
and
$W_0 := W_E$
and
![]() $M := N_G(W_0)$
. We accomplish the proof step by step.
$M := N_G(W_0)$
. We accomplish the proof step by step.
(1)
![]() $N_G(S) \le M$
.
$N_G(S) \le M$
.
Let
![]() $g \in N_G(S)$
. Clearly,
$g \in N_G(S)$
. Clearly,
![]() $E \in \mathcal {S}$
, and it is easy to note
$E \in \mathcal {S}$
, and it is easy to note
![]() $E^g$
still lies in
$E^g$
still lies in
![]() $\mathcal {S}$
. Lemma 7.6 implies that
$\mathcal {S}$
. Lemma 7.6 implies that
![]() $W_0 = W_{E^g}$
. On the other hand, we have
$W_0 = W_{E^g}$
. On the other hand, we have
![]() $(W_0)^g = W_{E^g}$
by Proposition 2.8 (i). So we have
$(W_0)^g = W_{E^g}$
by Proposition 2.8 (i). So we have
![]() $(W_0)^g = W_0$
and hence
$(W_0)^g = W_0$
and hence
![]() $g \in M$
.
$g \in M$
.
(2) Let y be an involution of S such that y is G-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < n$
. Then y is M-conjugate to
$2 \le j < n$
. Then y is M-conjugate to
![]() $t_j$
.
$t_j$
.
We have
![]() $\langle y \rangle \in \mathcal {S}$
. By Lemma 7.5 (i), there is a subgroup A of S with
$\langle y \rangle \in \mathcal {S}$
. By Lemma 7.5 (i), there is a subgroup A of S with
![]() $\langle y \rangle \le A$
,
$\langle y \rangle \le A$
,
![]() $A \in \mathcal {S}$
and
$A \in \mathcal {S}$
and
![]() $m(A) = 3$
. As a consequence of Lemma 3.22, there is an element g of G with
$m(A) = 3$
. As a consequence of Lemma 3.22, there is an element g of G with
![]() $A^g \le E$
. By Lemma 7.6 and Proposition 2.8 (i), we have
$A^g \le E$
. By Lemma 7.6 and Proposition 2.8 (i), we have
![]() $(W_0)^g = (W_A)^g = W_{A^g} = W_0$
. Thus,
$(W_0)^g = (W_A)^g = W_{A^g} = W_0$
. Thus,
![]() $g \in M$
.
$g \in M$
.
We have
![]() $y^g \in E$
, and
$y^g \in E$
, and
![]() $y^g$
is G-conjugate and hence
$y^g$
is G-conjugate and hence
![]() $PSL_n(q)$
-conjugate to
$PSL_n(q)$
-conjugate to
![]() $t_j$
. So we have
$t_j$
. So we have
![]() $y^g = t_B$
for some
$y^g = t_B$
for some
![]() $B \subseteq \lbrace 1, \dots , n \rbrace $
with
$B \subseteq \lbrace 1, \dots , n \rbrace $
with
![]() $|B| = j$
. From Lemma 3.23 (i), we see that
$|B| = j$
. From Lemma 3.23 (i), we see that
![]() $y^g = t_B$
is
$y^g = t_B$
is
![]() $N_{PSL_n(q)}(E)$
-conjugate and hence
$N_{PSL_n(q)}(E)$
-conjugate and hence
![]() $N_G(E)$
-conjugate to
$N_G(E)$
-conjugate to
![]() $t_j$
. As
$t_j$
. As
![]() $N_G(E) \le M$
, it follows that
$N_G(E) \le M$
, it follows that
![]() $y^g$
is M-conjugate to
$y^g$
is M-conjugate to
![]() $t_j$
. Hence, y is M-conjugate to
$t_j$
. Hence, y is M-conjugate to
![]() $t_j$
.
$t_j$
.
(3) Let y be an involution of S such that y is G-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < n$
. Then
$2 \le j < n$
. Then
![]() $C_G(y) \le M$
.
$C_G(y) \le M$
.
Because of (2), we may assume that
![]() $\langle y \rangle $
is fully
$\langle y \rangle $
is fully
![]() $\mathcal {F}_S(G)$
-centralized. Then, by Lemma 7.1,
$\mathcal {F}_S(G)$
-centralized. Then, by Lemma 7.1,
![]() $C_G(y)$
is generated by the normalizers
$C_G(y)$
is generated by the normalizers
![]() $N_{C_G(y)}(U)$
, where U is a subgroup of
$N_{C_G(y)}(U)$
, where U is a subgroup of
![]() $C_S(y)$
such that there exists
$C_S(y)$
such that there exists
![]() $B \le U$
with
$B \le U$
with
![]() $B \in \mathcal {S}$
and
$B \in \mathcal {S}$
and
![]() $m(B) \ge 3$
. It suffices to show that each such normalizer lies in M.
$m(B) \ge 3$
. It suffices to show that each such normalizer lies in M.
Let U and B be as above, and let
![]() $g \in N_{C_G(y)}(U)$
. By Lemma 7.6 and Proposition 2.8 (i), we have
$g \in N_{C_G(y)}(U)$
. By Lemma 7.6 and Proposition 2.8 (i), we have
![]() $(W_0)^g = (W_B)^g = W_{B^g} = W_0$
. Thus,
$(W_0)^g = (W_B)^g = W_{B^g} = W_0$
. Thus,
![]() $g \in M$
and hence
$g \in M$
and hence
![]() $N_{C_G(y)}(U) \le M$
, as required.
$N_{C_G(y)}(U) \le M$
, as required.
(4) Let y be an involution of S. Then
![]() $C_G(y) \le M$
.
$C_G(y) \le M$
.
We can see from Lemmas 3.14 and 3.15 that
![]() $Z(S)$
has an involution s which is G-conjugate to
$Z(S)$
has an involution s which is G-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < n$
. Let P be a Sylow
$2 \le j < n$
. Let P be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_G(y)$
with
$C_G(y)$
with
![]() $s \in P$
. By (1),
$s \in P$
. By (1),
![]() $s \in M$
and hence
$s \in M$
and hence
![]() $s \in P \cap M$
. Now let
$s \in P \cap M$
. Now let
![]() $r \in N_P(P \cap M)$
. Then
$r \in N_P(P \cap M)$
. Then
![]() $s^r \in P \cap M$
. As a consequence of (1) and (2),
$s^r \in P \cap M$
. As a consequence of (1) and (2),
![]() $s^r$
and s are M-conjugate to
$s^r$
and s are M-conjugate to
![]() $t_j$
. Therefore, there is some
$t_j$
. Therefore, there is some
![]() $m \in M$
with
$m \in M$
with
![]() $s^r = s^m$
. We have
$s^r = s^m$
. We have
![]() $rm^{-1} \in C_G(s)$
, and so
$rm^{-1} \in C_G(s)$
, and so
![]() $rm^{-1} \in M$
by (3). Hence,
$rm^{-1} \in M$
by (3). Hence,
![]() $r \in M$
. Consequently,
$r \in M$
. Consequently,
![]() $N_P(P \cap M) = P \cap M$
. It follows that
$N_P(P \cap M) = P \cap M$
. It follows that
![]() $P = P \cap M$
.
$P = P \cap M$
.
Let
![]() $U \le P$
with
$U \le P$
with
![]() $m(U) \ge 3$
, and let
$m(U) \ge 3$
, and let
![]() $g \in N_{C_G(y)}(U)$
. By Lemma 2.3, any
$g \in N_{C_G(y)}(U)$
. By Lemma 2.3, any
![]() $E_8$
-subgroup of S has an involution which is the image of an involution of
$E_8$
-subgroup of S has an involution which is the image of an involution of
![]() $SL_n(q)$
. Since
$SL_n(q)$
. Since
![]() $m(U) \ge 3$
, it follows that U has an element u which is G-conjugate to
$m(U) \ge 3$
, it follows that U has an element u which is G-conjugate to
![]() $t_k$
for some even
$t_k$
for some even
![]() $2 \le k < n$
. By the preceding paragraph,
$2 \le k < n$
. By the preceding paragraph,
![]() $u, u^g \in U \le P \le M$
. As a consequence of (1) and (2), u and
$u, u^g \in U \le P \le M$
. As a consequence of (1) and (2), u and
![]() $u^g$
are M-conjugate to
$u^g$
are M-conjugate to
![]() $t_k$
. So there is some
$t_k$
. So there is some
![]() $m \in M$
with
$m \in M$
with
![]() $u^g = u^m$
. Hence,
$u^g = u^m$
. Hence,
![]() $gm^{-1} \in C_G(u)$
. From (3), we see that
$gm^{-1} \in C_G(u)$
. From (3), we see that
![]() $C_G(u) \le M$
, and so
$C_G(u) \le M$
, and so
![]() $gm^{-1} \in M$
. Thus,
$gm^{-1} \in M$
. Thus,
![]() $g \in M$
and hence
$g \in M$
and hence
![]() $N_{C_G(y)}(U) \le M$
. Since
$N_{C_G(y)}(U) \le M$
. Since
![]() $C_G(y)$
is
$C_G(y)$
is
![]() $3$
-generated by Corollary 7.3, it follows that
$3$
-generated by Corollary 7.3, it follows that
![]() $C_G(y) \le M$
.
$C_G(y) \le M$
.
(5)
![]() $M = G.$
$M = G.$
Assume that
![]() $M \ne G$
. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11], we may deduce from (1) and (4) that M is strongly embedded in G, i.e.,
$M \ne G$
. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11], we may deduce from (1) and (4) that M is strongly embedded in G, i.e.,
![]() $M \cap M^g$
has odd order for any
$M \cap M^g$
has odd order for any
![]() $g \in G \setminus M$
. Applying [Reference Suzuki50, Chapter 6, 4.4], it follows that G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has at least two conjugacy classes of involutions. This contradiction shows that
$g \in G \setminus M$
. Applying [Reference Suzuki50, Chapter 6, 4.4], it follows that G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has at least two conjugacy classes of involutions. This contradiction shows that
![]() $M = G$
.
$M = G$
.
(6) Conclusion.
Let
![]() $y \in E^{\#}$
, and let J be a
$y \in E^{\#}$
, and let J be a
![]() $2$
-component of
$2$
-component of
![]() $C_G(y)$
. By Lemma 7.4,
$C_G(y)$
. By Lemma 7.4,
![]() $J/O(J)$
is locally balanced. So, by [Reference Gorenstein and Walter31, Corollary 5.6], G is balanced with respect to E. Proposition 2.8 (ii) implies that
$J/O(J)$
is locally balanced. So, by [Reference Gorenstein and Walter31, Corollary 5.6], G is balanced with respect to E. Proposition 2.8 (ii) implies that
![]() $W_0$
has odd order. By (5), we have
$W_0$
has odd order. By (5), we have
![]() $M = G$
and hence
$M = G$
and hence
![]() $W_0 \trianglelefteq G$
. As
$W_0 \trianglelefteq G$
. As
![]() $O(G) = 1$
by Hypothesis 5.1, it follows that
$O(G) = 1$
by Hypothesis 5.1, it follows that
![]() $W_0 = 1$
. So we have
$W_0 = 1$
. So we have
![]() $O(C_G(y)) = 1$
for all
$O(C_G(y)) = 1$
for all
![]() $y \in E^{\#}$
, and the statement of the proposition follows.
$y \in E^{\#}$
, and the statement of the proposition follows.
Proposition 7.7 implies that if
![]() $q^{*} = 3$
, then
$q^{*} = 3$
, then
![]() $K \cong SL_{n-2}^{\varepsilon }(3)$
and
$K \cong SL_{n-2}^{\varepsilon }(3)$
and
![]() $L \cong SL_2(3)$
. Our next goal is to find the isomorphism types of K and L for the case
$L \cong SL_2(3)$
. Our next goal is to find the isomorphism types of K and L for the case
![]() $q^{*} \ne 3$
.
$q^{*} \ne 3$
.
In general,
![]() $O(C_{PSL_n(q)}(t))$
is not trivial. So, if
$O(C_{PSL_n(q)}(t))$
is not trivial. So, if
![]() $q^{*}$
is not assumed to be
$q^{*}$
is not assumed to be
![]() $3$
, we have no chance to prove that
$3$
, we have no chance to prove that
![]() $O(C_G(t)) = 1$
. However, we will be able to show that
$O(C_G(t)) = 1$
. However, we will be able to show that
for any Klein four subgroup F of G consisting of elements of the form
![]() $t_A$
, where
$t_A$
, where
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. This will later enable us to determine the isomorphism types of K and L for the case
$A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. This will later enable us to determine the isomorphism types of K and L for the case
![]() $q^{*} \ne 3$
.
$q^{*} \ne 3$
.
7.3
 $2$
-balance of G
$2$
-balance of G
In this subsection, we prove that G is
![]() $2$
-balanced when
$2$
-balanced when
![]() $q^{*} \ne 3$
.
$q^{*} \ne 3$
.
Lemma 7.8. Set
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Let F be a Klein four subgroup of C. Then
. Let F be a Klein four subgroup of C. Then
![]() .
.
Proof. We closely follow arguments found in the proof of [Reference Gorenstein and Walter31, Theorem 5.2].
First, we consider the case that F has a nontrivial element y such that
centralizes
. Then
normalizes
and, as
,
also normalizes
. It follows that
Hence,
is a subgroup of
with odd order. By [Reference Kurzweil and Stellmacher37, 1.5.5],
normalizes
. It follows that
As
, this implies that
centralizes
. By definition of
, we have
. Consequently,
centralizes
![]() $\overline K$
.
$\overline K$
.
Now we treat the case that
![]() . For each subgroup or element X of C, let
. For each subgroup or element X of C, let
![]() $\widehat X$
denote the image of
$\widehat X$
denote the image of
![]() in
in
![]() . Since
. Since
![]() , we have
, we have
![]() , and so
, and so
![]() $\widehat F$
is a Klein four subgroup of
$\widehat F$
is a Klein four subgroup of
![]() $\widehat C$
. As
$\widehat C$
. As
![]() , we have that
, we have that
![]() is locally
is locally
![]() $2$
-balanced (see Lemma 3.49). Using this together with the fact that the group
$2$
-balanced (see Lemma 3.49). Using this together with the fact that the group
![]() is isomorphic to a subgroup of
is isomorphic to a subgroup of
![]() containing
containing
![]() , we may conclude that
, we may conclude that
![]() $\Delta _{\widehat C}(\widehat F) = 1$
. By [Reference Gorenstein and Walter31, Proposition 3.11], if X is a finite group, B a
$\Delta _{\widehat C}(\widehat F) = 1$
. By [Reference Gorenstein and Walter31, Proposition 3.11], if X is a finite group, B a
![]() $2$
-subgroup of X and
$2$
-subgroup of X and
![]() $N \trianglelefteq X$
, then the image of
$N \trianglelefteq X$
, then the image of
![]() $O(C_X(B))$
in
$O(C_X(B))$
in
![]() $X/N$
lies in
$X/N$
lies in
![]() $O(C_{X/N}(BN/N))$
. Thus, if y is an involution of F, then the image of
$O(C_{X/N}(BN/N))$
. Thus, if y is an involution of F, then the image of
![]() in
in
![]() $\widehat C$
lies in
$\widehat C$
lies in
![]() $O(C_{\widehat C}(\widehat y))$
. It follows that the image of
$O(C_{\widehat C}(\widehat y))$
. It follows that the image of
![]() in
in
![]() $\widehat C$
is contained in
$\widehat C$
is contained in
![]() $\Delta _{\widehat C}(\widehat F) = 1$
. Hence,
$\Delta _{\widehat C}(\widehat F) = 1$
. Hence,
![]() .
.
Lemma 7.9. Let
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Then
. Then
![]() is a
is a
![]() $2$
-group.
$2$
-group.
Proof. For convenience, we denote
![]() by
by
![]() . Since
. Since
![]() is core-free, we have that
is core-free, we have that
![]() is core-free. So it is enough to prove that
is core-free. So it is enough to prove that
![]() is
is
![]() $2$
-nilpotent. By [Reference Linckelmann39, Theorem 1.4], it suffices to show that
$2$
-nilpotent. By [Reference Linckelmann39, Theorem 1.4], it suffices to show that
![]() has a nilpotent
has a nilpotent
![]() $2$
-fusion system.
$2$
-fusion system.
Let X denote the subgroup of T consisting of all elements of T of the form
 $$ \begin{align*} \begin{pmatrix}A & \\ & B \end{pmatrix} Z(SL_n(q)) \end{align*} $$
$$ \begin{align*} \begin{pmatrix}A & \\ & B \end{pmatrix} Z(SL_n(q)) \end{align*} $$
with
![]() $A \in W \cap Z(GL_{n-2}(q))$
,
$A \in W \cap Z(GL_{n-2}(q))$
,
![]() $B \in V \cap Z(GL_2(q))$
and
$B \in V \cap Z(GL_2(q))$
and
![]() $\mathrm {det}(A) \mathrm {det}(B) = 1$
.
$\mathrm {det}(A) \mathrm {det}(B) = 1$
.
Let
![]() $A \in W$
and
$A \in W$
and
![]() $B \in V$
with
$B \in V$
with
![]() $\mathrm {det}(A)\mathrm {det}(B) = 1$
and
$\mathrm {det}(A)\mathrm {det}(B) = 1$
and
 $$ \begin{align*} m := \begin{pmatrix}A & \\ & B \end{pmatrix} Z(SL_n(q)) \in T. \end{align*} $$
$$ \begin{align*} m := \begin{pmatrix}A & \\ & B \end{pmatrix} Z(SL_n(q)) \in T. \end{align*} $$
Assume that
![]() centralizes
centralizes
![]() and
and
![]() . Then we have
. Then we have
![]() $A \in Z(GL_{n-2}(q))$
by Lemma 6.2. Since
$A \in Z(GL_{n-2}(q))$
by Lemma 6.2. Since
![]() centralizes
centralizes
![]() ,
,
![]() also centralizes
also centralizes
![]() . Thus, m centralizes
. Thus, m centralizes
![]() $X_2$
, and so B centralizes
$X_2$
, and so B centralizes
![]() $V \cap SL_2(q)$
. Lemma 3.17 implies that
$V \cap SL_2(q)$
. Lemma 3.17 implies that
![]() $B \in Z(GL_2(q))$
. So we have
$B \in Z(GL_2(q))$
. So we have
![]() $m \in X$
. Conversely, if
$m \in X$
. Conversely, if
![]() $A \in Z(GL_{n-2}(q))$
and
$A \in Z(GL_{n-2}(q))$
and
![]() $B \in Z(GL_2(q))$
, then
$B \in Z(GL_2(q))$
, then
![]() as a consequence of Lemmas 6.2 and 3.44. It follows that
as a consequence of Lemmas 6.2 and 3.44. It follows that
![]() .
.
Let
![]() $\mathcal {F} := \mathcal {F}_S(PSL_n(q)) = \mathcal {F}_S(G)$
. Since X is central in
$\mathcal {F} := \mathcal {F}_S(PSL_n(q)) = \mathcal {F}_S(G)$
. Since X is central in
![]() $C_{PSL_n(q)}(t)$
, the only subsystem of
$C_{PSL_n(q)}(t)$
, the only subsystem of
![]() $C_{\mathcal {F}}(\langle t \rangle )$
on X is the nilpotent fusion system on X. It follows that
$C_{\mathcal {F}}(\langle t \rangle )$
on X is the nilpotent fusion system on X. It follows that
![]() is nilpotent. So
is nilpotent. So
![]() has a nilpotent
has a nilpotent
![]() $2$
-fusion system, as required.
$2$
-fusion system, as required.
In the following lemma,
![]() $A_1$
and
$A_1$
and
![]() $A_2$
have the meanings given to them after Lemma 6.5.
$A_2$
have the meanings given to them after Lemma 6.5.
Lemma 7.10. Set
![]() $C := C_G(t)$
. Suppose that
$C := C_G(t)$
. Suppose that
![]() $q^{*} \ne 3$
. Then
$q^{*} \ne 3$
. Then
![]() $A_1$
,
$A_1$
,
![]() $A_2$
and L are the only
$A_2$
and L are the only
![]() $2$
-components of
$2$
-components of
![]() $C_C(u)$
. Moreover, the following hold:
$C_C(u)$
. Moreover, the following hold:
-
(i)
 $A_1$
is the only
$A_1$
is the only
 $2$
-component of
$2$
-component of
 $C_C(u)$
containing u.
$C_C(u)$
containing u. -
(ii)
 $A_2$
is the only
$A_2$
is the only
 $2$
-component of
$2$
-component of
 $C_C(u)$
containing neither u nor t.
$C_C(u)$
containing neither u nor t. -
(iii) L is the only
 $2$
-component of
$2$
-component of
 $C_C(u)$
containing t.
$C_C(u)$
containing t.
Proof. By definition,
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are
$A_2$
are
![]() $2$
-components of
$2$
-components of
![]() $C_C(u)$
. Also, it is clear from the definition of L (see Proposition 6.8) that L is a
$C_C(u)$
. Also, it is clear from the definition of L (see Proposition 6.8) that L is a
![]() $2$
-component of
$2$
-component of
![]() $C_C(u)$
.
$C_C(u)$
.
Set
![]() . As a consequence of Lemma 6.4,
. As a consequence of Lemma 6.4,
![]() and
and
![]() are the only
are the only
![]() $2$
-components of
$2$
-components of
![]() . Moreover,
. Moreover,
![]() is a component of
is a component of
![]() . So Lemma 2.5 shows that
. So Lemma 2.5 shows that
![]() ,
,
![]() and
and
![]() are the only
are the only
![]() $2$
-components of
$2$
-components of
![]() . As we have observed after Lemma 6.5, there is a bijection from the set of
. As we have observed after Lemma 6.5, there is a bijection from the set of
![]() $2$
-components of
$2$
-components of
![]() $C_C(u)$
to the set of
$C_C(u)$
to the set of
![]() $2$
-components of
$2$
-components of
![]() sending each
sending each
![]() $2$
-component A of
$2$
-component A of
![]() $C_C(u)$
to
$C_C(u)$
to
![]() . Therefore,
. Therefore,
![]() $A_1$
,
$A_1$
,
![]() $A_2$
and L are the only
$A_2$
and L are the only
![]() $2$
-components of
$2$
-components of
![]() $C_C(u)$
.
$C_C(u)$
.
It remains to prove (i), (ii) and (iii). We have
![]() $T_1 \le A_1$
by Lemma 6.6 and thus
$T_1 \le A_1$
by Lemma 6.6 and thus
![]() $u \in A_1$
. From the definition of L, it is clear that
$u \in A_1$
. From the definition of L, it is clear that
![]() $t \in L$
. Moreover,
$t \in L$
. Moreover,
![]() $u \not \in L$
since
$u \not \in L$
since
![]() is the only involution of
is the only involution of
![]() . Similarly,
. Similarly,
![]() $t \not \in A_1$
. Also, it is easy to see from Lemma 6.4 that u and t cannot be elements of
$t \not \in A_1$
. Also, it is easy to see from Lemma 6.4 that u and t cannot be elements of
![]() $A_2$
.
$A_2$
.
Lemma 7.11. Suppose that
![]() $q^{*} \ne 3$
. Let F be a Klein four subgroup of T. Then we have
$q^{*} \ne 3$
. Let F be a Klein four subgroup of T. Then we have
![]() $\Delta _G(F) \cap C_G(t) \le O(C_G(t))$
.
$\Delta _G(F) \cap C_G(t) \le O(C_G(t))$
.
Proof. Set
![]() $C := C_G(t)$
,
$C := C_G(t)$
,
![]() $D := \Delta _G(F) \cap C$
and
$D := \Delta _G(F) \cap C$
and
![]() . We are going to show that
. We are going to show that
![]() is trivial.
is trivial.
A direct calculation shows that
![]() $D \le \Delta _C(F)$
. For each
$D \le \Delta _C(F)$
. For each
![]() $a \in F^{\#}$
, we have
$a \in F^{\#}$
, we have
![]() as a consequence of Corollary 2.2. Therefore, we have
as a consequence of Corollary 2.2. Therefore, we have
![]() , and hence,
, and hence,
![]() . Lemma 7.8 implies that
. Lemma 7.8 implies that
![]() . In particular,
. In particular,
![]() . Fix a subgroup
. Fix a subgroup
![]() $D_0$
of
$D_0$
of
![]() $C_C(u)$
with
$C_C(u)$
with
![]() . Also, let
. Also, let
![]() $g \in G$
with
$g \in G$
with
![]() $u^g = t$
and
$u^g = t$
and
![]() $t^g = u$
(such an element exists by Lemma 6.7). Note that
$t^g = u$
(such an element exists by Lemma 6.7). Note that
![]() $(D_0)^g \le (C_C(u))^g = C_C(u)$
.
$(D_0)^g \le (C_C(u))^g = C_C(u)$
.
We accomplish the proof step by step.
(1)
![]() $A_1$
,
$A_1$
,
![]() $A_2$
and L are normal subgroups of
$A_2$
and L are normal subgroups of
![]() $C_C(u)$
.
$C_C(u)$
.
This is immediate from Lemma 7.10.
(2) There is a group isomorphism
![]() which maps
which maps
![]() to
to
![]() and
and
![]() to
to
![]() .
.
Let
![]() $\mathrm {Aut}_{D_0}(L/O(L))$
denote the image of
$\mathrm {Aut}_{D_0}(L/O(L))$
denote the image of
![]() $\mathrm {Aut}_{D_0}(L)$
under the natural group homomorphism
$\mathrm {Aut}_{D_0}(L)$
under the natural group homomorphism
![]() $\mathrm {Aut}(L) \rightarrow \mathrm {Aut}(L/O(L))$
. Also, let
$\mathrm {Aut}(L) \rightarrow \mathrm {Aut}(L/O(L))$
. Also, let
![]() $\mathrm {Aut}_{(D_0)^g}(A_1/O(A_1))$
denote the image of
$\mathrm {Aut}_{(D_0)^g}(A_1/O(A_1))$
denote the image of
![]() $\mathrm {Aut}_{(D_0)^g}(A_1)$
under the natural group homomorphism
$\mathrm {Aut}_{(D_0)^g}(A_1)$
under the natural group homomorphism
![]() $\mathrm {Aut}(A_1) \rightarrow \mathrm {Aut}(A_1/O(A_1))$
.
$\mathrm {Aut}(A_1) \rightarrow \mathrm {Aut}(A_1/O(A_1))$
.
From Lemma 7.10, it is clear that
![]() $(A_1)^{g^{-1}} = L$
. The group isomorphism
$(A_1)^{g^{-1}} = L$
. The group isomorphism
![]() $c_{g^{-1}}|_{A_1,L}$
induces a group isomorphism
$c_{g^{-1}}|_{A_1,L}$
induces a group isomorphism
![]() $A_1/O(A_1) \rightarrow L/O(L)$
, and this group isomorphism induces a group isomorphism
$A_1/O(A_1) \rightarrow L/O(L)$
, and this group isomorphism induces a group isomorphism
![]() $\mathrm {Aut}(A_1/O(A_1)) \rightarrow \mathrm {Aut}(L/O(L))$
. By a direct calculation, the group isomorphism just mentioned maps
$\mathrm {Aut}(A_1/O(A_1)) \rightarrow \mathrm {Aut}(L/O(L))$
. By a direct calculation, the group isomorphism just mentioned maps
![]() $\mathrm {Aut}_{(D_0)^g}(A_1/O(A_1))$
to
$\mathrm {Aut}_{(D_0)^g}(A_1/O(A_1))$
to
![]() $\mathrm {Aut}_{D_0}(L/O(L))$
and
$\mathrm {Aut}_{D_0}(L/O(L))$
and
![]() $\mathrm {Inn}(A_1/O(A_1))$
to
$\mathrm {Inn}(A_1/O(A_1))$
to
![]() $\mathrm {Inn}(L/O(L))$
.
$\mathrm {Inn}(L/O(L))$
.
We have
![]() . As
. As
![]() $SL_2(q^{*})$
is core-free, it follows that
$SL_2(q^{*})$
is core-free, it follows that
![]() $A_1 \cap O(C) = O(A_1)$
. So the natural group homomorphism
$A_1 \cap O(C) = O(A_1)$
. So the natural group homomorphism
![]() induces a group isomorphism
induces a group isomorphism
![]() . This group isomorphism induces a group isomorphism
. This group isomorphism induces a group isomorphism
![]() . By a direct calculation, the group isomorphism just mentioned maps
. By a direct calculation, the group isomorphism just mentioned maps
![]() $\mathrm {Aut}_{(D_0)^g}(A_1/O(A_1))$
to
$\mathrm {Aut}_{(D_0)^g}(A_1/O(A_1))$
to
![]() and
and
![]() $\mathrm {Inn}(A_1/O(A_1))$
to
$\mathrm {Inn}(A_1/O(A_1))$
to
![]() . In a very similar way, we obtain an isomorphism
. In a very similar way, we obtain an isomorphism
![]() which maps
which maps
![]() $\mathrm {Aut}_{D_0}(L/O(L))$
to
$\mathrm {Aut}_{D_0}(L/O(L))$
to
![]() and
and
![]() $\mathrm {Inn}(L/O(L))$
to
$\mathrm {Inn}(L/O(L))$
to
![]() .
.
As a consequence of the preceding observations, there is a group isomorphism
![]() which maps
which maps
![]() to
to
![]() and
and
![]() to
to
![]() , as asserted.
, as asserted.
(3)
![]() .
.
As observed above,
![]() centralizes
centralizes
![]() . In particular,
. In particular,
![]() centralizes
centralizes
![]() . This implies that
. This implies that
![]() $[D_0,A_2] \le O(C)$
. As
$[D_0,A_2] \le O(C)$
. As
![]() $D_0$
normalizes
$D_0$
normalizes
![]() $A_2$
by (1), we also have that
$A_2$
by (1), we also have that
![]() $[D_0,A_2] \le A_2$
. Consequently,
$[D_0,A_2] \le A_2$
. Consequently,
![]() $[D_0,A_2] \le O(A_2)$
. Because of Lemma 7.10, we have
$[D_0,A_2] \le O(A_2)$
. Because of Lemma 7.10, we have
![]() $(A_2)^g = A_2$
. It follows that
$(A_2)^g = A_2$
. It follows that
![]() $[(D_0)^g,A_2] \le O(A_2)$
. This easily implies
$[(D_0)^g,A_2] \le O(A_2)$
. This easily implies
![]() . As
. As
![]() by Lemma 6.4, we have
by Lemma 6.4, we have
![]() . It follows that
. It follows that
![]() . The three subgroups lemma [Reference Kurzweil and Stellmacher37, 1.5.6] implies
. The three subgroups lemma [Reference Kurzweil and Stellmacher37, 1.5.6] implies
![]() . Hence,
. Hence,
![]() centralizes
centralizes
![]() . By (1),
. By (1),
![]() normalizes
normalizes
![]() . Moreover,
. Moreover,
![]() has odd order since
has odd order since
![]() has odd order. The assertion now follows from Lemmas 6.4 (iii), 3.50 and 3.51.
has odd order. The assertion now follows from Lemmas 6.4 (iii), 3.50 and 3.51.
(4)
![]() .
.
As a consequence of (2) and (3), we have
. This implies
. By [Reference Kurzweil and Stellmacher37, 6.5.3],
. As observed above,
and hence
. It follows that
is a subgroup of
. By Lemma 7.9,
is a
![]() $2$
-group. As
$2$
-group. As
has odd order and
, this implies that
. Now we see that

(5) Conclusion.
As F is a Klein four subgroup of T, we have
![]() $F = \langle y_1, y_2 \rangle $
for two commuting involutions
$F = \langle y_1, y_2 \rangle $
for two commuting involutions
![]() $y_1$
and
$y_1$
and
![]() $y_2$
of T. For
$y_2$
of T. For
![]() $i \in \lbrace 1,2\rbrace $
, we have
$i \in \lbrace 1,2\rbrace $
, we have
 $$ \begin{align*} y_i = \begin{pmatrix} A_i & \\ & B_i \end{pmatrix} Z(SL_n(q)) \end{align*} $$
$$ \begin{align*} y_i = \begin{pmatrix} A_i & \\ & B_i \end{pmatrix} Z(SL_n(q)) \end{align*} $$
for some
![]() $A_i \in W$
and
$A_i \in W$
and
![]() $B_i \in V$
with
$B_i \in V$
with
![]() $\mathrm {det}(A_i) \mathrm {det}(B_i) = 1$
. Let
$\mathrm {det}(A_i) \mathrm {det}(B_i) = 1$
. Let
![]() $y_3 := y_1y_2, A_3 := A_1A_2$
and
$y_3 := y_1y_2, A_3 := A_1A_2$
and
![]() $B_3 := B_1B_2$
. As
$B_3 := B_1B_2$
. As
![]() $y_1, y_2, y_3$
are involutions, we have
$y_1, y_2, y_3$
are involutions, we have
![]() $(B_i)^2 \in Z(GL_2(q))$
for each
$(B_i)^2 \in Z(GL_2(q))$
for each
![]() $i \in \lbrace 1,2,3 \rbrace $
.
$i \in \lbrace 1,2,3 \rbrace $
.
It is easy to note that
. If
![]() $B \in V \cap SL_2(q)$
and
$B \in V \cap SL_2(q)$
and
 $$ \begin{align*} y := \begin{pmatrix} I_{n-2} & \\ & B \end{pmatrix} Z(SL_n(q)) \in X_2, \end{align*} $$
$$ \begin{align*} y := \begin{pmatrix} I_{n-2} & \\ & B \end{pmatrix} Z(SL_n(q)) \in X_2, \end{align*} $$
then
 $$ \begin{align*} y^{y_i} = \begin{pmatrix} I_{n-2} & \\ & B^{B_i} \end{pmatrix} Z(SL_n(q)) \end{align*} $$
$$ \begin{align*} y^{y_i} = \begin{pmatrix} I_{n-2} & \\ & B^{B_i} \end{pmatrix} Z(SL_n(q)) \end{align*} $$
for each
![]() $i \in \lbrace 1,2,3 \rbrace $
. Applying Lemma 3.52, we deduce that
$i \in \lbrace 1,2,3 \rbrace $
. Applying Lemma 3.52, we deduce that

So we have
by (4). This completes the proof.
Lemma 7.12. Suppose that
![]() $q^{*} \ne 3$
. Then G is
$q^{*} \ne 3$
. Then G is
![]() $2$
-balanced.
$2$
-balanced.
Proof. Let F be a Klein four subgroup of G, and let a be an involution of G centralizing F. We have to show that
![]() $\Delta _G(F) \cap C_G(a) \le O(C_G(a))$
.
$\Delta _G(F) \cap C_G(a) \le O(C_G(a))$
.
Assume that a is G-conjugate to t. Then there is some
![]() $g \in G$
with
$g \in G$
with
![]() $a^g = t$
and
$a^g = t$
and
![]() $F^g \le T$
. By Lemma 7.11, we have
$F^g \le T$
. By Lemma 7.11, we have
![]() $\Delta _G(F^g) \cap C_G(t) \le O(C_G(t))$
. Clearly,
$\Delta _G(F^g) \cap C_G(t) \le O(C_G(t))$
. Clearly,
![]() $\Delta _G(F)^g = \Delta _G(F^g)$
. It follows that
$\Delta _G(F)^g = \Delta _G(F^g)$
. It follows that
![]() $\Delta _G(F) \cap C_G(a) \le O(C_G(a))$
.
$\Delta _G(F) \cap C_G(a) \le O(C_G(a))$
.
Assume now that a is not G-conjugate to t. Let J be a
![]() $2$
-component of
$2$
-component of
![]() $C_G(a)$
. By Propositions 6.10, 6.11 and 6.13, either
$C_G(a)$
. By Propositions 6.10, 6.11 and 6.13, either
![]() $J/O(J) \cong SL_k^{\varepsilon }(q^{*})/O(SL_k^{\varepsilon }(q^{*}))$
for some
$J/O(J) \cong SL_k^{\varepsilon }(q^{*})/O(SL_k^{\varepsilon }(q^{*}))$
for some
![]() $k \ge 3$
, or
$k \ge 3$
, or
![]() $J/O(J)$
is isomorphic to a nontrivial quotient of
$J/O(J)$
is isomorphic to a nontrivial quotient of
![]() $SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
$SL_{\frac {n}{2}}^{\varepsilon _0}(q_0)$
for some nontrivial odd prime power
![]() $q_0$
and some
$q_0$
and some
![]() $\varepsilon _0 \in \lbrace +,- \rbrace $
. So
$\varepsilon _0 \in \lbrace +,- \rbrace $
. So
![]() $J/O(J)$
is locally
$J/O(J)$
is locally
![]() $2$
-balanced by Lemma 3.49. Applying [Reference Gorenstein and Walter31, Theorem 5.2], we may conclude that
$2$
-balanced by Lemma 3.49. Applying [Reference Gorenstein and Walter31, Theorem 5.2], we may conclude that
![]() $\Delta _{C_G(a)}(F) \le O(C_G(a))$
. A direct calculation shows that
$\Delta _{C_G(a)}(F) \le O(C_G(a))$
. A direct calculation shows that
![]() $\Delta _G(F) \cap C_G(a) \le \Delta _{C_G(a)}(F)$
. Hence,
$\Delta _G(F) \cap C_G(a) \le \Delta _{C_G(a)}(F)$
. Hence,
![]() $\Delta _G(F) \cap C_G(a) \le O(C_G(a))$
.
$\Delta _G(F) \cap C_G(a) \le O(C_G(a))$
.
7.4 The case
 $q^{*} \ne 3$
: triviality of
$q^{*} \ne 3$
: triviality of
 $\Delta _G(F)$
$\Delta _G(F)$
Lemma 7.13. Suppose that
![]() $q^{*} \ne 3$
. Assume moreover that
$q^{*} \ne 3$
. Assume moreover that
![]() $q \equiv 1 \ \mathrm {mod} \ 4$
or
$q \equiv 1 \ \mathrm {mod} \ 4$
or
![]() $n \ge 7$
. Then we have
$n \ge 7$
. Then we have
![]() $\Delta _G(F) = 1$
for each Klein four subgroup F of S.
$\Delta _G(F) = 1$
for each Klein four subgroup F of S.
Proof. We follow the pattern of the proof of [Reference Gorenstein and Walter31, Theorem 9.1].
For each elementary abelian
![]() $2$
-subgroup A of G of rank at least
$2$
-subgroup A of G of rank at least
![]() $3$
, we define
$3$
, we define
Let P and Q be elementary abelian subgroups of S of rank at least
![]() $3$
. We claim that
$3$
. We claim that
![]() $W_P = W_Q$
. By Corollary 3.34 (iii), S is
$W_P = W_Q$
. By Corollary 3.34 (iii), S is
![]() $3$
-connected. So there exist a natural number
$3$
-connected. So there exist a natural number
![]() $m \ge 1$
and a sequence
$m \ge 1$
and a sequence
such that
![]() $P_i$
,
$P_i$
,
![]() $1 \le i \le m$
, is an elementary abelian subgroup of S of rank at least
$1 \le i \le m$
, is an elementary abelian subgroup of S of rank at least
![]() $3$
and such that
$3$
and such that
for all
![]() $1 \le i < m$
. By Lemma 7.12, G is
$1 \le i < m$
. By Lemma 7.12, G is
![]() $2$
-balanced. Proposition 2.8 (ii) implies that
$2$
-balanced. Proposition 2.8 (ii) implies that
![]() $W_{P_i} = W_{P_{i+1}}$
for all
$W_{P_i} = W_{P_{i+1}}$
for all
![]() $1 \le i < m$
. Therefore,
$1 \le i < m$
. Therefore,
![]() $W_P = W_Q$
, as asserted.
$W_P = W_Q$
, as asserted.
We use
![]() $W_0$
to denote
$W_0$
to denote
![]() $W_P$
, where P is an elementary abelian subgroup of S of rank at least
$W_P$
, where P is an elementary abelian subgroup of S of rank at least
![]() $3$
. Let
$3$
. Let
![]() $M := N_G(W_0)$
. We accomplish the proof step by step.
$M := N_G(W_0)$
. We accomplish the proof step by step.
(1)
![]() $N_G(S) \le M$
.
$N_G(S) \le M$
.
Let
![]() $g \in N_G(S)$
. Take an elementary abelian subgroup P of S with
$g \in N_G(S)$
. Take an elementary abelian subgroup P of S with
![]() $m(P) \ge 3$
. By Proposition 2.8 (i), we have
$m(P) \ge 3$
. By Proposition 2.8 (i), we have
![]() $(W_0)^g = (W_P)^g = W_{P^g} = W_0$
. Thus,
$(W_0)^g = (W_P)^g = W_{P^g} = W_0$
. Thus,
![]() $g \in M$
.
$g \in M$
.
(2) Let x be an involution of S. Then
![]() $C_G(x) \le M$
.
$C_G(x) \le M$
.
By Corollary 3.35, there is an elementary abelian subgroup P of S with
![]() $x \in P$
and
$x \in P$
and
![]() $m(P) = 4$
. Clearly,
$m(P) = 4$
. Clearly,
![]() $P \le C_G(x)$
. Let R be a Sylow
$P \le C_G(x)$
. Let R be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_G(x)$
containing P. By Corollary 7.3,
$C_G(x)$
containing P. By Corollary 7.3,
![]() $C_G(x)$
is
$C_G(x)$
is
![]() $3$
-generated. Hence,
$3$
-generated. Hence,
![]() $C_G(x)$
is generated by the normalizers
$C_G(x)$
is generated by the normalizers
![]() $N_{C_G(x)}(U)$
, where
$N_{C_G(x)}(U)$
, where
![]() $U \le R$
and
$U \le R$
and
![]() $m(U) \ge 3$
. It suffices to show that each such normalizer lies in M.
$m(U) \ge 3$
. It suffices to show that each such normalizer lies in M.
So let U be a subgroup of R with
![]() $m(U) \ge 3$
, and let
$m(U) \ge 3$
, and let
![]() $g \in N_{C_G(x)}(U)$
. Let Q be an elementary abelian subgroup of U with
$g \in N_{C_G(x)}(U)$
. Let Q be an elementary abelian subgroup of U with
![]() $m(Q) = 3$
, and let
$m(Q) = 3$
, and let
![]() $h \in G$
with
$h \in G$
with
![]() $R^h \le S$
. Then
$R^h \le S$
. Then
![]() $W_{Q^h} = W_{Q^{gh}} = W_{P^h} = W_0$
. Proposition 2.8 (i) implies that
$W_{Q^h} = W_{Q^{gh}} = W_{P^h} = W_0$
. Proposition 2.8 (i) implies that
![]() $W_Q = W_{Q^g} = W_P = W_0$
. Applying Proposition 2.8 (i) again, it follows that
$W_Q = W_{Q^g} = W_P = W_0$
. Applying Proposition 2.8 (i) again, it follows that
![]() $(W_0)^g = (W_Q)^g = W_{Q^g} = W_0$
. Hence,
$(W_0)^g = (W_Q)^g = W_{Q^g} = W_0$
. Hence,
![]() $g \in M$
and thus
$g \in M$
and thus
![]() $N_{C_G(x)}(U) \le M$
.
$N_{C_G(x)}(U) \le M$
.
(3)
![]() $M = G$
.
$M = G$
.
Assume that
![]() $M \ne G$
. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11]; we may deduce from (1) and (2) that M is strongly embedded in G, i.e.,
$M \ne G$
. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11]; we may deduce from (1) and (2) that M is strongly embedded in G, i.e.,
![]() $M \cap M^g$
has odd order for any
$M \cap M^g$
has odd order for any
![]() $g \in G \setminus M$
. Applying [Reference Suzuki50, Chapter 6, 4.4], it follows that G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has at least two conjugacy classes of involutions. This contradiction shows that
$g \in G \setminus M$
. Applying [Reference Suzuki50, Chapter 6, 4.4], it follows that G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has at least two conjugacy classes of involutions. This contradiction shows that
![]() $M = G$
.
$M = G$
.
(4) Conclusion.
Let F be a Klein four subgroup of S. By Corollary 3.35, there is an elementary abelian subgroup P of S with
![]() $F \le P$
and
$F \le P$
and
![]() $m(P) = 4$
. Clearly,
$m(P) = 4$
. Clearly,
![]() $\Delta _G(F) \le W_P$
. Since G is
$\Delta _G(F) \le W_P$
. Since G is
![]() $2$
-balanced,
$2$
-balanced,
![]() $W_P$
has odd order by Proposition 2.8 (ii). Since
$W_P$
has odd order by Proposition 2.8 (ii). Since
![]() $W_P = W_0$
, we have
$W_P = W_0$
, we have
![]() $W_P \trianglelefteq G$
by (3). As
$W_P \trianglelefteq G$
by (3). As
![]() $O(G) = 1$
by Hypothesis 5.1, it follows that
$O(G) = 1$
by Hypothesis 5.1, it follows that
![]() $W_P = 1$
. Hence,
$W_P = 1$
. Hence,
![]() $\Delta _G(F) = 1$
.
$\Delta _G(F) = 1$
.
Next, we deal with the case that
![]() $n = 6$
,
$n = 6$
,
![]() $q \equiv 3 \mod 4$
and
$q \equiv 3 \mod 4$
and
![]() $q^{*} \ne 3$
. We show that, in this case,
$q^{*} \ne 3$
. We show that, in this case,
![]() $\Delta _G(F) = 1$
for each Klein four subgroup F of S consisting of elements of the form
$\Delta _G(F) = 1$
for each Klein four subgroup F of S consisting of elements of the form
![]() $t_A$
, where
$t_A$
, where
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. We need the following lemma.
$A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. We need the following lemma.
Lemma 7.14. Suppose that
![]() $q^{*} \ne 3$
. Set
$q^{*} \ne 3$
. Set
![]() $\ell := n-4$
. Let E be the subgroup of T consisting of all
$\ell := n-4$
. Let E be the subgroup of T consisting of all
![]() $t_A$
, where
$t_A$
, where
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. Let
$A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. Let
![]() $E_1$
denote the subgroup of
$E_1$
denote the subgroup of
![]() $X_1$
consisting of all
$X_1$
consisting of all
![]() $t_A$
, where A is a subset of
$t_A$
, where A is a subset of
![]() $\lbrace 1,\dots ,n-2 \rbrace $
of even order. Then we may choose elements
$\lbrace 1,\dots ,n-2 \rbrace $
of even order. Then we may choose elements
![]() $m_1, \dots , m_{\ell } \in N_K(E_1)$
and an
$m_1, \dots , m_{\ell } \in N_K(E_1)$
and an
![]() $E_8$
-subgroup
$E_8$
-subgroup
![]() $E_0$
of E with
$E_0$
of E with
Proof. Set
![]() $C := C_G(t)$
and
$C := C_G(t)$
and
![]() . Let
. Let
![]() $H := SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
. Let
$H := SL_{n-2}^{\varepsilon }(q^{*})/O(SL_{n-2}^{\varepsilon }(q^{*}))$
. Let
![]() $\widetilde {D}$
be the subgroup of
$\widetilde {D}$
be the subgroup of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
consisting of all diagonal matrices in
$SL_{n-2}^{\varepsilon }(q^{*})$
consisting of all diagonal matrices in
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
with diagonal entries in
$SL_{n-2}^{\varepsilon }(q^{*})$
with diagonal entries in
![]() $\lbrace 1, -1 \rbrace $
, and let D denote the image of
$\lbrace 1, -1 \rbrace $
, and let D denote the image of
![]() $\widetilde {D}$
in H. Denote by
$\widetilde {D}$
in H. Denote by
![]() $H_1$
the image of
$H_1$
the image of
 $$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-4}\end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left\lbrace \begin{pmatrix} A & \\ & I_{n-4}\end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
in H.
We claim that there is a group isomorphism
![]() which maps
which maps
![]() to D and
to D and
![]() to
to
![]() $H_1$
. By Lemma 6.4 (iii), there is a group isomorphism
$H_1$
. By Lemma 6.4 (iii), there is a group isomorphism
![]() under which
under which
![]() corresponds to
corresponds to
![]() $H_1$
. Since
$H_1$
. Since
![]() is the only involution of
is the only involution of
![]() , we have that
, we have that
![]() is the image of
is the image of
![]() $\mathrm {diag}(-1,-1,1,\dots ,1) \in SL_{n-2}^{\varepsilon }(q^{*})$
in H. Clearly,
$\mathrm {diag}(-1,-1,1,\dots ,1) \in SL_{n-2}^{\varepsilon }(q^{*})$
in H. Clearly,
![]() is elementary abelian of order
is elementary abelian of order
![]() $2^{n-3}$
. Using Lemma 3.22, we conclude that
$2^{n-3}$
. Using Lemma 3.22, we conclude that
![]() is H-conjugate to D. So there is some
is H-conjugate to D. So there is some
![]() $\alpha \in \mathrm {Inn}(H)$
mapping
$\alpha \in \mathrm {Inn}(H)$
mapping
![]() to D. We may assume that
to D. We may assume that
![]() $\alpha $
centralizes
$\alpha $
centralizes
![]() . Then
. Then
![]() ${H_1}^{\alpha } = H_1$
, and the isomorphism
${H_1}^{\alpha } = H_1$
, and the isomorphism
![]() $\psi := \varphi \alpha $
maps
$\psi := \varphi \alpha $
maps
![]() to D and
to D and
![]() to
to
![]() $H_1$
, as desired.
$H_1$
, as desired.
Using Lemma 3.39, we can find elements
![]() $x_1, \dots , x_{\ell } \in N_H(D)$
such that
$x_1, \dots , x_{\ell } \in N_H(D)$
such that
![]() $H = \langle H_1$
,
$H = \langle H_1$
,
![]() ${H_1}^{x_1}$
, …,
${H_1}^{x_1}$
, …,
![]() ${H_1}^{x_{\ell }} \rangle $
. Therefore, K has elements
${H_1}^{x_{\ell }} \rangle $
. Therefore, K has elements
![]() $m_1$
,
$m_1$
,
![]() $\dots $
,
$\dots $
,
![]() $m_{\ell }$
such that
$m_{\ell }$
such that
and
. From Lemma 2.1, we see that
. So we may assume
![]() $m_i \in N_K(E_1)$
for
$m_i \in N_K(E_1)$
for
![]() $i \in \lbrace 1, \dots , \ell \rbrace $
. Let
$i \in \lbrace 1, \dots , \ell \rbrace $
. Let
![]() $E_0 := \langle u, t_{\lbrace 3,4 \rbrace }, t_{\lbrace 4,5 \rbrace } \rangle $
. By Lemma 6.5, we have
$E_0 := \langle u, t_{\lbrace 3,4 \rbrace }, t_{\lbrace 4,5 \rbrace } \rangle $
. By Lemma 6.5, we have
. In particular,
normalizes
. Moreover,
centralizes
. We have
and
(see Lemma 6.4). Applying Lemma 3.44, we conclude that
. As
and
, we even have that
is a component of
. It follows that
Let
![]() $k \in K$
such that
$k \in K$
such that
. As
![]() $K \trianglelefteq C$
, we have
$K \trianglelefteq C$
, we have
![]() $[k,E_0] \le O(C) \cap K = O(K)$
. Thus,
$[k,E_0] \le O(C) \cap K = O(K)$
. Thus,
![]() $k O(K) \in C_{C/O(K)}(E_0O(K)/O(K))$
. By Lemma 2.1, there is an element
$k O(K) \in C_{C/O(K)}(E_0O(K)/O(K))$
. By Lemma 2.1, there is an element
![]() $z \in C_C(E_0)$
such that
$z \in C_C(E_0)$
such that
![]() $kO(K) = zO(K)$
. Observing that
$kO(K) = zO(K)$
. Observing that
![]() $z \in C_K(E_0)$
and that
$z \in C_K(E_0)$
and that
, we may conclude that
. If
![]() $1 \le i \le \ell $
, then
$1 \le i \le \ell $
, then
, where the second equality follows from Proposition 2.4. It follows that
This completes the proof.
Lemma 7.15. Suppose that
![]() $n = 6$
,
$n = 6$
,
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
and
$q \equiv 3 \ \mathrm {mod} \ 4$
and
![]() $q^{*} \ne 3$
. Let E denote the subgroup of S consisting of all
$q^{*} \ne 3$
. Let E denote the subgroup of S consisting of all
![]() $t_A$
, where A is a subset of
$t_A$
, where A is a subset of
![]() $\lbrace 1, \dots , n \rbrace $
of even order. Then
$\lbrace 1, \dots , n \rbrace $
of even order. Then
![]() $\Delta _G(F) = 1$
for any Klein four subgroup F of E.
$\Delta _G(F) = 1$
for any Klein four subgroup F of E.
Proof. We follow the pattern of the proof of [Reference Gorenstein and Walter31, Theorem 9.1].
Set
![]() $W_0 := \langle \Delta _G(F) \ \vert \ F \le E, m(F) = 2 \rangle $
and
$W_0 := \langle \Delta _G(F) \ \vert \ F \le E, m(F) = 2 \rangle $
and
![]() $M := N_G(W_0)$
. Since T is the image of
$M := N_G(W_0)$
. Since T is the image of
 $$ \begin{align*} \left \lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in W, B \in V, \mathrm{det}(A)\mathrm{det}(B) = 1 \right \rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} A & \\ & B \end{pmatrix} \ : \ A \in W, B \in V, \mathrm{det}(A)\mathrm{det}(B) = 1 \right \rbrace \end{align*} $$
in
![]() $PSL_n(q)$
, we have
$PSL_n(q)$
, we have
![]() $T \in \mathrm {Syl}_2(PSL_n(q))$
by Lemma 3.15. Hence,
$T \in \mathrm {Syl}_2(PSL_n(q))$
by Lemma 3.15. Hence,
![]() $S = T$
and thus
$S = T$
and thus
![]() $t \in Z(S)$
. By choice of W (see Section 5), we have
$t \in Z(S)$
. By choice of W (see Section 5), we have
 $$ \begin{align*} W = \left\lbrace\begin{pmatrix} A & \\ & B \\ \end{pmatrix} \ : \ A, B \in V \right \rbrace \cdot \left \langle \begin{pmatrix} & I_{2} \\ I_{2} & \\ \end{pmatrix} \right \rangle \end{align*} $$
$$ \begin{align*} W = \left\lbrace\begin{pmatrix} A & \\ & B \\ \end{pmatrix} \ : \ A, B \in V \right \rbrace \cdot \left \langle \begin{pmatrix} & I_{2} \\ I_{2} & \\ \end{pmatrix} \right \rangle \end{align*} $$
We accomplish the proof step by step.
(1) For each subgroup
![]() $E_0$
of E with order at least
$E_0$
of E with order at least
![]() $8$
, we have
$8$
, we have
![]() $N_G(E_0) \le M$
.
$N_G(E_0) \le M$
.
Clearly,
![]() $E \cong E_{16}$
. Therefore, the statement follows from the
$E \cong E_{16}$
. Therefore, the statement follows from the
![]() $2$
-balance of G (see Lemma 7.12) and Proposition 2.8 (ii).
$2$
-balance of G (see Lemma 7.12) and Proposition 2.8 (ii).
(2)
![]() $N_G(S) \le M$
.
$N_G(S) \le M$
.
First, we prove
![]() $S \le M$
. By (1), we have
$S \le M$
. By (1), we have
![]() $E \le M$
. As
$E \le M$
. As
![]() $q \equiv 3 \ \mathrm {mod} \ 4$
and
$q \equiv 3 \ \mathrm {mod} \ 4$
and
![]() $S = T$
, any element of S can be written as a product of an element of E and an element of S induced by a matrix of the form
$S = T$
, any element of S can be written as a product of an element of E and an element of S induced by a matrix of the form
 $$ \begin{align*} \begin{pmatrix} A & \\ & B \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} A & \\ & B \end{pmatrix} \end{align*} $$
with
![]() $A \in W \cap SL_4(q)$
and
$A \in W \cap SL_4(q)$
and
![]() $B \in V \cap SL_2(q)$
. So, in order to prove that
$B \in V \cap SL_2(q)$
. So, in order to prove that
![]() $S \le M$
, it suffices to show that each element of S induced by a matrix of this form lies in M. If
$S \le M$
, it suffices to show that each element of S induced by a matrix of this form lies in M. If
![]() $B \in V \cap SL_2(q)$
, then the image of
$B \in V \cap SL_2(q)$
, then the image of
 $$ \begin{align*} \begin{pmatrix} I_4 & \\ & B \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} I_4 & \\ & B \end{pmatrix} \end{align*} $$
in S centralizes the group
![]() $\langle t_{\lbrace 1,2 \rbrace }, t_{\lbrace 2,3 \rbrace }, t_{\lbrace 3,4 \rbrace } \rangle \cong E_8$
. So it is contained in M by (1). Hence, in order to prove that
$\langle t_{\lbrace 1,2 \rbrace }, t_{\lbrace 2,3 \rbrace }, t_{\lbrace 3,4 \rbrace } \rangle \cong E_8$
. So it is contained in M by (1). Hence, in order to prove that
![]() $S \le M$
, it suffices to show that if
$S \le M$
, it suffices to show that if
![]() $A \in W \cap SL_4(q)$
, then the image of
$A \in W \cap SL_4(q)$
, then the image of
 $$ \begin{align*} \begin{pmatrix} A & \\ & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} A & \\ & I_2 \end{pmatrix} \end{align*} $$
in S lies in M. So assume that
![]() $A \in W \cap SL_4(q)$
. By the structure of W, there are elements
$A \in W \cap SL_4(q)$
. By the structure of W, there are elements
![]() $M_1$
,
$M_1$
,
![]() $M_2$
of V such that
$M_2$
of V such that
![]() $\mathrm {det}(M_1) = \mathrm {det}(M_2)$
and
$\mathrm {det}(M_1) = \mathrm {det}(M_2)$
and
 $$ \begin{align*} A = \begin{pmatrix} M_1 & \\ & M_2 \end{pmatrix} \ \text{or} \ A = \begin{pmatrix} M_1 & \\ & M_2 \end{pmatrix} \begin{pmatrix} & I_2 \\ I_2 & \end{pmatrix}. \end{align*} $$
$$ \begin{align*} A = \begin{pmatrix} M_1 & \\ & M_2 \end{pmatrix} \ \text{or} \ A = \begin{pmatrix} M_1 & \\ & M_2 \end{pmatrix} \begin{pmatrix} & I_2 \\ I_2 & \end{pmatrix}. \end{align*} $$
The image of
 $$ \begin{align*} \begin{pmatrix} M_1 & & \\ & M_2 & \\ & & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} M_1 & & \\ & M_2 & \\ & & I_2 \end{pmatrix} \end{align*} $$
in S can be written as a product of an element of E and an element of S induced by a matrix of the form
 $$ \begin{align*} \begin{pmatrix} \widetilde{M_1} & & \\ & \widetilde{M_2} & \\ & & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \widetilde{M_1} & & \\ & \widetilde{M_2} & \\ & & I_2 \end{pmatrix} \end{align*} $$
with
![]() $\widetilde {M_1},\widetilde {M_2} \in V \cap SL_2(q)$
. The images of
$\widetilde {M_1},\widetilde {M_2} \in V \cap SL_2(q)$
. The images of
 $$ \begin{align*} \begin{pmatrix} \widetilde{M_1} & \\ & I_4 \end{pmatrix} \ \text{and} \ \begin{pmatrix} I_2 & & \\ & \widetilde{M_2} & \\ & & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} \widetilde{M_1} & \\ & I_4 \end{pmatrix} \ \text{and} \ \begin{pmatrix} I_2 & & \\ & \widetilde{M_2} & \\ & & I_2 \end{pmatrix} \end{align*} $$
in S centralize the groups
![]() $\langle t_{\lbrace 3,4 \rbrace }, t_{\lbrace 4,5 \rbrace }, t_{\lbrace 5,6 \rbrace } \rangle $
and
$\langle t_{\lbrace 3,4 \rbrace }, t_{\lbrace 4,5 \rbrace }, t_{\lbrace 5,6 \rbrace } \rangle $
and
![]() $\langle t_{\lbrace 1,2 \rbrace }, t_{\lbrace 2,5 \rbrace }, t_{\lbrace 5,6 \rbrace } \rangle $
, respectively. So they are elements of M. It follows that the image of
$\langle t_{\lbrace 1,2 \rbrace }, t_{\lbrace 2,5 \rbrace }, t_{\lbrace 5,6 \rbrace } \rangle $
, respectively. So they are elements of M. It follows that the image of
 $$ \begin{align*} \begin{pmatrix} M_1 & & \\ & M_2 & \\ & & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} M_1 & & \\ & M_2 & \\ & & I_2 \end{pmatrix} \end{align*} $$
in S lies in M. The image of the block matrix
 $$ \begin{align*} \begin{pmatrix} & I_2 & \\ I_2 & & \\ & & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} & I_2 & \\ I_2 & & \\ & & I_2 \end{pmatrix} \end{align*} $$
in S normalizes E and is thus contained in M. It follows that the image of
 $$ \begin{align*} \begin{pmatrix} A & \\ & I_2 \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} A & \\ & I_2 \end{pmatrix} \end{align*} $$
in S lies in M. Consequently,
![]() $S \le M$
.
$S \le M$
.
By Lemma 3.24,
![]() $\mathrm {Aut}_{PSL_n(q)}(S) = \mathrm {Inn}(S)$
. As
$\mathrm {Aut}_{PSL_n(q)}(S) = \mathrm {Inn}(S)$
. As
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, it follows that
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, it follows that
![]() $\mathrm {Aut}_G(S) = \mathrm {Inn}(S)$
, and so
$\mathrm {Aut}_G(S) = \mathrm {Inn}(S)$
, and so
![]() $N_G(S) = SC_G(S)$
. We have seen above that
$N_G(S) = SC_G(S)$
. We have seen above that
![]() $S \le M$
, and we have
$S \le M$
, and we have
![]() $C_G(S) \le M$
by (1). Hence,
$C_G(S) \le M$
by (1). Hence,
![]() $N_G(S) \le M$
.
$N_G(S) \le M$
.
(3)
![]() $C_G(t) \le M$
.
$C_G(t) \le M$
.
Let
![]() $E_1$
be the subgroup of
$E_1$
be the subgroup of
![]() $X_1$
consisting of all
$X_1$
consisting of all
![]() $t_A$
, where A is a subset of
$t_A$
, where A is a subset of
![]() $\lbrace 1, \dots , n-2 \rbrace $
of even order. As a consequence of Lemma 7.14, there is an
$\lbrace 1, \dots , n-2 \rbrace $
of even order. As a consequence of Lemma 7.14, there is an
![]() $E_8$
-subgroup
$E_8$
-subgroup
![]() $E_0$
of E such that
$E_0$
of E such that
![]() $K = \langle O(K), C_K(E_0), N_K(E_1) \rangle $
. By (1),
$K = \langle O(K), C_K(E_0), N_K(E_1) \rangle $
. By (1),
![]() $C_K(E_0)$
and
$C_K(E_0)$
and
![]() $N_K(E_1)$
are subgroups of M. By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
$N_K(E_1)$
are subgroups of M. By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
Therefore,
![]() $O(K) \le M$
by (1). Consequently,
$O(K) \le M$
by (1). Consequently,
![]() $K \le M$
. By the Frattini argument,
$K \le M$
. By the Frattini argument,
So it suffices to show that
![]() $N_{C_G(t)}(X_1) \le M$
. Since
$N_{C_G(t)}(X_1) \le M$
. Since
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we may conclude from Lemma 5.7 that
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we may conclude from Lemma 5.7 that
![]() $\mathrm {Aut}_{C_G(t)}(X_1)$
is a
$\mathrm {Aut}_{C_G(t)}(X_1)$
is a
![]() $2$
-group. Hence,
$2$
-group. Hence,
![]() $N_{C_G(t)}(X_1)/C_{C_G(t)}(X_1)$
is a
$N_{C_G(t)}(X_1)/C_{C_G(t)}(X_1)$
is a
![]() $2$
-group. As
$2$
-group. As
![]() $X_1 \trianglelefteq T = S \in \mathrm {Syl}_2(C_G(t))$
, it follows that
$X_1 \trianglelefteq T = S \in \mathrm {Syl}_2(C_G(t))$
, it follows that
![]() $N_{C_G(t)}(X_1) = S C_{C_G(t)}(X_1)$
. We have
$N_{C_G(t)}(X_1) = S C_{C_G(t)}(X_1)$
. We have
![]() $S \le M$
by (2), and
$S \le M$
by (2), and
![]() $C_{C_G(t)}(X_1) \le C_G(E_1) \le M$
by (1). Consequently,
$C_{C_G(t)}(X_1) \le C_G(E_1) \le M$
by (1). Consequently,
![]() $N_{C_G(t)}(X_1) \le M$
, as required.
$N_{C_G(t)}(X_1) \le M$
, as required.
(4) Let x be an involution of S which is G-conjugate to t. Then x is M-conjugate to t.
It is easy to see that if an element of T is
![]() $PSL_n(q)$
-conjugate to t, then it is
$PSL_n(q)$
-conjugate to t, then it is
![]() $C_{PSL_n(q)}(t)$
-conjugate to an element of E. As
$C_{PSL_n(q)}(t)$
-conjugate to an element of E. As
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
and
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
and
![]() $S = T$
, it follows that x is
$S = T$
, it follows that x is
![]() $C_G(t)$
-conjugate and hence M-conjugate to an element y of E. From Lemma 3.23, we see that if an element of E is
$C_G(t)$
-conjugate and hence M-conjugate to an element y of E. From Lemma 3.23, we see that if an element of E is
![]() $PSL_n(q)$
-conjugate to t, then it is
$PSL_n(q)$
-conjugate to t, then it is
![]() $N_{PSL_n(q)}(E)$
-conjugate to t. So, as
$N_{PSL_n(q)}(E)$
-conjugate to t. So, as
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we have that y is
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we have that y is
![]() $N_G(E)$
-conjugate to t. By (1),
$N_G(E)$
-conjugate to t. By (1),
![]() $N_G(E) \le M$
, and so x is M-conjugate to t.
$N_G(E) \le M$
, and so x is M-conjugate to t.
(5) Let x be an involution of S. Then
![]() $C_G(x) \le M$
.
$C_G(x) \le M$
.
Let R be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $C_G(x)$
with
$C_G(x)$
with
![]() $C_S(x) \le R$
. We have
$C_S(x) \le R$
. We have
![]() $t \in Z(S) \le C_S(x)$
and
$t \in Z(S) \le C_S(x)$
and
![]() $t \in M$
. Thus,
$t \in M$
. Thus,
![]() $t \in R \cap M$
. Let
$t \in R \cap M$
. Let
![]() $r \in N_R(R \cap M)$
. Then
$r \in N_R(R \cap M)$
. Then
![]() $y := t^r \in R \cap M$
. As a consequence of (4), y is M-conjugate to t. So there is an element m of M such that
$y := t^r \in R \cap M$
. As a consequence of (4), y is M-conjugate to t. So there is an element m of M such that
![]() $t^r = y = t^m$
. We have
$t^r = y = t^m$
. We have
![]() $rm^{-1} \in C_G(t) \le M$
by (3), and so
$rm^{-1} \in C_G(t) \le M$
by (3), and so
![]() $r \in R \cap M$
. Hence,
$r \in R \cap M$
. Hence,
![]() $N_R(R \cap M) = R \cap M$
, and thus,
$N_R(R \cap M) = R \cap M$
, and thus,
![]() $R = R \cap M$
.
$R = R \cap M$
.
By Corollary 7.3,
![]() $C_G(x)$
is
$C_G(x)$
is
![]() $3$
-generated. Therefore,
$3$
-generated. Therefore,
![]() $C_G(x)$
is generated by the normalizers
$C_G(x)$
is generated by the normalizers
![]() $N_{C_G(x)}(U)$
, where
$N_{C_G(x)}(U)$
, where
![]() $U \le R$
and
$U \le R$
and
![]() $m(U) \ge 3$
. It suffices to show that each such normalizer lies in M.
$m(U) \ge 3$
. It suffices to show that each such normalizer lies in M.
So let
![]() $U \le R$
with
$U \le R$
with
![]() $m(U) \ge 3$
, and let
$m(U) \ge 3$
, and let
![]() $g \in N_{C_G(x)}(U)$
. Take an elementary abelian subgroup Q of U of rank
$g \in N_{C_G(x)}(U)$
. Take an elementary abelian subgroup Q of U of rank
![]() $3$
. Lemma 2.3 shows that any
$3$
. Lemma 2.3 shows that any
![]() $E_8$
-subgroup of S has an involution which is the image of an involution of
$E_8$
-subgroup of S has an involution which is the image of an involution of
![]() $SL_n(q)$
. This implies that Q has an element s which is G-conjugate to t. Since
$SL_n(q)$
. This implies that Q has an element s which is G-conjugate to t. Since
![]() $s, s^g \in U \le R \le M$
, we see from (4) that s and
$s, s^g \in U \le R \le M$
, we see from (4) that s and
![]() $s^g$
are M-conjugate to t. So there are elements
$s^g$
are M-conjugate to t. So there are elements
![]() $m,m' \in M$
such that
$m,m' \in M$
such that
![]() $s = t^m$
and
$s = t^m$
and
![]() $s^g = t^{m'}$
. We have
$s^g = t^{m'}$
. We have
![]() $t^{m'} = s^g = (t^m)^g = t^{mg}$
. Thus,
$t^{m'} = s^g = (t^m)^g = t^{mg}$
. Thus,
![]() $mgm^{\prime -1} \in C_G(t) \le M$
, and hence,
$mgm^{\prime -1} \in C_G(t) \le M$
, and hence,
![]() $g \in M$
. It follows that
$g \in M$
. It follows that
![]() $N_{C_G(x)}(U) \le M$
.
$N_{C_G(x)}(U) \le M$
.
(6)
![]() $M = G$
.
$M = G$
.
Assume that
![]() $M \ne G$
. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11], we may deduce from (2) and (5) that M is strongly embedded in G, i.e.,
$M \ne G$
. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11], we may deduce from (2) and (5) that M is strongly embedded in G, i.e.,
![]() $M \cap M^g$
has odd order for any
$M \cap M^g$
has odd order for any
![]() $g \in G \setminus M$
. Applying [Reference Suzuki50, Chapter 6, 4.4], it follows that G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has precisely two conjugacy classes of involutions. This contradiction shows that
$g \in G \setminus M$
. Applying [Reference Suzuki50, Chapter 6, 4.4], it follows that G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has precisely two conjugacy classes of involutions. This contradiction shows that
![]() $M = G$
.
$M = G$
.
(7) Conclusion.
Let F be a Klein four subgroup of E. Clearly,
![]() $\Delta _G(F) \le W_0$
. By (6), we have
$\Delta _G(F) \le W_0$
. By (6), we have
![]() $W_0 \trianglelefteq G$
. Since G is
$W_0 \trianglelefteq G$
. Since G is
![]() $2$
-balanced,
$2$
-balanced,
![]() $W_0$
has odd order by Proposition 2.8 (ii). As
$W_0$
has odd order by Proposition 2.8 (ii). As
![]() $O(G) = 1$
by Hypothesis 5.1, it follows that
$O(G) = 1$
by Hypothesis 5.1, it follows that
![]() $W_0 = 1$
. Hence,
$W_0 = 1$
. Hence,
![]() $\Delta _G(F) = 1$
.
$\Delta _G(F) = 1$
.
7.5 Quasisimplicity of the
 $2$
-components of
$2$
-components of
 $C_G(t)$
$C_G(t)$
In this subsection, we determine the isomorphism types of K and L.
Lemma 7.16. Let x and y be two commuting involutions of G. Set
![]() $C := C_G(x)$
and
$C := C_G(x)$
and
![]() . Then any
. Then any
![]() $2$
-component of
$2$
-component of
![]() is a component of
is a component of
![]() .
.
Proof. By [Reference Gorenstein and Walter31, Corollary 3.2],
![]() . We know from Section 6 that
. We know from Section 6 that
![]() is a K-group, i.e., the composition factors of
is a K-group, i.e., the composition factors of
![]() are known finite simple groups. Applying [Reference Gorenstein25, Theorem 3.5], we conclude that
are known finite simple groups. Applying [Reference Gorenstein25, Theorem 3.5], we conclude that
![]() . Therefore, any
. Therefore, any
![]() $2$
-component of
$2$
-component of
![]() is a component of
is a component of
![]() . So any
. So any
![]() $2$
-component of
$2$
-component of
![]() is a component of
is a component of
![]() .
.
Instead of using [Reference Gorenstein25, Theorem 3.5], the lemma could be proved directly by using Corollary 3.47 (i) and the results of Section 6.
Proposition 7.17.
K is isomorphic to a quotient of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
by a central subgroup of odd order.
$SL_{n-2}^{\varepsilon }(q^{*})$
by a central subgroup of odd order.
Proof. The proof is inspired from the proof of [Reference Gorenstein and Walter31, Theorem 10.1].
For
![]() $q^{*} = 3$
, the proposition follows from Proposition 7.7. From now on, we assume that
$q^{*} = 3$
, the proposition follows from Proposition 7.7. From now on, we assume that
![]() $q^{*} \ne 3$
.
$q^{*} \ne 3$
.
Set
![]() $C := C_G(t)$
. Let E denote the subgroup of T consisting of all
$C := C_G(t)$
. Let E denote the subgroup of T consisting of all
![]() $t_A$
, where
$t_A$
, where
![]() $A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. We assume
$A \subseteq \lbrace 1, \dots , n \rbrace $
has even order. We assume
![]() $m_1, \dots , m_{\ell }$
, where
$m_1, \dots , m_{\ell }$
, where
![]() $\ell := n-4$
, to be elements of K and
$\ell := n-4$
, to be elements of K and
![]() $E_0$
to be an
$E_0$
to be an
![]() $E_8$
-subgroup of E with
$E_8$
-subgroup of E with
Such elements
![]() $m_1, \dots , m_{\ell }$
and such a subgroup
$m_1, \dots , m_{\ell }$
and such a subgroup
![]() $E_0$
exist by Lemma 7.14.
$E_0$
exist by Lemma 7.14.
The proof will be accomplished step by step.
(1) Let f be an involution of
![]() $E_0$
. Then
$E_0$
. Then
![]() $L_{2'}(C_K(E_0)) \le L_{2'}(C_C(f))$
.
$L_{2'}(C_K(E_0)) \le L_{2'}(C_C(f))$
.
As
![]() $K \trianglelefteq C$
, we have
$K \trianglelefteq C$
, we have
![]() $C_K(E_0) \trianglelefteq C_C(E_0)$
. This implies
$C_K(E_0) \trianglelefteq C_C(E_0)$
. This implies
![]() $L_{2'}(C_K(E_0)) \le L_{2'}(C_C(E_0))$
. By [Reference Gorenstein and Walter31, Theorem 3.1], we have
$L_{2'}(C_K(E_0)) \le L_{2'}(C_C(E_0))$
. By [Reference Gorenstein and Walter31, Theorem 3.1], we have
![]() $L_{2'}(C_{C_C(f)}(E_0)) \le L_{2'}(C_C(f))$
. Clearly,
$L_{2'}(C_{C_C(f)}(E_0)) \le L_{2'}(C_C(f))$
. Clearly,
![]() $C_{C_C(f)}(E_0) = C_C(E_0)$
. It follows that
$C_{C_C(f)}(E_0) = C_C(E_0)$
. It follows that
![]() $L_{2'}(C_K(E_0)) \le L_{2'}(C_C(E_0)) \le L_{2'}(C_C(f))$
.
$L_{2'}(C_K(E_0)) \le L_{2'}(C_C(E_0)) \le L_{2'}(C_C(f))$
.
(2) Let F be a Klein four subgroup of
![]() $E_0$
. Set
$E_0$
. Set
![]() $D := [C_{O(K)}(F),L_{2'}(C_K(E_0))]$
. Then
$D := [C_{O(K)}(F),L_{2'}(C_K(E_0))]$
. Then
![]() $D = 1$
.
$D = 1$
.
Clearly,
![]() $L_{2'}(C_K(E_0))$
normalizes
$L_{2'}(C_K(E_0))$
normalizes
![]() $C_{O(K)}(F)$
. Also,
$C_{O(K)}(F)$
. Also,
![]() $O^{2'}(L_{2'}(C_K(E_0))) = L_{2'}(C_K(E_0))$
, and
$O^{2'}(L_{2'}(C_K(E_0))) = L_{2'}(C_K(E_0))$
, and
![]() $C_{O(K)}(F)$
is a
$C_{O(K)}(F)$
is a
![]() $2'$
-group. Applying [Reference Gorenstein, Lyons and Solomon27, Proposition 4.3 (i)], we conclude that
$2'$
-group. Applying [Reference Gorenstein, Lyons and Solomon27, Proposition 4.3 (i)], we conclude that
![]() $D = [D,L_{2'}(C_K(E_0))]$
.
$D = [D,L_{2'}(C_K(E_0))]$
.
Now let f be an involution of F. We are going to show that
![]() $D \le O(C_G(f))$
. Set
$D \le O(C_G(f))$
. Set
![]() $M := L_{2'}(C_C(f))$
. By (1),
$M := L_{2'}(C_C(f))$
. By (1),
![]() $L_{2'}(C_K(E_0)) \le M$
. Also,
$L_{2'}(C_K(E_0)) \le M$
. Also,
![]() $D \le C_C(F) \le C_C(f)$
and
$D \le C_C(F) \le C_C(f)$
and
![]() $M \trianglelefteq C_C(f)$
. It follows that
$M \trianglelefteq C_C(f)$
. It follows that
![]() $D = [D,L_{2'}(C_K(E_0))] \le [C_C(f), M] \le M$
.
$D = [D,L_{2'}(C_K(E_0))] \le [C_C(f), M] \le M$
.
Let
![]() . By Corollary 2.2,
. By Corollary 2.2,
![]() . As a consequence of Proposition 2.4,
. As a consequence of Proposition 2.4,
![]() . Lemma 7.16 implies that
. Lemma 7.16 implies that
![]() . It easily follows that
. It easily follows that
![]() is central in
is central in
![]() .
.
From the definition of D, it is clear that
![]() $D \le O(K)$
. So we have
$D \le O(K)$
. So we have
![]() $D \le M \cap O(K) \le O(M)$
. It follows that
$D \le M \cap O(K) \le O(M)$
. It follows that
![]() . In particular,
. In particular,
![]() centralizes
centralizes
![]() . Thus,
. Thus,
![]() $D = [D,L_{2'}(C_K(E_0))] \le O(C_G(f))$
.
$D = [D,L_{2'}(C_K(E_0))] \le O(C_G(f))$
.
Since f was arbitrarily chosen, it follows that
![]() $D \le \Delta _G(F)$
. By Lemmas 7.13 and 7.15, we have
$D \le \Delta _G(F)$
. By Lemmas 7.13 and 7.15, we have
![]() $\Delta _G(F) = 1$
. Consequently,
$\Delta _G(F) = 1$
. Consequently,
![]() $D = 1$
, as wanted.
$D = 1$
, as wanted.
(3)
![]() $O(K) \le Z(K)$
.
$O(K) \le Z(K)$
.
By [Reference Gorenstein, Lyons and Solomon27, Proposition 11.23], we have
Because of (2), it follows that
![]() $O(K)$
centralizes
$O(K)$
centralizes
![]() $L_{2'}(C_K(E_0))$
. By choice of
$L_{2'}(C_K(E_0))$
. By choice of
![]() $E_0$
, we have
$E_0$
, we have
for some
![]() $m_1, \dots , m_{\ell } \in K$
. It follows that
$m_1, \dots , m_{\ell } \in K$
. It follows that
![]() $K = O(K)C_K(O(K))$
. Therefore,
$K = O(K)C_K(O(K))$
. Therefore,
![]() $C_K(O(K))$
has odd index in K. We have
$C_K(O(K))$
has odd index in K. We have
![]() $O^{2'}(K) = K$
since K is a
$O^{2'}(K) = K$
since K is a
![]() $2$
-component of C. It follows that
$2$
-component of C. It follows that
![]() $K = C_K(O(K))$
. Consequently,
$K = C_K(O(K))$
. Consequently,
![]() $O(K) \le Z(K)$
.
$O(K) \le Z(K)$
.
(4) Conclusion.
Applying [Reference Gorenstein, Lyons and Solomon27, Lemma 4.11], we deduce from (3) that K is a component of C. Therefore, K is quasisimple. We have
Applying Lemmas 3.1 and 3.2, we conclude that
![]() $K \cong SL_{n-2}^{\varepsilon }(q^{*})/Z$
for some central subgroup Z of
$K \cong SL_{n-2}^{\varepsilon }(q^{*})/Z$
for some central subgroup Z of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
. Using Proposition 3.19 or using the order formulas for
$SL_{n-2}^{\varepsilon }(q^{*})$
. Using Proposition 3.19 or using the order formulas for
![]() $\vert SL_{n-2}^{\varepsilon }(q^{*}) \vert $
and
$\vert SL_{n-2}^{\varepsilon }(q^{*}) \vert $
and
![]() $\vert SL_{n-2}(q) \vert $
given by [Reference Grove32, Proposition 1.1 and Corollary 11.29], we see that
$\vert SL_{n-2}(q) \vert $
given by [Reference Grove32, Proposition 1.1 and Corollary 11.29], we see that
Thus, Z has odd order.
Proposition 7.18. We have
![]() $L \cong SL_2(q^{*})$
and
$L \cong SL_2(q^{*})$
and
![]() $L \trianglelefteq C_G(t)$
. Moreover, L is the only normal subgroup of
$L \trianglelefteq C_G(t)$
. Moreover, L is the only normal subgroup of
![]() $C_G(t)$
which is isomorphic to
$C_G(t)$
which is isomorphic to
![]() $SL_2(q^{*})$
.
$SL_2(q^{*})$
.
Proof. For
![]() $q^{*} = 3$
, this follows from Propositions 7.7 and 6.8.
$q^{*} = 3$
, this follows from Propositions 7.7 and 6.8.
Assume now that
![]() $q^{*} \ne 3$
. Let
$q^{*} \ne 3$
. Let
![]() $\widetilde K := KO(C_G(t))$
. By the last statement in Proposition 2.4,
$\widetilde K := KO(C_G(t))$
. By the last statement in Proposition 2.4,
![]() $K = O^{2'}(\widetilde K)$
. Let
$K = O^{2'}(\widetilde K)$
. Let
![]() $i \in \lbrace 1,2 \rbrace $
. Since
$i \in \lbrace 1,2 \rbrace $
. Since
![]() $A_i$
is a
$A_i$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_{C_G(t)}(u)$
, we have
$C_{C_G(t)}(u)$
, we have
![]() $A_i = O^{2'}(A_i)$
. Also,
$A_i = O^{2'}(A_i)$
. Also,
![]() $A_i \le \widetilde K$
, and so
$A_i \le \widetilde K$
, and so
![]() $A_i \le O^{2'}(\widetilde K) = K$
. It follows that
$A_i \le O^{2'}(\widetilde K) = K$
. It follows that
![]() $A_i$
is a
$A_i$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_K(u)$
.
$C_K(u)$
.
By Proposition 7.17, we have
![]() $K \cong SL_{n-2}^{\varepsilon }(q^{*})/Z$
for some central subgroup Z of
$K \cong SL_{n-2}^{\varepsilon }(q^{*})/Z$
for some central subgroup Z of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
with odd order. It is easy to see that if m is a noncentral involution of
$SL_{n-2}^{\varepsilon }(q^{*})$
with odd order. It is easy to see that if m is a noncentral involution of
![]() $SL_{n-2}^{\varepsilon }(q^{*})/Z$
and J is a
$SL_{n-2}^{\varepsilon }(q^{*})/Z$
and J is a
![]() $2$
-component of its centralizer in
$2$
-component of its centralizer in
![]() $SL_{n-2}^{\varepsilon }(q^{*})/Z$
, then
$SL_{n-2}^{\varepsilon }(q^{*})/Z$
, then
![]() $J \cong SL_k^{\varepsilon }(q^{*})$
for some
$J \cong SL_k^{\varepsilon }(q^{*})$
for some
![]() $k \ge 2$
. Since u is a noncentral involution of K and
$k \ge 2$
. Since u is a noncentral involution of K and
![]() $A_1/O(A_1) \cong SL_2(q^{*})$
, it follows that
$A_1/O(A_1) \cong SL_2(q^{*})$
, it follows that
![]() $A_1 \cong SL_2(q^{*})$
. By definition of L (see Proposition 6.8), L is isomorphic to
$A_1 \cong SL_2(q^{*})$
. By definition of L (see Proposition 6.8), L is isomorphic to
![]() $A_1$
. So we have
$A_1$
. So we have
![]() $L \cong SL_2(q^{*})$
.
$L \cong SL_2(q^{*})$
.
Let
![]() $L_0$
be the
$L_0$
be the
![]() $2$
-component of
$2$
-component of
![]() $C_G(t)$
associated to
$C_G(t)$
associated to
![]() $LO(C_G(t))/O(C_G(t))$
. By [Reference Kurzweil and Stellmacher37, 6.5.2], we have
$LO(C_G(t))/O(C_G(t))$
. By [Reference Kurzweil and Stellmacher37, 6.5.2], we have
![]() $[L_0,K] = 1$
. Hence,
$[L_0,K] = 1$
. Hence,
![]() $L_0 \le C_{C_G(t)}(u)$
. So
$L_0 \le C_{C_G(t)}(u)$
. So
![]() $L_0$
is a
$L_0$
is a
![]() $2$
-component of
$2$
-component of
![]() $C_{C_G(t)}(u)$
. Clearly,
$C_{C_G(t)}(u)$
. Clearly,
![]() $A_1 \ne L_0 \ne A_2$
. Lemma 7.10 implies that
$A_1 \ne L_0 \ne A_2$
. Lemma 7.10 implies that
![]() $L_0 = L$
. From Proposition 6.8 (iii), we see that
$L_0 = L$
. From Proposition 6.8 (iii), we see that
![]() $L = L_0 \trianglelefteq C_G(t)$
.
$L = L_0 \trianglelefteq C_G(t)$
.
Proposition 6.8 (iii) also shows that K and L are the only
![]() $2$
-components of
$2$
-components of
![]() $C_G(t)$
. So L is the only normal subgroup of
$C_G(t)$
. So L is the only normal subgroup of
![]() $C_G(t)$
isomorphic to
$C_G(t)$
isomorphic to
![]() $SL_2(q^{*})$
.
$SL_2(q^{*})$
.
8 The subgroup
 $G_0$
$G_0$
Let A be a subset of
![]() $\lbrace 1, \dots , n \rbrace $
with order
$\lbrace 1, \dots , n \rbrace $
with order
![]() $2$
. Then
$2$
. Then
![]() $t_A$
is G-conjugate to t. Proposition 7.18 implies that
$t_A$
is G-conjugate to t. Proposition 7.18 implies that
![]() $C_G(t_A)$
has a unique normal subgroup isomorphic to
$C_G(t_A)$
has a unique normal subgroup isomorphic to
![]() $SL_2(q^{*})$
. We denote this subgroup by
$SL_2(q^{*})$
. We denote this subgroup by
![]() $L_{A}$
, and we define
$L_{A}$
, and we define
![]() $G_0$
to be the subgroup of G generated by the groups
$G_0$
to be the subgroup of G generated by the groups
![]() $L_A$
, where
$L_A$
, where
![]() $A = \lbrace i,i+1 \rbrace $
for some
$A = \lbrace i,i+1 \rbrace $
for some
![]() $1 \le i < n$
. We are going to prove that
$1 \le i < n$
. We are going to prove that
![]() $G_0 \trianglelefteq G$
and that
$G_0 \trianglelefteq G$
and that
![]() $G_0$
is isomorphic to a nontrivial quotient of
$G_0$
is isomorphic to a nontrivial quotient of
![]() $SL_n^{\varepsilon }(q^{*})$
. This will complete the proof of Theorem 5.2.
$SL_n^{\varepsilon }(q^{*})$
. This will complete the proof of Theorem 5.2.
By Proposition 7.17, K is isomorphic to a quotient of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
by a central subgroup of odd order. By the proof of Proposition 7.18,
$SL_{n-2}^{\varepsilon }(q^{*})$
by a central subgroup of odd order. By the proof of Proposition 7.18,
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are
$A_2$
are
![]() $2$
-components of
$2$
-components of
![]() $C_K(u)$
if
$C_K(u)$
if
![]() $q^{*} \ne 3$
.
$q^{*} \ne 3$
.
Lemma 8.1. Let
![]() $Z \le Z(SL_{n-2}^{\varepsilon }(q^{*}))$
with
$Z \le Z(SL_{n-2}^{\varepsilon }(q^{*}))$
with
![]() $K \cong H := SL_{n-2}^{\varepsilon }(q^{*})/Z$
. Let
$K \cong H := SL_{n-2}^{\varepsilon }(q^{*})/Z$
. Let
![]() $H_1$
be the image of
$H_1$
be the image of
 $$ \begin{align*} \left \lbrace \begin{pmatrix} A & \\ & I_{n-4} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} A & \\ & I_{n-4} \end{pmatrix} \ : \ A \in SL_2^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
in H and
![]() $H_2$
the image of
$H_2$
the image of
 $$ \begin{align*} \left \lbrace \begin{pmatrix} I_2 & \\ & A \end{pmatrix} \ : \ A \in SL_{n-4}^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} I_2 & \\ & A \end{pmatrix} \ : \ A \in SL_{n-4}^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
in H. Then there is a group isomorphism
![]() $\varphi : K \rightarrow H$
which maps
$\varphi : K \rightarrow H$
which maps
![]() $A_1$
to
$A_1$
to
![]() $H_1$
and
$H_1$
and
![]() $A_2$
to
$A_2$
to
![]() $H_2$
.
$H_2$
.
Proof. For
![]() $q^{*} = 3$
, this follows from Proposition 7.7 and Lemma 6.4 (iii).
$q^{*} = 3$
, this follows from Proposition 7.7 and Lemma 6.4 (iii).
Assume now that
![]() $q^{*} \ne 3$
. Let
$q^{*} \ne 3$
. Let
![]() $\varphi : K \rightarrow H$
be a group isomorphism. For each even natural number k with
$\varphi : K \rightarrow H$
be a group isomorphism. For each even natural number k with
![]() $2 \le k < n-2$
, let
$2 \le k < n-2$
, let
![]() $h_k$
be the image of
$h_k$
be the image of
 $$ \begin{align*} \begin{pmatrix} -I_k & \\ & I_{n-2-k} \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} -I_k & \\ & I_{n-2-k} \end{pmatrix} \end{align*} $$
in H. Since Z has odd order by Proposition 7.17, we have that any involution of H is the image of an involution of
![]() $SL_{n-2}^{\varepsilon }(q^{*})$
. Applying Lemmas 3.3 (i) and 3.4 (ii), we conclude that each noncentral involution of H is conjugate to
$SL_{n-2}^{\varepsilon }(q^{*})$
. Applying Lemmas 3.3 (i) and 3.4 (ii), we conclude that each noncentral involution of H is conjugate to
![]() $h_k$
for some even
$h_k$
for some even
![]() $2 \le k < n-2$
. As u is a noncentral involution of K, we may assume that
$2 \le k < n-2$
. As u is a noncentral involution of K, we may assume that
![]() $u^{\varphi } = h_k$
for some even
$u^{\varphi } = h_k$
for some even
![]() $2 \le k < n-2$
.
$2 \le k < n-2$
.
Let
![]() $\widetilde {H_1}$
be the image of
$\widetilde {H_1}$
be the image of
 $$ \begin{align*} \left \lbrace \begin{pmatrix} A & \\ & I_{n-2-k} \end{pmatrix} \ : \ A \in SL_k^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} A & \\ & I_{n-2-k} \end{pmatrix} \ : \ A \in SL_k^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
in H and
![]() $\widetilde {H_2}$
be the image of
$\widetilde {H_2}$
be the image of
 $$ \begin{align*} \left \lbrace \begin{pmatrix} I_k & \\ & A \end{pmatrix} \ : \ A \in SL_{n-2-k}^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \begin{pmatrix} I_k & \\ & A \end{pmatrix} \ : \ A \in SL_{n-2-k}^{\varepsilon}(q^{*}) \right \rbrace \end{align*} $$
in H. The
![]() $2$
-components of
$2$
-components of
![]() $C_H(h_k)$
are precisely the quasisimple members of
$C_H(h_k)$
are precisely the quasisimple members of
![]() $\lbrace \widetilde {H_1}, \widetilde {H_2} \rbrace $
. Also,
$\lbrace \widetilde {H_1}, \widetilde {H_2} \rbrace $
. Also,
![]() $h_k \in \widetilde {H_1}$
, but
$h_k \in \widetilde {H_1}$
, but
![]() $h_k \not \in \widetilde {H_2}$
. On the other hand,
$h_k \not \in \widetilde {H_2}$
. On the other hand,
![]() $A_1$
and
$A_1$
and
![]() $A_2$
are the
$A_2$
are the
![]() $2$
-components of
$2$
-components of
![]() $C_K(u)$
, and we have
$C_K(u)$
, and we have
![]() $u \in A_1$
. This implies
$u \in A_1$
. This implies
![]() $(A_1)^{\varphi } = \widetilde {H_1}$
and
$(A_1)^{\varphi } = \widetilde {H_1}$
and
![]() $(A_2)^{\varphi } = \widetilde {H_2}$
. Since
$(A_2)^{\varphi } = \widetilde {H_2}$
. Since
![]() $A_1 \cong L \cong SL_2(q^{*})$
, we have
$A_1 \cong L \cong SL_2(q^{*})$
, we have
![]() $k = 2$
, and hence,
$k = 2$
, and hence,
![]() $\widetilde {H_1} = H_1$
and
$\widetilde {H_1} = H_1$
and
![]() $\widetilde {H_2} = H_2$
.
$\widetilde {H_2} = H_2$
.
Lemma 8.2. Let
![]() $1 \le i < j < n$
. Set
$1 \le i < j < n$
. Set
![]() $A := \lbrace i,i+1 \rbrace $
and
$A := \lbrace i,i+1 \rbrace $
and
![]() $B:= \lbrace j,j+1 \rbrace $
. Then:
$B:= \lbrace j,j+1 \rbrace $
. Then:
-
(i) If
 $i+1 < j$
, then
$i+1 < j$
, then
 $[L_A,L_B] = 1$
.
$[L_A,L_B] = 1$
. -
(ii) Suppose that
 $j = i+1$
. Then there is a group isomorphism from
$j = i+1$
. Then there is a group isomorphism from
 $\langle L_A, L_B \rangle $
to
$\langle L_A, L_B \rangle $
to
 $SL_3^{\varepsilon }(q^{*})$
under which
$SL_3^{\varepsilon }(q^{*})$
under which
 $L_A$
corresponds to the subgroup of
$L_A$
corresponds to the subgroup of $$ \begin{align*} \left \lbrace \left( \begin{array}{c|c} M & \begin{matrix} 0 \\ 0 \end{matrix} \\ \hline \begin{matrix} 0 & 0 \end{matrix} & 1 \end{array} \right) \ : \ M \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \left( \begin{array}{c|c} M & \begin{matrix} 0 \\ 0 \end{matrix} \\ \hline \begin{matrix} 0 & 0 \end{matrix} & 1 \end{array} \right) \ : \ M \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
 $SL_3^{\varepsilon }(q^{*})$
and under which
$SL_3^{\varepsilon }(q^{*})$
and under which
 $L_B$
corresponds to the subgroup of
$L_B$
corresponds to the subgroup of $$ \begin{align*} \left \lbrace \left( \begin{array}{c|cc} 1 & \begin{matrix} 0 & 0 \end{matrix} \\ \hline \begin{matrix} 0 \\ 0 \end{matrix} & M \end{array} \right) \ : \ M \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
$$ \begin{align*} \left \lbrace \left( \begin{array}{c|cc} 1 & \begin{matrix} 0 & 0 \end{matrix} \\ \hline \begin{matrix} 0 \\ 0 \end{matrix} & M \end{array} \right) \ : \ M \in SL_2^{\varepsilon}(q^{*}) \right\rbrace \end{align*} $$
 $SL_3^{\varepsilon }(q^{*})$
.
$SL_3^{\varepsilon }(q^{*})$
.
-
(iii) Suppose that
 $1 \le i \le n-3$
and that
$1 \le i \le n-3$
and that
 $j = i+1$
. Set
$j = i+1$
. Set
 $k := i+2$
and
$k := i+2$
and
 $C := \lbrace k,k+1 \rbrace $
. Then
$C := \lbrace k,k+1 \rbrace $
. Then
 $\langle L_A, L_B, L_C \rangle $
is isomorphic to
$\langle L_A, L_B, L_C \rangle $
is isomorphic to
 $SL_4^{\varepsilon }(q^{*})$
.
$SL_4^{\varepsilon }(q^{*})$
.
Proof. To prove (i), (ii) and (iii), we first introduce some notation and make some preliminary observations. Let H,
![]() $H_1$
,
$H_1$
,
![]() $H_2$
and
$H_2$
and
![]() $\varphi $
be as in Lemma 8.1. For each
$\varphi $
be as in Lemma 8.1. For each
![]() $D \subseteq \lbrace 1, \dots , n-2\rbrace $
of even order, let
$D \subseteq \lbrace 1, \dots , n-2\rbrace $
of even order, let
![]() $h_D$
be the image of the matrix
$h_D$
be the image of the matrix
![]() $\mathrm {diag}(d_1,\dots , d_{n-2}) \in SL_{n-2}^{\varepsilon }(q^{*})$
in H, where
$\mathrm {diag}(d_1,\dots , d_{n-2}) \in SL_{n-2}^{\varepsilon }(q^{*})$
in H, where
![]() $d_{\ell } = -1$
if
$d_{\ell } = -1$
if
![]() $\ell \in D$
and
$\ell \in D$
and
![]() $d_{\ell } = 1$
if
$d_{\ell } = 1$
if
![]() $\ell \in \lbrace 1, \dots , n-2 \rbrace \setminus D$
. We have
$\ell \in \lbrace 1, \dots , n-2 \rbrace \setminus D$
. We have
![]() $u^{\varphi } = h_{\lbrace 1,2 \rbrace }$
as u and
$u^{\varphi } = h_{\lbrace 1,2 \rbrace }$
as u and
![]() $h_{\lbrace 1,2 \rbrace }$
are the unique involutions of
$h_{\lbrace 1,2 \rbrace }$
are the unique involutions of
![]() $A_1$
and
$A_1$
and
![]() $H_1 = (A_1)^{\varphi }$
, respectively.
$H_1 = (A_1)^{\varphi }$
, respectively.
Let J be the subgroup of H consisting of all
![]() $h_D$
, where
$h_D$
, where
![]() $D \subseteq \lbrace 1, \dots , n-2 \rbrace $
has even order, and let
$D \subseteq \lbrace 1, \dots , n-2 \rbrace $
has even order, and let
![]() $E_1$
denote the subgroup of
$E_1$
denote the subgroup of
![]() $X_1$
consisting of all
$X_1$
consisting of all
![]() $t_D$
, where
$t_D$
, where
![]() $D \subseteq \lbrace 1, \dots , n-2 \rbrace $
has even order. Then
$D \subseteq \lbrace 1, \dots , n-2 \rbrace $
has even order. Then
![]() $(E_1)^{\varphi }$
is an elementary abelian
$(E_1)^{\varphi }$
is an elementary abelian
![]() $2$
-subgroup of H of rank
$2$
-subgroup of H of rank
![]() $n-3$
. As a consequence of Lemma 3.22, there is an element
$n-3$
. As a consequence of Lemma 3.22, there is an element
![]() $h \in H$
such that
$h \in H$
such that
![]() $(E_1^{\varphi })^h = J$
. Then
$(E_1^{\varphi })^h = J$
. Then
![]() $(h_{\lbrace 1,2 \rbrace })^h = (u^{\varphi })^h \in (E_1^{\varphi })^h = J$
. Lemma 3.23 (i) shows that
$(h_{\lbrace 1,2 \rbrace })^h = (u^{\varphi })^h \in (E_1^{\varphi })^h = J$
. Lemma 3.23 (i) shows that
![]() $(h_{\lbrace 1,2 \rbrace })^h$
is
$(h_{\lbrace 1,2 \rbrace })^h$
is
![]() $N_H(J)$
-conjugate to
$N_H(J)$
-conjugate to
![]() $h_{\lbrace 1,2 \rbrace }$
. Therefore, we can assume that h centralizes
$h_{\lbrace 1,2 \rbrace }$
. Therefore, we can assume that h centralizes
![]() $h_{\lbrace 1,2 \rbrace }$
. Then
$h_{\lbrace 1,2 \rbrace }$
. Then
![]() $(H_1)^h = H_1$
and
$(H_1)^h = H_1$
and
![]() $(H_2)^h = H_2$
. Upon replacing
$(H_2)^h = H_2$
. Upon replacing
![]() $\varphi $
by
$\varphi $
by
![]() $\varphi c_h$
, we may thus assume that
$\varphi c_h$
, we may thus assume that
![]() $(E_1)^{\varphi } = J$
.
$(E_1)^{\varphi } = J$
.
We have
![]() $C_H(h_{\lbrace 1,2 \rbrace })' = H_1 \times H_2$
, and
$C_H(h_{\lbrace 1,2 \rbrace })' = H_1 \times H_2$
, and
![]() $H_1 \cong SL_2^{\varepsilon }(q^{*})$
and
$H_1 \cong SL_2^{\varepsilon }(q^{*})$
and
![]() $H_2 \cong SL_{n-4}^{\varepsilon }(q^{*})$
are indecomposable. Also,
$H_2 \cong SL_{n-4}^{\varepsilon }(q^{*})$
are indecomposable. Also,
![]() $(|H_1/H_1'|,|Z(H_2)|) = 1 = (|H_2/H_2'|,|Z(H_1)|)$
. So, by a consequence of the Krull–Remark–Schmidt theorem [Reference Huppert and Endliche Gruppen35, Kapitel I, Satz 12.6],
$(|H_1/H_1'|,|Z(H_2)|) = 1 = (|H_2/H_2'|,|Z(H_1)|)$
. So, by a consequence of the Krull–Remark–Schmidt theorem [Reference Huppert and Endliche Gruppen35, Kapitel I, Satz 12.6],
![]() $C_H(h_{\lbrace 1,2 \rbrace })' = H_1 \times H_2$
is the only decomposition of
$C_H(h_{\lbrace 1,2 \rbrace })' = H_1 \times H_2$
is the only decomposition of
![]() $C_H(h_{\lbrace 1,2 \rbrace })'$
into a direct product of indecomposable groups. This implies that
$C_H(h_{\lbrace 1,2 \rbrace })'$
into a direct product of indecomposable groups. This implies that
![]() $H_1$
is the only normal subgroup of
$H_1$
is the only normal subgroup of
![]() $C_H(h_{\lbrace 1,2 \rbrace })$
which contains
$C_H(h_{\lbrace 1,2 \rbrace })$
which contains
![]() $h_{\lbrace 1,2 \rbrace }$
and is isomorphic to
$h_{\lbrace 1,2 \rbrace }$
and is isomorphic to
![]() $SL_2^{\varepsilon }(q^{*})$
. For each
$SL_2^{\varepsilon }(q^{*})$
. For each
![]() $D \subseteq \lbrace 1, \dots , n-2 \rbrace $
of order
$D \subseteq \lbrace 1, \dots , n-2 \rbrace $
of order
![]() $2$
,
$2$
,
![]() $h_D$
and
$h_D$
and
![]() $h_{\lbrace 1,2 \rbrace }$
are conjugate, and so
$h_{\lbrace 1,2 \rbrace }$
are conjugate, and so
![]() $C_H(h_D)$
has a unique normal subgroup
$C_H(h_D)$
has a unique normal subgroup
![]() $H_D$
with
$H_D$
with
![]() $h_D \in H_D$
and
$h_D \in H_D$
and
![]() $H_D \cong SL_2^{\varepsilon }(q^{*})$
. Note that the groups
$H_D \cong SL_2^{\varepsilon }(q^{*})$
. Note that the groups
![]() $H_{\lbrace 1,2 \rbrace }, H_{\lbrace 2,3 \rbrace }, \dots , H_{\lbrace n-3,n-2 \rbrace }$
are the
$H_{\lbrace 1,2 \rbrace }, H_{\lbrace 2,3 \rbrace }, \dots , H_{\lbrace n-3,n-2 \rbrace }$
are the
![]() $SL_2^{\varepsilon }(q^{*})$
-subgroups of H corresponding to the
$SL_2^{\varepsilon }(q^{*})$
-subgroups of H corresponding to the
![]() $2 \times 2$
-blocks along the main diagonal.
$2 \times 2$
-blocks along the main diagonal.
Now let
![]() $D_0 \subseteq \lbrace 1, \dots , n-2 \rbrace $
with order
$D_0 \subseteq \lbrace 1, \dots , n-2 \rbrace $
with order
![]() $2$
. Then
$2$
. Then
![]() $(t_{D_0})^{\varphi } \in (E_1)^{\varphi } = J$
, and
$(t_{D_0})^{\varphi } \in (E_1)^{\varphi } = J$
, and
![]() $(t_{D_0})^{\varphi }$
is conjugate to
$(t_{D_0})^{\varphi }$
is conjugate to
![]() $u^{\varphi } = h_{\lbrace 1,2 \rbrace }$
. Thus,
$u^{\varphi } = h_{\lbrace 1,2 \rbrace }$
. Thus,
![]() $(t_{D_0})^{\varphi } = h_D$
for some
$(t_{D_0})^{\varphi } = h_D$
for some
![]() $D \subseteq \lbrace 1, \dots , n-2 \rbrace $
of order
$D \subseteq \lbrace 1, \dots , n-2 \rbrace $
of order
![]() $2$
. We claim that
$2$
. We claim that
![]() $L_{D_0} \le K$
and
$L_{D_0} \le K$
and
![]() $(L_{D_0})^{\varphi } = H_D$
. To see this, let
$(L_{D_0})^{\varphi } = H_D$
. To see this, let
![]() $k \in K$
with
$k \in K$
with
![]() $t_{D_0} = u^k = (t_{\lbrace 1,2 \rbrace })^k$
. Then
$t_{D_0} = u^k = (t_{\lbrace 1,2 \rbrace })^k$
. Then
![]() $L_{D_0} = (L_{\lbrace 1,2 \rbrace })^k = (A_1)^k \le K$
, where the last equality follows from the definition of L (see Proposition 6.8) and the definition of
$L_{D_0} = (L_{\lbrace 1,2 \rbrace })^k = (A_1)^k \le K$
, where the last equality follows from the definition of L (see Proposition 6.8) and the definition of
![]() $L_{\lbrace 1,2 \rbrace }$
. Since
$L_{\lbrace 1,2 \rbrace }$
. Since
![]() $L_{D_0} \trianglelefteq C_K(t_{D_0})$
,
$L_{D_0} \trianglelefteq C_K(t_{D_0})$
,
![]() $L_{D_0} \cong SL_2^{\varepsilon }(q^{*})$
and
$L_{D_0} \cong SL_2^{\varepsilon }(q^{*})$
and
![]() $t_{D_0} \in L_{D_0}$
, the previous paragraph implies that
$t_{D_0} \in L_{D_0}$
, the previous paragraph implies that
![]() $(L_{D_0})^{\varphi } = H_D$
, as claimed.
$(L_{D_0})^{\varphi } = H_D$
, as claimed.
We are now ready to prove (i), (ii) and (iii). To prove (i), suppose that
![]() $i+1 < j$
. As
$i+1 < j$
. As
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we see from Lemma 3.23 (i) that there is some
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we see from Lemma 3.23 (i) that there is some
![]() $g \in G$
with
$g \in G$
with
![]() $(t_A)^g = t_{\lbrace 1,2 \rbrace }$
and
$(t_A)^g = t_{\lbrace 1,2 \rbrace }$
and
![]() $(t_B)^g = t_{\lbrace 3,4 \rbrace }$
. As
$(t_B)^g = t_{\lbrace 3,4 \rbrace }$
. As
![]() $[L_A,L_B]^g = [(L_A)^g,(L_B)^g] = [L_{\lbrace 1,2 \rbrace },L_{\lbrace 3,4 \rbrace }]$
, we may assume that
$[L_A,L_B]^g = [(L_A)^g,(L_B)^g] = [L_{\lbrace 1,2 \rbrace },L_{\lbrace 3,4 \rbrace }]$
, we may assume that
![]() $A = \lbrace 1,2 \rbrace $
and
$A = \lbrace 1,2 \rbrace $
and
![]() $B = \lbrace 3,4 \rbrace $
. Then
$B = \lbrace 3,4 \rbrace $
. Then
![]() $(L_A)^{\varphi } = (A_1)^{\varphi } = H_1$
. Also,
$(L_A)^{\varphi } = (A_1)^{\varphi } = H_1$
. Also,
![]() $(t_B)^{\varphi } \in (A_2)^{\varphi } = H_2$
, and so
$(t_B)^{\varphi } \in (A_2)^{\varphi } = H_2$
, and so
![]() $(t_B)^{\varphi } = h_D$
for some
$(t_B)^{\varphi } = h_D$
for some
![]() $D \subseteq \lbrace 3, 4, \dots , n-2 \rbrace $
with
$D \subseteq \lbrace 3, 4, \dots , n-2 \rbrace $
with
![]() $|D| = 2$
. By the previous paragraph,
$|D| = 2$
. By the previous paragraph,
![]() $[L_A,L_B]^{\varphi } = [(L_A)^{\varphi },(L_B)^{\varphi }] = [H_1,H_D] = 1$
, and so
$[L_A,L_B]^{\varphi } = [(L_A)^{\varphi },(L_B)^{\varphi }] = [H_1,H_D] = 1$
, and so
![]() $[L_A,L_B] = 1$
, whence (i) holds.
$[L_A,L_B] = 1$
, whence (i) holds.
Assume now that
![]() $j = i+1$
. As
$j = i+1$
. As
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we see from Lemma 3.23 (i) that there is some
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we see from Lemma 3.23 (i) that there is some
![]() $g \in G$
with
$g \in G$
with
![]() $(t_A)^g = t_{\lbrace 1,2 \rbrace }$
and
$(t_A)^g = t_{\lbrace 1,2 \rbrace }$
and
![]() $(t_B)^g = t_{\lbrace 2,3 \rbrace }$
. As
$(t_B)^g = t_{\lbrace 2,3 \rbrace }$
. As
![]() $\langle L_A, L_B \rangle ^g = \langle (L_A)^g, (L_B)^g \rangle = \langle L_{\lbrace 1,2 \rbrace }, L_{\lbrace 2,3 \rbrace } \rangle $
, we may assume that
$\langle L_A, L_B \rangle ^g = \langle (L_A)^g, (L_B)^g \rangle = \langle L_{\lbrace 1,2 \rbrace }, L_{\lbrace 2,3 \rbrace } \rangle $
, we may assume that
![]() $A = \lbrace 1,2 \rbrace $
and
$A = \lbrace 1,2 \rbrace $
and
![]() $B = \lbrace 2,3 \rbrace $
. Let
$B = \lbrace 2,3 \rbrace $
. Let
![]() $D \subseteq \lbrace 1, \dots , n-2 \rbrace $
with
$D \subseteq \lbrace 1, \dots , n-2 \rbrace $
with
![]() $(t_B)^{\varphi } = h_D$
. We have
$(t_B)^{\varphi } = h_D$
. We have
![]() $|D| = 2$
by paragraph four and
$|D| = 2$
by paragraph four and
![]() $h_D \not \in (H_1 \cup H_2)$
since
$h_D \not \in (H_1 \cup H_2)$
since
![]() $t_B \not \in (A_1 \cup A_2)$
. Thus,
$t_B \not \in (A_1 \cup A_2)$
. Thus,
![]() $D = \lbrace k, \ell \rbrace $
for some
$D = \lbrace k, \ell \rbrace $
for some
![]() $k \in \lbrace 1,2 \rbrace $
and some
$k \in \lbrace 1,2 \rbrace $
and some
![]() $\ell \in \lbrace 3,4, \dots , n-2 \rbrace $
. Because of Lemma 3.23 (i), we may assume that
$\ell \in \lbrace 3,4, \dots , n-2 \rbrace $
. Because of Lemma 3.23 (i), we may assume that
![]() $k = 2$
and
$k = 2$
and
![]() $\ell = 3$
. Since
$\ell = 3$
. Since
![]() $(L_A)^{\varphi } = H_1 = H_{\lbrace 1,2 \rbrace }$
and
$(L_A)^{\varphi } = H_1 = H_{\lbrace 1,2 \rbrace }$
and
![]() $(L_B)^{\varphi } = H_{\lbrace 2,3 \rbrace }$
, we have proved (ii).
$(L_B)^{\varphi } = H_{\lbrace 2,3 \rbrace }$
, we have proved (ii).
Assume now that the hypotheses of (iii) are satisfied. Arguing as in the proof of (ii), we may assume that
![]() $A = \lbrace 1,2 \rbrace , B = \lbrace 2,3 \rbrace , C = \lbrace 3,4 \rbrace $
and
$A = \lbrace 1,2 \rbrace , B = \lbrace 2,3 \rbrace , C = \lbrace 3,4 \rbrace $
and
![]() $(t_B)^{\varphi } = h_{\lbrace 2,3 \rbrace }$
. Let
$(t_B)^{\varphi } = h_{\lbrace 2,3 \rbrace }$
. Let
![]() $D \subseteq \lbrace 1, \dots , n-2 \rbrace $
with
$D \subseteq \lbrace 1, \dots , n-2 \rbrace $
with
![]() $(t_C)^{\varphi } = h_D$
. By paragraph four, we have
$(t_C)^{\varphi } = h_D$
. By paragraph four, we have
![]() $|D| = 2$
. Also,
$|D| = 2$
. Also,
![]() $h_D \in (A_2)^{\varphi } = H_2$
, so
$h_D \in (A_2)^{\varphi } = H_2$
, so
![]() $D \cap \lbrace 1,2 \rbrace = \emptyset $
. We claim that
$D \cap \lbrace 1,2 \rbrace = \emptyset $
. We claim that
![]() $D \cap \lbrace 2,3 \rbrace = \lbrace 3 \rbrace $
. Assume not. Then
$D \cap \lbrace 2,3 \rbrace = \lbrace 3 \rbrace $
. Assume not. Then
![]() $D \cap \lbrace 1,2,3 \rbrace = \emptyset $
, and Lemma 3.23 (i) shows that there is an element of
$D \cap \lbrace 1,2,3 \rbrace = \emptyset $
, and Lemma 3.23 (i) shows that there is an element of
![]() $N_H(J)$
which interchanges
$N_H(J)$
which interchanges
![]() $h_{\lbrace 1,2 \rbrace }$
and
$h_{\lbrace 1,2 \rbrace }$
and
![]() $h_{\lbrace 2,3 \rbrace }$
and fixes
$h_{\lbrace 2,3 \rbrace }$
and fixes
![]() $h_D$
. So there is an element of
$h_D$
. So there is an element of
![]() $N_K(E_1)$
which interchanges u and
$N_K(E_1)$
which interchanges u and
![]() $t_{\lbrace 2,3 \rbrace }$
and fixes
$t_{\lbrace 2,3 \rbrace }$
and fixes
![]() $t_{\lbrace 3,4 \rbrace }$
. Having in mind that
$t_{\lbrace 3,4 \rbrace }$
. Having in mind that
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we see from Lemma 3.23 (ii) that
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, we see from Lemma 3.23 (ii) that
![]() $N_K(E_1)$
has no such element. This contradiction shows that
$N_K(E_1)$
has no such element. This contradiction shows that
![]() $D \cap \lbrace 2,3 \rbrace = \lbrace 3 \rbrace $
. By Lemma 3.23 (i), we may assume that
$D \cap \lbrace 2,3 \rbrace = \lbrace 3 \rbrace $
. By Lemma 3.23 (i), we may assume that
![]() $D = \lbrace 3,4 \rbrace $
. Now
$D = \lbrace 3,4 \rbrace $
. Now
![]() $\langle L_A, L_B, L_C \rangle ^{\varphi } = \langle H_{\lbrace 1,2 \rbrace }, H_{\lbrace 2,3 \rbrace }, H_{\lbrace 3,4 \rbrace } \rangle \cong SL_4^{\varepsilon }(q^{*})$
, and the proof of (iii) is complete.
$\langle L_A, L_B, L_C \rangle ^{\varphi } = \langle H_{\lbrace 1,2 \rbrace }, H_{\lbrace 2,3 \rbrace }, H_{\lbrace 3,4 \rbrace } \rangle \cong SL_4^{\varepsilon }(q^{*})$
, and the proof of (iii) is complete.
Proposition 8.3.
![]() $G_0$
is isomorphic to a nontrivial quotient of
$G_0$
is isomorphic to a nontrivial quotient of
![]() $SL_n^{\varepsilon }(q^{*})$
.
$SL_n^{\varepsilon }(q^{*})$
.
Proof. Assume that
![]() $\varepsilon = +$
. By Lemma 8.2, the groups
$\varepsilon = +$
. By Lemma 8.2, the groups
![]() $L_{\lbrace 1,2 \rbrace }, \dots , L_{\lbrace n-1,n \rbrace }$
form a weak Curtis–Tits system in G of type
$L_{\lbrace 1,2 \rbrace }, \dots , L_{\lbrace n-1,n \rbrace }$
form a weak Curtis–Tits system in G of type
![]() $SL_n(q^{*})$
(in the sense of [Reference Gorenstein, Lyons and Solomon29, p. 9]). Applying a version of the Curtis–Tits theorem, namely [Reference Gorenstein, Lyons and Solomon29, Chapter 13, Theorem 1.4], we conclude that
$SL_n(q^{*})$
(in the sense of [Reference Gorenstein, Lyons and Solomon29, p. 9]). Applying a version of the Curtis–Tits theorem, namely [Reference Gorenstein, Lyons and Solomon29, Chapter 13, Theorem 1.4], we conclude that
![]() $G_0$
is isomorphic to a quotient of
$G_0$
is isomorphic to a quotient of
![]() $SL_n(q^{*})$
.
$SL_n(q^{*})$
.
Assume now that
![]() $\varepsilon = -$
. Then Lemma 8.2 shows that
$\varepsilon = -$
. Then Lemma 8.2 shows that
![]() $G_0$
has a weak Phan system of rank
$G_0$
has a weak Phan system of rank
![]() $n-1$
over
$n-1$
over
![]() $\mathbb {F}_{{q^{*}}^2}$
(in the sense of [Reference Bennett and Shpectorov13, p. 288]). If
$\mathbb {F}_{{q^{*}}^2}$
(in the sense of [Reference Bennett and Shpectorov13, p. 288]). If
![]() $q^{*} \ne 3$
, then [Reference Bennett and Shpectorov13, Theorem 1.2] implies that
$q^{*} \ne 3$
, then [Reference Bennett and Shpectorov13, Theorem 1.2] implies that
![]() $G_0$
is isomorphic to a quotient of
$G_0$
is isomorphic to a quotient of
![]() $SU_n(q^{*})$
. If
$SU_n(q^{*})$
. If
![]() $q^{*} = 3$
, the same follows from [Reference Bennett and Shpectorov13, Theorem 1.3] and Lemma 8.2 (iii).
$q^{*} = 3$
, the same follows from [Reference Bennett and Shpectorov13, Theorem 1.3] and Lemma 8.2 (iii).
Lemma 8.4. Let R be a Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $G_0$
. Then
$G_0$
. Then
![]() $R \in \mathrm {Syl}_2(G)$
and
$R \in \mathrm {Syl}_2(G)$
and
![]() $\mathcal {F}_R(G_0) = \mathcal {F}_R(G)$
.
$\mathcal {F}_R(G_0) = \mathcal {F}_R(G)$
.
Proof. Since
![]() $q \sim \varepsilon q^{*}$
, we have that the
$q \sim \varepsilon q^{*}$
, we have that the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n^{\varepsilon }(q^{*})$
is isomorphic to the
$PSL_n^{\varepsilon }(q^{*})$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
(see Proposition 3.20). Clearly,
$PSL_n(q)$
(see Proposition 3.20). Clearly,
![]() $G_0/Z(G_0) \cong PSL_n^{\varepsilon }(q^{*})$
. So the
$G_0/Z(G_0) \cong PSL_n^{\varepsilon }(q^{*})$
. So the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $G_0/Z(G_0)$
is isomorphic to the
$G_0/Z(G_0)$
is isomorphic to the
![]() $2$
-fusion system of G. It easily follows that
$2$
-fusion system of G. It easily follows that
![]() $\vert G_0 \vert _2 = \vert G_0/Z(G_0) \vert _2 = \vert G \vert _2$
, and Lemma 2.11 shows that the
$\vert G_0 \vert _2 = \vert G_0/Z(G_0) \vert _2 = \vert G \vert _2$
, and Lemma 2.11 shows that the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $G_0$
is isomorphic to that of
$G_0$
is isomorphic to that of
![]() $G_0/Z(G_0)$
and hence to that of G. This completes the proof.
$G_0/Z(G_0)$
and hence to that of G. This completes the proof.
Lemma 8.5. The following hold.
-
(i) If
 $q^{*} \ne 3$
, then
$q^{*} \ne 3$
, then
 $O^{2'}(O^{2}(C_G(t))) = KL$
.
$O^{2'}(O^{2}(C_G(t))) = KL$
. -
(ii) If
 $q^{*} = 3$
, then
$q^{*} = 3$
, then
 $O^2(C_G(t)) = KL$
.
$O^2(C_G(t)) = KL$
.
Proof. Set
![]() $C := C_G(t)$
.
$C := C_G(t)$
.
Assume that
![]() $q^{*} \ne 3$
. Then
$q^{*} \ne 3$
. Then
![]() $KL$
is perfect. This implies that
$KL$
is perfect. This implies that
![]() $KL = O^{2'}(O^2(KL)) \le O^{2'}(O^{2}(C))$
. Since
$KL = O^{2'}(O^2(KL)) \le O^{2'}(O^{2}(C))$
. Since
![]() $T \cap KL = (T \cap K)(T \cap L) = X_1 X_2$
, Lemmas 5.4 and 2.11 show that
$T \cap KL = (T \cap K)(T \cap L) = X_1 X_2$
, Lemmas 5.4 and 2.11 show that
![]() $C/KL$
has a nilpotent
$C/KL$
has a nilpotent
![]() $2$
-fusion system. So
$2$
-fusion system. So
![]() $C/KL$
is
$C/KL$
is
![]() $2$
-nilpotent by [Reference Linckelmann39, Theorem 1.4]. This implies
$2$
-nilpotent by [Reference Linckelmann39, Theorem 1.4]. This implies
![]() $O^{2'}(O^{2}(C)) \le KL$
.
$O^{2'}(O^{2}(C)) \le KL$
.
We assume now that
![]() $q^{*} = 3$
. Then
$q^{*} = 3$
. Then
![]() $KL = O^2(KL)$
since K is perfect and
$KL = O^2(KL)$
since K is perfect and
![]() $L \cong SL_2(3)$
. Thus,
$L \cong SL_2(3)$
. Thus,
![]() $KL \le O^2(C)$
. In order to prove equality, it suffices to show that
$KL \le O^2(C)$
. In order to prove equality, it suffices to show that
![]() $C/KL$
is a
$C/KL$
is a
![]() $2$
-group. By Proposition 7.7 and Lemma 6.3 (i),
$2$
-group. By Proposition 7.7 and Lemma 6.3 (i),
![]() $C/KC_C(K)$
is a
$C/KC_C(K)$
is a
![]() $2$
-group. By [Reference Kurzweil and Stellmacher37, 6.5.2], we have
$2$
-group. By [Reference Kurzweil and Stellmacher37, 6.5.2], we have
![]() $L \le C_C(K)$
. It is enough to show that
$L \le C_C(K)$
. It is enough to show that
![]() $C_C(K)/L$
is a
$C_C(K)/L$
is a
![]() $2$
-group.
$2$
-group.
We have
![]() $O^2(C_{C}(K)) \cap T \le O^2(C_{C}(X_1)) \cap T = X_2$
by Lemma 5.6 and the hyperfocal subgroup theorem [Reference Craven18, Theorem 1.33]. On the other hand,
$O^2(C_{C}(K)) \cap T \le O^2(C_{C}(X_1)) \cap T = X_2$
by Lemma 5.6 and the hyperfocal subgroup theorem [Reference Craven18, Theorem 1.33]. On the other hand,
![]() $X_2 \le L = O^2(L) \le O^2(C_{C}(K))$
. Consequently,
$X_2 \le L = O^2(L) \le O^2(C_{C}(K))$
. Consequently,
![]() $X_2 = O^2(C_{C}(K)) \cap T \in \mathrm {Syl}_2(O^2(C_C(K)))$
. Set
$X_2 = O^2(C_{C}(K)) \cap T \in \mathrm {Syl}_2(O^2(C_C(K)))$
. Set
![]() $U := C_{O^2(C_C(K))}(X_2)$
. We have
$U := C_{O^2(C_C(K))}(X_2)$
. We have
![]() $X_2 \trianglelefteq C$
since
$X_2 \trianglelefteq C$
since
![]() $X_2$
is the unique Sylow
$X_2$
is the unique Sylow
![]() $2$
-subgroup of
$2$
-subgroup of
![]() $L \cong SL_2(3)$
. So we have
$L \cong SL_2(3)$
. So we have
![]() $U \trianglelefteq C$
. Hence,
$U \trianglelefteq C$
. Hence,
![]() $Z(X_2) = X_2 \cap U \in \mathrm {Syl}_2(U)$
. Applying [Reference Kurzweil and Stellmacher37, 7.2.2], we conclude that U is
$Z(X_2) = X_2 \cap U \in \mathrm {Syl}_2(U)$
. Applying [Reference Kurzweil and Stellmacher37, 7.2.2], we conclude that U is
![]() $2$
-nilpotent. We have
$2$
-nilpotent. We have
![]() $O(U) = 1$
since
$O(U) = 1$
since
![]() $U \trianglelefteq C$
and
$U \trianglelefteq C$
and
![]() $O(C) = 1$
by Proposition 7.7. It follows that
$O(C) = 1$
by Proposition 7.7. It follows that
![]() $U = Z(X_2)$
.
$U = Z(X_2)$
.
Clearly,
![]() $O^{2}(C_C(K))/U$
is isomorphic to a subgroup of
$O^{2}(C_C(K))/U$
is isomorphic to a subgroup of
![]() $\mathrm {Aut}(X_2)$
. We have
$\mathrm {Aut}(X_2)$
. We have
![]() $|O^{2}(C_C(K))/U|_2 = 4$
since
$|O^{2}(C_C(K))/U|_2 = 4$
since
![]() $Q_8 \cong X_2 \in \mathrm {Syl}_2(O^2(C_C(K)))$
and
$Q_8 \cong X_2 \in \mathrm {Syl}_2(O^2(C_C(K)))$
and
![]() $U = Z(X_2)$
. Also,
$U = Z(X_2)$
. Also,
![]() $|O^{2}(C_C(K))/U| \ge 12$
since
$|O^{2}(C_C(K))/U| \ge 12$
since
![]() $L \le O^2(C_C(K))$
. As
$L \le O^2(C_C(K))$
. As
![]() $\mathrm {Aut}(X_2) \cong \mathrm {Aut}(Q_8) \cong S_4$
by [Reference Kurzweil and Stellmacher37, 5.3.3], it follows that
$\mathrm {Aut}(X_2) \cong \mathrm {Aut}(Q_8) \cong S_4$
by [Reference Kurzweil and Stellmacher37, 5.3.3], it follows that
![]() $|O^{2}(C_C(K))/U| = 12$
. This implies
$|O^{2}(C_C(K))/U| = 12$
. This implies
![]() $O^2(C_C(K)) = L$
. So
$O^2(C_C(K)) = L$
. So
![]() $C_C(K)/L$
is a
$C_C(K)/L$
is a
![]() $2$
-group, as required.
$2$
-group, as required.
Lemma 8.6. We have
![]() $KL \le G_0$
.
$KL \le G_0$
.
Proof. We have
![]() $t \in X_2 \le L = L_{\lbrace n-1, n \rbrace } \le G_0$
. Let
$t \in X_2 \le L = L_{\lbrace n-1, n \rbrace } \le G_0$
. Let
![]() $R \in \mathrm {Syl}_2(G_0)$
with
$R \in \mathrm {Syl}_2(G_0)$
with
![]() $t \in R$
such that
$t \in R$
such that
![]() $\langle t \rangle $
is fully centralized in
$\langle t \rangle $
is fully centralized in
![]() $\mathcal {G} := \mathcal {F}_R(G_0)$
. By Lemma 8.4,
$\mathcal {G} := \mathcal {F}_R(G_0)$
. By Lemma 8.4,
![]() $R \in \mathrm {Syl}_2(G)$
and
$R \in \mathrm {Syl}_2(G)$
and
![]() $\mathcal {G} = \mathcal {F}_R(G)$
. Therefore,
$\mathcal {G} = \mathcal {F}_R(G)$
. Therefore,
![]() $C_R(t) \in \mathrm {Syl}_2(C_G(t))$
and
$C_R(t) \in \mathrm {Syl}_2(C_G(t))$
and
![]() $C_{\mathcal {G}}(\langle t \rangle ) = \mathcal {F}_{C_R(t)}(C_G(t))$
. Also,
$C_{\mathcal {G}}(\langle t \rangle ) = \mathcal {F}_{C_R(t)}(C_G(t))$
. Also,
![]() $T = C_S(t) \in \mathrm {Syl}_2(C_G(t))$
and
$T = C_S(t) \in \mathrm {Syl}_2(C_G(t))$
and
![]() $C_{\mathcal {F}_S(G)}(\langle t \rangle ) = \mathcal {F}_T(C_G(t))$
. So, by Lemma 5.3,
$C_{\mathcal {F}_S(G)}(\langle t \rangle ) = \mathcal {F}_T(C_G(t))$
. So, by Lemma 5.3,
![]() $C_{\mathcal {G}}(\langle t \rangle )$
has a component isomorphic to the
$C_{\mathcal {G}}(\langle t \rangle )$
has a component isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_{n-2}(q)$
.
$SL_{n-2}(q)$
.
Let
![]() $Z \le Z(SL_n^{\varepsilon }(q^{*}))$
with
$Z \le Z(SL_n^{\varepsilon }(q^{*}))$
with
![]() $G_0 \cong SL_n^{\varepsilon }(q^{*})/Z$
. By the proof of Lemma 8.4,
$G_0 \cong SL_n^{\varepsilon }(q^{*})/Z$
. By the proof of Lemma 8.4,
![]() $Z(G_0)$
has odd order.
$Z(G_0)$
has odd order.
Let
![]() $\widetilde x$
be an element of
$\widetilde x$
be an element of
![]() $SL_n^{\varepsilon }(q^{*})$
such that
$SL_n^{\varepsilon }(q^{*})$
such that
![]() $x := \widetilde x Z$
is an involution of
$x := \widetilde x Z$
is an involution of
![]() $SL_n^{\varepsilon }(q^{*})/Z$
. Set
$SL_n^{\varepsilon }(q^{*})/Z$
. Set
![]() $C := C_{SL_n^{\varepsilon }(q^{*})/Z}(x)$
. Noticing that the
$C := C_{SL_n^{\varepsilon }(q^{*})/Z}(x)$
. Noticing that the
![]() $2$
-components of C are precisely the images of the
$2$
-components of C are precisely the images of the
![]() $2$
-components of
$2$
-components of
![]() $C_{SL_n^{\varepsilon }(q^{*})}(\widetilde x)$
in
$C_{SL_n^{\varepsilon }(q^{*})}(\widetilde x)$
in
![]() $SL_n^{\varepsilon }(q^{*})/Z$
, one can see from Lemmas 3.3 and 3.4 that one of the following holds:
$SL_n^{\varepsilon }(q^{*})/Z$
, one can see from Lemmas 3.3 and 3.4 that one of the following holds:
-
(1)
 $q^{*} \ne 3$
,
$q^{*} \ne 3$
,
 $O^{2'}(O^2(C)) = K_0L_0$
, where
$O^{2'}(O^2(C)) = K_0L_0$
, where
 $K_0$
and
$K_0$
and
 $L_0$
are subnormal subgroups of C such that
$L_0$
are subnormal subgroups of C such that
 $K_0 \cong SL_{n-i}^{\varepsilon }(q^{*})$
and
$K_0 \cong SL_{n-i}^{\varepsilon }(q^{*})$
and
 $L_0 \cong SL_i^{\varepsilon }(q^{*})$
for some
$L_0 \cong SL_i^{\varepsilon }(q^{*})$
for some
 $1 \le i < n$
. Moreover, the
$1 \le i < n$
. Moreover, the
 $2$
-components of C are precisely the quasisimple members of
$2$
-components of C are precisely the quasisimple members of
 $\lbrace K_0, L_0 \rbrace $
.
$\lbrace K_0, L_0 \rbrace $
. -
(2)
 $q^{*} = 3$
,
$q^{*} = 3$
,
 $O^2(C) = K_0L_0$
, where
$O^2(C) = K_0L_0$
, where
 $K_0$
and
$K_0$
and
 $L_0$
are subnormal subgroups of C such that
$L_0$
are subnormal subgroups of C such that
 $K_0 \cong SL_{n-i}^{\varepsilon }(q^{*})$
and
$K_0 \cong SL_{n-i}^{\varepsilon }(q^{*})$
and
 $L_0 \cong SL_i^{\varepsilon }(q^{*})$
for some
$L_0 \cong SL_i^{\varepsilon }(q^{*})$
for some
 $1 \le i < n$
. Moreover, the
$1 \le i < n$
. Moreover, the
 $2$
-components of C are precisely the quasisimple members of
$2$
-components of C are precisely the quasisimple members of
 $\lbrace K_0, L_0 \rbrace $
.
$\lbrace K_0, L_0 \rbrace $
. -
(3) C has precisely one
 $2$
-component, and this
$2$
-component, and this
 $2$
-component is isomorphic to a nontrivial quotient of
$2$
-component is isomorphic to a nontrivial quotient of
 $SL_{n/2}((q^{*})^2)$
.
$SL_{n/2}((q^{*})^2)$
.
As seen above,
![]() $C_{\mathcal {G}}(\langle t \rangle ) = \mathcal {F}_{C_R(t)}(C_{G_0}(t))$
has a component isomorphic to the
$C_{\mathcal {G}}(\langle t \rangle ) = \mathcal {F}_{C_R(t)}(C_{G_0}(t))$
has a component isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $SL_{n-2}(q)$
. By Proposition 2.17, this component is induced by a
$SL_{n-2}(q)$
. By Proposition 2.17, this component is induced by a
![]() $2$
-component of
$2$
-component of
![]() $C_{G_0}(t)$
. In view of the preceding observations, we can conclude that
$C_{G_0}(t)$
. In view of the preceding observations, we can conclude that
![]() $C_{G_0}(t)$
has subgroups
$C_{G_0}(t)$
has subgroups
![]() $K_0$
and
$K_0$
and
![]() $L_0$
with
$L_0$
with
![]() $K_0 \cong SL_{n-2}^{\varepsilon }(q^{*})$
and
$K_0 \cong SL_{n-2}^{\varepsilon }(q^{*})$
and
![]() $L_0 \cong SL_2(q^{*})$
such that
$L_0 \cong SL_2(q^{*})$
such that
![]() $O^{2'}(O^2(C_{G_0}(t))) = K_0L_0$
if
$O^{2'}(O^2(C_{G_0}(t))) = K_0L_0$
if
![]() $q^{*} \ne 3$
and
$q^{*} \ne 3$
and
![]() $O^2(C_{G_0}(t)) = K_0 L_0$
if
$O^2(C_{G_0}(t)) = K_0 L_0$
if
![]() $q^{*} = 3$
.
$q^{*} = 3$
.
Clearly,
![]() $O^{2'}(O^2(C_{G_0}(t))) \le O^{2'}(O^2(C_G(t)))$
and
$O^{2'}(O^2(C_{G_0}(t))) \le O^{2'}(O^2(C_G(t)))$
and
![]() $O^2(C_{G_0}(t)) \le O^2(C_G(t))$
. Lemma 8.5 implies that
$O^2(C_{G_0}(t)) \le O^2(C_G(t))$
. Lemma 8.5 implies that
![]() $K_0 L_0 \le KL$
. If n is odd, then it is easy to see that
$K_0 L_0 \le KL$
. If n is odd, then it is easy to see that
![]() $\vert K_0 L_0 \vert = \vert K_0 \vert \vert L_0 \vert \ge \vert K \vert \vert L \vert = \vert KL \vert $
. If n is even, then one can easily see that
$\vert K_0 L_0 \vert = \vert K_0 \vert \vert L_0 \vert \ge \vert K \vert \vert L \vert = \vert KL \vert $
. If n is even, then one can easily see that
![]() $\vert K_0 L_0 \vert = \frac {1}{2} |K_0||L_0| \ge \frac {1}{2} |K||L| = |KL|$
. Consequently,
$\vert K_0 L_0 \vert = \frac {1}{2} |K_0||L_0| \ge \frac {1}{2} |K||L| = |KL|$
. Consequently,
![]() $K_0L_0 \le KL$
and
$K_0L_0 \le KL$
and
![]() $|K_0L_0| \ge |KL|$
. It follows that
$|K_0L_0| \ge |KL|$
. It follows that
![]() $KL = K_0L_0 \le G_0$
.
$KL = K_0L_0 \le G_0$
.
Corollary 8.7. Let x be an involution of
![]() $G_0$
which is G-conjugate to t. Let
$G_0$
which is G-conjugate to t. Let
![]() $L_0$
be the unique normal
$L_0$
be the unique normal
![]() $SL_2(q^{*})$
-subgroup of
$SL_2(q^{*})$
-subgroup of
![]() $C_G(x)$
, and let
$C_G(x)$
, and let
![]() $K_0$
be the component of
$K_0$
be the component of
![]() $C_G(x)$
different from
$C_G(x)$
different from
![]() $L_0$
. Then we have
$L_0$
. Then we have
![]() $K_0 L_0 \le G_0$
.
$K_0 L_0 \le G_0$
.
Proof. Since
![]() $t \in G_0$
, we see from Lemma 8.4 that there is some
$t \in G_0$
, we see from Lemma 8.4 that there is some
![]() $g \in G_0$
with
$g \in G_0$
with
![]() $x = t^g$
. Clearly,
$x = t^g$
. Clearly,
![]() $(K_0L_0) = (KL)^g$
, and so
$(K_0L_0) = (KL)^g$
, and so
![]() $K_0L_0 \le G_0$
by Lemma 8.6.
$K_0L_0 \le G_0$
by Lemma 8.6.
Lemma 8.8. We have
![]() $N_G(S) \le N_G(G_0)$
.
$N_G(S) \le N_G(G_0)$
.
Proof. Set
![]() $M := N_G(G_0)$
. Let
$M := N_G(G_0)$
. Let
![]() $s \in N_S(S \cap M)$
, and let
$s \in N_S(S \cap M)$
, and let
![]() $1 \le i \le n-1$
. We have
$1 \le i \le n-1$
. We have
![]() $t_{\lbrace i,i+1 \rbrace } \in S \cap L_{\lbrace i,i+1 \rbrace } \le S \cap G_0 \le S \cap M$
, and hence,
$t_{\lbrace i,i+1 \rbrace } \in S \cap L_{\lbrace i,i+1 \rbrace } \le S \cap G_0 \le S \cap M$
, and hence,
![]() $(t_{\lbrace i,i+1 \rbrace })^s \in S \cap M \le M$
. Since
$(t_{\lbrace i,i+1 \rbrace })^s \in S \cap M \le M$
. Since
![]() $G_0$
has odd index in M by Lemma 8.4, we even have
$G_0$
has odd index in M by Lemma 8.4, we even have
![]() $(t_{\lbrace i,i+1 \rbrace })^s \in G_0$
. Corollary 8.7 implies that
$(t_{\lbrace i,i+1 \rbrace })^s \in G_0$
. Corollary 8.7 implies that
![]() $(L_{\lbrace i,i+1 \rbrace })^s \le G_0$
. So we have
$(L_{\lbrace i,i+1 \rbrace })^s \le G_0$
. So we have
![]() $s \in M$
by the definition of
$s \in M$
by the definition of
![]() $G_0$
. Thus,
$G_0$
. Thus,
![]() $N_S(S \cap M) = S \cap M$
and hence
$N_S(S \cap M) = S \cap M$
and hence
![]() $S \le M$
. We have
$S \le M$
. We have
![]() $C_G(S) \le C_G(t_{\lbrace i,i+1 \rbrace }) \le N_G(L_{\lbrace i,i+1 \rbrace })$
for all
$C_G(S) \le C_G(t_{\lbrace i,i+1 \rbrace }) \le N_G(L_{\lbrace i,i+1 \rbrace })$
for all
![]() $1 \le i \le n-1$
. Thus,
$1 \le i \le n-1$
. Thus,
![]() $C_G(S) \le M$
. Using Lemma 3.24, we conclude that
$C_G(S) \le M$
. Using Lemma 3.24, we conclude that
![]() $N_G(S) = SC_G(S) \le M$
.
$N_G(S) = SC_G(S) \le M$
.
Lemma 8.9. If x is an involution of S, then
![]() $C_G(x) \le N_G(G_0)$
.
$C_G(x) \le N_G(G_0)$
.
Proof. Set
![]() $M := N_G(G_0)$
.
$M := N_G(G_0)$
.
We begin by proving that
![]() $C_G(t) \le M$
. We have
$C_G(t) \le M$
. We have
![]() $K \le G_0 \le M$
by Lemma 8.6 and
$K \le G_0 \le M$
by Lemma 8.6 and
![]() $C_G(t) = K N_{C_G(t)}(X_1)$
by the Frattini argument. Also,
$C_G(t) = K N_{C_G(t)}(X_1)$
by the Frattini argument. Also,
![]() $N_{C_G(t)}(X_1) = T C_{C_G(t)}(X_1)$
as a consequence of Lemma 5.7, and
$N_{C_G(t)}(X_1) = T C_{C_G(t)}(X_1)$
as a consequence of Lemma 5.7, and
![]() $T \le M$
by Lemma 8.8. So it suffices to show that
$T \le M$
by Lemma 8.8. So it suffices to show that
![]() $C_{C_G(t)}(X_1) \le M$
.
$C_{C_G(t)}(X_1) \le M$
.
Let
![]() $z \in C_{C_G(t)}(X_1)$
. In order to prove
$z \in C_{C_G(t)}(X_1)$
. In order to prove
![]() $z \in M$
, it is enough to show that
$z \in M$
, it is enough to show that
![]() $(L_{\lbrace i, i+1 \rbrace })^z \le G_0$
for all
$(L_{\lbrace i, i+1 \rbrace })^z \le G_0$
for all
![]() $1 \le i < n$
. If
$1 \le i < n$
. If
![]() $1 \le i < n$
and
$1 \le i < n$
and
![]() $i \ne n-2$
, we have
$i \ne n-2$
, we have
![]() $z \in C_G(t_{\lbrace i,i+1 \rbrace })$
and hence
$z \in C_G(t_{\lbrace i,i+1 \rbrace })$
and hence
![]() $(L_{\lbrace i,i+1 \rbrace })^z = L_{\lbrace i,i+1 \rbrace } \le G_0$
. It remains to show that
$(L_{\lbrace i,i+1 \rbrace })^z = L_{\lbrace i,i+1 \rbrace } \le G_0$
. It remains to show that
![]() $(L_{\lbrace n-2,n-1 \rbrace })^z \le G_0$
. Since
$(L_{\lbrace n-2,n-1 \rbrace })^z \le G_0$
. Since
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, there is some
$\mathcal {F}_S(G) = \mathcal {F}_S(PSL_n(q))$
, there is some
![]() $g \in G$
with
$g \in G$
with
![]() $t^g = u$
,
$t^g = u$
,
![]() $u^g = t$
and
$u^g = t$
and
![]() $(t_{\lbrace 2,3 \rbrace })^g = t_{\lbrace n-2,n-1 \rbrace }$
(see Lemma 3.23 (i)). From the definition of L (Proposition 6.8), we see that
$(t_{\lbrace 2,3 \rbrace })^g = t_{\lbrace n-2,n-1 \rbrace }$
(see Lemma 3.23 (i)). From the definition of L (Proposition 6.8), we see that
![]() $L_{\lbrace 1,2 \rbrace } = A_1 \le K$
. Since
$L_{\lbrace 1,2 \rbrace } = A_1 \le K$
. Since
![]() $u = t_{\lbrace 1,2 \rbrace }$
and
$u = t_{\lbrace 1,2 \rbrace }$
and
![]() $t_{\lbrace 2,3 \rbrace }$
are K-conjugate by Lemma 3.23 (i), we thus have
$t_{\lbrace 2,3 \rbrace }$
are K-conjugate by Lemma 3.23 (i), we thus have
![]() $L_{\lbrace 2,3 \rbrace } \le K \le L_{2'}(C_G(t))$
. Hence,
$L_{\lbrace 2,3 \rbrace } \le K \le L_{2'}(C_G(t))$
. Hence,
![]() $L_{\lbrace n-2,n-1 \rbrace } = (L_{\lbrace 2,3 \rbrace })^g \le L_{2'}(C_G(t))^g = L_{2'}(C_G(u))$
. Since z centralizes u, it follows that
$L_{\lbrace n-2,n-1 \rbrace } = (L_{\lbrace 2,3 \rbrace })^g \le L_{2'}(C_G(t))^g = L_{2'}(C_G(u))$
. Since z centralizes u, it follows that
![]() $(L_{\lbrace n-2,n-1 \rbrace })^z \le L_{2'}(C_G(u))$
. From Corollary 8.7, we see that
$(L_{\lbrace n-2,n-1 \rbrace })^z \le L_{2'}(C_G(u))$
. From Corollary 8.7, we see that
![]() $L_{2'}(C_G(u)) \le G_0$
. So we have
$L_{2'}(C_G(u)) \le G_0$
. So we have
![]() $(L_{\lbrace n-2,n-1 \rbrace })^z \le G_0$
, and it follows that
$(L_{\lbrace n-2,n-1 \rbrace })^z \le G_0$
, and it follows that
![]() $C_{C_G(t)}(X_1) \le M$
. Consequently,
$C_{C_G(t)}(X_1) \le M$
. Consequently,
![]() $C_G(t) \le M$
.
$C_G(t) \le M$
.
Since
![]() $G_0$
has odd index in M by Lemma 8.4, we see from Lemma 8.8 that
$G_0$
has odd index in M by Lemma 8.4, we see from Lemma 8.8 that
![]() $S \le G_0$
. Also,
$S \le G_0$
. Also,
![]() $\mathcal {F}_S(G_0) = \mathcal {F}_S(G)$
by Lemma 8.4. As
$\mathcal {F}_S(G_0) = \mathcal {F}_S(G)$
by Lemma 8.4. As
![]() $C_G(t) \le M$
, it follows that
$C_G(t) \le M$
, it follows that
![]() $C_G(x) \le M$
for any involution x of S which is G-conjugate to t.
$C_G(x) \le M$
for any involution x of S which is G-conjugate to t.
Assume now that x is an involution of S which is G-conjugate to
![]() $t_i$
for some even natural number i with
$t_i$
for some even natural number i with
![]() $4 \le i < n$
such that
$4 \le i < n$
such that
![]() $i \le \frac {n}{2}$
if n is even. We are going to show that
$i \le \frac {n}{2}$
if n is even. We are going to show that
![]() $C_G(x) \le M$
. Arguing by induction over i and using the preceding observations, we may assume that, for each even
$C_G(x) \le M$
. Arguing by induction over i and using the preceding observations, we may assume that, for each even
![]() $2 \le j < i$
and each involution y of S which is G-conjugate to
$2 \le j < i$
and each involution y of S which is G-conjugate to
![]() $t_j$
, we have
$t_j$
, we have
![]() $C_G(y) \le M$
. Furthermore, we may assume that
$C_G(y) \le M$
. Furthermore, we may assume that
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}_S(G)$
-centralized since
$\mathcal {F}_S(G)$
-centralized since
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(G_0)$
.
$\mathcal {F}_S(G) = \mathcal {F}_S(G_0)$
.
As a consequence of Lemma 7.1,
![]() $C_G(x)$
is generated by the normalizers
$C_G(x)$
is generated by the normalizers
![]() $N_{C_G(x)}(U)$
, where U is a subgroup of
$N_{C_G(x)}(U)$
, where U is a subgroup of
![]() $C_S(x)$
containing a G-conjugate of
$C_S(x)$
containing a G-conjugate of
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < i$
. We show that each such normalizer is contained in M. Thus, let U be a subgroup of
$2 \le j < i$
. We show that each such normalizer is contained in M. Thus, let U be a subgroup of
![]() $C_S(x)$
, and let y be an element of U which is G-conjugate to
$C_S(x)$
, and let y be an element of U which is G-conjugate to
![]() $t_j$
for some even
$t_j$
for some even
![]() $2 \le j < i$
. Also, let
$2 \le j < i$
. Also, let
![]() $g \in N_{C_G(x)}(U)$
. Then
$g \in N_{C_G(x)}(U)$
. Then
![]() $y^g \in U \le C_S(x) \le S$
. Since
$y^g \in U \le C_S(x) \le S$
. Since
![]() $\mathcal {F}_S(G_0) = \mathcal {F}_S(G)$
, we have that y and
$\mathcal {F}_S(G_0) = \mathcal {F}_S(G)$
, we have that y and
![]() $y^g$
are
$y^g$
are
![]() $G_0$
-conjugate. Hence, there is some
$G_0$
-conjugate. Hence, there is some
![]() $m \in G_0$
with
$m \in G_0$
with
![]() $y^g = y^m$
. We have
$y^g = y^m$
. We have
![]() $mg^{-1} \in C_G(y) \le M$
. This implies
$mg^{-1} \in C_G(y) \le M$
. This implies
![]() $g \in M$
since
$g \in M$
since
![]() $m \in G_0 \le M$
. So we have
$m \in G_0 \le M$
. So we have
![]() $N_{C_G(x)}(U) \le M$
and hence
$N_{C_G(x)}(U) \le M$
and hence
![]() $C_G(x) \le M$
.
$C_G(x) \le M$
.
Assume now that x is an arbitrary involution of S. We are going to prove that
![]() $C_G(x) \le M$
. Since
$C_G(x) \le M$
. Since
![]() $\mathcal {F}_S(G) = \mathcal {F}_S(G_0)$
, we may assume that
$\mathcal {F}_S(G) = \mathcal {F}_S(G_0)$
, we may assume that
![]() $\langle x \rangle $
is fully
$\langle x \rangle $
is fully
![]() $\mathcal {F}_S(G)$
-centralized. By Corollary 7.3,
$\mathcal {F}_S(G)$
-centralized. By Corollary 7.3,
![]() $C_G(x)$
is
$C_G(x)$
is
![]() $3$
-generated. Therefore,
$3$
-generated. Therefore,
![]() $C_G(x)$
is generated by the normalizers
$C_G(x)$
is generated by the normalizers
![]() $N_{C_G(x)}(U)$
, where
$N_{C_G(x)}(U)$
, where
![]() $U \le C_S(x)$
and
$U \le C_S(x)$
and
![]() $m(U) \ge 3$
. Take some
$m(U) \ge 3$
. Take some
![]() $U \le C_S(x)$
with
$U \le C_S(x)$
with
![]() $m(U) \ge 3$
. By Lemma 2.3, any
$m(U) \ge 3$
. By Lemma 2.3, any
![]() $E_8$
-subgroup of S has an involution which is the image of an involution of
$E_8$
-subgroup of S has an involution which is the image of an involution of
![]() $SL_n(q)$
. It follows that U has an element y which is G-conjugate to
$SL_n(q)$
. It follows that U has an element y which is G-conjugate to
![]() $t_k$
for some even
$t_k$
for some even
![]() $2 \le k < n$
. By the preceding observations,
$2 \le k < n$
. By the preceding observations,
![]() $C_G(y) \le M$
. Arguing as above, we can conclude that
$C_G(y) \le M$
. Arguing as above, we can conclude that
![]() $N_{C_G(x)}(U) \le M$
. It follows that
$N_{C_G(x)}(U) \le M$
. It follows that
![]() $C_G(x) \le M$
.
$C_G(x) \le M$
.
Proposition 8.10. We have
![]() $G_0 \trianglelefteq G$
.
$G_0 \trianglelefteq G$
.
Proof. Suppose that
![]() $M := N_G(G_0)$
is a proper subgroup of G. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11], we may deduce from Lemmas 8.8 and 8.9 that M is strongly embedded in G. Therefore, by [Reference Suzuki50, Chapter 6, 4.4], G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has at least two conjugacy classes of involutions. This contradiction shows that
$M := N_G(G_0)$
is a proper subgroup of G. By [Reference Gorenstein, Lyons and Solomon27, Proposition 17.11], we may deduce from Lemmas 8.8 and 8.9 that M is strongly embedded in G. Therefore, by [Reference Suzuki50, Chapter 6, 4.4], G has only one conjugacy class of involutions. On the other hand, we see from Proposition 3.5 that G has at least two conjugacy classes of involutions. This contradiction shows that
![]() $M = G$
. Hence,
$M = G$
. Hence,
![]() $G_0 \trianglelefteq G$
.
$G_0 \trianglelefteq G$
.
With Propositions 8.3 and 8.10, we have completed the proof of Theorem 5.2.
9 Proofs of the main results
Proof of Theorem A
By Section 4, Theorem A is true for
![]() $n \le 5$
.
$n \le 5$
.
Suppose now that
![]() $n \ge 6$
. Let q be a nontrivial odd prime power, and let G be a finite simple group satisfying (𝒞𝒦).
$n \ge 6$
. Let q be a nontrivial odd prime power, and let G be a finite simple group satisfying (𝒞𝒦).
Recall that a natural number
![]() $k \ge 6$
is said to satisfy
$k \ge 6$
is said to satisfy
![]() $P(k)$
if whenever
$P(k)$
if whenever
![]() $q_0$
is a nontrivial odd prime power and H is a finite simple group satisfying (𝒞𝒦) and realizing the
$q_0$
is a nontrivial odd prime power and H is a finite simple group satisfying (𝒞𝒦) and realizing the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_k(q_0)$
, we have
$PSL_k(q_0)$
, we have
![]() $H \cong PSL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$H \cong PSL_k^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $\varepsilon q^{*} \sim q_0$
. Theorem 5.2 shows that
$\varepsilon q^{*} \sim q_0$
. Theorem 5.2 shows that
![]() $P(k)$
is satisfied for all natural numbers
$P(k)$
is satisfied for all natural numbers
![]() $k \ge 6$
.
$k \ge 6$
.
Therefore, if the
![]() $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
, then condition (i) of Theorem A is satisfied.
$PSL_n(q)$
, then condition (i) of Theorem A is satisfied.
Conversely, if one of the conditions (i), (ii), (iii) of Theorem A is satisfied, then this can only be condition (i), and Proposition 3.20 implies that the
![]() $2$
-fusion system of G is isomorphic to the
$2$
-fusion system of G is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
Proof of Theorem B
Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number, where
$n \ge 2$
be a natural number, where
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \mod 8$
if
$7 \mod 8$
if
![]() $n = 2$
. Let G be a finite simple group and
$n = 2$
. Let G be a finite simple group and
![]() $S \in \mathrm {Syl}_2(G)$
. Suppose that
$S \in \mathrm {Syl}_2(G)$
. Suppose that
![]() $\mathcal {F}_S(G)$
has a normal subsystem
$\mathcal {F}_S(G)$
has a normal subsystem
![]() $\mathcal {E}$
on a subgroup T of S such that
$\mathcal {E}$
on a subgroup T of S such that
![]() $\mathcal {E}$
is isomorphic to the
$\mathcal {E}$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
and such that
$PSL_n(q)$
and such that
![]() $C_S(\mathcal {E}) = 1$
. We have to show that
$C_S(\mathcal {E}) = 1$
. We have to show that
![]() $\mathcal {F}_S(G)$
is isomorphic to the
$\mathcal {F}_S(G)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
By Lemma 3.21,
![]() $PSL_n(q)$
is not a Goldschmidt group. Applying [Reference Aschbacher9, Theorem 5.6.18], we conclude that
$PSL_n(q)$
is not a Goldschmidt group. Applying [Reference Aschbacher9, Theorem 5.6.18], we conclude that
![]() $\mathcal {E}$
is simple. We see from [Reference Broto, Møller and Oliver15, Theorem B] that
$\mathcal {E}$
is simple. We see from [Reference Broto, Møller and Oliver15, Theorem B] that
![]() $\mathcal {E}$
is tamely realized by some finite simple group of Lie type K.
$\mathcal {E}$
is tamely realized by some finite simple group of Lie type K.
By Theorem A, we have
![]() $K \cong PSL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
$K \cong PSL_n^{\varepsilon }(q^{*})$
for some nontrivial odd prime power
![]() $q^{*}$
and some
$q^{*}$
and some
![]() $\varepsilon \in \lbrace +,- \rbrace $
with
$\varepsilon \in \lbrace +,- \rbrace $
with
![]() $\varepsilon q^{*} \sim q$
.
$\varepsilon q^{*} \sim q$
.
By Propositions 3.40 and 3.42, we have that
![]() $\mathrm {Out}(K)$
is
$\mathrm {Out}(K)$
is
![]() $2$
-nilpotent. Now Proposition 2.20 implies that
$2$
-nilpotent. Now Proposition 2.20 implies that
![]() $\mathcal {F}_S(G)$
is tamely realized by a subgroup L of
$\mathcal {F}_S(G)$
is tamely realized by a subgroup L of
![]() $\mathrm {Aut}(K)$
containing
$\mathrm {Aut}(K)$
containing
![]() $\mathrm {Inn}(K)$
such that the index of
$\mathrm {Inn}(K)$
such that the index of
![]() $\mathrm {Inn}(K)$
in L is odd. By Lemma 3.57, the
$\mathrm {Inn}(K)$
in L is odd. By Lemma 3.57, the
![]() $2$
-fusion system of L is isomorphic to the
$2$
-fusion system of L is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $\mathrm {Inn}(K) \cong K$
and hence isomorphic to the
$\mathrm {Inn}(K) \cong K$
and hence isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
. So
$PSL_n(q)$
. So
![]() $\mathcal {F}_S(G)$
is isomorphic to the
$\mathcal {F}_S(G)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
Proof of Corollary C
Let q be a nontrivial odd prime power, and let
![]() $n \ge 2$
be a natural number, where
$n \ge 2$
be a natural number, where
![]() $q \equiv 1$
or
$q \equiv 1$
or
![]() $7 \mod 8$
if
$7 \mod 8$
if
![]() $n = 2$
. Let G be a finite simple group, and let S be a Sylow
$n = 2$
. Let G be a finite simple group, and let S be a Sylow
![]() $2$
-subgroup of G. Suppose that
$2$
-subgroup of G. Suppose that
![]() $F^{*}(\mathcal {F}_S(G))$
is isomorphic to the
$F^{*}(\mathcal {F}_S(G))$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
We have
![]() $F^{*}(\mathcal {F}_S(G)) \trianglelefteq \mathcal {F}_S(G)$
and
$F^{*}(\mathcal {F}_S(G)) \trianglelefteq \mathcal {F}_S(G)$
and
![]() $C_S(F^{*}(\mathcal {F}_S(G))) = Z(F^{*}(\mathcal {F}_S(G))) = 1$
. So Theorem B implies that
$C_S(F^{*}(\mathcal {F}_S(G))) = Z(F^{*}(\mathcal {F}_S(G))) = 1$
. So Theorem B implies that
![]() $\mathcal {F}_S(G)$
is isomorphic to the
$\mathcal {F}_S(G)$
is isomorphic to the
![]() $2$
-fusion system of
$2$
-fusion system of
![]() $PSL_n(q)$
.
$PSL_n(q)$
.
Acknowledgements
This paper is based on the author’s PhD thesis, written at the University of Aberdeen under the supervision of Professor Ellen Henke and Professor Benjamin Martin. The author is deeply grateful to them for their guidance and support. Moreover, the author would like to thank Professor Ron Solomon for helpful discussions. Last but not least, the author thanks the referee for many useful comments, which helped to improve the original version of this paper and to simplify some proofs.
Conflicts of Interests
None.