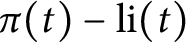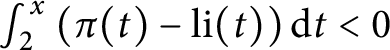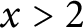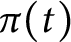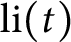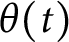1 Introduction
Let
$\pi (x)$
denote the number of primes less than or equal to x and
$$ \begin{align*} \operatorname{\mathrm{li}}(x)=\int_0^x\frac{1}{\log t}\mathrm{d}t. \end{align*} $$
In his celebrated 1859 article, Riemann [Reference Riemann21] remarked on the apparent truth of the inequality
$$ \begin{align*} \pi(x)<\operatorname{\mathrm{li}}(x), \end{align*} $$
for all
$x\geq 2$
. In 1903, Schmidt [Reference Schmidt25, p. 204] showed that such a result would imply the Riemann hypothesis. However, in 1914, Littlewood [Reference Littlewood16] managed to prove that
$\pi (x)-\operatorname {\textrm {li}}(x)$
changes sign infinitely often. More precisely, he showed that for some positive constant c, there are arbitrarily large values of x such that
$$ \begin{align*} \pi(x)-\operatorname{\mathrm{li}}(x)>\frac{c\sqrt{x}\log\log\log x}{\log x}\quad\text{and}\quad\pi(x)-\operatorname{\mathrm{li}}(x)<-\frac{c\sqrt{x}\log\log\log x}{\log x}. \end{align*} $$
It is an open problem to determine the smallest value of x such that
$\pi (x)>\operatorname {\textrm {li}}(x)$
. Large computations have shown that
$\pi (x)<\operatorname {\textrm {li}}(x)$
for all
$x\leq 10^{19}$
[Reference Büthe6, Theorem 2] and that the first sign change occurs before
$x=1.4\times 10^{316}$
[Reference Bays and Hudson1, Reference Saouter, Trudgian and Demichel24].
Although
$\pi (x)<\operatorname {\textrm {li}}(x)$
is not true in general, one can ask whether, in a precise sense,
$\pi (x)<\operatorname {\textrm {li}}(x)$
is true on average. Namely, several authors [Reference Ingham12–Reference Karatsuba14, Reference Pintz19, Reference Stechkin and Popov26] assert that the Riemann hypothesis implies
$$ \begin{align} \int_{2}^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t<0,\quad x>x_0, \end{align} $$
for some sufficiently large
$x_0$
. Pintz [Reference Pintz19] claims that (1.1) is in fact equivalent to the Riemann hypothesis and is likely to hold for all
$x>2$
under such assumptions. Using explicit bounds on prime-counting functions, we are able to prove this claim.
Theorem 1.1 The Riemann hypothesis is equivalent to the condition
$$ \begin{align} \int_{2}^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t<0,\quad\text{for all}\ x>2. \end{align} $$
We also prove an analogous result for the Chebyshev function
$$ \begin{align*} \theta(x)=\sum_{p\leq x}\log p. \end{align*} $$
Theorem 1.2 The Riemann hypothesis is equivalent to the condition
$$ \begin{align} \int_{2}^x\left(\theta(t)-t\right)\mathrm{d}t<0,\quad\text{for all}\ x>2. \end{align} $$
It is natural to ask whether a modification of (1.2) or (1.3) is true unconditionally. In this direction, we consider the weighted integrals
$$\begin{align}I_1(x,f)=\int_2^x(\pi(t)-\operatorname{\mathrm{li}}(t))f(t)\:\mathrm{d}t\quad\text{and}\quad I_2(x,f)=\int_2^x(\theta(t)-t)f(t)\:\mathrm{d}t \nonumber\\ \end{align}$$
for some choice of function
$f(t)$
. Given that one has to go quite far to find a value of t such thatFootnote
1
$\pi (t)-\operatorname {\textrm {li}}(t)>0$
, one should intuitively take
$f(t)$
to be positive and decreasing as to give more weight to the negative bias for small values of t. In [Reference Pintz19], Pintz considers
$f(t)=\exp (-\log ^2t/y)$
for sufficiently large y. However, using an explicit form of Mertens’ theorems, we show that
$I_1(x,f)<0$
and
$I_2(x,f)<0$
for the simpler and asymptotically larger function
$f(t)=1/t^2$
. Analogous results also hold for the prime-counting functions
$$ \begin{align*} \psi(x)=\sum_{p^m\leq x}\log p\quad\text{and}\quad\Pi(x)=\sum_{p^m\leq x}\frac{1}{m}. \end{align*} $$
Theorem 1.3 Unconditionally, we have
$$ \begin{align*} &\int_{2}^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t<0,\qquad \int_{2}^x\frac{\theta(t)-t}{t^2}\mathrm{d}t<0,\\ &\int_{2}^x\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t<0,\qquad \int_{2}^x\frac{\psi(t)-t}{t^2}\mathrm{d}t<0, \end{align*} $$
for all
$x>2$
.
Note that since
$\pi (t)<\Pi (t)$
and
$\theta (t)<\psi (t)$
, the apparent negative bias of
$\Pi (t)-\operatorname {\textrm {li}}(t)$
and
$\psi (t)-t$
is less pronounced than that of
$\pi (t)-\operatorname {\textrm {li}}(t)$
or
$\theta (t)-t$
. In fact,
$\int _2^x\Pi (t)-\operatorname {\textrm {li}}(t)\:\textrm {d}t$
and
$\int _2^x\psi (t)-t\:\textrm {d}t$
change sign infinitely often (see Lemma 2.8). Thus, unlike as in Theorem 1.3, Theorems 1.1 and 1.2 do not hold if
$\pi (t)$
and
$\theta (t)$
are replaced with
$\Pi (t)$
and
$\psi (t)$
, respectively.
Finally, we show that one cannot do much better than Theorem 1.3 without further knowledge of the location of the zeros of
$\zeta (s)$
.
Theorem 1.4 Let
$\omega =\sup \{\Re (s):\zeta (s)=0\}$
. If
$1/2<\omega \leq 1$
and
$c<1+\omega \leq 2$
, then
$$ \begin{align*} \int_2^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\mathrm{d}t=\Omega_+(1),\qquad\int_2^x\frac{\theta(t)-t}{t^c}\mathrm{dt}=\Omega_+(1),\\ \int_2^x\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\mathrm{d}t=\Omega_+(1),\qquad\int_2^x\frac{\psi(t)-t}{t^c}\mathrm{dt}=\Omega_+(1). \end{align*} $$
Here, as per usual, the notation
$g(x)=\Omega _+(1)$
means that there exist arbitrarily large values of x such that
$g(x)>0$
.
Remark 1.5 Despite the restrictions in Theorem 1.4, it is conceivable that one may be able to use a slightly (asymptotically) larger weight than
$f(t)=1/t^2$
in Theorem 1.3. For instance,
$f(t)=\log t/t^2$
. Such a result would most likely require the use of an explicit zero-free region, e.g., [Reference Mossinghoff and Trudgian18, Theorem 1] or [Reference Ford8, Theorem 5]. We do not pursue this here.
2 Useful lemmas
In this section, we list a series of useful lemmas. Most of the following results are explicit bounds on prime-counting functions which follow directly from existing results in the literature.
Lemma 2.1 [Reference Büthe6, Theorem 2]
For all
$2\leq x\leq 10^{19}$
,
$\pi (x)-\operatorname {\textrm {li}}(x)<0$
and
$\theta (x)-x<0$
.
Lemma 2.2 [Reference Rosser and Schoenfeld22, Equations (3.5), (3.6), (3.15), and (3.16)]
We have
$$ \begin{align} \frac{x}{\log x}&<\pi(x)<\frac{1.3x}{\log x},&x\geq 17, \end{align} $$
$$ \begin{align} x-\frac{x}{\log x}&<\theta(x)<x+\frac{0.5x}{\log x},&x\geq 41. \end{align} $$
Lemma 2.3 We have
$$ \begin{align} \Pi(x)-1.9x^{1/2}&<\pi(x)<\Pi(x)-x^{1/2}/\log x,&x\geq 17, \end{align} $$
$$ \begin{align} \psi(x)-1.5x^{1/2}&<\theta(x)<\psi(x)-0.98x^{1/2},&x\geq 121. \end{align} $$
Proof Let
$M=\lfloor \frac {\log x}{\log 2}\rfloor $
. Then,
$$ \begin{align*} \Pi(x)=\sum_{m=1}^M\frac{1}{m}\pi(x^{1/m})\leq\pi(x)+\frac{M}{2}\pi(x^{1/2})<\pi(x)+\frac{1.3}{\log 2}x^{1/2}<\pi(x)+1.9x^{1/2} \end{align*} $$
by Lemma 2.2. On the other hand,
$$ \begin{align*} \Pi(x)=\sum_{m=1}^M\frac{1}{m}\pi(x^{1/m})>\pi(x)+\frac{1}{2}\pi(x^{1/2})>\pi(x)+\frac{x^{1/2}}{\log x}, \end{align*} $$
as required. The inequalities in (2.4) then follow from equations (3.36) and (3.37) in [Reference Rosser and Schoenfeld22].▪
Lemma 2.4 For all
$x>1$
, we have
$$ \begin{align*} \operatorname{\mathrm{li}}(x)<\frac{x}{\log x}+\frac{2x}{\log^2x}. \end{align*} $$
Proof For
$x\geq 1{,}865$
, the result follows from [Reference Bennett, Martin, O’Bryant and Rechnitzer2, Lemma 5.9]. For smaller values of x, the result follows via simple computations.▪
Lemma 2.5 We have
$$ \begin{align*} -30{,}000&<\int_2^{3{,}000}\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t<-29{,}000,\\ -140{,}000&<\int_2^{3{,}000}\left(\theta(t)-t\right)\mathrm{d}t<-130{,}000,\\ -2{,}900&<\int_2^{3{,}000}\left(\psi(t)-t\right)\mathrm{d}t<-2{,}800. \end{align*} $$
Proof Follows by directly computing each integral on Mathematica.▪
Lemma 2.6 Assuming the Riemann hypothesis,
$\left |\int _2^x\left (\psi (t)-t\right )\textrm {d}t\right |\leq 0.08x^{3/2}$
for all
$x\geq 3{,}000$
.
Proof By [Reference Ingham12, Theorem 27],
$$ \begin{align*} \psi_1(x):=\int_{2}^x\psi(t)\:\mathrm{d}t=\frac{x^2}{2}-\sum_{\rho}\frac{x^{\rho+1}}{\rho(\rho+1)}-x\frac{\zeta'}{\zeta}(0)+\frac{\zeta'}{\zeta}(-1)-\sum_{r=1}^\infty\frac{x^{1-2r}}{2r(2r-1)}, \end{align*} $$
where the sum is taken over all nontrivial zeros
$\rho =\beta +i\gamma $
of the Riemann zeta function. First, we note that
$$ \begin{align*} \left|\sum_{\rho}\frac{x^{\rho+1}}{\rho(\rho+1)}\right|\leq x^{1+\omega}\sum_{\rho}\frac{1}{\gamma(\gamma+1)}\leq 0.04621x^{3/2}, \end{align*} $$
because
$\sum _{\rho }1/\gamma ^2=0.046209\ldots $
[Reference Brent, Platt and Trudgian3, Corollary 1]. Next,
$(\zeta '/\zeta )(0)=\log 2\pi $
[Reference Edwards7, Section 3.8] and
$(\zeta '/\zeta )(-1)=1.985\ldots $
as computed on Mathematica. Finally,
$$ \begin{align*} 0\leq\sum_{r=1}^\infty\frac{x^{1-2r}}{2r(2r-1)}\leq\frac{x}{2}\sum_{r=1}^\infty\frac{1}{x^{2r}}=\frac{x}{2(x^2-1)}. \end{align*} $$
Thus, noting that
$\frac {x^2}{2}=\int _2^x t\:\textrm {d}t+2$
,
$$ \begin{align*} \left|\int_2^x\left(\psi(t)-t\right)\mathrm{d}t\right|&\leq x^{3/2}\left(0.04621+\frac{\log(2\pi)}{x^{1/2}}+\frac{2+1.986}{x^{3/2}}+\frac{1}{2x^{1/2}(x^2-1)}\right)\\ &\leq 0.08x^{3/2}, \end{align*} $$
for all
$x\geq 3{,}000$
.▪
Lemma 2.7 (Cf. [Reference Ingham12, pp. 103–104])
Let
$Q(x)=\Pi (x)-\operatorname {\textrm {li}}(x)$
,
$R(x)=\psi (x)-x$
, and
$R_1(x)=\int _2^xR(t)\:\textrm {d}t$
. Then,
$$ \begin{align} Q(x)=\frac{R(x)}{\log x}+\frac{R_1(x)}{x\log^2x}+\int_{3{,}000}^x\left(\frac{R_1(t)}{t^2\log^2t}+\frac{2R_1(t)}{t^2\log^3t}\right)\mathrm{d}t+C, \end{align} $$
where
$$ \begin{align*} C=Q(3{,}000)-\frac{R(3{,}000)}{\log(3{,}000)}-\frac{R_1(3{,}000)}{3{,}000\log^2(3{,}000)}=-0.4351\ldots<0. \end{align*} $$
Proof Using integration by parts,
$$ \begin{align*} \operatorname{\mathrm{li}}(x)-\operatorname{\mathrm{li}}(3{,}000)=\frac{x}{\log x}+\int_{3{,}000}^{x}\frac{\mathrm{d}t}{\log^2t}-\frac{3{,}000}{\log(3{,}000)}, \end{align*} $$
so that by partial summation,
$$ \begin{align*} \Pi(x)-\Pi(3{,}000)=\operatorname{\mathrm{li}}(x)-\operatorname{\mathrm{li}}(3{,}000)+\frac{R(x)}{\log x}-\frac{R(3{,}000)}{\log (3{,}000)}+\int_{3{,}000}^x\frac{R(t)}{t\log^2t}\mathrm{d}t. \end{align*} $$
Hence,
$$ \begin{align*} Q(x)=\frac{R(x)}{\log x}+\int_{3{,}000}^x\frac{R(t)}{t\log^2t}\mathrm{d}t+Q(3{,}000)-\frac{R(3{,}000)}{\log(3{,}000)}. \end{align*} $$
A further application of integration by parts then gives the desired result.▪
Lemma 2.8 Let
$c\in \mathbb {R}$
and define
$$ \begin{align*} \Pi_{1,c}(x):=\int_2^x\frac{\Pi(t)}{t^c}\mathrm{d}t\quad\text{and}\quad\psi_{1,c}(x):=\int_2^x\frac{\psi(t)}{t^c}\mathrm{d}t. \end{align*} $$
If
$\omega =\sup \{\Re (s):\zeta (s)=0\}$
and
$c<1+\omega \leq 2$
, then for all
$\delta>0$
,
$$ \begin{align*} \Pi_{1,c}(x)-\int_2^x\frac{\operatorname{\mathrm{li}}(t)}{t^c}=\Omega_{\pm}(x^{1+\omega-c-\delta})\quad\text{and}\quad\psi_{1,c}(x)-\int_2^x\frac{t}{t^c}\mathrm{d}t=\Omega_{\pm}(x^{1+\omega-c-\delta}). \end{align*} $$
Proof We begin with the integral expression [Reference Ingham12, Equation (18), p. 18]
$$ \begin{align*} \log\zeta(s)=s\int_1^\infty\frac{\Pi(x)}{x^{s+1}}\mathrm{d}x,\quad\Re(s)>1. \end{align*} $$
Using integration by parts,
$$ \begin{align*} \int_1^\infty\frac{\Pi(x)}{x^{s+1}}\mathrm{d}x&=\int_1^\infty\frac{d\Pi_{1,c}(x)}{x^{s+1-c}}\\ &=\left[\frac{\Pi_{1,c}(x)}{x^{s+1-c}}\right]_1^\infty+(s+1-c)\int_1^\infty\frac{\Pi_{1,c}(x)}{x^{s+2-c}}\mathrm{d}x\\ &=(s+1-c)\int_1^\infty\frac{\Pi_{1,c}(x)}{x^{s+2-c}}\mathrm{d}x, \end{align*} $$
noting that since
$\Pi (x)=O(x)$
,
$$ \begin{align*} \left|\frac{\Pi_{1,c}(x)}{x^{s+1-c}}\right|=O\left(x^{c-1-\Re(s)}\int_2^xt^{1-c}\mathrm{d}t\right)=O(x^{1-\Re(s)})=o(1). \end{align*} $$
Hence,
$$ \begin{align} \log\zeta(s)=s(s+1-c)\int_1^\infty\frac{\Pi_{1,c}(x)}{x^{s+2-c}}\mathrm{d}x,\quad\Re(s)>1. \end{align} $$
Using an analogous argument with the integral expression [Reference Ingham12, Equation (17), p. 18]
$$ \begin{align*} -\frac{\zeta'(s)}{\zeta(s)}=s\int_1^\infty\frac{\psi(x)}{x^{s+1}}\mathrm{d}x,\quad\Re(s)>1, \end{align*} $$
one obtains
$$ \begin{align} -\frac{\zeta'(s)}{\zeta(s)}=s(s+1-c)\int_1^\infty\frac{\psi_{1,c}(x)}{x^{s+2-c}}\mathrm{d}x,\quad\Re(s)>1. \end{align} $$
Equipped with (2.6) and (2.7), one can then follow a standard argument (e.g., [Reference Broughan4, p. 80], [Reference Ingham12, pp. 90–91]) mutatis mutandis to obtain the desired result.▪
3 Proofs of Theorems 1.1 and 1.2
We begin with the case where the Riemann hypothesis is false. By Lemma 2.8 with
$c=0$
, there are arbitrarily large values of x such that
$\int _{2}^x\Pi (t)-\operatorname {\textrm {li}}(t)\:\textrm {d}t>Kx^{\kappa }$
for some positive constants
$K>0$
and
$\kappa>3/2$
. For such values of x, we then have by Lemma 2.3 that
$$ \begin{align*} \int_2^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t&=\int_{2}^{17}\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t+\int_{17}^{x}\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t\\ &>-\int_{17}^x1.9t^{1/2}\:\mathrm{d}t+\int_{17}^x\left(\Pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t+O(1)\\ &=Kx^\kappa+O(x^{3/2}). \end{align*} $$
Thus, there are arbitrarily large values of x such that
$$ \begin{align*} \int_2^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t>0, \end{align*} $$
as required. The same reasoning holds for the integral over
$\theta (t)-t$
using the corresponding bounds for
$\theta (t)$
in Lemmas 2.3 and 2.8.
Now, suppose the Riemann hypothesis is true. To show (1.2) and (1.3), it suffices to consider
$x>10^{19}$
in light of Lemma 2.1. We begin with the integral over
$\theta (t)-t$
. By Lemmas 2.3, 2.5, and 2.6, we have
$$ \begin{align*} &\int_{2}^x\left(\theta(t)-t\right)\mathrm{d}t=\int_{2}^{3{,}000}\left(\theta(t)-t\right)\mathrm{d}t+\int_{3{,}000}^x\left(\theta(t)-t\right)\mathrm{d}t\\ &\quad<-130{,}000-\int_{3{,}000}^x 0.98t^{1/2}\:\mathrm{d}t+\int_{3{,}000}^x\left(\psi(t)-t\right)\mathrm{d}t\\ &\quad<-130{,}000-\frac{1.96}{3}(x^{3/2}-(3{,}000)^{3/2})+0.08x^{3/2}-\int_{2}^{3{,}000}\left(\psi(t)-t\right)\mathrm{d}t\\ &\quad<-19{,}000-0.57x^{3/2}<0, \end{align*} $$
as required.
The integral over
$\pi (t)-\operatorname {\textrm {li}}(t)$
requires more work. First, we apply Lemmas 2.3, 2.5, and 2.7 to obtain
$$ \begin{align} \int_2^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t&<\int_2^{3{,}000}\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t+\int_{3{,}000}^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t\notag\\ &<-29{,}000-\int_{3{,}000}^x\frac{t^{1/2}}{\log t}\mathrm{d}t+\int_{3{,}000}^x\left(\Pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t\notag\\ &<-29{,}000-\int_{3{,}000}^x\frac{t^{1/2}}{\log t}\mathrm{d}t+\int_{3{,}000}^x\left(\frac{R(t)}{\log t}+\frac{R_1(t)}{t\log^2 t}\right.\notag\\ &\qquad\qquad\qquad+\left.\int_{3{,}000}^t\left(\frac{R_1(u)}{u^2\log^2u}+\frac{2R_1(u)}{u^2\log^3u}\mathrm{d}u\right)\right)\mathrm{d}t, \end{align} $$
using the notation from Lemma 2.7. Now, by integration by parts and Lemmas 2.5 and 2.6,
$$ \begin{align} \int_{3{,}000}^x\left(\frac{R(t)}{\log t}+\frac{R_1(t)}{t\log^2t}\right)\mathrm{d}t&=\frac{R_1(x)}{\log x}-\frac{R_1(3{,}000)}{\log(3{,}000)}+\int_{3{,}000}^x\frac{2R_1(t)}{t\log^2t}\mathrm{d}t\notag\\ &\leq 0.08 \frac{x^{3/2}}{\log x}+370+0.16\int_{3{,}000}^x\frac{t^{1/2}}{\log^2t}\mathrm{d}t. \end{align} $$
Next,
$$ \begin{align*} \int_{3{,}000}^t\left(\frac{R_1(u)}{u^2\log^2u}+\frac{2R_1(u)}{u^2\log^3u}\right)\mathrm{d}u&\leq 0.08\int_{3{,}000}^t\left(\frac{1}{u^{1/2}\log^2u}+\frac{2}{u^{1/2}\log^3u}\right)\mathrm{d}u\\ &\leq 0.08\int_{3{,}000}^t\frac{3}{u^{1/2}\log^2u}\mathrm{d}u. \end{align*} $$
Since
$u^{1/4}/\log ^2u$
is increasing for
$u\geq 3{,}000$
, we then have
$$ \begin{align*} 0.08\int_{3{,}000}^t\frac{3}{u^{1/2}\log^2u}\mathrm{d}u\leq 0.24\frac{t^{1/4}}{\log^2t}\int_{3{,}000}^t\frac{1}{u^{3/4}}\mathrm{d}u\leq 0.96\frac{t^{1/2}}{\log^2t}. \end{align*} $$
Thus,
$$ \begin{align} \int_{3{,}000}^t\left(\frac{R_1(u)}{u^2\log^2u}+\frac{2R_1(u)}{u^2\log^3u}\right)\mathrm{d}u\leq 0.96\frac{t^{1/2}}{\log^2 t}. \end{align} $$
Substituting (3.2) and (3.3) into (3.1) then gives
$$ \begin{align} \int_{2}^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t&<-28,630-\int_{3{,}000}^x\frac{t^{1/2}}{\log t}\mathrm{d}t+0.08\frac{x^{3/2}}{\log x}+1.12\int_{3{,}000}^x\frac{t^{1/2}}{\log^2 t}\mathrm{d}t. \end{align} $$
Now, using integration by parts,
$$ \begin{align} \int_{3{,}000}^x\frac{t^{1/2}}{\log t}\mathrm{d}t=\frac{2}{3}\frac{x^{3/2}}{\log x}-\frac{2}{3}\frac{(3{,}000)^{3/2}}{\log (3{,}000)}+\frac{2}{3}\int_{3{,}000}^x\frac{t^{1/2}}{\log^2t}\mathrm{d}t\geq\frac{2}{3}\frac{x^{3/2}}{\log x}-14{,}000. \end{align} $$
Moreover,
$$ \begin{align} 1.12\int_{3{,}000}^x\frac{t^{1/2}}{\log^2t}\mathrm{d}t\leq 1.12\frac{x^{1/4}}{\log^2x}\int_{3{,}000}^xt^{1/4}\:\mathrm{d}t\leq 0.9\frac{x^{3/2}}{\log^2x}. \end{align} $$
Applying (3.5) and (3.6), we have that (3.4) reduces to
$$ \begin{align*} \int_2^x\left(\pi(t)-\operatorname{\mathrm{li}}(t)\right)\mathrm{d}t<-14{,}000-0.58\frac{x^{3/2}}{\log x}+0.9\frac{x^{3/2}}{\log^2 x}<0, \end{align*} $$
as required.
4 Proof of Theorem 1.3
First, we note that, via a simple computation, all four integrals in question are negative for
$2<x\leq 200$
. Thus, we may assume throughout that
$x>200$
.
First, we deal with the integrals involving
$\pi (t)$
and
$\Pi (t)$
. By an explicit form of Mertens’ theorem [Reference Rosser and Schoenfeld22, Equation (3.20)], we have
$$ \begin{align} \sum_{p\leq x}\frac{1}{p}<\log\log x+B+\frac{1}{\log^2x}, \end{align} $$
where
$B=0.2614\ldots $
. Now, by partial summation and Lemma 2.2,
$$ \begin{align} \sum_{p\leq x}\frac{1}{p}=\frac{\pi(x)}{x}+\int_2^x\frac{\pi(t)}{t^2}\mathrm{d}t>\frac{1}{\log x}+\int_2^x\frac{\pi(t)}{t^2}\mathrm{d}t. \end{align} $$
Moreover, by integration by parts and Lemma 2.4,
$$ \begin{align} \log\log x=\int_e^x\frac{1}{t\log t}\mathrm{d}t&=\frac{\operatorname{\mathrm{li}}(x)}{x}-\frac{\operatorname{\mathrm{li}}(e)}{e}+\int_e^x\frac{\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t\notag\\ &\leq\frac{1}{\log x}+\frac{2}{\log^2x}-\frac{\operatorname{\mathrm{li}}(e)}{e}+\int_2^x\frac{\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t-\int_2^e\frac{\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t. \end{align} $$
Substituting (4.2) and (4.3) into (4.1) gives
$$ \begin{align} \qquad\int_2^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t<\frac{2.5}{\log^2x}+B-\frac{\operatorname{\mathrm{li}}(e)}{e}-\int_2^e\frac{\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t<\frac{3}{\log^2x}-0.62<0, \end{align} $$
as desired. For the integral involving
$\Pi (t)$
, we then note that by Lemma 2.3,
$$ \begin{align*} \int_2^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t&=\int_2^{200}\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t+\int_{200}^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t\\ &>-0.59+\int_{200}^x\frac{\Pi(t)-1.9t^{1/2}-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t\\ &=-0.59+\left(\frac{3.8}{\sqrt{x}}-\frac{3.8}{\sqrt{200}}\right)+\int_2^{x}\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad-\int_{2}^{200}\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t\\ &>\int_{2}^x\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t-0.56+\frac{3.8}{\sqrt{x}}. \end{align*} $$
Substituting this into (4.4) then gives
$$ \begin{align*} \int_{2}^x\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^2}\mathrm{d}t<-0.06-\frac{3.8}{\sqrt{x}}+\frac{3}{\log^2x}<0. \end{align*} $$
We argue similarly for the integrals involving
$\theta (t)$
and
$\psi (t)$
. In particular, we have [Reference Rosser and Schoenfeld22, Equation (3.23)]
$$ \begin{align*} \sum_{p\leq x}\frac{\log p}{p}<\log x+E+\frac{1}{\log x}, \end{align*} $$
where
$E=-1.332\ldots $
. Then, by Lemma 2.2,
$$ \begin{align*} \sum_{p\leq x}\frac{\log p}{p}=\frac{\theta(x)}{x}+\int_2^x\frac{\theta(t)}{t^2}\mathrm{d}t>1-\frac{1}{\log x}+\int_2^x\frac{\theta(t)}{t^2}\mathrm{d}t \end{align*} $$
and
$$ \begin{align*} \log(x)=\int_1^x\frac{1}{t}\mathrm{d}t=\int_2^x\frac{t}{t^2}\mathrm{d}t+\log 2. \end{align*} $$
Therefore,
$$ \begin{align} \int_2^x\frac{\theta(t)-t}{t^2}\mathrm{d}t<E-1+\log 2+\frac{1.5}{\log x}<-1.63+\frac{2}{\log x}<0, \end{align} $$
as required. The corresponding result for
$\psi (t)$
then follows similar to before by applying Lemma 2.3 to (4.5). In particular, we have that
$$ \begin{align*} \int_2^x\frac{\psi(t)-t}{t^2}\mathrm{d}t<-0.83-\frac{3}{\sqrt{x}}+\frac{2}{\log x}<0. \end{align*} $$
5 Proof of Theorem 1.4
The result for the integrals involving
$\Pi (t)$
and
$\psi (t)$
follows immediately from Lemma 2.8. For the integral involving
$\pi (t)$
, we first note that by Lemma 2.8, for any choice of
$\delta>0$
, there exist arbitrarily large values of x such that
$$ \begin{align*} \int_{2}^x\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\:\mathrm{d}t>Kx^{1+\omega-c-\delta}, \end{align*} $$
for some positive constant
$K>0$
. For such values of x, we then have by Lemma 2.3 that
$$ \begin{align} \int_2^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\:\mathrm{d}t&=\int_{2}^{17}\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\:\mathrm{d}t+\int_{17}^{x}\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\:\mathrm{d}t\notag\\ &>-\int_{17}^x1.9t^{1/2-c}\:\mathrm{d}t+\int_{17}^x\frac{\Pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\:\mathrm{d}t+O(1)\notag\\ &>-\int_{17}^x 1.9t^{1/2-c}\:\mathrm{d}t+Kx^{1+\omega-c-\delta}+O(1). \end{align} $$
The integral in (5.1) satisfies
$$ \begin{align*} \int_{17}^x1.9t^{1/2-c}\:\mathrm{d}t= \begin{cases} O(x^{3/2-c}),&c<3/2,\\ O(\log x),&c=3/2,\\ O(1),&3/2<c<1+\omega. \end{cases} \end{align*} $$
Thus, if we take any choice of
$\delta <\omega -1/2$
when
$c\leq 3/2$
, and
$\delta <1+\omega -c$
when
$3/2<c<1+\omega $
, we have
$$ \begin{align*} \int_2^x\frac{\pi(t)-\operatorname{\mathrm{li}}(t)}{t^c}\mathrm{d}t>0 \end{align*} $$
for arbitrarily large values of x as required. The same reasoning holds for the integral over
$(\theta (t)-t)/t^c$
using the corresponding bounds for
$\theta (t)$
in Lemmas 2.3 and 2.8.
6 Discussion and further work
The general idea in this paper was to consider averaged versions of arithmetic functions in order to gain insight into biases occurring in number theory. The functions
$\pi (t)-\operatorname {\textrm {li}}(t)$
and
$\theta (t)-t$
, in particular, exhibit an apparent negative bias, and our results reflect this.
There are many other biases occurring in number theory, and it would be interesting to consider averaged versions of these. For example, we have:
-
(a) The bias in Mertens’ theorems [Reference Büthe5, Reference Lamzouri15].
-
(b) The Chebyshev bias for primes in arithmetic progressions [Reference Granville and Martin10, Reference Rubinstein and Sarnak23].
-
(c) The bias of
$\lambda (n)$
and related functions [Reference Humphries11, Reference Martin, Mossinghoff and Trudgian17].
One could also attempt to extend our results to more general number fields. In this direction, it is worth noting that Garcia and Lee [Reference Garcia and Lee9] recently proved explicit versions of Mertens’ theorems for number fields. Using Garcia and Lee’s results could thus allow one to generalize Theorem 1.3, whose proof followed directly from an explicit version of Mertens’ theorems in the standard setting.
Acknowledgment
Thanks to my supervisor Tim Trudgian and colleagues Ethan, Michaela, and Shehzad for the fun and fruitful discussions on this project.
