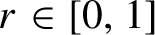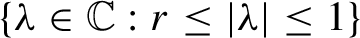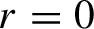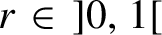1 Introduction
Soit E un espace vectoriel normé sur
![]() ${\mathbb {C}}$
. On appellera ici opérateur de E toute application linéaire continue
${\mathbb {C}}$
. On appellera ici opérateur de E toute application linéaire continue
![]() $u$
de E dans E. Il est dit rigide (respectivement uniformément rigide) quand il existe une suite strictement croissante
$u$
de E dans E. Il est dit rigide (respectivement uniformément rigide) quand il existe une suite strictement croissante
![]() $(n_{k})_{k\ge 1}$
d’entiers telle que pour tout x de E, on a
$(n_{k})_{k\ge 1}$
d’entiers telle que pour tout x de E, on a
![]() $\lim \nolimits _{k\rightarrow +\infty } u^{n_{k}}x=x$
(respectivement telle que
$\lim \nolimits _{k\rightarrow +\infty } u^{n_{k}}x=x$
(respectivement telle que
![]() $\lim \nolimits _{k\rightarrow +\infty } u^{n_{k}}={\rm id}_{E}$
dans l’espace vectoriel normé des opérateurs de E). On dira que
$\lim \nolimits _{k\rightarrow +\infty } u^{n_{k}}={\rm id}_{E}$
dans l’espace vectoriel normé des opérateurs de E). On dira que
![]() $(n_{k})_{k\ge 1}$
est une suite de rigidité de
$(n_{k})_{k\ge 1}$
est une suite de rigidité de
![]() $u$
(respectivement d’uniforme rigidité de
$u$
(respectivement d’uniforme rigidité de
![]() $u$
).
$u$
).
En 2014, Costakis, Manoussos et Parissis [Reference Costakis, Manoussos and Parissis2] ont entrepris une étude systématique des opérateurs rigides et uniformément rigides. Ils passent notamment en revue des familles classiques d’opérateurs (certaines familles d’opérateurs diagonaux, certaines familles d’opérateurs de composition, etc) et pour chacune d’entre elles, ils donnent un critère de rigidité, voire d’uniforme rigidité. Ils se demandent en particulier à quelle condition nécessaire et suffisante un endomorphisme de dimension finie est rigide, et de même pour uniformément rigide.
Poser la question, c’est y répondre. Encore faut il la poser! C’est tout le mérite de Costakis, Manoussos et Parissis de l’avoir fait.
Cela les amène à effectuer une démarche en trois temps. En notant
![]() ${\mathbb {U}}=\{z\in {\mathbb {C}} : |z|=1\}$
et
${\mathbb {U}}=\{z\in {\mathbb {C}} : |z|=1\}$
et
![]() $\sigma (u)$
le spectre de
$\sigma (u)$
le spectre de
![]() $u$
, ils donnent donc d’abord la preuve (voir le theorem 4.1 et la remark 4.3 de [Reference Costakis, Manoussos and Parissis2]) du théorème suivant.
$u$
, ils donnent donc d’abord la preuve (voir le theorem 4.1 et la remark 4.3 de [Reference Costakis, Manoussos and Parissis2]) du théorème suivant.
Théorème CMP. Soit
![]() $u$
un endomorphisme d’un
$u$
un endomorphisme d’un
![]() ${\mathbb {C}}$
espace vectoriel de dimension finie. Les conditions suivantes sont équivalentes:
${\mathbb {C}}$
espace vectoriel de dimension finie. Les conditions suivantes sont équivalentes:
-
(i)
 $u$
est rigide;
$u$
est rigide; -
(ii)
 $u$
est uniformément rigide;
$u$
est uniformément rigide; -
(iii)
 $u$
est diagonalisable et
$u$
est diagonalisable et
 $\sigma (u) \subset {\mathbb {U}}$
.
$\sigma (u) \subset {\mathbb {U}}$
.
Ils se demandent ensuite dans quelle mesure ce résultat s’étend à la dimension infinie. Dans cette direction, ils montrent (voir la proposition 2.19 de [Reference Costakis, Manoussos and Parissis2]) la proposition suivante.
Proposition CMP. Soit
![]() $u$
un opérateur uniformément rigide d’un espace de Banach complexe. Alors
$u$
un opérateur uniformément rigide d’un espace de Banach complexe. Alors
![]() $\sigma (u) \subset {\mathbb {U}}$
.
$\sigma (u) \subset {\mathbb {U}}$
.
(Nous donnons en Annexe 1 une preuve de ce résultat plus rapide que celle de [Reference Costakis, Manoussos and Parissis2].)
Enfin quid des opérateurs rigides? La proposition CMP s’étend-elle à ceux-ci? Dans leur question 2.20 ils posent deux questions précises.
Question 1. Est-ce que tous les opérateurs rigides sont inversibles?
Question 2. Est-ce que pour tout opérateur rigide et inversible, son inverse est rigide?
La réponse aux deux questions est négative. On y répond en donnant des exemples qui montrent que la proposition CMP ne s’étend pas aux opérateurs rigides.
Plus précisément, on rappelle qu’un opérateur de
![]() $\ell ^{2}(\mathbb {N}^{*})$
est dit diagonal quand sa matrice infinie dans la base orthonormale canonique de
$\ell ^{2}(\mathbb {N}^{*})$
est dit diagonal quand sa matrice infinie dans la base orthonormale canonique de
![]() $\ell ^{2}(\mathbb {N}^{*})$
est diagonale. Quand plus généralement, cette matrice est diagonale par blocs, tous finis, on dira que l’opérateur est diagonal par blocs. On a alors le théorème suivant.
$\ell ^{2}(\mathbb {N}^{*})$
est diagonale. Quand plus généralement, cette matrice est diagonale par blocs, tous finis, on dira que l’opérateur est diagonal par blocs. On a alors le théorème suivant.
Théorème. Pour tout
![]() $r\in [0,1]$
, il existe un opérateur diagonal par blocs de
$r\in [0,1]$
, il existe un opérateur diagonal par blocs de
![]() $\ell ^{2}(\mathbb {N}^{*})$
et rigide dont le spectre est
$\ell ^{2}(\mathbb {N}^{*})$
et rigide dont le spectre est
![]() $\{\lambda \in {\mathbb {C}} : r \le |\lambda | \le 1\}$
.
$\{\lambda \in {\mathbb {C}} : r \le |\lambda | \le 1\}$
.
Pour
![]() $r=0$
, un tel opérateur est non inversible. Cela répond donc négativement à la Question
$r=0$
, un tel opérateur est non inversible. Cela répond donc négativement à la Question
![]() $1$
. Signalons qu’après avoir prouvé notre théorème, nous avons été informés par Sophie Grivaux que l’existence d’opérateurs rigides dont le spectre est le disque unité fermé peut également être établie à partir du travail [Reference Grivaux and Roginskaya3].
$1$
. Signalons qu’après avoir prouvé notre théorème, nous avons été informés par Sophie Grivaux que l’existence d’opérateurs rigides dont le spectre est le disque unité fermé peut également être établie à partir du travail [Reference Grivaux and Roginskaya3].
Pour
![]() $r\in \, ]0,1[$
, l’inverse d’un tel opérateur n’est pas rigide. En effet son spectre est
$r\in \, ]0,1[$
, l’inverse d’un tel opérateur n’est pas rigide. En effet son spectre est
![]() $\{\lambda \in {\mathbb {C}} : 1\le |\lambda | \le r^{-1}\}$
. Or on sait que le spectre d’un opérateur rigide est inclus dans le disque unité fermé (voir l’Annexe 2 pour une preuve rapide qui utilise le théorème de Banach and Steinhaus). Cela répond donc négativement à la Question
$\{\lambda \in {\mathbb {C}} : 1\le |\lambda | \le r^{-1}\}$
. Or on sait que le spectre d’un opérateur rigide est inclus dans le disque unité fermé (voir l’Annexe 2 pour une preuve rapide qui utilise le théorème de Banach and Steinhaus). Cela répond donc négativement à la Question
![]() $2$
.
$2$
.
Nous avons donc utilisé que le rayon spectral d’un opérateur rigide est inférieur ou égal à un. Il est facile d’en déduire que dès que le Banach n’est pas réduit au vecteur nul, le rayon spectral d’un opérateur rigide est égal à un.
Toujours pour tout opérateur rigide
![]() $u$
d’un Banach, on a de plus que
$u$
d’un Banach, on a de plus que
Cela découle facilement du théorème de décomposition de Riesz (theorem D.2.1 de l’appendice D.2 de [Reference Bayart and Matheron1]) comme l’ont montré Costakis, Manoussos et Parissis à la proposition 2.11 de [Reference Costakis, Manoussos and Parissis2], sous une hypothèse plus faible que la rigidité. En réalité, la même argumentation avait déjà été utilisée par Kitai en 1982 pour établir que les opérateurs
![]() $u$
d’un Banach qui satisfont la propriété
$u$
d’un Banach qui satisfont la propriété
vérifient également la propriété (1.1) (voir le theorem 1.18 de [Reference Bayart and Matheron1]). Signalons au passage que les opérateurs qui vérifient (1.2) sont appelés hypercycliques et que le livre [Reference Bayart and Matheron1] de Bayart et Matheron constitue l’ouvrage de référence pour leur étude générale.
Le spectre d’un opérateur diagonal de
![]() $\ell ^{2}(\mathbb {N}^{*})$
est égal à l’adhérence de son spectre ponctuel (voir le problem 63 de [Reference Halmos4]). Or il est immédiat que le spectre ponctuel d’un opérateur rigide est inclus dans
$\ell ^{2}(\mathbb {N}^{*})$
est égal à l’adhérence de son spectre ponctuel (voir le problem 63 de [Reference Halmos4]). Or il est immédiat que le spectre ponctuel d’un opérateur rigide est inclus dans
![]() ${\mathbb {U}}$
. On ne peut donc pas puiser dans les opérateurs diagonaux pour traiter les cas du théorème correspondant à
${\mathbb {U}}$
. On ne peut donc pas puiser dans les opérateurs diagonaux pour traiter les cas du théorème correspondant à
![]() $0\le r<1$
. Nos exemples montrent que cela devient possible quand on élargit aux opérateurs diagonaux par blocs de
$0\le r<1$
. Nos exemples montrent que cela devient possible quand on élargit aux opérateurs diagonaux par blocs de
![]() $\ell ^{2}(\mathbb {N}^{*})$
.
$\ell ^{2}(\mathbb {N}^{*})$
.
Notre construction d’opérateurs diagonaux par blocs mais non diagonaux donne également un exemple quand
![]() $r=1$
, mais il y a alors plus simple. En effet un opérateur diagonal de
$r=1$
, mais il y a alors plus simple. En effet un opérateur diagonal de
![]() $\ell ^{2}(\mathbb {N}^{*})$
avec
$\ell ^{2}(\mathbb {N}^{*})$
avec
![]() $e^{i\pi \mathbb {Q}}$
comme ensemble de ses éléments diagonaux est rigide de spectre
$e^{i\pi \mathbb {Q}}$
comme ensemble de ses éléments diagonaux est rigide de spectre
![]() ${\mathbb {U}}$
.
${\mathbb {U}}$
.
2 Une famille d’opérateurs en dimension finie
On désigne par
![]() $\Omega $
l’ensemble des triplets
$\Omega $
l’ensemble des triplets
![]() $\omega =(p,q,\alpha )$
où
$\omega =(p,q,\alpha )$
où
![]() $(p,q)\in \mathbb {N}^{*2}$
et
$(p,q)\in \mathbb {N}^{*2}$
et
![]() $\alpha \in [1,+\infty [$
.
$\alpha \in [1,+\infty [$
.
Pour tout
![]() $\omega $
de
$\omega $
de
![]() $\Omega $
, on note n l’entier et
$\Omega $
, on note n l’entier et
![]() $\beta $
le réel appartenant à
$\beta $
le réel appartenant à
![]() $]0,1]$
définis par
$]0,1]$
définis par
et
Pour tout
![]() $\omega $
de
$\omega $
de
![]() $\Omega $
, on désigne par
$\Omega $
, on désigne par
![]() $\gamma =\gamma (\omega )$
le n-uplet
$\gamma =\gamma (\omega )$
le n-uplet
![]() $(\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})=(\gamma _{1}(\omega ),\gamma _{2}(\omega ), \ldots ,\gamma _{n}(\omega ))$
défini par
$(\gamma _{1},\gamma _{2},\ldots ,\gamma _{n})=(\gamma _{1}(\omega ),\gamma _{2}(\omega ), \ldots ,\gamma _{n}(\omega ))$
défini par
 $$ \begin{align*} \gamma_{j} = \bigg\{\!\! \begin{array}{ll} \alpha&(1\le j\le p),\\ \beta&(p+1\le j \le n). \end{array} \end{align*} $$
$$ \begin{align*} \gamma_{j} = \bigg\{\!\! \begin{array}{ll} \alpha&(1\le j\le p),\\ \beta&(p+1\le j \le n). \end{array} \end{align*} $$
On désigne par
![]() $(e_{1},e_{2},\ldots ,e_{n})$
la base canonique de
$(e_{1},e_{2},\ldots ,e_{n})$
la base canonique de
![]() ${\mathbb {C}}^{n}$
.
${\mathbb {C}}^{n}$
.
Les opérateurs que nous étudions dans ce chapitre sont les endomorphismes
![]() $v=v_{\omega }$
de
$v=v_{\omega }$
de
![]() ${\mathbb {C}}^{n}$
définis par
${\mathbb {C}}^{n}$
définis par
avec la convention
![]() $e_{n+j}=e_{j}$
. On convient également que
$e_{n+j}=e_{j}$
. On convient également que
![]() $\gamma _{n+j}=\gamma _{j}$
.
$\gamma _{n+j}=\gamma _{j}$
.
Lemme 2.1. Soit
![]() $\omega \in \Omega $
.
$\omega \in \Omega $
.
On a pour tous j et k vérifiant
![]() $1\le j\le n-1$
et
$1\le j\le n-1$
et
![]() $1\le k\le n$
$1\le k\le n$
Démonstration. On a
L’inégalité demandée est donc immédiate si
![]() $k+j-1\le n$
. Si
$k+j-1\le n$
. Si
![]() $k+j-1>n$
, on a d’après (2.1)
$k+j-1>n$
, on a d’après (2.1)
D’où
 $$ \begin{align*} \gamma_{k}\gamma_{k+1}\cdots \gamma_{k+j-1} &=(\gamma_{k}\gamma_{k+1}\cdots \gamma_{n})(\gamma_{1}\gamma_{2}\cdots\gamma_{k+j-1-n})\\[3pt] &\le (\gamma_{k-n+j}\gamma_{k-n+j+1} \cdots\gamma_{j})(\gamma_{1}\gamma_{2}\cdots\gamma_{k+j-1-n})\\[3pt] &=\gamma_{1}\gamma_{2}\cdots\gamma_{j}.\\[-34pt] \end{align*} $$
$$ \begin{align*} \gamma_{k}\gamma_{k+1}\cdots \gamma_{k+j-1} &=(\gamma_{k}\gamma_{k+1}\cdots \gamma_{n})(\gamma_{1}\gamma_{2}\cdots\gamma_{k+j-1-n})\\[3pt] &\le (\gamma_{k-n+j}\gamma_{k-n+j+1} \cdots\gamma_{j})(\gamma_{1}\gamma_{2}\cdots\gamma_{k+j-1-n})\\[3pt] &=\gamma_{1}\gamma_{2}\cdots\gamma_{j}.\\[-34pt] \end{align*} $$
Soit
![]() $\omega =(p,q,\alpha ) \in \Omega $
et
$\omega =(p,q,\alpha ) \in \Omega $
et
![]() $t>0$
. On note
$t>0$
. On note
![]() $\omega ^{2}=(p,q,\alpha ^{2})$
et
$\omega ^{2}=(p,q,\alpha ^{2})$
et
 $$ \begin{align*} S(\omega,t)=t^{n-1} \sum_{j=0}^{n-1} \frac{\gamma_{1}\gamma_{2}\cdots \gamma_{j}}{t^{j}}. \end{align*} $$
$$ \begin{align*} S(\omega,t)=t^{n-1} \sum_{j=0}^{n-1} \frac{\gamma_{1}\gamma_{2}\cdots \gamma_{j}}{t^{j}}. \end{align*} $$
Pour
![]() $\lambda \in {\mathbb {C}}$
, on note
$\lambda \in {\mathbb {C}}$
, on note
![]() $\rho =|\lambda |$
.
$\rho =|\lambda |$
.
Si
![]() $\lambda \not = 0$
, on note également pour
$\lambda \not = 0$
, on note également pour
![]() $v=v_{\omega }$
,
$v=v_{\omega }$
,
 $$ \begin{align*} \psi_{\lambda}(v) = \lambda^{n-1}\sum_{j=0}^{n-1} \bigg(\frac{v}{\lambda}\bigg)^{j}. \end{align*} $$
$$ \begin{align*} \psi_{\lambda}(v) = \lambda^{n-1}\sum_{j=0}^{n-1} \bigg(\frac{v}{\lambda}\bigg)^{j}. \end{align*} $$
On munit de plus
![]() ${\mathbb {C}}^{n}$
de sa structure usuelle d’espace hermitien qui fait de la base
${\mathbb {C}}^{n}$
de sa structure usuelle d’espace hermitien qui fait de la base
![]() $(e_{j})_{1 \le j\le n}$
une base orthonormale.
$(e_{j})_{1 \le j\le n}$
une base orthonormale.
Lemme 2.2. Soient
![]() $\omega \in \Omega $
,
$\omega \in \Omega $
,
![]() $\lambda \in {\mathbb {C}}^{*}$
et
$\lambda \in {\mathbb {C}}^{*}$
et
![]() $1\le j\le n-1$
. On a alors pour
$1\le j\le n-1$
. On a alors pour
![]() $v=v_{\omega }$
,
$v=v_{\omega }$
,
 $$ \begin{align} \|v^{j}\| = \|v^{j}(e_{1})\| = \gamma_{1}\gamma_{2}\cdots \gamma_{j},\end{align} $$
$$ \begin{align} \|v^{j}\| = \|v^{j}(e_{1})\| = \gamma_{1}\gamma_{2}\cdots \gamma_{j},\end{align} $$
Démonstration. On a
![]() $\gamma _{1}\gamma _{2}\cdots \gamma _{n}=1$
. On en déduit que
$\gamma _{1}\gamma _{2}\cdots \gamma _{n}=1$
. On en déduit que
![]() $v$
permute circulairement les vecteurs de la base
$v$
permute circulairement les vecteurs de la base
![]() $(e_{1},\gamma _{1}e_{2}, \gamma _{1}\gamma _{2}e_{3},\ldots , \gamma _{1}\gamma _{2}\cdots \gamma _{n-1}e_{n})$
de
$(e_{1},\gamma _{1}e_{2}, \gamma _{1}\gamma _{2}e_{3},\ldots , \gamma _{1}\gamma _{2}\cdots \gamma _{n-1}e_{n})$
de
![]() ${\mathbb {C}}^{n}$
. D’où (2.2).
${\mathbb {C}}^{n}$
. D’où (2.2).
On a
 $$ \begin{align*} v\psi_{\lambda}(v)=\lambda^{n} \sum_{j=1}^{n}(v/\lambda)^{j} = \lambda\psi_{\lambda}(v)+v^{n} -\lambda^{n} {\rm id} = \lambda\psi_{\lambda}(v)+(1-\lambda^{n}){\rm id} \end{align*} $$
$$ \begin{align*} v\psi_{\lambda}(v)=\lambda^{n} \sum_{j=1}^{n}(v/\lambda)^{j} = \lambda\psi_{\lambda}(v)+v^{n} -\lambda^{n} {\rm id} = \lambda\psi_{\lambda}(v)+(1-\lambda^{n}){\rm id} \end{align*} $$
d’après (2.2). Cela entraîne (2.3).
On a
![]() $\|v^{j}e_{1}\| = \gamma _{1}\gamma _{2}\cdots \gamma _{j}$
, d’où
$\|v^{j}e_{1}\| = \gamma _{1}\gamma _{2}\cdots \gamma _{j}$
, d’où
![]() $\|v^{j}\| \ge \gamma _{1}\gamma _{2}\cdots \gamma _{j}$
. Par ailleurs on a
$\|v^{j}\| \ge \gamma _{1}\gamma _{2}\cdots \gamma _{j}$
. Par ailleurs on a
 $$ \begin{align*} \bigg\|v^{j}\bigg(\displaystyle\sum_{k=1}^{n} x_{k}e_{k}\bigg)\bigg\|^{2} &=\bigg\|\displaystyle\sum_{k=1}^{n} x_{k} \gamma_{k}\gamma_{k+1}\cdots \gamma_{k+j-1}e_{k+j}\bigg\|^{2}\\ &= \displaystyle\sum_{k=1}^{n} (\gamma_{k}\gamma_{k+1} \cdots \gamma_{k+j-1} |x_{k}|)^{2} \le (\gamma_{1}\gamma_{2} \cdots \gamma_{j})^{2} \displaystyle\sum_{k=1}^{n} |x_{k}|^{2} \end{align*} $$
$$ \begin{align*} \bigg\|v^{j}\bigg(\displaystyle\sum_{k=1}^{n} x_{k}e_{k}\bigg)\bigg\|^{2} &=\bigg\|\displaystyle\sum_{k=1}^{n} x_{k} \gamma_{k}\gamma_{k+1}\cdots \gamma_{k+j-1}e_{k+j}\bigg\|^{2}\\ &= \displaystyle\sum_{k=1}^{n} (\gamma_{k}\gamma_{k+1} \cdots \gamma_{k+j-1} |x_{k}|)^{2} \le (\gamma_{1}\gamma_{2} \cdots \gamma_{j})^{2} \displaystyle\sum_{k=1}^{n} |x_{k}|^{2} \end{align*} $$
d’après le lemme 2.1 On a donc aussi
![]() $\|v^{j}\| \le \gamma _{1}\gamma _{2}\cdots \gamma _{j}$
, ce qui permet d’achever la preuve de (2.4).
$\|v^{j}\| \le \gamma _{1}\gamma _{2}\cdots \gamma _{j}$
, ce qui permet d’achever la preuve de (2.4).
En utilisant (2.4), on a
 $$ \begin{align*} \|\psi_{\lambda}(v)\|\le \rho^{n-1} \displaystyle\sum_{j=0}^{n-1} \|v^{j}\|/\rho^{j} = \rho^{n-1} \displaystyle\sum_{j=0}^{n-1} \frac{\gamma_{1}\gamma_{2}\cdots\gamma_{j}}{\rho^{j}} = S(\omega,\rho). \end{align*} $$
$$ \begin{align*} \|\psi_{\lambda}(v)\|\le \rho^{n-1} \displaystyle\sum_{j=0}^{n-1} \|v^{j}\|/\rho^{j} = \rho^{n-1} \displaystyle\sum_{j=0}^{n-1} \frac{\gamma_{1}\gamma_{2}\cdots\gamma_{j}}{\rho^{j}} = S(\omega,\rho). \end{align*} $$
3 Endomorphismes de
 ${\mathbb {C}}^{\mathbb {N}^{*}}$
et opérateurs de
${\mathbb {C}}^{\mathbb {N}^{*}}$
et opérateurs de
 $\ell ^{2}(\mathbb {N}^{*})$
, diagonaux par blocs
$\ell ^{2}(\mathbb {N}^{*})$
, diagonaux par blocs
On pose
![]() $\ell ^{2}:=\ell ^{2}(\mathbb {N}^{*})$
et on note
$\ell ^{2}:=\ell ^{2}(\mathbb {N}^{*})$
et on note
![]() $(\delta _{r})_{r\ge 1}$
sa base orthonormale canonique définie par
$(\delta _{r})_{r\ge 1}$
sa base orthonormale canonique définie par
 $$ \begin{align*} \delta_{r}(j) = \bigg\{\!\! \begin{array}{rl} 1 &\mathrm{si}\ j=r,\\ 0 &\mathrm{si}\ j\not= r. \end{array} \end{align*} $$
$$ \begin{align*} \delta_{r}(j) = \bigg\{\!\! \begin{array}{rl} 1 &\mathrm{si}\ j=r,\\ 0 &\mathrm{si}\ j\not= r. \end{array} \end{align*} $$
Pour alléger les notations, on écrit
![]() $\ll k\gg $
à la place de
$\ll k\gg $
à la place de
![]() $\ll k\ge 1\gg $
. On choisit une suite
$\ll k\ge 1\gg $
. On choisit une suite
![]() $n(1),n(2),\ldots $
d’entiers de
$n(1),n(2),\ldots $
d’entiers de
![]() $\mathbb {N}^{*}$
et on définit
$\mathbb {N}^{*}$
et on définit
![]() $s(1)$
,
$s(1)$
,
![]() $s(2),\ldots $
par les formules
$s(2),\ldots $
par les formules
et pour tout k
On note
On choisit pour tout k un endomorphisme
![]() $v_{k}$
de
$v_{k}$
de
![]() $E_{k}$
. En écrivant un vecteur générique y de
$E_{k}$
. En écrivant un vecteur générique y de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
sous la forme
${\mathbb {C}}^{\mathbb {N}^{*}}$
sous la forme
 $$ \begin{align*} y= \sum_{k} y_{k} \end{align*} $$
$$ \begin{align*} y= \sum_{k} y_{k} \end{align*} $$
avec
![]() $y_{k}\in E_{k}$
, on définit un endomorphisme
$y_{k}\in E_{k}$
, on définit un endomorphisme
![]() $v$
de
$v$
de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
par la formule
${\mathbb {C}}^{\mathbb {N}^{*}}$
par la formule
 $$ \begin{align*} v(y) = \sum_{k} v_{k}(y_{k}). \end{align*} $$
$$ \begin{align*} v(y) = \sum_{k} v_{k}(y_{k}). \end{align*} $$
On dira que
![]() $v$
est l’endomorphisme diagonal par blocs de
$v$
est l’endomorphisme diagonal par blocs de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par les endomorphismes
${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par les endomorphismes
![]() $v_{k}$
.
$v_{k}$
.
Dans le cas où
![]() $v(\ell ^{2}) \subset \ell ^{2}$
, on note
$v(\ell ^{2}) \subset \ell ^{2}$
, on note
![]() $u=v_{|\ell ^{2}}$
la restriction de
$u=v_{|\ell ^{2}}$
la restriction de
![]() $v$
à
$v$
à
![]() $\ell ^{2}$
, à la fois pour l’espace de départ et l’espace d’arrivée. On verra alors que
$\ell ^{2}$
, à la fois pour l’espace de départ et l’espace d’arrivée. On verra alors que
![]() $u$
est automatiquement continu. On dira que
$u$
est automatiquement continu. On dira que
![]() $u$
est l’opérateur diagonal par blocs de
$u$
est l’opérateur diagonal par blocs de
![]() $\ell ^{2}$
défini par les endomorphismes
$\ell ^{2}$
défini par les endomorphismes
![]() $v_{k}$
.
$v_{k}$
.
Le lemme suivant précise tout cela. Il généralise le cas des opérateurs diagonaux traité dans l’excellent livre [Reference Halmos4] de Halmos sur les Hilbert, aux problèmes 61 et 62.
Lemme 3.1. Soit
![]() $v$
un endomorphisme diagonal par blocs de
$v$
un endomorphisme diagonal par blocs de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par des endomorphismes
${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par des endomorphismes
![]() $v_{k}$
. Les conditions suivantes sont équivalentes:
$v_{k}$
. Les conditions suivantes sont équivalentes:
-
(i)
 $v(\ell ^{2}) \subset \ell ^{2}$
;
$v(\ell ^{2}) \subset \ell ^{2}$
; -
(ii)
 $\sup \nolimits _{k} \|v_{k}\| <+\infty $
.
$\sup \nolimits _{k} \|v_{k}\| <+\infty $
.
Quand ces conditions sont réalisées, on a pour
![]() $u:=v_{|\ell ^{2}}$
:
$u:=v_{|\ell ^{2}}$
:
-
(iii)
 $ \left\{ \begin {array}{ll} u \ {\it est}\ {\it continu}\\ et\\ \|u\| = \sup \limits _{k} \|v_{k}\|.\end {array}\right. $
$ \left\{ \begin {array}{ll} u \ {\it est}\ {\it continu}\\ et\\ \|u\| = \sup \limits _{k} \|v_{k}\|.\end {array}\right. $
Démonstration. (i)
![]() $\Rightarrow $
(ii) On raisonne par l’absurde; on suppose donc que
$\Rightarrow $
(ii) On raisonne par l’absurde; on suppose donc que
![]() $\sup \nolimits _{k} \|v_{k}\|=+\infty $
.
$\sup \nolimits _{k} \|v_{k}\|=+\infty $
.
On extrait une sous-suite
![]() $k_{n}$
pour laquelle
$k_{n}$
pour laquelle
![]() $\|v_{k_{n}}\|\ge n$
pour tout n. En choisissant y avec
$\|v_{k_{n}}\|\ge n$
pour tout n. En choisissant y avec
![]() $\|y_{k}\|=1/n$
et
$\|y_{k}\|=1/n$
et
![]() $\|v_{k}(y_{k})\| =\|v_{k}\|\cdot \|y_{k}\|$
quand
$\|v_{k}(y_{k})\| =\|v_{k}\|\cdot \|y_{k}\|$
quand
![]() $k=k_{n}$
, et
$k=k_{n}$
, et
![]() $y_{k}=0$
sinon, on voit que
$y_{k}=0$
sinon, on voit que
![]() $y\in \ell ^{2}$
et
$y\in \ell ^{2}$
et
![]() $v(y)\notin \ell ^{2}$
. Donc
$v(y)\notin \ell ^{2}$
. Donc
![]() $v(\ell ^{2})\not \subset \ell ^{2}$
.
$v(\ell ^{2})\not \subset \ell ^{2}$
.
(ii)
![]() $\Rightarrow $
[(i) et (iii)] Soit
$\Rightarrow $
[(i) et (iii)] Soit
![]() $y\in \ell ^{2}$
. On a
$y\in \ell ^{2}$
. On a
 $$ \begin{align*} \sum_{k} \|v(y_{k})\|^{2} \le \sum_{k} \|v_{k}\|^{2} \cdot \|y_{k}\|^{2} \le \sup_{k} \|v_{k}\|^{2} \cdot \|y\|^{2}. \end{align*} $$
$$ \begin{align*} \sum_{k} \|v(y_{k})\|^{2} \le \sum_{k} \|v_{k}\|^{2} \cdot \|y_{k}\|^{2} \le \sup_{k} \|v_{k}\|^{2} \cdot \|y\|^{2}. \end{align*} $$
Donc avec (ii),
![]() $v(\ell ^{2}) \subset \ell ^{2}$
,
$v(\ell ^{2}) \subset \ell ^{2}$
,
![]() $u=v_{|\ell ^{2}}$
est continu et
$u=v_{|\ell ^{2}}$
est continu et
 $$ \begin{align*} \|u\| \le \sup_{k} \|v_{k}\|. \end{align*} $$
$$ \begin{align*} \|u\| \le \sup_{k} \|v_{k}\|. \end{align*} $$
Par ailleurs, en considérant, pour chaque k, un vecteur
![]() $y_{k}$
de
$y_{k}$
de
![]() $E_{k}$
qui vérifie
$E_{k}$
qui vérifie
![]() $\|y_{k}\| =1$
et
$\|y_{k}\| =1$
et
![]() $\|v_{k}(y_{k})\|=\|v_{k}\|$
, on a
$\|v_{k}(y_{k})\|=\|v_{k}\|$
, on a
 $$ \begin{align*} \|u\| \ge \sup_{k} \|v_{k} (y_{k})\| = \sup_{k} \|v_{k}\|. \\[-42pt] \end{align*} $$
$$ \begin{align*} \|u\| \ge \sup_{k} \|v_{k} (y_{k})\| = \sup_{k} \|v_{k}\|. \\[-42pt] \end{align*} $$
Dans les deux lemmes suivants on suppose vérifiée la condition (ii) du lemme 3.1. La condition (i) est donc vérifiée et la lettre
![]() $u$
désignera implicitement l’opérateur diagonal par blocs
$u$
désignera implicitement l’opérateur diagonal par blocs
![]() $u=v_{|\ell ^{2}}$
.
$u=v_{|\ell ^{2}}$
.
Lemme 3.2. Soit
![]() $v$
un endomorphisme diagonal par blocs de
$v$
un endomorphisme diagonal par blocs de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par des endomorphismes
${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par des endomorphismes
![]() $v_{k}$
, tel que
$v_{k}$
, tel que
 $$ \begin{align*} \sup_{k} \|v_{k}\| <+\infty. \end{align*} $$
$$ \begin{align*} \sup_{k} \|v_{k}\| <+\infty. \end{align*} $$
Les conditions suivantes sont équivalentes:
-
(i)
 $u$
est inversible;
$u$
est inversible; -
(ii) pour tout k,
 $v_{k}$
est inversible, et Quand ces conditions sont réalisées, on a aussi
$v_{k}$
est inversible, et Quand ces conditions sont réalisées, on a aussi $$ \begin{align*} \sup_{k} \|v_{k}^{-1}\| <+\infty. \end{align*} $$
$$ \begin{align*} \sup_{k} \|v_{k}^{-1}\| <+\infty. \end{align*} $$
-
(iii)
 $\|u^{-1}\| = \sup _{k} \|v_{k}^{-1}\|$
.
$\|u^{-1}\| = \sup _{k} \|v_{k}^{-1}\|$
.
Démonstration. (i)
![]() $\Rightarrow $
[(ii) et (iii)] Supposons (i). On a alors pour tout k
$\Rightarrow $
[(ii) et (iii)] Supposons (i). On a alors pour tout k
 $$ \begin{align*} \ker v_{k} \subset \bigg(\prod_{j\ge 1} \ker v_{j}\bigg) \cap \ell^{2} = (\ker v) \cap \ell^{2} = \ker u=\{0\}. \end{align*} $$
$$ \begin{align*} \ker v_{k} \subset \bigg(\prod_{j\ge 1} \ker v_{j}\bigg) \cap \ell^{2} = (\ker v) \cap \ell^{2} = \ker u=\{0\}. \end{align*} $$
Donc
![]() $v_{k}$
est inversible. On en déduit que
$v_{k}$
est inversible. On en déduit que
![]() $v$
est inversible et
$v$
est inversible et
 $$ \begin{align} v^{-1} = (v_{k}^{-1})_{k}. \end{align} $$
$$ \begin{align} v^{-1} = (v_{k}^{-1})_{k}. \end{align} $$
Soit maintenant
![]() $y\in \ell ^{2}$
. Notons
$y\in \ell ^{2}$
. Notons
![]() $x=u^{-1}(y)$
. On a
$x=u^{-1}(y)$
. On a
![]() $v^{-1}(y) =v^{-1}(u(x)) =x\in \ell ^{2}$
. Donc
$v^{-1}(y) =v^{-1}(u(x)) =x\in \ell ^{2}$
. Donc
![]() $v^{-1}(\ell ^{2})\subset {\ell }^{2}$
et
$v^{-1}(\ell ^{2})\subset {\ell }^{2}$
et
 ${v^{-1}}_{|\ell ^{2}}={(v_{|\ell ^{2}})}^{-1}$
. En appliquant le lemme 3.1 à
${v^{-1}}_{|\ell ^{2}}={(v_{|\ell ^{2}})}^{-1}$
. En appliquant le lemme 3.1 à
![]() $v^{-1}$
, on a donc avec (3.4) que
$v^{-1}$
, on a donc avec (3.4) que
![]() $\sup \nolimits _{k} \|{v_{k}}^{-1}\| <+\infty $
,
$\sup \nolimits _{k} \|{v_{k}}^{-1}\| <+\infty $
,
 ${v^{-1}}_{|\ell ^{2}}$
est continu et
${v^{-1}}_{|\ell ^{2}}$
est continu et
 $$ \begin{align*} \|u^{-1}\| = \|v^{-1}{}_{|\ell^{2}}\| = \sup_{k} \|v_{k}^{-1}\|. \end{align*} $$
$$ \begin{align*} \|u^{-1}\| = \|v^{-1}{}_{|\ell^{2}}\| = \sup_{k} \|v_{k}^{-1}\|. \end{align*} $$
(ii)
![]() $\Rightarrow $
(i) Supposons (ii). On a alors
$\Rightarrow $
(i) Supposons (ii). On a alors
![]() $v$
inversible et (3.4) est vérifié. En appliquant le lemme 3.1 à
$v$
inversible et (3.4) est vérifié. En appliquant le lemme 3.1 à
![]() $v$
, on a
$v$
, on a
![]() $v(\ell ^{2}) \subset \ell ^{2}$
et
$v(\ell ^{2}) \subset \ell ^{2}$
et
![]() $u$
est continu. En l’appliquant cette fois à
$u$
est continu. En l’appliquant cette fois à
![]() $v^{-1}$
, on a
$v^{-1}$
, on a
![]() $v^{-1}(\ell ^{2}) \subset \ell ^{2}$
et
$v^{-1}(\ell ^{2}) \subset \ell ^{2}$
et
![]() $u^{-1}$
est continu. Il découle de tout cela que
$u^{-1}$
est continu. Il découle de tout cela que
![]() $u$
est inversible d’inverse
$u$
est inversible d’inverse
 $v^{-1}{}_{|\ell ^{2}}$
.
$v^{-1}{}_{|\ell ^{2}}$
.
On déduit immédiatement du lemme 3.2 le critère suivant d’appartenance au spectre.
Lemme 3.3. Soit
![]() $v$
un endomorphisme diagonal par blocs de
$v$
un endomorphisme diagonal par blocs de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par des endomorphismes
${\mathbb {C}}^{\mathbb {N}^{*}}$
défini par des endomorphismes
![]() $v_{k}$
, tel que
$v_{k}$
, tel que
 $$ \begin{align*} \sup_{k} \|v_{k}\| <+\infty. \end{align*} $$
$$ \begin{align*} \sup_{k} \|v_{k}\| <+\infty. \end{align*} $$
Soit
![]() $\lambda \in {\mathbb {C}}$
.
$\lambda \in {\mathbb {C}}$
.
Les conditions suivantes sont équivalentes:
-
(i)
 $\lambda \in \sigma (u)$
;
$\lambda \in \sigma (u)$
; -
(ii)
 $ \left\{ \begin {array}{ll} \lambda \in \bigcup \limits _{k} \sigma (v_{k})\\ ou\\ \lambda \notin \bigcup \limits _{k} \sigma (v_{k})\ et\ \sup \limits _{k} \|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| =+\infty. \end {array}\right. $
$ \left\{ \begin {array}{ll} \lambda \in \bigcup \limits _{k} \sigma (v_{k})\\ ou\\ \lambda \notin \bigcup \limits _{k} \sigma (v_{k})\ et\ \sup \limits _{k} \|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| =+\infty. \end {array}\right. $
Remarque 1. Dans le cas particulier des opérateurs diagonaux, le critère (ii) s’écrit de manière plus simple
 $$ \begin{align*} \lambda\in \overline{\bigcup_{k} \sigma(v_{k})} \end{align*} $$
$$ \begin{align*} \lambda\in \overline{\bigcup_{k} \sigma(v_{k})} \end{align*} $$
(voir le problème 63 de [Reference Halmos4]).
Remarque 2. Lorsque
![]() $v$
n’est pas pas inversible, écrivons par convention
$v$
n’est pas pas inversible, écrivons par convention
![]() $\|v^{-1}\|=+\infty $
. On peut alors écrire (ii) sous la forme plus concise,
$\|v^{-1}\|=+\infty $
. On peut alors écrire (ii) sous la forme plus concise,
-
(ii)’
 $ \sup _{k} \|(v_{k} -\lambda {\kern2pt}{\rm id})^{-1}\| = +\infty. $
$ \sup _{k} \|(v_{k} -\lambda {\kern2pt}{\rm id})^{-1}\| = +\infty. $
4 Une famille d’opérateurs diagonaux par blocs
On se donne une suite
![]() $\omega =(\omega (k))_{k\ge 3}=(\omega _{p(k),q(k),\alpha (k)})_{k\ge 3}$
d’éléments de l’ensemble
$\omega =(\omega (k))_{k\ge 3}=(\omega _{p(k),q(k),\alpha (k)})_{k\ge 3}$
d’éléments de l’ensemble
![]() $\Omega $
du chapitre 2. On pose
$\Omega $
du chapitre 2. On pose
![]() $n(1)=n(2)=1$
et
$n(1)=n(2)=1$
et
![]() $n(k)=p(k)+q(k)$
pour
$n(k)=p(k)+q(k)$
pour
![]() $k\ge 3$
. On définit les sous-espaces
$k\ge 3$
. On définit les sous-espaces
![]() $E_{k}$
pour
$E_{k}$
pour
![]() $k\ge 1$
par (3.1), (3.2) et (3.3).
$k\ge 1$
par (3.1), (3.2) et (3.3).
Pour tout
![]() $k\ge 3$
, on identifie
$k\ge 3$
, on identifie
![]() ${\mathbb {C}}^{n(k)}$
à
${\mathbb {C}}^{n(k)}$
à
![]() $E_{k}$
en envoyant la base canonique
$E_{k}$
en envoyant la base canonique
![]() $(e_{1},e_{2},\ldots , e_{n(k)})$
de
$(e_{1},e_{2},\ldots , e_{n(k)})$
de
![]() ${\mathbb {C}}^{n(k)}$
sur la base
${\mathbb {C}}^{n(k)}$
sur la base
![]() $(\delta _{s(k)},\delta _{s(k)+1},\ldots ,\delta _{s(k+1)-1})$
de
$(\delta _{s(k)},\delta _{s(k)+1},\ldots ,\delta _{s(k+1)-1})$
de
![]() $E_{k}$
. On définit alors l’endomorphisme diagonal par blocs
$E_{k}$
. On définit alors l’endomorphisme diagonal par blocs
![]() $v$
de
$v$
de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
par
${\mathbb {C}}^{\mathbb {N}^{*}}$
par
![]() $v_{1}={\rm id}_{|E_{1}}$
,
$v_{1}={\rm id}_{|E_{1}}$
,
![]() $v_{2}={\rm id}_{|E_{2}}$
et
$v_{2}={\rm id}_{|E_{2}}$
et
![]() $v_{k}=v_{\omega (k)}$
pour tout
$v_{k}=v_{\omega (k)}$
pour tout
![]() $k\ge 3$
. On dit que
$k\ge 3$
. On dit que
![]() $v$
est associé à
$v$
est associé à
![]() $\omega $
.
$\omega $
.
Lemme 4.1. Soit
![]() $\omega =(\omega _{p(k),q(k),\alpha (k)})_{k\ge 3}$
une suite d’éléments de
$\omega =(\omega _{p(k),q(k),\alpha (k)})_{k\ge 3}$
une suite d’éléments de
![]() $\Omega $
telle que la suite
$\Omega $
telle que la suite
![]() $(\alpha (k))_{k\ge 3}$
est bornée.
$(\alpha (k))_{k\ge 3}$
est bornée.
Alors l’endomorphisme par blocs
![]() $v$
de
$v$
de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
associé à
${\mathbb {C}}^{\mathbb {N}^{*}}$
associé à
![]() $\omega $
laisse stable
$\omega $
laisse stable
![]() $\ell ^{2}$
et
$\ell ^{2}$
et
![]() $u:=v_{|\ell ^{2}}$
est continu.
$u:=v_{|\ell ^{2}}$
est continu.
Démonstration. Cela découle de la combinaison du lemme 3.1 avec le point (2.4) du lemme 2.2 avec
![]() $j=1$
.
$j=1$
.
Notations. Dans les chapitres 5 et 6 qui suivent, une fois donnée une telle suite
![]() $\omega $
d’éléments de
$\omega $
d’éléments de
![]() $\Omega $
, on continuera à désigner par
$\Omega $
, on continuera à désigner par
![]() $v$
l’endomorphisme diagonal par blocs de
$v$
l’endomorphisme diagonal par blocs de
![]() ${\mathbb {C}}^{\mathbb {N}^{*}}$
associé à
${\mathbb {C}}^{\mathbb {N}^{*}}$
associé à
![]() $\omega $
, et par
$\omega $
, et par
![]() $u$
l’opérateur diagonal par blocs de
$u$
l’opérateur diagonal par blocs de
![]() $\ell ^{2}$
défini par
$\ell ^{2}$
défini par
![]() $u=v_{|\ell ^{2}}$
.
$u=v_{|\ell ^{2}}$
.
5 Spectre
Lemme 5.1. Soit
![]() $\omega =(\omega (k))_{k\ge 3}=(\omega _{p(k),q(k),\alpha (k)})_{k\ge 3}$
une suite d’éléments de
$\omega =(\omega (k))_{k\ge 3}=(\omega _{p(k),q(k),\alpha (k)})_{k\ge 3}$
une suite d’éléments de
![]() $\Omega $
telle que
$\Omega $
telle que
et
 $$ \begin{align} \lim_{k\rightarrow +\infty} \alpha(k) =1. \end{align} $$
$$ \begin{align} \lim_{k\rightarrow +\infty} \alpha(k) =1. \end{align} $$
Alors
où
 $$ \begin{align*} r=\sup \{s\in [0,1] : \mathit{la\ suite\ } (\alpha(k)^{p(k)} s^{q(k)})_{k\ge3}\ \textrm{est born}\acute{\mathrm{e}}\textrm{e}\}. \end{align*} $$
$$ \begin{align*} r=\sup \{s\in [0,1] : \mathit{la\ suite\ } (\alpha(k)^{p(k)} s^{q(k)})_{k\ge3}\ \textrm{est born}\acute{\mathrm{e}}\textrm{e}\}. \end{align*} $$
Dans la suite de cet article et en particulier pour la preuve de ce lemme, on utilise les notations suivantes. Soient f et g deux fonctions définies sur une partie D de
![]() $\mathbb {R}^{d}$
à valeurs dans
$\mathbb {R}^{d}$
à valeurs dans
![]() $\mathbb {R}^{+*}$
. On note
$\mathbb {R}^{+*}$
. On note
![]() $f\ll g$
(respectivement
$f\ll g$
(respectivement
![]() $f\gg g$
) pour signifier qu’il existe un réel positif K tel que pour tout élément x de D, on a
$f\gg g$
) pour signifier qu’il existe un réel positif K tel que pour tout élément x de D, on a
![]() $f(x)\le Kg(x) (\mathrm {respectivement} f(x) \ge Kg(x))$
. Si K dépend d’un paramètre
$f(x)\le Kg(x) (\mathrm {respectivement} f(x) \ge Kg(x))$
. Si K dépend d’un paramètre
![]() $\eta $
, c’est-à-dire est une fonction de
$\eta $
, c’est-à-dire est une fonction de
![]() $\eta $
, on écrira par exemple
$\eta $
, on écrira par exemple
![]() $f\ll _{\eta } g$
à la place de
$f\ll _{\eta } g$
à la place de
![]() $f\ll g$
.
$f\ll g$
.
Démonstration. C’est la combinaison du lemme 4.1 avec l’hypothèse (5.2), qui assure que
![]() $u$
est bien défini et continu.
$u$
est bien défini et continu.
D’après le point (2.2) du lemme 2.2, on a
 $$ \begin{align} \bigcup_{k\ge1} \sigma(v_{k}) = \bigcup_{k\ge1} \{z\in {\mathbb{C}} : z^{n(k)}=1\}. \end{align} $$
$$ \begin{align} \bigcup_{k\ge1} \sigma(v_{k}) = \bigcup_{k\ge1} \{z\in {\mathbb{C}} : z^{n(k)}=1\}. \end{align} $$
Soit
![]() $\lambda \in {\mathbb {C}}$
. On va maintenant discuter suivant les propriétés conjointes de
$\lambda \in {\mathbb {C}}$
. On va maintenant discuter suivant les propriétés conjointes de
![]() $\rho :=|\lambda |$
et de la suite
$\rho :=|\lambda |$
et de la suite
![]() $(\omega (k))_{k\ge 3} = (p(k),q(k),\alpha (k))_{k\ge 3}$
.
$(\omega (k))_{k\ge 3} = (p(k),q(k),\alpha (k))_{k\ge 3}$
.
1
![]() $^{\mathrm {er}}$
cas.
$^{\mathrm {er}}$
cas.
![]() $\rho>1$
. En utilisant successivement les formules (2.3) et (2.4) du lemme 2.2, et l’hypothèse (5.2), on a
$\rho>1$
. En utilisant successivement les formules (2.3) et (2.4) du lemme 2.2, et l’hypothèse (5.2), on a
 $$ \begin{align*} \|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| &= \dfrac{\|\psi_{\lambda}(v_{k})\|}{|1-\lambda^{n(k)}|} \ll_{\rho}\displaystyle \sum_{j=0}^{n(k)-1} \frac{\|v_{k}^{j}\|}{\rho^{j}} \\ &=\displaystyle\sum_{j=0}^{n(k)-1} \frac{\gamma_{1}(\omega(k))\gamma_{2}(\omega(k))\cdots\gamma_{j}(\omega(k))}{\rho^{j}} &\le \displaystyle\sum_{j=0}^{n(k)-1}\bigg(\dfrac{\alpha(k)}{\rho}\bigg)^{j} \ll_{\rho}\ 1. \end{align*} $$
$$ \begin{align*} \|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| &= \dfrac{\|\psi_{\lambda}(v_{k})\|}{|1-\lambda^{n(k)}|} \ll_{\rho}\displaystyle \sum_{j=0}^{n(k)-1} \frac{\|v_{k}^{j}\|}{\rho^{j}} \\ &=\displaystyle\sum_{j=0}^{n(k)-1} \frac{\gamma_{1}(\omega(k))\gamma_{2}(\omega(k))\cdots\gamma_{j}(\omega(k))}{\rho^{j}} &\le \displaystyle\sum_{j=0}^{n(k)-1}\bigg(\dfrac{\alpha(k)}{\rho}\bigg)^{j} \ll_{\rho}\ 1. \end{align*} $$
En utilisant (5.3) et le lemme 3.3, on en déduit que
Pour les 2
![]() $^{\grave{\mathrm{e}}\textrm {me}}$
et 3
$^{\grave{\mathrm{e}}\textrm {me}}$
et 3
![]() $^{\grave{\mathrm{e}}\textrm {me}}$
cas, on note
$^{\grave{\mathrm{e}}\textrm {me}}$
cas, on note
2
![]() $^{\textrm{i}\grave{{e}}{me}}$
cas.
$^{\textrm{i}\grave{{e}}{me}}$
cas.
![]() $0<\rho <1$
et la suite
$0<\rho <1$
et la suite
![]() $\alpha (k)^{p(k)}\rho ^{q(k)}$
n’est pas bornée. En utilisant successivement les formules (2.3) et (2.6) du lemme 2.2 on a
$\alpha (k)^{p(k)}\rho ^{q(k)}$
n’est pas bornée. En utilisant successivement les formules (2.3) et (2.6) du lemme 2.2 on a
 $$ \begin{align*} \|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| &\gg_{\rho} \|\psi_{\lambda}(v_{k})\| \ge \|\psi_{\lambda}(v_{k})(e_{1})\|\\[3pt] &= S^{1/2}(\omega(k)^{2},\rho^{2})\ge \alpha(k)^{p(k)} \rho^{q(k)-1}. \end{align*} $$
$$ \begin{align*} \|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| &\gg_{\rho} \|\psi_{\lambda}(v_{k})\| \ge \|\psi_{\lambda}(v_{k})(e_{1})\|\\[3pt] &= S^{1/2}(\omega(k)^{2},\rho^{2})\ge \alpha(k)^{p(k)} \rho^{q(k)-1}. \end{align*} $$
Donc
 $\sup \nolimits _{k\ge 1}\|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| =+\infty $
.
$\sup \nolimits _{k\ge 1}\|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| =+\infty $
.
Avec le lemme 3.3, on en déduit que
3
![]() $^{\grave{{e}}{me}}$
cas. Pour un certain réel
$^{\grave{{e}}{me}}$
cas. Pour un certain réel
![]() $\gamma $
, on a
$\gamma $
, on a
![]() $0\le \rho <\gamma <1$
et la suite
$0\le \rho <\gamma <1$
et la suite
![]() $\alpha (k)^{p(k)}\gamma ^{q(k)}$
est bornée. Si
$\alpha (k)^{p(k)}\gamma ^{q(k)}$
est bornée. Si
![]() $\rho =0$
, on a en utilisant successivement les formules (2.2) et (2.4) du lemme 2.2,
$\rho =0$
, on a en utilisant successivement les formules (2.2) et (2.4) du lemme 2.2,
 $$ \begin{align*} \|v_{k}^{-1}\| = \|v_{k}^{n(k)-1}\| &= \gamma_{1}(\omega(k))\gamma_{2}(\omega(k)) \cdots \gamma_{n(k)-1}(\omega(k))\\[3pt] &= 1/\beta(k) = \alpha(k)^{p(k)/q(k)}\\[3pt] &= \dfrac{1}{\gamma} (\alpha(k)^{p(k)} \gamma^{q(k)})^{1/q(k)} \ll_{\gamma} 1. \end{align*} $$
$$ \begin{align*} \|v_{k}^{-1}\| = \|v_{k}^{n(k)-1}\| &= \gamma_{1}(\omega(k))\gamma_{2}(\omega(k)) \cdots \gamma_{n(k)-1}(\omega(k))\\[3pt] &= 1/\beta(k) = \alpha(k)^{p(k)/q(k)}\\[3pt] &= \dfrac{1}{\gamma} (\alpha(k)^{p(k)} \gamma^{q(k)})^{1/q(k)} \ll_{\gamma} 1. \end{align*} $$
Si maintenant
![]() $\rho \not = 0$
, il existe un grand
$\rho \not = 0$
, il existe un grand
![]() $M>1$
et un petit
$M>1$
et un petit
![]() $\delta>0$
tels que si
$\delta>0$
tels que si
alors
En utilisant successivement les formules (2.3) et (2.5) du lemme 2.2 on a
 $$ \begin{align*} \|(v_{k} -\lambda {\kern2pt}{\rm id})^{-1}\| &\ll_{\rho} \|\psi_{\lambda}(v_{k})\| \le S(\omega_{k},\rho)\\ &\ll_{\rho} Q:= \alpha(k)^{p(k)}\rho^{q(k)} \displaystyle \sum_{j=0}^{q(k)-1}(\beta(k)/\rho)^{j}. \end{align*} $$
$$ \begin{align*} \|(v_{k} -\lambda {\kern2pt}{\rm id})^{-1}\| &\ll_{\rho} \|\psi_{\lambda}(v_{k})\| \le S(\omega_{k},\rho)\\ &\ll_{\rho} Q:= \alpha(k)^{p(k)}\rho^{q(k)} \displaystyle \sum_{j=0}^{q(k)-1}(\beta(k)/\rho)^{j}. \end{align*} $$
On a de plus
![]() $Q\ll _{\rho } 1$
. En effet pour les k tels que l’on a (5.6), cela résulte de (5.7). Et quand (5.6) n’est pas vérifiée, la somme dans Q est bornée, ainsi que la suite
$Q\ll _{\rho } 1$
. En effet pour les k tels que l’on a (5.6), cela résulte de (5.7). Et quand (5.6) n’est pas vérifiée, la somme dans Q est bornée, ainsi que la suite
![]() $\alpha (k)^{p(k)}\rho ^{q(k)}$
.
$\alpha (k)^{p(k)}\rho ^{q(k)}$
.
On déduit de tout cela que si
![]() $0\le \rho <\tilde {r}$
, alors
$0\le \rho <\tilde {r}$
, alors
![]() $\|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| \ll _{\rho }\, 1$
. En combinant avec (5.3) et le lemme 3.3, on obtient que
$\|(v_{k}-\lambda {\kern2pt}{\rm id})^{-1}\| \ll _{\rho }\, 1$
. En combinant avec (5.3) et le lemme 3.3, on obtient que
Par ailleurs on a
![]() $\sigma (v_{k}) \subset \sigma (u)$
pour tout
$\sigma (v_{k}) \subset \sigma (u)$
pour tout
![]() $k\ge 1$
. D’où avec (5.3)
$k\ge 1$
. D’où avec (5.3)
 $$ \begin{align} \bigcup_{k\ge 1} \{z \in {\mathbb{C}} : z^{n(k)}= 1\} \subset \sigma(u). \end{align} $$
$$ \begin{align} \bigcup_{k\ge 1} \{z \in {\mathbb{C}} : z^{n(k)}= 1\} \subset \sigma(u). \end{align} $$
On conclut la preuve du lemme 5.1, en utilisant l’hypothèse (5.1) et les propriétés du spectre
![]() $\sigma (u)$
que sont sa compacité, (5.4), (5.5), (5.8) et (5.9).
$\sigma (u)$
que sont sa compacité, (5.4), (5.5), (5.8) et (5.9).
6 Rigidité
Lemme 6.1. Soit
![]() $(p{(k),\alpha (k)})_{k\ge 3}$
une suite d’éléments de
$(p{(k),\alpha (k)})_{k\ge 3}$
une suite d’éléments de
![]() $\mathbb {N}^{*}\times [1,+\infty [$
avec pour tout
$\mathbb {N}^{*}\times [1,+\infty [$
avec pour tout
![]() $k\ge 3$
,
$k\ge 3$
,
![]() $(k-1)!\le p(k)<k!$
,
$(k-1)!\le p(k)<k!$
,
![]() $\alpha (k)$
décroissante et
$\alpha (k)$
décroissante et
![]() $\alpha (k+1)=1+O({1}/{k!})$
. On note
$\alpha (k+1)=1+O({1}/{k!})$
. On note
![]() $\omega =(\omega _{p(k),k!-p(k),\alpha (k)})_{k\ge 3}$
. Alors
$\omega =(\omega _{p(k),k!-p(k),\alpha (k)})_{k\ge 3}$
. Alors
![]() $u$
est rigide de suite de rigidité
$u$
est rigide de suite de rigidité
![]() $\ell !$
.
$\ell !$
.
Démonstration. C’est la combinaison du lemme 4.1 avec la décroissance de
![]() $\alpha (k)$
, qui assure que
$\alpha (k)$
, qui assure que
![]() $u$
est bien défini et continu.
$u$
est bien défini et continu.
Soit
![]() $y\in \ell ^{2}$
. On a en utilisant successivement les formules (2.2) et (2.4) du lemme 2.2, l’hypothèse sur
$y\in \ell ^{2}$
. On a en utilisant successivement les formules (2.2) et (2.4) du lemme 2.2, l’hypothèse sur
![]() $p(k)$
et les deux hypothèses sur
$p(k)$
et les deux hypothèses sur
![]() $\alpha (k)$
,
$\alpha (k)$
,
 $$ \begin{align*} \|(u^{\ell!}-{\rm id})y\|^{2} &= \displaystyle\sum_{k\ge \ell+1} \|(v_{k}^{\ell!}-{\rm id})y_{k}\|^{2}\\ &\le \displaystyle\sum_{k\ge \ell+1} \|v_{k}^{\ell!}-{\rm id}\|^{2} \|y_{k}\|^{2} \le 4 \displaystyle\sum_{k\ge \ell+1} \|v_{k}^{\ell!}\|^{2}\ \|y_{k}\|^{2}\\ &=4 \displaystyle\sum_{k\ge \ell+1} (\alpha(k))^{2\ell!} \|y_{k}\|^{2} \le 4 (\alpha(\ell+1))^{2\ell!} \displaystyle\sum_{k\ge \ell+1} \|y_{k}\|^{2}\\ &\ll\displaystyle\sum_{k\ge \ell+1} \|y_{k}\|^{2}. \end{align*} $$
$$ \begin{align*} \|(u^{\ell!}-{\rm id})y\|^{2} &= \displaystyle\sum_{k\ge \ell+1} \|(v_{k}^{\ell!}-{\rm id})y_{k}\|^{2}\\ &\le \displaystyle\sum_{k\ge \ell+1} \|v_{k}^{\ell!}-{\rm id}\|^{2} \|y_{k}\|^{2} \le 4 \displaystyle\sum_{k\ge \ell+1} \|v_{k}^{\ell!}\|^{2}\ \|y_{k}\|^{2}\\ &=4 \displaystyle\sum_{k\ge \ell+1} (\alpha(k))^{2\ell!} \|y_{k}\|^{2} \le 4 (\alpha(\ell+1))^{2\ell!} \displaystyle\sum_{k\ge \ell+1} \|y_{k}\|^{2}\\ &\ll\displaystyle\sum_{k\ge \ell+1} \|y_{k}\|^{2}. \end{align*} $$
On a donc
![]() $\lim \nolimits _{\ell \rightarrow +\infty } u^{\ell !}y=y$
.
$\lim \nolimits _{\ell \rightarrow +\infty } u^{\ell !}y=y$
.
7 Preuve du théorème
Pour tout
![]() $r\in [0,1]$
, on choisit l’opérateur par blocs
$r\in [0,1]$
, on choisit l’opérateur par blocs
![]() $u=v_{|\ell ^{2}}$
où
$u=v_{|\ell ^{2}}$
où
![]() $v$
est associé à
$v$
est associé à
et
 $$ \begin{align*} (q(k),\alpha(k)) = \left\{ \begin{array}{ll} \bigg(k,1+\dfrac{\log(1/r)}{(k-1)!}\bigg) &\mathrm{si} \ 0<r\le 1,\\\\[-5pt] \bigg(1,1+\dfrac{1}{(k-1)!}\bigg) &\mathrm{si}\ r=0. \end{array} \right. \end{align*} $$
$$ \begin{align*} (q(k),\alpha(k)) = \left\{ \begin{array}{ll} \bigg(k,1+\dfrac{\log(1/r)}{(k-1)!}\bigg) &\mathrm{si} \ 0<r\le 1,\\\\[-5pt] \bigg(1,1+\dfrac{1}{(k-1)!}\bigg) &\mathrm{si}\ r=0. \end{array} \right. \end{align*} $$
C’est en combinant les lemmes 5.1 et 6.1 que l’on vérifie que ce choix permet d’établir le théorème.
Remerciements
Nous remercions Etienne Matheron de nous avoir signalé l’article [Reference Costakis, Manoussos and Parissis2] de Costakis, Manoussos et Parissis, et Sophie Grivaux de nous avoir informé du lien entre son article [Reference Grivaux and Roginskaya3] avec Maria Roginskaya et le présent travail.
A Annexe
On utilisera pour cette annexe la notation
A.1 Preuve alternative de la Proposition CMP
Soit
![]() $u$
un opérateur d’un Banach et
$u$
un opérateur d’un Banach et
![]() $n\ge 1$
tels que
$n\ge 1$
tels que
On a alors
d’où
et
Maintenant si
![]() $u$
est uniformément rigide, il existe des entiers n arbitrairement grands vérifiant (A.1) et donc aussi (A.2). On en déduit que
$u$
est uniformément rigide, il existe des entiers n arbitrairement grands vérifiant (A.1) et donc aussi (A.2). On en déduit que
![]() $\sigma (u) \subset {\mathbb {U}}$
.
$\sigma (u) \subset {\mathbb {U}}$
.
A.2 Rayon spectral d’un opérateur rigide
Il résulte immédiatement d’un résultat de Müller de 1986 (voir theorem de [Reference Müller5]) que l’on a l’énoncé suivant.
Théorème M. Le rayon spectral d’un opérateur rigide est inférieur ou égal à un.
Preuve alternative du théorème M. Soit
![]() $u$
un opérateur rigide d’un Banach de suite de rigidité
$u$
un opérateur rigide d’un Banach de suite de rigidité
![]() $(n_{k})_{k\ge 1}$
. Alors pour tout élément x de E, la suite de vecteurs
$(n_{k})_{k\ge 1}$
. Alors pour tout élément x de E, la suite de vecteurs
![]() $(u^{n_{k}}x)_{k\ge 1}$
est bornée. D’après le théorème de Banach and Steinhaus, il existe un réel positif M tel que pour tout
$(u^{n_{k}}x)_{k\ge 1}$
est bornée. D’après le théorème de Banach and Steinhaus, il existe un réel positif M tel que pour tout
![]() $k\ge 1$
,
$k\ge 1$
,
On procède alors comme dans § A.1: on en déduit d’abord que pour tout
![]() $k\ge 1$
,
$k\ge 1$
,
puis
On conclut en faisant tendre k vers
![]() $+\infty $
.
$+\infty $
.