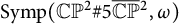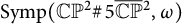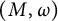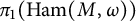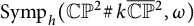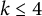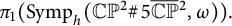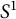1 Introduction
Let
![]() $(M, \omega )$
be a closed simply connected symplectic manifold. The symplectomorphism group
$(M, \omega )$
be a closed simply connected symplectic manifold. The symplectomorphism group
![]() $\operatorname {\mathrm{Symp}}(M, \omega )$
, equipped with the standard
$\operatorname {\mathrm{Symp}}(M, \omega )$
, equipped with the standard
![]() $C^\infty $
-topology, is an infinite-dimensional Fréchet Lie group. In general, symplectomorphism groups are viewed as intermediate objects between Lie groups and general groups of diffeomorphisms. Of course, this philosophy can be understood in many different ways. One interesting question is to compare the homotopy types of various symplectomorphism groups with those of compact Lie groups, and see to what extend their homotopical and algebraic properties are related. For instance, recall that if G is a compact Lie group, then any element of its fundamental group
$C^\infty $
-topology, is an infinite-dimensional Fréchet Lie group. In general, symplectomorphism groups are viewed as intermediate objects between Lie groups and general groups of diffeomorphisms. Of course, this philosophy can be understood in many different ways. One interesting question is to compare the homotopy types of various symplectomorphism groups with those of compact Lie groups, and see to what extend their homotopical and algebraic properties are related. For instance, recall that if G is a compact Lie group, then any element of its fundamental group
![]() $\pi _1(G)$
is represented by a continuous homomorphism
$\pi _1(G)$
is represented by a continuous homomorphism
![]() $S^1\to G$
. Therefore, it is natural to ask whether the same holds for symplectomorphism groups.
$S^1\to G$
. Therefore, it is natural to ask whether the same holds for symplectomorphism groups.
Question 1.1 Suppose that
![]() $\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))$
is nontrivial. Is every element represented by a continuous homomorphism
$\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))$
is nontrivial. Is every element represented by a continuous homomorphism
![]() $S^1 \mapsto \operatorname {\mathrm{Symp}}(M, \omega )$
(i.e., a circle action on M)? If not, can we characterize homotopy classes that are represented by circle actions?▪
$S^1 \mapsto \operatorname {\mathrm{Symp}}(M, \omega )$
(i.e., a circle action on M)? If not, can we characterize homotopy classes that are represented by circle actions?▪
In [Reference Kȩdra13], Kȩdra showed that the answer to the first part of the question is negative in general.
Theorem 1.2 [Reference Kȩdra13]
Let
![]() $(M, \omega )$
be a symplectic blowup (in a small ball) of a closed simply connected Kähler surface, which is neither a rational nor a ruled surface up to the blowup. Then
$(M, \omega )$
be a symplectic blowup (in a small ball) of a closed simply connected Kähler surface, which is neither a rational nor a ruled surface up to the blowup. Then
![]() $(M, \omega )$
admits no symplectic circle action, although
$(M, \omega )$
admits no symplectic circle action, although
![]() $\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))$
is nontrivial.
$\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))$
is nontrivial.
A concrete example is obtained by taking a K3 surface with any symplectic form. Another type of example was found by Buse in her work on symplectomorphism groups of irrational ruled surfaces [Reference Buse6, Proposition 3.3]. More precisely, although
![]() $\mathbb T^2 \times S^2$
admits Hamiltonian circle actions, she showed that there is an element
$\mathbb T^2 \times S^2$
admits Hamiltonian circle actions, she showed that there is an element
![]() $\gamma \in \pi _1 (\operatorname {\mathrm {Ham}} (\mathbb T^2 \times S^2))$
for which the rational Samelson product
$\gamma \in \pi _1 (\operatorname {\mathrm {Ham}} (\mathbb T^2 \times S^2))$
for which the rational Samelson product
![]() $[\gamma , \gamma ]_{\mathbb {Q}}$
does not vanish, which implies that
$[\gamma , \gamma ]_{\mathbb {Q}}$
does not vanish, which implies that
![]() $\gamma $
cannot be represented by such an action.
$\gamma $
cannot be represented by such an action.
In the present paper, we consider the symplectic rational surfaces
![]() $(\mathbb C\mathbb P^2\#\,n\overline { \mathbb C\mathbb P}\,\!^2, \omega )$
. For
$(\mathbb C\mathbb P^2\#\,n\overline { \mathbb C\mathbb P}\,\!^2, \omega )$
. For
![]() $1\leq n\leq 5$
, the topological group
$1\leq n\leq 5$
, the topological group
![]() $\operatorname {\mathrm{Symp}}_h(\mathbb C\mathbb P^2\#\,n\overline { \mathbb C\mathbb P}\,\!^2, \omega ) $
of symplectomorphisms that act trivially on homology has been studied by several authors (see [Reference Abreu, Granja and Kitchloo1–Reference Anjos and Eden3, Reference Anjos and Pinsonnault5, Reference Evans9, Reference Li, Li and Wu18, Reference Pinsonnault25, Reference Seidel28]). In the case
$\operatorname {\mathrm{Symp}}_h(\mathbb C\mathbb P^2\#\,n\overline { \mathbb C\mathbb P}\,\!^2, \omega ) $
of symplectomorphisms that act trivially on homology has been studied by several authors (see [Reference Abreu, Granja and Kitchloo1–Reference Anjos and Eden3, Reference Anjos and Pinsonnault5, Reference Evans9, Reference Li, Li and Wu18, Reference Pinsonnault25, Reference Seidel28]). In the case
![]() $n=5$
, Seidel [Reference Seidel28] and Evans [Reference Evans9] proved that, in the monotone case, this group is homotopy equivalent to the group of orientation-preserving diffeomorphisms of
$n=5$
, Seidel [Reference Seidel28] and Evans [Reference Evans9] proved that, in the monotone case, this group is homotopy equivalent to the group of orientation-preserving diffeomorphisms of
![]() $S^2$
preserving five points. Recently, Li, Li, and Wu in [Reference Li, Li and Wu18] completely determined the group of connected components of
$S^2$
preserving five points. Recently, Li, Li, and Wu in [Reference Li, Li and Wu18] completely determined the group of connected components of
![]() $\operatorname {\mathrm{Symp}}_{h}(\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2, \omega )$
, called the Torelli symplectic mapping class group, as well as the rank of its fundamental group, for any given symplectic form
$\operatorname {\mathrm{Symp}}_{h}(\mathbb C\mathbb P^2\#\,5\overline { \mathbb C\mathbb P}\,\!^2, \omega )$
, called the Torelli symplectic mapping class group, as well as the rank of its fundamental group, for any given symplectic form
![]() $\omega $
. In order to explain their results, which are of interest to us, we first recall the definition of reduced forms, and postpone further details to Section 2.3.
$\omega $
. In order to explain their results, which are of interest to us, we first recall the definition of reduced forms, and postpone further details to Section 2.3.
For
![]() $\mathbb {X}_n = \mathbb {CP}^2 \#\, n\overline { \mathbb C\mathbb P}\,\!^2$
, let
$\mathbb {X}_n = \mathbb {CP}^2 \#\, n\overline { \mathbb C\mathbb P}\,\!^2$
, let
![]() $\{ L, V_1, \ldots , V_n\}$
be a standard basis for
$\{ L, V_1, \ldots , V_n\}$
be a standard basis for
![]() $H_2(\mathbb {X}_n; \mathbb {Z})$
, where L is the class representing a line, and the
$H_2(\mathbb {X}_n; \mathbb {Z})$
, where L is the class representing a line, and the
![]() $V_i$
are the exceptional classes.
$V_i$
are the exceptional classes.
Definition 1.1 Consider
![]() $\mathbb {X}_n$
with the standard basis
$\mathbb {X}_n$
with the standard basis
![]() $\{ L, V_1, \ldots , V_n\}$
of
$\{ L, V_1, \ldots , V_n\}$
of
![]() $H_2(\mathbb {X}_n; \mathbb {Z})$
. Given a symplectic form
$H_2(\mathbb {X}_n; \mathbb {Z})$
. Given a symplectic form
![]() $\omega $
such that each class
$\omega $
such that each class
![]() $ L, V_1, \ldots , V_n$
has
$ L, V_1, \ldots , V_n$
has
![]() $\omega $
-area
$\omega $
-area
![]() $\nu , \delta _1, \ldots , \delta _n$
, then
$\nu , \delta _1, \ldots , \delta _n$
, then
![]() $\omega $
is called reduced if
$\omega $
is called reduced if
We recall in Section 2.3 why any symplectic form on
![]() $\mathbb {X}_n$
is diffeomorphic to a reduced one. Note that diffeomorphic symplectic forms yield homeomorphic symplectomorphism groups. Therefore, it suffices to understand the symplectomorphism group
$\mathbb {X}_n$
is diffeomorphic to a reduced one. Note that diffeomorphic symplectic forms yield homeomorphic symplectomorphism groups. Therefore, it suffices to understand the symplectomorphism group
![]() $\operatorname {\mathrm{Symp}}(\mathbb {X}_n, \omega )$
for any reduced form
$\operatorname {\mathrm{Symp}}(\mathbb {X}_n, \omega )$
for any reduced form
![]() $\omega $
. In this section, we also recall that
$\omega $
. In this section, we also recall that
![]() $(\mathbb {X}_n, \omega )$
can be naturally identified with
$(\mathbb {X}_n, \omega )$
can be naturally identified with
![]() $(n-1)$
-point blowups of the manifold
$(n-1)$
-point blowups of the manifold
![]() ${(S ^{2} \times S ^{2}, \mu \sigma \oplus \sigma )}$
, denoted by
${(S ^{2} \times S ^{2}, \mu \sigma \oplus \sigma )}$
, denoted by
![]() ${M}_{\mu ,c_1,\ldots ,c_{n-1}}$
, where
${M}_{\mu ,c_1,\ldots ,c_{n-1}}$
, where
![]() $\sigma $
denotes the standard symplectic form on
$\sigma $
denotes the standard symplectic form on
![]() $S^2$
that gives area 1 to the sphere,
$S^2$
that gives area 1 to the sphere,
![]() $\mu \geq 1$
, and
$\mu \geq 1$
, and
![]() $c_1, \ldots , c_{n-1}$
denote the capacities of the blowups.
$c_1, \ldots , c_{n-1}$
denote the capacities of the blowups.
If
![]() $n \leq 3$
, it is well known that the group
$n \leq 3$
, it is well known that the group
![]() $\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,\ldots ,c_{n}})$
is connected (see, for example, [Reference Li, Li and Wu17]) and it follows from [Reference Anjos and Eden3, Reference Anjos and Pinsonnault5, Reference Pinsonnault25] that the fundamental group of
$\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,\ldots ,c_{n}})$
is connected (see, for example, [Reference Li, Li and Wu17]) and it follows from [Reference Anjos and Eden3, Reference Anjos and Pinsonnault5, Reference Pinsonnault25] that the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_{h}({M}_{\mu ,c_1,\ldots ,c_{n}})$
is always generated by Hamiltonian circle actions. More precisely, in these cases, the full rational homotopy type of
$\operatorname {\mathrm{Symp}}_{h}({M}_{\mu ,c_1,\ldots ,c_{n}})$
is always generated by Hamiltonian circle actions. More precisely, in these cases, the full rational homotopy type of
![]() $\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,\ldots ,c_{n}})$
, with
$\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,\ldots ,c_{n}})$
, with
![]() $n \leq 3$
, is generated by loops in the fundamental group, represented by circle actions, via Samelson products. On the other hand, it was shown by Li and Li in [Reference Li and Li16] that if
$n \leq 3$
, is generated by loops in the fundamental group, represented by circle actions, via Samelson products. On the other hand, it was shown by Li and Li in [Reference Li and Li16] that if
![]() $n \leq 3$
, then
$n \leq 3$
, then
![]() $\pi _1(\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,\ldots ,c_{n}}))$
is a free abelian group.
$\pi _1(\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,\ldots ,c_{n}}))$
is a free abelian group.
In [Reference Li, Li and Wu18], the authors show that, in addition to the monotone case, there is a one-dimensional family of symplectic manifolds
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
for which the Torelli symplectic mapping class group
${M}_{\mu ,c_1,c_2,c_3,c_4}$
for which the Torelli symplectic mapping class group
![]() $\pi _0(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
is isomorphic to
$\pi _0(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
is isomorphic to
![]() $\pi _0(\operatorname {\mathrm {Diff}}^+(S^2,4))$
, where
$\pi _0(\operatorname {\mathrm {Diff}}^+(S^2,4))$
, where
![]() $\operatorname {\mathrm {Diff}}^+(S^2,4)$
is the group of orientation-preserving diffeomorphisms of
$\operatorname {\mathrm {Diff}}^+(S^2,4)$
is the group of orientation-preserving diffeomorphisms of
![]() $S^2$
preserving four points. This family is defined by the values
$S^2$
preserving four points. This family is defined by the values
![]() $ \mu>1$
and
$ \mu>1$
and
![]() $c_i= 1/2$
for all
$c_i= 1/2$
for all
![]() $ i \in \{1,2,3,4\}$
. From now on, we use the notation
$ i \in \{1,2,3,4\}$
. From now on, we use the notation
![]() ${M}_{\mu ,c_i=1/2}$
to denote this family of symplectic manifolds. For all the remaining symplectic forms, the group
${M}_{\mu ,c_i=1/2}$
to denote this family of symplectic manifolds. For all the remaining symplectic forms, the group
![]() $\pi _0(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
is trivial. Moreover, in [Reference Li, Li and Wu18, Section 5.3], the authors show that
$\pi _0(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
is trivial. Moreover, in [Reference Li, Li and Wu18, Section 5.3], the authors show that
![]() $\pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})) = \mathbb {Z}^5$
, and hence the fundamental group is a free abelian group.
$\pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})) = \mathbb {Z}^5$
, and hence the fundamental group is a free abelian group.
In this note, we study generators of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
. Our main result is the following theorem that gives a negative answer to the first part of Question 1.1.
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
. Our main result is the following theorem that gives a negative answer to the first part of Question 1.1.
Theorem 1.3 If
![]() $1 < \mu \leq \frac 32$
, then the set of all Hamiltonian circle actions generates a proper subgroup of rank 4 in the fundamental group of
$1 < \mu \leq \frac 32$
, then the set of all Hamiltonian circle actions generates a proper subgroup of rank 4 in the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
. Moreover, if
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
. Moreover, if
![]() $\mu>\frac 32$
, then
$\mu>\frac 32$
, then
![]() $\pi _1( \operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))\otimes \mathbb {Q}$
is generated by Hamiltonian circle actions.
$\pi _1( \operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))\otimes \mathbb {Q}$
is generated by Hamiltonian circle actions.
To the best of our knowledge, this is the first example of symplectic rational surface where the fundamental group of
![]() $\operatorname {\mathrm{Symp}} (\mathbb {X}_n, \omega )$
is not generated by circle actions. In Section 5, we discuss the existence of more symplectic forms
$\operatorname {\mathrm{Symp}} (\mathbb {X}_n, \omega )$
is not generated by circle actions. In Section 5, we discuss the existence of more symplectic forms
![]() $\omega $
in
$\omega $
in
![]() $\mathbb {X}_5$
for which a similar phenomenon may occur.
$\mathbb {X}_5$
for which a similar phenomenon may occur.
Remark 1.4 Although there is a generator of
![]() $\pi _1( \operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))\otimes \mathbb {Q}$
which cannot be represented by a Hamiltonian circle action when
$\pi _1( \operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))\otimes \mathbb {Q}$
which cannot be represented by a Hamiltonian circle action when
![]() $1 < \mu \leq \frac 32$
, one can find its quantum homology representative (see Proposition 4.12).
$1 < \mu \leq \frac 32$
, one can find its quantum homology representative (see Proposition 4.12).
Our techniques allows us to completely describe the elements of
![]() $\pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
that are represented by Hamiltonian circle actions, answering the second part of Question 1.1 as well. In particular, we obtain the following result.
$\pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
that are represented by Hamiltonian circle actions, answering the second part of Question 1.1 as well. In particular, we obtain the following result.
Theorem 1.5 For any value of
![]() $\mu>1$
, there exist infinitely many homotopy classes in the fundamental group
$\mu>1$
, there exist infinitely many homotopy classes in the fundamental group
![]() $\pi _1( \operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
that cannot be represented by Hamiltonian circle actions.
$\pi _1( \operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
that cannot be represented by Hamiltonian circle actions.
As a final remark, it seems very likely that Theorem 1.3 holds not only rationally but also in the integer case, that is, that the fundamental group
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
is generated by Hamiltonian circle actions whenever
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
is generated by Hamiltonian circle actions whenever
![]() $\mu> \frac 32$
. Although we are not able to prove this stronger claim, we note that our quantum homology calculations imply the existence of five circle actions representing homotopy classes in
$\mu> \frac 32$
. Although we are not able to prove this stronger claim, we note that our quantum homology calculations imply the existence of five circle actions representing homotopy classes in
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
that can be shown to be not only linearly independent but also primitive.
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
that can be shown to be not only linearly independent but also primitive.
1.1 Organization of the paper
In Section 2, we review the main tools we need to prove the theorems above, namely Karshon’s classification of Hamiltonian circle actions, Delzant’s classification of toric manifolds, and the definitions of the quantum homology ring of a symplectic manifold and of the Seidel morphism. We also recall the results of [Reference Li, Li and Wu18] regarding
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
of the symplectomorphism group
$\pi _1$
of the symplectomorphism group
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
relevant to our work. In Section 3, we give a presentation of the quantum homology ring
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
relevant to our work. In Section 3, we give a presentation of the quantum homology ring
![]() $QH_\ast ({M}_{\mu ,c_1,c_2,c_3,c_4})$
, that follows from applying the formulas for the quantum product on a rational surface obtained by Crauder and Miranda in [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7]. We dedicate Section 4 to obtaining our main results: we choose a tentative set of five generators of the rational fundamental group and prove, using the Seidel morphism, that these elements are linearly independent. We conclude this section giving a classification of all Hamiltonian circle actions on
$QH_\ast ({M}_{\mu ,c_1,c_2,c_3,c_4})$
, that follows from applying the formulas for the quantum product on a rational surface obtained by Crauder and Miranda in [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7]. We dedicate Section 4 to obtaining our main results: we choose a tentative set of five generators of the rational fundamental group and prove, using the Seidel morphism, that these elements are linearly independent. We conclude this section giving a classification of all Hamiltonian circle actions on
![]() ${M}_{\mu ,c_i=1/2}$
, which allows us to determine which homotopy class of loops can be represented by such an action.
${M}_{\mu ,c_i=1/2}$
, which allows us to determine which homotopy class of loops can be represented by such an action.
Finally, in the last section, we propose some further questions that arose naturally on the course of this work. Appendix A contains computations on the quantum ring, whereas Appendix B is devoted to the proof of an auxiliary relation between elements in
![]() $\pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
.
$\pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
.
2 Background
2.1 Hamiltonian circle actions, decorated graphs, and Delzant polygons
In the forthcoming sections, we will study loops in the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
. Since these loops will appear as Hamiltonian circle actions, we will make extensive use of Karshon’s classification of Hamiltonian circle actions and Delzant’s classification of toric actions on symplectic manifolds. For convenience, we give a quick overview on how these classifications work.
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
. Since these loops will appear as Hamiltonian circle actions, we will make extensive use of Karshon’s classification of Hamiltonian circle actions and Delzant’s classification of toric actions on symplectic manifolds. For convenience, we give a quick overview on how these classifications work.
Karshon’s classification [Reference Karshon10] yields a bijection between certain decorated graphs and
![]() $4$
-tuples
$4$
-tuples
![]() $(M^4,\omega ,\rho ,\Phi )$
consisting of a symplectic
$(M^4,\omega ,\rho ,\Phi )$
consisting of a symplectic
![]() $4$
-manifold
$4$
-manifold
![]() $(M^4,\omega )$
, and an effective Hamiltonian circle action
$(M^4,\omega )$
, and an effective Hamiltonian circle action
![]() $\rho $
with a given moment map
$\rho $
with a given moment map
![]() $ \Phi : M \rightarrow \mathbb {R}$
. Given such a tuple
$ \Phi : M \rightarrow \mathbb {R}$
. Given such a tuple
![]() $ (M^4, \omega , \rho , \Phi ) $
, the associated decorated graph is constructed as follows. Each component C of the fixed point set is either a single point or a symplectic surface, and fixed points on which the moment map is not extremal are isolated. For each such component C, there is a vertex
$ (M^4, \omega , \rho , \Phi ) $
, the associated decorated graph is constructed as follows. Each component C of the fixed point set is either a single point or a symplectic surface, and fixed points on which the moment map is not extremal are isolated. For each such component C, there is a vertex
![]() $\langle C \rangle $
, labeled by the real number
$\langle C \rangle $
, labeled by the real number
![]() $\Phi (C)$
. A vertex that corresponds to a fixed symplectic surface is said to be “fat” and is given two more labels: the area label
$\Phi (C)$
. A vertex that corresponds to a fixed symplectic surface is said to be “fat” and is given two more labels: the area label
![]() $\frac {1}{2 \pi } \int _{C} \omega $
, and the genus g of the surface. A
$\frac {1}{2 \pi } \int _{C} \omega $
, and the genus g of the surface. A
![]() $\mathbb {Z}_{k}$
-sphere is a gradient sphere in M on which
$\mathbb {Z}_{k}$
-sphere is a gradient sphere in M on which
![]() $ S^{1} $
acts with isotropy
$ S^{1} $
acts with isotropy
![]() $ \mathbb {Z}_{k} $
,
$ \mathbb {Z}_{k} $
,
![]() $k\geq 2$
. For each
$k\geq 2$
. For each
![]() $\mathbb {Z}_{k}$
-sphere containing two fixed points
$\mathbb {Z}_{k}$
-sphere containing two fixed points
![]() $ p $
and
$ p $
and
![]() $ q $
, the graph has an edge connecting the vertices
$ q $
, the graph has an edge connecting the vertices
![]() $ \langle p \rangle $
and
$ \langle p \rangle $
and
![]() $ \langle q \rangle $
labeled by the integer
$ \langle q \rangle $
labeled by the integer
![]() $ k $
.
$ k $
.
Labeled graphs associated with effective Hamiltonian circle actions are characterized by the following properties. If we order the vertices according to their moment map labels, then:
-
– there are exactly two extremal vertices;
-
– fat vertices are extremal, and if the graph contains two fat vertices, then their genus label must coincide;
-
– the area label of any fat vertex must be strictly positive;
-
– a vertex is connected to no more than two edges, and no edge is connected to a fat vertex;
-
– the moment map labels must be strictly monotone along each chain of edges;
-
– if
 $e_{1},\ldots ,e_{\ell }$
is a chain of edges, and if
$e_{1},\ldots ,e_{\ell }$
is a chain of edges, and if
 $k_{1},\ldots ,k_{\ell }$
are the orders of their stabilizers, then
$k_{1},\ldots ,k_{\ell }$
are the orders of their stabilizers, then
 $\gcd (k_{i}, k_{i+1}) = 1$
for
$\gcd (k_{i}, k_{i+1}) = 1$
for
 $i = 1,\ldots \ell -1$
, and
$i = 1,\ldots \ell -1$
, and
 $(k_{i-1} + k_{i+1})/k_{i}$
is an integer for
$(k_{i-1} + k_{i+1})/k_{i}$
is an integer for
 $i= 2,\ldots ,\ell -1$
.
$i= 2,\ldots ,\ell -1$
.
We call such graphs admissible.
Theorem 2.1 (Karshon [Reference Karshon10])
Each
![]() $4$
-tuple
$4$
-tuple
![]() $(M^4,\omega ,\rho ,\Phi )$
corresponds to a unique admissible labeled graph. Conversely, each admissible labeled graph corresponds to a
$(M^4,\omega ,\rho ,\Phi )$
corresponds to a unique admissible labeled graph. Conversely, each admissible labeled graph corresponds to a
![]() $4$
-tuple
$4$
-tuple
![]() $(M^4,\omega ,\rho ,\Phi )$
that is unique up to
$(M^4,\omega ,\rho ,\Phi )$
that is unique up to
![]() $S^1$
-equivariant symplectomorphisms preserving the moment map.
$S^1$
-equivariant symplectomorphisms preserving the moment map.
Furthermore, it can be shown that each Hamiltonian action on a four-dimensional manifold can be obtained from a circle action on a symplectic ruled surface by performing a sequence of
![]() $S^1$
-equivariant symplectic blowups. At the graph level, equivariant symplectic blowups correspond to the simple transformations pictured in Figures 1 and 2. Together with Lalonde–McDuff–Li–Liu’s uniqueness theorem [Reference Lalonde and McDuff14, Reference Li and Liu19] stating that any two cohomologous symplectic forms on blowups of ruled surfaces are diffeomorphic, this gives an effective algorithm to enumerate all effective circle actions on any given
$S^1$
-equivariant symplectic blowups. At the graph level, equivariant symplectic blowups correspond to the simple transformations pictured in Figures 1 and 2. Together with Lalonde–McDuff–Li–Liu’s uniqueness theorem [Reference Lalonde and McDuff14, Reference Li and Liu19] stating that any two cohomologous symplectic forms on blowups of ruled surfaces are diffeomorphic, this gives an effective algorithm to enumerate all effective circle actions on any given
![]() $4$
-manifold.
$4$
-manifold.

Figure 1: Blowing up at a point inside an invariant surface at the minimum value of
![]() $ \Phi $
.
$ \Phi $
.

Figure 2: Blowing up at an interior fixed point.
Since we are mainly interested in the continuous map
![]() $\rho :S^1\to \operatorname {\mathrm {Ham}}(M,\omega )$
, we do not need to keep track of the moment map associated with a Hamiltonian circle action. As any two moment maps only differ by a constant, we can either consider graphs only up to a uniform translation of their moment map labels, or normalize the moment map by setting
$\rho :S^1\to \operatorname {\mathrm {Ham}}(M,\omega )$
, we do not need to keep track of the moment map associated with a Hamiltonian circle action. As any two moment maps only differ by a constant, we can either consider graphs only up to a uniform translation of their moment map labels, or normalize the moment map by setting
![]() $\min _{x\in M} \Phi (x) =0$
. Finally, note that the reparameterization of the circle
$\min _{x\in M} \Phi (x) =0$
. Finally, note that the reparameterization of the circle
![]() $t\mapsto -t$
corresponds to changing the signs of the moment map labels.
$t\mapsto -t$
corresponds to changing the signs of the moment map labels.
There is an analogous classification of Hamiltonian toric actions that we now briefly describe in the special case of
![]() $4$
-manifolds. Given a
$4$
-manifolds. Given a
![]() $4$
-tuple
$4$
-tuple
![]() $(M^{4},\omega ,\rho ,\Phi )$
consisting of a symplectic
$(M^{4},\omega ,\rho ,\Phi )$
consisting of a symplectic
![]() $4$
-manifold
$4$
-manifold
![]() $(M,\omega )$
, an effective Hamiltonian toric action
$(M,\omega )$
, an effective Hamiltonian toric action
![]() $\rho :T^2\to \operatorname {\mathrm {Ham}}(M,\omega )$
, and a moment map
$\rho :T^2\to \operatorname {\mathrm {Ham}}(M,\omega )$
, and a moment map
![]() $\Phi :M\to \mathfrak {t}^*\simeq \mathbb {R}^2$
, the image
$\Phi :M\to \mathfrak {t}^*\simeq \mathbb {R}^2$
, the image
![]() $\Phi (M)$
is always a Delzant polygon, that is, a polygon satisfying the following three properties:
$\Phi (M)$
is always a Delzant polygon, that is, a polygon satisfying the following three properties:
-
– simplicity, i.e., there are two edges meeting each vertex;
-
– rationality, i.e., the edges meeting at the vertex
 $ p $
are rational in the sense that each edge is of the form
$ p $
are rational in the sense that each edge is of the form
 $ p + t u_{i} $
,
$ p + t u_{i} $
,
 $ t \in [0,\ell _i] $
, where
$ t \in [0,\ell _i] $
, where
 $ \ell _i \in \mathbb {R}$
and
$ \ell _i \in \mathbb {R}$
and
 $ u_{i} \in \mathbb {Z}^{2} $
;
$ u_{i} \in \mathbb {Z}^{2} $
; -
– smoothness, i.e., for each vertex, the corresponding
 $ u_{1} $
,
$ u_{1} $
,
 $ u_{2} $
can be chosen to be a
$ u_{2} $
can be chosen to be a
 $ \mathbb {Z} $
-basis of
$ \mathbb {Z} $
-basis of
 $ \mathbb {Z}^{2} $
.
$ \mathbb {Z}^{2} $
.
Moreover, the preimage in the manifold of a vertex of the polygon
![]() $ \Phi (M) $
is a fixed point for the torus action, whereas the preimage of an edge is an invariant 2-sphere. The preimage of the interior of the polygon consists of free torus orbits. These facts are explained in [Reference Delzant8].
$ \Phi (M) $
is a fixed point for the torus action, whereas the preimage of an edge is an invariant 2-sphere. The preimage of the interior of the polygon consists of free torus orbits. These facts are explained in [Reference Delzant8].
Delzant’s classification [Reference Delzant8] states that equivalence classes of
![]() $4$
-tuple
$4$
-tuple
![]() $(M^{4},\omega ,\rho ,\Phi )$
up to equivariant symplectomorphisms that preserve the moment maps are classified by Delzant polygons in
$(M^{4},\omega ,\rho ,\Phi )$
up to equivariant symplectomorphisms that preserve the moment maps are classified by Delzant polygons in
![]() $\mathbb {R}^2$
. If we disregard the moment map and only consider an effective toric action as an injective homomorphism
$\mathbb {R}^2$
. If we disregard the moment map and only consider an effective toric action as an injective homomorphism
![]() $\rho :\mathbb {T}^2\to \operatorname {\mathrm {Ham}}(M,\omega )$
, it is natural to declare two actions as equivalent if they only differ by a reparameterization of the torus or by a conjugation by an element of
$\rho :\mathbb {T}^2\to \operatorname {\mathrm {Ham}}(M,\omega )$
, it is natural to declare two actions as equivalent if they only differ by a reparameterization of the torus or by a conjugation by an element of
![]() $\operatorname {\mathrm{Symp}}(M,\omega )$
. In this setting, the classification theorem yields a bijection
$\operatorname {\mathrm{Symp}}(M,\omega )$
. In this setting, the classification theorem yields a bijection
 $$ \begin{gather*} \{\text{Conjugacy classes of toric actions on}~4\text{-manifolds up to reparameterizations}\}\\ \updownarrow\\ \{\text{Delzant polygons in~}\mathbb{R}^2 \text{~up to~} \operatorname{\mathrm{AGL}}(2;\mathbb{Z}) \text{~action}\}. \end{gather*} $$
$$ \begin{gather*} \{\text{Conjugacy classes of toric actions on}~4\text{-manifolds up to reparameterizations}\}\\ \updownarrow\\ \{\text{Delzant polygons in~}\mathbb{R}^2 \text{~up to~} \operatorname{\mathrm{AGL}}(2;\mathbb{Z}) \text{~action}\}. \end{gather*} $$
If we restrict the action to the subcircle
![]() $\{ e\} \times S^1$
, we get a compact four-dimensional
$\{ e\} \times S^1$
, we get a compact four-dimensional
![]() $S^1$
-space. The moment map for the
$S^1$
-space. The moment map for the
![]() $S^1$
-action is the composition of the
$S^1$
-action is the composition of the
![]() $\mathbb {T}^{2}$
-moment map with the projection
$\mathbb {T}^{2}$
-moment map with the projection
![]() $\mathbb {R}^2 \to \mathbb {R}$
to the second coordinate. The fixed surfaces are the preimages, under the
$\mathbb {R}^2 \to \mathbb {R}$
to the second coordinate. The fixed surfaces are the preimages, under the
![]() $\mathbb {T}^{2}$
-moment map, of the horizontal edges of the Delzant polygon. Such a surface has genus zero, and its normalized symplectic area is equal to the length of the corresponding horizontal edge. The isolated fixed points are the preimages of those vertices of the polygon that do not lie on horizontal edges. The
$\mathbb {T}^{2}$
-moment map, of the horizontal edges of the Delzant polygon. Such a surface has genus zero, and its normalized symplectic area is equal to the length of the corresponding horizontal edge. The isolated fixed points are the preimages of those vertices of the polygon that do not lie on horizontal edges. The
![]() $\mathbb {Z}_k$
-spheres,
$\mathbb {Z}_k$
-spheres,
![]() $k\geq 2$
, are the preimages of edges with slope
$k\geq 2$
, are the preimages of edges with slope
![]() $\pm k/b$
in a reduced form, where b is relatively prime to k. With this information, we can construct the graph for the
$\pm k/b$
in a reduced form, where b is relatively prime to k. With this information, we can construct the graph for the
![]() $S^1$
-space out of the Delzant polygon. This is explained by Karshon in [Reference Karshon10, Section 2.2]. Note that, similarly, we can restrict the toric action to the subcircle
$S^1$
-space out of the Delzant polygon. This is explained by Karshon in [Reference Karshon10, Section 2.2]. Note that, similarly, we can restrict the toric action to the subcircle
![]() $S^1 \times \{ e\}$
in order to obtain another compact four-dimensional
$S^1 \times \{ e\}$
in order to obtain another compact four-dimensional
![]() $S^1$
-space. In this case, the moment map for the
$S^1$
-space. In this case, the moment map for the
![]() $S^1$
-action is the composition of the
$S^1$
-action is the composition of the
![]() $\mathbb {T}^{2}$
-moment map with the projection
$\mathbb {T}^{2}$
-moment map with the projection
![]() $\mathbb {R}^2 \to \mathbb {R}$
to the first coordinate. This relation between polygons and decorated graphs will be particularly useful in the following subsections.
$\mathbb {R}^2 \to \mathbb {R}$
to the first coordinate. This relation between polygons and decorated graphs will be particularly useful in the following subsections.
2.2 Quantum homology and Seidel morphism
Following [Reference McDuff and Salamon23], consider the (small) quantum homology ring
![]() ${QH}_*(M; \Pi ) = H_*(M, \mathbb {Q}) \otimes _{\mathbb {Q}} \Pi $
with coefficients in the ring
${QH}_*(M; \Pi ) = H_*(M, \mathbb {Q}) \otimes _{\mathbb {Q}} \Pi $
with coefficients in the ring
![]() $\Pi := \Pi ^{\mathrm {univ}}[q,q^{-1}]$
where the q is a polynomial variable of degree 2 and
$\Pi := \Pi ^{\mathrm {univ}}[q,q^{-1}]$
where the q is a polynomial variable of degree 2 and
![]() $ \Pi ^{\mathrm {univ}},$
called the universal Novikov ring, is a generalized Laurent series ring in a variable t of degree 0:
$ \Pi ^{\mathrm {univ}},$
called the universal Novikov ring, is a generalized Laurent series ring in a variable t of degree 0:
 $$ \begin{align} \Pi^{\mathrm{univ}}:= \left\{ \sum_{\kappa \in \mathbb{R}} r_\kappa t^\kappa \,\big|\, r_\kappa \in \mathbb{Q}, \ \#\{ \kappa> c\mid r_\kappa \neq 0\} < \infty, \forall c \in \mathbb{R} \right \}\!. \end{align} $$
$$ \begin{align} \Pi^{\mathrm{univ}}:= \left\{ \sum_{\kappa \in \mathbb{R}} r_\kappa t^\kappa \,\big|\, r_\kappa \in \mathbb{Q}, \ \#\{ \kappa> c\mid r_\kappa \neq 0\} < \infty, \forall c \in \mathbb{R} \right \}\!. \end{align} $$
The quantum homology
![]() ${QH}_*(M; \Pi )$
is
${QH}_*(M; \Pi )$
is
![]() $\mathbb {Z}$
-graded so that
$\mathbb {Z}$
-graded so that
![]() $\deg (a \otimes q^d t^\kappa )= \deg (a) +2d$
with
$\deg (a \otimes q^d t^\kappa )= \deg (a) +2d$
with
![]() $a \in H_*(M)$
. The quantum intersection product
$a \in H_*(M)$
. The quantum intersection product
![]() $a*b \in {QH}_{i+j -\dim M}(M; \Pi )$
, of classes
$a*b \in {QH}_{i+j -\dim M}(M; \Pi )$
, of classes
![]() $a \in H_i(M)$
and
$a \in H_i(M)$
and
![]() $b \in H_j(M)$
, has the form
$b \in H_j(M)$
, has the form
where
![]() $H_2^S(M;\mathbb {Z})$
is the image of
$H_2^S(M;\mathbb {Z})$
is the image of
![]() $\pi _2(M)$
under the Hurewicz map. The homology class
$\pi _2(M)$
under the Hurewicz map. The homology class
![]() $(a*b)_B \in H_{i+j-\dim M +2c_1(B)}(M)$
is defined by the requirement that
$(a*b)_B \in H_{i+j-\dim M +2c_1(B)}(M)$
is defined by the requirement that
In this formula,
![]() $ \mathrm {GW}^M_{B,3}(a,b,c) \in \mathbb {Q}$
denotes the Gromov–Witten invariant that counts the number of spheres in M in class B that meet cycles representing the classes
$ \mathrm {GW}^M_{B,3}(a,b,c) \in \mathbb {Q}$
denotes the Gromov–Witten invariant that counts the number of spheres in M in class B that meet cycles representing the classes
![]() $a,b,c \in H_*(M)$
. The product
$a,b,c \in H_*(M)$
. The product
![]() $*$
is extended to
$*$
is extended to
![]() ${QH}_*(M)$
by linearity over
${QH}_*(M)$
by linearity over
![]() $\Pi $
, and is associative (see [Reference McDuff and Salamon23, Proposition 11.1.9] for a proof of this fact). It also respects the
$\Pi $
, and is associative (see [Reference McDuff and Salamon23, Proposition 11.1.9] for a proof of this fact). It also respects the
![]() $\mathbb {Z}$
-grading and gives
$\mathbb {Z}$
-grading and gives
![]() ${QH}_*(M)$
the structure of a graded commutative ring, with unit
${QH}_*(M)$
the structure of a graded commutative ring, with unit
![]() $[M]$
.
$[M]$
.
The Seidel morphism is a homomorphism
![]() $\mathcal {S}$
from
$\mathcal {S}$
from
![]() $\pi _1 (\operatorname {\mathrm {Ham}} (M, \omega ))$
to the degree
$\pi _1 (\operatorname {\mathrm {Ham}} (M, \omega ))$
to the degree
![]() $2n$
multiplicative units
$2n$
multiplicative units
![]() ${QH}_{2n}(M)^{\times }$
of the small quantum homology, first introduced by Seidel in [Reference Seidel27]. One way of thinking of it is to say that it “counts” pseudoholomorphic sections of the bundle
${QH}_{2n}(M)^{\times }$
of the small quantum homology, first introduced by Seidel in [Reference Seidel27]. One way of thinking of it is to say that it “counts” pseudoholomorphic sections of the bundle
![]() $M_\Lambda \to S^2$
associated with the loop
$M_\Lambda \to S^2$
associated with the loop
![]() $\Lambda \subset \operatorname {\mathrm {Ham}}(M,\omega )$
via the clutching construction (as in [Reference McDuff and Tolman24, Section 2]): let
$\Lambda \subset \operatorname {\mathrm {Ham}}(M,\omega )$
via the clutching construction (as in [Reference McDuff and Tolman24, Section 2]): let
![]() $(M, \omega )$
be a closed symplectic manifold and let
$(M, \omega )$
be a closed symplectic manifold and let
![]() $\Lambda =\{ \Lambda _\theta \}$
be a loop in
$\Lambda =\{ \Lambda _\theta \}$
be a loop in
![]() $\operatorname {\mathrm {Ham}}(M, \omega )$
based on identity. Denote by
$\operatorname {\mathrm {Ham}}(M, \omega )$
based on identity. Denote by
![]() $M_\Lambda $
the total space of the fibration over
$M_\Lambda $
the total space of the fibration over
![]() $S^2$
with fiber M which consists of two trivial fibrations over 2-discs, glued along their boundary via
$S^2$
with fiber M which consists of two trivial fibrations over 2-discs, glued along their boundary via
![]() $\Lambda $
. Namely, we consider
$\Lambda $
. Namely, we consider
![]() $S^2$
as the union of the two 2-discs
$S^2$
as the union of the two 2-discs
![]() $D_0$
and
$D_0$
and
![]() $D_\infty $
such that
$D_\infty $
such that
![]() $D_0$
is the closed unit disk centered at 0 in the Riemann sphere
$D_0$
is the closed unit disk centered at 0 in the Riemann sphere
![]() $S^2 = \mathbb {C} \cup \{ \infty \}$
and
$S^2 = \mathbb {C} \cup \{ \infty \}$
and
![]() $D_\infty $
is another copy of this disk, embedded in
$D_\infty $
is another copy of this disk, embedded in
![]() $S^2 = \mathbb {C} \cup \{ \infty \}$
, via the orientation reversing map
$S^2 = \mathbb {C} \cup \{ \infty \}$
, via the orientation reversing map
![]() $r\, e^{i\theta } \mapsto r^{-1} \, e^{i\theta }$
. The total space is
$r\, e^{i\theta } \mapsto r^{-1} \, e^{i\theta }$
. The total space is
This construction only depends on the homotopy class of
![]() $\Lambda $
. Moreover, the family (parameterized by
$\Lambda $
. Moreover, the family (parameterized by
![]() $S^2$
) of symplectic forms of the fibers can be extended to give a closed form,
$S^2$
) of symplectic forms of the fibers can be extended to give a closed form,
![]() $\Omega $
, on
$\Omega $
, on
![]() $M_\Lambda $
(see [Reference Sternberg29]). By adding to
$M_\Lambda $
(see [Reference Sternberg29]). By adding to
![]() $\Omega $
the pullback of a suitable area form on the base, we get a nondegenerate form. More precisely,
$\Omega $
the pullback of a suitable area form on the base, we get a nondegenerate form. More precisely,
![]() $\omega _{\Lambda ,\kappa } = \Omega + \kappa \cdot \pi ^*(\omega _0)$
is symplectic, where
$\omega _{\Lambda ,\kappa } = \Omega + \kappa \cdot \pi ^*(\omega _0)$
is symplectic, where
![]() $\omega _0$
is the standard symplectic form on
$\omega _0$
is the standard symplectic form on
![]() $S^2$
(with area 1),
$S^2$
(with area 1),
![]() $\pi $
is the projection to the base of the fibration, and
$\pi $
is the projection to the base of the fibration, and
![]() $\kappa $
is a big enough constant to make
$\kappa $
is a big enough constant to make
![]() $\omega _{\Lambda ,\kappa }$
nondegenerate. (Once chosen,
$\omega _{\Lambda ,\kappa }$
nondegenerate. (Once chosen,
![]() $\kappa $
will be omitted from the notation.)
$\kappa $
will be omitted from the notation.)
So we end up with the following Hamiltonian fibration:
In [Reference McDuff and Tolman24], McDuff and Tolman observed that, when
![]() $\Lambda $
is a circle action (with associated moment map
$\Lambda $
is a circle action (with associated moment map
![]() $\Phi _\Lambda $
), the clutching construction can be simplified since, then,
$\Phi _\Lambda $
), the clutching construction can be simplified since, then,
![]() $M_\Lambda $
can be seen as the quotient of
$M_\Lambda $
can be seen as the quotient of
![]() $M \times S^3$
by the diagonal action of
$M \times S^3$
by the diagonal action of
![]() $S^1$
,
$S^1$
,
![]() $e^{2\pi i \theta }\cdot (x,(z_1,z_2))=(\Lambda _\theta (x),(e^{2\pi i \theta } z_1, e^{2\pi i \theta } z_2))$
. The symplectic form also has an alternative description in
$e^{2\pi i \theta }\cdot (x,(z_1,z_2))=(\Lambda _\theta (x),(e^{2\pi i \theta } z_1, e^{2\pi i \theta } z_2))$
. The symplectic form also has an alternative description in
![]() $M \times _{S^1} S^3$
. Let
$M \times _{S^1} S^3$
. Let
![]() $\alpha \in \Omega ^1(S^3)$
be the standard contact form on
$\alpha \in \Omega ^1(S^3)$
be the standard contact form on
![]() $S^3$
such that
$S^3$
such that
![]() $d\alpha = \chi ^*(\omega _0)$
where
$d\alpha = \chi ^*(\omega _0)$
where
![]() $\chi : S^3 \to S^2$
is the Hopf map and
$\chi : S^3 \to S^2$
is the Hopf map and
![]() $\omega _0$
is the standard area form on
$\omega _0$
is the standard area form on
![]() $S^2$
with total area 1. For all
$S^2$
with total area 1. For all
![]() $c\in \mathbb {R}$
,
$c\in \mathbb {R}$
,
![]() $\omega +cd\alpha -d(\Phi _\Lambda \alpha )$
is a closed 2-form on
$\omega +cd\alpha -d(\Phi _\Lambda \alpha )$
is a closed 2-form on
![]() $M \times S^3$
which descends through the projection,
$M \times S^3$
which descends through the projection,
![]() $p: M \times S^3 \rightarrow M \times _{S^1} S^3$
, to a closed 2-form on
$p: M \times S^3 \rightarrow M \times _{S^1} S^3$
, to a closed 2-form on
![]() $M_\Lambda $
:
$M_\Lambda $
:
which extends
![]() $\Omega $
. Now, if
$\Omega $
. Now, if
![]() $c>\max \,\Phi _\Lambda $
,
$c>\max \,\Phi _\Lambda $
,
![]() $\omega _c$
is nondegenerate and coincides with
$\omega _c$
is nondegenerate and coincides with
![]() $\omega _{\Lambda ,\kappa }$
for some big enough
$\omega _{\Lambda ,\kappa }$
for some big enough
![]() $\kappa $
.
$\kappa $
.
A quantum class lying in the image of
![]() $\mathcal S$
is called a Seidel element. In [Reference McDuff and Tolman24], McDuff and Tolman were able to calculate the leading term of Seidel’s elements associated with Hamiltonian circle actions whose maximal fixed point component,
$\mathcal S$
is called a Seidel element. In [Reference McDuff and Tolman24], McDuff and Tolman were able to calculate the leading term of Seidel’s elements associated with Hamiltonian circle actions whose maximal fixed point component,
![]() $F_{\max }$
, is semi-free, that is, the action is semi-free on some neighborhood of
$F_{\max }$
, is semi-free, that is, the action is semi-free on some neighborhood of
![]() $F_{\max }$
. Recall that a circle action is semi-free if the stabilizer of every point is trivial or the whole circle. Moreover, when the codimension of
$F_{\max }$
. Recall that a circle action is semi-free if the stabilizer of every point is trivial or the whole circle. Moreover, when the codimension of
![]() $F_{\max }$
is 2, their result immediately ensures that if there exists an invariant almost complex structure J on M so that
$F_{\max }$
is 2, their result immediately ensures that if there exists an invariant almost complex structure J on M so that
![]() $(M,J)$
is Fano, i.e., so that there are no J-pseudoholomorphic spheres in M with nonpositive first Chern number, all the lower-order terms vanish. In the presence of J-pseudoholomorphic spheres with vanishing first Chern number, there is a priori no reason why arbitrarily large multiple coverings of such objects should not contribute to the Seidel elements. In fact, as explained in [Reference Anjos and Leclercq4], when the almost complex manifold
$(M,J)$
is Fano, i.e., so that there are no J-pseudoholomorphic spheres in M with nonpositive first Chern number, all the lower-order terms vanish. In the presence of J-pseudoholomorphic spheres with vanishing first Chern number, there is a priori no reason why arbitrarily large multiple coverings of such objects should not contribute to the Seidel elements. In fact, as explained in [Reference Anjos and Leclercq4], when the almost complex manifold
![]() $(M,J)$
is only numerically effective (NEF), i.e.,
$(M,J)$
is only numerically effective (NEF), i.e.,
![]() $c_1(B) \geq 0$
for every class
$c_1(B) \geq 0$
for every class
![]() $B \in H_2(M)$
with a J-holomorphic sphere representative, and not Fano, then there are indeed infinitely many contributions to the Seidel elements. More precisely, it is shown in [Reference Anjos and Leclercq4] that if M is a 4-toric manifold, then these quantum classes can still be expressed by explicit closed formulas. Moreover, these formulas only depend on the relative position of representatives of elements of
$B \in H_2(M)$
with a J-holomorphic sphere representative, and not Fano, then there are indeed infinitely many contributions to the Seidel elements. More precisely, it is shown in [Reference Anjos and Leclercq4] that if M is a 4-toric manifold, then these quantum classes can still be expressed by explicit closed formulas. Moreover, these formulas only depend on the relative position of representatives of elements of
![]() $\pi _2(M)$
with vanishing first Chern number as edges of the moment polygon. In particular, they are directly readable from the polygon.
$\pi _2(M)$
with vanishing first Chern number as edges of the moment polygon. In particular, they are directly readable from the polygon.
We now recall the precise results from [Reference Anjos and Leclercq4] that we will use in the forthcoming sections. Consider a four-dimensional closed symplectic manifold
![]() $(M,\omega )$
, endowed with a toric structure
$(M,\omega )$
, endowed with a toric structure
![]() $(\rho ,\Phi )$
. Suppose that the associated Delzant polygon
$(\rho ,\Phi )$
. Suppose that the associated Delzant polygon
![]() $P = \Phi (M)$
has
$P = \Phi (M)$
has
![]() $m \geq 4$
edges, and consider a Hamiltonian circle action
$m \geq 4$
edges, and consider a Hamiltonian circle action
![]() $\Lambda $
on
$\Lambda $
on
![]() $(M, \omega )$
, with moment map
$(M, \omega )$
, with moment map
![]() $\Phi _\Lambda $
, such that
$\Phi _\Lambda $
, such that
![]() $\Lambda $
is a subcircle of the toric action
$\Lambda $
is a subcircle of the toric action
![]() $\rho :\mathbb {T}^{2}\to \operatorname {\mathrm {Ham}}(M,\omega )$
.
$\rho :\mathbb {T}^{2}\to \operatorname {\mathrm {Ham}}(M,\omega )$
.
We assume additionally that the fixed point component of
![]() $\Lambda $
on which
$\Lambda $
on which
![]() $\Phi _\Lambda $
is maximal is a 2-sphere,
$\Phi _\Lambda $
is maximal is a 2-sphere,
![]() $F_{\max } \subset M$
, whose momentum image is an edge D of P. We denote by
$F_{\max } \subset M$
, whose momentum image is an edge D of P. We denote by
![]() $A \in H_2(M;\mathbb {Z})$
the homology class of
$A \in H_2(M;\mathbb {Z})$
the homology class of
![]() $F_{\max }$
and by
$F_{\max }$
and by
![]() $\Phi _{\max } = \Phi _\Lambda (F_{\max })$
.
$\Phi _{\max } = \Phi _\Lambda (F_{\max })$
.
In this case, McDuff–Tolman’s result [Reference McDuff and Tolman24, Theorem 1.10] ensures that the Seidel element associated with
![]() $\Lambda $
is
$\Lambda $
is
where
![]() $H_2^S(M;\mathbb {Z})^{>0}$
consists of the spherical classes of positive symplectic area, that is,
$H_2^S(M;\mathbb {Z})^{>0}$
consists of the spherical classes of positive symplectic area, that is,
![]() $\omega (B)>0$
and
$\omega (B)>0$
and
![]() $a_B\in H_*(M;\mathbb {Z})$
denotes the contribution of B. As mentioned above, when
$a_B\in H_*(M;\mathbb {Z})$
denotes the contribution of B. As mentioned above, when
![]() $(M,J)$
is Fano for some
$(M,J)$
is Fano for some
![]() $S^1$
-invariant
$S^1$
-invariant
![]() $\omega $
-compatible almost complex structure J, then all the lower-order terms vanish and we end up with
$\omega $
-compatible almost complex structure J, then all the lower-order terms vanish and we end up with
![]() $ \mathcal S(\Lambda )=A \otimes qt^{\Phi _{\max }}$
.
$ \mathcal S(\Lambda )=A \otimes qt^{\Phi _{\max }}$
.
In the non-Fano case, one has to be careful about the number and relative position of edges, in the vicinity of D, corresponding to spheres in M with vanishing first Chern number. We denote the number of such edges by
![]() $\mathcal {\#}\{c_1=0\}$
. We denote the edges and the corresponding homology classes in M in a cyclic way, that is, D, which, we denote by
$\mathcal {\#}\{c_1=0\}$
. We denote the edges and the corresponding homology classes in M in a cyclic way, that is, D, which, we denote by
![]() $D_m$
below, has neighboring edges
$D_m$
below, has neighboring edges
![]() $D_{m-1}$
on one side and
$D_{m-1}$
on one side and
![]() $D_{m+1}=D_1$
on the other, and they, respectively, induce classes
$D_{m+1}=D_1$
on the other, and they, respectively, induce classes
![]() $A_m$
,
$A_m$
,
![]() $A_{m-1}$
, and
$A_{m-1}$
, and
![]() $A_{m+1}=A_1$
in
$A_{m+1}=A_1$
in
![]() $H_2(M;\mathbb {Z})$
.
$H_2(M;\mathbb {Z})$
.
Figure 3 shows the relevant parts of the different polygons we need to consider. Dotted lines represent edges with positive first Chern number, and we indicate near each edge with nontrivial contribution the homology class of the corresponding sphere in M. For example, in Case (3c), only three homology classes contribute:
![]() $A_{m-1}$
,
$A_{m-1}$
,
![]() $A_m$
, and
$A_m$
, and
![]() $A_1$
;
$A_1$
;
![]() $A_{m-1}$
and
$A_{m-1}$
and
![]() $A_1$
have vanishing first Chern number while
$A_1$
have vanishing first Chern number while
![]() $c_1(A_m) \neq 0$
.
$c_1(A_m) \neq 0$
.

Figure 3: Cases appearing in Theorem 2.2.
Now, the following theorem gives the explicit expression of the Seidel element associated with
![]() $\Lambda $
when
$\Lambda $
when
![]() $\mathcal {\#}\{c_1=0\} \leq 2$
.
$\mathcal {\#}\{c_1=0\} \leq 2$
.
Theorem 2.2 [Reference Anjos and Leclercq4, Theorem 4.5]
Let
![]() $(M,\omega )$
be a four-dimensional closed symplectic manifold, endowed with a toric structure. With the notation described above, assume that the Delzant polygon P has
$(M,\omega )$
be a four-dimensional closed symplectic manifold, endowed with a toric structure. With the notation described above, assume that the Delzant polygon P has
![]() $m \geq 4$
edges, and that the fixed point component of the Hamiltonian action
$m \geq 4$
edges, and that the fixed point component of the Hamiltonian action
![]() $\Lambda $
on which
$\Lambda $
on which
![]() $\Phi _\Lambda $
is maximal is a 2-sphere,
$\Phi _\Lambda $
is maximal is a 2-sphere,
![]() $F_{\max } \subset M$
. Additionally, assume that
$F_{\max } \subset M$
. Additionally, assume that
![]() $(M,J)$
is NEF, for some
$(M,J)$
is NEF, for some
![]() $S^1$
-invariant
$S^1$
-invariant
![]() $\omega $
-compatible almost complex structure J. Then, in the cases described by Figure 3, the Seidel element associated with
$\omega $
-compatible almost complex structure J. Then, in the cases described by Figure 3, the Seidel element associated with
![]() $\Lambda $
is:
$\Lambda $
is:
-
(1)
 $ \displaystyle \mathcal S(\Lambda )=A_m\otimes qt^{\Phi _{\max }}$
;
$ \displaystyle \mathcal S(\Lambda )=A_m\otimes qt^{\Phi _{\max }}$
; -
(2a)
 $ \displaystyle \mathcal S(\Lambda )=A_m\otimes q\,\frac {t^{\Phi _{\max }}}{1-t^{-\omega (A_m)}}$
;
$ \displaystyle \mathcal S(\Lambda )=A_m\otimes q\,\frac {t^{\Phi _{\max }}}{1-t^{-\omega (A_m)}}$
; -
(2b)
 $ \displaystyle \mathcal S(\Lambda )=\left ( A_m\otimes q\,\frac {t^{\Phi _{\max }}}{1-t^{-\omega (A_m)}}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}} \right ) \frac {1}{1-t^{-\omega (A_m)-\omega (A_1)}} $
;
$ \displaystyle \mathcal S(\Lambda )=\left ( A_m\otimes q\,\frac {t^{\Phi _{\max }}}{1-t^{-\omega (A_m)}}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}} \right ) \frac {1}{1-t^{-\omega (A_m)-\omega (A_1)}} $
; -
(3a)
 $ \displaystyle \mathcal S(\Lambda )=A_m\otimes qt^{\Phi _{\max }}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}} $
;
$ \displaystyle \mathcal S(\Lambda )=A_m\otimes qt^{\Phi _{\max }}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}} $
; -
(3b)
 $ \displaystyle \mathcal S(\Lambda ) = A_m\otimes qt^{\Phi _{\max }}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}} $
$ \displaystyle \mathcal S(\Lambda ) = A_m\otimes qt^{\Phi _{\max }}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}} $
 $ \displaystyle \kern22pt -\left (A_1\otimes q\,\frac {t^{\Phi _{\max }}}{1-t^{-\omega (A_1)}}-A_2\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_2)}}{1-t^{-\omega (A_2)}}\right )\frac {t^{-\omega (A_1)-\omega (A_2)}}{1-t^{-\omega (A_1)-\omega (A_2)}}; $
$ \displaystyle \kern22pt -\left (A_1\otimes q\,\frac {t^{\Phi _{\max }}}{1-t^{-\omega (A_1)}}-A_2\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_2)}}{1-t^{-\omega (A_2)}}\right )\frac {t^{-\omega (A_1)-\omega (A_2)}}{1-t^{-\omega (A_1)-\omega (A_2)}}; $
-
(3c)
 $ \displaystyle \mathcal S(\Lambda )=A_m\otimes qt^{\Phi _{\max }}-A_{m-1}\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_{m-1})}}{1-t^{-\omega (A_{m-1})}}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}}.$
$ \displaystyle \mathcal S(\Lambda )=A_m\otimes qt^{\Phi _{\max }}-A_{m-1}\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_{m-1})}}{1-t^{-\omega (A_{m-1})}}-A_1\otimes q\,\frac {t^{\Phi _{\max }-\omega (A_1)}}{1-t^{-\omega (A_1)}}.$
2.3 The fundamental group of
 $\operatorname {\mbox{Symp}} ( {M}_{\mu ,c_1,c_2,c_3,c_4})$
$\operatorname {\mbox{Symp}} ( {M}_{\mu ,c_1,c_2,c_3,c_4})$
In this section, we recall the main results obtained by Li et al. [Reference Li, Li and Wu18] on the Torelli symplectic mapping class group and on the rank of the fundamental group of the group Symp
![]() $_{h}({M}_{\mu ,c_1,c_2,c_3,c_4}) $
of symplectomorphisms that act trivially on homology, for any given symplectic form.
$_{h}({M}_{\mu ,c_1,c_2,c_3,c_4}) $
of symplectomorphisms that act trivially on homology, for any given symplectic form.
First, note that diffeomorphic symplectic forms define symplectomorphism groups that are homeomorphic, and that symplectomorphism groups are invariant under rescalings of symplectic forms. Consequently, we can restrict ourselves to symplectic forms belonging to a fundamental domain for the action of
![]() $ \operatorname {\mathrm {Diff}} \times \mathbb {R_*} $
on the space
$ \operatorname {\mathrm {Diff}} \times \mathbb {R_*} $
on the space
![]() $ \Omega _{+} $
of orientation-compatible symplectic forms defined on the n-fold blowup
$ \Omega _{+} $
of orientation-compatible symplectic forms defined on the n-fold blowup
![]() $ \mathbb {X}_{n} $
. The cohomology class of a reduced class
$ \mathbb {X}_{n} $
. The cohomology class of a reduced class
![]() $\omega $
(see Definition 1.1 in the Introduction) is
$\omega $
(see Definition 1.1 in the Introduction) is
![]() $\nu L - \delta _1 V_1 - \cdots - \delta _n V_n$
. Let
$\nu L - \delta _1 V_1 - \cdots - \delta _n V_n$
. Let
![]() $\mathcal J_\omega $
be the space of compatible almost complex structures on
$\mathcal J_\omega $
be the space of compatible almost complex structures on
![]() $\mathbb {X}_n$
. For any
$\mathbb {X}_n$
. For any
![]() $J \in \mathcal J_\omega $
on
$J \in \mathcal J_\omega $
on
![]() $\mathbb {X}_n$
, the first Chern class
$\mathbb {X}_n$
, the first Chern class
![]() $c_1:= c_1 (TM) \in H^2(\mathbb {X}_n; \mathbb {Z})$
is the Poincaré dual to
$c_1:= c_1 (TM) \in H^2(\mathbb {X}_n; \mathbb {Z})$
is the Poincaré dual to
![]() $K:= 3L - \sum _i V_i$
. Let
$K:= 3L - \sum _i V_i$
. Let
![]() $\mathcal K$
be the symplectic cone of
$\mathcal K$
be the symplectic cone of
![]() $\mathbb {X}_n$
, that is,
$\mathbb {X}_n$
, that is,
Now, if C stands for the Poincaré dual of the symplectic cone of
![]() $ \mathbb {X}_{n} $
, then by uniqueness of symplectic blowups proved by McDuff in [Reference McDuff22], the diffeomorphism class of the form
$ \mathbb {X}_{n} $
, then by uniqueness of symplectic blowups proved by McDuff in [Reference McDuff22], the diffeomorphism class of the form
![]() $ \omega $
only depends on its cohomology class. Therefore, it is enough to describe a fundamental domain of the action of
$ \omega $
only depends on its cohomology class. Therefore, it is enough to describe a fundamental domain of the action of
![]() $ \operatorname {\mathrm {Diff}} \times \mathbb {R_*} $
on C. Moreover, the canonical class K is unique up to orientation-preserving diffeomorphisms [Reference Li and Liu20], so it suffices to describe the action of the diffeomorphisms fixing K,
$ \operatorname {\mathrm {Diff}} \times \mathbb {R_*} $
on C. Moreover, the canonical class K is unique up to orientation-preserving diffeomorphisms [Reference Li and Liu20], so it suffices to describe the action of the diffeomorphisms fixing K,
![]() $\operatorname {\mathrm {Diff}}_K$
, on
$\operatorname {\mathrm {Diff}}_K$
, on
where
![]() $ \Omega _{K}$
is the set of orientation-compatible symplectic forms with K as the symplectic canonical class. By the results in [Reference Li and Liu20], the set of reduced classes is a fundamental domain of
$ \Omega _{K}$
is the set of orientation-compatible symplectic forms with K as the symplectic canonical class. By the results in [Reference Li and Liu20], the set of reduced classes is a fundamental domain of
![]() $C_{K} ( \mathbb {X}_{n} )$
under the action of
$C_{K} ( \mathbb {X}_{n} )$
under the action of
![]() $ \operatorname {\mathrm {Diff}}_{K}$
. A proof of this result is also given in [Reference Karshon and Kessler11, Theorem 1.4]. We now consider the following change of basis in
$ \operatorname {\mathrm {Diff}}_{K}$
. A proof of this result is also given in [Reference Karshon and Kessler11, Theorem 1.4]. We now consider the following change of basis in
![]() $H_2(\mathbb {X}_n; \mathbb {Z})$
. Consider the symplectic manifold
$H_2(\mathbb {X}_n; \mathbb {Z})$
. Consider the symplectic manifold
![]() $(S^2 \times S^2, \mu \sigma \oplus \sigma )$
where the homology class of the base
$(S^2 \times S^2, \mu \sigma \oplus \sigma )$
where the homology class of the base
![]() $ B \in H _{2} ( S ^{2} \times S ^{2} )$
represented by
$ B \in H _{2} ( S ^{2} \times S ^{2} )$
represented by
![]() $ S ^{2} \times \{ pt \} $
has area
$ S ^{2} \times \{ pt \} $
has area
![]() $ \mu , $
and the homology class of the fiber
$ \mu , $
and the homology class of the fiber
![]() $ F \in H _{2} ( S ^{2} \times S ^{2} )$
represented by
$ F \in H _{2} ( S ^{2} \times S ^{2} )$
represented by
![]() $ \{ pt \} \times S ^{2} $
has area
$ \{ pt \} \times S ^{2} $
has area
![]() $ 1 $
. Recall that
$ 1 $
. Recall that
![]() ${M}_{\mu ,c_1,\ldots ,c_{n-1}}=(S^2 \times S^2 \#\, (n-1)\overline { \mathbb C\mathbb P}\,\!^2, \omega _{\mu ,c_1,\ldots , c_{n-1}})$
is obtained from
${M}_{\mu ,c_1,\ldots ,c_{n-1}}=(S^2 \times S^2 \#\, (n-1)\overline { \mathbb C\mathbb P}\,\!^2, \omega _{\mu ,c_1,\ldots , c_{n-1}})$
is obtained from
![]() $(S^2 \times S^2, \mu \sigma \oplus \sigma )$
, by performing
$(S^2 \times S^2, \mu \sigma \oplus \sigma )$
, by performing
![]() $n-1$
successive blowups of capacities
$n-1$
successive blowups of capacities
![]() $ c_{1}, \ldots , c_{n-1}$
. This can be naturally identified with
$ c_{1}, \ldots , c_{n-1}$
. This can be naturally identified with
![]() $(\mathbb {X}_n, \omega )$
. One easy way to understand the equivalence is as follows: let
$(\mathbb {X}_n, \omega )$
. One easy way to understand the equivalence is as follows: let
![]() $ \{ B, F, E_{1}, \ldots , E_{n-1} \} $
be the basis for
$ \{ B, F, E_{1}, \ldots , E_{n-1} \} $
be the basis for
![]() $H_{2}({M}_{\mu ,c_1,\ldots ,c_{n-1}}; \mathbb {Z}) $
where the
$H_{2}({M}_{\mu ,c_1,\ldots ,c_{n-1}}; \mathbb {Z}) $
where the
![]() $ E_{i}$
represent the exceptional spheres arising from the blowups. We identify L with
$ E_{i}$
represent the exceptional spheres arising from the blowups. We identify L with
![]() $ B+F-E_{1} $
,
$ B+F-E_{1} $
,
![]() $ V_{1}$
with
$ V_{1}$
with
![]() $ B - E_{1}$
,
$ B - E_{1}$
,
![]() $ V_{2} $
with
$ V_{2} $
with
![]() $ F - E_{1} $
, and
$ F - E_{1} $
, and
![]() $ V_{i} $
with
$ V_{i} $
with
![]() $ E_{i-1} $
, with
$ E_{i-1} $
, with
![]() $3 \leq i \leq n$
. Then the uniqueness of symplectic blowups due to McDuff (see [Reference McDuff22, Corollary 1.3]) implies that the symplectomorphism type of a symplectic blowup of a rational ruled manifold along an embedded ball of capacity
$3 \leq i \leq n$
. Then the uniqueness of symplectic blowups due to McDuff (see [Reference McDuff22, Corollary 1.3]) implies that the symplectomorphism type of a symplectic blowup of a rational ruled manifold along an embedded ball of capacity
![]() $ c \in (0,1) $
depends only on the capacity
$ c \in (0,1) $
depends only on the capacity
![]() $ c $
and not on the particular embedding used in obtaining the blowup. Using this result and after rescaling, we conclude that, for parameters satisfying the relations
$ c $
and not on the particular embedding used in obtaining the blowup. Using this result and after rescaling, we conclude that, for parameters satisfying the relations
there exists a symplectomorphism between two symplectic manifolds encoded by these parameters such that
Summarizing the above discussion, we showed that
Lemma 2.3 Every symplectic form on
![]() $S^2 \times S^2 \#\, (n-1)\overline { \mathbb C\mathbb P}\,\!^2$
is, after rescaling, diffeomorphic to a form Poincaré dual to
$S^2 \times S^2 \#\, (n-1)\overline { \mathbb C\mathbb P}\,\!^2$
is, after rescaling, diffeomorphic to a form Poincaré dual to
![]() $\mu B + F -c_1 E_1 - \cdots -c_{n-1} E_{n-1}$
with
$\mu B + F -c_1 E_1 - \cdots -c_{n-1} E_{n-1}$
with
Recall (see [Reference Li and Li16]) that the normalized reduced symplectic cone is defined as the space of reduced symplectic classes having area 1 on L, the line class. Note that cohomologous symplectic forms on a rational or ruled surface are diffeomorphic (cf. [Reference Lalonde and McDuff15, Reference Li and Liu20]). We represent such a class by
![]() $(1 | \delta _1, \ldots , \delta _n)$
, or
$(1 | \delta _1, \ldots , \delta _n)$
, or
![]() $(\delta _1, \ldots , \delta _n) \in \mathbb {R}^n.$
For
$(\delta _1, \ldots , \delta _n) \in \mathbb {R}^n.$
For
![]() $3 \leq n \leq 8$
, such a cone is a n-simplex with one facet removed, where the monotone class is one of the vertices, namely
$3 \leq n \leq 8$
, such a cone is a n-simplex with one facet removed, where the monotone class is one of the vertices, namely
![]() $M_n = (\frac 13, \ldots , \frac 13)$
. We are interested in the case when the manifold is
$M_n = (\frac 13, \ldots , \frac 13)$
. We are interested in the case when the manifold is
![]() $\mathbb {X}_5$
where the normalized reduced cone is convexly generated by five half-closed intervals
$\mathbb {X}_5$
where the normalized reduced cone is convexly generated by five half-closed intervals
![]() $\{MO,MA,MB,MC,MD\}$
, with vertices
$\{MO,MA,MB,MC,MD\}$
, with vertices
![]() $M= (\frac 13,\frac 13,\frac 13,\frac 13,\frac 13)$
, which corresponds to the monotone case,
$M= (\frac 13,\frac 13,\frac 13,\frac 13,\frac 13)$
, which corresponds to the monotone case,
![]() $O=(0,0,0,0,0)$
,
$O=(0,0,0,0,0)$
,
![]() $A=(1,0,0,0,0)$
,
$A=(1,0,0,0,0)$
,
![]() $B=(\frac 12,\frac 12, 0,0,0)$
,
$B=(\frac 12,\frac 12, 0,0,0)$
,
![]() $C=(\frac 13,\frac 13,\frac 13,0,0)$
, and
$C=(\frac 13,\frac 13,\frac 13,0,0)$
, and
![]() $D=(\frac 13,\frac 13,\frac 13,\frac 13,0)$
(for more details, see [Reference Li and Li16]).
$D=(\frac 13,\frac 13,\frac 13,\frac 13,0)$
(for more details, see [Reference Li and Li16]).
Let
![]() $N_\omega $
be the number of symplectic-2 spheres classes. Then Li, Li, and Wu proved the following.
$N_\omega $
be the number of symplectic-2 spheres classes. Then Li, Li, and Wu proved the following.
Theorem 2.4 [Reference Li, Li and Wu18, Theorem 1.2]
Consider
![]() $\mathbb {X}_5$
with any symplectic form
$\mathbb {X}_5$
with any symplectic form
![]() $\omega $
. Then the rank of the fundamental group of
$\omega $
. Then the rank of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h (\mathbb {X}_5, \omega )$
satisfies
$\operatorname {\mathrm{Symp}}_h (\mathbb {X}_5, \omega )$
satisfies
where the rank of
![]() $\pi _0 (\operatorname {\mathrm{Symp}}_h(\mathbb {X}_5, \omega ))$
means the rank of its abelianization.
$\pi _0 (\operatorname {\mathrm{Symp}}_h(\mathbb {X}_5, \omega ))$
means the rank of its abelianization.
Moreover, along the edge
![]() $MA$
, when
$MA$
, when
![]() $\nu =1, \delta _1> \delta _2 =\delta _3=\delta _4=\delta _5$
, and
$\nu =1, \delta _1> \delta _2 =\delta _3=\delta _4=\delta _5$
, and
![]() $\delta _1+ \delta _2 +\delta _3 =1$
, or equivalently, when
$\delta _1+ \delta _2 +\delta _3 =1$
, or equivalently, when
![]() $\mu> 1$
and
$\mu> 1$
and
![]() $c_1=c_2=c_3=c_4= 1/2$
, it follows from [Reference Li, Li and Wu18, Lemma 5.10] and its proof (in particular from sequence (37)) that
$c_1=c_2=c_3=c_4= 1/2$
, it follows from [Reference Li, Li and Wu18, Lemma 5.10] and its proof (in particular from sequence (37)) that
![]() $ \pi _1 (\operatorname {\mathrm{Symp}}_h (\mathbb {X}_5, \omega ))=\mathbb {Z}_5$
. This is the case we will study in detail in the forthcoming sections. In particular, we will show that a generating set of the fundamental group of
$ \pi _1 (\operatorname {\mathrm{Symp}}_h (\mathbb {X}_5, \omega ))=\mathbb {Z}_5$
. This is the case we will study in detail in the forthcoming sections. In particular, we will show that a generating set of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h(\mathbb {X}_5, \omega )$
can be realized by Hamiltonian circle actions except in some particular interval of values of
$\operatorname {\mathrm{Symp}}_h(\mathbb {X}_5, \omega )$
can be realized by Hamiltonian circle actions except in some particular interval of values of
![]() $\mu $
.
$\mu $
.
3 Quantum homology of
 ${M}_{\mu ,c_1,c_2,c_3,c_4}$
${M}_{\mu ,c_1,c_2,c_3,c_4}$
In [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7], Crauder and Miranda compute the quantum cohomology of a general rational surface, which includes the case of the blown-up manifold
![]() $\mathbb {CP}^2 \# 5 \overline {\mathbb {CP}^2}$
. Using Poincaré duality, this allows us to construct a presentation for the quantum homology ring
$\mathbb {CP}^2 \# 5 \overline {\mathbb {CP}^2}$
. Using Poincaré duality, this allows us to construct a presentation for the quantum homology ring
![]() $QH_\ast ({M}_{\mu ,c_1,c_2,c_3,c_4})$
, so that we can then compare different Seidel elements. The relations
$QH_\ast ({M}_{\mu ,c_1,c_2,c_3,c_4})$
, so that we can then compare different Seidel elements. The relations
 $$ \begin{align*}\begin{cases} L = B+F-E_1, \\ V_1 = B-E_1, \\ V_2 = F-E-1, \\ V_i = E_{i-1},~\mathrm{for}~ 2 \leq i \leq n, \end{cases} \end{align*} $$
$$ \begin{align*}\begin{cases} L = B+F-E_1, \\ V_1 = B-E_1, \\ V_2 = F-E-1, \\ V_i = E_{i-1},~\mathrm{for}~ 2 \leq i \leq n, \end{cases} \end{align*} $$
give an explicit way of translating information in terms of the classes
![]() $\{L, V_1, \ldots , V_n\}$
to one in terms of
$\{L, V_1, \ldots , V_n\}$
to one in terms of
![]() $\{B, F, E_1, \ldots , E_{n-1} \}$
.
$\{B, F, E_1, \ldots , E_{n-1} \}$
.
An explicit formula for the quantum product in terms of the classes
![]() $L, V_i$
is given in Proposition 5.3 of [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7]. The coefficients that appear in these can be computed with the help of the tables in Section 4 of [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7], giving us a closed formula for the products we are interested in. As an example, the product of two classes, different from the class of a single point
$L, V_i$
is given in Proposition 5.3 of [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7]. The coefficients that appear in these can be computed with the help of the tables in Section 4 of [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7], giving us a closed formula for the products we are interested in. As an example, the product of two classes, different from the class of a single point
![]() $p \in H_0(\mathbb {X}_5, \mathbb {Z})$
, in
$p \in H_0(\mathbb {X}_5, \mathbb {Z})$
, in
![]() $\mathbb {CP}^2 \# 5 \overline {\mathbb {CP}^2}$
, is given by
$\mathbb {CP}^2 \# 5 \overline {\mathbb {CP}^2}$
, is given by
 $$ \begin{align*} & (dL-\sum\limits_{i} m_i V_i) \ast (d'L-\sum\limits_{i} m^{\prime}_i V_i) = \left( dd' - \sum\limits_{i} m_i m^{\prime}_i \right) pt^{[p]} + \sum\limits_{k} m_k m^{\prime}_k V_k t^{[V_k]} \\+\ &\sum\limits_{j,k}(d-m_j-m_k)(d'-m^{\prime}_j-m^{\prime}_k)(L-V_j-V_k)t^{[L-V_j-V_k]} \\+\ &\left(2d-\sum_{i} m_i \right) \left(2d'-\sum_{i} m^{\prime}_i \right)(2L-V_1-V_2-V_3-V_4-V_5)t^{[2L-V_1-V_2-V_3-V_4-V_5]} \\+\ &\sum\limits_{j} (d-m_j)(d'-m^{\prime}_j)X t^{[L-V_j]} \\+\ &\sum_{j,k,l,n} (2d-m_j-m_k-m_l-m_n) (2d'-m^{\prime}_j-m^{\prime}_k-m^{\prime}_l-m^{\prime}_n) X t^{[2L-V_j-V_k-V_l-V_n]}, \end{align*} $$
$$ \begin{align*} & (dL-\sum\limits_{i} m_i V_i) \ast (d'L-\sum\limits_{i} m^{\prime}_i V_i) = \left( dd' - \sum\limits_{i} m_i m^{\prime}_i \right) pt^{[p]} + \sum\limits_{k} m_k m^{\prime}_k V_k t^{[V_k]} \\+\ &\sum\limits_{j,k}(d-m_j-m_k)(d'-m^{\prime}_j-m^{\prime}_k)(L-V_j-V_k)t^{[L-V_j-V_k]} \\+\ &\left(2d-\sum_{i} m_i \right) \left(2d'-\sum_{i} m^{\prime}_i \right)(2L-V_1-V_2-V_3-V_4-V_5)t^{[2L-V_1-V_2-V_3-V_4-V_5]} \\+\ &\sum\limits_{j} (d-m_j)(d'-m^{\prime}_j)X t^{[L-V_j]} \\+\ &\sum_{j,k,l,n} (2d-m_j-m_k-m_l-m_n) (2d'-m^{\prime}_j-m^{\prime}_k-m^{\prime}_l-m^{\prime}_n) X t^{[2L-V_j-V_k-V_l-V_n]}, \end{align*} $$
where
![]() $i,j,k,l,n$
always represent distinct indices,
$i,j,k,l,n$
always represent distinct indices,
![]() $X \in H_4(\mathbb {X}_5,\mathbb {Z})$
is the class of the manifold,
$X \in H_4(\mathbb {X}_5,\mathbb {Z})$
is the class of the manifold,
![]() $d \in \mathbb {Z}_{>0}, ~m_i, m^{\prime }_j \in \mathbb {Z}_{\geq 0}$
, and
$d \in \mathbb {Z}_{>0}, ~m_i, m^{\prime }_j \in \mathbb {Z}_{\geq 0}$
, and
![]() $t^{[A]}$
means t to the power of the negative symplectic area of the corresponding class A (in the symplectic viewpoint).
$t^{[A]}$
means t to the power of the negative symplectic area of the corresponding class A (in the symplectic viewpoint).
The next proposition gives a description of the ring
![]() $QH_\ast ({M}_{\mu ,c_i=1/2})$
. For the sake of simpler notation, let
$QH_\ast ({M}_{\mu ,c_i=1/2})$
. For the sake of simpler notation, let
 $$ \begin{align*} & b_{ij}= (B-E_i -E_j) \otimes q \, \frac{t^{\frac12}}{1-t^{1- \mu}}, \quad f_{ij}= (F-E_i -E_j) \otimes q \, \frac{t^{\frac12}}{1-t^{1- \mu}}, \quad \mbox{and} \\ & e_{i}= E_i \otimes q \, \frac{t^{\frac12}}{1-t^{1- \mu}}, \end{align*} $$
$$ \begin{align*} & b_{ij}= (B-E_i -E_j) \otimes q \, \frac{t^{\frac12}}{1-t^{1- \mu}}, \quad f_{ij}= (F-E_i -E_j) \otimes q \, \frac{t^{\frac12}}{1-t^{1- \mu}}, \quad \mbox{and} \\ & e_{i}= E_i \otimes q \, \frac{t^{\frac12}}{1-t^{1- \mu}}, \end{align*} $$
and, as before, let distinct letters in the indices correspond to distinct elements. Its proof is just computing the quantum products by the formula above and then translating them to a formula in terms of
![]() $\{B, F, E_1, \ldots , E_4\}$
. It follows from [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7, Proposition 5.3] that we have the presentation for
$\{B, F, E_1, \ldots , E_4\}$
. It follows from [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7, Proposition 5.3] that we have the presentation for
![]() $QH_\ast ({M}_{\mu ,c_i=1/2})$
given below.
$QH_\ast ({M}_{\mu ,c_i=1/2})$
given below.
Proposition 3.1 With the notation above, when
![]() $\mu> 1$
, as a
$\mu> 1$
, as a
![]() $\Pi ^{\mathrm {univ}}$
-algebra, we have
$\Pi ^{\mathrm {univ}}$
-algebra, we have
where
![]() $\Pi ^{\mathrm {univ}}$
is the universal Novikov ring and
$\Pi ^{\mathrm {univ}}$
is the universal Novikov ring and
![]() $I_{\mu ,c_i=1/2}$
is the ideal generated by
$I_{\mu ,c_i=1/2}$
is the ideal generated by
 $$ \begin{align*} & (1) \ b_{ij}b_{k\ell}=1; & & (7) \ f_{ij} f_{k\ell}=0; \\[2pt] & (2) \ b_{ij}b_{ik}=b_{ij} f_{ij} +f_{j\ell} +1; & & (8) \ f_{ij} f_{ik}= f_{ij} ( b_{ij} +1); \\[2pt] & (3)\ b_{ij}^2 = 2 b_{ij} f_{ij} + f_{ij} + f_{k\ell} + 1; & & (9) \ f_{ij}^2 = 2 f_{ij} ( b_{ij} +1);\\[2pt] & (4) \ f_{ik} ( b_{ij} +1)=0; & & (10) \ (f_{ij} + f_{k\ell} ) ( b_{ij} +1)=0; \\[2pt] & (5) \ b_{ij}\left(f_{ij} +e_i + \frac{t^{1-\mu}}{1-t^{1- \mu}}\right) = e_j+ \frac{t^{1-\mu}}{1-t^{1- \mu}}; & & (11) \ f_{ij}\left(b_{ij} +e_i + \frac{1}{1-t^{1- \mu}}\right) =0; \\[2pt]
& (6) \ b_{ij}\left(e_k + \frac{t^{1-\mu}}{1-t^{1- \mu}}\right) = f_{k\ell} + e_\ell+ \frac{t^{1-\mu}}{1-t^{1- \mu}};
& & (12) \ f_{ij} \left(e_k + \frac{t^{1-\mu}}{1-t^{1- \mu}}\right)=0;\\
& (13) \ e_ie_j = (2b_{ij}+2f_{k\ell}+e_k+e_\ell)\frac{t^{1-\mu}}{1-t^{1- \mu}} + \frac{2t^{1-\mu}+t^{2-2\mu}}{(1-t^{1- \mu})^2}; \\[2pt]
& (14) \ e_i^2 = b_{ij}f_{ij} +\frac{f_{ij}}{1-t^{1-\mu}} + (2b_{ij}+f_{k\ell}+2e_j)\frac{t^{1-\mu}}{1-t^{1- \mu}} + \frac{2t^{1-\mu}+t^{2-2\mu}}{(1-t^{1- \mu})^2}. \\[-42pt]
\end{align*} $$
$$ \begin{align*} & (1) \ b_{ij}b_{k\ell}=1; & & (7) \ f_{ij} f_{k\ell}=0; \\[2pt] & (2) \ b_{ij}b_{ik}=b_{ij} f_{ij} +f_{j\ell} +1; & & (8) \ f_{ij} f_{ik}= f_{ij} ( b_{ij} +1); \\[2pt] & (3)\ b_{ij}^2 = 2 b_{ij} f_{ij} + f_{ij} + f_{k\ell} + 1; & & (9) \ f_{ij}^2 = 2 f_{ij} ( b_{ij} +1);\\[2pt] & (4) \ f_{ik} ( b_{ij} +1)=0; & & (10) \ (f_{ij} + f_{k\ell} ) ( b_{ij} +1)=0; \\[2pt] & (5) \ b_{ij}\left(f_{ij} +e_i + \frac{t^{1-\mu}}{1-t^{1- \mu}}\right) = e_j+ \frac{t^{1-\mu}}{1-t^{1- \mu}}; & & (11) \ f_{ij}\left(b_{ij} +e_i + \frac{1}{1-t^{1- \mu}}\right) =0; \\[2pt]
& (6) \ b_{ij}\left(e_k + \frac{t^{1-\mu}}{1-t^{1- \mu}}\right) = f_{k\ell} + e_\ell+ \frac{t^{1-\mu}}{1-t^{1- \mu}};
& & (12) \ f_{ij} \left(e_k + \frac{t^{1-\mu}}{1-t^{1- \mu}}\right)=0;\\
& (13) \ e_ie_j = (2b_{ij}+2f_{k\ell}+e_k+e_\ell)\frac{t^{1-\mu}}{1-t^{1- \mu}} + \frac{2t^{1-\mu}+t^{2-2\mu}}{(1-t^{1- \mu})^2}; \\[2pt]
& (14) \ e_i^2 = b_{ij}f_{ij} +\frac{f_{ij}}{1-t^{1-\mu}} + (2b_{ij}+f_{k\ell}+2e_j)\frac{t^{1-\mu}}{1-t^{1- \mu}} + \frac{2t^{1-\mu}+t^{2-2\mu}}{(1-t^{1- \mu})^2}. \\[-42pt]
\end{align*} $$
▪
Remark 3.2 Of course, our description does not give a minimal set of generators nor is that the intention of Proposition 3.1. The generators were picked with the intent of simplifying the computations of the Seidel morphism and they also give some simple insight into the ring structure: for instance, relation
![]() $f_{ij} f_{k\ell }=0 $
implies that there are zero divisors.
$f_{ij} f_{k\ell }=0 $
implies that there are zero divisors.
4 Generators of
 $\pi _1(\operatorname {\mbox{Symp}}({M}_{\mu ,c_1,c_2,c_3,c_4}))$
$\pi _1(\operatorname {\mbox{Symp}}({M}_{\mu ,c_1,c_2,c_3,c_4}))$
4.1 Hamiltonian circle actions in
 ${M}_{\mu ,c_1,c_2,c_3,c_4}$
${M}_{\mu ,c_1,c_2,c_3,c_4}$
In this section, we list all equivalence classes of Hamiltonian circle actions on symplectic manifolds whose symplectic cohomology class belongs to the edge
![]() $MA$
of the reduced symplectic cone. Recall that, along this edge, we have
$MA$
of the reduced symplectic cone. Recall that, along this edge, we have
![]() $\mu> 1$
and
$\mu> 1$
and
![]() $c_1=c_2=c_3=c_4= 1/2$
. Recall also that Karshon’s classification [Reference Karshon10, Section 6.2] implies that every compact four-dimensional Hamiltonian
$c_1=c_2=c_3=c_4= 1/2$
. Recall also that Karshon’s classification [Reference Karshon10, Section 6.2] implies that every compact four-dimensional Hamiltonian
![]() $S^1$
-space can be obtained from a minimal space, which can be
$S^1$
-space can be obtained from a minimal space, which can be
![]() $\mathbb {CP}^2$
, a Hirzebruch surface, or an irrational ruled manifold (see [Reference Karshon10, Section 6.3]), by a sequence of equivariant symplectic blowups at fixed points. It follows that the only possible Hamiltonian circle actions on the symplectic manifolds belonging to the edge
$\mathbb {CP}^2$
, a Hirzebruch surface, or an irrational ruled manifold (see [Reference Karshon10, Section 6.3]), by a sequence of equivariant symplectic blowups at fixed points. It follows that the only possible Hamiltonian circle actions on the symplectic manifolds belonging to the edge
![]() $MA$
are the ones corresponding to the labeled graphs of Figure 4, where the values of a and b represent the symplectic area of the invariant spheres and depend on which sphere we perform the blowup. In our figures, we omit the genus label since, in our case, the invariant surfaces are always embedded spheres. Moreover, since the symplectic area of the spheres is positive, i.e.,
$MA$
are the ones corresponding to the labeled graphs of Figure 4, where the values of a and b represent the symplectic area of the invariant spheres and depend on which sphere we perform the blowup. In our figures, we omit the genus label since, in our case, the invariant surfaces are always embedded spheres. Moreover, since the symplectic area of the spheres is positive, i.e.,
![]() $a,b> 0$
, and
$a,b> 0$
, and
![]() $c_1=c_2=c_3=c_4= 1/2$
, then we can only have
$c_1=c_2=c_3=c_4= 1/2$
, then we can only have
![]() $a+b= 2\mu -2$
.
$a+b= 2\mu -2$
.

Figure 4: Graphs representing Hamiltonian circle actions on symplectic manifolds belonging to the ray
![]() $MA$
.
$MA$
.
4.2 Circle actions and homotopy classes of loops
A labeled graph only determines a circle action up to symplectomorphisms. Equivalently, a labeled graph defines a conjugacy class of circles in
![]() $\operatorname {\mathrm{Symp}}(M,\omega )$
. Consequently, any such graph defines an element of
$\operatorname {\mathrm{Symp}}(M,\omega )$
. Consequently, any such graph defines an element of
where the action is by conjugation. The analysis of this action is done in two stages.
For any symplectic manifold
![]() $(M,\omega )$
belonging to the ray
$(M,\omega )$
belonging to the ray
![]() $MA$
, the action of
$MA$
, the action of
![]() $\operatorname {\mathrm{Symp}}(M,\omega )$
on homology induces a short exact sequence
$\operatorname {\mathrm{Symp}}(M,\omega )$
on homology induces a short exact sequence
where
![]() $\operatorname {\mathrm {Aut}}_{c_1,[\omega ]}\left (H_2(M,\mathbb {Z})\right )$
is the group of automorphisms of the lattice
$\operatorname {\mathrm {Aut}}_{c_1,[\omega ]}\left (H_2(M,\mathbb {Z})\right )$
is the group of automorphisms of the lattice
![]() $H_2(M,\mathbb {Z})$
preserving the intersection form and the classes dual to
$H_2(M,\mathbb {Z})$
preserving the intersection form and the classes dual to
![]() $c_1(M,\omega )$
and
$c_1(M,\omega )$
and
![]() $[\omega ]$
. The fact that the map f is onto follows from three results in [Reference Li and Wu21] that we briefly recall. First, by [Reference Li and Wu21, Proposition 4.14], the group
$[\omega ]$
. The fact that the map f is onto follows from three results in [Reference Li and Wu21] that we briefly recall. First, by [Reference Li and Wu21, Proposition 4.14], the group
![]() $\operatorname {\mathrm {Aut}}_{c_1,[\omega ]}\left (H_2(M,\mathbb {Z})\right )$
is generated by reflections about spherical homology classes A satisfying three conditions:
$\operatorname {\mathrm {Aut}}_{c_1,[\omega ]}\left (H_2(M,\mathbb {Z})\right )$
is generated by reflections about spherical homology classes A satisfying three conditions:
![]() $A\cdot A=-2$
,
$A\cdot A=-2$
,
![]() $c_1(A)=0$
, and
$c_1(A)=0$
, and
![]() $\omega (A)=0$
. Such a class is called a
$\omega (A)=0$
. Such a class is called a
![]() $(K, [\omega ])$
-null spherical class, where K denotes the symplectic canonical class. Second, a symplectic Dehn twist along a Lagrangian sphere L induces the reflection
$(K, [\omega ])$
-null spherical class, where K denotes the symplectic canonical class. Second, a symplectic Dehn twist along a Lagrangian sphere L induces the reflection
![]() $R([L])$
in homology. Finally, the result follows from Proposition 5.6 in [Reference Li and Wu21] which proves existence of Lagrangian spheres representing
$R([L])$
in homology. Finally, the result follows from Proposition 5.6 in [Reference Li and Wu21] which proves existence of Lagrangian spheres representing
![]() $(K, [\omega ])$
-null spherical classes.
$(K, [\omega ])$
-null spherical classes.
In our case, along
![]() $MA$
, the automorphism group is isomorphic to the Weyl group
$MA$
, the automorphism group is isomorphic to the Weyl group
![]() $D_4$
given by the trivalent Dynkin diagram (see [Reference Li, Li and Wu18]). It is easy to see that it fixes the classes
$D_4$
given by the trivalent Dynkin diagram (see [Reference Li, Li and Wu18]). It is easy to see that it fixes the classes
![]() $2B+2F-E_1-E_2-E_3-E_4$
and F, whereas it acts transitively on the eight exceptional classes
$2B+2F-E_1-E_2-E_3-E_4$
and F, whereas it acts transitively on the eight exceptional classes
![]() ${E_1,\ldots ,E_4, F-E_1,\ldots ,F-E_4}$
. In particular, the only element of
${E_1,\ldots ,E_4, F-E_1,\ldots ,F-E_4}$
. In particular, the only element of
![]() $\operatorname {\mathrm {Aut}}_{c_1,[\omega ]}$
that fixes the four exceptional classes
$\operatorname {\mathrm {Aut}}_{c_1,[\omega ]}$
that fixes the four exceptional classes
![]() $E_i$
is the identity.
$E_i$
is the identity.
In order to keep track of the action of
![]() on Hamiltonian circle actions, we consider extended graphs as defined in [Reference Karshon10, Section 5, p. 33] decorated with homology labels. Starting with the standard labelled graph of Figure 4, we add extra (dotted) edges that represent free invariant spheres connecting each interior fixed point to extrema of the moment map. Each such sphere is the closure of a free
on Hamiltonian circle actions, we consider extended graphs as defined in [Reference Karshon10, Section 5, p. 33] decorated with homology labels. Starting with the standard labelled graph of Figure 4, we add extra (dotted) edges that represent free invariant spheres connecting each interior fixed point to extrema of the moment map. Each such sphere is the closure of a free
![]() $\mathbb {C}^*$
-orbit, where the
$\mathbb {C}^*$
-orbit, where the
![]() $\mathbb {C}^*$
action is defined from the choice of a generic
$\mathbb {C}^*$
action is defined from the choice of a generic
![]() $S^1$
-invariant almost-complex structure. Since the action of
$S^1$
-invariant almost-complex structure. Since the action of
![]() $\operatorname {\mathrm{Symp}}(M,\omega )$
preserves the genericity of almost-complex structures, an extended graph defines a configuration of invariant spheres that is well defined up to conjugation. We then label the edges of the extended graph with homology classes according to the sequence of blowups that is used to construct the Hamiltonian
$\operatorname {\mathrm{Symp}}(M,\omega )$
preserves the genericity of almost-complex structures, an extended graph defines a configuration of invariant spheres that is well defined up to conjugation. We then label the edges of the extended graph with homology classes according to the sequence of blowups that is used to construct the Hamiltonian
![]() $S^1$
-manifold. Geometrically, this amounts to labeling invariant spheres with their homology class following a specific sequence of equivariant blowups performed on
$S^1$
-manifold. Geometrically, this amounts to labeling invariant spheres with their homology class following a specific sequence of equivariant blowups performed on
![]() $\left (S^2\times S^2,\mu \sigma \otimes \sigma \right )$
, starting with the two fixed surfaces labeled
$\left (S^2\times S^2,\mu \sigma \otimes \sigma \right )$
, starting with the two fixed surfaces labeled
![]() $B=[S^2\times \operatorname {\mathrm {pt}}]$
and
$B=[S^2\times \operatorname {\mathrm {pt}}]$
and
![]() $F=[\operatorname {\mathrm {pt}}\times S^2]$
. The possible extended labeled graphs are shown in Figures 5–7. By construction, the group
$F=[\operatorname {\mathrm {pt}}\times S^2]$
. The possible extended labeled graphs are shown in Figures 5–7. By construction, the group
![]() $\operatorname {\mathrm{Symp}}(M,\omega )$
acts on its corresponding extended labeled graph with kernel
$\operatorname {\mathrm{Symp}}(M,\omega )$
acts on its corresponding extended labeled graph with kernel
![]() $\operatorname {\mathrm{Symp}}_h(M,\omega )$
. In our case, these extended labeled graphs classify
$\operatorname {\mathrm{Symp}}_h(M,\omega )$
. In our case, these extended labeled graphs classify
![]() $\operatorname {\mathrm{Symp}}_h$
-equivalence classes of
$\operatorname {\mathrm{Symp}}_h$
-equivalence classes of
![]() $S^1$
-manifolds on the edge
$S^1$
-manifolds on the edge
![]() $MA$
endowed with a given framing
$MA$
endowed with a given framing
![]() $\phi :H_2(M,\mathbb {Z})\to \mathbb {Z}\langle B,F,E_1,E_2,E_3,E_4\rangle \simeq \mathbb {Z}^{1,5}$
.
$\phi :H_2(M,\mathbb {Z})\to \mathbb {Z}\langle B,F,E_1,E_2,E_3,E_4\rangle \simeq \mathbb {Z}^{1,5}$
.

Figure 5: Family of graphs in the case
![]() $\mu>1$
.
$\mu>1$
.
Recall from [Reference Li, Li and Wu18] that, for
![]() $(M,\omega )$
belonging to the edge
$(M,\omega )$
belonging to the edge
![]() $MA$
, the symplectomorphism group
$MA$
, the symplectomorphism group
![]() $\operatorname {\mathrm{Symp}}_h(M,\omega )$
is not connected. Indeed,
$\operatorname {\mathrm{Symp}}_h(M,\omega )$
is not connected. Indeed,
![]() $\pi _0 (\operatorname {\mathrm{Symp}}_h(M,\omega ))= \pi _0(\operatorname {\mathrm {Diff}}^+(S^2,4))\simeq P_4(S^2) / \mathbb {Z}_2$
, where
$\pi _0 (\operatorname {\mathrm{Symp}}_h(M,\omega ))= \pi _0(\operatorname {\mathrm {Diff}}^+(S^2,4))\simeq P_4(S^2) / \mathbb {Z}_2$
, where
![]() $P_4(S^2)$
is the pure braid group of four strings in
$P_4(S^2)$
is the pure braid group of four strings in
![]() $S^2.$
Since an extended labeled graph only determines an element in
$S^2.$
Since an extended labeled graph only determines an element in
![]() $\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))/\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
, we have to understand how
$\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))/\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
, we have to understand how
![]() $\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
acts on
$\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
acts on
![]() $\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))$
. We postpone this analysis to Section 4.4.
$\pi _1(\operatorname {\mathrm{Symp}}(M,\omega ))$
. We postpone this analysis to Section 4.4.
4.3 Extended labeled graphs along the edge
 $MA$
$MA$
We now describe a finite set of one-parameter families of extended labeled graphs, parameterized by
![]() $\mu $
, that correspond to symplectic manifolds belonging to the edge
$\mu $
, that correspond to symplectic manifolds belonging to the edge
![]() $MA$
of the reduced symplectic cone. The number of elements in these families depends on the range of
$MA$
of the reduced symplectic cone. The number of elements in these families depends on the range of
![]() $\mu $
. As explained above, each such graph corresponds to a
$\mu $
. As explained above, each such graph corresponds to a
![]() $\operatorname {\mathrm{Symp}}_h(M,\omega )$
-conjugacy class of Hamiltonian circle actions.
$\operatorname {\mathrm{Symp}}_h(M,\omega )$
-conjugacy class of Hamiltonian circle actions.
Notice that these actions only exist as long as the symplectic area of the classes corresponding to the fixed spheres is positive. Assuming
![]() $1 <\mu \leq \frac 32$
, we have four circle actions represented by the graphs in Figure 5. We can consider for example:
$1 <\mu \leq \frac 32$
, we have four circle actions represented by the graphs in Figure 5. We can consider for example:
![]() $z_{0,12}, z_{0,13},z_{0,14}$
and
$z_{0,12}, z_{0,13},z_{0,14}$
and
![]() $z_1$
. We do not consider flips of these graphs as they represent actions which are inverse to these ones.
$z_1$
. We do not consider flips of these graphs as they represent actions which are inverse to these ones.
Remark 4.1 Note that removing the homology labels and the dotted edges from the graphs representing the four actions
![]() $z_{0,12}, z_{0,13},z_{0,14}$
, and
$z_{0,12}, z_{0,13},z_{0,14}$
, and
![]() $z_1$
, we get exactly the same underlying labeled graph. It follows that these four Hamiltonian circle actions are conjugated by symplectomorphisms that act nontrivially on homology.
$z_1$
, we get exactly the same underlying labeled graph. It follows that these four Hamiltonian circle actions are conjugated by symplectomorphisms that act nontrivially on homology.
Moreover, as we increase the value of
![]() $\mu $
, there are more classes that can be represented by the fixed spheres, as we see next. If we consider
$\mu $
, there are more classes that can be represented by the fixed spheres, as we see next. If we consider
![]() $ \mu> \frac 32 $
, then we can add the graphs in Figure 6 to the previous family. It should be clear that there are eight such graphs, because
$ \mu> \frac 32 $
, then we can add the graphs in Figure 6 to the previous family. It should be clear that there are eight such graphs, because
![]() $i,j, \ell ,m=1,2,3,4$
are all distinct. More precisely, we have the graphs representing the following actions:
$i,j, \ell ,m=1,2,3,4$
are all distinct. More precisely, we have the graphs representing the following actions:
![]() $z_{0,123},z_{0,124},z_{0,134},z_{0,234}$
and
$z_{0,123},z_{0,124},z_{0,134},z_{0,234}$
and
![]() $z_{1,1},z_{1,2}, z_{1,3},z_{1,4}$
.
$z_{1,1},z_{1,2}, z_{1,3},z_{1,4}$
.

Figure 6: New family of graphs if
![]() $\mu>\frac 32$
.
$\mu>\frac 32$
.
Then there are no more possible classes for the fixed symplectic spheres unless we consider
![]() $\mu>2$
. In this case, eight new circle actions appear, where the following pairs of classes are represented by the fixed spheres: B and
$\mu>2$
. In this case, eight new circle actions appear, where the following pairs of classes are represented by the fixed spheres: B and
![]() $B-E_1-E_2-E_3-E_4$
;
$B-E_1-E_2-E_3-E_4$
;
![]() $B-2F$
and
$B-2F$
and
![]() $B+2F-E_1-E_2-E_3-E_4$
; and
$B+2F-E_1-E_2-E_3-E_4$
; and
![]() $B-F-E_i-E_j$
and
$B-F-E_i-E_j$
and
![]() $B+F -E_\ell -E_m$
with
$B+F -E_\ell -E_m$
with
![]() $i,j,\ell , m =1,2,3,4$
all distinct. If we restrict the range of values of
$i,j,\ell , m =1,2,3,4$
all distinct. If we restrict the range of values of
![]() $\mu $
further, it is easy to see that the number of circle actions keeps increasing. More precisely, when
$\mu $
further, it is easy to see that the number of circle actions keeps increasing. More precisely, when
![]() $\mu $
passes
$\mu $
passes
![]() $k +\frac 12$
or
$k +\frac 12$
or
![]() $k+1$
, for
$k+1$
, for
![]() $k \in \mathbb {Z}_{\geq 1}$
, the number of actions always increases by 8. Therefore, we obtain the following proposition.
$k \in \mathbb {Z}_{\geq 1}$
, the number of actions always increases by 8. Therefore, we obtain the following proposition.
Proposition 4.2 The Hamiltonian circle actions on the symplectic manifolds belonging to the edge
![]() $MA$
of the reduced symplectic cone are the ones represented by the labeled graphs in Figure 7. In particular, these actions satisfy the following existence conditions:
$MA$
of the reduced symplectic cone are the ones represented by the labeled graphs in Figure 7. In particular, these actions satisfy the following existence conditions:
 $$\begin{align*} & \bullet z_k \ \mbox{exists} \ \mbox{iff} \ \mu>k \ \mbox{and} \ \mu > 2-k, \\ & \bullet z_{k,i} \ \mbox{exists} \ \mbox{iff} \ \mu > k +\frac12 \ \mbox{and} \ \mu > \frac32-k, \\ & \bullet z_{k,ij} \ \mbox{exists} \ \mbox{iff}\ \mu > k +1,\\ & \bullet z_{k,ijl} \ \mbox{exists} \ \mbox{iff} \ \mu > k +\frac32,\\ & \bullet z_{k,1234} \ \mbox{exists} \ \mbox{iff} \ \mu > k +2,\end{align*}$$
$$\begin{align*} & \bullet z_k \ \mbox{exists} \ \mbox{iff} \ \mu>k \ \mbox{and} \ \mu > 2-k, \\ & \bullet z_{k,i} \ \mbox{exists} \ \mbox{iff} \ \mu > k +\frac12 \ \mbox{and} \ \mu > \frac32-k, \\ & \bullet z_{k,ij} \ \mbox{exists} \ \mbox{iff}\ \mu > k +1,\\ & \bullet z_{k,ijl} \ \mbox{exists} \ \mbox{iff} \ \mu > k +\frac32,\\ & \bullet z_{k,1234} \ \mbox{exists} \ \mbox{iff} \ \mu > k +2,\end{align*}$$
where
![]() $k \in \mathbb {Z}_{\geq 0}$
and
$k \in \mathbb {Z}_{\geq 0}$
and
![]() $i,j,\ell ,m =1,2,3,4$
are all distinct.
$i,j,\ell ,m =1,2,3,4$
are all distinct.

Figure 7: Families of graphs of Hamiltonian
![]() $S^1$
-spaces encoded by the edge
$S^1$
-spaces encoded by the edge
![]() $MA$
.
$MA$
.
Remark 4.3 As we saw above, when
![]() $ 1 < \mu \leq \frac 32$
, there exist only four Hamiltonian circle actions:
$ 1 < \mu \leq \frac 32$
, there exist only four Hamiltonian circle actions:
![]() $z_{0,12}, z_{0,13},z_{0,14}$
, and
$z_{0,12}, z_{0,13},z_{0,14}$
, and
![]() $z_1$
, so there are not enough circle actions to generate the fundamental group. Then, when
$z_1$
, so there are not enough circle actions to generate the fundamental group. Then, when
![]() $\mu $
passes
$\mu $
passes
![]() $k+\frac 12$
, where
$k+\frac 12$
, where
![]() $k \geq 1$
, there exist eight more circle actions, namely
$k \geq 1$
, there exist eight more circle actions, namely
![]() $z_{k-1,123}, z_{k-1,124}, z_{k-1,134}, z_{k-1,234}$
, and
$z_{k-1,123}, z_{k-1,124}, z_{k-1,134}, z_{k-1,234}$
, and
![]() $z_{k,i}$
with
$z_{k,i}$
with
![]() $i=1,2,3,4$
, and when
$i=1,2,3,4$
, and when
![]() $\mu $
passes
$\mu $
passes
![]() $k+1$
, eight more circle actions appear:
$k+1$
, eight more circle actions appear:
![]() $z_{k-1,1234}$
,
$z_{k-1,1234}$
,
![]() $z_{k,12}, z_{k,13},z_{k,14},z_{k,23},z_{k,24},z_{k,34}$
, and
$z_{k,12}, z_{k,13},z_{k,14},z_{k,23},z_{k,24},z_{k,34}$
, and
![]() $z_{k+1}$
.
$z_{k+1}$
.
Remark 4.4 Although the number of Hamiltonian circle actions keeps increasing as the values of
![]() $\mu $
increase, we know by the work of Li et al. in [Reference Li, Li and Wu18] that the rank of
$\mu $
increase, we know by the work of Li et al. in [Reference Li, Li and Wu18] that the rank of
![]() $\pi _1$
remains constant as
$\pi _1$
remains constant as
![]() $\mu $
increases so there can only be at most five independent circle actions as elements of the fundamental group.
$\mu $
increases so there can only be at most five independent circle actions as elements of the fundamental group.
Remark 4.5 In the forthcoming sections, we prove that, for
![]() $\mu> \frac 32$
, the fundamental group
$\mu> \frac 32$
, the fundamental group
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))\otimes \mathbb {Q}$
is indeed generated by circle actions. We choose as a tentative set of generators the set consisting of the four circle actions
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))\otimes \mathbb {Q}$
is indeed generated by circle actions. We choose as a tentative set of generators the set consisting of the four circle actions
![]() $z_{0,12}, z_{0,13},z_{0,14}$
, and
$z_{0,12}, z_{0,13},z_{0,14}$
, and
![]() $z_1$
, which are the only ones that exist for all values of
$z_1$
, which are the only ones that exist for all values of
![]() $\mu $
plus the action
$\mu $
plus the action
![]() $z_{1,4}$
, which exists as soon as
$z_{1,4}$
, which exists as soon as
![]() $\mu $
passes
$\mu $
passes
![]() $\frac 32$
. The reason why we choose this action, among the new eight actions which appear when
$\frac 32$
. The reason why we choose this action, among the new eight actions which appear when
![]() $\mu $
passes
$\mu $
passes
![]() $\frac 32$
, is geometric and relates with the work of [Reference Li, Li and Wu18]. This action corresponds to a simultaneous rotation of all the spheres except the base in the configuration of seven exceptional spheres used in the proof of [Reference Li, Li and Wu18, Lemma 5.10], where the authors show that the rank of
$\frac 32$
, is geometric and relates with the work of [Reference Li, Li and Wu18]. This action corresponds to a simultaneous rotation of all the spheres except the base in the configuration of seven exceptional spheres used in the proof of [Reference Li, Li and Wu18, Lemma 5.10], where the authors show that the rank of
![]() $\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
is 5. While the first four actions fix spheres with self-intersection
$\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
is 5. While the first four actions fix spheres with self-intersection
![]() $-2$
, the action
$-2$
, the action
![]() $z_{1,4}$
fixes a
$z_{1,4}$
fixes a
![]() $-3$
self-intersection sphere in class
$-3$
self-intersection sphere in class
![]() $B-F-E_4$
.
$B-F-E_4$
.
4.4 The Seidel morphism along the edge
 $MA$
$MA$
In this subsection, we prove our first main theorem, namely Theorem 1.3. The proof relies on the computation of the Seidel elements associated with the circle actions
![]() $z_{0,1i}, i=2,3,4$
,
$z_{0,1i}, i=2,3,4$
,
![]() $z_1$
, and
$z_1$
, and
![]() $z_{1,4}$
, and on the fact that they are linearly independent in the subgroup of invertible elements of the quantum homology of the manifold
$z_{1,4}$
, and on the fact that they are linearly independent in the subgroup of invertible elements of the quantum homology of the manifold
![]() ${M}_{\mu ,c_i=1/2}$
.
${M}_{\mu ,c_i=1/2}$
.
4.4.1 Seidel elements and deformations
In order to describe the Seidel morphism
our strategy is to combine the invariance property of
![]() $\mathcal {S}$
under the natural
$\mathcal {S}$
under the natural
![]() $\operatorname {\mathrm{Symp}}_{h}(M,\omega )$
action, the invariance of Gromov–Witten invariants with respect to symplectic deformations, and Theorem 2.2, which describes certain Seidel elements associated with subcircles of toric actions on NEF symplectic manifolds.
$\operatorname {\mathrm{Symp}}_{h}(M,\omega )$
action, the invariance of Gromov–Witten invariants with respect to symplectic deformations, and Theorem 2.2, which describes certain Seidel elements associated with subcircles of toric actions on NEF symplectic manifolds.
More precisely, we first observe that the Seidel morphism
defined in Section 2.2 is invariant under the action of
![]() $\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
on
$\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
on
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega )$
. This follows from the definition of
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega )$
. This follows from the definition of
![]() $\mathcal {S}$
and, in the case of Hamiltonian circle actions, can be seen directly from the formula (2.3) given by McDuff and Tolman. In particular, given a Hamiltonian circle action
$\mathcal {S}$
and, in the case of Hamiltonian circle actions, can be seen directly from the formula (2.3) given by McDuff and Tolman. In particular, given a Hamiltonian circle action
![]() $\gamma :S^1\to \operatorname {\mathrm {Ham}}(M,\omega )$
, its image
$\gamma :S^1\to \operatorname {\mathrm {Ham}}(M,\omega )$
, its image
![]() $\mathcal {S}(\gamma )$
is determined by the labeled extended graph associated with
$\mathcal {S}(\gamma )$
is determined by the labeled extended graph associated with
![]() $\gamma $
.
$\gamma $
.
Next, consider a Hamiltonian circle action
![]() $\rho $
on
$\rho $
on
![]() ${M}_{\mu ,c_i=1/2}$
and the corresponding loop
${M}_{\mu ,c_i=1/2}$
and the corresponding loop
![]() $[\rho ]$
in
$[\rho ]$
in
![]() $\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2})$
. Let
$\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2})$
. Let
![]() $\Omega (\rho )$
be the space of all symplectic forms that are invariant under this action and write
$\Omega (\rho )$
be the space of all symplectic forms that are invariant under this action and write
![]() $\Omega _0(\rho )$
for the connected component of
$\Omega _0(\rho )$
for the connected component of
![]() $\omega _{\mu ,c_i=1/2}$
. A
$\omega _{\mu ,c_i=1/2}$
. A
![]() $\mathbb {Q}$
-generic symplectic form is a symplectic form whose cohomology class
$\mathbb {Q}$
-generic symplectic form is a symplectic form whose cohomology class
![]() $ [\mu ;c_1,\ldots ,c_4]$
is given by coefficients that are linearly independent over
$ [\mu ;c_1,\ldots ,c_4]$
is given by coefficients that are linearly independent over
![]() $\mathbb {Q}$
. One can show that invariant
$\mathbb {Q}$
. One can show that invariant
![]() $\mathbb {Q}$
-generic symplectic forms are dense in
$\mathbb {Q}$
-generic symplectic forms are dense in
![]() $\Omega _0(\rho )$
: let
$\Omega _0(\rho )$
: let
![]() $\omega $
be any invariant symplectic form and
$\omega $
be any invariant symplectic form and
![]() $\delta _i$
be invariant closed two forms whose cohomology classes are a basis for
$\delta _i$
be invariant closed two forms whose cohomology classes are a basis for
![]() $H^2(M,\mathbb {R})$
. Then, for sufficiently small
$H^2(M,\mathbb {R})$
. Then, for sufficiently small
![]() $c_i$
, the two forms
$c_i$
, the two forms
![]() $ \omega + \sum _i c_i\delta _i$
are invariant and symplectic. The result follows readily.
$ \omega + \sum _i c_i\delta _i$
are invariant and symplectic. The result follows readily.
The same argument shows that extended graphs whose moment map labels are small continuous perturbations of the labels associated with
![]() $\rho $
correspond to deformation equivalent symplectic forms invariant under the same circle action. Consequently, for any
$\rho $
correspond to deformation equivalent symplectic forms invariant under the same circle action. Consequently, for any
![]() $S^1$
-manifold
$S^1$
-manifold
![]() $(M,\omega ')$
associated with such an extended graph, there is no ambiguity as to what the Seidel element
$(M,\omega ')$
associated with such an extended graph, there is no ambiguity as to what the Seidel element
![]() $\mathcal {S}([\rho ])\in {QH}_{2n}(M,\omega ')^{\times }$
is.Footnote
1
$\mathcal {S}([\rho ])\in {QH}_{2n}(M,\omega ')^{\times }$
is.Footnote
1
We now observe that, due to deformation invariance of Gromov–Witten invariants, given any symplectic form
![]() $\omega '$
in
$\omega '$
in
![]() $\Omega _0(\rho )$
, the quantum homology ring
$\Omega _0(\rho )$
, the quantum homology ring
![]() ${QH}(M,\omega ')$
is obtained from the quantum ring of a
${QH}(M,\omega ')$
is obtained from the quantum ring of a
![]() $\mathbb {Q}$
-generic class
$\mathbb {Q}$
-generic class
![]() $\omega _{\mu ,c_1,c_2,c_3,c_4}$
by setting the values of the coefficients
$\omega _{\mu ,c_1,c_2,c_3,c_4}$
by setting the values of the coefficients
![]() $\mu ,c_1,c_2,c_3,c_4$
equal to those of
$\mu ,c_1,c_2,c_3,c_4$
equal to those of
![]() $\omega '$
. We thus have a natural specialization map
$\omega '$
. We thus have a natural specialization map
![]() ${QH}(M,\omega _{\mu ,c_1,c_2,c_3,c_4})\to {QH}(M,\omega ')$
, which sends the Seidel element of
${QH}(M,\omega _{\mu ,c_1,c_2,c_3,c_4})\to {QH}(M,\omega ')$
, which sends the Seidel element of
![]() $[\rho ]$
computed relatively to the generic form
$[\rho ]$
computed relatively to the generic form
![]() $\omega _{\mu ,c_1,c_2,c_3,c_4}$
to the one computed relatively to the form
$\omega _{\mu ,c_1,c_2,c_3,c_4}$
to the one computed relatively to the form
![]() $\omega '$
.
$\omega '$
.
Finally, we can apply the previous discussion starting with a Hamiltonian circle actions
![]() $\rho $
on
$\rho $
on
![]() ${M}_{\mu ,c_i=1/2}$
. From the above remarks, we can find a deformation equivalent
${M}_{\mu ,c_i=1/2}$
. From the above remarks, we can find a deformation equivalent
![]() $\mathbb {Q}$
-generic form
$\mathbb {Q}$
-generic form
![]() $\omega _{\mu ;c_1,c_2,c_3,c_4}$
such that the sizes of the blowups satisfy the inequalities
$\omega _{\mu ;c_1,c_2,c_3,c_4}$
such that the sizes of the blowups satisfy the inequalities
![]() $0 < c_4 < c_3 < c_2 < c_1 < c_i+c_j < 1 < \mu $
, with
$0 < c_4 < c_3 < c_2 < c_1 < c_i+c_j < 1 < \mu $
, with
![]() $i,j \in \{1,2,3,4\}$
distinct. Symplectic cohomology classes satisfying this condition are said to be reduced generic or, more simply, generic. By choosing the sizes carefully, we can embed the circle action
$i,j \in \{1,2,3,4\}$
distinct. Symplectic cohomology classes satisfying this condition are said to be reduced generic or, more simply, generic. By choosing the sizes carefully, we can embed the circle action
![]() $\rho $
into a toric action of a toric manifold that is NEF, and for which Theorem 2.2 applies. This allows us to compute the Seidel element of
$\rho $
into a toric action of a toric manifold that is NEF, and for which Theorem 2.2 applies. This allows us to compute the Seidel element of
![]() $\rho $
.
$\rho $
.
In what follows, we consider Hamiltonian actions fixing spheres in the same homology classes as the ones in Proposition 4.2 and we list in Figure 8 their graphs. Note that we use the same notation for the circle actions in the generic case as, for the circle actions along the edge
![]() $MA$
, we do not distinguish one case from the other with regard to notation.
$MA$
, we do not distinguish one case from the other with regard to notation.

Figure 8: Graphs of the circle actions
![]() $z_k$
,
$z_k$
,
![]() $z_{k,i}$
,
$z_{k,i}$
,
![]() $z_{k,ij}$
,
$z_{k,ij}$
,
![]() $z_{k,ijl}$
, and
$z_{k,ijl}$
, and
![]() $z_{k,1234}$
in the generic case.
$z_{k,1234}$
in the generic case.
4.4.2 Computing Seidel elements from toric actions
First, consider the actions
![]() $z_{0,12}, z_{0,13}, z_{0,14}$
and the polygon of Figure 9. The action
$z_{0,12}, z_{0,13}, z_{0,14}$
and the polygon of Figure 9. The action
![]() $z_{0,12}$
corresponds to the circle action whose moment map is the first component of the moment map associated with the toric action
$z_{0,12}$
corresponds to the circle action whose moment map is the first component of the moment map associated with the toric action
![]() $T_{0,12}$
, represented in this figure. Moreover, it is clear that the homology classes of the fixed spheres are
$T_{0,12}$
, represented in this figure. Moreover, it is clear that the homology classes of the fixed spheres are
![]() $B-E_1-E_2$
and
$B-E_1-E_2$
and
![]() $B-E_3-E_4$
. Then Theorem 2.2(2a) yields
$B-E_3-E_4$
. Then Theorem 2.2(2a) yields
where
![]() $\epsilon $
is the maximum of the momentum map of the action
$\epsilon $
is the maximum of the momentum map of the action
![]() $z_{0,12}$
,
$z_{0,12}$
,
![]() $\phi _{\mathrm {max}}(F_{\mathrm {max}})$
, where
$\phi _{\mathrm {max}}(F_{\mathrm {max}})$
, where
![]() $F_{\mathrm {max}}$
is the maximal 2-sphere whose momentum image is the edge in class
$F_{\mathrm {max}}$
is the maximal 2-sphere whose momentum image is the edge in class
![]() $B-E_3-E_4$
, in the normalized polygon. In general, we obtain
$B-E_3-E_4$
, in the normalized polygon. In general, we obtain
One can check that the normalized polygon yields
 $$ \begin{align*}\epsilon = \frac{c_j^3+ 3c_1^2-c_1^3+c_\ell^3+3c_i^2-c_i^3-3\mu}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)}.\end{align*} $$
$$ \begin{align*}\epsilon = \frac{c_j^3+ 3c_1^2-c_1^3+c_\ell^3+3c_i^2-c_i^3-3\mu}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)}.\end{align*} $$
Hence, if
![]() $c_i=1/2$
for all i, we obtain
$c_i=1/2$
for all i, we obtain
![]() $\epsilon = 1/2$
and
$\epsilon = 1/2$
and
 $$ \begin{align} \mathcal S (z_{0,1i})= [B-E_j-E_\ell] \otimes q \, \frac{t^{\frac12}}{1- t^{1-\mu}}, \quad \mbox{where} \quad j \neq \ell \neq i. \end{align} $$
$$ \begin{align} \mathcal S (z_{0,1i})= [B-E_j-E_\ell] \otimes q \, \frac{t^{\frac12}}{1- t^{1-\mu}}, \quad \mbox{where} \quad j \neq \ell \neq i. \end{align} $$
Note that the expression is well defined because
![]() $\mu>1$
.
$\mu>1$
.

Figure 9: Toric action
![]() $T_{0,12}$
.
$T_{0,12}$
.
Consider now the polygon of Figure 10, which represents a toric action on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
, and for which the homology classes of the edges are represented in the figure. The graph of the circle action obtained by the projection of the polygon onto the x-axis is also represented in Figure 10. Note that it becomes the action
${M}_{\mu ,c_1,c_2,c_3,c_4}$
, and for which the homology classes of the edges are represented in the figure. The graph of the circle action obtained by the projection of the polygon onto the x-axis is also represented in Figure 10. Note that it becomes the action
![]() $z_1$
defined in Figure 5 if
$z_1$
defined in Figure 5 if
![]() $c_i=1/2$
for all i.
$c_i=1/2$
for all i.

Figure 10: Toric action
![]() $T_1$
and its projection to the x-axis.
$T_1$
and its projection to the x-axis.
Now, Theorem 2.2(2a) gives
where in this case the maximum of the momentum map on the invariant sphere is given by
 $$ \begin{align*}\epsilon = \frac{-1 -c_1^3 + 3c_1^2 +3c_2^2-c_2^3 +3c_3^2 -c_3^3+3c_4^2-c_4^3+ 3c_1c_4^2-3c_3c_4^2-3\mu}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)},\end{align*} $$
$$ \begin{align*}\epsilon = \frac{-1 -c_1^3 + 3c_1^2 +3c_2^2-c_2^3 +3c_3^2 -c_3^3+3c_4^2-c_4^3+ 3c_1c_4^2-3c_3c_4^2-3\mu}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)},\end{align*} $$
which is simply equal to
![]() $1/2$
if
$1/2$
if
![]() $c_i=1/2$
for all i. Therefore, we obtain
$c_i=1/2$
for all i. Therefore, we obtain
 $$ \begin{align} \mathcal S(z_1)= [B+F-E_1-E_2-E_3-E_4] \otimes q \, \frac{t^{\frac12}}{1- t^{1-\mu}}. \end{align} $$
$$ \begin{align} \mathcal S(z_1)= [B+F-E_1-E_2-E_3-E_4] \otimes q \, \frac{t^{\frac12}}{1- t^{1-\mu}}. \end{align} $$
Finally, we compute the Seidel element of the circle action
![]() $z_{1,4}$
, seen as an element of the fundamental group of
$z_{1,4}$
, seen as an element of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,c_2,c_3,c_4})$
. In order to do that, first consider the Delzant polygon of Figure 11. It represents a toric action on
$\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,c_2,c_3,c_4})$
. In order to do that, first consider the Delzant polygon of Figure 11. It represents a toric action on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
and its projections onto the x-axis and the y-axis are represented in Figure 12. Note that the projection onto the x-axis corresponds to the graph of the action
${M}_{\mu ,c_1,c_2,c_3,c_4}$
and its projections onto the x-axis and the y-axis are represented in Figure 12. Note that the projection onto the x-axis corresponds to the graph of the action
![]() $z_{1,4}$
given in Figure 6. Let us denote the action whose graph is obtained by projection onto the y-axis by
$z_{1,4}$
given in Figure 6. Let us denote the action whose graph is obtained by projection onto the y-axis by
![]() $s_{1,4}$
.
$s_{1,4}$
.

Figure 11: Toric action
![]() $(z_{1,4}, s_{1,4})$
.
$(z_{1,4}, s_{1,4})$
.

Figure 12: Graphs of circle actions
![]() $z_{1,4}$
and
$z_{1,4}$
and
![]() $s_{1,4}$
, respectively.
$s_{1,4}$
, respectively.
Since
![]() $c_1(B-F-E_4)= -1 <0$
, the complex manifold corresponding to Figure 11 is not NEF and we cannot apply immediately Theorem 2.2 to compute the Seidel element of
$c_1(B-F-E_4)= -1 <0$
, the complex manifold corresponding to Figure 11 is not NEF and we cannot apply immediately Theorem 2.2 to compute the Seidel element of
![]() $z_{1,4}$
. Instead, we need to consider some auxiliary polygons for which the underlying complex manifolds are NEF and relate the circle actions represented on those polygons with the actions
$z_{1,4}$
. Instead, we need to consider some auxiliary polygons for which the underlying complex manifolds are NEF and relate the circle actions represented on those polygons with the actions
![]() $z_{1,4}$
and
$z_{1,4}$
and
![]() $s_{1,4}$
. More precisely, consider the Delzant polygon, on the left in Figure 13 and apply the
$s_{1,4}$
. More precisely, consider the Delzant polygon, on the left in Figure 13 and apply the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align} \left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right) \end{align} $$
$$ \begin{align} \left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right) \end{align} $$
to this polygon as well as to the polygon of Figure 11. Then consider the projection onto the y-axis of the two transformed polygons and denote the action obtained this way from the polygon of Figure 13 by
![]() $t_{1,4}$
. It is easy to check that the two graphs coincide, which implies that as elements of
$t_{1,4}$
. It is easy to check that the two graphs coincide, which implies that as elements of
![]() $\pi _1(\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,c_2,c_3,c_4}))$
the following identification holds
$\pi _1(\operatorname {\mathrm{Symp}}_h ({M}_{\mu ,c_1,c_2,c_3,c_4}))$
the following identification holds

Figure 13: Polygon representing an NEF complex manifold and its transformation by the
![]() $GL(2, \mathbb {Z})$
matrix (4.3).
$GL(2, \mathbb {Z})$
matrix (4.3).
On the other hand, consider the polygon on the left in Figure 14, which represents a toric action, denoted by
![]() $(x_1,y_1)$
, on
$(x_1,y_1)$
, on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
and its transformation by the same
${M}_{\mu ,c_1,c_2,c_3,c_4}$
and its transformation by the same
![]() $GL(2,\mathbb {Z})$
matrix (4.3). The projection of the transformed polygon onto the y-axis yields a graph that, up to translation, coincides with the graph of the action
$GL(2,\mathbb {Z})$
matrix (4.3). The projection of the transformed polygon onto the y-axis yields a graph that, up to translation, coincides with the graph of the action
![]() $s_{1,4}$
, which implies that
$s_{1,4}$
, which implies that
![]() $s_{1,4}=x_1+y_1.$
$s_{1,4}=x_1+y_1.$

Figure 14: Toric action
![]() $(x_1,y_1)$
and its transformation by the
$(x_1,y_1)$
and its transformation by the
![]() $GL(2, \mathbb {Z})$
matrix (4.3).
$GL(2, \mathbb {Z})$
matrix (4.3).
Note that, in Figure 14, we have
![]() $c_1(A) \geq 0$
for all homology classes A of the fixed spheres corresponding to edges of the polygon, so we can apply Theorem 2.2 to compute the Seidel element of
$c_1(A) \geq 0$
for all homology classes A of the fixed spheres corresponding to edges of the polygon, so we can apply Theorem 2.2 to compute the Seidel element of
![]() $s_{1,4}=x_1+y_1$
. Moreover, it follows from equation (4.4) that the Seidel element of
$s_{1,4}=x_1+y_1$
. Moreover, it follows from equation (4.4) that the Seidel element of
![]() $z_{1,4}$
is given by
$z_{1,4}$
is given by
More precisely, Theorem 2.2(3a) yields the Seidel elements of
![]() $t_{1,4}$
and
$t_{1,4}$
and
![]() $-s_{1,4}$
, which are readable directly from the polygons on the right in Figures 13 and 14.
$-s_{1,4}$
, which are readable directly from the polygons on the right in Figures 13 and 14.
 $$ \begin{align*} & \mathcal S(t_{1,4}) = E_2 \otimes q t^{\mu +1 -c_1-c_2 -\gamma} - (E_1-E_2) \otimes q \frac{t^{\mu + 1-2c_1-\gamma}}{1-t^{c_2-c_1}},\\ & \mathcal S(s_{1,4})^{-1} = E_3 \otimes q t^{\beta-c_3} - (F-E_3-E_4) \otimes q \frac{t^{\beta +c_4-1}}{1-t^{c_3+c_4-1}}, \end{align*} $$
$$ \begin{align*} & \mathcal S(t_{1,4}) = E_2 \otimes q t^{\mu +1 -c_1-c_2 -\gamma} - (E_1-E_2) \otimes q \frac{t^{\mu + 1-2c_1-\gamma}}{1-t^{c_2-c_1}},\\ & \mathcal S(s_{1,4})^{-1} = E_3 \otimes q t^{\beta-c_3} - (F-E_3-E_4) \otimes q \frac{t^{\beta +c_4-1}}{1-t^{c_3+c_4-1}}, \end{align*} $$
where the exponents of the higher degree terms, namely of
![]() $E_2$
and
$E_2$
and
![]() $E_3$
, are the maximal values of the momentum map for the normalized polygons. Therefore, one can check that
$E_3$
, are the maximal values of the momentum map for the normalized polygons. Therefore, one can check that
 $$ \begin{align*}\gamma = \frac{-1+ 3c_1^2 -3c_1^3 +3c_2^2 -3c_1c_2^2 -2c_2^3 +c_3^3 +c_4^3 +3c_1^2\mu+3c_2^2\mu -3\mu^2}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)}\end{align*} $$
$$ \begin{align*}\gamma = \frac{-1+ 3c_1^2 -3c_1^3 +3c_2^2 -3c_1c_2^2 -2c_2^3 +c_3^3 +c_4^3 +3c_1^2\mu+3c_2^2\mu -3\mu^2}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)}\end{align*} $$
and
 $$ \begin{align*}\beta=\frac{3c_1^2 -2c_1^3 +3c_2^2 -3c_1c_2^2 -c_2^3 +2c_3^3 +3c_4^2-3\mu +3c_1^2\mu+3c_2^2\mu -3\mu^2}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)}.\end{align*} $$
$$ \begin{align*}\beta=\frac{3c_1^2 -2c_1^3 +3c_2^2 -3c_1c_2^2 -c_2^3 +2c_3^3 +3c_4^2-3\mu +3c_1^2\mu+3c_2^2\mu -3\mu^2}{3(c_1^2+c_2^2+c_3^2+c_4^2-2\mu)}.\end{align*} $$
Using [Reference Crauder, Miranda, Dijkgraaf, Faber and van der Geer7, Proposition 5.3], we can now compute the quantum product (4.5) (we leave the details to the interested reader since it is a long and boring computation) and finally obtain
where the identity
![]() $\nVdash $
is the homology class of the manifold,
$\nVdash $
is the homology class of the manifold,
![]() $[\mathbb C\mathbb P^2\#\, 5\overline { \mathbb C\mathbb P^2}] \in H_4(\mathbb C\mathbb P^2\#\, 5\overline { \mathbb C\mathbb P^2}, \mathbb {Z})$
. In what follows, we will suppress the identity from the expressions in order to simplify the notation.
$[\mathbb C\mathbb P^2\#\, 5\overline { \mathbb C\mathbb P^2}] \in H_4(\mathbb C\mathbb P^2\#\, 5\overline { \mathbb C\mathbb P^2}, \mathbb {Z})$
. In what follows, we will suppress the identity from the expressions in order to simplify the notation.
If
![]() $c_i=1/2$
for all i, then
$c_i=1/2$
for all i, then
Note that this result agrees with McDuff–Tolman’s result as the leading term is given by the homology class of the edge where the action is maximal.
Remark 4.6 In a similar way, we can compute the Seidel element of the inverse of
![]() $z_{1,4}$
:
$z_{1,4}$
:
 $$ \begin{align} \begin{split} \mathcal S(z_{1,4})^{-1} = [(B-F -E_4)\otimes q & + [pt] \otimes q^2 \, t^{\frac32 - \mu} + (3F -E_1-E_2-E_3 +E_4)\otimes q\, t^{1 - \mu} \\ & + (B-E_4)\otimes q \, t^{2 - 2\mu} + t^{\frac12 - \mu}(1 + t^{2 - 2\mu})] \frac{t^{\frac{1-3\mu}{3(1-2\mu)}}}{(1-t^{1 - \mu})^4}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathcal S(z_{1,4})^{-1} = [(B-F -E_4)\otimes q & + [pt] \otimes q^2 \, t^{\frac32 - \mu} + (3F -E_1-E_2-E_3 +E_4)\otimes q\, t^{1 - \mu} \\ & + (B-E_4)\otimes q \, t^{2 - 2\mu} + t^{\frac12 - \mu}(1 + t^{2 - 2\mu})] \frac{t^{\frac{1-3\mu}{3(1-2\mu)}}}{(1-t^{1 - \mu})^4}. \end{split} \end{align} $$
Since all the possible Hamiltonian circle actions on
![]() ${M}_{\mu ,c_i=1/2}$
have semi-free maximal sets, the McDuff–Tolman result always applies. Observe that, when
${M}_{\mu ,c_i=1/2}$
have semi-free maximal sets, the McDuff–Tolman result always applies. Observe that, when
![]() $\mu> \frac 32$
, the leading term is the homology class
$\mu> \frac 32$
, the leading term is the homology class
![]() $B+F -E_4$
, corresponding to the homology class of the edge where the moment map is maximal, in accordance with the McDuff–Tolman formula. Otherwise, if
$B+F -E_4$
, corresponding to the homology class of the edge where the moment map is maximal, in accordance with the McDuff–Tolman formula. Otherwise, if
![]() $1 < \mu \leq \frac 32$
, the leading term is given by the class of a point, showing that the quantum homology class (4.7) is not the image of an effective Hamiltonian action under the Seidel homomorphism.
$1 < \mu \leq \frac 32$
, the leading term is given by the class of a point, showing that the quantum homology class (4.7) is not the image of an effective Hamiltonian action under the Seidel homomorphism.
4.4.3 Injectivity of the Seidel morphism for
 $\mu>3/2$
$\mu>3/2$
Proposition 4.7 Consider the circle actions
![]() $z_{0,1i}, i=2,3,4$
,
$z_{0,1i}, i=2,3,4$
,
![]() $z_1,$
and
$z_1,$
and
![]() $z_{1,4}$
, defined in Figure 7. If
$z_{1,4}$
, defined in Figure 7. If
![]() $\mu> \frac 32$
and
$\mu> \frac 32$
and
![]() $c_1=c_2=c_3=c_4=1/2$
, then the Seidel elements of these five circle actions generate a free subgroup of rank 5 in the group of invertible elements of the quantum homology.▪
$c_1=c_2=c_3=c_4=1/2$
, then the Seidel elements of these five circle actions generate a free subgroup of rank 5 in the group of invertible elements of the quantum homology.▪
Proof Using the notation of Section 3 for the quantum homology ring, the Seidel elements of these five circle actions are given by the following expressions:
 $$ \begin{align} \quad \ \ \ \mathcal S (z_1) = b_{12} + f_{34}, \quad \mathcal S (z_{1,4}) = \left( b_{12} + f_{34}+e_4 + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right) (1-t^{1-\mu})t^{\frac{1}{6(1-2\mu)}}. \hspace{-1pc} \end{align} $$
$$ \begin{align} \quad \ \ \ \mathcal S (z_1) = b_{12} + f_{34}, \quad \mathcal S (z_{1,4}) = \left( b_{12} + f_{34}+e_4 + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right) (1-t^{1-\mu})t^{\frac{1}{6(1-2\mu)}}. \hspace{-1pc} \end{align} $$
In order to show they are linearly independent, we first consider a simplification of the quantum algebra, namely, we set the
![]() $b_{ij},$
for all
$b_{ij},$
for all
![]() $i,j$
, equal to an element b, the
$i,j$
, equal to an element b, the
![]() $f_{ij}$
to f, and
$f_{ij}$
to f, and
![]() $e_j$
to e. Then the quantum homology algebra becomes isomorphic to the
$e_j$
to e. Then the quantum homology algebra becomes isomorphic to the
![]() $\Pi ^{\mathrm {univ}}$
-algebra
$\Pi ^{\mathrm {univ}}$
-algebra
where
![]() $I'$
is the ideal generated by
$I'$
is the ideal generated by
 $$ \begin{gather*} (1) \ f^2 = 0, \qquad (2) \ b^2 =1, \qquad (3) \ f(b+1)=0, \\ (4) \ f \left( e + \frac{t^{1-\mu}}{1-t^{1-\mu}} \right) = 0, \qquad (5) \ b \left( e + \frac{t^{1-\mu}}{1-t^{1-\mu}} \right) = f+ e + \frac{t^{1-\mu}}{1-t^{1-\mu}}, \\ (6) \ e^2 = 2(b+f+e) \frac{t^{1-\mu}}{1-t^{1-\mu}} + 2\frac{t^{1-\mu}}{(1-t^{1-\mu})^2} + \frac{t^{2-2\mu}}{(1-t^{1-\mu})^2}. \end{gather*} $$
$$ \begin{gather*} (1) \ f^2 = 0, \qquad (2) \ b^2 =1, \qquad (3) \ f(b+1)=0, \\ (4) \ f \left( e + \frac{t^{1-\mu}}{1-t^{1-\mu}} \right) = 0, \qquad (5) \ b \left( e + \frac{t^{1-\mu}}{1-t^{1-\mu}} \right) = f+ e + \frac{t^{1-\mu}}{1-t^{1-\mu}}, \\ (6) \ e^2 = 2(b+f+e) \frac{t^{1-\mu}}{1-t^{1-\mu}} + 2\frac{t^{1-\mu}}{(1-t^{1-\mu})^2} + \frac{t^{2-2\mu}}{(1-t^{1-\mu})^2}. \end{gather*} $$
Moreover, it is clear that the Seidel elements simplify to
 $$ \begin{gather*} \mathcal S(z_{0,12}) = \mathcal S (z_{0,13}) = \mathcal S (z_{0,14}) = b, \quad \mathcal S(z_1) = b +f, \\ \mbox{and} \quad \mathcal S(z_{1,4}) = \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)(1-t^{1-\mu})\, t^{\frac{1}{6(1-2\mu)}}. \end{gather*} $$
$$ \begin{gather*} \mathcal S(z_{0,12}) = \mathcal S (z_{0,13}) = \mathcal S (z_{0,14}) = b, \quad \mathcal S(z_1) = b +f, \\ \mbox{and} \quad \mathcal S(z_{1,4}) = \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)(1-t^{1-\mu})\, t^{\frac{1}{6(1-2\mu)}}. \end{gather*} $$
We postpone the proof of the next two lemmas to Appendix A.
Lemma 4.8 Consider the elements b,
![]() $b+f$
, and
$b+f$
, and
![]() $\left ( b + f + e + \frac {t^{1-\mu }}{1-t^{1-\mu }}\right )(1-t^{1-\mu })\, t^{\frac {1}{6(1-2\mu )}}$
contained in the subgroup of invertible elements of the algebra
$\left ( b + f + e + \frac {t^{1-\mu }}{1-t^{1-\mu }}\right )(1-t^{1-\mu })\, t^{\frac {1}{6(1-2\mu )}}$
contained in the subgroup of invertible elements of the algebra
![]() $ \Pi ^{\mathrm {univ}} [f,b,e]/ I'$
. They are linearly independent, that is, if
$ \Pi ^{\mathrm {univ}} [f,b,e]/ I'$
. They are linearly independent, that is, if
 $$ \begin{align*}b^\alpha \, (b+f)^\beta \, \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma \, t^{\frac{\gamma}{6(1-2\mu)}}=1, \quad \mbox{where} \quad \alpha, \beta, \gamma \in \mathbb{Z},\end{align*} $$
$$ \begin{align*}b^\alpha \, (b+f)^\beta \, \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma \, t^{\frac{\gamma}{6(1-2\mu)}}=1, \quad \mbox{where} \quad \alpha, \beta, \gamma \in \mathbb{Z},\end{align*} $$
then
![]() $\alpha =\beta =\gamma =0$
.
$\alpha =\beta =\gamma =0$
.
Lemma 4.9 The Seidel elements
![]() $b_{34}$
,
$b_{34}$
,
![]() $b_{24}$
, and
$b_{24}$
, and
![]() $b_{23}$
are linearly independent in the subgroup of invertible elements of the quantum homology
$b_{23}$
are linearly independent in the subgroup of invertible elements of the quantum homology
![]() ${QH}_4^\times ({M}_{\mu ,c_i=1/2})$
.
${QH}_4^\times ({M}_{\mu ,c_i=1/2})$
.
Now, putting together the two lemmas, it is easy to conclude that the five Seidel elements
![]() $\mathcal S (z_{0,12}), \mathcal S (z_{0,13}),$
$\mathcal S (z_{0,12}), \mathcal S (z_{0,13}),$
![]() $\mathcal S (z_{0,14}), \mathcal S (z_1)$
, and
$\mathcal S (z_{0,14}), \mathcal S (z_1)$
, and
![]() $ \mathcal S (z_{1,4})$
are linearly independent. If
$ \mathcal S (z_{1,4})$
are linearly independent. If
then
 $$ \begin{gather*} b_{34}^{\alpha_1}\ b_{24}^{\alpha_2}\ b_{23}^{\alpha_3}\ (b_{12} + f_{34})^\beta\ \left( b_{12} + f_{34}+e_4 + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma\, t^{\frac{\gamma}{6(1-2\mu)}}=1. \end{gather*} $$
$$ \begin{gather*} b_{34}^{\alpha_1}\ b_{24}^{\alpha_2}\ b_{23}^{\alpha_3}\ (b_{12} + f_{34})^\beta\ \left( b_{12} + f_{34}+e_4 + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma\, t^{\frac{\gamma}{6(1-2\mu)}}=1. \end{gather*} $$
Using the simplification above of the quantum homology algebra, one obtains
 $$ \begin{align*}b ^{\alpha_1+\alpha_2+\alpha_3}\, (b+f)^\beta \, \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma \, t^{\frac{\gamma}{6(1-2\mu)}}=1.\end{align*} $$
$$ \begin{align*}b ^{\alpha_1+\alpha_2+\alpha_3}\, (b+f)^\beta \, \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma \, t^{\frac{\gamma}{6(1-2\mu)}}=1.\end{align*} $$
From Lemma 4.8, we conclude that
![]() $\alpha _1+\alpha _2+\alpha _3=\beta =\gamma =0$
. Therefore,
$\alpha _1+\alpha _2+\alpha _3=\beta =\gamma =0$
. Therefore,
and Lemma 4.9 implies that
![]() $\alpha _1=\alpha _2=\alpha _3=0$
, so the five Seidel elements are linearly independent.
$\alpha _1=\alpha _2=\alpha _3=0$
, so the five Seidel elements are linearly independent.
Next, we study the action of
![]() $\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
on
$\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
on
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
.
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
.
Proposition 4.10 If
![]() $(M,\omega )$
belongs to the edge
$(M,\omega )$
belongs to the edge
![]() $MA$
of the reduced symplectic cone, and if
$MA$
of the reduced symplectic cone, and if
![]() $\mu>3/2$
, then the Seidel homomorphism is injective and the action of
$\mu>3/2$
, then the Seidel homomorphism is injective and the action of
![]() $\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
on
$\pi _0(\operatorname {\mathrm{Symp}}_h(M,\omega ))$
on
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
is trivial.▪
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
is trivial.▪
Proof The Seidel homomorphism factors through

Consider arbitrary lifts in
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))\simeq \mathbb {Z}^5$
of the five actions. By Proposition 4.7, these lifts generate a free subgroup of rank 5 in
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))\simeq \mathbb {Z}^5$
of the five actions. By Proposition 4.7, these lifts generate a free subgroup of rank 5 in
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))\simeq \mathbb {Z}^5$
on which the Seidel homomorphism
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))\simeq \mathbb {Z}^5$
on which the Seidel homomorphism
![]() $\mathcal {S}$
is injective. Consequently,
$\mathcal {S}$
is injective. Consequently,
![]() $\mathcal {S}$
is injective on the whole group
$\mathcal {S}$
is injective on the whole group
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
. Since
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
. Since
is also of rank
![]() $5$
, the triviality of the action follows readily.
$5$
, the triviality of the action follows readily.
Corollary 4.11 Each labeled extended graph in Figures 5–7 corresponds to a well-defined homotopy class in
![]() $\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
.
$\pi _1(\operatorname {\mathrm{Symp}}_0(M,\omega ))$
.
We now prove Theorem 1.3.
Proof Consider the extended labeled graph
![]() $z_{0,1i}$
,
$z_{0,1i}$
,
![]() $i=2,3,4$
,
$i=2,3,4$
,
![]() $z_1$
, and
$z_1$
, and
![]() $z_{1,4}$
of Figure 7. It follows from Corollary 4.11 that these graphs define five elements of
$z_{1,4}$
of Figure 7. It follows from Corollary 4.11 that these graphs define five elements of
![]() $\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
. By Proposition 4.7, these five elements are linearly independent. This proves the second statement of the theorem. The first statement follows immediately from Remark 4.3.
$\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2}))$
. By Proposition 4.7, these five elements are linearly independent. This proves the second statement of the theorem. The first statement follows immediately from Remark 4.3.
Note that the proof of Proposition 4.7 does not depend on the value of
![]() $\mu $
, in addition to the condition
$\mu $
, in addition to the condition
![]() $\mu>1$
. It follows that the five quantum homology classes
$\mu>1$
. It follows that the five quantum homology classes
![]() $b_{34}$
,
$b_{34}$
,
![]() $b_{24}$
,
$b_{24}$
,
![]() $b_{23}$
,
$b_{23}$
,
![]() $b_{12}+f_{34}$
, and
$b_{12}+f_{34}$
, and
 $$ \begin{align} \left( b_{12} + f_{34}+e_4 + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)(1-t^{1-\mu})\, t^{\frac{1}{6(1-2\mu)}} \end{align} $$
$$ \begin{align} \left( b_{12} + f_{34}+e_4 + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)(1-t^{1-\mu})\, t^{\frac{1}{6(1-2\mu)}} \end{align} $$
generate a free subgroup of rank 5 in the group of invertible elements of the quantum homology, for every
![]() $\mu>1$
. This observation proves the following result.
$\mu>1$
. This observation proves the following result.
Proposition 4.12 When
![]() $ 1 < \mu \leq \frac 32$
, the quantum class (
4.11
) is not contained in the
$ 1 < \mu \leq \frac 32$
, the quantum class (
4.11
) is not contained in the
![]() $\mathbb {Q}$
-subspace spanned by circle actions inside the
$\mathbb {Q}$
-subspace spanned by circle actions inside the
![]() $\mathbb {Q}$
-vector space formed by Seidel elements.▪
$\mathbb {Q}$
-vector space formed by Seidel elements.▪
4.5 Relations between Hamiltonian circle actions on
 ${M}_{\mu ,c_1,c_2,c_3,c_4}$
${M}_{\mu ,c_1,c_2,c_3,c_4}$
In this section, we prove our second main result. The main step is to obtain a classification of all circle actions in
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
, which also shows that although we have more and more circle actions on
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
, which also shows that although we have more and more circle actions on
![]() ${M}_{\mu ,c_i=1/2}$
as we increase the value of
${M}_{\mu ,c_i=1/2}$
as we increase the value of
![]() $\mu $
, they do not give new generators in the fundamental group of the symplectomorphism group
$\mu $
, they do not give new generators in the fundamental group of the symplectomorphism group
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
. We show this by describing relations between the loops
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_i=1/2})$
. We show this by describing relations between the loops
![]() $z_k$
,
$z_k$
,
![]() $z_{k,i}$
,
$z_{k,i}$
,
![]() $z_{k,ij}$
,
$z_{k,ij}$
,
![]() $z_{k,ijl}$
, and
$z_{k,ijl}$
, and
![]() $z_{k,1234}$
, described in Section 4.3, that come from embedding pairs of loops inside torus actions. The tools we use are Delzant’s classification of toric actions and Karshon’s classification of Hamiltonian circle actions. We always consider the actions in the generic case, that is, when
$z_{k,1234}$
, described in Section 4.3, that come from embedding pairs of loops inside torus actions. The tools we use are Delzant’s classification of toric actions and Karshon’s classification of Hamiltonian circle actions. We always consider the actions in the generic case, that is, when
![]() $0 < c_4 < c_3 < c_2 < c_1 < c_i+c_j < 1 < \mu $
, with
$0 < c_4 < c_3 < c_2 < c_1 < c_i+c_j < 1 < \mu $
, with
![]() $i,j \in \{1,2,3,4\}$
, in order to obtain the relations between the loops. As explained in Section 4.4.1, these relations between actions induce relations between Seidel elements in the quantum ring associated with the generic symplectic form. These relations map to similar relations in the quantum homology ring of
$i,j \in \{1,2,3,4\}$
, in order to obtain the relations between the loops. As explained in Section 4.4.1, these relations between actions induce relations between Seidel elements in the quantum ring associated with the generic symplectic form. These relations map to similar relations in the quantum homology ring of
![]() ${M}_{\mu ,c_i=1/2}$
. By injectivity of the Seidel homomorphism when
${M}_{\mu ,c_i=1/2}$
. By injectivity of the Seidel homomorphism when
![]() $\mu>3/2$
, we deduce that these relations hold in
$\mu>3/2$
, we deduce that these relations hold in
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
as well.
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
as well.
Consider the manifold
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
endowed with a toric action, which we denote by
${M}_{\mu ,c_1,c_2,c_3,c_4}$
endowed with a toric action, which we denote by
![]() $T_k$
, such that the momentum polygon is given in Figure 15. In addition to the homology classes indicated in the figure, it should be clear that the classes
$T_k$
, such that the momentum polygon is given in Figure 15. In addition to the homology classes indicated in the figure, it should be clear that the classes
![]() $E_3-E_4$
and
$E_3-E_4$
and
![]() $E_4$
are also represented in the bottom edges. Projecting onto the x-axis and the y-axis, we obtain the graphs in Figure 16 of the actions
$E_4$
are also represented in the bottom edges. Projecting onto the x-axis and the y-axis, we obtain the graphs in Figure 16 of the actions
![]() $z_k$
and
$z_k$
and
![]() $w_k$
, respectively, whose momentum maps are the first and second coordinates of the momentum map of the action
$w_k$
, respectively, whose momentum maps are the first and second coordinates of the momentum map of the action
![]() $T_k$
.
$T_k$
.

Figure 15: Toric action
![]() $T_k$
.
$T_k$
.

Figure 16: Graphs of the circle actions
![]() $z_k$
and
$z_k$
and
![]() $w_k$
, respectively.
$w_k$
, respectively.
Performing the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ j & -1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ j & -1 \end{array} \!\right)\end{align*} $$
to the polygon of Figure 15 yields a new polygon representing the same toric manifold. This new polygon has vertices
 $$ \begin{align*} & (1, j- \mu), \ (0, k-\mu), \ (0,0), \ (1-c_1, (j+k)(1-c_1)), \ (1-c_2, (j+k)(1-c_2)-c_1+c_2), \\ & (1-c_3, (j+k)(1-c_3)-c_1-c_2+2c_3), \ (1-c_4, (j+k)(1-c_4)-c_1-c_2-c_3+3c_4), \ \mbox{and} \\ & (1, j+k-c_1-c_2-c_3-c_4). \end{align*} $$
$$ \begin{align*} & (1, j- \mu), \ (0, k-\mu), \ (0,0), \ (1-c_1, (j+k)(1-c_1)), \ (1-c_2, (j+k)(1-c_2)-c_1+c_2), \\ & (1-c_3, (j+k)(1-c_3)-c_1-c_2+2c_3), \ (1-c_4, (j+k)(1-c_4)-c_1-c_2-c_3+3c_4), \ \mbox{and} \\ & (1, j+k-c_1-c_2-c_3-c_4). \end{align*} $$
Then perform the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ k & -1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ k & -1 \end{array} \!\right)\end{align*} $$
to the polygon of the toric action
![]() $T_j$
. It should be clear, looking at the coordinates of the two transformed polygons, that projecting both polygons onto the y-axis, we obtain the same graph, which implies that
$T_j$
. It should be clear, looking at the coordinates of the two transformed polygons, that projecting both polygons onto the y-axis, we obtain the same graph, which implies that
Now, consider the toric action
![]() $T_0$
on
$T_0$
on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the Delzant polygon of Figure 17. Consider also its projections, in Figure 18, to the x-axis and the y-axis representing circle actions that we denote by
${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the Delzant polygon of Figure 17. Consider also its projections, in Figure 18, to the x-axis and the y-axis representing circle actions that we denote by
![]() $(z_0, y_0)$
.
$(z_0, y_0)$
.

Figure 17: Toric action
![]() $T_0$
.
$T_0$
.

Figure 18: Graphs of circle actions
![]() $z_0$
and
$z_0$
and
![]() $y_0$
, respectively.
$y_0$
, respectively.
Again, performing the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -k & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -k & 1 \end{array} \!\right)\end{align*} $$
to the polygon of Figure 17 yields a new polygon representing the same toric manifold. This new polygon has vertices
 $$ \begin{align*} & (0, \mu), (1, \mu-k), (0,0), (1-c_1, -k(1-c_1)), (1-c_2, -k(1-c_2)+c_1-c_2), \\ & (1-c_3, -k(1-c_3)+c_1+c_2-2c_3), (1-c_4, -k(1-c_4)+c_1+c_2+c_3-3c_4), \ \mbox{and} \\ & (1, -k+c_1+c_2+c_3+c_4). \end{align*} $$
$$ \begin{align*} & (0, \mu), (1, \mu-k), (0,0), (1-c_1, -k(1-c_1)), (1-c_2, -k(1-c_2)+c_1-c_2), \\ & (1-c_3, -k(1-c_3)+c_1+c_2-2c_3), (1-c_4, -k(1-c_4)+c_1+c_2+c_3-3c_4), \ \mbox{and} \\ & (1, -k+c_1+c_2+c_3+c_4). \end{align*} $$
Therefore, projecting this new polygon onto the y-axis, it is easy to check that we obtain the graph of the circle action
![]() $w_k$
, which means we have the following identification:
$w_k$
, which means we have the following identification:
Combining equations (4.12) and (4.13) yields
Finally, setting
![]() $j=1$
implies that
$j=1$
implies that
Next, we use a similar argument in order to obtain more relations between other circle actions listed in Proposition 4.2. For that, we need to consider the toric action
![]() $T_{k,4}$
on
$T_{k,4}$
on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
, represented in the momentum polytope in Figure 19. Note that the two edges without homology labels represent the classes,
${M}_{\mu ,c_1,c_2,c_3,c_4}$
, represented in the momentum polytope in Figure 19. Note that the two edges without homology labels represent the classes,
![]() $E_2-E_3$
and
$E_2-E_3$
and
![]() $E_3$
.
$E_3$
.

Figure 19: Toric action
![]() $T_{k,4}$
.
$T_{k,4}$
.
Projecting onto the x- and y-axes, we obtain the graphs in Figure 20 of the actions
![]() $(z_{k,4},w_{k,4})$
, respectively, whose momentum maps are the first and second coordinates of the momentum map of the action
$(z_{k,4},w_{k,4})$
, respectively, whose momentum maps are the first and second coordinates of the momentum map of the action
![]() $T_{k,4}$
.
$T_{k,4}$
.

Figure 20: Graphs of the circle actions
![]() $z_{k,4}$
and
$z_{k,4}$
and
![]() $w_{k,4}$
.
$w_{k,4}$
.
Using the same argument as before, that is, performing the
![]() $GL(2, \mathbb {Z})$
transformation represented by the following matrix
$GL(2, \mathbb {Z})$
transformation represented by the following matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ j & -1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ j & -1 \end{array} \!\right)\end{align*} $$
on the polygon of Figure 19 yields a new polygon with vertices
 $$ \begin{align*} & (1, j+k-c_1-c_2-c_3), (1, j- \mu), (0, k-\mu), (0,-c_4), \ (c_4, (j+k)c_4), (1-c_1, (j+k)(1-c_1)), \\ & (1-c_2, (j+k)(1-c_2)-c_1+c_2), \ \mbox{and} \ (1-c_3, (j+k)(1-c_3)-c_1-c_2+2c_3). \end{align*} $$
$$ \begin{align*} & (1, j+k-c_1-c_2-c_3), (1, j- \mu), (0, k-\mu), (0,-c_4), \ (c_4, (j+k)c_4), (1-c_1, (j+k)(1-c_1)), \\ & (1-c_2, (j+k)(1-c_2)-c_1+c_2), \ \mbox{and} \ (1-c_3, (j+k)(1-c_3)-c_1-c_2+2c_3). \end{align*} $$
Interchanging the role of k and j and then projecting onto the y-axis, it follows that
Now, consider the toric action on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygon of Figure 21. Consider also its projections, in Figure 22, to the x- and y-axes representing circle actions that we denote by
${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygon of Figure 21. Consider also its projections, in Figure 22, to the x- and y-axes representing circle actions that we denote by
![]() $(z_{0,4}, y_{0,4})$
.
$(z_{0,4}, y_{0,4})$
.

Figure 21: Toric action
![]() $T_{0,4}$
.
$T_{0,4}$
.

Figure 22: Graphs of the circle actions
![]() $z_{0,4}$
and
$z_{0,4}$
and
![]() $y_{0,4}$
, respectively.
$y_{0,4}$
, respectively.
In this case, performing the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -k & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -k & 1 \end{array} \!\right)\end{align*} $$
to the polygon of Figure 21 yields a new polygon whose vertices are
 $$ \begin{align*} & (0, \mu), (1, \mu-k), (0,c_4), (c_4, -kc_4), (1-c_1, -k(1-c_1)), (1-c_2, -k(1-c_2)+c_1-c_2), \\ & (1-c_3, -k(1-c_3)+c_1+c_2-2c_3), \ \mbox{and} \ (1, -k+c_1+c_2+c_3). \end{align*} $$
$$ \begin{align*} & (0, \mu), (1, \mu-k), (0,c_4), (c_4, -kc_4), (1-c_1, -k(1-c_1)), (1-c_2, -k(1-c_2)+c_1-c_2), \\ & (1-c_3, -k(1-c_3)+c_1+c_2-2c_3), \ \mbox{and} \ (1, -k+c_1+c_2+c_3). \end{align*} $$
Therefore, projecting this new polygon onto the y-axis, it is clear that one obtains the graph of the circle action
![]() $w_{k,4}$
, which means we have the following relation:
$w_{k,4}$
, which means we have the following relation:
Combining equations (4.15) and (4.16) yields
and setting
![]() $j=1$
implies that
$j=1$
implies that
Therefore, it is clear that, in fact, we have the following identifications:
Using a similar argument three more times applied to the appropriate toric actions on the manifold
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
, it follows that the following identifications hold:
${M}_{\mu ,c_1,c_2,c_3,c_4}$
, it follows that the following identifications hold:
and
In what follows, we will often use the next proposition. The proof follows from techniques similar to the ones used to obtain the previous relations, so we postpone it to Appendix B.
Proposition 4.13 Consider the circle actions
![]() $z_0$
,
$z_0$
,
![]() $z_{0,i}, \ i=1,2,3,4$
,
$z_{0,i}, \ i=1,2,3,4$
,
![]() $z_{0,1i}, i=2,3,4$
,
$z_{0,1i}, i=2,3,4$
,
![]() $z_1$
, and
$z_1$
, and
![]() $z_{1,4}$
, defined in Figure 7 or 8 through their graphs, as elements of
$z_{1,4}$
, defined in Figure 7 or 8 through their graphs, as elements of
![]() $\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
. Then the following identifications hold:
$\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
. Then the following identifications hold:
and
![]() $z_{0}= 2z_1 -2z_{1,4} - z_{0,12}-z_{0,13}+ z_{0,14}$
.▪
$z_{0}= 2z_1 -2z_{1,4} - z_{0,12}-z_{0,13}+ z_{0,14}$
.▪
Putting together Proposition 4.13 with equations (4.14) and (4.17)–(4.20), we then obtain the following result.
Proposition 4.14 Consider the circle actions
![]() $z_{0,1i}, i=2,3,4$
,
$z_{0,1i}, i=2,3,4$
,
![]() $z_1$
, and
$z_1$
, and
![]() $z_{1,4}$
, defined in Figure 7 or 8 through their graphs, as elements of
$z_{1,4}$
, defined in Figure 7 or 8 through their graphs, as elements of
![]() $\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
. Let
$\pi _1 (\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
. Let
![]() $t= z_{0,12}+z_{0,13}- z_{0,14}$
. Then, for
$t= z_{0,12}+z_{0,13}- z_{0,14}$
. Then, for
![]() $k \in \mathbb {Z}_{\geq 0}$
and
$k \in \mathbb {Z}_{\geq 0}$
and
![]() $i,j=1,2,3,4$
with
$i,j=1,2,3,4$
with
![]() $i \neq j$
, we have the following identifications:
$i \neq j$
, we have the following identifications:
 $$ \begin{align*} & z_k= (2-k) z_1 + (k-1)(2z_{1,4} +t), & &z_{k,ij}=2kz_{1,4}-kz_1 +kt + z_{0,ij}, \\ & z_{k,1}= (2k-1)z_{1,4} + (1-k)z_1 +kt +z_{0,14}, & &z_{k,124}= (2k+1)z_{1,4}-(k+1)z_1 +kt + z_{0,12}, \\ & z_{k,2}= (2k-1)z_{1,4} + (1-k)z_1 +kt -z_{0,13}, & &z_{k,134}= (2k+1)z_{1,4}-(k+1)z_1 +kt + z_{0,13}, \\ & z_{k,3}= (2k-1)z_{1,4} + (1-k)z_1 +kt -z_{0,12}, & &z_{k,234}= (2k+1)z_{1,4}-(k+1)z_1 +kt - z_{0,14}, \\ & z_{k,4}= (2k-1)z_{1,4} + (1-k)z_1 +(k-1)t, & &z_{k,123}= (2k+1)z_{1,4}-(k+1)z_1 +(k+1)t, \end{align*} $$
$$ \begin{align*} & z_k= (2-k) z_1 + (k-1)(2z_{1,4} +t), & &z_{k,ij}=2kz_{1,4}-kz_1 +kt + z_{0,ij}, \\ & z_{k,1}= (2k-1)z_{1,4} + (1-k)z_1 +kt +z_{0,14}, & &z_{k,124}= (2k+1)z_{1,4}-(k+1)z_1 +kt + z_{0,12}, \\ & z_{k,2}= (2k-1)z_{1,4} + (1-k)z_1 +kt -z_{0,13}, & &z_{k,134}= (2k+1)z_{1,4}-(k+1)z_1 +kt + z_{0,13}, \\ & z_{k,3}= (2k-1)z_{1,4} + (1-k)z_1 +kt -z_{0,12}, & &z_{k,234}= (2k+1)z_{1,4}-(k+1)z_1 +kt - z_{0,14}, \\ & z_{k,4}= (2k-1)z_{1,4} + (1-k)z_1 +(k-1)t, & &z_{k,123}= (2k+1)z_{1,4}-(k+1)z_1 +(k+1)t, \end{align*} $$
and
![]() $z_{k,1234}=(2k+2)z_{1,4}-(k+2)z_1 +(k+1)t $
.▪
$z_{k,1234}=(2k+2)z_{1,4}-(k+2)z_1 +(k+1)t $
.▪
Remark 4.15 It is clear from the definition of the circle actions
![]() $z_{0,ij}$
that
$z_{0,ij}$
that
Thus, we get
which allows us to write
![]() $z_{k,ij}$
completely in terms of the chosen generators.
$z_{k,ij}$
completely in terms of the chosen generators.
Corollary 4.16 If
![]() $\mu> \frac 32$
, then there are loops in
$\mu> \frac 32$
, then there are loops in
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
which are not represented by circle actions, although the fundamental group, rationally, is generated by circle actions.
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
which are not represented by circle actions, although the fundamental group, rationally, is generated by circle actions.
Proof We use the classification of all circle actions on
![]() $\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2})$
obtained in Proposition 4.14 to show that those actions do not fill in the lattice
$\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2})$
obtained in Proposition 4.14 to show that those actions do not fill in the lattice
![]() $\mathbb {Z}^5$
. In fact, it is sufficient to look at the plane of the actions
$\mathbb {Z}^5$
. In fact, it is sufficient to look at the plane of the actions
![]() $z_{1,4}$
and
$z_{1,4}$
and
![]() $z_1$
. There we have five families of points defined by the pairs
$z_1$
. There we have five families of points defined by the pairs
![]() $(2k-2,2-k)$
,
$(2k-2,2-k)$
,
![]() $(2k-1,1-k)$
,
$(2k-1,1-k)$
,
![]() $(2k,-k)$
,
$(2k,-k)$
,
![]() $(2k+1,-(k+1))$
, and
$(2k+1,-(k+1))$
, and
![]() $(2k+2,-(k+2))$
. Each family is contained in one line with slope
$(2k+2,-(k+2))$
. Each family is contained in one line with slope
![]() $-\frac 12$
, whereas the y-intercepts are given by
$-\frac 12$
, whereas the y-intercepts are given by
![]() $1,\frac 12, 0, -\frac 12$
, and
$1,\frac 12, 0, -\frac 12$
, and
![]() $-1$
, respectively. We should also consider the integer multiples of these actions as they represent circle actions although they are not effective. The corresponding points lie in lines connecting the origin to the points representing the effective actions. The set of all these points clearly do not fill in the full lattice
$-1$
, respectively. We should also consider the integer multiples of these actions as they represent circle actions although they are not effective. The corresponding points lie in lines connecting the origin to the points representing the effective actions. The set of all these points clearly do not fill in the full lattice
![]() $\mathbb {Z}^2$
in this plane. For example, the primitive point
$\mathbb {Z}^2$
in this plane. For example, the primitive point
![]() $(2,3)$
is not contained in this set. Therefore, there are elements in
$(2,3)$
is not contained in this set. Therefore, there are elements in
![]() $\pi _1$
which cannot be represented by circle actions.
$\pi _1$
which cannot be represented by circle actions.
We now prove Theorem 1.5.
5 Further questions
In this paper, we deal with a particular case in the symplectic cone of
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
, namely the edge
${M}_{\mu ,c_1,c_2,c_3,c_4}$
, namely the edge
![]() $MA$
, when
$MA$
, when
![]() $\mu>1$
and
$\mu>1$
and
![]() $c_i=1/2$
for all
$c_i=1/2$
for all
![]() $i \in \{1,2,3,4 \}$
. A very natural question is whether there are other points in the symplectic cone where the fundamental group of
$i \in \{1,2,3,4 \}$
. A very natural question is whether there are other points in the symplectic cone where the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
is not generated Hamiltonian circle actions, similarly to what happens along some points of the edge
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
is not generated Hamiltonian circle actions, similarly to what happens along some points of the edge
![]() $MA$
. For example, it is possible to check that, along the edge
$MA$
. For example, it is possible to check that, along the edge
![]() $MD$
, where
$MD$
, where
![]() $\mu =1, c_1=c_2=c_3=1/2>c_4$
, there are no circle actions. On the one hand, there are no graphs representing Hamiltonian
$\mu =1, c_1=c_2=c_3=1/2>c_4$
, there are no circle actions. On the one hand, there are no graphs representing Hamiltonian
![]() $S^1$
-spaces along this edge. However, the graph only encodes equivariant blowups. Not having such graphs does not a priori rule out the possibility of exotic circle actions, obtained by equivariant blowups corresponding to parameters
$S^1$
-spaces along this edge. However, the graph only encodes equivariant blowups. Not having such graphs does not a priori rule out the possibility of exotic circle actions, obtained by equivariant blowups corresponding to parameters
![]() $\mu ',c_1',c_2',c_3',c_4'$
such that the symplectic manifold corresponding to these parameters is symplectomorphic to the symplectic manifold corresponding to the parameters
$\mu ',c_1',c_2',c_3',c_4'$
such that the symplectic manifold corresponding to these parameters is symplectomorphic to the symplectic manifold corresponding to the parameters
![]() $\mu ,c_1,c_2,c_3,c_4$
. On the other hand, exotic circle actions were ruled out, first, by Pinsonnault in [Reference Pinsonnault26] and later by Karshon, Kessler, and Pinsonnault in [Reference Karshon, Kessler and Pinsonnault12]. Note that if we forget the fourth blowup, this case corresponds to the monotone case in
$\mu ,c_1,c_2,c_3,c_4$
. On the other hand, exotic circle actions were ruled out, first, by Pinsonnault in [Reference Pinsonnault26] and later by Karshon, Kessler, and Pinsonnault in [Reference Karshon, Kessler and Pinsonnault12]. Note that if we forget the fourth blowup, this case corresponds to the monotone case in
![]() $\operatorname {\mathrm{Symp}}_h({S^2 \times S^2\#\,3\overline { \mathbb C\mathbb P}\,\!^2})$
and it is well known that there are no Hamiltonian circle actions in this case. In fact, this symplectomorphism group is contractible (see [Reference Evans9]). However, by the work of [Reference Li, Li and Wu18], we know that the rank of the fundamental group of
$\operatorname {\mathrm{Symp}}_h({S^2 \times S^2\#\,3\overline { \mathbb C\mathbb P}\,\!^2})$
and it is well known that there are no Hamiltonian circle actions in this case. In fact, this symplectomorphism group is contractible (see [Reference Evans9]). However, by the work of [Reference Li, Li and Wu18], we know that the rank of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}({M}_{\mu ,c_1,c_2,c_3,c_4})$
along the edge
$\operatorname {\mathrm{Symp}}({M}_{\mu ,c_1,c_2,c_3,c_4})$
along the edge
![]() $MD$
is 5, so none of these five generators can be represented by circle actions. Moreover, we believe that there is a neighborhood of the monotone point M, including points in the generic case, such that the generators of the fundamental group of
$MD$
is 5, so none of these five generators can be represented by circle actions. Moreover, we believe that there is a neighborhood of the monotone point M, including points in the generic case, such that the generators of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}({M}_{\mu ,c_1,c_2,c_3,c_4})$
cannot all be realized by circle actions. The main reason appears to be that one circle action of the type
$\operatorname {\mathrm{Symp}}({M}_{\mu ,c_1,c_2,c_3,c_4})$
cannot all be realized by circle actions. The main reason appears to be that one circle action of the type
![]() $z_{0,i}$
or
$z_{0,i}$
or
![]() $z_{1,i}$
for some
$z_{1,i}$
for some
![]() $i \in \{1,2,3,4 \}$
always have to be included in the set of generators, in order to have the required number of generators, but this implies that there must exist a fixed sphere with positive area in class
$i \in \{1,2,3,4 \}$
always have to be included in the set of generators, in order to have the required number of generators, but this implies that there must exist a fixed sphere with positive area in class
![]() $B-E_j-E_k- E_\ell $
or
$B-E_j-E_k- E_\ell $
or
![]() $B-F-E_i$
, that is,
$B-F-E_i$
, that is,
![]() $ \mu -c_j-c_k-c_\ell> 0$
or
$ \mu -c_j-c_k-c_\ell> 0$
or
![]() $\mu -1 -c_i>0$
, respectively. However, this condition does not necessarily hold for all points in the symplectic cone, in particular, for points close to the monotone point M.
$\mu -1 -c_i>0$
, respectively. However, this condition does not necessarily hold for all points in the symplectic cone, in particular, for points close to the monotone point M.
An alternative way of proving that there is an element of
![]() $ \pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
which cannot be represented by a circle action would be to compute the Samelson product of this loop with itself and check if it is nonzero, as done by Buse in [Reference Buse6, Proposition 3.3] (if it was generated by a circle action, this Samelson product would be trivially 0). Moreover, it would be interesting to know if this loop in
$ \pi _1(\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4}))$
which cannot be represented by a circle action would be to compute the Samelson product of this loop with itself and check if it is nonzero, as done by Buse in [Reference Buse6, Proposition 3.3] (if it was generated by a circle action, this Samelson product would be trivially 0). Moreover, it would be interesting to know if this loop in
![]() $\pi _1$
gives rise to new elements in higher homotopy groups, via iterated Samelson products. The problem with this approach is that it is not clear yet how to obtain the necessary information about the higher homotopy groups of
$\pi _1$
gives rise to new elements in higher homotopy groups, via iterated Samelson products. The problem with this approach is that it is not clear yet how to obtain the necessary information about the higher homotopy groups of
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
, which is fundamental to work on these ideas. The answer to these questions will be pursued in a different paper.
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
, which is fundamental to work on these ideas. The answer to these questions will be pursued in a different paper.
In another direction, it seems very likely that Theorem 1.4 holds not only rationally but also in the integer case, that is,
Conjecture 5.1 If
![]() $\mu> \frac 32$
, then the fundamental group
$\mu> \frac 32$
, then the fundamental group
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
is generated by Hamiltonian circle actions.▪
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
is generated by Hamiltonian circle actions.▪
In fact, it is possible to show that the Seidel elements of the classes of the actions
![]() $z_{0,12}$
,
$z_{0,12}$
,
![]() $z_{0,13}$
,
$z_{0,13}$
,
![]() $z_{0,14}$
,
$z_{0,14}$
,
![]() $z_1$
, and
$z_1$
, and
![]() $z_{1,4}$
, seen as elements of
$z_{1,4}$
, seen as elements of
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
, are primitive in the subgroup of invertible elements of the quantum homology of
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
, are primitive in the subgroup of invertible elements of the quantum homology of
![]() $\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2})$
. This result together with a geometric interpretation of the generators of
$\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2})$
. This result together with a geometric interpretation of the generators of
![]() $\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
given in [Reference Li, Li and Wu18, Lemma 5.10] might lead to a proof of this conjecture. We believe that this should involve a detailed analysis of the strata of the space of almost complex structures and the generators of their homology groups.
$\pi _1(\operatorname {\mathrm{Symp}}({M}_{\mu ,c_i=1/2}))$
given in [Reference Li, Li and Wu18, Lemma 5.10] might lead to a proof of this conjecture. We believe that this should involve a detailed analysis of the strata of the space of almost complex structures and the generators of their homology groups.
A Computations on the quantum ring
In this section, we prove Lemmas 4.8 and 4.9.
Proof (of Lemma 4.8) Recall that we wish to prove that the invertible elements b,
![]() $b+f$
, and
$b+f$
, and
![]() $\left ( b + f + e + \frac {t^{1-\mu }}{1-t^{1-\mu }}\right )(1-t^{1-\mu })\, t^{\frac {1}{6(1-2\mu )}}$
are linearly independent in the subgroup of invertible elements of the ring (4.10). Suppose that
$\left ( b + f + e + \frac {t^{1-\mu }}{1-t^{1-\mu }}\right )(1-t^{1-\mu })\, t^{\frac {1}{6(1-2\mu )}}$
are linearly independent in the subgroup of invertible elements of the ring (4.10). Suppose that
 $$ \begin{align*}b^\alpha \, (b+f)^\beta \, \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma \, t^{\frac{\gamma}{6(1-2\mu)}}=1, \quad \mbox{where} \quad \alpha, \beta, \gamma \in \mathbb{Z}.\end{align*} $$
$$ \begin{align*}b^\alpha \, (b+f)^\beta \, \left( b + f + e + \frac{t^{1-\mu}}{1-t^{1-\mu}}\right)^\gamma(1-t^{1-\mu})^\gamma \, t^{\frac{\gamma}{6(1-2\mu)}}=1, \quad \mbox{where} \quad \alpha, \beta, \gamma \in \mathbb{Z}.\end{align*} $$
Using the relations in the ideal
![]() $I'$
in (4.10), in particular relations (3) and (5), it follows that this is equivalent to
$I'$
in (4.10), in particular relations (3) and (5), it follows that this is equivalent to
because
![]() $f^2=0$
. Moreover, since
$f^2=0$
. Moreover, since
![]() $(1-\beta f)(1+\beta f)=1 $
, if
$(1-\beta f)(1+\beta f)=1 $
, if
![]() $\alpha +\beta +\gamma $
is even, then we obtain
$\alpha +\beta +\gamma $
is even, then we obtain
If
![]() $\gamma \geq 0$
, then it should be clear from relations in
$\gamma \geq 0$
, then it should be clear from relations in
![]() $I'$
, in particular, from relation (6), that we cannot never obtain the right-hand side of the last expression, since it is not possible to obtain such power on t, unless
$I'$
, in particular, from relation (6), that we cannot never obtain the right-hand side of the last expression, since it is not possible to obtain such power on t, unless
![]() $\gamma =0$
, which implies that
$\gamma =0$
, which implies that
![]() $\beta =0$
and then
$\beta =0$
and then
![]() $\alpha =0$
. If
$\alpha =0$
. If
![]() $\gamma \leq 0$
, then equation (A.1) is equivalent to
$\gamma \leq 0$
, then equation (A.1) is equivalent to
and again we can conclude that
![]() $\gamma =0$
. Similarly, if
$\gamma =0$
. Similarly, if
![]() $\alpha +\beta +\gamma $
is odd, we obtain
$\alpha +\beta +\gamma $
is odd, we obtain
and again we can conclude that
![]() $\gamma =\beta =0$
and
$\gamma =\beta =0$
and
![]() $\alpha +\beta +\gamma $
cannot be odd. This concludes the proof of the lemma.
$\alpha +\beta +\gamma $
cannot be odd. This concludes the proof of the lemma.
Proof (of Lemma 4.9) We first prove by induction on
![]() $n \in \mathbb {N}$
that
$n \in \mathbb {N}$
that
where
![]() $i,j,k,\ell \in \{1,2,3,4 \}$
are all distinct.
$i,j,k,\ell \in \{1,2,3,4 \}$
are all distinct.
Note that if
![]() $n=1$
, then (A.2) gives
$n=1$
, then (A.2) gives
![]() $b_{ij}^{2}= 2 b_{ij}f_{ij} + 1 f_{ij}+ f_{k\ell } $
, which agrees with relation (3) in Proposition 3.1. Moreover, it follows from relation (3) together with relations (8) and (11) that
$b_{ij}^{2}= 2 b_{ij}f_{ij} + 1 f_{ij}+ f_{k\ell } $
, which agrees with relation (3) in Proposition 3.1. Moreover, it follows from relation (3) together with relations (8) and (11) that
 $$ \begin{align*} b_{ij}^2f_{ij} & = 2 b_{ij}f_{ij}^2 + f_{ij}^2+ f_{ij}f_{k\ell} + f_{ij} \\ & = -f_{ij}^2 + f_{ij} \\ & = -2 b_{ij}f_{ij} - f_{ij}. \end{align*} $$
$$ \begin{align*} b_{ij}^2f_{ij} & = 2 b_{ij}f_{ij}^2 + f_{ij}^2+ f_{ij}f_{k\ell} + f_{ij} \\ & = -f_{ij}^2 + f_{ij} \\ & = -2 b_{ij}f_{ij} - f_{ij}. \end{align*} $$
Now, if we assume (A.2), then the previous equation together with relation (11) yields
 $$ \begin{align*} b_{ij}^{2(n+1)} & = b_{ij}^{2n}\, b_{ij} \\ & = n (2n \, b_{ij}^2f_{ij}+ (2n-1)f_{ij}b_{ij}+ f_{k\ell}b_{ij}) +b_{ij} = \\ & = n (2n (-2 b_{ij}f_{ij} - f_{ij}) + (2n-1)f_{ij}b_{ij} - f_{ij}b_{ij} - f_{ij}- f_{k\ell}) +b_{ij} \\ & = -n(2(n+1) b_{ij}f_{ij}+ (2n+1)f_{ij}+ f_{k\ell})+b_{ij}. \end{align*} $$
$$ \begin{align*} b_{ij}^{2(n+1)} & = b_{ij}^{2n}\, b_{ij} \\ & = n (2n \, b_{ij}^2f_{ij}+ (2n-1)f_{ij}b_{ij}+ f_{k\ell}b_{ij}) +b_{ij} = \\ & = n (2n (-2 b_{ij}f_{ij} - f_{ij}) + (2n-1)f_{ij}b_{ij} - f_{ij}b_{ij} - f_{ij}- f_{k\ell}) +b_{ij} \\ & = -n(2(n+1) b_{ij}f_{ij}+ (2n+1)f_{ij}+ f_{k\ell})+b_{ij}. \end{align*} $$
Similarly, it is easy to check that
Next, using (A.2) and (A.3), we compute
![]() $b_{ij}^{\alpha _1}\, b_{ik}^{\alpha _2}\, b_{jk}^{\alpha _3}$
, where
$b_{ij}^{\alpha _1}\, b_{ik}^{\alpha _2}\, b_{jk}^{\alpha _3}$
, where
![]() $\alpha _1,\alpha _2, \alpha _3 \in \mathbb {Z}$
, to conclude that indeed
$\alpha _1,\alpha _2, \alpha _3 \in \mathbb {Z}$
, to conclude that indeed
![]() $b_{ij}, b_{ik}, b_{jk}$
are linearly independent. Assume first that
$b_{ij}, b_{ik}, b_{jk}$
are linearly independent. Assume first that
![]() $\alpha _1,\alpha _2,\alpha _3 \geq 0$
and, in particular,
$\alpha _1,\alpha _2,\alpha _3 \geq 0$
and, in particular,
![]() $\alpha _i=2n_i$
, with
$\alpha _i=2n_i$
, with
![]() $n_i \in \mathbb {N}_0$
. Then
$n_i \in \mathbb {N}_0$
. Then
Recall relation (4) in Proposition 3.1:
![]() $b_{ij}f_{ik}=-f_{ik}$
. This yields
$b_{ij}f_{ik}=-f_{ik}$
. This yields
 $$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2} = & \, 4 n_1^2 \,n_2^2 \,f_{ij}f_{ik} -n_2 (2n_2-1) 2n_1^2 \, f_{ij}f_{ik} -n_1 (2n_1-1) 2n_2^2 \, f_{ij}f_{ik} - 2n_1^2 \,n_2 \, f_{ij}f_{j\ell} \\ & + 2n_1^2\, b_{ij}f_{ij} + n_1 (2n_1-1) \, n_2 (2n_2-1) \, f_{ij}f_{ik} + n_1 (2n_1-1) \,n_2 f_{ij}f_{j\ell} + n_1 (2n_1-1) \,f_{ij} \\ & - 2n_1 \, n_2^2 \,f_{ik}f_{k\ell} + n_1\,n_2 (2n_2-1) \,f_{ik}f_{k\ell} + n_1\, n_2\, f_{k\ell}f_{j\ell} + n_1\, f_{k\ell} + 2n_2^2\, b_{ik}f_{ik} \\ & + n_2 (2n_2-1) \, f_{ik} + n_2\, f_{j\ell} + 1 \\ = & \, n_1\, n_2 (f_{ij}f_{ik} -f_{ij}f_{j\ell} -f_{ik}f_{k\ell}+ f_{k\ell}f_{j\ell}) + 2\, n_1^2 b_{ij}f_{ij} + 2\, n_2^2 b_{ik}f_{ik} + n_1 (2n_1-1) \,f_{ij}\\ & + n_2 (2n_2-1) \, f_{ik} + n_1\, f_{k\ell} + n_2\, f_{j\ell} + 1 \\ = & \, 2\, n_1^2 b_{ij}f_{ij} + 2\, n_2^2 (b_{ij}f_{ij} + e_k -e_j) + n_1 (2n_1-1) \,f_{ij} + n_2 (2n_2-1) \, (f_{ij} +e_j-e_k) \\ & + n_1 (f_{ij} +e_i+e_j - e_k - e_l) + n_2 (f_{ij} +e_i- e_l) +1 \\ = & \, 2 (n_1^2 +n_2^2) f_{ij} (b_{ij} +1 ) + e_i(n_1+n_2) + e_j(n_1-n_2) -e_k(n_2-n_1) - e_\ell(n_1+n_2) +1, \end{align*} $$
$$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2} = & \, 4 n_1^2 \,n_2^2 \,f_{ij}f_{ik} -n_2 (2n_2-1) 2n_1^2 \, f_{ij}f_{ik} -n_1 (2n_1-1) 2n_2^2 \, f_{ij}f_{ik} - 2n_1^2 \,n_2 \, f_{ij}f_{j\ell} \\ & + 2n_1^2\, b_{ij}f_{ij} + n_1 (2n_1-1) \, n_2 (2n_2-1) \, f_{ij}f_{ik} + n_1 (2n_1-1) \,n_2 f_{ij}f_{j\ell} + n_1 (2n_1-1) \,f_{ij} \\ & - 2n_1 \, n_2^2 \,f_{ik}f_{k\ell} + n_1\,n_2 (2n_2-1) \,f_{ik}f_{k\ell} + n_1\, n_2\, f_{k\ell}f_{j\ell} + n_1\, f_{k\ell} + 2n_2^2\, b_{ik}f_{ik} \\ & + n_2 (2n_2-1) \, f_{ik} + n_2\, f_{j\ell} + 1 \\ = & \, n_1\, n_2 (f_{ij}f_{ik} -f_{ij}f_{j\ell} -f_{ik}f_{k\ell}+ f_{k\ell}f_{j\ell}) + 2\, n_1^2 b_{ij}f_{ij} + 2\, n_2^2 b_{ik}f_{ik} + n_1 (2n_1-1) \,f_{ij}\\ & + n_2 (2n_2-1) \, f_{ik} + n_1\, f_{k\ell} + n_2\, f_{j\ell} + 1 \\ = & \, 2\, n_1^2 b_{ij}f_{ij} + 2\, n_2^2 (b_{ij}f_{ij} + e_k -e_j) + n_1 (2n_1-1) \,f_{ij} + n_2 (2n_2-1) \, (f_{ij} +e_j-e_k) \\ & + n_1 (f_{ij} +e_i+e_j - e_k - e_l) + n_2 (f_{ij} +e_i- e_l) +1 \\ = & \, 2 (n_1^2 +n_2^2) f_{ij} (b_{ij} +1 ) + e_i(n_1+n_2) + e_j(n_1-n_2) -e_k(n_2-n_1) - e_\ell(n_1+n_2) +1, \end{align*} $$
where the step before the last follows from relations (2) and (9) in Proposition 3.1 and the definition of
![]() $f_{ij}$
and
$f_{ij}$
and
![]() $e_i$
. Similar computations then give
$e_i$
. Similar computations then give
 $$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,2 \,(n_1^2 +n_2^2+ n_3^2) f_{ij} (b_{ij} +1 ) + e_i(n_1+n_2-n_3) + e_j(n_1-n_2+n_3) \\ & +e_k(n_3+n_2-n_1) - e_\ell(n_1+n_2+n_3) +1. \end{align*} $$
$$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,2 \,(n_1^2 +n_2^2+ n_3^2) f_{ij} (b_{ij} +1 ) + e_i(n_1+n_2-n_3) + e_j(n_1-n_2+n_3) \\ & +e_k(n_3+n_2-n_1) - e_\ell(n_1+n_2+n_3) +1. \end{align*} $$
Now, it is clear that
![]() $b_{ij}^{\alpha _1}\, b_{ik}^{\alpha _2}\, b_{jk}^{\alpha _3}=1$
iff
$b_{ij}^{\alpha _1}\, b_{ik}^{\alpha _2}\, b_{jk}^{\alpha _3}=1$
iff
![]() $n_1=n_2=n_3=0$
. In the case
$n_1=n_2=n_3=0$
. In the case
![]() $\alpha _1= 2n_1+1$
,
$\alpha _1= 2n_1+1$
,
![]() $\alpha _2=2n_2$
, and
$\alpha _2=2n_2$
, and
![]() $\alpha _3=2n_3$
, analog computations yield
$\alpha _3=2n_3$
, analog computations yield
 $$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,-2 \,(n_1^2 +n_2^2+ n_3^2+n_1) f_{ij} (b_{ij} +1 ) - e_i(n_1+n_2-n_3) - e_j(n_1-n_2+n_3) \\ & - e_k(n_3+n_2-n_1) + e_\ell(n_1+n_2+n_3) + b_{ij}. \end{align*} $$
$$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,-2 \,(n_1^2 +n_2^2+ n_3^2+n_1) f_{ij} (b_{ij} +1 ) - e_i(n_1+n_2-n_3) - e_j(n_1-n_2+n_3) \\ & - e_k(n_3+n_2-n_1) + e_\ell(n_1+n_2+n_3) + b_{ij}. \end{align*} $$
If
![]() $\alpha _1= 2n_1+1$
,
$\alpha _1= 2n_1+1$
,
![]() $\alpha _2=2n_2+1$
, and
$\alpha _2=2n_2+1$
, and
![]() $\alpha _3=2n_3$
, then
$\alpha _3=2n_3$
, then
 $$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,[2 \,(n_1^2 +n_2^2+ n_3^2+n_1+n_2)+1] f_{ij} (b_{ij} +1 ) + e_i(n_1+n_2-n_3+1) \\ & + e_j(n_1-n_2+n_3) + e_k(n_3+n_2-n_1) - e_\ell(n_1+n_2+n_3+1) + 1. \end{align*} $$
$$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,[2 \,(n_1^2 +n_2^2+ n_3^2+n_1+n_2)+1] f_{ij} (b_{ij} +1 ) + e_i(n_1+n_2-n_3+1) \\ & + e_j(n_1-n_2+n_3) + e_k(n_3+n_2-n_1) - e_\ell(n_1+n_2+n_3+1) + 1. \end{align*} $$
Finally, if
![]() $\alpha _i= \, 2n_i+1 $
, one obtains
$\alpha _i= \, 2n_i+1 $
, one obtains
 $$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,-[2 \,(n_1^2 +n_2^2+ n_3^2+n_1+n_2+n_3)+1] f_{ij} (b_{ij} +1 ) - e_i(n_1+n_2-n_3) \\& - e_j(n_1-n_2+n_3) - e_k(n_3+n_2-n_1+1) - e_\ell(n_1+n_2+n_3+1) + b_{ij}. \end{align*} $$
$$ \begin{align*} b_{ij}^{\alpha_1}\, b_{ik}^{\alpha_2}\, b_{jk}^{\alpha_3} = & \,-[2 \,(n_1^2 +n_2^2+ n_3^2+n_1+n_2+n_3)+1] f_{ij} (b_{ij} +1 ) - e_i(n_1+n_2-n_3) \\& - e_j(n_1-n_2+n_3) - e_k(n_3+n_2-n_1+1) - e_\ell(n_1+n_2+n_3+1) + b_{ij}. \end{align*} $$
So it follows that
![]() $b_{ij}^{\alpha _1}\, b_{ik}^{\alpha _2}\, b_{jk}^{\alpha _3}=1$
iff
$b_{ij}^{\alpha _1}\, b_{ik}^{\alpha _2}\, b_{jk}^{\alpha _3}=1$
iff
![]() $\alpha _i=0$
for all i.
$\alpha _i=0$
for all i.
If
![]() $\alpha _m< 0$
, then we obtain similar expressions because
$\alpha _m< 0$
, then we obtain similar expressions because
![]() $b_{ij}^{\alpha _m}= b_{k\ell }^{-\alpha _m}$
. More precisely, in the case
$b_{ij}^{\alpha _m}= b_{k\ell }^{-\alpha _m}$
. More precisely, in the case
![]() $\alpha _m>0$
, the products above contain the term
$\alpha _m>0$
, the products above contain the term
![]() $n_m(e_i +e_j -e_k-e_\ell )$
, but if
$n_m(e_i +e_j -e_k-e_\ell )$
, but if
![]() $\alpha _m< 0$
, it is not hard to check that then the term is replaced by its symmetric
$\alpha _m< 0$
, it is not hard to check that then the term is replaced by its symmetric
![]() $n_m(-e_i -e_j +e_k + e_\ell )$
. Therefore, we prove that the elements
$n_m(-e_i -e_j +e_k + e_\ell )$
. Therefore, we prove that the elements
![]() $b_{ij}, b_{ik}, b_{jk}$
are linearly independent, and, in particular, we finish the proof of Lemma 4.9.
$b_{ij}, b_{ik}, b_{jk}$
are linearly independent, and, in particular, we finish the proof of Lemma 4.9.
B Proof of Proposition 4.13
This section is devoted to a proof of Proposition 4.13. First, we need to prove that the following identifications hold.
Lemma B.1 Consider the Hamiltonian circle actions
![]() $z_0, z_{0,1i}, z_{0,j}$
,
$z_0, z_{0,1i}, z_{0,j}$
,
![]() $ z_1$
, and
$ z_1$
, and
![]() $z_{1,4}$
, where
$z_{1,4}$
, where
![]() $i \in \{2,3,4\}$
and
$i \in \{2,3,4\}$
and
![]() $j \in \{1,2,3,4\}$
, whose graphs are represented in Figure 8, as elements of the fundamental group of
$j \in \{1,2,3,4\}$
, whose graphs are represented in Figure 8, as elements of the fundamental group of
![]() $\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
. Then we have the following relations:
$\operatorname {\mathrm{Symp}}_h({M}_{\mu ,c_1,c_2,c_3,c_4})$
. Then we have the following relations:
Proof In order to prove relation (B.1), we need to consider the two toric actions on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygons of Figure 23.
${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygons of Figure 23.

Figure 23: Auxiliary toric actions.
Note that, projecting onto the x-axis, we obtain the graphs of the circle actions
![]() $z_1$
on the left and
$z_1$
on the left and
![]() $z_{1,4}$
on the right. On the other hand, projecting onto the y-axis yields the graphs of two circle actions (see Figure 24) that we will denote by
$z_{1,4}$
on the right. On the other hand, projecting onto the y-axis yields the graphs of two circle actions (see Figure 24) that we will denote by
![]() $c_1$
and
$c_1$
and
![]() $c_{1,4}$
.
$c_{1,4}$
.

Figure 24: Graphs of the actions
![]() $c_1$
and
$c_1$
and
![]() $c_{1,4}$
.
$c_{1,4}$
.
It is easy to check that performing first a
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right)\end{align*} $$
to both polygons of Figure 23 and then a projection onto the y-axis, we obtain the same graph, which implies that the following identification holds:
Next, consider the polygons of Figure 25. Again, they represent particular toric actions on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
. We denote the circle actions whose graphs are obtained by projecting to the x- and y-axes by
${M}_{\mu ,c_1,c_2,c_3,c_4}$
. We denote the circle actions whose graphs are obtained by projecting to the x- and y-axes by
![]() $(a_1,b_1)$
and
$(a_1,b_1)$
and
![]() $(a_{1,4}, b_{1,4})$
. Since, clearly, the actions
$(a_{1,4}, b_{1,4})$
. Since, clearly, the actions
![]() $b_1$
and
$b_1$
and
![]() $b_{1,4}$
are represented by the same graph, it follows that
$b_{1,4}$
are represented by the same graph, it follows that
![]() $b_1=b_{1,4}$
. Next, performing a
$b_1=b_{1,4}$
. Next, performing a
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array} \!\right)\end{align*} $$
to both polygons and then projecting to the y-axis, we obtain the graphs of
![]() $c_1$
and
$c_1$
and
![]() $c_{1,4}$
. Therefore, as elements of
$c_{1,4}$
. Therefore, as elements of
![]() $\pi _1 (\operatorname {\mathrm{Symp}}_h( {M}_{\mu ,c_1,c_2,c_3,c_4}))$
, the following identifications hold:
$\pi _1 (\operatorname {\mathrm{Symp}}_h( {M}_{\mu ,c_1,c_2,c_3,c_4}))$
, the following identifications hold:
On the other hand, note that
![]() $a_1$
is the generator
$a_1$
is the generator
![]() $-z_{0,4}$
, whereas
$-z_{0,4}$
, whereas
![]() $a_{1,4}$
is
$a_{1,4}$
is
![]() $ -z_0$
. Therefore, we have
$ -z_0$
. Therefore, we have
Finally, substituting
![]() $c_1$
and
$c_1$
and
![]() $c_{1,4}$
in relation (B.6) and using
$c_{1,4}$
in relation (B.6) and using
![]() $b_1=b_{1,4}$
, we obtain the desired relation (B.1).
$b_1=b_{1,4}$
, we obtain the desired relation (B.1).

Figure 25: Toric actions
![]() $(a_1,b_1)$
and
$(a_1,b_1)$
and
![]() $(a_{1,4},b_{1,4})$
.
$(a_{1,4},b_{1,4})$
.
In order to prove the remaining relations in this lemma, we use an argument involving several auxiliary polygons representing different toric actions on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
that can be related between each other using Karshon’s and Delzant’s classifications. Since the argument is similar for all relations, we give the proof for relation (B.2) and leave the other proofs for the interested reader.
${M}_{\mu ,c_1,c_2,c_3,c_4}$
that can be related between each other using Karshon’s and Delzant’s classifications. Since the argument is similar for all relations, we give the proof for relation (B.2) and leave the other proofs for the interested reader.

Figure 26: Auxiliary Delzant polygons.
First, consider the toric actions on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygons of Figure 26. Denote the toric action in polygon
${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygons of Figure 26. Denote the toric action in polygon
![]() $n \in \{1,2,3,4,5,6\}$
in Figure 26 by
$n \in \{1,2,3,4,5,6\}$
in Figure 26 by
![]() $(x_n, y_n)$
. Projecting onto the x-axis to obtain the graph of
$(x_n, y_n)$
. Projecting onto the x-axis to obtain the graph of
![]() $x_n$
, using Karshon’s classification of Hamiltonian circle actions, it is clear that
$x_n$
, using Karshon’s classification of Hamiltonian circle actions, it is clear that
Moreover, applying the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right)\end{align*} $$
to the polygons 3, 4, 5, and 6 and then projecting onto the y-axis, it is easy to check that, as elements of the fundamental group, the following identifications hold:
Furthermore, the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 2 & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 2 & 1 \end{array} \!\right)\end{align*} $$
applied to the polygons 1 and 6 yields, after a projection onto the y-axis and a comparison of the graphs obtained, the following relation:
Next, consider the toric actions on
![]() ${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygons of Figure 27 and denote the toric action of polygon
${M}_{\mu ,c_1,c_2,c_3,c_4}$
represented in the polygons of Figure 27 and denote the toric action of polygon
![]() $n \in \{1,2,3,4,5,6\}$
by
$n \in \{1,2,3,4,5,6\}$
by
![]() $(s_n,t_n)$
. Applying to all these polygons, the
$(s_n,t_n)$
. Applying to all these polygons, the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ -1 & 1 \end{array} \!\right)\end{align*} $$
and then projecting onto the y-axis, it is easy to see that we obtain, as elements of the fundamental group of
![]() $\operatorname {\mathrm{Symp}} ({M}_{\mu ,c_1,c_2,c_3,c_4})$
, the following identification:
$\operatorname {\mathrm{Symp}} ({M}_{\mu ,c_1,c_2,c_3,c_4})$
, the following identification:
because the graphs obtained after the projection clearly coincide with the graphs of the actions
![]() $y_i$
. It is also clear that
$y_i$
. It is also clear that
since the graphs of these actions coincide in pairs. Finally, using the
![]() $GL(2, \mathbb {Z})$
transformation represented by the matrix
$GL(2, \mathbb {Z})$
transformation represented by the matrix
 $$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right)\end{align*} $$
$$ \begin{align*}\left (\!\begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \!\right)\end{align*} $$
applied to polygons 1 and 6 in Figure 27, we obtain the following identification:

Figure 27: Auxiliary Delzant polygons.
In order to finish the proof of relation (B.2), we just need to combine all the relations obtained above. More precisely, consider relation (B.10) and using first (B.11) and then (B.13), we get
From (B.7) and (B.9), it follows that
![]() $x_3-s_1=x_5+y_5-y_6-s_6.$
Then, using (B.11) to substitute
$x_3-s_1=x_5+y_5-y_6-s_6.$
Then, using (B.11) to substitute
![]() $y_5$
and
$y_5$
and
![]() $y_6$
in the previous equation yields
$y_6$
in the previous equation yields
![]() $x_3-s_1=x_5+t_5-s_5 -t_6.$
Hence, relations (B.7) and (B.12) imply that
$x_3-s_1=x_5+t_5-s_5 -t_6.$
Hence, relations (B.7) and (B.12) imply that
![]() $x_3-s_1= x_4-s_5.$
Finally, use first relation (B.8) to obtain
$x_3-s_1= x_4-s_5.$
Finally, use first relation (B.8) to obtain
![]() $y_4-y_3= s_1-s_5$
and then (B.11) one more time to get
$y_4-y_3= s_1-s_5$
and then (B.11) one more time to get
Now, notice that, using the notation for the circle actions defined in Figure 8, we have
so we proved the desired relation (B.2). This concludes the proof of the lemma.
Combining relations (B.1) and (B.2), we obtain one of the identifications in Proposition 4.13, namely
The remaining identifications in Proposition 4.13 follow from the previous relation together with relations (B.3)–(B.5). Therefore, we obtain
 $$ \begin{align*} z_{0,1}&= z_1 -z_{1,4} + z_{0,14}, \\ z_{0,2}&= z_1 -z_{1,4} - z_{0,13}, \\ z_{0,4}&= z_1 -z_{1,4} - z_{0,12}-z_{0,13}+ z_{0,14}. \end{align*} $$
$$ \begin{align*} z_{0,1}&= z_1 -z_{1,4} + z_{0,14}, \\ z_{0,2}&= z_1 -z_{1,4} - z_{0,13}, \\ z_{0,4}&= z_1 -z_{1,4} - z_{0,12}-z_{0,13}+ z_{0,14}. \end{align*} $$
Finally, using the last equation and relation (B.14) in relation (B.2), it follows that
This concludes the proof of Proposition 4.13.
Acknowledgment
The first and third authors are very grateful to Jun Li, Tian-Jun Li, and Weiwei Wu for showing and explaining to them their results in a preliminary version of [Reference Li, Li and Wu18]. The first author would also like to warmly thank Dusa McDuff for useful and enlightening discussions. The second and fourth authors kindly thank the support of the Gulbenkian Foundation which gave them the opportunity to take part on this work. Finally, we would like to thank the referees for their hard and thorough work in reviewing the paper. We greatly appreciate their comments and questions. Moreover, we think that the modifications based on their suggestions and corrections have vastly improved the paper.