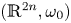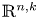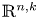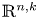1. Introduction
1.1 Coisotropic capacity
Recently, Lisi and Rieser [Reference Lisi and Rieser29] introduced the notion of a coisotropic capacity (i.e. a symplectic capacity relative to a coisotropic submanifold of a symplectic manifold), and discussed their motivations and backgrounds. Let $(M,\omega )$![]() be a symplectic manifold and $N\subset M$
be a symplectic manifold and $N\subset M$![]() a coisotropic submanifold. (In this paper all manifolds are assumed to be connected without special statements!) An equivalence relation $\sim$
a coisotropic submanifold. (In this paper all manifolds are assumed to be connected without special statements!) An equivalence relation $\sim$![]() on $N$
on $N$![]() was called a coisotropic equivalence relation if $x$
was called a coisotropic equivalence relation if $x$![]() and $y$
and $y$![]() are on the same leaf then $x\sim y$
are on the same leaf then $x\sim y$![]() (cf. [Reference Lisi and Rieser29, definition 1.4]). Special examples are the trivial relation defined by $x\sim y$
(cf. [Reference Lisi and Rieser29, definition 1.4]). Special examples are the trivial relation defined by $x\sim y$![]() for every pair $x, y\in N$
for every pair $x, y\in N$![]() and the so-called leaf relation defined by $x\sim y$
and the so-called leaf relation defined by $x\sim y$![]() if and only if $x$
if and only if $x$![]() and $y$
and $y$![]() are on the same leaf. For two tuples $(M_0, N_0, \omega _0, \sim _0)$
are on the same leaf. For two tuples $(M_0, N_0, \omega _0, \sim _0)$![]() and $(M_1, N_1, \omega _1, \sim _1)$
and $(M_1, N_1, \omega _1, \sim _1)$![]() as above, a relative symplectic embedding from $(M_0, N_0, \omega _0)$
as above, a relative symplectic embedding from $(M_0, N_0, \omega _0)$![]() to $(M_1, N_1, \omega _1)$
to $(M_1, N_1, \omega _1)$![]() is a symplectic embedding $\psi : (M_0, \omega _0)\to (M_1, \omega _1)$
is a symplectic embedding $\psi : (M_0, \omega _0)\to (M_1, \omega _1)$![]() satisfying $\psi ^{-1}(N_1) = N_0$
satisfying $\psi ^{-1}(N_1) = N_0$![]() [Reference Lisi and Rieser29, definition 1.5]. Such an embedding $\psi$
[Reference Lisi and Rieser29, definition 1.5]. Such an embedding $\psi$![]() is said to respect the pair of coisotropic equivalence relations $(\sim _0,\sim _1)$
is said to respect the pair of coisotropic equivalence relations $(\sim _0,\sim _1)$![]() if for every $x, y \in N_0$
if for every $x, y \in N_0$![]() ,
,
The standard symplectic space $(\mathbb {R}^{2n},\omega _0)$![]() has coisotropic linear subspaces
has coisotropic linear subspaces
for $k=0,\ldots,n$![]() , where we understand $\mathbb {R}^{n,0}=\{x\in \mathbb {R}^{2n}\,|\,x=(q_1,\ldots,q_n,0,\ldots,0)\}$
, where we understand $\mathbb {R}^{n,0}=\{x\in \mathbb {R}^{2n}\,|\,x=(q_1,\ldots,q_n,0,\ldots,0)\}$![]() . Denote by $\sim$
. Denote by $\sim$![]() the leaf relation on $\mathbb {R}^{n,k}$
the leaf relation on $\mathbb {R}^{n,k}$![]() , and by
, and by
Hereafter it is understood that $V_0^{n,0}=\{x\in \mathbb {R}^{2n}\,|\,x=(q_{1},\ldots,q_n,0,\ldots,0)\}=\mathbb {R}^{n,0}$![]() , $V^{n,n}_0=\{0\}$
, $V^{n,n}_0=\{0\}$![]() and $V^{n,0}_1=\{0\}$
and $V^{n,0}_1=\{0\}$![]() , $V^{n,n}_1=\mathbb {R}^{2n}$
, $V^{n,n}_1=\mathbb {R}^{2n}$![]() . Then $L_0^{n}:=V_0^{n,0}$
. Then $L_0^{n}:=V_0^{n,0}$![]() is a Lagrangian subspace, and two points $x, y\in \mathbb {R}^{n,k}$
is a Lagrangian subspace, and two points $x, y\in \mathbb {R}^{n,k}$![]() satisfy $x\sim y$
satisfy $x\sim y$![]() if and only if their difference $x-y$
if and only if their difference $x-y$![]() sits in $V_0^{n,k}$
sits in $V_0^{n,k}$![]() . Observe that $\mathbb {R}^{2n}$
. Observe that $\mathbb {R}^{2n}$![]() has the orthogonal decomposition $\mathbb {R}^{2n}=J_{2n}V^{n,k}_0\oplus \mathbb {R}^{n,k}=J_{2n}\mathbb {R}^{n,k}\oplus V^{n,k}_0$
has the orthogonal decomposition $\mathbb {R}^{2n}=J_{2n}V^{n,k}_0\oplus \mathbb {R}^{n,k}=J_{2n}\mathbb {R}^{n,k}\oplus V^{n,k}_0$![]() with respect to the standard inner product, where $J_{2n}$
with respect to the standard inner product, where $J_{2n}$![]() denotes the standard complex structure on $\mathbb {R}^{2n}$
denotes the standard complex structure on $\mathbb {R}^{2n}$![]() given by $(q_1,\ldots,q_n, p_1,\ldots, p_n)\mapsto (p_1,\ldots,p_n, -q_1,\ldots, -q_n)$
given by $(q_1,\ldots,q_n, p_1,\ldots, p_n)\mapsto (p_1,\ldots,p_n, -q_1,\ldots, -q_n)$![]() .
.
For $a\in \mathbb {R}$![]() we write ${\bf a}:=(0,\ldots,0,a)\in \mathbb {R}^{2n}$
we write ${\bf a}:=(0,\ldots,0,a)\in \mathbb {R}^{2n}$![]() . Denote by $B^{2n}({\bf a}, r)$
. Denote by $B^{2n}({\bf a}, r)$![]() and $B^{2n}(r)$
and $B^{2n}(r)$![]() the open balls of radius $r$
the open balls of radius $r$![]() centred at ${\bf a}$
centred at ${\bf a}$![]() and the origin in ${{\mathbb {R}}}^{2n}$
and the origin in ${{\mathbb {R}}}^{2n}$![]() respectively, and by
respectively, and by
($W^{2n}(R$![]() ) was written as $W(R)$
) was written as $W(R)$![]() in [Reference Lisi and Rieser29, definition 1.1]).
in [Reference Lisi and Rieser29, definition 1.1]).
According to [Reference Lisi and Rieser29, definition 1.7], a coisotropic capacity is a functor $c$![]() , which assigns to every tuple $(M,N,\omega, \sim )$
, which assigns to every tuple $(M,N,\omega, \sim )$![]() as above a non-negative (possibly infinite) number $c(M,N,\omega, \sim )$
as above a non-negative (possibly infinite) number $c(M,N,\omega, \sim )$![]() , such that the following conditions hold:
, such that the following conditions hold:
(i) Monotonicity. If there exists a relative symplectic embedding $\psi$
 from $(M_0, N_0, \omega _0, \sim _0)$
from $(M_0, N_0, \omega _0, \sim _0)$ to $(M_1, N_1, \omega _1, \sim _1)$
to $(M_1, N_1, \omega _1, \sim _1)$ respecting the coisotropic equivalence relations where $\dim M_0=\dim M_1$
respecting the coisotropic equivalence relations where $\dim M_0=\dim M_1$ , then $c(M_0,N_0,\omega _0, \sim _0) \leq c(M_1,N_1,\omega _1, \sim _1)$
, then $c(M_0,N_0,\omega _0, \sim _0) \leq c(M_1,N_1,\omega _1, \sim _1)$ .
.(ii) Conformality. $c(M,N,\alpha \omega, \sim )=|\alpha |c(M,N,\omega, \sim ),\ \forall \ \alpha \in \mathbb {R}\backslash \{0\}$
 .
.(iii) Non-triviality. With the leaf relation $\sim$
 it holds that for $k=0,\ldots,n-1$
it holds that for $k=0,\ldots,n-1$ ,
(1.5)\begin{equation} c(B^{2n}(1),B^{n,k}(1),\omega_0, \sim ) =\frac{\pi}{2}= c(W^{2n}(1),W^{n,k}(1),\omega_0, \sim ). \end{equation}
,
(1.5)\begin{equation} c(B^{2n}(1),B^{n,k}(1),\omega_0, \sim ) =\frac{\pi}{2}= c(W^{2n}(1),W^{n,k}(1),\omega_0, \sim ). \end{equation}
As remarked in [Reference Lisi and Rieser29, remark 1.9], any symplectic capacity cannot serve as a coisotropic capacity because of the non-triviality (iii).
From now on, we abbreviate $c(M,N,\omega,\sim )$![]() as $c(M,N,\omega )$
as $c(M,N,\omega )$![]() if $\sim$
if $\sim$![]() is the leaf relation on $N$
is the leaf relation on $N$![]() . In particular, for domains $D\subset \mathbb {R}^{2n}$
. In particular, for domains $D\subset \mathbb {R}^{2n}$![]() we also abbreviate $c(D, D\cap \mathbb {R}^{n,k},\omega _0)$
we also abbreviate $c(D, D\cap \mathbb {R}^{n,k},\omega _0)$![]() as $c(D, D\cap \mathbb {R}^{n,k})$
as $c(D, D\cap \mathbb {R}^{n,k})$![]() for simplicity.
for simplicity.
Given a ($n+k$![]() )-dimensional coisotropic submanifold $N$
)-dimensional coisotropic submanifold $N$![]() in a symplectic manifold $(M, \omega )$
in a symplectic manifold $(M, \omega )$![]() of dimension $2n$
of dimension $2n$![]() we defined in [Reference Jin and Lu26, definition 1.3]
we defined in [Reference Jin and Lu26, definition 1.3]

the relative Gromov width of $(M, N, \omega )$![]() . Here we always assume $k\in \{0,1\ldots,n-1\}$
. Here we always assume $k\in \{0,1\ldots,n-1\}$![]() . (If $k=n$
. (If $k=n$![]() then ${\it w}_G(N;M,\omega )$
then ${\it w}_G(N;M,\omega )$![]() is equal to the Gromov width ${\it w}_G(N,\omega |_N)$
is equal to the Gromov width ${\it w}_G(N,\omega |_N)$![]() of $(N,\omega |_N)$
of $(N,\omega |_N)$![]() .)
.)
When $k=0$![]() , $N$
, $N$![]() is a Lagrangian submanifold and this relative Gromov width was introduced by Barraud, Biran and Cornea [Reference Barraud and Cornea6–Reference Biran and Cornea9]. It is easily seen that ${\it w}_G$
is a Lagrangian submanifold and this relative Gromov width was introduced by Barraud, Biran and Cornea [Reference Barraud and Cornea6–Reference Biran and Cornea9]. It is easily seen that ${\it w}_G$![]() satisfies monotonicity, conformality and
satisfies monotonicity, conformality and
In fact ${\it w}_G(N;M,\omega )/2$![]() is the smallest coisotropic capacity by the nonsqueezing theorem in [Reference Lisi and Rieser29]. Rizell [Reference Rizell33] observed that the Lagrangian submanifolds of $\mathbb {C}^{3}$
is the smallest coisotropic capacity by the nonsqueezing theorem in [Reference Lisi and Rieser29]. Rizell [Reference Rizell33] observed that the Lagrangian submanifolds of $\mathbb {C}^{3}$![]() constructed by Ekholm, Eliashberg, Murphy and Smith [Reference Ekholm, Eliashberg, Murphy and Smith15] have infinite relative Gromov width.
constructed by Ekholm, Eliashberg, Murphy and Smith [Reference Ekholm, Eliashberg, Murphy and Smith15] have infinite relative Gromov width.
Similar to the construction of the Hofer–Zehnder capacity, Lisi and Rieser [Reference Lisi and Rieser29] constructed an analogue relative to a coisotropic submanifold, called the coisotropic Hofer–Zehnder capacity, and denoted by $c_{\rm LR}$![]() in this paper. By properties of this coisotropic capacity, they also studied symplectic embeddings relative to coisotropic constraints and got some corresponding dynamical results. The coisotropic capacity $c_{\rm LR}$
in this paper. By properties of this coisotropic capacity, they also studied symplectic embeddings relative to coisotropic constraints and got some corresponding dynamical results. The coisotropic capacity $c_{\rm LR}$![]() also played a key role in the proof of Humiliére–Leclercq–Seyfaddini's important rigidity result that symplectic homeomorphisms preserve coisotropic submanifolds and their characteristic foliations [Reference Humiliére, Leclercq and Seyfaddini21].
also played a key role in the proof of Humiliére–Leclercq–Seyfaddini's important rigidity result that symplectic homeomorphisms preserve coisotropic submanifolds and their characteristic foliations [Reference Humiliére, Leclercq and Seyfaddini21].
For the coisotropic capacity $c_{\rm LR}(D, D\cap \mathbb {R}^{n,k})$![]() of a bounded convex domain $D\subset \mathbb {R}^{2n}$
of a bounded convex domain $D\subset \mathbb {R}^{2n}$![]() , we [Reference Jin and Lu26] proved a representation formula, some interesting corollaries and corresponding versions of a Brunn–Minkowski type inequality by Artstein–Avidan and Ostrover and a theorem by Evgeni Neduv.
, we [Reference Jin and Lu26] proved a representation formula, some interesting corollaries and corresponding versions of a Brunn–Minkowski type inequality by Artstein–Avidan and Ostrover and a theorem by Evgeni Neduv.
1.2 A relative version of the Ekeland–Hofer capacity with respect to a coisotropic submanifold $\mathbb {R}^{n,k}$
Prompted by Gromov's work [Reference Gromov17], Ekeland and Hofer [Reference Ekeland and Hofer13, Reference Ekeland and Hofer14] constructed a sequence of symplectic invariants for subsets in the standard symplectic space $(\mathbb {R}^{2n},\omega _0)$![]() , the so-called Ekeland and Hofer symplectic capacities. (In this paper, the Ekeland and Hofer symplectic capacity always means the first Ekeland and Hofer symplectic capacity without special statements.) We introduced the generalized Ekeland–Hofer and the symmetric Ekeland–Hofer symplectic capacities and developed corresponding results [Reference Jin and Lu24, Reference Jin and Lu25]. The aim of this paper is to construct a coisotropic analogue of the Ekeland–Hofer capacity for subsets in $(\mathbb {R}^{2n},\omega _0)$
, the so-called Ekeland and Hofer symplectic capacities. (In this paper, the Ekeland and Hofer symplectic capacity always means the first Ekeland and Hofer symplectic capacity without special statements.) We introduced the generalized Ekeland–Hofer and the symmetric Ekeland–Hofer symplectic capacities and developed corresponding results [Reference Jin and Lu24, Reference Jin and Lu25]. The aim of this paper is to construct a coisotropic analogue of the Ekeland–Hofer capacity for subsets in $(\mathbb {R}^{2n},\omega _0)$![]() relative to a coisotropic submanifold $\mathbb {R}^{n,k}$
relative to a coisotropic submanifold $\mathbb {R}^{n,k}$![]() , the coisotropic Ekeland–Hofer capacity.
, the coisotropic Ekeland–Hofer capacity.
Fix an integer $0\le k\le n$![]() . For each subset $B\subset \mathbb {R}^{2n}$
. For each subset $B\subset \mathbb {R}^{2n}$![]() whose closure $\overline {B}$
whose closure $\overline {B}$![]() has nonempty intersection with $\mathbb {R}^{n,k}$
has nonempty intersection with $\mathbb {R}^{n,k}$![]() , we define a number $c^{n,k}(B)$
, we define a number $c^{n,k}(B)$![]() , called coisotropic Ekeland–Hofer capacity of $B$
, called coisotropic Ekeland–Hofer capacity of $B$![]() (though it does not satisfy the stronger monotonicity as in (i) above (1.5)), which is equal to the Ekeland–Hofer capacity of $B$
(though it does not satisfy the stronger monotonicity as in (i) above (1.5)), which is equal to the Ekeland–Hofer capacity of $B$![]() if $k=n$
if $k=n$![]() . The coisotropic capacity $c^{n,k}$
. The coisotropic capacity $c^{n,k}$![]() satisfies $c^{n,k}(B)=c^{n,k}(\overline {B})$
satisfies $c^{n,k}(B)=c^{n,k}(\overline {B})$![]() and the following:
and the following:
Proposition 1.1 Let $\lambda >0$![]() and $B\subset A\subset \mathbb {R}^{2n}$
and $B\subset A\subset \mathbb {R}^{2n}$![]() satisfy $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$
satisfy $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$![]() . Then
. Then
(i) (Monotonicity) $c^{n,k}(B)\le c^{n,k}(A)$
 .
.(ii) (Conformality) $c^{n,k}(\lambda B)=\lambda ^{2} c^{n,k}(B)$
 .
.(iii) (Exterior regularity) $c^{n,k}(B)=\inf \{c^{n,k}(U_\epsilon (B))\,|\,\epsilon >0\}$
 and so $c^{n,k}(B)=c^{n,k}(\overline {B}),$
and so $c^{n,k}(B)=c^{n,k}(\overline {B}),$ where $U_\epsilon (B)$
where $U_\epsilon (B)$ is the $\epsilon$
is the $\epsilon$ -neighbourhood of $B$
-neighbourhood of $B$ .
.(iv) (Translation invariance) $c^{n,k}(B+ w)=c^{n,k}(B)$
 for all $w\in \mathbb {R}^{n,k},$
for all $w\in \mathbb {R}^{n,k},$ where $B+w=\{z+w\,|\, z\in B\}$
where $B+w=\{z+w\,|\, z\in B\}$ .
.
The group ${\rm Sp}(2n)={\rm Sp}(2n,\mathbb {R})$![]() of symplectic matrices in $\mathbb {R}^{2n}$
of symplectic matrices in $\mathbb {R}^{2n}$![]() is a connected Lie group. Kun Shi shows in Appendix A that its subgroup
is a connected Lie group. Kun Shi shows in Appendix A that its subgroup
is also connected.
Theorem 1.2 (Symplectic invariance)
Let $B\subset \mathbb {R}^{2n}$![]() satisfy $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$
satisfy $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$![]() . Suppose that $\phi \in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$
. Suppose that $\phi \in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() satisfies for some $w_0\in \mathbb {R}^{n,k},$
satisfies for some $w_0\in \mathbb {R}^{n,k},$![]()
Then $c^{n,k}(\phi (B))=c^{n,k}(B)$![]() .
.
Corollary 1.3 For a subset $A\subset \mathbb {R}^{2n}$![]() satisfying $\overline {A}\cap \mathbb {R}^{n,k}\neq \emptyset,$
satisfying $\overline {A}\cap \mathbb {R}^{n,k}\neq \emptyset,$![]() suppose that there exists a star-shaped open neighbourhood $U$
suppose that there exists a star-shaped open neighbourhood $U$![]() of $\overline {A}$
of $\overline {A}$![]() with respect to some point $w_0\in \mathbb {R}^{n,k}$
with respect to some point $w_0\in \mathbb {R}^{n,k}$![]() and a symplectic embedding $\varphi$
and a symplectic embedding $\varphi$![]() from $U$
from $U$![]() to $\mathbb {R}^{2n}$
to $\mathbb {R}^{2n}$![]() such that
such that
Then $c^{n,k}(\varphi (A))=c^{n,k}(A)$![]() . In particular, for a subset $A\subset \mathbb {R}^{2n}$
. In particular, for a subset $A\subset \mathbb {R}^{2n}$![]() satisfying $\overline {A}\cap \mathbb {R}^{n,k}\neq \emptyset,$
satisfying $\overline {A}\cap \mathbb {R}^{n,k}\neq \emptyset,$![]() if it is star-shaped with respect to some point $w_0\in \mathbb {R}^{n,k}$
if it is star-shaped with respect to some point $w_0\in \mathbb {R}^{n,k}$![]() and there exists a symplectic embedding $\varphi$
and there exists a symplectic embedding $\varphi$![]() from some open neighbourhood $U$
from some open neighbourhood $U$![]() of $\overline {A}$
of $\overline {A}$![]() to $\mathbb {R}^{2n}$
to $\mathbb {R}^{2n}$![]() such that (1.7) holds, then $c^{n,k}(\varphi (A))=c^{n,k}(A)$
such that (1.7) holds, then $c^{n,k}(\varphi (A))=c^{n,k}(A)$![]() .
.
There exists a natural class of symplectic mappings satisfying the conditions in corollary 1.3. For $\epsilon >0$![]() small, let $\mathbb {R}^{n,k}_\epsilon =\{(q_1,\ldots, q_n, p_1,\ldots,p_n)\,|\, p_{k+1}^{2}+\cdots + p_n^{2}<\epsilon ^{2}\}$
small, let $\mathbb {R}^{n,k}_\epsilon =\{(q_1,\ldots, q_n, p_1,\ldots,p_n)\,|\, p_{k+1}^{2}+\cdots + p_n^{2}<\epsilon ^{2}\}$![]() , that is, the tubular open neighbourhood of $\mathbb {R}^{n,k}$
, that is, the tubular open neighbourhood of $\mathbb {R}^{n,k}$![]() of radius $\epsilon$
of radius $\epsilon$![]() . Let $U$
. Let $U$![]() be as in corollary 1.3, and let $H:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$
be as in corollary 1.3, and let $H:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$![]() be any smooth Hamiltonian that vanishes in $[0, 1]\times (\mathbb {R}^{n,k}_\epsilon \cap U)$
be any smooth Hamiltonian that vanishes in $[0, 1]\times (\mathbb {R}^{n,k}_\epsilon \cap U)$![]() . Suppose that $X_H$
. Suppose that $X_H$![]() can determine a $1$
can determine a $1$![]() -parameter family of symplectic mappings $\phi _H^{t}$
-parameter family of symplectic mappings $\phi _H^{t}$![]() for $t\in [0, 1]$
for $t\in [0, 1]$![]() as usual (e.g. this can be satisfied if $H$
as usual (e.g. this can be satisfied if $H$![]() has compact support). Then $\varphi :=(\psi _{w_0}\circ \phi _H^{1})|_U$
has compact support). Then $\varphi :=(\psi _{w_0}\circ \phi _H^{1})|_U$![]() satisfies the conditions in corollary 1.3, where $\psi _{w_0}\in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$
satisfies the conditions in corollary 1.3, where $\psi _{w_0}\in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() is the translation defined by $\psi _{w_0}(w)=w-w_0$
is the translation defined by $\psi _{w_0}(w)=w-w_0$![]() for $w\in \mathbb {R}^{2n}$
for $w\in \mathbb {R}^{2n}$![]() .
.
For a bounded convex domain $D$![]() in $(\mathbb {R}^{2n},\omega _0)$
in $(\mathbb {R}^{2n},\omega _0)$![]() with boundary $\mathcal {S}$
with boundary $\mathcal {S}$![]() , recall that a nonconstant absolutely continuous curve $z:[0,T]\to \mathbb {R}^{2n}$
, recall that a nonconstant absolutely continuous curve $z:[0,T]\to \mathbb {R}^{2n}$![]() (for some $T>0$
(for some $T>0$![]() ) is said to be a generalized characteristic on $\mathcal {S}$
) is said to be a generalized characteristic on $\mathcal {S}$![]() if $z([0,T])\subset \mathcal {S}$
if $z([0,T])\subset \mathcal {S}$![]() and $\dot {z}(t)\in J_{2n}N_\mathcal {S}(z(t))\ \hbox {a.e.}$
and $\dot {z}(t)\in J_{2n}N_\mathcal {S}(z(t))\ \hbox {a.e.}$![]() , where $N_\mathcal {S}(x)=\{y\in \mathbb {R}^{2n}\,|\, \langle u-x, y\rangle \le 0 \forall \ u\in D\}$
, where $N_\mathcal {S}(x)=\{y\in \mathbb {R}^{2n}\,|\, \langle u-x, y\rangle \le 0 \forall \ u\in D\}$![]() is the normal cone to $D$
is the normal cone to $D$![]() at $x\in \mathcal {S}$
at $x\in \mathcal {S}$![]() [Reference Jin and Lu24, definition 1.1]. When $D\cap \mathbb {R}^{n,k}\ne \emptyset$
[Reference Jin and Lu24, definition 1.1]. When $D\cap \mathbb {R}^{n,k}\ne \emptyset$![]() , such a generalized characteristic $z:[0,T]\to \mathcal {S}$
, such a generalized characteristic $z:[0,T]\to \mathcal {S}$![]() is called a generalized leafwise chord (abbreviated GLC) on $\mathcal {S}$
is called a generalized leafwise chord (abbreviated GLC) on $\mathcal {S}$![]() for $\mathbb {R}^{n,k}$
for $\mathbb {R}^{n,k}$![]() if $z(0), z(T)\in \mathbb {R}^{n,k}$
if $z(0), z(T)\in \mathbb {R}^{n,k}$![]() and $z(0)-z(T)\in V_0^{n,k}$
and $z(0)-z(T)\in V_0^{n,k}$![]() . (Generalized characteristics and generalized leafwise chords on $\mathcal {S}$
. (Generalized characteristics and generalized leafwise chords on $\mathcal {S}$![]() become characteristics and leafwise chords on $\mathcal {S}$
become characteristics and leafwise chords on $\mathcal {S}$![]() respectively if $\mathcal {S}$
respectively if $\mathcal {S}$![]() is of class $C^{1}$
is of class $C^{1}$![]() .) The action of a GLC $z:[0,T]\to \mathcal {S}$
.) The action of a GLC $z:[0,T]\to \mathcal {S}$![]() is defined by
is defined by
where $\langle \cdot,\cdot \rangle$![]() denotes the Euclid norm on $\mathbb {R}^{2n}$
denotes the Euclid norm on $\mathbb {R}^{2n}$![]() . As generalizations of representation formulas for the Ekeland–Hofer capacities of bounded convex domains we have:
. As generalizations of representation formulas for the Ekeland–Hofer capacities of bounded convex domains we have:
Theorem 1.4 Let $D\subset \mathbb {R}^{2n}$![]() be a bounded convex domain with $C^{1,1}$
be a bounded convex domain with $C^{1,1}$![]() boundary $S=\partial D$
boundary $S=\partial D$![]() . If $D\cap \mathbb {R}^{n,k}\ne \emptyset$
. If $D\cap \mathbb {R}^{n,k}\ne \emptyset$![]() $($
$($![]() and so $\partial D$
and so $\partial D$![]() contains at least two points of $\mathbb {R}^{n,k}),$
contains at least two points of $\mathbb {R}^{n,k}),$![]() then there exists a leafwise chord $x^{\ast }$
then there exists a leafwise chord $x^{\ast }$![]() on $\partial D$
on $\partial D$![]() for $\mathbb {R}^{n,k}$
for $\mathbb {R}^{n,k}$![]() such that
such that

Moreover, if $D\subset \mathbb {R}^{2n}$![]() is only a bounded convex domain such that $D\cap \mathbb {R}^{n,k}\ne \emptyset,$
is only a bounded convex domain such that $D\cap \mathbb {R}^{n,k}\ne \emptyset,$![]() then the above conclusions are still true after all words ‘leafwise chord’ are replaced by ‘generalized leafwise chord’.
then the above conclusions are still true after all words ‘leafwise chord’ are replaced by ‘generalized leafwise chord’.
This theorem may be false if the domain is not convex. Consider the following domain
where $0< r_1< r_2<\infty$![]() . Then by monotonicity of coisotropic Ekeland–Hofer capacity and theorem 1.4,
. Then by monotonicity of coisotropic Ekeland–Hofer capacity and theorem 1.4,
and

However, since $\partial A^{2n}(r_1, r_2)=\partial B^{2n-1}(r_1)\cup \partial B^{2n-1}(r_2)$![]() ,
,

Hence theorem 1.4 is false for $A^{2n}(r_1, r_2)$![]() .
.
Theorem 1.4 and [Reference Jin and Lu26, theorem 1.5] show that $c^{n,k}(D)=c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$![]() for a bounded convex domain $D\subset \mathbb {R}^{2n}$
for a bounded convex domain $D\subset \mathbb {R}^{2n}$![]() as in theorem 1.4. It follows from (3.18) and interior regularity of $c_{\rm LR}$
as in theorem 1.4. It follows from (3.18) and interior regularity of $c_{\rm LR}$![]() that
that
for any convex domain $D\subset \mathbb {R}^{2n}$![]() such that $D\cap \mathbb {R}^{n,k}\ne \emptyset$
such that $D\cap \mathbb {R}^{n,k}\ne \emptyset$![]() . Hence theorems 1.6, 1.12 and corollaries 1.7–1.10 in [Reference Jin and Lu26] are still true if $c_{\rm LR}$
. Hence theorems 1.6, 1.12 and corollaries 1.7–1.10 in [Reference Jin and Lu26] are still true if $c_{\rm LR}$![]() is replaced by suitable $c^{n,k}$
is replaced by suitable $c^{n,k}$![]() .
.
Moser [Reference Moser32] first studied Hamiltonian leafwise chords for understanding perturbations of Hamiltonian dynamical systems, his framework has been extended in many directions, which promotes the research of symplectic topology, see [Reference Albers and Frauenfelder3, Reference Albers and Momin4, Reference Dragnev12, Reference Ginzburg16, Reference Gürel18, Reference Hofer19, Reference Kang27, Reference Lisi and Rieser29, Reference Usher38, Reference Ziltener39] etc. Given two autonomous $C^{1,1}$![]() Hamiltonians $H, G:\mathbb {R}^{2n}\to \mathbb {R}$
Hamiltonians $H, G:\mathbb {R}^{2n}\to \mathbb {R}$![]() and a regular energy surface $G^{-1}(c')$
and a regular energy surface $G^{-1}(c')$![]() , one may ask the following natural mechanics problem: Is there a point on $G^{-1}(c')$
, one may ask the following natural mechanics problem: Is there a point on $G^{-1}(c')$![]() from which two particles start, move respectively along Hamiltonian trajectories of $X_H$
from which two particles start, move respectively along Hamiltonian trajectories of $X_H$![]() and $X_G$
and $X_G$![]() and after some finite time return to an intersection point of these two trajectories?
and after some finite time return to an intersection point of these two trajectories?
Suppose for some $c\in \mathbb {R}$![]() that $D_0:=\{z\in \mathbb {R}^{2n}\,|\, H(z)< c\}$
that $D_0:=\{z\in \mathbb {R}^{2n}\,|\, H(z)< c\}$![]() is a bounded convex domain whose intersection with $G^{-1}(c')$
is a bounded convex domain whose intersection with $G^{-1}(c')$![]() is a nonempty relative open subset in a $(2n-1)$
is a nonempty relative open subset in a $(2n-1)$![]() -dimensional coisotropic subspace $V$
-dimensional coisotropic subspace $V$![]() in $\mathbb {R}^{2n}$
in $\mathbb {R}^{2n}$![]() . Then theorem 1.4 implies an affirmative answer to the problem. In fact, since there exists a linear symplectic transformation $\Psi :(\mathbb {R}^{2n},\omega _0)\to (\mathbb {R}^{2n},\omega _0)$
. Then theorem 1.4 implies an affirmative answer to the problem. In fact, since there exists a linear symplectic transformation $\Psi :(\mathbb {R}^{2n},\omega _0)\to (\mathbb {R}^{2n},\omega _0)$![]() such that $\Psi (V)=\mathbb {R}^{n,n-1}$
such that $\Psi (V)=\mathbb {R}^{n,n-1}$![]() , we can replace $H$
, we can replace $H$![]() and $G$
and $G$![]() by $H\circ \Psi ^{-1}$
by $H\circ \Psi ^{-1}$![]() and $G\circ \Psi ^{-1}$
and $G\circ \Psi ^{-1}$![]() , respectively, and therefore reduce the question to the case $V=\mathbb {R}^{n,n-1}$
, respectively, and therefore reduce the question to the case $V=\mathbb {R}^{n,n-1}$![]() . The desired conclusion follows from theorem 1.4.
. The desired conclusion follows from theorem 1.4.
Theorem 1.4 is also closely related to the famous Arnold's chord conjecture in [Reference Arnol'd5, § 8]. Many cases for this problem have been proved to be true, see [Reference Abbas1, Reference Abbas2, Reference Cieliebak10, Reference Cristofaro-Gardiner and Hutchings11, Reference Hutchings and Taubes22, Reference Hutchings and Taubes23, Reference Merry30, Reference Mohnke31, Reference Rizell33–Reference Sandon35, Reference Ziltener40] etc. When $k=0$![]() , the intersection $S\cap \mathbb {R}^{n,0}$
, the intersection $S\cap \mathbb {R}^{n,0}$![]() is a closed $C^{1,1}$
is a closed $C^{1,1}$![]() Legendrian submanifold of dimension $n-1$
Legendrian submanifold of dimension $n-1$![]() in the contact manifold $S$
in the contact manifold $S$![]() with the standard contact form, which is diffeomorphic to the sphere $S^{n-1}$
with the standard contact form, which is diffeomorphic to the sphere $S^{n-1}$![]() , and theorem 1.4 affirms the conjecture in this case though for the smooth $S$
, and theorem 1.4 affirms the conjecture in this case though for the smooth $S$![]() it was proved by Mohnke [Reference Mohnke31] with a different method. Clearly, our result also gives the action of this chord.
it was proved by Mohnke [Reference Mohnke31] with a different method. Clearly, our result also gives the action of this chord.
As the Ekeland–Hofer capacity, $c^{n,k}$![]() satisfies the following product formulas, which play key roles for computations of $c_{\rm LR}$
satisfies the following product formulas, which play key roles for computations of $c_{\rm LR}$![]() and the proof of [Reference Jin and Lu26, theorem 1.12].
and the proof of [Reference Jin and Lu26, theorem 1.12].
Theorem 1.5 For convex domains $D_i\subset \mathbb {R}^{2n_i}$![]() containing the origin, $i=1,\ldots,m\ge 2,$
containing the origin, $i=1,\ldots,m\ge 2,$![]() and integers $0\le l_0\le n:=n_1+\cdots +n_m,$
and integers $0\le l_0\le n:=n_1+\cdots +n_m,$![]() $l_j=\max \{l_{j-1}-n_j,0\},$
$l_j=\max \{l_{j-1}-n_j,0\},$![]() $j=1,\ldots, m-1,$
$j=1,\ldots, m-1,$![]() it holds that
it holds that
Moreover, if all these domains $D_i$![]() are also bounded then
are also bounded then
Hereafter $\mathbb {R}^{2n_1}\times \mathbb {R}^{2n_2}\times \cdots \times \mathbb {R}^{2n_m}$![]() is identified with $\mathbb {R}^{2(n_1+\cdots +n_m)}$
is identified with $\mathbb {R}^{2(n_1+\cdots +n_m)}$![]() via
via

If $l_0=n$![]() then $l_i=\sum _{j>i}n_j$
then $l_i=\sum _{j>i}n_j$![]() and thus $\min \{n_i,l_{i-1}\}=n_i$
and thus $\min \{n_i,l_{i-1}\}=n_i$![]() for $i=1,\ldots,m$
for $i=1,\ldots,m$![]() . It follows that theorem 1.5 becomes theorem in [Reference Sikorav37, § 6.6]. We pointed out in [Reference Jin and Lu26, remark 1.11] that theorems 1.4, 1.5 and [Reference Jin and Lu26, theorem 1.5] can be combined together to improve some results therein.
. It follows that theorem 1.5 becomes theorem in [Reference Sikorav37, § 6.6]. We pointed out in [Reference Jin and Lu26, remark 1.11] that theorems 1.4, 1.5 and [Reference Jin and Lu26, theorem 1.5] can be combined together to improve some results therein.
Corollary 1.6 Let $S^{1}(r_i)$![]() be boundaries of discs $B^{2}(0,r_i)\subset \mathbb {R}^{2},$
be boundaries of discs $B^{2}(0,r_i)\subset \mathbb {R}^{2},$![]() $i=1,\ldots,n\ge 2,$
$i=1,\ldots,n\ge 2,$![]() and integers $0\le l_0\le n,$
and integers $0\le l_0\le n,$![]() $l_j=\max \{l_{j-1}-1,0\},$
$l_j=\max \{l_{j-1}-1,0\},$![]() $j=1,\ldots, n-1$
$j=1,\ldots, n-1$![]() . Then
. Then
Here $c^{1,1}(B^{2}(0,r_i))=\pi r_i^{2}$![]() and $c^{1,0}(B^{2}(0,r_i))=\pi r_i^{2}/2$
and $c^{1,0}(B^{2}(0,r_i))=\pi r_i^{2}/2$![]() . Precisely,
. Precisely,

Note that corollary 1.6 becomes [Reference Sikorav37, corollary 6.6] for $l_0=n$![]() .
.
Define $U^{2}(1)=\{(q_n,p_n)\in \mathbb {R}^{2}\,|\,q_n^{2}+p_n^{2}<1\;\hbox {or} -1< q_n<1 \hbox {and} p_n<0\}$![]() and
and
By (1.10) and [Reference Jin and Lu26, corollary 1.9] we obtain for $k=0,1,\ldots,n-1$![]() ,
,
The proof of theorem 1.5 relies partially on the representation of coisotropic Ekeland–Hofer capacity of convex domains given by theorem 1.4. It is possible that theorem 1.5 is still true for some product of non-convex domains. For integers $0\le l_0\le n:=n_1+ n_2$![]() and $l_1=\max \{l_0-n_1, 0\}$
and $l_1=\max \{l_0-n_1, 0\}$![]() , as the arguments below theorem 1.5 we can get
, as the arguments below theorem 1.5 we can get

and therefore

On the other hand

Hence (1.11) is also true for the produce of ${A^{2n_1}(r_1, r_2)}$![]() and $B^{2n_2}(r_3)$
and $B^{2n_2}(r_3)$![]() .
.
Recall that a vector field $X$![]() defined on an open set $U\subset \mathbb {R}^{2n}$
defined on an open set $U\subset \mathbb {R}^{2n}$![]() is called a Liouville vector field if $L_X\omega _0=\omega _0$
is called a Liouville vector field if $L_X\omega _0=\omega _0$![]() . A hypersurface $\mathcal {S}\subset \mathbb {R}^{2n}$
. A hypersurface $\mathcal {S}\subset \mathbb {R}^{2n}$![]() is said to be of restricted contact type if there exists a Liouville vector field $X$
is said to be of restricted contact type if there exists a Liouville vector field $X$![]() globally defined on $\mathbb {R}^{2n}$
globally defined on $\mathbb {R}^{2n}$![]() which is transversal to $\mathcal {S}$
which is transversal to $\mathcal {S}$![]() . Corresponding to the representation of the Ekeland–Hofer capacity of a bounded domain in $\mathbb {R}^{2n}$
. Corresponding to the representation of the Ekeland–Hofer capacity of a bounded domain in $\mathbb {R}^{2n}$![]() with boundary of restricted contact type we have:
with boundary of restricted contact type we have:
Theorem 1.7 Let $U\subset (\mathbb {R}^{2n},\omega _0)$![]() be a bounded domain with $C^{2n+2}$
be a bounded domain with $C^{2n+2}$![]() boundary $\mathcal {S}$
boundary $\mathcal {S}$![]() of restricted contact type. Suppose that $U$
of restricted contact type. Suppose that $U$![]() contains the origin and that there exists a globally defined $C^{2n+2}$
contains the origin and that there exists a globally defined $C^{2n+2}$![]() Liouville vector field $X$
Liouville vector field $X$![]() transversal to $\mathcal {S}$
transversal to $\mathcal {S}$![]() whose flow $\phi ^{t}$
whose flow $\phi ^{t}$![]() maps $\mathbb {R}^{n,k}$
maps $\mathbb {R}^{n,k}$![]() to $\mathbb {R}^{n,k}$
to $\mathbb {R}^{n,k}$![]() and preserves the leaf relation of $\mathbb {R}^{n,k}$
and preserves the leaf relation of $\mathbb {R}^{n,k}$![]() . Then
. Then
has empty interior and contains $c^{n,k}(U)=c^{n,k}(\mathcal {S})$![]() .
.
In order to show that $c^{n,k}$![]() is a coisotropic capacity (with the weaker monotonicity), we need to prove that $c^{n,k}$
is a coisotropic capacity (with the weaker monotonicity), we need to prove that $c^{n,k}$![]() satisfies the non-triviality as in (1.5). By theorem 1.4 we immediately obtain
satisfies the non-triviality as in (1.5). By theorem 1.4 we immediately obtain
Proposition 1.1(i) and (1.14) also lead to $c^{n,k}(W^{2n}(1))\ge c^{n,k}(U^{2n}(1))={\pi }/{2}$![]() directly. Using the extension monotonicity of $c_{\rm LR}$
directly. Using the extension monotonicity of $c_{\rm LR}$![]() in [Reference Lisi and Rieser29, lemma 2.4], Lisi and Rieser proved that
in [Reference Lisi and Rieser29, lemma 2.4], Lisi and Rieser proved that
above [Reference Lisi and Rieser29, proposition 3.1]. However, our proposition 1.1 and theorem 1.2 cannot yield such strong extension monotonicity for $c^{n,k}$![]() . Instead, we may use theorems 1.5 and 1.7 (though the latter does not hold for $c_{\rm LR}$
. Instead, we may use theorems 1.5 and 1.7 (though the latter does not hold for $c_{\rm LR}$![]() in general), to derive:
in general), to derive:
Theorem 1.8 For $k=0,\ldots,n-1,$![]() it holds that
it holds that
By this theorem, corollary 1.6 and theorem 1.2 we deduce:
Corollary 1.9 If $\min \{2\min _{i\le k}r_i^{2}, \min _{i>k}r_i^{2}\}>1$![]() for some $0< k< n,$
for some $0< k< n,$![]() then there is no $\phi \in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$
then there is no $\phi \in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() which satisfies $\phi (w)=w-w_0\ \forall \ w\in \mathbb {R}^{n,k}$
which satisfies $\phi (w)=w-w_0\ \forall \ w\in \mathbb {R}^{n,k}$![]() and ${\rm d}\phi (w_0)\in {\rm Sp}(2n,k)_0$
and ${\rm d}\phi (w_0)\in {\rm Sp}(2n,k)_0$![]() for some $w_0\in \mathbb {R}^{n,k},$
for some $w_0\in \mathbb {R}^{n,k},$![]() such that $\phi$
such that $\phi$![]() maps $S^{1}(r_1)\times \cdots \times S^{1}(r_n)$
maps $S^{1}(r_1)\times \cdots \times S^{1}(r_n)$![]() $= \{ (x_1, \ldots, x_n, y_1, \ldots, y_n) \in {{\mathbb {R}}}^{2n} \,|\, x_i^{2} + y_i^{2}=r_i^{2},\ i=1,\ldots,n\}$
$= \{ (x_1, \ldots, x_n, y_1, \ldots, y_n) \in {{\mathbb {R}}}^{2n} \,|\, x_i^{2} + y_i^{2}=r_i^{2},\ i=1,\ldots,n\}$![]() into $W^{2n}(1)$
into $W^{2n}(1)$![]() .
.
Under the assumptions of corollary 1.9 it is easy to see that there always exists a $\phi \in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() such that $\phi (S^{1}(r_1)\times \cdots \times S^{1}(r_n))\subset W^{2n}(1)$
such that $\phi (S^{1}(r_1)\times \cdots \times S^{1}(r_n))\subset W^{2n}(1)$![]() .
.
Let $\tau _0\in \mathcal {L}(\mathbb {R}^{2n})$![]() be the canonical involution on $\mathbb {R}^{2n}$
be the canonical involution on $\mathbb {R}^{2n}$![]() given by $\tau _0(x,y)=(x,-y)$
given by $\tau _0(x,y)=(x,-y)$![]() . For a subset $B\subset \mathbb {R}^{2n}$
. For a subset $B\subset \mathbb {R}^{2n}$![]() such that $\tau _0B=B$
such that $\tau _0B=B$![]() and $B\cap L^{n}_0\neq \emptyset$
and $B\cap L^{n}_0\neq \emptyset$![]() , let $c_{\rm EH,\tau _0}(B)$
, let $c_{\rm EH,\tau _0}(B)$![]() be the $\tau _0$
be the $\tau _0$![]() -symmetrical Ekeland–Hofer capacity constructed in [Reference Jin and Lu25]. We shall prove in § 8:
-symmetrical Ekeland–Hofer capacity constructed in [Reference Jin and Lu25]. We shall prove in § 8:
Theorem 1.10 The $\tau _0$![]() -symmetrical Ekeland–Hofer capacity $c_{\rm EH,\tau _0}(B)$
-symmetrical Ekeland–Hofer capacity $c_{\rm EH,\tau _0}(B)$![]() of each subset $B\subset \mathbb {R}^{2n}$
of each subset $B\subset \mathbb {R}^{2n}$![]() satisfying $\tau _0B=B$
satisfying $\tau _0B=B$![]() and $B\cap L^{n}_0\neq \emptyset$
and $B\cap L^{n}_0\neq \emptyset$![]() is greater than or equal to $c^{n,0}(B)$
is greater than or equal to $c^{n,0}(B)$![]() .
.
Structure of the paper. In § 2 we provide necessary variational preparations on the basis of [Reference Jin and Lu26, Reference Lisi and Rieser29]. In § 3 we give the definition of the coisotropic Ekeland–Hofer capacity and proofs of proposition 1.1, theorem 1.2 and corollary 1.3. In § 4 we prove theorem 1.4. In § 5 we prove a product formula, theorem 1.5. In § 6 we prove theorem 1.7 about the representation of the coisotropic capacity $c^{n,k}$![]() of a bounded domain in $\mathbb {R}^{2n}$
of a bounded domain in $\mathbb {R}^{2n}$![]() with boundary of restricted contact type. In § 7 we prove theorem 1.8.
with boundary of restricted contact type. In § 7 we prove theorem 1.8.
2. Variational preparations
We follow [Reference Jin and Lu26, Reference Lisi and Rieser29] to present necessary variational materials. Fix an integer $0\le k< n$![]() . Consider the Hilbert space defined in [Reference Lisi and Rieser29, definition 3.6]
. Consider the Hilbert space defined in [Reference Lisi and Rieser29, definition 3.6]

with $L^{2}$![]() -inner product. We proved in [Reference Jin and Lu26, proposition 2.3] that the Hilbert space $L^{2}_{n,k}$
-inner product. We proved in [Reference Jin and Lu26, proposition 2.3] that the Hilbert space $L^{2}_{n,k}$![]() is exactly $L^{2}([0,1],\mathbb {R}^{2n})$
is exactly $L^{2}([0,1],\mathbb {R}^{2n})$![]() . (If $k=n$
. (If $k=n$![]() this is clear as usual because $V^{n,n}_0=\{0\}$
this is clear as usual because $V^{n,n}_0=\{0\}$![]() and $V^{n,n}_1=\mathbb {R}^{2n}$
and $V^{n,n}_1=\mathbb {R}^{2n}$![]() .) For any real $s\ge 0$
.) For any real $s\ge 0$![]() we follow [Reference Lisi and Rieser29, definition 3.6] to define
we follow [Reference Lisi and Rieser29, definition 3.6] to define

Lemma 2.1 [Reference Lisi and Rieser29, lemmas 3.8, 3.9]
For each $s\ge 0,$![]() $H^{s}_{n,k}$
$H^{s}_{n,k}$![]() is a Hilbert space with the inner product
is a Hilbert space with the inner product
Furthermore, if $s>t,$![]() then the inclusion $\jmath :H^{s}_{n,k}\hookrightarrow H^{t}_{n,k}$
then the inclusion $\jmath :H^{s}_{n,k}\hookrightarrow H^{t}_{n,k}$![]() and its Hilbert adjoint $\jmath ^{\ast }:H^{t}_{n,k}\rightarrow H^{s}_{n,k}$
and its Hilbert adjoint $\jmath ^{\ast }:H^{t}_{n,k}\rightarrow H^{s}_{n,k}$![]() are compact.
are compact.
Let $\|\cdot \|_{s,n,k}$![]() denote the norm induced by $\langle \cdot,\cdot \rangle _{s,n,k}$
denote the norm induced by $\langle \cdot,\cdot \rangle _{s,n,k}$![]() . For $r\in \mathbb {N}$
. For $r\in \mathbb {N}$![]() or $r=\infty$
or $r=\infty$![]() let $C^{r}_{n,k}([0,1],\mathbb {R}^{2n})$
let $C^{r}_{n,k}([0,1],\mathbb {R}^{2n})$![]() denote the space of $C^{r}$
denote the space of $C^{r}$![]() maps $x:[0,1]\to \mathbb {R}^{2n}$
maps $x:[0,1]\to \mathbb {R}^{2n}$![]() such that $x(i)\in \mathbb {R}^{n,k}$
such that $x(i)\in \mathbb {R}^{n,k}$![]() , $i=0,1$
, $i=0,1$![]() , and $x(1)\sim x(0)$
, and $x(1)\sim x(0)$![]() , where $\sim$
, where $\sim$![]() is the leaf relation on $\mathbb {R}^{n,k}$
is the leaf relation on $\mathbb {R}^{n,k}$![]() . (Note: $H^{s}_{n,n}$
. (Note: $H^{s}_{n,n}$![]() is exactly the space $H^{s}$
is exactly the space $H^{s}$![]() on p. 83 of [Reference Hofer and Zehnder20]; $C^{r}_{n,n}([0,1],\mathbb {R}^{2n})$
on p. 83 of [Reference Hofer and Zehnder20]; $C^{r}_{n,n}([0,1],\mathbb {R}^{2n})$![]() is $C^{r}(\mathbb {R}/\mathbb {Z}, \mathbb {R}^{2n})$
is $C^{r}(\mathbb {R}/\mathbb {Z}, \mathbb {R}^{2n})$![]() .)
.)
Lemma 2.2 [Reference Lisi and Rieser29, lemma 3.10]
If $x\in H^{s}_{n,k}$![]() for $s>1/2+r$
for $s>1/2+r$![]() where $r$
where $r$![]() is an integer, then $x\in C^{r}_{n,k}([0,1],\mathbb {R}^{2n})$
is an integer, then $x\in C^{r}_{n,k}([0,1],\mathbb {R}^{2n})$![]() .
.
Lemma 2.3 [Reference Lisi and Rieser29, lemma 3.11]
$\jmath ^{\ast }(L^{2})\subset H^{1}_{n,k}$![]() and $\|\jmath ^{\ast }(y)\|_{1,n,k}\le \|y\|_{L^{2}}$
and $\|\jmath ^{\ast }(y)\|_{1,n,k}\le \|y\|_{L^{2}}$![]() .
.
Let
It has an orthogonal decomposition $E=E^{-}\oplus E^{0}\oplus E^{+}$![]() , where
, where

Let $P^{+}$![]() , $P^{0}$
, $P^{0}$![]() and $P^{-}$
and $P^{-}$![]() be the orthogonal projections to $E^{+}$
be the orthogonal projections to $E^{+}$![]() , $E^{0}$
, $E^{0}$![]() and $E^{-}$
and $E^{-}$![]() respectively. For $x\in E$
respectively. For $x\in E$![]() we write
we write
Define a functional $\mathfrak {a}:E\rightarrow \mathbb {R}$![]() by
by
Then there holds
(See [Reference Lisi and Rieser29].) The functional $\mathfrak {a}$![]() is differentiable with gradient $\nabla \mathfrak {a}(x)=x^{+}-x^{-}$
is differentiable with gradient $\nabla \mathfrak {a}(x)=x^{+}-x^{-}$![]() .
.
From now on we assume that for some $L>0$![]() ,
,
Then there exist positive real numbers $C_i$![]() , $i=1,2,3,4$
, $i=1,2,3,4$![]() , such that
, such that
for all $z\in \mathbb {R}^{2n}$![]() . Define functionals $\mathfrak {b}, \Phi _H: E\rightarrow \mathbb {R}$
. Define functionals $\mathfrak {b}, \Phi _H: E\rightarrow \mathbb {R}$![]() by
by
Lemma 2.4 [Reference Hofer and Zehnder20, § 3.3, lemma 4]
The functional $\mathfrak {b}$![]() is differentiable. Its gradient $\nabla \mathfrak {b}$
is differentiable. Its gradient $\nabla \mathfrak {b}$![]() is compact and satisfies a global Lipschitz condition on $E$
is compact and satisfies a global Lipschitz condition on $E$![]() . In particular, $\mathfrak {b}$
. In particular, $\mathfrak {b}$![]() is $C^{1,1}$
is $C^{1,1}$![]() .
.
Lemma 2.5 [Reference Jin and Lu26, lemma 2.8]
$x\in E$![]() is a critical point of $\Phi _H$
is a critical point of $\Phi _H$![]() if and only if $x\in C^{1}_{n,k}([0,1],\mathbb {R}^{2n})$
if and only if $x\in C^{1}_{n,k}([0,1],\mathbb {R}^{2n})$![]() and solves
and solves
Moreover, if $H$![]() is of class $C^{l}$
is of class $C^{l}$![]() $(l\ge 2)$
$(l\ge 2)$![]() then each critical point of $\Phi _H$
then each critical point of $\Phi _H$![]() on $E$
on $E$![]() is $C^{l}$
is $C^{l}$![]() .
.
Since $\nabla \Phi _H(x)=x^{+}-x^{-}-\nabla \mathfrak {b}(x)$![]() satisfies the global Lipschitz condition, it has a unique global flow $\mathbb {R}\times E\to E: (u,x)\mapsto \varphi _u(x)$
satisfies the global Lipschitz condition, it has a unique global flow $\mathbb {R}\times E\to E: (u,x)\mapsto \varphi _u(x)$![]() .
.
Lemma 2.6 [Reference Lisi and Rieser29, lemma 3.25]
$\varphi _u(x)$![]() has the following form
has the following form
where $K:\mathbb {R}\times E \to E$![]() is continuous and maps bounded sets into precompact sets.
is continuous and maps bounded sets into precompact sets.
This may follow from the proof of lemma 7 in [Reference Hofer and Zehnder20, § 3.3] directly.
3. The Ekeland–Hofer capacity relative to a coisotropic subspace
We closely follow Sikorav's approach [Reference Sikorav37] to the Ekeland–Hofer capacity in [Reference Ekeland and Hofer13]. Fix an integer $0\le k\le n$![]() . Let $E=H^{1/2}_{n,k}$
. Let $E=H^{1/2}_{n,k}$![]() be as in (2.3) and $S^{+}=\{x\in E^{+}\,|\,\|x\|_E=1\}$
be as in (2.3) and $S^{+}=\{x\in E^{+}\,|\,\|x\|_E=1\}$![]() .
.
Definition 3.1 A continuous map $\gamma :E\rightarrow E$![]() is called an admissible deformation if there exists a homotopy $(\gamma _u)_{0\le u\le 1}$
is called an admissible deformation if there exists a homotopy $(\gamma _u)_{0\le u\le 1}$![]() such that $\gamma _0={\rm id},$
such that $\gamma _0={\rm id},$![]() $\gamma _1=\gamma$
$\gamma _1=\gamma$![]() and satisfies
and satisfies
(i) $\forall u\in [0,1],$
 $\gamma _u(E\setminus (E^{-}\oplus E^{0}))\subset E\setminus (E^{-}\oplus E^{0}),$
$\gamma _u(E\setminus (E^{-}\oplus E^{0}))\subset E\setminus (E^{-}\oplus E^{0}),$ i.e. $\gamma _u(x)^{+}\neq 0$
i.e. $\gamma _u(x)^{+}\neq 0$ for any $x\in E$
for any $x\in E$ such that $x^{+}\neq 0$
such that $x^{+}\neq 0$ .
.(ii) $\gamma _u(x)=a(x,u)x^{+}+b(x,u)x^{0}+c(x,u)x^{-}+K(x,u),$
 where $(a,b,c,K)$
where $(a,b,c,K)$ is a continuous map from $E\times [0,1]$
is a continuous map from $E\times [0,1]$ to $(0,+\infty )^{3}\times E$
to $(0,+\infty )^{3}\times E$ and maps any closed bounded sets to compact sets.
and maps any closed bounded sets to compact sets.
Let $\Gamma _{n,k}$![]() be the set of all admissible deformations on $E$
be the set of all admissible deformations on $E$![]() . It is not hard to verify that the composition $\gamma \circ \tilde {\gamma } \in \Gamma _{n,k}$
. It is not hard to verify that the composition $\gamma \circ \tilde {\gamma } \in \Gamma _{n,k}$![]() for any $\gamma, \tilde {\gamma }\in \Gamma _{n,k}$
for any $\gamma, \tilde {\gamma }\in \Gamma _{n,k}$![]() . (If $k=n$
. (If $k=n$![]() , $\Gamma _{n,k}$
, $\Gamma _{n,k}$![]() is equal to $\Gamma$
is equal to $\Gamma$![]() in [Reference Sikorav37].) Corresponding to [Reference Sikorav37, § 3, proposition 1] or [Reference Ekeland and Hofer13, § II, proposition 1] we can easily prove the following intersection property.
in [Reference Sikorav37].) Corresponding to [Reference Sikorav37, § 3, proposition 1] or [Reference Ekeland and Hofer13, § II, proposition 1] we can easily prove the following intersection property.
Proposition 3.2 $\gamma (S^{+})\cap (E^{-}\oplus E^{0}\oplus \mathbb {R}_+e)\neq \emptyset$![]() for any $e\in E^{+}\setminus \{0\}$
for any $e\in E^{+}\setminus \{0\}$![]() and $\gamma \in \Gamma _{n,k}$
and $\gamma \in \Gamma _{n,k}$![]() .
.
Definition 3.3 For $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0}),$![]() the $\mathbb {R}^{n,k}$
the $\mathbb {R}^{n,k}$![]() -coisotropic capacity of $H$
-coisotropic capacity of $H$![]() is defined by
is defined by
where $\Phi _H$![]() is as in (2.5).
is as in (2.5).
By proposition 1 in [Reference Sikorav37, § 3.3], for any $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() there holds
there holds
where $z_1\in \mathbb {C}$![]() is the projection of $z\in \mathbb {C}^{n}\equiv \mathbb {C}\times \mathbb {C}^{n-1}$
is the projection of $z\in \mathbb {C}^{n}\equiv \mathbb {C}\times \mathbb {C}^{n-1}$![]() to $\mathbb {C}$
to $\mathbb {C}$![]() . Correspondingly, we have
. Correspondingly, we have
Proposition 3.4 For any $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() there holds
there holds
Proof. Let $e(t)={\rm e}^{\pi J_{2n}t}X$![]() , where $X\in V^{n,k}_0$
, where $X\in V^{n,k}_0$![]() and $|X|=1$
and $|X|=1$![]() . For any $x=y+\lambda e$
. For any $x=y+\lambda e$![]() , where $y\in E^{-}\oplus E^{0}$
, where $y\in E^{-}\oplus E^{0}$![]() and $\lambda >0$
and $\lambda >0$![]() , it holds that
, it holds that
and
It follows that

This and proposition 3.2 lead to
and hence (3.3) is proved.
A function $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() is called $\mathbb {R}^{n,k}$
is called $\mathbb {R}^{n,k}$![]() -admissible if it satisfies:
-admissible if it satisfies:
(H1) ${\rm Int}(H^{-1}(0))\ne \emptyset$
 and intersects with $\mathbb {R}^{n,k}$
and intersects with $\mathbb {R}^{n,k}$ ,
,(H2) there exists $z_0\in \mathbb {R}^{n,k}$
 , real numbers $a, b$
, real numbers $a, b$ such that $H(z)=a|z|^{2}+ \langle z, z_0\rangle + b$
such that $H(z)=a|z|^{2}+ \langle z, z_0\rangle + b$ outside a compact subset of $\mathbb {R}^{2n}$
outside a compact subset of $\mathbb {R}^{2n}$ , where $a>\pi$
, where $a>\pi$ for $k=n$
for $k=n$ , and $a>\pi /2$
, and $a>\pi /2$ for $0\le k< n$
for $0\le k< n$ .
.
Moreover, a $\mathbb {R}^{n,n}$![]() -admissible $H$
-admissible $H$![]() is said to be nonresonant if $a$
is said to be nonresonant if $a$![]() in (H2) does not belong to $\pi \mathbb {N}$
in (H2) does not belong to $\pi \mathbb {N}$![]() ; and a $\mathbb {R}^{n,k}$
; and a $\mathbb {R}^{n,k}$![]() -admissible $H$
-admissible $H$![]() with $k< n$
with $k< n$![]() is called strong nonresonant if $a$
is called strong nonresonant if $a$![]() in (H2) does not sit in $\mathbb {N}\pi /2$
in (H2) does not sit in $\mathbb {N}\pi /2$![]() .
.
Clearly, for any $\mathbb {R}^{n,k}$![]() -admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
-admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() , $\nabla H:\mathbb {R}^{2n}\to \mathbb {R}^{2n}$
, $\nabla H:\mathbb {R}^{2n}\to \mathbb {R}^{2n}$![]() satisfies a global Lipschitz condition.
satisfies a global Lipschitz condition.
Note that $c^{n,k}(H)<+\infty$![]() if $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
if $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfies
satisfies
for some constant $C$![]() , where $a=\pi$
, where $a=\pi$![]() for $k=n$
for $k=n$![]() , and $a=\pi /2$
, and $a=\pi /2$![]() for $0\le k< n$
for $0\le k< n$![]() . In particular, we have $c^{n,k}(H)<+\infty$
. In particular, we have $c^{n,k}(H)<+\infty$![]() for any $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
for any $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfying (H2). In fact, for $k=n$
satisfying (H2). In fact, for $k=n$![]() this can be derived from (3.2) (cf. [Reference Sikorav37]). For $0\le k< n$
this can be derived from (3.2) (cf. [Reference Sikorav37]). For $0\le k< n$![]() , since there exist constants $a>\pi /2, b$
, since there exist constants $a>\pi /2, b$![]() such that $H(z)\ge a|z|^{2}+\langle z,z_0\rangle +b$
such that $H(z)\ge a|z|^{2}+\langle z,z_0\rangle +b$![]() for all $z\in \mathbb {R}^{2n}$
for all $z\in \mathbb {R}^{2n}$![]() , using the inequality
, using the inequality
for any $0<\varepsilon < a-\frac {\pi }{2}$![]() , we deduce that
, we deduce that
Then proposition 3.4 leads to $c^{n,k}(H)<+\infty$![]() .
.
It is easy proved that $c^{n,k}(H)$![]() satisfies:
satisfies:
Proposition 3.5 Let $H, K\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfy (H1) and (H2). Then the following holds$:$
satisfy (H1) and (H2). Then the following holds$:$![]()
(i) (Monotonicity) If $H\le K$
 then $c^{n,k}(H)\ge c^{n,k}(K)$
then $c^{n,k}(H)\ge c^{n,k}(K)$ .
.(ii) (Continuity) $|c^{n,k}(H)-c^{n,k}(K)|\le \sup _{z\in \mathbb {R}^{2n}}|H(z)-K(z)|$
 .
.(iii) (Homogeneity) $c^{n,k}(\lambda ^{2}H(\cdot /\lambda ))=\lambda ^{2} c^{n,k}(H)$
 for $\lambda \ne 0$
for $\lambda \ne 0$ .
.
By proposition 2 in [Reference Sikorav37, § 3.3] the following proposition holds for $k=n$![]() .
.
Proposition 3.6 Suppose that $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfies
satisfies
for some $z_0\in \mathbb {R}^{n,k}$![]() and for constants $C_1>0$
and for constants $C_1>0$![]() and $C_2>0$
and $C_2>0$![]() . Then $c^{n,k}(H)>0$
. Then $c^{n,k}(H)>0$![]() . In particular, $c^{n,k}(H)>0$
. In particular, $c^{n,k}(H)>0$![]() for any $\mathbb {R}^{n,k}$
for any $\mathbb {R}^{n,k}$![]() -admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
-admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() .
.
Proof. We assume $k< n$![]() . For a constant $\varepsilon >0$
. For a constant $\varepsilon >0$![]() define $\gamma _\varepsilon \in \Gamma _{n,k}$
define $\gamma _\varepsilon \in \Gamma _{n,k}$![]() by $\gamma _\varepsilon (x)=z_0+\varepsilon x\ \forall \ x\in E$
by $\gamma _\varepsilon (x)=z_0+\varepsilon x\ \forall \ x\in E$![]() . We claim that
. We claim that
for sufficiently small $\varepsilon$![]() . Since
. Since
it suffices to prove that

Otherwise, suppose there exists a sequence $(x_j)\subset E$![]() and $d>0$
and $d>0$![]() satisfying
satisfying

Let $y_j={x_j}/{\|x_j\|_E}$![]() and hence $\|y_j\|_E=1$
and hence $\|y_j\|_E=1$![]() . Then lemma 2.1 implies that $(y_j)$
. Then lemma 2.1 implies that $(y_j)$![]() has a convergent subsequence in $L^{2}$
has a convergent subsequence in $L^{2}$![]() . By a standard result in $L^{p}$
. By a standard result in $L^{p}$![]() theory, we have $w\in L^{2}$
theory, we have $w\in L^{2}$![]() and a subsequence of $(y_j)$
and a subsequence of $(y_j)$![]() , still denoted by $(y_j)$
, still denoted by $(y_j)$![]() , such that $y_j(t)\rightarrow y(t)$
, such that $y_j(t)\rightarrow y(t)$![]() a.e. on $(0,1)$
a.e. on $(0,1)$![]() and that $|y_j(t)|\leq w(t)$
and that $|y_j(t)|\leq w(t)$![]() a.e. on $(0,1)$
a.e. on $(0,1)$![]() for each $j$
for each $j$![]() . It follows from (3.5) that
. It follows from (3.5) that

The first claim in (3.9) implies that $(x_j)$![]() has a subsequence such that $x_{j_l}(t)\rightarrow 0$
has a subsequence such that $x_{j_l}(t)\rightarrow 0$![]() , a.e. in $(0,1)$
, a.e. in $(0,1)$![]() . Hence the Lebesgue dominated convergence theorem leads to
. Hence the Lebesgue dominated convergence theorem leads to
This contradicts the second claim in (3.9).
For any fixed $\mathbb {R}^{n,k}$![]() -admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
-admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() , pick some $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}(H^{-1}(0))$
, pick some $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}(H^{-1}(0))$![]() . Since (H1) implies that $H$
. Since (H1) implies that $H$![]() vanishes near $z_0$
vanishes near $z_0$![]() , by (H2) and the Taylor expansion of $H$
, by (H2) and the Taylor expansion of $H$![]() at $z_0\in \mathbb {R}^{2n}$
at $z_0\in \mathbb {R}^{2n}$![]() , we have constants $C_1>0$
, we have constants $C_1>0$![]() and $C_2>0$
and $C_2>0$![]() such that $H$
such that $H$![]() satisfies (3.5).
satisfies (3.5).
By (3.2) and propositions 3.4 and 3.6 we see that $c^{n,k}(H)$![]() is a finite positive number for each $\mathbb {R}^{n,k}$
is a finite positive number for each $\mathbb {R}^{n,k}$![]() -admissible $H$
-admissible $H$![]() . The following is a generalization of lemma 3 in [Reference Sikorav37, § 3.4].
. The following is a generalization of lemma 3 in [Reference Sikorav37, § 3.4].
Lemma 3.7 Let $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfy (3.4) and (3.5). Then
satisfy (3.4) and (3.5). Then
where
Moreover, if $H$![]() is also of class $C^{2}$
is also of class $C^{2}$![]() and has bounded derivatives of second order, then $\mathcal {F}_{n,k}$
and has bounded derivatives of second order, then $\mathcal {F}_{n,k}$![]() is positive invariant under the flow $\varphi _u$
is positive invariant under the flow $\varphi _u$![]() of $\nabla \Phi _H$
of $\nabla \Phi _H$![]() $($
$($![]() which must exist as pointed out above in lemma 2.6).
which must exist as pointed out above in lemma 2.6).
Proof. Since $c^{n,k}(H)$![]() is a finite positive number by proposition 3.6, the first claim follows from the arguments above proposition 3.5.
is a finite positive number by proposition 3.6, the first claim follows from the arguments above proposition 3.5.
When $H$![]() has bounded derivatives of second order, (2.4) is satisfied naturally. Then $\nabla \Phi _H$
has bounded derivatives of second order, (2.4) is satisfied naturally. Then $\nabla \Phi _H$![]() satisfies the global Lipschitz condition, and thus has a unique global flow $\mathbb {R}\times E\to E: (u,x)\mapsto \varphi _u(x)$
satisfies the global Lipschitz condition, and thus has a unique global flow $\mathbb {R}\times E\to E: (u,x)\mapsto \varphi _u(x)$![]() satisfying lemma 2.6, that is, $\varphi _u(x)={\rm e}^{-u}x^{-}+x^{0}+{\rm e}^{u}x^{+}+\widetilde {K}(u,x)$
satisfying lemma 2.6, that is, $\varphi _u(x)={\rm e}^{-u}x^{-}+x^{0}+{\rm e}^{u}x^{+}+\widetilde {K}(u,x)$![]() , where $\widetilde {K}:\mathbb {R}\times E\rightarrow E$
, where $\widetilde {K}:\mathbb {R}\times E\rightarrow E$![]() is continuous and maps bounded sets into precompact sets. For a set $F=\gamma (S^{+})\in \mathcal {F}_{n,k}$
is continuous and maps bounded sets into precompact sets. For a set $F=\gamma (S^{+})\in \mathcal {F}_{n,k}$![]() with $\gamma \in \Gamma _{n,k}$
with $\gamma \in \Gamma _{n,k}$![]() , we have $\alpha :=\inf (\Phi _H|_{\gamma (S^{+})})>0$
, we have $\alpha :=\inf (\Phi _H|_{\gamma (S^{+})})>0$![]() by the definition of $\mathcal {F}_{n,k}$
by the definition of $\mathcal {F}_{n,k}$![]() . Let $\rho :\mathbb {R}\rightarrow [0,1]$
. Let $\rho :\mathbb {R}\rightarrow [0,1]$![]() be a smooth function such that $\rho (s)=0$
be a smooth function such that $\rho (s)=0$![]() for $s\le 0$
for $s\le 0$![]() and $\rho (s)=1$
and $\rho (s)=1$![]() for $s\ge \alpha$
for $s\ge \alpha$![]() . Define a vector field $V$
. Define a vector field $V$![]() on $E$
on $E$![]() by
by
Clearly $V$![]() is locally Lipschitz and has linear growth. These imply that $V$
is locally Lipschitz and has linear growth. These imply that $V$![]() has a unique global flow, denoted by $\Upsilon _u$
has a unique global flow, denoted by $\Upsilon _u$![]() . Moreover, it is obvious that $\Upsilon _u$
. Moreover, it is obvious that $\Upsilon _u$![]() has the same property as $\varphi _u$
has the same property as $\varphi _u$![]() described in lemma 2.6. For $x\in E^{-}\oplus E^{0}$
described in lemma 2.6. For $x\in E^{-}\oplus E^{0}$![]() , we have $\Phi _H(x)\le 0$
, we have $\Phi _H(x)\le 0$![]() and hence $V(x)=-x^{-}$
and hence $V(x)=-x^{-}$![]() , which implies that $\Upsilon _u(E^{-}\oplus E^{0})=E^{-}\oplus E^{0}$
, which implies that $\Upsilon _u(E^{-}\oplus E^{0})=E^{-}\oplus E^{0}$![]() and $\Upsilon _u(E\setminus E^{-}\oplus E^{0})=E\setminus E^{-}\oplus E^{0}$
and $\Upsilon _u(E\setminus E^{-}\oplus E^{0})=E\setminus E^{-}\oplus E^{0}$![]() since $\Upsilon _u$
since $\Upsilon _u$![]() is a homeomorphism for each $u\in \mathbb {R}$
is a homeomorphism for each $u\in \mathbb {R}$![]() . Therefore, $\Upsilon _u\in \Gamma _{n,k}$
. Therefore, $\Upsilon _u\in \Gamma _{n,k}$![]() for all $u\in \mathbb {R}$
for all $u\in \mathbb {R}$![]() .
.
Note that $V|_{\Phi _H^{-1}([\alpha,\infty ])}=\nabla \Phi _H(x)$![]() . For each $u\ge 0$
. For each $u\ge 0$![]() we have $\Upsilon _u(x)=\varphi _u(x)$
we have $\Upsilon _u(x)=\varphi _u(x)$![]() for any $x\in \Phi _H^{-1}([\alpha,\infty ])$
for any $x\in \Phi _H^{-1}([\alpha,\infty ])$![]() , and especially $\Upsilon _u(F)=\varphi _u(F)$
, and especially $\Upsilon _u(F)=\varphi _u(F)$![]() , that is, $(\Upsilon _u\circ \gamma )(S^{+})=\varphi _u(F)$
, that is, $(\Upsilon _u\circ \gamma )(S^{+})=\varphi _u(F)$![]() . Since $\Gamma _{n,k}$
. Since $\Gamma _{n,k}$![]() is closed for the composition operation and
is closed for the composition operation and
we obtain $\varphi _u(F)\in \mathcal {F}_{n,k}$![]() , that is, $\mathcal {F}_{n,k}$
, that is, $\mathcal {F}_{n,k}$![]() is positively invariant under the flow $\varphi _u$
is positively invariant under the flow $\varphi _u$![]() of $\nabla \Phi _H$
of $\nabla \Phi _H$![]() .
.
Clearly, a $\mathbb {R}^{n,k}$![]() -admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
-admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfies the conditions of lemma 3.7.
satisfies the conditions of lemma 3.7.
Theorem 3.8 If an $\mathbb {R}^{n,k}$![]() -admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
-admissible $H\in C^{2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() is nonresonant for $k=n,$
is nonresonant for $k=n,$![]() and strong nonresonant for $k< n,$
and strong nonresonant for $k< n,$![]() then $c^{n,k}(H)$
then $c^{n,k}(H)$![]() is a positive critical value of $\Phi _H$
is a positive critical value of $\Phi _H$![]() .
.
The case of $k=n$![]() was proved in [Reference Ekeland and Hofer13, § II, proposition 2] (see also [Reference Sikorav37, § 3.4, proposition 1]). It remains to prove the case $k< n$
was proved in [Reference Ekeland and Hofer13, § II, proposition 2] (see also [Reference Sikorav37, § 3.4, proposition 1]). It remains to prove the case $k< n$![]() . By lemma 2.4, the functional $\Phi _H$
. By lemma 2.4, the functional $\Phi _H$![]() is $C^{1,1}$
is $C^{1,1}$![]() and its gradient $\nabla \Phi _H$
and its gradient $\nabla \Phi _H$![]() satisfies a global Lipschitz condition on $E$
satisfies a global Lipschitz condition on $E$![]() . By a standard minimax argument, theorem 3.8 follows from lemma 3.7 and the following
. By a standard minimax argument, theorem 3.8 follows from lemma 3.7 and the following
Lemma 3.9 If an $\mathbb {R}^{n,k}$![]() -admissible $H\in C^{1}(\mathbb {R}^{2n},\mathbb {R}{\ge 0})$
-admissible $H\in C^{1}(\mathbb {R}^{2n},\mathbb {R}{\ge 0})$![]() is strong nonresonant, then each sequence $(x_j)\subset E$
is strong nonresonant, then each sequence $(x_j)\subset E$![]() with $\nabla \Phi _{H}(x_j)\to 0$
with $\nabla \Phi _{H}(x_j)\to 0$![]() has a convergent subsequence. In particular, $\Phi _H$
has a convergent subsequence. In particular, $\Phi _H$![]() satisfies the $($
satisfies the $($![]() PS$)$
PS$)$![]() condition.
condition.
Proof. The functional $\mathfrak {b}$![]() is differentiable. Its gradient $\nabla \mathfrak {b}$
is differentiable. Its gradient $\nabla \mathfrak {b}$![]() is compact and satisfies a global Lipschitz condition on $E$
is compact and satisfies a global Lipschitz condition on $E$![]() . Since $\nabla \Phi _{H}(x)=x^{+}-x^{-}-\nabla \mathfrak {b}(x)$
. Since $\nabla \Phi _{H}(x)=x^{+}-x^{-}-\nabla \mathfrak {b}(x)$![]() for any $x\in E$
for any $x\in E$![]() , we have
, we have
Case 1. $(x_j)$![]() is bounded in $E$
is bounded in $E$![]() . Then $(x^{0}_j)$
. Then $(x^{0}_j)$![]() is a bounded sequence in the space $\mathbb {R}^{n,k}$
is a bounded sequence in the space $\mathbb {R}^{n,k}$![]() of finite dimension. Hence $(x^{0}_j)$
of finite dimension. Hence $(x^{0}_j)$![]() has a convergent subsequence. Moreover, since $\nabla \mathfrak {b}$
has a convergent subsequence. Moreover, since $\nabla \mathfrak {b}$![]() is compact, $(\nabla \mathfrak {b}(x_j))$
is compact, $(\nabla \mathfrak {b}(x_j))$![]() has a convergent subsequence, and so both $(x_j^{+})$
has a convergent subsequence, and so both $(x_j^{+})$![]() and $(x_j^{-})$
and $(x_j^{-})$![]() have convergent subsequences in $E$
have convergent subsequences in $E$![]() . It follows that $(x_j)$
. It follows that $(x_j)$![]() has a convergent subsequence.Case 2. $(x_j)$
has a convergent subsequence.Case 2. $(x_j)$![]() is unbounded in $E$
is unbounded in $E$![]() . Without loss of generality, we may assume $\lim _{j\rightarrow +\infty }\|x_j\|_E=+\infty$
. Without loss of generality, we may assume $\lim _{j\rightarrow +\infty }\|x_j\|_E=+\infty$![]() . For $z_0\in \mathbb {R}^{n,k}$
. For $z_0\in \mathbb {R}^{n,k}$![]() defined as in (H2), let
defined as in (H2), let
Then $|y_j^{0}|\le \|y_j\|_E\le 1+|{z_0}/{2a}|$![]() , and (3.11) implies
, and (3.11) implies
Also by (H2) there exist constants $C_1$![]() and $C_2$
and $C_2$![]() such that
such that

that is, $(\nabla H(x_j)/\|x_j\|_E)$![]() is bounded in $L^{2}$
is bounded in $L^{2}$![]() . Hence the sequence $\jmath ^{\ast }( \nabla H(x_j)/\|x_j\|_E)$
. Hence the sequence $\jmath ^{\ast }( \nabla H(x_j)/\|x_j\|_E)$![]() is compact. (3.12) implies that $(y_j)$
is compact. (3.12) implies that $(y_j)$![]() has a convergent subsequence in $E$
has a convergent subsequence in $E$![]() . Without loss of generality, we may assume that $y_{j}\rightarrow y$
. Without loss of generality, we may assume that $y_{j}\rightarrow y$![]() in $E$
in $E$![]() . Since (H2) implies that $H(z)=Q(z):=a|z|^{2}+ \langle z, z_0\rangle + b$
. Since (H2) implies that $H(z)=Q(z):=a|z|^{2}+ \langle z, z_0\rangle + b$![]() for $|z|$
for $|z|$![]() sufficiently large, there exists a constant $C>0$
sufficiently large, there exists a constant $C>0$![]() such that $|\nabla H(z)-\nabla Q(z)|\leq C$
such that $|\nabla H(z)-\nabla Q(z)|\leq C$![]() for all $z\in \mathbb {R}^{2n}$
for all $z\in \mathbb {R}^{2n}$![]() . It follows that as $j\to \infty$
. It follows that as $j\to \infty$![]() ,
,

This implies that $\jmath ^{\ast }(\nabla H(x_k)/\|x_k\|_{E})$![]() tends to $\jmath ^{\ast }(\nabla Q(y))$
tends to $\jmath ^{\ast }(\nabla Q(y))$![]() in $E$
in $E$![]() , and thus we arrive at
, and thus we arrive at
Then $y$![]() is smooth and satisfies
is smooth and satisfies
Clearly $y(t)$![]() is given by
is given by
Since $\|y+({1}/{2a})z_0\|_{E}=1$![]() implies that $y+({1}/{2a})z_0$
implies that $y+({1}/{2a})z_0$![]() is nonconstant, using the boundary condition satisfied by $y$
is nonconstant, using the boundary condition satisfied by $y$![]() and the assumption that $z_0\in \mathbb {R}^{n,k}$
and the assumption that $z_0\in \mathbb {R}^{n,k}$![]() , we deduce that $2a\in m\mathbb {N}\pi$
, we deduce that $2a\in m\mathbb {N}\pi$![]() . This gives rise to a contradiction because $H$
. This gives rise to a contradiction because $H$![]() is strong non-resonant.
is strong non-resonant.
Corresponding to [Reference Sikorav37, § 3.5, lemma] we have
Lemma 3.10 Suppose that $H:\mathbb {R}^{2n}\to \mathbb {R}$![]() is of class $C^{2n+2}$
is of class $C^{2n+2}$![]() and that $\nabla H:\mathbb {R}^{2n}\to \mathbb {R}^{2n}$
and that $\nabla H:\mathbb {R}^{2n}\to \mathbb {R}^{2n}$![]() satisfies a global Lipschitz condition. Then the set of critical values of $\Phi _{H}$
satisfies a global Lipschitz condition. Then the set of critical values of $\Phi _{H}$![]() has empty interior in $\mathbb {R}$
has empty interior in $\mathbb {R}$![]() .
.
Proof. The method is similar to that of [Reference Jin and Lu26, lemma 3.5]. For clearness we give it in details. By lemma 2.4, $\Phi _H$![]() is $C^{1,1}$
is $C^{1,1}$![]() . Lemma 2.5 implies that all critical points of $\Phi _{H}$
. Lemma 2.5 implies that all critical points of $\Phi _{H}$![]() sit in $C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$
sit in $C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$![]() . Thus the restriction of $\Phi _{H}$
. Thus the restriction of $\Phi _{H}$![]() to $C^{1}_{n,k}([0,1],\mathbb {R}^{2n})$
to $C^{1}_{n,k}([0,1],\mathbb {R}^{2n})$![]() , denoted by $\hat \Phi _{H}$
, denoted by $\hat \Phi _{H}$![]() , and $\Phi _{H}$
, and $\Phi _{H}$![]() have the same critical value sets. As in the proof of [Reference Jin and Lu24, claim 4.4] we can deduce that $\hat \Phi _{H}$
have the same critical value sets. As in the proof of [Reference Jin and Lu24, claim 4.4] we can deduce that $\hat \Phi _{H}$![]() is of class $C^{2n+1}$
is of class $C^{2n+1}$![]() .
.
Let $P_0$![]() and $P_1$
and $P_1$![]() be the orthogonal projections of $\mathbb {R}^{2n}$
be the orthogonal projections of $\mathbb {R}^{2n}$![]() to the spaces $V_0^{n,k}$
to the spaces $V_0^{n,k}$![]() and $V_1^{2k}$
and $V_1^{2k}$![]() in (1.1) and (1.2), respectively. Take a smooth $g:[0,1]\rightarrow [0,1]$
in (1.1) and (1.2), respectively. Take a smooth $g:[0,1]\rightarrow [0,1]$![]() such that $g$
such that $g$![]() equals $1$
equals $1$![]() (resp. $0$
(resp. $0$![]() ) near $0$
) near $0$![]() (resp. $1$
(resp. $1$![]() ). Denote by $\phi ^{t}$
). Denote by $\phi ^{t}$![]() the flow of $X_{H}$
the flow of $X_{H}$![]() . Since $X_{H}$
. Since $X_{H}$![]() is $C^{2n+1}$
is $C^{2n+1}$![]() , we have a $C^{2n+1}$
, we have a $C^{2n+1}$![]() map
map
For any $z\in \mathbb {R}^{n,k}$![]() , since $\psi (0,z)=\phi ^{0}(z)=z$
, since $\psi (0,z)=\phi ^{0}(z)=z$![]() and $\psi (1,z)=P_0\phi ^{1}(z)+P_1z$
and $\psi (1,z)=P_0\phi ^{1}(z)+P_1z$![]() , we have
, we have
These and [Reference Jin and Lu24, corollary B.2] show that $\psi$![]() gives rise to a $C^{2n}$
gives rise to a $C^{2n}$![]() map
map
Hence $\Phi _{H}\circ \Omega : \mathbb {R}^{n,k}\to \mathbb {R}$![]() is of class $C^{2n}$
is of class $C^{2n}$![]() . By Sard's theorem we deduce that the critical value sets of $\Phi _{H}\circ \Omega$
. By Sard's theorem we deduce that the critical value sets of $\Phi _{H}\circ \Omega$![]() is nowhere dense (since $\dim \mathbb {R}^{n,k}<2n$
is nowhere dense (since $\dim \mathbb {R}^{n,k}<2n$![]() ).
).
Let $z\in \mathbb {R}^{n,k}$![]() be such that $\phi ^{1}(z)\in \mathbb {R}^{n,k}$
be such that $\phi ^{1}(z)\in \mathbb {R}^{n,k}$![]() and $\phi ^{1}(z)\sim z$
and $\phi ^{1}(z)\sim z$![]() . Then $P_0\phi ^{1}(z)-P_0z=\phi ^{1}(z)-z$
. Then $P_0\phi ^{1}(z)-P_0z=\phi ^{1}(z)-z$![]() and therefore $P_0\phi ^{1}(z)+P_1z=\phi ^{1}(z)$
and therefore $P_0\phi ^{1}(z)+P_1z=\phi ^{1}(z)$![]() , which implies $\psi (t,z)=\phi ^{t}(z) \forall \ t\in [0,1]$
, which implies $\psi (t,z)=\phi ^{t}(z) \forall \ t\in [0,1]$![]() .
.
For a critical point $y$![]() of $\Phi _H$
of $\Phi _H$![]() , that is, $y\in C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$
, that is, $y\in C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$![]() and solves $\dot {y}=J_{2n}\nabla H(y)=X_H(y)$
and solves $\dot {y}=J_{2n}\nabla H(y)=X_H(y)$![]() , with $z_y:=y(0)\in \mathbb {R}^{n,k}$
, with $z_y:=y(0)\in \mathbb {R}^{n,k}$![]() we have $y(t)=\phi ^{t}(z_y)\ \forall \ t\in [0,1]$
we have $y(t)=\phi ^{t}(z_y)\ \forall \ t\in [0,1]$![]() , which implies that $\phi ^{1}(z_y)\in \mathbb {R}^{n,k}$
, which implies that $\phi ^{1}(z_y)\in \mathbb {R}^{n,k}$![]() , $\phi ^{1}(z_y)\sim z_y$
, $\phi ^{1}(z_y)\sim z_y$![]() and therefore $y=\psi (\cdot,z_y)=\Omega (z_y)$
and therefore $y=\psi (\cdot,z_y)=\Omega (z_y)$![]() . Hence $z_y$
. Hence $z_y$![]() is a critical point of $\Phi _{H}\circ \Omega$
is a critical point of $\Phi _{H}\circ \Omega$![]() and $\Phi _{H}\circ \Omega (z_y)=\Phi _{H}(y)$
and $\Phi _{H}\circ \Omega (z_y)=\Phi _{H}(y)$![]() . Thus the critical value set of $\Phi _{H}$
. Thus the critical value set of $\Phi _{H}$![]() is contained in that of $\Phi _{H}\circ \Omega$
is contained in that of $\Phi _{H}\circ \Omega$![]() . The desired claim is obtained.
. The desired claim is obtained.
Having this lemma we can prove the following proposition, which corresponds to proposition 3 in [Reference Ekeland and Hofer13, § II].
Proposition 3.11 Let $H\in C^{2n+2}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() be $\mathbb {R}^{n,k}$
be $\mathbb {R}^{n,k}$![]() -admissible with $k< n$
-admissible with $k< n$![]() and strong nonresonant. Suppose that $[0,1]\ni s\mapsto \psi _s$
and strong nonresonant. Suppose that $[0,1]\ni s\mapsto \psi _s$![]() is a smooth homotopy of the identity in ${\rm Symp}(\mathbb {R}^{2n},\omega _0)$
is a smooth homotopy of the identity in ${\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() satisfying
satisfying
and
where $R>0$![]() and $[0,1]\ni s\mapsto w_s$
and $[0,1]\ni s\mapsto w_s$![]() is a smooth path in $\mathbb {R}^{n,k}$
is a smooth path in $\mathbb {R}^{n,k}$![]() . Then $s\mapsto c^{n,k}(H\circ \psi _s)$
. Then $s\mapsto c^{n,k}(H\circ \psi _s)$![]() is constant. Moreover, the same conclusion holds true if all $\psi _s$
is constant. Moreover, the same conclusion holds true if all $\psi _s$![]() are replaced by translations $\mathbb {R}^{2n}\ni z\mapsto z+ w_s,$
are replaced by translations $\mathbb {R}^{2n}\ni z\mapsto z+ w_s,$![]() where $[0,1]\ni s\mapsto w_s$
where $[0,1]\ni s\mapsto w_s$![]() is a smooth path in $\mathbb {R}^{n,k}$
is a smooth path in $\mathbb {R}^{n,k}$![]() . In particular, $c^{n,k}(H(\cdot + w))=c^{n,k}(H)$
. In particular, $c^{n,k}(H(\cdot + w))=c^{n,k}(H)$![]() for any $w\in \mathbb {R}^{n,k}$
for any $w\in \mathbb {R}^{n,k}$![]() .
.
Proof. By the assumptions each $H\circ \psi _s$![]() is also $\mathbb {R}^{n,k}$
is also $\mathbb {R}^{n,k}$![]() -admissible and strong nonresonant. Hence $c(H\circ \psi _s)$
-admissible and strong nonresonant. Hence $c(H\circ \psi _s)$![]() is a positive critical value for each $s$
is a positive critical value for each $s$![]() . Let $x\in E$
. Let $x\in E$![]() be a critical point of $\Phi _{H\circ \psi _s}$
be a critical point of $\Phi _{H\circ \psi _s}$![]() with critical value $c(H\circ \psi _s)$
with critical value $c(H\circ \psi _s)$![]() . Then $x\in C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$
. Then $x\in C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$![]() and solves $\dot {x}=J_{2n}\nabla (H\circ \psi _s)(x)=X_{H\circ \psi _s}(x)$
and solves $\dot {x}=J_{2n}\nabla (H\circ \psi _s)(x)=X_{H\circ \psi _s}(x)$![]() . Let $y_s=\psi _s\circ x$
. Let $y_s=\psi _s\circ x$![]() . Then $y_s\in C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$
. Then $y_s\in C^{2n+2}_{n,k}([0,1],\mathbb {R}^{2n})$![]() and satisfies
and satisfies
since ${\rm d}\psi _s(z)X_H(z)=X_{H}(\psi _s(z))$![]() for any $z\in \mathbb {R}^{2n}$
for any $z\in \mathbb {R}^{2n}$![]() by [Reference Hofer and Zehnder20, p. 9]. Therefore $y_s$
by [Reference Hofer and Zehnder20, p. 9]. Therefore $y_s$![]() is a critical point of $\Phi _H$
is a critical point of $\Phi _H$![]() on $E$
on $E$![]() . We claim that
. We claim that
Clearly, it suffices to prove the following equality:
Extend $x$![]() into a piecewise $C^{2n+2}$
into a piecewise $C^{2n+2}$![]() -smooth loop $x^{\ast }:[0, 2]\to \mathbb {R}^{2n}$
-smooth loop $x^{\ast }:[0, 2]\to \mathbb {R}^{2n}$![]() by setting $x^{\ast }(t)=(2-t)x(1)+(t-1)x(0)$
by setting $x^{\ast }(t)=(2-t)x(1)+(t-1)x(0)$![]() for any $1\le t\le 2$
for any $1\le t\le 2$![]() . We get a piecewise $C^{2n+2}$
. We get a piecewise $C^{2n+2}$![]() -smooth loop extending of $y_s$
-smooth loop extending of $y_s$![]() , $y_s^{\ast }=\psi _s(x^{\ast })$
, $y_s^{\ast }=\psi _s(x^{\ast })$![]() . Clearly, we can extend $x^{\ast }$
. Clearly, we can extend $x^{\ast }$![]() into a piecewise $C^{2n+2}$
into a piecewise $C^{2n+2}$![]() -smooth $u:D^{2}\to \mathbb {R}^{2n}$
-smooth $u:D^{2}\to \mathbb {R}^{2n}$![]() , where $D^{2}$
, where $D^{2}$![]() is a closed disc bounded by $\partial D^{2}\equiv [0,2]/\{0,2\}$
is a closed disc bounded by $\partial D^{2}\equiv [0,2]/\{0,2\}$![]() . Then $\psi _s\circ u:D^{2}\to \mathbb {R}^{2n}$
. Then $\psi _s\circ u:D^{2}\to \mathbb {R}^{2n}$![]() is piecewise $C^{2n+2}$
is piecewise $C^{2n+2}$![]() -smooth and $\psi _s\circ u|_{\partial D^{2}}=y_s^{\ast }$
-smooth and $\psi _s\circ u|_{\partial D^{2}}=y_s^{\ast }$![]() . Stokes theorem yields
. Stokes theorem yields

Moreover, for any $t\in [1,2]$![]() we have $\dot {x}^{\ast }(t)=x(0)-x(1)\in V_0^{n,k}$
we have $\dot {x}^{\ast }(t)=x(0)-x(1)\in V_0^{n,k}$![]() and $x^{\ast }(t)\in \mathbb {R}^{n,k}$
and $x^{\ast }(t)\in \mathbb {R}^{n,k}$![]() , and therefore $\langle -J_{2n}\dot {x}^{\ast }(t), x^{\ast }(t)\rangle =0$
, and therefore $\langle -J_{2n}\dot {x}^{\ast }(t), x^{\ast }(t)\rangle =0$![]() because $\mathbb {R}^{2n}$
because $\mathbb {R}^{2n}$![]() has the orthogonal decomposition $\mathbb {R}^{2n}=J_{2n}V^{n,k}_0\oplus \mathbb {R}^{n,k}$
has the orthogonal decomposition $\mathbb {R}^{2n}=J_{2n}V^{n,k}_0\oplus \mathbb {R}^{n,k}$![]() . Then (3.15) follows from these.
. Then (3.15) follows from these.
Since $s\mapsto c^{n,k}(H\circ \psi _s)$![]() is continuous by proposition 3.5, and a critical point $x$
is continuous by proposition 3.5, and a critical point $x$![]() of $\Phi _{H\circ \psi _s}$
of $\Phi _{H\circ \psi _s}$![]() with critical value $c(H\circ \psi _s)$
with critical value $c(H\circ \psi _s)$![]() yields a critical point $y_s$
yields a critical point $y_s$![]() of $\Phi _H$
of $\Phi _H$![]() on $E$
on $E$![]() satisfying (3.14), we deduce that each $c(H\circ \psi _s)$
satisfying (3.14), we deduce that each $c(H\circ \psi _s)$![]() is also a critical value of $\Phi _H$
is also a critical value of $\Phi _H$![]() . Lemma 3.10 shows that $s\mapsto c^{n,k}(H\circ \psi _s)$
. Lemma 3.10 shows that $s\mapsto c^{n,k}(H\circ \psi _s)$![]() must be constant.
must be constant.
Finally, let $\psi _s(z)=z+ w_s$![]() . It is clear that $H\circ \psi _s$
. It is clear that $H\circ \psi _s$![]() is $\mathbb {R}^{n,k}$
is $\mathbb {R}^{n,k}$![]() -admissible and strong nonresonant. Thus $c(H\circ \psi _s)$
-admissible and strong nonresonant. Thus $c(H\circ \psi _s)$![]() is a positive critical value. If $x\in E$
is a positive critical value. If $x\in E$![]() is a critical point of $\Phi _{H\circ \psi _s}$
is a critical point of $\Phi _{H\circ \psi _s}$![]() with critical value $c(H\circ \psi _s)$
with critical value $c(H\circ \psi _s)$![]() , then $y_s:=\psi _s\circ x$
, then $y_s:=\psi _s\circ x$![]() is a critical point of $\Phi _H$
is a critical point of $\Phi _H$![]() on $E$
on $E$![]() and (3.14) holds. Hence $s\mapsto c^{n,k}(H(\cdot + w_s))$
and (3.14) holds. Hence $s\mapsto c^{n,k}(H(\cdot + w_s))$![]() is constant.
is constant.
Let $\mathscr {F}_{n,k}(\mathbb {R}^{2n})=\{H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})\,|\,H\ \hbox {satisfies (H2)}\}$![]() . For each bounded subset $B\subset \mathbb {R}^{2n}$
. For each bounded subset $B\subset \mathbb {R}^{2n}$![]() such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$
such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$![]() , we define
, we define
Definition 3.12 For each bounded subset $B\subset \mathbb {R}^{2n}$![]() such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset,$
such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset,$![]()
is called the coisotropic Ekeland–Hofer capacity of $B$![]() $($
$($![]() relative to $\mathbb {R}^{n,k})$
relative to $\mathbb {R}^{n,k})$![]() . For any unbounded subset $B\subset \mathbb {R}^{2n}$
. For any unbounded subset $B\subset \mathbb {R}^{2n}$![]() such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset,$
such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset,$![]() its coisotropic Ekeland–Hofer capacity is defined by
its coisotropic Ekeland–Hofer capacity is defined by
Remark 3.13 When $k=n$![]() in the above definition, $c^{n,n}(B)$
in the above definition, $c^{n,n}(B)$![]() is the (first) Ekeland–Hofer capacity of $B$
is the (first) Ekeland–Hofer capacity of $B$![]() .
.
For each bounded $B\subset \mathbb {R}^{2n}$![]() such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$
such that $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$![]() , we write
, we write

Clearly, each $H\in \mathscr {E}_{n,k}(\mathbb {R}^{2n},B)$![]() satisfies (H1), and $\mathscr {E}_{n,k}(\mathbb {R}^{2n},B)$
satisfies (H1), and $\mathscr {E}_{n,k}(\mathbb {R}^{2n},B)$![]() is a cofinal family of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
is a cofinal family of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$![]() , that is, for any $H\in \mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
, that is, for any $H\in \mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$![]() there exists $G\in \mathscr {E}_{n,k}(\mathbb {R}^{2n},B)$
there exists $G\in \mathscr {E}_{n,k}(\mathbb {R}^{2n},B)$![]() such that $G\ge H$
such that $G\ge H$![]() . Moreover, for each $l\in \mathbb {N}\cup \{\infty \}$
. Moreover, for each $l\in \mathbb {N}\cup \{\infty \}$![]() the smaller subset $\mathscr {E}_{n,k}(\mathbb {R}^{2n},B)\cap C^{l}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
the smaller subset $\mathscr {E}_{n,k}(\mathbb {R}^{2n},B)\cap C^{l}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() is also a cofinal family of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
is also a cofinal family of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$![]() . By the definition, we immediately get:
. By the definition, we immediately get:
Proposition 3.14
(i) $c^{n,k}(B)=c^{n,k}(\overline {B})$
 .
.(ii) $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
 in (3.17) can be replaced by any cofinal subset of it.
in (3.17) can be replaced by any cofinal subset of it.(iii) Suppose that $\overline {B}\subset B^{2n}(R)$
 . For each $l\in \mathbb {N}\cup \{\infty \}$
. For each $l\in \mathbb {N}\cup \{\infty \}$ let $\mathscr {E}^{l}_{n,k}(\mathbb {R}^{2n},B)$
let $\mathscr {E}^{l}_{n,k}(\mathbb {R}^{2n},B)$ consist of $H\in \mathscr {F}_{n,k}(\mathbb {R}^{2n},B)\cap C^{l}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
consist of $H\in \mathscr {F}_{n,k}(\mathbb {R}^{2n},B)\cap C^{l}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$ for which there exists $z_0\in \mathbb {R}^{n,k},$
for which there exists $z_0\in \mathbb {R}^{n,k},$ real numbers $a, b$
real numbers $a, b$ such that $H(z)=a|z|^{2}+ \langle z, z_0\rangle + b$
such that $H(z)=a|z|^{2}+ \langle z, z_0\rangle + b$ outside the closed ball $\overline {B^{2n}(R)},$
outside the closed ball $\overline {B^{2n}(R)},$ where $a>\pi$
where $a>\pi$ and $a\notin \pi \mathbb {N}$
and $a\notin \pi \mathbb {N}$ for $k=n,$
for $k=n,$ and $a>\pi /2$
and $a>\pi /2$ and $a\notin \pi \mathbb {N}/2$
and $a\notin \pi \mathbb {N}/2$ for $0\le k< n$
for $0\le k< n$ . Then each $\mathscr {E}^{l}_{n,k}(\mathbb {R}^{2n},B)$
. Then each $\mathscr {E}^{l}_{n,k}(\mathbb {R}^{2n},B)$ is a cofinal subset of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
is a cofinal subset of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$ .
.
Proof. We only prove (iii). By (ii) it suffices to prove that for each given $H\in \mathscr {E}_{n,k}(\mathbb {R}^{2n},B)$![]() there exists $G\in \mathscr {E}^{l}_{n,k}(\mathbb {R}^{2n},B)$
there exists $G\in \mathscr {E}^{l}_{n,k}(\mathbb {R}^{2n},B)$![]() such that $G\ge H$
such that $G\ge H$![]() . We may assume that $H(z)=a|z|^{2}+ \langle z, z_0\rangle + b$
. We may assume that $H(z)=a|z|^{2}+ \langle z, z_0\rangle + b$![]() outside a larger closed ball $\overline {B^{2n}(R_1)}$
outside a larger closed ball $\overline {B^{2n}(R_1)}$![]() , where $a>\pi$
, where $a>\pi$![]() and $a\notin \pi \mathbb {N}$
and $a\notin \pi \mathbb {N}$![]() for $k=n$
for $k=n$![]() , and $a>\pi /2$
, and $a>\pi /2$![]() and $a\notin \pi \mathbb {N}/2$
and $a\notin \pi \mathbb {N}/2$![]() for $0\le k< n$
for $0\le k< n$![]() . Let $U_\epsilon (B)$
. Let $U_\epsilon (B)$![]() be the $\epsilon$
be the $\epsilon$![]() -neighbourhood of $B$
-neighbourhood of $B$![]() . We can also assume that $H$
. We can also assume that $H$![]() vanishes in $U_{2\epsilon }(B)$
vanishes in $U_{2\epsilon }(B)$![]() . Since $\overline {B^{2n}(R_1)}$
. Since $\overline {B^{2n}(R_1)}$![]() is compact, we may find numbers $a'>a$
is compact, we may find numbers $a'>a$![]() , $b'$
, $b'$![]() such that $a'\notin \pi \mathbb {N}$
such that $a'\notin \pi \mathbb {N}$![]() for $k=n$
for $k=n$![]() , $a'\notin \pi \mathbb {N}/2$
, $a'\notin \pi \mathbb {N}/2$![]() for $0\le k< n$
for $0\le k< n$![]() , and $a'|z|^{2}+ \langle z, z_0\rangle + b'\ge H(z)$
, and $a'|z|^{2}+ \langle z, z_0\rangle + b'\ge H(z)$![]() for all $z\in \mathbb {R}^{2n}$
for all $z\in \mathbb {R}^{2n}$![]() . Take a smooth function $f:\mathbb {R}^{2n}\to \mathbb {R}_{\ge 0}$
. Take a smooth function $f:\mathbb {R}^{2n}\to \mathbb {R}_{\ge 0}$![]() such that it equals to zero in $U_{\epsilon }(B)$
such that it equals to zero in $U_{\epsilon }(B)$![]() and $1$
and $1$![]() outside $U_{2\epsilon }(B)$
outside $U_{2\epsilon }(B)$![]() . Define $G(z):=f(z)(a'|z|^{2}+ \langle z, z_0\rangle + b')$
. Define $G(z):=f(z)(a'|z|^{2}+ \langle z, z_0\rangle + b')$![]() for $z\in \mathbb {R}^{2n}$
for $z\in \mathbb {R}^{2n}$![]() . Then $G\ge H$
. Then $G\ge H$![]() and $G\in \mathscr {E}^{\infty }_{n,k}(\mathbb {R}^{2n},B)$
and $G\in \mathscr {E}^{\infty }_{n,k}(\mathbb {R}^{2n},B)$![]() .
.
Remark 3.15 Let $\mathscr {H}_{n,k}(\mathbb {R}^{2n},B)$![]() consist of $H\in C^{\infty }(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
consist of $H\in C^{\infty }(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() which vanishes near $\overline {B}$
which vanishes near $\overline {B}$![]() and for which there exists $z_0\in \mathbb {R}^{n,k}$
and for which there exists $z_0\in \mathbb {R}^{n,k}$![]() and a real number $a$
and a real number $a$![]() such that $H(z)=a|z|^{2}$
such that $H(z)=a|z|^{2}$![]() outside a compact subset, where $a>\pi$
outside a compact subset, where $a>\pi$![]() and $a\notin \pi \mathbb {N}$
and $a\notin \pi \mathbb {N}$![]() for $k=n$
for $k=n$![]() , and $a>\pi /2$
, and $a>\pi /2$![]() and $a\notin \pi \mathbb {N}/2$
and $a\notin \pi \mathbb {N}/2$![]() for $0\le k< n$
for $0\le k< n$![]() . As in the proof of proposition 1.1 it is not hard to prove that $\mathscr {H}_{n,k}(\mathbb {R}^{2n},B)$
. As in the proof of proposition 1.1 it is not hard to prove that $\mathscr {H}_{n,k}(\mathbb {R}^{2n},B)$![]() is a cofinal subset of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
is a cofinal subset of $\mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$![]() . When $k=n$
. When $k=n$![]() this shows that Sikorav's approach [Reference Sikorav37] to the Ekeland–Hofer capacity in [Reference Ekeland and Hofer13] defines the same capacity.
this shows that Sikorav's approach [Reference Sikorav37] to the Ekeland–Hofer capacity in [Reference Ekeland and Hofer13] defines the same capacity.
Proof of proposition 1.1. Proposition 3.5(i)–(iii) lead to the first three claims. Let us prove (iv). We may assume that $B$![]() is bounded. By (3.17) we have a sequence $(H_j)\subset \mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$
is bounded. By (3.17) we have a sequence $(H_j)\subset \mathscr {F}_{n,k}(\mathbb {R}^{2n},B)$![]() such that $c^{n,k}(H_j)\to c^{n,k}(B)$
such that $c^{n,k}(H_j)\to c^{n,k}(B)$![]() . Note that $H_j(\cdot -w)\in \mathscr {F}_{n,k}(\mathbb {R}^{2n},B+w)$
. Note that $H_j(\cdot -w)\in \mathscr {F}_{n,k}(\mathbb {R}^{2n},B+w)$![]() for each $j$
for each $j$![]() . Hence
. Hence
by the final claim in proposition 3.11. The same reasoning leads to $c^{n,k}(B)=c^{n,k}(B+w+(-w))\le c^{n,k}(B+w)$![]() and so $c^{n,k}(B+w)=c^{n,k}(B)$
and so $c^{n,k}(B+w)=c^{n,k}(B)$![]() .
.
Proposition 3.16 (Relative monotonicity)
Let subsets $A, B\subset \mathbb {R}^{2n}$![]() satisfy $\overline {A}\cap \mathbb {R}^{n,k}\neq \emptyset$
satisfy $\overline {A}\cap \mathbb {R}^{n,k}\neq \emptyset$![]() and $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$
and $\overline {B}\cap \mathbb {R}^{n,k}\neq \emptyset$![]() . If there exists a smooth homotopy of the identity in ${\rm Symp}(\mathbb {R}^{2n},\omega _0)$
. If there exists a smooth homotopy of the identity in ${\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() as in proposition 3.11, $[0,1]\ni s\mapsto \psi _s,$
as in proposition 3.11, $[0,1]\ni s\mapsto \psi _s,$![]() such that $\psi _1(A)\subset B,$
such that $\psi _1(A)\subset B,$![]() then $c^{n,k}(A)=c^{n,k}(\psi _s(A))$
then $c^{n,k}(A)=c^{n,k}(\psi _s(A))$![]() for all $s\in [0,1]$
for all $s\in [0,1]$![]() , and in particular $c^{n,k}(A)\le c^{n,k}(B)$
, and in particular $c^{n,k}(A)\le c^{n,k}(B)$![]() by proposition 1.1(i).
by proposition 1.1(i).
Proof. Note that
is a one-to-one correspondence. Then

Here the third equality comes from proposition 3.11.
Proof of theorem 1.2. We may assume that $B$![]() is bounded, and complete the proof in two steps.
is bounded, and complete the proof in two steps.
Step 1. Prove $c^{n,k}(\Phi (B))=c^{n,k}(B)$![]() for every $\Phi \in {\rm Sp}(2n,k)$
for every $\Phi \in {\rm Sp}(2n,k)$![]() . Take a smooth path $[0, 1]\ni t\mapsto \Phi _t\in {\rm Sp}(2n,k)$
. Take a smooth path $[0, 1]\ni t\mapsto \Phi _t\in {\rm Sp}(2n,k)$![]() such that $\Phi _0=I_{2n}$
such that $\Phi _0=I_{2n}$![]() and $\Phi _1=\Phi$
and $\Phi _1=\Phi$![]() . We have a smooth function $[0,1]\times \mathbb {R}^{2n}\ni (t,z)\mapsto G_t(z)\in \mathbb {R}^{2n}$
. We have a smooth function $[0,1]\times \mathbb {R}^{2n}\ni (t,z)\mapsto G_t(z)\in \mathbb {R}^{2n}$![]() such that the path $\Phi _t$
such that the path $\Phi _t$![]() is generated by $X_{G_t}$
is generated by $X_{G_t}$![]() and that $G_t(z)=0\ \forall \ z\in \mathbb {R}^{n,k}$
and that $G_t(z)=0\ \forall \ z\in \mathbb {R}^{n,k}$![]() (see step 2 below). Since $\cup _{t\in [0, 1]}\Phi _t(\overline {B})$
(see step 2 below). Since $\cup _{t\in [0, 1]}\Phi _t(\overline {B})$![]() is compact, it can be contained in a ball $B^{2n}(0, R)$
is compact, it can be contained in a ball $B^{2n}(0, R)$![]() for some $R>0$
for some $R>0$![]() . Take a smooth cut function $\rho :\mathbb {R}^{2n}\to [0, 1]$
. Take a smooth cut function $\rho :\mathbb {R}^{2n}\to [0, 1]$![]() such that $\rho =1$
such that $\rho =1$![]() on $B^{2n}(0, 2R)$
on $B^{2n}(0, 2R)$![]() and $\rho =0$
and $\rho =0$![]() outside $B^{2n}(0, 3R)$
outside $B^{2n}(0, 3R)$![]() . Define a smooth function $\tilde {G}:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$
. Define a smooth function $\tilde {G}:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$![]() by $\tilde {G}(t,z)=\rho (z)G_t(z)$
by $\tilde {G}(t,z)=\rho (z)G_t(z)$![]() for $(t,z)\in [0,1]\times \mathbb {R}^{2n}$
for $(t,z)\in [0,1]\times \mathbb {R}^{2n}$![]() . Denote by $\psi _t$
. Denote by $\psi _t$![]() the Hamiltonian path generated by $\tilde {G}$
the Hamiltonian path generated by $\tilde {G}$![]() in ${\rm Ham}^{c}(\mathbb {R}^{2n},\omega _0)$
in ${\rm Ham}^{c}(\mathbb {R}^{2n},\omega _0)$![]() . Then $\psi _t(z)=\Phi _t(z)$
. Then $\psi _t(z)=\Phi _t(z)$![]() for all $(t,z)\in [0,1]\times B^{2n}(0, R)$
for all $(t,z)\in [0,1]\times B^{2n}(0, R)$![]() . Moreover each $\psi _t$
. Moreover each $\psi _t$![]() restricts to the identity on $\mathbb {R}^{n,k}$
restricts to the identity on $\mathbb {R}^{n,k}$![]() because $\tilde {G}(t,z)=\rho (z)G_t(z)=0$
because $\tilde {G}(t,z)=\rho (z)G_t(z)=0$![]() for all $(t,z)\in [0,1]\times \mathbb {R}^{n,k}$
for all $(t,z)\in [0,1]\times \mathbb {R}^{n,k}$![]() . Hence we obtain $c^{n,k}(\Phi (B))=c^{n,k}(\Phi _1(B))=c^{n,k}(B)$
. Hence we obtain $c^{n,k}(\Phi (B))=c^{n,k}(\Phi _1(B))=c^{n,k}(B)$![]() by proposition 3.16.
by proposition 3.16.
Step 2. Prove $c^{n,k}(\phi (B))=c^{n,k}(B)$![]() in case $w_0=0$
in case $w_0=0$![]() . Let $\Phi =({\rm d}\phi (0))^{-1}$
. Let $\Phi =({\rm d}\phi (0))^{-1}$![]() . Since $c^{n,k}(\Phi \circ \phi (B))=c^{n,k}(\phi (B))$
. Since $c^{n,k}(\Phi \circ \phi (B))=c^{n,k}(\phi (B))$![]() by step 1, and $\Phi \circ \phi (w)=w\ \forall \ w\in \mathbb {R}^{n,k}$
by step 1, and $\Phi \circ \phi (w)=w\ \forall \ w\in \mathbb {R}^{n,k}$![]() , replacing $\Phi \circ \phi$
, replacing $\Phi \circ \phi$![]() by $\phi$
by $\phi$![]() , we may assume ${\rm d}\phi (0)={\rm id}_{\mathbb {R}^{2n}}$
, we may assume ${\rm d}\phi (0)={\rm id}_{\mathbb {R}^{2n}}$![]() . Define a continuous path in ${\rm Symp}(\mathbb {R}^{2n},\omega _0)$
. Define a continuous path in ${\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() ,
,

which is smooth except possibly at $t=0$![]() . As in [Reference Schlenk36, proposition A.1] we can smoothen it with a smooth function $\eta :\mathbb {R}\to \mathbb {R}$
. As in [Reference Schlenk36, proposition A.1] we can smoothen it with a smooth function $\eta :\mathbb {R}\to \mathbb {R}$![]() defined by
defined by
where $e$![]() is the Euler number. Namely, defining $\phi _t(z):=\varphi _{\eta (t)}(z)$
is the Euler number. Namely, defining $\phi _t(z):=\varphi _{\eta (t)}(z)$![]() for $z\in \mathbb {R}^{2n}$
for $z\in \mathbb {R}^{2n}$![]() and $t\in \mathbb {R}$
and $t\in \mathbb {R}$![]() , we get a smooth path $\mathbb {R}\ni t\mapsto \phi _t\in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$
, we get a smooth path $\mathbb {R}\ni t\mapsto \phi _t\in {\rm Symp}(\mathbb {R}^{2n},\omega _0)$![]() such that
such that
Define $X_t(z)=(({{{\rm d}}}/{{{\rm d}}t})\phi _t)(\phi _t^{-1}(z))$![]() and
and
where the integral is along any piecewise smooth curve from $0$![]() to $z$
to $z$![]() in $\mathbb {R}^{2n}$
in $\mathbb {R}^{2n}$![]() . Then $\mathbb {R}\times \mathbb {R}^{2n}\ni (t,z)\mapsto H_t(z)\in \mathbb {R}$
. Then $\mathbb {R}\times \mathbb {R}^{2n}\ni (t,z)\mapsto H_t(z)\in \mathbb {R}$![]() is smooth and $X_t=X_{H_t}$
is smooth and $X_t=X_{H_t}$![]() . By the final condition in (3.21), for each $(t,z)\in \mathbb {R}\times \mathbb {R}^{n,k}$
. By the final condition in (3.21), for each $(t,z)\in \mathbb {R}\times \mathbb {R}^{n,k}$![]() we have $X_t(z)=0$
we have $X_t(z)=0$![]() and therefore $H_t(z)=0$
and therefore $H_t(z)=0$![]() . As in step 1, we can assume that $\cup _{t\in [0, 1]}\phi _t(\overline {B})$
. As in step 1, we can assume that $\cup _{t\in [0, 1]}\phi _t(\overline {B})$![]() is contained a ball $B^{2n}(0, R)$
is contained a ball $B^{2n}(0, R)$![]() . Take a smooth cut function $\rho :\mathbb {R}^{2n}\to [0, 1]$
. Take a smooth cut function $\rho :\mathbb {R}^{2n}\to [0, 1]$![]() as above, and define a smooth function $\tilde {H}:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$
as above, and define a smooth function $\tilde {H}:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$![]() by $\tilde {H}(t,z)=\rho (z)H_t(z)$
by $\tilde {H}(t,z)=\rho (z)H_t(z)$![]() for $(t,z)\in [0,1]\times \mathbb {R}^{2n}$
for $(t,z)\in [0,1]\times \mathbb {R}^{2n}$![]() . Then the Hamiltonian path $\psi _t$
. Then the Hamiltonian path $\psi _t$![]() generated by $\tilde {H}$
generated by $\tilde {H}$![]() in ${\rm Ham}^{c}(\mathbb {R}^{2n},\omega _0)$
in ${\rm Ham}^{c}(\mathbb {R}^{2n},\omega _0)$![]() satisfies
satisfies
It follows from proposition 3.16 that $c^{n,k}(\phi (B))=c^{n,k}(\psi _1(B))=c^{n,k}(B)$![]() as above.
as above.
Step 3. Prove $c^{n,k}(\phi (B))=c^{n,k}(B)$![]() in case $w_0\ne 0$
in case $w_0\ne 0$![]() . Define $\varphi (w)=\phi (w+w_0)$
. Define $\varphi (w)=\phi (w+w_0)$![]() for $w\in \mathbb {R}^{2n}$
for $w\in \mathbb {R}^{2n}$![]() . Then ${\rm d}\varphi (0)={\rm d}\phi (w_0)\in {\rm Sp}(2n,k)$
. Then ${\rm d}\varphi (0)={\rm d}\phi (w_0)\in {\rm Sp}(2n,k)$![]() and $\varphi (w)=\phi (w+w_0)=w \forall \ w\in \mathbb {R}^{n,k}$
and $\varphi (w)=\phi (w+w_0)=w \forall \ w\in \mathbb {R}^{n,k}$![]() . By step 2 we arrive at $c^{n,k}(\varphi (B-w_0))=c^{n,k}(B-w_0)$
. By step 2 we arrive at $c^{n,k}(\varphi (B-w_0))=c^{n,k}(B-w_0)$![]() . The desired equality follows because $\phi (B)=\varphi (B-w_0)$
. The desired equality follows because $\phi (B)=\varphi (B-w_0)$![]() and $c^{n,k}(B-w_0)= c^{n,k}(B)$
and $c^{n,k}(B-w_0)= c^{n,k}(B)$![]() by proposition 1.1.
by proposition 1.1.
Proof of corollary 1.3. As discussed above the proof is reduced to the case $w_0=0$![]() . Moreover we can assume that both sets $A$
. Moreover we can assume that both sets $A$![]() and $U$
and $U$![]() are bounded and that $U$
are bounded and that $U$![]() is also star-shaped with respect to the origin $0\in \mathbb {R}^{2n}$
is also star-shaped with respect to the origin $0\in \mathbb {R}^{2n}$![]() .
.
Next the proof can be completed following [Reference Schlenk36, proposition A.1]. Now $[0,1]\ni t\mapsto \phi _t(\cdot ):=\varphi _{\eta (t)}(\cdot )$![]() given by (3.19) and (3.20) is a smooth path of symplectic embeddings from $U$
given by (3.19) and (3.20) is a smooth path of symplectic embeddings from $U$![]() to $\mathbb {R}^{2n}$
to $\mathbb {R}^{2n}$![]() with properties
with properties
Thus $X_t(z):=(({{{\rm d}}}/{{{\rm d}}t})\phi _t)(\phi _t^{-1}(z))$![]() is a symplectic vector field defined on $\phi _t(U)$
is a symplectic vector field defined on $\phi _t(U)$![]() , and (3.22) (where the integral is along any piecewise smooth curve from $0$
, and (3.22) (where the integral is along any piecewise smooth curve from $0$![]() to $z$
to $z$![]() in $\phi _t(U)$
in $\phi _t(U)$![]() ) defines a smooth function $H_t$
) defines a smooth function $H_t$![]() on $\phi _t(U)$
on $\phi _t(U)$![]() in the present case. Observe that $H:\cup _{t\in [0,1]}(\{t\}\times \phi _t(U))\to \mathbb {R}$
in the present case. Observe that $H:\cup _{t\in [0,1]}(\{t\}\times \phi _t(U))\to \mathbb {R}$![]() defined by $H(t,z)=H_t(z)$
defined by $H(t,z)=H_t(z)$![]() is smooth and generates the path $\phi _t$
is smooth and generates the path $\phi _t$![]() . Since $K=\cup _{t\in [0,1]}\{t\}\times \phi _t(\overline {A})$
. Since $K=\cup _{t\in [0,1]}\{t\}\times \phi _t(\overline {A})$![]() is a compact subset in $[0,1]\times \mathbb {R}^{2n}$
is a compact subset in $[0,1]\times \mathbb {R}^{2n}$![]() we can choose a bounded and relative open neighbourhood $W$
we can choose a bounded and relative open neighbourhood $W$![]() of $K$
of $K$![]() in $[0,1]\times \mathbb {R}^{2n}$
in $[0,1]\times \mathbb {R}^{2n}$![]() such that $W\subset \cup _{t\in [0,1]}(\{t\}\times \phi _t(U))$
such that $W\subset \cup _{t\in [0,1]}(\{t\}\times \phi _t(U))$![]() . Take a smooth cut function $\chi :[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$
. Take a smooth cut function $\chi :[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$![]() such that $\chi |_K=1$
such that $\chi |_K=1$![]() and $\chi$
and $\chi$![]() vanishes outside $W$
vanishes outside $W$![]() . Define $\hat {H}:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$
. Define $\hat {H}:[0,1]\times \mathbb {R}^{2n}\to \mathbb {R}$![]() by $\hat {H}(t,z)=\chi (t,z)H(t,z)$
by $\hat {H}(t,z)=\chi (t,z)H(t,z)$![]() . It generates a smooth homotopy $\psi _t$
. It generates a smooth homotopy $\psi _t$![]() ($t\in [0,1]$
($t\in [0,1]$![]() ) of the identity in ${\rm Ham}^{c}(\mathbb {R}^{2n},\omega _0)$
) of the identity in ${\rm Ham}^{c}(\mathbb {R}^{2n},\omega _0)$![]() such that $\psi _t(z)=\phi _t(z)$
such that $\psi _t(z)=\phi _t(z)$![]() for all $(t,z)\in [0,1]\times A$
for all $(t,z)\in [0,1]\times A$![]() . Moreover, the final condition in (3.21) implies that $\mathbb {R}^{n,k}\cap U\subset \phi _t(U)$
. Moreover, the final condition in (3.21) implies that $\mathbb {R}^{n,k}\cap U\subset \phi _t(U)$![]() and $X_t(z)=0$
and $X_t(z)=0$![]() for any $t\in [0,1]$
for any $t\in [0,1]$![]() and $z\in \mathbb {R}^{n,k}\cap U$
and $z\in \mathbb {R}^{n,k}\cap U$![]() . Hence for any $(t,z)\in [0,1]\times \mathbb {R}^{n,k}$
. Hence for any $(t,z)\in [0,1]\times \mathbb {R}^{n,k}$![]() we have $\hat {H}(t,z)=\chi (t,z)H(t,z)=0$
we have $\hat {H}(t,z)=\chi (t,z)H(t,z)=0$![]() and so $\psi _t(z)=z$
and so $\psi _t(z)=z$![]() . Then proposition 3.16 leads to $c^{n,k}(A)= c^{n,k}(\psi _1(A))=c^{n,k}(\phi _1(A))=c^{n,k}(\varphi (A))$
. Then proposition 3.16 leads to $c^{n,k}(A)= c^{n,k}(\psi _1(A))=c^{n,k}(\phi _1(A))=c^{n,k}(\varphi (A))$![]() .
.
4. Proof of theorem 1.4
The case of $k=n$![]() was proved in [Reference Ekeland and Hofer13, Reference Ekeland and Hofer14, Reference Sikorav37]. We assume $k< n$
was proved in [Reference Ekeland and Hofer13, Reference Ekeland and Hofer14, Reference Sikorav37]. We assume $k< n$![]() below. By proposition 1.1(iv), $c^{n,k}(D)=c^{n,k}(D+w)$
below. By proposition 1.1(iv), $c^{n,k}(D)=c^{n,k}(D+w)$![]() for any $w\in \mathbb {R}^{n,k}$
for any $w\in \mathbb {R}^{n,k}$![]() . Moreover, for each $x\in C^{1}_{n,k}([0,1])$
. Moreover, for each $x\in C^{1}_{n,k}([0,1])$![]() there holds
there holds
Recalling that $D\cap \mathbb {R}^{n,k}\ne \emptyset$![]() , we may assume that $D$
, we may assume that $D$![]() contains the origin $0$
contains the origin $0$![]() below.
below.
Let $j_D$![]() be the Minkowski functional associated to $D$
be the Minkowski functional associated to $D$![]() , $H:=j_D^{2}$
, $H:=j_D^{2}$![]() and $H^{\ast }$
and $H^{\ast }$![]() be the Legendre transform of $H$
be the Legendre transform of $H$![]() . Then $\partial D=H^{-1}(1)$
. Then $\partial D=H^{-1}(1)$![]() , and there exists a constant $R\geq 1$
, and there exists a constant $R\geq 1$![]() such that
such that
for all $z\in \mathbb {R}^{2n}$![]() . Moreover $H$
. Moreover $H$![]() is $C^{1,1}$
is $C^{1,1}$![]() with uniformly Lipschitz constant.
with uniformly Lipschitz constant.
By [Reference Jin and Lu26, theorem 1.5]
contains a minimum number $\varrho$![]() , that is, there exists a leafwise chord $x^{\ast }$
, that is, there exists a leafwise chord $x^{\ast }$![]() on $\partial D$
on $\partial D$![]() for $\mathbb {R}^{n,k}$
for $\mathbb {R}^{n,k}$![]() such that $A(x^{\ast })=\min \Sigma ^{n,k}_{\partial D}=\varrho$
such that $A(x^{\ast })=\min \Sigma ^{n,k}_{\partial D}=\varrho$![]() . Actually, the arguments therein shows that there exists $w\in C^{1}_{n,k}([0,1])$
. Actually, the arguments therein shows that there exists $w\in C^{1}_{n,k}([0,1])$![]() such that
such that
Let us prove (1.8) and (1.9) by the following two steps. As done in [Reference Jin and Lu24, Reference Jin and Lu25] (see also step 4 below), by approximating arguments we can assume that $\partial D$![]() is smooth and strictly convex. In this case $\Sigma ^{n,k}_{\partial D}$
is smooth and strictly convex. In this case $\Sigma ^{n,k}_{\partial D}$![]() has no interior points in $\mathbb {R}$
has no interior points in $\mathbb {R}$![]() because of [Reference Jin and Lu26, lemma 3.5], and we give a complete proof though the ideas which are similar to those of the proof of [Reference Sikorav37] (and [Reference Jin and Lu25, theorem 1.11] and [Reference Jin and Lu24, theorem 1.17]).
because of [Reference Jin and Lu26, lemma 3.5], and we give a complete proof though the ideas which are similar to those of the proof of [Reference Sikorav37] (and [Reference Jin and Lu25, theorem 1.11] and [Reference Jin and Lu24, theorem 1.17]).
Step 1. Prove that $c^{n,k}(D)\ge \varrho$![]() . By the monotonicity of $c^{n,k}$
. By the monotonicity of $c^{n,k}$![]() it suffices to prove $c^{n,k}(\partial D)\ge \varrho$
it suffices to prove $c^{n,k}(\partial D)\ge \varrho$![]() . For a given $\epsilon >0$
. For a given $\epsilon >0$![]() , consider a cofinal family of $\mathcal {F}_{n,k}(\mathbb {R}^{2n},\partial D)$
, consider a cofinal family of $\mathcal {F}_{n,k}(\mathbb {R}^{2n},\partial D)$![]() ,
,
consisting of $\overline {H}=f\circ H$![]() , where $f\in C^{\infty }(\mathbb {R},\mathbb {R}_{\ge 0})$
, where $f\in C^{\infty }(\mathbb {R},\mathbb {R}_{\ge 0})$![]() satisfies
satisfies

and where $\alpha$![]() is required to satisfy for some constant $C>0$
is required to satisfy for some constant $C>0$![]()
because of (4.1) and ${\rm Int}(\Sigma ^{n,k}_{\partial D})=\emptyset$![]() .
.
Then each $\overline {H}\in \mathscr {E}^{n,k}_\epsilon (\mathbb {R}^{2n},\partial D)$![]() satisfies all conditions in lemma 3.7. Indeed, it belongs to $C^{\infty }(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
satisfies all conditions in lemma 3.7. Indeed, it belongs to $C^{\infty }(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() , restricts to zero near $\partial D$
, restricts to zero near $\partial D$![]() and thus satisfies (H1). Note that $f(s)=\alpha s+ \epsilon -\alpha s_0$
and thus satisfies (H1). Note that $f(s)=\alpha s+ \epsilon -\alpha s_0$![]() for $s\ge s_0$
for $s\ge s_0$![]() , where $s_0=\inf \{s>1\,|\, f(s)\ge \epsilon \}$
, where $s_0=\inf \{s>1\,|\, f(s)\ge \epsilon \}$![]() . (4.5) implies that $\overline {H}(z)\ge ({\pi }/{2})|z|^{2}-C'\ \forall \ z\in \mathbb {R}^{2n}$
. (4.5) implies that $\overline {H}(z)\ge ({\pi }/{2})|z|^{2}-C'\ \forall \ z\in \mathbb {R}^{2n}$![]() for some constant $C'>0$
for some constant $C'>0$![]() , and therefore $c^{n,k}(\overline {H})<+\infty$
, and therefore $c^{n,k}(\overline {H})<+\infty$![]() by the arguments above proposition 3.5. Moreover, it is clear that $\mathbb {R}^{n,k}\cap {\rm Int}(\overline {H}^{-1}(0))\ne \emptyset$
by the arguments above proposition 3.5. Moreover, it is clear that $\mathbb {R}^{n,k}\cap {\rm Int}(\overline {H}^{-1}(0))\ne \emptyset$![]() and $|\overline {H}_{zz}(z)|$
and $|\overline {H}_{zz}(z)|$![]() is bounded on $\mathbb {R}^{2n}$
is bounded on $\mathbb {R}^{2n}$![]() . Then (3.5) is satisfied with any $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}(\overline {H}^{-1}(0))$
. Then (3.5) is satisfied with any $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}(\overline {H}^{-1}(0))$![]() by the arguments at the end of proof of proposition 3.6. Hence $c^{n,k}(\overline {H})>0$
by the arguments at the end of proof of proposition 3.6. Hence $c^{n,k}(\overline {H})>0$![]() .
.
By combining proofs of lemma 3.9 and [Reference Jin and Lu26, lemma 3.7] we can obtain the first claim of the following.
Lemma 4.1 For every $\overline {H}\in \mathscr {E}^{n,k}_\epsilon (\mathbb {R}^{2n},\partial D),$![]() $\Phi _{\overline {H}}$
$\Phi _{\overline {H}}$![]() satisfies the $(PS)$
satisfies the $(PS)$![]() condition and hence $c^{n,k}(\overline {H})$
condition and hence $c^{n,k}(\overline {H})$![]() is a positive critical value of $\Phi _{\overline {H}}$
is a positive critical value of $\Phi _{\overline {H}}$![]() .
.
Lemma 4.2 For every $\overline {H}\in \mathscr {E}^{n,k}_\epsilon (\mathbb {R}^{2n},\partial D),$![]() any positive critical value $c$
any positive critical value $c$![]() of $\Phi _{\overline {H}}$
of $\Phi _{\overline {H}}$![]() is greater than $\min \Sigma ^{n,k}_{\partial D}-\epsilon$
is greater than $\min \Sigma ^{n,k}_{\partial D}-\epsilon$![]() . In particular, $c^{n,k}(\overline {H})>\min \Sigma ^{n,k}_{\partial D}-\epsilon$
. In particular, $c^{n,k}(\overline {H})>\min \Sigma ^{n,k}_{\partial D}-\epsilon$![]() .
.
Proof. For a critical point $x$![]() of $\Phi _{\overline {H}}$
of $\Phi _{\overline {H}}$![]() with positive critical values there holds
with positive critical values there holds
and $H(x(t))\equiv c_0$![]() (a positive constant). Since
(a positive constant). Since

we deduce $\beta :=f'(c_0)>0$![]() , and so $c_0>1$
, and so $c_0>1$![]() . Define $y(t)=({1}/{\sqrt {c_0}})x(t/\beta )$
. Define $y(t)=({1}/{\sqrt {c_0}})x(t/\beta )$![]() for $0\le t\le \beta$
for $0\le t\le \beta$![]() . Then
. Then
and therefore $f'(c_0)=\beta =A(y)\in \Sigma ^{n,k}_{\partial D}$![]() . By the definition of $f$
. By the definition of $f$![]() this implies $f(c_0)<\epsilon$
this implies $f(c_0)<\epsilon$![]() and so
and so
Since for any $\epsilon >0$![]() and $G\in \mathcal {F}_{n,k}(\mathbb {R}^{2n},\partial D)$
and $G\in \mathcal {F}_{n,k}(\mathbb {R}^{2n},\partial D)$![]() , there exists $\overline {H}\in \mathscr {E}^{n,k}_\epsilon (\mathbb {R}^{2n},\partial D)$
, there exists $\overline {H}\in \mathscr {E}^{n,k}_\epsilon (\mathbb {R}^{2n},\partial D)$![]() such that $\overline {H}\ge G$
such that $\overline {H}\ge G$![]() , we deduce that $c^{n,k}(G)\ge c^{n,k}(\overline{H})\ge \min \Sigma ^{n,k}_{\partial D}-\epsilon$
, we deduce that $c^{n,k}(G)\ge c^{n,k}(\overline{H})\ge \min \Sigma ^{n,k}_{\partial D}-\epsilon$![]() . Hence $c^{n,k}(\partial D)\ge \min \Sigma ^{n,k}_{\partial D}=\varrho$
. Hence $c^{n,k}(\partial D)\ge \min \Sigma ^{n,k}_{\partial D}=\varrho$![]() .
.
Step 2. Prove that $c^{n,k}(D)\le \varrho$![]() . Denote by $w^{\ast }$
. Denote by $w^{\ast }$![]() the projections of $w$
the projections of $w$![]() in (4.2) onto $E^{\ast }$
in (4.2) onto $E^{\ast }$![]() (according to the decomposition $E = E^{1/2} =E^{+}\oplus E^{-}\oplus E^{0}$
(according to the decomposition $E = E^{1/2} =E^{+}\oplus E^{-}\oplus E^{0}$![]() ), $\ast =0,-,+$
), $\ast =0,-,+$![]() . Then $w^{+}\ne 0$
. Then $w^{+}\ne 0$![]() . (Otherwise, a contradiction occurs because $1=A(w) = A(w^{0}\oplus w^{-}) =-\frac {1}{2}\|w^{-}\|^{2}$
. (Otherwise, a contradiction occurs because $1=A(w) = A(w^{0}\oplus w^{-}) =-\frac {1}{2}\|w^{-}\|^{2}$![]() .) Define $y:=w/\sqrt {\varrho }$
.) Define $y:=w/\sqrt {\varrho }$![]() . Then $y\in C^{1}_{n,k}([0,1])$
. Then $y\in C^{1}_{n,k}([0,1])$![]() satisfies $I(y)=1$
satisfies $I(y)=1$![]() and $A(y)={1}/{\varrho }$
and $A(y)={1}/{\varrho }$![]() . It follows from the definition of $H^{\ast }$
. It follows from the definition of $H^{\ast }$![]() that for any $\lambda \in \mathbb {R}$
that for any $\lambda \in \mathbb {R}$![]() and $x\in E$
and $x\in E$![]() ,
,
and so
In particular, taking $\lambda =\frac {1}{2} \int ^{1}_0\langle x(t), - J_{2n}\dot {y}(t)\rangle {\rm d}t$![]() we arrive at
we arrive at

Since $y^{+}=w^{+}/\sqrt {\varrho }\ne 0$![]() and $E^{-}\oplus E^{0}+\mathbb {R}_+y=E^{-}\oplus E^{0}\oplus \mathbb {R}_+y^{+}$
and $E^{-}\oplus E^{0}+\mathbb {R}_+y=E^{-}\oplus E^{0}\oplus \mathbb {R}_+y^{+}$![]() , by proposition 3.2(ii),
, by proposition 3.2(ii),
Fixing $\gamma \in \Gamma _{n,k}$![]() and $x\in \gamma (S^{+})\cap (E^{-}\oplus E^{0}+\mathbb {R}_+y)$
and $x\in \gamma (S^{+})\cap (E^{-}\oplus E^{0}+\mathbb {R}_+y)$![]() , write $x=x^{-0}+ sy=x^{-0}+ sy^{-0}+ sy^{+}$
, write $x=x^{-0}+ sy=x^{-0}+ sy^{-0}+ sy^{+}$![]() where $x^{-0}\in E^{-}\oplus E^{0}$
where $x^{-0}\in E^{-}\oplus E^{0}$![]() , and consider the polynomial
, and consider the polynomial
Since $\mathfrak {a}|_{E^{-}\oplus E^{0}}\le 0$![]() implies $P(-s)\le 0$
implies $P(-s)\le 0$![]() , and $\mathfrak {a}(y)=1/\varrho >0$
, and $\mathfrak {a}(y)=1/\varrho >0$![]() implies $P(t)\to +\infty$
implies $P(t)\to +\infty$![]() as $|t|\to +\infty$
as $|t|\to +\infty$![]() , there exists $t_0\in \mathbb {R}$
, there exists $t_0\in \mathbb {R}$![]() such that $P(t_0)=0$
such that $P(t_0)=0$![]() . It follows that
. It follows that

This and (4.6) lead to

In order to prove that that $c^{n,k}(D)\le \varrho$![]() , it suffices to prove that for any $\varepsilon >0$
, it suffices to prove that for any $\varepsilon >0$![]() there exists $\tilde {H}\in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, D)$
there exists $\tilde {H}\in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, D)$![]() such that $c^{n,k}(\tilde {H})< \varrho +\varepsilon$
such that $c^{n,k}(\tilde {H})< \varrho +\varepsilon$![]() , which is reduced to prove: for any given $\gamma \in \Gamma _{n,k}$
, which is reduced to prove: for any given $\gamma \in \Gamma _{n,k}$![]() there exists $x\in h(S^{+})$
there exists $x\in h(S^{+})$![]() such that
such that
Now for $\tau >0$![]() there exists $H_\tau \in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, D)$
there exists $H_\tau \in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, D)$![]() such that
such that
For $\gamma \in \Gamma _{n,k}$![]() choose $x\in h(S^{+})$
choose $x\in h(S^{+})$![]() satisfying (4.7). We shall prove that for $\tau >0$
satisfying (4.7). We shall prove that for $\tau >0$![]() large enough $\tilde {H}=H_\tau$
large enough $\tilde {H}=H_\tau$![]() satisfies the requirements.
satisfies the requirements.
• If $\int ^{1}_0H(x(t))\,{{\rm d}}t\le (1+\frac {\varepsilon }{\varrho })$
 , then by $H_\tau \ge 0$
, then by $H_\tau \ge 0$ and (4.7), we have
\[ \Phi_{H_\tau}(x)\le \mathfrak{a}(x)\le \varrho\int^{1}_0H(x(t))\,{{\rm d}}t\le \varrho\left(1+\frac{\varepsilon}{\varrho}\right)<\varrho+\varepsilon. \]
and (4.7), we have
\[ \Phi_{H_\tau}(x)\le \mathfrak{a}(x)\le \varrho\int^{1}_0H(x(t))\,{{\rm d}}t\le \varrho\left(1+\frac{\varepsilon}{\varrho}\right)<\varrho+\varepsilon. \]
• If $\int ^{1}_0H(x(t))\,{{\rm d}}t>(1+{\varepsilon }/{\varrho })$
 , then (4.9) implies
(4.10)\begin{align} \int^{1}_0H_\tau(x(t))\,{{\rm d}}t & \ge \tau\left(\int^{1}_0H(x(t))\,{{\rm d}}t- \left(1+\frac{\varepsilon}{2\varrho}\right)\right)\nonumber\\ & \ge \tau \frac{\varepsilon}{2a}\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1} \int^{1}_0H(x(t))\,{{\rm d}}t \end{align}because
, then (4.9) implies
(4.10)\begin{align} \int^{1}_0H_\tau(x(t))\,{{\rm d}}t & \ge \tau\left(\int^{1}_0H(x(t))\,{{\rm d}}t- \left(1+\frac{\varepsilon}{2\varrho}\right)\right)\nonumber\\ & \ge \tau \frac{\varepsilon}{2a}\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1} \int^{1}_0H(x(t))\,{{\rm d}}t \end{align}because \begin{align*} \left(1+\frac{\varepsilon}{2\varrho}\right)& = \left(1+\frac{\varepsilon}{2\varrho}\right)\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1} \left(1+\frac{\varepsilon}{\varrho}\right)\\ & < \left(1+\frac{\varepsilon}{2\varrho}\right) \left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}\int^{1}_0H(x(t))\,{{\rm d}}t \end{align*}and
\begin{align*} \left(1+\frac{\varepsilon}{2\varrho}\right)& = \left(1+\frac{\varepsilon}{2\varrho}\right)\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1} \left(1+\frac{\varepsilon}{\varrho}\right)\\ & < \left(1+\frac{\varepsilon}{2\varrho}\right) \left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}\int^{1}_0H(x(t))\,{{\rm d}}t \end{align*}and \begin{align*} 1-\left(1+\frac{\varepsilon}{2\varrho}\right)\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}&= \left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}\left[\left(1+\frac{\varepsilon}{\varrho}\right)- \left(1+\frac{\varepsilon}{2\varrho}\right)\right]\\ & = \frac{\varepsilon}{2\varrho}\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}. \end{align*}
\begin{align*} 1-\left(1+\frac{\varepsilon}{2\varrho}\right)\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}&= \left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}\left[\left(1+\frac{\varepsilon}{\varrho}\right)- \left(1+\frac{\varepsilon}{2\varrho}\right)\right]\\ & = \frac{\varepsilon}{2\varrho}\left(1+\frac{\varepsilon}{\varrho}\right)^{{-}1}. \end{align*}
Choose $\tau >0$![]() so large that the right side of the last equality is more than $\varrho$
so large that the right side of the last equality is more than $\varrho$![]() . Then
. Then
by (4.10), and hence (4.7) leads to
In summary, in the above two cases we have $\Phi _{H_\tau }(x)<\varrho +\varepsilon$![]() . (4.8) is proved.
. (4.8) is proved.
Step 3. Prove the final claim. By [Reference Jin and Lu26, theorem 1.5] we have
Using proposition 1.12 and corollary 2.41 in [Reference Krantz28] we can choose two sequences of $C^{\infty }$![]() strictly convex domains with boundaries, $(D^{+}_j)$
strictly convex domains with boundaries, $(D^{+}_j)$![]() and $(D^{-}_j)$
and $(D^{-}_j)$![]() , such that
, such that
(i) $D^{-}_1\subset D^{-}_2\subset \cdots \subset D$
 and $\cup ^{\infty }_{j=1}D^{-}_j=D$
and $\cup ^{\infty }_{j=1}D^{-}_j=D$ ,
,(ii) $D^{+}_1\supseteq D^{+}_2\supseteq \cdots \supseteq D$
 and $\cap ^{\infty }_{j=1}D^{+}_j=D$
and $\cap ^{\infty }_{j=1}D^{+}_j=D$ ,
,(iii) for any small neighbourhood $O$
 of $\partial D$
of $\partial D$ there exists an integer $N>0$
there exists an integer $N>0$ such that $\partial D^{+}_k\cup \partial D^{-}_k\subset O\ \forall \ k\ge N$
such that $\partial D^{+}_k\cup \partial D^{-}_k\subset O\ \forall \ k\ge N$ .
.
Now step 1–step 2 and [Reference Jin and Lu26, theorem 1.5] give rise to $c_{\rm LR}(D^{+}_j,D\cap \mathbb {R}^{n,k})=c^{n,k}(D^{+}_j)$![]() and $c_{\rm LR}(D^{-}_j,D\cap \mathbb {R}^{n,k})=c^{n,k}(D^{-}_j)$
and $c_{\rm LR}(D^{-}_j,D\cap \mathbb {R}^{n,k})=c^{n,k}(D^{-}_j)$![]() for each $j=1,2,\ldots$
for each $j=1,2,\ldots$![]() . We have also that the sequence $c_{\rm LR}(D^{+}_j,D\cap \mathbb {R}^{n,k})$
. We have also that the sequence $c_{\rm LR}(D^{+}_j,D\cap \mathbb {R}^{n,k})$![]() converges decreasingly to $c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$
converges decreasingly to $c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$![]() as $j\to \infty$
as $j\to \infty$![]() and that the sequence $c_{\rm LR}(D^{-}_j,D\cap \mathbb {R}^{n,k})$
and that the sequence $c_{\rm LR}(D^{-}_j,D\cap \mathbb {R}^{n,k})$![]() converges increasingly to $c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$
converges increasingly to $c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$![]() as $j\to \infty$
as $j\to \infty$![]() . Moreover for each $j$
. Moreover for each $j$![]() there holds $c^{n,k}(D^{-}_j)\le c^{n,k}(D)\le c^{n,k}(D^{+}_j)$
there holds $c^{n,k}(D^{-}_j)\le c^{n,k}(D)\le c^{n,k}(D^{+}_j)$![]() by the monotonicity of $c^{n,k}$
by the monotonicity of $c^{n,k}$![]() . These lead to $c^{n,k}(D)=c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$
. These lead to $c^{n,k}(D)=c_{\rm LR}(D,D\cap \mathbb {R}^{n,k})$![]() .
.
5. Proof of theorem 1.5
Clearly, the proof of theorem 1.5 can be reduced to the case that $m=2$![]() and all $D_i$
and all $D_i$![]() are also bounded. Moreover, by an approximation argument in step 3 of § 4 we only need to prove the following:
are also bounded. Moreover, by an approximation argument in step 3 of § 4 we only need to prove the following:
Theorem 5.1 For bounded strictly convex domains $D_i\subset \mathbb {R}^{2n_i}$![]() with $C^{2}$
with $C^{2}$![]() -smooth boundary and containing the origin, $i=1,2,$
-smooth boundary and containing the origin, $i=1,2,$![]() and any integer $0\le k\le n:=n_1+n_2$
and any integer $0\le k\le n:=n_1+n_2$![]() it holds that
it holds that

We first prove two lemmas. For convenience we write $E=H^{{1}/{2}}_{n,k}$![]() as $E_{n,k}$
as $E_{n,k}$![]() , and $E^{\ast }$
, and $E^{\ast }$![]() as $E^{\ast }_{n,k}$
as $E^{\ast }_{n,k}$![]() , $\ast =+,-, 0$
, $\ast =+,-, 0$![]() . As a generalization of lemma 2 in [Reference Sikorav37, § 6.6] we have:
. As a generalization of lemma 2 in [Reference Sikorav37, § 6.6] we have:
Lemma 5.2 Let $D\subset \mathbb {R}^{2n}$![]() be a bounded strictly convex domain with $C^{2}$
be a bounded strictly convex domain with $C^{2}$![]() -smooth boundary and containing $0$
-smooth boundary and containing $0$![]() . Then for any given integer $0\le k\le n,$
. Then for any given integer $0\le k\le n,$![]() function ${H}\in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, \partial D)$
function ${H}\in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, \partial D)$![]() and any $\epsilon >0$
and any $\epsilon >0$![]() there exists $\gamma \in \Gamma _{n,k}$
there exists $\gamma \in \Gamma _{n,k}$![]() such that
such that
where $B_{n,k}^{+}$![]() is the closed unit ball in $E_{n,k}^{+}$
is the closed unit ball in $E_{n,k}^{+}$![]() .
.
Proof. The case $k=n$![]() was proved in lemma 2 of [Reference Sikorav37, § 6.6]. We assume $k< n$
was proved in lemma 2 of [Reference Sikorav37, § 6.6]. We assume $k< n$![]() below. Let $S_{n,k}^{+}=\partial B_{n,k}^{+}$
below. Let $S_{n,k}^{+}=\partial B_{n,k}^{+}$![]() and $\mathscr {E}^{n,k}_{\epsilon /2}(\mathbb {R}^{2n},\partial D)$
and $\mathscr {E}^{n,k}_{\epsilon /2}(\mathbb {R}^{2n},\partial D)$![]() be as in (4.3). Replacing $H$
be as in (4.3). Replacing $H$![]() by a greater function we may assume $H\in \mathscr {E}^{n,k}_{\epsilon /2}(\mathbb {R}^{2n},\partial D)$
by a greater function we may assume $H\in \mathscr {E}^{n,k}_{\epsilon /2}(\mathbb {R}^{2n},\partial D)$![]() . Since $H=0$
. Since $H=0$![]() near $\partial {D}$
near $\partial {D}$![]() , by the arguments at the end of proof of proposition 3.6, the condition (3.5) may be satisfied with any $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}({H}^{-1}(0))$
, by the arguments at the end of proof of proposition 3.6, the condition (3.5) may be satisfied with any $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}({H}^{-1}(0))$![]() . Fix such a $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}({H}^{-1}(0))$
. Fix such a $z_0\in \mathbb {R}^{n,k}\cap {\rm Int}({H}^{-1}(0))$![]() . It follows that there exists $\alpha >0$
. It follows that there exists $\alpha >0$![]() such that
such that
(see (3.6)–(3.8) in the proof of proposition 3.6). Define $\gamma _\varepsilon :E_{n,k}\to E_{n,k}$![]() by $\gamma _\varepsilon (z)=z_0+ \alpha z$
by $\gamma _\varepsilon (z)=z_0+ \alpha z$![]() . It is easily seen that $\gamma _\varepsilon \in \Gamma _{n,k}$
. It is easily seen that $\gamma _\varepsilon \in \Gamma _{n,k}$![]() . The first inequality in (5.2) shows that $\gamma _\varepsilon (S^{+}_{n,k})$
. The first inequality in (5.2) shows that $\gamma _\varepsilon (S^{+}_{n,k})$![]() belongs to the set $\mathcal {F}_{n,k}=\{\gamma (S^{+}_{n,k})\,|\,\gamma \in \Gamma _{n,k} \text{ and}\ \inf (\Phi _H|_{\gamma (S^{+}_{n,k})})>0\}$
belongs to the set $\mathcal {F}_{n,k}=\{\gamma (S^{+}_{n,k})\,|\,\gamma \in \Gamma _{n,k} \text{ and}\ \inf (\Phi _H|_{\gamma (S^{+}_{n,k})})>0\}$![]() in (3.10). Lemma 3.7 shows that
in (3.10). Lemma 3.7 shows that
and $\mathcal {F}_{n,k}$![]() is positively invariant under the flow $\varphi _u$
is positively invariant under the flow $\varphi _u$![]() of $\nabla \Phi _H$
of $\nabla \Phi _H$![]() . Define $S_u=\varphi _u(z_0+\alpha S^{+}_{n,k})$
. Define $S_u=\varphi _u(z_0+\alpha S^{+}_{n,k})$![]() and ${\rm d}(H)=\sup _{u\ge 0}\inf (\Phi _{H}|_{S_u})$
and ${\rm d}(H)=\sup _{u\ge 0}\inf (\Phi _{H}|_{S_u})$![]() . It follows from these and (5.2) that
. It follows from these and (5.2) that
Since $\Phi _{H}$![]() satisfies the (PS) condition by lemma 4.1, ${\rm d}(H)$
satisfies the (PS) condition by lemma 4.1, ${\rm d}(H)$![]() is a positive critical value of $\Phi _{H}$
is a positive critical value of $\Phi _{H}$![]() , and ${\rm d}(H)\ge c^{n,k}(D)-\epsilon /2$
, and ${\rm d}(H)\ge c^{n,k}(D)-\epsilon /2$![]() by lemma 4.2. Moreover, by the definition of $d({H)}$
by lemma 4.2. Moreover, by the definition of $d({H)}$![]() there exists $r>0$
there exists $r>0$![]() such that $\Phi _{H}|_{S_r}\ge {\rm d}(H)-\epsilon /2$
such that $\Phi _{H}|_{S_r}\ge {\rm d}(H)-\epsilon /2$![]() and thus
and thus
Because $\Phi _{H}$![]() is nondecreasing along the flow $\varphi _u$
is nondecreasing along the flow $\varphi _u$![]() , we arrive at
, we arrive at
Define $\gamma :E_{n,k}\to E_{n,k}$![]() by $\gamma (x^{+}+x^{0}+x^{-})=\widetilde {\gamma }(x^{+})+x^{0}+x^{-}$
by $\gamma (x^{+}+x^{0}+x^{-})=\widetilde {\gamma }(x^{+})+x^{0}+x^{-}$![]() , where
, where

The first and second lines imply $\gamma (({\epsilon }/{2})B^{+}_{n,k})=(z_0+\alpha B^{+}_{n,k})$![]() and $\gamma (B^{+}_{n,k}\setminus ({\epsilon }/{2})B^{+}_{n,k})=\bigcup _{0\le u\le r}S_u$
and $\gamma (B^{+}_{n,k}\setminus ({\epsilon }/{2})B^{+}_{n,k})=\bigcup _{0\le u\le r}S_u$![]() , respectively, and so
, respectively, and so
the third line implies $\gamma (B^{+}_{n,k}\setminus \epsilon B^{+}_{n,k})=S_r$![]() . It follows from these, (5.2) and (5.3)–(5.4) that $\gamma$
. It follows from these, (5.2) and (5.3)–(5.4) that $\gamma$![]() satisfies (5.1).
satisfies (5.1).
Finally, we can also know that $\gamma \in \Gamma _{n,k}$![]() by considering the homotopy
by considering the homotopy
Lemma 5.3 Let integers $n_1, n_2\ge 1,$![]() $0\le k\le n:=n_1+n_2$
$0\le k\le n:=n_1+n_2$![]() . For a bounded strictly convex domain $D\subset \mathbb {R}^{2n_1}$
. For a bounded strictly convex domain $D\subset \mathbb {R}^{2n_1}$![]() with $C^{2}$
with $C^{2}$![]() smooth boundary $\mathcal {S}$
smooth boundary $\mathcal {S}$![]() and containing $0,$
and containing $0,$![]() it holds that
it holds that
Moreover, if $\Omega \subset \mathbb {R}^{2n_2}$![]() is a bounded strictly convex domain with $C^{2}$
is a bounded strictly convex domain with $C^{2}$![]() smooth boundary and containing $0,$
smooth boundary and containing $0,$![]() then
then
Proof. Let $H(z)=(j_D(z))^{2}$![]() for $z\in \mathbb {R}^{n_1}$
for $z\in \mathbb {R}^{n_1}$![]() and define
and define
By the definition and the monotonicity of $c^{n,k}$![]() we have
we have
Since the function $\mathbb {R}^{2n_1}\times \mathbb {R}^{2n_2}\ni (z,z')\mapsto G(z,z'):=H(z)+ (|z'|/R)^{2}\in \mathbb {R}$![]() is convex and of class $C^{1,1}$
is convex and of class $C^{1,1}$![]() , $E_R$
, $E_R$![]() is convex and $\mathcal {S}_R=\partial E_R$
is convex and $\mathcal {S}_R=\partial E_R$![]() is of class $C^{1,1}$
is of class $C^{1,1}$![]() . By theorem 1.4 we arrive at
. By theorem 1.4 we arrive at
Let $\lambda$![]() be a positive number and $u=(x,x'):[0,\lambda ]\rightarrow \mathcal {S}_R$
be a positive number and $u=(x,x'):[0,\lambda ]\rightarrow \mathcal {S}_R$![]() satisfy
satisfy
Namely, $u$![]() is a leafwise chord on $\mathcal {S}_R$
is a leafwise chord on $\mathcal {S}_R$![]() for $\mathbb {R}^{n,k}$
for $\mathbb {R}^{n,k}$![]() with action $\lambda$
with action $\lambda$![]() . Let $k_1=\min \{n_1,k\}$
. Let $k_1=\min \{n_1,k\}$![]() and $k_2=\max \{k-n_1,0\}$
and $k_2=\max \{k-n_1,0\}$![]() . Clearly, $k_1+k_2=k$
. Clearly, $k_1+k_2=k$![]() , and (5.6) is equivalent to the following
, and (5.6) is equivalent to the following
because $\mathbb {R}^{n,k}\equiv (\mathbb {R}^{n_1,k_1}\times \{0\}^{2n_2})+ (\{0\}^{2n_1}\times \mathbb {R}^{n_2,k_2})$![]() . Note that nonzero constant vectors cannot be solutions of (5.7) and (5.8) and that $H(z)$
. Note that nonzero constant vectors cannot be solutions of (5.7) and (5.8) and that $H(z)$![]() and $(|z'|/R)^{2}$
and $(|z'|/R)^{2}$![]() take constant values along solutions of (5.7) and (5.8), respectively. There exist three possibilities for solutions of (5.7) and (5.8):
take constant values along solutions of (5.7) and (5.8), respectively. There exist three possibilities for solutions of (5.7) and (5.8):
• $x\equiv 0$
 , $|x'|=R$
, $|x'|=R$ and so $2\lambda /R^{2}\in \pi \mathbb {N}$
and so $2\lambda /R^{2}\in \pi \mathbb {N}$ if $k< n_1+n_2$
if $k< n_1+n_2$ , and $2\lambda /R^{2}\in 2\pi \mathbb {N}$
, and $2\lambda /R^{2}\in 2\pi \mathbb {N}$ if $k=n_1+n_2$
if $k=n_1+n_2$ by (5.8).
by (5.8).• $x'\equiv 0$
 , $H(x)\equiv 1$
, $H(x)\equiv 1$ and so $\lambda \in \Sigma _\mathcal {S}^{n_1,\min \{n_1,k\}}$
and so $\lambda \in \Sigma _\mathcal {S}^{n_1,\min \{n_1,k\}}$ by (5.7).
by (5.7).• $H(x)\equiv \delta ^{2}\in (0,1)$
 and $|x'|^{2}=R^{2}(1-\delta ^{2})$
and $|x'|^{2}=R^{2}(1-\delta ^{2})$ , where $\delta >0$
, where $\delta >0$ . Then $y(t):=({1}/{\delta })x(t)$
. Then $y(t):=({1}/{\delta })x(t)$ and $y'(t):=x'(t/\delta )$
and $y'(t):=x'(t/\delta )$ satisfy respectively the following two lines:
\begin{align*} & \dot{y}=X_H(y)\quad\hbox{and}\quad y(\lambda), y(0)\in\mathbb{R}^{n_1,k_1},\quad y(\lambda)\sim y(0),\quad H(y)\equiv 1,\\ & \dot{y}'=2J_{2n_2}y'/R^{2}\quad\hbox{and}\quad y'(\lambda), y'(0)\in\mathbb{R}^{n_2, k_2},\quad y'(\lambda)\sim y'(0),\quad|y'|\equiv R. \end{align*}
satisfy respectively the following two lines:
\begin{align*} & \dot{y}=X_H(y)\quad\hbox{and}\quad y(\lambda), y(0)\in\mathbb{R}^{n_1,k_1},\quad y(\lambda)\sim y(0),\quad H(y)\equiv 1,\\ & \dot{y}'=2J_{2n_2}y'/R^{2}\quad\hbox{and}\quad y'(\lambda), y'(0)\in\mathbb{R}^{n_2, k_2},\quad y'(\lambda)\sim y'(0),\quad|y'|\equiv R. \end{align*}
Hence we have also $\lambda \in \Sigma _\mathcal {S}^{n_1,\min \{n_1,k\}}$![]() by the first line, and
by the first line, and
by the second line.
In summary, we always have
A solution $x$![]() of (5.7) siting on $\mathcal {S}$
of (5.7) siting on $\mathcal {S}$![]() gives a solution $u=(x,0)$
gives a solution $u=(x,0)$![]() of (5.6) on $\mathcal {S}_R$
of (5.6) on $\mathcal {S}_R$![]() . It follows that
. It follows that
for $R$![]() sufficiently large. (5.5) is proved.
sufficiently large. (5.5) is proved.
The second claim can be proved in the similar way.
Proof of theorem 5.1. Since $D_1\times D_2\subset D_1\times \mathbb {R}^{2n_2}$![]() and $D_1\times D_2\subset \mathbb {R}^{2n_1}\times D_2$
and $D_1\times D_2\subset \mathbb {R}^{2n_1}\times D_2$![]() , we get
, we get
by lemma 5.3. In order to prove the inverse direction inequality it suffices to prove
because $c^{n,k}(D_1\times D_2)\ge c^{n,k}(\partial D_1\times \partial D_2)$![]() by the monotonicity.
by the monotonicity.
We assume $n_1\le k$![]() . (The case $n_1>k$
. (The case $n_1>k$![]() is similar!) Then (5.11) becomes
is similar!) Then (5.11) becomes
because $c^{n_1,n_1}(D_1)=c_{\rm EH}(D_1)$![]() by definition. Note that for each ${H}\in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, \partial D_1\times \partial D_2)$
by definition. Note that for each ${H}\in \mathscr {F}_{n,k}(\mathbb {R}^{2n}, \partial D_1\times \partial D_2)$![]() we may choose $\widehat {H}_1\in \mathscr {F}_{n_1,n_1}(\mathbb {R}^{2n_1}, \partial D_1)$
we may choose $\widehat {H}_1\in \mathscr {F}_{n_1,n_1}(\mathbb {R}^{2n_1}, \partial D_1)$![]() and $\widehat {H}_2\in \mathscr {F}_{n_2,k-n_1}(\mathbb {R}^{2n_2}, \partial D_2)$
and $\widehat {H}_2\in \mathscr {F}_{n_2,k-n_1}(\mathbb {R}^{2n_2}, \partial D_2)$![]() such that
such that
Let $k_1=n_1$![]() and $k_2=n-k_1$
and $k_2=n-k_1$![]() . By lemma 5.2, for any
. By lemma 5.2, for any
and each $i\in \{1,2\}$![]() there exists $\gamma _i\in \Gamma _{n_i,k_i}$
there exists $\gamma _i\in \Gamma _{n_i,k_i}$![]() such that
such that
Put $\gamma =\gamma _1\times \gamma _2$![]() , which is in $\Gamma _{n,k}$
, which is in $\Gamma _{n,k}$![]() . Since for any $x=(x_1,x_2)\in S^{+}_{n,k}\subset B^{+}_{n_1,k_1}\times B^{+}_{n_2,k_2}$
. Since for any $x=(x_1,x_2)\in S^{+}_{n,k}\subset B^{+}_{n_1,k_1}\times B^{+}_{n_2,k_2}$![]() there exists some $j\in \{1,2\}$
there exists some $j\in \{1,2\}$![]() such that
such that
it follows from this and (5.13) that
and hence
This leads to (5.12) because $c^{n_1,n_1}(D_1)=c_{\rm EH}(D_1)$![]() .
.
6. Proof of theorem 1.7
6.1 The interior of $\Sigma _{\mathcal {S}}$ is empty
is empty
Let $\lambda :=\imath _X\omega _0$![]() , and $\lambda _0:=\frac {1}{2}(qdp-pdq)$
, and $\lambda _0:=\frac {1}{2}(qdp-pdq)$![]() , where $(q,p)$
, where $(q,p)$![]() is the standard coordinate on $\mathbb {R}^{2n}$
is the standard coordinate on $\mathbb {R}^{2n}$![]() .
.
Claim 6.1 For every leafwise chord on $\mathcal {S}$![]() for $\mathbb {R}^{n,k},$
for $\mathbb {R}^{n,k},$![]() $x:[0,T]\rightarrow \mathcal {S},$
$x:[0,T]\rightarrow \mathcal {S},$![]() there holds
there holds
Proof. Since $\mathcal {S}$![]() is of class $C^{2n+2}$
is of class $C^{2n+2}$![]() , so is $x$
, so is $x$![]() . Define $y:[0, T]\rightarrow \mathbb {R}^{n,k}$
. Define $y:[0, T]\rightarrow \mathbb {R}^{n,k}$![]() by $y(t)= tx(0)+(1-t)x(T)$
by $y(t)= tx(0)+(1-t)x(T)$![]() . As below (3.15) we can take a piecewise $C^{2n+2}$
. As below (3.15) we can take a piecewise $C^{2n+2}$![]() -smooth map $u$
-smooth map $u$![]() from a suitable closed disc $D^{2}$
from a suitable closed disc $D^{2}$![]() to $\mathbb {R}^{2n}$
to $\mathbb {R}^{2n}$![]() such that $u|\partial D^{2}$
such that $u|\partial D^{2}$![]() is equal to the loop $x\cup (-y)$
is equal to the loop $x\cup (-y)$![]() . Now it is easily checked that $\int _y \lambda _0=0$
. Now it is easily checked that $\int _y \lambda _0=0$![]() and hence
and hence
On the other hand, since the flow of $X$![]() maps $\mathbb {R}^{n,k}$
maps $\mathbb {R}^{n,k}$![]() to $\mathbb {R}^{n,k}$
to $\mathbb {R}^{n,k}$![]() , $X$
, $X$![]() is tangent to $\mathbb {R}^{n,k}$
is tangent to $\mathbb {R}^{n,k}$![]() and therefore $\omega _0(X,\dot {y})=0$
and therefore $\omega _0(X,\dot {y})=0$![]() , i.e. $y^{\ast }\lambda =0$
, i.e. $y^{\ast }\lambda =0$![]() . It follows that
. It follows that
Choosing $\varepsilon >0$![]() so small that $\mathbb {R}^{2n}\setminus \cup _{t\in (-\varepsilon, \varepsilon )}\phi ^{t}(\mathcal {S})$
so small that $\mathbb {R}^{2n}\setminus \cup _{t\in (-\varepsilon, \varepsilon )}\phi ^{t}(\mathcal {S})$![]() has two components, we obtain a very special parameterized family of $C^{2n+2}$
has two components, we obtain a very special parameterized family of $C^{2n+2}$![]() hypersurfaces modelled on $\mathcal {S}$
hypersurfaces modelled on $\mathcal {S}$![]() , given by
, given by
which is $C^{2n+2}$![]() because both $\mathcal {S}$
because both $\mathcal {S}$![]() and $X$
and $X$![]() are $C^{2n+2}$
are $C^{2n+2}$![]() . Define $U:=\cup _{t\in (-\varepsilon, \varepsilon )}\phi ^{t}(\mathcal {S})$
. Define $U:=\cup _{t\in (-\varepsilon, \varepsilon )}\phi ^{t}(\mathcal {S})$![]() and
and
if $w=\psi (\tau,z)\in U$![]() where $z\in \mathcal {S}$
where $z\in \mathcal {S}$![]() . This is $C^{2n+2}$
. This is $C^{2n+2}$![]() . Denote by $X_{K_\psi }$
. Denote by $X_{K_\psi }$![]() the Hamiltonian vector field of $K_\psi$
the Hamiltonian vector field of $K_\psi$![]() defined by $\omega _0(\cdot,X_{K_\psi })=dK_\psi$
defined by $\omega _0(\cdot,X_{K_\psi })=dK_\psi$![]() . Then it is not hard to prove
. Then it is not hard to prove
and for $w=\phi ^{\tau }(z)=\psi (\tau,z)\in U$![]() there holds
there holds
Let $\mathcal {S}_\tau :=\psi (\{\tau \}\times \mathcal {S})$![]() . Since $\phi ^{t}$
. Since $\phi ^{t}$![]() preserves the leaf of $\mathbb {R}^{n,k}$
preserves the leaf of $\mathbb {R}^{n,k}$![]() , $y:[0,T]\to \mathcal {S}_\tau$
, $y:[0,T]\to \mathcal {S}_\tau$![]() satisfies
satisfies
if and only if $y(t)=\phi ^{\tau } (x({\rm e}^{-\tau } t))$![]() , where $x:[0, {\rm e}^{-\tau } T]\to \mathcal {S}$
, where $x:[0, {\rm e}^{-\tau } T]\to \mathcal {S}$![]() satisfies
satisfies
In addition, $y(t)=\phi ^{\tau } (x({\rm e}^{-\tau } t))$![]() implies $\int _y\lambda ={\rm e}^{\tau }\int _x\lambda$
implies $\int _y\lambda ={\rm e}^{\tau }\int _x\lambda$![]() . By (6.1) and (6.3) we deduce
. By (6.1) and (6.3) we deduce

Fix $0<\delta <\varepsilon$![]() . Let ${\bf A}_\delta$
. Let ${\bf A}_\delta$![]() and ${\bf B}_\delta$
and ${\bf B}_\delta$![]() denote the unbounded and bounded components of $\mathbb {R}^{2n}\setminus \cup _{t\in (-\delta, \delta )}\phi ^{t}(\mathcal {S})$
denote the unbounded and bounded components of $\mathbb {R}^{2n}\setminus \cup _{t\in (-\delta, \delta )}\phi ^{t}(\mathcal {S})$![]() , respectively. Then $\psi (\{\tau \}\times \mathcal {S})\subset {\bf B}_\delta$
, respectively. Then $\psi (\{\tau \}\times \mathcal {S})\subset {\bf B}_\delta$![]() for $-\varepsilon <\tau <-\delta$
for $-\varepsilon <\tau <-\delta$![]() . Let $\mathscr {F}_{n,k}(\mathbb {R}^{2n})$
. Let $\mathscr {F}_{n,k}(\mathbb {R}^{2n})$![]() be given by (3.10). We call $H\in \mathscr {F}_{n,k}(\mathbb {R}^{2n})$
be given by (3.10). We call $H\in \mathscr {F}_{n,k}(\mathbb {R}^{2n})$![]() adapted to $\psi$
adapted to $\psi$![]() if
if

where $f:(-1,1)\to \mathbb {R}$![]() and $h:[0, \infty )\to \mathbb {R}$
and $h:[0, \infty )\to \mathbb {R}$![]() are smooth functions satisfying
are smooth functions satisfying
Clearly, $H$![]() defined by (6.4) is $C^{2n+2}$
defined by (6.4) is $C^{2n+2}$![]() and its gradient $\nabla H:\mathbb {R}^{2n}\to \mathbb {R}^{2n}$
and its gradient $\nabla H:\mathbb {R}^{2n}\to \mathbb {R}^{2n}$![]() satisfies a global Lipschitz condition.
satisfies a global Lipschitz condition.
Lemma 6.2
(i) If $x$
 is a nonconstant critical point of $\Phi _H$
is a nonconstant critical point of $\Phi _H$ on $E$
on $E$ such that $x(0)\in \psi (\{\tau \}\times \mathcal {S})$
such that $x(0)\in \psi (\{\tau \}\times \mathcal {S})$ for some $\tau \in (-\delta,\delta )$
for some $\tau \in (-\delta,\delta )$ satisfying $f'(\tau )>0,$
satisfying $f'(\tau )>0,$ then
\[ {\rm e}^{-\tau}f'(\tau)\in \Sigma_{\mathcal{S}}\quad\hbox{and}\quad \Phi_H(x)=f'(\tau)-f(\tau). \]
then
\[ {\rm e}^{-\tau}f'(\tau)\in \Sigma_{\mathcal{S}}\quad\hbox{and}\quad \Phi_H(x)=f'(\tau)-f(\tau). \]
(ii) If some $\tau \in (-\delta,\delta )$
 satisfies $f'(\tau )>0$
satisfies $f'(\tau )>0$ and ${\rm e}^{-\tau }f'(\tau )\in \Sigma _{\mathcal {S}},$
and ${\rm e}^{-\tau }f'(\tau )\in \Sigma _{\mathcal {S}},$ then there is a nonconstant critical point $x$
then there is a nonconstant critical point $x$ of $\Phi _H$
of $\Phi _H$ on $E$
on $E$ such that $x(0)\in \psi (\{\tau \}\times \mathcal {S})$
such that $x(0)\in \psi (\{\tau \}\times \mathcal {S})$ and $\Phi _H(x)=f'(\tau )-f(\tau )$
and $\Phi _H(x)=f'(\tau )-f(\tau )$ .
.
Proof. (i) By lemma 2.5 $x$![]() is $C^{2n+2}$
is $C^{2n+2}$![]() and satisfies $\dot {x}=X_H(x)=f'(\tau )X_{K_\psi }(x)$
and satisfies $\dot {x}=X_H(x)=f'(\tau )X_{K_\psi }(x)$![]() , $x(j)\in \mathbb {R}^{n,k}$
, $x(j)\in \mathbb {R}^{n,k}$![]() , $j=0,1$
, $j=0,1$![]() , and $x(1)\sim x(0)$
, and $x(1)\sim x(0)$![]() . Moreover $x(0)\in \psi (\{\tau \}\times \mathcal {S})$
. Moreover $x(0)\in \psi (\{\tau \}\times \mathcal {S})$![]() implies $H(x(1))=H(x(0))=f(\tau )$
implies $H(x(1))=H(x(0))=f(\tau )$![]() and therefore $x(1)\in \psi (\{\tau \}\times \mathcal {S})$
and therefore $x(1)\in \psi (\{\tau \}\times \mathcal {S})$![]() by the construction of $H$
by the construction of $H$![]() above. These show that $x$
above. These show that $x$![]() is a leafwise chord on $\psi (\{\tau \}\times \mathcal {S})$
is a leafwise chord on $\psi (\{\tau \}\times \mathcal {S})$![]() for $\mathbb {R}^{n,k}$
for $\mathbb {R}^{n,k}$![]() . By the arguments below (6.3), $[0,1]\ni t\mapsto y(t):=\phi ^{-\tau }(y(t))$
. By the arguments below (6.3), $[0,1]\ni t\mapsto y(t):=\phi ^{-\tau }(y(t))$![]() is a leafwise chord on $\mathcal {S}$
is a leafwise chord on $\mathcal {S}$![]() for $\mathbb {R}^{n,k}$
for $\mathbb {R}^{n,k}$![]() . It follows from (6.3) and (6.1) that
. It follows from (6.3) and (6.1) that

These show that ${\rm e}^{-\tau }f'(\tau )=A(y)\in \Sigma _{\mathcal {S}}$![]() . By (6.1) we have
. By (6.1) we have

(ii) By the assumption there exists $y:[0, 1]\to \mathcal {S}$![]() satisfying
satisfying
Hence $x(t)=\psi (\tau, y(t))=\phi ^{\tau }(y(t))$![]() satisfies
satisfies

By lemma 2.5, $x$![]() is a critical point of $\Phi _H$
is a critical point of $\Phi _H$![]() . Moreover $\Phi _H(x)=f'(\tau )-f(\tau )$
. Moreover $\Phi _H(x)=f'(\tau )-f(\tau )$![]() as in (i).
as in (i).
Proposition 6.3 Let $\mathcal {S}$![]() be as in theorem 1.7. Then the interior of $\Sigma _{\mathcal {S}}$
be as in theorem 1.7. Then the interior of $\Sigma _{\mathcal {S}}$![]() in $\mathbb {R}$
in $\mathbb {R}$![]() is empty.
is empty.
Proof. Otherwise, suppose that $T\in \Sigma _{\mathcal {S}}$![]() is an interior point of $\Sigma _{\mathcal {S}}$
is an interior point of $\Sigma _{\mathcal {S}}$![]() . Then for some small $0<\epsilon _1<\delta$
. Then for some small $0<\epsilon _1<\delta$![]() the open neighbourhood $O:=\{{\rm e}^{-\tau }T\,|\,\tau \in (-\epsilon _1,\epsilon _1)\}$
the open neighbourhood $O:=\{{\rm e}^{-\tau }T\,|\,\tau \in (-\epsilon _1,\epsilon _1)\}$![]() of $T$
of $T$![]() is contained in $\Sigma _{\mathcal {S}}$
is contained in $\Sigma _{\mathcal {S}}$![]() . Let us choose the function $f$
. Let us choose the function $f$![]() in (6.4) such that $f(u)=Tu+\overline {C}\ge 0\ \forall \ u\in [-\epsilon _1, \epsilon _1]$
in (6.4) such that $f(u)=Tu+\overline {C}\ge 0\ \forall \ u\in [-\epsilon _1, \epsilon _1]$![]() (by shrinking $0<\epsilon _1<\delta$
(by shrinking $0<\epsilon _1<\delta$![]() if necessary). By lemma 6.2(ii) we deduce
if necessary). By lemma 6.2(ii) we deduce
It follows that the critical value set of $\Phi _H$![]() has nonempty interior. This is a contradiction by lemma 3.10. Hence $\Sigma _{\mathcal {S}}$
has nonempty interior. This is a contradiction by lemma 3.10. Hence $\Sigma _{\mathcal {S}}$![]() has empty interior.
has empty interior.
6.2 $c^{n,k}(U)=c^{n,k}(\mathcal {S})$ belongs to $\Sigma _{\mathcal {S}}$
belongs to $\Sigma _{\mathcal {S}}$
This can be obtained by slightly modifying the proof of [Reference Sikorav37, theorem 7.5] (or [Reference Jin and Lu25, theorem 1.18] or [Reference Jin and Lu24, theorem 1.17]). For completeness we give it in detail. For $C>0$![]() large enough and $\delta >2\eta >0$
large enough and $\delta >2\eta >0$![]() small enough, define $H=H_{C,\eta }\in \mathscr {F}_{n,k}(\mathbb {R}^{2n})$
small enough, define $H=H_{C,\eta }\in \mathscr {F}_{n,k}(\mathbb {R}^{2n})$![]() adapted to $\psi$
adapted to $\psi$![]() as follows:
as follows:

where $B^{2n}(0,R)\supseteq \overline {\psi ((-\varepsilon,\varepsilon )\times \mathcal {S})}$![]() (the closure of $\psi ((-\varepsilon,\varepsilon )\times \mathcal {S})$
(the closure of $\psi ((-\varepsilon,\varepsilon )\times \mathcal {S})$![]() ), $f_{C,\eta }:(-\varepsilon, \varepsilon )\to \mathbb {R}$
), $f_{C,\eta }:(-\varepsilon, \varepsilon )\to \mathbb {R}$![]() and $h:[0, \infty )\to \mathbb {R}$
and $h:[0, \infty )\to \mathbb {R}$![]() are smooth functions satisfying
are smooth functions satisfying

We can choose such a family $H_{C,\eta }$![]() ($C\to +\infty$
($C\to +\infty$![]() , $\eta \to 0$
, $\eta \to 0$![]() ) to be cofinal in $\mathscr {F}^{n,k}(\mathbb {R}^{2n},\mathcal {S})$
) to be cofinal in $\mathscr {F}^{n,k}(\mathbb {R}^{2n},\mathcal {S})$![]() defined by (3.16) and also to have the property that
defined by (3.16) and also to have the property that
It follows that
By proposition 3.5(i) and (6.8), $\eta \le \eta '$![]() implies that $c^{n,k}(H_{C,\eta })\le c^{n,k}(H_{C,\eta '})$
implies that $c^{n,k}(H_{C,\eta })\le c^{n,k}(H_{C,\eta '})$![]() , and hence
, and hence
exists, and
i.e. $C\mapsto \Upsilon (C)$![]() is non-increasing. We claim
is non-increasing. We claim
In fact, for any $\epsilon >0$![]() there exists $\eta _0>0$
there exists $\eta _0>0$![]() and $C_0>0$
and $C_0>0$![]() such that $|c^{n,k}(H_{C,\eta })-c^{n,k}(\mathcal {S})|<\epsilon$
such that $|c^{n,k}(H_{C,\eta })-c^{n,k}(\mathcal {S})|<\epsilon$![]() for all $\eta <\eta _0$
for all $\eta <\eta _0$![]() and $C>C_0$
and $C>C_0$![]() . Letting $\eta \to 0$
. Letting $\eta \to 0$![]() leads to $|\Upsilon (C)-c^{n,k}(\mathcal {S})|\le \epsilon$
leads to $|\Upsilon (C)-c^{n,k}(\mathcal {S})|\le \epsilon$![]() for all $C>C_0$
for all $C>C_0$![]() . (6.10) holds.
. (6.10) holds.
Claim 6.4 Let $\overline {\Sigma _{\mathcal {S}}}$![]() be the closure of $\Sigma _{\mathcal {S}}$
be the closure of $\Sigma _{\mathcal {S}}$![]() . Then $\overline {\Sigma _{\mathcal {S}}}\subset \Sigma _{\mathcal {S}}\cup \{0\}$
. Then $\overline {\Sigma _{\mathcal {S}}}\subset \Sigma _{\mathcal {S}}\cup \{0\}$![]() .
.
Proof. In fact, let $\varphi ^{t}$![]() denote the flow of $X_{K_\psi }$
denote the flow of $X_{K_\psi }$![]() . It is not hard to prove
. It is not hard to prove
Suppose that $(T_k)\subset \Sigma _{\mathcal {S}}$![]() satisfy $T_k\to T_0\ge 0$
satisfy $T_k\to T_0\ge 0$![]() . Then there exists a sequence $(z_k)\subset \mathcal {S}\cap \mathbb {R}^{n,k}$
. Then there exists a sequence $(z_k)\subset \mathcal {S}\cap \mathbb {R}^{n,k}$![]() such that $\varphi ^{T_k}(z_k)\in \mathcal {S}\cap \mathbb {R}^{n,k}$
such that $\varphi ^{T_k}(z_k)\in \mathcal {S}\cap \mathbb {R}^{n,k}$![]() and $\varphi ^{T_k}(z_k)\sim z_k$
and $\varphi ^{T_k}(z_k)\sim z_k$![]() for $k=1,2,\ldots$
for $k=1,2,\ldots$![]() . Define $\gamma _k(t)=\varphi ^{T_kt}(z_k)$
. Define $\gamma _k(t)=\varphi ^{T_kt}(z_k)$![]() for $t\in [0,1]$
for $t\in [0,1]$![]() and $k\in \mathbb {N}$
and $k\in \mathbb {N}$![]() . Then $\dot {\gamma }_k(t)=T_kX_{K_\psi }(\gamma _k(t))$
. Then $\dot {\gamma }_k(t)=T_kX_{K_\psi }(\gamma _k(t))$![]() . By the Arzelá-Ascoli theorem $(\gamma _k)$
. By the Arzelá-Ascoli theorem $(\gamma _k)$![]() has a subsequence converging to some $\gamma _0$
has a subsequence converging to some $\gamma _0$![]() in $C^{\infty }([0, 1],\mathcal {S})$
in $C^{\infty }([0, 1],\mathcal {S})$![]() , which satisfies the following relations
, which satisfies the following relations

Hence $\gamma _0(t)=\varphi ^{T_0t}(z_0)$![]() and $T_0\in \Sigma _{\mathcal {S}}$
and $T_0\in \Sigma _{\mathcal {S}}$![]() if $T_0>0$
if $T_0>0$![]() . It follows that $\overline {\Sigma _{\mathcal {S}}}\subset \Sigma _{\mathcal {S}}\cup \{0\}$
. It follows that $\overline {\Sigma _{\mathcal {S}}}\subset \Sigma _{\mathcal {S}}\cup \{0\}$![]() .
.
Note that so far we do not use the assumption $a_H\notin \mathbb {N}\pi /2$![]() .
.
Claim 6.5 If $a_H\notin \mathbb {N}\pi /2$![]() then either $\Upsilon (C)\in \overline {\Sigma _{\mathcal {S}}}$
then either $\Upsilon (C)\in \overline {\Sigma _{\mathcal {S}}}$![]() or
or
Proof. Since $a_H\notin \mathbb {N}\pi /2$![]() , by theorem 3.8 we get that $c^{n,k}(H_{C,\eta })$
, by theorem 3.8 we get that $c^{n,k}(H_{C,\eta })$![]() is a positive critical value of $\Phi _{H_{C,\eta }}$
is a positive critical value of $\Phi _{H_{C,\eta }}$![]() and the associated critical point $x\in E$
and the associated critical point $x\in E$![]() gives rise to a nonconstant leafwise chord sitting in the interior of $U$
gives rise to a nonconstant leafwise chord sitting in the interior of $U$![]() . Then lemma 6.2(i) yields
. Then lemma 6.2(i) yields
where $f'_{C,\eta }(\tau )\in {\rm e}^{\tau }\Sigma _{\mathcal {S}}$![]() and $\eta <|\tau |<2\eta$
and $\eta <|\tau |<2\eta$![]() . Choose $C>0$
. Choose $C>0$![]() so large that $c^{n,k}(H_{C,\eta })< c^{n,k}(\mathcal {S})+1$
so large that $c^{n,k}(H_{C,\eta })< c^{n,k}(\mathcal {S})+1$![]() . By the choice of $f$
. By the choice of $f$![]() below (6.7) we get either $f_{C,\eta }(\tau )<\eta$
below (6.7) we get either $f_{C,\eta }(\tau )<\eta$![]() or $f_{C,\eta }(\tau )>C-\eta$
or $f_{C,\eta }(\tau )>C-\eta$![]() . Moreover $c^{n,k}(H_{C,\eta })>0$
. Moreover $c^{n,k}(H_{C,\eta })>0$![]() implies $f'_{C,\eta }(\tau )>f_{C,\eta }(\tau )\ge 0$
implies $f'_{C,\eta }(\tau )>f_{C,\eta }(\tau )\ge 0$![]() and so $\tau >0$
and so $\tau >0$![]() .
.
Take a sequence of positive numbers $\eta _n\to 0$![]() . By the arguments above, passing to a subsequence we have the following two cases.
. By the arguments above, passing to a subsequence we have the following two cases.
Case 1. For each $n\in \mathbb {N}$![]() , $c^{n,k}(H_{C,\eta _n})=f'_{C,\eta _n}(\tau _n)-f_{C,\eta _n}(\tau _n) ={\rm e}^{\tau _n}a_n-f_{C,\eta _n}(\tau _n)$
, $c^{n,k}(H_{C,\eta _n})=f'_{C,\eta _n}(\tau _n)-f_{C,\eta _n}(\tau _n) ={\rm e}^{\tau _n}a_n-f_{C,\eta _n}(\tau _n)$![]() , where $a_n\in \Sigma _\mathcal {S}$
, where $a_n\in \Sigma _\mathcal {S}$![]() , $0\le f_{C,\eta _n}(\tau _n)<\eta _n$
, $0\le f_{C,\eta _n}(\tau _n)<\eta _n$![]() and $\eta _n<\tau _n<2\eta _n$
and $\eta _n<\tau _n<2\eta _n$![]() .
.
Case 2. For each $n\in \mathbb {N}$![]() , $c^{n,k}(H_{C,\eta _n})=f'_{C,\eta _n}(\tau _n)-f_{C,\eta _n}(\tau _n) ={\rm e}^{\tau _n}a_n-f_{C,\eta _n}(\tau _n)={\rm e}^{\tau _n}a_n-C-(f_{C,\eta _n}(\tau _n) -C)$
, $c^{n,k}(H_{C,\eta _n})=f'_{C,\eta _n}(\tau _n)-f_{C,\eta _n}(\tau _n) ={\rm e}^{\tau _n}a_n-f_{C,\eta _n}(\tau _n)={\rm e}^{\tau _n}a_n-C-(f_{C,\eta _n}(\tau _n) -C)$![]() , where $a_n\in \Sigma _\mathcal {S}$
, where $a_n\in \Sigma _\mathcal {S}$![]() , $C-\eta _n< f_{C,\eta _n}(\tau _n)\le C$
, $C-\eta _n< f_{C,\eta _n}(\tau _n)\le C$![]() and $\eta _n<\tau _n<2\eta _n$
and $\eta _n<\tau _n<2\eta _n$![]() .
.
In case 1, since $c^{n,k}(H_{C,\eta _n})\to \Upsilon (C)$![]() by (6.9), the sequence $a_n={\rm e}^{-\tau _n}(c^{n,k} (H_{C,\eta _n})+f_{C,\eta _n}(\tau _n))$
by (6.9), the sequence $a_n={\rm e}^{-\tau _n}(c^{n,k} (H_{C,\eta _n})+f_{C,\eta _n}(\tau _n))$![]() is bounded. Passing to a subsequence we may assume $a_n\to a_C\in \overline {\Sigma _{\mathcal {S}}}$
is bounded. Passing to a subsequence we may assume $a_n\to a_C\in \overline {\Sigma _{\mathcal {S}}}$![]() . Then
. Then
because ${\rm e}^{-\tau _n}\to 1$![]() and $f_{C,\eta _n}(\tau _n)\to 0$
and $f_{C,\eta _n}(\tau _n)\to 0$![]() .
.
Similarly, we can prove $\Upsilon (C)+C=a_C\in \overline {\Sigma _{\mathcal {S}}}$![]() in case 2.
in case 2.
Step 1. Prove $c^{n,k}(\mathcal {S})\in \overline {\Sigma _{\mathcal {S}}}$![]() . Suppose that there exists an increasing sequence $C_n$
. Suppose that there exists an increasing sequence $C_n$![]() tending to $+\infty$
tending to $+\infty$![]() such that $C_n/R^{2}\notin \mathbb {N}\pi /2$
such that $C_n/R^{2}\notin \mathbb {N}\pi /2$![]() and $\Upsilon (C_n)\in \Sigma _{\mathcal {S}}$
and $\Upsilon (C_n)\in \Sigma _{\mathcal {S}}$![]() for each $n$
for each $n$![]() . Since $(\Upsilon (C_n))$
. Since $(\Upsilon (C_n))$![]() is non-increasing we conclude
is non-increasing we conclude
Otherwise, we have
Claim 6.6 Let $\bar {C}>0$![]() be as in (6.13). Then for any $C< C'$
be as in (6.13). Then for any $C< C'$![]() in $(\bar {C}, +\infty )$
in $(\bar {C}, +\infty )$![]() there holds
there holds
Its proof is carried out later. Since $\Xi :=\{C>\bar {C}\,|\, C\ \hbox{satisfying}\ C/R^{2}\notin \mathbb {N}\pi /2\}$![]() is dense in $(\bar {C}, +\infty )$
is dense in $(\bar {C}, +\infty )$![]() , it follows from claim 6.6 that $\Upsilon (C')+C'\le \Upsilon (C)+C$
, it follows from claim 6.6 that $\Upsilon (C')+C'\le \Upsilon (C)+C$![]() if $C'>C$
if $C'>C$![]() are in $\Xi$
are in $\Xi$![]() . Fix a $C^{\ast }\in \Xi$
. Fix a $C^{\ast }\in \Xi$![]() . Then $\Upsilon (C')+C'\le \Upsilon (C^{\ast })+C^{\ast }$
. Then $\Upsilon (C')+C'\le \Upsilon (C^{\ast })+C^{\ast }$![]() for all $C'\in \{C\in \Xi \,|\, C>C^{\ast }\}$
for all $C'\in \{C\in \Xi \,|\, C>C^{\ast }\}$![]() . Taking a sequence $(C_n')\subset \{C\in \Xi \,|\, C>C^{\ast }\}$
. Taking a sequence $(C_n')\subset \{C\in \Xi \,|\, C>C^{\ast }\}$![]() such that $C_n'\to +\infty$
such that $C_n'\to +\infty$![]() , we deduce that $\Upsilon (C_n')\to -\infty$
, we deduce that $\Upsilon (C_n')\to -\infty$![]() . This contradicts the fact that $\Upsilon (C_n')\to c^{n,k}(\mathcal {S})>0$
. This contradicts the fact that $\Upsilon (C_n')\to c^{n,k}(\mathcal {S})>0$![]() . Hence (6.13) does not hold! (6.12) is proved.
. Hence (6.13) does not hold! (6.12) is proved.
Proof of claim 6.6. By contradiction we assume that for some $C'>C>\overline {C}$![]() ,
,
Let us prove that (6.14) implies:

Clearly, this contradicts the facts that ${\rm Int}(\Sigma _{\mathcal {S}})=\emptyset$![]() and (6.11) holds for all large $C$
and (6.11) holds for all large $C$![]() satisfying $C/R^{2}\notin \mathbb {N}\pi /2$
satisfying $C/R^{2}\notin \mathbb {N}\pi /2$![]() .
.
It remains to prove (6.15). Put $\Delta _d=\{C''\in (C, C')\,|\, C''+\Upsilon (C'')>d\}$![]() . Since $\Upsilon (C')+C'>d$
. Since $\Upsilon (C')+C'>d$![]() and $\Upsilon (C')\le \Upsilon (C'')\le \Upsilon (C)$
and $\Upsilon (C')\le \Upsilon (C'')\le \Upsilon (C)$![]() for any $C''\in (C, C')$
for any $C''\in (C, C')$![]() we obtain $\Upsilon (C'')+C''>d$
we obtain $\Upsilon (C'')+C''>d$![]() if $C''\in (C, C')$
if $C''\in (C, C')$![]() is sufficiently close to $C'$
is sufficiently close to $C'$![]() . Hence $\Delta _d\ne \emptyset$
. Hence $\Delta _d\ne \emptyset$![]() . Set $C_0=\inf \Delta _d$
. Set $C_0=\inf \Delta _d$![]() . Then $C_0\in [C, C')$
. Then $C_0\in [C, C')$![]() .
.
Let $(C_n'')\subset \Delta _d$![]() satisfy $C_n''\downarrow C_0$
satisfy $C_n''\downarrow C_0$![]() . Since $\Upsilon (C_n'')\le \Upsilon (C_0)$
. Since $\Upsilon (C_n'')\le \Upsilon (C_0)$![]() , we have $d< C_n''+\Upsilon (C_n'')\le \Upsilon (C_0)+ C_n''$
, we have $d< C_n''+\Upsilon (C_n'')\le \Upsilon (C_0)+ C_n''$![]() for each $n\in \mathbb {N}$
for each $n\in \mathbb {N}$![]() , and thus $d\le \Upsilon (C_0)+C_0$
, and thus $d\le \Upsilon (C_0)+C_0$![]() by letting $n\to \infty$
by letting $n\to \infty$![]() .
.
We conclude $d=\Upsilon (C_0)+C_0$![]() , and so (6.15) is proved. By contradiction suppose that
, and so (6.15) is proved. By contradiction suppose that
Since $d>C+\Upsilon (C)$![]() , this implies $C\ne C_0$
, this implies $C\ne C_0$![]() and so $C_0>C$
and so $C_0>C$![]() . For $\hat {C}\in (C, C_0)$
. For $\hat {C}\in (C, C_0)$![]() , as $\Upsilon (\hat {C})\ge \Upsilon (C_0)$
, as $\Upsilon (\hat {C})\ge \Upsilon (C_0)$![]() we derive from (6.16) that $\Upsilon (\hat {C})+\hat {C}>d$
we derive from (6.16) that $\Upsilon (\hat {C})+\hat {C}>d$![]() if $\hat {C}$
if $\hat {C}$![]() is close to $C_0$
is close to $C_0$![]() . Hence such $\hat {C}$
. Hence such $\hat {C}$![]() belongs to $\Delta _d$
belongs to $\Delta _d$![]() , which contradicts $C_0=\inf \Delta _d$
, which contradicts $C_0=\inf \Delta _d$![]() .
.
Step 2. Prove $c^{n,k}(U)=c^{n,k}(\mathcal {S})$![]() . Note that $c^{n,k}(U)=\inf _{\eta >0, C>0}c^{n,k}(\hat {H}_{C,\eta })$
. Note that $c^{n,k}(U)=\inf _{\eta >0, C>0}c^{n,k}(\hat {H}_{C,\eta })$![]() , where
, where

where $B^{2n}(0,R)\supseteq \overline {\psi ((-\varepsilon,\varepsilon )\times \mathcal {S})}$![]() , $\hat {f}_{C,\eta }:(-\varepsilon, \varepsilon )\to \mathbb {R}$
, $\hat {f}_{C,\eta }:(-\varepsilon, \varepsilon )\to \mathbb {R}$![]() and $\hat {h}:[0, \infty )\to \mathbb {R}$
and $\hat {h}:[0, \infty )\to \mathbb {R}$![]() are smooth functions satisfying the following conditions
are smooth functions satisfying the following conditions

For $H_{C,\eta }$![]() in (6.7), choose an associated $\hat {H}_{C,\eta }$
in (6.7), choose an associated $\hat {H}_{C,\eta }$![]() , where $\hat {f}_{C,\eta }|_{[0,\infty )}={f}_{C,\eta }|_{[0,\infty )}$
, where $\hat {f}_{C,\eta }|_{[0,\infty )}={f}_{C,\eta }|_{[0,\infty )}$![]() and $\hat {h}_{C,\eta }={h}_{C,\eta }$
and $\hat {h}_{C,\eta }={h}_{C,\eta }$![]() . Consider $H_s=sH_{C,\eta }+(1-s)\hat {H}_{C,\eta }$
. Consider $H_s=sH_{C,\eta }+(1-s)\hat {H}_{C,\eta }$![]() , $0\le s\le 1$
, $0\le s\le 1$![]() , and put $\Phi _s(x):=\Phi _{H_s}(x)$
, and put $\Phi _s(x):=\Phi _{H_s}(x)$![]() for $x\in E$
for $x\in E$![]() .
.
It suffices to prove $c^{n,k}(H_0)=c^{n,k}(H_1)$![]() . If $x$
. If $x$![]() is a critical point of $\Phi _s$
is a critical point of $\Phi _s$![]() with $\Phi _s(x)>0$
with $\Phi _s(x)>0$![]() , as in lemma 6.2, we have $x([0,1])\in \mathcal {S}_\tau =\psi (\{\tau \}\times \mathcal {S})$
, as in lemma 6.2, we have $x([0,1])\in \mathcal {S}_\tau =\psi (\{\tau \}\times \mathcal {S})$![]() for some $\tau \in (\eta,2\eta )$
for some $\tau \in (\eta,2\eta )$![]() . The choice of $\hat {H}_{C,\eta }$
. The choice of $\hat {H}_{C,\eta }$![]() shows $H_s(x(t))\equiv {H}_{C,\eta }(x(t))$
shows $H_s(x(t))\equiv {H}_{C,\eta }(x(t))$![]() for $t\in [0,1]$
for $t\in [0,1]$![]() . This implies that each $\Phi _s$
. This implies that each $\Phi _s$![]() has the same positive critical value as $\Phi _{H_{C,\eta }}$
has the same positive critical value as $\Phi _{H_{C,\eta }}$![]() . By the continuity in proposition 3.5(ii), $s\mapsto c^{n,k}(H_s)$
. By the continuity in proposition 3.5(ii), $s\mapsto c^{n,k}(H_s)$![]() is continuous and takes values in the set of positive critical value of $\Phi _{H_{C,\eta }}$
is continuous and takes values in the set of positive critical value of $\Phi _{H_{C,\eta }}$![]() (which has measure zero by Sard's theorem). Hence $s\mapsto c^{n,k}(H_s)$
(which has measure zero by Sard's theorem). Hence $s\mapsto c^{n,k}(H_s)$![]() is constant. We get $c^{n,k}(\hat {H}_{C,\eta })=c^{n,k}(H_0)=c^{\Psi }_{\rm EH}(H_1)=c^{n,k}(H_{C,\eta })$
is constant. We get $c^{n,k}(\hat {H}_{C,\eta })=c^{n,k}(H_0)=c^{\Psi }_{\rm EH}(H_1)=c^{n,k}(H_{C,\eta })$![]() .
.
Summarizing the above arguments we have proved that $c^{n,k}(\mathcal {S})=c^{n,k}(U)\in \overline {\Sigma _{\mathcal {S}}}$![]() . Noting that $c^{n,k}(U)>0$
. Noting that $c^{n,k}(U)>0$![]() , we deduce $c^{n,k}(\mathcal {S})=c^{n,k}(U)\in \Sigma _{\mathcal {S}}$
, we deduce $c^{n,k}(\mathcal {S})=c^{n,k}(U)\in \Sigma _{\mathcal {S}}$![]() by claim 6.4.
by claim 6.4.
7. Proof of theorem 1.8
For $W^{2n}(1)$![]() in (1.3), note that $W^{2n}(1)\equiv \mathbb {R}^{2n-2}\times W^{2}(1)\supseteq \mathbb {R}^{2n-2}\times U^{2}(1)$
in (1.3), note that $W^{2n}(1)\equiv \mathbb {R}^{2n-2}\times W^{2}(1)\supseteq \mathbb {R}^{2n-2}\times U^{2}(1)$![]() via the identification under (1.12). For each integer $0\le k< n$
via the identification under (1.12). For each integer $0\le k< n$![]() , (1.14) and (1.11) yield
, (1.14) and (1.11) yield
We only need to prove the inverse direction of the inequality.
Fix a number $0<\varepsilon <\frac {1}{100}$![]() . For $N>2$
. For $N>2$![]() define
define
Let us smoothen $W^{2}(1)$![]() and $W^{2}(1,N)$
and $W^{2}(1,N)$![]() in the following way. Choose positive numbers $\delta _1, \delta _2\ll 1$
in the following way. Choose positive numbers $\delta _1, \delta _2\ll 1$![]() and a smooth even function $g:\mathbb {R}\to \mathbb {R}$
and a smooth even function $g:\mathbb {R}\to \mathbb {R}$![]() satisfying the following conditions:
satisfying the following conditions:
(i) $g(t)=\sqrt {1-t^{2}}$
 for $0\le t\le 1-\delta _1$
for $0\le t\le 1-\delta _1$ ,
,(ii) $g(t)=0$
 for $t\ge 1+\delta _2$
for $t\ge 1+\delta _2$ ,
,(iii) $g$
 is strictly monotone decreasing, and $g(t)\ge \sqrt {1-t^{2}}$
is strictly monotone decreasing, and $g(t)\ge \sqrt {1-t^{2}}$ for $1-\delta _1\le t\le 1$
for $1-\delta _1\le t\le 1$ .
.
Denote by
and by $W^{2}_{g}(1,N)$![]() the open subset in $\mathbb {R}^{2}(x_n,y_n)$
the open subset in $\mathbb {R}^{2}(x_n,y_n)$![]() surrounded by curves $y_n=g(x_n)$
surrounded by curves $y_n=g(x_n)$![]() , $y_n=-N$
, $y_n=-N$![]() , $x_n=N$
, $x_n=N$![]() and $x_n=-N$
and $x_n=-N$![]() (see figure 2). Then $W^{2}_{g}(1,N)$
(see figure 2). Then $W^{2}_{g}(1,N)$![]() contains $W^{2}(1,N)$
contains $W^{2}(1,N)$![]() , and we can require $\delta _1,\delta _2$
, and we can require $\delta _1,\delta _2$![]() so small that
so small that
Take another smooth function $h:[0, \infty )\to \mathbb {R}$![]() satisfying the following conditions:
satisfying the following conditions:
(iv) $h(0)={\varepsilon }/{2}$
 and $h(t)=0$
and $h(t)=0$ for $t>{\varepsilon }/{2}$
for $t>{\varepsilon }/{2}$ ,
,(v) $h'(t)<0$
 and $h''(t)>0$
and $h''(t)>0$ for any $t\in (0, {\varepsilon }/{2})$
for any $t\in (0, {\varepsilon }/{2})$ ,
,(vi) the curve $\{(t, h(t))\,|\, 0\le t\le {\varepsilon }/{2}\}$
 is symmetric with respect to line $s=t$
is symmetric with respect to line $s=t$ in $\mathbb {R}^{2}(s,t)$
in $\mathbb {R}^{2}(s,t)$ .
.
Let $\triangle _1$![]() be the closed domain in $\mathbb {R}^{2}(x_n,y_n)$
be the closed domain in $\mathbb {R}^{2}(x_n,y_n)$![]() surrounded by curves $y_n=h(x_n)$
surrounded by curves $y_n=h(x_n)$![]() , $y_n=0$
, $y_n=0$![]() and $x_n=0$
and $x_n=0$![]() (see figure 1). Denote by
(see figure 1). Denote by
Let $p_1=(N,0),\ p_2=(-N,0),\ p_3=(-N,-N),\ p_4=(N,-N)$![]() . Define
. Define
Then $W^{2}_{g,\varepsilon }(1,N)$![]() has smooth boundary (see figure 2) and
has smooth boundary (see figure 2) and

FIG. 1. Domains $\triangle _i$![]() , $i=1,2,3,4$
, $i=1,2,3,4$![]() .
.

FIG. 2. Domain $W^{2}_{g,\varepsilon }(1,N)$![]() .
.
For $n>1$![]() and $N>2$
and $N>2$![]() we define
we define

Clearly, $W^{2n}_{g,\varepsilon }(1, N)\subset W^{2n}_{g,\varepsilon }(1,M)$![]() for any $M>N>2$
for any $M>N>2$![]() , and each bounded subset of $W^{2n}_g(1)$
, and each bounded subset of $W^{2n}_g(1)$![]() can be contained in $W^{2n}_{g,\varepsilon }(1,N)$
can be contained in $W^{2n}_{g,\varepsilon }(1,N)$![]() for some large $N>2$
for some large $N>2$![]() . It follows that
. It follows that
Let us estimate $c^{n,k}(W^{2n}_{g,\varepsilon }(1,N))$![]() with theorem 1.7. Regrettably, $W^{2}_{g,\varepsilon }(1,N)$
with theorem 1.7. Regrettably, $W^{2}_{g,\varepsilon }(1,N)$![]() is not star-shaped with respect to the origin. Fortunately, it can be approximated arbitrarily by star-shaped domains with respect to the origin and with smooth boundary. Indeed, for a very small $0<\eta <\varepsilon$
is not star-shaped with respect to the origin. Fortunately, it can be approximated arbitrarily by star-shaped domains with respect to the origin and with smooth boundary. Indeed, for a very small $0<\eta <\varepsilon$![]() the set
the set
is the desired one.
Define $j_{g,N,\epsilon, \eta }:\mathbb {R}^{2}\to \mathbb {R}$![]() by
by
Then $j_{g,N,\epsilon,\eta }$![]() is positively homogeneous, and smooth in $\mathbb {R}^{2}\setminus \{0\}$
is positively homogeneous, and smooth in $\mathbb {R}^{2}\setminus \{0\}$![]() . For $(x,y)\in \mathbb {R}^{2n}$
. For $(x,y)\in \mathbb {R}^{2n}$![]() we write $(x,y)=(\hat {z},z_n)$
we write $(x,y)=(\hat {z},z_n)$![]() and define
and define
Then we have $W^{2n}_{g,\varepsilon,R_1}(1,N,\eta )\subset W^{2n}_{g,\varepsilon, R_2}(1,N,\eta )$![]() for $R_1< R_2$
for $R_1< R_2$![]() , and
, and
which implies by (3.18) that
Observe that for arbitrary $N>2$![]() and $R>0$
and $R>0$![]() we can shrink $0<\eta <\varepsilon$
we can shrink $0<\eta <\varepsilon$![]() so that there holds
so that there holds
where for $r>0$![]() ,
,
We obtain
Note that $W^{2n}_{g, \varepsilon, R}(1,N,\eta )$![]() is a star-shaped domain with respect to the origin and with smooth boundary $\mathcal {S}_{N, g, \varepsilon,R,\eta }$
is a star-shaped domain with respect to the origin and with smooth boundary $\mathcal {S}_{N, g, \varepsilon,R,\eta }$![]() transversal to the globally defined Liouville vector field $X(z)=z$
transversal to the globally defined Liouville vector field $X(z)=z$![]() . Since the flow $\phi ^{t}$
. Since the flow $\phi ^{t}$![]() of $X$
of $X$![]() , $\phi ^{t}(z)={\rm e}^{t}z$
, $\phi ^{t}(z)={\rm e}^{t}z$![]() , maps $\mathbb {R}^{n,k}$
, maps $\mathbb {R}^{n,k}$![]() to $\mathbb {R}^{n,k}$
to $\mathbb {R}^{n,k}$![]() and preserves the leaf relation of $\mathbb {R}^{n,k}$
and preserves the leaf relation of $\mathbb {R}^{n,k}$![]() , by theorem 1.7 we obtain
, by theorem 1.7 we obtain
where
Arguing as in the proof of (5.9) we get that
Hence for $R>N$![]() , by (7.4) we have
, by (7.4) we have
Let us compute $\Sigma _{\partial W^{2}_{g,\varepsilon }(1,N,\eta )}$![]() . Note that the part of $\partial W^{2}_{g,\varepsilon }(1,N)$
. Note that the part of $\partial W^{2}_{g,\varepsilon }(1,N)$![]() over the line $y_n=-\frac {\varepsilon }{2}$
over the line $y_n=-\frac {\varepsilon }{2}$![]() and between lines $x_n=-N$
and between lines $x_n=-N$![]() and $x_n=N$
and $x_n=N$![]() is $\{(x_n, f(x_n))\in \mathbb {R}^{2}\,|\, |x_n|\le N\}$
is $\{(x_n, f(x_n))\in \mathbb {R}^{2}\,|\, |x_n|\le N\}$![]() , where
, where

Let $t_0\in (0, \varepsilon /2)$![]() be the unique number satisfying $h(t_0)=\eta$
be the unique number satisfying $h(t_0)=\eta$![]() . Then there only exist two leafwise chords on $\partial W^{2}_{g,\varepsilon }(1,N,\eta )$
. Then there only exist two leafwise chords on $\partial W^{2}_{g,\varepsilon }(1,N,\eta )$![]() for $\mathbb {R}^{1,0}$
for $\mathbb {R}^{1,0}$![]() . One is the curve in $\mathbb {R}^{2}(x_n,y_n)$
. One is the curve in $\mathbb {R}^{2}(x_n,y_n)$![]() ,
,
and the other is $\gamma _2:=\partial W^{2}_{g,\varepsilon }(1,N,\eta )\setminus \gamma _1$![]() . Then $A(\gamma _1)$
. Then $A(\gamma _1)$![]() is equal to the area of the domain in $\mathbb {R}^{2}(x_n,y_n)$
is equal to the area of the domain in $\mathbb {R}^{2}(x_n,y_n)$![]() surrounded by curves $\gamma _1$
surrounded by curves $\gamma _1$![]() and $x_n$
and $x_n$![]() -axis, that is,
-axis, that is,

and

Hence $\Sigma _{\partial W^{2}_{g,\epsilon }(1,N,\eta )}=\{A(\gamma _1), A(\gamma _2)\}$![]() . Let us choose $N>2$
. Let us choose $N>2$![]() so large that $({\pi }/{2})N^{2}<2N^{2}-\varepsilon$
so large that $({\pi }/{2})N^{2}<2N^{2}-\varepsilon$![]() . Then (7.4), (7.5) and (7.7) lead to
. Then (7.4), (7.5) and (7.7) lead to
Note that $2N^{2}- 4{\rm Area}(\triangle _1)>2N^{2}-\varepsilon$![]() and that (7.1) implies
and that (7.1) implies
It follows from this, (7.6) and (7.8) that

For fixed $N$![]() and $\varepsilon$
and $\varepsilon$![]() we may choose $0<\eta <\varepsilon$
we may choose $0<\eta <\varepsilon$![]() so small that $2(N-t_0)\eta <{\varepsilon }/{2}$
so small that $2(N-t_0)\eta <{\varepsilon }/{2}$![]() . Then
. Then
From this and (7.2)–(7.3) we derive
and hence $c^{n,k}(W^{2n}(1))\le {\pi }/{2}$![]() by letting $\varepsilon \to 0+$
by letting $\varepsilon \to 0+$![]() .
.
8. Comparison to symmetrical Ekeland–Hofer capacities
For each $i=1,\ldots,n$![]() , let $e_i$
, let $e_i$![]() be the vector in $\mathbb {R}^{2n}$
be the vector in $\mathbb {R}^{2n}$![]() with $1$
with $1$![]() in the $i$
in the $i$![]() th position and $0$
th position and $0$![]() s elsewhere. Then $\{e_i\}_{i=1}^{n}$
s elsewhere. Then $\{e_i\}_{i=1}^{n}$![]() is an orthonormal basis for $L_0^{n}:=V_0^{n,0}=\{x\in \mathbb {R}^{2n}\,|\,x=(q_{1},\ldots,q_n,0,\ldots,0)\}=\mathbb {R}^{n,0}$
is an orthonormal basis for $L_0^{n}:=V_0^{n,0}=\{x\in \mathbb {R}^{2n}\,|\,x=(q_{1},\ldots,q_n,0,\ldots,0)\}=\mathbb {R}^{n,0}$![]() . It was proved in [Reference Jin and Lu26, corollary 2.2] that $L^{2}([0,1],\mathbb {R}^{2n})$
. It was proved in [Reference Jin and Lu26, corollary 2.2] that $L^{2}([0,1],\mathbb {R}^{2n})$![]() has an orthogonal basis
has an orthogonal basis
and every $x\in L^{2}([0,1],\mathbb {R}^{2n})$![]() can be uniquely expanded as form $x=\sum _{m\in \mathbb {Z}}{\rm e}^{m\pi tJ_{2n}}x_m$
can be uniquely expanded as form $x=\sum _{m\in \mathbb {Z}}{\rm e}^{m\pi tJ_{2n}}x_m$![]() , where $x_m\in L_0^{n}$
, where $x_m\in L_0^{n}$![]() for all $m\in \mathbb {Z}$
for all $m\in \mathbb {Z}$![]() and satisfies $\sum _{m\in \mathbb {Z}}|x_m|^{2}<\infty$
and satisfies $\sum _{m\in \mathbb {Z}}|x_m|^{2}<\infty$![]() . Noting that $V^{n,0}_1=\{0\}$
. Noting that $V^{n,0}_1=\{0\}$![]() , the spaces in (2.1) and (2.2) become, respectively,
, the spaces in (2.1) and (2.2) become, respectively,

and

for any real $s\ge 0$![]() . It follows that the space $\mathbb {E}$
. It follows that the space $\mathbb {E}$![]() in [Reference Jin and Lu25, § 1.2] is a subspace of $E=H^{1/2}_{n,0}$
in [Reference Jin and Lu25, § 1.2] is a subspace of $E=H^{1/2}_{n,0}$![]() in (2.3). Denote by $\widehat {\Gamma }$
in (2.3). Denote by $\widehat {\Gamma }$![]() the set of the admissible deformations on $\mathbb {E}$
the set of the admissible deformations on $\mathbb {E}$![]() (see [Reference Jin and Lu25, § 1.2]) and $\widehat {S}^{+}$
(see [Reference Jin and Lu25, § 1.2]) and $\widehat {S}^{+}$![]() the unit sphere in $\mathbb {E}$
the unit sphere in $\mathbb {E}$![]() . Then $\Gamma _{n,0}|_{\mathbb {E}}\subset \widehat {\Gamma }$
. Then $\Gamma _{n,0}|_{\mathbb {E}}\subset \widehat {\Gamma }$![]() and $\widehat {S}^{+}\subset S^{+}_{n,0}$
and $\widehat {S}^{+}\subset S^{+}_{n,0}$![]() . Note that each function $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$
. Note that each function $H\in C^{0}(\mathbb {R}^{2n},\mathbb {R}_{\ge 0})$![]() satisfying the conditions (H1), (H2) and (H3) below [Reference Jin and Lu25, definition 1.4] is naturally $\mathbb {R}^{n,0}$
satisfying the conditions (H1), (H2) and (H3) below [Reference Jin and Lu25, definition 1.4] is naturally $\mathbb {R}^{n,0}$![]() -admissible. Then
-admissible. Then

It follows that $c^{n,0}(B)\le c_{\rm EH,\tau _0}(B)$![]() for each $B\subset \mathbb {R}^{2n}$
for each $B\subset \mathbb {R}^{2n}$![]() intersecting with $\mathbb {R}^{n,0}$
intersecting with $\mathbb {R}^{n,0}$![]() .
.
Appendix A. Connectedness of the subgroup ${\rm Sp}(2n,k)\subset {\rm Sp}(2n)$ (by Kun ShiFootnote 1)
(by Kun ShiFootnote 1)
Let $e_1,\ldots, e_{2n}$![]() be the standard symplectic basis in the standard symplectic Euclidean space $(\mathbb {R}^{2n},\omega _0)$
be the standard symplectic basis in the standard symplectic Euclidean space $(\mathbb {R}^{2n},\omega _0)$![]() . Then $\omega _0(e_i,e_j)=\omega _0(e_{n+i},e_{n+j})=0$
. Then $\omega _0(e_i,e_j)=\omega _0(e_{n+i},e_{n+j})=0$![]() and $\omega _0(e_{i},e_{n+j})=\delta _{ij}$
and $\omega _0(e_{i},e_{n+j})=\delta _{ij}$![]() for all $1\le i,j\le n$
for all $1\le i,j\le n$![]() .
.
Claim A.1 $A\in {\rm Sp}(2n)$![]() belongs to ${\rm Sp}(2n,k)$
belongs to ${\rm Sp}(2n,k)$![]() if and only if
if and only if

for some $B_{(n-k)\times (n-k)}=(B_{(n-k)\times (n-k)})^{t}\in \mathbb {R}^{(n-k)\times (n-k)}$![]() . Consequently, $tA_0+(1-t)A_1\in {\rm Sp}(2n,k)$
. Consequently, $tA_0+(1-t)A_1\in {\rm Sp}(2n,k)$![]() for any $0\le t\le 1$
for any $0\le t\le 1$![]() and $A_i\in {\rm Sp}(2n,k),$
and $A_i\in {\rm Sp}(2n,k),$![]() $i=0,1$
$i=0,1$![]() . Specially, ${\rm Sp}(2n,k)$
. Specially, ${\rm Sp}(2n,k)$![]() is a connected subgroup of ${\rm Sp}(2n)$
is a connected subgroup of ${\rm Sp}(2n)$![]() .
.
The following proof of this claim is presented by Kun Shi.
Let $A\in {\rm Sp}(2n,k)$![]() . Then $Ae_i=e_i$
. Then $Ae_i=e_i$![]() for $i=1,\ldots,n+k$
for $i=1,\ldots,n+k$![]() . For $k< j\le n$
. For $k< j\le n$![]() , suppose $Ae_{n+j}=\sum ^{2n}_{s=1}a_{s(n+j)}e_s$
, suppose $Ae_{n+j}=\sum ^{2n}_{s=1}a_{s(n+j)}e_s$![]() , where $a_{st}\in \mathbb {R}$
, where $a_{st}\in \mathbb {R}$![]() . For $1\le j\le k$
. For $1\le j\le k$![]() and $k< l\le n$
and $k< l\le n$![]() , we may obtain
, we may obtain

by a straightforward computation. Similarly, for $1\le j\le n$![]() and $k< l\le n$
and $k< l\le n$![]() , we have
, we have

It follows from this and (A.2) that $Ae_{n+l}=e_{n+l}+ \sum ^{n}_{j=k+1}a_{j(n+l)}e_j$![]() . By substituting this and $Ae_{n+s}=e_{n+s}+ \sum ^{n}_{j=k+1}a_{j(n+s)}e_j$
. By substituting this and $Ae_{n+s}=e_{n+s}+ \sum ^{n}_{j=k+1}a_{j(n+s)}e_j$![]() into $\omega _0(e_{n+l},e_{n+s})=\omega _0(Ae_{n+l}, Ae_{n+s})$
into $\omega _0(e_{n+l},e_{n+s})=\omega _0(Ae_{n+l}, Ae_{n+s})$![]() we obtain $a_{j(n+l)}=a_{l(n+j)}$
we obtain $a_{j(n+l)}=a_{l(n+j)}$![]() for all $k< j,l\le n$
for all $k< j,l\le n$![]() .
.
Conversely, suppose that $A\in {\rm Sp}(2n)$![]() has form (A.1), that is, $A$
has form (A.1), that is, $A$![]() satisfies: $Ae_i=e_i$
satisfies: $Ae_i=e_i$![]() for $i=1,\ldots,n+k$
for $i=1,\ldots,n+k$![]() , and $Ae_{n+l}=e_{n+l}+ \sum ^{n}_{j=k+1}a_{j(n+l)}e_j$
, and $Ae_{n+l}=e_{n+l}+ \sum ^{n}_{j=k+1}a_{j(n+l)}e_j$![]() for $k< l\le n$
for $k< l\le n$![]() , where $a_{j(n+l)}=a_{l(n+j)}\in \mathbb {R}$
, where $a_{j(n+l)}=a_{l(n+j)}\in \mathbb {R}$![]() for $k< j,l\le n$
for $k< j,l\le n$![]() . Then it is easy to check that $A\in {\rm Sp}(2n,k)$
. Then it is easy to check that $A\in {\rm Sp}(2n,k)$![]() .
.
Acknowledgements
We are deeply grateful to the anonymous referees for giving very helpful comments and suggestions to improve the exposition.
Financial support
This study was partially supported by the NNSF 11271044 of China and the Fundamental Research Funds for Central Universities, Civil Aviation University of China, 3122021074.