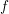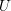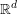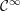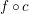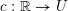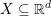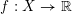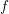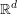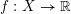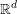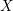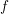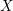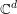1 Introduction
In this paper we study differentiability of functions defined on closed subsets of
![]() $\mathbb{R}^{d}$
. One way to endow an arbitrary set
$\mathbb{R}^{d}$
. One way to endow an arbitrary set
![]() $X$
with a smooth structure is by declaring which curves
$X$
with a smooth structure is by declaring which curves
![]() $\mathbb{R}\rightarrow X$
and which functions
$\mathbb{R}\rightarrow X$
and which functions
![]() $X\rightarrow \mathbb{R}$
should be smooth. Together with a natural compatibility condition, this leads to the notion of a Frölicher space; cf. [Reference Frölicher and KrieglFK88, Reference Kriegl and MichorKM97]. Here we study the Frölicher space generated by the inclusion of a closed set
$X\rightarrow \mathbb{R}$
should be smooth. Together with a natural compatibility condition, this leads to the notion of a Frölicher space; cf. [Reference Frölicher and KrieglFK88, Reference Kriegl and MichorKM97]. Here we study the Frölicher space generated by the inclusion of a closed set
![]() $X$
in
$X$
in
![]() $\mathbb{R}^{d}$
and some of its relatives. We will not use the terminology of Frölicher spaces in the paper but the connection is made precise in Remark 1.7.
$\mathbb{R}^{d}$
and some of its relatives. We will not use the terminology of Frölicher spaces in the paper but the connection is made precise in Remark 1.7.
1.1 Boman’s theorem and its relatives
Let
![]() $f:U\rightarrow \mathbb{R}$
be a function defined in an open subset
$f:U\rightarrow \mathbb{R}$
be a function defined in an open subset
![]() $U$
of
$U$
of
![]() $\mathbb{R}^{d}$
. Then
$\mathbb{R}^{d}$
. Then
![]() $f$
induces a mapping
$f$
induces a mapping
![]() $f_{\ast }:U^{\mathbb{R}}\rightarrow \mathbb{R}^{\mathbb{R}}$
,
$f_{\ast }:U^{\mathbb{R}}\rightarrow \mathbb{R}^{\mathbb{R}}$
,
![]() $f_{\ast }(c)=f\,\circ \,c$
, whose invariance properties encode the regularity of
$f_{\ast }(c)=f\,\circ \,c$
, whose invariance properties encode the regularity of
![]() $f$
.
$f$
.
Result 1.1 (Boman [Reference BomanBom67]).
A function
![]() $f:U\rightarrow \mathbb{R}$
is smooth (
$f:U\rightarrow \mathbb{R}$
is smooth (
![]() ${\mathcal{C}}^{\infty }$
) if and only if
${\mathcal{C}}^{\infty }$
) if and only if
![]() $f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},U)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
.
$f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},U)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
.
Similarly, Hölder differentiability can be characterized by
![]() $f_{\ast }$
; we denote by
$f_{\ast }$
; we denote by
![]() ${\mathcal{C}}^{k,\unicode[STIX]{x1D6FC}}$
, for
${\mathcal{C}}^{k,\unicode[STIX]{x1D6FC}}$
, for
![]() $k\in \mathbb{N}$
,
$k\in \mathbb{N}$
,
![]() $\unicode[STIX]{x1D6FC}\in (0,1]$
, the class of
$\unicode[STIX]{x1D6FC}\in (0,1]$
, the class of
![]() $k$
-times continuously differentiable functions whose partial derivatives of order
$k$
-times continuously differentiable functions whose partial derivatives of order
![]() $k$
satisfy a local
$k$
satisfy a local
![]() $\unicode[STIX]{x1D6FC}$
-Hölder condition.
$\unicode[STIX]{x1D6FC}$
-Hölder condition.
Result 1.2 [Reference Frölicher and KrieglFK88, Reference Faure and FrölicherFF89, Reference Kriegl and MichorKM97].
A function
![]() $f:U\rightarrow \mathbb{R}$
is of class
$f:U\rightarrow \mathbb{R}$
is of class
![]() ${\mathcal{C}}^{k,\unicode[STIX]{x1D6FC}}$
if and only if
${\mathcal{C}}^{k,\unicode[STIX]{x1D6FC}}$
if and only if
![]() $f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},U)\subseteq {\mathcal{C}}^{k,\unicode[STIX]{x1D6FC}}(\mathbb{R},\mathbb{R})$
.
$f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},U)\subseteq {\mathcal{C}}^{k,\unicode[STIX]{x1D6FC}}(\mathbb{R},\mathbb{R})$
.
Furthermore, there is an ultradifferentiable version of Boman’s theorem. We recall that, for a positive sequence
![]() $M=(M_{k})_{k\in \mathbb{N}}$
, the Denjoy–Carleman class (of Roumieu type)
$M=(M_{k})_{k\in \mathbb{N}}$
, the Denjoy–Carleman class (of Roumieu type)
![]() ${\mathcal{C}}^{M}(U,\mathbb{R}^{m})$
is the set of all functions
${\mathcal{C}}^{M}(U,\mathbb{R}^{m})$
is the set of all functions
![]() $f\in {\mathcal{C}}^{\infty }(U,\mathbb{R}^{m})$
such that for all compact
$f\in {\mathcal{C}}^{\infty }(U,\mathbb{R}^{m})$
such that for all compact
![]() $K\subseteq U$
,
$K\subseteq U$
,
The sequence
![]() $M$
is called non-quasianalytic if
$M$
is called non-quasianalytic if
![]() ${\mathcal{C}}^{M}$
contains non-trivial functions with compact support. If
${\mathcal{C}}^{M}$
contains non-trivial functions with compact support. If
![]() $M$
is log-convex, then
$M$
is log-convex, then
![]() ${\mathcal{C}}^{M}$
is stable under composition. We refer to § 2.1 for this and more on Denjoy–Carleman classes.
${\mathcal{C}}^{M}$
is stable under composition. We refer to § 2.1 for this and more on Denjoy–Carleman classes.
Result 1.3 [Reference Kriegl, Michor and RainerKMR09].
Assume that
![]() $M=(M_{k})$
is non-quasianalytic and log-convex. A function
$M=(M_{k})$
is non-quasianalytic and log-convex. A function
![]() $f:U\rightarrow \mathbb{R}$
is of class
$f:U\rightarrow \mathbb{R}$
is of class
![]() ${\mathcal{C}}^{M}$
if and only if
${\mathcal{C}}^{M}$
if and only if
![]() $f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},U)\subseteq {\mathcal{C}}^{M}(\mathbb{R},\mathbb{R})$
.
$f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},U)\subseteq {\mathcal{C}}^{M}(\mathbb{R},\mathbb{R})$
.
Remark 1.4. Boman actually showed that
![]() $f$
is smooth if and only if
$f$
is smooth if and only if
![]() $f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},U)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
, for some arbitrary non-quasianalytic log-convex sequence
$f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},U)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
, for some arbitrary non-quasianalytic log-convex sequence
![]() $M$
.
$M$
.
A glance at the proofs confirms that the curves along which the regularity in question is tested can be taken to have compact support.
A function
![]() $f:U\rightarrow \mathbb{R}$
with the property that
$f:U\rightarrow \mathbb{R}$
with the property that
![]() $f\,\circ \,c$
is real analytic (
$f\,\circ \,c$
is real analytic (
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D714}}$
) for all real analytic
${\mathcal{C}}^{\unicode[STIX]{x1D714}}$
) for all real analytic
![]() $c:\mathbb{R}\rightarrow U$
clearly does not need to be real analytic on
$c:\mathbb{R}\rightarrow U$
clearly does not need to be real analytic on
![]() $U\subseteq \mathbb{R}^{d}$
, let alone continuous; see [Reference Bierstone, Milman and ParusińskiBMP91]. But there is the following result.
$U\subseteq \mathbb{R}^{d}$
, let alone continuous; see [Reference Bierstone, Milman and ParusińskiBMP91]. But there is the following result.
Result 1.5 (Bochnak and Siciak [Reference BochnakBoc70, Reference SiciakSic70, Reference Bochnak and SiciakBS71]).
A function
![]() $f:U\rightarrow \mathbb{R}$
is real analytic if and only if
$f:U\rightarrow \mathbb{R}$
is real analytic if and only if
![]() $f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},U)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
and
$f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},U)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
and
![]() $f_{\ast }{\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},U)\subseteq {\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},\mathbb{R})$
.
$f_{\ast }{\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},U)\subseteq {\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},\mathbb{R})$
.
Actually, a smooth function
![]() $f\in {\mathcal{C}}^{\infty }(U)$
which is real analytic on affine lines is real analytic on
$f\in {\mathcal{C}}^{\infty }(U)$
which is real analytic on affine lines is real analytic on
![]() $U$
.
$U$
.
We remark that if
![]() $M=(M_{k})$
is quasianalytic such that
$M=(M_{k})$
is quasianalytic such that
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D714}}\subsetneq {\mathcal{C}}^{M}$
, then a
${\mathcal{C}}^{\unicode[STIX]{x1D714}}\subsetneq {\mathcal{C}}^{M}$
, then a
![]() ${\mathcal{C}}^{\infty }$
-function
${\mathcal{C}}^{\infty }$
-function
![]() $f:U\rightarrow \mathbb{R}$
which satisfies
$f:U\rightarrow \mathbb{R}$
which satisfies
![]() $f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},U)\subseteq {\mathcal{C}}^{M}(\mathbb{R},\mathbb{R})$
need not be of class
$f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},U)\subseteq {\mathcal{C}}^{M}(\mathbb{R},\mathbb{R})$
need not be of class
![]() ${\mathcal{C}}^{M}$
; see [Reference JaffeJaf16].
${\mathcal{C}}^{M}$
; see [Reference JaffeJaf16].
1.2 Arc-smooth functions
In this paper we investigate the validity of the above results on non-open subsets
![]() $X\subseteq \mathbb{R}^{d}$
. For arbitrary subsets
$X\subseteq \mathbb{R}^{d}$
. For arbitrary subsets
![]() $X\subseteq \mathbb{R}^{d}$
we define
$X\subseteq \mathbb{R}^{d}$
we define
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}^{\infty }(X) & := & \displaystyle \{f:X\rightarrow \mathbb{R}:f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},X)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})\},\nonumber\\ \displaystyle {\mathcal{A}}^{M}(X) & := & \displaystyle \{f:X\rightarrow \mathbb{R}:f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},X)\subseteq {\mathcal{C}}^{M}(\mathbb{R},\mathbb{R})\},\nonumber\\ \displaystyle {\mathcal{A}}_{M}^{\infty }(X) & := & \displaystyle \{f:X\rightarrow \mathbb{R}:f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},X)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})\},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}^{\infty }(X) & := & \displaystyle \{f:X\rightarrow \mathbb{R}:f_{\ast }{\mathcal{C}}^{\infty }(\mathbb{R},X)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})\},\nonumber\\ \displaystyle {\mathcal{A}}^{M}(X) & := & \displaystyle \{f:X\rightarrow \mathbb{R}:f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},X)\subseteq {\mathcal{C}}^{M}(\mathbb{R},\mathbb{R})\},\nonumber\\ \displaystyle {\mathcal{A}}_{M}^{\infty }(X) & := & \displaystyle \{f:X\rightarrow \mathbb{R}:f_{\ast }{\mathcal{C}}^{M}(\mathbb{R},X)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})\},\nonumber\end{eqnarray}$$
where we set
We call the elements of
![]() ${\mathcal{A}}^{\infty }(X)$
arc-smooth functions and those of
${\mathcal{A}}^{\infty }(X)$
arc-smooth functions and those of
![]() ${\mathcal{A}}^{M}(X)$
arc-
${\mathcal{A}}^{M}(X)$
arc-
![]() ${\mathcal{C}}^{M}$
functions on
${\mathcal{C}}^{M}$
functions on
![]() $X$
. We will also consider
$X$
. We will also consider
where
We will not speak of arc-analytic functions, since such are not assumed to be smooth in the literature.
Evidently,
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)\subseteq {\mathcal{A}}^{\infty }(X)\subseteq {\mathcal{A}}_{M}^{\infty }(X)\supseteq {\mathcal{A}}^{M}(X)$
. (We will see below that there is no hope of the analogue of Result 1.2 holding on even very simple non-open sets such as the closed half-space.)
${\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)\subseteq {\mathcal{A}}^{\infty }(X)\subseteq {\mathcal{A}}_{M}^{\infty }(X)\supseteq {\mathcal{A}}^{M}(X)$
. (We will see below that there is no hope of the analogue of Result 1.2 holding on even very simple non-open sets such as the closed half-space.)
With this notation, Results 1.1, 1.3, and 1.5 amount to
if
![]() $X\subseteq \mathbb{R}^{d}$
is a non-empty open set and
$X\subseteq \mathbb{R}^{d}$
is a non-empty open set and
![]() $M=(M_{k})$
is a non-quasianalytic log-convex sequence.
$M=(M_{k})$
is a non-quasianalytic log-convex sequence.
Remark 1.6. The identities (1.2) imply that, in the definition of
![]() ${\mathcal{A}}^{\infty }(X)$
,
${\mathcal{A}}^{\infty }(X)$
,
![]() ${\mathcal{A}}^{M}(X)$
, and
${\mathcal{A}}^{M}(X)$
, and
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)$
, we could equivalently replace the families of curves
${\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)$
, we could equivalently replace the families of curves
![]() $c:\mathbb{R}\rightarrow X$
by families of plots
$c:\mathbb{R}\rightarrow X$
by families of plots
![]() $p:U\rightarrow X$
(of the same regularity), where
$p:U\rightarrow X$
(of the same regularity), where
![]() $U$
is any open subset of
$U$
is any open subset of
![]() $\mathbb{R}^{e}$
with varying
$\mathbb{R}^{e}$
with varying
![]() $e$
.
$e$
.
Remark 1.7. Recall that a Frölicher space is a triple
![]() $(X,{\mathcal{C}}_{X},{\mathcal{F}}_{X})$
consisting of a set
$(X,{\mathcal{C}}_{X},{\mathcal{F}}_{X})$
consisting of a set
![]() $X$
, a subset
$X$
, a subset
![]() ${\mathcal{C}}_{X}\subseteq X^{\mathbb{R}}$
and a subset
${\mathcal{C}}_{X}\subseteq X^{\mathbb{R}}$
and a subset
![]() ${\mathcal{F}}_{X}\subseteq \mathbb{R}^{X}$
such that:
${\mathcal{F}}_{X}\subseteq \mathbb{R}^{X}$
such that:
(i)
 $f:X\rightarrow \mathbb{R}$
belongs to
$f:X\rightarrow \mathbb{R}$
belongs to
 ${\mathcal{F}}_{X}$
if and only if
${\mathcal{F}}_{X}$
if and only if
 $f\,\circ \,c\in {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
for all
$f\,\circ \,c\in {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
for all
 $c\in {\mathcal{C}}_{X}$
;
$c\in {\mathcal{C}}_{X}$
;(ii)
 $c:\mathbb{R}\rightarrow X$
belongs to
$c:\mathbb{R}\rightarrow X$
belongs to
 ${\mathcal{C}}_{X}$
if and only if
${\mathcal{C}}_{X}$
if and only if
 $f\,\circ \,c\in {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
for all
$f\,\circ \,c\in {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
for all
 $f\in {\mathcal{F}}_{X}$
.
$f\in {\mathcal{F}}_{X}$
.
Any subset
![]() ${\mathcal{F}}\subseteq \mathbb{R}^{X}$
generates a unique Frölicher space
${\mathcal{F}}\subseteq \mathbb{R}^{X}$
generates a unique Frölicher space
![]() $(X,{\mathcal{C}}_{X},{\mathcal{F}}_{X})$
by setting
$(X,{\mathcal{C}}_{X},{\mathcal{F}}_{X})$
by setting
In this paper we are investigating the Frölicher spaces generated by the inclusion map
![]() $\unicode[STIX]{x1D704}_{X}:X\rightarrow \mathbb{R}^{d}$
of subsets
$\unicode[STIX]{x1D704}_{X}:X\rightarrow \mathbb{R}^{d}$
of subsets
![]() $X$
of
$X$
of
![]() $\mathbb{R}^{d}$
, that is,
$\mathbb{R}^{d}$
, that is,
![]() $(X,{\mathcal{C}}^{\infty }(\mathbb{R},X),{\mathcal{A}}^{\infty }(X))$
. For suitable sets
$(X,{\mathcal{C}}^{\infty }(\mathbb{R},X),{\mathcal{A}}^{\infty }(X))$
. For suitable sets
![]() $X$
we try to identify the corresponding set of functions
$X$
we try to identify the corresponding set of functions
![]() ${\mathcal{F}}_{X}={\mathcal{A}}^{\infty }(X)$
. More on Frölicher spaces can be found in [Reference Frölicher and KrieglFK88, Reference Kriegl and MichorKM97].
${\mathcal{F}}_{X}={\mathcal{A}}^{\infty }(X)$
. More on Frölicher spaces can be found in [Reference Frölicher and KrieglFK88, Reference Kriegl and MichorKM97].
1.3 Admissible sets
Let
![]() $X\subseteq \mathbb{R}^{d}$
be an arbitrary subset. A function
$X\subseteq \mathbb{R}^{d}$
be an arbitrary subset. A function
![]() $f:X\rightarrow \mathbb{R}$
is said to be smooth if for each
$f:X\rightarrow \mathbb{R}$
is said to be smooth if for each
![]() $x\in X$
there exist a neighborhood
$x\in X$
there exist a neighborhood
![]() $U$
in
$U$
in
![]() $\mathbb{R}^{d}$
and a smooth function
$\mathbb{R}^{d}$
and a smooth function
![]() $F:U\rightarrow \mathbb{R}$
such that
$F:U\rightarrow \mathbb{R}$
such that
![]() $F|_{U\,\cap \,X}=f|_{U\,\cap \,X}$
. If
$F|_{U\,\cap \,X}=f|_{U\,\cap \,X}$
. If
![]() $X$
is open, then this notion of smoothness coincides with the usual one. We denote by
$X$
is open, then this notion of smoothness coincides with the usual one. We denote by
![]() ${\mathcal{C}}^{\infty }(X)$
the set of all smooth functions on
${\mathcal{C}}^{\infty }(X)$
the set of all smooth functions on
![]() $X$
.
$X$
.
Definition 1.8. A subset
![]() $X\subseteq \mathbb{R}^{d}$
is called
$X\subseteq \mathbb{R}^{d}$
is called
![]() ${\mathcal{A}}^{\infty }$
-admissible if
${\mathcal{A}}^{\infty }$
-admissible if
![]() ${\mathcal{A}}^{\infty }(X)={\mathcal{C}}^{\infty }(X)$
, that is, the arc-smooth functions on
${\mathcal{A}}^{\infty }(X)={\mathcal{C}}^{\infty }(X)$
, that is, the arc-smooth functions on
![]() $X$
are precisely the smooth functions.
$X$
are precisely the smooth functions.
Boman’s theorem states that open subsets
![]() $X\subseteq \mathbb{R}^{d}$
are
$X\subseteq \mathbb{R}^{d}$
are
![]() ${\mathcal{A}}^{\infty }$
-admissible. We will look for non-open
${\mathcal{A}}^{\infty }$
-admissible. We will look for non-open
![]() ${\mathcal{A}}^{\infty }$
-admissible sets. It follows from a result of Kriegl [Reference KrieglKri97] that closed convex subsets
${\mathcal{A}}^{\infty }$
-admissible sets. It follows from a result of Kriegl [Reference KrieglKri97] that closed convex subsets
![]() $X\subseteq \mathbb{R}^{d}$
with non-empty interior are
$X\subseteq \mathbb{R}^{d}$
with non-empty interior are
![]() ${\mathcal{A}}^{\infty }$
-admissible. It is natural to consider closed sets with dense interior.
${\mathcal{A}}^{\infty }$
-admissible. It is natural to consider closed sets with dense interior.
Definition 1.9. A non-empty closed subset
![]() $X$
of
$X$
of
![]() $\mathbb{R}^{d}$
is called fat if
$\mathbb{R}^{d}$
is called fat if
![]() $X=\overline{\operatorname{int}(X)}$
.
$X=\overline{\operatorname{int}(X)}$
.
If
![]() $X\subseteq \mathbb{R}^{d}$
is fat, then there are other natural possibilities for defining ‘smooth’ functions on
$X\subseteq \mathbb{R}^{d}$
is fat, then there are other natural possibilities for defining ‘smooth’ functions on
![]() $X$
which we compare in the following lemma.
$X$
which we compare in the following lemma.
Lemma 1.10. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed set. Consider the following conditions:
$X\subseteq \mathbb{R}^{d}$
be a fat closed set. Consider the following conditions:
(1) there exists
 $F\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
such that
$F\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
such that
 $F|_{X}=f$
;
$F|_{X}=f$
;(2)
 $f\in {\mathcal{C}}^{\infty }(X)$
;
$f\in {\mathcal{C}}^{\infty }(X)$
;(3)
 $f|_{\operatorname{int}(X)}\in {\mathcal{C}}^{\infty }(\operatorname{int}(X))$
and the Fréchet derivatives
$f|_{\operatorname{int}(X)}\in {\mathcal{C}}^{\infty }(\operatorname{int}(X))$
and the Fréchet derivatives
 $(f|_{\operatorname{int}(X)})^{(n)}$
of all orders have continuous extensions
$(f|_{\operatorname{int}(X)})^{(n)}$
of all orders have continuous extensions
 $f^{(n)}:X\rightarrow L_{n}(\mathbb{R}^{d},\mathbb{R})$
;
$f^{(n)}:X\rightarrow L_{n}(\mathbb{R}^{d},\mathbb{R})$
;(4)
 $f|_{\operatorname{int}(X)}\in {\mathcal{C}}^{\infty }(\operatorname{int}(X))$
and the directional derivatives
$f|_{\operatorname{int}(X)}\in {\mathcal{C}}^{\infty }(\operatorname{int}(X))$
and the directional derivatives
 $d_{v}^{n}f|_{\operatorname{int}(X)}$
for all
$d_{v}^{n}f|_{\operatorname{int}(X)}$
for all
 $v\in \mathbb{R}^{d}$
and all
$v\in \mathbb{R}^{d}$
and all
 $n\in \mathbb{N}$
have continuous extensions to
$n\in \mathbb{N}$
have continuous extensions to
 $X$
;
$X$
;(5)
 $f|_{\operatorname{int}(X)}\in {\mathcal{C}}^{\infty }(\operatorname{int}(X))$
and the partial derivatives
$f|_{\operatorname{int}(X)}\in {\mathcal{C}}^{\infty }(\operatorname{int}(X))$
and the partial derivatives
 $\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}f|_{\operatorname{int}(X)}$
for all
$\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}f|_{\operatorname{int}(X)}$
for all
 $\unicode[STIX]{x1D6FC}\in \mathbb{N}^{d}$
have continuous extensions to
$\unicode[STIX]{x1D6FC}\in \mathbb{N}^{d}$
have continuous extensions to
 $X$
.
$X$
.
Then
![]() $(1)\Rightarrow (2)\Rightarrow (3)\Leftrightarrow (4)\Leftrightarrow (5)$
. All five conditions are equivalent if
$(1)\Rightarrow (2)\Rightarrow (3)\Leftrightarrow (4)\Leftrightarrow (5)$
. All five conditions are equivalent if
![]() $X$
has the following regularity property.
$X$
has the following regularity property.
(6) For all
 $x\in X$
there exist
$x\in X$
there exist
 $m\in \mathbb{N}_{{>}0}$
,
$m\in \mathbb{N}_{{>}0}$
,
 $C>0$
, and a compact neighborhood
$C>0$
, and a compact neighborhood
 $K$
of
$K$
of
 $x$
in
$x$
in
 $X$
such that any two points
$X$
such that any two points
 $y_{1},y_{2}\in K$
can be joined by a rectifiable path
$y_{1},y_{2}\in K$
can be joined by a rectifiable path
 $\unicode[STIX]{x1D6FE}$
which lies in
$\unicode[STIX]{x1D6FE}$
which lies in
 $\operatorname{int}(X)$
, except perhaps for finitely many points, and has length
$\operatorname{int}(X)$
, except perhaps for finitely many points, and has length  $$\begin{eqnarray}\ell (\unicode[STIX]{x1D6FE})\leqslant C|y_{1}-y_{2}|^{1/m}.\end{eqnarray}$$
$$\begin{eqnarray}\ell (\unicode[STIX]{x1D6FE})\leqslant C|y_{1}-y_{2}|^{1/m}.\end{eqnarray}$$
Proof.
![]() $(1)\Rightarrow (2)\Rightarrow (3)$
are obvious.
$(1)\Rightarrow (2)\Rightarrow (3)$
are obvious.
![]() $(3)\Leftrightarrow (4)\Leftrightarrow (5)$
This follows from the fact that at points
$(3)\Leftrightarrow (4)\Leftrightarrow (5)$
This follows from the fact that at points
![]() $x\in \operatorname{int}(X)$
Fréchet, directional, and partial derivatives can be converted into one another in a linear way; cf. [Reference Kriegl and MichorKM97, Lemma 7.13].
$x\in \operatorname{int}(X)$
Fréchet, directional, and partial derivatives can be converted into one another in a linear way; cf. [Reference Kriegl and MichorKM97, Lemma 7.13].
![]() $(5)\Rightarrow (1)$
By the regularity property (6),
$(5)\Rightarrow (1)$
By the regularity property (6),
![]() $f$
defines a Whitney jet on
$f$
defines a Whitney jet on
![]() $X$
; see [Reference BierstoneBie80, Proposition 2.16]. So Whitney’s extension theorem implies (1).◻
$X$
; see [Reference BierstoneBie80, Proposition 2.16]. So Whitney’s extension theorem implies (1).◻
In general the implication
![]() $(5)\Rightarrow (1)$
is false; see Example 10.9.
$(5)\Rightarrow (1)$
is false; see Example 10.9.
Another natural condition for
![]() ${\mathcal{A}}^{\infty }$
-admissibility is the following; see Example 10.5.
${\mathcal{A}}^{\infty }$
-admissibility is the following; see Example 10.5.
Definition 1.11. A closed subset
![]() $X\subseteq \mathbb{R}^{d}$
is called simple if each
$X\subseteq \mathbb{R}^{d}$
is called simple if each
![]() $x\in X$
has a basis of neighborhoods
$x\in X$
has a basis of neighborhoods
![]() $\mathscr{U}$
such that
$\mathscr{U}$
such that
![]() $U\,\cap \,\operatorname{int}(X)$
is connected for all
$U\,\cap \,\operatorname{int}(X)$
is connected for all
![]() $U\in \mathscr{U}$
.
$U\in \mathscr{U}$
.
A function
![]() $f:X\rightarrow \mathbb{R}$
is said to be real analytic if for each
$f:X\rightarrow \mathbb{R}$
is said to be real analytic if for each
![]() $x\in X$
there exist a neighborhood
$x\in X$
there exist a neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
![]() $\mathbb{C}^{d}$
and a holomorphic function
$\mathbb{C}^{d}$
and a holomorphic function
![]() $F:U\rightarrow \mathbb{C}$
such that
$F:U\rightarrow \mathbb{C}$
such that
![]() $F|_{U\,\cap \,X}=f|_{U\,\cap \,X}$
. We denote by
$F|_{U\,\cap \,X}=f|_{U\,\cap \,X}$
. We denote by
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D714}}(X)$
the set of all real analytic functions on
${\mathcal{C}}^{\unicode[STIX]{x1D714}}(X)$
the set of all real analytic functions on
![]() $X$
.
$X$
.
If
![]() $M=(M_{k})$
is a positive sequence, we set
$M=(M_{k})$
is a positive sequence, we set
Note that we do not require that a function
![]() $f\in {\mathcal{C}}^{M}(X)$
is locally a restriction of a
$f\in {\mathcal{C}}^{M}(X)$
is locally a restriction of a
![]() ${\mathcal{C}}^{M}$
-function on
${\mathcal{C}}^{M}$
-function on
![]() $\mathbb{R}^{d}$
. We shall discuss in § 10.1 when a function in
$\mathbb{R}^{d}$
. We shall discuss in § 10.1 when a function in
![]() ${\mathcal{C}}^{M}(X)$
extends to a
${\mathcal{C}}^{M}(X)$
extends to a
![]() ${\mathcal{C}}^{M}$
-function on
${\mathcal{C}}^{M}$
-function on
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
Definition 1.12. A subset
![]() $X\subseteq \mathbb{R}^{d}$
is called
$X\subseteq \mathbb{R}^{d}$
is called
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible (respectively,
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible (respectively,
![]() ${\mathcal{A}}^{M}$
-admissible) if
${\mathcal{A}}^{M}$
-admissible) if
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)={\mathcal{C}}^{\unicode[STIX]{x1D714}}(X)$
(respectively,
${\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)={\mathcal{C}}^{\unicode[STIX]{x1D714}}(X)$
(respectively,
![]() ${\mathcal{A}}^{M}(X)={\mathcal{C}}^{M}(X)$
).
${\mathcal{A}}^{M}(X)={\mathcal{C}}^{M}(X)$
).
By the Bochnak–Siciak Theorem 1.5 and Result 1.3, all open subsets
![]() $X\subseteq \mathbb{R}^{d}$
are
$X\subseteq \mathbb{R}^{d}$
are
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible and
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible and
![]() ${\mathcal{A}}^{M}$
-admissible, for each log-convex non-quasianalytic
${\mathcal{A}}^{M}$
-admissible, for each log-convex non-quasianalytic
![]() $M$
.
$M$
.
1.4 Main results
Our results can be arranged in groups with respect to two criteria: regularity of the functions (smooth, real analytic, ultradifferentiable) and regularity of the domains (Hölder sets, fat subanalytic sets).
By a Hölder set we mean the closure of an open set which has the uniform cusp property of index
![]() $\unicode[STIX]{x1D6FC}$
for some
$\unicode[STIX]{x1D6FC}$
for some
![]() $0<\unicode[STIX]{x1D6FC}\leqslant 1$
. If
$0<\unicode[STIX]{x1D6FC}\leqslant 1$
. If
![]() $\unicode[STIX]{x1D6FC}=1$
we speak of a Lipschitz set. The collection of all Hölder sets in
$\unicode[STIX]{x1D6FC}=1$
we speak of a Lipschitz set. The collection of all Hölder sets in
![]() $\mathbb{R}^{d}$
is denoted by
$\mathbb{R}^{d}$
is denoted by
![]() $\mathscr{H}(\mathbb{R}^{d})$
. (We use the term Hölder set instead of domain, since the latter is usually reserved for open sets.) For precise definitions we refer to § 3.
$\mathscr{H}(\mathbb{R}^{d})$
. (We use the term Hölder set instead of domain, since the latter is usually reserved for open sets.) For precise definitions we refer to § 3.
The smooth case
Theorem 1.13. Every
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
is
$X\in \mathscr{H}(\mathbb{R}^{d})$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible. We even have
${\mathcal{A}}^{\infty }$
-admissible. We even have
for any non-quasianalytic log-convex positive sequence
![]() $M=(M_{k})$
.
$M=(M_{k})$
.
Theorem 1.13 is proved in § 4.
Theorem 1.14. Every simple fat closed subanalytic set
![]() $X\subseteq \mathbb{R}^{d}$
is
$X\subseteq \mathbb{R}^{d}$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible.
${\mathcal{A}}^{\infty }$
-admissible.
This is proved in § 5. The proof is based on the L-regular decomposition of subanalytic sets and the fact that fat closed subanalytic sets are uniformly polynomially cuspidal. It uses the result for Hölder sets (Theorem 1.13).
Remark 1.15. Hölder sets
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
and fat closed subanalytic subsets
$X\in \mathscr{H}(\mathbb{R}^{d})$
and fat closed subanalytic subsets
![]() $X\subseteq \mathbb{R}^{d}$
satisfy Lemma 1.10(6) and hence all items (1)–(5) in Lemma 1.10 are equivalent; cf. Proposition 3.8 and Theorem 5.6.
$X\subseteq \mathbb{R}^{d}$
satisfy Lemma 1.10(6) and hence all items (1)–(5) in Lemma 1.10 are equivalent; cf. Proposition 3.8 and Theorem 5.6.
Notice that the assumption that
![]() $X$
is simple is necessary; see Example 10.5. Hölder sets are always simple; see Proposition 3.9.
$X$
is simple is necessary; see Example 10.5. Hölder sets are always simple; see Proposition 3.9.
The real analytic case
Theorem 1.16. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. Let
$X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. Let
![]() $f\in {\mathcal{C}}^{\infty }(X)$
be real analytic on real analytic curves in
$f\in {\mathcal{C}}^{\infty }(X)$
be real analytic on real analytic curves in
![]() $X$
. Then
$X$
. Then
![]() $f$
extends to a holomorphic function defined on an open neighborhood of
$f$
extends to a holomorphic function defined on an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{C}^{d}$
.
$\mathbb{C}^{d}$
.
The proof of Theorem 1.16 (in § 6) is based on the uniformization theorem of subanalytic sets and a result of Eakin and Harris [Reference Eakin and HarrisEH77] (proved earlier by Gabriélov [Reference GabriélovGab73]). The following consequence will also be proved in § 6.
Corollary 1.17. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a closed set such that for all
$X\subseteq \mathbb{R}^{d}$
be a closed set such that for all
![]() $z\in \unicode[STIX]{x2202}X$
there is a closed fat subanalytic set
$z\in \unicode[STIX]{x2202}X$
there is a closed fat subanalytic set
![]() $X_{z}$
such that
$X_{z}$
such that
![]() $z\in X_{z}\subseteq X$
. Let
$z\in X_{z}\subseteq X$
. Let
![]() $f\in {\mathcal{C}}^{\infty }(X)$
be real analytic on real analytic curves in
$f\in {\mathcal{C}}^{\infty }(X)$
be real analytic on real analytic curves in
![]() $X$
. Then
$X$
. Then
![]() $f$
extends to a holomorphic function defined on an open neighborhood of
$f$
extends to a holomorphic function defined on an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{C}^{d}$
.
$\mathbb{C}^{d}$
.
Note that all Hölder sets satisfy the assumption in Corollary 1.17. Interestingly, for these results we need not assume that
![]() $X$
is simple (note that we already suppose that
$X$
is simple (note that we already suppose that
![]() $f\in {\mathcal{C}}^{\infty }(X)$
). Together with Theorems 1.13 and 1.14, we obtain the following corollary.
$f\in {\mathcal{C}}^{\infty }(X)$
). Together with Theorems 1.13 and 1.14, we obtain the following corollary.
Corollary 1.18. Every
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
and every simple fat closed subanalytic
$X\in \mathscr{H}(\mathbb{R}^{d})$
and every simple fat closed subanalytic
![]() $X\subseteq \mathbb{R}^{d}$
is
$X\subseteq \mathbb{R}^{d}$
is
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible.
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible.
The ultradifferentiable case
Let
![]() $M=(M_{k})$
be a non-quasianalytic log-convex positive sequence. For positive integers
$M=(M_{k})$
be a non-quasianalytic log-convex positive sequence. For positive integers
![]() $a$
let
$a$
let
![]() $M^{(a)}$
denote the sequence defined by
$M^{(a)}$
denote the sequence defined by
![]() $M_{k}^{(a)}:=M_{ak}$
.
$M_{k}^{(a)}:=M_{ak}$
.
Theorem 1.19. Let
![]() $M=(M_{k})$
be a non-quasianalytic log-convex positive sequence. Every Lipschitz set
$M=(M_{k})$
be a non-quasianalytic log-convex positive sequence. Every Lipschitz set
![]() $X\subseteq \mathbb{R}^{d}$
satisfies
$X\subseteq \mathbb{R}^{d}$
satisfies
![]() ${\mathcal{C}}^{M}(X)\subseteq {\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{M^{(2)}}(X)$
.
${\mathcal{C}}^{M}(X)\subseteq {\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{M^{(2)}}(X)$
.
A similar statement can be expected for Hölder sets (with the loss of regularity also depending on the Hölder index). We will not pursue this in this paper. Instead, combining our results with a result of [Reference Chaumat and CholletCC99, Reference Belotto da Silva, Bierstone and ChowBBC18], we show in Theorem 8.4 that for fat closed subanalytic sets the loss of regularity can be controlled in a precise way.
In an earlier version of the paper we claimed that every Lipschitz set
![]() $X\subseteq \mathbb{R}^{d}$
is
$X\subseteq \mathbb{R}^{d}$
is
![]() ${\mathcal{A}}^{M}$
-admissible. That is doubtful, but we do not have a counterexample.
${\mathcal{A}}^{M}$
-admissible. That is doubtful, but we do not have a counterexample.
1.5 Permanence of admissibility
The main results all concern subsets
![]() $X\subseteq \mathbb{R}^{d}$
with maximal dimension
$X\subseteq \mathbb{R}^{d}$
with maximal dimension
![]() $d$
. The following permanence properties yield further examples of admissible sets both of maximal dimension and of codimension at least
$d$
. The following permanence properties yield further examples of admissible sets both of maximal dimension and of codimension at least
![]() $1$
.
$1$
.
Proposition 1.20. Let
![]() $X\subseteq \mathbb{R}^{d}$
be
$X\subseteq \mathbb{R}^{d}$
be
![]() ${\mathcal{A}}^{\infty }$
-admissible. If
${\mathcal{A}}^{\infty }$
-admissible. If
![]() $U$
is an open neighborhood of
$U$
is an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{R}^{d}$
and
$\mathbb{R}^{d}$
and
![]() $\unicode[STIX]{x1D711}:U\rightarrow \mathbb{R}^{e}$
is a smooth embedding, then
$\unicode[STIX]{x1D711}:U\rightarrow \mathbb{R}^{e}$
is a smooth embedding, then
![]() $\unicode[STIX]{x1D711}(X)\subseteq \mathbb{R}^{e}$
is
$\unicode[STIX]{x1D711}(X)\subseteq \mathbb{R}^{e}$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible.
${\mathcal{A}}^{\infty }$
-admissible.
Proof. Let
![]() $Y:=\unicode[STIX]{x1D711}(X)$
. If
$Y:=\unicode[STIX]{x1D711}(X)$
. If
![]() $f\in {\mathcal{A}}^{\infty }(Y)$
, then
$f\in {\mathcal{A}}^{\infty }(Y)$
, then
![]() $g:=f\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\infty }(X)$
. Since
$g:=f\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{A}}^{\infty }(X)$
. Since
![]() $M:=\unicode[STIX]{x1D711}(U)$
is an embedded submanifold of
$M:=\unicode[STIX]{x1D711}(U)$
is an embedded submanifold of
![]() $\mathbb{R}^{e}$
, it suffices to show that for each
$\mathbb{R}^{e}$
, it suffices to show that for each
![]() $y\in Y$
there exist a neighborhood
$y\in Y$
there exist a neighborhood
![]() $V$
in
$V$
in
![]() $M$
and a smooth function
$M$
and a smooth function
![]() $F:V\rightarrow \mathbb{R}$
such that
$F:V\rightarrow \mathbb{R}$
such that
![]() $F|_{V\,\cap \,Y}=f|_{V\,\cap \,Y}$
.
$F|_{V\,\cap \,Y}=f|_{V\,\cap \,Y}$
.
Since
![]() $X$
is
$X$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible, for each
${\mathcal{A}}^{\infty }$
-admissible, for each
![]() $x\in X$
there exist a neighborhood
$x\in X$
there exist a neighborhood
![]() $W$
in
$W$
in
![]() $\mathbb{R}^{d}$
and a smooth function
$\mathbb{R}^{d}$
and a smooth function
![]() $G:W\rightarrow \mathbb{R}$
such that
$G:W\rightarrow \mathbb{R}$
such that
![]() $G|_{W\,\cap \,X}=g|_{W\,\cap \,X}$
. Taking
$G|_{W\,\cap \,X}=g|_{W\,\cap \,X}$
. Taking
![]() $U\,\cap \,W$
instead of
$U\,\cap \,W$
instead of
![]() $W$
, we may assume that
$W$
, we may assume that
![]() $W\subseteq U$
. Then
$W\subseteq U$
. Then
![]() $F:=G\,\circ \,\unicode[STIX]{x1D711}^{-1}|_{\unicode[STIX]{x1D711}(W)}$
is smooth on
$F:=G\,\circ \,\unicode[STIX]{x1D711}^{-1}|_{\unicode[STIX]{x1D711}(W)}$
is smooth on
![]() $V:=\unicode[STIX]{x1D711}(W)$
and satisfies
$V:=\unicode[STIX]{x1D711}(W)$
and satisfies
![]() $F|_{V\,\cap \,Y}=f|_{V\,\cap \,Y}$
.◻
$F|_{V\,\cap \,Y}=f|_{V\,\cap \,Y}$
.◻
The same proof yields the following proposition.
Proposition 1.21. Let
![]() $X\subseteq \mathbb{R}^{d}$
be
$X\subseteq \mathbb{R}^{d}$
be
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible. If
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible. If
![]() $U$
is an open neighborhood of
$U$
is an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{R}^{d}$
and
$\mathbb{R}^{d}$
and
![]() $\unicode[STIX]{x1D711}:U\rightarrow \mathbb{R}^{e}$
is a real analytic embedding, then
$\unicode[STIX]{x1D711}:U\rightarrow \mathbb{R}^{e}$
is a real analytic embedding, then
![]() $\unicode[STIX]{x1D711}(X)\subseteq \mathbb{R}^{e}$
is
$\unicode[STIX]{x1D711}(X)\subseteq \mathbb{R}^{e}$
is
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible.
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible.
In the ultradifferentiable case we have the following. Note that if
![]() $M=(M_{k})$
is log-convex, then
$M=(M_{k})$
is log-convex, then
![]() ${\mathcal{C}}^{M}$
is stable under composition and the
${\mathcal{C}}^{M}$
is stable under composition and the
![]() ${\mathcal{C}}^{M}$
inverse function theorem holds. If
${\mathcal{C}}^{M}$
inverse function theorem holds. If
![]() $N\subseteq \mathbb{R}^{e}$
is an embedded submanifold of class
$N\subseteq \mathbb{R}^{e}$
is an embedded submanifold of class
![]() ${\mathcal{C}}^{M}$
(i.e. the chart change maps are of class
${\mathcal{C}}^{M}$
(i.e. the chart change maps are of class
![]() ${\mathcal{C}}^{M}$
), then we define
${\mathcal{C}}^{M}$
), then we define
![]() ${\mathcal{C}}^{M}(N)$
to be the set of
${\mathcal{C}}^{M}(N)$
to be the set of
![]() $f\in {\mathcal{C}}^{\infty }(N)$
which are of class
$f\in {\mathcal{C}}^{\infty }(N)$
which are of class
![]() ${\mathcal{C}}^{M}$
in every local coordinate chart. If
${\mathcal{C}}^{M}$
in every local coordinate chart. If
![]() $Y\subseteq N$
, then let
$Y\subseteq N$
, then let
![]() ${\mathcal{C}}^{M}(Y)$
be the set of
${\mathcal{C}}^{M}(Y)$
be the set of
![]() ${\mathcal{C}}^{\infty }$
-functions on
${\mathcal{C}}^{\infty }$
-functions on
![]() $Y$
such that the defining estimates hold for all compact subsets in
$Y$
such that the defining estimates hold for all compact subsets in
![]() $Y$
in all local coordinate charts. The proof of Proposition 1.20 implies the following.
$Y$
in all local coordinate charts. The proof of Proposition 1.20 implies the following.
Proposition 1.22. Let
![]() $M=(M_{k})$
be non-quasianalytic and log-convex, and let
$M=(M_{k})$
be non-quasianalytic and log-convex, and let
![]() $N=(N_{k})$
be a sequence with
$N=(N_{k})$
be a sequence with
![]() $M\leqslant N$
. Assume that
$M\leqslant N$
. Assume that
![]() $X\subseteq \mathbb{R}^{d}$
satisfies
$X\subseteq \mathbb{R}^{d}$
satisfies
![]() ${\mathcal{C}}^{M}(X)\subseteq {\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{N}(X)$
. If
${\mathcal{C}}^{M}(X)\subseteq {\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{N}(X)$
. If
![]() $U$
is an open neighborhood of
$U$
is an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{R}^{d}$
and
$\mathbb{R}^{d}$
and
![]() $\unicode[STIX]{x1D711}:U\rightarrow \mathbb{R}^{e}$
is a
$\unicode[STIX]{x1D711}:U\rightarrow \mathbb{R}^{e}$
is a
![]() ${\mathcal{C}}^{M}$
-embedding, then
${\mathcal{C}}^{M}$
-embedding, then
![]() $Y:=\unicode[STIX]{x1D711}(X)\subseteq \mathbb{R}^{e}$
satisfies
$Y:=\unicode[STIX]{x1D711}(X)\subseteq \mathbb{R}^{e}$
satisfies
![]() ${\mathcal{C}}^{M}(Y)\subseteq {\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{N}(Y)$
.
${\mathcal{C}}^{M}(Y)\subseteq {\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{N}(Y)$
.
1.6 Sharpness of the results
We discuss in § 10.2 counterexamples which show that none of the conditions in the main results can in general be omitted without suitable replacement.
In particular, Example 10.4, which is based on a division theorem of [Reference Joris and PreissmannJP90], shows that the
![]() $\infty$
-flat cusp
$\infty$
-flat cusp
is not
![]() ${\mathcal{A}}^{\infty }$
-admissible; in this case
${\mathcal{A}}^{\infty }$
-admissible; in this case
![]() ${\mathcal{A}}^{\infty }(X)$
is strictly larger than
${\mathcal{A}}^{\infty }(X)$
is strictly larger than
![]() ${\mathcal{C}}^{\infty }(X)$
. Note, however, that for
${\mathcal{C}}^{\infty }(X)$
. Note, however, that for
![]() $Y:=\mathbb{R}^{2}\setminus \operatorname{int}(X)$
we have
$Y:=\mathbb{R}^{2}\setminus \operatorname{int}(X)$
we have
![]() $f\in {\mathcal{A}}^{\infty }(Y)$
if and only if
$f\in {\mathcal{A}}^{\infty }(Y)$
if and only if
![]() $f$
satisfies Lemma 1.10(3), but
$f$
satisfies Lemma 1.10(3), but
![]() ${\mathcal{A}}^{\infty }(Y)\neq {\mathcal{C}}^{\infty }(Y)$
; see Example 10.9.
${\mathcal{A}}^{\infty }(Y)\neq {\mathcal{C}}^{\infty }(Y)$
; see Example 10.9.
Interestingly, the analogue for finite differentiability (i.e. Result 1.2) fails even on convex fat closed sets such as the half-space; see Example 10.7, which is a consequence of Glaeser’s inequality.
1.7 Applications
As a corollary of the real analytic result (i.e. Theorem 1.16) we obtain that smooth solutions of real analytic equations on Hölder sets or closed fat subanalytic sets must be real analytic; see Theorem 9.1. Furthermore, we obtain sufficient conditions for the existence of real analytic solutions
![]() $g$
of the equation
$g$
of the equation
![]() $f=g\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(M)$
, where
$f=g\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(M)$
, where
![]() $\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
is a real analytic map defined on a real analytic manifold
$\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
is a real analytic map defined on a real analytic manifold
![]() $M$
; see Corollary 9.3.
$M$
; see Corollary 9.3.
The usefulness of the smooth result is illustrated by some consequences for the division of smooth functions (see Theorem 9.5) and for pseudo-immersions (see Theorem 9.6).
1.8 Structure of the paper
We recall facts on weight sequences and Denjoy–Carleman classes in § 2, and we revisit and adapt the
![]() ${\mathcal{C}}^{M}$
curve lemma which is an essential tool for proving some results of the paper. In § 3 we introduce Hölder sets and collect some of their properties. The proofs of Theorems 1.13, 1.14, 1.16 and 1.19 are given in §§ 4, 5, 6, and 7, respectively. In § 8 we discuss the ultradifferentiable case on subanalytic sets. Applications are given in § 9. The final § 10 contains complements, examples, and counterexamples.
${\mathcal{C}}^{M}$
curve lemma which is an essential tool for proving some results of the paper. In § 3 we introduce Hölder sets and collect some of their properties. The proofs of Theorems 1.13, 1.14, 1.16 and 1.19 are given in §§ 4, 5, 6, and 7, respectively. In § 8 we discuss the ultradifferentiable case on subanalytic sets. Applications are given in § 9. The final § 10 contains complements, examples, and counterexamples.
Some of the results of this paper were announced in [Reference RainerRai17].
2 A
 ${\mathcal{C}}^{M}$
-curve lemma
${\mathcal{C}}^{M}$
-curve lemma
This section is only of relevance for the ultradifferentiable results in the paper.
2.1 Weight sequences and Denjoy–Carleman classes
Let
![]() $M=(M_{k})_{k\in \mathbb{N}}$
be a positive sequence of reals. Let
$M=(M_{k})_{k\in \mathbb{N}}$
be a positive sequence of reals. Let
![]() $U\subseteq \mathbb{R}^{d}$
be open and let
$U\subseteq \mathbb{R}^{d}$
be open and let
![]() ${\mathcal{C}}^{M}(U,\mathbb{R}^{m})$
be the corresponding Denjoy–Carleman class (of Roumieu type) as defined in § 1.1.
${\mathcal{C}}^{M}(U,\mathbb{R}^{m})$
be the corresponding Denjoy–Carleman class (of Roumieu type) as defined in § 1.1.
If
![]() $N=(N_{k})$
is another positive sequence such that
$N=(N_{k})$
is another positive sequence such that
![]() $(M_{k}/N_{k})^{1/k}$
is bounded, then
$(M_{k}/N_{k})^{1/k}$
is bounded, then
![]() ${\mathcal{C}}^{M}(U)\subseteq {\mathcal{C}}^{N}(U)$
. The converse holds if
${\mathcal{C}}^{M}(U)\subseteq {\mathcal{C}}^{N}(U)$
. The converse holds if
![]() $k!M_{k}$
is logarithmically convex (log-convex for short). It follows that the class
$k!M_{k}$
is logarithmically convex (log-convex for short). It follows that the class
![]() ${\mathcal{C}}^{M}(U)$
is preserved by replacing
${\mathcal{C}}^{M}(U)$
is preserved by replacing
![]() $M=(M_{k})_{k}$
by
$M=(M_{k})_{k}$
by
![]() $(C^{k}M_{k})_{k}$
for some positive constant
$(C^{k}M_{k})_{k}$
for some positive constant
![]() $C$
.
$C$
.
We shall assume that the sequence
![]() $M$
is log-convex (which entails log-convexity of
$M$
is log-convex (which entails log-convexity of
![]() $k!M_{k}$
). We may assume that
$k!M_{k}$
). We may assume that
![]() $M_{0}=1$
and that
$M_{0}=1$
and that
![]() $M$
is increasing. Indeed, the sequence
$M$
is increasing. Indeed, the sequence
![]() $N_{k}:=C^{k}M_{k}/M_{0}$
for some constant
$N_{k}:=C^{k}M_{k}/M_{0}$
for some constant
![]() $C\geqslant M_{0}/M_{1}$
, is log-convex, increasing, satisfies
$C\geqslant M_{0}/M_{1}$
, is log-convex, increasing, satisfies
![]() $N_{0}=1$
, and
$N_{0}=1$
, and
![]() ${\mathcal{C}}^{M}(U)={\mathcal{C}}^{N}(U)$
. This motivates the following definition.
${\mathcal{C}}^{M}(U)={\mathcal{C}}^{N}(U)$
. This motivates the following definition.
Definition 2.1. An increasing log-convex sequence
![]() $M=(M_{k})$
with
$M=(M_{k})$
with
![]() $M_{0}=1$
is called a weight sequence.
$M_{0}=1$
is called a weight sequence.
The regularity properties of a weight sequence
![]() $M=(M_{k})$
entail stability properties of the class
$M=(M_{k})$
entail stability properties of the class
![]() ${\mathcal{C}}^{M}$
; cf. [Reference Rainer and SchindlRS16]. Of particular interest in this paper is the fact that, for a weight sequence
${\mathcal{C}}^{M}$
; cf. [Reference Rainer and SchindlRS16]. Of particular interest in this paper is the fact that, for a weight sequence
![]() $M$
, the composite of
$M$
, the composite of
![]() ${\mathcal{C}}^{M}$
mappings is
${\mathcal{C}}^{M}$
mappings is
![]() ${\mathcal{C}}^{M}$
. By the celebrated Denjoy–Carleman theorem, the condition
${\mathcal{C}}^{M}$
. By the celebrated Denjoy–Carleman theorem, the condition
holds if and only if
![]() ${\mathcal{C}}^{M}$
is non-quasianalytic, that is, the Borel mapping which sends germs at some point
${\mathcal{C}}^{M}$
is non-quasianalytic, that is, the Borel mapping which sends germs at some point
![]() $a$
of smooth functions to their infinite Taylor expansion at
$a$
of smooth functions to their infinite Taylor expansion at
![]() $a$
is not injective on
$a$
is not injective on
![]() ${\mathcal{C}}^{M}$
-germs. Then there exist non-trivial
${\mathcal{C}}^{M}$
-germs. Then there exist non-trivial
![]() ${\mathcal{C}}^{M}$
-functions with compact support. Note that (2.1) is equivalent to
${\mathcal{C}}^{M}$
-functions with compact support. Note that (2.1) is equivalent to
Definition 2.2. Let
![]() $M=(M_{k})$
be a weight sequence. We say that
$M=(M_{k})$
be a weight sequence. We say that
![]() $M$
is non-quasianalytic if it satisfies (2.1); otherwise it is said to be quasianalytic. A weight sequence
$M$
is non-quasianalytic if it satisfies (2.1); otherwise it is said to be quasianalytic. A weight sequence
![]() $M$
is called strongly non-quasianalytic if
$M$
is called strongly non-quasianalytic if
It is said to be of moderate growth if
A weight sequence is called strongly regular if it is strongly non-quasianalytic and of moderate growth.
Example 2.3. The Gevrey sequences
![]() $G_{k}^{s}=k!^{s}$
,
$G_{k}^{s}=k!^{s}$
,
![]() $s>0$
, which give rise to the Gevrey classes
$s>0$
, which give rise to the Gevrey classes
![]() ${\mathcal{C}}^{G^{s}}$
are strongly regular weight sequences. They appear naturally in the theory of (partial) differential equations. For
${\mathcal{C}}^{G^{s}}$
are strongly regular weight sequences. They appear naturally in the theory of (partial) differential equations. For
![]() $s=0$
we recover the real analytic functions
$s=0$
we recover the real analytic functions
![]() ${\mathcal{C}}^{G^{0}}={\mathcal{C}}^{\unicode[STIX]{x1D714}}$
which obviously form a quasianalytic class.
${\mathcal{C}}^{G^{0}}={\mathcal{C}}^{\unicode[STIX]{x1D714}}$
which obviously form a quasianalytic class.
Note that
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D714}}(U)\subseteq {\mathcal{C}}^{M}(U)\subseteq {\mathcal{C}}^{\infty }(U)$
for every weight sequence
${\mathcal{C}}^{\unicode[STIX]{x1D714}}(U)\subseteq {\mathcal{C}}^{M}(U)\subseteq {\mathcal{C}}^{\infty }(U)$
for every weight sequence
![]() $M$
. In fact, the Denjoy–Carleman classes form an a scale of spaces intermediate between the real analytic and the smooth functions.
$M$
. In fact, the Denjoy–Carleman classes form an a scale of spaces intermediate between the real analytic and the smooth functions.
2.2 The
 ${\mathcal{C}}^{M}$
curve lemma revisited
${\mathcal{C}}^{M}$
curve lemma revisited
We generalize the
![]() ${\mathcal{C}}^{M}$
curve lemma (see [Reference Kriegl, Michor and RainerKMR09, § 3.6] and [Reference Kriegl, Michor and RainerKMR11, § 2.5]) which was inspired by [Reference BomanBom67, Lemma 2].
${\mathcal{C}}^{M}$
curve lemma (see [Reference Kriegl, Michor and RainerKMR09, § 3.6] and [Reference Kriegl, Michor and RainerKMR11, § 2.5]) which was inspired by [Reference BomanBom67, Lemma 2].
Lemma 2.4. There are sequences
![]() $t_{k}\rightarrow t_{\infty }$
and
$t_{k}\rightarrow t_{\infty }$
and
![]() $s_{k}>0$
in
$s_{k}>0$
in
![]() $\mathbb{R}$
with the following property. For any non-quasianalytic weight sequence
$\mathbb{R}$
with the following property. For any non-quasianalytic weight sequence
![]() $M=(M_{k})$
and each
$M=(M_{k})$
and each
![]() $a\in \mathbb{N}_{{\geqslant}2}$
there is a real positive sequence
$a\in \mathbb{N}_{{\geqslant}2}$
there is a real positive sequence
![]() $\unicode[STIX]{x1D706}_{k}\rightarrow 0$
satisfying
$\unicode[STIX]{x1D706}_{k}\rightarrow 0$
satisfying
such that the following holds. Let
![]() $E$
be a Banach space. Let
$E$
be a Banach space. Let
![]() $c_{k}\in C^{\infty }(\mathbb{R},E)$
be a sequence such that
$c_{k}\in C^{\infty }(\mathbb{R},E)$
be a sequence such that
is bounded in
![]() $E$
, for every bounded interval
$E$
, for every bounded interval
![]() $I\subseteq \mathbb{R}$
. Then there exists a
$I\subseteq \mathbb{R}$
. Then there exists a
![]() ${\mathcal{C}}^{M}$
-curve
${\mathcal{C}}^{M}$
-curve
![]() $c:\mathbb{R}\rightarrow E$
with compact support and
$c:\mathbb{R}\rightarrow E$
with compact support and
![]() $c(t_{k}+t)=c_{k}(t)$
for
$c(t_{k}+t)=c_{k}(t)$
for
![]() $|t|\leqslant s_{k}$
.
$|t|\leqslant s_{k}$
.
Proof. There exists a non-quasianalytic weight sequence
![]() $L=(L_{k})$
such that
$L=(L_{k})$
such that
![]() $(M_{k}/L_{k})^{1/k}\rightarrow \infty$
(this follows, for example, from [Reference KomatsuKom79, Lemma 6]). Choose a
$(M_{k}/L_{k})^{1/k}\rightarrow \infty$
(this follows, for example, from [Reference KomatsuKom79, Lemma 6]). Choose a
![]() ${\mathcal{C}}^{L}$
-function
${\mathcal{C}}^{L}$
-function
![]() $\unicode[STIX]{x1D711}:\mathbb{R}\rightarrow [0,1]$
which is
$\unicode[STIX]{x1D711}:\mathbb{R}\rightarrow [0,1]$
which is
![]() $0$
on
$0$
on
![]() $\{t:|t|\geqslant 1/2\}$
and
$\{t:|t|\geqslant 1/2\}$
and
![]() $1$
on
$1$
on
![]() $\{t:|t|\leqslant 1/3\}$
.
$\{t:|t|\leqslant 1/3\}$
.
Let
![]() $T\in (0,1]$
and
$T\in (0,1]$
and
![]() $R>0$
. Assume that
$R>0$
. Assume that
![]() $\unicode[STIX]{x1D6FE}\in C^{\infty }(\mathbb{R},E)$
is such that
$\unicode[STIX]{x1D6FE}\in C^{\infty }(\mathbb{R},E)$
is such that
Then there exist
![]() $C,\unicode[STIX]{x1D70C}\geqslant 1$
such that for the curve
$C,\unicode[STIX]{x1D70C}\geqslant 1$
such that for the curve
![]() $c(t):=\unicode[STIX]{x1D711}(t/T)\unicode[STIX]{x1D6FE}(t)$
we have
$c(t):=\unicode[STIX]{x1D711}(t/T)\unicode[STIX]{x1D6FE}(t)$
we have
 $$\begin{eqnarray}\displaystyle \Vert c^{(\ell )}(t)\Vert & = & \displaystyle \biggl\|\mathop{\sum }_{j=0}^{\ell }\binom{\ell }{j}T^{-j}\unicode[STIX]{x1D711}^{(j)}\biggl(\frac{t}{T}\biggr)\unicode[STIX]{x1D6FE}^{(\ell -j)}(t)\biggr\|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle R\mathop{\sum }_{j=0}^{\ell }\binom{\ell }{j}T^{-j}C\unicode[STIX]{x1D70C}^{j}j!L_{j}\leqslant CR\biggl(1+\frac{\unicode[STIX]{x1D70C}}{T}\biggr)^{\ell }\ell !L_{\ell }\leqslant CR\biggl(\frac{2\unicode[STIX]{x1D70C}}{T}\biggr)^{\ell }\ell !L_{\ell }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Vert c^{(\ell )}(t)\Vert & = & \displaystyle \biggl\|\mathop{\sum }_{j=0}^{\ell }\binom{\ell }{j}T^{-j}\unicode[STIX]{x1D711}^{(j)}\biggl(\frac{t}{T}\biggr)\unicode[STIX]{x1D6FE}^{(\ell -j)}(t)\biggr\|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle R\mathop{\sum }_{j=0}^{\ell }\binom{\ell }{j}T^{-j}C\unicode[STIX]{x1D70C}^{j}j!L_{j}\leqslant CR\biggl(1+\frac{\unicode[STIX]{x1D70C}}{T}\biggr)^{\ell }\ell !L_{\ell }\leqslant CR\biggl(\frac{2\unicode[STIX]{x1D70C}}{T}\biggr)^{\ell }\ell !L_{\ell }.\end{eqnarray}$$
Choose a sequence
Now choose
![]() $\unicode[STIX]{x1D706}_{j}$
such that the following conditions are fulfilled:
$\unicode[STIX]{x1D706}_{j}$
such that the following conditions are fulfilled:
It suffices to take
![]() $\unicode[STIX]{x1D706}_{j}\leqslant \inf _{k}T_{j}^{k+1}M_{k}/L_{k}$
. Clearly, we may in addition require that
$\unicode[STIX]{x1D706}_{j}\leqslant \inf _{k}T_{j}^{k+1}M_{k}/L_{k}$
. Clearly, we may in addition require that
![]() $\unicode[STIX]{x1D706}_{j}$
tends to zero fast enough so that (2.5) holds.
$\unicode[STIX]{x1D706}_{j}$
tends to zero fast enough so that (2.5) holds.
By (2.6), there is
![]() $R>0$
such that
$R>0$
such that
Define
The summands have disjoint supports (the support of the
![]() $j$
th summand is contained in
$j$
th summand is contained in
![]() $[t_{j}-T_{j}/2,t_{j}+T_{j}/2]$
). Thus
$[t_{j}-T_{j}/2,t_{j}+T_{j}/2]$
). Thus
![]() $c$
is
$c$
is
![]() ${\mathcal{C}}^{\infty }$
on
${\mathcal{C}}^{\infty }$
on
![]() $\mathbb{R}\setminus \{t_{\infty }\}$
. By (2.7),
$\mathbb{R}\setminus \{t_{\infty }\}$
. By (2.7),
Consequently, by (2.9),
It follows that
![]() $c:\mathbb{R}\rightarrow E$
has compact support and is
$c:\mathbb{R}\rightarrow E$
has compact support and is
![]() ${\mathcal{C}}^{M}$
; cf. [Reference Kriegl and MichorKM97, Lemma 2.9] and [Reference Kriegl, Michor and RainerKMR09, Lemma 3.7].◻
${\mathcal{C}}^{M}$
; cf. [Reference Kriegl and MichorKM97, Lemma 2.9] and [Reference Kriegl, Michor and RainerKMR09, Lemma 3.7].◻
Remark 2.5. A similar statement holds for convenient vector spaces
![]() $E$
. The proof can be easily adapted to this case; cf. [Reference Kriegl, Michor and RainerKMR09] or [Reference Kriegl, Michor and RainerKMR11].
$E$
. The proof can be easily adapted to this case; cf. [Reference Kriegl, Michor and RainerKMR09] or [Reference Kriegl, Michor and RainerKMR11].
The next lemma is a variant of [Reference Kriegl and MichorKM97, Lemma 2.8]. Recall that, given some sequence
![]() $\unicode[STIX]{x1D707}_{k}\rightarrow \infty$
, a sequence
$\unicode[STIX]{x1D707}_{k}\rightarrow \infty$
, a sequence
![]() $x_{k}$
in
$x_{k}$
in
![]() $E$
is called
$E$
is called
![]() $\unicode[STIX]{x1D707}$
-convergent to
$\unicode[STIX]{x1D707}$
-convergent to
![]() $x$
if
$x$
if
![]() $\unicode[STIX]{x1D707}_{k}(x_{k}-x)$
is bounded.
$\unicode[STIX]{x1D707}_{k}(x_{k}-x)$
is bounded.
Lemma 2.6. For any non-quasianalytic weight sequence
![]() $M=(M_{k})$
there is a positive sequence
$M=(M_{k})$
there is a positive sequence
![]() $\unicode[STIX]{x1D706}_{k}\rightarrow 0$
such that the following holds. Let
$\unicode[STIX]{x1D706}_{k}\rightarrow 0$
such that the following holds. Let
![]() $E$
be a Banach space. Let
$E$
be a Banach space. Let
![]() $x_{n}\rightarrow x$
be
$x_{n}\rightarrow x$
be
![]() $1/\unicode[STIX]{x1D706}_{k}$
-convergent in
$1/\unicode[STIX]{x1D706}_{k}$
-convergent in
![]() $E$
. Then the infinite polygon through the
$E$
. Then the infinite polygon through the
![]() $x_{n}$
and
$x_{n}$
and
![]() $x$
can be parameterized as a
$x$
can be parameterized as a
![]() ${\mathcal{C}}^{M}$
-curve
${\mathcal{C}}^{M}$
-curve
![]() $c:\mathbb{R}\rightarrow E$
such that
$c:\mathbb{R}\rightarrow E$
such that
![]() $c(1/n)=x_{n}$
and
$c(1/n)=x_{n}$
and
![]() $c(0)=x$
.
$c(0)=x$
.
Proof. Let
![]() $L=(L_{k})$
be a non-quasianalytic weight sequence with
$L=(L_{k})$
be a non-quasianalytic weight sequence with
![]() $(M_{k}/L_{k})^{1/k}\rightarrow \infty$
. Set
$(M_{k}/L_{k})^{1/k}\rightarrow \infty$
. Set
![]() $T_{j}:=1/(j(j+1))$
and choose
$T_{j}:=1/(j(j+1))$
and choose
![]() $\unicode[STIX]{x1D706}_{j}$
such that the conditions (2.9) and (2.10) are satisfied. Let
$\unicode[STIX]{x1D706}_{j}$
such that the conditions (2.9) and (2.10) are satisfied. Let
![]() $\unicode[STIX]{x1D711}:\mathbb{R}\rightarrow [0,1]$
be a
$\unicode[STIX]{x1D711}:\mathbb{R}\rightarrow [0,1]$
be a
![]() ${\mathcal{C}}^{L}$
-function which vanishes on
${\mathcal{C}}^{L}$
-function which vanishes on
![]() $(-\infty ,0]$
and is
$(-\infty ,0]$
and is
![]() $1$
on
$1$
on
![]() $[1,\infty )$
. Let
$[1,\infty )$
. Let
![]() $t_{n}:=1/n$
and define
$t_{n}:=1/n$
and define
 $$\begin{eqnarray}c(t):=\left\{\begin{array}{@{}ll@{}}\displaystyle x\quad & \displaystyle \text{if }t\leqslant 0,\\ \displaystyle x_{n+1}+\unicode[STIX]{x1D711}\biggl(\frac{t-t_{n+1}}{t_{n}-t_{n+1}}\biggr)(x_{n}-x_{n+1})\quad & \displaystyle \text{if }t_{n+1}\leqslant t\leqslant t_{n},\\ x_{1}\quad & \text{if }t\geqslant 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}c(t):=\left\{\begin{array}{@{}ll@{}}\displaystyle x\quad & \displaystyle \text{if }t\leqslant 0,\\ \displaystyle x_{n+1}+\unicode[STIX]{x1D711}\biggl(\frac{t-t_{n+1}}{t_{n}-t_{n+1}}\biggr)(x_{n}-x_{n+1})\quad & \displaystyle \text{if }t_{n+1}\leqslant t\leqslant t_{n},\\ x_{1}\quad & \text{if }t\geqslant 1.\end{array}\right.\end{eqnarray}$$
Clearly,
![]() $c$
is
$c$
is
![]() ${\mathcal{C}}^{\infty }$
on
${\mathcal{C}}^{\infty }$
on
![]() $\mathbb{R}\setminus \{0\}$
. For
$\mathbb{R}\setminus \{0\}$
. For
![]() $t_{n+1}\leqslant t\leqslant t_{n}$
we have
$t_{n+1}\leqslant t\leqslant t_{n}$
we have
 $$\begin{eqnarray}\displaystyle c^{(k)}(t) & = & \displaystyle \unicode[STIX]{x1D711}^{(k)}\biggl(\frac{t-t_{n+1}}{t_{n}-t_{n+1}}\biggr)(n(n+1))^{k}(x_{n}-x_{n+1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D711}^{(k)}\biggl(\frac{t-t_{n+1}}{t_{n}-t_{n+1}}\biggr)\cdot \frac{\unicode[STIX]{x1D706}_{n}}{T_{n}^{k}}\cdot \frac{x_{n}-x_{n+1}}{\unicode[STIX]{x1D706}_{n}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c^{(k)}(t) & = & \displaystyle \unicode[STIX]{x1D711}^{(k)}\biggl(\frac{t-t_{n+1}}{t_{n}-t_{n+1}}\biggr)(n(n+1))^{k}(x_{n}-x_{n+1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D711}^{(k)}\biggl(\frac{t-t_{n+1}}{t_{n}-t_{n+1}}\biggr)\cdot \frac{\unicode[STIX]{x1D706}_{n}}{T_{n}^{k}}\cdot \frac{x_{n}-x_{n+1}}{\unicode[STIX]{x1D706}_{n}}.\nonumber\end{eqnarray}$$
Condition (2.10) guarantees that
![]() $c^{(k)}(t)\rightarrow 0$
as
$c^{(k)}(t)\rightarrow 0$
as
![]() $t\rightarrow 0$
for all
$t\rightarrow 0$
for all
![]() $k$
, and hence
$k$
, and hence
![]() $c$
is
$c$
is
![]() ${\mathcal{C}}^{\infty }$
on
${\mathcal{C}}^{\infty }$
on
![]() $\mathbb{R}$
. That
$\mathbb{R}$
. That
![]() $c$
is of class
$c$
is of class
![]() ${\mathcal{C}}^{M}$
follows from (2.9).◻
${\mathcal{C}}^{M}$
follows from (2.9).◻
3 Hölder sets
3.1 Uniform cusp property and Hölder sets
We denote by
![]() $B(x,\unicode[STIX]{x1D716}):=\{y\in \mathbb{R}^{d}:|x-y|<\unicode[STIX]{x1D716}\}$
the open ball with center
$B(x,\unicode[STIX]{x1D716}):=\{y\in \mathbb{R}^{d}:|x-y|<\unicode[STIX]{x1D716}\}$
the open ball with center
![]() $x$
and radius
$x$
and radius
![]() $\unicode[STIX]{x1D716}$
in
$\unicode[STIX]{x1D716}$
in
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
Definition 3.1 (Truncated open cusp).
Let us consider
![]() $\mathbb{R}^{d}=\mathbb{R}^{d-1}\times \mathbb{R}$
with the Euclidean coordinates
$\mathbb{R}^{d}=\mathbb{R}^{d-1}\times \mathbb{R}$
with the Euclidean coordinates
![]() $x=(x_{1},\ldots ,x_{d})=(x^{\prime },x_{d})$
. For
$x=(x_{1},\ldots ,x_{d})=(x^{\prime },x_{d})$
. For
![]() $0<\unicode[STIX]{x1D6FC}\leqslant 1$
and
$0<\unicode[STIX]{x1D6FC}\leqslant 1$
and
![]() $r,h>0$
, consider the truncated open cusp
$r,h>0$
, consider the truncated open cusp
For
![]() $\unicode[STIX]{x1D6FC}=1$
this is a truncated open cone.
$\unicode[STIX]{x1D6FC}=1$
this is a truncated open cone.
Definition 3.2 (Uniform cusp property).
Let
![]() $U\subseteq \mathbb{R}^{d}$
be an open set and let
$U\subseteq \mathbb{R}^{d}$
be an open set and let
![]() $\unicode[STIX]{x1D6FC}\in (0,1]$
. We say that
$\unicode[STIX]{x1D6FC}\in (0,1]$
. We say that
![]() $U$
has the uniform cusp property of index
$U$
has the uniform cusp property of index
![]() $\unicode[STIX]{x1D6FC}$
if for every
$\unicode[STIX]{x1D6FC}$
if for every
![]() $x\in \unicode[STIX]{x2202}U$
there exist
$x\in \unicode[STIX]{x2202}U$
there exist
![]() $\unicode[STIX]{x1D716}>0$
, a truncated open cusp
$\unicode[STIX]{x1D716}>0$
, a truncated open cusp
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,h)$
, and an orthogonal linear map
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,h)$
, and an orthogonal linear map
![]() $A\in \operatorname{O}(d)$
such that for all
$A\in \operatorname{O}(d)$
such that for all
![]() $y\in \overline{U}\,\cap \,B(x,\unicode[STIX]{x1D716})$
we have
$y\in \overline{U}\,\cap \,B(x,\unicode[STIX]{x1D716})$
we have
![]() $y+A\unicode[STIX]{x1D6E4}\subseteq U$
.
$y+A\unicode[STIX]{x1D6E4}\subseteq U$
.
Definition 3.3 (Hölder set).
By an
![]() $\unicode[STIX]{x1D6FC}$
-set we mean a closed fat set
$\unicode[STIX]{x1D6FC}$
-set we mean a closed fat set
![]() $X\subseteq \mathbb{R}^{d}$
such that
$X\subseteq \mathbb{R}^{d}$
such that
![]() $\operatorname{int}(X)$
has the uniform cusp property of index
$\operatorname{int}(X)$
has the uniform cusp property of index
![]() $\unicode[STIX]{x1D6FC}$
. We say that
$\unicode[STIX]{x1D6FC}$
. We say that
![]() $X\subseteq \mathbb{R}^{d}$
is a Hölder set if it is an
$X\subseteq \mathbb{R}^{d}$
is a Hölder set if it is an
![]() $\unicode[STIX]{x1D6FC}$
-set for some
$\unicode[STIX]{x1D6FC}$
-set for some
![]() $\unicode[STIX]{x1D6FC}\in (0,1]$
.
$\unicode[STIX]{x1D6FC}\in (0,1]$
.
We denote by
![]() $\mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
the collection of all
$\mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
the collection of all
![]() $\unicode[STIX]{x1D6FC}$
-sets in
$\unicode[STIX]{x1D6FC}$
-sets in
![]() $\mathbb{R}^{d}$
and by
$\mathbb{R}^{d}$
and by
the collection of all Hölder sets in
![]() $\mathbb{R}^{d}$
. Note that
$\mathbb{R}^{d}$
. Note that
![]() $\mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})\subseteq \mathscr{H}^{\unicode[STIX]{x1D6FD}}(\mathbb{R}^{d})$
if
$\mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})\subseteq \mathscr{H}^{\unicode[STIX]{x1D6FD}}(\mathbb{R}^{d})$
if
![]() $\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FD}$
.
Remark 3.4. A bounded open subset
![]() $U\subseteq \mathbb{R}^{d}$
has the uniform cusp property of index
$U\subseteq \mathbb{R}^{d}$
has the uniform cusp property of index
![]() $\unicode[STIX]{x1D6FC}$
if and only if
$\unicode[STIX]{x1D6FC}$
if and only if
![]() $U$
has Hölder boundary of index
$U$
has Hölder boundary of index
![]() $\unicode[STIX]{x1D6FC}$
with uniformly bounded Hölder constant; see [Reference Delfour and ZolésioDZ11, Theorem 6.9, p. 116] and [Reference GrisvardGri85, Theorem 1.2.2.2]. That means the following. At each boundary point
$\unicode[STIX]{x1D6FC}$
with uniformly bounded Hölder constant; see [Reference Delfour and ZolésioDZ11, Theorem 6.9, p. 116] and [Reference GrisvardGri85, Theorem 1.2.2.2]. That means the following. At each boundary point
![]() $p$
there is an orthogonal system of coordinates
$p$
there is an orthogonal system of coordinates
![]() $(x^{\prime },x_{d})$
and an
$(x^{\prime },x_{d})$
and an
![]() $\unicode[STIX]{x1D6FC}$
-Hölder function
$\unicode[STIX]{x1D6FC}$
-Hölder function
![]() $a=a(x^{\prime })$
such that in a neighborhood of
$a=a(x^{\prime })$
such that in a neighborhood of
![]() $p$
the boundary of
$p$
the boundary of
![]() $U$
is given by
$U$
is given by
![]() $\{x_{d}=a(x^{\prime })\}$
and the set
$\{x_{d}=a(x^{\prime })\}$
and the set
![]() $U$
is of the form
$U$
is of the form
![]() $\{x_{d}>a(x^{\prime })\}$
. There is a uniform bound for the Hölder constant of
$\{x_{d}>a(x^{\prime })\}$
. There is a uniform bound for the Hölder constant of
![]() $a$
which is independent of the boundary point
$a$
which is independent of the boundary point
![]() $p$
.
$p$
.
The boundary of an
![]() $\unicode[STIX]{x1D6FC}$
-set with
$\unicode[STIX]{x1D6FC}$
-set with
![]() $\unicode[STIX]{x1D6FC}<1$
can be quite irregular. It may have Hausdorff dimension strictly larger than
$\unicode[STIX]{x1D6FC}<1$
can be quite irregular. It may have Hausdorff dimension strictly larger than
![]() $d-1$
and hence its Hausdorff measure
$d-1$
and hence its Hausdorff measure
![]() ${\mathcal{H}}^{d-1}$
may be locally infinite. See [Reference Delfour and ZolésioDZ11, Theorem 6.10, p. 116].
${\mathcal{H}}^{d-1}$
may be locally infinite. See [Reference Delfour and ZolésioDZ11, Theorem 6.10, p. 116].
Example 3.5. (1) The set
![]() $X=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,|y|\leqslant x^{1/\unicode[STIX]{x1D6FC}}\}$
is an
$X=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,|y|\leqslant x^{1/\unicode[STIX]{x1D6FC}}\}$
is an
![]() $\unicode[STIX]{x1D6FC}$
-set.
$\unicode[STIX]{x1D6FC}$
-set.
(2) The set
![]() $X=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,x^{2}\leqslant y\leqslant 2x^{2}\}$
is not a Hölder set, but
$X=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,x^{2}\leqslant y\leqslant 2x^{2}\}$
is not a Hölder set, but
![]() $X$
is the image of the Hölder set
$X$
is the image of the Hölder set
![]() $\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,|y|\leqslant x^{2}/2\}$
under the diffeomorphism
$\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,|y|\leqslant x^{2}/2\}$
under the diffeomorphism
![]() $(x,y)\mapsto (x,y+3x^{2}/2)$
of
$(x,y)\mapsto (x,y+3x^{2}/2)$
of
![]() $\mathbb{R}^{2}$
.
$\mathbb{R}^{2}$
.
(3) The set
![]() $X=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,x^{3/2}\leqslant y\leqslant 2x^{3/2}\}$
is not a Hölder set and there is no smooth diffeomorphism of
$X=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,x^{3/2}\leqslant y\leqslant 2x^{3/2}\}$
is not a Hölder set and there is no smooth diffeomorphism of
![]() $\mathbb{R}^{2}$
which maps
$\mathbb{R}^{2}$
which maps
![]() $X$
to a Hölder set.
$X$
to a Hölder set.
(4) Let
![]() $C\subseteq [0,1]$
be the Cantor set and let
$C\subseteq [0,1]$
be the Cantor set and let
![]() $f:[0,1]\rightarrow \mathbb{R}$
be defined by
$f:[0,1]\rightarrow \mathbb{R}$
be defined by
![]() $f(x):=\operatorname{dist}(x,C)^{\unicode[STIX]{x1D6FC}}$
. Then the set
$f(x):=\operatorname{dist}(x,C)^{\unicode[STIX]{x1D6FC}}$
. Then the set
![]() $X=\{(x,y)\in \mathbb{R}^{2}:-1\leqslant x\leqslant 2,f(x)\leqslant y\leqslant 2\text{ if }x\in [0,1],0\leqslant y\leqslant 2\text{ if }x\not \in [0,1]\}$
is an
$X=\{(x,y)\in \mathbb{R}^{2}:-1\leqslant x\leqslant 2,f(x)\leqslant y\leqslant 2\text{ if }x\in [0,1],0\leqslant y\leqslant 2\text{ if }x\not \in [0,1]\}$
is an
![]() $\unicode[STIX]{x1D6FC}$
-set.
$\unicode[STIX]{x1D6FC}$
-set.
3.2
 $c^{\infty }$
-topology on Hölder sets
$c^{\infty }$
-topology on Hölder sets
The
![]() $c^{\infty }$
-topology on a locally convex space
$c^{\infty }$
-topology on a locally convex space
![]() $E$
is the final topology with respect to all smooth curves
$E$
is the final topology with respect to all smooth curves
![]() $c:\mathbb{R}\rightarrow E$
. The
$c:\mathbb{R}\rightarrow E$
. The
![]() $c^{\infty }$
-topology on
$c^{\infty }$
-topology on
![]() $\mathbb{R}^{d}$
coincides with the usual topology; cf. [Reference Kriegl and MichorKM97, Theorem 4.11]. The
$\mathbb{R}^{d}$
coincides with the usual topology; cf. [Reference Kriegl and MichorKM97, Theorem 4.11]. The
![]() $c^{\infty }$
-topology on a subset
$c^{\infty }$
-topology on a subset
![]() $X\subseteq E$
is the final topology with respect to all smooth curves
$X\subseteq E$
is the final topology with respect to all smooth curves
![]() $c:\mathbb{R}\rightarrow E$
satisfying
$c:\mathbb{R}\rightarrow E$
satisfying
![]() $c(\mathbb{R})\subseteq X$
.
$c(\mathbb{R})\subseteq X$
.
Proposition 3.6. Let
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
. Then the
$X\in \mathscr{H}(\mathbb{R}^{d})$
. Then the
![]() $c^{\infty }$
-topology of
$c^{\infty }$
-topology of
![]() $X$
coincides with the trace topology from
$X$
coincides with the trace topology from
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
Proof. Let
![]() $A\subseteq X$
be
$A\subseteq X$
be
![]() $c^{\infty }$
-closed in
$c^{\infty }$
-closed in
![]() $X$
. Let
$X$
. Let
![]() $\overline{A}$
be the closure of
$\overline{A}$
be the closure of
![]() $A$
in
$A$
in
![]() $\mathbb{R}^{d}$
. We have to show that
$\mathbb{R}^{d}$
. We have to show that
![]() $\overline{A}\,\cap \,X=\overline{A}\subseteq A$
. The converse implication is obvious.
$\overline{A}\,\cap \,X=\overline{A}\subseteq A$
. The converse implication is obvious.
Let
![]() $x\in \overline{A}$
. Then there is a sequence
$x\in \overline{A}$
. Then there is a sequence
![]() $x_{n}\in A$
which tends to
$x_{n}\in A$
which tends to
![]() $x$
. It suffices to find a smooth curve
$x$
. It suffices to find a smooth curve
![]() $c\in {\mathcal{C}}^{\infty }(\mathbb{R},X)$
passing through a subsequence of
$c\in {\mathcal{C}}^{\infty }(\mathbb{R},X)$
passing through a subsequence of
![]() $x_{n}$
and through
$x_{n}$
and through
![]() $x$
. Since
$x$
. Since
![]() $A$
is
$A$
is
![]() $c^{\infty }$
-closed in
$c^{\infty }$
-closed in
![]() $X$
, this shows
$X$
, this shows
![]() $x\in A$
.
$x\in A$
.
Since
![]() $X$
is an
$X$
is an
![]() $\unicode[STIX]{x1D6FC}$
-set, for some
$\unicode[STIX]{x1D6FC}$
-set, for some
![]() $0<\unicode[STIX]{x1D6FC}\leqslant 1$
, we may assume that there exist a neighborhood
$0<\unicode[STIX]{x1D6FC}\leqslant 1$
, we may assume that there exist a neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
![]() $X$
and a cusp
$X$
and a cusp
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,h)$
such that for all
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,h)$
such that for all
![]() $y\in U$
we have
$y\in U$
we have
![]() $y+\unicode[STIX]{x1D6E4}\subseteq \operatorname{int}(X)$
. By rescaling, we may assume that
$y+\unicode[STIX]{x1D6E4}\subseteq \operatorname{int}(X)$
. By rescaling, we may assume that
![]() $r=h=1$
.
$r=h=1$
.
Consider
![]() $C(y,r):=y+\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,r^{\unicode[STIX]{x1D6FC}})$
for
$C(y,r):=y+\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,r^{\unicode[STIX]{x1D6FC}})$
for
![]() $0<r\leqslant 1$
. It is easy to see that there is a universal constant
$0<r\leqslant 1$
. It is easy to see that there is a universal constant
![]() $c>0$
such that
$c>0$
such that
![]() $C(y_{1},r_{1})\,\cap \,C(y_{2},r_{2})\neq \emptyset$
provided that
$C(y_{1},r_{1})\,\cap \,C(y_{2},r_{2})\neq \emptyset$
provided that
![]() $|y_{1}-y_{2}|\leqslant c\min \{r_{1},r_{2}\}$
.
$|y_{1}-y_{2}|\leqslant c\min \{r_{1},r_{2}\}$
.
Choose a decreasing sequence
![]() $\unicode[STIX]{x1D707}_{n}$
which tends to
$\unicode[STIX]{x1D707}_{n}$
which tends to
![]() $0$
faster than any polynomial. By passing to a subsequence of
$0$
faster than any polynomial. By passing to a subsequence of
![]() $x_{n}$
(again denoted by
$x_{n}$
(again denoted by
![]() $x_{n}$
), we may assume that
$x_{n}$
), we may assume that
![]() $|x-x_{n}|\leqslant c\unicode[STIX]{x1D707}_{n+1}/2$
for all
$|x-x_{n}|\leqslant c\unicode[STIX]{x1D707}_{n+1}/2$
for all
![]() $n$
. Then, for all
$n$
. Then, for all
![]() $n$
,
$n$
,
Setting
![]() $C_{n}:=C(x_{n},\unicode[STIX]{x1D707}_{n})$
, this guarantees the existence of a sequence
$C_{n}:=C(x_{n},\unicode[STIX]{x1D707}_{n})$
, this guarantees the existence of a sequence
![]() $u_{n}$
such that
$u_{n}$
such that
![]() $u_{n+1}\in C_{n}\,\cap \,C_{n+1}$
for all
$u_{n+1}\in C_{n}\,\cap \,C_{n+1}$
for all
![]() $n$
. By construction,
$n$
. By construction,
![]() $x_{n}$
and
$x_{n}$
and
![]() $u_{n}$
tend to
$u_{n}$
tend to
![]() $x$
faster than any polynomial.
$x$
faster than any polynomial.

Figure 1. The polygon
![]() $P_{n}$
.
$P_{n}$
.
For
![]() $u\in C_{n}$
define
$u\in C_{n}$
define
![]() $\unicode[STIX]{x1D70B}_{n}(u):=x_{n}+u_{d}e_{d}$
(where
$\unicode[STIX]{x1D70B}_{n}(u):=x_{n}+u_{d}e_{d}$
(where
![]() $\{e_{i}\}$
is the standard basis in
$\{e_{i}\}$
is the standard basis in
![]() $\mathbb{R}^{d}$
). Consider the polygon
$\mathbb{R}^{d}$
). Consider the polygon
![]() $P_{n}$
through the points
$P_{n}$
through the points
![]() $u_{n}$
,
$u_{n}$
,
![]() $\unicode[STIX]{x1D70B}_{n}(u_{n})$
,
$\unicode[STIX]{x1D70B}_{n}(u_{n})$
,
![]() $x_{n}$
,
$x_{n}$
,
![]() $\unicode[STIX]{x1D70B}_{n}(u_{n+1})$
,
$\unicode[STIX]{x1D70B}_{n}(u_{n+1})$
,
![]() $u_{n+1}$
(see Figure 1). It is contained in
$u_{n+1}$
(see Figure 1). It is contained in
![]() $C_{n}$
. The infinite polygon consisting of the concatenation of all
$C_{n}$
. The infinite polygon consisting of the concatenation of all
![]() $P_{n}$
satisfies the assumptions of [Reference Kriegl and MichorKM97, Lemma 2.8] and can hence by parameterized by a smooth curve
$P_{n}$
satisfies the assumptions of [Reference Kriegl and MichorKM97, Lemma 2.8] and can hence by parameterized by a smooth curve
![]() $c$
which is contained in
$c$
which is contained in
![]() $X$
and satisfies
$X$
and satisfies
![]() $c(0)=x$
.◻
$c(0)=x$
.◻
Remark 3.7. It is not difficult to modify the proof in order to obtain the following result. Let
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
and let
$X\in \mathscr{H}(\mathbb{R}^{d})$
and let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence. Then the final topology on
$M=(M_{k})$
be a non-quasianalytic weight sequence. Then the final topology on
![]() $X$
with respect to all
$X$
with respect to all
![]() ${\mathcal{C}}^{M}$
-curves
${\mathcal{C}}^{M}$
-curves
![]() $c:\mathbb{R}\rightarrow \mathbb{R}^{d}$
with
$c:\mathbb{R}\rightarrow \mathbb{R}^{d}$
with
![]() $c(\mathbb{R})\subseteq X$
coincides with the trace topology from
$c(\mathbb{R})\subseteq X$
coincides with the trace topology from
![]() $\mathbb{R}^{d}$
. It suffices to take
$\mathbb{R}^{d}$
. It suffices to take
![]() $\unicode[STIX]{x1D707}_{n}:=\unicode[STIX]{x1D706}_{n}^{1/\unicode[STIX]{x1D6FC}}$
for the sequence
$\unicode[STIX]{x1D707}_{n}:=\unicode[STIX]{x1D706}_{n}^{1/\unicode[STIX]{x1D6FC}}$
for the sequence
![]() $\unicode[STIX]{x1D706}_{n}$
provided by Lemma 2.6.
$\unicode[STIX]{x1D706}_{n}$
provided by Lemma 2.6.
3.3 Further properties of Hölder sets
The following proposition is well known. We include a proof for the convenience of the reader.
Proposition 3.8. Let
![]() $X\in \mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
. Then for each
$X\in \mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
. Then for each
![]() $x\in X$
there exist a compact neighborhood
$x\in X$
there exist a compact neighborhood
![]() $K$
of
$K$
of
![]() $x$
in
$x$
in
![]() $X$
and a constant
$X$
and a constant
![]() $D>0$
such that any two points
$D>0$
such that any two points
![]() $y_{1},y_{2}\in K$
can be joined by a polygon
$y_{1},y_{2}\in K$
can be joined by a polygon
![]() $\unicode[STIX]{x1D6FE}$
contained in
$\unicode[STIX]{x1D6FE}$
contained in
![]() $K$
with
$K$
with
![]() $\unicode[STIX]{x2202}X\,\cap \,\unicode[STIX]{x1D6FE}\subseteq \{y_{1},y_{2}\}$
of length
$\unicode[STIX]{x2202}X\,\cap \,\unicode[STIX]{x1D6FE}\subseteq \{y_{1},y_{2}\}$
of length
Proof. Clearly each
![]() $x\in \operatorname{int}(X)$
has this property. Let
$x\in \operatorname{int}(X)$
has this property. Let
![]() $x\in \unicode[STIX]{x2202}X$
. We may assume that in a compact neighborhood
$x\in \unicode[STIX]{x2202}X$
. We may assume that in a compact neighborhood
![]() $K$
of
$K$
of
![]() $x$
the set
$x$
the set
![]() $X$
is the epigraph
$X$
is the epigraph
![]() $\{x_{d}\geqslant f(x^{\prime })\}$
of a
$\{x_{d}\geqslant f(x^{\prime })\}$
of a
![]() $\unicode[STIX]{x1D6FC}$
-Hölder function
$\unicode[STIX]{x1D6FC}$
-Hölder function
![]() $f$
with respect to an orthogonal system of coordinates
$f$
with respect to an orthogonal system of coordinates
![]() $(x^{\prime },x_{d})=(x_{1},\ldots ,x_{d})$
. For two points
$(x^{\prime },x_{d})=(x_{1},\ldots ,x_{d})$
. For two points
![]() $y_{1},y_{2}\in K$
consider the segments
$y_{1},y_{2}\in K$
consider the segments
![]() $S:=[y_{1},y_{2}]$
and
$S:=[y_{1},y_{2}]$
and
![]() $S^{\prime }:=[y_{1}^{\prime },y_{2}^{\prime }]$
. If
$S^{\prime }:=[y_{1}^{\prime },y_{2}^{\prime }]$
. If
![]() $(y_{1},y_{2})\subseteq K\,\cap \,\operatorname{int}(X)$
there is nothing to prove. Otherwise let
$(y_{1},y_{2})\subseteq K\,\cap \,\operatorname{int}(X)$
there is nothing to prove. Otherwise let
![]() $z^{\prime }\in S^{\prime }$
be such that
$z^{\prime }\in S^{\prime }$
be such that
![]() $f(z^{\prime })=\max _{y^{\prime }\in S^{\prime }}f(y^{\prime })$
and let
$f(z^{\prime })=\max _{y^{\prime }\in S^{\prime }}f(y^{\prime })$
and let
![]() $z=(z^{\prime },z_{d})$
with
$z=(z^{\prime },z_{d})$
with
![]() $z_{d}:=f(z^{\prime })+\unicode[STIX]{x1D716}|y_{1}-y_{2}|$
for some small
$z_{d}:=f(z^{\prime })+\unicode[STIX]{x1D716}|y_{1}-y_{2}|$
for some small
![]() $\unicode[STIX]{x1D716}>0$
such that
$\unicode[STIX]{x1D716}>0$
such that
![]() $z\in K\,\cap \,\operatorname{int}(X)$
. It is possible to choose
$z\in K\,\cap \,\operatorname{int}(X)$
. It is possible to choose
![]() $\unicode[STIX]{x1D716}$
such that it only depends on
$\unicode[STIX]{x1D716}$
such that it only depends on
![]() $K$
, not on
$K$
, not on
![]() $y_{1},y_{2}$
. We have
$y_{1},y_{2}$
. We have
![]() $(y_{i})_{d}\leqslant f(z^{\prime })$
and thus
$(y_{i})_{d}\leqslant f(z^{\prime })$
and thus
![]() $|(y_{i})_{d}-f(z^{\prime })|\leqslant |f(y_{i}^{\prime })-f(z^{\prime })|$
for at least one
$|(y_{i})_{d}-f(z^{\prime })|\leqslant |f(y_{i}^{\prime })-f(z^{\prime })|$
for at least one
![]() $i\in \{1,2\}$
, say for
$i\in \{1,2\}$
, say for
![]() $i=1$
. If
$i=1$
. If
![]() $(y_{2})_{d}\leqslant f(z^{\prime })$
, then the polygon with vertices
$(y_{2})_{d}\leqslant f(z^{\prime })$
, then the polygon with vertices
![]() $y_{1}$
,
$y_{1}$
,
![]() $(y_{1}^{\prime },z_{d})$
,
$(y_{1}^{\prime },z_{d})$
,
![]() $(y_{2}^{\prime },z_{d})$
,
$(y_{2}^{\prime },z_{d})$
,
![]() $y_{2}$
is contained in
$y_{2}$
is contained in
![]() $K$
, meets
$K$
, meets
![]() $\unicode[STIX]{x2202}X$
at most at one of the points
$\unicode[STIX]{x2202}X$
at most at one of the points
![]() $y_{i}$
, and has length
$y_{i}$
, and has length
 $$\begin{eqnarray}\displaystyle & & \displaystyle |(y_{1})_{d}-z_{d}|+|(y_{2})_{d}-z_{d}|+|y_{1}^{\prime }-y_{2}^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,|f(y_{1}^{\prime })-f(z^{\prime })|+|f(y_{2}^{\prime })-f(z^{\prime })|+2\unicode[STIX]{x1D716}|y_{1}-y_{2}|+|y_{1}^{\prime }-y_{2}^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C|y_{1}^{\prime }-z^{\prime }|^{\unicode[STIX]{x1D6FC}}+C|y_{2}^{\prime }-z^{\prime }|^{\unicode[STIX]{x1D6FC}}+(1+2\unicode[STIX]{x1D716})|y_{1}-y_{2}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,D|y_{1}-y_{2}|^{\unicode[STIX]{x1D6FC}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |(y_{1})_{d}-z_{d}|+|(y_{2})_{d}-z_{d}|+|y_{1}^{\prime }-y_{2}^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,|f(y_{1}^{\prime })-f(z^{\prime })|+|f(y_{2}^{\prime })-f(z^{\prime })|+2\unicode[STIX]{x1D716}|y_{1}-y_{2}|+|y_{1}^{\prime }-y_{2}^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,C|y_{1}^{\prime }-z^{\prime }|^{\unicode[STIX]{x1D6FC}}+C|y_{2}^{\prime }-z^{\prime }|^{\unicode[STIX]{x1D6FC}}+(1+2\unicode[STIX]{x1D716})|y_{1}-y_{2}|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,D|y_{1}-y_{2}|^{\unicode[STIX]{x1D6FC}},\nonumber\end{eqnarray}$$
for constants only depending on
![]() $K$
. If
$K$
. If
![]() $(y_{2})_{d}>f(z^{\prime })$
, then the segment joining
$(y_{2})_{d}>f(z^{\prime })$
, then the segment joining
![]() $z$
and
$z$
and
![]() $y_{2}$
is contained in
$y_{2}$
is contained in
![]() $K\,\cap \,\operatorname{int}(X)$
, and thus the polygon with vertices
$K\,\cap \,\operatorname{int}(X)$
, and thus the polygon with vertices
![]() $y_{1}$
,
$y_{1}$
,
![]() $(y_{1}^{\prime },z_{d})$
,
$(y_{1}^{\prime },z_{d})$
,
![]() $z$
,
$z$
,
![]() $y_{2}$
is contained in
$y_{2}$
is contained in
![]() $K$
, meets
$K$
, meets
![]() $\unicode[STIX]{x2202}X$
at most at one of the points
$\unicode[STIX]{x2202}X$
at most at one of the points
![]() $y_{i}$
, and has length
$y_{i}$
, and has length
 $$\begin{eqnarray}\displaystyle & & \displaystyle |(y_{1})_{d}-z_{d}|+|y_{2}-z|+|y_{1}^{\prime }-z^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,|f(y_{1}^{\prime })-f(z^{\prime })|+(1+\unicode[STIX]{x1D716})|y_{1}-y_{2}|+|y_{1}^{\prime }-y_{2}^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,D|y_{1}-y_{2}|^{\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle |(y_{1})_{d}-z_{d}|+|y_{2}-z|+|y_{1}^{\prime }-z^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,|f(y_{1}^{\prime })-f(z^{\prime })|+(1+\unicode[STIX]{x1D716})|y_{1}-y_{2}|+|y_{1}^{\prime }-y_{2}^{\prime }|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \,D|y_{1}-y_{2}|^{\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
This finishes the proof. ◻
Proposition 3.9. Every
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
is simple in the sense of Definition 1.11.
$X\in \mathscr{H}(\mathbb{R}^{d})$
is simple in the sense of Definition 1.11.
Proof. The proof of Proposition 3.8 implies that there is a basis of neighborhoods
![]() $\mathscr{U}$
of each
$\mathscr{U}$
of each
![]() $x\in X$
such that
$x\in X$
such that
![]() $\operatorname{int}(X)\,\cap \,U$
is path-connected for each
$\operatorname{int}(X)\,\cap \,U$
is path-connected for each
![]() $U\in \mathscr{U}$
.◻
$U\in \mathscr{U}$
.◻
4 Arc-smooth functions on Hölder sets
The aim of this section is to prove Theorem 1.13: Every
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
is
$X\in \mathscr{H}(\mathbb{R}^{d})$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible. We even have
${\mathcal{A}}^{\infty }$
-admissible. We even have
for any non-quasianalytic weight sequence
![]() $M=(M_{n})$
.
$M=(M_{n})$
.
Remark 4.1. For fat closed convex sets
![]() $X\subseteq \mathbb{R}^{d}$
,
$X\subseteq \mathbb{R}^{d}$
,
![]() ${\mathcal{A}}^{\infty }$
-admissibility follows from a result of Kriegl [Reference KrieglKri97]. The statement in [Reference KrieglKri97] is more general: Let
${\mathcal{A}}^{\infty }$
-admissibility follows from a result of Kriegl [Reference KrieglKri97]. The statement in [Reference KrieglKri97] is more general: Let
![]() $X$
be a convex subset of a convenient vector space
$X$
be a convex subset of a convenient vector space
![]() $E$
with non-empty interior. Then
$E$
with non-empty interior. Then
![]() $f\in {\mathcal{A}}^{\infty }(X)$
if and only if
$f\in {\mathcal{A}}^{\infty }(X)$
if and only if
![]() $f$
is smooth on
$f$
is smooth on
![]() $\operatorname{int}(X)$
and all Fréchet derivatives
$\operatorname{int}(X)$
and all Fréchet derivatives
![]() $(f|_{\operatorname{int}(X)})^{(n)}$
extend continuously to
$(f|_{\operatorname{int}(X)})^{(n)}$
extend continuously to
![]() $f^{(n)}:X\rightarrow L_{n}(E,\mathbb{R})$
with respect to the
$f^{(n)}:X\rightarrow L_{n}(E,\mathbb{R})$
with respect to the
![]() $c^{\infty }$
-topology of
$c^{\infty }$
-topology of
![]() $X$
. In general the
$X$
. In general the
![]() $c^{\infty }$
-topology is finer than the given locally convex topology.
$c^{\infty }$
-topology is finer than the given locally convex topology.
It is evident that
The second inclusion is by definition; the first inclusion is a simple consequence of the chain rule. Let us prove the other inclusions.
Lemma 4.2. Let
![]() $1\leqslant p\leqslant q$
be integers. For
$1\leqslant p\leqslant q$
be integers. For
![]() $x\in \mathbb{R}^{d}$
and
$x\in \mathbb{R}^{d}$
and
![]() $v=(v^{\prime },v_{d})\in \mathbb{R}^{d}$
let
$v=(v^{\prime },v_{d})\in \mathbb{R}^{d}$
let
![]() $c(t)=x+(t^{q}v^{\prime },t^{p}v_{d})$
, for
$c(t)=x+(t^{q}v^{\prime },t^{p}v_{d})$
, for
![]() $t$
in a neighborhood of
$t$
in a neighborhood of
![]() $0\in \mathbb{R}$
. Let
$0\in \mathbb{R}$
. Let
![]() $f$
be of class
$f$
be of class
![]() ${\mathcal{C}}^{q}$
in a neighborhood of the image of
${\mathcal{C}}^{q}$
in a neighborhood of the image of
![]() $c$
. Then
$c$
. Then
 $$\begin{eqnarray}\frac{(f\,\circ \,c)^{(k)}(0)}{k!}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{j!}f^{(j)}(x)((0,v_{d})^{j})\quad & \text{if }k=jp<q,\\ \displaystyle f^{\prime }(x)((v^{\prime },0))\quad & \text{if }k=q\not \in p\mathbb{N},\\ \displaystyle f^{\prime }(x)((v^{\prime },0))+\frac{1}{j!}f^{(j)}(x)((0,v_{d})^{j})\quad & \text{if }k=jp=q.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\frac{(f\,\circ \,c)^{(k)}(0)}{k!}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{j!}f^{(j)}(x)((0,v_{d})^{j})\quad & \text{if }k=jp<q,\\ \displaystyle f^{\prime }(x)((v^{\prime },0))\quad & \text{if }k=q\not \in p\mathbb{N},\\ \displaystyle f^{\prime }(x)((v^{\prime },0))+\frac{1}{j!}f^{(j)}(x)((0,v_{d})^{j})\quad & \text{if }k=jp=q.\end{array}\right.\end{eqnarray}$$
For all other
![]() $k<q$
we have
$k<q$
we have
![]() $(f\,\circ \,c)^{(k)}(0)=0$
.
$(f\,\circ \,c)^{(k)}(0)=0$
.
Proof. This follows easily from an inspection of the Faà di Bruno formula
 $$\begin{eqnarray}\frac{(f\,\circ \,c)^{(k)}(t)}{k!}=\mathop{\sum }_{j\geqslant 1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}_{i}>0 \\ \unicode[STIX]{x1D6FC}_{1}+\cdots +\unicode[STIX]{x1D6FC}_{j}=k}}\frac{f^{(j)}(c(t))}{j!}\biggl(\frac{c^{(\unicode[STIX]{x1D6FC}_{1})}(t)}{\unicode[STIX]{x1D6FC}_{1}!},\ldots ,\frac{c^{(\unicode[STIX]{x1D6FC}_{j})}(t)}{\unicode[STIX]{x1D6FC}_{j}!}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\frac{(f\,\circ \,c)^{(k)}(t)}{k!}=\mathop{\sum }_{j\geqslant 1}\mathop{\sum }_{\substack{ \unicode[STIX]{x1D6FC}_{i}>0 \\ \unicode[STIX]{x1D6FC}_{1}+\cdots +\unicode[STIX]{x1D6FC}_{j}=k}}\frac{f^{(j)}(c(t))}{j!}\biggl(\frac{c^{(\unicode[STIX]{x1D6FC}_{1})}(t)}{\unicode[STIX]{x1D6FC}_{1}!},\ldots ,\frac{c^{(\unicode[STIX]{x1D6FC}_{j})}(t)}{\unicode[STIX]{x1D6FC}_{j}!}\biggr)\end{eqnarray}$$
and the special form of
![]() $c$
.◻
$c$
.◻
Proposition 4.3. Let
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
and
$X\in \mathscr{H}(\mathbb{R}^{d})$
and
![]() $f\in {\mathcal{A}}^{\infty }(X)$
. Then
$f\in {\mathcal{A}}^{\infty }(X)$
. Then
![]() $f|_{\operatorname{int}(X)}$
is smooth and its derivative
$f|_{\operatorname{int}(X)}$
is smooth and its derivative
![]() $(f|_{\operatorname{int}(X)})^{\prime }$
extends uniquely to a mapping
$(f|_{\operatorname{int}(X)})^{\prime }$
extends uniquely to a mapping
![]() $f^{\prime }:X\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
which belongs to
$f^{\prime }:X\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
which belongs to
![]() ${\mathcal{A}}^{\infty }(X,L(\mathbb{R}^{d},\mathbb{R}))$
, that is,
${\mathcal{A}}^{\infty }(X,L(\mathbb{R}^{d},\mathbb{R}))$
, that is,
Proof. That
![]() $f|_{\operatorname{int}(X)}$
is smooth follows from Boman’s Theorem 1.1.
$f|_{\operatorname{int}(X)}$
is smooth follows from Boman’s Theorem 1.1.
There is
![]() $0<\unicode[STIX]{x1D6FC}\leqslant 1$
such that
$0<\unicode[STIX]{x1D6FC}\leqslant 1$
such that
![]() $X\in \mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
. Let
$X\in \mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
. Let
![]() $x\in \unicode[STIX]{x2202}X$
. We may assume that there exist a truncated open cusp
$x\in \unicode[STIX]{x2202}X$
. We may assume that there exist a truncated open cusp
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,h)$
and an open neighborhood
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{\unicode[STIX]{x1D6FC}}(r,h)$
and an open neighborhood
![]() $Y$
of
$Y$
of
![]() $x$
in X such that for all
$x$
in X such that for all
![]() $y\in Y$
we have
$y\in Y$
we have
![]() $y+\unicode[STIX]{x1D6E4}\subseteq \operatorname{int}(X)$
. It suffices to show that
$y+\unicode[STIX]{x1D6E4}\subseteq \operatorname{int}(X)$
. It suffices to show that
![]() $(f|_{Y\,\cap \,\operatorname{int}(X)})^{\prime }$
extends uniquely to a mapping
$(f|_{Y\,\cap \,\operatorname{int}(X)})^{\prime }$
extends uniquely to a mapping
![]() $f^{\prime }:Y\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
which belongs to
$f^{\prime }:Y\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
which belongs to
![]() ${\mathcal{A}}^{\infty }(Y,L(\mathbb{R}^{d},\mathbb{R}))$
.
${\mathcal{A}}^{\infty }(Y,L(\mathbb{R}^{d},\mathbb{R}))$
.
Let
![]() $p<q$
be positive integers such that
$p<q$
be positive integers such that
![]() $p/q\leqslant \unicode[STIX]{x1D6FC}$
and
$p/q\leqslant \unicode[STIX]{x1D6FC}$
and
![]() $q/p\not \in \mathbb{N}$
. Let
$q/p\not \in \mathbb{N}$
. Let
![]() $x\in Y$
and
$x\in Y$
and
![]() $v=(v^{\prime },v_{d})\in \unicode[STIX]{x1D6E4}$
. Then the curve
$v=(v^{\prime },v_{d})\in \unicode[STIX]{x1D6E4}$
. Then the curve
lies in
![]() $\operatorname{int}(X)$
for
$\operatorname{int}(X)$
for
![]() $0<|t|<1$
and
$0<|t|<1$
and
![]() $c_{x,v}(0)=x$
. Since
$c_{x,v}(0)=x$
. Since
![]() $f\in {\mathcal{A}}^{\infty }(X)$
,
$f\in {\mathcal{A}}^{\infty }(X)$
,
![]() $f\,\circ \,c_{x,v}$
is
$f\,\circ \,c_{x,v}$
is
![]() ${\mathcal{C}}^{\infty }$
.
${\mathcal{C}}^{\infty }$
.
Let
![]() $v\in \unicode[STIX]{x1D6E4}$
be fixed. We define
$v\in \unicode[STIX]{x1D6E4}$
be fixed. We define
This definition turns into a correct statement if
![]() $x\in \operatorname{int}(X)$
, by Lemma 4.2.
$x\in \operatorname{int}(X)$
, by Lemma 4.2.
We claim that
Let
![]() $\mathbb{R}\ni s\mapsto x(s)$
be a
$\mathbb{R}\ni s\mapsto x(s)$
be a
![]() ${\mathcal{C}}^{\infty }$
-curve in
${\mathcal{C}}^{\infty }$
-curve in
![]() $Y$
. Then
$Y$
. Then
![]() $(s,t)\mapsto c_{x(s),v}(t)$
is a smooth mapping near
$(s,t)\mapsto c_{x(s),v}(t)$
is a smooth mapping near
![]() $(0,0)$
with values in
$(0,0)$
with values in
![]() $X$
. Thus
$X$
. Thus
![]() $(s,t)\mapsto f(c_{x(s),v}(t))$
is smooth, by Boman’s Theorem 1.1. So, in particular,
$(s,t)\mapsto f(c_{x(s),v}(t))$
is smooth, by Boman’s Theorem 1.1. So, in particular,
![]() $s\mapsto \unicode[STIX]{x2202}_{t}^{k}|_{t=0}(f\,\circ \,c_{x(s),v}(t))$
is smooth for all
$s\mapsto \unicode[STIX]{x2202}_{t}^{k}|_{t=0}(f\,\circ \,c_{x(s),v}(t))$
is smooth for all
![]() $k$
. It follows that
$k$
. It follows that
![]() $s\mapsto f^{\prime }(x(s))(v)$
is smooth, which implies the claim.
$s\mapsto f^{\prime }(x(s))(v)$
is smooth, which implies the claim.
Let
![]() $s\mapsto x(s)$
be any
$s\mapsto x(s)$
be any
![]() ${\mathcal{C}}^{\infty }$
-curve in
${\mathcal{C}}^{\infty }$
-curve in
![]() $Y$
such that
$Y$
such that
![]() $x(s)\in \operatorname{int}(X)$
for
$x(s)\in \operatorname{int}(X)$
for
![]() $0<|s|\leqslant 1$
and
$0<|s|\leqslant 1$
and
![]() $x(0)=x_{0}$
. Then
$x(0)=x_{0}$
. Then
 $$\begin{eqnarray}\displaystyle f^{\prime }(x_{0})(v) & = & \displaystyle \frac{(f\,\circ \,c_{x_{0},v})^{(2p)}(0)}{(2p)!}+\frac{(f\,\circ \,c_{x_{0},v})^{(2q)}(0)}{(2q)!}\nonumber\\ \displaystyle & = & \displaystyle \lim _{s\rightarrow 0}\biggl(\frac{(f\,\circ \,c_{x(s),v})^{(2p)}(0)}{(2p)!}+\frac{(f\,\circ \,c_{x(s),v})^{(2q)}(0)}{(2q)!}\biggr)=\lim _{s\rightarrow 0}f^{\prime }(x(s))(v).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f^{\prime }(x_{0})(v) & = & \displaystyle \frac{(f\,\circ \,c_{x_{0},v})^{(2p)}(0)}{(2p)!}+\frac{(f\,\circ \,c_{x_{0},v})^{(2q)}(0)}{(2q)!}\nonumber\\ \displaystyle & = & \displaystyle \lim _{s\rightarrow 0}\biggl(\frac{(f\,\circ \,c_{x(s),v})^{(2p)}(0)}{(2p)!}+\frac{(f\,\circ \,c_{x(s),v})^{(2q)}(0)}{(2q)!}\biggr)=\lim _{s\rightarrow 0}f^{\prime }(x(s))(v).\nonumber\end{eqnarray}$$
Consequently, the given definition of
![]() $f^{\prime }(x_{0})(v)$
is the only possible extension of
$f^{\prime }(x_{0})(v)$
is the only possible extension of
![]() $f^{\prime }(\cdot )(v)$
to
$f^{\prime }(\cdot )(v)$
to
![]() $x_{0}$
which is continuous on
$x_{0}$
which is continuous on
![]() ${\mathcal{C}}^{\infty }$
-curves.
${\mathcal{C}}^{\infty }$
-curves.
Now let
![]() $v\in \mathbb{R}^{d}$
be arbitrary. Since
$v\in \mathbb{R}^{d}$
be arbitrary. Since
![]() $\unicode[STIX]{x1D6E4}$
is open, there exist
$\unicode[STIX]{x1D6E4}$
is open, there exist
![]() $\unicode[STIX]{x1D716}>0$
and
$\unicode[STIX]{x1D716}>0$
and
![]() $w\in \unicode[STIX]{x1D6E4}$
such that
$w\in \unicode[STIX]{x1D6E4}$
such that
![]() $\unicode[STIX]{x1D716}v+w\in \unicode[STIX]{x1D6E4}$
. For all
$\unicode[STIX]{x1D716}v+w\in \unicode[STIX]{x1D6E4}$
. For all
![]() $x\in Y\,\cap \,\operatorname{int}(X)$
, we have
$x\in Y\,\cap \,\operatorname{int}(X)$
, we have
and the right-hand side uniquely extends to points
![]() $x_{0}\in Y\,\cap \,\unicode[STIX]{x2202}X$
and satisfies (4.3), by the arguments above.
$x_{0}\in Y\,\cap \,\unicode[STIX]{x2202}X$
and satisfies (4.3), by the arguments above.
Thus, we define
![]() $f^{\prime }(x_{0})(v):=\lim _{s\rightarrow 0}f^{\prime }(x(s))(v)$
for some
$f^{\prime }(x_{0})(v):=\lim _{s\rightarrow 0}f^{\prime }(x(s))(v)$
for some
![]() ${\mathcal{C}}^{\infty }$
-curve
${\mathcal{C}}^{\infty }$
-curve
![]() $s\mapsto x(s)$
in
$s\mapsto x(s)$
in
![]() $Y$
with
$Y$
with
![]() $x(0)=x_{0}$
and
$x(0)=x_{0}$
and
![]() $x(s)\in \operatorname{int}(X)$
for
$x(s)\in \operatorname{int}(X)$
for
![]() $0<|s|\leqslant 1$
. Then
$0<|s|\leqslant 1$
. Then
![]() $f^{\prime }(x_{0})$
is linear as the pointwise limit of
$f^{\prime }(x_{0})$
is linear as the pointwise limit of
![]() $f^{\prime }(x(s))\in L(\mathbb{R}^{d},\mathbb{R})$
. The definition does not depend on the curve
$f^{\prime }(x(s))\in L(\mathbb{R}^{d},\mathbb{R})$
. The definition does not depend on the curve
![]() $x$
, since it is the unique extension for
$x$
, since it is the unique extension for
![]() $v\in \unicode[STIX]{x1D6E4}$
.
$v\in \unicode[STIX]{x1D6E4}$
.
Let us finally show that
![]() $f^{\prime }:Y\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
belongs to
$f^{\prime }:Y\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
belongs to
![]() ${\mathcal{A}}^{\infty }(Y,L(\mathbb{R}^{d},\mathbb{R}))$
. Let
${\mathcal{A}}^{\infty }(Y,L(\mathbb{R}^{d},\mathbb{R}))$
. Let
![]() $x:\mathbb{R}\rightarrow Y$
be a
$x:\mathbb{R}\rightarrow Y$
be a
![]() ${\mathcal{C}}^{\infty }$
-curve and let
${\mathcal{C}}^{\infty }$
-curve and let
![]() $v\in \mathbb{R}^{d}$
. It suffices to show that
$v\in \mathbb{R}^{d}$
. It suffices to show that
![]() $s\mapsto f^{\prime }(x(s))(v)$
is smooth. For
$s\mapsto f^{\prime }(x(s))(v)$
is smooth. For
![]() $v\in \unicode[STIX]{x1D6E4}$
this follows from (4.3). For general
$v\in \unicode[STIX]{x1D6E4}$
this follows from (4.3). For general
![]() $v$
,
$v$
,
![]() $f^{\prime }(x(s))(v)$
is a linear combination of
$f^{\prime }(x(s))(v)$
is a linear combination of
![]() $f^{\prime }(x(s))(v_{1})$
and
$f^{\prime }(x(s))(v_{1})$
and
![]() $f^{\prime }(x(s))(v_{2})$
for
$f^{\prime }(x(s))(v_{2})$
for
![]() $v_{i}\in \unicode[STIX]{x1D6E4}$
which locally is independent of
$v_{i}\in \unicode[STIX]{x1D6E4}$
which locally is independent of
![]() $s$
. The proof is complete.◻
$s$
. The proof is complete.◻
Corollary 4.4. Let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence. Let
$M=(M_{k})$
be a non-quasianalytic weight sequence. Let
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
and
$X\in \mathscr{H}(\mathbb{R}^{d})$
and
![]() $f\in {\mathcal{A}}_{M}^{\infty }(X)$
. Then
$f\in {\mathcal{A}}_{M}^{\infty }(X)$
. Then
![]() $f|_{\operatorname{int}(X)}$
is smooth and its derivative
$f|_{\operatorname{int}(X)}$
is smooth and its derivative
![]() $(f|_{\operatorname{int}(X)})^{\prime }$
extends uniquely to a mapping
$(f|_{\operatorname{int}(X)})^{\prime }$
extends uniquely to a mapping
![]() $f^{\prime }:X\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
which belongs to
$f^{\prime }:X\rightarrow L(\mathbb{R}^{d},\mathbb{R})$
which belongs to
![]() ${\mathcal{A}}_{M}^{\infty }(X,L(\mathbb{R}^{n},\mathbb{R}))$
, that is,
${\mathcal{A}}_{M}^{\infty }(X,L(\mathbb{R}^{n},\mathbb{R}))$
, that is,
Proof. The proof is the same with the only difference that we use
![]() ${\mathcal{C}}^{M}$
-curves (thanks to Remark 1.4); note that the curves
${\mathcal{C}}^{M}$
-curves (thanks to Remark 1.4); note that the curves
![]() $c_{x,v}$
are polynomial and thus of class
$c_{x,v}$
are polynomial and thus of class
![]() ${\mathcal{C}}^{M}$
.◻
${\mathcal{C}}^{M}$
.◻
Proof of Theorem 1.13.
Let
![]() $f\in {\mathcal{A}}^{\infty }(X)$
(respectively,
$f\in {\mathcal{A}}^{\infty }(X)$
(respectively,
![]() $f\in {\mathcal{A}}_{M}^{\infty }(X)$
). Proposition 4.3 and Corollary 4.4 imply by induction that the Fréchet derivatives
$f\in {\mathcal{A}}_{M}^{\infty }(X)$
). Proposition 4.3 and Corollary 4.4 imply by induction that the Fréchet derivatives
![]() $(f|_{\operatorname{int}(X)})^{(n)}$
of all orders have unique extensions
$(f|_{\operatorname{int}(X)})^{(n)}$
of all orders have unique extensions
![]() $f^{(n)}:X\rightarrow L_{n}(\mathbb{R}^{d},\mathbb{R})$
which satisfy
$f^{(n)}:X\rightarrow L_{n}(\mathbb{R}^{d},\mathbb{R})$
which satisfy
(respectively,
![]() $(f^{(n)})_{\ast }{\mathcal{C}}^{M}(\mathbb{R},X)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},L_{n}(\mathbb{R}^{d},\mathbb{R}))$
). So
$(f^{(n)})_{\ast }{\mathcal{C}}^{M}(\mathbb{R},X)\subseteq {\mathcal{C}}^{\infty }(\mathbb{R},L_{n}(\mathbb{R}^{d},\mathbb{R}))$
). So
![]() $f$
satisfies Lemma 1.10(3), since the
$f$
satisfies Lemma 1.10(3), since the
![]() $c^{\infty }$
-topology of
$c^{\infty }$
-topology of
![]() $X$
(respectively, the final topology on
$X$
(respectively, the final topology on
![]() $X$
with respect to all
$X$
with respect to all
![]() ${\mathcal{C}}^{M}$
-curves in
${\mathcal{C}}^{M}$
-curves in
![]() $X$
) coincides with the trace topology from
$X$
) coincides with the trace topology from
![]() $\mathbb{R}^{d}$
, by Proposition 3.6 (respectively, Remark 3.7). Thus
$\mathbb{R}^{d}$
, by Proposition 3.6 (respectively, Remark 3.7). Thus
![]() $f\in {\mathcal{C}}^{\infty }(X)$
, by Lemma 1.10 and Proposition 3.8.◻
$f\in {\mathcal{C}}^{\infty }(X)$
, by Lemma 1.10 and Proposition 3.8.◻
5 Arc-smooth functions on subanalytic sets
The goal of this section is to prove Theorem 1.14.
5.1 Subanalytic sets
Let
![]() $M$
be a real analytic manifold. A subset
$M$
be a real analytic manifold. A subset
![]() $X$
of
$X$
of
![]() $M$
is called subanalytic if for each
$M$
is called subanalytic if for each
![]() $x\in M$
there is an open neighborhood
$x\in M$
there is an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
![]() $M$
such that
$M$
such that
![]() $X\,\cap \,U$
is the projection of a relatively compact semianalytic subset of
$X\,\cap \,U$
is the projection of a relatively compact semianalytic subset of
![]() $M\times N$
, where
$M\times N$
, where
![]() $N$
is a real analytic manifold. Recall that a subset
$N$
is a real analytic manifold. Recall that a subset
![]() $X$
of a real analytic manifold
$X$
of a real analytic manifold
![]() $M$
is semianalytic if for each
$M$
is semianalytic if for each
![]() $x\in M$
there exist an open neighborhood
$x\in M$
there exist an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
in
$x$
in
![]() $M$
and finitely many real analytic functions
$M$
and finitely many real analytic functions
![]() $f_{ij},g_{ij}$
on
$f_{ij},g_{ij}$
on
![]() $U$
such that
$U$
such that
If
![]() $\dim M\leqslant 2$
, then the family of subanalytic sets in
$\dim M\leqslant 2$
, then the family of subanalytic sets in
![]() $M$
coincides with the family of semianalytic sets. In higher dimensions the family of subanalytic sets is essentially larger.
$M$
coincides with the family of semianalytic sets. In higher dimensions the family of subanalytic sets is essentially larger.
Henceforth we restrict to the case
![]() $M=\mathbb{R}^{d}$
.
$M=\mathbb{R}^{d}$
.
Theorem 5.1 (Rectilinearization of subanalytic sets [Reference HironakaHir73, Reference Bierstone and MilmanBM88, Reference ParusińskiPar94b]).
Let
![]() $X\subseteq \mathbb{R}^{d}$
be closed subanalytic. There exists a locally finite collection of real analytic mappings
$X\subseteq \mathbb{R}^{d}$
be closed subanalytic. There exists a locally finite collection of real analytic mappings
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}:U_{\unicode[STIX]{x1D6FC}}\rightarrow \mathbb{R}^{d}$
such that each
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}:U_{\unicode[STIX]{x1D6FC}}\rightarrow \mathbb{R}^{d}$
such that each
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}$
is the composite of a finite sequence of local blow-ups with smooth centers and:
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}$
is the composite of a finite sequence of local blow-ups with smooth centers and:
(i) each
 $U_{\unicode[STIX]{x1D6FC}}$
is diffeomorphic to
$U_{\unicode[STIX]{x1D6FC}}$
is diffeomorphic to
 $\mathbb{R}^{d}$
and there are compact subsets
$\mathbb{R}^{d}$
and there are compact subsets
 $K_{\unicode[STIX]{x1D6FC}}\subseteq U_{\unicode[STIX]{x1D6FC}}$
such that
$K_{\unicode[STIX]{x1D6FC}}\subseteq U_{\unicode[STIX]{x1D6FC}}$
such that
 $\bigcup _{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(K_{\unicode[STIX]{x1D6FC}})$
is a neighborhood of
$\bigcup _{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(K_{\unicode[STIX]{x1D6FC}})$
is a neighborhood of
 $X$
in
$X$
in
 $\mathbb{R}^{d}$
;
$\mathbb{R}^{d}$
;(ii) for each
 $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
 $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}^{-1}(X)$
is a union of quadrants in
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}^{-1}(X)$
is a union of quadrants in
 $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
A quadrant in
![]() $\mathbb{R}^{d}$
is a set
$\mathbb{R}^{d}$
is a set
where
![]() $I_{0}$
,
$I_{0}$
,
![]() $I_{-}$
,
$I_{-}$
,
![]() $I_{+}$
is any partition of
$I_{+}$
is any partition of
![]() $\{1,2,\ldots ,d\}$
.
$\{1,2,\ldots ,d\}$
.
5.2 Bounded fat subanalytic sets are uniformly polynomially cuspidal
This is due to Pawłucki and Pleśniak [Reference Pawłucki and PleśniakPP86]. We recall some steps of the proof which will be needed later.
Definition 5.2. A subset
![]() $X\subseteq \mathbb{R}^{d}$
is called uniformly polynomially cuspidal if there exist positive constants
$X\subseteq \mathbb{R}^{d}$
is called uniformly polynomially cuspidal if there exist positive constants
![]() $M,m>0$
and a positive integer
$M,m>0$
and a positive integer
![]() $n$
such that for all
$n$
such that for all
![]() $x\in \overline{X}$
there is a polynomial curve
$x\in \overline{X}$
there is a polynomial curve
![]() $h_{x}:\mathbb{R}\rightarrow \mathbb{R}^{d}$
of degree at most
$h_{x}:\mathbb{R}\rightarrow \mathbb{R}^{d}$
of degree at most
![]() $n$
with the following properties:
$n$
with the following properties:
(i)
 $h_{x}((0,1])\subseteq X$
and
$h_{x}((0,1])\subseteq X$
and
 $h_{x}(0)=x$
;
$h_{x}(0)=x$
;(ii)
 $\operatorname{dist}(h_{x}(t),\mathbb{R}^{d}\setminus X)\geqslant Mt^{m}$
for all
$\operatorname{dist}(h_{x}(t),\mathbb{R}^{d}\setminus X)\geqslant Mt^{m}$
for all
 $x\in X$
and all
$x\in X$
and all
 $t\in (0,1]$
.
$t\in (0,1]$
.
Remark 5.3. Every compact set
![]() $X\in \mathscr{H}(\mathbb{R}^{d})$
is uniformly polynomially cuspidal; this is clear by Definition 5.2. The converse is not true: for instance, the sets in Example 3.5(2) and (3) are uniformly polynomially cuspidal but not in
$X\in \mathscr{H}(\mathbb{R}^{d})$
is uniformly polynomially cuspidal; this is clear by Definition 5.2. The converse is not true: for instance, the sets in Example 3.5(2) and (3) are uniformly polynomially cuspidal but not in
![]() $\mathscr{H}(\mathbb{R}^{d})$
. The set
$\mathscr{H}(\mathbb{R}^{d})$
. The set
![]() $X$
in Example 10.9 is uniformly polynomially cuspidal but neither subanalytic nor in
$X$
in Example 10.9 is uniformly polynomially cuspidal but neither subanalytic nor in
![]() $\mathscr{H}(\mathbb{R}^{d})$
; cf. [Reference Pawłucki and PleśniakPP88, p. 284].
$\mathscr{H}(\mathbb{R}^{d})$
; cf. [Reference Pawłucki and PleśniakPP88, p. 284].
Theorem 5.4 [Reference Pawłucki and PleśniakPP86, Proposition 6.3].
Let
![]() $X$
be a bounded open subanalytic subset of
$X$
be a bounded open subanalytic subset of
![]() $\mathbb{R}^{d}$
. Then there is a map
$\mathbb{R}^{d}$
. Then there is a map
![]() $h:\overline{X}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
such that
$h:\overline{X}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
such that
![]() $h(x,t)$
is a polynomial in
$h(x,t)$
is a polynomial in
![]() $t$
with degree
$t$
with degree
![]() $n$
independent of
$n$
independent of
![]() $x\in \overline{X}$
with
$x\in \overline{X}$
with
![]() $h(x,0)=x$
for all
$h(x,0)=x$
for all
![]() $x\in \overline{X}$
,
$x\in \overline{X}$
,
![]() $h(\overline{X}\times (0,1])\subseteq X$
, and there exist positive constants
$h(\overline{X}\times (0,1])\subseteq X$
, and there exist positive constants
![]() $M,m$
such that
$M,m$
such that
We give a sketch of the proof in order to explicate the uniformity of
![]() $h_{x}$
which will be of importance later.
$h_{x}$
which will be of importance later.
The following is a corollary of the rectilinearization theorem.
Proposition 5.5 [Reference Pawłucki and PleśniakPP86, Proposition 6.3].
Let
![]() $X$
be a relatively compact subanalytic subset of
$X$
be a relatively compact subanalytic subset of
![]() $\mathbb{R}^{d}$
of pure dimension
$\mathbb{R}^{d}$
of pure dimension
![]() $d$
. Then there are a finite number of real analytic maps
$d$
. Then there are a finite number of real analytic maps
![]() $\unicode[STIX]{x1D711}_{j}:\mathbb{R}^{d}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
such that, for
$\unicode[STIX]{x1D711}_{j}:\mathbb{R}^{d}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
such that, for
![]() $I^{d}:=[-1,1]^{d}$
,
$I^{d}:=[-1,1]^{d}$
,
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{j}(I^{d}\times (0,1])\subseteq X\quad \text{for all }j, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\bigcup }_{j}\unicode[STIX]{x1D711}_{j}(I^{d}\times \{0\})=\overline{X}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{j}(I^{d}\times (0,1])\subseteq X\quad \text{for all }j, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\bigcup }_{j}\unicode[STIX]{x1D711}_{j}(I^{d}\times \{0\})=\overline{X}. & \displaystyle \nonumber\end{eqnarray}$$
Let
![]() $X$
be a bounded open subanalytic subset of
$X$
be a bounded open subanalytic subset of
![]() $\mathbb{R}^{d}$
. Let
$\mathbb{R}^{d}$
. Let
![]() $\unicode[STIX]{x1D711}_{j}$
be the maps provided by Proposition 5.5. Then, for each
$\unicode[STIX]{x1D711}_{j}$
be the maps provided by Proposition 5.5. Then, for each
![]() $j$
, the function
$j$
, the function
is subanalytic (cf. [Reference Bierstone and MilmanBM88, Remark 3.11]). By the Łojasiewicz inequality (cf. [Reference Bierstone and MilmanBM88, Theorem 6.4]), there exist positive constants
![]() $L,m$
such that
$L,m$
such that
The constants
![]() $L$
,
$L$
,
![]() $m$
may be assumed independent of
$m$
may be assumed independent of
![]() $j$
, by taking the minimum and maximum, respectively. Choose an integer
$j$
, by taking the minimum and maximum, respectively. Choose an integer
![]() $n\geqslant m$
and write
$n\geqslant m$
and write
where
![]() $T_{j}(y,\cdot )$
is the Taylor polynomial at
$T_{j}(y,\cdot )$
is the Taylor polynomial at
![]() $0$
of degree
$0$
of degree
![]() $n$
of
$n$
of
![]() $\unicode[STIX]{x1D711}_{j}(y,\cdot )$
and
$\unicode[STIX]{x1D711}_{j}(y,\cdot )$
and
![]() $Q_{j}:\mathbb{R}^{d}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
is real analytic. If we choose
$Q_{j}:\mathbb{R}^{d}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
is real analytic. If we choose
![]() $\unicode[STIX]{x1D6FF}\in (0,1]$
such that
$\unicode[STIX]{x1D6FF}\in (0,1]$
such that
![]() $|tQ_{j}(y,t)|\leqslant L/2$
for all
$|tQ_{j}(y,t)|\leqslant L/2$
for all
![]() $j$
,
$j$
,
![]() $y\in I^{d}$
, and
$y\in I^{d}$
, and
![]() $t\in [0,\unicode[STIX]{x1D6FF}]$
, then
$t\in [0,\unicode[STIX]{x1D6FF}]$
, then
Replacing
![]() $t$
by
$t$
by
![]() $\unicode[STIX]{x1D6FF}t$
, we obtain
$\unicode[STIX]{x1D6FF}t$
, we obtain
where
![]() $M:=L\unicode[STIX]{x1D6FF}^{m}/2$
. Clearly,
$M:=L\unicode[STIX]{x1D6FF}^{m}/2$
. Clearly,
![]() $\bigcup _{j}T_{j}(I^{d}\times \{0\})=\bigcup _{j}\unicode[STIX]{x1D711}_{j}(I^{d}\times \{0\})=\overline{X}$
. Theorem 5.4 follows.
$\bigcup _{j}T_{j}(I^{d}\times \{0\})=\bigcup _{j}\unicode[STIX]{x1D711}_{j}(I^{d}\times \{0\})=\overline{X}$
. Theorem 5.4 follows.
5.3 Fat closed subanalytic sets are
 $m$
-regular
$m$
-regular
Another property of fat closed subanalytic sets we need is the fact that they are
![]() $m$
-regular in the following sense.
$m$
-regular in the following sense.
Theorem 5.6 ([Reference BierstoneBie80, Theorem 6.17], [Reference HardtHar83], [Reference Bierstone and MilmanBM88, Theorem 6.10]).
Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. For each
$X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. For each
![]() $a\in X$
there exist a compact neighborhood
$a\in X$
there exist a compact neighborhood
![]() $K$
in
$K$
in
![]() $X$
, a constant
$X$
, a constant
![]() $C>0$
, and a positive integer
$C>0$
, and a positive integer
![]() $m$
such that any two points
$m$
such that any two points
![]() $x,y\in K$
can be joined by a semianalytic path
$x,y\in K$
can be joined by a semianalytic path
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $X$
which intersects
$X$
which intersects
![]() $\unicode[STIX]{x2202}X$
in at most finitely many points and satisfies
$\unicode[STIX]{x2202}X$
in at most finitely many points and satisfies
5.4 L-regular decomposition
Let us recall the L-regular decomposition of subanalytic sets.
First we introduce sets which are L-regular with respect to a given system of coordinates. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a subanalytic set of dimension
$X\subseteq \mathbb{R}^{d}$
be a subanalytic set of dimension
![]() $d$
. If
$d$
. If
![]() $d=1$
, then
$d=1$
, then
![]() $X$
is called L-regular if
$X$
is called L-regular if
![]() $X$
is a non-empty compact interval. If
$X$
is a non-empty compact interval. If
![]() $d>1$
, then
$d>1$
, then
![]() $X$
is L-regular if it is of the form
$X$
is L-regular if it is of the form
where
![]() $X^{\prime }\subseteq \mathbb{R}^{d-1}$
is L-regular and
$X^{\prime }\subseteq \mathbb{R}^{d-1}$
is L-regular and
![]() $f$
,
$f$
,
![]() $g$
are continuous subanalytic functions on
$g$
are continuous subanalytic functions on
![]() $X^{\prime }$
, analytic and satisfying
$X^{\prime }$
, analytic and satisfying
![]() $f<g$
on
$f<g$
on
![]() $\operatorname{int}(X^{\prime })$
with bounded partial derivatives of first order. If
$\operatorname{int}(X^{\prime })$
with bounded partial derivatives of first order. If
![]() $\dim X=k<d$
, then
$\dim X=k<d$
, then
![]() $X$
is L-regular if
$X$
is L-regular if
where
![]() $X^{\prime }\subseteq \mathbb{R}^{k}$
is L-regular,
$X^{\prime }\subseteq \mathbb{R}^{k}$
is L-regular,
![]() $\dim X^{\prime }=k$
, and
$\dim X^{\prime }=k$
, and
![]() $h$
is continuous subanalytic on
$h$
is continuous subanalytic on
![]() $X^{\prime }$
, analytic on
$X^{\prime }$
, analytic on
![]() $\operatorname{int}(X^{\prime })$
with bounded partial derivatives of first order.
$\operatorname{int}(X^{\prime })$
with bounded partial derivatives of first order.
In general a subanalytic set
![]() $X$
in
$X$
in
![]() $\mathbb{R}^{d}$
is said to be L-regular if it is L-regular with respect to some linear (or equivalently orthogonal) system of coordinates. It is called an L-regular cell if it is the relative interior of an L-regular set, that is, it is
$\mathbb{R}^{d}$
is said to be L-regular if it is L-regular with respect to some linear (or equivalently orthogonal) system of coordinates. It is called an L-regular cell if it is the relative interior of an L-regular set, that is, it is
![]() $\operatorname{int}(X)$
in case (5.1) and the graph of
$\operatorname{int}(X)$
in case (5.1) and the graph of
![]() $h$
restricted to
$h$
restricted to
![]() $\operatorname{int}(X^{\prime })$
in case (5.2). By definition, every point is a zero-dimensional L-regular cell.
$\operatorname{int}(X^{\prime })$
in case (5.2). By definition, every point is a zero-dimensional L-regular cell.
It is well known that L-regular sets and L-regular cells are quasiconvex (cf. [Reference KurdykaKur92], [Reference ParusińskiPar94a, Lemma 2.2], or [Reference Kurdyka and ParusińskiKP06]): there is a constant
![]() $C>0$
such that any two points
$C>0$
such that any two points
![]() $x,y$
in the set can be joined in the set by a subanalytic path of length at most
$x,y$
in the set can be joined in the set by a subanalytic path of length at most
![]() $C|x-y|$
.
$C|x-y|$
.
Theorem 5.7 [Reference KurdykaKur92, Reference Kurdyka and ParusińskiKP06, Reference PawłuckiPaw08].
Let
![]() $X\subseteq \mathbb{R}^{d}$
be a bounded subanalytic set. Then
$X\subseteq \mathbb{R}^{d}$
be a bounded subanalytic set. Then
![]() $X$
is a finite disjoint union of L-regular cells.
$X$
is a finite disjoint union of L-regular cells.
For the proof of Theorem 1.14 we need the following preparatory results.
Lemma 5.8. Let
![]() $[a,b]\subseteq \mathbb{R}$
be a non-trivial interval such that
$[a,b]\subseteq \mathbb{R}$
be a non-trivial interval such that
![]() $[a,b]=\bigcup _{i=1}^{k}F_{i}$
for closed sets
$[a,b]=\bigcup _{i=1}^{k}F_{i}$
for closed sets
![]() $F_{i}$
. If
$F_{i}$
. If
![]() $a\leqslant \sup F_{i}<b$
then there exists
$a\leqslant \sup F_{i}<b$
then there exists
![]() $j\neq i$
such that
$j\neq i$
such that
![]() $\sup F_{i}\in F_{j}$
and
$\sup F_{i}\in F_{j}$
and
![]() $\sup F_{i}<\sup F_{j}$
.
$\sup F_{i}<\sup F_{j}$
.
Proof. Fix
![]() $i$
and suppose that
$i$
and suppose that
![]() $t:=\sup F_{i}<b$
. There is a sequence
$t:=\sup F_{i}<b$
. There is a sequence
![]() $(t,b)\ni t_{n}\rightarrow t$
. After passing to a subsequence we may assume that
$(t,b)\ni t_{n}\rightarrow t$
. After passing to a subsequence we may assume that
![]() $t_{n}\in F_{j}$
for some fixed
$t_{n}\in F_{j}$
for some fixed
![]() $j\neq i$
. Since
$j\neq i$
. Since
![]() $F_{j}$
is closed,
$F_{j}$
is closed,
![]() $t\in F_{j}$
.◻
$t\in F_{j}$
.◻
Lemma 5.9. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. Let
$X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. Let
![]() $x\in \unicode[STIX]{x2202}X$
and suppose there is a basis of neighborhoods
$x\in \unicode[STIX]{x2202}X$
and suppose there is a basis of neighborhoods
![]() $\mathscr{U}$
of
$\mathscr{U}$
of
![]() $x$
such that
$x$
such that
![]() $U\,\cap \,\operatorname{int}(X)$
is connected for all
$U\,\cap \,\operatorname{int}(X)$
is connected for all
![]() $U\in \mathscr{U}$
. Then there exist
$U\in \mathscr{U}$
. Then there exist
![]() $U_{0}\in \mathscr{U}$
and a positive constant
$U_{0}\in \mathscr{U}$
and a positive constant
![]() $C$
such that the following holds. For all
$C$
such that the following holds. For all
![]() $U\in \mathscr{U}_{0}:=\{U\in \mathscr{U}:U\subseteq U_{0}\}$
and for any two points
$U\in \mathscr{U}_{0}:=\{U\in \mathscr{U}:U\subseteq U_{0}\}$
and for any two points
![]() $y,z\in U\,\cap \,\operatorname{int}(X)$
, there exists a rectifiable path
$y,z\in U\,\cap \,\operatorname{int}(X)$
, there exists a rectifiable path
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\operatorname{int}(X)$
which connects
$\operatorname{int}(X)$
which connects
![]() $y$
and
$y$
and
![]() $z$
and satisfies
$z$
and satisfies
Proof. We may assume that
![]() $X$
is bounded, by intersecting with a ball centered at
$X$
is bounded, by intersecting with a ball centered at
![]() $x$
. Let
$x$
. Let
![]() $U_{0}$
be any member of
$U_{0}$
be any member of
![]() $\mathscr{U}$
which is contained in this ball. By Theorem 5.7,
$\mathscr{U}$
which is contained in this ball. By Theorem 5.7,
![]() $\operatorname{int}(X)$
is a finite disjoint union of L-regular cells
$\operatorname{int}(X)$
is a finite disjoint union of L-regular cells
![]() $\{A_{1},\ldots ,A_{k}\}$
.
$\{A_{1},\ldots ,A_{k}\}$
.
Fix
![]() $U\in \mathscr{U}_{0}$
and let
$U\in \mathscr{U}_{0}$
and let
![]() $y,z\in U\,\cap \,\operatorname{int}(X)$
. Since
$y,z\in U\,\cap \,\operatorname{int}(X)$
. Since
![]() $U\,\cap \,\operatorname{int}(X)$
is connected, there is a path
$U\,\cap \,\operatorname{int}(X)$
is connected, there is a path
![]() $\unicode[STIX]{x1D70E}:[0,1]\rightarrow U\,\cap \,\operatorname{int}(X)$
with
$\unicode[STIX]{x1D70E}:[0,1]\rightarrow U\,\cap \,\operatorname{int}(X)$
with
![]() $\unicode[STIX]{x1D70E}(0)=y$
and
$\unicode[STIX]{x1D70E}(0)=y$
and
![]() $\unicode[STIX]{x1D70E}(1)=z$
. Then we have a finite disjoint union
$\unicode[STIX]{x1D70E}(1)=z$
. Then we have a finite disjoint union
![]() $[0,1]=\bigcup _{i=1}^{k}E_{i}$
, where
$[0,1]=\bigcup _{i=1}^{k}E_{i}$
, where
![]() $E_{i}:=\unicode[STIX]{x1D70E}^{-1}(A_{i})$
.
$E_{i}:=\unicode[STIX]{x1D70E}^{-1}(A_{i})$
.
Let
![]() $E_{i}^{\prime }$
be the set of limit points of
$E_{i}^{\prime }$
be the set of limit points of
![]() $E_{i}$
. Then
$E_{i}$
. Then
![]() $[0,1]=\bigcup _{i=1}^{k}E_{i}^{\prime }$
. Let
$[0,1]=\bigcup _{i=1}^{k}E_{i}^{\prime }$
. Let
![]() $i_{1}\in \{1,\ldots ,k\}$
be such that
$i_{1}\in \{1,\ldots ,k\}$
be such that
![]() $t_{0}:=0\in E_{i_{1}}^{\prime }$
. If
$t_{0}:=0\in E_{i_{1}}^{\prime }$
. If
![]() $t_{1}<1$
, then there exists
$t_{1}<1$
, then there exists
![]() $i_{2}\in \{1,\ldots ,k\}\setminus \{i_{1}\}$
such that
$i_{2}\in \{1,\ldots ,k\}\setminus \{i_{1}\}$
such that
![]() $t_{1}\in E_{i_{2}}^{\prime }$
and
$t_{1}\in E_{i_{2}}^{\prime }$
and
![]() $t_{2}:=\sup E_{i_{2}}^{\prime }>t_{1}$
, by Lemma 5.8. Moreover,
$t_{2}:=\sup E_{i_{2}}^{\prime }>t_{1}$
, by Lemma 5.8. Moreover,
![]() $[t_{1},b]=\bigcup _{j\neq i_{1}}E_{j}^{\prime }\,\cap \,[t_{1}\,\cap \,b]$
. If
$[t_{1},b]=\bigcup _{j\neq i_{1}}E_{j}^{\prime }\,\cap \,[t_{1}\,\cap \,b]$
. If
![]() $t_{2}<b$
we may apply Lemma 5.8 again and find
$t_{2}<b$
we may apply Lemma 5.8 again and find
![]() $i_{3}\in \{1,\ldots ,k\}\setminus \{i_{1},i_{2}\}$
such that
$i_{3}\in \{1,\ldots ,k\}\setminus \{i_{1},i_{2}\}$
such that
![]() $t_{2}\in E_{i_{3}}^{\prime }$
and
$t_{2}\in E_{i_{3}}^{\prime }$
and
![]() $t_{3}:=\sup E_{i_{3}}^{\prime }>t_{2}$
. This procedure ends after finitely many steps and gives a finite partition
$t_{3}:=\sup E_{i_{3}}^{\prime }>t_{2}$
. This procedure ends after finitely many steps and gives a finite partition
![]() $0=t_{0}<t_{1}<\cdots <t_{h-1}<t_{h}=1$
of
$0=t_{0}<t_{1}<\cdots <t_{h-1}<t_{h}=1$
of
![]() $[0,1]$
. The points
$[0,1]$
. The points
![]() $y=z_{0},z_{1},\ldots ,z_{h}=z$
, where
$y=z_{0},z_{1},\ldots ,z_{h}=z$
, where
![]() $z_{j}=\unicode[STIX]{x1D70E}(t_{j})$
, all lie in
$z_{j}=\unicode[STIX]{x1D70E}(t_{j})$
, all lie in
![]() $U\,\cap \,\operatorname{int}(X)$
. Let
$U\,\cap \,\operatorname{int}(X)$
. Let
![]() $\unicode[STIX]{x1D716}>0$
be sufficiently small such that the balls
$\unicode[STIX]{x1D716}>0$
be sufficiently small such that the balls
![]() $B_{j}:=B(z_{j},\unicode[STIX]{x1D716})$
are all contained in
$B_{j}:=B(z_{j},\unicode[STIX]{x1D716})$
are all contained in
![]() $U\,\cap \,\operatorname{int}(X)$
. For all
$U\,\cap \,\operatorname{int}(X)$
. For all
![]() $j=1,2,\ldots ,h-1$
, there exist
$j=1,2,\ldots ,h-1$
, there exist
![]() $z_{j}^{-}\in B_{j}\,\cap \,A_{i_{j}}$
and
$z_{j}^{-}\in B_{j}\,\cap \,A_{i_{j}}$
and
![]() $z_{j}^{+}\in B_{j}\,\cap \,A_{i_{j+1}}$
, by construction. Additionally, there exist
$z_{j}^{+}\in B_{j}\,\cap \,A_{i_{j+1}}$
, by construction. Additionally, there exist
![]() $z_{0}^{+}\in B_{0}\,\cap \,A_{i_{1}}$
and
$z_{0}^{+}\in B_{0}\,\cap \,A_{i_{1}}$
and
![]() $z_{h}^{-}\in B_{h}\,\cap \,A_{i_{h}}$
.
$z_{h}^{-}\in B_{h}\,\cap \,A_{i_{h}}$
.
Since the cells are quasiconvex, for all
![]() $j=1,2,\ldots ,h$
, there exist rectifiable paths
$j=1,2,\ldots ,h$
, there exist rectifiable paths
![]() $\unicode[STIX]{x1D6FE}_{j}\in A_{i_{j}}$
joining
$\unicode[STIX]{x1D6FE}_{j}\in A_{i_{j}}$
joining
![]() $z_{j-1}^{+}$
and
$z_{j-1}^{+}$
and
![]() $z_{j}^{-}$
such that
$z_{j}^{-}$
such that
where the constant
![]() $C_{j}$
depends only on
$C_{j}$
depends only on
![]() $A_{i_{j}}$
. Joining the paths
$A_{i_{j}}$
. Joining the paths
![]() $\unicode[STIX]{x1D6FE}_{j}$
with the line segments
$\unicode[STIX]{x1D6FE}_{j}$
with the line segments
![]() $[z_{0},z_{0}^{+}]$
,
$[z_{0},z_{0}^{+}]$
,
![]() $[z_{j}^{-},z_{j}^{+}]$
, for
$[z_{j}^{-},z_{j}^{+}]$
, for
![]() $j=1,\ldots ,h-1$
, and
$j=1,\ldots ,h-1$
, and
![]() $[z_{h}^{-},z_{h}]$
, we obtain a rectifiable path
$[z_{h}^{-},z_{h}]$
, we obtain a rectifiable path
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $\operatorname{int}(X)$
which connects
$\operatorname{int}(X)$
which connects
![]() $y$
and
$y$
and
![]() $z$
and has length
$z$
and has length
for a constant
![]() $C$
which depends only on the
$C$
which depends only on the
![]() $C_{j}$
and the number of cells
$C_{j}$
and the number of cells
![]() $k$
, since all points
$k$
, since all points
![]() $z_{j}$
,
$z_{j}$
,
![]() $z_{j}^{-}$
,
$z_{j}^{-}$
,
![]() $z_{j}^{+}$
lie in
$z_{j}^{+}$
lie in
![]() $U$
.◻
$U$
.◻
5.5 Proof of Theorem 1.14
The inclusion
![]() ${\mathcal{C}}^{\infty }(X)\subseteq {\mathcal{A}}^{\infty }(X)$
is clear.
${\mathcal{C}}^{\infty }(X)\subseteq {\mathcal{A}}^{\infty }(X)$
is clear.
Let
![]() $f\in {\mathcal{A}}^{\infty }(X)$
. Then
$f\in {\mathcal{A}}^{\infty }(X)$
. Then
![]() $f$
is smooth in
$f$
is smooth in
![]() $\operatorname{int}(X)$
, by Result 1.1. We must show that
$\operatorname{int}(X)$
, by Result 1.1. We must show that
![]() $f\in {\mathcal{C}}^{\infty }(X)$
. This is a local problem, so we may assume without loss of generality that
$f\in {\mathcal{C}}^{\infty }(X)$
. This is a local problem, so we may assume without loss of generality that
![]() $X$
is compact (by intersecting with a suitable ball). By Lemma 1.10 and Theorem 5.6, it suffices to show that
$X$
is compact (by intersecting with a suitable ball). By Lemma 1.10 and Theorem 5.6, it suffices to show that
![]() $f$
satisfies Lemma 1.10(3).
$f$
satisfies Lemma 1.10(3).
Fix
![]() $x\in \unicode[STIX]{x2202}X$
. By Theorem 5.4, there is a polynomial curve
$x\in \unicode[STIX]{x2202}X$
. By Theorem 5.4, there is a polynomial curve
![]() $h_{x}:\mathbb{R}\rightarrow \mathbb{R}^{d}$
of degree at most
$h_{x}:\mathbb{R}\rightarrow \mathbb{R}^{d}$
of degree at most
![]() $n$
with the properties:
$n$
with the properties:
(i)
 $h_{x}((0,1])\subseteq \operatorname{int}(X)$
and
$h_{x}((0,1])\subseteq \operatorname{int}(X)$
and
 $h_{x}(0)=x$
,
$h_{x}(0)=x$
,(ii)
 $\operatorname{dist}(h_{x}(t),\mathbb{R}^{d}\setminus X)\geqslant Mt^{m}$
for all
$\operatorname{dist}(h_{x}(t),\mathbb{R}^{d}\setminus X)\geqslant Mt^{m}$
for all
 $t\in (0,1]$
,
$t\in (0,1]$
,
where
![]() $n,M,m$
are independent of
$n,M,m$
are independent of
![]() $x$
and
$x$
and
![]() $t$
. Then there is a positive integer
$t$
. Then there is a positive integer
![]() $k=k(x)$
such that
$k=k(x)$
such that
![]() $h_{x}(t)-x=t^{k}\tilde{h}_{x}(t)$
, where
$h_{x}(t)-x=t^{k}\tilde{h}_{x}(t)$
, where
![]() $\tilde{h}_{x}(0)\neq 0$
. Set
$\tilde{h}_{x}(0)\neq 0$
. Set
![]() $v_{1}:=\tilde{h}_{x}(0)/|\tilde{h}_{x}(0)|\in S^{d-1}$
. Choose
$v_{1}:=\tilde{h}_{x}(0)/|\tilde{h}_{x}(0)|\in S^{d-1}$
. Choose
![]() $d-1$
directions
$d-1$
directions
![]() $v_{2},\ldots ,v_{d}\in S^{d-1}$
such that
$v_{2},\ldots ,v_{d}\in S^{d-1}$
such that
![]() $v_{1},v_{2},\ldots ,v_{d}$
are linearly independent and define
$v_{1},v_{2},\ldots ,v_{d}$
are linearly independent and define
for
![]() $t=(t_{1},\ldots ,t_{d})$
in the set
$t=(t_{1},\ldots ,t_{d})$
in the set
If
![]() $C:=M/(2(d-1))$
and
$C:=M/(2(d-1))$
and
![]() $\unicode[STIX]{x1D6FF}>0$
is chosen small enough, then
$\unicode[STIX]{x1D6FF}>0$
is chosen small enough, then
![]() $\unicode[STIX]{x1D6F9}_{x,v}$
is a diffeomorphism of
$\unicode[STIX]{x1D6F9}_{x,v}$
is a diffeomorphism of
![]() $Y$
onto the open subset
$Y$
onto the open subset
![]() $H_{x,v}:=\unicode[STIX]{x1D6F9}_{x,v}(Y)$
of
$H_{x,v}:=\unicode[STIX]{x1D6F9}_{x,v}(Y)$
of
![]() $\operatorname{int}(X)$
and it extends to a homeomorphism between
$\operatorname{int}(X)$
and it extends to a homeomorphism between
![]() $Y\cup \{0\}$
and
$Y\cup \{0\}$
and
![]() $H_{x,v}\cup \{x\}$
; indeed, by (2),
$H_{x,v}\cup \{x\}$
; indeed, by (2),
 $$\begin{eqnarray}\displaystyle \operatorname{dist}(\unicode[STIX]{x1D6F9}_{x,v}(t),\mathbb{R}^{d}\setminus X) & {\geqslant} & \displaystyle \operatorname{dist}(h_{x}(t_{1}),\mathbb{R}^{d}\setminus X)-|t_{2}|-\cdots -|t_{d}|\nonumber\\ \displaystyle & {>} & \displaystyle Mt_{1}^{m}-(d-1)Ct_{1}^{m}=\frac{M}{2}t_{1}^{m}>0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{dist}(\unicode[STIX]{x1D6F9}_{x,v}(t),\mathbb{R}^{d}\setminus X) & {\geqslant} & \displaystyle \operatorname{dist}(h_{x}(t_{1}),\mathbb{R}^{d}\setminus X)-|t_{2}|-\cdots -|t_{d}|\nonumber\\ \displaystyle & {>} & \displaystyle Mt_{1}^{m}-(d-1)Ct_{1}^{m}=\frac{M}{2}t_{1}^{m}>0,\nonumber\end{eqnarray}$$
for
![]() $t\in Y$
. Since
$t\in Y$
. Since
![]() $f$
is smooth in
$f$
is smooth in
![]() $\operatorname{int}(X)$
, we have
$\operatorname{int}(X)$
, we have
The left-hand side of (5.3) extends continuously to
![]() $t=0$
, since
$t=0$
, since
![]() $f\,\circ \,\unicode[STIX]{x1D6F9}_{x,v}\in {\mathcal{A}}^{\infty }(\overline{Y})$
and
$f\,\circ \,\unicode[STIX]{x1D6F9}_{x,v}\in {\mathcal{A}}^{\infty }(\overline{Y})$
and
![]() ${\mathcal{A}}^{\infty }(\overline{Y})={\mathcal{C}}^{\infty }(\overline{Y})$
, by Theorem 1.13, as
${\mathcal{A}}^{\infty }(\overline{Y})={\mathcal{C}}^{\infty }(\overline{Y})$
, by Theorem 1.13, as
![]() $\overline{Y}$
is a Hölder set. Since
$\overline{Y}$
is a Hölder set. Since
![]() $\unicode[STIX]{x1D6F9}_{x,v}$
is a homeomorphism
$\unicode[STIX]{x1D6F9}_{x,v}$
is a homeomorphism
![]() $Y\cup \{0\}\rightarrow H_{x,v}\cup \{x\}$
, we may conclude that the directional derivatives
$Y\cup \{0\}\rightarrow H_{x,v}\cup \{x\}$
, we may conclude that the directional derivatives
![]() $d_{v_{2}}^{\unicode[STIX]{x1D6FC}_{2}}\cdots d_{v_{d}}^{\unicode[STIX]{x1D6FC}_{d}}f$
,
$d_{v_{2}}^{\unicode[STIX]{x1D6FC}_{2}}\cdots d_{v_{d}}^{\unicode[STIX]{x1D6FC}_{d}}f$
,
![]() $\unicode[STIX]{x1D6FC}_{j}\geqslant 0$
, extend continuously from
$\unicode[STIX]{x1D6FC}_{j}\geqslant 0$
, extend continuously from
![]() $H_{x,v}$
to
$H_{x,v}$
to
![]() $x$
.
$x$
.
If we perturb the directions
![]() $v_{2},\ldots ,v_{d}$
a little such that
$v_{2},\ldots ,v_{d}$
a little such that
![]() $v_{1},v_{2},\ldots ,v_{d}$
remain linearly independent and take the intersection
$v_{1},v_{2},\ldots ,v_{d}$
remain linearly independent and take the intersection
![]() $H_{x}$
of the corresponding sets
$H_{x}$
of the corresponding sets
![]() $H_{x,v}$
, then
$H_{x,v}$
, then
![]() $H_{x}$
still is an open subset of
$H_{x}$
still is an open subset of
![]() $\operatorname{int}(X)$
with
$\operatorname{int}(X)$
with
![]() $h_{x}(t)\in H_{x}$
for small
$h_{x}(t)\in H_{x}$
for small
![]() $t>0$
and
$t>0$
and
![]() $x\in \overline{H}_{x}$
. Then
$x\in \overline{H}_{x}$
. Then
![]() $d_{w_{2}}^{\unicode[STIX]{x1D6FC}_{2}}\cdots d_{w_{d}}^{\unicode[STIX]{x1D6FC}_{d}}f$
,
$d_{w_{2}}^{\unicode[STIX]{x1D6FC}_{2}}\cdots d_{w_{d}}^{\unicode[STIX]{x1D6FC}_{d}}f$
,
![]() $\unicode[STIX]{x1D6FC}_{j}\geqslant 0$
, extend continuously from
$\unicode[STIX]{x1D6FC}_{j}\geqslant 0$
, extend continuously from
![]() $H_{x}$
to
$H_{x}$
to
![]() $x$
for all
$x$
for all
![]() $w_{2},\ldots ,w_{d}$
near
$w_{2},\ldots ,w_{d}$
near
![]() $v_{2},\ldots ,v_{d}$
. By Lemma 1.10, we infer that the Fréchet derivatives
$v_{2},\ldots ,v_{d}$
. By Lemma 1.10, we infer that the Fréchet derivatives
![]() $f^{(p)}$
of all orders of
$f^{(p)}$
of all orders of
![]() $f$
extend continuously from
$f$
extend continuously from
![]() $H_{x}$
to
$H_{x}$
to
![]() $x$
.
$x$
.
Thus for all
![]() $x\in \unicode[STIX]{x2202}X$
and
$x\in \unicode[STIX]{x2202}X$
and
![]() $p\in \mathbb{N}$
, we have a candidate for the Fréchet derivative
$p\in \mathbb{N}$
, we have a candidate for the Fréchet derivative
![]() $f^{(p)}(x)$
of
$f^{(p)}(x)$
of
![]() $f$
at
$f$
at
![]() $x$
and an open set
$x$
and an open set
![]() $H_{x}\subseteq \operatorname{int}(X)$
on which
$H_{x}\subseteq \operatorname{int}(X)$
on which
![]() $f^{(p)}(y)$
tends to this candidate as
$f^{(p)}(y)$
tends to this candidate as
![]() $y\rightarrow x$
. It remains to prove that the extension of
$y\rightarrow x$
. It remains to prove that the extension of
![]() $f^{(p)}$
to
$f^{(p)}$
to
![]() $X$
thus defined is continuous on
$X$
thus defined is continuous on
![]() $X$
. First we show that it is bounded.
$X$
. First we show that it is bounded.
Claim 1. For all
![]() $p\in \mathbb{N}$
,
$p\in \mathbb{N}$
,
![]() $f^{(p)}$
is bounded on
$f^{(p)}$
is bounded on
![]() $X$
.
$X$
.
Let
![]() $p\in \mathbb{N}$
be fixed. It suffices to show that
$p\in \mathbb{N}$
be fixed. It suffices to show that
![]() $f^{(p)}$
is bounded on
$f^{(p)}$
is bounded on
![]() $\operatorname{int}(X)$
(since
$\operatorname{int}(X)$
(since
![]() $X$
is fat). For contradiction suppose that there is a sequence
$X$
is fat). For contradiction suppose that there is a sequence
![]() $(x_{\ell })$
in
$(x_{\ell })$
in
![]() $\operatorname{int}(X)$
such that
$\operatorname{int}(X)$
such that
![]() $\Vert f^{(p)}(x_{\ell })\Vert _{L_{p}}\rightarrow \infty$
. Since
$\Vert f^{(p)}(x_{\ell })\Vert _{L_{p}}\rightarrow \infty$
. Since
![]() $X$
is compact, we may assume that
$X$
is compact, we may assume that
![]() $x_{\ell }\rightarrow x$
. Then
$x_{\ell }\rightarrow x$
. Then
![]() $x\in \unicode[STIX]{x2202}X$
, since we already know that
$x\in \unicode[STIX]{x2202}X$
, since we already know that
![]() $f$
is smooth on
$f$
is smooth on
![]() $\operatorname{int}(X)$
.
$\operatorname{int}(X)$
.
By Proposition 5.5, there are a finite number of real analytic maps
![]() $\unicode[STIX]{x1D711}_{j}:\mathbb{R}^{d}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
such that
$\unicode[STIX]{x1D711}_{j}:\mathbb{R}^{d}\times \mathbb{R}\rightarrow \mathbb{R}^{d}$
such that
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{j}(I^{d}\times (0,1])\subseteq \operatorname{int}(X)\quad \text{for all }j, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\bigcup }_{j}\unicode[STIX]{x1D711}_{j}(I^{d}\times \{0\})=X, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D711}_{j}(I^{d}\times (0,1])\subseteq \operatorname{int}(X)\quad \text{for all }j, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\bigcup }_{j}\unicode[STIX]{x1D711}_{j}(I^{d}\times \{0\})=X, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $I^{d}:=[-1,1]^{d}$
. After passing to a subsequence we may assume that
$I^{d}:=[-1,1]^{d}$
. After passing to a subsequence we may assume that
![]() $x_{\ell }\in \unicode[STIX]{x1D711}_{j_{0}}(I^{d}\times \{0\})$
for all
$x_{\ell }\in \unicode[STIX]{x1D711}_{j_{0}}(I^{d}\times \{0\})$
for all
![]() $\ell$
and some
$\ell$
and some
![]() $j_{0}$
. Choose
$j_{0}$
. Choose
![]() $y_{\ell }\in I^{d}$
such that
$y_{\ell }\in I^{d}$
such that
![]() $\unicode[STIX]{x1D711}_{j_{0}}(y_{\ell },0)=x_{\ell }$
. Since
$\unicode[STIX]{x1D711}_{j_{0}}(y_{\ell },0)=x_{\ell }$
. Since
![]() $I^{d}$
is compact, after passing to a subsequence we may assume that
$I^{d}$
is compact, after passing to a subsequence we may assume that
![]() $y_{\ell }\rightarrow y$
and in turn that this convergence is faster than any polynomial. The infinite polygon through the points
$y_{\ell }\rightarrow y$
and in turn that this convergence is faster than any polynomial. The infinite polygon through the points
![]() $y_{\ell }$
and
$y_{\ell }$
and
![]() $y$
can be parameterized by a smooth curve
$y$
can be parameterized by a smooth curve
![]() $c:\mathbb{R}\rightarrow I^{d}$
such that
$c:\mathbb{R}\rightarrow I^{d}$
such that
![]() $c(1/\ell )=y_{\ell }$
and
$c(1/\ell )=y_{\ell }$
and
![]() $c(0)=y$
(cf. [Reference Kriegl and MichorKM97, Lemma 2.8]). Then
$c(0)=y$
(cf. [Reference Kriegl and MichorKM97, Lemma 2.8]). Then
![]() $s\mapsto \unicode[STIX]{x1D711}_{j_{0}}(c(s),0)$
is a smooth curve in
$s\mapsto \unicode[STIX]{x1D711}_{j_{0}}(c(s),0)$
is a smooth curve in
![]() $X$
through the points
$X$
through the points
![]() $x_{\ell }$
and
$x_{\ell }$
and
![]() $x$
.
$x$
.
Since
![]() $\unicode[STIX]{x1D711}_{j_{0}}$
is real analytic, for small
$\unicode[STIX]{x1D711}_{j_{0}}$
is real analytic, for small
![]() $t_{1}$
we have
$t_{1}$
we have
![]() $\unicode[STIX]{x1D711}_{j_{0}}(y,t_{1})=x+t_{1}^{k}\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(y,t_{1})$
for some positive integer
$\unicode[STIX]{x1D711}_{j_{0}}(y,t_{1})=x+t_{1}^{k}\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(y,t_{1})$
for some positive integer
![]() $k$
and a real analytic map
$k$
and a real analytic map
![]() $\tilde{\unicode[STIX]{x1D711}}_{j_{0}}$
with
$\tilde{\unicode[STIX]{x1D711}}_{j_{0}}$
with
![]() $\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(y,0)\neq 0$
. Then
$\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(y,0)\neq 0$
. Then
![]() $\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,t_{1})\neq 0$
for
$\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,t_{1})\neq 0$
for
![]() $(z,t_{1})$
in a neighborhood of
$(z,t_{1})$
in a neighborhood of
![]() $(y,0)$
. Thus,
$(y,0)$
. Thus,
 $$\begin{eqnarray}v_{1}(z,t_{1}):=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\unicode[STIX]{x2202}_{t_{1}}\unicode[STIX]{x1D711}_{j_{0}}(z,t_{1})}{|\unicode[STIX]{x2202}_{t_{1}}\unicode[STIX]{x1D711}_{j_{0}}(z,t_{1})|}=\frac{k\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,t_{1})+t_{1}\tilde{\unicode[STIX]{x1D711}}_{j_{0}}^{\prime }(z,t_{1})}{|k\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,t_{1})+t_{1}\tilde{\unicode[STIX]{x1D711}}_{j_{0}}^{\prime }(z,t_{1})|}\quad & \text{if }t_{1}>0,\\ \displaystyle \frac{\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,0)}{|\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,0)|}\quad & \text{if }t_{1}=0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v_{1}(z,t_{1}):=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\unicode[STIX]{x2202}_{t_{1}}\unicode[STIX]{x1D711}_{j_{0}}(z,t_{1})}{|\unicode[STIX]{x2202}_{t_{1}}\unicode[STIX]{x1D711}_{j_{0}}(z,t_{1})|}=\frac{k\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,t_{1})+t_{1}\tilde{\unicode[STIX]{x1D711}}_{j_{0}}^{\prime }(z,t_{1})}{|k\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,t_{1})+t_{1}\tilde{\unicode[STIX]{x1D711}}_{j_{0}}^{\prime }(z,t_{1})|}\quad & \text{if }t_{1}>0,\\ \displaystyle \frac{\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,0)}{|\tilde{\unicode[STIX]{x1D711}}_{j_{0}}(z,0)|}\quad & \text{if }t_{1}=0,\end{array}\right.\end{eqnarray}$$
is continuous in
![]() $(z,t_{1})$
, where
$(z,t_{1})$
, where
![]() $t_{1}\geqslant 0$
, near
$t_{1}\geqslant 0$
, near
![]() $(y,0)$
. It follows that we can find an open set of directions
$(y,0)$
. It follows that we can find an open set of directions
![]() $v\in S^{d-1}$
such that
$v\in S^{d-1}$
such that
![]() $v_{1}(c(s),0)$
and
$v_{1}(c(s),0)$
and
![]() $v$
are linearly independent for
$v$
are linearly independent for
![]() $s$
near
$s$
near
![]() $0$
. For such
$0$
. For such
![]() $v$
,
$v$
,
is smooth for small
![]() $s\in \mathbb{R}$
,
$s\in \mathbb{R}$
,
![]() $t_{1}\geqslant 0$
, and
$t_{1}\geqslant 0$
, and
![]() $|t_{2}|\leqslant Ct_{1}^{m}$
, by the arguments in § 5.2 and the considerations in the first part of the proof. But this implies that
$|t_{2}|\leqslant Ct_{1}^{m}$
, by the arguments in § 5.2 and the considerations in the first part of the proof. But this implies that
![]() $d_{v}^{p}f(x_{\ell })$
is bounded for all such
$d_{v}^{p}f(x_{\ell })$
is bounded for all such
![]() $v$
, and hence
$v$
, and hence
![]() $f^{(p)}(x_{\ell })$
is bounded, a contradiction. Claim 1 is proved.
$f^{(p)}(x_{\ell })$
is bounded, a contradiction. Claim 1 is proved.
Claim 2. The Fréchet derivatives
![]() $f^{(p)}$
,
$f^{(p)}$
,
![]() $p\in \mathbb{N}$
, are continuous on
$p\in \mathbb{N}$
, are continuous on
![]() $X$
.
$X$
.
Let
![]() $x\in \unicode[STIX]{x2202}X$
and suppose that
$x\in \unicode[STIX]{x2202}X$
and suppose that
![]() $(x_{n})$
and
$(x_{n})$
and
![]() $(y_{n})$
are two sequences in
$(y_{n})$
are two sequences in
![]() $\operatorname{int}(X)$
both converging to
$\operatorname{int}(X)$
both converging to
![]() $x$
. By Lemma 5.9, for each
$x$
. By Lemma 5.9, for each
![]() $\unicode[STIX]{x1D716}>0$
there exists
$\unicode[STIX]{x1D716}>0$
there exists
![]() $n_{0}\in \mathbb{N}$
such that for all
$n_{0}\in \mathbb{N}$
such that for all
![]() $n\geqslant n_{0}$
the points
$n\geqslant n_{0}$
the points
![]() $x_{n}$
and
$x_{n}$
and
![]() $y_{n}$
can be joined by a rectifiable path
$y_{n}$
can be joined by a rectifiable path
![]() $\unicode[STIX]{x1D6FE}_{n}$
in
$\unicode[STIX]{x1D6FE}_{n}$
in
![]() $\operatorname{int}(X)$
with length
$\operatorname{int}(X)$
with length
![]() $\ell (\unicode[STIX]{x1D6FE}_{n})\leqslant \unicode[STIX]{x1D716}$
. Since
$\ell (\unicode[STIX]{x1D6FE}_{n})\leqslant \unicode[STIX]{x1D716}$
. Since
![]() $f$
is smooth in
$f$
is smooth in
![]() $\operatorname{int}(X)$
, we may apply the fundamental theorem of calculus and Claim 1 to conclude
$\operatorname{int}(X)$
, we may apply the fundamental theorem of calculus and Claim 1 to conclude
If we assume that the sequence
![]() $(x_{n})$
lies in
$(x_{n})$
lies in
![]() $H_{x}$
, we obtain that
$H_{x}$
, we obtain that
![]() $f^{(p)}(y)\rightarrow f^{(p)}(x)$
for all
$f^{(p)}(y)\rightarrow f^{(p)}(x)$
for all
![]() $\operatorname{int}(X)\ni y\rightarrow x$
. Finally, suppose that
$\operatorname{int}(X)\ni y\rightarrow x$
. Finally, suppose that
![]() $\unicode[STIX]{x2202}X\ni x_{n}\rightarrow x$
. Choose
$\unicode[STIX]{x2202}X\ni x_{n}\rightarrow x$
. Choose
![]() $y_{n}\in H_{x_{n}}\,\cap \,B(x_{n},1/n)$
. Then
$y_{n}\in H_{x_{n}}\,\cap \,B(x_{n},1/n)$
. Then
as
![]() $n\rightarrow \infty$
. This proves Claim 2 and hence the theorem. ◻
$n\rightarrow \infty$
. This proves Claim 2 and hence the theorem. ◻
6 The Bochnak–Siciak theorem on tame closed sets
In this section we prove Theorem 1.16. The strategy for the proof is the following. Since
![]() $f\in {\mathcal{C}}^{\infty }(X)$
, we can associate with every
$f\in {\mathcal{C}}^{\infty }(X)$
, we can associate with every
![]() $x\in X$
the formal Taylor series
$x\in X$
the formal Taylor series
![]() $F_{x}$
of
$F_{x}$
of
![]() $f$
at
$f$
at
![]() $x$
. Using a result of Eakin and Harris [Reference Eakin and HarrisEH77] and Gabriélov [Reference GabriélovGab73], we show that each
$x$
. Using a result of Eakin and Harris [Reference Eakin and HarrisEH77] and Gabriélov [Reference GabriélovGab73], we show that each
![]() $F_{x}$
is convergent and coincides with
$F_{x}$
is convergent and coincides with
![]() $f$
on their common domain. To prove that all
$f$
on their common domain. To prove that all
![]() $F_{x}$
glue together to give a global holomorphic extension we will use the following lemma.
$F_{x}$
glue together to give a global holomorphic extension we will use the following lemma.
Lemma 6.1. Let
![]() $X\subseteq \mathbb{R}^{d}$
be closed and let
$X\subseteq \mathbb{R}^{d}$
be closed and let
![]() $U\subseteq \mathbb{R}^{d}$
be open with
$U\subseteq \mathbb{R}^{d}$
be open with
![]() $U\,\cap \,X\neq \emptyset$
. Then there is an open subset
$U\,\cap \,X\neq \emptyset$
. Then there is an open subset
![]() $U_{0}$
of
$U_{0}$
of
![]() $U$
with
$U$
with
![]() $U_{0}\,\cap \,X=U\,\cap \,X$
and such that for all
$U_{0}\,\cap \,X=U\,\cap \,X$
and such that for all
![]() $x\in U_{0}$
and all
$x\in U_{0}$
and all
![]() $a\in A_{x}:=\{a\in X:|a-x|=\operatorname{dist}(x,X)\}$
we have
$a\in A_{x}:=\{a\in X:|a-x|=\operatorname{dist}(x,X)\}$
we have
![]() $[x,a]\subseteq U_{0}$
.
$[x,a]\subseteq U_{0}$
.
Proof. Set
![]() $U_{0}:=\{x\in U:[x,a]\subseteq U\text{ for all }a\in A_{x}\}$
. Then, for all
$U_{0}:=\{x\in U:[x,a]\subseteq U\text{ for all }a\in A_{x}\}$
. Then, for all
![]() $x\in U_{0}$
and all
$x\in U_{0}$
and all
![]() $a\in A_{x}$
, we have
$a\in A_{x}$
, we have
![]() $[x,a]\subseteq U_{0}$
. To see this, let
$[x,a]\subseteq U_{0}$
. To see this, let
![]() $y\in [x,a]$
. If
$y\in [x,a]$
. If
![]() $y=x$
there is nothing to prove. Otherwise
$y=x$
there is nothing to prove. Otherwise
![]() $A_{y}=\{a\}$
and
$A_{y}=\{a\}$
and
![]() $[y,a]\subseteq [x,a]\subseteq U$
(as in Figure 2).
$[y,a]\subseteq [x,a]\subseteq U$
(as in Figure 2).

Figure 2. If
![]() $y\in (x,a]$
and
$y\in (x,a]$
and
![]() $X\cap B(x,|x-a|)=\emptyset$
then
$X\cap B(x,|x-a|)=\emptyset$
then
![]() $X\cap B(y,|y-a|)=\emptyset$
.
$X\cap B(y,|y-a|)=\emptyset$
.
Clearly,
![]() $U_{0}\,\cap \,X=U\,\cap \,X$
. It remains to show that
$U_{0}\,\cap \,X=U\,\cap \,X$
. It remains to show that
![]() $U_{0}$
is open. To this end we first observe that if
$U_{0}$
is open. To this end we first observe that if
![]() $x_{n}\rightarrow x$
and
$x_{n}\rightarrow x$
and
![]() $A_{x_{n}}\ni a_{n}\rightarrow a$
, then
$A_{x_{n}}\ni a_{n}\rightarrow a$
, then
![]() $a\in A_{x}$
. This follows from letting
$a\in A_{x}$
. This follows from letting
![]() $n\rightarrow \infty$
in
$n\rightarrow \infty$
in
![]() $|x_{n}-a_{n}|=\operatorname{dist}(x_{n},X)$
, since
$|x_{n}-a_{n}|=\operatorname{dist}(x_{n},X)$
, since
![]() $X$
is closed.
$X$
is closed.
If
![]() $U_{0}$
is not open, then there exists a sequence
$U_{0}$
is not open, then there exists a sequence
![]() $x_{n}\rightarrow x$
, where
$x_{n}\rightarrow x$
, where
![]() $x_{n}\not \in U_{0}$
and
$x_{n}\not \in U_{0}$
and
![]() $x\in U_{0}$
. So, for all
$x\in U_{0}$
. So, for all
![]() $n$
, there exist
$n$
, there exist
![]() $a_{n}\in A_{x_{n}}$
and
$a_{n}\in A_{x_{n}}$
and
![]() $y_{n}\in [x_{n},a_{n}]\setminus U$
. After passing to a subsequence, we may assume that
$y_{n}\in [x_{n},a_{n}]\setminus U$
. After passing to a subsequence, we may assume that
![]() $a_{n}\rightarrow a\in A_{x}$
, by the observation above, and in turn that
$a_{n}\rightarrow a\in A_{x}$
, by the observation above, and in turn that
![]() $y_{n}\rightarrow y\in [x,a]$
. Since
$y_{n}\rightarrow y\in [x,a]$
. Since
![]() $x\in U_{0}$
we have
$x\in U_{0}$
we have
![]() $y\in U$
, a contradiction.◻
$y\in U$
, a contradiction.◻
Proof of Theorem 1.16.
Suppose that
![]() $X\subseteq \mathbb{R}^{d}$
is a fat closed subanalytic set. There exist an analytic manifold
$X\subseteq \mathbb{R}^{d}$
is a fat closed subanalytic set. There exist an analytic manifold
![]() $M$
and a proper analytic map
$M$
and a proper analytic map
![]() $\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
such that
$\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
such that
![]() $X=\unicode[STIX]{x1D711}(M)$
, by the uniformization theorem; see, for example, [Reference Bierstone and MilmanBM88]. Then
$X=\unicode[STIX]{x1D711}(M)$
, by the uniformization theorem; see, for example, [Reference Bierstone and MilmanBM88]. Then
![]() $f\,\circ \,\unicode[STIX]{x1D711}$
is
$f\,\circ \,\unicode[STIX]{x1D711}$
is
![]() ${\mathcal{C}}^{\infty }$
and real analytic on real analytic curves in
${\mathcal{C}}^{\infty }$
and real analytic on real analytic curves in
![]() $M$
. By the Bochnak–Siciak theorem (Result 1.5),
$M$
. By the Bochnak–Siciak theorem (Result 1.5),
![]() $f\,\circ \,\unicode[STIX]{x1D711}$
is analytic on
$f\,\circ \,\unicode[STIX]{x1D711}$
is analytic on
![]() $M$
. For each
$M$
. For each
![]() $x\in X$
there is
$x\in X$
there is
![]() $y\in \unicode[STIX]{x1D711}^{-1}(x)$
such that
$y\in \unicode[STIX]{x1D711}^{-1}(x)$
such that
![]() $\unicode[STIX]{x1D711}$
has generic rank
$\unicode[STIX]{x1D711}$
has generic rank
![]() $d$
at
$d$
at
![]() $y$
. By a result of Eakin and Harris [Reference Eakin and HarrisEH77] (proved earlier by Gabriélov [Reference GabriélovGab73]), the homomorphism
$y$
. By a result of Eakin and Harris [Reference Eakin and HarrisEH77] (proved earlier by Gabriélov [Reference GabriélovGab73]), the homomorphism
![]() $\unicode[STIX]{x1D711}^{\ast }$
of formal power series rings given by formal composition with
$\unicode[STIX]{x1D711}^{\ast }$
of formal power series rings given by formal composition with
![]() $\unicode[STIX]{x1D711}$
at
$\unicode[STIX]{x1D711}$
at
![]() $y$
is strongly injective, that is, the formal Taylor series
$y$
is strongly injective, that is, the formal Taylor series
![]() $F_{x}$
of
$F_{x}$
of
![]() $f$
at
$f$
at
![]() $x$
converges. It represents a holomorphic function
$x$
converges. It represents a holomorphic function
![]() $F_{x}$
in a neighborhood
$F_{x}$
in a neighborhood
![]() $U_{x}$
of
$U_{x}$
of
![]() $x$
in
$x$
in
![]() $\mathbb{C}^{d}$
which coincides with the real analytic function
$\mathbb{C}^{d}$
which coincides with the real analytic function
![]() $f|_{\operatorname{int}(X)}$
on
$f|_{\operatorname{int}(X)}$
on
![]() $\operatorname{int}(X)\,\cap \,U_{x}$
.
$\operatorname{int}(X)\,\cap \,U_{x}$
.
It remains to show that the
![]() $F_{x}$
piece together to give a global holomorphic extension of
$F_{x}$
piece together to give a global holomorphic extension of
![]() $f$
to a neighborhood of
$f$
to a neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{C}^{d}$
. We may assume that
$\mathbb{C}^{d}$
. We may assume that
where
![]() $U_{x}^{\mathbb{R}}\subseteq \mathbb{R}^{d}$
. We use Lemma 6.1 to replace each
$U_{x}^{\mathbb{R}}\subseteq \mathbb{R}^{d}$
. We use Lemma 6.1 to replace each
![]() $U_{x}^{\mathbb{R}}$
by the connected component of
$U_{x}^{\mathbb{R}}$
by the connected component of
![]() $(U_{x}^{\mathbb{R}})_{0}$
which contains
$(U_{x}^{\mathbb{R}})_{0}$
which contains
![]() $x$
(and leave the part of
$x$
(and leave the part of
![]() $U_{x}$
in
$U_{x}$
in
![]() $i\mathbb{R}^{d}$
unchanged). Thus we may assume that the cover
$i\mathbb{R}^{d}$
unchanged). Thus we may assume that the cover
![]() $\{U_{x}^{\mathbb{R}}\}$
of
$\{U_{x}^{\mathbb{R}}\}$
of
![]() $X$
has the property that for each
$X$
has the property that for each
![]() $z\in U_{x}^{\mathbb{R}}$
all segments
$z\in U_{x}^{\mathbb{R}}$
all segments
![]() $[z,a]$
,
$[z,a]$
,
![]() $a\in A_{z}$
, belong to
$a\in A_{z}$
, belong to
![]() $U_{x}^{\mathbb{R}}$
. By (6.1), each
$U_{x}^{\mathbb{R}}$
. By (6.1), each
![]() $U_{x}$
has the property that for
$U_{x}$
has the property that for
![]() $z+iw\in U_{x}$
also
$z+iw\in U_{x}$
also
![]() $z+itw\in U_{x}$
for all
$z+itw\in U_{x}$
for all
![]() $t\in [0,1]$
.
$t\in [0,1]$
.
Let
![]() $V$
be a connected component of
$V$
be a connected component of
![]() $U_{x}\,\cap \,U_{y}$
. It follows that if
$U_{x}\,\cap \,U_{y}$
. It follows that if
![]() $z+iw\in V$
, then
$z+iw\in V$
, then
![]() $z\in V^{\mathbb{R}}:=V\,\cap \,\mathbb{R}^{d}$
, and
$z\in V^{\mathbb{R}}:=V\,\cap \,\mathbb{R}^{d}$
, and
![]() $V^{\mathbb{R}}$
is a connected component of
$V^{\mathbb{R}}$
is a connected component of
![]() $U_{x}^{\mathbb{R}}\,\cap \,U_{y}^{\mathbb{R}}$
. Moreover,
$U_{x}^{\mathbb{R}}\,\cap \,U_{y}^{\mathbb{R}}$
. Moreover,
![]() $[z,a]\subseteq V^{\mathbb{R}}$
for all
$[z,a]\subseteq V^{\mathbb{R}}$
for all
![]() $a\in A_{z}\subseteq X$
. Since
$a\in A_{z}\subseteq X$
. Since
![]() $X=\overline{\operatorname{int}(X)}$
, the intersection
$X=\overline{\operatorname{int}(X)}$
, the intersection
![]() $V^{\mathbb{R}}\,\cap \,\operatorname{int}(X)$
is non-empty and on this set the holomorphic extensions
$V^{\mathbb{R}}\,\cap \,\operatorname{int}(X)$
is non-empty and on this set the holomorphic extensions
![]() $F_{x}$
and
$F_{x}$
and
![]() $F_{y}$
coincide with
$F_{y}$
coincide with
![]() $f$
. By the identity theorem,
$f$
. By the identity theorem,
![]() $F_{x}$
and
$F_{x}$
and
![]() $F_{y}$
coincide on
$F_{y}$
coincide on
![]() $V$
. Since the component
$V$
. Since the component
![]() $V$
of
$V$
of
![]() $U_{x}\,\cap \,U_{y}$
was arbitrary,
$U_{x}\,\cap \,U_{y}$
was arbitrary,
![]() $F_{x}$
and
$F_{x}$
and
![]() $F_{y}$
coincide on
$F_{y}$
coincide on
![]() $U_{x}\,\cap \,U_{y}$
.◻
$U_{x}\,\cap \,U_{y}$
.◻
Proof of Corollary 1.17.
The assumption for
![]() $X$
clearly implies that
$X$
clearly implies that
![]() $X=\overline{\operatorname{int}(X)}$
. For each boundary point
$X=\overline{\operatorname{int}(X)}$
. For each boundary point
![]() $z\in \unicode[STIX]{x2202}X$
there is a holomorphic function
$z\in \unicode[STIX]{x2202}X$
there is a holomorphic function
![]() $F_{z}$
defined in a neighborhood
$F_{z}$
defined in a neighborhood
![]() $U_{z}$
of
$U_{z}$
of
![]() $z$
in
$z$
in
![]() $\mathbb{C}^{d}$
which coincides with
$\mathbb{C}^{d}$
which coincides with
![]() $f$
on
$f$
on
![]() $U_{z}\,\cap \,\operatorname{int}(X)$
; this follows from Theorem 1.16 applied to the subanalytic set
$U_{z}\,\cap \,\operatorname{int}(X)$
; this follows from Theorem 1.16 applied to the subanalytic set
![]() $X_{z}$
. Using Lemma 6.1 as in the proof of Theorem 1.16, one easily concludes the assertion.◻
$X_{z}$
. Using Lemma 6.1 as in the proof of Theorem 1.16, one easily concludes the assertion.◻
7 Arc-
 ${\mathcal{C}}^{M}$
functions on Lipschitz sets
${\mathcal{C}}^{M}$
functions on Lipschitz sets
In this section we prove Theorem 1.19: All
![]() $X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
satisfy
$X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
satisfy
for any non-quasianalytic weight sequence
![]() $M=(M_{k})$
.
$M=(M_{k})$
.
It can be expected that a similar statement holds for
![]() $X\in \mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
, where
$X\in \mathscr{H}^{\unicode[STIX]{x1D6FC}}(\mathbb{R}^{d})$
, where
![]() $\unicode[STIX]{x1D6FC}<1$
, with a larger weight sequence
$\unicode[STIX]{x1D6FC}<1$
, with a larger weight sequence
![]() $N=N(\unicode[STIX]{x1D6FC},M)$
instead of
$N=N(\unicode[STIX]{x1D6FC},M)$
instead of
![]() $M^{(2)}$
. We do not pursue this question any further for
$M^{(2)}$
. We do not pursue this question any further for
![]() $\unicode[STIX]{x1D6FC}$
-sets, but results of this type for subanalytic sets are presented in § 8.
$\unicode[STIX]{x1D6FC}$
-sets, but results of this type for subanalytic sets are presented in § 8.
7.1 Reduction to an open set of directions
Let
![]() $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$
be smooth. The mixed partial derivatives of order
$f:\mathbb{R}^{2}\rightarrow \mathbb{R}$
be smooth. The mixed partial derivatives of order
![]() $k$
of
$k$
of
![]() $f$
at any point
$f$
at any point
![]() $x\in \mathbb{R}^{2}$
can be computed from directional derivatives of order
$x\in \mathbb{R}^{2}$
can be computed from directional derivatives of order
![]() $k$
of
$k$
of
![]() $f$
at
$f$
at
![]() $x$
by means of the identity
$x$
by means of the identity
The next lemma guarantees that the constants which appear in the process of solving these linear equations grow at most exponentially in
![]() $k$
and hence the class
$k$
and hence the class
![]() ${\mathcal{C}}^{M}$
is preserved; a similar lemma was proved in [Reference NeelonNee99].
${\mathcal{C}}^{M}$
is preserved; a similar lemma was proved in [Reference NeelonNee99].
Lemma 7.1. Let
![]() $-1\leqslant t_{0}<t_{1}<\cdots <t_{k}\leqslant 1$
be equidistant points such that
$-1\leqslant t_{0}<t_{1}<\cdots <t_{k}\leqslant 1$
be equidistant points such that
![]() $t_{k}-t_{0}=a$
. If
$t_{k}-t_{0}=a$
. If
![]() $x_{0},x_{1},\ldots ,x_{k}$
is a solution of the linear system of equations
$x_{0},x_{1},\ldots ,x_{k}$
is a solution of the linear system of equations
then we have
Proof. Let
![]() $P(t)=a_{0}+a_{1}t+\cdots +a_{k}t^{k}$
be the polynomial with coefficients
$P(t)=a_{0}+a_{1}t+\cdots +a_{k}t^{k}$
be the polynomial with coefficients
![]() $a_{j}=\binom{k}{j}x_{j}$
. Then the system (7.2) reads
$a_{j}=\binom{k}{j}x_{j}$
. Then the system (7.2) reads
By Lagrange’s interpolation formula (e.g. [Reference Rahman and SchmeisserRS02, (1.2.5)]),
 $$\begin{eqnarray}P(t)=\mathop{\sum }_{i=0}^{k}y_{i}\mathop{\prod }_{\substack{ j=0 \\ j\neq i}}^{k}\frac{t-t_{j}}{t_{i}-t_{j}},\end{eqnarray}$$
$$\begin{eqnarray}P(t)=\mathop{\sum }_{i=0}^{k}y_{i}\mathop{\prod }_{\substack{ j=0 \\ j\neq i}}^{k}\frac{t-t_{j}}{t_{i}-t_{j}},\end{eqnarray}$$
and therefore
 $$\begin{eqnarray}a_{m}=(-1)^{k-m}\mathop{\sum }_{i=0}^{k}y_{i}\unicode[STIX]{x1D70E}_{k-m}^{i}\mathop{\prod }_{\substack{ j=0 \\ j\neq i}}^{k}\frac{1}{t_{i}-t_{j}},\end{eqnarray}$$
$$\begin{eqnarray}a_{m}=(-1)^{k-m}\mathop{\sum }_{i=0}^{k}y_{i}\unicode[STIX]{x1D70E}_{k-m}^{i}\mathop{\prod }_{\substack{ j=0 \\ j\neq i}}^{k}\frac{1}{t_{i}-t_{j}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}_{j}^{i}$
is the
$\unicode[STIX]{x1D70E}_{j}^{i}$
is the
![]() $j$
th elementary symmetric polynomial in
$j$
th elementary symmetric polynomial in
![]() $(t_{\ell })_{\ell \neq i}$
. We have
$(t_{\ell })_{\ell \neq i}$
. We have
and hence, using
![]() $e^{-k}k^{k}\leqslant k!\leqslant k^{k}$
,
$e^{-k}k^{k}\leqslant k!\leqslant k^{k}$
,
 $$\begin{eqnarray}\mathop{\prod }_{\substack{ j=0 \\ j\neq i}}^{k}\frac{1}{|t_{i}-t_{j}|}=\frac{k^{k}}{a^{k}i!(k-i)!}\leqslant \biggl(\frac{2e}{a}\biggr)^{k},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\substack{ j=0 \\ j\neq i}}^{k}\frac{1}{|t_{i}-t_{j}|}=\frac{k^{k}}{a^{k}i!(k-i)!}\leqslant \biggl(\frac{2e}{a}\biggr)^{k},\end{eqnarray}$$
and
It follows that
which is (7.3). ◻
Proposition 7.2. Let
![]() $f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
be smooth. Let
$f:\mathbb{R}^{d}\rightarrow \mathbb{R}$
be smooth. Let
![]() $K\subseteq \mathbb{R}^{d}$
be compact and let
$K\subseteq \mathbb{R}^{d}$
be compact and let
![]() $M=(M_{k})$
be a positive sequence. The following assertions are equivalent:
$M=(M_{k})$
be a positive sequence. The following assertions are equivalent:
(1)
 $\exists C,\unicode[STIX]{x1D70C}>0\;\forall k\in \mathbb{N}\;\forall x\in K\;\forall v\in S^{d-1}:|d_{v}^{k}f(x)|\leqslant C\unicode[STIX]{x1D70C}^{k}k!\,M_{k};$
$\exists C,\unicode[STIX]{x1D70C}>0\;\forall k\in \mathbb{N}\;\forall x\in K\;\forall v\in S^{d-1}:|d_{v}^{k}f(x)|\leqslant C\unicode[STIX]{x1D70C}^{k}k!\,M_{k};$
(2) there exist
 $v_{0}\in S^{d-1}$
and
$v_{0}\in S^{d-1}$
and
 $r>0$
such that
$r>0$
such that  $$\begin{eqnarray}\exists C,\unicode[STIX]{x1D70C}>0\;\forall k\in \mathbb{N}\;\forall x\in K\;\forall v\in B(v_{0},r)\,\cap \,S^{d-1}:|d_{v}^{k}f(x)|\leqslant C\unicode[STIX]{x1D70C}^{k}k!\,M_{k};\end{eqnarray}$$
$$\begin{eqnarray}\exists C,\unicode[STIX]{x1D70C}>0\;\forall k\in \mathbb{N}\;\forall x\in K\;\forall v\in B(v_{0},r)\,\cap \,S^{d-1}:|d_{v}^{k}f(x)|\leqslant C\unicode[STIX]{x1D70C}^{k}k!\,M_{k};\end{eqnarray}$$
(3)
 $\exists C,\unicode[STIX]{x1D70C}>0\;\forall x\in K\;\forall \unicode[STIX]{x1D6FC}\in \mathbb{N}^{d}:|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}f(x)|\leqslant C\unicode[STIX]{x1D70C}^{|\unicode[STIX]{x1D6FC}|}|\unicode[STIX]{x1D6FC}|!\,M_{|\unicode[STIX]{x1D6FC}|}.$
$\exists C,\unicode[STIX]{x1D70C}>0\;\forall x\in K\;\forall \unicode[STIX]{x1D6FC}\in \mathbb{N}^{d}:|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}f(x)|\leqslant C\unicode[STIX]{x1D70C}^{|\unicode[STIX]{x1D6FC}|}|\unicode[STIX]{x1D6FC}|!\,M_{|\unicode[STIX]{x1D6FC}|}.$
The constants
![]() $C$
,
$C$
,
![]() $\unicode[STIX]{x1D70C}$
may differ from item to item, but they change in a uniform way which depends only on
$\unicode[STIX]{x1D70C}$
may differ from item to item, but they change in a uniform way which depends only on
![]() $r$
.
$r$
.
Proof. Let us first consider the case
![]() $d=2$
. In this case
$d=2$
. In this case
![]() $B:=B(v_{0},r)\,\cap \,S^{d-1}$
is an open arc
$B:=B(v_{0},r)\,\cap \,S^{d-1}$
is an open arc
![]() $I\subseteq S^{1}$
; let
$I\subseteq S^{1}$
; let
![]() $\ell (I)$
denote the length of
$\ell (I)$
denote the length of
![]() $I$
.
$I$
.
(1)
![]() $\Rightarrow$
(2) is trivial and (3)
$\Rightarrow$
(2) is trivial and (3)
![]() $\Rightarrow$
(1) follows easily from (7.1).
$\Rightarrow$
(1) follows easily from (7.1).
(2)
![]() $\Rightarrow$
(3) By a linear change of coordinates, we may assume that the arc
$\Rightarrow$
(3) By a linear change of coordinates, we may assume that the arc
![]() $I$
is symmetric about the
$I$
is symmetric about the
![]() $y$
-axis and, by shrinking
$y$
-axis and, by shrinking
![]() $I$
, we may also assume that its projection to the
$I$
, we may also assume that its projection to the
![]() $y$
-axis is contained in
$y$
-axis is contained in
![]() $\{(0,y):1/2\leqslant y\leqslant 1\}$
and that the estimates in (2) hold also at the endpoints of
$\{(0,y):1/2\leqslant y\leqslant 1\}$
and that the estimates in (2) hold also at the endpoints of
![]() $I$
. Let
$I$
. Let
![]() $(-a/2,a/2)$
be the projection of
$(-a/2,a/2)$
be the projection of
![]() $I$
to the
$I$
to the
![]() $x$
-axis and let
$x$
-axis and let
![]() $-a/2=t_{0}<t_{1}<\cdots <t_{k}=a/2$
be an equidistant partition. Apply Lemma 7.1 to the system (7.1) with the
$-a/2=t_{0}<t_{1}<\cdots <t_{k}=a/2$
be an equidistant partition. Apply Lemma 7.1 to the system (7.1) with the
![]() $k+1$
directions
$k+1$
directions
![]() $v_{i}=(t_{i},s_{i})$
,
$v_{i}=(t_{i},s_{i})$
,
![]() $i=0,\ldots ,k$
, in
$i=0,\ldots ,k$
, in
![]() $I$
; then
$I$
; then
![]() $1/2\leqslant s_{i}\leqslant 1$
. The statement about the uniform change of the constants follows from (7.3).
$1/2\leqslant s_{i}\leqslant 1$
. The statement about the uniform change of the constants follows from (7.3).
Now we consider the general case.
(1)
![]() $\Leftrightarrow$
(2) The statement follows by applying the two-dimensional analogue to every affine 2-plane
$\Leftrightarrow$
(2) The statement follows by applying the two-dimensional analogue to every affine 2-plane
![]() $\unicode[STIX]{x1D70B}$
containing the affine line
$\unicode[STIX]{x1D70B}$
containing the affine line
![]() $x+\mathbb{R}v_{0}$
. The change of the constants
$x+\mathbb{R}v_{0}$
. The change of the constants
![]() $C$
,
$C$
,
![]() $\unicode[STIX]{x1D70C}$
depends only on the length of the arcs defined by the intersection
$\unicode[STIX]{x1D70C}$
depends only on the length of the arcs defined by the intersection
![]() $\unicode[STIX]{x1D70B}\,\cap \,B$
which is independent of
$\unicode[STIX]{x1D70B}\,\cap \,B$
which is independent of
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
(1)
![]() $\Leftrightarrow$
(3) By the polarization formula [Reference Kriegl and MichorKM97, Lemma 7.13(1)], we have
$\Leftrightarrow$
(3) By the polarization formula [Reference Kriegl and MichorKM97, Lemma 7.13(1)], we have
which entails the assertion. ◻
7.2 Proof of Theorem 1.19
Let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence. Let
$M=(M_{k})$
be a non-quasianalytic weight sequence. Let
![]() $X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
. The inclusion
$X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
. The inclusion
![]() ${\mathcal{C}}^{M}(X)\subseteq {\mathcal{A}}^{M}(X)$
is an easy consequence of Faà di Bruno’s formula and log-convexity of
${\mathcal{C}}^{M}(X)\subseteq {\mathcal{A}}^{M}(X)$
is an easy consequence of Faà di Bruno’s formula and log-convexity of
![]() $M$
(cf. [Reference Rainer and SchindlRS14, Proposition 3.1]).
$M$
(cf. [Reference Rainer and SchindlRS14, Proposition 3.1]).
Let us prove
![]() ${\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{M^{(2)}}(X)$
. A function
${\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{M^{(2)}}(X)$
. A function
![]() $f\in {\mathcal{A}}^{M}(X)$
belongs to
$f\in {\mathcal{A}}^{M}(X)$
belongs to
![]() ${\mathcal{C}}^{\infty }(X)$
, by Theorem 1.13. Suppose for contradiction that
${\mathcal{C}}^{\infty }(X)$
, by Theorem 1.13. Suppose for contradiction that
![]() $f\not \in {\mathcal{C}}^{M^{(2)}}(X)$
. Then there is
$f\not \in {\mathcal{C}}^{M^{(2)}}(X)$
. Then there is
![]() $a\in X$
such that for all
$a\in X$
such that for all
![]() $\unicode[STIX]{x1D6FF},C,\unicode[STIX]{x1D70C}>0$
there exist
$\unicode[STIX]{x1D6FF},C,\unicode[STIX]{x1D70C}>0$
there exist
![]() $x\in X\,\cap \,B(a,\unicode[STIX]{x1D6FF})$
,
$x\in X\,\cap \,B(a,\unicode[STIX]{x1D6FF})$
,
![]() $v\in S^{d-1}$
, and
$v\in S^{d-1}$
, and
![]() $k\in \mathbb{N}$
with
$k\in \mathbb{N}$
with
We may assume that
![]() $a\in \unicode[STIX]{x2202}X$
(if
$a\in \unicode[STIX]{x2202}X$
(if
![]() $a\in \operatorname{int}(X)$
then the arguments in the proof of [Reference Kriegl, Michor and RainerKMR09, Theorem 3.9] lead to a contradiction). Since
$a\in \operatorname{int}(X)$
then the arguments in the proof of [Reference Kriegl, Michor and RainerKMR09, Theorem 3.9] lead to a contradiction). Since
![]() $X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
, we may suppose that there exist
$X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
, we may suppose that there exist
![]() $\unicode[STIX]{x1D716}>0$
and a truncated open cone
$\unicode[STIX]{x1D716}>0$
and a truncated open cone
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{1}(r,h)$
such that
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{d}^{1}(r,h)$
such that
By rescaling, we may assume that
![]() $r=h=1$
. Set
$r=h=1$
. Set
![]() $C(y,r):=y+\unicode[STIX]{x1D6E4}_{d}^{1}(r,r)$
for
$C(y,r):=y+\unicode[STIX]{x1D6E4}_{d}^{1}(r,r)$
for
![]() $0<r\leqslant 1$
. There is a universal constant
$0<r\leqslant 1$
. There is a universal constant
![]() $c>0$
such that
$c>0$
such that
![]() $C(y_{1},r_{1})\,\cap \,C(y_{2},r_{2})\neq \emptyset$
if
$C(y_{1},r_{1})\,\cap \,C(y_{2},r_{2})\neq \emptyset$
if
![]() $|y_{1}-y_{2}|<c\min \{r_{1},r_{2}\}$
.
$|y_{1}-y_{2}|<c\min \{r_{1},r_{2}\}$
.
Let
![]() $\unicode[STIX]{x1D706}_{k}{\searrow}0$
be the sequence associated with the sequence
$\unicode[STIX]{x1D706}_{k}{\searrow}0$
be the sequence associated with the sequence
![]() $M_{k}$
, by Lemma 2.4. By Proposition 7.2 and (7.4) (using
$M_{k}$
, by Lemma 2.4. By Proposition 7.2 and (7.4) (using
![]() $\unicode[STIX]{x1D6FF}:=c\unicode[STIX]{x1D706}_{n+1}/3$
,
$\unicode[STIX]{x1D6FF}:=c\unicode[STIX]{x1D706}_{n+1}/3$
,
![]() $C:=\unicode[STIX]{x1D706}_{n}^{-1}$
,
$C:=\unicode[STIX]{x1D706}_{n}^{-1}$
,
![]() $\unicode[STIX]{x1D70C}:=\unicode[STIX]{x1D706}_{n}^{-3}$
), there exist sequences
$\unicode[STIX]{x1D70C}:=\unicode[STIX]{x1D706}_{n}^{-3}$
), there exist sequences
![]() $x_{n}\in X\,\cap \,B(a,c\unicode[STIX]{x1D706}_{n+1}/3)$
,
$x_{n}\in X\,\cap \,B(a,c\unicode[STIX]{x1D706}_{n+1}/3)$
,
![]() $v_{n}\in S^{d-1}\,\cap \,\mathbb{R}_{+}\unicode[STIX]{x1D6E4}$
,
$v_{n}\in S^{d-1}\,\cap \,\mathbb{R}_{+}\unicode[STIX]{x1D6E4}$
,
![]() $k_{n}\in \mathbb{N}$
such that
$k_{n}\in \mathbb{N}$
such that
Let us set
![]() $C_{n}:=C(x_{n},\unicode[STIX]{x1D706}_{n})$
. Since
$C_{n}:=C(x_{n},\unicode[STIX]{x1D706}_{n})$
. Since
![]() $|x_{n}-x_{n+1}|<c\unicode[STIX]{x1D706}_{n+1}$
, there is a sequence
$|x_{n}-x_{n+1}|<c\unicode[STIX]{x1D706}_{n+1}$
, there is a sequence
![]() $u_{n}$
such that
$u_{n}$
such that
![]() $u_{n+1}\in C_{n}\,\cap \,C_{n+1}$
for all
$u_{n+1}\in C_{n}\,\cap \,C_{n+1}$
for all
![]() $n$
. Evidently,
$n$
. Evidently,
![]() $x_{n}$
and
$x_{n}$
and
![]() $u_{n}$
are both
$u_{n}$
are both
![]() $1/\unicode[STIX]{x1D706}_{n}$
-converging to
$1/\unicode[STIX]{x1D706}_{n}$
-converging to
![]() $a$
. We may assume that for all
$a$
. We may assume that for all
![]() $n\geqslant n_{0}$
we have
$n\geqslant n_{0}$
we have
![]() $C_{n}\subseteq \operatorname{int}(X)$
, by (7.5).
$C_{n}\subseteq \operatorname{int}(X)$
, by (7.5).
Without loss of generality assume that
![]() $a=0$
. Let
$a=0$
. Let
![]() $c_{n}(t)=x_{n}+t^{2}\unicode[STIX]{x1D706}_{n}v_{n}$
. Let
$c_{n}(t)=x_{n}+t^{2}\unicode[STIX]{x1D706}_{n}v_{n}$
. Let
![]() $T_{n}$
and
$T_{n}$
and
![]() $t_{n}$
be chosen as in (2.8), and let
$t_{n}$
be chosen as in (2.8), and let
![]() $\unicode[STIX]{x1D711}$
be the function used in the proof of Lemma 2.4. Define
$\unicode[STIX]{x1D711}$
be the function used in the proof of Lemma 2.4. Define
for
![]() $t\in [t_{n}-T_{n},t_{n}+T_{n}]$
(here
$t\in [t_{n}-T_{n},t_{n}+T_{n}]$
(here
![]() $\unicode[STIX]{x1D7D9}_{A}$
denotes the characteristic function of the set
$\unicode[STIX]{x1D7D9}_{A}$
denotes the characteristic function of the set
![]() $A$
); note that
$A$
); note that
![]() $t_{n}+T_{n}=t_{n+1}-T_{n+1}$
(see Figure 3).
$t_{n}+T_{n}=t_{n+1}-T_{n+1}$
(see Figure 3).

Figure 3. The curve
![]() $c$
in
$c$
in
![]() $C_{n-1}\cup C_{n}\cup C_{n+1}$
.
$C_{n-1}\cup C_{n}\cup C_{n+1}$
.
Extend
![]() $c$
by
$c$
by
![]() $c=0$
on
$c=0$
on
![]() $[t_{\infty },\infty )$
. Then
$[t_{\infty },\infty )$
. Then
![]() $c$
is
$c$
is
![]() ${\mathcal{C}}^{\infty }$
on
${\mathcal{C}}^{\infty }$
on
![]() $[t_{n_{0}}-T_{n_{0}},+\infty )\setminus \{t_{\infty }\}$
and
$[t_{n_{0}}-T_{n_{0}},+\infty )\setminus \{t_{\infty }\}$
and
![]() $c(t_{n}-T_{n})=u_{n}$
and
$c(t_{n}-T_{n})=u_{n}$
and
![]() $c(t_{n}+T_{n})=u_{n+1}$
. By construction,
$c(t_{n}+T_{n})=u_{n+1}$
. By construction,
![]() $c(t)\in C_{n}$
if
$c(t)\in C_{n}$
if
![]() $t\in [t_{n}-T_{n},t_{n}+T_{n}]$
and thus
$t\in [t_{n}-T_{n},t_{n}+T_{n}]$
and thus
![]() $c$
lies in
$c$
lies in
![]() $X$
. Since the curves
$X$
. Since the curves
![]() $c_{n}$
as well as
$c_{n}$
as well as
![]() $u_{n}$
satisfy (2.6), the proof of Lemma 2.4 implies that
$u_{n}$
satisfy (2.6), the proof of Lemma 2.4 implies that
![]() $c$
is a
$c$
is a
![]() ${\mathcal{C}}^{M}$
-curve.
${\mathcal{C}}^{M}$
-curve.
Then, since
![]() $f\in {\mathcal{A}}^{\infty }(X)$
, for all
$f\in {\mathcal{A}}^{\infty }(X)$
, for all
![]() $k$
,
$k$
,
Using (7.6), we may conclude
as
![]() $n\rightarrow \infty$
, contradicting the assumption
$n\rightarrow \infty$
, contradicting the assumption
![]() $f\in {\mathcal{A}}^{M}(X)$
.◻
$f\in {\mathcal{A}}^{M}(X)$
.◻
8 Arc-
 ${\mathcal{C}}^{M}$
functions on subanalytic sets
${\mathcal{C}}^{M}$
functions on subanalytic sets
Let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence. Let
$M=(M_{k})$
be a non-quasianalytic weight sequence. Let
![]() $X$
be a simple fat closed subanalytic set. We will see in this section that
$X$
be a simple fat closed subanalytic set. We will see in this section that
![]() ${\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{N}(X)$
for some other non-quasianalytic weight sequence
${\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{N}(X)$
for some other non-quasianalytic weight sequence
![]() $N$
which depends only on
$N$
which depends only on
![]() $M$
and
$M$
and
![]() $X$
(in an explicit way).
$X$
(in an explicit way).
8.1 Rectilinearization
We start with some simple observations. For arbitrary sets
![]() $Y\subseteq \mathbb{R}^{e}$
,
$Y\subseteq \mathbb{R}^{e}$
,
![]() $X\subseteq \mathbb{R}^{d}$
, we denote by
$X\subseteq \mathbb{R}^{d}$
, we denote by
![]() ${\mathcal{C}}^{\infty }(Y,X)$
the class of mappings
${\mathcal{C}}^{\infty }(Y,X)$
the class of mappings
![]() $\unicode[STIX]{x1D711}:Y\rightarrow X$
such that
$\unicode[STIX]{x1D711}:Y\rightarrow X$
such that
![]() $\unicode[STIX]{x1D711}_{i}\in {\mathcal{C}}^{\infty }(Y)$
for all components
$\unicode[STIX]{x1D711}_{i}\in {\mathcal{C}}^{\infty }(Y)$
for all components
![]() $\unicode[STIX]{x1D711}_{i}=\operatorname{pr}_{i}\,\circ \,\unicode[STIX]{x1D711}$
. Similarly for
$\unicode[STIX]{x1D711}_{i}=\operatorname{pr}_{i}\,\circ \,\unicode[STIX]{x1D711}$
. Similarly for
![]() ${\mathcal{C}}^{M}(Y,X)$
and
${\mathcal{C}}^{M}(Y,X)$
and
![]() ${\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y,X)$
.
${\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y,X)$
.
Lemma 8.1. Let
![]() $X\subseteq \mathbb{R}^{d}$
and
$X\subseteq \mathbb{R}^{d}$
and
![]() $Y\subseteq \mathbb{R}^{e}$
.
$Y\subseteq \mathbb{R}^{e}$
.
(1) If
 $\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\infty }(Y,X)$
and
$\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\infty }(Y,X)$
and
 ${\mathcal{A}}^{\infty }(Y)={\mathcal{C}}^{\infty }(Y)$
, then
${\mathcal{A}}^{\infty }(Y)={\mathcal{C}}^{\infty }(Y)$
, then
 $\unicode[STIX]{x1D711}^{\ast }{\mathcal{A}}^{\infty }(X)\subseteq {\mathcal{C}}^{\infty }(Y)$
.
$\unicode[STIX]{x1D711}^{\ast }{\mathcal{A}}^{\infty }(X)\subseteq {\mathcal{C}}^{\infty }(Y)$
.(2) If
 $\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y,X)$
and
$\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y,X)$
and
 ${\mathcal{A}}^{\unicode[STIX]{x1D714}}(Y)={\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y)$
, then
${\mathcal{A}}^{\unicode[STIX]{x1D714}}(Y)={\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y)$
, then
 $\unicode[STIX]{x1D711}^{\ast }{\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)\subseteq {\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y)$
.
$\unicode[STIX]{x1D711}^{\ast }{\mathcal{A}}^{\unicode[STIX]{x1D714}}(X)\subseteq {\mathcal{C}}^{\unicode[STIX]{x1D714}}(Y)$
.(3) If
 $\unicode[STIX]{x1D711}\in {\mathcal{C}}^{M}(Y,X)$
and
$\unicode[STIX]{x1D711}\in {\mathcal{C}}^{M}(Y,X)$
and
 ${\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{N}(Y)$
, then
${\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{N}(Y)$
, then
 $\unicode[STIX]{x1D711}^{\ast }{\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{N}(Y)$
.
$\unicode[STIX]{x1D711}^{\ast }{\mathcal{A}}^{M}(X)\subseteq {\mathcal{C}}^{N}(Y)$
.
Proof. We prove (1); (2) and (3) work similarly. Let
![]() $f\in {\mathcal{A}}^{\infty }(X)$
. Assume that
$f\in {\mathcal{A}}^{\infty }(X)$
. Assume that
![]() $f\,\circ \,\unicode[STIX]{x1D711}\not \in {\mathcal{C}}^{\infty }(Y)$
. Since
$f\,\circ \,\unicode[STIX]{x1D711}\not \in {\mathcal{C}}^{\infty }(Y)$
. Since
![]() ${\mathcal{C}}^{\infty }(Y)={\mathcal{A}}^{\infty }(Y)$
, there exists
${\mathcal{C}}^{\infty }(Y)={\mathcal{A}}^{\infty }(Y)$
, there exists
![]() $c\in {\mathcal{C}}^{\infty }(\mathbb{R},Y)$
such that
$c\in {\mathcal{C}}^{\infty }(\mathbb{R},Y)$
such that
![]() $f\,\circ \,\unicode[STIX]{x1D711}\,\circ \,c\not \in {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
. But
$f\,\circ \,\unicode[STIX]{x1D711}\,\circ \,c\not \in {\mathcal{C}}^{\infty }(\mathbb{R},\mathbb{R})$
. But
![]() $\unicode[STIX]{x1D711}\,\circ \,c$
is a
$\unicode[STIX]{x1D711}\,\circ \,c$
is a
![]() ${\mathcal{C}}^{\infty }$
-curve in
${\mathcal{C}}^{\infty }$
-curve in
![]() $X$
, contradicting
$X$
, contradicting
![]() $f\in {\mathcal{A}}^{\infty }(X)$
.◻
$f\in {\mathcal{A}}^{\infty }(X)$
.◻
Combining this lemma with the rectilinearization of subanalytic sets (see Theorem 5.1), we conclude the following result.
Theorem 8.2. Let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence. Let
$M=(M_{k})$
be a non-quasianalytic weight sequence. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. There is a locally finite collection of real analytic mappings
$X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. There is a locally finite collection of real analytic mappings
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}:U_{\unicode[STIX]{x1D6FC}}\rightarrow \mathbb{R}^{d}$
, where the
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}:U_{\unicode[STIX]{x1D6FC}}\rightarrow \mathbb{R}^{d}$
, where the
![]() $U_{\unicode[STIX]{x1D6FC}}$
are open sets in
$U_{\unicode[STIX]{x1D6FC}}$
are open sets in
![]() $\mathbb{R}^{d}$
, such that, for all
$\mathbb{R}^{d}$
, such that, for all
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
Proof. We use Theorem 5.1. Since
![]() $X=\overline{\operatorname{int}(X)}$
, we may assume that, for the quadrants
$X=\overline{\operatorname{int}(X)}$
, we may assume that, for the quadrants
![]() $Q(I_{0},I_{-},I_{+})$
whose union is
$Q(I_{0},I_{-},I_{+})$
whose union is
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}^{-1}(X)$
, we have
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}^{-1}(X)$
, we have
![]() $I_{0}=\emptyset$
. We claim that a union
$I_{0}=\emptyset$
. We claim that a union
![]() $Y$
of quadrants
$Y$
of quadrants
![]() $Q(\emptyset ,I_{-},I_{+})$
is
$Q(\emptyset ,I_{-},I_{+})$
is
![]() ${\mathcal{A}}^{\infty }$
- and
${\mathcal{A}}^{\infty }$
- and
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible. Furthermore, we claim that
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissible. Furthermore, we claim that
![]() $Y$
satisfies
$Y$
satisfies
![]() ${\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{M^{(2)}}(Y)$
. Then Lemma 8.1 implies the result.
${\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{M^{(2)}}(Y)$
. Then Lemma 8.1 implies the result.
![]() ${\mathcal{A}}^{\infty }$
-admissibility. By Theorem 1.13, each
${\mathcal{A}}^{\infty }$
-admissibility. By Theorem 1.13, each
![]() $Q=Q(\emptyset ,I_{-},I_{+})$
is
$Q=Q(\emptyset ,I_{-},I_{+})$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible. Any two different quadrants
${\mathcal{A}}^{\infty }$
-admissible. Any two different quadrants
![]() $Q_{1}$
,
$Q_{1}$
,
![]() $Q_{2}$
have non-empty intersection
$Q_{2}$
have non-empty intersection
![]() $\unicode[STIX]{x1D70B}$
which consists of a coordinate sector of dimension
$\unicode[STIX]{x1D70B}$
which consists of a coordinate sector of dimension
![]() $k\in \{0,\ldots ,d-1\}$
(for
$k\in \{0,\ldots ,d-1\}$
(for
![]() $k=0$
,
$k=0$
,
![]() $\unicode[STIX]{x1D70B}=\{0\}$
). Suppose that
$\unicode[STIX]{x1D70B}=\{0\}$
). Suppose that
![]() $\unicode[STIX]{x1D70B}$
is a coordinate sector of dimension
$\unicode[STIX]{x1D70B}$
is a coordinate sector of dimension
![]() $k$
. Let
$k$
. Let
![]() $v\in Q_{1}\cup Q_{2}$
be any vector perpendicular to
$v\in Q_{1}\cup Q_{2}$
be any vector perpendicular to
![]() $\unicode[STIX]{x1D70B}$
. Then
$\unicode[STIX]{x1D70B}$
. Then
![]() $\unicode[STIX]{x1D70E}_{v}:=\unicode[STIX]{x1D70B}+\mathbb{R}v$
is a (
$\unicode[STIX]{x1D70E}_{v}:=\unicode[STIX]{x1D70B}+\mathbb{R}v$
is a (
![]() $k+1$
)-dimensional closed convex set contained in
$k+1$
)-dimensional closed convex set contained in
![]() $Q_{1}\cup Q_{2}$
. We may conclude that
$Q_{1}\cup Q_{2}$
. We may conclude that
![]() $f|_{\unicode[STIX]{x1D70E}_{v}}\in {\mathcal{C}}^{\infty }(\unicode[STIX]{x1D70E}_{v})$
. Thus the directional derivatives
$f|_{\unicode[STIX]{x1D70E}_{v}}\in {\mathcal{C}}^{\infty }(\unicode[STIX]{x1D70E}_{v})$
. Thus the directional derivatives
![]() $d_{w}^{n}f$
of
$d_{w}^{n}f$
of
![]() $f$
of all orders
$f$
of all orders
![]() $n$
at points in
$n$
at points in
![]() $\unicode[STIX]{x1D70B}$
with direction
$\unicode[STIX]{x1D70B}$
with direction
![]() $w\in \bigcup _{v\in Q_{1}\cup Q_{2}}\unicode[STIX]{x1D70E}_{v}$
exist and are unique. These suffice to compute the partial derivatives of
$w\in \bigcup _{v\in Q_{1}\cup Q_{2}}\unicode[STIX]{x1D70E}_{v}$
exist and are unique. These suffice to compute the partial derivatives of
![]() $f$
of all orders at points in
$f$
of all orders at points in
![]() $\unicode[STIX]{x1D70B}$
. This proves that
$\unicode[STIX]{x1D70B}$
. This proves that
![]() $Q_{1}\cup Q_{2}$
is
$Q_{1}\cup Q_{2}$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible. The general case follows by induction. This also proves that we even have
${\mathcal{A}}^{\infty }$
-admissible. The general case follows by induction. This also proves that we even have
![]() ${\mathcal{A}}_{M}^{\infty }(Y)={\mathcal{C}}^{\infty }(Y)$
.
${\mathcal{A}}_{M}^{\infty }(Y)={\mathcal{C}}^{\infty }(Y)$
.
![]() ${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissibility. This follows from Theorem 1.16 and the fact that
${\mathcal{A}}^{\unicode[STIX]{x1D714}}$
-admissibility. This follows from Theorem 1.16 and the fact that
![]() $Y$
is
$Y$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible.
${\mathcal{A}}^{\infty }$
-admissible.
Finally, we show
![]() ${\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{M^{(2)}}(Y)$
. Since we already have
${\mathcal{A}}^{M}(Y)\subseteq {\mathcal{C}}^{M^{(2)}}(Y)$
. Since we already have
![]() ${\mathcal{A}}_{M}^{\infty }(Y)={\mathcal{C}}^{\infty }(Y)$
, it suffices to check that the estimates (1.1) (for
${\mathcal{A}}_{M}^{\infty }(Y)={\mathcal{C}}^{\infty }(Y)$
, it suffices to check that the estimates (1.1) (for
![]() $M^{(2)}$
instead of
$M^{(2)}$
instead of
![]() $M$
) hold for all
$M$
) hold for all
![]() $f\in {\mathcal{A}}^{M}(Y)$
and for each compact
$f\in {\mathcal{A}}^{M}(Y)$
and for each compact
![]() $K\subseteq Y$
. This is clear, since
$K\subseteq Y$
. This is clear, since
![]() $f|_{Q}\in {\mathcal{A}}^{M}(Q)\subseteq {\mathcal{C}}^{M^{(2)}}(Q)$
, by Theorem 1.19, for each of the finitely many quadrants
$f|_{Q}\in {\mathcal{A}}^{M}(Q)\subseteq {\mathcal{C}}^{M^{(2)}}(Q)$
, by Theorem 1.19, for each of the finitely many quadrants
![]() $Q$
which make up
$Q$
which make up
![]() $Y$
.◻
$Y$
.◻
8.2 Controlled loss of regularity
Let
![]() $M=(M_{k})$
be a weight sequence. Recall that, for positive integers
$M=(M_{k})$
be a weight sequence. Recall that, for positive integers
![]() $a$
,
$a$
,
![]() $M^{(a)}$
denotes the weight sequence defined by
$M^{(a)}$
denotes the weight sequence defined by
![]() $M_{k}^{(a)}:=M_{ak}$
.
$M_{k}^{(a)}:=M_{ak}$
.
Proposition 8.3. Let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence. Let
$M=(M_{k})$
be a non-quasianalytic weight sequence. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat compact subanalytic set. Then there is a positive integer
$X\subseteq \mathbb{R}^{d}$
be a fat compact subanalytic set. Then there is a positive integer
![]() $a$
, independent of
$a$
, independent of
![]() $M$
, such that
$M$
, such that
Proof. Let
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}$
be the finitely many mappings provided by Theorem 5.1. We may assume that the Jacobian determinant of each
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}$
be the finitely many mappings provided by Theorem 5.1. We may assume that the Jacobian determinant of each
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}$
is a monomial times a nowhere vanishing factor. Let
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}$
is a monomial times a nowhere vanishing factor. Let
![]() $f\in {\mathcal{C}}^{\infty }(X)\,\cap \,{\mathcal{A}}^{M}(X)$
. By Theorem 8.2,
$f\in {\mathcal{C}}^{\infty }(X)\,\cap \,{\mathcal{A}}^{M}(X)$
. By Theorem 8.2,
![]() $f\,\circ \,\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}\in {\mathcal{C}}^{M^{(2)}}(Y_{\unicode[STIX]{x1D6FC}})$
where
$f\,\circ \,\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}\in {\mathcal{C}}^{M^{(2)}}(Y_{\unicode[STIX]{x1D6FC}})$
where
![]() $Y_{\unicode[STIX]{x1D6FC}}$
is a union of quadrants in
$Y_{\unicode[STIX]{x1D6FC}}$
is a union of quadrants in
![]() $\mathbb{R}^{d}$
. By [Reference Belotto da Silva, Bierstone and ChowBBC18, Theorem 1.4], for each
$\mathbb{R}^{d}$
. By [Reference Belotto da Silva, Bierstone and ChowBBC18, Theorem 1.4], for each
![]() $\unicode[STIX]{x1D6FC}$
there is a positive integer
$\unicode[STIX]{x1D6FC}$
there is a positive integer
![]() $a_{\unicode[STIX]{x1D6FC}}$
such that
$a_{\unicode[STIX]{x1D6FC}}$
such that
![]() $f$
is of class
$f$
is of class
![]() ${\mathcal{C}}^{M^{(a_{\unicode[STIX]{x1D6FC}})}}$
on
${\mathcal{C}}^{M^{(a_{\unicode[STIX]{x1D6FC}})}}$
on
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(Y_{\unicode[STIX]{x1D6FC}})$
. It follows that
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D6FC}}(Y_{\unicode[STIX]{x1D6FC}})$
. It follows that
![]() $f\in {\mathcal{C}}^{M^{(a)}}(X)$
, where
$f\in {\mathcal{C}}^{M^{(a)}}(X)$
, where
![]() $a=\max _{\unicode[STIX]{x1D6FC}}a_{\unicode[STIX]{x1D6FC}}$
.◻
$a=\max _{\unicode[STIX]{x1D6FC}}a_{\unicode[STIX]{x1D6FC}}$
.◻
For
![]() $a\in \mathbb{R}_{{>}0}$
we may define the weight sequence
$a\in \mathbb{R}_{{>}0}$
we may define the weight sequence
![]() $M^{a}$
by
$M^{a}$
by
![]() $M_{k}^{a}:=(M_{k})^{a}$
. If
$M_{k}^{a}:=(M_{k})^{a}$
. If
![]() $M=(M_{k})$
has moderate growth (see (2.4)) and
$M=(M_{k})$
has moderate growth (see (2.4)) and
![]() $a$
is an integer, then there exists
$a$
is an integer, then there exists
![]() $C=C(a)$
such that
$C=C(a)$
such that
that is,
![]() $M^{(a)}$
and
$M^{(a)}$
and
![]() $M^{a}$
define the same Denjoy–Carleman class. Note also that
$M^{a}$
define the same Denjoy–Carleman class. Note also that
![]() $M^{a}$
has moderate growth whenever
$M^{a}$
has moderate growth whenever
![]() $M$
has.
$M$
has.
Assume that for each
![]() $a>0$
, the weight sequence
$a>0$
, the weight sequence
![]() $M^{a}$
is non-quasianalytic and define
$M^{a}$
is non-quasianalytic and define
Theorem 8.4. Let
![]() $M=(M_{k})$
be a weight sequence of moderate growth such that
$M=(M_{k})$
be a weight sequence of moderate growth such that
![]() $M^{a}$
is non-quasianalytic for all
$M^{a}$
is non-quasianalytic for all
![]() $a>0$
. Let
$a>0$
. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. Then
$X\subseteq \mathbb{R}^{d}$
be a fat closed subanalytic set. Then
If
![]() $X$
is simple, then
$X$
is simple, then
Proof. The inclusion
![]() $\widehat{{\mathcal{C}}}^{M}(X)\subseteq {\mathcal{C}}^{\infty }(X)\,\cap \,\widehat{{\mathcal{A}}}^{M}(X)$
is obvious. The converse inclusion follows from Proposition 8.3.◻
$\widehat{{\mathcal{C}}}^{M}(X)\subseteq {\mathcal{C}}^{\infty }(X)\,\cap \,\widehat{{\mathcal{A}}}^{M}(X)$
is obvious. The converse inclusion follows from Proposition 8.3.◻
Remark 8.5. Instead of [Reference Belotto da Silva, Bierstone and ChowBBC18, Theorem 1.4] one can also use the results of [Reference Chaumat and CholletCC99].
9 Applications
9.1 Solutions of real analytic equations
Theorem 9.1. Let
![]() $U\subseteq \mathbb{R}^{d+1}$
be open and let
$U\subseteq \mathbb{R}^{d+1}$
be open and let
![]() $H:U\rightarrow \mathbb{R}$
be a real analytic function (not identically zero). Let
$H:U\rightarrow \mathbb{R}$
be a real analytic function (not identically zero). Let
![]() $X\subseteq \mathbb{R}^{d}$
be a closed set such that for all
$X\subseteq \mathbb{R}^{d}$
be a closed set such that for all
![]() $z\in \unicode[STIX]{x2202}X$
there is a closed fat subanalytic set
$z\in \unicode[STIX]{x2202}X$
there is a closed fat subanalytic set
![]() $X_{z}$
such that
$X_{z}$
such that
![]() $z\in X_{z}\subseteq X$
; for example,
$z\in X_{z}\subseteq X$
; for example,
![]() $X$
itself is fat and subanalytic or a Hölder set. If
$X$
itself is fat and subanalytic or a Hölder set. If
![]() $f\in {\mathcal{C}}^{\infty }(X)$
satisfies
$f\in {\mathcal{C}}^{\infty }(X)$
satisfies
![]() $H(x,f(x))=0$
for all
$H(x,f(x))=0$
for all
![]() $x\in X$
, then
$x\in X$
, then
![]() $f$
extends to a holomorphic function on a neighborhood of
$f$
extends to a holomorphic function on a neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{C}^{d}$
.
$\mathbb{C}^{d}$
.
Proof. Suppose first that
![]() $X\subseteq \mathbb{R}^{d}$
is fat closed subanalytic. As in the proof of Theorem 1.16, there is a proper real analytic map
$X\subseteq \mathbb{R}^{d}$
is fat closed subanalytic. As in the proof of Theorem 1.16, there is a proper real analytic map
![]() $\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
with
$\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
with
![]() $X=\unicode[STIX]{x1D711}(M)$
. Then
$X=\unicode[STIX]{x1D711}(M)$
. Then
![]() $(z,y)\mapsto H(\unicode[STIX]{x1D711}(z),y)$
is not identically zero. By the classical version of this theorem (cf. [Reference BochnakBoc70, Reference SiciakSic70, Reference MalgrangeMal67]), we may conclude that
$(z,y)\mapsto H(\unicode[STIX]{x1D711}(z),y)$
is not identically zero. By the classical version of this theorem (cf. [Reference BochnakBoc70, Reference SiciakSic70, Reference MalgrangeMal67]), we may conclude that
![]() $z\mapsto (f\,\circ \,\unicode[STIX]{x1D711})(z)$
is real analytic on
$z\mapsto (f\,\circ \,\unicode[STIX]{x1D711})(z)$
is real analytic on
![]() $M$
. The proof of Theorem 1.16 (in § 6) then yields the assertion.
$M$
. The proof of Theorem 1.16 (in § 6) then yields the assertion.
In the general case, fix
![]() $z\in \unicode[STIX]{x2202}X$
and a closed fat subanalytic set
$z\in \unicode[STIX]{x2202}X$
and a closed fat subanalytic set
![]() $X_{z}$
with
$X_{z}$
with
![]() $z\in X_{z}\subseteq X$
. Then
$z\in X_{z}\subseteq X$
. Then
![]() $f|_{X_{z}}\in {\mathcal{C}}^{\infty }(X_{z})$
satisfies
$f|_{X_{z}}\in {\mathcal{C}}^{\infty }(X_{z})$
satisfies
![]() $H(x,f(x))=0$
for all
$H(x,f(x))=0$
for all
![]() $x\in X_{z}$
. Thus, by the first part of the proof,
$x\in X_{z}$
. Thus, by the first part of the proof,
![]() $f|_{X_{z}}$
extends to a holomorphic function on a neighborhood of
$f|_{X_{z}}$
extends to a holomorphic function on a neighborhood of
![]() $X_{z}$
in
$X_{z}$
in
![]() $\mathbb{C}^{d}$
. That these local extensions glue to the desired global extension follows from Lemma 6.1 as in the proof of Theorem 1.16.◻
$\mathbb{C}^{d}$
. That these local extensions glue to the desired global extension follows from Lemma 6.1 as in the proof of Theorem 1.16.◻
We obtain the following corollary for Nash functions, that is, real analytic functions
![]() $f:U\rightarrow \mathbb{R}$
defined in an open semialgebraic set
$f:U\rightarrow \mathbb{R}$
defined in an open semialgebraic set
![]() $U\subseteq \mathbb{R}^{d}$
which satisfy a non-trivial polynomial equation
$U\subseteq \mathbb{R}^{d}$
which satisfy a non-trivial polynomial equation
![]() $P(x,f(x))=0$
for all
$P(x,f(x))=0$
for all
![]() $x\in U$
.
$x\in U$
.
Corollary 9.2. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat closed semialgebraic set and let
$X\subseteq \mathbb{R}^{d}$
be a fat closed semialgebraic set and let
![]() $f:\operatorname{int}(X)\rightarrow \mathbb{R}$
be a Nash function whose partial derivatives of all orders extend continuously to the boundary of
$f:\operatorname{int}(X)\rightarrow \mathbb{R}$
be a Nash function whose partial derivatives of all orders extend continuously to the boundary of
![]() $X$
. Then
$X$
. Then
![]() $f$
is the restriction of a Nash function on an open neighborhood of
$f$
is the restriction of a Nash function on an open neighborhood of
![]() $X$
.
$X$
.
Proof. The extension of
![]() $f$
clearly also satisfies the defining polynomial equation.◻
$f$
clearly also satisfies the defining polynomial equation.◻
9.2 Composite real analytic functions
Suppose that
![]() $\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
is a real analytic map, where
$\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
is a real analytic map, where
![]() $M$
is a real analytic manifold. Assume that
$M$
is a real analytic manifold. Assume that
![]() $g\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
and
$g\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
and
![]() $f=g\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(M)$
. Let
$f=g\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(M)$
. Let
![]() $X:=\unicode[STIX]{x1D711}(M)$
. Our results yield a sufficient condition for
$X:=\unicode[STIX]{x1D711}(M)$
. Our results yield a sufficient condition for
![]() $g|_{X}$
to admit a real analytic extension to some open neighborhood of
$g|_{X}$
to admit a real analytic extension to some open neighborhood of
![]() $X$
.
$X$
.
Corollary 9.3. Let
![]() $\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
be real analytic and such that:
$\unicode[STIX]{x1D711}:M\rightarrow \mathbb{R}^{d}$
be real analytic and such that:
(i)
 $X:=\unicode[STIX]{x1D711}(M)$
is a fat closed subanalytic subset of
$X:=\unicode[STIX]{x1D711}(M)$
is a fat closed subanalytic subset of
 $\mathbb{R}^{d}$
;
$\mathbb{R}^{d}$
;(ii) each
 $c\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},X)$
admits a lifting
$c\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},X)$
admits a lifting
 $\tilde{c}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},M)$
, that is,
$\tilde{c}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(\mathbb{R},M)$
, that is,
 $c=\unicode[STIX]{x1D711}\,\circ \,\tilde{c}$
.
$c=\unicode[STIX]{x1D711}\,\circ \,\tilde{c}$
.
Then, for each
![]() $g\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
with
$g\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
with
![]() $g\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(M)$
, there exists a holomorphic function
$g\,\circ \,\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\unicode[STIX]{x1D714}}(M)$
, there exists a holomorphic function
![]() $G$
defined in an open neighborhood of
$G$
defined in an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{C}^{d}$
such that
$\mathbb{C}^{d}$
such that
![]() $g|_{X}=G|_{X}$
.
$g|_{X}=G|_{X}$
.
Proof. Follows from Theorem 1.16. ◻
Conditions for the existence of a smooth solution
![]() $g$
of the equation
$g$
of the equation
![]() $f=g\,\circ \,\unicode[STIX]{x1D711}$
have been intensively studied; see [Reference Bierstone and MilmanBM82, Reference Bierstone, Milman and PawłuckiBMP96, Reference Bierstone and MilmanBM98].
$f=g\,\circ \,\unicode[STIX]{x1D711}$
have been intensively studied; see [Reference Bierstone and MilmanBM82, Reference Bierstone, Milman and PawłuckiBMP96, Reference Bierstone and MilmanBM98].
Remark 9.4. For instance, the conditions of the corollary are satisfied in the following situation. Let
![]() $\unicode[STIX]{x1D70C}:G\rightarrow \operatorname{O}(V)$
be a coregular finite-dimensional orthogonal representation of a compact Lie group. Let
$\unicode[STIX]{x1D70C}:G\rightarrow \operatorname{O}(V)$
be a coregular finite-dimensional orthogonal representation of a compact Lie group. Let
![]() $\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{d})$
be a minimal system of generators of the algebra
$\unicode[STIX]{x1D70E}=(\unicode[STIX]{x1D70E}_{1},\ldots ,\unicode[STIX]{x1D70E}_{d})$
be a minimal system of generators of the algebra
![]() $\mathbb{R}[V]^{G}$
of
$\mathbb{R}[V]^{G}$
of
![]() $G$
-invariant polynomials. Schwarz’s theorem [Reference SchwarzSch75] (see also [Reference MatherMat77]) holds that for each
$G$
-invariant polynomials. Schwarz’s theorem [Reference SchwarzSch75] (see also [Reference MatherMat77]) holds that for each
![]() $G$
-invariant
$G$
-invariant
![]() $f\in {\mathcal{C}}^{\infty }(V)$
there exists
$f\in {\mathcal{C}}^{\infty }(V)$
there exists
![]() $g\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
such that
$g\in {\mathcal{C}}^{\infty }(\mathbb{R}^{d})$
such that
![]() $f=g\,\circ \,\unicode[STIX]{x1D70E}$
. The set
$f=g\,\circ \,\unicode[STIX]{x1D70E}$
. The set
![]() $X=\unicode[STIX]{x1D70E}(V)$
is closed semialgebraic and fat, by the assumption that
$X=\unicode[STIX]{x1D70E}(V)$
is closed semialgebraic and fat, by the assumption that
![]() $\unicode[STIX]{x1D70C}$
is coregular; cf. [Reference Procesi and SchwarzPS85]. Real analytic curves in
$\unicode[STIX]{x1D70C}$
is coregular; cf. [Reference Procesi and SchwarzPS85]. Real analytic curves in
![]() $X$
admit real analytic liftings to
$X$
admit real analytic liftings to
![]() $V$
, by [Reference Alekseevsky, Kriegl, Losik and MichorAKLM00] and [Reference Parusiński and RainerPR16, Theorem 4]. The corollary implies that every
$V$
, by [Reference Alekseevsky, Kriegl, Losik and MichorAKLM00] and [Reference Parusiński and RainerPR16, Theorem 4]. The corollary implies that every
![]() $G$
-invariant real analytic function
$G$
-invariant real analytic function
![]() $f$
on
$f$
on
![]() $V$
is of the form
$V$
is of the form
![]() $f=g\,\circ \,\unicode[STIX]{x1D70E}$
, where
$f=g\,\circ \,\unicode[STIX]{x1D70E}$
, where
![]() $g$
is a holomorphic function defined in an open neighborhood of
$g$
is a holomorphic function defined in an open neighborhood of
![]() $X$
in
$X$
in
![]() $\mathbb{C}^{d}$
. A more general result (with a different proof) is due to Luna [Reference LunaLun76].
$\mathbb{C}^{d}$
. A more general result (with a different proof) is due to Luna [Reference LunaLun76].
9.3 Division of smooth functions and pseudo-immersions
Statements about smooth functions on open sets can sometimes be reduced to corresponding statements for functions of one real variable, thanks to Boman’s Theorem 1.4. This principle extends to
![]() ${\mathcal{A}}^{\infty }$
-admissible sets. We illustrate this using two selected examples. The first concerns division of smooth functions.
${\mathcal{A}}^{\infty }$
-admissible sets. We illustrate this using two selected examples. The first concerns division of smooth functions.
Theorem 9.5. Suppose that
![]() $X$
is a Hölder set or a simple fat closed subanalytic subset of
$X$
is a Hölder set or a simple fat closed subanalytic subset of
![]() $\mathbb{R}^{d}$
. If
$\mathbb{R}^{d}$
. If
![]() $f,g:X\rightarrow \mathbb{C}$
satisfy
$f,g:X\rightarrow \mathbb{C}$
satisfy
(i)
 $g,fg,f^{m}\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
, and
$g,fg,f^{m}\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
, and(ii)
 $|f(x)|\leqslant C|g(x)|^{\unicode[STIX]{x1D6FC}}$
for all
$|f(x)|\leqslant C|g(x)|^{\unicode[STIX]{x1D6FC}}$
for all
 $x\in X$
,
$x\in X$
,
for some
![]() $m\in \mathbb{N}_{{\geqslant}1}$
and
$m\in \mathbb{N}_{{\geqslant}1}$
and
![]() $C,\unicode[STIX]{x1D6FC}>0$
, then
$C,\unicode[STIX]{x1D6FC}>0$
, then
![]() $f\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
.
$f\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
.
Proof. This follows from [Reference Joris and PreissmannJP90, Theorem 1] (which is precisely the case
![]() $X=\mathbb{R}$
), Theorems 1.13, and 1.14.◻
$X=\mathbb{R}$
), Theorems 1.13, and 1.14.◻
In [Reference Joris and PreissmannJP90] this theorem (for
![]() $X=\mathbb{R}$
) was used to prove that certain maps are pseudo-immersions. A
$X=\mathbb{R}$
) was used to prove that certain maps are pseudo-immersions. A
![]() ${\mathcal{C}}^{\infty }$
-map
${\mathcal{C}}^{\infty }$
-map
![]() $p:N\rightarrow M$
between
$p:N\rightarrow M$
between
![]() ${\mathcal{C}}^{\infty }$
-manifolds is a pseudo-immersion if for each continuous map
${\mathcal{C}}^{\infty }$
-manifolds is a pseudo-immersion if for each continuous map
![]() $f:P\rightarrow N$
, where
$f:P\rightarrow N$
, where
![]() $P$
is a
$P$
is a
![]() ${\mathcal{C}}^{\infty }$
-manifold,
${\mathcal{C}}^{\infty }$
-manifold,
![]() $p\,\circ \,f\in {\mathcal{C}}^{\infty }$
implies
$p\,\circ \,f\in {\mathcal{C}}^{\infty }$
implies
![]() $f\in {\mathcal{C}}^{\infty }$
; see also [Reference Joris and PreissmannJP87]. Pseudo-immersivity of a smooth map is a local property. So it is enough to consider germs of smooth maps
$f\in {\mathcal{C}}^{\infty }$
; see also [Reference Joris and PreissmannJP87]. Pseudo-immersivity of a smooth map is a local property. So it is enough to consider germs of smooth maps
![]() $p:(\mathbb{R}^{n},0)\rightarrow (\mathbb{R}^{m},0)$
. By Boman’s Theorem 1.1, the defining universal property must be checked only for smooth curves:
$p:(\mathbb{R}^{n},0)\rightarrow (\mathbb{R}^{m},0)$
. By Boman’s Theorem 1.1, the defining universal property must be checked only for smooth curves:
![]() $p$
is a pseudo-immersion if and only if for each (continuous) curve
$p$
is a pseudo-immersion if and only if for each (continuous) curve
![]() $c:\mathbb{R}\rightarrow \mathbb{R}^{n}$
we have the implication
$c:\mathbb{R}\rightarrow \mathbb{R}^{n}$
we have the implication
![]() $p\,\circ \,c\in {\mathcal{C}}^{\infty }\;\Longrightarrow \;c\in {\mathcal{C}}^{\infty }$
.
$p\,\circ \,c\in {\mathcal{C}}^{\infty }\;\Longrightarrow \;c\in {\mathcal{C}}^{\infty }$
.
Theorems 1.13 and 1.14 entail the following result.
Theorem 9.6. Let
![]() $p:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$
be a pseudo-immersion. Then the universal property of
$p:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$
be a pseudo-immersion. Then the universal property of
![]() $p$
extends to maps
$p$
extends to maps
![]() $f:X\rightarrow \mathbb{R}^{n}$
, where
$f:X\rightarrow \mathbb{R}^{n}$
, where
![]() $X\subseteq \mathbb{R}^{d}$
is
$X\subseteq \mathbb{R}^{d}$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible, in particular, for
${\mathcal{A}}^{\infty }$
-admissible, in particular, for
![]() $X$
a Hölder set or a simple fat closed subanalytic subset of
$X$
a Hölder set or a simple fat closed subanalytic subset of
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
For instance, if
![]() $f:X\rightarrow \mathbb{C}$
is continuous and
$f:X\rightarrow \mathbb{C}$
is continuous and
![]() $f^{2},f^{3}\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
, then
$f^{2},f^{3}\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
, then
![]() $f\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
. In addition, by Theorem 9.1, if at least one of
$f\in {\mathcal{C}}^{\infty }(X,\mathbb{C})$
. In addition, by Theorem 9.1, if at least one of
![]() $f^{2}$
or
$f^{2}$
or
![]() $f^{3}$
is real analytic, then also
$f^{3}$
is real analytic, then also
![]() $f$
is real analytic.
$f$
is real analytic.
10 Complements and examples
10.1
 ${\mathcal{C}}^{M}$
-extensions
${\mathcal{C}}^{M}$
-extensions
Let
![]() $X\subseteq \mathbb{R}^{d}$
be a Hölder set or a fat closed subanalytic set. By Lemma 1.10, Proposition 3.8, and Theorem 5.6, any function
$X\subseteq \mathbb{R}^{d}$
be a Hölder set or a fat closed subanalytic set. By Lemma 1.10, Proposition 3.8, and Theorem 5.6, any function
![]() $f:X\rightarrow \mathbb{R}$
which satisfies Lemma 1.10(3) extends to a
$f:X\rightarrow \mathbb{R}$
which satisfies Lemma 1.10(3) extends to a
![]() ${\mathcal{C}}^{\infty }$
-function on
${\mathcal{C}}^{\infty }$
-function on
![]() $\mathbb{R}^{d}$
. Let us investigate this in the ultradifferentiable case. For strongly regular weight sequences
$\mathbb{R}^{d}$
. Let us investigate this in the ultradifferentiable case. For strongly regular weight sequences
![]() $M$
there is a
$M$
there is a
![]() ${\mathcal{C}}^{M}$
-version of Whitney’s extension theorem [Reference BrunaBru80].
${\mathcal{C}}^{M}$
-version of Whitney’s extension theorem [Reference BrunaBru80].
Lemma 10.1. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a fat compact set either in
$X\subseteq \mathbb{R}^{d}$
be a fat compact set either in
![]() $\mathscr{H}(\mathbb{R}^{d})$
or subanalytic. Suppose there exist a positive integer
$\mathscr{H}(\mathbb{R}^{d})$
or subanalytic. Suppose there exist a positive integer
![]() $m$
and a constant
$m$
and a constant
![]() $D>0$
, such that any two points
$D>0$
, such that any two points
![]() $x,y\in X$
can be joined by a rectifiable path
$x,y\in X$
can be joined by a rectifiable path
![]() $\unicode[STIX]{x1D6FE}$
in
$\unicode[STIX]{x1D6FE}$
in
![]() $X$
and
$X$
and
Let
![]() $M$
be a weight sequence. Then each
$M$
be a weight sequence. Then each
![]() $f\in {\mathcal{C}}^{M}(X)$
defines a Whitney jet on
$f\in {\mathcal{C}}^{M}(X)$
defines a Whitney jet on
![]() $X$
of class
$X$
of class
![]() ${\mathcal{C}}^{N}$
where
${\mathcal{C}}^{N}$
where
![]() $N_{k}:=M_{mk}$
, that is, there exist constants
$N_{k}:=M_{mk}$
, that is, there exist constants
![]() $C,\unicode[STIX]{x1D70C}>0$
such that
$C,\unicode[STIX]{x1D70C}>0$
such that
where
Proof. Let
![]() $f\in {\mathcal{C}}^{M}(X)$
. Now (10.2) is clearly satisfied since we even have
$f\in {\mathcal{C}}^{M}(X)$
. Now (10.2) is clearly satisfied since we even have
Since
![]() $f$
has a smooth extension to
$f$
has a smooth extension to
![]() $\mathbb{R}^{d}$
,
$\mathbb{R}^{d}$
,
![]() $f$
defines a Whitney jet of class
$f$
defines a Whitney jet of class
![]() ${\mathcal{C}}^{\infty }$
on
${\mathcal{C}}^{\infty }$
on
![]() $X$
. We claim that
$X$
. We claim that
 $$\begin{eqnarray}|(R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y)|\leqslant \frac{(d\ell (\unicode[STIX]{x1D70E}))^{p+1-|\unicode[STIX]{x1D6FC}|}}{(p+1-|\unicode[STIX]{x1D6FC}|)!}\sup _{\substack{ \unicode[STIX]{x1D709}\in \unicode[STIX]{x1D70E} \\ |\unicode[STIX]{x1D6FE}|=p+1}}|f^{(\unicode[STIX]{x1D6FE})}(\unicode[STIX]{x1D709})|\end{eqnarray}$$
$$\begin{eqnarray}|(R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y)|\leqslant \frac{(d\ell (\unicode[STIX]{x1D70E}))^{p+1-|\unicode[STIX]{x1D6FC}|}}{(p+1-|\unicode[STIX]{x1D6FC}|)!}\sup _{\substack{ \unicode[STIX]{x1D709}\in \unicode[STIX]{x1D70E} \\ |\unicode[STIX]{x1D6FE}|=p+1}}|f^{(\unicode[STIX]{x1D6FE})}(\unicode[STIX]{x1D709})|\end{eqnarray}$$
for any rectifiable path
![]() $\unicode[STIX]{x1D70E}$
which joins
$\unicode[STIX]{x1D70E}$
which joins
![]() $x$
and
$x$
and
![]() $y$
. Then, by (10.1) and (10.4), there are constants
$y$
. Then, by (10.1) and (10.4), there are constants
![]() $C_{i},\unicode[STIX]{x1D70C}_{i}>0$
such that
$C_{i},\unicode[STIX]{x1D70C}_{i}>0$
such that
 $$\begin{eqnarray}\displaystyle |(R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y)| & {\leqslant} & \displaystyle |(R_{x}^{m(p+1)-1}f)^{\unicode[STIX]{x1D6FC}}(y)|+\biggl|\mathop{\sum }_{p-|\unicode[STIX]{x1D6FC}|<|\unicode[STIX]{x1D6FD}|<m(p+1)-|\unicode[STIX]{x1D6FC}|}\frac{f^{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})}(x)}{\unicode[STIX]{x1D6FD}!}(y-x)^{\unicode[STIX]{x1D6FD}}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle d^{m(p+1)-|\unicode[STIX]{x1D6FC}|}C\unicode[STIX]{x1D70C}^{m(p+1)}|\unicode[STIX]{x1D6FC}|!\,M_{m(p+1)}\ell (\unicode[STIX]{x1D70E})^{m(p+1)-|\unicode[STIX]{x1D6FC}|}\nonumber\\ \displaystyle & & \displaystyle +\,C_{1}\unicode[STIX]{x1D70C}_{1}^{m(p+1)}|\unicode[STIX]{x1D6FC}|!\,M_{m(p+1)}|x-y|^{p-|\unicode[STIX]{x1D6FC}|+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{2}\unicode[STIX]{x1D70C}_{2}^{m(p+1)}|\unicode[STIX]{x1D6FC}|!\,M_{m(p+1)}|x-y|^{p-|\unicode[STIX]{x1D6FC}|+1},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |(R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y)| & {\leqslant} & \displaystyle |(R_{x}^{m(p+1)-1}f)^{\unicode[STIX]{x1D6FC}}(y)|+\biggl|\mathop{\sum }_{p-|\unicode[STIX]{x1D6FC}|<|\unicode[STIX]{x1D6FD}|<m(p+1)-|\unicode[STIX]{x1D6FC}|}\frac{f^{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD})}(x)}{\unicode[STIX]{x1D6FD}!}(y-x)^{\unicode[STIX]{x1D6FD}}\biggr|\nonumber\\ \displaystyle & {\leqslant} & \displaystyle d^{m(p+1)-|\unicode[STIX]{x1D6FC}|}C\unicode[STIX]{x1D70C}^{m(p+1)}|\unicode[STIX]{x1D6FC}|!\,M_{m(p+1)}\ell (\unicode[STIX]{x1D70E})^{m(p+1)-|\unicode[STIX]{x1D6FC}|}\nonumber\\ \displaystyle & & \displaystyle +\,C_{1}\unicode[STIX]{x1D70C}_{1}^{m(p+1)}|\unicode[STIX]{x1D6FC}|!\,M_{m(p+1)}|x-y|^{p-|\unicode[STIX]{x1D6FC}|+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{2}\unicode[STIX]{x1D70C}_{2}^{m(p+1)}|\unicode[STIX]{x1D6FC}|!\,M_{m(p+1)}|x-y|^{p-|\unicode[STIX]{x1D6FC}|+1},\nonumber\end{eqnarray}$$
which is (10.3). To see (10.5) notice that, with
![]() $T_{x}^{p}f(y):=\sum _{|\unicode[STIX]{x1D6FD}|\leqslant p}((f^{(\unicode[STIX]{x1D6FD})}(x))/\unicode[STIX]{x1D6FD}!)(y-x)^{\unicode[STIX]{x1D6FD}}$
,
$T_{x}^{p}f(y):=\sum _{|\unicode[STIX]{x1D6FD}|\leqslant p}((f^{(\unicode[STIX]{x1D6FD})}(x))/\unicode[STIX]{x1D6FD}!)(y-x)^{\unicode[STIX]{x1D6FD}}$
,
By choosing a suitable parameterization, we may assume that
![]() $\unicode[STIX]{x1D70E}:[0,1]\rightarrow \mathbb{R}^{d}$
is an absolutely continuous curve from
$\unicode[STIX]{x1D70E}:[0,1]\rightarrow \mathbb{R}^{d}$
is an absolutely continuous curve from
![]() $x$
to
$x$
to
![]() $y$
such that
$y$
such that
![]() $|\unicode[STIX]{x1D70E}^{\prime }(t)|=\ell (\unicode[STIX]{x1D70E})$
for almost every
$|\unicode[STIX]{x1D70E}^{\prime }(t)|=\ell (\unicode[STIX]{x1D70E})$
for almost every
![]() $t$
. Then
$t$
. Then
 $$\begin{eqnarray}\displaystyle (R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y) & = & \displaystyle \int _{0}^{1}\unicode[STIX]{x2202}_{t}(T_{\unicode[STIX]{x1D70E}(t)}^{p-|\unicode[STIX]{x1D6FC}|}f^{(\unicode[STIX]{x1D6FC})}(y))\,dt\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=p-|\unicode[STIX]{x1D6FC}|}\frac{1}{\unicode[STIX]{x1D6FD}!}\mathop{\sum }_{i=1}^{d}f^{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+e_{i})}(\unicode[STIX]{x1D70E}(t))(y-\unicode[STIX]{x1D70E}(t))^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70E}_{i}^{\prime }(t)\,dt.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y) & = & \displaystyle \int _{0}^{1}\unicode[STIX]{x2202}_{t}(T_{\unicode[STIX]{x1D70E}(t)}^{p-|\unicode[STIX]{x1D6FC}|}f^{(\unicode[STIX]{x1D6FC})}(y))\,dt\nonumber\\ \displaystyle & = & \displaystyle \int _{0}^{1}\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=p-|\unicode[STIX]{x1D6FC}|}\frac{1}{\unicode[STIX]{x1D6FD}!}\mathop{\sum }_{i=1}^{d}f^{(\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}+e_{i})}(\unicode[STIX]{x1D70E}(t))(y-\unicode[STIX]{x1D70E}(t))^{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D70E}_{i}^{\prime }(t)\,dt.\nonumber\end{eqnarray}$$
By the Cauchy–Schwarz inequality,
Moreover,
![]() $|y-\unicode[STIX]{x1D70E}(t)|=|\unicode[STIX]{x1D70E}(1)-\unicode[STIX]{x1D70E}(t)|\leqslant \ell (\unicode[STIX]{x1D70E})(1-t)$
. Thus
$|y-\unicode[STIX]{x1D70E}(t)|=|\unicode[STIX]{x1D70E}(1)-\unicode[STIX]{x1D70E}(t)|\leqslant \ell (\unicode[STIX]{x1D70E})(1-t)$
. Thus
 $$\begin{eqnarray}|(R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y)|\leqslant \sqrt{d}\sup _{\substack{ \unicode[STIX]{x1D709}\in \unicode[STIX]{x1D70E} \\ |\unicode[STIX]{x1D6FE}|=p+1}}|f^{(\unicode[STIX]{x1D6FE})}(\unicode[STIX]{x1D709})|\ell (\unicode[STIX]{x1D70E})^{p+1-|\unicode[STIX]{x1D6FC}|}\int _{0}^{1}\frac{(1-t)^{p-|\unicode[STIX]{x1D6FC}|}}{(p-|\unicode[STIX]{x1D6FC}|)!}\,dt\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=p-|\unicode[STIX]{x1D6FC}|}\frac{|\unicode[STIX]{x1D6FD}|}{\unicode[STIX]{x1D6FD}!},\end{eqnarray}$$
$$\begin{eqnarray}|(R_{x}^{p}f)^{\unicode[STIX]{x1D6FC}}(y)|\leqslant \sqrt{d}\sup _{\substack{ \unicode[STIX]{x1D709}\in \unicode[STIX]{x1D70E} \\ |\unicode[STIX]{x1D6FE}|=p+1}}|f^{(\unicode[STIX]{x1D6FE})}(\unicode[STIX]{x1D709})|\ell (\unicode[STIX]{x1D70E})^{p+1-|\unicode[STIX]{x1D6FC}|}\int _{0}^{1}\frac{(1-t)^{p-|\unicode[STIX]{x1D6FC}|}}{(p-|\unicode[STIX]{x1D6FC}|)!}\,dt\mathop{\sum }_{|\unicode[STIX]{x1D6FD}|=p-|\unicode[STIX]{x1D6FC}|}\frac{|\unicode[STIX]{x1D6FD}|}{\unicode[STIX]{x1D6FD}!},\end{eqnarray}$$
which is (10.5). ◻
Corollary 10.2. Let
![]() $M=(M_{k})$
be a strongly regular weight sequence. For all
$M=(M_{k})$
be a strongly regular weight sequence. For all
![]() $X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
, the functions in
$X\in \mathscr{H}^{1}(\mathbb{R}^{d})$
, the functions in
![]() ${\mathcal{C}}^{M}(X)$
are precisely the functions which admit a
${\mathcal{C}}^{M}(X)$
are precisely the functions which admit a
![]() ${\mathcal{C}}^{M}$
-extension to
${\mathcal{C}}^{M}$
-extension to
![]() $\mathbb{R}^{d}$
.
$\mathbb{R}^{d}$
.
Proof. This follows from Lemma 10.1 and the
![]() ${\mathcal{C}}^{M}$
-version of Whitney’s extension theorem [Reference BrunaBru80], since a bounded Lipschitz set is quasiconvex, that is, (10.1) holds with
${\mathcal{C}}^{M}$
-version of Whitney’s extension theorem [Reference BrunaBru80], since a bounded Lipschitz set is quasiconvex, that is, (10.1) holds with
![]() $m=1$
; cf. Proposition 3.8.◻
$m=1$
; cf. Proposition 3.8.◻
Corollary 10.3. Let
![]() $M=(M_{k})$
be a non-quasianalytic weight sequence of moderate growth such that
$M=(M_{k})$
be a non-quasianalytic weight sequence of moderate growth such that
![]() $M^{a}$
is non-quasianalytic for each
$M^{a}$
is non-quasianalytic for each
![]() $a>0$
. Let
$a>0$
. Let
![]() $X\subseteq \mathbb{R}^{d}$
be a closed fat subanalytic subset. Then the functions in
$X\subseteq \mathbb{R}^{d}$
be a closed fat subanalytic subset. Then the functions in
![]() $\widehat{{\mathcal{C}}}^{M}(X)$
are precisely the functions which admit a
$\widehat{{\mathcal{C}}}^{M}(X)$
are precisely the functions which admit a
![]() $\widehat{{\mathcal{C}}}^{M}$
-extension to
$\widehat{{\mathcal{C}}}^{M}$
-extension to
![]() $\mathbb{R}^{d}$
. If
$\mathbb{R}^{d}$
. If
![]() $X$
is simple, they are precisely the functions in
$X$
is simple, they are precisely the functions in
![]() $\widehat{{\mathcal{A}}}^{M}(X)$
.
$\widehat{{\mathcal{A}}}^{M}(X)$
.
Proof. This follows from Theorems 8.4, 5.6, and Lemma 10.1. Indeed, Lemma 10.1 implies that each
![]() $f\in \widehat{{\mathcal{C}}}^{M}(X)$
defines a Whitney jet of class
$f\in \widehat{{\mathcal{C}}}^{M}(X)$
defines a Whitney jet of class
![]() $\widehat{{\mathcal{C}}}^{M}$
on
$\widehat{{\mathcal{C}}}^{M}$
on
![]() $X$
(the integer
$X$
(the integer
![]() $m$
of Lemma 10.1 is local but it is absorbed by
$m$
of Lemma 10.1 is local but it is absorbed by
![]() $\widehat{{\mathcal{C}}}^{M}$
). The extension theorem [Reference Chaumat and CholletCC98, Theorem 8] yields the required extension to
$\widehat{{\mathcal{C}}}^{M}$
). The extension theorem [Reference Chaumat and CholletCC98, Theorem 8] yields the required extension to
![]() $\mathbb{R}^{d}$
.◻
$\mathbb{R}^{d}$
.◻
10.2 Examples and counterexamples
The following examples complement the results and indicate their sharpness.
Example 10.4 (Infinitely flat fat cusps are not
 ${\mathcal{A}}^{\infty }$
-admissible).
${\mathcal{A}}^{\infty }$
-admissible).
Let
![]() $p:[0,\infty )\rightarrow [0,\infty )$
be a strictly increasing
$p:[0,\infty )\rightarrow [0,\infty )$
be a strictly increasing
![]() ${\mathcal{C}}^{\infty }$
-function which is infinitely flat at
${\mathcal{C}}^{\infty }$
-function which is infinitely flat at
![]() $0$
. Consider the set
$0$
. Consider the set
![]() $X:=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,0\leqslant y\leqslant p(x)\}$
and the function
$X:=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,0\leqslant y\leqslant p(x)\}$
and the function
![]() $f:X\rightarrow \mathbb{R}$
defined by
$f:X\rightarrow \mathbb{R}$
defined by
![]() $f(x,y)=\sqrt{x^{2}+y}$
. Clearly,
$f(x,y)=\sqrt{x^{2}+y}$
. Clearly,
![]() $f$
is
$f$
is
![]() ${\mathcal{C}}^{\infty }$
in the interior of
${\mathcal{C}}^{\infty }$
in the interior of
![]() $X$
but
$X$
but
![]() $\unicode[STIX]{x2202}_{y}f$
does not extend continuously to the origin.
$\unicode[STIX]{x2202}_{y}f$
does not extend continuously to the origin.
On the other hand,
![]() $f\in {\mathcal{A}}^{\infty }(X)$
. Let
$f\in {\mathcal{A}}^{\infty }(X)$
. Let
![]() $x,y:\mathbb{R}\rightarrow \mathbb{R}$
be
$x,y:\mathbb{R}\rightarrow \mathbb{R}$
be
![]() ${\mathcal{C}}^{\infty }$
-functions such that
${\mathcal{C}}^{\infty }$
-functions such that
![]() $(x(t),y(t))\in X$
for all
$(x(t),y(t))\in X$
for all
![]() $t\in \mathbb{R}$
. To see that
$t\in \mathbb{R}$
. To see that
![]() $f\in {\mathcal{A}}^{\infty }(X)$
it suffices to prove that there is a
$f\in {\mathcal{A}}^{\infty }(X)$
it suffices to prove that there is a
![]() ${\mathcal{C}}^{\infty }$
-function
${\mathcal{C}}^{\infty }$
-function
![]() $z:\mathbb{R}\rightarrow \mathbb{R}$
such that
$z:\mathbb{R}\rightarrow \mathbb{R}$
such that
![]() $y=x^{2}z$
.
$y=x^{2}z$
.
We use the following result due to [Reference Joris and PreissmannJP90, Theorem 7]. Let
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}:\mathbb{R}\rightarrow \mathbb{R}$
be such that
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}:\mathbb{R}\rightarrow \mathbb{R}$
be such that
![]() $\unicode[STIX]{x1D713}\in {\mathcal{C}}^{\infty }$
,
$\unicode[STIX]{x1D713}\in {\mathcal{C}}^{\infty }$
,
![]() $\unicode[STIX]{x1D711}\unicode[STIX]{x1D713}\in {\mathcal{C}}^{\infty }$
, and
$\unicode[STIX]{x1D711}\unicode[STIX]{x1D713}\in {\mathcal{C}}^{\infty }$
, and
![]() $|\unicode[STIX]{x1D711}|\leqslant |\unicode[STIX]{x1D713}|^{\unicode[STIX]{x1D6FC}}$
for some positive constant
$|\unicode[STIX]{x1D711}|\leqslant |\unicode[STIX]{x1D713}|^{\unicode[STIX]{x1D6FC}}$
for some positive constant
![]() $\unicode[STIX]{x1D6FC}$
. Then
$\unicode[STIX]{x1D6FC}$
. Then
![]() $\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\lfloor 2\unicode[STIX]{x1D6FC}\rfloor }$
.
$\unicode[STIX]{x1D711}\in {\mathcal{C}}^{\lfloor 2\unicode[STIX]{x1D6FC}\rfloor }$
.
We apply this result for
![]() $\unicode[STIX]{x1D713}=x^{2}$
and
$\unicode[STIX]{x1D713}=x^{2}$
and
The assumption
![]() $0\leqslant y\leqslant p(x)$
implies that for each
$0\leqslant y\leqslant p(x)$
implies that for each
![]() $n\in \mathbb{N}$
there is an interval
$n\in \mathbb{N}$
there is an interval
![]() $[0,\unicode[STIX]{x1D716}_{n})$
such that for all
$[0,\unicode[STIX]{x1D716}_{n})$
such that for all
![]() $x\in [0,\unicode[STIX]{x1D716}_{n})$
we have
$x\in [0,\unicode[STIX]{x1D716}_{n})$
we have
![]() $y\leqslant x^{2n+2}$
. We may conclude that
$y\leqslant x^{2n+2}$
. We may conclude that
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() ${\mathcal{C}}^{2n}$
on the set
${\mathcal{C}}^{2n}$
on the set
![]() $x^{-1}([0,\unicode[STIX]{x1D716}_{n}))$
. Clearly,
$x^{-1}([0,\unicode[STIX]{x1D716}_{n}))$
. Clearly,
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() ${\mathcal{C}}^{\infty }$
on the set
${\mathcal{C}}^{\infty }$
on the set
![]() $\{t\in \mathbb{R}:x(t)\neq 0\}$
. Thus
$\{t\in \mathbb{R}:x(t)\neq 0\}$
. Thus
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() ${\mathcal{C}}^{\infty }$
everywhere.
${\mathcal{C}}^{\infty }$
everywhere.
Example 10.5 (Necessity of simpleness).
Let
![]() $X_{1}=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,0\leqslant y\leqslant x\}$
and
$X_{1}=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,0\leqslant y\leqslant x\}$
and
![]() $X_{2}=\{(x,y)\in \mathbb{R}^{2}:0\leqslant x\leqslant y/2\}$
and set
$X_{2}=\{(x,y)\in \mathbb{R}^{2}:0\leqslant x\leqslant y/2\}$
and set
![]() $X=X_{1}\cup X_{2}$
. The function
$X=X_{1}\cup X_{2}$
. The function
![]() $f$
on
$f$
on
![]() $X$
defined by
$X$
defined by
![]() $f(x,y)=x$
if
$f(x,y)=x$
if
![]() $(x,y)\in X_{1}$
and
$(x,y)\in X_{1}$
and
![]() $f(x,y)=y$
if
$f(x,y)=y$
if
![]() $(x,y)\in X_{2}$
belongs to
$(x,y)\in X_{2}$
belongs to
![]() ${\mathcal{A}}^{\infty }(X)$
but clearly not to
${\mathcal{A}}^{\infty }(X)$
but clearly not to
![]() ${\mathcal{C}}^{\infty }(X)$
. This follows from the fact that a
${\mathcal{C}}^{\infty }(X)$
. This follows from the fact that a
![]() ${\mathcal{C}}^{\infty }$
-curve
${\mathcal{C}}^{\infty }$
-curve
![]() $c(t)$
in
$c(t)$
in
![]() $X$
must vanish of infinite order at each
$X$
must vanish of infinite order at each
![]() $t_{0}$
with
$t_{0}$
with
![]() $c(t_{0})\in X_{1}\,\cap \,X_{2}=\{0\}$
. Indeed, suppose that
$c(t_{0})\in X_{1}\,\cap \,X_{2}=\{0\}$
. Indeed, suppose that
![]() $c(t)=t^{p}\tilde{c}(t)$
with
$c(t)=t^{p}\tilde{c}(t)$
with
![]() $(a,b):=\tilde{c}(0)\neq 0$
and
$(a,b):=\tilde{c}(0)\neq 0$
and
![]() $c(t)\in X_{1}$
if
$c(t)\in X_{1}$
if
![]() $t\leqslant 0$
and
$t\leqslant 0$
and
![]() $c(t)\in X_{2}$
if
$c(t)\in X_{2}$
if
![]() $t\geqslant 0$
. If
$t\geqslant 0$
. If
![]() $p$
is even, it follows that
$p$
is even, it follows that
![]() $b\leqslant a\leqslant b/2$
which entails
$b\leqslant a\leqslant b/2$
which entails
![]() $a=b=0$
, a contradiction. If
$a=b=0$
, a contradiction. If
![]() $p$
is odd, we conclude that
$p$
is odd, we conclude that
![]() $0\leqslant a\leqslant 0$
,
$0\leqslant a\leqslant 0$
,
![]() $b\leqslant 0$
,
$b\leqslant 0$
,
![]() $a\leqslant b/2$
hence
$a\leqslant b/2$
hence
![]() $a=b=0$
again.
$a=b=0$
again.
A modification of this example shows that the assumption that
![]() $X$
is simple cannot be replaced by the weaker assumption that each
$X$
is simple cannot be replaced by the weaker assumption that each
![]() $x\in X$
has a neighborhood
$x\in X$
has a neighborhood
![]() $U$
such that
$U$
such that
![]() $U\,\cap \,\operatorname{int}(X)$
is connected: Let
$U\,\cap \,\operatorname{int}(X)$
is connected: Let
![]() $0<r<R$
, consider
$0<r<R$
, consider
![]() $X:=X_{1}\cup X_{2}\cup X_{3}$
, where
$X:=X_{1}\cup X_{2}\cup X_{3}$
, where
![]() $X_{3}=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,y\geqslant 0,x^{2}+y^{2}\geqslant R^{2}\}$
, and multiply
$X_{3}=\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,y\geqslant 0,x^{2}+y^{2}\geqslant R^{2}\}$
, and multiply
![]() $f$
with a smooth bump function which is
$f$
with a smooth bump function which is
![]() $1$
on
$1$
on
![]() $B(0,r)$
and has support in
$B(0,r)$
and has support in
![]() $B(0,R)$
.
$B(0,R)$
.
Nevertheless we have the following example.
Example 10.6. Let
![]() $X_{1}=\{(x,0)\in \mathbb{R}^{2}:x\geqslant 0\}$
and
$X_{1}=\{(x,0)\in \mathbb{R}^{2}:x\geqslant 0\}$
and
![]() $X_{2}=\{(0,y)\in \mathbb{R}^{2}:y\geqslant 0\}$
and set
$X_{2}=\{(0,y)\in \mathbb{R}^{2}:y\geqslant 0\}$
and set
![]() $X=X_{1}\cup X_{2}$
. Then
$X=X_{1}\cup X_{2}$
. Then
![]() $X$
is
$X$
is
![]() ${\mathcal{A}}^{\infty }$
-admissible. Indeed, let
${\mathcal{A}}^{\infty }$
-admissible. Indeed, let
![]() $f\in {\mathcal{A}}^{\infty }(X)$
. We may assume without loss of generality that
$f\in {\mathcal{A}}^{\infty }(X)$
. We may assume without loss of generality that
![]() $f(0,0)=1$
(by multiplying with or adding a constant). Now
$f(0,0)=1$
(by multiplying with or adding a constant). Now
![]() $f|_{X_{1}}$
(respectively,
$f|_{X_{1}}$
(respectively,
![]() $f|_{X_{2}}$
) has a
$f|_{X_{2}}$
) has a
![]() ${\mathcal{C}}^{\infty }$
-extension
${\mathcal{C}}^{\infty }$
-extension
![]() $F_{1}$
to
$F_{1}$
to
![]() $\mathbb{R}\times \{0\}$
(respectively,
$\mathbb{R}\times \{0\}$
(respectively,
![]() $F_{2}$
to
$F_{2}$
to
![]() $\{0\}\times \mathbb{R}$
), by Theorem 1.13, and
$\{0\}\times \mathbb{R}$
), by Theorem 1.13, and
![]() $F(x,y):=F_{1}(x)F_{2}(y)$
is a
$F(x,y):=F_{1}(x)F_{2}(y)$
is a
![]() ${\mathcal{C}}^{\infty }$
-extension of
${\mathcal{C}}^{\infty }$
-extension of
![]() $f$
.
$f$
.
Example 10.7 (There is no analogue for finite differentiability).
This is an interesting consequence of Glaeser’s inequality [Reference GlaeserGla63]: for
![]() $f:\mathbb{R}\rightarrow [0,\infty )$
,
$f:\mathbb{R}\rightarrow [0,\infty )$
,
Indeed, consider the closed half-space
![]() $X=\{x\in \mathbb{R}^{d}:x_{d}\geqslant 0\}$
and the function
$X=\{x\in \mathbb{R}^{d}:x_{d}\geqslant 0\}$
and the function
![]() $f:X\rightarrow \mathbb{R}$
given by
$f:X\rightarrow \mathbb{R}$
given by
![]() $f(x)=x_{d}^{k+1/2}$
. Then all partial derivatives of
$f(x)=x_{d}^{k+1/2}$
. Then all partial derivatives of
![]() $f$
up to order
$f$
up to order
![]() $k$
extend continuously by
$k$
extend continuously by
![]() $0$
to
$0$
to
![]() $\unicode[STIX]{x2202}X$
, and the partial derivatives of order
$\unicode[STIX]{x2202}X$
, and the partial derivatives of order
![]() $k$
are
$k$
are
![]() $1/2$
-Hölder continuous, but not better, near points of
$1/2$
-Hölder continuous, but not better, near points of
![]() $\unicode[STIX]{x2202}X$
. On the other hand, for each
$\unicode[STIX]{x2202}X$
. On the other hand, for each
![]() ${\mathcal{C}}^{k,1}$
-curve
${\mathcal{C}}^{k,1}$
-curve
![]() $c$
in
$c$
in
![]() $X$
with compact support, the composite
$X$
with compact support, the composite
![]() $(f\,\circ \,c)(t)=c_{d}(t)^{k+1/2}$
is
$(f\,\circ \,c)(t)=c_{d}(t)^{k+1/2}$
is
![]() ${\mathcal{C}}^{k}$
with
${\mathcal{C}}^{k}$
with
where
![]() $t\mapsto D_{k}(c(t))$
is Lipschitz. Since
$t\mapsto D_{k}(c(t))$
is Lipschitz. Since
![]() $\sqrt{c_{d}}$
is Lipschitz, by Glaeser’s inequality, we conclude that
$\sqrt{c_{d}}$
is Lipschitz, by Glaeser’s inequality, we conclude that
![]() $f\,\circ \,c$
is of class
$f\,\circ \,c$
is of class
![]() ${\mathcal{C}}^{k,1}$
.
${\mathcal{C}}^{k,1}$
.
We want to add that the images of pseudo-immersions (which are not immersions) yield examples of sets
![]() $X\subseteq \mathbb{R}^{d}$
which are not
$X\subseteq \mathbb{R}^{d}$
which are not
![]() ${\mathcal{A}}^{\infty }$
-admissible.
${\mathcal{A}}^{\infty }$
-admissible.
Example 10.8. If
![]() $\operatorname{gcd}(p,q)=1$
then the map
$\operatorname{gcd}(p,q)=1$
then the map
![]() $\unicode[STIX]{x1D711}:\mathbb{R}\ni t\mapsto (t^{p},t^{q})\in \mathbb{R}^{2}$
is a pseudo-immersion, by [Reference JorisJor82]; see also [Reference Joris and PreissmannJP87, Reference Joris and PreissmannJP90, Reference Duncan, Krantz and ParksDKP85, Reference Amemiya and MasudaAM89]. Now the function
$\unicode[STIX]{x1D711}:\mathbb{R}\ni t\mapsto (t^{p},t^{q})\in \mathbb{R}^{2}$
is a pseudo-immersion, by [Reference JorisJor82]; see also [Reference Joris and PreissmannJP87, Reference Joris and PreissmannJP90, Reference Duncan, Krantz and ParksDKP85, Reference Amemiya and MasudaAM89]. Now the function
![]() $f(x,y)=y^{1/q}$
belongs to
$f(x,y)=y^{1/q}$
belongs to
![]() ${\mathcal{A}}^{\infty }(\unicode[STIX]{x1D711}(\mathbb{R}))$
but has no smooth extension to
${\mathcal{A}}^{\infty }(\unicode[STIX]{x1D711}(\mathbb{R}))$
but has no smooth extension to
![]() $\mathbb{R}^{2}$
.
$\mathbb{R}^{2}$
.
The following example shows that there are closed fat sets
![]() $X\subseteq \mathbb{R}^{d}$
which satisfy
$X\subseteq \mathbb{R}^{d}$
which satisfy
Example 10.9. Let
![]() $X$
be the complement in
$X$
be the complement in
![]() $\mathbb{R}^{2}$
of the set
$\mathbb{R}^{2}$
of the set
![]() $\{(x,y)\in \mathbb{R}^{2}:x>0,|y|<e^{-1/x}\}$
. It is well known (cf. [Reference BierstoneBie80, Example 2.18]) that there exist functions
$\{(x,y)\in \mathbb{R}^{2}:x>0,|y|<e^{-1/x}\}$
. It is well known (cf. [Reference BierstoneBie80, Example 2.18]) that there exist functions
![]() $f:X\rightarrow \mathbb{R}$
which satisfy Lemma 1.10(3), but
$f:X\rightarrow \mathbb{R}$
which satisfy Lemma 1.10(3), but
![]() $f\not \in {\mathcal{C}}^{\infty }(X)$
.
$f\not \in {\mathcal{C}}^{\infty }(X)$
.
Let us show that for this
![]() $X$
the identity in (10.6) holds. To this end let
$X$
the identity in (10.6) holds. To this end let
![]() $h:\mathbb{R}\rightarrow \mathbb{R}$
be defined by
$h:\mathbb{R}\rightarrow \mathbb{R}$
be defined by
![]() $h(x)=0$
if
$h(x)=0$
if
![]() $x\leqslant 0$
and
$x\leqslant 0$
and
![]() $h(x)=e^{-1/x}$
if
$h(x)=e^{-1/x}$
if
![]() $x>0$
. Consider
$x>0$
. Consider
Then
![]() $X_{\pm }$
are
$X_{\pm }$
are
![]() $1$
-sets and hence are
$1$
-sets and hence are
![]() ${\mathcal{A}}^{\infty }$
-admissible, by Theorem 1.13.
${\mathcal{A}}^{\infty }$
-admissible, by Theorem 1.13.
Suppose
![]() $f\in {\mathcal{A}}^{\infty }(X)$
. Then
$f\in {\mathcal{A}}^{\infty }(X)$
. Then
![]() $f$
is smooth on
$f$
is smooth on
![]() $\operatorname{int}(X)$
. The restrictions
$\operatorname{int}(X)$
. The restrictions
![]() $f|_{X_{\pm }}$
belong to
$f|_{X_{\pm }}$
belong to
![]() ${\mathcal{A}}^{\infty }(X_{\pm })$
, respectively. So all their derivatives extend to the boundary arcs
${\mathcal{A}}^{\infty }(X_{\pm })$
, respectively. So all their derivatives extend to the boundary arcs
![]() $\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,\pm y=h(x)\}$
, respectively. It remains to check that the extensions of the derivatives of
$\{(x,y)\in \mathbb{R}^{2}:x\geqslant 0,\pm y=h(x)\}$
, respectively. It remains to check that the extensions of the derivatives of
![]() $f|_{X_{\pm }}$
coincide at the origin. But this is clear, since they are uniquely determined by the restriction of
$f|_{X_{\pm }}$
coincide at the origin. But this is clear, since they are uniquely determined by the restriction of
![]() $f$
to
$f$
to
![]() $X_{+}\,\cap \,X_{-}$
.
$X_{+}\,\cap \,X_{-}$
.
For the converse suppose that
![]() $f:X\rightarrow \mathbb{R}$
satisfies 1.10(3). We have to show that
$f:X\rightarrow \mathbb{R}$
satisfies 1.10(3). We have to show that
![]() $f\,\circ \,c$
is smooth for all smooth curves
$f\,\circ \,c$
is smooth for all smooth curves
![]() $c:\mathbb{R}\rightarrow X$
. Since
$c:\mathbb{R}\rightarrow X$
. Since
![]() $X_{\pm }$
are
$X_{\pm }$
are
![]() ${\mathcal{A}}^{\infty }$
-admissible, this is clear on the complement of
${\mathcal{A}}^{\infty }$
-admissible, this is clear on the complement of
![]() $c^{-1}(0)$
in
$c^{-1}(0)$
in
![]() $\mathbb{R}$
. Assume that
$\mathbb{R}$
. Assume that
![]() $c(0)=0$
. We claim that
$c(0)=0$
. We claim that
![]() $f\,\circ \,c$
is differentiable at
$f\,\circ \,c$
is differentiable at
![]() $0$
and the chain rule
$0$
and the chain rule
![]() $(f\,\circ \,c)^{\prime }(0)=f^{\prime }(0)(c^{\prime }(0))$
holds. The set
$(f\,\circ \,c)^{\prime }(0)=f^{\prime }(0)(c^{\prime }(0))$
holds. The set
![]() $X$
is star-shaped with respect to each point in
$X$
is star-shaped with respect to each point in
![]() $(-\infty ,0]$
.
$(-\infty ,0]$
.
For each
![]() $v\in X$
, the curve
$v\in X$
, the curve
![]() $\unicode[STIX]{x1D6FE}(t):=tv$
lies in
$\unicode[STIX]{x1D6FE}(t):=tv$
lies in
![]() $X$
for
$X$
for
![]() $0\leqslant t\leqslant 1$
. Moreover,
$0\leqslant t\leqslant 1$
. Moreover,
![]() $\unicode[STIX]{x1D6FE}_{s}(t):=\unicode[STIX]{x1D6FE}(t)+s^{2}(-1-\unicode[STIX]{x1D6FE}(t))$
lies in
$\unicode[STIX]{x1D6FE}_{s}(t):=\unicode[STIX]{x1D6FE}(t)+s^{2}(-1-\unicode[STIX]{x1D6FE}(t))$
lies in
![]() $X$
for
$X$
for
![]() $0\leqslant t\leqslant 1$
and
$0\leqslant t\leqslant 1$
and
![]() $|s|\leqslant 1$
. If
$|s|\leqslant 1$
. If
![]() $s\neq 0$
, then
$s\neq 0$
, then
![]() $\unicode[STIX]{x1D6FE}_{s}(t)\in \operatorname{int}(X)$
and hence
$\unicode[STIX]{x1D6FE}_{s}(t)\in \operatorname{int}(X)$
and hence
Letting
![]() $s\rightarrow 0$
and using that
$s\rightarrow 0$
and using that
![]() $f$
satisfies Lemma 1.10(3), we get
$f$
satisfies Lemma 1.10(3), we get
This tends to
![]() $f^{\prime }(\unicode[STIX]{x1D6FE}(0))(v)$
as
$f^{\prime }(\unicode[STIX]{x1D6FE}(0))(v)$
as
![]() $t\rightarrow 0$
.
$t\rightarrow 0$
.
Now for
![]() $0\leqslant s\leqslant 1$
and
$0\leqslant s\leqslant 1$
and
![]() $t\in \mathbb{R}$
we have
$t\in \mathbb{R}$
we have
![]() $s\cdot c(t)\in X$
. We may apply the last paragraph for
$s\cdot c(t)\in X$
. We may apply the last paragraph for
![]() $v=c(t)/t$
and obtain
$v=c(t)/t$
and obtain
which tends to
![]() $f^{\prime }(0)(c^{\prime }(0))$
, since
$f^{\prime }(0)(c^{\prime }(0))$
, since
![]() $f^{\prime }(uc(t))\rightarrow f^{\prime }(0)$
uniformly on the bounded set
$f^{\prime }(uc(t))\rightarrow f^{\prime }(0)$
uniformly on the bounded set
![]() $\{c(t)/t:t\text{ near }0\}$
. This proves the claim.
$\{c(t)/t:t\text{ near }0\}$
. This proves the claim.
By iteration we may conclude that
![]() $f\,\circ \,c$
is smooth; cf. the proof of [Reference Kriegl and MichorKM97, Theorem 24.5].
$f\,\circ \,c$
is smooth; cf. the proof of [Reference Kriegl and MichorKM97, Theorem 24.5].
Acknowledgements
I am grateful to Vincent Grandjean, Andreas Kriegl, and Adam Parusiński for helpful discussions. Kriegl contributed Lemma 6.1 and Example 10.6 and Parusiński suggested using the results on Hölder sets to attack subanalytic sets. In addition, I would like to thank the anonymous referees for their valuable comments.