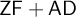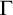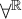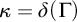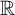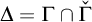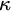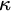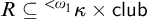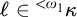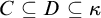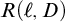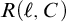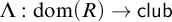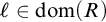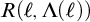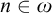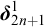1 Introduction
Club uniformization is a selection principle for club subsets of certain cardinals. These uniformization principles are useful in the study of combinatorics of partition measures under determinacy axioms.
If
![]() $X \subseteq \kappa $
and
$X \subseteq \kappa $
and
![]() $\epsilon \leq \kappa $
, then
$\epsilon \leq \kappa $
, then
![]() $[X]^\epsilon _*$
denote the set of increasing functions
$[X]^\epsilon _*$
denote the set of increasing functions
![]() $f : \epsilon \rightarrow X$
which have the correct type (everywhere discontinuous and has uniform cofinality
$f : \epsilon \rightarrow X$
which have the correct type (everywhere discontinuous and has uniform cofinality
![]() $\omega $
). The (correct type) partition relation
$\omega $
). The (correct type) partition relation
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
asserts that for all
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
asserts that for all
![]() $P \colon [\kappa ]^\epsilon _* \rightarrow 2$
, there exists an
$P \colon [\kappa ]^\epsilon _* \rightarrow 2$
, there exists an
![]() $i \in 2$
and a club subset
$i \in 2$
and a club subset
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f \in [C]^\epsilon _*$
,
$f \in [C]^\epsilon _*$
,
![]() $P(f) = i$
. (The correct type partition relation is essentially equivalent to the ordinary partition relation.)
$P(f) = i$
. (The correct type partition relation is essentially equivalent to the ordinary partition relation.)
Martin showed under
![]() $\mathsf {AD}$
that the partition relation
$\mathsf {AD}$
that the partition relation
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
holds. This implies that for each
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
holds. This implies that for each
![]() $\epsilon \leq {\omega _1}$
, the filter
$\epsilon \leq {\omega _1}$
, the filter
![]() $\mu _\epsilon $
defined on
$\mu _\epsilon $
defined on
![]() $[{\omega _1}]^\epsilon _*$
by
$[{\omega _1}]^\epsilon _*$
by
![]() $X \in \mu _\epsilon $
if and only if there is a club
$X \in \mu _\epsilon $
if and only if there is a club
![]() $C \subseteq {\omega _1}$
so that
$C \subseteq {\omega _1}$
so that
![]() $[C]^\epsilon _* \subseteq X$
is a countably complete ultrafilter. (See [Reference Chan1] for a survey of partition relations on
$[C]^\epsilon _* \subseteq X$
is a countably complete ultrafilter. (See [Reference Chan1] for a survey of partition relations on
![]() ${\omega _1}$
.) The study of the combinatorics of the partition measures
${\omega _1}$
.) The study of the combinatorics of the partition measures
![]() $\mu _\epsilon $
frequently requires the selection of clubs that witness
$\mu _\epsilon $
frequently requires the selection of clubs that witness
![]() $\mu _\epsilon $
-largeness or are homogeneous for partitions.
$\mu _\epsilon $
-largeness or are homogeneous for partitions.
The most challenging partition measure on
![]() ${\omega _1}$
is the strong partition measure
${\omega _1}$
is the strong partition measure
![]() $\mu _{\omega _1}$
. There are several interesting combinatorial questions surrounding the strong partition measure. For instance, is every function
$\mu _{\omega _1}$
. There are several interesting combinatorial questions surrounding the strong partition measure. For instance, is every function
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
continuous
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
continuous
![]() $\mu _{\omega _1}$
-almost everywhere. Another class of questions involve the stable theory of the strong partition measure. Since for each
$\mu _{\omega _1}$
-almost everywhere. Another class of questions involve the stable theory of the strong partition measure. Since for each
![]() $\epsilon \leq {\omega _1}$
,
$\epsilon \leq {\omega _1}$
,
![]() $\mu _\epsilon $
is an ultrafilter, for any sentence
$\mu _\epsilon $
is an ultrafilter, for any sentence
![]() $\varphi $
in the language
$\varphi $
in the language
![]() $\{\dot \in , \dot E\}$
(where
$\{\dot \in , \dot E\}$
(where
![]() $\dot \in $
is a binary relation symbol and
$\dot \in $
is a binary relation symbol and
![]() $\dot E$
is a unary relation symbol), either
$\dot E$
is a unary relation symbol), either
![]() $\mu _\epsilon $
-almost all f satisfies
$\mu _\epsilon $
-almost all f satisfies
![]() $L[f] \models \varphi $
or
$L[f] \models \varphi $
or
![]() $\mu _\epsilon $
-almost all f satisfies
$\mu _\epsilon $
-almost all f satisfies
![]() $L[f] \models \neg \varphi $
. The
$L[f] \models \neg \varphi $
. The
![]() $\epsilon $
-stable theory, denoted
$\epsilon $
-stable theory, denoted
![]() $\mathfrak {T}_\epsilon $
, is the collection of sentences
$\mathfrak {T}_\epsilon $
, is the collection of sentences
![]() $\varphi $
so that
$\varphi $
so that
![]() $\mu _\epsilon $
-almost all f satisfies
$\mu _\epsilon $
-almost all f satisfies
![]() $L[f] \models \varphi $
. One can naturally ask whether important statements of set theory, such as
$L[f] \models \varphi $
. One can naturally ask whether important statements of set theory, such as
![]() $\mathsf {GCH}$
, belong to the stable theory of the strong partition measure
$\mathsf {GCH}$
, belong to the stable theory of the strong partition measure
![]() $\mathfrak {T}_{\omega _1}$
.
$\mathfrak {T}_{\omega _1}$
.
To answer these types of questions concerning the strong partition measure, [Reference Chan and Jackson3, Theorem 3.10] proved under
![]() $\mathsf {AD}$
the almost everywhere short length club uniformization at
$\mathsf {AD}$
the almost everywhere short length club uniformization at
![]() ${\omega _1}$
: Let
${\omega _1}$
: Let
![]() $\mathsf {club}$
denote the collection of club subsets of
$\mathsf {club}$
denote the collection of club subsets of
![]() ${\omega _1}$
. For every relation
${\omega _1}$
. For every relation
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times \mathsf {club}$
which is
$R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times \mathsf {club}$
which is
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() $\mathsf {club}$
-coordinate (which means for all
$\mathsf {club}$
-coordinate (which means for all
![]() $\sigma \in [{\omega _1}]^{<{\omega _1}}_*$
and clubs
$\sigma \in [{\omega _1}]^{<{\omega _1}}_*$
and clubs
![]() $D \subseteq E$
,
$D \subseteq E$
,
![]() $R(\sigma ,E)$
implies
$R(\sigma ,E)$
implies
![]() $R(\sigma ,D)$
), then there is a club
$R(\sigma ,D)$
), then there is a club
![]() $C \subseteq {\omega _1}$
and a function
$C \subseteq {\omega _1}$
and a function
![]() $\Lambda : ([C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)) \rightarrow \mathsf {club}$
so that for all
$\Lambda : ([C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)) \rightarrow \mathsf {club}$
so that for all
![]() $\sigma \in [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)$
,
$\sigma \in [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)$
,
![]() $R(\sigma ,\Lambda (\sigma ))$
.
$R(\sigma ,\Lambda (\sigma ))$
.
To illustrate a typical application, [Reference Chan and Jackson3, Theorem 4.5] showed that under
![]() $\mathsf {AD}$
, every function
$\mathsf {AD}$
, every function
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is continuous
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is continuous
![]() $\mu _{\omega _1}$
-almost everywhere, which means there is a club
$\mu _{\omega _1}$
-almost everywhere, which means there is a club
![]() $C \subseteq {\omega _1}$
with the property that for all
$C \subseteq {\omega _1}$
with the property that for all
![]() $f \in [C]^{\omega _1}_*$
, there is an
$f \in [C]^{\omega _1}_*$
, there is an
![]() $\alpha < {\omega _1}$
so that for all
$\alpha < {\omega _1}$
so that for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $f \upharpoonright \alpha = g \upharpoonright \alpha $
, then
$f \upharpoonright \alpha = g \upharpoonright \alpha $
, then
![]() $\Phi (f) = \Phi (g)$
. Define a partition
$\Phi (f) = \Phi (g)$
. Define a partition
![]() $P \colon [{\omega _1}]^{\omega _1}_* \rightarrow 2$
by
$P \colon [{\omega _1}]^{\omega _1}_* \rightarrow 2$
by
![]() $P(f) = 0$
if and only if there exists an
$P(f) = 0$
if and only if there exists an
![]() $\alpha < {\omega _1}$
so that for all clubs
$\alpha < {\omega _1}$
so that for all clubs
![]() $D \subseteq {\omega _1}$
, there exists a
$D \subseteq {\omega _1}$
, there exists a
![]() $g \in [D]^{\omega _1}_*$
with
$g \in [D]^{\omega _1}_*$
with
![]() $\sup (f \upharpoonright \alpha ) < g(0)$
and
$\sup (f \upharpoonright \alpha ) < g(0)$
and
![]() $\Phi ((f\upharpoonright \alpha )\hat {\ }g) < g(0)$
. Since
$\Phi ((f\upharpoonright \alpha )\hat {\ }g) < g(0)$
. Since
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club C homogeneous for P. The most important step is to show that C is homogeneous for P taking value
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club C homogeneous for P. The most important step is to show that C is homogeneous for P taking value
![]() $0$
. Suppose otherwise. Define a relation
$0$
. Suppose otherwise. Define a relation
![]() $R \subseteq [C]^{<{\omega _1}}_* \times \mathsf {club}$
by
$R \subseteq [C]^{<{\omega _1}}_* \times \mathsf {club}$
by
![]() $R(\sigma ,D)$
if and only if for all
$R(\sigma ,D)$
if and only if for all
![]() $g \in [D]^{\omega _1}_*$
,
$g \in [D]^{\omega _1}_*$
,
![]() $\Phi (\sigma \hat {\ }g) \geq g(0)$
. C being homogeneous for P taking value
$\Phi (\sigma \hat {\ }g) \geq g(0)$
. C being homogeneous for P taking value
![]() $1$
implies
$1$
implies
![]() $\mathrm {dom}(R) = [C]^{<{\omega _1}}_*$
. Applying the almost everywhere club uniformization to R, there is a club
$\mathrm {dom}(R) = [C]^{<{\omega _1}}_*$
. Applying the almost everywhere club uniformization to R, there is a club
![]() $E \subseteq C$
and a function
$E \subseteq C$
and a function
![]() $\Lambda : [E]^{<{\omega _1}}_* \rightarrow \mathsf {club}$
so that for all
$\Lambda : [E]^{<{\omega _1}}_* \rightarrow \mathsf {club}$
so that for all
![]() $\sigma \in [E]^{<{\omega _1}}_*$
,
$\sigma \in [E]^{<{\omega _1}}_*$
,
![]() $R(\sigma ,\Lambda (\sigma ))$
. Using
$R(\sigma ,\Lambda (\sigma ))$
. Using
![]() $\Lambda $
, one can recursively construct a function
$\Lambda $
, one can recursively construct a function
![]() $h \in [E]^{\omega _1}_*$
so that for all
$h \in [E]^{\omega _1}_*$
so that for all
![]() $\alpha < {\omega _1}$
,
$\alpha < {\omega _1}$
,
![]() $R(h \upharpoonright \alpha , \Lambda (h \upharpoonright \alpha ))$
. By definition of R, this means that for all
$R(h \upharpoonright \alpha , \Lambda (h \upharpoonright \alpha ))$
. By definition of R, this means that for all
![]() $\alpha < {\omega _1}$
,
$\alpha < {\omega _1}$
,
![]() $\Phi (h) \geq h(\alpha )$
. Since h is an increasing function, this implies
$\Phi (h) \geq h(\alpha )$
. Since h is an increasing function, this implies
![]() $\Phi (h) \geq {\omega _1}$
which is impossible since
$\Phi (h) \geq {\omega _1}$
which is impossible since
![]() $\Phi $
takes values in
$\Phi $
takes values in
![]() ${\omega _1}$
. Thus C must be homogeneous for P taking value
${\omega _1}$
. Thus C must be homogeneous for P taking value
![]() $0$
and this will eventually lead to the
$0$
and this will eventually lead to the
![]() $\mu _{\omega _1}$
-almost everywhere continuity of
$\mu _{\omega _1}$
-almost everywhere continuity of
![]() $\Phi $
. Following this template, in forthcoming work by the authors, it is shown that many familiar statements of set theory like
$\Phi $
. Following this template, in forthcoming work by the authors, it is shown that many familiar statements of set theory like
![]() $\mathsf {GCH}$
belong to the stable theory
$\mathsf {GCH}$
belong to the stable theory
![]() $\mathfrak {T}_\epsilon $
for all
$\mathfrak {T}_\epsilon $
for all
![]() $\epsilon \leq {\omega _1}$
. It is also shown that for
$\epsilon \leq {\omega _1}$
. It is also shown that for
![]() $\mu _\epsilon $
-almost all f, there is a sequence of normal measures
$\mu _\epsilon $
-almost all f, there is a sequence of normal measures
![]() $\bar {\nu }_f$
with a discontinuous sequence of critical points
$\bar {\nu }_f$
with a discontinuous sequence of critical points
![]() $\bar {\kappa }$
so that f is a generic over
$\bar {\kappa }$
so that f is a generic over
![]() $L[\bar {\nu }_f]$
for a generalized Prikry forcing
$L[\bar {\nu }_f]$
for a generalized Prikry forcing
![]() $\bar {\mathbb {P}}_{\bar {\nu }_f}$
considered by Fuchs [Reference Fuchs4].
$\bar {\mathbb {P}}_{\bar {\nu }_f}$
considered by Fuchs [Reference Fuchs4].
The argument in [Reference Chan and Jackson3] to prove the almost everywhere short length club uniformization at
![]() ${\omega _1}$
(although it uses just
${\omega _1}$
(although it uses just
![]() $\mathsf {AD}$
) appears peculiar and inefficient in that it passes first through an everywhere club uniformization principle whose argument requires generic coding, category arguments, and uniformization for certain relations on
$\mathsf {AD}$
) appears peculiar and inefficient in that it passes first through an everywhere club uniformization principle whose argument requires generic coding, category arguments, and uniformization for certain relations on
![]() $\mathbb {R} \times \mathbb {R}$
. [Reference Chan and Jackson3, Theorem 3.7] shows that if
$\mathbb {R} \times \mathbb {R}$
. [Reference Chan and Jackson3, Theorem 3.7] shows that if
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times \mathsf {club}$
is a
$R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times \mathsf {club}$
is a
![]() $\subseteq $
-downward closed relation so that its coded version
$\subseteq $
-downward closed relation so that its coded version
![]() $\tilde R \subseteq \mathbb {R} \times \mathbb {R}$
has a uniformization, then there is a uniformization function
$\tilde R \subseteq \mathbb {R} \times \mathbb {R}$
has a uniformization, then there is a uniformization function
![]() $\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
for R.
$\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
for R.
![]() $\mathsf {AD}_{\mathbb {R}}$
is the determinacy of all games on
$\mathsf {AD}_{\mathbb {R}}$
is the determinacy of all games on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
is the determinacy of games on
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
is the determinacy of games on
![]() $\mathbb {R}$
where one of the two players must always make moves from
$\mathbb {R}$
where one of the two players must always make moves from
![]() $\omega $
. Kechris [Reference Kechris6] showed
$\omega $
. Kechris [Reference Kechris6] showed
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
is equivalent to
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
is equivalent to
![]() $\mathsf {AD}$
and all relations on
$\mathsf {AD}$
and all relations on
![]() $\mathbb {R} \times \mathbb {R}$
can be uniformized. The relationship between
$\mathbb {R} \times \mathbb {R}$
can be uniformized. The relationship between
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
,
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
,
![]() $\mathsf {AD}_{\mathbb {R}}$
, and all sets of reals being Suslin is open. However, Woodin has shown that if
$\mathsf {AD}_{\mathbb {R}}$
, and all sets of reals being Suslin is open. However, Woodin has shown that if
![]() $\mathsf {AD}$
and
$\mathsf {AD}$
and
![]() $\mathsf {DC}$
holds, then all three notions are equivalent.
$\mathsf {DC}$
holds, then all three notions are equivalent.
Thus assuming
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
, every
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
, every
![]() $\subseteq $
-downward closed relation
$\subseteq $
-downward closed relation
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}} \times \mathsf {club}$
can be uniformized everywhere on its domain. Using the Moschovakis coding lemma, a Martin good coding system for
$R \subseteq [{\omega _1}]^{<{\omega _1}} \times \mathsf {club}$
can be uniformized everywhere on its domain. Using the Moschovakis coding lemma, a Martin good coding system for
![]() ${}^{\omega _1}{\omega _1}$
, and the almost everywhere good code uniformization [Reference Chan1, Theorem 3.8], it can be shown that there is a club
${}^{\omega _1}{\omega _1}$
, and the almost everywhere good code uniformization [Reference Chan1, Theorem 3.8], it can be shown that there is a club
![]() $C \subseteq {\omega _1}$
so that
$C \subseteq {\omega _1}$
so that
![]() $R \cap ([C]^{<{\omega _1}}_* \times \mathsf {club})$
has a coded version
$R \cap ([C]^{<{\omega _1}}_* \times \mathsf {club})$
has a coded version
![]() $\tilde R$
which is projective and hence uniformizable under
$\tilde R$
which is projective and hence uniformizable under
![]() $\mathsf {AD}$
. The prior result [Reference Chan and Jackson3, Theorem 3.7] is then used to uniformize
$\mathsf {AD}$
. The prior result [Reference Chan and Jackson3, Theorem 3.7] is then used to uniformize
![]() $R \cap ([C]^{<{\omega _1}}_* \times \mathsf {club})$
. Moreover, everywhere short length club uniformization is not provable under
$R \cap ([C]^{<{\omega _1}}_* \times \mathsf {club})$
. Moreover, everywhere short length club uniformization is not provable under
![]() $\mathsf {AD}$
as it fails in
$\mathsf {AD}$
as it fails in
![]() $L(\mathbb {R})$
by [Reference Chan and Jackson3, Fact 3.9]. Thus the almost everywhere version is the best possible under
$L(\mathbb {R})$
by [Reference Chan and Jackson3, Fact 3.9]. Thus the almost everywhere version is the best possible under
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
Naturally one would like to study these properties at strong partition cardinals larger than
![]() ${\omega _1}$
such as the next strong partition cardinal
${\omega _1}$
such as the next strong partition cardinal
![]() $\boldsymbol {\delta }^1_3$
(or more generally the odd projective ordinals
$\boldsymbol {\delta }^1_3$
(or more generally the odd projective ordinals
![]() $\boldsymbol {\delta }_{2n + 1}^1$
) or the
$\boldsymbol {\delta }_{2n + 1}^1$
) or the
![]() $\Sigma _1$
-stable ordinals
$\Sigma _1$
-stable ordinals
![]() $\boldsymbol {\delta }_A$
for
$\boldsymbol {\delta }_A$
for
![]() $L(A,\mathbb {R})$
where
$L(A,\mathbb {R})$
where
![]() $A \subseteq \mathbb {R}$
. As in [Reference Chan and Jackson3], one would like to first prove the everywhere short length club uniformization at a strong partition cardinal
$A \subseteq \mathbb {R}$
. As in [Reference Chan and Jackson3], one would like to first prove the everywhere short length club uniformization at a strong partition cardinal
![]() $\delta> {\omega _1}$
. Numerous issues with generalization quickly arise. First, more general generic coding functions exist for many cardinals beyond
$\delta> {\omega _1}$
. Numerous issues with generalization quickly arise. First, more general generic coding functions exist for many cardinals beyond
![]() ${\omega _1}$
; however, these require that relevant sets possess scales. The stable ordinals
${\omega _1}$
; however, these require that relevant sets possess scales. The stable ordinals
![]() $\boldsymbol {\delta }_A$
generally are not associated with pointclasses with scales. The odd projective ordinals, however, still have generic coding functions. These generic coding functions are more technical than the simple generic coding function on
$\boldsymbol {\delta }_A$
generally are not associated with pointclasses with scales. The odd projective ordinals, however, still have generic coding functions. These generic coding functions are more technical than the simple generic coding function on
![]() ${\omega _1}$
, but a more substantial issue is that the generic coding function acts on
${\omega _1}$
, but a more substantial issue is that the generic coding function acts on
![]() ${}^\omega \delta $
. Thus category and generic coding arguments of [Reference Chan and Jackson3] would at best give an everywhere club uniformization for families indexed by countable sequences (which will be verified in this paper).
${}^\omega \delta $
. Thus category and generic coding arguments of [Reference Chan and Jackson3] would at best give an everywhere club uniformization for families indexed by countable sequences (which will be verified in this paper).
To obtain almost everywhere short length club uniformization at strong partition cardinals
![]() $\delta $
greater than
$\delta $
greater than
![]() ${\omega _1}$
under
${\omega _1}$
under
![]() $\mathsf {AD}$
(or
$\mathsf {AD}$
(or
![]() $\mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
), one would need to find scale-free arguments. [Reference Chan2] defines a notion of a good coding family for
$\mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
), one would need to find scale-free arguments. [Reference Chan2] defines a notion of a good coding family for
![]() $\delta $
which augments a good coding system for
$\delta $
which augments a good coding system for
![]() ${}^\delta \delta $
with a coding of the short functions on
${}^\delta \delta $
with a coding of the short functions on
![]() $\delta $
which interact under strict definability conditions. Moreover, this good coding family has a continuous function which merges a code for a short function and a good code for a full function and returns a good code so the short function overrides an initial segment of the original full function. [Reference Chan2] shows that
$\delta $
which interact under strict definability conditions. Moreover, this good coding family has a continuous function which merges a code for a short function and a good code for a full function and returns a good code so the short function overrides an initial segment of the original full function. [Reference Chan2] shows that
![]() ${\omega _1}$
, (and more generally for all
${\omega _1}$
, (and more generally for all
![]() $n \in \omega $
)
$n \in \omega $
)
![]() $\boldsymbol {\delta }_{2n + 1}^1$
, and the stable ordinals
$\boldsymbol {\delta }_{2n + 1}^1$
, and the stable ordinals
![]() $\boldsymbol {\delta }_A$
all possess very good coding families. It is then shown that a cardinal
$\boldsymbol {\delta }_A$
all possess very good coding families. It is then shown that a cardinal
![]() $\delta $
that possesses a very good coding family is a strong partition cardinal which also satisfies the almost everywhere short length club uniformization at
$\delta $
that possesses a very good coding family is a strong partition cardinal which also satisfies the almost everywhere short length club uniformization at
![]() $\delta $
.
$\delta $
.
The goal of this paper is to verify under suitable conditions that the everywhere countable length club uniformization holds at certain cardinals
![]() $\kappa $
. That is, for every relation
$\kappa $
. That is, for every relation
![]() $R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$
which is
$R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$
which is
![]() $\subseteq $
-downward closed (where
$\subseteq $
-downward closed (where
![]() $\mathsf {club}$
refers to the collection of club subsets of
$\mathsf {club}$
refers to the collection of club subsets of
![]() $\kappa $
), there is a uniformization function
$\kappa $
), there is a uniformization function
![]() $\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
. As mentioned above, this seems to be the best everywhere club uniformization result obtainable by the method of generic coding. In this general setting, one will encounter ordinal games so Suslin representations will be necessary to conclude the determinacy of such games. Moreover, one will need to find winning strategies uniformly which will require the ideas of the third periodicity theorem of Moschovakis. The main theorem is the following.
$\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
. As mentioned above, this seems to be the best everywhere club uniformization result obtainable by the method of generic coding. In this general setting, one will encounter ordinal games so Suslin representations will be necessary to conclude the determinacy of such games. Moreover, one will need to find winning strategies uniformly which will require the ideas of the third periodicity theorem of Moschovakis. The main theorem is the following.
Theorem 3.8. Assume
![]() $\mathsf {ZF} + \mathsf {AD}$
and all sets of reals are Suslin. Let
$\mathsf {ZF} + \mathsf {AD}$
and all sets of reals are Suslin. Let
![]() $\Gamma $
be a pointclass closed under
$\Gamma $
be a pointclass closed under
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
, and
$\vee $
, and
![]() $\forall ^{\mathbb {R}}$
with the scale property. Then the countable length everywhere club uniformization holds for
$\forall ^{\mathbb {R}}$
with the scale property. Then the countable length everywhere club uniformization holds for
![]() $\delta (\Gamma )$
. In particular, for all
$\delta (\Gamma )$
. In particular, for all
![]() $n \in \omega $
, the countable length everywhere club uniformization holds for
$n \in \omega $
, the countable length everywhere club uniformization holds for
![]() $\boldsymbol {\delta }^1_{2n + 1}$
.
$\boldsymbol {\delta }^1_{2n + 1}$
.
2 Basics
This section will collect some standard facts concerning games, Suslin representations, and generic codings. The reader familiar with this material can skim this section for some definitions and notations and refer back as necessary.
Definition 2.1. Let X be a set and
![]() $\kappa $
be an ordinal.
$\kappa $
be an ordinal.
![]() ${}^\kappa X$
is the set of all functions from
${}^\kappa X$
is the set of all functions from
![]() $\kappa $
into X.
$\kappa $
into X.
![]() ${}^{<\kappa } X$
is the set of all functions
${}^{<\kappa } X$
is the set of all functions
![]() $\ell : \epsilon \rightarrow X$
where
$\ell : \epsilon \rightarrow X$
where
![]() $\epsilon < \kappa $
. If
$\epsilon < \kappa $
. If
![]() $\ell : \epsilon \rightarrow X$
, then let
$\ell : \epsilon \rightarrow X$
, then let
![]() $|\ell | = \epsilon $
which is the length of
$|\ell | = \epsilon $
which is the length of
![]() $\ell $
. If
$\ell $
. If
![]() $s \in {}^{<\kappa }X$
and
$s \in {}^{<\kappa }X$
and
![]() $t \in {}^{<\kappa }X \cup {}^\kappa X$
, one write
$t \in {}^{<\kappa }X \cup {}^\kappa X$
, one write
![]() $s \subseteq t$
to indicate that t is an extension of s.
$s \subseteq t$
to indicate that t is an extension of s.
Let X be given the discrete topology and
![]() ${}^\omega X$
be given the product of the discrete topology. If
${}^\omega X$
be given the product of the discrete topology. If
![]() $s \in {}^{<\omega }X$
, then let
$s \in {}^{<\omega }X$
, then let
![]() $N^X_s = \{f \in {}^\omega X : s \subseteq f\}$
. The topology on
$N^X_s = \{f \in {}^\omega X : s \subseteq f\}$
. The topology on
![]() ${}^\omega X$
is equivalent to the topology generated by
${}^\omega X$
is equivalent to the topology generated by
![]() $\{N_s^X : s \in {}^{<\omega } X\}$
as a basis.
$\{N_s^X : s \in {}^{<\omega } X\}$
as a basis.
A tree on X is a set
![]() $T \subseteq {}^{<\omega } X$
which is closed under the substring relation
$T \subseteq {}^{<\omega } X$
which is closed under the substring relation
![]() $\subseteq $
. If T is a tree, let
$\subseteq $
. If T is a tree, let
![]() $[T] = \{f \in {}^\omega X : (\forall ^\omega n)(f \upharpoonright n \in T)\}$
. A set
$[T] = \{f \in {}^\omega X : (\forall ^\omega n)(f \upharpoonright n \in T)\}$
. A set
![]() $A \subseteq {}^\omega X$
is closed if and only if there is a tree T so that
$A \subseteq {}^\omega X$
is closed if and only if there is a tree T so that
![]() $A = [T]$
.
$A = [T]$
.
As common in descriptive set theory,
![]() $\mathbb {R}$
may be used to denote either
$\mathbb {R}$
may be used to denote either
![]() ${{}^\omega \omega }$
or
${{}^\omega \omega }$
or
![]() ${{}^\omega 2}$
.
${{}^\omega 2}$
.
Definition 2.2. A strategy on a set X is a function
![]() $\rho : {}^{<\omega }X \rightarrow X$
. The run of a strategy
$\rho : {}^{<\omega }X \rightarrow X$
. The run of a strategy
![]() $\rho _1$
against a strategy
$\rho _1$
against a strategy
![]() $\rho _2$
is denoted
$\rho _2$
is denoted
![]() $\rho _1 * \rho _2 \in {}^\omega X$
and it is defined recursively as follows: Suppose
$\rho _1 * \rho _2 \in {}^\omega X$
and it is defined recursively as follows: Suppose
![]() $\rho _1 * \rho _2 \upharpoonright n$
has been defined, if n is even, then
$\rho _1 * \rho _2 \upharpoonright n$
has been defined, if n is even, then
![]() $(\rho _1 * \rho _2)(n) = \rho _1(\rho _1 * \rho _2 \upharpoonright n)$
and if n is odd, then
$(\rho _1 * \rho _2)(n) = \rho _1(\rho _1 * \rho _2 \upharpoonright n)$
and if n is odd, then
![]() $(\rho _1 * \rho _2)(n) = \rho _2(\rho _1 * \rho _2 \upharpoonright n)$
.
$(\rho _1 * \rho _2)(n) = \rho _2(\rho _1 * \rho _2 \upharpoonright n)$
.
If
![]() $A \subseteq {}^\omega X$
, then one says that A (or the game on X with payoff set A) is determined if either there is a strategy
$A \subseteq {}^\omega X$
, then one says that A (or the game on X with payoff set A) is determined if either there is a strategy
![]() $\rho _1$
so that for all strategies
$\rho _1$
so that for all strategies
![]() $\rho _2$
,
$\rho _2$
,
![]() $\rho _1 * \rho _2 \in A$
or there is a strategy
$\rho _1 * \rho _2 \in A$
or there is a strategy
![]() $\rho _2$
so that for all strategies
$\rho _2$
so that for all strategies
![]() $\rho _1$
,
$\rho _1$
,
![]() $\rho _1 * \rho _2 \notin A$
. Intuitively, the game
$\rho _1 * \rho _2 \notin A$
. Intuitively, the game
![]() $G_A^X$
consists of Player 1 and Player 2 taking turns playing elements of X where Player 1 wins if and only if the joint infinite run belongs to A. Thus the determinacy of A is the existence of a winning strategy for one of the two players in this game.
$G_A^X$
consists of Player 1 and Player 2 taking turns playing elements of X where Player 1 wins if and only if the joint infinite run belongs to A. Thus the determinacy of A is the existence of a winning strategy for one of the two players in this game.
![]() $\mathsf {AD}_X$
is the statement that for all
$\mathsf {AD}_X$
is the statement that for all
![]() $A \subseteq {}^\omega X$
, A is determined (as a game on X). The common determinacy axioms are
$A \subseteq {}^\omega X$
, A is determined (as a game on X). The common determinacy axioms are
![]() $\mathsf {AD}_\omega $
(which is denoted simply
$\mathsf {AD}_\omega $
(which is denoted simply
![]() $\mathsf {AD}$
) and
$\mathsf {AD}$
) and
![]() $\mathsf {AD}_{\mathbb {R}}$
.
$\mathsf {AD}_{\mathbb {R}}$
.
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
is the determinacy of games on
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
is the determinacy of games on
![]() $\mathbb {R}$
where one player is required to play only elements of
$\mathbb {R}$
where one player is required to play only elements of
![]() $\omega $
.
$\omega $
.
If
![]() $x \in {}^\omega X$
, let
$x \in {}^\omega X$
, let
![]() $\rho _x$
be the strategy such that if
$\rho _x$
be the strategy such that if
![]() $s \in {}^{<\omega }\omega $
has length
$s \in {}^{<\omega }\omega $
has length
![]() $2n$
or
$2n$
or
![]() $2n + 1$
, then
$2n + 1$
, then
![]() $\rho _x(s) = x(n)$
. That is,
$\rho _x(s) = x(n)$
. That is,
![]() $\rho _x$
can be used as either a Player 1 or Player 2 strategy which simply outputs the bits of x on each turn.
$\rho _x$
can be used as either a Player 1 or Player 2 strategy which simply outputs the bits of x on each turn.
If
![]() $x \in {}^\omega X$
, let
$x \in {}^\omega X$
, let
![]() $x_{\mathrm {even}}, x_{\mathrm {odd}} \in {}^\omega X$
be defined by
$x_{\mathrm {even}}, x_{\mathrm {odd}} \in {}^\omega X$
be defined by
![]() $x_{\mathrm {even}}(k) = x(2k)$
and
$x_{\mathrm {even}}(k) = x(2k)$
and
![]() $x_{\mathrm {odd}}(k) = x(2k + 1)$
.
$x_{\mathrm {odd}}(k) = x(2k + 1)$
.
Let
![]() $\rho $
be a strategy. Define
$\rho $
be a strategy. Define
![]() $\Sigma ^1_\rho , \Sigma ^2_\rho : {}^\omega X \rightarrow {}^\omega X$
by
$\Sigma ^1_\rho , \Sigma ^2_\rho : {}^\omega X \rightarrow {}^\omega X$
by
![]() $\Sigma ^1_\rho (z) = \rho * \rho _z$
and
$\Sigma ^1_\rho (z) = \rho * \rho _z$
and
![]() $\Sigma ^2_\rho (z) = \rho _z * \rho $
. Define
$\Sigma ^2_\rho (z) = \rho _z * \rho $
. Define
![]() $\Xi ^1_\rho : {}^\omega X \rightarrow {}^\omega X$
by
$\Xi ^1_\rho : {}^\omega X \rightarrow {}^\omega X$
by
![]() $\Xi ^1_\rho (z) = (\Sigma ^1_\rho (z))_{\mathrm {even}} = (\rho * \rho _z)_{\mathrm {even}}$
.
$\Xi ^1_\rho (z) = (\Sigma ^1_\rho (z))_{\mathrm {even}} = (\rho * \rho _z)_{\mathrm {even}}$
.
![]() $\Xi ^1_\rho $
is a Lipschitz function which simply collects the moves of
$\Xi ^1_\rho $
is a Lipschitz function which simply collects the moves of
![]() $\rho $
(used as a Player 1 strategy) when played against
$\rho $
(used as a Player 1 strategy) when played against
![]() $\rho _z$
. Similar,
$\rho _z$
. Similar,
![]() $\Xi ^2_\rho : {}^\omega X \rightarrow {}^\omega X$
is defined by
$\Xi ^2_\rho : {}^\omega X \rightarrow {}^\omega X$
is defined by
![]() $\Xi ^2_\rho (z) = (\Sigma _\rho ^2(z))_{\mathrm {odd}} = (\rho _z * \rho )_{\mathrm {odd}}$
.
$\Xi ^2_\rho (z) = (\Sigma _\rho ^2(z))_{\mathrm {odd}} = (\rho _z * \rho )_{\mathrm {odd}}$
.
Observe that if
![]() $\Xi : {}^\omega X \rightarrow {}^\omega X$
is a Lipschitz continuous function, then there is a strategy
$\Xi : {}^\omega X \rightarrow {}^\omega X$
is a Lipschitz continuous function, then there is a strategy
![]() $\rho $
so that
$\rho $
so that
![]() $\Xi = \Xi ^2_\rho $
.
$\Xi = \Xi ^2_\rho $
.
The article will work implicitly under
![]() $\mathsf {ZF} + \mathsf {AD}$
and additional assumptions will be made explicit.
$\mathsf {ZF} + \mathsf {AD}$
and additional assumptions will be made explicit.
Next, one will review the necessary concepts concerning prewellordering and scales. See [Reference Kechris and Moschovakis7], [Reference Moschovakis10, Chapters 2, 4, and 6], and [Reference Jackson5, Section 2].
Definition 2.3. Pointclasses are collections of subsets of
![]() ${}^j\omega \times {}^k\mathbb {R}$
(for various
${}^j\omega \times {}^k\mathbb {R}$
(for various
![]() $j,k \in \omega $
) which are closed under continuous substitution. If
$j,k \in \omega $
) which are closed under continuous substitution. If
![]() $\Gamma $
is a pointclass, then
$\Gamma $
is a pointclass, then
![]() $\check \Gamma $
denotes the dual pointclass and
$\check \Gamma $
denotes the dual pointclass and
![]() $\Delta = \Gamma \cap \check \Gamma $
.
$\Delta = \Gamma \cap \check \Gamma $
.
Definition 2.4. A norm on a set A is a map
![]() $\phi : A \rightarrow \mathrm {ON}$
. The associated prewellordering on A is
$\phi : A \rightarrow \mathrm {ON}$
. The associated prewellordering on A is
![]() ${\preceq _\phi } \subseteq A \times A$
defined by
${\preceq _\phi } \subseteq A \times A$
defined by
![]() $x \preceq _\phi y$
if and only if
$x \preceq _\phi y$
if and only if
![]() $\phi (x) \leq \phi (y)$
. (The term norm and prewellordering will be used interchangeably.) The length of the prewellordering
$\phi (x) \leq \phi (y)$
. (The term norm and prewellordering will be used interchangeably.) The length of the prewellordering
![]() $\phi $
is the ordertype of
$\phi $
is the ordertype of
![]() $\phi [A]$
.
$\phi [A]$
.
Now suppose X is a set. Let
![]() $P \subseteq {}^\omega X$
and
$P \subseteq {}^\omega X$
and
![]() $\phi : P \rightarrow \mathrm {ON}$
be a norm on P. Define
$\phi : P \rightarrow \mathrm {ON}$
be a norm on P. Define
![]() ${\leq ^*_\phi } \subseteq {}^\omega X \times {}^\omega X$
by
${\leq ^*_\phi } \subseteq {}^\omega X \times {}^\omega X$
by
![]() $f \leq ^*_\phi g$
if and only if
$f \leq ^*_\phi g$
if and only if
![]() $f \in P \wedge (g \notin P \vee \phi (f) \leq \phi (g))$
and
$f \in P \wedge (g \notin P \vee \phi (f) \leq \phi (g))$
and
![]() ${<^*_\phi } \subseteq {}^\omega X \times {}^\omega X$
by
${<^*_\phi } \subseteq {}^\omega X \times {}^\omega X$
by
![]() $f <^*_\phi g$
if and only if
$f <^*_\phi g$
if and only if
![]() $f \in P \wedge (g \notin P \vee \phi (f) < \phi (g))$
.
$f \in P \wedge (g \notin P \vee \phi (f) < \phi (g))$
.
Let
![]() $\Gamma $
be a pointclass closed under
$\Gamma $
be a pointclass closed under
![]() $\wedge $
and
$\wedge $
and
![]() $\vee $
. Suppose
$\vee $
. Suppose
![]() $P \subseteq {{}^\omega \omega }$
and
$P \subseteq {{}^\omega \omega }$
and
![]() $\phi : P \rightarrow \mathrm {ON}$
is a prewellordering.
$\phi : P \rightarrow \mathrm {ON}$
is a prewellordering.
![]() $\phi $
is a
$\phi $
is a
![]() $\Gamma $
-norm if and only if
$\Gamma $
-norm if and only if
![]() $P \in \Gamma $
and
$P \in \Gamma $
and
![]() $\leq _\phi ^*, <_\phi ^* \in \Gamma $
.
$\leq _\phi ^*, <_\phi ^* \in \Gamma $
.
Let
![]() $\delta (\Gamma )$
be the supremum of the length of all prewellorderings
$\delta (\Gamma )$
be the supremum of the length of all prewellorderings
![]() $\phi $
on
$\phi $
on
![]() ${{}^\omega \omega }$
such that
${{}^\omega \omega }$
such that
![]() ${\preceq _\phi } \in \Delta $
.
${\preceq _\phi } \in \Delta $
.
![]() $\delta (\Gamma )$
is called the prewellordering ordinal of
$\delta (\Gamma )$
is called the prewellordering ordinal of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\Theta $
be the supremum of the length of all prewellorderings on
$\Theta $
be the supremum of the length of all prewellorderings on
![]() $\mathbb {R}$
. (Every ordinal considered in this article will be below
$\mathbb {R}$
. (Every ordinal considered in this article will be below
![]() $\Theta $
.)
$\Theta $
.)
Definition 2.5. Fix a recursive bijection
![]() $\mathsf {pair} : \omega \times \omega \rightarrow \omega $
. If
$\mathsf {pair} : \omega \times \omega \rightarrow \omega $
. If
![]() $x \in {{}^\omega \omega }$
and
$x \in {{}^\omega \omega }$
and
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $x^{[n]} \in {{}^\omega \omega }$
be defined by
$x^{[n]} \in {{}^\omega \omega }$
be defined by
![]() $x^{[n]}(k) = x(\mathsf {pair}(n,k))$
.
$x^{[n]}(k) = x(\mathsf {pair}(n,k))$
.
![]() $x^{[n]}$
is the
$x^{[n]}$
is the
![]() $n{\text {th}}$
-section of x.
$n{\text {th}}$
-section of x.
If
![]() $x \in {{}^\omega 2}$
, let
$x \in {{}^\omega 2}$
, let
![]() $\mathcal {R}_x \subseteq \omega \times \omega $
be defined by
$\mathcal {R}_x \subseteq \omega \times \omega $
be defined by
![]() $\mathcal {R}_x(a,b)$
if and only if
$\mathcal {R}_x(a,b)$
if and only if
![]() $x(\mathsf {pair}(a,b)) = 1$
.
$x(\mathsf {pair}(a,b)) = 1$
.
Let
![]() ${\mathrm {WO}}$
be the
${\mathrm {WO}}$
be the
![]() $\Pi _1^1$
-complete set of
$\Pi _1^1$
-complete set of
![]() $w \in \mathbb {R}$
so that
$w \in \mathbb {R}$
so that
![]() $\mathcal {R}_x$
is a wellordering. Let
$\mathcal {R}_x$
is a wellordering. Let
![]() ${\mathrm {ot}} : {\mathrm {WO}} \rightarrow {\omega _1}$
be the ordertype function.
${\mathrm {ot}} : {\mathrm {WO}} \rightarrow {\omega _1}$
be the ordertype function.
![]() ${\mathrm {ot}}$
is a
${\mathrm {ot}}$
is a
![]() $\Pi _1^1$
-norm on
$\Pi _1^1$
-norm on
![]() ${\mathrm {WO}}$
. If
${\mathrm {WO}}$
. If
![]() $w \in {\mathrm {WO}}$
and
$w \in {\mathrm {WO}}$
and
![]() $n \in \mathrm {field}(\mathcal {R}_w)$
, then let
$n \in \mathrm {field}(\mathcal {R}_w)$
, then let
![]() ${\mathrm {ot}}(w,n)$
denote the ordertype of n in
${\mathrm {ot}}(w,n)$
denote the ordertype of n in
![]() $\mathcal {R}_w$
. If
$\mathcal {R}_w$
. If
![]() $w \in {\mathrm {WO}}$
and
$w \in {\mathrm {WO}}$
and
![]() $\alpha < {\mathrm {ot}}(w)$
, then let
$\alpha < {\mathrm {ot}}(w)$
, then let
![]() $\mathsf {num}(w,\alpha )$
be the unique element of
$\mathsf {num}(w,\alpha )$
be the unique element of
![]() $\omega $
with ordertype
$\omega $
with ordertype
![]() $\alpha $
according to
$\alpha $
according to
![]() $\mathcal {R}_w$
.
$\mathcal {R}_w$
.
Definition 2.6. Let X be a set. A set
![]() $A \subseteq {}^\omega X$
is Suslin if and only if there is an ordinal
$A \subseteq {}^\omega X$
is Suslin if and only if there is an ordinal
![]() $\delta $
and a tree T on
$\delta $
and a tree T on
![]() $X \times \delta $
so that
$X \times \delta $
so that
![]() $A = \pi _1[[T]]$
, where
$A = \pi _1[[T]]$
, where
![]() $\pi _1 : {}^\omega X \times {}^\omega \delta \rightarrow {}^\omega X$
is the projection onto the first coordinate. T is called a Suslin representation for A. A set A is co-Suslin if and only if
$\pi _1 : {}^\omega X \times {}^\omega \delta \rightarrow {}^\omega X$
is the projection onto the first coordinate. T is called a Suslin representation for A. A set A is co-Suslin if and only if
![]() ${}^\omega X \setminus A$
is Suslin.
${}^\omega X \setminus A$
is Suslin.
Let X be a set and
![]() $A \subseteq {}^\omega X$
. A sequence of norms on A,
$A \subseteq {}^\omega X$
. A sequence of norms on A,
![]() $\bar \phi = \langle \phi _n : n \in \omega \rangle $
, is a semiscale if and only if for all
$\bar \phi = \langle \phi _n : n \in \omega \rangle $
, is a semiscale if and only if for all
![]() $f \in {}^\omega X$
and sequence
$f \in {}^\omega X$
and sequence
![]() $\bar {f} = \langle f_n : n \in \omega \rangle $
of elements in A so that
$\bar {f} = \langle f_n : n \in \omega \rangle $
of elements in A so that
-
(1)
 $f = \lim _{n \in \omega } f_n$
(in the natural topology on
$f = \lim _{n \in \omega } f_n$
(in the natural topology on
 ${}^\omega X$
) and
${}^\omega X$
) and -
(2) for all
 $n \in \omega $
, there is a
$n \in \omega $
, there is a
 $\lambda _n \in \mathrm {ON}$
so that
$\lambda _n \in \mathrm {ON}$
so that
 $\lim _{i \in \omega } \phi _n(f_i) = \lambda _n$
(i.e., is eventually constant taking value
$\lim _{i \in \omega } \phi _n(f_i) = \lambda _n$
(i.e., is eventually constant taking value
 $\lambda _n$
),
$\lambda _n$
),
one has that
![]() $f \in A$
.
$f \in A$
.
A semiscale
![]() $\bar \phi $
on A is good if and only if for any sequence
$\bar \phi $
on A is good if and only if for any sequence
![]() $\bar {f}$
which satisfies just (2) above, there is an
$\bar {f}$
which satisfies just (2) above, there is an
![]() $f \in {}^\omega X$
so that
$f \in {}^\omega X$
so that
![]() $f = \lim _{n \in \omega } f_n$
. A semiscale is very good if and only if it is good and for all
$f = \lim _{n \in \omega } f_n$
. A semiscale is very good if and only if it is good and for all
![]() $x,y \in A$
and
$x,y \in A$
and
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\phi _n(x) \leq \phi _n(y)$
implies that for all
$\phi _n(x) \leq \phi _n(y)$
implies that for all
![]() $m \leq n$
,
$m \leq n$
,
![]() $\phi _m(x) \leq \phi _m(y)$
.
$\phi _m(x) \leq \phi _m(y)$
.
A semiscale
![]() $\bar \phi $
on A is a scale if and only if it satisfies the lower semicontinuity property: Using the notations of (1) and (2) above, for all
$\bar \phi $
on A is a scale if and only if it satisfies the lower semicontinuity property: Using the notations of (1) and (2) above, for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\phi _n(f) \leq \lambda _n$
.
$\phi _n(f) \leq \lambda _n$
.
Every semiscale
![]() $\bar \phi $
on A yields a Suslin representation for A. Suppose a tree T on
$\bar \phi $
on A yields a Suslin representation for A. Suppose a tree T on
![]() $X \times \delta $
is a Suslin representation for A. If
$X \times \delta $
is a Suslin representation for A. If
![]() $f \in A$
, then the tree
$f \in A$
, then the tree
![]() $T_f = \{u \in {}^{<\omega }\delta : (f \upharpoonright |u|,u) \in T\}$
has an infinite path so let
$T_f = \{u \in {}^{<\omega }\delta : (f \upharpoonright |u|,u) \in T\}$
has an infinite path so let
![]() $L^T_f$
denote the leftmost path of
$L^T_f$
denote the leftmost path of
![]() $T_f$
. The canonical semiscale for A derived from T is
$T_f$
. The canonical semiscale for A derived from T is
![]() $\bar \varphi ^T = \langle \varphi ^T_n : n \in \omega \rangle $
defined by
$\bar \varphi ^T = \langle \varphi ^T_n : n \in \omega \rangle $
defined by
![]() $\varphi ^T_n(f) = L^T_f(n)$
. (See [Reference Moschovakis10, Theorem 2B.1].) Also every semiscale on A can be converted into a very good semiscale by a standard procedure (see [Reference Moschovakis10, Lemma 4E.2]).
$\varphi ^T_n(f) = L^T_f(n)$
. (See [Reference Moschovakis10, Theorem 2B.1].) Also every semiscale on A can be converted into a very good semiscale by a standard procedure (see [Reference Moschovakis10, Lemma 4E.2]).
Definition 2.7. Let
![]() $R \subseteq \mathbb {R} \times \mathbb {R}$
. A uniformization for R is a function
$R \subseteq \mathbb {R} \times \mathbb {R}$
. A uniformization for R is a function
![]() $\Phi : \mathrm {dom}(R) \rightarrow \mathbb {R}$
so that for all
$\Phi : \mathrm {dom}(R) \rightarrow \mathbb {R}$
so that for all
![]() $x \in \mathrm {dom}(R)$
,
$x \in \mathrm {dom}(R)$
,
![]() $R(x,\Phi (x))$
. Let
$R(x,\Phi (x))$
. Let
![]() $\mathsf {Uniformization}$
be the statement that every relation
$\mathsf {Uniformization}$
be the statement that every relation
![]() $R \subseteq \mathbb {R} \times \mathbb {R}$
has a uniformization.
$R \subseteq \mathbb {R} \times \mathbb {R}$
has a uniformization.
By a game argument,
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
implies
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
implies
![]() $\mathsf {Uniformization}$
. Since
$\mathsf {Uniformization}$
. Since
![]() $\mathsf {AD}_{\mathbb {R}}$
implies
$\mathsf {AD}_{\mathbb {R}}$
implies
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
,
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
,
![]() $\mathsf {AD}_{\mathbb {R}}$
also proves
$\mathsf {AD}_{\mathbb {R}}$
also proves
![]() $\mathsf {Uniformization}$
. Kechris [Reference Kechris6] showed that over
$\mathsf {Uniformization}$
. Kechris [Reference Kechris6] showed that over
![]() $\mathsf {AD}$
,
$\mathsf {AD}$
,
![]() $\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
and
$\mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
and
![]() $\mathsf {Uniformization}$
are equivalent. If
$\mathsf {Uniformization}$
are equivalent. If
![]() $R \subseteq \mathbb {R} \times \mathbb {R}$
has a Suslin representation, then R has a uniformization. Thus every set having a Suslin representation implies
$R \subseteq \mathbb {R} \times \mathbb {R}$
has a Suslin representation, then R has a uniformization. Thus every set having a Suslin representation implies
![]() $\mathsf {Uniformization}$
.
$\mathsf {Uniformization}$
.
![]() $\mathsf {AD}$
alone cannot establish any of these principles since
$\mathsf {AD}$
alone cannot establish any of these principles since
![]() $L(\mathbb {R}) \models \neg \mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
because the relation
$L(\mathbb {R}) \models \neg \mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
because the relation
![]() $S(x,y)$
if and only if y is not
$S(x,y)$
if and only if y is not
![]() $\mathrm {OD}_x$
cannot be uniformized in
$\mathrm {OD}_x$
cannot be uniformized in
![]() $L(\mathbb {R})$
. It is open whether these principles are equivalent over
$L(\mathbb {R})$
. It is open whether these principles are equivalent over
![]() $\mathsf {AD}$
; however, Woodin has shown they are equivalent over
$\mathsf {AD}$
; however, Woodin has shown they are equivalent over
![]() $\mathsf {AD} + \mathsf {DC}$
.
$\mathsf {AD} + \mathsf {DC}$
.
In this article, one will be concerned about the determinacy of certain games on ordinals. Generally, the determinacy of all games on uncountable ordinals is not consistent. However, the following result states that games with Suslin and co-Suslin payoff sets are determined.
Fact 2.8 [Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin9, Theorem 2.8].
Suppose
![]() $\kappa < \Theta $
. Let
$\kappa < \Theta $
. Let
![]() $A \subseteq {}^\omega \kappa $
and suppose that A is Suslin and co-Suslin. Then the game on
$A \subseteq {}^\omega \kappa $
and suppose that A is Suslin and co-Suslin. Then the game on
![]() $\kappa $
with payoff set A is determined.
$\kappa $
with payoff set A is determined.
To apply Fact 2.8, one will need to show some relevant ordinal games have Suslin and co-Suslin payoff sets. Moreover, it will be very important in certain instances to have that the Suslin representations are obtained uniformly from certain objects. Next, one will give some closure properties of Suslin representations with a particular focus on uniformity.
Fact 2.9. The class of Suslin subsets of
![]() ${}^\omega \kappa $
contains the open and closed subsets of
${}^\omega \kappa $
contains the open and closed subsets of
![]() ${}^\omega \kappa $
and is closed under countable unions, countable intersection, and projections. The Cartesian product of two Suslin subset of
${}^\omega \kappa $
and is closed under countable unions, countable intersection, and projections. The Cartesian product of two Suslin subset of
![]() ${}^\omega \kappa $
is a Suslin subset of
${}^\omega \kappa $
is a Suslin subset of
![]() ${}^\omega \kappa \times {}^\omega \kappa $
.
${}^\omega \kappa \times {}^\omega \kappa $
.
Fact 2.10. Let
![]() $\kappa $
be a cardinal. Let
$\kappa $
be a cardinal. Let
![]() $\epsilon < {\omega _1}$
,
$\epsilon < {\omega _1}$
,
![]() $w \in {\mathrm {WO}}$
with
$w \in {\mathrm {WO}}$
with
![]() ${\mathrm {ot}}(w) = \epsilon $
,
${\mathrm {ot}}(w) = \epsilon $
,
![]() $\nu < \kappa $
, and
$\nu < \kappa $
, and
![]() $\ell : \epsilon \rightarrow \nu $
. Define a relation
$\ell : \epsilon \rightarrow \nu $
. Define a relation
![]() $R^\nu _\ell \subseteq {}^\omega \nu $
by
$R^\nu _\ell \subseteq {}^\omega \nu $
by
![]() $R^\nu _\ell (g)$
if and only if
$R^\nu _\ell (g)$
if and only if
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
. Then
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
. Then
![]() $R^\nu _\ell $
is Suslin and co-Suslin uniformly in
$R^\nu _\ell $
is Suslin and co-Suslin uniformly in
![]() $\ell $
,
$\ell $
,
![]() $\nu $
, and w. The term “uniformly” means there are functions
$\nu $
, and w. The term “uniformly” means there are functions
![]() $\mathfrak {T}$
and
$\mathfrak {T}$
and
![]() $\mathfrak {U}$
so that whenever
$\mathfrak {U}$
so that whenever
![]() $\ell $
, w, and
$\ell $
, w, and
![]() $\nu $
have the above property,
$\nu $
have the above property,
![]() $\mathfrak {T}(\ell ,w,\nu )$
and
$\mathfrak {T}(\ell ,w,\nu )$
and
![]() $\mathfrak {U}(\ell ,w,\nu )$
are trees on
$\mathfrak {U}(\ell ,w,\nu )$
are trees on
![]() $\nu \times \kappa $
,
$\nu \times \kappa $
,
![]() $R^\nu _\ell = \pi _1[[\mathfrak {T}(\ell ,w,\nu )]]$
, and
$R^\nu _\ell = \pi _1[[\mathfrak {T}(\ell ,w,\nu )]]$
, and
![]() ${}^\omega \nu \setminus R^\nu _\ell = \pi _1[[\mathfrak {U}(\ell ,w,\nu )]]$
where
${}^\omega \nu \setminus R^\nu _\ell = \pi _1[[\mathfrak {U}(\ell ,w,\nu )]]$
where
![]() $\pi _1 : {}^\omega \nu \times {}^\omega \kappa \rightarrow {}^\omega \nu $
is the projection onto the first coordinate.
$\pi _1 : {}^\omega \nu \times {}^\omega \kappa \rightarrow {}^\omega \nu $
is the projection onto the first coordinate.
Proof Fix a bijection
![]() $\Upsilon : \kappa \rightarrow {}^{<\omega }\kappa $
with the property that for all
$\Upsilon : \kappa \rightarrow {}^{<\omega }\kappa $
with the property that for all
![]() $s,t \in {}^{<\omega }\kappa $
, if
$s,t \in {}^{<\omega }\kappa $
, if
![]() $s \subseteq t$
, then
$s \subseteq t$
, then
![]() $\Upsilon ^{-1}(s) \leq \Upsilon ^{-1}(t)$
. If
$\Upsilon ^{-1}(s) \leq \Upsilon ^{-1}(t)$
. If
![]() $s,t \in {}^{<\omega }\nu $
, then say that s is compatible with t if
$s,t \in {}^{<\omega }\nu $
, then say that s is compatible with t if
![]() $s \subseteq t$
or
$s \subseteq t$
or
![]() $t \subseteq s$
. Recall from Definition 2.5, if
$t \subseteq s$
. Recall from Definition 2.5, if
![]() $n \in \mathrm {field}(\mathcal {R}_w)$
where
$n \in \mathrm {field}(\mathcal {R}_w)$
where
![]() $\mathcal {R}_w$
is the wellordering coded by
$\mathcal {R}_w$
is the wellordering coded by
![]() $w \in {\mathrm {WO}}$
, then
$w \in {\mathrm {WO}}$
, then
![]() ${\mathrm {ot}}(w,n)$
is the rank of n in
${\mathrm {ot}}(w,n)$
is the rank of n in
![]() $\mathcal {R}_w$
.
$\mathcal {R}_w$
.
Let
![]() $S^\nu _\ell = {}^\omega \nu \setminus R^\nu _\ell $
. Note that
$S^\nu _\ell = {}^\omega \nu \setminus R^\nu _\ell $
. Note that
![]() $S^\nu _\ell $
is a countable union of closed sets in the topology of
$S^\nu _\ell $
is a countable union of closed sets in the topology of
![]() ${}^\omega \nu $
and thus has the following simple Suslin representation. Let U be a tree on
${}^\omega \nu $
and thus has the following simple Suslin representation. Let U be a tree on
![]() ${}^\omega \nu \times \omega $
defined by
${}^\omega \nu \times \omega $
defined by
![]() $(s,u) \in U$
if and only if
$(s,u) \in U$
if and only if
![]() $|s| = |u| = 0$
or there exists an
$|s| = |u| = 0$
or there exists an
![]() $m \in \mathrm {field}(\mathcal {R}_w)$
so that u is the constant sequence taking value m and
$m \in \mathrm {field}(\mathcal {R}_w)$
so that u is the constant sequence taking value m and
![]() $\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(s)$
. If
$\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(s)$
. If
![]() $m \in \omega $
, let
$m \in \omega $
, let
![]() $\bar {m} \in {}^\omega \omega $
be the constant infinite sequence taking value m. Note that if
$\bar {m} \in {}^\omega \omega $
be the constant infinite sequence taking value m. Note that if
![]() $g \in \pi _1[[U]]$
then there exists an
$g \in \pi _1[[U]]$
then there exists an
![]() $m \in \omega $
so that
$m \in \omega $
so that
![]() $(g,\bar {m}) \in [U]$
. So for all
$(g,\bar {m}) \in [U]$
. So for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $(g \upharpoonright n, \bar {m} \upharpoonright n) \in U$
which implies that for all
$(g \upharpoonright n, \bar {m} \upharpoonright n) \in U$
which implies that for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g \upharpoonright n)$
. Hence
$\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g \upharpoonright n)$
. Hence
![]() $\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g)$
and
$\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g)$
and
![]() $\neg (\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g))$
. Thus
$\neg (\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g))$
. Thus
![]() $S^\nu _\ell (g)$
. Conversely, suppose
$S^\nu _\ell (g)$
. Conversely, suppose
![]() $S^\nu _\ell (g)$
which means
$S^\nu _\ell (g)$
which means
![]() $\neg (\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g))$
. Since
$\neg (\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g))$
. Since
![]() ${\mathrm {ot}}(w) = \epsilon = |\ell |$
, there is some
${\mathrm {ot}}(w) = \epsilon = |\ell |$
, there is some
![]() $m \in \mathrm {field}(\mathcal {R}_w)$
so that
$m \in \mathrm {field}(\mathcal {R}_w)$
so that
![]() $\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g)$
. Then
$\ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g)$
. Then
![]() $(g,\bar {m}) \in [U]$
and thus
$(g,\bar {m}) \in [U]$
and thus
![]() $g \in \pi _1[[U]]$
. This shows that
$g \in \pi _1[[U]]$
. This shows that
![]() $S^\nu _\ell $
is Suslin and therefore
$S^\nu _\ell $
is Suslin and therefore
![]() $R^\nu _\ell $
is co-Suslin.
$R^\nu _\ell $
is co-Suslin.
Define a tree T on
![]() $\nu \times \kappa $
by
$\nu \times \kappa $
by
![]() $(s,u) \in T$
if and only if for all
$(s,u) \in T$
if and only if for all
![]() $k < |s|$
, the following holds:
$k < |s|$
, the following holds:
-
•
 $\Upsilon (u(k)) \in {}^{<\omega }\nu $
.
$\Upsilon (u(k)) \in {}^{<\omega }\nu $
. -
• If
 $k \notin \mathrm {field}(\mathcal {R}_w)$
, then
$k \notin \mathrm {field}(\mathcal {R}_w)$
, then
 $\Upsilon (u(k)) = \emptyset $
.
$\Upsilon (u(k)) = \emptyset $
. -
• If
 $k \in \mathrm {field}(\mathcal {R}_w)$
, then
$k \in \mathrm {field}(\mathcal {R}_w)$
, then
 $\ell ({\mathrm {ot}}(w,k))) \in \mathrm {rang}(\Upsilon (u(k)))$
.
$\ell ({\mathrm {ot}}(w,k))) \in \mathrm {rang}(\Upsilon (u(k)))$
. -
•
 $\Upsilon (u(k))$
is compatible with s.
$\Upsilon (u(k))$
is compatible with s.
Suppose
![]() $g \in \pi _1[[T]]$
. Then there exists an
$g \in \pi _1[[T]]$
. Then there exists an
![]() $h \in {}^\omega \kappa $
so that
$h \in {}^\omega \kappa $
so that
![]() $(g,h) \in [T]$
. Thus for all
$(g,h) \in [T]$
. Thus for all
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $\Upsilon (h(k)) \subseteq g$
and
$\Upsilon (h(k)) \subseteq g$
and
![]() $\ell ({\mathrm {ot}}(w,k)) \in \mathrm {rang}(\Upsilon (h(k)))$
. Hence
$\ell ({\mathrm {ot}}(w,k)) \in \mathrm {rang}(\Upsilon (h(k)))$
. Hence
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
which is equivalent to
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
which is equivalent to
![]() $R^\nu _\ell (g)$
. Conversely, suppose
$R^\nu _\ell (g)$
. Conversely, suppose
![]() $R^\nu _\ell (g)$
. Then
$R^\nu _\ell (g)$
. Then
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
. If
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
. If
![]() $n \in \mathrm {field}(\mathcal {R}_w)$
, let
$n \in \mathrm {field}(\mathcal {R}_w)$
, let
![]() $k_n$
be least
$k_n$
be least
![]() $k \in \omega $
with
$k \in \omega $
with
![]() $k> 0$
so that
$k> 0$
so that
![]() $g(k - 1) = \ell ({\mathrm {ot}}(w,n))$
. If
$g(k - 1) = \ell ({\mathrm {ot}}(w,n))$
. If
![]() $n \notin \mathrm {field}(\mathcal {R}_w)$
, then let
$n \notin \mathrm {field}(\mathcal {R}_w)$
, then let
![]() $k_n = 0$
. Let
$k_n = 0$
. Let
![]() $h(n) = \Upsilon ^{-1}(g \upharpoonright k_n)$
. Then
$h(n) = \Upsilon ^{-1}(g \upharpoonright k_n)$
. Then
![]() $(g,h) \in [T]$
. Thus
$(g,h) \in [T]$
. Thus
![]() $g \in \pi _1[[T]]$
. Observe that this explicit h is actually the leftmost branch,
$g \in \pi _1[[T]]$
. Observe that this explicit h is actually the leftmost branch,
![]() $L^T_g$
, of T corresponding to g. It has been shown that
$L^T_g$
, of T corresponding to g. It has been shown that
![]() $g \in \pi _1[[T]]$
if and only if
$g \in \pi _1[[T]]$
if and only if
![]() $R^\nu _\ell (g)$
, so
$R^\nu _\ell (g)$
, so
![]() $R^\nu _\ell $
is Suslin.
$R^\nu _\ell $
is Suslin.
Observe that both trees U and T are produced uniformly from
![]() $\ell $
,
$\ell $
,
![]() $\nu $
, and w. Let
$\nu $
, and w. Let
![]() $\mathfrak {U}(\ell ,w,\nu ) = U$
and
$\mathfrak {U}(\ell ,w,\nu ) = U$
and
![]() $\mathfrak {T}(\ell ,w,\nu ) = T$
.
$\mathfrak {T}(\ell ,w,\nu ) = T$
.
Fact 2.11. Assume the setting of Fact 2.10. Let
![]() $\bar \varphi ^{\ell ,w,\nu } = \langle \varphi ^{\ell ,w,\nu }_n : n \in \omega \rangle $
be the canonical semiscale derived from
$\bar \varphi ^{\ell ,w,\nu } = \langle \varphi ^{\ell ,w,\nu }_n : n \in \omega \rangle $
be the canonical semiscale derived from
![]() $\mathfrak {T}(\ell ,w,\nu ) ($
using the leftmost branch as in Definition 2.6
$\mathfrak {T}(\ell ,w,\nu ) ($
using the leftmost branch as in Definition 2.6
![]() $)$
and
$)$
and
![]() $\bar \varsigma ^{\ell ,w,\nu } = \langle \varsigma _n^{\ell ,w,\nu } : n \in \omega \rangle $
be the canonical semiscale derived from
$\bar \varsigma ^{\ell ,w,\nu } = \langle \varsigma _n^{\ell ,w,\nu } : n \in \omega \rangle $
be the canonical semiscale derived from
![]() $\mathfrak {U}(\ell ,w,\nu )$
. For all
$\mathfrak {U}(\ell ,w,\nu )$
. For all
![]() $n \in \omega $
, the norm relations
$n \in \omega $
, the norm relations
![]() $\leq _{\varphi _n^{\ell ,w,\nu }}^*$
,
$\leq _{\varphi _n^{\ell ,w,\nu }}^*$
,
![]() $<_{\varphi _n^{\ell ,w,\nu }}^*$
,
$<_{\varphi _n^{\ell ,w,\nu }}^*$
,
![]() $\leq _{\varsigma _n^{\ell ,w,\nu }}^*$
, and
$\leq _{\varsigma _n^{\ell ,w,\nu }}^*$
, and
![]() $<^*_{\varsigma _n^{\ell ,w,\nu }}$
are Suslin and co-Suslin.
$<^*_{\varsigma _n^{\ell ,w,\nu }}$
are Suslin and co-Suslin.
Proof The notation from the statement and proof of Fact 2.10 will be used. Note that from the definition of
![]() $\mathfrak {U}(\ell ,w,\nu )$
from Fact 2.10, the leftmost branch
$\mathfrak {U}(\ell ,w,\nu )$
from Fact 2.10, the leftmost branch
![]() $L^{\mathfrak {U}(\ell ,w,\nu )}_g$
is simply
$L^{\mathfrak {U}(\ell ,w,\nu )}_g$
is simply
![]() $\bar {m}$
where m is least so that
$\bar {m}$
where m is least so that
![]() $\ell ({\mathrm {ot}}(w,n)) \notin \mathrm {rang}(g)$
.
$\ell ({\mathrm {ot}}(w,n)) \notin \mathrm {rang}(g)$
.
For each
![]() $m \in \mathrm {field}(\mathcal {R}_w)$
, let
$m \in \mathrm {field}(\mathcal {R}_w)$
, let
![]() $E_m = \{g \in {}^\omega \nu : (\forall k < m)(k \in \mathrm {field}(\mathcal {R}_w) \Rightarrow \ell ({\mathrm {ot}}(w,k)) \in \mathrm {rang}(g)) \wedge \ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g)\}$
. If
$E_m = \{g \in {}^\omega \nu : (\forall k < m)(k \in \mathrm {field}(\mathcal {R}_w) \Rightarrow \ell ({\mathrm {ot}}(w,k)) \in \mathrm {rang}(g)) \wedge \ell ({\mathrm {ot}}(w,m)) \notin \mathrm {rang}(g)\}$
. If
![]() $m \notin \mathrm {field}(\mathcal {R}_w)$
, then let
$m \notin \mathrm {field}(\mathcal {R}_w)$
, then let
![]() $E_m = \emptyset $
. One can check that
$E_m = \emptyset $
. One can check that
![]() $E_m$
is Suslin and co-Suslin using arguments similar to Fact 2.10. Observe that for any
$E_m$
is Suslin and co-Suslin using arguments similar to Fact 2.10. Observe that for any
![]() $k \in \omega $
$k \in \omega $
 $$ \begin{align*}\leq^*_{\varsigma_k^{\ell,w,\nu}} = \left(\bigcup_{m \leq n} E_m \times E_n\right) \cup \left(\bigcup_{m \in \omega} E_m \times R^\nu_\ell\right)\end{align*} $$
$$ \begin{align*}\leq^*_{\varsigma_k^{\ell,w,\nu}} = \left(\bigcup_{m \leq n} E_m \times E_n\right) \cup \left(\bigcup_{m \in \omega} E_m \times R^\nu_\ell\right)\end{align*} $$
and
 $$ \begin{align*}<^*_{\varsigma_k^{\ell,w,\nu}} = \left(\bigcup_{m < n} E_m \times E_n\right) \cup \left(\bigcup_{m \in \omega} E_m \times R^\nu_\ell\right).\end{align*} $$
$$ \begin{align*}<^*_{\varsigma_k^{\ell,w,\nu}} = \left(\bigcup_{m < n} E_m \times E_n\right) \cup \left(\bigcup_{m \in \omega} E_m \times R^\nu_\ell\right).\end{align*} $$
These norm relations are Suslin and co-Suslin by Fact 2.9, Fact 2.10, and the earlier observations.
In the proof of Fact 2.10, one showed that if
![]() $f \in \pi _1[[\mathfrak {T}(\ell ,w,\nu )]]$
, then the leftmost branch
$f \in \pi _1[[\mathfrak {T}(\ell ,w,\nu )]]$
, then the leftmost branch
![]() $L^{\mathfrak {T}(\ell ,w,\nu )}_f$
is explicitly given by the following: For each
$L^{\mathfrak {T}(\ell ,w,\nu )}_f$
is explicitly given by the following: For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $k_n$
be the least
$k_n$
be the least
![]() $k \in \omega $
such that
$k \in \omega $
such that
![]() $f(k-1) = \ell ({\mathrm {ot}}(w,n))$
if
$f(k-1) = \ell ({\mathrm {ot}}(w,n))$
if
![]() $n \in \mathrm {field}(\mathcal {R}_w)$
and
$n \in \mathrm {field}(\mathcal {R}_w)$
and
![]() $k_n = 0$
if
$k_n = 0$
if
![]() $n \notin \mathrm {field}(\mathcal {R}_w)$
. Then
$n \notin \mathrm {field}(\mathcal {R}_w)$
. Then
![]() $L^{\mathfrak {T}(\ell ,w,\nu )}_f(n) = \Upsilon ^{-1}(f \upharpoonright k_n)$
.
$L^{\mathfrak {T}(\ell ,w,\nu )}_f(n) = \Upsilon ^{-1}(f \upharpoonright k_n)$
.
For each
![]() $n \in \mathrm {field}(\mathcal {R}_w)$
, let
$n \in \mathrm {field}(\mathcal {R}_w)$
, let
![]() $A_n \subseteq \kappa $
be the collection of
$A_n \subseteq \kappa $
be the collection of
![]() $\gamma $
so that
$\gamma $
so that
![]() $|\Upsilon (\gamma )|> 0$
,
$|\Upsilon (\gamma )|> 0$
,
![]() $\Upsilon (\gamma )(|\Upsilon (\gamma )| - 1) = \ell ({\mathrm {ot}}(w,n))$
, and for all
$\Upsilon (\gamma )(|\Upsilon (\gamma )| - 1) = \ell ({\mathrm {ot}}(w,n))$
, and for all
![]() $i < |\Upsilon (\gamma )| - 1$
,
$i < |\Upsilon (\gamma )| - 1$
,
![]() $\Upsilon (\gamma )(i) \neq \ell ({\mathrm {ot}}(w,n))$
. Define a tree
$\Upsilon (\gamma )(i) \neq \ell ({\mathrm {ot}}(w,n))$
. Define a tree
![]() $K_n$
on
$K_n$
on
![]() $\nu \times \nu \times \kappa \times \kappa $
by
$\nu \times \nu \times \kappa \times \kappa $
by
![]() $(s,t,u,v) \in K_n$
if and only if
$(s,t,u,v) \in K_n$
if and only if
![]() $u(0) \leq v(0)$
,
$u(0) \leq v(0)$
,
![]() $u(0),v(0) \in A_n$
,
$u(0),v(0) \in A_n$
,
![]() $\Upsilon (u(0))$
is compatible with s, and
$\Upsilon (u(0))$
is compatible with s, and
![]() $\Upsilon (v(0))$
is compatible with t. Define a tree
$\Upsilon (v(0))$
is compatible with t. Define a tree
![]() $J_n$
similarly with
$J_n$
similarly with
![]() $u(0) \leq v(0)$
replaced with
$u(0) \leq v(0)$
replaced with
![]() $u(0) < v(0)$
.
$u(0) < v(0)$
.
Note that if
![]() $f,g \in R^\nu _\ell $
, then
$f,g \in R^\nu _\ell $
, then
![]() $\varphi _n^{\ell ,w,\nu }(f) \leq \varphi _n^{\ell ,w,\nu }(g)$
if and only if
$\varphi _n^{\ell ,w,\nu }(f) \leq \varphi _n^{\ell ,w,\nu }(g)$
if and only if
![]() $L^{\mathfrak {T}(\ell ,w,\nu )}_f(n) \leq L^{\mathfrak {T}(\ell ,w,\nu )}_g(n)$
if and only if
$L^{\mathfrak {T}(\ell ,w,\nu )}_f(n) \leq L^{\mathfrak {T}(\ell ,w,\nu )}_g(n)$
if and only if
![]() $(\exists x,y)((f,g,x,y) \in [K_n])$
. Similarly, if
$(\exists x,y)((f,g,x,y) \in [K_n])$
. Similarly, if
![]() $f,g \in R^\nu _\ell $
, then
$f,g \in R^\nu _\ell $
, then
![]() $\varphi _n^{\ell ,w,\nu }(f) < \varphi _n^{\ell ,w,\nu }(g)$
if and only if
$\varphi _n^{\ell ,w,\nu }(f) < \varphi _n^{\ell ,w,\nu }(g)$
if and only if
![]() $L^{\mathfrak {T}(\ell ,w,\nu )}_f(n) < L^{\mathfrak {T}(\ell ,w,\nu )}_g(n)$
if and only if
$L^{\mathfrak {T}(\ell ,w,\nu )}_f(n) < L^{\mathfrak {T}(\ell ,w,\nu )}_g(n)$
if and only if
![]() $(\exists x,y)((f,g,x,y) \in [J_n])$
.
$(\exists x,y)((f,g,x,y) \in [J_n])$
.
Note that
![]() $f \leq ^*_{\varphi _n^{\ell ,w,\nu }} g$
if and only if
$f \leq ^*_{\varphi _n^{\ell ,w,\nu }} g$
if and only if
Also
![]() $\neg (f \leq ^*_{\varphi _n^{\ell ,w,\nu }} g)$
if and only if
$\neg (f \leq ^*_{\varphi _n^{\ell ,w,\nu }} g)$
if and only if
This shows that
![]() $\leq ^*_{\varphi _n^{\ell ,w,\nu }}$
is Suslin and co-Suslin by Fact 2.9 and Fact 2.10. A similar argument shows that
$\leq ^*_{\varphi _n^{\ell ,w,\nu }}$
is Suslin and co-Suslin by Fact 2.9 and Fact 2.10. A similar argument shows that
![]() $<^*_{\varphi _n^{\ell ,w,\nu }}$
is also Suslin and co-Suslin.
$<^*_{\varphi _n^{\ell ,w,\nu }}$
is also Suslin and co-Suslin.
Fact 2.12. [Reference Moschovakis10, 6E]; Moschovakis Third Periodicity Theorem) Assume
![]() $\mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
. Let
$\mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
. Let
![]() $\nu < \Theta $
. Let
$\nu < \Theta $
. Let
![]() $A \subseteq {}^\omega \nu $
be Suslin and
$A \subseteq {}^\omega \nu $
be Suslin and
![]() $\bar \varphi = \langle \varphi _n : n \in \omega \rangle $
be a very good semiscale on A. For each
$\bar \varphi = \langle \varphi _n : n \in \omega \rangle $
be a very good semiscale on A. For each
![]() $n \in \omega $
, odd
$n \in \omega $
, odd
![]() $m \in \omega $
, and
$m \in \omega $
, and
![]() $s,t \in {}^m\nu $
, define the game
$s,t \in {}^m\nu $
, define the game
![]() ${}^nH^s_t$
on
${}^nH^s_t$
on
![]() $\nu $
as in the following diagram.
$\nu $
as in the following diagram.

The game has two players called the first player and second player making moves in
![]() $\nu $
as indicated in the diagram. Say that the second player wins if and only if
$\nu $
as indicated in the diagram. Say that the second player wins if and only if
![]() $s\hat {\ }a \leq ^*_{\varphi _n} t\hat {\ }b$
.
$s\hat {\ }a \leq ^*_{\varphi _n} t\hat {\ }b$
.
Assume that Player 1 has a winning strategy in the game
![]() $G^\nu _A$
on
$G^\nu _A$
on
![]() $\nu $
with payoff set A. Assume for all
$\nu $
with payoff set A. Assume for all
![]() $n \in \omega $
, odd
$n \in \omega $
, odd
![]() $m \in \omega $
, and
$m \in \omega $
, and
![]() $s,t \in {}^m\nu $
, the games
$s,t \in {}^m\nu $
, the games
![]() ${}^nH^s_t$
are determined. Then uniformly from
${}^nH^s_t$
are determined. Then uniformly from
![]() $\nu $
, A, and the very good semiscale
$\nu $
, A, and the very good semiscale
![]() $\bar \varphi $
, one can obtain a strategy
$\bar \varphi $
, one can obtain a strategy
![]() $\sigma $
for Player 1 in
$\sigma $
for Player 1 in
![]() $G_A^\nu $
.
$G_A^\nu $
.
![]() $($
This means there is a function
$($
This means there is a function
![]() $\Phi $
so that whenever
$\Phi $
so that whenever
![]() $\nu $
, A, and
$\nu $
, A, and
![]() $\bar \varphi $
have the above property,
$\bar \varphi $
have the above property,
![]() $\Phi (\nu ,A,\bar \varphi )$
is a Player 1 winning strategy for
$\Phi (\nu ,A,\bar \varphi )$
is a Player 1 winning strategy for
![]() $G^\nu _A$
.
$G^\nu _A$
.
![]() $)$
$)$
Proof This result is essentially a coarse form of the Moschovakis third periodicity theorem for ordinal value games using the idea of the “best” strategy. (The definability estimates for the strategy will not be relevant here.) The uniformity statement will be essential so an explicit definition of the Player 1 winning strategy will be provided. The reader can see [Reference Moschovakis10, 6D and 6E] or [Reference Jackson5, Section 2] for the details.
For each odd m, let
![]() $W_m$
be the set of
$W_m$
be the set of
![]() $s \in {}^m\nu $
so that Player 1 can win in the game
$s \in {}^m\nu $
so that Player 1 can win in the game
![]() $G_A^\nu $
when s is an initial partial run (m being odd implies that Player 2 is the next player to respond). Since Player 1 is assumed to have a winning strategy, for all odd
$G_A^\nu $
when s is an initial partial run (m being odd implies that Player 2 is the next player to respond). Since Player 1 is assumed to have a winning strategy, for all odd
![]() $m \in \omega $
,
$m \in \omega $
,
![]() $W_m$
is nonempty. For
$W_m$
is nonempty. For
![]() $s,t \in W_m$
, define
$s,t \in W_m$
, define
![]() $s \preceq ^m_n t$
if and only if the second player has a winning strategy in
$s \preceq ^m_n t$
if and only if the second player has a winning strategy in
![]() ${}^n H^s_t$
. It can be shown that
${}^n H^s_t$
. It can be shown that
![]() $\preceq ^m_n$
is a prewellordering on
$\preceq ^m_n$
is a prewellordering on
![]() $W_m$
.
$W_m$
.
If
![]() $k \in \omega $
and
$k \in \omega $
and
![]() $u \in {}^{2k}\nu $
, then define
$u \in {}^{2k}\nu $
, then define
![]() $\sigma (u)$
to be the least
$\sigma (u)$
to be the least
![]() $\gamma < \nu $
so that
$\gamma < \nu $
so that
![]() $u\hat {\ }\gamma \in W_{2k + 1}$
and for all
$u\hat {\ }\gamma \in W_{2k + 1}$
and for all
![]() $\eta $
with
$\eta $
with
![]() $u\hat {\ }\eta \in W_{2k + 1}$
,
$u\hat {\ }\eta \in W_{2k + 1}$
,
![]() $u\hat {\ }\gamma \preceq ^{2k + 1}_k u \hat {\ }\eta $
. (If u is odd length, then let
$u\hat {\ }\gamma \preceq ^{2k + 1}_k u \hat {\ }\eta $
. (If u is odd length, then let
![]() $\sigma (u) = 0$
as this case is irrelevant because
$\sigma (u) = 0$
as this case is irrelevant because
![]() $\sigma $
is intended to be used as a Player 1’s strategy.) It can be shown that
$\sigma $
is intended to be used as a Player 1’s strategy.) It can be shown that
![]() $\sigma $
is a Player 1’s winning strategy in
$\sigma $
is a Player 1’s winning strategy in
![]() $G^\nu _A$
and is produced uniformly from
$G^\nu _A$
and is produced uniformly from
![]() $\nu $
, A, and
$\nu $
, A, and
![]() $\bar \varphi $
.
$\bar \varphi $
.
Fact 2.13. Let
![]() $\nu < \Theta $
. Let
$\nu < \Theta $
. Let
![]() $\Xi : {}^\omega \nu \rightarrow {}^\omega \omega $
be a Lipschitz continuous function. Suppose
$\Xi : {}^\omega \nu \rightarrow {}^\omega \omega $
be a Lipschitz continuous function. Suppose
![]() $\Gamma $
is a pointclass and
$\Gamma $
is a pointclass and
![]() $\Delta = \Gamma \cap \check \Gamma $
. Suppose there is a norm
$\Delta = \Gamma \cap \check \Gamma $
. Suppose there is a norm
![]() $\varphi : W \rightarrow \nu $
so that
$\varphi : W \rightarrow \nu $
so that
![]() $W \in \Delta $
and the associated prewellordering
$W \in \Delta $
and the associated prewellordering
![]() $\preceq _\varphi $
on W is also in
$\preceq _\varphi $
on W is also in
![]() $\Delta $
. Then
$\Delta $
. Then
![]() $\Xi [{}^\omega \nu ]$
is
$\Xi [{}^\omega \nu ]$
is
![]() $\exists ^{\mathbb {R}}\Delta $
.
$\exists ^{\mathbb {R}}\Delta $
.
Proof First, a simple coding of
![]() ${}^{<\omega }\nu $
by reals will be developed. Let
${}^{<\omega }\nu $
by reals will be developed. Let
![]() $\mathsf {finS}$
consist of reals z so that
$\mathsf {finS}$
consist of reals z so that
![]() $(\forall i < z^{[0]}(0))(z^{[{i + 1}]} \in W)$
. Let
$(\forall i < z^{[0]}(0))(z^{[{i + 1}]} \in W)$
. Let
![]() $\mathsf {finseq} : \mathsf {finS} \rightarrow {}^{<\omega }\nu $
by
$\mathsf {finseq} : \mathsf {finS} \rightarrow {}^{<\omega }\nu $
by
![]() $\mathsf {finseq}(z)$
be a sequence of length
$\mathsf {finseq}(z)$
be a sequence of length
![]() $z^{[0]}(0)$
and for all
$z^{[0]}(0)$
and for all
![]() $i < z^{[0]}(0)$
,
$i < z^{[0]}(0)$
,
![]() $\mathsf {finseq}(z)(i) = \varphi (z^{[i + 1]})$
. Note that
$\mathsf {finseq}(z)(i) = \varphi (z^{[i + 1]})$
. Note that
![]() $\mathsf {finseq}$
is a surjection of
$\mathsf {finseq}$
is a surjection of
![]() $\mathsf {finS}$
onto
$\mathsf {finS}$
onto
![]() ${}^{<\omega }\nu $
. The set
${}^{<\omega }\nu $
. The set
![]() $\mathsf {finS}$
is
$\mathsf {finS}$
is
![]() $\Delta $
. The expression “
$\Delta $
. The expression “
![]() $u \in \mathsf {finS}$
,
$u \in \mathsf {finS}$
,
![]() $i < |\mathsf {finseq}(u)|$
,
$i < |\mathsf {finseq}(u)|$
,
![]() $w \in W$
, and
$w \in W$
, and
![]() $\mathsf {finseq}(u)(i) = \varphi (w)$
” is
$\mathsf {finseq}(u)(i) = \varphi (w)$
” is
![]() $\Delta $
as a relation in the variables u, i, and w.
$\Delta $
as a relation in the variables u, i, and w.
Fix a bijection
![]() $\Upsilon : \nu \rightarrow {}^{<\omega }\nu $
. Next one will show that
$\Upsilon : \nu \rightarrow {}^{<\omega }\nu $
. Next one will show that
![]() $\Upsilon $
has a coded version which is
$\Upsilon $
has a coded version which is
![]() $\exists ^{\mathbb {R}}\Delta $
. Define
$\exists ^{\mathbb {R}}\Delta $
. Define
![]() $Z \subseteq W \times \mathsf {finS}$
by
$Z \subseteq W \times \mathsf {finS}$
by
![]() $Z(w,u)$
if and only if
$Z(w,u)$
if and only if
![]() $\Upsilon (\varphi (w)) = \mathsf {finseq}(u)$
. By the Moschovakis coding lemma ([Reference Moschovakis10, Section 7D] or [Reference Jackson5, Theorem 2.12]), there is a
$\Upsilon (\varphi (w)) = \mathsf {finseq}(u)$
. By the Moschovakis coding lemma ([Reference Moschovakis10, Section 7D] or [Reference Jackson5, Theorem 2.12]), there is a
![]() $\bar {Z} \in \exists ^{\mathbb {R}} \Delta $
so that
$\bar {Z} \in \exists ^{\mathbb {R}} \Delta $
so that
![]() $\bar {Z} \subseteq Z$
and for all
$\bar {Z} \subseteq Z$
and for all
![]() $\alpha < \nu $
,
$\alpha < \nu $
,
![]() $\bar {Z} \cap (\varphi ^{-1}[\{\alpha \}] \times \mathbb {R}) \neq \emptyset $
if and only if
$\bar {Z} \cap (\varphi ^{-1}[\{\alpha \}] \times \mathbb {R}) \neq \emptyset $
if and only if
![]() $Z \cap (\varphi ^{-1}[\{\alpha \}] \times \mathbb {R}) \neq \emptyset $
.
$Z \cap (\varphi ^{-1}[\{\alpha \}] \times \mathbb {R}) \neq \emptyset $
.
Since
![]() $\Xi $
is Lipschitz, there is a function
$\Xi $
is Lipschitz, there is a function
![]() $\tau : {}^{<\omega }\nu \rightarrow \omega $
so that
$\tau : {}^{<\omega }\nu \rightarrow \omega $
so that
![]() $\Xi = \Xi ^2_\tau $
using the notation of Definition 2.2. Define
$\Xi = \Xi ^2_\tau $
using the notation of Definition 2.2. Define
![]() $Y \subseteq W \times \omega $
by
$Y \subseteq W \times \omega $
by
![]() $Y(w,n)$
if and only if
$Y(w,n)$
if and only if
![]() $\tau (\Upsilon (\varphi (w))) = n$
. By the Moschovakis coding lemma, there is a
$\tau (\Upsilon (\varphi (w))) = n$
. By the Moschovakis coding lemma, there is a
![]() $\bar {Y} \in \exists ^{\mathbb {R}}\Delta $
so that
$\bar {Y} \in \exists ^{\mathbb {R}}\Delta $
so that
![]() $\bar {Y} \subseteq Y$
and for all
$\bar {Y} \subseteq Y$
and for all
![]() $\alpha < \nu $
,
$\alpha < \nu $
,
![]() $\bar {Y} \cap (\varphi ^{-1}[\{\alpha \}] \times \omega ) \neq \emptyset $
if and only if
$\bar {Y} \cap (\varphi ^{-1}[\{\alpha \}] \times \omega ) \neq \emptyset $
if and only if
![]() $Y \cap (\varphi ^{-1}[\{\alpha \}] \times \omega ) \neq \emptyset $
.
$Y \cap (\varphi ^{-1}[\{\alpha \}] \times \omega ) \neq \emptyset $
.
Now observe that
![]() $x \in \Xi [{}^\omega \nu ]$
if and only if there is an
$x \in \Xi [{}^\omega \nu ]$
if and only if there is an
![]() $f \in {}^\omega \nu $
so that
$f \in {}^\omega \nu $
so that
![]() $x = \Xi ^2_\tau (f)$
if and only if there is a
$x = \Xi ^2_\tau (f)$
if and only if there is a
![]() $y \in \mathbb {R}$
coding f in the sense that each
$y \in \mathbb {R}$
coding f in the sense that each
![]() $y^{[n]}$
codes
$y^{[n]}$
codes
![]() $f(n)$
and
$f(n)$
and
![]() $\Xi ^2_\tau (f) = x$
as expressed by the coding through
$\Xi ^2_\tau (f) = x$
as expressed by the coding through
![]() $\bar {Y}$
and
$\bar {Y}$
and
![]() $\bar {Z}$
. Formally,
$\bar {Z}$
. Formally,
![]() $x \in \Xi [{}^\omega \nu ]$
if and only if the conjunction of the following holds.
$x \in \Xi [{}^\omega \nu ]$
if and only if the conjunction of the following holds.
-
(1) For all
 $n \in \omega $
,
$n \in \omega $
,
 $y^{[n]} \in W$
.
$y^{[n]} \in W$
. -
(2) For all
 $n \in \omega $
, there exist
$n \in \omega $
, there exist
 $v,w \in W$
and there exists a
$v,w \in W$
and there exists a
 $u \in \mathsf {finS}$
so that
$u \in \mathsf {finS}$
so that
 $\varphi (v) = \varphi (w)$
,
$\varphi (v) = \varphi (w)$
,
 $|\mathsf {finseq}(u)| = n$
, and for all
$|\mathsf {finseq}(u)| = n$
, and for all
 $i < |\mathsf {finseq}(u)|$
,
$i < |\mathsf {finseq}(u)|$
,
 $\mathsf {finseq}(u)(i) = \varphi (y^{[i]})$
,
$\mathsf {finseq}(u)(i) = \varphi (y^{[i]})$
,
 $\bar {Z}(v,u)$
, and
$\bar {Z}(v,u)$
, and
 $\bar {Y}(w,x(n))$
.
$\bar {Y}(w,x(n))$
.
The above expression is
![]() $\exists ^{\mathbb {R}}\Delta $
by using the above observations.
$\exists ^{\mathbb {R}}\Delta $
by using the above observations.
Fact 2.14.
![]() $($
Boundedness Principle
$($
Boundedness Principle
![]() $)$
Suppose
$)$
Suppose
![]() $\Gamma $
is a pointclass closed under
$\Gamma $
is a pointclass closed under
![]() $\forall ^{\mathbb {R}}$
. Suppose
$\forall ^{\mathbb {R}}$
. Suppose
![]() $W \in \Gamma $
is a
$W \in \Gamma $
is a
![]() $\Gamma $
-complete set with a surjective
$\Gamma $
-complete set with a surjective
![]() $\Gamma $
-norm
$\Gamma $
-norm
![]() $\varphi : W \rightarrow \kappa $
. If
$\varphi : W \rightarrow \kappa $
. If
![]() $A \subseteq W$
and
$A \subseteq W$
and
![]() $A \in \check \Gamma $
, then there is a
$A \in \check \Gamma $
, then there is a
![]() $\delta < \kappa $
so that
$\delta < \kappa $
so that
![]() $\varphi [A] \subseteq \delta $
.
$\varphi [A] \subseteq \delta $
.
Fact 2.15.
![]() $($
Moschovakis [Reference Jackson5, Theorem 2.6 and Lemma 2.13]
$($
Moschovakis [Reference Jackson5, Theorem 2.6 and Lemma 2.13]
![]() $)$
Let
$)$
Let
![]() $\Gamma $
be a pointclass closed under
$\Gamma $
be a pointclass closed under
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
, and
$\vee $
, and
![]() $\forall ^{\mathbb {R}}$
with a
$\forall ^{\mathbb {R}}$
with a
![]() $\Gamma $
-complete set W and a
$\Gamma $
-complete set W and a
![]() $\Gamma $
-norm
$\Gamma $
-norm
![]() $\varphi $
on W. Then the length of
$\varphi $
on W. Then the length of
![]() $\varphi $
is
$\varphi $
is
![]() $\delta (\Gamma )$
and
$\delta (\Gamma )$
and
![]() $\delta (\Gamma )$
is a regular cardinal.
$\delta (\Gamma )$
is a regular cardinal.
Recall that under
![]() $\mathsf {AD}$
, Wadge’s lemma implies that every nonselfdual pointclass has complete sets. Solovay club coding techniques for
$\mathsf {AD}$
, Wadge’s lemma implies that every nonselfdual pointclass has complete sets. Solovay club coding techniques for
![]() ${\omega _1}$
under
${\omega _1}$
under
![]() $\mathsf {AD}$
can be extended to
$\mathsf {AD}$
can be extended to
![]() $\delta (\Gamma )$
when
$\delta (\Gamma )$
when
![]() $\Gamma $
is a nonselfdual pointclass closed under
$\Gamma $
is a nonselfdual pointclass closed under
![]() $\forall ^{\mathbb {R}}$
.
$\forall ^{\mathbb {R}}$
.
Fact 2.16. Let
![]() $\Gamma $
be a nonselfdual pointclass closed under
$\Gamma $
be a nonselfdual pointclass closed under
![]() $\forall ^{\mathbb {R}}$
. Let
$\forall ^{\mathbb {R}}$
. Let
![]() $\kappa = \delta (\Gamma )$
. Let W be a
$\kappa = \delta (\Gamma )$
. Let W be a
![]() $\Gamma $
-complete set with surjective
$\Gamma $
-complete set with surjective
![]() $\Gamma $
-norm
$\Gamma $
-norm
![]() $\varphi : W \rightarrow \kappa $
. Let
$\varphi : W \rightarrow \kappa $
. Let
![]() $\mathsf {clubcode} \subseteq \mathbb {R}$
consist of the strategies
$\mathsf {clubcode} \subseteq \mathbb {R}$
consist of the strategies
![]() $\tau $
with the property
$\tau $
with the property
If
![]() $\tau \in \mathsf {clubcode}$
, then let
$\tau \in \mathsf {clubcode}$
, then let
![]() $\mathfrak {C}_\tau $
is a club. If
$\mathfrak {C}_\tau $
is a club. If
![]() $C \subseteq \kappa $
is club, then there is a
$C \subseteq \kappa $
is club, then there is a
![]() $\tau \in \mathsf {clubcode}$
so that
$\tau \in \mathsf {clubcode}$
so that
![]() $\mathfrak {C}_\tau \subseteq C$
.
$\mathfrak {C}_\tau \subseteq C$
.
If
![]() $A \subseteq \mathsf {clubcode}$
is
$A \subseteq \mathsf {clubcode}$
is
![]() $\check \Gamma $
, then uniformly in A, one can produce a club C so that for all
$\check \Gamma $
, then uniformly in A, one can produce a club C so that for all
![]() $\tau \in A$
,
$\tau \in A$
,
![]() $C \subseteq \mathfrak {C}_\tau $
.
$C \subseteq \mathfrak {C}_\tau $
.
![]() $($
Uniformly here means there is a function
$($
Uniformly here means there is a function
![]() $\Upsilon $
so that whenever
$\Upsilon $
so that whenever
![]() $A \subseteq \mathsf {clubcode}$
is
$A \subseteq \mathsf {clubcode}$
is
![]() $\check \Gamma $
,
$\check \Gamma $
,
![]() $\Upsilon (A)$
is club with the property that for all
$\Upsilon (A)$
is club with the property that for all
![]() $\tau \in A$
,
$\tau \in A$
,
![]() $\Upsilon (A) \subseteq \mathfrak {C}_\tau $
.
$\Upsilon (A) \subseteq \mathfrak {C}_\tau $
.
![]() $)$
$)$
Proof These are proved using the boundedness principle (Fact 2.14). See [Reference Chan1, Fact 4.7] for a similar argument.
Definition 2.17. Let
![]() $\alpha \in {\omega _1}$
. If
$\alpha \in {\omega _1}$
. If
![]() $s \in {}^{<\omega }\alpha $
, let
$s \in {}^{<\omega }\alpha $
, let
![]() $N^\alpha _s = \{f \in {}^\omega \alpha : s \subseteq f\}$
. The topology on
$N^\alpha _s = \{f \in {}^\omega \alpha : s \subseteq f\}$
. The topology on
![]() ${}^\omega \alpha $
generated by
${}^\omega \alpha $
generated by
![]() $\{N_s^\alpha : s \in {}^{<\omega }\alpha \}$
as a basis is homeomorphic to
$\{N_s^\alpha : s \in {}^{<\omega }\alpha \}$
as a basis is homeomorphic to
![]() ${}^\omega \omega $
. Thus the familiar category notion can be formulated for
${}^\omega \omega $
. Thus the familiar category notion can be formulated for
![]() ${}^\omega \alpha $
in this topology. Let
${}^\omega \alpha $
in this topology. Let
![]() $\mathsf {surj}_\alpha $
be the collection of
$\mathsf {surj}_\alpha $
be the collection of
![]() $f \in {}^\omega \alpha $
such that
$f \in {}^\omega \alpha $
such that
![]() $f[\omega ] = \alpha $
, i.e., f is a surjection onto
$f[\omega ] = \alpha $
, i.e., f is a surjection onto
![]() $\alpha $
.
$\alpha $
.
![]() $\mathsf {surj}_\alpha $
is comeager in
$\mathsf {surj}_\alpha $
is comeager in
![]() ${}^\omega \alpha $
.
${}^\omega \alpha $
.
Recall that under
![]() $\mathsf {AD}$
, the category ideal has full wellordered additivity. That is, if
$\mathsf {AD}$
, the category ideal has full wellordered additivity. That is, if
![]() $\delta $
is an ordinal and
$\delta $
is an ordinal and
![]() $\langle X_\alpha : \alpha < \delta \rangle $
is a collection of meager subsets of
$\langle X_\alpha : \alpha < \delta \rangle $
is a collection of meager subsets of
![]() $\mathbb {R}$
, then
$\mathbb {R}$
, then
![]() $\bigcup _{\alpha < \delta } X_\alpha $
is a meager subset of
$\bigcup _{\alpha < \delta } X_\alpha $
is a meager subset of
![]() $\mathbb {R}$
. Thus the meager ideal on
$\mathbb {R}$
. Thus the meager ideal on
![]() ${}^\omega \alpha $
also has the full wellordered additivity.
${}^\omega \alpha $
also has the full wellordered additivity.
The following is the simplest example of the Kechris–Woodin generic coding function occurs at
![]() ${\omega _1}$
.
${\omega _1}$
.
Fact 2.18. There is a function
![]() $\mathfrak {G} : {}^\omega {\omega _1} \rightarrow {\mathrm {WO}}$
so that for all
$\mathfrak {G} : {}^\omega {\omega _1} \rightarrow {\mathrm {WO}}$
so that for all
![]() $\alpha < {\omega _1}$
, if
$\alpha < {\omega _1}$
, if
![]() $f \in \mathsf {surj}_\alpha $
, then
$f \in \mathsf {surj}_\alpha $
, then
![]() ${\mathrm {ot}}(\mathfrak {G}(f)) = \alpha $
.
${\mathrm {ot}}(\mathfrak {G}(f)) = \alpha $
.
Proof Let
![]() $A_f = \{n \in \omega : (\forall m)(m < n \Rightarrow f(m) \neq f(n))\}$
. Define
$A_f = \{n \in \omega : (\forall m)(m < n \Rightarrow f(m) \neq f(n))\}$
. Define
![]() $\mathfrak {G}(f) \in \mathbb {R}$
so that
$\mathfrak {G}(f) \in \mathbb {R}$
so that
![]() $\mathcal {R}_{\mathfrak {G}(f)}(a,b) = 1 \Leftrightarrow a,b \in A_f \wedge f(a) < f(b)$
. Note that the domain of
$\mathcal {R}_{\mathfrak {G}(f)}(a,b) = 1 \Leftrightarrow a,b \in A_f \wedge f(a) < f(b)$
. Note that the domain of
![]() $\mathcal {R}_{\mathfrak {G}(f)}$
is
$\mathcal {R}_{\mathfrak {G}(f)}$
is
![]() $A_f$
and
$A_f$
and
![]() $\mathfrak {G}(f) \in {\mathrm {WO}}$
. If
$\mathfrak {G}(f) \in {\mathrm {WO}}$
. If
![]() $f \in \mathsf {surj}_\alpha $
, then
$f \in \mathsf {surj}_\alpha $
, then
![]() $(A_f,\mathcal {R}_{\mathfrak {G}(f)})$
is order-isomorphic to
$(A_f,\mathcal {R}_{\mathfrak {G}(f)})$
is order-isomorphic to
![]() $\alpha $
.
$\alpha $
.
The following results are generalizations of the category boundedness arguments found in the proof of the main theorems in [Reference Chan and Jackson3].
Fact 2.19. Let
![]() $\nu < {\omega _1}$
and
$\nu < {\omega _1}$
and
![]() $\kappa $
be a cardinal with
$\kappa $
be a cardinal with
![]() ${\mathrm {cof}}(\kappa )> \omega $
. Suppose
${\mathrm {cof}}(\kappa )> \omega $
. Suppose
![]() $A \subseteq {}^\omega \nu $
is comeager in
$A \subseteq {}^\omega \nu $
is comeager in
![]() ${}^\omega \nu $
and
${}^\omega \nu $
and
![]() $\Phi : A \rightarrow \kappa $
. Then there is a
$\Phi : A \rightarrow \kappa $
. Then there is a
![]() $\delta < \kappa $
and a comeager
$\delta < \kappa $
and a comeager
![]() $B \subseteq A$
so that
$B \subseteq A$
so that
![]() $\Phi [B] \subseteq \delta $
.
$\Phi [B] \subseteq \delta $
.
Proof For each
![]() $\alpha < \kappa $
, let
$\alpha < \kappa $
, let
![]() $A_\alpha = \{f \in A : \Phi (f) = \alpha \}$
. Note that
$A_\alpha = \{f \in A : \Phi (f) = \alpha \}$
. Note that
![]() $A = \bigcup _{\alpha < \kappa } A_\alpha $
. Let
$A = \bigcup _{\alpha < \kappa } A_\alpha $
. Let
![]() $T = \{\alpha < \kappa : A_\alpha \text { is nonmeager}\}$
.
$T = \{\alpha < \kappa : A_\alpha \text { is nonmeager}\}$
.
![]() $\mathsf {AD}$
implies that a wellordered union of meager sets in
$\mathsf {AD}$
implies that a wellordered union of meager sets in
![]() ${}^\omega \nu $
is meager and since A is not meager,
${}^\omega \nu $
is meager and since A is not meager,
![]() $T \neq \emptyset $
. Since
$T \neq \emptyset $
. Since
![]() $\mathsf {AD}$
implies that all sets of reals have the Baire property and there are no uncountable sets of disjoint open subsets of
$\mathsf {AD}$
implies that all sets of reals have the Baire property and there are no uncountable sets of disjoint open subsets of
![]() ${}^\omega \nu $
, one has that T must be countable. Since
${}^\omega \nu $
, one has that T must be countable. Since
![]() ${\mathrm {cof}}(\kappa )> \omega $
,
${\mathrm {cof}}(\kappa )> \omega $
,
![]() $\sup (T) < \kappa $
. Let
$\sup (T) < \kappa $
. Let
![]() $\delta = \sup (T) + 1 < \kappa $
. Note that
$\delta = \sup (T) + 1 < \kappa $
. Note that
![]() $B = \bigcup _{\alpha < \delta } A_\alpha $
is comeager. By definition of B,
$B = \bigcup _{\alpha < \delta } A_\alpha $
is comeager. By definition of B,
![]() $\Phi [B] \subseteq \delta $
.
$\Phi [B] \subseteq \delta $
.
Fact 2.20. Let
![]() $\nu < {\omega _1}$
and
$\nu < {\omega _1}$
and
![]() $\kappa $
be cardinal with
$\kappa $
be cardinal with
![]() ${\mathrm {cof}}(\kappa )> \omega $
. Let
${\mathrm {cof}}(\kappa )> \omega $
. Let
![]() $\mathsf {club}$
be the set of club subsets of
$\mathsf {club}$
be the set of club subsets of
![]() $\kappa $
. Suppose
$\kappa $
. Suppose
![]() $A \subseteq {}^\omega \nu $
is comeager and
$A \subseteq {}^\omega \nu $
is comeager and
![]() $\Phi : A \rightarrow \mathsf {club}$
. Then uniformly from
$\Phi : A \rightarrow \mathsf {club}$
. Then uniformly from
![]() $\Phi $
, there is a club
$\Phi $
, there is a club
![]() $C \subseteq \kappa $
and a comeager set
$C \subseteq \kappa $
and a comeager set
![]() $B \subseteq A$
so that for all
$B \subseteq A$
so that for all
![]() $f \in B$
,
$f \in B$
,
![]() $C \subseteq \Phi (f)$
.
$C \subseteq \Phi (f)$
.
Proof If
![]() $X \subseteq \kappa $
and
$X \subseteq \kappa $
and
![]() $|X| = \kappa $
, then let
$|X| = \kappa $
, then let
![]() $\mathsf {enum}_X : \kappa \rightarrow X$
be the increasing enumeration of X. For
$\mathsf {enum}_X : \kappa \rightarrow X$
be the increasing enumeration of X. For
![]() $\alpha < \kappa $
, let
$\alpha < \kappa $
, let
![]() $E_\alpha : A \rightarrow \kappa $
be defined by
$E_\alpha : A \rightarrow \kappa $
be defined by
![]() $E_\alpha (f) = \mathsf {enum}_{\Phi (f)}(\alpha )$
. For
$E_\alpha (f) = \mathsf {enum}_{\Phi (f)}(\alpha )$
. For
![]() $\alpha < \delta < \kappa $
, let
$\alpha < \delta < \kappa $
, let
![]() $Y^\delta _\alpha = \{f \in A : E_\alpha (f) < \delta \}$
. Define
$Y^\delta _\alpha = \{f \in A : E_\alpha (f) < \delta \}$
. Define
![]() $K : \kappa \rightarrow \kappa $
by letting
$K : \kappa \rightarrow \kappa $
by letting
![]() $K(\alpha )$
be the least
$K(\alpha )$
be the least
![]() $\delta $
so that
$\delta $
so that
![]() $Y^\delta _\alpha $
is comeager. Note that for each
$Y^\delta _\alpha $
is comeager. Note that for each
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $K(\alpha )$
is well defined by Fact 2.19 applied to the function
$K(\alpha )$
is well defined by Fact 2.19 applied to the function
![]() $E_\alpha $
. Since for any
$E_\alpha $
. Since for any
![]() $f \in A$
,
$f \in A$
,
![]() $E_\alpha (f) \geq \alpha $
, one has that
$E_\alpha (f) \geq \alpha $
, one has that
![]() $K(\alpha )> \alpha $
. Also note that for any
$K(\alpha )> \alpha $
. Also note that for any
![]() $\alpha _0 \leq \alpha _1$
and
$\alpha _0 \leq \alpha _1$
and
![]() $f \in A$
,
$f \in A$
,
![]() $E_{\alpha _0}(f) \leq E_{\alpha _1}(f)$
and thus
$E_{\alpha _0}(f) \leq E_{\alpha _1}(f)$
and thus
![]() $K(\alpha _0) \leq K(\alpha _1)$
.
$K(\alpha _0) \leq K(\alpha _1)$
.
Let
![]() $C = \{\eta < \kappa : (\forall \xi < \eta )(K(\xi ) < \eta )\}$
. (Note that C is produced uniformly from
$C = \{\eta < \kappa : (\forall \xi < \eta )(K(\xi ) < \eta )\}$
. (Note that C is produced uniformly from
![]() $\Phi $
.) First, to show C is unbounded. Let
$\Phi $
.) First, to show C is unbounded. Let
![]() $\alpha < \kappa $
. Let
$\alpha < \kappa $
. Let
![]() $\alpha _0 = \alpha $
. If
$\alpha _0 = \alpha $
. If
![]() $\alpha _n$
has been defined, then let
$\alpha _n$
has been defined, then let
![]() $\alpha _{n + 1} = K(\alpha _n)$
. By the property of K mentioned above,
$\alpha _{n + 1} = K(\alpha _n)$
. By the property of K mentioned above,
![]() $\langle \alpha _n : n \in \omega \rangle $
is a strictly increasing sequence in
$\langle \alpha _n : n \in \omega \rangle $
is a strictly increasing sequence in
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\eta = \sup \{\alpha _n : n \in \omega \}$
and note that
$\eta = \sup \{\alpha _n : n \in \omega \}$
and note that
![]() $\alpha < \eta < \kappa $
since
$\alpha < \eta < \kappa $
since
![]() ${\mathrm {cof}}(\kappa )> \omega $
. Let
${\mathrm {cof}}(\kappa )> \omega $
. Let
![]() $\xi < \eta $
be arbitrary. There is an
$\xi < \eta $
be arbitrary. There is an
![]() $n \in \omega $
so that
$n \in \omega $
so that
![]() $\xi < \alpha _{n}$
. Since
$\xi < \alpha _{n}$
. Since
![]() $K(\xi ) \leq K(\alpha _n) = \alpha _{n + 1} < \eta $
, one has that
$K(\xi ) \leq K(\alpha _n) = \alpha _{n + 1} < \eta $
, one has that
![]() $K(\xi ) < \eta $
. Since
$K(\xi ) < \eta $
. Since
![]() $\xi < \eta $
was arbitrary,
$\xi < \eta $
was arbitrary,
![]() $\eta \in C$
. Next to show C is closed. Suppose
$\eta \in C$
. Next to show C is closed. Suppose
![]() $\eta $
is a limit point of C. Let
$\eta $
is a limit point of C. Let
![]() $\xi < \eta $
be arbitrary. Then there is an
$\xi < \eta $
be arbitrary. Then there is an
![]() $\eta ' \in C$
with
$\eta ' \in C$
with
![]() $\xi < \eta ' < \eta $
. Thus
$\xi < \eta ' < \eta $
. Thus
![]() $K(\xi ) < \eta ' < \eta $
. Since
$K(\xi ) < \eta ' < \eta $
. Since
![]() $\xi < \eta $
was arbitrary, one has that
$\xi < \eta $
was arbitrary, one has that
![]() $\eta \in C$
. It has been established that C is a club subset of
$\eta \in C$
. It has been established that C is a club subset of
![]() $\kappa $
.
$\kappa $
.
Fix
![]() $\eta \in C$
. For all
$\eta \in C$
. For all
![]() $\xi < \eta $
,
$\xi < \eta $
,
![]() $K(\xi ) < \eta $
so
$K(\xi ) < \eta $
so
![]() $Y^\eta _\xi $
is comeager. Let
$Y^\eta _\xi $
is comeager. Let
![]() $Y^\eta = \bigcap _{\xi < \eta } Y^\eta _\xi $
. Since wellordered intersection of comeager sets are comeager under
$Y^\eta = \bigcap _{\xi < \eta } Y^\eta _\xi $
. Since wellordered intersection of comeager sets are comeager under
![]() $\mathsf {AD}$
,
$\mathsf {AD}$
,
![]() $Y^\eta $
is comeager. Note that for each
$Y^\eta $
is comeager. Note that for each
![]() $f \in Y^\eta $
and
$f \in Y^\eta $
and
![]() $\xi < \eta $
,
$\xi < \eta $
,
![]() $\xi \leq E_\xi (f) < \eta $
. Since
$\xi \leq E_\xi (f) < \eta $
. Since
![]() $\xi < \eta $
is arbitrary,
$\xi < \eta $
is arbitrary,
![]() $E_\xi (f) = \mathsf {enum}_{\Phi (f)}(\xi ) \in \Phi (f)$
, and
$E_\xi (f) = \mathsf {enum}_{\Phi (f)}(\xi ) \in \Phi (f)$
, and
![]() $\Phi (f) \subseteq \kappa $
is a club, one must have that
$\Phi (f) \subseteq \kappa $
is a club, one must have that
![]() $\eta \in \Phi (f)$
. Thus for all
$\eta \in \Phi (f)$
. Thus for all
![]() $f \in Y^\eta $
,
$f \in Y^\eta $
,
![]() $\eta \in \Phi (f)$
. Now let
$\eta \in \Phi (f)$
. Now let
![]() $Y = \bigcap _{\eta \in C} Y^\eta $
. Again since a wellordering intersection of comeager sets is comeager under
$Y = \bigcap _{\eta \in C} Y^\eta $
. Again since a wellordering intersection of comeager sets is comeager under
![]() $\mathsf {AD}$
, Y is comeager. Take any
$\mathsf {AD}$
, Y is comeager. Take any
![]() $f \in Y$
. For any
$f \in Y$
. For any
![]() $\eta \in C$
,
$\eta \in C$
,
![]() $f \in Y^\eta $
. By the previous observation,
$f \in Y^\eta $
. By the previous observation,
![]() $\eta \in \Phi (f)$
. Since
$\eta \in \Phi (f)$
. Since
![]() $\eta \in C$
was arbitrary, one has shown that
$\eta \in C$
was arbitrary, one has shown that
![]() $C \subseteq \Phi (f)$
.
$C \subseteq \Phi (f)$
.
Next, the more general notion of a reliable ordinal and its associated Kechris–Woodin generic coding function will be defined.
Definition 2.21. [Reference Kechris and Woodin8] An ordinal
![]() $\lambda $
is reliable if and only if there is a
$\lambda $
is reliable if and only if there is a
![]() $W \subseteq \mathbb {R}$
and a scale
$W \subseteq \mathbb {R}$
and a scale
![]() $\bar \varphi = \langle \varphi _i : i \in \omega \rangle $
on W with the following properties.
$\bar \varphi = \langle \varphi _i : i \in \omega \rangle $
on W with the following properties.
-
• For all
 $n \in \omega $
,
$n \in \omega $
,
 $\varphi _n : W \rightarrow \lambda $
and
$\varphi _n : W \rightarrow \lambda $
and
 $\varphi _0 : W \rightarrow \lambda $
is surjective.
$\varphi _0 : W \rightarrow \lambda $
is surjective. -
• The norm relations
 $\leq ^*_{\varphi _0}$
and
$\leq ^*_{\varphi _0}$
and
 $<^*_{\varphi _0}$
are Suslin and co-Suslin.
$<^*_{\varphi _0}$
are Suslin and co-Suslin.
![]() $(W,\bar {\varphi })$
is called the witness to the reliability of
$(W,\bar {\varphi })$
is called the witness to the reliability of
![]() $\lambda $
.
$\lambda $
.
For
![]() $\xi < \lambda $
, say that
$\xi < \lambda $
, say that
![]() $S \subseteq \lambda $
is
$S \subseteq \lambda $
is
![]() $\xi $
-honest if and only if there is a
$\xi $
-honest if and only if there is a
![]() $w \in W$
such that
$w \in W$
such that
![]() $\varphi _0(w) = \xi $
and for all
$\varphi _0(w) = \xi $
and for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\varphi _n(w) \in S$
. A set
$\varphi _n(w) \in S$
. A set
![]() $S \subseteq \lambda $
is honest if and only if for all
$S \subseteq \lambda $
is honest if and only if for all
![]() $\xi \in S$
, S is
$\xi \in S$
, S is
![]() $\xi $
-honest. (Note that the notions of honest and
$\xi $
-honest. (Note that the notions of honest and
![]() $\xi $
-honest depend on the witness to reliability.)
$\xi $
-honest depend on the witness to reliability.)
Fact 2.22. Let
![]() $\lambda $
be a regular reliable cardinal as witnessed by
$\lambda $
be a regular reliable cardinal as witnessed by
![]() $(W,\bar {\varphi })$
. Then for any
$(W,\bar {\varphi })$
. Then for any
![]() $\alpha < \lambda $
, there exists an
$\alpha < \lambda $
, there exists an
![]() $\alpha '$
such that
$\alpha '$
such that
![]() $\alpha \leq \alpha ' < \lambda $
and
$\alpha \leq \alpha ' < \lambda $
and
![]() $\alpha '$
is honest.
$\alpha '$
is honest.
Proof For each
![]() $\xi < \lambda $
, there is a
$\xi < \lambda $
, there is a
![]() $\xi ' \geq \xi $
so that
$\xi ' \geq \xi $
so that
![]() $\xi '$
is
$\xi '$
is
![]() $\xi $
-honest. To see this, pick any
$\xi $
-honest. To see this, pick any
![]() $w \in W$
so that
$w \in W$
so that
![]() $\varphi _0(w) = \xi $
. Let
$\varphi _0(w) = \xi $
. Let
![]() $\xi ' = \sup \{\varphi _n(w) + 1 : n \in \omega \}$
.
$\xi ' = \sup \{\varphi _n(w) + 1 : n \in \omega \}$
.
![]() $\xi '$
is
$\xi '$
is
![]() $\xi $
-honest. Since
$\xi $
-honest. Since
![]() ${\mathrm {cof}}(\lambda )> \omega $
,
${\mathrm {cof}}(\lambda )> \omega $
,
![]() $\xi ' < \lambda $
. Let
$\xi ' < \lambda $
. Let
![]() $\Lambda : \lambda \rightarrow \lambda $
be defined by:
$\Lambda : \lambda \rightarrow \lambda $
be defined by:
![]() $\Lambda (\xi )$
is the least
$\Lambda (\xi )$
is the least
![]() $\xi '$
with
$\xi '$
with
![]() $\xi \leq \xi ' < \lambda $
and
$\xi \leq \xi ' < \lambda $
and
![]() $\xi '$
is
$\xi '$
is
![]() $\xi $
-honest.
$\xi $
-honest.
Let
![]() $\alpha _0 = \alpha $
. If
$\alpha _0 = \alpha $
. If
![]() $\alpha _n < \lambda $
has been defined, let
$\alpha _n < \lambda $
has been defined, let
![]() $\alpha _{n + 1} = \sup \Lambda [\alpha _n]$
. Note that
$\alpha _{n + 1} = \sup \Lambda [\alpha _n]$
. Note that
![]() $\alpha _{n + 1} < \lambda $
since
$\alpha _{n + 1} < \lambda $
since
![]() $\lambda $
is regular. Let
$\lambda $
is regular. Let
![]() $\alpha ' = \sup \{\alpha _n : n \in \omega \}$
and note that
$\alpha ' = \sup \{\alpha _n : n \in \omega \}$
and note that
![]() $\alpha ' < \lambda $
since
$\alpha ' < \lambda $
since
![]() $\lambda $
is regular. Now suppose
$\lambda $
is regular. Now suppose
![]() $\xi < \alpha '$
. There is some
$\xi < \alpha '$
. There is some
![]() $n \in \omega $
so that
$n \in \omega $
so that
![]() $\xi < \alpha _n$
. Since
$\xi < \alpha _n$
. Since
![]() $\Lambda (\xi ) \leq \alpha _{n + 1}$
, one has that
$\Lambda (\xi ) \leq \alpha _{n + 1}$
, one has that
![]() $\alpha _{n + 1}$
is
$\alpha _{n + 1}$
is
![]() $\xi $
-honest. Since
$\xi $
-honest. Since
![]() $\alpha _{n + 1} \subseteq \alpha '$
, one has that
$\alpha _{n + 1} \subseteq \alpha '$
, one has that
![]() $\alpha '$
is
$\alpha '$
is
![]() $\xi $
-honest. Since
$\xi $
-honest. Since
![]() $\xi < \alpha '$
was arbitrary, this shows that
$\xi < \alpha '$
was arbitrary, this shows that
![]() $\alpha '$
is honest.
$\alpha '$
is honest.
Fact 2.23 ([Reference Kechris and Woodin8, Lemma 1.1]; Kechris–Woodin generic coding).
Let
![]() $\lambda $
be a reliable ordinal with witness
$\lambda $
be a reliable ordinal with witness
![]() $(W,\bar \varphi )$
. Then there is a Lipschitz continuous function
$(W,\bar \varphi )$
. Then there is a Lipschitz continuous function
![]() $\mathfrak {F} : {}^\omega \lambda \rightarrow \mathbb {R}$
so that for all
$\mathfrak {F} : {}^\omega \lambda \rightarrow \mathbb {R}$
so that for all
![]() $f \in {}^\omega \lambda $
, for all
$f \in {}^\omega \lambda $
, for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\mathfrak {F}(f)^{[n]} \in W$
, and if
$\mathfrak {F}(f)^{[n]} \in W$
, and if
![]() $f[\omega ]$
is honest, then for all
$f[\omega ]$
is honest, then for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\varphi _0(\mathfrak {F}(f)^{[n]}) = f(n)$
.
$\varphi _0(\mathfrak {F}(f)^{[n]}) = f(n)$
.
Definition 2.24. Let
![]() $\mathsf {BS}$
consist of the collection of
$\mathsf {BS}$
consist of the collection of
![]() $z \in \mathbb {R}$
so that
$z \in \mathbb {R}$
so that
![]() $z^{[0]} \in {\mathrm {WO}}$
and for all
$z^{[0]} \in {\mathrm {WO}}$
and for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $(z^{[1]})^{[n]} \in {\mathrm {WO}}$
. If
$(z^{[1]})^{[n]} \in {\mathrm {WO}}$
. If
![]() $z \in \mathsf {BS}$
, then let
$z \in \mathsf {BS}$
, then let
![]() $\mathsf {seq}(z) \in {}^{<{\omega _1}}{\omega _1}$
be the sequence of length
$\mathsf {seq}(z) \in {}^{<{\omega _1}}{\omega _1}$
be the sequence of length
![]() ${\mathrm {ot}}(z^{[0]})$
such that for all
${\mathrm {ot}}(z^{[0]})$
such that for all
![]() $\alpha < {\mathrm {ot}}(z^{[0]})$
,
$\alpha < {\mathrm {ot}}(z^{[0]})$
,
![]() $\mathsf {seq}(z)(\alpha ) = {\mathrm {ot}}((z^{[1]})^{[\mathsf {num}(z^{[0]},\alpha )]})$
. Note that for all
$\mathsf {seq}(z)(\alpha ) = {\mathrm {ot}}((z^{[1]})^{[\mathsf {num}(z^{[0]},\alpha )]})$
. Note that for all
![]() $\ell \in {}^{<{\omega _1}}{\omega _1}$
, there is a
$\ell \in {}^{<{\omega _1}}{\omega _1}$
, there is a
![]() $z \in \mathsf {BS}$
so that
$z \in \mathsf {BS}$
so that
![]() $\mathsf {seq}(z) = \ell $
.
$\mathsf {seq}(z) = \ell $
.
Definition 2.25. Let
![]() $\lambda $
be an ordinal,
$\lambda $
be an ordinal,
![]() $W \subseteq \mathbb {R}$
, and
$W \subseteq \mathbb {R}$
, and
![]() $\varphi : W \rightarrow \lambda $
be a surjective norm. Let
$\varphi : W \rightarrow \lambda $
be a surjective norm. Let
![]() $\mathsf {CS}$
consist of those
$\mathsf {CS}$
consist of those
![]() $z \in {{}^\omega \omega }$
so that
$z \in {{}^\omega \omega }$
so that
![]() $z^{[0]} \in {\mathrm {WO}}$
and for all
$z^{[0]} \in {\mathrm {WO}}$
and for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $(z^{[1]})^{[n]} \in W$
.
$(z^{[1]})^{[n]} \in W$
.
For each
![]() $z \in \mathsf {CS}$
, let
$z \in \mathsf {CS}$
, let
![]() $\mathsf {cseq}(z)$
be the sequence in
$\mathsf {cseq}(z)$
be the sequence in
![]() $\lambda $
of length
$\lambda $
of length
![]() ${\mathrm {ot}}(z^{[0]})$
defined by
${\mathrm {ot}}(z^{[0]})$
defined by
![]() $\mathsf {cseq}(z)(\alpha ) = \varphi ((z^{[1]})^{[\mathsf {num}(z^{[0]},\alpha )]})$
. Note that for all
$\mathsf {cseq}(z)(\alpha ) = \varphi ((z^{[1]})^{[\mathsf {num}(z^{[0]},\alpha )]})$
. Note that for all
![]() $\ell \in {}^{<{\omega _1}}\lambda $
, there is a
$\ell \in {}^{<{\omega _1}}\lambda $
, there is a
![]() $z \in \mathsf {CS}$
so that
$z \in \mathsf {CS}$
so that
![]() $\mathsf {cseq}(z) = \ell $
.
$\mathsf {cseq}(z) = \ell $
.
3 Countable Length Everywhere Club Uniformization
Definition 3.1. If
![]() $\kappa $
is a cardinal, let
$\kappa $
is a cardinal, let
![]() $\mathsf {club}$
denote the collection of club subsets of
$\mathsf {club}$
denote the collection of club subsets of
![]() $\kappa $
. A relation
$\kappa $
. A relation
![]() $R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$
is
$R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$
is
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() $\mathsf {club}$
-coordinate if and only if for all
$\mathsf {club}$
-coordinate if and only if for all
![]() $\ell \in {}^{<{\omega _1}}\kappa $
and clubs
$\ell \in {}^{<{\omega _1}}\kappa $
and clubs
![]() $C \subseteq D$
,
$C \subseteq D$
,
![]() $R(\ell ,D)$
implies
$R(\ell ,D)$
implies
![]() $R(\ell ,C)$
. Let
$R(\ell ,C)$
. Let
![]() $\mathrm {dom}(R) = \{\ell \in {}^{<{\omega _1}}{\omega _1} : (\exists C \in \mathsf {club})R(\ell ,C)\}$
. A uniformization for R is a function
$\mathrm {dom}(R) = \{\ell \in {}^{<{\omega _1}}{\omega _1} : (\exists C \in \mathsf {club})R(\ell ,C)\}$
. A uniformization for R is a function
![]() $\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
so that for all
$\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
so that for all
![]() $\ell \in \mathrm {dom}(R)$
,
$\ell \in \mathrm {dom}(R)$
,
![]() $R(\ell ,\Lambda (\ell ))$
.
$R(\ell ,\Lambda (\ell ))$
.
Countable length everywhere club uniformization for
![]() $\kappa $
is the statement that for every
$\kappa $
is the statement that for every
![]() $R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$
which is
$R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$
which is
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() $\mathsf {club}$
-coordinate, there is a uniformization for R.
$\mathsf {club}$
-coordinate, there is a uniformization for R.
Fact 3.2 ([Reference Chan and Jackson3]; Countable Length Everywhere Club Uniformization for
 ${\omega _1}$
).
${\omega _1}$
).
Assume
![]() $\mathsf {ZF} + \mathsf {AD}$
. Let
$\mathsf {ZF} + \mathsf {AD}$
. Let
![]() $R \subseteq {}^{<{\omega _1}}{\omega _1} \times \mathsf {club}$
be
$R \subseteq {}^{<{\omega _1}}{\omega _1} \times \mathsf {club}$
be
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() $\mathsf {club}$
-coordinate. Let
$\mathsf {club}$
-coordinate. Let
![]() $\tilde R \subseteq \mathsf {BS} \times \mathsf {clubcode}$
be the coded version of R defined by
$\tilde R \subseteq \mathsf {BS} \times \mathsf {clubcode}$
be the coded version of R defined by
![]() $\tilde R (z,e)$
if and only if
$\tilde R (z,e)$
if and only if
![]() $R(\mathsf {seq}(z),\mathfrak {C}_e)$
. Assume
$R(\mathsf {seq}(z),\mathfrak {C}_e)$
. Assume
![]() $\tilde R$
has a uniformization (i.e., a function
$\tilde R$
has a uniformization (i.e., a function
![]() $\Phi : \mathrm {dom}(\tilde R) \rightarrow \mathbb {R}$
so that for all
$\Phi : \mathrm {dom}(\tilde R) \rightarrow \mathbb {R}$
so that for all
![]() $z \in \mathrm {dom}(\tilde R)$
,
$z \in \mathrm {dom}(\tilde R)$
,
![]() $\tilde R(z,\Phi (e)))$
. Then R has a uniformization.
$\tilde R(z,\Phi (e)))$
. Then R has a uniformization.
Thus, under
![]() $\mathsf {ZF} + \mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
, countable length everywhere club uniformization for
$\mathsf {ZF} + \mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
, countable length everywhere club uniformization for
![]() ${\omega _1}$
holds.
${\omega _1}$
holds.
![]() $L(\mathbb {R}) \models \neg \mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
. [Reference Chan and Jackson3] gives an example to show that countable length everywhere club uniformization for
$L(\mathbb {R}) \models \neg \mathsf {AD}_{\frac {1}{2}\mathbb {R}}$
. [Reference Chan and Jackson3] gives an example to show that countable length everywhere club uniformization for
![]() ${\omega _1}$
cannot hold in
${\omega _1}$
cannot hold in
![]() $L(\mathbb {R})$
and thus it is not provable under
$L(\mathbb {R})$
and thus it is not provable under
![]() $\mathsf {AD}$
alone.
$\mathsf {AD}$
alone.
The main result is a generalization of the countable length everywhere club uniformization for
![]() ${\omega _1}$
.
${\omega _1}$
.
Theorem 3.3. Assume
![]() $\mathsf {ZF} + \mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
. Let
$\mathsf {ZF} + \mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
. Let
![]() $\Gamma $
be a nonselfdual pointclass closed under
$\Gamma $
be a nonselfdual pointclass closed under
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
, and
$\vee $
, and
![]() $\forall ^{\mathbb {R}}$
. Let
$\forall ^{\mathbb {R}}$
. Let
![]() $\kappa = \delta (\Gamma )$
and assume that
$\kappa = \delta (\Gamma )$
and assume that
![]() $\kappa $
is reliable with witness
$\kappa $
is reliable with witness
![]() $(W,\bar \varphi )$
such that W is
$(W,\bar \varphi )$
such that W is
![]() $\Gamma $
-complete and
$\Gamma $
-complete and
![]() $\varphi _0 : W \rightarrow \kappa $
is a surjective
$\varphi _0 : W \rightarrow \kappa $
is a surjective
![]() $\Gamma $
-norm. Let
$\Gamma $
-norm. Let
![]() $\mathsf {CS}$
and
$\mathsf {CS}$
and
![]() $\mathsf {cseq}$
be the codings of
$\mathsf {cseq}$
be the codings of
![]() ${}^{<{\omega _1}}\kappa $
from Definition 2.25 defined relative to
${}^{<{\omega _1}}\kappa $
from Definition 2.25 defined relative to
![]() $\varphi _0$
. Let
$\varphi _0$
. Let
![]() $\mathsf {clubcode}$
and
$\mathsf {clubcode}$
and
![]() $\mathfrak {C}_e ($
for each
$\mathfrak {C}_e ($
for each
![]() $e \in \mathsf {clubcode})$
be the codings of club subsets of
$e \in \mathsf {clubcode})$
be the codings of club subsets of
![]() $\kappa $
from Definition 2.16 relative to
$\kappa $
from Definition 2.16 relative to
![]() $\Gamma $
and the
$\Gamma $
and the
![]() $\Gamma $
-norm
$\Gamma $
-norm
![]() $\varphi _0$
on the
$\varphi _0$
on the
![]() $\Gamma $
-complete set W.
$\Gamma $
-complete set W.
Let
![]() $R \subseteq [\kappa ]^{<{\omega _1}} \times \mathsf {club}$
be a
$R \subseteq [\kappa ]^{<{\omega _1}} \times \mathsf {club}$
be a
![]() $\subseteq $
-downward closed relation in the
$\subseteq $
-downward closed relation in the
![]() $\mathsf {club}$
-coordinate. Let
$\mathsf {club}$
-coordinate. Let
![]() $\tilde R \subseteq \mathsf {CS} \times \mathsf {clubcode}$
be the coded version of R defined by
$\tilde R \subseteq \mathsf {CS} \times \mathsf {clubcode}$
be the coded version of R defined by
![]() $\tilde R(z,e)$
if and only if
$\tilde R(z,e)$
if and only if
![]() $R(\mathsf {cseq}(z),\mathfrak {C}_e)$
. Assume that
$R(\mathsf {cseq}(z),\mathfrak {C}_e)$
. Assume that
![]() $\tilde R$
is Suslin and co-Suslin meaning there are trees
$\tilde R$
is Suslin and co-Suslin meaning there are trees
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $\omega \times \omega \times \zeta _0$
and
$\omega \times \omega \times \zeta _0$
and
![]() $\mathcal {S}$
on
$\mathcal {S}$
on
![]() $\omega \times \omega \times \zeta _1$
so that
$\omega \times \omega \times \zeta _1$
so that
![]() $\tilde R = \{(z,e) : (\exists f \in {}^\omega \zeta _0)((z,e,f) \in [T])\}$
and
$\tilde R = \{(z,e) : (\exists f \in {}^\omega \zeta _0)((z,e,f) \in [T])\}$
and
![]() $\mathbb {R} \times \mathbb {R} \setminus \tilde R = \{(z,e) : (\exists g \in {}^\omega \zeta _1)((z,e,f) \in [S])\}$
. Let
$\mathbb {R} \times \mathbb {R} \setminus \tilde R = \{(z,e) : (\exists g \in {}^\omega \zeta _1)((z,e,f) \in [S])\}$
. Let
![]() $\bar \phi = \langle \phi _n : n \in \omega \rangle $
be the canonical semiscale on
$\bar \phi = \langle \phi _n : n \in \omega \rangle $
be the canonical semiscale on
![]() $\tilde R$
derived from the Suslin representation
$\tilde R$
derived from the Suslin representation
![]() $\mathcal {T}$
for
$\mathcal {T}$
for
![]() $\tilde R$
as in Definition 2.6. Assume each norm relation
$\tilde R$
as in Definition 2.6. Assume each norm relation
![]() $\leq ^*_{\phi _n}$
is Suslin and co-Suslin. Then there is a
$\leq ^*_{\phi _n}$
is Suslin and co-Suslin. Then there is a
![]() $\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
so that for all
$\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
so that for all
![]() $\ell \in \mathrm {dom}(R)$
,
$\ell \in \mathrm {dom}(R)$
,
![]() $R(\ell ,\Lambda (\ell ))$
.
$R(\ell ,\Lambda (\ell ))$
.
Thus assuming
![]() $\mathsf {ZF} + \mathsf {AD}$
and all sets of reals are Suslin, countable length everywhere club uniformization holds for
$\mathsf {ZF} + \mathsf {AD}$
and all sets of reals are Suslin, countable length everywhere club uniformization holds for
![]() $\kappa $
with the above properties.
$\kappa $
with the above properties.
Proof By the hypothesis, each norm relation
![]() $\leq _{\phi _n}^*$
for
$\leq _{\phi _n}^*$
for
![]() $\tilde R$
is assumed to be Suslin and co-Suslin so there are trees
$\tilde R$
is assumed to be Suslin and co-Suslin so there are trees
![]() $\mathcal {P}$
on
$\mathcal {P}$
on
![]() $\omega \times \omega \times \lambda _0$
and
$\omega \times \omega \times \lambda _0$
and
![]() $\mathcal {Q}$
on
$\mathcal {Q}$
on
![]() $\omega \times \omega \times \lambda _1$
with
$\omega \times \omega \times \lambda _1$
with
![]() $\lambda _0,\lambda _1 < \Theta $
which project onto
$\lambda _0,\lambda _1 < \Theta $
which project onto
![]() $\leq ^*_{\phi _n}$
and its complement, respectively. By the Moschovakis coding lemma and
$\leq ^*_{\phi _n}$
and its complement, respectively. By the Moschovakis coding lemma and
![]() $\mathsf {AC}_\omega ^{\mathbb {R}}$
, one may find sequences
$\mathsf {AC}_\omega ^{\mathbb {R}}$
, one may find sequences
![]() $\langle \mathcal {P}_n : n \in \omega \rangle $
and
$\langle \mathcal {P}_n : n \in \omega \rangle $
and
![]() $\langle \mathcal {Q}_n : n \in \omega \rangle $
so that for each
$\langle \mathcal {Q}_n : n \in \omega \rangle $
so that for each
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\pi _1[[\mathcal {P}_n]] = {\leq ^*_{\phi _n}}$
and
$\pi _1[[\mathcal {P}_n]] = {\leq ^*_{\phi _n}}$
and
![]() $\pi _1[[\mathcal {Q}_n]] = \mathbb {R} \times \mathbb {R} \setminus {\leq ^*_{\phi _n}}$
.
$\pi _1[[\mathcal {Q}_n]] = \mathbb {R} \times \mathbb {R} \setminus {\leq ^*_{\phi _n}}$
.
Let
![]() $\ell \in \mathrm {dom}(R)$
. Recall that by Fact 2.15,
$\ell \in \mathrm {dom}(R)$
. Recall that by Fact 2.15,
![]() $\kappa = \delta (\Gamma )$
is a regular cardinal. By Fact 2.22, let
$\kappa = \delta (\Gamma )$
is a regular cardinal. By Fact 2.22, let
![]() $\nu _\ell $
be the least honest ordinal greater than
$\nu _\ell $
be the least honest ordinal greater than
![]() $\sup (\ell )$
. Let
$\sup (\ell )$
. Let
![]() $R^{\nu _\ell }_\ell \subseteq {}^\omega \nu _\ell $
be defined by
$R^{\nu _\ell }_\ell \subseteq {}^\omega \nu _\ell $
be defined by
![]() $R^{\nu _\ell }_\ell (g)$
if and only if
$R^{\nu _\ell }_\ell (g)$
if and only if
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
.
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
.
Fix
![]() $g \in {}^\omega \nu _\ell $
so that
$g \in {}^\omega \nu _\ell $
so that
![]() $R^{\nu _\ell }_\ell (g)$
. Fix
$R^{\nu _\ell }_\ell (g)$
. Fix
![]() $w \in {\mathrm {WO}}$
with
$w \in {\mathrm {WO}}$
with
![]() ${\mathrm {ot}}(w) = |\ell |$
. Let
${\mathrm {ot}}(w) = |\ell |$
. Let
![]() $\mathfrak {F}$
be the function from Fact 2.23. Let
$\mathfrak {F}$
be the function from Fact 2.23. Let
![]() $\mathfrak {r}(\ell ,g,w)$
be the unique real with the following properties.
$\mathfrak {r}(\ell ,g,w)$
be the unique real with the following properties.
-
• For all
 $n \in \omega $
, if
$n \in \omega $
, if
 $n \notin \mathrm {field}(\mathcal {R}_w)$
, then
$n \notin \mathrm {field}(\mathcal {R}_w)$
, then
 $\mathfrak {r}(\ell ,g,w)^{[n]} = \mathfrak {F}(g)^{[n]}$
.
$\mathfrak {r}(\ell ,g,w)^{[n]} = \mathfrak {F}(g)^{[n]}$
. -
• For
 $n \in \mathrm {field}(\mathcal {R}_w)$
, let
$n \in \mathrm {field}(\mathcal {R}_w)$
, let
 $i_n^g$
be the least k so that
$i_n^g$
be the least k so that
 $g(k) = \ell ({\mathrm {ot}}(w,n))$
. Then one has
$g(k) = \ell ({\mathrm {ot}}(w,n))$
. Then one has
 $\mathfrak {r}(\ell ,g,w)^{[n]} = \mathfrak {F}(g)^{[i^g_n]}$
.
$\mathfrak {r}(\ell ,g,w)^{[n]} = \mathfrak {F}(g)^{[i^g_n]}$
.
Let
![]() $\mathsf {extract}(\ell ,g,w)$
be the unique real z so that
$\mathsf {extract}(\ell ,g,w)$
be the unique real z so that
![]() $z^{[0]} = w$
,
$z^{[0]} = w$
,
![]() $z^{[1]} = \mathfrak {r}(\ell ,g,w)$
, and for all
$z^{[1]} = \mathfrak {r}(\ell ,g,w)$
, and for all
![]() $n> 1$
,
$n> 1$
,
![]() $z^{[n]} = \bar {0}$
, the constant
$z^{[n]} = \bar {0}$
, the constant
![]() $0$
sequence.
$0$
sequence.
Lemma 3.4. Let
![]() $E^{\ell ,w} : R^{\nu _\ell }_\ell \rightarrow \mathbb {R}$
be defined by
$E^{\ell ,w} : R^{\nu _\ell }_\ell \rightarrow \mathbb {R}$
be defined by
![]() $E^{\ell ,w}(g) = \mathsf {extract}(\ell ,g,w)$
. If
$E^{\ell ,w}(g) = \mathsf {extract}(\ell ,g,w)$
. If
![]() $\mathrm {rang}(g)$
is honest then
$\mathrm {rang}(g)$
is honest then
![]() $\mathsf {cseq}(\mathsf {extract}(\ell ,g,w)) = \ell $
.
$\mathsf {cseq}(\mathsf {extract}(\ell ,g,w)) = \ell $
.
Proof Assume
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
and g is honest. Let
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
and g is honest. Let
![]() $\alpha < |\ell |$
and
$\alpha < |\ell |$
and
![]() $n = \mathsf {num}(w,\alpha )$
(where
$n = \mathsf {num}(w,\alpha )$
(where
![]() $\mathsf {num}$
comes from Definition 2.5). Since
$\mathsf {num}$
comes from Definition 2.5). Since
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
,
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
,
![]() $i_n^g$
is defined with the property that
$i_n^g$
is defined with the property that
![]() $g(i^g_n) = \ell ({\mathrm {ot}}(w,n)) = \ell ({\mathrm {ot}}(w,\mathsf {num}(w,\alpha ))) = \ell (\alpha )$
. Since g is honest, one has that for all
$g(i^g_n) = \ell ({\mathrm {ot}}(w,n)) = \ell ({\mathrm {ot}}(w,\mathsf {num}(w,\alpha ))) = \ell (\alpha )$
. Since g is honest, one has that for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $g(n) = \varphi _0(\mathfrak {F}(g)^{[n]})$
. This implies that
$g(n) = \varphi _0(\mathfrak {F}(g)^{[n]})$
. This implies that
![]() $\mathsf {cseq}(\mathsf {extract}(\ell ,g,w)) = \ell $
.
$\mathsf {cseq}(\mathsf {extract}(\ell ,g,w)) = \ell $
.
Lemma 3.5. Let
![]() $\mathsf {graph}(E^{\ell ,w}) \subseteq R^{\nu _\ell }_\ell \times \mathbb {R}$
be defined as the graph of
$\mathsf {graph}(E^{\ell ,w}) \subseteq R^{\nu _\ell }_\ell \times \mathbb {R}$
be defined as the graph of
![]() $E^{\ell ,w}$
.
$E^{\ell ,w}$
.
![]() $\mathsf {graph}(E^{\ell ,w})$
is Suslin and co-Suslin uniformly in
$\mathsf {graph}(E^{\ell ,w})$
is Suslin and co-Suslin uniformly in
![]() $\ell $
and w. Moreover, the canonical semiscale derived from this Suslin representation as in Definition 2.6 has associated norm relations which are Suslin and co-Suslin.
$\ell $
and w. Moreover, the canonical semiscale derived from this Suslin representation as in Definition 2.6 has associated norm relations which are Suslin and co-Suslin.
Proof Note that although
![]() $E^{\ell ,w}$
is only defined on
$E^{\ell ,w}$
is only defined on
![]() $R^{\nu _\ell }_\ell $
, it is continuous on
$R^{\nu _\ell }_\ell $
, it is continuous on
![]() $R^{\nu _\ell }_\ell $
. For instance, for
$R^{\nu _\ell }_\ell $
. For instance, for
![]() $n \in \mathrm {field}(w)$
and
$n \in \mathrm {field}(w)$
and
![]() $g_0,g_1 \in {}^\omega \kappa $
, let
$g_0,g_1 \in {}^\omega \kappa $
, let
![]() $i_n^{g_0}$
and
$i_n^{g_0}$
and
![]() $i_n^{g_1}$
be the corresponding objects for
$i_n^{g_1}$
be the corresponding objects for
![]() $g_0$
and
$g_0$
and
![]() $g_1$
, respectively. If
$g_1$
, respectively. If
![]() $i_n^{g_0} = k$
and
$i_n^{g_0} = k$
and
![]() $g_0 \upharpoonright k + 1 = g_1 \upharpoonright k + 1$
, then
$g_0 \upharpoonright k + 1 = g_1 \upharpoonright k + 1$
, then
![]() $i_n^{g_0} = i_n^{g_1}$
. The continuity of
$i_n^{g_0} = i_n^{g_1}$
. The continuity of
![]() $E^{\ell ,w}$
follows from this observation and the fact that the generic coding function
$E^{\ell ,w}$
follows from this observation and the fact that the generic coding function
![]() $\mathfrak {F}$
is Lipschitz.
$\mathfrak {F}$
is Lipschitz.
The domain of
![]() $E^{\ell ,w}$
is
$E^{\ell ,w}$
is
![]() $R^{\nu _\ell }_\ell $
. Fact 2.10 and Fact 2.11 give an analogous result for
$R^{\nu _\ell }_\ell $
. Fact 2.10 and Fact 2.11 give an analogous result for
![]() $R^{\nu _\ell }_\ell $
. The proof of the lemma is quite similar to the arguments of these two facts. The details are left to the reader.
$R^{\nu _\ell }_\ell $
. The proof of the lemma is quite similar to the arguments of these two facts. The details are left to the reader.
Consider the game
![]() $G^w_\ell $
defined as follows.
$G^w_\ell $
defined as follows.

For all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $g(n) \in \nu _\ell $
. Player 1 plays
$g(n) \in \nu _\ell $
. Player 1 plays
![]() $g(2n)$
for all
$g(2n)$
for all
![]() $n \in \omega $
. Player 2 plays
$n \in \omega $
. Player 2 plays
![]() $g(2n + 1)$
for all
$g(2n + 1)$
for all
![]() $n \in \omega $
. Player 1 also plays
$n \in \omega $
. Player 1 also plays
![]() $e(n) \in \omega $
for all
$e(n) \in \omega $
for all
![]() $n \in \omega $
. After an infinite run, Player 1 and Player 2 together produce
$n \in \omega $
. After an infinite run, Player 1 and Player 2 together produce
![]() $g \in {}^\omega \nu _\ell $
and Player 1 alone produces
$g \in {}^\omega \nu _\ell $
and Player 1 alone produces
![]() $e \in \mathbb {R}$
. Player 1 wins
$e \in \mathbb {R}$
. Player 1 wins
![]() $G^w_\ell $
if and only if
$G^w_\ell $
if and only if
![]() $P^w_\ell (g)$
, where
$P^w_\ell (g)$
, where
![]() $P^w_\ell (g)$
is defined by the conjunction of the following.
$P^w_\ell (g)$
is defined by the conjunction of the following.
-
(1)
 $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
.
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
. -
(2)
 $\mathsf {extract}(\ell ,g,w) \in \mathrm {dom}(\tilde R)$
.
$\mathsf {extract}(\ell ,g,w) \in \mathrm {dom}(\tilde R)$
. -
(3)
 $\tilde R(\mathsf {extract}(\ell ,g,w),e)$
.
$\tilde R(\mathsf {extract}(\ell ,g,w),e)$
.
Lemma 3.6. The payoff set
![]() $P^w_\ell $
for the game
$P^w_\ell $
for the game
![]() $G^w_\ell $
is Suslin and co-Suslin uniformly in
$G^w_\ell $
is Suslin and co-Suslin uniformly in
![]() $\ell $
and w. Moreover, the semiscale derived from this Suslin representation as in Definition 2.6 is Suslin and co-Suslin.
$\ell $
and w. Moreover, the semiscale derived from this Suslin representation as in Definition 2.6 is Suslin and co-Suslin.
Proof (1) is Suslin and co-Suslin uniformly in
![]() $\ell $
and w by Fact 2.10 (and note that
$\ell $
and w by Fact 2.10 (and note that
![]() $\nu _\ell $
is defined uniformly from
$\nu _\ell $
is defined uniformly from
![]() $\ell $
). (2) is Suslin and co-Suslin uniformly from
$\ell $
). (2) is Suslin and co-Suslin uniformly from
![]() $\ell $
and w using this observation and Lemma 3.5. Similarly (3) is Suslin and co-Suslin uniformly from
$\ell $
and w using this observation and Lemma 3.5. Similarly (3) is Suslin and co-Suslin uniformly from
![]() $\ell $
and w using the tree
$\ell $
and w using the tree
![]() $\mathcal {T}$
and
$\mathcal {T}$
and
![]() $\mathcal {S}$
and Lemma 3.5. This establishes that the payoff set
$\mathcal {S}$
and Lemma 3.5. This establishes that the payoff set
![]() $P^w_\ell $
is Suslin and co-Suslin uniformly in
$P^w_\ell $
is Suslin and co-Suslin uniformly in
![]() $\ell $
and w. Using Fact 2.11 and Lemma 3.5, one can show each norm relation of the derived semiscale is Suslin and co-Suslin.
$\ell $
and w. Using Fact 2.11 and Lemma 3.5, one can show each norm relation of the derived semiscale is Suslin and co-Suslin.
The first part of Lemma 3.6 implies the ordinal game
![]() $G^w_\ell $
is determined by Fact 2.8.
$G^w_\ell $
is determined by Fact 2.8.
Lemma 3.7. Suppose
![]() $\tau $
is a Player 2 strategy for
$\tau $
is a Player 2 strategy for
![]() $G^w_\ell $
and
$G^w_\ell $
and
![]() $e \in \mathbb {R}$
. Then there is an
$e \in \mathbb {R}$
. Then there is an
![]() $h \in {}^\omega \nu _\ell $
with the following properties.
$h \in {}^\omega \nu _\ell $
with the following properties.
-
•
 $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
.
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
. -
• Let
 $h \oplus e \in {}^\omega \nu _\ell $
be defined by
$h \oplus e \in {}^\omega \nu _\ell $
be defined by
 $(h \oplus e)(n) = \langle h(n),e(n)\rangle $
. Let
$(h \oplus e)(n) = \langle h(n),e(n)\rangle $
. Let
 $(g,e) = \Sigma ^2_\tau (h \oplus e)$
.
$(g,e) = \Sigma ^2_\tau (h \oplus e)$
.
 $($
That is,
$($
That is,
 $(g,e)$
is the run of the game where Player 2 uses
$(g,e)$
is the run of the game where Player 2 uses
 $\tau $
against Player 1 using
$\tau $
against Player 1 using
 $\rho _{h \oplus e}$
. See Definition 2.2 for the notations associated with strategies.
$\rho _{h \oplus e}$
. See Definition 2.2 for the notations associated with strategies.
 $)$
Then
$)$
Then
 $\mathrm {rang}(g)$
is honest.
$\mathrm {rang}(g)$
is honest.
Suppose
![]() $\sigma $
is a Player 1 strategy for
$\sigma $
is a Player 1 strategy for
![]() $G^w_\ell $
. Then there is an
$G^w_\ell $
. Then there is an
![]() $h \in {}^\omega \nu _\ell $
with the following properties.
$h \in {}^\omega \nu _\ell $
with the following properties.
-
•
 $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
.
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
. -
• Let
 $(g,e) = \Sigma ^1_\sigma (h)$
. Then
$(g,e) = \Sigma ^1_\sigma (h)$
. Then
 $\mathrm {rang}(g)$
is honest.
$\mathrm {rang}(g)$
is honest.
Proof Fix a bijection
![]() $B : \omega \rightarrow |\ell |$
. Using
$B : \omega \rightarrow |\ell |$
. Using
![]() $\mathsf {AC}_\omega ^{\mathbb {R}}$
, find a sequence
$\mathsf {AC}_\omega ^{\mathbb {R}}$
, find a sequence
![]() $\langle x_n : n \in \omega \rangle $
in W so that for all
$\langle x_n : n \in \omega \rangle $
in W so that for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\varphi _0(x_n) = \ell (B(n))$
. Let
$\varphi _0(x_n) = \ell (B(n))$
. Let
![]() $\mathsf {pair} : \omega ^2 \rightarrow \omega $
be a bijection with the property that for all
$\mathsf {pair} : \omega ^2 \rightarrow \omega $
be a bijection with the property that for all
![]() $a,b,c \in \omega $
, if
$a,b,c \in \omega $
, if
![]() $\mathsf {pair}(a,b) = c$
, then
$\mathsf {pair}(a,b) = c$
, then
![]() $a,b \leq c$
and for all
$a,b \leq c$
and for all
![]() $a,b,c \in \omega $
, if
$a,b,c \in \omega $
, if
![]() $b < c$
, then
$b < c$
, then
![]() $\mathsf {pair}(a,b) < \mathsf {pair}(a,c)$
. Let
$\mathsf {pair}(a,b) < \mathsf {pair}(a,c)$
. Let
![]() $\pi _1 : \nu _\ell \rightarrow \nu _\ell $
be such that
$\pi _1 : \nu _\ell \rightarrow \nu _\ell $
be such that
![]() $\pi _1(\langle \alpha ,n\rangle ) = \alpha $
for all
$\pi _1(\langle \alpha ,n\rangle ) = \alpha $
for all
![]() $\alpha \in \nu _\ell $
and
$\alpha \in \nu _\ell $
and
![]() $n \in \omega $
. Now define a tree K on
$n \in \omega $
. Now define a tree K on
![]() $\mathbb {R}$
by
$\mathbb {R}$
by
![]() $s \in K$
if and only if the following holds.
$s \in K$
if and only if the following holds.
-
(1) For all
 $k < |s|$
,
$k < |s|$
,
 $s(k) \in W$
.
$s(k) \in W$
. -
(2) Let
 $n = |s|$
. Let
$n = |s|$
. Let
 $p_s : 2n \rightarrow \nu _\ell $
be defined as follows.
$p_s : 2n \rightarrow \nu _\ell $
be defined as follows.-
(a) For
 $k < n$
,
$k < n$
,  $$ \begin{align*}p_s(2k) = \begin{cases} \langle\varphi_j(x_i),e(k)\rangle, & \quad k = 2d \wedge d = \mathsf{pair}(i,j), \\ \langle\varphi_j(s(i)),e(k)\rangle, & \quad k = 2d + 1 \wedge d = \mathsf{pair}(i,j). \end{cases}\end{align*} $$
$$ \begin{align*}p_s(2k) = \begin{cases} \langle\varphi_j(x_i),e(k)\rangle, & \quad k = 2d \wedge d = \mathsf{pair}(i,j), \\ \langle\varphi_j(s(i)),e(k)\rangle, & \quad k = 2d + 1 \wedge d = \mathsf{pair}(i,j). \end{cases}\end{align*} $$
-
(b) For
 $k < n$
,
$k < n$
,
 $p_s(2k + 1)$
is the result of applying
$p_s(2k + 1)$
is the result of applying
 $\tau $
to the partial run
$\tau $
to the partial run
 $\langle p_s(j) : j < 2k + 1\rangle $
in
$\langle p_s(j) : j < 2k + 1\rangle $
in
 $G^w_\ell $
.
$G^w_\ell $
. -
(c) For each
 $k < n$
, if k is odd, then
$k < n$
, if k is odd, then
 $\varphi _0(s(k)) = p_s(k)$
and if k is even, then
$\varphi _0(s(k)) = p_s(k)$
and if k is even, then
 $\varphi _0(s(k)) = \pi _1(p_s(k))$
.
$\varphi _0(s(k)) = \pi _1(p_s(k))$
.
-
Observe that
![]() $p_s$
is continuous in the sense that if
$p_s$
is continuous in the sense that if
![]() $s \subseteq t$
, then
$s \subseteq t$
, then
![]() $p_t \upharpoonright 2|s| = p_s$
. The tree K is ordered by proper string extension
$p_t \upharpoonright 2|s| = p_s$
. The tree K is ordered by proper string extension
![]() $\subsetneq $
. One can check every node s of K can be strictly extended by appending some
$\subsetneq $
. One can check every node s of K can be strictly extended by appending some
![]() $y \in W$
so that
$y \in W$
so that
![]() $\varphi _0(y) = p_s(|s|)$
if
$\varphi _0(y) = p_s(|s|)$
if
![]() $|s|$
is odd and
$|s|$
is odd and
![]() $\varphi _0(y) = \pi _1(p_s(|s|))$
if
$\varphi _0(y) = \pi _1(p_s(|s|))$
if
![]() $|s|$
is even. By
$|s|$
is even. By
![]() $\mathsf {DC}_{\mathbb {R}}$
, there is an
$\mathsf {DC}_{\mathbb {R}}$
, there is an
![]() $f \in [K]$
. Let
$f \in [K]$
. Let
![]() $q = \bigcup _{n \in \omega } p_{f \upharpoonright n}$
. Let
$q = \bigcup _{n \in \omega } p_{f \upharpoonright n}$
. Let
![]() $h = \langle \pi _1(q(2n)) : n \in \omega \rangle $
. Let g be such that
$h = \langle \pi _1(q(2n)) : n \in \omega \rangle $
. Let g be such that
![]() $(g,e) = \Sigma _\tau ^2(h\oplus e)$
and observe that
$(g,e) = \Sigma _\tau ^2(h\oplus e)$
and observe that
![]() $\mathrm {rang}(g)$
is honest. To see this, note that by (1) and (2b), for all
$\mathrm {rang}(g)$
is honest. To see this, note that by (1) and (2b), for all
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $f(k) \in W$
and
$f(k) \in W$
and
![]() $\varphi _0(f(k)) = g(k)$
. Then the second case of (2a) will eventually include each
$\varphi _0(f(k)) = g(k)$
. Then the second case of (2a) will eventually include each
![]() $\varphi _j(f(k))$
for all
$\varphi _j(f(k))$
for all
![]() $j \in \omega $
into
$j \in \omega $
into
![]() $\mathrm {rang}(g)$
. Note that
$\mathrm {rang}(g)$
. Note that
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
by the first case of (2a).
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
by the first case of (2a).
![]() $\Sigma ^2_\tau (h \oplus e) = (g,e)$
by (2b). Thus h is the desired object.
$\Sigma ^2_\tau (h \oplus e) = (g,e)$
by (2b). Thus h is the desired object.
The argument for the second statement is quite similar.
Next one seeks to show that Player 1 has the winning strategy for
![]() $G^w_\ell $
. Suppose
$G^w_\ell $
. Suppose
![]() $\tau $
is a Player 2 strategy. Since
$\tau $
is a Player 2 strategy. Since
![]() $\ell \in \mathrm {dom}(R)$
, there is a club
$\ell \in \mathrm {dom}(R)$
, there is a club
![]() $C \subseteq \kappa $
so that
$C \subseteq \kappa $
so that
![]() $R(\ell ,C)$
. Pick any e so that
$R(\ell ,C)$
. Pick any e so that
![]() $\mathfrak {C}_e \subseteq C$
which is possible by Fact 2.16. Now by Lemma 3.7 pick an h so that
$\mathfrak {C}_e \subseteq C$
which is possible by Fact 2.16. Now by Lemma 3.7 pick an h so that
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
and if
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h)$
and if
![]() $(g,e) = \Sigma ^2_\tau (h \oplus e)$
is the run according to
$(g,e) = \Sigma ^2_\tau (h \oplus e)$
is the run according to
![]() $\tau $
where Player 1 plays
$\tau $
where Player 1 plays
![]() $(h(n),e(n))$
for its
$(h(n),e(n))$
for its
![]() $n{\text {th}}$
-move, then
$n{\text {th}}$
-move, then
![]() $\mathrm {rang}(g)$
is honest. Note that (1) of
$\mathrm {rang}(g)$
is honest. Note that (1) of
![]() $P^w_\ell $
clearly holds. By Lemma 3.4, one has
$P^w_\ell $
clearly holds. By Lemma 3.4, one has
![]() $\mathsf {cseq}(\mathsf {extract}(\ell ,g,w)) = \ell $
. Then
$\mathsf {cseq}(\mathsf {extract}(\ell ,g,w)) = \ell $
. Then
![]() $\mathsf {extract}(\ell ,g,w) \in \mathrm {dom}(\tilde R)$
and hence (2) of
$\mathsf {extract}(\ell ,g,w) \in \mathrm {dom}(\tilde R)$
and hence (2) of
![]() $P^w_\ell $
holds. Also (3) of
$P^w_\ell $
holds. Also (3) of
![]() $P^w_\ell $
is true since
$P^w_\ell $
is true since
![]() $\tilde R(\mathsf {extract}(\ell ,g,w),e)$
holds by choice of e. Thus Player 1 wins and hence
$\tilde R(\mathsf {extract}(\ell ,g,w),e)$
holds by choice of e. Thus Player 1 wins and hence
![]() $\tau $
cannot be a winning strategy for Player 2.
$\tau $
cannot be a winning strategy for Player 2.
This completes the argument that Player 2 cannot have a winning strategy in
![]() $G^w_\ell $
. By the determinacy of
$G^w_\ell $
. By the determinacy of
![]() $G^w_\ell $
, Player 1 has a winning strategy. Next, one will need to show that a winning strategy for
$G^w_\ell $
, Player 1 has a winning strategy. Next, one will need to show that a winning strategy for
![]() $G^w_\ell $
can be found uniformly in w and
$G^w_\ell $
can be found uniformly in w and
![]() $\ell $
.
$\ell $
.
Lemma 3.6 implies that
![]() $P^w_\ell $
has a Suslin representation whose derived semiscale has norm relations which are Suslin and co-Suslin. From these semiscales, one can construct a very good semiscale for
$P^w_\ell $
has a Suslin representation whose derived semiscale has norm relations which are Suslin and co-Suslin. From these semiscales, one can construct a very good semiscale for
![]() $P^w_\ell $
(uniformly in w and
$P^w_\ell $
(uniformly in w and
![]() $\ell $
) whose associated norm relations are all Suslin and co-Suslin. In the notation of Fact 2.12, this can be used to show that the payoff set of each game
$\ell $
) whose associated norm relations are all Suslin and co-Suslin. In the notation of Fact 2.12, this can be used to show that the payoff set of each game
![]() ${}^nH^s_t$
is Suslin and co-Suslin.
${}^nH^s_t$
is Suslin and co-Suslin.
![]() ${}^nH^s_t$
is determined by Fact 2.8. Fact 2.12 can now be applied to find, uniformly in w and
${}^nH^s_t$
is determined by Fact 2.8. Fact 2.12 can now be applied to find, uniformly in w and
![]() $\ell $
, a Player 1 winning strategy
$\ell $
, a Player 1 winning strategy
![]() $\sigma ^w_\ell $
in the game
$\sigma ^w_\ell $
in the game
![]() $G^w_\ell $
.
$G^w_\ell $
.
Functions
![]() $\varrho : {}^\omega \nu _\ell \rightarrow {}^\omega \nu _\ell $
and
$\varrho : {}^\omega \nu _\ell \rightarrow {}^\omega \nu _\ell $
and
![]() $\vartheta : {}^\omega \nu _\ell \rightarrow {{}^\omega \omega }$
will be defined so that if
$\vartheta : {}^\omega \nu _\ell \rightarrow {{}^\omega \omega }$
will be defined so that if
![]() $(g,e)$
is the resulting run in the game
$(g,e)$
is the resulting run in the game
![]() $G^w_\ell $
where Player 1 uses
$G^w_\ell $
where Player 1 uses
![]() $\sigma ^w_\ell $
against Player 2 using
$\sigma ^w_\ell $
against Player 2 using
![]() $\rho _h$
, then
$\rho _h$
, then
![]() $\varrho (h) = g$
and
$\varrho (h) = g$
and
![]() $\vartheta (h) = e$
. Formally, let
$\vartheta (h) = e$
. Formally, let
![]() $\pi _1 : \nu _\ell \times \omega \rightarrow \nu _\ell $
and
$\pi _1 : \nu _\ell \times \omega \rightarrow \nu _\ell $
and
![]() $\pi _2 : \nu _\ell \times \omega \rightarrow \omega $
be the projections onto the first and second coordinates, respectively. Define
$\pi _2 : \nu _\ell \times \omega \rightarrow \omega $
be the projections onto the first and second coordinates, respectively. Define
![]() $\varrho $
by
$\varrho $
by
 $$ \begin{align*}\varrho(h)(n) = \begin{cases} \pi_1(\Sigma^1_{\sigma^w_\ell}(h)(n)), & \quad n \text{ is even}, \\ \Sigma^1_{\sigma^w_\ell}(h)(n), & \quad n \text{ is odd}. \end{cases}\end{align*} $$
$$ \begin{align*}\varrho(h)(n) = \begin{cases} \pi_1(\Sigma^1_{\sigma^w_\ell}(h)(n)), & \quad n \text{ is even}, \\ \Sigma^1_{\sigma^w_\ell}(h)(n), & \quad n \text{ is odd}. \end{cases}\end{align*} $$
Define
![]() $\vartheta $
by
$\vartheta $
by
![]() $\vartheta (h)(n) = \pi _2(\Sigma ^1_{\sigma ^w_\ell }(h)(2n))$
. Both
$\vartheta (h)(n) = \pi _2(\Sigma ^1_{\sigma ^w_\ell }(h)(2n))$
. Both
![]() $\varrho $
and
$\varrho $
and
![]() $\vartheta $
are Lipschitz continuous functions and are produced uniformly from w and
$\vartheta $
are Lipschitz continuous functions and are produced uniformly from w and
![]() $\ell $
(since they depend only on
$\ell $
(since they depend only on
![]() $\sigma ^w_\ell $
).
$\sigma ^w_\ell $
).
Since
![]() $\sigma ^w_\ell $
is a Player 1 winning strategy in
$\sigma ^w_\ell $
is a Player 1 winning strategy in
![]() $G^w_\ell $
, one has by (1) of the payoff set
$G^w_\ell $
, one has by (1) of the payoff set
![]() $P^w_\ell $
that for all
$P^w_\ell $
that for all
![]() $g \in \varrho [{}^\omega \nu _\ell ]$
,
$g \in \varrho [{}^\omega \nu _\ell ]$
,
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
and thus
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(g)$
and thus
![]() $\mathsf {extract}(\ell ,g,w)$
is well defined. Also since
$\mathsf {extract}(\ell ,g,w)$
is well defined. Also since
![]() $\sigma ^w_\ell $
is a Player 1 winning strategy in
$\sigma ^w_\ell $
is a Player 1 winning strategy in
![]() $G^w_\ell $
, one has that
$G^w_\ell $
, one has that
![]() $\vartheta [{}^\omega \nu _\ell ] \subseteq \mathsf {clubcode}$
. Let
$\vartheta [{}^\omega \nu _\ell ] \subseteq \mathsf {clubcode}$
. Let
![]() $W_\ell = \varphi _0^{-1}[\nu _\ell ]$
and let
$W_\ell = \varphi _0^{-1}[\nu _\ell ]$
and let
![]() $\varphi _\ell : W_\ell \rightarrow \nu _\ell $
be defined by
$\varphi _\ell : W_\ell \rightarrow \nu _\ell $
be defined by
![]() $\varphi _\ell = \varphi _0 \upharpoonright W_\ell $
. Since
$\varphi _\ell = \varphi _0 \upharpoonright W_\ell $
. Since
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Gamma $
-norm, one has that the associated prewellordering
$\Gamma $
-norm, one has that the associated prewellordering
![]() $\preceq _{\varphi _\ell }$
belongs to
$\preceq _{\varphi _\ell }$
belongs to
![]() $\Delta $
. Fact 2.13 can now be applied to show
$\Delta $
. Fact 2.13 can now be applied to show
![]() $\vartheta [{}^\omega \nu _\ell ]$
is
$\vartheta [{}^\omega \nu _\ell ]$
is
![]() $\exists ^{\mathbb {R}}\Delta \subseteq \check \Gamma $
since
$\exists ^{\mathbb {R}}\Delta \subseteq \check \Gamma $
since
![]() $\Gamma $
is closed under
$\Gamma $
is closed under
![]() $\forall ^{\mathbb {R}}$
. By Fact 2.16, there is a club
$\forall ^{\mathbb {R}}$
. By Fact 2.16, there is a club
![]() $D \subseteq \kappa $
(produced uniformly from the set
$D \subseteq \kappa $
(produced uniformly from the set
![]() $\vartheta [{}^\omega \nu _\ell ]$
) with the property that for all
$\vartheta [{}^\omega \nu _\ell ]$
) with the property that for all
![]() $e \in \vartheta [{}^\omega \nu _\ell ]$
,
$e \in \vartheta [{}^\omega \nu _\ell ]$
,
![]() $D \subseteq \mathfrak {C}_e$
. By Lemma 3.7, one can find a sequence
$D \subseteq \mathfrak {C}_e$
. By Lemma 3.7, one can find a sequence
![]() $h^*$
so that
$h^*$
so that
![]() $\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h^*)$
and if
$\mathrm {rang}(\ell ) \subseteq \mathrm {rang}(h^*)$
and if
![]() $(g,e^*) = \Sigma ^1_{\sigma ^w_\ell }(h^*)$
is the run according to
$(g,e^*) = \Sigma ^1_{\sigma ^w_\ell }(h^*)$
is the run according to
![]() $\sigma ^w_\ell $
where Player 2 uses
$\sigma ^w_\ell $
where Player 2 uses
![]() $h^*$
, then
$h^*$
, then
![]() $\mathrm {rang}(g)$
is honest. By Lemma 3.4,
$\mathrm {rang}(g)$
is honest. By Lemma 3.4,
![]() $\mathsf {extract}(\ell ,g,w) = \ell $
. Thus since
$\mathsf {extract}(\ell ,g,w) = \ell $
. Thus since
![]() $e^* = \vartheta (h^*)$
,
$e^* = \vartheta (h^*)$
,
![]() $\tilde R(\ell ,\vartheta (h^*))$
and hence
$\tilde R(\ell ,\vartheta (h^*))$
and hence
![]() $R(\ell ,\mathfrak {C}_{\vartheta (h^*)})$
. Since
$R(\ell ,\mathfrak {C}_{\vartheta (h^*)})$
. Since
![]() $\vartheta (h^*) \in \vartheta [{}^\omega \nu _\ell ]$
, one has that
$\vartheta (h^*) \in \vartheta [{}^\omega \nu _\ell ]$
, one has that
![]() $D \subseteq \mathfrak {C}_{\vartheta (h^*)}$
. Since R is
$D \subseteq \mathfrak {C}_{\vartheta (h^*)}$
. Since R is
![]() $\subseteq $
-downward closed, one has that
$\subseteq $
-downward closed, one has that
![]() $R(\ell ,D)$
. Finally, observe that D is produced uniformly from w and
$R(\ell ,D)$
. Finally, observe that D is produced uniformly from w and
![]() $\ell \in \mathrm {dom}(R)$
.
$\ell \in \mathrm {dom}(R)$
.
By the uniformity observation, it has been shown that there is a function
![]() $\Psi $
so that whenever
$\Psi $
so that whenever
![]() $\ell \in \mathrm {dom}(R)$
and
$\ell \in \mathrm {dom}(R)$
and
![]() $w \in {\mathrm {WO}}$
with
$w \in {\mathrm {WO}}$
with
![]() ${\mathrm {ot}}(w) = |\ell |$
,
${\mathrm {ot}}(w) = |\ell |$
,
![]() $\Psi (\ell ,w) \in \mathsf {club}$
and
$\Psi (\ell ,w) \in \mathsf {club}$
and
![]() $R(\ell ,\Psi (\ell ,w))$
. One will need to remove the dependence on w.
$R(\ell ,\Psi (\ell ,w))$
. One will need to remove the dependence on w.
Fix
![]() $\ell \in \mathrm {dom}(R)$
. Observe that if
$\ell \in \mathrm {dom}(R)$
. Observe that if
![]() $f \in \mathsf {surj}_{|\ell |}$
, then
$f \in \mathsf {surj}_{|\ell |}$
, then
![]() $\mathfrak {G}(f) \in {\mathrm {WO}}_{|\ell |}$
where
$\mathfrak {G}(f) \in {\mathrm {WO}}_{|\ell |}$
where
![]() $\mathfrak {G}$
is the simple generic coding function at
$\mathfrak {G}$
is the simple generic coding function at
![]() ${\omega _1}$
from Fact 2.18. Let
${\omega _1}$
from Fact 2.18. Let
![]() $\Phi _\ell : \mathsf {surj}_{|\ell |} \rightarrow \mathsf {club}$
be defined by
$\Phi _\ell : \mathsf {surj}_{|\ell |} \rightarrow \mathsf {club}$
be defined by
![]() $\Phi _\ell (f) = \Psi (\ell ,\mathfrak {G}(f))$
. Note that for all
$\Phi _\ell (f) = \Psi (\ell ,\mathfrak {G}(f))$
. Note that for all
![]() $f \in \mathsf {surj}_{|\ell |}$
,
$f \in \mathsf {surj}_{|\ell |}$
,
![]() $R(\ell ,\Phi _\ell (f))$
. Since
$R(\ell ,\Phi _\ell (f))$
. Since
![]() $\mathsf {surj}_{|\ell |}$
is comeager in
$\mathsf {surj}_{|\ell |}$
is comeager in
![]() ${}^\omega |\ell |$
, Fact 2.20 states that one can find uniformly from
${}^\omega |\ell |$
, Fact 2.20 states that one can find uniformly from
![]() $\Phi _\ell $
(which was constructed uniformly from
$\Phi _\ell $
(which was constructed uniformly from
![]() $\ell $
), a comeager set
$\ell $
), a comeager set
![]() $B_{\ell } \subseteq \mathsf {surj}_{|\ell |}$
and club
$B_{\ell } \subseteq \mathsf {surj}_{|\ell |}$
and club
![]() $D_\ell \subseteq \kappa $
so that for all
$D_\ell \subseteq \kappa $
so that for all
![]() $f \in B_\ell $
,
$f \in B_\ell $
,
![]() $D_\ell \subseteq \Phi _\ell (f)$
. Pick any
$D_\ell \subseteq \Phi _\ell (f)$
. Pick any
![]() $f \in B_\ell $
. Since
$f \in B_\ell $
. Since
![]() $R(\ell ,\Phi _\ell (f))$
and R is
$R(\ell ,\Phi _\ell (f))$
and R is
![]() $\subseteq $
-downward closed, one has that
$\subseteq $
-downward closed, one has that
![]() $R(\ell ,D_\ell )$
.
$R(\ell ,D_\ell )$
.
By the uniformity of the construction, one can define
![]() $\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
by
$\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$
by
![]() $\Lambda (\ell ) = D_\ell $
. It has been shown that for all
$\Lambda (\ell ) = D_\ell $
. It has been shown that for all
![]() $\ell \in \mathrm {dom}(R)$
,
$\ell \in \mathrm {dom}(R)$
,
![]() $R(\ell ,\Lambda (\ell ))$
.
$R(\ell ,\Lambda (\ell ))$
.
![]() $\Lambda $
is the desired uniformization, and this completes the proof of the theorem.
$\Lambda $
is the desired uniformization, and this completes the proof of the theorem.
In particular, the following is a corollary of Theorem 3.3.
Theorem 3.8. Assume
![]() $\mathsf {ZF} + \mathsf {AD}$
and all sets of reals are Suslin. Let
$\mathsf {ZF} + \mathsf {AD}$
and all sets of reals are Suslin. Let
![]() $\Gamma $
be a pointclass closed under
$\Gamma $
be a pointclass closed under
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
, and
$\vee $
, and
![]() $\forall ^{\mathbb {R}}$
with the scale property. Then the countable length everywhere club uniformization holds for
$\forall ^{\mathbb {R}}$
with the scale property. Then the countable length everywhere club uniformization holds for
![]() $\delta (\Gamma )$
. In particular, for all
$\delta (\Gamma )$
. In particular, for all
![]() $n \in \omega $
, the countable length everywhere club uniformization holds for
$n \in \omega $
, the countable length everywhere club uniformization holds for
![]() $\boldsymbol {\delta }^1_{2n + 1}$
.
$\boldsymbol {\delta }^1_{2n + 1}$
.
Acknowledgments
The first author was supported by NSF grant DMS-1703708. The second author was supported by NSF grant DMS-1800323. The third author was supported by NSF grants DMS-1855757 and DMS-1945592.