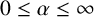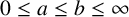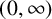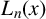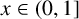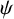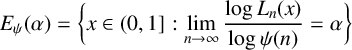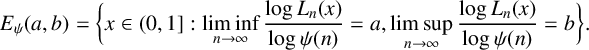1 Introduction
It is well known that every
![]() $x\in (0,1]$
admits an infinite Lüroth expansion of the form
$x\in (0,1]$
admits an infinite Lüroth expansion of the form
 $$ \begin{align} x=\frac{1}{d_1(x)}+\sum\limits_{n\geq2}\frac{1}{d_1(x)(d_1(x)-1)\cdots d_{n-1}(x)(d_{n-1}(x)-1)d_n(x)}, \end{align} $$
$$ \begin{align} x=\frac{1}{d_1(x)}+\sum\limits_{n\geq2}\frac{1}{d_1(x)(d_1(x)-1)\cdots d_{n-1}(x)(d_{n-1}(x)-1)d_n(x)}, \end{align} $$
where
![]() $d_n(x)\in \mathbb {N}$
for all
$d_n(x)\in \mathbb {N}$
for all
![]() $n\geq 1$
, which we write as
$n\geq 1$
, which we write as
![]() $x=[d_1(x),d_2(x),\ldots ]$
. Lüroth [Reference Lüroth12] showed that the Lüroth expansion can be induced by the Lüroth map
$x=[d_1(x),d_2(x),\ldots ]$
. Lüroth [Reference Lüroth12] showed that the Lüroth expansion can be induced by the Lüroth map
![]() $T:[0,1]\rightarrow [0,1]$
defined by
$T:[0,1]\rightarrow [0,1]$
defined by
 $$\begin{align*}T(x)= \begin{cases} 0 & \text{if }x=0, \\ \bigg\lfloor\dfrac{1}{x}\bigg\rfloor\bigg(\bigg(\bigg\lfloor\dfrac{1}{x}\bigg\rfloor+1\bigg)x-1\bigg) & \text{if }x\in(0,1]. \end{cases} \end{align*}$$
$$\begin{align*}T(x)= \begin{cases} 0 & \text{if }x=0, \\ \bigg\lfloor\dfrac{1}{x}\bigg\rfloor\bigg(\bigg(\bigg\lfloor\dfrac{1}{x}\bigg\rfloor+1\bigg)x-1\bigg) & \text{if }x\in(0,1]. \end{cases} \end{align*}$$
The digits
![]() $d_n:=d_n(x)$
in (1.1) are defined by
$d_n:=d_n(x)$
in (1.1) are defined by
where
![]() $\lfloor \cdot \rfloor $
denotes the integer part of some real number and
$\lfloor \cdot \rfloor $
denotes the integer part of some real number and
![]() $T^n$
stands for the nth iterate of
$T^n$
stands for the nth iterate of
![]() $T\ (T^0=\mathrm {Id}_{(0,1]})$
.
$T\ (T^0=\mathrm {Id}_{(0,1]})$
.
Clearly, the above algorithm gives
![]() $d_n\geq 2$
for each
$d_n\geq 2$
for each
![]() $n\geq 1$
. Conversely, it is shown in [Reference Galambos6] that any sequence of integers
$n\geq 1$
. Conversely, it is shown in [Reference Galambos6] that any sequence of integers
![]() $\{d_n\}_{n\geq 1}$
with
$\{d_n\}_{n\geq 1}$
with
![]() $d_n\geq 2$
for each
$d_n\geq 2$
for each
![]() $n\geq 1$
must be the Lüroth expansion of some
$n\geq 1$
must be the Lüroth expansion of some
![]() $x\in (0,1]$
. The Lüroth expansion has been studied extensively in the representation theory of real numbers, probability theory and dynamical systems (see [Reference Barreira and Iommi1, Reference Cao, Wu and Zhang2, Reference Fan, Liao, Ma and Wang5, Reference Hutchinson7] and the monograph of Dajani and Kraaikamp [Reference Dajani and Kraaikamp3]).
$x\in (0,1]$
. The Lüroth expansion has been studied extensively in the representation theory of real numbers, probability theory and dynamical systems (see [Reference Barreira and Iommi1, Reference Cao, Wu and Zhang2, Reference Fan, Liao, Ma and Wang5, Reference Hutchinson7] and the monograph of Dajani and Kraaikamp [Reference Dajani and Kraaikamp3]).
Given
![]() $x\in (0,1]$
, let
$x\in (0,1]$
, let
![]() $L_n(x)=\max \{d_1(x),d_2(x),\ldots ,d_n(x)\}$
be the largest digit among the first n terms of the Lüroth expansion of x. The first metrical result on
$L_n(x)=\max \{d_1(x),d_2(x),\ldots ,d_n(x)\}$
be the largest digit among the first n terms of the Lüroth expansion of x. The first metrical result on
![]() $L_n(x)$
was given by Galambos [Reference Galambos6] in 1976: for Lebesgue almost all
$L_n(x)$
was given by Galambos [Reference Galambos6] in 1976: for Lebesgue almost all
![]() $x\in (0,1]$
,
$x\in (0,1]$
,
 $$ \begin{align} \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=1. \end{align} $$
$$ \begin{align} \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=1. \end{align} $$
That is,
![]() $\log L_n(x)$
tends to infinity steadily with the speed
$\log L_n(x)$
tends to infinity steadily with the speed
![]() $\log n$
.
$\log n$
.
From the point of view of multifractal analysis, Shen et al. [Reference Shen, Yu and Zhou14] studied the level sets
 $$ \begin{align} \bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=\gamma\bigg\}, \quad \gamma\geq0, \end{align} $$
$$ \begin{align} \bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=\gamma\bigg\}, \quad \gamma\geq0, \end{align} $$
and showed that they have full Hausdorff dimension. Recently, Lin and Li [Reference Lin and Li11] generalised this result by considering the size of the sets for which the limit in (1.3) may not exist. More precisely, they proved that for
![]() $0\leq \alpha \leq \beta \leq \infty $
, the set
$0\leq \alpha \leq \beta \leq \infty $
, the set
 $$ \begin{align} \bigg\{x\in(0,1]: \liminf\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=\alpha, \limsup\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=\beta\bigg\} \end{align} $$
$$ \begin{align} \bigg\{x\in(0,1]: \liminf\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=\alpha, \limsup\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log n}=\beta\bigg\} \end{align} $$
has Hausdorff dimension one.
After (1.3) and (1.4), it is natural to wonder how large the sets are when
![]() $\log L_n(x)$
tends to infinity at a different rate. We will investigate the Hausdorff dimension of the sets when
$\log L_n(x)$
tends to infinity at a different rate. We will investigate the Hausdorff dimension of the sets when
![]() $\log L_n(x)$
grows with slowly increasing speed as defined below.
$\log L_n(x)$
grows with slowly increasing speed as defined below.
Definition 1.1 [Reference Jakimczuk8, Reference Jakimczuk9].
Let
![]() $f(x)$
be a function defined on the interval
$f(x)$
be a function defined on the interval
![]() $[c,\infty )$
such that
$[c,\infty )$
such that
![]() $f(x)>0$
,
$f(x)>0$
,
![]() $\lim _{x\rightarrow \infty }f(x)=\infty $
and with continuous derivative
$\lim _{x\rightarrow \infty }f(x)=\infty $
and with continuous derivative
![]() $f'(x)>0$
. We say the function
$f'(x)>0$
. We say the function
![]() $f(x)$
is slowly increasing if
$f(x)$
is slowly increasing if
![]() $ \lim _{x\rightarrow \infty }{xf'(x)}/{f(x)}=0. $
$ \lim _{x\rightarrow \infty }{xf'(x)}/{f(x)}=0. $
Slowly increasing functions were used recently by Jakimczuk [Reference Jakimczuk8, Reference Jakimczuk9] as a tool to study the asymptotic properties of Bell numbers. Typical slowly increasing functions are
![]() $\log x$
,
$\log x$
,
![]() $\log \log x$
,
$\log \log x$
,
![]() $\log ^2x$
,
$\log ^2x$
,
![]() ${\log x}/{\log \log x}$
. The elementary properties of slowly increasing functions will be presented in Section 2.
${\log x}/{\log \log x}$
. The elementary properties of slowly increasing functions will be presented in Section 2.
We complement the limit theorem (1.2) by studying the following two sets:
 $$\begin{align*}E_\psi(\alpha):=\bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=\alpha\bigg\}, \end{align*}$$
$$\begin{align*}E_\psi(\alpha):=\bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=\alpha\bigg\}, \end{align*}$$
 $$\begin{align*}E_\psi(a,b):=\bigg\{x\in(0,1]: \liminf\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=a, \limsup\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=b\bigg\}, \end{align*}$$
$$\begin{align*}E_\psi(a,b):=\bigg\{x\in(0,1]: \liminf\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=a, \limsup\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=b\bigg\}, \end{align*}$$
where
![]() $0\leq \alpha \leq \infty $
,
$0\leq \alpha \leq \infty $
,
![]() $0\leq a\leq b\leq \infty $
and
$0\leq a\leq b\leq \infty $
and
![]() $\psi $
is a positive function defined on
$\psi $
is a positive function defined on
![]() $(0,\infty )$
. We will establish the following two main theorems. We use
$(0,\infty )$
. We will establish the following two main theorems. We use
![]() $\dim _H$
to denote the Hausdorff dimension.
$\dim _H$
to denote the Hausdorff dimension.
Theorem 1.2. If the function
![]() $\log \psi $
is slowly increasing, then
$\log \psi $
is slowly increasing, then
![]() $\dim _HE_\psi (\alpha )=1$
for any real number
$\dim _HE_\psi (\alpha )=1$
for any real number
![]() $\alpha $
with
$\alpha $
with
![]() $0\leq \alpha \leq \infty $
.
$0\leq \alpha \leq \infty $
.
Theorem 1.3. If the function
![]() $\log \psi $
is slowly increasing, then
$\log \psi $
is slowly increasing, then
![]() $\dim _HE_\psi (a,b)=1$
for any real numbers
$\dim _HE_\psi (a,b)=1$
for any real numbers
![]() $a,b$
with
$a,b$
with
![]() $0\leq a\leq b\leq \infty $
.
$0\leq a\leq b\leq \infty $
.
In particular, we can take
![]() $\psi (x)=x^\gamma \ (\gamma>0)$
,
$\psi (x)=x^\gamma \ (\gamma>0)$
,
![]() $\psi (x)=x^{\log x}$
and
$\psi (x)=x^{\log x}$
and
![]() $\psi (x)=\log x$
in Theorem 1.3 to give the following result.
$\psi (x)=\log x$
in Theorem 1.3 to give the following result.
Corollary 1.4. If
![]() $0\leq a\leq b\leq \infty $
and
$0\leq a\leq b\leq \infty $
and
![]() $\gamma>0$
, then
$\gamma>0$
, then
Notice that if we take
![]() $\psi (n)=n$
in Theorems 1.2 and 1.3, then we obtain the special results
$\psi (n)=n$
in Theorems 1.2 and 1.3, then we obtain the special results
![]() $\dim _HE_{\psi }(\alpha )=\dim _HE_{\psi }(a,b)=1$
given in [Reference Lin and Li11, Reference Shen, Yu and Zhou14]. Theorem 1.3 also implies the following result.
$\dim _HE_{\psi }(\alpha )=\dim _HE_{\psi }(a,b)=1$
given in [Reference Lin and Li11, Reference Shen, Yu and Zhou14]. Theorem 1.3 also implies the following result.
Corollary 1.5. If the function
![]() $\log \psi $
is slowly increasing, the set
$\log \psi $
is slowly increasing, the set
 $$\begin{align*}\bigg\{x\in(0,1]:\liminf\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\log\psi(n)}<\limsup\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\log\psi(n)} \bigg\} \end{align*}$$
$$\begin{align*}\bigg\{x\in(0,1]:\liminf\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\log\psi(n)}<\limsup\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\log\psi(n)} \bigg\} \end{align*}$$
has full Hausdorff dimension.
For more results concerning the largest digits in Lüroth expansions and continued fraction expansions, see [Reference Liao and Rams10, Reference Song, Fang and Ma15–Reference Zhang and Ma17]. For the definitions and elementary properties of Hausdorff dimension, Falconer’s book [Reference Falconer4] is recommended.
2 Preliminaries
In this section, we will list some elementary results related to Lüroth expansions and present some notation and basic facts that will be used later.
Let
![]() $\{d_n\}_{n\geq 1}$
be a sequence of integers not less than
$\{d_n\}_{n\geq 1}$
be a sequence of integers not less than
![]() $2$
. We call
$2$
. We call
a cylinder of level n, whose endpoints and length denoted by
![]() $|I_n(d_1,\ldots ,d_n)|$
are determined by the following lemma.
$|I_n(d_1,\ldots ,d_n)|$
are determined by the following lemma.
Lemma 2.1 [Reference Galambos6].
Let
![]() $I_n(d_1,\ldots ,d_n)$
be a cylinder of level n. Then the left and right endpoints are
$I_n(d_1,\ldots ,d_n)$
be a cylinder of level n. Then the left and right endpoints are
 $$\begin{align*}\frac{1}{d_1}+\frac{1}{d_1(d_1-1)d_2}+\cdots+\prod\limits_{k=1}^{n-1}\frac{1}{d_k(d_k-1)}\frac{1}{d_n} \end{align*}$$
$$\begin{align*}\frac{1}{d_1}+\frac{1}{d_1(d_1-1)d_2}+\cdots+\prod\limits_{k=1}^{n-1}\frac{1}{d_k(d_k-1)}\frac{1}{d_n} \end{align*}$$
and
 $$\begin{align*}\frac{1}{d_1}+\frac{1}{d_1(d_1-1)d_2}+\cdots+\prod\limits_{k=1}^{n-1}\frac{1}{d_k(d_k-1)}\frac{1}{d_n}+\prod\limits_{k=1}^{n}\frac{1}{d_k(d_k-1)}. \end{align*}$$
$$\begin{align*}\frac{1}{d_1}+\frac{1}{d_1(d_1-1)d_2}+\cdots+\prod\limits_{k=1}^{n-1}\frac{1}{d_k(d_k-1)}\frac{1}{d_n}+\prod\limits_{k=1}^{n}\frac{1}{d_k(d_k-1)}. \end{align*}$$
As a result,
 $$\begin{align*}|I_n(d_1,\ldots,d_n)|=\prod\limits_{k=1}^{n}\frac{1}{d_k(d_k-1)}. \end{align*}$$
$$\begin{align*}|I_n(d_1,\ldots,d_n)|=\prod\limits_{k=1}^{n}\frac{1}{d_k(d_k-1)}. \end{align*}$$
For
![]() $m\in \mathbb {N}$
with
$m\in \mathbb {N}$
with
![]() $m\geq 2$
, write
$m\geq 2$
, write
![]() $\Sigma _m=\{2,3,\ldots ,m\}$
. Let
$\Sigma _m=\{2,3,\ldots ,m\}$
. Let
![]() $E_m$
be the set consisting of all points in
$E_m$
be the set consisting of all points in
![]() $(0,1]$
whose digits are less than m, that is,
$(0,1]$
whose digits are less than m, that is,
It is known that the set
![]() $E_m$
can be regarded as a self-similar set generated by contracting similarities
$E_m$
can be regarded as a self-similar set generated by contracting similarities
![]() $\{{x}/{a(a-1)}+{1}/{a}\}_{a=2}^{m}$
. The following lemma is a classic result which gives the dimension of
$\{{x}/{a(a-1)}+{1}/{a}\}_{a=2}^{m}$
. The following lemma is a classic result which gives the dimension of
![]() $E_m$
.
$E_m$
.
Lemma 2.2 [Reference Hutchinson7, Reference Shen and Liu13].
For any
![]() $m\geq 2$
,
$m\geq 2$
,
![]() $\dim _HE_m=s_m$
, where
$\dim _HE_m=s_m$
, where
![]() $s_m$
is the solution s of the equation
$s_m$
is the solution s of the equation
 $$\begin{align*}\sum\limits_{2\leq a\leq m}\bigg(\frac{1}{a(a-1)}\bigg)^s=1. \end{align*}$$
$$\begin{align*}\sum\limits_{2\leq a\leq m}\bigg(\frac{1}{a(a-1)}\bigg)^s=1. \end{align*}$$
Moreover,
![]() $\lim _{m\rightarrow \infty }s_m=1$
.
$\lim _{m\rightarrow \infty }s_m=1$
.
Next, we present a key tool which indicates that the Hausdorff dimensions of some specific sets are stationary to the dimension of
![]() $E_m$
under certain Hölder mappings defined below.
$E_m$
under certain Hölder mappings defined below.
Let
![]() $\mathbb {J}=\{n_1<n_2<\cdots \}\subset \mathbb {N}$
and
$\mathbb {J}=\{n_1<n_2<\cdots \}\subset \mathbb {N}$
and
![]() $f_{\mathbb {J}}: (0,1]\rightarrow (0,1]$
be a mapping satisfying
$f_{\mathbb {J}}: (0,1]\rightarrow (0,1]$
be a mapping satisfying
where the number
![]() $\overline {x}$
is obtained by deleting all
$\overline {x}$
is obtained by deleting all
![]() $\{d_{n_k}(x)\}_{k\geq 1}$
in the Lüroth expansion of x. For
$\{d_{n_k}(x)\}_{k\geq 1}$
in the Lüroth expansion of x. For
![]() $m\geq 2$
and
$m\geq 2$
and
![]() $\{a_n\}_{n\geq 1}$
a sequence of integers, set
$\{a_n\}_{n\geq 1}$
a sequence of integers, set
Lemma 2.3. Fix
![]() $m\geq 2$
and a set of positive integers
$m\geq 2$
and a set of positive integers
![]() $\mathbb {J}=\{n_1<n_2<\cdots \}$
. Let
$\mathbb {J}=\{n_1<n_2<\cdots \}$
. Let
![]() $\{a_k\}_{k\geq 1}$
be an increasing positive integer sequence satisfying
$\{a_k\}_{k\geq 1}$
be an increasing positive integer sequence satisfying
![]() $a_k\rightarrow \infty $
as
$a_k\rightarrow \infty $
as
![]() $k\rightarrow \infty $
and
$k\rightarrow \infty $
and
Then
![]() $ \dim _HF_m(\mathbb {J},\{a_k\})=\dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))=\dim _HE_m=s_m. $
$ \dim _HF_m(\mathbb {J},\{a_k\})=\dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))=\dim _HE_m=s_m. $
Proof. The main idea of the proof of Lemma 2.3 comes from [Reference Wu and Xu16]. Here we will modify the calculations in [Reference Shen, Yu and Zhou14] and give a sketch of the proof of this argument.
To estimate the dimension of
![]() $F_m(\mathbb {J},\{a_k\})$
, we shall use the terminology of symbolic space. For each
$F_m(\mathbb {J},\{a_k\})$
, we shall use the terminology of symbolic space. For each
![]() $n\geq 1$
, let
$n\geq 1$
, let
For any
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $(\sigma _1,\ldots ,\sigma _n)\in D_n$
, we call
$(\sigma _1,\ldots ,\sigma _n)\in D_n$
, we call
the fundamental interval of level n, where the union is taken over all
![]() $\sigma _{n+1}$
such that
$\sigma _{n+1}$
such that
![]() $(\sigma _1,\ldots ,\sigma _{n},\sigma _{n+1})\in D_{n+1}$
. Clearly,
$(\sigma _1,\ldots ,\sigma _{n},\sigma _{n+1})\in D_{n+1}$
. Clearly,
 $$\begin{align*}F_m(\mathbb{J},\{a_k\})=\bigcap\limits_{n\geq1}\bigcup\limits_{(\sigma_1,\ldots,\sigma_{n})\in D_n}I_n(\sigma_1,\ldots,\sigma_{n}) =\bigcap\limits_{n\geq1}\bigcup\limits_{(\sigma_1,\ldots,\sigma_{n})\in D_n}J_n(\sigma_1,\ldots,\sigma_{n}). \end{align*}$$
$$\begin{align*}F_m(\mathbb{J},\{a_k\})=\bigcap\limits_{n\geq1}\bigcup\limits_{(\sigma_1,\ldots,\sigma_{n})\in D_n}I_n(\sigma_1,\ldots,\sigma_{n}) =\bigcap\limits_{n\geq1}\bigcup\limits_{(\sigma_1,\ldots,\sigma_{n})\in D_n}J_n(\sigma_1,\ldots,\sigma_{n}). \end{align*}$$
By the definition of
![]() $f_{\mathbb {J}}$
with
$f_{\mathbb {J}}$
with
![]() $\mathbb {J}=\{n_k\}_{k\geq 1}$
, we can assume that
$\mathbb {J}=\{n_k\}_{k\geq 1}$
, we can assume that
![]() $n_k\leq n<n_{k+1}$
for some
$n_k\leq n<n_{k+1}$
for some
![]() ${k\in \mathbb {N}}$
. Then
${k\in \mathbb {N}}$
. Then
![]() $\overline {(\sigma _1,\ldots ,\sigma _{n})}:=f_{\mathbb {J}}((\sigma _1,\ldots ,\sigma _{n}))$
is obtained by deleting the k terms
$\overline {(\sigma _1,\ldots ,\sigma _{n})}:=f_{\mathbb {J}}((\sigma _1,\ldots ,\sigma _{n}))$
is obtained by deleting the k terms
![]() $\{\sigma _{n_i}\}_{i=1}^{k}$
in
$\{\sigma _{n_i}\}_{i=1}^{k}$
in
![]() $(\sigma _1,\ldots ,\sigma _{n})$
. Write
$(\sigma _1,\ldots ,\sigma _{n})$
. Write
Then we have the following claim.
Claim 1. For any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $N_0>0$
such that for all
$N_0>0$
such that for all
![]() $n\geq N_0$
and
$n\geq N_0$
and
![]() $(\sigma _1,\ldots ,\sigma _{n})\in D_n$
, we have
$(\sigma _1,\ldots ,\sigma _{n})\in D_n$
, we have
In fact, (2.1) implies that for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $N_0>0$
such that for all
$N_0>0$
such that for all
![]() $k>N_0$
, we have
$k>N_0$
, we have
![]() $k\log a_k<\tfrac {1}{2}\varepsilon \log 2 n_k$
. We can assume that
$k\log a_k<\tfrac {1}{2}\varepsilon \log 2 n_k$
. We can assume that
![]() $n_k\leq n<n_{k+1}$
and obtain
$n_k\leq n<n_{k+1}$
and obtain
 $$ \begin{align} |I_n(\sigma_1,\ldots,\sigma_{n})|^{\varepsilon}\leq\frac{1}{2^{(n-k)\varepsilon}}\leq\frac{1}{2^{n_{k}\varepsilon}}\leq\frac{1}{a_{k}^{2k}}. \end{align} $$
$$ \begin{align} |I_n(\sigma_1,\ldots,\sigma_{n})|^{\varepsilon}\leq\frac{1}{2^{(n-k)\varepsilon}}\leq\frac{1}{2^{n_{k}\varepsilon}}\leq\frac{1}{a_{k}^{2k}}. \end{align} $$
Since
![]() $\{a_k\}$
is increasing, (2.2) and Lemma 2.1 give
$\{a_k\}$
is increasing, (2.2) and Lemma 2.1 give
 $$ \begin{align*} |I_n(\sigma_1,\cdots,\sigma_{n})|&=|\overline{I_n}(\sigma_1,\ldots,\sigma_{n})| /{\sigma_{n_1}(\sigma_{n_1}-1)\cdots\sigma_{n_k}(\sigma_{n_k}-1)} \\ &\geq|\overline{I_n}(\sigma_1,\ldots,\sigma_{n})| /{a_k^{2k}} \\ &\geq|\overline{I_n}(\sigma_1,\ldots,\sigma_{n})|^{1+\varepsilon}. \end{align*} $$
$$ \begin{align*} |I_n(\sigma_1,\cdots,\sigma_{n})|&=|\overline{I_n}(\sigma_1,\ldots,\sigma_{n})| /{\sigma_{n_1}(\sigma_{n_1}-1)\cdots\sigma_{n_k}(\sigma_{n_k}-1)} \\ &\geq|\overline{I_n}(\sigma_1,\ldots,\sigma_{n})| /{a_k^{2k}} \\ &\geq|\overline{I_n}(\sigma_1,\ldots,\sigma_{n})|^{1+\varepsilon}. \end{align*} $$
Let x and y belong to the set
![]() $F_m(\mathbb {J},\{a_k\})$
with
$F_m(\mathbb {J},\{a_k\})$
with
![]() $x\neq y$
. It follows that there exists a largest integer n such that x and y are both contained in the same cylinder of level n. The next claim is devoted to estimating the distance between x and y, which is very similar to [Reference Shen, Yu and Zhou14, Lemma 3.3], so we omit the details.
$x\neq y$
. It follows that there exists a largest integer n such that x and y are both contained in the same cylinder of level n. The next claim is devoted to estimating the distance between x and y, which is very similar to [Reference Shen, Yu and Zhou14, Lemma 3.3], so we omit the details.
Claim 2. Let n be the largest level of the cylinders which contain both x and y. Then
 $$\begin{align*}|y-x|\geq\min\bigg\{\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^2\cdot a_n},\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^3}\bigg\}. \end{align*}$$
$$\begin{align*}|y-x|\geq\min\bigg\{\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^2\cdot a_n},\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^3}\bigg\}. \end{align*}$$
Therefore, when
![]() $x,y\in F_m(\mathbb {J},\{a_k\})$
with
$x,y\in F_m(\mathbb {J},\{a_k\})$
with
 $$\begin{align*}|x-y|<\min\limits_{(\sigma_1,\ldots,\sigma_{N_0})\in D_{N_0}}\bigg\{\frac{I_{N_0}(\sigma_1,\ldots,\sigma_{N_0})}{m^2 a_{N_0+2}}, \frac{I_{N_0}(\sigma_1,\ldots,\sigma_{N_0})}{m^3}\bigg\}, \end{align*}$$
$$\begin{align*}|x-y|<\min\limits_{(\sigma_1,\ldots,\sigma_{N_0})\in D_{N_0}}\bigg\{\frac{I_{N_0}(\sigma_1,\ldots,\sigma_{N_0})}{m^2 a_{N_0+2}}, \frac{I_{N_0}(\sigma_1,\ldots,\sigma_{N_0})}{m^3}\bigg\}, \end{align*}$$
we have
From these two claims and [Reference Falconer4, Proposition 2.3], we obtain
and so
![]() $\dim _HF_m(\mathbb {J},\{a_k\})\geq \dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))$
by letting
$\dim _HF_m(\mathbb {J},\{a_k\})\geq \dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))$
by letting
![]() $\varepsilon \rightarrow 0$
.
$\varepsilon \rightarrow 0$
.
To see that
![]() $\dim _HF_m(\mathbb {J},\{a_k\})\leq \dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))$
, it suffices to show that the mapping
$\dim _HF_m(\mathbb {J},\{a_k\})\leq \dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))$
, it suffices to show that the mapping
is
![]() $1$
-Hölder. For any
$1$
-Hölder. For any
![]() $y_1,y_2\in f_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))$
, let
$y_1,y_2\in f_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\}))$
, let
![]() $y_1,y_2\in I_{n}(\sigma _1,\ldots ,\sigma _{n})$
with
$y_1,y_2\in I_{n}(\sigma _1,\ldots ,\sigma _{n})$
with
![]() $\sigma _{n+1}(y_1)\neq \sigma _{n+1}(y_2)$
. Let
$\sigma _{n+1}(y_1)\neq \sigma _{n+1}(y_2)$
. Let
![]() $x_1=f_{\mathbb {J}}^{-1}(y_1),x_2=f_{\mathbb {J}}^{-1}(y_2)$
. By the definition of
$x_1=f_{\mathbb {J}}^{-1}(y_1),x_2=f_{\mathbb {J}}^{-1}(y_2)$
. By the definition of
![]() $f_{\mathbb {J}}^{-1}$
, we know that
$f_{\mathbb {J}}^{-1}$
, we know that
![]() $x_1$
and
$x_1$
and
![]() $x_2$
are obtained by inserting the sequence
$x_2$
are obtained by inserting the sequence
![]() $\{a_k\}_{k\geq 1}$
in the Lüroth expansions of
$\{a_k\}_{k\geq 1}$
in the Lüroth expansions of
![]() $y_1$
and
$y_1$
and
![]() $y_2$
at the positions
$y_2$
at the positions
![]() $\{n_{k}\}_{k\geq 1}$
, respectively. Let
$\{n_{k}\}_{k\geq 1}$
, respectively. Let
![]() $M\in \mathbb {N}$
be such that we can insert just M integers
$M\in \mathbb {N}$
be such that we can insert just M integers
![]() $\{a_{i}\}_{i=1}^{M}$
into the block
$\{a_{i}\}_{i=1}^{M}$
into the block
![]() $(\sigma _1,\ldots ,\sigma _{n})$
. Then
$(\sigma _1,\ldots ,\sigma _{n})$
. Then
![]() $x_1$
and
$x_1$
and
![]() $x_2$
have at least
$x_2$
have at least
![]() $n+M$
common digits in their Lüroth expansions. By Lemma 2.1,
$n+M$
common digits in their Lüroth expansions. By Lemma 2.1,
 $$ \begin{align*} \displaystyle |x_1-x_2|&\leq|I_{n+M}(\sigma_1,\ldots,\sigma_{n+M})| \\ \displaystyle &\leq|I_n(\sigma_1,\ldots,\sigma_{n})| /{\sigma_{n_1}(\sigma_{n_1}-1)\cdots\sigma_{n_k}(\sigma_{n_k}-1)} \\ \displaystyle &\leq\tfrac{1}{2}|I_n(\sigma_1,\ldots,\sigma_{n})|. \end{align*} $$
$$ \begin{align*} \displaystyle |x_1-x_2|&\leq|I_{n+M}(\sigma_1,\ldots,\sigma_{n+M})| \\ \displaystyle &\leq|I_n(\sigma_1,\ldots,\sigma_{n})| /{\sigma_{n_1}(\sigma_{n_1}-1)\cdots\sigma_{n_k}(\sigma_{n_k}-1)} \\ \displaystyle &\leq\tfrac{1}{2}|I_n(\sigma_1,\ldots,\sigma_{n})|. \end{align*} $$
However, similar to the argument in Claim 2, we also have
 $$\begin{align*}|y_1-y_2|\geq\min\bigg\{\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^2\cdot a_n},\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^3}\bigg\}. \end{align*}$$
$$\begin{align*}|y_1-y_2|\geq\min\bigg\{\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^2\cdot a_n},\frac{|I_n(\sigma_1,\ldots,\sigma_{n})|}{m^3}\bigg\}. \end{align*}$$
It follows that
showing that
![]() $f_{\mathbb {J}}^{-1}$
is
$f_{\mathbb {J}}^{-1}$
is
![]() $1$
-Hölder and
$1$
-Hölder and
![]() $ \dim _HF_m(\mathbb {J},\{a_k\})\leq \dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\})). $
$ \dim _HF_m(\mathbb {J},\{a_k\})\leq \dim _Hf_{\mathbb {J}}(F_m(\mathbb {J},\{a_k\})). $
We end this section by presenting the following lemma which exhibits some basic properties of slowly increasing functions.
Lemma 2.4 [Reference Jakimczuk8].
Let the functions
![]() $f(x)$
and
$f(x)$
and
![]() $g(x)$
be slowly increasing and
$g(x)$
be slowly increasing and
![]() $\gamma $
be a positive constant. Then,
$\gamma $
be a positive constant. Then,
-
(1) the function
 $f(x^\gamma )$
is slowly increasing;
$f(x^\gamma )$
is slowly increasing; -
(2) the function
 $f(x^\gamma g(x))$
is slowly increasing;
$f(x^\gamma g(x))$
is slowly increasing; -
(3)
 $\lim _{n\rightarrow \infty } {\log f(x)}/{\log x}=0;$
$\lim _{n\rightarrow \infty } {\log f(x)}/{\log x}=0;$
-
(4)
 $\lim _{n\rightarrow \infty }{f(x+1)}/{f(x)}=1.$
$\lim _{n\rightarrow \infty }{f(x+1)}/{f(x)}=1.$
3 Proofs
This section is devoted to the proofs of our main results. To prove Theorem 1.2, we will construct a suitable subset
![]() $F_{m}(\mathbb {J},\{a_k\})$
of
$F_{m}(\mathbb {J},\{a_k\})$
of
![]() $E_\psi (\alpha )$
, so that the result can be established by using Lemma 2.3. As for the proof of Theorem 1.3, since the nonexistence of the limit in
$E_\psi (\alpha )$
, so that the result can be established by using Lemma 2.3. As for the proof of Theorem 1.3, since the nonexistence of the limit in
![]() $E_\psi (a,b)$
describes the essence of the question compared with the known results, we need to carefully construct a nice Cantor subset in the lower bound estimations for the Hausdorff dimension. Our proof provides a convenient method to estimate the lower bound for the Hausdorff dimension, which is very different from the method used in [Reference Lin and Li11].
$E_\psi (a,b)$
describes the essence of the question compared with the known results, we need to carefully construct a nice Cantor subset in the lower bound estimations for the Hausdorff dimension. Our proof provides a convenient method to estimate the lower bound for the Hausdorff dimension, which is very different from the method used in [Reference Lin and Li11].
Proof of Theorem 1.2.
The proof is divided into three cases according as
![]() $\alpha =0$
,
$\alpha =0$
,
![]() $0<\alpha <\infty $
and
$0<\alpha <\infty $
and
![]() $\alpha =\infty $
.
$\alpha =\infty $
.
Case 1:
![]() $\alpha =0$
. In this case, it is clear that
$\alpha =0$
. In this case, it is clear that
![]() $E_m\subset E_\psi (0)$
. Therefore the result follows directly by Lemma 2.2.
$E_m\subset E_\psi (0)$
. Therefore the result follows directly by Lemma 2.2.
Case 2:
![]() $0<\alpha <\infty $
. Let
$0<\alpha <\infty $
. Let
![]() $m\geq 2$
and
$m\geq 2$
and
![]() $\{a_n\}_{n\geq 1}$
be a sequence of integers and recall the set
$\{a_n\}_{n\geq 1}$
be a sequence of integers and recall the set
defined in Lemma 2.3. Here we take
![]() $n_k=k^2$
and
$n_k=k^2$
and
![]() $a_k=\lfloor \psi (k^2)^\alpha \rfloor $
for each
$a_k=\lfloor \psi (k^2)^\alpha \rfloor $
for each
![]() $k\geq 1$
.
$k\geq 1$
.
On the one hand, for any
![]() $x\in F_m(\mathbb {J},\{a_k\})$
, if
$x\in F_m(\mathbb {J},\{a_k\})$
, if
![]() $k^2\leq n<(k+1)^2$
for some integer k, then
$k^2\leq n<(k+1)^2$
for some integer k, then
 $$\begin{align*}\frac{\log\lfloor\psi(k^2)^\alpha\rfloor}{\log\psi((k+1)^2)}\leq\frac{\log L_n(x)}{\log\psi(n)}\leq\frac{\log\lfloor\psi(k^2)^\alpha\rfloor}{\log\psi(k^2)}. \end{align*}$$
$$\begin{align*}\frac{\log\lfloor\psi(k^2)^\alpha\rfloor}{\log\psi((k+1)^2)}\leq\frac{\log L_n(x)}{\log\psi(n)}\leq\frac{\log\lfloor\psi(k^2)^\alpha\rfloor}{\log\psi(k^2)}. \end{align*}$$
From Lemma 2.4(1) and (4),
 $$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log\psi(k^2)}{\log\psi((k+1)^2)}=1. \end{align*}$$
$$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log\psi(k^2)}{\log\psi((k+1)^2)}=1. \end{align*}$$
Consequently,
 $$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=\alpha, \end{align*}$$
$$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}=\alpha, \end{align*}$$
which yields
![]() $F_m(\mathbb {J},\{a_k\})\subset E_\psi (\alpha )$
.
$F_m(\mathbb {J},\{a_k\})\subset E_\psi (\alpha )$
.
On the other hand, since
![]() $\log \psi $
is slowly increasing, Lemma 2.4(3) implies that
$\log \psi $
is slowly increasing, Lemma 2.4(3) implies that
 $$\begin{align*}\lim\limits_{k\rightarrow\infty}\frac{\log\log\psi(k)}{\log k}=0, \end{align*}$$
$$\begin{align*}\lim\limits_{k\rightarrow\infty}\frac{\log\log\psi(k)}{\log k}=0, \end{align*}$$
which ensures that for any
![]() $\varepsilon $
with
$\varepsilon $
with
![]() $0<\varepsilon <\tfrac {1}{2}$
and sufficiently large k,
$0<\varepsilon <\tfrac {1}{2}$
and sufficiently large k,
This gives
 $$\begin{align*}\lim\limits_{k\rightarrow\infty}\frac{k\log\lfloor\psi(k^2)^\alpha\rfloor}{k^2}\leq\lim\limits_{k\rightarrow\infty}\frac{\alpha\cdot k^{1+2\varepsilon}}{k^2}=0, \end{align*}$$
$$\begin{align*}\lim\limits_{k\rightarrow\infty}\frac{k\log\lfloor\psi(k^2)^\alpha\rfloor}{k^2}\leq\lim\limits_{k\rightarrow\infty}\frac{\alpha\cdot k^{1+2\varepsilon}}{k^2}=0, \end{align*}$$
that is, (2.1) in Lemma 2.3 holds. From Lemma 2.3,
and we obtain the result in Theorem 1.2 by letting
![]() $m\rightarrow \infty $
.
$m\rightarrow \infty $
.
Case 3:
![]() $\alpha =\infty $
. In this case, for each
$\alpha =\infty $
. In this case, for each
![]() $k\geq 1$
, we take
$k\geq 1$
, we take
in the definition of the set
![]() $F_m(\mathbb {J},\{a_k\})$
in Lemma 2.3.
$F_m(\mathbb {J},\{a_k\})$
in Lemma 2.3.
We show first that
![]() $F_m(\mathbb {J},\{a_k\})\subset E_\psi (\infty )$
. For every
$F_m(\mathbb {J},\{a_k\})\subset E_\psi (\infty )$
. For every
![]() $x\in F_m(\mathbb {J},\{a_k\})$
, since the functions
$x\in F_m(\mathbb {J},\{a_k\})$
, since the functions
![]() $\log \psi (x)$
and
$\log \psi (x)$
and
![]() $\log x$
are slowly increasing, Lemma 2.4(2) and (4) give
$\log x$
are slowly increasing, Lemma 2.4(2) and (4) give
 $$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log(\psi(k^2\log k))}{\log(\psi((k+1)^2\log(k+1)))}=1. \end{align*}$$
$$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log(\psi(k^2\log k))}{\log(\psi((k+1)^2\log(k+1)))}=1. \end{align*}$$
So if
![]() $\lfloor k^2\log k\rfloor \leq n<\lfloor (k+1)^2\log (k+1)\rfloor $
for some integer k, then
$\lfloor k^2\log k\rfloor \leq n<\lfloor (k+1)^2\log (k+1)\rfloor $
for some integer k, then
 $$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}\geq\lim\limits_{k\rightarrow\infty}\frac{(\log k)^{1/2}\cdot\log(\lfloor\psi(k^2\log k)\rfloor)} {\log(\psi(\lfloor(k+1)^2\log(k+1)\rfloor))}=\lim\limits_{k\rightarrow\infty}(\log k)^{1/2}=\infty, \end{align*}$$
$$\begin{align*}\lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\log\psi(n)}\geq\lim\limits_{k\rightarrow\infty}\frac{(\log k)^{1/2}\cdot\log(\lfloor\psi(k^2\log k)\rfloor)} {\log(\psi(\lfloor(k+1)^2\log(k+1)\rfloor))}=\lim\limits_{k\rightarrow\infty}(\log k)^{1/2}=\infty, \end{align*}$$
which means
![]() $F_m(\mathbb {J},\{a_k\})\subset E_\psi (\infty )$
.
$F_m(\mathbb {J},\{a_k\})\subset E_\psi (\infty )$
.
Next, (3.1) holds for any
![]() $\varepsilon $
with
$\varepsilon $
with
![]() $0<\varepsilon <\tfrac {1}{2}$
as in the last case, and we can check that (2.1) still holds here, namely
$0<\varepsilon <\tfrac {1}{2}$
as in the last case, and we can check that (2.1) still holds here, namely
 $$\begin{align*}\lim\limits_{k\rightarrow\infty}\frac{k\log\lfloor(\psi(k^2\log k))^{(\log k)^{{1}/{2}}}\rfloor}{\lfloor k^2\log k\rfloor} \leq\lim\limits_{k\rightarrow\infty}\frac{\log\psi(k^2\log k)}{k(\log k)^{{1}/{2}}}\leq\lim\limits_{k\rightarrow\infty}k^{2\varepsilon-1}(\log k)^{\varepsilon-{1}/{2}}=0. \end{align*}$$
$$\begin{align*}\lim\limits_{k\rightarrow\infty}\frac{k\log\lfloor(\psi(k^2\log k))^{(\log k)^{{1}/{2}}}\rfloor}{\lfloor k^2\log k\rfloor} \leq\lim\limits_{k\rightarrow\infty}\frac{\log\psi(k^2\log k)}{k(\log k)^{{1}/{2}}}\leq\lim\limits_{k\rightarrow\infty}k^{2\varepsilon-1}(\log k)^{\varepsilon-{1}/{2}}=0. \end{align*}$$
Hence, by Lemma 2.3,
Then we finish the proof of Theorem 1.2 by letting
![]() $m\rightarrow \infty $
.
$m\rightarrow \infty $
.
Proof of Theorem 1.3.
We give the proof of Theorem 1.3 for the case
![]() $0<a<b<\infty $
in detail. The argument for other cases involves minor modifications. In the following, we will write
$0<a<b<\infty $
in detail. The argument for other cases involves minor modifications. In the following, we will write
![]() $\phi :=\log \psi $
for simplicity.
$\phi :=\log \psi $
for simplicity.
Case 1:
![]() $0<a<b<\infty $
. Let
$0<a<b<\infty $
. Let
![]() $\phi $
be a slowly increasing function. Our strategy is to find a nice Cantor subset of
$\phi $
be a slowly increasing function. Our strategy is to find a nice Cantor subset of
![]() $E_\psi (a,b)$
with full Hausdorff dimension. To this end, we construct another slowly increasing function
$E_\psi (a,b)$
with full Hausdorff dimension. To this end, we construct another slowly increasing function
![]() $\widetilde {\phi }$
satisfying some specific properties with respect to
$\widetilde {\phi }$
satisfying some specific properties with respect to
![]() $\phi $
. Then the proof can be completed by using the result mentioned in Theorem 1.2.
$\phi $
. Then the proof can be completed by using the result mentioned in Theorem 1.2.
For
![]() $0<a<b<\infty $
, define
$0<a<b<\infty $
, define
![]() $\widetilde {\phi }(x)$
on
$\widetilde {\phi }(x)$
on
![]() $(0,\infty )$
such that
$(0,\infty )$
such that
![]() $\widetilde {\phi }(x)>0$
and, for any
$\widetilde {\phi }(x)>0$
and, for any
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
Proposition 3.1. Let
![]() $\phi (n)$
be slowly increasing and define the function
$\phi (n)$
be slowly increasing and define the function
![]() $\widetilde {\phi }$
as above. Then
$\widetilde {\phi }$
as above. Then
![]() $\widetilde {\phi }$
is also slowly increasing and
$\widetilde {\phi }$
is also slowly increasing and
 $$ \begin{align} \liminf\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=a,\quad \limsup\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=b. \end{align} $$
$$ \begin{align} \liminf\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=a,\quad \limsup\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=b. \end{align} $$
Proof. First,
![]() $0<a\cdot \phi \leq \widetilde {\phi }\leq b\cdot \phi $
and
$0<a\cdot \phi \leq \widetilde {\phi }\leq b\cdot \phi $
and
![]() $\widetilde {\phi }\rightarrow \infty $
as
$\widetilde {\phi }\rightarrow \infty $
as
![]() $x\rightarrow \infty $
. Next, we check that the function
$x\rightarrow \infty $
. Next, we check that the function
![]() $\widetilde {\phi }(x)$
has positive derivative. In fact,
$\widetilde {\phi }(x)$
has positive derivative. In fact,
 $$ \begin{align*} \widetilde{\phi}'(x)&=\bigg(\frac{a+b}{2}\phi(x)+\frac{b-a}{2}\phi(x)\sin\bigg(\frac{a}{b-a}\log\phi(x)\bigg)\bigg)' \\ &=\frac{a+b}{2}\phi'(x)+\frac{b-a}{2}\phi'(x)\sin\bigg(\frac{a}{b-a}\log\phi(x)\bigg) \\ &\quad +\frac{b-a}{2}\phi(x)\cos\bigg(\frac{a}{b-a}\log\phi(x)\bigg)\frac{a}{b-a}\cdot\phi^{-1}(x)\cdot\phi'(x) \\ &\geq\frac{a+b}{2}\phi'(x)-\frac{b-a}{2}\phi'(x)-\frac{a}{2}\phi'(x) =\frac{a}{2}\phi'(x)>0, \end{align*} $$
$$ \begin{align*} \widetilde{\phi}'(x)&=\bigg(\frac{a+b}{2}\phi(x)+\frac{b-a}{2}\phi(x)\sin\bigg(\frac{a}{b-a}\log\phi(x)\bigg)\bigg)' \\ &=\frac{a+b}{2}\phi'(x)+\frac{b-a}{2}\phi'(x)\sin\bigg(\frac{a}{b-a}\log\phi(x)\bigg) \\ &\quad +\frac{b-a}{2}\phi(x)\cos\bigg(\frac{a}{b-a}\log\phi(x)\bigg)\frac{a}{b-a}\cdot\phi^{-1}(x)\cdot\phi'(x) \\ &\geq\frac{a+b}{2}\phi'(x)-\frac{b-a}{2}\phi'(x)-\frac{a}{2}\phi'(x) =\frac{a}{2}\phi'(x)>0, \end{align*} $$
where the last inequality follows from the fact that
![]() $\phi $
is slowly increasing. The calculation also implies that
$\phi $
is slowly increasing. The calculation also implies that
 $$\begin{align*}\bigg|\frac{x\widetilde{\phi}'(x)}{\widetilde{\phi}(x)}\bigg| \leq \bigg| \frac{x}{a\phi(x)} \bigg(\frac{a+b}{2}\phi'(x)+\frac{b-a}{2}\phi'(x)+\frac{a}{2}\phi'(x)\bigg) \bigg| \rightarrow0 \quad \text{as } x\rightarrow\infty. \end{align*}$$
$$\begin{align*}\bigg|\frac{x\widetilde{\phi}'(x)}{\widetilde{\phi}(x)}\bigg| \leq \bigg| \frac{x}{a\phi(x)} \bigg(\frac{a+b}{2}\phi'(x)+\frac{b-a}{2}\phi'(x)+\frac{a}{2}\phi'(x)\bigg) \bigg| \rightarrow0 \quad \text{as } x\rightarrow\infty. \end{align*}$$
Therefore,
![]() $\widetilde {\phi }$
is also a slowly increasing function. By the construction of
$\widetilde {\phi }$
is also a slowly increasing function. By the construction of
![]() $\widetilde {\phi }$
, (3.2) holds immediately.
$\widetilde {\phi }$
, (3.2) holds immediately.
Let
![]() $\widetilde {\phi }=\log \widetilde {\psi }$
be the slowly increasing function defined above, where
$\widetilde {\phi }=\log \widetilde {\psi }$
be the slowly increasing function defined above, where
![]() $\widetilde {\psi }$
is a positive function defined on
$\widetilde {\psi }$
is a positive function defined on
![]() $(0,\infty )$
. We replace
$(0,\infty )$
. We replace
![]() $\widetilde {\phi }$
with
$\widetilde {\phi }$
with
![]() $\phi =\log \psi $
and take
$\phi =\log \psi $
and take
![]() $\alpha =1$
in the set
$\alpha =1$
in the set
![]() $E_\psi (\alpha )$
in Theorem 1.2. The Hausdorff dimension of the set
$E_\psi (\alpha )$
in Theorem 1.2. The Hausdorff dimension of the set
 $$\begin{align*}E_{\widetilde{\psi}}(1):=\bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\widetilde{\phi}(n)}=1\bigg\} \end{align*}$$
$$\begin{align*}E_{\widetilde{\psi}}(1):=\bigg\{x\in(0,1]: \lim\limits_{n\rightarrow\infty}\frac{\log L_n(x)}{\widetilde{\phi}(n)}=1\bigg\} \end{align*}$$
is full. The lower bound of
![]() $\dim _HE_\psi (a,b)$
follows directly by Proposition 3.1 and the fact that
$\dim _HE_\psi (a,b)$
follows directly by Proposition 3.1 and the fact that
![]() $E_{\widetilde {\psi }}(1)\subset E_\psi (a,b)$
. To see this, note that for any
$E_{\widetilde {\psi }}(1)\subset E_\psi (a,b)$
. To see this, note that for any
![]() $x\in E_{\widetilde {\psi }}(1)$
,
$x\in E_{\widetilde {\psi }}(1)$
,
 $$ \begin{align*} \liminf\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\phi(n)} &=\lim\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\widetilde{\phi}(n)}\cdot \liminf\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=a, \\ \limsup\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\phi(n)} &=\lim\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\widetilde{\phi}(n)}\cdot \limsup\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=b, \end{align*} $$
$$ \begin{align*} \liminf\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\phi(n)} &=\lim\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\widetilde{\phi}(n)}\cdot \liminf\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=a, \\ \limsup\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\phi(n)} &=\lim\limits_{n\rightarrow\infty}\frac{\log L_{n}(x)}{\widetilde{\phi}(n)}\cdot \limsup\limits_{n\rightarrow\infty}\frac{\widetilde{\phi}(n)}{\phi(n)}=b, \end{align*} $$
which means that
![]() $x\in E_\psi (a,b)$
.
$x\in E_\psi (a,b)$
.
Case 2:
![]() $0=a<b<\infty $
. The proof is similar to the case when
$0=a<b<\infty $
. The proof is similar to the case when
![]() $0<a<b<\infty $
. We only need to modify the construction of the function
$0<a<b<\infty $
. We only need to modify the construction of the function
![]() $\widetilde {\phi }$
to make sure that Proposition 3.1 still holds. We define
$\widetilde {\phi }$
to make sure that Proposition 3.1 still holds. We define
![]() $\widetilde {\phi }(x)$
on
$\widetilde {\phi }(x)$
on
![]() $(0,\infty )$
such that
$(0,\infty )$
such that
![]() $\widetilde {\phi }(x)>0$
by taking
$\widetilde {\phi }(x)>0$
by taking
 $$\begin{align*}\widetilde{\phi}(x)=\frac{b\phi(x)}{\log\log\phi(x)}+\frac{1}{2}b\phi(x)(\sin(\log\log\phi(x))+1). \end{align*}$$
$$\begin{align*}\widetilde{\phi}(x)=\frac{b\phi(x)}{\log\log\phi(x)}+\frac{1}{2}b\phi(x)(\sin(\log\log\phi(x))+1). \end{align*}$$
Equation (3.2) holds directly and we can check that
![]() $\widetilde {\phi }(x)$
satisfies
$\widetilde {\phi }(x)$
satisfies
![]() $\widetilde {\phi }'(x)>0$
and
$\widetilde {\phi }'(x)>0$
and
![]() $|{x\widetilde {\phi }'(x)}/{\widetilde {\phi }(x)}|\rightarrow 0$
as
$|{x\widetilde {\phi }'(x)}/{\widetilde {\phi }(x)}|\rightarrow 0$
as
![]() $x\rightarrow \infty $
. Thus
$x\rightarrow \infty $
. Thus
![]() $\widetilde {\phi }(x)$
is slowly increasing.
$\widetilde {\phi }(x)$
is slowly increasing.
For the remaining cases, the discussions run as before, so we only give the constructions of the slowly increasing functions
![]() $\widetilde {\phi }(x)$
as follows.
$\widetilde {\phi }(x)$
as follows.
Case 3:
![]() $0<a<b=\infty $
. Take
$0<a<b=\infty $
. Take
Case 4:
![]() $0=a<b=\infty $
. Take
$0=a<b=\infty $
. Take
 $$\begin{align*}\widetilde{\phi}(x)=\frac{\phi(x)}{\log\log\phi(x)}+\frac{1}{2}\phi(x)\log\phi(x)(\sin(\log\log\log\phi(x))+1). \end{align*}$$
$$\begin{align*}\widetilde{\phi}(x)=\frac{\phi(x)}{\log\log\phi(x)}+\frac{1}{2}\phi(x)\log\phi(x)(\sin(\log\log\log\phi(x))+1). \end{align*}$$
Case 5:
![]() $0<a=b<\infty $
. Take
$0<a=b<\infty $
. Take
![]() $ \widetilde {\phi }(x)=a\phi (x). $
$ \widetilde {\phi }(x)=a\phi (x). $
Case 6:
![]() $a=b=\infty $
. Take
$a=b=\infty $
. Take
![]() $ \widetilde {\phi }(x)=\phi (x)\log x. $
$ \widetilde {\phi }(x)=\phi (x)\log x. $
Case 7:
![]() $a=b=0$
. Take
$a=b=0$
. Take
![]() $ \widetilde {\phi }(x)=\log \phi (x). $
$ \widetilde {\phi }(x)=\log \phi (x). $
Acknowledgment
The authors wish to warmly thank the anonymous referee for the helpful suggestions to improve the readability of this paper.