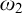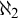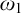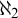1 Introduction
Shelah introduced countable support iterations of proper forcing notions, which enable us to obtain a large number of consistency results. But by technical limitations, the size of the continuum cannot be larger than
![]() $\aleph _2$
in such consistency results. Asperó and Mota introduced a new iteration technique for proper forcing notions that enables us to obtain some consistency results with the continuum larger than
$\aleph _2$
in such consistency results. Asperó and Mota introduced a new iteration technique for proper forcing notions that enables us to obtain some consistency results with the continuum larger than
![]() $\aleph _2$
. Asperó–Mota iterations are equipped with symmetric systems of models as side conditions, idea due to Todorčević (see, e.g., [Reference Todorčević12, Section 4]). The main ingredient is not only the use of symmetric systems of models but also symmetric systems of models with markers. Asperó–Mota iterations are used in the papers [Reference Asperó and Mota2–Reference Asperó and Mota5, Reference Miyamoto and Yorioka10, Reference Yorioka13]. In [Reference Asperó and Mota5, Reference Miyamoto and Yorioka10], the iterations require that markers of models in symmetric systems also have symmetry in a suitable sense (Definition 4.1
(el), (ho), (up), and (down)).
$\aleph _2$
. Asperó–Mota iterations are equipped with symmetric systems of models as side conditions, idea due to Todorčević (see, e.g., [Reference Todorčević12, Section 4]). The main ingredient is not only the use of symmetric systems of models but also symmetric systems of models with markers. Asperó–Mota iterations are used in the papers [Reference Asperó and Mota2–Reference Asperó and Mota5, Reference Miyamoto and Yorioka10, Reference Yorioka13]. In [Reference Asperó and Mota5, Reference Miyamoto and Yorioka10], the iterations require that markers of models in symmetric systems also have symmetry in a suitable sense (Definition 4.1
(el), (ho), (up), and (down)).
The Asperó–Mota iterations used in [Reference Miyamoto and Yorioka10] have length
![]() $\omega _2$
and are proper. The Asperó–Mota iterations used in [Reference Asperó and Mota5] have length beyond
$\omega _2$
and are proper. The Asperó–Mota iterations used in [Reference Asperó and Mota5] have length beyond
![]() $\omega _2$
and are claimed to be proper. The proof, however, contains a flaw, which has been acknowledged in personal communication. The problems of the proof from [Reference Asperó and Mota5] are generated by the fact that the iteration in the paper is greater than
$\omega _2$
and are claimed to be proper. The proof, however, contains a flaw, which has been acknowledged in personal communication. The problems of the proof from [Reference Asperó and Mota5] are generated by the fact that the iteration in the paper is greater than
![]() $\omega _2$
.Footnote
1
$\omega _2$
.Footnote
1
The forcing iteration in this paper deals with Asperó–Mota iterations with symmetric markers, like in [Reference Asperó and Mota5, Reference Miyamoto and Yorioka10]. We disclose a technical limitation of this type of iterations; in fact our results show that the length of Asperó–Mota iterations with symmetric markers in the style of [Reference Asperó and Mota5, Reference Miyamoto and Yorioka10] must be at most
![]() $\omega _2$
in order to ensure their properness.
$\omega _2$
in order to ensure their properness.
To achieve our goal, we consider a family of club subsets of
![]() $\omega _1$
. Specifically, it is proved that Asperó–Mota iteration can force a certain assertion, which is called (c) in this paper, concerning the existence of a family of club subsets of
$\omega _1$
. Specifically, it is proved that Asperó–Mota iteration can force a certain assertion, which is called (c) in this paper, concerning the existence of a family of club subsets of
![]() $\omega _1$
which cannot be diagonalized while preserving
$\omega _1$
which cannot be diagonalized while preserving
![]() $\aleph _2$
. The assertion was introduced by Justin Tatch Moore in personal communication and was inspired by the results in [Reference Abraham and Shelah1, Section 2]. Moreover, the natural proof of properness does not work when the length of the iteration is greater than
$\aleph _2$
. The assertion was introduced by Justin Tatch Moore in personal communication and was inspired by the results in [Reference Abraham and Shelah1, Section 2]. Moreover, the natural proof of properness does not work when the length of the iteration is greater than
![]() $\omega _2$
.
$\omega _2$
.
This paper is organized as follows. Section 2 is devoted to the basic facts of the assertion (c): In Section 2.1, the assertion (c) is introduced; in Section 2.2, we introduce forcing notions to force the assertion (c). Forcing notions stated in Section 2.2 consist of finite objects. This idea is applied to the Asperó–Mota iterations presented in this paper. The rest of the sections are devoted to our main goal, that is, to prove that the assertion (c) can be forced by Asperó–Mota iterations. In Section 3, we introduce relational structures with which we will equip our Asperó–Mota style iterations. This notion is necessary for symmetric systems with symmetric markers. We define our iteration in Section 4, and in Section 5 we prove that it forces (c). As part of this proof, we show that the iteration is proper whenever its length is at most
![]() $\omega _2$
. In the last section we explain why the proof of properness breaks down when the length of our the iteration is greater than
$\omega _2$
. In the last section we explain why the proof of properness breaks down when the length of our the iteration is greater than
![]() $\omega _2$
.
$\omega _2$
.
2 The assertion (c) and forcing (c) by finite approximations
2.1 The assertion (c)
Galvin showed that, if the Continuum Hypothesis holds, then for any family of
![]() $\aleph _2$
many club subsets of
$\aleph _2$
many club subsets of
![]() $\omega _1$
, there exists a subfamily of size
$\omega _1$
, there exists a subfamily of size
![]() $\aleph _1$
whose intersection is a club [Reference Baumgartner, Hajnal and Mate8, Section 3.2]. Abraham and Shelah showed that the assumption of CH in this theorem of Galvin is necessary. More precisely, they showed that it is consistent that there exists a family of
$\aleph _1$
whose intersection is a club [Reference Baumgartner, Hajnal and Mate8, Section 3.2]. Abraham and Shelah showed that the assumption of CH in this theorem of Galvin is necessary. More precisely, they showed that it is consistent that there exists a family of
![]() $\aleph _2$
many club subsets of
$\aleph _2$
many club subsets of
![]() $\omega _1$
such that the intersection of any uncountable subfamily is finite [Reference Abraham and Shelah1, Section 2]. (Notice that such a family cannot be diagonalized without collapsing
$\omega _1$
such that the intersection of any uncountable subfamily is finite [Reference Abraham and Shelah1, Section 2]. (Notice that such a family cannot be diagonalized without collapsing
![]() $\aleph _1$
.) They proved this consistency result by an involved forcing construction using countable objects and ccc forcing notions. Justin Tatch Moore introduced the assertion (c), which is inspired by this result of Abraham–Shelah. His assertion (c) can be forced by a countable support iteration of proper forcing notions.
$\aleph _1$
.) They proved this consistency result by an involved forcing construction using countable objects and ccc forcing notions. Justin Tatch Moore introduced the assertion (c), which is inspired by this result of Abraham–Shelah. His assertion (c) can be forced by a countable support iteration of proper forcing notions.
All definitions, propositions, and remarks in the subsection are due to Moore. Throughout the article, we assume the following.
Assumptions throughout the paper 2.1.
-
•
 $\mathcal {C} =\left \langle {C_\delta : \delta \in \omega _1 \cap \mathsf {Lim}}\right \rangle $
is a ladder system on
$\mathcal {C} =\left \langle {C_\delta : \delta \in \omega _1 \cap \mathsf {Lim}}\right \rangle $
is a ladder system on
 $\omega _1$
, that is, each
$\omega _1$
, that is, each
 $C_\delta $
is a cofinal subset of
$C_\delta $
is a cofinal subset of
 $\delta $
of order type
$\delta $
of order type
 $\omega $
; moreover, we suppose that each
$\omega $
; moreover, we suppose that each
 $C_\delta $
consists of successor ordinals (hence, for any limit ordinals
$C_\delta $
consists of successor ordinals (hence, for any limit ordinals
 $\delta $
and
$\delta $
and
 $\gamma $
in
$\gamma $
in
 $\omega _1$
with
$\omega _1$
with
 $\delta < \gamma $
,
$\delta < \gamma $
,
 $C_\delta \cap (\gamma +1) = C_\delta \cap \gamma $
),
$C_\delta \cap (\gamma +1) = C_\delta \cap \gamma $
), -
• the set
 $2^{<\omega } $
is equipped with the discrete topology, and
$2^{<\omega } $
is equipped with the discrete topology, and
 $\left ( 2^{<\omega } \right )^\omega $
is considered as the product space of copies of the discrete space
$\left ( 2^{<\omega } \right )^\omega $
is considered as the product space of copies of the discrete space
 $2^{<\omega } $
,
$2^{<\omega } $
, -
• for each
 $\nu \in \left ( 2^{<\omega } \right )^{<\omega }$
, we denote which is a basic open subset of the space
$\nu \in \left ( 2^{<\omega } \right )^{<\omega }$
, we denote which is a basic open subset of the space $$\begin{align*}[\nu] := \left\{{ g \in \left( 2^{<\omega} \right)^\omega : \nu \subseteq g}\right\} , \end{align*}$$
$$\begin{align*}[\nu] := \left\{{ g \in \left( 2^{<\omega} \right)^\omega : \nu \subseteq g}\right\} , \end{align*}$$
 $\left ( 2^{<\omega } \right )^\omega $
; here we recall that
$\left ( 2^{<\omega } \right )^\omega $
; here we recall that
 $\nu \subseteq g$
means that, for every
$\nu \subseteq g$
means that, for every
 $n \in \operatorname {dom}(\nu )$
,
$n \in \operatorname {dom}(\nu )$
,
 $\nu (n) = g(n)$
.
$\nu (n) = g(n)$
.
Definition 2.2. For a set X of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
and
$2^{<\omega }$
and
![]() $r\in 2^\omega $
, we say that a club subset E of
$r\in 2^\omega $
, we say that a club subset E of
![]() $\omega _1$
captures r relative to (
$\omega _1$
captures r relative to (
![]() $\mathcal {C}$
and) X if, for any limit point
$\mathcal {C}$
and) X if, for any limit point
![]() $\delta $
of E, there are
$\delta $
of E, there are
![]() $f\in X$
and
$f\in X$
and
![]() $\varepsilon \in \delta $
such that, for any
$\varepsilon \in \delta $
such that, for any
![]() $\xi \in (E\cap \delta )\setminus \varepsilon $
,
$\xi \in (E\cap \delta )\setminus \varepsilon $
,
![]() $f( \left | C_\delta \cap \xi \right |) \subseteq r$
.
$f( \left | C_\delta \cap \xi \right |) \subseteq r$
.
Proposition 2.3. Suppose that R is a set of reals and X is a set of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
of size
$2^{<\omega }$
of size
![]() $\aleph _1$
. If, for each
$\aleph _1$
. If, for each
![]() $r\in R$
, there exists a club subset
$r\in R$
, there exists a club subset
![]() $E_r$
of
$E_r$
of
![]() $\omega _1$
which captures r relative to X and if the set
$\omega _1$
which captures r relative to X and if the set
![]() $\left \{{ E_r : r\in R}\right \}$
can be diagonalized, then the size of R is not larger than
$\left \{{ E_r : r\in R}\right \}$
can be diagonalized, then the size of R is not larger than
![]() $\aleph _1$
.
$\aleph _1$
.
Proof. Suppose that a club subset E of
![]() $\omega _1$
diagonalizes all club sets
$\omega _1$
diagonalizes all club sets
![]() $E_r$
,
$E_r$
,
![]() $r\in R$
, (i.e., for each
$r\in R$
, (i.e., for each
![]() $r\in R$
,
$r\in R$
,
![]() $E\setminus E_r$
is bounded in
$E\setminus E_r$
is bounded in
![]() $\omega _1$
) and R is of size
$\omega _1$
) and R is of size
![]() $\geq \aleph _2$
. Then there exists
$\geq \aleph _2$
. Then there exists
![]() $\eta \in \omega _1$
such that the set
$\eta \in \omega _1$
such that the set
is of size
![]() $\geq \aleph _2$
. Let
$\geq \aleph _2$
. Let
![]() $\delta $
be a limit point of the set
$\delta $
be a limit point of the set
![]() $E\setminus \eta $
. Since X is of size
$E\setminus \eta $
. Since X is of size
![]() $\aleph _1$
, there are an injective function f in X and
$\aleph _1$
, there are an injective function f in X and
![]() $\varepsilon \in \delta $
such that
$\varepsilon \in \delta $
such that
![]() $\varepsilon \geq \eta $
and the set
$\varepsilon \geq \eta $
and the set
is of size
![]() $\geq \aleph _2$
. But then, for any
$\geq \aleph _2$
. But then, for any
![]() $r\in R"$
,
$r\in R"$
,
This contradicts the fact that
![]() $R"$
has at least two different reals.⊣
$R"$
has at least two different reals.⊣
Definition 2.4. Define the assertion (c) to be the statement that there are a set X of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
of size
$2^{<\omega }$
of size
![]() $\aleph _1$
and a collection of
$\aleph _1$
and a collection of
![]() $\aleph _2$
-many reals each one of which can be captured by a club of
$\aleph _2$
-many reals each one of which can be captured by a club of
![]() $\omega _1$
relative to X.
$\omega _1$
relative to X.
Remark 2.5. By Proposition 2.3, any collection of
![]() $\aleph _2$
many club subsets each of which captures a real r relative to X cannot be diagonalized in any outer model with the same
$\aleph _2$
many club subsets each of which captures a real r relative to X cannot be diagonalized in any outer model with the same
![]() $\aleph _2$
if all the r’s are distinct.
$\aleph _2$
if all the r’s are distinct.
Remark 2.6. Moore pointed out that, if X is a non-meager subset of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
and
$2^{<\omega }$
and
![]() $r\in 2^\omega $
, the forcing notion of all countable approximations to a club subset of
$r\in 2^\omega $
, the forcing notion of all countable approximations to a club subset of
![]() $\omega _1$
that captures r is proper and adds no new reals (however it may not be
$\omega _1$
that captures r is proper and adds no new reals (however it may not be
![]() $\sigma $
-closed). Moreover, if
$\sigma $
-closed). Moreover, if
![]() $\operatorname {\mathsf {CH}}$
holds, then it satisfies the
$\operatorname {\mathsf {CH}}$
holds, then it satisfies the
![]() $\aleph _2$
-proper isomorphic condition (
$\aleph _2$
-proper isomorphic condition (
![]() $\aleph _2$
-pic). Therefore, the assertion (c) can be forced by a countable support iteration.
$\aleph _2$
-pic). Therefore, the assertion (c) can be forced by a countable support iteration.
2.2 Forcing (c) by finite approximations
In this subsection, we deal with a forcing notion to force the assertion (c) different from the one referred to in Remark 2.6. Our forcing notion is equipped with models as side conditions [Reference Todorčević12, Section 4]. The proofs of the basic facts of this forcing notion should help the reader understand the machinery of the proofs dealing with our Asperó–Mota iteration in Section 5.
Suppose that X is a non-meager subset of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
, and
$2^{<\omega }$
, and
![]() $r\in 2^\omega $
. Let
$r\in 2^\omega $
. Let
![]() $\kappa := \left ( 2^{\aleph _0} \right )^+$
. Define
$\kappa := \left ( 2^{\aleph _0} \right )^+$
. Define
![]() $\mathfrak {M}(X,r)$
to be the set of countable elementary submodels of
$\mathfrak {M}(X,r)$
to be the set of countable elementary submodels of
![]() $H_\kappa $
which contain the set
$H_\kappa $
which contain the set
![]() $\left \{{\mathcal {C}, X, r}\right \}$
. Each member of
$\left \{{\mathcal {C}, X, r}\right \}$
. Each member of
![]() $\mathfrak {M}(X,r)$
is considered as a substructure of the structure
$\mathfrak {M}(X,r)$
is considered as a substructure of the structure
![]() $ \left \langle { H_\kappa ,\in , {\omega _1}, \mathcal {C}, X, r}\right \rangle $
. For each
$ \left \langle { H_\kappa ,\in , {\omega _1}, \mathcal {C}, X, r}\right \rangle $
. For each
![]() $M\in \mathfrak {M}(X,r)$
, the transitive collapse of M is considered as the structure
$M\in \mathfrak {M}(X,r)$
, the transitive collapse of M is considered as the structure
![]() $ \left \langle { \mathrm {trcl}(M),\in , {\omega _1}\cap M, \mathcal {C} \restriction M, X \cap M, r}\right \rangle $
, which is denoted by
$ \left \langle { \mathrm {trcl}(M),\in , {\omega _1}\cap M, \mathcal {C} \restriction M, X \cap M, r}\right \rangle $
, which is denoted by
![]() $\overline M$
.
$\overline M$
.
![]() $\Psi _M$
denotes the transitive collapsing map from M onto
$\Psi _M$
denotes the transitive collapsing map from M onto
![]() $\overline M$
. For each
$\overline M$
. For each
![]() $M\in \mathfrak {M}(X,r)$
, since M is countable and
$M\in \mathfrak {M}(X,r)$
, since M is countable and
![]() ${\omega _1}$
is of uncountable cofinality,
${\omega _1}$
is of uncountable cofinality,
![]() $\omega _1\cap M$
is a countable ordinal. And if M and
$\omega _1\cap M$
is a countable ordinal. And if M and
![]() $M'$
in
$M'$
in
![]() $\mathfrak {M}(X,r)$
have the same transitive collapse, then
$\mathfrak {M}(X,r)$
have the same transitive collapse, then
![]() $\omega _1\cap M=\omega _1\cap M'$
, and the composition
$\omega _1\cap M=\omega _1\cap M'$
, and the composition
![]() ${\Psi _{M'}}^{-1}\circ \Psi _M$
is an isomorphism from the structure
${\Psi _{M'}}^{-1}\circ \Psi _M$
is an isomorphism from the structure
![]() $ \left \langle { M,\in , {\omega _1}, \mathcal {C} , X , r}\right \rangle $
onto the structure
$ \left \langle { M,\in , {\omega _1}, \mathcal {C} , X , r}\right \rangle $
onto the structure
![]() $ \left \langle { M', \in , {\omega _1}, \mathcal {C} , X , r}\right \rangle\!. $
$ \left \langle { M', \in , {\omega _1}, \mathcal {C} , X , r}\right \rangle\!. $
In this subsection, we suppose
![]() $2^{\aleph _0} = \aleph _1$
. If M and
$2^{\aleph _0} = \aleph _1$
. If M and
![]() $M'$
in
$M'$
in
![]() $\mathfrak {M}(X,r)$
satisfy
$\mathfrak {M}(X,r)$
satisfy
![]() $\omega _1\cap M = \omega _1 \cap M'$
, then
$\omega _1\cap M = \omega _1 \cap M'$
, then
![]() $\mathbb {R} \cap M = \mathbb {R}\cap M'$
. So the set of Borel codes in M coincides with those in
$\mathbb {R} \cap M = \mathbb {R}\cap M'$
. So the set of Borel codes in M coincides with those in
![]() $M'$
. Therefore, for any
$M'$
. Therefore, for any
![]() $f\in \left ({2^{<\omega }}\right )^\omega $
, f is Cohen over M iff f is Cohen over
$f\in \left ({2^{<\omega }}\right )^\omega $
, f is Cohen over M iff f is Cohen over
![]() $M'$
. In this subsection, we identify a non-meager set X (which is of size
$M'$
. In this subsection, we identify a non-meager set X (which is of size
![]() $\aleph _1$
) with some fixed enumeration of X of length
$\aleph _1$
) with some fixed enumeration of X of length
![]() $\omega _1$
. Then, if M and
$\omega _1$
. Then, if M and
![]() $M'$
in
$M'$
in
![]() $\mathfrak {M}(X,r)$
satisfies
$\mathfrak {M}(X,r)$
satisfies
![]() $\omega _1\cap M = \omega _1 \cap M'$
, then
$\omega _1\cap M = \omega _1 \cap M'$
, then
![]() $X\cap M = X \cap M'$
. We notice that, for any
$X\cap M = X \cap M'$
. We notice that, for any
![]() $M \in \mathfrak {M}(X,r)$
and any
$M \in \mathfrak {M}(X,r)$
and any
![]() $f\in \left ( 2^{<\omega }\right )^\omega $
which is Cohen over M, the set
$f\in \left ( 2^{<\omega }\right )^\omega $
which is Cohen over M, the set
![]() $\left \{{ n \in \omega : f(n) \subseteq r}\right \}$
is infinite.
$\left \{{ n \in \omega : f(n) \subseteq r}\right \}$
is infinite.
In Section 4, we will define an Asperó–Mota iteration of forcing notions playing the same role as the following forcing notions.
Definition 2.7. Define the forcing notion
![]() $\mathbb {Q}(X,r)$
consisting of the triples
$\mathbb {Q}(X,r)$
consisting of the triples
![]() $p=\left \langle {\mathcal {N}_p^0, \mathcal {N}_p^1, A_p}\right \rangle $
such that
$p=\left \langle {\mathcal {N}_p^0, \mathcal {N}_p^1, A_p}\right \rangle $
such that
-
(sym)
 $\mathcal {N}_p^0 \cup \mathcal {N}_p^1$
is a finite subset of
$\mathcal {N}_p^0 \cup \mathcal {N}_p^1$
is a finite subset of
 $\mathfrak {M}(X,r)$
such that
$\mathfrak {M}(X,r)$
such that-
• for each
 $M,M'\in \mathcal {N}^0_p\cup \mathcal {N}^1_p$
, if
$M,M'\in \mathcal {N}^0_p\cup \mathcal {N}^1_p$
, if
 $\omega _1\cap M=\omega _1\cap M'$
, then
$\omega _1\cap M=\omega _1\cap M'$
, then
 $\overline M=\overline {M'}$
,
$\overline M=\overline {M'}$
, -
• for each
 $M, M'\in \mathcal {N}^0_p\cup \mathcal {N}^1_p$
, if
$M, M'\in \mathcal {N}^0_p\cup \mathcal {N}^1_p$
, if
 $\omega _1\cap M'<\omega _1\cap M$
, then there exists
$\omega _1\cap M'<\omega _1\cap M$
, then there exists
 $M"\in \mathcal {N}^0_p\cup \mathcal {N}^1_p$
such that
$M"\in \mathcal {N}^0_p\cup \mathcal {N}^1_p$
such that
 $\overline {M"}=\overline M$
and
$\overline {M"}=\overline M$
and
 $M'\in M"$
,
$M'\in M"$
,
-
-
(ob)
 $A_p$
is a finite set of tuples of the form
$A_p$
is a finite set of tuples of the form
 $\sigma = \left \langle {\varepsilon _\sigma , \delta _\sigma , \gamma _\sigma , f_\sigma }\right \rangle $
such that
$\sigma = \left \langle {\varepsilon _\sigma , \delta _\sigma , \gamma _\sigma , f_\sigma }\right \rangle $
such that
 $\varepsilon _\sigma , \delta _\sigma , \gamma _\sigma \in \omega _1$
,
$\varepsilon _\sigma , \delta _\sigma , \gamma _\sigma \in \omega _1$
,
 $\varepsilon _\sigma < \delta _\sigma < \gamma _\sigma $
, and
$\varepsilon _\sigma < \delta _\sigma < \gamma _\sigma $
, and
 $f_\sigma \in X$
,
$f_\sigma \in X$
, -
(ob-2)
-
• the set
 $\left \{{\delta _\sigma : \sigma \in A_p}\right \} $
includes the set
$\left \{{\delta _\sigma : \sigma \in A_p}\right \} $
includes the set
 $\left \{{\omega _1\cap N : N \in \mathcal {N}_p^0}\right \}$
, and the set
$\left \{{\omega _1\cap N : N \in \mathcal {N}_p^0}\right \}$
, and the set
 $\left \{{\gamma _\sigma : \sigma \in A_p}\right \} $
includes the set
$\left \{{\gamma _\sigma : \sigma \in A_p}\right \} $
includes the set
 $\left \{{\omega _1\cap M : M \in \mathcal {N}_p^1}\right \}$
,
$\left \{{\omega _1\cap M : M \in \mathcal {N}_p^1}\right \}$
, -
• for any
 $\sigma \in A_p$
and any
$\sigma \in A_p$
and any
 $N\in \mathcal {N}_p^0$
, if
$N\in \mathcal {N}_p^0$
, if
 $\omega _1\cap N = \delta _\sigma $
, then there exists
$\omega _1\cap N = \delta _\sigma $
, then there exists
 $M\in \mathcal {N}_p^1$
such that
$M\in \mathcal {N}_p^1$
such that
 $N \in M$
and
$N \in M$
and
 $\omega _1\cap M = \gamma _\sigma $
,
$\omega _1\cap M = \gamma _\sigma $
, -
• for any
 $\sigma \in A_p$
and any
$\sigma \in A_p$
and any
 $M\in \mathcal {N}_p^1$
, if
$M\in \mathcal {N}_p^1$
, if
 $\omega _1\cap M = \gamma _\sigma $
, then
$\omega _1\cap M = \gamma _\sigma $
, then
 $f_\sigma $
is Cohen over M,
$f_\sigma $
is Cohen over M, -
• for any
 $\sigma \in A_p$
and
$\sigma \in A_p$
and
 $N \in \mathcal {N}_p^0$
, if
$N \in \mathcal {N}_p^0$
, if
 $\delta _\sigma < \omega _1\cap N$
, then
$\delta _\sigma < \omega _1\cap N$
, then
 $\sigma \in N$
,
$\sigma \in N$
,
-
-
(cl) for any
 $\left \{{\sigma ,\tau }\right \}\in \left [A_p \right ]^2$
, either
$\left \{{\sigma ,\tau }\right \}\in \left [A_p \right ]^2$
, either
 $\gamma _\sigma < \delta _\tau $
or
$\gamma _\sigma < \delta _\tau $
or
 $\gamma _\tau < \delta _\sigma $
, and
$\gamma _\tau < \delta _\sigma $
, and -
(w) for any
 $\sigma \in A_p$
, if
$\sigma \in A_p$
, if
 $\delta _\sigma $
is a limit ordinal, then the set
$\delta _\sigma $
is a limit ordinal, then the set
 $\left \{{ n \in \omega : f_\sigma (n) \subseteq r }\right \}$
is infinite, and for any
$\left \{{ n \in \omega : f_\sigma (n) \subseteq r }\right \}$
is infinite, and for any
 $\tau \in A_p\setminus \left \{{\sigma }\right \}$
with
$\tau \in A_p\setminus \left \{{\sigma }\right \}$
with
 $\varepsilon _{\sigma } < \delta _\tau < \delta _\sigma $
,
$\varepsilon _{\sigma } < \delta _\tau < \delta _\sigma $
,
 $f_{\sigma } ( \left | C_{\delta _\sigma } \cap \delta _\tau \right |) \subseteq r$
and
$f_{\sigma } ( \left | C_{\delta _\sigma } \cap \delta _\tau \right |) \subseteq r$
and
 $f_{\sigma } ( \left | C_{\delta _\sigma } \cap (\gamma _\tau +1) \right |) \subseteq r$
,
$f_{\sigma } ( \left | C_{\delta _\sigma } \cap (\gamma _\tau +1) \right |) \subseteq r$
,
for each
![]() $p,q \in \mathbb {Q}(X,r)$
,
$p,q \in \mathbb {Q}(X,r)$
,
![]() $q \leq _{\mathbb {Q}(X,r)} p $
if
$q \leq _{\mathbb {Q}(X,r)} p $
if
![]() $\mathcal {N}_q^0 \supseteq \mathcal {N}_p^0$
,
$\mathcal {N}_q^0 \supseteq \mathcal {N}_p^0$
,
![]() $\mathcal {N}_q^1 \supseteq \mathcal {N}_p^1$
,
$\mathcal {N}_q^1 \supseteq \mathcal {N}_p^1$
,
![]() $A_q \supseteq A_p$
.
$A_q \supseteq A_p$
.
We notice that, for any
![]() $p\in \mathbb {Q}(X,r)$
, any
$p\in \mathbb {Q}(X,r)$
, any
![]() $N\in \mathcal {N}^0_p$
and any
$N\in \mathcal {N}^0_p$
and any
![]() $M \in \mathcal {N}^1_p$
,
$M \in \mathcal {N}^1_p$
,
![]() $\omega _1\cap N \neq \omega _1\cap M$
.
$\omega _1\cap N \neq \omega _1\cap M$
.
Lemma 2.8. For any non-meager set X of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
and any
$2^{<\omega }$
and any
![]() $r\in 2^\omega $
,
$r\in 2^\omega $
,
![]() $\mathbb {Q}(X,r)$
is proper.
$\mathbb {Q}(X,r)$
is proper.
Proof. Let
![]() $\theta $
be a large enough regular cardinal,
$\theta $
be a large enough regular cardinal,
![]() $N^*$
a countable elementary submodel of
$N^*$
a countable elementary submodel of
![]() $H_\theta $
which contains
$H_\theta $
which contains
![]() $\left \{{\mathcal {C}, X , r, H_{\kappa }}\right \}$
, and
$\left \{{\mathcal {C}, X , r, H_{\kappa }}\right \}$
, and
![]() $p \in \mathbb {Q}(X,r) \cap N^*$
. Let
$p \in \mathbb {Q}(X,r) \cap N^*$
. Let
![]() $M^*$
be a countable elementary submodel of
$M^*$
be a countable elementary submodel of
![]() $H_\theta $
which has the set
$H_\theta $
which has the set
![]() $\{N^*\}$
, and let
$\{N^*\}$
, and let
![]() $\varepsilon _* \in \omega _1\cap N^*$
such that
$\varepsilon _* \in \omega _1\cap N^*$
such that
![]() $\delta _\sigma <\varepsilon _*$
for every
$\delta _\sigma <\varepsilon _*$
for every
![]() $\sigma \in A_p$
. We denote
$\sigma \in A_p$
. We denote
![]() $N_* := N^* \cap H_{\kappa } $
and
$N_* := N^* \cap H_{\kappa } $
and
![]() $M_* := M^* \cap H_{\kappa } $
. Since X is non-meager and
$M_* := M^* \cap H_{\kappa } $
. Since X is non-meager and
![]() $M^*$
is countable, there exists a function
$M^*$
is countable, there exists a function
![]() $f_*$
in X which is Cohen over
$f_*$
in X which is Cohen over
![]() $M^*$
. Define
$M^*$
. Define
![]() $ \sigma _* := \left \langle {\varepsilon _* , \omega _1\cap N_* , \omega _1\cap M_* , f_* }\right \rangle $
and
$ \sigma _* := \left \langle {\varepsilon _* , \omega _1\cap N_* , \omega _1\cap M_* , f_* }\right \rangle $
and
![]() $ p^+ : = \left \langle {\mathcal {N}_p^0 \cup \left \{{N_*}\right \}, \mathcal {N}_p^1\cup \left \{{M_*}\right \}, A_p \cup \left \{{ \sigma _*}\right \} }\right \rangle. $
$ p^+ : = \left \langle {\mathcal {N}_p^0 \cup \left \{{N_*}\right \}, \mathcal {N}_p^1\cup \left \{{M_*}\right \}, A_p \cup \left \{{ \sigma _*}\right \} }\right \rangle. $
![]() $p^+$
is a condition of
$p^+$
is a condition of
![]() $\mathbb {Q}(X,r)$
, and hence is an extension of p.
$\mathbb {Q}(X,r)$
, and hence is an extension of p.
Let us show that
![]() $p^+$
is an
$p^+$
is an
![]() $N^*$
-generic condition of
$N^*$
-generic condition of
![]() $\mathbb {Q}(X,r)$
. Let
$\mathbb {Q}(X,r)$
. Let
![]() $\mathcal {D}$
be a predense subset of
$\mathcal {D}$
be a predense subset of
![]() $\mathbb {Q}(X,r)$
which belongs to
$\mathbb {Q}(X,r)$
which belongs to
![]() $N^*$
, and q an extension of
$N^*$
, and q an extension of
![]() $p^+$
in
$p^+$
in
![]() $\mathbb {Q}(X,r)$
. By extending q if necessary, we may assume that q is an extension of some member of
$\mathbb {Q}(X,r)$
. By extending q if necessary, we may assume that q is an extension of some member of
![]() $\mathcal {D}$
. Moreover, by extending q if necessary again, we may assume that the set
$\mathcal {D}$
. Moreover, by extending q if necessary again, we may assume that the set
![]() $\left ( \mathcal {N}_q^0 \cup \mathcal {N}_q^1 \right ) \cap N_*$
includes the set
$\left ( \mathcal {N}_q^0 \cup \mathcal {N}_q^1 \right ) \cap N_*$
includes the set
 $$ \begin{align*} { \begin{array}{r@{}l} \Big\{ \left( \left(\Psi_{N_*}\right)^{-1} \circ \Psi_{N} \right) (K) :{\ } & N\in\mathcal{N}_q^0 \text{ with }\omega_1\cap N = \omega_1\cap N_* , \\ & K \in \left(\mathcal{N}_q^0 \cup \mathcal{N}_q^1\right) \cap N \Big\}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \Big\{ \left( \left(\Psi_{N_*}\right)^{-1} \circ \Psi_{N} \right) (K) :{\ } & N\in\mathcal{N}_q^0 \text{ with }\omega_1\cap N = \omega_1\cap N_* , \\ & K \in \left(\mathcal{N}_q^0 \cup \mathcal{N}_q^1\right) \cap N \Big\}. \end{array} } \end{align*} $$
Define
![]() $\mathcal {E}$
to be the set of the conditions u of
$\mathcal {E}$
to be the set of the conditions u of
![]() $\mathbb {Q}(X,r) $
such that
$\mathbb {Q}(X,r) $
such that
-
• u is an extension of some member of
 $\mathcal {D}$
in
$\mathcal {D}$
in
 $\mathbb {Q}(X,r)$
,
$\mathbb {Q}(X,r)$
, -
•
 $\mathcal {N}_u^0 \cap N = \mathcal {N}_q^0 \cap N_*$
,
$\mathcal {N}_u^0 \cap N = \mathcal {N}_q^0 \cap N_*$
,
 $\mathcal {N}_u^1 \cap M = \mathcal {N}_q^1 \cap M_*$
(
$\mathcal {N}_u^1 \cap M = \mathcal {N}_q^1 \cap M_*$
(
 $= \mathcal {N}_q^1 \cap N_*$
), and
$= \mathcal {N}_q^1 \cap N_*$
), and
 $N \in M$
for some
$N \in M$
for some
 $N \in \mathcal {N}_u^0$
and some
$N \in \mathcal {N}_u^0$
and some
 $M \in \mathcal {N}_u^1$
,
$M \in \mathcal {N}_u^1$
, -
•
 $A_u \supseteq A_q\cap N_*$
, and, for any
$A_u \supseteq A_q\cap N_*$
, and, for any
 $\sigma \in A_u\setminus (A_q\cap N_*)$
and any
$\sigma \in A_u\setminus (A_q\cap N_*)$
and any
 $\tau \in A_q\setminus \left ( N_* \cup \left \{{ \sigma _* }\right \} \right )$
,
$\tau \in A_q\setminus \left ( N_* \cup \left \{{ \sigma _* }\right \} \right )$
,  $$\begin{align*}\max\left( C_{\delta_\tau}\cap N_* \right) < \delta_\sigma. \end{align*}$$
$$\begin{align*}\max\left( C_{\delta_\tau}\cap N_* \right) < \delta_\sigma. \end{align*}$$
Then
![]() $p^+ \in \mathcal {E}$
. Since the set
$p^+ \in \mathcal {E}$
. Since the set
belongs to
![]() $N^*$
, by elementarity of
$N^*$
, by elementarity of
![]() $N^*$
,
$N^*$
,
![]() $\mathcal {E}$
belongs to
$\mathcal {E}$
belongs to
![]() $N^*$
. We note that
$N^*$
. We note that
-
♠ if
 $u\in \mathcal {E} \cap N_*$
, then for any
$u\in \mathcal {E} \cap N_*$
, then for any
 $\sigma \in A_u\setminus (A_q\cap N_*)$
and any
$\sigma \in A_u\setminus (A_q\cap N_*)$
and any
 $\tau \in A_q\setminus \left ( N_* \cup \left \{{ \sigma _* }\right \} \right )$
,
$\tau \in A_q\setminus \left ( N_* \cup \left \{{ \sigma _* }\right \} \right )$
,  $$\begin{align*}C_{\delta_\tau}\cap \delta_\sigma = C_{\delta_\tau}\cap \gamma_\sigma = C_{\delta_\tau}\cap N_* = C_{\delta_\tau} \cap \delta_{\sigma_*}. \end{align*}$$
$$\begin{align*}C_{\delta_\tau}\cap \delta_\sigma = C_{\delta_\tau}\cap \gamma_\sigma = C_{\delta_\tau}\cap N_* = C_{\delta_\tau} \cap \delta_{\sigma_*}. \end{align*}$$
It follows from elementarity of
![]() $N^*$
that
$N^*$
that
-
♦ for any
 $\eta \in \omega _1\cap N_*$
, there exists
$\eta \in \omega _1\cap N_*$
, there exists
 $u\in \mathcal {E}\cap N^*$
such that, for every
$u\in \mathcal {E}\cap N^*$
such that, for every
 $\tau \in A_u \setminus (A_q\cap N_*)$
,
$\tau \in A_u \setminus (A_q\cap N_*)$
,
 $\eta < \delta _\tau $
, hence, for any
$\eta < \delta _\tau $
, hence, for any
 $n\in \omega $
, there exists
$n\in \omega $
, there exists
 $u\in \mathcal {E}\cap N^*$
such that, for every
$u\in \mathcal {E}\cap N^*$
such that, for every
 $\tau \in A_u \setminus (A_q\cap N_*)$
,
$\tau \in A_u \setminus (A_q\cap N_*)$
,
 $\left | C_{\omega _1\cap N_*}\cap \gamma _\tau \right | \geq \left | C_{\omega _1\cap N_*}\cap \delta _\tau \right | \geq n$
.
$\left | C_{\omega _1\cap N_*}\cap \gamma _\tau \right | \geq \left | C_{\omega _1\cap N_*}\cap \delta _\tau \right | \geq n$
.
Define Z to be the set of the functions g from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
such that there exists
$2^{<\omega }$
such that there exists
![]() $u\in \mathcal {E} \cap N^*$
which satisfies that for any
$u\in \mathcal {E} \cap N^*$
which satisfies that for any
![]() $\tau \in A_u\setminus \left ( A_q\cap N_* \right )$
,
$\tau \in A_u\setminus \left ( A_q\cap N_* \right )$
,
![]() $g ( \left | C_{\omega _1\cap N_* } \cap \delta _\tau \right |) \subseteq r$
and
$g ( \left | C_{\omega _1\cap N_* } \cap \delta _\tau \right |) \subseteq r$
and
![]() $g ( \left | C_{\omega _1\cap N_* } \cap (\gamma _\tau +1) \right |) \subseteq r$
. Since Z is defined from
$g ( \left | C_{\omega _1\cap N_* } \cap (\gamma _\tau +1) \right |) \subseteq r$
. Since Z is defined from
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $C_{\omega _1\cap N_*}$
(
$C_{\omega _1\cap N_*}$
(
![]() $= C_{\delta _{\sigma _*}}$
), and the set
$= C_{\delta _{\sigma _*}}$
), and the set
![]() $\left \{{\mathcal {E}, N^*, C_{\omega _1\cap N_*}}\right \}$
is in
$\left \{{\mathcal {E}, N^*, C_{\omega _1\cap N_*}}\right \}$
is in
![]() $M^*$
, Z belongs to
$M^*$
, Z belongs to
![]() $M^*$
. By the property
$M^*$
. By the property
![]() $\blacklozenge $
of
$\blacklozenge $
of
![]() $\mathcal {E} \cap N^*$
, Z is a dense open subset of the space
$\mathcal {E} \cap N^*$
, Z is a dense open subset of the space
![]() $\left ( 2^{<\omega } \right )^\omega $
. Since
$\left ( 2^{<\omega } \right )^\omega $
. Since
![]() $f_*$
is Cohen over
$f_*$
is Cohen over
![]() $M^*$
,
$M^*$
,
![]() $f_*$
belongs to Z. Let u be a witness that
$f_*$
belongs to Z. Let u be a witness that
![]() $f_*$
belongs to Z.
$f_*$
belongs to Z.
Define
![]() $u' =\left \langle {\mathcal {N}_{u'}^0, \mathcal {N}_{u'}^1, A_{u'}}\right \rangle $
such that
$u' =\left \langle {\mathcal {N}_{u'}^0, \mathcal {N}_{u'}^1, A_{u'}}\right \rangle $
such that
 $$\begin{align*}\begin{array}{r@{\ }l} \mathcal{N}_{u'}^0:= & \mathcal{N}_q^0 \cup \mathcal{N}_u^0 \\[5pt] & \cup \Big\{ \left( {\Psi_{N} }^{-1} \circ \Psi_{N_*} \right) (N') : N\in \mathcal{N}_q^0 \text{ with } \omega_1\cap N=\omega_1\cap N_*, N'\in \mathcal{N}_u^0 \Big\}, \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} \mathcal{N}_{u'}^0:= & \mathcal{N}_q^0 \cup \mathcal{N}_u^0 \\[5pt] & \cup \Big\{ \left( {\Psi_{N} }^{-1} \circ \Psi_{N_*} \right) (N') : N\in \mathcal{N}_q^0 \text{ with } \omega_1\cap N=\omega_1\cap N_*, N'\in \mathcal{N}_u^0 \Big\}, \end{array} \end{align*}$$
 $$\begin{align*}\begin{array}{r@{\ }l@{\ }l} \mathcal{N}_{u'}^1:= & \mathcal{N}_q^1 \cup \mathcal{N}_u^1 \\[5pt] & \cup \Big\{ \left( {\Psi_{M} }^{-1} \circ \Psi_{N_*} \right) (M') : & M\in \mathcal{N}_q^1 \text{ with } \omega_1\cap M=\omega_1\cap M_*, \\ && M'\in \mathcal{N}_u^1 \Big\}, \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l@{\ }l} \mathcal{N}_{u'}^1:= & \mathcal{N}_q^1 \cup \mathcal{N}_u^1 \\[5pt] & \cup \Big\{ \left( {\Psi_{M} }^{-1} \circ \Psi_{N_*} \right) (M') : & M\in \mathcal{N}_q^1 \text{ with } \omega_1\cap M=\omega_1\cap M_*, \\ && M'\in \mathcal{N}_u^1 \Big\}, \end{array} \end{align*}$$
Let us show that
![]() $u'$
is a condition of
$u'$
is a condition of
![]() $\mathbb {Q}(X,r)$
. Then it follows that
$\mathbb {Q}(X,r)$
. Then it follows that
![]() $u'$
is a common extension of q and u, which completes the proof. Since u and q satisfies (ob) and (ob-2), so does
$u'$
is a common extension of q and u, which completes the proof. Since u and q satisfies (ob) and (ob-2), so does
![]() $u'$
. Since
$u'$
. Since
![]() $A_{u'}$
is an end-extension of
$A_{u'}$
is an end-extension of
![]() $A_q\cap N_*$
and
$A_q\cap N_*$
and
![]() $u'\in N^*$
,
$u'\in N^*$
,
![]() $A_{u'}$
satisfies (cl). We will check two non-trivial cases of (w) for
$A_{u'}$
satisfies (cl). We will check two non-trivial cases of (w) for
![]() $u'$
. Suppose that
$u'$
. Suppose that
![]() $\sigma \in A_{u}\setminus (A_q\cap N_*)$
and
$\sigma \in A_{u}\setminus (A_q\cap N_*)$
and
![]() $\tau \in A_q\setminus \left ( N_* \cup \left \{{ \sigma _* }\right \} \right )$
. Then
$\tau \in A_q\setminus \left ( N_* \cup \left \{{ \sigma _* }\right \} \right )$
. Then
![]() $\delta _\sigma < \delta _\tau $
. If
$\delta _\sigma < \delta _\tau $
. If
![]() $\varepsilon _\tau < \delta _\sigma $
, then
$\varepsilon _\tau < \delta _\sigma $
, then
![]() $\varepsilon _\tau < \omega _1\cap N_*$
, and so, by
$\varepsilon _\tau < \omega _1\cap N_*$
, and so, by
![]() $\spadesuit $
,
$\spadesuit $
,
This takes care of one non-trivial case. Since u is a witness that
![]() $f_* \in Z$
,
$f_* \in Z$
,
and
This takes care of the other non-trivial case. Therefore,
![]() $A_{u'}$
satisfies (w).⊣
$A_{u'}$
satisfies (w).⊣
Proposition 2.9. For any non-meager set X of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
and any
$2^{<\omega }$
and any
![]() $r\in 2^\omega $
,
$r\in 2^\omega $
,
where
![]() $[\delta , \gamma ] := \left \{{\xi \in \gamma +1 : \delta \leq \xi }\right \}$
, and
$[\delta , \gamma ] := \left \{{\xi \in \gamma +1 : \delta \leq \xi }\right \}$
, and
![]() $\mathsf {Lim}$
denotes the class of the limit ordinals.
$\mathsf {Lim}$
denotes the class of the limit ordinals.
Proof. Let
![]() $p\in \mathbb {Q}(X,r)$
and
$p\in \mathbb {Q}(X,r)$
and
![]() $\xi \in \omega _1\cap \mathsf {Lim}$
. Suppose that
$\xi \in \omega _1\cap \mathsf {Lim}$
. Suppose that
![]() $\xi $
is not in the set
$\xi $
is not in the set
![]() $\displaystyle \bigcup _{\sigma \in A_p} \left [ \delta _\sigma , \gamma _\sigma \right ]$
and that there exists
$\displaystyle \bigcup _{\sigma \in A_p} \left [ \delta _\sigma , \gamma _\sigma \right ]$
and that there exists
![]() $\sigma _0 \in A_p$
such that
$\sigma _0 \in A_p$
such that
![]() $\gamma _{\sigma _0} < \xi $
. Since
$\gamma _{\sigma _0} < \xi $
. Since
![]() $\xi $
is a limit ordinal,
$\xi $
is a limit ordinal,
![]() $\gamma _{\sigma _0} +1 < \xi $
. We may assume that
$\gamma _{\sigma _0} +1 < \xi $
. We may assume that
![]() $\sigma _0$
is a largest tuple of
$\sigma _0$
is a largest tuple of
![]() $A_p$
with this property. Take
$A_p$
with this property. Take
![]() $f_0 \in X \cap \bigcap \mathcal {N}^0_p$
.
$f_0 \in X \cap \bigcap \mathcal {N}^0_p$
.
If there are no
![]() $\tau \in A_p$
such that
$\tau \in A_p$
such that
![]() $\xi < \delta _\tau $
, then let
$\xi < \delta _\tau $
, then let
![]() $\delta \in \xi $
be a successor ordinal such that
$\delta \in \xi $
be a successor ordinal such that
![]() $\gamma _\sigma < \delta < \xi $
for every
$\gamma _\sigma < \delta < \xi $
for every
![]() $\sigma \in A_p$
, and define
$\sigma \in A_p$
, and define
![]() $q:= \big \langle \mathcal {N}^0_p, \mathcal {N}^1_p, A_p\cup \left \{{ \left \langle {\gamma _{\sigma _0}, \delta , \xi +1, f_0}\right \rangle }\right \} \big \rangle $
. Suppose that
$q:= \big \langle \mathcal {N}^0_p, \mathcal {N}^1_p, A_p\cup \left \{{ \left \langle {\gamma _{\sigma _0}, \delta , \xi +1, f_0}\right \rangle }\right \} \big \rangle $
. Suppose that
![]() $\xi < \gamma _\tau $
for some
$\xi < \gamma _\tau $
for some
![]() $\tau \in A_p$
. Let
$\tau \in A_p$
. Let
![]() $\sigma _1\in A_p$
be the smallest tuple with the property that
$\sigma _1\in A_p$
be the smallest tuple with the property that
![]() $\xi < \gamma _{\sigma _1}$
. Then by our assumption,
$\xi < \gamma _{\sigma _1}$
. Then by our assumption,
![]() $\xi < \delta _{\sigma _1}$
. If
$\xi < \delta _{\sigma _1}$
. If
![]() $\delta _{\sigma _1}$
is a successor ordinal, then define
$\delta _{\sigma _1}$
is a successor ordinal, then define
![]() $q := \big \langle \mathcal {N}^0_p, \mathcal {N}^1_p, A_p\cup \left \{{ \left \langle {\gamma _{\sigma _0}, \gamma _{\sigma _0}+1, \delta _{\sigma _1} - 1 , f_0}\right \rangle }\right \} \big \rangle $
. If
$q := \big \langle \mathcal {N}^0_p, \mathcal {N}^1_p, A_p\cup \left \{{ \left \langle {\gamma _{\sigma _0}, \gamma _{\sigma _0}+1, \delta _{\sigma _1} - 1 , f_0}\right \rangle }\right \} \big \rangle $
. If
![]() $\delta _{\sigma _1}$
is a limit ordinal, then take
$\delta _{\sigma _1}$
is a limit ordinal, then take
![]() $\gamma \in \delta _{\sigma _1}$
such that, for any
$\gamma \in \delta _{\sigma _1}$
such that, for any
![]() $\tau \in A_p$
with
$\tau \in A_p$
with
![]() $\delta _\tau> \delta _{\sigma _1}$
, if
$\delta _\tau> \delta _{\sigma _1}$
, if
![]() $\delta _\tau $
is a limit ordinal, then
$\delta _\tau $
is a limit ordinal, then
It follows that, if
![]() $\varepsilon _\tau < \delta _{\sigma _1}$
, then
$\varepsilon _\tau < \delta _{\sigma _1}$
, then
![]() $f_\tau ( \left | C_{\delta _\tau } \cap (\gamma +1) \right |) \subseteq r$
. By extending
$f_\tau ( \left | C_{\delta _\tau } \cap (\gamma +1) \right |) \subseteq r$
. By extending
![]() $\gamma $
if necessary, we may assume that
$\gamma $
if necessary, we may assume that
This can be done because the set
![]() $ \{{n\in \omega : f_{\gamma _{\sigma _1}} (n) \subseteq r} \}$
is infinite. Define
$ \{{n\in \omega : f_{\gamma _{\sigma _1}} (n) \subseteq r} \}$
is infinite. Define
![]() $q := \big \langle \mathcal {N}^0_p, \mathcal {N}^1_p, A_p\cup \left \{{ \left \langle {\gamma _{\sigma _0}, \gamma _{\sigma _0}+1, \gamma , f_0}\right \rangle }\right \} \big \rangle $
.
$q := \big \langle \mathcal {N}^0_p, \mathcal {N}^1_p, A_p\cup \left \{{ \left \langle {\gamma _{\sigma _0}, \gamma _{\sigma _0}+1, \gamma , f_0}\right \rangle }\right \} \big \rangle $
.
In each case, q is a condition of
![]() $\mathbb {Q}(X,r)$
, and hence it is an extension of p in
$\mathbb {Q}(X,r)$
, and hence it is an extension of p in
![]() $\mathbb {Q}(X,r)$
and
$\mathbb {Q}(X,r)$
and
which finishes the proof.⊣
It follows from this proposition that
The following lemma shows that
![]() $\mathbb {Q}(X,r)$
almost preserves
$\mathbb {Q}(X,r)$
almost preserves
![]() $\sqsubseteq ^{\mathrm {Cohen}}$
in the sense of Goldstern [Reference Goldstern9, Section 6, Application 3] (see also [Reference Bartoszyński and Judah7, Section 6.3.C]). It follows that
$\sqsubseteq ^{\mathrm {Cohen}}$
in the sense of Goldstern [Reference Goldstern9, Section 6, Application 3] (see also [Reference Bartoszyński and Judah7, Section 6.3.C]). It follows that
![]() $\mathbb {Q}(X,r)$
preserves non-meager sets of reals (from [Reference Bartoszyński and Judah7, Lemmas 6.3.16 and 6.3.17]). This is necessary to guarantee that a countable support iteration of forcing notions of the form
$\mathbb {Q}(X,r)$
preserves non-meager sets of reals (from [Reference Bartoszyński and Judah7, Lemmas 6.3.16 and 6.3.17]). This is necessary to guarantee that a countable support iteration of forcing notions of the form
![]() $\mathbb {Q}(X,r)$
is still proper because the non-meagerness of X is used to prove properness of
$\mathbb {Q}(X,r)$
is still proper because the non-meagerness of X is used to prove properness of
![]() $\mathbb {Q}(X,r)$
. The preservation of
$\mathbb {Q}(X,r)$
. The preservation of
![]() $\sqsubseteq ^{\mathrm {Cohen}}$
is closed under countable support iterations [Reference Bartoszyński and Judah7, Theorems 6.1.13 and 6.3.20]. Therefore, for any non-meager set X of injective functions from
$\sqsubseteq ^{\mathrm {Cohen}}$
is closed under countable support iterations [Reference Bartoszyński and Judah7, Theorems 6.1.13 and 6.3.20]. Therefore, for any non-meager set X of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
, a countable support iteration of forcing notion of the form
$2^{<\omega }$
, a countable support iteration of forcing notion of the form
![]() $\mathbb {Q}(X,r)$
is still proper and forces X to be non-meager.
$\mathbb {Q}(X,r)$
is still proper and forces X to be non-meager.
Lemma 2.10. Let X be a non-meager set of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
,
$2^{<\omega }$
,
![]() $r\in 2^\omega $
,
$r\in 2^\omega $
,
![]() $\theta $
a regular cardinal such that
$\theta $
a regular cardinal such that
![]() $H_{\kappa } \in H_\theta $
, and
$H_{\kappa } \in H_\theta $
, and
![]() $\lambda $
a regular cardinal such that
$\lambda $
a regular cardinal such that
![]() $H_\theta \in H_{\lambda }$
. Then, for any countable elementary submodel
$H_\theta \in H_{\lambda }$
. Then, for any countable elementary submodel
![]() $N^*$
of
$N^*$
of
![]() $H_\lambda $
which contains the set
$H_\lambda $
which contains the set
![]() $\left \{{\mathcal {C}, X , r, H_{\kappa }, H_\theta }\right \}$
, any
$\left \{{\mathcal {C}, X , r, H_{\kappa }, H_\theta }\right \}$
, any
![]() $c \in 2^\omega $
which is Cohen over
$c \in 2^\omega $
which is Cohen over
![]() $N^*$
, and any
$N^*$
, and any
![]() $p \in \mathbb {Q}(X,r) \cap N^*$
, there exists an extension
$p \in \mathbb {Q}(X,r) \cap N^*$
, there exists an extension
![]() $p^+$
of p in
$p^+$
of p in
![]() $\mathbb {Q}(X,r)$
such that
$\mathbb {Q}(X,r)$
such that
![]() $p^+$
is an
$p^+$
is an
![]() $(N^*, \mathbb {Q}(X,r))$
-generic condition and
$(N^*, \mathbb {Q}(X,r))$
-generic condition and
Proof. As in the previous proof, let
![]() $N^*$
be a countable elementary submodel of
$N^*$
be a countable elementary submodel of
![]() $H_{\lambda }$
which contains
$H_{\lambda }$
which contains
![]() $\left \{{\mathcal {C}, X , r, H_{\kappa }, H_\theta , p}\right \}$
,
$\left \{{\mathcal {C}, X , r, H_{\kappa }, H_\theta , p}\right \}$
,
![]() $M^*$
a countable elementary submodel of
$M^*$
a countable elementary submodel of
![]() $H_\lambda $
which has the set
$H_\lambda $
which has the set
![]() $\{N^*\}$
,
$\{N^*\}$
,
![]() $\varepsilon _* \in \omega _1\cap N^*$
such that
$\varepsilon _* \in \omega _1\cap N^*$
such that
![]() $\delta ^p_\sigma <\varepsilon _*$
for every
$\delta ^p_\sigma <\varepsilon _*$
for every
![]() $\sigma \in A_p$
, and
$\sigma \in A_p$
, and
![]() $f_*$
a member of X which is Cohen over
$f_*$
a member of X which is Cohen over
![]() $M^*$
. Define
$M^*$
. Define
![]() $ \sigma _* := \left \langle {\varepsilon _* , \omega _1\cap N^*, \omega _1\cap M^*, f_* }\right \rangle $
and
$ \sigma _* := \left \langle {\varepsilon _* , \omega _1\cap N^*, \omega _1\cap M^*, f_* }\right \rangle $
and
We have shown in Lemma 2.8 that
![]() $p^+$
is
$p^+$
is
![]() $(N^*, \mathbb {Q}(X,r))$
-generic. Let us show that
$(N^*, \mathbb {Q}(X,r))$
-generic. Let us show that
Suppose not. Then there are a
![]() $\mathbb {Q}(X,r)$
-name
$\mathbb {Q}(X,r)$
-name
![]() $\dot F$
for a nowhere dense subset of
$\dot F$
for a nowhere dense subset of
![]() $2^{\omega }$
and
$2^{\omega }$
and
![]() $q\leq _{ \mathbb {Q}(X,r)} p$
such that
$q\leq _{ \mathbb {Q}(X,r)} p$
such that
![]() $\dot F \in N^*$
and
$\dot F \in N^*$
and
Define
![]() $\mathcal {D}$
to be the set of the conditions u of
$\mathcal {D}$
to be the set of the conditions u of
![]() $\mathbb {Q}(X,r)$
such that there are countable elementary submodels
$\mathbb {Q}(X,r)$
such that there are countable elementary submodels
![]() $N'$
and
$N'$
and
![]() $ M'$
of
$ M'$
of
![]() $H_\theta $
such that
$H_\theta $
such that
-
•
 $\left ( \mathcal {N}_u^0 \cup \mathcal {N}_u^1 \cup A_u \right ) \cap N' = \left ( \mathcal {N}_q^0 \cup \mathcal {N}_q^1 \cup A_q \right ) \cap N^*$
,
$\left ( \mathcal {N}_u^0 \cup \mathcal {N}_u^1 \cup A_u \right ) \cap N' = \left ( \mathcal {N}_q^0 \cup \mathcal {N}_q^1 \cup A_q \right ) \cap N^*$
, -
•
 $ \Big \{\mathcal {C}, X , r, H_{\kappa }, \dot F, \left \{{C_{\delta _\sigma } \cap N^* : \sigma \in A_q\setminus (N^* \cup \{\sigma _*\})}\right \}, \left \{{\varepsilon _\sigma : \sigma \in A_q}\right \} \cap N^* \Big \} $
$ \Big \{\mathcal {C}, X , r, H_{\kappa }, \dot F, \left \{{C_{\delta _\sigma } \cap N^* : \sigma \in A_q\setminus (N^* \cup \{\sigma _*\})}\right \}, \left \{{\varepsilon _\sigma : \sigma \in A_q}\right \} \cap N^* \Big \} $
 $\in N' \in M'$
,
$\in N' \in M'$
, -
•
 $N' \cap H_\kappa \in \mathcal {N}_u^0$
and
$N' \cap H_\kappa \in \mathcal {N}_u^0$
and
 $M' \cap H_\kappa \in \mathcal {N}_u^1$
, and
$M' \cap H_\kappa \in \mathcal {N}_u^1$
, and -
• there is a
 $\sigma \in A_u$
such that
$\sigma \in A_u$
such that
 $\omega _1\cap N' = \delta _\sigma $
and
$\omega _1\cap N' = \delta _\sigma $
and
 $\omega _1\cap M' = \gamma _\sigma $
.
$\omega _1\cap M' = \gamma _\sigma $
.
Then
![]() $q\in \mathcal {D} \in N^*$
. Since q is
$q\in \mathcal {D} \in N^*$
. Since q is
![]() $(N^*, \mathbb {Q}(X,r))$
-generic, there exists
$(N^*, \mathbb {Q}(X,r))$
-generic, there exists
![]() $u \in \mathcal {D}\cap N^*$
that is compatible with q in
$u \in \mathcal {D}\cap N^*$
that is compatible with q in
![]() $\mathbb {Q}(X,r)$
. Let
$\mathbb {Q}(X,r)$
. Let
![]() $q^+$
be a common extension of q and u in
$q^+$
be a common extension of q and u in
![]() $\mathbb {Q}(X,r)$
such that there are countable elementary submodels
$\mathbb {Q}(X,r)$
such that there are countable elementary submodels
![]() $N_0^*$
and
$N_0^*$
and
![]() $M_0^*$
of
$M_0^*$
of
![]() $H_\theta $
such that
$H_\theta $
such that
-
•
 $\left ( \mathcal {N}_u^0 \cup \mathcal {N}_u^1 \cup A_u \right ) \cap N_0^* = \left ( \mathcal {N}_q^0 \cup \mathcal {N}_q^1 \cup A_q \right ) \cap N^*$
,
$\left ( \mathcal {N}_u^0 \cup \mathcal {N}_u^1 \cup A_u \right ) \cap N_0^* = \left ( \mathcal {N}_q^0 \cup \mathcal {N}_q^1 \cup A_q \right ) \cap N^*$
, -
•
 $ \Big \{\mathcal {C}, X , r, H_{\kappa }, \dot F, \left \{{C_{\delta _\sigma } \cap N^* : \sigma \in A_q\setminus (N^* \cup \{\sigma _*\})}\right \}, \left \{{\varepsilon _\sigma : \sigma \in A_q}\right \} \cap N^* \Big \} $
$ \Big \{\mathcal {C}, X , r, H_{\kappa }, \dot F, \left \{{C_{\delta _\sigma } \cap N^* : \sigma \in A_q\setminus (N^* \cup \{\sigma _*\})}\right \}, \left \{{\varepsilon _\sigma : \sigma \in A_q}\right \} \cap N^* \Big \} $
 $\in N_0^* \in M_0^* \in N^*$
,
$\in N_0^* \in M_0^* \in N^*$
, -
•
 $N_0 := N_0^* \cap H_\kappa \in \mathcal {N}_{q^+}^0$
and
$N_0 := N_0^* \cap H_\kappa \in \mathcal {N}_{q^+}^0$
and
 $M_0 := M_0^* \cap H_\kappa \in \mathcal {N}_{q^+}^1$
, and
$M_0 := M_0^* \cap H_\kappa \in \mathcal {N}_{q^+}^1$
, and -
• there is a unique
 $\sigma _0 \in A_{q^+}$
such that
$\sigma _0 \in A_{q^+}$
such that
 $\omega _1\cap N_0 = \delta _{\sigma _0}$
and
$\omega _1\cap N_0 = \delta _{\sigma _0}$
and
 $\omega _1\cap M_0 = \gamma _{\sigma _0}$
.
$\omega _1\cap M_0 = \gamma _{\sigma _0}$
.
As seen in the previous lemma,
![]() $q^+$
is
$q^+$
is
![]() $(N_0^*, \mathbb {Q}(X,r))$
-generic. By extending
$(N_0^*, \mathbb {Q}(X,r))$
-generic. By extending
![]() $q^+$
if necessary, we may assume that the set
$q^+$
if necessary, we may assume that the set
![]() $\left ( \mathcal {N}_{q^+}^0 \cup \mathcal {N}_{q^+}^1 \right ) \cap N^*$
contains the set
$\left ( \mathcal {N}_{q^+}^0 \cup \mathcal {N}_{q^+}^1 \right ) \cap N^*$
contains the set
 $$\begin{align*}\begin{array}{r@{\ }l} \Big\{ \left( \left(\Psi_{N^* \cap H_\kappa}\right)^{-1} \circ \Psi_{N} \right) (K) : & N\in\mathcal{N}_{q^+}^0 \text{ with }\omega_1\cap N = \omega_1\cap N^*, \\ & K \in \left(\mathcal{N}_{q^+}^0 \cup \mathcal{N}_{q^+}^1\right) \cap N \Big\}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} \Big\{ \left( \left(\Psi_{N^* \cap H_\kappa}\right)^{-1} \circ \Psi_{N} \right) (K) : & N\in\mathcal{N}_{q^+}^0 \text{ with }\omega_1\cap N = \omega_1\cap N^*, \\ & K \in \left(\mathcal{N}_{q^+}^0 \cup \mathcal{N}_{q^+}^1\right) \cap N \Big\}. \end{array} \end{align*}$$
Let
![]() $\zeta _0 \in \omega _1\cap N_0$
be such that
$\zeta _0 \in \omega _1\cap N_0$
be such that
-
• for every
 $\sigma \in A_q\cap N_0$
(
$\sigma \in A_q\cap N_0$
(
 $= A_{q} \cap N^* = A_{q^+} \cap N_0$
),
$= A_{q} \cap N^* = A_{q^+} \cap N_0$
),
 $\gamma _\sigma < \zeta _0$
, and
$\gamma _\sigma < \zeta _0$
, and -
• for every
 $\sigma \in A_q \setminus N_0$
(then
$\sigma \in A_q \setminus N_0$
(then
 $\delta _\sigma \geq \omega _1\cap N^*> \omega _1\cap N_0 = \delta _{\sigma _0}$
),
$\delta _\sigma \geq \omega _1\cap N^*> \omega _1\cap N_0 = \delta _{\sigma _0}$
),-
– if
 $C_{\delta _\sigma }\cap N_0 \neq \emptyset $
, then
$C_{\delta _\sigma }\cap N_0 \neq \emptyset $
, then
 $ \max \left ( C_{\delta _\sigma }\cap N_0 \right ) < \zeta _0 $
, and
$ \max \left ( C_{\delta _\sigma }\cap N_0 \right ) < \zeta _0 $
, and -
– if
 $\varepsilon _\sigma < \omega _1\cap N_0$
, then
$\varepsilon _\sigma < \omega _1\cap N_0$
, then
 $\varepsilon _\sigma < \zeta _0$
.
$\varepsilon _\sigma < \zeta _0$
.
-
For each
![]() $\nu \in 2^{<\omega }$
, each
$\nu \in 2^{<\omega }$
, each
![]() $\eta \in \omega _1$
, and each
$\eta \in \omega _1$
, and each
![]() $x\in [\mathfrak {M}(X,r)]^{<\aleph _0}$
, define
$x\in [\mathfrak {M}(X,r)]^{<\aleph _0}$
, define
![]() $\mathcal {E}(\nu ,\eta , x)$
to be the set of the conditions u of
$\mathcal {E}(\nu ,\eta , x)$
to be the set of the conditions u of
![]() $\mathbb {Q}(X,r)$
such that
$\mathbb {Q}(X,r)$
such that
-
•
 $A_{u} \cap (\eta ^3\times X) = A_{q}\cap N_0 $
and, for any
$A_{u} \cap (\eta ^3\times X) = A_{q}\cap N_0 $
and, for any
 $\tau \in A_u \setminus (A_q\cap N_0)$
,
$\tau \in A_u \setminus (A_q\cap N_0)$
,
 $\delta _\tau \geq \eta $
,
$\delta _\tau \geq \eta $
, -
♦ the set
is equal to the set $$\begin{align*}\left\{{\left\langle{\varepsilon_\sigma, C_{ \delta_\sigma}\cap \eta, f_{\sigma} \restriction \left| C_{\delta_\sigma} \cap \eta \right| }\right\rangle : \sigma \in A_{u} \setminus \big( A_q \cap N_0\big) \text{ with } \varepsilon_\sigma < \eta}\right\} \end{align*}$$
$$\begin{align*}\left\{{\left\langle{\varepsilon_\sigma, C_{ \delta_\sigma}\cap \eta, f_{\sigma} \restriction \left| C_{\delta_\sigma} \cap \eta \right| }\right\rangle : \sigma \in A_{u} \setminus \big( A_q \cap N_0\big) \text{ with } \varepsilon_\sigma < \eta}\right\} \end{align*}$$
 $$\begin{align*}\left\{{\left\langle{\varepsilon_\sigma, C_{\delta_\sigma}\cap N_0, f_{\sigma} \restriction \left| C_{\delta_\sigma} \cap N_0 \right| }\right\rangle : \sigma \in A_q \setminus N_0 \text{ with } \varepsilon_\sigma < \zeta_0}\right\} , \end{align*}$$
$$\begin{align*}\left\{{\left\langle{\varepsilon_\sigma, C_{\delta_\sigma}\cap N_0, f_{\sigma} \restriction \left| C_{\delta_\sigma} \cap N_0 \right| }\right\rangle : \sigma \in A_q \setminus N_0 \text{ with } \varepsilon_\sigma < \zeta_0}\right\} , \end{align*}$$
-
• there are
 $N\in \mathcal {N}_u^0$
and
$N\in \mathcal {N}_u^0$
and
 $M\in \mathcal {N}_u^1$
such that
$M\in \mathcal {N}_u^1$
such that
 $x \in N $
,
$x \in N $
,
 $\mathcal {N}_u^0 \cap N = \mathcal {N}_{q}^0 \cap N_0$
,
$\mathcal {N}_u^0 \cap N = \mathcal {N}_{q}^0 \cap N_0$
,
 $ \omega _1\cap N = \min \left \{{\delta _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
,
$ \omega _1\cap N = \min \left \{{\delta _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
,
 $\mathcal {N}_u^1 \cap M = \mathcal {N}_{q}^1 \cap M_0$
(
$\mathcal {N}_u^1 \cap M = \mathcal {N}_{q}^1 \cap M_0$
(
 $=\mathcal {N}_{q}^1 \cap N_0$
),
$=\mathcal {N}_{q}^1 \cap N_0$
),
 $ \omega _1\cap M = \min \left \{{\gamma _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
, and
$ \omega _1\cap M = \min \left \{{\gamma _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
, and
 $N \in M$
,
$N \in M$
, -
•
 $u \Vdash _{\mathbb {Q}(X,r)}\!\!\!\text {"}\,\, \dot F \cap [\nu ] \neq \emptyset \,\text {"} .$
$u \Vdash _{\mathbb {Q}(X,r)}\!\!\!\text {"}\,\, \dot F \cap [\nu ] \neq \emptyset \,\text {"} .$
By the choice of
![]() $N_0^*$
, the set
$N_0^*$
, the set
belongs to
![]() $N_0$
. Define
$N_0$
. Define
 $$ \begin{align*} { \begin{array}{r@{\ }l} Y := \Big\{ a \in 2^\omega : & \text{ for any }k \in \omega, \text{ any }\eta\in \omega_1\setminus \zeta_0, \text{ and } \text{ any }x\in [\mathfrak{M}(X,r)]^{<\aleph_0}, \\ & \mathcal{E}(a\restriction k,\eta, x) \neq\emptyset \Big\}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{\ }l} Y := \Big\{ a \in 2^\omega : & \text{ for any }k \in \omega, \text{ any }\eta\in \omega_1\setminus \zeta_0, \text{ and } \text{ any }x\in [\mathfrak{M}(X,r)]^{<\aleph_0}, \\ & \mathcal{E}(a\restriction k,\eta, x) \neq\emptyset \Big\}. \end{array} } \end{align*} $$
Y also belongs to
![]() $N_0$
.
$N_0$
.
We claim that Y is nowhere dense in
![]() $2^{\omega }$
. Let
$2^{\omega }$
. Let
![]() $\nu $
be in
$\nu $
be in
![]() $2^{<\omega }$
. Take an extension
$2^{<\omega }$
. Take an extension
![]() $q'$
of
$q'$
of
![]() $q^+$
in
$q^+$
in
![]() $\mathbb {Q}(X,r)$
and an end extension
$\mathbb {Q}(X,r)$
and an end extension
![]() $\nu '$
of
$\nu '$
of
![]() $\nu $
in
$\nu $
in
![]() $2^{<\omega }$
such that
$2^{<\omega }$
such that
By extending
![]() $q'$
if necessary, we may assume that the set
$q'$
if necessary, we may assume that the set
![]() $\left ( \mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right ) \cap N_0$
includes the set
$\left ( \mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right ) \cap N_0$
includes the set
 $$\begin{align*}\begin{array}{r@{\ }l} \Big\{ \left( \left(\Psi_{N_0}\right)^{-1} \circ \Psi_{N} \right) (K) : & N\in\mathcal{N}_{q'}^0 \text{ with }\omega_1\cap N = \omega_1\cap N_0, \\ & K \in \left(\mathcal{N}_{q'}^0 \cup \mathcal{N}_{q'}^1\right) \cap N \Big\}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} \Big\{ \left( \left(\Psi_{N_0}\right)^{-1} \circ \Psi_{N} \right) (K) : & N\in\mathcal{N}_{q'}^0 \text{ with }\omega_1\cap N = \omega_1\cap N_0, \\ & K \in \left(\mathcal{N}_{q'}^0 \cup \mathcal{N}_{q'}^1\right) \cap N \Big\}. \end{array} \end{align*}$$
Let us show that
![]() $Y \cap [\nu '] =\emptyset $
. Suppose not. Then there exists
$Y \cap [\nu '] =\emptyset $
. Suppose not. Then there exists
![]() $a \in Y \cap [\nu '] $
. Let
$a \in Y \cap [\nu '] $
. Let
![]() $k\in \omega $
be such that
$k\in \omega $
be such that
![]() $\nu ' \subseteq a\restriction k$
, and let
$\nu ' \subseteq a\restriction k$
, and let
![]() $\zeta _1 \in \omega _1\cap N_0$
be such that
$\zeta _1 \in \omega _1\cap N_0$
be such that
-
• for every
 $\sigma \in A_{q'}\cap N_0$
,
$\sigma \in A_{q'}\cap N_0$
,
 $\gamma _\sigma < \zeta _1$
, and
$\gamma _\sigma < \zeta _1$
, and -
• for every
 $\sigma \in A_{q'} \setminus \left ( N_0 \cup \left \{{\sigma _0}\right \} \right )$
, if
$\sigma \in A_{q'} \setminus \left ( N_0 \cup \left \{{\sigma _0}\right \} \right )$
, if
 $C_{\delta _\sigma }\cap N_0 \neq \emptyset $
, then
$C_{\delta _\sigma }\cap N_0 \neq \emptyset $
, then
 $ \max \left ( C_{\delta _\sigma }\cap N_0 \right ) < \zeta _1 $
.
$ \max \left ( C_{\delta _\sigma }\cap N_0 \right ) < \zeta _1 $
.
Define Z to be the set of the functions h from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
such that there exists
$2^{<\omega }$
such that there exists
![]() $u\in \mathcal {E}(a \restriction k, \zeta _1, \left (\mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right )\cap N_0) \cap N_0^*$
which satisfies that, for any
$u\in \mathcal {E}(a \restriction k, \zeta _1, \left (\mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right )\cap N_0) \cap N_0^*$
which satisfies that, for any
![]() $\sigma \in A_{u} \setminus (A_q\cap N_0)$
,
$\sigma \in A_{u} \setminus (A_q\cap N_0)$
,
![]() $h ( \left | C_{\omega _1\cap N_0 } \cap \delta _\sigma \right |) \subseteq r$
and
$h ( \left | C_{\omega _1\cap N_0 } \cap \delta _\sigma \right |) \subseteq r$
and
![]() $h ( \left | C_{\omega _1\cap N_0 } \cap ( \gamma _\sigma +1) \right |) \subseteq r$
. Since
$h ( \left | C_{\omega _1\cap N_0 } \cap ( \gamma _\sigma +1) \right |) \subseteq r$
. Since
![]() $a\in Y $
, it follows from elementarity of
$a\in Y $
, it follows from elementarity of
![]() $N_0^*$
again that Z is a dense open subset of
$N_0^*$
again that Z is a dense open subset of
![]() $\left ( 2^{<\omega } \right )^\omega $
. We note that Z is in
$\left ( 2^{<\omega } \right )^\omega $
. We note that Z is in
![]() $M_0^*$
. Since
$M_0^*$
. Since
![]() $f_{\sigma _0}$
is Cohen over
$f_{\sigma _0}$
is Cohen over
![]() $M_0^*$
,
$M_0^*$
,
![]() $f_{\sigma _0} $
is in Z. Take
$f_{\sigma _0} $
is in Z. Take
![]() $u\in \mathcal {E}(a \restriction k, \zeta _1, \left ( \mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right ) \cap N_0) \cap N_0^*$
which witnesses
$u\in \mathcal {E}(a \restriction k, \zeta _1, \left ( \mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right ) \cap N_0) \cap N_0^*$
which witnesses
![]() $f_{\sigma _0} \in Z$
. So there are
$f_{\sigma _0} \in Z$
. So there are
![]() $N\in \mathcal {N}_u^0$
and
$N\in \mathcal {N}_u^0$
and
![]() $M\in \mathcal {N}_u^1$
such that
$M\in \mathcal {N}_u^1$
such that
![]() $ \omega _1\cap N = \min \left \{{\delta _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
,
$ \omega _1\cap N = \min \left \{{\delta _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
,
![]() $ \omega _1\cap M = \min \left \{{\gamma _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
,
$ \omega _1\cap M = \min \left \{{\gamma _\sigma : \sigma \in A_{u} \setminus (A_q \cap N_0)}\right \} $
,
![]() $\left ( \mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right ) \cap N_0 \in N \in M$
,
$\left ( \mathcal {N}_{q'}^0 \cup \mathcal {N}_{q'}^1 \right ) \cap N_0 \in N \in M$
,
![]() $\mathcal {N}_u^0 \cap N = \mathcal {N}_{q}^0 \cap N_0$
, and
$\mathcal {N}_u^0 \cap N = \mathcal {N}_{q}^0 \cap N_0$
, and
![]() $\mathcal {N}_u^1 \cap M = \mathcal {N}_{q}^1 \cap M_0$
. Then
$\mathcal {N}_u^1 \cap M = \mathcal {N}_{q}^1 \cap M_0$
. Then
and
Therefore, if
![]() $A_u\cup A_{q'}$
satisfies (w), as in the proof of properness of
$A_u\cup A_{q'}$
satisfies (w), as in the proof of properness of
![]() $\mathbb {Q}(X,r)$
, u and
$\mathbb {Q}(X,r)$
, u and
![]() $q'$
are compatible in
$q'$
are compatible in
![]() $\mathbb {Q}(X,r)$
. However, a common extension of u and
$\mathbb {Q}(X,r)$
. However, a common extension of u and
![]() $q'$
in
$q'$
in
![]() $\mathbb {Q}(X,r)$
forces both
$\mathbb {Q}(X,r)$
forces both
![]() $\dot F\cap [\nu '] =\emptyset $
and
$\dot F\cap [\nu '] =\emptyset $
and
![]() $\dot F \cap [ a\restriction k] \neq \emptyset $
, which contradicts
$\dot F \cap [ a\restriction k] \neq \emptyset $
, which contradicts
![]() $\nu ' \subseteq a\restriction k$
. Therefore, if
$\nu ' \subseteq a\restriction k$
. Therefore, if
![]() $A_u\cup A_{q'}$
satisfies (w), then
$A_u\cup A_{q'}$
satisfies (w), then
![]() $Y \cap [\nu '] = \emptyset $
.
$Y \cap [\nu '] = \emptyset $
.
We will show that
![]() $A_u\cup A_{q'}$
satisfies (w). The non-trivial case is that
$A_u\cup A_{q'}$
satisfies (w). The non-trivial case is that
![]() $\sigma \in A_u \setminus \left (A_q\cap N_0\right )$
such that
$\sigma \in A_u \setminus \left (A_q\cap N_0\right )$
such that
![]() $\varepsilon _\sigma < \zeta _1$
, and
$\varepsilon _\sigma < \zeta _1$
, and
![]() $\tau \in \left ( A_{q'} \cap N_0 \right ) \setminus A_q$
such that
$\tau \in \left ( A_{q'} \cap N_0 \right ) \setminus A_q$
such that
![]() $\varepsilon _\sigma < \delta _\tau $
. Then
$\varepsilon _\sigma < \delta _\tau $
. Then
![]() $\delta _\tau < \zeta _1 < \delta _\sigma $
. Moreover by
$\delta _\tau < \zeta _1 < \delta _\sigma $
. Moreover by
![]() $\blacklozenge $
, there exists
$\blacklozenge $
, there exists
![]() $\sigma ' \in A_q \setminus N_0$
such that
$\sigma ' \in A_q \setminus N_0$
such that
Then
![]() $\sigma ' \in A_q \subseteq A_{q^+} \subseteq A_{q'}$
. Since
$\sigma ' \in A_q \subseteq A_{q^+} \subseteq A_{q'}$
. Since
![]() $\tau \in A_{q'}\cap N_0$
,
$\tau \in A_{q'}\cap N_0$
,
![]() $\delta _\tau < \gamma _\tau < \zeta _1 <\omega _1\cap N_0$
. Thus
$\delta _\tau < \gamma _\tau < \zeta _1 <\omega _1\cap N_0$
. Thus
![]() $C_{\delta _\sigma }\cap \delta _\tau = C_{\delta _{\sigma '}}\cap \delta _\tau $
and
$C_{\delta _\sigma }\cap \delta _\tau = C_{\delta _{\sigma '}}\cap \delta _\tau $
and
![]() $C_{\delta _\sigma }\cap (\gamma _\tau +1) = C_{\delta _{\sigma '}}\cap (\gamma _\tau +1)$
. Thus, since
$C_{\delta _\sigma }\cap (\gamma _\tau +1) = C_{\delta _{\sigma '}}\cap (\gamma _\tau +1)$
. Thus, since
![]() $\left \{{\sigma ', \tau }\right \}\subseteq A_{q'}$
and
$\left \{{\sigma ', \tau }\right \}\subseteq A_{q'}$
and
![]() $\varepsilon _{\sigma '} = \varepsilon _\sigma < \delta _\tau < \omega _1\cap N_0 < \delta _{\sigma '}$
,
$\varepsilon _{\sigma '} = \varepsilon _\sigma < \delta _\tau < \omega _1\cap N_0 < \delta _{\sigma '}$
,
and
Since c is Cohen over
![]() $N^*$
,
$N^*$
,
![]() $c $
is not in
$c $
is not in
![]() $ Y$
. Thus, there are
$ Y$
. Thus, there are
![]() $k \in \omega $
,
$k \in \omega $
,
![]() $\eta \in \omega _1\setminus \zeta _0$
, and
$\eta \in \omega _1\setminus \zeta _0$
, and
![]() $x\in [\mathfrak {M}(X,r)]^{<\aleph _0}$
such that
$x\in [\mathfrak {M}(X,r)]^{<\aleph _0}$
such that
![]() $\mathcal {E}(c\restriction k,\eta , x) $
is empty. Since
$\mathcal {E}(c\restriction k,\eta , x) $
is empty. Since
![]() $c\restriction k \in N_0^*$
, by elementarity of
$c\restriction k \in N_0^*$
, by elementarity of
![]() $N_0^*$
, we may assume that
$N_0^*$
, we may assume that
![]() $\eta \in \left (\omega _1 \cap N_0^*\right ) \setminus \zeta _0$
, and
$\eta \in \left (\omega _1 \cap N_0^*\right ) \setminus \zeta _0$
, and
![]() $x\in [\mathfrak {M}(X,r)]^{<\aleph _0} \cap N_0^*$
. But then q belongs to
$x\in [\mathfrak {M}(X,r)]^{<\aleph _0} \cap N_0^*$
. But then q belongs to
![]() $\mathcal {E}(c\restriction k,\eta , x) $
, which is a contradiction.⊣
$\mathcal {E}(c\restriction k,\eta , x) $
, which is a contradiction.⊣
As in the proof of Proposition 5.1 that we will see later on, we can show that
![]() $\mathbb {Q}(X,r)$
has the
$\mathbb {Q}(X,r)$
has the
![]() $\aleph _2$
-chain condition (
$\aleph _2$
-chain condition (
![]() $\aleph _2$
-cc). Moreover, as in [Reference Todorčević12, Section 4], we can show that
$\aleph _2$
-cc). Moreover, as in [Reference Todorčević12, Section 4], we can show that
![]() $\mathbb {Q}(X,r)$
has the
$\mathbb {Q}(X,r)$
has the
![]() $\aleph _2$
-pic, which is defined by Shelah [Reference Shelah11, Chapter VIII, Section 2] (see also [Reference Todorčević12, Section 4]). The
$\aleph _2$
-pic, which is defined by Shelah [Reference Shelah11, Chapter VIII, Section 2] (see also [Reference Todorčević12, Section 4]). The
![]() $\aleph _2$
-pic is a stronger condition than the
$\aleph _2$
-pic is a stronger condition than the
![]() $\aleph _2$
-cc, and is closed under countable support iterations. Therefore, the following theorem is a consequence of the lemmas and observations in the present subsections.
$\aleph _2$
-cc, and is closed under countable support iterations. Therefore, the following theorem is a consequence of the lemmas and observations in the present subsections.
Theorem 2.11. Suppose that
![]() $2^{\aleph _0} = \aleph _1$
, X is a non-meager subset of injective functions from
$2^{\aleph _0} = \aleph _1$
, X is a non-meager subset of injective functions from
![]() $\omega $
into
$\omega $
into
![]() $2^{<\omega }$
, and some diamond principle (which is used in the book-keeping argument of a countable support iteration) holds. Then a countable support iteration of forcing notions of the form
$2^{<\omega }$
, and some diamond principle (which is used in the book-keeping argument of a countable support iteration) holds. Then a countable support iteration of forcing notions of the form
![]() $\mathbb {Q}(X,r)$
with some booking argument forces the assertion
(
c
)
.
$\mathbb {Q}(X,r)$
with some booking argument forces the assertion
(
c
)
.
3 Symmetric systems of relational structures
This section is similar to Section 4 of the paper [Reference Miyamoto and Yorioka10]. The idea of this section is due to Tadatoshi Miyamoto. The notion in this section will be used in the definition of our forcing notion which forces the assertion (c).
Assumptions throughout the paper 3.1. Throughout the rest of the paper, suppose that
-
•
 $2^{\aleph _0}=\aleph _1$
holds,
$2^{\aleph _0}=\aleph _1$
holds, -
•
 $\mathbb {R}$
stands for the set of real numbers, and
$\mathbb {R}$
stands for the set of real numbers, and
 $\vec {\mathbb {R}}$
is a fixed enumeration of
$\vec {\mathbb {R}}$
is a fixed enumeration of
 $\mathbb {R}$
,
$\mathbb {R}$
, -
• X is a non-meager set of injective functions from
 $\omega $
into
$\omega $
into
 $2^{<\omega }$
(of size
$2^{<\omega }$
(of size
 $\aleph _1$
),
$\aleph _1$
), -
•
 $\kappa $
is an uncountable regular cardinal such that
$\kappa $
is an uncountable regular cardinal such that
 $\kappa \geq \aleph _2$
and
$\kappa \geq \aleph _2$
and
 $2^{<\kappa }=\kappa $
,
$2^{<\kappa }=\kappa $
, -
•
 $\Phi $
is a surjection from
$\Phi $
is a surjection from
 $\kappa $
to
$\kappa $
to
 $H_\kappa $
such that for every
$H_\kappa $
such that for every
 $x\in H_\kappa $
,
$x\in H_\kappa $
,
 $\Phi ^{-1}[\{x\}]$
is unbounded in
$\Phi ^{-1}[\{x\}]$
is unbounded in
 $\kappa $
.
$\kappa $
.
If M and
![]() $M'$
are countable elementary submodels of
$M'$
are countable elementary submodels of
![]() $H_\kappa $
with the set
$H_\kappa $
with the set
![]() $\left \{{\vec {\mathbb R}}\right \}$
such that
$\left \{{\vec {\mathbb R}}\right \}$
such that
![]() $\omega _1\cap M = \omega _1 \cap M'$
, then
$\omega _1\cap M = \omega _1 \cap M'$
, then
![]() $\mathbb {R} \cap M = \mathbb {R}\cap M'$
. So, as in Section 2.2, the set of Borel codes in M coincides with the one in
$\mathbb {R} \cap M = \mathbb {R}\cap M'$
. So, as in Section 2.2, the set of Borel codes in M coincides with the one in
![]() $M'$
. Therefore, for any
$M'$
. Therefore, for any
![]() $f\in \left ({2^{<\omega }}\right )^\omega $
, f is Cohen over M iff f is Cohen over
$f\in \left ({2^{<\omega }}\right )^\omega $
, f is Cohen over M iff f is Cohen over
![]() $M'$
.
$M'$
.
Assumptions throughout the paper 3.2.
-
•
 $\vec {X} = \left \langle {f_\delta : \delta \in \omega _1}\right \rangle $
is an enumeration of X such that, for any countable elementary submodel M of
$\vec {X} = \left \langle {f_\delta : \delta \in \omega _1}\right \rangle $
is an enumeration of X such that, for any countable elementary submodel M of
 $H_\kappa $
which contains the set
$H_\kappa $
which contains the set
 $\left \{{\vec {\mathbb R}}\right \}$
,
$\left \{{\vec {\mathbb R}}\right \}$
,
 $f_{\omega _1\cap M}$
is Cohen over M.
$f_{\omega _1\cap M}$
is Cohen over M.
Definition 3.3.
![]() $\mathfrak {M}_0$
is the set of countable elementary submodels N of
$\mathfrak {M}_0$
is the set of countable elementary submodels N of
![]() $H_\kappa $
such that
$H_\kappa $
such that
![]() $\left \{{\vec {\mathbb {R}}, \vec X }\right \} \in N$
and the structure
$\left \{{\vec {\mathbb {R}}, \vec X }\right \} \in N$
and the structure
![]() $\left \langle {N, \in ,\Phi \cap N}\right \rangle $
is an elementary substructure of the structure
$\left \langle {N, \in ,\Phi \cap N}\right \rangle $
is an elementary substructure of the structure
![]() $\left \langle {H_\kappa ,\in ,\Phi }\right \rangle $
.
$\left \langle {H_\kappa ,\in ,\Phi }\right \rangle $
.
As in Section 2.2, we always consider the members of
![]() $\mathfrak {M}_0$
as substructures of the structure
$\mathfrak {M}_0$
as substructures of the structure
![]() $ \left \langle { H_\kappa ,\in , {\omega _1}, \vec {\mathbb {R}}, \vec X, \Phi }\right \rangle $
. For each
$ \left \langle { H_\kappa ,\in , {\omega _1}, \vec {\mathbb {R}}, \vec X, \Phi }\right \rangle $
. For each
![]() $M \in \mathfrak {M}_0$
, the transitive collapse of M is considered as the structure
$M \in \mathfrak {M}_0$
, the transitive collapse of M is considered as the structure
![]() $ \left \langle { \mathrm {trcl}(M),\in , {\omega _1}\cap M, \vec {\mathbb {R}}\cap M, \vec X \cap M, \overline {\Phi \cap M}}\right \rangle $
, which is denoted by
$ \left \langle { \mathrm {trcl}(M),\in , {\omega _1}\cap M, \vec {\mathbb {R}}\cap M, \vec X \cap M, \overline {\Phi \cap M}}\right \rangle $
, which is denoted by
![]() $\overline M$
, where
$\overline M$
, where
![]() $\overline {\Phi \cap M}$
is considered as the image, under the collapsing function of M, of
$\overline {\Phi \cap M}$
is considered as the image, under the collapsing function of M, of
![]() $\Phi \cap M$
. As in Section 2.2,
$\Phi \cap M$
. As in Section 2.2,
![]() $\Psi _M$
denotes the transitive collapsing map from M onto
$\Psi _M$
denotes the transitive collapsing map from M onto
![]() $\overline M$
. So when M and
$\overline M$
. So when M and
![]() $M'$
in
$M'$
in
![]() $\mathfrak {M}_0$
are isomorphic, the composition
$\mathfrak {M}_0$
are isomorphic, the composition
![]() ${\Psi _{M'}}^{-1}\circ \Psi _M$
is an isomorphism from the structure
${\Psi _{M'}}^{-1}\circ \Psi _M$
is an isomorphism from the structure
![]() $ \Big \langle M,\in , {\omega _1}, \vec {\mathbb {R}} , \vec X , \Phi \cap M \Big \rangle $
onto the structure
$ \Big \langle M,\in , {\omega _1}, \vec {\mathbb {R}} , \vec X , \Phi \cap M \Big \rangle $
onto the structure
![]() $ \Big \langle M', \in , {\omega _1}, \vec {\mathbb {R}} , \vec X , \Phi \cap M' \Big \rangle. $
$ \Big \langle M', \in , {\omega _1}, \vec {\mathbb {R}} , \vec X , \Phi \cap M' \Big \rangle. $
Definition 3.4. A finite subset
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathfrak {M}_0$
is called a symmetric system if
$\mathfrak {M}_0$
is called a symmetric system if
-
(ho) for each
 $M,M'\in \mathcal {M}$
, if
$M,M'\in \mathcal {M}$
, if
 $\omega _1\cap M=\omega _1\cap M'$
, then
$\omega _1\cap M=\omega _1\cap M'$
, then
 $\overline M=\overline {M'}$
,
$\overline M=\overline {M'}$
, -
(up) for each
 $M, M'\in \mathcal {M}$
, if
$M, M'\in \mathcal {M}$
, if
 $\omega _1\cap M'<\omega _1\cap M$
, then there exists
$\omega _1\cap M'<\omega _1\cap M$
, then there exists
 $M"\in \mathcal {M}$
such that
$M"\in \mathcal {M}$
such that
 $\overline {M"}=\overline M$
and
$\overline {M"}=\overline M$
and
 $M'\in M"$
,
$M'\in M"$
, -
(down) for each
 $M_0, M_1 \in \mathcal {M}$
and each
$M_0, M_1 \in \mathcal {M}$
and each
 $M'\in \mathcal {M}\cap M_0$
, if
$M'\in \mathcal {M}\cap M_0$
, if
 $\overline {M_0} =\overline {M_1}$
, then
$\overline {M_0} =\overline {M_1}$
, then
 $\left ({\Psi _{M_1}}^{-1}\circ \Psi _{M_0}\right ) (M')$
belongs to
$\left ({\Psi _{M_1}}^{-1}\circ \Psi _{M_0}\right ) (M')$
belongs to
 $\mathcal {M}$
, and
$\mathcal {M}$
, and -
(id) for each
 $M,M'\in \mathcal {M}$
, if
$M,M'\in \mathcal {M}$
, if
 $\omega _1\cap M=\omega _1\cap M'$
, then the function is the identity.
$\omega _1\cap M=\omega _1\cap M'$
, then the function is the identity. $$\begin{align*}\Big({\Psi_{M'}}^{-1}\circ\Psi_M\Big) \restriction ( M\cap M') \end{align*}$$
$$\begin{align*}\Big({\Psi_{M'}}^{-1}\circ\Psi_M\Big) \restriction ( M\cap M') \end{align*}$$
The requirement (id) comes from the Asperó–Mota iteration [Reference Asperó and Mota3]. This was used to show properness whenever the length of the iteration has uncountable cofinality. In this paper, the requirement (id) will be used in other places, for example, Propositions 3.10 and 3.11.
We will deal with symmetric systems of relational structures. To introduce such systems, we define the following notions, and mention some necessary propositions.
Definition 3.5. Let
![]() $( \mathbb {P}, \leq _{\mathbb {P}})$
be a forcing notion with the
$( \mathbb {P}, \leq _{\mathbb {P}})$
be a forcing notion with the
![]() $\kappa $
-chain condition such that
$\kappa $
-chain condition such that
![]() $\mathbb {P}\subseteq H_\kappa $
. We define the expanded relational structure by
$\mathbb {P}\subseteq H_\kappa $
. We define the expanded relational structure by
![]() $\mathbb {P}$
to the relational structure
$\mathbb {P}$
to the relational structure
where
-
•
 $H^{\mathbb {P}}_\kappa := V^{\mathbb {P}}\cap H_\kappa $
, where
$H^{\mathbb {P}}_\kappa := V^{\mathbb {P}}\cap H_\kappa $
, where
 $V^{\mathbb {P}}$
denotes the class of all
$V^{\mathbb {P}}$
denotes the class of all
 $\mathbb {P}$
-names,
$\mathbb {P}$
-names, -
•
 $R^{\mathbb {P}}_= :=\left \{{(p,\tau ,\pi )\in \left (\mathbb {P}\times V^{\mathbb {P}}\times V^{\mathbb {P}}\right )\cap H_\kappa : p\Vdash _{\mathbb {P}}\text {"} \tau =\pi \,\text {"}}\right \}$
, and
$R^{\mathbb {P}}_= :=\left \{{(p,\tau ,\pi )\in \left (\mathbb {P}\times V^{\mathbb {P}}\times V^{\mathbb {P}}\right )\cap H_\kappa : p\Vdash _{\mathbb {P}}\text {"} \tau =\pi \,\text {"}}\right \}$
, and -
•
 $R^{\mathbb {P}}_\in :=\left \{{(p,\tau ,\pi )\in \left (\mathbb {P}\times V^{\mathbb {P}}\times V^{\mathbb {P}}\right )\cap H_\kappa : p\Vdash _{\mathbb {P}}\text {"} \tau \in \pi \,\text {"}}\right \}$
.
$R^{\mathbb {P}}_\in :=\left \{{(p,\tau ,\pi )\in \left (\mathbb {P}\times V^{\mathbb {P}}\times V^{\mathbb {P}}\right )\cap H_\kappa : p\Vdash _{\mathbb {P}}\text {"} \tau \in \pi \,\text {"}}\right \}$
.
For each
![]() $M\in \mathfrak {M}_0$
, M is also considered as the substructure
$M\in \mathfrak {M}_0$
, M is also considered as the substructure
of the expanded relational structure by
![]() $\mathbb {P}$
, and we write
$\mathbb {P}$
, and we write
![]() $M\prec \mathbb {P}$
when the structure M is an elementary substructure of the expanded relational structure by
$M\prec \mathbb {P}$
when the structure M is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
The forcing notions we will define in Section 4 are not members of
![]() $H_\kappa $
, but subsets of
$H_\kappa $
, but subsets of
![]() $H_\kappa $
. The following can be proved in a similar way as in [Reference Shelah11, Chapter III, Section 2]. Here,
$H_\kappa $
. The following can be proved in a similar way as in [Reference Shelah11, Chapter III, Section 2]. Here,
![]() $p\in \mathbb {P}$
is called
$p\in \mathbb {P}$
is called
![]() $(M,\mathbb {P})$
-generic if, for any predense subset
$(M,\mathbb {P})$
-generic if, for any predense subset
![]() $\mathcal {D}\in M$
of
$\mathcal {D}\in M$
of
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\mathcal {D}\cap M$
is predense below p in
$\mathcal {D}\cap M$
is predense below p in
![]() $\mathbb {P}$
. For the proof of the following proposition, see, e.g., [Reference Shelah11, Chapter III, Theorem 2.11].
$\mathbb {P}$
. For the proof of the following proposition, see, e.g., [Reference Shelah11, Chapter III, Theorem 2.11].
Proposition 3.6. Suppose that
![]() $\mathbb {P}$
is a forcing notion with the
$\mathbb {P}$
is a forcing notion with the
![]() $\kappa $
-chain condition such that
$\kappa $
-chain condition such that
![]() $\mathbb {P}\subseteq H_\kappa $
.
$\mathbb {P}\subseteq H_\kappa $
.
-
1. If
 $\theta $
is a large enough regular cardinal for
$\theta $
is a large enough regular cardinal for
 $\mathbb {P}$
and
$\mathbb {P}$
and
 $M^*$
is a countable elementary submodel of
$M^*$
is a countable elementary submodel of
 $H_\theta $
which contains the set as a member, then
$H_\theta $
which contains the set as a member, then $$\begin{align*}\Big\{ H_\kappa,\in, \mathbb{P}, \leq_{\mathbb{P}}, \vec{\mathbb{R}}, \vec X, \Phi \Big\} \end{align*}$$
$$\begin{align*}\Big\{ H_\kappa,\in, \mathbb{P}, \leq_{\mathbb{P}}, \vec{\mathbb{R}}, \vec X, \Phi \Big\} \end{align*}$$
 $M^*\cap H_\kappa \in \mathfrak {M}_0$
and
$M^*\cap H_\kappa \in \mathfrak {M}_0$
and
 $M^*\cap H_\kappa \prec \mathbb {P}$
.
$M^*\cap H_\kappa \prec \mathbb {P}$
.
-
2. For any
 $M\in \mathfrak {M}_0$
with
$M\in \mathfrak {M}_0$
with
 $M\prec \mathbb {P}$
, and any
$M\prec \mathbb {P}$
, and any
 $p\in \mathbb {P}$
, the followings are equivalent:
$p\in \mathbb {P}$
, the followings are equivalent:-
• p is
 $(M,\mathbb {P})$
-generic,
$(M,\mathbb {P})$
-generic, -
•
 $p\Vdash _{\mathbb {P}} {"} M[\dot G]\cap {H_\kappa }^V = M{"}$
, where
$p\Vdash _{\mathbb {P}} {"} M[\dot G]\cap {H_\kappa }^V = M{"}$
, where
 ${H_\kappa }^V $
denotes
${H_\kappa }^V $
denotes
 $H_\kappa $
in the ground model, and
$H_\kappa $
in the ground model, and -
•
 $p\Vdash _{\mathbb {P}}{"} M[\dot G]\cap \kappa =M\cap \kappa{"}$
.
$p\Vdash _{\mathbb {P}}{"} M[\dot G]\cap \kappa =M\cap \kappa{"}$
.
-
-
3. For any
 $M\in \mathfrak {M}_0$
with
$M\in \mathfrak {M}_0$
with
 $M\prec \mathbb {P}$
,
$M\prec \mathbb {P}$
,  $$ \begin{align*} \begin{array}{r@{}l} \Vdash_{\mathbb{P}}\ \ &{"} \text{the structure } \\ & \Big\langle M[\dot G], \in \cap M[\dot G]^2, H_\kappa^ V\cap M[\dot G], \mathbb{P}\cap M[\dot G], \leq_{\mathbb{P}}\cap M[\dot G]^2, \dot G\cap M[\dot G], \\ &\hfill H^{\mathbb{P}}_\kappa \cap M[\dot G], R^{\mathbb{P}}_{=} \cap M[\dot G]^3, R^{\mathbb{P}}_\in \cap M[\dot G]^3, \vec{\mathbb{R}} , \vec X , \Phi \cap M[\dot G] \Big\rangle \\ & \text{ is an elementary substructure of the structure } \\ & \Big\langle H_\kappa^{V[\dot G]}, \in, H_\kappa^V, \mathbb{P}, \leq_{\mathbb{P}}, \dot G, H^{\mathbb{P}}_\kappa , R^{\mathbb{P}}_= , R^{\mathbb{P}}_\in , \vec{\mathbb{R}} , \vec{X}, \Phi \Big\rangle{"}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{r@{}l} \Vdash_{\mathbb{P}}\ \ &{"} \text{the structure } \\ & \Big\langle M[\dot G], \in \cap M[\dot G]^2, H_\kappa^ V\cap M[\dot G], \mathbb{P}\cap M[\dot G], \leq_{\mathbb{P}}\cap M[\dot G]^2, \dot G\cap M[\dot G], \\ &\hfill H^{\mathbb{P}}_\kappa \cap M[\dot G], R^{\mathbb{P}}_{=} \cap M[\dot G]^3, R^{\mathbb{P}}_\in \cap M[\dot G]^3, \vec{\mathbb{R}} , \vec X , \Phi \cap M[\dot G] \Big\rangle \\ & \text{ is an elementary substructure of the structure } \\ & \Big\langle H_\kappa^{V[\dot G]}, \in, H_\kappa^V, \mathbb{P}, \leq_{\mathbb{P}}, \dot G, H^{\mathbb{P}}_\kappa , R^{\mathbb{P}}_= , R^{\mathbb{P}}_\in , \vec{\mathbb{R}} , \vec{X}, \Phi \Big\rangle{"}. \end{array} \end{align*} $$
Notation 3.7. For
![]() $\alpha \in \kappa +1$
,
$\alpha \in \kappa +1$
,
![]() $n\in \omega $
, and a sequence
$n\in \omega $
, and a sequence
![]() $\left \langle {X_\xi ^i : i\in n, \xi \in \alpha }\right \rangle $
of subsets of
$\left \langle {X_\xi ^i : i\in n, \xi \in \alpha }\right \rangle $
of subsets of
![]() $H_\kappa $
, we denote
$H_\kappa $
, we denote
Then the tuple
![]() $\langle \!\langle X_\xi ^i : i\in n, \xi \in \alpha \rangle \!\rangle $
is also a subset of
$\langle \!\langle X_\xi ^i : i\in n, \xi \in \alpha \rangle \!\rangle $
is also a subset of
![]() $H_\kappa $
.
$H_\kappa $
.
Definition 3.8. Let
![]() $\alpha \in \kappa +1$
, and
$\alpha \in \kappa +1$
, and
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
a sequence of forcing notions such that
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
a sequence of forcing notions such that
![]() $\mathbb {P}_\xi \subseteq H_\kappa $
and
$\mathbb {P}_\xi \subseteq H_\kappa $
and
![]() $\mathbb {P}_\xi $
has the
$\mathbb {P}_\xi $
has the
![]() $\kappa $
-chain condition for each
$\kappa $
-chain condition for each
![]() $\xi \leq \alpha $
. We define the expanded relational structure by
$\xi \leq \alpha $
. We define the expanded relational structure by
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
to the structure
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
to the structure
For each
![]() $M\in \mathfrak {M}_0$
, M is also considered as the substructure
$M\in \mathfrak {M}_0$
, M is also considered as the substructure
 $$ \begin{align*} { \begin{array}{l} \Big\langle M, \in \cap M^2 , \mathbb{P}_\alpha\cap M, \leq_{\mathbb{P}_\alpha}\cap M^2, H^{\mathbb{P}_\alpha}_\kappa \cap M, R^{\mathbb{P}_\alpha}_= \cap M^3, R^{\mathbb{P}_\alpha}_\in \cap M^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap M, R^{\mathbb{P}_\xi}_= \cap M^3, R^{\mathbb{P}_\xi}_\in \cap M^3 : \xi \in \alpha \cap M \rangle\!\rangle \Big\rangle \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{l} \Big\langle M, \in \cap M^2 , \mathbb{P}_\alpha\cap M, \leq_{\mathbb{P}_\alpha}\cap M^2, H^{\mathbb{P}_\alpha}_\kappa \cap M, R^{\mathbb{P}_\alpha}_= \cap M^3, R^{\mathbb{P}_\alpha}_\in \cap M^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap M, R^{\mathbb{P}_\xi}_= \cap M^3, R^{\mathbb{P}_\xi}_\in \cap M^3 : \xi \in \alpha \cap M \rangle\!\rangle \Big\rangle \end{array} } \end{align*} $$
of the expanded relational structure by
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
, and we write
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
, and we write
![]() $M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
when the structure M is an elementary substructure of the expanded relational structure by
$M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
when the structure M is an elementary substructure of the expanded relational structure by
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
.
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
.
The following is a variation of Proposition 3.6 for iterated forcing.
Proposition 3.9. Suppose that
![]() $\alpha \in \kappa +1$
, and
$\alpha \in \kappa +1$
, and
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
is a sequence of forcing notions such that
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
is a sequence of forcing notions such that
![]() $\mathbb {P}_\xi \subseteq H_\kappa $
and
$\mathbb {P}_\xi \subseteq H_\kappa $
and
![]() $\mathbb {P}_\xi $
has the
$\mathbb {P}_\xi $
has the
![]() $\kappa $
-chain condition for each
$\kappa $
-chain condition for each
![]() $\xi \leq \alpha $
.
$\xi \leq \alpha $
.
-
1. If
 $\theta $
is a large enough regular cardinal for the iteration
$\theta $
is a large enough regular cardinal for the iteration
 $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
and
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
and
 $M^*$
is a countable elementary submodel of
$M^*$
is a countable elementary submodel of
 $H_\theta $
which contains the set as a member, then
$H_\theta $
which contains the set as a member, then $$\begin{align*}\Big\{ H_\kappa,\in, \left\langle{\mathbb{P}_\xi:\xi\leq\alpha}\right\rangle, \vec{\mathbb{R}} , \vec X , \Phi \Big\} \end{align*}$$
$$\begin{align*}\Big\{ H_\kappa,\in, \left\langle{\mathbb{P}_\xi:\xi\leq\alpha}\right\rangle, \vec{\mathbb{R}} , \vec X , \Phi \Big\} \end{align*}$$
 $M^*\cap H_\kappa \in \mathfrak {M}_0$
and
$M^*\cap H_\kappa \in \mathfrak {M}_0$
and
 $M^*\cap H_\kappa \prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
.
$M^*\cap H_\kappa \prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
.
-
2. If
 $\alpha <\kappa $
, then for any
$\alpha <\kappa $
, then for any
 $M\in \mathfrak {M}_0$
with
$M\in \mathfrak {M}_0$
with
 $M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
,
$M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
,
 $\alpha $
belongs to M.
$\alpha $
belongs to M. -
3. For any
 $M\in \mathfrak {M}_0$
with
$M\in \mathfrak {M}_0$
with
 $M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
and any
$M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
and any
 $\beta \in \alpha $
, if
$\beta \in \alpha $
, if
 $\beta \in M$
, then
$\beta \in M$
, then
 $M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \beta }\right \rangle $
.
$M\prec \left \langle {\mathbb {P}_\xi :\xi \leq \beta }\right \rangle $
.
The following is necessary for our symmetric systems of relational structures. This is the reason why we introduce the relational structures equipped with forcing notions that are subsets of
![]() $H_\kappa $
.
$H_\kappa $
.
Proposition 3.10. Suppose that
![]() $M, N_0,N_1\in \mathfrak {M}_0$
are elementary substructures of the expanded relational structure by
$M, N_0,N_1\in \mathfrak {M}_0$
are elementary substructures of the expanded relational structure by
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
,
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
,
![]() $N_0$
and
$N_0$
and
![]() $N_1$
are isomorphic as substructures of the expanded relational structure by the sequence
$N_1$
are isomorphic as substructures of the expanded relational structure by the sequence
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
(then the map
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
(then the map
![]() $\Psi ={\Psi _{N_1}}^{-1}\circ \Psi _{N_0}$
is the isomorphism from
$\Psi ={\Psi _{N_1}}^{-1}\circ \Psi _{N_0}$
is the isomorphism from
![]() $N_0$
onto
$N_0$
onto
![]() $N_1$
as substructures of the expanded relational structure by
$N_1$
as substructures of the expanded relational structure by
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
),
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
),
![]() $\beta \leq \alpha $
is such that
$\beta \leq \alpha $
is such that
![]() $\Psi (\beta )=\beta $
, and
$\Psi (\beta )=\beta $
, and
![]() $M\in \mathfrak {M}_0\cap N_0$
. Then
$M\in \mathfrak {M}_0\cap N_0$
. Then
-
• if
 $M\prec \left \langle {\mathbb {P}_\xi : \xi \leq \alpha }\right \rangle $
, then the structure is an elementary substructure of the structure
$M\prec \left \langle {\mathbb {P}_\xi : \xi \leq \alpha }\right \rangle $
, then the structure is an elementary substructure of the structure $$ \begin{align*} { \begin{array}{l} \Big\langle M, \in \cap M^2 , \mathbb{P}_\beta\cap M, \leq_{\mathbb{P}_\beta}\cap M^2, H^{\mathbb{P}_\beta}_\kappa \cap M, R^{\mathbb{P}_\beta}_= \cap M^3, R^{\mathbb{P}_\beta}_\in \cap M^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap M, R^{\mathbb{P}_\xi}_= \cap M^3, R^{\mathbb{P}_\xi}_\in \cap M^3 : \xi \in \beta \cap M \rangle\!\rangle \Big\rangle \end{array} } \end{align*} $$
and
$$ \begin{align*} { \begin{array}{l} \Big\langle M, \in \cap M^2 , \mathbb{P}_\beta\cap M, \leq_{\mathbb{P}_\beta}\cap M^2, H^{\mathbb{P}_\beta}_\kappa \cap M, R^{\mathbb{P}_\beta}_= \cap M^3, R^{\mathbb{P}_\beta}_\in \cap M^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap M, R^{\mathbb{P}_\xi}_= \cap M^3, R^{\mathbb{P}_\xi}_\in \cap M^3 : \xi \in \beta \cap M \rangle\!\rangle \Big\rangle \end{array} } \end{align*} $$
and $$ \begin{align*} { \begin{array}{l} \Big\langle {N_0}, \in \cap {N_0}^2 , \mathbb{P}_\beta\cap {N_0}, \leq_{\mathbb{P}_\beta}\cap {N_0}^2, H^{\mathbb{P}_\beta}_\kappa \cap {N_0}, R^{\mathbb{P}_\beta}_= \cap {N_0}^3, R^{\mathbb{P}_\beta}_\in \cap {N_0}^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap {N_0}, R^{\mathbb{P}_\xi}_= \cap {N_0}^3, R^{\mathbb{P}_\xi}_\in \cap {N_0}^3 : \xi \in \beta \cap {N_0} \rangle\!\rangle \Big\rangle , \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{l} \Big\langle {N_0}, \in \cap {N_0}^2 , \mathbb{P}_\beta\cap {N_0}, \leq_{\mathbb{P}_\beta}\cap {N_0}^2, H^{\mathbb{P}_\beta}_\kappa \cap {N_0}, R^{\mathbb{P}_\beta}_= \cap {N_0}^3, R^{\mathbb{P}_\beta}_\in \cap {N_0}^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap {N_0}, R^{\mathbb{P}_\xi}_= \cap {N_0}^3, R^{\mathbb{P}_\xi}_\in \cap {N_0}^3 : \xi \in \beta \cap {N_0} \rangle\!\rangle \Big\rangle , \end{array} }\end{align*} $$
-
•
 $ \Psi (M) \prec \left \langle {\mathbb {P}_\xi :\xi \leq \beta }\right \rangle $
, and the structure is an elementary substructure of the structure
$ \Psi (M) \prec \left \langle {\mathbb {P}_\xi :\xi \leq \beta }\right \rangle $
, and the structure is an elementary substructure of the structure $$ \begin{align*} { \begin{array}{l} \Big\langle \Psi(M), \in \cap \Psi(M)^2, \mathbb{P}_\beta\cap \Psi(M), \leq_{\mathbb{P}_\beta}\cap \Psi(M)^2, H^{\mathbb{P}_\beta}_\kappa \cap \Psi(M), R^{\mathbb{P}_\beta}_= \cap \Psi(M)^3, \\ R^{\mathbb{P}_\beta}_\in \cap \Psi(M)^3, \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap \Psi(M), R^{\mathbb{P}_\xi}_= \cap \Psi(M)^3, R^{\mathbb{P}_\xi}_\in \cap \Psi(M)^3 : \xi \in \beta \cap \Psi(M) \rangle\!\rangle \Big\rangle \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{l} \Big\langle \Psi(M), \in \cap \Psi(M)^2, \mathbb{P}_\beta\cap \Psi(M), \leq_{\mathbb{P}_\beta}\cap \Psi(M)^2, H^{\mathbb{P}_\beta}_\kappa \cap \Psi(M), R^{\mathbb{P}_\beta}_= \cap \Psi(M)^3, \\ R^{\mathbb{P}_\beta}_\in \cap \Psi(M)^3, \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap \Psi(M), R^{\mathbb{P}_\xi}_= \cap \Psi(M)^3, R^{\mathbb{P}_\xi}_\in \cap \Psi(M)^3 : \xi \in \beta \cap \Psi(M) \rangle\!\rangle \Big\rangle \end{array} }\end{align*} $$
 $$ \begin{align*} { \begin{array}{l} \Big\langle {N_1}, \in \cap {N_1}^2 , \mathbb{P}_\beta\cap {N_1}, \leq_{\mathbb{P}_\beta}\cap {N_1}^2, H^{\mathbb{P}_\beta}_\kappa \cap {N_1}, R^{\mathbb{P}_\beta}_= \cap {N_1}^3, R^{\mathbb{P}_\beta}_\in \cap {N_1}^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap {N_1}, R^{\mathbb{P}_\xi}_= \cap {N_1}^3, R^{\mathbb{P}_\xi}_\in \cap {N_1}^3 : \xi \in \beta \cap {N_1} \rangle\!\rangle \Big\rangle. \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{l} \Big\langle {N_1}, \in \cap {N_1}^2 , \mathbb{P}_\beta\cap {N_1}, \leq_{\mathbb{P}_\beta}\cap {N_1}^2, H^{\mathbb{P}_\beta}_\kappa \cap {N_1}, R^{\mathbb{P}_\beta}_= \cap {N_1}^3, R^{\mathbb{P}_\beta}_\in \cap {N_1}^3, \\ \hfill \langle\!\langle H^{\mathbb{P}_\xi}_\kappa \cap {N_1}, R^{\mathbb{P}_\xi}_= \cap {N_1}^3, R^{\mathbb{P}_\xi}_\in \cap {N_1}^3 : \xi \in \beta \cap {N_1} \rangle\!\rangle \Big\rangle. \end{array} }\end{align*} $$
The following is a key point of the proof of properness of our forcing notions.
Proposition 3.11. Suppose that
![]() $\alpha \in \omega _2\leq \kappa $
,
$\alpha \in \omega _2\leq \kappa $
,
![]() $N_0,N_1\in \mathfrak {M}_0$
, and
$N_0,N_1\in \mathfrak {M}_0$
, and
![]() $N_0$
and
$N_0$
and
![]() $N_1$
are isomorphic as the substructures of the expanded relational structure by
$N_1$
are isomorphic as the substructures of the expanded relational structure by
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
. Then
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
. Then
![]() $N_0\cap \alpha = N_1\cap \alpha $
.
$N_0\cap \alpha = N_1\cap \alpha $
.
Proof. Let us only show the case that
![]() $\alpha $
is uncountable. By our assumption,
$\alpha $
is uncountable. By our assumption,
![]() $\alpha \in N_0\cap N_1$
and
$\alpha \in N_0\cap N_1$
and
![]() $N_0\cap \omega _1 =N_1\cap \omega _1$
. Then there exists a bijection
$N_0\cap \omega _1 =N_1\cap \omega _1$
. Then there exists a bijection
![]() $f:\omega _1\to \alpha $
which is in both
$f:\omega _1\to \alpha $
which is in both
![]() $N_0$
and
$N_0$
and
![]() $N_1$
. Then
$N_1$
. Then
⊣
4 Definition of Asperó–Mota iteration to force (c)
In this section, we define our forcing notion
![]() $\mathbb {P}_\kappa $
that forces the assertion
(
c
)
.
$\mathbb {P}_\kappa $
that forces the assertion
(
c
)
.
![]() $\mathbb {P}_\kappa $
is defined by an Asperó–Mota iteration of forcing notions playing the same role as
$\mathbb {P}_\kappa $
is defined by an Asperó–Mota iteration of forcing notions playing the same role as
![]() $\mathbb {Q}(X,r)$
in Section 2.2.
$\mathbb {Q}(X,r)$
in Section 2.2.
We notice that, for each
![]() $M\in \mathfrak {M}_0$
and
$M\in \mathfrak {M}_0$
and
![]() $\alpha \in \kappa +1$
, any initial segment of
$\alpha \in \kappa +1$
, any initial segment of
![]() $\alpha \cap M$
is of the form
$\alpha \cap M$
is of the form
![]() $\beta \cap M$
for some
$\beta \cap M$
for some
![]() $\beta \in \alpha +1$
(which is not necessary unique). For each
$\beta \in \alpha +1$
(which is not necessary unique). For each
![]() $\alpha \in \kappa +1$
, we will define the forcing notion
$\alpha \in \kappa +1$
, we will define the forcing notion
![]() $\mathbb {P}_\alpha $
to be a subset of the set
$\mathbb {P}_\alpha $
to be a subset of the set
 $$\begin{align*}U_\alpha:= \begin{array}[t]{l} \left[ \mathfrak{M}_0 \right]^{<\aleph_0} \\[6pt] \times \displaystyle \left\{ \bigcup_{\left\langle{M,\beta}\right\rangle\in Z}\{M\}\times(\beta \cap M): Z\in [\mathfrak{M}_0\times (\alpha+1)]^{<\aleph_0} \right\} \\[-8pt] \\ \times \displaystyle \left( \bigcup_{D\in [\alpha]^{<\aleph_0}} \left( \left[ \omega_1\times \omega_1\times\omega_1 \right]^{<\omega} \right)^D \right). \end{array} \end{align*}$$
$$\begin{align*}U_\alpha:= \begin{array}[t]{l} \left[ \mathfrak{M}_0 \right]^{<\aleph_0} \\[6pt] \times \displaystyle \left\{ \bigcup_{\left\langle{M,\beta}\right\rangle\in Z}\{M\}\times(\beta \cap M): Z\in [\mathfrak{M}_0\times (\alpha+1)]^{<\aleph_0} \right\} \\[-8pt] \\ \times \displaystyle \left( \bigcup_{D\in [\alpha]^{<\aleph_0}} \left( \left[ \omega_1\times \omega_1\times\omega_1 \right]^{<\omega} \right)^D \right). \end{array} \end{align*}$$
Since
![]() $\mathfrak {M}_0$
is a subset of
$\mathfrak {M}_0$
is a subset of
![]() $H_\kappa $
, for each
$H_\kappa $
, for each
![]() $\alpha \in \kappa +1$
, the forcing notion
$\alpha \in \kappa +1$
, the forcing notion
![]() $\mathbb {P}_\alpha $
is a subset of
$\mathbb {P}_\alpha $
is a subset of
![]() $H_\kappa $
.
$H_\kappa $
.
To define
![]() $\mathbb {P}_\alpha $
, we introduce the following notation. For each
$\mathbb {P}_\alpha $
, we introduce the following notation. For each
![]() $\alpha \in \kappa +1$
and
$\alpha \in \kappa +1$
and
![]() $p=(\mathcal {N}_p, R_p, A_p)\in U_\alpha $
,
$p=(\mathcal {N}_p, R_p, A_p)\in U_\alpha $
,
-
•
 $\operatorname {dom}(R_p) :=\left \{{M : \text { there is } \zeta \in \alpha \text { so that } \left \langle {M,\zeta }\right \rangle \in R_p }\right \}$
,
$\operatorname {dom}(R_p) :=\left \{{M : \text { there is } \zeta \in \alpha \text { so that } \left \langle {M,\zeta }\right \rangle \in R_p }\right \}$
, -
•
 $\operatorname {ran}(R_p) :=\left \{{\zeta : \text { there is } M \in \mathfrak {M}_0 \text { so that } \left \langle {M,\zeta }\right \rangle \in R_p }\right \}$
,
$\operatorname {ran}(R_p) :=\left \{{\zeta : \text { there is } M \in \mathfrak {M}_0 \text { so that } \left \langle {M,\zeta }\right \rangle \in R_p }\right \}$
, -
• for each
 $I\subseteq \alpha $
,
$I\subseteq \alpha $
,  $$\begin{align*}{R_p}^{-1}[ I ] := \big\{M : \text{ there is }\ \zeta\in I\ \text{so that } \left\langle{M,\zeta}\right\rangle\in R_p \big\} , \end{align*}$$
$$\begin{align*}{R_p}^{-1}[ I ] := \big\{M : \text{ there is }\ \zeta\in I\ \text{so that } \left\langle{M,\zeta}\right\rangle\in R_p \big\} , \end{align*}$$
-
• for each
 $M\in \operatorname {dom}(R_p)$
,
$M\in \operatorname {dom}(R_p)$
,  $$\begin{align*}R_p(M):=\left\{{\zeta\in\operatorname{ran}(R_p): \left\langle{M,\zeta}\right\rangle\in R_p}\right\} \!, \end{align*}$$
$$\begin{align*}R_p(M):=\left\{{\zeta\in\operatorname{ran}(R_p): \left\langle{M,\zeta}\right\rangle\in R_p}\right\} \!, \end{align*}$$
-
• for each
 $\beta \in \alpha $
, define
$\beta \in \alpha $
, define
 $p\restriction \beta = (\mathcal {N}_{p\restriction \beta }, R_{p\restriction \beta },A_{p\restriction \beta })$
to be the member of
$p\restriction \beta = (\mathcal {N}_{p\restriction \beta }, R_{p\restriction \beta },A_{p\restriction \beta })$
to be the member of
 $U_\beta $
such that
$U_\beta $
such that-
–
 $\mathcal {N}_{p\restriction \beta } :=\mathcal {N}_p$
,
$\mathcal {N}_{p\restriction \beta } :=\mathcal {N}_p$
, -
–
 $ R_{p\restriction \beta } := R_p\cap \left (\mathfrak {M}_0\times \beta \right ) \!, $
and
$ R_{p\restriction \beta } := R_p\cap \left (\mathfrak {M}_0\times \beta \right ) \!, $
and -
–
 $A_{p\restriction \beta }:=A_p\restriction \beta $
, the restriction of the function
$A_{p\restriction \beta }:=A_p\restriction \beta $
, the restriction of the function
 $A_p$
to the set
$A_p$
to the set
 $\beta $
.
$\beta $
.
-
For
![]() $p\in U_\alpha $
and
$p\in U_\alpha $
and
![]() $M\in \mathcal {N}_p$
, members of the set
$M\in \mathcal {N}_p$
, members of the set
![]() $R_p(M)$
are called markers of M.
$R_p(M)$
are called markers of M.
We define a forcing notion
![]() $\mathbb {P}_\alpha $
satisfying the
$\mathbb {P}_\alpha $
satisfying the
![]() $\aleph _2$
-cc (under
$\aleph _2$
-cc (under
![]() $\operatorname {\mathsf {CH}}$
), by recursion on
$\operatorname {\mathsf {CH}}$
), by recursion on
![]() $\alpha \in \kappa +1$
. When we have defined the sequence
$\alpha \in \kappa +1$
. When we have defined the sequence
![]() $\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
of forcing notions, we will define the subset
$\left \langle {\mathbb {P}_\xi :\xi \leq \alpha }\right \rangle $
of forcing notions, we will define the subset
![]() $\mathfrak {M}_{\alpha }^P$
of
$\mathfrak {M}_{\alpha }^P$
of
![]() $\mathfrak {M}_{0}$
by
$\mathfrak {M}_{0}$
by
As in Proposition 3.9(2), if
![]() $\alpha \in \kappa $
and
$\alpha \in \kappa $
and
![]() $M\in \mathfrak {M}^P_\alpha $
, then
$M\in \mathfrak {M}^P_\alpha $
, then
![]() $\alpha \in M$
. As seen below, for each
$\alpha \in M$
. As seen below, for each
![]() $\alpha \in \kappa $
,
$\alpha \in \kappa $
,
![]() $\mathbb {P}_{\alpha }$
will be defined from the set
$\mathbb {P}_{\alpha }$
will be defined from the set
![]() $\mathbb {P}_\kappa $
can be considered as the direct limit of
$\mathbb {P}_\kappa $
can be considered as the direct limit of
![]() $\left \langle {\mathbb {P}_\alpha :\alpha \in \kappa }\right \rangle $
.
$\left \langle {\mathbb {P}_\alpha :\alpha \in \kappa }\right \rangle $
.
Definition 4.1. The forcing notion
![]() $\mathbb {P}_\alpha $
is defined by recursion on
$\mathbb {P}_\alpha $
is defined by recursion on
![]() $\alpha \in \kappa +1$
. However, each
$\alpha \in \kappa +1$
. However, each
![]() $\mathbb {P}_\alpha $
is defined uniformly.
$\mathbb {P}_\alpha $
is defined uniformly.
![]() $\mathbb {P}_\alpha $
consists of the members
$\mathbb {P}_\alpha $
consists of the members
![]() $p=(\mathcal {N}_p, R_p, A_p)$
of
$p=(\mathcal {N}_p, R_p, A_p)$
of
![]() $U_\alpha $
satisfying the following conditions:
$U_\alpha $
satisfying the following conditions:
-
(ob)
 $\bullet $
$\bullet $
 $\mathcal {N}_p$
is finite and forms a symmetric system, and
$\mathcal {N}_p$
is finite and forms a symmetric system, and-
•
 $\operatorname {dom}(R_p) \subseteq \mathcal {N}_p$
, and, for each
$\operatorname {dom}(R_p) \subseteq \mathcal {N}_p$
, and, for each
 $M\in \operatorname {dom}(R_p)$
,
$M\in \operatorname {dom}(R_p)$
,
 $R_p(M)$
is an initial segment of the set
$R_p(M)$
is an initial segment of the set
 $\alpha \cap M$
.
$\alpha \cap M$
.
-
-
(el) For each
 $\zeta \in \alpha $
,
$\zeta \in \alpha $
,
 ${R_p}^{-1}[\{ \zeta \}] \subseteq \mathfrak {M}^P_\zeta $
.
${R_p}^{-1}[\{ \zeta \}] \subseteq \mathfrak {M}^P_\zeta $
. -
(ho) For each
 $\zeta \in \alpha $
and each
$\zeta \in \alpha $
and each
 $M_0,M_1\in {R_p}^{-1}[\{ \zeta \}]$
, if
$M_0,M_1\in {R_p}^{-1}[\{ \zeta \}]$
, if
 $\omega _1\cap M_0=\omega _1\cap M_1$
, then the structure
$\omega _1\cap M_0=\omega _1\cap M_1$
, then the structure
 $\left \langle {M_0,\in , \vec {\mathbb {R}} , \vec X , \Phi \restriction M_0 , \langle \!\langle \mathbb {P}_\xi :\xi \in (\zeta +1)\cap M_0 \rangle \!\rangle }\right \rangle $
is isomorphic to the structure
$\left \langle {M_0,\in , \vec {\mathbb {R}} , \vec X , \Phi \restriction M_0 , \langle \!\langle \mathbb {P}_\xi :\xi \in (\zeta +1)\cap M_0 \rangle \!\rangle }\right \rangle $
is isomorphic to the structure
 $\left \langle {M_1,\in , \vec {\mathbb {R}} , \vec X , \Phi \restriction M_1 , \langle \!\langle \mathbb {P}_\xi :\xi \in (\zeta +1) \cap M_1 \rangle \!\rangle }\right \rangle $
.
$\left \langle {M_1,\in , \vec {\mathbb {R}} , \vec X , \Phi \restriction M_1 , \langle \!\langle \mathbb {P}_\xi :\xi \in (\zeta +1) \cap M_1 \rangle \!\rangle }\right \rangle $
. -
(up) For each
 $\zeta \in \alpha $
and each
$\zeta \in \alpha $
and each
 $M,N_0\in {R_p}^{-1}[\{ \zeta \}]$
, if
$M,N_0\in {R_p}^{-1}[\{ \zeta \}]$
, if
 $\omega _1\cap M <\omega _1\cap N_0$
, then there exists
$\omega _1\cap M <\omega _1\cap N_0$
, then there exists
 $N_1\in {R_p}^{-1}[\{\zeta \}]$
such that
$N_1\in {R_p}^{-1}[\{\zeta \}]$
such that
 $M\in N_1$
and
$M\in N_1$
and
 $\omega _1\cap N_1=\omega _1\cap N_0$
.
$\omega _1\cap N_1=\omega _1\cap N_0$
. -
(down) For each
 $\zeta \in \alpha $
and each
$\zeta \in \alpha $
and each
 $M,N_0,N_1\in {R_p}^{-1}[\{ \zeta \}]$
, if
$M,N_0,N_1\in {R_p}^{-1}[\{ \zeta \}]$
, if
 $M\in N_0$
and
$M\in N_0$
and
 $\omega _1\cap N_0=\omega _1\cap N_1$
, then
$\omega _1\cap N_0=\omega _1\cap N_1$
, then
 $\Big ({\Psi _{N_1}}^{-1}\circ \Psi _{N_0}\Big )(M) \in {R_p}^{-1}[\{\zeta \}]$
.
$\Big ({\Psi _{N_1}}^{-1}\circ \Psi _{N_0}\Big )(M) \in {R_p}^{-1}[\{\zeta \}]$
. -
(g) If
 $\xi \in \operatorname {dom}(A_p)$
and
$\xi \in \operatorname {dom}(A_p)$
and
 $p\restriction \xi $
belongs to
$p\restriction \xi $
belongs to
 $\mathbb {P}_\xi $
, then
$\mathbb {P}_\xi $
, then
 $\Phi (\xi )=\left \{{\dot r_\xi }\right \}$
such that
$\Phi (\xi )=\left \{{\dot r_\xi }\right \}$
such that
 $\dot r_\xi $
is a
$\dot r_\xi $
is a
 $\mathbb {P}_\xi $
-name for a function from
$\mathbb {P}_\xi $
-name for a function from
 $\omega $
into
$\omega $
into
 $2$
. Moreover,
$2$
. Moreover, -
(g-ob)
 $A_p(\xi )$
is a finite set of triples of the form
$A_p(\xi )$
is a finite set of triples of the form
 $\sigma = \left \langle {\varepsilon _\sigma , \delta _\sigma , \gamma _\sigma }\right \rangle $
such that
$\sigma = \left \langle {\varepsilon _\sigma , \delta _\sigma , \gamma _\sigma }\right \rangle $
such that
 $\varepsilon _\sigma \in \delta _\sigma \in \gamma _\sigma \in \omega _1$
,
$\varepsilon _\sigma \in \delta _\sigma \in \gamma _\sigma \in \omega _1$
, -
(g-ob-2) the set
 $\left \{{\delta _\sigma : \sigma \in A_p}\right \} $
includes the set
$\left \{{\delta _\sigma : \sigma \in A_p}\right \} $
includes the set
 $\left \{{\omega _1\cap N : N \in {R_p}^{-1}[\{\xi \}]}\right \}$
,
$\left \{{\omega _1\cap N : N \in {R_p}^{-1}[\{\xi \}]}\right \}$
, -
(g-cl) for each
 $\left \{{\sigma , \tau }\right \} \in \left [ A_p(\xi ) \right ]^2$
, either
$\left \{{\sigma , \tau }\right \} \in \left [ A_p(\xi ) \right ]^2$
, either
 $\gamma _\sigma < \delta _{\tau }$
or
$\gamma _\sigma < \delta _{\tau }$
or
 $\gamma _{\tau } < \delta _\sigma $
,
$\gamma _{\tau } < \delta _\sigma $
, -
(g-w) for any
 $\sigma \in A_p(\xi )$
, if
$\sigma \in A_p(\xi )$
, if
 $\delta _\sigma $
is a limit ordinal, then
$\delta _\sigma $
is a limit ordinal, then  $$ \begin{align*} \begin{array}{r@{}l} \kern-10pt p\restriction \xi \Vdash_{\mathbb{P}_\xi}\ \text{"} & \left\{{ n \in \omega : f_{\gamma_\sigma}(n) \subseteq \dot r_\xi}\right\} \text{ is infinite, and, for any }\tau \in A_p(\xi) \setminus \left\{{\sigma}\right\}\\ &\text{ with } \varepsilon_{\sigma} < \delta_\tau < \delta_\sigma, f_{\gamma_\sigma} ( \left| C_{\delta_\sigma} \cap \delta_{\tau} \right| ) \subseteq \dot r_\xi \text{ and }\\ & f_{\gamma_\sigma} ( \left| C_{\delta_\sigma} \cap (\gamma_{\tau} +1) \right| ) \subseteq \dot r_\xi \text{"} , \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{r@{}l} \kern-10pt p\restriction \xi \Vdash_{\mathbb{P}_\xi}\ \text{"} & \left\{{ n \in \omega : f_{\gamma_\sigma}(n) \subseteq \dot r_\xi}\right\} \text{ is infinite, and, for any }\tau \in A_p(\xi) \setminus \left\{{\sigma}\right\}\\ &\text{ with } \varepsilon_{\sigma} < \delta_\tau < \delta_\sigma, f_{\gamma_\sigma} ( \left| C_{\delta_\sigma} \cap \delta_{\tau} \right| ) \subseteq \dot r_\xi \text{ and }\\ & f_{\gamma_\sigma} ( \left| C_{\delta_\sigma} \cap (\gamma_{\tau} +1) \right| ) \subseteq \dot r_\xi \text{"} , \end{array} \end{align*} $$
-
(g-m) for each
 $\sigma \in A_p(\xi )$
and each
$\sigma \in A_p(\xi )$
and each
 $N\in {R_p}^{-1}[\{\xi \}]$
(that is,
$N\in {R_p}^{-1}[\{\xi \}]$
(that is,
 $\{N\}\times \big ( (\xi +1)\cap N\big ) \subseteq R_p$
) with
$\{N\}\times \big ( (\xi +1)\cap N\big ) \subseteq R_p$
) with
 $\omega _1\cap N = \delta _\sigma $
, there exists
$\omega _1\cap N = \delta _\sigma $
, there exists
 $M\in \mathcal {N}_p \cap \mathfrak {M}^P_\xi $
such that
$M\in \mathcal {N}_p \cap \mathfrak {M}^P_\xi $
such that-
•
 $N\in M$
,
$N\in M$
, -
•
 $\omega _1\cap M = \gamma _\sigma $
, and
$\omega _1\cap M = \gamma _\sigma $
, and -
•
 $\{M\}\times (\xi \cap M) \subseteq R_p$
(then, by (g-ob-2) and (g-cl),
$\{M\}\times (\xi \cap M) \subseteq R_p$
(then, by (g-ob-2) and (g-cl),
 $M \not \in {R_p}^{-1}[\{\xi \}]$
).
$M \not \in {R_p}^{-1}[\{\xi \}]$
).
-
-
By definition, we can check that, for each
![]() $p\in \mathbb {P}_\alpha $
and
$p\in \mathbb {P}_\alpha $
and
![]() $\zeta \in \alpha $
,
$\zeta \in \alpha $
,
![]() $p\restriction \zeta $
is a condition of
$p\restriction \zeta $
is a condition of
![]() $\mathbb {P}_\zeta $
. The order of
$\mathbb {P}_\zeta $
. The order of
![]() $\mathbb {P}_\alpha $
is defined as follows: For each
$\mathbb {P}_\alpha $
is defined as follows: For each
![]() $p,q\in \mathbb {P}_{\alpha }$
,
$p,q\in \mathbb {P}_{\alpha }$
,
![]() $q\leq _{\mathbb {P}_{\alpha }} p$
iff
$q\leq _{\mathbb {P}_{\alpha }} p$
iff
-
•
 $\mathcal {N}_q\supseteq \mathcal {N}_p$
,
$\mathcal {N}_q\supseteq \mathcal {N}_p$
, -
•
 $R_q\supseteq R_p$
,
$R_q\supseteq R_p$
, -
•
 $\operatorname {dom}(A_q)\supseteq \operatorname {dom}(A_p)$
,
$\operatorname {dom}(A_q)\supseteq \operatorname {dom}(A_p)$
, -
• for each
 $\xi \in \operatorname {dom}(A_p)$
,
$\xi \in \operatorname {dom}(A_p)$
,
 $A_q(\xi )\supseteq A_p(\xi )$
.
$A_q(\xi )\supseteq A_p(\xi )$
.
By definition, we can check that, for each
![]() $p,q\in \mathbb {P}_\alpha $
with
$p,q\in \mathbb {P}_\alpha $
with
![]() $q \leq _{\mathbb {P}_\alpha }p$
, and each
$q \leq _{\mathbb {P}_\alpha }p$
, and each
![]() $\zeta \in \alpha $
,
$\zeta \in \alpha $
,
![]() $q\restriction \zeta \leq _{\mathbb {P}_\zeta }p \restriction \zeta $
. By definition,
$q\restriction \zeta \leq _{\mathbb {P}_\zeta }p \restriction \zeta $
. By definition,
![]() $\mathbb {P}_\kappa $
is equivalent to the direct limit of
$\mathbb {P}_\kappa $
is equivalent to the direct limit of
![]() $\left \langle {\mathbb {P}_\alpha :\alpha \in \kappa }\right \rangle $
.
$\left \langle {\mathbb {P}_\alpha :\alpha \in \kappa }\right \rangle $
.
Lemma 4.2. Suppose that
![]() $\alpha ,\beta \in \kappa +1$
with
$\alpha ,\beta \in \kappa +1$
with
![]() $\beta <\alpha $
. Then
$\beta <\alpha $
. Then
![]() $\mathbb {P}_\beta $
can be completely embeddable into
$\mathbb {P}_\beta $
can be completely embeddable into
![]() $\mathbb {P}_\alpha $
.
$\mathbb {P}_\alpha $
.
Proof. By definition, any condition of
![]() $\mathbb {P}_\beta $
is also a condition of
$\mathbb {P}_\beta $
is also a condition of
![]() $\mathbb {P}_\alpha $
. Suppose that
$\mathbb {P}_\alpha $
. Suppose that
![]() $q\in \mathbb {P}_\beta $
,
$q\in \mathbb {P}_\beta $
,
![]() $p\in \mathbb {P}_\alpha $
, and
$p\in \mathbb {P}_\alpha $
, and
![]() $q\leq _{\mathbb {P}_\beta } p\restriction \beta $
. Then define
$q\leq _{\mathbb {P}_\beta } p\restriction \beta $
. Then define
We can check that r is a condition of
![]() $\mathbb {P}_\zeta $
. So r is an extension of p in
$\mathbb {P}_\zeta $
. So r is an extension of p in
![]() $\mathbb {P}_\alpha $
. Such an r is a canonical common extension of q and p in
$\mathbb {P}_\alpha $
. Such an r is a canonical common extension of q and p in
![]() $\mathbb {P}_\alpha $
. Hence the identity map from
$\mathbb {P}_\alpha $
. Hence the identity map from
![]() $\mathbb {P}_\beta $
into
$\mathbb {P}_\beta $
into
![]() $\mathbb {P}_\alpha $
is a complete embedding.⊣
$\mathbb {P}_\alpha $
is a complete embedding.⊣
Definition 4.3. For each
![]() $\xi \in \kappa $
, define the
$\xi \in \kappa $
, define the
![]() $\mathbb {P}_{\xi +1}$
-name
$\mathbb {P}_{\xi +1}$
-name
![]() $\dot E_\xi $
by
$\dot E_\xi $
by
Observation 4.4. It is proved in the next section that for each
![]() $\xi \in \omega _2$
,
$\xi \in \omega _2$
,
![]() $\mathbb {P}_\xi $
is proper. Then, as in the case of
$\mathbb {P}_\xi $
is proper. Then, as in the case of
![]() $\mathbb {Q}(X,r)$
in Section 2.2,
$\mathbb {Q}(X,r)$
in Section 2.2,
![]() $\dot E_\xi $
is a
$\dot E_\xi $
is a
![]() $\mathbb {P}_{\xi +1}$
-name for a club subset of
$\mathbb {P}_{\xi +1}$
-name for a club subset of
![]() $\omega _1$
. By the definition, for each
$\omega _1$
. By the definition, for each
![]() $\xi \in \omega _2$
, if
$\xi \in \omega _2$
, if
![]() $\Phi (\xi ) =\left \{{\dot r _\xi }\right \}$
and
$\Phi (\xi ) =\left \{{\dot r _\xi }\right \}$
and
![]() $\dot r_\xi $
is a
$\dot r_\xi $
is a
![]() $\mathbb {P}_\xi $
-name for a function from
$\mathbb {P}_\xi $
-name for a function from
![]() $\omega $
into
$\omega $
into
![]() $2$
, then
$2$
, then
![]() $\mathbb {P}_{\xi +1}$
forces that
$\mathbb {P}_{\xi +1}$
forces that
![]() $\dot E_\xi $
captures
$\dot E_\xi $
captures
![]() $\dot r_\xi $
relative to X.
$\dot r_\xi $
relative to X.
Observation 4.5. The requirement (g-cl) is necessary in the definition of
![]() $\mathbb {P}_\kappa $
to show Lemma 5.2. To show properness of
$\mathbb {P}_\kappa $
to show Lemma 5.2. To show properness of
![]() $\mathbb {P}_\alpha $
(for each
$\mathbb {P}_\alpha $
(for each
![]() $\alpha \leq \omega _2$
) equipped with (g-cl), we want the requirements (el), (ho), (up), and (down) in Definition 4.1. This is the reason why we introduced a symmetric system of relational structures.
$\alpha \leq \omega _2$
) equipped with (g-cl), we want the requirements (el), (ho), (up), and (down) in Definition 4.1. This is the reason why we introduced a symmetric system of relational structures.
5 Forcing (c) by
 $\mathbb {P}_{\omega _2}$
$\mathbb {P}_{\omega _2}$
Proposition 5.1. For every
![]() $\alpha \in \kappa +1$
,
$\alpha \in \kappa +1$
,
![]() $\mathbb {P}_\alpha $
has the
$\mathbb {P}_\alpha $
has the
![]() $\aleph _2$
-chain condition. In fact, every subset of
$\aleph _2$
-chain condition. In fact, every subset of
![]() $\mathbb {P}_\alpha $
of size
$\mathbb {P}_\alpha $
of size
![]() $\aleph _2$
has a pairwise compatible subset of size
$\aleph _2$
has a pairwise compatible subset of size
![]() $\aleph _2$
.
$\aleph _2$
.
Proof. Suppose that
![]() $\alpha \in \kappa +1$
and
$\alpha \in \kappa +1$
and
![]() $\left \{{p_\zeta : \zeta \in \omega _2}\right \}$
is a set of
$\left \{{p_\zeta : \zeta \in \omega _2}\right \}$
is a set of
![]() $\aleph _2$
-many conditions in
$\aleph _2$
-many conditions in
![]() $\mathbb {P}_\alpha $
. Recall that
$\mathbb {P}_\alpha $
. Recall that
![]() $\operatorname {\mathsf {CH}}$
holds (Assumption 3.1). By shrinking the set if necessary, we may assume that
$\operatorname {\mathsf {CH}}$
holds (Assumption 3.1). By shrinking the set if necessary, we may assume that
-
• the set
 $\left \{{\mathcal {N}_{p_\zeta } : \zeta \in \omega _2}\right \}$
forms a
$\left \{{\mathcal {N}_{p_\zeta } : \zeta \in \omega _2}\right \}$
forms a
 $\Delta $
-system,
$\Delta $
-system, -
• the set
 $\left \{{\operatorname {dom} (A_{p_\zeta }) : \zeta \in \omega _2}\right \}$
forms a
$\left \{{\operatorname {dom} (A_{p_\zeta }) : \zeta \in \omega _2}\right \}$
forms a
 $\Delta $
-system with root D,
$\Delta $
-system with root D, -
(•) the set
 $\displaystyle \left \{{ \left ( \bigcup \mathcal {N}_{p_\zeta } \right ) \cap \kappa : \zeta \in \omega _2}\right \}$
forms a
$\displaystyle \left \{{ \left ( \bigcup \mathcal {N}_{p_\zeta } \right ) \cap \kappa : \zeta \in \omega _2}\right \}$
forms a
 $\Delta $
-system with root K (which is a countable subset of
$\Delta $
-system with root K (which is a countable subset of
 $\kappa $
),
$\kappa $
), -
(•) for each
 $\xi \in K$
, the set does not depend on
$\xi \in K$
, the set does not depend on $$\begin{align*}\left\{{ \overline M : M\in {R_{p_\zeta }}^{-1}\big[\, [\xi,\kappa) \,\big] \cap\mathfrak{M}_\xi^P }\right\} \end{align*}$$
$$\begin{align*}\left\{{ \overline M : M\in {R_{p_\zeta }}^{-1}\big[\, [\xi,\kappa) \,\big] \cap\mathfrak{M}_\xi^P }\right\} \end{align*}$$
 $\zeta \in \omega _2$
,
$\zeta \in \omega _2$
,
-
(•) for each
 $\zeta \in \omega _2$
,
$\zeta \in \omega _2$
,
 $\left (\operatorname {dom}(A_{p_\zeta })\setminus D\right )\cap K=\emptyset $
,
$\left (\operatorname {dom}(A_{p_\zeta })\setminus D\right )\cap K=\emptyset $
, -
(•) for each
 $\zeta , \zeta ' \in \omega _2$
, each
$\zeta , \zeta ' \in \omega _2$
, each
 $M\in \mathcal {N}_{p_\zeta }$
and each
$M\in \mathcal {N}_{p_\zeta }$
and each
 $M'\in \mathcal {N}_{p_{\zeta '}}$
, if
$M'\in \mathcal {N}_{p_{\zeta '}}$
, if
 $\overline M=\overline {M'}$
, then
$\overline M=\overline {M'}$
, then
 $M\cap \kappa $
and
$M\cap \kappa $
and
 $M'\cap \kappa $
are order isomorphic and the corresponding isomorphism fixes
$M'\cap \kappa $
are order isomorphic and the corresponding isomorphism fixes
 $\kappa \cap M\cap M'$
(which is a subset of K)Footnote
2
, and
$\kappa \cap M\cap M'$
(which is a subset of K)Footnote
2
, and -
• for each
 $\xi \in D$
, the coordinate
$\xi \in D$
, the coordinate
 $A_{p_\zeta }(\xi ) \in \left [ \omega _1\times \omega _1\times \omega _1 \right ]^{<\aleph _0}$
does not depend on
$A_{p_\zeta }(\xi ) \in \left [ \omega _1\times \omega _1\times \omega _1 \right ]^{<\aleph _0}$
does not depend on
 $\zeta \in \omega _2$
.
$\zeta \in \omega _2$
.
Then we claim that for each distinct
![]() $\zeta $
and
$\zeta $
and
![]() $\zeta '$
,
$\zeta '$
,
![]() $p_\zeta $
and
$p_\zeta $
and
![]() $p_{\zeta '}$
are compatible in
$p_{\zeta '}$
are compatible in
![]() $\mathbb {P}_\alpha $
. To see this, let
$\mathbb {P}_\alpha $
. To see this, let
![]() $q \in U_\alpha $
such that
$q \in U_\alpha $
such that
-
•
 $\mathcal {N}_q:=\mathcal {N}_{p_\zeta }\cup \mathcal {N}_{p_{\zeta '}}$
,
$\mathcal {N}_q:=\mathcal {N}_{p_\zeta }\cup \mathcal {N}_{p_{\zeta '}}$
, -
•
 $R_q:=R_{p_\zeta }\cup R_{p_{\zeta '}}$
, and
$R_q:=R_{p_\zeta }\cup R_{p_{\zeta '}}$
, and -
•
 $A_q$
is the function with domain
$A_q$
is the function with domain
 $\operatorname {dom}(A_{p_\zeta })\cup \operatorname {dom}(A_{p_{\zeta '}})$
such that, for each
$\operatorname {dom}(A_{p_\zeta })\cup \operatorname {dom}(A_{p_{\zeta '}})$
such that, for each
 $\xi \in \operatorname {dom}(A_{p_\zeta })\cup \operatorname {dom}(A_{p_{\zeta '}})$
, (which is equal to
$\xi \in \operatorname {dom}(A_{p_\zeta })\cup \operatorname {dom}(A_{p_{\zeta '}})$
, (which is equal to $$\begin{align*}A_q(\xi):= A_{p_\zeta}(\xi)\cup A_{p_{\zeta'}}(\xi) \end{align*}$$
$$\begin{align*}A_q(\xi):= A_{p_\zeta}(\xi)\cup A_{p_{\zeta'}}(\xi) \end{align*}$$
 $A_{p_\zeta }(\xi )$
or
$A_{p_\zeta }(\xi )$
or
 $A_{p_{\zeta '}}(\xi )$
).
$A_{p_{\zeta '}}(\xi )$
).
Such a q is a canonical amalgamation of
![]() $p_\zeta $
and
$p_\zeta $
and
![]() $p_{\zeta '}$
. Then by the above items
$p_{\zeta '}$
. Then by the above items
![]() $(\boldsymbol \bullet )$
,
$(\boldsymbol \bullet )$
,
![]() $\mathcal {N}_q$
and
$\mathcal {N}_q$
and
![]() $R_q$
satisfy Definition 4.1
(ob), (el), (ho), (up), and (down). Recall that for each
$R_q$
satisfy Definition 4.1
(ob), (el), (ho), (up), and (down). Recall that for each
![]() $M\in \mathfrak {M}_0$
and each
$M\in \mathfrak {M}_0$
and each
![]() $\alpha \in \kappa $
, if
$\alpha \in \kappa $
, if
![]() $\alpha \not \in M$
, then
$\alpha \not \in M$
, then
![]() $M\not \in \mathfrak {M}_\alpha ^P$
. So for any
$M\not \in \mathfrak {M}_\alpha ^P$
. So for any
![]() $\left \{{\zeta ,\zeta '}\right \} \in \left [\omega _2\right ]^2$
and any
$\left \{{\zeta ,\zeta '}\right \} \in \left [\omega _2\right ]^2$
and any
![]() $\alpha \in \operatorname {dom}(A_{p_\zeta })\setminus D$
,
$\alpha \in \operatorname {dom}(A_{p_\zeta })\setminus D$
,
![]() $\operatorname {dom}(R_{p_{\zeta '}})\cap \mathfrak {M}_\alpha ^P =\emptyset $
, and hence
$\operatorname {dom}(R_{p_{\zeta '}})\cap \mathfrak {M}_\alpha ^P =\emptyset $
, and hence
![]() ${R_q}^{-1}[\{\alpha \}] = {R_{p_\zeta }}^{-1}[\{\alpha \}]$
. Therefore q satisfies (g). Thus q is a condition of
${R_q}^{-1}[\{\alpha \}] = {R_{p_\zeta }}^{-1}[\{\alpha \}]$
. Therefore q satisfies (g). Thus q is a condition of
![]() $\mathbb {P}_\alpha $
, and is a common extension of
$\mathbb {P}_\alpha $
, and is a common extension of
![]() $p_\zeta $
and
$p_\zeta $
and
![]() $p_{\zeta '}$
.⊣
$p_{\zeta '}$
.⊣
Lemma 5.2. Each
![]() $\alpha $
in
$\alpha $
in
![]() $\omega _2+1$
satisfies the following assertions.
$\omega _2+1$
satisfies the following assertions.
-
 $\mathsf {(p)}_\alpha $
: For any
$\mathsf {(p)}_\alpha $
: For any
 $p\in \mathbb {P}_{\alpha }$
and any
$p\in \mathbb {P}_{\alpha }$
and any
 $N\in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
such that
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
such that
 $\{N\}\times (\alpha \cap N) \subseteq R_p$
, p is
$\{N\}\times (\alpha \cap N) \subseteq R_p$
, p is
 $(N,\mathbb {P}_\alpha )$
-generic.
$(N,\mathbb {P}_\alpha )$
-generic. -
 $\mathsf {(C)}_\alpha $
: For any
$\mathsf {(C)}_\alpha $
: For any
 $p\in \mathbb {P}_{\alpha }$
and any
$p\in \mathbb {P}_{\alpha }$
and any
 $N \in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
such that
$N \in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
such that
 $\{N \}\times (\alpha \cap N) \subseteq R_p$
,
$\{N \}\times (\alpha \cap N) \subseteq R_p$
,  $$\begin{align*}p \Vdash_{\mathbb{P}_\alpha}\ {"} f_{\omega_1\cap N} \text{ is Cohen over } N[\dot G_{\mathbb{P}_\alpha}]{"}. \end{align*}$$
$$\begin{align*}p \Vdash_{\mathbb{P}_\alpha}\ {"} f_{\omega_1\cap N} \text{ is Cohen over } N[\dot G_{\mathbb{P}_\alpha}]{"}. \end{align*}$$
This is proved by induction on
![]() $\alpha \in \omega _2+1$
. A point is that, if
$\alpha \in \omega _2+1$
. A point is that, if
![]() $\alpha \in \omega _2+1$
,
$\alpha \in \omega _2+1$
,
![]() $p\in \mathbb {P}$
, and
$p\in \mathbb {P}$
, and
![]() $N\in \mathcal {N}_p$
, then
$N\in \mathcal {N}_p$
, then
![]() $R_p(N) \subseteq \omega _2$
. In the following proof, we will use Propositions 3.10 and 3.11 frequently.
$R_p(N) \subseteq \omega _2$
. In the following proof, we will use Propositions 3.10 and 3.11 frequently.
Proof of
 $\mathsf {(p)}_0$
.
$\mathsf {(p)}_0$
.
This proof is a standard proof in the context of the side condition method (see, e.g., [Reference Todorčević12, Lemma 4]), and similar to the proof in [Reference Miyamoto and Yorioka10]. Suppose that
![]() $p\in \mathbb {P}_0$
(then
$p\in \mathbb {P}_0$
(then
![]() $R_p=A_p=\emptyset $
),
$R_p=A_p=\emptyset $
),
![]() $N\in \mathcal {N}_p \cap \mathfrak {M}^P_0$
,
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_0$
,
![]() $\mathcal {D}\in N$
is a predense subset of
$\mathcal {D}\in N$
is a predense subset of
![]() $\mathbb {P}_0$
, and
$\mathbb {P}_0$
, and
![]() $q\leq _{\mathbb {P}_0} p$
. We notice that q is of the form
$q\leq _{\mathbb {P}_0} p$
. We notice that q is of the form
![]() $(\mathcal {N}_q,\emptyset , \emptyset )$
. It suffices to find
$(\mathcal {N}_q,\emptyset , \emptyset )$
. It suffices to find
![]() $u'\in \mathcal {D} \cap N$
which is compatible with q in
$u'\in \mathcal {D} \cap N$
which is compatible with q in
![]() $\mathbb {P}_0$
.
$\mathbb {P}_0$
.
By extending q if necessary, we may assume that there exists
![]() $u\in \mathcal {D}$
such that
$u\in \mathcal {D}$
such that
![]() $q\leq _{\mathbb {P}_0} u$
. Define
$q\leq _{\mathbb {P}_0} u$
. Define
 $$ \begin{align*} { \begin{array}{r@{}l} \mathcal{E}:=\Big\{r\in\mathbb{P}_0:{\ } & \text{there are }u' \in\mathcal{D} \text{ and } M\in \mathcal{N}_r \text{ such that }r\leq_{\mathbb{P}_0} u' \text{ and }\\ &\mathcal{N}_r\cap M = \mathcal{N}_q\cap N \Big\}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \mathcal{E}:=\Big\{r\in\mathbb{P}_0:{\ } & \text{there are }u' \in\mathcal{D} \text{ and } M\in \mathcal{N}_r \text{ such that }r\leq_{\mathbb{P}_0} u' \text{ and }\\ &\mathcal{N}_r\cap M = \mathcal{N}_q\cap N \Big\}. \end{array} } \end{align*} $$
Since the set
![]() $\mathcal {N}_q\cap N$
belongs to N,
$\mathcal {N}_q\cap N$
belongs to N,
![]() $\mathcal {E}$
is a definable class in the expanded relational structure by
$\mathcal {E}$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_0$
with parameters in N. Moreover, we note that
$\mathbb {P}_0$
with parameters in N. Moreover, we note that
![]() $q\in \mathcal {E}$
. So by elementarity of N, there exist
$q\in \mathcal {E}$
. So by elementarity of N, there exist
![]() $r\in \mathcal {E}\cap N$
and
$r\in \mathcal {E}\cap N$
and
![]() $u'\in \mathcal {D}\cap N$
such that
$u'\in \mathcal {D}\cap N$
such that
![]() $r\leq _{\mathbb {P}_0} u'$
. Define
$r\leq _{\mathbb {P}_0} u'$
. Define
![]() $q' \in U_0$
such that
$q' \in U_0$
such that
 $$\begin{align*}\begin{array}{r@{\ }l} \mathcal{N}_{q'}:= & \mathcal{N}_q \cup \mathcal{N}_r \\[5pt] & \cup \Big\{ \left( {\Psi_{M'} }^{-1} \circ \Psi_{N} \right) (M) : M'\in \mathcal{N}_q \text{ with } \omega_1\cap M'=\omega_1\cap N, M\in \mathcal{N}_r \Big\}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} \mathcal{N}_{q'}:= & \mathcal{N}_q \cup \mathcal{N}_r \\[5pt] & \cup \Big\{ \left( {\Psi_{M'} }^{-1} \circ \Psi_{N} \right) (M) : M'\in \mathcal{N}_q \text{ with } \omega_1\cap M'=\omega_1\cap N, M\in \mathcal{N}_r \Big\}. \end{array} \end{align*}$$
![]() $\mathcal {N}_{q'}$
forms a symmetric system.
$\mathcal {N}_{q'}$
forms a symmetric system.
![]() $q'$
is the canonical amalgamation of q and r. Therefore,
$q'$
is the canonical amalgamation of q and r. Therefore,
![]() $q'$
is a condition of
$q'$
is a condition of
![]() $\mathbb {P}_0$
and a common extension of q and r in
$\mathbb {P}_0$
and a common extension of q and r in
![]() $\mathbb {P}_0$
.
$\mathbb {P}_0$
.
![]() $\dashv$
$\dashv$
Proof of
 $\mathsf {(C)}_0$
.
$\mathsf {(C)}_0$
.
Suppose that
![]() $p\in \mathbb {P}_0$
,
$p\in \mathbb {P}_0$
,
![]() $N \in \mathcal {N}_p \cap \mathfrak {M}^P_0$
, and
$N \in \mathcal {N}_p \cap \mathfrak {M}^P_0$
, and
![]() $\left \{{\dot F_n: n\in \omega }\right \}$
is a set of
$\left \{{\dot F_n: n\in \omega }\right \}$
is a set of
![]() $\mathbb {P}_0$
-names for nowhere dense subsets of
$\mathbb {P}_0$
-names for nowhere dense subsets of
![]() $\left ({2^{<\omega }}\right )^\omega $
such that the sequence
$\left ({2^{<\omega }}\right )^\omega $
such that the sequence
![]() $\left \langle {\dot F_n: n\in \omega }\right \rangle $
belongs to
$\left \langle {\dot F_n: n\in \omega }\right \rangle $
belongs to
![]() $ N$
. Let us show that
$ N$
. Let us show that
Suppose not, and let q be an extension of p in
![]() $\mathbb {P}_0$
such that, for some
$\mathbb {P}_0$
such that, for some
![]() $n\in \omega $
,
$n\in \omega $
,
For each
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, each
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, each
![]() $x\in \left [ \mathfrak {M}^P_0 \right ]^{<\aleph _0}$
, and each
$x\in \left [ \mathfrak {M}^P_0 \right ]^{<\aleph _0}$
, and each
![]() $r\in \mathbb {P}_0$
, define
$r\in \mathbb {P}_0$
, define
![]() $\varphi _0(\nu , x, r)$
to be the assertion that there exists
$\varphi _0(\nu , x, r)$
to be the assertion that there exists
![]() $K \in \mathcal {N}_r$
such that
$K \in \mathcal {N}_r$
such that
-
•
 $\left \{{\omega _1\cap M : M\in \mathcal {N}_r\cap K }\right \} = \left \{{\omega _1\cap M : M\in \mathcal {N}_q \cap N }\right \} , $
$\left \{{\omega _1\cap M : M\in \mathcal {N}_r\cap K }\right \} = \left \{{\omega _1\cap M : M\in \mathcal {N}_q \cap N }\right \} , $
-
•
 $\mathcal {N}_q\cap N \subseteq \mathcal {N}_r \cap K $
,
$\mathcal {N}_q\cap N \subseteq \mathcal {N}_r \cap K $
, -
•
 $x\in K$
, and
$x\in K$
, and -
•
 $ r \Vdash _{\mathbb {P}_0}\!\!\!\text {"}\,\, \dot F_n \cap [ \nu ] \neq \emptyset \,\text {"} $
,
$ r \Vdash _{\mathbb {P}_0}\!\!\!\text {"}\,\, \dot F_n \cap [ \nu ] \neq \emptyset \,\text {"} $
,
and define
 $$ \begin{align*} { \begin{array}{r@{}l} Y:=\Big\{g\in \left({2^{<\omega}}\right)^\omega :{\ } & \text{for any }k\in \omega \text{ and any }x\in \left[ \mathfrak{M}^P_0 \right]^{<\aleph_0}, \text{ there is } r\in \mathbb{P}_0\\ &\text{ which satisfies } \varphi_0(g\restriction k, x , r)\Big\}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} Y:=\Big\{g\in \left({2^{<\omega}}\right)^\omega :{\ } & \text{for any }k\in \omega \text{ and any }x\in \left[ \mathfrak{M}^P_0 \right]^{<\aleph_0}, \text{ there is } r\in \mathbb{P}_0\\ &\text{ which satisfies } \varphi_0(g\restriction k, x , r)\Big\}. \end{array} } \end{align*} $$
Since
![]() $\left \{{\dot F_n, \mathcal {N}_p\cap N}\right \} \in N \in \mathfrak {M}^P_0$
, we have
$\left \{{\dot F_n, \mathcal {N}_p\cap N}\right \} \in N \in \mathfrak {M}^P_0$
, we have
![]() $Y\in N$
.
$Y\in N$
.
We claim that Y is nowhere dense. To show this, let
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
. Take
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
. Take
![]() $\nu ' \in \left ({2^{<\omega }}\right )^{<\omega }$
and
$\nu ' \in \left ({2^{<\omega }}\right )^{<\omega }$
and
![]() $s\leq _{ \mathbb {P}_0} q$
such that
$s\leq _{ \mathbb {P}_0} q$
such that
![]() $\nu \subseteq \nu '$
, and
$\nu \subseteq \nu '$
, and
Let us show that
![]() $Y \cap [\nu '] =\emptyset $
. If not, there exists
$Y \cap [\nu '] =\emptyset $
. If not, there exists
![]() $g\in Y \cap [\nu ']$
. Let
$g\in Y \cap [\nu ']$
. Let
![]() $k\in \omega $
be such that
$k\in \omega $
be such that
![]() $\nu ' \subseteq g\restriction k$
. Then there exists
$\nu ' \subseteq g\restriction k$
. Then there exists
![]() $r \in \mathbb {P}_0$
which satisfies
$r \in \mathbb {P}_0$
which satisfies
![]() $\varphi _0(g\restriction k, \mathcal {N}_s, r)$
. Let us fix
$\varphi _0(g\restriction k, \mathcal {N}_s, r)$
. Let us fix
![]() $K\in \mathcal {N}_r$
witness to
$K\in \mathcal {N}_r$
witness to
![]() $\varphi _0(g\restriction k, \mathcal {N}_s, r)$
. Define
$\varphi _0(g\restriction k, \mathcal {N}_s, r)$
. Define
![]() $r'\in U_0$
such that
$r'\in U_0$
such that
 $$\begin{align*}\begin{array}{r@{\ }l} \mathcal{N}_{r'}:= & \mathcal{N}_s \cup \mathcal{N}_r \\[5pt] & \cup \Big\{ \left( {\Psi_{M'} }^{-1} \circ \Psi_{K} \right) (M) : M'\in \mathcal{N}_r \text{ with } \omega_1\cap M'=\omega_1\cap K, M\in \mathcal{N}_s \Big\}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} \mathcal{N}_{r'}:= & \mathcal{N}_s \cup \mathcal{N}_r \\[5pt] & \cup \Big\{ \left( {\Psi_{M'} }^{-1} \circ \Psi_{K} \right) (M) : M'\in \mathcal{N}_r \text{ with } \omega_1\cap M'=\omega_1\cap K, M\in \mathcal{N}_s \Big\}. \end{array} \end{align*}$$
Then
![]() $r'$
is a common extension of s and r in
$r'$
is a common extension of s and r in
![]() $\mathbb {P}_0$
, and hence
$\mathbb {P}_0$
, and hence
which is a contradiction.
We claim that
![]() $f_{\omega _1\cap N}$
belongs to
$f_{\omega _1\cap N}$
belongs to
![]() $ Y$
. This contradicts the fact that
$ Y$
. This contradicts the fact that
![]() $f_{\omega _1\cap N}$
is Cohen over N. To show that
$f_{\omega _1\cap N}$
is Cohen over N. To show that
![]() $f_{\omega _1\cap N} \in Y$
, assume that
$f_{\omega _1\cap N} \in Y$
, assume that
![]() $f_{\omega _1\cap N} \not \in Y$
. Then there are
$f_{\omega _1\cap N} \not \in Y$
. Then there are
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $x\in \left [ \mathfrak {M}^P_0 \right ]^{<\aleph _0}$
such that there are no
$x\in \left [ \mathfrak {M}^P_0 \right ]^{<\aleph _0}$
such that there are no
![]() $r \in \mathbb {P}_0$
which satisfies
$r \in \mathbb {P}_0$
which satisfies
![]() $\varphi _0(f_{\omega _1\cap N} \restriction k, x , r)$
. Since
$\varphi _0(f_{\omega _1\cap N} \restriction k, x , r)$
. Since
![]() $f_{\omega _1\cap N} \restriction k\in N$
and N is an elementary substructure of the expanded relational structure by
$f_{\omega _1\cap N} \restriction k\in N$
and N is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}_0$
, there exists
$\mathbb {P}_0$
, there exists
![]() $x' \in \left [ \mathfrak {M}^P_0 \right ]^{<\aleph _0} \cap N$
such that there are no
$x' \in \left [ \mathfrak {M}^P_0 \right ]^{<\aleph _0} \cap N$
such that there are no
![]() $r \in \mathbb {P}_0$
which satisfies
$r \in \mathbb {P}_0$
which satisfies
![]() $\varphi _0(f_{\omega _1\cap N} \restriction k, x' , r)$
. However, q satisfies
$\varphi _0(f_{\omega _1\cap N} \restriction k, x' , r)$
. However, q satisfies
![]() $\varphi _0(f_{\omega _1\cap N} \restriction k, x' , q)$
, which is a contradiction.
$\varphi _0(f_{\omega _1\cap N} \restriction k, x' , q)$
, which is a contradiction.
![]() $\dashv$
$\dashv$
Proof of
 $\mathsf {(p)}_{\alpha +1}$
.
$\mathsf {(p)}_{\alpha +1}$
.
Suppose that
![]() $\alpha \in \omega _2$
,
$\alpha \in \omega _2$
,
![]() $p\in \mathbb {P}_{\alpha +1}$
,
$p\in \mathbb {P}_{\alpha +1}$
,
![]() $N\in \mathcal {N}_p \cap \mathfrak {M}^P_{\alpha +1}$
which satisfies that
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_{\alpha +1}$
which satisfies that
![]() $\{N\}\times ((\alpha +1)\cap N)\subseteq R_p$
,
$\{N\}\times ((\alpha +1)\cap N)\subseteq R_p$
,
![]() $\mathcal {D}\in N$
is a predense subset of
$\mathcal {D}\in N$
is a predense subset of
![]() $\mathbb {P}_{\alpha +1}$
, and
$\mathbb {P}_{\alpha +1}$
, and
![]() ${q\leq _{\mathbb {P}_{\alpha +1}} p}$
. By extending q if necessary, we may assume that q is an extension of some member of
${q\leq _{\mathbb {P}_{\alpha +1}} p}$
. By extending q if necessary, we may assume that q is an extension of some member of
![]() $\mathcal {D}$
. Since
$\mathcal {D}$
. Since
![]() $N \in \mathfrak {M}^P_{\alpha +1}$
, by Proposition 3.9(3) and the fact that
$N \in \mathfrak {M}^P_{\alpha +1}$
, by Proposition 3.9(3) and the fact that
![]() $\alpha + 1 \in N$
(hence
$\alpha + 1 \in N$
(hence
![]() $\alpha \in N$
),
$\alpha \in N$
),
![]() $N \in \mathfrak {M}^P_\alpha $
. So by the induction hypothesis
$N \in \mathfrak {M}^P_\alpha $
. So by the induction hypothesis
![]() $\mathsf {(p)}_\alpha $
,
$\mathsf {(p)}_\alpha $
,
![]() $q\restriction \alpha $
is
$q\restriction \alpha $
is
![]() $(N,\mathbb {P}_\alpha )$
-generic. It suffices to find
$(N,\mathbb {P}_\alpha )$
-generic. It suffices to find
![]() $u\in \mathbb {P}_{\alpha + 1} \cap N$
which is compatible with q in
$u\in \mathbb {P}_{\alpha + 1} \cap N$
which is compatible with q in
![]() $\mathbb {P}_{\alpha +1}$
such that u is an extension of some member of
$\mathbb {P}_{\alpha +1}$
such that u is an extension of some member of
![]() $\mathcal {D} \cap N$
. When
$\mathcal {D} \cap N$
. When
![]() $\alpha \not \in \operatorname {dom}(A_q)$
, the argument is similar to the proof of
$\alpha \not \in \operatorname {dom}(A_q)$
, the argument is similar to the proof of
![]() $\mathsf {(p)}_0$
. So we suppose that
$\mathsf {(p)}_0$
. So we suppose that
![]() $\alpha \in \operatorname {dom}(A_q)$
.
$\alpha \in \operatorname {dom}(A_q)$
.
Define
![]() $\mathcal {E}$
to be the set of the conditions u of
$\mathcal {E}$
to be the set of the conditions u of
![]() $\mathbb {P}_{\alpha +1} $
such that
$\mathbb {P}_{\alpha +1} $
such that
-
• u is an extension of some member of
 $\mathcal {D}$
in
$\mathcal {D}$
in
 $\mathbb {P}_{\alpha +1}$
,
$\mathbb {P}_{\alpha +1}$
, -
•
 $\mathcal {N}_u\cap M = \mathcal {N}_q\cap N$
and
$\mathcal {N}_u\cap M = \mathcal {N}_q\cap N$
and
 $A_u(\alpha )\cap M = A_q(\alpha )\cap N$
for some
$A_u(\alpha )\cap M = A_q(\alpha )\cap N$
for some
 $M\in {R_u}^{-1}[\{\alpha \}]$
, and
$M\in {R_u}^{-1}[\{\alpha \}]$
, and -
• for any
 $\sigma \in A_q(\alpha )\setminus N$
with
$\sigma \in A_q(\alpha )\setminus N$
with
 $\delta _\sigma> \omega _1\cap N$
and
$\delta _\sigma> \omega _1\cap N$
and
 $C_{\delta _\sigma }\cap N \neq \emptyset $
,
$C_{\delta _\sigma }\cap N \neq \emptyset $
,  $$\begin{align*}\max\left( C_{\delta_\sigma}\cap N \right) < \min \left\{{\delta_\tau : \tau \in A_u(\alpha) \setminus \left( A_q(\alpha) \cap N \right)}\right\}. \end{align*}$$
$$\begin{align*}\max\left( C_{\delta_\sigma}\cap N \right) < \min \left\{{\delta_\tau : \tau \in A_u(\alpha) \setminus \left( A_q(\alpha) \cap N \right)}\right\}. \end{align*}$$
Then
![]() $q\in \mathcal {E}$
, and
$q\in \mathcal {E}$
, and
![]() $\mathcal {E}$
is a definable class in the expanded relational structure by
$\mathcal {E}$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
with parameters
$\mathbb {P}_{\alpha +1}$
with parameters
![]() $\mathcal {D}$
,
$\mathcal {D}$
,
![]() $\mathcal {N}_q \cap N$
,
$\mathcal {N}_q \cap N$
,
![]() $A_q(\alpha )\cap N$
,
$A_q(\alpha )\cap N$
,
![]() $\{ C_{\delta _\sigma } \cap N : \sigma \in A_q(\alpha )\setminus N, \delta _\sigma> \omega _1\cap N \} $
, all of which are in N. Since
$\{ C_{\delta _\sigma } \cap N : \sigma \in A_q(\alpha )\setminus N, \delta _\sigma> \omega _1\cap N \} $
, all of which are in N. Since
![]() $q\restriction \alpha $
is
$q\restriction \alpha $
is
![]() $(N,\mathbb {P}_\alpha )$
-generic, for any
$(N,\mathbb {P}_\alpha )$
-generic, for any
![]() $\eta \in \omega _1\cap N$
,
$\eta \in \omega _1\cap N$
,
 $$ \begin{align*} { \begin{array}{r@{\ }l} \star \ q\restriction\alpha \Vdash_{\mathbb{P}_\alpha}\!\!\!&\text{"} \text{there exists }u\in \mathcal{E}\cap N \text{ such that } u\restriction \alpha \in \dot G_{\mathbb{P}_\alpha} \text{ and } \\ & \eta < \min \left\{{\delta_\tau : \tau \in A_u(\alpha) \setminus \left( A_q(\alpha) \cap N \right)}\right\}\! \text{"}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{\ }l} \star \ q\restriction\alpha \Vdash_{\mathbb{P}_\alpha}\!\!\!&\text{"} \text{there exists }u\in \mathcal{E}\cap N \text{ such that } u\restriction \alpha \in \dot G_{\mathbb{P}_\alpha} \text{ and } \\ & \eta < \min \left\{{\delta_\tau : \tau \in A_u(\alpha) \setminus \left( A_q(\alpha) \cap N \right)}\right\}\! \text{"}. \end{array} } \end{align*} $$
Define
![]() $\dot Z$
to be a
$\dot Z$
to be a
![]() $\mathbb {P}_\alpha $
-name such that
$\mathbb {P}_\alpha $
-name such that
 $$ \begin{align*} { \begin{array}{r@{}l} \Vdash_{\mathbb{P}_\alpha}\ \text{"} & \dot Z \text{ is the set of the functions }g \text{ from }\omega \text{ into }2^{<\omega} \text{ such that there exists}\\ &u\in \mathcal{E}\cap N \text{ such that } u\restriction \alpha \in \dot G_{\mathbb{P}_\alpha} \text{ and, for any } \tau \in A_u(\alpha) \setminus \left( A_q(\alpha)\cap N \right),\\ &g ( \left| C_{\omega_1\cap N } \cap \delta_\tau \right|) \subseteq \dot r_\alpha \text{ and } g ( \left| C_{\omega_1\cap N } \cap (\gamma_\tau +1) \right|) \subseteq \dot r_\alpha \text{"}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \Vdash_{\mathbb{P}_\alpha}\ \text{"} & \dot Z \text{ is the set of the functions }g \text{ from }\omega \text{ into }2^{<\omega} \text{ such that there exists}\\ &u\in \mathcal{E}\cap N \text{ such that } u\restriction \alpha \in \dot G_{\mathbb{P}_\alpha} \text{ and, for any } \tau \in A_u(\alpha) \setminus \left( A_q(\alpha)\cap N \right),\\ &g ( \left| C_{\omega_1\cap N } \cap \delta_\tau \right|) \subseteq \dot r_\alpha \text{ and } g ( \left| C_{\omega_1\cap N } \cap (\gamma_\tau +1) \right|) \subseteq \dot r_\alpha \text{"}. \end{array} } \end{align*} $$
By (g-ob-2), (g-cl), and
![]() $N\in {R_q}^{-1}[\{\alpha \}]$
, there exists the unique
$N\in {R_q}^{-1}[\{\alpha \}]$
, there exists the unique
![]() $\sigma _0 \in A_q(\alpha )$
such that
$\sigma _0 \in A_q(\alpha )$
such that
![]() $\delta _{\sigma _0} = \omega _1\cap N$
. By (g-m), we can take
$\delta _{\sigma _0} = \omega _1\cap N$
. By (g-m), we can take
![]() $M\in \mathcal {N}_q \cap \mathfrak {M}^P_\alpha $
such that
$M\in \mathcal {N}_q \cap \mathfrak {M}^P_\alpha $
such that
![]() $N \in M$
,
$N \in M$
,
![]() $\omega _1\cap M = \gamma _{\sigma _0}$
, and
$\omega _1\cap M = \gamma _{\sigma _0}$
, and
![]() $\{ M\}\times (\alpha \cap M)\subseteq R_q$
. By
$\{ M\}\times (\alpha \cap M)\subseteq R_q$
. By
![]() $\star $
above,
$\star $
above,
![]() $q \restriction \alpha \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\dot Z$
is dense open in
$q \restriction \alpha \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\dot Z$
is dense open in
![]() $\left ({2^{<\omega }}\right )^\omega $
”.
$\left ({2^{<\omega }}\right )^\omega $
”.
![]() $\dot Z$
is defined from the set
$\dot Z$
is defined from the set
![]() $\left \{{N, A_q(\alpha ) \cap N , C_{\omega _1\cap N}, \dot r_\alpha }\right \}$
(which is in M),
$\left \{{N, A_q(\alpha ) \cap N , C_{\omega _1\cap N}, \dot r_\alpha }\right \}$
(which is in M),
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\dot G_{\mathbb {P}_\alpha }$
, and is forced to be an open subset of
$\dot G_{\mathbb {P}_\alpha }$
, and is forced to be an open subset of
![]() $\left ({2^{<\omega }}\right )^\omega $
. Since M is an elementary substructure of the expanded relational structure by
$\left ({2^{<\omega }}\right )^\omega $
. Since M is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}_{\alpha }$
, by Proposition 5.1,
$\mathbb {P}_{\alpha }$
, by Proposition 5.1,
![]() $\dot Z$
can be considered as an element of M. By the induction hypothesis
$\dot Z$
can be considered as an element of M. By the induction hypothesis
![]() $\mathsf {(C)}_\alpha $
,
$\mathsf {(C)}_\alpha $
,
![]() $q \restriction \alpha \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\,\, f_{\omega _1\cap M}$
is Cohen over
$q \restriction \alpha \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\,\, f_{\omega _1\cap M}$
is Cohen over
![]() $M[\dot G_{\mathbb {P}_\alpha }]\,\text {"}$
. It follows that
$M[\dot G_{\mathbb {P}_\alpha }]\,\text {"}$
. It follows that
![]() $q \restriction \alpha \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\,\, f_{\omega _1\cap M} \in \dot Z \,\text {"}$
. Take
$q \restriction \alpha \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\,\, f_{\omega _1\cap M} \in \dot Z \,\text {"}$
. Take
![]() $r\in \mathbb {P}_\alpha $
and
$r\in \mathbb {P}_\alpha $
and
![]() $u\in \mathcal {E}\cap N$
such that
$u\in \mathcal {E}\cap N$
such that
![]() $r\leq _{\mathbb {P}_\alpha } q\restriction \alpha $
and
$r\leq _{\mathbb {P}_\alpha } q\restriction \alpha $
and
Let
![]() $r'$
be a common extension of r and
$r'$
be a common extension of r and
![]() $u\restriction \alpha $
. Define
$u\restriction \alpha $
. Define
![]() $q' \in U_{\alpha +1}$
such that
$q' \in U_{\alpha +1}$
such that
-
•
 $\mathcal {N}_{q'}:=\mathcal {N}_{r'}$
,
$\mathcal {N}_{q'}:=\mathcal {N}_{r'}$
, -
•
 $R_{q'}:=R_{r'}$
$R_{q'}:=R_{r'}$
 $$\begin{align*}\begin{array}{r@{\ }l} \cup \Big\{ \left\langle{\left( {\Psi_{M'} }^{-1} \circ \Psi_{N} \right) (K), \alpha}\right\rangle : & M' \in {R_q}^{-1}[\{\alpha\}] \text{ with } \omega_1\cap M' = \omega_1\cap N, \\ & K \in {R_u}^{-1}[\{\alpha\}] \setminus {R_q}^{-1}[\{\alpha\}] \Big\} , \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} \cup \Big\{ \left\langle{\left( {\Psi_{M'} }^{-1} \circ \Psi_{N} \right) (K), \alpha}\right\rangle : & M' \in {R_q}^{-1}[\{\alpha\}] \text{ with } \omega_1\cap M' = \omega_1\cap N, \\ & K \in {R_u}^{-1}[\{\alpha\}] \setminus {R_q}^{-1}[\{\alpha\}] \Big\} , \end{array} \end{align*}$$
-
•
 $A_{q'}\restriction \alpha := A_{r'}$
, and
$A_{q'}\restriction \alpha := A_{r'}$
, and -
•
 $A_{q'}(\alpha ) = A_u(\alpha ) \cup A_q(\alpha )$
.
$A_{q'}(\alpha ) = A_u(\alpha ) \cup A_q(\alpha )$
.
We claim that
![]() $q'$
is a condition of
$q'$
is a condition of
![]() $\mathbb {P}_{\alpha +1}$
. Since
$\mathbb {P}_{\alpha +1}$
. Since
![]() $q'\restriction \alpha = r'$
,
$q'\restriction \alpha = r'$
,
![]() $q'\restriction \alpha $
is a condition of
$q'\restriction \alpha $
is a condition of
![]() $\mathbb {P}_\alpha $
. Since
$\mathbb {P}_\alpha $
. Since
![]() $q\in \mathbb {P}_{\alpha +1}$
,
$q\in \mathbb {P}_{\alpha +1}$
,
![]() $u \in \mathbb {P}_{\alpha +1} \cap N$
,
$u \in \mathbb {P}_{\alpha +1} \cap N$
,
![]() $N\in \mathfrak {M}^P_{\alpha +1}$
, and
$N\in \mathfrak {M}^P_{\alpha +1}$
, and
![]() $\alpha \in \omega _2$
, by Propositions 3.10 and 3.11,
$\alpha \in \omega _2$
, by Propositions 3.10 and 3.11,
![]() ${R_{q'}}^{-1}[\{\alpha \}]$
satisfies (el), (ho), (up), and (down). Since q and u are conditions of
${R_{q'}}^{-1}[\{\alpha \}]$
satisfies (el), (ho), (up), and (down). Since q and u are conditions of
![]() $\mathbb {P}_{\alpha +1}$
,
$\mathbb {P}_{\alpha +1}$
,
![]() $A_{q'}(\alpha )$
satisfies (g-ob), (g-ob-2), and (g-cl). It follows from the choice of r and u that
$A_{q'}(\alpha )$
satisfies (g-ob), (g-ob-2), and (g-cl). It follows from the choice of r and u that
![]() $A_{q'}(\alpha )$
satisfies (g-w). Moreover, by
$A_{q'}(\alpha )$
satisfies (g-w). Moreover, by
![]() $\alpha \in \omega _2$
and Proposition 3.10,
$\alpha \in \omega _2$
and Proposition 3.10,
![]() $A_{q'}(\alpha )$
satisfies (g-m). Therefore
$A_{q'}(\alpha )$
satisfies (g-m). Therefore
![]() $q'$
is a condition of
$q'$
is a condition of
![]() $\mathbb {P}_{\alpha +1}$
. So
$\mathbb {P}_{\alpha +1}$
. So
![]() $q'$
is a common extension of q and u in
$q'$
is a common extension of q and u in
![]() $\mathbb {P}_{\alpha +1}$
. By elementarity of N and the fact that
$\mathbb {P}_{\alpha +1}$
. By elementarity of N and the fact that
![]() $u\in \mathcal {E} \cap N$
, u is an extension of some member of
$u\in \mathcal {E} \cap N$
, u is an extension of some member of
![]() $\mathcal {D}\cap N$
in
$\mathcal {D}\cap N$
in
![]() $\mathbb {P}_{\alpha +1}$
.
$\mathbb {P}_{\alpha +1}$
.
![]() $\dashv$
$\dashv$
The following proposition will be used in the rest of the proof.
Proposition 5.3. Suppose that
![]() $\alpha \in \omega _2$
,
$\alpha \in \omega _2$
,
![]() $\mathsf {(p)}_{\alpha +1}$
holds,
$\mathsf {(p)}_{\alpha +1}$
holds,
![]() $p\in \mathbb {P}_{\alpha +1}$
,
$p\in \mathbb {P}_{\alpha +1}$
,
![]() $N\in \mathcal {N}_p \cap \mathfrak {M}^P_{\alpha +1}$
such that
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_{\alpha +1}$
such that
![]() $\{N\}\times ((\alpha +1)\cap N)\subseteq R_p$
, and
$\{N\}\times ((\alpha +1)\cap N)\subseteq R_p$
, and
![]() $\mathcal {D}$
is a definable class in the expanded relational structure by
$\mathcal {D}$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
with parameters in N such that
$\mathbb {P}_{\alpha +1}$
with parameters in N such that
![]() $p\in \mathcal {D}$
. Then there exists
$p\in \mathcal {D}$
. Then there exists
![]() $q\in \mathcal {D}\cap N$
which is compatible with p in
$q\in \mathcal {D}\cap N$
which is compatible with p in
![]() $\mathbb {P}_{\alpha +1}$
.
$\mathbb {P}_{\alpha +1}$
.
Proof of Proposition 5.3.
Define
![]() $\mathcal {D}'$
to be the set of the conditions u of
$\mathcal {D}'$
to be the set of the conditions u of
![]() $\mathbb {P}_{\alpha +1}$
such that either
$\mathbb {P}_{\alpha +1}$
such that either
![]() $u\in \mathcal {D}$
or u is incompatible with any element of
$u\in \mathcal {D}$
or u is incompatible with any element of
![]() $\mathcal {D}$
in
$\mathcal {D}$
in
![]() $\mathbb {P}_{\alpha +1}$
. Then
$\mathbb {P}_{\alpha +1}$
. Then
![]() $\mathcal {D}'$
is a predense subset of
$\mathcal {D}'$
is a predense subset of
![]() $\mathbb {P}_{\alpha +1}$
. Since N is an elementary substructure of the expanded relational structure by
$\mathbb {P}_{\alpha +1}$
. Since N is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
, by Proposition 5.1, there exists a maximal antichain
$\mathbb {P}_{\alpha +1}$
, by Proposition 5.1, there exists a maximal antichain
![]() $\mathcal {A}$
in N that is a subset of
$\mathcal {A}$
in N that is a subset of
![]() $\mathcal {D}'$
. By
$\mathcal {D}'$
. By
![]() $\mathsf {(p)}_{\alpha +1}$
, p is
$\mathsf {(p)}_{\alpha +1}$
, p is
![]() $(N,\mathbb {P}_{\alpha +1})$
-generic. So there exists
$(N,\mathbb {P}_{\alpha +1})$
-generic. So there exists
![]() $q\in \mathcal {A} \cap N$
such that q is compatible with p in
$q\in \mathcal {A} \cap N$
such that q is compatible with p in
![]() $\mathbb {P}_{\alpha +1}$
. Since
$\mathbb {P}_{\alpha +1}$
. Since
![]() $p \in \mathcal {D}$
, q has to be in
$p \in \mathcal {D}$
, q has to be in
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
![]() $\dashv$
$\dashv$
The following proof has similarities with the proof of Lemma 2.10 (although it is not identical to it).
Proof of
 $\mathsf {(C)}_{\alpha +1}$
.
$\mathsf {(C)}_{\alpha +1}$
.
Suppose that
![]() $p\in \mathbb {P}_{\alpha +1}$
,
$p\in \mathbb {P}_{\alpha +1}$
,
![]() $N\in \mathcal {N}_p \cap \mathfrak {M}^P_{\alpha +1}$
which satisfies that
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_{\alpha +1}$
which satisfies that
![]() $\{N\}\times ((\alpha +1)\cap N)\subseteq R_p$
, and
$\{N\}\times ((\alpha +1)\cap N)\subseteq R_p$
, and
![]() $\left \{{\dot F_n: n\in \omega }\right \}$
is a set of
$\left \{{\dot F_n: n\in \omega }\right \}$
is a set of
![]() $\mathbb {P}_{\alpha +1}$
-names for nowhere dense subsets of
$\mathbb {P}_{\alpha +1}$
-names for nowhere dense subsets of
![]() $\left ({2^{<\omega }}\right )^\omega $
such that
$\left ({2^{<\omega }}\right )^\omega $
such that
![]() $\left \{{\dot F_n: n\in \omega }\right \} \in N$
. Let us show that
$\left \{{\dot F_n: n\in \omega }\right \} \in N$
. Let us show that
![]() $p \Vdash _{\mathbb {P}_{\alpha +1}} \!\!\!\text {"}\,\, f_{\omega _1\cap N} \not \in \bigcup _{n\in \omega } \dot F_n \,\text {"}$
.
$p \Vdash _{\mathbb {P}_{\alpha +1}} \!\!\!\text {"}\,\, f_{\omega _1\cap N} \not \in \bigcup _{n\in \omega } \dot F_n \,\text {"}$
.
Suppose not, and let
![]() $q\leq _{\mathbb {P}_{\alpha +1}} p$
and
$q\leq _{\mathbb {P}_{\alpha +1}} p$
and
![]() $n\in \omega $
be such that
$n\in \omega $
be such that
Let
![]() $\sigma _N \in A_q(\alpha )$
be such that
$\sigma _N \in A_q(\alpha )$
be such that
![]() $\delta _{\sigma _N} = \omega _1\cap N$
.
$\delta _{\sigma _N} = \omega _1\cap N$
.
Only in this paragraph, for each set x (in the ground model), we denote by
![]() $\check x$
the canonical
$\check x$
the canonical
![]() $\mathbb {P}_\alpha $
-name which represents the set x in the forcing extension. For each
$\mathbb {P}_\alpha $
-name which represents the set x in the forcing extension. For each
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
![]() $A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, define
$A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, define
![]() $\dot \Sigma '(\nu , A)$
to be the
$\dot \Sigma '(\nu , A)$
to be the
![]() $\mathbb {P}_\alpha $
-name which consists of all the pairs
$\mathbb {P}_\alpha $
-name which consists of all the pairs
![]() $\left \langle {u, \check B}\right \rangle $
such that
$\left \langle {u, \check B}\right \rangle $
such that
-
•
 $u\in \mathbb {P}_\alpha $
and
$u\in \mathbb {P}_\alpha $
and
 $B\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
,
$B\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, -
• there exists
 $u'\in \mathbb {P}_{\alpha +1}$
such that
$u'\in \mathbb {P}_{\alpha +1}$
such that-
–
 $u\leq _{\mathbb {P}_\alpha }u'\restriction \alpha $
,
$u\leq _{\mathbb {P}_\alpha }u'\restriction \alpha $
, -
–
 ${R_q}^{-1}[\{\alpha \}]\cap N \subseteq {R_{u'}}^{-1}[\{\alpha \}]$
,
${R_q}^{-1}[\{\alpha \}]\cap N \subseteq {R_{u'}}^{-1}[\{\alpha \}]$
, -
–
 $A_{u'}(\alpha ) = A \cup B$
,
$A_{u'}(\alpha ) = A \cup B$
, -
– for any
 $\sigma \in A$
and any
$\sigma \in A$
and any
 $\tau \in B$
,
$\tau \in B$
,
 $\delta _\sigma < \delta _\tau $
, and
$\delta _\sigma < \delta _\tau $
, and -
–
 $ u' \Vdash _{\mathbb {P}_{\alpha +1}}\!\!\!\text {"}\,\, \dot F_n \cap [\nu ] = \emptyset \,\text {"} $
(here we omit the check-notation for
$ u' \Vdash _{\mathbb {P}_{\alpha +1}}\!\!\!\text {"}\,\, \dot F_n \cap [\nu ] = \emptyset \,\text {"} $
(here we omit the check-notation for
 $\mathbb {P}_{\alpha +1}$
).
$\mathbb {P}_{\alpha +1}$
).
-
For each
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
![]() $A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
,
$A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
,
![]() $\dot \Sigma '(\nu , A) $
is a definable class in the expanded relational structure by
$\dot \Sigma '(\nu , A) $
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
with parameters in
$\mathbb {P}_{\alpha +1}$
with parameters in
![]() $H(\kappa )$
. Moreover, if
$H(\kappa )$
. Moreover, if
![]() $A\in N$
, then
$A\in N$
, then
![]() $\dot \Sigma '(\nu , A) $
is a definable class in the expanded relational structure by
$\dot \Sigma '(\nu , A) $
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
with parameters in N. By Proposition 5.1, there exists
$\mathbb {P}_{\alpha +1}$
with parameters in N. By Proposition 5.1, there exists
![]() $\Sigma \in H(\kappa )$
such that
$\Sigma \in H(\kappa )$
such that
-
•
 $\Sigma \subseteq \left ({2^{<\omega }}\right )^{<\omega } \times [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0} \times \mathbb {P}_\alpha \times [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
,
$\Sigma \subseteq \left ({2^{<\omega }}\right )^{<\omega } \times [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0} \times \mathbb {P}_\alpha \times [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, -
• for each
 $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
 $A, B\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, the set
$A, B\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, the set
 $\mathcal {A}(\nu ,A,B) := \left \{{u\in \mathbb {P}_\alpha : \left \langle {\nu , A, u, B}\right \rangle \in \Sigma }\right \}$
is a maximal antichain (of size
$\mathcal {A}(\nu ,A,B) := \left \{{u\in \mathbb {P}_\alpha : \left \langle {\nu , A, u, B}\right \rangle \in \Sigma }\right \}$
is a maximal antichain (of size
 $\aleph _1$
), and, for each
$\aleph _1$
), and, for each
 $u\in \mathcal {A}(\nu ,A,B)$
, either
$u\in \mathcal {A}(\nu ,A,B)$
, either
 $\left \langle {u, \check B}\right \rangle \in \dot \Sigma '(\nu ,A)$
, or no extension v of u in
$\left \langle {u, \check B}\right \rangle \in \dot \Sigma '(\nu ,A)$
, or no extension v of u in
 $\mathbb {P}_\alpha $
satisfies
$\mathbb {P}_\alpha $
satisfies
 $\left \langle {v, \check B}\right \rangle \in \dot \Sigma '(\nu ,A)$
.
$\left \langle {v, \check B}\right \rangle \in \dot \Sigma '(\nu ,A)$
.
Since N is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
, we may assume that
$\mathbb {P}_{\alpha +1}$
, we may assume that
![]() $\Sigma \in N$
. For each
$\Sigma \in N$
. For each
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
![]() $A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, define
$A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
, define
![]() $\dot \Sigma (\nu ,A) $
to be the
$\dot \Sigma (\nu ,A) $
to be the
![]() $\mathbb {P}_\alpha $
-name such that
$\mathbb {P}_\alpha $
-name such that
 $$\begin{align*}\dot \Sigma(\nu,A) := \bigcup_{B\in [\omega_1\times\omega_1\times\omega_1]^{<\aleph_0}} \left\{{\left\langle{u, \check B}\right\rangle : u \in \mathcal{A}(\nu,A, B) \text{ and } \left\langle{u, \check B}\right\rangle\in \dot \Sigma'(\nu,A)}\right\}. \end{align*}$$
$$\begin{align*}\dot \Sigma(\nu,A) := \bigcup_{B\in [\omega_1\times\omega_1\times\omega_1]^{<\aleph_0}} \left\{{\left\langle{u, \check B}\right\rangle : u \in \mathcal{A}(\nu,A, B) \text{ and } \left\langle{u, \check B}\right\rangle\in \dot \Sigma'(\nu,A)}\right\}. \end{align*}$$
Then, the sequence
![]() $\left \langle {\dot \Sigma (\nu ,A) : \nu \in \left ({2^{<\omega }}\right )^{<\omega }, A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0} }\right \rangle $
belongs to N, and, for each
$\left \langle {\dot \Sigma (\nu ,A) : \nu \in \left ({2^{<\omega }}\right )^{<\omega }, A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0} }\right \rangle $
belongs to N, and, for each
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
and each
![]() $A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
,
$A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}$
,
![]() $\Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\dot \Sigma (\nu ,A) = \dot \Sigma '(\nu ,A) \,\text {"}$
. From now on, we omit the check-notation in the forcing language.
$\Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}\dot \Sigma (\nu ,A) = \dot \Sigma '(\nu ,A) \,\text {"}$
. From now on, we omit the check-notation in the forcing language.
Since
![]() $\{N\}\times ( (\alpha +1)\cap N) \subseteq R_q$
, by
$\{N\}\times ( (\alpha +1)\cap N) \subseteq R_q$
, by
![]() $\mathsf {(p)}_{\alpha +1}$
and Proposition 5.3, there exists
$\mathsf {(p)}_{\alpha +1}$
and Proposition 5.3, there exists
![]() $q'\in \mathbb {P}_{\alpha +1}\cap N$
such that
$q'\in \mathbb {P}_{\alpha +1}\cap N$
such that
-
•
 $q'$
is compatible with q in
$q'$
is compatible with q in
 $\mathbb {P}_{\alpha +1}$
,
$\mathbb {P}_{\alpha +1}$
, -
•
 ${R_q}^{-1}[\{\alpha \}]\cap N \subseteq {R_{q'}}^{-1}[\{\alpha \}]$
,
${R_q}^{-1}[\{\alpha \}]\cap N \subseteq {R_{q'}}^{-1}[\{\alpha \}]$
, -
• there exists
 $N_0 \in {R_{q'}}^{-1}[\{\alpha \}]$
such that
$N_0 \in {R_{q'}}^{-1}[\{\alpha \}]$
such that-
–
 $A_{q'}(\alpha ) \cap N_0 = A_q(\alpha ) \cap N$
,
$A_{q'}(\alpha ) \cap N_0 = A_q(\alpha ) \cap N$
, -
– the set
is equal to the set $$\begin{align*}\begin{array}{r@{\ }l} \big\{ \left\langle{ \varepsilon_\sigma, C_{\delta_\sigma} \cap N_0 , f_{\gamma_\sigma} \restriction \left| C_{\delta_\sigma} \cap N_0 \right| }\right\rangle : & \sigma \in A_{q'}(\alpha)\setminus N_0 \text{ with } \varepsilon_\sigma \in N_0 \\ & \&\ \delta_\sigma\neq \omega_1\cap N_0 \big\} \end{array}\end{align*}$$
and
$$\begin{align*}\begin{array}{r@{\ }l} \big\{ \left\langle{ \varepsilon_\sigma, C_{\delta_\sigma} \cap N_0 , f_{\gamma_\sigma} \restriction \left| C_{\delta_\sigma} \cap N_0 \right| }\right\rangle : & \sigma \in A_{q'}(\alpha)\setminus N_0 \text{ with } \varepsilon_\sigma \in N_0 \\ & \&\ \delta_\sigma\neq \omega_1\cap N_0 \big\} \end{array}\end{align*}$$
and $$\begin{align*}\left\{{ \left\langle{ \varepsilon_\sigma, C_{\delta_\sigma} \cap N, f_{\gamma_\sigma} \restriction \left| C_{\delta_\sigma} \cap N \right| }\right\rangle : \sigma \in A_{q}(\alpha) \setminus (N \cup\left\{{\sigma_N}\right\}) \text{ with } \varepsilon_\sigma \in N}\right\} , \end{align*}$$
$$\begin{align*}\left\{{ \left\langle{ \varepsilon_\sigma, C_{\delta_\sigma} \cap N, f_{\gamma_\sigma} \restriction \left| C_{\delta_\sigma} \cap N \right| }\right\rangle : \sigma \in A_{q}(\alpha) \setminus (N \cup\left\{{\sigma_N}\right\}) \text{ with } \varepsilon_\sigma \in N}\right\} , \end{align*}$$
-
–
 $N_0$
contains the sets
$N_0$
contains the sets
 $\left \{{\varepsilon _\sigma : \sigma \in A_{q}(\alpha ) \setminus N }\right \}\cap N $
,
$\left \{{\varepsilon _\sigma : \sigma \in A_{q}(\alpha ) \setminus N }\right \}\cap N $
,
 $\{C_{\gamma _\sigma }\cap N : \sigma \in A_{q}(\alpha ) \setminus (N \cup \left \{{\sigma _N}\right \}) \}$
and
$\{C_{\gamma _\sigma }\cap N : \sigma \in A_{q}(\alpha ) \setminus (N \cup \left \{{\sigma _N}\right \}) \}$
and
 $\Big \langle \dot \Sigma (\nu ,A) : \nu \in \left ({2^{<\omega }}\right )^{<\omega }, A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0} \Big \rangle $
as members.
$\Big \langle \dot \Sigma (\nu ,A) : \nu \in \left ({2^{<\omega }}\right )^{<\omega }, A\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0} \Big \rangle $
as members.
-
Let
![]() $q^+$
be a common extension of
$q^+$
be a common extension of
![]() $q'$
and q in
$q'$
and q in
![]() $\mathbb {P}_{\alpha +1}$
. We notice that
$\mathbb {P}_{\alpha +1}$
. We notice that
![]() $N_0$
contains the set
$N_0$
contains the set
![]() $\big \{ C_{\omega _1\cap N } \cap N_0 , f_{\gamma _{\sigma _N}} \restriction \left (\left | C_{\omega _1\cap N } \cap N_0 \right | + 1 \right ) \big \}$
and
$\big \{ C_{\omega _1\cap N } \cap N_0 , f_{\gamma _{\sigma _N}} \restriction \left (\left | C_{\omega _1\cap N } \cap N_0 \right | + 1 \right ) \big \}$
and
In a similar way as in the definition of
![]() $\dot \Sigma '(\nu ,A)$
before, we have a
$\dot \Sigma '(\nu ,A)$
before, we have a
![]() $\mathbb {P}_\alpha $
-name
$\mathbb {P}_\alpha $
-name
![]() $\dot Z$
for a subset of
$\dot Z$
for a subset of
![]() $\left ({2^{<\omega }}\right )^{\omega }$
such that
$\left ({2^{<\omega }}\right )^{\omega }$
such that
![]() $\dot Z$
is a definable class in the expanded relational structure by
$\dot Z$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
with parameters in N and, for any
$\mathbb {P}_{\alpha +1}$
with parameters in N and, for any
![]() $u\in \mathbb {P}_\alpha $
and any
$u\in \mathbb {P}_\alpha $
and any
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, if
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, if
![]() $u\Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}[\nu ]\subseteq \dot Z \,\text {"}$
, then there exists
$u\Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}[\nu ]\subseteq \dot Z \,\text {"}$
, then there exists
![]() $u'\in \mathbb {P}_{\alpha +1}$
such that
$u'\in \mathbb {P}_{\alpha +1}$
such that
-
•
 $u \leq _{\mathbb {P}_\alpha } u' \restriction \alpha $
,
$u \leq _{\mathbb {P}_\alpha } u' \restriction \alpha $
, -
•
 $u' \leq _{\mathbb {P}_{\alpha +1}} q'$
,
$u' \leq _{\mathbb {P}_{\alpha +1}} q'$
, -
• for each
 $\tau \in A_{u'}(\alpha )\cap N_0$
, if
$\tau \in A_{u'}(\alpha )\cap N_0$
, if
 $\varepsilon _{\sigma _N} < \delta _\tau $
, then
$\varepsilon _{\sigma _N} < \delta _\tau $
, then
 $\gamma _{\tau }+1 < \omega _1\cap N_0$
and
$\gamma _{\tau }+1 < \omega _1\cap N_0$
and  $$\begin{align*}u'\restriction \alpha \Vdash_{\mathbb{P}_\alpha}\ \text{"} f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap \delta_\tau \right|) \subseteq \dot r_\alpha \text{ and } f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap (\gamma_\tau +1) \right|) \subseteq \dot r_\alpha \text{"} , \end{align*}$$
$$\begin{align*}u'\restriction \alpha \Vdash_{\mathbb{P}_\alpha}\ \text{"} f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap \delta_\tau \right|) \subseteq \dot r_\alpha \text{ and } f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap (\gamma_\tau +1) \right|) \subseteq \dot r_\alpha \text{"} , \end{align*}$$
-
•
 $A_{u'}(\alpha )$
has
$A_{u'}(\alpha )$
has
 $\sigma $
such that
$\sigma $
such that
 $\delta _\sigma =\omega _1\cap N_0$
, and
$\delta _\sigma =\omega _1\cap N_0$
, and -
•
 $u' \Vdash _{\mathbb {P}_{\alpha +1}}\!\!\!\text {"}\,\, \dot F_n \cap [\nu ] = \emptyset \,\text {"}$
.
$u' \Vdash _{\mathbb {P}_{\alpha +1}}\!\!\!\text {"}\,\, \dot F_n \cap [\nu ] = \emptyset \,\text {"}$
.
Now
![]() $\dot F_n$
is a
$\dot F_n$
is a
![]() $\mathbb {P}_{\alpha +1}$
-name for a nowhere dense subset of
$\mathbb {P}_{\alpha +1}$
-name for a nowhere dense subset of
![]() $\left ({2^{<\omega }}\right )^{\omega }$
,
$\left ({2^{<\omega }}\right )^{\omega }$
,
![]() $\sigma _N\in A_{q^+}(\alpha )$
,
$\sigma _N\in A_{q^+}(\alpha )$
,
![]() ${A_{q^+}}(\alpha )$
has
${A_{q^+}}(\alpha )$
has
![]() $\sigma $
such that
$\sigma $
such that
![]() $\delta _\sigma =\omega _1\cap N_0$
, and
$\delta _\sigma =\omega _1\cap N_0$
, and
![]() $q^+ \leq _{\mathbb {P}_{\alpha +1}} q'$
, so
$q^+ \leq _{\mathbb {P}_{\alpha +1}} q'$
, so
Since
![]() $\dot Z$
is a definable class in the expanded relational structure by
$\dot Z$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
with parameters in N, by Proposition 5.1,
$\mathbb {P}_{\alpha +1}$
with parameters in N, by Proposition 5.1,
![]() $\dot Z$
can be considered as an element of N. So by
$\dot Z$
can be considered as an element of N. So by
![]() $\mathsf {(C)}_\alpha $
,
$\mathsf {(C)}_\alpha $
,
Thus, there are
![]() $r\leq _{\mathbb {P}_\alpha } q^+\restriction \alpha $
and
$r\leq _{\mathbb {P}_\alpha } q^+\restriction \alpha $
and
![]() $k\in \omega $
such that
$k\in \omega $
such that
Let
![]() $u_0\in \mathbb {P}_{\alpha +1}$
be a witness to
$u_0\in \mathbb {P}_{\alpha +1}$
be a witness to
![]() $r \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}[f_{\omega _1\cap N}\restriction k ] \subseteq \dot Z \,\text {"} $
. Then
$r \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}[f_{\omega _1\cap N}\restriction k ] \subseteq \dot Z \,\text {"} $
. Then
Let
![]() $\zeta _0 \in \omega _1\cap N_0$
be such that
$\zeta _0 \in \omega _1\cap N_0$
be such that
-
• for any
 $\tau \in A_{u_0}(\alpha )\cap N_0$
,
$\tau \in A_{u_0}(\alpha )\cap N_0$
,
 $\gamma _\tau < \zeta _0$
,
$\gamma _\tau < \zeta _0$
, -
• for any
 $\sigma \in A_q(\alpha ) \setminus N$
,
$\sigma \in A_q(\alpha ) \setminus N$
,-
– if
 $\varepsilon _\sigma \in N$
, then
$\varepsilon _\sigma \in N$
, then
 $\varepsilon _\sigma < \zeta _0$
, and
$\varepsilon _\sigma < \zeta _0$
, and -
–
 $C_{\delta _\sigma }\cap N_0 \subseteq \zeta _0$
.
$C_{\delta _\sigma }\cap N_0 \subseteq \zeta _0$
.
-
Since
![]() $\{N_0\}\times (\alpha \cap N_0) \subseteq R_{q^+} \subseteq R_r$
, by
$\{N_0\}\times (\alpha \cap N_0) \subseteq R_{q^+} \subseteq R_r$
, by
![]() $\mathsf {(p)}_\alpha $
, r is
$\mathsf {(p)}_\alpha $
, r is
![]() $(N_0, \mathbb {P}_\alpha )$
-generic. Since the set
$(N_0, \mathbb {P}_\alpha )$
-generic. Since the set
![]() $\left \{{f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0}\right \}$
is in
$\left \{{f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0}\right \}$
is in
![]() $N_0$
,
$N_0$
,
![]() $\dot \Sigma (f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0) $
is also in
$\dot \Sigma (f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0) $
is also in
![]() $N_0$
. Moreover,
$N_0$
. Moreover,
![]() $A_{u_0}(\alpha )\setminus N_0 $
has
$A_{u_0}(\alpha )\setminus N_0 $
has
![]() $\sigma $
such that
$\sigma $
such that
![]() $\delta _\sigma =\omega _1\cap N_0$
, which is larger than
$\delta _\sigma =\omega _1\cap N_0$
, which is larger than
![]() $\zeta _0$
. Hence, by Proposition 5.3, there are
$\zeta _0$
. Hence, by Proposition 5.3, there are
![]() $r'\leq _{\mathbb {P}_\alpha } r$
and
$r'\leq _{\mathbb {P}_\alpha } r$
and
![]() $B\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}\cap N_0$
such that
$B\in [\omega _1\times \omega _1\times \omega _1]^{<\aleph _0}\cap N_0$
such that
-
• for every
 $\tau \in B$
,
$\tau \in B$
,
 $\zeta _0 < \delta _\tau $
, and
$\zeta _0 < \delta _\tau $
, and -
•
 $r' \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}B \in \dot \Sigma (f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0) \,\text {"} $
.
$r' \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}B \in \dot \Sigma (f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0) \,\text {"} $
.
Since
![]() $\{N\}\times (\alpha \cap N) \subseteq R_{q^+} \subseteq R_{r'}$
, by
$\{N\}\times (\alpha \cap N) \subseteq R_{q^+} \subseteq R_{r'}$
, by
![]() $\mathsf {(p)}_\alpha $
,
$\mathsf {(p)}_\alpha $
,
![]() $r'$
is
$r'$
is
![]() $(N, \mathbb {P}_\alpha )$
-generic. Since N is an elementary substructure of the expanded relational structure by
$(N, \mathbb {P}_\alpha )$
-generic. Since N is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}_{\alpha +1}$
, there exists
$\mathbb {P}_{\alpha +1}$
, there exists
![]() $u_1 \in \mathbb {P}_{\alpha +1}\cap N$
which witnesses
$u_1 \in \mathbb {P}_{\alpha +1}\cap N$
which witnesses
![]() $r' \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}B \in \dot \Sigma (f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0) \,\text {"} $
. Then
$r' \Vdash _{\mathbb {P}_\alpha }\!\!\!\text {"}B \in \dot \Sigma (f_{\omega _1\cap N}\restriction k, A_{u_0}(\alpha )\cap N_0) \,\text {"} $
. Then
![]() $r'$
is a common extension of
$r'$
is a common extension of
![]() $u_1$
and
$u_1$
and
![]() $q\restriction \alpha $
in
$q\restriction \alpha $
in
![]() $\mathbb {P}_\alpha $
. Define
$\mathbb {P}_\alpha $
. Define
![]() $s\in U_{\alpha +1}$
such that
$s\in U_{\alpha +1}$
such that
-
•
 $\mathcal {N}_{s} := \mathcal {N}_{r'}$
,
$\mathcal {N}_{s} := \mathcal {N}_{r'}$
, -
•
 $R_{s}:=R_{u_1}\cup R_{q} $
$R_{s}:=R_{u_1}\cup R_{q} $
 $\cup \Big \{$
$\cup \Big \{$
 $\begin {array}[t]{@{}l@{\,}c@{\,}l} \left \langle {\left ( {\Psi _{M'} }^{-1} \circ \Psi _{N} \right ) (K), \alpha }\right \rangle & : & M'\in {R_{q}}^{-1}[\{\alpha \}] \text { with } \omega _1\cap M' = \omega _1\cap N, \\ & & K\in {R_{u_1}}^{-1}[\{\alpha \}] \Big \} , \end {array}$
$\begin {array}[t]{@{}l@{\,}c@{\,}l} \left \langle {\left ( {\Psi _{M'} }^{-1} \circ \Psi _{N} \right ) (K), \alpha }\right \rangle & : & M'\in {R_{q}}^{-1}[\{\alpha \}] \text { with } \omega _1\cap M' = \omega _1\cap N, \\ & & K\in {R_{u_1}}^{-1}[\{\alpha \}] \Big \} , \end {array}$
-
•
 $A_{s}\restriction \alpha := A_{r'}$
, and
$A_{s}\restriction \alpha := A_{r'}$
, and -
•
 $A_{s}(\alpha ) := A_{u_1}(\alpha ) \cup A_{q}(\alpha )$
.
$A_{s}(\alpha ) := A_{u_1}(\alpha ) \cup A_{q}(\alpha )$
.
Now
![]() $s\restriction \alpha =r' \in \mathbb {P}_\alpha $
. Since
$s\restriction \alpha =r' \in \mathbb {P}_\alpha $
. Since
![]() $u_1\in N$
and
$u_1\in N$
and
![]() ${R_s}^{-1}[\{\alpha \}]$
satisfies (el), (ho), (up), and (down).
${R_s}^{-1}[\{\alpha \}]$
satisfies (el), (ho), (up), and (down).
![]() $A_s(\alpha )$
satisfies (g-ob), (g-ob-2), (g-cl), and (g-m). We will check that
$A_s(\alpha )$
satisfies (g-ob), (g-ob-2), (g-cl), and (g-m). We will check that
![]() $A_s(\alpha )$
satisfies (g-w). Since
$A_s(\alpha )$
satisfies (g-w). Since
![]() $u_1\leq _{\mathbb {P}_{\alpha +1}} q'$
,
$u_1\leq _{\mathbb {P}_{\alpha +1}} q'$
,
By the choice of
![]() $u_1$
,
$u_1$
,
Let
![]() $\tau \in A_{u_1}(\alpha )$
and
$\tau \in A_{u_1}(\alpha )$
and
![]() $\sigma \in A_q(\alpha )\setminus (N\cup \left \{{\sigma _N}\right \})$
. Then there exists
$\sigma \in A_q(\alpha )\setminus (N\cup \left \{{\sigma _N}\right \})$
. Then there exists
![]() $\sigma ' \in A_{q'}(\alpha )\setminus N_0 $
such that
$\sigma ' \in A_{q'}(\alpha )\setminus N_0 $
such that
So if
![]() $\varepsilon _\sigma < \delta _\tau $
, then, since
$\varepsilon _\sigma < \delta _\tau $
, then, since
![]() $u_1\leq _{\mathbb {P}_{\alpha +1}} q'$
,
$u_1\leq _{\mathbb {P}_{\alpha +1}} q'$
,
 $$\begin{align*}\begin{array}{r@{\ }l} u_1\restriction \alpha \Vdash_{\mathbb{P}_\alpha}\ \text{"} &\!\! f_{\gamma_{\sigma}} ( \left| C_{\delta_\sigma} \cap \delta_\tau \right|) = f_{\gamma_{\sigma'}} ( \left| C_{\delta_{\sigma'}} \cap \delta_\tau \right|) \subseteq \dot r_\alpha \text{ and } \\ & f_{\gamma_{\sigma}} ( \left| C_{\delta_\sigma} \cap (\gamma_\tau +1) \right|) = f_{\gamma_{\sigma'}} ( \left| C_{\delta_{\sigma'}} \cap (\gamma_\tau +1) \right|) \subseteq \dot r_\alpha \text{"}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} u_1\restriction \alpha \Vdash_{\mathbb{P}_\alpha}\ \text{"} &\!\! f_{\gamma_{\sigma}} ( \left| C_{\delta_\sigma} \cap \delta_\tau \right|) = f_{\gamma_{\sigma'}} ( \left| C_{\delta_{\sigma'}} \cap \delta_\tau \right|) \subseteq \dot r_\alpha \text{ and } \\ & f_{\gamma_{\sigma}} ( \left| C_{\delta_\sigma} \cap (\gamma_\tau +1) \right|) = f_{\gamma_{\sigma'}} ( \left| C_{\delta_{\sigma'}} \cap (\gamma_\tau +1) \right|) \subseteq \dot r_\alpha \text{"}. \end{array} \end{align*}$$
Let
![]() $\tau '\in A_{u_1}(\alpha )\cap N_0$
. By the choice of
$\tau '\in A_{u_1}(\alpha )\cap N_0$
. By the choice of
![]() $u_1$
, if
$u_1$
, if
![]() $\varepsilon _{\sigma _N} < \delta _\tau $
, then
$\varepsilon _{\sigma _N} < \delta _\tau $
, then
Let
![]() $\tau "\in A_{u_1}(\alpha )\setminus N_0$
. Then
$\tau "\in A_{u_1}(\alpha )\setminus N_0$
. Then
![]() $\zeta _0 < \delta _{\tau "}$
, and hence
$\zeta _0 < \delta _{\tau "}$
, and hence
![]() $C_{\omega _1\cap N } \cap \delta _{\tau "} = C_{\omega _1\cap N } \cap (\gamma _{\tau "}+1) = C_{\omega _1\cap N } \cap N_0$
. Since
$C_{\omega _1\cap N } \cap \delta _{\tau "} = C_{\omega _1\cap N } \cap (\gamma _{\tau "}+1) = C_{\omega _1\cap N } \cap N_0$
. Since
![]() $r' \leq _{\mathbb {P}_\alpha } q^+\restriction \alpha $
,
$r' \leq _{\mathbb {P}_\alpha } q^+\restriction \alpha $
,
 $$\begin{align*}\begin{array}{r@{\ }l} r' \Vdash_{\mathbb{P}_\alpha}\ \text{"} &\!\! f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap \delta_{\tau"} \right|) = f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap (\gamma_{\tau"}+1) \right|) \\[4pt] & = f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap N_0 \right|) \subseteq \dot r_\alpha \text{"}. \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} r' \Vdash_{\mathbb{P}_\alpha}\ \text{"} &\!\! f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap \delta_{\tau"} \right|) = f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap (\gamma_{\tau"}+1) \right|) \\[4pt] & = f_{\gamma_{\sigma_N}} ( \left| C_{\omega_1\cap N } \cap N_0 \right|) \subseteq \dot r_\alpha \text{"}. \end{array} \end{align*}$$
Thus
![]() $A_s(\alpha )$
satisfies (g-w). Therefore s is a condition of
$A_s(\alpha )$
satisfies (g-w). Therefore s is a condition of
![]() $\mathbb {P}_{\alpha +1}$
. It follows that s is a common extension of
$\mathbb {P}_{\alpha +1}$
. It follows that s is a common extension of
![]() $u_1$
and q. However, then
$u_1$
and q. However, then
which is a contradiction, and finishes the proof of
![]() $\mathsf {(C)}_{\alpha +1}$
.
$\mathsf {(C)}_{\alpha +1}$
.
![]() $\dashv$
$\dashv$
We will use Proposition 5.5 in the proof of
![]() $\mathsf {(p)}_{\alpha }$
and
$\mathsf {(p)}_{\alpha }$
and
![]() $\mathsf {(C)}_{\alpha }$
for a limit ordinal
$\mathsf {(C)}_{\alpha }$
for a limit ordinal
![]() $\alpha $
.
$\alpha $
.
Proposition 5.4. Suppose that
![]() $\alpha \in \omega _2+1$
,
$\alpha \in \omega _2+1$
,
![]() $\mathsf {(p)}_{\beta }$
and
$\mathsf {(p)}_{\beta }$
and
![]() $\mathsf {(C)}_\beta $
hold for every
$\mathsf {(C)}_\beta $
hold for every
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
![]() $p\in \mathbb {P}_{\alpha }$
,
$p\in \mathbb {P}_{\alpha }$
,
![]() $\xi \in \operatorname {dom}(A_p)$
,
$\xi \in \operatorname {dom}(A_p)$
,
![]() $M\in {R_p}^{-1}[\{\xi \}] \cap \mathfrak {M}^P_{\xi +1}$
, and
$M\in {R_p}^{-1}[\{\xi \}] \cap \mathfrak {M}^P_{\xi +1}$
, and
![]() $N\in \mathfrak {M}^P_{\xi } \cap M$
contains the set
$N\in \mathfrak {M}^P_{\xi } \cap M$
contains the set
![]() $ \left \{{ \mathcal {N}_p\cap M , \left \langle {A_p(\zeta )\cap M : \zeta \in \operatorname {dom}(A_p) \cap (\xi +1) \cap M}\right \rangle }\right \} $
and is such that, for every
$ \left \{{ \mathcal {N}_p\cap M , \left \langle {A_p(\zeta )\cap M : \zeta \in \operatorname {dom}(A_p) \cap (\xi +1) \cap M}\right \rangle }\right \} $
and is such that, for every
![]() $\zeta \in \operatorname {dom}(A_p)\cap (\xi +1) \cap N$
and every
$\zeta \in \operatorname {dom}(A_p)\cap (\xi +1) \cap N$
and every
![]() $\sigma \in A_p(\zeta )$
with
$\sigma \in A_p(\zeta )$
with
![]() $\varepsilon _\sigma < \omega _1 \cap N < \delta _\sigma $
,
$\varepsilon _\sigma < \omega _1 \cap N < \delta _\sigma $
,
Then there is some
![]() $q\leq _{\mathbb {P}_{\xi +1}} p\restriction (\xi +1)$
such that
$q\leq _{\mathbb {P}_{\xi +1}} p\restriction (\xi +1)$
such that
![]() $\left \langle {N, \xi }\right \rangle \in R_q$
and
$\left \langle {N, \xi }\right \rangle \in R_q$
and
![]() $A_q = A_p \cup \{\sigma \}$
for some
$A_q = A_p \cup \{\sigma \}$
for some
![]() $\sigma $
with
$\sigma $
with
![]() $\delta _\sigma = \omega _1\cap N$
.
$\delta _\sigma = \omega _1\cap N$
.
Proof of Proposition 5.4.
We will prove this by induction on
![]() $\xi $
. Let
$\xi $
. Let
![]() $\xi _0 : = \max \big ( \operatorname {dom}(A_p) \cap \xi \cap M \big )$
. Note that
$\xi _0 : = \max \big ( \operatorname {dom}(A_p) \cap \xi \cap M \big )$
. Note that
![]() $\xi _0 \in N$
, and hence
$\xi _0 \in N$
, and hence
![]() $N \in \mathfrak {M}^P_{\xi _0}\cap M$
. By the induction hypothesis, there exists
$N \in \mathfrak {M}^P_{\xi _0}\cap M$
. By the induction hypothesis, there exists
![]() $p_0 \leq _{\mathbb {P}_{\xi _0+1}} p\restriction (\xi _0+1)$
such that
$p_0 \leq _{\mathbb {P}_{\xi _0+1}} p\restriction (\xi _0+1)$
such that
![]() $N \in {R_{p_0}}^{-1}[\{\xi _0 \}]$
. Let
$N \in {R_{p_0}}^{-1}[\{\xi _0 \}]$
. Let
![]() $p_0' = \left \langle { \mathcal {N}_{p_0}, R_{p_0} \cup R_p, A_{p_0} \cup \left ( A_p \restriction [\xi _0+1, \xi ) \right )}\right \rangle $
, which is a canonical common extension of
$p_0' = \left \langle { \mathcal {N}_{p_0}, R_{p_0} \cup R_p, A_{p_0} \cup \left ( A_p \restriction [\xi _0+1, \xi ) \right )}\right \rangle $
, which is a canonical common extension of
![]() $p_0$
and p in
$p_0$
and p in
![]() $\mathbb {P}_\xi $
. Since
$\mathbb {P}_\xi $
. Since
![]() $p_0'$
is
$p_0'$
is
![]() $(M, \mathbb {P}_{\xi +1})$
-generic, by Proposition 5.3, we can take an extension
$(M, \mathbb {P}_{\xi +1})$
-generic, by Proposition 5.3, we can take an extension
![]() $p_1 \leq _{\mathbb {P}_{\xi +1}} p_0'$
and
$p_1 \leq _{\mathbb {P}_{\xi +1}} p_0'$
and
![]() $N_1 \in {R_{p_1}}^{-1}[\{\xi \}] \cap M$
which contains N as a member. Then, by (g-ob-2) and (g-w), for every
$N_1 \in {R_{p_1}}^{-1}[\{\xi \}] \cap M$
which contains N as a member. Then, by (g-ob-2) and (g-w), for every
![]() $\zeta \in \operatorname {dom}(A_{p_1}) \cap N$
and every
$\zeta \in \operatorname {dom}(A_{p_1}) \cap N$
and every
![]() $\sigma \in A_{p_1}(\zeta )$
with
$\sigma \in A_{p_1}(\zeta )$
with
![]() $\varepsilon _\sigma < \omega _1 \cap N_1 < \delta _\sigma $
,
$\varepsilon _\sigma < \omega _1 \cap N_1 < \delta _\sigma $
,
Recall that, for each limit ordinal
![]() $\delta $
,
$\delta $
,
![]() $C_\delta \cap \omega _1\cap N_1 = C_\delta \cap (\omega _1\cap N_1 +1)$
. Take
$C_\delta \cap \omega _1\cap N_1 = C_\delta \cap (\omega _1\cap N_1 +1)$
. Take
![]() $\varepsilon \in \omega _1\cap N$
such that
$\varepsilon \in \omega _1\cap N$
such that
Define
![]() $q \in U_{\xi + 1}$
such that
$q \in U_{\xi + 1}$
such that
![]() $\mathcal {N}_q := \mathcal {N}_{p_1}$
,
$\mathcal {N}_q := \mathcal {N}_{p_1}$
,
 $$\begin{align*}\begin{array}{r@{\ }l} R_q := R_{p_1\restriction \xi} \cup \Big\{ \left\langle{\left( {\Psi_{K} }^{-1} \circ \Psi_{M} \right) (N), \xi}\right\rangle : & K\in {R_{p}}^{-1}[\{\xi\}] \\ & \text{ with } \omega_1\cap K = \omega_1\cap M \Big\} , \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }l} R_q := R_{p_1\restriction \xi} \cup \Big\{ \left\langle{\left( {\Psi_{K} }^{-1} \circ \Psi_{M} \right) (N), \xi}\right\rangle : & K\in {R_{p}}^{-1}[\{\xi\}] \\ & \text{ with } \omega_1\cap K = \omega_1\cap M \Big\} , \end{array}\end{align*}$$
![]() $A_q \restriction \xi := A_{p_1}\restriction \xi $
, and
$A_q \restriction \xi := A_{p_1}\restriction \xi $
, and
By Propositions 3.10 and 3.11,
![]() $R_{q}$
satisfies (el), (ho), (up), and (down) in Definition 4.1. By
$R_{q}$
satisfies (el), (ho), (up), and (down) in Definition 4.1. By
![]() $\mathsf {(C)}_\xi $
and the fact that
$\mathsf {(C)}_\xi $
and the fact that
![]() $\{N_1\}\times (\xi \cap N_1) \subseteq R_{p_1\restriction \xi } \subseteq R_q$
,
$\{N_1\}\times (\xi \cap N_1) \subseteq R_{p_1\restriction \xi } \subseteq R_q$
,
 $$ \begin{align*} {\begin{array}{r@{\ }l} q\restriction\xi \Vdash_{\mathbb{P}_\xi}\!\!\!&\text{"} f_{\omega_1\cap N_1} \text{ is Cohen over } N_1[\dot G_{\mathbb{P}_\xi}] \text{ and }\dot r_\xi \in N_1, \text{ hence }\\ &\left\{{n\in \omega : f_{\omega_1\cap N_1}(n) \subseteq \dot r_\xi}\right\} \text{ is infinite"}. \end{array}} \end{align*} $$
$$ \begin{align*} {\begin{array}{r@{\ }l} q\restriction\xi \Vdash_{\mathbb{P}_\xi}\!\!\!&\text{"} f_{\omega_1\cap N_1} \text{ is Cohen over } N_1[\dot G_{\mathbb{P}_\xi}] \text{ and }\dot r_\xi \in N_1, \text{ hence }\\ &\left\{{n\in \omega : f_{\omega_1\cap N_1}(n) \subseteq \dot r_\xi}\right\} \text{ is infinite"}. \end{array}} \end{align*} $$
Moreover, by the roles of
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $N_1$
,
$N_1$
,
![]() $A_{q}(\xi )$
satisfies (g-ob), (g-ob-2) (g-cl), and (g-w). By the role of the set
$A_{q}(\xi )$
satisfies (g-ob), (g-ob-2) (g-cl), and (g-w). By the role of the set
![]() $N_1 $
,
$N_1 $
,
![]() $A_{q}(\xi )$
satisfies (g-m) for
$A_{q}(\xi )$
satisfies (g-m) for
![]() $R_{q}$
. Therefore, q is a condition of
$R_{q}$
. Therefore, q is a condition of
![]() $\mathbb {P}_{\xi +1}$
. This q is what we want. (We notice that
$\mathbb {P}_{\xi +1}$
. This q is what we want. (We notice that
![]() $q\restriction \xi $
is an extension of
$q\restriction \xi $
is an extension of
![]() $p_1\restriction \xi $
in
$p_1\restriction \xi $
in
![]() $\mathbb {P}_\xi $
; however, q may not be an extension of
$\mathbb {P}_\xi $
; however, q may not be an extension of
![]() $p_1$
in
$p_1$
in
![]() $\mathbb {P}_{\xi +1}$
.)
$\mathbb {P}_{\xi +1}$
.)
![]() $\dashv$
$\dashv$
Proposition 5.5. Suppose that
![]() $\alpha \in \omega _2+1$
,
$\alpha \in \omega _2+1$
,
![]() $\mathsf {(p)}_{\beta }$
and
$\mathsf {(p)}_{\beta }$
and
![]() $\mathsf {(C)}_\beta $
hold for every
$\mathsf {(C)}_\beta $
hold for every
![]() $\beta <\alpha $
,
$\beta <\alpha $
,
![]() $q,r\in \mathbb {P}_{\alpha }$
, and
$q,r\in \mathbb {P}_{\alpha }$
, and
![]() $\xi < \alpha $
is such that
$\xi < \alpha $
is such that
-
•
 $q\restriction \xi $
and
$q\restriction \xi $
and
 $r\restriction \xi $
are compatible in
$r\restriction \xi $
are compatible in
 $\mathbb {P}_{\xi }$
,
$\mathbb {P}_{\xi }$
, -
•
 $\xi \not \in \operatorname {dom}(A_q)$
and
$\xi \not \in \operatorname {dom}(A_q)$
and
 $\xi \in \operatorname {dom}(A_r)$
,
$\xi \in \operatorname {dom}(A_r)$
, -
• there exists
 $N \in {R_q}^{-1}[\{\xi \}]$
such that
$N \in {R_q}^{-1}[\{\xi \}]$
such that
 $r\in N$
and, for any
$r\in N$
and, for any
 $M\in {R_q}^{-1}[\{\xi \}]$
,
$M\in {R_q}^{-1}[\{\xi \}]$
,
 $\omega _1\cap M \geq \omega _1\cap N$
and
$\omega _1\cap M \geq \omega _1\cap N$
and
 $M \in \mathfrak {M}^P_{\xi +1}$
.
$M \in \mathfrak {M}^P_{\xi +1}$
.
Then there exists a common extension
![]() $q' \in \mathbb {P}_{\xi +1}$
of
$q' \in \mathbb {P}_{\xi +1}$
of
![]() $q\restriction (\xi +1)$
and
$q\restriction (\xi +1)$
and
![]() $r\restriction (\xi +1)$
in
$r\restriction (\xi +1)$
in
![]() $\mathbb {P}_{\xi +1}$
such that
$\mathbb {P}_{\xi +1}$
such that
Proof of Proposition 5.5.
Let
![]() $p_{-1} \in \mathbb {P}_{\xi +1}$
be such that
$p_{-1} \in \mathbb {P}_{\xi +1}$
be such that
-
•
 $p_{-1}\restriction \xi $
is a common extension of
$p_{-1}\restriction \xi $
is a common extension of
 $q\restriction \xi $
and
$q\restriction \xi $
and
 $r\restriction \xi $
in
$r\restriction \xi $
in
 $\mathbb {P}_\xi $
,
$\mathbb {P}_\xi $
, -
•
 $p_{-1}$
is an extension of r in
$p_{-1}$
is an extension of r in
 $\mathbb {P}_{\xi +1}$
,
$\mathbb {P}_{\xi +1}$
, -
•
 ${R_{p_{-1}}}^{-1}[\{\xi \}] = {R_{r}}^{-1}[\{\xi \}]$
, and
${R_{p_{-1}}}^{-1}[\{\xi \}] = {R_{r}}^{-1}[\{\xi \}]$
, and -
•
 $A_{p_{-1}}(\xi ) = A_r(\xi )$
.
$A_{p_{-1}}(\xi ) = A_r(\xi )$
.
Take a maximal
![]() $\in $
-chain
$\in $
-chain
![]() $\left \{{M_i : i \leq n}\right \}$
of
$\left \{{M_i : i \leq n}\right \}$
of
![]() ${R_q}^{-1}[\{\xi \}]$
such that
${R_q}^{-1}[\{\xi \}]$
such that
![]() $M_0 = N$
. For each
$M_0 = N$
. For each
![]() $i\leq n$
, since
$i\leq n$
, since
![]() $\{M_i\}\times (\xi \cap M_i) \subseteq R_{p_{-1}}$
, for every
$\{M_i\}\times (\xi \cap M_i) \subseteq R_{p_{-1}}$
, for every
![]() $\zeta \in \operatorname {dom}(A_{p_{-1}})\cap \xi \cap M_i$
and every
$\zeta \in \operatorname {dom}(A_{p_{-1}})\cap \xi \cap M_i$
and every
![]() $\sigma \in A_{p_{-1}}(\zeta )$
with
$\sigma \in A_{p_{-1}}(\zeta )$
with
![]() $\varepsilon _\sigma < \omega _1 \cap M_i < \delta _\sigma $
,
$\varepsilon _\sigma < \omega _1 \cap M_i < \delta _\sigma $
,
By using Proposition 5.4
![]() $(n+1)$
times repeatedly, for each
$(n+1)$
times repeatedly, for each
![]() $i\leq n$
, we can construct an extension
$i\leq n$
, we can construct an extension
![]() $p_i \in \mathbb {P}_{\xi +1}$
such that
$p_i \in \mathbb {P}_{\xi +1}$
such that
-
•
 $p_i\restriction \xi $
is an extension of
$p_i\restriction \xi $
is an extension of
 $p_{i-1}$
,
$p_{i-1}$
, -
•
 $\left \langle {M_i, \xi }\right \rangle \in R_{p_{i}}$
, and
$\left \langle {M_i, \xi }\right \rangle \in R_{p_{i}}$
, and -
•
 $A_{p_i}(\xi ) = A_{p_{i-1}}(\xi ) \cup \left \{{\sigma _i}\right \}$
for some
$A_{p_i}(\xi ) = A_{p_{i-1}}(\xi ) \cup \left \{{\sigma _i}\right \}$
for some
 $\sigma _i$
such that
$\sigma _i$
such that
 $\delta _{\sigma _i} = \omega _1\cap M_i$
.
$\delta _{\sigma _i} = \omega _1\cap M_i$
.
Then
![]() $p_{n}$
is what we want.
$p_{n}$
is what we want.
![]() $\dashv$
$\dashv$
Proof of
 $\mathsf {(p)}_{\alpha }$
for a limit ordinal
$\mathsf {(p)}_{\alpha }$
for a limit ordinal
 $\alpha $
.
$\alpha $
.
Suppose that
![]() $\alpha \in \omega _2+1$
is a limit ordinal,
$\alpha \in \omega _2+1$
is a limit ordinal,
![]() $p\in \mathbb {P}_{\alpha }$
,
$p\in \mathbb {P}_{\alpha }$
,
![]() $N\in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
satisfies that
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
satisfies that
![]() $\{N\}\times (\alpha \cap N) \subseteq R_p$
,
$\{N\}\times (\alpha \cap N) \subseteq R_p$
,
![]() $\mathcal {D} \in N$
is a predense subset of
$\mathcal {D} \in N$
is a predense subset of
![]() $\mathbb {P}_{\alpha }$
, and
$\mathbb {P}_{\alpha }$
, and
![]() $q\leq _{\mathbb {P}_{\alpha }} p$
is an extension of some member of
$q\leq _{\mathbb {P}_{\alpha }} p$
is an extension of some member of
![]() $\mathcal {D}$
. By extending q if necessary, we may assume that there exists
$\mathcal {D}$
. By extending q if necessary, we may assume that there exists
![]() $u\in \mathcal {D}$
such that
$u\in \mathcal {D}$
such that
![]() $q\leq _{\mathbb {P}_\alpha }u$
. It suffices to find
$q\leq _{\mathbb {P}_\alpha }u$
. It suffices to find
![]() $u'\in \mathcal {D}\cap N$
which is compatible with q in
$u'\in \mathcal {D}\cap N$
which is compatible with q in
![]() $\mathbb {P}_{\alpha }$
. We have the case when
$\mathbb {P}_{\alpha }$
. We have the case when
![]() $\alpha $
has uncountable cofinality and the case when it has countable cofinality. In the latter case,
$\alpha $
has uncountable cofinality and the case when it has countable cofinality. In the latter case,
![]() $\alpha \cap N$
is cofinal in
$\alpha \cap N$
is cofinal in
![]() $\alpha $
and hence we can take
$\alpha $
and hence we can take
![]() $\beta \in \alpha \cap N$
such that
$\beta \in \alpha \cap N$
such that
![]() $\max (\operatorname {dom}(A_q))<\beta $
. But we may not be able to take such a
$\max (\operatorname {dom}(A_q))<\beta $
. But we may not be able to take such a
![]() $\beta $
in the former case, that is, it may happen that
$\beta $
in the former case, that is, it may happen that
![]() $\operatorname {dom}(A_q)$
is not bounded by
$\operatorname {dom}(A_q)$
is not bounded by
![]() $\sup (\alpha \cap N)$
. So we need more argument for the former case than for the latter case.
$\sup (\alpha \cap N)$
. So we need more argument for the former case than for the latter case.
Suppose that
![]() $\alpha $
is of uncountable cofinality and
$\alpha $
is of uncountable cofinality and
![]() $\operatorname {dom}(A_q) \not \subseteq \sup (\alpha \cap N)$
. (If
$\operatorname {dom}(A_q) \not \subseteq \sup (\alpha \cap N)$
. (If
![]() $\operatorname {dom}(A_q) \subseteq \sup (\alpha \cap N)$
, then the proof will be simpler, same to the proof of the case that
$\operatorname {dom}(A_q) \subseteq \sup (\alpha \cap N)$
, then the proof will be simpler, same to the proof of the case that
![]() $\alpha $
is of countable cofinality.) Since
$\alpha $
is of countable cofinality.) Since
![]() $\mathcal {N}_q$
forms a symmetric system, for each
$\mathcal {N}_q$
forms a symmetric system, for each
![]() $M'\in \mathcal {N}_q$
with
$M'\in \mathcal {N}_q$
with
![]() $\omega _1\cap M'<\omega _1\cap N$
, there exists
$\omega _1\cap M'<\omega _1\cap N$
, there exists
![]() $M\in \mathcal {N}_q$
such that
$M\in \mathcal {N}_q$
such that
![]() $\omega _1\cap M=\omega _1\cap N$
and
$\omega _1\cap M=\omega _1\cap N$
and
![]() $M'\in M$
, and then, by the requirement (id) in Definition 3.4,
$M'\in M$
, and then, by the requirement (id) in Definition 3.4,
 $$\begin{align*}\begin{array}{r@{\ }c@{\ }l} \sup(M'\cap N\cap \alpha) & = & \sup(\left({\Psi_{{N\cap H_\kappa}}}^{-1}\circ \Psi_M\right)(M')\cap M\cap\alpha) \\[0.5em] & \leq & \sup(\left({\Psi_{{N\cap H_\kappa}}}^{-1}\circ \Psi_M\right)(M')\cap\alpha). \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r@{\ }c@{\ }l} \sup(M'\cap N\cap \alpha) & = & \sup(\left({\Psi_{{N\cap H_\kappa}}}^{-1}\circ \Psi_M\right)(M')\cap M\cap\alpha) \\[0.5em] & \leq & \sup(\left({\Psi_{{N\cap H_\kappa}}}^{-1}\circ \Psi_M\right)(M')\cap\alpha). \end{array} \end{align*}$$
Since N thinks that the set
![]() $\left ({\Psi _{{N\cap H_\kappa }}}^{-1}\circ \Psi _M\right )(M')$
is countable and
$\left ({\Psi _{{N\cap H_\kappa }}}^{-1}\circ \Psi _M\right )(M')$
is countable and
![]() $\alpha $
is of uncountable cofinality,
$\alpha $
is of uncountable cofinality,
So there are large enough
![]() $\beta \in \alpha \cap N$
and
$\beta \in \alpha \cap N$
and
![]() $\zeta \in \omega _1\cap N$
, which means that
$\zeta \in \omega _1\cap N$
, which means that
-
•
 $\max (\operatorname {dom}(A_q)\cap \sup (\alpha \cap N))<\beta $
,
$\max (\operatorname {dom}(A_q)\cap \sup (\alpha \cap N))<\beta $
, -
•
 $\max (\big \{\sup (R_q(M)) : M\in \operatorname {dom}(R_q)\big \}\cap N)<\beta $
,
$\max (\big \{\sup (R_q(M)) : M\in \operatorname {dom}(R_q)\big \}\cap N)<\beta $
, -
• for every
 $M'\in \mathcal {N}_q$
with
$M'\in \mathcal {N}_q$
with
 $\omega _1\cap M'<\omega _1\cap N$
,
$\omega _1\cap M'<\omega _1\cap N$
,  $$\begin{align*}\sup(M'\cap N\cap \alpha)<\beta , \end{align*}$$
$$\begin{align*}\sup(M'\cap N\cap \alpha)<\beta , \end{align*}$$
-
•
 $\left \{{\omega _1\cap M : M \in \mathcal {N}_q \cap N }\right \} \subseteq \zeta $
,
$\left \{{\omega _1\cap M : M \in \mathcal {N}_q \cap N }\right \} \subseteq \zeta $
, -
• for any
 $\xi \in \operatorname {dom}(A_q) \cap N$
and any
$\xi \in \operatorname {dom}(A_q) \cap N$
and any
 $\sigma \in A_q(\xi ) \cap N$
,
$\sigma \in A_q(\xi ) \cap N$
,
 $\gamma _\sigma < \zeta $
.
$\gamma _\sigma < \zeta $
.
By the second and the third requirements on
![]() $\beta $
, we observe that
$\beta $
, we observe that
-
〈1〉 for every
 $\xi \in [\beta , \alpha )\cap N$
and every
$\xi \in [\beta , \alpha )\cap N$
and every
 $K\in \mathcal {N}_q$
with
$K\in \mathcal {N}_q$
with
 $\omega _1\cap K<\omega _1\cap N$
,
$\omega _1\cap K<\omega _1\cap N$
,
 $ K\not \in \mathfrak {M}_\xi ^P $
(because if K was in
$ K\not \in \mathfrak {M}_\xi ^P $
(because if K was in
 $\mathfrak {M}_\xi ^P$
,
$\mathfrak {M}_\xi ^P$
,
 $\xi $
would be in K).
$\xi $
would be in K).
Define
 $$ \begin{align*} { \begin{array}{r@{}l} \mathcal{E}:=\Big\{r\restriction\beta:{\ } & r\in \mathbb{P}_\alpha \text{ such that }\\ &\bullet\ \text{ there exists }u\in\mathcal{D} \text{ so that }r\leq_{\mathbb{P}_\alpha} u, \text{ and }\\ &\bullet\ \left\{{\omega_1\cap K:K\in\mathcal{N}_r}\right\}\cap \zeta =\left\{{\omega_1\cap K:K\in\mathcal{N}_q}\right\}\cap N \Big\}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \mathcal{E}:=\Big\{r\restriction\beta:{\ } & r\in \mathbb{P}_\alpha \text{ such that }\\ &\bullet\ \text{ there exists }u\in\mathcal{D} \text{ so that }r\leq_{\mathbb{P}_\alpha} u, \text{ and }\\ &\bullet\ \left\{{\omega_1\cap K:K\in\mathcal{N}_r}\right\}\cap \zeta =\left\{{\omega_1\cap K:K\in\mathcal{N}_q}\right\}\cap N \Big\}. \end{array} } \end{align*} $$
We notice that
![]() $q\restriction \beta \in \mathcal {E}$
and
$q\restriction \beta \in \mathcal {E}$
and
![]() $\mathcal {E}$
is a definable class in the expanded relational structure by
$\mathcal {E}$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_\alpha $
with parameters in N. By Proposition 3.9, since
$\mathbb {P}_\alpha $
with parameters in N. By Proposition 3.9, since
![]() $\beta \in N\in \mathfrak {M}^P_\alpha $
,
$\beta \in N\in \mathfrak {M}^P_\alpha $
,
![]() $N\in \mathfrak {M}^P_\beta $
. Moreover, it follows that
$N\in \mathfrak {M}^P_\beta $
. Moreover, it follows that
So, by the induction hypothesis
![]() $\mathsf {(p)}_\beta $
,
$\mathsf {(p)}_\beta $
,
![]() $q\restriction \beta $
is
$q\restriction \beta $
is
![]() $(N,\mathbb {P}_\beta )$
-generic. Hence there exists
$(N,\mathbb {P}_\beta )$
-generic. Hence there exists
![]() $p_1$
in the set
$p_1$
in the set
![]() $\mathcal {E}\cap N$
which is compatible with the condition
$\mathcal {E}\cap N$
which is compatible with the condition
![]() $q\restriction \beta $
in
$q\restriction \beta $
in
![]() $\mathbb {P}_\beta $
. Let
$\mathbb {P}_\beta $
. Let
![]() $r\in \mathbb {P}_\alpha \cap N$
and
$r\in \mathbb {P}_\alpha \cap N$
and
![]() $u\in \mathcal {D}\cap N$
witness that
$u\in \mathcal {D}\cap N$
witness that
![]() $p_1\in \mathcal {E}$
.
$p_1\in \mathcal {E}$
.
Let us show that q and r are compatible in
![]() $\mathbb {P}_\alpha $
, which finishes the proof of this case. Let
$\mathbb {P}_\alpha $
, which finishes the proof of this case. Let
![]() $p_2\in \mathbb {P}_\beta $
be a common extension of
$p_2\in \mathbb {P}_\beta $
be a common extension of
![]() $q\restriction \beta $
and
$q\restriction \beta $
and
![]() $p_1$
(
$p_1$
(
![]() $=r\restriction \beta $
). We note that
$=r\restriction \beta $
). We note that
![]() $\operatorname {dom}(A_{p_2})\subseteq \beta $
and
$\operatorname {dom}(A_{p_2})\subseteq \beta $
and
-
〈2〉
 $ \operatorname {dom}(A_q)\cap \operatorname {dom}(A_r)\cap [\beta ,\alpha ) =\emptyset $
, more precisely,
$ \operatorname {dom}(A_q)\cap \operatorname {dom}(A_r)\cap [\beta ,\alpha ) =\emptyset $
, more precisely,
because
![]() $\operatorname {dom}(A_r)\subseteq N$
and
$\operatorname {dom}(A_r)\subseteq N$
and
![]() $\max (\operatorname {dom}(A_q)\cap \sup (\alpha \cap N))<\beta $
. Since
$\max (\operatorname {dom}(A_q)\cap \sup (\alpha \cap N))<\beta $
. Since
![]() $r\in N$
,
$r\in N$
,
-
〈3〉
 $\mathcal {N}_r\subseteq N$
,
$\mathcal {N}_r\subseteq N$
, -
〈4〉 for each
 $\xi \in \left [ \beta , \alpha \right )\cap N$
,
$\xi \in \left [ \beta , \alpha \right )\cap N$
,-
– if
 $\xi \in \operatorname {dom}(A_r)$
, then
$\xi \in \operatorname {dom}(A_r)$
, then
 $A_r(\xi )\subseteq N$
,
$A_r(\xi )\subseteq N$
, -
–
 $ \left \{{K\in {R_{q}}^{-1}\big [\,[\xi ,\alpha )\,\big ] \cap \mathfrak {M}_\xi ^P: \omega _1\cap K<\omega _1\cap N}\right \} =\emptyset $
(which follows from
$ \left \{{K\in {R_{q}}^{-1}\big [\,[\xi ,\alpha )\,\big ] \cap \mathfrak {M}_\xi ^P: \omega _1\cap K<\omega _1\cap N}\right \} =\emptyset $
(which follows from
 $\langle $
1
$\langle $
1
 $\rangle $
), and
$\rangle $
), and -
– if
 $M\in {R_q}^{-1}[\{\xi \}]$
, then
$M\in {R_q}^{-1}[\{\xi \}]$
, then
 $\omega _1\cap M \geq \omega _1\cap N$
and
$\omega _1\cap M \geq \omega _1\cap N$
and
 $\sup (R_q(M)) \geq \sup (\alpha \cap N)$
(by the role of
$\sup (R_q(M)) \geq \sup (\alpha \cap N)$
(by the role of
 $\beta $
), and hence
$\beta $
), and hence
 $M \in {R_q}^{-1}[\{\xi +1\}] \subseteq \mathfrak {M}^P_{\xi +1}$
,
$M \in {R_q}^{-1}[\{\xi +1\}] \subseteq \mathfrak {M}^P_{\xi +1}$
,
and
-
-
〈5〉 for each
 $\xi \in \left [ \beta , \alpha \right )\setminus N$
,
$\xi \in \left [ \beta , \alpha \right )\setminus N$
,
 $ \mathcal {N}_r\cap \mathfrak {M}_\xi ^P = \emptyset $
, in fact, no element of
$ \mathcal {N}_r\cap \mathfrak {M}_\xi ^P = \emptyset $
, in fact, no element of
 $\mathcal {N}_r$
contains
$\mathcal {N}_r$
contains
 $\xi $
as a member.
$\xi $
as a member.
Let
![]() $\xi _0 := \min \big ( \operatorname {dom}(A_r) \setminus \beta \big )$
. Define
$\xi _0 := \min \big ( \operatorname {dom}(A_r) \setminus \beta \big )$
. Define
![]() $p_2' \in U_{\xi _0}$
such that
$p_2' \in U_{\xi _0}$
such that
-
•
 $R_{p_2'} := \begin {array}[t]{l@{\,}l} R_{p_2} \cup R_{q\restriction \xi _0} \\ \cup \Big \{ \left \langle {\left ( {\Psi _{M} }^{-1} \circ \Psi _{N} \right ) (K) , \xi }\right \rangle : & \left \langle {K, \xi }\right \rangle \in R_{r\restriction \xi _0}, \ M\in {R_{q}}^{-1}[\{\xi \}] \\ & \text {with } \omega _1\cap M = \omega _1\cap N \Big \} , \end {array} $
$R_{p_2'} := \begin {array}[t]{l@{\,}l} R_{p_2} \cup R_{q\restriction \xi _0} \\ \cup \Big \{ \left \langle {\left ( {\Psi _{M} }^{-1} \circ \Psi _{N} \right ) (K) , \xi }\right \rangle : & \left \langle {K, \xi }\right \rangle \in R_{r\restriction \xi _0}, \ M\in {R_{q}}^{-1}[\{\xi \}] \\ & \text {with } \omega _1\cap M = \omega _1\cap N \Big \} , \end {array} $
-
•
 $\mathcal {N}_{p_2'} := \operatorname {dom}(R_{p_2'}) $
, and
$\mathcal {N}_{p_2'} := \operatorname {dom}(R_{p_2'}) $
, and -
•
 $A_{p_2'} := A_{p_2}$
.
$A_{p_2'} := A_{p_2}$
.
Now
![]() $\operatorname {dom}(A_r) \cap \xi _0 = \operatorname {dom}(A_r) \cap \beta $
and
$\operatorname {dom}(A_r) \cap \xi _0 = \operatorname {dom}(A_r) \cap \beta $
and
![]() $\operatorname {dom}(A_q) \cap \xi _0 = \operatorname {dom}(A_q) \cap \beta $
. By Propositions 3.10 and 3.11 and the fact that
$\operatorname {dom}(A_q) \cap \xi _0 = \operatorname {dom}(A_q) \cap \beta $
. By Propositions 3.10 and 3.11 and the fact that
![]() $\alpha \in \omega _2$
,
$\alpha \in \omega _2$
,
![]() $R_{p_2'}$
satisfies (el), (ho), (up), and (down) in Definition 4.1, and so
$R_{p_2'}$
satisfies (el), (ho), (up), and (down) in Definition 4.1, and so
![]() $p_2'$
is a condition of
$p_2'$
is a condition of
![]() $\mathbb {P}_{\xi _0}$
. Hence
$\mathbb {P}_{\xi _0}$
. Hence
![]() $p_2'$
is a common extension of
$p_2'$
is a common extension of
![]() $r\restriction \xi _0$
and
$r\restriction \xi _0$
and
![]() $q\restriction \xi _0$
.
$q\restriction \xi _0$
.
By
![]() $\langle $
4
$\langle $
4
![]() $\rangle $
, we can apply Proposition 5.5 to find a common extension
$\rangle $
, we can apply Proposition 5.5 to find a common extension
![]() $q_{\xi _0}' $
of
$q_{\xi _0}' $
of
![]() $p_2'$
,
$p_2'$
,
![]() $r\restriction (\xi _0+1)$
, and
$r\restriction (\xi _0+1)$
, and
![]() $q \restriction (\xi _0 +1)$
in
$q \restriction (\xi _0 +1)$
in
![]() $\mathbb {P}_{\xi _0+1}$
. Let
$\mathbb {P}_{\xi _0+1}$
. Let
![]() $\left \{{\xi _i : i \leq m}\right \}$
be the increasing enumeration of the set
$\left \{{\xi _i : i \leq m}\right \}$
be the increasing enumeration of the set
![]() $\operatorname {dom}(A_r)\setminus \beta $
. By
$\operatorname {dom}(A_r)\setminus \beta $
. By
![]() $\langle $
4
$\langle $
4
![]() $\rangle $
again, for each
$\rangle $
again, for each
![]() $i \leq m$
with
$i \leq m$
with
![]() $i\neq 0$
, we can apply Proposition 5.5 to find a common extension
$i\neq 0$
, we can apply Proposition 5.5 to find a common extension
![]() $q_{\xi _i}'$
of
$q_{\xi _i}'$
of
![]() $q_{\xi _{i-1}}'$
,
$q_{\xi _{i-1}}'$
,
![]() $r\restriction (\xi _i+1)$
, and
$r\restriction (\xi _i+1)$
, and
![]() $q \restriction (\xi _i +1)$
in
$q \restriction (\xi _i +1)$
in
![]() $\mathbb {P}_{\xi _i+1}$
.
$\mathbb {P}_{\xi _i+1}$
.
Define
![]() $q^{\prime }_\alpha \in U_\alpha $
such that
$q^{\prime }_\alpha \in U_\alpha $
such that
-
•
 $ R_{q^{\prime }_\alpha }:= R_{q^{\prime }_{\xi _m}}\cup R_q$
$ R_{q^{\prime }_\alpha }:= R_{q^{\prime }_{\xi _m}}\cup R_q$
 $$\begin{align*}\begin{array}{r} \cup \bigcup \Big\{ \left\{{\left( {\Psi_{M} }^{-1} \circ \Psi_{N} \right) (K)}\right\} \times \left( (\zeta+1)\cap \left( {\Psi_{M} }^{-1} \circ \Psi_{N} \right) (K) \right) : \hspace{3em} \ \\ \hfill \zeta \geq \beta, \left\langle{K,\zeta}\right\rangle \in R_r, \left\langle{M,\zeta}\right\rangle\in R_q \text{ with } \omega_1\cap M =\omega_1\cap N \Big\} , \end{array} \end{align*}$$
$$\begin{align*}\begin{array}{r} \cup \bigcup \Big\{ \left\{{\left( {\Psi_{M} }^{-1} \circ \Psi_{N} \right) (K)}\right\} \times \left( (\zeta+1)\cap \left( {\Psi_{M} }^{-1} \circ \Psi_{N} \right) (K) \right) : \hspace{3em} \ \\ \hfill \zeta \geq \beta, \left\langle{K,\zeta}\right\rangle \in R_r, \left\langle{M,\zeta}\right\rangle\in R_q \text{ with } \omega_1\cap M =\omega_1\cap N \Big\} , \end{array} \end{align*}$$
-
•
 $ \mathcal {N}_{q_\alpha '}:= \operatorname {dom}(R_{q_\alpha '}), $
and
$ \mathcal {N}_{q_\alpha '}:= \operatorname {dom}(R_{q_\alpha '}), $
and -
•
 $A_{q_\alpha '} := A_{q^{\prime }_{\xi _m}}\cup \left ( A_q \restriction [\beta , \alpha ) \right ) $
.
$A_{q_\alpha '} := A_{q^{\prime }_{\xi _m}}\cup \left ( A_q \restriction [\beta , \alpha ) \right ) $
.
By Propositions 3.10 and 3.11 and the fact that
![]() $\alpha \in \omega _2$
again,
$\alpha \in \omega _2$
again,
![]() $R_{q_\alpha '}$
satisfies (el), (ho), (up), and (down) in Definition 4.1. By
$R_{q_\alpha '}$
satisfies (el), (ho), (up), and (down) in Definition 4.1. By
![]() $\langle $
5
$\langle $
5
![]() $\rangle $
, for each
$\rangle $
, for each
![]() $\xi \in \operatorname {dom}(A_q) \cap [\beta ,\alpha )$
,
$\xi \in \operatorname {dom}(A_q) \cap [\beta ,\alpha )$
,
![]() $A_{p_\alpha '}(\xi )$
satisfies (g) for
$A_{p_\alpha '}(\xi )$
satisfies (g) for
![]() $R_{q_\alpha '}$
. Therefore,
$R_{q_\alpha '}$
. Therefore,
![]() $q_\alpha '$
is a condition of
$q_\alpha '$
is a condition of
![]() $\mathbb {P}_\alpha $
, and so is a common extension of r and q in
$\mathbb {P}_\alpha $
, and so is a common extension of r and q in
![]() $\mathbb {P}_\alpha $
. This finishes the proof of this case.
$\mathbb {P}_\alpha $
. This finishes the proof of this case.
Suppose that
![]() $\alpha $
is of countable cofinality. Take a large enough ordinal
$\alpha $
is of countable cofinality. Take a large enough ordinal
![]() $\beta \in \alpha \cap N$
, which means that
$\beta \in \alpha \cap N$
, which means that
-
•
 $\max (\operatorname {dom}(A_q)) <\beta $
, and
$\max (\operatorname {dom}(A_q)) <\beta $
, and -
• for each
 $M\in \operatorname {dom}({R_q})$
, either
$M\in \operatorname {dom}({R_q})$
, either
 $R_q(M)\subseteq \beta $
or
$R_q(M)\subseteq \beta $
or
 $R_q(M)$
is cofinal in
$R_q(M)$
is cofinal in
 $\alpha $
,
$\alpha $
,
and define
 $$ \begin{align*} { \begin{array}{r@{}l} \mathcal{E}:=\Big\{r\restriction\beta:{\ } & r\in \mathbb{P}_\alpha \text{ such that}\\ &\bullet\ \text{ there exists }u'\in\mathcal{D} \text{ so that }r\leq_{\mathbb{P}_\alpha} u',\\ &\bullet\ \operatorname{dom}(A_r)\subseteq \beta, \text{ and }\\ &\bullet\ \text{ for each }M\in {\mathcal{N}_r}, \text{ either }R_r(M)\subseteq\beta \text{ or }R_r(M) \text{ is } \text{ cofinal in }\alpha \Big\}. \end{array} } \end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \mathcal{E}:=\Big\{r\restriction\beta:{\ } & r\in \mathbb{P}_\alpha \text{ such that}\\ &\bullet\ \text{ there exists }u'\in\mathcal{D} \text{ so that }r\leq_{\mathbb{P}_\alpha} u',\\ &\bullet\ \operatorname{dom}(A_r)\subseteq \beta, \text{ and }\\ &\bullet\ \text{ for each }M\in {\mathcal{N}_r}, \text{ either }R_r(M)\subseteq\beta \text{ or }R_r(M) \text{ is } \text{ cofinal in }\alpha \Big\}. \end{array} } \end{align*} $$
We note that
![]() $q\in \mathcal {E}$
and
$q\in \mathcal {E}$
and
![]() $\mathcal {E}$
is a definable class in the expanded relational structure by
$\mathcal {E}$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_\alpha $
with parameters in N. By the induction hypothesis
$\mathbb {P}_\alpha $
with parameters in N. By the induction hypothesis
![]() $\mathsf {(p)}_\beta $
and the fact that
$\mathsf {(p)}_\beta $
and the fact that
![]() $\beta \in N\in \mathfrak {M}_\alpha ^P$
,
$\beta \in N\in \mathfrak {M}_\alpha ^P$
,
![]() $q\restriction \beta $
is
$q\restriction \beta $
is
![]() $(N,\mathbb {P}_\beta )$
-generic. So there exists
$(N,\mathbb {P}_\beta )$
-generic. So there exists
![]() $p_1\in \mathcal {E}\cap N$
which is compatible with the condition
$p_1\in \mathcal {E}\cap N$
which is compatible with the condition
![]() $q\restriction \beta $
in
$q\restriction \beta $
in
![]() $\mathbb {P}_\beta $
. Let
$\mathbb {P}_\beta $
. Let
![]() $r\in \mathbb {P}_\alpha \cap N$
and
$r\in \mathbb {P}_\alpha \cap N$
and
![]() $u' \in \mathcal {D} \cap N$
witness that
$u' \in \mathcal {D} \cap N$
witness that
![]() $p_1\in \mathcal {E}$
, and let
$p_1\in \mathcal {E}$
, and let
![]() $p_2\in \mathbb {P}_\beta $
be a common extension of
$p_2\in \mathbb {P}_\beta $
be a common extension of
![]() $q\restriction \beta $
and
$q\restriction \beta $
and
![]() $p_1$
(
$p_1$
(
![]() $=r\restriction \beta $
).
$=r\restriction \beta $
).
Define
![]() $q' \in U_\alpha $
such that
$q' \in U_\alpha $
such that
-
•
 $ R_{q'}:= R_{p_2}\cup R_r \cup R_{q} $
$ R_{q'}:= R_{p_2}\cup R_r \cup R_{q} $
 $ \kern20pt \cup \bigcup \Big \{ \left \{{\left ( {\Psi _{M} }^{-1} \circ \Psi _{N} \right ) (K)}\right \} \times \left ( \alpha \cap \left ( {\Psi _{M} }^{-1} \circ \Psi _{N} \right ) (K) \right ) : $
$ \kern20pt \cup \bigcup \Big \{ \left \{{\left ( {\Psi _{M} }^{-1} \circ \Psi _{N} \right ) (K)}\right \} \times \left ( \alpha \cap \left ( {\Psi _{M} }^{-1} \circ \Psi _{N} \right ) (K) \right ) : $
 $ \kern20pt \xi \geq \beta , \left \langle {K,\xi }\right \rangle \in R_r, \left \langle {M,\xi }\right \rangle \in R_q \text { with } \omega _1\cap M =\omega _1\cap N \Big \}, $
$ \kern20pt \xi \geq \beta , \left \langle {K,\xi }\right \rangle \in R_r, \left \langle {M,\xi }\right \rangle \in R_q \text { with } \omega _1\cap M =\omega _1\cap N \Big \}, $
-
•
 $\mathcal {N}_{q'}:=\operatorname {dom}(R_{q'})$
, and
$\mathcal {N}_{q'}:=\operatorname {dom}(R_{q'})$
, and -
•
 $A_{q'} := A_{p_2}$
.
$A_{q'} := A_{p_2}$
.
Then
![]() $q'$
is a condition of
$q'$
is a condition of
![]() $\mathbb {P}_\alpha $
, and is a common extension of q, r, and
$\mathbb {P}_\alpha $
, and is a common extension of q, r, and
![]() $u'$
in
$u'$
in
![]() $\mathbb {P}_\alpha $
.
$\mathbb {P}_\alpha $
.
![]() $\dashv$
$\dashv$
The following proof is similar to one of Lemma 2.10.
Proof of
 $\mathsf {(C)}_{\alpha }$
for a limit ordinal
$\mathsf {(C)}_{\alpha }$
for a limit ordinal
 $\alpha $
.
$\alpha $
.
Suppose that
![]() $\alpha \in \omega _2+1$
is a limit ordinal,
$\alpha \in \omega _2+1$
is a limit ordinal,
![]() $p\in \mathbb {P}_{\alpha }$
,
$p\in \mathbb {P}_{\alpha }$
,
![]() $N\in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
satisfies that
$N\in \mathcal {N}_p \cap \mathfrak {M}^P_\alpha $
satisfies that
![]() $\{N\}\times (\alpha \cap N)\subseteq R_p$
, and
$\{N\}\times (\alpha \cap N)\subseteq R_p$
, and
![]() $\left \{{\dot F_n: n\in \omega }\right \}$
is a set of
$\left \{{\dot F_n: n\in \omega }\right \}$
is a set of
![]() $\mathbb {P}_\alpha $
-names for nowhere dense subsets of
$\mathbb {P}_\alpha $
-names for nowhere dense subsets of
![]() $\left ({2^{<\omega }}\right )^\omega $
such that
$\left ({2^{<\omega }}\right )^\omega $
such that
![]() $\left \{{\dot F_n: n\in \omega }\right \} \in N$
. Let us show that
$\left \{{\dot F_n: n\in \omega }\right \} \in N$
. Let us show that
![]() $p \Vdash _{\mathbb {P}_{\alpha }} \!\!\!\text {"} f_{\omega _1\cap N} \not \in \bigcup _{n\in \omega } \dot F_n \,\text {"}$
.
$p \Vdash _{\mathbb {P}_{\alpha }} \!\!\!\text {"} f_{\omega _1\cap N} \not \in \bigcup _{n\in \omega } \dot F_n \,\text {"}$
.
Suppose not, and let
![]() $q\leq _{\mathbb {P}_{\alpha }} p$
and
$q\leq _{\mathbb {P}_{\alpha }} p$
and
![]() $n\in \omega $
be such that
$n\in \omega $
be such that
As in the proof of
![]() $\mathsf {(p)}_\alpha $
when
$\mathsf {(p)}_\alpha $
when
![]() $\alpha $
is a limit ordinal, we need to separate two cases.
$\alpha $
is a limit ordinal, we need to separate two cases.
Suppose that
![]() $\alpha $
is of uncountable cofinality and
$\alpha $
is of uncountable cofinality and
![]() $\operatorname {dom}(A_q) \not \subseteq \sup (\alpha \cap N)$
. Let
$\operatorname {dom}(A_q) \not \subseteq \sup (\alpha \cap N)$
. Let
![]() $\beta \in \alpha \cap N$
and
$\beta \in \alpha \cap N$
and
![]() $\zeta \in \omega _1\cap N$
be large enough ordinals for the condition q as in the proof of
$\zeta \in \omega _1\cap N$
be large enough ordinals for the condition q as in the proof of
![]() $\mathsf {(p)}_\alpha $
. By the induction hypothesis
$\mathsf {(p)}_\alpha $
. By the induction hypothesis
![]() $\mathsf {(p)_\beta }$
and the fact that
$\mathsf {(p)_\beta }$
and the fact that
![]() $\beta \in N \in \mathfrak {M}^P_\alpha $
,
$\beta \in N \in \mathfrak {M}^P_\alpha $
,
![]() $q\restriction \beta $
is
$q\restriction \beta $
is
![]() $(N,\mathbb {P}_\beta )$
-generic. For each
$(N,\mathbb {P}_\beta )$
-generic. For each
![]() $\nu \in \left ( 2^{<\omega } \right )^{<\omega }$
, each
$\nu \in \left ( 2^{<\omega } \right )^{<\omega }$
, each
![]() $\beta ' \in \alpha \setminus \beta $
, each
$\beta ' \in \alpha \setminus \beta $
, each
![]() $\eta \in \omega _1$
and each
$\eta \in \omega _1$
and each
![]() $u\in \mathbb {P}_\alpha $
, define
$u\in \mathbb {P}_\alpha $
, define
![]() $\varphi _\alpha (\nu , \beta ', \eta , u)$
to be the assertion that
$\varphi _\alpha (\nu , \beta ', \eta , u)$
to be the assertion that
-
•
 $\operatorname {dom}(A_u) \cap \beta ' = \operatorname {dom}(A_p) \cap \beta $
,
$\operatorname {dom}(A_u) \cap \beta ' = \operatorname {dom}(A_p) \cap \beta $
, -
•
 $ \left \{{\omega _1\cap K:K\in \mathcal {N}_u }\right \} \cap \eta =\left \{{\omega _1\cap K:K\in \mathcal {N}_q }\right \} \cap N $
, and
$ \left \{{\omega _1\cap K:K\in \mathcal {N}_u }\right \} \cap \eta =\left \{{\omega _1\cap K:K\in \mathcal {N}_q }\right \} \cap N $
, and -
•
 $ u \Vdash _{\mathbb {P}_{\alpha }}\!\!\!\text {"}\dot F_n \cap [\nu ] \neq \emptyset \,\text {"}. $
$ u \Vdash _{\mathbb {P}_{\alpha }}\!\!\!\text {"}\dot F_n \cap [\nu ] \neq \emptyset \,\text {"}. $
Define a
![]() $\mathbb {P}_\beta $
-name
$\mathbb {P}_\beta $
-name
![]() $\dot Y$
such that
$\dot Y$
such that
 $$ \begin{align*} { \begin{array}{r@{\ }l} \Vdash_{\mathbb{P}_\beta}\ \text{"} \dot Y = \Big\{ g \in \left({2^{<\omega}}\right)^\omega : & \text{ for any }k\in \omega, \text{ any }\beta'\in \alpha \setminus \beta, \text{ and } \text{ any }\eta \in \omega_1\setminus \zeta,\\ &\text{ there exists }u\in \mathbb{P}_{\alpha} \text{ such that } u\restriction \beta \in \dot G_{\mathbb{P}_{\beta}} \text{ and}\\ &\varphi_\alpha( g \restriction k, \beta', \eta, u) \Big\} \text{"}. \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{r@{\ }l} \Vdash_{\mathbb{P}_\beta}\ \text{"} \dot Y = \Big\{ g \in \left({2^{<\omega}}\right)^\omega : & \text{ for any }k\in \omega, \text{ any }\beta'\in \alpha \setminus \beta, \text{ and } \text{ any }\eta \in \omega_1\setminus \zeta,\\ &\text{ there exists }u\in \mathbb{P}_{\alpha} \text{ such that } u\restriction \beta \in \dot G_{\mathbb{P}_{\beta}} \text{ and}\\ &\varphi_\alpha( g \restriction k, \beta', \eta, u) \Big\} \text{"}. \end{array} }\end{align*} $$
Then
![]() $\dot Y$
is a definable class in the expanded relational structure by
$\dot Y$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_\alpha $
with parameters in N.
$\mathbb {P}_\alpha $
with parameters in N.
![]() $\dot Y$
is forced to be a closed subset of
$\dot Y$
is forced to be a closed subset of
![]() $\left ({2^{<\omega }}\right )^\omega $
. So by Proposition 5.1,
$\left ({2^{<\omega }}\right )^\omega $
. So by Proposition 5.1,
![]() $\dot Y$
can be considered as an element of N.
$\dot Y$
can be considered as an element of N.
We claim that
Let
![]() $r \leq _{\mathbb {P}_\beta } q \restriction \beta $
and
$r \leq _{\mathbb {P}_\beta } q \restriction \beta $
and
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, and let
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, and let
![]() $q'$
be a common extension of both r and q in
$q'$
be a common extension of both r and q in
![]() $\mathbb {P}_{\alpha }$
. Then there are
$\mathbb {P}_{\alpha }$
. Then there are
![]() $q"\leq _{\mathbb {P}_\alpha } q'$
and an end-extension
$q"\leq _{\mathbb {P}_\alpha } q'$
and an end-extension
![]() $\nu '$
of
$\nu '$
of
![]() $\nu $
in
$\nu $
in
![]() $\left ({2^{<\omega }}\right )^{<\omega }$
such that
$\left ({2^{<\omega }}\right )^{<\omega }$
such that
![]() $q"\restriction \beta $
is an extension of r in
$q"\restriction \beta $
is an extension of r in
![]() $\mathbb {P}_\beta $
. Let us show that
$\mathbb {P}_\beta $
. Let us show that
Assume not. Let
![]() $\dot g$
a
$\dot g$
a
![]() $\mathbb {P}_\beta $
-name such that
$\mathbb {P}_\beta $
-name such that
Take
![]() $s\leq _{\mathbb {P}_{\beta }} q"\restriction \beta $
,
$s\leq _{\mathbb {P}_{\beta }} q"\restriction \beta $
,
![]() $k\in \omega $
, and
$k\in \omega $
, and
![]() $\nu " \in \left ({2^{<\omega }}\right )^{<\omega }$
such that
$\nu " \in \left ({2^{<\omega }}\right )^{<\omega }$
such that
Let
![]() $\beta '\in (\alpha \cap N)\setminus \beta $
and let
$\beta '\in (\alpha \cap N)\setminus \beta $
and let
![]() $\eta \in (\omega _1\cap N) \setminus \zeta $
be large enough ordinals for
$\eta \in (\omega _1\cap N) \setminus \zeta $
be large enough ordinals for
![]() $q"$
as in the proof of
$q"$
as in the proof of
![]() $\mathsf {(p)}_\alpha $
. By the definition of
$\mathsf {(p)}_\alpha $
. By the definition of
![]() $\dot Y$
,
$\dot Y$
,
![]() $\left \{{\dot Y, \beta ', \eta , \nu "}\right \} \in N$
, and the fact that
$\left \{{\dot Y, \beta ', \eta , \nu "}\right \} \in N$
, and the fact that
![]() $q"\restriction \beta $
is also
$q"\restriction \beta $
is also
![]() $(N, \mathbb {P}_{\beta })$
-generic and that N is an elementary substructure of the expanded relational structure by
$(N, \mathbb {P}_{\beta })$
-generic and that N is an elementary substructure of the expanded relational structure by
![]() $\mathbb {P}_\alpha $
, there exists an extension
$\mathbb {P}_\alpha $
, there exists an extension
![]() $s'$
of s in
$s'$
of s in
![]() $\mathbb {P}_{\beta }$
and
$\mathbb {P}_{\beta }$
and
![]() $u\in \mathbb {P}_\alpha \cap N$
such that
$u\in \mathbb {P}_\alpha \cap N$
such that
![]() $s' \leq _{\mathbb {P}_{\beta }} u\restriction {\beta } $
and
$s' \leq _{\mathbb {P}_{\beta }} u\restriction {\beta } $
and
![]() $\varphi _\alpha (\nu ", \beta ', \eta , u)$
. As in the proof of
$\varphi _\alpha (\nu ", \beta ', \eta , u)$
. As in the proof of
![]() $\mathsf {(p)}_\alpha $
, by the roles of
$\mathsf {(p)}_\alpha $
, by the roles of
![]() $\beta '$
and
$\beta '$
and
![]() $\eta $
, we can build a common extension t of
$\eta $
, we can build a common extension t of
![]() $s'$
,
$s'$
,
![]() $q"$
, and u in
$q"$
, and u in
![]() $\mathbb {P}_{\alpha }$
. (To build t, for each coordinate
$\mathbb {P}_{\alpha }$
. (To build t, for each coordinate
![]() $\xi $
in
$\xi $
in
![]() $\left (\operatorname {dom}(A_{q"}) \cup \operatorname {dom}(A_u) \right ) \cap [\beta , \sup (\alpha \cap N))$
, we construct a preparatory condition
$\left (\operatorname {dom}(A_{q"}) \cup \operatorname {dom}(A_u) \right ) \cap [\beta , \sup (\alpha \cap N))$
, we construct a preparatory condition
![]() $t_\xi \in \mathbb {P}_{\xi +1}$
like
$t_\xi \in \mathbb {P}_{\xi +1}$
like
![]() $q_{\xi _i}'$
as in the proof of
$q_{\xi _i}'$
as in the proof of
![]() $\mathsf {(p)}_\alpha $
.) Then
$\mathsf {(p)}_\alpha $
.) Then
which is a contradiction.
We claim that
This contradicts the induction hypothesis
![]() $\mathsf {(C)}_\beta $
, and finishes the proof of this case.
$\mathsf {(C)}_\beta $
, and finishes the proof of this case.
Assume not. Then there exists
![]() $r\leq _{\mathbb {P}_\beta } q \restriction \beta $
such that
$r\leq _{\mathbb {P}_\beta } q \restriction \beta $
such that
By extending r if necessary, we may assume that there are
![]() $k\in \omega $
,
$k\in \omega $
,
![]() $\beta ' \in \alpha \setminus \beta $
, and
$\beta ' \in \alpha \setminus \beta $
, and
![]() $\eta \in \omega _1\setminus \zeta $
such that
$\eta \in \omega _1\setminus \zeta $
such that
By the induction hypothesis
![]() $\mathsf {(p)}_\beta $
, r is
$\mathsf {(p)}_\beta $
, r is
![]() $(N,\mathbb {P}_\beta )$
-generic. So by extending r again if necessary, we may assume that
$(N,\mathbb {P}_\beta )$
-generic. So by extending r again if necessary, we may assume that
![]() $\beta '\in (\alpha \cap N)\setminus \beta $
and
$\beta '\in (\alpha \cap N)\setminus \beta $
and
![]() $\eta \in (\omega _1\cap N) \setminus \zeta $
. However, then
$\eta \in (\omega _1\cap N) \setminus \zeta $
. However, then
which is a contradiction.
Suppose that
![]() $\alpha $
is of countable cofinality. The proof below is similar to the one in the case of uncountable cofinality. The differences are the necessary property of
$\alpha $
is of countable cofinality. The proof below is similar to the one in the case of uncountable cofinality. The differences are the necessary property of
![]() $\beta $
and the definition of
$\beta $
and the definition of
![]() $\dot Y$
. Let
$\dot Y$
. Let
![]() $\beta \in \alpha \cap N$
be a large enough ordinal as in the proof of
$\beta \in \alpha \cap N$
be a large enough ordinal as in the proof of
![]() $\mathsf {(p)}_\alpha $
. Let
$\mathsf {(p)}_\alpha $
. Let
![]() $\zeta \in \omega _1\cap N$
be such that
$\zeta \in \omega _1\cap N$
be such that
For each
![]() $\nu \in \left ( 2^{<\omega } \right )^{<\omega }$
, each
$\nu \in \left ( 2^{<\omega } \right )^{<\omega }$
, each
![]() $\eta \in \omega _1$
, and each
$\eta \in \omega _1$
, and each
![]() $u\in \mathbb {P}_\alpha $
, define
$u\in \mathbb {P}_\alpha $
, define
![]() $\varphi _\alpha (\nu , \eta , u)$
to be the assertion that
$\varphi _\alpha (\nu , \eta , u)$
to be the assertion that
-
•
 $\operatorname {dom}(A_u) \subseteq \beta $
,
$\operatorname {dom}(A_u) \subseteq \beta $
, -
• for each
 $M\in {\mathcal {N}_u}$
, either
$M\in {\mathcal {N}_u}$
, either
 $R_u(M)\subseteq \beta $
or
$R_u(M)\subseteq \beta $
or
 $R_u(M)$
is cofinal in
$R_u(M)$
is cofinal in
 $\alpha $
,
$\alpha $
, -
•
 $ \left \{{\omega _1\cap K:K\in \mathcal {N}_u }\right \} \cap \eta =\left \{{\omega _1\cap K:K\in \mathcal {N}_q }\right \} \cap N $
, and
$ \left \{{\omega _1\cap K:K\in \mathcal {N}_u }\right \} \cap \eta =\left \{{\omega _1\cap K:K\in \mathcal {N}_q }\right \} \cap N $
, and -
•
 $ u \Vdash _{\mathbb {P}_{\alpha }}\!\!\!\text {"}\dot F_n \cap [\nu ] \neq \emptyset \,\text {"} , $
$ u \Vdash _{\mathbb {P}_{\alpha }}\!\!\!\text {"}\dot F_n \cap [\nu ] \neq \emptyset \,\text {"} , $
and define
![]() $\dot Y$
to be a
$\dot Y$
to be a
![]() $\mathbb {P}_\beta $
-name such that
$\mathbb {P}_\beta $
-name such that
 $$ \begin{align*} { \begin{array}{r@{\ }l} \Vdash_{\mathbb{P}_\beta}\ \text{"} \dot Y = \Big\{ g \in \left({2^{<\omega}}\right)^\omega : & \text{ for any }k\in\omega \text{ and } \text{ any }\eta\in \omega_1\setminus \zeta, \text{ there exists }u\in \mathbb{P}_{\alpha}\\ &\text{ such that } u\restriction \beta \in \dot G_{\mathbb{P}_\beta} \text{ and } \varphi_\alpha(g \restriction k, \eta, u) \Big\}\text{"}. \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{r@{\ }l} \Vdash_{\mathbb{P}_\beta}\ \text{"} \dot Y = \Big\{ g \in \left({2^{<\omega}}\right)^\omega : & \text{ for any }k\in\omega \text{ and } \text{ any }\eta\in \omega_1\setminus \zeta, \text{ there exists }u\in \mathbb{P}_{\alpha}\\ &\text{ such that } u\restriction \beta \in \dot G_{\mathbb{P}_\beta} \text{ and } \varphi_\alpha(g \restriction k, \eta, u) \Big\}\text{"}. \end{array} }\end{align*} $$
Then
![]() $\dot Y$
is a definable class in the expanded relational structure by
$\dot Y$
is a definable class in the expanded relational structure by
![]() $\mathbb {P}_\alpha $
with parameters in N, and is forced to be a closed subset of
$\mathbb {P}_\alpha $
with parameters in N, and is forced to be a closed subset of
![]() $\left ({2^{<\omega }}\right )^\omega $
. So by Proposition 5.1,
$\left ({2^{<\omega }}\right )^\omega $
. So by Proposition 5.1,
![]() $\dot Y$
can be considered as an element of N.
$\dot Y$
can be considered as an element of N.
We claim that
Let
![]() $r \leq _{\mathbb {P}_\beta } q \restriction \beta $
and
$r \leq _{\mathbb {P}_\beta } q \restriction \beta $
and
![]() $\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, and let
$\nu \in \left ({2^{<\omega }}\right )^{<\omega }$
, and let
![]() $q'$
be a common extension of both r and q in
$q'$
be a common extension of both r and q in
![]() $\mathbb {P}_{\alpha }$
. Then there are
$\mathbb {P}_{\alpha }$
. Then there are
![]() $q"\leq _{\mathbb {P}_\alpha } q'$
and an end-extension
$q"\leq _{\mathbb {P}_\alpha } q'$
and an end-extension
![]() $\nu '$
of
$\nu '$
of
![]() $\nu $
in
$\nu $
in
![]() $\left ({2^{<\omega }}\right )^{<\omega }$
such that
$\left ({2^{<\omega }}\right )^{<\omega }$
such that
![]() $q"\restriction \beta $
is an extension of r in
$q"\restriction \beta $
is an extension of r in
![]() $\mathbb {P}_\beta $
. Let us show that
$\mathbb {P}_\beta $
. Let us show that
Assume not, and let
![]() $\dot g$
be a
$\dot g$
be a
![]() $\mathbb {P}_\beta $
-name such that
$\mathbb {P}_\beta $
-name such that
Take
![]() $s\leq _{\mathbb {P}_{\beta }} q"\restriction \beta $
,
$s\leq _{\mathbb {P}_{\beta }} q"\restriction \beta $
,
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $\nu " \in \left ({2^{<\omega }}\right )^{<\omega }$
such that
$\nu " \in \left ({2^{<\omega }}\right )^{<\omega }$
such that
Take
![]() $\eta \in \omega _1\cap N$
such that
$\eta \in \omega _1\cap N$
such that
![]() $\eta \geq \zeta $
and, for any
$\eta \geq \zeta $
and, for any
![]() $\xi \in \operatorname {dom}(A_{q"})\cap [\beta , \alpha )\cap N$
(then
$\xi \in \operatorname {dom}(A_{q"})\cap [\beta , \alpha )\cap N$
(then
![]() $N\in R_{q"}[\{\xi \}]$
) and any
$N\in R_{q"}[\{\xi \}]$
) and any
![]() $\sigma \in A_{q"}(\xi ) \cap N$
,
$\sigma \in A_{q"}(\xi ) \cap N$
,
![]() $\gamma _\sigma < \eta $
. As in the previous case, we take an extension s of
$\gamma _\sigma < \eta $
. As in the previous case, we take an extension s of
![]() $q" \restriction \beta $
in
$q" \restriction \beta $
in
![]() $\mathbb {P}_\beta $
and
$\mathbb {P}_\beta $
and
![]() $u\in \mathbb {P}_\alpha \cap N$
such that
$u\in \mathbb {P}_\alpha \cap N$
such that
![]() $s \leq _{\mathbb {P}_\beta } u\restriction \beta $
and
$s \leq _{\mathbb {P}_\beta } u\restriction \beta $
and
![]() $\varphi _\alpha (\nu ", \eta , u)$
. For any
$\varphi _\alpha (\nu ", \eta , u)$
. For any
![]() $\xi \in \operatorname {dom}(A_{q"}) \cap [\beta ,\alpha )$
,
$\xi \in \operatorname {dom}(A_{q"}) \cap [\beta ,\alpha )$
,
-
• if
 $\xi \in N$
, then
$\xi \in N$
, then-
–
 $N\in {R_{q"}}^{-1}[\{\xi \}] \cap \mathfrak {M}^P_{\xi +1}$
,
$N\in {R_{q"}}^{-1}[\{\xi \}] \cap \mathfrak {M}^P_{\xi +1}$
, -
–
 ${R_u}^{-1}[\{\xi \}] = {R_u}^{-1}[\{\xi +1\}] \subseteq \mathfrak {M}^P_{\xi +1}$
(because u satisfies
${R_u}^{-1}[\{\xi \}] = {R_u}^{-1}[\{\xi +1\}] \subseteq \mathfrak {M}^P_{\xi +1}$
(because u satisfies
 $\varphi _\alpha (\nu ", \eta , u)$
),
$\varphi _\alpha (\nu ", \eta , u)$
), -
–
 $\left \{{\omega _1\cap M : M \in {R_u}^{-1}[\{\xi \}]}\right \} \cap \eta \subseteq \left \{{\delta _\sigma : \sigma \in A_{q"}(\xi )}\right \}$
,
$\left \{{\omega _1\cap M : M \in {R_u}^{-1}[\{\xi \}]}\right \} \cap \eta \subseteq \left \{{\delta _\sigma : \sigma \in A_{q"}(\xi )}\right \}$
, -
– for any
 $\sigma \in A_q(\xi )\cap N$
,
$\sigma \in A_q(\xi )\cap N$
,
 $\gamma _\sigma < \eta $
, and
$\gamma _\sigma < \eta $
, and -
–
 $\max \left \{{\omega _1\cap M : M \in {R_u}^{-1}[\{\xi \}]}\right \} < \omega _1\cap N$
,
$\max \left \{{\omega _1\cap M : M \in {R_u}^{-1}[\{\xi \}]}\right \} < \omega _1\cap N$
,
-
-
• if
 $\xi \not \in N$
, by Proposition 3.11 and the fact that
$\xi \not \in N$
, by Proposition 3.11 and the fact that
 $u\in N$
,
$u\in N$
,
 ${R_u}^{-1}[\{\xi \}] = \emptyset $
.
${R_u}^{-1}[\{\xi \}] = \emptyset $
.
Hence, as the construction of
![]() $q^{\prime }_{\xi _m}$
in the proof of
$q^{\prime }_{\xi _m}$
in the proof of
![]() $\mathsf {(p)}_\alpha $
before, we can find a common extension t of s, u, and
$\mathsf {(p)}_\alpha $
before, we can find a common extension t of s, u, and
![]() $q"$
. But then t forces a contradiction.
$q"$
. But then t forces a contradiction.
We claim that
This contradicts the induction hypothesis
![]() $\mathsf {(C)}_\beta $
, and finishes the proof of this case.
$\mathsf {(C)}_\beta $
, and finishes the proof of this case.
Assume not, then there exists
![]() $r\leq _{\mathbb {P}_\beta } q \restriction \beta $
such that
$r\leq _{\mathbb {P}_\beta } q \restriction \beta $
such that
By extending r if necessary, we may assume that there are
![]() $k\in \omega $
and
$k\in \omega $
and
![]() $\eta \in \omega _1\setminus \zeta $
such that
$\eta \in \omega _1\setminus \zeta $
such that
By the induction hypothesis
![]() $\mathsf {(p)}_\beta $
, r is
$\mathsf {(p)}_\beta $
, r is
![]() $(N,\mathbb {P}_\beta )$
-generic. So by extending r again if necessary, we may assume that
$(N,\mathbb {P}_\beta )$
-generic. So by extending r again if necessary, we may assume that
![]() $\eta \in \left ( \omega _1 \setminus \zeta \right ) \cap N$
. However then
$\eta \in \left ( \omega _1 \setminus \zeta \right ) \cap N$
. However then
which is a contradiction.
![]() $\dashv$
$\dashv$
Lemma 5.6. For any
![]() $\mathbb {P}_{\omega _2}$
-name
$\mathbb {P}_{\omega _2}$
-name
![]() $\dot r$
for a member of
$\dot r$
for a member of
![]() $2^\omega $
,
$2^\omega $
,
Proof.
![]() $\dot E_\xi $
is defined in Definition 4.3. By Proposition 5.1, we may assume that
$\dot E_\xi $
is defined in Definition 4.3. By Proposition 5.1, we may assume that
![]() $\dot r$
belongs to
$\dot r$
belongs to
![]() $H(\kappa )$
. Let
$H(\kappa )$
. Let
![]() $p\in \mathbb {P}_{\omega _2}$
. Take
$p\in \mathbb {P}_{\omega _2}$
. Take
![]() $\alpha \in \omega _2$
such that
$\alpha \in \omega _2$
such that
![]() $\Phi (\alpha ) = \left \{{ \dot r_\alpha }\right \} = \left \{{\dot r}\right \}$
, and
$\Phi (\alpha ) = \left \{{ \dot r_\alpha }\right \} = \left \{{\dot r}\right \}$
, and
![]() $\operatorname {ran}(R_p) \subseteq \alpha $
. Then
$\operatorname {ran}(R_p) \subseteq \alpha $
. Then
![]() $\operatorname {dom}(A_p) \subseteq \alpha $
.
$\operatorname {dom}(A_p) \subseteq \alpha $
.
Let
![]() $\theta $
be a large enough regular cardinal for the forcing notion
$\theta $
be a large enough regular cardinal for the forcing notion
![]() $\mathbb {P}_{\alpha +1}$
. Take any
$\mathbb {P}_{\alpha +1}$
. Take any
![]() $\varepsilon \in \omega _1$
, and take countable elementary submodels
$\varepsilon \in \omega _1$
, and take countable elementary submodels
![]() $N_0^*$
and
$N_0^*$
and
![]() $N^*_1$
of
$N^*_1$
of
![]() $H_\theta $
such that
$H_\theta $
such that
![]() $\left \{{\vec {\mathbb {R}}, \vec X, H_\kappa , \mathbb {P}_\alpha , p, \alpha , \varepsilon }\right \} \in N^*_0 \in N^*_1$
. Then both
$\left \{{\vec {\mathbb {R}}, \vec X, H_\kappa , \mathbb {P}_\alpha , p, \alpha , \varepsilon }\right \} \in N^*_0 \in N^*_1$
. Then both
![]() $N^*_0 \cap H_\kappa $
and
$N^*_0 \cap H_\kappa $
and
![]() $N^*_1 \cap H_\kappa $
are in
$N^*_1 \cap H_\kappa $
are in
![]() $\mathfrak {M}^P_\alpha \cap \mathfrak {M}^P_{\alpha + 1} $
. By Proposition 5.4, there exists an extension q of p in
$\mathfrak {M}^P_\alpha \cap \mathfrak {M}^P_{\alpha + 1} $
. By Proposition 5.4, there exists an extension q of p in
![]() $\mathbb {P}_{\alpha +1}$
such that
$\mathbb {P}_{\alpha +1}$
such that
![]() ${R_q}^{-1}[\{\alpha \}] = \left \{{ N_0^* \cap H_\kappa }\right \}$
and
${R_q}^{-1}[\{\alpha \}] = \left \{{ N_0^* \cap H_\kappa }\right \}$
and
![]() $A_q(\alpha ) = \left \{{\left \langle {\varepsilon , \omega _1\cap N^*_0, \omega _1\cap N^*_1 }\right \rangle }\right \}$
. Then, by Lemma 5.2,
$A_q(\alpha ) = \left \{{\left \langle {\varepsilon , \omega _1\cap N^*_0, \omega _1\cap N^*_1 }\right \rangle }\right \}$
. Then, by Lemma 5.2,
![]() $\mathbb {P}_{\alpha +1}$
is proper and q is
$\mathbb {P}_{\alpha +1}$
is proper and q is
![]() $(N_0^*\cap H_\kappa , \mathbb {P}_{\alpha +1})$
-generic. So as seen in Observation 4.4,
$(N_0^*\cap H_\kappa , \mathbb {P}_{\alpha +1})$
-generic. So as seen in Observation 4.4,
⊣
Since
![]() $\mathbb {P}_{\omega _2}$
forces that
$\mathbb {P}_{\omega _2}$
forces that
![]() $2^{\aleph _0}=\aleph _2$
, we conclude the following.
$2^{\aleph _0}=\aleph _2$
, we conclude the following.
Theorem 5.7.
![]() $\mathbb {P}_{\omega _2}$
forces the assertion
(
c
)
.
$\mathbb {P}_{\omega _2}$
forces the assertion
(
c
)
.
6 Properness and the length of the iteration
For each
![]() $\xi \in \kappa $
, define the
$\xi \in \kappa $
, define the
![]() $\mathbb {P}_{\xi +1}$
-name
$\mathbb {P}_{\xi +1}$
-name
![]() $\dot S_\xi $
by
$\dot S_\xi $
by
Let
![]() $p\in \mathbb {P}_{\omega _2}$
and
$p\in \mathbb {P}_{\omega _2}$
and
![]() $\xi \in \operatorname {dom}(A_p)$
(then
$\xi \in \operatorname {dom}(A_p)$
(then
![]() $\xi \in \omega _2$
). If M belongs to
$\xi \in \omega _2$
). If M belongs to
![]() ${R_p}^{-1}[\{\xi \}]$
, that is,
${R_p}^{-1}[\{\xi \}]$
, that is,
![]() $\{ M \} \times \big ( (\xi + 1) \cap M \big ) \subseteq R_p$
, then
$\{ M \} \times \big ( (\xi + 1) \cap M \big ) \subseteq R_p$
, then
Moreover, if M also belongs to
![]() $\mathfrak {M}^P_{\xi +1}$
, then p is
$\mathfrak {M}^P_{\xi +1}$
, then p is
![]() $(M,\mathbb {P}_{\xi +1})$
-generic by Lemma 5.2, and therefore
$(M,\mathbb {P}_{\xi +1})$
-generic by Lemma 5.2, and therefore
We notice that
If
![]() $\Phi (\xi ) =\left \{{\dot r _\xi }\right \}$
and
$\Phi (\xi ) =\left \{{\dot r _\xi }\right \}$
and
![]() $\dot r_\xi $
is a
$\dot r_\xi $
is a
![]() $\mathbb {P}_\xi $
-name for a function from
$\mathbb {P}_\xi $
-name for a function from
![]() $\omega $
into
$\omega $
into
![]() $2$
, then
$2$
, then
 $$ \begin{align*} { \begin{array}{r@{}l} \Vdash_{\mathbb{P}_{\xi+1}}\ \text{"} & \text{ the set } \dot{S}_\xi \text{ is a stationary subset of }\omega_1, \text{ and captures }r \text{ relative to }X,\\ &\text{ that is, for any limit point }\delta \text{ of }\dot S_\xi \text{ (which means that } \delta \in \dot{S}_\xi \text{ and }\\ &\dot{S}_\xi \cap \delta \text{ is cofinal in }\delta), \text{ there exists }f\in X \text{ and }\varepsilon \in \delta \text{ such that, for any}\\ & \xi \in (\dot{S}_\xi \cap \delta) \setminus \varepsilon, f ( \left| C_{\delta } \cap \xi \right|) \subseteq r \text{"}. \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \Vdash_{\mathbb{P}_{\xi+1}}\ \text{"} & \text{ the set } \dot{S}_\xi \text{ is a stationary subset of }\omega_1, \text{ and captures }r \text{ relative to }X,\\ &\text{ that is, for any limit point }\delta \text{ of }\dot S_\xi \text{ (which means that } \delta \in \dot{S}_\xi \text{ and }\\ &\dot{S}_\xi \cap \delta \text{ is cofinal in }\delta), \text{ there exists }f\in X \text{ and }\varepsilon \in \delta \text{ such that, for any}\\ & \xi \in (\dot{S}_\xi \cap \delta) \setminus \varepsilon, f ( \left| C_{\delta } \cap \xi \right|) \subseteq r \text{"}. \end{array} }\end{align*} $$
Suppose that
![]() $p\in \mathbb {P}_{\omega _2}$
,
$p\in \mathbb {P}_{\omega _2}$
,
![]() $\xi , \zeta \in \operatorname {dom}(A_p)$
with
$\xi , \zeta \in \operatorname {dom}(A_p)$
with
![]() $\xi <\zeta $
, and
$\xi <\zeta $
, and
![]() $M\in {R_p}^{-1}[\{\zeta \}]$
(then p forces
$M\in {R_p}^{-1}[\{\zeta \}]$
(then p forces
![]() $\omega _1\cap M$
to be in
$\omega _1\cap M$
to be in
![]() $\dot S_\zeta $
). If
$\dot S_\zeta $
). If
![]() $\xi \in M$
, then
$\xi \in M$
, then
Therefore, by Proposition 3.10 and the requirements (ho) and (up) in the definition of
![]() $\mathbb {P}_\alpha $
,
$\mathbb {P}_\alpha $
,
Therefore,
![]() $\mathbb {P}_{\omega _2}$
forces that there are
$\mathbb {P}_{\omega _2}$
forces that there are
![]() $R\in \left [ 2^\omega \right ]^{\aleph _2}$
and a sequence
$R\in \left [ 2^\omega \right ]^{\aleph _2}$
and a sequence
![]() $\left \langle {S_\xi : \xi \in \omega _2}\right \rangle $
of stationary subsets of
$\left \langle {S_\xi : \xi \in \omega _2}\right \rangle $
of stationary subsets of
![]() $\omega _1$
such that
$\omega _1$
such that
-
• for each
 $r\in R$
, there exists
$r\in R$
, there exists
 $\xi \in \omega _2$
such that
$\xi \in \omega _2$
such that
 $S_\xi $
captures r relative to X.
$S_\xi $
captures r relative to X. -
• for each
 $\xi , \zeta \in \omega _2$
, if
$\xi , \zeta \in \omega _2$
, if
 $\xi < \zeta $
, then
$\xi < \zeta $
, then
 $S_\zeta \setminus S_\xi $
is bounded in
$S_\zeta \setminus S_\xi $
is bounded in
 $\omega _1$
.
$\omega _1$
.
As in the proof of Proposition 2.3, the set
![]() $\left \{{S_\xi : \xi \in \omega _2}\right \}$
cannot be diagonalized by any stationary subset of
$\left \{{S_\xi : \xi \in \omega _2}\right \}$
cannot be diagonalized by any stationary subset of
![]() $\omega _1$
without collapsing
$\omega _1$
without collapsing
![]() $\aleph _2$
. This observation leads to the following conclusion.
$\aleph _2$
. This observation leads to the following conclusion.
Lemma 6.1. If
![]() $\kappa>\omega _2$
, then
$\kappa>\omega _2$
, then
![]() $\mathsf {(p)}_{\omega _2+1}$
in Lemma 5.2 fails.
$\mathsf {(p)}_{\omega _2+1}$
in Lemma 5.2 fails.
This suggests that
![]() $\mathbb {P}_{\omega _2 +1}$
should not be proper.
$\mathbb {P}_{\omega _2 +1}$
should not be proper.
Proof. Suppose that
![]() $\mathsf {(p)}_{\omega _2+1}$
in Lemma 5.2 holds. Then, as we have already proved,
$\mathsf {(p)}_{\omega _2+1}$
in Lemma 5.2 holds. Then, as we have already proved,
![]() $\dot S_{\omega _2}$
is a
$\dot S_{\omega _2}$
is a
![]() $\mathbb {P}_{\omega _2+1}$
-name for a stationary subset of
$\mathbb {P}_{\omega _2+1}$
-name for a stationary subset of
![]() $\omega _1$
. For each
$\omega _1$
. For each
![]() $\eta \in \omega _2$
, the set of conditions p of
$\eta \in \omega _2$
, the set of conditions p of
![]() $\mathbb {P}_{\omega _2+1}$
such that there are
$\mathbb {P}_{\omega _2+1}$
such that there are
![]() $M\in \mathcal {N}_p$
and
$M\in \mathcal {N}_p$
and
![]() $\xi \in \omega _2\setminus \eta $
such that
$\xi \in \omega _2\setminus \eta $
such that
![]() $\{\xi , \omega _2\} \in M$
,
$\{\xi , \omega _2\} \in M$
,
![]() $\{M\}\times \big ( (\omega _2+1) \cap M\big ) \subseteq R_p$
, and
$\{M\}\times \big ( (\omega _2+1) \cap M\big ) \subseteq R_p$
, and
![]() $\left \{{\xi , \omega _2}\right \} \subseteq \operatorname {dom}(A_p)$
is dense in
$\left \{{\xi , \omega _2}\right \} \subseteq \operatorname {dom}(A_p)$
is dense in
![]() $\mathbb {P}_{\omega _2+1}$
. Therefore
$\mathbb {P}_{\omega _2+1}$
. Therefore
 $$ \begin{align*} { \begin{array}{r@{}l} \Vdash_{\mathbb{P}_{{\omega_2}+1}}\ \text{"} & \left\{{\xi : \exists p\in \dot G_{\mathbb{P}_{{\omega_2}+1}} \left( \xi \in \operatorname{dom}(A_p)\cap {\omega_2} \right)}\right\} \text{ is of size }\aleph_2, \\[10pt] & \dot S_{\omega_2} \text{ is a stationary subset of }\omega_1 \text{ and diagonalizes the set } \\[5pt] & \left\{{\dot S_\xi : \exists p\in \dot G_{\mathbb{P}_{{\omega_2}+1}} \left( \xi \in \operatorname{dom}(A_p)\cap {\omega_2} \right)}\right\} \text{"}. \end{array} }\end{align*} $$
$$ \begin{align*} { \begin{array}{r@{}l} \Vdash_{\mathbb{P}_{{\omega_2}+1}}\ \text{"} & \left\{{\xi : \exists p\in \dot G_{\mathbb{P}_{{\omega_2}+1}} \left( \xi \in \operatorname{dom}(A_p)\cap {\omega_2} \right)}\right\} \text{ is of size }\aleph_2, \\[10pt] & \dot S_{\omega_2} \text{ is a stationary subset of }\omega_1 \text{ and diagonalizes the set } \\[5pt] & \left\{{\dot S_\xi : \exists p\in \dot G_{\mathbb{P}_{{\omega_2}+1}} \left( \xi \in \operatorname{dom}(A_p)\cap {\omega_2} \right)}\right\} \text{"}. \end{array} }\end{align*} $$
However, this is a contradiction.⊣
Remark 6.2. There are reasons to suspect that
![]() $\mathbb {P}_\alpha $
, for
$\mathbb {P}_\alpha $
, for
![]() $\alpha> \omega _2$
, may fail to be proper, even disregarding the working parts of the forcing. Suppose that the length of the iteration is
$\alpha> \omega _2$
, may fail to be proper, even disregarding the working parts of the forcing. Suppose that the length of the iteration is
![]() $\omega _2+1$
,
$\omega _2+1$
,
![]() $q\in \mathbb {P}_{\omega _2+1}$
,
$q\in \mathbb {P}_{\omega _2+1}$
,
![]() $\{M,N\}\subseteq {R_q}^{-1}[\{\omega _2\}]$
,
$\{M,N\}\subseteq {R_q}^{-1}[\{\omega _2\}]$
,
![]() $r\in \mathbb {P}_{\omega _2+1}\cap N$
which is a nice copy of q inside N as in the proof of
$r\in \mathbb {P}_{\omega _2+1}\cap N$
which is a nice copy of q inside N as in the proof of
![]() $\mathsf {(p)}_\alpha $
for a limit ordinal
$\mathsf {(p)}_\alpha $
for a limit ordinal
![]() $\alpha $
,
$\alpha $
,
![]() $\left \{{M_0,M_1,M_2,M_3}\right \}\subseteq {R_r}^{-1}[\{\omega _2\}]\setminus M$
such that
$\left \{{M_0,M_1,M_2,M_3}\right \}\subseteq {R_r}^{-1}[\{\omega _2\}]\setminus M$
such that
![]() $M_2 \in M_0$
,
$M_2 \in M_0$
,
![]() $M_3\in M_1$
,
$M_3\in M_1$
,
![]() $M_0\cap \omega _1 =M_1\cap \omega _1$
,
$M_0\cap \omega _1 =M_1\cap \omega _1$
,
![]() $M_2\cap \omega _1 =M_3\cap \omega _1$
, and
$M_2\cap \omega _1 =M_3\cap \omega _1$
, and
![]() $M_i':=\left ({\Psi _M}^{-1}\circ \Psi _N\right )(M_i) \in \mathcal {N}_{q'}\setminus \left (\mathcal {N}_q\cup \mathcal {N}_r\right )$
for each
$M_i':=\left ({\Psi _M}^{-1}\circ \Psi _N\right )(M_i) \in \mathcal {N}_{q'}\setminus \left (\mathcal {N}_q\cup \mathcal {N}_r\right )$
for each
![]() $i\in \{0,1,2,3\}$
, as in the following figure.
$i\in \{0,1,2,3\}$
, as in the following figure.

Then
![]() $\left \{{M_0',M_1',M_2',M_3'}\right \}\subseteq {R_{q'}}^{-1}[\{\omega _2\}]$
, and
$\left \{{M_0',M_1',M_2',M_3'}\right \}\subseteq {R_{q'}}^{-1}[\{\omega _2\}]$
, and
![]() ${R_{q'}}^{-1}[\{\omega _2\}]$
forms a symmetric system. Let
${R_{q'}}^{-1}[\{\omega _2\}]$
forms a symmetric system. Let
![]() $\zeta \in \alpha $
. It should be satisfied that
$\zeta \in \alpha $
. It should be satisfied that
![]() ${R_{q'}}^{-1}[\{\zeta \}] \subseteq \mathfrak {M}^P_\zeta $
and
${R_{q'}}^{-1}[\{\zeta \}] \subseteq \mathfrak {M}^P_\zeta $
and
![]() ${R_{q'}}^{-1}[\{\zeta \}]$
forms a symmetric system. Now we have no guarantees that the assertion
${R_{q'}}^{-1}[\{\zeta \}]$
forms a symmetric system. Now we have no guarantees that the assertion
![]() ${R_{q'}}^{-1}[\{\zeta \}] \subseteq \mathfrak {M}^P_\zeta $
is true. And even if this is true, since Proposition 3.11 may fail for
${R_{q'}}^{-1}[\{\zeta \}] \subseteq \mathfrak {M}^P_\zeta $
is true. And even if this is true, since Proposition 3.11 may fail for
![]() $\alpha =\omega _2$
,
$\alpha =\omega _2$
,
![]() ${R_{q'}}^{-1}[\{\zeta \}] $
may fail to form a symmetric system. For example, it may happen that
${R_{q'}}^{-1}[\{\zeta \}] $
may fail to form a symmetric system. For example, it may happen that
![]() $\zeta \in M_1'$
,
$\zeta \in M_1'$
,
![]() $\zeta \in M_2'$
(hence
$\zeta \in M_2'$
(hence
![]() $\zeta \in M_0'$
), and
$\zeta \in M_0'$
), and
![]() $\zeta \not \in M_3'$
. Then
$\zeta \not \in M_3'$
. Then
![]() $ {R_{q'}}^{-1}[\{\zeta \}]$
does not satisfy (down). Therefore, in this case, q and r may fail to be compatible in
$ {R_{q'}}^{-1}[\{\zeta \}]$
does not satisfy (down). Therefore, in this case, q and r may fail to be compatible in
![]() $\mathbb {P}_{\omega _2+1}$
.
$\mathbb {P}_{\omega _2+1}$
.
7 Acknowledgments
In the workshop “Set theory of the Reals” at Casa Matemática Oaxaca, I asked Justin Tatch Moore about assertions which imply that the size of the continuum is
![]() $\aleph _2$
. The aim of my question was to find some types of Asperó–Mota iterations whose length is greater than
$\aleph _2$
. The aim of my question was to find some types of Asperó–Mota iterations whose length is greater than
![]() $\omega _2$
and not proper. He gave me the idea presented in Section 2.1. He encouraged me to complete this paper and assisted me on the draft of the introduction. I am very thankful to him.
$\omega _2$
and not proper. He gave me the idea presented in Section 2.1. He encouraged me to complete this paper and assisted me on the draft of the introduction. I am very thankful to him.
I would also like to thank Diego A. Mejía and Tadatoshi Miyamoto for many useful comments on an earlier draft of the paper. To conclude, I am grateful to the referee for many worthwhile comments.