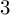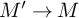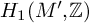1 Introduction
In [Reference Sun20], Sun showed that any closed hyperbolic
![]() $3$
-manifold virtually contains any prescribed finite subgroup in homological torsion. Sun used the immersed almost-Fuchsian surfaces of Kahn and Markovic [Reference Kahn and Markovic14] to construct immersed
$3$
-manifold virtually contains any prescribed finite subgroup in homological torsion. Sun used the immersed almost-Fuchsian surfaces of Kahn and Markovic [Reference Kahn and Markovic14] to construct immersed
![]() $\pi _1$
-injective
$\pi _1$
-injective
![]() $2$
-complexes. By using Agol’s result that the fundamental groups of closed hyperbolic
$2$
-complexes. By using Agol’s result that the fundamental groups of closed hyperbolic
![]() $3$
-manifolds are virtually compact special [Reference Agol2] and the implications on virtual retractions to quasi-convex subgroups, Sun finds for any closed hyperbolic
$3$
-manifolds are virtually compact special [Reference Agol2] and the implications on virtual retractions to quasi-convex subgroups, Sun finds for any closed hyperbolic
![]() $3$
-manifold a finite cover containing the prescribed finite abelian group as a direct factor in homology [Reference Sun20, Theorem 1.5].
$3$
-manifold a finite cover containing the prescribed finite abelian group as a direct factor in homology [Reference Sun20, Theorem 1.5].
Since the Kahn–Markovic construction requires that the manifolds be closed, Sun’s results do not apply to hyperbolic
![]() $3$
-manifolds with cusps. Indeed, Sun asked whether his result applied also to finite-volume hyperbolic 3-manifolds with cusps. In this paper, we extend the results of Sun to a larger class of
$3$
-manifolds with cusps. Indeed, Sun asked whether his result applied also to finite-volume hyperbolic 3-manifolds with cusps. In this paper, we extend the results of Sun to a larger class of
![]() $3$
-manifolds which includes all finite-volume hyperbolic
$3$
-manifolds which includes all finite-volume hyperbolic
![]() $3$
-manifolds, giving a positive answer to [Reference Sun20, Question 1.8].
$3$
-manifolds, giving a positive answer to [Reference Sun20, Question 1.8].
Theorem 1.1. Suppose that M is an irreducible
![]() $3$
-manifold with empty or toroidal boundary which has at least one hyperbolic piece in its geometric decomposition and that A is a finite abelian group. There is a finite cover
$3$
-manifold with empty or toroidal boundary which has at least one hyperbolic piece in its geometric decomposition and that A is a finite abelian group. There is a finite cover
![]() $N \to M$
so that
$N \to M$
so that
![]() $H_1(N;\mathbb {Z})$
has a direct factor isomorphic to A.
$H_1(N;\mathbb {Z})$
has a direct factor isomorphic to A.
Prior to Theorem 1.1, Friedl and Herrmann used [Reference Sun20] and a result of Hadari [Reference Hadari10] to show that for any such M and any
![]() $k>0$
there is finite cover
$k>0$
there is finite cover
![]() $N \to M$
with
$N \to M$
with
![]() $\left |{\mathrm {Tor}} H_1(N;\mathbb {Z})\right |>k$
[Reference Friedl and Herrmann7, Theorem 1.3]. Independently, Liu showed that any such M admits a finite cover
$\left |{\mathrm {Tor}} H_1(N;\mathbb {Z})\right |>k$
[Reference Friedl and Herrmann7, Theorem 1.3]. Independently, Liu showed that any such M admits a finite cover
![]() $N' \to M$
with
$N' \to M$
with
![]() $\left |{\mathrm {Tor}} H_1(N';\mathbb {Z})\right |\neq 0$
[Reference Liu16, Corollary 1.4].
$\left |{\mathrm {Tor}} H_1(N';\mathbb {Z})\right |\neq 0$
[Reference Liu16, Corollary 1.4].
The key case in the proof of Theorem 1.1 is the case of finite-volume hyperbolic
![]() $3$
-manifolds. We follow the strategy of [Reference Sun20] but give an independent proof which simplifies and generalizes Sun’s results. We replace Sun’s use of the results of Kahn and Markovic [Reference Kahn and Markovic14] with those of Kahn and Wright [Reference Kahn and Wright15] and replace some arguments of Sun with an elementary argument using coverings of surfaces. We then apply virtual retraction properties of relatively quasi-convex subgroups in relatively hyperbolic groups to deduce both the case where M is finite-volume hyperbolic and also to reduce the general case to this one. Cooper and Futer [Reference Cooper and Futer6] independently obtained similar results to those of [Reference Kahn and Wright15] on constructing many closed immersed
$3$
-manifolds. We follow the strategy of [Reference Sun20] but give an independent proof which simplifies and generalizes Sun’s results. We replace Sun’s use of the results of Kahn and Markovic [Reference Kahn and Markovic14] with those of Kahn and Wright [Reference Kahn and Wright15] and replace some arguments of Sun with an elementary argument using coverings of surfaces. We then apply virtual retraction properties of relatively quasi-convex subgroups in relatively hyperbolic groups to deduce both the case where M is finite-volume hyperbolic and also to reduce the general case to this one. Cooper and Futer [Reference Cooper and Futer6] independently obtained similar results to those of [Reference Kahn and Wright15] on constructing many closed immersed
![]() $\pi _1$
-injective quasi-Fuchsian surfaces in finite-volume hyperbolic
$\pi _1$
-injective quasi-Fuchsian surfaces in finite-volume hyperbolic
![]() $3$
-manifolds with cusps. However, our arguments rely on the additional control on the quasi-conformal constants and the holonomies in the Kahn–Wright constructions.
$3$
-manifolds with cusps. However, our arguments rely on the additional control on the quasi-conformal constants and the holonomies in the Kahn–Wright constructions.
A hybrid hyperbolic manifold is constructed either by inbreeding (c.f. [Reference Agol1, Reference Belolipetsky and Thomson4]) or interbreeding (c.f. [Reference Gromov and Piatetski-Shapiro8]) arithmetic hyperbolic manifolds. For
![]() $n>3$
every arithmetic hyperbolic n-manifold N of simplest type contains a totally geodesic arithmetic hyperbolic
$n>3$
every arithmetic hyperbolic n-manifold N of simplest type contains a totally geodesic arithmetic hyperbolic
![]() $3$
-manifold M (coming from restrictions of the associated quadratic form). By [Reference Bergeron, Haglund and Wise3, §9], we get the following corollary (some of these cases follow from [Reference Sun20]).
$3$
-manifold M (coming from restrictions of the associated quadratic form). By [Reference Bergeron, Haglund and Wise3, §9], we get the following corollary (some of these cases follow from [Reference Sun20]).
Corollary 1.2. Suppose that
![]() $n>3$
and N is a finite-volume hyperbolic n-manifold which is either arithmetic of simplest type or a hybrid. Then if A is a finite abelian group, there is a finite cover
$n>3$
and N is a finite-volume hyperbolic n-manifold which is either arithmetic of simplest type or a hybrid. Then if A is a finite abelian group, there is a finite cover
![]() $N_1\to N$
so that
$N_1\to N$
so that
![]() $H_1(N_1;\mathbb {Z})$
has a direct factor isomorphic to A.
$H_1(N_1;\mathbb {Z})$
has a direct factor isomorphic to A.
2 Quasi-isometric embeddings
Our first goal is to prove Theorem 1.1 in the case of a noncompact finite-volume hyperbolic
![]() $3$
-manifold. In Section 6, we deduce the general case from this case. In this section, we record some elementary facts about quasi-isometries and hyperbolic spaces.
$3$
-manifold. In Section 6, we deduce the general case from this case. In this section, we record some elementary facts about quasi-isometries and hyperbolic spaces.
Definition 2.1. Let
![]() $k, \lambda , \kappa $
be constants, and let
$k, \lambda , \kappa $
be constants, and let
![]() $X,Y$
be metric spaces. A map
$X,Y$
be metric spaces. A map
![]() $f \colon \thinspace X \to Y$
is a k–local
$f \colon \thinspace X \to Y$
is a k–local
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding if for all
$(\lambda ,\kappa )$
-quasi-isometric embedding if for all
![]() $x \in X$
the map
$x \in X$
the map
is a
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding.
$(\lambda ,\kappa )$
-quasi-isometric embedding.
The following is essentially [Reference Kahn and Wright15, Theorem A.20].
Proposition 2.2. For all
![]() $\delta $
, for all
$\delta $
, for all
![]() $\kappa \ge 0$
and all
$\kappa \ge 0$
and all
![]() $\lambda \ge 1$
, there exist
$\lambda \ge 1$
, there exist
![]() $k,\lambda ',\kappa '$
so that if Y is a
$k,\lambda ',\kappa '$
so that if Y is a
![]() $\delta $
–hyperbolic metric space and X is a geodesic metric space, then any k-local
$\delta $
–hyperbolic metric space and X is a geodesic metric space, then any k-local
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding
$(\lambda ,\kappa )$
-quasi-isometric embedding
![]() $f \colon \thinspace X \to Y$
is a
$f \colon \thinspace X \to Y$
is a
![]() $(\lambda ',\kappa ')$
-quasi-isometric embedding.
$(\lambda ',\kappa ')$
-quasi-isometric embedding.
Proof. Since X and Y are geodesic metric spaces, distances in X and Y are calculated by geodesics. Therefore, we can apply the standard local-to-global result for quasi-geodesics (see, for example, [Reference Coornaert, Delzant and Papadopoulos5, Theorem 3.1.4, p.25]).
2.1 Half-planes
Let
![]() $\theta \in (0,\pi ]$
. The space
$\theta \in (0,\pi ]$
. The space
![]() $P_\theta $
is the subspace of
$P_\theta $
is the subspace of
![]() ${\mathbb H} ^3$
obtained from gluing two totally geodesic half-planes together along their boundary geodesic, meeting at angle
${\mathbb H} ^3$
obtained from gluing two totally geodesic half-planes together along their boundary geodesic, meeting at angle
![]() $\theta $
. There is a natural embedding
$\theta $
. There is a natural embedding
![]() $p_\theta \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
given by mapping the positive y-axis to the boundary geodesic of the two half-planes (we consider
$p_\theta \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
given by mapping the positive y-axis to the boundary geodesic of the two half-planes (we consider
![]() ${\mathbb H} ^2$
in the upper half-space model as a subset of
${\mathbb H} ^2$
in the upper half-space model as a subset of
![]() ${\mathbb R}^2$
). The image of these boundary geodesics is the pleating locus for
${\mathbb R}^2$
). The image of these boundary geodesics is the pleating locus for
![]() $p_\theta $
.
$p_\theta $
.
Lemma 2.3. Given
![]() $\theta \in (0,\pi ]$
, there exists
$\theta \in (0,\pi ]$
, there exists
![]() $\kappa _\theta \ge 0$
so that for all
$\kappa _\theta \ge 0$
so that for all
![]() $\theta _0 \in [\theta ,\pi ]$
the map
$\theta _0 \in [\theta ,\pi ]$
the map
![]() $p_{\theta _0}$
is a
$p_{\theta _0}$
is a
![]() $(1,\kappa _\theta )$
-quasi-isometric embedding.
$(1,\kappa _\theta )$
-quasi-isometric embedding.
Proof. We show that it suffices to take
 $$ \begin{align*}\kappa_\theta = 2 \cdot \operatorname{\mathrm{arccosh}} \left( \frac{1}{\sin\left(\frac{\theta}{2}\right)} \right). \end{align*} $$
$$ \begin{align*}\kappa_\theta = 2 \cdot \operatorname{\mathrm{arccosh}} \left( \frac{1}{\sin\left(\frac{\theta}{2}\right)} \right). \end{align*} $$
Indeed, suppose that
![]() $a,b \in {\mathbb H} ^2$
, let
$a,b \in {\mathbb H} ^2$
, let
![]() $\overline {a} = p_\theta (a)$
and
$\overline {a} = p_\theta (a)$
and
![]() $\overline {b} = p_\theta (b)$
and consider the image of the geodesic segment
$\overline {b} = p_\theta (b)$
and consider the image of the geodesic segment
![]() $[a,b]$
in
$[a,b]$
in
![]() $p_\theta ({\mathbb H} ^2)$
. If the sign of the x-coordinates of a and b are the same, then
$p_\theta ({\mathbb H} ^2)$
. If the sign of the x-coordinates of a and b are the same, then
![]() $[a,b]$
maps to a geodesic segment in
$[a,b]$
maps to a geodesic segment in
![]() ${\mathbb H} ^3$
and
${\mathbb H} ^3$
and
![]() $d_{{\mathbb H} ^3}(\overline {a},\overline {b}) = d_{{\mathbb H} ^2}(a,b)$
in this case.
$d_{{\mathbb H} ^3}(\overline {a},\overline {b}) = d_{{\mathbb H} ^2}(a,b)$
in this case.
Suppose then that the signs of the x-coordinates of a and b are different, and let
![]() $c \in [a,b]$
have x-coordinate
$c \in [a,b]$
have x-coordinate
![]() $0$
. Let
$0$
. Let
![]() $\overline {c} = p_\theta (c)$
. Then
$\overline {c} = p_\theta (c)$
. Then
![]() $p_\theta ([a,b])$
consists of two geodesic segments
$p_\theta ([a,b])$
consists of two geodesic segments
![]() $[\overline {a},\overline {c}]$
and
$[\overline {a},\overline {c}]$
and
![]() $[\overline {c},\overline {b}]$
meeting at some angle
$[\overline {c},\overline {b}]$
meeting at some angle
![]() $\eta \ge \theta $
.
$\eta \ge \theta $
.
Consider the geodesic triangle
![]() $\Delta $
in
$\Delta $
in
![]() ${\mathbb H} ^3$
with vertices
${\mathbb H} ^3$
with vertices
![]() $\overline {a},\overline {b},\overline {c}$
, and let e be the distance from
$\overline {a},\overline {b},\overline {c}$
, and let e be the distance from
![]() $\overline {c}$
to the geodesic
$\overline {c}$
to the geodesic
![]() $[\overline {a},\overline {b}]$
. The shortest geodesic from
$[\overline {a},\overline {b}]$
. The shortest geodesic from
![]() $\overline {c}$
to
$\overline {c}$
to
![]() $[\overline {a},\overline {b}]$
cuts
$[\overline {a},\overline {b}]$
cuts
![]() $\Delta $
into two right-angled hyperbolic triangles, one of which has angle at
$\Delta $
into two right-angled hyperbolic triangles, one of which has angle at
![]() $\overline {c}$
at least
$\overline {c}$
at least
![]() $\frac {\theta }{2}$
. We thus have a hyperbolic triangle with side lengths
$\frac {\theta }{2}$
. We thus have a hyperbolic triangle with side lengths
![]() $e_1,e_2,e_3$
, say, where the angle opposite
$e_1,e_2,e_3$
, say, where the angle opposite
![]() $e_3$
is
$e_3$
is
![]() $\frac {\pi }{2}$
, and the angle opposite
$\frac {\pi }{2}$
, and the angle opposite
![]() $e_2$
is at
$e_2$
is at
![]() $\overline {c}$
and is
$\overline {c}$
and is
![]() $E_2 \ge \frac {\theta }{2}$
. Let
$E_2 \ge \frac {\theta }{2}$
. Let
![]() $E_1$
be the angle opposite the side of length
$E_1$
be the angle opposite the side of length
![]() $e_1$
.
$e_1$
.

Figure 1 The proof of Lemma 2.3
The second hyperbolic law of cosines says
so
 $$\begin{align*}\cosh(e_1) = \frac{\cos(E_1)}{\sin(E_2)} \le \frac{1}{\sin\left( \frac{\theta}{2}\right)}. \end{align*}$$
$$\begin{align*}\cosh(e_1) = \frac{\cos(E_1)}{\sin(E_2)} \le \frac{1}{\sin\left( \frac{\theta}{2}\right)}. \end{align*}$$
Let
![]() $d_1 = d_{{\mathbb H} ^3}(\overline {a},\overline {c})$
and
$d_1 = d_{{\mathbb H} ^3}(\overline {a},\overline {c})$
and
![]() $d_2 = d_{{\mathbb H} ^3}(\overline {c},\overline {b})$
. Observe that
$d_2 = d_{{\mathbb H} ^3}(\overline {c},\overline {b})$
. Observe that
![]() $d_{{\mathbb H} ^2}(a,b) = d_1 + d_2$
. It is clear that
$d_{{\mathbb H} ^2}(a,b) = d_1 + d_2$
. It is clear that
 $$\begin{align*}d_1+d_2 -2 \operatorname{\mathrm{arccosh}} \left( \frac{1}{\sin\left( \frac{\theta}{2}\right)}\right) \le d_{{\mathbb H} ^3}(\overline{a},\overline{b}) \le d_1 + d_2 , \end{align*}$$
$$\begin{align*}d_1+d_2 -2 \operatorname{\mathrm{arccosh}} \left( \frac{1}{\sin\left( \frac{\theta}{2}\right)}\right) \le d_{{\mathbb H} ^3}(\overline{a},\overline{b}) \le d_1 + d_2 , \end{align*}$$
and the result follows.
3 Kahn–Wright surfaces
From this section until the end of Section 5, let N be a (noncompact) finite-volume hyperbolic
![]() $3$
-manifold. We remark that our proof of Theorem 1.1 works in the compact hyperbolic setting also without changes and is simpler in some ways than Sun’s in this case.
$3$
-manifold. We remark that our proof of Theorem 1.1 works in the compact hyperbolic setting also without changes and is simpler in some ways than Sun’s in this case.
The set of closed geodesics in
![]() $N={\mathbb H} ^3/\Gamma $
is in 1-to-1 correspondence with the set of conjugacy classes of loxodromic elements in
$N={\mathbb H} ^3/\Gamma $
is in 1-to-1 correspondence with the set of conjugacy classes of loxodromic elements in
![]() $\Gamma $
. For a closed geodesic
$\Gamma $
. For a closed geodesic
![]() $\alpha $
in N (with corresponding conjugacy class
$\alpha $
in N (with corresponding conjugacy class
![]() $[\gamma ]\subset \Gamma $
), let
$[\gamma ]\subset \Gamma $
), let
![]() $\ell (\alpha )$
denote the length of
$\ell (\alpha )$
denote the length of
![]() $\alpha $
(the translation length of
$\alpha $
(the translation length of
![]() $\gamma $
) and
$\gamma $
) and
![]() $\theta (\alpha )$
the holonomy class of
$\theta (\alpha )$
the holonomy class of
![]() $\alpha $
(the rotation angle of
$\alpha $
(the rotation angle of
![]() $\gamma $
around its axis).
$\gamma $
around its axis).
3.1 Pre-good curves
Later in the section, we give a brief discussion of the construction of surfaces due to Kahn and Wright in [Reference Kahn and Wright15]. However, we first give a lemma which proves the existence of certain well-behaved geodesics whose
![]() $n^{\mathrm {th}}$
powers will become part of the Kahn–Wright surface. In the next section, we take a cover of the Kahn–Wright surface, cut along a lift of this
$n^{\mathrm {th}}$
powers will become part of the Kahn–Wright surface. In the next section, we take a cover of the Kahn–Wright surface, cut along a lift of this
![]() $n^{\mathrm {th}}$
power, and then quotient by the
$n^{\mathrm {th}}$
power, and then quotient by the
![]() $n^{\mathrm {th}}$
root of the two resulting boundary curves, to form a complex
$n^{\mathrm {th}}$
root of the two resulting boundary curves, to form a complex
![]() $X_n$
. This construction is similar to Sun’s in [Reference Sun20] and forms the basis of the proof of Theorem 1.1 in the finite-volume hyperbolic case. The following is an analogue in the finite-volume case of Sun’s [Reference Sun20, Lemma 2.9]. In order to use this geodesic in Kahn and Wright’s construction, it is important to control its height, a measure of how far it goes into a cusp neighborhood. See [Reference Kahn and Wright15,
$X_n$
. This construction is similar to Sun’s in [Reference Sun20] and forms the basis of the proof of Theorem 1.1 in the finite-volume hyperbolic case. The following is an analogue in the finite-volume case of Sun’s [Reference Sun20, Lemma 2.9]. In order to use this geodesic in Kahn and Wright’s construction, it is important to control its height, a measure of how far it goes into a cusp neighborhood. See [Reference Kahn and Wright15,
![]() $\S 3$
] for the definition of height in the following statement.
$\S 3$
] for the definition of height in the following statement.
Lemma 3.1. For
![]() $n\in {\mathbb N}, \epsilon>0$
,
$n\in {\mathbb N}, \epsilon>0$
,
![]() $\mu>\frac {1}{2}$
, there exists
$\mu>\frac {1}{2}$
, there exists
![]() $R_0$
so that for all
$R_0$
so that for all
![]() $R> R_0$
there exists a geodesic
$R> R_0$
there exists a geodesic
![]() $\alpha _0$
in N of height at most
$\alpha _0$
in N of height at most
![]() $\mu \log R$
such that
$\mu \log R$
such that
![]() $\left | \ell (\alpha _0)-\frac {2R}{n} \right |<\frac {\epsilon }{n}$
and
$\left | \ell (\alpha _0)-\frac {2R}{n} \right |<\frac {\epsilon }{n}$
and
![]() $\left | \theta (\alpha _0)-\frac {2\pi }{n} \right |<\frac {\epsilon }{n}$
.
$\left | \theta (\alpha _0)-\frac {2\pi }{n} \right |<\frac {\epsilon }{n}$
.
Proof. For a closed subset
![]() $\Omega $
of
$\Omega $
of
![]() ${\mathrm {SO}}(2)$
and
${\mathrm {SO}}(2)$
and
![]() $T> 0$
, let
$T> 0$
, let
As noted in [Reference Kahn and Wright15, §3.1], an application of the Margulis argument shows that
which in this case follows, for example, from [Reference Margulis, Mohammadi and Oh18, Theorem 1.1] by setting
![]() $\varphi :=1_{\Omega }$
the indicator function on
$\varphi :=1_{\Omega }$
the indicator function on
![]() ${\mathrm {SO}}(2)$
(see also [Reference Gangolli and Warner9]).
${\mathrm {SO}}(2)$
(see also [Reference Gangolli and Warner9]).
Considering geodesics
![]() $\alpha \in {\mathcal G}(2R/n+\epsilon /n,\Omega )\setminus {\mathcal G}(2R/n-\epsilon /n,\Omega )$
, where
$\alpha \in {\mathcal G}(2R/n+\epsilon /n,\Omega )\setminus {\mathcal G}(2R/n-\epsilon /n,\Omega )$
, where
![]() $\Omega $
is the interval
$\Omega $
is the interval
![]() $(\frac {2\pi }{n}-\frac {\epsilon }{n},\frac {2\pi }{n}+\frac {\epsilon }{n})$
, we have
$(\frac {2\pi }{n}-\frac {\epsilon }{n},\frac {2\pi }{n}+\frac {\epsilon }{n})$
, we have
 $$ \begin{align} \#\left\{ \alpha : \left| \ell(\alpha_0)-\frac{2R}{n} \right|<\frac{\epsilon}{n} \text{ and } \left| \theta(\alpha_0)-\frac{2\pi}{n} \right|<\frac{\epsilon}{n} \right\} \sim \mu_\epsilon\frac{e^{4R/n}}{4R}. \end{align} $$
$$ \begin{align} \#\left\{ \alpha : \left| \ell(\alpha_0)-\frac{2R}{n} \right|<\frac{\epsilon}{n} \text{ and } \left| \theta(\alpha_0)-\frac{2\pi}{n} \right|<\frac{\epsilon}{n} \right\} \sim \mu_\epsilon\frac{e^{4R/n}}{4R}. \end{align} $$
The arguments in the proof of [Reference Kahn and Wright15, Lemma 3.1] apply to show that, as R grows, the proportion of those
![]() $\alpha $
with height larger than
$\alpha $
with height larger than
![]() $\mu \log R$
shrinks since
$\mu \log R$
shrinks since
![]() $\mu> \frac {1}{2}$
. In particular, for sufficiently large R, one can find
$\mu> \frac {1}{2}$
. In particular, for sufficiently large R, one can find
![]() $\alpha _0$
as needed.
$\alpha _0$
as needed.
Note that
![]() $\alpha _0$
may be chosen to be primitive. In the language of Kahn and Wright,
$\alpha _0$
may be chosen to be primitive. In the language of Kahn and Wright,
![]() $\alpha _0^n$
is an
$\alpha _0^n$
is an
![]() $(R,\epsilon )$
-good curve.
$(R,\epsilon )$
-good curve.
Definition 3.2. Fix
![]() $n \in {\mathbb N}$
and also
$n \in {\mathbb N}$
and also
![]() $R, \epsilon $
. An
$R, \epsilon $
. An
![]() $(R,\epsilon ,n)$
-pre-good curve in N is a geodesic
$(R,\epsilon ,n)$
-pre-good curve in N is a geodesic
![]() $\alpha _0$
satisfying the conclusion of Lemma 3.1 for
$\alpha _0$
satisfying the conclusion of Lemma 3.1 for
![]() $\mu = 1$
.
$\mu = 1$
.
We remark that Kahn and Wright allow curves to have height at most
![]() $50\log (R)$
before needing to be ‘cut-off’, so certainly curves of height at most
$50\log (R)$
before needing to be ‘cut-off’, so certainly curves of height at most
![]() $\log R$
are fine. Lemma 3.1 asserts that, for fixed n and
$\log R$
are fine. Lemma 3.1 asserts that, for fixed n and
![]() $\epsilon $
, for large enough R, there exists an
$\epsilon $
, for large enough R, there exists an
![]() $(R,\epsilon ,n)$
-pre-good curve (in fact there are many).
$(R,\epsilon ,n)$
-pre-good curve (in fact there are many).
3.2 The construction of Kahn and Wright
In [Reference Kahn and Wright15], Kahn and Wright build certain quasi-Fuchsian immersed surfaces in N out of pieces called good pants and good hamster wheels. Each good pant and good hamster wheel is immersed in N and has geodesic boundary components, which are referred to as cuffs.
The construction in [Reference Kahn and Wright15] depends on choices of parameters R (sufficiently large) and
![]() $\epsilon> 0$
(sufficiently small). A pant is a sphere with three holes, and a hamster wheel is a sphere with
$\epsilon> 0$
(sufficiently small). A pant is a sphere with three holes, and a hamster wheel is a sphere with
![]() $R+2$
holes,
$R+2$
holes,
![]() $2$
of which are special. Pants and hamster wheels are good if all cuffs have complex length within
$2$
of which are special. Pants and hamster wheels are good if all cuffs have complex length within
![]() $\epsilon $
of
$\epsilon $
of
![]() $2R$
and perfect if they are exactly
$2R$
and perfect if they are exactly
![]() $2R$
.
$2R$
.
We postpone for now the choice of the parameters R and
![]() $\epsilon $
in order to discuss the construction. Kahn and Wright also specify another pair of parameters called ‘cutoff heights’, and the purpose of Lemma 3.1 above is to ensure that we can find an
$\epsilon $
in order to discuss the construction. Kahn and Wright also specify another pair of parameters called ‘cutoff heights’, and the purpose of Lemma 3.1 above is to ensure that we can find an
![]() $\alpha _0$
whose height stays below the cutoff heights and whose
$\alpha _0$
whose height stays below the cutoff heights and whose
![]() $n^{\mathrm {th}}$
power is a good curve.
$n^{\mathrm {th}}$
power is a good curve.
Suppose that we find a curve
![]() $\alpha _0$
as in Lemma 3.1 so that
$\alpha _0$
as in Lemma 3.1 so that
![]() $\alpha = \alpha _0^n$
is an
$\alpha = \alpha _0^n$
is an
![]() $(R,\epsilon )$
-good curve and so that the height of
$(R,\epsilon )$
-good curve and so that the height of
![]() $\alpha _0$
(and hence
$\alpha _0$
(and hence
![]() $\alpha $
) is at most
$\alpha $
) is at most
![]() $\log R$
. Then Kahn and Wright build a surface S out of good pants and good hamster wheels, and
$\log R$
. Then Kahn and Wright build a surface S out of good pants and good hamster wheels, and
![]() $\alpha $
appears as a cuff on at least one (in fact many) of these pieces.
$\alpha $
appears as a cuff on at least one (in fact many) of these pieces.
Let
![]() $H_R = \{ (x,y) \in {\mathbb H} ^2 \mid x \ge 0\}$
and
$H_R = \{ (x,y) \in {\mathbb H} ^2 \mid x \ge 0\}$
and
![]() $H_L = \{ (x,y) \in {\mathbb H} ^2 \mid x \le 0 \}$
, and let
$H_L = \{ (x,y) \in {\mathbb H} ^2 \mid x \le 0 \}$
, and let
![]() $m= \{ (x,y) \in {\mathbb H} ^2 \mid x = 0 \} = H_R \cap H_L$
.
$m= \{ (x,y) \in {\mathbb H} ^2 \mid x = 0 \} = H_R \cap H_L$
.
Consider
![]() $\alpha _0 \colon \thinspace {\mathbb S}^1 \to N$
as a map from the circle to N parametrized proportional to arc length, and let
$\alpha _0 \colon \thinspace {\mathbb S}^1 \to N$
as a map from the circle to N parametrized proportional to arc length, and let
![]() $u = \alpha _0(1)$
. Let
$u = \alpha _0(1)$
. Let
![]() $\phi _n \colon \thinspace {\mathbb S}^1 \to {\mathbb S}^1$
be the connected n-fold covering map, and let
$\phi _n \colon \thinspace {\mathbb S}^1 \to {\mathbb S}^1$
be the connected n-fold covering map, and let
![]() $\alpha \colon \thinspace {\mathbb S}^1 \to N$
be the composition
$\alpha \colon \thinspace {\mathbb S}^1 \to N$
be the composition
![]() $\alpha _0 \circ \phi _n$
. Suppose
$\alpha _0 \circ \phi _n$
. Suppose
![]() $f \colon \thinspace S_0 \looparrowright N$
is a Kahn–Wright surface and that there is a map
$f \colon \thinspace S_0 \looparrowright N$
is a Kahn–Wright surface and that there is a map
![]() $C \colon \thinspace {\mathbb S}^1 \to S_0$
so
$C \colon \thinspace {\mathbb S}^1 \to S_0$
so
![]() $\alpha = f \circ C$
. Let
$\alpha = f \circ C$
. Let
![]() $\phi _n^{-1}(u) = \{ u_1, \ldots , u_n \}$
, and note that there are n different points
$\phi _n^{-1}(u) = \{ u_1, \ldots , u_n \}$
, and note that there are n different points
![]() $\{ a_1, \ldots , a_n \}$
on
$\{ a_1, \ldots , a_n \}$
on
![]() $S_0$
, so
$S_0$
, so
![]() $f(a_i) = \alpha (u_i)$
for each i.
$f(a_i) = \alpha (u_i)$
for each i.
Choose a basepoint
![]() $b \in {\mathbb H} ^3$
, and let
$b \in {\mathbb H} ^3$
, and let
![]() $\pi \colon \thinspace ({\mathbb H} ^3,b) \to (N,u)$
be the based universal covering map. Fix a basepoint
$\pi \colon \thinspace ({\mathbb H} ^3,b) \to (N,u)$
be the based universal covering map. Fix a basepoint
![]() $c \in {\mathbb H} ^2$
, and for each i, let
$c \in {\mathbb H} ^2$
, and for each i, let
![]() $\tau _i \colon \thinspace ({\mathbb H} ^2, c) \to (S_0,a_i)$
be a based universal cover so that
$\tau _i \colon \thinspace ({\mathbb H} ^2, c) \to (S_0,a_i)$
be a based universal cover so that
![]() $\tau _i(m) = C({\mathbb S}^1)$
.
$\tau _i(m) = C({\mathbb S}^1)$
.
The map f elevates to n distinct (based) maps:
so that for each i we have
![]() $\pi \circ \widetilde {f_i} = f \circ \tau _i$
.
$\pi \circ \widetilde {f_i} = f \circ \tau _i$
.
Now, for a pair
![]() $i \ne j$
from
$i \ne j$
from
![]() $\{ 1 ,\ldots , n \}$
, we have
$\{ 1 ,\ldots , n \}$
, we have
![]() $\widetilde {f_i}(m) = \widetilde {f_j}(m)$
. Thus, we can take the two maps
$\widetilde {f_i}(m) = \widetilde {f_j}(m)$
. Thus, we can take the two maps
![]() $\widetilde {f_i}|_{H_R}$
and
$\widetilde {f_i}|_{H_R}$
and
![]() $\widetilde {f_j}|_{H_R}$
and glue them together via an orientation-preserving isometry along the boundary to get a continuous map
$\widetilde {f_j}|_{H_R}$
and glue them together via an orientation-preserving isometry along the boundary to get a continuous map
![]() $\widetilde {f}_{i,j}^{H_R} \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
, and similarly for the two maps restricted to
$\widetilde {f}_{i,j}^{H_R} \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
, and similarly for the two maps restricted to
![]() $H_L$
to get a continuous map
$H_L$
to get a continuous map
![]() $\widetilde {f}_{i,j}^{H_L}$
.
$\widetilde {f}_{i,j}^{H_L}$
.
Kahn and Wright prove that, for appropriate choices of parameters, their surface, built as an assembly of good pants and good hamster wheels, is close to an assembly of perfect pants and perfect hamster wheels and that the map which takes the ‘good’ assembly to the ‘perfect’ assembly is compliant (see [Reference Kahn and Wright15, §A.5]), which in particular means that it takes cuffs to cuffs. For a perfect assembly with cuff
![]() $\alpha $
, the construction analogous to the
$\alpha $
, the construction analogous to the
![]() $\widetilde {f}_{i,j}$
leads to pairs of totally geodesic half-planes glued along their boundary geodesic, namely to a map
$\widetilde {f}_{i,j}$
leads to pairs of totally geodesic half-planes glued along their boundary geodesic, namely to a map
![]() $p_\theta $
for some
$p_\theta $
for some
![]() $\theta $
. Thus, the map that takes the good assembly to the perfect assembly induces a map between
$\theta $
. Thus, the map that takes the good assembly to the perfect assembly induces a map between
![]() $\widetilde {f}_{i,j}^{H_R} \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
and some map
$\widetilde {f}_{i,j}^{H_R} \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
and some map
![]() $p_\theta \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
, and this map takes m to the pleating locus for
$p_\theta \colon \thinspace {\mathbb H} ^2 \to {\mathbb H} ^3$
, and this map takes m to the pleating locus for
![]() $p_\theta $
.
$p_\theta $
.
Our first task is to bound
![]() $\theta $
away from
$\theta $
away from
![]() $0$
, and our second is to show that the two maps are close. The sense in which they are close will be that of [Reference Kahn and Wright15, p. 554]—being of
$0$
, and our second is to show that the two maps are close. The sense in which they are close will be that of [Reference Kahn and Wright15, p. 554]—being of
![]() $\epsilon _0$
-bounded distortion to distance D for appropriate choice of
$\epsilon _0$
-bounded distortion to distance D for appropriate choice of
![]() $\epsilon _0$
and D.
$\epsilon _0$
and D.
Denote the angles of the maps
![]() $p_\theta $
induced by i, j and
$p_\theta $
induced by i, j and
![]() $H_R$
by
$H_R$
by
![]() $\theta (i,j,H_R)$
and for i, j and
$\theta (i,j,H_R)$
and for i, j and
![]() $H_L$
by
$H_L$
by
![]() $\theta (i,j,H_L)$
.
$\theta (i,j,H_L)$
.
The following is a summary of the above discussion and also of [Reference Kahn and Wright15, Theorem A.18]. In the following statement,
![]() $R_0$
is the constant from the statement of Lemma 3.1 (with values n,
$R_0$
is the constant from the statement of Lemma 3.1 (with values n,
![]() $\epsilon _0$
and
$\epsilon _0$
and
![]() $\mu = 1$
, respectively).
$\mu = 1$
, respectively).
Theorem 3.3. Fix
![]() $n \in {\mathbb N}$
. For all D there exist C,
$n \in {\mathbb N}$
. For all D there exist C,
![]() $\epsilon _0$
and
$\epsilon _0$
and
![]() $R_1> R_0$
so that for all
$R_1> R_0$
so that for all
![]() $\epsilon \in (0,\epsilon _0)$
and all
$\epsilon \in (0,\epsilon _0)$
and all
![]() $R> R_1$
and any
$R> R_1$
and any
![]() $(n,R,\epsilon )$
-pre-good curve
$(n,R,\epsilon )$
-pre-good curve
![]() $\alpha _0$
there exists a Kahn–Wright surface
$\alpha _0$
there exists a Kahn–Wright surface
![]() $f \colon \thinspace S_0 \looparrowright N$
containing
$f \colon \thinspace S_0 \looparrowright N$
containing
![]() $\alpha = \alpha _0^n$
as a cuff, constructed as an
$\alpha = \alpha _0^n$
as a cuff, constructed as an
![]() $(R,\epsilon )$
-good assembly.
$(R,\epsilon )$
-good assembly.
For each
![]() $i,j \in \{ 1,\ldots , n \}$
with
$i,j \in \{ 1,\ldots , n \}$
with
![]() $i \ne j$
, we have the following:
$i \ne j$
, we have the following:
-
(1) For any point v which lies within D of m in
 ${\mathbb H} ^2$
, we have and
${\mathbb H} ^2$
, we have and $$\begin{align*}d\left(\widetilde{f}_{i,j}^{H_L}(v),p_{\theta(i,j,H_L)}(v) \right) , d\left(\widetilde{f}_{i,j}^{H_R}(v),p_{\theta(i,j,H_R)}(v) \right) < C\epsilon \end{align*}$$
$$\begin{align*}d\left(\widetilde{f}_{i,j}^{H_L}(v),p_{\theta(i,j,H_L)}(v) \right) , d\left(\widetilde{f}_{i,j}^{H_R}(v),p_{\theta(i,j,H_R)}(v) \right) < C\epsilon \end{align*}$$
-
(2) For any point
 $z \in {\mathbb H} ^2$
lying at distance at least D from m, the maps
$z \in {\mathbb H} ^2$
lying at distance at least D from m, the maps
 $\widetilde {f}_{i,j}^{H_L}$
and
$\widetilde {f}_{i,j}^{H_L}$
and
 $\widetilde {f}_{i,j}^{H_R}$
restricted to the ball of radius D about z are
$\widetilde {f}_{i,j}^{H_R}$
restricted to the ball of radius D about z are
 $(1+C\epsilon ,C\epsilon )$
-quasi-isometric embeddings.
$(1+C\epsilon ,C\epsilon )$
-quasi-isometric embeddings.
Moreover, we have
The following is an easy consequence of Theorem 3.3 and Lemma 2.3. In the following statement
![]() $\epsilon _D$
is the constant from Theorem 3.3 applied to n and D,
$\epsilon _D$
is the constant from Theorem 3.3 applied to n and D,
![]() $R_0$
is the constant from Lemma 3.1 applied with choices n,
$R_0$
is the constant from Lemma 3.1 applied with choices n,
![]() $\epsilon _D$
and
$\epsilon _D$
and
![]() $\mu = 1$
, and
$\mu = 1$
, and
![]() $R_1$
is the constant then obtained from Theorem 3.3.
$R_1$
is the constant then obtained from Theorem 3.3.
Corollary 3.4. Fix
![]() $n \in {\mathbb N}$
. There exist
$n \in {\mathbb N}$
. There exist
![]() $\lambda ,\kappa $
so that for any D there exist
$\lambda ,\kappa $
so that for any D there exist
![]() $R_D> R_1, R_0$
and
$R_D> R_1, R_0$
and
![]() $\epsilon _D> 0$
so that for any
$\epsilon _D> 0$
so that for any
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $f \colon \thinspace S_0 \looparrowright N$
as in Theorem 3.3 with
$f \colon \thinspace S_0 \looparrowright N$
as in Theorem 3.3 with
![]() $R> R_D$
and any
$R> R_D$
and any
![]() $\epsilon \in (0,\epsilon _D)$
the maps
$\epsilon \in (0,\epsilon _D)$
the maps
![]() $\widetilde {f}_{i,j}^{H_R}$
and
$\widetilde {f}_{i,j}^{H_R}$
and
![]() $\widetilde {f}_{i,j}^{H_L}$
are D-local
$\widetilde {f}_{i,j}^{H_L}$
are D-local
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding.
$(\lambda ,\kappa )$
-quasi-isometric embedding.
Now, choose
![]() $D, \lambda _1,\kappa _1$
so that any D–local
$D, \lambda _1,\kappa _1$
so that any D–local
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding from
$(\lambda ,\kappa )$
-quasi-isometric embedding from
![]() ${\mathbb H} ^2$
to
${\mathbb H} ^2$
to
![]() ${\mathbb H} ^3$
is a global
${\mathbb H} ^3$
is a global
![]() $(\lambda _1,\kappa _1)$
-quasi-isometric embedding (see Proposition 2.2). This D then gives
$(\lambda _1,\kappa _1)$
-quasi-isometric embedding (see Proposition 2.2). This D then gives
![]() $R_D$
and
$R_D$
and
![]() $\epsilon _D$
as above.
$\epsilon _D$
as above.
Lemma 3.1 proves that there is an
![]() $(n,R_D,\epsilon _D)$
-pre-good curve
$(n,R_D,\epsilon _D)$
-pre-good curve
![]() $\alpha _0$
, and the construction from [Reference Kahn and Wright15] proves that there is an
$\alpha _0$
, and the construction from [Reference Kahn and Wright15] proves that there is an
![]() $f \colon \thinspace S_0 \to N$
with
$f \colon \thinspace S_0 \to N$
with
![]() $\alpha = \alpha _0^n$
as a cuff satisfying the conclusions of Theorem 3.3 and Corollary 3.4, with
$\alpha = \alpha _0^n$
as a cuff satisfying the conclusions of Theorem 3.3 and Corollary 3.4, with
![]() $R= R_D$
.
$R= R_D$
.
We fix this map
![]() $f \colon \thinspace S_0 \looparrowright N$
, along with n, D,
$f \colon \thinspace S_0 \looparrowright N$
, along with n, D,
![]() $R_D$
,
$R_D$
,
![]() $\epsilon _D$
,
$\epsilon _D$
,
![]() $\alpha _0$
,
$\alpha _0$
,
![]() $\alpha =\alpha _0^n$
,
$\alpha =\alpha _0^n$
,
![]() $\kappa $
and
$\kappa $
and
![]() $\epsilon $
as chosen above for the next two sections.
$\epsilon $
as chosen above for the next two sections.
4 The space
 $X_n$
$X_n$
By standard separability properties of surface groups, we may find a cover
![]() $S \to S_0$
to which
$S \to S_0$
to which
![]() $\alpha $
lifts as a nonseparating simple closed curve and so that:
$\alpha $
lifts as a nonseparating simple closed curve and so that:
-
(1) The injectivity radius of S is at least
 $\max \{ 2D, \lambda _1\kappa _1 \}$
, and
$\max \{ 2D, \lambda _1\kappa _1 \}$
, and -
(2) The lift of
 $\alpha $
to S is contained in an embedded collar of width at least
$\alpha $
to S is contained in an embedded collar of width at least
 $\max \{ 2D, \lambda _1\kappa _1 \}$
.
$\max \{ 2D, \lambda _1\kappa _1 \}$
.
Given the surface S, we build a space
![]() $X_n$
which immerses into N, exactly as in [Reference Sun20]. Passing from
$X_n$
which immerses into N, exactly as in [Reference Sun20]. Passing from
![]() $S_0$
to S before constructing
$S_0$
to S before constructing
![]() $X_n$
makes the proof that
$X_n$
makes the proof that
![]() $X_n$
is
$X_n$
is
![]() $\pi _1$
-injective with quasi-convex image much simpler than Sun’s proof from [Reference Sun20,
$\pi _1$
-injective with quasi-convex image much simpler than Sun’s proof from [Reference Sun20,
![]() $\S 4$
]. Let C denote the image of
$\S 4$
]. Let C denote the image of
![]() $\alpha $
in S, and let
$\alpha $
in S, and let
![]() $\phi ^n_C \colon \thinspace C \to \mathbb {S}^1$
be an n-to-
$\phi ^n_C \colon \thinspace C \to \mathbb {S}^1$
be an n-to-
![]() $1$
covering map, and let
$1$
covering map, and let
![]() $\tau _C \colon \thinspace C \to C$
be a deck transformation. We may choose
$\tau _C \colon \thinspace C \to C$
be a deck transformation. We may choose
![]() $\phi ^n_C$
so that
$\phi ^n_C$
so that
![]() $\tau $
is an isometry.
$\tau $
is an isometry.
Definition 4.1. The space
![]() $X_n(S,C)$
is defined by cutting S along C to get a surface
$X_n(S,C)$
is defined by cutting S along C to get a surface
![]() $S_1$
with two boundary components, denoted
$S_1$
with two boundary components, denoted
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, and taking the quotient of
$C_2$
, and taking the quotient of
![]() $S_1$
by the relation generated by
$S_1$
by the relation generated by
![]() $c \sim \tau _{C_i}(c)$
for
$c \sim \tau _{C_i}(c)$
for
![]() $c \in C_i$
and
$c \in C_i$
and
![]() $i = 1,2$
.
$i = 1,2$
.
Suppose that S is equipped with a hyperbolic metric, and consider the induced metric on
![]() $S_1$
. Since the maps
$S_1$
. Since the maps
![]() $\tau _{C_i}$
are isometries, there is a natural induced quotient metric on
$\tau _{C_i}$
are isometries, there is a natural induced quotient metric on
![]() $X_n(S,C)$
, which is locally isometric to
$X_n(S,C)$
, which is locally isometric to
![]() ${\mathbb H} ^2$
away from the images of the
${\mathbb H} ^2$
away from the images of the
![]() $C_i$
.
$C_i$
.
The following result is clear from the construction of S from
![]() $S_0$
.
$S_0$
.
Lemma 4.2. The injectivity radius of
![]() $X_n$
is at least
$X_n$
is at least
![]() $\max \{ 2D, \lambda _1\kappa _1 \}$
.
$\max \{ 2D, \lambda _1\kappa _1 \}$
.
Let
![]() $S_1$
be the surface obtained from S by cutting along C, and let
$S_1$
be the surface obtained from S by cutting along C, and let
![]() $C_1, C_2$
be the boundary components of
$C_1, C_2$
be the boundary components of
![]() $S_1$
. Let
$S_1$
. Let
![]() $q \colon \thinspace S_1 \to X_n$
be the defining quotient map, and let
$q \colon \thinspace S_1 \to X_n$
be the defining quotient map, and let
![]() $\overline {C_i} = q(C_i)$
for
$\overline {C_i} = q(C_i)$
for
![]() $i = 1,2$
.
$i = 1,2$
.
Because in S the curve C has an embedded collar of width at least
![]() $2D$
, for any
$2D$
, for any
![]() $i,j \in \{ 1, 2\}$
, any two distinct elevations of
$i,j \in \{ 1, 2\}$
, any two distinct elevations of
![]() $\overline {C_i}$
and
$\overline {C_i}$
and
![]() $\overline {C_j}$
to
$\overline {C_j}$
to
![]() $\widetilde {X_n}$
are at distance at least
$\widetilde {X_n}$
are at distance at least
![]() $4D$
from each other.
$4D$
from each other.
Definition 4.3. Suppose that
![]() ${\mathcal A} = \{ Z_1, \ldots , Z_m \}$
is a finite collection of metric spaces and that
${\mathcal A} = \{ Z_1, \ldots , Z_m \}$
is a finite collection of metric spaces and that
![]() $k> 0$
. A metric space Z is k-modeled on
$k> 0$
. A metric space Z is k-modeled on
![]() ${\mathcal A}$
if for every
${\mathcal A}$
if for every
![]() $z \in Z$
there is an i so that the ball of radius k about z is isometric to a ball in
$z \in Z$
there is an i so that the ball of radius k about z is isometric to a ball in
![]() $Z_i$
.
$Z_i$
.
Recall
![]() $H_R = \{ (x,y) \mid x \ge 0, y> 0 \}$
is the (closed) half-hyperbolic plane (in the upper half-space model). Let
$H_R = \{ (x,y) \mid x \ge 0, y> 0 \}$
is the (closed) half-hyperbolic plane (in the upper half-space model). Let
![]() $W_n$
be the space obtained from n copies of
$W_n$
be the space obtained from n copies of
![]() $H_R$
glued along the boundary geodesics (by an isometry).
$H_R$
glued along the boundary geodesics (by an isometry).
Lemma 4.4. The space
![]() $\widetilde {X_n}$
is D-modeled on
$\widetilde {X_n}$
is D-modeled on
![]() $W_n$
.
$W_n$
.
Proof. Let
![]() $x \in \widetilde {X_n}$
, and consider the covering map
$x \in \widetilde {X_n}$
, and consider the covering map
![]() $\pi \colon \thinspace \widetilde {X_n} \to X_n$
.
$\pi \colon \thinspace \widetilde {X_n} \to X_n$
.
Case 1:
![]() $d(\pi (x),\{ \overline {C_1}, \overline {C_2} \} ) \le D$
.
$d(\pi (x),\{ \overline {C_1}, \overline {C_2} \} ) \le D$
.
In this case, in
![]() $\widetilde {X_n}$
there is a unique elevation of some
$\widetilde {X_n}$
there is a unique elevation of some
![]() $\overline {C_i}$
which lies within D of x. Let y be a point in this elevation so
$\overline {C_i}$
which lies within D of x. Let y be a point in this elevation so
![]() $d(x,y) \le D$
. Then
$d(x,y) \le D$
. Then
![]() $B_{D}(x) \subseteq B_{2D}(y)$
, and
$B_{D}(x) \subseteq B_{2D}(y)$
, and
![]() $B_{2D}(y)$
is isometric to a ball of radius
$B_{2D}(y)$
is isometric to a ball of radius
![]() $2D$
in
$2D$
in
![]() $W_n$
.
$W_n$
.
Case 2:
![]() $d(\pi (x), \{ \overline {C_1}, \overline {C_2} \} )> D$
.
$d(\pi (x), \{ \overline {C_1}, \overline {C_2} \} )> D$
.
In this case, there is no elevation of either
![]() $\overline {C_i}$
which lies within D of x, and
$\overline {C_i}$
which lies within D of x, and
![]() $B_{D}(x)$
is isometric to a ball of radius D in
$B_{D}(x)$
is isometric to a ball of radius D in
![]() ${\mathbb H} ^2$
(and so in
${\mathbb H} ^2$
(and so in
![]() $W_n$
).
$W_n$
).
By construction, the immersion
![]() $f_1 \colon \thinspace S \to N$
obtained from composing the covering map
$f_1 \colon \thinspace S \to N$
obtained from composing the covering map
![]() $S \to S_0$
with
$S \to S_0$
with
![]() $f \colon \thinspace S_0 \looparrowright N$
yields an immersion
$f \colon \thinspace S_0 \looparrowright N$
yields an immersion
![]() $g \colon \thinspace X_n \looparrowright N$
. Let
$g \colon \thinspace X_n \looparrowright N$
. Let
![]() $\widetilde {g} \colon \thinspace \widetilde {X_n} \to {\mathbb H} ^3$
be the induced map on universal covers.
$\widetilde {g} \colon \thinspace \widetilde {X_n} \to {\mathbb H} ^3$
be the induced map on universal covers.
Two points
![]() $x, y$
in
$x, y$
in
![]() $\widetilde {X_n}$
at distance at most D either lie in an isometrically embedded copy of a half-space from
$\widetilde {X_n}$
at distance at most D either lie in an isometrically embedded copy of a half-space from
![]() ${\mathbb H} ^2$
,= or else in two different ‘sheets’ of a copy of
${\mathbb H} ^2$
,= or else in two different ‘sheets’ of a copy of
![]() $W_n$
. In either case, it follows immediately from Corollary 3.4 that
$W_n$
. In either case, it follows immediately from Corollary 3.4 that
![]() $\widetilde {g}$
is a D–local
$\widetilde {g}$
is a D–local
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding. Thus,
$(\lambda ,\kappa )$
-quasi-isometric embedding. Thus,
Theorem 4.5. The map
![]() $\widetilde {g} \colon \thinspace \widetilde {X_n} \to {\mathbb H} ^3$
is a D-local
$\widetilde {g} \colon \thinspace \widetilde {X_n} \to {\mathbb H} ^3$
is a D-local
![]() $(\lambda ,\kappa )$
-quasi-isometric embedding and hence is a (global)
$(\lambda ,\kappa )$
-quasi-isometric embedding and hence is a (global)
![]() $(\lambda _1,\kappa _1)$
-quasi-isometric embedding.
$(\lambda _1,\kappa _1)$
-quasi-isometric embedding.
In particular, since the injectivity radius of
![]() $X_n$
is at least
$X_n$
is at least
![]() $\lambda _1\kappa _1$
the map g is
$\lambda _1\kappa _1$
the map g is
![]() $\pi _1$
-injective, and
$\pi _1$
-injective, and
![]() $g_\ast (\pi _1(X_n))$
is relatively quasi-convex in
$g_\ast (\pi _1(X_n))$
is relatively quasi-convex in
![]() $\pi _1(N)$
. Moreover,
$\pi _1(N)$
. Moreover,
![]() $g_\ast (\pi _1(X_n))$
does not intersect any (conjugate of) the cusp subgroups of
$g_\ast (\pi _1(X_n))$
does not intersect any (conjugate of) the cusp subgroups of
![]() $\pi _1(N)$
.
$\pi _1(N)$
.
5 Virtual retractions and the proof of Theorem 1.1 in the hyperbolic case
In this section, we prove Theorem 1.1 in case of a (noncompact) finite-volume hyperbolic
![]() $3$
-manifold N. Let
$3$
-manifold N. Let
![]() $\Gamma = \pi _1(N)$
. By [Reference Wise22, Theorem 17.14],
$\Gamma = \pi _1(N)$
. By [Reference Wise22, Theorem 17.14],
![]() $\pi _1(N)$
is the fundamental group of a compact virtually special cube complex X. Let
$\pi _1(N)$
is the fundamental group of a compact virtually special cube complex X. Let
![]() $\Gamma ' \le \Gamma $
be a finite-index subgroup so that the cover of X corresponding to
$\Gamma ' \le \Gamma $
be a finite-index subgroup so that the cover of X corresponding to
![]() $\Gamma '$
is special, and let
$\Gamma '$
is special, and let
![]() $N_1$
be the cover of N corresponding to
$N_1$
be the cover of N corresponding to
![]() $\Gamma '$
. As in Section 4, construct an immersion
$\Gamma '$
. As in Section 4, construct an immersion
![]() $g \colon \thinspace X_n \to N_1$
. Note that
$g \colon \thinspace X_n \to N_1$
. Note that
![]() $(\Gamma ',{\mathcal P})$
is relatively hyperbolic, where
$(\Gamma ',{\mathcal P})$
is relatively hyperbolic, where
![]() ${\mathcal P}$
consists of the (abelian) cusp subgroups.
${\mathcal P}$
consists of the (abelian) cusp subgroups.
Let
![]() $H = g_\ast \left ( \pi _1(X_n) \right ) \le \pi _1(N_1) = \Gamma '$
. The subgroup H is relatively quasi-convex in
$H = g_\ast \left ( \pi _1(X_n) \right ) \le \pi _1(N_1) = \Gamma '$
. The subgroup H is relatively quasi-convex in
![]() $\Gamma '$
, and so by [Reference Haglund and Wise12, Corollary 6.7] (we use the formulation as in [Reference Przytycki and Wise19, Theorem 6.3]) that H is a virtual retract of
$\Gamma '$
, and so by [Reference Haglund and Wise12, Corollary 6.7] (we use the formulation as in [Reference Przytycki and Wise19, Theorem 6.3]) that H is a virtual retract of
![]() $\Gamma '$
. Let
$\Gamma '$
. Let
![]() $\Gamma ''$
be a finite-index subgroup of
$\Gamma ''$
be a finite-index subgroup of
![]() $\Gamma '$
which retracts onto H. Let
$\Gamma '$
which retracts onto H. Let
![]() $N_2$
be the finite cover of
$N_2$
be the finite cover of
![]() $N_1$
corresponding to
$N_1$
corresponding to
![]() $\Gamma ''$
. As in [Reference Sun20, Proposition 3.7], we have the induced maps on homology:
$\Gamma ''$
. As in [Reference Sun20, Proposition 3.7], we have the induced maps on homology:
Therefore, since
![]() $r\circ g_*=id_H$
,
$r\circ g_*=id_H$
,
![]() $H_1(X_n;{\mathbb Z})={\mathbb Z}^{2\cdot \mathrm {genus}(S)+1}\oplus {\mathbb Z} / n{\mathbb Z}$
is a direct factor of
$H_1(X_n;{\mathbb Z})={\mathbb Z}^{2\cdot \mathrm {genus}(S)+1}\oplus {\mathbb Z} / n{\mathbb Z}$
is a direct factor of
![]() $H_1(N_2;{\mathbb Z})$
. In particular,
$H_1(N_2;{\mathbb Z})$
. In particular,
![]() ${\mathbb Z} / n{\mathbb Z}$
is a direct factor of
${\mathbb Z} / n{\mathbb Z}$
is a direct factor of
![]() $H_1(N_2;{\mathbb Z})$
, and this proves the hyperbolic case of Theorem 1.1 in the case that A is finite cyclic.
$H_1(N_2;{\mathbb Z})$
, and this proves the hyperbolic case of Theorem 1.1 in the case that A is finite cyclic.
Given a finite abelian group A, induction on the rank k of A also works as in [Reference Sun20, Proposition 3.9] as follows. Let
![]() $A=A_1\oplus {\mathbb Z}/n_{k+1}{\mathbb Z}$
, where
$A=A_1\oplus {\mathbb Z}/n_{k+1}{\mathbb Z}$
, where
![]() $A_1=\oplus _{i=1}^k{\mathbb Z}/n_i{\mathbb Z}$
. Suppose by induction that
$A_1=\oplus _{i=1}^k{\mathbb Z}/n_i{\mathbb Z}$
. Suppose by induction that
![]() $H_1 \le \Gamma '$
is a relatively quasi-convex free product of images of
$H_1 \le \Gamma '$
is a relatively quasi-convex free product of images of
![]() $\pi _1\left ( X_{n_i} \right )$
(for
$\pi _1\left ( X_{n_i} \right )$
(for
![]() $i = 1, \ldots , k$
) and that
$i = 1, \ldots , k$
) and that
![]() $H_2=(g_{k+1})_*\left ( \pi _1(X_{n_{k+1}})\right ) \le \Gamma '$
. Choose any
$H_2=(g_{k+1})_*\left ( \pi _1(X_{n_{k+1}})\right ) \le \Gamma '$
. Choose any
![]() $\gamma \in \Gamma '$
whose fixed points in
$\gamma \in \Gamma '$
whose fixed points in
![]() $\partial {\mathbb H} ^3$
are disjoint from both limit sets
$\partial {\mathbb H} ^3$
are disjoint from both limit sets
![]() $\Lambda (H_1)$
and
$\Lambda (H_1)$
and
![]() $\Lambda (H_2)$
. Then after conjugating
$\Lambda (H_2)$
. Then after conjugating
![]() $H_2$
by some sufficiently high power
$H_2$
by some sufficiently high power
![]() $\gamma ^m$
, the first Klein–Maskit combination theorem [Reference Maskit17] applies (note that by [Reference Christopher Hruska11, Corollary 1.3] a subgroup is relatively quasi-convex if and only if it is geometrically finite). Since
$\gamma ^m$
, the first Klein–Maskit combination theorem [Reference Maskit17] applies (note that by [Reference Christopher Hruska11, Corollary 1.3] a subgroup is relatively quasi-convex if and only if it is geometrically finite). Since
![]() $H_2$
is relatively quasi-convex, the free product
$H_2$
is relatively quasi-convex, the free product
![]() $H_1*\gamma ^mH_2\gamma ^{-m}$
is also a relatively quasi-convex subgroup of
$H_1*\gamma ^mH_2\gamma ^{-m}$
is also a relatively quasi-convex subgroup of
![]() $\Gamma '$
isomorphic to the abstract group
$\Gamma '$
isomorphic to the abstract group
![]() $H_1*H_2$
. The proof of the hyperbolic case of Theorem 1.1 for a general finite abelian A then follows exactly as in the case of a finite cyclic A above.
$H_1*H_2$
. The proof of the hyperbolic case of Theorem 1.1 for a general finite abelian A then follows exactly as in the case of a finite cyclic A above.
6 Nonhyperbolic manifolds
We now prove Theorem 1.1 in general. To that end, suppose that M is an irreducible
![]() $3$
-manifold which has at least one hyperbolic piece in its geometric decomposition and that A is a finite abelian group. By [Reference Przytycki and Wise19, Theorem 1.1], there exists a
$3$
-manifold which has at least one hyperbolic piece in its geometric decomposition and that A is a finite abelian group. By [Reference Przytycki and Wise19, Theorem 1.1], there exists a
![]() $\operatorname {CAT}(0)$
cube complex X equipped with a free
$\operatorname {CAT}(0)$
cube complex X equipped with a free
![]() $\pi _1(M)$
–action so that there are finitely many orbits of hyperplanes and so that
$\pi _1(M)$
–action so that there are finitely many orbits of hyperplanes and so that
![]() has a finite special cover. Let
has a finite special cover. Let
![]() $\Gamma _1 \le \pi (M)$
be a finite-index subgroup corresponding to the finite special cover of
$\Gamma _1 \le \pi (M)$
be a finite-index subgroup corresponding to the finite special cover of
![]() , and let
, and let
![]() $M_1$
be the finite cover of M corresponding to
$M_1$
be the finite cover of M corresponding to
![]() $\Gamma _1$
. Let
$\Gamma _1$
. Let
![]() $M_h$
be a hyperbolic piece in the geometric decomposition of
$M_h$
be a hyperbolic piece in the geometric decomposition of
![]() $M_1$
, and let
$M_1$
, and let
![]() $\Gamma _h := \pi _1(M_h) \le \pi _1(M_1)$
(basepoints/conjugacy classes are not important here). According to the construction in the previous sections, there is a relatively quasi-convex subgroup H of
$\Gamma _h := \pi _1(M_h) \le \pi _1(M_1)$
(basepoints/conjugacy classes are not important here). According to the construction in the previous sections, there is a relatively quasi-convex subgroup H of
![]() $\Gamma _h$
so that A is a direct factor of
$\Gamma _h$
so that A is a direct factor of
![]() $H_1(H;{\mathbb Z})$
. Theorem 1.1 then follows immediately from the following result. This result is presumably known to the experts, but we were unable to find it in the literature.
$H_1(H;{\mathbb Z})$
. Theorem 1.1 then follows immediately from the following result. This result is presumably known to the experts, but we were unable to find it in the literature.
Proposition 6.1. There is a finite-index subgroup
![]() $\Gamma _0 \le \pi _1(M_1)$
so that
$\Gamma _0 \le \pi _1(M_1)$
so that
![]() $H \le \Gamma _0$
and H is a retract of
$H \le \Gamma _0$
and H is a retract of
![]() $\Gamma _0$
.
$\Gamma _0$
.
Proof. Let
![]() $\widetilde {M_h} \le \widetilde {M}$
be the (
$\widetilde {M_h} \le \widetilde {M}$
be the (
![]() $\Gamma _h$
–invariant) universal cover of
$\Gamma _h$
–invariant) universal cover of
![]() $M_h$
inside the universal cover of M. The space X is built via a wallspace construction on
$M_h$
inside the universal cover of M. The space X is built via a wallspace construction on
![]() $\widetilde {M}$
as in [Reference Hruska and Wise13]. As in [Reference Hruska and Wise13, §3.4], we can associate to
$\widetilde {M}$
as in [Reference Hruska and Wise13]. As in [Reference Hruska and Wise13, §3.4], we can associate to
![]() $\widetilde {M_h}$
a hemiwallspace consisting of those half-spaces in
$\widetilde {M_h}$
a hemiwallspace consisting of those half-spaces in
![]() $\widetilde {M}$
which intersect
$\widetilde {M}$
which intersect
![]() $\widetilde {M_h}$
(see [Reference Hruska and Wise13, Example 3.20]. This builds a
$\widetilde {M_h}$
(see [Reference Hruska and Wise13, Example 3.20]. This builds a
![]() $\Gamma _h$
-invariant convex subcomplex
$\Gamma _h$
-invariant convex subcomplex
![]() $X_h$
of X by [Reference Hruska and Wise13, Lemma 3.24].
$X_h$
of X by [Reference Hruska and Wise13, Lemma 3.24].
By [Reference Przytycki and Wise19, Theorem 2.1], the surfaces of the cubulation intersecting
![]() $M_h$
all intersect
$M_h$
all intersect
![]() $M_h$
in a geometrically finite surface. Therefore, by [Reference Hruska and Wise13, Theorem 7.10], the
$M_h$
in a geometrically finite surface. Therefore, by [Reference Hruska and Wise13, Theorem 7.10], the
![]() $\Gamma _h$
–action on
$\Gamma _h$
–action on
![]() $X_h$
is (free and) co-sparse (see [Reference Sageev and Wise21, Definition 7.1]).
$X_h$
is (free and) co-sparse (see [Reference Sageev and Wise21, Definition 7.1]).
According to [Reference Sageev and Wise21, Theorem 7.2] inside of
![]() $X_h$
there is an H-invariant convex subcomplex Z upon which H acts co-sparsely. In fact, since H does not intersect any of the parabolic subgroups of
$X_h$
there is an H-invariant convex subcomplex Z upon which H acts co-sparsely. In fact, since H does not intersect any of the parabolic subgroups of
![]() $\Gamma _h$
, the subcomplex Z found in [Reference Sageev and Wise21, Theorem 7.2] is H-cocompact (this follow immediately from the proof).
$\Gamma _h$
, the subcomplex Z found in [Reference Sageev and Wise21, Theorem 7.2] is H-cocompact (this follow immediately from the proof).
Since
![]() is special, it follows from [Reference Haglund and Wise12, Corollary 6.7] (we use the formulation as in [Reference Przytycki and Wise19, Theorem 6.3]) that H is a virtual retract of
is special, it follows from [Reference Haglund and Wise12, Corollary 6.7] (we use the formulation as in [Reference Przytycki and Wise19, Theorem 6.3]) that H is a virtual retract of
![]() $\Gamma _1$
.
$\Gamma _1$
.
Acknowledgements
The first author is supported in part by NSF grant DMS 1803094 and by MSRI. The second author is supported in part by NSF grant DMS 1904913.
Competing Interests
None.