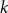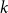1. Introduction
This paper studies improper vertex colourings of graphs with bounded monochromatic degree or bounded monochromatic component size. This topic has been extensively studied recently [Reference Alon, Ding, Oporowski and Vertigan1–Reference Dujmović, Esperet, Morin, Walczak and Wood6, Reference Dvořák and Norin7, Reference Edwards, Kang, Kim, Oum and Seymour8, Reference Esperet and Joret9–Reference Mohar, Reed and Wood18, Reference Norin, Scott, Seymour and Wood19–Reference van den Heuvel and Wood21]; see [Reference Wood22] for a survey.
A
![]() $k$
-colouring of a graph
$k$
-colouring of a graph
![]() $G$
is a function that assigns one of
$G$
is a function that assigns one of
![]() $k$
colours to each vertex of
$k$
colours to each vertex of
![]() $G$
. In a coloured graph, a monochromatic component is a connected component of the subgraph induced by all the vertices of one colour.
$G$
. In a coloured graph, a monochromatic component is a connected component of the subgraph induced by all the vertices of one colour.
A colouring has defect
![]() $d$
if each monochromatic component has maximum degree at most
$d$
if each monochromatic component has maximum degree at most
![]() $d$
. The defective chromatic number of a graph class
$d$
. The defective chromatic number of a graph class
![]() $\mathcal{G}$
, denoted by
$\mathcal{G}$
, denoted by
![]() $\chi _{\Delta }(\mathcal{G})$
, is the minimum integer
$\chi _{\Delta }(\mathcal{G})$
, is the minimum integer
![]() $k$
such that, for some integer
$k$
such that, for some integer
![]() $d$
, every graph in
$d$
, every graph in
![]() $\mathcal{G}$
is
$\mathcal{G}$
is
![]() $k$
-colourable with defect
$k$
-colourable with defect
![]() $d$
.
$d$
.
A colouring has clustering
![]() $c$
if each monochromatic component has at most
$c$
if each monochromatic component has at most
![]() $c$
vertices. The clustered chromatic number of a graph class
$c$
vertices. The clustered chromatic number of a graph class
![]() $\mathcal{G}$
, denoted by
$\mathcal{G}$
, denoted by
![]() $\chi _{\star }(\mathcal{G})$
, is the minimum integer
$\chi _{\star }(\mathcal{G})$
, is the minimum integer
![]() $k$
such that, for some integer
$k$
such that, for some integer
![]() $c$
, every graph in
$c$
, every graph in
![]() $\mathcal{G}$
has a
$\mathcal{G}$
has a
![]() $k$
-colouring with clustering
$k$
-colouring with clustering
![]() $c$
. We shall consider such colourings, where the goal is to minimise the number of colours, without optimising the clustering value.
$c$
. We shall consider such colourings, where the goal is to minimise the number of colours, without optimising the clustering value.
Every colouring of a graph with clustering
![]() $c$
has defect
$c$
has defect
![]() $c-1$
. Thus,
$c-1$
. Thus,
![]() $ \chi _{\Delta }(\mathcal{G}) \leqslant \chi _{\star }(\mathcal{G})$
for every class
$ \chi _{\Delta }(\mathcal{G}) \leqslant \chi _{\star }(\mathcal{G})$
for every class
![]() $\mathcal{G}$
.
$\mathcal{G}$
.
The following is a well-known and important example in defective and clustered graph colouring. Let
![]() $T$
be a rooted tree. The depth of
$T$
be a rooted tree. The depth of
![]() $T$
is the maximum number of vertices on a root–to–leaf path in
$T$
is the maximum number of vertices on a root–to–leaf path in
![]() $T$
. The closure of
$T$
. The closure of
![]() $T$
is obtained from
$T$
is obtained from
![]() $T$
by adding an edge between every ancestor and descendant in
$T$
by adding an edge between every ancestor and descendant in
![]() $T$
. For
$T$
. For
![]() $h,k\geqslant 1$
, let
$h,k\geqslant 1$
, let
![]() $C\langle{h,k}\rangle$
be the closure of the complete
$C\langle{h,k}\rangle$
be the closure of the complete
![]() $k$
-ary tree of depth
$k$
-ary tree of depth
![]() $h$
, as illustrated in Figure 1.
$h$
, as illustrated in Figure 1.

Figure 1. The standard example
![]() $C\langle{4,2}\rangle$
.
$C\langle{4,2}\rangle$
.
It is well known and easily proved (see [Reference Wood22]) that there is no
![]() $(h-1)$
-colouring of
$(h-1)$
-colouring of
![]() $C\langle{h,k}\rangle$
with defect
$C\langle{h,k}\rangle$
with defect
![]() $k-1$
, which implies there is no
$k-1$
, which implies there is no
![]() $(h-1)$
-colouring of
$(h-1)$
-colouring of
![]() $C\langle{h,k}\rangle$
with clustering
$C\langle{h,k}\rangle$
with clustering
![]() $k$
. This says that if a graph class
$k$
. This says that if a graph class
![]() $\mathcal{G}$
includes
$\mathcal{G}$
includes
![]() $C\langle{h,k}\rangle$
for all
$C\langle{h,k}\rangle$
for all
![]() $k$
, then the defective chromatic number and the clustered chromatic number are at least
$k$
, then the defective chromatic number and the clustered chromatic number are at least
![]() $h$
. Put another way, define the tree-closure-number of a graph class
$h$
. Put another way, define the tree-closure-number of a graph class
![]() $\mathcal{G}$
to be
$\mathcal{G}$
to be
then
Our main result, Theorem 1 below, establishes a converse result for minor-closed classes with bounded treedepth. First we explain these terms. A graph
![]() $H$
is a minor of a graph
$H$
is a minor of a graph
![]() $G$
if a graph isomorphic to
$G$
if a graph isomorphic to
![]() $H$
can be obtained from some subgraph of
$H$
can be obtained from some subgraph of
![]() $G$
by contracting edges. A class of graphs
$G$
by contracting edges. A class of graphs
![]() $\mathcal{M}$
is minor-closed if for every graph
$\mathcal{M}$
is minor-closed if for every graph
![]() $G\in \mathcal{M}$
every minor of
$G\in \mathcal{M}$
every minor of
![]() $G$
is in
$G$
is in
![]() $\mathcal{M}$
, and
$\mathcal{M}$
, and
![]() $\mathcal{M}$
is proper minor-closed if, in addition, some graph is not in
$\mathcal{M}$
is proper minor-closed if, in addition, some graph is not in
![]() $\mathcal{M}$
. The connected treedepth of a graph
$\mathcal{M}$
. The connected treedepth of a graph
![]() $H$
, denoted by
$H$
, denoted by
![]() $\overline{\rm td}(H)$
, is the minimum depth of a rooted tree
$\overline{\rm td}(H)$
, is the minimum depth of a rooted tree
![]() $T$
such that
$T$
such that
![]() $H$
is a subgraph of the closure of
$H$
is a subgraph of the closure of
![]() $T$
. This definition is a variant of the more commonly used definition of the treedepth of
$T$
. This definition is a variant of the more commonly used definition of the treedepth of
![]() $H$
, denoted by
$H$
, denoted by
![]() $\text{td}(H)$
, which equals the maximum connected treedepth of the connected components of
$\text{td}(H)$
, which equals the maximum connected treedepth of the connected components of
![]() $H$
. (See [Reference Nešetřil and Ossona de Mendez23] for background on treedepth.) If
$H$
. (See [Reference Nešetřil and Ossona de Mendez23] for background on treedepth.) If
![]() $H$
is connected, then
$H$
is connected, then
![]() $\text{td}(H)=\overline{\rm td}(H)$
. In fact,
$\text{td}(H)=\overline{\rm td}(H)$
. In fact,
![]() $\text{td}(H)=\overline{\rm td}(H)$
unless
$\text{td}(H)=\overline{\rm td}(H)$
unless
![]() $H$
has two connected components
$H$
has two connected components
![]() $H_1$
and
$H_1$
and
![]() $H_2$
with
$H_2$
with
![]() $\text{td}(H_1)=\text{td}(H_2)=\text{td}(H)$
, in which case
$\text{td}(H_1)=\text{td}(H_2)=\text{td}(H)$
, in which case
![]() $\overline{\rm td}(H)=\text{td}(H)+1$
. It is convenient to work with connected treedepth to avoid this distinction. A class of graphs has bounded treedepth if there exists a constant
$\overline{\rm td}(H)=\text{td}(H)+1$
. It is convenient to work with connected treedepth to avoid this distinction. A class of graphs has bounded treedepth if there exists a constant
![]() $c$
such that every graph in the class has treedepth at most
$c$
such that every graph in the class has treedepth at most
![]() $c$
.
$c$
.
Theorem 1.
For every minor-closed class
![]() $\mathcal{G}$
with bounded treedepth,
$\mathcal{G}$
with bounded treedepth,
Our second result concerns pathwidth. A path-decomposition of a graph
![]() $G$
consists of a sequence
$G$
consists of a sequence
![]() $(B_1,\ldots,B_n)$
, where each
$(B_1,\ldots,B_n)$
, where each
![]() $B_i$
is a subset of
$B_i$
is a subset of
![]() $V(G)$
called a bag, such that for every vertex
$V(G)$
called a bag, such that for every vertex
![]() $v\in V(G)$
, the set
$v\in V(G)$
, the set
![]() $\{i\in [1,n]\;:\; v\in B_i\}$
is an interval, and for every edge
$\{i\in [1,n]\;:\; v\in B_i\}$
is an interval, and for every edge
![]() $vw\in E(G)$
there is a bag
$vw\in E(G)$
there is a bag
![]() $B_i$
containing both
$B_i$
containing both
![]() $v$
and
$v$
and
![]() $w$
. Here
$w$
. Here
![]() $[a,b]\;:\!=\;\{a,a+1,\ldots,b\}$
. The width of a path decomposition
$[a,b]\;:\!=\;\{a,a+1,\ldots,b\}$
. The width of a path decomposition
![]() $(B_1,\ldots,B_n)$
is
$(B_1,\ldots,B_n)$
is
![]() $\max \{|B_i|\;:\; i\in [1,n] \}-1$
. The pathwidth of a graph
$\max \{|B_i|\;:\; i\in [1,n] \}-1$
. The pathwidth of a graph
![]() $G$
is the minimum width of a path-decomposition of
$G$
is the minimum width of a path-decomposition of
![]() $G$
. Note that paths (and more generally caterpillars) have pathwidth 1. A class of graphs has bounded pathwidth if there exists a constant
$G$
. Note that paths (and more generally caterpillars) have pathwidth 1. A class of graphs has bounded pathwidth if there exists a constant
![]() $c$
such that every graph in the class has pathwidth at most
$c$
such that every graph in the class has pathwidth at most
![]() $c$
.
$c$
.
Theorem 2.
For every minor-closed class
![]() $\mathcal{G}$
with bounded pathwidth,
$\mathcal{G}$
with bounded pathwidth,
Theorems 1 and 2 are, respectively, proved in Sections 2 and 3. These results are best possible and partially resolve a number of conjectures from the literature, as we now explain.
Ossona de Mendez et al. [Reference Ossona de Mendez, Oum and Wood20] studied the defective chromatic number of minor-closed classes. For a graph
![]() $H$
, let
$H$
, let
![]() $\mathcal{M}_H$
be the class of
$\mathcal{M}_H$
be the class of
![]() $H$
-minor-free graphs (that is, not containing
$H$
-minor-free graphs (that is, not containing
![]() $H$
as a minor). Ossona de Mendez et al. [Reference Ossona de Mendez, Oum and Wood20] proved the lower bound,
$H$
as a minor). Ossona de Mendez et al. [Reference Ossona de Mendez, Oum and Wood20] proved the lower bound,
![]() $\chi _{\Delta }(\mathcal{M}_H) \geqslant \overline{\rm td}(H)-1$
and conjectured that equality holds.
$\chi _{\Delta }(\mathcal{M}_H) \geqslant \overline{\rm td}(H)-1$
and conjectured that equality holds.
Conjecture 3 ([Reference Ossona de Mendez, Oum and Wood20]). For every graph
![]() $H$
,
$H$
,
Conjecture 3 is known to hold in some special cases. Edwards et al. [Reference Edwards, Kang, Kim, Oum and Seymour8] proved it if
![]() $H=K_t$
; that is,
$H=K_t$
; that is,
![]() $\chi _{\Delta }(\mathcal{M}_{K_t})=t-1$
, which can be thought of as a defective version of Hadwiger’s Conjecture; see [Reference van den Heuvel and Wood21] for an improved bound on the defect in this case. Ossona de Mendez et al. [Reference Ossona de Mendez, Oum and Wood20] proved Conjecture 3 if
$\chi _{\Delta }(\mathcal{M}_{K_t})=t-1$
, which can be thought of as a defective version of Hadwiger’s Conjecture; see [Reference van den Heuvel and Wood21] for an improved bound on the defect in this case. Ossona de Mendez et al. [Reference Ossona de Mendez, Oum and Wood20] proved Conjecture 3 if
![]() $\overline{\rm td}(H)\leqslant 3$
or if
$\overline{\rm td}(H)\leqslant 3$
or if
![]() $H$
is a complete bipartite graph. In particular,
$H$
is a complete bipartite graph. In particular,
![]() $\chi _{\Delta }(\mathcal{M}_{K_{s,t}})=\min \{s,t\}$
.
$\chi _{\Delta }(\mathcal{M}_{K_{s,t}})=\min \{s,t\}$
.
Norin et al. [Reference Norin, Scott, Seymour and Wood19] studied the clustered chromatic number of minor-closed classes. They showed that for each
![]() $k\geqslant 2$
, there is a graph
$k\geqslant 2$
, there is a graph
![]() $H$
with treedepth
$H$
with treedepth
![]() $k$
and connected treedepth
$k$
and connected treedepth
![]() $k$
such that
$k$
such that
![]() $\chi _{\star }(\mathcal{M}_{H}) \geqslant 2k-2$
. Their proof in fact constructs a set
$\chi _{\star }(\mathcal{M}_{H}) \geqslant 2k-2$
. Their proof in fact constructs a set
![]() $\mathcal{X}$
of graphs in
$\mathcal{X}$
of graphs in
![]() $\mathcal{M}_H$
with bounded pathwidth (at most
$\mathcal{M}_H$
with bounded pathwidth (at most
![]() $2k-3$
to be precise) such that
$2k-3$
to be precise) such that
![]() $\chi _{\star }(\mathcal{X}) \geqslant 2k-2$
. Thus, the upper bound on
$\chi _{\star }(\mathcal{X}) \geqslant 2k-2$
. Thus, the upper bound on
![]() $\chi _{\star }(\mathcal{G})$
in Theorem 2 is best possible.
$\chi _{\star }(\mathcal{G})$
in Theorem 2 is best possible.
Norin et al. [Reference Norin, Scott, Seymour and Wood19] conjectured the following converse upper bound (analogous to Conjecture 3):
Conjecture 4 ([Reference Norin, Scott, Seymour and Wood19]). For every graph
![]() $H$
,
$H$
,
While Conjectures 3 and 4 remain open, Norin et al. [Reference Norin, Scott, Seymour and Wood19] showed in the following theorem that
![]() $\chi _{\Delta }(\mathcal{M}_H)$
and
$\chi _{\Delta }(\mathcal{M}_H)$
and
![]() $\chi _{\star }(\mathcal{M}_H)$
are controlled by the treedepth of
$\chi _{\star }(\mathcal{M}_H)$
are controlled by the treedepth of
![]() $H$
:
$H$
:
Theorem 5 ([Reference Norin, Scott, Seymour and Wood19]). For every graph
![]() $H$
,
$H$
,
![]() $\chi _{\star }(\mathcal{M}_H)$
is tied to the (connected) treedepth of
$\chi _{\star }(\mathcal{M}_H)$
is tied to the (connected) treedepth of
![]() $H$
. In particular,
$H$
. In particular,
Theorem 1 gives a much more precise bound than Theorem 5 under the extra assumption of bounded treedepth.
Our third main result concerns fractional colourings. For real
![]() $t \geqslant 1$
, a graph
$t \geqslant 1$
, a graph
![]() $G$
is fractionally
$G$
is fractionally
![]() $t$
-colourable with clustering
$t$
-colourable with clustering
![]() $c$
if there exist
$c$
if there exist
![]() $Y_1,Y_2, \ldots, Y_s \subseteq V(G)$
and
$Y_1,Y_2, \ldots, Y_s \subseteq V(G)$
and
![]() $\alpha _1,\ldots,\alpha _s \in [0,1]$
such thatFootnote
1
:
$\alpha _1,\ldots,\alpha _s \in [0,1]$
such thatFootnote
1
:
-
Every component of
 $G[Y_i]$
has at most
$G[Y_i]$
has at most
 $c$
vertices,
$c$
vertices, -
 $\sum _{i=1}^s \alpha _i \leqslant t$
,
$\sum _{i=1}^s \alpha _i \leqslant t$
, -
 $\sum _{i\,:v \in Y_i}\alpha _i \geqslant 1$
for every
$\sum _{i\,:v \in Y_i}\alpha _i \geqslant 1$
for every
 $v \in V(G)$
.
$v \in V(G)$
.
The fractional clustered chromatic number
![]() $\chi ^f_{\star }(\mathcal{G})$
of a graph class
$\chi ^f_{\star }(\mathcal{G})$
of a graph class
![]() $\mathcal{G}$
is the infimum of
$\mathcal{G}$
is the infimum of
![]() $t\gt 0$
such that there exists
$t\gt 0$
such that there exists
![]() $c=c(t,\mathcal{G})$
such that every
$c=c(t,\mathcal{G})$
such that every
![]() $G \in \mathcal{G}$
is fractionally
$G \in \mathcal{G}$
is fractionally
![]() $t$
-colourable with clustering
$t$
-colourable with clustering
![]() $c$
.
$c$
.
Fractionally
![]() $t$
-colourable with defect
$t$
-colourable with defect
![]() $d$
and fractional defective chromatic number
$d$
and fractional defective chromatic number
![]() $\chi ^f_{\Delta }(\mathcal{G})$
are defined in exactly the same way, except the condition on the component size of
$\chi ^f_{\Delta }(\mathcal{G})$
are defined in exactly the same way, except the condition on the component size of
![]() $G[Y_i]$
is replaced by “the maximum degree of
$G[Y_i]$
is replaced by “the maximum degree of
![]() $G[Y_i]$
is at most
$G[Y_i]$
is at most
![]() $d$
”.
$d$
”.
The following theorem determines the fractional clustered chromatic number and fractional defective chromatic number of any proper minor-closed class.
Theorem 6.
For every proper minor-closed class
![]() $\mathcal{G}$
,
$\mathcal{G}$
,
This result is proved in Section 4.
We now give an interesting example of Theorem 6.
Corollary 7.
For every surface
![]() $\Sigma$
, if
$\Sigma$
, if
![]() $\mathcal{G}_\Sigma$
is the class of graphs embeddable in
$\mathcal{G}_\Sigma$
is the class of graphs embeddable in
![]() $\Sigma$
, then
$\Sigma$
, then
Proof. Note that
![]() $C\langle{3,k}\rangle$
is planar for all
$C\langle{3,k}\rangle$
is planar for all
![]() $k$
. Thus,
$k$
. Thus,
![]() $\text{tcn}(\mathcal{G}_\Sigma )\geqslant 4$
. Say
$\text{tcn}(\mathcal{G}_\Sigma )\geqslant 4$
. Say
![]() $\Sigma$
has Euler genus
$\Sigma$
has Euler genus
![]() $g$
. It follows from Euler’s formula that
$g$
. It follows from Euler’s formula that
![]() $K_{3,2g+3}\not \in \mathcal{G}_\Sigma$
. Since
$K_{3,2g+3}\not \in \mathcal{G}_\Sigma$
. Since
![]() $K_{3,2g+3} \subseteq C\langle{4,2g+3}\rangle$
, we have
$K_{3,2g+3} \subseteq C\langle{4,2g+3}\rangle$
, we have
![]() $C\langle{4,2g+3}\rangle \not \in \mathcal{G}_\Sigma$
. Thus,
$C\langle{4,2g+3}\rangle \not \in \mathcal{G}_\Sigma$
. Thus,
![]() $\text{tcn}(\mathcal{G}_\Sigma )= 4$
. The result follows from Theorem 6.
$\text{tcn}(\mathcal{G}_\Sigma )= 4$
. The result follows from Theorem 6.
In contrast to Corollary 7, Dvořák and Norin [Reference Dvořák and Norin7] proved that
![]() $\chi _{\star }(\mathcal{G}_\Sigma )=4$
. Note that Archdeacon [Reference Archdeacon2] proved that
$\chi _{\star }(\mathcal{G}_\Sigma )=4$
. Note that Archdeacon [Reference Archdeacon2] proved that
![]() $\chi _{\Delta }(\mathcal{G}_\Sigma )=3$
; see [Reference Cowen, Goddard and Jesurum5] for an improved bound on the defect.
$\chi _{\Delta }(\mathcal{G}_\Sigma )=3$
; see [Reference Cowen, Goddard and Jesurum5] for an improved bound on the defect.
2. Treedepth
Say
![]() $G$
is a subgraph of the closure of some rooted tree
$G$
is a subgraph of the closure of some rooted tree
![]() $T$
. For each vertex
$T$
. For each vertex
![]() $v\in V(T)$
, let
$v\in V(T)$
, let
![]() $T_v$
be the maximal subtree of
$T_v$
be the maximal subtree of
![]() $T$
rooted at
$T$
rooted at
![]() $v$
(consisting of
$v$
(consisting of
![]() $v$
and all its descendants), and let
$v$
and all its descendants), and let
![]() $G[T_v]$
be the subgraph of
$G[T_v]$
be the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $V(T_v)$
.
$V(T_v)$
.
The weak closure of a rooted tree
![]() $T$
is the graph
$T$
is the graph
![]() $G$
with vertex set
$G$
with vertex set
![]() $V(T)$
, where two vertices
$V(T)$
, where two vertices
![]() $v,w\in V(T)$
are adjacent in
$v,w\in V(T)$
are adjacent in
![]() $G$
whenever
$G$
whenever
![]() $v$
is a leaf of
$v$
is a leaf of
![]() $T$
and
$T$
and
![]() $w$
is an ancestor of
$w$
is an ancestor of
![]() $v$
in
$v$
in
![]() $T$
. As illustrated in Figure 2, let
$T$
. As illustrated in Figure 2, let
![]() $W\langle{h,k}\rangle$
be the weak closure of the complete
$W\langle{h,k}\rangle$
be the weak closure of the complete
![]() $k$
-ary tree of height
$k$
-ary tree of height
![]() $h$
.
$h$
.

Figure 2. The weak closure
![]() $W\langle{4,2}\rangle$
.
$W\langle{4,2}\rangle$
.
Note that
![]() $W\langle{h,k}\rangle$
is a proper subgraph of
$W\langle{h,k}\rangle$
is a proper subgraph of
![]() $C\langle{h,k}\rangle$
for
$C\langle{h,k}\rangle$
for
![]() $h\geqslant 3$
. On the other hand, Norin et al. [Reference Norin, Scott, Seymour and Wood19] showed that
$h\geqslant 3$
. On the other hand, Norin et al. [Reference Norin, Scott, Seymour and Wood19] showed that
![]() $W\langle{h,k}\rangle$
contains
$W\langle{h,k}\rangle$
contains
![]() $C\langle{h,k-1}\rangle$
as a minor for all
$C\langle{h,k-1}\rangle$
as a minor for all
![]() $h,k\geqslant 2$
. Therefore, Theorem 1 is an immediate consequence of the following lemma.
$h,k\geqslant 2$
. Therefore, Theorem 1 is an immediate consequence of the following lemma.
Lemma 8.
For all
![]() $d,k,h\in \mathbb{N}$
there exists
$d,k,h\in \mathbb{N}$
there exists
![]() $c=c(d,k,h)\in \mathbb{N}$
such that for every graph
$c=c(d,k,h)\in \mathbb{N}$
such that for every graph
![]() $G$
with treedepth at most
$G$
with treedepth at most
![]() $d$
, either
$d$
, either
![]() $G$
contains a
$G$
contains a
![]() $W\langle{h,k}\rangle$
-minor or
$W\langle{h,k}\rangle$
-minor or
![]() $G$
is
$G$
is
![]() $(h-1)$
-colourable with clustering
$(h-1)$
-colourable with clustering
![]() $c$
.
$c$
.
Proof. Throughout this proof,
![]() $d$
,
$d$
,
![]() $k$
and
$k$
and
![]() $h$
are fixed, and we make no attempt to optimise
$h$
are fixed, and we make no attempt to optimise
![]() $c$
.
$c$
.
We may assume that
![]() $G$
is connected. So
$G$
is connected. So
![]() $G$
is a subgraph of the closure of some rooted tree of depth at most
$G$
is a subgraph of the closure of some rooted tree of depth at most
![]() $d$
. Choose a tree
$d$
. Choose a tree
![]() $T$
of depth at most
$T$
of depth at most
![]() $d$
rooted at some vertex
$d$
rooted at some vertex
![]() $r$
, such that
$r$
, such that
![]() $G$
is a subgraph of the closure of
$G$
is a subgraph of the closure of
![]() $T$
, and subject to this,
$T$
, and subject to this,
![]() $\sum _{v\in V(T)} \text{dist}_T(v,r)$
is minimal. Suppose that
$\sum _{v\in V(T)} \text{dist}_T(v,r)$
is minimal. Suppose that
![]() $G[T_v]$
is disconnected for some vertex
$G[T_v]$
is disconnected for some vertex
![]() $v$
in
$v$
in
![]() $T$
. Choose such a vertex
$T$
. Choose such a vertex
![]() $v$
at maximum distance from r. Since
$v$
at maximum distance from r. Since
![]() $G$
is connected,
$G$
is connected,
![]() $v\neq r$
. By the choice of
$v\neq r$
. By the choice of
![]() $v$
, for each child
$v$
, for each child
![]() $w$
of
$w$
of
![]() $v$
, the subgraph
$v$
, the subgraph
![]() $G[T_w]$
is connected. Thus, for some child
$G[T_w]$
is connected. Thus, for some child
![]() $w$
of
$w$
of
![]() $v$
, there is no edge in
$v$
, there is no edge in
![]() $G$
joining
$G$
joining
![]() $v$
and
$v$
and
![]() $G[T_w]$
. Let
$G[T_w]$
. Let
![]() $u$
be the parent of
$u$
be the parent of
![]() $v$
. Let
$v$
. Let
![]() $T'$
be obtained from
$T'$
be obtained from
![]() $T$
by deleting the edge
$T$
by deleting the edge
![]() $vw$
and adding the edge
$vw$
and adding the edge
![]() $uw$
, so that
$uw$
, so that
![]() $w$
is a child of
$w$
is a child of
![]() $u$
in
$u$
in
![]() $T'$
. Note that
$T'$
. Note that
![]() $G$
is a subgraph of the closure of
$G$
is a subgraph of the closure of
![]() $T'$
(since
$T'$
(since
![]() $v$
has no neighbour in
$v$
has no neighbour in
![]() $G[T_w]$
). Moreover,
$G[T_w]$
). Moreover,
![]() $\text{dist}_{T'}(x,r) = \text{dist}_T(x,r)-1$
for every vertex
$\text{dist}_{T'}(x,r) = \text{dist}_T(x,r)-1$
for every vertex
![]() $x\in V(T_w)$
, and
$x\in V(T_w)$
, and
![]() $\text{dist}_{T'}(y,r) = \text{dist}_T(y,r)$
for every vertex
$\text{dist}_{T'}(y,r) = \text{dist}_T(y,r)$
for every vertex
![]() $y\in V(T)\setminus V(T_w)$
. Hence,
$y\in V(T)\setminus V(T_w)$
. Hence,
![]() $\sum _{v\in V(T')} \text{dist}_{T'}(v,r)\lt \sum _{v\in V(T)} \text{dist}_T(v,r)$
, which contradicts our choice of
$\sum _{v\in V(T')} \text{dist}_{T'}(v,r)\lt \sum _{v\in V(T)} \text{dist}_T(v,r)$
, which contradicts our choice of
![]() $T$
. Therefore,
$T$
. Therefore,
![]() $G[T_v]$
is connected for every vertex
$G[T_v]$
is connected for every vertex
![]() $v$
of
$v$
of
![]() $T$
.
$T$
.
Consider each vertex
![]() $v\in V(T)$
. Define the level
$v\in V(T)$
. Define the level
![]() $\ell (v)\;:\!=\; \text{dist}_T(r,v) \in [0,d-1]$
. Let
$\ell (v)\;:\!=\; \text{dist}_T(r,v) \in [0,d-1]$
. Let
![]() $T^+_v$
be the subtree of
$T^+_v$
be the subtree of
![]() $T$
consisting of
$T$
consisting of
![]() $T_v$
plus the
$T_v$
plus the
![]() $vr$
-path in
$vr$
-path in
![]() $T$
, and let
$T$
, and let
![]() $G[T^+_v]$
be the subgraph of
$G[T^+_v]$
be the subgraph of
![]() $G$
induced by
$G$
induced by
![]() $V(T^+_v)$
. For a subtree
$V(T^+_v)$
. For a subtree
![]() $X$
of
$X$
of
![]() $T$
rooted at vertex
$T$
rooted at vertex
![]() $v$
, define the level
$v$
, define the level
![]() $\ell (X)\;:\!=\;\ell (v)$
.
$\ell (X)\;:\!=\;\ell (v)$
.
A ranked graph (for fixed
![]() $d$
) is a triple
$d$
) is a triple
![]() $(H,L,\preceq )$
where:
$(H,L,\preceq )$
where:
-
 $H$
is a graph,
$H$
is a graph, -
 $L\;:\;V(H)\rightarrow [0,d-1]$
is a function,
$L\;:\;V(H)\rightarrow [0,d-1]$
is a function, -
 $\preceq$
is a partial order on
$\preceq$
is a partial order on
 $V(H)$
such that
$V(H)$
such that
 $L(v) \lt L(w)$
whenever
$L(v) \lt L(w)$
whenever
 $v \prec w$
.
$v \prec w$
.
Here and throughout this proof,
![]() $v\prec w$
means that
$v\prec w$
means that
![]() $v\preceq w$
and
$v\preceq w$
and
![]() $v\neq w$
. Up to isomorphism, the number of ranked graphs on
$v\neq w$
. Up to isomorphism, the number of ranked graphs on
![]() $n$
vertices is at most
$n$
vertices is at most
![]() $2^{\binom{n}{2}}\,d^n\, 3^{\binom{n}{2}}$
. For a vertex
$2^{\binom{n}{2}}\,d^n\, 3^{\binom{n}{2}}$
. For a vertex
![]() $v$
of
$v$
of
![]() $T$
, a ranked graph
$T$
, a ranked graph
![]() $(H,L,\preceq )$
is said to be contained in
$(H,L,\preceq )$
is said to be contained in
![]() $G[T^+_v]$
if there is an isomorphism
$G[T^+_v]$
if there is an isomorphism
![]() $\phi$
from
$\phi$
from
![]() $H$
to some subgraph of
$H$
to some subgraph of
![]() $G[T^+_v]$
such that:
$G[T^+_v]$
such that:
-
(A) for each vertex
 $v\in V(H)$
we have
$v\in V(H)$
we have
 $L(v)=\ell (\phi (v))$
, and
$L(v)=\ell (\phi (v))$
, and -
(B) for all distinct vertices
 $v,w\in V(H)$
we have that
$v,w\in V(H)$
we have that
 $v\prec w$
if and only if
$v\prec w$
if and only if
 $\phi (v)$
is an ancestor of
$\phi (v)$
is an ancestor of
 $\phi (w)$
in
$\phi (w)$
in
 $T$
.
$T$
.
Say
![]() $(H,L,\preceq )$
is a ranked graph and
$(H,L,\preceq )$
is a ranked graph and
![]() $i\in [0,d-1]$
. Below we define the
$i\in [0,d-1]$
. Below we define the
![]() $i$
-splice of
$i$
-splice of
![]() $(H,L,\preceq )$
to be a particular ranked graph
$(H,L,\preceq )$
to be a particular ranked graph
![]() $(H',L',\preceq{\kern-2pt}')$
, which (intuitively speaking) is obtained from
$(H',L',\preceq{\kern-2pt}')$
, which (intuitively speaking) is obtained from
![]() $(H,L,\preceq )$
by copying
$(H,L,\preceq )$
by copying
![]() $k$
times the subgraph of
$k$
times the subgraph of
![]() $H$
induced by the vertices
$H$
induced by the vertices
![]() $v$
with
$v$
with
![]() $L(v)\gt i$
. Formally, let
$L(v)\gt i$
. Formally, let
 \begin{align*} V(H') \;:\!=\; & \{ (v,0) \;:\; v \in V(H), L(v) \in [0,i] \} \;\cup \\ & \{ (v,j) \;:\; v \in V(H), L(v) \in [i+1,d], j \in [1,k] \}.\\ E(H') \;:\!=\; & \{ (v,0)(w,0) \;:\; vw \in E(H), L(v) \in [0,i], L(w) \in [0,i] \} \;\cup \\ & \{ (v,0)(w,j) \;:\; vw \in E(H), L(v) \in [0,i], L(w) \in [i+1,d], j \in [1,k] \} \; \cup \\ & \{ (v,j)(w,j) \;:\; vw \in E(H), L(v)\in [i+1,d], L(w) \in [i+1,d], j \in [1,k] \}. \end{align*}
\begin{align*} V(H') \;:\!=\; & \{ (v,0) \;:\; v \in V(H), L(v) \in [0,i] \} \;\cup \\ & \{ (v,j) \;:\; v \in V(H), L(v) \in [i+1,d], j \in [1,k] \}.\\ E(H') \;:\!=\; & \{ (v,0)(w,0) \;:\; vw \in E(H), L(v) \in [0,i], L(w) \in [0,i] \} \;\cup \\ & \{ (v,0)(w,j) \;:\; vw \in E(H), L(v) \in [0,i], L(w) \in [i+1,d], j \in [1,k] \} \; \cup \\ & \{ (v,j)(w,j) \;:\; vw \in E(H), L(v)\in [i+1,d], L(w) \in [i+1,d], j \in [1,k] \}. \end{align*}
Define
![]() $L'((v,j)) \;:\!=\; L(v)$
for every vertex
$L'((v,j)) \;:\!=\; L(v)$
for every vertex
![]() $(v,j)\in V(H')$
. Now define the following partial order
$(v,j)\in V(H')$
. Now define the following partial order
![]() $\preceq{\kern-2pt}'$
on
$\preceq{\kern-2pt}'$
on
![]() $V(H')$
:
$V(H')$
:
-
 $(v,j)\preceq{\kern-2pt}' (v,j)$
for all
$(v,j)\preceq{\kern-2pt}' (v,j)$
for all
 $(v,j)\in V(H')$
;
$(v,j)\in V(H')$
; -
if
 $v \prec w$
and
$v \prec w$
and
 $L(v),L(w) \in [0,i]$
, then
$L(v),L(w) \in [0,i]$
, then
 $(v,0) \prec ' (w,0)$
;
$(v,0) \prec ' (w,0)$
; -
if
 $v \prec w$
and
$v \prec w$
and
 $L(v)\in [0,i]$
and
$L(v)\in [0,i]$
and
 $L(w) \in [i+1,d]$
, then
$L(w) \in [i+1,d]$
, then
 $(v,0) \prec ' (w,j)$
for all
$(v,0) \prec ' (w,j)$
for all
 $j\in [1,k]$
; and
$j\in [1,k]$
; and -
if
 $v \prec w$
and
$v \prec w$
and
 $L(v),L(w) \in [i+1,d]$
, then
$L(v),L(w) \in [i+1,d]$
, then
 $(v,j) \prec ' (w,j)$
for all
$(v,j) \prec ' (w,j)$
for all
 $j\in [1,k]$
.
$j\in [1,k]$
.
Note that if
![]() $(v,a)\prec ' (w,b)$
, then
$(v,a)\prec ' (w,b)$
, then
![]() $a\leqslant b$
and
$a\leqslant b$
and
![]() $v\prec w$
(implying
$v\prec w$
(implying
![]() $(L(v)\lt L(w)$
). It follows that
$(L(v)\lt L(w)$
). It follows that
![]() $\prec '$
is a partial order on
$\prec '$
is a partial order on
![]() $V(H')$
such that
$V(H')$
such that
![]() $L'((v,a)) \lt L'((w,b))$
whenever
$L'((v,a)) \lt L'((w,b))$
whenever
![]() $(v,a) \prec ' (w,b)$
. Thus,
$(v,a) \prec ' (w,b)$
. Thus,
![]() $(H',L',\preceq{\kern-2pt}')$
is a ranked graph.
$(H',L',\preceq{\kern-2pt}')$
is a ranked graph.
For
![]() $\ell \in [0,d-1]$
, let
$\ell \in [0,d-1]$
, let
For each vertex
![]() $v$
of
$v$
of
![]() $T$
, define the profile of
$T$
, define the profile of
![]() $v$
to be the set of all ranked graphs
$v$
to be the set of all ranked graphs
![]() $(H,L,\preceq )$
contained in
$(H,L,\preceq )$
contained in
![]() $G[T_v^+]$
such that
$G[T_v^+]$
such that
![]() $|V(H)| \leqslant N_{\ell (v)}$
. Note that if
$|V(H)| \leqslant N_{\ell (v)}$
. Note that if
![]() $v$
is a descendant of
$v$
is a descendant of
![]() $u$
, then the profile of
$u$
, then the profile of
![]() $v$
is a subset of the profile of
$v$
is a subset of the profile of
![]() $u$
. For
$u$
. For
![]() $\ell \in [0,d-1]$
, if
$\ell \in [0,d-1]$
, if
![]() $N=N_\ell$
then let
$N=N_\ell$
then let
Then there are at most
![]() $M_\ell$
possible profiles of a vertex at level
$M_\ell$
possible profiles of a vertex at level
![]() $\ell$
.
$\ell$
.
We now partition
![]() $V(T)$
into subtrees. Each subtree is called a group. (At the end of the proof, vertices in a single group will be assigned the same colour.) We assign vertices to groups in non-increasing order of their distance from the root. Initialise this process by placing each leaf
$V(T)$
into subtrees. Each subtree is called a group. (At the end of the proof, vertices in a single group will be assigned the same colour.) We assign vertices to groups in non-increasing order of their distance from the root. Initialise this process by placing each leaf
![]() $v$
of
$v$
of
![]() $T$
into a singleton group. We now show how to determine the group of a non-leaf vertex. Let
$T$
into a singleton group. We now show how to determine the group of a non-leaf vertex. Let
![]() $v$
be a vertex not assigned to a group at maximum distance from
$v$
be a vertex not assigned to a group at maximum distance from
![]() $r$
. So each child of
$r$
. So each child of
![]() $v$
is assigned to a group. Let
$v$
is assigned to a group. Let
![]() $Y_v$
be the set of children
$Y_v$
be the set of children
![]() $y$
of
$y$
of
![]() $v$
, such that the number of children of
$v$
, such that the number of children of
![]() $v$
that have the same profile as
$v$
that have the same profile as
![]() $y$
is in the range
$y$
is in the range
![]() $[1,k-1]$
. If
$[1,k-1]$
. If
![]() $Y_v =\emptyset$
start a new singleton group
$Y_v =\emptyset$
start a new singleton group
![]() $\{v\}$
. If
$\{v\}$
. If
![]() $Y_v\neq \emptyset$
then merge all the groups rooted at vertices in
$Y_v\neq \emptyset$
then merge all the groups rooted at vertices in
![]() $Y_v$
into one group including
$Y_v$
into one group including
![]() $v$
. This defines our partition of
$v$
. This defines our partition of
![]() $V(T)$
into groups. Each group
$V(T)$
into groups. Each group
![]() $X$
is rooted at the vertex in
$X$
is rooted at the vertex in
![]() $X$
closest to
$X$
closest to
![]() $r$
in
$r$
in
![]() $T$
. A group
$T$
. A group
![]() $Y$
is above a distinct group
$Y$
is above a distinct group
![]() $X$
if the root of
$X$
if the root of
![]() $Y$
is on the path in
$Y$
is on the path in
![]() $T$
from the root of
$T$
from the root of
![]() $X$
to
$X$
to
![]() $r$
.
$r$
.
The next claim is the key to the remainder of the proof.
Claim 1.
Let
![]() $uv\in E(T)$
where
$uv\in E(T)$
where
![]() $u$
is the parent of
$u$
is the parent of
![]() $v$
, and
$v$
, and
![]() $u$
is in a different group to
$u$
is in a different group to
![]() $v$
. Then for every ranked graph
$v$
. Then for every ranked graph
![]() $(H,L,\preceq )$
in the profile of
$(H,L,\preceq )$
in the profile of
![]() $v$
, the
$v$
, the
![]() $\ell (u)$
-splice of
$\ell (u)$
-splice of
![]() $(H,L,\preceq )$
is in the profile of
$(H,L,\preceq )$
is in the profile of
![]() $u$
.
$u$
.
Proof. Since
![]() $(H,L,\preceq )$
is in the profile of
$(H,L,\preceq )$
is in the profile of
![]() $v$
, there is an isomorphism
$v$
, there is an isomorphism
![]() $\phi$
from
$\phi$
from
![]() $H$
to some subgraph of
$H$
to some subgraph of
![]() $G[T^+_v]$
such that for each vertex
$G[T^+_v]$
such that for each vertex
![]() $x\in V(H)$
we have
$x\in V(H)$
we have
![]() $L(x)=\ell (\phi (x))$
, and for all distinct vertices
$L(x)=\ell (\phi (x))$
, and for all distinct vertices
![]() $x,y\in V(H)$
we have that
$x,y\in V(H)$
we have that
![]() $x\prec y$
if and only if
$x\prec y$
if and only if
![]() $\phi (x)$
is an ancestor of
$\phi (x)$
is an ancestor of
![]() $\phi (y)$
in
$\phi (y)$
in
![]() $T$
.
$T$
.
Since
![]() $u$
and
$u$
and
![]() $v$
are in different groups, there are
$v$
are in different groups, there are
![]() $k$
children
$k$
children
![]() $y_1,\ldots,y_k$
of
$y_1,\ldots,y_k$
of
![]() $u$
(one of which is
$u$
(one of which is
![]() $v$
) such that the profiles of
$v$
) such that the profiles of
![]() $y_1,\ldots,y_k$
are equal. Thus,
$y_1,\ldots,y_k$
are equal. Thus,
![]() $(H,L,\preceq )$
is in the profile of each of
$(H,L,\preceq )$
is in the profile of each of
![]() $y_1,\ldots,y_k$
. That is, for each
$y_1,\ldots,y_k$
. That is, for each
![]() $j\in [1,k]$
, there is an isomorphism
$j\in [1,k]$
, there is an isomorphism
![]() $\phi _j$
from
$\phi _j$
from
![]() $H$
to some subgraph of
$H$
to some subgraph of
![]() $G[T^+_{y_j}]$
such that for each vertex
$G[T^+_{y_j}]$
such that for each vertex
![]() $x\in V(H)$
we have
$x\in V(H)$
we have
![]() $L(x)=\ell (\phi _j(x))$
, and for all distinct vertices
$L(x)=\ell (\phi _j(x))$
, and for all distinct vertices
![]() $x,y\in V(H)$
we have that
$x,y\in V(H)$
we have that
![]() $x\prec y$
if and only if
$x\prec y$
if and only if
![]() $\phi _j(x)$
is an ancestor of
$\phi _j(x)$
is an ancestor of
![]() $\phi _j(y)$
in
$\phi _j(y)$
in
![]() $T$
.
$T$
.
Let
![]() $(H',L',\preceq{\kern-2pt}')$
be the
$(H',L',\preceq{\kern-2pt}')$
be the
![]() $\ell (u)$
-splice of
$\ell (u)$
-splice of
![]() $(H,L,\preceq )$
. We now define a function
$(H,L,\preceq )$
. We now define a function
![]() $\phi '$
from
$\phi '$
from
![]() $V(H')$
to
$V(H')$
to
![]() $V( G[ T^+_u] )$
. For each vertex
$V( G[ T^+_u] )$
. For each vertex
![]() $(x,0)$
of
$(x,0)$
of
![]() $H'$
(thus with
$H'$
(thus with
![]() $x\in V(H)$
and
$x\in V(H)$
and
![]() $L(x)\in [0,\ell (u)]$
), define
$L(x)\in [0,\ell (u)]$
), define
![]() $\phi '((x,0)) \;:\!=\; \phi (x)$
. For every other vertex
$\phi '((x,0)) \;:\!=\; \phi (x)$
. For every other vertex
![]() $(x,j)$
of
$(x,j)$
of
![]() $H'$
(thus with
$H'$
(thus with
![]() $x\in V(H)$
and
$x\in V(H)$
and
![]() $L(x)\in [\ell (u)+1,d-1]$
and
$L(x)\in [\ell (u)+1,d-1]$
and
![]() $j\in [1,k]$
), define
$j\in [1,k]$
), define
![]() $\phi '((x,j)) \;:\!=\; \phi _j(x)$
.
$\phi '((x,j)) \;:\!=\; \phi _j(x)$
.
We now show that
![]() $\phi '$
is an isomorphism from
$\phi '$
is an isomorphism from
![]() $H'$
to a subgraph of
$H'$
to a subgraph of
![]() $G[T^+_u]$
. Consider an edge
$G[T^+_u]$
. Consider an edge
![]() $(x,a)(y,b)$
of
$(x,a)(y,b)$
of
![]() $H'$
. Thus,
$H'$
. Thus,
![]() $xy\in E(H)$
. It suffices to show that
$xy\in E(H)$
. It suffices to show that
![]() $\phi '((x,a))\phi '((y,b))\in E(G[T^+_u])$
. First suppose that
$\phi '((x,a))\phi '((y,b))\in E(G[T^+_u])$
. First suppose that
![]() $a=b=0$
. So
$a=b=0$
. So
![]() $L(x)\in [0,\ell (u)]$
and
$L(x)\in [0,\ell (u)]$
and
![]() $L(y)\in [0,\ell (u)]$
. Thus
$L(y)\in [0,\ell (u)]$
. Thus
![]() $\phi '((x,a))=\phi (x)$
and
$\phi '((x,a))=\phi (x)$
and
![]() $\phi '((y,b))=\phi (y)$
. Since
$\phi '((y,b))=\phi (y)$
. Since
![]() $\phi$
is an isomorphism to a subgraph of
$\phi$
is an isomorphism to a subgraph of
![]() $G[ T^+_v]$
, we have
$G[ T^+_v]$
, we have
![]() $\phi (x)\phi (y) \in E(G[ T^+_v] )$
, which is a subgraph of
$\phi (x)\phi (y) \in E(G[ T^+_v] )$
, which is a subgraph of
![]() $G[ T^+_u]$
. Hence,
$G[ T^+_u]$
. Hence,
![]() $\phi '((x,a))\phi '((y,b)) \in E(G[ T^+_u] )$
, as desired. Now suppose that
$\phi '((x,a))\phi '((y,b)) \in E(G[ T^+_u] )$
, as desired. Now suppose that
![]() $a=0$
and
$a=0$
and
![]() $b\in [1,k]$
. Thus,
$b\in [1,k]$
. Thus,
![]() $\phi '((x,a))=\phi (x)$
and
$\phi '((x,a))=\phi (x)$
and
![]() $\phi '((y,b))=\phi _b(y)$
. Moreover, both
$\phi '((y,b))=\phi _b(y)$
. Moreover, both
![]() $\ell (\phi (x))$
and
$\ell (\phi (x))$
and
![]() $\ell (\phi _b(x))$
equal
$\ell (\phi _b(x))$
equal
![]() $L(x)\in [0,\ell (u)]$
. There is only vertex
$L(x)\in [0,\ell (u)]$
. There is only vertex
![]() $z$
in
$z$
in
![]() $T^+_v$
with
$T^+_v$
with
![]() $\ell (z)$
equal to a specific number in
$\ell (z)$
equal to a specific number in
![]() $[0,\ell (u)]$
. Thus,
$[0,\ell (u)]$
. Thus,
![]() $\phi '((x,a))=\phi (x)=\phi _b(x)$
(
$\phi '((x,a))=\phi (x)=\phi _b(x)$
(
![]() $=z$
). Since
$=z$
). Since
![]() $\phi _b$
is an isomorphism to a subgraph of
$\phi _b$
is an isomorphism to a subgraph of
![]() $G[ T^+_{y_b}]$
, we have
$G[ T^+_{y_b}]$
, we have
![]() $\phi _b(x)\phi _b(y) \in E(G[ T^+_{y_b}] )$
, which is a subgraph of
$\phi _b(x)\phi _b(y) \in E(G[ T^+_{y_b}] )$
, which is a subgraph of
![]() $G[ T^+_u]$
. Hence,
$G[ T^+_u]$
. Hence,
![]() $\phi '((x,a))\phi '((y,b)) \in E(G[ T^+_u] )$
, as desired. Finally, suppose that
$\phi '((x,a))\phi '((y,b)) \in E(G[ T^+_u] )$
, as desired. Finally, suppose that
![]() $a=b\in [1,k]$
. Thus,
$a=b\in [1,k]$
. Thus,
![]() $\phi '((x,a))=\phi _a(x)$
and
$\phi '((x,a))=\phi _a(x)$
and
![]() $\phi '((y,b))=\phi _b(y)=\phi _a(y)$
. Since
$\phi '((y,b))=\phi _b(y)=\phi _a(y)$
. Since
![]() $\phi _a$
is an isomorphism to a subgraph of
$\phi _a$
is an isomorphism to a subgraph of
![]() $G[ T^+_{y_a}]$
, we have
$G[ T^+_{y_a}]$
, we have
![]() $\phi _a(x)\phi _a(y) \in E(G[ T^+_{y_a}] )$
, which is a subgraph of
$\phi _a(x)\phi _a(y) \in E(G[ T^+_{y_a}] )$
, which is a subgraph of
![]() $G[ T^+_u]$
. Hence,
$G[ T^+_u]$
. Hence,
![]() $\phi '((x,a))\phi '((y,b)) \in E(G[ T^+_u] )$
, as desired. This shows that
$\phi '((x,a))\phi '((y,b)) \in E(G[ T^+_u] )$
, as desired. This shows that
![]() $\phi '$
is an isomorphism from
$\phi '$
is an isomorphism from
![]() $H'$
to a subgraph of
$H'$
to a subgraph of
![]() $G[T^+_u]$
.
$G[T^+_u]$
.
We now verify property (A) for
![]() $(H',L',\preceq{\kern-2pt}')$
. For each vertex
$(H',L',\preceq{\kern-2pt}')$
. For each vertex
![]() $(x,0)$
of
$(x,0)$
of
![]() $H'$
(thus with
$H'$
(thus with
![]() $x\in V(H)$
and
$x\in V(H)$
and
![]() $L(x)\in [0,\ell (u)]$
) we have
$L(x)\in [0,\ell (u)]$
) we have
![]() $L'((x,0))=L(x)= \ell (\phi (x)) = \ell (\phi '((x,0)))$
, as desired. For every other vertex
$L'((x,0))=L(x)= \ell (\phi (x)) = \ell (\phi '((x,0)))$
, as desired. For every other vertex
![]() $(x,j)$
of
$(x,j)$
of
![]() $H'$
(thus with
$H'$
(thus with
![]() $x\in V(H)$
and
$x\in V(H)$
and
![]() $L(x)\in [\ell (u)+1,d-1]$
and
$L(x)\in [\ell (u)+1,d-1]$
and
![]() $j\in [1,k]$
) we have
$j\in [1,k]$
) we have
![]() $L'((x,j))=L(x)= \ell (\phi _j(x)) = \ell (\phi '((x,j)))$
, as desired. Hence, property (A) is satisfied for
$L'((x,j))=L(x)= \ell (\phi _j(x)) = \ell (\phi '((x,j)))$
, as desired. Hence, property (A) is satisfied for
![]() $(H',L',\preceq{\kern-2pt}')$
.
$(H',L',\preceq{\kern-2pt}')$
.
We now verify property (B) for
![]() $(H',L',\preceq{\kern-2pt}')$
. Consider distinct vertices
$(H',L',\preceq{\kern-2pt}')$
. Consider distinct vertices
![]() $(x,a),(y,b)\in V(H')$
. First suppose that
$(x,a),(y,b)\in V(H')$
. First suppose that
![]() $a=0$
and
$a=0$
and
![]() $b=0$
. Then
$b=0$
. Then
![]() $(x,a) \prec ' (y,b)$
if and only if
$(x,a) \prec ' (y,b)$
if and only if
![]() $x \prec y$
if and only if
$x \prec y$
if and only if
![]() $\phi (x)$
is an ancestor of
$\phi (x)$
is an ancestor of
![]() $\phi (y)$
in
$\phi (y)$
in
![]() $T$
if and only if
$T$
if and only if
![]() $\phi '((x,a))$
is an ancestor of
$\phi '((x,a))$
is an ancestor of
![]() $\phi '((y,b))$
in
$\phi '((y,b))$
in
![]() $T$
, as desired. Now suppose that
$T$
, as desired. Now suppose that
![]() $a=0$
and
$a=0$
and
![]() $b\in [1,k]$
. Then
$b\in [1,k]$
. Then
![]() $(x,a) \prec ' (y,b)$
if and only if
$(x,a) \prec ' (y,b)$
if and only if
![]() $x \prec y$
if and only if
$x \prec y$
if and only if
![]() $\phi (x)$
is an ancestor of
$\phi (x)$
is an ancestor of
![]() $\phi _b(y)$
in
$\phi _b(y)$
in
![]() $T$
if and only if
$T$
if and only if
![]() $\phi '((x,a))$
is an ancestor of
$\phi '((x,a))$
is an ancestor of
![]() $\phi '((y,b))$
in
$\phi '((y,b))$
in
![]() $T$
, as desired. Now suppose that
$T$
, as desired. Now suppose that
![]() $a=b\in [1,k]$
. Then
$a=b\in [1,k]$
. Then
![]() $(x,a) \prec ' (y,b)$
if and only if
$(x,a) \prec ' (y,b)$
if and only if
![]() $x \prec y$
if and only if
$x \prec y$
if and only if
![]() $\phi _a(x)$
is an ancestor of
$\phi _a(x)$
is an ancestor of
![]() $\phi _b(y)$
in
$\phi _b(y)$
in
![]() $T$
if and only if
$T$
if and only if
![]() $\phi '((x,a))$
is an ancestor of
$\phi '((x,a))$
is an ancestor of
![]() $\phi '((y,b))$
in
$\phi '((y,b))$
in
![]() $T$
, as desired. Finally, suppose that
$T$
, as desired. Finally, suppose that
![]() $a,b\in [1,k]$
and
$a,b\in [1,k]$
and
![]() $a\neq b$
. Then
$a\neq b$
. Then
![]() $(x,a)$
and
$(x,a)$
and
![]() $(y,b)$
are incomparable under
$(y,b)$
are incomparable under
![]() $\prec '$
, and
$\prec '$
, and
![]() $\phi '((x,a))$
and
$\phi '((x,a))$
and
![]() $\phi '((y,b))$
in
$\phi '((y,b))$
in
![]() $T$
are unrelated in
$T$
are unrelated in
![]() $T$
, as desired. Hence, property (B) is satisfied for
$T$
, as desired. Hence, property (B) is satisfied for
![]() $(H',L',\preceq{\kern-2pt}')$
.
$(H',L',\preceq{\kern-2pt}')$
.
So
![]() $\phi '$
is an isomorphism from
$\phi '$
is an isomorphism from
![]() $H'$
to a subgraph of
$H'$
to a subgraph of
![]() $G[T^+_u]$
satisfying properties (A) and (B). Thus
$G[T^+_u]$
satisfying properties (A) and (B). Thus
![]() $(H',L',\preceq{\kern-2pt}')$
is contained in
$(H',L',\preceq{\kern-2pt}')$
is contained in
![]() $G[T^+_u]$
, as desired. Since
$G[T^+_u]$
, as desired. Since
![]() $(H,L,\preceq )$
is in the profile of
$(H,L,\preceq )$
is in the profile of
![]() $v$
, we have
$v$
, we have
![]() $|V(H)| \leqslant (d+1)(h-1)(k+1)^{h-\ell (v)}$
. Since
$|V(H)| \leqslant (d+1)(h-1)(k+1)^{h-\ell (v)}$
. Since
![]() $|V(H')|\leqslant (k+1) |V(H)|$
and
$|V(H')|\leqslant (k+1) |V(H)|$
and
![]() $\ell (u)=\ell (v)-1$
, we have
$\ell (u)=\ell (v)-1$
, we have
![]() $|V(H')| \leqslant (d+1)(h-1)(k+1)^{h+1-\ell (v)} = (d+1)(h-1)(k+1)^{h-\ell (u)}$
. Thus,
$|V(H')| \leqslant (d+1)(h-1)(k+1)^{h+1-\ell (v)} = (d+1)(h-1)(k+1)^{h-\ell (u)}$
. Thus,
![]() $(H',L',\preceq{\kern-2pt}')$
is in the profile of
$(H',L',\preceq{\kern-2pt}')$
is in the profile of
![]() $u$
.
$u$
.
The proof now divides into two cases. If some group
![]() $X_0$
is adjacent in
$X_0$
is adjacent in
![]() $G$
to at least
$G$
to at least
![]() $h-1$
other groups above
$h-1$
other groups above
![]() $X_0$
, then we show that
$X_0$
, then we show that
![]() $G$
contains
$G$
contains
![]() $W\langle{h,k}\rangle$
as a minor. Otherwise, every group
$W\langle{h,k}\rangle$
as a minor. Otherwise, every group
![]() $X$
is adjacent in
$X$
is adjacent in
![]() $G$
to at most
$G$
to at most
![]() $h-2$
other groups above
$h-2$
other groups above
![]() $X$
, in which case we show that
$X$
, in which case we show that
![]() $G$
is
$G$
is
![]() $(h-1)$
-colourable with bounded clustering.
$(h-1)$
-colourable with bounded clustering.
Finding the minor
Suppose that some group
![]() $X_0$
is adjacent in
$X_0$
is adjacent in
![]() $G$
to at least
$G$
to at least
![]() $h-1$
other groups
$h-1$
other groups
![]() $X_1,\ldots,X_{h-1}$
above
$X_1,\ldots,X_{h-1}$
above
![]() $X_0$
. We now show that
$X_0$
. We now show that
![]() $G$
contains
$G$
contains
![]() $W\langle{h,k}\rangle$
as a minor; refer to Figure 3. For
$W\langle{h,k}\rangle$
as a minor; refer to Figure 3. For
![]() $i\in [1,h-1]$
, since
$i\in [1,h-1]$
, since
![]() $X_i$
is above
$X_i$
is above
![]() $X_0$
, the root
$X_0$
, the root
![]() $v_i$
of
$v_i$
of
![]() $X_i$
is on the
$X_i$
is on the
![]() $v_0r$
-path in
$v_0r$
-path in
![]() $T$
. Without loss of generality,
$T$
. Without loss of generality,
![]() $v_0,v_1,\ldots,v_{h-1}$
appear in this order on the
$v_0,v_1,\ldots,v_{h-1}$
appear in this order on the
![]() $v_0r$
-path in
$v_0r$
-path in
![]() $T$
. For
$T$
. For
![]() $i\in [1,h-1]$
, let
$i\in [1,h-1]$
, let
![]() $w_i$
be a vertex in
$w_i$
be a vertex in
![]() $X_i$
adjacent to some vertex
$X_i$
adjacent to some vertex
![]() $z_i$
in
$z_i$
in
![]() $X_0$
; since
$X_0$
; since
![]() $G$
is a subgraph of the closure of
$G$
is a subgraph of the closure of
![]() $T$
,
$T$
,
![]() $w_i$
is on the
$w_i$
is on the
![]() $v_0r$
-path in
$v_0r$
-path in
![]() $T$
. For
$T$
. For
![]() $i\in [0,h-2]$
, let
$i\in [0,h-2]$
, let
![]() $u_i$
be the parent of
$u_i$
be the parent of
![]() $v_i$
in
$v_i$
in
![]() $T$
(which exists since
$T$
(which exists since
![]() $v_{h-2}\neq r$
). So
$v_{h-2}\neq r$
). So
![]() $u_i$
is not in
$u_i$
is not in
![]() $X_i$
(but may be in
$X_i$
(but may be in
![]() $X_{i+1}$
). Note that
$X_{i+1}$
). Note that
![]() $v_0,u_0,w_1,v_1,u_1,\ldots,w_{h-2},v_{h-2},u_{h-2},w_{h-1},v_{h-1}$
appear in this order on the
$v_0,u_0,w_1,v_1,u_1,\ldots,w_{h-2},v_{h-2},u_{h-2},w_{h-1},v_{h-1}$
appear in this order on the
![]() $v_0r$
-path in
$v_0r$
-path in
![]() $T$
, where
$T$
, where
![]() $v_0,v_1,\ldots,v_{h-1}$
are distinct (since they are in distinct groups).
$v_0,v_1,\ldots,v_{h-1}$
are distinct (since they are in distinct groups).
Let
![]() $P_j$
be the
$P_j$
be the
![]() $z_jr$
-path in
$z_jr$
-path in
![]() $T$
for
$T$
for
![]() $j\in [1,h-1]$
. Let
$j\in [1,h-1]$
. Let
![]() $H_0$
be the graph with
$H_0$
be the graph with
![]() $V(H_0)\;:\!=\;V( P_1\cup \ldots \cup P_{h-1} )$
and
$V(H_0)\;:\!=\;V( P_1\cup \ldots \cup P_{h-1} )$
and
![]() $E(H_0) \;:\!=\; \{z_jw_j\;:\;j\in [1,h-1]\}$
. Define the function
$E(H_0) \;:\!=\; \{z_jw_j\;:\;j\in [1,h-1]\}$
. Define the function
![]() $L_0\;:\;V(H_0)\to [0,d-1]$
by
$L_0\;:\;V(H_0)\to [0,d-1]$
by
![]() $L_0(x)\;:\!=\;\ell (x)$
for each
$L_0(x)\;:\!=\;\ell (x)$
for each
![]() $x\in V(H_0)$
. Define the partial order
$x\in V(H_0)$
. Define the partial order
![]() $\preceq _0$
on
$\preceq _0$
on
![]() $V(H_0)$
, where
$V(H_0)$
, where
![]() $x\prec _0 y$
if and only if
$x\prec _0 y$
if and only if
![]() $x$
is ancestor of
$x$
is ancestor of
![]() $y$
in
$y$
in
![]() $T$
. Thus,
$T$
. Thus,
![]() $(H_0,L_0,\preceq _0)$
is a ranked graph. By construction,
$(H_0,L_0,\preceq _0)$
is a ranked graph. By construction,
![]() $(H_0,L_0,\preceq _0\!)$
is contained in
$(H_0,L_0,\preceq _0\!)$
is contained in
![]() $G[T^+_{v_0}]$
. Since
$G[T^+_{v_0}]$
. Since
![]() $H_0$
has less than
$H_0$
has less than
![]() $(d+1)(h-1)$
vertices,
$(d+1)(h-1)$
vertices,
![]() $H_0$
is in the profile of
$H_0$
is in the profile of
![]() $v_0$
. For
$v_0$
. For
![]() $i=0,1,\ldots,h-2$
, let
$i=0,1,\ldots,h-2$
, let
![]() $(H_{i+1},L_{i+1},\prec _{i+1})$
be the
$(H_{i+1},L_{i+1},\prec _{i+1})$
be the
![]() $\ell (u_i)$
-splice of
$\ell (u_i)$
-splice of
![]() $(H_i,L_i,\prec _i\!)$
.
$(H_i,L_i,\prec _i\!)$
.
By induction on
![]() $i$
, using Claim 1 at each step and since
$i$
, using Claim 1 at each step and since
![]() $G[T^+_{u_i}]\subseteq G[T^+_{v_{i+1}}\!]$
, we conclude that for each
$G[T^+_{u_i}]\subseteq G[T^+_{v_{i+1}}\!]$
, we conclude that for each
![]() $i\in [0,h-1]$
, the ranked graph
$i\in [0,h-1]$
, the ranked graph
![]() $(H_i,L_i,\preceq _i)$
is in the profile of
$(H_i,L_i,\preceq _i)$
is in the profile of
![]() $v_i$
. In particular,
$v_i$
. In particular,
![]() $(H_{h-1},L_{h-1},\prec _{h-1})$
is in the profile of
$(H_{h-1},L_{h-1},\prec _{h-1})$
is in the profile of
![]() $v_{h-1}$
, and
$v_{h-1}$
, and
![]() $H_{h-1}$
is isomorphic to a subgraph of
$H_{h-1}$
is isomorphic to a subgraph of
![]() $G$
. Note that each vertex of
$G$
. Note that each vertex of
![]() $H_{h-1}$
is of the form
$H_{h-1}$
is of the form
![]() $(((\ldots (x,d_1),d_2),\ldots ),d_{h-1})$
for some
$(((\ldots (x,d_1),d_2),\ldots ),d_{h-1})$
for some
![]() $x\in V(H_0)$
and
$x\in V(H_0)$
and
![]() $d_1,\ldots,d_{h-1}\in [0,k]$
. For brevity, call such a vertex
$d_1,\ldots,d_{h-1}\in [0,k]$
. For brevity, call such a vertex
![]() $x\langle{d_1,\ldots,d_{h-1}\rangle }$
. Note that if
$x\langle{d_1,\ldots,d_{h-1}\rangle }$
. Note that if
![]() $x=w_j$
for some
$x=w_j$
for some
![]() $j\in [1,h-1]$
, then
$j\in [1,h-1]$
, then
![]() $d_1=\ldots =d_j=0$
(since
$d_1=\ldots =d_j=0$
(since
![]() $w_j$
is above
$w_j$
is above
![]() $u_i$
whenever
$u_i$
whenever
![]() $i\lt j$
, and
$i\lt j$
, and
![]() $(H_{i+1},L_{i+1},\prec _{i+1}\!)$
is the
$(H_{i+1},L_{i+1},\prec _{i+1}\!)$
is the
![]() $\ell (u_i)$
-splice of
$\ell (u_i)$
-splice of
![]() $(H_i,L_i,\preceq _i\!)$
).
$(H_i,L_i,\preceq _i\!)$
).

Figure 3. Construction of a
![]() $W\langle{4,k}\rangle$
minor (where
$W\langle{4,k}\rangle$
minor (where
![]() $u_i$
might be in
$u_i$
might be in
![]() $X_{i+1}$
).
$X_{i+1}$
).
For
![]() $x\in V(H_0)$
, let
$x\in V(H_0)$
, let
![]() $\Lambda _x$
be the set of vertices
$\Lambda _x$
be the set of vertices
![]() $x\langle{d_1,\ldots,d_{h-1}\rangle }$
in
$x\langle{d_1,\ldots,d_{h-1}\rangle }$
in
![]() $H_{h-1}$
. By construction, no two vertices in
$H_{h-1}$
. By construction, no two vertices in
![]() $\Lambda _x$
are comparable under
$\Lambda _x$
are comparable under
![]() $\preceq _{h-1}$
. Therefore, by property (B),
$\preceq _{h-1}$
. Therefore, by property (B),
![]() $V(T_a)\cap V(T_b)=\emptyset$
for all distinct
$V(T_a)\cap V(T_b)=\emptyset$
for all distinct
![]() $a,b\in \Lambda _x$
. In particular,
$a,b\in \Lambda _x$
. In particular,
![]() $V(T_{a})\cap V(T_b)=\emptyset$
for all distinct
$V(T_{a})\cap V(T_b)=\emptyset$
for all distinct
![]() $a,b\in \Lambda _{v_0}$
. As proved above,
$a,b\in \Lambda _{v_0}$
. As proved above,
![]() $G[T_a]$
is connected for each
$G[T_a]$
is connected for each
![]() $a\in V(T)$
. Let
$a\in V(T)$
. Let
![]() $G'$
be the graph obtained from
$G'$
be the graph obtained from
![]() $G$
by contracting
$G$
by contracting
![]() $G[T_a]$
into a single vertex
$G[T_a]$
into a single vertex
![]() $\alpha{\kern-1pt}\langle{d_1,\ldots,d_{h-1}\rangle }$
, for each
$\alpha{\kern-1pt}\langle{d_1,\ldots,d_{h-1}\rangle }$
, for each
![]() $a=v_0\langle{d_1,\ldots,d_{h-1}\rangle } \in \Lambda _{v_0}$
. So
$a=v_0\langle{d_1,\ldots,d_{h-1}\rangle } \in \Lambda _{v_0}$
. So
![]() $G'$
is a minor of
$G'$
is a minor of
![]() $G$
.
$G$
.
Let
![]() $U$
be the tree with vertex set
$U$
be the tree with vertex set
where the parent of
![]() $(0,\ldots,0,d_{j+1},d_{j+2},\ldots,d_{h-1})$
is
$(0,\ldots,0,d_{j+1},d_{j+2},\ldots,d_{h-1})$
is
![]() $(0,\ldots,0,d_{j+2},\ldots,d_{h-1})$
. Then
$(0,\ldots,0,d_{j+2},\ldots,d_{h-1})$
. Then
![]() $U$
is isomorphic to the complete
$U$
is isomorphic to the complete
![]() $k$
-tree of height
$k$
-tree of height
![]() $h$
rooted at
$h$
rooted at
![]() $\langle 0,\ldots,0\rangle$
. We now show that the weak closure of
$\langle 0,\ldots,0\rangle$
. We now show that the weak closure of
![]() $U$
is a subgraph of
$U$
is a subgraph of
![]() $G$
′, where each vertex
$G$
′, where each vertex
![]() $\langle 0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle$
of
$\langle 0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle$
of
![]() $U$
with
$U$
with
![]() $j\in [1,h-1]$
is mapped to vertex
$j\in [1,h-1]$
is mapped to vertex
![]() $w_j\langle 0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle$
of
$w_j\langle 0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle$
of
![]() $G'$
, and each other vertex
$G'$
, and each other vertex
![]() $\langle d_1,\ldots,d_{h-1}\rangle$
of
$\langle d_1,\ldots,d_{h-1}\rangle$
of
![]() $U$
is mapped to
$U$
is mapped to
![]() $\alpha \langle d_1,\ldots,d_{h-1}\rangle$
of
$\alpha \langle d_1,\ldots,d_{h-1}\rangle$
of
![]() $G'$
. For all
$G'$
. For all
![]() $d_1,\ldots,d_{h-1}\in [1,k]$
and
$d_1,\ldots,d_{h-1}\in [1,k]$
and
![]() $j\in [1,h-1]$
the vertex
$j\in [1,h-1]$
the vertex
![]() $z_j\langle{d_1,\ldots,d_{h-1}\rangle }$
of
$z_j\langle{d_1,\ldots,d_{h-1}\rangle }$
of
![]() $G$
is contracted into the vertex
$G$
is contracted into the vertex
![]() $\alpha \langle{d_1,\ldots,d_{h-1}\rangle }$
of
$\alpha \langle{d_1,\ldots,d_{h-1}\rangle }$
of
![]() $G'$
. By construction,
$G'$
. By construction,
![]() $z_j\langle{d_1,\ldots,d_{h-1}\rangle }$
is adjacent to
$z_j\langle{d_1,\ldots,d_{h-1}\rangle }$
is adjacent to
![]() $w_j\langle{0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle }$
in
$w_j\langle{0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle }$
in
![]() $G$
. So
$G$
. So
![]() $\alpha \langle{d_1,\ldots,d_{h-1}\rangle }$
is adjacent to
$\alpha \langle{d_1,\ldots,d_{h-1}\rangle }$
is adjacent to
![]() $w_j\langle{0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle }$
in
$w_j\langle{0,\ldots,0,d_{j+1},\ldots,d_{h-1}\rangle }$
in
![]() $G'$
. This implies that the weak closure of
$G'$
. This implies that the weak closure of
![]() $U$
(that is,
$U$
(that is,
![]() $W\langle{h,k}\rangle$
) is isomorphic to a subgraph of
$W\langle{h,k}\rangle$
) is isomorphic to a subgraph of
![]() $G$
’, and is therefore a minor of
$G$
’, and is therefore a minor of
![]() $G$
.
$G$
.
Finding the colouring
Now assume that every group
![]() $X$
is adjacent in
$X$
is adjacent in
![]() $G$
to at most
$G$
to at most
![]() $h-2$
other groups above
$h-2$
other groups above
![]() $X$
. Then
$X$
. Then
![]() $(h-1)$
-colour the groups in order of distance from the root, such that every group
$(h-1)$
-colour the groups in order of distance from the root, such that every group
![]() $X$
is assigned a colour different from the colours assigned to the neighbouring groups above
$X$
is assigned a colour different from the colours assigned to the neighbouring groups above
![]() $X$
. Assign each vertex within a group the same colour as that assigned to the whole group. This defines an
$X$
. Assign each vertex within a group the same colour as that assigned to the whole group. This defines an
![]() $(h-1)$
-colouring of
$(h-1)$
-colouring of
![]() $G$
.
$G$
.
Consider the function
![]() $s\;:\;[0,d-1]\to \mathbb{N}$
recursively defined by
$s\;:\;[0,d-1]\to \mathbb{N}$
recursively defined by
 \begin{equation*} s(\ell ) \;:\!=\; \begin {cases} 1 & \text { if }\ell =d-1\\ (k-1) \cdot M_{\ell +1} \cdot s(\ell +1) & \text { if } \ell \in [0,d-2]. \end {cases} \end{equation*}
\begin{equation*} s(\ell ) \;:\!=\; \begin {cases} 1 & \text { if }\ell =d-1\\ (k-1) \cdot M_{\ell +1} \cdot s(\ell +1) & \text { if } \ell \in [0,d-2]. \end {cases} \end{equation*}
Then every group at level
![]() $\ell$
has at most
$\ell$
has at most
![]() $s(\ell )$
vertices. By construction, our
$s(\ell )$
vertices. By construction, our
![]() $(h-1)$
-colouring of
$(h-1)$
-colouring of
![]() $G$
has clustering
$G$
has clustering
![]() $s(0)$
, which is bounded by a function of
$s(0)$
, which is bounded by a function of
![]() $d$
,
$d$
,
![]() $k$
and
$k$
and
![]() $h$
, as desired.
$h$
, as desired.
3. Pathwidth
The following lemma of independent interest is the key to proving Theorem 2. Note that Eppstein [Reference Eppstein24] independently discovered the same result (with a slightly weaker bound on the path length). The decomposition method in the proof has been previously used, for example, by Dujmović, Joret, Kozik, and Wood [Reference Dujmović, Joret, Kozik and Wood25, Lemma 17].
Lemma 9.
Every graph with pathwidth at most
![]() $w$
has a vertex 2-colouring such that each monochromatic path has at most
$w$
has a vertex 2-colouring such that each monochromatic path has at most
![]() $(w+3)^w$
vertices.
$(w+3)^w$
vertices.
Proof. We proceed by induction on
![]() $w\geqslant 1$
. Every graph with pathwidth 1 is a caterpillar, and is thus properly 2-colourable. Now assume
$w\geqslant 1$
. Every graph with pathwidth 1 is a caterpillar, and is thus properly 2-colourable. Now assume
![]() $w\geqslant 2$
and the result holds for graphs with pathwidth at most
$w\geqslant 2$
and the result holds for graphs with pathwidth at most
![]() $w-1$
. Let
$w-1$
. Let
![]() $G$
be a graph with pathwidth at most
$G$
be a graph with pathwidth at most
![]() $w$
. Let
$w$
. Let
![]() $(B_1,\ldots,B_n)$
be a path-decomposition of
$(B_1,\ldots,B_n)$
be a path-decomposition of
![]() $G$
with width at most
$G$
with width at most
![]() $w$
. Let
$w$
. Let
![]() $t_1,t_2,\ldots,t_m$
be a maximal sequence such that
$t_1,t_2,\ldots,t_m$
be a maximal sequence such that
![]() $t_1=1$
and for each
$t_1=1$
and for each
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
![]() $t_i$
is the minimum integer such that
$t_i$
is the minimum integer such that
![]() $B_{t_i} \cap B_{t_{i-1}}=\emptyset$
. For odd
$B_{t_i} \cap B_{t_{i-1}}=\emptyset$
. For odd
![]() $i$
, colour every vertex in
$i$
, colour every vertex in
![]() $B_{t_i}$
‘red’. For even
$B_{t_i}$
‘red’. For even
![]() $i$
, colour every vertex in
$i$
, colour every vertex in
![]() $B_{t_i}$
‘blue’. Since
$B_{t_i}$
‘blue’. Since
![]() $B_{t_i} \cap B_{t_{i-1}}=\emptyset$
for
$B_{t_i} \cap B_{t_{i-1}}=\emptyset$
for
![]() $i\geqslant 2$
, no vertex is coloured twice. Let
$i\geqslant 2$
, no vertex is coloured twice. Let
![]() $G'$
be the subgraph of
$G'$
be the subgraph of
![]() $G$
induced by the uncoloured vertices. By the choice of
$G$
induced by the uncoloured vertices. By the choice of
![]() $B_{t_i}$
, for
$B_{t_i}$
, for
![]() $i\geqslant 2$
each bag
$i\geqslant 2$
each bag
![]() $B_j$
with
$B_j$
with
![]() $j\in [t_{i-1}+1,t_i-1]$
intersects
$j\in [t_{i-1}+1,t_i-1]$
intersects
![]() $B_{t_{i-1}}$
. Thus,
$B_{t_{i-1}}$
. Thus,
![]() $(B_1\cap V(G'),\ldots,B_n\cap V(G'))$
is a path-decomposition of
$(B_1\cap V(G'),\ldots,B_n\cap V(G'))$
is a path-decomposition of
![]() $G'$
of width at most
$G'$
of width at most
![]() $w-1$
. By induction,
$w-1$
. By induction,
![]() $G'$
has a vertex 2-colouring such that each monochromatic path has at most
$G'$
has a vertex 2-colouring such that each monochromatic path has at most
![]() $(w+3)^{w-1}$
vertices. Since
$(w+3)^{w-1}$
vertices. Since
![]() $B_{t_i}\cup B_{t_{i+2}}$
separates
$B_{t_i}\cup B_{t_{i+2}}$
separates
![]() $B_{t_i+1}\cup \ldots \cup B_{t_{i+2}-1}$
from the rest of
$B_{t_i+1}\cup \ldots \cup B_{t_{i+2}-1}$
from the rest of
![]() $G$
, each monochromatic component of
$G$
, each monochromatic component of
![]() $G$
is contained in
$G$
is contained in
![]() $B_{t_i+1}\cup \ldots \cup B_{t_{i+2}-1}$
for some
$B_{t_i+1}\cup \ldots \cup B_{t_{i+2}-1}$
for some
![]() $i\in [0,n-2]$
. Consider a monochromatic path
$i\in [0,n-2]$
. Consider a monochromatic path
![]() $P$
in
$P$
in
![]() $G[ B_{t_i+1}\cup \ldots \cup B_{t_{i+2}-1} ]$
. Then
$G[ B_{t_i+1}\cup \ldots \cup B_{t_{i+2}-1} ]$
. Then
![]() $P$
has at most
$P$
has at most
![]() $w+1$
vertices in
$w+1$
vertices in
![]() $B_{t_{i+1}}$
. Note that
$B_{t_{i+1}}$
. Note that
![]() $P- B_{t_{i+1}}$
is contained in
$P- B_{t_{i+1}}$
is contained in
![]() $G'$
. Thus,
$G'$
. Thus,
![]() $P$
consists of up to
$P$
consists of up to
![]() $w+2$
monochromatic subpaths in
$w+2$
monochromatic subpaths in
![]() $G'$
plus
$G'$
plus
![]() $w+1$
vertices in
$w+1$
vertices in
![]() $B_{t_{i+1}}$
. Hence,
$B_{t_{i+1}}$
. Hence,
![]() $P$
has at most
$P$
has at most
![]() $(w+2) (w+3)^{w-1} + (w+1) \lt (w+3)^{w}$
vertices.
$(w+2) (w+3)^{w-1} + (w+1) \lt (w+3)^{w}$
vertices.
Nešetřil and Ossona de Mendez [Reference Nešetřil and Ossona de Mendez23] showed that if a graph
![]() $G$
contains no path on
$G$
contains no path on
![]() $k$
vertices, then
$k$
vertices, then
![]() $\text{td}(G)\lt k$
(since
$\text{td}(G)\lt k$
(since
![]() $G$
is a subgraph of the closure of a DFS spanning tree with height at most
$G$
is a subgraph of the closure of a DFS spanning tree with height at most
![]() $k$
). Thus Lemma 9 implies:
$k$
). Thus Lemma 9 implies:
Corollary 10.
Every graph with pathwidth at most
![]() $w$
has a vertex 2-colouring such that each monochromatic component has treedepth at most
$w$
has a vertex 2-colouring such that each monochromatic component has treedepth at most
![]() $(w+3)^w$
.
$(w+3)^w$
.
Proof of Theorem 2.Let
![]() $\mathcal{G}$
be a minor-closed class of graphs, each with pathwidth at most
$\mathcal{G}$
be a minor-closed class of graphs, each with pathwidth at most
![]() $w$
. Let
$w$
. Let
![]() $h$
be the minimum integer such that
$h$
be the minimum integer such that
![]() $C\langle{h,k}\rangle \not \in \mathcal{G}$
for some
$C\langle{h,k}\rangle \not \in \mathcal{G}$
for some
![]() $k\in \mathbb{N}$
. Consider
$k\in \mathbb{N}$
. Consider
![]() $G\in \mathcal{G}$
. Thus,
$G\in \mathcal{G}$
. Thus,
![]() $W\langle{h,k+1}\rangle$
is not a minor of
$W\langle{h,k+1}\rangle$
is not a minor of
![]() $G$
(since
$G$
(since
![]() $C\langle{h,k}\rangle$
is a minor of
$C\langle{h,k}\rangle$
is a minor of
![]() $W\langle{h,k+1}\rangle$
, as noted above). By Corollary 10,
$W\langle{h,k+1}\rangle$
, as noted above). By Corollary 10,
![]() $G$
has a vertex 2-colouring such that each monochromatic component
$G$
has a vertex 2-colouring such that each monochromatic component
![]() $H$
of
$H$
of
![]() $G$
has treedepth at most
$G$
has treedepth at most
![]() $(w+3)^w$
. Thus,
$(w+3)^w$
. Thus,
![]() $W\langle{h,k+1}\rangle$
is not a minor of
$W\langle{h,k+1}\rangle$
is not a minor of
![]() $H$
. By Lemma 8,
$H$
. By Lemma 8,
![]() $H$
is
$H$
is
![]() $(h-1)$
-colourable with clustering
$(h-1)$
-colourable with clustering
![]() $c((w+3)^w,k+1,h)$
. Taking a product colouring,
$c((w+3)^w,k+1,h)$
. Taking a product colouring,
![]() $G$
is
$G$
is
![]() $(2h-2)$
-colourable with clustering
$(2h-2)$
-colourable with clustering
![]() $c((w+3)^w,k+1,h)$
. Hence,
$c((w+3)^w,k+1,h)$
. Hence,
![]() $ \chi _{\Delta }(\mathcal{G}) \leqslant \chi _{\star }(\mathcal{G}) \leqslant 2h-2$
.
$ \chi _{\Delta }(\mathcal{G}) \leqslant \chi _{\star }(\mathcal{G}) \leqslant 2h-2$
.
Note that Lemma 9 cannot be extended to the setting of bounded tree-width graphs: Esperet and Joret (see [[Reference Liu and Oum14], Theorem 4.1]) proved that for all positive integers
![]() $w$
and
$w$
and
![]() $d$
there exists a graph
$d$
there exists a graph
![]() $G$
with tree-width at most
$G$
with tree-width at most
![]() $w$
such that for every
$w$
such that for every
![]() $w$
-colouring of
$w$
-colouring of
![]() $G$
there exists a monochromatic component of
$G$
there exists a monochromatic component of
![]() $G$
with diameter greater than
$G$
with diameter greater than
![]() $d$
(and thus with a monochromatic path on more than
$d$
(and thus with a monochromatic path on more than
![]() $d$
vertices, and thus with treedepth at least
$d$
vertices, and thus with treedepth at least
![]() $\log _2 d$
).
$\log _2 d$
).
4. Fractional colouring
This section proves Theorem 6. The starting point is the following key result of Dvořák and Sereni [Reference Dvořák and Sereni26].Footnote 2
Theorem 11 ([Reference Dvořák and Sereni26]). For every proper minor-closed class
![]() $\mathcal{G}$
and every
$\mathcal{G}$
and every
![]() $\delta \gt 0$
there exists
$\delta \gt 0$
there exists
![]() $d \in \mathbb{N}$
satisfying the following. For every
$d \in \mathbb{N}$
satisfying the following. For every
![]() $G \in \mathcal{G}$
there exist
$G \in \mathcal{G}$
there exist
![]() $s \in \mathbb{N}$
and
$s \in \mathbb{N}$
and
![]() $X_1,X_2, \ldots, X_s \subseteq V(G)$
such that:
$X_1,X_2, \ldots, X_s \subseteq V(G)$
such that:
-
•
 $\mathrm{td}(G[X_i]) \leqslant d$
, and
$\mathrm{td}(G[X_i]) \leqslant d$
, and
-
• every
 $v \in V(G)$
belongs to at least
$v \in V(G)$
belongs to at least
 $(1 - \delta )s$
of these sets.
$(1 - \delta )s$
of these sets.
We now prove a lower bound on the fractional defective chromatic number of the closure of complete trees of given height.
Lemma 12.
Let
![]() $\mathcal{C}_h \;:\!=\; \{C \langle h,k\rangle \}_{k \in \mathbb{N}}$
. Then
$\mathcal{C}_h \;:\!=\; \{C \langle h,k\rangle \}_{k \in \mathbb{N}}$
. Then
![]() $\chi ^f_{\Delta}{\kern-2pt}(\mathcal{C}_h) \geqslant h$
.
$\chi ^f_{\Delta}{\kern-2pt}(\mathcal{C}_h) \geqslant h$
.
Proof. We show by induction on
![]() $h$
that if
$h$
that if
![]() $C \langle h,k\rangle$
is fractionally
$C \langle h,k\rangle$
is fractionally
![]() $t$
-colourable with defect
$t$
-colourable with defect
![]() $d$
, then
$d$
, then
![]() $t\geqslant h - (h-1)d/k$
. This clearly implies the lemma. The base case
$t\geqslant h - (h-1)d/k$
. This clearly implies the lemma. The base case
![]() $h=1$
is trivial.
$h=1$
is trivial.
For the induction step, suppose that
![]() $G\;:\!=\;C \langle h,k\rangle$
is fractionally
$G\;:\!=\;C \langle h,k\rangle$
is fractionally
![]() $t$
-colourable with defect
$t$
-colourable with defect
![]() $d$
. Thus, there exist
$d$
. Thus, there exist
![]() $Y_1,Y_2, \ldots, Y_s \subseteq V(G)$
and
$Y_1,Y_2, \ldots, Y_s \subseteq V(G)$
and
![]() $\alpha _1,\ldots,\alpha _s \in [0,1]$
such that:
$\alpha _1,\ldots,\alpha _s \in [0,1]$
such that:
-
every component of
 $G[Y_i]$
has maximum degree at most
$G[Y_i]$
has maximum degree at most
 $d$
,
$d$
, -
 $\sum _{i=1}^s \alpha _i \leqslant t$
, and
$\sum _{i=1}^s \alpha _i \leqslant t$
, and -
 $\sum _{i{\kern1pt}:v \in Y_i}\alpha _i \geqslant 1$
for every
$\sum _{i{\kern1pt}:v \in Y_i}\alpha _i \geqslant 1$
for every
 $v \in V(G)$
.
$v \in V(G)$
.
Let
![]() $r$
be the vertex of
$r$
be the vertex of
![]() $G$
corresponding to the root of the complete
$G$
corresponding to the root of the complete
![]() $k$
-ary tree and let
$k$
-ary tree and let
![]() $H_1,\ldots,H_k$
be the components of
$H_1,\ldots,H_k$
be the components of
![]() $G - r$
. Then each
$G - r$
. Then each
![]() $H_i$
is isomorphic to
$H_i$
is isomorphic to
![]() $C \langle h-1,k\rangle$
. Let
$C \langle h-1,k\rangle$
. Let
![]() $J_0 \;:\!=\; \{j \;:\; r \in Y_j \}$
, and let
$J_0 \;:\!=\; \{j \;:\; r \in Y_j \}$
, and let
![]() $J_i \;:\!=\; \{j \;:\; Y_j \cap V(H_i) \neq \emptyset \}$
for
$J_i \;:\!=\; \{j \;:\; Y_j \cap V(H_i) \neq \emptyset \}$
for
![]() $i\in [1,k]$
. Denote
$i\in [1,k]$
. Denote
![]() $\sum _{j \in J_i} \alpha _j$
by
$\sum _{j \in J_i} \alpha _j$
by
![]() $\alpha (J_i)$
for brevity. Thus,
$\alpha (J_i)$
for brevity. Thus,
![]() $\alpha (J_0) \geqslant 1$
. For
$\alpha (J_0) \geqslant 1$
. For
![]() $i\in [1,k]$
, the subgraph
$i\in [1,k]$
, the subgraph
![]() $H_i$
is
$H_i$
is
![]() $\alpha (J_i)$
-colourable with defect
$\alpha (J_i)$
-colourable with defect
![]() $d$
, and thus
$d$
, and thus
![]() $\alpha (J_i) \geqslant h-1 - (h-2)d/k$
by the induction hypothesis. Thus,
$\alpha (J_i) \geqslant h-1 - (h-2)d/k$
by the induction hypothesis. Thus,
 \begin{equation*} (k-d)\alpha (J_0) + \sum _{i=1}^{k}\alpha (J_i) \geqslant (k-d)+k(h-1) - (h-2)d = kh-(h-1)d. \end{equation*}
\begin{equation*} (k-d)\alpha (J_0) + \sum _{i=1}^{k}\alpha (J_i) \geqslant (k-d)+k(h-1) - (h-2)d = kh-(h-1)d. \end{equation*}
If
![]() $j \in J_0$
then
$j \in J_0$
then
![]() $Y_j$
intersects at most
$Y_j$
intersects at most
![]() $d$
of
$d$
of
![]() $H_1,\ldots,H_k$
(since
$H_1,\ldots,H_k$
(since
![]() $G[Y_j]$
has maximum degree at most
$G[Y_j]$
has maximum degree at most
![]() $d$
). Thus, every
$d$
). Thus, every
![]() $\alpha _j$
appears with coefficient at most
$\alpha _j$
appears with coefficient at most
![]() $k$
in the left side of the above inequality, implying
$k$
in the left side of the above inequality, implying
 \begin{equation*} (k-d)\alpha (J_0) + \sum _{i=1}^{k}\alpha (J_i) \leqslant k \sum _{i=1}^s \alpha _i \leqslant kt. \end{equation*}
\begin{equation*} (k-d)\alpha (J_0) + \sum _{i=1}^{k}\alpha (J_i) \leqslant k \sum _{i=1}^s \alpha _i \leqslant kt. \end{equation*}
Combining the above inequalities yields the claimed bound on
![]() $t$
.
$t$
.
Proof of Theorem 6.By Lemma 12,
It remains to show that
![]() $\chi ^f_{\star }(\mathcal{G}) \leqslant \text{tcn}(\mathcal{G}) -1$
. Equivalently, we need to show that for all
$\chi ^f_{\star }(\mathcal{G}) \leqslant \text{tcn}(\mathcal{G}) -1$
. Equivalently, we need to show that for all
![]() $h,k \in \mathbb{N}$
and
$h,k \in \mathbb{N}$
and
![]() $\varepsilon \gt 0$
, if
$\varepsilon \gt 0$
, if
![]() $C\langle{h,k}\rangle \not \in \mathcal{G}$
then there exists
$C\langle{h,k}\rangle \not \in \mathcal{G}$
then there exists
![]() $c$
such that every graph in
$c$
such that every graph in
![]() $\mathcal{G}$
is fractionally
$\mathcal{G}$
is fractionally
![]() $(h-1+\varepsilon )$
-colourable with clustering
$(h-1+\varepsilon )$
-colourable with clustering
![]() $c$
. This is trivial for
$c$
. This is trivial for
![]() $h=1$
, and so we assume
$h=1$
, and so we assume
![]() $h \geqslant 2$
.
$h \geqslant 2$
.
Let
![]() $d \in \mathbb{N}$
satisfy the conclusion of Theorem 11 for the class
$d \in \mathbb{N}$
satisfy the conclusion of Theorem 11 for the class
![]() $\mathcal{G}$
and
$\mathcal{G}$
and
![]() $\delta = 1 - \frac{1}{1+\varepsilon/(h-1)}$
. Choose
$\delta = 1 - \frac{1}{1+\varepsilon/(h-1)}$
. Choose
![]() $c=c(d,k+1,h)$
to satisfy the conclusion of Lemma 8. We show that
$c=c(d,k+1,h)$
to satisfy the conclusion of Lemma 8. We show that
![]() $c$
is as desired.
$c$
is as desired.
Consider
![]() $G \in \mathcal{G}$
. By the choice of
$G \in \mathcal{G}$
. By the choice of
![]() $d$
there exists
$d$
there exists
![]() $s \in \mathbb{N}$
and
$s \in \mathbb{N}$
and
![]() $X_1,X_2, \ldots, X_s \subseteq V(G)$
such that:
$X_1,X_2, \ldots, X_s \subseteq V(G)$
such that:
-
 $\text{td}(G[X_i]) \leqslant d$
, and
$\text{td}(G[X_i]) \leqslant d$
, and -
every
 $v \in V(G)$
belongs to at least
$v \in V(G)$
belongs to at least
 $(1 - \delta )s$
of these sets.
$(1 - \delta )s$
of these sets.
Since
![]() $C\langle{h,k}\rangle \not \in \mathcal{G}$
, we have
$C\langle{h,k}\rangle \not \in \mathcal{G}$
, we have
![]() $W\langle{h,k+1}\rangle \not \in \mathcal{G}$
, and by the choice of
$W\langle{h,k+1}\rangle \not \in \mathcal{G}$
, and by the choice of
![]() $c$
, for each
$c$
, for each
![]() $i\in [1,s]$
there exists a partition
$i\in [1,s]$
there exists a partition
![]() $(Y^1_i,Y^2_i,\ldots,Y^{h-1}_i)$
of
$(Y^1_i,Y^2_i,\ldots,Y^{h-1}_i)$
of
![]() $X_i$
such that every component of
$X_i$
such that every component of
![]() $G[Y^j_i]$
has at most
$G[Y^j_i]$
has at most
![]() $c$
vertices. Every vertex of
$c$
vertices. Every vertex of
![]() $G$
belongs to at least
$G$
belongs to at least
![]() $(1 - \delta )s$
sets
$(1 - \delta )s$
sets
![]() $Y^{j}_i$
where
$Y^{j}_i$
where
![]() $i\in [1,s]$
and
$i\in [1,s]$
and
![]() $j\in [1,h-1]$
. Considering these sets with equal coefficients
$j\in [1,h-1]$
. Considering these sets with equal coefficients
![]() $\alpha ^{j}_i \;:\!=\; \frac{1}{(1 - \delta )s}$
, we conclude that
$\alpha ^{j}_i \;:\!=\; \frac{1}{(1 - \delta )s}$
, we conclude that
![]() $G$
is fractionally
$G$
is fractionally
![]() $\frac{h-1}{1-\delta }$
-colourable with clustering
$\frac{h-1}{1-\delta }$
-colourable with clustering
![]() $c$
, as desired (since
$c$
, as desired (since
![]() $\frac{h-1}{1-\delta }=h-1+\varepsilon$
).
$\frac{h-1}{1-\delta }=h-1+\varepsilon$
).
Acknowledgement
This work was partially completed while SN was visiting Monash University supported by a Robert Bartnik Visiting Fellowship. SN thanks the School of Mathematics at Monash University for its hospitality. Thanks to the referee for several helpful comments.