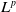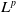1. Introduction
It is an interesting problem in geometry and topology to find sufficient conditions on the manifold for the space of harmonic k-forms to be trivial. The nonexistence of nontrivial
![]() $L^2$
harmonic 1-forms on a complete noncompact submanifold has been studied by many geometers.
$L^2$
harmonic 1-forms on a complete noncompact submanifold has been studied by many geometers.
Palmer [Reference Palmer23] proved that a complete minimal hypersurface in the Euclidean space
![]() $\mathbb{R}^{n+1}$
has no nontrivial
$\mathbb{R}^{n+1}$
has no nontrivial
![]() $L^2$
harmonic 1-forms. Thereafter, using the Bochner’s vanishing technique, Miyaoka [Reference Miyaoka22] obtained the nonexistence of nontrivial
$L^2$
harmonic 1-forms. Thereafter, using the Bochner’s vanishing technique, Miyaoka [Reference Miyaoka22] obtained the nonexistence of nontrivial
![]() $L^2$
harmonic 1-forms on complete orientable noncompact stable minimal hypersurface in a Riemannnian manifold with nonnegative sectional curvature. Later, this result was extended to more general ambient spaces [Reference Lam16, Reference Li and Wang20, Reference Matheus21]. When the curvature of the ambient manifold is negative, Seo [Reference Seo28] proved that such a vanishing theorem holds for a complete stable minimal hypersurface in
$L^2$
harmonic 1-forms on complete orientable noncompact stable minimal hypersurface in a Riemannnian manifold with nonnegative sectional curvature. Later, this result was extended to more general ambient spaces [Reference Lam16, Reference Li and Wang20, Reference Matheus21]. When the curvature of the ambient manifold is negative, Seo [Reference Seo28] proved that such a vanishing theorem holds for a complete stable minimal hypersurface in
![]() $\mathbb{H}^{n+1}$
with a further assumption about the first eigenvalue of Laplacian (
$\mathbb{H}^{n+1}$
with a further assumption about the first eigenvalue of Laplacian (
![]() $\lambda_1 \gt (2n-1)(n-1)$
). Dung and Seo [Reference Dung and Seo8] dealed with case of the curvature of the ambient manifold is pinched and obtained the corresponding vanishing result for a complete noncompact stable non-totally geodesic minimal hypersurface in Riemannian manifold N with
$\lambda_1 \gt (2n-1)(n-1)$
). Dung and Seo [Reference Dung and Seo8] dealed with case of the curvature of the ambient manifold is pinched and obtained the corresponding vanishing result for a complete noncompact stable non-totally geodesic minimal hypersurface in Riemannian manifold N with
![]() $K\leq K_N(K\leq 0)$
and
$K\leq K_N(K\leq 0)$
and
![]() $\lambda_1(M)\gt -K(2n-1)(n-1)$
.
$\lambda_1(M)\gt -K(2n-1)(n-1)$
.
A natural question is that how about the nonexistence results of nontrivial
![]() $L^p(peq 2)$
harmonic 1-forms? Yau [Reference Yau33] proved that there is no nonconstant
$L^p(peq 2)$
harmonic 1-forms? Yau [Reference Yau33] proved that there is no nonconstant
![]() $L^p(1<p<\infty)$
harmonic function on a complete Riemannian manifold. Later, Li and Schoen [Reference Li and Schoen19] proved that Yau’s result is valid for
$L^p(1<p<\infty)$
harmonic function on a complete Riemannian manifold. Later, Li and Schoen [Reference Li and Schoen19] proved that Yau’s result is valid for
![]() $L^p(0<p<\infty)$
harmonic functions on a complete manifold with nonnegative Ricci curvature. For
$L^p(0<p<\infty)$
harmonic functions on a complete manifold with nonnegative Ricci curvature. For
![]() $L^p$
harmonic forms, Greene and Wu [Reference Greene and Wu12, Reference Greene and Wu13] presented a vanishing theorem for the complete Riemannian manifolds or Kähler manifolds of nonnegative curvature. Recently, under the stability assumption, Seo [Reference Seo26] obtained that there is no nontrivial
$L^p$
harmonic forms, Greene and Wu [Reference Greene and Wu12, Reference Greene and Wu13] presented a vanishing theorem for the complete Riemannian manifolds or Kähler manifolds of nonnegative curvature. Recently, under the stability assumption, Seo [Reference Seo26] obtained that there is no nontrivial
![]() $L^{2p}$
harmonic 1-form on a stable minimal hypersurface
$L^{2p}$
harmonic 1-form on a stable minimal hypersurface
![]() $M^n$
of Riemannian manifold N with
$M^n$
of Riemannian manifold N with
![]() $K_N\geq K(K\leq 0)$
, provided
$K_N\geq K(K\leq 0)$
, provided
![]() $\lambda_1(M)>\frac{-2n(n-1)^2p^2K}{2n-[(n-1)p-n]^2}$
for
$\lambda_1(M)>\frac{-2n(n-1)^2p^2K}{2n-[(n-1)p-n]^2}$
for
![]() $0<p<\frac{n}{n-1}+\sqrt{2n}$
. Moreover, Dung and Seo [Reference Dung and Seo9] studied the same topic on a complete
$0<p<\frac{n}{n-1}+\sqrt{2n}$
. Moreover, Dung and Seo [Reference Dung and Seo9] studied the same topic on a complete
![]() $\delta$
-stability hypersurface in a Riemannian manifold with nonnegative sectional curvature. The first author and Lv [Reference Chao and Lv6] also investigated the nonexistence of nontrivial
$\delta$
-stability hypersurface in a Riemannian manifold with nonnegative sectional curvature. The first author and Lv [Reference Chao and Lv6] also investigated the nonexistence of nontrivial
![]() $L^{p}$
harmonic 1-form of a complete
$L^{p}$
harmonic 1-form of a complete
![]() $\delta$
-stable hypersurface with weighted Poincaré inequality in a Riemannian manifold with sectional curvature bounded below by a nonpositive function. Most recently, without the stability assumption, Choi and Seo [Reference Choi and Seo7] proved the following finiteness theorem.
$\delta$
-stable hypersurface with weighted Poincaré inequality in a Riemannian manifold with sectional curvature bounded below by a nonpositive function. Most recently, without the stability assumption, Choi and Seo [Reference Choi and Seo7] proved the following finiteness theorem.
Theorem 1.1 ([Reference Choi and Seo7]). Let N be an
![]() $(n + 1)$
-dimensional complete simply connected Riemannian manifold with sectional curvature
$(n + 1)$
-dimensional complete simply connected Riemannian manifold with sectional curvature
![]() $K_N$
satisfying
$K_N$
satisfying
![]() $-k^2 \leq K_N \leq 0$
for a nonzero constant k. Let M be an
$-k^2 \leq K_N \leq 0$
for a nonzero constant k. Let M be an
![]() $n(n\geq3)$
-dimensional complete noncompact minimal hypersurface with finite index in N. For
$n(n\geq3)$
-dimensional complete noncompact minimal hypersurface with finite index in N. For
![]() $\frac{n-2}{n-1}<p<\frac{n}{n-1}$
, assume that
$\frac{n-2}{n-1}<p<\frac{n}{n-1}$
, assume that
Then,
![]() $\dim H^1(L^{2p}(M))<\infty$
.
$\dim H^1(L^{2p}(M))<\infty$
.
In this paper, removing the minimality assumption of M in Theorem 1.1, we can obtain the following finiteness result.
Theorem 1.2. Let N be an
![]() $(n + 1)$
-dimensional complete simply connected Riemannian manifold with sectional curvature
$(n + 1)$
-dimensional complete simply connected Riemannian manifold with sectional curvature
![]() $K_N$
satisfying
$K_N$
satisfying
![]() $-k^2 \leq K_N \leq 0$
for a nonzero constant k. Let M be an n-dimensional
$-k^2 \leq K_N \leq 0$
for a nonzero constant k. Let M be an n-dimensional
![]() $(3\leq n\leq6)$
complete noncompact hypersurface with
$(3\leq n\leq6)$
complete noncompact hypersurface with
![]() $(\!\int_M H^n)^{\frac{2}{n}}<\frac{1}{S(n)}$
and finite index in N, where S(n) is the Sobolev constant. For
$(\!\int_M H^n)^{\frac{2}{n}}<\frac{1}{S(n)}$
and finite index in N, where S(n) is the Sobolev constant. For
![]() $\frac{n-2}{n-1}<p<\frac{2}{\sqrt{n-1}}$
, assume that
$\frac{n-2}{n-1}<p<\frac{2}{\sqrt{n-1}}$
, assume that
![]() $|A|$
is bounded and
$|A|$
is bounded and
 \begin{equation*}\lambda_1(M)>\max\!\left\{\frac{(n-1)^2k^2p^2}{(n-1)p-n+2}, \frac{n\sqrt{n-1}k^2p}{2-p\sqrt{n-1}}\right\}.\end{equation*}
\begin{equation*}\lambda_1(M)>\max\!\left\{\frac{(n-1)^2k^2p^2}{(n-1)p-n+2}, \frac{n\sqrt{n-1}k^2p}{2-p\sqrt{n-1}}\right\}.\end{equation*}
Then,
![]() $\dim H^1(L^{2p}(M))<\infty$
.
$\dim H^1(L^{2p}(M))<\infty$
.
Corollary 1.3. Let M be an n-dimensional
![]() $(3\leq n\leq4)$
complete noncompact hypersurface with finite index in hyperbolic space
$(3\leq n\leq4)$
complete noncompact hypersurface with finite index in hyperbolic space
![]() $\mathbb{H}^{n+1}$
. If
$\mathbb{H}^{n+1}$
. If
![]() $\lambda_1(M)>\frac{n\sqrt{n-1}}{2-\sqrt{n-1}}$
and
$\lambda_1(M)>\frac{n\sqrt{n-1}}{2-\sqrt{n-1}}$
and
![]() $(\!\int_M H^n)^{\frac{2}{n}}<\frac{1}{S(n)}$
, where S(n) is the Sobolev constant, then
$(\!\int_M H^n)^{\frac{2}{n}}<\frac{1}{S(n)}$
, where S(n) is the Sobolev constant, then
![]() $\dim H^1(L^{2}(M))<\infty$
. Moreover, M has finitely many ends.
$\dim H^1(L^{2}(M))<\infty$
. Moreover, M has finitely many ends.
We say that an n-dimensional complete Riemannian manifold M has property
![]() $(\mathcal{P}_\rho)$
, if a weighted Poincaré inequality is valid on M with some nonnegative weight function
$(\mathcal{P}_\rho)$
, if a weighted Poincaré inequality is valid on M with some nonnegative weight function
![]() $\rho(x)$
, namely
$\rho(x)$
, namely
Moreover, the
![]() $\rho$
-metric, defined by
$\rho$
-metric, defined by
![]() $ds^2_\rho=\rho ds^2_M$
is complete. In particular, if
$ds^2_\rho=\rho ds^2_M$
is complete. In particular, if
![]() $\lambda_1(M)$
is assumed to be positive, then obviously M possesses property
$\lambda_1(M)$
is assumed to be positive, then obviously M possesses property
![]() $(\mathcal{P}_\rho)$
with
$(\mathcal{P}_\rho)$
with
![]() $\rho=\lambda_1(M)$
. So, the notion of property
$\rho=\lambda_1(M)$
. So, the notion of property
![]() $(\mathcal{P}_\rho)$
may be viewed as a generalization of the assumption
$(\mathcal{P}_\rho)$
may be viewed as a generalization of the assumption
![]() $\lambda_1(M)>0$
. Recently, Sang and Thanh [Reference Sang and Thanh25] proved that a complete noncompact stable minimal hypersurface with property (
$\lambda_1(M)>0$
. Recently, Sang and Thanh [Reference Sang and Thanh25] proved that a complete noncompact stable minimal hypersurface with property (
![]() $\mathcal{P}_\rho$
) in Riemannian manifold N has no nontrivial
$\mathcal{P}_\rho$
) in Riemannian manifold N has no nontrivial
![]() $L^2$
harmonic 1-form if the sectional curvature of N satisfies
$L^2$
harmonic 1-form if the sectional curvature of N satisfies
![]() $K_{N}(x)\geq -\frac{(1-\tau)\rho(x)}{(2n-1)(n-1)},0<\tau\leq 1$
and
$K_{N}(x)\geq -\frac{(1-\tau)\rho(x)}{(2n-1)(n-1)},0<\tau\leq 1$
and
![]() $\rho(x)$
satisfies certain growth condition. Motivated by [Reference Chao, Hui and Bai4, Reference Chao and Lv5, Reference Chao and Lv6, Reference Dung and Seo9, Reference Sang and Thanh25], we can obtain an another improvement of Theorem 1.1. More precisely, we have the following theorem.
$\rho(x)$
satisfies certain growth condition. Motivated by [Reference Chao, Hui and Bai4, Reference Chao and Lv5, Reference Chao and Lv6, Reference Dung and Seo9, Reference Sang and Thanh25], we can obtain an another improvement of Theorem 1.1. More precisely, we have the following theorem.
Theorem 1.4. Let
![]() $M^n(3\leq n\leq 6)$
be a complete noncompact hypersurface with property
$M^n(3\leq n\leq 6)$
be a complete noncompact hypersurface with property
![]() $(\mathcal{P}_\rho)$
in an
$(\mathcal{P}_\rho)$
in an
![]() $(n+1)$
-dimensional Riemannian manifold N. Assume that
$(n+1)$
-dimensional Riemannian manifold N. Assume that
![]() $\rho$
is bounded and
$\rho$
is bounded and
for some
![]() $\tau\;:\;\frac{122-51\sqrt{5}}{12+4\sqrt{5}}<\tau\leq 1$
. If M has finite index, then
$\tau\;:\;\frac{122-51\sqrt{5}}{12+4\sqrt{5}}<\tau\leq 1$
. If M has finite index, then
![]() $\dim H^1(L^{2p}(M))<\infty$
for any constant p satisfying
$\dim H^1(L^{2p}(M))<\infty$
for any constant p satisfying
![]() $C_1(n,\tau)<p<C_2(n,\tau),$
where
$C_1(n,\tau)<p<C_2(n,\tau),$
where
 \begin{align*}C_0&=\frac{(2\sqrt{n-1}+n)(1-\tau)}{(2n-1)(n-1)},\\[5pt]C_1(n,\tau)&=\frac{2\Big(1-\sqrt{1-\frac{n-2}{2\sqrt{n-1}}(1+C_0)}\Big)}{\sqrt{n-1}(1+C_0)}, \\[5pt]C_2(n,\tau)&=\frac{2\Big(1+\sqrt{1-\frac{n-2}{2\sqrt{n-1}}(1+C_0)}\Big)}{\sqrt{n-1}(1+C_0)}.\end{align*}
\begin{align*}C_0&=\frac{(2\sqrt{n-1}+n)(1-\tau)}{(2n-1)(n-1)},\\[5pt]C_1(n,\tau)&=\frac{2\Big(1-\sqrt{1-\frac{n-2}{2\sqrt{n-1}}(1+C_0)}\Big)}{\sqrt{n-1}(1+C_0)}, \\[5pt]C_2(n,\tau)&=\frac{2\Big(1+\sqrt{1-\frac{n-2}{2\sqrt{n-1}}(1+C_0)}\Big)}{\sqrt{n-1}(1+C_0)}.\end{align*}
when
![]() $\tau=1$
, we have
$\tau=1$
, we have
Corollary 1.5. Let
![]() $M^n(3\leq n\leq 6)$
be a complete noncompact hypersurface with property
$M^n(3\leq n\leq 6)$
be a complete noncompact hypersurface with property
![]() $(\mathcal{P}_\rho)$
in
$(\mathcal{P}_\rho)$
in
![]() $\mathbb{R}^{n+1}$
. If M has finite index and
$\mathbb{R}^{n+1}$
. If M has finite index and
![]() $\rho$
is bounded, then
$\rho$
is bounded, then
![]() $\dim H^1(L^{2p}(M))<\infty$
for any constant p satisfying
$\dim H^1(L^{2p}(M))<\infty$
for any constant p satisfying
![]() $C_1(n)<p<C_2(n),$
where
$C_1(n)<p<C_2(n),$
where
 \begin{align*}C_1(n)&=\frac{2}{\sqrt{n-1}}\left(1-\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right), \\[5pt]C_2(n)&=\frac{2}{\sqrt{n-1}}\left(1+\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right).\end{align*}
\begin{align*}C_1(n)&=\frac{2}{\sqrt{n-1}}\left(1-\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right), \\[5pt]C_2(n)&=\frac{2}{\sqrt{n-1}}\left(1+\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right).\end{align*}
Moreover, we can prove a similar finiteness theorem for
![]() $L^{p}$
harmonic 1-forms on complete noncompact hypersurfaces with property
$L^{p}$
harmonic 1-forms on complete noncompact hypersurfaces with property
![]() $(\mathcal{P}_\rho)$
as Theorem 1.4 except the condition that the lower bound of
$(\mathcal{P}_\rho)$
as Theorem 1.4 except the condition that the lower bound of
![]() $K_N$
depends on
$K_N$
depends on
![]() $n, p,\rho$
. More precisely, we have
$n, p,\rho$
. More precisely, we have
Theorem 1.6. Let
![]() $N^{n+1}$
be an
$N^{n+1}$
be an
![]() $(n+1)$
-dimensional Riemannian manifold, and
$(n+1)$
-dimensional Riemannian manifold, and
![]() $M^n (3\leq n\leq 6)$
be a complete noncompact hypersurface satisfying weighted Poincaré inequality
$M^n (3\leq n\leq 6)$
be a complete noncompact hypersurface satisfying weighted Poincaré inequality
![]() $(\mathcal{P}_\rho)$
for some nonnegative bounded function
$(\mathcal{P}_\rho)$
for some nonnegative bounded function
![]() $\rho$
in N. If M has finite index and
$\rho$
in N. If M has finite index and
where p satisfies
 \begin{equation*}\frac{2}{\sqrt{n-1}}\left(1-\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right)<p<\frac{2}{\sqrt{n-1}}\left(1+\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right).\end{equation*}
\begin{equation*}\frac{2}{\sqrt{n-1}}\left(1-\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right)<p<\frac{2}{\sqrt{n-1}}\left(1+\sqrt{1-\frac{n-2}{2\sqrt{n-1}}}\;\right).\end{equation*}
Then,
![]() $\dim H^1(L^{2p}(M))<\infty$
.
$\dim H^1(L^{2p}(M))<\infty$
.
2. Some lemmas
In this section, we will recall some useful results which will be adopted in the proof of main theorems. The most basic one is the following Weitzenböck formula.
Lemma 2.1 ([Reference Li18]). Given a Riemannian manifold
![]() $M^n$
, for any 1-form
$M^n$
, for any 1-form
![]() $\omega$
on
$\omega$
on
![]() $M^n$
, we have
$M^n$
, we have
where
![]() $\omega^{\sharp}$
is the dual vector field of
$\omega^{\sharp}$
is the dual vector field of
![]() $\omega$
.
$\omega$
.
Besides, the Kato inequality is also a fundamental technique.
Lemma 2.2 ([Reference Calderbank, Gauduchon and Herzlich1]). Given a Riemannian manifold
![]() $M^n$
, for any closed and coclosed k-form
$M^n$
, for any closed and coclosed k-form
![]() $\omega$
on
$\omega$
on
![]() $M^n$
, we have
$M^n$
, we have
 \begin{equation*}|\nabla \omega|^2\geq (1+C_{n,k})|\nabla |\omega||^2, \quad where \quad C_{n,k}=\begin{cases}\dfrac{1}{n-k},\quad 1\leq k\leq\dfrac{n}{2}.\\[12pt] \dfrac{1}{k},\quad \dfrac{n}{2}\leq k \leq n-1.\end{cases}\end{equation*}
\begin{equation*}|\nabla \omega|^2\geq (1+C_{n,k})|\nabla |\omega||^2, \quad where \quad C_{n,k}=\begin{cases}\dfrac{1}{n-k},\quad 1\leq k\leq\dfrac{n}{2}.\\[12pt] \dfrac{1}{k},\quad \dfrac{n}{2}\leq k \leq n-1.\end{cases}\end{equation*}
What’s more, Shiohama and Xu [Reference Shiohama and Xu29] proved the following estimation on the Ricci curvature of submanifold.
Lemma 2.3 ([Reference Shiohama and Xu29]). Let M be an n-dimensional complete immersed hypersurface in a Riemannian manifold N. If all the sectional curvatures of N are bounded pointwise from below by a function k, then
where H is the mean curvature and A is the second fundamental form of M.
We should note in [Reference Shiohama and Xu29], the author assumed that all the sectional curvatures of N are bounded below by a constant k. But according to his argument, this assumption was only used in the end of the proof; hence, this method can be used to prove the above lemma without any change. Under the same assumption, the following lemma estimates the right hand side of (2.1).
Lemma 2.4 ([Reference Chao and Lv6]). Let
![]() $M^n$
be an n-dimensional orientable submanifold in Riemannian manifold N. We have
$M^n$
be an n-dimensional orientable submanifold in Riemannian manifold N. We have
Definition 2.5. Let
![]() $M^n$
be an n-dimensional orientable hypersurface in a Riemannian manifold N. We say M is stable if the following inequality
$M^n$
be an n-dimensional orientable hypersurface in a Riemannian manifold N. We say M is stable if the following inequality
holds for any
![]() $\eta\in C^{\infty}_0(M)$
, where
$\eta\in C^{\infty}_0(M)$
, where
![]() $u$
is a unit normal vector field on M,
$u$
is a unit normal vector field on M,
![]() $\overline{{\rm Ric}}$
is the Ricci curvature of N, and A is the second fundamental form of M.
$\overline{{\rm Ric}}$
is the Ricci curvature of N, and A is the second fundamental form of M.
Now, we will give a condition to ensure that the volume of Riemannian manifold to be infinite.
Lemma 2.6 ([Reference Dung and Seo9]). Let M be a complete oriented noncompact immersed hypersurface in a complete Riemannian manifold
![]() $N^{n+1}$
with nonnegative sectional curvature. If the stability inequality (2.3) holds on M, then the volume of M is infinite.
$N^{n+1}$
with nonnegative sectional curvature. If the stability inequality (2.3) holds on M, then the volume of M is infinite.
In addition, the following Hoffman-Spruck inequality generalizes the Poincaré inequality and relates it to the Sobolev inequality.
Lemma 2.7 ([Reference Hoffman and Spruck14]). Let
![]() $x\;:\;M^n\hookrightarrow N$
be an isometric immersion of a complete manifold M in a complete simply connected manifold N with nonpositive sectional curvature. Then, the following inequality holds:
$x\;:\;M^n\hookrightarrow N$
be an isometric immersion of a complete manifold M in a complete simply connected manifold N with nonpositive sectional curvature. Then, the following inequality holds:
for all nonnegative
![]() $C^1$
-functions
$C^1$
-functions
![]() $h\;:\;M^n\rightarrow \mathbb{R}$
with compact support, where S(n) is the Sobolev constant, which is positive and only depends on n.
$h\;:\;M^n\rightarrow \mathbb{R}$
with compact support, where S(n) is the Sobolev constant, which is positive and only depends on n.
The following Cauchy inequality gives the
![]() $L^2$
upper bound of a nonnegative sub-eigenfunction.
$L^2$
upper bound of a nonnegative sub-eigenfunction.
Lemma 2.8 ([Reference Li18]). Let M be an n-dimensional complete noncompact Riemannian manifold. For
![]() $x \in M$
and a constant
$x \in M$
and a constant
![]() $\kappa \geq 0$
, we assume that the Ricci curvature of M satisfies
$\kappa \geq 0$
, we assume that the Ricci curvature of M satisfies
on the geodesic ball
![]() $B_x(4r)$
centered at p with radius 4r. Let
$B_x(4r)$
centered at p with radius 4r. Let
![]() $0 < \delta < \frac{1}{2}$
and
$0 < \delta < \frac{1}{2}$
and
![]() $\lambda > 0$
be two fixed constants. Then there exists a positive constant
$\lambda > 0$
be two fixed constants. Then there exists a positive constant
![]() $C = C(r, \delta, \lambda, \kappa)$
so that if any nonnegative function
$C = C(r, \delta, \lambda, \kappa)$
so that if any nonnegative function
![]() $\eta \in C^{\infty}(B_x(2r))$
satisfying the differential inequality
$\eta \in C^{\infty}(B_x(2r))$
satisfying the differential inequality
![]() $\triangle\eta\geq-\lambda\eta$
, then
$\triangle\eta\geq-\lambda\eta$
, then
The last lemma associates the
![]() $L^2$
and
$L^2$
and
![]() $L^{\infty}$
norms of harmonic forms with the dimension of the space of harmonic forms.
$L^{\infty}$
norms of harmonic forms with the dimension of the space of harmonic forms.
Lemma 2.9 ([Reference Li17, Reference Pigola, Rigoli and Setti24]). Let K be a finite dimensional subspace of
![]() $L^{2p}$
harmonic q-forms on an m-dimensional complete noncompact Riemannian manifold M for any
$L^{2p}$
harmonic q-forms on an m-dimensional complete noncompact Riemannian manifold M for any
![]() $p > 0$
. Then, there exists
$p > 0$
. Then, there exists
![]() $\eta \in K$
such that
$\eta \in K$
such that
 \begin{equation*}(\dim K)^{\min\{1,p\}}\int_{B_x(r)}|\eta|^{2p}\leq \operatorname{Vol}\!(B_x(r))\cdot\min\left\{ \left(\begin{array}{c}m\\[5pt] q \end{array}\right), \dim K\right\}^{\min\{1,p\}}\cdot\sup_{B_x(r)}|\eta|^{2p},\end{equation*}
\begin{equation*}(\dim K)^{\min\{1,p\}}\int_{B_x(r)}|\eta|^{2p}\leq \operatorname{Vol}\!(B_x(r))\cdot\min\left\{ \left(\begin{array}{c}m\\[5pt] q \end{array}\right), \dim K\right\}^{\min\{1,p\}}\cdot\sup_{B_x(r)}|\eta|^{2p},\end{equation*}
for any
![]() $x \in M$
and
$x \in M$
and
![]() $r > 0$
.
$r > 0$
.
3. Proofs of the theorems
Proof of Theorem 1.2. Let
![]() $\omega$
be a
$\omega$
be a
![]() $L^{2p}$
harmonic 1-form. Using the Weitzenböck formula and the Kato inequality, we can get that
$L^{2p}$
harmonic 1-form. Using the Weitzenböck formula and the Kato inequality, we can get that
Under our hypothesis on the sectional curvature of N, we can estimate the Ricci curvature of M by using Lemmas 2.3 and 2.4:
 \begin{align*} {\rm Ric}_M &\geq -(n-1)k^2+\frac{2(n-1)-n\sqrt{n-1}}{2n}|A|^2-\frac{n-1}{n}|A|^2 \\[5pt]&=-(n-1)k^2-\frac{\sqrt{n-1}}{2}|A|^2.\end{align*}
\begin{align*} {\rm Ric}_M &\geq -(n-1)k^2+\frac{2(n-1)-n\sqrt{n-1}}{2n}|A|^2-\frac{n-1}{n}|A|^2 \\[5pt]&=-(n-1)k^2-\frac{\sqrt{n-1}}{2}|A|^2.\end{align*}
Thus equation (3.1) becomes
Furthermore, using (3.2) we have that
 \begin{align} |\omega|^p\triangle |\omega|^p &=|\omega|^p\Big(p(p-1)|\omega|^{p-2}|\nabla |\omega||^2+p |\omega|^{p-1}\triangle |\omega|\Big) \\[5pt] &=\frac{p-1}{p}|\nabla |\omega|^p|^2+p|\omega|^{2p-2}|\omega|\triangle|\omega| \\[5pt] &\geq \Big(1-\frac{n-2}{(n-1)p}\Big)|\nabla |\omega|^p|^2- \frac{p\sqrt{n-1}}{2}|A|^2|\omega|^{2p}-(n-1)k^2p|\omega|^{2p}.\end{align}
\begin{align} |\omega|^p\triangle |\omega|^p &=|\omega|^p\Big(p(p-1)|\omega|^{p-2}|\nabla |\omega||^2+p |\omega|^{p-1}\triangle |\omega|\Big) \\[5pt] &=\frac{p-1}{p}|\nabla |\omega|^p|^2+p|\omega|^{2p-2}|\omega|\triangle|\omega| \\[5pt] &\geq \Big(1-\frac{n-2}{(n-1)p}\Big)|\nabla |\omega|^p|^2- \frac{p\sqrt{n-1}}{2}|A|^2|\omega|^{2p}-(n-1)k^2p|\omega|^{2p}.\end{align}
Since M has finite index, there exists a compact subset
![]() $\Omega\subset M$
such that
$\Omega\subset M$
such that
![]() $M\backslash\Omega$
is stable ([Reference Fischer-Colbrie10, Reference Tysk31]). Without loss of generality, we assume that
$M\backslash\Omega$
is stable ([Reference Fischer-Colbrie10, Reference Tysk31]). Without loss of generality, we assume that
![]() $\Omega = B_x(R_0)$
. Then, according to Definition 2.5, for any compactly supported Lipschitz function
$\Omega = B_x(R_0)$
. Then, according to Definition 2.5, for any compactly supported Lipschitz function
![]() $\eta$
on
$\eta$
on
![]() $M\backslash\ \!B_x(R_0)$
,
$M\backslash\ \!B_x(R_0)$
,
The assumption on the sectional curvature of N implies that
![]() $\overline{{\rm Ric}}(u,u)\geq -nk^2$
and
$\overline{{\rm Ric}}(u,u)\geq -nk^2$
and
for all compactly supported Lipschitz function
![]() $\eta$
on
$\eta$
on
![]() $M \backslash B_x(R_0)$
. Replacing
$M \backslash B_x(R_0)$
. Replacing
![]() $\eta$
by
$\eta$
by
![]() $\eta |\omega|^p$
in (3.4), we get
$\eta |\omega|^p$
in (3.4), we get
Moreover, the domain monotonicity of eigenvalues implies that
for any compactly supported Lipschitz function
![]() $\eta$
on
$\eta$
on
![]() $M \backslash B_x(R_0)$
. Replacing
$M \backslash B_x(R_0)$
. Replacing
![]() $\eta$
by
$\eta$
by
![]() $\eta |\omega|^p$
in this inequality and using (3.5), we have
$\eta |\omega|^p$
in this inequality and using (3.5), we have
and
 \begin{align}\int_{M \backslash B_x(R_0)}&|A|^2\eta^2 |\omega|^{2p}\leq \Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}|\nabla(\eta |\omega|^p)|^2 \\[5pt]&=\Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}\!\Big(\eta^2|\nabla|\omega|^p|^2+|\nabla\eta|^2|\omega|^{2p}+2\eta|\omega|^p\langle\nabla\eta,\nabla|\omega|^p\rangle\Big).\end{align}
\begin{align}\int_{M \backslash B_x(R_0)}&|A|^2\eta^2 |\omega|^{2p}\leq \Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}|\nabla(\eta |\omega|^p)|^2 \\[5pt]&=\Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}\!\Big(\eta^2|\nabla|\omega|^p|^2+|\nabla\eta|^2|\omega|^{2p}+2\eta|\omega|^p\langle\nabla\eta,\nabla|\omega|^p\rangle\Big).\end{align}
Applying the divergence theorem, we get
Therefore,
 \begin{align*}\int_{M \backslash B_x(R_0)}|A|^2\eta^2 |\omega|^{2p}&\leq \Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p} \\[5pt]&\;\;\;-\Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\Big(1-\frac{n-2}{(n-1)p}\Big)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2 \\[5pt]&\;\;\;+\Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}\Big(\frac{p\sqrt{n-1}}{2}|A|^2+(n-1)k^2p\Big)\eta^2|\omega|^{2p}.\end{align*}
\begin{align*}\int_{M \backslash B_x(R_0)}|A|^2\eta^2 |\omega|^{2p}&\leq \Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p} \\[5pt]&\;\;\;-\Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\Big(1-\frac{n-2}{(n-1)p}\Big)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2 \\[5pt]&\;\;\;+\Big(1+\frac{nk^2}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}\Big(\frac{p\sqrt{n-1}}{2}|A|^2+(n-1)k^2p\Big)\eta^2|\omega|^{2p}.\end{align*}
Therefore, the assumption on
![]() $\lambda_1(M)$
implies
$\lambda_1(M)$
implies
 \begin{align}\Big(1-\frac{n-2}{(n-1)p}\Big)&\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2 \\[5pt]&\leq \int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}+(n-1)k^2p\int_{M \backslash B_x(R_0)}\eta^2|\omega|^{2p} \\[5pt]&\quad +\left(\frac{p\sqrt{n-1}}{2}-\frac{1}{1+\frac{nk^2}{\lambda_1(M)}}\right)\int_{M \backslash B_x(R_0)}|A|^2\eta^2|\omega|^{2p} \\[5pt]&\leq \int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}+(n-1)k^2p\int_{M \backslash B_x(R_0)}\eta^2|\omega|^{2p}.\end{align}
\begin{align}\Big(1-\frac{n-2}{(n-1)p}\Big)&\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2 \\[5pt]&\leq \int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}+(n-1)k^2p\int_{M \backslash B_x(R_0)}\eta^2|\omega|^{2p} \\[5pt]&\quad +\left(\frac{p\sqrt{n-1}}{2}-\frac{1}{1+\frac{nk^2}{\lambda_1(M)}}\right)\int_{M \backslash B_x(R_0)}|A|^2\eta^2|\omega|^{2p} \\[5pt]&\leq \int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}+(n-1)k^2p\int_{M \backslash B_x(R_0)}\eta^2|\omega|^{2p}.\end{align}
On the other hand, applying Young’s inequality in (3.6), we obtain
for any
![]() $\varepsilon>0$
. Combining this with (3.10), we get
$\varepsilon>0$
. Combining this with (3.10), we get
 \begin{align*}\Big(1-\frac{n-2}{(n-1)p}&-\frac{(n-1)k^2p(1+\varepsilon)}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2\\[5pt]&\leq\Big(1+\frac{(n-1)k^2p}{\lambda_1(M)}\cdot\frac{1+\varepsilon}{\varepsilon}\Big)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}.\end{align*}
\begin{align*}\Big(1-\frac{n-2}{(n-1)p}&-\frac{(n-1)k^2p(1+\varepsilon)}{\lambda_1(M)}\Big)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2\\[5pt]&\leq\Big(1+\frac{(n-1)k^2p}{\lambda_1(M)}\cdot\frac{1+\varepsilon}{\varepsilon}\Big)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}.\end{align*}
Using the assumption on
![]() $\lambda_1(M)$
, we choose a sufficiently small
$\lambda_1(M)$
, we choose a sufficiently small
![]() $\varepsilon > 0$
such that
$\varepsilon > 0$
such that
Then we have
for some positive constant
![]() $C_1$
which depends only on p, n, k and
$C_1$
which depends only on p, n, k and
![]() $\lambda_1(M)$
. Moreover, from Lemma 2.7 and Hölder inequality, we obtain
$\lambda_1(M)$
. Moreover, from Lemma 2.7 and Hölder inequality, we obtain
 \begin{align}\Big(\int_{M \backslash B_x(R_0)}(\eta|\omega|^p)^{\frac{2n}{n-2}}\Big)^{\frac{n-2}{n}}&\leq S(n)\int_{M \backslash B_x(R_0)}\big(|\nabla (\eta|\omega|^p)|^2+\eta^2|\omega|^{2p}|H|^2\big) \\[5pt]&\leq 2S(n)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2 \\[5pt]&\quad +2S(n)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p} \\[5pt]&\quad +S(n)\Big(\int_{M \backslash B_x(R_0)} |H|^n\Big)^{\frac{2}{n}}\Big(\int_{M \backslash B_x(R_0)} (\eta|\omega|^p)^{\frac{2n}{n-2}}\Big)^{\frac{n-2}{n}},\end{align}
\begin{align}\Big(\int_{M \backslash B_x(R_0)}(\eta|\omega|^p)^{\frac{2n}{n-2}}\Big)^{\frac{n-2}{n}}&\leq S(n)\int_{M \backslash B_x(R_0)}\big(|\nabla (\eta|\omega|^p)|^2+\eta^2|\omega|^{2p}|H|^2\big) \\[5pt]&\leq 2S(n)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2 \\[5pt]&\quad +2S(n)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p} \\[5pt]&\quad +S(n)\Big(\int_{M \backslash B_x(R_0)} |H|^n\Big)^{\frac{2}{n}}\Big(\int_{M \backslash B_x(R_0)} (\eta|\omega|^p)^{\frac{2n}{n-2}}\Big)^{\frac{n-2}{n}},\end{align}
i.e.
 \begin{align}\Big(1-S(n)&\|H\|^2_{L^n(M)}\Big)\Big(\int_{M \backslash B_x(R_0)} (\eta|\omega|^p)^{\frac{2n}{n-2}}\Big)^{\frac{n-2}{n}} \\[5pt]&\leq 2S(n)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2+2S(n)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}.\end{align}
\begin{align}\Big(1-S(n)&\|H\|^2_{L^n(M)}\Big)\Big(\int_{M \backslash B_x(R_0)} (\eta|\omega|^p)^{\frac{2n}{n-2}}\Big)^{\frac{n-2}{n}} \\[5pt]&\leq 2S(n)\int_{M \backslash B_x(R_0)}\eta^2|\nabla |\omega|^p|^2+2S(n)\int_{M \backslash B_x(R_0)}|\nabla\eta|^2|\omega|^{2p}.\end{align}
Combining (3.11) and (3.13) and the assumption
![]() $1-S(n)\|H\|^2_{L^n(M)}>0$
, we get
$1-S(n)\|H\|^2_{L^n(M)}>0$
, we get
for some positive constant
![]() $C_2$
. Now we choose our test function
$C_2$
. Now we choose our test function
![]() $0 \leq \eta \leq 1$
as in [Reference Choi and Seo7]: given
$0 \leq \eta \leq 1$
as in [Reference Choi and Seo7]: given
![]() $R > R_0 + 1$
,
$R > R_0 + 1$
,
 \begin{equation*}\eta=\left\{ \begin{array}{ll} 1, & on\;B_x(R)\backslash B_x(R_0+1) \\[5pt] 0, & on\;B_x(R_0)\cup(M\backslash B_x(2R)), \end{array} \right.\end{equation*}
\begin{equation*}\eta=\left\{ \begin{array}{ll} 1, & on\;B_x(R)\backslash B_x(R_0+1) \\[5pt] 0, & on\;B_x(R_0)\cup(M\backslash B_x(2R)), \end{array} \right.\end{equation*}
![]() $|\nabla\eta|\leq C_3$
on
$|\nabla\eta|\leq C_3$
on
![]() $B_x(R_0+1)\backslash B_x(R_0)$
and
$B_x(R_0+1)\backslash B_x(R_0)$
and
![]() $|\nabla\eta|\leq \frac{C_3}{R}$
on
$|\nabla\eta|\leq \frac{C_3}{R}$
on
![]() $B_x(2R)\backslash B_x(R)$
. Applying this test function
$B_x(2R)\backslash B_x(R)$
. Applying this test function
![]() $\eta$
to (3.14), we get
$\eta$
to (3.14), we get
Letting
![]() $R\rightarrow\infty$
and using the assumption that
$R\rightarrow\infty$
and using the assumption that
![]() $\displaystyle \int_M |\omega|^{2p}<\infty$
, we obtain
$\displaystyle \int_M |\omega|^{2p}<\infty$
, we obtain
Then, using Hölder inequality and (3.15), we conclude that
 \begin{align}\int_{B_x(R_0+2) \backslash B_x(R_0+1)}|\omega|^{2p} &\leq \big({\rm Vol}(B_x(R_0+2))\big)^{\frac{2}{n}}\Big(\int_{B_x(R_0+2) \backslash B_x(R_0+1)} |\omega|^{\frac{2np}{n-2}}\Big)^{\frac{n-2}{n}} \\[5pt]&\leq C_4\cdot \big({\rm Vol}(B_x(R_0+2))\big)^{\frac{2}{n}} \int_{B_x(R_0+1) \backslash B_x(R_0)}|\omega|^{2p}.\end{align}
\begin{align}\int_{B_x(R_0+2) \backslash B_x(R_0+1)}|\omega|^{2p} &\leq \big({\rm Vol}(B_x(R_0+2))\big)^{\frac{2}{n}}\Big(\int_{B_x(R_0+2) \backslash B_x(R_0+1)} |\omega|^{\frac{2np}{n-2}}\Big)^{\frac{n-2}{n}} \\[5pt]&\leq C_4\cdot \big({\rm Vol}(B_x(R_0+2))\big)^{\frac{2}{n}} \int_{B_x(R_0+1) \backslash B_x(R_0)}|\omega|^{2p}.\end{align}
Adding
![]() $\displaystyle \int_{B_x(R_0+1) \backslash B_x(R_0)}|\omega|^{2p}$
to both sides of (3.16), we get
$\displaystyle \int_{B_x(R_0+1) \backslash B_x(R_0)}|\omega|^{2p}$
to both sides of (3.16), we get
Again adding
![]() $\displaystyle \int_{B_x(R_0)}|\omega|^{2p}$
to both sides infers
$\displaystyle \int_{B_x(R_0)}|\omega|^{2p}$
to both sides infers
On the other hand, since
![]() $|\omega|$
satisfies the differential inequality (3.3), Lemma 2.8 implies that
$|\omega|$
satisfies the differential inequality (3.3), Lemma 2.8 implies that
for some positive constant
![]() $C_6=C_6(\delta, n, k, {\rm Vol}(B_x(R_0+2)), \sup_{B_x(R_0+2)}|A|^2)$
. For a sufficiently small
$C_6=C_6(\delta, n, k, {\rm Vol}(B_x(R_0+2)), \sup_{B_x(R_0+2)}|A|^2)$
. For a sufficiently small
![]() $\delta > 0$
such that
$\delta > 0$
such that
![]() $(1-\delta)(R_0+2) > R_0 + 1$
,
$(1-\delta)(R_0+2) > R_0 + 1$
,
Together with (3.17), we have
for some positive constant
![]() $C_7=C_7(n,p,k,R_0,\lambda_1(M),S(n),{\rm Vol}(B_x(R_0+2)))$
. In what follows, as in [Reference Choi and Seo7], we consider any finite dimensional subspace
$C_7=C_7(n,p,k,R_0,\lambda_1(M),S(n),{\rm Vol}(B_x(R_0+2)))$
. In what follows, as in [Reference Choi and Seo7], we consider any finite dimensional subspace
![]() $K\subset H^1(L^{2p}(M))$
. According to Lemma 2.9, we see that there exists an
$K\subset H^1(L^{2p}(M))$
. According to Lemma 2.9, we see that there exists an
![]() $L^{2p}$
harmonic 1-form
$L^{2p}$
harmonic 1-form
![]() $\omega\subset K$
such that
$\omega\subset K$
such that
From (3.18), we have
which implies that
![]() $\dim K$
is bounded by a fixed constant. Since K is an arbitrary subspace of finite dimension, we get that
$\dim K$
is bounded by a fixed constant. Since K is an arbitrary subspace of finite dimension, we get that
![]() $\dim H^1(L^{2p}(M))<\infty$
.
$\dim H^1(L^{2p}(M))<\infty$
.
Proof of Theorem 1.4. Let
![]() $\omega$
be a
$\omega$
be a
![]() $L^{2p}$
harmonic 1-form. Using Weitzenböck formula and Kato inequality, we can get that
$L^{2p}$
harmonic 1-form. Using Weitzenböck formula and Kato inequality, we can get that
Under our hypothesis on the sectional curvature of N, we can estimate the Ricci curvature of M by using Lemmas 2.3 and 2.4:
 \begin{align*} {\rm Ric}_M &\geq -(n-1)\frac{(1-\tau)\rho}{(2n-1)(n-1)}+(n-1)H^2-\frac{n-1}{n}|\Phi|^2-\frac{(n-2)\sqrt{n(n-1)}}{n}|H||\Phi| \\[5pt] &=-\frac{(1-\tau)\rho}{2n-1}+2(n-1)H^2-\frac{(n-2)\sqrt{n(n-1)}}{n}|H|\sqrt{|A|^2-nH^2}-\frac{n-1}{n}|A|^2 \\[5pt] &\geq -\frac{(1-\tau)\rho}{2n-1}+\frac{2(n-1)-n\sqrt{n-1}}{2n}|A|^2-\frac{n-1}{n}|A|^2 \\[5pt]&=-\frac{(1-\tau)\rho}{2n-1}-\frac{\sqrt{n-1}}{2}|A|^2.\end{align*}
\begin{align*} {\rm Ric}_M &\geq -(n-1)\frac{(1-\tau)\rho}{(2n-1)(n-1)}+(n-1)H^2-\frac{n-1}{n}|\Phi|^2-\frac{(n-2)\sqrt{n(n-1)}}{n}|H||\Phi| \\[5pt] &=-\frac{(1-\tau)\rho}{2n-1}+2(n-1)H^2-\frac{(n-2)\sqrt{n(n-1)}}{n}|H|\sqrt{|A|^2-nH^2}-\frac{n-1}{n}|A|^2 \\[5pt] &\geq -\frac{(1-\tau)\rho}{2n-1}+\frac{2(n-1)-n\sqrt{n-1}}{2n}|A|^2-\frac{n-1}{n}|A|^2 \\[5pt]&=-\frac{(1-\tau)\rho}{2n-1}-\frac{\sqrt{n-1}}{2}|A|^2.\end{align*}
Thus, equation (3.19) becomes
Given any
![]() $\alpha>0$
, using (3.20) we have that
$\alpha>0$
, using (3.20) we have that
 \begin{align} |\omega|^\alpha\triangle |\omega|^\alpha &=|\omega|^\alpha\Big(\alpha(\alpha-1)|\omega|^{\alpha-2}|\nabla |\omega||^2+\alpha |\omega|^{\alpha-1}\triangle |\omega|\Big) \\[5pt] &=\frac{\alpha-1}{\alpha}|\nabla |\omega|^\alpha|^2+\alpha|\omega|^{2\alpha-2}|\omega|\triangle|\omega| \\[5pt] &\geq \Big(1-\frac{n-2}{(n-1)\alpha}\Big)|\nabla |\omega|^\alpha|^2- \frac{\alpha\sqrt{n-1}}{2}|A|^2|\omega|^{2\alpha}-\frac{(1-\tau)\rho\alpha}{2n-1}|\omega|^{2\alpha}.\end{align}
\begin{align} |\omega|^\alpha\triangle |\omega|^\alpha &=|\omega|^\alpha\Big(\alpha(\alpha-1)|\omega|^{\alpha-2}|\nabla |\omega||^2+\alpha |\omega|^{\alpha-1}\triangle |\omega|\Big) \\[5pt] &=\frac{\alpha-1}{\alpha}|\nabla |\omega|^\alpha|^2+\alpha|\omega|^{2\alpha-2}|\omega|\triangle|\omega| \\[5pt] &\geq \Big(1-\frac{n-2}{(n-1)\alpha}\Big)|\nabla |\omega|^\alpha|^2- \frac{\alpha\sqrt{n-1}}{2}|A|^2|\omega|^{2\alpha}-\frac{(1-\tau)\rho\alpha}{2n-1}|\omega|^{2\alpha}.\end{align}
Since M has finite index, as in the proof of Theorem 1.2, we assume that
![]() $M\backslash B_x(R_0)$
is stable. In other words,
$M\backslash B_x(R_0)$
is stable. In other words,
for all compactly supported Lipschitz function
![]() $\eta$
on
$\eta$
on
![]() $M \backslash B_x(R_0)$
. Replacing
$M \backslash B_x(R_0)$
. Replacing
![]() $\eta$
by
$\eta$
by
![]() $|\omega|^{(s+1)\alpha}\eta$
in (3.22) and applying the lower bound of sectional curvature of N allow us to conclude that
$|\omega|^{(s+1)\alpha}\eta$
in (3.22) and applying the lower bound of sectional curvature of N allow us to conclude that
 \begin{align} \int_{M \backslash B_x(R_0)}& |A|^2|\omega|^{2(s+1)\alpha}\eta^2 \\[5pt]&\leq \int_{M \backslash B_x(R_0)} |\nabla (|\omega|^{(s+1)\alpha}\eta)|^2+\frac{n(1-\tau)}{(2n-1)(n-1)}\int_{M \backslash B_x(R_0)}\rho |\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &=(s+1)^2\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2+\int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2\\[5pt] &\quad+2(s+1)\int_{M \backslash B_x(R_0)} |\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle \\[5pt] &\quad+\frac{n(1-\tau)}{(2n-1)(n-1)}\int_{M \backslash B_x(R_0)}\rho |\omega|^{2(s+1)\alpha}\eta^2.\end{align}
\begin{align} \int_{M \backslash B_x(R_0)}& |A|^2|\omega|^{2(s+1)\alpha}\eta^2 \\[5pt]&\leq \int_{M \backslash B_x(R_0)} |\nabla (|\omega|^{(s+1)\alpha}\eta)|^2+\frac{n(1-\tau)}{(2n-1)(n-1)}\int_{M \backslash B_x(R_0)}\rho |\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &=(s+1)^2\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2+\int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2\\[5pt] &\quad+2(s+1)\int_{M \backslash B_x(R_0)} |\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle \\[5pt] &\quad+\frac{n(1-\tau)}{(2n-1)(n-1)}\int_{M \backslash B_x(R_0)}\rho |\omega|^{2(s+1)\alpha}\eta^2.\end{align}
On the other hand, for
![]() $s>0$
and a smooth function
$s>0$
and a smooth function
![]() $\eta$
with compactly support in M, multiplying both sides of the inequality (3.21) by
$\eta$
with compactly support in M, multiplying both sides of the inequality (3.21) by
![]() $|\omega|^{2s\alpha}\eta^2$
and integrating over M, we obtain that
$|\omega|^{2s\alpha}\eta^2$
and integrating over M, we obtain that
 \begin{align*} &\quad\Big(1-\frac{n-2}{(n-1)\alpha}\Big)\int_{M \backslash B_x(R_0)}|\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2 \\[5pt] &\leq\int_{M \backslash B_x(R_0)}|\omega|^{(2s+1)\alpha}\eta^2\triangle|\omega|^\alpha+ \frac{\alpha \sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)}|A|^2|\omega|^{2(s+1)\alpha}\eta^2\\[5pt]&\quad+\frac{\alpha (1-\tau)}{2n-1}\int_{M \backslash B_x(R_0)}\rho|\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &=-(2s+1)\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2-2\int_{M \backslash B_x(R_0)} \eta|\omega|^{(2s+1)\alpha}\langle \nabla \eta,\nabla |\omega|^\alpha\rangle \\[5pt] &\quad+\frac{\alpha\sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)}|A|^2|\omega|^{2(s+1)\alpha}\eta^2+\frac{\alpha (1-\tau)}{2n-1}\int_{M \backslash B_x(R_0)}\rho|\omega|^{2(s+1)\alpha}\eta^2,\end{align*}
\begin{align*} &\quad\Big(1-\frac{n-2}{(n-1)\alpha}\Big)\int_{M \backslash B_x(R_0)}|\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2 \\[5pt] &\leq\int_{M \backslash B_x(R_0)}|\omega|^{(2s+1)\alpha}\eta^2\triangle|\omega|^\alpha+ \frac{\alpha \sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)}|A|^2|\omega|^{2(s+1)\alpha}\eta^2\\[5pt]&\quad+\frac{\alpha (1-\tau)}{2n-1}\int_{M \backslash B_x(R_0)}\rho|\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &=-(2s+1)\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2-2\int_{M \backslash B_x(R_0)} \eta|\omega|^{(2s+1)\alpha}\langle \nabla \eta,\nabla |\omega|^\alpha\rangle \\[5pt] &\quad+\frac{\alpha\sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)}|A|^2|\omega|^{2(s+1)\alpha}\eta^2+\frac{\alpha (1-\tau)}{2n-1}\int_{M \backslash B_x(R_0)}\rho|\omega|^{2(s+1)\alpha}\eta^2,\end{align*}
i.e.
 \begin{align} &\quad\Big(2(s+1)-\frac{n-2}{(n-1)\alpha}\Big)\int_{M \backslash B_x(R_0)}|\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2 \\[5pt] &\leq-2\int_{M \backslash B_x(R_0)} \eta|\omega|^{(2s+1)\alpha}\langle \nabla \eta,\nabla |\omega|^\alpha\rangle+\frac{\alpha\sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)}|A|^2|\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &\quad+\frac{\alpha (1-\tau)}{2n-1}\int_{M \backslash B_x(R_0)}\rho|\omega|^{2(s+1)\alpha}\eta^2.\end{align}
\begin{align} &\quad\Big(2(s+1)-\frac{n-2}{(n-1)\alpha}\Big)\int_{M \backslash B_x(R_0)}|\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2 \\[5pt] &\leq-2\int_{M \backslash B_x(R_0)} \eta|\omega|^{(2s+1)\alpha}\langle \nabla \eta,\nabla |\omega|^\alpha\rangle+\frac{\alpha\sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)}|A|^2|\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &\quad+\frac{\alpha (1-\tau)}{2n-1}\int_{M \backslash B_x(R_0)}\rho|\omega|^{2(s+1)\alpha}\eta^2.\end{align}
Combining (3.24) with (3.23), we obtain that
 \begin{align} &\quad \Big(2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot (s+1)^2\Big)\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2 \\[5pt] &\leq \frac{\alpha \sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2+E\int_{M \backslash B_x(R_0)} \rho |\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &\quad +\big(\alpha\sqrt{n-1}\cdot (s+1)-2\big)\int_{M \backslash B_x(R_0)}|\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle,\end{align}
\begin{align} &\quad \Big(2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot (s+1)^2\Big)\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2 \\[5pt] &\leq \frac{\alpha \sqrt{n-1}}{2}\int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2+E\int_{M \backslash B_x(R_0)} \rho |\omega|^{2(s+1)\alpha}\eta^2 \\[5pt] &\quad +\big(\alpha\sqrt{n-1}\cdot (s+1)-2\big)\int_{M \backslash B_x(R_0)}|\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle,\end{align}
where
From the assumption of weighted Poincaré inequality (1.1), we obtain that
 \begin{align} \int_{M \backslash B_x(R_0)} \rho (|\omega|^{2(s+1)\alpha}\eta^2)&\leq \int_{M \backslash B_x(R_0)} |\nabla (|\omega|^{(s+1)\alpha}\eta)|^2 \\[5pt] &=(s+1)^2\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2+\int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2 \\[5pt] &\quad+2(s+1)\int_{M \backslash B_x(R_0)}|\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle.\end{align}
\begin{align} \int_{M \backslash B_x(R_0)} \rho (|\omega|^{2(s+1)\alpha}\eta^2)&\leq \int_{M \backslash B_x(R_0)} |\nabla (|\omega|^{(s+1)\alpha}\eta)|^2 \\[5pt] &=(s+1)^2\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2+\int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2 \\[5pt] &\quad+2(s+1)\int_{M \backslash B_x(R_0)}|\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle.\end{align}
Plugging (3.26) into (3.25) implies that
where
 \begin{align*} &B=2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)^2-E(s+1)^2, \\[5pt] &C=\frac{\alpha \sqrt{n-1}}{2}+E, \\[5pt] &D=\frac{\alpha\sqrt{n-1}}{2}\cdot(1+s)-1+E(s+1). \end{align*}
\begin{align*} &B=2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)^2-E(s+1)^2, \\[5pt] &C=\frac{\alpha \sqrt{n-1}}{2}+E, \\[5pt] &D=\frac{\alpha\sqrt{n-1}}{2}\cdot(1+s)-1+E(s+1). \end{align*}
For any
![]() $\varepsilon>0$
, using Cauchy-Schwarz inequality, we can rewrite equation (3.27) as
$\varepsilon>0$
, using Cauchy-Schwarz inequality, we can rewrite equation (3.27) as
Now let
![]() $p=(s+1)\alpha$
, we see that
$p=(s+1)\alpha$
, we see that
 \begin{align}&\quad B=2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)^2-E(s+1)^2 \\[5pt]&=\frac{1}{\alpha}\Big\{2p-\frac{n-2}{n-1}-\frac{p^2\sqrt{n-1}}{2}-\left(\frac{n\sqrt{n-1}}{2}+n-1\right)\frac{(1-\tau)p^2}{(2n-1)(n-1)}\Big\} \\[5pt]&=\frac{1}{\alpha}\Big\{2p-\frac{n-2}{n-1}-\frac{\sqrt{n-1}}{2}\Big[1+\Big(n+2\sqrt{n-1}\Big)\frac{(1-\tau)}{(2n-1)(n-1)}\Big]p^2\Big\}.\end{align}
\begin{align}&\quad B=2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)^2-E(s+1)^2 \\[5pt]&=\frac{1}{\alpha}\Big\{2p-\frac{n-2}{n-1}-\frac{p^2\sqrt{n-1}}{2}-\left(\frac{n\sqrt{n-1}}{2}+n-1\right)\frac{(1-\tau)p^2}{(2n-1)(n-1)}\Big\} \\[5pt]&=\frac{1}{\alpha}\Big\{2p-\frac{n-2}{n-1}-\frac{\sqrt{n-1}}{2}\Big[1+\Big(n+2\sqrt{n-1}\Big)\frac{(1-\tau)}{(2n-1)(n-1)}\Big]p^2\Big\}.\end{align}
Let
then the discriminant of f(p) is
when
![]() $2\leq n\leq 6$
and
$2\leq n\leq 6$
and
![]() $\frac{122-51\sqrt{5}}{12+4\sqrt5}< \tau\leq 1$
. Consequently, the condition
$\frac{122-51\sqrt{5}}{12+4\sqrt5}< \tau\leq 1$
. Consequently, the condition
![]() $C_1<p<C_2$
allows us to conclude that
$C_1<p<C_2$
allows us to conclude that
![]() $f(p)>0$
, or equivalently
$f(p)>0$
, or equivalently
![]() $B>0$
. Therefore, for a sufficiently small
$B>0$
. Therefore, for a sufficiently small
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
![]() $B -|D|\varepsilon>0.$
Then, the inequality (3.28) becomes
$B -|D|\varepsilon>0.$
Then, the inequality (3.28) becomes
for some positive constant
![]() $C_0=C_0(n,p,\tau)$
. Then following the same method as in Theorem 1.2, we can obtain
$C_0=C_0(n,p,\tau)$
. Then following the same method as in Theorem 1.2, we can obtain
![]() $\dim H^1(L^{2p}(M))<\infty$
.
$\dim H^1(L^{2p}(M))<\infty$
.
Remark 3.1. If we assume further that
![]() $index(M)=0$
(i.e. M is stable) in Theorem 1.4, then
$index(M)=0$
(i.e. M is stable) in Theorem 1.4, then
![]() $H^1(L^{2p}(M))$
is trivial [Reference Chao and Lv6].
$H^1(L^{2p}(M))$
is trivial [Reference Chao and Lv6].
Proof of Theorem 1.6. Let
![]() $K_N\geq -k\rho$
, where
$K_N\geq -k\rho$
, where
![]() $k<\frac{4p(n-1)-2(n-2)-(n-1)\sqrt{n-1}p^2}{p^2(n-1)(2n-2+n\sqrt{n-1})}$
. Similarly as in the proof of Theorem 1.4, we can obtain that
$k<\frac{4p(n-1)-2(n-2)-(n-1)\sqrt{n-1}p^2}{p^2(n-1)(2n-2+n\sqrt{n-1})}$
. Similarly as in the proof of Theorem 1.4, we can obtain that
 \begin{align*} \widetilde{B}\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2&\leq \widetilde{C} \int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2\\[5pt]&\quad+2\widetilde{D}\int_{M \backslash B_x(R_0)} |\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle\end{align*}
\begin{align*} \widetilde{B}\int_{M \backslash B_x(R_0)} |\omega|^{2s\alpha}|\nabla |\omega|^\alpha|^2\eta^2&\leq \widetilde{C} \int_{M \backslash B_x(R_0)} |\omega|^{2(s+1)\alpha}|\nabla \eta|^2\\[5pt]&\quad+2\widetilde{D}\int_{M \backslash B_x(R_0)} |\omega|^{(2s+1)\alpha}\eta\langle \nabla \eta,\nabla |\omega|^\alpha\rangle\end{align*}
for any compactly supported nonconstant Lipschitz function
![]() $\eta$
on
$\eta$
on
![]() $M \backslash B_x(R_0)$
, where
$M \backslash B_x(R_0)$
, where
 \begin{align*} &\widetilde{B}=2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)^2-\widetilde{E}(s+1)^2, \\[5pt] &\widetilde{C}=\frac{\alpha \sqrt{n-1}}{2}+\widetilde{E}, \\[5pt] &\widetilde{D}=\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)-1+\widetilde{E}(s+1),\\[5pt] &\widetilde{E}=\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)k\alpha.\end{align*}
\begin{align*} &\widetilde{B}=2(s+1)-\frac{n-2}{(n-1)\alpha}-\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)^2-\widetilde{E}(s+1)^2, \\[5pt] &\widetilde{C}=\frac{\alpha \sqrt{n-1}}{2}+\widetilde{E}, \\[5pt] &\widetilde{D}=\frac{\alpha\sqrt{n-1}}{2}\cdot(s+1)-1+\widetilde{E}(s+1),\\[5pt] &\widetilde{E}=\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)k\alpha.\end{align*}
For any
![]() $\varepsilon>0$
, applying Cauchy-Schwarz inequality, we have that
$\varepsilon>0$
, applying Cauchy-Schwarz inequality, we have that
Let
![]() $p=(s+1)\alpha,$
then we have
$p=(s+1)\alpha,$
then we have
Let
![]() $\widetilde{f}(p)=-(n-1)\sqrt{n-1}p^2+4(n-1)p-2(n-2)$
, then the discriminant of
$\widetilde{f}(p)=-(n-1)\sqrt{n-1}p^2+4(n-1)p-2(n-2)$
, then the discriminant of
![]() $\widetilde{f}(p)$
is
$\widetilde{f}(p)$
is
which is satisfied when
![]() $3\leq n\leq 6$
. Thus from the assumption on p, we see that
$3\leq n\leq 6$
. Thus from the assumption on p, we see that
![]() $\widetilde{f}(p)>0$
. Moreover, the condition
$\widetilde{f}(p)>0$
. Moreover, the condition
![]() $k<\frac{4p(n-1)-2(n-2)-(n-1)\sqrt{n-1}p^2}{p^2(n-1)(2n-2+n\sqrt{n-1})}$
allow us to conclude that
$k<\frac{4p(n-1)-2(n-2)-(n-1)\sqrt{n-1}p^2}{p^2(n-1)(2n-2+n\sqrt{n-1})}$
allow us to conclude that
 \begin{align*} \widetilde{B}&=\frac{1}{\alpha}\Big\{2p-\frac{n-2}{n-1}-\frac{p^2\sqrt{n-1}}{2}-\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)kp^2\Big\} \\[5pt] &=\frac{1}{\alpha}\Big\{\frac{4(n-1)p-2(n-2)-(n-1)\sqrt{n-1}p^2}{2(n-1)}-\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)kp^2\Big\} \\[5pt] &=\frac{1}{\alpha}\Big\{\frac{\widetilde{f}(p)}{2(n-1)}-\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)kp^2\Big\}>0.\end{align*}
\begin{align*} \widetilde{B}&=\frac{1}{\alpha}\Big\{2p-\frac{n-2}{n-1}-\frac{p^2\sqrt{n-1}}{2}-\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)kp^2\Big\} \\[5pt] &=\frac{1}{\alpha}\Big\{\frac{4(n-1)p-2(n-2)-(n-1)\sqrt{n-1}p^2}{2(n-1)}-\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)kp^2\Big\} \\[5pt] &=\frac{1}{\alpha}\Big\{\frac{\widetilde{f}(p)}{2(n-1)}-\Big(\frac{n\sqrt{n-1}}{2}+n-1\Big)kp^2\Big\}>0.\end{align*}
Therefore, for a sufficiently small
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
![]() $\widetilde{B}-|\widetilde{D}|\varepsilon>0$
. Using same argument as before, we can complete the proof of Theorem 1.6.
$\widetilde{B}-|\widetilde{D}|\varepsilon>0$
. Using same argument as before, we can complete the proof of Theorem 1.6.
Acknowledgements
The first author is supported by the Natural Science Foundation of Jiangsu Province (No.BK20161412), and the second author is supported by the Natural Science Foundation of Jiangsu Province (No.BK20160661) and the National Natural Science Foundation of China No.12001099.