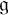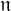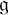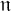Introduction
The theory of representations of a finite-dimensional complex Lie algebra
![]() $\mathfrak {g}$
on a Banach space and, more generally, Lie-algebra homomorphisms from
$\mathfrak {g}$
on a Banach space and, more generally, Lie-algebra homomorphisms from
![]() $\mathfrak {g}$
to a Banach algebra, unexpectedly turned out to be not as trivial as it might seem at first glance (see the book [Reference Beltiţă and Şabac7]). Indeed, in the solvable case, all irreducible representations of
$\mathfrak {g}$
to a Banach algebra, unexpectedly turned out to be not as trivial as it might seem at first glance (see the book [Reference Beltiţă and Şabac7]). Indeed, in the solvable case, all irreducible representations of
![]() $\mathfrak {g}$
are one-dimensional. Moreover, it was proved by Taylor that in the semisimple case, all (not only irreducible) representations of
$\mathfrak {g}$
are one-dimensional. Moreover, it was proved by Taylor that in the semisimple case, all (not only irreducible) representations of
![]() $\mathfrak {g}$
are finite dimensional [Reference Taylor23]. Nevertheless, a general representation on a Banach space can be quite complicated even when
$\mathfrak {g}$
are finite dimensional [Reference Taylor23]. Nevertheless, a general representation on a Banach space can be quite complicated even when
![]() $\mathfrak {g}$
is nilpotent.
$\mathfrak {g}$
is nilpotent.
Here we consider arbitrary finite-dimensional Lie algebras but restrict to representations (and homomorphisms) with range generating a Banach algebra satisfying a polynomial identity (a PI-algebra). We give an answer to the question: When does a Banach algebra that is a completion of the universal enveloping algebra
![]() $U(\mathfrak {g})$
satisfy a PI? We do this by providing several necessary and sufficient conditions (algebraic and analytic) in terms of the nilpotent radical
$U(\mathfrak {g})$
satisfy a PI? We do this by providing several necessary and sufficient conditions (algebraic and analytic) in terms of the nilpotent radical
![]() $\mathfrak {n}$
of
$\mathfrak {n}$
of
![]() $\mathfrak {g}$
(Theorems 1 and 2). We also include some examples, which show how the criterion works in concrete cases.
$\mathfrak {g}$
(Theorems 1 and 2). We also include some examples, which show how the criterion works in concrete cases.
According to the nature of the conditions, the argument can be divided in two parts, algebraic and analytic. The proof of the algebraic part is based on two results in algebraic PI-theory, a theorem of Bahturin [Reference Bahturin6] on PI-quotients in the semisimple case and the Braun–Kemer–Razmyslov theorem on the nilpotency of the Jacobson radical. In the proof of the analytic part, we use a result of Turovskii [Reference Turovskii and Maksudov24] on topological nilpotency, the theorem of Taylor on semisimple Lie algebras mentioned above and a small piece of the theory of generalised scalar operators.
This study was initially motivated by noncommutative spectral theory. In [Reference Dosiev (Dosi)13], Dosi considered a Fréchet algebra
![]() $\mathfrak {F}_{\mathfrak {g}}$
, ‘the algebra of formally-radical functions’, associated with a nilpotent Lie algebra
$\mathfrak {F}_{\mathfrak {g}}$
, ‘the algebra of formally-radical functions’, associated with a nilpotent Lie algebra
![]() $\mathfrak {g}$
. His goal was applications to noncommutative spectral theory (see [Reference Dosi10, Reference Dosi11, Reference Dosi12, Reference Dosiev (Dosi)14]). (Dosi’s construction is extended to the case of a general solvable Lie algebra in the author’s article [Reference Aristov3]. It is also shown there that
$\mathfrak {g}$
. His goal was applications to noncommutative spectral theory (see [Reference Dosi10, Reference Dosi11, Reference Dosi12, Reference Dosiev (Dosi)14]). (Dosi’s construction is extended to the case of a general solvable Lie algebra in the author’s article [Reference Aristov3]. It is also shown there that
![]() $\mathfrak {F}_{\mathfrak {g}}$
is an Arens–Michael algebra, that is, it can be approximated by Banach algebras.) It is proved in [Reference Dosiev (Dosi)13, Lemma 4] that in the nilpotent case, an embedding
$\mathfrak {F}_{\mathfrak {g}}$
is an Arens–Michael algebra, that is, it can be approximated by Banach algebras.) It is proved in [Reference Dosiev (Dosi)13, Lemma 4] that in the nilpotent case, an embedding
![]() $\mathfrak {g}$
to a Banach algebra B can be extended to a continuous homomorphism
$\mathfrak {g}$
to a Banach algebra B can be extended to a continuous homomorphism
![]() $\mathfrak {F}_{\mathfrak {g}}\to B$
if and only if
$\mathfrak {F}_{\mathfrak {g}}\to B$
if and only if
![]() $\mathfrak {g}$
is supernilpotent, that is, every element of
$\mathfrak {g}$
is supernilpotent, that is, every element of
![]() $[\mathfrak {g},\mathfrak {g}]$
(which is equal to
$[\mathfrak {g},\mathfrak {g}]$
(which is equal to
![]() $\mathfrak {n}$
in this case) is associatively nilpotent. This paper comes from a desire to understand what form this condition can take in the general case. Our main results show that the property to satisfy a PI, which is formally weaker that the supernilpotency, is reasonable in this context.
$\mathfrak {n}$
in this case) is associatively nilpotent. This paper comes from a desire to understand what form this condition can take in the general case. Our main results show that the property to satisfy a PI, which is formally weaker that the supernilpotency, is reasonable in this context.
This paper is just the beginning of work on PI-completions. As a continuation of the study, we discuss such completions of the algebra of analytic functionals on a complex Lie group in subsequent articles [Reference Aristov4, Reference Aristov5], which contain the following topics: a generalisation of Theorem 1, a relationship with large-scale geometry and a decomposition into an analytic smash product.
Statement of the main results
An associative algebra A (in our case, over a field, which usually is
![]() $\mathbb {C}$
) satisfies a polynomial identity (in short, a PI-algebra) if there is a nontrivial noncommutative polynomial p (that is, an element of a free algebra on n generators) such that
$\mathbb {C}$
) satisfies a polynomial identity (in short, a PI-algebra) if there is a nontrivial noncommutative polynomial p (that is, an element of a free algebra on n generators) such that
![]() $p(a_1,\ldots ,a_n)=0$
for all
$p(a_1,\ldots ,a_n)=0$
for all
![]() $a_1,\ldots ,a_n\in A$
. PI-algebras can be both unital and nonunital, but we usually assume that associative algebras are unital unless otherwise stated. Banach PI-algebras are discussed in [Reference Krupnik19, Reference Müller and Zemánek21], but we do not use the results contained there. For up-to-date information on general PI-algebras, see [Reference Aljadeff, Giambruno, Procesi and Regev1] or [Reference Kanel-Belov, Karasik and Rowen18].
$a_1,\ldots ,a_n\in A$
. PI-algebras can be both unital and nonunital, but we usually assume that associative algebras are unital unless otherwise stated. Banach PI-algebras are discussed in [Reference Krupnik19, Reference Müller and Zemánek21], but we do not use the results contained there. For up-to-date information on general PI-algebras, see [Reference Aljadeff, Giambruno, Procesi and Regev1] or [Reference Kanel-Belov, Karasik and Rowen18].
The nilpotent radical
![]() $\mathfrak {n}$
of a Lie algebra
$\mathfrak {n}$
of a Lie algebra
![]() $\mathfrak {g}$
is the intersection of the kernels of all irreducible representations of
$\mathfrak {g}$
is the intersection of the kernels of all irreducible representations of
![]() $\mathfrak {g}$
(see [Reference Bourbaki8, Ch. I, Section 5.3, Definition 3, page 44] or [Reference Dixmier9, Section 1.7.2, page 27].
$\mathfrak {g}$
(see [Reference Bourbaki8, Ch. I, Section 5.3, Definition 3, page 44] or [Reference Dixmier9, Section 1.7.2, page 27].
The following two theorems are our main results.
Theorem 1. Suppose that
![]() $\mathfrak {g}$
is a finite-dimensional complex Lie subalgebra of a Banach algebra B. Let
$\mathfrak {g}$
is a finite-dimensional complex Lie subalgebra of a Banach algebra B. Let
![]() $\|\cdot \|$
denote the norm on B and
$\|\cdot \|$
denote the norm on B and
![]() $\mathfrak {n}$
the nilpotent radical of
$\mathfrak {n}$
the nilpotent radical of
![]() $\mathfrak {g}$
. If B is generated by
$\mathfrak {g}$
. If B is generated by
![]() $\mathfrak {g}$
as a Banach algebra, then the following conditions are equivalent:
$\mathfrak {g}$
as a Banach algebra, then the following conditions are equivalent:
-
(1) B is a PI-algebra;
-
(2a) every element of
 $\mathfrak {n}$
is nilpotent;
$\mathfrak {n}$
is nilpotent; -
(2b) the nonunital associative subalgebra of B generated by
 $\mathfrak {n}$
is nilpotent;
$\mathfrak {n}$
is nilpotent; -
(3a)
 $e^b-1$
is nilpotent for every
$e^b-1$
is nilpotent for every
 $b\in \mathfrak {n}$
;
$b\in \mathfrak {n}$
; -
(3b) there is
 $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
 $e^b-1$
is nilpotent of degree at most d for every
$e^b-1$
is nilpotent of degree at most d for every
 $b\in \mathfrak {n}$
;
$b\in \mathfrak {n}$
; -
(4) there are
 $C>0$
and
$C>0$
and
 $\alpha>0$
such that
$\alpha>0$
such that
 $\|e^b\|\le C (1+\|b\|)^\alpha $
for every
$\|e^b\|\le C (1+\|b\|)^\alpha $
for every
 $b\in \mathfrak {n}$
.
$b\in \mathfrak {n}$
.
Note that the conditions (2b) and (3b) are the uniform versions of the point-wise conditions (2a) and (3a).
In Theorem 1, we assume that
![]() $\mathfrak {g}$
is embedded into B. Is not hard to extend the result to the case of an arbitrary Lie-algebra homomorphism
$\mathfrak {g}$
is embedded into B. Is not hard to extend the result to the case of an arbitrary Lie-algebra homomorphism
![]() $\mathfrak {g}\to B$
(or equivalently, a homomorphism
$\mathfrak {g}\to B$
(or equivalently, a homomorphism
![]() $U(\mathfrak {g})\to B$
). Namely, the following result holds.
$U(\mathfrak {g})\to B$
). Namely, the following result holds.
Theorem 2. Suppose that
![]() $\mathfrak {g}$
is a finite-dimensional complex Lie algebra, B is a Banach algebra and
$\mathfrak {g}$
is a finite-dimensional complex Lie algebra, B is a Banach algebra and
![]() $\theta \!:U(\mathfrak {g})\to B$
is a homomorphism of associative algebras. Let
$\theta \!:U(\mathfrak {g})\to B$
is a homomorphism of associative algebras. Let
![]() $\|\cdot \|$
be the norm on B,
$\|\cdot \|$
be the norm on B,
![]() $|\cdot |$
a norm on
$|\cdot |$
a norm on
![]() $\mathfrak {n}$
and
$\mathfrak {n}$
and
![]() $U(\mathfrak {n})_0$
the augmentation ideal of
$U(\mathfrak {n})_0$
the augmentation ideal of
![]() $U(\mathfrak {n})$
, that is, the kernel of the trivial representation. If
$U(\mathfrak {n})$
, that is, the kernel of the trivial representation. If
![]() $\theta $
has dense range, then the following conditions are equivalent:
$\theta $
has dense range, then the following conditions are equivalent:
-
(1) B is a PI-algebra;
-
(2a)
 $\theta (\eta )$
is nilpotent for every
$\theta (\eta )$
is nilpotent for every
 $\eta \in \mathfrak {n}$
;
$\eta \in \mathfrak {n}$
; -
(2b) the nonunital associative algebra
 $\theta (U(\mathfrak {n})_0)$
is nilpotent;
$\theta (U(\mathfrak {n})_0)$
is nilpotent; -
(3a)
 $e^{\theta (\eta )}-1$
is nilpotent for every
$e^{\theta (\eta )}-1$
is nilpotent for every
 $\eta \in \mathfrak {n}$
;
$\eta \in \mathfrak {n}$
; -
(3b) there is
 $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
 $e^{\theta (\eta )}-1$
is nilpotent of degree at most d for every
$e^{\theta (\eta )}-1$
is nilpotent of degree at most d for every
 $\eta \in \mathfrak {n}$
;
$\eta \in \mathfrak {n}$
; -
(4) there are
 $C>0$
and
$C>0$
and
 $\alpha>0$
such that
$\alpha>0$
such that
 $\|e^{\theta (\eta )}\|\le C (1+|\eta |)^\alpha $
for every
$\|e^{\theta (\eta )}\|\le C (1+|\eta |)^\alpha $
for every
 $\eta \in \mathfrak {n}$
.
$\eta \in \mathfrak {n}$
.
The proof of Theorem 2 is placed after the proof of Theorem 1, to which we now turn.
The algebraic argument
As mentioned in the Introduction, the proof of the theorem is divided into two parts, algebraic and analytic. The algebraic part is in the following proposition.
Proposition 3. Let
![]() $\mathfrak {g}$
be a finite-dimensional Lie subalgebra of an associative algebra A over a field of characteristic
$\mathfrak {g}$
be a finite-dimensional Lie subalgebra of an associative algebra A over a field of characteristic
![]() $0$
,
$0$
,
![]() $\mathfrak {s}$
a Levi subalgebra and
$\mathfrak {s}$
a Levi subalgebra and
![]() $\mathfrak {n}$
the nilpotent radical of
$\mathfrak {n}$
the nilpotent radical of
![]() $\mathfrak {g}$
. Suppose that A is generated by
$\mathfrak {g}$
. Suppose that A is generated by
![]() $\mathfrak {g}$
as an associative algebra. Then A is a PI-algebra if and only if the unital subalgebra generated by
$\mathfrak {g}$
as an associative algebra. Then A is a PI-algebra if and only if the unital subalgebra generated by
![]() $\mathfrak {s}$
is finite dimensional and every element of
$\mathfrak {s}$
is finite dimensional and every element of
![]() $\mathfrak {n}$
is nilpotent.
$\mathfrak {n}$
is nilpotent.
For the proof, we need three lemmas.
Lemma 4. Let A be an associative algebra over a field,
![]() $\mathfrak {g}$
a finite-dimensional Lie subalgebra that generates A as an associative algebra and
$\mathfrak {g}$
a finite-dimensional Lie subalgebra that generates A as an associative algebra and
![]() $\mathfrak {n}$
the nilpotent radical of
$\mathfrak {n}$
the nilpotent radical of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
-
(A) Then
 $\mathfrak {n}$
is contained in the Jacobson radical of A.
$\mathfrak {n}$
is contained in the Jacobson radical of A. -
(B) If, in addition, A is a PI-algebra, then
 $\mathfrak {n}$
is associatively nilpotent, that is, there is
$\mathfrak {n}$
is associatively nilpotent, that is, there is
 $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
 $b_1\ldots b_d=0$
for all
$b_1\ldots b_d=0$
for all
 $b_1,\ldots , b_d\in \mathfrak {n}$
.
$b_1,\ldots , b_d\in \mathfrak {n}$
.
The proof of part (B) is based on a deep result in PI-theory, the Braun–Kemer– Razmyslov theorem on the nilpotency of the Jacobson radical.
Proof. It is obvious that A is a quotient of
![]() $U(\mathfrak {g})$
and, in particular, finitely generated.
$U(\mathfrak {g})$
and, in particular, finitely generated.
(A) Recall that the Jacobson radical,
![]() $\mathop {\mathrm {Rad}} A$
, of A is the intersection of the kernels of all irreducible representations of A. However, the nilpotent radical
$\mathop {\mathrm {Rad}} A$
, of A is the intersection of the kernels of all irreducible representations of A. However, the nilpotent radical
![]() $\mathfrak {n}$
of the Lie algebra
$\mathfrak {n}$
of the Lie algebra
![]() $\mathfrak {g}$
is the intersection of the kernels of all irreducible representations of
$\mathfrak {g}$
is the intersection of the kernels of all irreducible representations of
![]() $\mathfrak {g}$
. Since irreducible representations of
$\mathfrak {g}$
. Since irreducible representations of
![]() $U(\mathfrak {g})$
are in one-to-one correspondence with irreducible representations of
$U(\mathfrak {g})$
are in one-to-one correspondence with irreducible representations of
![]() $\mathfrak {g}$
and every irreducible representation of A can be lifted to an irreducible representation of
$\mathfrak {g}$
and every irreducible representation of A can be lifted to an irreducible representation of
![]() $U(\mathfrak {g})$
, it follows that
$U(\mathfrak {g})$
, it follows that
![]() $\mathfrak {n}\subset \mathop {\mathrm {Rad}} A$
.
$\mathfrak {n}\subset \mathop {\mathrm {Rad}} A$
.
(B) The Braun–Kemer–Razmyslov theorem asserts that the Jacobson radical of a finitely generated PI-algebra over a commutative Jacobson ring (in particular, over a field) is nilpotent [Reference Kanel-Belov, Karasik and Rowen18, Theorem 4.0.1, page 149]. This completes the proof.
A theorem of Wedderburn asserts that a finite-dimensional associative algebra over a field (of arbitrary characteristic) with linear basis consisting of nilpotent elements is nilpotent (see, for example, [Reference Herstein16, Theorem 2.3.1, page 56]). We need a more general result in characteristic
![]() $0$
: if
$0$
: if
![]() $\mathfrak {h}$
is a Lie subalgebra of an associative algebra and
$\mathfrak {h}$
is a Lie subalgebra of an associative algebra and
![]() $\mathfrak {h}$
is generated by finitely many associatively nilpotent elements, then the nonunital associative subalgebra generated by the solvable radical of
$\mathfrak {h}$
is generated by finitely many associatively nilpotent elements, then the nonunital associative subalgebra generated by the solvable radical of
![]() $\mathfrak {h}$
is nilpotent [Reference Herstein, Small and Winter17, Theorem 8]. In particular, we have the following lemma.
$\mathfrak {h}$
is nilpotent [Reference Herstein, Small and Winter17, Theorem 8]. In particular, we have the following lemma.
Lemma 5. Let
![]() $A_0$
be a nonunital associative algebra over a field of characteristic
$A_0$
be a nonunital associative algebra over a field of characteristic
![]() $0$
. Suppose that
$0$
. Suppose that
![]() $A_0$
is generated by a nilpotent Lie subalgebra
$A_0$
is generated by a nilpotent Lie subalgebra
![]() $\mathfrak {h}$
. If every element of
$\mathfrak {h}$
. If every element of
![]() $\mathfrak {h}$
is nilpotent, then so is
$\mathfrak {h}$
is nilpotent, then so is
![]() $A_0$
.
$A_0$
.
Remark 6. In [Reference Dosi10, Lemma 2.2], Dosi gave a direct proof of the lemma in the particular case when
![]() $\mathfrak {h}=[\mathfrak {g},\mathfrak {g}]$
for a nilpotent
$\mathfrak {h}=[\mathfrak {g},\mathfrak {g}]$
for a nilpotent
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
Lemma 7. An extension of a PI-algebra (over an arbitrary commutative ring) by an ideal that is a PI-algebra is also a PI-algebra.
Proof. Let I be an ideal of an algebra A. Suppose that
![]() $A/I$
and I satisfy polynomial identities p and q, respectively. Let n and m be the numbers of variables in p and q, respectively. If
$A/I$
and I satisfy polynomial identities p and q, respectively. Let n and m be the numbers of variables in p and q, respectively. If
![]() $a_{ij}\in A$
(
$a_{ij}\in A$
(
![]() $i=1,\ldots ,n$
,
$i=1,\ldots ,n$
,
![]() $j=1,\ldots ,m$
), then
$j=1,\ldots ,m$
), then
![]() $p(a_{1j},\ldots ,a_{nj})\in I$
for every j because
$p(a_{1j},\ldots ,a_{nj})\in I$
for every j because
![]() $p(a_{1j}+I,\ldots ,a_{nj}+I)\subset I$
. Hence,
$p(a_{1j}+I,\ldots ,a_{nj}+I)\subset I$
. Hence,
![]() $q(p(a_{11},\ldots ,a_{n1}),\ldots ,p(a_{1m},\ldots ,a_{nm}))=0$
. It is easy to see that since p and q are not trivial, this noncommutative polynomial is not trivial. Thus A is a PI-algebra.
$q(p(a_{11},\ldots ,a_{n1}),\ldots ,p(a_{1m},\ldots ,a_{nm}))=0$
. It is easy to see that since p and q are not trivial, this noncommutative polynomial is not trivial. Thus A is a PI-algebra.
Proof of Proposition 3
Denote by S the unital subalgebra of A generated by
![]() $\mathfrak {s}$
and suppose that A is a PI-algebra. Then S is a quotient of
$\mathfrak {s}$
and suppose that A is a PI-algebra. Then S is a quotient of
![]() $U(\mathfrak {s})$
and satisfies a PI. Since we work in characteristic
$U(\mathfrak {s})$
and satisfies a PI. Since we work in characteristic
![]() $0$
and
$0$
and
![]() $\mathfrak {s}$
is semisimple, we can apply a result of Bahturin, which asserts that every quotient of
$\mathfrak {s}$
is semisimple, we can apply a result of Bahturin, which asserts that every quotient of
![]() $U(\mathfrak {s})$
that is a PI-algebra is finite dimensional (see [Reference Bahturin6, Theorem 1 and Corollary]). In particular, S is finite dimensional. However, it follows from Lemma 4 that every element of
$U(\mathfrak {s})$
that is a PI-algebra is finite dimensional (see [Reference Bahturin6, Theorem 1 and Corollary]). In particular, S is finite dimensional. However, it follows from Lemma 4 that every element of
![]() $\mathfrak {n}$
is nilpotent. The necessity is proved.
$\mathfrak {n}$
is nilpotent. The necessity is proved.
Suppose now that S is finite dimensional and every element of
![]() $\mathfrak {n}$
is nilpotent. Denote by I the ideal of A generated by
$\mathfrak {n}$
is nilpotent. Denote by I the ideal of A generated by
![]() $\mathfrak {n}$
. From Lemma 7, it suffices to show that I and
$\mathfrak {n}$
. From Lemma 7, it suffices to show that I and
![]() $A/I$
are PI-algebras.
$A/I$
are PI-algebras.
Denote by
![]() $A_0$
the nonunital subalgebra of A generated by
$A_0$
the nonunital subalgebra of A generated by
![]() $\mathfrak {n}$
and by
$\mathfrak {n}$
and by
![]() $U(\mathfrak {n})_0$
the augmentation ideal of
$U(\mathfrak {n})_0$
the augmentation ideal of
![]() $U(\mathfrak {n})$
. Note that
$U(\mathfrak {n})$
. Note that
![]() $\mathfrak {n}$
is a nilpotent Lie algebra. So by Lemma 5, there is a
$\mathfrak {n}$
is a nilpotent Lie algebra. So by Lemma 5, there is a
![]() $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
![]() $A_0^d=0$
. Since
$A_0^d=0$
. Since
![]() $\mathfrak {n}$
is a Lie ideal of
$\mathfrak {n}$
is a Lie ideal of
![]() $\mathfrak {g}$
, it easily follows that
$\mathfrak {g}$
, it easily follows that
![]() $U(\mathfrak {g})U(\mathfrak {n})_0=U(\mathfrak {n})_0 U(\mathfrak {g})$
. Then,
$U(\mathfrak {g})U(\mathfrak {n})_0=U(\mathfrak {n})_0 U(\mathfrak {g})$
. Then,
![]() $(U(\mathfrak {g})U(\mathfrak {n})_0)^d\subset U(\mathfrak {n})_0^d U(\mathfrak {g})$
and therefore
$(U(\mathfrak {g})U(\mathfrak {n})_0)^d\subset U(\mathfrak {n})_0^d U(\mathfrak {g})$
and therefore
![]() $I^d=A_0^d A=0$
. Hence, I is nilpotent and, in particular, a PI-algebra.
$I^d=A_0^d A=0$
. Hence, I is nilpotent and, in particular, a PI-algebra.
On the other hand, being reductive,
![]() $\mathfrak {g}/\mathfrak {n}$
is a direct sum of a semisimple summand and an abelian summand
$\mathfrak {g}/\mathfrak {n}$
is a direct sum of a semisimple summand and an abelian summand
![]() $\mathfrak {a}$
[Reference Dixmier9, Proposition 1.7.3, page 27]. Note that the restriction of the map
$\mathfrak {a}$
[Reference Dixmier9, Proposition 1.7.3, page 27]. Note that the restriction of the map
![]() $\mathfrak {g}\to \mathfrak {g}/\mathfrak {n}$
to
$\mathfrak {g}\to \mathfrak {g}/\mathfrak {n}$
to
![]() $\mathfrak {s}$
is injective and so we can identify the semisimple summand in
$\mathfrak {s}$
is injective and so we can identify the semisimple summand in
![]() $\mathfrak {g}/\mathfrak {n}$
with
$\mathfrak {g}/\mathfrak {n}$
with
![]() $\mathfrak {s}$
. Consider the naturally defined homomorphisms
$\mathfrak {s}$
. Consider the naturally defined homomorphisms
![]() $S\to A\to A/I$
and
$S\to A\to A/I$
and
![]() $U(\mathfrak {a})\to U(\mathfrak {g}/\mathfrak {n})\to A/I$
. Their ranges commute since
$U(\mathfrak {a})\to U(\mathfrak {g}/\mathfrak {n})\to A/I$
. Their ranges commute since
![]() $U(\mathfrak {s})$
and
$U(\mathfrak {s})$
and
![]() $U(\mathfrak {a})$
commute in
$U(\mathfrak {a})$
commute in
![]() $U(\mathfrak {g}/\mathfrak {n})$
and the diagram
$U(\mathfrak {g}/\mathfrak {n})$
and the diagram

is commutative. By the universal property of tensor products of associative algebras, we have the induced homomorphism
![]() $S\otimes U(\mathfrak {a})\to A/I$
. This homomorphism is surjective because
$S\otimes U(\mathfrak {a})\to A/I$
. This homomorphism is surjective because
![]() $A/I$
and
$A/I$
and
![]() $S\otimes U(\mathfrak {a})$
are quotients of
$S\otimes U(\mathfrak {a})$
are quotients of
![]() $U(\mathfrak {g})/(U(\mathfrak {g})U(\mathfrak {n})_0)$
and
$U(\mathfrak {g})/(U(\mathfrak {g})U(\mathfrak {n})_0)$
and
![]() $U(\mathfrak {s})\otimes U(\mathfrak {a})$
, respectively, and the last two algebras are isomorphic being isomorphic to
$U(\mathfrak {s})\otimes U(\mathfrak {a})$
, respectively, and the last two algebras are isomorphic being isomorphic to
![]() $U(\mathfrak {g}/\mathfrak {n})$
. By Regev’s theorem [Reference Kanel-Belov, Karasik and Rowen18, Theorem 3.4.7, page 138], the class of PI-algebras is stable under tensor products. Thus,
$U(\mathfrak {g}/\mathfrak {n})$
. By Regev’s theorem [Reference Kanel-Belov, Karasik and Rowen18, Theorem 3.4.7, page 138], the class of PI-algebras is stable under tensor products. Thus,
![]() $S\otimes U(\mathfrak {a})$
is a PI-algebra since it is the tensor product of a finite-dimensional and abelian algebra. Being a quotient of a PI-algebra,
$S\otimes U(\mathfrak {a})$
is a PI-algebra since it is the tensor product of a finite-dimensional and abelian algebra. Being a quotient of a PI-algebra,
![]() $A/I$
also satisfies a PI. This completes the proof of the sufficiency.
$A/I$
also satisfies a PI. This completes the proof of the sufficiency.
The analytic argument
Now we turn to auxiliary lemmas, which are needed in the analytic part of the proof of Theorem 1. The first lemma is a corollary of a result of Turovskii in [Reference Turovskii and Maksudov24].
Lemma 8. Suppose that the hypotheses in Theorem 1 hold. Then
![]() $\mathfrak {n}\subset \mathop {\mathrm {Rad}} B$
.
$\mathfrak {n}\subset \mathop {\mathrm {Rad}} B$
.
Proof. Note that
![]() $\mathfrak {n}=[\mathfrak {g},\mathfrak {r}]$
, where
$\mathfrak {n}=[\mathfrak {g},\mathfrak {r}]$
, where
![]() $\mathfrak {r}$
is the solvable radical of
$\mathfrak {r}$
is the solvable radical of
![]() $\mathfrak {g}$
[Reference Dixmier9, Proposition 1.7.1, page 26]. Turovskii’s theorem [Reference Turovskii and Maksudov24] asserts that
$\mathfrak {g}$
[Reference Dixmier9, Proposition 1.7.1, page 26]. Turovskii’s theorem [Reference Turovskii and Maksudov24] asserts that
![]() $[\mathfrak {g},\mathfrak {h}]\subset \mathop {\mathrm {Rad}} B$
for every solvable ideal
$[\mathfrak {g},\mathfrak {h}]\subset \mathop {\mathrm {Rad}} B$
for every solvable ideal
![]() $\mathfrak {h}$
of
$\mathfrak {h}$
of
![]() $\mathfrak {g}$
(for a proof, see [Reference Beltiţă and Şabac7, Section 24, Theorem 1, page 130]). By putting
$\mathfrak {g}$
(for a proof, see [Reference Beltiţă and Şabac7, Section 24, Theorem 1, page 130]). By putting
![]() $\mathfrak {h}=\mathfrak {r}$
, we have the result.
$\mathfrak {h}=\mathfrak {r}$
, we have the result.
An element of a Banach algebra is topologically nilpotent if
![]() $\|b^n\|^{1/n}\to 0$
as
$\|b^n\|^{1/n}\to 0$
as
![]() $n\to \infty $
.
$n\to \infty $
.
Lemma 9. Let b be a topologically nilpotent element of a Banach algebra. Then b is nilpotent if and only if
![]() $e^b-1$
is nilpotent. Moreover, b has degree of nilpotency at most d if and only if
$e^b-1$
is nilpotent. Moreover, b has degree of nilpotency at most d if and only if
![]() $e^b-1$
does.
$e^b-1$
does.
Proof. Put
![]() $r\!:=e^b-1$
. If
$r\!:=e^b-1$
. If
![]() $b^d=0$
for some
$b^d=0$
for some
![]() $d\in \mathbb {N}$
, then
$d\in \mathbb {N}$
, then
![]() $r=b+\cdots + b^{d-1}/(d-1)!$
and therefore
$r=b+\cdots + b^{d-1}/(d-1)!$
and therefore
![]() $r^d=0$
.
$r^d=0$
.
Suppose now that there is
![]() $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
![]() $r^d=0$
. Since b is topologically nilpotent, its spectrum is
$r^d=0$
. Since b is topologically nilpotent, its spectrum is
![]() $\{0\}$
. Let f be the function on
$\{0\}$
. Let f be the function on
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
![]() $f(z)=(e^z-1)/z$
when
$f(z)=(e^z-1)/z$
when
![]() $z\ne 0$
and
$z\ne 0$
and
![]() $f(0)=1$
. Since f is holomorphic, it follows from the spectral mapping theorem [Reference Helemskii15, Theorem 2.2.23] that the spectrum of
$f(0)=1$
. Since f is holomorphic, it follows from the spectral mapping theorem [Reference Helemskii15, Theorem 2.2.23] that the spectrum of
![]() $f(b)$
is
$f(b)$
is
![]() $\{1\}$
and therefore
$\{1\}$
and therefore
![]() $f(b)$
is invertible. Since
$f(b)$
is invertible. Since
![]() $bf(b)=e^b-1=r$
and
$bf(b)=e^b-1=r$
and
![]() $r^d=0$
, we have
$r^d=0$
, we have
![]() $b^df(b)^d=0$
. Since
$b^df(b)^d=0$
. Since
![]() $f(b)$
is invertible,
$f(b)$
is invertible,
![]() $b^d=0$
.
$b^d=0$
.
Lemma 10. Let r be a topologically nilpotent element of a Banach algebra with the norm
![]() $\|\cdot \|$
. Then the following conditions are equivalent:
$\|\cdot \|$
. Then the following conditions are equivalent:
-
(1) there are
 $C>0$
and
$C>0$
and
 $\alpha>0$
such that
$\alpha>0$
such that
 $\|(1+r)^k\|\le C(1+ |k|)^\alpha $
for all
$\|(1+r)^k\|\le C(1+ |k|)^\alpha $
for all
 $k\in \mathbb {Z}$
;
$k\in \mathbb {Z}$
; -
(2) r is nilpotent.
Moreover, we can assume that C and
![]() $\alpha $
depend only on
$\alpha $
depend only on
![]() $\|r\|$
and the degree of nilpotency of r.
$\|r\|$
and the degree of nilpotency of r.
Note that
![]() $(1+r)^k$
is well defined for negative k because the spectrum of r is
$(1+r)^k$
is well defined for negative k because the spectrum of r is
![]() $\{0\}$
.
$\{0\}$
.
Proof. If (1) holds, then
![]() $1+r$
is generalised scalar [Reference Laursen and Neumann20, Theorem 1.5.12, page 66], that is, admits a
$1+r$
is generalised scalar [Reference Laursen and Neumann20, Theorem 1.5.12, page 66], that is, admits a
![]() $C^\infty $
-functional calculus on
$C^\infty $
-functional calculus on
![]() $\mathbb {C}$
. (This result and the proposition cited below are stated for operators but, in fact, the arguments for them use only the Banach algebra structure.) Shifting by a number does not change the property of being generalised scalar. Thus, r is both topologically nilpotent and generalised scalar. It follows from [Reference Laursen and Neumann20, Proposition 1.5.10, page 64] that r is nilpotent.
$\mathbb {C}$
. (This result and the proposition cited below are stated for operators but, in fact, the arguments for them use only the Banach algebra structure.) Shifting by a number does not change the property of being generalised scalar. Thus, r is both topologically nilpotent and generalised scalar. It follows from [Reference Laursen and Neumann20, Proposition 1.5.10, page 64] that r is nilpotent.
However, if r is nilpotent, then we immediately have the desired estimate for positive k with constants
![]() $C>0$
and
$C>0$
and
![]() $\alpha>0$
depending only on the degree of nilpotency of r, say d, and
$\alpha>0$
depending only on the degree of nilpotency of r, say d, and
![]() $\|r\|$
. To prove it for negative k, note that
$\|r\|$
. To prove it for negative k, note that
![]() $(1+r)^{-1}=1+r'$
for some nilpotent
$(1+r)^{-1}=1+r'$
for some nilpotent
![]() $r'$
whose degree of nilpotency and norm depend only on d and
$r'$
whose degree of nilpotency and norm depend only on d and
![]() $\|r\|$
. It follows that (1) holds with C and
$\|r\|$
. It follows that (1) holds with C and
![]() $\alpha $
also depending only on d and
$\alpha $
also depending only on d and
![]() $\|r\|$
.
$\|r\|$
.
Proof of Theorem 1
We show that (1)
![]() $\Leftrightarrow $
(2a) and (2a)
$\Leftrightarrow $
(2a) and (2a)
![]() $\Rightarrow $
(2b)
$\Rightarrow $
(2b)
![]() $\Rightarrow $
(3b)
$\Rightarrow $
(3b)
![]() $\Rightarrow $
(4)
$\Rightarrow $
(4)
![]() $\Rightarrow $
(3a)
$\Rightarrow $
(3a)
![]() $\Rightarrow $
(2a). Let
$\Rightarrow $
(2a). Let
![]() $\mathfrak {s}$
be a Levi subalgebra of
$\mathfrak {s}$
be a Levi subalgebra of
![]() $\mathfrak {g}$
, A the associative unital subalgebra of B generated by
$\mathfrak {g}$
, A the associative unital subalgebra of B generated by
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $A_0$
the nonunital subalgebra of A generated by
$A_0$
the nonunital subalgebra of A generated by
![]() $\mathfrak {n}$
.
$\mathfrak {n}$
.
(1)
![]() $\Leftrightarrow $
(2a). Since
$\Leftrightarrow $
(2a). Since
![]() $\mathfrak {s}$
is semisimple, it follows from a result of Taylor [Reference Taylor23] (see also [Reference Beltiţă and Şabac7] or [Reference Aristov2]) that the image of
$\mathfrak {s}$
is semisimple, it follows from a result of Taylor [Reference Taylor23] (see also [Reference Beltiţă and Şabac7] or [Reference Aristov2]) that the image of
![]() $U(\mathfrak {s})$
in a Banach algebra is finite dimensional. Being dense in B, the subalgebra A satisfies a PI if and only if so does B. Applying Proposition 3 to A, we conclude that (1) and (2a) are equivalent.
$U(\mathfrak {s})$
in a Banach algebra is finite dimensional. Being dense in B, the subalgebra A satisfies a PI if and only if so does B. Applying Proposition 3 to A, we conclude that (1) and (2a) are equivalent.
(2a)
![]() $\Rightarrow $
(2b). Applying Lemma 5 to
$\Rightarrow $
(2b). Applying Lemma 5 to
![]() $A_0$
shows that A is nilpotent when every element of
$A_0$
shows that A is nilpotent when every element of
![]() $\mathfrak {n}$
is nilpotent.
$\mathfrak {n}$
is nilpotent.
(2b)
![]() $\Rightarrow $
(3b). Suppose that
$\Rightarrow $
(3b). Suppose that
![]() $A_0$
is nilpotent, that is, there is
$A_0$
is nilpotent, that is, there is
![]() $d\in \mathbb {N}$
such that
$d\in \mathbb {N}$
such that
![]() $A_0^d=0$
. In particular, every b in
$A_0^d=0$
. In particular, every b in
![]() $\mathfrak {n}$
is of degree of nilpotency at most d and so is
$\mathfrak {n}$
is of degree of nilpotency at most d and so is
![]() $e^b-1$
by Lemma 9.
$e^b-1$
by Lemma 9.
(3b)
![]() $\Rightarrow $
(4). Let d be a positive integer such that
$\Rightarrow $
(4). Let d be a positive integer such that
![]() $e^b-1$
is nilpotent of degree at most d for every
$e^b-1$
is nilpotent of degree at most d for every
![]() $b\in \mathfrak {n}$
. Applying the implication (2)
$b\in \mathfrak {n}$
. Applying the implication (2)
![]() $\Rightarrow $
(1) in Lemma 10 shows that there are constants
$\Rightarrow $
(1) in Lemma 10 shows that there are constants
![]() $C>0$
and
$C>0$
and
![]() $\alpha>0$
such that
$\alpha>0$
such that
when
![]() $\|e^b-1\|\le 1$
. Therefore, there is
$\|e^b-1\|\le 1$
. Therefore, there is
![]() $\varepsilon>0$
such that (4.1) holds when
$\varepsilon>0$
such that (4.1) holds when
![]() $\|b\|\le \varepsilon $
.
$\|b\|\le \varepsilon $
.
Now fix a nonzero element b of
![]() $\mathfrak {n}$
. Take
$\mathfrak {n}$
. Take
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $(k-1)\varepsilon \le \|b\|\le k\varepsilon $
and put
$(k-1)\varepsilon \le \|b\|\le k\varepsilon $
and put
![]() $b'\!:=k^{-1}b$
. Then
$b'\!:=k^{-1}b$
. Then
![]() $\|b'\|\le \varepsilon $
and
$\|b'\|\le \varepsilon $
and
Since
![]() $k\le 1+\varepsilon ^{-1}\|b\|$
, we have
$k\le 1+\varepsilon ^{-1}\|b\|$
, we have
Combining this with (4.2) shows that there is
![]() $C'>0$
such that
$C'>0$
such that
![]() $\|e^b\|\le C' (1+\|b\|)^\alpha $
and
$\|e^b\|\le C' (1+\|b\|)^\alpha $
and
![]() $C'$
is independent in b.
$C'$
is independent in b.
(4)
![]() $\Rightarrow $
(3a). Suppose that for some
$\Rightarrow $
(3a). Suppose that for some
![]() $C>0$
and
$C>0$
and
![]() $\alpha>0$
, the inequality
$\alpha>0$
, the inequality
![]() $\|e^{b}\|\le C (1+\|b\|)^\alpha $
holds when
$\|e^{b}\|\le C (1+\|b\|)^\alpha $
holds when
![]() $b\in \mathfrak {n}$
. We claim that
$b\in \mathfrak {n}$
. We claim that
![]() $r\!:=e^b-1$
is topologically nilpotent whenever
$r\!:=e^b-1$
is topologically nilpotent whenever
![]() $b\in \mathfrak {n}$
. Indeed, Lemma 8 implies that
$b\in \mathfrak {n}$
. Indeed, Lemma 8 implies that
![]() $b\in \mathop {\mathrm {Rad}} B$
. Note that
$b\in \mathop {\mathrm {Rad}} B$
. Note that
![]() $r=\sum _{n=1}^{\infty }{b^n}/{n!}$
and
$r=\sum _{n=1}^{\infty }{b^n}/{n!}$
and
![]() $\mathop {\mathrm {Rad}} B$
is closed. So r is also contained in
$\mathop {\mathrm {Rad}} B$
is closed. So r is also contained in
![]() $\mathop {\mathrm {Rad}} B$
. Being an element of the radical of a Banach algebra, r is topologically nilpotent.
$\mathop {\mathrm {Rad}} B$
. Being an element of the radical of a Banach algebra, r is topologically nilpotent.
Further, it follows from the assumption that
for every
![]() $k\in \mathbb {Z}$
. So by the implication (1)
$k\in \mathbb {Z}$
. So by the implication (1)
![]() $\Rightarrow $
(2) in Lemma 10, r is nilpotent.
$\Rightarrow $
(2) in Lemma 10, r is nilpotent.
(3a)
![]() $\Rightarrow $
(2a). Suppose that
$\Rightarrow $
(2a). Suppose that
![]() $e^b-1$
is nilpotent for every
$e^b-1$
is nilpotent for every
![]() $b\in \mathfrak {n}$
. Then it follows immediately from Lemma 9 that b is nilpotent.
$b\in \mathfrak {n}$
. Then it follows immediately from Lemma 9 that b is nilpotent.
This completes the proof of Theorem 1.
Proof of Theorem 2
To deduce Theorem 2 from Theorem 1, note that every Lie-algebra homomorphism
![]() $\phi \!:\mathfrak {g}_1\to \mathfrak {g}_2$
maps the nilpotent radical of
$\phi \!:\mathfrak {g}_1\to \mathfrak {g}_2$
maps the nilpotent radical of
![]() $\mathfrak {g}_1$
into the nilpotent radical of
$\mathfrak {g}_1$
into the nilpotent radical of
![]() $\mathfrak {g}_2$
. If, in addition,
$\mathfrak {g}_2$
. If, in addition,
![]() $\phi $
is surjective, then so is the Lie-algebra homomorphism
$\phi $
is surjective, then so is the Lie-algebra homomorphism
![]() $\mathfrak {r}_1\to \mathfrak {r}_2$
of the solvable radicals (see, for example, [Reference Aristov3, Lemma 4.10]). Since the nilpotent radicals of
$\mathfrak {r}_1\to \mathfrak {r}_2$
of the solvable radicals (see, for example, [Reference Aristov3, Lemma 4.10]). Since the nilpotent radicals of
![]() $\mathfrak {g}_1$
and
$\mathfrak {g}_1$
and
![]() $\mathfrak {g}_2$
coincide respectively with
$\mathfrak {g}_2$
coincide respectively with
![]() $[\mathfrak {g}_1,\mathfrak {r}_1]$
and
$[\mathfrak {g}_1,\mathfrak {r}_1]$
and
![]() $[\mathfrak {g}_2,\mathfrak {r}_1]$
(see the reference in the proof of Lemma 8), we have a surjective Lie-algebra homomorphism of the nilpotent radicals. Thus, (1), (2a), (2b), (3a) and (3b) are equivalent since so are the corresponding conditions in Theorem 1.
$[\mathfrak {g}_2,\mathfrak {r}_1]$
(see the reference in the proof of Lemma 8), we have a surjective Lie-algebra homomorphism of the nilpotent radicals. Thus, (1), (2a), (2b), (3a) and (3b) are equivalent since so are the corresponding conditions in Theorem 1.
The proof of the implication (4)
![]() $\Rightarrow $
(3a) is a slight modification of the argument for the corresponding implication in Theorem 1. First note that there is
$\Rightarrow $
(3a) is a slight modification of the argument for the corresponding implication in Theorem 1. First note that there is
![]() $K>0$
such that
$K>0$
such that
Then writing
![]() $\theta (\eta )$
instead of b and using (4.3), we deduce from the inequality
$\theta (\eta )$
instead of b and using (4.3), we deduce from the inequality
![]() $\|e^{\theta (\eta )}\|\le C (1+|\eta |)^\alpha $
for
$\|e^{\theta (\eta )}\|\le C (1+|\eta |)^\alpha $
for
![]() $\eta \in \mathfrak {n}$
that
$\eta \in \mathfrak {n}$
that
and then apply Lemma 10.
Finally, if (1) holds, then so does (4) in Theorem 1 for elements b of the form
![]() $\theta (\eta )$
with
$\theta (\eta )$
with
![]() $\eta \in \mathfrak {n}$
. It follows from (4.3) that (4) in Theorem 2 is also satisfied.
$\eta \in \mathfrak {n}$
. It follows from (4.3) that (4) in Theorem 2 is also satisfied.
Some examples
There are many finite-dimensional Lie algebras such that every completion of the universal enveloping algebra with respect to a submultiplicative prenorm (that is, every completion that is a Banach algebra) satisfies a polynomial identity. The two simplest cases follow.
Proposition 11. If a finite-dimensional complex Lie algebra
![]() $\mathfrak {g}$
is reductive, then every completion of
$\mathfrak {g}$
is reductive, then every completion of
![]() $U(\mathfrak {g})$
with respect to a submultiplicative prenorm satisfies a PI.
$U(\mathfrak {g})$
with respect to a submultiplicative prenorm satisfies a PI.
Proof. Since
![]() $\mathfrak {g}$
is reductive, the nilpotent radical is trivial. Thus by Theorem 2, every completion of
$\mathfrak {g}$
is reductive, the nilpotent radical is trivial. Thus by Theorem 2, every completion of
![]() $U(\mathfrak {g})$
with respect to a submultiplicative prenorm satisfies a PI.
$U(\mathfrak {g})$
with respect to a submultiplicative prenorm satisfies a PI.
Proposition 12. Let
![]() $\mathfrak {g}$
be a two-dimensional nonabelian complex Lie algebra. Then every completion of
$\mathfrak {g}$
be a two-dimensional nonabelian complex Lie algebra. Then every completion of
![]() $U(\mathfrak {g})$
with respect to a submultiplicative prenorm satisfies a PI.
$U(\mathfrak {g})$
with respect to a submultiplicative prenorm satisfies a PI.
Proof. There is a basis
![]() $e_1,e_2$
in
$e_1,e_2$
in
![]() $\mathfrak {g}$
such that
$\mathfrak {g}$
such that
![]() $[e_1,e_2]=e_2$
. Note that
$[e_1,e_2]=e_2$
. Note that
![]() $\mathfrak {n}=[\mathfrak {g},\mathfrak {g}]=\mathbb {C} e_2$
. Let B be a Banach-algebra completion of
$\mathfrak {n}=[\mathfrak {g},\mathfrak {g}]=\mathbb {C} e_2$
. Let B be a Banach-algebra completion of
![]() $U(\mathfrak {g})$
and
$U(\mathfrak {g})$
and
![]() $\pi $
the corresponding Lie-algebra homomorphism from
$\pi $
the corresponding Lie-algebra homomorphism from
![]() $\mathfrak {g}$
to B. It is not hard to see that
$\mathfrak {g}$
to B. It is not hard to see that
![]() $\pi (e_2)$
is nilpotent (see, for example, [Reference Pirkovskii22, Example 5.1]). Then B satisfies a PI by Theorem 2.
$\pi (e_2)$
is nilpotent (see, for example, [Reference Pirkovskii22, Example 5.1]). Then B satisfies a PI by Theorem 2.
However, there are Lie algebras whose universal enveloping algebra admits a completion that does not satisfy a PI. Here we give a particular case.
Proposition 13. Let
![]() $\mathfrak {g}$
be a nonabelian nilpotent complex Lie algebra
$\mathfrak {g}$
be a nonabelian nilpotent complex Lie algebra
![]() $\mathfrak {g}$
. Then there is a submultiplicative prenorm on
$\mathfrak {g}$
. Then there is a submultiplicative prenorm on
![]() $U(\mathfrak {g})$
such that the completion does not satisfy a PI.
$U(\mathfrak {g})$
such that the completion does not satisfy a PI.
Proof. Since
![]() $\mathfrak {g}$
is nonabelian and nilpotent, there is a sequence
$\mathfrak {g}$
is nonabelian and nilpotent, there is a sequence
![]() $(\theta _n)$
of representations of
$(\theta _n)$
of representations of
![]() $U(\mathfrak {g})$
on (finite-dimensional) Hilbert spaces such that the sequence
$U(\mathfrak {g})$
on (finite-dimensional) Hilbert spaces such that the sequence
![]() $(d_n)$
of the corresponding degrees of nilpotency of
$(d_n)$
of the corresponding degrees of nilpotency of
![]() $\theta _n(\mathfrak {n})$
is unbounded (see, for example, [Reference Aristov3, Proposition 4.14 and Lemma 4.16]). Using renormalisation, we can assume that the set
$\theta _n(\mathfrak {n})$
is unbounded (see, for example, [Reference Aristov3, Proposition 4.14 and Lemma 4.16]). Using renormalisation, we can assume that the set
![]() $\{\|\theta _n(e_j)\|\}$
, where
$\{\|\theta _n(e_j)\|\}$
, where
![]() $e_1,\ldots ,e_k$
are algebraic generators of
$e_1,\ldots ,e_k$
are algebraic generators of
![]() $\mathfrak {g}$
, is bounded for every j. Then the infinite sum
$\mathfrak {g}$
, is bounded for every j. Then the infinite sum
![]() $\theta \!:=\oplus _{n=1}^\infty \theta _n$
is a well-defined representation of
$\theta \!:=\oplus _{n=1}^\infty \theta _n$
is a well-defined representation of
![]() $U(\mathfrak {g})$
on a Hilbert space. Since for every
$U(\mathfrak {g})$
on a Hilbert space. Since for every
![]() $p\in \mathbb {N}_+$
there are
$p\in \mathbb {N}_+$
there are
![]() $n\in \mathbb {N}_+$
and
$n\in \mathbb {N}_+$
and
![]() $\eta \in \mathfrak {n}$
such that
$\eta \in \mathfrak {n}$
such that
![]() $\theta _n(\eta )^p\ne 0$
, the completion of the range of
$\theta _n(\eta )^p\ne 0$
, the completion of the range of
![]() $\theta $
does not satisfy a PI by Theorem 2.
$\theta $
does not satisfy a PI by Theorem 2.
For a general criterion, see the follow-up paper [Reference Aristov5].