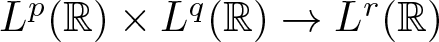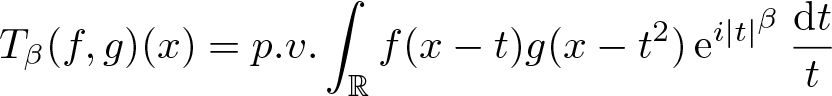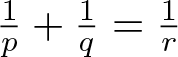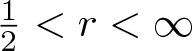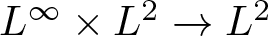1. Introduction
The main task of the present paper is to determine the boundedness of the following bilinear oscillatory operators along parabola
 \begin{equation*}
T_\beta(f, g)(x)=p.v.\int_{{\mathbb R}} f(x-t)g(x-t^{2})\,{\rm e}^{i |t|^{\beta}}\,\frac{{\rm d}t}{t},\
\end{equation*}
\begin{equation*}
T_\beta(f, g)(x)=p.v.\int_{{\mathbb R}} f(x-t)g(x-t^{2})\,{\rm e}^{i |t|^{\beta}}\,\frac{{\rm d}t}{t},\
\end{equation*}with β > 1 or β < 0. The main result is as follows.
Theorem 1.1. Assume β is real number such that β < 0 or β > 1. We have
for
 \begin{equation}
\frac{1}{r}=\frac{1}{p}+\frac{1}{q}, \quad p, q\gt1, \quad \frac{1}{2} \lt r\lt\infty
\end{equation}
\begin{equation}
\frac{1}{r}=\frac{1}{p}+\frac{1}{q}, \quad p, q\gt1, \quad \frac{1}{2} \lt r\lt\infty
\end{equation}and the constant ![]() $C_{\beta, r, p, q}\lt\infty$ depending only on
$C_{\beta, r, p, q}\lt\infty$ depending only on ![]() $\beta, p, q$ and r.
$\beta, p, q$ and r.
In [Reference Fan and Li4], Fan and Li proved that T β is bounded from ![]() $L^\infty\times L^2$ to L 2 with
$L^\infty\times L^2$ to L 2 with ![]() $\beta\lt-1$. In the same paper, the authors raised an open question to set up the
$\beta\lt-1$. In the same paper, the authors raised an open question to set up the ![]() $L^p\times L^q\to L^r$ boundedness for T β with
$L^p\times L^q\to L^r$ boundedness for T β with ![]() $(p,q,r)$ satisfying Equation (1.2) for β < 0. In this paper, we give a confirm answer to this question. T β is an oscillatory form of the bilinear Hilbert transform along the parabola, which is defined as
$(p,q,r)$ satisfying Equation (1.2) for β < 0. In this paper, we give a confirm answer to this question. T β is an oscillatory form of the bilinear Hilbert transform along the parabola, which is defined as
 \begin{equation*}
H_{t^2}(f,g)(x)=p.v.\int_{\mathbb {R}}f(x-t)g(x-t^2)\,\frac{{\rm d}t}{t}
\end{equation*}
\begin{equation*}
H_{t^2}(f,g)(x)=p.v.\int_{\mathbb {R}}f(x-t)g(x-t^2)\,\frac{{\rm d}t}{t}
\end{equation*}for f and g in the Schwartz class ![]() $\mathcal{S}(\mathbb{R})$ whose boundedness was obtained by Li [Reference Li11] and Li and Xiao [Reference Li and Xiao12]. Our main interest is to explore how the oscillatory term
$\mathcal{S}(\mathbb{R})$ whose boundedness was obtained by Li [Reference Li11] and Li and Xiao [Reference Li and Xiao12]. Our main interest is to explore how the oscillatory term ![]() ${\rm e}^{i|\xi|^\beta}$ effects the boundedness of the operator. To make the idea clear, we start with the well-known bilinear Hilbert transform
${\rm e}^{i|\xi|^\beta}$ effects the boundedness of the operator. To make the idea clear, we start with the well-known bilinear Hilbert transform
 \begin{equation*}H(f,g)(x)=p.v.\int f(x-t)g(x+t)\,\frac{{\rm d}t}{t}.\end{equation*}
\begin{equation*}H(f,g)(x)=p.v.\int f(x-t)g(x+t)\,\frac{{\rm d}t}{t}.\end{equation*}By Fourier transform, the bilinear Hilbert transform can be written (informly) as
 \begin{equation*}H(f,g)(x)=i\int_{\mathbb R^2}\hat{f}(\xi)\hat{g}(\eta)\,{\rm sgn}(\eta-\xi)\,{\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi \,{\rm d}\eta.\end{equation*}
\begin{equation*}H(f,g)(x)=i\int_{\mathbb R^2}\hat{f}(\xi)\hat{g}(\eta)\,{\rm sgn}(\eta-\xi)\,{\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi \,{\rm d}\eta.\end{equation*} Here sgn(x) denotes the Sign function. The line ![]() $\xi=\eta$, the set of the critical points of sgn
$\xi=\eta$, the set of the critical points of sgn![]() $(\xi-\eta)$, is called the resonance set. We say that the functions f resonates with g on the resonance set. If we have some suitable decay estimate away from the line, the bilinear Hilbert transform is almost a product of f and g. We could obtain the boundedness of the bilinear Hilbert transform. However, this problem becomes very subtle since the line
$(\xi-\eta)$, is called the resonance set. We say that the functions f resonates with g on the resonance set. If we have some suitable decay estimate away from the line, the bilinear Hilbert transform is almost a product of f and g. We could obtain the boundedness of the bilinear Hilbert transform. However, this problem becomes very subtle since the line ![]() $\xi=\eta$ is modulation-invariant. This is the main obstacle to obtain the boundedness of the bilinear Hilbert transform. The boundedness of such bilinear transform was conjectured by Calderón and motivated by the study of the Cauchy integrals on Lipschitz curves. In the 1990s, this conjecture was verified by Lacey and Thiele in a breakthrough pair of papers [Reference Lacey and Thiele9, Reference Lacey and Thiele10]. In their works, a systematic and delicate method was developed, inspired by the famous works of Carleson [Reference Carleson1] and Fefferman [Reference Fefferman5], which is nowadays referred as the method of time–frequency analysis. Over the past two decades, this method has emerged as a powerful analytic tool to handle problems that are related to multilinear analysis.
$\xi=\eta$ is modulation-invariant. This is the main obstacle to obtain the boundedness of the bilinear Hilbert transform. The boundedness of such bilinear transform was conjectured by Calderón and motivated by the study of the Cauchy integrals on Lipschitz curves. In the 1990s, this conjecture was verified by Lacey and Thiele in a breakthrough pair of papers [Reference Lacey and Thiele9, Reference Lacey and Thiele10]. In their works, a systematic and delicate method was developed, inspired by the famous works of Carleson [Reference Carleson1] and Fefferman [Reference Fefferman5], which is nowadays referred as the method of time–frequency analysis. Over the past two decades, this method has emerged as a powerful analytic tool to handle problems that are related to multilinear analysis.
We write (informally) the multiplier of ![]() $H_{t^2}$ as
$H_{t^2}$ as
 \begin{equation*}m(\xi,\eta)=p.v.\int {\rm e}^{i(t\xi+t^2\eta)}\,\frac{{\rm d}t}{t}.\end{equation*}
\begin{equation*}m(\xi,\eta)=p.v.\int {\rm e}^{i(t\xi+t^2\eta)}\,\frac{{\rm d}t}{t}.\end{equation*}The extra curvature of t 2 breaks down the modulation invariant of the operators. The tools in oscillatory integral such as van der Corput’s lemma and method of stationary phase work well. Along this direction, there are plenty of literatures studying how the curvature of a general curve effects the boundedness of bilinear Hilbert transform along a general curve (replacing the parabola t 2 by a general curve γ). We refer the readers to the recent paper [Reference Li and Yu13] and the references in it.
The multiplier of the bilinear oscillatory integral T β can be written (informally) as
 \begin{equation*}m(\xi,\eta)=p.v.\int {\rm e}^{i(t\xi+t^2\eta+|t|^\beta)}\,\frac{{\rm d}t}{t}.\end{equation*}
\begin{equation*}m(\xi,\eta)=p.v.\int {\rm e}^{i(t\xi+t^2\eta+|t|^\beta)}\,\frac{{\rm d}t}{t}.\end{equation*} Except the curvature of t 2, the oscillatory term ![]() ${\rm e}^{i|t|^\beta}$ also effects the distribution of the singular points. Thus, there is the competition between t 2 and
${\rm e}^{i|t|^\beta}$ also effects the distribution of the singular points. Thus, there is the competition between t 2 and ![]() ${\rm e}^{i|t|^\beta}$. As one may find out in § 2, β < 0 affects when
${\rm e}^{i|t|^\beta}$. As one may find out in § 2, β < 0 affects when ![]() $|t|\lt1$ and β > 0 places a rule for
$|t|\lt1$ and β > 0 places a rule for ![]() $|t|\gt1$. The main contribution of this paper is to elaborate the competition. For this reason, we need to consider different cases carefully.
$|t|\gt1$. The main contribution of this paper is to elaborate the competition. For this reason, we need to consider different cases carefully.
The bilinear oscillatory integrals studied in this paper are the combination of the bilinear Hilbert transform along curve ![]() $H_{t^2}$ and the oscillatory operators
$H_{t^2}$ and the oscillatory operators
 \begin{equation*}T_\beta f(x):=p.v.\int f(x-t)\, {\rm e}^{i|t|^\beta}\,\frac{{\rm d}t}{t}.\end{equation*}
\begin{equation*}T_\beta f(x):=p.v.\int f(x-t)\, {\rm e}^{i|t|^\beta}\,\frac{{\rm d}t}{t}.\end{equation*}These operators are excluded in Cardelón–Zygmund type operators (see [Reference Fefferman and Stein6, 7, Reference Sjölin15, Reference Wainger16]). Moreover, for the case β > 1, let us assume for a moment β = 3. We believe our result may share some light on the boundedness of the trilinear Hilbert transform:
 \begin{equation*}H(f,g,h)(x):=p.v.\int f(x-t)g(x-t^2)h(x-t^3)\,\frac{{\rm d}t}{t},\end{equation*}
\begin{equation*}H(f,g,h)(x):=p.v.\int f(x-t)g(x-t^2)h(x-t^3)\,\frac{{\rm d}t}{t},\end{equation*}but we do not pursue this issue in this paper.
2. Strategy of the proof
In this section, we explain the strategy of the proof. We split the bilinear operator T β into two parts:
 \begin{equation*}
T_{\beta,\leq1}(f, g)(x)=p.v.\int_{-1}^1 f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}
\end{equation*}
\begin{equation*}
T_{\beta,\leq1}(f, g)(x)=p.v.\int_{-1}^1 f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}
\end{equation*}and
 \begin{equation*}
T_{\beta,\geq1}(f, g)(x)=\int_{|t|\ge 1} f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}.
\end{equation*}
\begin{equation*}
T_{\beta,\geq1}(f, g)(x)=\int_{|t|\ge 1} f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}.
\end{equation*} It is sufficient to prove that they map ![]() $L^p\times L^q$ to L r under the condition (1.2). When
$L^p\times L^q$ to L r under the condition (1.2). When ![]() $|t|\leq 1$, the term
$|t|\leq 1$, the term ![]() ${\rm e}^{i|t|^{\beta}}$ behaves like 1 if β > 0, and when
${\rm e}^{i|t|^{\beta}}$ behaves like 1 if β > 0, and when ![]() $|t|\geq1$,
$|t|\geq1$, ![]() ${\rm e}^{i|t|^\beta}\sim 1$ if β < 0. Hence, we compare them with
${\rm e}^{i|t|^\beta}\sim 1$ if β < 0. Hence, we compare them with
 \begin{equation*}
H_{\leq1}(f,g)(x)=p.v.\int_{-1}^1f(x-t)g(x-t^2)\,\frac{{\rm d}t}{t}
\end{equation*}
\begin{equation*}
H_{\leq1}(f,g)(x)=p.v.\int_{-1}^1f(x-t)g(x-t^2)\,\frac{{\rm d}t}{t}
\end{equation*}and
 \begin{equation*}
H_{\geq1}(f,g)(x)=\int_{|t|\geq1}f(x-t)g(x-t^2)\,\frac{{\rm d}t}{t},
\end{equation*}
\begin{equation*}
H_{\geq1}(f,g)(x)=\int_{|t|\geq1}f(x-t)g(x-t^2)\,\frac{{\rm d}t}{t},
\end{equation*}respectively. Their sum is the bilinear Hilbert transform
 \begin{equation*}
H(f, g)(x)=p.v.\int_{\mathbb {R}} f(x-t)g(x- t^2)\,\frac{{\rm d}t}{t}.
\end{equation*}
\begin{equation*}
H(f, g)(x)=p.v.\int_{\mathbb {R}} f(x-t)g(x- t^2)\,\frac{{\rm d}t}{t}.
\end{equation*} From Li [Reference Li11] and Li and Xiao [Reference Li and Xiao12], we know that ![]() $H,$
$H,$ ![]() $H_{\leq 1}$ and
$H_{\leq 1}$ and ![]() $H_{\geq1}$ are
$H_{\geq1}$ are ![]() $L^p\times L^q$ to L r bounded for
$L^p\times L^q$ to L r bounded for ![]() $p, q, r$ satisfying Equation (1.2).
$p, q, r$ satisfying Equation (1.2).
When ![]() $\beta \geq 1$, by Taylor’s formula,
$\beta \geq 1$, by Taylor’s formula,
 \begin{equation}
T_{\beta,\leq 1}(f, g)(x)-H_{\leq1}(f, g)(x)=\sum_{n=1}^{\infty} \int_{|t|\le 1} f(x-t)g(x- t^2) \frac{i^n |t|^{n\beta}}{n!}\,\frac{{\rm d}t}{t}.
\end{equation}
\begin{equation}
T_{\beta,\leq 1}(f, g)(x)-H_{\leq1}(f, g)(x)=\sum_{n=1}^{\infty} \int_{|t|\le 1} f(x-t)g(x- t^2) \frac{i^n |t|^{n\beta}}{n!}\,\frac{{\rm d}t}{t}.
\end{equation} The boundedness of ![]() $T_{\beta, \leq1}$ is reduced to set up the boundedness of
$T_{\beta, \leq1}$ is reduced to set up the boundedness of
 \begin{equation}
M_0(f,g)(x)=\int_{|t|\leq 1}f(x-t)g(x-t^2)\,{\rm d}t
\end{equation}
\begin{equation}
M_0(f,g)(x)=\int_{|t|\leq 1}f(x-t)g(x-t^2)\,{\rm d}t
\end{equation}under condition (1.2).
When β < 0, we use Taylor’s formula again,
 \begin{equation}
T_{\beta,\geq1}(f, g)(x)-H_{\geq1}(f, g)(x)=\sum_{n=1}^{\infty} \int_{|t|\ge 1} f(x-t)g(x- t^2) \frac{i^n |t|^{n\beta}}{n!}\,\frac{{\rm d}t}{t}.
\end{equation}
\begin{equation}
T_{\beta,\geq1}(f, g)(x)-H_{\geq1}(f, g)(x)=\sum_{n=1}^{\infty} \int_{|t|\ge 1} f(x-t)g(x- t^2) \frac{i^n |t|^{n\beta}}{n!}\,\frac{{\rm d}t}{t}.
\end{equation} We decompose  $\frac{1}{t}=\sum_{j\in\mathbb{Z}}\rho_j(t)$, where
$\frac{1}{t}=\sum_{j\in\mathbb{Z}}\rho_j(t)$, where ![]() $\rho: {\mathbb R}\to {\mathbb R}$ is a non-negative smooth bump function supported on
$\rho: {\mathbb R}\to {\mathbb R}$ is a non-negative smooth bump function supported on ![]() $[-3,
-1]\cup [1, 3]$ and
$[-3,
-1]\cup [1, 3]$ and ![]() $\rho_j(t)=2^j\rho(2^jt)$. It is sufficient to set up the uniform boundedness of
$\rho_j(t)=2^j\rho(2^jt)$. It is sufficient to set up the uniform boundedness of
 \begin{equation}
M_j(f, g)(x)=\int_{{\mathbb R}} f(x-t)g(x-t^2)\rho_j(t)\,{\rm d}t \quad j\leq 1.
\end{equation}
\begin{equation}
M_j(f, g)(x)=\int_{{\mathbb R}} f(x-t)g(x-t^2)\rho_j(t)\,{\rm d}t \quad j\leq 1.
\end{equation}Li and Xiao [Reference Li and Xiao12] have already set up the following bilinear estimates.
Lemma 2.1. For every p, q and r satisfying Equation (1.2), we have
with a bound uniform in ![]() $j\in {\mathbb Z}$.
$j\in {\mathbb Z}$.
Using Equations (2.2) and (2.3) and Lemma 2.1, we can obtain the following result.
Proposition 2.1. For every p, q and r satisfying Equation (1.2), we have
and
Proof. The β > 1 case is clear. We only give the proof for β < 0. According to Equation (2.3), we have
 \begin{equation*}
\begin{split}
\left|T_{\beta,\geq1}(f, g)(x)-H_{\geq1}(f, g)(x)\right|\leq&\sum^\infty_{n=1}\frac{1}{n!}\int_{|t|\geq1}\left|f(x-t)g(x-t^2)\right||t|^{n\beta-1}\,{\rm d}t\\
&\leq\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}\int \left|f(x-t)g(x-t^2)\right||t|^{n\beta}\rho_j(t)\,{\rm d}t\\
&\leq\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}2^{-jn\beta}\int \left|f(x-t)g(x-t^2)\right|\rho_j(t)\,{\rm d}t\\
&=\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}2^{-jn\beta}M_j(f,g)(x).
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\left|T_{\beta,\geq1}(f, g)(x)-H_{\geq1}(f, g)(x)\right|\leq&\sum^\infty_{n=1}\frac{1}{n!}\int_{|t|\geq1}\left|f(x-t)g(x-t^2)\right||t|^{n\beta-1}\,{\rm d}t\\
&\leq\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}\int \left|f(x-t)g(x-t^2)\right||t|^{n\beta}\rho_j(t)\,{\rm d}t\\
&\leq\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}2^{-jn\beta}\int \left|f(x-t)g(x-t^2)\right|\rho_j(t)\,{\rm d}t\\
&=\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}2^{-jn\beta}M_j(f,g)(x).
\end{split}
\end{equation*} By the triangle inequality, when ![]() $r\geq1$, we have
$r\geq1$, we have
 \begin{equation*}
\left\|T_{\beta,\geq1}\right\|_r\leq\left\|H_{\geq1}(f,g)\right\|_r+\left(\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}2^{-jn\beta}\right)\sup_j\left\|M_j(f,g)\right\|_r.
\end{equation*}
\begin{equation*}
\left\|T_{\beta,\geq1}\right\|_r\leq\left\|H_{\geq1}(f,g)\right\|_r+\left(\sum^\infty_{n=1}\frac{1}{n!}\sum_{j\leq1}2^{-jn\beta}\right)\sup_j\left\|M_j(f,g)\right\|_r.
\end{equation*} When  $\frac{1}{2}\lt r\lt1$, we have
$\frac{1}{2}\lt r\lt1$, we have
 \begin{equation*}
\left\|T_{\beta,\geq1}\right\|_r\leq\left\|H_{\geq1}(f,g)\right\|_r+\left[\sum^\infty_{n=1}\left(\frac{1}{n!}\right)^r\sum_{j\leq1}2^{-jn\beta r}\right]^{\frac{1}{r}}\sup_j\left\|M_j(f,g)\right\|_r.
\end{equation*}
\begin{equation*}
\left\|T_{\beta,\geq1}\right\|_r\leq\left\|H_{\geq1}(f,g)\right\|_r+\left[\sum^\infty_{n=1}\left(\frac{1}{n!}\right)^r\sum_{j\leq1}2^{-jn\beta r}\right]^{\frac{1}{r}}\sup_j\left\|M_j(f,g)\right\|_r.
\end{equation*}By Lemma 2.1 and noticing that β < 0, we can finish the proof.
We now consider the following bilinear operators:
 \begin{equation*}
T_{\beta,\leq1}(f, g)(x)=p.v.\int_{-1}^1 f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}\quad\text{for}\ \beta\lt0
\end{equation*}
\begin{equation*}
T_{\beta,\leq1}(f, g)(x)=p.v.\int_{-1}^1 f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}\quad\text{for}\ \beta\lt0
\end{equation*}and
 \begin{equation*}
T_{\beta,\geq1}(f, g)(x)=\int_{|t|\ge 1} f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}\quad\text{for}\ \beta\gt1.
\end{equation*}
\begin{equation*}
T_{\beta,\geq1}(f, g)(x)=\int_{|t|\ge 1} f(x-t)g(x- t^{2})\,{\rm e}^{i|t|^{\beta}}\,\frac{{\rm d}t}{t}\quad\text{for}\ \beta\gt1.
\end{equation*} In this step, the cancellation of the Hilbert kernel  $p.v.\frac{1}{t}$ will not play a role. One can as well replace it by
$p.v.\frac{1}{t}$ will not play a role. One can as well replace it by ![]() $\frac{1}{|t|}$ and prove the same bounds. Under this consideration, we define for any
$\frac{1}{|t|}$ and prove the same bounds. Under this consideration, we define for any ![]() $j\ge1$
$j\ge1$
 \begin{equation*}
T_{\beta,j}(f, g)(x)=\int_{{\mathbb R}} f(x-2^{j}t) g(x-2^{2j} t^2)\,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\quad\text{for}\ \beta\gt1
\end{equation*}
\begin{equation*}
T_{\beta,j}(f, g)(x)=\int_{{\mathbb R}} f(x-2^{j}t) g(x-2^{2j} t^2)\,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\quad\text{for}\ \beta\gt1
\end{equation*}and
 \begin{equation}
T_{\beta,j}(f, g)(x)=\int_{{\mathbb R}} f(x-2^{-j}t) g(x-2^{-2j} t^2)\,{\rm e}^{i2^{-\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\quad\text{for}\,\beta\lt0.
\end{equation}
\begin{equation}
T_{\beta,j}(f, g)(x)=\int_{{\mathbb R}} f(x-2^{-j}t) g(x-2^{-2j} t^2)\,{\rm e}^{i2^{-\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\quad\text{for}\,\beta\lt0.
\end{equation}As a corollary of Lemma 2.1, we have
Theorem 2.1. Let β < 0 or β > 1,  $r\geq\frac{1}{2}$,
$r\geq\frac{1}{2}$, ![]() $p\ge1,\ q\ge1$, with
$p\ge1,\ q\ge1$, with  $\frac{1}{p}+\frac{1}{q}=\frac{1}{r}$, there is a constant C independent of j and the coefficients of
$\frac{1}{p}+\frac{1}{q}=\frac{1}{r}$, there is a constant C independent of j and the coefficients of ![]() $p,\ q$, such that
$p,\ q$, such that
Notice that
 \begin{equation*}
T_{\beta,\ge1}(f,g)(x)=\sum_{j\geq 1}T_{\beta,j}(f, g)(x) \quad \beta\gt1
\end{equation*}
\begin{equation*}
T_{\beta,\ge1}(f,g)(x)=\sum_{j\geq 1}T_{\beta,j}(f, g)(x) \quad \beta\gt1
\end{equation*}and
 \begin{equation*}
T_{\beta,\leq1}(f,g)(x)=\sum_{j\geq 1}T_{\beta,j}(f, g)(x) \quad \beta\lt0.
\end{equation*}
\begin{equation*}
T_{\beta,\leq1}(f,g)(x)=\sum_{j\geq 1}T_{\beta,j}(f, g)(x) \quad \beta\lt0.
\end{equation*}The main aim of this paper becomes to set up the following result.
Proposition 2.2. For every p, q and r satisfying Equation (1.2), β > 1 or β < 0, we have
 \begin{equation}
\left\|\sum_{j\in \mathbb N} T_{\beta,j} (f, g) \right\|_r \lesssim \left\|f\right\|_p \left\|g\right\|_q
\end{equation}
\begin{equation}
\left\|\sum_{j\in \mathbb N} T_{\beta,j} (f, g) \right\|_r \lesssim \left\|f\right\|_p \left\|g\right\|_q
\end{equation}with a constant depending only on β, p, q and r.
To prove Proposition 2.2, it is sufficient to show that
 \begin{equation*}
\left\|T_{\beta,j}(f,g)\right\|_r\lesssim_\epsilon 2^{-\epsilon j}\left\|f\right\|_{p}\left\|g\right\|_{q}\quad\,j\geq1.
\end{equation*}
\begin{equation*}
\left\|T_{\beta,j}(f,g)\right\|_r\lesssim_\epsilon 2^{-\epsilon j}\left\|f\right\|_{p}\left\|g\right\|_{q}\quad\,j\geq1.
\end{equation*}Noticing the uniform estimate (2.6), we can further reduce our aim to set up the following estimate.
Theorem 2.2. Suppose β > 1 or β < 0 and ![]() $j\geq 1$, there exists ϵ > 0 such that
$j\geq 1$, there exists ϵ > 0 such that
Let us take β > 1, for example, and rewrite
 \begin{equation*}
T_{\beta,j}(f,g)(x)=\int_{\mathbb R^2} \hat{f}(\xi)\hat{g}(\eta)m_{j}(\xi,\eta)\,{\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi\,{\rm d}\eta
\end{equation*}
\begin{equation*}
T_{\beta,j}(f,g)(x)=\int_{\mathbb R^2} \hat{f}(\xi)\hat{g}(\eta)m_{j}(\xi,\eta)\,{\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi\,{\rm d}\eta
\end{equation*}with
 \begin{equation*}
m_j(\xi, \eta)=\int_{{\mathbb R}} \rho(t) {\rm e}^{i(2^{j}t\xi+2^{2j} t^2\eta+2^{\beta j}|t|^{\beta})}\,{\rm d}t.
\end{equation*}
\begin{equation*}
m_j(\xi, \eta)=\int_{{\mathbb R}} \rho(t) {\rm e}^{i(2^{j}t\xi+2^{2j} t^2\eta+2^{\beta j}|t|^{\beta})}\,{\rm d}t.
\end{equation*} The main idea is to obtain a suitable decay estimate of the bilinear multiplier ![]() $m_j(\xi,\eta)$, in which the critical points of the phase function
$m_j(\xi,\eta)$, in which the critical points of the phase function
 \begin{equation*}\phi_{j,\xi,\eta}(t)=2^{\beta j}(2^{(1-\beta)j} \xi t+2^{(2-\beta)j}\eta t^2+|t|^\beta)\end{equation*}
\begin{equation*}\phi_{j,\xi,\eta}(t)=2^{\beta j}(2^{(1-\beta)j} \xi t+2^{(2-\beta)j}\eta t^2+|t|^\beta)\end{equation*}in the support of ρ play the crucial role. Thus, depending on the sizes of ![]() $2^{(1-\beta)j}\xi$ and
$2^{(1-\beta)j}\xi$ and ![]() $2^{(2-\beta)j}\eta$, the following decompositions will be natural.
$2^{(2-\beta)j}\eta$, the following decompositions will be natural.
Let ![]() $\Phi: {\mathbb R}\to {\mathbb R}$ be a Schwartz function such that
$\Phi: {\mathbb R}\to {\mathbb R}$ be a Schwartz function such that ![]() $\widehat{\Phi}$ is a non-negative bump function supported on
$\widehat{\Phi}$ is a non-negative bump function supported on ![]() $[-3, -1]\cup [1, 3]$ and satisfies
$[-3, -1]\cup [1, 3]$ and satisfies
 \begin{equation*}
\sum_k \widehat{\Phi}\left(\frac{\xi}{2^k}\right)=1 \quad \text{for every }\ \xi\neq 0.
\end{equation*}
\begin{equation*}
\sum_k \widehat{\Phi}\left(\frac{\xi}{2^k}\right)=1 \quad \text{for every }\ \xi\neq 0.
\end{equation*} For a function ![]() $f: {\mathbb R}\to {\mathbb R}$, we define
$f: {\mathbb R}\to {\mathbb R}$, we define
 \begin{equation*}
P_k f(x):=f_k(x):=\int_{{\mathbb R}} \widehat{f}(\xi) \widehat{\Phi}\left(\frac{\xi}{2^k}\right)\, {\rm e}^{ix\xi}\,{\rm d}\xi,
\end{equation*}
\begin{equation*}
P_k f(x):=f_k(x):=\int_{{\mathbb R}} \widehat{f}(\xi) \widehat{\Phi}\left(\frac{\xi}{2^k}\right)\, {\rm e}^{ix\xi}\,{\rm d}\xi,
\end{equation*}and
 \begin{equation*}
P_{\le k} f(x):=f_{\le k}(x):=\int_{{\mathbb R}} \widehat{f}(\xi) \left(\sum_{k^{\prime} \le k}\widehat{\Phi}\left(\frac{x}{2^{k^{\prime}}}\right)\right)\,{\rm e}^{ix\xi}\,{\rm d}\xi.
\end{equation*}
\begin{equation*}
P_{\le k} f(x):=f_{\le k}(x):=\int_{{\mathbb R}} \widehat{f}(\xi) \left(\sum_{k^{\prime} \le k}\widehat{\Phi}\left(\frac{x}{2^{k^{\prime}}}\right)\right)\,{\rm e}^{ix\xi}\,{\rm d}\xi.
\end{equation*} For fixed ![]() $j\geq 1$, we decompose
$j\geq 1$, we decompose
 \begin{equation*}
T_{\beta,j}(f,g)(x)=\sum_{m,m^{\prime} \in{\mathbb Z}} T_{j,m,m^{\prime}}(f,g)(x)
\end{equation*}
\begin{equation*}
T_{\beta,j}(f,g)(x)=\sum_{m,m^{\prime} \in{\mathbb Z}} T_{j,m,m^{\prime}}(f,g)(x)
\end{equation*}with
 \begin{equation*}
T_{j,m,m^{\prime}}(f,g)(x)=\int_{{\mathbb R}^2} \hat{f}(\xi)\hat{\Phi}\left(\frac{\xi}{2^{(\beta-1)j+m}}\right)
\hat{g}(\eta)\hat{\Phi}\left(\frac{\eta}{2^{(\beta-2)j+m^{\prime}}}\right)m_j(\xi,\eta){\rm e}^{i(\xi+\eta)x}\,{\rm d}\xi \,{\rm d}\eta.
\end{equation*}
\begin{equation*}
T_{j,m,m^{\prime}}(f,g)(x)=\int_{{\mathbb R}^2} \hat{f}(\xi)\hat{\Phi}\left(\frac{\xi}{2^{(\beta-1)j+m}}\right)
\hat{g}(\eta)\hat{\Phi}\left(\frac{\eta}{2^{(\beta-2)j+m^{\prime}}}\right)m_j(\xi,\eta){\rm e}^{i(\xi+\eta)x}\,{\rm d}\xi \,{\rm d}\eta.
\end{equation*}It equals to
 \begin{equation*}
\int_{{\mathbb R}} P_{\beta j-j+m}f(x-2^{j}t) P_{\beta j-2j+m^{\prime}}g(x-2^{2j} t^2){\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t.
\end{equation*}
\begin{equation*}
\int_{{\mathbb R}} P_{\beta j-j+m}f(x-2^{j}t) P_{\beta j-2j+m^{\prime}}g(x-2^{2j} t^2){\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t.
\end{equation*}Let C β be a large positive integer depending only on β. Define
 \begin{equation*}
\begin{split}
& \Lambda_1=\{\iota \in {\mathbb Z}\big| \iota \le -\beta j\},\\
& \Lambda_2=\{\iota \in {\mathbb Z}\big| -\beta j\le \iota \le -C_{\beta}\},\\
& \Lambda_3=\{\iota\in {\mathbb Z}\big| -C_{\beta}\le \iota\le C_{\beta}\},\\
& \Lambda_4=\{\iota \in {\mathbb Z}\big| \iota\ge C_{\beta}\}.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \Lambda_1=\{\iota \in {\mathbb Z}\big| \iota \le -\beta j\},\\
& \Lambda_2=\{\iota \in {\mathbb Z}\big| -\beta j\le \iota \le -C_{\beta}\},\\
& \Lambda_3=\{\iota\in {\mathbb Z}\big| -C_{\beta}\le \iota\le C_{\beta}\},\\
& \Lambda_4=\{\iota \in {\mathbb Z}\big| \iota\ge C_{\beta}\}.
\end{split}
\end{equation*}We will consider several cases according to where m and mʹ take values from. The construction of the proof is stated in the following table.

In § 3, § 4, § 5, § 6 and § 7, for technical reasons, we need the condition β ≠ 2. As we pointed out, the curvature of the curve t 2 and the oscillatory term ![]() ${\rm e}^{i|\xi|^\beta}$ are used to isolate the critical points in the frequency space. But if β = 2, this isolation disappears. However, this case can be reduced to the
${\rm e}^{i|\xi|^\beta}$ are used to isolate the critical points in the frequency space. But if β = 2, this isolation disappears. However, this case can be reduced to the ![]() $H_{t^2}$.
$H_{t^2}$.
 \begin{equation*}
\begin{split}
T(f,g)(x)& =p.v.\int_{\mathbb{R}} f(x-t)g(x-t^2)\,{\rm e}^{it^2}\,\frac{{\rm d}t}{t}\\
&=p.v.\int_{\mathbb{R}}f(x-t)g(x-t^2)\,{\rm e}^{ix}{\rm e}^{i(t^2-x)}\,\frac{{\rm d}t}{t}\\
&={\rm e}^{ix}p.v.\int_{\mathbb{R}}f(x-t)g_e(x-t^2)\,\frac{{\rm d}t}{t}={\rm e}^{ix}H_{t^2}(f,g_e)(x),
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
T(f,g)(x)& =p.v.\int_{\mathbb{R}} f(x-t)g(x-t^2)\,{\rm e}^{it^2}\,\frac{{\rm d}t}{t}\\
&=p.v.\int_{\mathbb{R}}f(x-t)g(x-t^2)\,{\rm e}^{ix}{\rm e}^{i(t^2-x)}\,\frac{{\rm d}t}{t}\\
&={\rm e}^{ix}p.v.\int_{\mathbb{R}}f(x-t)g_e(x-t^2)\,\frac{{\rm d}t}{t}={\rm e}^{ix}H_{t^2}(f,g_e)(x),
\end{split}
\end{equation*}where ![]() $g_e(x)={\rm e}^{ix}g(x)$ and
$g_e(x)={\rm e}^{ix}g(x)$ and ![]() $\|g_e\|_p=\|g\|_p$. The boundedness of
$\|g_e\|_p=\|g\|_p$. The boundedness of ![]() $H_{t^2}$ was already known.
$H_{t^2}$ was already known.
3. The case of  $m\in \Lambda_1$ or
$m\in \Lambda_1$ or  $m^{\prime}\in \Lambda_1$: contribution from extremely low frequencies
$m^{\prime}\in \Lambda_1$: contribution from extremely low frequencies
In the section, we consider the case of ![]() $m\in \Lambda_1$ or
$m\in \Lambda_1$ or ![]() $m^{\prime} \in \Lambda_1$. We take
$m^{\prime} \in \Lambda_1$. We take ![]() $m\in\Lambda_1$ as an example. The other case can be handled similarly.
$m\in\Lambda_1$ as an example. The other case can be handled similarly.
We write
 \begin{equation*}
\sum_{m\in \Lambda_1, m^{\prime} \in {\mathbb Z}} T_{j, m, m^{\prime}}(f, g)=T_{\beta,j} (P_{\le -j}f, g).
\end{equation*}
\begin{equation*}
\sum_{m\in \Lambda_1, m^{\prime} \in {\mathbb Z}} T_{j, m, m^{\prime}}(f, g)=T_{\beta,j} (P_{\le -j}f, g).
\end{equation*}By Fourier transform, it equals to
 \begin{equation}
\iint_{{\mathbb R}\times {\mathbb R}} \widehat{P_{\le -j}f}(\xi) \widehat{g}(\eta) m_j(\xi, \eta) {\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi\, {\rm d}\eta.
\end{equation}
\begin{equation}
\iint_{{\mathbb R}\times {\mathbb R}} \widehat{P_{\le -j}f}(\xi) \widehat{g}(\eta) m_j(\xi, \eta) {\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi\, {\rm d}\eta.
\end{equation}By Taylor’s formula,
 \begin{equation}
m_j(\xi, \eta)=\int_{{\mathbb R}} \left(\sum_{n=0}^{\infty} \frac{i^n (2^{j}\xi)^n}{n!} \right) \,{\rm e}^{i\left(2^{2j}t^2\eta+2^{\beta j}|t|^{\beta}\right)}\rho(t)t^n\,{\rm d}t.
\end{equation}
\begin{equation}
m_j(\xi, \eta)=\int_{{\mathbb R}} \left(\sum_{n=0}^{\infty} \frac{i^n (2^{j}\xi)^n}{n!} \right) \,{\rm e}^{i\left(2^{2j}t^2\eta+2^{\beta j}|t|^{\beta}\right)}\rho(t)t^n\,{\rm d}t.
\end{equation} Fix an ![]() $n\in\mathbb{N}$,
$n\in\mathbb{N}$,
 \begin{equation*} \left|\int_{\mathbb{R}}\dfrac{(it)^n}{n!}\,{\rm e}^{i2^{2j}t^2\eta}\,{\rm e}^{i2^{\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right|=\frac{1}{n!}\left|\int_{\mathbb{R}}{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)r^n\,{\rm d}t\right|, \end{equation*}
\begin{equation*} \left|\int_{\mathbb{R}}\dfrac{(it)^n}{n!}\,{\rm e}^{i2^{2j}t^2\eta}\,{\rm e}^{i2^{\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right|=\frac{1}{n!}\left|\int_{\mathbb{R}}{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)r^n\,{\rm d}t\right|, \end{equation*}where ![]() $\phi(t)=2^{2j-\beta j}\eta t^2+|t|^{\beta}.$ Since
$\phi(t)=2^{2j-\beta j}\eta t^2+|t|^{\beta}.$ Since
by van der Corput’s lemma, we have
 \begin{equation*}
\left|\int_{\mathbb{R}}\,{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)t^n\,{\rm d}t\right| \lesssim n2^{-\beta j/3}.
\end{equation*}
\begin{equation*}
\left|\int_{\mathbb{R}}\,{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)t^n\,{\rm d}t\right| \lesssim n2^{-\beta j/3}.
\end{equation*}By Hölder’s inequality, it is easy to obtain
 \begin{equation*}
\begin{split}
& \left\|\left[\int_{{\mathbb R}} \widehat{P_{\le -j}f}(\xi) (2^{j}\xi)^n\,{\rm e}^{ix\xi} \,{\rm d}\xi\right] \left[ \int_{{\mathbb R}} \widehat{g}(\eta)
\left(\int_{{\mathbb R}} \,{\rm e}^{i\left(2^{2j}t^2\eta+2^{\beta j}|t|^{\beta}\right)}\rho(t)t^n\,{\rm d}t\right) \,{\rm e}^{i x\eta}\,{\rm d}\eta\right]\right\|_1\\
& \lesssim 2^{-\beta j/3} \|f\|_2 \|g\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left\|\left[\int_{{\mathbb R}} \widehat{P_{\le -j}f}(\xi) (2^{j}\xi)^n\,{\rm e}^{ix\xi} \,{\rm d}\xi\right] \left[ \int_{{\mathbb R}} \widehat{g}(\eta)
\left(\int_{{\mathbb R}} \,{\rm e}^{i\left(2^{2j}t^2\eta+2^{\beta j}|t|^{\beta}\right)}\rho(t)t^n\,{\rm d}t\right) \,{\rm e}^{i x\eta}\,{\rm d}\eta\right]\right\|_1\\
& \lesssim 2^{-\beta j/3} \|f\|_2 \|g\|_2.
\end{split}
\end{equation*} We finish the proof of the case ![]() $m\in \Lambda_1$.
$m\in \Lambda_1$.
4. The case of  $m, m^{\prime}\in \Lambda_3$
$m, m^{\prime}\in \Lambda_3$
In this section, we consider the case ![]() $m,m^{\prime}\in\Lambda_3$. Without loss of generality, we assume that
$m,m^{\prime}\in\Lambda_3$. Without loss of generality, we assume that ![]() $m=m^{\prime}=0$. The main result of this section is the following decay estimate.
$m=m^{\prime}=0$. The main result of this section is the following decay estimate.
Proposition 4.1. For ![]() $\beta\gt1,j\geq 0$, we have
$\beta\gt1,j\geq 0$, we have
 \begin{equation*}
\left\|T_{\beta,j} (P_{\beta j-j}f, P_{\beta j-2j}g)\right\|_1 \lesssim 2^{-\epsilon j} \left\|f\right\|_2 \left\|g\right\|_2
\end{equation*}
\begin{equation*}
\left\|T_{\beta,j} (P_{\beta j-j}f, P_{\beta j-2j}g)\right\|_1 \lesssim 2^{-\epsilon j} \left\|f\right\|_2 \left\|g\right\|_2
\end{equation*}for some ϵ > 0 depending only on β.
Proof. By rescaling, it is sufficient to prove
 \begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2)\,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\left\|f\right\|_2 \left\|g\right\|_2,
\end{equation*}
\begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2)\,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\left\|f\right\|_2 \left\|g\right\|_2,
\end{equation*}where ![]() $f=P_{\beta j} f$ and
$f=P_{\beta j} f$ and ![]() $g=P_{(\beta-1)j}g$.
$g=P_{(\beta-1)j}g$.
Using the standard localization argument, we can localize the integrals into small intervals. More precisely, for fixed ![]() $j\geq1$, we split
$j\geq1$, we split ![]() $\mathbb{R}$ into disjoint intervals
$\mathbb{R}$ into disjoint intervals ![]() $\cup_{i}I_i$ with
$\cup_{i}I_i$ with ![]() $I_i=[i2^j,(i+1)2^j),i\in{\mathbb Z}$. We set
$I_i=[i2^j,(i+1)2^j),i\in{\mathbb Z}$. We set
where χ is the characteristic function. For ![]() $\forall x\in I_i,\ \text{and}\ |t|\leq1$, if
$\forall x\in I_i,\ \text{and}\ |t|\leq1$, if ![]() $|x-t|\in I_{i^{\prime}} $, then we have
$|x-t|\in I_{i^{\prime}} $, then we have ![]() $|i-i^{\prime}|\lt2$. Similarly, if
$|i-i^{\prime}|\lt2$. Similarly, if ![]() $|x-2^jt|\in I_{i^{\prime\prime}} $, we also have
$|x-2^jt|\in I_{i^{\prime\prime}} $, we also have ![]() $|i-i^{\prime\prime}|\lt2$.
$|i-i^{\prime\prime}|\lt2$.
 \begin{equation*}
\begin{split}
& \int_{\mathbb{R}}\left|\int f(x-t)g(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& =\sum_{i\in{\mathbb Z}}\int_{I_i}\left|\int f(x-t)g(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& \leq\sum_{i\in{\mathbb Z}}\sum_{|i-i^{\prime}|\lt2}\sum_{|i-i^{\prime\prime}|\lt2}\int_{I_i}\left|\int f_{I_{i^{\prime}}}(x-t)g_{I_{i^{\prime\prime}}}(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& \leq C\sum_{i\in{\mathbb Z}}\int_{I_i}\left|\int f_{I_i}(x-t)g_{I_i}(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& \leq C\sum_{i\in{\mathbb Z}}2^{\frac{j}{2}}\left\|\int f_{I_i}(x-t)g_{I_i}(x-2^jt^2)\rho(t)\,{\rm d}t\right\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \int_{\mathbb{R}}\left|\int f(x-t)g(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& =\sum_{i\in{\mathbb Z}}\int_{I_i}\left|\int f(x-t)g(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& \leq\sum_{i\in{\mathbb Z}}\sum_{|i-i^{\prime}|\lt2}\sum_{|i-i^{\prime\prime}|\lt2}\int_{I_i}\left|\int f_{I_{i^{\prime}}}(x-t)g_{I_{i^{\prime\prime}}}(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& \leq C\sum_{i\in{\mathbb Z}}\int_{I_i}\left|\int f_{I_i}(x-t)g_{I_i}(x-2^jt^2)\rho(t)\,{\rm d}t\right|{\rm d}x\\
& \leq C\sum_{i\in{\mathbb Z}}2^{\frac{j}{2}}\left\|\int f_{I_i}(x-t)g_{I_i}(x-2^jt^2)\rho(t)\,{\rm d}t\right\|_2.
\end{split}
\end{equation*}By Cauchy-Schwarz, it is sufficient to prove
 \begin{equation*}
\left\|\int f(x-t)g(x-2^jt^2)\,{\rm e}^{i2^{\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right\|_2\lesssim 2^{-\varepsilon j}2^{-j/2}\|f\|_2\|g\|_2.
\end{equation*}
\begin{equation*}
\left\|\int f(x-t)g(x-2^jt^2)\,{\rm e}^{i2^{\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right\|_2\lesssim 2^{-\varepsilon j}2^{-j/2}\|f\|_2\|g\|_2.
\end{equation*}By Fourier transform, it equals to show that
 \begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{j}t^2 \eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+\eta)\,{\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{j}t^2 \eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+\eta)\,{\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation}By Hölder’s inequality, the left hand side of Equation (4.1) can be bounded by
 \begin{equation*}
2^{(\beta-1) j/2}\|g\|_2 \left\| \int \widehat{f}(\xi) \left[\int_{{\mathbb R}}\,{\rm e}^{it\xi+i2^jt^2\eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right] \widehat{h}(\xi+\eta)\,{\rm d}\xi\right\|_{L^{\infty}_{\eta}}.
\end{equation*}
\begin{equation*}
2^{(\beta-1) j/2}\|g\|_2 \left\| \int \widehat{f}(\xi) \left[\int_{{\mathbb R}}\,{\rm e}^{it\xi+i2^jt^2\eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right] \widehat{h}(\xi+\eta)\,{\rm d}\xi\right\|_{L^{\infty}_{\eta}}.
\end{equation*} Here, since ![]() $supp \hat{g}\subset \{|\eta|\sim 2^{(\beta-1)j}\}$, we have
$supp \hat{g}\subset \{|\eta|\sim 2^{(\beta-1)j}\}$, we have ![]() $\|\widehat{g}\|_1\lesssim2^{(\beta-1)j/2}\|\widehat{g}\|_2$. We consider the following term
$\|\widehat{g}\|_1\lesssim2^{(\beta-1)j/2}\|\widehat{g}\|_2$. We consider the following term
 \begin{equation*}
\int_{{\mathbb R}}{\rm e}^{it\xi+i2^jt^2\eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t=\int_{{\mathbb R}}{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)\,{\rm d}t,
\end{equation*}
\begin{equation*}
\int_{{\mathbb R}}{\rm e}^{it\xi+i2^jt^2\eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t=\int_{{\mathbb R}}{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)\,{\rm d}t,
\end{equation*}where ![]() $\phi(t)=2^{-\beta j}t\xi+2^{j-\beta j}t^2\eta+|t|^\beta$ for
$\phi(t)=2^{-\beta j}t\xi+2^{j-\beta j}t^2\eta+|t|^\beta$ for ![]() $|\xi|\sim 2^{\beta j}, |\eta|\sim 2^{(\beta-1)j}$. Since β ≠ 2, for any fixed ξ and η,
$|\xi|\sim 2^{\beta j}, |\eta|\sim 2^{(\beta-1)j}$. Since β ≠ 2, for any fixed ξ and η, ![]() $\phi^{\prime}(t)$ and
$\phi^{\prime}(t)$ and ![]() $\phi^{\prime\prime}(t)$ cannot be zero at the same point. By van der Corput’s lemma and the method of stationary phase, we obtain
$\phi^{\prime\prime}(t)$ cannot be zero at the same point. By van der Corput’s lemma and the method of stationary phase, we obtain
 \begin{equation*}
\left|\int_{{\mathbb R}}{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)\,{\rm d}t\right|\lesssim2^{-\beta j/2}.
\end{equation*}
\begin{equation*}
\left|\int_{{\mathbb R}}{\rm e}^{i2^{\beta j}\phi(t)}\rho(t)\,{\rm d}t\right|\lesssim2^{-\beta j/2}.
\end{equation*}Since β > 1, we can finish the proof.
5. The cases where phase functions admit no critical points
In this section, we study several cases. In these cases, the corresponding phase function does not admit any critical point. These cases are ![]() $(m\in
\Lambda_2, m^{\prime}\in \Lambda_2)$,
$(m\in
\Lambda_2, m^{\prime}\in \Lambda_2)$, ![]() $(m\in \Lambda_2, m^{\prime}\in \Lambda_4)$,
$(m\in \Lambda_2, m^{\prime}\in \Lambda_4)$, ![]() $(m\in \Lambda_4, m^{\prime}\in \Lambda_2)$,
$(m\in \Lambda_4, m^{\prime}\in \Lambda_2)$, ![]() $(m\in \Lambda_3, m^{\prime}\in
\Lambda_4)$ and
$(m\in \Lambda_3, m^{\prime}\in
\Lambda_4)$ and ![]() $(m\in \Lambda_4, m^{\prime}\in \Lambda_3)$. The proofs for all these cases are similar. We only present the proof of the case
$(m\in \Lambda_4, m^{\prime}\in \Lambda_3)$. The proofs for all these cases are similar. We only present the proof of the case ![]() $m\in \Lambda_3, m^{\prime}\in \Lambda_4$.
$m\in \Lambda_3, m^{\prime}\in \Lambda_4$.
Without loss of generality, we take m = 0. By the triangle inequality, it is sufficient to prove that
 \begin{equation}
\left\|T_{j, 0, m^{\prime}}(f, g)\right\|_1 \lesssim 2^{-(j+m^{\prime})}\left\|f\right\|_2 \left\|g\right\|_2.\end{equation}
\begin{equation}
\left\|T_{j, 0, m^{\prime}}(f, g)\right\|_1 \lesssim 2^{-(j+m^{\prime})}\left\|f\right\|_2 \left\|g\right\|_2.\end{equation} Let ![]() $\tilde{m}_j$ be defined by
$\tilde{m}_j$ be defined by
 \begin{equation*}
\tilde{m}_j(\xi,\eta)=\int\rho(t)\,{\rm e}^{i2^{\beta j\tilde{\phi}_{\xi,\eta}(t)}}\,{\rm d}t,
\end{equation*}
\begin{equation*}
\tilde{m}_j(\xi,\eta)=\int\rho(t)\,{\rm e}^{i2^{\beta j\tilde{\phi}_{\xi,\eta}(t)}}\,{\rm d}t,
\end{equation*}where
 \begin{equation*}
\tilde{\phi}_{\xi,\eta}(t)=\xi t+2^{m^{\prime}}\eta t^2+|t|^\beta.
\end{equation*}
\begin{equation*}
\tilde{\phi}_{\xi,\eta}(t)=\xi t+2^{m^{\prime}}\eta t^2+|t|^\beta.
\end{equation*} Then the fact that ![]() $m^{\prime}\gt C_\beta$ gives
$m^{\prime}\gt C_\beta$ gives
 \begin{equation*}
|\tilde{\phi}^{\prime}_{\xi,\eta}(t)|\gtrsim2^{m^{\prime}},\qquad \text{for}\ t\in \text{supp}\rho.
\end{equation*}
\begin{equation*}
|\tilde{\phi}^{\prime}_{\xi,\eta}(t)|\gtrsim2^{m^{\prime}},\qquad \text{for}\ t\in \text{supp}\rho.
\end{equation*}By integration by parts, for every large integer M, it holds that
 \begin{equation*}
|\tilde{m}_j(\xi, \eta)| \lesssim_{M,\beta} 2^{-M(j+m')}.
\end{equation*}
\begin{equation*}
|\tilde{m}_j(\xi, \eta)| \lesssim_{M,\beta} 2^{-M(j+m')}.
\end{equation*}It is straightforward to check that
 \begin{equation*}
2^{j+m^{\prime}} m_j(\xi, \eta) \widehat{\Phi}\left(\frac{\xi}{2^{\beta j-j}}\right) \widehat{\Phi}\left(\frac{\eta}{2^{\beta j-2j+m^{\prime}}}\right)
\end{equation*}
\begin{equation*}
2^{j+m^{\prime}} m_j(\xi, \eta) \widehat{\Phi}\left(\frac{\xi}{2^{\beta j-j}}\right) \widehat{\Phi}\left(\frac{\eta}{2^{\beta j-2j+m^{\prime}}}\right)
\end{equation*}is a Coifman–Meyer multiplier, see [Reference Coifman and Meyer2] and [Reference Coifman and Meyer3]. This finishes the proof of the desired Equation (5.1).
6. The case of  $m\in \Lambda_2, m^{\prime}\in \Lambda_3$
$m\in \Lambda_2, m^{\prime}\in \Lambda_3$
We assume again that ![]() $m^{\prime}=0$. Recall that
$m^{\prime}=0$. Recall that ![]() $-\beta j\le m\le -C_{\beta}$. We will show the following:
$-\beta j\le m\le -C_{\beta}$. We will show the following:
Proposition 6.1. It holds that
 \begin{equation}
\left\|T_{\beta,j}\left(P_{\beta j-j+m}f ,P_{\beta j-2j}g\right)\right\|_1\lesssim_\epsilon 2^{-\epsilon j}\left\|f\right\|_2\left\|g\right\|_2
\end{equation}
\begin{equation}
\left\|T_{\beta,j}\left(P_{\beta j-j+m}f ,P_{\beta j-2j}g\right)\right\|_1\lesssim_\epsilon 2^{-\epsilon j}\left\|f\right\|_2\left\|g\right\|_2
\end{equation}for some ϵ > 0 depending only on β and ![]() $-\beta j\le m\le -C_{\beta}$.
$-\beta j\le m\le -C_{\beta}$.
When Equation (6.1) is true, by Cauchy–Schwarz, we have
 \begin{equation*}
\sum_{-\beta j\leq m\le -C_\beta }\left\|T_{\beta,j}\left(P_{\beta j-j+m}f ,P_{\beta j-2j}g\right)\right\|_1\lesssim_\epsilon 2^{-\epsilon j}\#(M_{j,\beta})^\frac12\left\|f\right\|_2\left\|g\right\|_2,
\end{equation*}
\begin{equation*}
\sum_{-\beta j\leq m\le -C_\beta }\left\|T_{\beta,j}\left(P_{\beta j-j+m}f ,P_{\beta j-2j}g\right)\right\|_1\lesssim_\epsilon 2^{-\epsilon j}\#(M_{j,\beta})^\frac12\left\|f\right\|_2\left\|g\right\|_2,
\end{equation*}with ![]() $M_{j,\beta}=\{m\in {\mathbb Z}; -\beta j\leq m\leq -C_\beta\}$ and
$M_{j,\beta}=\{m\in {\mathbb Z}; -\beta j\leq m\leq -C_\beta\}$ and
 \begin{equation*}
\#(M_{j,\beta})\lesssim_{\epsilon_1} 2^{\epsilon_1 j}
\end{equation*}
\begin{equation*}
\#(M_{j,\beta})\lesssim_{\epsilon_1} 2^{\epsilon_1 j}
\end{equation*}hold for j large enough. By taking ![]() $\epsilon_1\ll \epsilon$, we obtain our aim.
$\epsilon_1\ll \epsilon$, we obtain our aim.
Proof of Proposition 6.1
By rescaling, it is sufficient to prove
 \begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2) {\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\left\|f\right\|_2 \left\|g\right\|_2,
\end{equation*}
\begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2) {\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\left\|f\right\|_2 \left\|g\right\|_2,
\end{equation*}where ![]() $f=P_{m} f$ and
$f=P_{m} f$ and ![]() $g=P_{(\beta-1)j}g$ with
$g=P_{(\beta-1)j}g$ with ![]() $0\le m\le \beta j-C_{\beta}$.
$0\le m\le \beta j-C_{\beta}$.
By the localization argument above, it equals to set up
 \begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2) \,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_2 \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2
\|g\|_2.
\end{equation*}
\begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2) \,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_2 \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2
\|g\|_2.
\end{equation*}By turning to the Fourier side and the duality, we need to show
 \begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{j}t^2 \eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm
d}t \right] \widehat{h}(\xi+\eta)\, {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{j}t^2 \eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm
d}t \right] \widehat{h}(\xi+\eta)\, {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation}This will be finished in several subsections.
6.1. The case of  $0\lt m\le (\beta-1)j-C_\beta$
$0\lt m\le (\beta-1)j-C_\beta$
To prove Equation (6.2), it is equivalent to prove
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}\left(2^{m-\beta j}t\xi+t^2
\eta+|t|^{\beta}\right)}\rho(t)\,{\rm d}t \right] \widehat{h}(2^{m-(\beta-1)j}\xi+\eta) {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-\frac{j+m}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}\left(2^{m-\beta j}t\xi+t^2
\eta+|t|^{\beta}\right)}\rho(t)\,{\rm d}t \right] \widehat{h}(2^{m-(\beta-1)j}\xi+\eta) {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-\frac{j+m}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}for f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$.
$[-3, -1]\cup [1, 3]$.
We set the phase function
 \begin{equation*}
\phi_{\xi, \eta}(t)=2^{m-\beta j}t\xi+t^2 \eta+|t|^{\beta}.
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)=2^{m-\beta j}t\xi+t^2 \eta+|t|^{\beta}.
\end{equation*}Let t 0 denote the critical point of it. By the method of stationary phase, it is enough to prove
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta)\,{\rm e}^{i2^{\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}\left(2^{-(\beta-1)j+m}\xi+\eta\right)
\,{\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j}2^{\frac{(\beta-1)j-m}{2}} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta)\,{\rm e}^{i2^{\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}\left(2^{-(\beta-1)j+m}\xi+\eta\right)
\,{\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j}2^{\frac{(\beta-1)j-m}{2}} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}Changing the variables
the left hand side is comparable to
 \begin{equation*}
\left|\iint_{{\mathbb R}^2} \widehat{f}(u-v) \widehat{g}(b_1u+b_2v)\,{\rm e}^{i2^{\beta j}\phi_{u-v, b_1u+b_2v}(t_0)} \widehat{h}(u) \,{\rm d}u\,{\rm d}v\right|.
\end{equation*}
\begin{equation*}
\left|\iint_{{\mathbb R}^2} \widehat{f}(u-v) \widehat{g}(b_1u+b_2v)\,{\rm e}^{i2^{\beta j}\phi_{u-v, b_1u+b_2v}(t_0)} \widehat{h}(u) \,{\rm d}u\,{\rm d}v\right|.
\end{equation*}Here
By Hölder’s inequality, it is sufficient to prove
 \begin{equation*}
\begin{split}
& \left\| \int_{{\mathbb R}} \widehat{f}(u-v) \widehat{g}(b_1u+b_2v)\,{\rm e}^{i2^{\beta j}\phi_{u-v, b_1u+b_2v}(t_0)}\,{\rm d}v\right\|_{L^2_{u}}^2\\
& \lesssim 2^{-\epsilon j} 2^{(\beta-1)j-m}\|f\|_2^2\|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left\| \int_{{\mathbb R}} \widehat{f}(u-v) \widehat{g}(b_1u+b_2v)\,{\rm e}^{i2^{\beta j}\phi_{u-v, b_1u+b_2v}(t_0)}\,{\rm d}v\right\|_{L^2_{u}}^2\\
& \lesssim 2^{-\epsilon j} 2^{(\beta-1)j-m}\|f\|_2^2\|g\|_2^2.
\end{split}
\end{equation*}We expand the left hand side as
 \begin{equation*}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \widehat{f}(u-v_1) \widehat{g}(b_1u+b_2v_1)\,{\rm e}^{i2^{\beta j}\phi_{u-v_1, b_1u+b_2v_1}(t_0)}\\
& \left.\overline{\widehat{f}(u-v_2)} \overline{\widehat{g}(b_1u+b_2v_2)} \,{\rm e}^{i2^{\beta j}\phi_{u-v_2, b_1u+b_2v_2}(t_0)}\,{\rm d}v_1 \,{\rm d}v_2\right]{\rm d}u.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \widehat{f}(u-v_1) \widehat{g}(b_1u+b_2v_1)\,{\rm e}^{i2^{\beta j}\phi_{u-v_1, b_1u+b_2v_1}(t_0)}\\
& \left.\overline{\widehat{f}(u-v_2)} \overline{\widehat{g}(b_1u+b_2v_2)} \,{\rm e}^{i2^{\beta j}\phi_{u-v_2, b_1u+b_2v_2}(t_0)}\,{\rm d}v_1 \,{\rm d}v_2\right]{\rm d}u.
\end{split}
\end{equation*}Changing the variables
we obtain
 \begin{equation}
\begin{split}
& \int\!\left[\iint_{{\mathbb R}^2}\!\! F_{\tau}(u-v) G_{\tau}(b_1u+b_2v)\,{\rm e}^{i2^{\beta j}(\phi_{u-v, b_1u+b_2v}(t_0)-\phi_{u-v-\tau,
b_1u+b_2v+b_2\tau}(t_0))}\,{\rm d}\xi \,{\rm d}\eta\right] {\rm d}\tau\\
& = \int\left[\iint_{{\mathbb R}^2} F_{\tau}(u) G_{\tau}(v) \,{\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v+b_2\tau}(t_0))}\,{\rm d}u\, {\rm d}v\right] {\rm d}\tau,
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \int\!\left[\iint_{{\mathbb R}^2}\!\! F_{\tau}(u-v) G_{\tau}(b_1u+b_2v)\,{\rm e}^{i2^{\beta j}(\phi_{u-v, b_1u+b_2v}(t_0)-\phi_{u-v-\tau,
b_1u+b_2v+b_2\tau}(t_0))}\,{\rm d}\xi \,{\rm d}\eta\right] {\rm d}\tau\\
& = \int\left[\iint_{{\mathbb R}^2} F_{\tau}(u) G_{\tau}(v) \,{\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v+b_2\tau}(t_0))}\,{\rm d}u\, {\rm d}v\right] {\rm d}\tau,
\end{split}
\end{equation}where
 \begin{equation*}
F_\tau(\cdot)=\widehat{f}(\cdot)\overline{\widehat{f}(\cdot-\tau)}\qquad
G_\tau(\cdot)=\widehat{g}(\cdot)\overline{\widehat{g}(\cdot-\tau)}.
\end{equation*}
\begin{equation*}
F_\tau(\cdot)=\widehat{f}(\cdot)\overline{\widehat{f}(\cdot-\tau)}\qquad
G_\tau(\cdot)=\widehat{g}(\cdot)\overline{\widehat{g}(\cdot-\tau)}.
\end{equation*}Let us denote
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}To proceed, we will use the following Hörmander’s oscillatory integral estimates.
Lemma 6.1. [Reference Hörmander8, Reference Phong and Stein14]
Let ![]() $a: {\mathbb R}^2\to {\mathbb R}$ be an amplitude supported on
$a: {\mathbb R}^2\to {\mathbb R}$ be an amplitude supported on ![]() $[0, 1]^2$ with
$[0, 1]^2$ with ![]() $\|a\|_{C^4}\lesssim 1$. Let
$\|a\|_{C^4}\lesssim 1$. Let ![]() $\Psi: {\mathbb R}^2\to {\mathbb R}$ be a phase function with
$\Psi: {\mathbb R}^2\to {\mathbb R}$ be a phase function with
Then
 \begin{equation*}
\left|\iint_{{\mathbb R}^2} {\rm e}^{i N \Psi(x, y)}a(x, y)f(x)g(y)\,{\rm d}x\, {\rm d}y\right| \lesssim N^{-1/2}\|f\|_2 \|g\|_2
\end{equation*}
\begin{equation*}
\left|\iint_{{\mathbb R}^2} {\rm e}^{i N \Psi(x, y)}a(x, y)f(x)g(y)\,{\rm d}x\, {\rm d}y\right| \lesssim N^{-1/2}\|f\|_2 \|g\|_2
\end{equation*}for smooth functions f and g.
Proof of Lemma 6.1
Let us denote
 \begin{equation*}T_Nf(x)=\int_{\mathbb R}{\rm e}^{iN\Psi(x,y)}a(x,y)f(y)\,{\rm d}y.\end{equation*}
\begin{equation*}T_Nf(x)=\int_{\mathbb R}{\rm e}^{iN\Psi(x,y)}a(x,y)f(y)\,{\rm d}y.\end{equation*}It is equivalent to set up
 \begin{equation*}\|T_Nf\|_{L^2}\lesssim N^{-1/2}\|f\|_{L^2}\end{equation*}
\begin{equation*}\|T_Nf\|_{L^2}\lesssim N^{-1/2}\|f\|_{L^2}\end{equation*}with f supported in ![]() $[0,1]$. We rewrite
$[0,1]$. We rewrite
 \begin{equation*}
\|T_Nf\|^2_2=\int T_Nf(x)\overline{T_Nf}(x)\,{\rm d}x=\iint_{\mathbb{R}^2}a_N(y,z)f(y)\overline{f(z)}\,{\rm d}y\,{\rm d}z,
\end{equation*}
\begin{equation*}
\|T_Nf\|^2_2=\int T_Nf(x)\overline{T_Nf}(x)\,{\rm d}x=\iint_{\mathbb{R}^2}a_N(y,z)f(y)\overline{f(z)}\,{\rm d}y\,{\rm d}z,
\end{equation*}where
 \begin{equation*}
a_N(y,z)=\int {\rm e}^{iN(\Psi(x,y)-\Psi(x,z))}a(x,y)\overline{a(x,z)}\,{\rm d}x.
\end{equation*}
\begin{equation*}
a_N(y,z)=\int {\rm e}^{iN(\Psi(x,y)-\Psi(x,z))}a(x,y)\overline{a(x,z)}\,{\rm d}x.
\end{equation*}By Taylor’s formula, we have
 \begin{equation*}
\begin{split}
&\left|\partial/\partial x\left(\Psi\left(x,y\right)-\Psi\left(x,z\right)\right)\right|\\
=&\left|\Psi^{\prime\prime}_{xy}\left(x,z\right)\left|y-z\right|+\frac{\Psi^{\prime\prime\prime}_{xy^2}\left(x,z\right)}{2}\left|y-z\right|^2+o\left(\left|y-z\right|^2\right)\right|\\
\geq &c|y-z|.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left|\partial/\partial x\left(\Psi\left(x,y\right)-\Psi\left(x,z\right)\right)\right|\\
=&\left|\Psi^{\prime\prime}_{xy}\left(x,z\right)\left|y-z\right|+\frac{\Psi^{\prime\prime\prime}_{xy^2}\left(x,z\right)}{2}\left|y-z\right|^2+o\left(\left|y-z\right|^2\right)\right|\\
\geq &c|y-z|.
\end{split}
\end{equation*}Since
 \begin{equation*}
|a_N(y,z)|=\left|\int_0^1{\rm e}^{iN(\Psi(x,y)-\Psi(x,z))}a(x,y)\overline{a(x,z)}\,{\rm d}x\right|\leq1,
\end{equation*}
\begin{equation*}
|a_N(y,z)|=\left|\int_0^1{\rm e}^{iN(\Psi(x,y)-\Psi(x,z))}a(x,y)\overline{a(x,z)}\,{\rm d}x\right|\leq1,
\end{equation*}integration by parts shows that
 \begin{equation*}
|a_N(y,z)|\lesssim\frac{1}{(1+N|y-z|)^2}.
\end{equation*}
\begin{equation*}
|a_N(y,z)|\lesssim\frac{1}{(1+N|y-z|)^2}.
\end{equation*}We obtain
 \begin{equation*}
\int|a_N(y,z)|{\rm d}y \lt CN^{-1},\qquad \int|a_N(y,z)|{\rm d}z \lt CN^{-1}.
\end{equation*}
\begin{equation*}
\int|a_N(y,z)|{\rm d}y \lt CN^{-1},\qquad \int|a_N(y,z)|{\rm d}z \lt CN^{-1}.
\end{equation*}We now use Hölder’s inequality to obtain
 \begin{equation*}\|T_Nf\|_2^2\leq \left(\int a_N(y,z)f(z)\,{\rm d}z\right)^{\frac12}\|f\|_{2}\leq\int_y\frac{{\rm d}y}{(1+N|y|)^2}\|f\|_{2}^2\lesssim N^{-1}\|f\|_2^2.\end{equation*}
\begin{equation*}\|T_Nf\|_2^2\leq \left(\int a_N(y,z)f(z)\,{\rm d}z\right)^{\frac12}\|f\|_{2}\leq\int_y\frac{{\rm d}y}{(1+N|y|)^2}\|f\|_{2}^2\lesssim N^{-1}\|f\|_2^2.\end{equation*}Therefore, we finish the proof.
Lemma 6.2. Under the above notation, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{(m-\beta j)}\tau \hfill & \text{if } \beta\neq 3\\
2^{2m-2\beta j}\tau \hfill & \text{if } \beta=3
\end{cases}
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{(m-\beta j)}\tau \hfill & \text{if } \beta\neq 3\\
2^{2m-2\beta j}\tau \hfill & \text{if } \beta=3
\end{cases}
\end{equation}and
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau
\end{equation}for every ![]() $j\gg 1$.
$j\gg 1$.
Proof of Lemma 6.2
We assume that ![]() $t_0\gt0$, and when
$t_0\gt0$, and when ![]() $t_0\lt0$, the proof is similar. Because
$t_0\lt0$, the proof is similar. Because ![]() $t_0(u,v)$ is the critical point of the phase function
$t_0(u,v)$ is the critical point of the phase function ![]() $\phi_{u, v}(t)$,
$\phi_{u, v}(t)$,
 \begin{equation*}
\phi^{\prime}_{u, v}(t_0)=2^{m-\beta j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}
\begin{equation*}
\phi^{\prime}_{u, v}(t_0)=2^{m-\beta j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}Thus, we have
 \begin{equation*}
\frac{\partial t_0}{\partial u}=\frac{-2^{m-\beta j}}{\phi^{\prime\prime}_{u, v}(t_0)}
\end{equation*}
\begin{equation*}
\frac{\partial t_0}{\partial u}=\frac{-2^{m-\beta j}}{\phi^{\prime\prime}_{u, v}(t_0)}
\end{equation*}and
 \begin{equation*}
\frac{\partial t_0}{\partial v}=\frac{-2t_0}{\phi^{\prime\prime}_{u, v}(t_0)}.
\end{equation*}
\begin{equation*}
\frac{\partial t_0}{\partial v}=\frac{-2t_0}{\phi^{\prime\prime}_{u, v}(t_0)}.
\end{equation*}By the chain rule, we have
 \begin{equation*}
\frac{\partial Q}{\partial u}=2^{m-\beta j}t_0(u,v)
\end{equation*}
\begin{equation*}
\frac{\partial Q}{\partial u}=2^{m-\beta j}t_0(u,v)
\end{equation*}and
 \begin{equation*}
\frac{\partial Q}{\partial v}=t^2_0(u,v).
\end{equation*}
\begin{equation*}
\frac{\partial Q}{\partial v}=t^2_0(u,v).
\end{equation*}By a direct calculation,
 \begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m-\beta j+1}t_0}{2v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}
\begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m-\beta j+1}t_0}{2v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}Hence,
 \begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u,v)=-2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial u}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \big)}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u,v)=-2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial u}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \big)}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}The relation between v and t 0 is given by
 \begin{equation*}
2^{m-\beta j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}
\begin{equation*}
2^{m-\beta j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}Here we used the fact that β ≠ 2.
 \begin{equation}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial v}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\big)-2t_0}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation}
\begin{equation}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial v}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\big)-2t_0}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation}By an implicit function calculation,
 \begin{equation*}
2t_0+2v\, \frac{\partial t_0}{\partial v}+\beta (\beta-1) t_0^{\beta-2}\,\frac{\partial t_0}{\partial v}=0.
\end{equation*}
\begin{equation*}
2t_0+2v\, \frac{\partial t_0}{\partial v}+\beta (\beta-1) t_0^{\beta-2}\,\frac{\partial t_0}{\partial v}=0.
\end{equation*}Therefore,
 \begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2t_0}{2v+\beta(\beta-1)t_0^{\beta-2}}.
\end{equation*}
\begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2t_0}{2v+\beta(\beta-1)t_0^{\beta-2}}.
\end{equation*}Hence,
 \begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2t_0 \right|\\
&=2\left|\frac{4t_0v+\beta(\beta-1)(4-\beta)t_0^{\beta-1}}{2v+\beta(\beta-1)t_0^{\beta-2}}\right|\\
& \approx \left|4t_0v +\beta(\beta-1)(4-\beta)t_0^{\beta-1} \right|.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2t_0 \right|\\
&=2\left|\frac{4t_0v+\beta(\beta-1)(4-\beta)t_0^{\beta-1}}{2v+\beta(\beta-1)t_0^{\beta-2}}\right|\\
& \approx \left|4t_0v +\beta(\beta-1)(4-\beta)t_0^{\beta-1} \right|.
\end{split}
\end{equation}We notice that
 \begin{equation*}
2t_0v=-2^{m-\beta j}u-\beta t_0^{\beta-1},
\end{equation*}
\begin{equation*}
2t_0v=-2^{m-\beta j}u-\beta t_0^{\beta-1},
\end{equation*}where ![]() $2^{m-\beta j}\ll1$. According to the above equation, we have
$2^{m-\beta j}\ll1$. According to the above equation, we have
When β ≠ 3, we have ![]() $(6.7)\approx 1$. When β = 3, we have
$(6.7)\approx 1$. When β = 3, we have ![]() $(6.6)\approx 2^{2m-5 j}$. By the mean value theorem, we have
$(6.6)\approx 2^{2m-5 j}$. By the mean value theorem, we have
 \begin{equation*}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} (u,v)\right|=\left|\frac{\partial^3Q}{\partial u \partial^2 v}(u,v+\theta\tau)\right|\tau
\end{equation*}
\begin{equation*}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} (u,v)\right|=\left|\frac{\partial^3Q}{\partial u \partial^2 v}(u,v+\theta\tau)\right|\tau
\end{equation*}for some ![]() $\theta\in[0,1]$. Therefore, Equation (6.4) can be proved. To prove Equations(6.5), it suffices to prove that
$\theta\in[0,1]$. Therefore, Equation (6.4) can be proved. To prove Equations(6.5), it suffices to prove that
 \begin{equation*}
\left\|\frac{\partial^3 Q}{\partial^2 u \partial v} \right\|_{C^2}\lesssim 1,
\end{equation*}
\begin{equation*}
\left\|\frac{\partial^3 Q}{\partial^2 u \partial v} \right\|_{C^2}\lesssim 1,
\end{equation*}and
 \begin{equation*}
\left\|\frac{\partial^3 Q}{\partial u \partial^2 v} \right\|_{C^2}\lesssim
1.
\end{equation*}
\begin{equation*}
\left\|\frac{\partial^3 Q}{\partial u \partial^2 v} \right\|_{C^2}\lesssim
1.
\end{equation*}Both are straightforward to check. Therefore, Equation (6.5) is true.
To bound Equation (6.3), we write it as
 \begin{equation*}
(6.3)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0},
\end{equation*}
\begin{equation*}
(6.3)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0},
\end{equation*}for some τ 0 will be decided soon. The former term can be bounded by
 \begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} F_{\tau}(u) G_{\tau}(v) \,{\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v+b_2\tau}(t_0))}\,{\rm d}\xi\,{\rm d}\eta\right| \le |\tau_0| \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} F_{\tau}(u) G_{\tau}(v) \,{\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v+b_2\tau}(t_0))}\,{\rm d}\xi\,{\rm d}\eta\right| \le |\tau_0| \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}For the latter term, when β ≠ 3, we bound it by
 \begin{equation*}
\begin{split}
&2^{-\frac{\beta j}{2}}2^{\frac{-(m-\beta j)}{2}} \tau_0^{-\frac{1}{2}}\int \left[\int_{{\mathbb
R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm d}u\right]^{1/2} \left[\int_{{\mathbb R}}
\left|\widehat{g}(v)\overline{\widehat{g}(b_1v+b_2\tau)}\right|^2\,{\rm d}v
\right]^{1/2} \,{\rm d}\tau\\
& \le 2^{-\frac{\beta j}{2}}2^{\frac{-(m-\beta j)}{2}} \tau_0^{-\frac{1}{2}}{b_2}^{\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&2^{-\frac{\beta j}{2}}2^{\frac{-(m-\beta j)}{2}} \tau_0^{-\frac{1}{2}}\int \left[\int_{{\mathbb
R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm d}u\right]^{1/2} \left[\int_{{\mathbb R}}
\left|\widehat{g}(v)\overline{\widehat{g}(b_1v+b_2\tau)}\right|^2\,{\rm d}v
\right]^{1/2} \,{\rm d}\tau\\
& \le 2^{-\frac{\beta j}{2}}2^{\frac{-(m-\beta j)}{2}} \tau_0^{-\frac{1}{2}}{b_2}^{\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} Choosing  $\tau_0=2^{-\frac{\beta j}{3}+\frac{1}{3}j}$ will finish the proof.
$\tau_0=2^{-\frac{\beta j}{3}+\frac{1}{3}j}$ will finish the proof.
When β = 3, for the latter term, we bound it by
 \begin{equation*}
\begin{split}
&2^{-\frac{3 j}{2}}2^{\frac{-(2m-6 j)}{2}} \tau_0^{-\frac{1}{2}}\int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm
d}u\right]^{1/2} \left[\int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(b_1v+b_2\tau)}\right|^2\,{\rm d}v \right]^{1/2}\, {\rm d}\tau\\
& \le 2^{-\frac{3 j}{2}}2^{\frac{-2m+6j}{2}} \tau_0^{-\frac{1}{2}}{b_2}^{\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&2^{-\frac{3 j}{2}}2^{\frac{-(2m-6 j)}{2}} \tau_0^{-\frac{1}{2}}\int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm
d}u\right]^{1/2} \left[\int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(b_1v+b_2\tau)}\right|^2\,{\rm d}v \right]^{1/2}\, {\rm d}\tau\\
& \le 2^{-\frac{3 j}{2}}2^{\frac{-2m+6j}{2}} \tau_0^{-\frac{1}{2}}{b_2}^{\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} Choosing  $\tau_0=2^{-\frac{1}{3}m+\frac{1}{3}j}$ will finish the proof.
$\tau_0=2^{-\frac{1}{3}m+\frac{1}{3}j}$ will finish the proof.
6.2. The case of  $ (\beta-1)j-C_{\beta}\le m\le (\beta -1)j+C_\beta$
$ (\beta-1)j-C_{\beta}\le m\le (\beta -1)j+C_\beta$
For convenience, we assume that ![]() $m=(\beta-1)j$. To prove Equation (6.2), it is equivalent to prove
$m=(\beta-1)j$. To prove Equation (6.2), it is equivalent to prove
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}(2^{-j}t\xi+t^2 \eta+|t|^{\beta})}\rho(t)\,{\rm d}t \right] {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-\frac{\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}(2^{-j}t\xi+t^2 \eta+|t|^{\beta})}\rho(t)\,{\rm d}t \right] {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-\frac{\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}for all functions f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$. Denote
$[-3, -1]\cup [1, 3]$. Denote
 \begin{equation*}
\phi_{\xi, \eta}(t)=2^{-j}t\xi+t^2 \eta+|t|^{\beta}.
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)=2^{-j}t\xi+t^2 \eta+|t|^{\beta}.
\end{equation*}Let t 0 denote the critical point of it. By the same argument as in last subsection, we face to estimate
 \begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} F_{\tau}(u) H_{\tau}(v) {\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v-\tau}(t_0))}\,{\rm d}u \,{\rm d}v\right] {\rm d}\tau
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} F_{\tau}(u) H_{\tau}(v) {\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v-\tau}(t_0))}\,{\rm d}u \,{\rm d}v\right] {\rm d}\tau
\end{split}
\end{equation}where
 \begin{equation*}
F_\tau(\cdot)=\widehat{f}(\cdot)\overline{\widehat{f}(\cdot-\tau)},\qquad
H_\tau(\cdot)=\widehat{h}(\cdot)\overline{\widehat{h}(\cdot-\tau)}.
\end{equation*}
\begin{equation*}
F_\tau(\cdot)=\widehat{f}(\cdot)\overline{\widehat{f}(\cdot-\tau)},\qquad
H_\tau(\cdot)=\widehat{h}(\cdot)\overline{\widehat{h}(\cdot-\tau)}.
\end{equation*}Let us denote
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v-\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v-\tau).
\end{equation*}Lemma 6.3. Under the above notation, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{-j}\tau \hfill & \text{if } \beta\neq 3,\\
2^{-2 j}\tau \hfill & \text{if } \beta=3,
\end{cases}
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{-j}\tau \hfill & \text{if } \beta\neq 3,\\
2^{-2 j}\tau \hfill & \text{if } \beta=3,
\end{cases}
\end{equation}and
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau
\end{equation}for every ![]() $j\gg 1$.
$j\gg 1$.
Proof of Lemma 6.3
As the same argument in § 6.2, we have
 \begin{equation*}
\frac{\partial^2 Q}{\partial u\partial v}(\xi, \eta)=-\frac{2^{-j+1}t_0}{2v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}
\begin{equation*}
\frac{\partial^2 Q}{\partial u\partial v}(\xi, \eta)=-\frac{2^{-j+1}t_0}{2v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}Hence,
 \begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{- j+1} \frac{\frac{\partial t_0}{\partial u}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \big)}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{- j+1} \frac{\frac{\partial t_0}{\partial u}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \big)}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}The relation between v and t 0 is given by
 \begin{equation*}
2^{- j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}
\begin{equation*}
2^{- j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}Here we also used the fact that β ≠ 2. Let
 \begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{-j+1} \frac{\frac{\partial t_0}{\partial v}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\big)-2t_0}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{-j+1} \frac{\frac{\partial t_0}{\partial v}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\big)-2t_0}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}We have
 \begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2t_0}{2v+\beta(\beta-1)t_0^{\beta-2}}
\end{equation*}
\begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2t_0}{2v+\beta(\beta-1)t_0^{\beta-2}}
\end{equation*}and
 \begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2v+\beta\left(\beta-1\right)\left(3-\beta\right)t_0^{\beta-2}\right)-2t_0 \right|\\
& \approx \left|4v +\beta\left(\beta-1\right)\left(4-\beta\right)t_0^{\beta-2} \right|.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2v+\beta\left(\beta-1\right)\left(3-\beta\right)t_0^{\beta-2}\right)-2t_0 \right|\\
& \approx \left|4v +\beta\left(\beta-1\right)\left(4-\beta\right)t_0^{\beta-2} \right|.
\end{split}
\end{equation} When β ≠ 3, we have (6.11) ![]() $\approx 1$. When β = 3, we have (6.11)
$\approx 1$. When β = 3, we have (6.11) ![]() $\approx 2^{- j}$. Equations (6.9) and (6.10) can be proved by the mean value theorem.
$\approx 2^{- j}$. Equations (6.9) and (6.10) can be proved by the mean value theorem.
To estimate Equation (6.8), as before, we decompose it as
 \begin{equation*}
(6.8)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0},
\end{equation*}
\begin{equation*}
(6.8)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0},
\end{equation*}with τ 0 being given soon. The former term can be bounded by
 \begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} F_{\tau}(u) H_{\tau}(v) {\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v-\tau}(t_0))}\,{\rm
d}\xi\,{\rm d}\eta\right| \le|\tau_0| \|f\|_2^2 \|h\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} F_{\tau}(u) H_{\tau}(v) {\rm e}^{i2^{\beta j}(\phi_{u, v}(t_0)-\phi_{u-\tau, v-\tau}(t_0))}\,{\rm
d}\xi\,{\rm d}\eta\right| \le|\tau_0| \|f\|_2^2 \|h\|_2^2.
\end{split}
\end{equation*}For the latter term, when β ≠ 3, we bound it by
 \begin{equation*}
\begin{split}
&2^{-\frac{\beta j}{2}} (2^{-j}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm
d}u\right]^{1/2} \left[\int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(v-\tau)}\right|^2\,{\rm d}\eta \right]^{1/2} {\rm d}\tau\\
& \le 2^{-\frac{\beta j}{2}}(2^{-j}\tau_0)^{-\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&2^{-\frac{\beta j}{2}} (2^{-j}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm
d}u\right]^{1/2} \left[\int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(v-\tau)}\right|^2\,{\rm d}\eta \right]^{1/2} {\rm d}\tau\\
& \le 2^{-\frac{\beta j}{2}}(2^{-j}\tau_0)^{-\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} We can finish the proof by setting  $\tau_0=2^{-\frac{(\beta-1)j}{3}}$.
$\tau_0=2^{-\frac{(\beta-1)j}{3}}$.
When β = 3, we bound it by
 \begin{equation*}
\begin{split}
& 2^{-\frac{\beta j}{2}} (2^{-2j}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(\xi)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm d}u\right]^{1/2}
\left[\int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(v-\tau)}\right|^2 \,{\rm d}\eta \right]^{1/2}\, {\rm d}\tau\\
& \le 2^{-\frac{\beta j}{2}}(2^{-2j}\tau_0)^{-\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& 2^{-\frac{\beta j}{2}} (2^{-2j}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(\xi)\overline{\widehat{f}(u-\tau)}\right|^2\,{\rm d}u\right]^{1/2}
\left[\int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(v-\tau)}\right|^2 \,{\rm d}\eta \right]^{1/2}\, {\rm d}\tau\\
& \le 2^{-\frac{\beta j}{2}}(2^{-2j}\tau_0)^{-\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} We set  $\tau_0=2^{-\frac{j}{3}}$ and finish this proof.
$\tau_0=2^{-\frac{j}{3}}$ and finish this proof.
6.3. The case of  $ (\beta-1)j+C_{\beta}\le m\le \beta j-C_\beta$
$ (\beta-1)j+C_{\beta}\le m\le \beta j-C_\beta$
As before, we need to set up
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}\left(2^{m-\beta j}t\xi+t^2
\eta+|t|^{\beta}\right)}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+2^{(\beta-1)j-m}\eta){\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{-\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}\left(2^{m-\beta j}t\xi+t^2
\eta+|t|^{\beta}\right)}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+2^{(\beta-1)j-m}\eta){\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{-\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}for f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$. Let t 0 denote the critical point of
$[-3, -1]\cup [1, 3]$. Let t 0 denote the critical point of
 \begin{equation*}
\phi_{\xi, \eta}(t)=2^{m-\beta j}t\xi+t^2 \eta+|t|^{\beta}.
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)=2^{m-\beta j}t\xi+t^2 \eta+|t|^{\beta}.
\end{equation*}By the same argument, we need to estimate
 \begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \left.\widehat{f}(u)\overline{\widehat{f}(u-{b}\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)} {\rm e}^{i2^{\beta j}(\phi_{u,v
}(t_0)-\phi_{u-{b}\tau, v+\tau}(t_0))}\,{\rm d}u \,{\rm d}v\right] {\rm d}\tau.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \left.\widehat{f}(u)\overline{\widehat{f}(u-{b}\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)} {\rm e}^{i2^{\beta j}(\phi_{u,v
}(t_0)-\phi_{u-{b}\tau, v+\tau}(t_0))}\,{\rm d}u \,{\rm d}v\right] {\rm d}\tau.
\end{split}
\end{equation}with ![]() $b=2^{(\beta-1)j-m}$. Let
$b=2^{(\beta-1)j-m}$. Let
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}We can finish the estimate of Equation (6.12) with the following.
Lemma 6.4. Under the above notation and the assumption that β > 1, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{m-\beta j}\tau \hfill & \text{if } \beta\neq 3\\
2^{2(m-3j)}\tau \hfill & \text{if } \beta=3
\end{cases}
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{m-\beta j}\tau \hfill & \text{if } \beta\neq 3\\
2^{2(m-3j)}\tau \hfill & \text{if } \beta=3
\end{cases}
\end{equation}for every ![]() $j\gg 1$. Moreover,
$j\gg 1$. Moreover,
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}Proof of Lemma 6.4
By a direct calculation, we have
 \begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m-\beta j+1}t_0}{2v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}
\begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m-\beta j+1}t_0}{2v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}Hence,
 \begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial u}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \big)}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial u}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \big)}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}The relation between v and t 0 is given by
 \begin{equation*}
2^{m-\beta j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}
\begin{equation*}
2^{m-\beta j}u+2t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}We obtain
 \begin{equation*}
2^{m-\beta j}+2v\, \frac{\partial t_0}{\partial u}+\beta (\beta-1)t_0^{\beta-2}\,\frac{\partial t_0}{\partial u}=0.
\end{equation*}
\begin{equation*}
2^{m-\beta j}+2v\, \frac{\partial t_0}{\partial u}+\beta (\beta-1)t_0^{\beta-2}\,\frac{\partial t_0}{\partial u}=0.
\end{equation*}Here we used the fact that β ≠ 2.
 \begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial v}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\big)-2t_0}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m-\beta j+1} \frac{\frac{\partial t_0}{\partial v}\big(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\big)-2t_0}{(2v+\beta(\beta-1)t_0^{\beta-2})^2}.
\end{equation*}By a implicit function calculation, we obtain
 \begin{equation*}
2t_0+2v\, \frac{\partial t_0}{\partial v}+\beta (\beta-1) t^{\beta-2}\,\frac{\partial t_0}{\partial v}=0.
\end{equation*}
\begin{equation*}
2t_0+2v\, \frac{\partial t_0}{\partial v}+\beta (\beta-1) t^{\beta-2}\,\frac{\partial t_0}{\partial v}=0.
\end{equation*}Therefore, we have
 \begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2t_0}{2v+\beta(\beta-1)t_0^{\beta-2}}
\end{equation*}
\begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2t_0}{2v+\beta(\beta-1)t_0^{\beta-2}}
\end{equation*}and
 \begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2t_0 \right|\\
& \approx \left|4v +\beta(\beta-1)(4-\beta)t_0^{\beta-2} \right|.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2t_0 \right|\\
& \approx \left|4v +\beta(\beta-1)(4-\beta)t_0^{\beta-2} \right|.
\end{split}
\end{equation} When β ≠ 3, we have (6.15) ![]() $\approx 1$. When β = 3, we have (6.15)
$\approx 1$. When β = 3, we have (6.15) ![]() $\approx 2^{m-3 j}$. We can finish Equations (6.13) and (6.14) in the same way as above.
$\approx 2^{m-3 j}$. We can finish Equations (6.13) and (6.14) in the same way as above.
With the above estimates, we can finish the estimate of Equation (6.12) in the same way.
 \begin{equation*}
(6.12) = \int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0}.
\end{equation*}
\begin{equation*}
(6.12) = \int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0}.
\end{equation*}The former term can be bounded by
 \begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} \widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)} \,{\rm e}^{i2^{\beta
j}(\phi_{u, v}(t_0)-\phi_{u-b\tau, v+\tau}(t_0))}\,{\rm d}u \,{\rm d}v\right|\\
& \le \tau_0| \iint_{{\mathbb R}^2}|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}|du dv \le|\tau_0| \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} \widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)} \,{\rm e}^{i2^{\beta
j}(\phi_{u, v}(t_0)-\phi_{u-b\tau, v+\tau}(t_0))}\,{\rm d}u \,{\rm d}v\right|\\
& \le \tau_0| \iint_{{\mathbb R}^2}|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}|du dv \le|\tau_0| \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}For the latter term, when β ≠ 3, we bound it by
 \begin{equation*}
\begin{split}
& 2^{-\beta j/2}(2^{m-\beta j
}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)}|^2\,{\rm d}u\right]^{1/2} \left[\int_{{\mathbb R}}
\left|\widehat{g}(v)\overline{\widehat{g}(v+\tau)}\right|^2 \,{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{-\beta j/2}(2^{m-\beta j}\tau_0)^{-\frac{1}{2}} 2^{\frac{(\beta-1)j-m}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& 2^{-\beta j/2}(2^{m-\beta j
}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)}|^2\,{\rm d}u\right]^{1/2} \left[\int_{{\mathbb R}}
\left|\widehat{g}(v)\overline{\widehat{g}(v+\tau)}\right|^2 \,{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{-\beta j/2}(2^{m-\beta j}\tau_0)^{-\frac{1}{2}} 2^{\frac{(\beta-1)j-m}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} We can finish our proof by setting  $\tau_0=\frac{-2m+\beta j-j}{3}$. The proof for the case β = 3 is more or less the same; for the latter term, we bound it by
$\tau_0=\frac{-2m+\beta j-j}{3}$. The proof for the case β = 3 is more or less the same; for the latter term, we bound it by
 \begin{equation*}
\begin{split}
& 2^{-3 j/2}(2^{2m-6 j
}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)}\right|^2\,{\rm d}u\right]^{1/2}
\left[\int_{{\mathbb R}}
|\widehat{g}(v)\overline{\widehat{g}(v+\tau)}|^2 \,{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{-3 j/2}(2^{2m-6 j}\tau_0)^{-\frac{1}{2}} 2^{\frac{2j-m}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& 2^{-3 j/2}(2^{2m-6 j
}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)}\right|^2\,{\rm d}u\right]^{1/2}
\left[\int_{{\mathbb R}}
|\widehat{g}(v)\overline{\widehat{g}(v+\tau)}|^2 \,{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{-3 j/2}(2^{2m-6 j}\tau_0)^{-\frac{1}{2}} 2^{\frac{2j-m}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} We can finish the proof by setting  $\tau_0=2^{-m+\frac{5j}{3}}$.
$\tau_0=2^{-m+\frac{5j}{3}}$.
7. The cases of  $(m\in \Lambda_3, m^{\prime}\in \Lambda_2)$ and
$(m\in \Lambda_3, m^{\prime}\in \Lambda_2)$ and  $(m\in \Lambda_4, m^{\prime}\in \Lambda_4)$
$(m\in \Lambda_4, m^{\prime}\in \Lambda_4)$
In this section, we show the case ![]() $(m\in \Lambda_3, m^{\prime}\in \Lambda_2)$. The proof of the case
$(m\in \Lambda_3, m^{\prime}\in \Lambda_2)$. The proof of the case ![]() $(m\in \Lambda_4, m^{\prime}\in \Lambda_4)$ is almost the same and will be left out. As before, it is sufficient to show (after a rescaling) that
$(m\in \Lambda_4, m^{\prime}\in \Lambda_4)$ is almost the same and will be left out. As before, it is sufficient to show (after a rescaling) that
 \begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2)\,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\|f\|_2 \|g\|_2,
\end{equation*}
\begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2)\,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\|f\|_2 \|g\|_2,
\end{equation*}where ![]() $f=P_{\beta j} f$ and
$f=P_{\beta j} f$ and ![]() $g=P_{m^{\prime}+\beta j-j}g$ with
$g=P_{m^{\prime}+\beta j-j}g$ with ![]() $-j\le m^{\prime}\le (\beta-1)j-C_{\beta}$. By the localization argument as above, it equals to show
$-j\le m^{\prime}\le (\beta-1)j-C_{\beta}$. By the localization argument as above, it equals to show
 \begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2) \,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_2 \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2
\|g\|_2.
\end{equation*}
\begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{j}t^2) \,{\rm e}^{i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_2 \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2
\|g\|_2.
\end{equation*}By Fourier transform,
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{j}t^2 \eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t \right]
\widehat{h}(\xi+\eta) \,{\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{j}t^2 \eta+i2^{\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t \right]
\widehat{h}(\xi+\eta) \,{\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{-j/2} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}By scaling,
 \begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}(t\xi+2^{m^{\prime}-(\beta-1)j}t^2
\eta+|t|^{\beta})}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+2^{m-\beta j}\eta) {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{-m- j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{\beta j}(t\xi+2^{m^{\prime}-(\beta-1)j}t^2
\eta+|t|^{\beta})}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+2^{m-\beta j}\eta) {\rm d}\xi \,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{-m- j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation}for f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$.
$[-3, -1]\cup [1, 3]$.
Let t 0 denote the critical point of the phase function
 \begin{equation*}
\phi_{\xi, \eta}(t)=t\xi+2^{m^{\prime}-(\beta-1)j}t^2 \eta+|t|^{\beta}.
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)=t\xi+2^{m^{\prime}-(\beta-1)j}t^2 \eta+|t|^{\beta}.
\end{equation*}Changing the variables,
 \begin{equation*}
\xi+2^{m^{\prime}-\beta j}\eta\to u,\qquad \eta=v,
\end{equation*}
\begin{equation*}
\xi+2^{m^{\prime}-\beta j}\eta\to u,\qquad \eta=v,
\end{equation*}the left hand side of Equation (7.1) becomes
 \begin{equation*}
\left|\iint_{{\mathbb R}^2} \widehat{f}(u-2^{m-\beta j}v) \widehat{g}(v)\, {\rm e}^{i2^{\beta j}\phi_{u-2^{(\beta-1)j-m}v, v}(t_0)} \widehat{h}(u)\,{\rm d}u\, {\rm d}v\right|.
\end{equation*}
\begin{equation*}
\left|\iint_{{\mathbb R}^2} \widehat{f}(u-2^{m-\beta j}v) \widehat{g}(v)\, {\rm e}^{i2^{\beta j}\phi_{u-2^{(\beta-1)j-m}v, v}(t_0)} \widehat{h}(u)\,{\rm d}u\, {\rm d}v\right|.
\end{equation*}Denote
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}By the same argument as before, it is sufficient to prove
 \begin{equation}
\begin{split}
& \left|\int\left[\iint_{{\mathbb R}^2} \widehat{f}(u)\overline{\widehat{f}(u-2^{m^{\prime}-\beta j}\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}\, {\rm
e}^{i2^{\beta j}\widetilde{Q_{\tau}}(u, v)}\,{\rm d}u\,{\rm d}v\right] {\rm d}\tau\right|\\
& \lesssim 2^{-\epsilon j} 2^{(\beta-1)j-m'}\|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\int\left[\iint_{{\mathbb R}^2} \widehat{f}(u)\overline{\widehat{f}(u-2^{m^{\prime}-\beta j}\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}\, {\rm
e}^{i2^{\beta j}\widetilde{Q_{\tau}}(u, v)}\,{\rm d}u\,{\rm d}v\right] {\rm d}\tau\right|\\
& \lesssim 2^{-\epsilon j} 2^{(\beta-1)j-m'}\|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation}Lemma 7.1. With the same notation, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{2m^{\prime}-2\beta j+2j}\tau \hfill & \text{if } \beta\neq 4\\
2^{3m^{\prime}-9j} \tau \hfill & \text{if } \beta=4
\end{cases}
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim
\begin{cases}
2^{2m^{\prime}-2\beta j+2j}\tau \hfill & \text{if } \beta\neq 4\\
2^{3m^{\prime}-9j} \tau \hfill & \text{if } \beta=4
\end{cases}
\end{equation}and
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau
\end{equation}for every ![]() $j\gg 1$.
$j\gg 1$.
The proof of the lemma is exactly the same as in the last section; we omit the proof. With this lemma, we can obtain Equation (7.2) in the same way as before.
8. The case of β < 0
According to Equation (2.5), in this section, we will consider the operator
 \begin{equation*}
T_{\beta,j}(f,g)(x)=\int_{\mathbb{R}}f(x-2^{-j}t)g(x-2^{-2j}t^2)\,{\rm e}^{i2^{-\beta j}|t|^\beta}\rho(t)\,{\rm d}t,
\end{equation*}
\begin{equation*}
T_{\beta,j}(f,g)(x)=\int_{\mathbb{R}}f(x-2^{-j}t)g(x-2^{-2j}t^2)\,{\rm e}^{i2^{-\beta j}|t|^\beta}\rho(t)\,{\rm d}t,
\end{equation*}where β < 0 and ![]() $j\geq 1$.
$j\geq 1$.
As before, we decompose the frequencies of f and g and estimate
 \begin{equation*}
T_{j, m, m^{\prime}}(f, g)(x)=\int_{{\mathbb R}} P_{-\beta j+j+m}f(x-2^{-j}t) P_{-\beta j+2j+m'}g(x-2^{-2j} t^2)\,{\rm e}^{i2^{-\beta
j}|t|^{\beta}}\rho(t)\,{\rm d}t.
\end{equation*}
\begin{equation*}
T_{j, m, m^{\prime}}(f, g)(x)=\int_{{\mathbb R}} P_{-\beta j+j+m}f(x-2^{-j}t) P_{-\beta j+2j+m'}g(x-2^{-2j} t^2)\,{\rm e}^{i2^{-\beta
j}|t|^{\beta}}\rho(t)\,{\rm d}t.
\end{equation*}Define
 \begin{equation*}
\begin{split}
& \Omega_1=\{\iota \in {{\mathbb Z}}\big| \iota \le \beta j\},\\
& \Omega_2=\{\iota \in {{\mathbb Z}}\big| \beta j\le \iota \le -C_{\beta}\},\\
& \Omega_3=\{\iota\in {{\mathbb Z}}\big| -C_{\beta}\le \iota\le C_{\beta}\},\\
& \Omega_4=\{\iota \in {{\mathbb Z}}\big| \iota\ge C_{\beta}\},
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \Omega_1=\{\iota \in {{\mathbb Z}}\big| \iota \le \beta j\},\\
& \Omega_2=\{\iota \in {{\mathbb Z}}\big| \beta j\le \iota \le -C_{\beta}\},\\
& \Omega_3=\{\iota\in {{\mathbb Z}}\big| -C_{\beta}\le \iota\le C_{\beta}\},\\
& \Omega_4=\{\iota \in {{\mathbb Z}}\big| \iota\ge C_{\beta}\},
\end{split}
\end{equation*}where C β is a large positive integer that depends only on β. Similarly, depending on which set m belongs to and which set mʹ belongs to, we have 16 cases. These cases will be considered in § 9–§ 13.
9. The case of  $m\in \Omega_1$ or
$m\in \Omega_1$ or  $m^{\prime}\in\Omega_1$
$m^{\prime}\in\Omega_1$
In this case, the situation is similar as in § 3. When m is extremely small, the function ![]() $P_{-\beta j+j+m}f(x-2^{-j}t)$ is essentially the same as
$P_{-\beta j+j+m}f(x-2^{-j}t)$ is essentially the same as ![]() $P_{-\beta j+j+m}f(x)$. Therefore,
$P_{-\beta j+j+m}f(x)$. Therefore, ![]() $T_{j, m, m^{\prime}}(f, g)$ can be viewed as a product. We write
$T_{j, m, m^{\prime}}(f, g)$ can be viewed as a product. We write
 \begin{equation*}
\sum_{m\in \Omega_1, m^{\prime}\in {\mathbb Z}} T_{j, m, m^{\prime}}(f, g)=T_{\beta,j} (P_{\le j}f, g).
\end{equation*}
\begin{equation*}
\sum_{m\in \Omega_1, m^{\prime}\in {\mathbb Z}} T_{j, m, m^{\prime}}(f, g)=T_{\beta,j} (P_{\le j}f, g).
\end{equation*}Turning to the Fourier side, we face
 \begin{equation*}
\iint_{{\mathbb R}\times {\mathbb R}} \widehat{P_{\le j}f}(\xi) \widehat{g}(\eta) m_j(\xi, \eta)\,{\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi \,{\rm d}\eta.
\end{equation*}
\begin{equation*}
\iint_{{\mathbb R}\times {\mathbb R}} \widehat{P_{\le j}f}(\xi) \widehat{g}(\eta) m_j(\xi, \eta)\,{\rm e}^{ix(\xi+\eta)}\,{\rm d}\xi \,{\rm d}\eta.
\end{equation*}By Taylor’s formula, we have
 \begin{equation*}
m_j(\xi, \eta)=\int_{{\mathbb R}} \left(\sum_{n=0}^{\infty} \frac{i^n (2^{-j}\xi)^n}{n!} \right){\rm e}^{i(2^{-2j}t^2\eta+2^{-\beta
j}|t|^{\beta})}\rho(t)t^n\,{\rm d}t.
\end{equation*}
\begin{equation*}
m_j(\xi, \eta)=\int_{{\mathbb R}} \left(\sum_{n=0}^{\infty} \frac{i^n (2^{-j}\xi)^n}{n!} \right){\rm e}^{i(2^{-2j}t^2\eta+2^{-\beta
j}|t|^{\beta})}\rho(t)t^n\,{\rm d}t.
\end{equation*} Fix ![]() $n\in\mathbb{N}$, we consider the term
$n\in\mathbb{N}$, we consider the term
 \begin{equation*} \left|\int_{\mathbb{R}}\dfrac{(i2^{-j}\xi)^n}{n!}{\rm e}^{i2^{-2j}t^2\eta}{\rm e}^{i2^{-\beta j}|t|^\beta}\rho(t)t^n\,{\rm
d}t\right|\leq\frac{1}{n!}\left|\int_{\mathbb{R}}{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}\rho(t)t^n\,{\rm d}t\right|, \end{equation*}
\begin{equation*} \left|\int_{\mathbb{R}}\dfrac{(i2^{-j}\xi)^n}{n!}{\rm e}^{i2^{-2j}t^2\eta}{\rm e}^{i2^{-\beta j}|t|^\beta}\rho(t)t^n\,{\rm
d}t\right|\leq\frac{1}{n!}\left|\int_{\mathbb{R}}{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}\rho(t)t^n\,{\rm d}t\right|, \end{equation*}with ![]() $\phi_{\xi,\eta}(t)=2^{-2j+ \beta j}\eta t^2+|t|^{\beta}.$
$\phi_{\xi,\eta}(t)=2^{-2j+ \beta j}\eta t^2+|t|^{\beta}.$
Noticing that  $|\phi^{\prime\prime\prime}_{\xi,\eta}(t)|\gtrsim1$, by van der Corput’s lemma, we have
$|\phi^{\prime\prime\prime}_{\xi,\eta}(t)|\gtrsim1$, by van der Corput’s lemma, we have
 \begin{equation*}
\left|\int_{\mathbb{R}}{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}\rho(t)t^n\,{\rm d}t\right| \lesssim n2^{\frac{\beta j}{3}}.
\end{equation*}
\begin{equation*}
\left|\int_{\mathbb{R}}{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}\rho(t)t^n\,{\rm d}t\right| \lesssim n2^{\frac{\beta j}{3}}.
\end{equation*} We sum up according to ![]() $n\in\mathbb N$ and by Hölder’s inequality,
$n\in\mathbb N$ and by Hölder’s inequality,
 \begin{equation*}
\begin{split}
& \left\|\left[\int_{{\mathbb R}} \widehat{P_{\le j}f}(\xi) (2^{-j}\xi)^n {\rm e}^{ix\xi}\,{\rm d}\xi\right] \left[ \int_{{\mathbb R}} \widehat{g}(\eta)
\left(\int_{{\mathbb R}} {\rm e}^{i(2^{-2j}t^2\eta+2^{-\beta j}|t|^{\beta})}\rho(t)t^n\,{\rm d}t\right) {\rm e}^{i x\eta}{\rm d}\eta\right]\right\|_1\\
& \lesssim 2^{\frac{\beta j}{3}} \|f\|_2 \|g\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left\|\left[\int_{{\mathbb R}} \widehat{P_{\le j}f}(\xi) (2^{-j}\xi)^n {\rm e}^{ix\xi}\,{\rm d}\xi\right] \left[ \int_{{\mathbb R}} \widehat{g}(\eta)
\left(\int_{{\mathbb R}} {\rm e}^{i(2^{-2j}t^2\eta+2^{-\beta j}|t|^{\beta})}\rho(t)t^n\,{\rm d}t\right) {\rm e}^{i x\eta}{\rm d}\eta\right]\right\|_1\\
& \lesssim 2^{\frac{\beta j}{3}} \|f\|_2 \|g\|_2.
\end{split}
\end{equation*} We finish the proof of the case ![]() $m\in \Omega_1$. The case
$m\in \Omega_1$. The case ![]() $m^{\prime}\in\Omega_1$ can be estimated in the same way.
$m^{\prime}\in\Omega_1$ can be estimated in the same way.
10. The case of  $m, m^{\prime}\in \Omega_3$
$m, m^{\prime}\in \Omega_3$
In this section, without loss of generality, we assume that ![]() $m=m^{\prime}=0$.
$m=m^{\prime}=0$.
Proposition 10.1. For β < 0, it holds that
for some ϵ > 0 depending only on β.
Proof. By rescaling, it suffices to prove
 \begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{-j}t^2)\, {\rm e}^{i2^{-\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\|f\|_2 \|g\|_2,
\end{equation*}
\begin{equation*}
\left\|\int_{{\mathbb R}} f(x-t) g(x-2^{-j}t^2)\, {\rm e}^{i2^{-\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right\|_1 \lesssim 2^{-\epsilon j}\|f\|_2 \|g\|_2,
\end{equation*} where ![]() $f=P_{-\beta j} f$ and
$f=P_{-\beta j} f$ and ![]() $g=P_{(-\beta+1)j}g$.
$g=P_{(-\beta+1)j}g$.
By the localization argument as above, it is sufficient to set up
 \begin{equation*}
\left\|\int f(x-t)g(x-2^{-j}t^2)\,{\rm e}^{i2^{-\beta j}|t|^\beta}\rho(t)dt\right\|_2\lesssim 2^{-\epsilon j}\|f\|_2\|g\|_2.
\end{equation*}
\begin{equation*}
\left\|\int f(x-t)g(x-2^{-j}t^2)\,{\rm e}^{i2^{-\beta j}|t|^\beta}\rho(t)dt\right\|_2\lesssim 2^{-\epsilon j}\|f\|_2\|g\|_2.
\end{equation*}Turning to the Fourier side and applying duality, it equals to show that
 \begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{-j}t^2 \eta+i2^{-\beta
j}|t|^{\beta}}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{it\xi+i2^{-j}t^2 \eta+i2^{-\beta
j}|t|^{\beta}}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation}By scaling, it can be rewritten as
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}}{\rm e}^{i2^{-\beta j}(t\xi+t^2 \eta+|t|^{\beta})}\rho(t)\,{\rm d}t
\right] \widehat{h}(2^{-j}\xi+\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}}{\rm e}^{i2^{-\beta j}(t\xi+t^2 \eta+|t|^{\beta})}\rho(t)\,{\rm d}t
\right] \widehat{h}(2^{-j}\xi+\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}for f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$.
$[-3, -1]\cup [1, 3]$.
By the method of stationary phase, it is enough to prove
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta)\, {\rm e}^{i2^{-\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}(2^{-j}\xi+\eta) {\rm d}\xi
{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta)\, {\rm e}^{i2^{-\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}(2^{-j}\xi+\eta) {\rm d}\xi
{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}Here
 \begin{equation*}
\phi_{\xi, \eta}(t)= t\xi+t^2 \eta+|t|^{\beta}
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)= t\xi+t^2 \eta+|t|^{\beta}
\end{equation*}and t 0 is the critical point of it. By applying change of variables and denoting ![]() $ b=2^{-j},
$ it is sufficient to show that
$ b=2^{-j},
$ it is sufficient to show that
 \begin{equation*}
\left\| \int_{{\mathbb R}} \widehat{f}(u) \widehat{g}(v-bu)\, {\rm e}^{i2^{-\beta j}\phi_{u, v-bu}(t_0)}\,{\rm d}u\right\|_{L^2_{v}}^2 \lesssim 2^{-\epsilon j}\|f\|_2^2\|g\|_2^2.
\end{equation*}
\begin{equation*}
\left\| \int_{{\mathbb R}} \widehat{f}(u) \widehat{g}(v-bu)\, {\rm e}^{i2^{-\beta j}\phi_{u, v-bu}(t_0)}\,{\rm d}u\right\|_{L^2_{v}}^2 \lesssim 2^{-\epsilon j}\|f\|_2^2\|g\|_2^2.
\end{equation*}We expand the left hand side as
 \begin{equation*}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \widehat{f}(u_1) \widehat{g}(v-bu_1)\,{\rm e}^{i2^{-\beta j}\phi_{u_1, v-bu_1}(t_0)}\\
&\left. \overline{\widehat{f}(u_2)} \overline{\widehat{g}(v-bu_2)}\, {\rm e}^{-i2^{-\beta j}\phi_{u_2, v-bu_2}(t_0)}\,{\rm d}u_1 \,{\rm d}u_2\right]{\rm d}v.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \widehat{f}(u_1) \widehat{g}(v-bu_1)\,{\rm e}^{i2^{-\beta j}\phi_{u_1, v-bu_1}(t_0)}\\
&\left. \overline{\widehat{f}(u_2)} \overline{\widehat{g}(v-bu_2)}\, {\rm e}^{-i2^{-\beta j}\phi_{u_2, v-bu_2}(t_0)}\,{\rm d}u_1 \,{\rm d}u_2\right]{\rm d}v.
\end{split}
\end{equation*}By changing the variables
we obtain
 \begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \left.\widehat{f}(u)\overline{\widehat{f}(u+\tau)} \widehat{g}(v)\overline{\widehat{g}(v-b\tau)} \,{\rm e}^{i2^{\beta j}(\phi_{u,v
}(t_0)-\phi_{u+\tau, v-b\tau}(t_0))}\,{\rm d}u\,{\rm d}v\right] {\rm d}\tau.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \left.\widehat{f}(u)\overline{\widehat{f}(u+\tau)} \widehat{g}(v)\overline{\widehat{g}(v-b\tau)} \,{\rm e}^{i2^{\beta j}(\phi_{u,v
}(t_0)-\phi_{u+\tau, v-b\tau}(t_0))}\,{\rm d}u\,{\rm d}v\right] {\rm d}\tau.
\end{split}
\end{equation}Let us denote
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}Lemma 10.1. With the above notation, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim\tau
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim\tau
\end{equation}and
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}As in last section, we omit the proof of the lemma. It can be proved in the same way. With this lemma, Equation (10.1) can be proved easily.
11. The cases where phase functions admit no critical points
This section contains several cases ![]() $(m\in \Omega_2, m^{\prime}\in \Omega_2)$,
$(m\in \Omega_2, m^{\prime}\in \Omega_2)$, ![]() $(m\in \Omega_2, m^{\prime}\in \Omega_4)$,
$(m\in \Omega_2, m^{\prime}\in \Omega_4)$, ![]() $(m\in \Omega_4, m^{\prime}\in \Omega_2)$,
$(m\in \Omega_4, m^{\prime}\in \Omega_2)$, ![]() $(m\in
\Omega_3, m^{\prime}\in \Omega_4)$ and
$(m\in
\Omega_3, m^{\prime}\in \Omega_4)$ and ![]() $(m\in \Omega_4, m^{\prime}\in \Omega_3)$. The proofs for all these cases are similar. We only present the proof of the case
$(m\in \Omega_4, m^{\prime}\in \Omega_3)$. The proofs for all these cases are similar. We only present the proof of the case ![]() $m\in
\Omega_3, m^{\prime}\in \Omega_4$.
$m\in
\Omega_3, m^{\prime}\in \Omega_4$.
Without loss of generality, we assume m = 0. As in § 5, we consider the multiplier ![]() $m_j(\xi,\eta)$, which is given by
$m_j(\xi,\eta)$, which is given by
 \begin{equation*}
m_j(\xi,\eta)=\int\rho(t)\,{\rm e}^{i2^{-\beta j}(\xi t+2^{m^{\prime}}\eta t^2+|t|^\beta)}\,{\rm d}t.
\end{equation*}
\begin{equation*}
m_j(\xi,\eta)=\int\rho(t)\,{\rm e}^{i2^{-\beta j}(\xi t+2^{m^{\prime}}\eta t^2+|t|^\beta)}\,{\rm d}t.
\end{equation*}By integration by parts, for every large integer M, it holds that
 \begin{equation*}
|m_j(\xi,\eta)|\lesssim 2^{-M(j+m^{\prime})}.
\end{equation*}
\begin{equation*}
|m_j(\xi,\eta)|\lesssim 2^{-M(j+m^{\prime})}.
\end{equation*}With this estimate, we can finish the proof by the same argument as in § 5.
12. The case of  $m\in{\Omega_2,\ m^{\prime}\in{\Omega_3}}$
$m\in{\Omega_2,\ m^{\prime}\in{\Omega_3}}$
Without loss of generality, we assume that ![]() $m^{\prime}=0$. We need to show that
$m^{\prime}=0$. We need to show that
 \begin{equation}
\begin{split}
&\iint_{\mathbb{R}^2}\hat{f}(\xi)\hat{g}(\eta)\left[\int_{\mathbb{R}}{\rm e}^{it\xi+i2^{-j}t^2\eta+i2^{-\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right]\hat{h}(\xi+\eta)\,{\rm d}\xi\,{\rm d}\eta\\
&\lesssim 2^{-\epsilon j}\|f\|_2\|g\|_2\|h\|_2,
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\iint_{\mathbb{R}^2}\hat{f}(\xi)\hat{g}(\eta)\left[\int_{\mathbb{R}}{\rm e}^{it\xi+i2^{-j}t^2\eta+i2^{-\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right]\hat{h}(\xi+\eta)\,{\rm d}\xi\,{\rm d}\eta\\
&\lesssim 2^{-\epsilon j}\|f\|_2\|g\|_2\|h\|_2,
\end{split}
\end{equation}where ![]() $f=P_{m-\beta j} f$ and
$f=P_{m-\beta j} f$ and ![]() $g=P_{(-\beta+1)j}g$ with
$g=P_{(-\beta+1)j}g$ with ![]() $\beta j\le m\le -C_{\beta}$. By Hölder’s inequality, the left hand side of Equation (12.1) can be bounded by
$\beta j\le m\le -C_{\beta}$. By Hölder’s inequality, the left hand side of Equation (12.1) can be bounded by
 \begin{equation*}
2^{\frac{m-\beta j}{2}}\|\hat{f}\|_2 \left\| \int \widehat{g}(\eta) \left[\int_{{\mathbb R}}{\rm e}^{it\xi+i2^{-j}t^2\eta+i2^{-\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right]
\widehat{h}(\xi+\eta){\rm d}\eta\right\|_{L^{\infty}_{\xi}}.
\end{equation*}
\begin{equation*}
2^{\frac{m-\beta j}{2}}\|\hat{f}\|_2 \left\| \int \widehat{g}(\eta) \left[\int_{{\mathbb R}}{\rm e}^{it\xi+i2^{-j}t^2\eta+i2^{-\beta j}|t|^{\beta}}\rho(t)\,{\rm d}t\right]
\widehat{h}(\xi+\eta){\rm d}\eta\right\|_{L^{\infty}_{\xi}}.
\end{equation*} Here, because  $supp\hat{f}\subset \{\xi:|\xi|\sim2^{m-\beta j}\}$, we have the fact that
$supp\hat{f}\subset \{\xi:|\xi|\sim2^{m-\beta j}\}$, we have the fact that  $\|\widehat{f}\|_1\lesssim2^{(m-\beta j)/2}\|\widehat{f}\|_2$.
$\|\widehat{f}\|_1\lesssim2^{(m-\beta j)/2}\|\widehat{f}\|_2$.
We note that
 \begin{equation*}
m_j(\xi, \eta)=\int_{\mathbb{R}}\rho(t)\,{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}{\rm d}t,
\end{equation*}
\begin{equation*}
m_j(\xi, \eta)=\int_{\mathbb{R}}\rho(t)\,{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}{\rm d}t,
\end{equation*}with ![]() $\phi_{\xi,\eta}(t)=2^{\beta j}t\xi+2^{\beta j-j}t^2\eta+|t|^\beta$. Since
$\phi_{\xi,\eta}(t)=2^{\beta j}t\xi+2^{\beta j-j}t^2\eta+|t|^\beta$. Since  $ 2^{\beta j}\leq|2^{\beta j}\xi|\leq2^{-C_\beta},\ |\eta|\sim 2^{(-\beta+1
)j}$,
$ 2^{\beta j}\leq|2^{\beta j}\xi|\leq2^{-C_\beta},\ |\eta|\sim 2^{(-\beta+1
)j}$,  $\phi^{\prime}_{\xi,\eta}(t)$ and
$\phi^{\prime}_{\xi,\eta}(t)$ and  $\phi^{\prime\prime}_{\xi,\eta}(t)$ cannot be zero at same point. By van der Corput’s lemma, we obtain
$\phi^{\prime\prime}_{\xi,\eta}(t)$ cannot be zero at same point. By van der Corput’s lemma, we obtain
 \begin{equation*}
\left|\int_{{\mathbb R}}\,{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}\rho(t)\,{\rm d}t\right|\lesssim2^{\beta j/2}.
\end{equation*}
\begin{equation*}
\left|\int_{{\mathbb R}}\,{\rm e}^{i2^{-\beta j}\phi_{\xi,\eta}(t)}\rho(t)\,{\rm d}t\right|\lesssim2^{\beta j/2}.
\end{equation*}Notice that β < 0, it is enough to obtain the expected estimate.
13. The cases of  $m\in{\Omega_3,\ m^{\prime}\in{\Omega_2}} $ and
$m\in{\Omega_3,\ m^{\prime}\in{\Omega_2}} $ and  $m\in \Omega_4,\ m\in\Omega_4$
$m\in \Omega_4,\ m\in\Omega_4$
In this section, we consider the case ![]() $(m\in{\Omega_3,\ m^{\prime}\in{\Omega_2}} )$. The proof of (
$(m\in{\Omega_3,\ m^{\prime}\in{\Omega_2}} )$. The proof of (![]() $m\in \Omega_4,\ m\in\Omega_4$) is similar and will be left out. Without loss of generality, we assume m = 0. By the same argument as in § 7, we need to show
$m\in \Omega_4,\ m\in\Omega_4$) is similar and will be left out. Without loss of generality, we assume m = 0. By the same argument as in § 7, we need to show
 \begin{equation}
\begin{split}
&\left|\iint_{\mathbb{R}^2}\hat{f}(\xi)\hat{g}(\eta)\left[\int_{\mathbb{R}}{\rm e}^{it\xi+i2^{-j}t^2\eta+i2^{-\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right]\hat{h}(\xi+\eta){\rm d}\xi {\rm d}\eta\right|\\
&\lesssim 2^{-\varepsilon j}\|f\|_2\|g\|_2\|h\|_2,
\end{split}
\end{equation}
\begin{equation}
\begin{split}
&\left|\iint_{\mathbb{R}^2}\hat{f}(\xi)\hat{g}(\eta)\left[\int_{\mathbb{R}}{\rm e}^{it\xi+i2^{-j}t^2\eta+i2^{-\beta j}|t|^\beta}\rho(t)\,{\rm d}t\right]\hat{h}(\xi+\eta){\rm d}\xi {\rm d}\eta\right|\\
&\lesssim 2^{-\varepsilon j}\|f\|_2\|g\|_2\|h\|_2,
\end{split}
\end{equation}where ![]() $f=P_{-\beta j} f$ and
$f=P_{-\beta j} f$ and ![]() $g=P_{m^{\prime}-\beta j+j}g$. We will consider two cases.
$g=P_{m^{\prime}-\beta j+j}g$. We will consider two cases.
13.1.  $\beta j\lt m^{\prime}\leqslant-j$
$\beta j\lt m^{\prime}\leqslant-j$
It is equivalent to show
 \begin{equation*}
\begin{split}
&\left| \iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{-\beta j}(t\xi+2^{m^{\prime}}t^2
\eta+|t|^{\beta})}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+2^{m^{\prime}+j}\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{-m'+\beta j-j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
&\left| \iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{-\beta j}(t\xi+2^{m^{\prime}}t^2
\eta+|t|^{\beta})}\rho(t)\,{\rm d}t \right] \widehat{h}(\xi+2^{m^{\prime}+j}\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{-m'+\beta j-j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}for f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$. By the method of stationary phase, it is enough to prove that
$[-3, -1]\cup [1, 3]$. By the method of stationary phase, it is enough to prove that
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) {\rm e}^{i2^{-\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}(\xi+2^{m^{\prime}+j}\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j}2^{\frac{-m^{\prime}-j}{2}} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) {\rm e}^{i2^{-\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}(\xi+2^{m^{\prime}+j}\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j}2^{\frac{-m^{\prime}-j}{2}} \|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}Here t 0 is the critical point of
 \begin{equation*}
\phi_{\xi, \eta}(t)=t\xi+2^{m^{\prime}}t^2 \eta+|t|^{\beta}.
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)=t\xi+2^{m^{\prime}}t^2 \eta+|t|^{\beta}.
\end{equation*} By changing the variables and setting  $ b=2^{m'+j},
$ it is sufficient to prove that
$ b=2^{m'+j},
$ it is sufficient to prove that
 \begin{equation*}
\left\| \int_{{\mathbb R}} \widehat{f}(u-{b}v) \widehat{g}(v) {\rm e}^{i2^{-\beta j}\phi_{u-{b}v, v}(t_0)}{\rm d}v\right\|_{L^2_{u}}^2 \lesssim 2^{-\epsilon j}2^{\frac{-m^{\prime}-j}{2}}\|f\|_2^2\|g\|_2^2.
\end{equation*}
\begin{equation*}
\left\| \int_{{\mathbb R}} \widehat{f}(u-{b}v) \widehat{g}(v) {\rm e}^{i2^{-\beta j}\phi_{u-{b}v, v}(t_0)}{\rm d}v\right\|_{L^2_{u}}^2 \lesssim 2^{-\epsilon j}2^{\frac{-m^{\prime}-j}{2}}\|f\|_2^2\|g\|_2^2.
\end{equation*}We expand the left hand side,
 \begin{equation*}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \widehat{f}(u-{b}v_1) \widehat{g}(v_1)\, {\rm e}^{i2^{-\beta j}\phi_{u-{b}v_1, v_1}(t_0)}\\
& \left.\overline{\widehat{f}(u-{b}v_2)} \overline{\widehat{g}(v_2)} \,{\rm e}^{-i2^{-\beta j}\phi_{u-{b}v_2, v_2}(t_0)}\,{\rm d}v_1 \,{\rm d}v_2\right]{\rm d}u.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \widehat{f}(u-{b}v_1) \widehat{g}(v_1)\, {\rm e}^{i2^{-\beta j}\phi_{u-{b}v_1, v_1}(t_0)}\\
& \left.\overline{\widehat{f}(u-{b}v_2)} \overline{\widehat{g}(v_2)} \,{\rm e}^{-i2^{-\beta j}\phi_{u-{b}v_2, v_2}(t_0)}\,{\rm d}v_1 \,{\rm d}v_2\right]{\rm d}u.
\end{split}
\end{equation*}By changing variables
we obtain
 \begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2}\right. & \left.\widehat{f}(u)\overline{\widehat{f}(u-{b}\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}\,{\rm e}^{i2^{-\beta j}(\phi_{u, }(t_0)-\phi_{\xi-{b}\tau, \eta+\tau}(t_0))}{\rm d}\xi \,{\rm d}\eta\right] {\rm d}\tau.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2}\right. & \left.\widehat{f}(u)\overline{\widehat{f}(u-{b}\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}\,{\rm e}^{i2^{-\beta j}(\phi_{u, }(t_0)-\phi_{\xi-{b}\tau, \eta+\tau}(t_0))}{\rm d}\xi \,{\rm d}\eta\right] {\rm d}\tau.
\end{split}
\end{equation}Let us denote
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}We can also set up the following key estimates as before.
Lemma 13.1. Under the above notation and the assumption that β < 0, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim2^{2m^{\prime}}\tau.
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim2^{2m^{\prime}}\tau.
\end{equation}Moreover,
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}Proof of Lemma 13.1
By a direct calculation, we have
 \begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m^{\prime} +1}t_0}{2^{m^{\prime}+1}v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}
\begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m^{\prime} +1}t_0}{2^{m^{\prime}+1}v+\beta(\beta-1)|t_0| ^{\beta-2}}.
\end{equation*}Hence,
 \begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial
u}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \right)}{\left(2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}\right)^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial
u}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2} \right)}{\left(2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}\right)^2}.
\end{equation*}The relation between v and t 0 is given by
 \begin{equation*}
u+2^{m^{\prime}+1}t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}
\begin{equation*}
u+2^{m^{\prime}+1}t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}We obtain
 \begin{equation*}
1+2^{m^{\prime}+1}v \frac{\partial t_0}{\partial u}+\beta (\beta-1)t_0^{\beta-2}\frac{\partial t_0}{\partial u}=0.
\end{equation*}
\begin{equation*}
1+2^{m^{\prime}+1}v \frac{\partial t_0}{\partial u}+\beta (\beta-1)t_0^{\beta-2}\frac{\partial t_0}{\partial u}=0.
\end{equation*}A simple calculation shows that
 \begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial v}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2^{m^{\prime}+1}t_0}{\left(2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}\right)^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial v}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2^{m^{\prime}+1}t_0}{\left(2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}\right)^2}.
\end{equation*}On the other side, we have
 \begin{equation*}
2^{m^{\prime}+1}t_0+2^{m^{\prime}+1}v \,\frac{\partial t_0}{\partial v}+\beta (\beta-1) t^{\beta-2}\,\frac{\partial t_0}{\partial v}=0.
\end{equation*}
\begin{equation*}
2^{m^{\prime}+1}t_0+2^{m^{\prime}+1}v \,\frac{\partial t_0}{\partial v}+\beta (\beta-1) t^{\beta-2}\,\frac{\partial t_0}{\partial v}=0.
\end{equation*}Therefore, we have
 \begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2^{m^{\prime}+1}t_0}{2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}}.
\end{equation*}
\begin{equation*}
\frac{\partial t_0}{\partial v}=-\frac{2^{m^{\prime}+1}t_0}{2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}}.
\end{equation*}Hence,
 \begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2^{m^{\prime}+1}t_0 \right|\\
& \approx \left|2^{m^{\prime}+2}v +\beta(\beta-1)(4-\beta)t_0^{\beta-2} \right|\approx1.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \left|\frac{\partial t_0}{\partial v}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2^{m^{\prime}+1}t_0 \right|\\
& \approx \left|2^{m^{\prime}+2}v +\beta(\beta-1)(4-\beta)t_0^{\beta-2} \right|\approx1.
\end{split}
\end{equation}Equation (13.3) follows from the mean value theorem. Equation (13.4) can also be proved in the same way.
We estimate Equation (13.2) in the same way as before.
 \begin{equation*}
(13.2)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0}.
\end{equation*}
\begin{equation*}
(13.2)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0}.
\end{equation*}The former term can be bounded by
 \begin{equation*}
\begin{split}
& \tau_0 \sup_{\tau} \left|\iint_{{\mathbb R}^2} \widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)} \,{\rm
e}^{i2^{-\beta j}(\phi_{u, v}(t_0)-\phi_{u-b\tau, v+\tau}(t_0))}\,{\rm d}u\,{\rm d}v\right|\\
& \le \tau_0 \iint_{{\mathbb R}^2}\left|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}\right|{\rm d}u\,{\rm
d}v \le|\tau_0| \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \tau_0 \sup_{\tau} \left|\iint_{{\mathbb R}^2} \widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)} \,{\rm
e}^{i2^{-\beta j}(\phi_{u, v}(t_0)-\phi_{u-b\tau, v+\tau}(t_0))}\,{\rm d}u\,{\rm d}v\right|\\
& \le \tau_0 \iint_{{\mathbb R}^2}\left|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)} \widehat{g}(v)\overline{\widehat{g}(v+\tau)}\right|{\rm d}u\,{\rm
d}v \le|\tau_0| \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}For the latter term, when β < 0, we bound it by
 \begin{equation*}
\begin{split}
& 2^{\beta j/2}(2^{2m^{\prime}
}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)}\right|^2\,{\rm d}u\right]^{1/2} \left[\int_{{\mathbb R}}
\left|\widehat{g}(v)\overline{\widehat{g}(v+\tau)}\right|^2 \,{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{\beta j/2}(2^{2m^{\prime}}\tau_0)^{-\frac{1}{2}}b^{\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& 2^{\beta j/2}(2^{2m^{\prime}
}\tau_0)^{-\frac{1}{2}} \int \left[\int_{{\mathbb R}}\left|\widehat{f}(u)\overline{\widehat{f}(u-b\tau)}\right|^2\,{\rm d}u\right]^{1/2} \left[\int_{{\mathbb R}}
\left|\widehat{g}(v)\overline{\widehat{g}(v+\tau)}\right|^2 \,{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{\beta j/2}(2^{2m^{\prime}}\tau_0)^{-\frac{1}{2}}b^{\frac{1}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} We can finish the proof by setting  $\tau_0=2^{\frac{\beta j}{3}-\frac{m^{\prime}}{3}+\frac{j}{3}}$.
$\tau_0=2^{\frac{\beta j}{3}-\frac{m^{\prime}}{3}+\frac{j}{3}}$.
13.2.  $-j\lt{m^{\prime}}\lt-C_\beta$
$-j\lt{m^{\prime}}\lt-C_\beta$
As before, we need to set up
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{-\beta j}(t\xi+2^{m^{\prime}}t^2 \eta+|t|^{\beta})}\rho(t)\,{\rm d}t
\right] \widehat{h}(2^{-m^{\prime}-j}\xi+\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) \left[\int_{{\mathbb R}} {\rm e}^{i2^{-\beta j}(t\xi+2^{m^{\prime}}t^2 \eta+|t|^{\beta})}\rho(t)\,{\rm d}t
\right] \widehat{h}(2^{-m^{\prime}-j}\xi+\eta) {\rm d}\xi\,{\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j} 2^{\frac{\beta j}{2}} \|f\|_2 \|g\|_2 \|h\|_2
\end{split}
\end{equation*}for f and g whose frequencies support on ![]() $[-3, -1]\cup [1, 3]$. By the method of stationary phase, it is enough to prove that
$[-3, -1]\cup [1, 3]$. By the method of stationary phase, it is enough to prove that
 \begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) {\rm e}^{i2^{-\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}(2^{-m^{\prime}-j}\xi+\eta) {\rm d}\xi\, {\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j}\|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& \left|\iint_{{\mathbb R}^2} \widehat{f}(\xi) \widehat{g}(\eta) {\rm e}^{i2^{-\beta j}\phi_{\xi, \eta}(t_0)} \widehat{h}(2^{-m^{\prime}-j}\xi+\eta) {\rm d}\xi\, {\rm d}\eta\right|\\
& \lesssim 2^{-\epsilon j}\|f\|_2 \|g\|_2 \|h\|_2.
\end{split}
\end{equation*}As before, t 0 is the critical point of
 \begin{equation*}
\phi_{\xi, \eta}(t)=t\xi+2^{m^{\prime}}t^2 \eta+|t|^{\beta}.
\end{equation*}
\begin{equation*}
\phi_{\xi, \eta}(t)=t\xi+2^{m^{\prime}}t^2 \eta+|t|^{\beta}.
\end{equation*} By changing the variables and taking ![]() $ b=2^{-m^{\prime}-j}$, it is sufficient to prove that
$ b=2^{-m^{\prime}-j}$, it is sufficient to prove that
 \begin{equation*}
\left\| \int_{{\mathbb R}} \widehat{f}(u) \widehat{g}(v-bu) \,{\rm e}^{i2^{-\beta j}\phi_{u, v-bu}(t_0)}\,{\rm d}v\right\|_{L^2_{v}}^2 \lesssim 2^{-\epsilon
j}\|f\|_2^2\|g\|_2^2.
\end{equation*}
\begin{equation*}
\left\| \int_{{\mathbb R}} \widehat{f}(u) \widehat{g}(v-bu) \,{\rm e}^{i2^{-\beta j}\phi_{u, v-bu}(t_0)}\,{\rm d}v\right\|_{L^2_{v}}^2 \lesssim 2^{-\epsilon
j}\|f\|_2^2\|g\|_2^2.
\end{equation*}We expand the left hand side and change the variables to obtain
 \begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \left.\widehat{f}(u)\overline{\widehat{f}(u+\tau)} \widehat{g}(v)\overline{\widehat{g}(v-b\tau)} {\rm e}^{i2^{-\beta j}(\phi_{u,v
}(t_0)-\phi_{u+\tau, v-b\tau}(t_0))}\,{\rm d}u\,{\rm d}v\right] {\rm d}\tau.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\int\left[\iint_{{\mathbb R}^2} \right.& \left.\widehat{f}(u)\overline{\widehat{f}(u+\tau)} \widehat{g}(v)\overline{\widehat{g}(v-b\tau)} {\rm e}^{i2^{-\beta j}(\phi_{u,v
}(t_0)-\phi_{u+\tau, v-b\tau}(t_0))}\,{\rm d}u\,{\rm d}v\right] {\rm d}\tau.
\end{split}
\end{equation}Let us denote
and
 \begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}
\begin{equation*}
\widetilde{Q_{\tau}}(u, v):=Q(u, v)-Q(u, v+\tau).
\end{equation*}Lemma 13.2. With these notation, we have
 \begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim2^{2m^{\prime}}\tau
\end{equation}
\begin{equation}
\left|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right|\gtrsim2^{2m^{\prime}}\tau
\end{equation}and
 \begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}
\begin{equation}
\left\|\frac{\partial^2 \widetilde{Q_{\tau}}}{\partial u \partial v} \right\|_{C^2}\lesssim
\tau.
\end{equation}Proof of Lemma 13.2
By a direct calculation, we have
 \begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m^{\prime}+1}t_0}{\phi^{\prime\prime}_{u,v}(t_0)}.
\end{equation*}
\begin{equation*}
\frac{\partial^2 Q}{\partial u \partial v}(u, v)=-\frac{2^{m^{\prime}+1}t_0}{\phi^{\prime\prime}_{u,v}(t_0)}.
\end{equation*}Hence,
 \begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial u}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}
\right)}{(\phi^{\prime\prime}_{u,v}(t_0))^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial^2 u \partial v}(u, v)=-2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial u}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}
\right)}{(\phi^{\prime\prime}_{u,v}(t_0))^2}.
\end{equation*}The relation between v and t 0 is given by
 \begin{equation*}
u+2^{m^{\prime}+1}t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}
\begin{equation*}
u+2^{m^{\prime}+1}t_0v+\beta t_0^{\beta-1}=0.
\end{equation*}A simple calculation shows that
 \begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial
v}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2^{m^{\prime}+1}t_0}{\left(2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}\right)^2}.
\end{equation*}
\begin{equation*}
\frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)= -2^{m^{\prime}+1} \frac{\frac{\partial t_0}{\partial
v}\left(2^{m^{\prime}+1}v+\beta(\beta-1)(3-\beta)t_0^{\beta-2}\right)-2^{m^{\prime}+1}t_0}{\left(2^{m^{\prime}+1}v+\beta(\beta-1)t_0^{\beta-2}\right)^2}.
\end{equation*}By an implicit function calculation, we obtain
 \begin{equation*}
\left| \frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)\right|\approx \left|2^{m^{\prime}+1} v+\beta(\beta-1)(4-\beta)t_0^{\beta-2}
\right|\approx2^{2m^{\prime}}.
\end{equation*}
\begin{equation*}
\left| \frac{\partial^3 Q}{\partial u \partial^2 v}(u, v)\right|\approx \left|2^{m^{\prime}+1} v+\beta(\beta-1)(4-\beta)t_0^{\beta-2}
\right|\approx2^{2m^{\prime}}.
\end{equation*}Equation (13.7) can be proved as before. Equation (13.8) will also be proved in the same way.
We then write
 \begin{equation*}
(13.6)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0}.
\end{equation*}
\begin{equation*}
(13.6)=\int_{|\tau|\le \tau_0}+\int_{|\tau|\ge \tau_0}.
\end{equation*}The former term can be bounded by
 \begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} \widehat{f}(u)\widehat{f}(u +\tau) \widehat{g}(v)\widehat{g}(v-b\tau) {\rm e}^{i2^{-\beta
j}\widetilde{Q_{\tau}}(u, v)}{\rm d}u {\rm d}v\right|\\
& \le |\tau_0| \iint_{{\mathbb R}^2}\left|\widehat{f}(u)\overline{\widehat{f}(u+\tau)} \widehat{g}(v)\overline{\widehat{g}(v-b\tau)}\right|{\rm d}u\,{\rm d}v \le |\tau_0|
\|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& |\tau_0| \sup_{\tau} \left|\iint_{{\mathbb R}^2} \widehat{f}(u)\widehat{f}(u +\tau) \widehat{g}(v)\widehat{g}(v-b\tau) {\rm e}^{i2^{-\beta
j}\widetilde{Q_{\tau}}(u, v)}{\rm d}u {\rm d}v\right|\\
& \le |\tau_0| \iint_{{\mathbb R}^2}\left|\widehat{f}(u)\overline{\widehat{f}(u+\tau)} \widehat{g}(v)\overline{\widehat{g}(v-b\tau)}\right|{\rm d}u\,{\rm d}v \le |\tau_0|
\|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}For the latter term is bounded by
 \begin{equation*}
\begin{split}
& 2^{\frac{\beta j}{2}}\left(2^{2m^{\prime}}\tau_0\right)^{-\frac{1}{2}}\int \left[\int_{{\mathbb R}}|\widehat{f}(u)\overline{\widehat{f}(u+\tau)}|^2{\rm d}u\right]^{1/2}
\left[ \int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(v-b\tau)}\right|{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{\frac{\beta j}{2}}(2^{2m^{\prime}}\tau_0)^{-\frac{1}{2}}2^{\frac{-m^{\prime}- j}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*}
\begin{equation*}
\begin{split}
& 2^{\frac{\beta j}{2}}\left(2^{2m^{\prime}}\tau_0\right)^{-\frac{1}{2}}\int \left[\int_{{\mathbb R}}|\widehat{f}(u)\overline{\widehat{f}(u+\tau)}|^2{\rm d}u\right]^{1/2}
\left[ \int_{{\mathbb R}} \left|\widehat{g}(v)\overline{\widehat{g}(v-b\tau)}\right|{\rm d}v \right]^{1/2} {\rm d}\tau\\
& \le 2^{\frac{\beta j}{2}}(2^{2m^{\prime}}\tau_0)^{-\frac{1}{2}}2^{\frac{-m^{\prime}- j}{2}} \|f\|_2^2 \|g\|_2^2.
\end{split}
\end{equation*} We can finish the proof by setting  $\tau_0=2^\frac{\beta j-3m^{\prime}-j}{3}$.
$\tau_0=2^\frac{\beta j-3m^{\prime}-j}{3}$.
Acknowledgments
The authors thank Shaoming Guo for valuable and encouraging discussions about this paper.
Funding statement
Junfeng Li is supported by NSFC (grant number 12071052) and the Fundamental Research Funds for the Central Universities. Guoliang Li is supported by Nature Science Fundation of China (NSFC) (grant number 12271232).