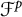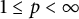1 Introduction
Let
![]() $\beta $
be a positive real number. The Gaussian measure on the complex plane
$\beta $
be a positive real number. The Gaussian measure on the complex plane
![]() $\mathbb {C}$
is defined as
$\mathbb {C}$
is defined as
where
![]() $dA$
is the Euclidean area measure. The Fock space
$dA$
is the Euclidean area measure. The Fock space
![]() $\mathcal {F}_{}^p:=\mathcal {F}_{\pi }^p$
, where
$\mathcal {F}_{}^p:=\mathcal {F}_{\pi }^p$
, where
![]() $1\leq p<\infty $
, is the collection of entire functions
$1\leq p<\infty $
, is the collection of entire functions
![]() $f : \mathbb {C} \rightarrow \mathbb {C}$
such that
$f : \mathbb {C} \rightarrow \mathbb {C}$
such that
 $$\begin{align*}\|f\|_{p}:= \left( \int_{\mathbb{C}}\left|f(z)\right|{}^p d\mu_{p\pi}(z)\right)^{\frac{1}{p}}<\infty. \end{align*}$$
$$\begin{align*}\|f\|_{p}:= \left( \int_{\mathbb{C}}\left|f(z)\right|{}^p d\mu_{p\pi}(z)\right)^{\frac{1}{p}}<\infty. \end{align*}$$
The space
![]() $\mathcal {F}^p$
endowed with the norm
$\mathcal {F}^p$
endowed with the norm
![]() $\|.\|_{p}$
is a vector Banach space, for every
$\|.\|_{p}$
is a vector Banach space, for every
![]() $p\geq 1$
. For the particular case when
$p\geq 1$
. For the particular case when
![]() $p=2$
,
$p=2$
,
![]() $\mathcal {F}_{}^2$
is a reproducing kernel Hilbert space with the reproducing kernel given by
$\mathcal {F}_{}^2$
is a reproducing kernel Hilbert space with the reproducing kernel given by
For instance, see the textbook [Reference Zhu19, Chapitre 2] and the references therein.
A countable set
![]() $Z=\{z_{n}\}_{n\in \mathbb {N}}\subseteq \mathbb {C}$
is called a zero set for
$Z=\{z_{n}\}_{n\in \mathbb {N}}\subseteq \mathbb {C}$
is called a zero set for
![]() $\mathcal {F}_{}^p$
if there exists a function
$\mathcal {F}_{}^p$
if there exists a function
![]() $f\in \mathcal {F}_{}^p \backslash \{0\}$
such that the zero set
$f\in \mathcal {F}_{}^p \backslash \{0\}$
such that the zero set
![]() $\{z\in \mathbb {C}\ :\ f(z)=0\}$
of
$\{z\in \mathbb {C}\ :\ f(z)=0\}$
of
![]() $f,$
counting multiplicities, coincides with Z. We say that Z is a uniqueness set for
$f,$
counting multiplicities, coincides with Z. We say that Z is a uniqueness set for
![]() $\mathcal {F}_{}^p$
if the unique function of
$\mathcal {F}_{}^p$
if the unique function of
![]() $\mathcal {F}^p$
that vanishes on Z is the zero function. It is known that a complete characterization, of zero and uniqueness sets for the Fock spaces, still remains an open question, and we refer to [Reference Aadi, Bouya and Omari1, Reference Mishko and Wick13, Reference Zhu18, Reference Zhu19].
$\mathcal {F}^p$
that vanishes on Z is the zero function. It is known that a complete characterization, of zero and uniqueness sets for the Fock spaces, still remains an open question, and we refer to [Reference Aadi, Bouya and Omari1, Reference Mishko and Wick13, Reference Zhu18, Reference Zhu19].
Due to the distinctiveness of Fock spaces among other spaces of analytic functions, there exist particular sets, uniqueness set with zero excess. These are those uniqueness sets that they become zero sets by removing just one point. Numerous examples of uniqueness sets with zero excess are known for
![]() $\mathcal {F}^p$
. The first typical example is the square lattice for
$\mathcal {F}^p$
. The first typical example is the square lattice for
![]() $\mathcal {F}^{p}$
, when
$\mathcal {F}^{p}$
, when
![]() $2<p<\infty $
, and the square lattice without one point for every
$2<p<\infty $
, and the square lattice without one point for every
![]() $1<p\leq 2$
. More generally, for every
$1<p\leq 2$
. More generally, for every
![]() $0\leq \nu \leq 1$
, the sequence
$0\leq \nu \leq 1$
, the sequence
![]() $\Gamma _\nu $
is a uniqueness set with zero excess for
$\Gamma _\nu $
is a uniqueness set with zero excess for
![]() $\mathcal {F}^p$
, for every
$\mathcal {F}^p$
, for every
![]() $\frac {2}{1+\nu }< p < \frac {2}{\nu }$
, where
$\frac {2}{1+\nu }< p < \frac {2}{\nu }$
, where
and where
![]() $\mathcal {I}_\nu :=\left (\mathbb {Z}\times (\mathbb {Z} \backslash \{0\})\right )\cup \left (\mathbb {Z}_{-}\times \{0\}\right )\cup \{(m+\nu ,0)\}_{m\geq 0}$
(see [Reference Lyubarskii11, Reference Zhu18]). It is simple to see that
$\mathcal {I}_\nu :=\left (\mathbb {Z}\times (\mathbb {Z} \backslash \{0\})\right )\cup \left (\mathbb {Z}_{-}\times \{0\}\right )\cup \{(m+\nu ,0)\}_{m\geq 0}$
(see [Reference Lyubarskii11, Reference Zhu18]). It is simple to see that
![]() $\Gamma _\nu $
is a separated sequence in the complex plan and of critical density for
$\Gamma _\nu $
is a separated sequence in the complex plan and of critical density for
![]() $\mathcal {F}_{}^p$
in the study of interpolating and sampling problems (see, for example, [Reference Seip16, Reference Zhu18, Reference Zhu19]). Motivated by the results in [Reference Horowitz8, Reference Omari14, Reference Zhu18], we are interested in the study of a stability problem of sequences
$\mathcal {F}_{}^p$
in the study of interpolating and sampling problems (see, for example, [Reference Seip16, Reference Zhu18, Reference Zhu19]). Motivated by the results in [Reference Horowitz8, Reference Omari14, Reference Zhu18], we are interested in the study of a stability problem of sequences
![]() $\Gamma _\nu $
, for every
$\Gamma _\nu $
, for every
![]() $0\leq \nu \leq 1$
.
$0\leq \nu \leq 1$
.
The second kind of uniqueness sets with zero excess for
![]() $\mathcal {F}_{}^p$
is an example of a nonseparated sequence localized at the real and imaginary lines. It constitutes the zero set of the sin-cardinal type function
$\mathcal {F}_{}^p$
is an example of a nonseparated sequence localized at the real and imaginary lines. It constitutes the zero set of the sin-cardinal type function
 $$ \begin{align} S(z):=(z^2-1)\frac{\sin\big(\frac{\pi}{2}z^2 \big)}{\pi z^2},\quad z\in\mathbb{C}, \end{align} $$
$$ \begin{align} S(z):=(z^2-1)\frac{\sin\big(\frac{\pi}{2}z^2 \big)}{\pi z^2},\quad z\in\mathbb{C}, \end{align} $$
and it is given by
This sequence was constructed by Ascensi, Lyubarski, and Seip in [Reference Ascensi, Lyubarskii and Seip2] for the Hilbert case. It is still of the same kind for
![]() $\mathcal {F}_{}^p$
, for every
$\mathcal {F}_{}^p$
, for every
![]() $1<p<\infty $
.
$1<p<\infty $
.
As in the work of the second author in [Reference Omari14], we are interested in the study of a stability problem of the sequences
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma _\nu $
, for every
$\Gamma _\nu $
, for every
![]() $0\leq \nu \leq 1$
, for the spaces
$0\leq \nu \leq 1$
, for the spaces
![]() $\mathcal {F}^p$
, and for a fixed
$\mathcal {F}^p$
, and for a fixed
![]() $1<p<\infty $
. Namely, if
$1<p<\infty $
. Namely, if
![]() $\Lambda =\{\lambda _\sigma \ :\ \sigma \in \Sigma \}$
is a sequence of complex numbers, where
$\Lambda =\{\lambda _\sigma \ :\ \sigma \in \Sigma \}$
is a sequence of complex numbers, where
![]() $\Sigma =\Gamma $
or
$\Sigma =\Gamma $
or
![]() $\Gamma _\nu $
, we write
$\Gamma _\nu $
, we write
![]() $\lambda _\sigma =\sigma e^{\delta _\sigma }e^{i\theta _\sigma }$
, where
$\lambda _\sigma =\sigma e^{\delta _\sigma }e^{i\theta _\sigma }$
, where
![]() $\delta _\sigma , \theta _\sigma \in \mathbb {R}$
for every
$\delta _\sigma , \theta _\sigma \in \mathbb {R}$
for every
![]() $\sigma \in \Sigma $
. We are interesting in giving optimal conditions on
$\sigma \in \Sigma $
. We are interesting in giving optimal conditions on
![]() $(\delta _\sigma )$
and
$(\delta _\sigma )$
and
![]() $(\theta _\sigma )$
for which
$(\theta _\sigma )$
for which
![]() $\Lambda $
fails to be a uniqueness set with zero excess for
$\Lambda $
fails to be a uniqueness set with zero excess for
![]() $\mathcal {F}^p$
, for a fixed
$\mathcal {F}^p$
, for a fixed
![]() $1<p<\infty $
. Before stating our main results, we need some notations. For
$1<p<\infty $
. Before stating our main results, we need some notations. For
![]() $\Lambda :=\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\ :\ \gamma \in \Gamma _\nu \}$
, we denote
$\Lambda :=\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\ :\ \gamma \in \Gamma _\nu \}$
, we denote
 $$ \begin{align*}\hat{\delta}(\Lambda):=\liminf_{R\rightarrow \infty} \frac{1}{\log R} \sum_{|\gamma|\leq R}\delta_\gamma\ \ \mbox{and}\ \ \delta(\Lambda):=\limsup_{R\rightarrow \infty} \frac{1}{\log R} \sum_{|\gamma|\leq R}\delta_\gamma.\end{align*} $$
$$ \begin{align*}\hat{\delta}(\Lambda):=\liminf_{R\rightarrow \infty} \frac{1}{\log R} \sum_{|\gamma|\leq R}\delta_\gamma\ \ \mbox{and}\ \ \delta(\Lambda):=\limsup_{R\rightarrow \infty} \frac{1}{\log R} \sum_{|\gamma|\leq R}\delta_\gamma.\end{align*} $$
Our first main result in this paper is the following theorem.
Theorem 1.1 Let
![]() $0\leq \nu \leq 1$
, and let
$0\leq \nu \leq 1$
, and let
![]() $\Lambda =\{\lambda _\gamma \}_{\gamma \in \Gamma _\nu }$
be a sequence of complex numbers. We write
$\Lambda =\{\lambda _\gamma \}_{\gamma \in \Gamma _\nu }$
be a sequence of complex numbers. We write
![]() $\lambda _\gamma = \gamma e^{\delta _\gamma }e^{i\theta _\gamma }$
, for every
$\lambda _\gamma = \gamma e^{\delta _\gamma }e^{i\theta _\gamma }$
, for every
![]() $\gamma \in \Gamma _\nu $
, where
$\gamma \in \Gamma _\nu $
, where
![]() $\delta _\gamma ,\theta _\gamma \in \mathbb {R}$
. If
$\delta _\gamma ,\theta _\gamma \in \mathbb {R}$
. If
-
(1)
 $\Lambda $
is separated,
$\Lambda $
is separated, -
(2) the sequences
 $(\gamma ^2\delta _\gamma )_{\gamma \in \Gamma _\nu }$
and
$(\gamma ^2\delta _\gamma )_{\gamma \in \Gamma _\nu }$
and
 $(\gamma ^2\theta _\gamma )_{\gamma \in \Gamma _\nu }$
are bounded, and
$(\gamma ^2\theta _\gamma )_{\gamma \in \Gamma _\nu }$
are bounded, and -
(3)
 $$ \begin{align*}\nu-\frac{2}{p}<\hat{\delta}(\Lambda) \leq \delta(\Lambda) < \nu+1-\frac{2}{p},\end{align*} $$
$$ \begin{align*}\nu-\frac{2}{p}<\hat{\delta}(\Lambda) \leq \delta(\Lambda) < \nu+1-\frac{2}{p},\end{align*} $$
then
![]() $\Lambda $
is a uniqueness set with zero excess for
$\Lambda $
is a uniqueness set with zero excess for
![]() $\mathcal {F}^p$
, whenever
$\mathcal {F}^p$
, whenever
![]() $\frac {2}{1+\nu }<p < \frac {2}{\nu }$
.
$\frac {2}{1+\nu }<p < \frac {2}{\nu }$
.
Now, for the Ascensi–Lyubarskii–Seip sequence
![]() $\Gamma $
, if
$\Gamma $
, if
![]() $\Lambda :=\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\ :\ \gamma \in \Gamma \}$
is a sequence of
$\Lambda :=\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\ :\ \gamma \in \Gamma \}$
is a sequence of
![]() $\mathbb {C}$
, we will denote by
$\mathbb {C}$
, we will denote by
![]() $\Delta _n$
the quantity
$\Delta _n$
the quantity
Our second main result is the following.
Theorem 1.2 Let
![]() $\Gamma :=\left \{\pm \sqrt {2n},\ \pm i\sqrt {2n} \ :\ n\geq 1\right \}\cup \{\pm 1\}$
, and let
$\Gamma :=\left \{\pm \sqrt {2n},\ \pm i\sqrt {2n} \ :\ n\geq 1\right \}\cup \{\pm 1\}$
, and let
![]() $\Lambda =\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\kern1pt{:} \gamma \in \Gamma \}$
be a sequence of complex numbers. Suppose that:
$\Lambda =\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\kern1pt{:} \gamma \in \Gamma \}$
be a sequence of complex numbers. Suppose that:
-
(1) There exists
 $c>0$
such that
$c>0$
such that
 $\left |\lambda _\gamma - \lambda _{\gamma '}\right | \geq c/\min \{|\gamma |,|\gamma '|\}$
, for every
$\left |\lambda _\gamma - \lambda _{\gamma '}\right | \geq c/\min \{|\gamma |,|\gamma '|\}$
, for every
 $\gamma , \gamma ' \in \Gamma $
.
$\gamma , \gamma ' \in \Gamma $
. -
(2) The sequences
 $(\gamma ^2\delta _\gamma )_{\gamma \in \Gamma }$
and
$(\gamma ^2\delta _\gamma )_{\gamma \in \Gamma }$
and
 $(\gamma ^2\theta _\gamma )_{\gamma \in \Gamma }$
are bounded.
$(\gamma ^2\theta _\gamma )_{\gamma \in \Gamma }$
are bounded. -
(3)
 $\Delta (\Lambda ) := \underset {n\rightarrow \infty }{\limsup }\ \frac {1}{\log n} \left |\underset {k=1}{\overset {n}{\sum }} \Delta _k\right |< \frac {1}{2\max \{p,q\}}$
, where q is the Hölder conjugate number of p.
$\Delta (\Lambda ) := \underset {n\rightarrow \infty }{\limsup }\ \frac {1}{\log n} \left |\underset {k=1}{\overset {n}{\sum }} \Delta _k\right |< \frac {1}{2\max \{p,q\}}$
, where q is the Hölder conjugate number of p.
Then,
![]() $\Lambda $
is a uniqueness set with a zero excess for
$\Lambda $
is a uniqueness set with a zero excess for
![]() $\mathcal {F}^p$
, where
$\mathcal {F}^p$
, where
![]() $1<p<\infty $
.
$1<p<\infty $
.
Another extreme case of sequences, we are interesting in, is motivated by the zero set of the sin-cardinal type function
 $$\begin{align*}s(z)=\frac{\sin\big(\frac{\pi}{2} z^2\big)}{z^2} \in\mathcal{F}^{p}.\end{align*}$$
$$\begin{align*}s(z)=\frac{\sin\big(\frac{\pi}{2} z^2\big)}{z^2} \in\mathcal{F}^{p}.\end{align*}$$
The zero set of s, denoted by
![]() $Z(s)$
, is a zero sequence for
$Z(s)$
, is a zero sequence for
![]() $\mathcal {F}^p$
, for every
$\mathcal {F}^p$
, for every
![]() $1\leq p<\infty $
. However, if we remove the subset which belongs to the imaginary axis from
$1\leq p<\infty $
. However, if we remove the subset which belongs to the imaginary axis from
![]() $Z(s)$
, the remaining part is not a zero set anymore for
$Z(s)$
, the remaining part is not a zero set anymore for
![]() $\mathcal {F}^{p}$
. Such result can be viewed as a consequence of Lindelöf’s theorem (see [Reference Boas5, Theorem 2.10.1]). Therefore, a natural question is: which zero set for
$\mathcal {F}^{p}$
. Such result can be viewed as a consequence of Lindelöf’s theorem (see [Reference Boas5, Theorem 2.10.1]). Therefore, a natural question is: which zero set for
![]() $\mathcal {F}^{p}$
remains a zero set too for
$\mathcal {F}^{p}$
remains a zero set too for
![]() $\mathcal {F}^{p}$
, even an infinite subset was removed?
$\mathcal {F}^{p}$
, even an infinite subset was removed?
Actually, the example above is a variant to the one given by Zhu in [Reference Zhu17]. This phenomenon is one of the main deference between Fock spaces and Hardy spaces and even Bergman spaces of the unit disk where zero sets are well stable [Reference Duren6, Reference Hedenmalm, Korenblum and Zhu7].
In the following theorem, we give a complete description of zero sets for which all their subsequences are also zero sets for
![]() $\mathcal {F}^p.$
$\mathcal {F}^p.$
Theorem 1.3 Let
![]() $Z =\{z_n\}_{n\in \mathbb {N}}$
be a zero set for
$Z =\{z_n\}_{n\in \mathbb {N}}$
be a zero set for
![]() $\mathcal {F}^p$
,
$\mathcal {F}^p$
,
![]() $1\leq p<\infty $
. The following statements are equivalents:
$1\leq p<\infty $
. The following statements are equivalents:
-
(1) Every subset of Z is a zero set for
 $\mathcal {F}^p$
.
$\mathcal {F}^p$
. -
(2) Z satisfies
(5) $$ \begin{align} \underset{n\in\mathbb{N}}{\sum}\frac{1}{|z_n|^2} < \infty. \end{align} $$
$$ \begin{align} \underset{n\in\mathbb{N}}{\sum}\frac{1}{|z_n|^2} < \infty. \end{align} $$
Before stating the proofs of our main results, we give first some remarks:
-
(1) In Theorem 1.1, if
 $\nu =1$
, we then get
$\nu =1$
, we then get
 $1<p<2$
. Actually, the result remains valid for
$1<p<2$
. Actually, the result remains valid for
 $p=2$
, and this case was treated in [Reference Omari14]. Theorem 1.1 gives a result analogous to those related to complete interpolating sequences for the Paley–Wiener spaces (see [Reference Avdonin3, Reference Lyubarskii and Seip12]), and small Fock spaces [Reference Baranov, Dumont, Hartmann and Kellay4, Reference Omari15].
$p=2$
, and this case was treated in [Reference Omari14]. Theorem 1.1 gives a result analogous to those related to complete interpolating sequences for the Paley–Wiener spaces (see [Reference Avdonin3, Reference Lyubarskii and Seip12]), and small Fock spaces [Reference Baranov, Dumont, Hartmann and Kellay4, Reference Omari15]. -
(2) Note that if there exists a positive integer N such that
(6)then $$ \begin{align} \underset{n\geq 0}{\sup}\ \frac{n+1}{N}\left|\underset{k=n+1}{\overset{n+N}{\sum}}\Delta_k\right|<\frac{1}{2\max\{p,q\}}, \end{align} $$
$$ \begin{align} \underset{n\geq 0}{\sup}\ \frac{n+1}{N}\left|\underset{k=n+1}{\overset{n+N}{\sum}}\Delta_k\right|<\frac{1}{2\max\{p,q\}}, \end{align} $$
 $\underset {N\rightarrow \infty }{\limsup } \frac {1}{\log N}\left |\underset {k=0}{\overset {N}{\sum }}\Delta _k\right |<\frac {1}{2\max \{p,q\}}$
and the converse is not true (see [Reference Omari14, Lemma 5.4]). On the other hand, in Theorem 1.2, for
$\underset {N\rightarrow \infty }{\limsup } \frac {1}{\log N}\left |\underset {k=0}{\overset {N}{\sum }}\Delta _k\right |<\frac {1}{2\max \{p,q\}}$
and the converse is not true (see [Reference Omari14, Lemma 5.4]). On the other hand, in Theorem 1.2, for
 $p=2$
, we have
$p=2$
, we have
 $q=2$
. This case was treated in [Reference Omari14]. Theorem 1.2 with the Avdonin-type condition (6) appears like the result proved by Lyubarskii and Seip in [Reference Lyubarskii and Seip12] concerning complete interpolating sequences for Paley–Wiener spaces. Such result generalizes those by Kadets and Avdonin for the Hilbert case (see [Reference Avdonin3, Reference Kadets9]).
$q=2$
. This case was treated in [Reference Omari14]. Theorem 1.2 with the Avdonin-type condition (6) appears like the result proved by Lyubarskii and Seip in [Reference Lyubarskii and Seip12] concerning complete interpolating sequences for Paley–Wiener spaces. Such result generalizes those by Kadets and Avdonin for the Hilbert case (see [Reference Avdonin3, Reference Kadets9]).
-
(3) The conditions on the sequences
 $(\delta _\gamma )$
and
$(\delta _\gamma )$
and
 $(\theta _\gamma )$
in Theorem 1.1 are optimal. The proof is similar to Theorem 1.5 and Proposition 5.3 in [Reference Omari14].
$(\theta _\gamma )$
in Theorem 1.1 are optimal. The proof is similar to Theorem 1.5 and Proposition 5.3 in [Reference Omari14]. -
(4) An interesting fact appears in the proof of Theorem 1.2 (namely Lemma 2.2) is a confirmation of the result which confirms that
 $\mathcal {F}^{p}$
and
$\mathcal {F}^{p}$
and
 $\mathcal {F}^{q}$
,
$\mathcal {F}^{q}$
,
 $p>q$
, do not share the same zero sets, a result that we have already got in [Reference Aadi, Bouya and Omari1]. We provided a sequence with positive Beurling uniform density, while the example that we can construct here, by a precise choice of
$p>q$
, do not share the same zero sets, a result that we have already got in [Reference Aadi, Bouya and Omari1]. We provided a sequence with positive Beurling uniform density, while the example that we can construct here, by a precise choice of
 $\delta $
, is of null lower Beurling density.
$\delta $
, is of null lower Beurling density.
We end this section with some words on notation: throughout this paper, the notation
![]() $A\lesssim B$
means that
$A\lesssim B$
means that
![]() $A\leq cB$
for a certain positive constant c, and the notation
$A\leq cB$
for a certain positive constant c, and the notation
![]() $A\asymp B$
will be used to say that
$A\asymp B$
will be used to say that
![]() $A\lesssim B$
and
$A\lesssim B$
and
![]() $B\lesssim A$
hold in the same time. The paper is organized as follows: in the next section, we state some key lemmas containing estimates of some modified infinite products. Section 3 is devoted to prove Theorems 1.1 and 1.2. Theorem 1.3 will be proved in the last section.
$B\lesssim A$
hold in the same time. The paper is organized as follows: in the next section, we state some key lemmas containing estimates of some modified infinite products. Section 3 is devoted to prove Theorems 1.1 and 1.2. Theorem 1.3 will be proved in the last section.
2 Some lemmas
In this section, we introduce some modified Weierstrass products. These functions will play an important role in the proof of our main results. First, we recall that for every
![]() $0\leq \nu \leq 1$
, the sequence
$0\leq \nu \leq 1$
, the sequence
![]() $\Gamma _\nu =\{\gamma _{m,n}\ :\ m,n\in \mathbb {Z}\}$
is given by
$\Gamma _\nu =\{\gamma _{m,n}\ :\ m,n\in \mathbb {Z}\}$
is given by
If
![]() $\Lambda =\{\lambda _{m,n}\ :\ m,n\in \mathbb {Z}\}$
is a sequence of complex numbers, we will write
$\Lambda =\{\lambda _{m,n}\ :\ m,n\in \mathbb {Z}\}$
is a sequence of complex numbers, we will write
![]() $\lambda _{m,n}:=\gamma _{m,n} e^{\delta _{m,n}}e^{i\theta _{m,n}}$
, where
$\lambda _{m,n}:=\gamma _{m,n} e^{\delta _{m,n}}e^{i\theta _{m,n}}$
, where
![]() $\delta _{m,n}, \theta _{m,n} \in \mathbb {R}$
, for every
$\delta _{m,n}, \theta _{m,n} \in \mathbb {R}$
, for every
![]() $m,n\in \mathbb {Z}$
. We associate with
$m,n\in \mathbb {Z}$
. We associate with
![]() $\Lambda $
the following infinite product
$\Lambda $
the following infinite product
 $$ \begin{align*}G_{\Lambda}(z) := (z-\lambda_{0,0})\prod_{m,n\in\mathbb{Z}}\ ^{\prime} \left(1-\frac{z}{\lambda_{m,n}}\right)\exp\left[\frac{z}{\gamma_{m,n}}+\frac{z^2}{2\gamma_{m,n}^2}\right],\quad z\in\mathbb{C}.\end{align*} $$
$$ \begin{align*}G_{\Lambda}(z) := (z-\lambda_{0,0})\prod_{m,n\in\mathbb{Z}}\ ^{\prime} \left(1-\frac{z}{\lambda_{m,n}}\right)\exp\left[\frac{z}{\gamma_{m,n}}+\frac{z^2}{2\gamma_{m,n}^2}\right],\quad z\in\mathbb{C}.\end{align*} $$
The product with the prime is taken over all integers m and n such that
![]() $(m, n) \neq (0, 0)$
. The following lemma provides an estimates of the function
$(m, n) \neq (0, 0)$
. The following lemma provides an estimates of the function
![]() $G_{\Lambda} $
.
$G_{\Lambda} $
.
Lemma 2.1 [Reference Omari14, Lemma 3.2]
If
![]() $\Lambda $
satisfies the conditions of Theorem 1.1,
$\Lambda $
satisfies the conditions of Theorem 1.1,
![]() $G_{\Lambda} $
is an entire function vanishing exactly on
$G_{\Lambda} $
is an entire function vanishing exactly on
![]() $\Lambda $
and verifying
$\Lambda $
and verifying
 $$ \begin{align*}\frac{(1+|\operatorname{Im}(z)|)^M}{(1+|z|)^{\nu-\hat{\delta}+M}} \operatorname{dist}(z,\Lambda) \lesssim |G_{\Lambda}(z)|e^{-\frac{\pi}{2}|z|^2} \lesssim \frac{(1+|z|)^{-\nu+\delta+M}}{(1+|\operatorname{Im}(z)|)^M} \operatorname{dist}(z,\Lambda), \ z\in\mathbb{C},\end{align*} $$
$$ \begin{align*}\frac{(1+|\operatorname{Im}(z)|)^M}{(1+|z|)^{\nu-\hat{\delta}+M}} \operatorname{dist}(z,\Lambda) \lesssim |G_{\Lambda}(z)|e^{-\frac{\pi}{2}|z|^2} \lesssim \frac{(1+|z|)^{-\nu+\delta+M}}{(1+|\operatorname{Im}(z)|)^M} \operatorname{dist}(z,\Lambda), \ z\in\mathbb{C},\end{align*} $$
for some positive constant M, where
![]() $\delta =\delta (\Lambda )+\varepsilon $
and
$\delta =\delta (\Lambda )+\varepsilon $
and
![]() $\hat {\delta }=\hat {\delta }(\Lambda )-\varepsilon $
for a positive
$\hat {\delta }=\hat {\delta }(\Lambda )-\varepsilon $
for a positive
![]() $\varepsilon $
small enough.
$\varepsilon $
small enough.
On the other hand, for the Ascensi–Lyubarskii–Seip sequence given in [Reference Ascensi, Lyubarskii and Seip2] by
we associate the modified sin-cardinal function
![]() $G_{\Gamma} (z):=\frac {z^2-1}{\pi z^2}\sin \left (\frac {\pi }{2}z^2\right )$
. Now, if
$G_{\Gamma} (z):=\frac {z^2-1}{\pi z^2}\sin \left (\frac {\pi }{2}z^2\right )$
. Now, if
![]() $\Lambda =\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\ :\ \gamma \in \Gamma \}$
is a sequence of complex numbers, we associate with
$\Lambda =\{\lambda _\gamma :=\gamma e^{\delta _\gamma }e^{i\theta _\gamma }\ :\ \gamma \in \Gamma \}$
is a sequence of complex numbers, we associate with
![]() $\Lambda $
the infinite product
$\Lambda $
the infinite product
 $$ \begin{align*}G_{\Lambda}(z):=\lim_{r\rightarrow\infty}\prod_{\lambda\in\lambda,\ |\lambda|\leq r} \left(1-\frac{z}{\lambda}\right),\quad z\in\mathbb{C}.\end{align*} $$
$$ \begin{align*}G_{\Lambda}(z):=\lim_{r\rightarrow\infty}\prod_{\lambda\in\lambda,\ |\lambda|\leq r} \left(1-\frac{z}{\lambda}\right),\quad z\in\mathbb{C}.\end{align*} $$
According to the proof of [Reference Omari14, Theorem 1.10], we have the following lemma that gives an estimate of the function
![]() $G_{\Lambda} $
.
$G_{\Lambda} $
.
Lemma 2.2 If
![]() $\Lambda $
satisfies the conditions of Theorem 1.2, the infinite product
$\Lambda $
satisfies the conditions of Theorem 1.2, the infinite product
![]() $G_{\Lambda} $
converges uniformly on every compact set of
$G_{\Lambda} $
converges uniformly on every compact set of
![]() $\mathbb {C}$
and verifies
$\mathbb {C}$
and verifies
 $$\begin{align*}\frac{\operatorname{dist}(z,\Lambda)}{\operatorname{dist}(z,\Gamma)}\frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}|G_{\Gamma}(z)|\lesssim |G_{\Lambda}(z)|, \end{align*}$$
$$\begin{align*}\frac{\operatorname{dist}(z,\Lambda)}{\operatorname{dist}(z,\Gamma)}\frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}|G_{\Gamma}(z)|\lesssim |G_{\Lambda}(z)|, \end{align*}$$
 $$\begin{align*}|G_{\Lambda}(z)| \lesssim \frac{\operatorname{dist}(z,\Lambda)}{\operatorname{dist}(z,\Gamma)}\frac{(1+|z|)^{2\delta+2M}}{(1+|\operatorname{Im} z^2|)^M}|G_{\Gamma}(z)|, \end{align*}$$
$$\begin{align*}|G_{\Lambda}(z)| \lesssim \frac{\operatorname{dist}(z,\Lambda)}{\operatorname{dist}(z,\Gamma)}\frac{(1+|z|)^{2\delta+2M}}{(1+|\operatorname{Im} z^2|)^M}|G_{\Gamma}(z)|, \end{align*}$$
for every
![]() $z\in \mathbb {C} \backslash \Gamma $
, where
$z\in \mathbb {C} \backslash \Gamma $
, where
![]() $\delta =\Delta (\Lambda )+\varepsilon $
for a small positive
$\delta =\Delta (\Lambda )+\varepsilon $
for a small positive
![]() $\varepsilon .$
$\varepsilon .$
3 Proofs of Theorems 1.1 and 1.2
This section is devoted to the proofs of Theorem 1.1 and 1.2.
3.1 Proof of Theorem 1.1
First, we show that
![]() $\Lambda \backslash \{\lambda \}$
is a zero set for
$\Lambda \backslash \{\lambda \}$
is a zero set for
![]() $\mathcal {F}^p$
, for some fixed (any)
$\mathcal {F}^p$
, for some fixed (any)
![]() $\lambda \in \Lambda $
. To this end, it suffices to prove that
$\lambda \in \Lambda $
. To this end, it suffices to prove that
![]() $\frac {G_{\Lambda} }{z-\lambda }$
belongs to
$\frac {G_{\Lambda} }{z-\lambda }$
belongs to
![]() $\mathcal {F}^p$
. Indeed, by Lemma 2.1, we have
$\mathcal {F}^p$
. Indeed, by Lemma 2.1, we have
 $$ \begin{align*} \int_{\mathbb{C}} \left|\frac{G_{\Lambda}(z)}{z-\lambda}e^{-\frac{\pi}{2}|z|^2}\right|^p dA(z) & \lesssim \int_{\mathbb{C}} \frac{(1+|z|)^{p(-1-\nu+\delta+M)}}{(1+|\operatorname{Im}(z)|)^{pM}} dA(z)\\ & \asymp \int_{\mathbb{C}} \frac{1}{(1+|z|)^{p(1+\nu-\delta)}}dA(z), \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}} \left|\frac{G_{\Lambda}(z)}{z-\lambda}e^{-\frac{\pi}{2}|z|^2}\right|^p dA(z) & \lesssim \int_{\mathbb{C}} \frac{(1+|z|)^{p(-1-\nu+\delta+M)}}{(1+|\operatorname{Im}(z)|)^{pM}} dA(z)\\ & \asymp \int_{\mathbb{C}} \frac{1}{(1+|z|)^{p(1+\nu-\delta)}}dA(z), \end{align*} $$
and the last integral converges if and only if
![]() $p(1+\nu -\delta )>2$
. In view of the third assumption, the integral converges. Hence,
$p(1+\nu -\delta )>2$
. In view of the third assumption, the integral converges. Hence,
![]() $\frac {G_{\Lambda} }{z-\lambda } \in \mathcal {F}^{p}$
(obviously,
$\frac {G_{\Lambda} }{z-\lambda } \in \mathcal {F}^{p}$
(obviously,
![]() $z\mapsto \frac {G_{\Lambda} (z)}{z-\lambda }$
is an entire function).
$z\mapsto \frac {G_{\Lambda} (z)}{z-\lambda }$
is an entire function).
Second, we prove that
![]() $\Lambda $
is a uniqueness set for
$\Lambda $
is a uniqueness set for
![]() $\mathcal {F}^p$
. Let F be a function of
$\mathcal {F}^p$
. Let F be a function of
![]() $\mathcal {F}^p$
that vanishes on
$\mathcal {F}^p$
that vanishes on
![]() $\Lambda $
. Then there exists an entire function h such that
$\Lambda $
. Then there exists an entire function h such that
![]() $F=hG_{\Lambda} $
. According to the estimates of
$F=hG_{\Lambda} $
. According to the estimates of
![]() $G_{\Lambda} $
in Lemma 2.1, we have
$G_{\Lambda} $
in Lemma 2.1, we have
 $$ \begin{align*} |h(z)|\frac{(1+|\operatorname{Im}(z)|)^M}{(1+|z|)^{\nu-\hat{\delta}+M}} \operatorname{dist}(z,\Lambda) & \lesssim \left|h(z)G_{\Lambda}(z)\right|e^{-\frac{\pi}{2}|z|^2} = |F(z)|e^{-\frac{\pi}{2}|z|^2} \lesssim 1. \end{align*} $$
$$ \begin{align*} |h(z)|\frac{(1+|\operatorname{Im}(z)|)^M}{(1+|z|)^{\nu-\hat{\delta}+M}} \operatorname{dist}(z,\Lambda) & \lesssim \left|h(z)G_{\Lambda}(z)\right|e^{-\frac{\pi}{2}|z|^2} = |F(z)|e^{-\frac{\pi}{2}|z|^2} \lesssim 1. \end{align*} $$
This implies that h is a polynomial of z, and we denote later by k its degree. Integrating the last inequality with respect to the measure
![]() $dA(z)$
, we get
$dA(z)$
, we get
 $$ \begin{align*} \int_{\mathbb{C}} \left|F(z)e^{-\frac{\pi}{2}|z|^2} \right|^p dA(z) & \gtrsim \int_{\mathbb{C}} |h(z)|^p\frac{(1+|\operatorname{Im}(z)|)^{pM}}{(1+|z|)^{p(\nu-\hat{\delta}+M)}} \operatorname{dist}(z,\Lambda)^pdA(z)\\ & \asymp \int_{\mathbb{C}} \frac{(1+|\operatorname{Im}(z)|)^{pM}}{(1+|z|)^{p(\nu-k-\hat{\delta}+M)}}dA(z) \\ & \asymp \int_{\mathbb{C}} \frac{1}{(1+|z|)^{p(\nu-k-\hat{\delta})}}dA(z). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}} \left|F(z)e^{-\frac{\pi}{2}|z|^2} \right|^p dA(z) & \gtrsim \int_{\mathbb{C}} |h(z)|^p\frac{(1+|\operatorname{Im}(z)|)^{pM}}{(1+|z|)^{p(\nu-\hat{\delta}+M)}} \operatorname{dist}(z,\Lambda)^pdA(z)\\ & \asymp \int_{\mathbb{C}} \frac{(1+|\operatorname{Im}(z)|)^{pM}}{(1+|z|)^{p(\nu-k-\hat{\delta}+M)}}dA(z) \\ & \asymp \int_{\mathbb{C}} \frac{1}{(1+|z|)^{p(\nu-k-\hat{\delta})}}dA(z). \end{align*} $$
The last integral converges if and only if
![]() $p(\nu -k-\hat {\delta })>2$
, and this implies that
$p(\nu -k-\hat {\delta })>2$
, and this implies that
![]() $k+\hat {\delta }<\nu -2/p$
. This is in contradiction with the assumption
$k+\hat {\delta }<\nu -2/p$
. This is in contradiction with the assumption
![]() $\nu -2/p < \hat {\delta }(\Lambda )$
. Thus, h is zero and F too. This completes the proof of Theorem 1.1.
$\nu -2/p < \hat {\delta }(\Lambda )$
. Thus, h is zero and F too. This completes the proof of Theorem 1.1.
3.2 Proof of Theorem 1.2.
First, we need the lemma below, which is analogous to Lemma 3.4 in [Reference Omari14], we include the proof for completeness. We denote
 $$\begin{align*}d\nu_{p,\alpha,\beta}(z)=\Big(\frac{1+|z|^2}{1+|\operatorname{Im} z^2|}\Big)^{\alpha p}\frac{1}{(1+|z|)^{p\beta}} e^{-\frac{p\pi}{2}|z|^2}dA(z),\end{align*}$$
$$\begin{align*}d\nu_{p,\alpha,\beta}(z)=\Big(\frac{1+|z|^2}{1+|\operatorname{Im} z^2|}\Big)^{\alpha p}\frac{1}{(1+|z|)^{p\beta}} e^{-\frac{p\pi}{2}|z|^2}dA(z),\end{align*}$$
where
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are two real numbers.
$\beta $
are two real numbers.
Lemma 3.1 Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two real numbers. The sin-cardinal type function
$\beta $
be two real numbers. The sin-cardinal type function
![]() $G_{\Gamma} $
belongs to
$G_{\Gamma} $
belongs to
![]() $L^p(\mathbb {C},d\nu _{p,\alpha ,\beta })$
if and only if
$L^p(\mathbb {C},d\nu _{p,\alpha ,\beta })$
if and only if
![]() $\beta>\frac {1}{p}$
.
$\beta>\frac {1}{p}$
.
Proof Let
![]() $1\leq p<\infty $
. Recall that
$1\leq p<\infty $
. Recall that
It follows that,
![]() $G_{\Gamma }$
belongs to
$G_{\Gamma }$
belongs to
![]() $L^{p}(\mathbb {C}, d\nu _{p,\alpha ,\beta })$
if and only if
$L^{p}(\mathbb {C}, d\nu _{p,\alpha ,\beta })$
if and only if
![]() $\sinh \left (\frac {\pi }{2}z^2\right )$
does. This is equivalent to
$\sinh \left (\frac {\pi }{2}z^2\right )$
does. This is equivalent to
 $$\begin{align*}\int_{\mathbb{C}} \left(\frac{e^{\frac{\pi}{2} |\operatorname{Im} z^2|} }{1+|z|^{\beta}}\right)^{p} \left(\frac{1+|z|^2}{1+|\operatorname{Im} z^2|}\right)^{p \alpha } e^{-\frac{p \pi}{2}|z|^{2}}dA(z)<\infty. \end{align*}$$
$$\begin{align*}\int_{\mathbb{C}} \left(\frac{e^{\frac{\pi}{2} |\operatorname{Im} z^2|} }{1+|z|^{\beta}}\right)^{p} \left(\frac{1+|z|^2}{1+|\operatorname{Im} z^2|}\right)^{p \alpha } e^{-\frac{p \pi}{2}|z|^{2}}dA(z)<\infty. \end{align*}$$
Using the Tonelli theorem, we obtain
 $$ \begin{align} I & := \int_{|z|>1} \frac{1}{(1+|z|)^{p\beta-2p\alpha}} \frac{1}{(1+|\operatorname{Im} z^2|)^{p\alpha}} e^{-\frac{p\pi}{2} (|z|^2-|\operatorname{Im} z^2|)}dA(z)\nonumber \\ &\asymp 8 \int_{1}^{\infty} \int_{0}^{x} \frac{e^{-\frac{p\pi}{2} (x-y)^{2} } } {(x^2+y^2)^{p(\beta-2\alpha)/2}} \frac{1}{(1+xy)^{p \alpha} } dy dx. \end{align} $$
$$ \begin{align} I & := \int_{|z|>1} \frac{1}{(1+|z|)^{p\beta-2p\alpha}} \frac{1}{(1+|\operatorname{Im} z^2|)^{p\alpha}} e^{-\frac{p\pi}{2} (|z|^2-|\operatorname{Im} z^2|)}dA(z)\nonumber \\ &\asymp 8 \int_{1}^{\infty} \int_{0}^{x} \frac{e^{-\frac{p\pi}{2} (x-y)^{2} } } {(x^2+y^2)^{p(\beta-2\alpha)/2}} \frac{1}{(1+xy)^{p \alpha} } dy dx. \end{align} $$
On the other hand, we have
 $$ \begin{align} \int_{0}^{x} \frac{e^{-\frac{p\pi}{2} (x-y)^{2} }} {(x^2+y^2)^{p(\beta-2\alpha)/2}} \frac{1}{(1+xy)^{p \alpha}} dy & \asymp \frac{1}{x^{p(\beta-2\alpha)}}\int_{0}^{\infty} \frac{e^{-\frac{p\pi}{2} y^{2} }}{ (1+x^2-xy)^{p \alpha}}\chi_{[0,x]}(y) dy. \end{align} $$
$$ \begin{align} \int_{0}^{x} \frac{e^{-\frac{p\pi}{2} (x-y)^{2} }} {(x^2+y^2)^{p(\beta-2\alpha)/2}} \frac{1}{(1+xy)^{p \alpha}} dy & \asymp \frac{1}{x^{p(\beta-2\alpha)}}\int_{0}^{\infty} \frac{e^{-\frac{p\pi}{2} y^{2} }}{ (1+x^2-xy)^{p \alpha}}\chi_{[0,x]}(y) dy. \end{align} $$
Combining (7) and (8), we obtain
 $$ \begin{align*} I & \asymp \int_1^\infty \int_0^\infty \frac{1}{x^{p(\beta-2\alpha)}} \frac{e^{-\frac{p\pi}{2} y^2}}{ (1+x^2-xy)^{p\alpha} }\chi_{[0,x]}(y) dx dy\\ & = \int_{0}^{\infty} e^{-\frac{p\pi}{2} y^{2} } \int_{\max\{1,y\}}^{\infty} \frac{1}{ x^{p(\beta-2\alpha)}(1+x^2-xy)^{p \alpha} } dxdy. \end{align*} $$
$$ \begin{align*} I & \asymp \int_1^\infty \int_0^\infty \frac{1}{x^{p(\beta-2\alpha)}} \frac{e^{-\frac{p\pi}{2} y^2}}{ (1+x^2-xy)^{p\alpha} }\chi_{[0,x]}(y) dx dy\\ & = \int_{0}^{\infty} e^{-\frac{p\pi}{2} y^{2} } \int_{\max\{1,y\}}^{\infty} \frac{1}{ x^{p(\beta-2\alpha)}(1+x^2-xy)^{p \alpha} } dxdy. \end{align*} $$
Consequently, the integral needed converges if and only if
converges too. That is, if and only if,
![]() $\beta>\frac {1}{p}$
.
$\beta>\frac {1}{p}$
.
Now, we can start the proof of Theorem 1.2. First, we will show that
![]() $\Lambda \backslash \{\lambda \}$
is a zero set for
$\Lambda \backslash \{\lambda \}$
is a zero set for
![]() $\mathcal {F}^p$
, for fixed
$\mathcal {F}^p$
, for fixed
![]() $\lambda \in \Lambda $
, and for every
$\lambda \in \Lambda $
, and for every
![]() $1<p<\infty $
. To do this, it suffices to prove that
$1<p<\infty $
. To do this, it suffices to prove that
![]() $\frac {G_{\Lambda} }{z-\lambda }$
belongs to
$\frac {G_{\Lambda} }{z-\lambda }$
belongs to
![]() $\mathcal {F}^p$
. According to Lemma 2.2 and by a subharmonicity argument, we have
$\mathcal {F}^p$
. According to Lemma 2.2 and by a subharmonicity argument, we have
 $$ \begin{align*} \int_{\mathbb{C}}\left|\frac{G_{\Lambda}(z)}{z-\lambda}e^{-\frac{\pi}{2}|z|^2}\right|^p dA(z) & \asymp \int_{\mathbb{C}}\left|\frac{G_{\Lambda}(z)}{z-\lambda}\frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)}e^{-\frac{\pi}{2}|z|^2}\right|^p dA(z) \\ & \lesssim \int_{\mathbb{C}} |G_{\Gamma}(z)|^p\left(\frac{1+|z|^2}{1+|\operatorname{Im} z^2|}\right)^{pM}\frac{e^{-\frac{p\pi}{2}|z|^2}}{(1+|z|)^{p(1-2\delta)}}dA(z)\\ & = \int_{\mathbb{C}} |G_{\Gamma}(z)|^pd\nu_{p,M,1-2\delta}(z). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}\left|\frac{G_{\Lambda}(z)}{z-\lambda}e^{-\frac{\pi}{2}|z|^2}\right|^p dA(z) & \asymp \int_{\mathbb{C}}\left|\frac{G_{\Lambda}(z)}{z-\lambda}\frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)}e^{-\frac{\pi}{2}|z|^2}\right|^p dA(z) \\ & \lesssim \int_{\mathbb{C}} |G_{\Gamma}(z)|^p\left(\frac{1+|z|^2}{1+|\operatorname{Im} z^2|}\right)^{pM}\frac{e^{-\frac{p\pi}{2}|z|^2}}{(1+|z|)^{p(1-2\delta)}}dA(z)\\ & = \int_{\mathbb{C}} |G_{\Gamma}(z)|^pd\nu_{p,M,1-2\delta}(z). \end{align*} $$
By Lemma 3.1, the last integral converges since
![]() $2\delta <1-\frac {1}{p}=\frac {1}{q}.$
$2\delta <1-\frac {1}{p}=\frac {1}{q}.$
To prove that
![]() $\Lambda $
is a uniqueness set for
$\Lambda $
is a uniqueness set for
![]() $\mathcal {F}^p$
,
$\mathcal {F}^p$
,
![]() $1<p<\infty $
, let F be a function of
$1<p<\infty $
, let F be a function of
![]() $\mathcal {F}^p$
that vanishes on
$\mathcal {F}^p$
that vanishes on
![]() $\Lambda $
. Write
$\Lambda $
. Write
![]() $F(z)=h(z)G_{\Lambda} (z)$
, for some entire function h. Again, by Lemma 2.2, we have
$F(z)=h(z)G_{\Lambda} (z)$
, for some entire function h. Again, by Lemma 2.2, we have
 $$ \begin{align} |F(z)| \frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)} \gtrsim |h(z)G_{\Gamma}(z)| \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}. \end{align} $$
$$ \begin{align} |F(z)| \frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)} \gtrsim |h(z)G_{\Gamma}(z)| \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}. \end{align} $$
Integrating both sides of the last inequality over
![]() $\mathbb {C}$
with respect to the measure
$\mathbb {C}$
with respect to the measure
![]() $d\mu _{p\pi }(z)=e^{-\frac {p\pi }{2}|z|^2}dA(z)$
,
$d\mu _{p\pi }(z)=e^{-\frac {p\pi }{2}|z|^2}dA(z)$
,
 $$ \begin{align*} \int_{\mathbb{C}}\left|F(z)\right|^p d\mu_{p\pi}(z) & \asymp \int_{\mathbb{C}}\left|F(z)\frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)} \right|^p d\mu_{p\pi}(z) \\ & \gtrsim \int_{\mathbb{C}} \left|h(z)G_{\Gamma}(z) \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z)\\ & \gtrsim \int_{\mathbb{C}} \left| \frac{h(z)G_{\Gamma}(z)}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}\left|F(z)\right|^p d\mu_{p\pi}(z) & \asymp \int_{\mathbb{C}}\left|F(z)\frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)} \right|^p d\mu_{p\pi}(z) \\ & \gtrsim \int_{\mathbb{C}} \left|h(z)G_{\Gamma}(z) \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z)\\ & \gtrsim \int_{\mathbb{C}} \left| \frac{h(z)G_{\Gamma}(z)}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z). \end{align*} $$
In the second line, we have used a subharmonicity argument. Since
![]() $2\delta < \frac {1}{\max \{p,q\}}\leq \frac {1}{2}$
, then for a fixed
$2\delta < \frac {1}{\max \{p,q\}}\leq \frac {1}{2}$
, then for a fixed
![]() $\gamma \in \Gamma $
, we have
$\gamma \in \Gamma $
, we have
 $$ \begin{align*} \int_{\mathbb{C}} \left| \frac{h(z)G_{\Gamma}(z)}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z) & \gtrsim \int_{\mathbb{C}} \left| \frac{h(z)G_{\Gamma}(z)}{(z-\gamma)P_{2M}(z)}\right|^p d\mu_{p\pi}(z), \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}} \left| \frac{h(z)G_{\Gamma}(z)}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z) & \gtrsim \int_{\mathbb{C}} \left| \frac{h(z)G_{\Gamma}(z)}{(z-\gamma)P_{2M}(z)}\right|^p d\mu_{p\pi}(z), \end{align*} $$
where
![]() $P_{2M}$
is a polynomial of degree
$P_{2M}$
is a polynomial of degree
![]() $\lfloor 2M\rfloor +1$
, that vanishes on
$\lfloor 2M\rfloor +1$
, that vanishes on
![]() $\lfloor 2M\rfloor +1$
points of
$\lfloor 2M\rfloor +1$
points of
![]() ${\Gamma \backslash \{\gamma \}}$
. This implies that the function
${\Gamma \backslash \{\gamma \}}$
. This implies that the function
![]() $z\mapsto \frac {h(z)G_{\Gamma} (z)}{(z-\gamma )P_{2M}(z)}$
belongs to
$z\mapsto \frac {h(z)G_{\Gamma} (z)}{(z-\gamma )P_{2M}(z)}$
belongs to
![]() $\mathcal {F}^p$
. Since the sequence
$\mathcal {F}^p$
. Since the sequence
![]() $\Gamma \backslash \{\gamma \}$
is a maximal zero sequence for
$\Gamma \backslash \{\gamma \}$
is a maximal zero sequence for
![]() $\mathcal {F}^p$
, then h must be a polynomial of degree less than
$\mathcal {F}^p$
, then h must be a polynomial of degree less than
![]() $\lfloor 2M\rfloor +1$
(see [Reference Zhu18, Reference Zhu19]). Suppose that h is not zero and denote by k its degree. Now, return to (9) and integrate both sides over
$\lfloor 2M\rfloor +1$
(see [Reference Zhu18, Reference Zhu19]). Suppose that h is not zero and denote by k its degree. Now, return to (9) and integrate both sides over
![]() $\mathbb {C}$
with respect to the measure
$\mathbb {C}$
with respect to the measure
![]() $d\mu _{p\pi }$
again, and we obtain
$d\mu _{p\pi }$
again, and we obtain
 $$ \begin{align*} \int_{\mathbb{C}}|F(z)|^p d\mu_{p\pi}(z) & \asymp \int_C\left|F(z)\frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)} \right|^p d\mu_{p\pi}(z) \\ & \gtrsim \int_{\mathbb{C}} \left|h(z)G_{\Gamma}(z) \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z)\\ & \asymp \int_{\mathbb{C}} \left|G_{\Gamma}(z) \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M-k}}\right|^p d\mu_{p\pi}(z)\\ & = \int_{\mathbb{C}}|G_{\Gamma}(z)|^p d\nu_{p,-M,2\delta-k}(z). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{C}}|F(z)|^p d\mu_{p\pi}(z) & \asymp \int_C\left|F(z)\frac{\operatorname{dist}(z,\Gamma)}{\operatorname{dist}(z,\Lambda)} \right|^p d\mu_{p\pi}(z) \\ & \gtrsim \int_{\mathbb{C}} \left|h(z)G_{\Gamma}(z) \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M}}\right|^p d\mu_{p\pi}(z)\\ & \asymp \int_{\mathbb{C}} \left|G_{\Gamma}(z) \frac{(1+|\operatorname{Im} z^2|)^M}{(1+|z|)^{2\delta+2M-k}}\right|^p d\mu_{p\pi}(z)\\ & = \int_{\mathbb{C}}|G_{\Gamma}(z)|^p d\nu_{p,-M,2\delta-k}(z). \end{align*} $$
By Lemma 3.1, the latter integral converges if and only if
![]() $2\delta -k>1/p$
. Since
$2\delta -k>1/p$
. Since
![]() $\delta <1/(2p)$
, we then get
$\delta <1/(2p)$
, we then get
This is a contradiction. Hence, h and F are zero. Therefore,
![]() $\Lambda $
is a uniqueness set for
$\Lambda $
is a uniqueness set for
![]() $\mathcal {F}^p$
. This completes the proof of Theorem 1.2.
$\mathcal {F}^p$
. This completes the proof of Theorem 1.2.
4 Proof of Theorem 1.3
The proof of Theorem 1.3 is essentially based on Lindelöf’s theorem below. First, we recall some main tools very useful for our proof, and we refer to [Reference Boas5, Reference Levin10] for more details. If f is an entire function and r is a positive real number, we denote
![]() $ M(r,f)$
the maximum modulus of f on the circle
$ M(r,f)$
the maximum modulus of f on the circle
![]() $|z|=r$
:
$|z|=r$
:
The order of f is given by the quantity
 $$\begin{align*}\rho_{f}:=\underset{r\rightarrow\infty}{\limsup}\ \frac{\log\log M(r,f)}{\log(r)}.\end{align*}$$
$$\begin{align*}\rho_{f}:=\underset{r\rightarrow\infty}{\limsup}\ \frac{\log\log M(r,f)}{\log(r)}.\end{align*}$$
Always, we have
![]() $0\leq \rho _{f}\leq \infty $
. In the case
$0\leq \rho _{f}\leq \infty $
. In the case
![]() $0<\rho _{f} <\infty $
, the type of f is defined as
$0<\rho _{f} <\infty $
, the type of f is defined as
Let
![]() $Z=\{z_n\}_{n\in \mathbb {N}}$
be the zero set of an entire function f. Following [Reference Boas5], the convergence exponent of the sequence
$Z=\{z_n\}_{n\in \mathbb {N}}$
be the zero set of an entire function f. Following [Reference Boas5], the convergence exponent of the sequence
![]() $Z=\{z_n\}_{n\in \mathbb {N}}$
(excluding
$Z=\{z_n\}_{n\in \mathbb {N}}$
(excluding
![]() $0$
if it belongs to Z) is defined as the infimum of all positive numbers s such that
$0$
if it belongs to Z) is defined as the infimum of all positive numbers s such that
and it will be denoted by
![]() $\rho _1$
(for short, the convergence exponent of f). A consequence of Jensen’s formula gives the following relations among the order
$\rho _1$
(for short, the convergence exponent of f). A consequence of Jensen’s formula gives the following relations among the order
![]() $\rho _f$
and the exponent of convergence
$\rho _f$
and the exponent of convergence
![]() $\rho _1$
of an entire function f (see [Reference Boas5] for complete proof):
$\rho _1$
of an entire function f (see [Reference Boas5] for complete proof):
The following theorem characterizes entire functions of integral order and of finite type.
Theorem 4.1 (Lindelöf [Reference Boas5])
If
![]() $\rho $
is a positive integer, the entire function f of order
$\rho $
is a positive integer, the entire function f of order
![]() $\rho _f=\rho $
is of finite type if and only if:
$\rho _f=\rho $
is of finite type if and only if:
-
(1)
 $n(r)=O(r^{\rho _f})$
, where
$n(r)=O(r^{\rho _f})$
, where
 $n(r)$
is the number of zeros of f in the disk
$n(r)$
is the number of zeros of f in the disk
 $|z|\leq r$
, counting multiplicity, and
$|z|\leq r$
, counting multiplicity, and -
(2) the sums
(12)are bounded, where $$ \begin{align} S(r) := \sum_{|z_n|\leq r}\frac{1}{z_n^\rho} \end{align} $$
$$ \begin{align} S(r) := \sum_{|z_n|\leq r}\frac{1}{z_n^\rho} \end{align} $$
 $\{z_n\}_{n}$
is the zero sequence of f.
$\{z_n\}_{n}$
is the zero sequence of f.
In the sequel, our constructions are based on dividing the complex plane into sectors with some defined opening aperture. To this end, for a given two angles
![]() $\beta \in (-\pi ,\pi ]$
and
$\beta \in (-\pi ,\pi ]$
and
![]() $\theta \in (0,\pi ]$
, define
$\theta \in (0,\pi ]$
, define
The following lemma will be of prominent role in the proof of Theorem 1.3 later on.
Lemma 4.2 Let
![]() $1\leq p<\infty $
. If
$1\leq p<\infty $
. If
![]() $Z=\{z_n\}_{n\in \mathbb {N}}$
is a zero set for
$Z=\{z_n\}_{n\in \mathbb {N}}$
is a zero set for
![]() $\mathcal {F}^{p}_{}$
such that
$\mathcal {F}^{p}_{}$
such that
![]() $Z\subset \mathcal {S}(\beta ,\theta )$
for some
$Z\subset \mathcal {S}(\beta ,\theta )$
for some
![]() $0\leq \theta <\frac {\pi }{4}$
and
$0\leq \theta <\frac {\pi }{4}$
and
![]() $\beta \in (-\pi ,\pi ]$
, then Z satisfies
$\beta \in (-\pi ,\pi ]$
, then Z satisfies
Proof Without loss of generality, we may suppose
![]() $\beta =0$
. Aiming to come to a contradiction, assume that
$\beta =0$
. Aiming to come to a contradiction, assume that
If g is a function in
![]() $\mathcal {F}^{p}_{}$
with
$\mathcal {F}^{p}_{}$
with
![]() $Z(g)=Z$
, then by [Reference Zhu19, Theorem 5.1], for every
$Z(g)=Z$
, then by [Reference Zhu19, Theorem 5.1], for every
![]() $\epsilon>0$
, we have
$\epsilon>0$
, we have
Thus,
![]() $Z=\{z_n\}_{n\in \mathbb {N}}$
is of convergence exponent
$Z=\{z_n\}_{n\in \mathbb {N}}$
is of convergence exponent
![]() $\rho _1=2$
. Combining (11), (14), and (15), we obtain
$\rho _1=2$
. Combining (11), (14), and (15), we obtain
Hence, g is of order
![]() $2$
, and of type
$2$
, and of type
![]() $\tau _{g}$
less than or equal to
$\tau _{g}$
less than or equal to
![]() $\frac {\pi }{2}$
. Since g is of integral order, Lindelöf’s theorem applies. Writing
$\frac {\pi }{2}$
. Since g is of integral order, Lindelöf’s theorem applies. Writing
![]() $z_n=|z_n|e^{i\theta _n}$
,
$z_n=|z_n|e^{i\theta _n}$
,
![]() $n\in \mathbb {N}$
, a straightforward calculation gives
$n\in \mathbb {N}$
, a straightforward calculation gives
 $$ \begin{align*} |S(r)|^2 & = \left|\underset{|z_n|\leq r}{\sum} \frac{1}{z_n^2}\right|^2=\left|\underset{|z_n|\leq r}{\sum} \frac{e^{-2i\theta_n}}{|z_n|^2}\right|^2 \\ & = \left|\underset{|z_n|\leq r}{\sum} \frac{\cos\big(2\theta_n\big)-i\sin\big(2\theta_n\big)}{|z_n|^2}\right|^2\\ & = \left(\underset{|z_n|\leq r}{\sum} \frac{\cos\big(2\theta_n\big)}{|z_n|^2}\right)^2 + \left(\underset{|z_n|\leq r}{\sum} \frac{\sin\big(2\theta_n\big)}{|z_n|^2}\right)^2 \\ & \geq \left(\underset{|z_n|\leq r}{\sum} \frac{\cos\big(2\theta_n\big)}{|z_n|^2}\right)^2 \\ & \geq \cos^2(2\theta)\left(\underset{|z_n|\leq r}{\sum} \frac{1}{|z_n|^2}\right)^2 \longrightarrow\infty, \qquad \mbox{as} \ r\rightarrow \infty. \end{align*} $$
$$ \begin{align*} |S(r)|^2 & = \left|\underset{|z_n|\leq r}{\sum} \frac{1}{z_n^2}\right|^2=\left|\underset{|z_n|\leq r}{\sum} \frac{e^{-2i\theta_n}}{|z_n|^2}\right|^2 \\ & = \left|\underset{|z_n|\leq r}{\sum} \frac{\cos\big(2\theta_n\big)-i\sin\big(2\theta_n\big)}{|z_n|^2}\right|^2\\ & = \left(\underset{|z_n|\leq r}{\sum} \frac{\cos\big(2\theta_n\big)}{|z_n|^2}\right)^2 + \left(\underset{|z_n|\leq r}{\sum} \frac{\sin\big(2\theta_n\big)}{|z_n|^2}\right)^2 \\ & \geq \left(\underset{|z_n|\leq r}{\sum} \frac{\cos\big(2\theta_n\big)}{|z_n|^2}\right)^2 \\ & \geq \cos^2(2\theta)\left(\underset{|z_n|\leq r}{\sum} \frac{1}{|z_n|^2}\right)^2 \longrightarrow\infty, \qquad \mbox{as} \ r\rightarrow \infty. \end{align*} $$
This contradicts Lindelöf’s Theorem 4.1. As a conclusion,
 $$ \begin{align*} \underset{n=0}{\overset{\infty}{\sum}}\ \frac{1}{|z_n|^2}\ < \infty.\\[-44pt] \end{align*} $$
$$ \begin{align*} \underset{n=0}{\overset{\infty}{\sum}}\ \frac{1}{|z_n|^2}\ < \infty.\\[-44pt] \end{align*} $$
Remark 1 We mention that the constant
![]() $\frac {\pi }{4}$
, which appears in Lemma 4.2, is the best possible. A counterexample is given by the zero set of the sin-cardinal function
$\frac {\pi }{4}$
, which appears in Lemma 4.2, is the best possible. A counterexample is given by the zero set of the sin-cardinal function
 $$\begin{align*}s(z)=\frac{\sin(\frac{\pi}{2}z^2)}{z^2}\in\mathcal{F}^{p}.\end{align*}$$
$$\begin{align*}s(z)=\frac{\sin(\frac{\pi}{2}z^2)}{z^2}\in\mathcal{F}^{p}.\end{align*}$$
Now, we can prove Theorem 1.3.
4.1 Proof of Theorem 1.3.
Let
![]() $Z=\{z_n\}_{n\in \mathbb {N}}$
be a sequence of complex numbers which is a zero sequence for
$Z=\{z_n\}_{n\in \mathbb {N}}$
be a sequence of complex numbers which is a zero sequence for
![]() $\mathcal {F}^{p}_{}$
and satisfies (5). If
$\mathcal {F}^{p}_{}$
and satisfies (5). If
![]() $Z'$
is any subsequence of Z, then it is a zero sequence too for
$Z'$
is any subsequence of Z, then it is a zero sequence too for
![]() $\mathcal {F}^{p}_{}$
by the sufficient condition [Reference Zhu19, Theorem 5.3]. Therefore, Z belongs to the desired class.
$\mathcal {F}^{p}_{}$
by the sufficient condition [Reference Zhu19, Theorem 5.3]. Therefore, Z belongs to the desired class.
Conversely, let Z be a zero sequence for
![]() $\mathcal {F}^{p}_{}$
with the property: every subset of Z is also a zero set for
$\mathcal {F}^{p}_{}$
with the property: every subset of Z is also a zero set for
![]() $\mathcal {F}^p$
. Now, we divide the sequence Z into eight subsets, by writing
$\mathcal {F}^p$
. Now, we divide the sequence Z into eight subsets, by writing
 $$\begin{align*}\displaystyle Z=\bigcup_{k=0}^{7}Z_k,\end{align*}$$
$$\begin{align*}\displaystyle Z=\bigcup_{k=0}^{7}Z_k,\end{align*}$$
where for each
![]() $0\leq k\leq 7$
,
$0\leq k\leq 7$
,
and
![]() $\varepsilon $
is an arbitrary small positive number in
$\varepsilon $
is an arbitrary small positive number in
![]() $(0,\frac {\pi }{8})$
. By the assumption, each
$(0,\frac {\pi }{8})$
. By the assumption, each
![]() $Z_{k}$
,
$Z_{k}$
,
![]() $k\in \{0,1,\ldots ,7\}$
is a zero set for
$k\in \{0,1,\ldots ,7\}$
is a zero set for
![]() $\mathcal {F}^{p}$
. We conclude by Lemma 4.2.
$\mathcal {F}^{p}$
. We conclude by Lemma 4.2.
Acknowledgment
The authors are deeply grateful to Professor O. El-Fallah (Faculty of Sciences, Mohammed V University in Rabat) for many helpful discussions, suggestions, and remarks. Moreover, they thank Professor Brett D. Wick (Washington University - St. Louis, USA) for drawing our attention to his work with Mishko Mitkovski about uniqueness sets for Fock spaces.