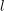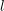1 Introduction
In its most elementary form, Bezout’s theorem states that a subset of
![]() $\mathbb{C}^{n}$
defined by equations
$\mathbb{C}^{n}$
defined by equations
![]() $P_{1},\ldots ,P_{n}$
of respective degrees
$P_{1},\ldots ,P_{n}$
of respective degrees
![]() $d_{1},\ldots ,d_{n}$
can have at most
$d_{1},\ldots ,d_{n}$
can have at most
![]() $d_{1}\cdots d_{n}$
isolated points. Various generalizations of this statement have been proposed. For example, the Bernstein–Kushnirenko–Khovanskii theorem estimates the number of isolated points in terms of the mixed volume of the Newton polytopes
$d_{1}\cdots d_{n}$
isolated points. Various generalizations of this statement have been proposed. For example, the Bernstein–Kushnirenko–Khovanskii theorem estimates the number of isolated points in terms of the mixed volume of the Newton polytopes
![]() $\unicode[STIX]{x1D6E5}(P_{1}),\ldots ,\unicode[STIX]{x1D6E5}(P_{n})$
. As a consequence of the Bezout theorem and its generalizations, whenever a set defined within the algebraic category happens to be finite, one can produce effective estimates for the size of the set (which often turn out to be fairly accurate).
$\unicode[STIX]{x1D6E5}(P_{1}),\ldots ,\unicode[STIX]{x1D6E5}(P_{n})$
. As a consequence of the Bezout theorem and its generalizations, whenever a set defined within the algebraic category happens to be finite, one can produce effective estimates for the size of the set (which often turn out to be fairly accurate).
In this paper we consider generalizations of Bezout’s bound for systems of differential equations. The fundamental question is as follows: given a system of algebraic conditions on an
![]() $n$
-tuple of functions and their first
$n$
-tuple of functions and their first
![]() $l$
derivatives, which admits finitely many solutions, can one estimate the number of solutions in terms of the degrees of the equations involved?
$l$
derivatives, which admits finitely many solutions, can one estimate the number of solutions in terms of the degrees of the equations involved?
This question has been considered by Hrushovski and Pillay in [Reference Hrushovski and PillayHP00]. Their result, quoted in Theorem 2 below, is a powerful analog of the Bezout theorem which similarly allows one to translate qualitative finiteness results obtained using differential-algebraic and model-theoretic methods into effective estimates (two examples of a diophantine nature are discussed below).
The explicit estimate in Theorem 2 is stated in terms of slightly different algebraic data than our naive formulation of the Bezout bound, making it difficult to make a direct comparison. Nonetheless, it is clear that the Bezout bound has two advantages. First, the Bezout bound and its various generalizations are singly-exponential with respect to the ambient dimension, whereas Theorem 2 admits doubly-exponential growth. Second, assuming for example that all equations involved have degree
![]() $d$
, the Bezout bound is a polynomial in
$d$
, the Bezout bound is a polynomial in
![]() $d$
with exponent equal to the ambient dimension. This is the natural asymptotic for solutions of
$d$
with exponent equal to the ambient dimension. This is the natural asymptotic for solutions of
![]() $n$
-dimensional systems of equations, and is known of course to be optimal in the algebraic context. The bound of Theorem 2 depends polynomially on the degree as well, but the exponent can in general be much larger than the ambient dimension (indeed, exponentially large).
$n$
-dimensional systems of equations, and is known of course to be optimal in the algebraic context. The bound of Theorem 2 depends polynomially on the degree as well, but the exponent can in general be much larger than the ambient dimension (indeed, exponentially large).
Our principal result is an estimate which recovers the two asymptotic properties above in the differential algebraic context. The statements are presented in §1.2, with formulations in terms of degrees and, more generally, mixed volumes of Newton polytopes.
Theorem 2 has been applied to produce effective bounds for some diophantine counting problems:
-
(i) In [Reference Hrushovski and PillayHP00] Theorem 2 was used to derive bounds on the number of transcendental lattice points on algebraic subvarieties of semi-abelian varieties. In particular, in the case of the two-dimensional torus this allowed the authors to produce doubly-exponential bounds for a counting problem due to Bombieri, improving the previous repeated-exponential bounds obtained by Buium [Reference BuiumBui95b].
-
(ii) More recently, Theorem 2 has been used in [Reference Freitag and ScanlonFS14] to derive bounds on the number of intersections between isogeny classes of elliptic curves and algebraic varieties. In particular, in the two-dimensional case this allowed the authors to produce doubly-exponential bounds for a counting problem due to Mazur.
Both of these applications follow the same principal strategy, inspired by the work of Buium [Reference BuiumBui92, Reference BuiumBui93] (see [Reference PillayPil97, Reference ScanlonSca01] for surveys). Namely, given a counting problem of a diophantine nature (over
![]() $\mathbb{C}$
, for example) one first expands the structure by adjoining to
$\mathbb{C}$
, for example) one first expands the structure by adjoining to
![]() $\mathbb{C}$
a differential operator making it into a differentially-closed field with field of constants
$\mathbb{C}$
a differential operator making it into a differentially-closed field with field of constants
![]() $\bar{\mathbb{Q}}$
. One then writes a system of differential algebraic conditions satisfied by the solutions of the diophantine problem. Finally, one shows (and this is naturally the deeper step involving arguments specific to the problem at hand) that the system, while possibly admitting more solutions than the original diophantine problem, still admits finitely many solutions.
$\bar{\mathbb{Q}}$
. One then writes a system of differential algebraic conditions satisfied by the solutions of the diophantine problem. Finally, one shows (and this is naturally the deeper step involving arguments specific to the problem at hand) that the system, while possibly admitting more solutions than the original diophantine problem, still admits finitely many solutions.
After carrying out the steps above, one can use Theorem 2 to produce an explicit estimate for the number of solutions of the diophantine problem. In §5 we apply our estimates to obtain refined (singly-exponential) bounds for problems (i) and (ii) above.
1.1 Setup and notation
Let
![]() $K$
denote a differentially-closed field of characteristic zero with a derivation
$K$
denote a differentially-closed field of characteristic zero with a derivation
![]() $D$
, and
$D$
, and
![]() $K_{0}$
its field of constants. Let
$K_{0}$
its field of constants. Let
![]() $M$
denote an ambient space, which we will take to be either an affine space
$M$
denote an ambient space, which we will take to be either an affine space
![]() $K^{n}$
or a Zariski open dense subset thereof. Denote by
$K^{n}$
or a Zariski open dense subset thereof. Denote by
![]() $\unicode[STIX]{x1D709}$
a coordinate on
$\unicode[STIX]{x1D709}$
a coordinate on
![]() $M$
. We define the
$M$
. We define the
![]() $l$
th prolongation as
$l$
th prolongation as
![]() $M^{(l)}=M\times K^{nl}$
, and denote by
$M^{(l)}=M\times K^{nl}$
, and denote by
![]() $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{(0)},\unicode[STIX]{x1D709}^{(1)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
coordinates on
$\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}^{(0)},\unicode[STIX]{x1D709}^{(1)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
coordinates on
![]() $M^{(l)}$
. For simplicity of notation we denote
$M^{(l)}$
. For simplicity of notation we denote
![]() $s:=\dim M^{(l)}=n(l+1)$
. We denote by
$s:=\dim M^{(l)}=n(l+1)$
. We denote by
![]() $\unicode[STIX]{x1D70B}_{M}:M^{(l)}\rightarrow M$
the projection onto
$\unicode[STIX]{x1D70B}_{M}:M^{(l)}\rightarrow M$
the projection onto
![]() $M$
. If there is no ambiguity we omit
$M$
. If there is no ambiguity we omit
![]() $M$
from this notation.
$M$
from this notation.
For any
![]() $x\in M$
, denote by
$x\in M$
, denote by
![]() $x^{(l)}\in M^{(l)}$
the
$x^{(l)}\in M^{(l)}$
the
![]() $l$
-jet of
$l$
-jet of
![]() $x$
, i.e. the element
$x$
, i.e. the element
![]() $(x,\ldots ,D^{l}x)$
. We denote by
$(x,\ldots ,D^{l}x)$
. We denote by
![]() ${\mathcal{J}}^{l}(M)\subset M^{(l)}$
the set of all
${\mathcal{J}}^{l}(M)\subset M^{(l)}$
the set of all
![]() $l$
-jets in
$l$
-jets in
![]() $M^{(l)}$
,
$M^{(l)}$
,
Let
![]() $\unicode[STIX]{x1D6FA}^{(l)}\subset M^{(l)}$
denote a Zariski open dense subset of
$\unicode[STIX]{x1D6FA}^{(l)}\subset M^{(l)}$
denote a Zariski open dense subset of
![]() $M^{(l)}$
(we include
$M^{(l)}$
(we include
![]() $l$
in the notation
$l$
in the notation
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
in the interest of clarity, but this is in fact an arbitrary open dense set). If we do not explicitly specify
$\unicode[STIX]{x1D6FA}^{(l)}$
in the interest of clarity, but this is in fact an arbitrary open dense set). If we do not explicitly specify
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
then it is taken to be equal to
$\unicode[STIX]{x1D6FA}^{(l)}$
then it is taken to be equal to
![]() $M^{(l)}$
.
$M^{(l)}$
.
Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a Zariski closed set. We view
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a Zariski closed set. We view
![]() $S$
as a system of algebraic-differential conditions on
$S$
as a system of algebraic-differential conditions on
![]() $M$
. We say that
$M$
. We say that
![]() $x\in M$
is a solution for
$x\in M$
is a solution for
![]() $S$
if
$S$
if
![]() $x^{(l)}\in S$
. We define the reduction of
$x^{(l)}\in S$
. We define the reduction of
![]() $S$
, denoted
$S$
, denoted
![]() ${\mathcal{R}}(S)\subset S$
, to be
${\mathcal{R}}(S)\subset S$
, to be
where
![]() $\operatorname{Clo}$
denotes Zariski closure. In other words, the reduction of
$\operatorname{Clo}$
denotes Zariski closure. In other words, the reduction of
![]() $S$
is the Zariski closure of the set of jets of the solutions of
$S$
is the Zariski closure of the set of jets of the solutions of
![]() $S$
. If
$S$
. If
![]() $S$
admits finitely many solutions then
$S$
admits finitely many solutions then
![]() ${\mathcal{R}}(S)$
is the set consisting of their jets. In this case we denote the number of solutions by
${\mathcal{R}}(S)$
is the set consisting of their jets. In this case we denote the number of solutions by
![]() ${\mathcal{N}}(S)$
.
${\mathcal{N}}(S)$
.
Example 1. Suppose
![]() $M=K^{2}$
with coordinates
$M=K^{2}$
with coordinates
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
, and consider the set
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}$
, and consider the set
![]() $S\subset M^{(1)}$
given by the conditions
$S\subset M^{(1)}$
given by the conditions
![]() $\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}=1$
and
$\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}=1$
and
![]() $\unicode[STIX]{x1D709}^{(1)}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}^{(1)}=1$
. Then
$\unicode[STIX]{x1D709}^{(1)}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}^{(1)}=1$
. Then
![]() $\dim S=2$
. However, it is clear that
$\dim S=2$
. However, it is clear that
![]() $S$
admits no solutions, since deriving the first condition we see that any solution must also satisfy
$S$
admits no solutions, since deriving the first condition we see that any solution must also satisfy
![]() $\unicode[STIX]{x1D709}^{(1)}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}^{(1)}=0$
, contradicting the second condition. Thus
$\unicode[STIX]{x1D709}^{(1)}\unicode[STIX]{x1D702}+\unicode[STIX]{x1D709}\unicode[STIX]{x1D702}^{(1)}=0$
, contradicting the second condition. Thus
![]() ${\mathcal{R}}(S)=\emptyset$
.
${\mathcal{R}}(S)=\emptyset$
.
In [Reference Hrushovski and PillayHP00], Hrushovski and Pillay considered the problem of estimating
![]() ${\mathcal{N}}(S)$
in terms of the algebraic degree of
${\mathcal{N}}(S)$
in terms of the algebraic degree of
![]() $S$
. In particular, using differential algebraic methods, they have established the following estimate.
$S$
. In particular, using differential algebraic methods, they have established the following estimate.
Theorem 2 [Reference Hrushovski and PillayHP00, Proposition 3.1].
Let
![]() $X\subset M$
and
$X\subset M$
and
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be Zariski closed. Denote
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be Zariski closed. Denote
![]() $m:=\dim X$
. Denote
$m:=\dim X$
. Denote
![]() $T=S\cap \unicode[STIX]{x1D70B}^{-1}(X)$
and suppose that
$T=S\cap \unicode[STIX]{x1D70B}^{-1}(X)$
and suppose that
![]() $T$
admits finitely many solutions. Then
$T$
admits finitely many solutions. Then
1.2 Statement of our results
Recall that for a Laurent polynomial
![]() $P$
in the
$P$
in the
![]() $\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables (over
$\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables (over
![]() $K$
), its Newton polytope denoted
$K$
), its Newton polytope denoted
![]() $\unicode[STIX]{x1D6E5}(P)$
is defined to be the convex hull of the set of exponents (of terms with non-zero coefficients) of
$\unicode[STIX]{x1D6E5}(P)$
is defined to be the convex hull of the set of exponents (of terms with non-zero coefficients) of
![]() $P$
, viewed as a subset of
$P$
, viewed as a subset of
![]() $\mathbb{R}^{s}$
. We say that
$\mathbb{R}^{s}$
. We say that
![]() $\unicode[STIX]{x1D6E5}$
is a lattice polytope if it is obtained as the Newton polytope of some Laurent polynomial. We will denote by
$\unicode[STIX]{x1D6E5}$
is a lattice polytope if it is obtained as the Newton polytope of some Laurent polynomial. We will denote by
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{(j)}}$
the standard simplex in the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}^{(j)}}$
the standard simplex in the
![]() $\unicode[STIX]{x1D709}^{(j)}$
variables, and by
$\unicode[STIX]{x1D709}^{(j)}$
variables, and by
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
the standard simplex in the
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
the standard simplex in the
![]() $\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables.
$\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables.
Recall that for
![]() $s$
convex bodies
$s$
convex bodies
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s}$
in
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s}$
in
![]() $\mathbb{R}^{s}$
, their mixed volume is defined to be
$\mathbb{R}^{s}$
, their mixed volume is defined to be
The mixed volume is symmetric and multilinear, and generates the volume function in the sense that
![]() $V(\unicode[STIX]{x1D6E5},\ldots ,\unicode[STIX]{x1D6E5})=\operatorname{Vol}(\unicode[STIX]{x1D6E5})$
. In fact, these properties completely determine the mixed volume function.
$V(\unicode[STIX]{x1D6E5},\ldots ,\unicode[STIX]{x1D6E5})=\operatorname{Vol}(\unicode[STIX]{x1D6E5})$
. In fact, these properties completely determine the mixed volume function.
The following classical Bernstein–Kushnirenko–Khovanskii (BKK) theorem relates the number of solutions of a system of polynomial equations to the mixed volume of their Newton polytopes.
Theorem 3 [Reference KušnirenkoKuš76, Reference BernsteinBer75].
Let
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s}$
be lattice polytopes in
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{s}$
be lattice polytopes in
![]() $\mathbb{R}^{s}$
. Then for any tuple
$\mathbb{R}^{s}$
. Then for any tuple
![]() $P_{1},\ldots ,P_{s}$
with
$P_{1},\ldots ,P_{s}$
with
![]() $\unicode[STIX]{x1D6E5}(P_{i})=\unicode[STIX]{x1D6E5}_{i}$
, the system of equations
$\unicode[STIX]{x1D6E5}(P_{i})=\unicode[STIX]{x1D6E5}_{i}$
, the system of equations
![]() $P_{1}=\cdots =P_{s}=0$
admits at most
$P_{1}=\cdots =P_{s}=0$
admits at most
![]() $\unicode[STIX]{x1D707}$
isolated solutions in
$\unicode[STIX]{x1D707}$
isolated solutions in
![]() $(K^{\ast })^{s}$
, where
$(K^{\ast })^{s}$
, where
and
![]() $V(\cdots \,)$
denotes the mixed volume. Moreover, for a sufficiently generic choice of the tuple
$V(\cdots \,)$
denotes the mixed volume. Moreover, for a sufficiently generic choice of the tuple
![]() $P_{i}$
the bound
$P_{i}$
the bound
![]() $\unicode[STIX]{x1D707}$
is attained.
$\unicode[STIX]{x1D707}$
is attained.
Remark 4. Under some mild conditions, the BKK estimate also bounds the number of zeros in
![]() $K^{s}$
. For instance, this is true if each
$K^{s}$
. For instance, this is true if each
![]() $\unicode[STIX]{x1D6E5}_{i}$
is the convex hull of a finite co-ideal
$\unicode[STIX]{x1D6E5}_{i}$
is the convex hull of a finite co-ideal
![]() $I_{i}\subset \mathbb{Z}_{{\geqslant}0}$
(since in this case one can always, after a generic translation, assume that none of the solutions lie on the coordinate axes). We will refer to such polytopes as co-ideal polytopes. The common case of the polytope of polynomials with bounded degree or multi-degree certainly satisfies this condition.
$I_{i}\subset \mathbb{Z}_{{\geqslant}0}$
(since in this case one can always, after a generic translation, assume that none of the solutions lie on the coordinate axes). We will refer to such polytopes as co-ideal polytopes. The common case of the polytope of polynomials with bounded degree or multi-degree certainly satisfies this condition.
Our results can be applied either to
![]() $(K^{\ast })^{s}$
or to
$(K^{\ast })^{s}$
or to
![]() $K^{s}$
, but in the latter case we always assume that all polytopes involved are co-ideal polytopes.
$K^{s}$
, but in the latter case we always assume that all polytopes involved are co-ideal polytopes.
Our main result is an analog of the first part of the BKK theorem. Namely, for a system of algebraic-differential conditions
![]() $S$
admitting finitely many solution, we estimate the number of solutions in terms of a mixed volume of the Newton polytopes associated to the equations defining
$S$
admitting finitely many solution, we estimate the number of solutions in terms of a mixed volume of the Newton polytopes associated to the equations defining
![]() $S$
. Note that our various formulations are stated in terms of the degrees/polytopes of the equations defining
$S$
. Note that our various formulations are stated in terms of the degrees/polytopes of the equations defining
![]() $S$
, whereas Theorem 2 is stated in terms of the algebraic degree of
$S$
, whereas Theorem 2 is stated in terms of the algebraic degree of
![]() $S$
as a variety. The proofs of the various statements are given in §4.
$S$
as a variety. The proofs of the various statements are given in §4.
Remark 5. The reader unfamiliar with the theory of Newton polytopes may wish to assume on first reading that the Newton polytopes under consideration are of the form
![]() $d\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
(this amounts to requiring that the polynomial equations in the
$d\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
(this amounts to requiring that the polynomial equations in the
![]() $\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables have degree bounded by
$\unicode[STIX]{x1D709}^{(0)},\ldots ,\unicode[STIX]{x1D709}^{(l)}$
variables have degree bounded by
![]() $d$
). Not much will be lost by considering only this special case, where the BKK theorem reduces to the Bezout theorem. In particular, the use of the BKK theorem is not essential for obtaining the single-exponential asymptotics of the constants in all of our results.
$d$
). Not much will be lost by considering only this special case, where the BKK theorem reduces to the Bezout theorem. In particular, the use of the BKK theorem is not essential for obtaining the single-exponential asymptotics of the constants in all of our results.
We begin with a formulation valid for complete intersections (for a slightly more general form valid for flat limits of complete intersections, see Proposition 29).
Theorem 6. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a complete intersection defined by polynomials with Newton polytopes
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a complete intersection defined by polynomials with Newton polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
, and suppose that
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
, and suppose that
![]() ${\mathcal{N}}(S)<\infty$
. Denote
${\mathcal{N}}(S)<\infty$
. Denote
Then
where
![]() $\unicode[STIX]{x1D6FF}:=s-k$
.
$\unicode[STIX]{x1D6FF}:=s-k$
.
We note that the factor of
![]() $s!$
in
$s!$
in
![]() $C_{s,k}$
is the usual factor appearing in the BKK theorem. The additional factor is an artifact of our construction and could certainly be improved somewhat.
$C_{s,k}$
is the usual factor appearing in the BKK theorem. The additional factor is an artifact of our construction and could certainly be improved somewhat.
We next present a result valid for arbitrary varieties rather than complete intersections.
Theorem 7. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety with
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety with
![]() ${\mathcal{N}}(S)<\infty$
. Suppose that:
${\mathcal{N}}(S)<\infty$
. Suppose that:
-
(i)
 $S$
is contained in a complete intersection defined by polynomials with Newton polytopes
$S$
is contained in a complete intersection defined by polynomials with Newton polytopes
 $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
;
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
; -
(ii)
 $S$
is set-theoretically cut out by equations whose Newton polytopes are contained in a polytope
$S$
is set-theoretically cut out by equations whose Newton polytopes are contained in a polytope
 $\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. To simplify the notation we write
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. To simplify the notation we write
 $\unicode[STIX]{x1D6E5}_{j}=\unicode[STIX]{x1D6E5}$
for
$\unicode[STIX]{x1D6E5}_{j}=\unicode[STIX]{x1D6E5}$
for
 $j>k$
.
$j>k$
.
Denote
Then
In particular, assuming
![]() $\unicode[STIX]{x1D6E5}_{j}\subset \unicode[STIX]{x1D6E5}$
for
$\unicode[STIX]{x1D6E5}_{j}\subset \unicode[STIX]{x1D6E5}$
for
![]() $j=1,\ldots ,k$
, we have
$j=1,\ldots ,k$
, we have
As an immediate consequence we obtain the following analog of the Kushnirenko theorem.
Corollary 8. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety of top dimension
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety of top dimension
![]() $s-k$
cut out by equations whose Newton polytopes are contained in a polytope
$s-k$
cut out by equations whose Newton polytopes are contained in a polytope
![]() $\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. Suppose that
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. Suppose that
![]() $S$
admits finitely many solutions. Then
$S$
admits finitely many solutions. Then
Proof. Let
![]() ${\mathcal{P}}$
denote the given collection of polynomials with Newton polytopes contained in
${\mathcal{P}}$
denote the given collection of polynomials with Newton polytopes contained in
![]() $\unicode[STIX]{x1D6E5}$
which set theoretically cut out
$\unicode[STIX]{x1D6E5}$
which set theoretically cut out
![]() $S$
. We define a sequence of polynomials
$S$
. We define a sequence of polynomials
![]() $P_{1},\ldots ,P_{k}\in {\mathcal{P}}$
as follows: for
$P_{1},\ldots ,P_{k}\in {\mathcal{P}}$
as follows: for
![]() $j=1$
let
$j=1$
let
![]() $P_{1}\in {\mathcal{P}}$
be a non-zero polynomial; for
$P_{1}\in {\mathcal{P}}$
be a non-zero polynomial; for
![]() $j<k$
and assuming
$j<k$
and assuming
![]() $P_{j}$
is already constructed, let
$P_{j}$
is already constructed, let
![]() $P_{j+1}\in {\mathcal{P}}$
be any polynomial which is not identically vanishing on any component of
$P_{j+1}\in {\mathcal{P}}$
be any polynomial which is not identically vanishing on any component of
![]() $\{P_{1}=\cdots =P_{j}=0\}$
. Such a polynomial must exist since otherwise a component of
$\{P_{1}=\cdots =P_{j}=0\}$
. Such a polynomial must exist since otherwise a component of
![]() $\{P_{1}=\cdots =P_{j}=0\}$
is a component of
$\{P_{1}=\cdots =P_{j}=0\}$
is a component of
![]() $S$
, which is ruled out by our assumption on the dimension of
$S$
, which is ruled out by our assumption on the dimension of
![]() $S$
.
$S$
.
It follows by an easy induction that the intersection
![]() $P_{1}=\cdots =P_{k}=0$
is a complete intersection and the claim of the theorem now follows by application of Theorem 7.◻
$P_{1}=\cdots =P_{k}=0$
is a complete intersection and the claim of the theorem now follows by application of Theorem 7.◻
More generally, for systems admitting infinitely many solutions we have similar estimates for the degree of their reduction. Here the degree of an irreducible variety in
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
is defined to be the number of intersections with a generic affine-linear space of complementary dimension, and this notion is extended by linearity to arbitrary (possible mixed-dimensional) varieties. We give an analog of the second part of Theorem 7 (but the other part extends in a similar manner).
$\unicode[STIX]{x1D6FA}^{(l)}$
is defined to be the number of intersections with a generic affine-linear space of complementary dimension, and this notion is extended by linearity to arbitrary (possible mixed-dimensional) varieties. We give an analog of the second part of Theorem 7 (but the other part extends in a similar manner).
Theorem 9. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
and suppose that:
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
and suppose that:
-
(i)
 $S$
is contained in a complete-intersection defined by polynomials with Newton polytopes
$S$
is contained in a complete-intersection defined by polynomials with Newton polytopes
 $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
;
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
; -
(ii)
 $S$
is set-theoretically cut out by equations whose Newton polytopes are contained in a polytope
$S$
is set-theoretically cut out by equations whose Newton polytopes are contained in a polytope
 $\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
.
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
.
Assume further that
![]() $\unicode[STIX]{x1D6E5}_{j}\subset \unicode[STIX]{x1D6E5}$
for
$\unicode[STIX]{x1D6E5}_{j}\subset \unicode[STIX]{x1D6E5}$
for
![]() $j=1,\ldots ,k$
. Then
$j=1,\ldots ,k$
. Then
The proof of the following corollary is similar to that of Corollary 8.
Corollary 10. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety of top dimension
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be any variety of top dimension
![]() $s-k$
cut out by equations whose Newton polytope are contained in a polytope
$s-k$
cut out by equations whose Newton polytope are contained in a polytope
![]() $\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. Then
$\unicode[STIX]{x1D6E5}\supset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
. Then
Finally, we record a statement with a formulation more similar to that of Theorem 2. In particular, it shows that for a fixed system of differential conditions
![]() $S$
, the number of solutions within a variety
$S$
, the number of solutions within a variety
![]() $X$
defined by equations of degrees bounded by
$X$
defined by equations of degrees bounded by
![]() $d_{X}$
grows asymptotically like
$d_{X}$
grows asymptotically like
![]() $d_{X}^{n}$
, which is the expected order of growth (even in a purely algebraic context).
$d_{X}^{n}$
, which is the expected order of growth (even in a purely algebraic context).
Corollary 11. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety of top dimension
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety of top dimension
![]() $s-k$
cut out by equations of degrees at most
$s-k$
cut out by equations of degrees at most
![]() $d_{S}$
and
$d_{S}$
and
![]() $X\subset M$
be a variety cut out by equations of degrees at most
$X\subset M$
be a variety cut out by equations of degrees at most
![]() $d_{X}\geqslant d_{S}$
. Denote
$d_{X}\geqslant d_{S}$
. Denote
![]() $T=S\cap \unicode[STIX]{x1D70B}^{-1}(X)$
and suppose that
$T=S\cap \unicode[STIX]{x1D70B}^{-1}(X)$
and suppose that
![]() $T$
admits finitely many solutions. Then
$T$
admits finitely many solutions. Then
More generally, without the assumption that
![]() $T$
admits finitely many solutions, we have
$T$
admits finitely many solutions, we have
Proof. We let
![]() $\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{s}$
denote the polytope obtained from the polytope
$\unicode[STIX]{x1D6E5}\subset \mathbb{R}^{s}$
denote the polytope obtained from the polytope
![]() $d_{S}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
by stretching each of the coordinates
$d_{S}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
by stretching each of the coordinates
![]() $\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n})$
by a factor of
$\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n})$
by a factor of
![]() $d_{X}/d_{S}$
. In particular,
$d_{X}/d_{S}$
. In particular,
![]() $\unicode[STIX]{x1D6E5}$
contains both
$\unicode[STIX]{x1D6E5}$
contains both
![]() $d_{S}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
and
$d_{S}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)}$
and
![]() $d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
, i.e. it contains the Newton polytopes of the given equations for
$d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
, i.e. it contains the Newton polytopes of the given equations for
![]() $S$
and
$S$
and
![]() $\unicode[STIX]{x1D70B}^{-1}(X)$
. It remains to note that
$\unicode[STIX]{x1D70B}^{-1}(X)$
. It remains to note that
1.3 Elementary differential algebraic constructions
For any Zariski closed set
![]() $V\subset M$
we define the
$V\subset M$
we define the
![]() $l$
th prolongation
$l$
th prolongation
![]() $V^{(l)}\subset M^{(l)}$
to be the Zariski closure of
$V^{(l)}\subset M^{(l)}$
to be the Zariski closure of
![]() $\{x^{(l)}:x\in V\}$
. The prolongation of a finite union of closed sets is clearly equal to the union of their prolongations. Moreover, by a theorem of Kolchin [Reference KolchinKol73], the prolongation of an irreducible set is itself irreducible.
$\{x^{(l)}:x\in V\}$
. The prolongation of a finite union of closed sets is clearly equal to the union of their prolongations. Moreover, by a theorem of Kolchin [Reference KolchinKol73], the prolongation of an irreducible set is itself irreducible.
The following encapsulates a key property of differentially closed fields.
Fact 12 [Reference Hrushovski and PillayHP00, Fact 3.7].
Let
![]() $V$
denote an irreducible variety and
$V$
denote an irreducible variety and
![]() $W\subset V^{(1)}$
an irreducible variety which projects dominantly on
$W\subset V^{(1)}$
an irreducible variety which projects dominantly on
![]() $V$
. Then for any non-empty Zariski open subset
$V$
. Then for any non-empty Zariski open subset
![]() $U\subset W$
there exists
$U\subset W$
there exists
![]() $x\in V$
with
$x\in V$
with
![]() $x^{(1)}\in U$
.
$x^{(1)}\in U$
.
We denote
![]() ${M^{(l)}}^{(1)}:=(M^{(l)})^{(1)}$
, and similarly for
${M^{(l)}}^{(1)}:=(M^{(l)})^{(1)}$
, and similarly for
![]() ${x^{(l)}}^{(1)}$
. We have a canonical variety
${x^{(l)}}^{(1)}$
. We have a canonical variety
![]() $\unicode[STIX]{x1D6EF}\subset {M^{(l)}}^{(1)}$
defined to be the Zariski closure of
$\unicode[STIX]{x1D6EF}\subset {M^{(l)}}^{(1)}$
defined to be the Zariski closure of
![]() $\{{x^{(l)}}^{(1)}:x\in M\}$
. It is given by the equations
$\{{x^{(l)}}^{(1)}:x\in M\}$
. It is given by the equations
![]() ${\unicode[STIX]{x1D709}^{(k)}}^{(0)}={\unicode[STIX]{x1D709}^{(k-1)}}^{(1)}$
for
${\unicode[STIX]{x1D709}^{(k)}}^{(0)}={\unicode[STIX]{x1D709}^{(k-1)}}^{(1)}$
for
![]() $k=1,\ldots ,l$
.
$k=1,\ldots ,l$
.
Proposition 13. The points
![]() $y\in M^{(l)}$
that satisfy
$y\in M^{(l)}$
that satisfy
![]() $y^{(1)}\in \unicode[STIX]{x1D6EF}$
are precisely the points of the form
$y^{(1)}\in \unicode[STIX]{x1D6EF}$
are precisely the points of the form
![]() $x^{(l)}$
for some
$x^{(l)}$
for some
![]() $x\in M$
.
$x\in M$
.
Proof. Let
![]() $y=(x_{0},x_{1},\ldots ,x_{l})$
with
$y=(x_{0},x_{1},\ldots ,x_{l})$
with
![]() $y^{(1)}=(y,Dy)\in \unicode[STIX]{x1D6EF}$
. It follows that
$y^{(1)}=(y,Dy)\in \unicode[STIX]{x1D6EF}$
. It follows that
![]() $x_{k}=Dx_{k-1}$
for
$x_{k}=Dx_{k-1}$
for
![]() $k=1,\ldots ,l$
, so
$k=1,\ldots ,l$
, so
![]() $y=(x_{0})^{(l)}$
as claimed. The other direction is obvious.◻
$y=(x_{0})^{(l)}$
as claimed. The other direction is obvious.◻
Lemma 14. Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety admitting finitely many solutions. Then
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety admitting finitely many solutions. Then
![]() $S^{(1)}\cap \unicode[STIX]{x1D6EF}$
does not project dominantly on any positive-dimensional component of
$S^{(1)}\cap \unicode[STIX]{x1D6EF}$
does not project dominantly on any positive-dimensional component of
![]() $S$
. More generally, the same holds if
$S$
. More generally, the same holds if
![]() ${\mathcal{R}}(S)$
does not contain any component of
${\mathcal{R}}(S)$
does not contain any component of
![]() $S$
.
$S$
.
Proof. It is enough to check the case of
![]() $S$
irreducible (and positive-dimensional). Let
$S$
irreducible (and positive-dimensional). Let
![]() $U=\unicode[STIX]{x1D6FA}^{(l)}\setminus {\mathcal{R}}(S)$
. By assumption,
$U=\unicode[STIX]{x1D6FA}^{(l)}\setminus {\mathcal{R}}(S)$
. By assumption,
![]() $U\cap S$
is open dense in
$U\cap S$
is open dense in
![]() $S$
.
$S$
.
Assume toward contradiction that
![]() $S^{(1)}\cap \unicode[STIX]{x1D6EF}$
projects dominantly on
$S^{(1)}\cap \unicode[STIX]{x1D6EF}$
projects dominantly on
![]() $S$
. Then some irreducible component
$S$
. Then some irreducible component
![]() $W$
of this intersection projects dominantly on
$W$
of this intersection projects dominantly on
![]() $S$
as well. Thus we can apply Fact 12 to the non-empty open subset
$S$
as well. Thus we can apply Fact 12 to the non-empty open subset
![]() $W\cap \unicode[STIX]{x1D70B}^{-1}(U)$
and deduce that there exists
$W\cap \unicode[STIX]{x1D70B}^{-1}(U)$
and deduce that there exists
![]() $y\in U$
with
$y\in U$
with
![]() $y^{(1)}\in S^{(1)}\cap \unicode[STIX]{x1D6EF}$
. But by Proposition 13 such
$y^{(1)}\in S^{(1)}\cap \unicode[STIX]{x1D6EF}$
. But by Proposition 13 such
![]() $y$
is of the form
$y$
is of the form
![]() $z^{(l)}$
for some
$z^{(l)}$
for some
![]() $z\in M$
, and hence
$z\in M$
, and hence
![]() $z$
is another solution of
$z$
is another solution of
![]() $S$
, contradicting the definition of
$S$
, contradicting the definition of
![]() $U$
.◻
$U$
.◻
1.4 Overview of the proof
1.4.1 The reduction of dimension
Let
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety of positive dimension admitting finitely many solutions, and let
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
be a variety of positive dimension admitting finitely many solutions, and let
![]() $\widetilde{S}:=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6FA}^{(l)}}(S^{(1)}\cap \unicode[STIX]{x1D6EF})$
. Then by Lemma 14 we have
$\widetilde{S}:=\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D6FA}^{(l)}}(S^{(1)}\cap \unicode[STIX]{x1D6EF})$
. Then by Lemma 14 we have
![]() $\dim \widetilde{S}<\dim S$
. If
$\dim \widetilde{S}<\dim S$
. If
![]() $x\in M$
is any solution of
$x\in M$
is any solution of
![]() $S$
, then
$S$
, then
![]() $x^{(l)}\in S$
and hence
$x^{(l)}\in S$
and hence
![]() ${x^{(l)}}^{(1)}\in S^{(1)}\cap \unicode[STIX]{x1D6EF}$
, so
${x^{(l)}}^{(1)}\in S^{(1)}\cap \unicode[STIX]{x1D6EF}$
, so
![]() $x^{(l)}\in \widetilde{S}$
. That is,
$x^{(l)}\in \widetilde{S}$
. That is,
![]() $x$
is also a solution of
$x$
is also a solution of
![]() $\widetilde{S}$
. Since
$\widetilde{S}$
. Since
![]() $\widetilde{S}\subset S$
we conclude that
$\widetilde{S}\subset S$
we conclude that
![]() ${\mathcal{N}}(S)={\mathcal{N}}(\widetilde{S})$
.
${\mathcal{N}}(S)={\mathcal{N}}(\widetilde{S})$
.
Repeating this reduction
![]() $s$
times, one is eventually reduced to counting the number of solutions of a zero-dimensional variety, which is certainly bounded by the number of points in the variety. This is similar to the approach employed in [Reference Hrushovski and PillayHP00]. In order to obtain good effective estimates it is thus necessary to have an effective description of
$s$
times, one is eventually reduced to counting the number of solutions of a zero-dimensional variety, which is certainly bounded by the number of points in the variety. This is similar to the approach employed in [Reference Hrushovski and PillayHP00]. In order to obtain good effective estimates it is thus necessary to have an effective description of
![]() $\widetilde{S}$
in terms of
$\widetilde{S}$
in terms of
![]() $S$
, and the key step is obtaining an effective description of
$S$
, and the key step is obtaining an effective description of
![]() $S^{(1)}$
.
$S^{(1)}$
.
1.4.2 An approximation for the first prolongation
We now work with an arbitrary ambient space
![]() $N$
, and the reader should keep in mind that eventually we will take this ambient space to be
$N$
, and the reader should keep in mind that eventually we will take this ambient space to be
![]() $M^{(l)}$
or its open dense subset
$M^{(l)}$
or its open dense subset
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
$\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
![]() $N$
by
$N$
by
![]() $\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D701}$
.
If
![]() $V\subset N$
is an effectively smooth complete intersection defined by
$V\subset N$
is an effectively smooth complete intersection defined by
![]() $k$
polynomial equations
$k$
polynomial equations
![]() $\{P_{j}\}$
with a given Newton polytope
$\{P_{j}\}$
with a given Newton polytope
![]() $\unicode[STIX]{x1D6E5}$
, then one can explicitly write
$\unicode[STIX]{x1D6E5}$
, then one can explicitly write
![]() $2k$
equations in
$2k$
equations in
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}$
for
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}$
for
![]() $V^{(1)}$
, with (essentially) the same Newton polytope in
$V^{(1)}$
, with (essentially) the same Newton polytope in
![]() $\unicode[STIX]{x1D701}$
and linear in
$\unicode[STIX]{x1D701}$
and linear in
![]() $\unicode[STIX]{x1D701}^{(1)}$
. However, this system of equations degenerates if
$\unicode[STIX]{x1D701}^{(1)}$
. However, this system of equations degenerates if
![]() $V$
is a non-smooth intersection.
$V$
is a non-smooth intersection.
Our proof is based on the following idea. We embed
![]() $V$
as the zero fiber
$V$
as the zero fiber
![]() $V=X_{0}$
of a flat family
$V=X_{0}$
of a flat family
![]() $X$
whose generic fiber is a complete intersection. Making a small perturbation, we may also assume that the generic fiber is smooth. We write the system of
$X$
whose generic fiber is a complete intersection. Making a small perturbation, we may also assume that the generic fiber is smooth. We write the system of
![]() $2k$
equations as above (now depending on an extra deformation parameter
$2k$
equations as above (now depending on an extra deformation parameter
![]() $e$
), obtaining a family
$e$
), obtaining a family
![]() $\unicode[STIX]{x1D70F}(X)$
. It turns out that the limit
$\unicode[STIX]{x1D70F}(X)$
. It turns out that the limit
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
, while not necessarily equal to
$\unicode[STIX]{x1D70F}(X)_{0}$
, while not necessarily equal to
![]() $V^{(1)}$
, still approximates it rather well: the two agree over an open dense set. To conclude, if
$V^{(1)}$
, still approximates it rather well: the two agree over an open dense set. To conclude, if
![]() $V$
is a limit of a family of complete intersections of a given Newton polytope, then the same is essentially true for
$V$
is a limit of a family of complete intersections of a given Newton polytope, then the same is essentially true for
![]() $V^{(1)}$
(at least in an open dense set).
$V^{(1)}$
(at least in an open dense set).
1.4.3 Conclusion
Returning now to the notation of §1.4.1, we show that if
![]() $S$
was the limit of a family of complete intersections with a given Newton polytope, then the same is true for
$S$
was the limit of a family of complete intersections with a given Newton polytope, then the same is true for
![]() $\widetilde{S}$
(with a slightly larger Newton polytope). We may now repeat the construction
$\widetilde{S}$
(with a slightly larger Newton polytope). We may now repeat the construction
![]() $s$
times and eventually obtain the limit of a zero-dimensional variety. Of course, the number of points of such a limit is bounded by the number of points of the generic fiber, which may now be estimated with the help of the BKK theorem.
$s$
times and eventually obtain the limit of a zero-dimensional variety. Of course, the number of points of such a limit is bounded by the number of points of the generic fiber, which may now be estimated with the help of the BKK theorem.
2 Smooth approximations and flat families
In this section we denote the ambient space by
![]() $N$
and its dimension by
$N$
and its dimension by
![]() $n$
. The reader should keep in mind that eventually we will take this ambient space to be
$n$
. The reader should keep in mind that eventually we will take this ambient space to be
![]() $M^{(l)}$
or its open dense subset
$M^{(l)}$
or its open dense subset
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
$\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
![]() $N$
by
$N$
by
![]() $\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D701}$
.
2.1 The
 $\unicode[STIX]{x1D70F}$
-variety associated to a flat family
$\unicode[STIX]{x1D70F}$
-variety associated to a flat family
Let
![]() $V\subset N$
be given by
$V\subset N$
be given by
We define
![]() $\unicode[STIX]{x1D70F}(V)\subset N^{(1)}$
to be
$\unicode[STIX]{x1D70F}(V)\subset N^{(1)}$
to be
where
![]() $P^{D}$
is the polynomial obtained by applying
$P^{D}$
is the polynomial obtained by applying
![]() $D$
to each coefficient of
$D$
to each coefficient of
![]() $P$
. It follows from the chain rule that
$P$
. It follows from the chain rule that
![]() $V^{(1)}\subset \unicode[STIX]{x1D70F}(V)$
. Moreover, if
$V^{(1)}\subset \unicode[STIX]{x1D70F}(V)$
. Moreover, if
![]() $V$
is effectively smooth (i.e. the differentials
$V$
is effectively smooth (i.e. the differentials
![]() $dP_{1},\ldots ,dP_{k}$
are linearly independent at every point of
$dP_{1},\ldots ,dP_{k}$
are linearly independent at every point of
![]() $V$
) then equality holds [Reference Hrushovski and PillayHP00, Remark 3.5(3)], and in particular
$V$
) then equality holds [Reference Hrushovski and PillayHP00, Remark 3.5(3)], and in particular
![]() $\unicode[STIX]{x1D70F}(V)$
has pure codimension
$\unicode[STIX]{x1D70F}(V)$
has pure codimension
![]() $2k$
in
$2k$
in
![]() $N^{(1)}$
(assuming
$N^{(1)}$
(assuming
![]() $V$
is non-empty).
$V$
is non-empty).
Recall that a variety
![]() $X\subset N\times \mathbb{A}_{K}$
is flat over
$X\subset N\times \mathbb{A}_{K}$
is flat over
![]() $\mathbb{A}_{K}$
if and only if every component of
$\mathbb{A}_{K}$
if and only if every component of
![]() $X$
projects dominantly on
$X$
projects dominantly on
![]() $\mathbb{A}_{K}$
. For general
$\mathbb{A}_{K}$
. For general
![]() $X$
, we denote by
$X$
, we denote by
![]() ${\mathcal{F}}(X)$
the flat family obtained by removing any component which projects to a point in
${\mathcal{F}}(X)$
the flat family obtained by removing any component which projects to a point in
![]() $\mathbb{A}_{K}$
. For any
$\mathbb{A}_{K}$
. For any
![]() $\unicode[STIX]{x1D700}\in \mathbb{A}_{K}$
we denote by
$\unicode[STIX]{x1D700}\in \mathbb{A}_{K}$
we denote by
![]() $X_{\unicode[STIX]{x1D700}}$
the
$X_{\unicode[STIX]{x1D700}}$
the
![]() $\unicode[STIX]{x1D700}$
-fiber of
$\unicode[STIX]{x1D700}$
-fiber of
![]() $X$
.
$X$
.
Consider now a variety
![]() $X\subset N\times \mathbb{A}_{K}$
given by
$X\subset N\times \mathbb{A}_{K}$
given by
where
![]() $e$
denotes a coordinate on
$e$
denotes a coordinate on
![]() $\mathbb{A}_{K}$
. We say that
$\mathbb{A}_{K}$
. We say that
![]() $X$
is a generic complete intersection if the generic fiber
$X$
is a generic complete intersection if the generic fiber
![]() $X_{\unicode[STIX]{x1D700}}$
has pure codimension
$X_{\unicode[STIX]{x1D700}}$
has pure codimension
![]() $k$
. We define
$k$
. We define
![]() $\unicode[STIX]{x1D70F}(X)\subset N^{(1)}\times \mathbb{A}_{K}$
to be
$\unicode[STIX]{x1D70F}(X)\subset N^{(1)}\times \mathbb{A}_{K}$
to be
For generic
![]() $\unicode[STIX]{x1D700}\in K_{0}$
,
$\unicode[STIX]{x1D700}\in K_{0}$
,
![]() $\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}}$
is just
$\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}}$
is just
![]() $\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}})$
. The following subsection establishes a precise sense in which
$\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}})$
. The following subsection establishes a precise sense in which
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
, obtained as the limit of these generic fibers, approximates
$\unicode[STIX]{x1D70F}(X)_{0}$
, obtained as the limit of these generic fibers, approximates
![]() $(X_{0})^{(1)}$
.
$(X_{0})^{(1)}$
.
2.2 Approximation of the first prolongation
In this section it will be convenient for us to assume that the field
![]() $K$
has an analytic realization. We therefore assume that the field of constants
$K$
has an analytic realization. We therefore assume that the field of constants
![]() $K_{0}$
is a subfield of
$K_{0}$
is a subfield of
![]() $\mathbb{C}$
, and that all functions involved in the definition of any of the varieties we consider have been embedded in the field of meromorphic functions on the disc
$\mathbb{C}$
, and that all functions involved in the definition of any of the varieties we consider have been embedded in the field of meromorphic functions on the disc
![]() $\mathbb{D}$
(this is always possible by a result of Seidenberg [Reference SeidenbergSei58, Reference SeidenbergSei69]). Thus we may consider
$\mathbb{D}$
(this is always possible by a result of Seidenberg [Reference SeidenbergSei58, Reference SeidenbergSei69]). Thus we may consider
![]() $K$
-varieties as analytic sets.
$K$
-varieties as analytic sets.
We begin with a simple lemma.
Lemma 15. Let
![]() $X\subset N\times \mathbb{A}_{K}$
be a flat family, and
$X\subset N\times \mathbb{A}_{K}$
be a flat family, and
![]() $x\in X_{0}$
. Then for any sequence
$x\in X_{0}$
. Then for any sequence
![]() $\unicode[STIX]{x1D700}_{i}\in K_{0}$
with
$\unicode[STIX]{x1D700}_{i}\in K_{0}$
with
![]() $\unicode[STIX]{x1D700}_{i}\rightarrow 0$
, there exists a sequence of
$\unicode[STIX]{x1D700}_{i}\rightarrow 0$
, there exists a sequence of
![]() $K$
-points
$K$
-points
![]() $x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
, holomorphic in a common disc and converging uniformly to
$x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
, holomorphic in a common disc and converging uniformly to
![]() $x$
.
$x$
.
Proof. Intersecting with generic linear functionals vanishing at
![]() $x$
, one can reduce the problem to the case that
$x$
, one can reduce the problem to the case that
![]() $X$
is a curve. Moreover, changing coordinate
$X$
is a curve. Moreover, changing coordinate
![]() $e\rightarrow e^{\unicode[STIX]{x1D708}}$
, we may assume that the curve is irreducible, smooth and transversal to
$e\rightarrow e^{\unicode[STIX]{x1D708}}$
, we may assume that the curve is irreducible, smooth and transversal to
![]() $e$
at
$e$
at
![]() $x$
in the
$x$
in the
![]() $K$
-sense, i.e. for generic
$K$
-sense, i.e. for generic
![]() $t$
. We restrict the disc
$t$
. We restrict the disc
![]() $\mathbb{D}$
to make this true for every
$\mathbb{D}$
to make this true for every
![]() $t$
.
$t$
.
Consider the intersection
![]() $X\cap \{e=\unicode[STIX]{x1D700}_{i}\}$
. This is a zero-dimensional set, and for sufficiently small
$X\cap \{e=\unicode[STIX]{x1D700}_{i}\}$
. This is a zero-dimensional set, and for sufficiently small
![]() $\unicode[STIX]{x1D700}_{i}$
contains precisely one solution
$\unicode[STIX]{x1D700}_{i}$
contains precisely one solution
![]() $x_{i}$
near
$x_{i}$
near
![]() $x$
. All
$x$
. All
![]() $x_{i}$
are
$x_{i}$
are
![]() $K$
-points and, moreover, are in fact defined over the field of definition of
$K$
-points and, moreover, are in fact defined over the field of definition of
![]() $X$
. Therefore they may be viewed as (a priori, ramified) holomorphic functions on
$X$
. Therefore they may be viewed as (a priori, ramified) holomorphic functions on
![]() $\mathbb{D}$
. But in fact
$\mathbb{D}$
. But in fact
![]() $x_{i}(t)$
is well defined for
$x_{i}(t)$
is well defined for
![]() $t\in \mathbb{D}$
, and thus no ramification can occur and the functions
$t\in \mathbb{D}$
, and thus no ramification can occur and the functions
![]() $x_{i}(t)$
are holomorphic in
$x_{i}(t)$
are holomorphic in
![]() $\mathbb{D}$
. Finally,
$\mathbb{D}$
. Finally,
![]() $x_{i}$
converges pointwise to
$x_{i}$
converges pointwise to
![]() $x$
by definition, and it follows by standard arguments that convergence is uniform (perhaps on a smaller disc).◻
$x$
by definition, and it follows by standard arguments that convergence is uniform (perhaps on a smaller disc).◻
We remark that since the Zariski topology is coarser than the analytic
![]() $\mathbb{C}$
-topology, the converse also holds: if
$\mathbb{C}$
-topology, the converse also holds: if
![]() $x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
is a sequence of
$x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
is a sequence of
![]() $K$
points holomorphic on a disc
$K$
points holomorphic on a disc
![]() $\mathbb{D}$
and converging uniformly to
$\mathbb{D}$
and converging uniformly to
![]() $x\in K$
, then any Zariski closed set containing
$x\in K$
, then any Zariski closed set containing
![]() $x_{i}$
for every
$x_{i}$
for every
![]() $i$
must contain
$i$
must contain
![]() $x$
.
$x$
.
Proposition 16. Let
![]() $X$
be a generic complete intersection as in (19). Then we have
$X$
be a generic complete intersection as in (19). Then we have
![]() $(X_{0})^{(1)}\subset \unicode[STIX]{x1D70F}(X)_{0}$
.
$(X_{0})^{(1)}\subset \unicode[STIX]{x1D70F}(X)_{0}$
.
Proof. Since
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
is closed by definition, it is enough to prove that for every
$\unicode[STIX]{x1D70F}(X)_{0}$
is closed by definition, it is enough to prove that for every
![]() $x\in X_{0}$
, we have
$x\in X_{0}$
, we have
![]() $x^{(1)}\in \unicode[STIX]{x1D70F}(X)_{0}$
. Let
$x^{(1)}\in \unicode[STIX]{x1D70F}(X)_{0}$
. Let
![]() $x\in X_{0}$
. Since the family
$x\in X_{0}$
. Since the family
![]() $X$
is flat, we can choose by Lemma 15 a sequence
$X$
is flat, we can choose by Lemma 15 a sequence
![]() $x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
with
$x_{i}\in X_{\unicode[STIX]{x1D700}_{i}}$
with
![]() $\unicode[STIX]{x1D700}_{i}\in K_{0}$
and
$\unicode[STIX]{x1D700}_{i}\in K_{0}$
and
![]() $\unicode[STIX]{x1D700}_{i}\rightarrow 0$
, converging uniformly to
$\unicode[STIX]{x1D700}_{i}\rightarrow 0$
, converging uniformly to
![]() $x$
. Then
$x$
. Then
![]() $(x_{i})^{(1)}$
converges uniformly to
$(x_{i})^{(1)}$
converges uniformly to
![]() $x^{(l)}$
(in an appropriate disc). Since
$x^{(l)}$
(in an appropriate disc). Since
![]() $(X_{\unicode[STIX]{x1D700}_{i}})^{(1)}\subset \unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})$
and
$(X_{\unicode[STIX]{x1D700}_{i}})^{(1)}\subset \unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})$
and
![]() $\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})=\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
by the remark following (20), we have
$\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})=\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
by the remark following (20), we have
![]() $(x_{i})^{(1)}\in \unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
. Since
$(x_{i})^{(1)}\in \unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
. Since
![]() $\unicode[STIX]{x1D70F}(X)$
is closed we conclude that
$\unicode[STIX]{x1D70F}(X)$
is closed we conclude that
![]() $x^{(l)}\in \unicode[STIX]{x1D70F}(X)_{0}$
as claimed.◻
$x^{(l)}\in \unicode[STIX]{x1D70F}(X)_{0}$
as claimed.◻
For a variety
![]() $V\subset N$
as in (17), we can describe
$V\subset N$
as in (17), we can describe
![]() $\unicode[STIX]{x1D70F}(V)$
at effectively smooth points in terms of complex tangent spaces. Indeed, let
$\unicode[STIX]{x1D70F}(V)$
at effectively smooth points in terms of complex tangent spaces. Indeed, let
![]() $x\in V$
be an effectively smooth
$x\in V$
be an effectively smooth
![]() $K$
-point. Then
$K$
-point. Then
![]() $V$
is smooth as a complex variety at
$V$
is smooth as a complex variety at
![]() $x(t)$
for generic
$x(t)$
for generic
![]() $t$
and we have the equivalence
$t$
and we have the equivalence
where the right-hand side is understood to hold for generic
![]() $t$
. In particular, if
$t$
. In particular, if
![]() $V$
is any variety then one can choose a system of equations such that it becomes effectively smooth at every smooth point. Thus, since we know that
$V$
is any variety then one can choose a system of equations such that it becomes effectively smooth at every smooth point. Thus, since we know that
![]() $\unicode[STIX]{x1D70F}(V)$
agrees with
$\unicode[STIX]{x1D70F}(V)$
agrees with
![]() $V^{(1)}$
over the effectively smooth locus, we conclude that for every smooth point
$V^{(1)}$
over the effectively smooth locus, we conclude that for every smooth point
![]() $x\in V$
we also have
$x\in V$
we also have
The following proposition establishes a partial converse to Proposition 16.
Proposition 17. Let
![]() $X$
be a generic complete intersection as in (19) such that the generic fiber
$X$
be a generic complete intersection as in (19) such that the generic fiber
![]() $X_{\unicode[STIX]{x1D700}}$
is effectively smooth. Then there is an open dense set
$X_{\unicode[STIX]{x1D700}}$
is effectively smooth. Then there is an open dense set
![]() $U\subset X_{0}$
such that
$U\subset X_{0}$
such that
Before proving this proposition, we illustrate with the following example.

Figure 1. Degeneration of
![]() $\unicode[STIX]{x1D70F}(X)$
in Example 18.
$\unicode[STIX]{x1D70F}(X)$
in Example 18.
Example 18. Consider
![]() $X\subset \mathbb{A}_{K}^{2}\times \mathbb{A}_{K}$
given by
$X\subset \mathbb{A}_{K}^{2}\times \mathbb{A}_{K}$
given by
![]() $y^{2}=ex$
(see Figure 1). Since the family is defined by an equation with constant coefficients,
$y^{2}=ex$
(see Figure 1). Since the family is defined by an equation with constant coefficients,
![]() $(X_{0})^{(1)}$
agrees with the tangent bundle of
$(X_{0})^{(1)}$
agrees with the tangent bundle of
![]() $X_{0}$
. For generic
$X_{0}$
. For generic
![]() $\unicode[STIX]{x1D700}$
, the fiber
$\unicode[STIX]{x1D700}$
, the fiber
![]() $X_{\unicode[STIX]{x1D700}}$
is an effectively smooth parabola, and for
$X_{\unicode[STIX]{x1D700}}$
is an effectively smooth parabola, and for
![]() $\unicode[STIX]{x1D700}$
constant
$\unicode[STIX]{x1D700}$
constant
![]() $\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}}$
agrees with the tangent bundle of this parabola.
$\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}}$
agrees with the tangent bundle of this parabola.
The fiber
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
is the flat limit of
$\unicode[STIX]{x1D70F}(X)_{0}$
is the flat limit of
![]() $\unicode[STIX]{x1D70F}(X)_{e}$
. Since
$\unicode[STIX]{x1D70F}(X)_{e}$
. Since
![]() $\unicode[STIX]{x2202}_{y}$
is tangent to
$\unicode[STIX]{x2202}_{y}$
is tangent to
![]() $X_{\unicode[STIX]{x1D700}}$
at
$X_{\unicode[STIX]{x1D700}}$
at
![]() $(x,y)=(0,0)$
for any
$(x,y)=(0,0)$
for any
![]() $\unicode[STIX]{x1D700}$
, the fiber of
$\unicode[STIX]{x1D700}$
, the fiber of
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
over this point contains
$\unicode[STIX]{x1D70F}(X)_{0}$
over this point contains
![]() $\unicode[STIX]{x2202}_{y}$
. Thus
$\unicode[STIX]{x2202}_{y}$
. Thus
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
is strictly larger than the tangent bundle of
$\unicode[STIX]{x1D70F}(X)_{0}$
is strictly larger than the tangent bundle of
![]() $X_{0}$
. However, over any point of
$X_{0}$
. However, over any point of
![]() $U:=X_{0}\setminus \{(0,0)\}$
, one can easily check that the limit of
$U:=X_{0}\setminus \{(0,0)\}$
, one can easily check that the limit of
![]() $X_{\unicode[STIX]{x1D700}}$
agrees with the tangent bundle of
$X_{\unicode[STIX]{x1D700}}$
agrees with the tangent bundle of
![]() $X_{0}$
.
$X_{0}$
.
Proof of Proposition 17.
To avoid confusion, in this proof we make the convention that
![]() $p$
denotes
$p$
denotes
![]() $\mathbb{C}$
-points, whereas
$\mathbb{C}$
-points, whereas
![]() $x$
denotes
$x$
denotes
![]() $K$
-points.
$K$
-points.
Since the map
![]() $e$
is flat on
$e$
is flat on
![]() $X$
(over
$X$
(over
![]() $K$
), it follows that for generic
$K$
), it follows that for generic
![]() $t$
there are no components of
$t$
there are no components of
![]() $X$
contained in the
$X$
contained in the
![]() $e=0$
fiber. After restricting to a disc where this holds, the map
$e=0$
fiber. After restricting to a disc where this holds, the map
![]() $e:X\rightarrow \mathbb{C}$
can be viewed as a flat map over
$e:X\rightarrow \mathbb{C}$
can be viewed as a flat map over
![]() $\mathbb{C}$
. By a theorem of Hironaka [Reference HironakaHir77], there exists an analytic stratification
$\mathbb{C}$
. By a theorem of Hironaka [Reference HironakaHir77], there exists an analytic stratification
![]() $\{Z_{\unicode[STIX]{x1D6FC}}\}$
of
$\{Z_{\unicode[STIX]{x1D6FC}}\}$
of
![]() $X_{0}$
with the following property: for any sequence of points
$X_{0}$
with the following property: for any sequence of points
![]() $p_{i}\in X$
converging to
$p_{i}\in X$
converging to
![]() $p\in Z_{\unicode[STIX]{x1D6FC}}$
, if
$p\in Z_{\unicode[STIX]{x1D6FC}}$
, if
![]() $X_{e(p_{i})}$
is smooth at
$X_{e(p_{i})}$
is smooth at
![]() $p_{i}$
and
$p_{i}$
and
![]() $T_{p_{i}}X_{e(p_{i})}$
converges to a limit
$T_{p_{i}}X_{e(p_{i})}$
converges to a limit
![]() $T$
, then
$T$
, then
![]() $T_{p}Z_{\unicode[STIX]{x1D6FC}}\subset T$
. This is a somewhat weaker form of Thom’s
$T_{p}Z_{\unicode[STIX]{x1D6FC}}\subset T$
. This is a somewhat weaker form of Thom’s
![]() $A_{e}$
-condition, which will suffice for our purposes. We fix such a stratification, and let
$A_{e}$
-condition, which will suffice for our purposes. We fix such a stratification, and let
![]() $Z_{0}$
denote the (union of) top-dimensional strata.
$Z_{0}$
denote the (union of) top-dimensional strata.
The following observation is the key geometric idea for the proof. Let
![]() $p_{i}\in X$
be any sequence of points converging to
$p_{i}\in X$
be any sequence of points converging to
![]() $p\in Z_{0}$
with
$p\in Z_{0}$
with
![]() $X_{e(p_{i})}$
smooth at
$X_{e(p_{i})}$
smooth at
![]() $p_{i}$
and
$p_{i}$
and
![]() $v_{i}\in T_{p_{i}}X_{e(p_{i})}$
a sequence of tangent vectors converging to a vector
$v_{i}\in T_{p_{i}}X_{e(p_{i})}$
a sequence of tangent vectors converging to a vector
![]() $v$
. Then
$v$
. Then
![]() $v\in T_{p}X_{0}$
. Indeed, one can always pass to a subsequence such that
$v\in T_{p}X_{0}$
. Indeed, one can always pass to a subsequence such that
![]() $T_{p_{i}}X_{e(p_{i})}$
converges to some limit
$T_{p_{i}}X_{e(p_{i})}$
converges to some limit
![]() $T$
, and hence
$T$
, and hence
![]() $T_{p}Z_{0}\subset T$
. But since the dimensions of these sets agree, in fact
$T_{p}Z_{0}\subset T$
. But since the dimensions of these sets agree, in fact
![]() $T_{p}X_{0}=T_{p}Z_{0}=T$
, and in particular
$T_{p}X_{0}=T_{p}Z_{0}=T$
, and in particular
![]() $v\in T$
implies
$v\in T$
implies
![]() $v\in T_{p}X_{0}$
.
$v\in T_{p}X_{0}$
.
We know by Proposition 16 that
![]() $(X_{0})^{(1)}\subset \unicode[STIX]{x1D70F}(X)_{0}$
. The set of points in
$(X_{0})^{(1)}\subset \unicode[STIX]{x1D70F}(X)_{0}$
. The set of points in
![]() $X_{0}$
such that the
$X_{0}$
such that the
![]() $\unicode[STIX]{x1D70B}$
-fibers of these two sets are equal is
$\unicode[STIX]{x1D70B}$
-fibers of these two sets are equal is
![]() $K$
-constructible. Thus, if it does not contain an open dense set it must be contained in a closed set of strictly smaller dimension. Therefore it will suffice to establish the claim over any analytic open dense set
$K$
-constructible. Thus, if it does not contain an open dense set it must be contained in a closed set of strictly smaller dimension. Therefore it will suffice to establish the claim over any analytic open dense set
![]() $U$
. We will establish it with
$U$
. We will establish it with
![]() $U=Z_{0}$
. Thus, let
$U=Z_{0}$
. Thus, let
![]() $(x,v)\in \unicode[STIX]{x1D70F}(X)_{0}$
with
$(x,v)\in \unicode[STIX]{x1D70F}(X)_{0}$
with
![]() $x\in Z_{0}$
, and we will prove that
$x\in Z_{0}$
, and we will prove that
![]() $(x,v)\in (X_{0})^{(1)}$
.
$(x,v)\in (X_{0})^{(1)}$
.
Since
![]() $\unicode[STIX]{x1D70F}(X)$
is flat by definition, we may by Lemma 15 choose a sequence
$\unicode[STIX]{x1D70F}(X)$
is flat by definition, we may by Lemma 15 choose a sequence
![]() $\unicode[STIX]{x1D700}_{i}\in K_{0}$
with
$\unicode[STIX]{x1D700}_{i}\in K_{0}$
with
![]() $\unicode[STIX]{x1D700}_{i}\rightarrow 0$
and a sequence
$\unicode[STIX]{x1D700}_{i}\rightarrow 0$
and a sequence
![]() $(x_{i},v_{i})\in \unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
such that
$(x_{i},v_{i})\in \unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}$
such that
![]() $(x_{i},v_{i})$
are defined in a common disc
$(x_{i},v_{i})$
are defined in a common disc
![]() $\mathbb{D}$
and converge uniformly to
$\mathbb{D}$
and converge uniformly to
![]() $(x,v)$
. By assumption, we may take the fibers
$(x,v)$
. By assumption, we may take the fibers
![]() $X_{\unicode[STIX]{x1D700}_{i}}$
to be effectively smooth. Also, by the remark following (20) we may assume that
$X_{\unicode[STIX]{x1D700}_{i}}$
to be effectively smooth. Also, by the remark following (20) we may assume that
![]() $\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}=\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})$
. We conclude from (21) that
$\unicode[STIX]{x1D70F}(X)_{\unicode[STIX]{x1D700}_{i}}=\unicode[STIX]{x1D70F}(X_{\unicode[STIX]{x1D700}_{i}})$
. We conclude from (21) that
for generic
![]() $t$
.
$t$
.
For
![]() $t$
outside a countable set, each fiber
$t$
outside a countable set, each fiber
![]() $X_{\unicode[STIX]{x1D700}_{i}}$
is effectively smooth (over
$X_{\unicode[STIX]{x1D700}_{i}}$
is effectively smooth (over
![]() $\mathbb{C}$
) at
$\mathbb{C}$
) at
![]() $x_{i}(t)$
. By the key geometric observation above it now follows that
$x_{i}(t)$
. By the key geometric observation above it now follows that
for generic
![]() $t$
. Thus (22) gives
$t$
. Thus (22) gives
![]() $(x,v)\in (X_{0})^{(1)}$
as claimed.◻
$(x,v)\in (X_{0})^{(1)}$
as claimed.◻
Corollary 19. Let
![]() $X$
be a generic complete intersection as in (19) and suppose that the generic fiber
$X$
be a generic complete intersection as in (19) and suppose that the generic fiber
![]() $X_{\unicode[STIX]{x1D700}}$
is effectively smooth. Then every component of
$X_{\unicode[STIX]{x1D700}}$
is effectively smooth. Then every component of
![]() $(X_{0})^{(1)}$
is a component of
$(X_{0})^{(1)}$
is a component of
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
.
$\unicode[STIX]{x1D70F}(X)_{0}$
.
Proof. Indeed, if
![]() $Z_{1},\ldots ,Z_{r}$
denote the components of
$Z_{1},\ldots ,Z_{r}$
denote the components of
![]() $X_{0}$
then they each have codimension
$X_{0}$
then they each have codimension
![]() $k$
(since
$k$
(since
![]() $X$
is a flat family of pure codimension
$X$
is a flat family of pure codimension
![]() $k$
), and
$k$
), and
![]() $Z_{i}^{(1)}$
are the components of
$Z_{i}^{(1)}$
are the components of
![]() $(X_{0})^{(1)}$
. In particular,
$(X_{0})^{(1)}$
. In particular,
![]() $\unicode[STIX]{x1D70B}^{-1}(U)$
is dense in each
$\unicode[STIX]{x1D70B}^{-1}(U)$
is dense in each
![]() $Z_{i}^{(1)}$
(for
$Z_{i}^{(1)}$
(for
![]() $U$
given in Proposition 17), and since
$U$
given in Proposition 17), and since
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
agrees with
$\unicode[STIX]{x1D70F}(X)_{0}$
agrees with
![]() $(X_{0})^{(1)}$
over
$(X_{0})^{(1)}$
over
![]() $\unicode[STIX]{x1D70B}^{-1}(U)$
it follows that each
$\unicode[STIX]{x1D70B}^{-1}(U)$
it follows that each
![]() $Z_{i}^{(1)}$
is also a component of
$Z_{i}^{(1)}$
is also a component of
![]() $\unicode[STIX]{x1D70F}(X)_{0}$
.◻
$\unicode[STIX]{x1D70F}(X)_{0}$
.◻
3 Constructions with flat families
Once again, in this section we denote the ambient space by
![]() $N$
and its dimension by
$N$
and its dimension by
![]() $n$
. The reader should keep in mind that eventually we will take this ambient space to be
$n$
. The reader should keep in mind that eventually we will take this ambient space to be
![]() $M^{(l)}$
or its open dense subset
$M^{(l)}$
or its open dense subset
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
$\unicode[STIX]{x1D6FA}^{(l)}$
. To avoid confusion we denote the coordinates on
![]() $N$
by
$N$
by
![]() $\unicode[STIX]{x1D701}$
.
$\unicode[STIX]{x1D701}$
.
When speaking about the Newton polytope of a polynomial in
![]() $K[\unicode[STIX]{x1D701},e]$
we mean the Newton polytope in the
$K[\unicode[STIX]{x1D701},e]$
we mean the Newton polytope in the
![]() $\unicode[STIX]{x1D701}$
variables obtained for a generic value of
$\unicode[STIX]{x1D701}$
variables obtained for a generic value of
![]() $e$
.
$e$
.
3.1 General lemmas on perturbations and intersections in flat families
The following proposition shows that the
![]() $0$
-fiber of a flat family is not changed if one makes a sufficiently small perturbation of the family, i.e. a perturbation of sufficiently high order in
$0$
-fiber of a flat family is not changed if one makes a sufficiently small perturbation of the family, i.e. a perturbation of sufficiently high order in
![]() $e$
.
$e$
.
Proposition 20. Let
![]() $X\subset N\times \mathbb{A}_{K}^{2}$
be a variety, and suppose that every component of
$X\subset N\times \mathbb{A}_{K}^{2}$
be a variety, and suppose that every component of
![]() $X$
projects dominantly on
$X$
projects dominantly on
![]() $\mathbb{A}_{K}^{2}$
. Then the flat limit at the origin of
$\mathbb{A}_{K}^{2}$
. Then the flat limit at the origin of
![]() $X_{s,t}$
(as a variety) along
$X_{s,t}$
(as a variety) along
![]() $\unicode[STIX]{x1D6E4}=\{t=0\}\subset \mathbb{A}_{K}^{2}$
is the same as the flat limit at the origin along any smooth curve
$\unicode[STIX]{x1D6E4}=\{t=0\}\subset \mathbb{A}_{K}^{2}$
is the same as the flat limit at the origin along any smooth curve
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \mathbb{A}_{K}^{2}$
sufficiently tangent to
$\unicode[STIX]{x1D6E4}^{\prime }\subset \mathbb{A}_{K}^{2}$
sufficiently tangent to
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Proof. We may assume that
![]() $X$
is irreducible. Denote the projection to
$X$
is irreducible. Denote the projection to
![]() $\mathbb{A}_{K}^{2}$
by
$\mathbb{A}_{K}^{2}$
by
![]() $\unicode[STIX]{x1D702}$
. Recall that
$\unicode[STIX]{x1D702}$
. Recall that
![]() $N$
is an open dense subset of some projective space
$N$
is an open dense subset of some projective space
![]() $\mathbb{C}P^{S}$
. Let
$\mathbb{C}P^{S}$
. Let
![]() $\bar{X}$
denote the closure of
$\bar{X}$
denote the closure of
![]() $X$
in
$X$
in
![]() $\mathbb{C}P^{S}\times \mathbb{A}_{K}^{2}$
, which clearly projects dominantly to
$\mathbb{C}P^{S}\times \mathbb{A}_{K}^{2}$
, which clearly projects dominantly to
![]() $\mathbb{A}_{K}^{2}$
as well.
$\mathbb{A}_{K}^{2}$
as well.
Consider the map
![]() $\unicode[STIX]{x1D6F7}$
taking a pair
$\unicode[STIX]{x1D6F7}$
taking a pair
![]() $(s,t)$
to the fiber
$(s,t)$
to the fiber
![]() $X_{s,t}:=\bar{X}\cap \unicode[STIX]{x1D702}^{-1}(s,t)$
with its cycle structure in the Chow variety parametrizing cycles of degree
$X_{s,t}:=\bar{X}\cap \unicode[STIX]{x1D702}^{-1}(s,t)$
with its cycle structure in the Chow variety parametrizing cycles of degree
![]() $\deg X$
in
$\deg X$
in
![]() $\mathbb{C}P^{S}$
. This is a rational map defined over the (open dense) locus
$\mathbb{C}P^{S}$
. This is a rational map defined over the (open dense) locus
![]() $U=\mathbb{A}_{K}^{2}\setminus \unicode[STIX]{x1D6F4}$
such that the intersection above is proper. We have
$U=\mathbb{A}_{K}^{2}\setminus \unicode[STIX]{x1D6F4}$
such that the intersection above is proper. We have
![]() $\operatorname{codim}\unicode[STIX]{x1D6F4}\geqslant 2$
(otherwise
$\operatorname{codim}\unicode[STIX]{x1D6F4}\geqslant 2$
(otherwise
![]() $\dim \unicode[STIX]{x1D702}^{-1}(\unicode[STIX]{x1D6F4})=\dim X$
, which is ruled out by the hypotheses). Thus
$\dim \unicode[STIX]{x1D702}^{-1}(\unicode[STIX]{x1D6F4})=\dim X$
, which is ruled out by the hypotheses). Thus
![]() $\unicode[STIX]{x1D6F7}$
is defined on both
$\unicode[STIX]{x1D6F7}$
is defined on both
![]() $\unicode[STIX]{x1D6E4}$
and
$\unicode[STIX]{x1D6E4}$
and
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
except for possibly finitely many exceptions where they intersect
$\unicode[STIX]{x1D6E4}^{\prime }$
except for possibly finitely many exceptions where they intersect
![]() $\unicode[STIX]{x1D6F4}$
.
$\unicode[STIX]{x1D6F4}$
.
In projective coordinates on the Chow variety, we have
where
![]() $[\widetilde{X}]$
denotes the Chow form of the flat limit of
$[\widetilde{X}]$
denotes the Chow form of the flat limit of
![]() $X_{s,t}$
along
$X_{s,t}$
along
![]() $\unicode[STIX]{x1D6E4}$
(with its cycle structure). Thus
$\unicode[STIX]{x1D6E4}$
(with its cycle structure). Thus
We see that if
![]() $t=O(s^{\unicode[STIX]{x1D708}+1})$
along
$t=O(s^{\unicode[STIX]{x1D708}+1})$
along
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
then the limit of
$\unicode[STIX]{x1D6E4}^{\prime }$
then the limit of
![]() $X_{s,t}$
along
$X_{s,t}$
along
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
is also equal to
$\unicode[STIX]{x1D6E4}^{\prime }$
is also equal to
![]() $[\widetilde{X}]$
as a cycle. In particular, these cycles intersect
$[\widetilde{X}]$
as a cycle. In particular, these cycles intersect
![]() $N$
in the same set, proving the claim.◻
$N$
in the same set, proving the claim.◻
Remark 21. Let
![]() $U$
denote a Zariski open subset in the space of
$U$
denote a Zariski open subset in the space of
![]() $n$
-tuples of polynomials with a given Newton polytope. Proposition 20 implies, in particular, that one may deform a given complete intersection family (19) to make
$n$
-tuples of polynomials with a given Newton polytope. Proposition 20 implies, in particular, that one may deform a given complete intersection family (19) to make
![]() $P_{i}(\unicode[STIX]{x1D701},e)\in U$
for generic values of
$P_{i}(\unicode[STIX]{x1D701},e)\in U$
for generic values of
![]() $e$
, without changing the fiber
$e$
, without changing the fiber
![]() $X_{0}$
. Indeed, consider
$X_{0}$
. Indeed, consider
![]() $\widetilde{P}_{i}=P_{i}+sQ_{i}$
where
$\widetilde{P}_{i}=P_{i}+sQ_{i}$
where
![]() $Q_{i}$
denotes some tuple of polynomials from the space. Then taking
$Q_{i}$
denotes some tuple of polynomials from the space. Then taking
![]() $s=e^{\unicode[STIX]{x1D708}}$
for sufficiently large
$s=e^{\unicode[STIX]{x1D708}}$
for sufficiently large
![]() $\unicode[STIX]{x1D708}$
ensures that the families defined by
$\unicode[STIX]{x1D708}$
ensures that the families defined by
![]() $\{P_{i}\}$
and
$\{P_{i}\}$
and
![]() $\{\widetilde{P}_{i}\}$
have the same
$\{\widetilde{P}_{i}\}$
have the same
![]() $0$
-fiber, whereas an appropriate (generic) choice of
$0$
-fiber, whereas an appropriate (generic) choice of
![]() $Q_{i}$
ensures that
$Q_{i}$
ensures that
![]() $\{\widetilde{P}_{i}\}\in U$
for generic
$\{\widetilde{P}_{i}\}\in U$
for generic
![]() $e$
.
$e$
.
For instance, in conjunction with the Bertini theorem, this implies that one can make the generic fiber effectively smooth.
If
![]() $X$
is a flat family and
$X$
is a flat family and
![]() $P\in K[\unicode[STIX]{x1D701}]$
is such that
$P\in K[\unicode[STIX]{x1D701}]$
is such that
![]() $\{P=0\}$
intersects
$\{P=0\}$
intersects
![]() $X_{0}$
properly, then the family
$X_{0}$
properly, then the family
![]() $Y={\mathcal{F}}\big[X\cap \{P=0\}\big]$
satisfies
$Y={\mathcal{F}}\big[X\cap \{P=0\}\big]$
satisfies
![]() $Y_{0}=X_{0}\cap \{P=0\}$
. However, if the intersection is not proper, one cannot in general predict the structure of
$Y_{0}=X_{0}\cap \{P=0\}$
. However, if the intersection is not proper, one cannot in general predict the structure of
![]() $Y_{0}$
. The following proposition shows that under a technical modification, one can guarantee that
$Y_{0}$
. The following proposition shows that under a technical modification, one can guarantee that
![]() $Y_{0}$
is given by the intersection between
$Y_{0}$
is given by the intersection between
![]() $\{P=0\}$
and those components of
$\{P=0\}$
and those components of
![]() $X_{0}$
that meet it properly.
$X_{0}$
that meet it properly.
Proposition 22. Let
![]() $X\subset N\times \mathbb{A}_{K}$
be a generic complete intersection and
$X\subset N\times \mathbb{A}_{K}$
be a generic complete intersection and
![]() $P\in K[\unicode[STIX]{x1D701}]$
. Define
$P\in K[\unicode[STIX]{x1D701}]$
. Define
![]() $Y,\widetilde{Y}$
by
$Y,\widetilde{Y}$
by
where
![]() $\unicode[STIX]{x1D708}$
is a sufficiently large natural number.
$\unicode[STIX]{x1D708}$
is a sufficiently large natural number.
Then
![]() $\widetilde{Y}_{0}=Y_{0}$
. In particular, if
$\widetilde{Y}_{0}=Y_{0}$
. In particular, if
![]() $X_{0}=C\cup C^{\prime }$
where
$X_{0}=C\cup C^{\prime }$
where
![]() $C^{\prime }$
denotes the union of components of
$C^{\prime }$
denotes the union of components of
![]() $X_{0}$
where
$X_{0}$
where
![]() $P$
vanishes identically and
$P$
vanishes identically and
![]() $C$
the rest, then
$C$
the rest, then
![]() $Y_{0}=C\cap \{P=0\}$
.
$Y_{0}=C\cap \{P=0\}$
.
Proof. The first part of the statement is simply Proposition 20 applied to the family
![]() $(X\times \mathbb{A}_{K}^{s})\cap \{P=s\}$
(with
$(X\times \mathbb{A}_{K}^{s})\cap \{P=s\}$
(with
![]() $e$
in place of
$e$
in place of
![]() $t$
). For the second part it suffices to compute
$t$
). For the second part it suffices to compute
![]() $\widetilde{Y}_{0}$
by noting that
$\widetilde{Y}_{0}$
by noting that
![]() $\{P=e^{1/\unicode[STIX]{x1D708}}\}$
intersects
$\{P=e^{1/\unicode[STIX]{x1D708}}\}$
intersects
![]() $C$
properly and does not intersect
$C$
properly and does not intersect
![]() $C^{\prime }$
at all (in the affine space).◻
$C^{\prime }$
at all (in the affine space).◻

Figure 2. The different families in Example 23.
We remark that the use of the ramified factor
![]() $e^{1/\unicode[STIX]{x1D708}}$
is merely a notational convenience, to avoid reparametrizing the original family
$e^{1/\unicode[STIX]{x1D708}}$
is merely a notational convenience, to avoid reparametrizing the original family
![]() $X$
. One could of course obtain an honest polynomial family by passing to a new deformation parameter.
$X$
. One could of course obtain an honest polynomial family by passing to a new deformation parameter.
Example 23. Consider
![]() $X\subset \mathbb{C}^{2}\times \mathbb{C}$
given by
$X\subset \mathbb{C}^{2}\times \mathbb{C}$
given by
![]() $xy=e$
, and
$xy=e$
, and
![]() $P=x$
(see Figure 2). Then
$P=x$
(see Figure 2). Then
![]() $X_{0}$
has two components, the
$X_{0}$
has two components, the
![]() $x$
- and
$x$
- and
![]() $y$
-axes. The former intersects
$y$
-axes. The former intersects
![]() $\{P=0\}$
properly at the origin, whereas the latter intersects
$\{P=0\}$
properly at the origin, whereas the latter intersects
![]() $\{P=0\}$
non-properly.
$\{P=0\}$
non-properly.
If we consider the family
![]() $Y={\mathcal{F}}(X\cap \{P=0\})$
we obtain
$Y={\mathcal{F}}(X\cap \{P=0\})$
we obtain
![]() $Y_{0}=\emptyset$
. If we consider
$Y_{0}=\emptyset$
. If we consider
![]() $Y={\mathcal{F}}(X\cap \{P=e\})$
we obtain
$Y={\mathcal{F}}(X\cap \{P=e\})$
we obtain
![]() $Y_{0}=\{(0,1)\}$
. Finally, if we consider
$Y_{0}=\{(0,1)\}$
. Finally, if we consider
![]() $Y={\mathcal{F}}(X\cap \{P=e^{\unicode[STIX]{x1D6FC}}\})$
where
$Y={\mathcal{F}}(X\cap \{P=e^{\unicode[STIX]{x1D6FC}}\})$
where
![]() $0<\unicode[STIX]{x1D6FC}<1$
, then we obtain
$0<\unicode[STIX]{x1D6FC}<1$
, then we obtain
![]() $Y=\{(0,0)\}$
, which is the intersection between the
$Y=\{(0,0)\}$
, which is the intersection between the
![]() $x$
-axis and
$x$
-axis and
![]() $\{P=0\}$
as predicted by Proposition 22.
$\{P=0\}$
as predicted by Proposition 22.
3.2 Projections and reduction of dimension
We begin with a simple lemma on linear elimination of variables. Let
![]() $P\in K[\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}]$
be a polynomial with
$P\in K[\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}]$
be a polynomial with
![]() $\deg _{\unicode[STIX]{x1D701}^{(1)}}P\leqslant 1$
. The homogenization
$\deg _{\unicode[STIX]{x1D701}^{(1)}}P\leqslant 1$
. The homogenization
![]() $\widetilde{P}$
of
$\widetilde{P}$
of
![]() $P$
is the polynomial in one extra variable,
$P$
is the polynomial in one extra variable,
![]() $\unicode[STIX]{x1D701}_{0}^{(1)},\ldots ,\unicode[STIX]{x1D701}_{n}^{(1)}$
, where the free term of
$\unicode[STIX]{x1D701}_{0}^{(1)},\ldots ,\unicode[STIX]{x1D701}_{n}^{(1)}$
, where the free term of
![]() $P$
is multiplied by
$P$
is multiplied by
![]() $\unicode[STIX]{x1D701}_{0}^{(1)}$
.
$\unicode[STIX]{x1D701}_{0}^{(1)}$
.
Lemma 24. Let
and let
![]() $\widetilde{P}_{1},\ldots ,\widetilde{P}_{n+1}$
denote their homogenization, and
$\widetilde{P}_{1},\ldots ,\widetilde{P}_{n+1}$
denote their homogenization, and
![]() $W\subset N\times \mathbb{P}_{K}^{n}$
the variety they define.
$W\subset N\times \mathbb{P}_{K}^{n}$
the variety they define.
Let
![]() $R$
denote the determinant of the
$R$
denote the determinant of the
![]() $(n+1)\times (n+1)$
matrix whose
$(n+1)\times (n+1)$
matrix whose
![]() $j$
th row is given by the
$j$
th row is given by the
![]() $n+1$
coefficients of
$n+1$
coefficients of
![]() $\widetilde{P}_{j}$
, viewed as a linear form in the variables
$\widetilde{P}_{j}$
, viewed as a linear form in the variables
![]() $\unicode[STIX]{x1D701}_{0}^{(1)},\ldots ,\unicode[STIX]{x1D701}_{n}^{(1)}$
. Then
$\unicode[STIX]{x1D701}_{0}^{(1)},\ldots ,\unicode[STIX]{x1D701}_{n}^{(1)}$
. Then
![]() $\unicode[STIX]{x1D6E5}(R)\subset \sum _{j=1}^{n+1}\unicode[STIX]{x1D6E5}_{j}$
and
$\unicode[STIX]{x1D6E5}(R)\subset \sum _{j=1}^{n+1}\unicode[STIX]{x1D6E5}_{j}$
and
![]() $\unicode[STIX]{x1D70B}(W)=\{R=0\}$
.
$\unicode[STIX]{x1D70B}(W)=\{R=0\}$
.
Proof. The points of
![]() $\unicode[STIX]{x1D70B}(W)$
correspond to points
$\unicode[STIX]{x1D70B}(W)$
correspond to points
![]() $\unicode[STIX]{x1D701}\in N$
such that the linear forms
$\unicode[STIX]{x1D701}\in N$
such that the linear forms
![]() $\widetilde{P}_{j}$
have a common kernel in
$\widetilde{P}_{j}$
have a common kernel in
![]() $\mathbb{P}_{K}^{n}$
– the locus of which corresponds to the zeros of the determinant
$\mathbb{P}_{K}^{n}$
– the locus of which corresponds to the zeros of the determinant
![]() $R$
.◻
$R$
.◻
Lemma 25. Let
and
define a generic complete intersection
![]() $X\subset N^{(1)}\times \mathbb{A}_{K}$
,
$X\subset N^{(1)}\times \mathbb{A}_{K}$
,
Denote by
![]() $W$
the union of the components
$W$
the union of the components
![]() $C$
of
$C$
of
![]() $X_{0}$
such that
$X_{0}$
such that
![]() $\operatorname{codim}\unicode[STIX]{x1D70B}(C)>k$
. Then there exist
$\operatorname{codim}\unicode[STIX]{x1D70B}(C)>k$
. Then there exist
![]() $R\in K[\unicode[STIX]{x1D701},e]$
and a generic complete intersection
$R\in K[\unicode[STIX]{x1D701},e]$
and a generic complete intersection
![]() $Y$
,
$Y$
,
such that
![]() $\unicode[STIX]{x1D70B}(W)\subset Y_{0}$
.
$\unicode[STIX]{x1D70B}(W)\subset Y_{0}$
.
Proof. We prove the claim by reverse induction on
![]() $l$
, starting with the case
$l$
, starting with the case
![]() $l\geqslant n+1$
. In this case
$l\geqslant n+1$
. In this case
![]() $W=X_{0}$
. We replace
$W=X_{0}$
. We replace
![]() $Q_{1},\ldots ,Q_{n+1}$
by their small generic perturbation (keeping the same Newton polytope). By Proposition 20 this does not change
$Q_{1},\ldots ,Q_{n+1}$
by their small generic perturbation (keeping the same Newton polytope). By Proposition 20 this does not change
![]() $X_{0}$
. We can thus assume without loss of generality that the generic fiber of
$X_{0}$
. We can thus assume without loss of generality that the generic fiber of
![]() $V\subset N\times \mathbb{P}_{K}^{n}\times \mathbb{A}_{K}$
cut out by
$V\subset N\times \mathbb{P}_{K}^{n}\times \mathbb{A}_{K}$
cut out by
![]() $P_{1},\ldots ,P_{k}$
and the homogenizations of
$P_{1},\ldots ,P_{k}$
and the homogenizations of
![]() $Q_{1},\ldots ,Q_{n+1}$
has codimension
$Q_{1},\ldots ,Q_{n+1}$
has codimension
![]() $n+k+1$
. Applying Lemma 24 to
$n+k+1$
. Applying Lemma 24 to
![]() $Q_{1},\ldots ,Q_{n+1}$
, we thus obtain
$Q_{1},\ldots ,Q_{n+1}$
, we thus obtain
![]() $R$
giving a generic complete intersection (34). By construction the generic fiber
$R$
giving a generic complete intersection (34). By construction the generic fiber
![]() $Y_{\unicode[STIX]{x1D700}}$
contains
$Y_{\unicode[STIX]{x1D700}}$
contains
![]() $\unicode[STIX]{x1D70B}(X_{\unicode[STIX]{x1D700}})$
, and it follows that
$\unicode[STIX]{x1D70B}(X_{\unicode[STIX]{x1D700}})$
, and it follows that
![]() $Y_{0}$
contains
$Y_{0}$
contains
![]() $\unicode[STIX]{x1D70B}(X_{0})$
as claimed.
$\unicode[STIX]{x1D70B}(X_{0})$
as claimed.
We now consider the case
![]() $l\leqslant n$
. Then for any component
$l\leqslant n$
. Then for any component
![]() $C\subset W$
, the generic fiber of
$C\subset W$
, the generic fiber of
![]() $\unicode[STIX]{x1D70B}:C\rightarrow \unicode[STIX]{x1D70B}(C)$
has dimension at least
$\unicode[STIX]{x1D70B}:C\rightarrow \unicode[STIX]{x1D70B}(C)$
has dimension at least
![]() $n+1-l\geqslant 1$
. Let
$n+1-l\geqslant 1$
. Let
![]() $\ell$
be a generic affine-linear form in the
$\ell$
be a generic affine-linear form in the
![]() $\unicode[STIX]{x1D701}^{(1)}$
variables. Then
$\unicode[STIX]{x1D701}^{(1)}$
variables. Then
![]() $\{\ell =0\}$
meets
$\{\ell =0\}$
meets
![]() $X_{0}$
properly, and, taking
$X_{0}$
properly, and, taking
![]() $Q_{l+1}$
to be
$Q_{l+1}$
to be
![]() $\ell$
, we obtain a new family
$\ell$
, we obtain a new family
![]() $X^{\prime }$
such that
$X^{\prime }$
such that
Moreover,
since
![]() $\{\ell =0\}$
meets the generic fiber of
$\{\ell =0\}$
meets the generic fiber of
![]() $\unicode[STIX]{x1D70B}:C\rightarrow \unicode[STIX]{x1D70B}(C)$
. Since this is true for any component
$\unicode[STIX]{x1D70B}:C\rightarrow \unicode[STIX]{x1D70B}(C)$
. Since this is true for any component
![]() $C\subset W$
(with sufficiently generic
$C\subset W$
(with sufficiently generic
![]() $\ell$
), the claim follows by induction with the new family
$\ell$
), the claim follows by induction with the new family
![]() $X^{\prime }$
and
$X^{\prime }$
and
![]() $\unicode[STIX]{x1D6E5}_{l+1}=\{0\}$
.◻
$\unicode[STIX]{x1D6E5}_{l+1}=\{0\}$
.◻
The following lemma provides the main inductive step in our estimates.
Lemma 26. Let
![]() $X\subset N\times \mathbb{A}_{K}$
given by
$X\subset N\times \mathbb{A}_{K}$
given by
be a generic complete intersection. Let
![]() ${\mathcal{S}}\subset N^{(1)}$
be a variety defined by equations which are affine-linear in
${\mathcal{S}}\subset N^{(1)}$
be a variety defined by equations which are affine-linear in
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}$
. Suppose that
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{(1)}$
. Suppose that
![]() $(X_{0})^{(1)}\cap {\mathcal{S}}$
does not project dominantly on any component of
$(X_{0})^{(1)}\cap {\mathcal{S}}$
does not project dominantly on any component of
![]() $X_{0}$
. Then there exist
$X_{0}$
. Then there exist
with
![]() $\unicode[STIX]{x1D6E5}(\widetilde{P}_{j})\subset \unicode[STIX]{x1D6E5}_{j}$
for
$\unicode[STIX]{x1D6E5}(\widetilde{P}_{j})\subset \unicode[STIX]{x1D6E5}_{j}$
for
![]() $j=1,\ldots ,k$
and
$j=1,\ldots ,k$
and
such that
is a generic complete intersection and
![]() $\unicode[STIX]{x1D70B}((X_{0})^{(1)}\cap {\mathcal{S}})\subset Y_{0}\subset X_{0}$
.
$\unicode[STIX]{x1D70B}((X_{0})^{(1)}\cap {\mathcal{S}})\subset Y_{0}\subset X_{0}$
.
Proof. By Proposition 20 any sufficiently small perturbation of
![]() $P_{1},\ldots ,P_{k}$
does not change
$P_{1},\ldots ,P_{k}$
does not change
![]() $X_{0}$
. We fix such a perturbation making the generic fiber of the family effectively smooth (without changing the Newton polytopes). Without loss of generality we may assume that the family
$X_{0}$
. We fix such a perturbation making the generic fiber of the family effectively smooth (without changing the Newton polytopes). Without loss of generality we may assume that the family
![]() $P_{1},\ldots ,P_{k}$
is already in this form.
$P_{1},\ldots ,P_{k}$
is already in this form.
We let
![]() $Z^{0}$
denote the family
$Z^{0}$
denote the family
![]() $\unicode[STIX]{x1D70F}(X)$
. Recall that it is a generic complete intersection defined by the vanishing of
$\unicode[STIX]{x1D70F}(X)$
. Recall that it is a generic complete intersection defined by the vanishing of
![]() $P_{1},\ldots ,P_{k}$
and another set of
$P_{1},\ldots ,P_{k}$
and another set of
![]() $k$
equations
$k$
equations
![]() $Q_{1},\ldots ,Q_{k}$
with
$Q_{1},\ldots ,Q_{k}$
with
![]() $\unicode[STIX]{x1D6E5}(Q_{j})\subset (\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}})\times \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}^{(1)}}$
. By Corollary 19 every component of
$\unicode[STIX]{x1D6E5}(Q_{j})\subset (\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}})\times \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}^{(1)}}$
. By Corollary 19 every component of
![]() $(X_{0})^{(1)}$
is also a component of
$(X_{0})^{(1)}$
is also a component of
![]() $Z_{0}^{0}$
. Moreover, any extra components do not project dominantly on a component of
$Z_{0}^{0}$
. Moreover, any extra components do not project dominantly on a component of
![]() $X_{0}$
by Proposition 17.
$X_{0}$
by Proposition 17.
For
![]() $j=1,\ldots ,n-k+1$
we define
$j=1,\ldots ,n-k+1$
we define
![]() $Z^{j}$
to be the family obtained from
$Z^{j}$
to be the family obtained from
![]() $Z^{j-1}$
by intersecting with a generic linear combination
$Z^{j-1}$
by intersecting with a generic linear combination
![]() $\widetilde{Q}^{j}$
of the given equations of
$\widetilde{Q}^{j}$
of the given equations of
![]() ${\mathcal{S}}$
, using Proposition 22. We define
${\mathcal{S}}$
, using Proposition 22. We define
![]() $R^{j},Y^{j}$
by applying Lemma 25 to
$R^{j},Y^{j}$
by applying Lemma 25 to
![]() $Z^{j}$
. We have
$Z^{j}$
. We have
![]() $\unicode[STIX]{x1D6E5}(R_{j})\subset \unicode[STIX]{x1D6E4}$
. Finally, we take
$\unicode[STIX]{x1D6E5}(R_{j})\subset \unicode[STIX]{x1D6E4}$
. Finally, we take
![]() $\widetilde{P}_{k+1}=R_{1}\cdots R_{n-k+1}$
which gives
$\widetilde{P}_{k+1}=R_{1}\cdots R_{n-k+1}$
which gives
![]() $Y=Y^{1}\cup \cdots \cup Y^{n-k+1}$
.
$Y=Y^{1}\cup \cdots \cup Y^{n-k+1}$
.
Let
![]() $C$
be a component of
$C$
be a component of
![]() $(X_{0})^{(1)}$
. Then it is also a component of
$(X_{0})^{(1)}$
. Then it is also a component of
![]() $Z_{0}^{0}$
. Since
$Z_{0}^{0}$
. Since
![]() $C$
projects dominantly on a component of
$C$
projects dominantly on a component of
![]() $X_{0}$
, it cannot be contained in
$X_{0}$
, it cannot be contained in
![]() ${\mathcal{S}}$
. Hence by genericity
${\mathcal{S}}$
. Hence by genericity
![]() $C^{\prime }:=C\cap \{\widetilde{Q}^{1}=0\}$
is strictly contained in
$C^{\prime }:=C\cap \{\widetilde{Q}^{1}=0\}$
is strictly contained in
![]() $C$
, and by Proposition 22 we have
$C$
, and by Proposition 22 we have
![]() $C^{\prime }\subset Z_{0}^{1}$
. Moreover, clearly
$C^{\prime }\subset Z_{0}^{1}$
. Moreover, clearly
![]() $C^{\prime }\cap {\mathcal{S}}=C\cap {\mathcal{S}}$
. Thus it will suffice to prove that
$C^{\prime }\cap {\mathcal{S}}=C\cap {\mathcal{S}}$
. Thus it will suffice to prove that
Now let
![]() $C$
be any component of
$C$
be any component of
![]() $Z_{0}^{1}$
. If
$Z_{0}^{1}$
. If
![]() $\operatorname{codim}(\unicode[STIX]{x1D70B}(C))>k$
then
$\operatorname{codim}(\unicode[STIX]{x1D70B}(C))>k$
then
where the middle inclusion follows from Lemma 25. Otherwise,
![]() $C$
projects dominantly on a component of
$C$
projects dominantly on a component of
![]() $X_{0}$
, so it again cannot be contained in
$X_{0}$
, so it again cannot be contained in
![]() ${\mathcal{S}}$
. Again by genericity
${\mathcal{S}}$
. Again by genericity
![]() $C^{\prime }:=C\cap \{\widetilde{Q}^{2}=0\}$
is strictly contained in
$C^{\prime }:=C\cap \{\widetilde{Q}^{2}=0\}$
is strictly contained in
![]() $C$
, and by Proposition 22 we have
$C$
, and by Proposition 22 we have
![]() $C^{\prime }\subset Z_{0}^{2}$
. Moreover, clearly
$C^{\prime }\subset Z_{0}^{2}$
. Moreover, clearly
![]() $C\cap {\mathcal{S}}=C^{\prime }\cap {\mathcal{S}}$
. Thus it will suffice to prove that
$C\cap {\mathcal{S}}=C^{\prime }\cap {\mathcal{S}}$
. Thus it will suffice to prove that
We repeat this process until
![]() $Z_{0}^{n-k+1}$
. At this point every component has dimension at most
$Z_{0}^{n-k+1}$
. At this point every component has dimension at most
![]() $n-k-1$
even before the
$n-k-1$
even before the
![]() $\unicode[STIX]{x1D70B}$
projection, and thus projects to a set of codimension greater than
$\unicode[STIX]{x1D70B}$
projection, and thus projects to a set of codimension greater than
![]() $k$
. As in (42) it then follows that
$k$
. As in (42) it then follows that
for every component
![]() $C$
of
$C$
of
![]() $Z_{0}^{n-k+1}$
, thus concluding the proof.◻
$Z_{0}^{n-k+1}$
, thus concluding the proof.◻
Remark 27. If the polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are co-ideal polytopes (see Remark 4) then they are stable under differentiations. In this case in the definition of
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
are co-ideal polytopes (see Remark 4) then they are stable under differentiations. In this case in the definition of
![]() $\unicode[STIX]{x1D6E4}$
in (39) one can replace
$\unicode[STIX]{x1D6E4}$
in (39) one can replace
![]() $(n+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}$
by
$(n+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}$
by
![]() $(n-k+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}$
. For such polytopes, all of our main results remain valid with this refined definition of
$(n-k+1)\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D701}}$
. For such polytopes, all of our main results remain valid with this refined definition of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
4 Proofs of the main estimates
In this section we prove our main results on the number of isolated solutions of a differential system of equations and the degree of its reduction. Recall the notation of §1.1. In particular,
![]() $M$
denotes our ambient space, which is a Zariski open subset of
$M$
denotes our ambient space, which is a Zariski open subset of
![]() $K^{n}$
;
$K^{n}$
;
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
denotes a Zariski open subset of the prolongation
$\unicode[STIX]{x1D6FA}^{(l)}$
denotes a Zariski open subset of the prolongation
![]() $M^{(l)}$
; and
$M^{(l)}$
; and
![]() $s:=\dim \unicode[STIX]{x1D6FA}^{(l)}=n(l+1)$
. We begin with a lemma demonstrating the application of Lemma 26 to this context.
$s:=\dim \unicode[STIX]{x1D6FA}^{(l)}=n(l+1)$
. We begin with a lemma demonstrating the application of Lemma 26 to this context.
Lemma 28. Let
![]() $X\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be a generic complete intersection family, and suppose that
$X\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be a generic complete intersection family, and suppose that
![]() $(X_{0})^{(1)}\cap \unicode[STIX]{x1D6EF}$
does not project dominantly on any component of
$(X_{0})^{(1)}\cap \unicode[STIX]{x1D6EF}$
does not project dominantly on any component of
![]() $X_{0}$
. Then the family
$X_{0}$
. Then the family
![]() $Y$
defined by applying Lemma 26 to
$Y$
defined by applying Lemma 26 to
![]() $X$
with
$X$
with
![]() $N=\unicode[STIX]{x1D6FA}^{(l)}$
and
$N=\unicode[STIX]{x1D6FA}^{(l)}$
and
![]() ${\mathcal{S}}=\unicode[STIX]{x1D6EF}$
satisfies
${\mathcal{S}}=\unicode[STIX]{x1D6EF}$
satisfies
![]() $X_{0}\cap {\mathcal{J}}^{l}(M)=Y_{0}\cap {\mathcal{J}}^{l}(M)$
.
$X_{0}\cap {\mathcal{J}}^{l}(M)=Y_{0}\cap {\mathcal{J}}^{l}(M)$
.
Proof. Since
![]() $Y_{0}\subset X_{0}$
, one inclusion is obvious. In the other direction, let
$Y_{0}\subset X_{0}$
, one inclusion is obvious. In the other direction, let
![]() $x^{(l)}\in X_{0}$
. Then
$x^{(l)}\in X_{0}$
. Then
![]() ${x^{(l)}}^{(1)}\in (X_{0})^{(1)}\cap \unicode[STIX]{x1D6EF}$
so by Lemma 26
${x^{(l)}}^{(1)}\in (X_{0})^{(1)}\cap \unicode[STIX]{x1D6EF}$
so by Lemma 26
![]() $x^{(l)}=\unicode[STIX]{x1D70B}({x^{(l)}}^{(1)})\in Y_{0}$
as well.◻
$x^{(l)}=\unicode[STIX]{x1D70B}({x^{(l)}}^{(1)})\in Y_{0}$
as well.◻
We now prove our result for the case that
![]() $S$
is a fiber
$S$
is a fiber
![]() $X_{0}$
of a generic complete intersection family
$X_{0}$
of a generic complete intersection family
![]() $X$
. In particular, the following proposition implies (and generalizes) Theorem 6.
$X$
. In particular, the following proposition implies (and generalizes) Theorem 6.
Proposition 29. Let
![]() $X\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be a generic complete intersection family defined by polynomials with Newton polytopes
$X\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be a generic complete intersection family defined by polynomials with Newton polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
, and suppose that
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
, and suppose that
![]() $X_{0}$
admits finitely many solutions. Denote
$X_{0}$
admits finitely many solutions. Denote
Then
where
![]() $\unicode[STIX]{x1D6FF}:=s-k$
.
$\unicode[STIX]{x1D6FF}:=s-k$
.
Proof. Let
![]() $X(0)=X$
. As long as
$X(0)=X$
. As long as
![]() $X(j)_{0}$
has positive dimension, we define
$X(j)_{0}$
has positive dimension, we define
![]() $X(j+1)$
to be the family obtained by applying Lemma 26 to
$X(j+1)$
to be the family obtained by applying Lemma 26 to
![]() $X(j)$
with the ambient space
$X(j)$
with the ambient space
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
and
$\unicode[STIX]{x1D6FA}^{(l)}$
and
![]() $S=\unicode[STIX]{x1D6EF}$
. The lemma is applicable by application of Lemma 14, since
$S=\unicode[STIX]{x1D6EF}$
. The lemma is applicable by application of Lemma 14, since
![]() $X(j)_{0}$
admits finitely many solutions. We denote the extra equation obtained in this processFootnote
1
by
$X(j)_{0}$
admits finitely many solutions. We denote the extra equation obtained in this processFootnote
1
by
![]() $R_{j+1}$
. By Lemma 28 we have
$R_{j+1}$
. By Lemma 28 we have
![]() ${\mathcal{N}}(X(j+1)_{0})={\mathcal{N}}(X(j)_{0})$
.
${\mathcal{N}}(X(j+1)_{0})={\mathcal{N}}(X(j)_{0})$
.
The Newton polytope of
![]() $R_{j}$
is contained in
$R_{j}$
is contained in
![]() $(\unicode[STIX]{x1D6FF}+2)^{j}\unicode[STIX]{x1D6E4}$
, as one can see by the following simple induction:
$(\unicode[STIX]{x1D6FF}+2)^{j}\unicode[STIX]{x1D6E4}$
, as one can see by the following simple induction:
Eventually we obtain the zero-dimensional variety
![]() $X(\unicode[STIX]{x1D6FF})$
. From the above we conclude that
$X(\unicode[STIX]{x1D6FF})$
. From the above we conclude that
![]() ${\mathcal{N}}(X_{0})={\mathcal{N}}(X(\unicode[STIX]{x1D6FF})_{0})$
, which is certainly bounded by the number of points in
${\mathcal{N}}(X_{0})={\mathcal{N}}(X(\unicode[STIX]{x1D6FF})_{0})$
, which is certainly bounded by the number of points in
![]() $X(\unicode[STIX]{x1D6FF})_{0}$
. Since the number of points of a flat limit is certainly bounded by the number of points of the generic fiber, we have by the BKK theorem
$X(\unicode[STIX]{x1D6FF})_{0}$
. Since the number of points of a flat limit is certainly bounded by the number of points of the generic fiber, we have by the BKK theorem
as claimed. ◻
We now prove our result for arbitrary varieties
![]() $S\subset \unicode[STIX]{x1D6FA}^{(l)}$
.
$S\subset \unicode[STIX]{x1D6FA}^{(l)}$
.
Proof of Theorem 7.
Let
![]() $X(k)\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be the (constant) family cut out by the given equations with Newton polytopes
$X(k)\subset \unicode[STIX]{x1D6FA}^{(l)}\times \mathbb{A}_{K}$
be the (constant) family cut out by the given equations with Newton polytopes
![]() $\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
.
$\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{k}$
.
For
![]() $j\geqslant k$
, let
$j\geqslant k$
, let
![]() $P_{j}$
denote a generic linear combination of the given equations with Newton polytope
$P_{j}$
denote a generic linear combination of the given equations with Newton polytope
![]() $\unicode[STIX]{x1D6E5}$
defining
$\unicode[STIX]{x1D6E5}$
defining
![]() $S$
. Define
$S$
. Define
![]() $X(j+1)$
to be the family obtained by application of Proposition 22 to
$X(j+1)$
to be the family obtained by application of Proposition 22 to
![]() $X(j)$
and
$X(j)$
and
![]() $P_{j}$
. Write
$P_{j}$
. Write
![]() $X(j)_{0}=A(j)\cup B(j)$
, where
$X(j)_{0}=A(j)\cup B(j)$
, where
![]() $A(j)$
denotes the union of the components of
$A(j)$
denotes the union of the components of
![]() $X(j)_{0}$
that are contained in
$X(j)_{0}$
that are contained in
![]() $S$
, and
$S$
, and
![]() $B(j)$
the rest.
$B(j)$
the rest.
The number of solutions of
![]() $S$
which are contained in
$S$
which are contained in
![]() $C(j)=A(j)\setminus B(j)$
is bounded by
$C(j)=A(j)\setminus B(j)$
is bounded by
Indeed,
![]() $C(j)$
is the flat limit of the family
$C(j)$
is the flat limit of the family
![]() $X(j)$
in the ambient space
$X(j)$
in the ambient space
![]() $\unicode[STIX]{x1D6FA}^{(l)}\setminus B(j)$
, and the bound thus follows from Proposition 29. The claim of the theorem will follow once we show that
$\unicode[STIX]{x1D6FA}^{(l)}\setminus B(j)$
, and the bound thus follows from Proposition 29. The claim of the theorem will follow once we show that
![]() $S=C(k)\cup \cdots \cup C(s)$
.
$S=C(k)\cup \cdots \cup C(s)$
.
Let
![]() $x\in S$
, and we will show that it belongs to some
$x\in S$
, and we will show that it belongs to some
![]() $C(j)$
. Certainly
$C(j)$
. Certainly
![]() $x\in X(k)_{0}$
. If
$x\in X(k)_{0}$
. If
![]() $X\not \in B(k)$
, we are done. Otherwise
$X\not \in B(k)$
, we are done. Otherwise
![]() $x$
is contained in some component
$x$
is contained in some component
![]() $G\subset X(k)_{0}$
with
$G\subset X(k)_{0}$
with
![]() $G\not \subset S$
, and we may assume by genericity that
$G\not \subset S$
, and we may assume by genericity that
![]() $P_{k}$
does not vanish identically on
$P_{k}$
does not vanish identically on
![]() $G$
. Then according to Proposition 22,
$G$
. Then according to Proposition 22,
![]() $X(k+1)_{0}$
contains
$X(k+1)_{0}$
contains
![]() $G\cap \{P_{k}=0\}$
, and, in particular,
$G\cap \{P_{k}=0\}$
, and, in particular,
![]() $x\in X(k+1)_{0}$
.
$x\in X(k+1)_{0}$
.
We continue in the same manner. The process must stop at
![]() $j=s$
(if not before), because at this point
$j=s$
(if not before), because at this point
![]() $X(j)_{0}$
consists of isolated points, so
$X(j)_{0}$
consists of isolated points, so
![]() $x\in X(j)_{0}$
implies
$x\in X(j)_{0}$
implies
![]() $x\in C(j)$
.◻
$x\in C(j)$
.◻
Finally, we prove the more general Theorem 9.
Proof of Theorem 9.
We indicate the minor changes required in the proofs of Proposition 29 and Theorem 7.
The proof of Proposition 29 carries out verbatim as long as
![]() $X(j)_{0}$
does not have a component which is a component of
$X(j)_{0}$
does not have a component which is a component of
![]() ${\mathcal{R}}(S)$
. Let
${\mathcal{R}}(S)$
. Let
![]() $S(j)\subset {\mathcal{R}}(S)$
denote the components of codimension
$S(j)\subset {\mathcal{R}}(S)$
denote the components of codimension
![]() $j$
. Then these are also components of
$j$
. Then these are also components of
![]() $X(j)_{0}$
, and their degrees can be bounded by the BKK theorem. We then define
$X(j)_{0}$
, and their degrees can be bounded by the BKK theorem. We then define
![]() $X(j+1)$
in the same way, but restricting the ambient space to
$X(j+1)$
in the same way, but restricting the ambient space to
![]() $\unicode[STIX]{x1D6FA}^{(l)}\setminus (S(1)\cup \cdots \cup S(j))$
. This insures that Lemma 26 is again applicable. It remain only to note that the degree of the remaining components of
$\unicode[STIX]{x1D6FA}^{(l)}\setminus (S(1)\cup \cdots \cup S(j))$
. This insures that Lemma 26 is again applicable. It remain only to note that the degree of the remaining components of
![]() ${\mathcal{R}}(S)$
in the new ambient space is the same as the degree in the original ambient space. The proof is thus concluded by induction. The resulting bound has an extra multiplicative factor of
${\mathcal{R}}(S)$
in the new ambient space is the same as the degree in the original ambient space. The proof is thus concluded by induction. The resulting bound has an extra multiplicative factor of
![]() $s-k+1$
corresponding to the fact that we separately bound the degree in each dimension.Footnote
2
$s-k+1$
corresponding to the fact that we separately bound the degree in each dimension.Footnote
2
We can now carry out the proof of Theorem 7 in the same way, noting that since
![]() $S=C(k)\cup \cdots \cup C(s)$
, any component of
$S=C(k)\cup \cdots \cup C(s)$
, any component of
![]() ${\mathcal{R}}(S)$
must be a component of
${\mathcal{R}}(S)$
must be a component of
![]() ${\mathcal{R}}(C(j))$
for some
${\mathcal{R}}(C(j))$
for some
![]() $j=k,\ldots ,s$
.◻
$j=k,\ldots ,s$
.◻
5 Diophantine applications
In the papers [Reference Hrushovski and PillayHP00, Reference Freitag and ScanlonFS14] the effective estimate of Theorem 2 has been used to derive estimates for some counting problems of a diophantine nature. In this section we illustrate our result by improving the estimates presented in these papers.
In this section we assume that
![]() $K=\mathbb{C}$
, and the differentiation operator
$K=\mathbb{C}$
, and the differentiation operator
![]() $D$
is chosen such that the field of constants is
$D$
is chosen such that the field of constants is
![]() $k=\bar{\mathbb{Q}}$
.
$k=\bar{\mathbb{Q}}$
.
5.1 Transcendental points in subvarieties of semi-abelian varieties
Recall that a semi-abelian variety is an extension of an abelian variety by a torus. Let
![]() $A$
be a semi-abelian variety and
$A$
be a semi-abelian variety and
![]() $\unicode[STIX]{x1D6E4}\subset A$
a subgroup of finite rational rank
$\unicode[STIX]{x1D6E4}\subset A$
a subgroup of finite rational rank
![]() $r:=\dim _{\mathbb{Q}}\unicode[STIX]{x1D6E4}\otimes \mathbb{Q}$
. Finally, let
$r:=\dim _{\mathbb{Q}}\unicode[STIX]{x1D6E4}\otimes \mathbb{Q}$
. Finally, let
![]() $X$
be a subvariety of
$X$
be a subvariety of
![]() $A$
.
$A$
.
In [Reference Hrushovski and PillayHP00] effective bounds are given on the number of points in the intersection
![]() $X\cap \unicode[STIX]{x1D6E4}$
under various conditions on
$X\cap \unicode[STIX]{x1D6E4}$
under various conditions on
![]() $\unicode[STIX]{x1D6E4},X$
. The estimates are presented in terms of the following data. Suppose that
$\unicode[STIX]{x1D6E4},X$
. The estimates are presented in terms of the following data. Suppose that
![]() $A$
has dimension
$A$
has dimension
![]() $n$
and is defined over
$n$
and is defined over
![]() $k$
. We assume that
$k$
. We assume that
![]() $A$
is embedded as a locally closed subset of a projective space
$A$
is embedded as a locally closed subset of a projective space
![]() $\mathbb{C}P^{N}$
. Let
$\mathbb{C}P^{N}$
. Let
![]() $\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{n}$
be a basis of translation-invariant differential forms on
$\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{n}$
be a basis of translation-invariant differential forms on
![]() $A$
.
$A$
.
We assume that
![]() $A$
is covered by
$A$
is covered by
![]() $t$
affine charts, and that each
$t$
affine charts, and that each
![]() $\unicode[STIX]{x1D714}_{i}$
is given in each chart by a polynomial in the local coordinates
$\unicode[STIX]{x1D714}_{i}$
is given in each chart by a polynomial in the local coordinates
![]() $x_{1},\ldots ,x_{N}$
and
$x_{1},\ldots ,x_{N}$
and
![]() $dx_{1},\ldots ,dx_{n}$
. Let
$dx_{1},\ldots ,dx_{n}$
. Let
![]() $d_{A}$
be the maximal degree of the equations defining
$d_{A}$
be the maximal degree of the equations defining
![]() $A$
in any of the charts, and
$A$
in any of the charts, and
![]() $d_{\unicode[STIX]{x1D714}}$
be the maximal degree of any of the polynomials defining
$d_{\unicode[STIX]{x1D714}}$
be the maximal degree of any of the polynomials defining
![]() $\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{n}$
in any of the charts. Finally, let
$\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{n}$
in any of the charts. Finally, let
![]() $d_{X}$
denote an upper bound on the degrees of the equations defining
$d_{X}$
denote an upper bound on the degrees of the equations defining
![]() $X$
in any of the charts. We assume for simplicity of the formulation that
$X$
in any of the charts. We assume for simplicity of the formulation that
![]() $d_{X}\geqslant d_{A}$
.
$d_{X}\geqslant d_{A}$
.
The following is a refined form of the main result of [Reference Hrushovski and PillayHP00].
Theorem 30 (Cf. [Reference Hrushovski and PillayHP00, Theorem 1.1]).
Suppose
![]() $A,X$
are defined over
$A,X$
are defined over
![]() $k$
and there exist no positive-dimensional subvarieties
$k$
and there exist no positive-dimensional subvarieties
![]() $X_{1},X_{2}\subset A$
such that
$X_{1},X_{2}\subset A$
such that
![]() $X_{1}+X_{2}\subset X$
. Then
$X_{1}+X_{2}\subset X$
. Then
where
Proof. In [Reference Hrushovski and PillayHP00] it is shown that
![]() $\unicode[STIX]{x1D6E4}$
is contained in a finite-dimensional differential algebraic subgroup
$\unicode[STIX]{x1D6E4}$
is contained in a finite-dimensional differential algebraic subgroup
![]() $G$
of
$G$
of
![]() $A$
such that
$A$
such that
![]() $B:=(X\cap G)\setminus X(k)$
is finite. It is therefore enough to bound the number of points in
$B:=(X\cap G)\setminus X(k)$
is finite. It is therefore enough to bound the number of points in
![]() $B$
. Moreover, it is shown that in each of the affine charts on
$B$
. Moreover, it is shown that in each of the affine charts on
![]() $A$
, the group
$A$
, the group
![]() $G$
can be written in the form
$G$
can be written in the form
where
![]() $V\subset (K^{N})^{(r)}$
is a variety defined by equations of degrees bounded by
$V\subset (K^{N})^{(r)}$
is a variety defined by equations of degrees bounded by
![]() $d_{\unicode[STIX]{x1D714}}$
.
$d_{\unicode[STIX]{x1D714}}$
.
We will apply Theorem 7 with parameters
 $$\begin{eqnarray}\displaystyle M & = & \displaystyle K^{N},\nonumber\\ \displaystyle l & = & \displaystyle r,\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}^{(r)} & = & \displaystyle M^{(r)}\setminus \{\unicode[STIX]{x1D709}^{(1)}=0\},\nonumber\\ \displaystyle S & = & \displaystyle \unicode[STIX]{x1D6FA}^{(r)}\cap V\cap \unicode[STIX]{x1D70B}^{-1}(X).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M & = & \displaystyle K^{N},\nonumber\\ \displaystyle l & = & \displaystyle r,\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}^{(r)} & = & \displaystyle M^{(r)}\setminus \{\unicode[STIX]{x1D709}^{(1)}=0\},\nonumber\\ \displaystyle S & = & \displaystyle \unicode[STIX]{x1D6FA}^{(r)}\cap V\cap \unicode[STIX]{x1D70B}^{-1}(X).\nonumber\end{eqnarray}$$
Since
![]() $S$
is contained in
$S$
is contained in
![]() $\unicode[STIX]{x1D70B}^{-1}(A)$
which has codimension
$\unicode[STIX]{x1D70B}^{-1}(A)$
which has codimension
![]() $N-n$
and is cut out by equations of degree at most
$N-n$
and is cut out by equations of degree at most
![]() $d_{A}$
, we can apply Theorem 7 with
$d_{A}$
, we can apply Theorem 7 with
We note that
![]() $\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime }$
where
$\unicode[STIX]{x1D6E5}\subset \unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime }$
where
![]() $\unicode[STIX]{x1D6E5}^{\prime }=2d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
and
$\unicode[STIX]{x1D6E5}^{\prime }=2d_{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}$
and
![]() $\unicode[STIX]{x1D6E5}^{\prime \prime }$
is the polytope of polynomials of degree
$\unicode[STIX]{x1D6E5}^{\prime \prime }$
is the polytope of polynomials of degree
![]() $d_{\unicode[STIX]{x1D714}}$
in
$d_{\unicode[STIX]{x1D714}}$
in
![]() $\unicode[STIX]{x1D709}^{(1)},\ldots ,\unicode[STIX]{x1D709}^{(r)}$
.
$\unicode[STIX]{x1D709}^{(1)},\ldots ,\unicode[STIX]{x1D709}^{(r)}$
.
Finally,
![]() $S$
admits finitely many solutions, and by Theorem 7 we have
$S$
admits finitely many solutions, and by Theorem 7 we have
 $$\begin{eqnarray}\displaystyle {\mathcal{N}}(S) & {\leqslant} & \displaystyle E_{s,N-n}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{N-n},\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime },\ldots ,\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle E_{s,N-n}\binom{s-N+n}{n}V\biggl(\underbrace{d_{A}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}}_{N-n\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}^{\prime }}_{n\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}^{\prime \prime }}_{s-N\text{ times}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle E_{s,N-n}\binom{s-N+n}{n}d_{A}^{N-n}(2d_{X})^{n}d_{\unicode[STIX]{x1D714}}^{N-n}V(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)},\ldots ,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)})\nonumber\\ \displaystyle & = & \displaystyle E_{s,N-n}\binom{s-N+n}{n}2^{n}(s!)^{-1}d_{A}^{N-n}d_{\unicode[STIX]{x1D714}}^{s-N}d_{X}^{n},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{N}}(S) & {\leqslant} & \displaystyle E_{s,N-n}V(\unicode[STIX]{x1D6E5}_{1},\ldots ,\unicode[STIX]{x1D6E5}_{N-n},\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime },\ldots ,\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D6E5}^{\prime \prime })\nonumber\\ \displaystyle & = & \displaystyle E_{s,N-n}\binom{s-N+n}{n}V\biggl(\underbrace{d_{A}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}}_{N-n\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}^{\prime }}_{n\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}^{\prime \prime }}_{s-N\text{ times}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle E_{s,N-n}\binom{s-N+n}{n}d_{A}^{N-n}(2d_{X})^{n}d_{\unicode[STIX]{x1D714}}^{N-n}V(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)},\ldots ,\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(l)})\nonumber\\ \displaystyle & = & \displaystyle E_{s,N-n}\binom{s-N+n}{n}2^{n}(s!)^{-1}d_{A}^{N-n}d_{\unicode[STIX]{x1D714}}^{s-N}d_{X}^{n},\nonumber\end{eqnarray}$$
where in the second equality we expand the mixed volume by multilinearity and use the fact that the value is non-zero if and only if
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
appears exactly
$\unicode[STIX]{x1D6E5}^{\prime }$
appears exactly
![]() $n$
times.◻
$n$
times.◻
We note, in particular, that the bound of Theorem 30 is singly-exponential with respect to
![]() $N$
and
$N$
and
![]() $r$
, and has the natural asymptotic
$r$
, and has the natural asymptotic
![]() $d_{X}^{n}$
with respect to
$d_{X}^{n}$
with respect to
![]() $d_{X}$
. We also remark that since
$d_{X}$
. We also remark that since
![]() $A$
is smooth, the arguments of this paper could have been applied with small changes in the ambient space
$A$
is smooth, the arguments of this paper could have been applied with small changes in the ambient space
![]() $A$
rather than
$A$
rather than
![]() $K^{N}$
, leading to somewhat better estimates.
$K^{N}$
, leading to somewhat better estimates.
We next present a version of Theorem 30 for a torus. This result may be seen as an analog of the Kushnirenko theorem. Similar analogs of the BKK theorem involving mixed volumes can be obtained in a similar manner.
Theorem 31. Let
![]() $A=(\mathbb{C}^{\ast })^{n}$
and let
$A=(\mathbb{C}^{\ast })^{n}$
and let
![]() $X\subset A$
be defined over
$X\subset A$
be defined over
![]() $k$
by equations with Newton polytope
$k$
by equations with Newton polytope
![]() $\unicode[STIX]{x1D6E5}$
. Suppose that there exist no positive-dimensional subvarieties
$\unicode[STIX]{x1D6E5}$
. Suppose that there exist no positive-dimensional subvarieties
![]() $X_{1},X_{2}\subset A$
such that
$X_{1},X_{2}\subset A$
such that
![]() $X_{1}+X_{2}\subset X$
. Then
$X_{1}+X_{2}\subset X$
. Then
Proof. We embed
![]() $A$
in
$A$
in
![]() $\mathbb{C}^{2n}=\mathbb{C}[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{n}]$
with the equations
$\mathbb{C}^{2n}=\mathbb{C}[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{n}]$
with the equations
![]() $x_{i}y_{i}=1$
. Then the invariant forms
$x_{i}y_{i}=1$
. Then the invariant forms
![]() $dx_{i}/x_{i}$
become polynomials of degree
$dx_{i}/x_{i}$
become polynomials of degree
![]() $2$
, so
$2$
, so
![]() $d_{A}=d_{\unicode[STIX]{x1D714}}=2$
. The proof proceeds in a manner analogous to the proof of Theorem 30.◻
$d_{A}=d_{\unicode[STIX]{x1D714}}=2$
. The proof proceeds in a manner analogous to the proof of Theorem 30.◻
A special case with
![]() $n=2$
in Theorem 31 is of some particular interest. It has been considered by Buium [Reference BuiumBui95b] who gave an iterated-exponential bound, answering a question posed by Bombieri. The bound was improved in [Reference Hrushovski and PillayHP00] to a doubly-exponential bound as follows.
$n=2$
in Theorem 31 is of some particular interest. It has been considered by Buium [Reference BuiumBui95b] who gave an iterated-exponential bound, answering a question posed by Bombieri. The bound was improved in [Reference Hrushovski and PillayHP00] to a doubly-exponential bound as follows.
Theorem 32 [Reference Hrushovski and PillayHP00, Corollary 1.2].
Let
![]() $f\in \bar{\mathbb{Q}}[x,y]$
be an irreducible polynomial of degree
$f\in \bar{\mathbb{Q}}[x,y]$
be an irreducible polynomial of degree
![]() $d$
, whose zero locus in
$d$
, whose zero locus in
![]() $(\mathbb{C}^{\ast })^{2}$
is not a translate of a torus. Let
$(\mathbb{C}^{\ast })^{2}$
is not a translate of a torus. Let
![]() $\unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$
be a subgroup of rational rank
$\unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$
be a subgroup of rational rank
![]() $r$
. Then
$r$
. Then
From Theorem 31 we obtain the following.
Theorem 33. Let
![]() $f\in \bar{\mathbb{Q}}[x,y]$
be an irreducible polynomial with Newton polygon
$f\in \bar{\mathbb{Q}}[x,y]$
be an irreducible polynomial with Newton polygon
![]() $\unicode[STIX]{x1D6E5}$
, whose zero-locus in
$\unicode[STIX]{x1D6E5}$
, whose zero-locus in
![]() $(\mathbb{C}^{\ast })^{2}$
is not a translate of a torus. Let
$(\mathbb{C}^{\ast })^{2}$
is not a translate of a torus. Let
![]() $\unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$
be a subgroup of rational rank
$\unicode[STIX]{x1D6E4}\subset \mathbb{C}^{\ast }$
be a subgroup of rational rank
![]() $r$
. Then
$r$
. Then
We note, in particular, that the bound of Theorem 32 is singly-exponential in
![]() $r$
, and if we assume that
$r$
, and if we assume that
![]() $\deg f=d$
then
$\deg f=d$
then
![]() $\operatorname{Vol}(\unicode[STIX]{x1D6E5})=d^{2}/2$
.
$\operatorname{Vol}(\unicode[STIX]{x1D6E5})=d^{2}/2$
.
We also present a refined form of [Reference Hrushovski and PillayHP00, Theorem 1.1], replacing the condition on
![]() $X$
in Theorem 31 by a condition on the lattice
$X$
in Theorem 31 by a condition on the lattice
![]() $\unicode[STIX]{x1D6E4}$
. For simplicity we present the result in the context of the torus, although the proof works in general in the same way as the proof of Theorem 30.
$\unicode[STIX]{x1D6E4}$
. For simplicity we present the result in the context of the torus, although the proof works in general in the same way as the proof of Theorem 30.
Theorem 34. Let
![]() $A=(\mathbb{C}^{\ast })^{n}$
and let
$A=(\mathbb{C}^{\ast })^{n}$
and let
![]() $X\subset A$
be defined by equations with Newton polytope
$X\subset A$
be defined by equations with Newton polytope
![]() $\unicode[STIX]{x1D6E5}$
, and suppose that it does not contain a translate of a non-trivial subtorus. Suppose that
$\unicode[STIX]{x1D6E5}$
, and suppose that it does not contain a translate of a non-trivial subtorus. Suppose that
![]() $\unicode[STIX]{x1D6E4}\cap A(k)=\{0\}$
. Then
$\unicode[STIX]{x1D6E4}\cap A(k)=\{0\}$
. Then
Proof. In [Reference Hrushovski and PillayHP00, Lemma 6.1] it is shown that
![]() $\unicode[STIX]{x1D6E4}$
is contained in a finite-dimensional differential algebraic subgroup
$\unicode[STIX]{x1D6E4}$
is contained in a finite-dimensional differential algebraic subgroup
![]() $G$
of
$G$
of
![]() $(K^{\ast })^{n}$
such that
$(K^{\ast })^{n}$
such that
![]() $X\cap G$
intersects only finitely many translates
$X\cap G$
intersects only finitely many translates
![]() $c_{1}(k^{\ast })^{n},\ldots ,c_{\unicode[STIX]{x1D708}}(k^{\ast })^{n}$
of
$c_{1}(k^{\ast })^{n},\ldots ,c_{\unicode[STIX]{x1D708}}(k^{\ast })^{n}$
of
![]() $(k^{\ast })^{n}$
. By the assumption on
$(k^{\ast })^{n}$
. By the assumption on
![]() $\unicode[STIX]{x1D6E4}$
, each such translate intersects
$\unicode[STIX]{x1D6E4}$
, each such translate intersects
![]() $\unicode[STIX]{x1D6E4}$
at most once, so it will suffice to give a bound on
$\unicode[STIX]{x1D6E4}$
at most once, so it will suffice to give a bound on
![]() $\unicode[STIX]{x1D708}$
.
$\unicode[STIX]{x1D708}$
.
We choose
![]() $M,\unicode[STIX]{x1D6FA}^{(r)}$
as in the proof of Theorem 30 and write
$M,\unicode[STIX]{x1D6FA}^{(r)}$
as in the proof of Theorem 30 and write
![]() $X\cap G$
as the set of solutions of a variety
$X\cap G$
as the set of solutions of a variety
![]() $S\subset \unicode[STIX]{x1D6FA}^{(r)}$
. The logarithmic derivative
$S\subset \unicode[STIX]{x1D6FA}^{(r)}$
. The logarithmic derivative
![]() $l(x)=(Dx)/x$
takes a different value
$l(x)=(Dx)/x$
takes a different value
![]() $l(c_{j})$
on each of the translates
$l(c_{j})$
on each of the translates
![]() $c_{j}(k^{\ast })^{n}$
, so the solutions of
$c_{j}(k^{\ast })^{n}$
, so the solutions of
![]() $S$
are contained in a union of
$S$
are contained in a union of
![]() $\unicode[STIX]{x1D708}$
disjoint planes
$\unicode[STIX]{x1D708}$
disjoint planes
![]() $\unicode[STIX]{x1D709}^{(1)}=c_{j}\unicode[STIX]{x1D709}$
in
$\unicode[STIX]{x1D709}^{(1)}=c_{j}\unicode[STIX]{x1D709}$
in
![]() $\unicode[STIX]{x1D6FA}^{(r)}$
(and meets each of them). Then the same is true for the Zariski closure
$\unicode[STIX]{x1D6FA}^{(r)}$
(and meets each of them). Then the same is true for the Zariski closure
![]() ${\mathcal{R}}(S)$
, and it is thus enough to bound the degree of this variety. The result now follows by Theorem 9.◻
${\mathcal{R}}(S)$
, and it is thus enough to bound the degree of this variety. The result now follows by Theorem 9.◻
5.2 Isogeny classes of elliptic curves
Denote by
![]() $E_{x}$
the elliptic curve with
$E_{x}$
the elliptic curve with
![]() $j$
-invariant
$j$
-invariant
![]() $x\in \mathbb{C}$
. We write
$x\in \mathbb{C}$
. We write
![]() $E_{x}\sim E_{y}$
when
$E_{x}\sim E_{y}$
when
![]() $E_{x}$
is isogenous to
$E_{x}$
is isogenous to
![]() $E_{y}$
. We denote
$E_{y}$
. We denote
and more generally, for
![]() $\bar{x}\in \mathbb{C}^{n}$
,
$\bar{x}\in \mathbb{C}^{n}$
,
In [Reference Freitag and ScanlonFS14] the authors, following a question of Mazur, consider the following problem: given a non-identity automorphism
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\mathbb{C}P^{1}$
and
$\mathbb{C}P^{1}$
and
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}$
, estimate the number of elliptic curves
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
, estimate the number of elliptic curves
![]() $E_{\unicode[STIX]{x1D70C}}$
satisfying
$E_{\unicode[STIX]{x1D70C}}$
satisfying
![]() $E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
$E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
![]() $E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
. In particular, they obtain the following estimate.
$E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
. In particular, they obtain the following estimate.
Theorem 35 [Reference Freitag and ScanlonFS14, §6.1].
Assume
![]() $\unicode[STIX]{x1D70F}$
is transcendental and set
$\unicode[STIX]{x1D70F}$
is transcendental and set
Then the size of
![]() $S$
, i.e. the number of elliptic curves
$S$
, i.e. the number of elliptic curves
![]() $E_{\unicode[STIX]{x1D70C}}$
satisfying
$E_{\unicode[STIX]{x1D70C}}$
satisfying
![]() $E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
$E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
![]() $E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
, is at mostFootnote
3
$E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
, is at mostFootnote
3
![]() $2^{24}36^{7}\simeq 10^{18}$
.
$2^{24}36^{7}\simeq 10^{18}$
.
The proof of this theorem, as in §5.1, is based on the introduction of a differential algebraic construction. Namely, recall that the Schwartzian operator is defined by
where we interpret this as an operator on our differentially closed field
![]() $\mathbb{C}$
, and write
$\mathbb{C}$
, and write
![]() $x^{\prime }$
as a shorthand for
$x^{\prime }$
as a shorthand for
![]() $Dx$
. We introduce the differential operator
$Dx$
. We introduce the differential operator
which is a third order algebraic differential operator vanishing on Klein’s j-invariant
![]() $j$
[Reference BuiumBui95a]. Let
$j$
[Reference BuiumBui95a]. Let
![]() $\unicode[STIX]{x1D70F}\in \mathbb{C}$
be transcendental (i.e., non-constant with respect to our chosen differential structure). By a theorem of Buium [Reference BuiumBui95a], the set
$\unicode[STIX]{x1D70F}\in \mathbb{C}$
be transcendental (i.e., non-constant with respect to our chosen differential structure). By a theorem of Buium [Reference BuiumBui95a], the set
![]() $\unicode[STIX]{x1D712}^{-1}(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F}))$
is the Kolchin closure of
$\unicode[STIX]{x1D712}^{-1}(\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F}))$
is the Kolchin closure of
![]() $\operatorname{Iso}(\unicode[STIX]{x1D70F})$
. One may therefore attempt to study the set
$\operatorname{Iso}(\unicode[STIX]{x1D70F})$
. One may therefore attempt to study the set
![]() $S$
in (59) by considering the (possibly larger) set
$S$
in (59) by considering the (possibly larger) set
Of course, even if the set
![]() $S$
is finite (which is not an obvious assertion), it is not clear a priori that the set
$S$
is finite (which is not an obvious assertion), it is not clear a priori that the set
![]() $Z$
must also be finite. However, in [Reference Freitag and ScanlonFS14, §6.1] it is proven that this is indeed the case. Since
$Z$
must also be finite. However, in [Reference Freitag and ScanlonFS14, §6.1] it is proven that this is indeed the case. Since
![]() $Z$
is a set given by differential algebraic conditions, it is thus possible to estimate its size using the methods of [Reference Hrushovski and PillayHP00], and this is carried out in [Reference Freitag and ScanlonFS14] to give Theorem 35.
$Z$
is a set given by differential algebraic conditions, it is thus possible to estimate its size using the methods of [Reference Hrushovski and PillayHP00], and this is carried out in [Reference Freitag and ScanlonFS14] to give Theorem 35.
We now apply our results, specifically Theorem 6, to estimate the size of
![]() $Z$
. We begin by expressing
$Z$
. We begin by expressing
![]() $Z$
as the set of solutions of a variety of differential conditions
$Z$
as the set of solutions of a variety of differential conditions
![]() $S$
. Let
$S$
. Let
![]() $\unicode[STIX]{x1D6FC}\cdot z=(az+b)/(cz+d)$
. We choose
$\unicode[STIX]{x1D6FC}\cdot z=(az+b)/(cz+d)$
. We choose
![]() $M=\mathbb{C}^{2}$
,
$M=\mathbb{C}^{2}$
,
![]() $l=3$
and let
$l=3$
and let
![]() $\unicode[STIX]{x1D6FA}^{(l)}$
be the open dense subset of
$\unicode[STIX]{x1D6FA}^{(l)}$
be the open dense subset of
![]() $M^{(l)}$
obtained by removing the polar divisor of
$M^{(l)}$
obtained by removing the polar divisor of
![]() $\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D709}$
(i.e.
$\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D709}$
(i.e.
![]() $\{c\unicode[STIX]{x1D709}+d=0\}$
) as well as the polar divisors of
$\{c\unicode[STIX]{x1D709}+d=0\}$
) as well as the polar divisors of
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})$
and
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D702})$
.
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D702})$
.
We write six explicit equations for
![]() $S$
. The first is given by
$S$
. The first is given by
![]() $P_{1}:(c\unicode[STIX]{x1D709}+d)\unicode[STIX]{x1D702}=a\unicode[STIX]{x1D709}+b$
. We obtain the next three equations
$P_{1}:(c\unicode[STIX]{x1D709}+d)\unicode[STIX]{x1D702}=a\unicode[STIX]{x1D709}+b$
. We obtain the next three equations
![]() $P_{2},P_{3},P_{4}$
by taking the first three derivatives of
$P_{2},P_{3},P_{4}$
by taking the first three derivatives of
![]() $P_{1}$
with respect to
$P_{1}$
with respect to
![]() $D$
(and replacing
$D$
(and replacing
![]() $D\unicode[STIX]{x1D709}$
by
$D\unicode[STIX]{x1D709}$
by
![]() $\unicode[STIX]{x1D709}^{(1)}$
, etc.). One can easily check that these equations define a complete intersection (in fact, they define the third prolongation of the graph of
$\unicode[STIX]{x1D709}^{(1)}$
, etc.). One can easily check that these equations define a complete intersection (in fact, they define the third prolongation of the graph of
![]() $\unicode[STIX]{x1D6FC}$
: at this point it is essential that we removed the polar divisor
$\unicode[STIX]{x1D6FC}$
: at this point it is essential that we removed the polar divisor
![]() $c\unicode[STIX]{x1D709}+d=0$
). Clearly
$c\unicode[STIX]{x1D709}+d=0$
). Clearly
![]() $\unicode[STIX]{x1D6E5}(P_{j})\subset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}$
for
$\unicode[STIX]{x1D6E5}(P_{j})\subset \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}$
for
![]() $j=1,2,3,4$
.
$j=1,2,3,4$
.
The next two equations
![]() $P_{5},P_{6}$
are given by
$P_{5},P_{6}$
are given by
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D70F})$
and
![]() $\unicode[STIX]{x1D712}(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F})$
respectively, where we clear out all the denominators. We have
$\unicode[STIX]{x1D712}(\unicode[STIX]{x1D702})=\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F})$
respectively, where we clear out all the denominators. We have
![]() $\unicode[STIX]{x1D6E5}(P_{5})\subset 6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}$
and
$\unicode[STIX]{x1D6E5}(P_{5})\subset 6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}$
and
![]() $\unicode[STIX]{x1D6E5}(P_{6})\subset 6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}$
. Since these equations are linear in
$\unicode[STIX]{x1D6E5}(P_{6})\subset 6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}$
. Since these equations are linear in
![]() $\unicode[STIX]{x1D709}^{(3)}$
and
$\unicode[STIX]{x1D709}^{(3)}$
and
![]() $\unicode[STIX]{x1D702}^{(3)}$
respectively, it is not hard to check that they are each irreducible (this was already noted in [Reference Freitag and ScanlonFS14, §5.2]). It follows that
$\unicode[STIX]{x1D702}^{(3)}$
respectively, it is not hard to check that they are each irreducible (this was already noted in [Reference Freitag and ScanlonFS14, §5.2]). It follows that
![]() $P_{1},\ldots ,P_{6}$
define a complete intersection. Indeed, otherwise
$P_{1},\ldots ,P_{6}$
define a complete intersection. Indeed, otherwise
![]() $P_{1},\ldots ,P_{5}$
would imply
$P_{1},\ldots ,P_{5}$
would imply
![]() $P_{6}$
. But
$P_{6}$
. But
![]() $P_{5}$
, being an equation of order 3, admits infinitely many solutions
$P_{5}$
, being an equation of order 3, admits infinitely many solutions
![]() $z$
, and for each of these
$z$
, and for each of these
![]() $(z,\unicode[STIX]{x1D6FC}\cdot z)$
would be a solution of
$(z,\unicode[STIX]{x1D6FC}\cdot z)$
would be a solution of
![]() $P_{1},\ldots ,P_{5}$
and hence also of
$P_{1},\ldots ,P_{5}$
and hence also of
![]() $P_{6}$
, contradicting the fact that
$P_{6}$
, contradicting the fact that
![]() $S$
has finitely many solutions.
$S$
has finitely many solutions.
Finally, we apply Theorem 6 to
![]() $S$
. In computing
$S$
. In computing
![]() $\unicode[STIX]{x1D6E4}$
we also take into account Remark 27,
$\unicode[STIX]{x1D6E4}$
we also take into account Remark 27,
and
 $$\begin{eqnarray}\displaystyle {\mathcal{N}}(S) & {\leqslant} & \displaystyle 4^{3}\cdot 8!V\biggl(\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{4\text{ times}},6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)},6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)},\underbrace{13(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)})}_{2\text{ times}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{6}6^{2}13^{2}\cdot 8!V\biggl(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)},\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)},\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{6\text{ times}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 2^{6}6^{2}13^{2}\binom{6}{3}\cdot 8!V\biggl(\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}}_{4\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{4\text{ times}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 2^{6}6^{2}13^{2}\binom{6}{3}=2^{10}\cdot 3^{3}\cdot 13^{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{N}}(S) & {\leqslant} & \displaystyle 4^{3}\cdot 8!V\biggl(\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{4\text{ times}},6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)},6\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)},\underbrace{13(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)})}_{2\text{ times}}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{6}6^{2}13^{2}\cdot 8!V\biggl(\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)},\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)},\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}+\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{6\text{ times}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 2^{6}6^{2}13^{2}\binom{6}{3}\cdot 8!V\biggl(\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D709}}^{(3)}}_{4\text{ times}},\underbrace{\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D702}}^{(3)}}_{4\text{ times}}\biggr)\nonumber\\ \displaystyle & = & \displaystyle 2^{6}6^{2}13^{2}\binom{6}{3}=2^{10}\cdot 3^{3}\cdot 13^{2}.\nonumber\end{eqnarray}$$
In conclusion, we have the following result.
Theorem 36 (Cf. Theorem 35).
Assume
![]() $\unicode[STIX]{x1D70F}$
is transcendental. Then the number of elliptic curves
$\unicode[STIX]{x1D70F}$
is transcendental. Then the number of elliptic curves
![]() $E_{\unicode[STIX]{x1D70C}}$
satisfying
$E_{\unicode[STIX]{x1D70C}}$
satisfying
![]() $E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
$E_{\unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D70F}}$
and
![]() $E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
is at most
$E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70C}}\sim E_{\unicode[STIX]{x1D6FC}\cdot \unicode[STIX]{x1D70F}}$
is at most
![]() $2^{10}\cdot 3^{3}\cdot 13^{2}\simeq 5\times 10^{6}$
.
$2^{10}\cdot 3^{3}\cdot 13^{2}\simeq 5\times 10^{6}$
.
Remark 37. One could have derived a bound directly using Theorem 7 without the derivation of the extra equations
![]() $P_{2},P_{3},P_{4}$
and the fact that the intersection with
$P_{2},P_{3},P_{4}$
and the fact that the intersection with
![]() $P_{5}$
and
$P_{5}$
and
![]() $P_{6}$
is complete. We presented this more detailed approach because it gives a somewhat better estimate, and also to illustrate a computation involving mixed volumes in Theorem 6.
$P_{6}$
is complete. We presented this more detailed approach because it gives a somewhat better estimate, and also to illustrate a computation involving mixed volumes in Theorem 6.
The computation above could certainly be improved somewhat: by using the precise Newton polytopes of
![]() $P_{1},\ldots ,P_{6}$
; by accurately computing the resulting mixed volumes; and by following the proof of Theorem 6 where various inaccurate estimates were invariably made.
$P_{1},\ldots ,P_{6}$
; by accurately computing the resulting mixed volumes; and by following the proof of Theorem 6 where various inaccurate estimates were invariably made.
Generalizing to varieties of arbitrary dimension and degree, [Reference Freitag and ScanlonFS14] gives the following result.
Corollary 38 [Reference Freitag and ScanlonFS14, Corollary 6.9].
Let
![]() $V\subset \mathbb{C}^{n}$
be a Zariski closed set of dimension
$V\subset \mathbb{C}^{n}$
be a Zariski closed set of dimension
![]() $m$
and
$m$
and
![]() $\bar{\unicode[STIX]{x1D70F}}\in \mathbb{C}^{n}$
an
$\bar{\unicode[STIX]{x1D70F}}\in \mathbb{C}^{n}$
an
![]() $n$
-tuple of transcendental numbers. Let
$n$
-tuple of transcendental numbers. Let
![]() $W$
denote the Zariski closure of
$W$
denote the Zariski closure of
![]() $V\cap \operatorname{Iso}(\bar{\unicode[STIX]{x1D70F}})$
. Then
$V\cap \operatorname{Iso}(\bar{\unicode[STIX]{x1D70F}})$
. Then
![]() $W$
is a weakly-special variety, and (see footnote 3 on page 886)
$W$
is a weakly-special variety, and (see footnote 3 on page 886)
We refer the reader to [Reference Freitag and ScanlonFS14] for the definition of a weakly special variety. As for the degree estimate, the proof of this corollary proceeds in a manner analogous to the proof of Theorem 35. Arguing in a manner analogous to the proof of Theorem 36 and using Theorem 9, we obtain the following result.
Corollary 39. Let
![]() $V\subset \mathbb{C}^{n}$
be a Zariski closed set defined by equations of degree
$V\subset \mathbb{C}^{n}$
be a Zariski closed set defined by equations of degree
![]() $d$
, and
$d$
, and
![]() $\bar{\unicode[STIX]{x1D70F}}\in \mathbb{C}^{n}$
an
$\bar{\unicode[STIX]{x1D70F}}\in \mathbb{C}^{n}$
an
![]() $n$
-tuple of transcendental numbers. Let
$n$
-tuple of transcendental numbers. Let
![]() $W$
denote the Zariski closure of
$W$
denote the Zariski closure of
![]() $V\cap \operatorname{Iso}(\bar{\unicode[STIX]{x1D70F}})$
. Then
$V\cap \operatorname{Iso}(\bar{\unicode[STIX]{x1D70F}})$
. Then
![]() $\deg W\leqslant G_{n}d^{n}$
where
$\deg W\leqslant G_{n}d^{n}$
where
![]() $G_{n}$
is an explicit constant, singly-exponential in
$G_{n}$
is an explicit constant, singly-exponential in
![]() $n$
.
$n$
.
In conclusion, we remark that the estimates in terms of degrees in this section could be generalized to estimates in terms of volumes of Newton polytopes, with the proofs extending verbatim.
Acknowledgements
I would like to express my gratitude to Ehud Hrushovski for suggesting the problem studied in this paper to me and for invaluable discussions. I also wish to thank Omar Leon Sanchez for his useful suggestions during the preparation of this manuscript. Finally, I wish to thank the anonymous referee for many helpful suggestions.