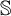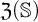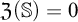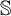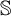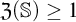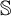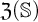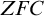1 Introduction
Equivalence of behavior, or bisimilarity in any of its flavors, is a fundamental concept in the study of processes, logic, and many other areas of Computer Science and Mathematics. In the case of discrete (countable) processes, many formalizations of the concept result to be equivalent and it can be completely described by using some form of modal logic—the well-known Hennessy–Milner property.
As soon as one leaves the realm of discrete processes, the question of defining and characterizing behavior turns into a problem with various (sometimes unexpected) mathematical edges. For the case of labelled Markov processes (LMP) [Reference Desharnais3], the first issue to be taken care of is that the concept of probability and measure cannot be defined for all subsets of the state space. Hence the complexity of state spaces (in the sense of Descriptive Set Theory [Reference Kechris7]) plays an important role.
A notable consequence is that an LMP admits two generally different notions of equivalence of behavior between its states: state bisimilarity and event bisimilarity. The first one can be considered as an appropriate generalization to continuous spaces of Larsen and Skou’s probabilistic bisimilarity. On the other hand, event bisimilarity can be characterized by a very simple and natural modal logic
$\mathcal {L}$
defined by the following grammar:
$$\begin{align*}\phi \mathrel{\mathop:}= \top \mid \phi_1 \land \phi_2 \mid \langle a \rangle_{>q}\phi, \end{align*}$$
where a ranges over possible actions of the interpreting LMP and q over rationals between
$0$
and
$1$
; the formula
$\langle a \rangle _{>q}\phi $
holds on states at which the probability of reaching another state satisfying
$\phi $
after an a transition is greater than q.
Despite its simplicity, this logic also characterizes state bisimilarity for wide classes of LMPs (thus, the two types of bisimilarities coincide). Desharnais, Edalat and Panangaden [Reference Desharnais, Edalat and Panangaden4] showed (building on Edalat’s categorical result [Reference Edalat6]) that the category of generalized LMP over analytic state spaces has the Hennessy–Milner property with respect to
$\mathcal {L}$
. This result was later strengthened by Doberkat [Reference Doberkat5] in that it applies to the original category of LMP. Recently, Pachl and the second author extended the result to LMP over universally measurable state spaces [Reference Pachl and Sánchez Terraf9].
But if regularity assumptions on the state spaces are omitted, the Hennessy–Milner property is lost (see [Reference Sánchez Terraf10] by the second author). It is therefore of interest to understand how state bisimilarity differs from the event one for LMP over general measurable spaces. Zhou proposed in [Reference Zhou12] one way to quantify this difference, by expressing state bisimilarity as the greatest fixed point of an operator
$\mathcal {O}$
and pointed out an LMP for which more than
$\omega $
iterates of
$\mathcal {O}$
are needed to reach it.
In this paper, we study the operator
$\mathcal {O}$
in a general setting, a dual version
$\mathcal {G}$
of it, and the hierarchy of relations and
$\sigma $
-algebras respectively induced by them. We then define the Zhou ordinal
$\mathfrak {Z}(\mathbb {S})$
of an LMP
$\mathbb {S}$
to be the number of iterates needed to reach state bisimilarity when one starts from the event one. After reviewing some basic material in Section 2, we develop the general theory of the operators
$\mathcal {O}$
and
$\mathcal {G}$
in Section 3. In Section 4 we focus on the class
$\mathcal {S}$
of LMP over separable metrizable spaces, “separable LMP” for short, and the supremum of the Zhou ordinals of such processes,
$\mathfrak {Z}(\mathcal {S})$
. One of our main results is that
$\mathfrak {Z}(\mathcal {S})$
is a limit ordinal of uncountable cofinality (and hence at least
$\omega _1$
). In Section 5, we construct a family of LMPs
$\{\mathbb {S}(\beta ) \mid \beta \leq \omega _1\}$
having
$\mathfrak {Z}(\mathbb {S}(\beta ))= \beta $
when
$\beta $
is a limit ordinal; these processes are separable for countable
$\beta $
. We also discuss the consistency with the axioms of set theory that the bound
$\omega _1$
is actually attained by a separable LMP. Finally, some further directions are pointed out in Section 6.
2 Preliminaries
An algebra over a set S is a nonempty family of subsets of S closed under finite unions and complementation. It is a
$\sigma $
-algebra if it is also closed under countable unions. Given an arbitrary family
$\mathcal {U}$
of subsets of S, we use
$\sigma (\mathcal {U})$
to denote the least
$\sigma $
-algebra over S containing
$\mathcal {U}$
. Let
$(S,\Sigma )$
be a measurable space, i.e., a set S with a
$\sigma $
-algebra
$\Sigma $
over S. We say that
$(S,\Sigma )$
(or
$\Sigma $
) is countably generated if there is some countable family
$\mathcal {U}\subseteq \Sigma $
such that
$\Sigma =\sigma (\mathcal {U})$
. A subspace of the measurable space
$(S,\Sigma )$
consists of a subset
$Y\subseteq S$
with the relative
$\sigma $
-algebra
. Notice that if
$\Sigma =\sigma (\mathcal {U})$
, then
. If
$(S_1,\Sigma _1),(S_2,\Sigma _2)$
are two measurable spaces, we say that
$f:S_1\to S_2$
is
$\underline{(\Sigma _1,\Sigma _2)\text{-}\mathrm{measurable}}$
if
$f^{-1}(A)\in \Sigma _1$
for all
$A\in \Sigma _2$
.
Assume now that
$V\subseteq S$
. We will use
$\Sigma _V$
to denote
$\sigma (\Sigma \cup \{V\})$
, the extension of
$\Sigma $
by the set V. It is immediate that
$\Sigma _V=\{(B_1\cap V)\cup (B_2\cap V^c)\mid B_1,B_2\in \Sigma \}$
. It is obvious that if
$\Sigma $
is countably generated so is
$\Sigma _V$
. The sum of two measurable spaces
$(S_1,\Sigma _1)$
and
$(S_2,\Sigma _2)$
is
$(S_1\oplus S_2,\Sigma _1\oplus \Sigma _2)$
, with the following abuse of notation:
$S_1\oplus S_2$
is the disjoint union (direct sum qua sets) and
$\Sigma _1\oplus \Sigma _2\mathrel {\mathop :}=\{Q_1\oplus Q_2\mid Q_i \in \Sigma _i\}$
. If Y is a topological space,
$\mathcal {B}(Y)$
will denote the
$\sigma $
-algebra generated by the open sets in Y; hence
$(Y,\mathcal {B}(Y))$
is a measurable space, the Borel space of Y. We say that a family of sets
$\mathcal {F}\subseteq \mathcal {P}(S)$
separates points if for every pair of distinct points
$x,y$
in S, there is some
$A\in \mathcal {F}$
with
$x\in A$
and
$y \notin A$
. We have the following proposition.
Proposition 1. [Reference Kechris7, Proposition 12.1]
Let
$(S,\Sigma )$
be a measurable space. The following are equivalent
$:$
-
1.
$(S,\Sigma )$
is isomorphic to some
$(Y,\mathcal {B}(Y))$
, where Y is separable metrizable. -
2.
$(S,\Sigma )$
is isomorphic to some
$(Y,\mathcal {B}(Y))$
for
$Y\subseteq [0,1]$
. -
3.
$(S,\Sigma )$
is countably generated and separates points.
A class
$\mathcal {M}$
of subsets of S is monotone if it is closed under the formation of monotone unions and intersections. Halmos’ Monotone Class Theorem will be frequently used in this work.
Theorem 2. [Reference Billingsley1, Theorem 3.4]
If
$\mathcal {F}$
is an algebra of sets and
$\mathcal {M}$
is a monotone class, then
$\mathcal {F}\subseteq \mathcal {M}$
implies
$\sigma (\mathcal {F})\subseteq \mathcal {M}$
.
Given a measurable space
$(S,\Sigma )$
, a subprobability measure on S is a
$[0,1]$
-valued set function
$\mu $
defined on
$\Sigma $
such that
$\mu (0)=0$
and for any pairwise disjoint collection
$\{A_n\mid n\in \omega \}\subseteq \Sigma $
, we have
$\mu (\bigcup _{n\in \omega }A_n)=\sum _{n\in \omega }\mu (A_n)$
. In addition, for probability measures we require
$\mu (S)=1$
. If
$\Sigma \subseteq \Sigma '$
and
$\mu ,\mu '$
are measures defined on
$(S,\Sigma ),(S,\Sigma ')$
respectively, we say that
$\mu '$
extends
$\mu $
to
$(S,\Sigma ')$
when
. A key idea in the construction of examples is the possibility of extending a measure in the following particular way:
Theorem 3. Let
$\mu $
be a finite measure defined in
$(S,\Sigma )$
and let
$V \subseteq S$
be a non-
$\mu $
-measurable set. Then there are extensions
$\mu _0$
and
$\mu _1$
of
$\mu $
to
$\Sigma _V$
such that
$\mu _0(V)\neq \mu _1(V)$
.
Definition 4. A
$\underline{\mathrm{Markov\ kernel}}$
on
$(S,\Sigma )$
is a function
$\tau :S\times \Sigma \rightarrow [0,1]$
such that for each fixed
$s \in S$
,
$\tau (s,\cdot ):\Sigma \rightarrow [0,1]$
is a subprobability measure, and for each fixed set
$X \in \Sigma $
,
$\tau (\cdot ,X):S \rightarrow [0,1]$
is
$(\Sigma ,\mathcal {B}[0,1])$
-measurable.
These kernels will play the role of transition functions in the processes we define next. Let L be a countable set.
Definition 5. A
$\underline{\mathrm{labelled\ Markov\ process (LMP)}}$
with
$\underline{\mathrm{label\ set}} \ L$
is a triple
$\mathbb {S}=(S,\Sigma ,\{\tau _a \mid a \in L\})$
, where S is a set of
$\underline{\mathrm{states}}$
,
$\Sigma $
is a
$\sigma $
-algebra over S, and for each
$a\in L$
,
$\tau _a:S \times \Sigma \rightarrow [0,1]$
is a Markov kernel. An LMP is said to be
$\underline{\mathrm{separable}}$
if its state space is countably generated and separates points.
By Proposition 1, the restriction to separable LMP is equivalent to studying processes whose state space is a subset of Euclidean space.
Example 6. We will now present the LMP
$\mathbb {U}$
, which was introduced (under the name
$\mathbf {S_3}$
) in [Reference Sánchez Terraf10]. This will be an important example throughout this paper to illustrate concepts and motivate constructions. From this point onwards, I will denote the open interval
$(0,1)$
,
$\mathfrak {m}$
will be the Lebesgue measure on I and
$\mathcal {B}_V$
will be the
$\sigma $
-algebra
$\sigma (\mathcal {B}(I) \cup \{V\})$
, where V is a Lebesgue non-measurable subset of
$I $
. By Theorem 3 we have two extensions
$\mathfrak {m}_0$
and
$\mathfrak {m}_1$
of
$\mathfrak {m}$
such that
$\mathfrak {m}_0(V)\neq \mathfrak {m}_1(V)$
. Also, let
$\{q_n\}_{n\in \omega }$
be an enumeration of the rationals in I and define
$B_n \mathrel {\mathop :}= (0,q_n)$
; hence
$\{B_n\mid n\in \omega \}$
is a countable generating family of
$\mathcal {B}(I )$
.
Let
$s,t,x \notin I $
be mutually distinct; we may view
$\mathfrak {m}_0$
and
$\mathfrak {m}_1$
as measures defined on the sum
$I \oplus \{s,t,x\}$
, supported on
$I $
. The label set will be
$L\mathrel {\mathop :}= \omega \cup \{\infty \}$
. Now define
$\mathbb {U}=(U,\Upsilon ,\{\tau _n \mid n\in L\})$
such that
$$ \begin{align*} (U,\Upsilon)& \mathrel{\mathop:}= (I \oplus\{s,t,x\},\mathcal{B}_V\oplus \mathcal{P}(\{s,t,x\})), \\ \tau_n(r,A) &\mathrel{\mathop:}= \chi_{B_n}(r)\cdot \delta_x(A),\\ \tau_{\infty}(r,A)&\mathrel{\mathop:}= \chi_{\{s\}}(r)\cdot \mathfrak{m}_0(A)+\chi_{\{t\}}(r)\cdot \mathfrak{m}_1(A), \end{align*} $$
when
$n\in \omega $
and
$A\in \Upsilon $
. This defines an LMP since for all r,
$0\leq \chi _{B_a}(r) \leq 1$
and
${0\leq \chi _{\{s\}}(r) + \chi _{\{t\}}(r) \leq 1}$
and we infer measurability because
$\tau _l(\cdot ,A)$
is always a linear combination of measurable functions.
The dynamics of this process goes intuitively as follows: The states s and t can only make an
$\infty $
-labelled transition to a “uniformly distributed” state in
$I $
, but they disagree on the probability of reaching
$V\subseteq I$
. Then, each point of
$B_n\subseteq I$
can make an n-transition to x. Finally, x can make no transition at all (see Figure 1).
Figure 1 The LMP
$\mathbb {U}$
.
For R a symmetric relation over S, we say that
$A \subseteq S$
is R-closed if
$\{s\in S \mid \exists x\in A \; x\mathrel {R}s\} \subseteq A$
. If
$\Gamma \subseteq \mathcal {P}(S)$
, we denote by
$\Gamma (R)$
the family of all R-closed sets in
$\Gamma $
. Note that if
$\Gamma $
is a
$\sigma $
-algebra, then
$\Gamma (R)$
is a sub-
$\sigma $
-algebra of
$\Gamma $
. We also define a new relation
$\mathcal {R}(\Gamma )$
consisting of all pairs
$(s,t)$
such that
$\forall A \in \Gamma \; (s \in A \leftrightarrow t \in A)$
.
Definition 7. Fix an LMP
$\mathbb {S}=(S,\Sigma ,\{\tau _a\mid a\in L\})$
. A
$\underline{\mathrm{state\ bisimulation}} \ R$
on
$\mathbb {S}$
is a symmetric relation on S such that
$\forall a\in L \; \tau _a(s,C)=\tau _a(t,C)$
whenever
$s\mathrel {R}t$
and
$C \in \Sigma (R)$
. We say that s and t are
$\underline{\mathrm{state\ bisimilar}}$
, denoted by
$s\sim _s t$
, if there exists some state bisimulation R such that
$s\mathrel {R}t$
. The relation
$\sim _s$
is called
$\underline{\mathrm{state\ bisimilarity}}$
.
Definition 8. Let
$\mathbb {S}=(S,\Sigma ,\{\tau _a \mid a\in L\})$
be an LMP and
$\Lambda \subseteq \Sigma $
.
$\Lambda $
is
$\underline{\mathrm{stable}}$
with respect to
$\mathbb {S}$
if for all
$A \in \Lambda $
,
$r \in [0,1]\cap \mathbb {Q}$
and
$a \in L$
, we have
$\{s : \tau _a(s,A)>r\} \in \Lambda $
.
Note that for a sub-
$\sigma $
-algebra
$\Lambda \subseteq \Sigma $
,
$\Lambda $
is stable if and only if
is an LMP.
Definition 9. Let
$\mathbb {S}=(S,\Sigma ,\{\tau _a \mid a\in L\})$
be an LMP. A relation R on S will be called an
$\underline{\mathrm{event\ bisimulation}}$
if there exists a stable sub-
$\sigma $
-algebra
$\Lambda \subseteq \Sigma $
such that
$R=\mathcal {R}(\Lambda )$
.
Two states s and t of an LMP are
$\underline{\mathrm{event\ bisimilar}}$
, denoted by
$s\sim _e t$
, if there exists some event bisimulation R such that
$s\mathrel {R}t$
. The relation
$\sim _e$
is called
$\underline{\mathrm{event\ bisimilarity}}$
.
To illustrate these concepts with the LMP
$\mathbb {U}$
, one can show that
$\Xi \mathrel {\mathop :}= \sigma (\mathcal {B}(I) \cup \{\{s,t\},\{x\}\})$
is a stable
$\sigma $
-algebra; hence s and t are event bisimilar. However they are not state bisimilar as V is
$\mathcal {R}(\sim _s)$
-closed and
$\tau _{\infty }(s,V)\neq \tau _{\infty }(t,V)$
. See [Reference Sánchez Terraf10] for details.
Recall the modal logic
$\mathcal {L}$
presented in the Introduction. We spell out the formal interpretation of the modalities:
$s \models \langle a \rangle _{>q}\phi $
on the LMP
$(S,\Sigma ,\{\tau _a \mid a\in L\})$
if and only if there exists
$A \in \Sigma $
such that for all
$s' \in A$
,
$s' \models \phi $
and
$\tau _a(s,A)> q$
. Given a formula
$\phi $
we write
to denote the set of states satisfying
$\phi $
. It can be proved by induction that each of these sets is measurable. We write
for the collection of sets
; we have the following logical characterization of event bisimilarity.
Theorem 10. [Reference Danos, Desharnais, Laviolette and Panangaden2, Proposition 5.5 and Corollary 5.6]
For an LMP
$(S,\Sigma ,\{\tau _a \mid a\in L\})$
,
is the smallest stable
$\sigma $
-algebra included in
$\Sigma $
. Therefore the logic
$\mathcal {L}$
characterizes event bisimilarity, in symbols
.
The last equality follows easily from the fact that
$\mathcal {R}(\sigma (\mathcal {F}))=\mathcal {R}(\mathcal {F})$
holds for any family of sets
$\mathcal {F}$
.
Regarding
$\mathbb {U}$
, the
$\sigma $
-algebra
$\Xi $
turns out to be
; therefore
${\sim _e}=\textrm {id}_U\cup \{(s,t),(t,s)\}$
. This further implies that
${\sim _s}=\textrm {id}_U$
given that it can be proved that
${\sim _s}\subseteq {\sim _e}$
is always the case and, as noted before, s and t are not state-bisimilar. Consequently, this is an example where state bisimilarity is properly contained in event bisimilarity. In fact, the LMP
$\mathbb {U}$
was introduced in [Reference Sánchez Terraf10] to show that event bisimilarity and state bisimilarity differ in LMP over general measurable spaces. In this work it will serve as a seed for several constructions to be performed in Section 4.
3 The operators
$\mathcal {O}$
and
$\mathcal {G}$
Fix a Markov process
$\mathbb {S}=(S,\Sigma ,\{\tau _a\mid a\in L\})$
. We will work with the operators defined in [Reference Zhou12], and we introduce a new one,
$\mathcal {G}$
:
Definition 11. Let
$\Lambda \subseteq \Sigma $
and
$R \subseteq S\times S$
.
-
• The relation
$\mathcal {R}^T(\Lambda )$
is given by
$$\begin{align*}(s,t) \in \mathcal{R}^T(\Lambda) \iff \forall a\in L \; \forall E\in \Lambda \; \tau_a(s,E)=\tau_a(t,E). \end{align*}$$
-
•
$\mathcal {O}(R)\mathrel {\mathop :}= \mathcal {R}^T(\Sigma (R))$
. -
•
$\mathcal {G}(\Lambda )\mathrel {\mathop :}= \Sigma (\mathcal {R}^T(\Lambda ))$
.
Note that
$\mathcal {O}(R)$
is always an equivalence relation for any R and if
$\Lambda $
is a
$\sigma $
-algebra, then
$\mathcal {G}(\Lambda )$
is too. The motivating idea behind the definition of
$\mathcal {R}^T$
is to relate states that are probabilistically indistinguishable with respect to a fixed set of “tests,” here given by the family
$\Lambda $
of events. An equivalence relation R on the set of states induces naturally
$\Sigma (R)$
, the R-closed sets in
$\Sigma $
, as a family of tests. It follows that R is a state bisimulation if and only if
$R\subseteq \mathcal {R}^T(\Sigma (R)) = \mathcal {O}(R)$
.
Example 12. Let us do some simple calculations with the operator
$\mathcal {O}$
concerning the LMP
$\mathbb {U}$
. If
$\nabla $
denotes the total relation
$U\times U$
,
$$\begin{align*}\mathcal{O}(\nabla)=\mathcal{R}^T(\Upsilon (\nabla))=\mathcal{R}^T(\{\varnothing,U\})= \textrm{id}_U\cup\{(s,t),(t,s)\}={\sim_e}. \end{align*}$$
Also, because
$V \in \Upsilon (\sim _e)$
,
$$\begin{align*}\mathcal{O}(\sim_e)=\mathcal{R}^T(\Upsilon(\sim_e))=\textrm{id}_U={\sim_s}. \end{align*}$$
We highlight the fact that a single application of
$\mathcal {O}$
from the event bisimilarity
$\sim _e$
leads to state bisimilarity
$\sim _s$
.
In the next proposition we collect some basic facts on the operators defined up to this point; most of them appear in [Reference Zhou12].
Proposition 13. Let
$\Lambda , \Lambda '\subseteq \Sigma $
be sub-
$\sigma $
-algebras and
$R, R'\subseteq S\times S$
.
-
1.
$\Lambda \subseteq \Sigma (\mathcal {R}(\Lambda ))$
. -
2.
$R\subseteq \mathcal {R}(\Sigma (R))$
. -
3. If
$\Lambda \subseteq \Lambda '$
, then
$\mathcal {R}(\Lambda )\supseteq \mathcal {R}(\Lambda ')$
and
$\mathcal {R}^T(\Lambda )\supseteq \mathcal {R}^T(\Lambda ')$
. -
4. If
$R\subseteq R'$
, then
$\Sigma (R)\supseteq \Sigma (R')$
. -
5.
$\mathcal {R}(\Sigma (\mathcal {R}(\Lambda )))=\mathcal {R}(\Lambda )$
. -
6.
$\mathcal {O}$
and
$\mathcal {G}$
are monotone operators. -
7. R is a state bisimulation iff
$(S,\Sigma (R),\{\tau _a\mid a \in L\})$
is an LMP. -
8. If
$\Lambda $
is stable, then
$\mathcal {R}(\Lambda )\subseteq \mathcal {R}^T(\Lambda )$
.
We will also need some basic material on fixpoint theory. We work with von Neumann ordinals, viz.
$\alpha = \{\gamma : \gamma < \alpha \}$
. If
$F:A\to A$
is a function on a complete lattice A, we define the iterates of F by
$F^0(x)\mathrel {\mathop :}= x$
,
$F^{\alpha +1}(x)\mathrel {\mathop :}= F(F^{\alpha }(x))$
,
$F^{\lambda }(x)\mathrel {\mathop :}=\bigwedge _{\alpha <\lambda }F^{\alpha }(x)$
if
$\lambda $
is a limit ordinal, and
$F^{\infty }(x)=\bigwedge _{\lambda }F^{\lambda }(x)$
. We say that x is a pre-fixpoint (resp. post-fixpoint) of F if
$F(x)\leq x$
(resp.
$x\leq F(x)$
).
Proposition 14. [Reference Sangiorgi11, Exercise 2.8.10]
Let
$F:A\to A$
be a monotone function on a complete lattice A. If x is a pre-fixpoint of F, then
$F^{\infty }(x)$
is the greatest fixpoint of F below x. Furthermore, this fixed point is reached at an ordinal
$\alpha $
such that
$|\alpha |\leq |A|$
.
As in Zhou’s work [Reference Zhou12] we will construct chains of relations and of
$\sigma $
-algebras using the operators
$\mathcal {O}$
and
$\mathcal {G}$
. The next result will be an aid in showing that
(resp.
) is a post(pre)-fixpoint of
$\mathcal {G}$
(
$\mathcal {O}$
).
Lemma 15.
.
Proof. Since
is stable, we have
by Proposition 13(8). We prove the other inclusion by structural induction on formulas. Suppose that
. If
, then
$s \in A \Leftrightarrow t \in A$
. The case
is also trivial from the IH. For the case
, observe that the hypothesis
implies
. Then, the
$\sigma $
-algebra
$\mathcal {A}_{s,t}\mathrel {\mathop :}= \{A\in \Sigma \mid s\in A \Leftrightarrow t\in A\}$
includes
. We conclude that
, i.e.,
.
Corollary 16.
and
$\mathcal {O}(\sim _e)\subseteq {\sim _e}$
.
Proof. Since
$\Sigma \circ \mathcal {R}$
is expansive by Proposition 13(1), the previous lemma implies that
. Moreover, by antimonotonicity of
$\mathcal {R}^T$
we obtain the result for
$\mathcal {O}$
:
The inclusions
$\mathcal {O}(R)\subseteq R$
and
$\Lambda \subseteq \mathcal {G}(\Lambda )$
do not hold in general for arbitrary R and
$\Lambda $
. For example, if
$\tau $
is null for all arguments,
$\mathcal {O}(R) =S\times S$
for any relation R and analogously for
$\mathcal {G}$
.
Given a relation R we define a transfinite sequence of equivalence relations using the operator
$\mathcal {O}$
:
-
•
$\mathcal {O}^0(R)\mathrel {\mathop :}= R$
. -
•
$\mathcal {O}^{\alpha +1}(R)\mathrel {\mathop :}= \mathcal {O}(\mathcal {O}^{\alpha }(R))$
. -
•
$\mathcal {O}^{\lambda }(R)\mathrel {\mathop :}= \bigcap _{\alpha < \lambda }\mathcal {O}^{\alpha }(R)$
if
$\lambda $
is a limit.
Similarly, if
$\Lambda \subseteq \Sigma $
is a
$\sigma $
-algebra,
$\mathcal {G}$
generates a family of
$\sigma $
-algebras given by:
-
•
$\mathcal {G}^0(\Lambda )\mathrel {\mathop :}= \Lambda $
. -
•
$\mathcal {G}^{\alpha +1}(\Lambda )\mathrel {\mathop :}= \mathcal {G}(\mathcal {G}^{\alpha }(\Lambda ))$
. -
•
$\mathcal {G}^{\lambda }(\Lambda )\mathrel {\mathop :}= \sigma (\bigcup _{\alpha < \lambda } \mathcal {G}{^{\alpha }}(\Lambda ))$
if
$\lambda $
is a limit ordinal.
Note that in the limit case of this last definition we must take the generated
$\sigma $
-algebra since the union of a countable chain of
$\sigma $
-algebras is not in general a
$\sigma $
-algebra.
Let
$\Sigma _0 \subseteq \Sigma $
be a sub-
$\sigma $
-algebra and
$R_0\subseteq S\times S$
a relation. From the iterates of
$\mathcal {O}$
and
$\mathcal {G}$
we define new
$\sigma $
-algebras and relations.
Definition 17. For every ordinal
$\alpha $
let
$\Sigma _{\alpha }\mathrel {\mathop :}= \mathcal {G}^{\alpha }(\Sigma _0)$
and
$R_{\alpha }\mathrel {\mathop :}= \mathcal {O}^{\alpha }(R_0)$
.
It is clear that if
$\alpha <\lambda $
, then
$R_{\lambda }\subseteq R_{\alpha }$
since
$R_{\lambda }=\mathcal {O}^{\lambda }(R_0)=\bigcap _{\beta < \lambda }\mathcal {O}^{\beta }(R_0)=\bigcap _{\beta < \lambda }R_{\beta }\subseteq R_{\alpha }$
. It is also easy to verify from the definitions that
$\Sigma _{\alpha } \subseteq \Sigma _{\lambda }$
. We are interested in determining what other relationships hold among these relations and
$\sigma $
-algebras. We are mainly concerned in the case in which
and when
$R_0$
is the relation of event bisimilarity; then by Lemma 15 we have
$R_0=\mathcal {R}^T(\Sigma _0)$
.
Proposition 18. If
$R_0=\mathcal {R}^T(\Sigma _0)$
, then for all
$\alpha $
,
$R_{\alpha } = \mathcal {R}^T(\Sigma _{\alpha })$
.
Proof. By induction on
$\alpha $
. The case
$\alpha =0$
is included in the hypothesis. Now assume that it holds for
$\alpha $
. We calculate as follows:
$R_{\alpha +1}\ {=}\ \mathcal {O}^{\alpha +1}(R_0)\ {=}\ \mathcal {O}(\mathcal {O}^{\alpha }(R_0))\ {=}\ \mathcal {O}(R_{\alpha })=\mathcal {R}^T(\Sigma (R_{\alpha }))\ {=}\ \mathcal {R}^T(\Sigma (\mathcal {R}^T(\Sigma _{\alpha })))\ {=}\ \mathcal {R}^T(\mathcal {G}(\Sigma _{\alpha }))\ {=}\ \mathcal {R}^T(\mathcal {G}(\mathcal {G}^{\alpha }(\Sigma _0))\ {=}\ \mathcal {R}^T(\mathcal {G}^{\alpha +1}(\Sigma _0)){=}\mathcal {R}^T(\Sigma _{\alpha +1})$
. Then it holds for
$\alpha +1$
.
Suppose now that the result holds for all
$\alpha <\lambda $
, with
$\lambda $
a limit ordinal. We have
$R_{\lambda }=\mathcal {O}^{\lambda }(R_0)=\bigcap _{\alpha <\lambda }\mathcal {O}^{\alpha }(R_0)=\bigcap _{\alpha <\lambda }R_{\alpha }=\bigcap _{\alpha <\lambda }\mathcal {R}^T(\Sigma _{\alpha })$
. We will prove that the last term equals
$\mathcal {R}^T(\bigcup _{\alpha <\lambda }\Sigma _{\alpha })$
. Let
$s,t \in S$
. Then
$$ \begin{align*} (s,t) \in \textstyle\bigcap_{\alpha<\lambda}\mathcal{R}^T(\Sigma_{\alpha}) &\Leftrightarrow \forall \alpha<\lambda \, \forall a\in L\,\forall Q \ (Q\in\Sigma_{\alpha} \Rightarrow \tau_a(s,Q)=\tau_a(t,Q)) \\ &\Leftrightarrow \forall a\in L\, \forall Q \, \forall \alpha<\lambda \, (Q \in \Sigma_{\alpha} \Rightarrow \tau_a(s,Q)=\tau_a(t,Q))\\ &\Leftrightarrow \forall a\in L\,\forall Q \, (\exists \alpha<\lambda \, Q \in \Sigma_{\alpha} \Rightarrow \tau_a(s,Q)=\tau_a(t,Q)) \\ &\Leftrightarrow \forall a\in L\,\forall Q \, (Q \in \textstyle \bigcup_{\alpha<\lambda}\Sigma_{\alpha} \Rightarrow \tau_a(s,Q)=\tau_a(t,Q)) \\ &\Leftrightarrow (s,t) \in \mathcal{R}^T(\textstyle \bigcup_{\alpha<\lambda}\Sigma_{\alpha}). \end{align*} $$
Claim.
$\mathcal {R}^T(\bigcup _{\alpha <\lambda }\Sigma _{\alpha })=\mathcal {R}^T(\sigma (\bigcup _{\alpha <\lambda }\Sigma _{\alpha }))$
.
With this we can conclude since
$$\begin{align*}\textstyle\mathcal{R}^T(\sigma(\bigcup_{\alpha<\lambda}\Sigma_{\alpha}))=\mathcal{R}^T(\sigma(\bigcup_{\alpha<\lambda}\mathcal{G}^{\alpha}(\Sigma_0)))=\mathcal{R}^T(\mathcal{G}^{\lambda}(\Sigma_0))=\mathcal{R}^T(\Sigma_{\lambda}). \end{align*}$$
Now we prove the claim. Let
$s,t \in S$
such that
$(s,t)\in \mathcal {R}^T(\bigcup _{\alpha <\lambda }\Sigma _{\alpha })$
. We define
${\mathcal {D}_{s,t}\mathrel {\mathop :}=\{A\in \Sigma \mid \forall a\in L, \, \tau _a(s,A)=\tau _a(t,A)\}}$
. We check that
$\mathcal {D}_{s,t}$
is a monotone class on S. If
$\{A_i\}_{i\in \omega }$
is an increasing family of subsets S such that
$A_i\in \mathcal {D}_{s,t}$
, upper continuity of the measures
$\tau _a(s,\cdot )$
and
$\tau _a(t,\cdot )$
implies
$$\begin{align*}\tau_a(s,\textstyle \bigcup_{i\in\omega}A_i)=\lim_i\tau_a(s,A_i)=\lim_i\tau_a(t,A_i)=\tau_a(t,\textstyle \bigcup_{i\in\omega}A_i). \end{align*}$$
We argue similarly for an intersection of a decreasing family in
$\mathcal {D}_{s,t}$
by using lower continuity of the (finite) measures involved. Since, by hypothesis,
$\bigcup _{\alpha <\lambda }\Sigma _{\alpha } \subseteq \mathcal {D}_{s,t}$
and moreover, the family
$\bigcup _{\alpha <\lambda }\Sigma _{\alpha }$
is an algebra of subsets of S, the Monotone Class Theorem yields
$\sigma (\bigcup _{\alpha <\lambda }\Sigma _{\alpha })\subseteq \mathcal {D}_{s,t}$
.
Since the reverse inclusion
$\mathcal {R}^T(\bigcup _{\alpha <\lambda }\Sigma _{\alpha })\supseteq \mathcal {R}^T(\sigma (\bigcup _{\alpha <\lambda }\Sigma _{\alpha }))$
is trivial, we have the result.
Corollary 19. If
$R_0=\mathcal {R}^T(\Sigma _0)$
, then for all
$\alpha $
,
$\Sigma (R_{\alpha })=\Sigma _{\alpha +1}$
.
Proof. Unfolding definitions,
$$\begin{align*}\Sigma(R_{\alpha})= \Sigma(\mathcal{R}^T(\Sigma_{\alpha}))= \Sigma(\mathcal{R}^T(\mathcal{G}^{\alpha}(\Sigma_0))) =\mathcal{G}(\mathcal{G}^{\alpha}(\Sigma_0))=\mathcal{G}^{\alpha+1}(\Sigma_0)=\Sigma_{\alpha+1}. \end{align*}$$
Proposition 20. If
$R_0=\mathcal {R}(\Sigma _0)=\mathcal {R}^T(\Sigma _0)$
, then for all
$\alpha $
,
$R_{\alpha +1}\subseteq R_{\alpha }$
.
Proof. We work by induction on
$\alpha $
. By using the antimonotonicity of
$\mathcal {R}^T$
and
$\Sigma (\mathcal {R}(\Sigma _0))\supseteq \Sigma _0$
we have
$$\begin{align*}R_1=\mathcal{O}(R_0)=\mathcal{R}^T(\Sigma(R_0))=\mathcal{R}^T(\Sigma(\mathcal{R}(\Sigma_0)))\subseteq \mathcal{R}^T(\Sigma_0)=R_0. \end{align*}$$
This shows the base case. Assume the result for
$\alpha $
, then by applying the monotonicity of
$\mathcal {O}$
to the IH, we have
$R_{\alpha +2}=\mathcal {O}(R_{\alpha +1})\subseteq \mathcal {O}(R_{\alpha })=R_{\alpha +1}$
.
For limit
$\lambda $
we observe that for all
$\alpha <\lambda $
monotonicity of
$\mathcal {O}$
and IH ensure
${R_{\lambda +1}=\mathcal {O}(R_{\lambda })\subseteq \mathcal {O}(R_{\alpha })=R_{\alpha +1}\subseteq R_{\alpha }}$
. Then,
$R_{\lambda +1}\subseteq \bigcap _{\alpha < \lambda }R_{\alpha }=R_{\lambda }$
.
Corollary 21. If
$R_0=\mathcal {R}(\Sigma _0)=\mathcal {R}^T(\Sigma _0)$
, then for all
$\alpha $
,
$\Sigma _{\alpha }\subseteq \Sigma _{\alpha +1}$
.
Proof. For
$\alpha =0$
we observe that
$\Sigma _0\subseteq \Sigma (\mathcal {R}(\Sigma _0))=\Sigma (\mathcal {R}^T(\Sigma _0))=\mathcal {G}(\Sigma _0)=\Sigma _1$
. For successor ordinals, we use Propositions 18 and 20 to obtain
$$\begin{align*}\Sigma_{\alpha+1}=\mathcal{G}(\Sigma_{\alpha})=\Sigma(\mathcal{R}^T(\Sigma_{\alpha}))=\Sigma(R_{\alpha})\subseteq\Sigma(R_{\alpha+1})=\Sigma_{\alpha+2}. \end{align*}$$
Finally, for the limit case, observe that for all
$\alpha <\lambda $
,
$\Sigma _{\alpha }\subseteq \Sigma _{\lambda }$
; then by IH and monotonicity of
$\mathcal {G}$
we have
$\Sigma _{\alpha }\subseteq \Sigma _{\alpha +1}=\mathcal {G}(\Sigma _{\alpha })\subseteq \mathcal {G}(\Sigma _{\lambda })=\Sigma _{\lambda +1}$
. Therefore
$\Sigma _{\lambda }=\sigma (\bigcup _{\alpha < \lambda }\Sigma _{\alpha })\subseteq \Sigma _{\lambda +1}$
.
In the following, for any
$Q\in \Sigma $
,
${\langle a \rangle _{\leq q}}Q$
will denote the set
$\{s\in S \mid \tau _a(s,Q)\leq q \}$
. Similarly for the other order relations.
Note 22. If
$\Theta $
is a
$\sigma $
-algebra, a relation
$\mathcal {R}^T(\Theta )$
is of the form
$\mathcal {R}(\mathcal {F})$
for some subfamily
$\mathcal {F}$
of
$\Sigma $
: If
$\Gamma $
is any algebra such that
$\sigma (\Gamma )=\Theta $
, then
$$\begin{align*}s\mathrel{\mathcal{R}^T(\Theta)}t \iff (s,t)\in \mathcal{R}(\{{\langle a \rangle_{\leq q}}Q \mid a\in L,\, q\in\mathbb{Q},\, Q\in \Gamma\}). \end{align*}$$
Let
$\mathcal {F}$
the family on the right-hand side, namely
$\{{\langle a \rangle _{\leq q}}Q \mid a\in L,\, q\in \mathbb {Q},\, Q\in \Gamma \}$
. If
$(s,t)\in \mathcal {R}^T(\Theta )$
, then for any
$a\in L$
,
$q\in \mathbb {Q}$
and
$Q\in \Theta $
, we have
$s\in {\langle a \rangle _{\leq q}}Q$
iff
$\tau _a(s,Q)\leq q$
iff
$\tau _a(t,Q)\leq q$
iff
$t\in {\langle a \rangle _{\leq q}}Q$
. Conversely, suppose that
$(s,t)\in \mathcal {R}(\mathcal {F})$
. Since
$\mathcal {D}_{s,t}=\{Q\in \Theta \mid \forall a\in L, \, \tau _a(s,Q)=\tau _a(t,Q)\}$
is a monotone class and
$\Gamma $
is a generating algebra for
$\Theta $
such that
$\Gamma \subseteq \mathcal {D}_{s,t}$
, the Monotone Class Theorem yields
$\Theta =\sigma (\Gamma )\subseteq \mathcal {D}_{s,t}$
for every
$a\in L$
.
Proposition 23. If
$R_0=\mathcal {R}(\Sigma _0)=\mathcal {R}^T(\Sigma _0)$
, then for all limit ordinals
$\lambda $
,
$\mathcal {R}(\Sigma _{\lambda })=\mathcal {R}^T(\Sigma _{\lambda })$
.
Proof. By Note 22 there is some
$\Lambda \subseteq \Sigma $
such that
$\mathcal {R}^T(\Sigma _{\alpha })=\mathcal {R}(\Lambda )$
. From Proposition 13(5) it follows that
$$\begin{align*}\mathcal{R}^T(\Sigma_{\alpha})=\mathcal{R}(\Sigma(\mathcal{R}^T(\Sigma_{\alpha})))=\mathcal{R}(\mathcal{G}(\Sigma_{\alpha}))=\mathcal{R}(\Sigma_{\alpha+1})\subseteq \mathcal{R}(\Sigma_{\alpha}). \end{align*}$$
If
$\lambda $
is a limit ordinal,
$\Sigma _{\alpha +1}\subseteq \Sigma _{\lambda }$
holds for all
$\alpha <\lambda $
and hence
$\mathcal {R}(\Sigma _{\lambda })\subseteq \mathcal {R}(\Sigma _{\alpha +1})=\mathcal {R}^T(\Sigma _{\alpha })=R_{\alpha }$
. Then,
$\mathcal {R}(\Sigma _{\lambda })\subseteq \bigcap _{\alpha <\lambda }R_{\alpha }=R_{\lambda }=\mathcal {R}^T(\Sigma _{\lambda })=\mathcal {R}(\Sigma _{\lambda +1})\subseteq \mathcal {R}(\Sigma _{\lambda })$
and the result follows.
In Section 5 we will construct an LMP for which
$\mathcal {R}(\Sigma _{\alpha +1})\supsetneq \mathcal {R}^T(\Sigma _{\alpha +1})$
, and hence the previous equality does not hold for successor ordinals in general.
In the case
$R_0=\mathcal {R}(\Sigma _0)=\mathcal {R}^T(\Sigma _0)$
, we may summarize the results up to this point in Figure 2:
Figure 2 Chains of relations and
$\sigma $
-algebras induced by
$\mathcal {O}$
and
$\mathcal {G}$
(
$\lambda $
limit).
Corollary 24. For a limit ordinal
$\lambda $
, if
$\Sigma (\mathcal {R}(\Sigma _{\lambda }))=\Sigma _{\lambda }$
, then
$\mathcal {R}(\Sigma _{\lambda })$
is a state bisimulation.
Proof.
$\mathcal {R}^T(\Sigma (\mathcal {R}(\Sigma _{\lambda })))=\mathcal {R}^T(\Sigma _{\lambda })=\mathcal {R}(\Sigma _{\lambda })$
. Therefore
$\mathcal {R}(\Sigma _{\lambda })$
is a state bisimulation.
We add an observation about Figure 2: If
$\mathcal {G}(\Gamma )=\Gamma $
, then
$\mathcal {O}(\mathcal {R}^T(\Gamma ))=\mathcal {R}^T\Sigma (\mathcal {R}^T(\Gamma ))=\mathcal {R}^T(\mathcal {G}(\Gamma ))=\mathcal {R}^T(\Gamma )$
. This means that a fixpoint in the lower part forces a fixpoint in the upper part. By using the example in [Reference Sánchez Terraf10] it can be seen that the converse does not hold.
Lemma 25. Let
$\Lambda $
be a sub-
$\sigma $
-algebra of
$\Sigma $
such that
$\Sigma (\mathcal {R}(\Lambda ))=\Lambda $
. The following are equivalent
$:$
-
1.
$\Lambda $
is stable. -
2.
$\mathcal {R}(\Lambda ) \subseteq \mathcal {R}^T(\Lambda )$
. -
3.
$\mathcal {R}(\Lambda )$
is a state bisimulation.
Proof.
1 implies 2 by Proposition 13(8). For 2
$\Rightarrow $
3, observe that
$\mathcal {R}(\Lambda )\subseteq \mathcal {R}^T(\Lambda )=\mathcal {R}^T(\Sigma (\mathcal {R}(\Lambda )))$
and this means that
$\mathcal {R}(\Lambda )$
is a state bisimulation.
By virtue of Proposition 13, Item 7 implies
$(S,\Sigma (\mathcal {R}(\Lambda )),\tau )$
is an LMP, but then
$\Sigma (\mathcal {R}(\Lambda ))=\Lambda $
is stable.
Example. The hypothesis is necessary
$:$
On
$[0,1]$
, take
$\Sigma =\mathcal {B}([0,1])$
,
$\Lambda $
to be the countable-cocountable
$\sigma $
-algebra and
$\tau (x,A)\mathrel {\mathop :}= \delta _x(A)$
for
$x\in [0,\frac {1}{2}]$
and
$\tau (x,A)\mathrel {\mathop :}= \frac {1}{2} \delta _x(A)$
if
$x\in (\frac {1}{2},1]$
. Then
$\Sigma (\mathcal {R}(\Lambda ))=\Sigma \neq \Lambda $
,
$\mathcal {R}(\Lambda )=\textrm {id}_{[0,1]}=\mathcal {R}^T(\Lambda )$
and
$\Lambda $
is not stable since, e.g.,
$\{x \mid \tau (x,[0,1])>\frac {1}{2}\}=[0,\frac {1}{2}]\notin \Lambda $
. This example shows that 2 does not imply 1 in general. Since the identity relation is a state bisimulation, we also conclude that 3 does not imply 1 in general.
The
$\sigma $
-algebra
$\Sigma _{\omega }$
corresponding to the LMP to be presented in Section 5, satisfies
$\mathcal {R}^T(\Sigma _{\omega })=\mathcal {R}(\Sigma _{\omega })$
but
$\mathcal {R}(\Sigma _{\omega })$
is not a state bisimulation. Hence 2 does not imply 3 in general. This example has a stable
$\Sigma _0$
but
$R_0=\mathcal {R}(\Sigma _0)$
is not state bisimulation; hence 1 does not imply 3.
We now aim to prove that
$\Sigma _{\lambda }$
is stable for limit
$\lambda $
. With the notation introduced before Note 22, we observe that
$\Gamma $
is stable if and only if
$\forall a \in L \; \forall q \in \mathbb {Q} \; \forall Q\in \Gamma \; \langle a \rangle _{\leq q}Q \in \Gamma $
. Given a label a, we define the following set:
$$\begin{align*}\mathcal{A}_a \mathrel{\mathop:}= \{Q\in \Sigma \mid \forall q \in \mathbb{Q} \, (\langle a\rangle_{\leq q}Q \in \Sigma_{\lambda} \, \wedge \, \langle a \rangle_{<q}Q \in \Sigma_{\lambda})\}. \end{align*}$$
Then, to show that
$\Sigma _{\lambda }$
is stable it is enough to prove
$\Sigma _{\lambda } \subseteq \mathcal {A}_a$
for all
$a\in L$
.
Lemma 26. If
$\lambda $
is a limit ordinal, then
$\forall a \in L \, \forall \alpha <\lambda \; \Sigma _{\alpha } \subseteq \mathcal {A}_a$
.
Proof. Let
$\alpha <\lambda $
and
$Q\in \Sigma _{\alpha }$
. We will show that for every label
$a\in L$
and for all
$q\in \mathbb {Q}$
the sets
$\langle a\rangle _{\leq q}Q$
and
$\langle a\rangle _{<q}Q$
are in
$\Sigma _{\alpha +1}=\Sigma (\mathcal {R}^T(\Sigma _{\alpha }))\subseteq \Sigma _{\lambda }$
. Since
$\tau _a(\cdot ,Q)$
is measurable,
$\langle a\rangle _{\leq q}Q=\tau _a(\cdot , Q)^{-1}((0,q]) \in \Sigma $
. To check that
$\langle a\rangle _{\leq q}Q$
is
$\mathcal {R}^T(\Sigma _{\alpha })$
-closed, note that
$$ \begin{align*} s\mathrel{\mathcal{R}^T(\Sigma_{\alpha})}t &\iff \forall a\in L \, \forall A\in \Sigma_{\alpha} \; \tau_a(s,A)=\tau_a(t,A) \\ &\iff \forall a\in L \, \forall A\in \Sigma_{\alpha} \, \forall q\in \mathbb{Q} \; (\tau_a(s,A)\leq q \text{ iff } \tau_a(t,A)\leq q) \\ & \iff \forall a\in L \, \forall A\in \Sigma_{\alpha} \, \forall q\in \mathbb{Q} \; (s\in \langle a \rangle_{\leq q}A \text{ iff } t\in \langle a \rangle_{\leq q}A). \end{align*} $$
The proof for
$\langle a \rangle _{<q}Q$
is similar.
Lemma 27.
-
1. If
$\{A_n\}_{n \in \omega }$
is a non-decreasing sequence of measurable sets, then for all
$a\in L$
and for all
$q\in \mathbb {Q}$
,
$\langle a \rangle _{\leq q}\bigcup _{n\in \omega }A_n=\bigcap _{n\in \omega }\langle a \rangle _{\leq q}A_n$
. -
2. If
$\{B_n\}_{n\in \omega }$
is a non-increasing sequence of measurable sets, then for all
$a\in L$
and for all
$q\in \mathbb {Q}$
,
$\langle a \rangle _{< q}\bigcap _{n\in \omega }B_n=\bigcup _{n\in \omega }\langle a \rangle _{<q}B_n$
. -
3.
$\mathcal {A}_a$
is a monotone class.
Proof.
-
1. In general, if
$A\subseteq B$
, then
$\langle a \rangle _{\leq q}B\subseteq \langle a \rangle _{\leq q}A$
by monotonicity of measures. Thus we have (
$\subseteq $
). For (
$\supseteq $
), if
$s\in S$
satisfies
$\forall n\in \omega \, \tau _a(s,A_n)\leq q$
, the continuity of the measure
$\tau _a(s,\cdot )$
yields
$\tau _a(s,\bigcup _{n\in \omega }A_n)=\lim \tau _a(s,A_n)\leq q$
. -
2. Similarly to 1,
$$\begin{align*}\textstyle\bigcap_{n\in\omega}B_n\subseteq B_m &\implies \langle a \rangle_{<q}\bigcap_{n\in\omega}B_n\supseteq \langle a \rangle_{<q}B_m \\&\implies \langle a \rangle_{<q}\bigcap_{n\in\omega}B_n \supseteq \bigcup_{m\in\omega} \langle a \rangle_{<q}B_m. \end{align*}$$
For the other inclusion, if
$s\in \langle a \rangle _{<q}\bigcap _{n\in \omega }B_n $
, continuity of the measure
$\tau _a(s,\cdot )$
implies
$q>\tau _a(s,\bigcap _{n\in \omega }B_n)=\lim \tau (s,B_n)$
. Then, there exists
$n\in \omega $
such that
$\tau _a(s,B_n)<q$
and hence
$s\in \langle a \rangle _{<q}B_n$
. -
3. Let
$\{A_n\}_{n \in \omega }\subseteq \mathcal {A}_a$
be a non-decreasing sequence of sets. Let
$q\in \mathbb {Q}$
; part 1 allows us to conclude
$\langle a \rangle _{\leq q}\bigcup _{n\in \omega }A_n=\bigcap _{n\in \omega }\langle a \rangle _{\leq q}A_n\in \Sigma _{\lambda }$
and also
$$\begin{align*}\textstyle \langle a \rangle _{<q}\bigcup_{n\in \omega}A_n\kern1.2pt{=}\kern1.2pt\bigcup_{m\in\omega}\langle a \rangle_{\leq q-1/m}(\bigcup_{n\in \omega}A_n)\kern1.2pt{=}\kern1.2pt\bigcup_{m\in\omega}\bigcap_{n\in \omega}(\langle a \rangle_{\leq q-1/m}A_n) \kern1.2pt{\in}\kern1.2pt \Sigma_{\lambda}. \end{align*}$$
Then,
$\bigcup _{n\in \omega }A_n \in \mathcal {A}_a$
.Now let
$\{B_n\}_{n \in \omega }\subseteq \mathcal {A}_a$
be non-increasing and let
$q\in \mathbb {Q}$
. The second part yields
$\langle a \rangle _{<q}\bigcap _{n\in \omega }B_n=\bigcup _{n\in \omega }\langle a \rangle _{<q}B_n\in \Sigma _{\lambda }$
and also
$$\begin{align*}\textstyle \langle a \rangle _{\leq q}\bigcap_{n\in \omega}B_n\kern1.2pt{=}\kern1.2pt\bigcap_{m\in\omega}\langle a \rangle_{<q+1/m}(\bigcap_{n\in \omega}B_n)\kern1.2pt{=}\bigcap_{m\in\omega}\bigcup_{n\in \omega}(\langle a \rangle_{<q+1/m}B_n) \kern1.2pt{\in}\kern1.2pt \Sigma_{\lambda}. \end{align*}$$
Then,
$\bigcap _{n\in \omega }B_n \in \mathcal {A}_a$
.
Theorem 28.
$\Sigma _{\lambda }$
is a stable
$\sigma $
-algebra for any limit ordinal
$\lambda $
.
4 The Zhou Ordinal
Zhou expressed state bisimilarity as a fixpoint:
Theorem 29. [Reference Zhou12, Theorem 3.4]
State bisimilarity
$\sim _s$
is the greatest fixpoint of
$\mathcal {O}$
.
By direct application of Proposition 14 we get the following:
Theorem 30. Let R be an equivalence relation on S such that
${\sim _s}\subseteq R$
and
$\mathcal {O}(R)\subseteq R$
, then there exists an ordinal
$\alpha $
such that
$|\alpha |\leq |S|$
and
$\mathcal {O}^{\alpha }(R)={\sim _s}$
.
Corollary 31. [Reference Zhou12, Theorem 4.1]
State bisimilarity
$\sim _s$
can be obtained by iterating
$\mathcal {O}$
from the total relation or from event bisimilarity
$\sim _e$
.
Thanks to this result we may define the following concept.
Definition 32. The
$\underline{\mathrm{Zhou\ ordinal}}$
of an LMP
$\mathbb {S}$
, denoted
$\mathfrak {Z}(\mathbb {S})$
, is the minimum
$\alpha $
such that
$\mathcal {O}^{\alpha }(\sim _e)={\sim _s}$
. The Zhou ordinal of a class
$\mathcal {A}$
of processes, denoted
$\mathfrak {Z}(\mathcal {A})$
, is the supremum of the class
$\{\mathfrak {Z}(\mathbb {S})\mid \mathbb {S}\in \mathcal {A}\}$
if it is bounded or
$\infty $
otherwise.
We will focus on the study of the Zhou ordinal of the class
$\mathcal {S}$
of separable LMPs. It is immediate that it is bounded by the cardinal successor of
${\left |\mathbb {R}\right |}$
.
Lemma 33.
$\mathfrak {Z}(\mathcal {S})\leq (2^{\aleph _0})^+$
.
Proof. Every separable metrizable space S satisfies
${\left |S\right |}\leq 2^{\aleph _0}$
, and hence the bound follows from Theorem 30.
Next we provide the last technical ingredient for the constructions to be performed for our main Theorems 37 and 38. It a simple though essential device to enlarge a given LMP in such a way that the original structure is “isolated” and it does not produce any side effect on the enlargement.
Suppose that
$\mathbb {T}=(T,\Sigma ,\{\tau _a\mid a\in L\})$
is an LMP with label set L. Let
$e\notin T$
be a new state and let
be an expansion of the label set by two new actions. Over the measurable space
$(T^{\ast },\Sigma ^{\ast })\mathrel {\mathop :}= (T\oplus \{e\},\Sigma \oplus \{\{e\},\varnothing \})$
, we define a new LMP
$\mathbb {T}^{\ast }$
with kernels
given by
It is clear that
$\mathbb {T}^{\ast }$
is an LMP. The kernel
$\tau _{\triangledown }$
allows, with probability
$1$
, a transition to e from each state
$t\in T$
, and
only loops around e.
The use of a new state and two extra kernels (instead of just a single new kernel) stems from the fact that in this way it is immediate that
$\mathcal {R}^T$
(as a set operator) is the same, modulo e, for
$\mathbb {T}$
and
$\mathbb {T}^{\ast }$
. This has the following consequence, which will be used in the sequel.
Lemma 34. The Zhou ordinal is invariant under the map
$\mathbb {T}\mapsto \mathbb {T}^{\ast }$
, namely:
$\mathfrak {Z}(\mathbb {T}^{\ast }) =\mathfrak {Z}(\mathbb {T})$
.
The
$\mathbb {T}\mapsto \mathbb {T}^{\ast }$
construction will be used in conjunction with the next lemma, where
$\bar {S}$
is the intended enlargement that we referred to above.
Lemma 35. Let
$\mathbb {S}=(S,\Sigma ,\{\tau _a\mid a\in L\})$
be an LMP and let
$\mathbb {S'}=(S',\Sigma ',\{\tau ^{\prime }_a\mid a\in L\})$
be an LMP over a direct sum
$(S',\Sigma ')=(S\oplus \bar {S},\Sigma \oplus \bar {\Sigma })$
such that
$:$
-
• For all
$r\in S$
and
$a\in L$
,
$\tau ^{\prime }_a(r,Q)=\tau _a(r,Q\cap S)$
. -
•
and
. -
•
$S\in \Sigma ^{\prime }_0$
.
Then
(equivalently,
) and
hold for every
$\alpha \geq 0$
.
Regarding the equation that involves
$R^{\prime }_{\alpha }$
, it says that to know such relation it is enough to determine it in each direct summand separately. One interpretation of this is that whenever
$S\in \Sigma ^{\prime }_0$
, no relevant information about
$\mathbb {S}$
is lost in the direct sum.
The proofs of the main results of this section are based on further analysis of the LMP
$\mathbb {U}$
from Example 6, which was the first example of a process with positive Zhou ordinal. Actually,
$\mathfrak {Z}(\mathbb {U})=1$
as highlighted in Example 12.
A key idea behind the definition of
$\mathbb {U}$
is that the non-measurable set V is essentially the only set that distinguishes
$\mathfrak {m}_0$
from
$\mathfrak {m}_1$
and hence s from t. This V can become “available” when all the rational intervals can be used to separate points in
$I=(0,1)$
. From this approach one can control the unveiling of V using
$B_n=(0,q_n)$
to become “available as tests” simultaneously or in parallel, and this is the reason why state bisimilarity is reached in one step in
$\mathbb {U}$
. The same pattern will be used in Theorem 37. On the other hand a serial approach to the uncovering of the family
$\{B_n\}$
will be followed in the proof of Theorem 38.
We will prove our first important result about
$\mathfrak {Z}(\mathcal {S})$
, namely, that it is a limit ordinal. In order to do this we first give the construction of an LMP that will play an essential role in the aforementioned result. Since we will be exclusively concerned with the Zhou ordinal from now on,
$\Sigma _0$
will always be the least stable
$\sigma $
-algebra
of the LMP in consideration and
$R_0 \mathrel {\mathop :}= \mathcal {R}(\Sigma _0)$
.
Start with any
$\mathbb {T}$
such that
$\mathfrak {Z}(\mathbb {T})=\alpha +1$
. Consider the LMP
$\mathbb {T}^{\ast }$
constructed in (1), that for simplicity we will denote by
. By Lemma 34,
$\mathfrak {Z}(\mathbb {S})=\alpha +1$
. Let
$z,y \in S\mathbin \smallsetminus\{e\}$
be such that
$z \mathrel {R_{\alpha }} y$
but
. Then there exist
$A_0\in \Sigma _{\alpha +1}\setminus \Sigma _{\alpha }$
and
$n\in \omega $
such that
$\tau _n(z,A_0)\neq \tau _n(y,A_0)$
. We now define a new process: Let
where
We will call
$\Sigma '$
the
$\sigma $
-algebra of
$\mathbb {S}'$
and anything referred to this LMP will be primed:
$\Sigma ^{\prime }_{\alpha }, R^{\prime }_{\alpha }, \sim ^{\prime }_s$
.
This new process will act as an amalgam of
$\mathbb {S}$
and
$\mathbb {U}$
with x replaced by S: Each state in I behaves either as z or y according to the label
$m\in \omega $
, and the process continues inside
$\mathbb {S}$
afterwards. Labels
$\triangledown $
and
allow to separate the LMP
$\mathbb {S}$
from the rest in such a way that its behavior is independent of the enlargement. If that were not the case, event bisimilarity could identify states of S and
$I\cup \{s,t\}$
, and therefore restrict the sets that appear in
. Observe that
$\mathbb {S}'$
will end up with infinitely many different kernels, even though
$\mathbb {S}$
had only finitely many. Also note that for
$r\in I$
, there are only three possible values of
$\tau '(r,Q)$
:
$\tau _n(z,Q\cap S)$
,
$\tau _n(y,Q\cap S)$
or
$0$
; this is very similar to
$\mathbb {U}$
, where there were only two possible values of
$\tau _n(r,Q)$
.
Lemma 36.
$\mathbb {S}'$
is an LMP. Moreover,
and
.
Proof. To show that
$\mathbb {S}'$
is an LMP, we only need to check that
$\tau ^{\prime }_a$
is a Markov kernel for every
.
If
$Q\in \Sigma '$
, measurability of
$\tau ^{\prime }_m(\cdot ,Q)$
follows from the fact that
$\tau _m(\cdot ,Q\cap S)$
is measurable for all
$m\in \omega $
and from the measurability of the sets
$(0,q_m)$
and
$\{s,t\}$
. Measurability of
$\tau ^{\prime }_{\Box }(\cdot ,Q)$
for
only depends on the measurability of the characteristic functions involved. Finally, for fixed
$r\in S'$
, all maps
$\tau ^{\prime }_a(r,\cdot )$
are clearly subprobability measures.
For the second statement, consider the LMP obtained by adding the zero kernel with
$\infty $
label to
$\mathbb {S}$
. This operation does not modify
$R_{\alpha }$
nor
$\Sigma _{\alpha }$
. Moreover, it is immediate that for all
$r\in S$
and labels a,
$\tau ^{\prime }_a(r,Q)=\tau _a(r,Q\cap S)$
holds. Note that also
$S\in \Sigma _0'$
, since
. In this way, we may apply Lemma 35 to
$\mathbb {S}$
and the measurable space
$(I \oplus \{s,t\},\mathcal {B}_V\oplus \mathcal {P}(\{s,t\}))$
to obtain the result.
We are now ready to prove the previously announced result.
Theorem 37.
$\mathfrak {Z}(\mathcal {S})$
is a limit ordinal.
Proof. First observe that
$\mathfrak {Z}(\mathcal {S})>0$
as shown in [Reference Sánchez Terraf10]. Suppose by way of contradiction that
$\mathfrak {Z}(\mathcal {S})=\alpha +1$
for some
$\alpha \geq 0$
. Then there must exist a separable LMP
$\mathbb {T}$
such that
$\mathfrak {Z}(\mathbb {T})=\alpha +1$
. Now consider the LMP
$\mathbb {S'}$
as in the previous construction. We show that
$\mathfrak {Z}(\mathbb {S}')\geq \alpha +2$
. To see this it is enough to prove that
$s\mathrel {R^{\prime }_{\alpha +1}}t$
but
. For the first condition, let us show that
. Let
$Q\in \Sigma ^{\prime }_{\alpha +1}=\Sigma '(\mathcal {R}^T(\Sigma ^{\prime }_{\alpha }))$
and assume
$Q\cap I \neq \varnothing $
; we show that
$Q\cap I =I $
. Let
$r_0\in Q\cap I $
and
$r\in I $
. Suppose that
; then there exist
$m\in \omega $
and
$B\in \Sigma ^{\prime }_{\alpha }$
such that
$\tau ^{\prime }_m(r_0,B)\neq \tau ^{\prime }_m(r,B)$
, i.e.,
$\tau _m(z,B\cap S)\neq \tau _m(y,B\cap S)$
. By Lemma 36,
$B\cap S\in \Sigma _{\alpha }$
, then
; but this is absurd since we chose
$z,y$
in such a way they are indeed related. It follows that
$r_0\mathrel {\mathcal {R}^T(\Sigma ^{\prime }_{\alpha })} r$
and since Q is
$\mathcal {R}^T(\Sigma ^{\prime }_{\alpha })$
-closed,
$r\in Q\cap I $
. Note that this yields
. To show
$(s,t) \in R^{\prime }_{\alpha +1}=\mathcal {R}^T(\Sigma ^{\prime }_{\alpha +1})$
, consider
$\varnothing \neq Q\in \Sigma ^{\prime }_{\alpha +1}$
. By the previous calculation,
$Q\cap I =I $
; therefore
$\tau ^{\prime }_{\infty }(s,Q)=1=\tau ^{\prime }_{\infty }(t,Q)$
. For the remaining labels
we have
$\tau ^{\prime }_a(s,Q)=0=\tau ^{\prime }_a(t,Q)$
.
We now show that
. Recall that we had chosen
$z,y$
and
$A_0\in \Sigma _{\alpha +1}\setminus \Sigma _{\alpha }$
such that
$\tau _n(z,A_0)\neq \tau _n(y,A_0)$
for some
$n\in \omega $
. By Lemma 36,
$A_0\in \Sigma ^{\prime }_{\alpha +1}$
and from this we conclude
. We also observe that
; therefore
. Then we have
$V\in \Sigma ^{\prime }_{\alpha +2}$
and using that set with the transition labelled by
$\infty $
we obtain
.
It can be deduced from the proof of the previous theorem that from every separable process with Zhou ordinal
$\alpha +1$
another one can be constructed with ordinal equal to
$\alpha +2$
. In spite of this, this construction does not allow to construct a process with positive Zhou ordinal from one having null Zhou ordinal (i.e., having the Hennessy–Milner property).
In the next theorem, the cofinality
$\operatorname {cf} (\lambda )$
of a limit ordinal
$\lambda $
is the least order type (equivalently, the least cardinal) of an unbounded subset of
$\lambda $
.
Theorem 38.
$\operatorname {cf}(\mathfrak {Z}(\mathcal {S}))>\omega $
.
Proof. Towards a contradiction, suppose that for every
$m\in \omega $
we have a separable
$\mathbb {S}_m=(S^m,\Sigma ^m,\{\tau _n^m \}_{n\in \omega })$
with label set
$\{(m,n)\mid n\in \omega \}$
such that
$\zeta _m\mathrel {\mathop :}=\mathfrak {Z}(\mathbb {S}_m)$
satisfy
$\sup _{m\in \omega }\zeta _m=\mathfrak {Z}(\mathcal {S})$
. We will assume that these LMPs have gone through the construction given in (1); this way each process now has two distinguished labels, which for ease of reference we call
$(m,\triangledown )$
and
, that allow them to be differentiated from each other with formulas.
We can assume
$\zeta _0>0$
and also that
$\{\zeta _m\}_{m\in \omega }$
is a strictly increasing sequence; for convenience, we set
$\zeta _{-1}\mathrel {\mathop :}= 0$
. In this way
$\zeta _{m-1}<\zeta _m$
for all
$m\geq 0$
, and hence we can choose
$x_m, y_m \in S^m$
such that
$x_m \mathrel {R^m_{\zeta _{m-1}}} y_m$
but
. Then there is a set
$A_m \in \Sigma _{\zeta _m}^m\mathbin \smallsetminus \Sigma _{\zeta _{m-1}}^m$
such that for some
$i\in \omega $
we have
$\tau _i^m(x_m,A_m)\neq \tau _i^m(y_m,A_m)$
. By reordering the labels of the Markov kernels, we can assume that
$i\in \omega $
is exactly m.
Let us define a new LMP with label set
$L\mathrel {\mathop :}=\{(m,n)\mid m,n\in \omega \}\cup \{\infty \}$
:
where the kernels are given by
$$\begin{align*}\tilde{\tau}_{\infty}(r,Q) = \chi_{\{s\}}(r)\cdot \mathfrak{m}_0(Q\cap I )+\chi_{\{t\}}(r)\cdot \mathfrak{m}_1(Q\cap I). \end{align*}$$
In this case the LMP
$\mathbb {S}$
is an amalgam of the sum of all of the
$\mathbb {S}^m$
and
$\mathbb {U}$
. The sets
$(0,q_n) = B_n$
will become available successively, using a serial approach to uncovering the non-measurable set V. In this way we can surpass the limit of the Zhou ordinals of the
$\mathbb {S}^m$
.
We will call
$(S,\Sigma )$
the measurable space of
$\mathbb {S}$
. It is easy to see that this indeed defines an LMP and the separability of the base space follows from the separability of each of the countably many summands that make it up. We will show that
$\mathfrak {Z}(\mathbb {S})\geq \mathfrak {Z}(\mathcal {S})+1$
, reaching a contradiction. For this, it is enough to verify that
$(s,t)\in R_{\mathfrak {Z}(\mathcal {S})}\mathbin \smallsetminus R_{\mathfrak {Z}(\mathcal {S})+1}$
. This will be implied by the facts
and
$V \in \Sigma _{\mathfrak {Z}(\mathcal {S})+1}\mathbin \smallsetminus \Sigma _{\mathfrak {Z}(\mathcal {S})}$
which in turn are a consequence of the equality
for all
$\eta \leq \mathfrak {Z}(\mathcal {S})$
, where
$\Theta _{\eta }$
is the
$\sigma $
-algebra on
$I $
generated by the intervals
$\{(0,q_m)\mid \zeta _m<\eta \}$
.
Before proving this, we notice that for each
$m\in \omega $
, we can add to
$\mathbb {S}^m$
zero kernels
$\tau ^m_{\infty },\tau ^j_n \ (j\neq m)$
and get the property
$\forall r\in S \ \forall a\in L \ \tilde {\tau }_a(r,Q)=\tau _a(r,Q\cap S)$
, while not changing
$\Sigma ^m_{\eta }$
nor
$R^m_{\eta }$
. Also, thanks to the distinguished labels
$(m,\triangledown )$
and
(which cannot correspond to the label
$(m,m)$
in
$\mathbb {S}^m$
), we have
. This way, all the hypotheses of Lemma 35 are satisfied. Then, for each
$m\in \omega $
and
$\eta $
we have
and
. Using the fact that there are countably many summands and also that
$I,\{s,t\}\in \Sigma _0\subseteq \Sigma _{\eta }$
(because
), for all
$\eta $
we can conclude
So all we have to do now is to show by induction on
$\eta $
that
. If
$\eta =0$
, then obviously
$\Theta _0=\{\varnothing ,I \}$
, so we have to show that
is trivial. In order to do this, it is enough to show that
$\{Q\in \Sigma _0\mid Q\cap I \in \{\varnothing ,I \}\}$
is stable. Assume that
$Q\in \Sigma _0$
satisfies
$ Q \cap I \in \{\varnothing ,I \}$
and
$({\langle a \rangle _{>q}}Q) \cap I \neq \varnothing $
; hence
$a=(m,n)$
for some
$m,n\in \omega $
(since it is obvious from the definition of
$\tilde {\tau }_{\infty }$
that
$a\neq \infty $
). Then there is
$r\in I $
such that
$\tilde {\tau }^m_n(r, Q )>q$
. It follows that
$m=n$
; otherwise the kernel would equal zero.
From
$ Q \in \Sigma _0$
we have
$Q \cap S^m\in \Sigma ^m_0\subseteq \Sigma ^m_{\zeta _{m-1}}$
and considering
$x_m \mathrel {R}_{\zeta _{m-1}} y_m$
, we conclude that
$\tilde {\tau }^m_m(\cdot , Q)$
is constant on I. This yields
$r'\in {\langle a \rangle _{>q}}Q$
for every
$r'\in I$
. This shows that
$\{Q\in \Sigma _0\mid Q\cap I \in \{\varnothing ,I \}\}$
is stable. As this class is easily seen to be a
$\sigma $
-algebra, we have
and therefore the result holds for
$\eta =0$
.
Assume now that
. Notice that the kernels in
$\mathbb {S}$
only depend on one, and only one, of the restrictions to
$S^m$
and
$I $
, and use this together with the IH to obtain
As
$\mathcal {R}^T(\Theta _{\eta })= (S\mathbin \smallsetminus\{s,t\}\times S\mathbin \smallsetminus\{s,t\})\cup \{(s,t),(t,s)\}$
, then
$R_{\eta }$
is the disjoint union
. Therefore,
$A\subseteq I$
is
$R_{\eta }$
-closed iff it is
$\mathcal {R}^T(\bigoplus _{m\in \omega }\Sigma ^m_{\eta })$
-closed. Also, from the choice of
$x_m,y_m$
we deduce that
. From this we have
For the limit case, assume
for all
$\eta <\lambda $
. Then we have the following calculation:
This concludes the proof by induction of Equation (2) and thus ends the proof of the theorem.
Corollary 39.
$\mathfrak {Z}(\mathcal {S})\geq \omega _1$
.
5 The example
In this section we construct, for each ordinal
$\beta \leq \omega _1$
, an LMP
$\mathbb {S}(\beta )$
such that for
$\beta $
limit,
$\mathfrak {Z}(\mathbb {S}(\beta ))= \beta $
. For this, we take the set
$I \times \beta $
together with the product
$\sigma $
-algebra
$\Sigma \mathrel {\mathop :}= \mathcal {B}_V \otimes \mathcal {P}(\beta )$
where V denotes a Lebesgue non-measurable set.
Let
$\{C_n\}_{n\geq 2}$
be the family of open rational intervals included in
$I $
and set
$C_0\mathrel {\mathop :}= V$
and
$C_1\mathrel {\mathop :}= V^c$
; we have that
$\{C_n\}_{n\in \omega }$
generates
$\mathcal {B}_V$
. We now define a hierarchy of sets
$\boldsymbol {\Sigma }_{\xi }^{V}(I)$
totally analogous to the Borel hierarchy.
$\boldsymbol {\Sigma }_1^{V}(I)$
is the family of (countable) unions of sets in
$\{C_n\}_{n\in \omega }$
. The members of
$\boldsymbol {\Pi }_{\xi }^{V}(I)$
are the complements of sets in
$\boldsymbol {\Sigma }_{\xi }^{V}(I)$
and
$\boldsymbol {\Sigma }_{\xi }^{V}(I)\mathrel {\mathop :}=\bigl \{\bigcup _{n\in \omega }A_n\mid A_n\in \boldsymbol {\Pi }_{\xi _n}^{V}(I), \xi _n<\xi \bigr \}$
, for
$\xi>1$
. Note that
$\boldsymbol {\Sigma }_1^{V}(I)$
includes all the open subsets of I and their unions with V.
Given
$Q\subseteq I\times \beta $
, the sections of Q are the sets
$Q_{\alpha }\mathrel {\mathop :}=\{r\mid (r,\alpha )\in Q\}$
for
$\alpha <\beta $
(to avoid confusion we will only use greek subindices for sections). Sometimes we will call
$Q_{\alpha }$
“
$\alpha $
-section” to make the ordinal explicit. The sets
$I\times \{\alpha \}$
will be called fibers. For Q in
$\mathcal {B}_V \otimes \mathcal {P}(\beta )$
, each section
$Q_{\alpha }$
lies in
$\boldsymbol {\Sigma }_{\xi }^{V}(I)$
for some
$\xi $
. We say that the complexity of Q at
$\alpha $
is
$\operatorname {comp}(Q,\alpha ) \mathrel {\mathop :}=\min \bigl \{\xi \mid Q_{\alpha }\in \boldsymbol {\Sigma }_{\xi }^{V}(I)\bigr \}$
, and the (total) complexity of Q is
$\operatorname {comp}(Q) \mathrel {\mathop :}= \sup _{\alpha <\beta }\operatorname {comp}(Q,\alpha )$
. Sets in
$\mathcal {B}_V\otimes \mathcal {P}(\beta )$
can be characterized in terms of this complexity measure.
Lemma 40.
$Q\in \mathcal {B}_V\otimes \mathcal {P}(\beta )$
if and only if
$\operatorname {comp}(Q)<\omega _1$
.
Proof. (
$\Rightarrow $
) Let us verify that
$\mathcal {A}=\{A\subseteq I\times \beta \mid \operatorname {comp}(A) < \omega _1\}$
is a
$\sigma $
-algebra. Assume
$A \in \mathcal {A}$
. Since
$\operatorname {comp}(A^c,\alpha )\leq \operatorname {comp}(A,\alpha )+1$
then
$A^c \in \mathcal {A}$
. Now assume that
$\{A_n\}_{n\in \omega }\subseteq \mathcal {A}$
. Then
$\alpha _n \mathrel {\mathop :}= \operatorname {comp}(A_n)<\omega _1$
for all
$n \in \omega $
. From this it follows that
$\operatorname {comp}(\bigcup _{n \in \omega }A_n) \leq \sup _{n \in \omega } (\alpha _n + 1) < \omega _1$
, and therefore
$\mathcal {A}$
is a
$\sigma $
-algebra. Since
$\mathcal {A}$
includes all the measurable rectangles, we have
$\mathcal {B}_V \otimes \mathcal {P}(\beta )\subseteq \mathcal {A}$
.
(
$\Leftarrow $
) We show by induction on
$\xi $
that
$\operatorname {comp}(Q)=\xi <\omega _1 \implies Q\in \mathcal {B}_V\otimes \mathcal {P}(\beta )$
. If
$\operatorname {comp}(Q)=1$
, then for all
$\alpha <\beta $
,
$Q_{\alpha }=\bigcup \{C_n\mid C_n\subseteq Q_{\alpha }\}$
and therefore
$Q=\bigcup _{n\in \omega }(C_n\times \{\alpha \mid C_n\subseteq Q_{\alpha }\})\in \mathcal {B}_V\otimes \mathcal {P}(\beta )$
. Assume the result for all
$\eta $
with
$\eta <\xi <\omega _1$
and, moreover, assume
$\operatorname {comp}(Q)=\xi $
. Then
$\forall \alpha <\beta $
,
$Q_{\alpha }\in \boldsymbol {\Sigma }_{\xi }^{V}(I)$
. Hence
$Q_{\alpha }=\bigcup _{n<\omega }A^{\alpha }_n$
for some
$A^{\alpha }_n \in \boldsymbol {\Pi }_{\xi _n(\alpha )}^V(I)\subseteq \boldsymbol {\Sigma }_{\xi _n(\alpha )+1}^{V}(I)$
and
$\xi _n(\alpha )<\xi $
is non-decreasing. Let
$\{\theta _n\}_{n\in \omega }$
such that
$\theta _n+1$
is a non-decreasing sequence with limit
$\xi $
. If we set
$\tilde {A}^{\alpha }_n=\bigcup _{m\leq n}\{A^{\alpha }_m\mid A^{\alpha }_m\in \boldsymbol {\Sigma }^V_{\theta _n}(I)\}$
, then we have
$\forall \alpha \; \tilde {A}^{\alpha }_n \in \boldsymbol {\Sigma }^V_{\theta _n}(I)$
and
$Q_{\alpha }=\bigcup _{n\in \omega }\tilde {A}^{\alpha }_n$
. By the IH, for every
$n\in \omega $
,
$\mathcal {B}_V \otimes \mathcal {P}(\beta )$
contains the sets
$C_n = \bigcup _{\alpha <\beta }(\tilde {A}^{\alpha }_n\times \{\alpha \})$
whose
$\alpha $
-section is
$\tilde {A}^{\alpha }_n$
, with complexity
$\theta _n<\xi $
. It follows that
$Q=\bigcup _{n\in \omega }C_n \in \mathcal {B}_V \otimes \mathcal {P}(\beta )$
.
We now define a denumerable family of Markov kernels. As before, fix an enumeration
$\{q_n\}_{n\in \omega }$
of the rational numbers in
$I $
. Define
$\alpha _n(0)\mathrel {\mathop :}= 0$
(
$n\in \omega $
); and for each successor ordinal
$\eta +1$
, let
$\alpha _n(\eta +1)\mathrel {\mathop :}=\eta $
(
$n \in \omega $
). For limit
$\lambda $
we choose
$\{\alpha _n(\lambda )\}_{n\in \omega }$
to be a strictly increasing cofinal sequence in
$\lambda - \{0\}$
of order type
$\omega $
.
Recall that Theorem 3 gives us two extensions
$\mathfrak {m}_0$
and
$\mathfrak {m}_1$
of the Lebesgue measure
$\mathfrak {m}$
such that
$\mathfrak {m}_0(V)\neq \mathfrak {m}_1(V)$
. For each
$n\in \omega $
define
$\tau _n:(I\times \beta )\times (\mathcal {B}_V\otimes \mathcal {P}(\beta )) \to [0,1]$
as follows:
Here
$A_{\alpha _n(\eta )}$
is the
$\alpha _n(\eta )$
-section of A defined before Lemma 40. As in the previous results, the definition of the kernels is motivated by the process
$\mathbb {U}$
. The two “behaviors” that we described, in parallel and serial, are mimicked (by virtue of the definition of
$\alpha _n(\eta )$
) at successor and limit ordinals
$\eta $
, respectively.
Lemma 41. For each
$n \in \omega $
,
$\tau _n$
is a Markov kernel.
Proof. It is clear that for fixed
$(x,\eta )$
, the map
$\tau _n((x,\eta ),\cdot ): \mathcal {B}_V \otimes \mathcal {P}(\beta ) \to [0,1]$
is a subprobability measure. Let
$A \in \mathcal {B}_V\otimes \mathcal {P}(\beta )$
; we want to show that
$\tau _n(\cdot ,A)$
is measurable. For this, fix
$q \in \mathbb {Q}\cap [0,1]$
and consider the set
$\{(x,\alpha )\in I\times \beta \mid \tau _n((x,\alpha ),A)<q\}$
. By inspection of the definition of
$\tau _n$
in each fiber, we obtain that this set is the union of the following ones:
$$ \begin{align*} &\{(x,0) \mid x \cdot \mathfrak{m}_0(A_0)<q\},\quad \bigcup_{\eta < \beta}\{(0,q_n)\times \{\eta+1\} \mid \mathfrak{m}_0(A_{\eta})<q\}, \\ &\bigcup_{\eta < \beta}\{[q_n,1)\times \{\eta+1\} \mid \mathfrak{m}_1(A_{\eta})<q\},\quad \bigcup_{\lambda < \beta}\{(0,q_n)\times \{\lambda\} \mid \mathfrak{m}_0(A_{\alpha_n(\lambda)})<q\}, \\ &\bigcup_{\lambda < \beta}\{[q_n,1)\times \{\lambda\} \mid \mathfrak{m}_1(A_{\alpha_n(\lambda)})<q\}. \end{align*} $$
Observe that each section of this union is either open or closed. Then it is measurable in the product space by Lemma 40.
Hence we have an LMP
$$\begin{align*}\mathbb{S}(\beta) \mathrel{\mathop:}= \bigl( I \times \beta,\; \mathcal{B}_V \otimes \mathcal{P}(\beta),\; \{\tau_n\}_{n\in\omega} \bigr) \end{align*}$$
for each
$\beta \leq \omega _1$
.
Lemma 42. State bisimilarity
$\sim _s$
on
$\mathbb {S}(\beta )$
is the identity.
Proof. We will show by induction that for all
$1\leq \eta \leq \beta $
,
is the identity. For the case
$\eta =1$
, we observe that if
$(x,0)\neq (x',0)$
, then for any
$n \in \omega $
$$\begin{align*}\tau_n((x,0),I\times \beta)=x\neq x'=\tau_n((x',0),I\times \beta) \end{align*}$$
holds. Assume now that the result holds for
$\eta $
and that
$\eta +1\leq \beta $
. By inductive hypothesis
is the identity. It is enough to consider states
$(x,\alpha )\neq (x',\eta )$
for some
$\alpha \leq \eta $
. We analyze the case
$\alpha < \eta $
first. The IH guarantees that every
$(r,\gamma )$
is only
$\sim _s$
-related to itself when
$\gamma <\eta $
; since
$\alpha _n(\eta )<\eta $
, it follows that the measurable set
$A(n)\mathrel {\mathop :}=(I\times \{\alpha _n(\eta )\})\cup (I\times \{\xi \mid \eta \leq \xi <\beta \})$
is an element of
$\Sigma (\sim _s)$
for every
$n\in \omega $
. If
$\eta =1$
, then
$\alpha =0$
, and in such case
$\tau _n((x,\eta ),A(n))=\tau _n((x,\eta ),I\times \beta )=1>x' =\tau _n((x',0),A(n))$
holds for any
$n\in \omega $
. For
$\eta>1$
, there exists
$n\in \omega $
such that
$\alpha _n(\eta )\neq \alpha _n(\alpha )$
and we have
$$\begin{align*}\tau_n((x,\eta),A(n)) =\mathfrak{m}_i(A(n)_{\alpha_n(\eta)})=\mathfrak{m}_i(I)=1\neq 0= \tau_n((x',\alpha),A(n)). \end{align*}$$
Suppose now that
$\eta =\alpha $
and
$x\neq x'$
; without loss of generality we can choose
${n \in \omega }$
such that
$x<q_n<x'$
. Again, since
$\alpha _n(\eta )=\alpha _n(\alpha )<\eta $
, the inductive hypothesis guarantees that the set
$A\mathrel {\mathop :}= (V\times \{\alpha _n(\eta )\}) \cup (I \times \{\xi \mid \eta \leq \xi <\beta \})$
is in
$\Sigma (\sim _s)$
. But then
$$\begin{align*}\tau_n((x,\eta),A) =\mathfrak{m}_0(A_{\alpha_n(\eta)})=\mathfrak{m}_0(V)\neq \mathfrak{m}_1(V)=\mathfrak{m}_1(A_{\alpha_n(\alpha)})=\tau_n((x',\alpha),A). \end{align*}$$
This shows that the claim is also true for
$\eta +1$
. Finally, assume
$\lambda $
is a limit ordinal. Since
, the result follows easily from the IH.
We now calculate a bound for the event bisimilarity,
. We define
$$\begin{align*}\Lambda\mathrel{\mathop:}= \{A\subseteq I\times\beta \mid A_0 \in\mathcal{B}(I) \wedge \forall \alpha>0 \, (A_{\alpha} \in \{\varnothing,I\})\}. \end{align*}$$
Lemma 43.
.
Proof. It is clear that
$\Lambda $
is a
$\sigma $
-algebra, and now we verify that it is stable. Let
$A \in \Lambda $
and
$q\in \mathbb {Q}\cap I $
. By the same reasoning as in the proof of Lemma 41,
$\{(x,\alpha )\in I\times \beta \mid \tau _n((x,\alpha ),A)<q\} \in \Lambda $
since it is Borel in the 0-fiber and, since
$\mathfrak {m}_0(A_{\eta })=\mathfrak {m}_1(A_{\eta })$
for all
$\eta>0$
, the remaining sections are either
$\varnothing $
or I. From this it follows that
$\Lambda $
is stable. Since
is the least stable
$\sigma $
-algebra by Theorem 10, then
.
This bound is rather close to
, as the following result shows.
Lemma 44. For all
$\alpha <\beta $
,
.
Proof. For the case
$\alpha =0$
we observe that for any
$n\in \omega $
$\{(x,\eta )\mid \tau _n((x,\eta ),I\times \beta )<q\}=(0,q)\times \{0\}$
, and this set is in
because this
$\sigma $
-algebra is stable. If we choose
$q=1$
we obtain the first case.
Now assume that for a given
$\eta <\beta $
,
for all
$\alpha <\eta $
. For a fixed
$n\in \omega $
, since
$\alpha _n(\eta )<\eta $
, the following set is in
:
$\{(x,\xi )\mid \tau _n((x,\xi ),I\times \{\alpha _n(\eta )\})<q\}=\bigcup _{\alpha < \beta }\{I\times \{\alpha \}\mid \alpha _n(\alpha )\neq \alpha _n(\eta )\}=I\times (\{\eta \}\cup \{\alpha <\beta \mid \alpha _n(\alpha )=\alpha _n(\eta )\})^c$
. By taking complements in the right-hand side we obtain
. But
since for
$\alpha \neq \eta $
there exists
$n\in \omega $
such that
$\alpha _n(\alpha )\neq \alpha _n(\eta )$
. This completes the inductive step.
The next lemma gives some information about the
$\sigma $
-algebra
$\mathcal {G}^{\xi }(\Lambda )$
. Given
$\eta <\beta $
and a
$\sigma $
-algebra
$\mathcal {A}$
, we will denote by
$\mathcal {A}|_{\eta }$
the restriction
, i.e., the
$\sigma $
-algebra of
$\eta $
-sections of elements of
$\mathcal {A}$
.
Lemma 45. If
$\eta $
satisfies
$\beta> \eta \geq \xi $
, then
$\mathcal {G}^{\xi }(\Lambda )|_{\eta }\subseteq \mathcal {B}(I)$
. Also,
$\mathcal {G}^{\xi }(\Lambda )|_{\zeta +1}$
is trivial whenever
$\xi <\zeta +1<\beta $
.
Proof. By induction on
$\xi $
. If
$\xi =0$
, then
$\mathcal {G}^0(\Lambda )=\Lambda $
and by its definition,
$\Lambda |_{\eta }\subseteq \mathcal {B}(I)$
. Now suppose that the result holds for
$\xi \geq 0$
and take
$\eta \geq \xi +1$
. Let
$A\in \mathcal {G}^{\xi +1}(\Lambda )=\mathcal {G}(\mathcal {G}^{\xi }(\Lambda ))= \Sigma (\mathcal {R}^{T}(\mathcal {G}^{\xi }(\Lambda )))$
, i.e.,
$A \in \mathcal {B}_V\otimes \mathcal {P}(\beta )$
is
$\mathcal {R}^{T}(\mathcal {G}^{\xi }(\Lambda ))$
-closed and therefore it is closed under this relation in each fiber. We aim to prove that
$A_{\eta }$
is Borel. We distinguish two cases: If
$\eta $
is
$\zeta +1$
for some
$\zeta $
, then
$\zeta \geq \xi $
and by the IH
$\mathcal {G}^{\xi }(\Lambda )|_{\zeta }$
consists of Borel sets. Hence, for any set
$D \in \mathcal {G}^{\xi }(\Lambda )$
, any
$n\in \omega $
, and any
$x\in I$
,
$\tau _n((x,\eta ),D)=\mathfrak {m}(D_{\eta -1})$
. In consequence, if
$A_{\eta } \neq \varnothing $
, then it must be the case that
${A_{\eta }=I}$
because this set is
$\mathcal {R}^{T}(\mathcal {G}^{\xi }(\Lambda ))$
-closed. Moreover, the second claim in the statement of the lemma follows.
If
$\eta $
is a limit ordinal, we cannot argue as before because to determine the relation
$\mathcal {R}^{T}(\mathcal {G}^{\xi }(\Lambda ))$
we need to know the sections
$D_{\alpha _n(\eta )}$
of the elements in
$\mathcal {G}^{\xi }(\Lambda )$
, and it might be the case that
$\alpha _n(\eta )<\xi $
. Nevertheless,
$\{n\in \omega \mid \alpha _n(\eta )<\xi \}$
is finite and for the rest of the naturals m,
$\tau _m$
does not distinguish points in
$A_{\eta }$
since by the IH
$D_{\alpha _n(\eta )}$
is Borel. Now, if
$\alpha _n(\eta )<\xi $
,
$\tau _n$
can only distinguish points between
$[0,q_n)$
and
$[q_n,1]$
; in consequence,
$\mathcal {G}^{\xi +1}(\Lambda )|_{\eta }$
is the
$\sigma $
-algebra generated by such intervals, which is clearly included in the Borel
$\sigma $
-algebra. This finishes the case
$\xi +1$
.
For case of
$\xi $
limit, the IH ensures that for all
$\gamma < \xi $
and
$\eta \geq \gamma $
,
$\mathcal {G}^{\gamma }(\Lambda )|_{\eta }\subseteq \mathcal {B}(I)$
. Hence, if
$\eta \geq \xi $
, then
$\eta>\gamma $
and this yields
$\mathcal {G}^{\xi }(\Lambda )|_{\eta }=\sigma \bigl (\bigcup _{\gamma <\xi } \mathcal {G}^{\gamma }(\Lambda )\bigr )|_{\eta }= \sigma (\bigcup _{\gamma <\xi }\mathcal {G}^{\gamma }(\Lambda )|_{\eta }) \subseteq \mathcal {B}(I)$
.
Corollary 46. If
$\beta>\eta +1\geq \xi $
, then
is the total relation. In consequence
$\mathfrak {Z}(\mathbb {S}(\beta ))\geq \beta $
if
$\beta $
is limit, and
$\mathfrak {Z}(\mathbb {S}(\zeta +1))\geq \zeta $
for all
$\zeta $
.
Proof. Combining the inclusion in Lemma 43 with the monotonicity of
$\mathcal {G}$
, we see that
and by Lemma 45
$\Sigma _{\xi }|_{\eta }$
also consists of Borel sets if
$\eta \geq \xi $
. As a consequence,
$\mathcal {O}^{\xi }(\sim _e)=R_{\xi }\supseteq \mathcal {R}^T(\Sigma _{\xi })$
restricted to
$I\times \{\eta +1\}$
is the total relation because the measures
$\mathfrak {m}_i$
cannot distinguish points if the allowed sets are Borel. For the last assertion, take
$\xi =\eta +1$
for any
$\xi <\beta $
in the limit case. For the second case, take
$\xi =\eta =\zeta -1$
if
$\zeta $
is not limit. Otherwise, suppose by way of a contradiction that
$\mathfrak {Z}(\mathbb {S}(\zeta +1))<\zeta $
and choose any
$\eta $
such that
$\mathfrak {Z}(\mathbb {S}(\zeta +1))<\eta <\zeta $
, then
is the total relation. This is a contradiction because
$\sim _s$
is the identity.
The following lemma will provide a more detailed analysis of the relations
$R_{\alpha }$
.
Lemma 47. For all
$\alpha <\beta $
,
is the identity and
$V\times \{\alpha \}$
is in
$\Sigma (R_{\alpha })$
.
Proof. For the case
$\alpha =0$
, we note that
; hence, for any
$q\in \mathbb {Q}$
,
. Given that
$\tau _n((s,0),I\times \beta )=s \cdot \mathfrak {m}_0(I) = s < 1$
, if
$s<t$
, then for any
$q\in \mathbb {Q}$
between s and t we have
. Then,
. This shows that
$R_0={\sim _e}$
is the identity on
$I \times \{0\}$
. Moreover, if
$\eta>0$
and
$x \in I$
, then for any n,
$\tau _n((x,\eta ),I\times \beta )=1$
and hence
$((s,0),(x,\eta )) \notin {\sim _e}$
. As a consequence, the set
$V\times \{0\} \in \mathcal {B}_V \otimes \mathcal {P}(\beta )$
is
${\sim _e}$
-closed. Note that, since
${\sim _e}\supseteq R_{\alpha }$
for any
$\alpha $
, the previous sentence shows that the
$R_{\alpha }$
-class of a point
$(s,0)$
is the singleton
$\{(s,0)\}$
.
Assume now that
$\alpha +1<\beta $
and the result holds for
$\alpha $
. Thanks to the inclusion
$R_{\alpha +1}\subseteq R_{\alpha }$
, the IH ensures that
is the identity relation and the set
$V\times \{\alpha \}$
is in
$\Sigma (R_{\alpha })$
. If
$s < t$
, we choose
$n\in \omega $
such that
$s < q_n < t$
and thus
$\tau _n((s,\alpha +1),V\times \{\alpha \})=\mathfrak {m}_0(V)\neq \mathfrak {m}_1(V)=\tau _n((t,\alpha +1),V\times \{\alpha \})$
. Moreover, the same set
$V\times \{\alpha \}$
serves as a test to distinguish points in the
$(\alpha +1)$
-section and the previous ones:
$\tau _n((s,\alpha +1),V\times \{\alpha \})>0 =\tau ((t,\eta ),V\times \{\alpha \})$
for any
$\eta <\alpha +1$
. Therefore
is also the identity. To show that
$V \times \{\alpha +1\} \in \Sigma (R_{\alpha +1})$
it is enough to prove that
$((s,\alpha +1),(t,\eta )) \notin R_{\alpha +1}$
if
$\alpha +1 < \eta $
. For this we use the same
$V \times \{\alpha \}$
provided by the IH. If
$\eta $
is a successor ordinal, for any
$n \ \tau _n((t,\eta ),V \times \{\alpha \})=0$
holds and if
$\eta $
is limit, we choose
$n\in \omega $
such that
$\alpha _n(\eta )\neq \alpha $
and again we obtain
$\tau _n((t,\eta ),V \times \{\alpha \})=0$
.
It remains to check the limit case. Assume that
$\lambda <\beta $
is a limit ordinal and the result holds for every
$\alpha <\lambda $
. Since
$R_{\lambda }=\bigcap _{\alpha <\lambda }R_{\alpha }\subseteq R_{\alpha }$
,
must be the identity by the IH. From this we conclude that
is the identity relation. If
$s<t$
, let
$q_n \in \mathbb {Q}$
such that
$s<q_n<t$
. By IH,
$V\times \{\alpha _n(\lambda )\} \in \Sigma (R_{\alpha _n(\lambda )})$
and therefore the inequality
$\tau _n((s,\lambda ),V\times \{\alpha _n(\lambda )\})\neq \tau _n((t,\lambda ),V\times \{\alpha _n(\lambda )\})$
allows us to conclude that
$((s,\lambda ),(t,\lambda ))\notin R_{\alpha _n(\lambda )+1}\supseteq R_{\lambda }$
. Now, if
$\eta \neq \lambda $
, we choose n such that
$\alpha _n(\eta )\neq \alpha _n(\lambda )$
and we have
$\tau _n((s,\lambda ),V\times \{\alpha _n(\lambda )\})>0=\tau _n((t,\eta ),V\times \{\alpha _n(\lambda )\})$
. As before
$((s,\lambda ),(t,\eta ))\notin R_{\alpha _n(\lambda )+1}\supseteq R_{\lambda }$
. It follows that
is the identity and
$V\times \{\lambda \}$
is in
$\Sigma (R_{\lambda })$
.
Corollary 48.
$\mathfrak {Z}(\mathbb {S}(\zeta +1))\leq \zeta $
. If
$\beta $
is a limit ordinal, then
$\mathfrak {Z}(\mathbb {S}(\beta ))\leq \beta $
.
Proof. The first statement follows directly from Lemma 47 by taking
$\alpha =\zeta $
. For the second one, if
$\beta $
is a limit ordinal
$\forall \alpha <\beta $
$R_{\alpha }\supseteq R_{\beta }$
, then if
equals the identity,
is also the identity. Therefore
is the identity and
$\mathfrak {Z}(S(\beta ))\leq \beta $
.
Theorem 49. For a limit
$\beta \leq \omega _1$
,
$\mathfrak {Z}(\mathbb {S}(\beta ))=\beta $
, and if
$\beta <\omega _1$
,
$\mathfrak {Z}(\mathbb {S}(\beta +1))=\beta $
.
From this we have another proof of Corollary 39, since it is elementary to check that for countable
$\beta $
,
$\mathbb {S}(\beta )$
is separable.
We close this section by studying the possible dependency of the value of
$\mathfrak {Z}(\mathcal {S})$
under different set-theoretical hypotheses (consistent relative to Zermelo–Fraenkel set theory).
Assuming the Continuum Hypothesis (
$\mathit {CH}$
) we have
$2^{\aleph _0}=\aleph _1<2^{\aleph _1}$
and in consequence the space
$(I\times \omega _1,\mathcal {B}_V\otimes \mathcal {P}(\omega _1))$
is not separable. Indeed, there are
$2^{\aleph _1}=\left \vert {\mathcal {P}(\omega _1)}\right \vert $
subsets of
$\omega _1$
and each of them defines a different measurable set in the product
$\sigma $
-algebra, but the cardinal of a countably generated
$\sigma $
-algebra is at most
$2^{\aleph _0}$
.
On the other hand, if we assume Martin’s Axiom (
$\mathit {MA}$
) and the negation of
$\mathit {CH}$
, any uncountable subset
$X\subseteq \mathbb {R}$
with cardinality less than
$2^{\aleph _0}$
is a Q-set (see, e.g., [Reference Miller8]), viz. one such that all of its subsets are relative
$G_{\delta }$
. If we choose X such that
${\left |X\right |}=\aleph _1$
, the relative topology has a countable base (the relativization of such a base for
$\mathbb {R}$
) and it generates
$\mathcal {P}(X)$
as a
$\sigma $
-algebra since X is a Q-set. Then,
$\mathcal {P}(X)\cong \mathcal {P}(\omega _1)$
is separable and in consequence
$(I\times \omega _1,\mathcal {B}_V\otimes \mathcal {P}(\omega _1))$
, the state space of
$\mathbb {S}(\omega _1)$
, also is. In this context the bound in Corollary 39 is attained.
6 Conclusion
The Zhou ordinal provides a measure of the failure of the Hennessy–Milner property on labelled Markov processes over general measurable spaces. The general study of this ordinal on processes over separable metrizable spaces has opened several questions.
The proof of Theorem 37 shows in particular that given a process
$\mathbb {S}$
with
$\mathfrak {Z}(\mathbb {S})\geq \alpha $
, we can construct a second one
$\mathbb {S'}$
with
$\mathfrak {Z}(\mathbb {S'})=\alpha +1$
, whenever
$\alpha $
is a successor ordinal. But we actually do not know how to obtain this result for general
$\alpha $
. This is even clearer for
$\alpha =0$
: The construction of the initial counterexample from [Reference Sánchez Terraf10] does not follow the pattern of what we do in the passage from
$\alpha +1$
to
$\alpha +2$
. The same happens with the proof of the Theorem 38. Given
$\{\mathbb {S}_{\alpha }\}_{\alpha <\beta }$
with
$\beta $
limit, the second general question is to construct in a natural way some
$\mathbb {S}_{\beta }$
such that
$\mathfrak {Z}(\mathbb {S}_{\beta })=\sup _{\alpha <\beta } \mathfrak {Z}(\mathbb {S}_{\alpha })$
. For the case of countable
$\beta $
, we obtain a process
$\mathbb {T}$
with
$\mathfrak {Z}(\mathbb {T})\geq \sup _{\alpha <\beta } \mathfrak {Z}(\mathbb {S}_{\alpha })$
(actually, strictly greater).
It is to be noted that the last inequality can be upgraded to an equality by passing to an appropriate quotient. We know how to perform this construction to get a process with Zhou ordinal a limit
$\beta $
from one with a larger ordinal, but this needs further study in general. Another avenue to pursue is the characterization of event bisimilarity on the processes
$\mathbb {S}(\alpha )$
. It can be proved that our proposed bound
$\Lambda $
is indeed equal to
for countable
$\alpha $
; also
is always countably generated. But consistently,
$\Lambda $
on
$\mathbb {S}(\omega _1)$
is not.
As the main open question, we did not settle if
$\mathfrak {Z}(\mathcal {S})$
is actually a (regular) cardinal. An early conjecture was that
$\mathfrak {Z}(\mathcal {S}) =\omega _1$
(unconditionally), but this is now counterintuitive in view of the existence of a separable LMP with such ordinal under
$\mathit {MA}+\neg \mathit {CH}$
. It is also to be noted that if we were able to pass from any process with ordinal
$\alpha $
to one with ordinal
$\alpha +1$
, the same set-theoretical assumptions would let us conclude
$\mathfrak {Z}(\mathcal {S}) \geq \omega _1\cdot 2$
by Theorem 38. To put it in focus, (consistently) finding a separable
$\mathbb {S}$
with
$\mathfrak {Z}(\mathbb {S})\geq \omega _1+1$
is the next question to address.
Acknowledgements
We are very grateful for the referee’s useful suggestions and detailed reading. The second author wants to thank Chunlai Zhou for early discussions on this material during Dagstuhl Seminar 12411 on Coalgebraic Logics.
Funding
Authors supported by Secyt-UNC project 33620180100465CB.
