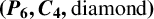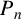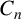1 Introduction
A graph is an ordered pair
$G=(V,E)$
, where V is a set and E is a collection of 2-subsets of V. Elements of V are referred to as vertices and elements of E are edges. All our graphs are finite and have no loops or multiple edges. If there is a risk of confusion, then the sets V and E will be denoted as
$V(G)$
and
$E(G)$
, respectively. For classical graph theory, we use the standard notation, following Bondy and Murty [Reference Bondy and Murty1] and West [Reference West19]. If X is a set of vertices in G, denote by
$G[X]$
the subgraph of G whose vertex set is X and whose edge set consists of all edges of G which have both ends in X. For any
$x\in V( G)$
, let
$N(x)$
denote the set of all neighbours of x in G and let
$d_G(x ):=|N(x)|$
. The neighbourhood
$N (X)$
of a subset
$X\subseteq V(G)$
is the set of vertices in
$V(G)\backslash X$
which are adjacent to a vertex of X.
A clique in a graph is a set of pairwise adjacent vertices and a stable set is a set of pariwise nonadjacent vertices. A k-colouring of a graph G is a mapping
$\varphi :V(G)\to \{1,2,\ldots ,k\}$
such that
$\varphi (u)\neq \varphi (v)$
whenever u and v are adjacent in G. Equivalently, a k-colouring of G is a partition of
$V(G)$
into k stable sets. A graph is k-colourable if it admits a k-colouring. The chromatic number of a graph G, denoted by
$\chi (G)$
, is the minimum number k for which G is k-colourable. The clique number of G, denoted by
$\omega (G)$
, is the size of the largest clique in G. Obviously,
$\chi (H)\geq \omega (H)$
for any induced subgraph H of G. However, the difference
$\chi (H)-\omega (H)$
may be arbitrarily large as there are triangle-free graphs with arbitrarily large chromatic number (see [Reference Mycielski15]). Furthermore, Erdős [Reference Erdős6] showed that for any positive integers k and l there exists a graph G with
$\chi (G)>k$
whose shortest cycle has length at least l.
The complement
$\bar {G}$
of a graph G has the same vertex set as G, and distinct vertices
$u,v$
are adjacent in
$\bar {G}$
just when they are not adjacent in G. A hole of G is an induced subgraph of G which is a cycle of length at least four, and a hole is said to be an odd hole if it has odd length. An
$anti$
-
$hole$
of G is an induced subgraph of G whose complement is a hole in
$\bar {G}$
. Given a graph with large chromatic number, it is natural to ask whether it must contain induced subgraphs with particular properties. A family
$\mathcal {F}$
of graphs is said to be
$\chi $
-
$bounded$
if there exists a function f such that
$\chi (H)\leq f(\omega (H))$
for every graph H in
$\mathcal {F}$
. The function f is called a
$\chi $
-
$bounding$
function of
$\mathcal {F}$
. If f is a linear function of
$\omega $
, then we say that
$\mathcal {F}$
is linearly
$\chi $
-bounded. The notion of
$\chi $
-bounded families was introduced by Gy
$\acute {\mathrm {a}}$
rf
$\acute {\mathrm {a}}$
s [Reference Gyárfás10] in 1987. Since then, it has received considerable attention for
$\mathcal {F}$
-free graphs. See [Reference Scott and Seymour17, Reference Scott and Seymour18] for further details.
We say that a graph G contains a graph H if H is isomorphic to an induced subgraph of G. A graph G is H-free if it does not contain H. For a family
$\mathcal {F}$
of graphs, G is
$\mathcal {F}$
-free if G is H-free for every
$H\in \mathcal {F}$
; when
$\mathcal {F}$
has two elements
$H_1$
and
$H_2$
, we simply write G is
$(H_1,H_2)$
-free instead of
$\{H_1,H_2\}$
-free. If
$\mathcal {F}$
is a finite family of graphs, and if
$\mathcal {C}$
is the class of
$\mathcal {F}$
-free graphs which is
$\chi $
-bounded, then by a classical result of Erdős [Reference Erdős6], at least one member of
$\mathcal {F}$
is a forest (see also [Reference Gyárfás10]). A graph G is perfect if
$\chi (H)=\omega (H)$
for each induced subgraph H of G. A chordless cycle of length
$2k+1, k\geq 2$
, satisfies
$3 =\chi>\omega = 2$
, and its complement satisfies
$k+1=\chi>\omega =k$
. These graphs are therefore imperfect. The strong perfect graph theorem [Reference Chudnovsky, Robertson, Seymour and Thomas4] says that the class of graphs without odd holes or odd anti-holes is linearly
$\chi $
-bounded and the
$\chi $
-bounding function is the identity function
$f(x) = x$
. If we only forbid odd holes, then the resulting class remains
$\chi $
-bounded, but the best known
$\chi $
-bounding function is not linear [Reference Scott and Seymour17]. In recent years, there has been an ongoing project led by Scott and Seymour that aims to determine the existence of
$\chi $
-bounding functions for classes of graphs without holes of various lengths (see the recent survey [Reference Scott and Seymour18]).
Let
$P_n,C_n$
and
$K_n$
denote the path, cycle and complete graph on n vertices, respectively. Gy
$\acute {\mathrm {a}}$
rf
$\acute {\mathrm {a}}$
s [Reference Gyárfás10] showed that the class of
$P_t$
-free graphs is
$\chi $
-bounded. Gravier et al. [Reference Gravier, Hoàng and Maffray9] improved Gy
$\acute {\mathrm {a}}$
rf
$\acute {\mathrm {a}}$
s’s bound slightly by proving that every
$P_t$
-free graph G satisfies
$\chi (G)\leq (t-2)^{\omega (G)-1}$
. It is well known that every
$P_4$
-free graph is perfect. The preceding result implies that every
$P_5$
-free graph G satisfies
$\chi (G)\leq 3^{\omega (G)-1}$
. The problem of determining whether the class of
$P_5$
-free graphs admits a polynomial
$\chi $
-bounding function remains open, and it is remarked in [Reference Kierstead, Penrice and Trotter14] (without proof) that the known
$\chi $
-bounding functions f for this class of graphs satisfy
$c(\omega ^2/\log \omega )\leq f(\omega )\leq 2^\omega $
. So the recent focus is on obtaining
$\chi $
-bounding functions for some classes of
$P_5$
-free graphs. Chudnovsky and Sivaraman [Reference Chudnovsky and Sivaraman5] showed that every
$(P_5, C_5)$
-free graph G satisfies
$\chi (G)\leq 2^{\omega (G)-1}$
, and that every
$(P_5, \mathrm {bull})$
-free graph G satisfies
$\chi (G)\leq \binom {\omega (G)+1}{2}$
. Schiermeyer [Reference Schiermeyer16] showed that every
$(P_5, H)$
-free graph G satisfies
$\chi (G)\leq \omega (G)^2$
, for some special graphs H. Char and Karthick [Reference Char and Karthick3] showed that every
$(P_5$
, 4-wheel)-free graph G satisfies
$\chi (G)\leq \tfrac 32\omega ( G)$
. Gaspers and Huang in [Reference Gaspers and Huang7] proved that every
$(P_6, C_4)$
-free graph G has
$\chi (G)\leq \tfrac 32\omega (G)$
. This
$\tfrac 32$
bound was improved recently by Karthick and Maffray [Reference Karthick and Maffray12] to
$\chi (G)\leq \tfrac 54\omega (G)$
. Karthick and Maffray [Reference Karthick and Maffray11] also showed that every
$(P_5$
, diamond)-free graph G satisfies
$\chi (G)\leq \omega (G)+1$
, where the diamond is the complete graph on four vertices minus one edge. For the family of
$(P_6$
, diamond)-free graphs, Karthick and Mishra [Reference Karthick and Mishra13] showed that every
$(P_6, \mbox {diamond})$
-free graph G satisfies
$\chi (G)\leq 2\omega (G)+5$
. In the same paper, they proved that every
$(P_6, \mbox {diamond}, K_4)$
-free graph is 6-colourable. In 2021, Cameron et al. [Reference Cameron, Huang and Merkel2] improved the
$\chi $
-bounding function of
$(P_6, \mbox {diamond})$
-free graphs to
$\omega (G)+3$
. In a recent paper [Reference Goedgebeur, Huang, Ju and Merkel8], Goedgebeur et al. proved that every
$(P_6, \mbox {diamond})$
-free graph G satisfies
$\chi (G)\leq \max \{6,\omega (G)\}$
.
We investigate the chromatic number of
$(P_6,C_4, \mbox {diamond})$
-free graphs. We do this by reducing the problem to imperfect
$(P_6,C_4, \mbox {diamond})$
-free graphs via the strong perfect graph theorem, dividing the imperfect graphs into several cases and giving a proper colouring for each case. More precisely, the result is stated in the following theorem.
Theorem 1.1. Let G be a
$(P_6,C_4, \mbox {diamond})$
-free graph. Then
$\chi (G)\leq \max \{3,\omega (G)\}$
.
We end this section by setting up the notation that we will be using. Let X and Y be any two subsets of
$V(G)$
. We write
$[X,Y]$
to denote the set of edges that have one end in X and other end in Y. We say that X is complete to Y or
$[X,Y]$
is complete if every vertex in X is adjacent to every vertex in Y; and X is anti-complete to Y if
$[X,Y]=\emptyset $
. If X is a singleton, say
$\{u\}$
, we simply write u is complete (anti-complete) to Y instead of writing
$\{u\}$
is complete (anti-complete) to Y.
2
$(P_6,C_4, \mbox {diamond})$
-free graphs
One of the most celebrated theorems in graph theory is the strong perfect graph theorem [Reference Chudnovsky, Robertson, Seymour and Thomas4].
Theorem 2.1. A graph is perfect if and only if it does not contain an odd hole or an odd anti-hole as an induced subgraph.
Karthick and Maffray [Reference Karthick and Maffray12] proved the following lemma.
Lemma 2.2. Let G be any
$(P_6,C_4)$
-free graph. Then
$\chi (G)\leq \lceil \tfrac 54\omega (G)\rceil $
.
We first study the structure of imperfect
$(P_6,C_4, \mbox {diamond})$
-free graphs. Since a
$P_6$
-free graph contains no hole of length at least 7, and a diamond-free graph contains no anti-hole of length at least 7, by Theorem 2.1, we have the following result.
Lemma 2.3. Every imperfect
$(P_6,C_4, \mbox {diamond})$
-free graph contains an induced
$C_5$
.
Let
$G = (V,E)$
be an imperfect
$(P_6,C_4, \mbox {diamond})$
-free graph that contains an induced
$C_5$
. Denote the vertex set of this
$C_5$
by
$\mathcal {P}:= \{u_1,u_2,u_3,u_4,u_5\}$
and its edge set by
$\{u_1u_2,u_2u_3,u_3u_4,u_4u_5,u_5u_1\}$
. Define the sets.
$$ \begin{align*}\mathcal{N}_1:=\{u\in V(G)\backslash\mathcal{P}:N(u)\cap\mathcal{P}\neq\emptyset\} \quad\mbox{and}\quad \mathcal{N}_2:=V(G)\backslash(\mathcal{N}_1\cup\mathcal{P}).\end{align*} $$
It is straightforward to see that
$V(G)=\mathcal {P}\cup \mathcal {N}_1\cup \mathcal {N}_2$
.
From now on, every subscript is taken modulo 5. Since G is diamond-free and
$C_4$
-free, we may assume that each vertex in
$\mathcal {N}_1$
is either adjacent to exactly one vertex in
$\mathcal {P}$
or exactly two consecutive vertices in
$\mathcal {P}$
. That is,
$\mathcal {N}_1$
can be partitioned into two subsets
$$ \begin{align*}A_i:=\{u\in \mathcal{N}_1:N(u)\cap \mathcal{P}=\{u_i\}\} \quad\mbox{and}\quad B_{i,i+1}:=\{u\in \mathcal{N}_1:N(u)\cap \mathcal{P}=\{u_i,u_{i+1}\}\}.\end{align*} $$
Let
$A:=\bigcup _{i=1}^5 A_i$
and
$B:=\bigcup _{i=1}^5 B_{i,i+1}$
so that
$N(\mathcal {P})=A\cup B$
and
$V(G)=\mathcal {P}\cup A \cup B~\cup ~\mathcal {N}_2$
.
We now claim that
$\mathcal {N}_2$
is empty. For otherwise, suppose that there is a vertex
$z\in \mathcal {N}_2$
. Then z has a neighbour
$x\in A\cup B$
since G is connected. Without loss of generality, we may assume that x is adjacent to
$u_i$
, but adjacent to none of
$u_{i+2},u_{i+3}$
and
$u_{i+4}$
. Then
$\{z,x,u_i,u_{i+2},u_{i+3},u_{i+4}\}$
induces a
$P_6$
. However, this is a contradiction and so
$V(G)=\mathcal {P}\cup A \cup B$
.
We next observe a few useful properties of the sets A and B before proceeding with the proof of the theorem.
-
M1. For any
$v\in V(G)$
,
$N(v)$
induces a
$P_3$
-free graph, so each
$G[A_i]$
is the disjoint union of complete graphs for all
$i\in [5]$
. This follows directly from the fact that G is diamond-free. -
M2. The set
$A_i$
is anti-complete to
$A_{i+1}$
for all
$i\in [5]$
. For if
$a_1\in A_i$
and
$a_2\in A_{i+1}$
are adjacent, then
$\{a_1,a_2,u_{i},u_{i+1}\}$
induces a
$C_4$
and
$\{a_1,a_2,u_{i+1},u_{i+2},u_{i+3},u_{i+4}\}$
induces a
$P_6$
, which is a contradiction. -
M3. The set
$A_i$
is complete to
$A_{i+2}$
for all
$i\in [5]$
. For if
$a_1\in A_i$
and
$a_2\in A_{i+2}$
are not adjacent, then
$\{a_1,a_2,u_{i-2},u_{i-1},u_i,u_{i+2}\}$
induces a
$P_6$
, which is a contradiction. -
M4. Each
$G[B_{i, i+1}]$
is a clique for all
$i\in [5]$
. For if
$b_1,b_2\in B_{i,i+1}$
are not adjacent, then
$\{b_1,b_2,u_i,u_{i+1}\}$
induces a diamond, which is a contradiction. -
M5. The set
$B=B_{i,i+1}\cup B_{i+2,i+3}$
for some i. It suffices to show that for each i at least one of
$B_{i, i+1},B_{i-1, i}$
is empty. Suppose the contrary. Let
$b_1\in B_{i, i+1}$
and
$b_2\in B_{i-1, i}$
. Then, either
$\{b_1,b_2,u_i,u_{i+1}\}$
induces a diamond if
$b_1b_2\in E$
or
$\{b_1,b_2,u_{i-1},u_{i+1},u_{i+2},u_{i+3}\}$
induces a
$P_6$
if
$b_1b_2\notin E$
, which is a contradiction. -
M6. The set
$B_{i,i+1}$
is anti-complete to
$A_i\cup A_{i+1}$
for all
$i\in [5]$
. By symmetry, it suffices to show that
$B_{i, i+1}$
is anti-complete to
$A_i$
. If
$a\in A_i$
and
$b\in B_{i, i+1}$
are adjacent, then
$\{a,b,u_i,u_{i+1}\}$
induces a diamond, which is a contradiction. -
M7. Either
$B_{i,i+1}=\emptyset $
or
$A_{i-1}\cup A_{i+2}=\emptyset $
for all
$i\in [5]$
. To the contrary, assume that
$a\in A_{i+2}$
and
$b\in B_{i,i+1}$
. If a and b are adjacent, then
$\{a,b,u_{i+1},u_{i+2}\}$
induces a
$C_4$
, which is a contradiction. If a and b are not adjacent, then
$\{a,b,u_i,u_{i+2},u_{i+3},u_{i+4}\}$
induces a
$P_6$
, which is a contradiction. The case with
$a\in A_{i-1}$
is symmetric. -
M8. If
$A_i$
contains an edge, then
$A_{i+2}=A_{i+3}=B_{i+1,i+2}=B_{i-2,i-1}=\emptyset $
for all
$i\in [5]$
. Suppose that
$A_i$
contains an edge
$a_1a_2$
. If there is a vertex x in
$A_{i+2}\cup A_{i+3}$
, then x is adjacent to
$a_1$
and
$a_2$
by
$\mathrm{M}3$
. Then
$\{x,a_1,a_2,u_i\}$
induces a diamond, which is a contradiction. Since
$A_i\neq \emptyset $
, it follows that
$B_{i+1,i+2}=B_{i-2,i-1}=\emptyset $
by
$\mathrm{M}7$
. -
M9. If
$A_i\neq \emptyset $
, then each of
$B_{i+1,i+2}=B_{i-2,i-1}=\emptyset $
for all
$i\in [5]$
. This follows directly from
$\mathrm{M}7$
. -
M10. The set
$B_{i,i+1}$
is anti-complete to
$B_{i+2,i+3}$
for all
$i\in [5]$
. For if
$b_1\in B_{i,i+1}$
and
$b_2\in B_{i+2,i+3}$
are such that
$b_1$
and
$b_2$
are adjacent, then
$\{b_1,b_2,u_{i+1},u_{i+2}\}$
induces a
$C_4$
, which is a contradiction.
3 Proof of Theorem 1.1
In this section, we show that every
$(P_6,C_4, \mbox {diamond})$
-free graph G is
$(\omega (G)+1)$
- colourable and G is
$\omega({G})$
-colourable if
$\omega \geq 3$
. The following lemma can be verified routinely.
Lemma 3.1 (Cameron et al. [Reference Cameron, Huang and Merkel2]).
Let G be a graph that can be partitioned into two cliques X and Y such that the edges between X and Y form a matching. If
$\max \{|X|,|Y|\}\leq k$
for some integer
$k\geq 2$
, then G is k-colourable.
To prove Theorem 1.1, we shall use induction on the number of vertices in G. The proof follows the pretty idea presented in [Reference Cameron, Huang and Merkel2]. Two nonadjacent vertices x and y in a graph G are
$comparable$
if
$N(x)\subseteq N(y)$
or
$N(y)\subseteq N(x)$
. The major work lies in proving the following auxiliary theorem.
Theorem 3.2. Let G be a connected
$(P_6,C_4,\mbox {diamond})$
-free graph without clique cutsets and comparable vertices. Then
$\chi (G)\leq \max \{3,\omega (G)\}$
.
Proof. Let
$G=(V,E)$
be a graph satisfying the assumptions of the theorem. In what follows, we let
$\omega $
denote the clique number of a graph under consideration. If
${\omega \leq 2}$
, then the theorem follows from Lemma 2.2. Therefore, we can assume that
$\omega \geq 3$
. Aiming for a contradiction, we assume that G is imperfect and hence it contains an induced
$C_5$
by Lemma 2.3, say
$\mathcal {P}:=\{u_1,u_2,u_3,u_4,u_5\}$
(in order). Define the sets
$\mathcal {P},A,B,A_i$
and
$B_{i,i+1}$
for each
$i\in \{1,2,3,4,5\}$
as before. By
$\mathrm{M}5$
, we may assume that
$B=B_{2,3}\cup B_{4,5}$
. The idea is to colour
$\mathcal {P}\cup A\cup B_{2,3}\cup B_{4,5}$
using exactly
$\omega $
colours. We consider several cases. In each case, we give a desired colouring explicitly. In the following, when we say that we colour a set, say X, with a certain colour a, we mean that we colour each vertex in X with that colour a. We now proceed by considering the following cases.
Case 1.
$A_1$
contains an edge. By
$\mathrm{M}8$
,
$A_3=A_4=B_{2,3}=B_{4,5}=\emptyset $
. Since
$B_{2,3}=B_{4,5}=\emptyset $
, B is empty, that is,
$V(G)=\mathcal {P}\cup A$
. Furthermore,
$A_1$
is anti-complete to
$A_2\cup A_5$
by
$\mathrm{M}2$
, and
$A_2$
and
$A_5$
are complete to each other by
$\mathrm{M}3$
. Now we can colour
$\mathcal {P}\cup A$
as follows.
-
(i)
$A_2$
contains an edge (so that
$A_5=\emptyset $
by
$\mathrm{M}8$
).-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$1,2,1,2,3$
in order. -
• Colour each component of
$A_1$
with colours in
$\{2, 3,\ldots ,\omega \}$
. -
• Colour each component of
$A_2$
with colours in
$\{1,3,4,\ldots ,\omega \}$
.
-
-
(ii)
$A_2$
is stable.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$2,1,2,3,1$
in order. -
• Colour each component of
$A_1$
with colours in
$\{1,3,4,\ldots ,\omega \}$
. -
• If
$A_5$
contains an edge, then
$A_2=\emptyset $
by
$\mathrm{M}8$
and we colour each component of
$A_5$
with colours in
$\{2,3,\ldots ,\omega \}$
. Otherwise, colour
$A_5$
with colour 2 if
$A_5\neq \emptyset $
and colour
$A_2$
with colour 3 if
$A_2\neq \emptyset $
.
-
We note that this colouring is well defined. Since the components of
$A_1$
and
$A_2$
are cliques of size at most
$\omega -1$
, every vertex is coloured with some colour. We now show that this is an
$\omega $
-colouring of
$\mathcal {P}\cup A$
. Observe first that each trivial component of
$A_1$
is coloured with colour 2. By
$\mathrm{M}1$
, the colouring is proper on
$\mathcal {P}\cup A$
. This proves that the colouring is a proper colouring.
Case 2.
$A_1$
is stable but not empty. By
$\mathrm{M}8$
, there are no edges in
$A_3$
and
$A_4$
. By
$\mathrm{M}9$
,
$B_{2,3}=B_{4,5}=\emptyset $
, that is,
$V(G)=\mathcal {P}\cup A$
. If both
$A_2$
and
$A_5$
are stable sets or both
$A_2$
and
$A_5$
are empty, then
$\omega =2$
, which is a contradiction. If
$A_2$
is stable but not empty, then
$A_5$
contains no edges by
$\mathrm{M}8$
, which is a contradiction to
$\omega \geq 3$
. Therefore, it follows from
$\mathrm{M}2$
that the following gives an
$\omega $
-colouring of
$\mathcal {P}\cup A$
.
-
(i)
$A_2$
contains an edge (so that
$A_4=A_5=\emptyset $
by
$\mathrm{M}8$
).-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$2,1,2,1,3$
in order. -
• Colour
$A_1$
and
$A_3$
with colours 1 and 3, respectively. -
• Colour each component of
$A_2$
with colours in
$\{2,3,\ldots ,\omega \}$
.
-
-
(ii)
$A_2$
is empty. (Note that
$A_5$
must contains an edge in this case since
$\omega \geq 3$
, and hence
$A_3=\emptyset $
by
$\mathrm{M}8$
.)-
• Colour
$\{u_1,u_2,u_3,u_4,u_5\}$
with colours
$2,1,2,3,1$
in order. -
• Colour
$A_1$
and
$A_4$
with colour 1 and 2 (if
$A_4\neq \emptyset $
), respectively. -
• Colour each component of
$A_5$
with colours in
$\{2,3,\ldots ,\omega \}$
.
-
By
$\mathrm{M}2$
and
$\mathrm{M}3$
, it is easily verified that the colouring is proper.
Case 3.
$A_1$
is empty. In this case, we further consider the following two subcases.
Subcase 3.1.
$A_{2}$
contains an edge. By
$\mathrm{M}8$
,
$A_4=A_5=\emptyset $
. By
$\mathrm{M}9$
,
$A_3\neq \emptyset $
and
$B_{4,5}\neq \emptyset $
cannot occur simultaneously. That is, either
$A_3$
is empty or
$B_{4,5}$
is empty.
If
$A_3\neq \emptyset $
, then
$B_{4,5}=\emptyset $
by
$\mathrm{M}9$
. That is,
$V(G)=\mathcal {P}\cup A_2\cup A_3\cup B_{2,3}$
. Consider the following colouring of
$\mathcal {P}\cup A_2\cup A_3\cup B_{2,3}$
.
-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$1,2,1,2,3$
in order. -
• Colour each component of
$A_2$
with colours in
$\{1,3,4,\ldots ,\omega \}$
. -
• Colour each component of
$A_3$
with colours in
$\{2,3,\ldots ,\omega \}$
. -
• Colour vertices in
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
By
$\mathrm{M}4$
,
$|B_{2,3}|\leq \omega -2$
. An argument similar to that in Case 1 shows that the above is a proper
$\omega $
-colouring of
$\mathcal {P}\cup A_2\cup A_3\cup B_{2,3}$
.
Suppose now that
$A_3$
is empty. That is,
$V(G)=\mathcal {P}\cup A_2\cup B_{2,3}\cup B_{4,5}$
. Since G is diamond-free, the edges (if there are any) between
$B_{4,5}$
and each component of
$A_2$
form a matching. Consider the following colouring of
$\mathcal {P}\cup A\cup B_{2,3}\cup B_{4,5}$
.
-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,1,2,1,2$
in order. -
• Colour each component of
$A_2$
with colours in
$\{2,3,\ldots ,\omega \}$
. By Lemma 3.1, there exists an
$(\omega -2)$
-colouring of
$B_{4,5}$
with colours in
$\{3,4,\ldots ,\omega \}$
by permuting colours in
$A_2$
(if necessary). -
• By
$\mathrm{M}10$
, it is easily verified that there exists an
$(\omega -2)$
-colouring of
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
Since
$B_{2,3}$
and
$A_2$
are anti-complete by
$\mathrm{M}6$
, the above colouring gives a proper
$\omega $
-colouring of
$\mathcal {P}\cup A_2\cup B_{2,3}\cup B_{4,5}$
.
Subcase 3.2.
$A_{2}$
is stable but not empty. Suppose first that
$A_3$
contains an edge. By
$\mathrm{M}8$
,
$A_5= B_{4,5} =\emptyset $
. By
$\mathrm{M}8$
,
$A_4$
contains no edges since
$A_{2}\neq \emptyset $
.
If
$A_4$
is empty, one can easily verify that the following is a proper
$\omega $
-colouring of
$\mathcal {P}\cup A\cup B_{2,3}\cup B_{4,5}$
.
-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$1,2,1,3,2$
in order. -
• Colour
$A_2$
with 1 and colour each component of
$A_3$
with colours in
$\{2,3,\ldots ,\omega \}$
. -
• Colour vertices in
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
If
$A_4$
is stable but not empty, then
$B_{2,3} =\emptyset $
by
$\mathrm{M}9$
. That is,
$V(G)=\mathcal {P}\cup A$
. One can obtain a proper colouring of
$\mathcal {P}\cup A$
as follows.
-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$1,2,1,3,2$
in order. -
• Colour
$A_2$
and
$A_4$
with colours 3 and 2, respectively, and colour each component of
$A_3$
with colours in
$\{2,3,\ldots ,\omega \}$
.
Now suppose that
$A_3$
is stable but not empty. Then, by
$\mathrm{M}9$
,
$B_{4,5}=\emptyset $
, and by
$\mathrm{M}8$
, both
$A_4$
and
$A_5$
are stable since
$A_2\neq \emptyset $
. So, each
$A_i$
is stable for
$2\leq i\leq 5$
. We can obtain a proper colouring of
$\mathcal {P}\cup A\cup B$
as follows.
-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$1,2,1,3,2$
in order. -
• Colour
$A_2,A_3,A_4$
and
$A_5$
with colours 3, 3, 2 and 1, respectively, and colour each component of
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
Therefore, we may suppose that
$A_3=\emptyset $
. Then, by
$\mathrm{M}8$
, both
$A_4$
and
$A_5$
are stable since
$A_2\neq \emptyset $
and, by
$\mathrm{M}9$
, either
$A_4=\emptyset $
or
$B_{2,3}=\emptyset $
. Now we consider the following two colourings.
-
(i)
$A_4=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,2,1,2,1$
in order. -
• Colour
$A_2$
and
$A_5$
with colours 1 and 2, respectively. -
• By
$\mathrm{M}10$
, there exists an
$(\omega -2)$
-colouring of
$B_{2,3}\cup B_{4,5}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
-
-
(ii)
$A_4\neq \emptyset $
, that is,
$B_{2,3}=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,2,1,2,1$
in order. -
• Colour
$A_2,A_4$
and
$A_5$
with colours 1, 3 and 2, respectively. -
• By
$\mathrm{M}4$
, there exists an
$(\omega -2)$
-colouring of
$B_{4,5}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
-
By
$\mathrm{M}4$
and
$\mathrm{M}10$
, one can easily verify that the above is a proper
$\omega $
-colouring of
$\mathcal {P}\cup A\cup B_{2,3}\cup B_{4,5}$
.
Subcase 3.3.
$A_{2}$
is empty. Suppose first that
$A_3$
contains an edge. By
$\mathrm{M}8$
,
$A_5= B_{4,5} =\emptyset $
. By
$\mathrm{M}9$
, either
$A_4=\emptyset $
or
$B_{2,3}=\emptyset $
. We consider the following two colourings.
-
(i)
$A_4=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,2,1,2,1$
in order. -
• Colour each component of
$A_3$
with colours in
$\{2,3,\ldots ,\omega \}$
. -
• Colour vertices in
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
-
-
(ii)
$A_4\neq \emptyset $
, that is,
$B_{2,3}=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$2,3,1,2,1$
in order. -
• Colour each component of
$A_3$
with colours in
$\{2,3,\ldots ,\omega \}$
. -
• Colour each component of
$A_4$
with colours in
$\{1,3,4,\ldots ,\omega \}$
.
-
One can easily verify that the above is a proper
$\omega $
-colouring of
$\mathcal {P}\cup A\cup B_{2,3}\cup B_{4,5}$
.
Now suppose that
$A_3$
is stable but not empty. Then, by
$\mathrm{M}9$
,
$B_{4,5}$
is empty and, by
$\mathrm{M}8$
,
$A_5$
is stable. We consider the following two colourings.
-
(i)
$A_4=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,1,2,1,2$
in order. -
• Colour
$A_3$
and
$A_5$
with colours 1 and 3, respectively. -
• Colour vertices in
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
-
-
(ii)
$A_4\neq \emptyset $
, that is,
$B_{2,3}=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$1,3,2,1,2$
in order. -
• Colour
$A_3$
and
$A_5$
with colours 1 and 3, respectively, and colour each component of
$A_4$
with colours in
$\{2,3,\ldots ,\omega \}$
.
-
By
$\mathrm{M}2$
and
$\mathrm{M}3$
, one can easily verify that the above is a proper
$\omega $
-colouring of
$\mathcal {P}\cup A\cup B_{2,3}\cup B_{4,5}$
.
Finally, we suppose that
$A_3$
is empty. That is,
$V(G)=\mathcal {P}\cup A_4\cup A_5\cup B_{2,3}\cup B_{4,5}$
. By
$\mathrm{M}9$
, either
$A_4=\emptyset $
or
$B_{2,3}=\emptyset $
. Since G is diamond-free, the edges (if there are any) between
$B_{2,3}$
and each component of
$A_5$
form a matching. Consider the following two colourings of
$\mathcal {P}\cup A_4\cup A_5\cup B_{2,3}\cup B_{4,5}$
.
-
(i)
$A_4=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,2,1,2,1$
in order. -
• Colour each component of
$A_{5}$
with colours in
$\{2,3,\ldots ,\omega \}$
. -
• By Lemma 3.1, there exists an
$(\omega -2)$
-colouring of
$B_{2,3}$
with colours in
$\{3,4,\ldots ,\omega \}$
by permuting colours in
$A_5$
(if necessary). -
• Colour vertices in
$B_{4,5}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
-
-
(ii)
$A_4\neq \emptyset $
, that is,
$B_{2,3}=\emptyset $
.-
• Colour
$\mathcal {P}:=u_1,u_2,u_3,u_4,u_5$
with colours
$3,1,2,1,2$
in order. -
• Colour each component of
$A_4$
with colours in
$\{2,3,\ldots ,\omega \}$
. -
• Colour each component of
$A_5$
with colours in
$\{1,3,4,\ldots ,\omega \}$
. -
• Colour
$B_{4,5}$
with colours in
$\{3,4,\ldots ,\omega \}$
.
-
Since
$B_{2,3}$
and
$A_2$
are anti-complete, the above colouring gives a proper
$\omega $
-colouring of
$\mathcal {P}\cup A_4\cup A_5\cup B_{2,3}\cup B_{4,5}$
. This concludes the proof of Theorem 3.2.
Now we can easily deduce Theorem 1.1.
Proof of Theorem 1.1.
If
$\omega \leq 2$
, then the theorem follows from Lemma 2.2. Therefore, we can assume that
$\omega \geq 3$
and we prove the theorem by induction on
$|V|$
. We may assume that G is connected. For otherwise, the theorem holds by applying the inductive hypothesis to each connected component of G. If G contains a clique cutset S, that is,
$G[V-S]$
is the disjoint union of two subgraphs
$X_1$
and
$X_2$
, then
$\chi (G)=\max \{\,\chi (G[V(X_1)\cup S]),\chi (G[V(X_2)\cup S])\}$
directly from the inductive hypothesis. If G contains two nonadjacent vertices x and y such that
$N(y)\subseteq N(x)$
, then
$\chi (G)=\chi (G[V-\{y\}])$
and
$\omega (G) =\omega (G[V-\{y\}])$
, and the theorem holds by applying the inductive hypothesis to
$G[V-\{y\}]$
. Therefore, we can assume that G is a connected graph with no pair of comparable vertices and no clique cutsets. Thus, the theorem follows directly from Theorem 3.2.
