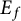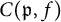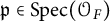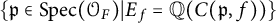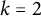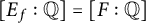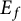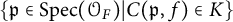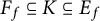1 Introduction
The study of the Fourier coefficients of modular forms is an active area of research in number theory. It is well known that, for any primitive form f over
$\mathbb {Q}$
, the Fourier coefficients of f generate a number field
$E_f$
. In [Reference Koo, Stein and WieseKSW08], Koo, Stein, and Wiese proved that the set of primes p for which the pth Fourier coefficient of f generates
$E_f$
has density 1, if f does not have any nontrivial inner twists. To the best of the authors’ knowledge, the analogous question is still open for Hilbert modular forms, which is the objective of our study in this article.
For a primitive form f over a totally real number field F, let
$E_f$
denote the number field generated by the Fourier coefficients
$C(\mathfrak {p}, f)(\mathfrak {p} \in P)$
of f, where
$P= \mathrm {Spec}(\mathcal {O}_F)$
, the set of all prime ideals of
$\mathcal {O}_F$
(cf. [Reference TaylorShi78]). We first state a result, for primitive forms f over F of weight
$2$
, the set of
$\mathfrak {p} \in P$
with
$\mathbb {Q}(C(\mathfrak {p},f))=E_f$
has Dirichlet density
$1$
, if
$[F : \mathbb {Q}]=[E_f : \mathbb {Q}]$
is an odd prime (cf. Theorem 3.1). We then state and prove a general result for primitive forms f of weight k (cf. Theorem 3.6), under some assumptions on the image of the residual Galois representations
$\bar {\rho }_{f, \lambda }$
attached to f and
$\lambda \in \mathrm {Spec}(\mathcal {O}_{E_f})$
(cf. equation (2.2)). We then show that these assumptions on the image of
$\bar {\rho }_{f, \lambda }$
are satisfied for primitive forms f over F of weight
$2$
, if
$[F : \mathbb {Q}]=[E_f : \mathbb {Q}]$
is an odd prime (cf. Theorem 3.1). The proof of Theorem 3.1 depends on the works of Dimitrov (cf. [Reference DimitrovDim05]), Dimitrov and Dieulefait (cf. [Reference Dieulefait and DimitrovDD06]). We continue a similar study for
$F_f$
, the fixed field of
$E_f$
by the set of all inner twists of f, and show that the set of
$\mathfrak {p} \in P$
with
$\mathbb {Q}(C^\ast (\mathfrak {p},f))=F_f$
has density
$1$
(cf. Section 2.1 for the definition of
$C^\ast (\mathfrak {p},f)$
).
This article builds on the ideas of Koo et al. in [Reference Koo, Stein and WieseKSW08] for primitive forms over
$\mathbb {Q}$
. One of the vital ingredients in the proof of [Reference Koo, Stein and WieseKSW08, Theorem 1.1] is a theorem of Ribet (cf. [Reference SerreRib85, Theorem 3.1]), where he explicitly described the image of l-adic residual Galois representation
$\bar {\rho }_{f,l}$
attached to primitive form f and a prime l. This result played a crucial role in obtaining certain sharp bounds for the images of
$\bar {\rho }_{f,l}$
, which was helpful in their proof. Unfortunately, in our context, an analog of Ribet’s result does not seem to exist in the literature. In order to get a similar sharp bound for the images of
$\bar {\rho }_{f,\lambda }$
, we have to work with some assumptions (cf. equation (3.1)). This explains the reason for our assumptions in Theorems 3.1 and 3.6. Using L-functions and modular forms database (LMFDB), we produce examples of primitive forms f of parallel weight
$2$
in support of Theorem 3.1 (cf. Examples 4–6).
We also calculate the density of
$\mathfrak {p} \in P$
for which
$C(\mathfrak {p}, f) \in K$
, where
$K \subseteq E_f$
is a subfield. This density depends on whether
$F_f \subseteq K$
or not. If
$F_f \not \subseteq K$
, then it is zero (cf. Lemma 4.1); otherwise, it is nonzero and completely determined by the inner twists of f associated with K (cf. Proposition 4.3).
1.1 Structure of the article
The article is organized as follows. In Section 2, we collate all the preliminaries that are required to prove our main theorems (cf. Theorems 3.1 and 3.6). We also introduce the notion of inner twists and study their properties quite elaborately. In Section 3, we state and prove Theorem 3.1 and its generalization (cf. Theorem 3.6) for primitive forms f over F of parallel weight
$2$
and weight k, respectively. We also prove analogous results for
$F_f$
and study their consequences. In Section 4, we calculate the Dirichlet density of
$\mathfrak {p} \in P$
with
$C(\mathfrak {p}, f) \in K$
for any field K with
$K \subseteq E_f$
.
2 Preliminaries
Let F be a totally real number field of degree n. Let
$\mathcal {O}_F$
,
$\mathfrak {n}$
, and
$\mathfrak {D}$
denote the ring of integers, an ideal, and the absolute different of F, respectively.
2.1 Notations
Throughout this article, we fix to use the following notations.
-
• Let
$\mathbb {P}$
denote the set of all primes in
$\mathbb {Z}$
,
$P=\mathrm {Spec}(\mathcal {O}_F)$
. -
• Let
$k=(k_1,k_2,\ldots ,k_n) \in \mathbb {Z}^n$
such that
$k_i\geq 2$
and
$k_1\equiv k_2 \equiv \cdots \equiv k_n \pmod 2$
. Let
$k_0 := \mathrm {max}\{k_1,k_2,\ldots ,k_n \}$
,
$n_0=k_0-2.$
-
• For any number field K, denote
$G_K:= \mathrm {Gal}(\bar {K}/K).$
Let L be a subfield of K. For a prime ideal
$\mathfrak {q}$
in K lying above
$\mathfrak {p}=\mathfrak {q} \cap L$
in L, let
$\mathrm {e}(\mathfrak {q}/\mathfrak {p})$
and
$\mathrm {f}(\mathfrak {q}/\mathfrak {p})$
denote the ramification degree and inertia degree of
$\mathfrak {q}$
over
$\mathfrak {p}$
, respectively.
For any Hecke character
$\Psi $
of F with conductor dividing
$\mathfrak {n}$
and infinity-type
$2-k_0$
, let
$S_k(\mathfrak {n}, \Psi )$
denote the space of all Hilbert modular newforms over F of weight k, level
$\mathfrak {n}$
, and character
$\Psi $
. A primitive form is a normalized Hecke eigenform in the space of newforms. The ideal character corresponding to
$\Psi $
of F is denoted by
$\Psi ^\ast .$
For a primitive form
$f\in S_k(\mathfrak {n}, \Psi )$
, let
$C(\mathfrak {b},f)$
denote the Fourier coefficient of f corresponding to an integral ideal
$\mathfrak {b}$
of
$\mathcal {O}_F$
and
$C^\ast (\mathfrak {b} , f):=\frac {{C(\mathfrak {b}, f)}^2}{\Psi ^\ast (\mathfrak {b})}$
for all ideal
$\mathfrak {b}$
with
$(\mathfrak {b}, \mathfrak {n})=1$
. Write
$E_f=\mathbb {Q}(C(\mathfrak {b}, f)),\ F_f=\mathbb {Q}(C^\ast (\mathfrak {b} , f))$
, where
$\mathfrak {b}$
runs over all the integral ideals of
$\mathcal {O}_F$
with
$(\mathfrak {b}, \mathfrak {n})=1$
. Let
$\mathcal {P}_f :=\mathrm {Spec}(\mathcal {O}_{E_f})$
, the set of all prime ideals of
$\mathcal {O}_{E_f}$
. For any two subfields
$F_1, F_2$
such that
$\mathbb {Q} \subseteq F_2 \subseteq F_1 \subseteq E_f$
, we let
$$ \begin{align*}\mathrm{f}_{\lambda, F_1, F_2} := \mathrm{f}(\lambda \cap F_1 / \lambda \cap F_2)\end{align*} $$
for
$\lambda \in \mathcal {P}_f$
. The following proposition describes some properties of
$E_f$
.
Proposition 2.1 [Reference TaylorShi78]
Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a primitive form of weight k, level
$\mathfrak {n}$
, and character
$\Psi $
with coefficient field
$E_f$
. Then:
-
(1)
$E_f$
is a finite Galois extension of
$\mathbb {Q}$
. -
(2)
$\Psi ^\ast (\mathfrak {m}) \in E_f$
, for all ideals
$\mathfrak {m} \subseteq \mathcal {O}_F$
. -
(3)
$E_f$
is either a totally real or a complex multiplication (CM) field. -
(4)
$E_f = \mathbb {Q} (\{C(\mathfrak {p},f)\}_{\mathfrak {p} \in S})$
, where
$S \subseteq P$
with
$S^c$
is finite. -
(5)
$\overline {C(\mathfrak {p},f)}={\Psi ^\ast (\mathfrak {p})}^{-1}C(\mathfrak {p},f)$
for all
$\mathfrak {p} \in P$
with
$(\mathfrak {p},\mathfrak {n})=1$
.
2.2 Galois representations attached to
${\boldsymbol{f}}$
Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a primitive form of weight k, level
$\mathfrak {n}$
, and character
$\Psi $
with coefficient field
$E_f$
. For
$\lambda \in \mathcal {P}_f$
, by the works of Ohta, Carayol, Blasius-Rogawski, and Taylor (cf. [Tay89] for more details), there exists a continuous Galois representation
$$ \begin{align*}\rho_{f,\lambda} : G_F \rightarrow \mathrm{GL}_2(E_{f,\lambda}),\end{align*} $$
which is absolutely irreducible, totally odd, and unramified outside
$\mathfrak {n} q$
, where
$q \in \mathbb {P}$
is the rational prime lying below
$\lambda $
. Here,
$E_{f,\lambda }$
denote the completion of
$E_f$
at
$\lambda $
. For all primes
$\mathfrak {p}$
of
$\mathcal {O}_F$
with
$(\mathfrak {p}, \mathfrak {n} q)=1$
, we have
$$ \begin{align} \mathrm{tr}(\rho_{f,\lambda}(\mathrm{Frob}_{\mathfrak{p}}))=C(\mathfrak{p},f)\ \mathrm{and} \ \det(\rho_{f,\lambda}(\mathrm{Frob}_{\mathfrak{p}}))=\Psi^\ast(\mathfrak{p}) {N(\mathfrak{p})}^{k_0-1} \end{align} $$
(cf. [Reference CarayolCar86]). By taking a Galois stable lattice, we define
$$ \begin{align} \bar{\rho}_{f, \lambda} := \rho_{f,\lambda} \pmod \lambda: G_F \rightarrow \mathrm{GL}_2(\mathbb{F}_\lambda) \end{align} $$
whose semi-simplification is independent of the choice of a lattice. We conclude this section by recalling the Chebotarev density theorem (cf. [Reference Shemanske and WallingSer81]).
Theorem 2.2 Let C be a conjugacy class of
$G :=\bar {\rho }_{f, \lambda }(G_F)$
. The natural density of
$\{\mathfrak {p}\in P : [\bar {\rho }_{f, \lambda }(\mathrm {Frob}_{\mathfrak {p}})]_G=C\}$
is
$\frac {|C|}{|G|}$
.
2.3 Inner twists and its properties
We now define inner twists associated with a primitive form and describe some of its properties. This notion is quite useful in Section 4.
Let
$f \in S_k(\mathfrak {n}, \Psi )$
be a primitive form defined over F. For any Hecke character
$\Phi $
of F, let
$f_{\Phi }$
denote the twist of f by
$\Phi $
(cf. [Reference ShimuraSW93, Section 5]). The Fourier coefficients of f and
$f_{\Phi }$
are related as follows.
Proposition 2.3 [Reference ShimuraSW93, Proposition 5.1]
Let
$f, f_\Phi $
be as above. If
$\mathfrak {n}_0$
and
$\mathfrak {m}_0$
are the conductors of
$\Psi $
and
$\Phi $
, respectively, then
$f_\Phi \in S_k \big (\mathrm {lcm}(\mathfrak {n},\mathfrak {m}_0 \mathfrak {n}_0, \mathfrak {m}_0^2), \Psi \Phi ^2\big )$
and
$C(\mathfrak {m},f_\Phi )=\Phi ^\ast (\mathfrak {m})C(\mathfrak {m},f)$
for all ideals
$\mathfrak {m}$
of
$\mathcal {O}_F$
.
Definition 2.4 We say a primitive form f is said to be of CM type, if there exists a nontrivial Hecke character
$\Phi $
of F such that
$C(\mathfrak {p}, f)=\Phi ^\ast (\mathfrak {p})C(\mathfrak {p}, f)$
for almost all prime ideals
$\mathfrak {p}$
of
$\mathcal {O}_F$
. We say that f is non-CM if f is not of CM type.
We are now ready to define inner twists.
Definition 2.5 (Inner twists)
Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a non-CM primitive form over F. For any Hecke character
$\Phi $
of F, we say that the twist
$f_\Phi $
of f is inner if there exists a field automorphism
$\gamma : E_f \rightarrow E_f$
such that
$\gamma (C(\mathfrak {p},f))=C(\mathfrak {p}, f_\Phi )$
for almost all prime ideals
$\mathfrak {p}$
of
$\mathcal {O}_F$
.
Remark 2.6 For any primitive form f, the identity map
$\mathrm {id} : E_f \rightarrow E_f$
induces an inner twist of f and we refer to it as the trivial inner twist of f.
Let
$\Gamma \leq \mathrm {Aut}(E_f)$
denote the subgroup of
$\gamma $
associated with all the inner twists of f. Let
$F_f := E_f^{\Gamma }$
, the fixed field of
$E_f$
by
$\Gamma $
. By Galois theory,
$E_f$
is a finite Galois extension of
$F_f$
. Some properties of
$F_f$
are given below.
Lemma 2.7 The field
$F_f$
is totally real and
$C^\ast (\mathfrak {p},f) \in \mathbb {Q}(C(\mathfrak {p},f)).$
Proof By Proposition 2.1, we have
$C^\ast (\mathfrak {p},f) =C(\mathfrak {p},f)\overline {C(\mathfrak {p},f)}$
. This shows that
$F_f$
is totally real. By Proposition 2.1, if
$E_f$
is totally real, then
$C^\ast (\mathfrak {p},f)={C(\mathfrak {p},f)}^2 \in \mathbb {Q}(C(\mathfrak {p},f))$
. If
$E_f$
is a CM field, then
$\mathbb {Q}(C(\mathfrak {p},f))$
is preserved under complex conjugation. Hence,
$C^\ast (\mathfrak {p},f) =C(\mathfrak {p},f)\overline {C(\mathfrak {p},f)} \in \mathbb {Q}(C(\mathfrak {p},f))$
.
We now examine the existence of trivial, nontrivial inner twists for any primitive form f.
Lemma 2.8 If
$f \in S_k(\mathfrak {n}, \Psi ) $
is a non-CM primitive form over F with a nontrivial Hecke character
$\Psi $
, then f has a nontrivial inner twist.
Proof Let
$\sigma : E_f\rightarrow E_f$
be an automorphism defined by
$\sigma (x)=\overline {x}$
, for all
$x \in E_f$
. By Proposition 2.1, we have
$\sigma (C(\mathfrak {p},f))={\Psi ^* (\mathfrak {p})}^{-1}C(\mathfrak {p},f)$
for all
$\mathfrak {p}$
with
$(\mathfrak {p},\mathfrak {n})=1$
. By Proposition 2.3, f has a nontrivial inner twist given by
$(\Psi ^*)^{-1}$
.
We now give some examples of primitive forms with a nontrivial inner twist.
Example 1 Consider a non-CM primitive form f labeled as
$\texttt {2.2.8.1-41.1-a}$
in [Reference MarcusLMFDB], defined over
$F=\mathbb {Q}(\sqrt {2})$
of weight
$(2, 2)$
, level
$[41,\; 41,\; 2\sqrt {2}-7]$
, and with trivial character. The coefficient field
$E_f = \mathbb {Q}(\sqrt {2})$
and
$F_f=\mathbb {Q}$
.
Example 2 Consider a non-CM primitive form f labeled as
$\texttt {2.2.12.1-13.1-a}$
in [Reference MarcusLMFDB], defined over
$F=\mathbb {Q}(\sqrt {3})$
of weight
$(2, 2)$
, level
$[13,\; 13,\; \sqrt {3}+4]$
, and with trivial character. The coefficient field
$E_f = \mathbb {Q}(\sqrt {2})$
and
$F_f=\mathbb {Q}$
.
Example 3 Consider a non-CM primitive form f labeled as
$\texttt {2.2.24.1-9.1-a}$
in [Reference MarcusLMFDB], defined over
$F=\mathbb {Q}(\sqrt {6})$
of weight
$(2, 2)$
, level
$[9,\; 3,\; 3]$
, and with trivial character. The coefficient field
$E_f = \mathbb {Q}(\sqrt {6})$
and
$F_f=\mathbb {Q}$
.
In Examples 1–3, the coefficient field
$E_f \neq F_f$
. Hence, these primitive forms f have a nontrivial inner twist.
Lemma 2.9 Suppose
$f\in S_k(\mathfrak {n}, \Psi )$
is a non-CM primitive form over F with
$[E_f : \mathbb {Q}]$
is an odd prime. If
$E_f$
is totally real, then f does not have any nontrivial inner twists. If
$\Psi = \Psi _0$
is a trivial character, then
$E_f$
is totally real.
Proof Let
$\mathfrak {p} \in P$
be a prime with
$(\mathfrak {p}, \mathfrak {n})=1$
. Since
$E_f$
is totally real,
${C(\mathfrak {p}, f)}^2 \in F_f$
. Since
$[E_f : \mathbb {Q}]$
is prime, the field
$F_f$
is either
$\mathbb {Q}$
or
$E_f$
. If
$F_f =\mathbb {Q},$
then
$[\mathbb {Q}(C(\mathfrak {p}, f)) : \mathbb {Q}]$
is either
$1$
or
$2 $
. This contradicts to that
$[E_f : \mathbb {Q}]$
is an odd prime. Therefore,
$F_f = E_f$
. Hence, f does not have any nontrivial inner twists.
3 Statement and proof of the main theorem
In this section, we shall state and prove the main theorem of this article.
Theorem 3.1 (Main Theorem)
Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a primitive form defined over F of parallel weight
$2$
, level
$\mathfrak {n}$
, and character
$\Psi $
, which is not a theta series. Let
$E_f$
denote the coefficient field of f. Suppose
$[F : \mathbb {Q}]=[E_f : \mathbb {Q}]$
is an odd prime. Then,
$$ \begin{align*}\delta_D \left( \big \{ \mathfrak{p}\in P : \mathbb{Q} \big (C(\mathfrak{p},f) \big ) =E_f \big \} \right) = 1,\end{align*} $$
where
$\delta _D(S)$
denotes the Dirichlet density of
$S \subseteq P$
.
3.1 Images of the residual Galois representations
We now determine the images of the residual Galois representations attached to primitive forms of parallel weight
$2$
. The work of Dimitrov in [Reference DimitrovDim05] is quite influential in this section.
Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a primitive form defined over F of weight
$k=(k_1, k_2, \ldots , k_n)$
, level
$\mathfrak {n}$
, and character
$\Psi $
. Recall that
$k_0=\max \{k_1, \ldots , k_n \}$
and
$\omega _q$
is the mod q cyclotomic character. Then,
$\bar {\Psi }{\omega _q}^{k_0-2}$
is a character on
$G_F$
. Let
$\hat {F}$
be the compositum of the Galois closure of F in
$\bar {\mathbb {Q}}$
and the subfield of
$\bar {\mathbb {Q}}$
given by
$(\bar {F})^{\mathrm {Ker}(\bar {\Psi }{\omega _q}^{k_0-2})}$
. Then,
$\hat {F}$
is a Galois extension of F and
$G_{\hat {F}} \unlhd G_F$
. A combination of Propositions 3.8 and 3.9 in [Reference DimitrovDim05] would imply the following proposition.
Proposition 3.2 Let f be a primitive form which is not a theta series. For almost all
$q \in \mathbb {P}$
, there exists a power
$\hat {q}$
of q such that either
$$ \begin{align*}\bar{\rho}_{f, \lambda}(G_{\hat{F}}) \simeq \big\{g \in \mathrm{GL}_2(\mathbb{F}_{\hat{q}}) : \det(g) \in (\mathbb{F}_q^{\times})^{k_0-1}\big\} \end{align*} $$
or
$$ \begin{align*}\bar{\rho}_{f, \lambda}(G_{\hat{F}}) \simeq \big \{g \in \mathbb{F}_{\hat{q}^2}^{\times} \mathrm{GL}_2(\mathbb{F}_{\hat{q}}) : \det(g) \in (\mathbb{F}_q^{\times})^{k_0-1}\big \}\end{align*} $$
holds.
3.2 Key proposition in the proof of Theorem 3.1
We will now determine the image of
$\bar {\rho }_{f, \lambda }$
for primitive forms f in Theorem 3.1. More precisely, we have
Proposition 3.3 Let
$f\in S_k(\mathfrak {n}, \Psi )$
be as in Theorem
3.1
. For any
$\lambda \in \mathrm {Spec}(\mathcal {O}_{E_f})$
lying above q, we have
$$ \begin{align*}\bar{\rho}_{f, \lambda}(G_{F}) \simeq \{\gamma \in \mathrm{GL}_2(\mathbb{F}_{q^{d}}) : \det(\gamma)\in {\mathbb{F}_q^\times} \},\end{align*} $$
for infinitely many
$q \in \mathbb {P}$
with
$d=\mathrm {f}(\lambda / q)$
.
Before we start the proof of Proposition 3.3, we recall some necessary results.
Proposition 3.4 [Reference RibetMar77]
Let
$K/ \mathbb {Q}$
be a cyclic Galois extension of degree n. For
$1 \leq r\mid n$
, let
$S_r := \{q \in \mathbb {P}: e(\lambda |q)=1\ \&\ \mathrm {f}(\lambda /q)=r \ \mathit {for\ some\ prime\ ideal}\ \lambda |q\}$
. Then,
$\delta _D\left ( S_r \right ) = \frac {\varphi (r)}{n}$
.
Corollary 3.5 Let f be as in Theorem
3.1
. Then, there exists infinitely many primes
$q \in \mathbb {P}$
which are inert in both F and
$E_f$
.
For
$q\in \mathbb {P}$
, let
$\lambda $
be a prime ideal of
$\mathcal {O}_{E_f}$
lying above q.
Proof of Proposition 3.3
We adopt the technique in [Reference Dieulefait and DimitrovDD06, Theorem 3.1] to prove this proposition. In our case,
$k_0=2$
,
$\Psi = \Psi _{\mathrm {triv}}$
, and hence
$G_{\hat {F}}=G_F$
. By Proposition 3.2, for all primes
$q \gg 1$
, there exists a power
$\hat {q}$
of q, and we have either
$ \bar {\rho }_{f, \lambda }(G_F) \simeq \big \{g \in \mathrm {GL}_2(\mathbb {F}_{\hat {q}}) : \det (g) \in \mathbb {F}_q^{\times }\big \} ,$
or
$ \bar {\rho }_{f, \lambda }(G_F) \simeq \big \{g \in \mathbb {F}_{\hat {q}^2}^{\times } \mathrm {GL}_2(\mathbb {F}_{\hat {q}}) : \det (g) \in \mathbb {F}_q^{\times }\big \}$
. We now show that the latter case will not occur.
Suppose that
$ \bar {\rho }_{f, \lambda }(G_F) \simeq \{\gamma \in \mathbb {F}_{\hat {q}^2}^\times \mathrm {GL}_2(\mathbb {F}_{\hat {q}}) : \det (\gamma )\in \mathbb {F}_q^{\times } \}$
for some prime power
$\hat {q}$
of q with
$q \gg 1$
. By the argument in the proof of [Reference DimitrovDim05, Proposition 3.9], we get that
$\mathbb {F}_q \subseteq \mathbb {F}_{\hat {q}^2} \subseteq \mathbb {F}_\lambda $
. However, this cannot happen because d is odd and
$2 |[\mathbb {F}_\lambda :\mathbb {F}_q]$
. Therefore,
$$ \begin{align*}\bar{\rho}_{f, \lambda}(G_F) \simeq \big\{g \in \mathrm{GL}_2(\mathbb{F}_{\hat{q}}) : \det(g) \in \mathbb{F}_q^{\times} \big\}\end{align*} $$
for
$q \in \mathbb {P}$
with
$q \gg 1$
. Now, choose a prime
$q \in \mathbb {P}$
which is inert in both F and
$E_f$
. Let
$\upsilon \in P$
be the unique prime in F that lying above q, and let
$I_\upsilon $
be the inertia group at
$\upsilon $
. By [Reference DimitrovDim05, Corollary 2.13] or by the discussion before [Reference Dieulefait and DimitrovDD06, Proposition 1], the possible tame characters for
$\bar {\rho }_{f, \lambda }|I_\upsilon $
are of level d or
$2d$
, since
$d=\mathrm {f}(\upsilon |q)$
. Hence, we have
$\mathbb {F}_{q^d} \subseteq \mathbb {F}_{\hat {q}} \subseteq \mathbb {F}_\lambda $
. By Corollary 3.5, there exists infinitely many such primes. Since
$\mathrm {f}(\lambda |q)=d$
, the tame characters of level
$2d$
cannot occur in
$\bar {\rho }_{f, \lambda }|I_\upsilon $
, and therefore
$\mathbb {F}_{q^{d}} = \mathbb {F}_{\hat {q}} =\mathbb {F}_\lambda $
. Therefore, we have
$$ \begin{align*}\bar{\rho}_{f, \lambda}(G_F) \simeq \big\{g \in \mathrm{GL}_2(\mathbb{F}_{q^d}) : \det(g) \in \mathbb{F}_q^{\times} \big\}\end{align*} $$
for infinitely many
$q \in \mathbb {P}$
with
$\mathrm {f}(\lambda / q)= \mathrm {f}(\upsilon / q)=d$
. We are done with the proof.
3.3 A result for primitive forms of weight
$\boldsymbol{k}$
In this section, we prove Theorem 3.1 for primitive forms of weight k. If k is of parallel weight
$2$
and
$[F : \mathbb {Q}]=[E_f : \mathbb {Q}]$
is an odd prime, then we show that the assumptions in Theorem 3.6 are satisfied. Hence, Theorem 3.1 is a consequence of Theorem 3.6.
Theorem 3.6 Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a primitive form defined over F of weight k, level
$\mathfrak {n}$
, and character
$\Psi $
. For any subfield
$\mathbb {Q} \subseteq L \subsetneq E_f$
, assume that
$$ \begin{align} \bar{\rho}_{f, \lambda}(G_{\hat{F}}) \supseteq \{\gamma \in \mathrm{GL}_2(\mathbb{F}_{q^{\mathrm{f}}}) : \det(\gamma)\in (\mathbb{F}_q^{\times})^{k_0-1} \}\ \mathrm{with\ } \mathrm{f} = \mathrm{f}(\lambda| q), \end{align} $$
for infinitely many
$\lambda \in \mathcal {P}_f$
with
$\mathrm {f}_{\lambda , E_f, L}>1$
, where
$q \in \mathbb {P}$
lying below
$\lambda $
. Then,
$$ \begin{align*}\delta_D \left( \big \{ \mathfrak{p} \in P :\, C(\mathfrak{p}, f)\in L \big \} \right) = 0\end{align*} $$
for all proper subfields L of
$E_f$
.
The following proposition (cf. [Reference Koo, Stein and WieseKSW08, Proposition 2.1(c)]) is helpful in the proof of Theorem 3.6.
Proposition 3.7 Let
$R\subseteq \tilde {R}$
be two subgroups of
$\mathbb {F}_{q^r}^\times $
for some
$q\in \mathbb {P}$
and
$r \in \mathbb {N}$
. Let
$G\subseteq \{g \in \mathrm {GL}_2(\mathbb {F}_{q^r}) : \det (g) \in \tilde {R} \} \leq \mathrm {GL}_2(\mathbb {F}_{q^r})$
. Let
$P(x)=x^2-ax+b \in \mathbb {F}_{q^r}[x]$
. Then,
$\sum _{C}|C|\leq 2 |\tilde {R}/R|(q^2+q)$
, where the sum carries over all the conjugacy classes C of G with characteristic polynomial equals to
$P(x)$
.
Proof of Theorem 3.6
Let
$\mathcal {O}_{E_f}, \mathcal {O}_L $
denote the ring of integers of
$E_f, L$
, respectively. Let T be the set of all
$\lambda \in \mathrm {Spec}(\mathcal {O}_{E_f})$
such that equation (3.1) holds. By assumption, T is an infinite set. For any
$Q \in T$
, let
$Q_L, q$
be the prime ideals of
$\mathcal {O}_{L}, \mathbb {Z}$
lying below Q, respectively. Let
$\mathbb {F}_{q^r}=\mathcal {O}_{L}/Q_L,\ \mathbb {F}_{q^{rm}}=\mathcal {O}_{E_f}/Q$
for some
$r\geq 1, m\geq 2$
.
Let
$R:=(\mathbb {F}_q^{\times })^{k_0-1}$
,
$W \leq \mathbb {F}_{q^{rm}}^\times $
denote the image of
$\Psi ^\ast $
mod Q and
$\tilde {R}:= \langle R,W \rangle $
, the subgroup of
$\mathbb {F}_{q^{rm}}^\times $
generated by R and W. Then,
$|R| \leq q-1, \; |W|\leq |(\mathcal {O}_E / \mathfrak {n})^\times |$
, and hence
$ |\tilde {R}|\leq |R||W|$
. Let
$G:= \bar {\rho }_{f,Q}(G_F)$
be the image of residual Q-adic Galois representation
$\bar {\rho }_{f, Q}$
. By equations (2.1) and (2.2),
$G \leq \{g \in \mathrm {GL}_2(\mathbb {F}_{q^{rm}}) : \text {det}(g) \in \tilde {R} \}$
is a subgroup.
Let
$M_Q:=\bigsqcup _C \{ \mathfrak {p}\in P : [\bar {\rho }_{f, Q}(\mathrm {Frob}_{\mathfrak {p}})]_G=C\}$
, where C carries over all the conjugacy classes of G with characteristic polynomial
$x^2-ax+b \in \mathbb {F}_{q^{rm}}[x]$
such that
$ a \in \mathbb {F}_{q^r}$
and
$ b\in \tilde {R}$
. There are at most
$q^r|R||W|$
such polynomials. By equation (2.1), we have
$a \equiv C(\mathfrak {p},f) \pmod Q$
. Since
$ a \in \mathbb {F}_{q^r}$
, we get
$C(\mathfrak {p},f) \pmod Q \in \mathbb {F}_{q^r} $
. Hence,
$$ \begin{align} M_Q \supseteq \{\mathfrak{p}\in P \, :\, C(\mathfrak{p}, f)\pmod{Q} \in \mathbb{F}_{q^r} \}. \end{align} $$
By Theorem 2.2, we have
$\delta _D (M_Q)=\sum _{C}\frac {|C|}{|G|}$
. Now, by Proposition 3.7, we get
$$ \begin{align} \delta_D (M_Q)\leq \frac{q^r|R||W|\times 2 |\tilde{R}/R|(q^2+q)}{|G|} = \frac{2|R||W|^2q^r(q^2+q)}{|G|}. \end{align} $$
Since
$G_F \supseteq G_{\hat {F}}$
, by equation (3.1), we get a lower bound to
$|G|$
as
$$ \begin{align} |G|\geq |R|\times |\mathrm{SL}_2(\mathbb{F}_{q^{rm}})|. \end{align} $$
Combine equations (3.4) and (3.3) to get
$$ \begin{align*}\delta_D (M_Q)\leq \frac{2|W|^2|R| q^r(q^2+q)}{|R|\times |\mathrm{SL}_2(\mathbb{F}_{q^{rm}})|}= \frac{2|W|^2{q^{r+3}}}{q^{3rm}(q-1)}.\end{align*} $$
Since
$m\geq 2, r\geq 1$
, we get
$\delta _D (M_Q)\leq O\left (\frac {1}{q^2}\right )$
. Since T is an infinite set, q is unbounded. The inclusion of the sets in equation (3.2) implies
$\big \{ \mathfrak {p} \in P :\, C (\mathfrak {p}, f)\in L \big \} \subseteq \bigcap _{Q \in T} M_Q $
. Therefore, we have
$$ \begin{align*} \delta_D \left( \big \{ \mathfrak{p} \in P :\, C(\mathfrak{p}, f)\in L \big \} \right) = 0. \end{align*} $$
This completes the proof of Theorem 3.6.
The above theorem holds even if the inclusion in equation (3.1) holds up to conjugation.
Corollary 3.8 Let f be as in Theorem
3.6
, which satisfies equation (3.1) for any subfield
$\mathbb {Q} \subseteq L \subsetneq E_f$
. Then,
$\delta _D \left ( \big \{ \mathfrak {p}\in P : \mathbb {Q} \big (C(\mathfrak {p},f) \big ) =E_f \big \} \right ) = 1.$
Proof Let
$\mathfrak {p}\in P$
be a prime ideal with
$ \mathbb {Q} \big (C(\mathfrak {p},f) \big ) \subsetneq E_f $
. Then,
$C(\mathfrak {p},f) \in L$
for some proper subfield L of
$E_f$
. Since
$[E_f:\mathbb {Q}]$
is a finite separable extension, there are only finitely many subfields between
$\mathbb {Q}$
and
$E_f$
. By Theorem 3.6, we have
$\delta _D \left ( \big \{ \mathfrak {p}\in P : \mathbb {Q} \big (C(\mathfrak {p},f) \big ) \subsetneq E_f \big \} \right ) =0.$
This completes the proof of the corollary.
We have some remarks to make.
-
• By the definition of a CM primitive form f, the density of
$\mathfrak {p} \in P$
for which
$C(\mathfrak {p},f)=0$
is at least
$\frac {1}{2}$
. -
• For a non-CM primitive form f, the density of primes
$\mathfrak {p}$
for which
$C(\mathfrak {p},f) = 0$
is
$0$
. This is a special case of the famous Sato–Tate equidistribution theorem of Barnet-Lamb, Gee, and Geraghty [Reference Barnet-Lamb, Gee and GeraghtyBGG11, Corollary 7.17] (cf. [Reference Dalal and KumarDK20, Theorem 4.4] for more details).
The assumption (3.1) of Theorem 3.6 implies
$E_f \neq \mathbb {Q}$
and the set of
$\mathfrak {p} \in P$
with
$\mathbb {Q} \big (C(\mathfrak {p},f) \big ) = E_f$
has density
$1$
(cf. Corollary 3.8) implies that the form f has to be non-CM.
3.4 The proof of Theorem 3.1 with supporting examples
In this section, we give a proof of Theorem 3.1 and provide some examples of f in support of it.
Proof of Theorem 3.1
Since
$[E_f : \mathbb {Q}]$
is an odd prime, the only proper subfield L of
$E_f$
is
$\mathbb {Q}$
. By Proposition 3.3, f satisfies the assumption (3.1) of Theorem 3.6. Hence, by Corollary 3.8, the proof of Theorem 3.1 follows.
We now give some examples of primitive forms f in support of Theorem 3.1.
Example 4 Consider a non-CM primitive form f defined over
$F=\mathbb {Q}(\zeta _7)^+$
with generator
$\omega $
having minimal polynomial
$x^3-x^2-2x+1$
, with weight
$(2, 2,2)$
, level
$[167,\; 167,\; \omega ^2+\omega -8]$
, and with trivial character. This Hilbert modular form f is labeled as
$\texttt {3.3.49.1-167.1-a}$
in [Reference MarcusLMFDB]. The coefficient field
$E_f$
of f is
$\mathbb {Q}(\alpha )$
, where
$\alpha $
is a root of the irreducible polynomial
$x^3-x^2-4x-1 \in \mathbb {Q}[x]$
.
Example 5 Consider a non-CM primitive form f defined over
$F=\mathbb {Q}(\zeta _9)^+$
with generator
$\omega $
having minimal polynomial
$x^3-3x-1$
, with weight
$(2, 2,2)$
, level
$[71,\; 71,\; \omega ^2+\omega -7]$
, and with trivial character. This Hilbert modular form f is labeled as
$\texttt {3.3.81.1-71.1-a}$
in [Reference MarcusLMFDB]. The coefficient field
$E_f$
of f is
$\mathbb {Q}(\beta )$
, where
$\beta $
is a root of the irreducible polynomial
$x^3-x^2-4x+3 \in \mathbb {Q}[x]$
.
Example 6 Consider a non-CM primitive form f defined over
$F=\mathbb {Q}(\zeta _7)^+$
with generator
$\omega $
having minimal polynomial
$x^3-x^2-2x+1$
, with weight
$(2, 2,2)$
, level
$[239,\; 239,\; 6\omega ^2-5\omega -7]$
, and with trivial character. This Hilbert modular form f is labeled as
$\texttt {3.3.49.1-239.1-a}$
in [Reference MarcusLMFDB]. The coefficient field
$E_f$
of f is
$\mathbb {Q}(\theta )$
, where
$\theta $
is a root of the irreducible polynomial
$x^3-12x-8 \in \mathbb {Q}[x]$
.
The primitive forms f in Examples 4–6 are of parallel weight
$2$
with
$[F : \mathbb {Q}]= [E_f:\mathbb {Q}]=3$
, and hence they satisfy the hypothesis of Theorem 3.1. Moreover,
$E_f$
is totally real, so by Lemma 2.9, these primitive forms f do not have any nontrivial inner twists.
3.5 Computation of some Dirichlet density for
$\boldsymbol{F}_{\kern-1pt\boldsymbol{f}}$
In this section, we shall state and prove a variant of Theorem 3.6 and Corollary 3.8 for
$F_f$
. In fact, we compute the Dirichlet density of the set
$\big \{ \mathfrak {p} \in P :\, \mathbb {Q}\left (C^\ast (\mathfrak {p}, f)\right )=F_f \big \}.$
Theorem 3.9 Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a primitive form defined over F of weight k, level
$\mathfrak {n}$
, and character
$\Psi $
. For any subfield
$\mathbb {Q} \subseteq L \subsetneq F_f$
, assume that
$$ \begin{align} \bar{\rho}_{f, \lambda}(G_{\hat{F}}) \supseteq \{\gamma \in \mathrm{GL}_2(\mathbb{F}_{q^{\mathrm{f}}}) : \det(\gamma)\in (\mathbb{F}_q^{\times})^{k_0-1} \}\ \mathrm{with\ } \mathrm{f} = \mathrm{f}_{\lambda, F_f, \mathbb{Q}}, \end{align} $$
for infinitely many
$\lambda \in \mathcal {P}_f$
with
$\mathrm {f}_{\lambda , F_f, L}>1$
, where
$q \in \mathbb {P}$
lying below
$\lambda $
. Then,
$$ \begin{align*}\delta_D \left( \big \{ \mathfrak{p} \in P :\, C^\ast(\mathfrak{p}, f)\in L \big \} \right) = 0.\end{align*} $$
The above theorem holds even if the inclusion in equation (3.5) holds up to conjugation.
Proof In this proof, we follow the notations as in Theorem 3.6. Let
$\mathcal {O}_{F_f}$
be the ring of integers of
$F_f$
. For any
$Q \in T$
, let
$Q_F$
be the prime ideal of
$\mathcal {O}_{F_f}$
lying below Q. Let
$\mathcal {O}_{L}/Q_L=\mathbb {F}_{q^{r}}, \mathcal {O}_{F_f}/Q_F= \mathbb {F}_{q^{rm}}$
, and
$ \mathcal {O}_{E_f}/ Q= \mathbb {F}_{q^{rms}}$
for some
$r\geq 1,\ m\geq 2$
, and
$s\geq 1$
. Then,
$G\subseteq \{g \in \mathrm {GL}_2(\mathbb {F}_{q^{rms}}) : \det (g) \in \tilde {R} \}$
. Now, arguing as in the proof of Theorem 3.6, we get
$\delta _D (M_Q)\leq \frac {4|W|^3{q^{r+3}}}{q^{3rm}(q-1)}.$
Since
$m\geq 2, r\geq 1$
, we get
$\delta _D (M_Q)\leq O\left (\frac {1}{q^2}\right )$
. Therefore, we have
$$ \begin{align*} \delta_D \left(\{ \mathfrak{p} \in P :\, C^\ast(\mathfrak{p}, f)\in L \big \}\right)=0. \end{align*} $$
This completes the proof of Theorem 3.9.
Corollary 3.10 Let f be as in Theorem
3.9
, which satisfies equation (3.5) for any subfield
$\mathbb {Q} \subseteq L \subsetneq F_f$
. Then,
$$ \begin{align*}\delta_D \left( \big \{ \mathfrak{p}\in P : \mathbb{Q} \big (C^\ast(\mathfrak{p},f) \big ) =F_f \big \} \right) = 1.\end{align*} $$
Proof Suppose
$\mathfrak {p}\in P$
is a prime such that
$L=\mathbb {Q} \big (C^\ast (\mathfrak {p},f) \big ) \subsetneq F_f $
is a proper subfield of
$F_f$
. Since
$[F_f:\mathbb {Q}]$
is a finite separable extension, there are only finitely many subfields between
$\mathbb {Q}$
and
$F_f$
, and by Theorem 3.9, we get
$$ \begin{align*}\delta_D \left( \big \{ \mathfrak{p}\in P : \mathbb{Q} \big (C^\ast(\mathfrak{p},f) \big ) \subsetneq F_f \big \} \right) =0.\end{align*} $$
This completes the proof of the corollary.
Corollary 3.11 Let f and
$\bar {\rho }_{f, \lambda }$
be as in Theorem
3.9
. Then, we have
$$ \begin{align*}\delta_D \left( \big \{ \mathfrak{p}\in P : F_f \subseteq \mathbb{Q}(C(\mathfrak{p},f)) \big \} \right) = 1.\end{align*} $$
Proof Suppose
$\mathfrak {p} \in P$
with
$\mathbb {Q}(C^\ast (\mathfrak {p},f) )=F_f$
. From Lemma 2.7, we have
$F_f=\mathbb {Q}(C^\ast (\mathfrak {p},f) ) \subseteq \mathbb {Q}(C(\mathfrak {p},f))$
. Corollary 3.10 implies the result.
In Examples 4–6, we have that
$E_f$
and F are of degree
$3$
over
$\mathbb {Q}$
and
$E_f=F_f$
. Since there are no proper subfields of
$F_f$
, by Proposition 3.3, we conclude that these examples satisfy the hypothesis (3.5) of Theorem 3.9.
4 Computation of the Dirichlet density for subfields of
$\boldsymbol{E}_{\boldsymbol{f}}$
In Section 3, we computed the Dirichlet density of
$\mathfrak {p} \in P$
such that
$C(\mathfrak {p}, f)$
,
$C^\ast (\mathfrak {p}, f)$
generate
$E_f$
,
$F_f$
, respectively. In this section, for any subfield K of
$E_f$
, we compute the Dirichlet density of the set
$\big \{\mathfrak {p} \in P : \mathbb {Q} \big (C(\mathfrak {p},f)\big )= K \big \}$
. It is quite surprising that this density depends on whether
$F_f \subseteq K$
or not.
We now calculate the density of
$\mathfrak {p}\in P$
such that
$C(\mathfrak {p},f)\in K$
when
$F_f \nsubseteq K$
. The following lemma is an analog of [Reference Koo, Stein and WieseKSW08, Corollary 1.3(a)].
Lemma 4.1 Let f be as in Theorem
3.9
. Let
$K \subseteq E_f$
be a subfield such that
$F_f \nsubseteq K$
. Then,
$ \delta _D \left ( \big \{\mathfrak {p} \in P : C(\mathfrak {p},f) \in K \big \}\right )= \delta _D \left ( \big \{\mathfrak {p} \in P : \mathbb {Q} \big (C(\mathfrak {p},f)\big )= K \big \}\right ) =0.$
Proof Since
$F_f \nsubseteq K$
, we get
$ \big \{\mathfrak {p} \in P : C(\mathfrak {p},f) \in K \big \} \subseteq \big \{ \mathfrak {p}\in P : F_f \nsubseteq \mathbb {Q}(C(\mathfrak {p}, f))\big \}$
. The proof now follows from Corollary 3.11.
Let
$\Gamma ^\prime =\{\gamma _1,\dots ,\gamma _r\}$
be a subgroup of the inner twists
$\Gamma $
associated with f. Let
$\Psi _{\gamma _1},\dots , \Psi _{\gamma _r}$
be the corresponding Hecke characters, and their ideal Hecke characters
$\Psi _{\gamma _1}^\ast ,\dots , \Psi _{\gamma _r}^\ast $
can be thought of as characters on
$G_F$
. For each
$i\in \{1, 2, \ldots , r\}$
, define
$H_{\gamma _i} :=\mathrm {Ker}(\Psi _{\gamma _i}^\ast )$
and set
$H^{\Gamma ^\prime } :=\bigcap _{i=1}^{r} H_{\gamma _i} \leq G_F$
. Let
$K_{H^{\Gamma ^\prime }}$
denote the fixed field of
$H^{\Gamma ^\prime }.$
In particular,
$F\subseteq K_{H^{\Gamma ^\prime }} \subseteq \bar {F}$
.
Lemma 4.2 Let
$\Gamma ^\prime , H^{\Gamma ^\prime }$
, and
$ K_{H^{\Gamma ^\prime }}$
be as above. Then,
$$ \begin{align*}\{ \mathfrak{p} \in P : \mathfrak{p} \ \textrm{splits completely in}\ K_{H^{\Gamma^\prime}} \}= \{ \mathfrak{p} \in P : \Psi_\gamma^\ast(\mathfrak{p})=1,\ \forall \gamma \in \Gamma^\prime \big \}.\end{align*} $$
Proof Let
$m= [K_{H^{\Gamma ^\prime }}: F]$
.
$$ \begin{align*} & \{ \mathfrak{p} \in P : \ \mathfrak{p}\ \text{splits completely in}\ K_{H^{\Gamma^\prime}}\}\\ & = \{ \mathfrak{p} \in P :\ \mathfrak{p}= \mathfrak{p}_1 \mathfrak{p}_2 \dots \mathfrak{p}_m \text{ for prime ideals } \mathfrak{p}_j \ \text{in} \ K_{H^{\Gamma^\prime}} \ \text{with} \ 1\leq j \leq m\} \\ &=\{ \mathfrak{p} \in P : \ \Psi_{\gamma_i}^\ast(\mathfrak{p}_j)=1\ \forall i \in \{1,2, \dots, r\},\ \forall j\in \{1,2, \dots, m\} \}\\ & =\{ \mathfrak{p} \in P : \ \Psi_{\gamma_i}^\ast(\mathfrak{p})=1\ \forall i\in \{1,2, \dots, r\}\}. \end{align*} $$
This completes the proof of the lemma.
We are now in a position to compute the density of the set
$\big \{\mathfrak {p} \in P: C(\mathfrak {p},f) \in K \big \}$
if
$F_f \subseteq K$
. The following proposition generalizes [Reference Koo, Stein and WieseKSW08, Corollary 1.3(b)] to primitive forms.
Proposition 4.3 Let
$f\in S_k(\mathfrak {n}, \Psi )$
be a non-CM primitive form defined over F. For any subfield K with
$F_f \subseteq K \subseteq E_f$
, there exists a subgroup
$\Gamma '$
of
$\Gamma $
such that
$K=E_f^{\Gamma '}$
and
$ \delta _D \left ( \big \{ \mathfrak {p} \in P : C(\mathfrak {p},f) \in K \big \}\right ) =\frac {1}{[K_{H^{\Gamma '}}: F]}$
.
Proof Since
$E_f/F_f$
is Galois, there exists
$\Gamma ' \subseteq \Gamma $
such that
$K=E_f^{\Gamma '}$
. Hence,
$$ \begin{align*} \begin{aligned} \{\mathfrak{p} \in P : C(\mathfrak{p},f) \in K \} &=\{\mathfrak{p} \in P : \gamma(C(\mathfrak{p},f))= C(\mathfrak{p},f) \text{ for all } \gamma \in \Gamma^\prime \} \\ &=\{\mathfrak{p} \in P : \Psi_\gamma^\ast(\mathfrak{p}) C(\mathfrak{p},f)= C(\mathfrak{p},f) \text{ for all } \gamma \in \Gamma^\prime \}. \end{aligned} \end{align*} $$
Since
$\delta _D \left ( \big \{\mathfrak {p} \in P : C(\mathfrak {p},f)=0 \big \}\right )=0$
(cf. [Reference Dalal and KumarDK20, Theorem 4.4(1)]) and by Chebotarev density theorem, we have
$$ \begin{align*} \begin{aligned} &\delta_D \left( \big \{\mathfrak{p} \in P : \Psi_\gamma^\ast(\mathfrak{p}) C(\mathfrak{p},f)= C(\mathfrak{p},f)\ \textrm{for all}\ \gamma \in \Gamma' \big \} \right) \\ &\qquad \qquad = \delta_D \left( \big \{ \mathfrak{p} \in P : \Psi_\gamma^\ast(\mathfrak{p})=1\ \textrm{for all}\ \gamma \in \Gamma' \big \} \right) \\ &\qquad \qquad \underset{\mathrm{Lemma}~(4.2)}{=} \delta_D \left( \big\{\mathfrak{p} \in P : \mathfrak{p} \text{ splits completely in } K_{H^{\Gamma'}} \big \} \right) =\frac{1}{[K_{H^{\Gamma'}}: F]}. \end{aligned} \end{align*} $$
This completes the proof of the proposition.
The following corollary is an application of Proposition 4.3 and an analog of [Reference Koo, Stein and WieseKSW08, Corollary 1.4].
Corollary 4.4 Let f, K be as in Proposition
4.3
and
$K=E_f^{\Gamma '}$
for
$\Gamma ' \leq \Gamma $
. Then,
$$ \begin{align*} &\delta_D \left( \big \{ \mathfrak{p} \in P : \mathbb{Q} \big( C(\mathfrak{p},f) \big) =K \big \} \right) \\ &\qquad = \delta_D \left( \big \{ \mathfrak{p} \in P : \Psi_\gamma^\ast(\mathfrak{p})=1, \; \forall \gamma \in \Gamma' \ \mathrm{and}\ \Psi_\omega^\ast(\mathfrak{p})\neq 1, \; \forall \omega \in \Gamma - \Gamma' \big \} \right). \end{align*} $$
These results illustrate that the Dirichlet density of
$\mathfrak {p} \in P$
such that
$\mathbb {Q}(C(\mathfrak {p}, f)) = K$
, with
$F_f \subseteq K \subseteq E_f$
, is determined by the inner twists of f associated with K.
Acknowledgment
The authors are thankful to the editor for his constant support. The authors are grateful to the anonymous referee for the valuable mathematical suggestions and comments which improved our article substantially.
