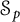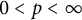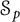1 Introduction
Let
$\text {Hol}(\mathbb {D})$
be the set of holomorphic functions on the open unit disk
$\mathbb {D}$
of the complex plane
$\mathbb {C}$
. For an analytic self-map
$\varphi $
on
$\mathbb {D}$
, we consider the composition operator
$$ \begin{align*}C_{\varphi} f := f \circ \varphi, \quad f\in\text{Hol}(\mathbb{D}).\end{align*} $$
For general information on composition operators on spaces of analytic functions, we refer the reader to the monographs by Shapiro [Reference Shapiro26] and Cowen and MacCluer [Reference Cowen and MacCluer9]. Boundedness, compactness, and membership in Schatten ideals of composition operators are the goals of several papers on various spaces of analytic functions (see, for instance, [Reference El-Fallah and ElIbbaoui10, Reference Lefèvre, Li, Queffélec and Rodríguez-Piazza16, Reference Pau and Pérez21, Reference Sarason and Silva24, Reference Zorboska27]). Recall that, for
$p>0$
, the Schatten p-ideal of a separable Hilbert space
$\mathcal {H}$
, denoted by
$\mathcal {S}_{p}(\mathcal {H})$
, consists of compact operators T on
$\mathcal {H}$
for which the sequence of singular values
$s_n(T)$
belongs to
$\ell ^p$
.
For
$\alpha>-1$
, let
${\mathcal {H}}_{\alpha }$
be the weighted analytic space given by
$$ \begin{align*}{\mathcal{H}}_\alpha= \left\{f \in \text{Hol}(\mathbb{D}): \int_{\mathbb{D}} |f'(z)|^{2}\,dA_{\alpha}(z)<\infty \right\},\end{align*} $$
where
$dA_{\alpha }(z)=(1-|z|^2)^\alpha \,dA(z).$
As usual,
$dA(z):= dx dy / \pi $
,
$z=x+\textit {i} y$
, is the normalized Lebesgue area measure on
$\mathbb {D}$
. For
$\alpha \in (-1,1)$
,
${\mathcal {H}}_{\alpha }$
is the standard Dirichlet space and is denoted by
$\mathcal {D}_\alpha $
.
${\mathcal {H}}_{1}$
is the classical Hardy space
$H^{2}$
. For
$\alpha>1$
,
${\mathcal {H}}_{\alpha }$
is the standard Bergman space
$A_{\alpha -2}^{2}$
. Recall that
$$ \begin{align*}A_{\beta}^{2}:=\left\{ f \in \text{Hol}(\mathbb{D}):\int_{\mathbb{D}}|f(z)|^{2}\,dA_{\beta}(z)<\infty\right\},\quad\beta>-1.\end{align*} $$
Littlewood’s subordination principle guarantees the boundedness of
$C_\varphi $
on the Hardy space
$H^{2}$
(see, for example, [Reference Shapiro26]). The compactness of
$C_{\varphi }$
on
$H^{2}$
has been characterized in [Reference Shapiro25] by Shapiro. For
$\alpha \geq 1$
, Luecking and Zhu obtained in [Reference Luecking and Zhu19] a characterization for a composition operator
$C_{\varphi }$
to be in
$ S_{p}\left ( \mathcal {H}_\alpha \right )$
for
$p>0$
. Pau and Pérez in [Reference Pau and Pérez21] gave an analogous characterization for the standard Dirichlet spaces
$\mathcal {D}_\alpha $
,
$\alpha \in (0,1)$
.
Let
$\varphi $
be an analytic self map of
$\mathbb {D}$
, and let
$\alpha>-1$
. The Nevanlinna counting function
$N_{\varphi ,\alpha }$
of
$\varphi $
associated with
$\mathcal {H} _{\alpha }$
is defined by
$$ \begin{align*}N_{\varphi,\alpha}(w)= \sum_{w=\varphi(z)}\left(1-|z|^2\right)^\alpha \quad\text{ if}\,\,\,w\in \varphi(\mathbb{D}); \qquad N_{\varphi,\alpha}(w)=0 \quad\text{ if}\,\,\,w\notin \varphi(\mathbb{D}) .\end{align*} $$
We summarize the results obtained in [Reference Luecking and Zhu19, Reference Pau and Pérez21] as follows. Let
$\alpha>0$
and
$p> 0$
. Then
$$ \begin{align} C_{\varphi} \in S_p \left(\mathcal {H} _{\alpha}\right)\Longleftrightarrow\displaystyle\int_{ \mathbb{D} } \left( \frac{N_{\varphi,\alpha}(w)}{ \left(1-|w|\right)^{\alpha}}\right)^{p/2}d\lambda(w)<\infty, \end{align} $$
where
$ d\lambda (z):=dA(z)/\left ( 1-|z|^2\right ) ^2 $
is the Möbius invariant measure on
$\mathbb {D}$
.
A weight on
$\mathbb {D}$
is a function
$\omega : \mathbb {D} \to (0, +\infty )$
which is integrable with respect to
$dA$
. If
$\omega : [0,1) \to (0, +\infty )$
is a radial weight, then we extend it to
$\mathbb {D}$
by setting
$\omega (z) = \omega (|z|)$
. The weighted Dirichlet space
$\mathcal {D}_{\omega }$
associated with a weight
$\omega $
on
$\mathbb {D}$
is defined by
$$ \begin{align*}\mathcal{D}_{\omega} = \left\{ f \in \text{Hol} (\mathbb{D}): \ \mathcal{D}_{\omega}(f): = \left( \displaystyle \displaystyle\int_{\mathbb{D}}|f'(z)|^2\omega (z)dA(z)\right)^{1/2} <\infty \right\}. \end{align*} $$
The space
$\mathcal {D}_{\omega }$
endowed with the norm
$ \|f\|^2_{\mathcal {D}_\omega }:=|f(0)|^2+\mathcal {D}_{\omega }(f)^2 $
is a Hilbert space (see Lemma 2.1).
For
$p>1$
, let
$\mathcal {C}_{p}$
be the set of weights
$\omega $
such that, for some
$\alpha \in (0,1)$
(or equivalently for all
$\alpha \in (0,1)$
, see [Reference Luecking18]), we have
$$\begin{align*}\left(\int_{\Delta(z,\alpha)}\omega dA \right)^{1/p} \left(\int_{\Delta(z,\alpha)}\omega^{-p'/p} dA \right)^{1/p'} \lesssim |\Delta(z,\alpha)|,\ z\in\mathbb{D}, \end{align*}$$
where
$\Delta (z,\alpha ) = \{w\in \mathbb {D}:\,\, |z-w|< \alpha (1-|z|^2))\}$
and
$1/p+1/p'=1$
. Here and throughout the paper, for a Borel set
$\Delta $
of
$\mathbb {D}$
,
$|\Delta |$
denotes the Lebesgue measure of
$\Delta $
. As usual, for real positive quantities A and B,
$A \lesssim B$
means that there is an absolute constant
$C>0$
such that
$A \leq C B$
. If
$A \lesssim B$
and
$B \lesssim A$
both hold, then we write
$A \asymp B$
.
We denote
$$\begin{align*}\tilde{\omega}(z) =\frac{1}{\left( 1-|z|^2\right)^2}\int_{\Delta(z,1/2)}\omega(\zeta)dA(\zeta), \ z\in \mathbb{D}, \end{align*}$$
and, for
$t\geq 0$
, let
$$ \begin{align*} \omega_{t}(z) =\int_{ \mathbb{D}}\frac{\omega(w)(1-|z|^2)^{t}}{|1-\overline{w}z|^{2+t}}dA(w), \ z\in \mathbb{D}. \end{align*} $$
For
$p>1$
and
$t\ge 0$
, a weight
$\omega $
is said to belong to the class
$\mathcal {C}_{p,t}$
if
$\omega \in \mathcal {C}_{p}$
and
$\omega _t \lesssim \tilde {\omega }$
. The class of such weights is introduced by Bourass and Marrhich in [Reference Bourass and Marrhich7]. In this paper, based on results obtained in [Reference Bourass and Marrhich7], we obtain characterizations of boundedness, compactness, and Schatten classes membership for composition operators on
$\mathcal {D}_{\omega }$
,
$\omega \in \mathcal {C}_{p,t}$
. Our results cover Bekollé–Bonami weights, superharmonic weights, and the radial admissible weights introduced by Kellay and Lefèvre in [Reference Kellay and Lefèvre15].
In particular, we are interested in perturbed superharmonic weights on
$\mathbb {D}$
. Let
$u\in \mathcal {C}^2(\mathbb {D})$
be a positive superharmonic function on
$\mathbb {D}$
. Recall that u admits the representation
$$ \begin{align} u(z)= \int_{\mathbb D}\log \left| \frac{1-\overline{\zeta}z}{z-\zeta}\right|\frac{d\sigma(\zeta)}{1-|\zeta|^2} +P_\nu(z)=: S_\sigma(z)+P_\nu(z), \end{align} $$
for a unique finite positive Borel measure
$\sigma $
on
$\mathbb {D}$
and a unique finite positive Borel measure
$\nu $
on the unit circle
$\mathbb {T}:=\partial \mathbb {D}$
(see [Reference Aleman2]). Here,
$$ \begin{align*}P_\nu (z) := \int_{\mathbb{T}} \frac{1 - |z|^2}{| 1 - \overline{\xi}z |^2} d \nu(\xi)\end{align*} $$
is the Poisson transform of the measure
$\nu $
on
$\mathbb {T}$
. Let
$\omega $
be a weight of the form
$\omega (z) = (1-|z|^2)^\alpha u(z), \alpha>-1$
. The space
$\mathcal {D}_\omega $
is called the perturbed superharmonically weighted Dirichlet space. We adopt the notation
$\mathcal {D}_{\sigma }$
(resp.
$\mathcal {D}_{\nu }$
) instead of
$\mathcal {D}_{S_\sigma }$
(resp.
$\mathcal {D}_{P_\nu }$
). The generalized Nevanlinna counting function of
$\varphi $
associated with a weight
$\omega $
is defined by
$$ \begin{align*} N_{\varphi,\omega}(w) = \sum_{w=\varphi(z)} \omega(z) \;\; \text{if } w \in \varphi(\mathbb{D}); \;\; N_{\varphi , \omega}(w) = 0 \;\; \text{if } w \notin \varphi(\mathbb{D}). \end{align*} $$
We write
$N_{\varphi , \nu }$
instead of
$N_{\varphi , P_\nu }$
. In [Reference Sarason and Silva24], Sarason and Silva characterized boundedness and compactness of operators
$C_\varphi \colon \mathcal {D}_{\nu } \to \mathcal {D}_{\nu }$
in terms of
$N_{\varphi , \nu }$
. They proved that
$C_\varphi $
is bounded (resp. compact) on
$\mathcal D _\nu $
if and only if
$$\begin{align*}\int_{\Delta_w} \frac{N_{\varphi , \nu}(z)}{P_\nu (z)} dA(z) = O(|\Delta_w|)\qquad \text{(resp. } \ o(|\Delta_w|)\ \text{as}\ |w|\to 1^-), \end{align*}$$
where
$\Delta _w=\Delta (w,\frac 12)$
. In [Reference El-Fallah, Mahzouli, Marrhich and Naqos12], El-Fallah, Mahzouli, Marrhich, and Naqos proved that
$C_{\varphi } \in \mathcal {S}_{p}(\mathcal {D}_\nu ),$
for
$p>0$
, if and only if
$$ \begin{align*} \sum_{n= 0}^{+\infty} \sum_{j= 0}^{2^n-1} \left ( \frac{ 1}{|R_{n,j}|}\int_{R_{n,j}} \frac{N_{\varphi , \nu}(z)}{P_\nu (z)} dA(z)\right )^{\frac{p}{2}} < \infty, \end{align*} $$
where
$$\begin{align*}R _{n,j} := \left\{ re^{it}:\ \frac{1}{2^{n+1}}< 1- r\leq \frac{1}{2^{n}} \mbox{ and } \frac{2\pi j}{ 2^{n}}\leq t < \frac{2\pi(j+1)}{2^{n}}\ \right\}, \quad n\in \mathbb{N}\ \text{and}\ 0\leq j \leq 2^n-1, \end{align*}$$
are the dyadic disks.
On the space
$\mathcal {D}_{\sigma }$
, Bao, Göğüş, and Pouliasis [Reference Bao, Göğüş and Pouliasis5] proved that
$C_\varphi $
is bounded (resp. compact) if and only if
$$\begin{align*}\check{N}_{\varphi,\sigma}(w) = O(U_\sigma(w))\qquad (\text{resp. } \ o(U_\sigma(w))\ \text{as}\ (|w|\to 1^-)), \end{align*}$$
with
$U_\sigma (z) = \displaystyle \int _{ \mathbb {D} } \frac {1-|z|^2}{|1-\overline {\zeta }z|^2} d\sigma (\zeta )$
and
$$ \begin{align*} \check{N}_{\varphi,\sigma}(w) = \sum_{w=\varphi(z)} U_\sigma(z) \;\; \text{if } w \in \varphi(\mathbb{D}); \;\; \check N_{\varphi , \sigma}(w) = 0 \;\; \text{if } w \notin \varphi(\mathbb{D}). \end{align*} $$
We will characterize boundedness, compactness, and Schatten classes membership of composition operators on perturbed superharmonically weighted Dirichlet spaces
$\mathcal {D}_\omega $
with
$\omega (z) = (1-|z|^2)^\alpha \left (S_\sigma (z) + P_\nu (z)\right )$
. In particular, we prove that
$C_\varphi : \mathcal {D}_\sigma \to \mathcal {D}_\sigma $
belongs to
$\mathcal {S}_p(\mathcal {D}_\sigma )$
, for
$p>0$
, if and only if
$$\begin{align*}\displaystyle\int_{ \mathbb{D} }\left( \frac{\check{N}_{\varphi,\sigma}(z)}{U_\sigma(z)}\right)^{p/2}d\lambda(z)<\infty. \end{align*}$$
In this paper, we are interested also in composition operators on weighted Bergman spaces. In particular, we extend the result obtained by Constantin in [Reference Constantin8] concerning the membership of
$C_\varphi $
to
$\mathcal {S}_p(A^2_{\omega })$
, for
$p\ge 2$
and in the Bekollé–Bonami weights setting, to all
$p>0$
and for
$\omega \in \mathcal {C}_{p,t}$
.
Throughout this paper, we decompose
$\mathbb {D}$
by using the disks
$ \Delta (z,r) $
,
$0<r<1$
. The sets
$\Delta (z,r)$
give a
$(\rho ,\delta )-$
lattice of
$\mathbb {D}$
for
$\rho (z)=(1-|z|^2)/2$
and for some choice of
$\delta $
. Let
$\left ( \Delta (z_n,\delta )\right )_n$
be the corresponding
$(\rho ,\delta )-$
lattice of
$\mathbb {D}$
, and let
$(\Delta _{n})_n$
be an enumeration of
$\Delta (z_n,\delta )$
. Let
$b>1$
such that
$b\Delta _n=\Delta (z_n,b\delta )$
is a covering of
$\mathbb {D}$
of finite multiplicity (see [Reference El-Fallah, Mahzouli, Marrhich and Naqos11, Proposition 3.1] and [Reference Oleinik20] for details and generalization).
2 Composition operators on weighted Dirichlet spaces
2.1 General results
Suppose that
$\omega $
is a weight such that
$\omega \in \mathcal {C}_{p_0,t}$
for some
$p_0>1$
and
$t\ge 0$
. The weighted Bergman space associated with
$\omega $
is defined by
$$ \begin{align*}A^2_\omega = \left\{ f \in \text{Hol} (\mathbb{D}): \ \|f\|_{A^2_\omega}: =\left( \displaystyle\int_{\mathbb{D}}|f(z)|^2\omega (z)dA(z)\right)^{1/2} <\infty \right\}. \end{align*} $$
Notice that
$A^2_\omega $
is a reproducing kernel Hilbert space since each point evaluation
$e_z:A^2_\omega \to \mathbb {C}$
, which takes f to
$f(z)$
, is a bounded linear functional on
$A^2_\omega $
(see [Reference Bourass and Marrhich7]). The reproducing kernel of
$A^2_\omega $
will be denoted by
$K^\omega $
. The Toeplitz operator
$T_\mu $
, associated with a positive Borel measure
$\mu $
on
$\mathbb {D}$
, acting on
$A^2_\omega $
is the transformation
$$ \begin{align*}T_{ \mu } f(z) = \int_{\mathbb{D}}f(\zeta) K^\omega(z, \zeta) \omega(\zeta) d\mu(\zeta), \quad f\in A^2_\omega,\mbox{ } z\in\mathbb{D}. \end{align*} $$
In the sequel, for a positive Borel measure
$\mu $
on
$\mathbb {D}$
, we denote
$ d\mu _\omega =\omega d\mu $
. The following results are proved in [Reference Bourass and Marrhich7].
Theorem A Let
$\mu $
be a finite positive Borel measure on
$\mathbb D$
. The following assertions are equivalent.
-
(1) The Toeplitz operator
$T_\mu $
is bounded (resp. compact) on
$A^2_\omega $
. -
(2)
$\mu _\omega (\Delta _n) = O\left ( A_\omega (\Delta _n)\right ) $
(resp.
$\mu _\omega (\Delta _n) = o\left ( A_\omega (\Delta _n)\right ) $
),
$n\to \infty $
.
Theorem B Let
$\mu $
be a finite positive Borel measure on
$\mathbb D$
such that
$T_{\mu } $
is compact on
$A^2_{\omega }$
, and let
$p>0$
. Then
$T_\mu $
belongs to
$\mathcal {S}_p(A^2_\omega )$
if and only if
$$ \begin{align*}\displaystyle \sum _{n=0}^{\infty} \left( \frac{\mu_\omega (\Delta_{n})}{A_\omega(\Delta_n)}\right)^p<\infty. \end{align*} $$
We will apply Theorems A and B to characterize boundedness, compactness, and Schatten class composition operators on
$\mathcal {D}_\omega $
. The following lemma, which implies, in particular, that
$\left ( \mathcal {D}_\omega , \|\textbf {.}\|_{\mathcal {D}_\omega }\right ) $
is a Hilbert space, will be needed for the proof of next result.
Lemma 2.1 Suppose that
$\omega $
is a weight such that
$\omega \in \mathcal {C}_{p}$
for some
$p>1$
. Then, each point evaluation is bounded on
$\left ( \mathcal {D}_\omega , \|\textbf {.}\|_{\mathcal {D}_\omega }\right ) $
.
Proof Fix z in
$\mathbb {D}$
, and let
$f \in \mathcal {D}_\omega $
. We have
$ \left |f(z) - f(0)\right |{}^2 \leq \displaystyle \int _{0}^{1} \left |f'(sz)\right |{}^2 ds. $
Since
$f' \in A^2_\omega $
and
$\omega \in \mathcal {C}_{p}$
, then
$$ \begin{align*}|f'(sz)|^{2}\lesssim \frac{1}{(1-|sz|^2)^2\tilde{\omega}(sz)} \|f'\|^2_{_{A^2_{\omega}}},\mbox{ }s\in[0,1] \end{align*} $$
(see [Reference Aleman and Constantin3] or [Reference Bourass and Marrhich7]). Let
$r\in (|z|,1)$
. We have
$$ \begin{align*}\displaystyle\inf_{w\in[0,z]}\tilde{\omega}(w) \ge \displaystyle\inf_{w\in \Delta(0,r)}\tilde{\omega}(w)\gtrsim \tilde{\omega}(0)>0, \end{align*} $$
since
$\tilde {\omega }(w)\asymp \tilde {\omega }(0)$
when
$w\in \Delta (0,r)$
(see Lemma
$2.2$
in [Reference Constantin8]). We obtain
$$ \begin{align*} \left|f(z) - f(0)\right|{}^2 \lesssim \|f'\|^2_{A^2_\omega}\displaystyle \int_{0}^{1}\dfrac{1}{(1-|sz|^2)^2\tilde{\omega}(sz)}ds \lesssim \|f'\|^2_{A^2_\omega} \le \|f\|^2_{\mathcal{D}_\omega}. \end{align*} $$
Consequently,
$ |f(z)|^2 \lesssim \left |f(z) - f(0)\right |{}^2 + |f(0)|^2 \lesssim \|f\|^2_{\mathcal {D}_\omega }. $
Theorem 2.2 Suppose that
$\omega $
is a weight such that
$\omega \in \mathcal {C}_{p_0,t}$
for some
$p_0>1$
and
$t\ge 0$
. Let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
. Then:
-
(1)
$C_\varphi $
is bounded on
$\mathcal {D}_\omega $
if and only if
$$ \begin{align*}\int_{\Delta_n} N_{\varphi,\omega}(z) dA(z)\lesssim \int_{\Delta_n} \omega(z) dA(z),\quad n\in\mathbb{N}. \end{align*} $$
-
(2)
$C_\varphi $
is compact on
$\mathcal {D}_\omega $
if and only if
$$ \begin{align*}\int_{\Delta_n} N_{\varphi,\omega}(z) dA(z)= o\left(\int_{\Delta_n} \omega(z) dA(z) \right) ,\quad (n\to\infty). \end{align*} $$
Proof Suppose that
$C_\varphi $
is bounded on
$\mathcal {D}_\omega $
. Let
$V_{\omega } : \mathcal {D}_{\omega } \rightarrow A^{2}_{\omega } $
be the bounded operator defined by
$V_{\omega } f = f'$
, and let
$D_{\varphi ,\omega }: A^{2}_{\omega } \rightarrow A^{2}_{\omega }$
be the operator defined by
$$ \begin{align*}D_{\varphi,\omega}f:=V_{\omega} C_{\varphi} V_{\omega}^{*}f.\end{align*} $$
By a direct calculation, we have
$ D_{\varphi ,\omega }f=\varphi '.f\circ \varphi , f\in A^2_{\omega }. $
The operator
$D_{\varphi ,\omega }^\ast D_{\varphi ,\omega }$
is then bounded on
$A^{2}_{\omega }$
. For
$f \in A^{2}_{\omega }$
, the change of variable formula [Reference Aleman1] gives
$$ \begin{align*} D_{\varphi,\omega}^{*} D_{\varphi,\omega} f(z) &= \langle D_{\varphi,\omega} f, D_{\varphi,\omega} K^{\omega}_{z} \rangle_{A^{2}_{\omega}}\\ &= \int_{\mathbb{D}} f(\xi) \overline{K_{z}^{\omega}(\xi)} \omega(\xi) d\omega_{\varphi}(\xi)\\ &= T_{\omega_\varphi} f(z), \end{align*} $$
where
$\omega _\varphi $
is the measure defined on
$\mathbb {D}$
by
$ d\omega _\varphi =\frac {N_{\varphi ,\omega }}{\omega } dA. $
It follows that
$T_{\omega _\varphi }$
is bounded on
$A^{2}_{\omega }$
. By
$(1)$
of Theorem A, we deduce that
$$ \begin{align} \int_{\Delta_n} N_{\varphi,\omega}(z) dA(z)\lesssim \int_{\Delta_n} \omega(z) dA(z),\quad n\in\mathbb{N}. \end{align} $$
Conversely, assume that (2.1) holds, and let
$f\in \mathcal {D}_\omega $
. By using once again the change of variable formula, we get
$$ \begin{align*} \|C_\varphi f\|^2_{\mathcal{D}_\omega}&=\left|f(\varphi(0)) \right|{}^2+\left\langle T_{\omega_\varphi}f',f' \right\rangle_{A^{2}_{\omega}} \\ &\le \left|f(\varphi(0)) \right|{}^2+\left\| T_{\omega_\varphi} \right\| \left\|f'\right\|^2_{A^{2}_{\omega}}\\ &\lesssim \left|f(\varphi(0)) \right|{}^2+ \|f\|^2_{\mathcal{D}_\omega}. \end{align*} $$
By Lemma 2.1, we deduce that
$ \|C_\varphi f\|^2_{\mathcal {D}_\omega } \lesssim \|f\|^2_{\mathcal {D}_\omega },$
$f\in \mathcal {D}_\omega. $
Therefore,
$C_\varphi $
is bounded on
$\mathcal {D}_\omega $
.
To prove the second assertion, we may assume that
$C_\varphi $
is bounded on
$\mathcal {D}_\omega $
. We have
$$ \begin{align} C_{\varphi}f=V^{*}_{\omega} D_{\varphi,\omega} V_{\omega}f+Kf,\quad f\in\mathcal{D}_\omega, \end{align} $$
where
$Kf(z)=f(\varphi (0))$
,
$f\in \mathcal {D}_\omega $
, and
$z\in \mathbb {D}$
. Since K is bounded on
$\mathcal {D}_\omega $
by Lemma 2.1 then, by definition of
$D_{\varphi ,\omega }$
on the one hand and by (2.2) on the other hand,
$C_\varphi $
is compact on
$\mathcal {D}_\omega $
if and only if
$D_{\varphi ,\omega }$
is compact on
$A^2_\omega $
. In other words,
$C_\varphi $
is compact on
$\mathcal {D}_\omega $
if and only if
$T_{\omega _\varphi }$
is compact on
$A^{2}_{\omega }$
. The result follows now by
$(2)$
of Theorem A.
Theorem 2.3 Suppose that
$\omega $
is a weight such that
$\omega \in \mathcal {C}_{p_0,t}$
for some
$p_0>1$
and
$t\ge 0$
. Assume that
$\varphi $
is an analytic self-map of
$\mathbb {D}$
such that
$C_\varphi $
is compact on
$\mathcal {D}_\omega $
. Then
$C_\varphi $
belongs to
$\mathcal {S}_p(\mathcal {D}_\omega )$
, for
$p>0$
, if and only if
$$ \begin{align*}\displaystyle \sum_{n=0}^{\infty} \left( \frac{\int_{\Delta_n} N_{\varphi,\omega}(z) dA(z)}{ \int_{\Delta_n} \omega(z) dA(z)} \right)^{p/2}<\infty. \end{align*} $$
Proof Note that
$C_\varphi $
belongs to
$\mathcal {S}_p(\mathcal {D}_\omega )$
if and only if
$D_{\varphi ,\omega }$
belongs to
$\mathcal {S}_{p}(A^{2}_{\omega })$
by (2.2). Since
$$ \begin{align*} D_{\varphi,\omega}^{*} D_{\varphi,\omega} f =T_{\omega_\varphi} f,\quad f\in A^{2}_{\omega}, \end{align*} $$
then
$C_\varphi \in \mathcal {S}_p(\mathcal {D}_\omega )$
if and only if
$T_{\omega _\varphi }\in \mathcal {S}_{\frac {p}{2}}(A^{2}_{\omega })$
. The result follows by Theorem B.
If
$\omega $
is a weight such that for some (equivalently for all)
$r\in (0,1)$
, we have
$$ \begin{align} \omega (z)\asymp \omega (w), \ w\in\Delta(z,r), \end{align} $$
then
$\omega \in \mathcal {C}_{p}$
for all
$p>1$
. Moreover, under the condition (2.3), we have
$$ \begin{align*}\frac{1}{|\Delta(z,\delta)|}\int_{\Delta(z,\delta)} \omega(\zeta)dA(\zeta)\asymp\omega(z), \ z\in\mathbb{D}\end{align*} $$
for all
$\delta \in (0,1)$
. In this case, Theorems 2.2 and 2.3 can be reduced to the following result.
Corollary 2.4 Let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
. Suppose that
$\omega $
is a weight satisfying (2.3) and such that
$\omega _{t}\lesssim \omega $
for some
$t\ge 0$
. Then:
-
(1)
$C_\varphi $
is bounded on
$\mathcal {D}_\omega $
if and only if
$$ \begin{align*}\frac{1}{|\Delta_{n}|}\int_{\Delta_n} \frac{N_{\varphi,\omega}(z)}{\omega(z)} dA(z)= O(1),\quad\forall n\in\mathbb{N}. \end{align*} $$
-
(2)
$C_\varphi $
is compact on
$\mathcal {D}_\omega $
if and only if
$$ \begin{align*}\frac{1}{|\Delta_{n}|}\int_{\Delta_n} \frac{N_{\varphi,\omega}(z)}{\omega(z)} dA(z)= o(1) ,\quad (n\to\infty). \end{align*} $$
-
(3)
$C_\varphi $
belongs to
$\mathcal {S}_p(\mathcal {D}_\omega )$
, for
$p>0$
, if and only if
$$ \begin{align*}\displaystyle \sum_{n=0}^{\infty} \left( \frac{1}{|\Delta_{n}|}\int_{\Delta_n} \frac{N_{\varphi,\omega}(z)}{\omega(z)} dA(z) \right)^{p/2}<\infty. \end{align*} $$
2.2 Radial weights
A radial weight
$\omega $
in
$\mathcal {C}^2[0,1)$
is called admissible if:
$(\mathcal {W}_1) \omega $
is nonincreasing.
$(\mathcal {W}_2)$
$\omega (r)(1-r)^{-(1+\delta )}$
is nondecreasing for some
$\delta>0$
.
$(\mathcal {W}_3) \displaystyle \lim _{r\to 1^{-}}\omega (r)=0$
.
$(\mathcal {W}_4)$
One of the two properties of convexity is fulfilled
$$\begin{align*}\begin{cases} (\mathcal{W}_4^{(I)}): \omega \mbox{ is convex and }\displaystyle\lim_{r\to 1^{-}}\omega'(r)=0,\\ (\mathcal{W}_4^{(II)}): \omega \mbox{ is concave}. \end{cases} \end{align*}$$
If
$\omega $
satisfies
$(\mathcal {W}_1)$
–
$(\mathcal {W}_3)$
and
$(\mathcal {W}_4^{(I)})$
(resp.
$(\mathcal {W}_4^{(II)})$
), then we say that
$\omega $
is
$(I)$
-admissible (resp.
$(II)$
-admissible). Kellay and Lefèvre [Reference Kellay and Lefèvre15] proved the following result.
Theorem C
-
(1) Let
$\omega $
be a
$(II)$
-admissible weight. Then
$C_\varphi $
is bounded on
$\mathcal {D}_\omega $
if and only if
$N_{\varphi ,\omega }(z)=O\left ( \omega (z)\right ), z\in \mathbb {D}$
. -
(2) Let
$\omega $
be an admissible weight. Then
$C_\varphi $
is compact on
$\mathcal {D}_\omega $
if and only if
$N_{\varphi ,\omega }(z)=o\left ( \omega (z)\right ), |z|\to 1^-$
.
As noticed in [Reference Kellay and Lefèvre15],
$C_\varphi $
is always bounded on
$\mathcal {D}_\omega $
if
$\omega $
is an
$(I)$
-admissible weight. We describe in the following theorem the membership of
$C_\varphi $
in
$\mathcal {S}_p(\mathcal {D}_\omega )$
for admissible weights.
Theorem 2.5 Let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
, and let
$\omega $
be an admissible weight. Then
$C_\varphi $
belongs to
$\mathcal {S}_p(\mathcal {D}_\omega )$
, for
$p>0$
, if and only if
$$ \begin{align} \int_{\mathbb D}\left( \frac{ N_{\varphi,\omega}(z)}{\omega(z)}\right) ^{p/2}d\lambda(z)<\infty. \end{align} $$
Proof Let z in
$\mathbb {D}$
, and let
$w\in \Delta (z,r)$
. Suppose that
$|z|\le |w|$
. By
$(\mathcal {W}_1)$
, we have
$\omega (z)\ge \omega (w)$
, and by
$(\mathcal {W}_2)$
, we have
$$ \begin{align*}\omega(z)=\frac{\omega(z)}{(1-|z|)^{\delta+1}}(1-|z|)^{\delta+1}\le \frac{\omega(w)}{(1-|w|)^{\delta+1}}(1-|z|)^{\delta+1}\asymp \omega(w), \end{align*} $$
where
$\delta $
is the constant in
$(\mathcal {W}_2)$
. Similarly, we have
$\omega (z)\asymp \omega (w)$
if
$|w|\le |z|$
. Therefore,
$\omega $
satisfies the condition (2.3). On the other hand, the conditions
$(\mathcal {W}_1)$
and
$(\mathcal {W}_2)$
imply that
$\omega _{2+2\delta }\lesssim \omega $
(see [Reference Kellay and Lefèvre15, Lemma 2.4]). By
$(3)$
of Corollary 2.4, it follows that
$C_\varphi $
belongs to
$\mathcal {S}_p(\mathcal {D}_\omega )$
, for
$p>0$
, if and only if
$$ \begin{align} \displaystyle \sum_{n=0}^{\infty} \left( \frac{1}{|\Delta_{n}|}\int_{\Delta_n} \frac{N_{\varphi,\omega}(z)}{\omega(z)} dA(z) \right)^{p/2}<\infty. \end{align} $$
Now, since
$N_{\varphi ,\omega }$
satisfies the sub-mean-value property, that is,
$$ \begin{align} N_{\varphi , \omega}(z)\lesssim \frac{1}{|\Delta(z,r)|}\int_{\Delta(z,r)} N_{\varphi , \omega}(w) dA(w),\quad z\in\mathbb{D} \end{align} $$
(see Lemmas 2.2 and 2.3 in [Reference Kellay and Lefèvre15]), then, similarly to the proof of Theorem 2.9, the condition (2.5) is equivalent to the condition (2.4).
2.3 Remarks and examples
$\bullet $
A radial weight
$\omega $
is called almost standard if
$\omega $
satisfies
$(\mathcal {W}_1)$
–
$(\mathcal {W}_3)$
. In the recent paper [Reference Esmaeili and Kellay13], Esmaeili and Kellay studied the boundedness and the compactness of weighted composition operators on Bergman and Dirichlet spaces associated with almost standard weights. As noticed in the proof of Theorem 2.5, every almost standard weight satisfies (2.3) and
$\omega _{2+2\delta }\lesssim \omega $
. Therefore, Corollary 2.4 can be applied for any almost standard weight.
$\bullet $
Let
$\omega $
be a weight on
$\mathbb {D}$
such that there are constants
$s\in (-1,0)$
and
$\eta \geq 0$
for which
$$ \begin{align} \omega_{s,\eta}(z):= \int_{ \mathbb{D}}\frac{\omega(\xi)(1-|\xi|^2)^s (1-|z|^2)^{\eta}}{|1-\overline{\xi}z|^{2+s+\eta}}dA(\xi)\lesssim \omega(z),\quad z\in \mathbb{D}. \end{align} $$
This condition is similar to the one that appears in [Reference Bao, Wulan and Zhu6]. Note that any standard weight
$\omega _{\alpha }(z)= (1-|z|^2)^{\alpha }$
, for
$\alpha>-1$
, satisfies the condition (2.7) since for
$s\in (\max (-1,-1-\alpha ),0)$
and
$\eta>\max (0,\alpha )$
, we have
$$ \begin{align*} \int_{ \mathbb{D}}\frac{(1-|z|^2)^{\alpha+s}}{|1-\overline{w}z|^{2+s+\eta}}dA(z)\asymp (1-|w|^2)^{\alpha-\eta},\quad w\in\mathbb{D}. \end{align*} $$
The following lemma is stated in [Reference Bourass and Marrhich7].
Lemma A Let
$\omega $
be a weight satisfying (2.7) for some constants
$s\in (-1,0)$
and
$\eta \geq 0$
. Then
$\omega $
satisfies (2.7) for all
$s'>s$
and
$\beta>\eta $
.
Let
$1<p,p'<\infty $
such that
$\frac {1}{p}+\frac {1}{p'}=1$
, and let
$\eta> -1$
. The class of Bekollé–Bonami weights
$B_p(\eta )$
consists of weights
$\omega $
such that
$$\begin{align*}\left(\int_{S(\theta,h)}\omega dA_\eta \right) \left(\int_{S(\theta,h)}\omega^{-p'/p} dA_\eta \right)^{p/p'} \lesssim \left(A_\eta(S(\theta,h)) \right)^p \end{align*}$$
for any Carleson square
$$\begin{align*}S(\theta,h) :=\left\lbrace re^{ i \alpha}:1-h<r<1,\; |\theta-\alpha|<h/2 \right\rbrace,\quad\theta\in[0,2\pi],\;h\in (0,1). \end{align*}$$
Note that if
$\frac {\omega }{(1-|z|^2)^\eta }\in B_{p}(\eta )$
, for some
$p>1$
and
$\eta>-1$
, then
$\omega \in \mathcal {C}_{p,t}$
for all
$t\geq p(\eta +2)-2$
(see [Reference Aleman and Constantin3, Lemma 2.1]).
If
$\omega $
is a weight on
$\mathbb {D}$
that satisfies (2.7), then by Lemma A,
$\omega _{\eta }\lesssim \omega $
for some
$\eta \geq 0$
. Using Corollary 4.4 from [Reference Aleman, Pott and Reguera4] (see the proof of
$(c)\Rightarrow (b)$
), we find that
$(1-|z|^2)^{-\eta }\omega $
belongs to
$B_p(\eta )$
for all
$p>1$
. We conclude that if
$\omega $
satisfies (2.7), then
$\omega \in \mathcal {C}_{p,t}$
for all
$p>1$
and some
$t\geq 0$
. As examples, we consider here weights which appear in [Reference Bao, Wulan and Zhu6]. Let
$\mu $
be a finite positive Borel mesure on
$\mathbb {D}$
and
$b\in \mathbb {R}$
such that
$\int _{ \mathbb {D}}(1-|w|^2)^bd\mu (w)<\infty $
. Let
$\nu $
be a finite positive Borel measure on
$\mathbb {T}$
. Let
$a>-1$
, and let
$c<a+2$
. Using Lemma
$2.5$
in [Reference Fàbrega and Ortega14], one can verify that the weight
$$ \begin{align*}\omega(z) = (1-|z|^2)^a\left( \int_{\mathbb{D}}\frac{(1-|w|^2)^b}{|1-z\overline{w}|^c} d\mu(w)+ \int_{\mathbb{T}}\frac{d\nu(\zeta) }{|1-\overline{\zeta}z|^c} \right)\end{align*} $$
satisfies the condition (2.7) for all
$\eta>a$
and
$c-a-2<s<0$
. Notice that the previous weight satisfies, in addition, the condition (2.3).
Remark 2.6 Let
$\omega $
be a weight satisfying (2.7) with
$s\in (-1,0)$
and
$t\ge 0$
. Then
$(1-|z|^2)^\alpha \omega $
satisfies (2.7) for all
$\alpha>s$
. Indeed, if
$\alpha>0$
, then for
$\epsilon \in (0,1)$
such that
$\alpha -\epsilon>0$
and
$\beta \ge t+\alpha -\epsilon $
we have by Lemma A
$$\begin{align*}\int_{ \mathbb{D}}\frac{\omega (z)(1-|z|^2)^{\alpha-\epsilon}(1-|w|^2)^{\beta-\alpha+\epsilon}}{|1-\overline{w}z|^{2+\beta}}dA(z)\lesssim\omega(w). \end{align*}$$
If
$\alpha \in (s,0)$
, then for
$s'=s-\alpha $
and
$\beta =t+\alpha +1$
once again by Lemma A, we obtain
$$ \begin{align*} \int_{ \mathbb{D}}\frac{\omega (z)(1-|z|^2)^{\alpha+s'}(1-|w|^2)^{\beta}}{|1-\overline{w}z|^{2+s'+\beta}}dA(z) &=\int_{ \mathbb{D}}\frac{\omega (z)(1-|z|^2)^{s}(1-|w|^2)^{t+\alpha+1}}{|1-\overline{w}z|^{3+s+t}}dA(z)\\ &\lesssim (1-|w|^2)^{\alpha}\omega(w). \end{align*} $$
2.4 Composition operators on Dirichlet spaces induced by perturbed superharmonic weights
In this subsection, we examine the case of perturbed superharmonic weights. We begin with the following proposition.
Proposition 2.7 Let
$\omega \in \mathcal {C}^2(\mathbb {D})$
be a positive superharmonic function on
$\mathbb {D}$
. Then
$(1-|z|^2)^\alpha \omega $
verifies (2.7) for all
$\alpha>-1$
.
Proof Let
$\sigma $
and
$\nu $
be the unique finite positive Borel measures on
$\mathbb {D}$
and
$\mathbb {T}$
, respectively, such that
$\omega = S_\sigma +P_\nu $
. It is proved in [Reference Liu, Chacón and Lou17] that
$P_\nu $
satisfies (2.7) for all
$s>-1$
and
$t>1$
. On the other hand, note that for
$s\in (-1,0)$
and
$t>1$
, we have
$$ \begin{align*} \int_{\mathbb D}\frac{(1-|z|^2)^s}{|1-\overline{w}z|^{2+s+t}}\log \left| \frac{1-\overline{\zeta}z}{z-\zeta}\right|dA(z) &\asymp \int_{\mathbb D} \frac{(1-|z|^2)^s}{|1-\overline{w}z|^{2+s+t}}\left( 1-\left| \frac{z-\zeta}{1-\overline{\zeta}z}\right|{}^2\right)dA(z)\\ &= (1-|\zeta|^2)\int_{\mathbb D} \frac{(1-|z|^2)^{s+1}}{|1-\overline{w}z|^{2+s+t} |1-\overline{\zeta}z|^{2}}dA(z)\\ &\lesssim \frac{(1-|\zeta|^2)}{(1-|w|^2)^{t-1}|1-\overline{\zeta}w|^{2}}. \end{align*} $$
Therefore, for
$s\in (-1,0)$
and
$t>1$
, we have
$$ \begin{align*} \int_{ \mathbb{D}}\frac{S_\sigma (z)(1-|z|^2)^s}{|1-\overline{w}z|^{2+s+t}}dA(w) &= \int_{ \mathbb{D}}\left( \int_{\mathbb D}\log \left| \frac{1-\overline{\zeta}z}{z-\zeta}\right| \frac{d\sigma(\zeta)}{1-|\zeta|^2}\right) \frac{(1-|z|^2)^s}{|1-\overline{w}z|^{2+s+t}}dA(z)\\ &=\int_{ \mathbb{D}}\left( \int_{\mathbb D}\frac{(1-|z|^2)^s}{|1-\overline{w}z|^{2+s+t}}\log \left| \frac{1-\overline{\zeta}z}{z-\zeta}\right|dA(z)\right) \frac{d\sigma(\zeta)}{1-|\zeta|^2}\\ &\lesssim \frac{1}{(1-|w|^2)^{t}}\int_{ \mathbb{D}} \left( \frac{(1-|\zeta|^2)(1-|w|^2)}{|1-\overline{\zeta}w|^{2}}\right) \frac{d\sigma(\zeta)}{1-|\zeta|^2}\\ &\lesssim \frac{S_\sigma(w)}{(1-|w|^2)^{t}}. \end{align*} $$
Thus,
$S_\sigma $
satisfies (2.7). It follows that
$S_\sigma +P_\nu $
satisfies (2.7) for all
$s>-1$
and
$t>1$
. Therefore, by Remark 2.6,
$(1-|z|^2)^\alpha \omega $
verifies (2.7) for all
$\alpha>-1$
.
In the rest of this subsection, let
$ \omega (z)=(1-|z|^2)^\alpha \left ( S_\sigma (z)+P_\nu (z)\right ), $
for a fixed
$\alpha>-1$
and finite positive Borel measures
$\sigma $
and
$\nu $
on
$\mathbb {D}$
and
$\mathbb {T}$
, respectively. Let
$\check {\omega }$
be the weight given by
$ \check {\omega }(z)=(1-|z|^2)^\alpha \left ( U_\sigma (z)+ P_\nu (z)\right ),\quad z\in \mathbb {D}. $
Theorem 2.8 Let
$\omega $
and
$\check {\omega }$
be as given above, and let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
. The following assertions hold.
-
(1)
$C_\varphi $
is bounded (resp. compact) on
$\mathcal {D}_\omega $
if and only if
$$ \begin{align*}\frac{1}{|\Delta_n|}\int_{\Delta_{n}} \frac{N_{\varphi , \check{\omega}}(z)}{\check{\omega} (z)} dA(z)=O( 1),\quad\left( \mbox{resp. }o(1)\mbox{ as } n\to\infty\right). \end{align*} $$
-
(2)
$C_\varphi $
belongs to
$\mathcal {S}_p(\mathcal {D}_\omega )$
,
$p>0$
, if and only if
$$ \begin{align*}\sum_{n= 0}^{+\infty} \left ( \frac{ 1}{|\Delta_{n}|}\int_{\Delta_{n}} \frac{N_{\varphi , \check{\omega}}(z)}{\check{\omega} (z)} dA(z)\right )^{\frac{p}{2}} < \infty. \end{align*} $$
Proof Let
$f\in \mathcal {D}_\omega $
. We have
$$ \begin{align*} &\mathcal{D}_\omega(f)-\displaystyle \displaystyle\int_{\mathbb{D}}|f'(z)|^2 (1-|z|^2)^\alpha P_\nu (z)dA(z)\\ &= \displaystyle\int_{\mathbb{D}} \displaystyle\int_{\mathbb{D}}|f'(z)|^2 (1-|z|^2)^\alpha \log \left| \frac{1-\overline{\zeta}z}{z-\zeta}\right| dA(z) \frac{d\sigma(\zeta)}{1-|\zeta|^2}\\ &\asymp \displaystyle\int_{\mathbb{D}} \displaystyle\int_{\mathbb{D}} |f'(z)|^2 (1-|z|^2)^\alpha \left( 1-\left|\frac{z-\zeta}{1-\overline{\zeta}z} \right|{}^2\right) dA(z) \frac{d\sigma(\zeta)}{1-|\zeta|^2} \\ &= \displaystyle\int_{\mathbb{D}} \displaystyle\int_{\mathbb{D}} |f'(z)|^2 (1-|z|^2)^\alpha \frac{1-|z|^2}{|1-\overline{\zeta}z|^2} dA(z) d\sigma(\zeta)\\ &= \displaystyle\int_{\mathbb{D}}|f'(z)|^2 (1-|z|^2)^\alpha U_\sigma(z)dA(z). \end{align*} $$
It follows that
$\mathcal {D}_{\omega }=\mathcal {D}_{\check {\omega }}$
with equivalent norms. Therefore,
$C_\varphi $
is bounded (resp. compact) on
$\mathcal {D}_\omega $
if and only if
$C_\varphi $
is bounded (resp. compact) on
$\mathcal {D}_{\check \omega }$
. Taking into account that
$\check {\omega }(z)\asymp \check {\omega }(z_n)$
, for
$z\in \Delta _n$
, the first assertion follows by combining Proposition 2.7, Lemma A, and
$(1)$
and
$(2)$
of Corollary 2.4.
For the proof of the second assertion, note that since
$\mathcal {D}_{\omega }=\mathcal {D}_{\check {\omega }}$
with equivalent norms then the operator
$I: \mathcal {D}_{\omega }\to \mathcal {D}_{\check {\omega }}$
which takes f to f is bounded and invertible. It follows that
$I^{\ast }$
, the adjoint of I defined by
$ \left \langle I^{\ast } f,g \right \rangle _{\mathcal {D}_{\omega }} =\left \langle f,Ig \right \rangle _{\mathcal {D}_{\check {\omega }}} $
is bounded and invertible on
$\mathcal {D}_{\check {\omega }}$
. This implies
$$ \begin{align*}I^{\ast} \left( C_{\varphi,\mathcal{D}_{\check{\omega}}}\right) ^\ast\left( C_{\varphi,\mathcal{D}_{\check{\omega}}}\right) I \asymp \left( C_{\varphi,\mathcal{D}_{\omega}}\right) ^\ast\left( C_{\varphi,\mathcal{D}_{\omega}}\right),\end{align*} $$
where
$C_{\varphi ,\mathcal {D}_{\omega }}$
is the operator
$C_\varphi :\mathcal {D}_{\check {\omega }}\to \mathcal {D}_{\check {\omega }}$
and
$C_{\varphi ,\mathcal {D}_{\omega }}$
is the operator
$C_\varphi :\mathcal {D}_{\omega }\to \mathcal {D}_{\omega }$
. It follows that if
$C_{\varphi ,\mathcal {D}_{\omega }}$
is compact, then
$C_{\varphi ,\mathcal {D}_{\omega }}$
belongs to
$\mathcal {S}_p(\mathcal {D}_{\omega })$
if and only if
$C_{\varphi ,\mathcal {D}_{\check {\omega }}}$
belongs to
$\mathcal {S}_p(\mathcal {D}_{\check {\omega }})$
. Hence, using once again Proposition 2.7, Lemma A, and
$(3)$
of Corollary 2.4, we obtain the second assertion of the theorem.
The following theorem extend the result obtained by Pau and Pérez [Reference Pau and Pérez21, Theorem 4.1] in standard Dirichlet spaces setting to the Green potential of the Riesz measure of any positive superharmonic function. Recall that
$$ \begin{align*} \check N_{\varphi,\sigma}(w) = \sum_{w=\varphi(z)} U_\sigma(z) \;\; \text{if } w \in \varphi(\mathbb{D}) \;\;; \;\; \check N_{\varphi , \sigma}(w) = 0 \;\; \text{if } w \notin \varphi(\mathbb{D}). \end{align*} $$
Theorem 2.9 Let
$p>0$
, and let
$\varphi $
be an analytic self-map of
$\mathbb D$
. Let
$\sigma $
be a finite positive measure on
$\mathbb {D}$
. Then,
$C_{\varphi }$
belongs to
$ \mathcal {S}_{p}(\mathcal {D}_\sigma )$
if and only if
$$ \begin{align*}\int_{\mathbb D}\left( \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)}\right) ^{p/2}d\lambda(z)<\infty.\end{align*} $$
Proof By Theorem 2.8, we have
$$ \begin{align*}C_{\varphi} \in \mathcal{S}_{p}(\mathcal{D}_{\sigma}) \Longleftrightarrow \sum_{n= 0}^{+\infty} \left(\frac{1}{\vert \Delta_n \vert}\int_{\Delta_n} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \right)^{p/2} < \infty. \end{align*} $$
Therefore, it suffices to show that
$$ \begin{align*}\frac{1}{\vert \Delta_n \vert}\displaystyle\int_{\Delta_n} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \in \ell^{p/2} \Longleftrightarrow \frac{\check N_{\varphi,\sigma}(w)}{U_\sigma}\in L^{p/2}(\mathbb{D},d\lambda).\end{align*} $$
We use for the proof some standard arguments. First, we prove that for all
$p> 0$
, we have
$$ \begin{align} \check N_{\varphi , \sigma}(z)^p\lesssim \frac{1}{|\Delta(z,r)|}\int_{\Delta(z,r)} \check N_{\varphi , \sigma}(w)^p dA(w),\quad z\in\mathbb{D}. \end{align} $$
The function
$\check N_{\varphi , \sigma }$
satisfies the sub-mean-value property, that is,
$$ \begin{align*}\check N_{\varphi , \sigma}(z)\lesssim \frac{1}{|\Delta(z,r)|}\int_{\Delta(z,r)} \check N_{\varphi , \sigma}(w) dA(w),\quad z\in\mathbb{D} \end{align*} $$
(see [Reference Bao, Göğüş and Pouliasis5, Lemma 5.2]). Therefore, there exists a subharmonic function u on
$\mathbb {D}$
such that
$ N_{\varphi , \sigma }\le u$
on
$\mathbb {D}$
and
$u= N_{\varphi , \sigma }$
almost everywhere on
$\mathbb {D}$
(see [Reference Luecking and Zhu19]. Since
$$ \begin{align*} u(z)^p\lesssim \frac{1}{|\Delta(z,r)|}\int_{\Delta(z,r)}u(w)^p dA(w),\quad z\in\mathbb{D}, \end{align*} $$
by [Reference Luecking and Zhu19, Lemma 3], we obtain (2.8). Now, we have
$$ \begin{align*} \int_{\mathbb D}\left( \frac{\check N_{\varphi,\sigma}(w)}{U_\sigma(w)}\right) ^{p/2}d\lambda(w) &\asymp \sum_{n= 0}^{+\infty} \int_{\Delta_n}\left( \frac{\check N_{\varphi,\sigma}(w)}{U_\sigma(w)}\right) ^{p/2}d\lambda(w). \end{align*} $$
Taking into account that
$U_\sigma (w)\asymp U_\sigma (z)$
if
$w\in \Delta _n$
and
$z\in b\Delta _n$
, the inequality (2.8) gives
$$ \begin{align*} \int_{\mathbb D}\left( \frac{\check N_{\varphi,\sigma}(w)}{U_\sigma(w)}\right) ^{p/2}d\lambda(w) &\lesssim \sum_{n= 0}^{+\infty} \int_{\Delta_n}\left( \frac{1}{\vert \Delta_n \vert}\int_{b\Delta_n} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \right) ^{p/2}d\lambda(w)\\ &\asymp \sum_{n= 0}^{+\infty} \left( \frac{1}{\vert \Delta_n \vert}\int_{b\Delta_n} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \right) ^{p/2}. \end{align*} $$
Since
$\left ( b\Delta _n\right ) _n$
is a covering of
$\mathbb {D}$
of finite multiplicity, then for all n there exist
$n_1,n_2,\ldots ,n_N$
such that
$b\Delta _n\subset \displaystyle \cup _{k=1}^{N} \Delta _{n_k}$
, for some
$N\in \mathbb {N}^\ast $
not depending on n. Hence,
$$ \begin{align*}\displaystyle\int _{b\Delta_{n}} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z)\lesssim \displaystyle\int_{\Delta_{m_n}} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z), \end{align*} $$
where
$m_n$
is such that
$\displaystyle \int _{\Delta _{m_n}} \frac {\check N_{\varphi ,\sigma }(z)}{U_\sigma (z)} dA(z)=\displaystyle \max _{1\le k\le N}\displaystyle \int _{\Delta _{n_k}} \frac {\check N_{\varphi ,\sigma }(z)}{U_\sigma (z)} dA(z)$
. Therefore,
$$ \begin{align*} \int_{\mathbb D}\left( \frac{\check N_{\varphi,\sigma}(w)}{U_\sigma(w)}\right) ^{p/2}d\lambda(w) &\lesssim \sum_{n= 0}^{+\infty} \left( \frac{1}{\vert \Delta_n \vert}\int_{\Delta_{m_n}} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \right) ^{p/2}\\ & \le \sum_{n= 0}^{+\infty} \left( \frac{1}{\vert \Delta_n \vert}\int_{\Delta_{n}} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \right) ^{p/2}. \end{align*} $$
On the other hand, let
$\zeta _n\in \overline {\Delta }_{n}$
such that
$ \dfrac {\check N_{\varphi ,\sigma }(\zeta _n)}{U_\sigma (\zeta _n)}=\displaystyle \sup _{z\in \Delta _{n}} \dfrac {\check N_{\varphi ,\sigma }(z)}{U_\sigma (z)}. $
We have
$$ \begin{align*} \sum_{n= 0}^{+\infty} \left( \frac{1}{\vert \Delta_n \vert}\int_{\Delta_{n}} \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)} dA(z) \right) ^{p/2} &\lesssim \sum_{n= 0}^{+\infty} \left( \frac{\check N_{\varphi,\sigma}(\zeta_n)}{U_\sigma(\zeta_n)}\right)^{p/2}\\ &\lesssim \sum_{n= 0}^{+\infty} \frac{1}{\vert \Delta_n \vert}\int_{b\Delta_{n}} \left( \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)}\right) ^{p/2} dA(z)\\ &\asymp \sum_{n= 0}^{+\infty} \int_{b\Delta_{n}} \left( \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)}\right) ^{p/2} d\lambda(z)\\ &\asymp \int_{\mathbb D}\left( \frac{\check N_{\varphi,\sigma}(z)}{U_\sigma(z)}\right) ^{p/2}d\lambda(z). \end{align*} $$
The proof is complete.
3 Composition operators on weighted Bergman spaces
3.1 Radial weights
Let
$\omega :[0,1)\to (0,\infty )$
be a continuous radial weight. We associate with
$\omega $
, the weight
$\omega _{\ast }$
defined by
$$ \begin{align*}\omega_{\ast}(r)=\int_{r}^{1}(t-r)\omega(t)dt. \end{align*} $$
As pointed in [Reference Kellay and Lefèvre15],
$A_\omega ^2=\mathcal {D}_{\omega _\ast }$
with equivalent norms and
$\omega _{\ast }$
always satisfies
$(\mathcal {W}_1)$
,
$(\mathcal {W}_3)$
, and
$(\mathcal {W}_4^{(I)})$
. Therefore, as a consequence of Theorem 2.5, we have the following result.
Theorem 3.1 Let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
, and let
$p>0$
. Let
$\omega $
be a continuous radial weight such that
$\omega _{\ast }$
satisfies
$(\mathcal {W}_2)$
. Then
$$ \begin{align*} C_\varphi\in \mathcal{S}_p(A^2_\omega)\Longleftrightarrow\int_{\mathbb D}\left( \frac{ N_{\varphi,\omega_\ast}(z)}{\omega_\ast(z)}\right) ^{p/2}d\lambda(z)<\infty. \end{align*} $$
Corollary 3.2 Let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
, and let
$p>0$
. Let
$\omega $
be a continuous radial weight such that
$\omega _{\ast }$
satisfies
$(\mathcal {W}_2)$
fore some
$\delta>0$
. The following assertions hold.
-
(1) If
$C_\varphi $
belongs to
$\mathcal {S}_p(H^2)$
, then
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_\omega )$
. -
(2) If
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_\omega )$
, then
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_{\delta -1})$
.
Proof Since
$\omega _{\ast }$
satisfies
$(\mathcal {W}_2)$
and always satisfies
$(\mathcal {W}_1)$
then, by [Reference Kellay and Lefèvre15, Lemma 2.1], each composition operator induced by the symbol
$q_{\varphi (0)}(z)=\frac {\varphi (0)-z}{1-\overline {\varphi (0)}z}$
is bounded on
$A_\omega ^2=\mathcal {D}_{\omega _\ast }$
. It is also known that each composition operator induced by
$q_{\varphi (0)}$
is bounded on
$\mathcal {H} _{\alpha }$
. Hence, by standard arguments, we may assume without loss of generality that
$\varphi (0)=0$
. The condition
$(\mathcal {W}_2)$
gives
$$ \begin{align*}\frac{\omega_{\ast}(r)}{\omega_{\ast}(t)}\le \left( \frac{1-r}{1-t}\right)^{1+\delta},\quad 0\leq r \leq t <1. \end{align*} $$
On the other hand, by a direct calculation,
$s\in [0,1)\to \frac {\omega _{\ast }(s)}{1-s}$
is a nonincreasing function. It follows that
$$ \begin{align*}\frac{\omega_{\ast}(r)}{\omega_{\ast}(t)}\ge \frac{1-r}{1-t},\quad 0\leq r \leq t <1. \end{align*} $$
Let
$z\in \varphi (\mathbb {D})$
and
$w\in \mathbb {D}$
such that
$\varphi (w)=z$
. By Schwarz’s lemma and the above inequalities, we obtain
$$\begin{align*}\left(\frac{1-|w|^2}{1-|z|^2}\right)^{\delta+1} \lesssim \frac{\omega_\ast\left(w\right)}{\omega_\ast(z)}\lesssim \frac{1-|w|^2}{1-|z|^2}. \end{align*}$$
It follows that
$$ \begin{align} \frac{N_{\varphi,\delta+1}(z)}{(1-|z|^2)^{\delta+1}} \lesssim \frac{N_{\varphi,\omega_\ast}(z)}{\omega_{\ast}(z)}\lesssim \frac{N_{\varphi,1}(z)}{(1-|z|^2)},\quad z\in\mathbb{D}. \end{align} $$
The assertions of the corollary are obtained by combining Theorem 3.1 and (1.1).
A radial weight
$\omega $
belongs to the class
$\hat {D}$
if
$ \displaystyle \int _{r}^{1}\omega (s)ds\lesssim \displaystyle \int _{\frac {1+r}{2}}^{1}\omega (s)ds, r\in [0,1).$
Peláez and Rättyä obtained in [Reference Peláez and Rättyä23], a trace class criteria for Toeplitz operators on Dirichlet spaces associated with regular weights and they obtained that, for
$\omega \in \hat {D}$
,
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_\omega )$
, for
$p>0$
, if and only if
$$ \begin{align*} \int_{\mathbb D}\left( \frac{ N_{\varphi,\omega^\ast}(z)}{\omega^\ast(z)}\right) ^{p/2}d\lambda(z)<\infty, \end{align*} $$
where
$ \omega ^{\ast }(r):=\int _{r}^{1}s\log \left (\frac {s}{r} \right )\omega (s)ds$
,
$r\in (0,1). $
We point out that Lemma
$2.4$
in [Reference Kellay and Lefèvre15] and Theorem 2.5 for
$(I)$
-admissible weights still hold if we replace the condition
$(\mathcal {W}_2)$
by the following one:
$$ \begin{align*}(\mathcal{W}^\prime_2) \mbox{ there is } \delta>0\mbox{ such that } \omega(r)(1-r)^{-(1+\delta)}\lesssim \omega(t)(1-t)^{-(1+\delta)},\quad 0\leq r \leq t <1.\end{align*} $$
Theorem 3.1 can be applied to continuous weights belonging to
$\hat {D}$
thanks to the following lemma.
Lemma 3.3 If
$\omega $
belongs to
$\hat {D}$
, then
$\omega _{\ast }$
satisfies
$(\mathcal {W}^\prime _2)$
.
Proof Assume that
$\omega $
belongs to
$\hat {D}$
. We have
$$ \begin{align*} \omega_{\ast}(r)\ge \int_{\frac{1+r}{2}}^{1}(t-r)\omega(t)dt \gtrsim (1-r)\int_{\frac{1+r}{2}}^{1}\omega(t)dt \gtrsim (1-r)\int_{r}^{1}\omega(t)dt. \end{align*} $$
It follows that
$\omega _{\ast }(r)\asymp (1-r)\int _{r}^{1}\omega (t)dt$
. On the other hand, since
$\omega \in \hat {D}$
, there exists a constant
$\delta>0$
such that
$$ \begin{align*} \int_{r}^{1} \omega(s)ds \lesssim \left(\frac{1-r}{1-t}\right)^\delta \int_{t}^{1} \omega(s)ds,\quad 0\leq r \leq t <1 \end{align*} $$
(see [Reference Peláez22]). We obtain
$$ \begin{align*} \frac{\omega_{\ast}(r)}{(1-r)^{\delta+1}} \asymp \frac{1}{(1-r)^{\delta}} \int_{r}^{1}\omega(s)ds \lesssim \frac{1}{(1-t)^{\delta}} \int_{t}^{1}\omega(s)ds \asymp \frac{\omega_{\ast}(t)}{(1-t)^{\delta+1}}, \end{align*} $$
for
$0\leq r \leq t <1$
.
3.2 General case
Let
$\omega $
be a weight not necessarily radial and consider the composition operator
$C_\varphi : A^2_\omega \to A^2_\omega $
. For the weights
$\omega $
such that
$\frac {\omega }{(1-|z|^2)^\eta }\in B_{p_0}(\eta )$
for some
$p_0>1$
and
$\eta>-1$
, Constantin [Reference Constantin8] characterized boundedness, compactness, and membership of
$C_\varphi $
in
$\mathcal {S}_p(A^2_\omega )$
, for
$p\ge 2$
, in terms of the pullback measure of
$\omega dA$
under
$\varphi $
.
If
$C_\varphi $
is bounded on
$A^2_\omega $
then
$ C_\varphi ^\ast C_\varphi = T_{\frac {1}{\omega }d\mu }$
with
$\mu (E)=A_\omega \left ( \varphi ^{-1}(E)\right )$
for any Borel subset E of
$\mathbb {D}$
. Using Theorem B, we obtain the following result, which extend [Reference Constantin8, Theorem 6.2].
Theorem 3.4 Let
$\omega $
be a weight in
$\omega \in \mathcal {C}_{p_0,t}$
for some
$p_0>1$
and
$t\ge 0$
. Assume that
$\varphi $
is an analytic self-map of
$\mathbb {D}$
such that
$C_\varphi $
is compact on
$A^2_{\omega }$
. Then
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_{\omega })$
, for
$p>0$
, if and only if
$$ \begin{align*}\displaystyle \sum_{n=0}^{\infty} \left( \frac{\int_{\varphi^{-1}(\Delta_n)} \omega(z) dA(z)}{ \int_{\Delta_n} \omega(z) dA(z)} \right)^{p/2}<\infty. \end{align*} $$
In particular, if
$\omega $
is an almost standard weight, then
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_{\omega })$
if and only if
$$ \begin{align*}\displaystyle \sum_{n=0}^{\infty} \left( \frac{A_\omega \left( \varphi^{-1}(\Delta_{n})\right)}{ (1-|z_n|^2)^2 \omega(z_n) } \right)^{p/2}<\infty. \end{align*} $$
Note that, when
$\omega $
is an almost standard weight,
$C_\varphi $
is bounded (resp. compact) on
$A^2_\omega $
if and only if
$A_\omega \left ( \varphi ^{-1}(\Delta _{z})\right )= O\left ( (1-|z|^2)^2 \omega (z) \right ) \left ( \mbox { resp. } o\left ( (1-|z|^2)^2 \omega (z) \right )\right ), |z|\to 1^-. $
Here, we characterize boundedness, compactness, and membership of
$C_\varphi $
in
$\mathcal {S}_p(A^2_\omega )$
, for
$\omega $
in some class
$\mathcal {C}_{p_0,t}$
, in terms of Nevanlinna counting function. Denote
$\omega _{[2]}=(1-|z|^2)^2\omega .$
Theorem 3.5 Let
$\varphi $
be an analytic self-map of
$\mathbb {D}$
, and let
$p>0$
. Suppose that
$\omega $
is a weight such that
$\omega \in \mathcal {C}_{p_0,t}$
for some
$p_0>1$
and
$t\ge 0$
. Then:
-
(1)
$C_\varphi $
is bounded on
$A^2_\omega $
if and only if
$$ \begin{align*}\frac{1}{|\Delta_{n}|}\int_{\Delta_n} N_{\varphi,\omega_{[2]}}(z) dA(z)\lesssim \int_{\Delta_n} \omega(z) dA(z),\quad\forall n\in\mathbb{N}. \end{align*} $$
-
(2)
$C_\varphi $
is compact on
$A^2_\omega $
if and only if
$$ \begin{align*}\frac{1}{|\Delta_{n}|}\int_{\Delta_n} N_{\varphi,\omega_{[2]}}(z) dA(z)= o\left(\int_{\Delta_n} \omega(z) dA(z) \right) ,\quad (n\to\infty). \end{align*} $$
-
(3)
$C_\varphi $
belongs to
$\mathcal {S}_p(A^2_{\omega })$
if and only if
$$ \begin{align*}\displaystyle \sum_{n=0}^{\infty} \left( \frac{\frac{1}{|\Delta_{n}|}\int_{\Delta_n} N_{\varphi,\omega_{[2]}}(z) dA(z)}{ \int_{\Delta_n} \omega(z) dA(z)} \right)^{p/2}<\infty. \end{align*} $$
Proof Note that, since
$\omega \in \mathcal {C}_{p_0,t}$
for some
$p_0>1$
and
$t\ge 0$
, we have the following Littlewood–Paley estimates:
$$ \begin{align} \|f\|_{A^2_\omega}^2\asymp \left|f(0) \right|{}^2 + \displaystyle \displaystyle\int_{\mathbb{D}}|f'(z)|^2(1-|z|^2)^2\omega (z)dA(z) ,\quad f\in \text{Hol} (\mathbb{D}) \end{align} $$
(see [Reference Bourass and Marrhich7]). Therefore,
$$ \begin{align*} \int_{ \mathbb{D}}|C_\varphi f(z)|^2 \omega(z)dA(z)\asymp |f(\varphi(0))|^2+ \int_{ \mathbb{D}}|(C_\varphi f)'(z)|^2\omega_{[2]}(z)dA(z), \quad f\in \text{Hol} (\mathbb{D}). \end{align*} $$
It follows that
${C_\varphi }:A^2_\omega \to A^2_\omega $
is bounded (resp. compact) if and only if
${C_\varphi }:\mathcal {D}_{\omega _{[2]}}\to \mathcal {D}_{\omega _{[2]}}$
is bounded (resp. compact). Also, note that if
$\omega \in \mathcal {C}_{p_0,t}$
, then
$\omega _{[2]}\in \mathcal {C}_{p_0,t+2}$
. By Theorem 2.2, we obtain the first and the second assertions of the theorem.
By (3.2), the operator
$X: A^2_\omega \to \mathcal {D}_{\omega _{[2]}}$
defined by
$Xf=f$
is bounded and invertible. Similarly to the proof of the second assertion of Theorem 2.8, it follows that
${C_\varphi }:A^2_{\omega }\to A^2_{\omega }$
belongs to
$\mathcal {S}_p(A^2_\omega )$
if and only if
${C_\varphi }:\mathcal {D}_{\omega _{[2]}}\to \mathcal {D}_{\omega _{[2]}}$
belongs to
$\mathcal {S}_p(\mathcal {D}_{\omega _{[2]}})$
. Hence, by Theorem 2.3, we obtain the third assertion of the theorem.
Remark 3.6 Let
$\alpha>-1$
. Luecking and Zhu proved in [Reference Luecking and Zhu19] that the condition
$$ \begin{align*}\left( \frac{1-|z|^2}{1-|\varphi(z)|^2}\right)^{2+\alpha}\in L^{p/2}(\mathbb{D},d\lambda) \end{align*} $$
is necessary when
$p\ge 2$
and sufficient when
$p\le 2$
for
$C_\varphi $
to be in
$\mathcal {S}_p(A^2_\alpha )$
. Suppose that
$\omega $
is a weight in
$\mathcal {C}_{p_0 ,t}$
for some
$p_0>1$
and
$t\ge 0$
. It is proved in [Reference Bourass and Marrhich7] that
$A^2_\omega =A^2_{\tilde \omega }$
with
$\Vert f \Vert _{A^2_\omega } \asymp \Vert f \Vert _{A^2_{\tilde \omega }}$
for all
$f\in Hol(\mathbb {D})$
. It is proved also in [Reference Bourass and Marrhich7] that
$A^2_{\tilde \omega }$
is a reproducing kernel space with kernel
$K^{\tilde {\omega }}$
satisfying
$$ \begin{align*}\Vert K^{\tilde{\omega}}_{z} \Vert_{A^2_{\tilde{\omega}}}^{2} \asymp \frac{1}{(1 - \vert z \vert^{2})^{ 2} \tilde{\omega} (z)},\quad z\in\mathbb{D}. \end{align*} $$
Since
$C_\varphi \in \mathcal {S}_p(A^2_\omega )$
if and only if
$C_\varphi \in \mathcal {S}_p(A^2_{\tilde {\omega }})$
, using the same argument given in [Reference Luecking and Zhu19], we obtain that the condition
$$ \begin{align} \frac{\int_{\Delta(z,(1-|z|^2)/2)} \omega(\zeta)dA(\zeta)}{\int_{\Delta(\varphi(z),(1-|\varphi(z)|^2)/2)} \omega(\zeta)dA(\zeta)}\in L^{p/2}(\mathbb{D},d\lambda) \end{align} $$
is necessary when
$p\ge 2$
and sufficient when
$p\le 2$
for
$C_\varphi $
to be in
$\mathcal {S}_p(A^2_{\omega })$
. Note that if in addition
$\omega $
verifies (2.3), then the condition (3.3) is equivalent to
$$ \begin{align*} \frac{(1-|z|^2)^2 \omega(z)}{(1-|\varphi(z)|^2)^2 \omega(\varphi(z))}\in L^{p/2}(\mathbb{D},d\lambda). \end{align*} $$
Acknowledgment
The authors would like to thank Professor Omar El-Fallah for helpful discussions.
