2.1. Geometrical set-up

The considered set-up is a modified generic swirl combustor consisting of a plenum, swirler and mixing tube. A cutaway view of the LES set-up is shown in figure 1(a) and a streamwise cut is shown in figure 1(b). The set-up consists of the straight end-section of the upstream plenum, the radial swirl generator and the mixing tube. The swirl generator was equipped with one central air inlet (indicated by the vertical dashed line) that creates a non-swirling axial jet. The swirler comprises eight radial-tangential air inlets (indicated by the horizontal dashed lines), which introduce the swirling flow with a geometric swirl number (Leuckel Reference Leuckel1967) of ${S}_{g} = 0.7$. The mixing tube has a diameter of $D = 34$ mm and, with the extended exhaust tube, a length of $L = 7.5D$. The upstream plenum has a diameter and axial length of $4.4D$. The simulations and experiments were performed at isothermal ($T = 293$ K) and ambient pressure ($p = 101\ 325$ Pa) operating conditions. The mass flow rate was $\dot {m} = 104\ {\rm kg}\ {\rm h}^{-1}$, corresponding to a bulk flow velocity of $U \approx 26\ {\rm m}\ {\rm s}^{-1}$. The Reynolds number of the swirling pipe flow in the mixing tube with respect to its diameter and bulk velocity was $Re = UD/\nu \approx 58\ 000$, with $\nu$ being the kinematic viscosity.

Figure 1. Large-eddy simulation set-up of the swirling pipe flow as (a) cutaway view and (b) streamwise cut with the origin of coordinates at the upstream end of the mixing tube ($x=0$) and at the mixing tube centreline ($y=0$). The inlet and outlet of the simulation domain are at the leftmost and rightmost boundary, respectively.

2.2. Large-eddy simulation

The LES was conducted with the compressible AVBP code from CERFACS and IFPEN. The domain was discretized with approximately $31$ million triangular cells. Time stepping was performed using a two-step Taylor–Galerkin scheme (Colin & Rudgyard Reference Colin and Rudgyard2000), which is third-order accurate in space and time. Subgrid turbulence was accounted for by using the $\sigma$-model (Nicoud et al. Reference Nicoud, Toda, Cabrit, Bose and Lee2011). At the inlet, a constant velocity profile with a mass flow rate of $\dot {m} = 104\ {\rm kg}\ {\rm h}^{-1}$ was set; at the outlet, a constant pressure of 101 325 Pa. Characteristic boundary conditions were applied at the inlet and outlet of the domain (Poinsot & Lele Reference Poinsot and Lele1992). The relaxation coefficient at the inlet was chosen as $10^4$ to ensure a close adherence to the prescribed mass flow value. According to Selle, Nicoud & Poinsot (Reference Selle, Nicoud and Poinsot2004), this results in a reflection cutoff frequency for acoustic waves of approximately $800$ Hz. The relaxation coefficient at the outlet was set to $10^3$, resulting in an acoustically transmissive boundary condition with a cutoff frequency of approximately $80$ Hz. All walls were assumed to be no-slip and adiabatic. The Courant–Friedrichs–Lewy number was set to $0.75$. The simulation was performed for a total time of $0.03$ s, which corresponds to approximately four mixing tube flow-through times. The axisymmetric mean flow field was obtained by averaging along the temporal and the azimuthal direction. Only marginal changes of the numerical solution were found when repeating the simulation with an increased mesh resolution of $101$ million cells. The associated mean field changes had negligible effects on the optimal response and forcing modes of the RA.

2.3. Experimental measurements

For validation of the LES mean flow and the linear model, two experimental datasets are used. The primarily considered dataset of Bluemner, Paschereit & Oberleithner (Reference Bluemner, Paschereit and Oberleithner2019) has the exact same operating conditions and set-up as the LES, but with an added trombone section upstream of the plenum. The LES provides the time- and phase-averaged velocity fields of the axial and radial components in a streamwise section. Four loudspeakers located upstream of the plenum were used for acoustically exciting the flow at various frequencies and at a target amplitude of $10\,\%$ of the bulk velocity. This target amplitude ensures a sufficiently large but still linear flow response, which was cross-checked with prior microphone measurements. Two-dimensional (2-D), two-component, time-resolved PIV was performed for measuring the velocity fields. For this, the mixing tube was made of borosilicate glass for optical access and the light sheet was aligned with the mixing tube's centreline. The effective measurement region reached from $x/D \approx 1.35$ to $x/D \approx 4$. The sampling frequency was $2027$ Hz with a measurement time of approximately $1$ s. A second dataset of Müller et al. (Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022) is considered to obtain the time- and phase-averaged velocity fields of the azimuthal component in cross-wise sections, which were not recorded in the first dataset introduced above. The second dataset has a very similar set-up but with a shorter mixing tube length of $4.4D$ and a combustion chamber attached downstream. In the second experiment, the operating conditions were at a slightly lower mass flow rate with a bulk velocity of $U \approx 21\ {\rm m}\ {\rm s}^{-1}$, corresponding to a Reynolds number of $Re \approx 47\ 000$. For further details of both experimental set-ups, the reader is referred to the respective studies.

2.4. Time-averaged flow field and validation of the LES

The time-averaged flow field is briefly characterized and the accuracy of the LES is evaluated with regard to the experimentally measured data. For the remainder of this paper, the velocity vector $\boldsymbol {u} = (u, v, w)^\mathrm {T}$ is defined by the components of axial, radial and azimuthal velocity, respectively. However, strictly speaking, we will show transverse instead of radial and out-of-plane instead of azimuthal velocities for the sake of visuals.

Figure 2 shows the contours of time-averaged velocity for all three components in the mixing tube of the LES, downstream of the central nozzle and the tangential swirler inlet (indicated by the dashed line between the black dots). At the central nozzle, a strong jet is evident for the axial component, introducing strong shear and velocity gradients. This jet joins with the tangentially and radially introduced flow from the swirler, as visible for the radial component. For the azimuthal component, a prominent region of very high swirl can be observed. Figure 3 compares the mean axial and azimuthal velocity profiles between LES and the two experiments for five different axial positions. The overall agreement is good. However, the LES overestimates the diffusive behaviour of the flow, as indicated by the increasingly homogeneous velocity profiles in the downstream direction. The azimuthal component reveals a region of nearly solid-body rotation for $|y/D| < 0.3$, which is almost fully developed at $x/D = 2.2$.

Figure 2. Contours of the time-averaged LES flow field of the swirling pipe flow inside the mixing tube for (a) axial velocity, (b) radial velocity and (c) azimuthal velocity.

Figure 3. Profiles of the time-averaged LES flow field of the swirling pipe flow for (a) axial velocity and (b) azimuthal velocity compared against two experimental datasets (Bluemner et al. Reference Bluemner, Paschereit and Oberleithner2019; Müller et al. Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022) and plug flow with solid-body rotation. Grey shaded area indicates region of approximate solid-body rotation in the swirling pipe flow and coincides with the radial domain size of the plug flow with solid-body rotation.

The discrepancies between LES and experiment may be attributed to a mismatch of the pressure drop across the swirler. This pressure drop is critical since a false prediction can lead to an incorrect mass flow split between the central and tangential air inlet that disagrees with the experiment. Even slight errors in this mass flow split can have a large impact on the LES flow field inside the mixing tube. As mentioned in § 2.2, another LES for more than triple the mesh resolution was performed, but only marginal changes for the mean fields and negligible impact on the RA results were found. Due to these diminishing returns, we did not see any substantial benefit in further pursuing an exhaustive LES study.

3.1. Phase average

To extract the coherent fluctuation part, a phase-averaging procedure is conducted. The phase average of the velocity field $\langle \boldsymbol {u}(\boldsymbol {x},t) \rangle$ is defined by

(3.2)\begin{equation} \langle \boldsymbol{u}(\boldsymbol{x},t) \rangle = \lim_{N\to\infty} \frac{1}{N} \sum_{n=1}^{N} \boldsymbol{u}(\boldsymbol{x},t + n\tau) ,\end{equation}

where $\tau$ is the characteristic period of the oscillation with the angular frequency $\omega = 2{\rm \pi} /\tau$, in which the frequency is related to the instantaneous phase angle $\varphi$ of the oscillation with $\varphi \propto \omega t$. In practice, the phase-averaging in (3.2) cannot be computed continuously in $t$. Instead, the time signal is partitioned into segments, in which each segment corresponds to a phase angle bin. The loudspeaker input signal is used for a reference phase angle and a complete period of oscillation is divided into $N_\varphi = 16$ phase bins. The PIV snapshots are sorted to each of these phase bins $\varphi _j$ and averaged subsequently, yielding a phase-averaged field $\langle \boldsymbol {u} \rangle _j$ for each given phase angle bin. The coherent fluctuation is retrieved by

(3.3)\begin{equation} \boldsymbol{\widetilde{u}}_j = \langle \boldsymbol{u} \rangle_j - \boldsymbol{\overline{u}} .\end{equation}

Finally, the coherent fluctuation is transformed into frequency space with

(3.4)\begin{equation} \skew2\hat{\boldsymbol{u}} = \frac{1}{N_\varphi} \sum_{j=1}^{N_\varphi} \boldsymbol{\widetilde{u}}_j \, \mathrm{e}^{-\mathrm{i}\varphi_j}. \end{equation}

This is done to filter out any higher harmonics and to obtain a defined spatial phase angle $\varphi _{\boldsymbol x} = \operatorname {atan2}({\rm Im}(\skew2\hat {\boldsymbol {u}}),{\rm Re}(\skew2\hat {\boldsymbol {u}}))$ required for computing the phase velocity in § 3.3.

3.2. Separation of acoustic and hydrodynamic response

The acoustic forcing of the loudspeakers in the upstream part of the test rig triggers a general flow response that can be decomposed into an acoustic wave that travels at the speed of sound and a hydrodynamic wave that travels at typical convective time scales. For examination of the swirl fluctuations that travel at the order of the convective flow, we are only interested in the hydrodynamic part and we disregard the acoustic part. It has to be noted that an acoustic wave can be physically converted into a hydrodynamic wave as briefly described in § 1 with regard to the swirler, and that the distinction between acoustic and hydrodynamic response is a local property and therefore a function of space.

Due to the very low Mach number of $Ma < 0.1$ in the swirling pipe flow, the phase velocity of the hydrodynamic modes $c_{ph,h}$ is expected to be much lower than the phase velocity of the acoustics $c_{ph,a}$, i.e. $c_{ph,h} \ll c_{ph,a}$. In turn, the axial wavenumber of the hydrodynamics $k_{x,{h}}$ is much greater than the axial wavenumber of the acoustics $k_{x,{a}}$, i.e. $k_{x,{h}} \gg k_{x,{a}}$. This can be exploited when doing a spatial Fourier decomposition. Taking into account that the axial length of the swirling pipe flow's region of interest is significantly lower than the acoustic wavelengths, we can assume that the acoustics are largely contained in the wavenumber bin of $k_x = 0$. This particular wavenumber is, thus, filtered in the spectral domain. Additionally, all negative wavenumbers $k_x < 0$ are filtered as well to discard all upstream travelling waves. The remaining spectral coefficients are inverse Fourier transformed to obtain the purely hydrodynamic part of the downstream travelling coherent fluctuations.

3.3. Phase and group velocity

For fully characterizing the spatio-temporal structure of the coherent fluctuations associated with the swirl fluctuations, their propagation and dispersion needs to be examined. This is done by computing the phase and group velocity, reading

(3.5)\begin{equation} c_{ph} = \frac{\omega}{k_x} \end{equation}

and

(3.6)\begin{equation} c_{g} = \frac{\partial \omega}{\partial k_x},\end{equation}

where we only consider the axial velocity component. For a given angular frequency $\omega = 2{\rm \pi} f$, the angular axial wavenumber $k_x$ is in general a function of space, meaning that both phase and group velocity are local quantities. For simplicity, we will focus on the phase and group velocity on the centreline that is spatially averaged between $x/D = 1.3$ and $2.2$. The axial wavenumber is computed with $k_x = \overline {\partial \varphi _x(x,y=0) / \partial x}$, where $\varphi _x$ is the axial phase angle of the axial component of the complex mode $\hat {u}$, and the $\overline {({\cdot })}$ operator denotes the spatial average. To compute the group velocity, a power law is fitted to the axial wavenumber distribution and used to analytically calculate the group velocity according to (3.6).

4.1. Resolvent analysis

The linear model is based on a global RA, which is essentially an optimal response analysis of the forced linearized Navier–Stokes equations, accomplished by a singular value decomposition of the resolvent operator (Farrell & Ioannou Reference Farrell and Ioannou2001). The global RA allows us to examine the spatial evolution of an optimal perturbation in the frequency domain.

The starting point for deriving the global RA equations is the Navier–Stokes equations of the coherent fluctuation, (4.2). Assuming the azimuthal direction to be homogeneous and the mean flow to be axisymmetric, we substitute a normal mode ansatz into (4.2) with harmonic fluctuations in $\theta$ and $t$,

(4.3)\begin{equation} \boldsymbol{\widetilde{q}}(x,r,\theta,t) = \skew2\hat{\boldsymbol{q}}(x,r) \, \mathrm{e}^{\mathrm{i}(m\theta - \omega t)} + \textrm{c.c.} , \end{equation}

in which $\skew2\hat {\boldsymbol {q}}$ is the complex amplitude function that describes the spatial mode shape, $\mathrm {c.c.}$ is the complex conjugate, $m \in \mathbb {Z}$ is the azimuthal wavenumber and $\omega \in \mathbb {R}$ is the angular frequency. The nonlinear terms and the external forcing are not set to zero, and both terms are lumped into a general forcing term

(4.4)\begin{equation} \boldsymbol{f} ={-} \boldsymbol{\nabla} \boldsymbol{\cdot} (\boldsymbol{\widetilde{u}}\,\boldsymbol{\widetilde{u}} -\overline{\boldsymbol{\widetilde{u}}\,\boldsymbol{\widetilde{u}}}) + \boldsymbol{g} . \end{equation}

The general forcing term can then be interpreted as being intrinsic due to turbulence (McKeon & Sharma Reference McKeon and Sharma2010), being external due to an external excitation (Jovanović & Bamieh Reference Jovanović and Bamieh2005), or both. The resulting Navier–Stokes equations in the spectral domain then read

(4.5) \begin{equation} {-}\mathrm{i} \omega \boldsymbol{\mathsf{B}} {\skew2\hat{\boldsymbol{q}}} + \boldsymbol{\mathcal{L}}(m,\boldsymbol{\overline{u}}) \skew2\hat{\boldsymbol{q}} = [- \widehat{(\boldsymbol{u}'' \boldsymbol{\cdot} \boldsymbol{\nabla}) \boldsymbol{u}''} + \,\skew2\hat{\boldsymbol{f}}, \ 0]^{\mathrm{T}} ,\end{equation}

where $\boldsymbol{\mathsf{B}}$ is a restriction operator and $\boldsymbol {\mathcal {L}}$ is the 2-D linearized Navier–Stokes operator. Both expressions are given in Appendix B.

The unknown term of the coherent Reynolds stress tensor on the right-hand side of (4.5) is separated ad hoc into a purely dissipative, energy-draining and a residual energy-donating part (Kuhn et al. Reference Kuhn, Müller, Oberleithner, Knechtel and Soria2022). The latter is absorbed in the remaining forcing term and the former, dissipative part is modelled by a Boussinesq-like eddy viscosity approach (Reau & Tumin Reference Reau and Tumin2002) in the form of

(4.6) \begin{equation} {-}\widetilde{\boldsymbol{u}''\boldsymbol{u}''} = 2 \overline{\nu}_{t} \widetilde{\boldsymbol{\mathsf{S}}} + 2 \widetilde{\nu}_{t} \overline{\boldsymbol{\mathsf{S}}} - \tfrac{2}{3} \widetilde{k} \boldsymbol{\mathsf{I}} ,\end{equation}

where $\overline {\boldsymbol{\mathsf{S}}} = 1/2 (\boldsymbol {\nabla } + \nabla ^\mathrm {T}) \overline {\boldsymbol {u}}$ and $\widetilde {\boldsymbol{\mathsf{S}}} = 1/2 (\boldsymbol {\nabla } + \nabla ^\mathrm {T}) \widetilde {\boldsymbol {u}}$ are the mean and coherent strain rate tensor, respectively, $\overline {\nu }_{t}$ and $\widetilde {\nu }_{t}$ are the mean and coherent eddy viscosity, respectively, $\widetilde {k}$ is the coherent kinetic energy and $\boldsymbol{\mathsf{I}}$ is the identity tensor. We assume a frozen eddy viscosity ($\widetilde {\nu }_{t} = 0$) and neglect fluctuations of the turbulent kinetic energy ($\widetilde {k} = 0$), and extract the mean eddy viscosity from the mean Reynolds stresses (Tammisola & Juniper Reference Tammisola and Juniper2016) via a least-squares fit (Ivanova, Noll & Aigner Reference Ivanova, Noll and Aigner2013):

(4.7)\begin{equation} \overline{\nu}_{t} = \frac{\langle -\overline{\boldsymbol{u}'' \boldsymbol{u}''} + 2/3 k'' \boldsymbol{\mathsf{I}} , \overline{\boldsymbol{\mathsf{S}}} \rangle_{F}}{2 \langle \overline{\boldsymbol{\mathsf{S}}} , \overline{\boldsymbol{\mathsf{S}}} \rangle_{F}} , \end{equation}

where $\langle {\cdot } , {\cdot } \rangle _{F}$ is the Frobenius inner product, $\overline {\boldsymbol {u}'' \boldsymbol {u}''}$ is the Reynolds stress tensor and $k''$ is the turbulent kinetic energy, both of the incoherent, stochastic part. To include the turbulence model, the molecular viscosity $\nu$ is then substituted by an effective viscosity $\nu _{eff} = \nu + \overline {\nu }_{t}$ within the linearized Navier–Stokes operator $\boldsymbol {\mathcal {L}}$ of (4.5). Figure 4 shows the eddy viscosity obtained from the LES and normalized with the molecular viscosity. Subsequently, (4.5) are discretized and recast as an input–output problem (Sipp & Marquet Reference Sipp and Marquet2013),

(4.8)\begin{equation} \skew2\hat{\boldsymbol{u}} = \boldsymbol{\mathcal{R}} \,\skew2\hat{\boldsymbol{f}} , \end{equation}

where $\boldsymbol {\mathcal {R}} = \boldsymbol{\mathsf{P}}^\mathrm {T}(- \mathrm {i}\omega \boldsymbol{\mathsf{B}} - \boldsymbol {\mathcal {L}})^{-1}\boldsymbol{\mathsf{P}}$ is a linear operator acting as a transfer function in the spectral domain that relates the input forcing $\,\skew2\hat{\boldsymbol{f}}$ to the output response $\skew2\hat {\boldsymbol {u}}$. The transfer function $\boldsymbol {\mathcal {R}}$ is called the resolvent operator. Here, $\boldsymbol{\mathsf{P}}^\mathrm {T}$ is a restriction operator and $\boldsymbol{\mathsf{P}}$ is a prolongation operator that are required to exclude the continuity equation and the pressure term from the forcing. The restriction operator can, furthermore, be used to restrict the forcing to a subset of the spatial domain. The full expressions of these operators are given in Appendix B.

Figure 4. Eddy viscosity normalized with kinematic molecular viscosity.

One way to put (4.8) into effect is to conduct an input–output analysis. As such, the forcing $\,\skew2\hat{\boldsymbol{f}}$ needs to be known explicitly. In the present case, there are two approaches for specifying the forcing structure. The ‘upstream approach’ would specify the acoustic forcing upstream of the swirler that requires to include the complete swirler geometry. This would be formally simple, but numerically expensive since the full compressible three-dimensional linearized equations would need to be considered. The ‘downstream approach’ would specify the resulting forcing downstream of the swirler, in which the forcing is assumed to be the result of an acoustic-convective mode conversion process caused by the interaction of the acoustic wave with the swirler. This would be numerically much more viable, although formally difficult due to uncertainties related to the assumptions of how the mode conversion process takes place (e.g. the proposed actuator disk model as in Palies et al. Reference Palies, Durox, Schuller and Candel2011a).

An alternative way to put (4.8) into effect is to conduct an RA, in which the resolvent operator $\boldsymbol {\mathcal {R}}$ itself is directly analysed. In the RA, (4.8) is treated as an optimization problem, searching for the largest possible, marginally (or neutrally) stable flow response to any forcing (in an energy norm sense) of an otherwise globally stable eigenvalue spectrum (Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). We will still presume any forcing to be hydrodynamic in the sense that the acoustic excitation has generated significant hydrodynamic fluctuations through an acoustic-convective mode conversion process inside the swirler as suggested in Palies et al. (Reference Palies, Durox, Schuller and Candel2011a). However, the exact forcing structure does not need to be known in contrast to the input–output analysis. The parameter to maximize is the gain function $\sigma ^2$ defined as

(4.9)\begin{equation} \sigma^2 = \frac{\langle \skew2\hat{\boldsymbol{u}}, \skew2\hat{\boldsymbol{u}} \rangle}{\langle\,\skew2\hat{\boldsymbol{f}},\,\skew2\hat{\boldsymbol{f}} \rangle} , \end{equation}

which can be rearranged to yield a singular value decomposition of the resolvent operator (Farrell & Ioannou Reference Farrell and Ioannou2001; Sipp & Marquet Reference Sipp and Marquet2013). Here, $\langle {\cdot },{\cdot }\rangle$ is the norm-inducing $L^2$ inner product in complex vector space defined as $\langle \boldsymbol {a} , \boldsymbol {b} \rangle = \int _V \boldsymbol {a}^* \boldsymbol{\cdot} \boldsymbol {b}\, \mathrm {d}V$, $({\cdot })^*$ denoting complex conjugation. The right singular vectors form an orthonormal basis of optimal forcing modes $\hat {\boldsymbol {\varPhi }}_j$. The left singular vectors are the orthonormal optimal response modes $\hat {\boldsymbol {\varPsi }}_j$ that satisfy $\skew2\hat {\boldsymbol {u}} = \sum _j \hat {\boldsymbol {\varPsi }}_j \sigma _j \langle \hat {\boldsymbol {\varPhi }}_j , \,\skew2\hat{\boldsymbol{f}} \rangle$. The inner product $\langle \hat {\boldsymbol {\varPhi }}_j , \,\skew2\hat{\boldsymbol{f}} \rangle$ is the projection of the actual forcing $\,\skew2\hat{\boldsymbol{f}}$ onto the optimal forcing modes $\hat {\boldsymbol {\varPhi }}_j$. We consider two different types of forcings, namely volume forcing and boundary forcing. The volume forcing allows the forcing to act on the entire domain. The boundary forcing allows the forcing only to act at certain boundaries of the domain. In the present case, we will consider the boundary forcing to act at the tangential air inlet only (see figure 1b). The squared singular values quantify the optimal gain function, $\sigma _j^2$. They are ranked with respect to their magnitude. The gain magnitude is a measure for the importance of the related optimal forcing and response modes. As a result, if the leading optimal gain, $\sigma _1^2$, is of significantly higher magnitude than all remaining gains and if the forcing $\,\skew2\hat{\boldsymbol{f}}$ does not show any preference in projection towards the suboptimal forcing modes $\hat {\boldsymbol {\varPhi }}_{j>1}$, the resolvent is low-rank, and the leading mode governs most of the response dynamics and all remaining suboptimal modes can be neglected (Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016). The spatial shape of the Fourier mode $\skew2\hat {\boldsymbol {u}}$ is then well approximated by

(4.10)\begin{equation} \skew2\hat{\boldsymbol{u}} \approx \hat{\boldsymbol{\varPsi}}_1 \sigma_1 \langle \hat{\boldsymbol{\varPhi}}_1, \,\skew2\hat{\boldsymbol{f}} \rangle.\end{equation}

5.1. Global resolvent analysis and phenomenological interpretation of inertial waves

Figure 6 displays the resolvent gain distribution as a function of non-dimensional frequency $f^* = f\delta /U$. Shown are the two leading modes that correspond to two different branches we will designate as S1 and F1.

Figure 6. Resolvent gain distribution for the global RA in the plug flow with solid-body rotation.

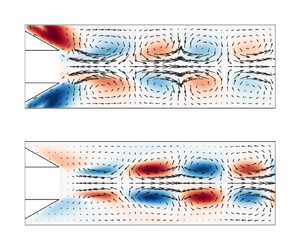
Figure 7 shows the spatial shape of the optimal response mode for the two leading optimal response modes at the non-dimensional frequency $f^* = 0.16$ at an arbitrary phase angle. The figure illustrates the existence of two modes that are distinguished from each other by their large difference in wavelength. The short wavelength mode we will designate as a slow-travelling wave belonging to the ‘S branch’, whereas the long wavelength mode we will designate as a fast-travelling wave belonging to the ‘F branch’. Furthermore, a number is designated to every mode on each branch separately with respect to the resolvent gain rank in ascending order, i.e. S1 for the leading mode on the S branch and F1 for the leading mode on the F branch. For both S1 and F1 modes, the vectors indicate the axial and radial fluctuations. Since the modes are axisymmetric distributions with $m=0$, the vectors indicate the presence of vortex rings whose axes of rotation are the azimuthal coordinate curves (i.e. curves with $x=\textrm {const.}$, $r=\textrm {const.}$) that alternate in the clockwise and counter-clockwise directions. The contours of azimuthal fluctuation $\hat {w}$ reveal an additional rotational motion that is superposed to these vortex rings whose axis of rotation is the axial centreline (i.e. $r=0$). Thus, the vortex rings are additionally spinning around the centreline, alternating in the clockwise and counter-clockwise directions. This spinning is induced by the Coriolis force because of the radial displacement of the fluid. Due to spatial quadrature of the imaginary counterpart (not shown in figure 7), the vortices are, furthermore, convected downstream.

Figure 7. Optimal response modes in the plug flow with solid-body rotation at $f^*=0.16$ for the (a) slow-travelling inertial wave S1 and (b) fast-travelling inertial wave F1, with vector arrows indicating axial and radial fluctuations and contours indicating the respective velocity fluctuations.

At low frequencies, the slow-travelling wave S1 has a higher gain than the fast-travelling wave F1 (see figure 6). With increasing frequency, the gain of S1 decreases sharply and falls below the gain of F1, which remains almost constant. However, it should be noted that the gain curves depend on the domain length considered. This makes it difficult to draw conclusions about which mode actually dominates the dynamics. This is attributed to the arbitrary domain truncation in the axial direction, although the parallel flow is supposed to be infinite in the $x$-direction. The shorter the domain, the lower the gain of F1 becomes compared with S1 due to the larger wavelengths of F1 being increasingly more constricted. This applies especially to F1 structures at low frequencies. In other words, when the flow is homogeneous in the $x$-direction and the domain is arbitrarily truncated in this direction, this leads to ambiguous results concerning which mode dominates. Notwithstanding, this does not diminish the capability of the global RA to model the leading inertial wave. Moreover, the domain truncation will be less of a problem for the swirling pipe flow case, where the flow is highly non-parallel and physically meaningful boundary conditions exist.

Figure 8 displays the magnitude of the S1 and F1 response modes for the axial, radial and azimuthal velocity components. Comparing the mode shapes of the slow- and fast-travelling modes, it can be observed that the mode shapes are very similar. For S1 (and thus, F1), the axial component peaks on the centreline and exhibits additional subpeaks at the walls. The radial and azimuthal components peak in between the centreline and the walls. The axial fluctuations have the highest amplitudes, followed by the azimuthal and radial fluctuations. The displayed mode shapes are very characteristic for axisymmetric inertial waves (Albayrak et al. Reference Albayrak, Juniper and Polifke2019).

Figure 8. Optimal response modes in the plug flow with solid-body rotation at $f^*=0.16$ identified as inertial waves of the (a) slow-travelling branch S1 and (b) fast-travelling branch F1.

The propagation behaviour of the two leading optimal response modes S1 and F1 is presented in figures 9(a) and 9(b). The distribution of each mode's non-dimensional phase velocity $c_{ph}^* = c_{ph}/U = 2{\rm \pi} f^*/k_x^*$ in figure 9(a) demonstrates the existence of slow- and fast-travelling modes for the entire frequency range. The figure further shows that the S1 and F1 are modes with a phase velocity lower and higher than the bulk velocity, respectively. For both branches, the phase velocity is almost constant for the entire frequency range and very weakly converging towards $c_{ph}^* \to 1$ with increasing frequency. Since all modes are only weakly dispersive, the group velocity in figure 9(b) has very comparable trends as the phase velocity.

Figure 9. Propagation of leading optimal response modes in the plug flow with solid-body rotation on the centreline ($y/D = 0$) characterized by (a) phase velocity over frequency and (b) group velocity over frequency.

All of these observed features such as two-branch structure, dispersion relation and spatial mode shape clearly indicate that the rotating plug flow supports inertial waves (Gallaire & Chomaz Reference Gallaire and Chomaz2003; Albayrak et al. Reference Albayrak, Juniper and Polifke2019). The RA models these inertial waves as forced convective modes. The conclusion that we have only inertial wave modes in this type of flow can be further corroborated when conducting a linear stability analysis. It provides an alternative view on how to model and interpret these coherent structures. We decide here against a detailed global stability analysis since the spectrum is globally stable and the convective amplifier behaviour is better captured by a local spatial stability analysis. The results of this stability analysis are discussed in Appendix A. It reveals that the inertial waves of S1 and F1 can also be viewed as convectively stable eigenmodes that belong to a larger family of inertial waves on the S and F branch. In the local stability framework, the S1 and F1 are the modes with the smallest spatial decay rate and thus can be expected to be the most dominant response when forced. The results of the stability analysis also agree very well with the observations in Albayrak et al. (Reference Albayrak, Juniper and Polifke2019), further demonstrating that inertial waves are the only modes present in this type of flow.

6.1. Global resolvent analysis and comparison with experimental measurements

In the following, the results from the global RA in the swirling pipe flow are presented and compared with the phase-averaged fields from the experiment and the global RA of the rotating plug flow case. Figure 10 shows, from top to bottom, the modelled coherent fluctuations of the flow response at $f^* = 0.16$ based on the leading optimal response mode from the global RA for (a) the plug flow with solid-body rotation (S1) and (b) the swirling pipe flow, and (c) the measured flow response for the acoustically excited flow in the experiment. On the left, the coherent axial velocity fluctuation for a fixed phase angle is shown. On the right, the magnitude of the coherent azimuthal fluctuation is shown for the three measured cross-sections.

Figure 10. Flow response at $f^*=0.16$ obtained by the (a) volume-forced RA of the plug flow with solid-body rotation (S1), (b) boundary-forced RA of the swirling pipe flow, (c) phase average from the acoustically excited experiments (Bluemner et al. Reference Bluemner, Paschereit and Oberleithner2019; Müller et al. Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022); first column, axial velocity fluctuation at arbitrary phase angle; remaining columns, magnitude of azimuthal velocity fluctuation.

The leading mode of the RA for the swirling pipe flow case (figure 10b) originates at the swirler and shows a five-peak structure from wall to wall for the axial component and a four-peak structure from wall to wall in the azimuthal component. The axial response mode predicted from the RA agrees very well with the experimental measurement shown in figure 10(c). Comparing the magnitude of the azimuthal response, also a close correspondence can be seen. Deviations are noticeable close to the wall where fluctuations are very strong and more pronounced in the experiment than in the RA. Most importantly, both the global RA and the experiments reveal only a single branch of waves that will be shown to be travelling slower than the centreline velocity further below. The global RA of the swirling pipe flow does not detect any fast-travelling waves in the subleading response modes, and the phase-averaged fields from the experiment only reveal short wavelengths as well.

The coherent fluctuations of the swirling pipe flow are now compared with the coherent fluctuations of the plug flow with solid-body rotation. Figure 10(a) shows the leading S1 inertial wave of the plug flow with solid-body rotation at equal Reynolds number, swirl number and frequency. Evidently, the axial wavelength is very similar to the swirling pipe flow configuration. The rotating plug flow case features a three-peak structure from wall to wall for the axial component and a two-peak structure from wall to wall in the azimuthal component. Since the swirling pipe mean flow is not homogeneous in the $x$-direction, and has large axial and radial velocity gradients in contrast to the rotating plug flow case, the coherent structure is exposed to larger changes throughout the swirling pipe flow and the radial distribution of the mode is altered including additional peaks close to the wall.

Figure 11 shows the magnitude of the spatial modes for the slow-travelling mode S1 to further corroborate the similarities between the three considered cases. Within the region of solid-body rotation ($|y/D < 0.3|$), the overall peak distribution of the modes is very similar among all three cases. In the experiment, additional peaks in the wall region occur that the RA is also able to capture. With regard to the magnitude ratios among the three velocity components, the rotating plug flow predicts slightly different values compared with the RA of the swirling pipe flow. In the swirling pipe flow, the relative magnitude of radial and azimuthal fluctuations is larger in relation to the axial fluctuation. This agrees well with the experiment for the azimuthal component. For the axial component, the RA of the swirling pipe flow underestimates the relative magnitude compared with the experiment. Notwithstanding, the large similarities between both RA results and the experiment clearly suggest that the coherent structure of the swirling pipe flow closely resembles a typical slow-travelling inertial wave.

Figure 11. Optimal response modes in the swirling pipe flow at $x/D = 2.2$ and $f^*=0.16$, identified as inertial waves of the slow-travelling branch S1, compared with optimal response mode in the plug flow with solid-body rotation and with experiment.

At last, we analyse the spatio-temporal structure of the inertial-wave-driven coherent structures by examining their propagation through the mixing tube. Figure 12 compares the phase and group velocity on the centreline for the RA-based swirling pipe flow modes with the rotating plug flow modes as well as the experimental measurements spatially averaged between $x/D = 1.3$ and $2.2$. The phase and group velocity are normalized with the centreline velocity that is likewise averaged between $x/D = 1.3$ and $2.2$. Both phase and group velocity of RA and experiment agree very well. Moreover, the phase and group velocity are evidently lower than one and close to the velocity values of the rotating pipe flow's S1 branch, in major contrast to the velocity values of the F1 branch that are larger than one (see figure 9). This demonstrates that in the RA as well as the experiment, only inertial waves of the S branch are found.

Figure 12. Propagation of the inertial waves in the swirling pipe flow on the centreline ($y/D = 0$) characterized by (a) phase velocity (black curve shows power law fit) and (b) group velocity, both averaged between $x/D = 1.3$ and $2.2$.

In summary, we observe that the flow response measured in the forced experiments consists only of slow-travelling inertial waves and no evidence for the existence of fast-travelling waves are found. Likewise, the global RA selects the S branch and reproduces the measured response fairly well regarding mode shape, amplitude distribution and propagation velocity. The remaining deviations might be rooted in the fact that the RA predicts the optimally forced structures, while the experiments show the response to a specific acoustic forcing.

7.1. Role of boundary, volume and optimal forcing

In § 6, RA was conducted assuming an optimal boundary forcing at the swirler. Boundary forcing can be interpreted as a periodic perturbation that is introduced upstream at a particular boundary from where its convective evolution is tracked throughout the domain. This means that perturbations are coming from outside into the domain, which aligns with our assumption that the hydrodynamic fluctuations are generated inside the swirler through an acoustic-convective mode conversion process (Palies et al. Reference Palies, Durox, Schuller and Candel2011a). By that, the convective amplification and decay of a locally introduced perturbation is considered. Although this optimal boundary forcing does not necessarily correspond to a physically realizable forcing, the dominance of one particular linear mechanism over all remaining ones in the swirling pipe flow still leads to a very similar response mode when the non-optimal true forcing is present. This dominance is indeed at hand in the swirling pipe flow case and it can be determined by considering the gain distribution of the volume-forced RA (see § 4.1 and Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016).

Figure 13 displays the gain distribution for the first three most amplified modes of the volume-forced RA. There is a sufficiently large gain separation between the leading and the subleading modes. Thus, the actual forcing structure to trigger the leading response mode is only secondary since the actual response is directly proportional to the square root of the gain value, $\sigma$, as stated in (4.10). In other words, the response is not sensitive to the structure of the actually applied forcing and is heavily dominated by the leading optimal response mode, even though the forcing may not be optimal or may not even act in the entire domain. This explains why the response with arbitrary boundary forcing at the swirler leads to a very similar result compared with the response with volume forcing (which has not been shown yet for brevity). The gain separation, resulting in the system being virtually agnostic to the actual forcing structure, further demonstrates that the flow inside the swirler (and the associated mode conversion process) does not need to be included in the linearized model and why the 2-D-based RA excluding the swirler is justified.

Figure 13. Resolvent gain distribution for volume-forced RA in the swirling pipe flow.

On a physics level, the large gain separation is equivalent to an amplification mechanism being significantly more dominant than any other in the flow (Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). In the swirling pipe flow, this mechanism is associated with the S branch of the inertial wave mode. The acoustic forcing, which is non-optimal, may excite a number of different response modes. However, due to its apparently high receptivity, only the S branch inertial wave is significantly amplified. This explains why the optimal response of the RA is a good representation of the actual response to acoustic forcing measured in the experiment.

7.2. Forcing–response coupling and driving of the inertial wave

The interplay and coupling of forcing and response of the coherent structures associated with the inertial waves is considered next to understand what drives these structures.

Figure 14(a) shows the optimal forcing and response modes at $f^* = 0.16$ for an arbitrary phase angle for the plug flow with solid-body rotation. The vectors indicate axial and radial fluctuations, and the contours represent azimuthal fluctuations. Evidently, the modes are highly similar. This is the effect of a very weak convective-type non-normality, which leads to a weak spatial separation and virtually zero phase shift of forcing and response (Chomaz Reference Chomaz2005; Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). In simple terms, the response has to be directly triggered by the forcing since no convective instability mechanism amplifies the fluctuations.

Figure 14. Optimal forcing and response modes at $f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow, with vector arrows indicating axial and radial fluctuations and contours indicating azimuthal fluctuations.

Figure 14(b) displays the optimal forcing and response modes for the volume-forced RA in the swirling pipe flow. The picture is qualitatively similar to the rotating plug flow case with virtually zero phase shift between the modes. However, the location of highest magnitude in forcing and response is spatially strongly separated, in contrast to the rotating plug flow case where it roughly coincides. This spatial separation indicates a stronger convective-type non-normality than in the rotating plug flow (Chomaz Reference Chomaz2005). The forcing in the swirling pipe flow case resides mainly close to the swirler and is the strongest in the azimuthal component. In the downstream direction, the forcing becomes weaker, shifts towards the centreline and aligns with the region of approximate solid-body rotation, $\lvert y/D \rvert < 0.3$. For the response, the largest amplitudes are reached further downstream and are also mainly present in the region of approximate solid-body rotation. This is different to the boundary forcing case, where high amplitudes also occur close to the walls (see figure 10b).

Overall, the structure of the optimal forcing and response modes in the swirling pipe flow show that inertial waves are most effectively amplified by azimuthal, i.e. swirl, fluctuations at the swirler outlet. This explains why the RA using boundary forcing agrees so well with the measured flow response, and more generally why inertial waves are actually very effective in propagating swirl fluctuations, since the strong optimal forcing close to the swirler indicates a high receptivity (Sipp & Marquet Reference Sipp and Marquet2013).

7.3. Structural sensitivity of the resolvent gain

The coupling between forcing and response is now examined quantitatively by considering the structural sensitivity tensor $\boldsymbol{\mathsf{S}}$ of the gain $\sigma ^2$ with regard to small perturbations of the 2-D linearized Navier–Stokes operator $\boldsymbol {\mathcal {L}}$, which is defined by (Qadri & Schmid Reference Qadri and Schmid2017)

(7.1)\begin{equation} \boldsymbol{\mathsf{S}} = \nabla_{\boldsymbol{\mathcal{L}}} \sigma = \sigma^2 {\rm Re} ( \,\skew2\hat{\boldsymbol{f}} \otimes \skew2\hat{\boldsymbol{u}}^* ),\end{equation}

where $\otimes$ denotes the dyadic product defined by $\boldsymbol {a} \otimes \boldsymbol {b} = \boldsymbol {a} \boldsymbol {b}^\mathrm {T}$. The structural sensitivity quantifies the effect of a localized perturbation of the linearized Navier–Stokes operator $\boldsymbol {\mathcal {L}}$ contained in the resolvent operator $\boldsymbol {\mathcal {R}}$ that leads to a drift of the resolvent gain $\sigma ^2$. In other words, the structural sensitivity identifies the coupling between forcing and response that causes this drift. A larger drift means the stronger the coupling must be. The structural sensitivity provides a $3 \times 3$ tensor that reveals how each component of the optimal forcing mode couples with each component of the optimal response mode.

Figure 15(a) shows each component of the structural sensitivity tensor of the rotating plug flow case at $f^* = 0.16$ that characterizes the forcing–response coupling. The forcing contribution is ordered row by row and the response contribution is ordered column by column (first row, axial forcing; second row, radial forcing, etc.; first column, axial response, etc.). Note the individual colour map range for each of the sensitivity components and the normalization with the maximum component value of the sensitivity tensor in the displayed domain extents. Evidently, the most dominant forcing-response coupling occurs between axial forcing and axial response, ${\mathsf{S}}_{xx}$: a forcing in the momentum equation in the $x$-direction leads to a response in the velocity fluctuation of the $x$-component. Essentially, these are the axial fluctuations of the aforementioned inertial wave's vortex rings that are driven through an axial forcing in the centreline region. Another direct coupling occurs between azimuthal forcing and response (${\mathsf{S}}_{\theta \theta }$), as already observed in figure 14(a). This direct coupling as well as the cross-coupling terms ${\mathsf{S}}_{x\theta }$ and ${\mathsf{S}}_{\theta x}$ are approximately one order of magnitude lower than ${\mathsf{S}}_{xx}$. The remaining components such as ${\mathsf{S}}_{xr}$, ${\mathsf{S}}_{rx}$, ${\mathsf{S}}_{r\theta }$ and ${\mathsf{S}}_{\theta r}$ are lower but not necessarily negligible. The former two describe a coupling between axial forcing and radial response (and vice versa) whereas the latter two describe a coupling between radial forcing and azimuthal response (and vice versa). Figure 15(b) displays the structural sensitivity for the swirling pipe flow. The general picture is very similar. The strongest coupling occurs again in ${\mathsf{S}}_{xx}$, followed by an ${\mathsf{S}}_{\theta \theta }$ and ${\mathsf{S}}_{x\theta }$ as well as ${\mathsf{S}}_{\theta x}$. The relative magnitudes of these components are of the same order of magnitude as in the rotating plug flow. However, the other cross-couplings ${\mathsf{S}}_{xr}$, ${\mathsf{S}}_{rx}$, ${\mathsf{S}}_{r\theta }$ and ${\mathsf{S}}_{\theta r}$ are significantly increased by more than one order of magnitude. This indicates a fundamental difference in the physical mechanisms behind the forcing–response couplings in the swirling pipe flow, which are further explored in the following.

Figure 15. Forcing–response coupling at $f^* = 0.16$ quantified with the structural sensitivity tensor $\boldsymbol{\mathsf{S}}$ of the resolvent gain for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.

A large value of ${\mathsf{S}}_{xx}$ is equivalent to a large sensitivity of the resolvent gain with respect to changes of the linear operator component $\mathcal {L}_{xx}$, per definition (see (7.1) and Qadri & Schmid Reference Qadri and Schmid2017). This component is mainly governed by convective and dissipative terms (see (B1a)). This implies that small changes to the convective and dissipative terms have a large impact on the resolvent gain. This also applies to the other main diagonal elements $\mathcal {L}_{rr}$ and $\mathcal {L}_{\theta \theta }$ which also contain convective and dissipative terms. Likewise, the off-diagonal elements of the sensitivity tensor are largely influenced by the corresponding off-diagonal elements of $\boldsymbol {\mathcal {L}}$ that contain terms associated with the production of fluctuations. For example, ${\mathsf{S}}_{\theta r}$ quantifies the sensitivity of $\mathcal {L}_{\theta r}$ that contains the Coriolis term $(\overline {w}/r) \hat {v}$ and the strain rate term $(\partial \overline {w}/\partial r) \hat {v}$ responsible for the production of inertial waves.

The influence of selected terms in $\boldsymbol {\mathcal {L}}$ on the structural sensitivity $\boldsymbol{\mathsf{S}}$ is now further corroborated by comparing their magnitudes between rotating plug flow and swirling pipe flow. In the rotating plug flow in figure 16(a), the axial convection term contained in $\mathcal {L}_{xx}$ is much more dominant than the radial-azimuthal strain rate plus Coriolis term contained in $\mathcal {L}_{\theta r}$. This explains the strong sensitivity in ${\mathsf{S}}_{xx}$. Moreover, since there is no axial-radial strain rate in $\mathcal {L}_{xr}$, this term is zero. When examining the same terms for the swirling pipe flow case in figure 16(b), the balance between these individual terms is significantly different. The Coriolis and radial-azimuthal strain rate term are of the same order of magnitude as the convection term. Additionally, the axial-radial strain rate term is not zero any longer, and large in the region where the jets of the central hole and tangential swirler merge. The significant increase of shear and Coriolis effects in the swirling pipe flow explain the large increase in the off-diagonal sensitivity components observed in figure 15(b). The strong shear being mainly located in the upstream region also explains why many of the sensitivity components peak in that region.

Figure 16. Momentum terms for axial convection in $\mathcal {L}_{xx}$ (left), axial-radial strain rate in $\mathcal {L}_{xr}$ (mid), and radial-azimuthal strain rate plus Coriolis effect in $\mathcal {L}_{\theta r}$ (right) at $f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.

Thus, the coherent fluctuations of the plug flow with solid-body rotation and swirling pipe flow largely share similar coupling mechanisms, further demonstrating that the identified response modes of the swirling pipe flow are indeed inertial waves. However, the shear in the swirling pipe flow case, caused by the merging of central and radial jet, increases the component-type non-normality (Marquet et al. Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009; Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018) and intensifies the inertial wave amplification significantly compared with the rotating plug flow case.

7.4. Energy budgets

At last, we examine parts of the coherent kinetic energy budget terms to reveal how and where the inertial wave gains energy. For this, the energy source terms of the energy budgets are considered, namely the production term and the additional source term due to the forcing on the right-hand side of (4.5). These terms are readily obtained by contracting the momentum equations of the spectral linearized Navier–Stokes equations, (4.5), with the complex-conjugated spectral response mode $\skew2\hat {\boldsymbol {u}}^*$ and only retaining the real part (Symon et al. Reference Symon, Illingworth and Marusic2021). The production term is then given by

(7.2)\begin{equation} \mathcal{P} = {\rm Re} ( \skew2\hat{\boldsymbol{u}}^* \boldsymbol{\cdot} (\skew2\hat{\boldsymbol{u}} \boldsymbol{\cdot} \boldsymbol{\nabla})\boldsymbol{\overline{u}} ). \end{equation}

It quantifies the energy transfer from the mean field to the coherent field due to linear amplification mechanisms. The energy forcing term is given by

(7.3)\begin{equation} \mathcal{F} = {\rm Re} ( \skew2\hat{\boldsymbol{u}}^* \boldsymbol{\cdot} \,\skew2\hat{\boldsymbol{f}} ), \end{equation}

which quantifies the energy gain due to intrinsic (turbulent) and external forcing (see § 4.1). The full expressions are provided in Appendix C.

Figure 17(a) shows the energy production $\mathcal {P}$ and energy forcing terms $\mathcal {F}$ normalized with their summated maximum value $(\mathcal {P} + \mathcal {F})_{max}$ for the rotating plug flow at $f^* = 0.16$. The production peaks in the centre of the solid-body region and consists essentially of the production due to the Coriolis force, $\hat {w}^*\hat {v} (\overline {w}/r)$. Evidently, the production is just a very small fraction of the total energy gain and the energy forcing term is the main contributor (note the different ranges of the colour bars). Therefore, the forcing is vital for sustaining the inertial wave. This is in line with the results of the sensitivity tensor, in which a Coriolis term is active but comparably low, leading to a low forcing–response coupling.

Figure 17. Coherent kinetic energy production and energy forcing term at $f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.

For the swirling pipe flow, shown in figure 17(b), the contributions are switched. The energy gain from production is increased significantly due to the strong shear at $x/D \approx 1$ where the jets from the central hole and the swirler merge. The forcing distribution shows that fluctuations are initially triggered close to the swirler. From there, they first pass through the region of high shear where they are strongly amplified. Downstream, the perturbations are convected as inertial waves as they pass through the region of solid-body rotation. The amount of energy added by the forcing is comparably low. Thus, in the swirling pipe flow case, the forcing inside the mixing tube is secondary in triggering and driving the inertial waves.

In summary, the coherent structures of the plug flow with solid-body rotation and the swirling pipe flow share similar coupling mechanisms. The mode selection process in the swirling pipe flow is primarily governed by the immediate region close to the swirler where the optimal forcing and, thus, receptivity (Sipp & Marquet Reference Sipp and Marquet2013) of the inertial waves is high. However, whereas in the rotating plug flow case the forcing is essential for sustaining inertial waves, in the swirling pipe flow case, the shear-driven production is mainly responsible for providing energy. The lower magnitude of the energy forcing term is related to a smaller projection of the response mode onto the forcing mode per definition (see (7.3)) that suggests an increased component-type non-normality due to the additional shear (Chomaz Reference Chomaz2005; Symon et al. Reference Symon, Illingworth and Marusic2021).