No CrossRef data available.
Published online by Cambridge University Press: 23 June 2023
In this paper, we investigate the thermal evolution in a one-dimensional bagasse stockpile. The mathematical model involves four unknowns: the temperature, oxygen content, liquid water content and water vapour content. We first nondimensionalize the model to identify dominant terms and so simplify the system. We then calculate solutions for the approximate and full system. It is shown that under certain conditions spontaneous combustion will occur. Most importantly, we show that spontaneous combustion can be avoided by sequential building. To be specific, in a situation where, say, a 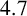 $4.7\,$m stockpile can spontaneously combust, we could construct a
$4.7\,$m stockpile can spontaneously combust, we could construct a 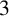 $3\,$m pile and then some days later add another
$3\,$m pile and then some days later add another 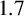 $1.7\,$m to produce a stable
$1.7\,$m to produce a stable 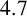 $4.7\,$m pile.
$4.7\,$m pile.