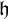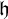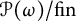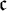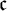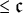1 Introduction
A collection
${\mathfrak A} = \{ {\cal A}_\gamma : \gamma < \vartheta \}$
of mad (maximal almost disjoint) families of subsets of the natural numbers
$\omega $
is called a refining matrix of height
$\vartheta $
if:
-
•
${\cal A}_\delta $
refines
${\cal A}_\gamma $
for
$\delta \geq \gamma $
, i.e., for all
$A \in {\cal A}_\delta $
, there is
$B \in {\cal A}_\gamma $
with
$A \subseteq ^* B$
, and -
• there is no common refinement of the
${\cal A}_\gamma $
, i.e., no mad family
${\cal A}$
refining all the
${\cal A}_\gamma $
.
${\mathfrak A}$
is a base matrix if it is a refining matrix and
$\bigcup _{\gamma < \vartheta } {\cal A}_\gamma $
is dense in
${\cal P} (\omega ) / {\mathrm {fin}}$
, i.e., for all
$B \in [\omega ]^\omega $
, there are
$\gamma < \vartheta $
and
$A \in {\cal A}_\gamma $
with
$A \subseteq ^* B$
. The distributivity number
${\mathfrak h}$
of
${\cal P} (\omega ) / {\mathrm {fin}}$
is the least cardinal
$\kappa $
such that
${\cal P} (\omega ) / {\mathrm {fin}}$
as a forcing notion is not
$\kappa $
-distributive; equivalently, it is the least
$\kappa $
such that there is a collection
${\mathfrak A}$
of size
$\kappa $
of mad families without common refinement. Clearly, a refining matrix must have height at least
${\mathfrak h}$
, and it is easy to see that there is one of height
${\mathfrak h}$
and none of regular height
$> {\mathfrak c}$
. Furthermore, if there is a refining matrix of height
$\vartheta $
, then there is one of height
$cf (\vartheta )$
so that it suffices to consider regular heights. A famous theorem of Balcar, Pelant, and Simon [Reference Balcar, Pelant and SimonBPS] (see also [Reference Blass, Foreman and KanamoriBl, Theorem 6.20]) says that there is even a base matrix of height
${\mathfrak h}$
. It is natural to ask whether there can consistently be refining (base) matrices of other heights, and in interesting recent work, Fischer, Koelbing, and Wohofsky [Reference Fischer, Koelbing and WohofskyFKW1] proved that it is consistent that
${\mathfrak h} = \omega _1$
and there is a refining matrix of height
$\vartheta \leq {\mathfrak c}$
, where
$\vartheta> \omega _1$
is regular, all of whose maximal branches are cofinal (see Section 2 for a formal definition). We show the following theorems.
Theorem A If
${\mathfrak c}$
is regular, then there is a base matrix of height
${\mathfrak c}$
.
Theorem B In the Cohen and random models, there are base matrices of any regular uncountable height
$\leq {\mathfrak c}$
.
This answers Questions 7.5 and 7.7 of [Reference Fischer, Koelbing and WohofskyFKW1]. Note that our results are incomparable with the one of the latter work. Their construction does not give a base matrix (in fact, by another result of Fischer, Koelbing, and Wohofsky [Reference Fischer, Koelbing and WohofskyFKW2], a base matrix of height
$> {\mathfrak h}$
always has some non-cofinal maximal branches, though one may still ask whether one can get such a base matrix in which some maximal branches are cofinal), whereas ours necessarily gives non-cofinal maximal branches. In fact, in the Cohen and random models,
${\mathfrak h} = \omega _1$
is the only cardinal
$\vartheta $
for which there is a refining (base) matrix of height
$\vartheta $
all of whose maximal branches are cofinal, and higher refining matrices have no cofinal branches at all (this follows from Fact 1).
2 Preliminaries
The Cohen model (resp. random model) is the model obtained by adding at least
$\omega _2$
many Cohen (resp. random) reals to a model of the continuum hypothesis CH [Reference Bartoszyński and JudahBJ].
For
$A,B \subseteq \omega $
, we say A is almost contained in B, and write
$A \subseteq ^* B$
, if
$A \setminus B$
is finite.
$A \subsetneq ^* B$
if
$A \subseteq ^* B$
and
$B \setminus A$
is infinite. For an ordinal
$\vartheta _0$
,
$\{ A_\gamma : \gamma < \vartheta _0 \}$
is a
$\subseteq ^*$
-decreasing chain of length
$\vartheta _0$
if
$A_\delta \subseteq ^* A_\gamma $
for all
$\gamma < \delta < \vartheta _0$
.
$\subsetneq ^*$
-decreasing chains are defined analogously. For a refining matrix
${\mathfrak A} = \{ {\cal A}_\gamma : \gamma < \vartheta \}$
and an ordinal
$\vartheta _0 \leq \vartheta $
,
$\{ A_\gamma : \gamma < \vartheta _0 \}$
is a branch in
${\mathfrak A}$
if it is a
$\subseteq ^*$
-decreasing chain and
$A_\gamma \in {\cal A}_\gamma $
for
$\gamma < \vartheta _0$
. A branch is maximal if it cannot be properly extended to a longer branch. A branch is cofinal if
$\vartheta _0 = \vartheta $
. Every cofinal branch is maximal, but there may be maximal branches that are not cofinal.
Fact 1 (Folklore)
There are no
$\subsetneq ^*$
-decreasing chains of length
$\omega _2$
in
${\cal P} (\omega )$
in the Cohen and random models.
This is proved by an isomorphism-of-names argument using the homogeneity of the Cohen or random algebra.
For
$A,B \in [\omega ]^\omega $
, A splits B if both
$A \cap B$
and
$B \setminus A$
are infinite.
${\cal X} \subseteq [\omega ]^\omega $
is a splitting family if every
$B \in [\omega ]^\omega $
is split by a member of
${\cal X}$
. The splitting number
${\mathfrak s}$
is the least size of a splitting family. It is well known that
${\mathfrak h} \leq {\mathfrak s}$
([Reference Blass, Foreman and KanamoriBl] or [Reference HalbeisenHa]).
Fact 2 (Folklore [see [Reference Blass, Foreman and KanamoriBl]; see also [Reference HalbeisenHa, Proposition 22.13] for Cohen forcing])
After adding at least
$\omega _1$
Cohen or random reals to a model of ZFC,
${\mathfrak s} = \omega _1$
. (In fact, the first
$\omega _1$
generics are a witness for
${\mathfrak s}$
.)
We will prove the following.
Main Theorem 3 Assume
$\vartheta \leq {\mathfrak c}$
is a regular cardinal and
-
(A) either there is no
$\subsetneq ^*$
-decreasing chain of length
$\vartheta $
in
${\cal P} (\omega )$
, -
(B) or
${\mathfrak s} \leq \vartheta $
.
Then there is a base matrix of height
$\vartheta $
.
Clearly, Theorem A follows from part (B) of the main theorem. (We note, however, that splitting families and
${\mathfrak s} \leq {\mathfrak c}$
are not needed in this case [see the comment at the beginning of the proof of Main Claim 5].) Theorem B follows from either (A) or (B) in view of Facts 1 and 2. Note that part (B) implies that in many other models of set theory there are base matrices of height
$\vartheta $
for any regular
$\vartheta $
between
${\mathfrak h}$
and
${\mathfrak c}$
, e.g., in the Hechler model (this satisfies
${\mathfrak s} = \omega _1$
by [Reference Baumgartner and DordalBD]; see also [Reference Blass, Foreman and KanamoriBl]), or in any extension by at least
$\omega _1$
Cohen or random reals (Fact 2). The former is, and the latter may be (depending on the ground model), a model for the failure of (A). We do not know whether (A)
$+ \neg $
(B) is consistent but conjecture that it is. This clearly implies
${\mathfrak s} \geq {\mathfrak b}^{++}$
, where
${\mathfrak b}$
is the unbounding number (which is known to be consistent; see [Reference Brendle and FischerBF]).
3 Proof of main theorem
By recursion on
$\alpha < {\mathfrak c}$
, we shall construct sets
$\Omega _\gamma \subseteq {\mathfrak c}$
and families
${\cal A}_\gamma = \{ A_{\gamma , \alpha } : \alpha \in \Omega _\gamma \}$
,
$\gamma < \vartheta $
, such that:
-
(I) All
${\cal A}_\gamma $
are mad. -
(II) If
$\gamma < \delta < \vartheta $
and
$\beta \in \Omega _\delta $
, then there is
$\alpha \leq \beta $
in
$\Omega _\gamma $
such that
$A_{\delta ,\beta } \subseteq ^* A_{\gamma ,\alpha }$
. -
(III) For all
$B \in [\omega ]^\omega $
, there are
$\gamma < \vartheta $
and
$\alpha \in \Omega _\gamma $
such that
$A_{\gamma ,\alpha } \subseteq ^* B$
.
This is clearly sufficient. In case (B), let
$\{ S_\zeta : \zeta < \nu \}$
be a splitting family with
$\nu \leq \vartheta $
. Let
$\{ (X_\alpha , \xi _\alpha ) : \alpha < {\mathfrak c} \}$
list all pairs
$(X,\xi ) \in [\omega ]^\omega \times \vartheta $
. At stage
$\alpha $
of the construction, we will have sets
$\{ \Omega _\gamma \cap \alpha : \gamma < \vartheta \}$
, ordinals
$\{ \eta _\beta : \beta < \alpha \}$
below
$\vartheta $
, and families
$\{ \{ A_{\gamma ,\beta } : \beta \in \Omega _\gamma \cap \alpha \} : \gamma < \vartheta \}$
such that:
-
(iα)
${\cal A}^\alpha _\gamma : = \{ A_{\gamma ,\beta } : \beta \in \Omega _\gamma \cap \alpha \}$
is almost disjoint for
$\gamma < \vartheta $
. -
(iiα) For all
$\beta < \alpha $
, the set
$\{ \gamma : \beta \in \Omega _\gamma \}$
is the interval of ordinals
$[\eta _\beta , \max ( \eta _\beta , \xi _\beta ) ]$
and-
– for
$\gamma \in [ \eta _\beta , \max ( \eta _\beta , \xi _\beta ) ]$
,
$A_{\gamma ,\beta } = A_{\eta _\beta ,\beta }$
, and -
– for
$\gamma < \eta _\beta $
, there is
$\beta ' < \beta $
in
$\Omega _\gamma $
such that
$A_{\eta _\beta , \beta } \subsetneq ^* A_{\gamma , \beta '}$
.
-
-
(iiiα) For all
$\beta < \alpha $
,
$A_{\eta _\beta , \beta } \subsetneq ^* X_\beta $
and, in case (B),
$A_{\eta _\beta ,\beta } \subseteq ^* S_\zeta $
or
$A_{\eta _\beta ,\beta } \subseteq ^* \omega \setminus S_\zeta $
, where
$\zeta $
is minimal such that
$S_\zeta $
splits
$A_{\gamma , \beta '}$
whenever
$\gamma < \eta _\beta $
and
$\beta ' \in \Omega _\gamma \cap \beta $
are such that
$A_{\eta _\beta , \beta } \subsetneq ^* A_{\gamma , \beta '}$
.
Let us first see that this suffices for completing the proof: indeed, (II) and (III) follow from (ii
$_\alpha $
) and (iii
$_\alpha $
), respectively. To see (I), fix
$\gamma < \vartheta $
and
$Y \in [\omega ]^\omega $
. Then there is
$\alpha < {\mathfrak c}$
such that
$(Y,\gamma ) = (X_\alpha , \xi _\alpha )$
. So
$A_{\max (\eta _\alpha , \xi _\alpha ), \alpha } = A_{\eta _\alpha , \alpha } \subseteq ^* Y$
by (ii
$_{\alpha + 1}$
) and (iii
$_{\alpha + 1}$
) and
$A_{\max (\eta _\alpha , \xi _\alpha ), \alpha } \subseteq ^* A_{\gamma , \beta } $
for some
$\beta \leq \alpha $
by (ii
$_{\alpha + 1}$
). Thus
$Y \cap A_{\gamma , \beta }$
is infinite, as required.
Next, we notice that, for
$\alpha = 0$
and for limit
$\alpha $
, there is nothing to show. Hence it suffices to describe the successor step, that is, the construction at stage
$\alpha + 1$
, and to prove that (i
$_{\alpha + 1}$
) through (iii
$_{\alpha + 1}$
) still hold. Assume
$Y \subseteq ^* X_\alpha \cap A_{\gamma ,\beta }$
for some
$\gamma < \vartheta $
and
$\beta \in \Omega _\gamma \cap \alpha $
, and let
$\delta $
be such that
$\gamma < \delta < \vartheta $
. We say that Y splits at
$\delta $
if:
-
• for all
$\gamma ' $
with
$\gamma \leq \gamma ' < \delta $
, there is
$\beta \in \Omega _{\gamma '} \cap \alpha $
such that
$Y \subseteq ^* A_{\gamma ' , \beta }$
, and -
• there is no
$\beta \in \Omega _\delta \cap \alpha $
such that
$Y \subseteq ^* A_{\delta ,\beta }$
.
We say Y splits below
$\gamma _0> \gamma $
if there is
$\delta $
with
$\gamma < \delta < \gamma _0$
such that Y splits at
$\delta $
. For infinite
$Y \subseteq X_\alpha $
, call
${\cal A}^\alpha _\gamma {\upharpoonright } Y$
mad if
$\{ Y \cap A_{\gamma ,\beta } : \beta \in \Omega _\gamma \cap \alpha $
and
$| Y \cap A_{\gamma , \beta } | = \aleph _0 \}$
is a mad family below Y. The following is crucial for our construction.
Crucial Lemma 4 Let
$\gamma _0 \leq \vartheta $
be an ordinal, and let
$Y_0 \subseteq X_\alpha $
be infinite. Assume
-
(mad)
${\cal A}^\alpha _\gamma {\upharpoonright } Y_0$
is mad for all
$\gamma < \gamma _0$
.
Then there are
$\gamma < \gamma _0$
,
$\beta \in \Omega _\gamma \cap \alpha $
, and an infinite
$Y \subseteq ^* Y_0 \cap A_{\gamma ,\beta }$
that does not split below
$\gamma _0$
.
Proof We make a proof by contradiction. Assume
-
(split) if
$Z \subseteq ^* Y_0 \cap A_{\gamma ,\beta } $
, for some
$\gamma < \gamma _0$
and
$\beta \in \Omega _\gamma \cap \alpha $
, then Z splits below
$\gamma _0$
.
By recursion on
$n\in \omega $
, we construct infinite sets
$( Y^0_s : s \in 2^{<\omega } )$
and
$(Y_s : s \in 2^{<\omega } )$
, as well as ordinals
$(\delta ^0_s : s \in 2^{<\omega } )$
and
$(\delta _n : n \in \omega )$
such that:
-
(a)
$Y_s \subseteq Y^0_s$
and
$Y^0_{s \,{}\hat {}\, i} \subseteq Y_s$
for
$i \in \{ 0,1 \}$
. -
(b)
$\delta _n = \max \{ \delta ^0_s : |s| = n \} < \gamma _0$
and
$\delta ^0_{s \,{}\hat {}\, i}> \delta _{|s|}$
for
$i \in \{ 0, 1 \}$
. -
(c)
$Y_s$
splits at
$\delta ^0_s$
and there are distinct
$\beta , \beta ' \in \Omega _{\delta ^0_s} \cap \alpha $
such that
$Y^0_{s \,{}\hat {}\, 0} = Y_s \cap A_{\delta ^0_s, \beta }$
and
$Y^0_{s \,{}\hat {}\, 1} = Y_s \cap A_{\delta ^0_s, \beta '}$
(in particular,
$Y^0_{s \,{}\hat {}\, 0} \cap Y^0_{s \,{}\hat {}\, 1}$
is finite). -
(d)
$Y_{s \,{}\hat {}\, i} = Y^0_{s \,{}\hat {}\, i} \cap A_{\delta _{|s|} , \beta }$
for some
$\beta \in \Omega _{\delta _{|s|}} \cap \alpha $
, for
$i \in \{ 0,1 \}$
.
We verify that we can carry out the construction. In the basic step
$n = 0$
and
$s = \langle \rangle $
, by (mad), let
$Y_{\langle \rangle } = Y^0_{\langle \rangle } : = Y_0 \cap A_{0,\beta }$
for some
$\beta \in \Omega _0 \cap \alpha $
such that this intersection is infinite. By clause (split), we know that there is
$\delta _0 = \delta ^0_{\langle \rangle }$
with
$0 < \delta _0 < \gamma _0$
such that
$Y_{\langle \rangle }$
splits at
$\delta _0$
.
Suppose
$Y_s^0, Y_s$
, and
$\delta ^0_s$
have been constructed for
$|s| = n$
and
$\delta _n = \max \{ \delta ^0_s: |s| = n \} < \gamma _0$
are such that (a) through (d) hold. We thus know that
$Y_s$
splits at
$\delta ^0_s$
and, by the definition of splitting and clause (mad), we can find distinct
$\beta , \beta ' \in \Omega _{\delta ^0_s} \cap \alpha $
such that
$Y^0_{s \,{}\hat {}\, 0}: = Y_s \cap A_{\delta ^0_s, \beta }$
and
$Y^0_{s \,{}\hat {}\, 1} : = Y_s \cap A_{\delta ^0_s, \beta '}$
are infinite. Using again (mad), we see that for
$i \in \{ 0,1 \}$
there is
$\beta \in \Omega _{\delta _n} \cap \alpha $
such that
$Y_{s \,{}\hat {}\, i} : = Y^0_{s \,{}\hat {}\, i} \cap A_{\delta _{n} , \beta }$
is infinite. Again by (split), there is
$\delta ^0_{s\,{}\hat {}\, i}$
,
$i \in \{ 0,1\}$
, with
$\delta _n < \delta ^0_{s\,{}\hat {}\, i} < \gamma _0$
such that
$Y_{s \,{}\hat {}\, i} $
splits at
$\delta ^0_{s \,{}\hat {}\, i}$
. Finally, let
$\delta _{n+1} : = \max \{ \delta ^0_{s \,{}\hat {}\, i} : |s| = n$
and
$i \in \{ 0,1 \} \} < \gamma _0$
. This completes the construction.
Let
$\delta _\omega = \bigcup _n \delta _n$
. Clearly
$\delta _\omega \leq \gamma _0$
is a limit ordinal of countable cofinality. Next, for
$f \in 2^\omega $
, let
$Y_f$
be a pseudointersection of the
$Y_{f {\upharpoonright } n}$
,
$n \in \omega $
. If possible, choose
$\beta _f \in \Omega _{\delta _\omega } \cap \alpha $
such that
$Y_f \cap A_{\delta _\omega , \beta _f}$
is infinite. By (a) and (c) in this construction and by (ii
$_\alpha $
), we see that if
$f \neq f'$
then
$\beta _f \neq \beta _{f'}$
. However,
$\Omega _{\delta _\omega } \cap \alpha $
has size strictly less than
${\mathfrak c}$
, and therefore there is
$f \in 2^\omega $
for which there is no such
$\beta _f$
. Since
$Y_f \subseteq ^* Y_0$
by construction, this implies that
${\cal A}^\alpha _{\delta _\omega } {\upharpoonright } Y_0$
is not mad and, by (mad),
$\gamma _0 = \delta _\omega $
. This means, however, that any
$Y_f$
contradicts (split). This completes the proof of the crucial lemma.
We next show:
Main Claim 5 There is
$\gamma < \vartheta $
such that
${\cal A}^\alpha _\gamma {\upharpoonright } X_\alpha $
is not mad.
Proof Note that, in case
$\vartheta = {\mathfrak c}$
, there is nothing to show because by (ii
$_\alpha $
) we see that a tail of the sequence
$(\Omega _\gamma \cap \alpha : \gamma < \vartheta )$
is empty, and therefore so is
${\cal A}^\alpha _\gamma $
(in fact, the proof of Theorem A is quite a bit simpler than the general argument: there is no need to list the
$\xi _\alpha $
, we may simply let
$\xi _\alpha = \alpha $
,
$\eta _\alpha $
will always be
$\leq \alpha $
, and the splitting family is unnecessary).
Hence assume
$\vartheta < {\mathfrak c}$
. By way of contradiction, suppose all
${\cal A}^\alpha _\gamma {\upharpoonright } X_\alpha $
are mad. By the crucial lemma with
$\gamma _0 = \vartheta $
and
$Y_0 = X_\alpha $
, we know that there are
$\gamma < \vartheta $
,
$\beta \in \Omega _\gamma \cap \alpha $
and an infinite
$Y \subseteq ^* X_\alpha \cap A_{\gamma ,\beta }$
that does not split below
$\vartheta $
. This means for all
$\delta $
with
$\gamma \leq \delta < \vartheta $
there is
$\beta \in \Omega _\delta \cap \alpha $
such that
$Y \subseteq ^* A_{\delta ,\beta }$
. By (i
$_\alpha $
) and (ii
$_\alpha $
), we see that there must be a strictly increasing sequence
$(\beta _\varepsilon : \varepsilon < \vartheta )$
of ordinals below
$\alpha $
such that for
$\varepsilon '> \varepsilon $
,
-
•
$\eta _{\beta _{\varepsilon '}}> \max ( \eta _{\beta _\varepsilon } , \xi _{\beta _\varepsilon } )$
and
$Y \subsetneq ^* A_{\eta _{\beta _{\varepsilon '}} , \beta _{\varepsilon '}} \subsetneq ^* A_{\eta _{\beta _{\varepsilon }} , \beta _{\varepsilon }}$
.
In case (A), this contradicts the initial assumption that there are no
$\subsetneq ^*$
-decreasing chains of length
$\vartheta $
in
${\cal P} (\omega )$
. So assume we are in case (B). Define a sequence
$(\zeta _\varepsilon : \varepsilon < \vartheta )$
of ordinals below
$\nu $
such that
-
•
$\zeta _\varepsilon $
is minimal such that
$S_{\zeta _\varepsilon }$
splits all
$A_{\eta _{\beta _{\varepsilon '}} , \beta _{\varepsilon '}}$
for
$\varepsilon ' < \varepsilon $
.
Using (iii
$_\alpha $
), we see that
$S_{\zeta _\varepsilon }$
does not split
$A_{\eta _{\beta _{\varepsilon }} , \beta _{\varepsilon }}$
. Therefore, the sequence must be strictly increasing, which is impossible (and thus contradictory) in case
$\nu < \vartheta $
. If
$\nu = \vartheta $
note that there cannot be any
$\zeta $
such that
$S_\zeta $
splits Y, contradicting the initial assumption that the
$S_\zeta $
form a splitting family. This final contradiction establishes the main claim.
We now let
$\eta _\alpha : = \min \{ \gamma : {\cal A}^\alpha _\gamma {\upharpoonright } X_\alpha $
is not mad
$\} < \vartheta $
. Choose
$Y_0 \subseteq X_\alpha $
infinite and almost disjoint from all members of
${\cal A}^\alpha _{\eta _\alpha }$
. Note that
${\cal A}^\alpha _\gamma {\upharpoonright } Y_0$
is mad for all
$\gamma < \eta _\alpha $
. Thus, by the crucial lemma with
$\gamma _0 = \eta _\alpha $
, we know there are
$\gamma < \eta _\alpha $
,
$\beta \in \Omega _\gamma \cap \alpha $
, and an infinite
$Y \subseteq ^* Y_0 \cap A_{\gamma ,\beta }$
that does not split below
$\eta _\alpha $
. Then,
-
(⋆) for all
$\delta $
with
$\gamma \leq \delta < \eta _\alpha $
, there is
$\beta = \beta _\delta \in \Omega _\delta \cap \alpha $
such that
$Y \subseteq ^* A_{\delta ,\beta }$
.
Choose infinite
$A_{\eta _\alpha ,\alpha } \subsetneq ^* Y$
. In case (B), choose
$\zeta < \nu $
minimal such that
$S_\zeta $
splits all
$A_{\delta , \beta _\delta }$
with
$\gamma \leq \delta < \eta _\alpha $
. If
$Y \cap S_\zeta $
is infinite, additionally require
$A_{\eta _\alpha ,\alpha } \subsetneq ^* Y \cap S_\zeta $
. (If not, we will automatically have
$A_{\eta _\alpha ,\alpha } \subsetneq ^* \omega \setminus S_\zeta $
.)
Next, for all
$\gamma $
with
$\eta _\alpha \leq \gamma \leq \max (\eta _\alpha ,\xi _\alpha )$
, we let
$A_{\gamma ,\alpha } = A_{\eta _\alpha , \alpha }$
. Also put
$$\begin{align*}\Omega_\gamma \cap ( \alpha + 1) = \left\{ \begin{array}{ll} \Omega_\gamma \cap \alpha, & \mbox{ if } \gamma < \eta_\alpha \mbox{ or } \gamma> \max (\eta_\alpha,\xi_\alpha), \\ (\Omega_\gamma \cap \alpha) \cup \{ \alpha \}, & \mbox{ if } \eta_\alpha \leq \gamma \leq \max (\eta_\alpha,\xi_\alpha). \end{array} \right. \end{align*}$$
Then clauses (i
$_{\alpha +1}$
) and (iii
$_{\alpha + 1}$
) are immediate, and (ii
$_{\alpha +1}$
) follows from
$(\star )$
. This completes the proof of the main theorem.
4 Further remarks and questions
Obviously, the main remaining problem is whether the spectrum of heights of base matrices can be non-convex on regular cardinals.
Question 6 Is it consistent that for some regular
$\vartheta $
with
${\mathfrak h} < \vartheta < {\mathfrak c}$
there is no base (refining) matrix of height
$\vartheta $
?
The simplest instance would be
${\mathfrak h} = \omega _1$
and
${\mathfrak c} = \omega _3$
with no base (refining) matrix of height
$\omega _2$
. By (B) in Main Theorem 3, this would imply
${\mathfrak s} = \omega _3$
.
As the referee remarked, another constellation for a nontrivial spectrum, which would be convex, might be a model where
${\mathfrak s} = {\mathfrak c}$
is singular and there is a regular cardinal
$\kappa \geq {\mathfrak h}$
with
$\kappa < {\mathfrak c}$
such that the spectrum consists exactly of the regular cardinals in the interval
$[{\mathfrak h} , \kappa ]$
. It is unknown, however, whether
${\mathfrak s} = {\mathfrak c} $
singular is consistent at all. The consistency of singular
${\mathfrak s}$
was shown by Dow and Shelah [Reference Dow and ShelahDS], but in their model,
${\mathfrak c}$
is at least
${\mathfrak s}^+$
.
The proof of Main Theorem 3 may look a little like cheating because we do not refine our mad families everywhere when going to the next level. Thus, let us say
${\mathfrak A} = \{ {\cal A}_\gamma : \gamma < \vartheta \}$
is a strict base (refining) matrix if it is a base (refining) matrix and for any
$\gamma < \delta < \vartheta $
and any
$A \in {\cal A}_\delta $
there is
$B \in {\cal A}_\gamma $
with
$A \subsetneq ^* B$
. We then obtain the following.
Proposition 7 Assume
$\vartheta \leq {\mathfrak c}$
is a regular cardinal such that there are
$\subsetneq ^*$
-decreasing chains of length
$\alpha $
in
${\cal P} (\omega )$
for any
$\alpha < \vartheta $
and
-
(A) either there is no
$\subsetneq ^*$
-decreasing chain of length
$\vartheta $
in
${\cal P} (\omega )$
, -
(B) or
${\mathfrak s} \leq \vartheta $
.
Then there is a strict base matrix of height
$\vartheta $
.
Proof sketch
Modify the proof of Main Theorem 3 by attaching a
$\subsetneq ^*$
-decreasing chain of length
$\zeta _\beta + 1$
to the set
$\{ \gamma : \beta \in \Omega _\gamma \} = [ \eta _\beta , \max (\eta _\beta , \xi _\beta ) ]$
, where
$\eta _\beta + \zeta _\beta = \max (\eta _\beta , \xi _\beta )$
. This is clearly possible by assumption.
To analyze this a bit further, let
${\mathfrak {ds}}$
denote the least ordinal
$\alpha $
such that there is no
$\subsetneq ^*$
-decreasing chain of length
$\alpha $
in
${\cal P} (\omega )$
. It is easy to see that
${\mathfrak {ds}}$
is a regular cardinal with
${\mathfrak b}^+ \leq {\mathfrak {ds}} \leq {\mathfrak c}^+$
. Put
$\vartheta _0 = \min \{ {\mathfrak {ds}} , {\mathfrak c} \}$
, and assume
$\vartheta _0$
is regular. Then:
-
(1) there are strict base matrices of heights
${\mathfrak h}$
and
$\vartheta _0$
, and -
(2) all strict refining matrices have height between
${\mathfrak h}$
and
$\vartheta _0$
.
To see (1), use the previous proposition for height
$\vartheta _0$
, and note that the original construction of [Reference Balcar, Pelant and SimonBPS] gives a strict base matrix of height
${\mathfrak h}$
. (2) is obvious. We leave it to the reader to verify that Proposition 7 implies the corresponding versions of Theorems A and B.
Corollary 8 If
${\mathfrak c} \leq \omega _2$
, then there is a strict base matrix of height
${\mathfrak c}$
.
Corollary 9 Let
$\vartheta $
be a regular uncountable cardinal. In the Cohen and random models, the following are equivalent:
-
(i)
$\vartheta \in \{ \omega _1 , \omega _2 \}$
. -
(ii) There is a strict base matrix of height
$\vartheta $
. -
(iii) There is a strict refining matrix of height
$\vartheta $
.
To see, e.g., Corollary 9, note that by Fact 1,
${\mathfrak {ds}} = \omega _2$
in either model, and use (1) and (2) above.
Acknowledgment
We thank Marlene Koelbing and Wolfgang Wohofsky for several illuminating comments which improved the presentation of the paper. We are also very grateful to the referee for many corrections and helpful suggestions.
