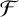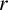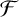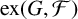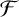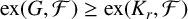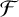1. Introduction
Let G be a graph. We denote the set of vertices of G by
$V(G)$
, the number of edges of G by
$e(G)$
and its chromatic number by
$\chi (G)$
. We say that a graph G is k-critical if
$\chi (G)=k$
and
$\chi (H)<\chi (G)$
for every proper subgraph H of G. Let
$\mathcal {F}$
be a family of graphs. The Turán number of
$\mathcal {F}$
is defined by
${\mathrm {ex}}(G,\mathcal {F})=\max \{e(H):H\subseteq G \ \mbox {and}\ H\ \mbox {is}\ \mathcal {F}\mbox {-free}\}$
. When
$\mathcal {F}=\{F\}$
, we simply write
${\mathrm {ex}}(G,F)$
. Turán [Reference Turán11] determined the exact value of
${\mathrm {ex}}(K_n,K_t)$
, which can be thought of as the first major result in extremal graph theory. Since then, the Turán problem has attracted much attention. A well-known result is the Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits5, Reference Erdős and Stone6], which gives the asymptotic Turán number of all nonbipartite graphs. It states that
$$ \begin{align*}{\mathrm{ex}}(K_n,F)=\bigg(\frac{\chi(F)-2}{\chi(F)-1}\bigg)\frac{n^2}{2}+o(n^2).\end{align*} $$
When F is a bipartite graph, it is natural to consider
${\mathrm {ex}}(K_{m,n},F)$
, replacing the host graph
$K_n$
with a complete bipartite graph
$K_{m,n}$
(the so-called Zarankiewicz problem). More generally, the host graph can also be replaced by other graphs. Frankl and Rödl [Reference Frankl and Rödl9] studied
${\mathrm {ex}}(G,F)$
in the case when G is a random graph. Dowden [Reference Dowden3] considered the Turán problem when the host graph G is a planar graph. Erdős [Reference Erdős, Erdős and Bollabás4] studied the problem
${\mathrm {ex}}(Q_n,F)$
, where
$Q_n$
is the hypercube graph.
Inspired by these problems, Briggs and Cox [Reference Briggs and Cox2] introduced a dual problem called the inverse Turán problem. That is, for a given set
$\mathcal {F}$
, if its Turán number is bounded, then what is the behaviour of the set of host graphs
$$ \begin{align*}\mathcal{G}(k,\mathcal{F})=\{G: {\mathrm{ex}}(G,\mathcal{F})< k\}.\end{align*} $$
The most interesting problem is to study the maximum size of the graphs in
$\mathcal {G}(k,\mathcal {F})$
. Let
$\varepsilon (k,\mathcal {F})=\sup \{e(G):{\mathrm {ex}}(G,\mathcal {F})< k\}$
. In [Reference Briggs and Cox2], Briggs and Cox obtained the asymptotic value of
$\varepsilon (k,F)$
for all nonbipartite graphs and determined the exact value of
$\varepsilon (k,\mathcal {F})$
when
$\mathcal {F}=\{C_3,C_4,C_5,\ldots \}$
or
$\mathcal {F}=\{C_4,C_6,C_8,\ldots \}$
. For a path or an even cycle, Győri et al. [Reference Győri, Salia, Tompkins and Zamora10] obtained results about the order of magnitude of
$\varepsilon (k,F)$
, in several cases. Before this problem was formally raised, there were several papers dealing with the function
$\varepsilon (k,\mathcal {F})$
in a different form, for example,
$\mathcal {F}=\{C_3,C_5,C_7,\ldots \}$
by Alon [Reference Alon1],
$\mathcal {F}=\{C_3,C_4,\ldots ,C_{2r+1}\}$
and
$\mathcal {F}=\{C_4,C_6,\ldots ,C_{2r}\}$
by Foucaud et al. [Reference Foucaud, Krivelevich and Perarnau8] and
$\mathcal {F}=\{K_3, P_4\}$
by Ferneyhough et al. [Reference Ferneyhough, Haas, Hanson and MacGillivray7].
At the end of [Reference Briggs and Cox2], Briggs and Cox also suggested investigating the maximum chromatic number of the graphs in
$\mathcal {G}(k,\mathcal {F})$
:
$$ \begin{align*}\varphi(k,\mathcal{F})=\sup\{\kern1.5pt\chi(G): {\mathrm{ex}}(G,\mathcal{F})<k\}.\end{align*} $$
The third author and Chen [Reference Zhu and Chen12] determined the value of
$\varphi (k,\mathcal {F})$
for families of graphs of diameter at most
$2$
.
Theorem 1.1 (Zhu and Chen [Reference Zhu and Chen12])
Let
$\mathcal {F}$
be a family of graphs, each member of which has diameter at most
$2$
. Then,
$$ \begin{align*}\varphi (k,\mathcal{F})=\max\{r: {\mathrm{ex}}(K_r,\mathcal{F})<k\}.\end{align*} $$
At the same time, they proposed the following conjecture.
Conjecture 1.2 (Zhu and Chen [Reference Zhu and Chen12])
For any
$F\neq 2K_2$
,
$$ \begin{align*}\varphi (k,F)=\max\{r: {\mathrm{ex}}(K_r,F)<k\}.\end{align*} $$
In this note, we continue this work and prove the following theorem which implies that Conjecture 1.2 is true for all connected graphs.
Theorem 1.3. Let
$\mathcal {F}$
be a family of connected graphs and r an integer. For any graph G with
$\chi (G)=r$
,
$$ \begin{align*}{\mathrm{ex}}(G,\mathcal{F})\ge {\mathrm{ex}}(K_r,\mathcal{F}).\end{align*} $$
If some r-chromatic graph G is contained in
$\{G: {\mathrm {ex}}(G,\mathcal {F})< k\}$
, then by Theorem 1.3,
$K_r$
is also in
$\{G: {\mathrm {ex}}(G,\mathcal {F})< k\}$
. Hence we obtain the following corollary.
Corollary 1.4. If F is a connected graph, then
$$ \begin{align*}\varphi (k,F)=\max\{r: {\mathrm{ex}}(K_r,F)<k\}.\end{align*} $$
2. Proof of Theorem 1.3
Let G be a graph with chromatic number r and let c:
$V(G) \to [r]$
be a proper vertex-colouring of G. We use
$C_i$
to denote the set of vertices assigned colour i and let
$c_i=|C_i|$
. Without loss of generality, we may assume
$c_1\leq c_2\leq \cdots \leq c_r$
. We call
$(c_1,c_2,\ldots ,c_r)$
the colour-sequence of c. Let c and
$c'$
be two different proper colourings of G. We say
$(c_1,c_2,\ldots ,c_r) < (c^{\prime }_1,c^{\prime }_2,\ldots ,c^{\prime }_r)$
if
$c_j<c^{\prime }_j$
for
$j=\max \{i:c_i\neq c^{\prime }_i\}$
. For convenience, we simply write
$c<c'$
. We first prove a lemma which will be used in the proof of Theorem 1.3.
Lemma 2.1. Let G be any graph with
$\chi (G)=r$
and let c be a proper vertex colouring of G such that its colour-sequence
$(c_1,c_2,\ldots ,c_r)$
is minimal. Then
$V(G)$
has a partition
$\{V_1,V_2,\ldots , V_s\}$
such that:
-
(i)
$|V_i| \leq r$
; -
(ii)
$s \leq c_r$
; -
(iii)
$\sum _{i=1}^{s} e(G[V_i]) \geq \binom {r}{2}$
.
Proof. We prove this lemma by induction on r. If
$r=2$
, the result is trivially true. Let
$r\ge 3 $
and suppose that the lemma holds for all
$r'<r$
. Let G be an r-chromatic graph on n vertices and c be a vertex-colouring of G such that the colour-sequence
$(c_1,c_2,\ldots ,c_r)$
is minimal. It is easy to see that
$c_r\ge \lceil n/r\rceil $
. Now let
$G'$
be an r-critical subgraph of G and
$c'$
be the minimum vertex-colouring of
$G'$
with colour-sequence
$(c^{\prime }_1,c^{\prime }_2,\ldots ,c^{\prime }_r)$
and colour classes
$\{C^{\prime }_1,\ldots ,C^{\prime }_r\}$
. If
$c'$
is restricted to the subgraph
$G'[C^{\prime }_1\cup \cdots \cup C^{\prime }_{r-1}]$
, it is still a minimal proper vertex colouring of
$G'-C^{\prime }_r$
and the colour-sequence is
$(c^{\prime }_1,\ldots ,c^{\prime }_{r-1})$
. Thus, by the induction hypothesis,
$G'-C^{\prime }_r$
has a partition
$V_1',\ldots,V^{\prime }_{s'}$
such that (i)
$|V^{\prime }_i| \leq r-1$
, (ii)
$s' \leq c^{\prime }_{r-1}$
and (iii)
$\sum _{i=1}^{s'} e(G'[V^{\prime }_i]) \geq \binom {r-1}{2}$
.
For each
$v\in C^{\prime }_r$
and
$i\le s'$
, let
$e_{G'}(v,V^{\prime }_i)$
denote the number of edges in
$G'$
having v as one endvertex and having the other endvertex in
$V^{\prime }_i$
. Observe that
$$ \begin{align*}s' \leq c^{\prime}_{r-1}\le c^{\prime}_r.\end{align*} $$
We choose
$s'$
vertices
$\{v_1,\ldots , v_{s'}\}$
from
$C^{\prime }_r$
step by step by the following greedy algorithm. Suppose we have found
$\{v_1,\ldots , v_{i-1}\}$
from
$C^{\prime }_r$
,
$i\le s'$
. Then we choose
$v_{i}$
from
$C^{\prime }_r\setminus \{v_1,\ldots , v_{i-1}\}$
such that
$e_{G'}(v_i,V^{\prime }_i)$
is the maximum among all remaining vertices. Consider the last vertex
$v_{s'}$
we choose. Since in each step
$e_{G'}(v_i,V^{\prime }_i)$
is maximal and
$C^{\prime }_r$
is independent in
$G'$
, we have
$$ \begin{align} d_{G'}(v_{s'})=\sum_{i=1}^{s'}e_{G'}(v_{s'},V^{\prime}_i)\le \sum_{i=1}^{s'}e_{G'}(v_{i},V^{\prime}_i). \end{align} $$
Suppose
$C^{\prime }_r\setminus \{v_1,v_2,\ldots ,v_{s'}\} = \{v_{s'+1},\ldots ,v_{c^{\prime }_r}\}$
and let
$V_{i} = V_{i}'\cup \{v_i\}$
for
$ 1\le i\le s'$
and
$V_j=\{v_j\}$
for
$s'+1\le j\le c^{\prime }_r$
. Then
$V_1,V_2,\ldots ,V_{s'},V_{s'+1},\ldots ,V_{c^{\prime }_r}$
is a partition of
$V(G')$
with
$|V_i| \leq r$
. Furthermore, by (2.1),
$$ \begin{align*}\begin{split} \sum_{i=1}^{c^{\prime}_r} e(G'[V_i]) &= \sum_{i=1}^{s'} e(G'[V^{\prime}_i]) + \sum_{i=1}^{s'} e_{G'}(v_i,V^{\prime}_i)\\ &\geq \binom{r-1}{2} + \sum_{i=1}^{s'} e_{G'}(v_s,V^{\prime}_i) \geq \binom{r-1}{2} + \delta(G') \geq \binom{r}{2}.\\ \end{split}\end{align*} $$
The last inequality holds because
$G'$
is r-critical and so
$\delta (G')\ge r-1$
.
It is possible that
$V_1,V_2,\ldots ,V_{c^{\prime }_r}$
is not a partition of
$V(G)$
. In this case, we take the additional sets
$V_{c^{\prime }_r+1},\ldots ,V_{c_r}$
if
$c_r>c^{\prime }_r$
and put the remaining vertices
$V(G)-V(G')$
into
$V_1,V_2,\ldots ,V_{c_r}$
in such a way that
$|V_i|\le r$
holds for each i. This can be done because
$r\cdot c_r\ge r\lceil n/r\rceil \ge n$
. Finally,
$V(G)=\bigcup _{i=1}^{c_r} V_i$
is a partition satisfying conditions (i)–(iii).
Proof of Theorem 1.3
Now, let G be an r-chromatic graph and suppose
$V_1,\ldots ,V_s$
is a partition of
$V(G)$
satisfying the properties in Lemma 2.1. For any
$i\in [s]$
, let K be the complete graph on the vertex set
$V_i$
and let T be a randomly chosen copy of an extremal graph for
${\mathrm {ex}}(K,\mathcal {F})$
. Let H be the subgraph of
$G[V_i]$
with the edge set
$\{uv\in E(G[V_i]):uv\in E(T)\}$
. Then,
$$ \begin{align*}\begin{split} {\mathrm{ex}}(G[V_i],\mathcal{F})\ge\mathbb{ E}(e(H))=e(G[V_i])\frac{{\mathrm{ex}}(K_r,\mathcal{F})}{\binom{r}{2}}, \end{split}\end{align*} $$
where
$\mathbb { E}(e(H))$
denotes the expectation of
$e(H)$
. Because all graphs in
$\mathcal {F}$
are connected,
$$ \begin{align*} {\mathrm{ex}}(G,\mathcal{F}) \geq \sum_{i=1}^{s} {\mathrm{ex}}(G[V_i],\mathcal{F}) \geq \sum_{i=1}^{s}e(G[V_i])\frac{{\mathrm{ex}}(K_r,\mathcal{F})}{\binom{r}{2}} \geq {\mathrm{ex}}(K_r,\mathcal{F}). \end{align*} $$
This completes the proof of Theorem 1.3.
Acknowledgement
This work was done while the authors were studying at the MTA Rényi Institute as visiting students, supported by the Chinese Scholarship Council.
