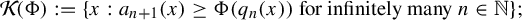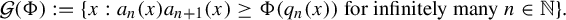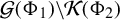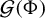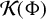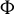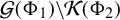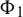1 Introduction
Diophantine approximation aims at quantitative analysis on how well irrational numbers can be approximated by rational numbers. Dirichlet’s theorem is the first non-trivial quantitative result in this aspect and is the starting point of metric Diophantine approximation.
Theorem 1.1. (Dirichlet [Reference Schmidt19])
Let
$x\in \mathbb {R}$
. For any positive number
$Q> 1$
, there exists an integer q with
$1\le q< Q$
, such that
$$ \begin{align*} \|qx\|\le \frac{1}{Q},\quad {\mathrm{i.e.}}\quad \min_{1\le q<Q, q\in \mathbb N}\|qx\|\le \frac{1}{Q}, \end{align*} $$
where
$\|\cdot \|$
denotes the distance to integers
$\mathbb Z$
.
As a corollary, one has the following.
Corollary 1.2. For any real number x, there are infinitely many integers
$q\in \mathbb N$
, such that
$$ \begin{align*} \|qx\|< 1/q. \end{align*} $$
The result in Theorem 1.1 is called the uniform Dirichlet theorem and the result in Corollary 1.2 is called the asymptotic Dirichlet theorem. The study of the improvability of Dirichlet’s theorem opens up the metric theory in Diophantine approximation.
-
• The improvability of the asymptotic theorem leads to the
$\psi $
well-approximable set The metric theory of
$$ \begin{align*} \mathcal{W}(\psi)=\{x\in [0,1): \|qx\|<\psi(q) \ {\text{for infinitely many}\ q\in \mathbb N}\}. \end{align*} $$
$\mathcal {W}(\psi )$
and its variants constitute the major topic in metric Diophantine approximation [Reference Sprindzuk20]. For examples, Khintchine’s theorem [Reference Khintchine10], Jarník’s theorem [Reference Jarník9], the mass transference principle [Reference Beresnevich and Velani2], the Duffin–Schaeffer conjecture [Reference Koukoulopoulos and Maynard15] etc.
-
• The improvability of the asymptotic theorem leads to the Dirichlet improvable set
The work of Davenport and Schmidt [Reference Davenport and Schmidt4] draw one’s attention to the improvability of Dirichlet’s theorem itself instead of its corollary. For examples, uniformly well approximable sets [Reference Kim and Liao12], uniform Diophantine exponent [Reference Bugeaud, Cheung and Chevallier3], homogeneous and inhomogeneous Dirichlet improvability [Reference Kleinbock and Wadleigh13, Reference Kleinbock and Wadleigh14] etc.
$$ \begin{align*} \mathcal{D}(\psi)=\{x\in [0,1]: \min_{1\le q<Q}\|qx\|\le \psi(Q) \ {\text{for all}\ Q\gg 1}\}. \end{align*} $$
As far as one-dimensional Diophantine approximation is concerned, the continued fraction expansion plays a significant role. Indeed, the metric theories, including Lebesgue measure and Hausdorff dimension, of the sets
$\mathcal {W}(\psi )$
and
$ \mathcal {D}(\psi )$
are both studied via continued fractions at the very beginning.
Let
$x={[a_1(x),a_2(x),\ldots ]}$
be the continued fraction of x, and
$p_n(x)/q_n(x)$
be the nth convergent of x. Then by the best rational approximation of the convergents, more precisely,
$$ \begin{align*} \min_{1\le q<q_{n+1}(x)}\|qx\|=\|q_n(x)\cdot x\|, \end{align*} $$
the sets
$\mathcal {W}(\psi )$
and
$\mathcal {D}(\psi )$
can be rewritten by changing q to
$q_n(x)$
and Q to
$q_{n+1}(x)$
. Easy calculation leads to the following sets:
$$ \begin{align*} \mathcal{K}(\Phi_2)&=\{x\in [0,1): a_{n+1}(x)\ge \Phi_2(q_n(x)) \ {\text{for infinitely many}\ n\in \mathbb N}\},\\ \mathcal{G}(\Phi_1)&=\{x\in [0,1): a_n(x)a_{n+1}(x)\ge \Phi_1(q_n(x)) \ {\text{for infinitely many}\ n\in \mathbb N}\}. \end{align*} $$
(Later we use i.m. for infinitely many.) By taking
$$ \begin{align*} \Phi_2(q)=\frac{1}{\psi(q)q} \quad{\text{and}}\quad \Phi_1(q)=\frac{\psi(q)q}{1-\psi(q)q}, \end{align*} $$
one has the inclusions
$$ \begin{align*} \mathcal{K}(\Phi_2)\subset \mathcal{W}(\psi)\subset \mathcal{K}\big(\tfrac{1}{2}\Phi_2\big) \quad {\text{and}}\quad \mathcal{G}(\Phi_1)\subset \mathcal{D}^c(\psi)\subset \mathcal{G}\big(\tfrac{1}{4}\Phi_1\big), \end{align*} $$
where
$\mathcal {D}^c$
means the complement set of
$\mathcal {D}$
.
Based on these relations, Khintchine [Reference Khintchine10] (or see his monograph [Reference Khintchine11]) presented the Lebesgue measure of
$\mathcal {W}(\psi )$
and Jarník [Reference Jarník9] showed its Hausdorff measure; for
$\mathcal {D}^c(\psi )$
, its Lebesgue measure is given by Kleinbock and Wadleigh [Reference Kleinbock and Wadleigh13] and the Hausdorff measure and dimension result is given by Hussain et al [Reference Hussian, Kleinbock, Wadleigh and Wang7].
The close relation between the sets
$\mathcal {K}(\Phi _2)$
and
$\mathcal {G}(\Phi _1)$
is disclosed in proving the Hausdorff measure theory of
$\mathcal {D}^c(\psi )$
.
Theorem 1.3. (Hussain et al [Reference Hussian, Kleinbock, Wadleigh and Wang7])
Let
$\psi $
be a non-increasing positive function with
$t\psi (t)<1$
for all large t. Then for any
$0\leq s<1$
,
$$ \begin{align*} \mathcal{H}^s(\mathcal{D}^c(\psi))=\begin {cases} 0 \ & {\mathrm{if }} \sum\limits_{t} {t}\bigg(\dfrac{1}{{t^2\Phi_{1}({t})}} \bigg)^s < \infty; \\[2ex] \infty \ & {\mathrm{if }} \sum\limits_{t} {t}\bigg(\dfrac{1}{{t^2\Phi_{1}({t})}} \bigg)^s = \infty. \end {cases}\end{align*} $$
More precisely, the divergence theory is followed by just using the simple fact that
$$ \begin{align*} \mathcal{K}(\Phi)\subset \mathcal{G}(\Phi) \end{align*} $$
and the following Jarník’s theorem.
Theorem 1.4. (Jarník [Reference Jarník9])
Let
$\Phi : \mathbb N\to \mathbb R^+$
be a non-decreasing positive function. Then for any
$0\leq s<1$
,
$$ \begin{align*} \mathcal{H}^s(\mathcal{K}(\Phi))=\begin {cases} 0 \ & {\mathrm{if }} \sum\limits_{t} {t}\bigg(\dfrac{1}{{t^2\Phi({t})}} \bigg)^s < \infty; \\[2ex] \infty \ & {\mathrm{if }} \sum\limits_{t} {t}\bigg(\dfrac{1}{{t^2\Phi({t})}} \bigg)^s = \infty. \end {cases}\end{align*} $$
So
$\dim _{\mathrm H} (\mathcal {G}(\Phi ))=\dim _{\mathrm H} (\mathcal {K}(\Phi ))$
. It is surprising that the subset
$\mathcal {K}(\Phi )$
can give the right dimension of
$\mathcal {G}(\Phi )$
from below. So it is desirable to know how much is the difference between
$\mathcal {K}(\Phi )$
and
$\mathcal {G}(\Phi )$
.
Theorem 1.5. (Bakhtawar, Bos and Hussain [Reference Bakhtawar, Bos and Hussain1])
Let
$\Phi :\mathbb N\to \mathbb {R}^+$
be a non-decreasing function. Then
$$ \begin{align} \dim_{\mathrm H}(\mathcal{G}(\Phi)\!\setminus\! \mathcal{K}(\Phi))=\dim_{\mathrm H} (\mathcal{K}(\Phi)). \end{align} $$
To prove the equality in equation (1.1), the
$\le $
direction is trivial since
$\dim _{\mathrm H} (\mathcal {G}(\Phi ))=\dim _{\mathrm H} (\mathcal {K}(\Phi ))$
; for the
$\ge $
direction, one considers the following subset:
$$ \begin{align*} \Big\{x\in [0,1): a_n(x)&=4,\ a_{n+1}(x)\ge \frac{\Phi(q_n(x))}{4}, {\text{i.m. }} n\in \mathbb N; \\ & \quad {\text{and}}\ a_{n+1}(x)< \Phi(q_n(x)) \ {\text{for all }} n\in \mathbb N \Big\}. \end{align*} $$
Since there is already enough room for the choice of
$a_{n+1}(x)$
and such a room is almost the same as in finding the lower bound of the dimension of
$\mathcal {K}(\Phi )$
(see for example [Reference Wang, Wu and Xu22]), it should be imagined that this subset should have the same dimension as
$\mathcal {K}(\Phi )$
.
Roughly speaking, only the term
$a_{n+1}(x)$
contributes the dimension of
$\mathcal {G}(\Phi )$
while
$a_n(x)$
does not. One main reason is that the restriction
$a_{n+1}(x)\le \Phi (q_n(x))$
is too loose that it is already sufficient to ask that
$a_{n+1}(x)$
is large and
$a_n(x)$
behaves almost freely.
However, if
$a_{n+1}(x)$
cannot be very large, then
$a_n(x)$
must contribute to realize that
$a_{n}(x)a_{n+1}(x)$
is large enough. So to have a better understanding about how
$a_n(x)$
and
$a_{n+1}(x)$
contribute to the dimension of
$\mathcal {G}(\Phi )$
, we consider the following difference set:
$$ \begin{align*} \mathcal{G}(\Phi_1)\!\setminus\! \mathcal{K}(\Phi_2)&= \{x\in [0,1): a_n(x) a_{n+1}(x)\ge {\Phi_1(q_n(x))}, {\text{i.m. }} n\in \mathbb N; \\ & \qquad {\text{and}}\ a_{n+1}(x)< \Phi_2(q_n(x)) \ {\text{for all }} n\in \mathbb N {\text{ large}} \}. \end{align*} $$
When
$\Phi _2\le \Phi _1$
, both
$a_n(x)$
and
$a_{n+1}(x)$
have to contribute to realize
$a_n(x)a_{n+1}(x)\ge \Phi _1(q_n(x))$
. Then there will be a selection about how to choose
$a_n(x)$
and
$a_{n+1}(x)$
separately: equal or non-equal growth rate, which would be the optimal choice? The general principle of how
$a_n(x)$
and
$a_{n+1}(x)$
are chosen will be explained in detail in the proof. Moreover, one will see that a minor change on
$\Phi $
will cause a big difference on the dimension.
We ask
$\Phi _1$
and
$\Phi _2$
to take the form as Jarník’s original theorem, that is,
$\Phi _i(q)=q^{t_i}$
and write
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
for the set
$\mathcal {G}(\Phi _1)\!\setminus\! \mathcal {K}(\Phi _2)$
.
Theorem 1.6. For any
$t_1, t_2>0$
:
-
• when
$t_1>t_2+{t_2}/({1+t_2})$
,
$$ \begin{align*}\mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)=\emptyset;\end{align*} $$
-
• when
$t_1=t_2+{t_2}/({1+t_2})$
,
$$ \begin{align*}\mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)=\emptyset;\end{align*} $$
-
• when
$t_2<t_1<t_2+{t_2}/({1+t_2})$
,
$$ \begin{align*} \dim_{\mathrm H} (\mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2))= 1-\frac{t_1}{2+t_2}; \end{align*} $$
-
• when
$t_1\le t_2$
,
$$ \begin{align*} \dim_{\mathrm H} (\mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2))=\frac{2}{2+t_1}. \end{align*} $$
We separate the case
$t_1=t_2+{t_2}/({1+t_2})$
from the others, mainly because a different situation will happen for this case. We give two examples to illustrate this. Denote
$$ \begin{align*} E_1=\{x\in [0,1): a_n(x)a_{n+1}(x)&\ge q_n(x)^{t_1}, {{\text{i.m.}}}\ n\in \mathbb N, \\ &\quad a_{n+1}(x)< q_n(x)^{t_2} \ {\text{for all}}\ n\in \mathbb N \ {\text{large}}\}, \\ E_2=\{x\in [0,1): a_n(x)a_{n+1}(x)&\ge 4^{-t_1}q_n(x)^{t_1}, {{\text{i.m.}}}\ n\in \mathbb N, \\ &\quad a_{n+1}(x)< 3q_n(x)^{t_2}\ {\text{for all}}\ n\in \mathbb N \ {\text{large}}\}. \end{align*} $$
The first set
$E_1$
is nothing but
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
. We duplicate it here mainly for comparison.
Proposition 1.7. If
$t_1=t_2+{t_2}/({1+t_2})$
, then
$$ \begin{align*}E_1=\emptyset,\quad \dim_{\mathrm H} E_2=1-\frac{t_1}{2+t_2}.\end{align*} $$
These two examples illustrate that as far as the general functions
$\Phi _i$
are concerned, minor change on the function will lead to a big difference between the dimensions. So it is almost hopeless to give a unified formula for the dimension of the set
$\mathcal {G}(\Phi _1)\!\setminus\! \mathcal {K}(\Phi _2)$
(the formula is hopeful only when
$\Phi _2$
is good). Therefore for simplicity, we ask
$\Phi _i$
to behave regularly instead of arbitrarily.
Theorem 1.8. Let
$\Phi _1,\Phi _2$
be two non-decreasing functions. Assume that
$$ \begin{align*} \lim_{q\to\infty}\frac{\log \Phi_1(q)}{\log q}=t_1, \quad \lim_{q\to\infty}\frac{\log \Phi_2(q)}{\log q}=t_2. \end{align*} $$
Then the following:
-
• when
$t_1>t_2+{t_2}/({1+t_2})$
,
$$ \begin{align*}\mathcal{G}(\Phi_1)\!\setminus\! \mathcal{K}(\Phi_2)=\emptyset;\end{align*} $$
-
• when
$t_2<t_1<t_2+{t_2}/({1+t_2})$
,
$$ \begin{align*} \dim_{\mathrm H} (\mathcal{G}(\Phi_1)\!\setminus\! \mathcal{K}(\Phi_2))= 1-\frac{t_1}{2+t_2}; \end{align*} $$
-
• when
$t_1\le t_2$
,
$$ \begin{align*} \dim_{\mathrm H} (\mathcal{G}(\Phi_1)\!\setminus\! \mathcal{K}(\Phi_2))=\frac{2}{2+t_1}. \end{align*} $$
Even though only special functions are considered here, the proof below will be sufficient to illustrate how the partial quotients
$a_n(x)$
and
$a_{n+1}(x)$
contribute to the dimension of
$\mathcal {G}(\Phi )$
.
Throughout the paper, denote by
$\mathcal {H}^{s}$
the s-dimensional Hausdorff measure,
$\dim _{\mathrm H}$
the Hausdorff dimension and ‘cl’ the closure of a set. We use
$a\ll b$
,
$a\gg b$
and
$a\asymp b$
respectively to mean that
$0<a/b\le e_{1}$
,
$a/b\ge e_{2}>0$
and
$e_2 \le a/b\le e_{1}$
for unspecified positive constants
$e_{1},e_{2}$
.
2 Preliminaries
In this section, we shall collect some basic properties about continued fractions for later use. For more properties, one is referred to the monographs [Reference Iosifescu and Kraaikamp8, Reference Khintchine11].
Continued fraction expansion is induced by the Gauss transformation
$T:[0,1)\to [0,1)$
given by
$$ \begin{align*} T(0):=0, \quad T(x)=\frac{1}{x}\ ({\text{mod}\ 1}),\quad x\in (0,1). \end{align*} $$
Then every irrational number
$x\in [0,1)$
can be uniquely expanded into an infinite continued fraction:
$$ \begin{align*} x=\cfrac{1}{a_{1}(x)+\cfrac{1}{a_{2}(x)+\ddots}}:=[a_1(x),a_2(x),\ldots], \end{align*} $$
where
$a_{1}(x)=\lfloor 1/x\rfloor $
and
$a_{n}(x)=a_{1}(T^{n-1}(x))$
for
$n\ge 2$
are called the partial quotients of x. The finite truncation
$$ \begin{align*} \frac{p_{n}(x)}{q_{n}(x)}=[a_{1}(x),\ldots,a_{n}(x)] \end{align*} $$
is called the nth convergent of x.
The numerator and denominator of a convergent can be determined by the recursive relation: for any
$k\ge 1$
,
$$ \begin{align} p_{k}(x)=a_{k}(x)p_{k-1}(x)+p_{k-2}(x),\ \ q_{k}(x)=a_{k}(x)q_{k-1}(x)+q_{k-2}(x), \end{align} $$
with the conventions
$p_{0}=0$
,
$q_{0}=1$
,
$p_{-1}=1$
,
$q_{-1}=0$
.
For simplicity, we write
$$ \begin{align}p_n(x)=p_{n}(a_{1},\ldots,a_{n})=p_{n}, \ \ q_{n}(x)=q_n(a_{1},\ldots,a_{n})=q_{n}\end{align} $$
when the partial quotients
$a_1,\ldots , a_n$
are clear.
Lemma 2.1. Let
$a_1,\ldots ,a_n, b_1,\ldots , b_m$
be integers in
$\mathbb N$
. For any
$1\le k\le n$
, one has
$$ \begin{align} q_{n}\ge 2^{(n-1)/2},\quad{\text{and}}\quad p_{n-1}q_n-p_nq_{n-1}=(-1)^n, \end{align} $$
$$ \begin{align} 1\le \frac{q_{n+m}(a_{1},\ldots,a_{n},b_{1},\ldots,b_{m})}{q_{n}(a_{1},\ldots,a_{n})\cdot q_{m}(b_1,\ldots,b_m)}\le 2. \end{align} $$
For any positive integers
$a_{1},\ldots ,a_{n}$
, define
$$ \begin{align*} I_{n}(a_{1},\ldots,a_{n}):=\{x\in[0,1):a_{1}(x)=a_{1},\ldots,a_{n}(x)=a_{n}\} \end{align*} $$
and call it
$\textit {a cylinder of order }n$
. The length of a cylinder and its position in
$[0,1)$
is demonstrated in the following propositions.
Proposition 2.2. (Khintchine [Reference Khintchine11])
For any
$n\ge 1$
and
$(a_{1},\ldots ,a_{n})\in \mathbb {N}^{n}$
,
$p_{k},q_{k}$
are defined recursively by equation (2.1) for
$0\le k\le n$
. Then
$$ \begin{align}I_{n}(a_{1},\ldots,a_{n})= \begin{cases} \bigg[\dfrac{p_{n}}{q_{n}},\dfrac{p_{n}+p_{n-1}}{q_{n}+q_{n-1}}\bigg) &\text{if}\ n\textrm{ is even},\\[12pt] \bigg(\dfrac{p_{n}+p_{n-1}}{q_{n}+q_{n-1}},\dfrac{p_{n}}{q_{n}}\bigg] & \text{if}\ n\text{ is odd}.\\ \end{cases} \end{align} $$
Therefore, the length of a cylinder of order n is given by
$$ \begin{align*} |I_{n}(a_{1},\ldots,a_{n})|=\dfrac{1}{q_{n}(q_{n}+q_{n-1})}. \end{align*} $$
Since every number in
$[0,1)$
has continued fraction expansion, then
$$ \begin{align*} [0, 1)=\bigcup_{a_1,\ldots, a_n}I_n(a_1,\ldots,a_n). \end{align*} $$
Thus,
$$ \begin{align} 1\le \sum_{a_1,\ldots,a_n}\frac{1}{q_n^2(a_1,\ldots,a_n)}\le 2. \end{align} $$
Proposition 2.3. (Khintchine [Reference Khintchine11])
Let
$I_n=I_n(a_1,\ldots , a_n)$
be a cylinder of order n, which is partitioned into sub-cylinders
$\{I_{n+1}(a_1,\ldots ,a_n, a_{n+1}): a_{n+1}\in \mathbb N\}$
. When n is odd, these sub-cylinders are positioned from left to right, as
$a_{n+1}$
increases from 1 to
$\infty $
; when n is even, they are positioned from right to left.
Next, we introduce the mass distribution principle which is the classic method in estimating the Hausdorff dimension of a set from below.
Proposition 2.4. [Reference Falconer5]
Let E be a Borel set and
$\mu $
be a measure with
$\mu (E)>0$
. Suppose that for some
$s>0$
, there exist constants
$c>0, r_o>0$
such that for any
$x\in E$
and
$r<r_o$
,
$$ \begin{align} \mu(B(x,r))\le cr^{s}, \end{align} $$
where
$B(x,r)$
denotes an open ball centered at x and radius r, then
$\dim _{\mathrm H} E\ge s$
.
At the end, we give some dimensional numbers which are related to the dimension of the set of points with bounded partial quotients.
For any integer M, define
$$ \begin{align*}E_M=\{x\in [0,1): 1\le a_n(x)\le M \ {\text{for all}}\ n\ge 1\}.\end{align*} $$
For each integer N, define
$\tilde {s}_{N}(M)$
to be the solution to the equation
$$ \begin{align*} \sum_{1\le a_1,\ldots,a_N\le M}\bigg(\frac{1}{q_N^{2}(a_1,\ldots, a_N)}\bigg)^{s}=1. \end{align*} $$
Proposition 2.5. (Good [Reference Good6])
The limit of
$\tilde {s}_N(M)$
as
$N\to \infty $
exists and
$$ \begin{align*} \dim_{\mathrm H} E_M=\lim_{N\to\infty}\tilde{s}_N(M):=\tilde{s}(M).\end{align*} $$
It is well known that the set of points with bounded partial quotients (that is, the set of badly approximable points) is of Hausdorff dimension 1 (see [Reference Schmidt18]). Thus,
$$ \begin{align*} \lim_{M\to\infty}\dim_{\mathrm H} E_M=1, \quad {\mathrm{i.e.}}\quad \lim_{M\to \infty}\tilde{s}_M=1. \end{align*} $$
These two results can also be seen by using the words from dynamical systems. More precisely, a pressure function with a continuous potential can be approximated by the pressure functions restricted to the sub-systems in continued fractions (see for example Mauldin and Urbański [Reference Mauldin and Urbański16] or their monograph [Reference Mauldin and Urbański17]).
3 A Cantor set
This section is devoted to dealing with the dimension of a Cantor set which is highly related to the dimension of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
and also may have its own interest and applications to other problems in continued fractions. Bear in mind the notation in equation (2.2).
Let
$\alpha _{1},\alpha _{2}>0$
be two positive numbers. Denote by
$E(\alpha _{1},\alpha _{2})$
the set
$$ \begin{align*} \{x\in [0,1):c_{1}q_{n-1}^{\alpha_{1}}(x)&\le a_{n}(x)< 2c_{1}q_{n-1}^{\alpha_{1}}(x),c_{2}q_{n}^{\alpha_{2}}(x)\\&\le a_{n+1}(x)< 2c_{2}q_{n}^{\alpha_{2}}(x), \textrm{i.m.}\ n\in \mathbb N\} \end{align*} $$
where
$c_{1},c_{2}$
are positive constants.
One will see how the growth of
$a_n(x)$
and
$a_{n+1}(x)$
affects the dimension of
$E(\alpha _1,\alpha _2)$
. For notational simplicity, we take
$c_1=c_2=1$
and the other case can be done with verbal modifications; if an integer n is assumed to be a real number
$\xi $
, we mean
$n=\lfloor \xi \rfloor $
; in the definition of
$E(\alpha _1,\alpha _2)$
, there are
$q_{n-1}^{\alpha _1}$
many choices of
$a_n(x)$
.
Theorem 3.1. For any
$\alpha _{1},\alpha _{2}>0$
,
$$ \begin{align*} \dim_{H}E(\alpha_{1},\alpha_{2})=\min\bigg\{\frac{2}{\alpha_{1}+2},\frac{\alpha_{1}+2}{(\alpha_{1}+1)(\alpha_{2}+2)}\bigg\}. \end{align*} $$
The proof of Theorem 3.1 is split into two parts: upper bound and lower bound.
3.1 Upper bound
Because of the limsup nature, there are natural coverings for
$E(\alpha _1,\alpha _2)$
. For each
$n\ge 1$
, define
$$ \begin{align*} E_n=\{x\in [0,1): q_{n-1}^{\alpha_1}(x)\le a_{n}(x)< 2q_{n-1}^{\alpha_1}(x), q_{n}^{\alpha_2}(x)\le a_{n+1}(x)< 2q_{n}^{\alpha_2}(x)\}. \end{align*} $$
Then
$$ \begin{align*} E(\alpha_1,\alpha_2)=\bigcap_{N=1}^{\infty}\bigcup_{n=N}^{\infty}E_n\subset \bigcup_{n=N}^{\infty}E_n. \end{align*} $$
So in the following, we search for the potential optimal cover of
$E_n$
for each
$n\ge N$
.
By decomposing the unit interval into the collection of
$(n-1)$
th order cylinders, one has
$$ \begin{align*} E_n&=\bigcup_{a_1,\ldots,a_{n-1}\in \mathbb N}\{x\in [0,1): a_i(x)=a_{i}, 1\le i<n, q_{n-1}^{\alpha_1}\le a_{n}(x)< 2q_{n-1}^{\alpha_1},\\ &\quad q_{n}^{\alpha_2}\le a_{n+1}(x)< 2q_{n}^{\alpha_2}\}. \end{align*} $$
Then there are two potential optimal covers.
-
• Cover type I. For any integers
$a_1,\ldots ,a_{n-1}\in \mathbb N$
, define which is an interval of length
$$ \begin{align*} J_{n-1}(a_1,\ldots,a_{n-1})=\bigcup_{q_{n-1}^{\alpha_1}\le a_{n}< 2q_{n-1}^{\alpha_1}}I_n(a_1,\ldots,a_n), \end{align*} $$
Then,
$$ \begin{align*} |J_{n-1}(a_1,\ldots,a_{n-1})|=\sum_{q_{n-1}^{\alpha_1}\le a_{n}< 2q_{n-1}^{\alpha_1}}\bigg|\frac{p_n}{q_n}-\frac{p_n+p_{n-1}}{q_n+q_{n-1}}\bigg|\asymp \frac{1}{q_{n-1}^{\alpha_1+2}}. \end{align*} $$
Therefore, an s-dimensional Hausdorff measure of
$$ \begin{align*}E_n\subset \bigcup_{a_1,\ldots, a_{n-1}}J_{n-1}(a_1,\ldots,a_{n-1}).\end{align*} $$
$E(\alpha _1,\alpha _2)$
can be estimated as Recall equation (2.6) where
$$ \begin{align*} \mathcal{H}^s(E(\alpha_1,\alpha_2))&\le\liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}|J_{n-1}(a_1,\ldots,a_{n-1})|^s\\ &\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\frac{1}{q_{n-1}^{(\alpha_1+2)s}}. \end{align*} $$
Thus for any
$$ \begin{align*} \sum_{a_1,\ldots,a_{n-1}}\frac{1}{q_{n-1}^2}\le 2, \quad {\text{and}}\ q_{n-1}\ge 2^{(n-2)/2}. \end{align*} $$
$\epsilon>0$
and by taking
$s=({2+2\epsilon })/({\alpha _1+2})$
, it follows that This shows that
$$ \begin{align*} \mathcal{H}^s(E(\alpha_1,\alpha_2))&\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\bigg(\frac{1}{q_{n-1}^{2}}\cdot \frac{1}{2^{(n-2)\epsilon}}\bigg)\\&\le 2\liminf_{N\to\infty}\sum_{n=N}^{\infty}\frac{1}{2^{(n-2)\epsilon}}<\infty. \end{align*} $$
$$ \begin{align*} \dim_{\mathrm H} E(\alpha_1,\alpha_2)\le \frac{2}{\alpha_1+2}. \end{align*} $$
-
• Cover type II. For any integers
$a_1,\ldots ,a_{n-1}\in \mathbb N$
and
$q_{n-1}^{\alpha _1}\le a_{n}< 2q_{n-1}^{\alpha _1}$
, define which is an interval of length
$$ \begin{align*} J_{n}(a_1,\ldots,a_{n})=\bigcup_{q_{n}^{\alpha_2}\le a_{n+1}< 2q_{n}^{\alpha_2}}I_{n+1}(a_1,\ldots,a_{n+1}), \end{align*} $$
Then,
$$ \begin{align*} |J_{n}(a_1,\ldots,a_{n})|\asymp \frac{1}{q_{n}^{\alpha_2+2}}. \end{align*} $$
Therefore, an s-dimensional Hausdorff measure of
$$ \begin{align*}E_n\subset \bigcup_{a_1,\ldots, a_{n-1}}\bigcup_{q_{n-1}^{\alpha_1}\le a_{n}< 2q_{n-1}^{\alpha_1}}J_{n}(a_1,\ldots,a_{n}).\end{align*} $$
$E(\alpha _1,\alpha _2)$
can be estimated as Recall that
$$ \begin{align*} \mathcal{H}^s(E(\alpha_1,\alpha_2))&\le\liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\sum_{q_{n-1}^{\alpha_1}\le a_{n}< 2q_{n-1}^{\alpha_1}}|J_{n}(a_1,\ldots,a_{n})|^s\\ &\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\sum_{q_{n-1}^{\alpha_1}\le a_{n}< 2q_{n-1}^{\alpha_1}}\frac{1}{q_{n}^{(\alpha_2+2)s}}. \end{align*} $$
Thus it follows that
$$ \begin{align*} q_n=a_nq_{n-1}+q_{n-2}\ge a_nq_{n-1}. \end{align*} $$
Then with a similar choice of s and the argument as in the first case, one has
$$ \begin{align*} \mathcal{H}^s(E(\alpha_1,\alpha_2))&\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\frac{q_{n-1}^{\alpha_1}}{q_{n-1}^{(1+\alpha_1)(\alpha_2+2)s}}. \end{align*} $$
$$ \begin{align*} \dim_{\mathrm H} E(\alpha_1,\alpha_2)\le \frac{2+\alpha_1}{(1+\alpha_1)(2+\alpha_2)}. \end{align*} $$
In summary, we have shown that
$$ \begin{align*} \dim_{H}E(\alpha_{1},\alpha_{2})\le \min\bigg\{\frac{2}{\alpha_{1}+2},\frac{\alpha_{1}+2}{(\alpha_{1}+1)(\alpha_{2}+2)}\bigg\}. \end{align*} $$
3.2 Lower bound
We use the mass distribution principle (Proposition 2.4) to search for the lower bound of the dimension of
$E(\alpha _1, \alpha _2)$
: define a measure supported on
$E(\alpha _1,\alpha _2)$
and then estimate the Hölder exponent of
$\mu $
.
Recall
$\alpha _1>0$
. For any integers
$N, M$
, define the dimensional number
$s=s_N(M)$
as the solution to
$$ \begin{align} \sum_{1\le a_1,\ldots,a_N\le M}{\frac{1}{q_N^{(2+\alpha_1)s}}}=1. \end{align} $$
Then by Proposition 2.5, one has
$$ \begin{align} \lim_{M\to\infty}\lim_{N\to \infty}s_N(M)=\frac{2}{\alpha_1+2}. \end{align} $$
So fix
$\epsilon>0$
and then choose integers
$M,N$
sufficiently large such that
$$ \begin{align*} s>\frac{2}{\alpha_1+2}-\epsilon, \ \ (2^{(N-1)/2})^{{\epsilon}/{2}}\ge 2^{100}.\end{align*} $$
Fix a sequence of largely sparse integers
$\{l_k\}_{k\ge 1}$
, say,
$$ \begin{align*} l_k\gg e^{l_1+\cdots+l_{k-1}}, {\text{and take}}\ n_k-n_{k-1}=l_kN+1 \quad \text{for all }\ k\ge 1, \end{align*} $$
such that
$$ \begin{align} (2^{\ell_{k}(N-1)/2})^{{\epsilon}/{2}}\ge \prod_{t=1}^{k-1}(M+1)^{\ell_t N(1+\alpha_2)^{k-t}(1+\alpha_1)^{k-t}}. \end{align} $$
Then define a subset of
$E(\alpha _1, \alpha _2)$
as
$$ \begin{align} E&=\{x\in [0,1): q_{n_k-1}(x)^{\alpha_1}\le a_{n_k}(x)<2 q_{n_k-1}(x)^{\alpha_1}, q_{n_k}(x)^{\alpha_2}\le a_{n_k+1}(x)\nonumber\\ & <2q_{n_k}(x)^{\alpha_2}\ {\text{for all}} \ k\ge 1; {\text{and}}\ a_n(x)\in \{1,\ldots, M\} \ {\text{for other}\ n\in \mathbb N}\}. \end{align} $$
For ease of notation, we perform the following.
-
• Use a symbolic space defined as
$D_0=\{\emptyset \}$
, and for any
$n\ge 1$
, which is just the collection of the prefix of the points in E.
$$ \begin{align*} D_n&=\{(a_1,\ldots, a_n)\in \mathbb N^n: q_{n_k-1}^{\alpha_1}\le a_{n_k}<2q_{n_k-1}^{\alpha_1}, q_{n_k}^{\alpha_2}\le a_{n_k+1}<2q_{n_k}^{\alpha_2}\ \\ &\quad{\text{for all}} \ k\ge 1 \ {\text{with}} \ {n_k}, n_{k}+1\le n; {\text{and}}\ a_j\in \{1,\ldots, M\} \ {\text{for other}\ j\le n}\}, \end{align*} $$
-
• Use
$\mathcal U$
to denote the following collection of finite words of length N: In the following, we always use w to denote a generic word in
$$ \begin{align*} \mathcal U=\{w=(\sigma_1,\ldots, \sigma_N): 1\le \sigma_i\le M, 1\le i\le N\}. \end{align*} $$
$\mathcal U$
.
3.2.1 Cantor structure of E
For any
$(a_1,\ldots , a_n)\in D_n$
, define
$$ \begin{align*} J_n(a_1,\ldots,a_n)=\bigcup_{a_{n+1}: (a_1,\ldots,a_n, a_{n+1})\in D_{n+1}}I_{n+1}(a_1,\ldots,a_n, a_{n+1}) \end{align*} $$
and call it a basic cylinder of order n. More precisely, for each
$k\ge 0$
:
-
• when
$n_{k-1}+1\le n<n_{k}-1$
(by viewing
$n_0=0$
),
$$ \begin{align*} J_n(a_1,\ldots,a_n)=\bigcup_{1\le a_{n+1}\le M}I_{n+1}(a_1,\ldots,a_n, a_{n+1}); \end{align*} $$
-
• when
$n=n_{k}-1$
or
$n=n_k$
,
$$ \begin{align*} J_{n_k-1}(a_1,\ldots,a_{n_k-1})&=\bigcup_{q_{n_k-1}^{\alpha_1}\le a_{n_k}< 2 q_{n_k-1}^{\alpha_1}}I_{n_k}(a_1,\ldots,a_n, a_{n_k}),\\ J_{n_k}(a_1,\ldots,a_{n_k})&=\bigcup_{q_{n_k}^{\alpha_2}\le a_{n_k+1}< 2 q_{n_k}^{\alpha_2}}I_{n_k+1}(a_1,\ldots,a_n, a_{n_k+1}). \end{align*} $$
Then define
$$ \begin{align*} \mathcal{F}_n=\bigcup_{(a_1,\ldots,a_n)\in D_n}J_n(a_1,\ldots,a_n) \end{align*} $$
and call it level n of the Cantor set E. It is clear that
$$ \begin{align*} E=\bigcap_{n=1}^{\infty}\mathcal{F}_n=\bigcap_{n=1}^{\infty}\bigcup_{(a_1,\ldots,a_n)\in D_n}J_n(a_1,\ldots,a_n). \end{align*} $$
We have the following observations about the length and gaps of the basic cylinders.
Lemma 3.2. (Gap estimation)
Denote by
$G_n(a_1,\ldots , a_n)$
the gap between
$J_n(a_1,\ldots , a_n)$
and other basic cylinders of order n. Then
$$ \begin{align*} G_n(a_1,\ldots, a_n)\ge \frac{1}{M}\cdot |J_n(a_1,\ldots,a_n)|. \end{align*} $$
Proof. This can be observed from the positions of the cylinders in Proposition 2.3. Recall the definition of
$J_n$
given above and note that different cylinders
$I_n$
are disjoint. When
$n=n_k-1$
or
$n=n_k$
, the basic cylinder
$J_n$
lies in the middle part of
$I_n$
, so there are large gaps between
$J_n$
with other basic cylinders of order n. For other n, note that
$$ \begin{align*} \bigcup_{a>M}I_{n+1}(a_1,\ldots,a_n, a) \end{align*} $$
falls in the gap of
$J_n(a_1,\ldots ,a_n)$
and other basic cylinders in its right/left side (when n is odd/even). Then one needs only estimate the length of these gaps. A detailed proof can be found in [Reference Wang and Wu21] or [Reference Wang, Wu and Xu22].
Recall the definition of
$\mathcal U$
. Every element
$x\in E$
can be written as the form
$$ \begin{align*} x=[w_1^{(1)},\ldots, w_{\ell_1}^{(1)}, a_{n_1}, a_{n_1+1}, & w_1^{(2)},\ldots, w_{\ell_2}^{(2)}, a_{n_2},a_{n_2+1},\\ \ldots, & w_1^{(k)},\ldots, w_{\ell_k}^{(k)}, a_{n_k},a_{n_k+1},\ldots], \end{align*} $$
where
$w_i^{(k)}\in \mathcal U$
for all
$1\le i\le \ell _k, k\ge 1,$
and
$$ \begin{align*} \ q_{n_t-1}^{\alpha_1}\le a_{n_t}< 2q_{n_t-1}^{\alpha_1}, \ \ \ q_{n_t}^{\alpha_2}\le a_{n_t+1}< 2q_{n_t}^{\alpha_2}\ {\text{for all}}\ t\ge 1. \end{align*} $$
We estimate the length of basic cylinders
$J_n(x)$
for all
$n\ge 1$
. For
$n_k+1\le n< n_{k+1}-1$
, we have
$$ \begin{align*} |J_n(x)|=\bigg|\frac{p_n+p_{n-1}}{q_n+q_{n-1}}-\frac{(M+1)p_n+p_{n-1}}{(M+1)q_n+q_{n-1}}\bigg| =\frac{M}{(q_n+q_{n-1})((M+1)q_n+q_{n-1})}\ge \frac{1}{8q_n^2}, \end{align*} $$
and similarly,
$$ \begin{align*} |J_{n_{k}-1}(x)|= \frac{q_{n_k-1}^{\alpha_1}}{(q_{n_k-1}^{\alpha_1}q_{n_k-1}+q_{n_k-2})(2q_{n_k-1}^{\alpha_1}q_{n_k-1}+q_{n_k-2})}, \end{align*} $$
so
$$ \begin{align*} \bigg(\frac{1}{q_{n_{k}-1}(x)}\bigg)^{\alpha_1+2}>|J_{n_{k}-1}(x)|\ge \frac{1}{8}\cdot \bigg(\frac{1}{q_{n_{k}-1}(x)}\bigg)^{\alpha_1+2}, \end{align*} $$
$$ \begin{align*} \bigg(\frac{1}{q_{n_k-1}}\bigg)^{(a_1+1)(\alpha_2+2)}&\ge \bigg(\frac{1}{q_{n_{k}}(x)}\bigg)^{\alpha_2+2}>|J_{n_{k}}(x)|\\ &\ge \frac{1}{8}\cdot \bigg(\frac{1}{q_{n_{k}}(x)}\bigg)^{\alpha_2+2}\ge \frac{1}{2^{7+2\alpha_2}}\bigg(\frac{1}{q_{n_k-1}}\bigg)^{(a_1+1)(\alpha_2+2)}. \end{align*} $$
Here for the last inequality, we used
$q_{n_k-1}^{\alpha _1}\le a_{n_k}<2q_{n_k-1}^{\alpha _1}$
.
Recall equation (3.3) for the choice of the largely sparse sequence
$\{\ell _k\}$
. Consequently, we have the following lemma.
Lemma 3.3. (Length estimation)
Let
$x\in E$
and an integer n with
$n_k-1\le n< n_{k+1}-1$
.
-
•
$n=n_{k}-1$
, (3.5)
$$ \begin{align}|J_{n_{k}-1}(x)|\ge \frac{1}{2^3}\cdot \frac{1}{q_{n_k-1}^{\alpha_1+2}}&\ge \frac{1}{2^3}\cdot \bigg(\frac{1}{2^{\ell_{k}}}\cdot \prod_{i=1}^{\ell_{k}}\frac{1}{q_N(w_i^{(k)})}\cdot \frac{1}{q_{n_{k-1}+1}}\bigg)^{\alpha_1+2}\nonumber\\ &\ge \bigg(\prod_{i=1}^{\ell_{k}}\frac{1}{q_N(w_i^{(k)})}\bigg)^{(\alpha_1+2)(1+\epsilon)}.\end{align} $$
-
•
$n=n_k$
, (3.6)
$$ \begin{align} |J_{n_k}(x)|\ge \frac{1}{2^3}\frac{1}{q_{n_k}^{\alpha_2+2}}\ge \frac{1}{2^3}\cdot \frac{1}{4^{2+\alpha_2}}\cdot \frac{1}{q_{n_k-1}^{(\alpha_1+1)(\alpha_2+2)}}. \end{align} $$
-
•
$n=n_k+1$
, (3.7)
$$ \begin{align} |J_{n_k+1}(x)|\ge \frac{1}{2^3}\cdot \frac{1}{q_{n_k+1}^2}\ge \frac{1}{2^7}\cdot \frac{1}{q_{n_k}^{2(1+\alpha_2)}}. \end{align} $$
-
• For each
$1\le \ell <\ell _{k+1}$
, (3.8)
$$ \begin{align}|J_{n_k+1+\ell N}(x)|&\ge \frac{1}{2^3}\cdot \bigg(\frac{1}{2^{2\ell}}\cdot \prod_{i=1}^{\ell}\frac{1}{q_N^2(w_i^{(k+1)})}\bigg)\cdot \frac{1}{q_{n_k+1}^2}\nonumber\\[6pt] &\ge \bigg(\prod_{i=1}^{\ell}\frac{1}{q_N^2(w_i^{(k+1)})}\bigg)^{1+\epsilon}\cdot \frac{1}{q_{n_k+1}^2}.\end{align} $$
-
• For
$n_k+1+(\ell -1)N\le n<n_k+1+\ell N$
with
$1\le \ell \le \ell _{k+1}$
, (3.9)where
$$ \begin{align} |J_{n}(x)|\ge c\cdot |J_{n_k+1+(\ell-1)N}(x)|, \end{align} $$
$c=c(M, N)$
is an absolute constant.
Proof. Applying equation (2.4) in Lemma 2.1 for
$\ell _k$
times allows us to arrive the third inequality in equation (3.5), while the last inequality just follows from the choice of
$\ell _k$
and
$\epsilon $
in equation (3.3).
For the relation in (3.9), one notes that the partial quotients are all bounded by M except at the positions
$n=n_k, n_{k}+1$
. The constant c can be taken as
$$ \begin{align*} \frac{1}{2^3}\cdot \bigg(\frac{1}{M+1}\bigg)^{2N}.\\[-42pt] \end{align*} $$
3.3 Mass distribution
We define a probability measure supported on the Cantor set E. Still express an element
$x\in E$
as
$$ \begin{align*} x=[w_1^{(1)},\ldots, w_{\ell_1}^{(1)}, &a_{n_1}, a_{n_1+1}, w_1^{(2)},\ldots, w_{\ell_2}^{(2)}, a_{n_2},a_{n_2+1},\\[3pt] &\ldots, w_1^{(k)},\ldots, w_{\ell_k}^{(k)}, {a_{n_k},a_{n_k+1}},\ldots], \end{align*} $$
where
$$ \begin{align*} {w_{i}^{(k)}\in \mathcal U \ {\text{for all}}\ i, k\in \mathbb{N}}, \ {\text{and}}\ q_{n_t-1}^{\alpha_1}\le a_{n_t}< 2q_{n_t-1}^{\alpha_1}, \ q_{n_t}^{\alpha_2}\le a_{n_t+1}< 2q_{n_t}^{\alpha_2} \ {\text{for all}}\ t\ge 1. \end{align*} $$
We define the measure along the basic cylinders
$J_n(x)$
containing x as follows.
-
• Let
$n\le n_1+1$
:-
– for each
$1\le \ell \le \ell _1$
, define Recall the definition of s (see equation (3.1)) and then once
$$ \begin{align*} \mu(J_{Nl}(x))=\prod_{i=1}^{\ell}\bigg(\frac{1}{q_N(w_i^{(1)})}\bigg)^{(\alpha_1+2)s}. \end{align*} $$
$\mu $
is a measure, it is a probability measure. Because of the arbitrariness of x, this defines the measure on all basic cylinders of order
$\ell N$
;
-
– for each integer n with
$(\ell -1)N<n<\ell N$
for some
$1\le \ell \le \ell _1$
, define where the summation is over all basic cylinders of order
$$ \begin{align*} \mu(J_n(x))=\sum_{J_{\ell N}\subset J_n(x)}\mu(J_{\ell N}(x)) \end{align*} $$
$\ell N$
contained in
$J_{n}(x)$
. This is designed to ensure the consistency of a measure;
-
– when
$n=n_1$
. Note that
$n_1=\ell _1 N+1$
, then define
$$ \begin{align*} \mu(J_{n_1}(x))=\frac{1}{q_{n_1-1}^{\alpha_1}}\mu(J_{n_1-1}(x))=\frac{1}{q_{n_1-1}^{\alpha_1}} \prod_{l=1}^{\ell_1}\frac{1}{q_N(w_l^{(1)})^{(\alpha_1+2)s}}; \end{align*} $$
-
– when
$n=n_1+1$
, define
$$ \begin{align*} \mu(J_{n_1+1}(x))=\frac{1}{q_{n_1}^{\alpha_2}}\cdot \mu(J_{n_1}(x))=\frac{1}{q_{n_1}^{\alpha_2}}\cdot\frac{1}{q_{n_1-1}^{\alpha_1}} \prod_{l=1}^{\ell_1}\frac{1}{q_N(w_l^{(1)})^{(\alpha_1+2)s}}. \end{align*} $$
-
-
• Let
$n_{k-1}+1<n\le n_{k}+1$
. Assume the measure of all basic cylinders of order
$n_{k-1}+1$
has been defined:-
– for each
$1\le \ell \le \ell _{k}$
, define (3.10)
$$ \begin{align} \mu(J_{n_{k-1}+1+N\ell}(x))&=\bigg(\prod_{i=1}^{\ell}\frac{1}{q_N(w_i^{(k)})^{(\alpha_1+2)s}}\bigg)\cdot \mu(J_{n_{k-1}+1}(x)); \end{align} $$
-
– for each integer n with
$n_{k-1}+1+(\ell -1)N<n<n_{k-1}+1+\ell N$
for some
$1\le \ell \le \ell _k$
, define
$$ \begin{align*} \mu(J_n(x))=\sum_{J_{n_{k-1}+1+\ell N}(x)\subset J_n(x)}\mu(J_{n_{k-1}+1+\ell N}(x)); \end{align*} $$
-
– for each
$n=n_k$
and
$n=n_k+1$
, define (3.11)
$$ \begin{align} \mu(J_{n_{k}}(x))&=\frac{1}{q_{n_{k}-1}^{\alpha_1}}\cdot \mu(J_{n_{k}-1}(x)), \ \ \mu(J_{n_k+1}(x))=\frac{1}{q_{n_k}^{\alpha_2}}\cdot \mu(J_{n_k}(x)); \end{align} $$
-
– define the measure of the basic cylinders of other orders as the summation of the measure of its offsprings to ensure the consistency of a measure.
-
Look at equation (3.10) for the measure of a basic cylinder of order
$n_k+1+\ell N$
and its predecessor of order
$n_k+1+(\ell -1)N$
: the former has one more term than the latter, that is the term
$$ \begin{align*} \bigg(\frac{1}{q_N(w_{\ell}^{(k+1)})}\bigg)^{(\alpha_1+2)s}, \end{align*} $$
which is uniformly bounded. Thus there is an absolute constant
$c>0$
, such that for each integer n:
-
• when
$n_k+1+(\ell -1)N\le n\le n_k+1+\ell N$
, (3.12)
$$ \begin{align}\mu(J_n(x))\ge c\cdot \mu(J_{n_k+1+(\ell-1)N}(x));\end{align} $$
-
• when
$n\ne n_k-1$
and
$n\ne n_{k}$
, (3.13)
$$ \begin{align} \mu(J_{n+1}(x))\ge c\cdot \mu(J_n(x)). \end{align} $$
3.4 Hölder exponent of
$\mu $
: for basic cylinders
We compare the measure with the length of
$J_{n}(x)$
.
-
(1) When
$n={n_{k}-1}$
. Recall equations (3.5) and (3.10) on the length and measure of
$J_{n_k-1}$
. It follows that
$$ \begin{align*} \mu(J_{n_k-1})\le \prod_{i=1}^{\ell_k}\frac{1}{q_N(w_i^{(k)})^{(\alpha_1+2)s}}\le |J_{n_k-1}(x)|^{{s}/({1+\epsilon})}\le \bigg(\frac{1}{q_{n_k-1}^{\alpha_1+2}}\bigg)^{{s}/({1+\epsilon})}. \end{align*} $$
-
(2) When
$n=n_k$
. Recall equations (3.11) and (3.6). where t is chosen as
$$ \begin{align*} \mu(J_{n_k}(x))=\frac{1}{q_{n_k-1}^{\alpha_1}}\cdot \mu(J_{n_k-1}(x))&\le \frac{1}{q_{n_k-1}^{\alpha_1}}\cdot \bigg(\frac{1}{q_{n_k-1}^{\alpha_1+2}}\bigg)^{{s}/({1+\epsilon})}:=\bigg(\frac{1}{q_{n_k-1}^{(\alpha_1+1)(\alpha_2+2)}}\bigg)^t\\ &\le c |J_{n_k}(x)|^t\le c \cdot \bigg(\frac{1}{q_{n_k}^{\alpha_2+2}}\bigg)^t, \end{align*} $$
$$ \begin{align*} t=\frac{\alpha_1+(\alpha_1+2){s}/({1+\epsilon})}{(\alpha_1+1)(\alpha_2+2)}. \end{align*} $$
-
(3) When
$n=n_k+1$
. Recall equations (3.11) and (3.7). Note that
$0\le t\le 1$
.
$$ \begin{align*} \mu(J_{n_{k}+1}(x))&=\frac{1}{q_{n_k}^{\alpha_2}}\cdot \mu(J_{n_k}(x))\le \frac{1}{q_{n_k}^{\alpha_2}}\cdot c \cdot \bigg(\frac{1}{q_{n_k}^{\alpha_2+2}}\bigg)^t \\ &\le c \bigg(\frac{1}{q_{n_k}^{2\alpha_2+2}}\bigg)^t\le c_2 |J_{n_k+1}(x)|^{t}\le c_2\bigg(\frac{1}{q_{n_k+1}^2}\bigg)^t. \end{align*} $$
-
(4) When
$n=n_k+1+\ell N$
for some
$1\le \ell \le \ell _k$
. Recall equations (3.5) and (3.10).
$$ \begin{align*} \mu(J_{n_k+1+\ell N})&=\prod_{i=1}^{\ell}\frac{1}{q_N(w_i^{(k+1)})^{(\alpha_1+2)s}}\cdot \mu(J_{n_{k}+1}(x))\\ &\le c_2 \cdot \prod_{i=1}^{\ell}\frac{1}{q_N(w_i^{(k+1)})^{2s}} \cdot \bigg(\frac{1}{q_{n_{k}+1}^2}\bigg)^t \quad {\text{(by neglecting}\ \alpha_1)}. \end{align*} $$
Recall equation (3.8) for the length of
$J_{n_k+1+\ell N}$
. It follows that
$$ \begin{align*} \mu(J_{n_k+1+\ell N}(x))\le c_2 |J_{n_k+1+\ell N}(x)|^{\min\{{s}/({1+\epsilon}), t\}}. \end{align*} $$
-
(5) Remaining cases. Then we are in the case that
$n_k+1<n<n_{k+1}-1$
. Let
$1\le \ell \le \ell _{k+1}$
be the integer such that
$n_k+1+(\ell -1)N<n<n_k+1+\ell N$
. Recall equation (3.9). Then
$$ \begin{align*} \mu(J_{n}(x))&\le \mu(J_{n_k+1+(\ell-1)N}(x))\le c_2 |J_{n_k+1+(\ell-1)N}(x)|^{\min\{{s}/({1+\epsilon}), t\}}\\ &\le c_2\cdot c\cdot |J_n(x)|^{\min\{{s}/({1+\epsilon}), t\}}. \end{align*} $$
In summary, we have shown that for some absolute constant
$c_3$
, for any
$n\ge 1$
and
$x\in E$
,
$$ \begin{align} \mu(J_n(x))\le c_3\cdot |J_n(x)|^{\min\{{s}/({1+\epsilon}), t\}}. \end{align} $$
3.5 Hölder exponent of
$\mu $
: for a general ball
Write
$$ \begin{align*} s_o=\min\bigg\{\frac{s}{1+\epsilon}, t\bigg\}. \end{align*} $$
Recall Lemma 3.2 about the relation of the gap and the length of the basic cylinders:
$$ \begin{align*} G_n(x)\ge \frac{1}{M}\cdot |J_n(x)|. \end{align*} $$
We consider the measure of a general ball
$B(x,r)$
with
$x\in E$
and r small. Let
$n\ge 1$
be the integer such that
$$ \begin{align*} G_{n+1}(x)\le r<G_{n}(x). \end{align*} $$
Then the ball
$B(x,r)$
can only intersect one basic cylinder of order n, that is, the basic cylinder
$J_n(x)$
, and so all the basic cylinders of order
$n+1$
which have non-empty intersection with
$B(x,r)$
are all contained in
$J_n(x)$
.
Let k be the integer such that
$$ \begin{align*} n_{k-1}+1\le n<n_{k}+1. \end{align*} $$
-
(1) When
$n_{k-1}+1\le n<n_{k}-1$
. By equations (3.13) and (3.14), it follows that
$$ \begin{align*} \mu(B(x,r))&\le \mu(J_n(x))\le c\cdot \mu(J_{n+1}(x))\le c\cdot c_3\cdot |J_{n+1}(x)|^{s_o}\\&\le c\cdot c_3\cdot M\cdot (G_{n+1}(x))^{s_o}\le c\cdot c_3\cdot M\cdot r^{s_o}. \end{align*} $$
-
(2) When
$n=n_{k}-1$
. The ball
$B(x,r)$
can only intersect the basic cylinder
$J_{n_k-1}(x)$
of order
$n_k-1$
. Now we estimate how many basic cylinders of order
$n_k$
are contained in
$J_{n_k-1}(x)$
and intersected with the ball
$B(x,r)$
.We write a general basic cylinder of order
$n_k$
contained in
$J_{n_k-1}(x)$
as It is clear that for each a, the basic cylinder
$$ \begin{align*} J_{n_k}(u, a) \quad {\text{with}}\ q_{n_k-1}^{\alpha_1}\le a<2q_{n_k-1}^{\alpha_1}. \end{align*} $$
$J_{n_{k}}(u,a)$
is contained in the cylinder
$I_{n_k}(u,a)$
and the latter interval is of length
${1}/{q_{n_k}(q_{n_k}+q_{n_k-1})}$
with
$$ \begin{align*} \frac{1}{q_{n_k-1}(u)^{2\alpha_1+2}}\ge \frac{1}{q_{n_k}(q_{n_k}+q_{n_k-1})}\ge \frac{1}{2^5}\cdot \frac{1}{q_{n_k-1}(u)^{2\alpha_1+2}}. \end{align*} $$
-
• When
Then the ball
$$ \begin{align*} r<\frac{1}{2^5}\cdot \frac{1}{q_{n_k-1}(u)^{2\alpha_1+2}}. \end{align*} $$
$B(x,r)$
can intersect at most three cylinders
$I_{n_k}(u,a)$
and so three basic cylinders
$J_{n_k}(u,a)$
. Note that all those basic cylinders are of the same
$\mu $
-measure, thus
$$ \begin{align*} \mu(B(x,r))&\le 3\mu(J_{n_k}(x))\le 3 \cdot c_3\cdot |J_{n_k}(x)|^{s_o}\\ &\le 3\cdot c_3\cdot M\cdot G_{n+1}(x)^{s_o}\le 3\cdot c_3\cdot M\cdot r^{s_o}. \end{align*} $$
-
• When
The number of cylinders
$$ \begin{align*} r\ge \frac{1}{2^5}\cdot \frac{1}{q_{n_k-1}(u)^{2\alpha_1+2}}. \end{align*} $$
$I_{n_k}(u,a)$
for which the ball
$B(x,r)$
can intersect is at most so at most this number of basic cylinders of order
$$ \begin{align*} {2^6\cdot r}\cdot q_{n_k-1}(u)^{2\alpha_1+2}+2\le {2^7\cdot r}\cdot q_{n_k-1}(u)^{2\alpha_1+2}, \end{align*} $$
$n_k$
can intersect
$B(x,r)$
. Thus,
$$ \begin{align*} \hspace{-1.5pc} \mu(B(x,r))&\le \min\bigg\{\mu(J_{n_k-1}(x)), {2^7\cdot r}\cdot q_{n_k-1}(u)^{2\alpha_1+2}\cdot \bigg(\frac{1}{q_{n_k-1}^{\alpha_1}}\cdot \mu(J_{n_k-1}(x))\bigg)\bigg\}\\ &\le c_3\cdot |J_{n_k-1}|^{s_o}\cdot \min\{1, {2^7\cdot r}\cdot q_{n_k-1}(u)^{\alpha_1+2}\}\\ &\le c_3\cdot \bigg(\frac{1}{q_{n_k-1}(u)^{\alpha_1+2}}\bigg)^{s_o}\cdot 1^{1-s_o}\cdot (2^7\cdot {r}\cdot q_{n_k-1}(u)^{\alpha_1+2})^{s_o}\\ &=c_4 \cdot r^{s_o}. \end{align*} $$
-
-
(3) When
$n=n_k$
. By changing
$n_k-1$
and
$\alpha _1$
in case (2) to
$n_k$
and
$\alpha _2$
respectively and then following the same argument as in case (2), we can arrive at the same conclusion.
We conclude by mass distribution principle (Proposition 2.4) that
$$ \begin{align} \dim_{\mathrm H} E\ge \min\bigg\{\frac{s}{1+\epsilon}, \ \frac{\alpha_1+(\alpha_1+2){s}/({1+\epsilon})}{(\alpha_1+1)(\alpha_2+2)}\bigg\}. \end{align} $$
Recall equation (3.2) on
$s=s_N(M)$
. Letting
$N\to \infty $
as then
$M\to \infty $
, we arrive at
$$ \begin{align*} \dim_{\mathrm H} E(\alpha_1, \alpha_2)\ge \min\bigg\{\frac{2}{\alpha_1+2}, \ \frac{\alpha_1+2}{(\alpha_1+1)(\alpha_2+2)}\bigg\}. \end{align*} $$
This finishes the proof.
4 Simple facts for
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
4.1 The condition for
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
non-empty
Recall that
$$ \begin{align*} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)&= \{x\in [0,1): a_n(x) a_{n+1}(x)\ge {q_n(x)^{t_1}}, {\text{i.m. }} n\in \mathbb N; \\ & \quad {\text{and}}\ a_{n+1}(x)< q_n(x)^{t_2} \ {\text{for all}\ n\in \mathbb N\ \text{large}} \}. \end{align*} $$
It is clear that if
$t_1$
is very large and
$t_2$
is very small, one must have
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)=\emptyset $
. So there should be some boundary value between
$t_1$
and
$t_2$
ensuring the non-empty of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
.
Lemma 4.1. When
$t_1>t_2+{t_2}/({1+t_2})$
, the set
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
is empty.
Proof. It is sufficient to show that under the restriction that
$a_{n+1}< q_n^{t_2}$
for all n large, one ultimately has
$$ \begin{align*} a_na_{n+1}<q_n^{t_1}. \end{align*} $$
It should be easy to see that
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
is non-empty when
$t_1\le t_2$
. So in the following, we ask
$t_1>t_2$
. Thus,
$$ \begin{align*} a_na_{n+1}<q_n^{t_1} \! \Longleftarrow &\ a_n<q_n^{t_1-t_2}\\ \! \Longleftarrow &\ a_n<a_n^{t_1-t_2}q_{n-1}^{t_1-t_2}\Longleftarrow\ a_n^{1-t_1+t_2}<q_{n-1}^{t_1-t_2}. \end{align*} $$
This is obviously true if
$t_1-t_2\ge 1$
, so assume that
$t_1-t_2<1$
. Let us continue the above argument.
$$ \begin{align*} a_na_{n+1}<q_n^{t_1} \!\Longleftarrow &\ q_{n-1}^{t_2(1-t_1+t_2)}<q_{n-1}^{t_1-t_2}\\ \!\Longleftarrow &\ t_2(1-t_1+t_2)<{t_1-t_2}\Longleftrightarrow\ t_1>t_2+\frac{t_2}{1+t_2}. \end{align*} $$
In conclusion, we have shown the desired claim.
5 Hausdorff dimension of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
when
$t_2<t_1<t_2+{t_2}/({1+t_2})$
5.1 Lower bound
First we give some rough words for finding a suitable subset of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
. Initially, we separate the restriction posed on the product
$a_na_{n+1}$
. This leads us to consider the following set:
$$ \begin{align*} F:=\{x: a_n\ {\asymp}\ q_{n-1}^{\alpha_1}, a_{n+1}\ {\asymp}\ q_n^{\alpha_2}, {\text{i.m. }} n\in \mathbb N, {\text{and}}\ 1\le a_n\le M \ {\text{for all other}}\ n\in \mathbb N\}. \end{align*} $$
We hope that F is a subset of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
and at the same time, the dimension of F should be as large as possible.
-
• It is clear that the smaller
$\alpha _1, \alpha _2$
will result in a larger dimension of F. So, we may choose
$\alpha _1, \alpha _2$
satisfying Combining with
$$ \begin{align*} q_{n-1}^{\alpha_1}q_n^{\alpha_2}=q_n^{t_1}. \end{align*} $$
$q_n\ {\asymp }\ a_n q_{n-1}$
, one has that (5.1)
$$ \begin{align} q_{n-1}^{\alpha_1} q_{n-1}^{(1+\alpha_1)\alpha_2}=q_{n-1}^{(1+\alpha_1)t_1}&\Leftrightarrow \alpha_1+(1+\alpha_1)\alpha_2=(1+\alpha_1)t_1\nonumber\\& \Leftrightarrow \alpha_2=t_1-\frac{\alpha_1}{1+\alpha_1}. \end{align} $$
-
• However, we need that
$\alpha _1< t_2$
and
$\alpha _2< t_2$
which gives the range of
$\alpha _1, \alpha _2$
. More precisely, (5.2)
$$ \begin{align} \hspace{-2pc} \text{`}\alpha_1< t_2, \alpha_2< t_2\text{'} &\Longleftrightarrow\ \text{`}\alpha_1< t_2, \ \alpha_2=t_1-\frac{\alpha_1}{1+\alpha_1}< t_2\text{'} \nonumber \\ &\Longleftrightarrow\ \text{`}\frac{t_1-t_2}{1-t_1+t_2}< \alpha_1< t_2\text{'} \quad(\text{expressed in the range of}\ \alpha_1) \end{align} $$
(5.3)
$$ \begin{align} \Longleftrightarrow\ t_1-\frac{t_2}{1+t_2}< \alpha_2< t_2 \quad(\text{expressed in the range of}\ \alpha_2). \hspace{-2.4pc} \end{align} $$
Now we give a rigorous argument in defining a subset of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
. Recall the set defined in equation (3.4) with a suitable choice of the constants c in
$E(\alpha _1, \alpha _2)$
:
$$ \begin{align} E=\{x: q_{n_k-1}(x)^{\alpha_1} & \le a_{n_k}(x)<2 q_{n_k-1}(x)^{\alpha_1}, \ 2^{2t_1}q_{n_k}(x)^{\alpha_2} \nonumber \\ &\le a_{n_k+1}(x)<2^{2t_1+1}q_{n_k}(x)^{\alpha_2} \nonumber\\ \ {\text{for all}} \ k&\ge 1;\ {\text{and}}\ a_n(x)\in \{1,\ldots, M\} \ {\text{for other}\ n\in \mathbb N}\}. \end{align} $$
Proposition 5.1. For any pair
$(\alpha _1, \alpha _2)$
satisfying equations (5.1) and (5.2), for any integer sequence
$\{n_k\}_{k\ge 1}$
, the set E in equation (5.4) is a subset of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
and thus
$$ \begin{align*} \dim_{\mathrm H} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)\ge \min\bigg\{\frac{2}{\alpha_1+2}, \ \frac{\alpha_1+2}{(\alpha_1+1)(\alpha_2+2)}\bigg\}. \end{align*} $$
Proof. The fact that
$a_n(x)q_{n-1}(x)\le q_n(x)\le 2a_n(x)q_{n-1}(x)$
will be used. Take a general element
$x \in E$
. We check that
$x\in \mathcal {G}(t_1)$
but
$x\not \in \mathcal {K}(t_2)$
.
-
•
$x\in \mathcal {G}(t_1)$
. This is done by checking that (5.5)More precisely, on one hand,
$$ \begin{align} a_{n_k}(x)a_{n_k+1}(x)\ge q_{n_k}(x)^{t_1} \quad {\text{for all}}\ k\ge 1. \end{align} $$
On the other hand,
$$ \begin{align*} a_{n_k}(x)a_{n_k+1}(x)&\ge q_{n_k-1}^{\alpha_1}\cdot 2^{2t_1}\cdot q_{n_k}^{\alpha_2}\ge2^{2t_1}\cdot q_{n_k-1}^{\alpha_1}(a_{n_k}q_{n_k-1})^{\alpha_2}\\&\ge 2^{2t_1}\cdot q_{n_k-1}^{\alpha_1}\cdot q_{n_k-1}^{(\alpha_1+1)\alpha_2}. \end{align*} $$
Then the inequality in equation (5.5) follows by recalling the first equivalence in equation (5.1).
$$ \begin{align*} q_{n_k}^{t_1}\le (2a_{n_k}q_{n_k-1})^{t_1}\le 2^{2t_1}\cdot q_{n_k-1}^{(\alpha_1+1)t_1}. \end{align*} $$
-
•
$x\not \in \mathcal {K}(t_2)$
. This is clear since
$\alpha _1<t_2, \alpha _2<t_2$
by equation (5.2).
The dimensional result follows directly by recalling the dimension of E in equation (3.15).
We claim that the second term is the minimal one under the condition in equation (5.1).
Lemma 5.2. Under the condition in equation (5.1), one has
$$ \begin{align*} \min\bigg\{\frac{2}{2+\alpha_1}, \ \frac{2+\alpha_1}{(1+\alpha_1)(2+\alpha_2)}\bigg\}=\frac{2+\alpha_1}{(1+\alpha_1)(2+\alpha_2)}. \end{align*} $$
Proof. At first, rewrite the relationship between
$\alpha _1$
and
$\alpha _2$
:
$$ \begin{align*} \alpha_2=t_1-1+\frac{1}{1+\alpha_1}, \ {\text{so}}\ \frac{1}{1+\alpha_1}=\alpha_2-t_1+1. \end{align*} $$
Thus,
$$ \begin{align*} \frac{2+\alpha_1}{(1+\alpha_1)(2+\alpha_2)}&=\frac{1}{(1+\alpha_1)(2+\alpha_2)}+\frac{1}{2+\alpha_2}\\ &=\frac{\alpha_2-t_1+1}{\alpha_2+2}+\frac{1}{2+\alpha_2}=1-\frac{t_1}{2+\alpha_2}. \end{align*} $$
As a consequence,
$$ \begin{align*} &\frac{2}{2+\alpha_1}\ge \frac{2+\alpha_1}{(1+\alpha_1)(2+\alpha_2)} \Longleftrightarrow\ \frac{2}{2+\alpha_1}\ge 1-\frac{t_1}{2+\alpha_2}\\ \Longleftrightarrow &\ \frac{t_1}{2+\alpha_2}\ge \frac{\alpha_1}{2+\alpha_1}\Longleftrightarrow\ t_1(1+\frac{2}{\alpha_1})\ge {2+\alpha_2}=t_1+1+\frac{1}{\alpha_1+1}\\ \Longleftrightarrow &\ \frac{2t_1}{\alpha_1}\ge 1+\frac{1}{1+\alpha_1}\Longleftrightarrow\ 2t_1\ge \alpha_1+\frac{\alpha_1}{\alpha_1+1}. \end{align*} $$
Let
$$ \begin{align*} f(x)=x+\frac{x}{1+x}=x+1-\frac{1}{1+x}, \quad x\in[0,t_2]. \end{align*} $$
Clearly f is increasing with respect to x and when
$x=t_2$
, it attains its maximal value
$$ \begin{align*} t_2+\frac{t_2}{1+t_2}. \end{align*} $$
So, what we need is to show that
$$ \begin{align*} &2t_1\ge t_2+\frac{t_2}{1+t_2} \Longleftarrow 2t_2\ge t_2+\frac{t_2}{1+t_2}\\ \Longleftarrow &\ 2\ge 1+\frac{1}{1+t_2}, \end{align*} $$
which is clearly true.
As a consequence,
$$ \begin{align*} \dim_{\mathrm H} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)&\ge \sup\bigg\{1-\frac{t_1}{2+\alpha_2}: t_1-\frac{t_2}{1+t_2}\le \alpha_2\le t_2\bigg\}\\ &=1-\frac{t_1}{2+t_2}. \end{align*} $$
In other words, the supremum is achieved at
$\alpha _2=t_2$
.
5.2 Upper bound
Recall that the lower bound of
$\dim _{\mathrm H} \mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
given above is attained at
$$ \begin{align*}\alpha_2=t_2, \quad \alpha_1=\frac{t_1-t_2}{1+t_2-t_1}.\end{align*} $$
Lemma 5.3. For any
$x\in [0,1)$
,
$$ \begin{align*}a_n(x)a_{n+1}(x)\ge q_n^{t_1}(x), \ a_{n+1}(x)< q_n^{t_2}(x)\Longrightarrow a_n(x)\ge q_{n-1}(x)^{({t_1-t_2})/({1+t_2-t_1})}.\end{align*} $$
Proof.
$$ \begin{align*} q_n^{t_1}\le a_n a_{n+1}\le a_n q_n^{t_2}&\Longrightarrow q_n^{t_1-t_2}\le a_n\Longrightarrow a_n^{t_1-t_2}q_{n-1}^{t_1-t_2}\le a_n\\ &\Longrightarrow q_{n-1}^{t_1-t_2}\le a_n^{1-t_1+t_2}\Longrightarrow a_n\ge q_{n-1}^{({t_1-t_2})/({1+t_2-t_1})}.\\[-2.5pc] \end{align*} $$
This lemma almost convinces us that the lower bound given above is the right dimension of
$\dim _{\mathrm H} \mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
. Denote
$\alpha _1=({t_1-t_2})/({1+t_2-t_1})$
. Lemma 5.3 implies that
$$ \begin{align*} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)&\subset \bigg\{x: a_n(x)\ge q_{n-1}(x)^{({t_1-t_2})/({1+t_2-t_1})}, a_{n+1}(x)\\& \qquad \ge \frac{q_n(x)^{t_1}}{a_n(x)}, {{\text{i.m.}}}\ n\in \mathbb N\bigg\}:=\mathcal{G}. \end{align*} $$
Fix
$s>1-{t_1}/({2+t_2})$
. At first, it is easy to check that
$$ \begin{align*} s(1+t_1)>1&\Longleftrightarrow\ s>\frac{1}{1+t_1}\Longleftrightarrow\ 1-\frac{t_1}{2+t_2}>\frac{1}{1+t_1}\\ &\Longleftrightarrow\ \frac{t_1}{1+t_1}>\frac{t_1}{2+t_2}\Longleftrightarrow\ 2+t_2>1+t_1\\ &\Longleftrightarrow\ 1+t_2>t_1. \end{align*} $$
The last inequality is clearly true since we are in the case that
$$ \begin{align*} t_1\le t_2+\frac{t_2}{1+t_2}. \end{align*} $$
Now we search an upper bound of the dimension of
$\mathcal {G}$
. Still due to the limsup nature, there is a natural cover of
$\mathcal {G}$
. For any
$a_1,\ldots , a_n\in \mathbb N$
, define
$$ \begin{align*} J_n(a_1,\ldots,a_n)=\bigcup_{a_{n+1}\ge q_n^{t_1}/a_n}I_{n+1}(a_1,\ldots, a_n, a_{n+1}), \end{align*} $$
which is of length
$$ \begin{align*} |J_n(a_1,\ldots,a_n)|\asymp \frac{a_n}{q_n^{2+t_1}}\asymp\frac{1}{q_{n-1}^{2+t_1}a_n^{1+t_1}}. \end{align*} $$
It is clear that
$$ \begin{align*} \mathcal{G}=\bigcup_{N=1}^{\infty}\bigcup_{n=N}^{\infty}\bigcup_{a_1,\ldots,a_{n-1}\in \mathbb N}\bigcup_{a_n\ge q_{n-1}^{\alpha_1}}J_n(a_1,\ldots,a_n). \end{align*} $$
Thus, the s-dimensional Hausdorff measure of
$\mathcal {G}$
can be estimated as
$$ \begin{align*} \mathcal{H}^s(\mathcal{G})&\le \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\sum_{a_n\ge q_{n-1}^{\alpha_1}}\bigg(\frac{1}{q_{n-1}^{2+t_1}a_n^{1+t_1}}\bigg)^s\\ &\ll \liminf_{N\to\infty}\sum_{n=N}^{\infty}\sum_{a_1,\ldots,a_{n-1}}\bigg(\frac{1}{q_{n-1}^{2+t_1}}\bigg)^s\bigg(\frac{1}{q_{n-1}^{\alpha_1[(1+t_1)s-1]}}\bigg), \end{align*} $$
where we used the fact that
$s(1+t_1)>1$
. The above series converges if
$$ \begin{align*} (2+t_1)s+\alpha_1[(1+t_1)s-1]>2&\Longleftrightarrow\ (2+t_1)s+\alpha_1(1+t_1)s>\alpha_1+2\\ &\Longleftrightarrow\ s>\frac{\alpha_1+2}{2+t_1+\alpha_1(1+t_1)}.\end{align*} $$
Substituting the choice of
$\alpha _1$
into the last term gives that
$$ \begin{align*} \frac{\alpha_1+2}{2+t_1+\alpha_1(1+t_1)}&=\frac{({t_1-t_2})/({1+t_2-t_1})+2}{1+(1+t_1)(1+\alpha_1)}=\frac{({1}/({1+t_2-t_1}))+1}{1+(1+t_1)\frac{1}{1+t_2-t_1}}\\ &=\frac{2+t_2-t_1}{1+t_2-t_1+1+t_1}=\frac{2+t_2-t_1}{2+t_2}\\ &=1-\frac{t_1}{2+t_2}. \end{align*} $$
This is what we choose about s. As a conclusion, we have shown that
$$ \begin{align*} \dim_{\mathrm H} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)\le \dim_{\mathrm H} \mathcal{G}\le 1-\frac{t_1}{2+t_2}. \end{align*} $$
6 Hausdorff dimension of
$\mathcal {G}(t_1)\!\setminus\! \mathcal {K}(t_2)$
when
$t_1\le t_2$
-
(1) When
$t_1=t_2$
. In this case, for any
$t'$
with
$t_2+{t_2}/({1+t_2})>t'>t_1=t_2$
, we have that Thus
$$ \begin{align*}\mathcal{G}(t')\!\setminus\! \mathcal{K}(t_2)\subset \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2).\end{align*} $$
then letting
$$ \begin{align*} \dim_{\mathrm H} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)\ge 1-\frac{t'}{2+t_2}, \end{align*} $$
$t'\to t_1$
gives the lower bound. The upper bound is clear, since Thus we have
$$ \begin{align*} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)\subset \mathcal{G}(t_1). \end{align*} $$
$$ \begin{align*} \dim_{\mathrm H} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)=\frac{2}{t_1+2}. \end{align*} $$
-
(2) When
$t_1<t_2$
. Take
$t_2'=t_1$
, that is, we decrease
$t_2$
to
$t_2'$
. Then Then we are in case (1). So,
$$ \begin{align*} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2')\subset \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2). \end{align*} $$
The upper bound of the dimension is trival since it is always bounded by
$$ \begin{align*} \dim_{\mathrm H} \mathcal{G}(t_1)\!\setminus\! \mathcal{K}(t_2)\ge \frac{2}{t_1+2}. \end{align*} $$
$\dim _{\mathrm H} \mathcal {G}(t_1)$
.
7 The two examples
Assume that
$$ \begin{align*}t_1=t_2+\frac{t_2}{1+t_2}.\end{align*} $$
$\bullet $
Example 1.
$$ \begin{align*} E_1=\{x\in [0,1): a_n(x)a_{n+1}(x)&\ge q_n(x)^{t_1}, {\text{i.m.}}\ n\in \mathbb N, \\ &\ \ a_{n+1}(x)< q_n(x)^{t_2} \quad {\text{for all}} \ n\in \mathbb N \ {\text{large}}\}. \end{align*} $$
We show that
$E_1$
is an empty set. The proof is rather the same as that for case
$t_1>t_2+{t_2}/({1+t_2})$
. Let
$x\in [0,1)$
and assume that for all
$n\gg 1$
,
$a_{n+1}(x)< q_n(x)^{t_2}$
. Then
$$ \begin{align*} a_na_{n+1}<q_n^{t_1} \Longleftarrow &\ a_n(x) \cdot q_n(x)^{t_2}<q_n(x)^{t_1}\\ \Longleftarrow &\ a_n(x)<q_n(x)^{t_1-t_2}\Longleftarrow a_n(x)\le (a_n(x)q_{n-1}(x))^{t_1-t_2}\\ \Longleftarrow &\ a_n(x)^{1-(t_1-t_2)}\le q_{n-1}(x)^{t_1-t_2}\Longleftarrow q_{n-1}(x)^{t_2(1-t_1+t_2)}\le (q_{n-1}(x))^{t_1-t_2}\\ \Longleftarrow &\ 1\le 1 \end{align*} $$
by noticing that
$$ \begin{align*} t_2(1-t_1+t_2)=t_1-t_2\Leftrightarrow t_1=t_2+\frac{t_2}{1+t_2}. \end{align*} $$
$\bullet $
Example 2.
$$ \begin{align*} E_2=\{x\in [0,1): a_n(x)a_{n+1}(x)&\ge 4^{-t_1}q_n(x)^{t_1}, {{\text{i.m.}}}\ n\in \mathbb N, \\ &\ \ a_{n+1}(x)\le 3q_n(x)^{t_2}, {\text{ for all}} \ n\in \mathbb N \ {\text{large}}\}. \end{align*} $$
Choose
$\alpha _2=t_2$
and
$\alpha _1$
such that
$\alpha _2=t_1-{\alpha _1}/({1+\alpha _1})$
(in fact,
$\alpha _1=t_2$
too). Then consider the set
$$ \begin{align*} F:= \{x: q_{n-1}(x)^{\alpha_1}\le a_n(x)<2 q_{n-1}(x)^{\alpha_1}, &\ q_n(x)^{\alpha_2} \le a_{n+1}(x)< 2q_n(x)^{\alpha_2}, {\text{i.m.}} \ n\in \mathbb N;\\ &\ {\text{and}}\ 1 \le a_n(x)\le M \ {\text{for all other}}\ n\in \mathbb N\}. \end{align*} $$
We show that F is a subset of
$E_2$
. Let
$x\in F$
. At first,
$$ \begin{align*} q_n(x)\le 2a_n(x) q_{n-1}(x)\le 4q_{n-1}(x)^{1+\alpha_1}\Longrightarrow q_{n-1}(x)\ge (q_n(x)/4)^{{1}/({1+\alpha_1})}. \end{align*} $$
Therefore,
-
• the first requirement in
$E_2$
:
$$ \begin{align*} a_n(x)a_{n+1}(x)&\ge q_{n-1}(x)^{\alpha_1}q_n(x)^{\alpha_2}\ge \bigg(\frac{q_n(x)}{4}\bigg)^{{\alpha_1}/({1+\alpha_1})}\cdot q_n(x)^{\alpha_2}\\ &\ge \bigg(\frac{q_n(x)}{4}\bigg)^{\alpha_2+{\alpha_1}/({1+\alpha_1})}=4^{-t_1}q_n(x)^{t_1}. \end{align*} $$
-
• The second requirement in
$E_2$
: the relation between
$t_1$
and
$t_2$
and the choice of
$\alpha _1, \alpha _2$
yield that
$\alpha _1=\alpha _2=t_2$
. So it is clear
$$ \begin{align*} a_{n+1}(x)<2q_n(x)^{\alpha_2}\le 3 q_n(x)^{t_2}, \ \ a_n(x)< 2q_{n-1}(x)^{\alpha_1}\le 3 q_{n-1}(x)^{t_2}. \end{align*} $$
This means that F is a subset of E, so we have that
$$ \begin{align*} \dim_{\mathrm H} E\ge 1-\frac{t_1}{2+t_2}. \end{align*} $$
The upper bound of the dimension of
$E_2$
is clear by the result for the case
$t_1<t_2+{t_2}/({1+t_2})$
, since
$E_2$
is enlarged if we decrease the value of
$t_1$
.
Acknowledgements
The authors show their sincere appreciations to the referee for careful reading and helpful comments. This work is supported by NSFC of China (No.11831007, 11871208).
