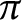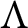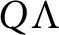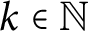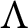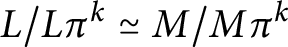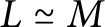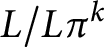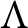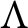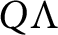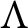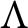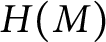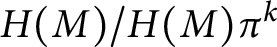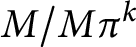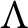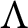1 Introduction
Let R be a discrete valuation domain with maximal ideal generated by
![]() $\pi $
and field of fractions Q. Let
$\pi $
and field of fractions Q. Let
![]() $\Lambda $
be an order over R (i.e., an R-algebra that is finitely generated and projective as an R-module) such that
$\Lambda $
be an order over R (i.e., an R-algebra that is finitely generated and projective as an R-module) such that
![]() $Q\Lambda $
is a separable Q-algebra. For example,
$Q\Lambda $
is a separable Q-algebra. For example,
![]() $\Lambda =RG$
, where G is a finite group and R is a discrete valuation domain whose field of fractions is characteristic zero. Maranda’s theorem (see [Reference Maranda13], [Reference Curtis and Reiner5, Theorem 30.14]) states that there exists
$\Lambda =RG$
, where G is a finite group and R is a discrete valuation domain whose field of fractions is characteristic zero. Maranda’s theorem (see [Reference Maranda13], [Reference Curtis and Reiner5, Theorem 30.14]) states that there exists
![]() $k_0\in \mathbb {N}$
such that for all
$k_0\in \mathbb {N}$
such that for all
![]() $k\geq k_0+1$
and
$k\geq k_0+1$
and
![]() $\Lambda $
-lattices
$\Lambda $
-lattices
![]() $L,M$
,
$L,M$
,
![]() $L/L\pi ^k\cong M/M\pi ^k$
implies
$L/L\pi ^k\cong M/M\pi ^k$
implies
![]() $L\cong M$
and if R is complete then L indecomposable implies
$L\cong M$
and if R is complete then L indecomposable implies
![]() $L/L\pi ^k$
is indecomposable.
$L/L\pi ^k$
is indecomposable.
For any
![]() $M\in \textrm {Mod}\text {-}\Lambda $
,
$M\in \textrm {Mod}\text {-}\Lambda $
,
![]() $M/M\pi ^k$
may be naturally viewed as a module over the
$M/M\pi ^k$
may be naturally viewed as a module over the
![]() $R/R\pi ^k$
-Artin algebra
$R/R\pi ^k$
-Artin algebra
![]() $\Lambda _k:=\Lambda /\Lambda \pi ^k$
. In this paper, we study the functor from the category of R-torsion-free
$\Lambda _k:=\Lambda /\Lambda \pi ^k$
. In this paper, we study the functor from the category of R-torsion-free
![]() $\Lambda $
-modules to the category of
$\Lambda $
-modules to the category of
![]() $\Lambda _k$
-modules which sends M to
$\Lambda _k$
-modules which sends M to
![]() $M/M\pi ^k$
for k sufficiently large. In particular, in Section 3, we extend Maranda’s theorem to a class of R-reduced R-torsion-free pure-injective
$M/M\pi ^k$
for k sufficiently large. In particular, in Section 3, we extend Maranda’s theorem to a class of R-reduced R-torsion-free pure-injective
![]() $\Lambda $
-modules and show that this functor preserves pure-injective hulls.
$\Lambda $
-modules and show that this functor preserves pure-injective hulls.
Pure-injective modules generalize injective modules, and they are “injective relative to pure embeddings.” They correspond, via the tensor embedding, exactly to the injective objects in the category of additive functors from the category of finitely presented modules to abelian groups. Topologically, they are characterized as direct summands of compact Hausdorff modules. Pure-injective modules play a prominent role in the model theory of modules because every module is an elementary substructure of its pure-injective hull. Every module is elementarily equivalent to a direct sum of indecomposable pure-injective modules, so the indecomposable pure-injective modules may be viewed as the building blocks of the module category up to elementary equivalence.
The set of isomorphism types of (right) indecomposable pure-injective modules over a ring S is equipped with the topology whose closed sets correspond to definable subcategories of
![]() $\textrm {Mod}\text {-}S$
. The resulting space is called the (right) Ziegler spectrum
$\textrm {Mod}\text {-}S$
. The resulting space is called the (right) Ziegler spectrum
![]() $\textrm {Zg}_S$
of S. This space captures the majority of model-theoretic information about
$\textrm {Zg}_S$
of S. This space captures the majority of model-theoretic information about
![]() $\textrm {Mod}\text {-}S$
.
$\textrm {Mod}\text {-}S$
.
From the perspective of model theory of modules, the natural nonfinitely-presented generalization of a
![]() $\Lambda $
-lattice is an R-torsion-free
$\Lambda $
-lattice is an R-torsion-free
![]() $\Lambda $
-module. This is because the smallest definable subcategory of
$\Lambda $
-module. This is because the smallest definable subcategory of
![]() $\textrm {Mod}\text {-}\Lambda $
containing all (right)
$\textrm {Mod}\text {-}\Lambda $
containing all (right)
![]() $\Lambda $
-lattices is exactly the category,
$\Lambda $
-lattices is exactly the category,
![]() $\text {Tf}_\Lambda $
, of (right) R-torsion-free
$\text {Tf}_\Lambda $
, of (right) R-torsion-free
![]() $\Lambda $
-modules. We write
$\Lambda $
-modules. We write
![]() ${_\Lambda }\text {Tf}$
for the category of R-torsion-free left
${_\Lambda }\text {Tf}$
for the category of R-torsion-free left
![]() $\Lambda $
-modules. Furthermore, the closed set of indecomposable pure-injective modules which are R-torsion-free is called the torsion-free part of the Ziegler spectrum of
$\Lambda $
-modules. Furthermore, the closed set of indecomposable pure-injective modules which are R-torsion-free is called the torsion-free part of the Ziegler spectrum of
![]() $\Lambda $
and is denoted by
$\Lambda $
and is denoted by
 $\textrm {Zg}_\Lambda ^{tf}$
. (This space is studied in [Reference Gregory, L’Innocente and Toffalori8, Reference Marcja, Prest and Toffalori14, Reference Puninski and Toffalori20].)
$\textrm {Zg}_\Lambda ^{tf}$
. (This space is studied in [Reference Gregory, L’Innocente and Toffalori8, Reference Marcja, Prest and Toffalori14, Reference Puninski and Toffalori20].)
An alternative nonfinitely-presented version of a
![]() $\Lambda $
-lattice, the generalized lattice, was introduced in [Reference Butler, Campbell and Kovács4] and further studied in [Reference Příhoda and Puninski19, Reference Rump23].
$\Lambda $
-lattice, the generalized lattice, was introduced in [Reference Butler, Campbell and Kovács4] and further studied in [Reference Příhoda and Puninski19, Reference Rump23].
We must exclude the R-divisible R-torsion-free
![]() $\Lambda $
-modules from our generalization of Maranda’s theorem because if D is divisible then
$\Lambda $
-modules from our generalization of Maranda’s theorem because if D is divisible then
![]() $D/D\pi ^k=0$
. However, every R-torsion-free
$D/D\pi ^k=0$
. However, every R-torsion-free
![]() $\Lambda $
-module decomposes as a direct sum
$\Lambda $
-module decomposes as a direct sum
![]() $D\oplus N$
of an R-divisible module D and an R-reduced module N, i.e.,
$D\oplus N$
of an R-divisible module D and an R-reduced module N, i.e.,
![]() $\bigcap _{i\in \mathbb {N}}N\pi ^i=0$
. Thus, by restricting our generalization of Maranda’s theorem further to the class of R-reduced R-torsion-free
$\bigcap _{i\in \mathbb {N}}N\pi ^i=0$
. Thus, by restricting our generalization of Maranda’s theorem further to the class of R-reduced R-torsion-free
![]() $\Lambda $
-modules, we do not lose anything because the R-divisible R-torsion-free
$\Lambda $
-modules, we do not lose anything because the R-divisible R-torsion-free
![]() $\Lambda $
-modules are just
$\Lambda $
-modules are just
![]() $Q\Lambda $
-modules and, by assumption,
$Q\Lambda $
-modules and, by assumption,
![]() $Q\Lambda $
is semisimple.
$Q\Lambda $
is semisimple.
In Section 3, with
![]() $k_0$
as in the classical version of Maranda’s theorem, we prove the following theorems.
$k_0$
as in the classical version of Maranda’s theorem, we prove the following theorems.
Theorem 3.4 Let
![]() $M,N$
be R-torsion-free R-reduced pure-injective
$M,N$
be R-torsion-free R-reduced pure-injective
![]() $\Lambda $
-modules. If
$\Lambda $
-modules. If
![]() $M/M\pi ^k\cong N/N\pi ^k$
for some
$M/M\pi ^k\cong N/N\pi ^k$
for some
![]() $k\geq k_0+1$
, then
$k\geq k_0+1$
, then
![]() $M\cong N$
.
$M\cong N$
.
Theorem 3.5 Let
![]() $k\geq k_0+1$
. If N is an indecomposable R-torsion-free R-reduced pure-injective
$k\geq k_0+1$
. If N is an indecomposable R-torsion-free R-reduced pure-injective
![]() $\Lambda $
-module, then
$\Lambda $
-module, then
![]() $N/N\pi ^k$
is indecomposable.
$N/N\pi ^k$
is indecomposable.
Unlike in the classical version of Theorem 3.5, we do not need to assume that R is complete. However,
![]() $\Lambda $
-lattices are pure-injective if and only if R is complete. So this is not unexpected.
$\Lambda $
-lattices are pure-injective if and only if R is complete. So this is not unexpected.
Using results from [Reference Gregory, L’Innocente and Toffalori8], which are applications of Maranda’s theorem for
![]() $\Lambda $
-lattices, we get the following.
$\Lambda $
-lattices, we get the following.
Theorem 3.8 Let
![]() $k\geq k_0+1$
. Suppose that M is R-torsion-free and R-reduced. If
$k\geq k_0+1$
. Suppose that M is R-torsion-free and R-reduced. If
![]() $u:M\rightarrow H(M)$
is the pure-injective hull of M, then
$u:M\rightarrow H(M)$
is the pure-injective hull of M, then
![]() $\overline {u}:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
is the pure-injective hull of
$\overline {u}:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
is the pure-injective hull of
![]() $M/M\pi ^k$
.
$M/M\pi ^k$
.
Our proofs of these theorems and their applications rely on the fact that the functor taking
![]() $M\in \text {Tf}_\Lambda $
to
$M\in \text {Tf}_\Lambda $
to
![]() $M/M\pi ^k\in \textrm {Mod}\text {-}\Lambda /\Lambda \pi ^k$
, which, for k sufficiently large, we will refer to as Maranda’s functor, is an interpretation functor. The original definition (see Section 2) of an interpretation functor came out of the model-theoretic notion of an interpretation. However, from an algebraic perspective, interpretation functors are just additive functors which commute with direct limits and direct products.
$M/M\pi ^k\in \textrm {Mod}\text {-}\Lambda /\Lambda \pi ^k$
, which, for k sufficiently large, we will refer to as Maranda’s functor, is an interpretation functor. The original definition (see Section 2) of an interpretation functor came out of the model-theoretic notion of an interpretation. However, from an algebraic perspective, interpretation functors are just additive functors which commute with direct limits and direct products.
Thanks to Maranda’s theorem, in order to get information about the category of
![]() $\Lambda $
-lattices, we may instead study a subcategory of the category of modules over the Artin algebra
$\Lambda $
-lattices, we may instead study a subcategory of the category of modules over the Artin algebra
![]() $\Lambda /\Lambda \pi ^k$
. The drawback of both the classical version of Maranda’s theorem and our extended version is that
$\Lambda /\Lambda \pi ^k$
. The drawback of both the classical version of Maranda’s theorem and our extended version is that
![]() ${\textrm {mod}}\text {-}\Lambda _k$
, respectively,
${\textrm {mod}}\text {-}\Lambda _k$
, respectively,
![]() $\textrm {Mod}\text {-}\Lambda _k$
, is almost always significantly more complicated than the category of
$\textrm {Mod}\text {-}\Lambda _k$
, is almost always significantly more complicated than the category of
![]() $\Lambda $
-lattices, respectively,
$\Lambda $
-lattices, respectively,
![]() $\text {Tf}_\Lambda $
. For instance, the order
$\text {Tf}_\Lambda $
. For instance, the order
 $\mathbb {Z}_{(p)}C(p^2)$
is of finite lattice type (see [Reference Butler3]), but the category of
$\mathbb {Z}_{(p)}C(p^2)$
is of finite lattice type (see [Reference Butler3]), but the category of
 $\mathbb {Z}_{(p)}/p^2\mathbb {Z}_{(p)}$
-free finitely generated
$\mathbb {Z}_{(p)}/p^2\mathbb {Z}_{(p)}$
-free finitely generated
 $\mathbb {Z}_{(p)}/p^2\mathbb {Z}_{(p)}C(p^2)$
-modules is wild [Reference Bondarenko1].
$\mathbb {Z}_{(p)}/p^2\mathbb {Z}_{(p)}C(p^2)$
-modules is wild [Reference Bondarenko1].
Despite the above, we will see in Sections 4 and 5 that being able to move from
![]() $\text {Tf}_\Lambda $
to a module category over an Artin algebra has useful applications.
$\text {Tf}_\Lambda $
to a module category over an Artin algebra has useful applications.
We now describe the applications in Sections 4 and 5, which are largely independent of each other. Section 4 presents applications of Theorem 3.8 to pure-injectives and pure-injective hulls in
![]() $\text {Tf}_{\Lambda }$
. We give the following characterization of pure-injective R-torsion-free
$\text {Tf}_{\Lambda }$
. We give the following characterization of pure-injective R-torsion-free
![]() $\Lambda $
-modules.
$\Lambda $
-modules.
Theorem 4.6 Let
![]() $M\in \text {Tf}_\Lambda $
. Then M is pure-injective if and only if
$M\in \text {Tf}_\Lambda $
. Then M is pure-injective if and only if
-
(1)
 $M/M\pi ^k$
is pure-injective for all
$M/M\pi ^k$
is pure-injective for all
 $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and -
(2) M is pure-injective as an R-module.
We also give information about the pure-injective hull of an R-reduced R-torsion-free module M in terms of pure-injective hulls of
![]() $M/M\pi ^k$
for all
$M/M\pi ^k$
for all
![]() $k\geq k_0+1$
. In particular, when M is reduced, R-torsion-free, and
$k\geq k_0+1$
. In particular, when M is reduced, R-torsion-free, and
![]() $M/M\pi ^k$
is pure-injective for all
$M/M\pi ^k$
is pure-injective for all
![]() $k\in \mathbb {N}$
, we show (Theorem 4.6) that the pure-injective hull of M is the inverse limit of the
$k\in \mathbb {N}$
, we show (Theorem 4.6) that the pure-injective hull of M is the inverse limit of the
![]() $\Lambda $
-modules
$\Lambda $
-modules
![]() $M/M\pi ^k$
along the canonical projections.
$M/M\pi ^k$
along the canonical projections.
We use these results to answer the questions at the end of [Reference Puninski and Toffalori20]. In particular, we describe the pure-injective hulls of the Prüfer-like modules, denoted T in [Reference Puninski and Toffalori20]. We show that these pure-injective hulls are indecomposable and hence are points of the
 $\widehat {\mathbb {Z}_{(2)}}$
-torsion-free part of the Ziegler spectrum of the
$\widehat {\mathbb {Z}_{(2)}}$
-torsion-free part of the Ziegler spectrum of the
 $\widehat {\mathbb {Z}_{(2)}}$
-order
$\widehat {\mathbb {Z}_{(2)}}$
-order
 $\widehat {\mathbb {Z}_{(2)}}C_2\times C_2$
. As far as we are aware, until now, the only points of
$\widehat {\mathbb {Z}_{(2)}}C_2\times C_2$
. As far as we are aware, until now, the only points of
 $\textrm {Zg}_\Lambda ^{tf}$
, for any order
$\textrm {Zg}_\Lambda ^{tf}$
, for any order
![]() $\Lambda $
, which have been explicitly described as modules are
$\Lambda $
, which have been explicitly described as modules are
![]() $\widehat {\Lambda }$
-lattices, where
$\widehat {\Lambda }$
-lattices, where
![]() $\widehat {R}$
is the completion of R and
$\widehat {R}$
is the completion of R and
![]() $\widehat {\Lambda }:=\widehat {R}\otimes \Lambda $
, and the R-divisible modules, which are just the indecomposable
$\widehat {\Lambda }:=\widehat {R}\otimes \Lambda $
, and the R-divisible modules, which are just the indecomposable
![]() $Q\Lambda $
-modules.
$Q\Lambda $
-modules.
The theme of Section 5 is connections between
![]() $\text {Tf}_\Lambda $
and
$\text {Tf}_\Lambda $
and
![]() ${_\Lambda }\text {Tf}$
. Here, we extend our setting to include the case where R is a Dedekind domain with field of fractions Q and
${_\Lambda }\text {Tf}$
. Here, we extend our setting to include the case where R is a Dedekind domain with field of fractions Q and
![]() $\Lambda $
is an R-order such that
$\Lambda $
is an R-order such that
![]() $Q\Lambda $
is a separable Q-algebra. We write
$Q\Lambda $
is a separable Q-algebra. We write
![]() ${_S}\textrm {Zg}$
for the left Ziegler spectrum of S and
${_S}\textrm {Zg}$
for the left Ziegler spectrum of S and
![]() ${_\Lambda }\textrm {Zg}^{tf}$
for the torsion-free part of the left Ziegler spectrum of
${_\Lambda }\textrm {Zg}^{tf}$
for the torsion-free part of the left Ziegler spectrum of
![]() $\Lambda $
.
$\Lambda $
.
Herzog [Reference Herzog9] showed that for any ring S, the lattice of open subsets of
![]() $\textrm {Zg}_S$
and the lattice of open subsets of
$\textrm {Zg}_S$
and the lattice of open subsets of
![]() ${_S}\textrm {Zg}$
are isomorphic. Applying Herzog’s result directly to
${_S}\textrm {Zg}$
are isomorphic. Applying Herzog’s result directly to
![]() $\textrm {Zg}_\Lambda $
shows that the lattice of open subsets of
$\textrm {Zg}_\Lambda $
shows that the lattice of open subsets of
 $\textrm {Zg}_\Lambda ^{tf}$
is isomorphic to the lattice of open subsets of the closed subset of R-divisible modules in
$\textrm {Zg}_\Lambda ^{tf}$
is isomorphic to the lattice of open subsets of the closed subset of R-divisible modules in
![]() ${_\Lambda }\textrm {Zg}$
. Despite this, we are able to show (Theorem 5.2) that the lattice of open subsets of
${_\Lambda }\textrm {Zg}$
. Despite this, we are able to show (Theorem 5.2) that the lattice of open subsets of
 $\textrm {Zg}^{tf}_\Lambda $
is also isomorphic, in a natural way, to the lattice of open subsets of
$\textrm {Zg}^{tf}_\Lambda $
is also isomorphic, in a natural way, to the lattice of open subsets of
![]() ${_\Lambda }\textrm {Zg}^{tf}$
. This is the main result of Section 5.
${_\Lambda }\textrm {Zg}^{tf}$
. This is the main result of Section 5.
We finish Section 5 by showing (Corollary 5.19) that the m-dimension of the lattice of (right) pp formulas of
![]() $\Lambda $
with respect to the theory of
$\Lambda $
with respect to the theory of
![]() $\text {Tf}_{\Lambda }$
is equal to the m-dimension of the lattice of (left) pp formulas of
$\text {Tf}_{\Lambda }$
is equal to the m-dimension of the lattice of (left) pp formulas of
![]() $\Lambda $
with respect to the theory of
$\Lambda $
with respect to the theory of
![]() ${_\Lambda }\text {Tf}$
. As a consequence, we show (Corollary 5.20) that the Krull–Gabriel dimension of
${_\Lambda }\text {Tf}$
. As a consequence, we show (Corollary 5.20) that the Krull–Gabriel dimension of
![]() $(\text {Latt}_{\Lambda },\text {Ab})^{fp}$
is equal to the Krull–Gabriel dimension of
$(\text {Latt}_{\Lambda },\text {Ab})^{fp}$
is equal to the Krull–Gabriel dimension of
![]() $({_\Lambda }\text {Latt},\text {Ab})^{fp}$
, where
$({_\Lambda }\text {Latt},\text {Ab})^{fp}$
, where
![]() $\text {Latt}_{\Lambda }$
is the category of right
$\text {Latt}_{\Lambda }$
is the category of right
![]() $\Lambda $
-lattices and
$\Lambda $
-lattices and
![]() ${_\Lambda }\text {Latt}$
is the category of left
${_\Lambda }\text {Latt}$
is the category of left
![]() $\Lambda $
-lattices.
$\Lambda $
-lattices.
Before starting the main body of the paper, the reader should be warned that the word lattice has two meanings in this paper; the first, a particular type of
![]() $\Lambda $
-module and the second a partially ordered set with meets and joins. Since these objects are so different in character, it should not cause confusion.
$\Lambda $
-module and the second a partially ordered set with meets and joins. Since these objects are so different in character, it should not cause confusion.
2 Preliminaries
We start by introducing some notation and basic definitions relating to orders. For a general introduction to orders and their categories of lattices, we suggest [Reference Curtis and Reiner5].
Let R be a Dedekind domain. We assume throughout that R is not a field. An R-order
![]() $\Lambda $
is an R-algebra which is finitely generated and R-torsion-free as an R-module. A
$\Lambda $
is an R-algebra which is finitely generated and R-torsion-free as an R-module. A
![]() $\Lambda $
-lattice is a finitely generated
$\Lambda $
-lattice is a finitely generated
![]() $\Lambda $
-module which is R-torsion-free. We will write
$\Lambda $
-module which is R-torsion-free. We will write
![]() $\text {Latt}_\Lambda $
(respectively,
$\text {Latt}_\Lambda $
(respectively,
![]() ${_\Lambda }\text {Latt}$
) for the category of right (respectively, left)
${_\Lambda }\text {Latt}$
) for the category of right (respectively, left)
![]() $\Lambda $
-lattices and
$\Lambda $
-lattices and
![]() $\text {Tf}_\Lambda $
(respectively,
$\text {Tf}_\Lambda $
(respectively,
![]() ${_\Lambda }\text {Tf}$
) for the category of right (respectively, left) R-torsion-free modules.
${_\Lambda }\text {Tf}$
) for the category of right (respectively, left) R-torsion-free modules.
Let
![]() $\text {Max}R$
denote the set of nonzero prime ideals of R. If
$\text {Max}R$
denote the set of nonzero prime ideals of R. If
![]() $P\in \text {Max}R$
, then
$P\in \text {Max}R$
, then
![]() $\Lambda _P$
, the localization of
$\Lambda _P$
, the localization of
![]() $\Lambda $
at the multiplicative set
$\Lambda $
at the multiplicative set
![]() $R\backslash P$
, is an
$R\backslash P$
, is an
![]() $R_P$
-order. Let
$R_P$
-order. Let
![]() $\widehat {R_P}$
and
$\widehat {R_P}$
and
![]() $\widehat {\Lambda _P}$
denote the P-adic completions of
$\widehat {\Lambda _P}$
denote the P-adic completions of
![]() $R_P$
and
$R_P$
and
![]() $\Lambda _P$
, respectively. Note that
$\Lambda _P$
, respectively. Note that
![]() $\widehat {\Lambda _P}$
is an
$\widehat {\Lambda _P}$
is an
![]() $\widehat {R_P}$
-order. If
$\widehat {R_P}$
-order. If
![]() $L\in \text {Latt}_\Lambda $
and
$L\in \text {Latt}_\Lambda $
and
![]() $P\in \text {Max}R$
, then
$P\in \text {Max}R$
, then
![]() $L_P$
will denote
$L_P$
will denote
![]() $R_P\otimes _RL$
. If
$R_P\otimes _RL$
. If
![]() $L\in \text {Latt}_\Lambda $
, then
$L\in \text {Latt}_\Lambda $
, then
![]() $\widehat {L_P}$
will denote the P-adic completion of L. Note that if
$\widehat {L_P}$
will denote the P-adic completion of L. Note that if
![]() $L\in \text {Latt}_\Lambda $
, then
$L\in \text {Latt}_\Lambda $
, then
![]() $L_P$
is a
$L_P$
is a
![]() $\Lambda _P$
-lattice and
$\Lambda _P$
-lattice and
![]() $\widehat {L_P}$
is a
$\widehat {L_P}$
is a
![]() $\widehat {\Lambda _P}$
-lattice.
$\widehat {\Lambda _P}$
-lattice.
We will assume that
![]() $Q\Lambda $
is a separable Q-algebra. This is used in two principal ways: first, it is an assumption of Maranda’s theorem for lattices over orders (see [Reference Curtis and Reiner5, 30.12]), and second, it implies that for all nonzero prime ideals
$Q\Lambda $
is a separable Q-algebra. This is used in two principal ways: first, it is an assumption of Maranda’s theorem for lattices over orders (see [Reference Curtis and Reiner5, 30.12]), and second, it implies that for all nonzero prime ideals
![]() $P\lhd R$
,
$P\lhd R$
,
![]() $\widehat {Q}\widehat {\Lambda _P}=\widehat {Q}\Lambda $
is a semisimple
$\widehat {Q}\widehat {\Lambda _P}=\widehat {Q}\Lambda $
is a semisimple
![]() $\widehat {Q}$
-algebra, where
$\widehat {Q}$
-algebra, where
![]() $\widehat {Q}$
denotes the field of fractions of
$\widehat {Q}$
denotes the field of fractions of
![]() $\widehat {R_P}$
.
$\widehat {R_P}$
.
We now give a summary of the notions from model theory of modules that will be used in this paper. For a more detailed introduction, the reader is referred to [Reference Prest15, Reference Prest17].
We will write
![]() $\mathbf {x}$
for tuples of variables and likewise
$\mathbf {x}$
for tuples of variables and likewise
![]() $\mathbf {m}$
for tuples of elements in a module.
$\mathbf {m}$
for tuples of elements in a module.
Let S be a ring. A (right) pp-n-formula is a formula in the language of S-modules of the form
where A is an
![]() $(l+n)\times m$
matrix with entries from S,
$(l+n)\times m$
matrix with entries from S,
![]() $\mathbf {y}$
is an l-tuple of variables,
$\mathbf {y}$
is an l-tuple of variables,
![]() $\mathbf {x}$
is an n-tuple of variables, and
$\mathbf {x}$
is an n-tuple of variables, and
![]() $l,n,m$
are natural numbers.
$l,n,m$
are natural numbers.
If
![]() $M\in \textrm {Mod}\text {-}S$
and
$M\in \textrm {Mod}\text {-}S$
and
![]() $\phi $
is a pp-n-formula, then we write
$\phi $
is a pp-n-formula, then we write
![]() $\phi (M)$
for the solution set of
$\phi (M)$
for the solution set of
![]() $\phi $
in M. For any pp-n-formula
$\phi $
in M. For any pp-n-formula
![]() $\phi $
and S-module M,
$\phi $
and S-module M,
![]() $\phi (M)$
is an
$\phi (M)$
is an
![]() $\textrm {End}(M)$
-submodule of
$\textrm {End}(M)$
-submodule of
![]() $M^n$
under the diagonal action of
$M^n$
under the diagonal action of
![]() $\textrm {End}(M)$
on
$\textrm {End}(M)$
on
![]() $M^n$
.
$M^n$
.
After identifying (right) pp-n-formulas
![]() $\phi ,\psi $
such that
$\phi ,\psi $
such that
![]() $\phi (M)=\psi (M)$
for all
$\phi (M)=\psi (M)$
for all
![]() $M\in \textrm {Mod}\text {-}S$
, the set of pp-n-formulas becomes a lattice under inclusion of solution sets, i.e.,
$M\in \textrm {Mod}\text {-}S$
, the set of pp-n-formulas becomes a lattice under inclusion of solution sets, i.e.,
![]() $\psi \leq \phi $
if
$\psi \leq \phi $
if
![]() $\psi (M)\subseteq \psi (M)$
for all
$\psi (M)\subseteq \psi (M)$
for all
![]() $M\in \textrm {Mod}\text {-}S$
. We denote this lattice by
$M\in \textrm {Mod}\text {-}S$
. We denote this lattice by
![]() $\textrm {pp}_S^n$
and the left module version by
$\textrm {pp}_S^n$
and the left module version by
![]() ${_S}\textrm {pp}^n$
. If X is a collection of (right) S-modules, then we write
${_S}\textrm {pp}^n$
. If X is a collection of (right) S-modules, then we write
![]() $\textrm {pp}_S^nX$
for the quotient of
$\textrm {pp}_S^nX$
for the quotient of
![]() $\textrm {pp}_S^n$
under the equivalence relation
$\textrm {pp}_S^n$
under the equivalence relation
![]() $\phi \sim _{X}\psi $
if
$\phi \sim _{X}\psi $
if
![]() $\phi (M)=\psi (M)$
for all
$\phi (M)=\psi (M)$
for all
![]() $M\in X$
.
$M\in X$
.
For
![]() $\phi ,\psi \in \textrm {pp}_S^n$
, we will write
$\phi ,\psi \in \textrm {pp}_S^n$
, we will write
![]() $\phi +\psi $
for the join (least upper bound) of
$\phi +\psi $
for the join (least upper bound) of
![]() $\phi $
and
$\phi $
and
![]() $\psi $
in
$\psi $
in
![]() $\textrm {pp}_S^n$
and
$\textrm {pp}_S^n$
and
![]() $\phi \wedge \psi $
for the meet (greatest lower bound) of
$\phi \wedge \psi $
for the meet (greatest lower bound) of
![]() $\phi $
and
$\phi $
and
![]() $\psi $
in
$\psi $
in
![]() $\textrm {pp}_S^n$
. Note that, for all
$\textrm {pp}_S^n$
. Note that, for all
![]() $M\in \textrm {Mod}\text {-}S$
,
$M\in \textrm {Mod}\text {-}S$
,
![]() $(\phi +\psi )(M)=\phi (M)+\psi (M)$
and
$(\phi +\psi )(M)=\phi (M)+\psi (M)$
and
![]() $(\phi \wedge \psi )(M)=\phi (M)\cap \psi (M)$
.
$(\phi \wedge \psi )(M)=\phi (M)\cap \psi (M)$
.
A pp- n-pair, written
![]() $\phi \, / \,\psi $
, is a pair of pp-n-formulas
$\phi \, / \,\psi $
, is a pair of pp-n-formulas
![]() $\phi ,\psi $
such that
$\phi ,\psi $
such that
![]() $\phi (M)\supseteq \psi (M)$
for all S-modules M. If
$\phi (M)\supseteq \psi (M)$
for all S-modules M. If
![]() $\phi \, / \,\psi $
is a pp-n-pair, then we write
$\phi \, / \,\psi $
is a pp-n-pair, then we write
![]() $[\psi ,\phi ]$
for the interval in
$[\psi ,\phi ]$
for the interval in
![]() $\textrm {pp}_S^n$
, that is, the set of
$\textrm {pp}_S^n$
, that is, the set of
![]() $\sigma \in \textrm {pp}_S^n$
such that
$\sigma \in \textrm {pp}_S^n$
such that
![]() $\psi \leq \sigma \leq \phi $
. If X is a collection of (right) S-modules, we will write
$\psi \leq \sigma \leq \phi $
. If X is a collection of (right) S-modules, we will write
![]() $[\psi ,\phi ]_X$
for the corresponding interval in
$[\psi ,\phi ]_X$
for the corresponding interval in
![]() $\textrm {pp}_S^nX$
.
$\textrm {pp}_S^nX$
.
If
![]() $\mathbf {m}$
is an n-tuple of elements from a module M, then the pp-type of
$\mathbf {m}$
is an n-tuple of elements from a module M, then the pp-type of
![]() $\mathbf {m}$
is the set of pp-n-formulas
$\mathbf {m}$
is the set of pp-n-formulas
![]() $\phi $
such that
$\phi $
such that
![]() $\mathbf {m}\in \phi (M)$
. If
$\mathbf {m}\in \phi (M)$
. If
![]() $M\in {\textrm {mod}}\text {-}S$
and
$M\in {\textrm {mod}}\text {-}S$
and
![]() $\mathbf {m}$
is an n-tuple of elements from M, then [Reference Prest17, Lemma 1.2.6] there exists
$\mathbf {m}$
is an n-tuple of elements from M, then [Reference Prest17, Lemma 1.2.6] there exists
![]() $\phi \in \textrm {pp}_S^n$
such that
$\phi \in \textrm {pp}_S^n$
such that
![]() $\psi $
is in the pp-type of
$\psi $
is in the pp-type of
![]() $\mathbf {m}$
if and only if
$\mathbf {m}$
if and only if
![]() $\psi \geq \phi $
. In this case, we say that
$\psi \geq \phi $
. In this case, we say that
![]() $\phi $
generates the pp-type of
$\phi $
generates the pp-type of
![]() $\mathbf {m}$
.
$\mathbf {m}$
.
For each
![]() $n\in \mathbb {N}$
, Prest defined a lattice anti-isomorphism
$n\in \mathbb {N}$
, Prest defined a lattice anti-isomorphism
![]() $D:\textrm {pp}_S^n\rightarrow {_S}\textrm {pp}^n$
(see [Reference Prest15, Theorem 8.21], [Reference Prest17, Section 1.3.1]). As is standard, we denote its inverse
$D:\textrm {pp}_S^n\rightarrow {_S}\textrm {pp}^n$
(see [Reference Prest15, Theorem 8.21], [Reference Prest17, Section 1.3.1]). As is standard, we denote its inverse
![]() ${_S}\textrm {pp}^n\rightarrow \textrm {pp}_S^n$
also by D. Apart from the fact that for
${_S}\textrm {pp}^n\rightarrow \textrm {pp}_S^n$
also by D. Apart from the fact that for
![]() $a\in S$
,
$a\in S$
,
![]() $D(xa=0)$
is
$D(xa=0)$
is
![]() $a|x$
and
$a|x$
and
![]() $D(a|x)$
is
$D(a|x)$
is
![]() $ax=0$
, we will not need to explicitly take the dual of a pp formula here, so we will not give its definition.
$ax=0$
, we will not need to explicitly take the dual of a pp formula here, so we will not give its definition.
An embedding
![]() $f:M\rightarrow N$
is a pure-embedding if for all
$f:M\rightarrow N$
is a pure-embedding if for all
![]() $\phi \in \textrm {pp}_S^1$
,
$\phi \in \textrm {pp}_S^1$
,
![]() $\phi (N)\cap f(M)=f(\phi (M))$
. Equivalently, for all
$\phi (N)\cap f(M)=f(\phi (M))$
. Equivalently, for all
![]() $L\in S\text {-}{\textrm {mod}}$
,
$L\in S\text {-}{\textrm {mod}}$
,
![]() $f\otimes -: M\otimes L\rightarrow N\otimes L$
is an embedding. We say N is pure-injective if every pure-embedding
$f\otimes -: M\otimes L\rightarrow N\otimes L$
is an embedding. We say N is pure-injective if every pure-embedding
![]() $g:N\rightarrow M$
is a split embedding. Equivalently, N is pure-injective if and only if it is algebraically compact [Reference Prest17, Theorem 4.3.11]. That is, for all
$g:N\rightarrow M$
is a split embedding. Equivalently, N is pure-injective if and only if it is algebraically compact [Reference Prest17, Theorem 4.3.11]. That is, for all
![]() $n\in \mathbb {N}$
, if for each
$n\in \mathbb {N}$
, if for each
![]() $i\in \mathcal {I}$
,
$i\in \mathcal {I}$
,
![]() $\mathbf {a_i}\in N$
is an n-tuple and
$\mathbf {a_i}\in N$
is an n-tuple and
![]() $\phi _i$
is a pp-n-formula, then
$\phi _i$
is a pp-n-formula, then
![]() $\bigcap _{i\in \mathcal {I}}\mathbf {a_i}+\phi _i(N)=\emptyset $
implies there is some finite subset
$\bigcap _{i\in \mathcal {I}}\mathbf {a_i}+\phi _i(N)=\emptyset $
implies there is some finite subset
![]() $\mathcal {I}'$
of
$\mathcal {I}'$
of
![]() $\mathcal {I}$
with
$\mathcal {I}$
with
![]() $\bigcap _{i\in \mathcal {I}'}\mathbf {a_i}+\phi _i(N)=\emptyset $
.
$\bigcap _{i\in \mathcal {I}'}\mathbf {a_i}+\phi _i(N)=\emptyset $
.
We will write
![]() $\textrm {pinj}_S$
(respectively,
$\textrm {pinj}_S$
(respectively,
![]() ${_S}\textrm {pinj}$
) for the set of (isomorphism types of) indecomposable pure-injective right (respectively, left) S-modules.
${_S}\textrm {pinj}$
) for the set of (isomorphism types of) indecomposable pure-injective right (respectively, left) S-modules.
We say a pure-embedding
![]() $i:M\rightarrow N$
with N pure-injective is a pure-injective hull of M if for every other pure-embedding
$i:M\rightarrow N$
with N pure-injective is a pure-injective hull of M if for every other pure-embedding
![]() $g:M\rightarrow K$
where K is pure-injective, there is a pure-embedding
$g:M\rightarrow K$
where K is pure-injective, there is a pure-embedding
![]() $h:N\rightarrow K$
such that
$h:N\rightarrow K$
such that
![]() $hi=g$
. The pure-injective hull of M is unique up to isomorphism over M, and we will write
$hi=g$
. The pure-injective hull of M is unique up to isomorphism over M, and we will write
![]() $H(M)$
for any module N such that the inclusion of M in N is a pure-injective hull of M.
$H(M)$
for any module N such that the inclusion of M in N is a pure-injective hull of M.
The following lemma will be used in Section 5. Its proof is exactly as in [Reference Marcja, Prest and Toffalori14, Lemma 3.1].
Lemma 2.1 Let M be a
![]() $\Lambda $
-lattice. The pure-injective hull of M is isomorphic to
$\Lambda $
-lattice. The pure-injective hull of M is isomorphic to
![]() $\prod _{P\in \text {Max}R}\widehat {M_P}$
.
$\prod _{P\in \text {Max}R}\widehat {M_P}$
.
A full subcategory of a module category
![]() $\textrm {Mod}\text {-}S$
is a definable subcategory if it satisfies the equivalent conditions in the following theorem.
$\textrm {Mod}\text {-}S$
is a definable subcategory if it satisfies the equivalent conditions in the following theorem.
Theorem 2.2 [Reference Prest17, Theorem 3.4.7]
The following statements are equivalent for
![]() $\mathcal {X}$
a full subcategory of
$\mathcal {X}$
a full subcategory of
![]() $\textrm {Mod}\text {-}S$
.
$\textrm {Mod}\text {-}S$
.
-
(1) There exists a set of pp-pairs
 $\{\phi _i/\psi _i\ \vert \ i\in I\}$
such that
$\{\phi _i/\psi _i\ \vert \ i\in I\}$
such that
 $M\in \mathcal {X}$
if and only if
$M\in \mathcal {X}$
if and only if
 $\phi _i(M)=\psi _i(M)$
for all
$\phi _i(M)=\psi _i(M)$
for all
 $i\in I$
.
$i\in I$
. -
(2)
 $\mathcal {X}$
is closed under direct products, direct limits, and pure submodules.
$\mathcal {X}$
is closed under direct products, direct limits, and pure submodules. -
(3)
 $\mathcal {X}$
is closed under direct products, reduced products, and pure submodules.
$\mathcal {X}$
is closed under direct products, reduced products, and pure submodules. -
(4)
 $\mathcal {X}$
is closed under direct products, ultrapowers, and pure submodules.
$\mathcal {X}$
is closed under direct products, ultrapowers, and pure submodules.
For an R-order
![]() $\Lambda $
, a particularly important definable subcategory is,
$\Lambda $
, a particularly important definable subcategory is,
![]() $\text {Tf}_\Lambda $
, the class of all R-torsion-free
$\text {Tf}_\Lambda $
, the class of all R-torsion-free
![]() $\Lambda $
-modules. It is the class of
$\Lambda $
-modules. It is the class of
![]() $\Lambda $
-modules such that for all nonzero
$\Lambda $
-modules such that for all nonzero
![]() $r\in R$
, the solution set of
$r\in R$
, the solution set of
![]() $xr=0$
in M is equal to the solution set of
$xr=0$
in M is equal to the solution set of
![]() $x=0$
in M.
$x=0$
in M.
Given a class of modules
![]() $\mathcal {C}$
, let
$\mathcal {C}$
, let
![]() $\langle \mathcal {C}\rangle $
denote the smallest definable subcategory containing
$\langle \mathcal {C}\rangle $
denote the smallest definable subcategory containing
![]() $\mathcal {C}$
. Since all modules in
$\mathcal {C}$
. Since all modules in
![]() $\text {Tf}_\Lambda $
are direct unions of their finitely generated submodules and a finitely generated R-torsion-free module is a
$\text {Tf}_\Lambda $
are direct unions of their finitely generated submodules and a finitely generated R-torsion-free module is a
![]() $\Lambda $
-lattice,
$\Lambda $
-lattice,
![]() $\langle \text {Latt}_\Lambda \rangle =\text {Tf}_\Lambda $
.
$\langle \text {Latt}_\Lambda \rangle =\text {Tf}_\Lambda $
.
If
![]() $\mathcal {C}\subseteq \textrm {Mod}\text {-}S$
, then we will write
$\mathcal {C}\subseteq \textrm {Mod}\text {-}S$
, then we will write
![]() $\textrm {pinj}(\mathcal {C})$
for the set of (isomorphism types of) indecomposable pure-injective S-modules contained in
$\textrm {pinj}(\mathcal {C})$
for the set of (isomorphism types of) indecomposable pure-injective S-modules contained in
![]() $\mathcal {C}$
. By [Reference Prest17, Corollary 5.1.4], definable subcategories of
$\mathcal {C}$
. By [Reference Prest17, Corollary 5.1.4], definable subcategories of
![]() $\textrm {Mod}\text {-}S$
are determined by the indecomposable pure-injective S-modules they contain, i.e.,
$\textrm {Mod}\text {-}S$
are determined by the indecomposable pure-injective S-modules they contain, i.e.,
![]() $\mathcal {C}=\langle \textrm {pinj}(\mathcal {C})\rangle $
.
$\mathcal {C}=\langle \textrm {pinj}(\mathcal {C})\rangle $
.
The (right) Ziegler spectrum of a ring S, denoted
![]() $\textrm {Zg}_S$
, is a topological space whose points are isomorphism classes of indecomposable pure-injective (right) S-modules and which has a basis of open sets given by
$\textrm {Zg}_S$
, is a topological space whose points are isomorphism classes of indecomposable pure-injective (right) S-modules and which has a basis of open sets given by
where
![]() $\varphi ,\psi $
range over (right) pp-
$\varphi ,\psi $
range over (right) pp-
![]() $1$
-formulas. We write
$1$
-formulas. We write
![]() ${_S}\textrm {Zg}$
for the left Ziegler spectrum of S.
${_S}\textrm {Zg}$
for the left Ziegler spectrum of S.
The sets
![]() $(\phi \, / \,\psi )$
are compact, in particular,
$(\phi \, / \,\psi )$
are compact, in particular,
![]() $\textrm {Zg}_S$
is compact.
$\textrm {Zg}_S$
is compact.
From (i) of Theorem 2.2, it is clear that if
![]() $\mathcal {X}$
is a definable subcategory of
$\mathcal {X}$
is a definable subcategory of
![]() $\textrm {Mod}\text {-}S$
, then
$\textrm {Mod}\text {-}S$
, then
![]() $\mathcal {X}\cap \textrm {pinj}_S$
is a closed subset of
$\mathcal {X}\cap \textrm {pinj}_S$
is a closed subset of
![]() $\textrm {Zg}_S$
and that all closed subsets of
$\textrm {Zg}_S$
and that all closed subsets of
![]() $\textrm {Zg}_S$
arise in this way. Since definable subcategories are determined by the indecomposable pure-injective modules they contain, if
$\textrm {Zg}_S$
arise in this way. Since definable subcategories are determined by the indecomposable pure-injective modules they contain, if
![]() $\mathcal {X},\mathcal {Y}$
definable subcategories of
$\mathcal {X},\mathcal {Y}$
definable subcategories of
![]() $\textrm {Mod}\text {-}S$
, then
$\textrm {Mod}\text {-}S$
, then
![]() $\mathcal {X}\cap \textrm {Zg}_S=\mathcal {Y}\cap \textrm {Zg}_S$
if and only if
$\mathcal {X}\cap \textrm {Zg}_S=\mathcal {Y}\cap \textrm {Zg}_S$
if and only if
![]() $\mathcal {X}=\mathcal {Y}$
. Thus, there is an inclusion preserving correspondence between the closed subsets of
$\mathcal {X}=\mathcal {Y}$
. Thus, there is an inclusion preserving correspondence between the closed subsets of
![]() $\textrm {Zg}_S$
and the definable subcategories of
$\textrm {Zg}_S$
and the definable subcategories of
![]() $\textrm {Mod}\text {-}S$
. If
$\textrm {Mod}\text {-}S$
. If
![]() $\mathcal {X}$
is a definable subcategory of
$\mathcal {X}$
is a definable subcategory of
![]() $\textrm {Mod}\text {-}S$
, then we will write
$\textrm {Mod}\text {-}S$
, then we will write
![]() $\textrm {Zg}(\mathcal {X})$
for the Ziegler spectrum of
$\textrm {Zg}(\mathcal {X})$
for the Ziegler spectrum of
![]() $\mathcal {X}$
, that is,
$\mathcal {X}$
, that is,
![]() $\mathcal {X}\cap \textrm {Zg}_S$
with the topology inherited from
$\mathcal {X}\cap \textrm {Zg}_S$
with the topology inherited from
![]() $\textrm {Zg}_S$
. When
$\textrm {Zg}_S$
. When
![]() $\Lambda $
is an R-order, we will write
$\Lambda $
is an R-order, we will write
 $\textrm {Zg}_\Lambda ^{tf}$
(respectively,
$\textrm {Zg}_\Lambda ^{tf}$
(respectively,
![]() ${_\Lambda }\textrm {Zg}^{tf}$
) for
${_\Lambda }\textrm {Zg}^{tf}$
) for
![]() $\textrm {Zg}(\text {Tf}_\Lambda )$
(respectively,
$\textrm {Zg}(\text {Tf}_\Lambda )$
(respectively,
![]() $\textrm {Zg}({_\Lambda }\text {Tf})$
).
$\textrm {Zg}({_\Lambda }\text {Tf})$
).
We finish this section by introducing interpretation functors and proving a result about them which we will need in Section 5.
Let
![]() $\mathcal {C}\subseteq \textrm {Mod}\text {-}S$
and
$\mathcal {C}\subseteq \textrm {Mod}\text {-}S$
and
![]() $\mathcal {D}\subseteq \textrm {Mod}\text {-}T$
be definable subcategories. Let
$\mathcal {D}\subseteq \textrm {Mod}\text {-}T$
be definable subcategories. Let
![]() $\phi /\psi $
be a pp-m-pair over S and for each
$\phi /\psi $
be a pp-m-pair over S and for each
![]() $t\in T$
, let
$t\in T$
, let
![]() $\rho _t(\overline {x},\overline {y})$
be a pp-
$\rho _t(\overline {x},\overline {y})$
be a pp-
![]() $2m$
-formula such that for each
$2m$
-formula such that for each
![]() $M\in \mathcal {C}$
, the solution set
$M\in \mathcal {C}$
, the solution set
![]() $\rho _t(M,M)\subseteq M^m\times M^m$
defines an endomorphism
$\rho _t(M,M)\subseteq M^m\times M^m$
defines an endomorphism
![]() $\rho _t^M$
of the abelian group
$\rho _t^M$
of the abelian group
![]() $\phi (M)/\psi (M)$
and such that
$\phi (M)/\psi (M)$
and such that
![]() $\phi (M)/\psi (M)$
is a T-module in
$\phi (M)/\psi (M)$
is a T-module in
![]() $\mathcal {D}$
when for all
$\mathcal {D}$
when for all
![]() $t\in T$
, the action of t on
$t\in T$
, the action of t on
![]() $\phi (M)/\psi (M)$
is given by
$\phi (M)/\psi (M)$
is given by
![]() $\rho ^M_t$
. In this situation,
$\rho ^M_t$
. In this situation,
![]() $(\phi /\psi ;(\rho _t)_{t\in T})$
defines an additive functor
$(\phi /\psi ;(\rho _t)_{t\in T})$
defines an additive functor
![]() $I:\mathcal {C}\rightarrow \mathcal {D}$
. Following [Reference Prest16], we call any functor equivalent to one defined in this way an interpretation functor.
$I:\mathcal {C}\rightarrow \mathcal {D}$
. Following [Reference Prest16], we call any functor equivalent to one defined in this way an interpretation functor.
From the definition, it is clear that for
![]() $k\in \mathbb {N}$
, the functor
$k\in \mathbb {N}$
, the functor
![]() $I:\text {Tf}_\Lambda \rightarrow \textrm {Mod}\text {-}\Lambda /\pi ^k\Lambda $
which sends
$I:\text {Tf}_\Lambda \rightarrow \textrm {Mod}\text {-}\Lambda /\pi ^k\Lambda $
which sends
![]() $M\in \text {Tf}_\Lambda $
to
$M\in \text {Tf}_\Lambda $
to
![]() $M/M\pi ^k$
is an interpretation functor. We will consider another interpretation functor, Butler’s functor, at the end of Section 4.
$M/M\pi ^k$
is an interpretation functor. We will consider another interpretation functor, Butler’s functor, at the end of Section 4.
The following theorem, due to Prest in full generality and Krause in a special case, gives a completely algebraic characterization of interpretation functors.
Theorem 2.3 [Reference Krause11, Theorem 7.2], [Reference Prest18, Corollary 25.3]
An additive functor
![]() $I:\mathcal {C}\rightarrow \mathcal {D}$
is an interpretation functor if and only if it commutes with direct products and direct limits.
$I:\mathcal {C}\rightarrow \mathcal {D}$
is an interpretation functor if and only if it commutes with direct products and direct limits.
There are many ways to see that interpretation functors preserve pure-injectivity. Working with pp formulas, it is easiest to show that interpretation functors preserve algebraic compactness by translating systems of cosets of solution sets of pp formulas for
![]() $IN$
into a system of cosets of solution sets of pp formulas for N via I. For the more categorically minded, the most direct route is to use the fact [Reference Prest17, Theorem 4.3.6] that a module M is pure-injective if and only if for any cardinal
$IN$
into a system of cosets of solution sets of pp formulas for N via I. For the more categorically minded, the most direct route is to use the fact [Reference Prest17, Theorem 4.3.6] that a module M is pure-injective if and only if for any cardinal
![]() $\kappa $
, the summation map
$\kappa $
, the summation map
![]() $\Sigma _M:M^{(\kappa )}\rightarrow M$
factors through the canonical embedding of
$\Sigma _M:M^{(\kappa )}\rightarrow M$
factors through the canonical embedding of
![]() $M^{(\kappa )}$
into
$M^{(\kappa )}$
into
![]() $M^{\kappa }$
. Note that since interpretation functors are additive and commute with direct limits, they commute with infinite direct sums. One sees that
$M^{\kappa }$
. Note that since interpretation functors are additive and commute with direct limits, they commute with infinite direct sums. One sees that
![]() $I\Sigma _M$
is the summation map
$I\Sigma _M$
is the summation map
![]() $\Sigma _{IM}:IM^{(\kappa )}\rightarrow IM$
because it is the unique map which is the identity when composed with the component maps
$\Sigma _{IM}:IM^{(\kappa )}\rightarrow IM$
because it is the unique map which is the identity when composed with the component maps
![]() $IM$
into
$IM$
into
![]() $IM^{(\kappa )}$
.
$IM^{(\kappa )}$
.
Define
![]() $\ker I$
to be the definable subcategory of objects
$\ker I$
to be the definable subcategory of objects
![]() $L\in \mathcal {C}$
such that
$L\in \mathcal {C}$
such that
![]() $IL=0$
. For
$IL=0$
. For
![]() $\mathcal {D}'$
a definable subcategory of
$\mathcal {D}'$
a definable subcategory of
![]() $\mathcal {D}$
, let
$\mathcal {D}$
, let
![]() $I^{-1}\mathcal {D}'$
be the definable subcategory of objects
$I^{-1}\mathcal {D}'$
be the definable subcategory of objects
![]() $L\in \mathcal {C}$
such that
$L\in \mathcal {C}$
such that
![]() $IL\in \mathcal {D}'$
.
$IL\in \mathcal {D}'$
.
The following lemma is used in various places in the literature. It follows easily from (3) of Theorem 2.2.
Lemma 2.4 Let
![]() $I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor and
$I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor and
![]() $\mathcal {C}'$
a definable subcategory of
$\mathcal {C}'$
a definable subcategory of
![]() $\mathcal {C}$
. Then the closure of
$\mathcal {C}$
. Then the closure of
![]() $I\mathcal {C}'$
under pure-subobjects is a definable subcategory of
$I\mathcal {C}'$
under pure-subobjects is a definable subcategory of
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 2.5 Let
![]() $I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor such that for all
$I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor such that for all
![]() $N\in \textrm {pinj}(\mathcal {C})$
,
$N\in \textrm {pinj}(\mathcal {C})$
,
![]() $IN=0$
, or
$IN=0$
, or
![]() $IN\in \textrm {pinj}(\mathcal {D})$
and if
$IN\in \textrm {pinj}(\mathcal {D})$
and if
![]() $N,M\in \textrm {pinj}(\mathcal {C})$
,
$N,M\in \textrm {pinj}(\mathcal {C})$
,
![]() $IN,IM\neq 0$
, and
$IN,IM\neq 0$
, and
![]() $IN\cong IM$
, then
$IN\cong IM$
, then
![]() $N\cong M$
.
$N\cong M$
.
-
(i) If
 $\mathcal {C}'$
is a definable subcategory of
$\mathcal {C}'$
is a definable subcategory of
 $\mathcal {C}$
containing
$\mathcal {C}$
containing
 $\ker I$
, then
$\ker I$
, then
 $I^{-1}\langle I\mathcal {C}'\rangle =\mathcal {C}'$
.
$I^{-1}\langle I\mathcal {C}'\rangle =\mathcal {C}'$
. -
(ii) If
 $\mathcal {D}'$
is a definable subcategory of
$\mathcal {D}'$
is a definable subcategory of
 $\langle I\mathcal {C}\rangle $
, then
$\langle I\mathcal {C}\rangle $
, then
 $\langle I(I^{-1}\mathcal {D}')\rangle =\mathcal {D}'$
.
$\langle I(I^{-1}\mathcal {D}')\rangle =\mathcal {D}'$
.
Proof
![]() $(\mathrm{i})$
Suppose
$(\mathrm{i})$
Suppose
![]() $M\in \mathcal {C}'$
. Then
$M\in \mathcal {C}'$
. Then
![]() $IM\in \langle I\mathcal {C}' \rangle $
. So
$IM\in \langle I\mathcal {C}' \rangle $
. So
![]() $M\in I^{-1}\langle I\mathcal {C}'\rangle $
.
$M\in I^{-1}\langle I\mathcal {C}'\rangle $
.
Suppose
![]() $N\in \textrm {pinj}(\mathcal {C})$
and
$N\in \textrm {pinj}(\mathcal {C})$
and
![]() $N\in I^{-1}\langle I\mathcal {C}'\rangle $
. If
$N\in I^{-1}\langle I\mathcal {C}'\rangle $
. If
![]() $IN=0$
, then
$IN=0$
, then
![]() $N\in \mathcal {C}'$
, since
$N\in \mathcal {C}'$
, since
![]() $\ker I\subseteq \mathcal {C}'$
. So we may assume that
$\ker I\subseteq \mathcal {C}'$
. So we may assume that
![]() $IN\neq 0$
and
$IN\neq 0$
and
![]() $IN$
is a pure-subobject of
$IN$
is a pure-subobject of
![]() $IL$
for some
$IL$
for some
![]() $L\in \mathcal {C}'$
by Lemma 2.4. Since N is pure-injective, so is
$L\in \mathcal {C}'$
by Lemma 2.4. Since N is pure-injective, so is
![]() $IN$
. Hence,
$IN$
. Hence,
![]() $IN$
is a direct summand of
$IN$
is a direct summand of
![]() $IL$
. By the hypotheses on I,
$IL$
. By the hypotheses on I,
![]() $IN$
is indecomposable. So by [Reference Prest17, Proposition 18.2.24], there exists
$IN$
is indecomposable. So by [Reference Prest17, Proposition 18.2.24], there exists
![]() $L'\in \textrm {pinj}(\mathcal {C}')$
such that
$L'\in \textrm {pinj}(\mathcal {C}')$
such that
![]() $IN$
is a direct summand of
$IN$
is a direct summand of
![]() $IL'$
. By the hypothesis on I,
$IL'$
. By the hypothesis on I,
![]() $IL'$
is indecomposable and hence
$IL'$
is indecomposable and hence
![]() $IN\cong IL'$
. By the other hypothesis on I,
$IN\cong IL'$
. By the other hypothesis on I,
![]() $L'\cong N$
. Thus,
$L'\cong N$
. Thus,
![]() $N\in \mathcal {C}'$
, as required.
$N\in \mathcal {C}'$
, as required.
Since definable subcategories are determined by the indecomposable pure-injective modules they contain,
![]() $I^{-1}\langle I\mathcal {C}'\rangle \subseteq \mathcal {C}'$
.
$I^{-1}\langle I\mathcal {C}'\rangle \subseteq \mathcal {C}'$
.
![]() $(\mathrm{ii})$
Suppose
$(\mathrm{ii})$
Suppose
![]() $\mathcal {D}'$
is a definable subcategory of
$\mathcal {D}'$
is a definable subcategory of
![]() $\langle I\mathcal {C}\rangle $
. Since
$\langle I\mathcal {C}\rangle $
. Since
![]() $\mathcal {D}'$
is a definable subcategory,
$\mathcal {D}'$
is a definable subcategory,
![]() $\langle I(I^{-1}\mathcal {D}')\rangle \subseteq \mathcal {D}'$
if and only if
$\langle I(I^{-1}\mathcal {D}')\rangle \subseteq \mathcal {D}'$
if and only if
![]() $ I(I^{-1}\mathcal {D}')\subseteq \mathcal {D}'$
. Take
$ I(I^{-1}\mathcal {D}')\subseteq \mathcal {D}'$
. Take
![]() $M\in I^{-1}\mathcal {D}'$
. By definition,
$M\in I^{-1}\mathcal {D}'$
. By definition,
![]() $IM\in \mathcal {D}'$
. So
$IM\in \mathcal {D}'$
. So
![]() $ I(I^{-1}\mathcal {D}')\subseteq \mathcal {D}'$
.
$ I(I^{-1}\mathcal {D}')\subseteq \mathcal {D}'$
.
We now show that
![]() $\mathcal {D}'\subseteq \langle I(I^{-1}\mathcal {D}') \rangle $
. Suppose
$\mathcal {D}'\subseteq \langle I(I^{-1}\mathcal {D}') \rangle $
. Suppose
![]() $N\in \textrm {pinj}(\mathcal {D}')$
. Since
$N\in \textrm {pinj}(\mathcal {D}')$
. Since
![]() $\mathcal {D}'\subseteq \langle I\mathcal {C}\rangle $
, by Lemma 2.4, there exists
$\mathcal {D}'\subseteq \langle I\mathcal {C}\rangle $
, by Lemma 2.4, there exists
![]() $L\in \mathcal {C}$
such that N is pure-subobject of
$L\in \mathcal {C}$
such that N is pure-subobject of
![]() $IL$
. Thus, N is a direct summand of
$IL$
. Thus, N is a direct summand of
![]() $IL$
. By [Reference Prest17, Proposition 18.2.24], we may assume L is also indecomposable pure-injective. Thus,
$IL$
. By [Reference Prest17, Proposition 18.2.24], we may assume L is also indecomposable pure-injective. Thus,
![]() $N\cong IL$
. So
$N\cong IL$
. So
![]() $L\in I^{-1}\mathcal {D}'$
and
$L\in I^{-1}\mathcal {D}'$
and
![]() $N\cong IL\in I(I^{-1}\mathcal {D}')$
, as required.▪
$N\cong IL\in I(I^{-1}\mathcal {D}')$
, as required.▪
Corollary 2.6 Let
![]() $I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor such that for all
$I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor such that for all
![]() $N\in \textrm {pinj}(\mathcal {C})$
,
$N\in \textrm {pinj}(\mathcal {C})$
,
![]() $IN=0$
, or
$IN=0$
, or
![]() $IN\in \textrm {pinj}(\mathcal {D})$
and if
$IN\in \textrm {pinj}(\mathcal {D})$
and if
![]() $N,M\in \textrm {pinj}(\mathcal {C})$
,
$N,M\in \textrm {pinj}(\mathcal {C})$
,
![]() $IN,IM\neq 0$
, and
$IN,IM\neq 0$
, and
![]() $IN\cong IM$
, then
$IN\cong IM$
, then
![]() $N\cong M$
. The maps
$N\cong M$
. The maps
and
give a inclusion preserving bijective correspondence between definable subcategories in
![]() $\langle I\mathcal {C}\rangle $
and definable subcategories of
$\langle I\mathcal {C}\rangle $
and definable subcategories of
![]() $\mathcal {C}$
containing
$\mathcal {C}$
containing
![]() $\ker I$
.
$\ker I$
.
Proof We have shown that if
![]() $\mathcal {C}'$
is a definable subcategory of
$\mathcal {C}'$
is a definable subcategory of
![]() $\mathcal {C}$
containing
$\mathcal {C}$
containing
![]() $\ker I$
, then
$\ker I$
, then
![]() $I^{-1}\langle I\mathcal {C}'\rangle =\mathcal {C}'$
, and if
$I^{-1}\langle I\mathcal {C}'\rangle =\mathcal {C}'$
, and if
![]() $\mathcal {D}'$
is a definable subcategory of
$\mathcal {D}'$
is a definable subcategory of
![]() $\langle I\mathcal {C}'\rangle $
, then
$\langle I\mathcal {C}'\rangle $
, then
![]() $\langle I(I^{-1}\mathcal {D}')\rangle =\mathcal {D}'$
.
$\langle I(I^{-1}\mathcal {D}')\rangle =\mathcal {D}'$
.
That this correspondence is inclusion preserving follows directly from its definition.▪
The following is very close to [Reference Krause11, Theorem 7.8], [Reference Prest16, Theorem 3.19], and [Reference Prest17, Corollary 18.2.26], but our hypotheses are slightly different. This statement will be needed in Section 5.
Proposition 2.7 Let
![]() $I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor such that for all
$I:\mathcal {C}\rightarrow \mathcal {D}$
be an interpretation functor such that for all
![]() $N\in \textrm {pinj}(\mathcal {C})$
,
$N\in \textrm {pinj}(\mathcal {C})$
,
![]() $IN=0$
, or
$IN=0$
, or
![]() $IN\in \textrm {pinj}(\mathcal {D})$
and if
$IN\in \textrm {pinj}(\mathcal {D})$
and if
![]() $N,M\in \textrm {pinj}(\mathcal {C})$
,
$N,M\in \textrm {pinj}(\mathcal {C})$
,
![]() $IN,IM\neq 0$
, and
$IN,IM\neq 0$
, and
![]() $IN\cong IM$
, then
$IN\cong IM$
, then
![]() $N\cong M$
. The assignment
$N\cong M$
. The assignment
![]() $N\mapsto IN$
induces a homeomorphism between
$N\mapsto IN$
induces a homeomorphism between
![]() $\textrm {Zg}(\mathcal {C})\backslash \ker I$
and its image in
$\textrm {Zg}(\mathcal {C})\backslash \ker I$
and its image in
![]() $\textrm {Zg}(\mathcal {D})$
which is closed.
$\textrm {Zg}(\mathcal {D})$
which is closed.
Proof Suppose
![]() $L\in \langle I\mathcal {C}\rangle \cap \textrm {Zg}(\mathcal {D})$
. Then L is a pure-subobject of some
$L\in \langle I\mathcal {C}\rangle \cap \textrm {Zg}(\mathcal {D})$
. Then L is a pure-subobject of some
![]() $IN$
for some
$IN$
for some
![]() $N\in \textrm {Zg}(\mathcal {C})$
. By hypothesis on I,
$N\in \textrm {Zg}(\mathcal {C})$
. By hypothesis on I,
![]() $IN$
is indecomposable. So
$IN$
is indecomposable. So
![]() $L\cong IN$
. Thus, the closed set
$L\cong IN$
. Thus, the closed set
![]() $\langle I\mathcal {C}\rangle \cap \textrm {Zg}(\mathcal {D})$
is the image of
$\langle I\mathcal {C}\rangle \cap \textrm {Zg}(\mathcal {D})$
is the image of
![]() $\textrm {Zg}(\mathcal {C})\backslash \ker I$
under I.
$\textrm {Zg}(\mathcal {C})\backslash \ker I$
under I.
Suppose X is a closed subset of
![]() $\textrm {Zg}(\mathcal {D})$
contained in
$\textrm {Zg}(\mathcal {D})$
contained in
![]() $I\textrm {Zg}(\mathcal {C})$
. Let
$I\textrm {Zg}(\mathcal {C})$
. Let
![]() $\mathcal {X}$
be the definable subcategory of
$\mathcal {X}$
be the definable subcategory of
![]() $\mathcal {D}$
generated by X. Let
$\mathcal {D}$
generated by X. Let
![]() $\mathcal {Y}:=I^{-1}\mathcal {X}$
and
$\mathcal {Y}:=I^{-1}\mathcal {X}$
and
![]() $Y:=\mathcal {Y}\cap \textrm {Zg}(\mathcal {C})$
. Since
$Y:=\mathcal {Y}\cap \textrm {Zg}(\mathcal {C})$
. Since
![]() $\mathcal {X}\subseteq \langle I\mathcal {C}\rangle $
,
$\mathcal {X}\subseteq \langle I\mathcal {C}\rangle $
,
![]() $IL\in \mathcal {X}$
if and only if
$IL\in \mathcal {X}$
if and only if
![]() $L\in \mathcal {Y}$
by Lemma 2.5. So
$L\in \mathcal {Y}$
by Lemma 2.5. So
![]() $N\in Y$
if and only if
$N\in Y$
if and only if
![]() $IN\in X$
. Thus,
$IN\in X$
. Thus,
![]() $N\mapsto IN$
is continuous.
$N\mapsto IN$
is continuous.
Suppose Y is a closed subset of
![]() $\textrm {Zg}(\mathcal {C})$
. We may replace Y by the closed subset
$\textrm {Zg}(\mathcal {C})$
. We may replace Y by the closed subset
![]() $Y\cup (\ker I\cap \textrm {Zg}(\mathcal {C}))$
without changing its intersection with
$Y\cup (\ker I\cap \textrm {Zg}(\mathcal {C}))$
without changing its intersection with
![]() $\textrm {Zg}(\mathcal {C})\backslash \ker I$
. Let
$\textrm {Zg}(\mathcal {C})\backslash \ker I$
. Let
![]() $\mathcal {Y}$
be the definable subcategory of
$\mathcal {Y}$
be the definable subcategory of
![]() $\mathcal {C}$
generated by Y, and let
$\mathcal {C}$
generated by Y, and let
![]() $X=\langle I\mathcal {Y}\rangle \cap \textrm {Zg}(\mathcal {D})$
. Now,
$X=\langle I\mathcal {Y}\rangle \cap \textrm {Zg}(\mathcal {D})$
. Now,
![]() $N\in \mathcal {Y}$
if and only
$N\in \mathcal {Y}$
if and only
![]() $N\in I^{-1}\langle I\mathcal {Y}\rangle $
by Lemma 2.5. So
$N\in I^{-1}\langle I\mathcal {Y}\rangle $
by Lemma 2.5. So
![]() $N\in Y$
if and only if
$N\in Y$
if and only if
![]() $IN\in X$
. Thus, the inverse of
$IN\in X$
. Thus, the inverse of
![]() $N\mapsto IN$
is continuous.▪
$N\mapsto IN$
is continuous.▪
3 Maranda’s functor
Throughout this section, R will be a discrete valuation domain with field of fractions Q and maximal ideal generated by
![]() $\pi $
, and
$\pi $
, and
![]() $\Lambda $
will be an R-order such that
$\Lambda $
will be an R-order such that
![]() $Q\Lambda $
is a separable Q-algebra.
$Q\Lambda $
is a separable Q-algebra.
The basis of Maranda’s theorem is the existenceFootnote
1
of a nonnegative integer l such that for all
![]() $\Lambda $
-lattices L and M,
$\Lambda $
-lattices L and M,
Throughout this section, let
![]() $k_0$
be the smallest such nonnegative integer. We will call this natural number Maranda’s constant (for
$k_0$
be the smallest such nonnegative integer. We will call this natural number Maranda’s constant (for
![]() $\Lambda $
as an R-order).
$\Lambda $
as an R-order).
Note that since
![]() $\Lambda $
is Noetherian,
$\Lambda $
is Noetherian,
![]() $\textrm {Ext}^1(L,-)$
is finitely presented as a functor in
$\textrm {Ext}^1(L,-)$
is finitely presented as a functor in
![]() $({\textrm {mod}}\text {-}\Lambda ,\text {Ab})$
(see [Reference Prest17, Theorem 10.2.35]). Hence,
$({\textrm {mod}}\text {-}\Lambda ,\text {Ab})$
(see [Reference Prest17, Theorem 10.2.35]). Hence,
![]() $\pi ^{k_0}\textrm {Ext}^1(L,-)$
is also finitely presented. Since
$\pi ^{k_0}\textrm {Ext}^1(L,-)$
is also finitely presented. Since
![]() $\text {Tf}_{\Lambda }$
is the smallest definable subcategory containing
$\text {Tf}_{\Lambda }$
is the smallest definable subcategory containing
![]() $\text {Latt}_\Lambda $
,
$\text {Latt}_\Lambda $
,
![]() $\pi ^{k_0}\textrm {Ext}^1(L,N)=0$
for all
$\pi ^{k_0}\textrm {Ext}^1(L,N)=0$
for all
![]() $L\in \text {Latt}_\Lambda $
and
$L\in \text {Latt}_\Lambda $
and
![]() $N\in \text {Tf}_{\Lambda }$
.
$N\in \text {Tf}_{\Lambda }$
.
Throughout this section, when
![]() $k\in \mathbb {N}$
is clear from the context, for
$k\in \mathbb {N}$
is clear from the context, for
![]() $M\in \textrm {Mod}\text {-}\Lambda $
and
$M\in \textrm {Mod}\text {-}\Lambda $
and
![]() $m\in M$
, we will often write
$m\in M$
, we will often write
![]() $\overline {M}$
for
$\overline {M}$
for
![]() $M/M\pi ^k$
and
$M/M\pi ^k$
and
![]() $\overline {m}$
for
$\overline {m}$
for
![]() $m+M\pi ^k$
. If
$m+M\pi ^k$
. If
![]() $f:M\rightarrow N\in \textrm {Mod}\text {-}\Lambda $
, then we will write
$f:M\rightarrow N\in \textrm {Mod}\text {-}\Lambda $
, then we will write
![]() $\overline {f}$
for the induced homomorphism from
$\overline {f}$
for the induced homomorphism from
![]() $M/M\pi ^k$
to
$M/M\pi ^k$
to
![]() $N/N\pi ^k$
. This is to allow us to use subscripts on modules as indices and to ease readability. We will write
$N/N\pi ^k$
. This is to allow us to use subscripts on modules as indices and to ease readability. We will write
![]() $\Lambda _k$
for the ring
$\Lambda _k$
for the ring
![]() $\Lambda /\pi ^k\Lambda $
.
$\Lambda /\pi ^k\Lambda $
.
The proof of the next lemma can easily be extracted from the proof of [Reference Curtis and Reiner5, Theorem 30.14].
Lemma 3.1 Let
![]() $L\in \text {Latt}_\Lambda $
and
$L\in \text {Latt}_\Lambda $
and
![]() $M\in \text {Tf}_\Lambda $
. If
$M\in \text {Tf}_\Lambda $
. If
![]() $k\geq k_0+1$
, then for all
$k\geq k_0+1$
, then for all
![]() $g\in \textrm {Hom}_{\Lambda _k}(L/L\pi ^k,M/M\pi ^k)$
, there exists
$g\in \textrm {Hom}_{\Lambda _k}(L/L\pi ^k,M/M\pi ^k)$
, there exists
![]() $h\in \textrm {Hom}_\Lambda (L,M)$
such that for all
$h\in \textrm {Hom}_\Lambda (L,M)$
such that for all
![]() $m\in L$
,
$m\in L$
,
 $\pi ^{k-k_0}+\Lambda \pi ^k|\overline {h(m)}-g(\overline {m})$
.
$\pi ^{k-k_0}+\Lambda \pi ^k|\overline {h(m)}-g(\overline {m})$
.
The following proposition is key to proving both parts of our extension of Maranda’s theorem.
Proposition 3.2 Let
![]() $M,N$
be R-torsion-free
$M,N$
be R-torsion-free
![]() $\Lambda $
-modules with N pure-injective. If
$\Lambda $
-modules with N pure-injective. If
![]() $k\geq k_0+1$
, then for all
$k\geq k_0+1$
, then for all
![]() $g\in \textrm {Hom}_{\Lambda _k}(M/M\pi ^k,N/N\pi ^k)$
, there exists
$g\in \textrm {Hom}_{\Lambda _k}(M/M\pi ^k,N/N\pi ^k)$
, there exists
![]() $h\in \textrm {Hom}_\Lambda (M,N)$
such that for all
$h\in \textrm {Hom}_\Lambda (M,N)$
such that for all
![]() $m\in M$
,
$m\in M$
,
 $\pi ^{k-k_0}+\Lambda \pi ^k|\overline {h(m)}-g(\overline {m})$
.
$\pi ^{k-k_0}+\Lambda \pi ^k|\overline {h(m)}-g(\overline {m})$
.
Proof Since
![]() $M\in \text {Tf}_\Lambda $
, there exists a directed system of
$M\in \text {Tf}_\Lambda $
, there exists a directed system of
![]() $\Lambda $
-lattices
$\Lambda $
-lattices
![]() $L_i$
for
$L_i$
for
![]() $i\in I$
and
$i\in I$
and
![]() $\sigma _{ij}:L_i\rightarrow L_j$
for
$\sigma _{ij}:L_i\rightarrow L_j$
for
![]() $i\leq j\in I$
such that M is the direct limit of this directed system. Let
$i\leq j\in I$
such that M is the direct limit of this directed system. Let
![]() $f_i:L_i\rightarrow M$
be the component maps.
$f_i:L_i\rightarrow M$
be the component maps.
Our aim is to find
![]() $h_i:L_i\rightarrow N$
for all
$h_i:L_i\rightarrow N$
for all
![]() $i\in I$
such that
$i\in I$
such that
![]() $h_i=h_j\sigma _{ij}$
and for all
$h_i=h_j\sigma _{ij}$
and for all
![]() $a\in L_i$
,
$a\in L_i$
,
 $\pi ^{k-k_0}+\Lambda \pi ^k|\overline {h_i(a)}-g(\overline {f_i(a)})$
.
$\pi ^{k-k_0}+\Lambda \pi ^k|\overline {h_i(a)}-g(\overline {f_i(a)})$
.
If we can do this, then there exists
![]() $h:M\rightarrow N$
such that
$h:M\rightarrow N$
such that
![]() $h_i=hf_i$
for all
$h_i=hf_i$
for all
![]() $i\in I$
. This homomorphism is then as required by the statement of the proposition for the following reasons. For all
$i\in I$
. This homomorphism is then as required by the statement of the proposition for the following reasons. For all
![]() $m\in M$
, there exist
$m\in M$
, there exist
![]() $i\in I$
and
$i\in I$
and
![]() $a\in L_i$
such that
$a\in L_i$
such that
![]() $f_i(a)=m$
. So
$f_i(a)=m$
. So
 $$ \begin{align*}\overline{h(m)}-g(\overline{m})=\overline{hf_i(a)}-g(\overline{f_i(a)})=\overline{h_i(a)}-g(\overline{f_i(a)})\end{align*} $$
$$ \begin{align*}\overline{h(m)}-g(\overline{m})=\overline{hf_i(a)}-g(\overline{f_i(a)})=\overline{h_i(a)}-g(\overline{f_i(a)})\end{align*} $$
is divisible by
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
.
$\pi ^{k-k_0}+\Lambda \pi ^k$
.
For each
![]() $i\in I$
, let
$i\in I$
, let
![]() $\epsilon _i:L_i\rightarrow N$
be such that for all
$\epsilon _i:L_i\rightarrow N$
be such that for all
![]() $a\in L_i$
,
$a\in L_i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {\epsilon _i(a)}-g(\overline {f_i(a)})$
. Such an
$\overline {\epsilon _i(a)}-g(\overline {f_i(a)})$
. Such an
![]() $\epsilon _i$
exists by Lemma 3.1 since
$\epsilon _i$
exists by Lemma 3.1 since
![]() $L_i$
is a
$L_i$
is a
![]() $\Lambda $
-lattice.
$\Lambda $
-lattice.
Let
![]() $\mathbf {c_i}:=(c_{i1},\ldots , c_{il_i})$
generate
$\mathbf {c_i}:=(c_{i1},\ldots , c_{il_i})$
generate
![]() $L_i$
as an R-module, and let
$L_i$
as an R-module, and let
![]() $\phi _i$
generate the pp-type of
$\phi _i$
generate the pp-type of
![]() $\mathbf {c_i}$
. Note that
$\mathbf {c_i}$
. Note that
![]() $\mathbf {m}\in \phi _i(N)$
if and only if there exists a
$\mathbf {m}\in \phi _i(N)$
if and only if there exists a
![]() $q:L_i\rightarrow N$
such that
$q:L_i\rightarrow N$
such that
![]() $q(\mathbf {c_i})=\mathbf {m}$
.
$q(\mathbf {c_i})=\mathbf {m}$
.
Let
 $$ \begin{align*}\chi_i(x_1,\ldots, x_{l_i}):=\phi_i(x_1,\ldots,x_{l_i})\wedge\bigwedge_{j=1}^{l_i}\pi^{k-k_0}|x_j.\end{align*} $$
$$ \begin{align*}\chi_i(x_1,\ldots, x_{l_i}):=\phi_i(x_1,\ldots,x_{l_i})\wedge\bigwedge_{j=1}^{l_i}\pi^{k-k_0}|x_j.\end{align*} $$
We now show that
![]() $\mathbf {m}-\epsilon _i(\mathbf {c_i})\in \chi _i(N)$
if and only if there exists a homomorphism
$\mathbf {m}-\epsilon _i(\mathbf {c_i})\in \chi _i(N)$
if and only if there exists a homomorphism
![]() $q\in \textrm {Hom}(L_i,N)$
such that
$q\in \textrm {Hom}(L_i,N)$
such that
![]() $q(\mathbf {c_i})=\mathbf {m}$
and for all
$q(\mathbf {c_i})=\mathbf {m}$
and for all
![]() $a\in L_i$
,
$a\in L_i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {q(a)}-g(\overline {f_i(a)})$
.
$\overline {q(a)}-g(\overline {f_i(a)})$
.
Suppose
![]() $\mathbf {m}-\epsilon _i(\mathbf {c}_i)\in \chi _i(N)$
. Since
$\mathbf {m}-\epsilon _i(\mathbf {c}_i)\in \chi _i(N)$
. Since
![]() $\epsilon _i(\mathbf {c_i})\in \phi _i(N)$
,
$\epsilon _i(\mathbf {c_i})\in \phi _i(N)$
,
![]() $\mathbf {m}\in \phi _i(N)$
, and hence there exists
$\mathbf {m}\in \phi _i(N)$
, and hence there exists
![]() $q\in \textrm {Hom}(L_i,N)$
such that
$q\in \textrm {Hom}(L_i,N)$
such that
![]() $q(\mathbf {c_i})=\mathbf {m}$
. For each
$q(\mathbf {c_i})=\mathbf {m}$
. For each
![]() $1\leq j\leq l_i$
,
$1\leq j\leq l_i$
,
![]() $\pi ^{k-k_0}$
divides
$\pi ^{k-k_0}$
divides
![]() $q(c_{ij})-\epsilon _i(c_{ij})=m_j-\epsilon _i(c_{ij})$
. By definition of
$q(c_{ij})-\epsilon _i(c_{ij})=m_j-\epsilon _i(c_{ij})$
. By definition of
![]() $\epsilon _i$
,
$\epsilon _i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {\epsilon _i(c_{ij})}-g(\overline {f_i(c_{ij})})$
. So
$\overline {\epsilon _i(c_{ij})}-g(\overline {f_i(c_{ij})})$
. So
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {q(c_{ij})}-g(\overline {f_i(c_{ij})})$
for
$\overline {q(c_{ij})}-g(\overline {f_i(c_{ij})})$
for
![]() $1\leq j\leq l_i$
. Since
$1\leq j\leq l_i$
. Since
![]() $\mathbf {c_i}$
generates
$\mathbf {c_i}$
generates
![]() $L_i$
,
$L_i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {q(a)}-g(\overline {f_i(a)})$
for all
$\overline {q(a)}-g(\overline {f_i(a)})$
for all
![]() $a\in L_i$
.
$a\in L_i$
.
Now, suppose that
![]() $q\in \textrm {Hom}(L_i,N)$
is such that
$q\in \textrm {Hom}(L_i,N)$
is such that
![]() $q(\mathbf {c_i})=\mathbf {m}$
and that for all
$q(\mathbf {c_i})=\mathbf {m}$
and that for all
![]() $a\in L_i$
,
$a\in L_i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {q(a)}-g(\overline {f_i(a)})$
. Then
$\overline {q(a)}-g(\overline {f_i(a)})$
. Then
![]() $\mathbf {m}-\epsilon _i(\mathbf {c_i})=(q-\epsilon _i)(\mathbf {c_i})\in \phi _i(N)$
. By definition of
$\mathbf {m}-\epsilon _i(\mathbf {c_i})=(q-\epsilon _i)(\mathbf {c_i})\in \phi _i(N)$
. By definition of
![]() $\epsilon _i$
,
$\epsilon _i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {\epsilon _i(a)}-g(\overline {f_i(a)})$
for all
$\overline {\epsilon _i(a)}-g(\overline {f_i(a)})$
for all
![]() $a\in L_i$
. So
$a\in L_i$
. So
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {q(a)}-\overline {\epsilon _i(a)}$
for all
$\overline {q(a)}-\overline {\epsilon _i(a)}$
for all
![]() $a\in L_i$
. Since
$a\in L_i$
. Since
![]() $k\geq k-k_0$
,
$k\geq k-k_0$
,
![]() $\pi ^{k-k_0}$
divides
$\pi ^{k-k_0}$
divides
![]() $q(a)-\epsilon _i(a)$
for all
$q(a)-\epsilon _i(a)$
for all
![]() $a\in L_i$
. So, in particular,
$a\in L_i$
. So, in particular,
![]() $\pi ^{k-k_0}$
divides
$\pi ^{k-k_0}$
divides
![]() $q(c_{ij})-\epsilon _i(c_{ij})=m_j-\epsilon _i(c_{ij})$
for all
$q(c_{ij})-\epsilon _i(c_{ij})=m_j-\epsilon _i(c_{ij})$
for all
![]() $1\leq j\leq l_i$
. Thus,
$1\leq j\leq l_i$
. Thus,
![]() $\mathbf {m}-\epsilon _i(c_i)\in \chi _i(N)$
, as required.
$\mathbf {m}-\epsilon _i(c_i)\in \chi _i(N)$
, as required.
For
![]() $i\leq j\in I$
, let
$i\leq j\in I$
, let
 $\mathbf {t_{ij}}\in R^{l_j\times l_i}$
be such that
$\mathbf {t_{ij}}\in R^{l_j\times l_i}$
be such that
![]() $\sigma _{ij}(\mathbf {c_i})=\mathbf {c_j}\cdot \mathbf {t_{ij}}$
.
$\sigma _{ij}(\mathbf {c_i})=\mathbf {c_j}\cdot \mathbf {t_{ij}}$
.
Consider the system of linear equations and cosets of pp-definable subsets
for
![]() $i\in I$
and
$i\in I$
and
for
![]() $i\leq j\in I$
.
$i\leq j\in I$
.
Let
![]() $I_0\subseteq I$
be a finite subset of I. Since I is directed, by adding an element to
$I_0\subseteq I$
be a finite subset of I. Since I is directed, by adding an element to
![]() $I_0$
if necessary, we may assume that there is a
$I_0$
if necessary, we may assume that there is a
![]() $p\in I_0$
such that
$p\in I_0$
such that
![]() $i\leq p$
for all
$i\leq p$
for all
![]() $i\in I_0$
.
$i\in I_0$
.
Let
![]() $\mathbf {m_p}=\epsilon _p(\mathbf {c_p})$
and for
$\mathbf {m_p}=\epsilon _p(\mathbf {c_p})$
and for
![]() $i\in I_0$
, and let
$i\in I_0$
, and let
![]() $\mathbf {m_i}=\mathbf {m_p}\cdot \mathbf {t_{ip}}$
. Then
$\mathbf {m_i}=\mathbf {m_p}\cdot \mathbf {t_{ip}}$
. Then
for all
![]() $i\in I_0$
.
$i\in I_0$
.
Suppose that
![]() $i\leq j\in I_0$
. Then
$i\leq j\in I_0$
. Then
![]() $\sigma _{ip}=\sigma _{jp}\circ \sigma _{ij}$
. So
$\sigma _{ip}=\sigma _{jp}\circ \sigma _{ij}$
. So
Thus,
![]() $(\mathbf {m_i})_{i\in I_0}$
satisfies
$(\mathbf {m_i})_{i\in I_0}$
satisfies
![]() $(2)_{ij}$
for all
$(2)_{ij}$
for all
![]() $i\leq j\in I_0$
.
$i\leq j\in I_0$
.
We now need to show that for all
![]() $i\in I_0$
,
$i\in I_0$
,
![]() $\mathbf {m_i}-\epsilon _i(\mathbf {c_i})\in \chi _i(N)$
. Let
$\mathbf {m_i}-\epsilon _i(\mathbf {c_i})\in \chi _i(N)$
. Let
![]() $q:=\epsilon _p\circ \sigma _{ip}$
. Then
$q:=\epsilon _p\circ \sigma _{ip}$
. Then
![]() $q(\mathbf {c_i})=\epsilon _p( \sigma _{ip}(\mathbf {c_i}))=\mathbf {m_i}$
; furthermore, by definition of
$q(\mathbf {c_i})=\epsilon _p( \sigma _{ip}(\mathbf {c_i}))=\mathbf {m_i}$
; furthermore, by definition of
![]() $\epsilon _p$
, for all
$\epsilon _p$
, for all
![]() $a\in L_i$
,
$a\in L_i$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {\epsilon _p(\sigma _{ip}(a))}-g(\overline {f_p(\sigma _{ip}(a))})=q(a)-g(\overline {f_i(a)})$
. Thus, using the characterization of the solution set of
$\overline {\epsilon _p(\sigma _{ip}(a))}-g(\overline {f_p(\sigma _{ip}(a))})=q(a)-g(\overline {f_i(a)})$
. Thus, using the characterization of the solution set of
![]() $\chi _i(N)$
proved earlier,
$\chi _i(N)$
proved earlier,
![]() $\mathbf {m_i}-\epsilon _i(\mathbf {c_i})\in \chi _i(N)$
.
$\mathbf {m_i}-\epsilon _i(\mathbf {c_i})\in \chi _i(N)$
.
Since the system of equations
![]() $(1)_i$
and
$(1)_i$
and
![]() $(2)_{ij}$
is finitely solvable and N is pure-injective, there exists
$(2)_{ij}$
is finitely solvable and N is pure-injective, there exists
![]() $(\mathbf {m_i})_{i\in I}$
with
$(\mathbf {m_i})_{i\in I}$
with
![]() $\mathbf {m_i}\in N$
satisfying
$\mathbf {m_i}\in N$
satisfying
![]() $(1)_{i}$
and
$(1)_{i}$
and
![]() $(2)_{ij}$
for all
$(2)_{ij}$
for all
![]() $i\leq j\in I$
. For each
$i\leq j\in I$
. For each
![]() $i\in I$
, let
$i\in I$
, let
![]() $h_i:L_i\rightarrow N$
be the homomorphism which sends
$h_i:L_i\rightarrow N$
be the homomorphism which sends
![]() $\mathbf {c_i}$
to
$\mathbf {c_i}$
to
![]() $\mathbf {m_i}$
. Condition
$\mathbf {m_i}$
. Condition
![]() $(2)_{ij}$
ensures that for all
$(2)_{ij}$
ensures that for all
![]() $i\leq j\in I$
,
$i\leq j\in I$
,
![]() $h_i=h_j\circ \sigma _{ij}$
. This is because
$h_i=h_j\circ \sigma _{ij}$
. This is because
![]() $h_j(\sigma _{ij}(\mathbf {c_i}))=h_j(\mathbf {c_j}\cdot \mathbf {t_{ij}})=h_j(\mathbf {c_j})\cdot \mathbf {t_{ij}}=\mathbf {m_j}\cdot \mathbf {t_{ij}}=\mathbf {m_i}$
. Condition
$h_j(\sigma _{ij}(\mathbf {c_i}))=h_j(\mathbf {c_j}\cdot \mathbf {t_{ij}})=h_j(\mathbf {c_j})\cdot \mathbf {t_{ij}}=\mathbf {m_j}\cdot \mathbf {t_{ij}}=\mathbf {m_i}$
. Condition
![]() $(1)_i$
ensures that
$(1)_i$
ensures that
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {h_i(a)}-g(\overline {f_i(a)})$
for all
$\overline {h_i(a)}-g(\overline {f_i(a)})$
for all
![]() $a\in L_i$
.▪
$a\in L_i$
.▪
Lemma 3.3 Let
![]() $N\in \textrm {Mod}\text {-}\Lambda _k$
, and let
$N\in \textrm {Mod}\text {-}\Lambda _k$
, and let
![]() $g,\sigma \in \textrm {End} N$
. Suppose that for all
$g,\sigma \in \textrm {End} N$
. Suppose that for all
![]() $m\in N$
,
$m\in N$
,
![]() $\pi +\Lambda \pi ^k|\sigma (m)$
. Then
$\pi +\Lambda \pi ^k|\sigma (m)$
. Then
![]() $g-\sigma $
is an isomorphism if and only if g is an isomorphism.
$g-\sigma $
is an isomorphism if and only if g is an isomorphism.
Proof Suppose that g is an isomorphism. Then
![]() $(g-\sigma )g^{-1}=\text {Id}_N-\sigma g^{-1}$
. Let
$(g-\sigma )g^{-1}=\text {Id}_N-\sigma g^{-1}$
. Let
![]() $h:=\sigma g^{-1}$
and
$h:=\sigma g^{-1}$
and
![]() $f:=\text {Id}_N+h+\cdots h^{k-1}$
. Since
$f:=\text {Id}_N+h+\cdots h^{k-1}$
. Since
![]() $\pi +\Lambda \pi ^k|\sigma (m)$
for all
$\pi +\Lambda \pi ^k|\sigma (m)$
for all
![]() $m\in N$
,
$m\in N$
,
![]() $h^k=0$
. Thus,
$h^k=0$
. Thus,
![]() $(\text {Id}_N-h)\circ f=f\circ (\text {Id}_N-h)=\text {Id}_N$
. So
$(\text {Id}_N-h)\circ f=f\circ (\text {Id}_N-h)=\text {Id}_N$
. So
![]() $(g-\sigma )g^{-1}f=\text {Id}_N$
and
$(g-\sigma )g^{-1}f=\text {Id}_N$
and
![]() $g^{-1}f(g-\sigma )=g^{-1}f(g-\sigma )g^{-1}g=\text {Id}_N$
. Therefore,
$g^{-1}f(g-\sigma )=g^{-1}f(g-\sigma )g^{-1}g=\text {Id}_N$
. Therefore,
![]() $g-\sigma $
is an isomorphism. For the converse, note that for all
$g-\sigma $
is an isomorphism. For the converse, note that for all
![]() $m\in N$
,
$m\in N$
,
![]() $\pi +\Lambda \pi ^k|-\sigma (m)$
. Thus, the implication we have just proved also shows that if
$\pi +\Lambda \pi ^k|-\sigma (m)$
. Thus, the implication we have just proved also shows that if
![]() $g-\sigma $
is an isomorphism, then
$g-\sigma $
is an isomorphism, then
![]() $g=(g-\sigma )-(-\sigma )$
is an isomorphism.▪
$g=(g-\sigma )-(-\sigma )$
is an isomorphism.▪
Theorem 3.4 Let
![]() $M,N\in \text {Tf}_\Lambda $
be R-reduced and pure-injective. If
$M,N\in \text {Tf}_\Lambda $
be R-reduced and pure-injective. If
![]() $M/M\pi ^k\cong N/N\pi ^k$
for some
$M/M\pi ^k\cong N/N\pi ^k$
for some
![]() $k\geq k_0+1$
, then
$k\geq k_0+1$
, then
![]() $M\cong N$
.
$M\cong N$
.
Proof We first show that if
![]() $f:M\rightarrow N$
is such that
$f:M\rightarrow N$
is such that
![]() $\overline {f}:\overline {M}\rightarrow \overline {N}$
is an isomorphism, then f is an isomorphism.
$\overline {f}:\overline {M}\rightarrow \overline {N}$
is an isomorphism, then f is an isomorphism.
Suppose
![]() $\overline {f}$
is an isomorphism and
$\overline {f}$
is an isomorphism and
![]() $f(m)=0$
. If
$f(m)=0$
. If
![]() $m\neq 0$
, then since M is reduced, there exists
$m\neq 0$
, then since M is reduced, there exists
![]() $n\in M$
and l a nonnegative integer such that
$n\in M$
and l a nonnegative integer such that
![]() $m=n\pi ^l$
where
$m=n\pi ^l$
where
![]() $\pi $
does not divide n. Since N is R-torsion-free,
$\pi $
does not divide n. Since N is R-torsion-free,
![]() $f(m)=f(n)\pi ^l=0$
implies
$f(m)=f(n)\pi ^l=0$
implies
![]() $f(n)=0$
. So
$f(n)=0$
. So
![]() $\overline {f}(\overline {n})=0$
. Therefore,
$\overline {f}(\overline {n})=0$
. Therefore,
![]() $\overline {n}=0$
. This implies
$\overline {n}=0$
. This implies
![]() $\pi $
divides n, contradicting our assumption. So
$\pi $
divides n, contradicting our assumption. So
![]() $m=0$
. Therefore, f is injective.
$m=0$
. Therefore, f is injective.
We now show that f is surjective. Since
![]() $\overline {f}$
is surjective, for all
$\overline {f}$
is surjective, for all
![]() $n\in N$
, there exists
$n\in N$
, there exists
![]() $m\in M$
such that
$m\in M$
such that
![]() $n-f(m)\in N\pi ^k$
. Suppose
$n-f(m)\in N\pi ^k$
. Suppose
![]() $m_l$
is such that
$m_l$
is such that
![]() $n-f(m_l)\in N\pi ^{lk}$
. Let
$n-f(m_l)\in N\pi ^{lk}$
. Let
![]() $a\pi ^{lk}=n-f(m_l)$
. There exists
$a\pi ^{lk}=n-f(m_l)$
. There exists
![]() $b\in M$
such that
$b\in M$
such that
![]() $a-f(b)\in N\pi ^{k}$
. Thus,
$a-f(b)\in N\pi ^{k}$
. Thus,
![]() $a\pi ^{lk}-f(b)\pi ^{lk}\in N\pi ^{(l+1)k}$
. So
$a\pi ^{lk}-f(b)\pi ^{lk}\in N\pi ^{(l+1)k}$
. So
![]() $n-f(b\pi ^{lk}+m_l) \in N\pi ^{(l+1)k}$
and
$n-f(b\pi ^{lk}+m_l) \in N\pi ^{(l+1)k}$
and
![]() $(b\pi ^{lk}+m_l)-m_l\in M\pi ^{lk}$
. So there exists a sequence
$(b\pi ^{lk}+m_l)-m_l\in M\pi ^{lk}$
. So there exists a sequence
![]() $(m_l)_{l\in \mathbb {N}}$
in M such that for all
$(m_l)_{l\in \mathbb {N}}$
in M such that for all
![]() $l\in \mathbb {N}$
,
$l\in \mathbb {N}$
,
![]() $n-f(m_l)\in N\pi ^{lk}$
and
$n-f(m_l)\in N\pi ^{lk}$
and
![]() $m_{l+1}-m_l\in M\pi ^{lk}$
. Since M is pure-injective, there exists an
$m_{l+1}-m_l\in M\pi ^{lk}$
. Since M is pure-injective, there exists an
![]() $m\in M$
such that
$m\in M$
such that
![]() $m-m_l\in M\pi ^{kl}$
for all
$m-m_l\in M\pi ^{kl}$
for all
![]() $l\in \mathbb {N}$
. Thus,
$l\in \mathbb {N}$
. Thus,
![]() $f(m)-n=f(m-m_l)-(n-f(m_l))\in N\pi ^{kl}$
for all
$f(m)-n=f(m-m_l)-(n-f(m_l))\in N\pi ^{kl}$
for all
![]() $l\in \mathbb {N}$
. Since N is reduced,
$l\in \mathbb {N}$
. Since N is reduced,
![]() $f(m)=n$
.
$f(m)=n$
.
Suppose that
![]() $g:\overline {M}\rightarrow \overline {N}$
is an isomorphism with inverse
$g:\overline {M}\rightarrow \overline {N}$
is an isomorphism with inverse
![]() $h:\overline {N}\rightarrow \overline {M}$
. There exists
$h:\overline {N}\rightarrow \overline {M}$
. There exists
![]() $e\in \textrm {Hom}_{\Lambda }(M,N)$
such that for all
$e\in \textrm {Hom}_{\Lambda }(M,N)$
such that for all
![]() $m\in M$
,
$m\in M$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^{k}$
divides
$\pi ^{k-k_0}+\Lambda \pi ^{k}$
divides
 $\overline {e(m)}-g(\overline {m})$
and
$\overline {e(m)}-g(\overline {m})$
and
![]() $f\in \textrm {Hom}_{\Lambda }(N,M)$
such that for all
$f\in \textrm {Hom}_{\Lambda }(N,M)$
such that for all
![]() $m\in N$
,
$m\in N$
,
![]() $\pi ^{k-k_0}+\Lambda \pi ^k$
divides
$\pi ^{k-k_0}+\Lambda \pi ^k$
divides
 $\overline {f(m)}-h(\overline {m})$
. Since
$\overline {f(m)}-h(\overline {m})$
. Since
![]() $\overline {f}\circ \overline {e}= (\overline {f}-h)\circ (\overline {e}-g)+(\overline {f}-h)\circ g+ h\circ (\overline {e}-g)+h\circ g$
, Lemma 3.3 implies that
$\overline {f}\circ \overline {e}= (\overline {f}-h)\circ (\overline {e}-g)+(\overline {f}-h)\circ g+ h\circ (\overline {e}-g)+h\circ g$
, Lemma 3.3 implies that
![]() $\overline {f}\circ \overline {e}$
is an isomorphism. Similarly, we can show that
$\overline {f}\circ \overline {e}$
is an isomorphism. Similarly, we can show that
![]() $\overline {e}\circ \overline {f}$
is an isomorphism. Thus,
$\overline {e}\circ \overline {f}$
is an isomorphism. Thus,
![]() $\overline {e}$
and
$\overline {e}$
and
![]() $\overline {f}$
are both isomorphisms. So the above arguments imply that e and f are both isomorphisms.▪
$\overline {f}$
are both isomorphisms. So the above arguments imply that e and f are both isomorphisms.▪
Theorem 3.5 Let
![]() $k\geq k_0+1$
. If N is an indecomposable R-torsion-free R-reduced pure-injective
$k\geq k_0+1$
. If N is an indecomposable R-torsion-free R-reduced pure-injective
![]() $\Lambda $
-module, then
$\Lambda $
-module, then
![]() $N/N\pi ^k$
is indecomposable.
$N/N\pi ^k$
is indecomposable.
Proof We will show that for all
![]() $f\in \textrm {End} \overline {N}$
, either f is an isomorphism, or
$f\in \textrm {End} \overline {N}$
, either f is an isomorphism, or
![]() $1-f$
is an isomorphism. Hence,
$1-f$
is an isomorphism. Hence,
![]() $\textrm {End} \overline {N}$
is local.
$\textrm {End} \overline {N}$
is local.
Proposition 3.2 implies that the homomorphism sending
![]() $f\in \textrm {End} N$
to
$f\in \textrm {End} N$
to
![]() $\overline {f}\in \textrm {End}\overline {N}$
induces a surjective ring homomorphism from
$\overline {f}\in \textrm {End}\overline {N}$
induces a surjective ring homomorphism from
![]() $\textrm {End} N$
to
$\textrm {End} N$
to
![]() $\textrm {End} \overline {N}/\{g\in \textrm {End} \overline {N} \ \vert \ g(n)\in \overline {N}\pi \text { for all } n\in \overline {N} \}$
.
$\textrm {End} \overline {N}/\{g\in \textrm {End} \overline {N} \ \vert \ g(n)\in \overline {N}\pi \text { for all } n\in \overline {N} \}$
.
Suppose
![]() $f\in \textrm {End} \overline {N}$
is not an isomorphism. There exist
$f\in \textrm {End} \overline {N}$
is not an isomorphism. There exist
![]() $g\in \textrm {End} N$
and
$g\in \textrm {End} N$
and
![]() $\sigma \in \textrm {End} \overline {N}$
such that
$\sigma \in \textrm {End} \overline {N}$
such that
![]() $f=\overline {g}+\sigma $
and
$f=\overline {g}+\sigma $
and
![]() $\sigma (n)\in \overline {N}\pi $
for all
$\sigma (n)\in \overline {N}\pi $
for all
![]() $n\in \overline {N}$
. By Lemma 3.3,
$n\in \overline {N}$
. By Lemma 3.3,
![]() $\overline {g}$
is not an isomorphism, and hence neither is g. Since
$\overline {g}$
is not an isomorphism, and hence neither is g. Since
![]() $\textrm {End} N$
is local,
$\textrm {End} N$
is local,
![]() $\text {Id}_N-g$
is an isomorphism. Thus,
$\text {Id}_N-g$
is an isomorphism. Thus,
![]() $\text {Id}_{\overline {N}}-\overline {g}$
is an isomorphism. So, by Lemma 3.3,
$\text {Id}_{\overline {N}}-\overline {g}$
is an isomorphism. So, by Lemma 3.3,
![]() $\text {Id}_{\overline {N}}-f=\text {Id}_{\overline {N}}-(\overline {g}+\sigma )$
is an isomorphism, as required.▪
$\text {Id}_{\overline {N}}-f=\text {Id}_{\overline {N}}-(\overline {g}+\sigma )$
is an isomorphism, as required.▪
We now show that Maranda’s functor preserves pure-injective hulls. The proof uses somewhat different techniques to those used so far and relies on [Reference Gregory, L’Innocente and Toffalori8, Proposition 4.6]. In order to avoid introducing various definitions that will not be used in the rest of this paper, we state only the part of that proposition which we need.
Proposition 3.6 Let
![]() $k\geq k_0+1$
. For all
$k\geq k_0+1$
. For all
![]() $\psi \in [\pi ^{k-k_0}|\mathbf {x},\mathbf {x}=\mathbf {x}]\subseteq \textrm {pp}^n_{\Lambda }$
, there exists
$\psi \in [\pi ^{k-k_0}|\mathbf {x},\mathbf {x}=\mathbf {x}]\subseteq \textrm {pp}^n_{\Lambda }$
, there exists
 $\widehat {\psi }\in [\pi ^{k-k_0}+\Lambda \pi ^k|\mathbf {x},\mathbf {x}=\mathbf {x}]\subseteq \textrm {pp}_{\Lambda _k}^n$
such that for all
$\widehat {\psi }\in [\pi ^{k-k_0}+\Lambda \pi ^k|\mathbf {x},\mathbf {x}=\mathbf {x}]\subseteq \textrm {pp}_{\Lambda _k}^n$
such that for all
![]() $M\in \text {Tf}_\Lambda $
and
$M\in \text {Tf}_\Lambda $
and
![]() $\mathbf {m}\in M$
,
$\mathbf {m}\in M$
,
![]() $\mathbf {m}\in \psi (M)$
if and only if
$\mathbf {m}\in \psi (M)$
if and only if
![]() $\mathbf {m}+M\pi ^k\in \widehat {\psi }(M/M\pi ^k)$
.
$\mathbf {m}+M\pi ^k\in \widehat {\psi }(M/M\pi ^k)$
.
The following useful lemma was communicated to me by Prest.
Lemma 3.7 Let
![]() $M\in \textrm {Mod}\text {-}S$
,
$M\in \textrm {Mod}\text {-}S$
,
![]() $H(M)$
be its pure-injective hull, and let
$H(M)$
be its pure-injective hull, and let
![]() $\mathbf {b}\in H(M)$
be an n-tuple. Suppose that
$\mathbf {b}\in H(M)$
be an n-tuple. Suppose that
![]() $\mathbf {b}\in \phi (H(M))\backslash \bigcup _{i=1}^l\psi _i(H(M))$
, where
$\mathbf {b}\in \phi (H(M))\backslash \bigcup _{i=1}^l\psi _i(H(M))$
, where
![]() $\phi ,\psi _1,\ldots ,\psi _n$
are pp-n-formulas. There exist an n-tuple
$\phi ,\psi _1,\ldots ,\psi _n$
are pp-n-formulas. There exist an n-tuple
![]() $\mathbf {b}'\in M$
and a pp-n-formula
$\mathbf {b}'\in M$
and a pp-n-formula
![]() $\theta $
such that
$\theta $
such that
![]() $\theta (\mathbf {b}'-\mathbf {b})$
holds and
$\theta (\mathbf {b}'-\mathbf {b})$
holds and
 $$ \begin{align*}H(M)\models \theta(\mathbf{b}'-\mathbf{y})\rightarrow \phi(\mathbf{y})\wedge\bigwedge_{i=1}^n\neg\psi_i(\mathbf{y}).\end{align*} $$
$$ \begin{align*}H(M)\models \theta(\mathbf{b}'-\mathbf{y})\rightarrow \phi(\mathbf{y})\wedge\bigwedge_{i=1}^n\neg\psi_i(\mathbf{y}).\end{align*} $$
Proof Let
![]() $\mathbf {b}\in H(M)$
. Suppose that
$\mathbf {b}\in H(M)$
. Suppose that
![]() $\mathbf {b}\in \phi (H(M))$
and
$\mathbf {b}\in \phi (H(M))$
and
![]() $\mathbf {b}\notin \bigcup _{i=1}^l\psi _i(H(M))$
.
$\mathbf {b}\notin \bigcup _{i=1}^l\psi _i(H(M))$
.
By [Reference Prest15, Lemma 4.1] and [Reference Prest15, Theorem 4.10(c)], there exist
![]() $\mathbf {a}\in M$
and a pp formula
$\mathbf {a}\in M$
and a pp formula
![]() $\chi (\mathbf {x},\mathbf {y})$
such that
$\chi (\mathbf {x},\mathbf {y})$
such that
![]() $\chi (\mathbf {a},\mathbf {b})$
holds in
$\chi (\mathbf {a},\mathbf {b})$
holds in
![]() $H(M)$
and
$H(M)$
and
 $$ \begin{align*}H(M)\models\chi(\mathbf{a},\mathbf{y})\rightarrow \phi(\mathbf{y})\wedge\bigwedge_{i=1}^n\neg\psi_i(\mathbf{y}).\end{align*} $$
$$ \begin{align*}H(M)\models\chi(\mathbf{a},\mathbf{y})\rightarrow \phi(\mathbf{y})\wedge\bigwedge_{i=1}^n\neg\psi_i(\mathbf{y}).\end{align*} $$
Since
![]() $H(M)$
is an elementary extension of M, there exists
$H(M)$
is an elementary extension of M, there exists
![]() $\mathbf {b}'\in M$
such that
$\mathbf {b}'\in M$
such that
![]() $\chi (\mathbf {a},\mathbf {b}')$
holds in M and hence in
$\chi (\mathbf {a},\mathbf {b}')$
holds in M and hence in
![]() $H(M)$
. Thus,
$H(M)$
. Thus,
![]() $\chi (\mathbf {0},\mathbf {b}'-\mathbf {b})$
holds in
$\chi (\mathbf {0},\mathbf {b}'-\mathbf {b})$
holds in
![]() $H(M)$
. Set
$H(M)$
. Set
![]() $\theta (\mathbf {z}):=\chi (\mathbf {0},\mathbf {z})$
. So
$\theta (\mathbf {z}):=\chi (\mathbf {0},\mathbf {z})$
. So
![]() $\theta (\mathbf {b}'-\mathbf {b})$
holds in
$\theta (\mathbf {b}'-\mathbf {b})$
holds in
![]() $H(M)$
.
$H(M)$
.
Suppose
![]() $\mathbf {c}\in H(M)$
and
$\mathbf {c}\in H(M)$
and
![]() $\theta (\mathbf {b}'-\mathbf {c})$
holds in
$\theta (\mathbf {b}'-\mathbf {c})$
holds in
![]() $H(M)$
. Then
$H(M)$
. Then
![]() $\chi (\mathbf {a},\mathbf {c})$
holds in
$\chi (\mathbf {a},\mathbf {c})$
holds in
![]() $H(M)$
. Thus,
$H(M)$
. Thus,
![]() $\phi (\mathbf {c})\wedge \bigwedge _{i=1}^l\neg \psi _i(\mathbf {c})$
holds in
$\phi (\mathbf {c})\wedge \bigwedge _{i=1}^l\neg \psi _i(\mathbf {c})$
holds in
![]() $H(M)$
. So
$H(M)$
. So
![]() $\theta (\mathbf {b}'-\mathbf {b})$
holds and
$\theta (\mathbf {b}'-\mathbf {b})$
holds and
 $$ \begin{align*}H(M)\models \theta(\mathbf{b}'-\mathbf{y})\rightarrow \phi(\mathbf{y})\wedge\bigwedge_{i=1}^l\neg\psi_i(\mathbf{y}).\\[-39pt]\end{align*} $$
$$ \begin{align*}H(M)\models \theta(\mathbf{b}'-\mathbf{y})\rightarrow \phi(\mathbf{y})\wedge\bigwedge_{i=1}^l\neg\psi_i(\mathbf{y}).\\[-39pt]\end{align*} $$
▪
The following theorem is motivated by [Reference Prest16, Lemma 3.16].
Theorem 3.8 Let
![]() $k\geq k_0+1$
and
$k\geq k_0+1$
and
![]() $M\in \text {Tf}_\Lambda $
. If
$M\in \text {Tf}_\Lambda $
. If
![]() $u:M\rightarrow H(M)$
is a pure-injective hull of M, then the induced map
$u:M\rightarrow H(M)$
is a pure-injective hull of M, then the induced map
![]() $\overline {u}:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
is a pure-injective hull for
$\overline {u}:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
is a pure-injective hull for
![]() $M/M\pi ^k$
.
$M/M\pi ^k$
.
Proof We identify M with its image in
![]() $H(M)$
. Our aim is to show that for all
$H(M)$
. Our aim is to show that for all
![]() $b\in H(M)$
with
$b\in H(M)$
with
![]() $\overline {b}\neq 0$
, there exists
$\overline {b}\neq 0$
, there exists
![]() $a\in M$
and
$a\in M$
and
 $\chi (x,y)\in \textrm {pp}^2_{\Lambda _k}$
such that
$\chi (x,y)\in \textrm {pp}^2_{\Lambda _k}$
such that
 $\chi (\overline {a},\overline {b})$
holds in
$\chi (\overline {a},\overline {b})$
holds in
![]() $H(M)/H(M)\pi ^k$
and
$H(M)/H(M)\pi ^k$
and
![]() $\chi (\overline {a},\overline {0})$
does not hold in
$\chi (\overline {a},\overline {0})$
does not hold in
![]() $H(M)/H(M)\pi ^k$
.
$H(M)/H(M)\pi ^k$
.
Suppose that
![]() $\pi $
does not divide
$\pi $
does not divide
![]() $b\in H(M)$
. Since
$b\in H(M)$
. Since
![]() $H(M)$
is the pure-injective hull of M, by Lemma 3.7, there exist
$H(M)$
is the pure-injective hull of M, by Lemma 3.7, there exist
![]() $a\in M$
and a pp formula
$a\in M$
and a pp formula
![]() $\theta (x)\in \textrm {pp}^1_\Lambda $
such that
$\theta (x)\in \textrm {pp}^1_\Lambda $
such that
![]() $\theta (a-b)$
holds in
$\theta (a-b)$
holds in
![]() $H(M)$
and
$H(M)$
and
![]() $\theta (a-x)\rightarrow \neg \pi |x$
. Let
$\theta (a-x)\rightarrow \neg \pi |x$
. Let
![]() $\Delta (x):=\theta (x)+\pi |x$
. Then
$\Delta (x):=\theta (x)+\pi |x$
. Then
![]() $\Delta (a-b)$
holds in
$\Delta (a-b)$
holds in
![]() $H(M)$
, and for all
$H(M)$
, and for all
![]() $c\in H(M)$
,
$c\in H(M)$
,
![]() $\Delta (a-c\pi )$
does not hold. Let
$\Delta (a-c\pi )$
does not hold. Let
![]() $\widehat {\Delta }$
be as in Proposition 3.6. So
$\widehat {\Delta }$
be as in Proposition 3.6. So
![]() $\widehat {\Delta }(\overline {a}-\overline {b})$
holds in
$\widehat {\Delta }(\overline {a}-\overline {b})$
holds in
![]() $H(M)/H(M)\pi ^k$
.
$H(M)/H(M)\pi ^k$
.
Now, suppose that
![]() $e\in H(M)\backslash H(M)\pi ^k$
,
$e\in H(M)\backslash H(M)\pi ^k$
,
![]() $e=b\pi ^n$
, and
$e=b\pi ^n$
, and
![]() $\pi $
does not divide b. Note that this implies
$\pi $
does not divide b. Note that this implies
![]() $n<k$
. Let
$n<k$
. Let
![]() $\Delta $
and
$\Delta $
and
![]() $a\in M$
be as in the previous paragraph, i.e.,
$a\in M$
be as in the previous paragraph, i.e.,
![]() $\Delta \geq \pi |x$
,
$\Delta \geq \pi |x$
,
![]() $\Delta (a-b)$
holds in
$\Delta (a-b)$
holds in
![]() $H(M)$
, and for all
$H(M)$
, and for all
![]() $c\in H(M)$
,
$c\in H(M)$
,
![]() $\Delta (a-c\pi )$
does not hold. Let
$\Delta (a-c\pi )$
does not hold. Let
 $\chi (x,y):=\exists z \ \widehat {\Delta }(x-z)\wedge y=z\pi ^n\in \textrm {pp}^2_{\Lambda _k}$
. Suppose that
$\chi (x,y):=\exists z \ \widehat {\Delta }(x-z)\wedge y=z\pi ^n\in \textrm {pp}^2_{\Lambda _k}$
. Suppose that
![]() $\chi (\overline {a},\overline {0})$
holds. Then there exists
$\chi (\overline {a},\overline {0})$
holds. Then there exists
![]() $d\in H(M)$
such that
$d\in H(M)$
such that
![]() $\overline {d}\pi ^n=\overline {0}$
and
$\overline {d}\pi ^n=\overline {0}$
and
![]() $\widehat {\Delta }(\overline {a}-\overline {d})$
holds. But then
$\widehat {\Delta }(\overline {a}-\overline {d})$
holds. But then
![]() $d\pi ^n\in H(M)\pi ^k$
. Since M and hence
$d\pi ^n\in H(M)\pi ^k$
. Since M and hence
![]() $H(M)$
and R-torsion-free,
$H(M)$
and R-torsion-free,
![]() $d\in H(M)\pi ^{k-n}$
. This contradicts the definition of
$d\in H(M)\pi ^{k-n}$
. This contradicts the definition of
![]() $\Delta $
. Thus,
$\Delta $
. Thus,
![]() $\chi (\overline {a},\overline {e})$
holds and
$\chi (\overline {a},\overline {e})$
holds and
![]() $\chi (\overline {a},\overline {0})$
does not hold in
$\chi (\overline {a},\overline {0})$
does not hold in
![]() $H(M)/H(M)\pi ^k$
.
$H(M)/H(M)\pi ^k$
.
Suppose that
![]() $H(M)/H(M)\pi ^k=N\oplus N'$
and
$H(M)/H(M)\pi ^k=N\oplus N'$
and
![]() $M/M\pi ^k\subseteq N$
. If
$M/M\pi ^k\subseteq N$
. If
![]() $\overline {c}\in H(M)/H(M)\pi ^k$
is nonzero, then we have shown that there exist
$\overline {c}\in H(M)/H(M)\pi ^k$
is nonzero, then we have shown that there exist
![]() $\overline {a}\in \overline {M}$
and
$\overline {a}\in \overline {M}$
and
 $\chi (x,y)\in \textrm {pp}_{\Lambda _k}^2$
such that
$\chi (x,y)\in \textrm {pp}_{\Lambda _k}^2$
such that
![]() $\chi (\overline {a},\overline {c})$
holds and
$\chi (\overline {a},\overline {c})$
holds and
![]() $\chi (\overline {a},\overline {0})$
does not hold. Since the solution sets of pp formulas commute with direct sums, this implies that if
$\chi (\overline {a},\overline {0})$
does not hold. Since the solution sets of pp formulas commute with direct sums, this implies that if
![]() $\overline {c}\in N'$
, then
$\overline {c}\in N'$
, then
![]() $\overline {c}=\overline {0}$
. Thus,
$\overline {c}=\overline {0}$
. Thus,
![]() $N'$
is the zero module, and
$N'$
is the zero module, and
![]() $H(M)/H(M)\pi ^k$
is the pure-injective hull of
$H(M)/H(M)\pi ^k$
is the pure-injective hull of
![]() $M/M\pi ^k$
.▪
$M/M\pi ^k$
.▪
4 Pure-injectives and pure-injective hulls
As in the previous section, R will be a discrete valuation domain with field of fractions Q and maximal ideal generated by
![]() $\pi $
, and
$\pi $
, and
![]() $\Lambda $
will be an R-order such that
$\Lambda $
will be an R-order such that
![]() $Q\Lambda $
is a separable Q-algebra.
$Q\Lambda $
is a separable Q-algebra.
We start this section by showing that the pure-injective hull of an R-reduced R-torsion-free
![]() $\Lambda $
-module is R-reduced. The proof of the following remark is the same as [Reference Marcja, Prest and Toffalori14, Claim 2, p. 1128].
$\Lambda $
-module is R-reduced. The proof of the following remark is the same as [Reference Marcja, Prest and Toffalori14, Claim 2, p. 1128].
Remark 4.1 If
![]() $M\in \text {Tf}_\Lambda $
is R-divisible, then M is injective as a
$M\in \text {Tf}_\Lambda $
is R-divisible, then M is injective as a
![]() $\Lambda $
-module.
$\Lambda $
-module.
This allows us to deduce that all
![]() $M\in \text {Tf}_\Lambda $
decompose as the direct sum of the divisible part
$M\in \text {Tf}_\Lambda $
decompose as the direct sum of the divisible part
![]() $D_M$
of M and an R-reduced module. Explicitly, let
$D_M$
of M and an R-reduced module. Explicitly, let
It is easy to check that
![]() $D_M$
is R-divisible. So, since R-divisible R-torsion-free
$D_M$
is R-divisible. So, since R-divisible R-torsion-free
![]() $\Lambda $
-modules are injective,
$\Lambda $
-modules are injective,
![]() $D_M$
is a direct summand of M. Hence,
$D_M$
is a direct summand of M. Hence,
![]() $M\cong D_M\oplus M/D_M$
. Now, note that if
$M\cong D_M\oplus M/D_M$
. Now, note that if
![]() $m\in M$
and
$m\in M$
and
![]() $\pi ^n|m+D_M$
for all
$\pi ^n|m+D_M$
for all
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
![]() $\pi ^n|m$
for all
$\pi ^n|m$
for all
![]() $n\in \mathbb {N}$
. Thus,
$n\in \mathbb {N}$
. Thus,
![]() $M/D_M$
is R-reduced.
$M/D_M$
is R-reduced.
Lemma 4.2 Let S be a ring,
![]() $C,M,E\in \textrm {Mod}\text {-}S$
, and E injective. Suppose that
$C,M,E\in \textrm {Mod}\text {-}S$
, and E injective. Suppose that
![]() $C,E\subseteq M$
and
$C,E\subseteq M$
and
![]() $C\cap E=\{0\}$
. There exists
$C\cap E=\{0\}$
. There exists
![]() $N'\subseteq M$
such that
$N'\subseteq M$
such that
![]() $C\subseteq N'$
and
$C\subseteq N'$
and
![]() $N'\oplus E=M$
.
$N'\oplus E=M$
.
Proof Using injectivity of E, there is an
![]() $f:M\rightarrow E$
such that
$f:M\rightarrow E$
such that
![]() $f|_C=0$
and
$f|_C=0$
and
![]() $f|_E=\text {Id}_E$
. So
$f|_E=\text {Id}_E$
. So
![]() $C\subseteq \ker f$
and
$C\subseteq \ker f$
and
![]() $M=E\oplus \ker f$
.▪
$M=E\oplus \ker f$
.▪
Lemma 4.3 If
![]() $C\in \text {Tf}_\Lambda $
is R-reduced, then
$C\in \text {Tf}_\Lambda $
is R-reduced, then
![]() $H(C)$
is R-reduced.
$H(C)$
is R-reduced.
Proof Since
![]() $Q\Lambda $
is separable,
$Q\Lambda $
is separable,
![]() $H(C)=N\oplus D_{H(C)}$
. Since C is pure in
$H(C)=N\oplus D_{H(C)}$
. Since C is pure in
![]() $H(C)$
and C is reduced,
$H(C)$
and C is reduced,
![]() $C\cap D_{H(C)}=\{0\}$
. By Lemma 4.2, there exists
$C\cap D_{H(C)}=\{0\}$
. By Lemma 4.2, there exists
![]() $N'\subseteq H(C)$
such that
$N'\subseteq H(C)$
such that
![]() $N'\oplus D_{H(C)}=H(C)$
and
$N'\oplus D_{H(C)}=H(C)$
and
![]() $C\subseteq N'$
. Since N and
$C\subseteq N'$
. Since N and
![]() $N'$
are isomorphic,
$N'$
are isomorphic,
![]() $N'$
is reduced. Since
$N'$
is reduced. Since
![]() $N'$
is a direct summand of
$N'$
is a direct summand of
![]() $H(C)$
and
$H(C)$
and
![]() $C\subseteq N'\subseteq H(C)$
,
$C\subseteq N'\subseteq H(C)$
,
![]() $N'=H(C)$
. Thus,
$N'=H(C)$
. Thus,
![]() $H(C)$
is R-reduced.▪
$H(C)$
is R-reduced.▪
Definition 4.1 If M is a
![]() $\Lambda $
-module, then let
$\Lambda $
-module, then let
![]() $M^*$
denote the inverse limit along the canonical maps
$M^*$
denote the inverse limit along the canonical maps
![]() $M/M\pi ^{n+1}\rightarrow M/M\pi ^n$
.
$M/M\pi ^{n+1}\rightarrow M/M\pi ^n$
.
Remark 4.4 If
![]() $M\in \textrm {Mod}\text {-}\Lambda $
is R-reduced and pure-injective as an R-module, then the canonical map
$M\in \textrm {Mod}\text {-}\Lambda $
is R-reduced and pure-injective as an R-module, then the canonical map
![]() $v:M\rightarrow M^*$
, induced by the quotient maps from M to
$v:M\rightarrow M^*$
, induced by the quotient maps from M to
![]() $M/M\pi ^n$
, is an isomorphism of
$M/M\pi ^n$
, is an isomorphism of
![]() $\Lambda $
-modules.
$\Lambda $
-modules.
Proof Since M is R-reduced, v is an embedding. Since M is pure-injective as an R-module (equivalently, algebraically compact), v is surjective.▪
Theorem 4.5 Let
![]() $M\in \text {Tf}_\Lambda $
. Then M is pure-injective if and only if
$M\in \text {Tf}_\Lambda $
. Then M is pure-injective if and only if
-
(1)
 $M/M\pi ^k$
is pure-injective for all
$M/M\pi ^k$
is pure-injective for all
 $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and -
(2) M is pure-injective as an R-module.
Proof Certainly, if M is pure-injective, then conditions
![]() $(1)$
and
$(1)$
and
![]() $(2)$
hold.
$(2)$
hold.
So suppose that
![]() $(1)$
and
$(1)$
and
![]() $(2)$
hold. We know that M is isomorphic to
$(2)$
hold. We know that M is isomorphic to
![]() $D_M\oplus N$
and that
$D_M\oplus N$
and that
![]() $D_M$
is injective. Thus, M is pure-injective if and only if N is pure-injective. Moreover, if conditions
$D_M$
is injective. Thus, M is pure-injective if and only if N is pure-injective. Moreover, if conditions
![]() $(1)$
and
$(1)$
and
![]() $(2)$
hold for M, then they also hold of N. Let
$(2)$
hold for M, then they also hold of N. Let
![]() $H(N)$
be the pure-injective hull of N. Since
$H(N)$
be the pure-injective hull of N. Since
![]() $N/N\pi ^k$
is pure-injective, Theorem 3.8 implies that
$N/N\pi ^k$
is pure-injective, Theorem 3.8 implies that
![]() $H(N)/H(N)\pi ^k=N/N\pi ^k$
. By Lemma 4.3,
$H(N)/H(N)\pi ^k=N/N\pi ^k$
. By Lemma 4.3,
![]() $H(N)$
is reduced, and hence is isomorphic to
$H(N)$
is reduced, and hence is isomorphic to
![]() $H(N)^*\cong N^*$
. Since N is reduced and pure-injective as an R-module,
$H(N)^*\cong N^*$
. Since N is reduced and pure-injective as an R-module,
![]() $N\cong N^*$
. Thus,
$N\cong N^*$
. Thus,
![]() $N\cong H(N)$
and is hence pure-injective. Thus,
$N\cong H(N)$
and is hence pure-injective. Thus,
![]() $M=D_M\oplus N$
is also pure-injective.▪
$M=D_M\oplus N$
is also pure-injective.▪
Theorem 4.6 Let
![]() $M\in \text {Tf}_\Lambda $
be R-reduced, and suppose that
$M\in \text {Tf}_\Lambda $
be R-reduced, and suppose that
![]() $M/M\pi ^n$
is pure-injective for all
$M/M\pi ^n$
is pure-injective for all
![]() $n\in \mathbb {N}$
. Then the canonical map
$n\in \mathbb {N}$
. Then the canonical map
![]() $v:M\rightarrow M^*$
is the pure-injective hull of M.
$v:M\rightarrow M^*$
is the pure-injective hull of M.
Proof Let
![]() $u:M\rightarrow H(M)$
be a pure-injective hull of M. For each
$u:M\rightarrow H(M)$
be a pure-injective hull of M. For each
![]() $k\in \mathbb {N}$
, let
$k\in \mathbb {N}$
, let
![]() $u_k:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
be the homomorphism induced by u. For each
$u_k:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
be the homomorphism induced by u. For each
![]() $k\geq k_0+1$
,
$k\geq k_0+1$
,
![]() $u_k:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
is the pure-injective hull of
$u_k:M/M\pi ^k\rightarrow H(M)/H(M)\pi ^k$
is the pure-injective hull of
![]() $M/M\pi ^k$
. Since
$M/M\pi ^k$
. Since
![]() $M/M\pi ^k$
is pure-injective,
$M/M\pi ^k$
is pure-injective,
![]() $u_k$
is an isomorphism. The maps
$u_k$
is an isomorphism. The maps
![]() $u_k$
induce an isomorphism
$u_k$
induce an isomorphism
![]() $w:M^*\rightarrow H(M)^*$
. Since M and hence, by Lemma 4.3,
$w:M^*\rightarrow H(M)^*$
. Since M and hence, by Lemma 4.3,
![]() $H(M)$
are reduced,
$H(M)$
are reduced,
![]() $H(M)\cong H(M)^*$
. Viewing
$H(M)\cong H(M)^*$
. Viewing
![]() $H(M)^*$
as a submodule of
$H(M)^*$
as a submodule of
![]() $\prod _{i\in \mathbb {N}}H(M)/H(M)\pi ^i$
, for all
$\prod _{i\in \mathbb {N}}H(M)/H(M)\pi ^i$
, for all
![]() $m\in M$
,
$m\in M$
,
![]() $wv(m)=(u(m)+H(M)\pi ^i)_{i\in \mathbb {N}}$
. Thus,
$wv(m)=(u(m)+H(M)\pi ^i)_{i\in \mathbb {N}}$
. Thus,
![]() $v=w^{-1}u$
.▪
$v=w^{-1}u$
.▪
The same argument as used in the proof above shows that for any R-reduced
![]() $M\in \text {Tf}_\Lambda $
, the pure-injective hull of M is
$M\in \text {Tf}_\Lambda $
, the pure-injective hull of M is
 $\varprojlim H(M/M\pi ^i)$
along some surjective homomorphisms
$\varprojlim H(M/M\pi ^i)$
along some surjective homomorphisms
![]() $p_i:H(M/M\pi ^{i+1})\rightarrow H(M/M\pi ^i)$
. Unfortunately, it is not clear how to explicitly describe the homomorphisms
$p_i:H(M/M\pi ^{i+1})\rightarrow H(M/M\pi ^i)$
. Unfortunately, it is not clear how to explicitly describe the homomorphisms
![]() $p_i$
beyond saying that
$p_i$
beyond saying that
![]() $\ker p_i=H(M/M\pi ^{i+1})\pi ^{i}$
.
$\ker p_i=H(M/M\pi ^{i+1})\pi ^{i}$
.
For the rest of this section, we focus on an application of Theorem 4.6. We will calculate the pure-injective hull of the direct limit at the “top” of a generalized tube in
![]() $\text {Latt}_\Lambda $
. This will allow us to describe certain points of
$\text {Latt}_\Lambda $
. This will allow us to describe certain points of
 $\textrm {Zg}_\Lambda ^{tf}$
as modules when
$\textrm {Zg}_\Lambda ^{tf}$
as modules when
 $\Lambda =\widehat {\mathbb {Z}}_{(2)}C_2\times C_2$
and answer the questions at the end of [Reference Puninski and Toffalori20].
$\Lambda =\widehat {\mathbb {Z}}_{(2)}C_2\times C_2$
and answer the questions at the end of [Reference Puninski and Toffalori20].
Following Krause in [Reference Krause12], we define a generalized tube in
![]() ${\textrm {mod}}\text {-}S$
to be a sequence of tuples
${\textrm {mod}}\text {-}S$
to be a sequence of tuples
![]() $\mathcal {T}:=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
where
$\mathcal {T}:=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
where
![]() $M_i\in {\textrm {mod}}\text {-}S$
,
$M_i\in {\textrm {mod}}\text {-}S$
,
![]() $M_0=0$
,
$M_0=0$
,
![]() $f_i:M_{i+1}\rightarrow M_i$
, and
$f_i:M_{i+1}\rightarrow M_i$
, and
![]() $g_i:M_i\rightarrow M_{i+1}$
such that for every
$g_i:M_i\rightarrow M_{i+1}$
such that for every
![]() $i\in \mathbb {N}$
,
$i\in \mathbb {N}$
,

is a pushout and a pullback.
We will show that if
![]() $\mathcal {T}$
is a generalized tube in
$\mathcal {T}$
is a generalized tube in
![]() $\text {Latt}_\Lambda $
, then its image, denoted
$\text {Latt}_\Lambda $
, then its image, denoted
![]() $\mathcal {T}_k$
, in
$\mathcal {T}_k$
, in
![]() ${\textrm {mod}}\text {-}\Lambda _k$
is a generalized tube.
${\textrm {mod}}\text {-}\Lambda _k$
is a generalized tube.
Recall that a diagram

is a pushout and a pullback if and only if

is an exact sequence.
We say a generalized tube
![]() $(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
is trivial if
$(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
is trivial if
![]() $M_i=0$
for all
$M_i=0$
for all
![]() $i\in \mathbb {N}_0$
.
$i\in \mathbb {N}_0$
.
Remark 4.7 If
![]() $(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
is a nontrivial generalized tube, then there exists
$(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
is a nontrivial generalized tube, then there exists
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $g_i$
is not an epimorphism for all
$g_i$
is not an epimorphism for all
![]() $i\geq n$
.
$i\geq n$
.
Proof Let
![]() $n\in \mathbb {N}$
be least such that
$n\in \mathbb {N}$
be least such that
![]() $M_n\neq 0$
. Then
$M_n\neq 0$
. Then
![]() $g_{n-1}$
is not an epimorphism. Since the pushout of an epimorphism is an epimorphism,
$g_{n-1}$
is not an epimorphism. Since the pushout of an epimorphism is an epimorphism,
![]() $g_{i}$
is not an epimorphism for all
$g_{i}$
is not an epimorphism for all
![]() $i\geq n-1$
.▪
$i\geq n-1$
.▪
The following remark seems like it should be false because certainly Maranda’s functor does not send monomorphisms between lattices to monomorphisms. Consider the exact sequence below. Since M is projective as an R-module and
![]() $\beta $
is surjective, there exists
$\beta $
is surjective, there exists
![]() $\gamma \in \textrm {Hom}_R(M,N)$
such that
$\gamma \in \textrm {Hom}_R(M,N)$
such that
![]() $\beta \gamma =\text {Id}_M$
. Thus, the exact sequence is split when viewed as an exact sequence of R-modules. Therefore, the second sequence is a split exact sequence of
$\beta \gamma =\text {Id}_M$
. Thus, the exact sequence is split when viewed as an exact sequence of R-modules. Therefore, the second sequence is a split exact sequence of
![]() $R_k$
-modules. Hence, it is an exact sequence of
$R_k$
-modules. Hence, it is an exact sequence of
![]() $\Lambda _k$
-modules.
$\Lambda _k$
-modules.
Remark 4.8 If

is an exact sequence of
![]() $\Lambda $
-lattices, then
$\Lambda $
-lattices, then

is an exact sequence of
![]() $\Lambda _k$
-modules.
$\Lambda _k$
-modules.
It follows that if
![]() $\mathcal {T}$
is a generalized tube of
$\mathcal {T}$
is a generalized tube of
![]() $\Lambda $
-lattices, then
$\Lambda $
-lattices, then
 $\mathcal {T}_k:=((M_i)_k,\overline {f_i},\overline {g_i})_{i\in \mathbb {N}_0}$
is a generalized tube of finitely presented
$\mathcal {T}_k:=((M_i)_k,\overline {f_i},\overline {g_i})_{i\in \mathbb {N}_0}$
is a generalized tube of finitely presented
![]() $\Lambda _k$
-modules.
$\Lambda _k$
-modules.
Given a generalized tube
![]() $\mathcal {T}=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
, define
$\mathcal {T}=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
, define
![]() $\mathcal {T}[\infty ]$
to be the direct limit along the embeddings
$\mathcal {T}[\infty ]$
to be the direct limit along the embeddings
![]() $g_i:M_i\rightarrow M_{i+1}$
. Note that if
$g_i:M_i\rightarrow M_{i+1}$
. Note that if
![]() $\mathcal {T}$
is trivial, then
$\mathcal {T}$
is trivial, then
![]() $\mathcal {T}[\infty ]=0$
.
$\mathcal {T}[\infty ]=0$
.
Recall that a module
![]() $M\in \textrm {Mod}\text {-}S$
is
$M\in \textrm {Mod}\text {-}S$
is
![]() $\Sigma $
-pure-injective if
$\Sigma $
-pure-injective if
![]() $M^{(\kappa )}$
is pure-injective for every cardinal
$M^{(\kappa )}$
is pure-injective for every cardinal
![]() $\kappa $
. Equivalently [Reference Prest17, Theorem 4.4.5], M is
$\kappa $
. Equivalently [Reference Prest17, Theorem 4.4.5], M is
![]() $\Sigma $
-pure-injective if and only if
$\Sigma $
-pure-injective if and only if
![]() $\textrm {pp}^1_SM$
has the descending chain condition.
$\textrm {pp}^1_SM$
has the descending chain condition.
Proposition 4.9 Let
![]() $\mathcal {T}=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
be a nontrivial generalized tube in
$\mathcal {T}=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
be a nontrivial generalized tube in
![]() $\text {Latt}_\Lambda $
. Then
$\text {Latt}_\Lambda $
. Then
-
(i)
 $\mathcal {T}[\infty ]$
is R-torsion-free and R-reduced,
$\mathcal {T}[\infty ]$
is R-torsion-free and R-reduced, -
(ii)
 $\mathcal {T}[\infty ]$
is not pure-injective,
$\mathcal {T}[\infty ]$
is not pure-injective, -
(iii) for all
 $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
 $\mathcal {T}[\infty ]/\mathcal {T}[\infty ]\pi ^k$
is
$\mathcal {T}[\infty ]/\mathcal {T}[\infty ]\pi ^k$
is
 $\Sigma $
-pure-injective, and
$\Sigma $
-pure-injective, and -
(iv)
 $\mathcal {T}[\infty ]^*$
is the pure-injective hull of
$\mathcal {T}[\infty ]^*$
is the pure-injective hull of
 $\mathcal {T}[\infty ]$
.
$\mathcal {T}[\infty ]$
.
Proof (i) and (ii): As a direct limit of lattices,
![]() $\mathcal {T}[\infty ]$
is R-torsion-free. Each
$\mathcal {T}[\infty ]$
is R-torsion-free. Each
![]() $g_i$
is split when viewed as a homomorphism of R-modules. Since
$g_i$
is split when viewed as a homomorphism of R-modules. Since
![]() $\mathcal {T}$
is nontrivial, there exists an
$\mathcal {T}$
is nontrivial, there exists an
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $g_i$
is not an isomorphism for all
$g_i$
is not an isomorphism for all
![]() $i\geq n$
. Therefore,
$i\geq n$
. Therefore,
![]() $\mathcal {T}[\infty ]$
is isomorphic to
$\mathcal {T}[\infty ]$
is isomorphic to
![]() $R^{(\aleph _0)}$
as an R-module. So
$R^{(\aleph _0)}$
as an R-module. So
![]() $\mathcal {T}[\infty ]$
is reduced. Since R is not
$\mathcal {T}[\infty ]$
is reduced. Since R is not
![]() $\Sigma $
-pure-injective as a module over itself [Reference Prest17, Theorem 4.4.8],
$\Sigma $
-pure-injective as a module over itself [Reference Prest17, Theorem 4.4.8],
![]() $R^{(\aleph _0)}$
is not pure-injective as an R-module, and hence
$R^{(\aleph _0)}$
is not pure-injective as an R-module, and hence
![]() $\mathcal {T}[\infty ]$
is not pure-injective as a
$\mathcal {T}[\infty ]$
is not pure-injective as a
![]() $\Lambda $
-module.
$\Lambda $
-module.
(iii): Krause shows [Reference Krause12, Proposition 8.3] that if
![]() $\mathcal {T}$
is a generalized tube in the category of finitely presented modules over an Artin algebra, then
$\mathcal {T}$
is a generalized tube in the category of finitely presented modules over an Artin algebra, then
![]() $\mathcal {T}[\infty ]$
is
$\mathcal {T}[\infty ]$
is
![]() $\Sigma $
-pure-injective. Since Maranda’s functor commutes with direct limits and sends generalized tubes to generalized tubes, if
$\Sigma $
-pure-injective. Since Maranda’s functor commutes with direct limits and sends generalized tubes to generalized tubes, if
![]() $\mathcal {T}=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
is a generalized tube in
$\mathcal {T}=(M_i,f_i,g_i)_{i\in \mathbb {N}_0}$
is a generalized tube in
![]() $\text {Latt}_\Lambda $
, then
$\text {Latt}_\Lambda $
, then
![]() $\mathcal {T}_k[\infty ]=\mathcal {T}[\infty ]/\mathcal {T}[\infty ]\pi ^k$
. Thus,
$\mathcal {T}_k[\infty ]=\mathcal {T}[\infty ]/\mathcal {T}[\infty ]\pi ^k$
. Thus,
![]() $\mathcal {T}[\infty ]/\mathcal {T}[\infty ]\pi ^k$
is
$\mathcal {T}[\infty ]/\mathcal {T}[\infty ]\pi ^k$
is
![]() $\Sigma $
-pure-injective.
$\Sigma $
-pure-injective.
(iv): Follows directly from (i), (iii), and Theorem 4.6.▪
When R is complete and
![]() $Q\Lambda $
is a separable Q-algebra, the category of
$Q\Lambda $
is a separable Q-algebra, the category of
![]() $\Lambda $
-lattices has almost split sequences (see [Reference Roggenkamp and Schmidt22]). A stable tube is an Auslander–Reiten component of the form
$\Lambda $
-lattices has almost split sequences (see [Reference Roggenkamp and Schmidt22]). A stable tube is an Auslander–Reiten component of the form
![]() $\mathbb {Z} A_{\infty }/\tau ^n$
, and we call n the rank of the tube. Explicitly, a stable tube of rank n has points
$\mathbb {Z} A_{\infty }/\tau ^n$
, and we call n the rank of the tube. Explicitly, a stable tube of rank n has points
![]() $S_i[j]$
for
$S_i[j]$
for
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $j\in \mathbb {N}$
. We read the index
$j\in \mathbb {N}$
. We read the index
![]() $i\ {\textrm {mod}} \ n$
. For all
$i\ {\textrm {mod}} \ n$
. For all
![]() $i,j\in \mathbb {N}$
, a stable tube has a single (trivially valued) arrow
$i,j\in \mathbb {N}$
, a stable tube has a single (trivially valued) arrow
![]() $S_i[j]\rightarrow S_i[j+1]$
and a single (trivially valued) arrow
$S_i[j]\rightarrow S_i[j+1]$
and a single (trivially valued) arrow
![]() $S_i[j+1]\rightarrow S_{i+1}[j]$
. We will identify the points with (the isomorphism type of) the
$S_i[j+1]\rightarrow S_{i+1}[j]$
. We will identify the points with (the isomorphism type of) the
![]() $\Lambda $
-lattice they represent. As for Artin algebras, generalized tubes can be constructed from stable tubes using the following two facts.
$\Lambda $
-lattice they represent. As for Artin algebras, generalized tubes can be constructed from stable tubes using the following two facts.
-
• If
 $A,B,C\in \text {Latt}_\Lambda $
are indecomposable and pairwise nonisomorphic and
$A,B,C\in \text {Latt}_\Lambda $
are indecomposable and pairwise nonisomorphic and
 $u:A\rightarrow B$
and
$u:A\rightarrow B$
and
 $v:A\rightarrow C$
are irreducible morphisms, then there is
$v:A\rightarrow C$
are irreducible morphisms, then there is
 $w:A\rightarrow D$
such that
$w:A\rightarrow D$
such that
 $(u \ v \ w)^T:A\rightarrow B\oplus C\oplus D$
is left minimal almost split.
$(u \ v \ w)^T:A\rightarrow B\oplus C\oplus D$
is left minimal almost split. -
• If
 $u:S_i[j]\rightarrow S_{i}[j+1]$
is an irreducible map,
$u:S_i[j]\rightarrow S_{i}[j+1]$
is an irreducible map,
 $w:S_i[j]\rightarrow W$
, and
$w:S_i[j]\rightarrow W$
, and
 $W\in \text {Latt}_\Lambda $
is indecomposable and is not isomorphic to any of
$W\in \text {Latt}_\Lambda $
is indecomposable and is not isomorphic to any of
 $S_i[j],S_{i+1}[j-1],\ldots ,S_{i+(j-1)}[1]$
, then there exists
$S_i[j],S_{i+1}[j-1],\ldots ,S_{i+(j-1)}[1]$
, then there exists
 $\gamma :S_i[j+1]\rightarrow W$
such that
$\gamma :S_i[j+1]\rightarrow W$
such that
 $w=\gamma u$
.
$w=\gamma u$
.
Krause [Reference Krause12, Theorem 9.1] showed that if
![]() $\mathcal {T}$
is a stable tube (of rank n) in the module category of an Artin algebra, with the labeling of modules as above, then for each
$\mathcal {T}$
is a stable tube (of rank n) in the module category of an Artin algebra, with the labeling of modules as above, then for each
![]() $1\leq i\leq n$
, the direct limit
$1\leq i\leq n$
, the direct limit
 $\varinjlim S_i[j]$
is an indecomposable pure-injective. For stable tubes in categories of lattices, we know (Proposition 4.9) that
$\varinjlim S_i[j]$
is an indecomposable pure-injective. For stable tubes in categories of lattices, we know (Proposition 4.9) that
 $\oplus _{i=1}^n\varinjlim S_i[j]$
has a pure-injective hull
$\oplus _{i=1}^n\varinjlim S_i[j]$
has a pure-injective hull
 $(\oplus _{i=1}^n\varinjlim S_i[j])^*$
. Hence, the pure-injective hull of
$(\oplus _{i=1}^n\varinjlim S_i[j])^*$
. Hence, the pure-injective hull of
 $\varinjlim S_i[j]$
is
$\varinjlim S_i[j]$
is
 $(\varinjlim S_i[j])^*$
. This raises the following question.
$(\varinjlim S_i[j])^*$
. This raises the following question.
Question Let R be a complete discrete valuation domain with field of fractions Q, and let
![]() $\Lambda $
be an order R such that
$\Lambda $
be an order R such that
![]() $Q\Lambda $
is a separable Q-algebra. If T is a direct limit up a ray of irreducible monomorphisms in a stable tube in
$Q\Lambda $
is a separable Q-algebra. If T is a direct limit up a ray of irreducible monomorphisms in a stable tube in
![]() $\text {Latt}_\Lambda $
, then is
$\text {Latt}_\Lambda $
, then is
![]() $T^*$
indecomposable?▪
$T^*$
indecomposable?▪
We are able to answer this question positively for the
![]() $\widehat {\mathbb {Z}_2}$
-order
$\widehat {\mathbb {Z}_2}$
-order
![]() $\Gamma :=\widehat {\mathbb {Z}_2}C_2\times C_2$
. The torsion-free part of the Ziegler spectrum of
$\Gamma :=\widehat {\mathbb {Z}_2}C_2\times C_2$
. The torsion-free part of the Ziegler spectrum of
![]() $\Gamma $
was described in [Reference Puninski and Toffalori20]. However, the points were not described as modules.
$\Gamma $
was described in [Reference Puninski and Toffalori20]. However, the points were not described as modules.
We start by explaining the setup. Let
![]() $e_1,e_2,e_3,e_4$
be the primitive orthogonal idempotents as in [Reference Puninski and Toffalori20]. Using these idempotents, Butler [Reference Butler2] defined a full functor
$e_1,e_2,e_3,e_4$
be the primitive orthogonal idempotents as in [Reference Puninski and Toffalori20]. Using these idempotents, Butler [Reference Butler2] defined a full functor
![]() $\Delta $
from the category of b-reduced
$\Delta $
from the category of b-reduced
![]() $\Gamma $
-lattices to the category of finite-dimensional vector spaces over
$\Gamma $
-lattices to the category of finite-dimensional vector spaces over
![]() $\mathbb {F}_2$
with four distinguished subspaces. A
$\mathbb {F}_2$
with four distinguished subspaces. A
![]() $\widehat {\mathbb {Z}_2}$
-torsion-free
$\widehat {\mathbb {Z}_2}$
-torsion-free
![]() $\Gamma $
-module M is b-reduced if
$\Gamma $
-module M is b-reduced if
![]() $M\cap Me_i=2Me_i$
for all
$M\cap Me_i=2Me_i$
for all
![]() $1\leq i\leq 4$
. Note that, since
$1\leq i\leq 4$
. Note that, since
![]() $e_i\notin \widehat {\mathbb {Z}_2}C_2\times C_2$
,
$e_i\notin \widehat {\mathbb {Z}_2}C_2\times C_2$
,
![]() $Me_i$
and
$Me_i$
and
![]() $M2e_i$
are calculated inside
$M2e_i$
are calculated inside
![]() $\widehat {\mathbb {Q}_2}M$
. Puninski and Toffalori extended this functor to the category of b-reduced
$\widehat {\mathbb {Q}_2}M$
. Puninski and Toffalori extended this functor to the category of b-reduced
![]() $\widehat {\mathbb {Z}_2}$
-torsion-free modules and showed [Reference Puninski and Toffalori20, Theorem 5.4] that it is full on
$\widehat {\mathbb {Z}_2}$
-torsion-free modules and showed [Reference Puninski and Toffalori20, Theorem 5.4] that it is full on
![]() $\widehat {\mathbb {Z}_2}$
-torsion-free b-reduced pure-injective
$\widehat {\mathbb {Z}_2}$
-torsion-free b-reduced pure-injective
![]() $\Gamma $
-modules.
$\Gamma $
-modules.
Let M be a b-reduced
![]() $\widehat {\mathbb {Z}_2}$
-torsion-free
$\widehat {\mathbb {Z}_2}$
-torsion-free
![]() $\widehat {\mathbb {Z}_2}C_2\times C_2$
-module. Define
$\widehat {\mathbb {Z}_2}C_2\times C_2$
-module. Define
![]() $M^\star :=Me_1\oplus \cdots \oplus Me_4$
. Then
$M^\star :=Me_1\oplus \cdots \oplus Me_4$
. Then
![]() $\Delta (M):=(V;V_1,V_2,V_3,V_4)$
, where
$\Delta (M):=(V;V_1,V_2,V_3,V_4)$
, where
![]() $V:=M^\star /M$
and
$V:=M^\star /M$
and
![]() $V_i:=Me_i+M/M\cong Me_i/M\cap Me_i=Me_i/2Me_i$
.
$V_i:=Me_i+M/M\cong Me_i/M\cap Me_i=Me_i/2Me_i$
.
The category of finite-dimensional vector spaces over
![]() $\mathbb {F}_2$
with four distinguished subspaces may be identified with a full subcategory of modules over the path algebra
$\mathbb {F}_2$
with four distinguished subspaces may be identified with a full subcategory of modules over the path algebra
![]() $\mathbb {F}_2\widetilde {D}_4$
. The only indecomposable representations which are not in this full subcategory are the simple injective
$\mathbb {F}_2\widetilde {D}_4$
. The only indecomposable representations which are not in this full subcategory are the simple injective
![]() $\mathbb {F}_2\widetilde {D}_4$
-modules. We will make this identification and consider
$\mathbb {F}_2\widetilde {D}_4$
-modules. We will make this identification and consider
![]() $\Delta $
as a functor to
$\Delta $
as a functor to
![]() $\textrm {Mod}\text {-}\mathbb {F}_2\widetilde {D}_4$
.
$\textrm {Mod}\text {-}\mathbb {F}_2\widetilde {D}_4$
.
As observed by Puninski and Toffalori, just from the construction, one can see that
![]() $\Delta $
is an interpretation functor. Note that if M is b-reduced and
$\Delta $
is an interpretation functor. Note that if M is b-reduced and
![]() $\widehat {\mathbb {Z}_2}$
-torsion-free, then
$\widehat {\mathbb {Z}_2}$
-torsion-free, then
![]() $\Delta (M)=0$
if and only if M is
$\Delta (M)=0$
if and only if M is
![]() $\widehat {\mathbb {Z}_2}$
-divisible.
$\widehat {\mathbb {Z}_2}$
-divisible.
Dieterich, in [Reference Dieterich6], showed that
![]() $\Delta $
induced an isomorphism from the Auslander–Reiten quiver of
$\Delta $
induced an isomorphism from the Auslander–Reiten quiver of
![]() $\mathbb {F}_2\widetilde {D}_4$
with all projective points removed and all simple injective modules removed and the Auslander–Reiten quiver of
$\mathbb {F}_2\widetilde {D}_4$
with all projective points removed and all simple injective modules removed and the Auslander–Reiten quiver of
![]() $\text {Latt}_{\Gamma }$
restricted to the b-reduced lattices. Using this, he was able [Reference Dieterich6, Proposition 3.4] to compute the full Auslander–Reiten quiver of
$\text {Latt}_{\Gamma }$
restricted to the b-reduced lattices. Using this, he was able [Reference Dieterich6, Proposition 3.4] to compute the full Auslander–Reiten quiver of
![]() $\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
. Moreover, see the proof of [Reference Dieterich6, Lemma 2.2] and [Reference Dieterich6, Proposition 3.4],
$\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
. Moreover, see the proof of [Reference Dieterich6, Lemma 2.2] and [Reference Dieterich6, Proposition 3.4],
![]() $\Delta $
induces a bimodule isomorphism between
$\Delta $
induces a bimodule isomorphism between
![]() $\text {Irr}_{\text {Latt}_{\Gamma }}(M,L)$
and
$\text {Irr}_{\text {Latt}_{\Gamma }}(M,L)$
and
![]() $\text {Irr}_{\mathbb {F}_2\widetilde {D}_4}(\Delta (M),\Delta (L))$
for all
$\text {Irr}_{\mathbb {F}_2\widetilde {D}_4}(\Delta (M),\Delta (L))$
for all
![]() $L,M$
indecomposable b-reduced
$L,M$
indecomposable b-reduced
![]() $\Gamma $
-lattices. In particular,
$\Gamma $
-lattices. In particular,
![]() $\Delta $
sends irreducible morphisms between indecomposable b-reduced
$\Delta $
sends irreducible morphisms between indecomposable b-reduced
![]() $\Gamma $
-lattices to irreducible morphisms in
$\Gamma $
-lattices to irreducible morphisms in
![]() ${\textrm {mod}}\text {-}\mathbb {F}_2\widetilde {D}_4$
. This implies that the Auslander–Reiten quiver of
${\textrm {mod}}\text {-}\mathbb {F}_2\widetilde {D}_4$
. This implies that the Auslander–Reiten quiver of
![]() $\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
has infinitely many stable tubes of rank
$\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
has infinitely many stable tubes of rank
![]() $1$
and rank
$1$
and rank
![]() $3$
stable tubes of rank
$3$
stable tubes of rank
![]() $2$
and
$2$
and
![]() $\Delta $
sends each stable tube in
$\Delta $
sends each stable tube in
![]() $\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
to a stable tube in
$\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
to a stable tube in
![]() ${\textrm {mod}}\text {-}\mathbb {F}_2\widetilde {D}_4$
.
${\textrm {mod}}\text {-}\mathbb {F}_2\widetilde {D}_4$
.
Keeping our notation as above, let
![]() $S_i[j]$
be the lattices in a stable tube of rank
$S_i[j]$
be the lattices in a stable tube of rank
![]() $n=1$
or
$n=1$
or
![]() $n=2$
in
$n=2$
in
![]() $\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
. Fix
$\text {Latt}_{\widehat {\mathbb {Z}_2}C_2\times C_2}$
. Fix
![]() $1\leq i\leq n$
and for each
$1\leq i\leq n$
and for each
![]() $j\in \mathbb {N}$
let
$j\in \mathbb {N}$
let
![]() $w_j:S_i[j]\rightarrow S_i[j+1]$
be an irreducible map. Let
$w_j:S_i[j]\rightarrow S_i[j+1]$
be an irreducible map. Let
 $S_i[\infty ]:=\varinjlim S_i[j]$
be the direct limit along the maps
$S_i[\infty ]:=\varinjlim S_i[j]$
be the direct limit along the maps
![]() $w_j$
. Then
$w_j$
. Then
 $\Delta S_i[\infty ] =\varinjlim \Delta S_i[j]$
is pure-injective and indecomposable by [Reference Krause12, Theorem 9.1] since
$\Delta S_i[\infty ] =\varinjlim \Delta S_i[j]$
is pure-injective and indecomposable by [Reference Krause12, Theorem 9.1] since
![]() $\Delta $
sends stable tubes to stable tubes. Since
$\Delta $
sends stable tubes to stable tubes. Since
![]() $\Delta $
is full on pure-injective modules, by [Reference Prest16, Lemmas 3.15 and 3.16],Footnote
2
it preserves pure-injective hulls. Thus,
$\Delta $
is full on pure-injective modules, by [Reference Prest16, Lemmas 3.15 and 3.16],Footnote
2
it preserves pure-injective hulls. Thus,
![]() $\Delta (S_i[\infty ])\cong \Delta (S_i[\infty ]^*)$
. Since
$\Delta (S_i[\infty ])\cong \Delta (S_i[\infty ]^*)$
. Since
![]() $S_i[\infty ]^*$
is reduced and
$S_i[\infty ]^*$
is reduced and
![]() $\Delta (S_i[\infty ]^*)$
is indecomposable,
$\Delta (S_i[\infty ]^*)$
is indecomposable,
![]() $S_i[\infty ]^*$
is indecomposable.
$S_i[\infty ]^*$
is indecomposable.
So, finally, for each quasi-simple S at the base of a tube (i.e.,
![]() $S_i[1]$
for some stable tube), the S-prüfer point in [Reference Puninski and Toffalori20, Theorem 6.1] is
$S_i[1]$
for some stable tube), the S-prüfer point in [Reference Puninski and Toffalori20, Theorem 6.1] is
![]() $S[\infty ]^*$
, where
$S[\infty ]^*$
, where
![]() $S[\infty ]$
is the direct limit up a ray of irreducible monomorphisms starting at S.
$S[\infty ]$
is the direct limit up a ray of irreducible monomorphisms starting at S.
The module T in Question 6.2 of [Reference Puninski and Toffalori20] is indecomposable but not pure-injective; however, its pure-injective hull is indecomposable (and
![]() $\widehat {\mathbb {Z}_2}$
-reduced).
$\widehat {\mathbb {Z}_2}$
-reduced).
5 Duality
Throughout this section, let R be a Dedekind domain which is not a field, Q its field of fractions,
![]() $\Lambda $
an R-order, and
$\Lambda $
an R-order, and
![]() $Q\Lambda $
a separable Q-algebra. The main aim of this section is to show that the lattice of open sets of
$Q\Lambda $
a separable Q-algebra. The main aim of this section is to show that the lattice of open sets of
 $\textrm {Zg}_\Lambda ^{tf}$
is isomorphic to the lattice of open sets of
$\textrm {Zg}_\Lambda ^{tf}$
is isomorphic to the lattice of open sets of
![]() ${_\Lambda }\textrm {Zg}^{tf}$
. We will also show, by other methods, that the m-dimension of
${_\Lambda }\textrm {Zg}^{tf}$
. We will also show, by other methods, that the m-dimension of
![]() $\textrm {pp}^1_\Lambda (\text {Tf}_{\Lambda })$
is equal to the m-dimension of
$\textrm {pp}^1_\Lambda (\text {Tf}_{\Lambda })$
is equal to the m-dimension of
![]() ${_\Lambda }\textrm {pp}^1({_\Lambda }\text {Tf})$
and that the Krull–Gabriel dimension of
${_\Lambda }\textrm {pp}^1({_\Lambda }\text {Tf})$
and that the Krull–Gabriel dimension of
![]() $(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
is equal to the Krull–Gabriel dimension of
$(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
is equal to the Krull–Gabriel dimension of
![]() $({_\Lambda }\text {Latt},\text {Ab})^{fp}$
.
$({_\Lambda }\text {Latt},\text {Ab})^{fp}$
.
5.1 Duality for the R-reduced part of
 $\textrm {Zg}_{\Lambda }^{tf}$
when R is a discrete valuation domain
$\textrm {Zg}_{\Lambda }^{tf}$
when R is a discrete valuation domain
Throughout this subsection, R will be a discrete valuation domain, k will be a natural number strictly greater than Maranda’s constant for
![]() $\Lambda $
as an R-order, and
$\Lambda $
as an R-order, and
![]() $I:\text {Tf}_\Lambda \rightarrow \textrm {Mod}\text {-}\Lambda _k$
(respectively,
$I:\text {Tf}_\Lambda \rightarrow \textrm {Mod}\text {-}\Lambda _k$
(respectively,
![]() $I:{_\Lambda }\text {Tf}\rightarrow \Lambda _k\text {-}\textrm {Mod}$
) will be Maranda’s functor.
$I:{_\Lambda }\text {Tf}\rightarrow \Lambda _k\text {-}\textrm {Mod}$
) will be Maranda’s functor.
Maranda’s functor
![]() $I:\text {Tf}_\Lambda \rightarrow \textrm {Mod}\text {-}\Lambda _k$
is an interpretation functor. The kernel of I is the definable subcategory of R-divisible modules. Since
$I:\text {Tf}_\Lambda \rightarrow \textrm {Mod}\text {-}\Lambda _k$
is an interpretation functor. The kernel of I is the definable subcategory of R-divisible modules. Since
![]() $Q\Lambda $
is separable, by Remark 4.1 and the discussion just below it, all indecomposable pure-injective modules in
$Q\Lambda $
is separable, by Remark 4.1 and the discussion just below it, all indecomposable pure-injective modules in
![]() $\text {Tf}_\Lambda $
are either R-reduced or R-divisible modules. When
$\text {Tf}_\Lambda $
are either R-reduced or R-divisible modules. When
![]() $\Lambda $
is an order over a discrete valuation domain R, we will write
$\Lambda $
is an order over a discrete valuation domain R, we will write
 $\textrm {Zg}^{rtf}_\Lambda $
for the subset of R-reduced modules in
$\textrm {Zg}^{rtf}_\Lambda $
for the subset of R-reduced modules in
 $\textrm {Zg}_\Lambda ^{tf}$
. We have shown in Section 3 that if
$\textrm {Zg}_\Lambda ^{tf}$
. We have shown in Section 3 that if
![]() $N,M\in \text {Tf}_\Lambda $
are R-reduced and pure-injective, then
$N,M\in \text {Tf}_\Lambda $
are R-reduced and pure-injective, then
![]() $IN\cong IM$
implies
$IN\cong IM$
implies
![]() $N\cong M$
and that if N is also indecomposable, then so is
$N\cong M$
and that if N is also indecomposable, then so is
![]() $IN$
. Thus, Proposition 2.7 gives us the following theorem.
$IN$
. Thus, Proposition 2.7 gives us the following theorem.
Theorem 5.1 The map which sends
 $N\in \textrm {Zg}_\Lambda ^{rtf}$
to
$N\in \textrm {Zg}_\Lambda ^{rtf}$
to
 $N/N\pi ^k\in \textrm {Zg}_{\Lambda _k}$
induces a homeomorphism onto its image which is closed.
$N/N\pi ^k\in \textrm {Zg}_{\Lambda _k}$
induces a homeomorphism onto its image which is closed.
In theory, the above theorem could be used to give a description of
 $\textrm {Zg}_\Lambda ^{rtf}$
and hence
$\textrm {Zg}_\Lambda ^{rtf}$
and hence
 $\textrm {Zg}_\Lambda ^{tf}$
based on a description of
$\textrm {Zg}_\Lambda ^{tf}$
based on a description of
![]() $\textrm {Zg}_{\Lambda _k}$
. However, as explained in Section 1,
$\textrm {Zg}_{\Lambda _k}$
. However, as explained in Section 1,
![]() $\textrm {Zg}_{\Lambda _k}$
is generally much more complicated than
$\textrm {Zg}_{\Lambda _k}$
is generally much more complicated than
 $\textrm {Zg}_\Lambda ^{tf}$
.
$\textrm {Zg}_\Lambda ^{tf}$
.
Based on Prest’s duality for pp formulas, Herzog defined a lattice isomorphism between the lattice of open subsets of
![]() $\textrm {Zg}_S$
and the lattice of open subsets of
$\textrm {Zg}_S$
and the lattice of open subsets of
![]() ${_S}\textrm {Zg}$
.
${_S}\textrm {Zg}$
.
Theorem 5.2 [Reference Herzog9]
There is a lattice isomorphism D between that lattice of open subsets of
![]() $\mathrm{Zg}_S$
(respectively,
$\mathrm{Zg}_S$
(respectively,
![]() ${_S}\mathrm{Zg}$
) and the lattice of open subsets of
${_S}\mathrm{Zg}$
) and the lattice of open subsets of
![]() ${_S}\mathrm{Zg}$
(respectively,
${_S}\mathrm{Zg}$
(respectively,
![]() $\mathrm{Zg}_S$
), which is given on basic open sets by
$\mathrm{Zg}_S$
), which is given on basic open sets by
for
![]() $\phi ,\psi $
pp-
$\phi ,\psi $
pp-
![]() $1$
-formulas. Moreover,
$1$
-formulas. Moreover,
![]() $D^2$
is the identity map.
$D^2$
is the identity map.
It is unknown if this lattice isomorphism is always induced by a homeomorphism.
If X is a closed subset of
![]() $\textrm {Zg}_S$
, then we will write
$\textrm {Zg}_S$
, then we will write
![]() $DX$
for
$DX$
for
![]() ${_S}\textrm {Zg}\backslash D(\textrm {Zg}_S\backslash X)$
. Since closed subsets of
${_S}\textrm {Zg}\backslash D(\textrm {Zg}_S\backslash X)$
. Since closed subsets of
![]() $\textrm {Zg}_S$
are in correspondence with the definable subcategories of
$\textrm {Zg}_S$
are in correspondence with the definable subcategories of
![]() $\textrm {Mod}\text {-}S$
, this isomorphism also defines an inclusion preserving bijection between the definable subcategories of
$\textrm {Mod}\text {-}S$
, this isomorphism also defines an inclusion preserving bijection between the definable subcategories of
![]() $\textrm {Mod}\text {-}S$
and
$\textrm {Mod}\text {-}S$
and
![]() $S\text {-}\textrm {Mod}$
. If
$S\text {-}\textrm {Mod}$
. If
![]() $\mathcal {X}\subseteq \textrm {Mod}\text {-}S$
is a definable subcategory, then we will write
$\mathcal {X}\subseteq \textrm {Mod}\text {-}S$
is a definable subcategory, then we will write
![]() $D\mathcal {X}$
for the corresponding definable subcategory of
$D\mathcal {X}$
for the corresponding definable subcategory of
![]() $S\text {-}\textrm {Mod}$
.
$S\text {-}\textrm {Mod}$
.
Herzog’s duality can be applied to closed subspaces of
![]() $\textrm {Zg}_S$
as follows. Let X be a closed subset of
$\textrm {Zg}_S$
as follows. Let X be a closed subset of
![]() $\textrm {Zg}_S$
. Open subsets of
$\textrm {Zg}_S$
. Open subsets of
![]() $\textrm {Zg}_S$
containing
$\textrm {Zg}_S$
containing
![]() $\textrm {Zg}_S\backslash X$
are in bijective correspondence with open subsets of X equipped with the subspace topology via the map
$\textrm {Zg}_S\backslash X$
are in bijective correspondence with open subsets of X equipped with the subspace topology via the map
![]() $U\mapsto U\cap X$
. If U is an open subset of
$U\mapsto U\cap X$
. If U is an open subset of
![]() $\textrm {Zg}_S$
containing
$\textrm {Zg}_S$
containing
![]() $\textrm {Zg}_S\backslash X$
, then
$\textrm {Zg}_S\backslash X$
, then
![]() $DU$
is an open subset of
$DU$
is an open subset of
![]() ${_S}\textrm {Zg}$
containing
${_S}\textrm {Zg}$
containing
![]() ${_S}\textrm {Zg}\backslash DX$
. Thus, D induces a lattice isomorphism between the lattice of open sets of X and the lattice of open sets of
${_S}\textrm {Zg}\backslash DX$
. Thus, D induces a lattice isomorphism between the lattice of open sets of X and the lattice of open sets of
![]() $DX$
both equipped with the appropriate subspace topology.
$DX$
both equipped with the appropriate subspace topology.
Herzog’s isomorphism D sends the definable subcategory
![]() $\text {Tf}_\Lambda $
to the definable subcategory of R-divisible
$\text {Tf}_\Lambda $
to the definable subcategory of R-divisible
![]() $\Lambda $
-modules. Thus, directly applying Herzog’s duality does not give an isomorphism between the open subsets of
$\Lambda $
-modules. Thus, directly applying Herzog’s duality does not give an isomorphism between the open subsets of
 $\textrm {Zg}_\Lambda ^{tf}$
and
$\textrm {Zg}_\Lambda ^{tf}$
and
![]() ${_\Lambda }\textrm {Zg}^{tf}$
. With this in mind, we instead use the right module version of Maranda’s functor I to move to
${_\Lambda }\textrm {Zg}^{tf}$
. With this in mind, we instead use the right module version of Maranda’s functor I to move to
![]() $\textrm {Mod}\text {-}\Lambda _k$
, then we apply D there, and then we use the left module version of Maranda’s functor to move back to
$\textrm {Mod}\text {-}\Lambda _k$
, then we apply D there, and then we use the left module version of Maranda’s functor to move back to
![]() ${_\Lambda }\text {Tf}$
. This will give us an isomorphism between the lattice of open subsets of
${_\Lambda }\text {Tf}$
. This will give us an isomorphism between the lattice of open subsets of
 $\textrm {Zg}_\Lambda ^{rtf}$
and
$\textrm {Zg}_\Lambda ^{rtf}$
and
![]() ${_\Lambda }\textrm {Zg}^{rtf}$
.
${_\Lambda }\textrm {Zg}^{rtf}$
.
Our first step is to show that
![]() $\langle I\text {Tf}_\Lambda \rangle =D\langle I{_\Lambda }\text {Tf}\rangle $
.
$\langle I\text {Tf}_\Lambda \rangle =D\langle I{_\Lambda }\text {Tf}\rangle $
.
The contravariant functor
induces an equivalence between the category of right
![]() $\Lambda $
-lattices and the opposite of the category of left
$\Lambda $
-lattices and the opposite of the category of left
![]() $\Lambda $
-lattices (see [Reference Roggenkamp21, Section IX 2.2]). If M is right
$\Lambda $
-lattices (see [Reference Roggenkamp21, Section IX 2.2]). If M is right
![]() $\Lambda $
-lattice, denote the left
$\Lambda $
-lattice, denote the left
![]() $\Lambda $
-lattice
$\Lambda $
-lattice
![]() $\textrm {Hom}_R(M,R)$
by
$\textrm {Hom}_R(M,R)$
by
![]() $M^{\dagger }$
.
$M^{\dagger }$
.
The ring
![]() $\Lambda /\pi ^n\Lambda $
is an
$\Lambda /\pi ^n\Lambda $
is an
![]() $R/\pi ^nR$
-Artin algebra. For all S-Artin algebras
$R/\pi ^nR$
-Artin algebra. For all S-Artin algebras
![]() $\mathcal {A}$
, there is a duality between
$\mathcal {A}$
, there is a duality between
![]() ${\textrm {mod}}\text {-}\mathcal {A}$
and
${\textrm {mod}}\text {-}\mathcal {A}$
and
![]() $\mathcal {A}\text {-}{\textrm {mod}}$
given by
$\mathcal {A}\text {-}{\textrm {mod}}$
given by
![]() $\textrm {Hom}_S(-,E)$
where E is the injective hull of
$\textrm {Hom}_S(-,E)$
where E is the injective hull of
![]() $S/\textrm {rad}(S)$
. We will write
$S/\textrm {rad}(S)$
. We will write
![]() $M^*$
for
$M^*$
for
![]() $\textrm {Hom}(M,E)$
. If
$\textrm {Hom}(M,E)$
. If
![]() $S=R/\pi ^nR$
, then
$S=R/\pi ^nR$
, then
![]() $S/\textrm {rad}(S)=R/\pi R$
. One can check, using Baer’s criterion, that
$S/\textrm {rad}(S)=R/\pi R$
. One can check, using Baer’s criterion, that
![]() $R/\pi ^nR$
is injective as an S-module. The map which sends
$R/\pi ^nR$
is injective as an S-module. The map which sends
![]() $a+\pi R\in R/\pi R$
to
$a+\pi R\in R/\pi R$
to
![]() $a\pi ^{n-1}+\pi ^n R\in R/\pi ^nR$
embeds
$a\pi ^{n-1}+\pi ^n R\in R/\pi ^nR$
embeds
![]() $R/\pi R$
into the socle of
$R/\pi R$
into the socle of
![]() $R/\pi ^nR$
which is simple. Thus,
$R/\pi ^nR$
which is simple. Thus,
![]() $E=R/\pi ^nR$
is the injective hull of
$E=R/\pi ^nR$
is the injective hull of
![]() $S/\textrm {rad}(S)=R/\pi R$
.
$S/\textrm {rad}(S)=R/\pi R$
.
We will now show that if L is a right
![]() $\Lambda $
-lattice, then
$\Lambda $
-lattice, then
![]() $(IL)^*=IL^\dagger $
.
$(IL)^*=IL^\dagger $
.
Lemma 5.3 If M is a right
![]() $\Lambda $
-lattice and
$\Lambda $
-lattice and
![]() $n\in \mathbb {N}$
, then
$n\in \mathbb {N}$
, then
Proof For
![]() $f\in \textrm {Hom}_R(M,R)$
, let
$f\in \textrm {Hom}_R(M,R)$
, let
 $\overline {f}:M/M\pi ^n\rightarrow R/\pi ^nR \in \textrm {Hom}_{R/\pi ^nR}(M/M\pi ^n, R/\pi ^nR)$
be the homomorphism which sends
$\overline {f}:M/M\pi ^n\rightarrow R/\pi ^nR \in \textrm {Hom}_{R/\pi ^nR}(M/M\pi ^n, R/\pi ^nR)$
be the homomorphism which sends
![]() $m+M\pi ^n$
to
$m+M\pi ^n$
to
![]() $f(m)+\pi ^nR$
.
$f(m)+\pi ^nR$
.
Let
![]() $\Phi :\textrm {Hom}_R(M,R)\rightarrow \textrm {Hom}_{R/\pi ^nR}(M/M\pi ^n,R/\pi ^nR)$
be defined by
$\Phi :\textrm {Hom}_R(M,R)\rightarrow \textrm {Hom}_{R/\pi ^nR}(M/M\pi ^n,R/\pi ^nR)$
be defined by
![]() $\Phi (f)=\overline {f}$
. It is clear that
$\Phi (f)=\overline {f}$
. It is clear that
![]() $\Phi $
is a homomorphism of left
$\Phi $
is a homomorphism of left
![]() $\Lambda $
-modules. Since M is projective as an R-module,
$\Lambda $
-modules. Since M is projective as an R-module,
![]() $\Phi $
is surjective.
$\Phi $
is surjective.
If
![]() $\Phi (f)=0$
, then for all
$\Phi (f)=0$
, then for all
![]() $m\in M$
,
$m\in M$
,
![]() $\pi ^n|f(m)$
. For all
$\pi ^n|f(m)$
. For all
![]() $m\in M$
, let
$m\in M$
, let
![]() $g(m)\in M$
be such that
$g(m)\in M$
be such that
![]() $g(m)\pi ^n=f(m)$
. Since M is R-torsion-free, the choice of
$g(m)\pi ^n=f(m)$
. Since M is R-torsion-free, the choice of
![]() $g(m)$
is unique. From this, it follows easily that g is a homomorphism of R-modules. Thus, if
$g(m)$
is unique. From this, it follows easily that g is a homomorphism of R-modules. Thus, if
![]() $\Phi (f)=0$
, then
$\Phi (f)=0$
, then
![]() $f\in \pi ^n\textrm {Hom}_R(M,R)$
.▪
$f\in \pi ^n\textrm {Hom}_R(M,R)$
.▪
The next remark follows from the fact (see [Reference Prest17, Corollary 1.3.13] for instance) that if
![]() $\mathcal {A}$
is an Artin algebra,
$\mathcal {A}$
is an Artin algebra,
![]() $\phi /\psi $
is a pp-pair, and M is a finite length
$\phi /\psi $
is a pp-pair, and M is a finite length
![]() $\mathcal {A}$
-module, then
$\mathcal {A}$
-module, then
![]() $\phi (M)=\psi (M)$
if and only if
$\phi (M)=\psi (M)$
if and only if
![]() $D\phi (M^*)=D\psi (M^*)$
.
$D\phi (M^*)=D\psi (M^*)$
.
Remark 5.4 Suppose that
![]() $\mathcal {A}$
is an Artin algebra and
$\mathcal {A}$
is an Artin algebra and
![]() $\{M_i \ \vert \ i\in I\}$
is a set of finite length right
$\{M_i \ \vert \ i\in I\}$
is a set of finite length right
![]() $\mathcal {A}$
-modules. Then
$\mathcal {A}$
-modules. Then
Lemma 5.5 The following equalities hold.
Proof (1) and (5). These hold because all
![]() $N\in \text {Tf}_{\Lambda }$
are direct limits of
$N\in \text {Tf}_{\Lambda }$
are direct limits of
![]() $\Lambda $
-lattices, all
$\Lambda $
-lattices, all
![]() $\Lambda $
-lattices are direct sums of indecomposable
$\Lambda $
-lattices are direct sums of indecomposable
![]() $\Lambda $
-lattices, and I commutes with direct limits.
$\Lambda $
-lattices, and I commutes with direct limits.
(2) For all (right)
![]() $\Lambda $
-lattices
$\Lambda $
-lattices
![]() $L^{\dagger \dagger }\cong L$
and
$L^{\dagger \dagger }\cong L$
and
![]() $L^{\dagger }$
is a (left)
$L^{\dagger }$
is a (left)
![]() $\Lambda $
-lattice. (3) holds by Lemma 5.3 and (4) holds by Remark 5.4.▪
$\Lambda $
-lattice. (3) holds by Lemma 5.3 and (4) holds by Remark 5.4.▪
Herzog’s duality D gives an isomorphism from the lattice of open sets of
![]() $\textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
to the lattice of open sets of
$\textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
to the lattice of open sets of
![]() $\textrm {Zg}(D\langle I\text {Tf}_{\Lambda }\rangle )$
. By Lemma 5.5,
$\textrm {Zg}(D\langle I\text {Tf}_{\Lambda }\rangle )$
. By Lemma 5.5,
![]() $D\langle I\text {Tf}_{\Lambda }\rangle =\langle I{_\Lambda }\text {Tf}\rangle $
.
$D\langle I\text {Tf}_{\Lambda }\rangle =\langle I{_\Lambda }\text {Tf}\rangle $
.
If U is an open subset of
 $\textrm {Zg}_\Lambda ^{rtf}$
(respectively,
$\textrm {Zg}_\Lambda ^{rtf}$
(respectively,
![]() ${_\Lambda }\textrm {Zg}^{rtf}$
), then write
${_\Lambda }\textrm {Zg}^{rtf}$
), then write
![]() $IU$
for the set of all
$IU$
for the set of all
![]() $IN$
where
$IN$
where
![]() $N\in U$
.
$N\in U$
.
Definition 5.1 Let U be an open subset of
 $\textrm {Zg}_\Lambda ^{rtf}$
. Define
$\textrm {Zg}_\Lambda ^{rtf}$
. Define
 $$ \begin{align*}dU:=\{N\in {_\Lambda}\textrm{Zg}^{rtf} \ \vert \ IN\in DIU \}. \end{align*} $$
$$ \begin{align*}dU:=\{N\in {_\Lambda}\textrm{Zg}^{rtf} \ \vert \ IN\in DIU \}. \end{align*} $$
By Theorem 5.1,
![]() $IU$
is an open subset of
$IU$
is an open subset of
![]() $\textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
. So
$\textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
. So
![]() $DIU$
is an open subset of
$DIU$
is an open subset of
![]() $\textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
. Again by Theorem 5.1, the set of
$\textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
. Again by Theorem 5.1, the set of
![]() $N\in {_\Lambda }\textrm {Zg}^{rtf}$
such that
$N\in {_\Lambda }\textrm {Zg}^{rtf}$
such that
![]() $IN\in DIU$
is an open subset of
$IN\in DIU$
is an open subset of
![]() ${_\Lambda }\textrm {Zg}^{rtf}$
.
${_\Lambda }\textrm {Zg}^{rtf}$
.
Proposition 5.6 The map d between the lattice of open sets of
 $\textrm {Zg}_\Lambda ^{rtf}$
and
$\textrm {Zg}_\Lambda ^{rtf}$
and
![]() ${_\Lambda }\textrm {Zg}^{rtf}$
is a lattice isomorphism.
${_\Lambda }\textrm {Zg}^{rtf}$
is a lattice isomorphism.
Proof The homeomorphism from Theorem 5.1 sends an open subset U of
 $\textrm {Zg}_\Lambda ^{rtf}$
to
$\textrm {Zg}_\Lambda ^{rtf}$
to
![]() $IU\subseteq \textrm {Zg}(\langle I\text {Tf}_\Lambda \rangle )$
. So the map sending U to
$IU\subseteq \textrm {Zg}(\langle I\text {Tf}_\Lambda \rangle )$
. So the map sending U to
![]() $IU$
is a lattice isomorphism. By Lemma 5.5, Herzog’s duality gives a lattice isomorphism between the open subsets of
$IU$
is a lattice isomorphism. By Lemma 5.5, Herzog’s duality gives a lattice isomorphism between the open subsets of
![]() $\textrm {Zg}(\langle I\text {Tf}_\Lambda \rangle )$
and the lattice of open subset of
$\textrm {Zg}(\langle I\text {Tf}_\Lambda \rangle )$
and the lattice of open subset of
![]() $\textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
. Thus, the map which sends an open subset U of
$\textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
. Thus, the map which sends an open subset U of
 $\textrm {Zg}_\Lambda ^{rtf}$
to
$\textrm {Zg}_\Lambda ^{rtf}$
to
![]() $DIU\subseteq \textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
is a lattice isomorphism. Finally, the inverse of the homeomorphism from Theorem 5.1 sends an open subset of
$DIU\subseteq \textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
is a lattice isomorphism. Finally, the inverse of the homeomorphism from Theorem 5.1 sends an open subset of
![]() $W\subseteq \textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
to the set of all
$W\subseteq \textrm {Zg}(\langle I{_\Lambda }\text {Tf}\rangle )$
to the set of all
![]() $N\in {_\Lambda }\textrm {Zg}^{rtf}$
such that
$N\in {_\Lambda }\textrm {Zg}^{rtf}$
such that
![]() $IN\in W$
. So this map is also a lattice isomorphism. Since d is the composition of these three lattice isomorphisms, d is also a lattice isomorphism.▪
$IN\in W$
. So this map is also a lattice isomorphism. Since d is the composition of these three lattice isomorphisms, d is also a lattice isomorphism.▪
If
![]() $\Lambda $
is an order over a complete discrete valuation domain, then the
$\Lambda $
is an order over a complete discrete valuation domain, then the
![]() $\Lambda $
-lattices are pure-injective (see [Reference Gregory, L’Innocente and Toffalori8, Proposition 2.2] for instance). When R is not complete, we can instead consider the lattices over the
$\Lambda $
-lattices are pure-injective (see [Reference Gregory, L’Innocente and Toffalori8, Proposition 2.2] for instance). When R is not complete, we can instead consider the lattices over the
![]() $\widehat {R}$
-order
$\widehat {R}$
-order
![]() $\widehat {\Lambda }$
. Then the
$\widehat {\Lambda }$
. Then the
![]() $\widehat {\Lambda }$
-lattices are pure-injective as
$\widehat {\Lambda }$
-lattices are pure-injective as
![]() $\widehat {\Lambda }$
-modules and hence also as
$\widehat {\Lambda }$
-modules and hence also as
![]() $\Lambda $
-modules. Moreover, if L is an indecomposable
$\Lambda $
-modules. Moreover, if L is an indecomposable
![]() $\widehat {\Lambda }$
-lattice, then, since L is R-reduced, L is also indecomposable as a
$\widehat {\Lambda }$
-lattice, then, since L is R-reduced, L is also indecomposable as a
![]() $\Lambda $
-module (see [Reference Marcja, Prest and Toffalori14, Remark 1] for a proof over group rings that also works in our context).
$\Lambda $
-module (see [Reference Marcja, Prest and Toffalori14, Remark 1] for a proof over group rings that also works in our context).
Proposition 5.7 Let R be a discrete valuation domain and
![]() $\Lambda $
an R-order. If L is an indecomposable right
$\Lambda $
an R-order. If L is an indecomposable right
![]() $\widehat {\Lambda }$
-lattice, then for all open sets
$\widehat {\Lambda }$
-lattice, then for all open sets
 $U\subseteq \textrm {Zg}_\Lambda ^{rtf}$
,
$U\subseteq \textrm {Zg}_\Lambda ^{rtf}$
,
![]() $L\in U$
if and only if
$L\in U$
if and only if
![]() $L^{\dagger }\in dU$
where
$L^{\dagger }\in dU$
where
 $L^\dagger :=\textrm {Hom}_{\widehat {R}}(L,\widehat {R})$
.
$L^\dagger :=\textrm {Hom}_{\widehat {R}}(L,\widehat {R})$
.
Proof First note that
![]() $IL$
is finite-length as a
$IL$
is finite-length as a
![]() $\Lambda _k$
-module. Since
$\Lambda _k$
-module. Since
![]() $\Lambda _k$
is an Artin algebra, if
$\Lambda _k$
is an Artin algebra, if
![]() $M\in \textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
is finite-length, then for all open subsets U of
$M\in \textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
is finite-length, then for all open subsets U of
![]() $\textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
,
$\textrm {Zg}(\langle I\text {Tf}_{\Lambda }\rangle )$
,
![]() $M\in U$
if and only if
$M\in U$
if and only if
![]() $M^*\in DU$
(see [Reference Prest17, Corollary 1.3.13]). So, if L is an indecomposable right
$M^*\in DU$
(see [Reference Prest17, Corollary 1.3.13]). So, if L is an indecomposable right
![]() $\widehat {\Lambda }$
-lattice, then
$\widehat {\Lambda }$
-lattice, then
![]() $L\in U$
if and only if
$L\in U$
if and only if
![]() $IL\in IU$
and
$IL\in IU$
and
![]() $IL\in IU$
if and only if
$IL\in IU$
if and only if
![]() $(IL)^*\in DIU$
. By Lemma 5.3,
$(IL)^*\in DIU$
. By Lemma 5.3,
![]() $(IL)^*=IL^\dagger $
, so
$(IL)^*=IL^\dagger $
, so
![]() $(IL)^*\in DIU$
if and only if
$(IL)^*\in DIU$
if and only if
![]() $L^\dagger \in dU$
. So
$L^\dagger \in dU$
. So
![]() $L\in U$
if and only if
$L\in U$
if and only if
![]() $L^\dagger \in dU$
.▪
$L^\dagger \in dU$
.▪
5.2 Duality for
 $\textrm {Zg}_\Lambda ^{tf}$
$\textrm {Zg}_\Lambda ^{tf}$
We now work to extend Proposition 5.6 in two ways concurrently. We extend the isomorphism to an isomorphism between the lattices of open subsets of
 $\textrm {Zg}_\Lambda ^{tf}$
and
$\textrm {Zg}_\Lambda ^{tf}$
and
![]() ${_\Lambda }\textrm {Zg}^{tf}$
and we extend the statement to the case where R is a Dedekind domain (which is not a field).
${_\Lambda }\textrm {Zg}^{tf}$
and we extend the statement to the case where R is a Dedekind domain (which is not a field).
In order to do this, we need to recall some key features of
 $\textrm {Zg}_\Lambda ^{tf}$
from [Reference Gregory, L’Innocente and Toffalori8]. As explained in [Reference Gregory, L’Innocente and Toffalori8, Section 3], for each
$\textrm {Zg}_\Lambda ^{tf}$
from [Reference Gregory, L’Innocente and Toffalori8]. As explained in [Reference Gregory, L’Innocente and Toffalori8, Section 3], for each
![]() $P\in \text {Max}R$
, the canonical homomorphism
$P\in \text {Max}R$
, the canonical homomorphism
![]() $\Lambda \rightarrow \Lambda _P$
induces, via restriction of scalars, an embedding of
$\Lambda \rightarrow \Lambda _P$
induces, via restriction of scalars, an embedding of
 $\textrm {Zg}^{tf}_{\Lambda _P}$
into
$\textrm {Zg}^{tf}_{\Lambda _P}$
into
 $\textrm {Zg}^{tf}_{\Lambda }$
and the image of this embedding is closed. We identify
$\textrm {Zg}^{tf}_{\Lambda }$
and the image of this embedding is closed. We identify
 $\textrm {Zg}^{tf}_{\Lambda _P}$
with its image. Moreover, for all
$\textrm {Zg}^{tf}_{\Lambda _P}$
with its image. Moreover, for all
 $N\in \textrm {Zg}_\Lambda ^{tf}$
, there exists a
$N\in \textrm {Zg}_\Lambda ^{tf}$
, there exists a
![]() $P\in \text {Max}R$
such that
$P\in \text {Max}R$
such that
 $N\in \textrm {Zg}^{tf}_{\Lambda _P}$
. So
$N\in \textrm {Zg}^{tf}_{\Lambda _P}$
. So
 $$ \begin{align*}\textrm{Zg}_{\Lambda}^{tf}=\bigcup_{P\in\text{Max}R}\textrm{Zg}_{\Lambda_P}^{tf}.\end{align*} $$
$$ \begin{align*}\textrm{Zg}_{\Lambda}^{tf}=\bigcup_{P\in\text{Max}R}\textrm{Zg}_{\Lambda_P}^{tf}.\end{align*} $$
Finally, if
![]() $N\in \textrm {Zg}_{\Lambda _P}$
for all
$N\in \textrm {Zg}_{\Lambda _P}$
for all
![]() $P\in \text {Max}R$
, then N is R-divisible and hence may be viewed as a module over
$P\in \text {Max}R$
, then N is R-divisible and hence may be viewed as a module over
![]() $Q\Lambda $
. Since
$Q\Lambda $
. Since
![]() $Q\Lambda $
is separable, hence semisimple, all indecomposable R-divisible modules, when viewed as
$Q\Lambda $
is separable, hence semisimple, all indecomposable R-divisible modules, when viewed as
![]() $Q\Lambda $
-modules, are simple.
$Q\Lambda $
-modules, are simple.
For each
![]() $P\in \text {Max}R$
, let
$P\in \text {Max}R$
, let
![]() $P|x$
denote the pp formula
$P|x$
denote the pp formula
![]() $\exists y_1,\ldots ,y_n \ x=\sum _{i=1}^ny_ir_i$
, where
$\exists y_1,\ldots ,y_n \ x=\sum _{i=1}^ny_ir_i$
, where
![]() $r_1,\ldots r_n$
generate P. In all
$r_1,\ldots r_n$
generate P. In all
![]() $\Lambda $
-modules M,
$\Lambda $
-modules M,
![]() $P|x$
defines the subset
$P|x$
defines the subset
![]() $MP$
. If
$MP$
. If
![]() $P,P'\in \text {Max}R$
are not equal, then
$P,P'\in \text {Max}R$
are not equal, then
![]() $\left (x=x/P|x\right )\cap \left (x=x/P'|x\right )$
is empty. For all
$\left (x=x/P|x\right )\cap \left (x=x/P'|x\right )$
is empty. For all
 $N\in \textrm {Zg}_\Lambda ^{tf}$
, either N is R-divisible or
$N\in \textrm {Zg}_\Lambda ^{tf}$
, either N is R-divisible or
![]() $N\in \left (x=x/P|x\right )$
for some
$N\in \left (x=x/P|x\right )$
for some
![]() $P\in \text {Max}R$
. So
$P\in \text {Max}R$
. So
 $$ \begin{align*}\textrm{Zg}_\Lambda^{tf}=\textrm{Zg}_{Q\Lambda}\cup\bigcup_{P\in\text{Max}R}\left(x=x/P|x\right)\!.\end{align*} $$
$$ \begin{align*}\textrm{Zg}_\Lambda^{tf}=\textrm{Zg}_{Q\Lambda}\cup\bigcup_{P\in\text{Max}R}\left(x=x/P|x\right)\!.\end{align*} $$
Note that
 $\left (x=x/P|x\right )=\textrm {Zg}^{tf}_{\Lambda _P}\backslash \textrm {Zg}_{Q\Lambda }$
. Under the assumption that
$\left (x=x/P|x\right )=\textrm {Zg}^{tf}_{\Lambda _P}\backslash \textrm {Zg}_{Q\Lambda }$
. Under the assumption that
![]() $Q\Lambda $
is a semisimple Q-algebra, this means that
$Q\Lambda $
is a semisimple Q-algebra, this means that
![]() $\left (x=x/P|x\right )$
is the set of
$\left (x=x/P|x\right )$
is the set of
![]() $R_P$
-reduced indecomposable pure-injective
$R_P$
-reduced indecomposable pure-injective
![]() $\Lambda _P$
-modules. For this reason, we will write
$\Lambda _P$
-modules. For this reason, we will write
 $\textrm {Zg}^{rtf}_{\Lambda _P}$
for this set. Note that this notation matches that of the previous section when
$\textrm {Zg}^{rtf}_{\Lambda _P}$
for this set. Note that this notation matches that of the previous section when
![]() $\Lambda $
is an order over a discrete valuation domain.
$\Lambda $
is an order over a discrete valuation domain.
Theorem 5.8 [Reference Gregory, L’Innocente and Toffalori8, Theorem 3.1]
Let R be a Dedekind domain with field of fractions Q, and
![]() $\Lambda $
an R-order such that
$\Lambda $
an R-order such that
![]() $Q\Lambda $
is semisimple. If
$Q\Lambda $
is semisimple. If
 $N \in \textrm {Zg}_\Lambda ^{tf}$
, then either
$N \in \textrm {Zg}_\Lambda ^{tf}$
, then either
-
• N is a simple
 $Q\Lambda $
-module or
$Q\Lambda $
-module or -
• there is some maximal ideal P of R such that
 $N \in \textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
and N is
$N \in \textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
and N is
 $R_P$
-reduced.
$R_P$
-reduced.
Moreover, if
 $N\in \textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
is
$N\in \textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
is
![]() $R_P$
-reduced, then
$R_P$
-reduced, then
 $N\in \textrm {Zg}_\Lambda ^{tf}$
.
$N\in \textrm {Zg}_\Lambda ^{tf}$
.
This theorem means that if
![]() $Q\Lambda $
is separable, then the
$Q\Lambda $
is separable, then the
![]() $R_P$
-reduced points of
$R_P$
-reduced points of
 $\textrm {Zg}_\Lambda ^{tf}$
can be identified with the
$\textrm {Zg}_\Lambda ^{tf}$
can be identified with the
![]() $\widehat {R_P}$
-reduced (equivalently,
$\widehat {R_P}$
-reduced (equivalently,
![]() $R_P$
-reduced) points of
$R_P$
-reduced) points of
 $\textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
. Following [Reference Marcja, Prest and Toffalori14], it is shown in [Reference Gregory, L’Innocente and Toffalori8, Theorem 3.3] that the topology on the set of
$\textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
. Following [Reference Marcja, Prest and Toffalori14], it is shown in [Reference Gregory, L’Innocente and Toffalori8, Theorem 3.3] that the topology on the set of
![]() $R_P$
-reduced points of
$R_P$
-reduced points of
 $\textrm {Zg}_\Lambda ^{tf}$
is the same whether it is viewed as a subspace of
$\textrm {Zg}_\Lambda ^{tf}$
is the same whether it is viewed as a subspace of
 $\textrm {Zg}_{\Lambda _P}^{tf}$
or
$\textrm {Zg}_{\Lambda _P}^{tf}$
or
 $\textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
. Thus, we may identify
$\textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
. Thus, we may identify
 $\textrm {Zg}^{rtf}_{\Lambda _P}$
and
$\textrm {Zg}^{rtf}_{\Lambda _P}$
and
 $\textrm {Zg}^{rtf}_{\widehat {\Lambda _P}}$
.
$\textrm {Zg}^{rtf}_{\widehat {\Lambda _P}}$
.
We have already mentioned in Section 5.1 that a
![]() $\widehat {\Lambda _P}$
-lattice is pure-injective. Therefore, the restrictions of indecomposable
$\widehat {\Lambda _P}$
-lattice is pure-injective. Therefore, the restrictions of indecomposable
![]() $\widehat {\Lambda _P}$
-lattices to
$\widehat {\Lambda _P}$
-lattices to
![]() $\Lambda $
are points in
$\Lambda $
are points in
 $\textrm {Zg}_\Lambda ^{tf}$
.
$\textrm {Zg}_\Lambda ^{tf}$
.
From now on, if
![]() $P\in \text {Max}R$
, then let
$P\in \text {Max}R$
, then let
![]() $d_P$
denote the isomorphism between the lattice of open subsets of
$d_P$
denote the isomorphism between the lattice of open subsets of
 $ \textrm {Zg}_{\Lambda _P}^{rtf}$
and of
$ \textrm {Zg}_{\Lambda _P}^{rtf}$
and of
![]() ${_{\Lambda _P}}\textrm {Zg}^{rtf}$
induced by d for
${_{\Lambda _P}}\textrm {Zg}^{rtf}$
induced by d for
![]() $\Lambda _P$
. Patching the
$\Lambda _P$
. Patching the
![]() $d_P$
together as
$d_P$
together as
![]() $P\in \text {Max}R$
varies will give us an isomorphism between the open subset of
$P\in \text {Max}R$
varies will give us an isomorphism between the open subset of
 $\bigcup _{P\in \text {Max}R}\textrm {Zg}_{\Lambda _P}^{rtf}\subseteq \textrm {Zg}_\Lambda ^{tf}$
and the open subsets of
$\bigcup _{P\in \text {Max}R}\textrm {Zg}_{\Lambda _P}^{rtf}\subseteq \textrm {Zg}_\Lambda ^{tf}$
and the open subsets of
![]() $\bigcup _{P\in \text {Max}R}{_{\Lambda _P}}\textrm {Zg}^{rtf}\subseteq {_\Lambda }\textrm {Zg}^{tf}$
. Thus, we just need to know what to do with open subsets which contain R-divisible points.
$\bigcup _{P\in \text {Max}R}{_{\Lambda _P}}\textrm {Zg}^{rtf}\subseteq {_\Lambda }\textrm {Zg}^{tf}$
. Thus, we just need to know what to do with open subsets which contain R-divisible points.
Let
![]() $e_1,\ldots ,e_n$
be a complete set of centrally primitive orthogonal idempotents for
$e_1,\ldots ,e_n$
be a complete set of centrally primitive orthogonal idempotents for
![]() $Q\Lambda $
. For each
$Q\Lambda $
. For each
![]() $1\leq i\leq n$
,
$1\leq i\leq n$
,
![]() $e_iQ\Lambda $
is isomorphic as a right
$e_iQ\Lambda $
is isomorphic as a right
![]() $Q\Lambda $
-module to
$Q\Lambda $
-module to
 $S_i^{(\alpha _i)}$
for some simple right
$S_i^{(\alpha _i)}$
for some simple right
![]() $Q\Lambda $
-module
$Q\Lambda $
-module
![]() $S_i$
and if
$S_i$
and if
![]() $S_i\cong S_j$
then
$S_i\cong S_j$
then
![]() $i=j$
.
$i=j$
.
Lemma 5.9 [Reference Gregory, L’Innocente and Toffalori8, Lemma 2.7]
Let
 $N\in \textrm {Zg}_\Lambda ^{tf}$
and
$N\in \textrm {Zg}_\Lambda ^{tf}$
and
![]() $S\in \textrm {Zg}_{Q\Lambda }$
. If S is a direct summand of
$S\in \textrm {Zg}_{Q\Lambda }$
. If S is a direct summand of
![]() $QN$
, then S is in the closure of N. In particular, if N is a closed point in
$QN$
, then S is in the closure of N. In particular, if N is a closed point in
 $\textrm {Zg}_\Lambda ^{tf}$
, then
$\textrm {Zg}_\Lambda ^{tf}$
, then
![]() $N\in \textrm {Zg}_{Q\Lambda }$
.
$N\in \textrm {Zg}_{Q\Lambda }$
.
Lemma 5.10 Let D be a Dedekind domain with field of fractions Q, and let
![]() $\Lambda $
be an order over D such that
$\Lambda $
be an order over D such that
![]() $Q\Lambda $
is semisimple. Let
$Q\Lambda $
is semisimple. Let
![]() $e\in Q\Lambda $
be a centrally primitive idempotent, let S be the simple right
$e\in Q\Lambda $
be a centrally primitive idempotent, let S be the simple right
![]() $Q\Lambda $
-module corresponding to e, and suppose that
$Q\Lambda $
-module corresponding to e, and suppose that
![]() $d\in D$
is such that
$d\in D$
is such that
![]() $ed\in \Lambda $
. The following are equivalent for all
$ed\in \Lambda $
. The following are equivalent for all
 $N\in \textrm {Zg}_\Lambda ^{tf}$
.
$N\in \textrm {Zg}_\Lambda ^{tf}$
.
-
(1)
 $N\in \left (xd(1-e)=0/x=0\right )$
.
$N\in \left (xd(1-e)=0/x=0\right )$
. -
(2) S is a direct summand of
 $QN$
.
$QN$
. -
(3) S is in the closure of N.
Proof
![]() $(1)\Rightarrow (2)$
Suppose
$(1)\Rightarrow (2)$
Suppose
![]() $md(1-e)=0$
and
$md(1-e)=0$
and
![]() $m\neq 0$
. Then, as an element of
$m\neq 0$
. Then, as an element of
![]() $QN$
viewed as a
$QN$
viewed as a
![]() $Q\Lambda $
-module,
$Q\Lambda $
-module,
![]() $m(1-e)=0$
. Thus,
$m(1-e)=0$
. Thus,
![]() $m=me$
. The kernel of the homomorphism from
$m=me$
. The kernel of the homomorphism from
![]() $Q\Lambda $
to
$Q\Lambda $
to
![]() $QN$
sending
$QN$
sending
![]() $1$
to m contains
$1$
to m contains
![]() $(1-e)Q\Lambda $
and thus induces a nonzero homomorphism from
$(1-e)Q\Lambda $
and thus induces a nonzero homomorphism from
![]() $eQ\Lambda $
to
$eQ\Lambda $
to
![]() $QN$
. Thus, S is a submodule and hence a direct summand of
$QN$
. Thus, S is a submodule and hence a direct summand of
![]() $QN$
.
$QN$
.
![]() $(2)\Rightarrow (3)$
This is Lemma 5.9.
$(2)\Rightarrow (3)$
This is Lemma 5.9.
![]() $(3)\Rightarrow (1)$
Suppose S is in the closure of N. Since
$(3)\Rightarrow (1)$
Suppose S is in the closure of N. Since
![]() $eQ\Lambda (1-e)d=0$
,
$eQ\Lambda (1-e)d=0$
,
![]() $S \in \left (xd(1-e)=0/x=0\right )$
. Thus,
$S \in \left (xd(1-e)=0/x=0\right )$
. Thus,
![]() $N\in \left (xd(1-e)=0/x=0\right )$
.▪
$N\in \left (xd(1-e)=0/x=0\right )$
.▪
Note that the above shows that the set of points specializing to a closed point in
 $\textrm {Zg}_\Lambda ^{tf}$
is an open set. For
$\textrm {Zg}_\Lambda ^{tf}$
is an open set. For
![]() $S\in \textrm {Zg}_{Q\Lambda }$
, we will write
$S\in \textrm {Zg}_{Q\Lambda }$
, we will write
![]() $\mathcal {V}(S)$
for the open set of points whose closure contains S.
$\mathcal {V}(S)$
for the open set of points whose closure contains S.
Corollary 5.11 Let U be an open subset of
 $\textrm {Zg}_{\Lambda }^{tf}$
. Then
$\textrm {Zg}_{\Lambda }^{tf}$
. Then
 $$ \begin{align*}U=\bigcup_{P}(U\cap \textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{S\in \lambda(U)}\mathcal{V}(S),\end{align*} $$
$$ \begin{align*}U=\bigcup_{P}(U\cap \textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{S\in \lambda(U)}\mathcal{V}(S),\end{align*} $$
where
 $\lambda (U):=U\cap \textrm {Zg}_{Q\Lambda }$
.
$\lambda (U):=U\cap \textrm {Zg}_{Q\Lambda }$
.
Proof If
 $N\in \textrm {Zg}_{\Lambda }^{tf}$
, then either
$N\in \textrm {Zg}_{\Lambda }^{tf}$
, then either
 $N\in \textrm {Zg}^{rtf}_{\Lambda _P}$
for some
$N\in \textrm {Zg}^{rtf}_{\Lambda _P}$
for some
![]() $P\in \text {Max}R$
or
$P\in \text {Max}R$
or
![]() $N\in \textrm {Zg}_{Q\Lambda }$
. So, since for all
$N\in \textrm {Zg}_{Q\Lambda }$
. So, since for all
![]() $S\in \textrm {Zg}_{Q\Lambda }$
,
$S\in \textrm {Zg}_{Q\Lambda }$
,
![]() $S\in \mathcal {V}(S)$
,
$S\in \mathcal {V}(S)$
,
 $U\subseteq \bigcup _{P}(U\cap \textrm {Zg}^{rtf}_{\Lambda _P})\cup \bigcup _{S\in \lambda (U)}\mathcal {V}(S)$
.
$U\subseteq \bigcup _{P}(U\cap \textrm {Zg}^{rtf}_{\Lambda _P})\cup \bigcup _{S\in \lambda (U)}\mathcal {V}(S)$
.
Suppose
![]() $S\in \lambda (U)$
and
$S\in \lambda (U)$
and
![]() $N\in \mathcal {V}(S)$
. Then S is in the closure of N. Hence,
$N\in \mathcal {V}(S)$
. Then S is in the closure of N. Hence,
![]() $N\in U$
. Thus,
$N\in U$
. Thus,
![]() $\mathcal {V}(S)\subseteq U$
. So
$\mathcal {V}(S)\subseteq U$
. So
 $U\supseteq \bigcup _{P}(U\cap \textrm {Zg}^{rtf}_{\Lambda _P})\cup \bigcup _{S\in \lambda (U)}\mathcal {V}(S)$
.▪
$U\supseteq \bigcup _{P}(U\cap \textrm {Zg}^{rtf}_{\Lambda _P})\cup \bigcup _{S\in \lambda (U)}\mathcal {V}(S)$
.▪
For each simple
![]() $Q\Lambda $
-module S, we now consider where to send the open set
$Q\Lambda $
-module S, we now consider where to send the open set
![]() $\mathcal {V}(S)$
. In particular, we need to calculate the image of
$\mathcal {V}(S)$
. In particular, we need to calculate the image of
 $\mathcal {V}(S)\cap \textrm {Zg}^{rtf}_{\Lambda _P}$
under
$\mathcal {V}(S)\cap \textrm {Zg}^{rtf}_{\Lambda _P}$
under
![]() $d_P$
for each
$d_P$
for each
![]() $P\in \text {Max}R$
.
$P\in \text {Max}R$
.
Lemma 5.12 Let R be a discrete valuation domain and
![]() $\Lambda $
an R-order. For all
$\Lambda $
an R-order. For all
![]() $M\in \text {Latt}_\Lambda $
,
$M\in \text {Latt}_\Lambda $
,
![]() $Q\textrm {Hom}_R(M,R)$
and
$Q\textrm {Hom}_R(M,R)$
and
![]() $\textrm {Hom}_Q(MQ,Q)$
are isomorphic as
$\textrm {Hom}_Q(MQ,Q)$
are isomorphic as
![]() $Q\Lambda $
-modules.
$Q\Lambda $
-modules.
Proof Let
![]() $\Delta :\textrm {Hom}_R(M,R)\rightarrow \textrm {Hom}_Q(MQ,Q)$
be defined by setting
$\Delta :\textrm {Hom}_R(M,R)\rightarrow \textrm {Hom}_Q(MQ,Q)$
be defined by setting
![]() $\Delta (f)(m\cdot q)=f(m)\cdot q$
for all
$\Delta (f)(m\cdot q)=f(m)\cdot q$
for all
![]() $m\in M$
and
$m\in M$
and
![]() $q\in Q$
. A quick computation shows that for all
$q\in Q$
. A quick computation shows that for all
![]() $f\in \textrm {Hom}_R(M,R)$
,
$f\in \textrm {Hom}_R(M,R)$
,
![]() $\Delta (f)$
is a well-defined element of
$\Delta (f)$
is a well-defined element of
![]() $\textrm {Hom}_Q(MQ,Q)$
and
$\textrm {Hom}_Q(MQ,Q)$
and
![]() $\Delta $
is an injective homomorphism of left
$\Delta $
is an injective homomorphism of left
![]() $\Lambda $
-modules. Since
$\Lambda $
-modules. Since
![]() $\textrm {Hom}_Q(MQ,Q)$
is Q-divisible,
$\textrm {Hom}_Q(MQ,Q)$
is Q-divisible,
![]() $\Delta $
extends to an injective homomorphism
$\Delta $
extends to an injective homomorphism
![]() $\Delta '$
from
$\Delta '$
from
![]() $Q\textrm {Hom}_R(M,R)$
to
$Q\textrm {Hom}_R(M,R)$
to
![]() $\textrm {Hom}_Q(MQ,Q)$
.
$\textrm {Hom}_Q(MQ,Q)$
.
Suppose that M is rank n. Then
![]() $\dim _Q MQ=\dim _Q\textrm {Hom}_Q(MQ,Q)=\dim _Q Q\textrm {Hom}_R(M,R)=n$
. Thus,
$\dim _Q MQ=\dim _Q\textrm {Hom}_Q(MQ,Q)=\dim _Q Q\textrm {Hom}_R(M,R)=n$
. Thus,
![]() $\Delta '$
is an injective homomorphism between two n-dimensional Q-vector spaces and hence is surjective.▪
$\Delta '$
is an injective homomorphism between two n-dimensional Q-vector spaces and hence is surjective.▪
Lemma 5.13 Let R be a discrete valuation domain. Let
![]() $L\in \text {Latt}_\Lambda $
, e a central idempotent of
$L\in \text {Latt}_\Lambda $
, e a central idempotent of
![]() $Q\Lambda $
, and
$Q\Lambda $
, and
![]() $d\in R$
be such that
$d\in R$
be such that
![]() $ed\in \Lambda $
. Then
$ed\in \Lambda $
. Then
![]() $L\in \left (x(e-1)d=0/x=0\right )$
if and only if
$L\in \left (x(e-1)d=0/x=0\right )$
if and only if
![]() $L^\dagger \in \left ((e-1)dx=0/x=0\right )$
.
$L^\dagger \in \left ((e-1)dx=0/x=0\right )$
.
Proof Suppose
![]() $L\in \left (x(e-1)d=0/x=0\right )$
. Then there exists
$L\in \left (x(e-1)d=0/x=0\right )$
. Then there exists
![]() $a\in QL\backslash \{0\}$
such that
$a\in QL\backslash \{0\}$
such that
![]() $a(e-1)=0$
. By Lemma 5.12,
$a(e-1)=0$
. By Lemma 5.12,
![]() $Q\textrm {Hom}_R(L,R)\cong \textrm {Hom}_Q(QL,Q)$
. Thus, we need to show that there exists
$Q\textrm {Hom}_R(L,R)\cong \textrm {Hom}_Q(QL,Q)$
. Thus, we need to show that there exists
![]() $0\neq f\in \textrm {Hom}_Q(QL,Q)$
such that
$0\neq f\in \textrm {Hom}_Q(QL,Q)$
such that
![]() $(e-1)\cdot f=0$
. Since e is central,
$(e-1)\cdot f=0$
. Since e is central,
![]() $QL=QLe\oplus QL(e-1)$
and
$QL=QLe\oplus QL(e-1)$
and
![]() $QLe\neq 0$
. Take
$QLe\neq 0$
. Take
![]() $f\in \textrm {Hom}_Q(QL,Q)$
such that f is zero on
$f\in \textrm {Hom}_Q(QL,Q)$
such that f is zero on
![]() $QL(e-1)$
and nonzero on
$QL(e-1)$
and nonzero on
![]() $QLe$
. Then for all
$QLe$
. Then for all
![]() $m\in QL$
,
$m\in QL$
,
![]() $(e-1)\cdot f(m)=f(m(e-1))=0$
, but
$(e-1)\cdot f(m)=f(m(e-1))=0$
, but
![]() $f\neq 0$
. Thus, there exists
$f\neq 0$
. Thus, there exists
![]() $b\in QL^\dagger \backslash \{0\}$
such that
$b\in QL^\dagger \backslash \{0\}$
such that
![]() $(e-1)\cdot b=0$
. There exists
$(e-1)\cdot b=0$
. There exists
![]() $r\in R\backslash \{0\}$
such that
$r\in R\backslash \{0\}$
such that
![]() $rb\in L^\dagger $
and
$rb\in L^\dagger $
and
![]() $(e-1)d\cdot rb=0$
. So
$(e-1)d\cdot rb=0$
. So
![]() $L^\dagger \in \left ((e-1)dx=0/x=0\right )$
.▪
$L^\dagger \in \left ((e-1)dx=0/x=0\right )$
.▪
Lemma 5.14 Let
![]() $a\in \Lambda $
. The set of indecomposable
$a\in \Lambda $
. The set of indecomposable
![]() $\widehat {\Lambda _P}$
-lattices, as
$\widehat {\Lambda _P}$
-lattices, as
![]() $P\in \text {Max}R$
varies, is dense in
$P\in \text {Max}R$
varies, is dense in
 $\textrm {Zg}_\Lambda ^{tf}\backslash \left (xa=0/x=0\right )$
.
$\textrm {Zg}_\Lambda ^{tf}\backslash \left (xa=0/x=0\right )$
.
Proof Suppose that
 $\left (\phi /\psi \right )\cap (\textrm {Zg}_\Lambda ^{tf}\backslash \left (xa=0/x=0\right ))\neq \emptyset $
. Pick
$\left (\phi /\psi \right )\cap (\textrm {Zg}_\Lambda ^{tf}\backslash \left (xa=0/x=0\right ))\neq \emptyset $
. Pick
 $N\in \left (\phi /\psi \right )\cap (\textrm {Zg}_\Lambda ^{tf}\backslash \left (xa=0/x=0\right ))$
. Since N is a direct union of its finitely generated submodules, there exists a finitely generated submodule L of N such that
$N\in \left (\phi /\psi \right )\cap (\textrm {Zg}_\Lambda ^{tf}\backslash \left (xa=0/x=0\right ))$
. Since N is a direct union of its finitely generated submodules, there exists a finitely generated submodule L of N such that
![]() $\phi (L)\supsetneq \psi (L)$
. Since L is a submodule of N, L is R-torsion-free and
$\phi (L)\supsetneq \psi (L)$
. Since L is a submodule of N, L is R-torsion-free and
![]() $\textrm {ann}_La=0$
. Thus,
$\textrm {ann}_La=0$
. Thus,
![]() $\phi (H(L))\supsetneq \psi (H(L))$
and
$\phi (H(L))\supsetneq \psi (H(L))$
and
![]() $\textrm {ann}_{H(L)}a=0$
. Since
$\textrm {ann}_{H(L)}a=0$
. Since
![]() $H(L)$
is isomorphic to
$H(L)$
is isomorphic to
![]() $\prod _{P\in \text {Max}R}\widehat {L_P}$
by Lemma 2.1, for all
$\prod _{P\in \text {Max}R}\widehat {L_P}$
by Lemma 2.1, for all
![]() $P\in \text {Max}R$
,
$P\in \text {Max}R$
,
![]() $\textrm {ann}_{\widehat {L_P}}a=0$
, and there exists
$\textrm {ann}_{\widehat {L_P}}a=0$
, and there exists
![]() $P\in \text {Max}R$
such that
$P\in \text {Max}R$
such that
 $\phi (\widehat {L_P})\supsetneq \psi (\widehat {L_P})$
. Thus, there exist a
$\phi (\widehat {L_P})\supsetneq \psi (\widehat {L_P})$
. Thus, there exist a
![]() $P\in \text {Max}R$
and a
$P\in \text {Max}R$
and a
![]() $\widehat {\Lambda _P}$
-lattice M such that
$\widehat {\Lambda _P}$
-lattice M such that
![]() $\phi (M)\supsetneq \psi (M)$
and
$\phi (M)\supsetneq \psi (M)$
and
![]() $\textrm {ann}_Ma=0$
. Since the category of
$\textrm {ann}_Ma=0$
. Since the category of
![]() $\widehat {\Lambda _P}$
-lattices is Krull–Schmidt, it follows that there exists an indecomposable
$\widehat {\Lambda _P}$
-lattices is Krull–Schmidt, it follows that there exists an indecomposable
![]() $\widehat {\Lambda _P}$
-lattice with the required properties.▪
$\widehat {\Lambda _P}$
-lattice with the required properties.▪
The following is proved in the case that R is a discrete valuation domain in [Reference Marcja, Prest and Toffalori14].
Corollary 5.15 The set of indecomposable
![]() $\widehat {\Lambda _P}$
-lattices, as
$\widehat {\Lambda _P}$
-lattices, as
![]() $P\in \text {Max}R$
varies, is a dense subset of
$P\in \text {Max}R$
varies, is a dense subset of
 $\textrm {Zg}^{tf}_{\Lambda }$
, and each
$\textrm {Zg}^{tf}_{\Lambda }$
, and each
![]() $\widehat {\Lambda _P}$
-lattice is isolated in
$\widehat {\Lambda _P}$
-lattice is isolated in
 $\textrm {Zg}^{tf}_{\Lambda }$
. Therefore, all isolated points in
$\textrm {Zg}^{tf}_{\Lambda }$
. Therefore, all isolated points in
 $\textrm {Zg}_\Lambda ^{tf}$
are
$\textrm {Zg}_\Lambda ^{tf}$
are
![]() $\widehat {\Lambda _P}$
-lattices for some
$\widehat {\Lambda _P}$
-lattices for some
![]() $P\in \text {Max}R$
.
$P\in \text {Max}R$
.
Proof Density is a special case of Lemma 5.14. It is shown in [Reference Gregory, L’Innocente and Toffalori8, Lemma 2.4] that the indecomposable
![]() $\widehat {\Lambda _P}$
-lattices are isolated in
$\widehat {\Lambda _P}$
-lattices are isolated in
 $\textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
. As explained just after Theorem 5.8, we may identify
$\textrm {Zg}^{tf}_{\widehat {\Lambda _P}}$
. As explained just after Theorem 5.8, we may identify
 $\textrm {Zg}^{rtf}_{\widehat {\Lambda _P}}$
with
$\textrm {Zg}^{rtf}_{\widehat {\Lambda _P}}$
with
 $\textrm {Zg}^{rtf}_{\Lambda _P}$
. Thus, the
$\textrm {Zg}^{rtf}_{\Lambda _P}$
. Thus, the
![]() $\widehat {\Lambda _P}$
-lattices are isolated in
$\widehat {\Lambda _P}$
-lattices are isolated in
 $\textrm {Zg}^{rtf}_{\Lambda _P}$
. Finally, viewed as a subspace of
$\textrm {Zg}^{rtf}_{\Lambda _P}$
. Finally, viewed as a subspace of
 $\textrm {Zg}^{tf}_\Lambda $
,
$\textrm {Zg}^{tf}_\Lambda $
,
 $\textrm {Zg}^{rtf}_{\Lambda _P}$
is equal to the open set
$\textrm {Zg}^{rtf}_{\Lambda _P}$
is equal to the open set
![]() $\left (x=x/P|x\right )$
. Thus, the indecomposable
$\left (x=x/P|x\right )$
. Thus, the indecomposable
![]() $\widehat {\Lambda _P}$
-lattices are isolated in
$\widehat {\Lambda _P}$
-lattices are isolated in
 $\textrm {Zg}^{tf}_{\Lambda }$
. The final statement follows from the first two statements.▪
$\textrm {Zg}^{tf}_{\Lambda }$
. The final statement follows from the first two statements.▪
Recall that for each
![]() $P\in \text {Max} R$
,
$P\in \text {Max} R$
,
![]() $d_P$
is the isomorphism between the lattice of open subsets of
$d_P$
is the isomorphism between the lattice of open subsets of
 $ \textrm {Zg}_{\Lambda _P}^{rtf}$
and of
$ \textrm {Zg}_{\Lambda _P}^{rtf}$
and of
![]() ${_{\Lambda _P}}\textrm {Zg}^{rtf}$
defined in Section 5.1.
${_{\Lambda _P}}\textrm {Zg}^{rtf}$
defined in Section 5.1.
Lemma 5.16 For all simple
![]() $Q\Lambda $
-modules S and all
$Q\Lambda $
-modules S and all
![]() $P\in \text {Max}R$
,
$P\in \text {Max}R$
,
 $$ \begin{align*}d_P(\mathcal{V}(S)\cap\textrm{Zg}^{rtf}_{\Lambda_P})=\mathcal{V}(S^*)\cap {_{\Lambda_P}}\textrm{Zg}^{rtf}.\end{align*} $$
$$ \begin{align*}d_P(\mathcal{V}(S)\cap\textrm{Zg}^{rtf}_{\Lambda_P})=\mathcal{V}(S^*)\cap {_{\Lambda_P}}\textrm{Zg}^{rtf}.\end{align*} $$
Proof We first show that if L is an indecomposable right
![]() $\widehat {\Lambda _P}$
-lattice and S is a simple right
$\widehat {\Lambda _P}$
-lattice and S is a simple right
![]() $Q\Lambda $
-module, then
$Q\Lambda $
-module, then
![]() $L\in \mathcal {V}(S)$
if and only if
$L\in \mathcal {V}(S)$
if and only if
![]() $L^\dagger \in \mathcal {V}(S^*)$
. Let e be a centrally primitive idempotent of
$L^\dagger \in \mathcal {V}(S^*)$
. Let e be a centrally primitive idempotent of
![]() $Q\Lambda $
corresponding to S. Note that e is central and idempotent as an element of
$Q\Lambda $
corresponding to S. Note that e is central and idempotent as an element of
![]() $\widehat {Q_P}\widehat {\Lambda }$
. We have shown in Lemma 5.13 that
$\widehat {Q_P}\widehat {\Lambda }$
. We have shown in Lemma 5.13 that
![]() $L\in \left (x(e-1)d=0/x=0\right )$
if and only if
$L\in \left (x(e-1)d=0/x=0\right )$
if and only if
![]() $L^\dagger \in \left ((e-1)dx=0/x=0\right )$
. So it is enough to show that
$L^\dagger \in \left ((e-1)dx=0/x=0\right )$
. So it is enough to show that
![]() $\left ((e-1)dx=0/x=0\right )=\mathcal {V}(S^*)$
. However, this is clear because certainly
$\left ((e-1)dx=0/x=0\right )=\mathcal {V}(S^*)$
. However, this is clear because certainly
![]() $(e-1)S^*=0$
, and thus e is a centrally primitive idempotent corresponding to
$(e-1)S^*=0$
, and thus e is a centrally primitive idempotent corresponding to
![]() $S^*$
.
$S^*$
.
Since, by Lemma 5.14, the indecomposable right
![]() $\widehat {\Lambda _P}$
-lattices are dense in the closed subset
$\widehat {\Lambda _P}$
-lattices are dense in the closed subset
 $\textrm {Zg}_{\Lambda _P}^{rtf}\backslash \left (x(e-1)d=0/x=0\right )$
of
$\textrm {Zg}_{\Lambda _P}^{rtf}\backslash \left (x(e-1)d=0/x=0\right )$
of
 $\textrm {Zg}_{\Lambda _P}^{rtf}$
,
$\textrm {Zg}_{\Lambda _P}^{rtf}$
,
 $$ \begin{align*}\textrm{Zg}_{\Lambda_P}^{rtf}\backslash\left(x(e-1)d=0/x=0\right)\subseteq \textrm{Zg}_{\Lambda_P}^{rtf}\backslash d_P(\left((e-1)dx=0/x=0\right)\cap {_{\Lambda_P}}\textrm{Zg}^{rtf}).\end{align*} $$
$$ \begin{align*}\textrm{Zg}_{\Lambda_P}^{rtf}\backslash\left(x(e-1)d=0/x=0\right)\subseteq \textrm{Zg}_{\Lambda_P}^{rtf}\backslash d_P(\left((e-1)dx=0/x=0\right)\cap {_{\Lambda_P}}\textrm{Zg}^{rtf}).\end{align*} $$
So
![]() $d_P(\left ((e-1)dx=0/x=0\right )\cap {_{\Lambda _P}}\textrm {Zg}^{rtf})\subseteq \left (x(e-1)d=0/x=0\right )$
. The same argument using left
$d_P(\left ((e-1)dx=0/x=0\right )\cap {_{\Lambda _P}}\textrm {Zg}^{rtf})\subseteq \left (x(e-1)d=0/x=0\right )$
. The same argument using left
![]() $\widehat {\Lambda _P}$
-lattices shows that
$\widehat {\Lambda _P}$
-lattices shows that
 $$ \begin{align*}d_P(\left(x(e-1)d=0/x=0\right)\cap \textrm{Zg}_{\Lambda_P}^{rtf})\subseteq \left((e-1)dx=0/x=0\right).\end{align*} $$
$$ \begin{align*}d_P(\left(x(e-1)d=0/x=0\right)\cap \textrm{Zg}_{\Lambda_P}^{rtf})\subseteq \left((e-1)dx=0/x=0\right).\end{align*} $$
So, since
![]() $d_P^2$
is the identity,
$d_P^2$
is the identity,
 $$ \begin{align*} d_P(\left(x(e-1)d=0/x=0\right)\cap\textrm{Zg}_{\Lambda_P}^{rtf})=\left((e-1)dx=0/x=0\right)\cap {_{\Lambda_P}}\textrm{Zg}^{rtf}.\\[-37pt] \end{align*} $$
$$ \begin{align*} d_P(\left(x(e-1)d=0/x=0\right)\cap\textrm{Zg}_{\Lambda_P}^{rtf})=\left((e-1)dx=0/x=0\right)\cap {_{\Lambda_P}}\textrm{Zg}^{rtf}.\\[-37pt] \end{align*} $$
▪
Definition 5.2 Let U be an open subset of
 $\textrm {Zg}_\Lambda ^{tf}$
. Define
$\textrm {Zg}_\Lambda ^{tf}$
. Define
 $$ \begin{align*}dU:=\bigcup_{P\in\text{Max}R}d_P(U\cap\textrm{Zg}_{\Lambda_P}^{rtf})\cup\bigcup_{S\in \lambda(U)}\mathcal{V}(S^*),\end{align*} $$
$$ \begin{align*}dU:=\bigcup_{P\in\text{Max}R}d_P(U\cap\textrm{Zg}_{\Lambda_P}^{rtf})\cup\bigcup_{S\in \lambda(U)}\mathcal{V}(S^*),\end{align*} $$
where
 $\lambda (U):=U\cap \textrm {Zg}_{Q\Lambda }$
.
$\lambda (U):=U\cap \textrm {Zg}_{Q\Lambda }$
.
We will also use d to denote the analogous map for open subsets of
![]() ${_\Lambda }\textrm {Zg}^{tf}$
.
${_\Lambda }\textrm {Zg}^{tf}$
.
Theorem 5.17 Let R be a Dedekind domain, Q its field of fractions, and
![]() $\Lambda $
an R-order with
$\Lambda $
an R-order with
![]() $Q\Lambda $
a separable Q-algebra.
$Q\Lambda $
a separable Q-algebra.
The mapping d is an isomorphism between the lattice of open sets of
 $\textrm {Zg}_\Lambda ^{tf}$
and
$\textrm {Zg}_\Lambda ^{tf}$
and
![]() ${_\Lambda }\textrm {Zg}^{tf}$
such that
${_\Lambda }\textrm {Zg}^{tf}$
such that
-
(1) if L is an indecomposable right
 $\widehat {\Lambda _P}$
-lattice, then for all open sets
$\widehat {\Lambda _P}$
-lattice, then for all open sets
 $U\subseteq \textrm {Zg}_\Lambda ^{tf}$
,
$U\subseteq \textrm {Zg}_\Lambda ^{tf}$
,
 $L\in U$
if and only if
$L\in U$
if and only if
 $L^{\dagger }\in dU$
, and
$L^{\dagger }\in dU$
, and -
(2) for all open sets
 $U\subseteq \textrm {Zg}_\Lambda ^{tf}$
, if S is a simple
$U\subseteq \textrm {Zg}_\Lambda ^{tf}$
, if S is a simple
 $Q\Lambda $
-module, then
$Q\Lambda $
-module, then
 $S\in U$
if and only if
$S\in U$
if and only if
 $S^*\in dU$
.
$S^*\in dU$
.
Proof Let U be an open subset of
 $\textrm {Zg}_\Lambda ^{tf}$
. We start by showing that for all open subsets
$\textrm {Zg}_\Lambda ^{tf}$
. We start by showing that for all open subsets
 $U\subseteq \textrm {Zg}_\Lambda ^{tf}$
,
$U\subseteq \textrm {Zg}_\Lambda ^{tf}$
,
![]() $d^2U=U$
. So
$d^2U=U$
. So
 $$ \begin{align*} d^2U &= d[\bigcup_{P}d_P(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{S\in \lambda(U)}\mathcal{V}(S^*)] \\ &= \bigcup_{P}d_P[d_P(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{S\in U}\mathcal{V}(S^*)\cap{_{\Lambda_P}}\textrm{Zg}^{rtf}]\cup \bigcup_{S\in \lambda(U)}\mathcal{V}(S)\\ &= \bigcup_{P}d_P^2(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{P}\bigcup_{S\in \lambda(U)}d_P[\mathcal{V}(S^*)\cap{_{\Lambda_P}}\textrm{Zg}^{rtf}]\cup \bigcup_{S\in \lambda(U)}\mathcal{V}(S)\\ &= \bigcup_{P}(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup \bigcup_{S\in \lambda(U)}\mathcal{V}(S) \\ &= U. \end{align*} $$
$$ \begin{align*} d^2U &= d[\bigcup_{P}d_P(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{S\in \lambda(U)}\mathcal{V}(S^*)] \\ &= \bigcup_{P}d_P[d_P(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{S\in U}\mathcal{V}(S^*)\cap{_{\Lambda_P}}\textrm{Zg}^{rtf}]\cup \bigcup_{S\in \lambda(U)}\mathcal{V}(S)\\ &= \bigcup_{P}d_P^2(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup\bigcup_{P}\bigcup_{S\in \lambda(U)}d_P[\mathcal{V}(S^*)\cap{_{\Lambda_P}}\textrm{Zg}^{rtf}]\cup \bigcup_{S\in \lambda(U)}\mathcal{V}(S)\\ &= \bigcup_{P}(U\cap\textrm{Zg}^{rtf}_{\Lambda_P})\cup \bigcup_{S\in \lambda(U)}\mathcal{V}(S) \\ &= U. \end{align*} $$
The first two equalities follow from the definition of d. The third is true because each
![]() $d_P$
is a lattice homomorphism. The fourth follows from Lemma 5.16 and the fifth follows from Corollary 5.11.
$d_P$
is a lattice homomorphism. The fourth follows from Lemma 5.16 and the fifth follows from Corollary 5.11.
Thus, d gives a bijection between the lattice of open subsets of
 $\textrm {Zg}_\Lambda ^{tf}$
and
$\textrm {Zg}_\Lambda ^{tf}$
and
![]() ${_\Lambda }\textrm {Zg}^{tf}$
. We now just need to show that d preserves inclusion.
${_\Lambda }\textrm {Zg}^{tf}$
. We now just need to show that d preserves inclusion.
Suppose
![]() $U\subseteq W$
are open subsets of
$U\subseteq W$
are open subsets of
 $\textrm {Zg}_\Lambda ^{tf}$
. Then
$\textrm {Zg}_\Lambda ^{tf}$
. Then
![]() $\lambda (U)\subseteq \lambda (W)$
and
$\lambda (U)\subseteq \lambda (W)$
and
 $U\cap \textrm {Zg}^{rtf}_{\Lambda _P}\subseteq W\cap \textrm {Zg}^{rtf}_{\Lambda _P}$
for all
$U\cap \textrm {Zg}^{rtf}_{\Lambda _P}\subseteq W\cap \textrm {Zg}^{rtf}_{\Lambda _P}$
for all
![]() $P\in \text {Max}(R)$
. So
$P\in \text {Max}(R)$
. So
 $d_P(U\cap \textrm {Zg}^{rtf}_{\Lambda _P})\subseteq d_P(W\cap \textrm {Zg}^{rtf}_{\Lambda _P})$
for all
$d_P(U\cap \textrm {Zg}^{rtf}_{\Lambda _P})\subseteq d_P(W\cap \textrm {Zg}^{rtf}_{\Lambda _P})$
for all
![]() $P\in \text {Max}R$
. For all open sets U,
$P\in \text {Max}R$
. For all open sets U,
![]() $S\in \lambda (U)$
if and only if
$S\in \lambda (U)$
if and only if
![]() $S^*\in \lambda (dU)$
. So
$S^*\in \lambda (dU)$
. So
![]() $\lambda (U)\subseteq \lambda (W)$
implies
$\lambda (U)\subseteq \lambda (W)$
implies
![]() $\lambda (dU)\subseteq \lambda (dW)$
. Therefore,
$\lambda (dU)\subseteq \lambda (dW)$
. Therefore,
![]() $dU\subseteq dW$
.
$dU\subseteq dW$
.
Finally,
![]() $(1)$
holds for d by Proposition 5.6 and
$(1)$
holds for d by Proposition 5.6 and
![]() $(2)$
holds by definition of d.▪
$(2)$
holds by definition of d.▪
We finish this section with a different aspect of duality.
Corollary 5.18 Let R be a discrete valuation domain with maximal ideal generated by
![]() $\pi $
. The lattices
$\pi $
. The lattices
![]() $[\pi |x,x=x]_{\text {Tf}_\Lambda }$
and
$[\pi |x,x=x]_{\text {Tf}_\Lambda }$
and
![]() $[\pi |x,x=x]_{{_\Lambda }\text {Tf}}$
are anti-isomorphic.
$[\pi |x,x=x]_{{_\Lambda }\text {Tf}}$
are anti-isomorphic.
Proof Let
![]() $k> k_0$
, and let
$k> k_0$
, and let
![]() $p=\pi +\pi ^k\Lambda $
. By Proposition 3.6,
$p=\pi +\pi ^k\Lambda $
. By Proposition 3.6,
![]() $[\pi |x,x=x]_{\text {Tf}_\Lambda }$
is isomorphic to
$[\pi |x,x=x]_{\text {Tf}_\Lambda }$
is isomorphic to
![]() $[p|x,x=x]_{\langle I\text {Tf}_\Lambda \rangle }$
and
$[p|x,x=x]_{\langle I\text {Tf}_\Lambda \rangle }$
and
![]() $[\pi |x,x=x]_{{_\Lambda }\text {Tf}}$
is isomorphic to
$[\pi |x,x=x]_{{_\Lambda }\text {Tf}}$
is isomorphic to
![]() $[p|x,x=x]_{\langle I{_\Lambda }\text {Tf}\rangle }$
. So, it is enough to show that
$[p|x,x=x]_{\langle I{_\Lambda }\text {Tf}\rangle }$
. So, it is enough to show that
![]() $[p|x,x=x]_{\langle I\text {Tf}_\Lambda \rangle }$
is anti-isomorphic to
$[p|x,x=x]_{\langle I\text {Tf}_\Lambda \rangle }$
is anti-isomorphic to
![]() $[p|x,x=x]_{\langle I{_\Lambda }\text {Tf}\rangle }$
.
$[p|x,x=x]_{\langle I{_\Lambda }\text {Tf}\rangle }$
.
We have seen in Lemma 5.5 that
![]() $D\langle I\text {Tf}_\Lambda \rangle =\langle I{_\Lambda }\text {Tf} \rangle $
. Thus, Prest’s duality for pp formulas gives an anti-isomorphism between
$D\langle I\text {Tf}_\Lambda \rangle =\langle I{_\Lambda }\text {Tf} \rangle $
. Thus, Prest’s duality for pp formulas gives an anti-isomorphism between
 $\textrm {pp}^1_{\Lambda _k}(\langle I\text {Tf}_\Lambda \rangle )$
and
$\textrm {pp}^1_{\Lambda _k}(\langle I\text {Tf}_\Lambda \rangle )$
and
![]() ${_{\Lambda _k}}\textrm {pp}^1(\langle I{_\Lambda }\text {Tf} \rangle )$
. Thus,
${_{\Lambda _k}}\textrm {pp}^1(\langle I{_\Lambda }\text {Tf} \rangle )$
. Thus,
![]() $[p|x,x=x]_{\langle I\text {Tf}_\Lambda \rangle }$
is anti-isomorphic to
$[p|x,x=x]_{\langle I\text {Tf}_\Lambda \rangle }$
is anti-isomorphic to
![]() $[x=0,px=0]_{\langle I{_\Lambda }\text {Tf} \rangle }$
.
$[x=0,px=0]_{\langle I{_\Lambda }\text {Tf} \rangle }$
.
The formula
![]() $y=xp^{k-1}$
induces a lattice isomorphism between the intervals
$y=xp^{k-1}$
induces a lattice isomorphism between the intervals
![]() $[xp^{k-1}=0,x=x]$
and
$[xp^{k-1}=0,x=x]$
and
![]() $[y=0,p^{k-1}|y]$
of
$[y=0,p^{k-1}|y]$
of
 $\textrm {pp}^1_{\Lambda _k}$
defined by
$\textrm {pp}^1_{\Lambda _k}$
defined by
 $$ \begin{align*}\phi(x)\mapsto \exists x (y=xp^{k-1}\wedge \phi(x)) \end{align*} $$
$$ \begin{align*}\phi(x)\mapsto \exists x (y=xp^{k-1}\wedge \phi(x)) \end{align*} $$
(see the proof of Goursat’s lemma [Reference Ziegler24, Lemma 8.9]). On
![]() $\langle I{_\Lambda }\text {Tf} \rangle $
,
$\langle I{_\Lambda }\text {Tf} \rangle $
,
![]() $p^{k-1}x=0$
is equivalent to
$p^{k-1}x=0$
is equivalent to
![]() $p|x$
and
$p|x$
and
![]() $p^{k-1}|y$
is equivalent to
$p^{k-1}|y$
is equivalent to
![]() $py=0$
. Thus,
$py=0$
. Thus,
![]() $[x=0,px=0]_{\langle I{_\Lambda }\text {Tf} \rangle }$
is isomorphic to
$[x=0,px=0]_{\langle I{_\Lambda }\text {Tf} \rangle }$
is isomorphic to
![]() $[p|x,x=x]_{\langle I{_\Lambda }\text {Tf} \rangle }$
.▪
$[p|x,x=x]_{\langle I{_\Lambda }\text {Tf} \rangle }$
.▪
For the definition of the m-dimension of a modular lattice, see [Reference Prest17, Section 7.2].
Corollary 5.19 Suppose R is a Dedekind domain with field of fractions Q,
![]() $\Lambda $
is an R-order, and
$\Lambda $
is an R-order, and
![]() $Q\Lambda $
is separable. The m-dimensions of
$Q\Lambda $
is separable. The m-dimensions of
![]() $\textrm {pp}_\Lambda ^1(\text {Tf}_{\Lambda })$
and
$\textrm {pp}_\Lambda ^1(\text {Tf}_{\Lambda })$
and
![]() ${_\Lambda }\textrm {pp}^1({_\Lambda }\text {Tf})$
are equal.
${_\Lambda }\textrm {pp}^1({_\Lambda }\text {Tf})$
are equal.
Proof For each
![]() $P\in \text {Max}R$
, by [Reference Gregory, L’Innocente and Toffalori8, Corollary 3.8], the m-dimension of
$P\in \text {Max}R$
, by [Reference Gregory, L’Innocente and Toffalori8, Corollary 3.8], the m-dimension of
 $\textrm {pp}_{\Lambda _P}^1(\text {Tf}_{\Lambda _P})$
is equal to the m-dimension of
$\textrm {pp}_{\Lambda _P}^1(\text {Tf}_{\Lambda _P})$
is equal to the m-dimension of
![]() $[P|x,x=x]_{\text {Tf}_{\Lambda _P}}$
plus
$[P|x,x=x]_{\text {Tf}_{\Lambda _P}}$
plus
![]() $1$
. Since
$1$
. Since
![]() $R_P$
is discrete valuation domain, by Corollary 5.18, the m-dimension of
$R_P$
is discrete valuation domain, by Corollary 5.18, the m-dimension of
![]() $[P|x,x=x]_{\text {Tf}_{\Lambda _P}}$
is equal to the m-dimension of
$[P|x,x=x]_{\text {Tf}_{\Lambda _P}}$
is equal to the m-dimension of
![]() $[P|x,x=x]_{{_{\Lambda _P}}\text {Tf}}$
. Thus, by [Reference Gregory, L’Innocente and Toffalori8, Corollary 3.8],
$[P|x,x=x]_{{_{\Lambda _P}}\text {Tf}}$
. Thus, by [Reference Gregory, L’Innocente and Toffalori8, Corollary 3.8],
![]() ${_{\Lambda _P}}\textrm {pp}^1({_{\Lambda _P}}\text {Tf})$
has m-dimension equal to the m-dimension of
${_{\Lambda _P}}\textrm {pp}^1({_{\Lambda _P}}\text {Tf})$
has m-dimension equal to the m-dimension of
![]() $[P|x,x=x]_{\text {Tf}_{\Lambda _P}}$
plus
$[P|x,x=x]_{\text {Tf}_{\Lambda _P}}$
plus
![]() $1$
, i.e., equal to the m-dimension of
$1$
, i.e., equal to the m-dimension of
 $\textrm {pp}_{\Lambda _P}^1(\text {Tf}_{\Lambda _P})$
.
$\textrm {pp}_{\Lambda _P}^1(\text {Tf}_{\Lambda _P})$
.
By [Reference Gregory, L’Innocente and Toffalori8, Remark 3.9], the m-dimension of
![]() $\textrm {pp}_\Lambda ^1(\text {Tf}_{\Lambda })$
(respectively,
$\textrm {pp}_\Lambda ^1(\text {Tf}_{\Lambda })$
(respectively,
![]() ${_\Lambda }\textrm {pp}^1({_\Lambda }\text {Tf})$
) is equal to the supremum of the m-dimensions of
${_\Lambda }\textrm {pp}^1({_\Lambda }\text {Tf})$
) is equal to the supremum of the m-dimensions of
 $\textrm {pp}_{\Lambda _P}^1(\text {Tf}_{\Lambda _P})$
(respectively,
$\textrm {pp}_{\Lambda _P}^1(\text {Tf}_{\Lambda _P})$
(respectively,
![]() ${_{\Lambda _P}}\textrm {pp}^1({_{\Lambda _P}}\text {Tf})$
) where
${_{\Lambda _P}}\textrm {pp}^1({_{\Lambda _P}}\text {Tf})$
) where
![]() $P\in \text {Max}R$
.▪
$P\in \text {Max}R$
.▪
We now translate the above corollary into a result about the Krull–Gabriel dimensions of
![]() $(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
and
$(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
and
![]() $({_\Lambda }\text {Latt},\text {Ab})^{fp}$
. See [Reference Geigle7, Definition 2.1] for a definition of the Krull–Gabriel dimension of a (skeletally) small abelian category.
$({_\Lambda }\text {Latt},\text {Ab})^{fp}$
. See [Reference Geigle7, Definition 2.1] for a definition of the Krull–Gabriel dimension of a (skeletally) small abelian category.
Recall that a full subcategory
![]() $\mathcal {C} \subseteq {\textrm {mod}}\text {-}S$
which is closed under isomorphism, finite direct sums, and direct summands is covariantly finite in
$\mathcal {C} \subseteq {\textrm {mod}}\text {-}S$
which is closed under isomorphism, finite direct sums, and direct summands is covariantly finite in
![]() ${\textrm {mod}}\text {-}S$
if for each
${\textrm {mod}}\text {-}S$
if for each
![]() $M\in {\textrm {mod}}\text {-}S$
there exists a homomorphism
$M\in {\textrm {mod}}\text {-}S$
there exists a homomorphism
![]() $f_M:M\rightarrow M_{\mathcal {C}}$
with
$f_M:M\rightarrow M_{\mathcal {C}}$
with
![]() $M_{\mathcal {C}}\in \mathcal {C}$
such that all homomorphisms
$M_{\mathcal {C}}\in \mathcal {C}$
such that all homomorphisms
![]() $g:M\rightarrow L$
with
$g:M\rightarrow L$
with
![]() $L\in \mathcal {C}$
, factor through
$L\in \mathcal {C}$
, factor through
![]() $f_M$
. For
$f_M$
. For
![]() $M\in {\textrm {mod}}\text {-}\Lambda $
, let
$M\in {\textrm {mod}}\text {-}\Lambda $
, let
![]() $\text {tor} M$
denote the submodule
$\text {tor} M$
denote the submodule
![]() $\{m\in M \ \vert \ \text { there exists }r\in R\backslash \{0\} \text { with } mr=0\}$
consisting of R-torsion elements of M. Then
$\{m\in M \ \vert \ \text { there exists }r\in R\backslash \{0\} \text { with } mr=0\}$
consisting of R-torsion elements of M. Then
![]() $M/\text {tor} M\in \text {Latt}_\Lambda $
and for any
$M/\text {tor} M\in \text {Latt}_\Lambda $
and for any
![]() $L\in \text {Latt}_\Lambda $
and
$L\in \text {Latt}_\Lambda $
and
![]() $g:M\rightarrow L$
,
$g:M\rightarrow L$
,
![]() $\text {tor} M\subseteq \ker g$
. Hence, g factors through the canonical surjection
$\text {tor} M\subseteq \ker g$
. Hence, g factors through the canonical surjection
![]() $f_M:M\rightarrow M/\text {tor} M$
. Therefore,
$f_M:M\rightarrow M/\text {tor} M$
. Therefore,
![]() $\text {Latt}_\Lambda $
is covariantly finite in
$\text {Latt}_\Lambda $
is covariantly finite in
![]() ${\textrm {mod}}\text {-}\Lambda $
.
${\textrm {mod}}\text {-}\Lambda $
.
If
![]() $\mathcal {C}\subseteq {\textrm {mod}}\text {-}S$
is a covariantly finite subcategory, then
$\mathcal {C}\subseteq {\textrm {mod}}\text {-}S$
is a covariantly finite subcategory, then
![]() $(\mathcal {C},\text {Ab})^{fp}$
is equivalent to
$(\mathcal {C},\text {Ab})^{fp}$
is equivalent to
![]() $({\textrm {mod}}\text {-}S,\text {Ab})^{fp}/\mathcal {S}(\mathcal {C})$
, the Serre localization of
$({\textrm {mod}}\text {-}S,\text {Ab})^{fp}/\mathcal {S}(\mathcal {C})$
, the Serre localization of
![]() $({\textrm {mod}}\text {-}S,\text {Ab})^{fp}$
at the Serre subcategory
$({\textrm {mod}}\text {-}S,\text {Ab})^{fp}$
at the Serre subcategory
See [Reference Herzog10] for details.
By [Reference Prest17, Corollary 13.2.2], the Krull–Gabriel dimension of
![]() $(\mathcal {C},\text {Ab})^{fp}/\mathcal {S}(\mathcal {C})$
is equal to the m-dimension of
$(\mathcal {C},\text {Ab})^{fp}/\mathcal {S}(\mathcal {C})$
is equal to the m-dimension of
![]() $\textrm {pp}^1_S(\langle \mathcal {C} \rangle )$
.
$\textrm {pp}^1_S(\langle \mathcal {C} \rangle )$
.
Applying this to
![]() $\text {Latt}_\Lambda $
as a covariantly finite subcategory of
$\text {Latt}_\Lambda $
as a covariantly finite subcategory of
![]() ${\textrm {mod}}\text {-}\Lambda $
, we get that the Krull–Gabriel dimension of
${\textrm {mod}}\text {-}\Lambda $
, we get that the Krull–Gabriel dimension of
![]() $(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
is equal to the m-dimension of
$(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
is equal to the m-dimension of
![]() $\textrm {pp}_\Lambda ^1\text {Tf}_\Lambda $
. Thus, we get the following corollary to Corollary 5.19.
$\textrm {pp}_\Lambda ^1\text {Tf}_\Lambda $
. Thus, we get the following corollary to Corollary 5.19.
Corollary 5.20 Suppose R is a Dedekind domain with field of fractions Q,
![]() $\Lambda $
is an R-order, and
$\Lambda $
is an R-order, and
![]() $Q\Lambda $
is separable. The Krull–Gabriel dimension of
$Q\Lambda $
is separable. The Krull–Gabriel dimension of
![]() $(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
is equal to the Krull–Gabriel dimension of
$(\text {Latt}_\Lambda ,\text {Ab})^{fp}$
is equal to the Krull–Gabriel dimension of
![]() $({_\Lambda }\text {Latt},\text {Ab})^{fp}$
.
$({_\Lambda }\text {Latt},\text {Ab})^{fp}$
.
Acknowledgment
I would like to thank Carlo Toffalori for reading an early version of the results in Sections 3 and 5, and more generally for support and encouragement during this project. I would also like to thank the anonymous referee for many helpful comments which have improved the readability of this article.