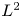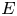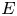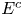1. Introduction
In this paper, we are interested in the exponential decay property of the KdV equation on the real line $\mathbb {R}$
Here, $u(x,\,t)$
is a real-valued function on $\mathbb {R}\times \mathbb {R}^{+}$
, the function $a(x)$
satisfies the condition
In the case $a(x)=0$
, (1.1) reduces to the classical KdV equation, which models the unidirectional propagation of small-amplitude long waves in nonlinear dispersive systems. If we multiply (1.1) by $2u$
and integrate over $\mathbb {R}$
, then
This, and condition $a(x)\geq 0$
, clearly implies that $\|u(\cdot\,,t )\|_{L^{2}(\mathbb {R})}\leq \|u_0\|_{L^{2}(\mathbb {R})}$
for all $t\geq 0$
. Moreover, if $a(x)\geq a_0>0$
for all $x\in \mathbb {R}$
, then (1.2) gives the decay bound
Thus, the term $au$
is called a damping in the literature. Now an interesting question arises naturally, whether the exponential decay as (1.3) holds if
is satisfied only on a subset $E\subset \mathbb {R}$
? In this case, the term $au$
is referred to a localized damping.
Similar problems for KdV type equations on bounded domains have been studied extensively, we refer to e.g. [Reference Capistrano-Filho3, Reference Laurent, Rosier and Zhang14, Reference Linares and Pazoto15, Reference Menzala, Vasconcellos and Zuazua17–Reference Panthee and Vielma Leal19, Reference Pazoto21, Reference Rosier23] and the survey [Reference Rosier and Zhang24]. But much less is known for the KdV equation on unbounded domains. For the KdV equation posed on $(x,\,t)\in \mathbb {R}^{2}_+$
, the exponential decay of the $L^{2}(\mathbb {R}_+)$
norm was proved in [Reference Linares and Pazoto16] when (A2) holds on $E=(0,\,\delta )\bigcup (L,\,+\infty )$
for some $0<\delta < L$
. The same result was obtained in [Reference Pazoto and Rosier22] under a weaker localized damping, namely (A2) holds only on $E=(L,\,+\infty )$
for some $L>0$
. For the KdV equation on $(x,\,t)\in \mathbb {R}\times \mathbb {R}_+$
, namely (1.1), the exponential decay was established in [Reference Cavalcanti, Cavalcanti, Faminskii and Natali4] with damping on $E=(-\infty,\,-L)\bigcup (L,\,+\infty )$
. If one considers the KdV equation with strong dissipation
called the Korteweg–de Vries–Burgers equation, then the exponential decay holds with an indefinite damping, namely $a(x)$
may change sign, see [Reference Cavalcanti, Cavalcanti, Komornik and Rodrigues5, Reference Gallego and Pazoto7, Reference Komornik and Pignotti9].
In this article, the main goal is to consider the following question: To what extent the set $E$
can be small so that the exponential decay holds for KdV equations with damping on $E$
. First of all, we give a sufficient and necessary condition for the exponential decay of the linear KdV equation.
Theorem 1.1 Assume that (A1) holds. Then the following are equivalent:
(1) There exist constants $C,\,\lambda >0$
so that
\[ \|u({\cdot},t)\|_{L^{2}(\mathbb{R})}\leq C{\rm e}^{-\lambda t}\|u_0\|_{L^{2}(\mathbb{R})}, \quad \forall t\geq 0 \]holds for all solutions of the initial value problem (IVP) $\partial _tu+\partial _x^{3}u+a(x)u=0,\, u(x,0)=u_0(x)\in L^{2}(\mathbb {R}).$(2) There exists a constant $L>0$
so that
(1.4)\begin{equation} \inf_{x\in \mathbb{R}}\int_{x-L}^{x+L}a(y){{\rm d}}y>0. \end{equation}
As noted in [Reference Green8], under assumption (A1), condition (1.4) is equivalent to (A2) for some $a_0>0$
and a thick set $E$
. Recall that (see e.g. [Reference Wang, Wang, Zhang and Zhang29]) a measurable set $E\subset \mathbb {R}$
is thick, if there exists $L>0$
so that
Here and below, we use $|E|$
to denote the Lebesgue measure of $E$
. Based on theorem 1.1 and the contraction mapping principle, we give the exponential decay for the KdV equation (1.1) with small data.
Theorem 1.2 (Decay for small data)
Assume that (A1) holds and (A2) holds on a thick set $E$
. Then there exist constants $C>0,\, \lambda >0,\,\delta >0$
such that
holds for all solutions of (1.1) with data $\|u_0\|_{L^{2}(\mathbb {R})}\leq \delta$
.
To obtain the exponential decay for large data, we need to strength the damping effect. To state our result, we first introduce a set class. A set $E\subset \mathbb {R}$
is said to be satisfying the network control condition (NCC), named after [Reference Burq and Joly2], if there exist constants $r,\,L>0$
so that
Clearly, a set satisfying NCC is a thick set, but a thick set could not satisfy NCC, see figure 1.
Remark 1.3 In figure 1, the set consisting of red intervals is a typical thick set. It has a fixed positive Lebesgue measure on every $[n,\,n+1]$
, but it does not contain an interval with given length simultaneously on all $[n,\,n+1],\, n\in \mathbb {Z}$
. The union of blue intervals is a typical set satisfying NCC.
FIG. 1. Comparison of thick set with NCC.
The set class satisfying NCC in higher dimensions (the definition is the same except minor modifications) was first introduced to study the observability of the Kolmogorov equation [Reference Le Rousseau and Moyano10] (see also [Reference Duan, Wang and Zhang6] for observability of heat equations).
Theorem 1.4 (Decay for general data)
Assume that (A1) holds and (A2) holds on $E,$
where $E$
satisfies NCC and the complement set $E^{c}$
has a finite Lebesgue measure. Then for every $R>0,$
there exist constants $C,\,\lambda >0$
depending only on $R$
and $a(x)$
so that
holds for all solutions $u$
of IVP (1.1) with initial data satisfying $\|u_0\|_{L^{2}(\mathbb {R})}\leq R$
.
Note that if $E$
is the complement of a compact set, then $E$
satisfies NCC and $m(E^{c})<\infty$
. However, if
then $E$
satisfies NCC and $m(E^{c})<\infty$
, but $E^{c}$
cannot be contained in a compact set, see figure 2. Therefore, theorem 1.4 improves the results in [Reference Cavalcanti, Cavalcanti, Faminskii and Natali4] in the sense that the exponential decay holds with localized damping on more general sets. In fact, to obtain exponential decay results established in [Reference Cavalcanti, Cavalcanti, Faminskii and Natali4], it is assumed that the damping effect holds on the complement of a compact set (see the blue set in figure 2). On the other hand, conditions in theorem 1.4 allows no damping to occur on some small gaps at infinity (see the red set in figure 2).
FIG. 2. Damping domain considered in [Reference Cavalcanti, Cavalcanti, Faminskii and Natali4] vs damping domain considered in theorem 1.4.
Let us describe briefly the applications of conditions established on the set $E$
and the main arguments to prove theorem 1.4.
(1) $E$
satisfies NCC. This condition is necessary to show the propagation of regularity for the operator $\mathbb {L}=\partial _t+\partial _x^{3}$. Roughly speaking, let $u$ be a solution of the equation $\mathbb {L}u=f$ with a smooth $f$, then $u$ is smooth on $\mathbb {R}$ if $u$ is smooth on $E$. We refer to lemma 4.3 for precise statements.(2) $m(E^{c})<\infty.$
This condition is necessary to establish the compactness of sequence $u_n\in L^{2}(0,\,T; L^{2}(E^{c}))$, where $u_n$ is the solution of IVP (1.1) with initial data $u_{0n}$ bounded in $L^{2}(\mathbb {R})$. Combining the compactness and the propagation of regularity, we show that the solution of (1.1) enjoys the observability
\[ \int_0^{T}\int_\mathbb{R}|u(x,t)|^{2}{{\rm d}}x {{\rm d}}t\leq C\int_0^{T}\int_\mathbb{R} a(x)|u(x,t)|^{2}{{\rm d}}x {{\rm d}}t. \]Then the exponential decay follows from a standard argument.
The notation used in this paper is standard. We only point out that we use $A\lesssim B$
to denote $A\leq CB$
for some constant $C>0$
, which may vary from place to place.
The paper is organized as follows. In § 2, we show theorem 1.1. The proof of theorem 1.2 is given in § 3. Finally, in § 4, the propagation of regularity and an observability inequality are established to prove theorem 1.4.
2. Exponential decay for linear KdV
Assume that $0\leq a(x)\in L^{\infty }(\mathbb {R})$
. Consider the linear operator $A: H^{3}(\mathbb {R})\mapsto L^{2}(\mathbb {R})$
Clearly, we have
This shows that $-A$
is dissipative. According to Lumer–Phillips theorem [Reference Pazy20], $-A$
generates a $C_0$
semigroup of contractions in $L^{2}(\mathbb {R})$
, namely
This will be improved to an exponential decay upper bound if $a$
satisfies some further damping conditions.
Theorem 2.1 Assume that (A1) holds and (A2) holds on a thick set $E$
. Then there exist constants $C,\,\lambda >0$
depending only on $a$
and $E$
so that
Proof. The result has been stated in [Reference Wang and Zhou31] without proof. We give a sketch here for the reader's convenience. Let $E$
be a thick set. Based on the uncertainty principle of the Fourier transform, one can show that (see [Reference Wang and Zhou31, lemma 2.3]) there exists a constant $c_1>0$
so that for all $\tau \in \mathbb {R},\, u\in H^{3}(\mathbb {R})$
,
Since $a\in L^{\infty }(\mathbb {R})$
, by the triangular inequality
By assumption (A2), $a(x)\geq a_0$
on $E$
, we have
It follows from (2.1)–(2.3) that for some $c_2>0$
Moreover, taking the $L^{2}(\mathbb {R})$
inner product and using (A1), we find
Plugging (2.5) into (2.4) and using Cauchy–Schwartz, we infer that for all $\varepsilon >0$
,
Taking $\varepsilon =\varepsilon _0>0$
small enough such that $c_2\varepsilon _0\leq {c_1}/{2}$
, then we deduce from (2.6) that
where $c_3>0$
is a constant independent of $\tau$
. This implies that the resolvent set $\rho (A)\supset {{\rm i}}\mathbb {R}$
and $\sup _{\tau \in \mathbb {R}}\|(A+{{\rm i}} \tau )^{-1}\|_{L^{2}(\mathbb {R})\to L^{2}(\mathbb {R})}<\infty$
. Thus according to Gearhart–Pruss–Huang criteria [Reference Huang11], the desired decay holds.
Proof of theorem 1.1. Assume that (A1) holds. We divide the proof into two steps.
(2)$\Longrightarrow$
(1). First, following [Reference Green8], we show that the condition $(2)$
implies that (A2) holds on a thick set $E$
. In fact, if $(2)$
holds, then there exists $\gamma >0$
, so that
Fix $x\in \mathbb {R}$
. For every $\varepsilon >0$
, we consider the set
It follows from (2.7) that
Choose $\varepsilon =\varepsilon _0:={\gamma }/{4L}$
. It follows from (2.8) and the definition of $\Sigma ^{c}_\varepsilon$
that
Since $x$
can be chosen arbitrarily, we conclude that the set $\{y\in \mathbb {R}: a(y)\geq \varepsilon _0\}$
is a thick set. Now according to theorem 2.1, $(1)$
holds.
(1)$\Longrightarrow$
(2). Assume that $(1)$
holds for some constants $C,\,\lambda >0$
, then
where $A=\partial _x^{3}+a(x)$
with domain $D(A)=H^{3}(\mathbb {R})$
. According to Gearhart–Pruss– Huang criteria [Reference Huang11], we have
In particular, letting $\tau =0$
, this implies $\|A^{-1}\|_{L^{2}(\mathbb {R})\to L^{2}(\mathbb {R})}<\infty$
. In other words, there exists a constant $c>0$
so that
Now we are going to test (2.9) with a sequence of functions
Fix $\varepsilon >0$
. Clearly,
for some constant $c_0>0$
independent of $\varepsilon$
. Moreover, we compute
which implies that
This gives that for some constant $c_1>0$
independent of $\varepsilon$
It follows from (2.9)–(2.11) that
Choosing $\varepsilon =\varepsilon _0$
such that $c_1\varepsilon _0^{{3}/{2}}={cc_0}/{2}$
in (2.12), we find
for every $L>0$
. Note that for some $c_2>0$
we have
Choosing $L=L_0$
so that $c_2\|a\|_{L^{\infty }(\mathbb {R})}{\rm e}^{-({\varepsilon _0}/{2})L^{2}}\leq {cc_0}/{4}$
, we deduce from (2.13)–(2.14) that
Squaring both sides of (2.15) and using Cauchy–Schwarz inequality, we infer that
It follows from (2.16) that
with $\gamma = \left (\frac {cc_0}{4}\right )^{2}\frac {1}{\sqrt {\varepsilon _0} \|a\|_{L^{\infty }(\mathbb {R})}}>0$
.
Now for every $x_0\in \mathbb {R}$
, if we testing (2.9) with
then, similar to (2.17), we have
This shows that $(2)$
holds. Thus the proof is complete.
3. Exponential decay with small data
First we recall some estimates in Bourgain spaces. Let $s,\,b\in \mathbb {R}$
, the Bourgain spaces $X^{s,b}$
are defined by the norm
where $\widehat {u}(\xi,\,\tau )$
is the space–time Fourier transform of $u$
, given by
For an open interval $I$
on $\mathbb {R}$
, the restriction in time Bourgain spaces $X^{s,b}_{I}$
are endowed with the norm
Let $\{W(t)\}_{t\in \mathbb {R}}$
be the Airy group, given by
where $c$
is an absolute constant.
Lemma 3.1 Assume that $I=(0,\,\delta )$
with $0<\delta \leq 1$
and $s\geq 0$
.
(1) If $b>{1}/{2},$
then
(3.2)\begin{align} & \|W(t)u_0\|_{X^{s,b}_{I}}\lesssim_b \|u_0\|_{H^{s}(\mathbb{R})}, \end{align}(3.3)\begin{align} & \left\|\int_0^{t} W(t-\tau)f({\cdot},\tau){{\rm d}} \tau\right\|_{X^{s,b}_{I}}\lesssim_b \|f\|_{X^{s,b-1}_{I}}. \end{align}(2) If $-({1}/{2})< b\leq b'<1/2$
, then
(3.4)\begin{equation} \|u\|_{X^{s, b}_{(-\delta,\delta)}} \lesssim_{s,b,b'} \delta^{b'-b}\|u\|_{X^{s, b'}_{I}}. \end{equation}(3) If ${1}/{2}< b\leq b'\leq {3}/{4}$
, then
(3.5)\begin{equation} \|\partial_x(uv)\|_{X^{s,b'-1}_{I}}\lesssim_{s,b}\|u\|_{X^{s,b}_{I}}\|v\|_{X^{s,b}_{I}}. \end{equation}
Proof. See [Reference Wang and Huang30].
The item $(1)$
of lemma 3.1 can be understood as some estimates of the Airy group $W(t)$
in Bourgain spaces. Now we give some similar estimates of ${\rm e}^{-tA}$
, $A=\partial _x^{3}+a(x)$
, based on lemma 3.1.
Lemma 3.2 Assume that $a\in L^{\infty }(\mathbb {R}),$
$I=(0,\,\delta )$
and $b\in ({1}/{2},\,1]$
. Then for some small $\delta =\delta (b,\,\|a\|_{L^{\infty }})>0,$
we have
Proof. By Duhamel formula we have
Taking $X^{0,b}_{I}$
norm on both sides of (3.8), using $(1)$
of lemma 3.1, we find
where $C=C(b)>0$
. Since $b\leq 1$
, noting $X^{0,0}=L^{2}_{t,x}$
, we have
where in the last step we used $(2)$
of lemma 3.1, and $C'>0$
is a constant depending on $b$
and $\|a\|_{L^{\infty }}$
, but independent of $\delta$
. It follows from (3.9)–(3.10) that
If we take $\delta$
small such that $CC'\delta ^{b}\leq {1}/{2}$
, then the last term of (3.11) can be absorbed by the left hand side, we have
This proves (3.6) for such $\delta$
.
To prove (3.7), we apply the identity
with $f=\partial _x(uv)$
, similar to the above argument, we obtain
This proves (3.7) for $\delta$
small enough.
Lemma 3.2 holds for the interval $I$
with small length. Now we extend it to general intervals.
Lemma 3.3 Assume that (A1) holds and (A2) holds on a thick set $E$
. Let $T>0,$
$I=(0,\,T)$
and $b\in ({1}/{2},\,1]$
. Then there exists $C=C(b,\,\|a\|_{L^{\infty }})>0$
we have
Proof. In the case $T\leq \delta$
, (3.12) and (3.12) follows from (3.6) and (3.7), respectively. So we assume $T>\delta$
now. The proof then mainly relies on the following inequality: for all $s\geq 0,\, b\in ({1}/{2},\,1],\,\delta >0$
and $t_0\in \mathbb {R}$
,
See [Reference Wu32, lemma 6.2] for a proof.
To prove (3.12), choose an integer $k\geq 1$
so that $k\delta \geq T$
. Then $(0,\,T)\subset (0,\,k\delta )$
, using (3.14) repeatedly, we find
But by (3.6) again, we have
where in the last step we used theorem 2.1. This, together with (3.15), gives
with some $C>0$
depending on $\delta$
and $b$
. This proves (3.12).
To show (3.13), we choose $k$
so that $(k-1)\delta < T\leq k\delta$
. Then by (3.14) and (3.7),
This proves (3.13).
Now we can prove theorem 1.2.
Proof of theorem 1.2. By Duhamel principle, we can rewrite the KdV equation (1.1) into an integral form
Taking $L^{2}(\mathbb {R})$
norm on both sides of (3.16), using theorem 2.1 and the embedding $X^{0,b}_{(0,T)}\hookrightarrow L^{\infty }(0,\,T;L^{2}(\mathbb {R}))$
when $b>{1}/{2}$
, we find for all $T>0$
for some $C_0>{1}/{2}$
, where in the last step we used (3.13).
Now fix a large $T>0$
so that
Then (3.17) becomes
Moreover, taking $X^{0,b}_{(0,T)}$
norm on both sides of (3.16), using lemma 3.3, we obtain
Now consider the map $\Gamma$
on the ball
The estimate (3.20) shows that if $u\in \mathcal {B}$
then
Moreover, if $u,\,v\in \mathcal {B}$
, then
Thanks to (3.22)–(3.23), if $\|u_0\|_{L^{2}(\mathbb {R})}$
is small enough, say,
then $\Gamma \mathcal {B} \subset \mathcal {B}$
and $\|\Gamma u-\Gamma v\|_{X^{0,b}_{(0,T)}}\leq ({1}/{2})\|u-v\|_{X^{0,b}_{(0,T)}}$
, thus $\Gamma$
is a contraction mapping on $\mathcal {B}$
. So equation (3.16) has a unique solution $u\subset \mathcal {B}$
. This, together with the bound (3.19), gives that
Assume further that
so that $4C_2^{2}C_1(T+1)\|u_0\|^{2}_{L^{2}(\mathbb {R})}\leq ({1}/{2}){\rm e}^{-({\lambda }/{2}) T}\|u_0\|_{L^{2}(\mathbb {R})}$
, then (3.25) becomes
By induction, we find that for all $n\geq 1$
if $\|u_0\|_{L^{2}(\mathbb {R})}\leq \delta = \min \{\delta _1,\,\delta _2\}$
. Then by the semigroup property, we infer that
for some constants $C',\,\lambda '>0$
. This completes the proof of theorem 1.2.
4. Exponential decay for general data
4.1 A unique continuation
This subsection is devoted to the following unique continuation property (UCP) of the KdV equation, which is a key step to establish the exponential decay for general data.
Proposition 4.1 Let $T>0$
and $E$
be a set satisfying NCC. Assume that $u\in X^{0,({1}/{2})+}_{(0,T)}$
is a solution of the KdV equation
and $u(x,\,t)=0$
on $E\times (0,\,T)$
. Then
The proof of this result relies on the following unique continuation property, stated explicitly in [Reference Zhang33], that follows from the results in [Reference Saut and Scheurer25].
Lemma 4.2 Let $T>0$
. Assume that $u\in L^{\infty }(0,\,T;H^{3}(\mathbb {R}))$
is a solution of the KdV equation
and $u=0$
on an open subset of $\mathbb {R}\times (0,\,T)$
, then
Note that proposition 4.1 does not follow from lemma 4.2 directly, since the solution, $u\in X^{0,({1}/{2})+}_{(0,T)}$
, has not higher enough regularity. To overcome this difficulty, we need to first establish the propagation of regularity for the operator $\partial _t+\partial _x^{3}$
on $\mathbb {R}$
.
Lemma 4.3 Let $T>0,$
$r\geq 0$
and $f\in X^{r,-({1}/{2})}_{(0,T)}$
. Let $u\in X^{r,{1}/{2}}_{(0,T)}$
be a solution of
If $E\subset \mathbb {R}$
satisfies NCC and $u\in L^{2}_{loc}(0,\,T;H^{r+{1}/{2}}(E)),$
then $u\in L^{2}_{loc}(0,\,T; H^{r+{1}/{2}}(\mathbb {R}))$
.
Roughly speaking, lemma 4.3 means that the solution of the linear KdV equation has higher regularity on a set satisfying NCC, then the solution automatically has higher regularity on the whole space $\mathbb {R}$
. This result is inspired by the work of [Reference Laurent, Rosier and Zhang14], in which the propagation of regularity for the linear KdV equation on torus $\mathbb {T}$
is proved, when $E$
is an open subset of $\mathbb {T}$
. In [Reference Laurent, Rosier and Zhang14], the proof relies on a partition of unity
where $\chi$
is a smooth cutoff function supported on the open set $E$
, and the sum is taken over for finite terms. However, the set $E$
, satisfying NCC, may have complicated structure, so it is not clear whether the corresponding partition of unity exists or not. Even though, we shall use the following lemma instead, which is sufficient for our purpose.
Lemma 4.4 Assume that $E$
satisfy NCC. Then there exist constants $L_0>0,\,m_0\in \mathbb {N}$
and a smooth function $\chi \in C^{\infty }(\mathbb {R})$
such that the support $supp\, \chi \subset E,$
$|\partial _x^{k}\chi |\leq C_k$
for all $k\in \mathbb {N},$
and
Proof. By definition, for some constants $r,\,L>0$
we have
Without loss of generality, we assume that $L> 2r$
. Clearly, there exists $n_0\in \mathbb {Z}$
so that $|x_{n_0}|\leq L$
. Then
We set
Similarly, for every $j\in \mathbb {Z}$
, there exists an interval
Clearly, we have
Now let $\chi _0\in C_c^{\infty }(I_0)$
(the set of smooth functions with compact support) so that
Moreover, we define for every $j\in \mathbb {Z}$
and
Now we show that $\chi$
enjoys the desired property. First, ${\rm supp} \, \chi \subset E$
follows from (4.3) and (4.5)–(4.7). Moreover, for every $x\in \mathbb {R}$
, by (4.2), all terms in the sum of (4.7) vanish except at most one term, so
and at the same time we have
Since $\chi _0=1$
on a subinterval of $[-6L,\,6L]$
with length $r$
, then for some $\mathbb {N}\ni m_0\geq 6L/r$
we have
Similarly,
Let $L_0=r$
. It follows from (4.8)–(4.10) that
This completes the proof.
Proof of lemma 4.3. Fix $T>0$
. We assume, without loss of generality, that $0\leq r<1$
. Otherwise, we consider the equation
instead, where $k$
is a positive integer. We divide the proof into three steps.
Step 1. Let $\phi \in C_c^{\infty }(0,\,T)$
and $\varphi \in C^{\infty }(\mathbb {R})$
so that $|\partial _x^{k}\varphi |\leq C_k,\, \forall k\in \mathbb {N}$
. We claim that
Here and in the rest of the proof, $J^{s}$
is defined by the Fourier transform as $\widehat {J^{s}f}=(1+|\xi |)^{s}\widehat {f}(\xi )$
, $(\cdot,\,\cdot )$
denotes the inner product in $L^{2}(0,\,T;L^{2}(\mathbb {R}))$
.
In fact, let $\mathbb {L}=\partial _t+\partial _x^{3}$
and $\mathbb {A}=\phi (t)J^{2r-1}\varphi$
. Then using Parseval's identity, we have
where $\mathbb {A}^{*}=\varphi (x)J^{2r-1}\phi (t)$
is the dual operator of $\mathbb {A}$
, the commutator $[A,\,B]=AB-BA$
as usual. Since $\mathbb {L}u=f\in X^{r,-({1}/{2})}_{(0,T)}$
, we infer that
By (A.1) in the appendix, we also have $|(\phi '(t)J^{2r-1}\varphi u,\, u)|\leq C$
. So by (4.12),
A direct computation gives that
Similar to (A.1), we have
Thus, the claim (4.11) follows from (4.13).
Step 2. For any $\phi \in C_c^{\infty }(0,\,T)$
, $\chi \in C^{\infty }(\mathbb {R})$
with support ${\rm supp}\, \chi \subset E$
and $|\partial _x^{k} \chi |\leq C_k$
, we claim that
In fact, we rewrite
where
From assumption $u\in L_{loc}^{2}(0,\,T;H^{r+{1}/{2}}(E))$
, we infer $\chi \partial _x^{2}u\in L^{2}_{loc}(0,\,T; H^{r-({3}/{2})}(\mathbb {R}))$
, thus
Moreover, using the fact $u\in L^{2}(0,\,T;H^{r}(\mathbb {R}))$
and (A.2)–(A.3), one can show that $|I_2|\leq C$
. This proves the claim (4.14).
Step 3. Complete the proof. Let $\chi \in C^{\infty }$
be the cutoff function constructed in lemma 4.4. For every $x_0\in \mathbb {R}$
, define a function $\varphi$
by Fourier transform
By the Fourier inversion, this implies that
We apply (4.11) with $\partial _x\varphi$
given by (4.15), and use (4.14) to find that
Since $0\leq r<1$
we infer
Noting $J^{2}=1-\partial _x^{2}$
we get from (4.16) that
We rewrite
and use the bound $|(\phi (t)J^{r+{1}/{2}}u,\,[J^{r-({3}/{2})},\,\chi ^{2}(\cdot +x_0)]J^{2}u)|\leq C\|u\|^{2}_{L^{2}_{loc}(0,\,T;H^{r}(\mathbb {R}))}\leq C$
(follows from (A.4)), we deduce from (4.17) that
Applying (4.18) with $x_0=\{lL_0\}_{l=-m_0}^{m_0}$
, noting (4.1), we conclude that
This shows that $u\in L^{2}_{loc}(0,\,T;H^{r+{1}/{2}}(\mathbb {R}))$
, and completes the proof.
Remark 4.5 Very recently, Panthee and Vielma Leal have established in [Reference Panthee and Vielma Leal19] the propagation of regularity in Bourgain's spaces for the Benjamin equation on a periodic domain.
Corollary 4.6 Let $T>0$
and $u\in X^{0,({1}/{2})+}_{(0,T)}$
be a solution of the KdV equation
If $E$
satisfies NCC and $u(x,\,t)=0$
for $(x,\,t)\in E\times (0,\,T),$
then $u\in L^{2}_{loc}(0,\,T;H^{\infty }(\mathbb {R}))$
.
Remark 4.7 Here and below $X^{0,({1}/{2})+}=X^{0,({1}/{2})+\varepsilon }$
with an arbitrarily small ${\varepsilon >0}$
.
Proof. Rewrite the KdV equation as
with $f=-u\partial _xu$
. Since $u\in X^{0,({1}/{2})+}_{(0,T)}$
, by the bilinear estimate (3.5),
Since $u(x,\,t)=0$
for $(x,\,t)\in E\times (0,\,T)$
, we have of course $u\in L^{2}_{loc}(0,\,T;H^{\infty }(E))$
. By lemma 4.3, we obtain
Let $t_0\in (0,\,T)$
so that $u(t_0)\in H^{{1}/{2}}(\mathbb {R})$
. Then we find the solution $u$
of (4.19) satisfies
Similarly, using lemma 4.3 repeatedly, we conclude that $u\in L^{2}_{loc}(0,\,T;H^{\infty }(\mathbb {R}))$
.
Proof of proposition 4.1. According to corollary 4.6, we know that $u\in L^{2}_{loc}(0,\,T; H^{\infty }(\mathbb {R}))$
. Since $u(x,\,t)=0$
for $(x,\,t)\in E\times (0,\,T)$
and $E$
contains an open set in $\mathbb {R}$
, so $u=0$
on an open set in $\mathbb {R}\times (0,\,T)$
, then by the UCP in lemma 4.2, we conclude that $u \equiv 0$
.
4.2 Proof of theorem 1.4
Let $W(t)={\rm e}^{-t\partial _x^{3}}$
be the Airy group. Then we have the sharp Kato smoothing effect [Reference Kenig, Ponce and Vega12, theorem 4.1]
The estimate (4.20) can be reformulated in Bourgain space as (see [Reference Kenig, Ponce and Vega13, p. 5])
The bound (4.21) will be used to derive the compactness of some sequences later.
Proposition 4.8 Assume that $0\leq a(x)\in L^{\infty }(\mathbb {R})$
. Then the IVP (1.1) has a unique global solution $u\in C([0,\,\infty );L^{2}(\mathbb {R}))$
. Moreover, for every $T>0$
Proof. Thanks to lemma 3.1, using the contraction principle one can show that there exists a unique solution $u\in X^{0,({1}/{2})+}_{(0,\delta )}$
of (1.1) with the bound
where the life span
is small enough. Multiplying (1.1) by $u$
and integrating over $\mathbb {R}$
we obtain
which, together with the fact $a(x)\geq 0$
, implies that
Thus we can take $u(\delta )$
as a new data, to find a solution on $(\delta,\,2\delta )$
so that $\|u\|_{X^{0,({1}/{2})+}_{(\delta,2\delta )}}\leq 2\|u_0\|_{L^{2}(\mathbb {R})}$
. Repeat this process, we find that for every $T>0$
This completes the proof.
Corollary 4.9 Assume that $0\leq a(x)\in L^{\infty }(\mathbb {R})$
. Let $u$
be the solution of (1.1) obtained in proposition 4.8. Then for every $T>0$
and for every measurable set $\Omega \subset \mathbb {R}$
where $|\Omega |$
denotes the Lebesgue measure of $\Omega$
.
Proof. Fix $T>0$
. Combining (4.21) and proposition 4.8 we obtain
From this, we use Hölder inequality to find
Then we conclude (4.23) by Fubini theorem.
Now we prove an observability inequality, which means that we can recover the solution of the KdV equation if we observe the solution on $E\times (0,\,T)$
when $E$
satisfies NCC and $E^{c}$
has a finite Lebesgue measure.
Lemma 4.10 Let $R,\,T>0$
and let $E$
satisfy NCC, $|E^{c}|<\infty$
. Assume that (A1) and (A2) hold. Then there exist a constant $C=C(R,\,T,\,a)>0$
such that for all $\|u_0\|_{L^{2}(\mathbb {R})}\leq R,$
the solution $u$
of the IVP (1.1) satisfies
Proof. Following [Reference Cavalcanti, Cavalcanti, Faminskii and Natali4], we argue by contradiction. Assume that there exists a sequence solutions $u_k$
of the KdV equation (1.1), with initial data $\|u_{0k}\|_{L^{2}(\mathbb {R})}\leq R$
, such that
Define
Then
and $v_k$
is a solution of
with initial data
It follows from (4.25)–(4.26) that
This, since $a(x)\geq a_0>0$
for all $x\in E$
, gives that
Moreover, multiplying (4.28) with $v_k$
and integrating over $\mathbb {R}\times (0,\,t)$
and changing the order of integration, we obtain
Integrating (4.31) with respect to $t$
over $[0,\,T]$
, we obtain
This, together with (4.27) and (4.29), shows that
Furthermore, it follows from the bound (4.22) that
This, together with (4.26), gives that
since $\|u_{0k}\|_{L^{2}(\mathbb {R})}\leq R$
for all $k$
. Thanks to (4.32) and (4.33), by the well posedness of (4.28), we have
By our assumption, the complement set $E^{c}$
has finite Lebesgue measure, ${|E^{c}|<\infty}$
. Thanks to (4.32) and (4.33), we can apply corollary 4.9 to obtain that
Combining (4.27) and (4.35) we find that $v_k$
is uniformly bounded in $L^{2}(0,\,T;H^{1}(E^{c}))$
. Also, using equation (4.28), we get that $(v_k)_t$
is uniformly bounded in $L^{2}(0,\,T;H^{-2}(E^{c}))$
. Since $|E^{c}|<\infty$
, it is easy to see that
then according to [Reference Berger and Martin1, theorem 2.8], the embedding $H^{1}(E^{c})\hookrightarrow L^{2}(E^{c})$
is compact. Thus, by Aubin–Lions theorem, there exists a subsequence, still denoted by $v_k$
, so that $v_k\to v$
in $L^{2}((0,\,T)\times E^{c})$
. On the other hand, it follows from (4.30) that $v_k\to 0$
in $L^{2}((0,\,T)\times E)$
. These show that
with $\|v\|_{X^{0,({1}/{2})+}_{(0,T)}}\leq C$
(by (4.34)) and
We assume that $\alpha _k\to \alpha \geq 0$
. Let $\phi (x,\,t)$
be a function such that $\phi \in C([0,\,T]; H^{3}(\mathbb {R}))$
, $\phi _t\in C([0,\,T];L^{2}(\mathbb {R}))$
with $\phi |_{t=0}=\phi |_{t=T}=0$
. Testing (4.28) with $\phi$
we get
Now, taking the limit as $k\rightarrow \infty$
in (4.38), and applying (4.36)–(4.37) we arrive at
where we used the fact that $\int _0^{T}\int _\mathbb {R} a(x)v_k(x,\,t)\phi (x,\,t){{\rm d}}x {{\rm d}}t\to 0$
as $k\to \infty$
, which follows from (4.29) and the inequality
The identity (4.39) means that $v(x,\,t)\in X^{0,({1}/{2})+}_{(0,T)}$
is a weak solution of
Moreover, by (4.37) we have $v|_{E\times (0,T)}=0$
.
If $\alpha =0$
, then equation (4.40) becomes $\partial _tv+\partial ^{3}_xv=0$
. Since $v=0$
on an open set in $(x,\,t)\in \mathbb {R}\times (0,\,T)$
, according to [Reference Zhang33, corollary 3.1], we have $v\equiv 0$
.
If $\alpha >0$
, set $V(x,\,t)=v(cx,\,c^{3}t)$
with $c=\alpha ^{-({1}/{2})}$
, then $V\in X^{0,({1}/{2})+}_{(0,c^{-3}T)}$
is a solution of
Moreover, we have $V|_{c^{-1}E\times (0,\,c^{-3}T)}=0$
, where $c^{-1}E=\{c^{-1}x: x\in E\}$
. It is easy to see that $c^{-1}E$
also satisfies NCC. Then by the unique continuation property in proposition 4.1 for the KdV equation, we get $V \equiv 0$
and thus $v \equiv 0$
.
In both cases, we arrive at the conclusion $v \equiv 0$
. However, this contradicts to (4.27). Therefore, (4.24) holds.
Proof of theorem 1.4. Let $T>0$
and $\|u_0\|_{L^{2}(\mathbb {R})}\leq R$
. Multiplying (1.1) by $u$
and integrating over $\mathbb {R}\times (0,\,T)$
, we get
Since $E$
satisfies NCC, it follows from lemma 4.10 that
where $c>0$
is a constant depending only on $T,\,R$
and the damping coefficient $a(x)$
. Moreover, since $a(x)\geq 0$
, we have $\|u(\cdot,\,t)\|_{L^{2}(\mathbb {R})}\leq \|u(\cdot,\,t')\|_{L^{2}(\mathbb {R})}$
for all $t\geq t'$
, which implies that
Combining (4.41)–(4.43), we infer that
with $\alpha ={1}/{(1+2cT)}\in (0,\,1)$
. By iteration we have for all $n\geq 1$
This gives the exponential decay clearly.
Acknowledgements
We owe our sincere thanks to the referees for their careful reading and insightful comments which have deeply improved the presentation of this work. Wang is supported by the National Natural Science Foundation of China under grant No. 12171442, and the Fundamental Research Funds for the Central Universities, China University of Geosciences (Wuhan) under grant No. CUGSX01. Zhou is supported by the National Natural Science Foundation of China under grant No. 11901067, the Natural Science Foundation of Chongqing under grant No. cstc2020jcyj-msxmX0623, and the Fundamental Research Funds for the Central Universities under grant No. 2021CDJQY-009.
Appendix A. Appendix
In this section, we prove some technical estimates used in lemma 4.3.
Let $b(x,\,\xi )$
be a smooth function on $\mathbb {R}^{2}$
. Define the pseudo-differential operator
where $D={{\rm i}}^{-1}\partial _x$
, $\widehat {f}$
denotes the Fourier transform of $f$
, $\mathscr {S}(\mathbb {R})$
the Schwartz class. The function $b(x,\,\xi )$
is called the symbol of the operator $b(x,\,D)$
. In particular, letting $b(x,\,\xi )=(1+|\xi |^{2})^{s/2}$
, $s\in \mathbb {R}$
, we recover the definition of the fractional Laplacian $J^{s}=(1-\partial _x^{2})^{s/2}$
. The Sobolev space $H^{s}(\mathbb {R})$
is an Hilbert space endowed with the norm
Let $m\in \mathbb {R}$
. We say a smooth function $b(x,\,\xi )$
belongs to $S^{m}$
if for all $\alpha,\,\beta \in \mathbb {N}$
An important result on the class $S^{m}$
is given in the following lemma, see [Reference Taylor27, proposition 5.5, p. 20].
Lemma A.1 Let $m,\,s\in \mathbb {R}$
and $b\in S^{m}$
. Then $b(x,\,D)$
is bounded from $H^{s}(\mathbb {R})$
to $H^{s-m}(\mathbb {R})$
.
We say $\varphi \in C^{\infty }_b$
if for all $\alpha \in \mathbb {N}$
Lemma A.2 Let $m\in \mathbb {R}$
and $\varphi \in C^{\infty }_b$
. Then
Proof. It is equivalent to show that
Note that the symbol of $\varphi J^{-m}$
is $b(x,\,\xi )=\varphi (x)(1+|\xi |^{2})^{-m/2}$
, and it is easy to see that $b(x,\,\xi )\in S^{-m}$
, then the desired bound follows from lemma A.1.
Lemma A.3 Let $m,\,s\in \mathbb {R}$
and $\varphi \in C^{\infty }_b$
. Then
Proof. By the definition of commutator, we have
where $b_1(x,\,\xi )=\varphi (x)(1+|\xi |^{2})^{-m/2}$
and $b_2(x,\,\xi )$
is the symbol of $J^{m}(\varphi \cdot )$
. According to the calculus of pseudo-differential operators, see e.g. [Reference Stein26, theorem 2, p. 237],
with $c(x,\,\xi )\in S^{-m-1}$
. Thus the symbol of $[\varphi,\,J^{m}]$
, equals to $c(x,\,\xi )$
, belongs to $S^{-m-1}$
. Then the lemma follows from lemma A.1.
Now we prove the results used in the proof of lemma 4.3.
Lemma A.4 Let $r\geq 0$
and $\varphi,\,\chi \in C_b^{\infty }$
. Then the following bounds hold:
Proof. By Cauchy–Schwarz inequality and lemma A.1, we have
This proves (A.1). Since
we also have $\|\chi \partial _x^{2}u\|_{H^{r-2}(\mathbb {R})}\leq C\|u\|_{H^{r}(\mathbb {R})}$
by lemma A.1, and $\|[\chi,\,J^{r+{1}/{2}}]u\|_{H^{{1}/{2}}(\mathbb {R})} \leq C\|u\|_{H^{r}(\mathbb {R})}$
by lemma A.2. Thus (A.2) holds.
Finally, we provide a multiplication property of Bourgain space $X^{s,b}$
.
Lemma A.5 Let $-1\leq b\leq 1,$
$s\in \mathbb {R}$
and $\varphi \in C_b^{\infty }$
. Then for all $u\in X^{s,b}$
Similarly, for every $T>0$
, we have $\|\varphi (x) u\|_{X_{(0,T)}^{s-2|b|,b}}\lesssim \|u\|_{X_{(0,T)}^{s,b}}.$
Proof. The proof is the same as that in [Reference Laurent, Rosier and Zhang14, lemma 3.4], we only give a sketch here. By duality and interpolation arguments, it suffices to consider the cases $b=0$
and $b=1$
.
In the case $b=0$
, (A.5) follows from lemma A.2 clearly.
In the case $b=1$
, we first observe that
where $\Upsilon =\|\varphi u\|_{X^{s-2,0}}+\|3\partial _x\varphi \partial _x^{2}u+3\partial _x^{2}\varphi \partial _xu+\partial _x^{3}\varphi u\|_{X^{s-2,0}}$
. Using lemma A.2 again, we deduce from (A.6) that
Thus (A.5) also holds.
Remark A.6 If $\phi \in C_c^{\infty }(\mathbb {R})$
, then $\phi (t)$
maps $X^{s,b}$
into $X^{s,b}$
, see [Reference Tao28, lemma 2.11, p. 101]. In other words, the Bourgain space is stable with the multiplication by a compact supported smooth function of time $t$
. However, as lemma A.5 indicates, some regularity index is lost with the multiplication by a smooth function of spatial variable $x$
. The loss is unavoidable, see the example in [Reference Laurent, Rosier and Zhang14, lemma 3.4]. Anyway, the lemma is sufficient for our purpose in this paper.
