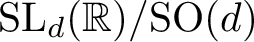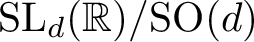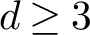1 Introduction
Let Y be a closed Riemann manifold, and let
![]() $\mathscr {B}=\{\psi _i\}$
be an orthonormal basis of
$\mathscr {B}=\{\psi _i\}$
be an orthonormal basis of
![]() $L^2(Y)$
consisting of Laplacian eigenfunctions
$L^2(Y)$
consisting of Laplacian eigenfunctions
![]() $\Delta \psi _i=\lambda _i\psi _i$
. A subsequence
$\Delta \psi _i=\lambda _i\psi _i$
. A subsequence
 $\left \{\psi _{i_j}\right \}$
of
$\left \{\psi _{i_j}\right \}$
of
![]() $\mathscr {B}$
is called quantum ergodic if, for every degree 0 pseudo-differential operator A on Y with principal symbol
$\mathscr {B}$
is called quantum ergodic if, for every degree 0 pseudo-differential operator A on Y with principal symbol
![]() $a\in C(S^*Y)$
, we have
$a\in C(S^*Y)$
, we have

Here
![]() $\mu _L$
is the Liouville measure on the cosphere bundle
$\mu _L$
is the Liouville measure on the cosphere bundle
![]() $S^*Y$
and
$S^*Y$
and
indicates normalization by the volume. The quantum ergodicity theorem of Šnirelman [Reference Silberman and Venkatesh32], Zelditch [Reference Zelditch35], and Colin de Verdière [Reference Colin de Verdière10] states that if the geodesic flow on
![]() $S^*Y$
is ergodic, one may extract from
$S^*Y$
is ergodic, one may extract from
![]() $\mathscr {B}$
a density
$\mathscr {B}$
a density
![]() $1$
quantum ergodic subsequence. More precisely, they show
$1$
quantum ergodic subsequence. More precisely, they show

as
![]() $\lambda \rightarrow \infty $
, where
$\lambda \rightarrow \infty $
, where
![]() $N(\lambda )=\lvert \{i: \lambda _i\leq \lambda \}\rvert $
.
$N(\lambda )=\lvert \{i: \lambda _i\leq \lambda \}\rvert $
.
In this paper we are concerned with a version of quantum ergodicity where, in contrast to the foregoing semiclassical statement, in which the manifold is fixed and the eigenvalue goes to infinity (the large-frequency regime), we allow the manifold to vary while keeping the eigenvalue constrained to a fixed spectral window (the large-spacial regime).
The most natural setting in which one can formulate such variation is in the Gromov–Hausdorff space of pointed locally compact spaces – or, rather, its space of probability measures – where one has a notion of convergence due to Benjamini and Schramm [Reference Benjamini and Schramm5]. Here one may consider a sequence of manifolds which converge, almost everywhere, to their common universal cover. Under certain auxiliary conditions, the question of quantum ergodicity for Benjamini–Schramm convergent sequences was recently settled for a large class of rank
![]() $1$
symmetric spaces [Reference Abert, Bergeron and Le Masson2, Reference Le Masson and Sahlsten24]. The aim of the present paper is to address this question for higher-rank locally symmetric spaces; for the most part we restrict ourselves to compact quotients associated with
$1$
symmetric spaces [Reference Abert, Bergeron and Le Masson2, Reference Le Masson and Sahlsten24]. The aim of the present paper is to address this question for higher-rank locally symmetric spaces; for the most part we restrict ourselves to compact quotients associated with
![]() $\operatorname {SL}_d({\mathbb R})$
.
$\operatorname {SL}_d({\mathbb R})$
.
1.1 The setting of locally symmetric spaces
As our setting will henceforth be that of locally symmetric spaces, we begin by commenting on some of their particular features in higher rank, and reviewing what is known for their quantum ergodic properties in the large-frequency regime.
We let S be a Riemannian globally symmetric space of noncompact type: nonpositively curved and having no Euclidean de Rham local factor. We may write
![]() $S=G/K$
, where G is a connected semisimple Lie group with finite center and K is a maximal compact subgroup. The rank of S is defined to be the dimension of a maximal flat subspace in S; equivalently, it is the dimension of a maximal split torus A in G.
$S=G/K$
, where G is a connected semisimple Lie group with finite center and K is a maximal compact subgroup. The rank of S is defined to be the dimension of a maximal flat subspace in S; equivalently, it is the dimension of a maximal split torus A in G.
In rank
![]() $1$
, S is of strictly negative curvature, and A gives rise to the geodesic flow on the cosphere bundle of S via the identification of the latter with
$1$
, S is of strictly negative curvature, and A gives rise to the geodesic flow on the cosphere bundle of S via the identification of the latter with
![]() $G/M$
, where M is the centralizer of A in K. It is important to note, however, that when the rank is strictly greater than
$G/M$
, where M is the centralizer of A in K. It is important to note, however, that when the rank is strictly greater than
![]() $1$
, such as for
$1$
, such as for
![]() $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
when
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
when
![]() $d\geq 3$
, the curvature of S, while nonpositive, can vanish, as indeed any geodesic triangle in a maximal flat will be Euclidean.
$d\geq 3$
, the curvature of S, while nonpositive, can vanish, as indeed any geodesic triangle in a maximal flat will be Euclidean.
Now let
![]() $\Gamma \subset G$
be a uniform lattice in G and form
$\Gamma \subset G$
be a uniform lattice in G and form
![]() $Y=\Gamma \backslash S$
, a compact locally symmetric space with geometry S. In higher rank, due to the presence of maximal flats, the geodesic flow is not ergodic on the cosphere bundle of Y. For this reason, the quantum ergodic statement (1) cannot hold, as it is known to be equivalent with the ergodicity of the geodesic flow [Reference Zelditch36, Theorem 1].
$Y=\Gamma \backslash S$
, a compact locally symmetric space with geometry S. In higher rank, due to the presence of maximal flats, the geodesic flow is not ergodic on the cosphere bundle of Y. For this reason, the quantum ergodic statement (1) cannot hold, as it is known to be equivalent with the ergodicity of the geodesic flow [Reference Zelditch36, Theorem 1].
Nevertheless, the higher-rank split torus A does act ergodically – in fact it is mixing – on
![]() $\Gamma \backslash G$
, and this is enough for one to expect similar quantum ergodic phenomena to that of Šnirelman’s theorem, at least if one refines the notion of eigenfunction as follows.
$\Gamma \backslash G$
, and this is enough for one to expect similar quantum ergodic phenomena to that of Šnirelman’s theorem, at least if one refines the notion of eigenfunction as follows.
Recall that a Maass form on Y is a function
![]() $\psi \in L^2(Y)$
which is a joint eigenfunction of the algebra
$\psi \in L^2(Y)$
which is a joint eigenfunction of the algebra
![]() $\mathscr {D}(S)$
of left-G-invariant differential operators on S. Since
$\mathscr {D}(S)$
of left-G-invariant differential operators on S. Since
![]() $\Delta \in \mathscr {D}(S)$
a Maass form is again a Laplacian eigenfunction, but in higher rank,
$\Delta \in \mathscr {D}(S)$
a Maass form is again a Laplacian eigenfunction, but in higher rank,
![]() $L^2(Y)$
can be further diagonalized. A Maass form
$L^2(Y)$
can be further diagonalized. A Maass form
![]() $\psi $
gives rise to an algebra homomorphism
$\psi $
gives rise to an algebra homomorphism
![]() $\chi \in \operatorname {Hom}_{{\mathbb C}-{\textrm {alg}}}(\mathscr {D}(S),{\mathbb C})$
verifying
$\chi \in \operatorname {Hom}_{{\mathbb C}-{\textrm {alg}}}(\mathscr {D}(S),{\mathbb C})$
verifying
![]() $D\psi =\chi (D)\psi $
for all
$D\psi =\chi (D)\psi $
for all
![]() $D\in \mathscr {D}(S)$
. The Harish-Chandra homomorphism allows one to realize
$D\in \mathscr {D}(S)$
. The Harish-Chandra homomorphism allows one to realize
![]() $\chi $
as the Weyl group orbit of an element
$\chi $
as the Weyl group orbit of an element
![]() $\nu $
in
$\nu $
in
![]() $\mathfrak {a}^*_{\mathbb C}$
, the complexification of the dual of the Lie algebra
$\mathfrak {a}^*_{\mathbb C}$
, the complexification of the dual of the Lie algebra
![]() $\mathfrak {a}$
of A. We call
$\mathfrak {a}$
of A. We call
![]() $\nu $
the spectral parameter of
$\nu $
the spectral parameter of
![]() $\psi $
.
$\psi $
.
One can then formulate a natural extension of formula (1) for Maass forms on Y with growing spectral parameter. To the best of our knowledge, this form of quantum ergodicity has not yet been established, although recent work by Nelson and Venkatesh [Reference Nelson and Venkatesh28] on microlocal analysis and representation theory should shed light on this problem.
Remark 1.1. There are of course harder conjectures that one can formulate here, such as quantum unique ergodicity [Reference Lindenstrauss25, Conjecture 1.2]. In the arithmetic setting, certain higher-rank congruence manifolds have been shown to satisfy the arithmetic quantum unique ergodicity property [Reference Shem–Tov30, Reference Šnirelman31], a generalization of the work (and techniques) of Lindenstrauss [Reference Lindenstrauss26] (see also [Reference Silberman and Venkatesh33]). We will not make further comments on this active line of research, and refer the reader instead to [Reference Le Masson and Sahlsten24, §1.3] for a discussion of a conjectural strengthening of quantum ergodicity for varying manifolds.
1.2 Our main result
We now pass to the large-spacial regime for higher-rank locally symmetric spaces
![]() $Y=\Gamma \backslash S$
, and allow
$Y=\Gamma \backslash S$
, and allow
![]() $\Gamma $
to vary along a nonconjugate sequence of torsion-free uniform lattices with growing covolume.
$\Gamma $
to vary along a nonconjugate sequence of torsion-free uniform lattices with growing covolume.
We furthermore require that the sequence
![]() $\Gamma $
be uniformly discrete, a property which we now recall. Let d be the Riemannian distance on S. Then the local injectivity radius about a point
$\Gamma $
be uniformly discrete, a property which we now recall. Let d be the Riemannian distance on S. Then the local injectivity radius about a point
![]() $x\in Y$
is the quantity
$x\in Y$
is the quantity
 $$ \begin{align*} \operatorname{InjRad}_\Gamma(x)=\frac12\min\{ d(x,\gamma.x): 1\neq \gamma\in \Gamma\}. \end{align*} $$
$$ \begin{align*} \operatorname{InjRad}_\Gamma(x)=\frac12\min\{ d(x,\gamma.x): 1\neq \gamma\in \Gamma\}. \end{align*} $$
The global injectivity radius
![]() $\operatorname {InjRad}(Y)$
is the infimum of
$\operatorname {InjRad}(Y)$
is the infimum of
![]() $\operatorname {InjRad}_\Gamma (x)$
over all
$\operatorname {InjRad}_\Gamma (x)$
over all
![]() $x\in Y$
; this is strictly positive, since Y is compact. We say that that a sequence of uniform torsion-free lattices
$x\in Y$
; this is strictly positive, since Y is compact. We say that that a sequence of uniform torsion-free lattices
![]() $\Gamma _n$
is uniformly discrete if
$\Gamma _n$
is uniformly discrete if
![]() $\operatorname {InjRad}(Y_n)$
is bounded away from zero. A conjecture of Margulis [Reference Margulis27] states that this is automatic in higher rank; this is a weak form of the Lehmer conjecture on monic integral polynomials.
$\operatorname {InjRad}(Y_n)$
is bounded away from zero. A conjecture of Margulis [Reference Margulis27] states that this is automatic in higher rank; this is a weak form of the Lehmer conjecture on monic integral polynomials.
Our precise result is as follows. We refer to §3.1 for any unexplained notation.
Theorem 1.1. Set
![]() $d\geq 3$
. Let
$d\geq 3$
. Let
![]() $\Gamma _n\subset \operatorname {SL}_d({\mathbb R})$
be a uniformly discrete sequence of torsion-free cocompact lattices such that
$\Gamma _n\subset \operatorname {SL}_d({\mathbb R})$
be a uniformly discrete sequence of torsion-free cocompact lattices such that
![]() $\operatorname {vol}(Y_n)\rightarrow \infty $
as
$\operatorname {vol}(Y_n)\rightarrow \infty $
as
![]() $n\rightarrow \infty $
, where
$n\rightarrow \infty $
, where
![]() $Y_n=\Gamma _n\backslash \operatorname {SL}_d({\mathbb R})/{\mathrm{SO}}(d)$
. Let
$Y_n=\Gamma _n\backslash \operatorname {SL}_d({\mathbb R})/{\mathrm{SO}}(d)$
. Let
![]() $a_n$
be a sequence of uniformly bounded, measurable functions on
$a_n$
be a sequence of uniformly bounded, measurable functions on
![]() $Y_n$
.
$Y_n$
.
There is
![]() $\varrho>1$
such that for sufficiently regular
$\varrho>1$
such that for sufficiently regular
![]() $\nu \in i\mathfrak {a}^*$
, we have
$\nu \in i\mathfrak {a}^*$
, we have

as
![]() $n\rightarrow \infty $
, where
$n\rightarrow \infty $
, where
denotes the normalization of the integral by the volume of
![]() $Y_n$
,
$Y_n$
,
is the ball of radius
![]() $\varrho $
in the unramified tempered spectrum, and
$\varrho $
in the unramified tempered spectrum, and
 $$ \begin{align} N(B_0(\nu,\varrho),\Gamma_n)=\left\lvert\left\{j: \nu_j^{(n)}\in B_0(\nu,\varrho)\right\}\right\rvert. \end{align} $$
$$ \begin{align} N(B_0(\nu,\varrho),\Gamma_n)=\left\lvert\left\{j: \nu_j^{(n)}\in B_0(\nu,\varrho)\right\}\right\rvert. \end{align} $$
This extends to higher rank the rank
![]() $1$
version of the same result in [Reference Le Masson and Sahlsten24] (for hyperbolic surfaces) and [Reference Abert, Bergeron and Le Masson2] (for higher-dimensional hyperbolic manifolds), which themselves built upon the breakthrough results of Anantharaman and Le Masson [Reference Arantharaman and Le Masson3] for large regular graphs. All of these works imposed the following additional hypotheses:
$1$
version of the same result in [Reference Le Masson and Sahlsten24] (for hyperbolic surfaces) and [Reference Abert, Bergeron and Le Masson2] (for higher-dimensional hyperbolic manifolds), which themselves built upon the breakthrough results of Anantharaman and Le Masson [Reference Arantharaman and Le Masson3] for large regular graphs. All of these works imposed the following additional hypotheses:
-
(i) The manifolds (or graphs)
 $Y_n$
converge to S in the sense of Benjamini and Schramm: for every
$Y_n$
converge to S in the sense of Benjamini and Schramm: for every
 $R>0$
, we have as
$R>0$
, we have as $$ \begin{align*} \frac{\operatorname{vol}\left((Y_n)_{\leq R}\right)}{\operatorname{vol}(Y_n)}\rightarrow 0 \end{align*} $$
$$ \begin{align*} \frac{\operatorname{vol}\left((Y_n)_{\leq R}\right)}{\operatorname{vol}(Y_n)}\rightarrow 0 \end{align*} $$
 $n\rightarrow \infty $
, where the R-thin part of
$n\rightarrow \infty $
, where the R-thin part of
 $Y_n$
is defined as (3)
$Y_n$
is defined as (3) $$ \begin{align} (Y_n)_{\leq R}=\left\{x\in Y_n: \operatorname{InjRad}_{\Gamma_n}(x)\leq R\right\}. \end{align} $$
$$ \begin{align} (Y_n)_{\leq R}=\left\{x\in Y_n: \operatorname{InjRad}_{\Gamma_n}(x)\leq R\right\}. \end{align} $$
-
(ii) The
 $Y_n$
have a uniform spectral gap.
$Y_n$
have a uniform spectral gap.
The proof of Theorem 1.1 also requires those properties, but they are automatic in higher rank (see [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, §4] and [Reference Kazhdan20]).
We note that in [Reference Abert, Bergeron and Le Masson2] the large-frequency regime for Laplacian eigenfunctions was interpreted as the Benjamini–Schramm convergence to Euclidean space via a rescaling of the Riemannian metric.
Remark 1.2. We point out two differences between the quantum ergodicity theorem of [Reference Abert, Bergeron and Le Masson2] for rank
![]() $1$
spaces and the higher-rank version we present in Theorem 1.1. In contrast to our result, the authors of [Reference Abert, Bergeron and Le Masson2] allow for two more general features:
$1$
spaces and the higher-rank version we present in Theorem 1.1. In contrast to our result, the authors of [Reference Abert, Bergeron and Le Masson2] allow for two more general features:
-
(a) They allow the spectral window to shrink with n, thereby isolating in the large-n limit a fixed tempered eigenvalue for the universal cover. This added flexibility was also present in [Reference Arantharaman and Le Masson3, Theorem 1.3].
-
(b) They take more general operators than scalar multiplication by functions
 $a_n$
. This more advanced formulation was first put forward in [Reference Arantharaman and Le Masson3, Theorem 1.7], using the pseudo-differential calculus for trees developed in [Reference Le Masson23].
$a_n$
. This more advanced formulation was first put forward in [Reference Arantharaman and Le Masson3, Theorem 1.7], using the pseudo-differential calculus for trees developed in [Reference Le Masson23].
Our Theorem 1.1 therefore more closely resembles the main results of [Reference Brooks, Le Masson and Lindenstrauss8, Reference Le Masson and Sahlsten24], in which neither of these two features is present. By taking more elaborate test functions, we believe we can incorporate (a) into our setup. By contrast, we have so far been unable to extend (b) to this higher-rank setting.
1.3 Comments on the proof
To prove the theorem we first reduce the assertion to several intermediate statements, as explained in §2. This reduction roughly follows along the lines of [Reference Le Masson and Sahlsten24] and the subsequent [Reference Abert, Bergeron and Le Masson2]. To establish these intermediate results, however, we need several new ideas to deal with a number of issues that arise only in rank
![]() $2$
or higher:
$2$
or higher:
-
• The first main reduction step involves the use of a normalized averaging operator on
 $S=G/K$
(a kind of wave propagation) with expanding support
$S=G/K$
(a kind of wave propagation) with expanding support
 $C_t$
,
$C_t$
,
 $t\rightarrow \infty $
. At a later critical point we need to estimate from above the volume of intersections
$t\rightarrow \infty $
. At a later critical point we need to estimate from above the volume of intersections
 $C_t\cap g C_t$
with
$C_t\cap g C_t$
with
 $g\in G$
. In [Reference Abert, Bergeron and Le Masson2, Reference Le Masson and Sahlsten24] they work with
$g\in G$
. In [Reference Abert, Bergeron and Le Masson2, Reference Le Masson and Sahlsten24] they work with
 $C_t$
being the metric ball
$C_t$
being the metric ball
 $B_t$
in S of radius t, and exploit the fact that S is a
$B_t$
in S of radius t, and exploit the fact that S is a
 $\text {CAT}(-1)$
space in rank
$\text {CAT}(-1)$
space in rank
 $1$
. In higher rank, S is only a
$1$
. In higher rank, S is only a
 $\text {CAT}(0)$
space, and working with intersection of metric balls becomes problematic. We therefore need to define new types of
$\text {CAT}(0)$
space, and working with intersection of metric balls becomes problematic. We therefore need to define new types of
 $C_t$
that look more ‘polytopal’ and are easier to work with in higher rank (see equation (15) and §5.5).
$C_t$
that look more ‘polytopal’ and are easier to work with in higher rank (see equation (15) and §5.5). -
• We need to establish a suitable lower bound for certain averages of spherical functions. In rank
 $1$
, this can be dealt with in a relatively straightforward manner, as the elementary spherical functions are basically linear combinations of trigonometric functions in one variable. In higher rank, we need to deal with linear combinations of exponential functions in several variables, which makes the analysis much more delicate (see §4). The techniques of §4 might also be of interest in other contexts.
$1$
, this can be dealt with in a relatively straightforward manner, as the elementary spherical functions are basically linear combinations of trigonometric functions in one variable. In higher rank, we need to deal with linear combinations of exponential functions in several variables, which makes the analysis much more delicate (see §4). The techniques of §4 might also be of interest in other contexts.
Additionally, we need to establish a type of local Weyl law/limit multiplicity for the
![]() $Y_n$
that gives a lower count for the number of eigenvalues locally around sufficiently regular points in the spectrum of
$Y_n$
that gives a lower count for the number of eigenvalues locally around sufficiently regular points in the spectrum of
![]() $Y_n$
. We only need the sharp lower bound in the level aspect stated in formula (7), but along the way we prove a stronger version that also yields the right order in the spectral parameter; for the exact statement, see Proposition 2.1. Such a result is also necessary for the rank
$Y_n$
. We only need the sharp lower bound in the level aspect stated in formula (7), but along the way we prove a stronger version that also yields the right order in the spectral parameter; for the exact statement, see Proposition 2.1. Such a result is also necessary for the rank
![]() $1$
situation, but involves a much more careful analysis of the nontempered spectrum in higher rank.
$1$
situation, but involves a much more careful analysis of the nontempered spectrum in higher rank.
2 Outline of proof and reduction steps
In this section, we shall reduce the proof of Theorem 1.1 to that of two auxiliary estimates: one spectral, one geometric. Let
![]() $G=\operatorname {SL}_d({\mathbb R})$
and
$G=\operatorname {SL}_d({\mathbb R})$
and
![]() $K=\textrm {SO}(d)$
. As a preliminary step, we note that by replacing
$K=\textrm {SO}(d)$
. As a preliminary step, we note that by replacing
![]() $a_n$
with
$a_n$
with
 , we may suppose that the measurable, right-K-invariant functions
, we may suppose that the measurable, right-K-invariant functions
![]() $a_n$
on
$a_n$
on
![]() $\Gamma _n\backslash G$
satisfy
$\Gamma _n\backslash G$
satisfy
 $$ \begin{align} \int_{\Gamma_n\backslash G} a_n=0 \quad \text{and}\quad \lVert a_n\rVert_\infty\leq 1. \end{align} $$
$$ \begin{align} \int_{\Gamma_n\backslash G} a_n=0 \quad \text{and}\quad \lVert a_n\rVert_\infty\leq 1. \end{align} $$
Under that assumption it will then be enough to prove
 $$ \begin{align} \frac{1}{N(B_0(\nu,\varrho),\Gamma_n)}\sum_{j:\nu_j^{(n)}\in B_0(\nu,\varrho)} \left\lvert\left\langle a_n\psi_j^{(n)}, \psi_j^{(n)}\right\rangle_{L^2(Y_n)}\right\rvert^2\rightarrow 0 \end{align} $$
$$ \begin{align} \frac{1}{N(B_0(\nu,\varrho),\Gamma_n)}\sum_{j:\nu_j^{(n)}\in B_0(\nu,\varrho)} \left\lvert\left\langle a_n\psi_j^{(n)}, \psi_j^{(n)}\right\rangle_{L^2(Y_n)}\right\rvert^2\rightarrow 0 \end{align} $$
as
![]() $n\rightarrow \infty $
. The rest of the paper is devoted to establishing formula (5).
$n\rightarrow \infty $
. The rest of the paper is devoted to establishing formula (5).
2.1 Spectral estimate
We shall first need to control the spectral counting function defined in equation (2). This is provided in the following result, to be proved in §3 (see [Reference Abert, Bergeron and Le Masson2] for a more abstract approach, in rank
![]() $1$
, using the limit-multiplicity result of [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1]):
$1$
, using the limit-multiplicity result of [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1]):
Proposition 2.1. Let G be a connected noncompact simple Lie group with finite center, and K a maximal compact subgroup. Let
![]() $S=G/K$
be the associated irreducible Riemannian globally symmetric space of noncompact type. Let
$S=G/K$
be the associated irreducible Riemannian globally symmetric space of noncompact type. Let
![]() $\Gamma _n$
be a sequence of uniformly discrete, torsion-free, cocompact lattices in G such that
$\Gamma _n$
be a sequence of uniformly discrete, torsion-free, cocompact lattices in G such that
![]() $Y_n=\Gamma _n\backslash S$
converges, in the sense of Benjamini and Schramm, to S. There exist
$Y_n=\Gamma _n\backslash S$
converges, in the sense of Benjamini and Schramm, to S. There exist
![]() $0<\varrho _1<1<\varrho _2$
such that the following holds: Fix
$0<\varrho _1<1<\varrho _2$
such that the following holds: Fix
![]() $\epsilon>0$
, and let
$\epsilon>0$
, and let
![]() $\nu \in i\mathfrak {a}^*$
be
$\nu \in i\mathfrak {a}^*$
be
![]() $\varepsilon $
-regular. Then
$\varepsilon $
-regular. Then
 $$ \begin{align} N(B(\nu,\varrho_1),\Gamma_n)\ll \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\ll_\varepsilon N(B(\nu,\varrho_2),\Gamma_n), \end{align} $$
$$ \begin{align} N(B(\nu,\varrho_1),\Gamma_n)\ll \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\ll_\varepsilon N(B(\nu,\varrho_2),\Gamma_n), \end{align} $$
where
![]() $B(\nu ,\varrho )=\left \{\lambda \in \mathfrak {a}_{\mathbb C}^*\mid \lVert \lambda - \nu \rVert _2<\varrho \right \}$
, and
$B(\nu ,\varrho )=\left \{\lambda \in \mathfrak {a}_{\mathbb C}^*\mid \lVert \lambda - \nu \rVert _2<\varrho \right \}$
, and
 $N(B(\nu ,\varrho ),\Gamma _n)=\left \lvert \left \{j\mid \nu _j^{(n)}\in B(\nu ,\varrho )\right \}\right \rvert $
is the counting function.
$N(B(\nu ,\varrho ),\Gamma _n)=\left \lvert \left \{j\mid \nu _j^{(n)}\in B(\nu ,\varrho )\right \}\right \rvert $
is the counting function.
We shall only make use of Proposition 2.1 in the form
for a sufficiently regular spectral parameter
![]() $\nu $
. Indeed formula (7) follows from the second estimate in formula (6) using the fact that
$\nu $
. Indeed formula (7) follows from the second estimate in formula (6) using the fact that
 $\tilde \beta (\nu )\geq 1$
for all
$\tilde \beta (\nu )\geq 1$
for all
![]() $\nu \in i\mathfrak {a}^*$
. See §3.1 for our notational conventions on the dependence on the implied constants on the assumption of sufficient regularity.
$\nu \in i\mathfrak {a}^*$
. See §3.1 for our notational conventions on the dependence on the implied constants on the assumption of sufficient regularity.
We note that Proposition 2.1 is stated for general symmetric spaces S. By contrast, we have restricted the setting of the next two results, Theorems 2.2 and 2.3, to the symmetric space
![]() $S=\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
.
$S=\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
.
2.2 The averaging subset
Following [Reference Brooks, Le Masson and Lindenstrauss8, Reference Le Masson and Sahlsten24], the main idea behind formula (5) is the strategic use of a self-adjoint normalized averaging operator which on one hand acts nondecreasingly on the spectral average (Theorem 2.2) and on the other hand has small Hilbert–Schmidt norm (Theorem 2.3). This idea can be traced back to the work of Brooks, Le Masson, and Lindenstrauss [Reference Brooks, Le Masson and Lindenstrauss8], which presents an alternative proof of [Reference Arantharaman and Le Masson3, Theorem 1.3], using discrete normalized averaging operators.
In the following we give a definition of an exhaustive sequence of sets
![]() $E_t\subset \operatorname {SL}_d({\mathbb R})$
, which we shall use in our averaging operators. The difficulty in higher rank is finding a set
$E_t\subset \operatorname {SL}_d({\mathbb R})$
, which we shall use in our averaging operators. The difficulty in higher rank is finding a set
![]() $E_t$
which satisfies simultaneously the desired spectral and geometric properties (in rank
$E_t$
which satisfies simultaneously the desired spectral and geometric properties (in rank
![]() $1$
, the obvious choice of a Riemannian metric ball is shown to work in [[Reference Abert, Bergeron and Le Masson2], Reference Le Masson and Sahlsten24]).
$1$
, the obvious choice of a Riemannian metric ball is shown to work in [[Reference Abert, Bergeron and Le Masson2], Reference Le Masson and Sahlsten24]).
We begin by introducing some notation. Let
![]() $\mathfrak {g}$
be the trace
$\mathfrak {g}$
be the trace
![]() $0$
matrices in
$0$
matrices in
![]() $M_d({\mathbb R})$
. Let
$M_d({\mathbb R})$
. Let
be the standard Cartan subalgebra of diagonal matrices. Let
![]() $W=N_K(\mathfrak {a})/Z_K(\mathfrak {a})$
be the Weyl group of
$W=N_K(\mathfrak {a})/Z_K(\mathfrak {a})$
be the Weyl group of
![]() $(\mathfrak {a},\mathfrak {g})$
; the action of
$(\mathfrak {a},\mathfrak {g})$
; the action of
![]() $W\simeq S_d$
on
$W\simeq S_d$
on
![]() $\mathfrak {a}$
is by permutation of the coordinates. Let
$\mathfrak {a}$
is by permutation of the coordinates. Let
![]() $\mathfrak {a}^+$
be the standard positive Weyl chamber in
$\mathfrak {a}^+$
be the standard positive Weyl chamber in
![]() $\mathfrak {a}$
given by
$\mathfrak {a}$
given by
![]() $X_1>X_2>\dotsb >X_d$
. For a vector
$X_1>X_2>\dotsb >X_d$
. For a vector
![]() $X\in \mathfrak {a}$
we will write
$X\in \mathfrak {a}$
we will write
The W-invariant norm
![]() $\lVert \cdot \rVert _\infty $
on
$\lVert \cdot \rVert _\infty $
on
![]() $\mathfrak {a}$
induces a subadditive bi-K-invariant norm on
$\mathfrak {a}$
induces a subadditive bi-K-invariant norm on
![]() $G=\operatorname {SL}_d({\mathbb R})$
via the Cartan decomposition
$G=\operatorname {SL}_d({\mathbb R})$
via the Cartan decomposition
 $G=K\exp \left (\overline {\mathfrak {a}^+}\right )K$
. Namely, if
$G=K\exp \left (\overline {\mathfrak {a}^+}\right )K$
. Namely, if
![]() $g\in G$
with
$g\in G$
with
![]() $g\in K e^X K$
, then we write
$g\in K e^X K$
, then we write
![]() $\lvert g\rvert = \lVert X\rVert _\infty $
. We have
$\lvert g\rvert = \lVert X\rVert _\infty $
. We have
![]() $\lvert g\rvert \geq 0$
,
$\lvert g\rvert \geq 0$
,
 $\left \lvert g^{-1}\right \rvert =\lvert g\rvert $
, and
$\left \lvert g^{-1}\right \rvert =\lvert g\rvert $
, and
![]() $\lvert g_1g_2\rvert \leq \lvert g_1\rvert +\lvert g_2\rvert $
.
$\lvert g_1g_2\rvert \leq \lvert g_1\rvert +\lvert g_2\rvert $
.
With this notation, we put
This is the averaging set we shall use for our wave propagator. One may view
![]() $E_t$
as a radially invariant subset of the symmetric space
$E_t$
as a radially invariant subset of the symmetric space
![]() $G/K$
. See §2.5 for more commentary on the nature of
$G/K$
. See §2.5 for more commentary on the nature of
![]() $E_t$
.
$E_t$
.
2.3 The two main results
We now define
 $$ \begin{align*} k_t=\frac{1}{\sqrt{m_G(E_t)}}\textbf{ 1}_{E_t}. \end{align*} $$
$$ \begin{align*} k_t=\frac{1}{\sqrt{m_G(E_t)}}\textbf{ 1}_{E_t}. \end{align*} $$
Let
![]() $\rho _{\Gamma \backslash G}$
denote the right-regular representation of G on
$\rho _{\Gamma \backslash G}$
denote the right-regular representation of G on
![]() $L^2(\Gamma \backslash G)$
, and consider the wave-propagation operator on
$L^2(\Gamma \backslash G)$
, and consider the wave-propagation operator on
![]() $L^2(\Gamma \backslash G)$
given by
$L^2(\Gamma \backslash G)$
given by
From
![]() $E_t^{-1}=E_t$
it follows that
$E_t^{-1}=E_t$
it follows that
![]() $k_t$
is a self-adjoint operator. For a measurable right-K-invariant function a on
$k_t$
is a self-adjoint operator. For a measurable right-K-invariant function a on
![]() $\Gamma \backslash G$
satisfying equation (4), and for
$\Gamma \backslash G$
satisfying equation (4), and for
![]() $\tau>0$
, we consider the time average
$\tau>0$
, we consider the time average
 $$ \begin{align} \textbf{ A}(\tau)=\frac{1}{\tau}\int_0^\tau U_taU_t dt. \end{align} $$
$$ \begin{align} \textbf{ A}(\tau)=\frac{1}{\tau}\int_0^\tau U_taU_t dt. \end{align} $$
In §4 we shall prove the following spectral estimate:
Theorem 2.2 spectral estimate
Let
![]() $S=\operatorname {SL}_d({\mathbb R})/{\mathrm{SO}}(d)$
. Let
$S=\operatorname {SL}_d({\mathbb R})/{\mathrm{SO}}(d)$
. Let
![]() $\Gamma $
a cocompact lattice in
$\Gamma $
a cocompact lattice in
![]() $\operatorname {SL}_d({\mathbb R})$
, and put
$\operatorname {SL}_d({\mathbb R})$
, and put
![]() $Y=\Gamma \backslash S$
. Let
$Y=\Gamma \backslash S$
. Let
![]() $\Omega \subseteq i\mathfrak {a}^*$
be compact. There exist constants
$\Omega \subseteq i\mathfrak {a}^*$
be compact. There exist constants
![]() $c,\tau _0>0$
, depending on
$c,\tau _0>0$
, depending on
![]() $\Omega $
, such that for
$\Omega $
, such that for
![]() $\tau \ge \tau _0$
, we have
$\tau \ge \tau _0$
, we have
 $$ \begin{align*} \sum_{j: \nu_j\in\Omega} \left\lvert\left\langle a\psi_j, \psi_j\right\rangle_{L^2(Y)}\right\rvert^2\leq c \sum_{j: \nu_j\in\Omega} \left\lvert\left\langle \textbf{ A}(\tau)\psi_j , \psi_j\right\rangle_{L^2(Y)}\right\rvert^2. \end{align*} $$
$$ \begin{align*} \sum_{j: \nu_j\in\Omega} \left\lvert\left\langle a\psi_j, \psi_j\right\rangle_{L^2(Y)}\right\rvert^2\leq c \sum_{j: \nu_j\in\Omega} \left\lvert\left\langle \textbf{ A}(\tau)\psi_j , \psi_j\right\rangle_{L^2(Y)}\right\rvert^2. \end{align*} $$
In §5 we shall use the Nevo mean ergodic theorem [Reference Nevo29] (see also [Reference Gorodnik and Nevo15, Theorem 4.1]) to prove the following geometric estimate. Recall that the Hilbert–Schmidt norm of a bounded operator
![]() $\mathbf {A}$
on a separable Hilbert space H is given by
$\mathbf {A}$
on a separable Hilbert space H is given by
 $$ \begin{align*} \lVert\textbf{ A}\rVert_{\textrm{HS}}^2=\sum_i \left\lvert\langle \textbf{ A} e_i,e_i\rangle\right\rvert^2, \end{align*} $$
$$ \begin{align*} \lVert\textbf{ A}\rVert_{\textrm{HS}}^2=\sum_i \left\lvert\langle \textbf{ A} e_i,e_i\rangle\right\rvert^2, \end{align*} $$
where
![]() $\{e_i\}$
is any orthonormal basis of H.
$\{e_i\}$
is any orthonormal basis of H.
Theorem 2.3 geometric estimate
Let
![]() $S=\operatorname {SL}_d({\mathbb R})/{\mathrm{SO}}(d)$
. Let
$S=\operatorname {SL}_d({\mathbb R})/{\mathrm{SO}}(d)$
. Let
![]() $\Gamma $
be a cocompact torsion-free lattice in
$\Gamma $
be a cocompact torsion-free lattice in
![]() $\operatorname {SL}_d({\mathbb R})$
, and put
$\operatorname {SL}_d({\mathbb R})$
, and put
![]() $Y=\Gamma \backslash S$
. Let a be a measurable function on
$Y=\Gamma \backslash S$
. Let a be a measurable function on
![]() $L^2(\Gamma \backslash S)$
. There are constants
$L^2(\Gamma \backslash S)$
. There are constants
![]() $b, c_1,c_2>0$
, depending only on d, such that for
$b, c_1,c_2>0$
, depending only on d, such that for
![]() $\tau>0$
,
$\tau>0$
,
 $$ \begin{align*} \lVert\textbf{ A}(\tau)\rVert_{\textrm{ HS}}^2\ll_b \frac{\lVert a\rVert_2^2}{\tau}+ \frac{e^{c_1\tau}}{\operatorname{InjRad}(Y)^{\dim S}}\operatorname{vol}\left((\Gamma\backslash G)_{\leq c_2(2\tau+b)}\right)\lVert a\rVert_\infty^2. \end{align*} $$
$$ \begin{align*} \lVert\textbf{ A}(\tau)\rVert_{\textrm{ HS}}^2\ll_b \frac{\lVert a\rVert_2^2}{\tau}+ \frac{e^{c_1\tau}}{\operatorname{InjRad}(Y)^{\dim S}}\operatorname{vol}\left((\Gamma\backslash G)_{\leq c_2(2\tau+b)}\right)\lVert a\rVert_\infty^2. \end{align*} $$
2.4 Reduction to two main results
We now deduce the main estimate (5) from the foregoing results.
We first note that if
![]() $\nu \in i\mathfrak {a}^*$
is sufficiently regular in the sense that
$\nu \in i\mathfrak {a}^*$
is sufficiently regular in the sense that
![]() $\left \lvert \left \langle \nu ,\alpha ^\vee \right \rangle \right \rvert \ge C_\varrho $
for all simple roots
$\left \lvert \left \langle \nu ,\alpha ^\vee \right \rangle \right \rvert \ge C_\varrho $
for all simple roots
![]() $\alpha $
, with
$\alpha $
, with
![]() $C_\varrho>0$
a sufficiently large constant depending on
$C_\varrho>0$
a sufficiently large constant depending on
![]() $\varrho $
, then
$\varrho $
, then
 $\left \{j\mid \nu _j^{(n)}\in B_0(\nu ,\varrho )\right \}=\left \{j\mid \nu _j^{(n)}\in B(\nu ,\varrho )\right \}$
because of formula (23). By the lower bound (7), which follows from Proposition 2.1, it suffices to prove an upper bound for
$\left \{j\mid \nu _j^{(n)}\in B_0(\nu ,\varrho )\right \}=\left \{j\mid \nu _j^{(n)}\in B(\nu ,\varrho )\right \}$
because of formula (23). By the lower bound (7), which follows from Proposition 2.1, it suffices to prove an upper bound for
 $$ \begin{align*} \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\sum_{j: \nu_j^{(n)}\in B(\nu,\varrho)} \left\lvert\left\langle a_n\psi_j^{(n)}, \psi_j^{(n)}\right\rangle_{L^2\left(Y_n\right)}\right\rvert^2. \end{align*} $$
$$ \begin{align*} \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\sum_{j: \nu_j^{(n)}\in B(\nu,\varrho)} \left\lvert\left\langle a_n\psi_j^{(n)}, \psi_j^{(n)}\right\rangle_{L^2\left(Y_n\right)}\right\rvert^2. \end{align*} $$
From Theorem 2.2, it follows that for
![]() $\tau \geq \tau _0$
,
$\tau \geq \tau _0$
,
 $$ \begin{align*} \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\sum_{j: \nu_j^{(n)}\in B\left(\nu,\varrho\right)} \left\lvert\left\langle a_n\psi_j^{(n)}, \psi_j^{(n)}\right\rangle_{L^2(Y_n)}\right\rvert^2 \ll \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\left\lVert \textbf{ A}^{(n)}(\tau)\right\rVert_{\textrm{ HS}}^2. \end{align*} $$
$$ \begin{align*} \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\sum_{j: \nu_j^{(n)}\in B\left(\nu,\varrho\right)} \left\lvert\left\langle a_n\psi_j^{(n)}, \psi_j^{(n)}\right\rangle_{L^2(Y_n)}\right\rvert^2 \ll \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\left\lVert \textbf{ A}^{(n)}(\tau)\right\rVert_{\textrm{ HS}}^2. \end{align*} $$
We now apply Theorem 2.3 to the right-hand side. To bound the first term, we use the estimate
![]() $\lVert a_n\rVert _2^2\leq \lVert a_n\rVert _\infty ^2 \operatorname {vol}(\Gamma _n\backslash G)$
along with the uniform boundedness of
$\lVert a_n\rVert _2^2\leq \lVert a_n\rVert _\infty ^2 \operatorname {vol}(\Gamma _n\backslash G)$
along with the uniform boundedness of
![]() $a_n$
. For the second term we insert the bound
$a_n$
. For the second term we insert the bound
![]() $\operatorname {InjRad}(Y_n)\gg 1$
coming from the uniformly discrete hypothesis in the statement of Theorem 1.1. We obtain
$\operatorname {InjRad}(Y_n)\gg 1$
coming from the uniformly discrete hypothesis in the statement of Theorem 1.1. We obtain
 $$ \begin{align} \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\left\lVert\textbf{ A}^{(n)}(\tau_n)\right\rVert_{\textrm{ HS}}^2\ll \frac{1}{\tau_n}+ e^{c_1\tau_n}\frac{\operatorname{vol}\left((\Gamma_n\backslash G)_{\leq c_2\left(2\tau_n+b\right)}\right)}{\operatorname{vol} (\Gamma_n\backslash G)}. \end{align} $$
$$ \begin{align} \frac{1}{\operatorname{vol} (\Gamma_n\backslash G)}\left\lVert\textbf{ A}^{(n)}(\tau_n)\right\rVert_{\textrm{ HS}}^2\ll \frac{1}{\tau_n}+ e^{c_1\tau_n}\frac{\operatorname{vol}\left((\Gamma_n\backslash G)_{\leq c_2\left(2\tau_n+b\right)}\right)}{\operatorname{vol} (\Gamma_n\backslash G)}. \end{align} $$
We know from [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, §4] that for any sequence
![]() $\Gamma _n$
for which
$\Gamma _n$
for which
![]() $\operatorname {vol}(\Gamma _n\backslash G)\rightarrow \infty $
, the space
$\operatorname {vol}(\Gamma _n\backslash G)\rightarrow \infty $
, the space
![]() $\Gamma _n\backslash G/K$
converges in the sense of Benjamini and Schramm to
$\Gamma _n\backslash G/K$
converges in the sense of Benjamini and Schramm to
![]() $G/K=\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
(recall our assumption that
$G/K=\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
(recall our assumption that
![]() $d\geq 3$
). We deduce that there is a sequence
$d\geq 3$
). We deduce that there is a sequence
![]() $R_n\rightarrow \infty $
such that
$R_n\rightarrow \infty $
such that
 $$ \begin{align} \frac{\operatorname{vol}\left((\Gamma_n\backslash G)_{\leq R_n}\right)}{\operatorname{vol}(\Gamma_n\backslash G)}\rightarrow 0 \end{align} $$
$$ \begin{align} \frac{\operatorname{vol}\left((\Gamma_n\backslash G)_{\leq R_n}\right)}{\operatorname{vol}(\Gamma_n\backslash G)}\rightarrow 0 \end{align} $$
as
![]() $n\rightarrow \infty $
. Given this sequence
$n\rightarrow \infty $
. Given this sequence
![]() $R_n$
, we let
$R_n$
, we let
![]() $r_n>0$
be a sequence such that
$r_n>0$
be a sequence such that
-
(i)
 $r_n\rightarrow \infty $
as
$r_n\rightarrow \infty $
as
 $n\rightarrow \infty $
and
$n\rightarrow \infty $
and -
(ii)
 $e^{c_1 r_n}\frac {\operatorname {vol}\left ((\Gamma _n\backslash G)_{\leq c_2\left (2r_n+b\right )}\right )}{\operatorname {vol}(\Gamma _n\backslash G)}\rightarrow 0$
as
$e^{c_1 r_n}\frac {\operatorname {vol}\left ((\Gamma _n\backslash G)_{\leq c_2\left (2r_n+b\right )}\right )}{\operatorname {vol}(\Gamma _n\backslash G)}\rightarrow 0$
as
 $n\rightarrow \infty $
.
$n\rightarrow \infty $
.
Taking
![]() $\tau _n=r_n$
, both terms in formula (11) go to
$\tau _n=r_n$
, both terms in formula (11) go to
![]() $0$
with n, establishing formula (5).
$0$
with n, establishing formula (5).
Remark 2.1. One could deduce an effective rate of convergence in Theorem 1.1 for congruence subgroups
![]() $\Gamma _n$
of
$\Gamma _n$
of
![]() $\operatorname {SL}_d({\mathbb Z})$
by inserting, in place of the
$\operatorname {SL}_d({\mathbb Z})$
by inserting, in place of the
![]() $o(1)$
result in formula (12), the explicit bounds on the R-thin part for such sequences proved in [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, Theorem 5.2].
$o(1)$
result in formula (12), the explicit bounds on the R-thin part for such sequences proved in [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, Theorem 5.2].
2.5 Remarks on the averaging subset
We now make several remarks about
![]() $E_t$
:
$E_t$
:
(i) In rank
![]() $1$
, the set
$1$
, the set
![]() $E_t$
recovers the metric ball centered at
$E_t$
recovers the metric ball centered at
![]() $i\in \mathbb {H}$
of radius
$i\in \mathbb {H}$
of radius
![]() $2t$
for the hyperbolic metric
$2t$
for the hyperbolic metric
 $\left (dx^2+dy^2\right )/y^2$
on the upper half-plane
$\left (dx^2+dy^2\right )/y^2$
on the upper half-plane
![]() $\mathbb {H}=\operatorname {SL}_2({\mathbb R})/\textrm {SO}(2)$
.
$\mathbb {H}=\operatorname {SL}_2({\mathbb R})/\textrm {SO}(2)$
.
(ii) In higher rank, the set
![]() $E_t$
differs substantially from a metric ball centered at the identity for the metric induced by the trace form
$E_t$
differs substantially from a metric ball centered at the identity for the metric induced by the trace form
 $\operatorname {Tr}\left (X^\top Y\right )$
(a constant multiple of the Killing form) on
$\operatorname {Tr}\left (X^\top Y\right )$
(a constant multiple of the Killing form) on
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
To see this, let us first compare a geodesic ball and the set
![]() $E_t$
by means of the Cartan decomposition of
$E_t$
by means of the Cartan decomposition of
![]() $G=\operatorname {SL}_d({\mathbb R})$
. Let
$G=\operatorname {SL}_d({\mathbb R})$
. Let
![]() $\mathscr {B}=\left \{X\in \mathfrak {a}: \lVert X\rVert _2\leq 1\right \}$
, where
$\mathscr {B}=\left \{X\in \mathfrak {a}: \lVert X\rVert _2\leq 1\right \}$
, where
 $\lVert X\rVert _2^2=\operatorname {tr}\left (X^2\right )=X_1^2+\dotsb +X_d^2$
. The geodesic ball
$\lVert X\rVert _2^2=\operatorname {tr}\left (X^2\right )=X_1^2+\dotsb +X_d^2$
. The geodesic ball
![]() $B_t$
of radius
$B_t$
of radius
![]() $t>0$
centered at the origin is given by
$t>0$
centered at the origin is given by
 $$ \begin{align} B_t=K\exp \left(\mathscr{B}_t^+\right) K, \end{align} $$
$$ \begin{align} B_t=K\exp \left(\mathscr{B}_t^+\right) K, \end{align} $$
where
![]() $\mathscr {B}_t^+=t\mathscr {B}\cap \overline {\mathfrak {a}^+}$
(see [Reference Bekka and Mayer4, Proposition 4.2]). On the other hand, let
$\mathscr {B}_t^+=t\mathscr {B}\cap \overline {\mathfrak {a}^+}$
(see [Reference Bekka and Mayer4, Proposition 4.2]). On the other hand, let
Note that
![]() ${\mathscr P}$
is a bounded convex polytope in
${\mathscr P}$
is a bounded convex polytope in
![]() $\mathfrak {a}$
, being the intersection of the half-planes
$\mathfrak {a}$
, being the intersection of the half-planes
![]() $\pm X_i\leq 1$
. It is clear that
$\pm X_i\leq 1$
. It is clear that
 $$ \begin{align} E_t=K\exp\left({\mathscr P}_t^+\right)K, \end{align} $$
$$ \begin{align} E_t=K\exp\left({\mathscr P}_t^+\right)K, \end{align} $$
where
![]() ${\mathscr P}^+_t=t{\mathscr P}\cap \overline {\mathfrak {a}^+}$
. One sees from equations (13) and (15) that an element in
${\mathscr P}^+_t=t{\mathscr P}\cap \overline {\mathfrak {a}^+}$
. One sees from equations (13) and (15) that an element in
![]() $B_t$
or
$B_t$
or
![]() $E_t$
has Cartan radial component contained to, respectively, an expanding ball or a dilated W-invariant polytope in
$E_t$
has Cartan radial component contained to, respectively, an expanding ball or a dilated W-invariant polytope in
![]() $\mathfrak {a}$
.
$\mathfrak {a}$
.
(iii) Related to the foregoing description is the difference in the volume asymptotics between
![]() $B_t$
and
$B_t$
and
![]() $E_t$
. Both are expressed, naturally, with respect to the half-sum of the positive roots
$E_t$
. Both are expressed, naturally, with respect to the half-sum of the positive roots
![]() $\rho \in \mathfrak {a}^*$
, as that quantity governs the Jacobian factor in the Cartan decomposition of the Haar measure on G (see §4.1).
$\rho \in \mathfrak {a}^*$
, as that quantity governs the Jacobian factor in the Cartan decomposition of the Haar measure on G (see §4.1).
For the geodesic ball, a result of Knieper [Reference Knieper21], valid more generally for irreducible Riemannian symmetric spaces
![]() $S=G/K$
of noncompact type, states that
$S=G/K$
of noncompact type, states that
 $$ \begin{align} m_G(B_t)\asymp t^{(r-1)/2}e^{2t\lVert\rho\rVert_2}, \end{align} $$
$$ \begin{align} m_G(B_t)\asymp t^{(r-1)/2}e^{2t\lVert\rho\rVert_2}, \end{align} $$
where r is the rank of S. On the other hand, we show in Corollary A.4 that, for
![]() $G=\operatorname {SL}_d({\mathbb R})$
,
$G=\operatorname {SL}_d({\mathbb R})$
,
 $$ \begin{align*} m_G(E_t)\sim c_2 e^{2t\left\langle \rho, X^0\right\rangle},\quad t\rightarrow\infty, \end{align*} $$
$$ \begin{align*} m_G(E_t)\sim c_2 e^{2t\left\langle \rho, X^0\right\rangle},\quad t\rightarrow\infty, \end{align*} $$
where
![]() $X^0\in {\mathscr P}^+$
is the unique point satisfying
$X^0\in {\mathscr P}^+$
is the unique point satisfying
 $$ \begin{align} \left\langle \rho, X^0\right\rangle=\max_{X\in{\mathscr P}^+}\langle\rho,X\rangle. \end{align} $$
$$ \begin{align} \left\langle \rho, X^0\right\rangle=\max_{X\in{\mathscr P}^+}\langle\rho,X\rangle. \end{align} $$
One can compute that
 $$ \begin{align} \lVert\rho\rVert_2=\left\langle\rho,\frac{\rho}{\lVert\rho\rVert_2}\right\rangle=\sqrt{d\left(d^2-1\right)/12}, \end{align} $$
$$ \begin{align} \lVert\rho\rVert_2=\left\langle\rho,\frac{\rho}{\lVert\rho\rVert_2}\right\rangle=\sqrt{d\left(d^2-1\right)/12}, \end{align} $$
whereas using Lemma A.1, we have
 $$ \begin{align*} \left\langle\rho,\frac{X^0}{\left\lVert X^0\right\rVert_2}\right\rangle=\begin{cases} d^{3/2}/4, & d \text{ even},\\ (d+1)(d-1)^{1/2}/4, & d \text{ odd}. \end{cases} \end{align*} $$
$$ \begin{align*} \left\langle\rho,\frac{X^0}{\left\lVert X^0\right\rVert_2}\right\rangle=\begin{cases} d^{3/2}/4, & d \text{ even},\\ (d+1)(d-1)^{1/2}/4, & d \text{ odd}. \end{cases} \end{align*} $$
We have normalized by
 $\left \lVert X^0\right \rVert _2$
so that
$\left \lVert X^0\right \rVert _2$
so that
![]() $B_t$
is the smallest geodesic ball containing
$B_t$
is the smallest geodesic ball containing
![]() $E_{t/\left \lVert X^0\right \rVert _2}$
. We see that the exponential volume growth of
$E_{t/\left \lVert X^0\right \rVert _2}$
. We see that the exponential volume growth of
![]() $B_t$
in
$B_t$
in
![]() $\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
is of order
$\operatorname {SL}_d({\mathbb R})/\textrm {SO}(d)$
is of order
 $2t \sqrt {d^3/12}$
, whereas that of
$2t \sqrt {d^3/12}$
, whereas that of
![]() $E_{t/\left \lVert X^0\right \rVert _2}$
is of order
$E_{t/\left \lVert X^0\right \rVert _2}$
is of order
 $2t\sqrt {d^3/16}$
, which is smaller by a factor of
$2t\sqrt {d^3/16}$
, which is smaller by a factor of
![]() $\sqrt {3}/2$
.
$\sqrt {3}/2$
.
(iv) Another norm that one often considers in the context of
![]() $G=\operatorname {SL}_d({\mathbb R})$
is the restriction to
$G=\operatorname {SL}_d({\mathbb R})$
is the restriction to
![]() $\operatorname {SL}_d({\mathbb R})\subset M_d({\mathbb R})$
of the Frobenius norm, defined on
$\operatorname {SL}_d({\mathbb R})\subset M_d({\mathbb R})$
of the Frobenius norm, defined on
![]() $M_d({\mathbb R})$
as
$M_d({\mathbb R})$
as
 $\lVert g\rVert ^2=\operatorname {tr}\left (g^\top g\right )$
, where
$\lVert g\rVert ^2=\operatorname {tr}\left (g^\top g\right )$
, where
![]() $g^\top $
is the transpose of g. Note that
$g^\top $
is the transpose of g. Note that
 $\left \lVert g^{-1}\right \rVert \neq \lVert g\rVert $
in general. Since invariance under inversion is important for the self-adjointness of the propagator
$\left \lVert g^{-1}\right \rVert \neq \lVert g\rVert $
in general. Since invariance under inversion is important for the self-adjointness of the propagator
![]() $U_t$
from equation (9), we define the Frobenius ball as
$U_t$
from equation (9), we define the Frobenius ball as
 $$ \begin{align} \boldsymbol{E}_t=\left\{g\in G: \max\left\{\lVert g\rVert,\left\lVert g^{-1}\right\rVert\right\}\leq e^t\right\}. \end{align} $$
$$ \begin{align} \boldsymbol{E}_t=\left\{g\in G: \max\left\{\lVert g\rVert,\left\lVert g^{-1}\right\rVert\right\}\leq e^t\right\}. \end{align} $$
From the point of view of their large-scale geometry, the Frobenius balls are similar to the sets
![]() $E_t$
from equation (8). Indeed, in the proof of Proposition 5.8 we show that
$E_t$
from equation (8). Indeed, in the proof of Proposition 5.8 we show that
![]() $m_G(E_t)\asymp m_G(\boldsymbol {E}_t)$
. Moreover, the very statement of Proposition 5.8, which is a key component of Theorem 2.3, holds equally well for
$m_G(E_t)\asymp m_G(\boldsymbol {E}_t)$
. Moreover, the very statement of Proposition 5.8, which is a key component of Theorem 2.3, holds equally well for
![]() $\boldsymbol {E}_t$
. On the other hand, because they are not defined by their radial Cartan component, Frobenius balls are not amenable to our proof of Theorem 2.2.
$\boldsymbol {E}_t$
. On the other hand, because they are not defined by their radial Cartan component, Frobenius balls are not amenable to our proof of Theorem 2.2.
3 Weyl-type law
Our aim in this section is to prove Proposition 2.1. Throughout this section only, we let G denote a connected noncompact simple Lie group with finite center and K a maximal compact subgroup.
3.1 Notation
The notation we introduce here will be consistent with that already introduced for the particular case of
![]() $G=\operatorname {SL}_d({\mathbb R})$
and
$G=\operatorname {SL}_d({\mathbb R})$
and
![]() $K=\textrm {SO}(d)$
.
$K=\textrm {SO}(d)$
.
Let
![]() $\theta $
be the Cartan involution on G for which
$\theta $
be the Cartan involution on G for which
![]() $K=G^\theta $
. Let
$K=G^\theta $
. Let
![]() $\Theta $
be its differential and let
$\Theta $
be its differential and let
![]() $\mathfrak {g}={\mathfrak p}\oplus {\mathfrak k}$
be the Cartan decomposition of the Lie algebra
$\mathfrak {g}={\mathfrak p}\oplus {\mathfrak k}$
be the Cartan decomposition of the Lie algebra
![]() $\mathfrak {g}$
of G into the
$\mathfrak {g}$
of G into the
![]() $\pm 1$
eigenspaces of
$\pm 1$
eigenspaces of
![]() $\Theta $
. We may identify
$\Theta $
. We may identify
![]() ${\mathfrak k}$
with the Lie algebra of K.
${\mathfrak k}$
with the Lie algebra of K.
Let
![]() $\kappa (X,Y)=\operatorname {tr}(\operatorname {ad} X\operatorname {ad} Y)$
denote the Killing form on
$\kappa (X,Y)=\operatorname {tr}(\operatorname {ad} X\operatorname {ad} Y)$
denote the Killing form on
![]() $\mathfrak {g}$
. Then
$\mathfrak {g}$
. Then
![]() $-\kappa (X,\Theta Y)$
defines an
$-\kappa (X,\Theta Y)$
defines an
![]() $\operatorname {Ad}_K$
-invariant inner product on
$\operatorname {Ad}_K$
-invariant inner product on
![]() $\mathfrak {g}$
, which induces a left-invariant Haar measure on G, denoted
$\mathfrak {g}$
, which induces a left-invariant Haar measure on G, denoted
![]() $dg$
or
$dg$
or
![]() $m_G$
.
$m_G$
.
The Killing form defines an
![]() $\operatorname {Ad}_K$
-invariant inner product
$\operatorname {Ad}_K$
-invariant inner product
![]() $\langle \cdot ,\cdot \rangle $
on
$\langle \cdot ,\cdot \rangle $
on
![]() ${\mathfrak p}$
, and in particular on
${\mathfrak p}$
, and in particular on
![]() $\mathfrak {a}$
, the maximal abelian subalgebra of
$\mathfrak {a}$
, the maximal abelian subalgebra of
![]() ${\mathfrak p}$
. Let
${\mathfrak p}$
. Let
![]() $W=N_K(\mathfrak {a})/Z_K(\mathfrak {a})$
be the Weyl group. Let
$W=N_K(\mathfrak {a})/Z_K(\mathfrak {a})$
be the Weyl group. Let
![]() $\lVert \cdot \rVert _2$
denote the W-invariant normFootnote
1
on
$\lVert \cdot \rVert _2$
denote the W-invariant normFootnote
1
on
![]() $\mathfrak {a}$
induced by
$\mathfrak {a}$
induced by
![]() $\langle \cdot ,\cdot \rangle $
.
$\langle \cdot ,\cdot \rangle $
.
Let
![]() $\Phi \subset \mathfrak {a}^*$
denote the system of roots for the adjoint action of
$\Phi \subset \mathfrak {a}^*$
denote the system of roots for the adjoint action of
![]() $\mathfrak {a}$
on
$\mathfrak {a}$
on
![]() $\mathfrak {g}$
. For
$\mathfrak {g}$
. For
![]() $\alpha \in \Phi $
, let
$\alpha \in \Phi $
, let
![]() $\mathfrak {g}_\alpha $
denote the corresponding root space. Let
$\mathfrak {g}_\alpha $
denote the corresponding root space. Let
![]() ${\mathfrak m}\subset \mathfrak {g}$
be the centralizer of
${\mathfrak m}\subset \mathfrak {g}$
be the centralizer of
![]() $\mathfrak {a}$
in
$\mathfrak {a}$
in
![]() $\mathfrak {g}$
. Then we have the root-space decomposition
$\mathfrak {g}$
. Then we have the root-space decomposition
 $$ \begin{align*} \mathfrak{g}={\mathfrak m}\oplus\mathfrak{a}\oplus\bigoplus_{\alpha\in\Phi}\mathfrak{g}_\alpha. \end{align*} $$
$$ \begin{align*} \mathfrak{g}={\mathfrak m}\oplus\mathfrak{a}\oplus\bigoplus_{\alpha\in\Phi}\mathfrak{g}_\alpha. \end{align*} $$
Choose a positive system of roots
![]() $\Phi ^+$
in
$\Phi ^+$
in
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $\Delta \subseteq \Phi ^+$
be the set of simple roots.
$\Delta \subseteq \Phi ^+$
be the set of simple roots.
Let
![]() $\mathfrak {a}^*=\mathrm {Hom}(\mathfrak {a},{\mathbb R})$
be the dual vector space of
$\mathfrak {a}^*=\mathrm {Hom}(\mathfrak {a},{\mathbb R})$
be the dual vector space of
![]() $\mathfrak {a}$
. We may identify
$\mathfrak {a}$
. We may identify
![]() $\mathfrak {a}$
with
$\mathfrak {a}$
with
![]() $\mathfrak {a}^*$
via the Killing form. We again denote by
$\mathfrak {a}^*$
via the Killing form. We again denote by
![]() $\lVert \cdot \rVert _2$
the induced norm on
$\lVert \cdot \rVert _2$
the induced norm on
![]() $\mathfrak {a}^*$
and extend it to a complex bilinear form on the complexification
$\mathfrak {a}^*$
and extend it to a complex bilinear form on the complexification
![]() $\mathfrak {a}^*_{\mathbb C}=\mathfrak {a}^*\otimes _{\mathbb R}{\mathbb C}$
. We call
$\mathfrak {a}^*_{\mathbb C}=\mathfrak {a}^*\otimes _{\mathbb R}{\mathbb C}$
. We call
![]() $\nu \in i\mathfrak {a}^*$
regular if
$\nu \in i\mathfrak {a}^*$
regular if
![]() $\langle \alpha ,\nu \rangle \neq 0$
for all
$\langle \alpha ,\nu \rangle \neq 0$
for all
![]() $\alpha \in \Delta $
, and for
$\alpha \in \Delta $
, and for
![]() $c>0$
we call
$c>0$
we call
![]() $\nu \in i\mathfrak {a}^* c$
-regular if
$\nu \in i\mathfrak {a}^* c$
-regular if
![]() $\lvert \langle \alpha ,\nu \rangle \rvert \ge c$
for all
$\lvert \langle \alpha ,\nu \rangle \rvert \ge c$
for all
![]() $\alpha \in \Phi ^+$
. An element
$\alpha \in \Phi ^+$
. An element
![]() $\nu \in i\mathfrak {a}^*$
is sufficiently regular if there exists a sufficiently regular
$\nu \in i\mathfrak {a}^*$
is sufficiently regular if there exists a sufficiently regular
![]() $c>0$
(which may vary at each occurrence) such that
$c>0$
(which may vary at each occurrence) such that
![]() $\nu $
is c-regular. Unless otherwise noted, implied constants for statements valid for sufficiently regular
$\nu $
is c-regular. Unless otherwise noted, implied constants for statements valid for sufficiently regular
![]() $\nu $
can depend on the value of c.
$\nu $
can depend on the value of c.
Let
![]() ${\mathfrak n}=\sum _{\alpha \in \Phi ^+} \mathfrak {g}_\alpha $
and write
${\mathfrak n}=\sum _{\alpha \in \Phi ^+} \mathfrak {g}_\alpha $
and write
![]() $N=\exp {\mathfrak n}$
. Then we have the Iwasawa decomposition
$N=\exp {\mathfrak n}$
. Then we have the Iwasawa decomposition
![]() $G=NAK$
, where
$G=NAK$
, where
![]() $A=\exp \mathfrak {a}$
, which gives rise to the Iwasawa projection
$A=\exp \mathfrak {a}$
, which gives rise to the Iwasawa projection
along the A component.
We may decompose the Riemannian Haar measure
![]() $dg$
on G according to the Iwasawa decomposition. We let
$dg$
on G according to the Iwasawa decomposition. We let
![]() $da$
denote the Haar measure on A obtained by pushing forward the Lebesgue measure on
$da$
denote the Haar measure on A obtained by pushing forward the Lebesgue measure on
![]() $\mathfrak {a}$
by means of the exponential. We let
$\mathfrak {a}$
by means of the exponential. We let
![]() $dk$
denote the probability Haar measure
$dk$
denote the probability Haar measure
![]() $dk$
on K. We normalize the left-invariant Haar measure
$dk$
on K. We normalize the left-invariant Haar measure
![]() $du$
on N as in [Reference Duistermaat, Kolk and Varadarajan12, §3.1]. As usual, we put
$du$
on N as in [Reference Duistermaat, Kolk and Varadarajan12, §3.1]. As usual, we put
 $$ \begin{align*} \rho=\frac12\operatorname{tr}\left(\operatorname{ad}(\mathfrak{a})\rvert_{\mathfrak n}\right)=\frac12\sum_{\alpha\in\Phi^+}(\dim\mathfrak{g}_\alpha) \alpha. \end{align*} $$
$$ \begin{align*} \rho=\frac12\operatorname{tr}\left(\operatorname{ad}(\mathfrak{a})\rvert_{\mathfrak n}\right)=\frac12\sum_{\alpha\in\Phi^+}(\dim\mathfrak{g}_\alpha) \alpha. \end{align*} $$
Then we have [Reference Gangolli and Varadarajan14, Proposition 2.4.10]
Since A normalizes N and
![]() $\det \operatorname {Ad}(a)\rvert _{\mathfrak n}=e^{2\rho \left (H_0(a)\right )}$
,
$\det \operatorname {Ad}(a)\rvert _{\mathfrak n}=e^{2\rho \left (H_0(a)\right )}$
,
in the decomposition
![]() $G=ANK$
.
$G=ANK$
.
Recall the Cartan decomposition
 $G=K\exp \left (\overline {\mathfrak {a}^+}\right )K$
, where
$G=K\exp \left (\overline {\mathfrak {a}^+}\right )K$
, where
![]() $\overline {\mathfrak {a}^+}$
denotes the closure of the (open) positive Weyl chamber
$\overline {\mathfrak {a}^+}$
denotes the closure of the (open) positive Weyl chamber
![]() $\mathfrak {a}^+=\left \{X\in \mathfrak {a}: \alpha (X)>0\;\forall \,\alpha \in \Phi ^+\right \}$
. We have the following decomposition of the Riemannian Haar measure
$\mathfrak {a}^+=\left \{X\in \mathfrak {a}: \alpha (X)>0\;\forall \,\alpha \in \Phi ^+\right \}$
. We have the following decomposition of the Riemannian Haar measure
![]() $dg$
into the Cartan decomposition:
$dg$
into the Cartan decomposition:
Here,
![]() $\operatorname {vol}(K)$
is the Riemannian volume on K for the measure induced by the inner product
$\operatorname {vol}(K)$
is the Riemannian volume on K for the measure induced by the inner product
![]() $-\kappa (X,Y)$
on
$-\kappa (X,Y)$
on
![]() $\mathfrak {k}$
, and similarly with
$\mathfrak {k}$
, and similarly with
![]() $\operatorname {vol}(K/M)$
. Finally,
$\operatorname {vol}(K/M)$
. Finally,
![]() $J(X)$
is the Jacobian factor, given by
$J(X)$
is the Jacobian factor, given by
 $$ \begin{align} J(X)=\prod_{\alpha\in\Phi^+} \sinh(\alpha(X))^{\dim\mathfrak{g}_\alpha},\quad X\in\overline{\mathfrak{a}^+} \end{align} $$
$$ \begin{align} J(X)=\prod_{\alpha\in\Phi^+} \sinh(\alpha(X))^{\dim\mathfrak{g}_\alpha},\quad X\in\overline{\mathfrak{a}^+} \end{align} $$
(see [Reference Gangolli and Varadarajan14, Proposition 2.4.11]).
Let
![]() $P_0$
be the normalizer of
$P_0$
be the normalizer of
![]() ${\mathfrak m}\oplus \mathfrak {a}\oplus {\mathfrak n}$
in G. Then
${\mathfrak m}\oplus \mathfrak {a}\oplus {\mathfrak n}$
in G. Then
![]() $P_0$
has Langlands decomposition
$P_0$
has Langlands decomposition
![]() $P_0=MAN$
, where M is the centralizer of A in G. For
$P_0=MAN$
, where M is the centralizer of A in G. For
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
, let
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
, let
![]() $\pi _\lambda $
denote the unique unramified irreducible subquotient of
$\pi _\lambda $
denote the unique unramified irreducible subquotient of
 $\mathrm {Ind}_{P_0}^G\left (1\otimes e^\lambda \otimes 1\right )$
. Let
$\mathrm {Ind}_{P_0}^G\left (1\otimes e^\lambda \otimes 1\right )$
. Let
be the spherical unitary dual of G. Furthermore, let
 $$ \begin{align*} \mathfrak{a}^*_{\textrm{ hm}}=\bigcup_{w\in W}\left\{\lambda\in\mathfrak{a}^*_{\mathbb C}: w\lambda=-\bar\lambda\right\} \end{align*} $$
$$ \begin{align*} \mathfrak{a}^*_{\textrm{ hm}}=\bigcup_{w\in W}\left\{\lambda\in\mathfrak{a}^*_{\mathbb C}: w\lambda=-\bar\lambda\right\} \end{align*} $$
denote the spherical Hermitian dual of G [Reference Lapid and Müller22, §3.3]. Let
![]() $i\mathfrak {a}$
be the subspace of
$i\mathfrak {a}$
be the subspace of
![]() $\mathfrak {a}_{\mathbb C}^*$
consisting of
$\mathfrak {a}_{\mathbb C}^*$
consisting of
![]() $\lambda $
taking on purely imaginary values. We may write
$\lambda $
taking on purely imaginary values. We may write
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
uniquely as
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
uniquely as
![]() $\lambda =\operatorname {Re}\lambda +\operatorname {Im}\lambda \in \mathfrak {a}^*\oplus i\mathfrak {a}^*$
. We have
$\lambda =\operatorname {Re}\lambda +\operatorname {Im}\lambda \in \mathfrak {a}^*\oplus i\mathfrak {a}^*$
. We have
For
![]() $\mu \in i\mathfrak {a}^*$
and
$\mu \in i\mathfrak {a}^*$
and
![]() $r>0$
, we let
$r>0$
, we let
denote the ball of radius r about
![]() $\mu $
in the tempered spectrum
$\mu $
in the tempered spectrum
![]() $i\mathfrak {a}^*$
. When
$i\mathfrak {a}^*$
. When
![]() $r=1$
we write
$r=1$
we write
![]() $B_0(\mu )$
for
$B_0(\mu )$
for
![]() $B_0(\mu ,1)$
. We also write
$B_0(\mu ,1)$
. We also write
for the ball of radius r around
![]() $\mu $
in
$\mu $
in
![]() $\mathfrak {a}^*_{\mathbb C}$
.
$\mathfrak {a}^*_{\mathbb C}$
.
3.2 Plancherel density and the
 $\mathbf {c}$
-function
$\mathbf {c}$
-function
We denote by
![]() $\beta $
the density function for the Plancherel measure on the spherical unitary dual, which can be identified with
$\beta $
the density function for the Plancherel measure on the spherical unitary dual, which can be identified with
 $\mathfrak {a}^*_{\mathrm {un}}\big /W$
. Then
$\mathfrak {a}^*_{\mathrm {un}}\big /W$
. Then
![]() $\beta $
is a W-invariant function supported on
$\beta $
is a W-invariant function supported on
![]() $i\mathfrak {a}^*$
that can be described as a product of
$i\mathfrak {a}^*$
that can be described as a product of
![]() $\Gamma $
-functions [Reference Helgason17, Ch. IV, §6]. Following [Reference Lapid and Müller22], we put
$\Gamma $
-functions [Reference Helgason17, Ch. IV, §6]. Following [Reference Lapid and Müller22], we put
 $$ \begin{align*} \tilde\beta(t,\lambda)=\prod_{\alpha\in\Phi^+}\left(t+\left\lvert\left\langle \lambda,\alpha^\vee\right\rangle \right\rvert\right)^{\dim\mathfrak{g}_\alpha}, \quad \lambda\in i\mathfrak{a}^*, \ t\geq 1, \end{align*} $$
$$ \begin{align*} \tilde\beta(t,\lambda)=\prod_{\alpha\in\Phi^+}\left(t+\left\lvert\left\langle \lambda,\alpha^\vee\right\rangle \right\rvert\right)^{\dim\mathfrak{g}_\alpha}, \quad \lambda\in i\mathfrak{a}^*, \ t\geq 1, \end{align*} $$
and
 $\tilde \beta (\lambda )=\tilde \beta (1,\lambda )$
. From [Reference Helgason17, Ch. IV, Theorem 6.14] and standard estimates for the
$\tilde \beta (\lambda )=\tilde \beta (1,\lambda )$
. From [Reference Helgason17, Ch. IV, Theorem 6.14] and standard estimates for the
![]() $\Gamma $
-function, it follows that
$\Gamma $
-function, it follows that
 $\beta (\lambda )\ll \tilde \beta (\lambda )$
for all
$\beta (\lambda )\ll \tilde \beta (\lambda )$
for all
![]() $\lambda \in i\mathfrak {a}^*$
. Since
$\lambda \in i\mathfrak {a}^*$
. Since
 $$ \begin{align*} 1+\left\lvert\left\langle t\lambda +\mu,\alpha^\vee\right\rangle \right\rvert &\le 1+ t \left\lvert\left\langle \lambda ,\alpha^\vee\right\rangle \right\rvert + \left\lvert\left\langle\mu,\alpha^\vee\right\rangle \right\rvert \\ &\le t (1+ \lVert\lambda\rVert_2) +\left\lvert\left\langle\mu,\alpha^\vee\right\rangle \right\rvert \le (1+ \lVert\lambda\rVert_2)\left(t +\left\lvert\left\langle\mu,\alpha^\vee\right\rangle \right\rvert\right) \end{align*} $$
$$ \begin{align*} 1+\left\lvert\left\langle t\lambda +\mu,\alpha^\vee\right\rangle \right\rvert &\le 1+ t \left\lvert\left\langle \lambda ,\alpha^\vee\right\rangle \right\rvert + \left\lvert\left\langle\mu,\alpha^\vee\right\rangle \right\rvert \\ &\le t (1+ \lVert\lambda\rVert_2) +\left\lvert\left\langle\mu,\alpha^\vee\right\rangle \right\rvert \le (1+ \lVert\lambda\rVert_2)\left(t +\left\lvert\left\langle\mu,\alpha^\vee\right\rangle \right\rvert\right) \end{align*} $$
for all
![]() $\lambda ,\mu \in i\mathfrak {a}^*$
and
$\lambda ,\mu \in i\mathfrak {a}^*$
and
![]() $t\geq 1$
, we get
$t\geq 1$
, we get
 $$ \begin{align} \tilde\beta(t\lambda+\mu)\ll (1+\lVert\lambda\rVert_2)^{\dim\mathfrak{n}} \tilde\beta(t,\mu) \end{align} $$
$$ \begin{align} \tilde\beta(t\lambda+\mu)\ll (1+\lVert\lambda\rVert_2)^{\dim\mathfrak{n}} \tilde\beta(t,\mu) \end{align} $$
for all such
![]() $\lambda $
,
$\lambda $
,
![]() $\mu $
, and t.
$\mu $
, and t.
The Harish-Chandra
![]() $\mathbf {c}$
-function
$\mathbf {c}$
-function
![]() $\mathbf {c}:\mathfrak {a}^*_{\mathbb C}\longrightarrow {\mathbb C}$
for G asymptotically describes the behavior of the elementary spherical functions
$\mathbf {c}:\mathfrak {a}^*_{\mathbb C}\longrightarrow {\mathbb C}$
for G asymptotically describes the behavior of the elementary spherical functions
 $\phi _\lambda \left (e^H\right )$
of G as the group parameter H grows. The quantity
$\phi _\lambda \left (e^H\right )$
of G as the group parameter H grows. The quantity
![]() $\mathbf {c}(\lambda )$
depends only on the root system of G, and can be explicitly computed as described in [Reference Helgason17, Ch. IV, Theorem 6.14]. Up to normalization, the Plancherel density
$\mathbf {c}(\lambda )$
depends only on the root system of G, and can be explicitly computed as described in [Reference Helgason17, Ch. IV, Theorem 6.14]. Up to normalization, the Plancherel density
![]() $\beta (\lambda )$
equals
$\beta (\lambda )$
equals
![]() $\lvert \mathbf {c}(\lambda )\rvert ^{-2}$
for
$\lvert \mathbf {c}(\lambda )\rvert ^{-2}$
for
![]() $\lambda \in i\mathfrak {a}^*$
.
$\lambda \in i\mathfrak {a}^*$
.
3.3 Test functions
For
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
, let
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
, let
 $$ \begin{align*} \varphi_\lambda(g)=\int_K e^{\left\langle \lambda + \rho, H_0\left(kg\right)\right\rangle} dk \end{align*} $$
$$ \begin{align*} \varphi_\lambda(g)=\int_K e^{\left\langle \lambda + \rho, H_0\left(kg\right)\right\rangle} dk \end{align*} $$
denote the spherical function on G with spectral parameter
![]() $\lambda $
. Here
$\lambda $
. Here
![]() $H_0:G\longrightarrow \mathfrak {a}$
is the Iwasawa projection. Let
$H_0:G\longrightarrow \mathfrak {a}$
is the Iwasawa projection. Let
![]() $C^\infty _c(G // K)$
be the space of complex-valued bi-K-invariant functions on G. The Harish-Chandra transform of a function
$C^\infty _c(G // K)$
be the space of complex-valued bi-K-invariant functions on G. The Harish-Chandra transform of a function
![]() $k\in C^\infty _c(G // K)$
is defined to be
$k\in C^\infty _c(G // K)$
is defined to be
 $$ \begin{align*} \hat{k}(\lambda)=\int_G \varphi_\lambda(g) k(g)dg. \end{align*} $$
$$ \begin{align*} \hat{k}(\lambda)=\int_G \varphi_\lambda(g) k(g)dg. \end{align*} $$
For
![]() $t>0$
, let
$t>0$
, let
![]() $\mathscr {B}_t$
denote the ball of radius t centered at
$\mathscr {B}_t$
denote the ball of radius t centered at
![]() $0$
in
$0$
in
![]() $\mathfrak {a}$
with respect to the usual Euclidean norm
$\mathfrak {a}$
with respect to the usual Euclidean norm
![]() $\lVert \cdot \rVert _2$
. Let
$\lVert \cdot \rVert _2$
. Let
![]() $G_{\leq t}=K\exp \mathscr {B}_t K$
. Let
$G_{\leq t}=K\exp \mathscr {B}_t K$
. Let
![]() $C^\infty _c(G // K)_{\leq t}$
denote the space of smooth compactly supported bi-K-invariant functions on G, supported on
$C^\infty _c(G // K)_{\leq t}$
denote the space of smooth compactly supported bi-K-invariant functions on G, supported on
![]() $G_{\leq t}$
. Let
$G_{\leq t}$
. Let
![]() $\mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t$
denote the class of Paley–Wiener functions of exponential type t. The Paley–Wiener theorem with supports (see [Reference Gangolli13, Theorem 3.5]) states that the Harish-Chandra transform is a topological isomorphism
$\mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t$
denote the class of Paley–Wiener functions of exponential type t. The Paley–Wiener theorem with supports (see [Reference Gangolli13, Theorem 3.5]) states that the Harish-Chandra transform is a topological isomorphism
 $C^\infty _c(G // K)_{\leq t}\xrightarrow {\sim } \mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t^W$
of Fréchet spaces. The inverse map sends
$C^\infty _c(G // K)_{\leq t}\xrightarrow {\sim } \mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t^W$
of Fréchet spaces. The inverse map sends
 $h\in \mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t^W$
to
$h\in \mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t^W$
to
 $$ \begin{align*} \frac{1}{\lvert W\rvert}\int_{i\mathfrak{a}^*}h(\mu)\varphi_\mu(g)\beta(\mu)d\mu. \end{align*} $$
$$ \begin{align*} \frac{1}{\lvert W\rvert}\int_{i\mathfrak{a}^*}h(\mu)\varphi_\mu(g)\beta(\mu)d\mu. \end{align*} $$
In particular, for
![]() $k\in C_c^\infty (G // K)$
we have
$k\in C_c^\infty (G // K)$
we have
 $$ \begin{align} k(e)=\frac{1}{\lvert W\rvert}\int_{i\mathfrak{a}^*}\hat{k}(\mu)\beta(\mu)d\mu. \end{align} $$
$$ \begin{align} k(e)=\frac{1}{\lvert W\rvert}\int_{i\mathfrak{a}^*}\hat{k}(\mu)\beta(\mu)d\mu. \end{align} $$
We shall need a Paley–Wiener function concentrating about
![]() $\nu $
and verifying certain positivity properties.
$\nu $
and verifying certain positivity properties.
Lemma 3.1 [Reference Brumley and Marshall9, §4]
For
![]() $t\geq 1$
and
$t\geq 1$
and
![]() $\nu \in i\mathfrak {a}^*$
, there is
$\nu \in i\mathfrak {a}^*$
, there is
![]() whose Harish-Chandra transform
whose Harish-Chandra transform
 $h_{\nu ,t}\in \mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t^W$
satisfies the following:
$h_{\nu ,t}\in \mathscr {PW}\left (\mathfrak {a}^*_{\mathbb C}\right )_t^W$
satisfies the following:
-
(1)
 $h_{\nu ,t}$
is real and nonnegative on
$h_{\nu ,t}$
is real and nonnegative on
 $\mathfrak {a}^*_{\mathrm {hm}}$
.
$\mathfrak {a}^*_{\mathrm {hm}}$
. -
(2) For all
 $\lambda \in \mathfrak {a}^*_{\mathrm {un}}$
we have
$\lambda \in \mathfrak {a}^*_{\mathrm {un}}$
we have  $$ \begin{align*} h_{\nu,t}(\lambda)\ll_A (1+\lVert(\operatorname{Im}\lambda-\nu)/t\rVert_2)^{-A}. \end{align*} $$
$$ \begin{align*} h_{\nu,t}(\lambda)\ll_A (1+\lVert(\operatorname{Im}\lambda-\nu)/t\rVert_2)^{-A}. \end{align*} $$
-
(3) There are constants
 $0<c_1,c_2<1$
such that for
$0<c_1,c_2<1$
such that for
 $\lambda \in \mathfrak {a}_{\mathrm {un}}^*$
with
$\lambda \in \mathfrak {a}_{\mathrm {un}}^*$
with
 $\lVert \operatorname {Im}\lambda -\nu \rVert _2\leq c_1t$
, we have
$\lVert \operatorname {Im}\lambda -\nu \rVert _2\leq c_1t$
, we have
 $c_2\leq h_{\nu ,t}(\lambda )\leq 2$
.
$c_2\leq h_{\nu ,t}(\lambda )\leq 2$
. -
(4)
 $k_{\nu ,t}(g)\ll \tilde \beta (\nu )t^r(1+\lVert \nu \rVert _2 d(g,K))^{-1/2}$
, where
$k_{\nu ,t}(g)\ll \tilde \beta (\nu )t^r(1+\lVert \nu \rVert _2 d(g,K))^{-1/2}$
, where
 $r=\dim \mathfrak {a}$
.
$r=\dim \mathfrak {a}$
.
3.4 Proof of Proposition 2.1.
Recall that for
![]() $\nu \in i\mathfrak {a}^*$
and
$\nu \in i\mathfrak {a}^*$
and
![]() $c>0$
, we denote by
$c>0$
, we denote by
![]() $B(\nu , c)$
the ball
$B(\nu , c)$
the ball
![]() $\left \{\lambda \in \mathfrak {a}_{\mathbb C}^*\mid \lVert \lambda -\nu \rVert _2\le c\right \}$
in
$\left \{\lambda \in \mathfrak {a}_{\mathbb C}^*\mid \lVert \lambda -\nu \rVert _2\le c\right \}$
in
![]() $\mathfrak {a}_{\mathbb C}^*$
. Moreover, for any set
$\mathfrak {a}_{\mathbb C}^*$
. Moreover, for any set
![]() $\Omega \subseteq \mathfrak {a}^*_{\mathbb C}$
, we write
$\Omega \subseteq \mathfrak {a}^*_{\mathbb C}$
, we write
 $N(\Omega ,\Gamma _n)=\left \lvert \left \{j\mid \nu _j^{(n)}\in \Omega \right \}\right \rvert $
.
$N(\Omega ,\Gamma _n)=\left \lvert \left \{j\mid \nu _j^{(n)}\in \Omega \right \}\right \rvert $
.
In the notation of Lemma 3.1, we write
![]() $h_\nu =h_{\nu ,1}$
and
$h_\nu =h_{\nu ,1}$
and
![]() $k_\nu =k_{\nu ,1}$
. Then
$k_\nu =k_{\nu ,1}$
. Then
 $$ \begin{align*} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) = \operatorname{vol}(\Gamma_n\backslash G) k_\nu(1) + \int_{\Gamma_n\backslash G} \sum_{\substack{\gamma\in \Gamma_n\\\gamma \neq 1}} k_\nu\left(g^{-1}\gamma g\right) dg, \end{align*} $$
$$ \begin{align*} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) = \operatorname{vol}(\Gamma_n\backslash G) k_\nu(1) + \int_{\Gamma_n\backslash G} \sum_{\substack{\gamma\in \Gamma_n\\\gamma \neq 1}} k_\nu\left(g^{-1}\gamma g\right) dg, \end{align*} $$
where
![]() $\Lambda _n$
denotes the spectrum of
$\Lambda _n$
denotes the spectrum of
![]() $\Gamma _n\backslash G$
(each
$\Gamma _n\backslash G$
(each
![]() $\lambda $
appearing with its respective multiplicity).
$\lambda $
appearing with its respective multiplicity).
To deal with the second term, we use Lemma 3.1(4), as well as the support condition on
![]() $k_\nu $
, to deduce
$k_\nu $
, to deduce
 $$ \begin{align*} \int_{\Gamma_n\backslash G} \sum_{\substack{\gamma\in \Gamma_n\\\gamma \neq 1}} k_\nu\left(g^{-1}\gamma g\right) dg\ll \tilde\beta(\nu)\int_{\Gamma_n\backslash G} \lvert\{\gamma\in \Gamma_n\smallsetminus\{1\}: d(g,\gamma g)\leq 1\}\rvert dg. \end{align*} $$
$$ \begin{align*} \int_{\Gamma_n\backslash G} \sum_{\substack{\gamma\in \Gamma_n\\\gamma \neq 1}} k_\nu\left(g^{-1}\gamma g\right) dg\ll \tilde\beta(\nu)\int_{\Gamma_n\backslash G} \lvert\{\gamma\in \Gamma_n\smallsetminus\{1\}: d(g,\gamma g)\leq 1\}\rvert dg. \end{align*} $$
As
![]() $\Gamma _n$
is torsion free, the inner sum is empty for all
$\Gamma _n$
is torsion free, the inner sum is empty for all
![]() $g\in (\Gamma _n\backslash G)_{>1}$
, so that it suffices to bound
$g\in (\Gamma _n\backslash G)_{>1}$
, so that it suffices to bound
 $$ \begin{align*} \int_{(\Gamma_n\backslash G)_{\leq 1}} N_R(g)dg, \end{align*} $$
$$ \begin{align*} \int_{(\Gamma_n\backslash G)_{\leq 1}} N_R(g)dg, \end{align*} $$
where
For
![]() $g\in (\Gamma _n\backslash G)_{\leq 1}$
we apply [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, Lemma 6.18], which provides a constant
$g\in (\Gamma _n\backslash G)_{\leq 1}$
we apply [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, Lemma 6.18], which provides a constant
![]() $C>0$
, depending only on G, such that
$C>0$
, depending only on G, such that
 $N_R(g)\leq C \operatorname {InjRad}_{\Gamma _n}(g)^{-\dim S}$
. The uniform discreteness of the (torsion-free)
$N_R(g)\leq C \operatorname {InjRad}_{\Gamma _n}(g)^{-\dim S}$
. The uniform discreteness of the (torsion-free)
![]() $\Gamma _n$
implies that
$\Gamma _n$
implies that
 $\operatorname {InjRad}_{\Gamma _n}(g)^{-1} \ll 1$
, uniformly in n and g. Taking these estimates together, we get
$\operatorname {InjRad}_{\Gamma _n}(g)^{-1} \ll 1$
, uniformly in n and g. Taking these estimates together, we get
 $$ \begin{align} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) =\operatorname{vol}(\Gamma_n\backslash G)k_\nu(1) +O\left(\tilde\beta(\nu)\operatorname{vol}(\Gamma_n\backslash G)_{\leq 1}\right). \end{align} $$
$$ \begin{align} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) =\operatorname{vol}(\Gamma_n\backslash G)k_\nu(1) +O\left(\tilde\beta(\nu)\operatorname{vol}(\Gamma_n\backslash G)_{\leq 1}\right). \end{align} $$
Furthermore, we have
 $$ \begin{align} k_\nu(1)\asymp_\epsilon \tilde\beta(\nu), \end{align} $$
$$ \begin{align} k_\nu(1)\asymp_\epsilon \tilde\beta(\nu), \end{align} $$
where only the lower bound depends on
![]() $\varepsilon $
. Indeed, the upper bound results from Lemma 3.1(4). To obtain the lower bound, one applies the Plancherel inversion formula (25) and Lemma 3.1(1) and (3) to get
$\varepsilon $
. Indeed, the upper bound results from Lemma 3.1(4). To obtain the lower bound, one applies the Plancherel inversion formula (25) and Lemma 3.1(1) and (3) to get
 $$ \begin{align*} k_\nu(1)\geq \int_{\substack{\lambda\in i\mathfrak{a}^*\\ \lVert\lambda-\nu\rVert_2\leq\delta}} h_\nu(\lambda)\beta(\lambda)d\lambda\geq c_2\int_{\substack{\lambda\in i\mathfrak{a}^*\\ \lVert\lambda-\nu\rVert_2\leq\delta}}\beta(\lambda)d\lambda, \end{align*} $$
$$ \begin{align*} k_\nu(1)\geq \int_{\substack{\lambda\in i\mathfrak{a}^*\\ \lVert\lambda-\nu\rVert_2\leq\delta}} h_\nu(\lambda)\beta(\lambda)d\lambda\geq c_2\int_{\substack{\lambda\in i\mathfrak{a}^*\\ \lVert\lambda-\nu\rVert_2\leq\delta}}\beta(\lambda)d\lambda, \end{align*} $$
for any
![]() $0<\delta <c_1$
. Recall that
$0<\delta <c_1$
. Recall that
![]() $\nu \in i\mathfrak {a}^*$
is
$\nu \in i\mathfrak {a}^*$
is
![]() $\varepsilon $
-regular. Taking
$\varepsilon $
-regular. Taking
![]() $\delta $
small enough, we may assume that the
$\delta $
small enough, we may assume that the
![]() $\lambda \in i\mathfrak {a}^*$
such that
$\lambda \in i\mathfrak {a}^*$
such that
![]() $\lVert \lambda -\nu \rVert _2\leq \delta $
are
$\lVert \lambda -\nu \rVert _2\leq \delta $
are
![]() $\varepsilon /2$
-regular. Then the lower bound follows from the inequality
$\varepsilon /2$
-regular. Then the lower bound follows from the inequality
 $\beta (\lambda )\gg _\varepsilon \tilde \beta (\lambda )$
for such
$\beta (\lambda )\gg _\varepsilon \tilde \beta (\lambda )$
for such
![]() $\lambda $
(see [Reference Duistermaat, Kolk and Varadarajan12, (3.44a)]).
$\lambda $
(see [Reference Duistermaat, Kolk and Varadarajan12, (3.44a)]).
From formulas (27) and (28), it follows that
 $$ \begin{align*} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) \asymp_\varepsilon \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\left(1+O\left(\frac{\operatorname{vol}(\Gamma_n\backslash G)_{\leq 1}}{\operatorname{vol}(\Gamma_n\backslash G)}\right)\right), \end{align*} $$
$$ \begin{align*} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) \asymp_\varepsilon \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\left(1+O\left(\frac{\operatorname{vol}(\Gamma_n\backslash G)_{\leq 1}}{\operatorname{vol}(\Gamma_n\backslash G)}\right)\right), \end{align*} $$
where only the lower bound depends on
![]() $\varepsilon $
. By the Benjamini–Schramm assumption, we have
$\varepsilon $
. By the Benjamini–Schramm assumption, we have
![]() $\operatorname {vol}(\Gamma _n\backslash G)_{\leq 1}=o(\operatorname {vol}(\Gamma _n\backslash G))$
as
$\operatorname {vol}(\Gamma _n\backslash G)_{\leq 1}=o(\operatorname {vol}(\Gamma _n\backslash G))$
as
![]() $n\rightarrow \infty $
. Thus for n large enough we have
$n\rightarrow \infty $
. Thus for n large enough we have
 $$ \begin{align} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) \asymp_\varepsilon \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu). \end{align} $$
$$ \begin{align} \sum_{\lambda\in \Lambda_n}h_\nu(\lambda) \asymp_\varepsilon \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu). \end{align} $$
For the first bound in formula (6), it suffices at this point to take
![]() $\varrho _1=c_1$
, apply Lemma 3.1(1) and (3), and then quote the upper bound in formula (29) to get
$\varrho _1=c_1$
, apply Lemma 3.1(1) and (3), and then quote the upper bound in formula (29) to get
 $$ \begin{align*} N(B(\nu,c_1),\Gamma_n)\leq c_2 \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\lambda-\nu\rVert_2\leq c_1}}h_\nu(\lambda)\leq c_2\sum_{\lambda\in \Lambda_n}h_\nu(\lambda) \ll \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu). \end{align*} $$
$$ \begin{align*} N(B(\nu,c_1),\Gamma_n)\leq c_2 \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\lambda-\nu\rVert_2\leq c_1}}h_\nu(\lambda)\leq c_2\sum_{\lambda\in \Lambda_n}h_\nu(\lambda) \ll \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu). \end{align*} $$
For the second bound in formula (6), we must show that the left-hand side in formula (29) approximates
![]() $N(B(\nu ,\varrho ),\Gamma _n)$
, for some
$N(B(\nu ,\varrho ),\Gamma _n)$
, for some
![]() $\varrho>0$
.
$\varrho>0$
.
A crucial ingredient for passing from a smooth count as before to a sharp count will be a good upper bound on
![]() $N(B(\mu ,t),\Gamma _n)$
, for any center
$N(B(\mu ,t),\Gamma _n)$
, for any center
![]() $\mu \in i\mathfrak {a}^*$
and any
$\mu \in i\mathfrak {a}^*$
and any
![]() $t\geq 1$
. This is proved similarly to the preceding analysis. Indeed, from Lemma 3.1 and the preceding geometric argument, we obtain
$t\geq 1$
. This is proved similarly to the preceding analysis. Indeed, from Lemma 3.1 and the preceding geometric argument, we obtain
 $$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\\lVert\operatorname{Im}\lambda-\mu\rVert_2\leq t}} 1\ll \sum_{\lambda\in\Lambda_n}h_{\mu,c_1^{-1}t}(\lambda)=\operatorname{vol}(\Gamma_n\backslash G) k_{\mu,c_1^{-1}t}(1) + o\left(\operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\mu) t^r \right). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\\lVert\operatorname{Im}\lambda-\mu\rVert_2\leq t}} 1\ll \sum_{\lambda\in\Lambda_n}h_{\mu,c_1^{-1}t}(\lambda)=\operatorname{vol}(\Gamma_n\backslash G) k_{\mu,c_1^{-1}t}(1) + o\left(\operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\mu) t^r \right). \end{align*} $$
Now
 $k_{\mu ,t}(1)\ll \tilde \beta (\mu )t^r$
from Lemma 3.1(4). We conclude that (for n large enough)
$k_{\mu ,t}(1)\ll \tilde \beta (\mu )t^r$
from Lemma 3.1(4). We conclude that (for n large enough)
 $$ \begin{align} N(B'(\mu,t),\Gamma_n)\ll \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\mu)t^r, \end{align} $$
$$ \begin{align} N(B'(\mu,t),\Gamma_n)\ll \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\mu)t^r, \end{align} $$
where
![]() $B'(\mu ,t)=\left \{\lambda \in \mathfrak {a}^*_{\mathbb C}\mid \lVert \operatorname {Im} \lambda - \mu \rVert _2\le t\right \}$
. We now return to the left-hand side of formula (29). We first claim the following:
$B'(\mu ,t)=\left \{\lambda \in \mathfrak {a}^*_{\mathbb C}\mid \lVert \operatorname {Im} \lambda - \mu \rVert _2\le t\right \}$
. We now return to the left-hand side of formula (29). We first claim the following:
Lemma 3.2. For every
![]() $\varrho>1$
,
$\varrho>1$
,
 $$ \begin{align} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im} \lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda) \ll_A \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\varrho^{-A}. \end{align} $$
$$ \begin{align} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im} \lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda) \ll_A \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\varrho^{-A}. \end{align} $$
Proof. To prove formula (31) we cover
![]() $\{\lambda \in i\mathfrak {a}^*: \lVert \lambda -\nu \rVert _2>\varrho \}$
by balls of unit radius with centers based at an affine lattice
$\{\lambda \in i\mathfrak {a}^*: \lVert \lambda -\nu \rVert _2>\varrho \}$
by balls of unit radius with centers based at an affine lattice
![]() $\Lambda \subset i\mathfrak {a}^*$
containing
$\Lambda \subset i\mathfrak {a}^*$
containing
![]() $\nu $
. Let
$\nu $
. Let
![]() $A(\nu ,\varrho )$
denote the set of all
$A(\nu ,\varrho )$
denote the set of all
![]() $\lambda \in \Lambda $
such that the ball of radius
$\lambda \in \Lambda $
such that the ball of radius
![]() $1$
in
$1$
in
![]() $i\mathfrak {a}^*$
around
$i\mathfrak {a}^*$
around
![]() $\lambda $
is entirely contained in the ball of radius
$\lambda $
is entirely contained in the ball of radius
![]() $\varrho $
in
$\varrho $
in
![]() $i\mathfrak {a}^*$
around
$i\mathfrak {a}^*$
around
![]() $\nu $
.
$\nu $
.
For any fixed
![]() $\mu \in \Lambda -A(\nu ,\varrho )$
, we bound the contribution of
$\mu \in \Lambda -A(\nu ,\varrho )$
, we bound the contribution of
![]() $\lambda \in \Lambda _n$
for which
$\lambda \in \Lambda _n$
for which
![]() $\operatorname {Im}\lambda \in B(\mu )$
by using Lemma 3.1(2) to get
$\operatorname {Im}\lambda \in B(\mu )$
by using Lemma 3.1(2) to get
 $$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im}\lambda-\mu\rVert_2\leq 1}}h_\nu(\lambda) \ll_A (1+\lVert\mu-\nu\rVert_2)^{-A}N(B'(\mu,1),\Gamma_n). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im}\lambda-\mu\rVert_2\leq 1}}h_\nu(\lambda) \ll_A (1+\lVert\mu-\nu\rVert_2)^{-A}N(B'(\mu,1),\Gamma_n). \end{align*} $$
Using formula (30) with
![]() $t=1$
and summing over
$t=1$
and summing over
![]() $\mu \in \Lambda - A(\nu , \varrho )$
we get
$\mu \in \Lambda - A(\nu , \varrho )$
we get
 $$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im}\lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda)\ll_A \operatorname{vol}(\Gamma_n\backslash G)\sum_{\mu\in\Lambda- A\left(\nu, \varrho\right)} (1+\lVert\mu-\nu\rVert_2)^{-A}\tilde\beta(\mu). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im}\lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda)\ll_A \operatorname{vol}(\Gamma_n\backslash G)\sum_{\mu\in\Lambda- A\left(\nu, \varrho\right)} (1+\lVert\mu-\nu\rVert_2)^{-A}\tilde\beta(\mu). \end{align*} $$
Now by formula (24) we have
 $\tilde \beta (\mu )\ll (1+\lVert \mu -\nu \rVert _2)^{\dim {\mathfrak n}}\tilde \beta (\nu )$
, so that
$\tilde \beta (\mu )\ll (1+\lVert \mu -\nu \rVert _2)^{\dim {\mathfrak n}}\tilde \beta (\nu )$
, so that
 $$ \begin{align*} \sum_{\lVert\operatorname{Im} \lambda-\nu\rVert_2>\varrho}h_\nu(\lambda)\ll_A \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\sum_{\mu\in\Lambda-A\left(\nu,\varrho\right)}(1+\lVert\mu-\nu\rVert_2)^{-A + \dim {\mathfrak n}}. \end{align*} $$
$$ \begin{align*} \sum_{\lVert\operatorname{Im} \lambda-\nu\rVert_2>\varrho}h_\nu(\lambda)\ll_A \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\sum_{\mu\in\Lambda-A\left(\nu,\varrho\right)}(1+\lVert\mu-\nu\rVert_2)^{-A + \dim {\mathfrak n}}. \end{align*} $$
For
![]() $\varrho $
sufficiently large, this last sum is at most
$\varrho $
sufficiently large, this last sum is at most
 $O_A\left (\varrho ^{-A + \dim {\mathfrak n}}\right )$
, as desired.
$O_A\left (\varrho ^{-A + \dim {\mathfrak n}}\right )$
, as desired.
From this lemma, we want to deduce the following estimate:
 $$ \begin{align} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda) \ll_A \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\varrho^{-A}. \end{align} $$
$$ \begin{align} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda) \ll_A \operatorname{vol}(\Gamma_n\backslash G)\tilde\beta(\nu)\varrho^{-A}. \end{align} $$
For this we split the sum on the left-hand side into three parts:
 $$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im} \lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda) + \sum_{\substack{\lambda\in\Lambda_n\\ \varrho^2-\lVert\rho\rVert_2^2< \lVert\operatorname{Im}\lambda-\nu\rVert_2^2\le \varrho^2 \\ \lVert\operatorname{Re} \lambda\rVert_2^2> \varrho^2-\lVert\operatorname{Im}\lambda-\nu\rVert_2^2 }}h_\nu(\lambda) + \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im} \lambda-\nu\rVert_2^2\le \varrho^2-\lVert\rho\rVert_2^2 \\ \lVert\operatorname{Re} \lambda\rVert_2^2> \varrho^2-\lVert\operatorname{Im}\lambda-\nu\rVert_2^2 }}h_\nu(\lambda). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im} \lambda-\nu\rVert_2>\varrho}}h_\nu(\lambda) + \sum_{\substack{\lambda\in\Lambda_n\\ \varrho^2-\lVert\rho\rVert_2^2< \lVert\operatorname{Im}\lambda-\nu\rVert_2^2\le \varrho^2 \\ \lVert\operatorname{Re} \lambda\rVert_2^2> \varrho^2-\lVert\operatorname{Im}\lambda-\nu\rVert_2^2 }}h_\nu(\lambda) + \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\operatorname{Im} \lambda-\nu\rVert_2^2\le \varrho^2-\lVert\rho\rVert_2^2 \\ \lVert\operatorname{Re} \lambda\rVert_2^2> \varrho^2-\lVert\operatorname{Im}\lambda-\nu\rVert_2^2 }}h_\nu(\lambda). \end{align*} $$
Using Lemma 3.2, the first sum can be bounded by
 $\ll _A \operatorname {vol}(\Gamma _n\backslash G) \tilde \beta (\nu ) \varrho ^{-A}$
. The third sum is in fact empty: The conditions on the real and complex parts of
$\ll _A \operatorname {vol}(\Gamma _n\backslash G) \tilde \beta (\nu ) \varrho ^{-A}$
. The third sum is in fact empty: The conditions on the real and complex parts of
![]() $\lambda $
imply that
$\lambda $
imply that
![]() $\lVert \operatorname {Re}\lambda \rVert _2> \lVert \rho \rVert _2$
, which is not possible for
$\lVert \operatorname {Re}\lambda \rVert _2> \lVert \rho \rVert _2$
, which is not possible for
![]() $\lambda $
in the spectrum of
$\lambda $
in the spectrum of
![]() $L^2(\Gamma _n\backslash G)$
, by formula (23). Finally, for the second term, we extend the sum to all
$L^2(\Gamma _n\backslash G)$
, by formula (23). Finally, for the second term, we extend the sum to all
![]() $\lambda \in \Lambda _n$
with
$\lambda \in \Lambda _n$
with
![]() $\lVert \operatorname {Im} \lambda -\nu \rVert _2^2\ge \varrho ^2-\lVert \rho \rVert _2^2$
. This is possible because
$\lVert \operatorname {Im} \lambda -\nu \rVert _2^2\ge \varrho ^2-\lVert \rho \rVert _2^2$
. This is possible because
![]() $h_\nu (\lambda )$
is nonzero on the unitary spectrum, by Lemma 3.1. Hence we can use Lemma 3.2 to bound this term by
$h_\nu (\lambda )$
is nonzero on the unitary spectrum, by Lemma 3.1. Hence we can use Lemma 3.2 to bound this term by
 $\ll _A \left (\varrho ^2-\lVert \rho \rVert _2^2\right )^{-A/2}$
.
$\ll _A \left (\varrho ^2-\lVert \rho \rVert _2^2\right )^{-A/2}$
.
We deduce from the lower bound in formula (29), as well as from formula (32) that with
![]() $A>1$
fixed and
$A>1$
fixed and
![]() $\varrho $
large enough with respect to the implied constant,
$\varrho $
large enough with respect to the implied constant,
 $$ \begin{align*} \sum_{\substack{\lambda\in \Lambda_n\\\lVert\lambda-\nu\rVert_2\leq \varrho}}h_\nu(\lambda)\gg_\varepsilon \operatorname{vol}(\Gamma_n\backslash G) \tilde\beta(\nu). \end{align*} $$
$$ \begin{align*} \sum_{\substack{\lambda\in \Lambda_n\\\lVert\lambda-\nu\rVert_2\leq \varrho}}h_\nu(\lambda)\gg_\varepsilon \operatorname{vol}(\Gamma_n\backslash G) \tilde\beta(\nu). \end{align*} $$
On the other hand, by applying Lemma 3.1(3) we have
 $$ \begin{align*} N(B(\nu,\varrho),\Gamma_n)\gg \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\lambda-\nu\rVert_2\leq \varrho}}h_\nu(\lambda). \end{align*} $$
$$ \begin{align*} N(B(\nu,\varrho),\Gamma_n)\gg \sum_{\substack{\lambda\in\Lambda_n\\ \lVert\lambda-\nu\rVert_2\leq \varrho}}h_\nu(\lambda). \end{align*} $$
Combing these yields the second bound in formula (6), with
![]() $\varrho _2=\varrho $
. □
$\varrho _2=\varrho $
. □
4 Spectral side
We now return to the setting of
![]() $G=\operatorname {SL}_d({\mathbb R})$
and prove Theorem 2.2. In the course of the proof, we will make use of both Appendices A and B.
$G=\operatorname {SL}_d({\mathbb R})$
and prove Theorem 2.2. In the course of the proof, we will make use of both Appendices A and B.
We first examine how
![]() $k_t$
acts on eigenfunctions
$k_t$
acts on eigenfunctions
![]() $\psi _\lambda $
. The Harish-Chandra transform of
$\psi _\lambda $
. The Harish-Chandra transform of
![]() $k_t$
is given by
$k_t$
is given by
 $$ \begin{align} h_t(\lambda)=\frac{1}{\sqrt{m_G(E_t)}}\int_{E_t} \varphi_\lambda(g)\, dg. \end{align} $$
$$ \begin{align} h_t(\lambda)=\frac{1}{\sqrt{m_G(E_t)}}\int_{E_t} \varphi_\lambda(g)\, dg. \end{align} $$
Then, recalling the definition (9), we have
which follows from the doubling formula of elementary spherical functions.
Let
![]() $\mathbf {A}(\tau )$
be the time-averaging operator of equation (10). Since
$\mathbf {A}(\tau )$
be the time-averaging operator of equation (10). Since
![]() $k_t$
is self-adjoint, we have
$k_t$
is self-adjoint, we have
 $$ \begin{align*} \left|\langle \textbf{ A}(\tau)\psi_\lambda , \psi_\lambda\rangle_{L^2(Y)}\right|{}^2=\left(\frac{1}{\tau}\int_0^\tau \lvert h_t(\lambda)\rvert^2 dt\right)^2 \left\lvert\langle a\psi_\lambda, \psi_\lambda\rangle_{L^2(Y)}\right\rvert^2. \end{align*} $$
$$ \begin{align*} \left|\langle \textbf{ A}(\tau)\psi_\lambda , \psi_\lambda\rangle_{L^2(Y)}\right|{}^2=\left(\frac{1}{\tau}\int_0^\tau \lvert h_t(\lambda)\rvert^2 dt\right)^2 \left\lvert\langle a\psi_\lambda, \psi_\lambda\rangle_{L^2(Y)}\right\rvert^2. \end{align*} $$
To prove Theorem 2.2, it will therefore be enough to show that
![]() $\lvert h_t(\lambda )\rvert $
is bounded away from
$\lvert h_t(\lambda )\rvert $
is bounded away from
![]() $0$
on average over t. More precisely, we prove the following higher-rank generalization of [Reference Abert, Bergeron and Le Masson2, §8.1]:
$0$
on average over t. More precisely, we prove the following higher-rank generalization of [Reference Abert, Bergeron and Le Masson2, §8.1]:
Proposition 4.1. Let
![]() $G=\operatorname {SL}_d({\mathbb R})$
. Given a compact nonempty set
$G=\operatorname {SL}_d({\mathbb R})$
. Given a compact nonempty set
![]() $\Omega \subseteq i\mathfrak {a}^*$
, there exist constants
$\Omega \subseteq i\mathfrak {a}^*$
, there exist constants
![]() $C,\tau _0>0$
, depending on
$C,\tau _0>0$
, depending on
![]() $\Omega $
, such that for every
$\Omega $
, such that for every
![]() $\tau \ge \tau _0$
and
$\tau \ge \tau _0$
and
![]() $\lambda \in \Omega $
,
$\lambda \in \Omega $
,
 $$ \begin{align*} \frac{1}{\tau}\int_0^\tau \lvert h_t(\lambda)\rvert^2 dt \ge C. \end{align*} $$
$$ \begin{align*} \frac{1}{\tau}\int_0^\tau \lvert h_t(\lambda)\rvert^2 dt \ge C. \end{align*} $$
4.1 Main idea of proof
We begin by writing the integral defining
![]() $h_t$
in polar coordinates, according to the Cartan decomposition. Recall the averaging set
$h_t$
in polar coordinates, according to the Cartan decomposition. Recall the averaging set
![]() $E_t$
from §2.2 and its polar decomposition (15). Letting
$E_t$
from §2.2 and its polar decomposition (15). Letting
 $f_\lambda (X)=e^{\left \langle \rho ,X\right \rangle }\varphi _\lambda \left (e^X\right )$
, and using the Cartan measure decomposition (21), we find that equation (33) becomes
$f_\lambda (X)=e^{\left \langle \rho ,X\right \rangle }\varphi _\lambda \left (e^X\right )$
, and using the Cartan measure decomposition (21), we find that equation (33) becomes
 $$ \begin{align} h_t(\lambda)=\frac{c_C}{\sqrt{m_G(E_t)}}\int_{\mathscr{P}_t^+} f_\lambda(X)J(X)e^{-\left\langle\rho,X\right\rangle}dX. \end{align} $$
$$ \begin{align} h_t(\lambda)=\frac{c_C}{\sqrt{m_G(E_t)}}\int_{\mathscr{P}_t^+} f_\lambda(X)J(X)e^{-\left\langle\rho,X\right\rangle}dX. \end{align} $$
The idea of the proof of Proposition 4.1 is to replace
![]() $f_\lambda $
by the main term
$f_\lambda $
by the main term
![]() $\Phi _\lambda $
, discussed later, of its Harish-Chandra asymptotic expansion relative to the Levi determined by
$\Phi _\lambda $
, discussed later, of its Harish-Chandra asymptotic expansion relative to the Levi determined by
![]() $X^0$
, defined in equation (17). We do this by showing in Appendix A (see Lemma A.2) that
$X^0$
, defined in equation (17). We do this by showing in Appendix A (see Lemma A.2) that
![]() $\mathscr {P}^+$
is the intersection with
$\mathscr {P}^+$
is the intersection with
![]() $\overline {\mathfrak {a}^+}$
of a translated cone
$\overline {\mathfrak {a}^+}$
of a translated cone
![]() $\mathscr {C}=X^0+\mathscr {C}^0$
in
$\mathscr {C}=X^0+\mathscr {C}^0$
in
![]() $\mathfrak {a}$
. We then show that when
$\mathfrak {a}$
. We then show that when
![]() $\lambda $
is taken to be rational,
$\lambda $
is taken to be rational,
![]() $\Phi _\lambda $
behaves like a sum of characters in the direction of
$\Phi _\lambda $
behaves like a sum of characters in the direction of
![]() $X^0$
. An argument using linear independence of characters then yields the result. We carry out this argument in this section, using some combinatorial results which we establish in Appendix B.
$X^0$
. An argument using linear independence of characters then yields the result. We carry out this argument in this section, using some combinatorial results which we establish in Appendix B.
4.2 The main term and periodicity
We wish to replace
![]() $f_\lambda $
by the main term in its Harish-Chandra expansion. This is possible thanks to Proposition 4.2. To state it, we must introduce some notation beyond that of §3.1. For simplicity, we continue to take
$f_\lambda $
by the main term in its Harish-Chandra expansion. This is possible thanks to Proposition 4.2. To state it, we must introduce some notation beyond that of §3.1. For simplicity, we continue to take
![]() $G=\operatorname {SL}_d({\mathbb R})$
, although Proposition 4.2 applies more generally.
$G=\operatorname {SL}_d({\mathbb R})$
, although Proposition 4.2 applies more generally.
A Levi subgroup of G will be called semistandard if it contains A. Let
![]() $\Delta _0\subseteq \Delta $
be a (possibly empty) subset of the set of simple roots, and let
$\Delta _0\subseteq \Delta $
be a (possibly empty) subset of the set of simple roots, and let
![]() $\Phi ^+_0$
be the subset of
$\Phi ^+_0$
be the subset of
![]() $\Phi ^+$
generated by
$\Phi ^+$
generated by
![]() $\Delta _0$
. The sets
$\Delta _0$
. The sets
![]() $\Delta _0$
correspond to semistandard Levi subgroups
$\Delta _0$
correspond to semistandard Levi subgroups
![]() $M\subseteq G$
such that
$M\subseteq G$
such that
![]() $\Phi ^+_0$
is the set of positive roots of A on M. With this identification,
$\Phi ^+_0$
is the set of positive roots of A on M. With this identification,
![]() $\Delta _0=\emptyset $
corresponds to
$\Delta _0=\emptyset $
corresponds to
![]() $M=A$
and
$M=A$
and
![]() $\Delta _0=\Delta $
to
$\Delta _0=\Delta $
to
![]() $M=G$
.
$M=G$
.
For fixed
![]() $\Delta _0$
and corresponding M, we further introduce the following notation:
$\Delta _0$
and corresponding M, we further introduce the following notation:
-
•
 $\rho ^M$
is the half-sum of all
$\rho ^M$
is the half-sum of all
 $\alpha \in \Phi _0^+$
;
$\alpha \in \Phi _0^+$
; -
•
 $W^M$
is the Weyl group of A in M;
$W^M$
is the Weyl group of A in M; -
•
 $\mathbf {c}^M$
denotes the Harish-Chandra
$\mathbf {c}^M$
denotes the Harish-Chandra
 $\mathbf {c}$
-function for
$\mathbf {c}$
-function for
 $\Phi _0^+$
;
$\Phi _0^+$
; -
•
 $\varphi ^M_\lambda $
is the spherical function on M for
$\varphi ^M_\lambda $
is the spherical function on M for
 $\lambda \in \mathfrak {a}_{\mathbb C}^*$
– that is,
$\lambda \in \mathfrak {a}_{\mathbb C}^*$
– that is,  $$ \begin{align*} \varphi^M_\lambda(m)= \int_{K\cap M} e^{\left\langle \lambda + \rho^M, H_0(km)\right\rangle} dk; \end{align*} $$
$$ \begin{align*} \varphi^M_\lambda(m)= \int_{K\cap M} e^{\left\langle \lambda + \rho^M, H_0(km)\right\rangle} dk; \end{align*} $$
-
• for
 $X\in \mathfrak {a}$
,
$X\in \mathfrak {a}$
,
 $\lambda \in \mathfrak {a}_{\mathbb C}^*$
, and
$\lambda \in \mathfrak {a}_{\mathbb C}^*$
, and
 $t>0$
, let
$t>0$
, let
 $f_\lambda ^M(t,X)= e^{\left \langle \rho ^M,tX\right \rangle } \varphi _\lambda ^M\left (e^{tX}\right )$
and (setting
$f_\lambda ^M(t,X)= e^{\left \langle \rho ^M,tX\right \rangle } \varphi _\lambda ^M\left (e^{tX}\right )$
and (setting
 $t=1$
) let
$t=1$
) let  $$ \begin{align*} f_\lambda^M(X)=e^{\left\langle \rho^M,X\right\rangle} \varphi_\lambda^M\left(e^X\right); \end{align*} $$
$$ \begin{align*} f_\lambda^M(X)=e^{\left\langle \rho^M,X\right\rangle} \varphi_\lambda^M\left(e^X\right); \end{align*} $$
-
•
 $\mathfrak {a}_M$
is the common null space of all
$\mathfrak {a}_M$
is the common null space of all
 $\alpha \in \Phi _0^+$
, and
$\alpha \in \Phi _0^+$
, and
 $\mathfrak {a}^M$
is its orthocomplement in
$\mathfrak {a}^M$
is its orthocomplement in
 $\mathfrak {a}$
relative to the inner product
$\mathfrak {a}$
relative to the inner product
 $\langle X, Y\rangle =\operatorname {tr} XY$
.
$\langle X, Y\rangle =\operatorname {tr} XY$
.
We follow the standard practice of omitting the superscript M from the notation whenever
![]() $M=G$
. In this way we recover the
$M=G$
. In this way we recover the
![]() $f_\lambda (X)$
introduced earlier. Other than G, the only Levi which will be of importance to us throughout this section is the centralizer of
$f_\lambda (X)$
introduced earlier. Other than G, the only Levi which will be of importance to us throughout this section is the centralizer of
![]() $X^0$
in G. Henceforth, we shall take M to be the centralizer of
$X^0$
in G. Henceforth, we shall take M to be the centralizer of
![]() $X^0$
in G, and
$X^0$
in G, and
![]() $\Delta _0$
such that it corresponds to M. In this case,
$\Delta _0$
such that it corresponds to M. In this case,
![]() $X^0\in \mathfrak {a}_M$
.
$X^0\in \mathfrak {a}_M$
.
For
![]() $\lambda \in i\mathfrak {a}^*$
regular, we define
$\lambda \in i\mathfrak {a}^*$
regular, we define
 $$ \begin{align} \Phi_\lambda(X) = \sum_{w\in W^M\backslash W} \frac{\textbf{ c}(w\lambda)}{\textbf{ c}^M(w\lambda)} f^M_{w\lambda}(X). \end{align} $$
$$ \begin{align} \Phi_\lambda(X) = \sum_{w\in W^M\backslash W} \frac{\textbf{ c}(w\lambda)}{\textbf{ c}^M(w\lambda)} f^M_{w\lambda}(X). \end{align} $$
In fact, we can define
![]() $\Phi _\lambda (X)$
for any regular
$\Phi _\lambda (X)$
for any regular
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
for which the
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
for which the
![]() $\mathbf {c}(w\lambda )$
do not have a pole. We can make this more precise, as follows. For a real number
$\mathbf {c}(w\lambda )$
do not have a pole. We can make this more precise, as follows. For a real number
![]() $\eta>0$
, let
$\eta>0$
, let
![]() $A_\eta \subseteq \mathfrak {a}^*$
denote the convex hull of the Weyl group orbit of
$A_\eta \subseteq \mathfrak {a}^*$
denote the convex hull of the Weyl group orbit of
![]() $\eta \rho $
. Define
$\eta \rho $
. Define
![]() ${\mathscr T}_\eta \subseteq \mathfrak {a}^*_{\mathbb C}$
to be the set of all
${\mathscr T}_\eta \subseteq \mathfrak {a}^*_{\mathbb C}$
to be the set of all
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
with
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
with
![]() $\operatorname {Re}\lambda \in A_\eta $
. Let
$\operatorname {Re}\lambda \in A_\eta $
. Let
![]() $\eta $
be so small that for every positive root
$\eta $
be so small that for every positive root
![]() $\alpha $
and all
$\alpha $
and all
![]() $\lambda \in {\mathscr T}_\eta $
, we have
$\lambda \in {\mathscr T}_\eta $
, we have
![]() $\left \langle \operatorname {Re}\lambda , \alpha ^\vee \right \rangle \not \in {\mathbb Z}\smallsetminus \{0\}$
. We fix such a
$\left \langle \operatorname {Re}\lambda , \alpha ^\vee \right \rangle \not \in {\mathbb Z}\smallsetminus \{0\}$
. We fix such a
![]() $0<\eta <1$
from now on (we will make our choice more precise later). Note that
$0<\eta <1$
from now on (we will make our choice more precise later). Note that
![]() ${\mathscr T}_\eta $
is W-invariant by construction. We may extend the definition of
${\mathscr T}_\eta $
is W-invariant by construction. We may extend the definition of
![]() $\Phi _\lambda (X)$
in equation (35) to
$\Phi _\lambda (X)$
in equation (35) to
![]() $\lambda \in {\mathscr T}_\eta $
regular and
$\lambda \in {\mathscr T}_\eta $
regular and
![]() $X\in \mathfrak {a}$
. Indeed, the
$X\in \mathfrak {a}$
. Indeed, the
![]() $\mathbf {c}$
-function is nonzero on
$\mathbf {c}$
-function is nonzero on
![]() $\mathfrak {a}^*_{\mathbb C}$
and does not have any poles for regular
$\mathfrak {a}^*_{\mathbb C}$
and does not have any poles for regular
![]() $\lambda \in {\mathscr T}_\eta $
, by our choice of
$\lambda \in {\mathscr T}_\eta $
, by our choice of
![]() $\eta $
.
$\eta $
.
The relevance of
![]() $\Phi _\lambda (X)$
is apparent from the next result, due to Trombi and Varadarajan [Reference Trombi and Varadarajan34, Theorem 2.11.2], providing the full asymptotic expansion of the spherical function. We have taken the exact statement from [Reference Gangolli and Varadarajan14, Theorem 5.9.4]. This extends to all
$\Phi _\lambda (X)$
is apparent from the next result, due to Trombi and Varadarajan [Reference Trombi and Varadarajan34, Theorem 2.11.2], providing the full asymptotic expansion of the spherical function. We have taken the exact statement from [Reference Gangolli and Varadarajan14, Theorem 5.9.4]. This extends to all
![]() $X\in \mathfrak {a}$
the asymptotic expansion proved by Harish-Chandra and Gangolli for conical subsets of regular elements.
$X\in \mathfrak {a}$
the asymptotic expansion proved by Harish-Chandra and Gangolli for conical subsets of regular elements.
Proposition 4.2. Let
![]() $\Omega \subseteq i\mathfrak {a}^*$
be a compact set and
$\Omega \subseteq i\mathfrak {a}^*$
be a compact set and
![]() $c>0$
. Then there exist
$c>0$
. Then there exist
![]() $C>0$
and
$C>0$
and
![]() $m\ge 0$
such that for all
$m\ge 0$
such that for all
![]() $H\in \overline {\mathfrak {a}^+}$
with
$H\in \overline {\mathfrak {a}^+}$
with
![]() $\beta _{\Delta _0}(H)\ge c$
, where
$\beta _{\Delta _0}(H)\ge c$
, where
 $$ \begin{align*} \beta_{\Delta_0}(H)=\min_{\alpha\in \Delta\smallsetminus \Delta_0} \alpha(H), \end{align*} $$
$$ \begin{align*} \beta_{\Delta_0}(H)=\min_{\alpha\in \Delta\smallsetminus \Delta_0} \alpha(H), \end{align*} $$
and for every regular
![]() $\lambda \in \Omega $
, we have
$\lambda \in \Omega $
, we have
 $$ \begin{align*} \left\lvert f_\lambda(H) - \Phi_\lambda(H) \right\rvert \le C (1+\lVert H\rVert_2)^m e^{-2\beta_{\Delta_0}(H)}. \end{align*} $$
$$ \begin{align*} \left\lvert f_\lambda(H) - \Phi_\lambda(H) \right\rvert \le C (1+\lVert H\rVert_2)^m e^{-2\beta_{\Delta_0}(H)}. \end{align*} $$
We now describe the key periodicity property of
![]() $\Phi _\lambda (X)$
. For this we need the following definition:
$\Phi _\lambda (X)$
. For this we need the following definition:
Definition 4.3. We say that
![]() $\lambda \in i\mathfrak {a}^*$
is rational if
$\lambda \in i\mathfrak {a}^*$
is rational if
 $i\left \langle w\lambda , X^0\right \rangle \in {\mathbb Q}$
for all
$i\left \langle w\lambda , X^0\right \rangle \in {\mathbb Q}$
for all
![]() $w\in W$
.
$w\in W$
.
If
![]() $\lambda $
is rational, we can choose
$\lambda $
is rational, we can choose
![]() $\tau _1\in {\mathbb R}_{>0}$
such that
$\tau _1\in {\mathbb R}_{>0}$
such that
 $\tau _1 \left \langle w\lambda , X^0\right \rangle \in 2i\pi {\mathbb Z}$
for all
$\tau _1 \left \langle w\lambda , X^0\right \rangle \in 2i\pi {\mathbb Z}$
for all
![]() $w\in W$
. Recall the definition of
$w\in W$
. Recall the definition of
![]() ${\mathscr C}$
from Lemma A.2.
${\mathscr C}$
from Lemma A.2.
Lemma 4.4. Let
![]() $\lambda \in i\mathfrak {a}^*$
be rational and let
$\lambda \in i\mathfrak {a}^*$
be rational and let
![]() $\tau _1$
be defined as before. Set
$\tau _1$
be defined as before. Set
![]() $\tau _n = n\tau _1$
for
$\tau _n = n\tau _1$
for
![]() $n\in {\mathbb N}$
. Then for every
$n\in {\mathbb N}$
. Then for every
![]() $Y\in {\mathscr C}$
,
$Y\in {\mathscr C}$
,
![]() $t\ge 0$
, and
$t\ge 0$
, and
![]() $n\in {\mathbb N}$
, we have
$n\in {\mathbb N}$
, we have
 $$ \begin{align*} \Phi_\lambda\left(Y + (t+\tau_n)X^0\right) = \Phi_\lambda\left(Y+ tX^0\right). \end{align*} $$
$$ \begin{align*} \Phi_\lambda\left(Y + (t+\tau_n)X^0\right) = \Phi_\lambda\left(Y+ tX^0\right). \end{align*} $$
Proof. By the definition of
![]() $\tau _1$
, it follows that
$\tau _1$
, it follows that
![]() $e^{\left \langle \lambda , \left (t+\tau _n\right )X^0\right \rangle } =e^{\left \langle \lambda , tX^0\right \rangle }$
for every
$e^{\left \langle \lambda , \left (t+\tau _n\right )X^0\right \rangle } =e^{\left \langle \lambda , tX^0\right \rangle }$
for every
![]() $n\in {\mathbb N}$
. Further, note that since
$n\in {\mathbb N}$
. Further, note that since
 $\left \langle \rho ^M,X^0\right \rangle =0$
and
$\left \langle \rho ^M,X^0\right \rangle =0$
and
 $H_0\left (ke^{Y+tX^0}\right )=tX^0+H\left (ke^Y\right )$
for
$H_0\left (ke^{Y+tX^0}\right )=tX^0+H\left (ke^Y\right )$
for
![]() $k\in K\cap M$
, we have
$k\in K\cap M$
, we have
 $$ \begin{align*} \varphi_\lambda^M\left(e^{Y+tX^0}\right)=e^{\left\langle \rho^M+\lambda,tX^0\right\rangle}\varphi_\lambda^M\left(e^Y\right)=e^{\left\langle \lambda,tX^0\right\rangle}\varphi_\lambda^M\left(e^Y\right). \end{align*} $$
$$ \begin{align*} \varphi_\lambda^M\left(e^{Y+tX^0}\right)=e^{\left\langle \rho^M+\lambda,tX^0\right\rangle}\varphi_\lambda^M\left(e^Y\right)=e^{\left\langle \lambda,tX^0\right\rangle}\varphi_\lambda^M\left(e^Y\right). \end{align*} $$
Thus
 $$ \begin{align} f^M_\lambda\left(Y+ tX^0\right) = e^{\left\langle \lambda, tX^0\right\rangle} f^M_\lambda(Y). \end{align} $$
$$ \begin{align} f^M_\lambda\left(Y+ tX^0\right) = e^{\left\langle \lambda, tX^0\right\rangle} f^M_\lambda(Y). \end{align} $$
Applying these two formulas for every
![]() $w\lambda $
,
$w\lambda $
,
![]() $w\in W^M\backslash W$
, yields the assertion.
$w\in W^M\backslash W$
, yields the assertion.
4.3 Convergence of an integral
To take advantage of Lemma 4.4, we shall need to replace the integration domain
![]() $\mathscr {P}_t^+$
in equation (34) by the translated cone
$\mathscr {P}_t^+$
in equation (34) by the translated cone
![]() $\mathscr {C}$
. Note that the Jacobian factor (22) can be alternatively written as
$\mathscr {C}$
. Note that the Jacobian factor (22) can be alternatively written as
 $$ \begin{align} J(X)=2^{-\dim\mathfrak{n}}\sum_{w\in W} \sigma(w) e^{2\left\langle w\rho, X\right\rangle}, \quad X\in\overline{\mathfrak{a}^+}, \end{align} $$
$$ \begin{align} J(X)=2^{-\dim\mathfrak{n}}\sum_{w\in W} \sigma(w) e^{2\left\langle w\rho, X\right\rangle}, \quad X\in\overline{\mathfrak{a}^+}, \end{align} $$
where
![]() $\sigma (w)\in \{\pm 1\}$
denotes the signature of w. With this in mind, for
$\sigma (w)\in \{\pm 1\}$
denotes the signature of w. With this in mind, for
![]() $t>0$
and
$t>0$
and
![]() $\lambda \in {\mathscr T}_\eta $
, we put
$\lambda \in {\mathscr T}_\eta $
, we put
 $$ \begin{align*} I(t,\lambda)=\int_{{\mathscr C}^0} \Phi_\lambda\left(Y + tX^0\right) e^{\left\langle \rho, Y\right\rangle} dY \end{align*} $$
$$ \begin{align*} I(t,\lambda)=\int_{{\mathscr C}^0} \Phi_\lambda\left(Y + tX^0\right) e^{\left\langle \rho, Y\right\rangle} dY \end{align*} $$
whenever it converges.
We now address this question of convergence. From the defining expression for
![]() $\Phi _\lambda $
in equation (35), it will be enough to understand the convergence of the integral
$\Phi _\lambda $
in equation (35), it will be enough to understand the convergence of the integral
 $$ \begin{align*} J(t,\lambda) =\int_{{\mathscr C}^0} f^M_{\lambda}\left(Y+ tX^0\right) e^{\left\langle \rho, Y\right\rangle} dY. \end{align*} $$
$$ \begin{align*} J(t,\lambda) =\int_{{\mathscr C}^0} f^M_{\lambda}\left(Y+ tX^0\right) e^{\left\langle \rho, Y\right\rangle} dY. \end{align*} $$
Lemma 4.5. There is
![]() $0<\eta <1$
such that for every
$0<\eta <1$
such that for every
![]() $\lambda \in {\mathscr T}_\eta $
and
$\lambda \in {\mathscr T}_\eta $
and
![]() $t\ge 0$
, the integral defining
$t\ge 0$
, the integral defining
![]() $J(t,\lambda )$
converges absolutely.
$J(t,\lambda )$
converges absolutely.
Proof. We first observe that it suffices to consider
![]() $t=0$
. Indeed, from equation (36) it follows that
$t=0$
. Indeed, from equation (36) it follows that
 $$ \begin{align} J(t,\lambda) = e^{ t \left\langle \lambda, X^0\right\rangle} J(\lambda), \end{align} $$
$$ \begin{align} J(t,\lambda) = e^{ t \left\langle \lambda, X^0\right\rangle} J(\lambda), \end{align} $$
where we have put
![]() $J(\lambda )=J(0,\lambda )$
. There should be no confusion between the integral
$J(\lambda )=J(0,\lambda )$
. There should be no confusion between the integral
![]() $J(\lambda )$
and the Jacobian factor
$J(\lambda )$
and the Jacobian factor
![]() $J(X)$
from equation (22), due to the different nature of their arguments.
$J(X)$
from equation (22), due to the different nature of their arguments.
Set
![]() $Y\in {\mathscr C}^0$
and write
$Y\in {\mathscr C}^0$
and write
![]() $Y= Y_M+Y^M$
, with
$Y= Y_M+Y^M$
, with
![]() $Y_M\in \mathfrak {a}_M$
and
$Y_M\in \mathfrak {a}_M$
and
![]() $Y^M\in \mathfrak {a}^M$
. Then
$Y^M\in \mathfrak {a}^M$
. Then
 $$ \begin{align} f^M_{\lambda}(Y) = e^{\left\langle \rho^M, Y\right\rangle} \varphi_\lambda^M\left(e^Y\right) = e^{\left\langle\lambda, Y_M\right\rangle} e^{\left\langle \rho^M, Y^M\right\rangle} \varphi_\lambda^M\left(e^{Y^M}\right). \end{align} $$
$$ \begin{align} f^M_{\lambda}(Y) = e^{\left\langle \rho^M, Y\right\rangle} \varphi_\lambda^M\left(e^Y\right) = e^{\left\langle\lambda, Y_M\right\rangle} e^{\left\langle \rho^M, Y^M\right\rangle} \varphi_\lambda^M\left(e^{Y^M}\right). \end{align} $$
Proposition B.1 then immediately yields the bound
 $\left \lvert e^{\left \langle \lambda , Y_M\right \rangle }\right \rvert \leq e^{-\eta C\left \langle \rho ,Y\right \rangle }$
on the first factor on the right-hand side.
$\left \lvert e^{\left \langle \lambda , Y_M\right \rangle }\right \rvert \leq e^{-\eta C\left \langle \rho ,Y\right \rangle }$
on the first factor on the right-hand side.
To bound the remaining two factors, we first let
![]() $Y^M_+$
be a point in the
$Y^M_+$
be a point in the
![]() $W^M$
-orbit of
$W^M$
-orbit of
![]() $Y^M$
lying in
$Y^M$
lying in
![]() $\overline {\mathfrak {a}^{M,+}}$
. Then by [Reference Jorgenson and Lang19, Ch. X, §2, Proposition 2.2, Theorem 2.8], we have
$\overline {\mathfrak {a}^{M,+}}$
. Then by [Reference Jorgenson and Lang19, Ch. X, §2, Proposition 2.2, Theorem 2.8], we have
 $$ \begin{align*} \left\lvert\varphi_\lambda^M\left(e^{Y^M}\right)\right\rvert \le \varphi_{\operatorname{Re} \lambda}^M\left(e^{Y^M}\right) &= \varphi_{\operatorname{Re} \lambda}^M\left(e^{Y^M_+}\right)\\ & \le \max_{w\in W^M} e^{\left\langle w{\textrm{Re}} \lambda, Y^M_+\right\rangle} \varphi_0^M\left(e^{Y^M_+}\right) \\ & \ll \max_{w\in W^M} e^{\left\langle w{\textrm{Re}} \lambda, Y^M_+\right\rangle} e^{-\left\langle \rho^M, Y^M_+\right\rangle} \left(1+\left\lVert Y^M_+\right\rVert_2\right)^{\dim\mathfrak{n}}. \end{align*} $$
$$ \begin{align*} \left\lvert\varphi_\lambda^M\left(e^{Y^M}\right)\right\rvert \le \varphi_{\operatorname{Re} \lambda}^M\left(e^{Y^M}\right) &= \varphi_{\operatorname{Re} \lambda}^M\left(e^{Y^M_+}\right)\\ & \le \max_{w\in W^M} e^{\left\langle w{\textrm{Re}} \lambda, Y^M_+\right\rangle} \varphi_0^M\left(e^{Y^M_+}\right) \\ & \ll \max_{w\in W^M} e^{\left\langle w{\textrm{Re}} \lambda, Y^M_+\right\rangle} e^{-\left\langle \rho^M, Y^M_+\right\rangle} \left(1+\left\lVert Y^M_+\right\rVert_2\right)^{\dim\mathfrak{n}}. \end{align*} $$
Now
 $\left \lVert Y^M_+\right \rVert _2 = \left \lVert Y^M\right \rVert _2$
and
$\left \lVert Y^M_+\right \rVert _2 = \left \lVert Y^M\right \rVert _2$
and
 $\left \langle \rho ^M, Y^M\right \rangle \le \left \langle \rho ^M, Y^M_+\right \rangle $
. Thus there is a
$\left \langle \rho ^M, Y^M\right \rangle \le \left \langle \rho ^M, Y^M_+\right \rangle $
. Thus there is a
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align*} \left\lvert e^{\left\langle \rho^M, Y^M\right\rangle} \varphi_\lambda^M\left(e^{Y^M}\right)\right\rvert \leq c \max_{w\in W^M} e^{\left\langle w\operatorname{Re} \lambda, Y^M_+\right\rangle} \left(1+\left\lVert Y^M\right\rVert_2\right)^{\dim\mathfrak{n}}. \end{align*} $$
$$ \begin{align*} \left\lvert e^{\left\langle \rho^M, Y^M\right\rangle} \varphi_\lambda^M\left(e^{Y^M}\right)\right\rvert \leq c \max_{w\in W^M} e^{\left\langle w\operatorname{Re} \lambda, Y^M_+\right\rangle} \left(1+\left\lVert Y^M\right\rVert_2\right)^{\dim\mathfrak{n}}. \end{align*} $$
Using the W-invariance of
![]() $\langle \cdot ,\cdot \rangle $
and
$\langle \cdot ,\cdot \rangle $
and
![]() $Y^M= Y-Y_M$
, we obtain
$Y^M= Y-Y_M$
, we obtain
 $$ \begin{align*} \max_{w\in W^M} \left\langle w\operatorname{Re} \lambda, Y^M_+\right\rangle=\max_{w\in W^M} \left\langle w\operatorname{Re} \lambda, Y^M\right\rangle \leq \max_{w\in W} \lvert\langle w \operatorname{Re} \lambda, Y\rangle\rvert+\max_{w\in W} \lvert\langle w \operatorname{Re} \lambda, Y_M\rangle\rvert. \end{align*} $$
$$ \begin{align*} \max_{w\in W^M} \left\langle w\operatorname{Re} \lambda, Y^M_+\right\rangle=\max_{w\in W^M} \left\langle w\operatorname{Re} \lambda, Y^M\right\rangle \leq \max_{w\in W} \lvert\langle w \operatorname{Re} \lambda, Y\rangle\rvert+\max_{w\in W} \lvert\langle w \operatorname{Re} \lambda, Y_M\rangle\rvert. \end{align*} $$
Note that
![]() $w\operatorname {Re}\lambda =\operatorname {Re} w\lambda $
and
$w\operatorname {Re}\lambda =\operatorname {Re} w\lambda $
and
![]() $w\lambda \in \mathcal {T}_\eta $
. Using Remark A.1, we have
$w\lambda \in \mathcal {T}_\eta $
. Using Remark A.1, we have
![]() $ \lvert \langle \operatorname {Re} \lambda , Y\rangle \rvert \ll -\eta \langle \rho , Y\rangle $
for all
$ \lvert \langle \operatorname {Re} \lambda , Y\rangle \rvert \ll -\eta \langle \rho , Y\rangle $
for all
![]() $\lambda \in {\mathscr T}_\eta $
and
$\lambda \in {\mathscr T}_\eta $
and
![]() $Y\in \mathscr {C}^0$
. From this and Proposition B.1, we deduce that there is a constant
$Y\in \mathscr {C}^0$
. From this and Proposition B.1, we deduce that there is a constant
![]() $C'>0$
, depending only on d, such that
$C'>0$
, depending only on d, such that
 $$ \begin{align*} \max_{w\in W^M} \left\langle w\operatorname{Re} \lambda, Y^M_+\right\rangle \le - \eta C'\langle\rho, Y\rangle. \end{align*} $$
$$ \begin{align*} \max_{w\in W^M} \left\langle w\operatorname{Re} \lambda, Y^M_+\right\rangle \le - \eta C'\langle\rho, Y\rangle. \end{align*} $$
Similarly, we can find
![]() $c>0$
such that
$c>0$
such that
 $\left \lVert Y^M\right \rVert _2 \le c \lVert Y\rVert _2$
. Hence if
$\left \lVert Y^M\right \rVert _2 \le c \lVert Y\rVert _2$
. Hence if
![]() $\eta>0$
is sufficiently small, then it follows from equation (39) and our estimates that for some
$\eta>0$
is sufficiently small, then it follows from equation (39) and our estimates that for some
![]() $c'>0$
,
$c'>0$
,
 $$ \begin{align*} \left\lvert f^M_{\lambda}(Y)\right\rvert \le c' e^{-\frac{1}{2}\left\langle \rho, Y\right\rangle}(1+\lVert Y\rVert_2)^{\dim\mathfrak{n}}. \end{align*} $$
$$ \begin{align*} \left\lvert f^M_{\lambda}(Y)\right\rvert \le c' e^{-\frac{1}{2}\left\langle \rho, Y\right\rangle}(1+\lVert Y\rVert_2)^{\dim\mathfrak{n}}. \end{align*} $$
We therefore obtain
 $$ \begin{align*} \int_{{\mathscr C}^0} \left\lvert f^M_{\lambda}(Y) e^{\left\langle \rho, Y\right\rangle}\right\rvert dY \le \int_{{\mathscr C}^0} e^{\left\langle \frac{1}{2} \rho, Y\right\rangle} (1+\lVert Y\rVert_2)^{\dim\mathfrak{n}} dY. \end{align*} $$
$$ \begin{align*} \int_{{\mathscr C}^0} \left\lvert f^M_{\lambda}(Y) e^{\left\langle \rho, Y\right\rangle}\right\rvert dY \le \int_{{\mathscr C}^0} e^{\left\langle \frac{1}{2} \rho, Y\right\rangle} (1+\lVert Y\rVert_2)^{\dim\mathfrak{n}} dY. \end{align*} $$
Using Remark A.1 we see that this last integral is finite. Thus the integral defining
![]() $J(\lambda )$
, and hence
$J(\lambda )$
, and hence
![]() $J(t,\lambda )$
, converges absolutely.
$J(t,\lambda )$
, converges absolutely.
It follows that for
![]() $\lambda \in {\mathscr T}_\eta $
we have
$\lambda \in {\mathscr T}_\eta $
we have
 $$ \begin{align} I(t,\lambda) = \sum_{w\in W^M\backslash W} \frac{\textbf{ c}(w\lambda)}{\textbf{ c}^M(w\lambda)} J(w\lambda) e^{t \left\langle w\lambda , X^0\right\rangle}, \end{align} $$
$$ \begin{align} I(t,\lambda) = \sum_{w\in W^M\backslash W} \frac{\textbf{ c}(w\lambda)}{\textbf{ c}^M(w\lambda)} J(w\lambda) e^{t \left\langle w\lambda , X^0\right\rangle}, \end{align} $$
where, we recall,
![]() $J(\lambda )=J(0,\lambda )$
.
$J(\lambda )=J(0,\lambda )$
.
4.4 Main-term replacement
Having established that
![]() $I(t,\lambda )$
is well defined, we now show, using Proposition 4.2, that
$I(t,\lambda )$
is well defined, we now show, using Proposition 4.2, that
![]() $h_t(\lambda )$
can be approximated by
$h_t(\lambda )$
can be approximated by
![]() $I(t,\lambda )$
.
$I(t,\lambda )$
.
Proposition 4.6. There are
![]() $c, C>0$
such that for regular
$c, C>0$
such that for regular
![]() $\lambda \in i\mathfrak {a}^*$
,
$\lambda \in i\mathfrak {a}^*$
,
 $$ \begin{align*} h_t(\lambda)=C I(t,\lambda)+O_\lambda\left(e^{-ct}\right). \end{align*} $$
$$ \begin{align*} h_t(\lambda)=C I(t,\lambda)+O_\lambda\left(e^{-ct}\right). \end{align*} $$
Before we prove this proposition, we establish the following lemma (see Lemma A.2 for the definition of the
![]() $\beta _i^{\vee }$
):
$\beta _i^{\vee }$
):
Lemma 4.7. Set
![]() $0<\eta <1$
and define
$0<\eta <1$
and define
![]() ${\mathscr E}= X^0 -\sum _{i=1}^r [0,\eta ]\beta _i^\vee = \sum _{i=1}^r [1-\eta , 1]\beta _i^\vee $
and
${\mathscr E}= X^0 -\sum _{i=1}^r [0,\eta ]\beta _i^\vee = \sum _{i=1}^r [1-\eta , 1]\beta _i^\vee $
and
![]() ${\mathscr E}^+ = {\mathscr E}\cap {\mathscr P}^+$
. Then if
${\mathscr E}^+ = {\mathscr E}\cap {\mathscr P}^+$
. Then if
![]() $\eta $
is sufficiently small, we have the following:
$\eta $
is sufficiently small, we have the following:
-
(i) For every V in the closure
 $\overline {{\mathscr P}^+\smallsetminus {\mathscr E}^+}$
of
$\overline {{\mathscr P}^+\smallsetminus {\mathscr E}^+}$
of
 ${\mathscr P}^+\smallsetminus {\mathscr E}^+$
, we have (41)for some
${\mathscr P}^+\smallsetminus {\mathscr E}^+$
, we have (41)for some $$ \begin{align} \langle \rho, V\rangle \le \left\langle\rho, X^0\right\rangle -\delta \end{align} $$
$$ \begin{align} \langle \rho, V\rangle \le \left\langle\rho, X^0\right\rangle -\delta \end{align} $$
 $\delta =\delta (\eta )>0$
uniform in all V.
$\delta =\delta (\eta )>0$
uniform in all V.
-
(ii) Let
 $\Delta ^M\subseteq \Delta $
denote the subset of simple roots in M. Then there exists
$\Delta ^M\subseteq \Delta $
denote the subset of simple roots in M. Then there exists
 $c=c(\eta )>0$
such that for every
$c=c(\eta )>0$
such that for every
 $X\in {\mathscr E}$
and
$X\in {\mathscr E}$
and
 $\alpha \in \Delta \smallsetminus \Delta ^M$
, we have
$\alpha \in \Delta \smallsetminus \Delta ^M$
, we have
 $\alpha (X)\ge c$
.
$\alpha (X)\ge c$
.
Proof. Since
![]() $X^0$
is the unique point in
$X^0$
is the unique point in
![]() ${\mathscr P}^+$
at which the linear map
${\mathscr P}^+$
at which the linear map
![]() $X\mapsto \langle \rho , X\rangle $
attains its maximum, and
$X\mapsto \langle \rho , X\rangle $
attains its maximum, and
![]() $\overline {{\mathscr P}^+\smallsetminus {\mathscr E}^+}$
is closed, it will suffice to show that every point in
$\overline {{\mathscr P}^+\smallsetminus {\mathscr E}^+}$
is closed, it will suffice to show that every point in
![]() $\overline {{\mathscr P}^+\smallsetminus {\mathscr E}^+}$
is bounded away from
$\overline {{\mathscr P}^+\smallsetminus {\mathscr E}^+}$
is bounded away from
![]() $X^0$
. But this is clear, since
$X^0$
. But this is clear, since
 ${\mathscr P}^+ =\left (X^0 -\sum _{i=1}^r [0,\infty )\beta _i^\vee \right )\cap \mathfrak {a}^+$
by Lemma A.2. Note that this argument holds for any
${\mathscr P}^+ =\left (X^0 -\sum _{i=1}^r [0,\infty )\beta _i^\vee \right )\cap \mathfrak {a}^+$
by Lemma A.2. Note that this argument holds for any
![]() $0<\eta <1$
, with the resulting constant
$0<\eta <1$
, with the resulting constant
![]() $\delta $
of course depending on
$\delta $
of course depending on
![]() $\eta $
.
$\eta $
.
For the second part, we note that for every
![]() $\alpha \in \Delta \smallsetminus \Delta ^M$
, we have
$\alpha \in \Delta \smallsetminus \Delta ^M$
, we have
 $\alpha \left (X^0\right ) = 2$
. Hence if
$\alpha \left (X^0\right ) = 2$
. Hence if
![]() $\eta $
is chosen sufficiently small, each such
$\eta $
is chosen sufficiently small, each such
![]() $\alpha $
stays bounded away from
$\alpha $
stays bounded away from
![]() $0$
on
$0$
on
![]() ${\mathscr E}$
so that (ii) follows.
${\mathscr E}$
so that (ii) follows.
Proof of Proposition 4.6. Let
 $$ \begin{align*} G(t,\lambda)=e^{-t\left\langle\rho, X^0\right\rangle} \int_{{\mathscr P}^+_t} f_\lambda(X) e^{\left\langle \rho, X\right\rangle} dX. \end{align*} $$
$$ \begin{align*} G(t,\lambda)=e^{-t\left\langle\rho, X^0\right\rangle} \int_{{\mathscr P}^+_t} f_\lambda(X) e^{\left\langle \rho, X\right\rangle} dX. \end{align*} $$
From equations (34) and (37), as well as the volume computation in Corollary A.4, we have
 $$ \begin{align*} h_t(\lambda)=C G(t,\lambda)+O\left(e^{-c_1t}\right) \end{align*} $$
$$ \begin{align*} h_t(\lambda)=C G(t,\lambda)+O\left(e^{-c_1t}\right) \end{align*} $$
for some
![]() $c_1, C>0$
. Next, let
$c_1, C>0$
. Next, let
![]() ${\mathscr E}^+$
be defined as in Lemma 4.7 with
${\mathscr E}^+$
be defined as in Lemma 4.7 with
![]() $\eta $
sufficiently small. Put
$\eta $
sufficiently small. Put
 $$ \begin{align*} H(t,\lambda)= \int_{t{\mathscr E}^+} f_\lambda(X) e^{\left\langle\rho, X- tX^0\right\rangle} dX. \end{align*} $$
$$ \begin{align*} H(t,\lambda)= \int_{t{\mathscr E}^+} f_\lambda(X) e^{\left\langle\rho, X- tX^0\right\rangle} dX. \end{align*} $$
Then
![]() $G(t, \lambda )=H(t,\lambda ) + O\left (e^{-c_2t}\right )$
for some absolute constant
$G(t, \lambda )=H(t,\lambda ) + O\left (e^{-c_2t}\right )$
for some absolute constant
![]() $c_2>0$
, by Lemma 4.7(i).
$c_2>0$
, by Lemma 4.7(i).
Note that by Lemma 4.7, for any
![]() $X\in t{\mathscr E}$
we have
$X\in t{\mathscr E}$
we have
![]() $\alpha (X)\ge ct$
for
$\alpha (X)\ge ct$
for
![]() $\alpha \in \Delta \smallsetminus \Delta ^M$
. Using Lemma 4.7(ii) and Proposition 4.2, there exists
$\alpha \in \Delta \smallsetminus \Delta ^M$
. Using Lemma 4.7(ii) and Proposition 4.2, there exists
![]() $c_3>0$
such that
$c_3>0$
such that
for every
![]() $X\in t{\mathscr E}^+$
and every regular
$X\in t{\mathscr E}^+$
and every regular
![]() $\lambda \in i\mathfrak {a}^*$
. Hence, for regular
$\lambda \in i\mathfrak {a}^*$
. Hence, for regular
![]() $\lambda \in i\mathfrak {a}^*$
, we have
$\lambda \in i\mathfrak {a}^*$
, we have
 $$ \begin{align*} H(t,\lambda)&= \int_{t{\mathscr E}^+} \Phi_\lambda(X) e^{\left\langle\rho, X- tX^0\right\rangle} dX + O_\lambda\left(e^{-c_3t}\right)\\ &= \int_{t{\mathscr E}^+- tX^0} \Phi_\lambda\left(Y + tX^0\right) e^{\left\langle \rho, Y\right\rangle} dY+O_\lambda\left(e^{-c_3t}\right) \end{align*} $$
$$ \begin{align*} H(t,\lambda)&= \int_{t{\mathscr E}^+} \Phi_\lambda(X) e^{\left\langle\rho, X- tX^0\right\rangle} dX + O_\lambda\left(e^{-c_3t}\right)\\ &= \int_{t{\mathscr E}^+- tX^0} \Phi_\lambda\left(Y + tX^0\right) e^{\left\langle \rho, Y\right\rangle} dY+O_\lambda\left(e^{-c_3t}\right) \end{align*} $$
after a change of variables. Noting that
![]() $t{\mathscr E}^+- tX^0\subseteq {\mathscr C}^0$
, we can then extend the integral to all of
$t{\mathscr E}^+- tX^0\subseteq {\mathscr C}^0$
, we can then extend the integral to all of
![]() ${\mathscr C}^0$
, incurring an additional error of
${\mathscr C}^0$
, incurring an additional error of
![]() $O_\lambda \left (e^{-c_4t}\right )$
, for some
$O_\lambda \left (e^{-c_4t}\right )$
, for some
![]() $c_4>0$
.□
$c_4>0$
.□
4.5 A nonvanishing result
We now show that
![]() $I(t,\lambda )$
is generically nonvanishing on
$I(t,\lambda )$
is generically nonvanishing on
![]() $i\mathfrak {a}^*$
. This will follow from the absolute convergence of
$i\mathfrak {a}^*$
. This will follow from the absolute convergence of
![]() $I(t,\lambda )$
, the periodic behavior of
$I(t,\lambda )$
, the periodic behavior of
![]() $\Phi _\lambda $
along
$\Phi _\lambda $
along
![]() $X^0$
for rational
$X^0$
for rational
![]() $\lambda $
, and a linear-independence-of-characters argument.
$\lambda $
, and a linear-independence-of-characters argument.
Proposition 4.8. There exists a finite number of hyperplanes
![]() ${\mathscr H}_1,\dotsc , {\mathscr H}_N\subseteq i\mathfrak {a}^*$
and a locally finite collection
${\mathscr H}_1,\dotsc , {\mathscr H}_N\subseteq i\mathfrak {a}^*$
and a locally finite collection
![]() ${\mathscr D}$
of
${\mathscr D}$
of
![]() $(d-2)$
-dimensional manifolds in
$(d-2)$
-dimensional manifolds in
![]() $i\mathfrak {a}^*$
such that for every
$i\mathfrak {a}^*$
such that for every
there exists
![]() $t=t_\lambda \ge 0$
with
$t=t_\lambda \ge 0$
with
![]() $I(t,\lambda )\neq 0$
.
$I(t,\lambda )\neq 0$
.
Proof. Let
![]() $\eta>0$
be sufficiently small and at most as large as in Lemma 4.5. We first claim that there exists a locally finite collection of
$\eta>0$
be sufficiently small and at most as large as in Lemma 4.5. We first claim that there exists a locally finite collection of
![]() $(d-2)$
-dimensional complex manifolds
$(d-2)$
-dimensional complex manifolds
![]() $\mathcal {Z}\subseteq {\mathscr T}_\eta $
such that
$\mathcal {Z}\subseteq {\mathscr T}_\eta $
such that
![]() $J(t,w\lambda )\neq 0$
for all
$J(t,w\lambda )\neq 0$
for all
![]() $\lambda \in {\mathscr T}_\eta \smallsetminus {\mathscr D}$
,
$\lambda \in {\mathscr T}_\eta \smallsetminus {\mathscr D}$
,
![]() $w\in W$
, and
$w\in W$
, and
![]() $t\ge 0$
. Indeed, for fixed
$t\ge 0$
. Indeed, for fixed
![]() $m\in M$
, the map
$m\in M$
, the map
![]() $\lambda \mapsto \varphi _\lambda ^M(m)$
is holomorphic in
$\lambda \mapsto \varphi _\lambda ^M(m)$
is holomorphic in
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
. Since the integral defining
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
. Since the integral defining
![]() $J(t,\lambda )$
converges absolutely,
$J(t,\lambda )$
converges absolutely,
![]() $J(t,\lambda )$
is in fact a holomorphic function for
$J(t,\lambda )$
is in fact a holomorphic function for
![]() $\lambda \in {\mathscr T}_\eta $
. From the nonvanishing at
$\lambda \in {\mathscr T}_\eta $
. From the nonvanishing at
![]() $\lambda =0$
,
$\lambda =0$
,
 $$ \begin{align*} J(t,0)=\int_{{\mathscr C}^0} e^{\left\langle \rho+\rho^M, Y\right\rangle} \varphi_0^M\left(e^Y\right) dY \neq0, \end{align*} $$
$$ \begin{align*} J(t,0)=\int_{{\mathscr C}^0} e^{\left\langle \rho+\rho^M, Y\right\rangle} \varphi_0^M\left(e^Y\right) dY \neq0, \end{align*} $$
it follows that
![]() $J(t,\lambda )$
does not vanish identically in
$J(t,\lambda )$
does not vanish identically in
![]() $\lambda $
, hence its zero set
$\lambda $
, hence its zero set
![]() $\mathcal {Z}= \{\lambda \in {\mathscr T}_\eta \mid J(t, \lambda )=0\}$
is a locally finite union of
$\mathcal {Z}= \{\lambda \in {\mathscr T}_\eta \mid J(t, \lambda )=0\}$
is a locally finite union of
![]() $(d-2)$
-dimensional complex manifolds. Put
$(d-2)$
-dimensional complex manifolds. Put
![]() ${\mathscr D} = \mathcal {Z}\cap i\mathfrak {a}^*$
.
${\mathscr D} = \mathcal {Z}\cap i\mathfrak {a}^*$
.
By our choice of
![]() $\eta $
,
$\eta $
,
![]() $\mathbf {c}(w\lambda )/\mathbf {c}^M(w\lambda )$
has no pole for regular
$\mathbf {c}(w\lambda )/\mathbf {c}^M(w\lambda )$
has no pole for regular
![]() $\lambda $
in
$\lambda $
in
![]() ${\mathscr T}_\eta $
. Let
${\mathscr T}_\eta $
. Let
![]() ${\mathscr T}_\eta '$
denote the set of all regular
${\mathscr T}_\eta '$
denote the set of all regular
![]() $\lambda \in {\mathscr T}_\eta \smallsetminus \mathcal {D}$
such that
$\lambda \in {\mathscr T}_\eta \smallsetminus \mathcal {D}$
such that
 $\left \langle \lambda , w^{-1}X^0\right \rangle \neq \left \langle \lambda , v^{-1}X^0\right \rangle $
for all
$\left \langle \lambda , w^{-1}X^0\right \rangle \neq \left \langle \lambda , v^{-1}X^0\right \rangle $
for all
![]() $w, v\in W^M\backslash W$
,
$w, v\in W^M\backslash W$
,
![]() $w\neq v$
. Then
$w\neq v$
. Then
![]() ${\mathscr T}_\eta '$
is in fact dense in
${\mathscr T}_\eta '$
is in fact dense in
![]() ${\mathscr T}_\eta $
, since
${\mathscr T}_\eta $
, since
![]() $w^{-1}X^0\neq v^{-1} X^0$
for all
$w^{-1}X^0\neq v^{-1} X^0$
for all
![]() $w\neq v$
,
$w\neq v$
,
![]() $w, v\in W^M\backslash W$
, so that we can obtain
$w, v\in W^M\backslash W$
, so that we can obtain
![]() ${\mathscr T}_\eta '$
by removing the hyperplanes
${\mathscr T}_\eta '$
by removing the hyperplanes
 $\left \{\lambda \mid \left \langle \lambda , w^{-1}X^0\right \rangle = \left \langle \lambda , v^{-1}X^0\right \rangle \right \}$
for each
$\left \{\lambda \mid \left \langle \lambda , w^{-1}X^0\right \rangle = \left \langle \lambda , v^{-1}X^0\right \rangle \right \}$
for each
![]() $v\neq w$
in
$v\neq w$
in
![]() $W^M\backslash W$
.
$W^M\backslash W$
.
Recall the expansion (40). By the definition of
![]() ${\mathscr T}_\eta '$
, the phases
${\mathscr T}_\eta '$
, the phases
 $\left \langle w\lambda , X^0\right \rangle $
,
$\left \langle w\lambda , X^0\right \rangle $
,
![]() $w\in W^M\backslash W$
, are pairwise distinct for
$w\in W^M\backslash W$
, are pairwise distinct for
![]() $\lambda \in {\mathscr T}_\eta '$
. We can therefore apply [Reference Harish-Chandra16, Lemma 56] (see also [Reference Jorgenson and Lang19, Ch. VIII, Lemma 0.1]) to the sum over
$\lambda \in {\mathscr T}_\eta '$
. We can therefore apply [Reference Harish-Chandra16, Lemma 56] (see also [Reference Jorgenson and Lang19, Ch. VIII, Lemma 0.1]) to the sum over
![]() $w\in W^M\backslash W$
to obtain, for each
$w\in W^M\backslash W$
to obtain, for each
![]() $\lambda \in {\mathscr T}_\eta '$
,
$\lambda \in {\mathscr T}_\eta '$
,
 $$ \begin{align*} \limsup_{t\rightarrow \infty} \left\lvert I(t,\lambda)\right\rvert^2 \ge \sum_{w\in W^M\backslash W} \left\lvert\frac{\textbf{ c}(w\lambda)}{\textbf{ c}^M(w\lambda)} J(w\lambda)\right\rvert^2. \end{align*} $$
$$ \begin{align*} \limsup_{t\rightarrow \infty} \left\lvert I(t,\lambda)\right\rvert^2 \ge \sum_{w\in W^M\backslash W} \left\lvert\frac{\textbf{ c}(w\lambda)}{\textbf{ c}^M(w\lambda)} J(w\lambda)\right\rvert^2. \end{align*} $$
Now for each
![]() $w\in W$
and
$w\in W$
and
![]() $\lambda \in {\mathscr T}_\eta '$
, the terms
$\lambda \in {\mathscr T}_\eta '$
, the terms
 $\frac {\mathbf {c}(w\lambda )}{\mathbf {c}^M(w\lambda )} J(w\lambda )$
are nonzero, and hence for each
$\frac {\mathbf {c}(w\lambda )}{\mathbf {c}^M(w\lambda )} J(w\lambda )$
are nonzero, and hence for each
![]() $\lambda \in {\mathscr T}_\eta '$
there exists
$\lambda \in {\mathscr T}_\eta '$
there exists
![]() $t=t_\lambda $
such that
$t=t_\lambda $
such that
![]() $I(t, \lambda )\neq 0$
.
$I(t, \lambda )\neq 0$
.
4.6 Final arguments
We now finish the proof of Proposition 4.1.
By enlarging
![]() $\Omega $
if necessary, we can assume that
$\Omega $
if necessary, we can assume that
![]() $\overline {\Omega ^\circ } = \Omega $
. Let
$\overline {\Omega ^\circ } = \Omega $
. Let
![]() ${\mathscr H}_1,\dotsc , {\mathscr H}_N$
and
${\mathscr H}_1,\dotsc , {\mathscr H}_N$
and
![]() ${\mathscr D}$
be as in Proposition 4.8. If necessary, we add in more hyperplanes such that the complement of their union in
${\mathscr D}$
be as in Proposition 4.8. If necessary, we add in more hyperplanes such that the complement of their union in
![]() $i\mathfrak {a}^*$
consists of regular points only. Then the set of rational
$i\mathfrak {a}^*$
consists of regular points only. Then the set of rational
![]() $\lambda $
in
$\lambda $
in
is dense in
![]() $\Omega $
. Since
$\Omega $
. Since
 $\lambda \mapsto \frac {1}{T}\int _0^T \lvert h_t(\lambda )\rvert ^2$
is a continuous function, and
$\lambda \mapsto \frac {1}{T}\int _0^T \lvert h_t(\lambda )\rvert ^2$
is a continuous function, and
![]() $\Omega $
is compact, Proposition 4.1 follows from the next result:
$\Omega $
is compact, Proposition 4.1 follows from the next result:
Lemma 4.9. For every rational
there exists
![]() $T_0>0$
depending on
$T_0>0$
depending on
![]() $\lambda $
such that for all
$\lambda $
such that for all
![]() $T>T_0$
, we have
$T>T_0$
, we have
 $$ \begin{align*} \frac{1}{T}\int_0^T \lvert h_t(\lambda)\rvert^2 dt>0. \end{align*} $$
$$ \begin{align*} \frac{1}{T}\int_0^T \lvert h_t(\lambda)\rvert^2 dt>0. \end{align*} $$
Proof. Recall the definition of ‘rational’ from Definition 4.3. Let
![]() $\tau _1\in {\mathbb R}_{>0}$
(depending on
$\tau _1\in {\mathbb R}_{>0}$
(depending on
![]() $\lambda $
) and
$\lambda $
) and
![]() $\tau _n=n\tau _1$
for
$\tau _n=n\tau _1$
for
![]() $n\in {\mathbb N}$
be as in the statement of Lemma 4.4. By Proposition 4.8 we can choose
$n\in {\mathbb N}$
be as in the statement of Lemma 4.4. By Proposition 4.8 we can choose
![]() $t_0\ge 0$
such that
$t_0\ge 0$
such that
![]() $I(t_0,\lambda )=:a\neq 0$
. Write
$I(t_0,\lambda )=:a\neq 0$
. Write
![]() $t_n=t_0+\tau _n$
for
$t_n=t_0+\tau _n$
for
![]() $n\in {\mathbb N}$
. Note that by Lemma 4.4, we have
$n\in {\mathbb N}$
. Note that by Lemma 4.4, we have
![]() $I(t+\tau _n,\lambda )=I(t,\lambda )$
for all
$I(t+\tau _n,\lambda )=I(t,\lambda )$
for all
![]() $t\ge 0$
and all
$t\ge 0$
and all
![]() $n\in {\mathbb N}$
. Thus
$n\in {\mathbb N}$
. Thus
![]() $I(t_n,\lambda )=a$
, and we can find a small
$I(t_n,\lambda )=a$
, and we can find a small
![]() $\epsilon>0$
such that for every
$\epsilon>0$
such that for every
![]() $n\in {\mathbb N}$
and every
$n\in {\mathbb N}$
and every
![]() $s\in (t_n-\epsilon , t_n+\epsilon )$
, we have
$s\in (t_n-\epsilon , t_n+\epsilon )$
, we have
From Lemma 4.6 we may choose
![]() $T_0>0$
so large that
$T_0>0$
so large that
![]() $\lvert h_t(\lambda ) - I(t,\lambda )\rvert <\lvert a\rvert /4$
for all
$\lvert h_t(\lambda ) - I(t,\lambda )\rvert <\lvert a\rvert /4$
for all
![]() $t\ge T_0$
. Let
$t\ge T_0$
. Let
![]() $N\in {\mathbb N}$
be such that
$N\in {\mathbb N}$
be such that
![]() $t_n-\epsilon \ge T_0$
for all
$t_n-\epsilon \ge T_0$
for all
![]() $n\ge N$
. Then for every
$n\ge N$
. Then for every
![]() $n\ge N$
, we have
$n\ge N$
, we have
for all
![]() $s\in (t_n-\epsilon , t_n+\epsilon )$
. We therefore get, for
$s\in (t_n-\epsilon , t_n+\epsilon )$
. We therefore get, for
![]() $T>2T_0 + \tau _1$
, that
$T>2T_0 + \tau _1$
, that
 $$ \begin{align*} \frac{1}{T}\int_0^T \lvert h_t(\lambda)\rvert^2 dt \gg \frac{1}{T}\sum_{n=N}^{\left(T-1-t_0\right)/\tau_1} \int_{-\epsilon}^\epsilon \left\lvert h_{t_n+s}(\lambda)\right\rvert^2 ds \gg_{\lambda} \frac{T-T_0}{T} \lvert a\rvert^2>0, \end{align*} $$
$$ \begin{align*} \frac{1}{T}\int_0^T \lvert h_t(\lambda)\rvert^2 dt \gg \frac{1}{T}\sum_{n=N}^{\left(T-1-t_0\right)/\tau_1} \int_{-\epsilon}^\epsilon \left\lvert h_{t_n+s}(\lambda)\right\rvert^2 ds \gg_{\lambda} \frac{T-T_0}{T} \lvert a\rvert^2>0, \end{align*} $$
as we wanted to show.
5 Geometric side
The aim of this section is to prove Theorem 2.3. The essential feature of the geometric side is the ergodic properties of the sets
![]() $gE_t\cap E_t$
in the quotient
$gE_t\cap E_t$
in the quotient
![]() $\Gamma \backslash G$
, as
$\Gamma \backslash G$
, as
![]() $t>0$
and
$t>0$
and
![]() $g\in G$
vary.
$g\in G$
vary.
5.1 A general bound
In this section, we return to the general setting of §3, with
![]() $S=G/K$
and
$S=G/K$
and
![]() $\Gamma $
a given torsion-free cocompact lattice in G.
$\Gamma $
a given torsion-free cocompact lattice in G.
For
![]() $g,h\in G$
, let
$g,h\in G$
, let
![]() $N_R(g,h)$
denote the number of
$N_R(g,h)$
denote the number of
![]() $\gamma \in \Gamma $
for which
$\gamma \in \Gamma $
for which
![]() $d(g, \gamma h)\le R$
. This generalizes the notation
$d(g, \gamma h)\le R$
. This generalizes the notation
![]() $N_R(g)$
from equation (26) when
$N_R(g)$
from equation (26) when
![]() $g=h$
. Let
$g=h$
. Let
![]() $N_\Gamma (R)=\sup _{\left (g,h\right )}N_R(g,h)$
.
$N_\Gamma (R)=\sup _{\left (g,h\right )}N_R(g,h)$
.
Lemma 5.1. There exists
![]() $c>0$
, independent of R and
$c>0$
, independent of R and
![]() $\Gamma $
, such that
$\Gamma $
, such that
Proof. Note that
![]() $N_R(g,h) = N_R(g,\gamma h)$
for all
$N_R(g,h) = N_R(g,\gamma h)$
for all
![]() $\gamma \in \Gamma $
, so that we can assume that h is such that
$\gamma \in \Gamma $
, so that we can assume that h is such that
![]() $d(g,h)=\min _{\gamma \in \Gamma } d(g, \gamma h)$
. If
$d(g,h)=\min _{\gamma \in \Gamma } d(g, \gamma h)$
. If
![]() $d(g,h)>R$
, then
$d(g,h)>R$
, then
![]() $N_R(g,h)=0$
, so that we can assume
$N_R(g,h)=0$
, so that we can assume
![]() $d(g, h)\le R$
.
$d(g, h)\le R$
.
Now if
![]() $\gamma \in \Gamma $
is such that
$\gamma \in \Gamma $
is such that
![]() $d(g,\gamma h)\le R$
, then
$d(g,\gamma h)\le R$
, then
so that
![]() $N_R(g,h)\le N_{2R}(h,h)$
. Applying [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, Lemma 6.18] to
$N_R(g,h)\le N_{2R}(h,h)$
. Applying [Reference Abert, Bergeron, Biringer, Gelander, Nikolov, Raimbault and Samet1, Lemma 6.18] to
![]() $N_{2R}(h,h)$
gives the assertion of the lemma.
$N_{2R}(h,h)$
gives the assertion of the lemma.
The following lemma is an adaptation of [Reference Le Masson and Sahlsten24, Lemma 5.1] to our setting. Recall the geodesic balls
![]() $B_t$
, first introduced in equation (13) in the setting of
$B_t$
, first introduced in equation (13) in the setting of
![]() $G=\operatorname {SL}_d({\mathbb R})$
, but more generally defined for all G using the same notation.
$G=\operatorname {SL}_d({\mathbb R})$
, but more generally defined for all G using the same notation.
Lemma 5.2. There is
![]() $c>0$
, depending only on G, such that the following holds. Let
$c>0$
, depending only on G, such that the following holds. Let
![]() $R>0$
, and let
$R>0$
, and let
![]() $K\in C(G\times G)$
be invariant under the diagonal action of
$K\in C(G\times G)$
be invariant under the diagonal action of
![]() $\Gamma $
and satisfy
$\Gamma $
and satisfy
 $\left \{g^{-1}h: (g,h)\in \mathrm {supp}(K)\right \} \subset B_R$
. Let
$\left \{g^{-1}h: (g,h)\in \mathrm {supp}(K)\right \} \subset B_R$
. Let
![]() $\bf {K}$
be an integral operator on
$\bf {K}$
be an integral operator on
![]() $L^2(\Gamma \backslash G)$
with kernel K. Then
$L^2(\Gamma \backslash G)$
with kernel K. Then
 $$ \begin{align*} \lVert\textbf{ K}\rVert_{\textrm{ HS}}^2\leq \int_{\Gamma\backslash G} \int_{G}\lvert K(g,h)\rvert^2 dg dh+O\left(\frac{e^{cR}}{\operatorname{InjRad}(\Gamma\backslash S)^{\dim S}}\operatorname{vol}\left((\Gamma\backslash G)_{\leq 2R}\right)\lVert K\rVert_\infty^2\right). \end{align*} $$
$$ \begin{align*} \lVert\textbf{ K}\rVert_{\textrm{ HS}}^2\leq \int_{\Gamma\backslash G} \int_{G}\lvert K(g,h)\rvert^2 dg dh+O\left(\frac{e^{cR}}{\operatorname{InjRad}(\Gamma\backslash S)^{\dim S}}\operatorname{vol}\left((\Gamma\backslash G)_{\leq 2R}\right)\lVert K\rVert_\infty^2\right). \end{align*} $$
Proof. By definition, we have
 $$ \begin{align*} \lVert \textbf{ K}\rVert_{\textrm{ HS}}^2=\int_{\Gamma\backslash G}\int_{\Gamma\backslash G} \left\lvert\sum_{\gamma\in \Gamma}K(g,\gamma h)\right\rvert^2 dg dh. \end{align*} $$
$$ \begin{align*} \lVert \textbf{ K}\rVert_{\textrm{ HS}}^2=\int_{\Gamma\backslash G}\int_{\Gamma\backslash G} \left\lvert\sum_{\gamma\in \Gamma}K(g,\gamma h)\right\rvert^2 dg dh. \end{align*} $$
Let
![]() $D\subset G$
be a fundamental domain for
$D\subset G$
be a fundamental domain for
![]() $\Gamma $
. We decompose D into its
$\Gamma $
. We decompose D into its
![]() $2R$
-thin and -thick parts
$2R$
-thin and -thick parts
![]() $D=D_{\leq 2R}\cup D_{>2R}$
, where, similar to equation (3), we have put
$D=D_{\leq 2R}\cup D_{>2R}$
, where, similar to equation (3), we have put
From the support condition on K, it follows that if
![]() $K(g,\gamma h)\neq 0$
then
$K(g,\gamma h)\neq 0$
then
![]() $d(g,\gamma h)\leq R$
.
$d(g,\gamma h)\leq R$
.
Now suppose that
![]() $h\in D_{>2R}$
and
$h\in D_{>2R}$
and
![]() $\gamma ,\delta \in \Gamma $
,
$\gamma ,\delta \in \Gamma $
,
![]() $\gamma \neq \delta $
, are such that
$\gamma \neq \delta $
, are such that
![]() $d(g,\gamma h)\le R$
and
$d(g,\gamma h)\le R$
and
![]() $d(g, \delta h)\le R$
. Then
$d(g, \delta h)\le R$
. Then
![]() $d(\gamma h, \delta h)\le d(g, \gamma h) + d(g, \delta h)\le 2R$
, but
$d(\gamma h, \delta h)\le d(g, \gamma h) + d(g, \delta h)\le 2R$
, but
![]() $d(\gamma h, \delta h)>2R$
, since
$d(\gamma h, \delta h)>2R$
, since
![]() $h\in D_{>2R}$
, leading to a contradiction. Hence there exists at most one
$h\in D_{>2R}$
, leading to a contradiction. Hence there exists at most one
![]() $\gamma \in \Gamma $
with
$\gamma \in \Gamma $
with
![]() $K(g,\gamma h)\neq 0$
. In this way,
$K(g,\gamma h)\neq 0$
. In this way,
 $$ \begin{align*} \left\lvert\sum_{\gamma\in\Gamma} K(g,\gamma h)\right\rvert^2=\sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2, \end{align*} $$
$$ \begin{align*} \left\lvert\sum_{\gamma\in\Gamma} K(g,\gamma h)\right\rvert^2=\sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2, \end{align*} $$
so that
 $$ \begin{align*} \int_{D_{> 2R}}\int_D \left\lvert\sum_{\gamma\in\Gamma} K(g,\gamma h)\right\rvert^2 dg dh&=\int_{D_{> 2R}}\int_D \sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2 dgdh\\ &\leq \int_D\int_D \sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2 dg dh\\ &= \int_G\int_D \lvert K(g,h)\rvert^2 dg dh\\ & =\int_{\Gamma\backslash G}\int_G \lvert K(g, h)\rvert^2dhdg. \end{align*} $$
$$ \begin{align*} \int_{D_{> 2R}}\int_D \left\lvert\sum_{\gamma\in\Gamma} K(g,\gamma h)\right\rvert^2 dg dh&=\int_{D_{> 2R}}\int_D \sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2 dgdh\\ &\leq \int_D\int_D \sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2 dg dh\\ &= \int_G\int_D \lvert K(g,h)\rvert^2 dg dh\\ & =\int_{\Gamma\backslash G}\int_G \lvert K(g, h)\rvert^2dhdg. \end{align*} $$
To deal with the
![]() $2R$
-thin part, we use Cauchy–Schwarz and the support condition on K to obtain
$2R$
-thin part, we use Cauchy–Schwarz and the support condition on K to obtain
 $$ \begin{align*} \left\lvert\sum_{\gamma\in\Gamma} K(g,\gamma h)\right\rvert^2 \leq N_\Gamma(R)\sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2. \end{align*} $$
$$ \begin{align*} \left\lvert\sum_{\gamma\in\Gamma} K(g,\gamma h)\right\rvert^2 \leq N_\Gamma(R)\sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2. \end{align*} $$
The factor
![]() $N_\Gamma (R)$
is bounded by Lemma 5.1. Furthermore,
$N_\Gamma (R)$
is bounded by Lemma 5.1. Furthermore,
 $$ \begin{align*} & \int_{(\Gamma\backslash G)_{\leq 2R}}\int_{\Gamma\backslash G} \sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2 dg dh \\ &\leq \sup_{g\in \Gamma \backslash G, h\in G}\lvert K(g, h)\rvert^2\int_{(\Gamma\backslash G)_{\leq 2R}}\int_{\Gamma\backslash G} \sum_{\gamma\in\Gamma} \textbf{ 1}_{B_R}\left(g^{-1}\gamma h\right) dg dh. \end{align*} $$
$$ \begin{align*} & \int_{(\Gamma\backslash G)_{\leq 2R}}\int_{\Gamma\backslash G} \sum_{\gamma\in\Gamma} \lvert K(g,\gamma h)\rvert^2 dg dh \\ &\leq \sup_{g\in \Gamma \backslash G, h\in G}\lvert K(g, h)\rvert^2\int_{(\Gamma\backslash G)_{\leq 2R}}\int_{\Gamma\backslash G} \sum_{\gamma\in\Gamma} \textbf{ 1}_{B_R}\left(g^{-1}\gamma h\right) dg dh. \end{align*} $$
By unfolding and changing variables, we have
 $$ \begin{align*} \int_{\Gamma\backslash G} \sum_{\gamma\in\Gamma} \textbf{ 1}_{B_R}\left(g^{-1}\gamma h\right) dg= \int_G \textbf{ 1}_{B_R}\left(g^{-1} h\right) dg=m_G(B_R)=c_C\int_{\mathscr{B}_R^+}J(X)dX, \end{align*} $$
$$ \begin{align*} \int_{\Gamma\backslash G} \sum_{\gamma\in\Gamma} \textbf{ 1}_{B_R}\left(g^{-1}\gamma h\right) dg= \int_G \textbf{ 1}_{B_R}\left(g^{-1} h\right) dg=m_G(B_R)=c_C\int_{\mathscr{B}_R^+}J(X)dX, \end{align*} $$
the last equality coming from the Cartan measure decomposition (21). The Jacobian factor satisfies
![]() $J(X)\ll e^{2\left \langle \rho ,X\right \rangle }\ll e^{2R\lVert \rho \rVert _2}$
for
$J(X)\ll e^{2\left \langle \rho ,X\right \rangle }\ll e^{2R\lVert \rho \rVert _2}$
for
![]() $X\in \mathscr {B}^+$
, using equation (37). From this one deducesFootnote
2
that
$X\in \mathscr {B}^+$
, using equation (37). From this one deducesFootnote
2
that
![]() $m_G(B_R)\ll R^r e^{2R\lVert \rho \rVert _2}$
, which is enough to complete the proof.
$m_G(B_R)\ll R^r e^{2R\lVert \rho \rVert _2}$
, which is enough to complete the proof.
5.2 Description of the kernel of
 $\mathbf {A}(\tau )$
$\mathbf {A}(\tau )$
We return to the setting of
![]() $G=\operatorname {SL}_d({\mathbb R})$
. We would like to apply Lemma 5.2 to our operator
$G=\operatorname {SL}_d({\mathbb R})$
. We would like to apply Lemma 5.2 to our operator
![]() $\mathbf {A}(\tau )$
on
$\mathbf {A}(\tau )$
on
![]() $L^2(\Gamma \backslash G)$
from equation (10). For this we shall need a description of its kernel, which we shall denote by
$L^2(\Gamma \backslash G)$
from equation (10). For this we shall need a description of its kernel, which we shall denote by
![]() $A(\tau )$
; it is a continuous function on
$A(\tau )$
; it is a continuous function on
![]() $\Gamma \backslash (G\times G)$
.
$\Gamma \backslash (G\times G)$
.
Lemma 5.3. The kernel of
![]() $\mathbf {A}(\tau )$
is
$\mathbf {A}(\tau )$
is
 $$ \begin{align} A(\tau)(g,h)=\frac{1}{\tau}\int_0^\tau \frac{1}{m_G(E_t)}\int_{gE_t\cap hE_t} a(x) dxdt. \end{align} $$
$$ \begin{align} A(\tau)(g,h)=\frac{1}{\tau}\int_0^\tau \frac{1}{m_G(E_t)}\int_{gE_t\cap hE_t} a(x) dxdt. \end{align} $$
Proof. By definition, the action of
![]() $U_taU_t$
on
$U_taU_t$
on
![]() $f\in L^2(\Gamma \backslash G)$
is given by
$f\in L^2(\Gamma \backslash G)$
is given by
 $$ \begin{align*} (U_taU_t)f(g)=\frac{1}{m_G(E_t)}\int_{E_t}a(gh_1)\int_{E_t} f(gh_1 h_2)dh_2 dh_1. \end{align*} $$
$$ \begin{align*} (U_taU_t)f(g)=\frac{1}{m_G(E_t)}\int_{E_t}a(gh_1)\int_{E_t} f(gh_1 h_2)dh_2 dh_1. \end{align*} $$
We set
![]() $x=gh_1$
and
$x=gh_1$
and
![]() $h=xh_2$
, apply Fubini, and use
$h=xh_2$
, apply Fubini, and use
![]() $E_t^{-1}=E_t$
to obtain
$E_t^{-1}=E_t$
to obtain
 $$ \begin{align*} (U_taU_t)f(g)&=\frac{1}{m_G(E_t)}\int_{gE_t} a(x)\int_{xE_t} f(h)dh dx\\ &=\int_G\left( \frac{1}{m_G(E_t)}\int_{gE_t\cap hE_t} a(x) dx\right)f(h)dh. \end{align*} $$
$$ \begin{align*} (U_taU_t)f(g)&=\frac{1}{m_G(E_t)}\int_{gE_t} a(x)\int_{xE_t} f(h)dh dx\\ &=\int_G\left( \frac{1}{m_G(E_t)}\int_{gE_t\cap hE_t} a(x) dx\right)f(h)dh. \end{align*} $$
Averaging over t yields the claim.
5.3 Support and
 $\sup $
of
$\sup $
of
 $\mathbf {A}(\tau )$
$\mathbf {A}(\tau )$
In order to bound the second term in Lemma 5.2, we shall need to estimate the support and the supremum of the kernel function
![]() $A(\tau )$
. This is accomplished in the next result, which is the higher-rank generalization of [Reference Abert, Bergeron and Le Masson2, Lemma 26]. We recall the norm
$A(\tau )$
. This is accomplished in the next result, which is the higher-rank generalization of [Reference Abert, Bergeron and Le Masson2, Lemma 26]. We recall the norm
![]() $\lvert \cdot \rvert $
on
$\lvert \cdot \rvert $
on
![]() $G=\operatorname {SL}_d({\mathbb R})$
introduced in §2.2 and defining the sets
$G=\operatorname {SL}_d({\mathbb R})$
introduced in §2.2 and defining the sets
![]() $E_t$
.
$E_t$
.
Proposition 5.4. There exists a constant
![]() $b>0$
depending only on d such that
$b>0$
depending only on d such that
![]() $gE_t\cap hE_t$
is empty unless
$gE_t\cap hE_t$
is empty unless
 $\left \lvert h^{-1}g\right \rvert \le 2t+b$
. In particular,
$\left \lvert h^{-1}g\right \rvert \le 2t+b$
. In particular,
![]() $A(\tau )(g, h)=0$
unless
$A(\tau )(g, h)=0$
unless
 $\left \lvert h^{-1}g\right \rvert \le 2\tau +b$
. Further,
$\left \lvert h^{-1}g\right \rvert \le 2\tau +b$
. Further,
 $$ \begin{align*} \sup_{g, h\in G}\lvert A(\tau)(g, h)\rvert^2\le \lVert a\rVert_\infty^2. \end{align*} $$
$$ \begin{align*} \sup_{g, h\in G}\lvert A(\tau)(g, h)\rvert^2\le \lVert a\rVert_\infty^2. \end{align*} $$
Proof. We begin by establishing the following:
Claim: For
![]() $x\in \operatorname {SL}_d({\mathbb R})$
, we have
$x\in \operatorname {SL}_d({\mathbb R})$
, we have
![]() $\left \lvert x_{ij}\right \rvert \leq e^{\lvert x\rvert }$
. Moreover, there exists a constant
$\left \lvert x_{ij}\right \rvert \leq e^{\lvert x\rvert }$
. Moreover, there exists a constant
![]() $c>0$
depending only on d, such that for every
$c>0$
depending only on d, such that for every
![]() $x=\left (x_{ij}\right )\in \operatorname {SL}_d({\mathbb R})$
and every
$x=\left (x_{ij}\right )\in \operatorname {SL}_d({\mathbb R})$
and every
![]() $i\in \{1,\dotsc ,d\}$
there exists
$i\in \{1,\dotsc ,d\}$
there exists
![]() $j\in \{1,\dotsc , d\}$
with
$j\in \{1,\dotsc , d\}$
with
![]() $\left \lvert x_{ij}\right \rvert \ge c e^{-\lvert x\rvert }$
.
$\left \lvert x_{ij}\right \rvert \ge c e^{-\lvert x\rvert }$
.
Proof of claim: Write
![]() $x= k e^Z l$
, with
$x= k e^Z l$
, with
![]() $k=\left (k_{ij}\right )$
,
$k=\left (k_{ij}\right )$
,
![]() $l = \left (l_{ij}\right ) \in K=\textrm {SO}(d)$
, and
$l = \left (l_{ij}\right ) \in K=\textrm {SO}(d)$
, and
![]() $Z\in \overline {\mathfrak {a}^+}$
. Let
$Z\in \overline {\mathfrak {a}^+}$
. Let
![]() $\kappa _i=(k_{i1},\dotsc , k_{id})$
and
$\kappa _i=(k_{i1},\dotsc , k_{id})$
and
![]() $\lambda _j= \left (l_{1j},\dotsc , l_{dj}\right )\in {\mathbb R}^d$
, for
$\lambda _j= \left (l_{1j},\dotsc , l_{dj}\right )\in {\mathbb R}^d$
, for
![]() $i,j=1,\dotsc ,d$
. Let
$i,j=1,\dotsc ,d$
. Let
![]() $\langle \cdot , \cdot \rangle $
denote the standard inner product on
$\langle \cdot , \cdot \rangle $
denote the standard inner product on
![]() ${\mathbb R}^d$
. Then
${\mathbb R}^d$
. Then
![]() $\kappa _1,\dotsc ,\kappa _d$
and
$\kappa _1,\dotsc ,\kappa _d$
and
![]() $\lambda _1,\dotsc , \lambda _d$
are both orthonormal bases of
$\lambda _1,\dotsc , \lambda _d$
are both orthonormal bases of
![]() ${\mathbb R}^d$
, and
${\mathbb R}^d$
, and
 $x_{ij}=\left \langle \kappa _i,\lambda _j e^Z\right \rangle $
. In particular, by Cauchy and Schwarz we have
$x_{ij}=\left \langle \kappa _i,\lambda _j e^Z\right \rangle $
. In particular, by Cauchy and Schwarz we have
 $$ \begin{align*} \left\lvert x_{ij}\right\rvert=\left\lvert\left\langle\kappa_i,\lambda_j e^Z\right\rangle\right\rvert\leq \left\lVert\lambda_j e^Z\right\rVert^{1/2}\leq e^{\lVert Z\rVert_\infty}=e^{\lvert x\rvert}, \end{align*} $$
$$ \begin{align*} \left\lvert x_{ij}\right\rvert=\left\lvert\left\langle\kappa_i,\lambda_j e^Z\right\rangle\right\rvert\leq \left\lVert\lambda_j e^Z\right\rVert^{1/2}\leq e^{\lVert Z\rVert_\infty}=e^{\lvert x\rvert}, \end{align*} $$
proving the first statement.
For the second statement, we begin by observing that for every
![]() $j=1,\dotsc ,d$
we have
$j=1,\dotsc ,d$
we have
 $$ \begin{align*} \left\langle\kappa_i, \kappa_i e^Z\right\rangle=\sum_{j=1}^de^{Z_j}k_{ij}^2\geq \left(\min_j e^{Z_j}\right)\lVert\kappa_i\rVert^2=\min_j e^{Z_j}\ge e^{-\lVert Z\rVert_\infty}=e^{-\lvert x\rvert}. \end{align*} $$
$$ \begin{align*} \left\langle\kappa_i, \kappa_i e^Z\right\rangle=\sum_{j=1}^de^{Z_j}k_{ij}^2\geq \left(\min_j e^{Z_j}\right)\lVert\kappa_i\rVert^2=\min_j e^{Z_j}\ge e^{-\lVert Z\rVert_\infty}=e^{-\lvert x\rvert}. \end{align*} $$
Writing
![]() $\kappa _i$
as a linear combination
$\kappa _i$
as a linear combination
![]() $\kappa _i= a_1\lambda _1+\dotsb + a_d \lambda _d$
, we obtain
$\kappa _i= a_1\lambda _1+\dotsb + a_d \lambda _d$
, we obtain
 $$ \begin{align*} e^{-\lvert x\rvert} \le \left\langle\kappa_i, \kappa_i e^Z\right\rangle \le \sum_{j=1}^d \left\lvert a_j\right\rvert \left\lvert\left\langle\kappa_i, \lambda_j e^Z\right\rangle\right\rvert. \end{align*} $$
$$ \begin{align*} e^{-\lvert x\rvert} \le \left\langle\kappa_i, \kappa_i e^Z\right\rangle \le \sum_{j=1}^d \left\lvert a_j\right\rvert \left\lvert\left\langle\kappa_i, \lambda_j e^Z\right\rangle\right\rvert. \end{align*} $$
Note that the
![]() $a_i$
are uniformly bounded, since k and l are contained in a compact set. Hence there exist
$a_i$
are uniformly bounded, since k and l are contained in a compact set. Hence there exist
![]() $c>0$
and
$c>0$
and
![]() $j\in \{1,\dotsc , d\}$
such that
$j\in \{1,\dotsc , d\}$
such that
 $$ \begin{align*} \left\lvert x_{ij}\right\rvert=\left\lvert\left\langle\kappa_i, \lambda_j e^Z\right\rangle \right\rvert \ge c e^{-\lvert x\rvert}, \end{align*} $$
$$ \begin{align*} \left\lvert x_{ij}\right\rvert=\left\lvert\left\langle\kappa_i, \lambda_j e^Z\right\rangle \right\rvert \ge c e^{-\lvert x\rvert}, \end{align*} $$
as claimed.
Continuing with the proof of the proposition, suppose that there exists
![]() $y\in h^{-1}gE_t\cap E_t$
. We can assume without loss that
$y\in h^{-1}gE_t\cap E_t$
. We can assume without loss that
![]() $h^{-1} g= e^Y$
for some suitable
$h^{-1} g= e^Y$
for some suitable
![]() $Y=(Y_1,\dotsc , Y_n)\in \overline {\mathfrak {a}^+}$
.
$Y=(Y_1,\dotsc , Y_n)\in \overline {\mathfrak {a}^+}$
.
Since
![]() $y\in E_t$
, the first part of the claim shows that
$y\in E_t$
, the first part of the claim shows that
![]() $\left \lvert y_{ij}\right \rvert \le e^t$
for all
$\left \lvert y_{ij}\right \rvert \le e^t$
for all
![]() $i,j=1,\dotsc , d$
. Moreover, since
$i,j=1,\dotsc , d$
. Moreover, since
![]() $y\in e^YE_t$
, we can write
$y\in e^YE_t$
, we can write
![]() $y=e^Y x $
for some
$y=e^Y x $
for some
![]() $x\in E_t$
. Then
$x\in E_t$
. Then
![]() $y_{ij} = e^{Y_i} x_{ij}$
, and the second part of the claim shows that for every i there is a
$y_{ij} = e^{Y_i} x_{ij}$
, and the second part of the claim shows that for every i there is a
![]() $j_i$
such that
$j_i$
such that
![]() $\left \lvert x_{i j_i}\right \rvert \ge ce^{-t}$
. Putting this together, we obtain
$\left \lvert x_{i j_i}\right \rvert \ge ce^{-t}$
. Putting this together, we obtain
![]() $e^t \ge c e^{Y_i} e^{-t}$
, so that
$e^t \ge c e^{Y_i} e^{-t}$
, so that
![]() $e^{Y_i}\le c^{-1} e^{2t}$
.
$e^{Y_i}\le c^{-1} e^{2t}$
.
By similar arguments, we also know that
![]() $\left \lvert x_{ij}\right \rvert \le e^t$
for all
$\left \lvert x_{ij}\right \rvert \le e^t$
for all
![]() $i,j$
, and that for every i there exists
$i,j$
, and that for every i there exists
![]() $j_i'$
with
$j_i'$
with
 $e^{Y_i}\left \lvert x_{i j_i'}\right \rvert =\left \lvert y_{i j_i'}\right \rvert \ge ce^{-t}$
– that is,
$e^{Y_i}\left \lvert x_{i j_i'}\right \rvert =\left \lvert y_{i j_i'}\right \rvert \ge ce^{-t}$
– that is,
![]() $e^Y_i \ge c e^{-2t}$
.
$e^Y_i \ge c e^{-2t}$
.
These two inequalities together imply the first assertion of the corollary, and hence also the assertion of the support of
![]() $A(\tau )$
. The last assertion, on the
$A(\tau )$
. The last assertion, on the
![]() $\sup $
of
$\sup $
of
![]() $A(\tau )$
, is a direct consequence of the definition (42).
$A(\tau )$
, is a direct consequence of the definition (42).
Recall from §2.5(iii) that
![]() $E_t\subset B_{t\left \lVert X^0\right \rVert _2}$
. It then follows from Proposition 5.4 that we can take
$E_t\subset B_{t\left \lVert X^0\right \rVert _2}$
. It then follows from Proposition 5.4 that we can take
 $R=\left \lVert X^0\right \rVert (2\tau +b)$
in Lemma 5.2. Inserting this and the
$R=\left \lVert X^0\right \rVert (2\tau +b)$
in Lemma 5.2. Inserting this and the
![]() $\sup $
norm bound of Proposition 5.4 into Lemma 5.2, we obtain the second term in Theorem 2.3.
$\sup $
norm bound of Proposition 5.4 into Lemma 5.2, we obtain the second term in Theorem 2.3.
5.4 First term
To establish Theorem 2.3, it remains to estimate the first term in Lemma 5.2, for the operator
![]() $\mathbf {A}(\tau )$
with kernel
$\mathbf {A}(\tau )$
with kernel
![]() $A(\tau )$
.
$A(\tau )$
.
For a measurable set
![]() $E\subseteq G$
, we write
$E\subseteq G$
, we write
![]() $\rho _{\Gamma \backslash G}(E)$
for the action by convolution of the normalized characteristic function of E on
$\rho _{\Gamma \backslash G}(E)$
for the action by convolution of the normalized characteristic function of E on
![]() $L^2(\Gamma \backslash G)$
. Thus
$L^2(\Gamma \backslash G)$
. Thus
 $$ \begin{align*} \rho_{\Gamma\backslash G}(E)f(x)=\frac{1}{m_G(E)}\int_E f(xg)dg. \end{align*} $$
$$ \begin{align*} \rho_{\Gamma\backslash G}(E)f(x)=\frac{1}{m_G(E)}\int_E f(xg)dg. \end{align*} $$
We shall in particular be interested in this operator for sets of the form
![]() $gE_t\cap E_t$
.
$gE_t\cap E_t$
.
We begin with the following elementary upper bound on the quantity
 $$ \begin{align*} \mathscr{A}(\tau)=\int_{\Gamma\backslash G} \int_G\lvert A(\tau)(g,h)\rvert^2 dg dh. \end{align*} $$
$$ \begin{align*} \mathscr{A}(\tau)=\int_{\Gamma\backslash G} \int_G\lvert A(\tau)(g,h)\rvert^2 dg dh. \end{align*} $$
Lemma 5.5. For all
![]() $\tau> 0$
, we have
$\tau> 0$
, we have
 $$ \begin{align*} \mathscr{A}(\tau)\leq \frac{1}{\tau^2}\int_{E_{2\tau+b}}\left(\int_{\max\left\{0,\left(\lvert g\rvert-b\right)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)}{m_G(E_t)}\left\lVert \rho_{\Gamma\backslash G}(gE_t\cap E_t)a\right\rVert_{L^2(\Gamma\backslash G)}dt\right)^2dg, \end{align*} $$
$$ \begin{align*} \mathscr{A}(\tau)\leq \frac{1}{\tau^2}\int_{E_{2\tau+b}}\left(\int_{\max\left\{0,\left(\lvert g\rvert-b\right)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)}{m_G(E_t)}\left\lVert \rho_{\Gamma\backslash G}(gE_t\cap E_t)a\right\rVert_{L^2(\Gamma\backslash G)}dt\right)^2dg, \end{align*} $$
where
![]() $b>0$
is as in Proposition 5.4.
$b>0$
is as in Proposition 5.4.
Proof. From the definition (42) of
![]() $A(\tau )$
, we see that
$A(\tau )$
, we see that
 $$ \begin{align*} \mathscr{A}(\tau)=\frac{1}{\tau^2}\int_{\Gamma\backslash G}\int_G\left\lvert\int_0^\tau \frac{1}{m_G(E_t)}\int_{gE_t\cap hE_t}a(x)dx dt\right\rvert^2 dgdh. \end{align*} $$
$$ \begin{align*} \mathscr{A}(\tau)=\frac{1}{\tau^2}\int_{\Gamma\backslash G}\int_G\left\lvert\int_0^\tau \frac{1}{m_G(E_t)}\int_{gE_t\cap hE_t}a(x)dx dt\right\rvert^2 dgdh. \end{align*} $$
Changing variables
![]() $x\mapsto hx$
and
$x\mapsto hx$
and
![]() $g\mapsto h^{-1}g$
, this is
$g\mapsto h^{-1}g$
, this is
 $$ \begin{align*} \frac{1}{\tau^2}\int_{\Gamma\backslash G}\int_G\left\lvert\int_0^\tau \frac{1}{m_G(E_t)}\int_{gE_t\cap E_t}a(hx)dx dt\right\rvert^2 dg dh. \end{align*} $$
$$ \begin{align*} \frac{1}{\tau^2}\int_{\Gamma\backslash G}\int_G\left\lvert\int_0^\tau \frac{1}{m_G(E_t)}\int_{gE_t\cap E_t}a(hx)dx dt\right\rvert^2 dg dh. \end{align*} $$
In view of Proposition 5.4, the integral over
![]() $g\in G$
may be truncated at
$g\in G$
may be truncated at
![]() $\lvert g\rvert \leq 2\tau +b$
, and the lower range of the t integral may be truncated at
$\lvert g\rvert \leq 2\tau +b$
, and the lower range of the t integral may be truncated at
![]() $\max \{0,\lvert g\rvert -b)/2\}$
. Furthermore,
$\max \{0,\lvert g\rvert -b)/2\}$
. Furthermore,
 $$ \begin{align*} \frac{1}{m_G(E_t)}\int_{gE_t\cap E_t}a(hx)dx&=\frac{m_G(gE_t\cap E_t)}{m_G(E_t)}\frac{1}{m_G(gE_t\cap E_t)}\int_{gE_t\cap E_t}a(hx)dx\\ &=\frac{m_G(gE_t\cap E_t)}{m_G(E_t)}\left(\rho_{\Gamma\backslash G}(gE_t\cap E_t)a\right)(h). \end{align*} $$
$$ \begin{align*} \frac{1}{m_G(E_t)}\int_{gE_t\cap E_t}a(hx)dx&=\frac{m_G(gE_t\cap E_t)}{m_G(E_t)}\frac{1}{m_G(gE_t\cap E_t)}\int_{gE_t\cap E_t}a(hx)dx\\ &=\frac{m_G(gE_t\cap E_t)}{m_G(E_t)}\left(\rho_{\Gamma\backslash G}(gE_t\cap E_t)a\right)(h). \end{align*} $$
We conclude the proof by an application of the Minkowski integral inequality.
We briefly return to the level of generality of §3, and let G denote a connected noncompact simple Lie group with finite center. Let
![]() $(\pi ,V_\pi )$
be a unitary representation of G. We recall that the integrability exponent
$(\pi ,V_\pi )$
be a unitary representation of G. We recall that the integrability exponent
![]() $q(\pi )$
of
$q(\pi )$
of
![]() $\pi $
is defined as
$\pi $
is defined as
A classical result of Borel and Wallach [Reference Borel and Wallach6], Cowling [Reference Cowling11], and Howe and Moore [Reference Howe and Moore18] states that
![]() $\pi $
has a spectral gap precisely when
$\pi $
has a spectral gap precisely when
![]() $q(\pi )<\infty $
; we can effectively take this as our definition of the spectral gap in our setting.
$q(\pi )<\infty $
; we can effectively take this as our definition of the spectral gap in our setting.
Nevo [Reference Nevo29] (see also [Reference Gorodnik and Nevo15, Theorem 4.1]) has proved a mean ergodic theorem for measure-preserving actions G on a probability space
![]() $(X,\mu )$
whose associated unitary representation
$(X,\mu )$
whose associated unitary representation
![]() $L^2_0(X,\mu )$
has a spectral gap. We shall be interested in the action of G on
$L^2_0(X,\mu )$
has a spectral gap. We shall be interested in the action of G on
![]() $X=\Gamma \backslash G$
by right translation, where
$X=\Gamma \backslash G$
by right translation, where
![]() $\Gamma <G$
is a lattice. The associated unitary representation is then
$\Gamma <G$
is a lattice. The associated unitary representation is then
 $\rho _{\Gamma \backslash G}^0$
, the restriction of the right-regular representation
$\rho _{\Gamma \backslash G}^0$
, the restriction of the right-regular representation
![]() $\rho _{\Gamma \backslash G}$
to the subspace
$\rho _{\Gamma \backslash G}$
to the subspace
![]() $L^2_0(\Gamma \backslash G)$
of
$L^2_0(\Gamma \backslash G)$
of
![]() $L^2(\Gamma \backslash G)$
consisting of functions f with
$L^2(\Gamma \backslash G)$
consisting of functions f with
 $\int _{\Gamma \backslash G} f=0$
. In this setting, they show the following result:
$\int _{\Gamma \backslash G} f=0$
. In this setting, they show the following result:
Proposition 5.6 Nevo
Let G be a connected noncompact simple Lie group with finite center. Let
![]() $\Gamma <G$
be a lattice. Then there are constants
$\Gamma <G$
be a lattice. Then there are constants
![]() $\theta ,C>0$
, depending on the integrability exponents of
$\theta ,C>0$
, depending on the integrability exponents of
 $\rho _{\Gamma \backslash G}^0$
, such that for any measurable
$\rho _{\Gamma \backslash G}^0$
, such that for any measurable
![]() $E\subseteq G$
of finite measure, we have
$E\subseteq G$
of finite measure, we have
 $$ \begin{align*} \left\lVert\rho_{\Gamma\backslash G}^0(E)\right\rVert_2 \leq C m_G(E)^{-\theta}. \end{align*} $$
$$ \begin{align*} \left\lVert\rho_{\Gamma\backslash G}^0(E)\right\rVert_2 \leq C m_G(E)^{-\theta}. \end{align*} $$
A famous result of Kazhdan [Reference Kazhdan20] states that when G furthermore has rank at least
![]() $2$
,
$2$
,
 $$ \begin{align*} \sup_{\pi: \pi^G=0} q(\pi)<\infty, \end{align*} $$
$$ \begin{align*} \sup_{\pi: \pi^G=0} q(\pi)<\infty, \end{align*} $$
the supremum running over all unitary representations of G having no G-invariant vectors. In this case, the constants of Proposition 5.6 can be taken independently of
![]() $\Gamma $
. In particular, this is true of
$\Gamma $
. In particular, this is true of
![]() $G=\operatorname {SL}_d({\mathbb R})$
for
$G=\operatorname {SL}_d({\mathbb R})$
for
![]() $d\geq 3$
.
$d\geq 3$
.
We thus return to
![]() $G=\operatorname {SL}_d({\mathbb R})$
, for
$G=\operatorname {SL}_d({\mathbb R})$
, for
![]() $d\geq 3$
, and again require
$d\geq 3$
, and again require
![]() $\Gamma <\operatorname {SL}_d({\mathbb R})$
to be a uniform lattice. Recall that
$\Gamma <\operatorname {SL}_d({\mathbb R})$
to be a uniform lattice. Recall that
![]() $a\in L^2_0(\Gamma \backslash G)$
. We can therefore apply Proposition 5.6 to estimate the quantity
$a\in L^2_0(\Gamma \backslash G)$
. We can therefore apply Proposition 5.6 to estimate the quantity
 $$ \begin{align*} \left\lVert\rho_{\Gamma\backslash G}(gE_t\cap E_t)a\right\rVert_{L^2(\Gamma\backslash G)}= \left\lVert\rho_{\Gamma\backslash G}^0(gE_t\cap E_t)a\right\rVert_{L^2_0(\Gamma\backslash G)} \end{align*} $$
$$ \begin{align*} \left\lVert\rho_{\Gamma\backslash G}(gE_t\cap E_t)a\right\rVert_{L^2(\Gamma\backslash G)}= \left\lVert\rho_{\Gamma\backslash G}^0(gE_t\cap E_t)a\right\rVert_{L^2_0(\Gamma\backslash G)} \end{align*} $$
appearing in Lemma 5.5. Hence there is
![]() $\theta>0$
, depending only on d, such that
$\theta>0$
, depending only on d, such that
 $$ \begin{align*} \mathscr{A}(\tau) \ll \frac{\lVert a\rVert_{L^2(\Gamma\backslash G)}^2}{\tau^2}\int_{E_{2\tau+b}}\left(\int_{\max\left\{0,\left(\lvert g\rvert-b\right)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)^{1-\theta}}{m_G(E_t)} dt\right)^2dg. \end{align*} $$
$$ \begin{align*} \mathscr{A}(\tau) \ll \frac{\lVert a\rVert_{L^2(\Gamma\backslash G)}^2}{\tau^2}\int_{E_{2\tau+b}}\left(\int_{\max\left\{0,\left(\lvert g\rvert-b\right)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)^{1-\theta}}{m_G(E_t)} dt\right)^2dg. \end{align*} $$
To conclude the proof of Theorem 2.3, it suffices to show the following estimate:
Proposition 5.7. Let
![]() $g\in G$
. Then for
$g\in G$
. Then for
![]() $\tau \gg 1$
we have
$\tau \gg 1$
we have
 $$ \begin{align*} \int_{E_{2\tau+b}}\left(\int_{\max\left\{0,\left(\lvert g\rvert-b\right)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)^{1-\theta}}{m_G(E_t)} dt\right)^2dg\ll \tau, \end{align*} $$
$$ \begin{align*} \int_{E_{2\tau+b}}\left(\int_{\max\left\{0,\left(\lvert g\rvert-b\right)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)^{1-\theta}}{m_G(E_t)} dt\right)^2dg\ll \tau, \end{align*} $$
the implied constant depending on d.
The main point in the proof of this result is an estimate on the intersection volumes
![]() $m_G(gE_t\cap E_t)$
, proved in the next subsection.
$m_G(gE_t\cap E_t)$
, proved in the next subsection.
5.5 Intersection volumes
We seek to prove the following estimate on the intersection volumes
 $m_G\left (e^YE_t\cap E_t\right )$
. See §2.5 for a discussion of some geometric aspects.
$m_G\left (e^YE_t\cap E_t\right )$
. See §2.5 for a discussion of some geometric aspects.
Proposition 5.8. Set
![]() $Y\in \mathfrak {a}^+$
and
$Y\in \mathfrak {a}^+$
and
![]() $t>0$
. Then
$t>0$
. Then
 $$ \begin{align} m_G\left(e^YE_t\cap E_t \right)\ll e^{-\left\langle \rho, Y\right\rangle}m_G(E_t). \end{align} $$
$$ \begin{align} m_G\left(e^YE_t\cap E_t \right)\ll e^{-\left\langle \rho, Y\right\rangle}m_G(E_t). \end{align} $$
Proof. Recall the definition of the Frobenius norm
![]() $\lVert \cdot \rVert $
from §2.5(iv) and the Frobenius ball
$\lVert \cdot \rVert $
from §2.5(iv) and the Frobenius ball
![]() $\boldsymbol {E}_t$
from equation (19). We claim that
$\boldsymbol {E}_t$
from equation (19). We claim that
Note that
![]() $\lVert \cdot \rVert $
is bi-K-invariant, so that if
$\lVert \cdot \rVert $
is bi-K-invariant, so that if
![]() $g=k_1 e^X k_2$
, where
$g=k_1 e^X k_2$
, where
![]() $X=(X_1,\dotsc ,X_d)\in \mathfrak {a}$
, then
$X=(X_1,\dotsc ,X_d)\in \mathfrak {a}$
, then
![]() $\lVert g\rVert ^2=e^{2X_1}+\dotsb +e^{2X_d}$
. Thus we may write
$\lVert g\rVert ^2=e^{2X_1}+\dotsb +e^{2X_d}$
. Thus we may write
![]() $\boldsymbol {E}_t=K\exp (\boldsymbol {P}_t) K$
, where
$\boldsymbol {E}_t=K\exp (\boldsymbol {P}_t) K$
, where
 $$ \begin{align*} \boldsymbol{P}_t=\left\{X=(X_1,\dotsc ,X_d)\in\mathfrak{a}: \max\left\{e^{2X_1}+\dotsb +e^{2X_d}, e^{-2X_1}+\dotsb +e^{-2X_d}\right\}\leq e^{2t}\right\}. \end{align*} $$
$$ \begin{align*} \boldsymbol{P}_t=\left\{X=(X_1,\dotsc ,X_d)\in\mathfrak{a}: \max\left\{e^{2X_1}+\dotsb +e^{2X_d}, e^{-2X_1}+\dotsb +e^{-2X_d}\right\}\leq e^{2t}\right\}. \end{align*} $$
We therefore wish to establish formula (44) for the sets
![]() $\boldsymbol {P}_t$
and
$\boldsymbol {P}_t$
and
![]() ${\mathscr P}_t=t{\mathscr P}$
, where
${\mathscr P}_t=t{\mathscr P}$
, where
![]() ${\mathscr P}$
is defined in equation (14):
${\mathscr P}$
is defined in equation (14):
-
⊳ If
 $\lvert X_i\rvert \leq t$
for all i, we have
$\lvert X_i\rvert \leq t$
for all i, we have
 $\max \left \{e^{2X_1}+\dotsb +e^{2X_d}, e^{-2X_1}+\dotsb +e^{-2X_d}\right \}\leq de^{2t}$
, so that
$\max \left \{e^{2X_1}+\dotsb +e^{2X_d}, e^{-2X_1}+\dotsb +e^{-2X_d}\right \}\leq de^{2t}$
, so that
 ${\mathscr P}_t\subseteq \boldsymbol {P}_{t+\log \sqrt {d}}$
.
${\mathscr P}_t\subseteq \boldsymbol {P}_{t+\log \sqrt {d}}$
. -
⊲ In the other direction, if
 $\max \left \{e^{2X_1}+\dotsb +e^{2X_d}, e^{-2X_1}+\dotsb +e^{-2X_d}\right \}\leq e^{2t}$
, then
$\max \left \{e^{2X_1}+\dotsb +e^{2X_d}, e^{-2X_1}+\dotsb +e^{-2X_d}\right \}\leq e^{2t}$
, then
 $\lvert X_i\rvert \leq t$
for all i, so that
$\lvert X_i\rvert \leq t$
for all i, so that
 $\boldsymbol {P}_t\subseteq {\mathscr P}_t$
.
$\boldsymbol {P}_t\subseteq {\mathscr P}_t$
.
It is now enough to prove formula (43) with
![]() $E_t$
replaced by
$E_t$
replaced by
![]() $\boldsymbol {E}_t$
. Indeed, suppose that
$\boldsymbol {E}_t$
. Indeed, suppose that
 $$ \begin{align} m_G\left(e^Y\boldsymbol{E}_t\cap \boldsymbol{E}_t\right)\ll e^{-\left\langle\rho,Y\right\rangle}m_G(\boldsymbol{E}_t) \end{align} $$
$$ \begin{align} m_G\left(e^Y\boldsymbol{E}_t\cap \boldsymbol{E}_t\right)\ll e^{-\left\langle\rho,Y\right\rangle}m_G(\boldsymbol{E}_t) \end{align} $$
for any
![]() $Y\in \mathfrak {a}$
. We use formula (44) to bound
$Y\in \mathfrak {a}$
. We use formula (44) to bound
![]() $m_G(e^YE_t\cap E_t)$
by
$m_G(e^YE_t\cap E_t)$
by
 $m_G(e^Y\boldsymbol {E}_{t+\log \sqrt {d}}\cap \boldsymbol {E}_{t+\log \sqrt {d}})$
. Inserting the estimate (45) and the inclusions (44) again, we find
$m_G(e^Y\boldsymbol {E}_{t+\log \sqrt {d}}\cap \boldsymbol {E}_{t+\log \sqrt {d}})$
. Inserting the estimate (45) and the inclusions (44) again, we find
 $$ \begin{align*} m_G\left(e^Y\boldsymbol{E}_{t+\log\sqrt{d}}\cap \boldsymbol{E}_{t+\log\sqrt{d}}\right) \ll e^{-\left\langle\rho,Y\right\rangle}m_G\left(\boldsymbol{E}_{t+\log\sqrt{d}}\right)\leq e^{-\left\langle\rho,Y\right\rangle}m_G\left(E_{t+\log\sqrt{d}}\right). \end{align*} $$
$$ \begin{align*} m_G\left(e^Y\boldsymbol{E}_{t+\log\sqrt{d}}\cap \boldsymbol{E}_{t+\log\sqrt{d}}\right) \ll e^{-\left\langle\rho,Y\right\rangle}m_G\left(\boldsymbol{E}_{t+\log\sqrt{d}}\right)\leq e^{-\left\langle\rho,Y\right\rangle}m_G\left(E_{t+\log\sqrt{d}}\right). \end{align*} $$
Since
 $m_G\left (E_{t+\log \sqrt {d}}\right )\asymp m_G(E_t)$
, by Corollary A.4, we have reduced formula (43) to formula (45).
$m_G\left (E_{t+\log \sqrt {d}}\right )\asymp m_G(E_t)$
, by Corollary A.4, we have reduced formula (43) to formula (45).
We prove formula (45) using the Iwasawa decomposition
![]() $G=ANK$
from §3.1. Let
$G=ANK$
from §3.1. Let
![]() $g=auk$
so that
$g=auk$
so that
![]() $\lVert g\rVert =\lVert au\rVert $
and
$\lVert g\rVert =\lVert au\rVert $
and
 $\left \lVert g^{-1}\right \rVert =\left \lVert u^{-1}a^{-1}\right \rVert $
. Now
$\left \lVert g^{-1}\right \rVert =\left \lVert u^{-1}a^{-1}\right \rVert $
. Now
![]() $\lVert au\rVert ^2$
just equals the sum of all the squares of the matrix entries of
$\lVert au\rVert ^2$
just equals the sum of all the squares of the matrix entries of
![]() $au$
, so that
$au$
, so that
![]() $\lVert au\rVert =\lVert g\rVert \le e^t$
immediately implies that
$\lVert au\rVert =\lVert g\rVert \le e^t$
immediately implies that
![]() $\lVert a\rVert \le e^t$
and
$\lVert a\rVert \le e^t$
and
![]() $\lVert au-a\rVert \le e^t$
. Similarly,
$\lVert au-a\rVert \le e^t$
. Similarly,
 $\left \lVert g^{-1}\right \rVert \le e^t$
implies
$\left \lVert g^{-1}\right \rVert \le e^t$
implies
 $\left \lVert a^{-1}\right \rVert \le e^t$
and
$\left \lVert a^{-1}\right \rVert \le e^t$
and
 $\left \lVert u^{-1} a^{-1}- a^{-1}\right \rVert \le e^t$
. Thus we obtain the inclusion
$\left \lVert u^{-1} a^{-1}- a^{-1}\right \rVert \le e^t$
. Thus we obtain the inclusion
 $$ \begin{align*} \boldsymbol{E}_t\subseteq \left\{g=auk\in G: \lVert a\rVert, \left\lVert a^{-1}\right\rVert, \lVert au-a\rVert, \left\lVert u^{-1}a^{-1}-a^{-1}\right\rVert \leq e^t\right\}. \end{align*} $$
$$ \begin{align*} \boldsymbol{E}_t\subseteq \left\{g=auk\in G: \lVert a\rVert, \left\lVert a^{-1}\right\rVert, \lVert au-a\rVert, \left\lVert u^{-1}a^{-1}-a^{-1}\right\rVert \leq e^t\right\}. \end{align*} $$
Applying the same argument to
![]() $e^Yg$
, for
$e^Yg$
, for
![]() $Y\in \mathfrak {a}$
, and dropping the last two conditions,
$Y\in \mathfrak {a}$
, and dropping the last two conditions,
 $$ \begin{align*} e^Y\boldsymbol{E}_t\subseteq \left\{g=auk\in G:\left\lVert e^{-Y}a\right\rVert, \left\lVert e^Ya^{-1}\right\rVert \leq e^t\right\}. \end{align*} $$
$$ \begin{align*} e^Y\boldsymbol{E}_t\subseteq \left\{g=auk\in G:\left\lVert e^{-Y}a\right\rVert, \left\lVert e^Ya^{-1}\right\rVert \leq e^t\right\}. \end{align*} $$
We conclude that
 $m_G\left (e^Y\boldsymbol {E}_t\cap \boldsymbol {E}_t\right )\leq I(Y,t)$
, where
$m_G\left (e^Y\boldsymbol {E}_t\cap \boldsymbol {E}_t\right )\leq I(Y,t)$
, where
 $$ \begin{align*} I(Y,t)= \int\limits_{\substack{\left\lVert e^{\pm A}\right\rVert\leq e^t\\ \left\lVert e^{\pm (A-Y)}\right\rVert\leq e^t}} \int\limits_{\substack{\left\lVert e^Au-e^A\right\rVert\leq e^t\\ \left\lVert u^{-1}e^{-A}-e^{-A}\right\rVert\leq e^t}}du dA. \end{align*} $$
$$ \begin{align*} I(Y,t)= \int\limits_{\substack{\left\lVert e^{\pm A}\right\rVert\leq e^t\\ \left\lVert e^{\pm (A-Y)}\right\rVert\leq e^t}} \int\limits_{\substack{\left\lVert e^Au-e^A\right\rVert\leq e^t\\ \left\lVert u^{-1}e^{-A}-e^{-A}\right\rVert\leq e^t}}du dA. \end{align*} $$
Changing variables
![]() $u\mapsto e^Au-e^A+I$
in the U-integration, we obtain
$u\mapsto e^Au-e^A+I$
in the U-integration, we obtain
 $$ \begin{align*} I(Y,t)= I_U(t) \int\limits_{\substack{\left\lVert e^{\pm A}\right\rVert\leq e^t\\ \left\lVert e^{\pm (A-Y)}\right\rVert\leq e^t}} e^{-\left\langle\rho,A\right\rangle}dA, \end{align*} $$
$$ \begin{align*} I(Y,t)= I_U(t) \int\limits_{\substack{\left\lVert e^{\pm A}\right\rVert\leq e^t\\ \left\lVert e^{\pm (A-Y)}\right\rVert\leq e^t}} e^{-\left\langle\rho,A\right\rangle}dA, \end{align*} $$
where
 $I_U(t)=m_U\left (u\in U: \lVert u-I\rVert , \left \lVert u^{-1}-I\right \rVert \leq e^t\right )$
. Changing variables
$I_U(t)=m_U\left (u\in U: \lVert u-I\rVert , \left \lVert u^{-1}-I\right \rVert \leq e^t\right )$
. Changing variables
![]() $A\mapsto A-Y$
in the A-integration and dropping a condition, we obtain
$A\mapsto A-Y$
in the A-integration and dropping a condition, we obtain
 $$ \begin{align*} \int\limits_{\substack{\left\lVert e^{\pm A}\right\rVert\leq e^t\\ \left\lVert e^{\pm (A-Y)}\right\rVert\leq e^t}} e^{-\left\langle\rho,A\right\rangle}dA&= e^{-\left\langle \rho,Y\right\rangle} \int\limits_{\substack{\left\lVert e^{\pm (A+Y)}\right\rVert\leq e^t\\ \left\lVert e^{\pm A}\right\rVert\leq e^t}} e^{-\left\langle\rho,A\right\rangle}dA\\ &\leq e^{-\left\langle \rho,Y\right\rangle}\int\limits_{\left\lVert e^{\pm A}\right\rVert\leq e^t} e^{-\left\langle\rho,A\right\rangle}dA. \end{align*} $$
$$ \begin{align*} \int\limits_{\substack{\left\lVert e^{\pm A}\right\rVert\leq e^t\\ \left\lVert e^{\pm (A-Y)}\right\rVert\leq e^t}} e^{-\left\langle\rho,A\right\rangle}dA&= e^{-\left\langle \rho,Y\right\rangle} \int\limits_{\substack{\left\lVert e^{\pm (A+Y)}\right\rVert\leq e^t\\ \left\lVert e^{\pm A}\right\rVert\leq e^t}} e^{-\left\langle\rho,A\right\rangle}dA\\ &\leq e^{-\left\langle \rho,Y\right\rangle}\int\limits_{\left\lVert e^{\pm A}\right\rVert\leq e^t} e^{-\left\langle\rho,A\right\rangle}dA. \end{align*} $$
We write this last integral as
![]() $I_A(t)$
. Using equation (20), this establishes
$I_A(t)$
. Using equation (20), this establishes
 $$ \begin{align} m_G\left(e^Y\boldsymbol{E}_t\cap \boldsymbol{E}_t\right)\leq c_I e^{-\left\langle \rho,Y\right\rangle}I_A(t)I_U(t). \end{align} $$
$$ \begin{align} m_G\left(e^Y\boldsymbol{E}_t\cap \boldsymbol{E}_t\right)\leq c_I e^{-\left\langle \rho,Y\right\rangle}I_A(t)I_U(t). \end{align} $$
We now go in reverse. For
![]() $A\in \mathfrak {a}$
, we change variables
$A\in \mathfrak {a}$
, we change variables
![]() $u\mapsto e^{-A}u-e^{-A}+I$
to obtain
$u\mapsto e^{-A}u-e^{-A}+I$
to obtain
 $$ \begin{align*} e^{-\left\langle \rho,A\right\rangle}I_U(t)=m_U\left(u\in U: \left\lVert e^Au-e^A\right\rVert, \left\lVert u^{-1}e^{-A}-e^{-A}\right\rVert\leq e^t\right), \end{align*} $$
$$ \begin{align*} e^{-\left\langle \rho,A\right\rangle}I_U(t)=m_U\left(u\in U: \left\lVert e^Au-e^A\right\rVert, \left\lVert u^{-1}e^{-A}-e^{-A}\right\rVert\leq e^t\right), \end{align*} $$
so that
 $$ \begin{align*} I_A(t)I_U(t)=\int\limits_{\left\lVert e^{\pm A}\right\rVert\leq e^t} \int\limits_{\left\lVert\left(e^Au\right)^{\pm 1}-e^{\pm A}\right\rVert\leq e^t} du dA. \end{align*} $$
$$ \begin{align*} I_A(t)I_U(t)=\int\limits_{\left\lVert e^{\pm A}\right\rVert\leq e^t} \int\limits_{\left\lVert\left(e^Au\right)^{\pm 1}-e^{\pm A}\right\rVert\leq e^t} du dA. \end{align*} $$
Again by the triangle inequality and equation (20), this gives
 $$ \begin{align*} I_A(t)I_U(t)\leq \iint\limits_{\left\lVert(au)^{\pm 1}\right\rVert\leq 2e^t} da du=c_I^{-1}m_G\left(\boldsymbol{E}_{t+\log 2}\right)\asymp m_G(\boldsymbol{E}_t). \end{align*} $$
$$ \begin{align*} I_A(t)I_U(t)\leq \iint\limits_{\left\lVert(au)^{\pm 1}\right\rVert\leq 2e^t} da du=c_I^{-1}m_G\left(\boldsymbol{E}_{t+\log 2}\right)\asymp m_G(\boldsymbol{E}_t). \end{align*} $$
Combining this last inequality with formula (46) yields formula (45).
5.6 Proof of Proposition 5.7
From Proposition 5.8 and Lemma A.4 we have, for
![]() $Y\in \mathfrak {a}^+$
,
$Y\in \mathfrak {a}^+$
,
 $$ \begin{align*} \frac{m_G\left(e^YE_t\cap E_t\right)^{1-\theta}}{m_G(E_t)}\ll e^{-(1-\theta)\left\langle \rho, Y\right\rangle}m_G(E_t)^{-\theta} \ll e^{-(1-\theta)\left\langle \rho, Y\right\rangle}e^{-t\theta \left\langle 2\rho, X^0\right\rangle}, \end{align*} $$
$$ \begin{align*} \frac{m_G\left(e^YE_t\cap E_t\right)^{1-\theta}}{m_G(E_t)}\ll e^{-(1-\theta)\left\langle \rho, Y\right\rangle}m_G(E_t)^{-\theta} \ll e^{-(1-\theta)\left\langle \rho, Y\right\rangle}e^{-t\theta \left\langle 2\rho, X^0\right\rangle}, \end{align*} $$
so that, using equation (15),
 $$ \begin{align*} &\int_{E_{2\tau+b}} \left(\int_{\max\left\{0,(\lvert g\rvert-b)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)^{1-\theta}}{m_G(E_t)} dt\right)^2dg\\ &\qquad\ll\int_{\mathscr{P}_{2\tau+b}^+}\left(\int_{\max\left\{0,\left(\lVert Y\rVert_\infty-b\right)/2\right\}}^\tau e^{-t\theta\left\langle 2\rho,X^0\right\rangle} dt\right)^2e^{-(1-\theta)\left\langle 2\rho, Y\right\rangle}J(Y)dY. \end{align*} $$
$$ \begin{align*} &\int_{E_{2\tau+b}} \left(\int_{\max\left\{0,(\lvert g\rvert-b)/2\right\}}^\tau \frac{m_G(gE_t\cap E_t)^{1-\theta}}{m_G(E_t)} dt\right)^2dg\\ &\qquad\ll\int_{\mathscr{P}_{2\tau+b}^+}\left(\int_{\max\left\{0,\left(\lVert Y\rVert_\infty-b\right)/2\right\}}^\tau e^{-t\theta\left\langle 2\rho,X^0\right\rangle} dt\right)^2e^{-(1-\theta)\left\langle 2\rho, Y\right\rangle}J(Y)dY. \end{align*} $$
Inserting
![]() $J(X)\ll e^{2\left \langle \rho ,X\right \rangle }$
for
$J(X)\ll e^{2\left \langle \rho ,X\right \rangle }$
for
![]() $X\in \mathfrak {a}^+$
from equation (37) and evaluating the t-integral, we majorize the foregoing expression by
$X\in \mathfrak {a}^+$
from equation (37) and evaluating the t-integral, we majorize the foregoing expression by
 $$ \begin{align*} \int_{\mathscr{P}_{2\tau+b}^+} e^{-\max\left\{0,\lVert Y\rVert_\infty-b\right\}\theta\left\langle 2\rho,X^0\right\rangle} e^{\theta\left\langle 2\rho, Y\right\rangle}dY. \end{align*} $$
$$ \begin{align*} \int_{\mathscr{P}_{2\tau+b}^+} e^{-\max\left\{0,\lVert Y\rVert_\infty-b\right\}\theta\left\langle 2\rho,X^0\right\rangle} e^{\theta\left\langle 2\rho, Y\right\rangle}dY. \end{align*} $$
We break up the last integral as
![]() $I_1+I_2$
, according to
$I_1+I_2$
, according to
 $\mathfrak {a}_1^+=\mathscr {P}_{b}^+$
and
$\mathfrak {a}_1^+=\mathscr {P}_{b}^+$
and
 $$ \begin{align*} \mathfrak{a}_2^+(\tau)&=\left\{Y\in\mathfrak{a}^+: b\leq \lVert Y\rVert_\infty\leq 2\tau+b\right\}. \end{align*} $$
$$ \begin{align*} \mathfrak{a}_2^+(\tau)&=\left\{Y\in\mathfrak{a}^+: b\leq \lVert Y\rVert_\infty\leq 2\tau+b\right\}. \end{align*} $$
Since
![]() $\mathfrak {a}^+_1$
is independent of
$\mathfrak {a}^+_1$
is independent of
![]() $\tau $
(as is the integrand), we have
$\tau $
(as is the integrand), we have
![]() $I_1\ll 1$
. Next, we have
$I_1\ll 1$
. Next, we have
 $$ \begin{align*} I_2\ll \int_{\mathfrak{a}_2^+(\tau)} e^{2\theta\left(\left\langle \rho,Y\right\rangle -\lVert Y\rVert_\infty\left\langle \rho,X^0\right\rangle\right)}dY. \end{align*} $$
$$ \begin{align*} I_2\ll \int_{\mathfrak{a}_2^+(\tau)} e^{2\theta\left(\left\langle \rho,Y\right\rangle -\lVert Y\rVert_\infty\left\langle \rho,X^0\right\rangle\right)}dY. \end{align*} $$
We will drop several of the conditions on Y in the course of the proof to simplify the integral.
Write
![]() $\tau ' = 2\tau +b$
. We distinguish the cases of d being even and odd. Define
$\tau ' = 2\tau +b$
. We distinguish the cases of d being even and odd. Define
 $$ \begin{align} s =\begin{cases} d/2 &\text{if}\ d\ \text{is even},\\ (d+1)/2 &\text{if}\ d\ \text{is odd}. \end{cases} \end{align} $$
$$ \begin{align} s =\begin{cases} d/2 &\text{if}\ d\ \text{is even},\\ (d+1)/2 &\text{if}\ d\ \text{is odd}. \end{cases} \end{align} $$
We first assume that
![]() $d\geq 3$
is odd. We can write Y in the integral as
$d\geq 3$
is odd. We can write Y in the integral as
with
![]() $\tau '\ge a_1\ge \dotsb \ge a_s\ge 0$
and
$\tau '\ge a_1\ge \dotsb \ge a_s\ge 0$
and
![]() $\tau '\ge b_1\ge \dotsb \ge b_s\ge 0$
. Then
$\tau '\ge b_1\ge \dotsb \ge b_s\ge 0$
. Then
![]() $\langle \rho , Y\rangle = \sum _{i=1}^s (s-i) (a_i+b_i)$
, and using Lemma A.1,
$\langle \rho , Y\rangle = \sum _{i=1}^s (s-i) (a_i+b_i)$
, and using Lemma A.1,
 $\left \langle \rho , X^0 \right \rangle = 2 A$
with
$\left \langle \rho , X^0 \right \rangle = 2 A$
with
![]() $A=\sum _{i=1}^s(s-i)$
. Moreover,
$A=\sum _{i=1}^s(s-i)$
. Moreover,
![]() $\lVert Y\rVert _\infty = \max \{a_1, b_1\}$
. Hence
$\lVert Y\rVert _\infty = \max \{a_1, b_1\}$
. Hence
 $$ \begin{align*} I_2(\tau)\ll \int\dotsi\int e^{2\theta\left( \sum_{i=1}^s (s-i) \left(a_i+b_i\right)- 2A\max\left\{a_1,b_1\right\}\right)}, \end{align*} $$
$$ \begin{align*} I_2(\tau)\ll \int\dotsi\int e^{2\theta\left( \sum_{i=1}^s (s-i) \left(a_i+b_i\right)- 2A\max\left\{a_1,b_1\right\}\right)}, \end{align*} $$
where the integral runs over
 $$ \begin{align*} \left\{ a_1,\dotsc, a_s, b_1,\dotsc, b_s\bigg\vert \begin{aligned} \tau'\ge a_1\ge0,\; a_1\ge a_2\ge0,\; & \dotsc,\; a_{s-1}\ge a_s\ge0,\\ \tau'\ge b_1\ge0,\; b_1\ge b_2\ge0,\; & \dotsc,\; b_{s-1}\ge b_s\ge0. \end{aligned} \right\} \end{align*} $$
$$ \begin{align*} \left\{ a_1,\dotsc, a_s, b_1,\dotsc, b_s\bigg\vert \begin{aligned} \tau'\ge a_1\ge0,\; a_1\ge a_2\ge0,\; & \dotsc,\; a_{s-1}\ge a_s\ge0,\\ \tau'\ge b_1\ge0,\; b_1\ge b_2\ge0,\; & \dotsc,\; b_{s-1}\ge b_s\ge0. \end{aligned} \right\} \end{align*} $$
We now integrate first
![]() $a_s$
and
$a_s$
and
![]() $b_s$
, and continue successively with
$b_s$
, and continue successively with
![]() $a_{s-1},\dotsc , a_2$
and
$a_{s-1},\dotsc , a_2$
and
![]() $b_{s-1},\dotsc , b_2$
, until only
$b_{s-1},\dotsc , b_2$
, until only
![]() $a_1$
and
$a_1$
and
![]() $b_1$
remain to be integrated. In this way we obtain
$b_1$
remain to be integrated. In this way we obtain
 $$ \begin{align*} I_2(\tau)\ll\iint_0^{\tau'} e^{2\theta A\left(a_1+b_1 - 2\max\left\{a_1, b_1\right\}\right)} da_1 db_1 &= \iint_0^{\tau'} e^{- 2\theta A\left\lvert a_1-b_1\right\rvert} da_1 db_1 \\ & = 2\tau' \int_0^{\tau'} e^{- 2\theta Ax}\, dx \ll \tau. \end{align*} $$
$$ \begin{align*} I_2(\tau)\ll\iint_0^{\tau'} e^{2\theta A\left(a_1+b_1 - 2\max\left\{a_1, b_1\right\}\right)} da_1 db_1 &= \iint_0^{\tau'} e^{- 2\theta A\left\lvert a_1-b_1\right\rvert} da_1 db_1 \\ & = 2\tau' \int_0^{\tau'} e^{- 2\theta Ax}\, dx \ll \tau. \end{align*} $$
If d is even, then
![]() $d\ge 4$
and
$d\ge 4$
and
![]() $s\ge 2$
. We can write
$s\ge 2$
. We can write
![]() $Y= (a_1,\dotsc , a_s, -b_s, \dotsc , -b_1)$
, with
$Y= (a_1,\dotsc , a_s, -b_s, \dotsc , -b_1)$
, with
![]() $\tau '\ge a_1\ge \dotsb \ge a_s\ge 0$
,
$\tau '\ge a_1\ge \dotsb \ge a_s\ge 0$
,
![]() $\tau '\ge b_1\ge \dotsb \ge b_s\ge 0$
, and
$\tau '\ge b_1\ge \dotsb \ge b_s\ge 0$
, and
Then
![]() $\lVert Y\rVert _\infty = \max \{a_1, b_1\}$
and
$\lVert Y\rVert _\infty = \max \{a_1, b_1\}$
and
 $$ \begin{align*} \langle \rho, Y\rangle = \sum_{i=1}^s (s-i+1/2)(a_i+b_i)= \sum_{i=1}^s (s-i+1)a_i + \sum_{i=1}^{s-1} (s-i)b_i, \end{align*} $$
$$ \begin{align*} \langle \rho, Y\rangle = \sum_{i=1}^s (s-i+1/2)(a_i+b_i)= \sum_{i=1}^s (s-i+1)a_i + \sum_{i=1}^{s-1} (s-i)b_i, \end{align*} $$
where we have used equation (48) to replace
![]() $b_s$
. Furthermore, using Lemma A.1, we have
$b_s$
. Furthermore, using Lemma A.1, we have
 $\left \langle \rho , X^0\right \rangle =A+ B$
, where we have put
$\left \langle \rho , X^0\right \rangle =A+ B$
, where we have put
 $$ \begin{align*} A=\sum_{i=1}^s (s-i+1)\quad\text{and}\quad B= \sum_{i=1}^s (s-i). \end{align*} $$
$$ \begin{align*} A=\sum_{i=1}^s (s-i+1)\quad\text{and}\quad B= \sum_{i=1}^s (s-i). \end{align*} $$
Extending the domain of integration if necessary, we obtain
 $$ \begin{align*} I_2(\tau)\leq \int\dotsi\int e^{2\theta\left(\sum_{i=1}^s (s-i+1)a_i + \sum_{i=1}^{s-1} (s-i)b_i - (A+B)\max\left\{a_1,b_1\right\}\right)}, \end{align*} $$
$$ \begin{align*} I_2(\tau)\leq \int\dotsi\int e^{2\theta\left(\sum_{i=1}^s (s-i+1)a_i + \sum_{i=1}^{s-1} (s-i)b_i - (A+B)\max\left\{a_1,b_1\right\}\right)}, \end{align*} $$
where the integral runs over
 $$ \begin{align*} \left\{ a_1,\dotsc, a_s, b_1,\dotsc, b_{s-1}\bigg\vert \begin{aligned} \tau'\ge a_1\ge0,\; a_1\ge a_2\ge0,\; & \dotsc,\; a_{s-1} \ge a_s\ge0,\\ \tau'\ge b_1\ge0,\; b_1\ge b_2\ge0,\; & \dotsc,\; b_{s-2}\ge b_{s-1}\ge0 \end{aligned} \right\}. \end{align*} $$
$$ \begin{align*} \left\{ a_1,\dotsc, a_s, b_1,\dotsc, b_{s-1}\bigg\vert \begin{aligned} \tau'\ge a_1\ge0,\; a_1\ge a_2\ge0,\; & \dotsc,\; a_{s-1} \ge a_s\ge0,\\ \tau'\ge b_1\ge0,\; b_1\ge b_2\ge0,\; & \dotsc,\; b_{s-2}\ge b_{s-1}\ge0 \end{aligned} \right\}. \end{align*} $$
As before, we successively integrate over
![]() $a_s,a_{s-1},\dotsc , a_2$
and
$a_s,a_{s-1},\dotsc , a_2$
and
![]() $b_{s-1}, b_{s-2},\dotsc , b_2$
, obtaining
$b_{s-1}, b_{s-2},\dotsc , b_2$
, obtaining
 $$ \begin{align*} I_2(\tau)\ll\iint_{0}^{\tau'} e^{2\theta \left( Aa_1 + Bb_1 - (A+B)\max\left\{a_1, b_1\right\}\right)} da_1 db_1 \le \iint_{0}^{\tau'} e^{-2\theta B \left\lvert a_1-b_1\right\rvert} da_1 db_1 \ll \tau, \end{align*} $$
$$ \begin{align*} I_2(\tau)\ll\iint_{0}^{\tau'} e^{2\theta \left( Aa_1 + Bb_1 - (A+B)\max\left\{a_1, b_1\right\}\right)} da_1 db_1 \le \iint_{0}^{\tau'} e^{-2\theta B \left\lvert a_1-b_1\right\rvert} da_1 db_1 \ll \tau, \end{align*} $$
as desired.□
Appendix A Cones and volumes
Recall the definition of
![]() ${\mathscr P}^+$
and
${\mathscr P}^+$
and
![]() $E_t$
in §2.2. Our goal is to write
$E_t$
in §2.2. Our goal is to write
![]() ${\mathscr P}^+$
as the intersection of
${\mathscr P}^+$
as the intersection of
![]() $\overline {\mathfrak {a}^+}$
with a suitable cone in
$\overline {\mathfrak {a}^+}$
with a suitable cone in
![]() $\mathfrak {a}$
and to calculate the asymptotic volume of the set
$\mathfrak {a}$
and to calculate the asymptotic volume of the set
![]() $E_t$
.
$E_t$
.
A.1 Cones
We will identify
![]() $\mathfrak {a}$
as before with the subspace of
$\mathfrak {a}$
as before with the subspace of
![]() ${\mathbb R}^d$
consisting of all vectors
${\mathbb R}^d$
consisting of all vectors
![]() $X=(X_1,\dotsc , X_d)$
with
$X=(X_1,\dotsc , X_d)$
with
![]() $X_1+\dotsb +X_d=0$
. We also identify
$X_1+\dotsb +X_d=0$
. We also identify
![]() $\mathfrak {a}$
with the set of all trace
$\mathfrak {a}$
with the set of all trace
![]() $0$
diagonal matrices whenever convenient.
$0$
diagonal matrices whenever convenient.
Lemma A.1. Let
![]() $X^0\in {\mathscr P}$
be any point in
$X^0\in {\mathscr P}$
be any point in
![]() ${\mathscr P}$
satisfying
${\mathscr P}$
satisfying
 $$ \begin{align*} \left\langle X^0, \rho\right\rangle = \max_{X\in{\mathscr P}^+} \langle X, \rho\rangle. \end{align*} $$
$$ \begin{align*} \left\langle X^0, \rho\right\rangle = \max_{X\in{\mathscr P}^+} \langle X, \rho\rangle. \end{align*} $$
Let
![]() $\{e_1,\dotsc , e_d\}$
denote the usual standard basis of
$\{e_1,\dotsc , e_d\}$
denote the usual standard basis of
![]() ${\mathbb R}^d$
. Then
${\mathbb R}^d$
. Then
 $$ \begin{align} X^0 = \begin{cases} e_1+\dotsb + e_s - e_{s+1}-\dotsb - e_d &\text{if}\ d\ \text{is even},\\ e_1+\dotsb + e_{s-1} - e_{s+1}-\dotsb -e_d &\text{if}\ d\ \text{is odd}, \end{cases} \end{align} $$
$$ \begin{align} X^0 = \begin{cases} e_1+\dotsb + e_s - e_{s+1}-\dotsb - e_d &\text{if}\ d\ \text{is even},\\ e_1+\dotsb + e_{s-1} - e_{s+1}-\dotsb -e_d &\text{if}\ d\ \text{is odd}, \end{cases} \end{align} $$
where s is defined in equation (47). In particular,
![]() $X^0$
is unique.
$X^0$
is unique.
Proof. We write the half-sum of positive roots
![]() $\rho \in \mathfrak {a}^*$
in coordinates as
$\rho \in \mathfrak {a}^*$
in coordinates as
 $\rho = (\rho _1,\dotsc , \rho _d)\in {\mathbb R}^d\simeq \left ({\mathbb R}^d\right )^*$
, where
$\rho = (\rho _1,\dotsc , \rho _d)\in {\mathbb R}^d\simeq \left ({\mathbb R}^d\right )^*$
, where
![]() $\rho _1+\dotsb +\rho _d=0$
. We have
$\rho _1+\dotsb +\rho _d=0$
. We have
![]() $\rho _1\ge \dotsb \ge \rho _d$
and
$\rho _1\ge \dotsb \ge \rho _d$
and
![]() $\rho _i=-\rho _{d+1-i}$
for every
$\rho _i=-\rho _{d+1-i}$
for every
![]() $i\le d/2$
, so that if d is odd, then
$i\le d/2$
, so that if d is odd, then
![]() $\rho _{(d+1)/2}=0$
. Let
$\rho _{(d+1)/2}=0$
. Let
![]() $X=(X_1,\dotsc , X_d)\in {\mathscr P}$
. Then
$X=(X_1,\dotsc , X_d)\in {\mathscr P}$
. Then
 $$ \begin{align*} \langle X, \rho\rangle = \sum_{i\le d/2} (X_i - X_{d+1-i}) \rho_i. \end{align*} $$
$$ \begin{align*} \langle X, \rho\rangle = \sum_{i\le d/2} (X_i - X_{d+1-i}) \rho_i. \end{align*} $$
Since
![]() $X\in {\mathscr P}$
, we have
$X\in {\mathscr P}$
, we have
![]() $-2\le X_i-X_{d+1-i}\le 2$
. Furthermore,
$-2\le X_i-X_{d+1-i}\le 2$
. Furthermore,
![]() $\rho _i>0$
for
$\rho _i>0$
for
![]() $i\le d/2$
, so this sum is maximized for
$i\le d/2$
, so this sum is maximized for
![]() $X_i=1$
and
$X_i=1$
and
![]() $X_{d+1-i}=-1$
. This proves our assertion for d even. For d odd, we finally note that
$X_{d+1-i}=-1$
. This proves our assertion for d even. For d odd, we finally note that
![]() $X_1+\dotsb +X_d=0$
forces
$X_1+\dotsb +X_d=0$
forces
![]() $X_{(d+1)/2}=0$
.
$X_{(d+1)/2}=0$
.
Lemma A.2. There is a basis
![]() $\mu _1,\dotsc ,\mu _{d-1}\in \mathfrak {a}^*$
such that
$\mu _1,\dotsc ,\mu _{d-1}\in \mathfrak {a}^*$
such that
 $\mu _i\left (X^0\right )=1$
,
$\mu _i\left (X^0\right )=1$
,
![]() $i=1,\dotsc , d-1$
, and
$i=1,\dotsc , d-1$
, and
![]() ${\mathscr P}^+=\mathscr {C}\cap \overline {\mathfrak {a}^+}$
, where
${\mathscr P}^+=\mathscr {C}\cap \overline {\mathfrak {a}^+}$
, where
In particular, if
![]() $\left \{\beta _i^\vee \right \}$
is the basis in
$\left \{\beta _i^\vee \right \}$
is the basis in
![]() $\mathfrak {a}$
which is dual to
$\mathfrak {a}$
which is dual to
![]() $\{\mu _i\}$
, then
$\{\mu _i\}$
, then
 $$ \begin{align*} \mathscr{C}^0=\left\{\sum_{i=1}^{d-1} x_i \beta_i^{\vee}: \forall \; i\; x_i\leq 0 \right\} \end{align*} $$
$$ \begin{align*} \mathscr{C}^0=\left\{\sum_{i=1}^{d-1} x_i \beta_i^{\vee}: \forall \; i\; x_i\leq 0 \right\} \end{align*} $$
and
![]() $ X^0= \beta _1^\vee +\dotsb + \beta _{d-1}^\vee $
.
$ X^0= \beta _1^\vee +\dotsb + \beta _{d-1}^\vee $
.
Proof. Note that
We rewrite this using the system of fundamental weights
![]() $\varpi _i\in \mathfrak {a}^*$
:
$\varpi _i\in \mathfrak {a}^*$
:
Since
 $\varpi _1\left (X^0\right )=\varpi _{d-1}\left (X^0\right )=1$
, we can put
$\varpi _1\left (X^0\right )=\varpi _{d-1}\left (X^0\right )=1$
, we can put
![]() $\mu _1=\varpi _1$
and
$\mu _1=\varpi _1$
and
![]() $\mu _{d-1}=\varpi _{d-1}$
. The strategy is then to complete
$\mu _{d-1}=\varpi _{d-1}$
. The strategy is then to complete
![]() $\{\mu _1,\mu _{d-1}\}$
to a basis of linear forms
$\{\mu _1,\mu _{d-1}\}$
to a basis of linear forms
![]() $\{\mu _i\}$
in such a way that
$\{\mu _i\}$
in such a way that
-
(1)
 $\mu _i\left (X^0\right )=1$
for all
$\mu _i\left (X^0\right )=1$
for all
 $i=1,\dotsc , d-1$
and
$i=1,\dotsc , d-1$
and -
(2) the conditions
 $X\in \overline {\mathfrak {a}^+}$
and
$X\in \overline {\mathfrak {a}^+}$
and
 $\mu _1(X),\mu _{d-1}(X)\leq 1$
, imply
$\mu _1(X),\mu _{d-1}(X)\leq 1$
, imply
 $\mu _i(X)\leq 1$
for
$\mu _i(X)\leq 1$
for
 $i=2,\dotsc ,d-2$
.
$i=2,\dotsc ,d-2$
.
In this case, property (1) shows that
 $$ \begin{align*} \mathscr{C} = X^0+\mathscr{C}^0=\left\{X\in\mathfrak{a}\mid \forall \ i:\, \mu_i\left(X - X^0\right)\le 0\right\}=\{X\in\mathfrak{a}\mid \forall \ i:\, \mu_i(X)\le 1\}, \end{align*} $$
$$ \begin{align*} \mathscr{C} = X^0+\mathscr{C}^0=\left\{X\in\mathfrak{a}\mid \forall \ i:\, \mu_i\left(X - X^0\right)\le 0\right\}=\{X\in\mathfrak{a}\mid \forall \ i:\, \mu_i(X)\le 1\}, \end{align*} $$
and then property (2) combines with equation (51) to establish
![]() ${\mathscr P}^+=\mathscr {C} \cap \overline {\mathfrak {a}^+}$
.
${\mathscr P}^+=\mathscr {C} \cap \overline {\mathfrak {a}^+}$
.
Note that relative to the standard basis
![]() $\{e_i\}$
of
$\{e_i\}$
of
![]() ${\mathbb R}^d$
,
${\mathbb R}^d$
,
![]() $\mu _1$
is the (restriction to
$\mu _1$
is the (restriction to
![]() $\mathfrak {a}$
of the) first coordinate functional and
$\mathfrak {a}$
of the) first coordinate functional and
![]() $\mu _{d-1}$
is minus the (restriction to
$\mu _{d-1}$
is minus the (restriction to
![]() $\mathfrak {a}$
of the) last coordinate functional. Thus if the
$\mathfrak {a}$
of the) last coordinate functional. Thus if the
![]() $\pm \mu _i$
, for
$\pm \mu _i$
, for
![]() $i=2,\dotsc , d-2$
, are a linearly independent subset of the remaining
$i=2,\dotsc , d-2$
, are a linearly independent subset of the remaining
![]() $d-2$
coordinate functionals, then (2) follows from the fact that
$d-2$
coordinate functionals, then (2) follows from the fact that
![]() $1\geq X_1\geq \dotsb \geq X_d\geq -1$
implies
$1\geq X_1\geq \dotsb \geq X_d\geq -1$
implies
![]() $\pm X_i\leq 1$
. To ensure property (1), we simply need to choose the sign suitably and avoid the
$\pm X_i\leq 1$
. To ensure property (1), we simply need to choose the sign suitably and avoid the
![]() $(d+1)/2$
coordinate for odd d. Thus for d odd we put
$(d+1)/2$
coordinate for odd d. Thus for d odd we put
 $$ \begin{align*} \mu_i = \begin{cases} \varpi_i-\varpi_{i-1} &\text{if } 2\le i\le s-1,\\ \varpi_i-\varpi_{i+1} &\text{if } s\le i \le d-2,\\ \end{cases} \end{align*} $$
$$ \begin{align*} \mu_i = \begin{cases} \varpi_i-\varpi_{i-1} &\text{if } 2\le i\le s-1,\\ \varpi_i-\varpi_{i+1} &\text{if } s\le i \le d-2,\\ \end{cases} \end{align*} $$
and for d even we put
 $$ \begin{align*} \mu_i = \begin{cases} \varpi_i-\varpi_{i-1} &\text{if } 2\leq i\le s,\\ \varpi_{i}-\varpi_{i+1} &\text{if } s+1\leq i\leq d-2, \end{cases} \end{align*} $$
$$ \begin{align*} \mu_i = \begin{cases} \varpi_i-\varpi_{i-1} &\text{if } 2\leq i\le s,\\ \varpi_{i}-\varpi_{i+1} &\text{if } s+1\leq i\leq d-2, \end{cases} \end{align*} $$
where s is defined in equation (47). Using the definition (49) of
![]() $X^0$
, we quickly verify property (1).
$X^0$
, we quickly verify property (1).
Remark A.1. Using the explicit description of the basis
![]() $\{\mu _i\}_{1\le i\le d-1}$
, one can easily see that writing
$\{\mu _i\}_{1\le i\le d-1}$
, one can easily see that writing
![]() $\rho $
as a linear combination of the
$\rho $
as a linear combination of the
![]() $\mu _i$
results in all the coefficients being positive integers. Hence if
$\mu _i$
results in all the coefficients being positive integers. Hence if
![]() $Y\in {\mathscr C}^0$
, then
$Y\in {\mathscr C}^0$
, then
![]() $\langle \rho , Y\rangle <0$
.
$\langle \rho , Y\rangle <0$
.
A.2 Volumes
Proposition A.3. Suppose
![]() $P\subseteq \overline {\mathfrak {a}^+}$
is a convex polytope. Let
$P\subseteq \overline {\mathfrak {a}^+}$
is a convex polytope. Let
![]() $V_P$
denote the vertices of P, and suppose that
$V_P$
denote the vertices of P, and suppose that
![]() $V_P\ni X\mapsto \langle \rho , X\rangle $
takes its maximum at exactly one vertex
$V_P\ni X\mapsto \langle \rho , X\rangle $
takes its maximum at exactly one vertex
![]() $v_0\in V_P$
. Then there exist
$v_0\in V_P$
. Then there exist
![]() $c, \delta>0$
such that
$c, \delta>0$
such that
 $$ \begin{align} \int_{P_t} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX = c e^{t\left\langle\rho, v_0\right\rangle}\left(1 + O\left(e^{-t\delta}\right)\right) \end{align} $$
$$ \begin{align} \int_{P_t} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX = c e^{t\left\langle\rho, v_0\right\rangle}\left(1 + O\left(e^{-t\delta}\right)\right) \end{align} $$
as
![]() $t\rightarrow \infty $
. Here
$t\rightarrow \infty $
. Here
![]() $P_t=\{tX\mid X\in P\}$
and
$P_t=\{tX\mid X\in P\}$
and
![]() $\sigma (w)$
denotes the signature of
$\sigma (w)$
denotes the signature of
![]() $w\in W$
.
$w\in W$
.
Before starting the proof of this proposition, we note that
 $$ \begin{align*} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle}\ge 0 \end{align*} $$
$$ \begin{align*} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle}\ge 0 \end{align*} $$
for all
![]() $X\in \overline {\mathfrak {a}^+}$
because of the convexity of the exponential function.
$X\in \overline {\mathfrak {a}^+}$
because of the convexity of the exponential function.
Proof. First note that
![]() $\langle w\rho , X\rangle \le \langle \rho , X\rangle $
for all
$\langle w\rho , X\rangle \le \langle \rho , X\rangle $
for all
![]() $X\in \overline {\mathfrak {a}^+}$
, and in fact
$X\in \overline {\mathfrak {a}^+}$
, and in fact
![]() $\langle w\rho , X\rangle < \langle \rho , X\rangle $
if
$\langle w\rho , X\rangle < \langle \rho , X\rangle $
if
![]() $X\in \mathfrak {a}^+$
. If P is not simple, we divide it into disjoint simple polytopes
$X\in \mathfrak {a}^+$
. If P is not simple, we divide it into disjoint simple polytopes
![]() $P^1,\dotsc , P^r$
whose respective sets of vertices we denote by
$P^1,\dotsc , P^r$
whose respective sets of vertices we denote by
![]() $V^1,\dotsc , V^r$
. The vertices
$V^1,\dotsc , V^r$
. The vertices
![]() $V_P$
are contained in the union
$V_P$
are contained in the union
 $\bigcup _j V^j$
. By Brion’s formula [Reference Brion and Vergne7], there exist nonzero coefficients
$\bigcup _j V^j$
. By Brion’s formula [Reference Brion and Vergne7], there exist nonzero coefficients
![]() $a_v^j\in {\mathbb R}$
,
$a_v^j\in {\mathbb R}$
,
![]() $j=1,\dotsc , r$
,
$j=1,\dotsc , r$
,
![]() $v\in V^j$
, such that
$v\in V^j$
, such that
 $$ \begin{align*} \int_{P_t^j} e^{\left\langle w\rho, X\right\rangle} dX = \sum_{v\in V^j} a_v^je^{t\left\langle w\rho, v\right\rangle}. \end{align*} $$
$$ \begin{align*} \int_{P_t^j} e^{\left\langle w\rho, X\right\rangle} dX = \sum_{v\in V^j} a_v^je^{t\left\langle w\rho, v\right\rangle}. \end{align*} $$
We can find
![]() $\delta>0$
such that for every j and
$\delta>0$
such that for every j and
![]() $v\in V^j$
,
$v\in V^j$
,
![]() $\langle w\rho , v\rangle \le \langle \rho , v_0\rangle -\delta $
unless
$\langle w\rho , v\rangle \le \langle \rho , v_0\rangle -\delta $
unless
![]() $w^{-1}v = v_0$
. Hence,
$w^{-1}v = v_0$
. Hence,
 $$ \begin{align} \int_{P_t} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX = \left(\sum_{\substack{j,v, w:\\ w^{-1}v=v_0}} a_v^j \sigma(w)\right) e^{t\left\langle \rho, v_0\right\rangle}. \end{align} $$
$$ \begin{align} \int_{P_t} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX = \left(\sum_{\substack{j,v, w:\\ w^{-1}v=v_0}} a_v^j \sigma(w)\right) e^{t\left\langle \rho, v_0\right\rangle}. \end{align} $$
It remains to argue that this last sum in brackets is a positive number. If
![]() $v_0$
is such that
$v_0$
is such that
![]() $\langle w\rho , v\rangle = \langle \rho , v_0\rangle $
if and only if
$\langle w\rho , v\rangle = \langle \rho , v_0\rangle $
if and only if
![]() $w=1$
and
$w=1$
and
![]() $v=v_0$
, then the left-hand side of equation (52) tends to
$v=v_0$
, then the left-hand side of equation (52) tends to
![]() $+\infty $
as
$+\infty $
as
![]() $t\rightarrow \infty $
. Moreover, the sum on the right-hand side of equation (53) has exactly one nonzero term in that situation, which consequently must be positive. If
$t\rightarrow \infty $
. Moreover, the sum on the right-hand side of equation (53) has exactly one nonzero term in that situation, which consequently must be positive. If
![]() $v_0$
does not satisfy this condition, we choose another polytope
$v_0$
does not satisfy this condition, we choose another polytope
![]() $P'\subseteq P$
with regular vertices (i.e.,
$P'\subseteq P$
with regular vertices (i.e.,
![]() $V_{P'}\subseteq \mathfrak {a}^+$
) that are sufficiently close to the original vertices of P. Then
$V_{P'}\subseteq \mathfrak {a}^+$
) that are sufficiently close to the original vertices of P. Then
 $$ \begin{align*} \int_{P_t} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX \le \int_{P_t'} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX, \end{align*} $$
$$ \begin{align*} \int_{P_t} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX \le \int_{P_t'} \sum_{w\in W} \sigma(w) e^{\left\langle w\rho, X\right\rangle} dX, \end{align*} $$
and the right-hand side grows like
![]() $ce^{tc'}$
for suitable
$ce^{tc'}$
for suitable
![]() $c>0$
and
$c>0$
and
![]() $\langle \rho ,v_0\rangle \ge c'>\langle \rho , v_0\rangle -\delta $
, provided
$\langle \rho ,v_0\rangle \ge c'>\langle \rho , v_0\rangle -\delta $
, provided
![]() $P'$
is chosen sufficiently close to P. This proves that the sum in brackets on the right-hand side of equation (53) is a positive number.
$P'$
is chosen sufficiently close to P. This proves that the sum in brackets on the right-hand side of equation (53) is a positive number.
We apply the foregoing result to estimate the volume of
![]() $E_t$
.
$E_t$
.
Corollary A.4. There exist
![]() $c, \delta>0$
such that we have
$c, \delta>0$
such that we have
 $$ \begin{align*} m_G(E_t)= c e^{2t\left\langle \rho, X^0\right\rangle}\left(1+ O\left(e^{-t\delta}\right)\right) \end{align*} $$
$$ \begin{align*} m_G(E_t)= c e^{2t\left\langle \rho, X^0\right\rangle}\left(1+ O\left(e^{-t\delta}\right)\right) \end{align*} $$
as
![]() $t\rightarrow \infty $
.
$t\rightarrow \infty $
.
Proof. By Cartan decomposition, we have
 $$ \begin{align*} m_G(E_t) = \int_{P_t} J(X) dX = 2^{-\dim\mathfrak{n}}\int_{P_t} \sum_{w\in W} \sigma(w) e^{2\left\langle w\rho, X\right\rangle} dX \end{align*} $$
$$ \begin{align*} m_G(E_t) = \int_{P_t} J(X) dX = 2^{-\dim\mathfrak{n}}\int_{P_t} \sum_{w\in W} \sigma(w) e^{2\left\langle w\rho, X\right\rangle} dX \end{align*} $$
where
![]() $\sigma (w)$
denotes the signature of w. The assertion of the lemma then follows from Proposition A.3.
$\sigma (w)$
denotes the signature of w. The assertion of the lemma then follows from Proposition A.3.
Appendix B Angles and inner products
The purpose of this appendix is to prove the following result, used in the course of the proof of Lemma 4.5.
Recall the notation of that lemma. Let
![]() $X^0$
be as in equation (17) and let M denote its centralizer in G. For
$X^0$
be as in equation (17) and let M denote its centralizer in G. For
![]() $Y\in \mathfrak {a}$
we write
$Y\in \mathfrak {a}$
we write
![]() $Y= Y_M+Y^M$
for unique
$Y= Y_M+Y^M$
for unique
![]() $Y_M\in \mathfrak {a}_M$
and
$Y_M\in \mathfrak {a}_M$
and
![]() $Y^M\in \mathfrak {a}^M$
. As before, for
$Y^M\in \mathfrak {a}^M$
. As before, for
![]() $\eta>0$
we write
$\eta>0$
we write
![]() ${\mathscr T}_\eta $
for the set of all
${\mathscr T}_\eta $
for the set of all
![]() $\lambda \in \mathfrak {a}^*_{\mathbb C}$
such that
$\lambda \in \mathfrak {a}^*_{\mathbb C}$
such that
![]() $\operatorname {Re}\lambda $
lies in the convex hull of the Weyl group orbit of
$\operatorname {Re}\lambda $
lies in the convex hull of the Weyl group orbit of
![]() $\eta \rho $
. The cone
$\eta \rho $
. The cone
![]() ${\mathscr C}^0$
is defined in Lemma A.2.
${\mathscr C}^0$
is defined in Lemma A.2.
Proposition B.1. There are constants
![]() $C_1, C_2>0$
, depending only on d, such that for every
$C_1, C_2>0$
, depending only on d, such that for every
![]() $Y\in {\mathscr C}^0$
,
$Y\in {\mathscr C}^0$
,
![]() $\lambda \in {\mathscr T}_\eta $
, and
$\lambda \in {\mathscr T}_\eta $
, and
![]() $w\in W$
, we have
$w\in W$
, we have
-
(i)
 $\lvert \langle w \rho , Y_M\rangle \rvert \leq - C_1\langle \rho , Y\rangle $
and
$\lvert \langle w \rho , Y_M\rangle \rvert \leq - C_1\langle \rho , Y\rangle $
and -
(ii)
 $\lvert \langle \operatorname {Re}\lambda , Y_M\rangle \rvert \leq - C_2\eta \langle \rho , Y_M\rangle $
.
$\lvert \langle \operatorname {Re}\lambda , Y_M\rangle \rvert \leq - C_2\eta \langle \rho , Y_M\rangle $
.
In particular, there is a constant
![]() $C>0$
, depending only on d, such that for all
$C>0$
, depending only on d, such that for all
![]() $Y\in {\mathscr C}^0$
and
$Y\in {\mathscr C}^0$
and
![]() $\lambda \in {\mathscr T}_\eta $
, we have
$\lambda \in {\mathscr T}_\eta $
, we have
To prove the proposition we shall work abstractly with linear forms on the Euclidean space
![]() ${\mathbb R}^d$
, equipped with its standard inner product. Namely, we make the usual identification of the standard Cartan subalgebra
${\mathbb R}^d$
, equipped with its standard inner product. Namely, we make the usual identification of the standard Cartan subalgebra
![]() $\mathfrak {a}_0$
of
$\mathfrak {a}_0$
of
![]() $\mathfrak {gl}_d({\mathbb R})$
with
$\mathfrak {gl}_d({\mathbb R})$
with
![]() ${\mathbb R}^d$
, so that
${\mathbb R}^d$
, so that
![]() $\mathfrak {a}=\mathfrak {a}_0^G$
identifies with the trace
$\mathfrak {a}=\mathfrak {a}_0^G$
identifies with the trace
![]() $0$
hyperplane
$0$
hyperplane
 $$ \begin{align*} {\mathscr H}=\left\{X=(X_1,\dotsc, X_d)\in{\mathbb R}^d : X_1+\dotsb + X_d = 0\right\}. \end{align*} $$
$$ \begin{align*} {\mathscr H}=\left\{X=(X_1,\dotsc, X_d)\in{\mathbb R}^d : X_1+\dotsb + X_d = 0\right\}. \end{align*} $$
We are interested in the linear form
![]() $L(Y) = \langle \rho , Y\rangle $
on
$L(Y) = \langle \rho , Y\rangle $
on
![]() ${\mathbb R}^d$
or
${\mathbb R}^d$
or
![]() ${\mathscr H}$
. It will be convenient to define a cone
${\mathscr H}$
. It will be convenient to define a cone
![]() ${\mathscr C}'$
in
${\mathscr C}'$
in
![]() ${\mathbb R}^d$
such that
${\mathbb R}^d$
such that
![]() ${\mathscr C}'\cap {\mathscr H}$
coincides with the cone
${\mathscr C}'\cap {\mathscr H}$
coincides with the cone
![]() $-{\mathscr C}^0$
of Proposition A.2. Property (i) will then follow from a similar maximizing property of L on
$-{\mathscr C}^0$
of Proposition A.2. Property (i) will then follow from a similar maximizing property of L on
![]() ${\mathscr C}'$
. Property (ii) requires bounds on the angles that the vectors in
${\mathscr C}'$
. Property (ii) requires bounds on the angles that the vectors in
![]() $-{\mathscr C}^0$
can form with
$-{\mathscr C}^0$
can form with
![]() $X^0$
, which we deduce from the relative position of
$X^0$
, which we deduce from the relative position of
![]() $X^0$
with
$X^0$
with
![]() $\mathscr {H}$
.
$\mathscr {H}$
.
B.1 Positive linear forms
Let
![]() $\{e_1,\dotsc , e_d\}$
denote the standard basis of
$\{e_1,\dotsc , e_d\}$
denote the standard basis of
![]() ${\mathbb R}^d$
.
${\mathbb R}^d$
.
Definition B.2. If d is even, let
![]() ${\mathscr C}'\subset {\mathbb R}^d$
be the closed orthant
${\mathscr C}'\subset {\mathbb R}^d$
be the closed orthant
 $$ \begin{align*} {\mathscr C}'={\textrm{cone}}_{{\mathbb R}_{\geq 0}}\left\{e_1,\dotsc, e_{d/2}, -e_{d/2+1},\dotsc, -e_d\right\}. \end{align*} $$
$$ \begin{align*} {\mathscr C}'={\textrm{cone}}_{{\mathbb R}_{\geq 0}}\left\{e_1,\dotsc, e_{d/2}, -e_{d/2+1},\dotsc, -e_d\right\}. \end{align*} $$
If d is odd, let
![]() ${\mathscr C}'={\mathscr O}^+\cup {\mathscr O}^-\subset {\mathbb R}^d$
be the union of the closed orthants
${\mathscr C}'={\mathscr O}^+\cup {\mathscr O}^-\subset {\mathbb R}^d$
be the union of the closed orthants
 $$ \begin{align*} {\mathscr O}^+&=\textrm{ cone}_{{\mathbb R}_{\geq 0}}\{e_1,\dotsc, e_{(d+1)/2-1}, e_{(d+1)/2}, -e_{(d+1)/2+1},\dotsc, -e_d\},\\ {\mathscr O}^-&=\textrm{ cone}_{{\mathbb R}_{\geq 0}}\{e_1,\dotsc, e_{(d+1)/2-1}, -e_{(d+1)/2}, -e_{(d+1)/2+1}, \dotsc, -e_d\}. \end{align*} $$
$$ \begin{align*} {\mathscr O}^+&=\textrm{ cone}_{{\mathbb R}_{\geq 0}}\{e_1,\dotsc, e_{(d+1)/2-1}, e_{(d+1)/2}, -e_{(d+1)/2+1},\dotsc, -e_d\},\\ {\mathscr O}^-&=\textrm{ cone}_{{\mathbb R}_{\geq 0}}\{e_1,\dotsc, e_{(d+1)/2-1}, -e_{(d+1)/2}, -e_{(d+1)/2+1}, \dotsc, -e_d\}. \end{align*} $$
Remark B.1. Recall the explicit description of
![]() $X^0\in {\mathbb R}^d$
as given in equation (49) (in Appendix A). If
$X^0\in {\mathbb R}^d$
as given in equation (49) (in Appendix A). If
![]() $V_d$
denotes the set of vertices of the unit cube
$V_d$
denotes the set of vertices of the unit cube
![]() $[-1,1]^d$
, then
$[-1,1]^d$
, then
![]() $\pm X^0\in V_d$
for d even and
$\pm X^0\in V_d$
for d even and
 $\pm X^0\pm e_{(d+1)/2}\in V_d$
for d odd. In particular, when d is odd,
$\pm X^0\pm e_{(d+1)/2}\in V_d$
for d odd. In particular, when d is odd,
![]() $-X^0$
lies on the edge of
$-X^0$
lies on the edge of
![]() $[-1,1]^d$
connecting the vertices
$[-1,1]^d$
connecting the vertices
 $X^0\pm e_{(d+1)/2}$
. We deduce that the origin of
$X^0\pm e_{(d+1)/2}$
. We deduce that the origin of
![]() ${\mathbb R}^d$
is a vertex of
${\mathbb R}^d$
is a vertex of
![]() $-X^0+[-1,1]^d$
if d is even, and it is the midpoint of an edge of
$-X^0+[-1,1]^d$
if d is even, and it is the midpoint of an edge of
![]() $-X^0+[-1,1]^d$
if d is odd.
$-X^0+[-1,1]^d$
if d is odd.
It is easy to see that when d is even,
![]() $-{\mathscr C}'$
is the unique orthant in
$-{\mathscr C}'$
is the unique orthant in
![]() ${\mathbb R}^d$
containing
${\mathbb R}^d$
containing
![]() $-X^0+[-1,1]^d$
, and when d is odd,
$-X^0+[-1,1]^d$
, and when d is odd,
![]() $-X^0+[-1,1]^d\subset -{\mathscr C}'$
.
$-X^0+[-1,1]^d\subset -{\mathscr C}'$
.
Remark B.2. If d is even, then
![]() ${\mathscr C}'$
does not contain any nontrivial linear subspace, and if d is odd, the only nontrivial linear subspace of
${\mathscr C}'$
does not contain any nontrivial linear subspace, and if d is odd, the only nontrivial linear subspace of
![]() ${\mathscr C}'$
is the
${\mathscr C}'$
is the
![]() $1$
-dimensional space
$1$
-dimensional space
![]() ${\mathbb R} e_{(d+1)/2}$
.
${\mathbb R} e_{(d+1)/2}$
.
Definition B.3. We call a linear form
![]() $L:{\mathbb R}^d\longrightarrow {\mathbb R}$
positive if it is nonnegative on
$L:{\mathbb R}^d\longrightarrow {\mathbb R}$
positive if it is nonnegative on
![]() ${\mathscr C}'$
and either positive on
${\mathscr C}'$
and either positive on
![]() ${\mathscr C}'\smallsetminus \{0\}$
if d is even or positive on
${\mathscr C}'\smallsetminus \{0\}$
if d is even or positive on
![]() ${\mathscr C}'\smallsetminus {\mathbb R} e_{(d+1)/2}$
if d is odd.
${\mathscr C}'\smallsetminus {\mathbb R} e_{(d+1)/2}$
if d is odd.
Let
![]() ${\mathscr L}\subseteq {\mathbb R}^d$
denote the ray
${\mathscr L}\subseteq {\mathbb R}^d$
denote the ray
![]() ${\mathbb R}_{\ge 0} X^0$
. Since
${\mathbb R}_{\ge 0} X^0$
. Since
![]() $X^0\in {\mathscr C}'$
, and
$X^0\in {\mathscr C}'$
, and
![]() ${\mathscr C}'$
is a cone, we have
${\mathscr C}'$
is a cone, we have
![]() ${\mathscr L}\subset {\mathscr C}'$
.
${\mathscr L}\subset {\mathscr C}'$
.
We identify the space of linear forms on
![]() ${\mathbb R}^d$
with
${\mathbb R}^d$
with
 $\left ({\mathbb R}^d\right )^*\simeq {\mathbb R}^d$
via the dual basis to
$\left ({\mathbb R}^d\right )^*\simeq {\mathbb R}^d$
via the dual basis to
![]() $\{e_1,\dotsc , e_d\}$
. If L is a linear form, written as
$\{e_1,\dotsc , e_d\}$
. If L is a linear form, written as
![]() $L=(L_1,\dotsc , L_d)$
with respect to this identification, and
$L=(L_1,\dotsc , L_d)$
with respect to this identification, and
![]() $\sigma \in S_d$
is a permutation, we define the linear form
$\sigma \in S_d$
is a permutation, we define the linear form
![]() $\sigma L$
by the rule
$\sigma L$
by the rule
 $\sigma L:=\left (L_{\sigma (1)},\dotsc , L_{\sigma (d)}\right )$
. We make the following identification:
$\sigma L:=\left (L_{\sigma (1)},\dotsc , L_{\sigma (d)}\right )$
. We make the following identification:
Lemma B.4. Let
 $L\in \left ({\mathbb R}^d\right )^*$
be a positive linear form. Let
$L\in \left ({\mathbb R}^d\right )^*$
be a positive linear form. Let
![]() $L'$
be a form in the closed convex hull of
$L'$
be a form in the closed convex hull of
 $\{\sigma L:\sigma \in S_d\}\subseteq \left ({\mathbb R}^d\right )^*$
. Then for all
$\{\sigma L:\sigma \in S_d\}\subseteq \left ({\mathbb R}^d\right )^*$
. Then for all
![]() $X\in {\mathscr L}$
, we have
$X\in {\mathscr L}$
, we have
![]() $L'(X)\le L(X)$
.
$L'(X)\le L(X)$
.
Proof. A linear form
![]() $L=(L_1,\dotsc , L_d)$
is positive if and only if
$L=(L_1,\dotsc , L_d)$
is positive if and only if
 $$ \begin{align*} \begin{cases} L_1,\dotsc, L_{d/2}>0, \ L_{d/2+1},\dotsc, L_d<0, & \text{if}\ d\ \text{is even},\\ L_1,\dotsc, L_{(d+1)/2-1}>0, \ L_{(d+1)/2}=0, \ L_{(d+1)/2+1},\dotsc, L_d<0, &\text{if}\ d\ \text{is odd}. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} L_1,\dotsc, L_{d/2}>0, \ L_{d/2+1},\dotsc, L_d<0, & \text{if}\ d\ \text{is even},\\ L_1,\dotsc, L_{(d+1)/2-1}>0, \ L_{(d+1)/2}=0, \ L_{(d+1)/2+1},\dotsc, L_d<0, &\text{if}\ d\ \text{is odd}. \end{cases} \end{align*} $$
It follows that for such L we have
 $L\left (X^0\right ) = \lvert L_1\rvert +\dotsb + \lvert L_d\rvert $
, and hence
$L\left (X^0\right ) = \lvert L_1\rvert +\dotsb + \lvert L_d\rvert $
, and hence
 $\sigma L\left (X^0\right )\le L\left (X^0\right )$
for every
$\sigma L\left (X^0\right )\le L\left (X^0\right )$
for every
![]() $\sigma \in S_d$
. Hence if
$\sigma \in S_d$
. Hence if
![]() $L'$
is in the closed convex hull of
$L'$
is in the closed convex hull of
![]() $\{\sigma L:\sigma \in S_d\}$
in
$\{\sigma L:\sigma \in S_d\}$
in
 $\left ({\mathbb R}^d\right )^*$
, we also have
$\left ({\mathbb R}^d\right )^*$
, we also have
 $L'\left (X^0\right )\le L\left (X^0\right )$
.
$L'\left (X^0\right )\le L\left (X^0\right )$
.
B.2 Hyperplane intersections
We now put
![]() ${\mathscr C}'' = {\mathscr C}'\cap {\mathscr H}$
.
${\mathscr C}'' = {\mathscr C}'\cap {\mathscr H}$
.
Lemma B.5.
![]() ${\mathscr C}''$
is a convex cone in
${\mathscr C}''$
is a convex cone in
![]() ${\mathbb R}^d$
of dimension
${\mathbb R}^d$
of dimension
![]() $d-1$
that satisfies
$d-1$
that satisfies
![]() ${\mathscr C}''\cap (-{\mathscr C}'')=\{0\}$
. Moreover, there exists
${\mathscr C}''\cap (-{\mathscr C}'')=\{0\}$
. Moreover, there exists
![]() $\gamma>0$
such that the angle between any nonzero vector in
$\gamma>0$
such that the angle between any nonzero vector in
![]() ${\mathscr C}''$
and the vector
${\mathscr C}''$
and the vector
![]() $X^0$
is at most
$X^0$
is at most
![]() $\pi /2-\gamma $
.
$\pi /2-\gamma $
.
Proof. The first part of the lemma follows directly from the description of
![]() ${\mathscr C}'$
in Definition B.2, coupled with Remark B.2.
${\mathscr C}'$
in Definition B.2, coupled with Remark B.2.
For the assertion on the bound of the angles, we proceed as follows: If d is even, then
![]() ${\mathscr C}'$
is just a single orthant in
${\mathscr C}'$
is just a single orthant in
![]() ${\mathbb R}^d$
, hence the angle between any two vectors is bounded by
${\mathbb R}^d$
, hence the angle between any two vectors is bounded by
![]() $\pi /2$
. Since
$\pi /2$
. Since
![]() $X^0$
does not lie on the boundary of
$X^0$
does not lie on the boundary of
![]() ${\mathscr C}'$
, there exists
${\mathscr C}'$
, there exists
![]() $\gamma>0$
such that the angle between
$\gamma>0$
such that the angle between
![]() $X^0$
and any vector in
$X^0$
and any vector in
![]() ${\mathscr C}'$
is bounded from above by
${\mathscr C}'$
is bounded from above by
![]() $\pi /2-\gamma $
.
$\pi /2-\gamma $
.
For d odd, recall that
![]() ${\mathscr C}'={\mathscr O}^+\cup {\mathscr O}^-$
and
${\mathscr C}'={\mathscr O}^+\cup {\mathscr O}^-$
and
![]() $X^0\in {\mathscr O}^+\cap {\mathscr O}^-$
, hence the angle between
$X^0\in {\mathscr O}^+\cap {\mathscr O}^-$
, hence the angle between
![]() $X^0$
and any vector in
$X^0$
and any vector in
![]() ${\mathscr C}'$
is at most
${\mathscr C}'$
is at most
![]() $\pi /2$
. Moreover, it is readily seen from the explicit descriptions of
$\pi /2$
. Moreover, it is readily seen from the explicit descriptions of
![]() $X^0$
and
$X^0$
and
![]() ${\mathscr O}^\pm $
that the only vectors in
${\mathscr O}^\pm $
that the only vectors in
![]() ${\mathscr C}'$
that are orthogonal to
${\mathscr C}'$
that are orthogonal to
![]() $X^0$
are the vectors on the line
$X^0$
are the vectors on the line
![]() ${\mathbb R} e_{(d+1)/2}$
. Since
${\mathbb R} e_{(d+1)/2}$
. Since
![]() $e_{(d+1)/2}\not \in {\mathscr H}$
and
$e_{(d+1)/2}\not \in {\mathscr H}$
and
![]() ${\mathscr C}''={\mathscr C}'\cap {\mathscr H}$
is closed, the angle between
${\mathscr C}''={\mathscr C}'\cap {\mathscr H}$
is closed, the angle between
![]() $X^0$
and nonzero vectors in
$X^0$
and nonzero vectors in
![]() ${\mathscr C}''$
must be bounded from above by
${\mathscr C}''$
must be bounded from above by
![]() $\pi /2-\gamma $
for some
$\pi /2-\gamma $
for some
![]() $\gamma>0$
.
$\gamma>0$
.
Note that
![]() ${\mathscr L}\subset {\mathscr C}''$
, since
${\mathscr L}\subset {\mathscr C}''$
, since
![]() $X^0\in \mathscr {H}$
.
$X^0\in \mathscr {H}$
.
Proposition B.6. Let
![]() ${\mathscr M}\subseteq {\mathscr H}$
be a vector subspace that is orthogonal to
${\mathscr M}\subseteq {\mathscr H}$
be a vector subspace that is orthogonal to
![]() ${\mathscr L}$
. Then for every
${\mathscr L}$
. Then for every
![]() $X\in {\mathscr L}$
, the section
$X\in {\mathscr L}$
, the section
is compact. Moreover, if
![]() ${\mathscr M}$
is of dimension
${\mathscr M}$
is of dimension
![]() $d-2$
, then
$d-2$
, then
 $$ \begin{align*} {\mathscr C}'' = \bigcup_{X\in{\mathscr L}} \left((X+{\mathscr M})\cap {\mathscr C}''\right), \end{align*} $$
$$ \begin{align*} {\mathscr C}'' = \bigcup_{X\in{\mathscr L}} \left((X+{\mathscr M})\cap {\mathscr C}''\right), \end{align*} $$
and writing
![]() $X= rX^0$
for a suitable
$X= rX^0$
for a suitable
![]() $r\ge 0$
, we have
$r\ge 0$
, we have
 $(X+{\mathscr M})\cap {\mathscr C}'' = r\left (\left (X^0+{\mathscr M}\right )\cap {\mathscr C}''\right )$
.
$(X+{\mathscr M})\cap {\mathscr C}'' = r\left (\left (X^0+{\mathscr M}\right )\cap {\mathscr C}''\right )$
.
Proof. Follows from Lemma B.5.
B.3 Application to linear forms
In the following lemma, we shall take L to be a positive linear form in the sense of Definition B.3, and
![]() ${\mathscr M}\subseteq {\mathscr H}$
a vector space of dimension
${\mathscr M}\subseteq {\mathscr H}$
a vector space of dimension
![]() $d-2$
which is orthogonal to
$d-2$
which is orthogonal to
![]() ${\mathscr L}$
:
${\mathscr L}$
:
Lemma B.7. There exists a constant
![]() $c>0$
such that
$c>0$
such that
![]() $L(X+Z)\le c L(X)$
for all
$L(X+Z)\le c L(X)$
for all
![]() $X\in {\mathscr L}$
and
$X\in {\mathscr L}$
and
![]() $Z\in {\mathscr M}$
with
$Z\in {\mathscr M}$
with
![]() $X+Z\in {\mathscr C}''$
.
$X+Z\in {\mathscr C}''$
.
Proof. For fixed
![]() $X\in {\mathscr L}$
, the set of all
$X\in {\mathscr L}$
, the set of all
![]() $Z\in {\mathscr M}$
such that
$Z\in {\mathscr M}$
such that
![]() $X+Z\in {\mathscr C}''$
is compact by Proposition B.6. In particular, there is
$X+Z\in {\mathscr C}''$
is compact by Proposition B.6. In particular, there is
![]() $D\subseteq {\mathscr M}$
compact such that
$D\subseteq {\mathscr M}$
compact such that
 $\left (X^0+ {\mathscr M}\right )\cap {\mathscr C}'' = X^0 + D$
. Hence any
$\left (X^0+ {\mathscr M}\right )\cap {\mathscr C}'' = X^0 + D$
. Hence any
![]() $X+Z\in {\mathscr C}''$
with
$X+Z\in {\mathscr C}''$
with
![]() $X\in {\mathscr L}$
and
$X\in {\mathscr L}$
and
![]() $Z\in {\mathscr M}$
can be written as
$Z\in {\mathscr M}$
can be written as
![]() $X+ Z= r X^0 + rZ'$
for some suitable
$X+ Z= r X^0 + rZ'$
for some suitable
![]() $r\ge 0$
and
$r\ge 0$
and
![]() $Z'\in D$
. Putting
$Z'\in D$
. Putting
 $$ \begin{align*} c= 1+ \frac{\max_{Z'\in D} L(Z')}{L\left(X^0\right)}, \end{align*} $$
$$ \begin{align*} c= 1+ \frac{\max_{Z'\in D} L(Z')}{L\left(X^0\right)}, \end{align*} $$
we then get
 $L(X+ Z) = r L\left (X^0\right ) + r L(Z') \le c L(X)$
.
$L(X+ Z) = r L\left (X^0\right ) + r L(Z') \le c L(X)$
.
B.4 Proof of Proposition B.1
We now apply the previous results to our situation. Namely, we identify
![]() $\mathfrak {a}_0$
with
$\mathfrak {a}_0$
with
![]() ${\mathbb R}^d$
as usual so that
${\mathbb R}^d$
as usual so that
![]() $\mathfrak {a}=\mathfrak {a}_0^G$
is the hyperplane
$\mathfrak {a}=\mathfrak {a}_0^G$
is the hyperplane
![]() ${\mathscr H}$
. The cone
${\mathscr H}$
. The cone
![]() ${\mathscr C}''= {\mathscr C}'\cap {\mathscr H}$
then coincides with the cone
${\mathscr C}''= {\mathscr C}'\cap {\mathscr H}$
then coincides with the cone
![]() $-{\mathscr C}^0$
that we considered in Appendix A, and
$-{\mathscr C}^0$
that we considered in Appendix A, and
![]() $X^0$
coincides with the vector of the same name from Appendix A.
$X^0$
coincides with the vector of the same name from Appendix A.
We consider the linear form
![]() $L(Y) = \langle \rho , Y\rangle $
,
$L(Y) = \langle \rho , Y\rangle $
,
![]() $Y\in {\mathscr C}$
. Let
$Y\in {\mathscr C}$
. Let
![]() $\mathfrak {a}_M\subseteq \mathfrak {a}$
be as before. Then
$\mathfrak {a}_M\subseteq \mathfrak {a}$
be as before. Then
![]() ${\mathbb R} X^0\subseteq \mathfrak {a}_M$
. In fact, if d is even, then
${\mathbb R} X^0\subseteq \mathfrak {a}_M$
. In fact, if d is even, then
![]() $\mathfrak {a}_M={\mathbb R} X^0$
and
$\mathfrak {a}_M={\mathbb R} X^0$
and
![]() $\mathfrak {a}^M$
is orthogonal to
$\mathfrak {a}^M$
is orthogonal to
![]() $\mathfrak {a}_M$
of dimension
$\mathfrak {a}_M$
of dimension
![]() $d-2$
. If d is odd, then
$d-2$
. If d is odd, then
![]() $\mathfrak {a}_M$
has dimension
$\mathfrak {a}_M$
has dimension
![]() $2$
. In that case, let
$2$
. In that case, let
![]() $V\subseteq \mathfrak {a}_M$
be the orthogonal complement to the line
$V\subseteq \mathfrak {a}_M$
be the orthogonal complement to the line
![]() ${\mathbb R} X^0$
so that
${\mathbb R} X^0$
so that
![]() $V\oplus \mathfrak {a}^M$
is orthogonal to
$V\oplus \mathfrak {a}^M$
is orthogonal to
![]() ${\mathbb R} X^0$
of dimension
${\mathbb R} X^0$
of dimension
![]() $d-2$
.
$d-2$
.
As before, if
![]() $Y\in {\mathscr C}''$
, we write
$Y\in {\mathscr C}''$
, we write
![]() $Y=Y_M + Y^M$
for unique
$Y=Y_M + Y^M$
for unique
![]() $Y_M\in \mathfrak {a}_M$
and
$Y_M\in \mathfrak {a}_M$
and
![]() $Y^M\in \mathfrak {a}^M$
. If d is even, then
$Y^M\in \mathfrak {a}^M$
. If d is even, then
![]() $Y_M\in {\mathbb R}_{\ge 0} X^0$
, and if d is odd, we can uniquely write
$Y_M\in {\mathbb R}_{\ge 0} X^0$
, and if d is odd, we can uniquely write
![]() $Y_M = Y_M' + Y_M''$
with unique
$Y_M = Y_M' + Y_M''$
with unique
![]() $Y_M'\in {\mathbb R}_{\ge 0} X^0$
and
$Y_M'\in {\mathbb R}_{\ge 0} X^0$
and
![]() $Y_M''\in V$
.
$Y_M''\in V$
.
Having set up the notation, we now note that
![]() $\langle \rho , \cdot \rangle $
vanishes on V, and hence Proposition B.1
(i) is an immediate consequence of Lemma B.4.
$\langle \rho , \cdot \rangle $
vanishes on V, and hence Proposition B.1
(i) is an immediate consequence of Lemma B.4.
For part (ii), we first note that by the definition of
![]() ${\mathscr T}_\eta $
,
${\mathscr T}_\eta $
,
![]() $\operatorname {Re}\lambda $
is contained in the convex hull of the Weyl group orbit of
$\operatorname {Re}\lambda $
is contained in the convex hull of the Weyl group orbit of
![]() $\eta \rho $
so that
$\eta \rho $
so that
 $\left \langle \operatorname {Re}\lambda , wX^0\right \rangle \le \eta \left \langle \rho , X^0 \right \rangle $
, by Lemma B.7, for every
$\left \langle \operatorname {Re}\lambda , wX^0\right \rangle \le \eta \left \langle \rho , X^0 \right \rangle $
, by Lemma B.7, for every
![]() $w\in W$
. This establishes part (ii) for d even. For d odd, we have
$w\in W$
. This establishes part (ii) for d even. For d odd, we have
![]() $\eta \langle \rho , Y_M\rangle = \eta \left \langle \rho , Y_M'\right \rangle \ge \left \langle \operatorname {Re}\lambda , Y_M ' \right \rangle $
, since
$\eta \langle \rho , Y_M\rangle = \eta \left \langle \rho , Y_M'\right \rangle \ge \left \langle \operatorname {Re}\lambda , Y_M ' \right \rangle $
, since
![]() $\langle \rho , \cdot \rangle $
vanishes on V. Taking
$\langle \rho , \cdot \rangle $
vanishes on V. Taking
![]() $Y_M'=X^0$
, the possible
$Y_M'=X^0$
, the possible
![]() $Y_M''$
lie in a compact set so that
$Y_M''$
lie in a compact set so that
![]() $\left \langle \operatorname {Re}\lambda , Y_M'' \right \rangle $
is bounded from above by
$\left \langle \operatorname {Re}\lambda , Y_M'' \right \rangle $
is bounded from above by
![]() $\eta c$
for c some absolute constant. Scaling
$\eta c$
for c some absolute constant. Scaling
![]() $Y_M'=X^0$
by a scalar, the compact set of
$Y_M'=X^0$
by a scalar, the compact set of
![]() $Y_M''$
gets scaled by the same scalar. Hence there is
$Y_M''$
gets scaled by the same scalar. Hence there is
![]() $C>0$
such that for any
$C>0$
such that for any
![]() $Y\in {\mathscr C}''$
, we have
$Y\in {\mathscr C}''$
, we have
![]() $\langle \operatorname {Re}\lambda , Y_M\rangle \le \eta C \langle \rho , Y_M\rangle $
□
$\langle \operatorname {Re}\lambda , Y_M\rangle \le \eta C \langle \rho , Y_M\rangle $
□
Acknowledgments
The first author was supported by ANR grant 14-CE25.
Competing Interest
None.