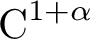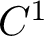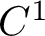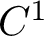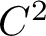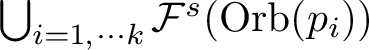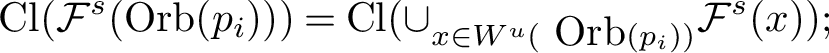1 Introduction and statement of results
Physical measures were introduced in the 1970s by Bowen, Ruelle and Sinai to study the large time behavior of Lebesgue typical points for Axiom A attractors. Such systems do not preserve volume (or any measure that is equivalent to the volume) due to the contraction near the attractor. For this reason, those measures are often supported on a zero-volume subset of the manifold but capture the behavior of points in a large set with positive Lebesgue measure. More precisely, an invariant measure
![]() $\mu $
is called a physical measure if the set
$\mu $
is called a physical measure if the set
 $$ \begin{align*}{\mathcal B}(\mu):=\left\{x\in M: \frac{1}{n}\sum_{i=0}^{n-1}\delta_{f^i(x)}\overset{weak *}{\longrightarrow}\mu\right\} \end{align*} $$
$$ \begin{align*}{\mathcal B}(\mu):=\left\{x\in M: \frac{1}{n}\sum_{i=0}^{n-1}\delta_{f^i(x)}\overset{weak *}{\longrightarrow}\mu\right\} \end{align*} $$
has positive volume. This set is known as the basin of
![]() $\mu $
. For Axiom A attractors, many properties of physical measures were studied by many different authors. We refer the readers to the review paper [Reference Young55] and the book [Reference Bonatti, Díaz and Viana10] for more details.
$\mu $
. For Axiom A attractors, many properties of physical measures were studied by many different authors. We refer the readers to the review paper [Reference Young55] and the book [Reference Bonatti, Díaz and Viana10] for more details.
It is also known that the physical measures of Axiom A attractors have strong statistical properties, one of the most important of which is the decay of correlations. It can be seen as the speed at which the system loses dependence and starts to behave like a random system. To be more precise, we have the following definition.
Definition 1.1. Given observables
![]() $\phi ,\psi : M\to \mathbb {R}$
, we define the correlation function with respect to a measure
$\phi ,\psi : M\to \mathbb {R}$
, we define the correlation function with respect to a measure
![]() $\mu $
as
$\mu $
as
 $$ \begin{align*}C_\mu(\phi,\psi\circ f^n)= \left| \int \phi(\psi\circ f^n)d\mu -\int \phi d\mu \int \psi d\mu \right|\quad \text{for } n\geq 1.\end{align*} $$
$$ \begin{align*}C_\mu(\phi,\psi\circ f^n)= \left| \int \phi(\psi\circ f^n)d\mu -\int \phi d\mu \int \psi d\mu \right|\quad \text{for } n\geq 1.\end{align*} $$
We say that the system has decay of correlations if for all
![]() $\phi $
and
$\phi $
and
![]() $\psi $
in some families of functions,
$\psi $
in some families of functions,
![]() $C_\mu (\phi ,\psi \circ f^n)$
converges to zero as n goes to infinity.
$C_\mu (\phi ,\psi \circ f^n)$
converges to zero as n goes to infinity.
With that we are ready to introduce the main application of the results in this article.
Theorem A. Let f be a
![]() $C^2$
partially hyperbolic, volume-preserving diffeomorphism with 1-dimensional center. Assume that f is accessible and that the center Lyapunov exponent of the volume is nonvanishing. Then f has exponential decay of correlations: there is
$C^2$
partially hyperbolic, volume-preserving diffeomorphism with 1-dimensional center. Assume that f is accessible and that the center Lyapunov exponent of the volume is nonvanishing. Then f has exponential decay of correlations: there is
![]() $d>0$
such that
$d>0$
such that
for all Hölder continuous
![]() $\phi :M\to {\mathbb R}$
, and
$\phi :M\to {\mathbb R}$
, and
![]() $\psi \in L^\infty (\operatorname {vol})$
.
$\psi \in L^\infty (\operatorname {vol})$
.
This theorem generalises [Reference Burns and Wilkinson18, Corollary 0.2], where it is shown that every
![]() $C^2$
accessible, partially hyperbolic diffeomorphism with 1-dimensional center is ergodic and has K-property. We remark that such systems are abundant; see the discussion in Subsection 3.2. Also note that the hyperbolicity assumption in the previous theorem (nonvanishing center exponent) is rather weak, yet we obtain a strong statistical property in the form of fast decay of correlations, central limit theorem and exponential large deviation control (the latter two results are the natural consequences of the decay of correlations; see [Reference Alves and Li2] and [Reference Gouëzel28]).
$C^2$
accessible, partially hyperbolic diffeomorphism with 1-dimensional center is ergodic and has K-property. We remark that such systems are abundant; see the discussion in Subsection 3.2. Also note that the hyperbolicity assumption in the previous theorem (nonvanishing center exponent) is rather weak, yet we obtain a strong statistical property in the form of fast decay of correlations, central limit theorem and exponential large deviation control (the latter two results are the natural consequences of the decay of correlations; see [Reference Alves and Li2] and [Reference Gouëzel28]).
By [Reference Yang52, Section 8], if f is a
![]() $C^2$
partially hyperbolic, volume-preserving diffeomorphism with 1-dimensional center and
$C^2$
partially hyperbolic, volume-preserving diffeomorphism with 1-dimensional center and
![]() $\lambda ^c(\operatorname {vol})\ne 0$
, then either f or
$\lambda ^c(\operatorname {vol})\ne 0$
, then either f or
![]() $f^{-1}$
has a mostly expanding center. The rest of this article is devoted to a general theory on such diffeomorphisms. In particular, Theorem A is a direct consequence of Theorem G.
$f^{-1}$
has a mostly expanding center. The rest of this article is devoted to a general theory on such diffeomorphisms. In particular, Theorem A is a direct consequence of Theorem G.
1.1 Diffeomorphisms with a mostly expanding center
Shortly after the physical measures were introduced for Axiom A attractors, a program for investigating the physical measures of diffeomorphisms beyond uniform hyperbolicity was initiated by Alves, Bonatti and Viana in a sequence of papers, such as [Reference Alves, Bonatti and Viana1, Reference Bonatti and Viana11], to name but a few. They introduced several classes of systems for which physical measures exist, and the number of physical measures is finite. Among them are diffeomorphisms with a mostly contracting center and diffeomorphisms with a mostly expanding center. In this article, we are particularly interested in the latter class.
Diffeomorphisms with a mostly expanding center are, roughly speaking, partially hyperbolic diffeomorphisms whose center Lyapunov exponents are positive. This class of systems was introduced by Alves, Bonatti and Viana ([Reference Alves, Bonatti and Viana1]) using a different, more technical definition. Later, another definition was given by Dolgopyat [Reference Dolgopyat25] and more recently by Andersson and Vásquez [Reference Andersson and Vásquez3]. In [Reference Andersson and Vásquez3], they also proposed the latter, somewhat stronger, definition as the official definition of having a mostly expanding center, which we will follow in this article.
We call a diffeomorphism f partially hyperbolic if there exists a decomposition
![]() $TM = E^s \oplus E^c \oplus E^u$
of the tangent bundle
$TM = E^s \oplus E^c \oplus E^u$
of the tangent bundle
![]() $TM$
into three continuous invariant subbundles
$TM$
into three continuous invariant subbundles
![]() $E^s_x$
and
$E^s_x$
and
![]() $E^c_x$
and
$E^c_x$
and
![]() $E^u_x$
such that
$E^u_x$
such that
![]() $Df \mid E^s$
is a uniform contraction,
$Df \mid E^s$
is a uniform contraction,
![]() $Df\mid E^u$
is a uniform expansion and
$Df\mid E^u$
is a uniform expansion and
![]() $Df \mid E^c$
lies in between them:
$Df \mid E^c$
lies in between them:
 $$ \begin{align*}\frac{\|Df(x)v^s\|}{\|Df(x)v^c\|} \le \frac 12 \quad\text{and}\quad \frac{\|Df(x)v^c\|}{\|Df(x)v^u\|} \le \frac 12 \end{align*} $$
$$ \begin{align*}\frac{\|Df(x)v^s\|}{\|Df(x)v^c\|} \le \frac 12 \quad\text{and}\quad \frac{\|Df(x)v^c\|}{\|Df(x)v^u\|} \le \frac 12 \end{align*} $$
for any unit vectors
![]() $v^s\in E^s_x$
,
$v^s\in E^s_x$
,
![]() $v^c\in E^c_x$
,
$v^c\in E^c_x$
,
![]() $v^u\in E^u_x$
and any
$v^u\in E^u_x$
and any
![]() $x\in M$
. This notation was proposed by Brin and Pesin [Reference Brin and Pesin14] and Pugh and Shub [Reference Pugh and Shub44] independently as early as the 1970s. In this article, we will assume that both
$x\in M$
. This notation was proposed by Brin and Pesin [Reference Brin and Pesin14] and Pugh and Shub [Reference Pugh and Shub44] independently as early as the 1970s. In this article, we will assume that both
![]() $E^s$
and
$E^s$
and
![]() $E^u$
bundles are nontrivial. In this case, it is well known (see, for example, [Reference Hirsch, Pugh and Shub31]) that
$E^u$
bundles are nontrivial. In this case, it is well known (see, for example, [Reference Hirsch, Pugh and Shub31]) that
![]() $E^*$
,
$E^*$
,
![]() $*=s,u$
can be integrated into foliations
$*=s,u$
can be integrated into foliations
![]() $\mathcal F^{*}$
,
$\mathcal F^{*}$
,
![]() $*=s,u$
, whose leaves are as smooth as the diffeomorphism f. A partially hyperbolic diffeomorphism f is called accessible if any point
$*=s,u$
, whose leaves are as smooth as the diffeomorphism f. A partially hyperbolic diffeomorphism f is called accessible if any point
![]() $x\in M$
can be reached from any other point
$x\in M$
can be reached from any other point
![]() $y\in M$
by an
$y\in M$
by an
![]() $su$
-path, a concatenation of finitely many subpaths, each of which lies entirely in a single leaf of
$su$
-path, a concatenation of finitely many subpaths, each of which lies entirely in a single leaf of
![]() ${\mathcal F}^s$
or a single leaf of
${\mathcal F}^s$
or a single leaf of
![]() ${\mathcal F}^u$
.
${\mathcal F}^u$
.
As shown by Bonatti, Díaz and Viana [Reference Bonatti, Díaz and Viana10] and Dolgopyat [Reference Dolgopyat24], physical measures of any
![]() $C^{1+\alpha }$
partially hyperbolic diffeomorphism should be a Gibbs u-state, meaning that the conditional measures of
$C^{1+\alpha }$
partially hyperbolic diffeomorphism should be a Gibbs u-state, meaning that the conditional measures of
![]() $\mu $
with respect to the partition into local strongly unstable manifolds are absolutely continuous with respect to the Lebesgue measure along the unstable leaves.
$\mu $
with respect to the partition into local strongly unstable manifolds are absolutely continuous with respect to the Lebesgue measure along the unstable leaves.
Definition 1.2. A partially hyperbolic diffeomorphism
![]() $f: M\to M$
is mostly expanding along the central direction if f has positive central Lyapunov exponents almost everywhere with respect to every Gibbs u-state for f.
$f: M\to M$
is mostly expanding along the central direction if f has positive central Lyapunov exponents almost everywhere with respect to every Gibbs u-state for f.
This definition is comparable to diffeomorphisms with a mostly contracting center (see, for example, [Reference Dolgopyat, Viana and Yang26]) and share similar properties with the latter. In particular,
![]() $C^1$
openness of the partially hyperbolic diffeomorphisms with a mostly expanding center was recently proved in [Reference Yang52]. Note, however, that the inverse of a diffeomorphism with a mostly expanding center may not be mostly contracting. This is because the space of Gibbs u-states of f could be very different from that of
$C^1$
openness of the partially hyperbolic diffeomorphisms with a mostly expanding center was recently proved in [Reference Yang52]. Note, however, that the inverse of a diffeomorphism with a mostly expanding center may not be mostly contracting. This is because the space of Gibbs u-states of f could be very different from that of
![]() $f^{-1}$
.
$f^{-1}$
.
A list of examples for partially hyperbolic diffeomorphisms with a mostly expanding center will be provided in Section 3.
1.2 Index-
 ${\bf \dim (E^{cu})}$
skeleton
${\bf \dim (E^{cu})}$
skeleton
In this article, we will introduce a topological structure of f, known as the skeleton, and use it to study the structure of physical measures of f. To this end, for a
![]() $C^1$
partially hyperbolic diffeomorphism f with partially hyperbolic splitting
$C^1$
partially hyperbolic diffeomorphism f with partially hyperbolic splitting
![]() $E^{s}\oplus E^{c}\oplus E^u$
, we denote by
$E^{s}\oplus E^{c}\oplus E^u$
, we denote by
![]() $i_{cu}=\dim (E^{cu})$
and
$i_{cu}=\dim (E^{cu})$
and
![]() $i_s=\dim (E^s)$
, where
$i_s=\dim (E^s)$
, where
![]() $E^{cu}= E^c\oplus E^u$
.
$E^{cu}= E^c\oplus E^u$
.
Definition 1.3.
Footnote
1
We say that
![]() ${\mathcal S}$
is an index
${\mathcal S}$
is an index
![]() $i_{s}$
skeleton of f if
$i_{s}$
skeleton of f if
![]() ${\mathcal S}=\{p_1,\cdots , p_k\}$
consists of finitely many hyperbolic saddles with stable index
${\mathcal S}=\{p_1,\cdots , p_k\}$
consists of finitely many hyperbolic saddles with stable index
![]() $i_s$
such that
$i_s$
such that
-
(a)
 $\bigcup _{i=1,\cdots k}{\mathcal F}^s(\mbox {Orb}(p_i))$
is dense in M;
$\bigcup _{i=1,\cdots k}{\mathcal F}^s(\mbox {Orb}(p_i))$
is dense in M; -
(b)
 ${\mathcal S}$
does not have a proper subset that satisfies property (a).
${\mathcal S}$
does not have a proper subset that satisfies property (a).
A set
![]() ${\mathcal S}$
consisting of finitely many hyperbolic saddles with stable index
${\mathcal S}$
consisting of finitely many hyperbolic saddles with stable index
![]() $i_s$
and satisfying (a) above is called a pre-skeleton .
$i_s$
and satisfying (a) above is called a pre-skeleton .
Let us observe that, in general, a partially hyperbolic diffeomorphism may not have any skeleton, because it may not have any hyperbolic periodic orbit at all. Even if it admits a set of periodic points such that the union of their stable manifolds is dense, such a set may have infinite cardinality. However, we will see in Section 4 that if f does have a skeleton, then all skeletons of f (with the same index) must have the same cardinality (Lemma 4.4). Furthermore, every pre-skeleton of f contains a skeleton (Lemma 4.5).
Finally, in Proposition 6.8 we will show that if f is
![]() $C^{1+\alpha }$
with a mostly expanding center (or if f is
$C^{1+\alpha }$
with a mostly expanding center (or if f is
![]() $C^1$
and close to a
$C^1$
and close to a
![]() $C^{1+\alpha }$
diffeomorphism with a mostly contracting center), then f has an index
$C^{1+\alpha }$
diffeomorphism with a mostly contracting center), then f has an index
![]() $i_s$
skeleton. Furthermore, in Section 7 we will see that the skeletons are robust under
$i_s$
skeleton. Furthermore, in Section 7 we will see that the skeletons are robust under
![]() $C^1$
topology, in the sense that the continuation of a skeleton of f is a pre-skeleton for nearby
$C^1$
topology, in the sense that the continuation of a skeleton of f is a pre-skeleton for nearby
![]() $C^1$
maps. Note, however, that this property requires f to have a mostly expanding center, unlike the skeletons in [Reference Dolgopyat, Viana and Yang26].
$C^1$
maps. Note, however, that this property requires f to have a mostly expanding center, unlike the skeletons in [Reference Dolgopyat, Viana and Yang26].
The main result of this article shows that for such diffeomorphisms, skeletons provide rich geometrical information on the physical measures of f.
For simplicity, we will frequently suppress the dependence on the Hölder index
![]() $\alpha $
and write
$\alpha $
and write
![]() $C^{1+}$
, because the Hölder index
$C^{1+}$
, because the Hölder index
![]() $\alpha $
does not play any particular role.
$\alpha $
does not play any particular role.
Theorem B. Let f be a
![]() $C^{1+}$
diffeomorphism with a mostly expanding center. Then f admits an index
$C^{1+}$
diffeomorphism with a mostly expanding center. Then f admits an index
![]() $i_s$
skeleton. Moreover, let
$i_s$
skeleton. Moreover, let
![]() ${\mathcal S}=\{p_1,\cdots ,p_k\}$
be any index
${\mathcal S}=\{p_1,\cdots ,p_k\}$
be any index
![]() $i_s$
skeleton of f; then for each
$i_s$
skeleton of f; then for each
![]() $p_i\in {\mathcal S}$
there exists a distinct physical measure
$p_i\in {\mathcal S}$
there exists a distinct physical measure
![]() $\mu _i$
such that
$\mu _i$
such that
-
(1) both the closure of
 $W^u(Orb(p_i))$
and the homoclinic class of the orbit
$W^u(Orb(p_i))$
and the homoclinic class of the orbit
 $\mbox {Orb}(p_i)$
coincide with
$\mbox {Orb}(p_i)$
coincide with
 $\operatorname {supp}(\mu _i)$
;
$\operatorname {supp}(\mu _i)$
; -
(2) the closure of
 ${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of the basin of the measure
${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of the basin of the measure
 $\mu _i$
.
$\mu _i$
.
In particular, the number of physical measures of f is precisely
![]() $k=\#{\mathcal S}$
. Moreover,
$k=\#{\mathcal S}$
. Moreover,
for
![]() $1 \leq i \neq j \leq k$
, where
$1 \leq i \neq j \leq k$
, where
![]() ${\mathcal B}(\mu _i)$
is the basin of
${\mathcal B}(\mu _i)$
is the basin of
![]() $\mu _i$
.
$\mu _i$
.
It is worth noting that the finiteness of the physical measures was known since the work of Alves, Bonatti and Viana [Reference Alves, Bonatti and Viana1]. However, Theorem B above provides a more detailed description on the geometric structure of the physical measures, which allows us to keep track of those measures as we perturb the system.
Remark 1.4. From the proof of Theorem B, we have more detailed description on the basins of
![]() $\mu _i$
: for every
$\mu _i$
: for every
![]() $p_i\in {\mathcal S}$
, we write
$p_i\in {\mathcal S}$
, we write
 $$ \begin{align*}{\mathcal O}_i=\bigcup_{x\in W^u(\mbox{Orb}(p_i))} {\mathcal F}^s(x);\end{align*} $$
$$ \begin{align*}{\mathcal O}_i=\bigcup_{x\in W^u(\mbox{Orb}(p_i))} {\mathcal F}^s(x);\end{align*} $$
then
![]() ${\mathcal O}_i$
contains an open neighbourhood of
${\mathcal O}_i$
contains an open neighbourhood of
![]() $\mbox {Orb}(p_i)$
. We are going to show that
$\mbox {Orb}(p_i)$
. We are going to show that
![]() ${\mathcal O}_i$
is open and dense in
${\mathcal O}_i$
is open and dense in
![]() $\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))=\mbox {Cl}({\mathcal B}(\mu _i)))$
. Moreover,
$\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))=\mbox {Cl}({\mathcal B}(\mu _i)))$
. Moreover,
![]() ${\mathcal B}(\mu _i)$
is a full-volume subset of
${\mathcal B}(\mu _i)$
is a full-volume subset of
![]() ${\mathcal O}_i$
, and
${\mathcal O}_i$
, and
![]() ${\mathcal O}_i\cap {\mathcal O}_j=\emptyset $
for
${\mathcal O}_i\cap {\mathcal O}_j=\emptyset $
for
![]() $1\leq i\neq j\leq k$
. This shows that the basin of different physical measures is topologically separated.
$1\leq i\neq j\leq k$
. This shows that the basin of different physical measures is topologically separated.
We would like to mention that the idea of using homoclinic classes to study measures was initiated by [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures30]; see also [Reference Dolgopyat, Viana and Yang26] and [Reference Buzzi, Crovisier and Sarig19] for recent similar results.
As a corollary of the previous theorem, we are going to show that any iteration of f still has a mostly expanding center; furthermore, the number of physical measures of
![]() $f^k$
is determined by the skeleton of f.
$f^k$
is determined by the skeleton of f.
Corollary C. Let f be a
![]() $C^{1+}$
partially diffeomorphism with a mostly expanding center and
$C^{1+}$
partially diffeomorphism with a mostly expanding center and
![]() ${\mathcal S}=\{p_1,\cdots ,p_k\}$
be any index
${\mathcal S}=\{p_1,\cdots ,p_k\}$
be any index
![]() $i_s$
skeleton of f. Then for any
$i_s$
skeleton of f. Then for any
![]() $n>0$
,
$n>0$
,
![]() $f^n$
has a mostly expanding center and has finitely many physical measures with number bounded by
$f^n$
has a mostly expanding center and has finitely many physical measures with number bounded by
 $$ \begin{align} P=\prod_{i=1}^k \pi(p_i), \text{ where } \pi(p_i) \text{ denotes the period of }p_i. \end{align} $$
$$ \begin{align} P=\prod_{i=1}^k \pi(p_i), \text{ where } \pi(p_i) \text{ denotes the period of }p_i. \end{align} $$
Moreover, every physical measure of
![]() $f^P$
is Bernoulli.
$f^P$
is Bernoulli.
Recall that for
![]() $C^2$
diffeomorphisms, every hyperbolic measure that is mixing has the Bernoulli property [Reference Pesin42, Reference Chernov and Haskell22]. Here we will provide a direct proof using the general work of Ornstein and Weiss [Reference Ornstein and Weiss41] and later show that the physical measures of
$C^2$
diffeomorphisms, every hyperbolic measure that is mixing has the Bernoulli property [Reference Pesin42, Reference Chernov and Haskell22]. Here we will provide a direct proof using the general work of Ornstein and Weiss [Reference Ornstein and Weiss41] and later show that the physical measures of
![]() $f^P$
are indeed exponentially mixing.
$f^P$
are indeed exponentially mixing.
1.3 Perturbation of physical measures
It was shown in [Reference Yang52] that partially hyperbolic diffeomorphisms with a mostly expanding center are
![]() $C^1$
open; that is, if a
$C^1$
open; that is, if a
![]() $C^{1+}$
diffeomorphism f has a mostly expanding center, then any
$C^{1+}$
diffeomorphism f has a mostly expanding center, then any
![]() $C^{1+}$
diffeomorphism g that is sufficiently
$C^{1+}$
diffeomorphism g that is sufficiently
![]() $C^1$
close to f also has a mostly expanding center. In the following we will analyse how the physical measures vary with respect to the
$C^1$
close to f also has a mostly expanding center. In the following we will analyse how the physical measures vary with respect to the
![]() $C^{1+}$
diffeomorphisms in
$C^{1+}$
diffeomorphisms in
![]() $C^1$
topology, which generalises a similar result of Andersson and Vásquez ([Reference Andersson and Vásquez4]) under
$C^1$
topology, which generalises a similar result of Andersson and Vásquez ([Reference Andersson and Vásquez4]) under
![]() $C^{1+\alpha }$
topology. The key observation here is that physical measures of f are associated with skeletons, which behaves well under
$C^{1+\alpha }$
topology. The key observation here is that physical measures of f are associated with skeletons, which behaves well under
![]() $C^1$
topology.
$C^1$
topology.
Theorem D. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center. Then there exists a
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center. Then there exists a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
of f such that the number of physical measures depends upper semi-continuously in
${\mathcal U}$
of f such that the number of physical measures depends upper semi-continuously in
![]() $C^1$
topology among diffeomorphisms in
$C^1$
topology among diffeomorphisms in
![]() $\mbox { Diff}^{1+}(M)\cap {\mathcal U}$
. Moreover, the number of physical measures is locally constant and the physical measures vary continuously in the weak* topology on a
$\mbox { Diff}^{1+}(M)\cap {\mathcal U}$
. Moreover, the number of physical measures is locally constant and the physical measures vary continuously in the weak* topology on a
![]() $C^1$
open and dense subset
$C^1$
open and dense subset
![]() ${\mathcal U}^\circ \subset {\mathcal U}$
.
${\mathcal U}^\circ \subset {\mathcal U}$
.
Indeed, the skeletons of f provide even more information on the physical measures for
![]() $C^1$
perturbed
$C^1$
perturbed
![]() $C^{1+}$
diffeomorphisms. In particular, the skeletons allow us to describe how the physical measures bifurcate as the diffeomorphism changes. To this end, we write
$C^{1+}$
diffeomorphisms. In particular, the skeletons allow us to describe how the physical measures bifurcate as the diffeomorphism changes. To this end, we write
![]() $p_i(g)$
the continuation of the hyperbolic saddle
$p_i(g)$
the continuation of the hyperbolic saddle
![]() $p_i$
for g in a
$p_i$
for g in a
![]() $C^1$
neighbourhood of f. Theorem D is a direct consequence of the following, more technical, result.
$C^1$
neighbourhood of f. Theorem D is a direct consequence of the following, more technical, result.
Theorem E. Let f be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center and
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center and
![]() ${\mathcal S}=\{p_1,\cdots , p_k\}$
be a skeleton of f. There exists a
${\mathcal S}=\{p_1,\cdots , p_k\}$
be a skeleton of f. There exists a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
of f such that, for any
${\mathcal U}$
of f such that, for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
, there is a subset of
$g\in {\mathcal U}$
, there is a subset of
![]() ${\mathcal S}(g) =\{p_1(g),\cdots , p_k(g)\}$
that is a skeleton. Consequently, for
${\mathcal S}(g) =\{p_1(g),\cdots , p_k(g)\}$
that is a skeleton. Consequently, for
![]() $g\in \mbox {Diff}^{1+}(M)\cap {\mathcal U}$
, the number of physical measures of g is no larger than the number of physical measures of f. Moreover, these two numbers coincide if and only if there is no heteroclinic intersection within
$g\in \mbox {Diff}^{1+}(M)\cap {\mathcal U}$
, the number of physical measures of g is no larger than the number of physical measures of f. Moreover, these two numbers coincide if and only if there is no heteroclinic intersection within
![]() $\{p_i(g)\}$
. In this case, each physical measure of g is close to some physical measure of f in the weak-* topology.
$\{p_i(g)\}$
. In this case, each physical measure of g is close to some physical measure of f in the weak-* topology.
In addition, restricted to any subset of
![]() ${\mathcal V}\subset {\mathcal U}$
where the number of physical measures is constant, the supports of the physical measures and the closures of their basins vary in a lower semi-continuous fashion, in the sense of the Hausdorff topology.
${\mathcal V}\subset {\mathcal U}$
where the number of physical measures is constant, the supports of the physical measures and the closures of their basins vary in a lower semi-continuous fashion, in the sense of the Hausdorff topology.
1.4 Existence of physical measures for
 $C^1$
generic diffeomorphisms
$C^1$
generic diffeomorphisms
Previously, the study of physical measures mainly focused on maps that are sufficiently smooth; that is, with
![]() $C^{1+}$
regularity. Recently, the new technique developed in [Reference Hua, Yang and Yang32, Reference Crovisier, Yang and Zhang23] enables us to shows the existence of physical measure for a large family of
$C^{1+}$
regularity. Recently, the new technique developed in [Reference Hua, Yang and Yang32, Reference Crovisier, Yang and Zhang23] enables us to shows the existence of physical measure for a large family of
![]() $C^1$
diffeomorphisms, such as those with a mostly contacting center.
$C^1$
diffeomorphisms, such as those with a mostly contacting center.
In this article, we will further show the existence of physical measures for
![]() $C^1$
generic diffeomorphisms close to a partially hyperbolic diffeomorphism f that has a mostly expanding center.
$C^1$
generic diffeomorphisms close to a partially hyperbolic diffeomorphism f that has a mostly expanding center.
Before stating the main theorem of this section, we need the following definition.
Definition 1.5. A set
![]() $\Lambda $
of a homeomorphism f is Lyapunov stable if there is a sequence of open neighbourhoods
$\Lambda $
of a homeomorphism f is Lyapunov stable if there is a sequence of open neighbourhoods
![]() $U_1\supset U_2\supset \cdots $
such that
$U_1\supset U_2\supset \cdots $
such that
-
(a)
 $\bigcap U_i=\Lambda $
;
$\bigcap U_i=\Lambda $
; -
(b)
 $f^n(U_{i+1})\subset U_i$
for any
$f^n(U_{i+1})\subset U_i$
for any
 $n,i\geq 1$
.
$n,i\geq 1$
.
A set being Lyapunov stable means that points starting near
![]() $\Lambda $
will not travel too far away from this set under forward iterations of f. However, this does not mean that
$\Lambda $
will not travel too far away from this set under forward iterations of f. However, this does not mean that
![]() $\Lambda $
is an attractor.
$\Lambda $
is an attractor.
We have the following
![]() $C^1$
locally generic result, which generalises Theorem E. We state it as a standalone result because the techniques involved are quite different from Theorem E.
$C^1$
locally generic result, which generalises Theorem E. We state it as a standalone result because the techniques involved are quite different from Theorem E.
Recall that a set
![]() ${\mathcal R}$
is called residual if it is a countable intersection of open and dense sets.
${\mathcal R}$
is called residual if it is a countable intersection of open and dense sets.
Theorem F. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center and
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center and
![]() ${\mathcal S}=\{p_1,\cdots , p_k\}$
be a skeleton of f. Then there exists a
${\mathcal S}=\{p_1,\cdots , p_k\}$
be a skeleton of f. Then there exists a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
of f and a
${\mathcal U}$
of f and a
![]() $C^1$
residual subset
$C^1$
residual subset
![]() ${\mathcal R}\subset {\mathcal U}$
such that every
${\mathcal R}\subset {\mathcal U}$
such that every
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal R}$
admits finitely many physical measures whose basins have full volume. The number of physical measures of g coincides with the cardinality of its skeleton, which is no more than the number of physical measures of f. Moreover, the physical measures of g are supported on disjoint Lyapunov stable chain recurrent classes, each of which is the homoclinic class of some saddle in its skeleton.
$g\in {\mathcal R}$
admits finitely many physical measures whose basins have full volume. The number of physical measures of g coincides with the cardinality of its skeleton, which is no more than the number of physical measures of f. Moreover, the physical measures of g are supported on disjoint Lyapunov stable chain recurrent classes, each of which is the homoclinic class of some saddle in its skeleton.
1.5 Statistical properties
To study the speed of decay of correlations for systems beyond uniformly hyperbolic, in [Reference Young53] Young used a type of Markov partition with infinitely many symbols to build towers for systems with nonuniform hyperbolic behavior. These structures are commonly referred to as Gibbs-Markov-Young (GMY) structures (see, for instance, [Reference Alves and Li2].) It is well known that such maps have exponential speed of decay of correlations whenever the GMY structure has exponentially small tails. By Alves and Li in [Reference Alves and Li2], which is built on the work of Gouëzel [Reference Gouëzel28], the latter case happens if the center bundle has certain expansion and, moreover, the tail of hyperbolic times is exponentially small.
We are going to show that Alves and Li’s criterion can be applied to partially hyperbolic diffeomorphisms with a mostly expanding center and, in particular, we prove exponential decay of correlations and exponential large deviations for the physical measures of f, provided that f has a mostly expanding center.
Theorem G. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center,
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center,
![]() ${\mathcal S}=\{p_1,\cdots ,p_k\}$
be a skeleton of f and
${\mathcal S}=\{p_1,\cdots ,p_k\}$
be a skeleton of f and
 $P=\prod _{i=1}^k \pi (p_i)$
. Then for every physical measure
$P=\prod _{i=1}^k \pi (p_i)$
. Then for every physical measure
![]() $\mu $
of
$\mu $
of
![]() $f^P$
, there is
$f^P$
, there is
![]() $d>0$
such that
$d>0$
such that
 $$ \begin{align*}C_\mu(\phi,\psi\circ f^{Pn})={\mathcal O}(e^{-dn})\end{align*} $$
$$ \begin{align*}C_\mu(\phi,\psi\circ f^{Pn})={\mathcal O}(e^{-dn})\end{align*} $$
for Hölder continuous
![]() $\phi : M\to \mathbb {R}$
, and
$\phi : M\to \mathbb {R}$
, and
![]() $\psi \in L^\infty (\mu )$
.
$\psi \in L^\infty (\mu )$
.
Corollary H. Under the assumptions of Theorem G, for every physical measure
![]() $\mu $
of
$\mu $
of
![]() $f^P$
and any Hölder continuous function
$f^P$
and any Hölder continuous function
![]() $\phi $
, the following limit exists:
$\phi $
, the following limit exists:
 $$ \begin{align*}\sigma^2=\lim_{n\to \infty} \frac{1}{n}\int \left(\sum_{j=0}^{n-1}\phi\circ f^{jP} -n\int \phi d\mu\right)^2d\mu.\end{align*} $$
$$ \begin{align*}\sigma^2=\lim_{n\to \infty} \frac{1}{n}\int \left(\sum_{j=0}^{n-1}\phi\circ f^{jP} -n\int \phi d\mu\right)^2d\mu.\end{align*} $$
Moreover, if
![]() $\sigma ^2>0$
, then there is a rate function
$\sigma ^2>0$
, then there is a rate function
![]() $c(\varepsilon )>0$
such that
$c(\varepsilon )>0$
such that
 $$ \begin{align*}\lim_{n\to \infty} \frac{1}{n}\log \mu\left(\left| \sum_{j=0}^{n-1}\phi\circ f^{jP} -n\int \phi d\mu \right| \geq \varepsilon\right)=-c(\varepsilon).\end{align*} $$
$$ \begin{align*}\lim_{n\to \infty} \frac{1}{n}\log \mu\left(\left| \sum_{j=0}^{n-1}\phi\circ f^{jP} -n\int \phi d\mu \right| \geq \varepsilon\right)=-c(\varepsilon).\end{align*} $$
1.6 Robustly transitive partially hyperbolic diffeomorphisms
The diffeomorphisms with a mostly expanding center also provide a new mechanism to describe the topological transitivity property. To make this article more complete, we collect two results from two other papers without giving their proof. For more details, see the related papers and the references therein.
Theorem I ([Reference Yang52])
Let f be a
![]() $C^{1+}$
volume-preserving, partially hyperbolic diffeomorphism with a 1-dimensional center. Suppose that f is accessible and the center exponent is not vanishing; then f is
$C^{1+}$
volume-preserving, partially hyperbolic diffeomorphism with a 1-dimensional center. Suppose that f is accessible and the center exponent is not vanishing; then f is
![]() $C^1$
robustly transitive; that is, every diffeomorphism g is transitive for g in a
$C^1$
robustly transitive; that is, every diffeomorphism g is transitive for g in a
![]() $C^1$
neighbourhood f, which is not necessarily volume preserving.
$C^1$
neighbourhood f, which is not necessarily volume preserving.
Theorem J ([Reference Ures, Viana and Yang49])
Let f be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center such that the stable foliation
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center such that the stable foliation
![]() ${\mathcal F}^s$
is minimal. Then there is a
${\mathcal F}^s$
is minimal. Then there is a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
of f such that the stable foliation of any
${\mathcal U}$
of f such that the stable foliation of any
![]() $g\in {\mathcal U}$
is minimal.
$g\in {\mathcal U}$
is minimal.
1.7 Structure of the article
This article is organised as follows: In Section 2 we introduce the main tool of this article: a special space of probability measures, denoted by
![]() $\operatorname {G}(f)$
, which is defined using the partial entropy along unstable leaves. This space will serve as the candidate space of physical measures.
$\operatorname {G}(f)$
, which is defined using the partial entropy along unstable leaves. This space will serve as the candidate space of physical measures.
Section 3 contains all the existing examples of diffeomorphisms with a mostly expanding center, as far as the author is aware. In particular, we collect some very recent examples from [Reference Yang52].
In Section 4, we provide some geometrical properties of skeletons, assuming that such structure exists (which will not be proven until Section 6). In particular, we will show that every skeleton of f must have the same cardinality and provide a useful criterion for the existence of a skeleton to be used in later sections.
Section 5 consists of a direct proof on the existence of physical measures for
![]() $C^{1+}$
diffeomorphisms with a mostly expanding center. More important, we show that the space
$C^{1+}$
diffeomorphisms with a mostly expanding center. More important, we show that the space
![]() $\operatorname {G}(f)$
is a finite-dimensional simplex that varies upper semi-continuously with respect to the diffeomorphism in
$\operatorname {G}(f)$
is a finite-dimensional simplex that varies upper semi-continuously with respect to the diffeomorphism in
![]() $C^1$
topology; moreover, every extreme point of
$C^1$
topology; moreover, every extreme point of
![]() $\operatorname {G}(f)$
is an ergodic physical measure of f.
$\operatorname {G}(f)$
is an ergodic physical measure of f.
The proof of Theorems B and E occupies the next two sections. We will carefully analyse the nonuniform expanding of f along
![]() $E^c$
using hyperbolic times and use the shadowing lemma of Liao to show the existence of skeletons. We then build a one-to-one correspondence between elements of a skeleton and the physical measures of f, and show that physical measures bifurcate as heteroclinic intersections are created between different elements of a skeleton. Then in Section 7, we generalise the result of Theorem E to generic
$E^c$
using hyperbolic times and use the shadowing lemma of Liao to show the existence of skeletons. We then build a one-to-one correspondence between elements of a skeleton and the physical measures of f, and show that physical measures bifurcate as heteroclinic intersections are created between different elements of a skeleton. Then in Section 7, we generalise the result of Theorem E to generic
![]() $C^1$
diffeomorphisms near f.
$C^1$
diffeomorphisms near f.
1.8 On the regularity assumption
Throughout this article, the regularity assumption on f is changed several times between
![]() $C^1$
and
$C^1$
and
![]() $C^{1+}$
. For the convenience of the readers, we summarise those changes below:
$C^{1+}$
. For the convenience of the readers, we summarise those changes below:
-
(1) Having a mostly contracting center requires the diffeomorphism to be
 $C^{1+};$
as a result, the initial diffeomorphism f is always assumed to be
$C^{1+};$
as a result, the initial diffeomorphism f is always assumed to be
 $C^{1+}$
.
$C^{1+}$
. -
(2) The topology is always
 $C^1$
. Throughout this article,
$C^1$
. Throughout this article,
 ${\mathcal U}$
is a neighbourhood of f under
${\mathcal U}$
is a neighbourhood of f under
 $C^1$
topology;
$C^1$
topology; -
(3) The geometrical properties of skeletons only require the diffeomorphism to be
 $C^1$
; this involves Section 4, Subsection 6.2 and certain parts of Section 7.
$C^1$
; this involves Section 4, Subsection 6.2 and certain parts of Section 7. -
(4) The physical measure having absolutely continuous conditional measure on the unstable leaves and the stable holonomy being absolutely continuous requires
 $C^{1+}$
regularity, as shown in the classical theory of physical measures. This affects Section 5, Subsection 6.3, certain parts of Section 7 and Section 9.
$C^{1+}$
regularity, as shown in the classical theory of physical measures. This affects Section 5, Subsection 6.3, certain parts of Section 7 and Section 9. -
(5) Section 8 deals with
 $C^1$
generic diffeomorphisms in
$C^1$
generic diffeomorphisms in
 ${\mathcal U}$
and thus only requires
${\mathcal U}$
and thus only requires
 $C^1$
smoothness.
$C^1$
smoothness.
2 Preliminary
In this section, we introduce some necessary notations and results that will be used later. Throughout this section, we assume f to be a partially hyperbolic diffeomorphism on the manifold M and
![]() $\mu $
an invariant probability measure of f. In Subsection 2.1 we will assume f to be
$\mu $
an invariant probability measure of f. In Subsection 2.1 we will assume f to be
![]() $C^{1+}$
for the discussion on the Gibbs u-states. In Subsections 2.2 and 2.3, f is assumed to be
$C^{1+}$
for the discussion on the Gibbs u-states. In Subsections 2.2 and 2.3, f is assumed to be
![]() $C^1$
only.
$C^1$
only.
2.1 Gibbs u-states
Following Pesin and Sinai [Reference Pesin and Sinai43] and Bonatti and Viana [Reference Bonatti and Viana11] (see also [Reference Bonatti, Díaz and Viana10, Chapter 11]), we call Gibbs u-state any invariant probability measure whose conditional probabilities (Rokhlin [Reference Rokhlin45]) along strongly unstable leaves are absolutely continuous with respect to the Lebesgue measure on the leaves. In fact, assuming that the derivative
![]() $Df$
is Hölder continuous, the Gibbs-u state always exists, and the densities with respect to Lebesgue measures along unstable plaques are continuous. Moreover, the densities vary continuously with respect to the strongly unstable leaves. As a consequence, the space of Gibbs u-states of f, denoted by
$Df$
is Hölder continuous, the Gibbs-u state always exists, and the densities with respect to Lebesgue measures along unstable plaques are continuous. Moreover, the densities vary continuously with respect to the strongly unstable leaves. As a consequence, the space of Gibbs u-states of f, denoted by
![]() $\mbox {Gibbs}^u(\cdot )$
, is compact relative to the weak-* topology in the probability space.
$\mbox {Gibbs}^u(\cdot )$
, is compact relative to the weak-* topology in the probability space.
The set of Gibbs u-states plays important roles in the study of physical measures for partially hyperbolic diffeomorphisms. The proofs for the following basic properties of Gibbs u-states can be found in the book of Bonatti, Díaz and Viana [Reference Bonatti, Díaz and Viana10, Subsection 11.2] (see also Dolgopyat [Reference Dolgopyat24]):
Proposition 2.1. Suppose that f is a
![]() $C^{1+}$
partially hyperbolic diffeomorphism; then
$C^{1+}$
partially hyperbolic diffeomorphism; then
-
(1)
 $\mbox {Gibbs}^u(f)$
is nonempty, weak* compact and convex. Ergodic components of Gibbs u-states are Gibbs u-states.
$\mbox {Gibbs}^u(f)$
is nonempty, weak* compact and convex. Ergodic components of Gibbs u-states are Gibbs u-states. -
(2) The support of every Gibbs u-state is
 ${\mathcal F}^u$
-saturated; that is, it consists of entire strongly unstable leaves.
${\mathcal F}^u$
-saturated; that is, it consists of entire strongly unstable leaves. -
(3) For Lebesgue almost every point x in any disk inside some strongly unstable leaf, every accumulation point of
 $\frac {1}{n}\sum _{j=0}^{n-1}\delta _{f^j(x)}$
is a Gibbs u-state.
$\frac {1}{n}\sum _{j=0}^{n-1}\delta _{f^j(x)}$
is a Gibbs u-state. -
(4) Every physical measure of f is a Gibbs u-state; conversely, every ergodic Gibbs u-state whose center Lyapunov exponents are negative is a physical measure.
The semi-continuity of Gibbs u-states with respect to
![]() $C^{1+}$
diffeomorphisms under
$C^{1+}$
diffeomorphisms under
![]() $C^1$
topology was recently proved by the author of this article in [Reference Yang52].
$C^1$
topology was recently proved by the author of this article in [Reference Yang52].
Proposition 2.2. Suppose that
![]() $f_n$
(
$f_n$
(
![]() $n=1,\cdots , \infty $
) and f are
$n=1,\cdots , \infty $
) and f are
![]() $C^{1+}$
partially hyperbolic diffeomorphisms such that
$C^{1+}$
partially hyperbolic diffeomorphisms such that
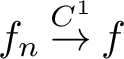 $f_n\overset {C^1}{\to } f$
. Then
$f_n\overset {C^1}{\to } f$
. Then
where the convergence is in the Hausdorff topology of the probability space.
The following lemma shows the relation between the Gibbs u-states of a diffeomorphism and its iterations.
Lemma 2.3. For any
![]() $n>0$
,
$n>0$
,
![]() $\mbox {Gibbs}^u(f)\subset \mbox {Gibbs}^u(f^n)$
. Conversely, let
$\mbox {Gibbs}^u(f)\subset \mbox {Gibbs}^u(f^n)$
. Conversely, let
![]() $\nu $
be any Gibbs u-state of
$\nu $
be any Gibbs u-state of
![]() $f^n$
; then
$f^n$
; then
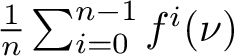 $\frac {1}{n}\sum _{i=0}^{n-1}f^i(\nu )$
is a Gibbs u-state of f.
$\frac {1}{n}\sum _{i=0}^{n-1}f^i(\nu )$
is a Gibbs u-state of f.
Proof. Let
![]() $\mu $
be a Gibbs u-state of f; then it is also an invariant probability of
$\mu $
be a Gibbs u-state of f; then it is also an invariant probability of
![]() $f^n$
. Because f and
$f^n$
. Because f and
![]() $f^n$
share the same unstable foliation,
$f^n$
share the same unstable foliation,
![]() $\mu $
must have the same disintegration along the unstable plaques. Then it follows from the definition that
$\mu $
must have the same disintegration along the unstable plaques. Then it follows from the definition that
![]() $\mu $
is also a Gibbs u-state of
$\mu $
is also a Gibbs u-state of
![]() $f^n$
.
$f^n$
.
On the other hand, it is clear that
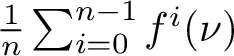 $\frac {1}{n}\sum _{i=0}^{n-1}f^i(\nu )$
is an invariant probability of f. By a similar argument as above,
$\frac {1}{n}\sum _{i=0}^{n-1}f^i(\nu )$
is an invariant probability of f. By a similar argument as above,
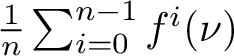 $\frac {1}{n}\sum _{i=0}^{n-1}f^i(\nu )$
is a Gibbs u-state of f. □
$\frac {1}{n}\sum _{i=0}^{n-1}f^i(\nu )$
is a Gibbs u-state of f. □
2.2 Partial entropy along unstable foliation
In this section, we give the precise definition of the partial metric entropy of
![]() $\mu $
along the unstable foliation
$\mu $
along the unstable foliation
![]() ${\mathcal F}^u$
of f, which depends on a special class of measurable partitions. The partial entropy has been proven to be a powerful tool in the study of partially hyperbolic diffeomorphisms, thanks to its semi-continuity in the
${\mathcal F}^u$
of f, which depends on a special class of measurable partitions. The partial entropy has been proven to be a powerful tool in the study of partially hyperbolic diffeomorphisms, thanks to its semi-continuity in the
![]() $C^1$
topology.
$C^1$
topology.
Definition 2.4. We say that a measurable partition
![]() $\xi $
of M is
$\xi $
of M is
![]() $\mu $
-subordinate to the
$\mu $
-subordinate to the
![]() ${\mathcal F}$
-foliation if for
${\mathcal F}$
-foliation if for
![]() $\mu $
-a.e. x, we have
$\mu $
-a.e. x, we have
-
(1)
 $\xi (x)\subset {\mathcal F}(x)$
and
$\xi (x)\subset {\mathcal F}(x)$
and
 $\xi (x)$
has uniformly small diameter inside
$\xi (x)$
has uniformly small diameter inside
 ${\mathcal F}(x)$
;
${\mathcal F}(x)$
; -
(2)
 $\xi (x)$
contains an open neighbourhood of x inside the leaf
$\xi (x)$
contains an open neighbourhood of x inside the leaf
 ${\mathcal F}(x)$
;
${\mathcal F}(x)$
; -
(3)
 $\xi $
is an increasing partition, meaning that
$\xi $
is an increasing partition, meaning that
 $\xi \prec f\xi $
.
$\xi \prec f\xi $
.
Ledrappier and Strelcyn [Reference Ledrappier and Strelcyn34] proved that the Pesin unstable lamination admits some
![]() $\mu $
-subordinate measurable partition. The following result is contained in Lemma 3.1.2 of Ledrappier and Young [Reference Ledrappier and Young35].
$\mu $
-subordinate measurable partition. The following result is contained in Lemma 3.1.2 of Ledrappier and Young [Reference Ledrappier and Young35].
Lemma 2.5. For any measurable partitions
![]() $\xi _1$
and
$\xi _1$
and
![]() $\xi _2$
that are
$\xi _2$
that are
![]() $\mu $
-subordinate to
$\mu $
-subordinate to
![]() ${\mathcal F}$
, we have
${\mathcal F}$
, we have
![]() $h_\mu (f,\xi _1)=h_\mu (f,\xi _2)$
.
$h_\mu (f,\xi _1)=h_\mu (f,\xi _2)$
.
This allows us to define the partial entropy of
![]() $\mu $
using any
$\mu $
using any
![]() $\mu $
-subordinate partition.
$\mu $
-subordinate partition.
Definition 2.6. For a
![]() $C^1$
partially hyperbolic diffeomorphism f and an invariant measure
$C^1$
partially hyperbolic diffeomorphism f and an invariant measure
![]() $\mu $
, the partial
$\mu $
, the partial
![]() $\mu $
-entropy along unstable foliation
$\mu $
-entropy along unstable foliation
![]() ${\mathcal F}^u$
, which we denote by
${\mathcal F}^u$
, which we denote by
![]() $h_\mu (f,{\mathcal F}^u)$
, is defined to be
$h_\mu (f,{\mathcal F}^u)$
, is defined to be
![]() $h_\mu (f,\xi )$
for any
$h_\mu (f,\xi )$
for any
![]() $\mu $
-subordinate partition
$\mu $
-subordinate partition
![]() $\xi $
.
$\xi $
.
Proposition 2.7 ([Reference Yang52])
The partial entropy
![]() $h_\mu (f,{\mathcal F}^u)$
varies upper semi-continuously with respect to the measures and maps in
$h_\mu (f,{\mathcal F}^u)$
varies upper semi-continuously with respect to the measures and maps in
![]() $C^1$
topology.
$C^1$
topology.
Although partially entropies are well defined for
![]() $C^1$
diffeomorphisms and behave well under
$C^1$
diffeomorphisms and behave well under
![]() $C^1$
topology, one still need higher regularity such as
$C^1$
topology, one still need higher regularity such as
![]() $C^2$
or at least
$C^2$
or at least
![]() $C^{1+}$
in order to relate it with other quantities such as Lyapunov exponents or Gibbs u-states. The following upper bound for the partial entropy along the unstable foliation
$C^{1+}$
in order to relate it with other quantities such as Lyapunov exponents or Gibbs u-states. The following upper bound for the partial entropy along the unstable foliation
![]() ${\mathcal F}^u$
follows [Reference Ledrappier and Young35, Reference Ledrappier and Young36].
${\mathcal F}^u$
follows [Reference Ledrappier and Young35, Reference Ledrappier and Young36].
Proposition 2.8. Let f be
![]() $C^{1+}$
and
$C^{1+}$
and
![]() $\mu $
be an invariant probability measure of f; then
$\mu $
be an invariant probability measure of f; then
 $$ \begin{align*}h_\mu(f,{\mathcal F}^u)\leq\int \log \operatorname{Jac}^u(x) d\mu(x).\end{align*} $$
$$ \begin{align*}h_\mu(f,{\mathcal F}^u)\leq\int \log \operatorname{Jac}^u(x) d\mu(x).\end{align*} $$
Moreover,
 $$ \begin{align} h_\mu(f,{\mathcal F}^u)=\int \log \operatorname{Jac}^u(x) d\mu(x) \end{align} $$
$$ \begin{align} h_\mu(f,{\mathcal F}^u)=\int \log \operatorname{Jac}^u(x) d\mu(x) \end{align} $$
if and only if
![]() $\mu $
is a Gibbs u-state of f.
$\mu $
is a Gibbs u-state of f.
Proof. The inequality follows by [Reference Ledrappier and Young36, Theorem
![]() ${C}^{\prime }$
] when f is
${C}^{\prime }$
] when f is
![]() $\operatorname {C}^2$
. It was pointed out by [Reference Brown15] that the same inequality goes well for
$\operatorname {C}^2$
. It was pointed out by [Reference Brown15] that the same inequality goes well for
![]() $\operatorname {C}^{1+}$
diffeomorphism.
$\operatorname {C}^{1+}$
diffeomorphism.
The second part was stated in [Reference Ledrappier33, Theorem 3.4]. □
The following equality was built in [Reference Ledrappier and Young36, Proposition 5.1] when f is
![]() $\operatorname {C}^2$
. As explained above, it also holds under the general situation assuming only
$\operatorname {C}^2$
. As explained above, it also holds under the general situation assuming only
![]() $C^{1+}$
.
$C^{1+}$
.
Proposition 2.9. Let
![]() $\mu $
be a probability measure of f such that all of the center exponents of
$\mu $
be a probability measure of f such that all of the center exponents of
![]() $\mu $
are nonpositive. Then
$\mu $
are nonpositive. Then
2.3 Other invariant measure subspaces
Proposition 2.1 (4) states that when f is
![]() $C^{1+}$
, Gibbs u-states are the natural candidates of the physical measures of f. However, this statement falls apart when f is only
$C^{1+}$
, Gibbs u-states are the natural candidates of the physical measures of f. However, this statement falls apart when f is only
![]() $C^1$
. Here let us recall that the main result of [Reference Hua, Yang and Yang32] (see also [Reference Crovisier, Yang and Zhang23]) shows that for
$C^1$
. Here let us recall that the main result of [Reference Hua, Yang and Yang32] (see also [Reference Crovisier, Yang and Zhang23]) shows that for
![]() $C^1$
diffeomorphisms, every limit point of the empirical measures at Lebesgue almost every point must satisfy ((2), Proposition 2.8). However, such measures may not be Gibbs u-states due to the lack of Pesin’s formula for
$C^1$
diffeomorphisms, every limit point of the empirical measures at Lebesgue almost every point must satisfy ((2), Proposition 2.8). However, such measures may not be Gibbs u-states due to the lack of Pesin’s formula for
![]() $C^1$
diffeomorphisms. To this end, we introduce two candidate spaces of physical measures for such f. See [Reference Hua, Yang and Yang32], [Reference Crovisier, Yang and Zhang23] and [Reference Catsigeras, Cerminara and Enrich Pesin21] for their properties.
$C^1$
diffeomorphisms. To this end, we introduce two candidate spaces of physical measures for such f. See [Reference Hua, Yang and Yang32], [Reference Crovisier, Yang and Zhang23] and [Reference Catsigeras, Cerminara and Enrich Pesin21] for their properties.
Definition 2.10. We define
-
(A1)
 $$ \begin{align*} \operatorname{G}^u(f)=\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(f,{\mathcal F}^u)\geq \int \log(\det(Df\mid_{E^u(x)}))d\mu(x)\}; \end{align*} $$
$$ \begin{align*} \operatorname{G}^u(f)=\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(f,{\mathcal F}^u)\geq \int \log(\det(Df\mid_{E^u(x)}))d\mu(x)\}; \end{align*} $$
-
(A2)
where $$ \begin{align*} \operatorname{G}^{cu}(f)=\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(f)\geq \int \log(\det(Df\mid_{E^{cu}(x)}))d\mu(x)\} \end{align*} $$
$$ \begin{align*} \operatorname{G}^{cu}(f)=\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(f)\geq \int \log(\det(Df\mid_{E^{cu}(x)}))d\mu(x)\} \end{align*} $$
 $E^{cu}=E^c\oplus E^u$
.
$E^{cu}=E^c\oplus E^u$
.
We write
Remark 2.11.
-
(a) When f is
 $C^{1+}$
, by Ledrappier [Reference Ledrappier33],
$C^{1+}$
, by Ledrappier [Reference Ledrappier33],
 $\operatorname {G}^u(f)=\operatorname {Gibbs}^u(f)$
.
$\operatorname {G}^u(f)=\operatorname {Gibbs}^u(f)$
. -
(b) By the Ruelle’s inequality for partial entropy (see, for instance, [Reference Wang, Wang and Zhu51]), one can replace the inequality in the definition of
 $\operatorname {G}^u$
by the equality However, the definition of
$\operatorname {G}^u$
by the equality However, the definition of $$ \begin{align*}\operatorname{G}^u(f)=\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(f,{\mathcal F}^u)= \int \log(\det(Df\mid_{E^u(x)}))d\mu(x)\}.\end{align*} $$
$$ \begin{align*}\operatorname{G}^u(f)=\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(f,{\mathcal F}^u)= \int \log(\det(Df\mid_{E^u(x)}))d\mu(x)\}.\end{align*} $$
 $\operatorname {G}^{cu}$
remains unchanged due to the possibility of having negative Lyapunov exponents in
$\operatorname {G}^{cu}$
remains unchanged due to the possibility of having negative Lyapunov exponents in
 $E^c$
.
$E^c$
.
We first observe that the spaces above are nonempty; moreover, the space
![]() $\operatorname {G}(f)$
contains all of the candidates of physical measures.
$\operatorname {G}(f)$
contains all of the candidates of physical measures.
Proposition 2.12. For every
![]() $C^1$
partially hyperbolic diffeomorphism f, there is a full-volume subset
$C^1$
partially hyperbolic diffeomorphism f, there is a full-volume subset
![]() $\Gamma $
such that for any
$\Gamma $
such that for any
![]() $x\in \Gamma $
, any limit point of the sequence
$x\in \Gamma $
, any limit point of the sequence
 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}$
belongs to
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}$
belongs to
![]() $\operatorname {G}(f)$
.
$\operatorname {G}(f)$
.
Proof. By [Reference Catsigeras, Cerminara and Enrich Pesin21], for x belonging to a full-volume subset, any limit of the sequence
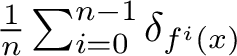 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}$
belongs to
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}$
belongs to
![]() $G^{cu}$
. Moreover, by [Reference Crovisier, Yang and Zhang23, Reference Hua, Yang and Yang32], for x belonging to a full-volume subset, any limit of the sequence
$G^{cu}$
. Moreover, by [Reference Crovisier, Yang and Zhang23, Reference Hua, Yang and Yang32], for x belonging to a full-volume subset, any limit of the sequence
 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}$
belongs to
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}$
belongs to
![]() $G^{u}$
. We conclude the proof by taking the intersection of the two full-volume subsets. □
$G^{u}$
. We conclude the proof by taking the intersection of the two full-volume subsets. □
The following property shows that
![]() $\operatorname {G}^u(\cdot )$
shares similar properties with
$\operatorname {G}^u(\cdot )$
shares similar properties with
![]() $\mbox {Gibbs}^u(\cdot )$
(Proposition 2.1).
$\mbox {Gibbs}^u(\cdot )$
(Proposition 2.1).
Proposition 2.13 ([Reference Hua, Yang and Yang32] [Propositions 3.1, 3.5])
The space
![]() $\operatorname {G}^u(f)$
is convex, compact and varies in a upper semi-continuous way with respect to the partially hyperbolic diffeomorphisms under
$\operatorname {G}^u(f)$
is convex, compact and varies in a upper semi-continuous way with respect to the partially hyperbolic diffeomorphisms under
![]() $C^1$
topology. Moreover, for any invariant measure
$C^1$
topology. Moreover, for any invariant measure
![]() $\mu \in \operatorname {G}^u(f)$
, every ergodic component of its ergodic decomposition still belongs to
$\mu \in \operatorname {G}^u(f)$
, every ergodic component of its ergodic decomposition still belongs to
![]() $\operatorname {G}^u(f)$
.
$\operatorname {G}^u(f)$
.
We need to observe that, in general, the space
![]() $\operatorname {G}(f)$
may not have such properties (especially when it comes to the ergodic components). Indeed, in Proposition 5.17, we will show that the above properties hold for
$\operatorname {G}(f)$
may not have such properties (especially when it comes to the ergodic components). Indeed, in Proposition 5.17, we will show that the above properties hold for
![]() $\operatorname {G}(g)$
when g is
$\operatorname {G}(g)$
when g is
![]() $C^1$
close to f which is
$C^1$
close to f which is
![]() $C^{1+}$
with a mostly expanding center.
$C^{1+}$
with a mostly expanding center.
3 Examples of partially hyperbolic diffeomorphisms with a mostly expanding center
For a long time (before [Reference Yang52]), there were only two known examples of diffeomorphisms with a mostly expanding center (under the definition that is used in this article, which is stronger than that in [Reference Alves, Bonatti and Viana1]). These examples are due to Mañé [Reference Mañé39] (see [Reference Alves, Bonatti and Viana1] and [Reference Andersson and Vásquez3, Section 6]) and Dolgopyat [Reference Dolgopyat25]. We list these examples below, as well as some new examples provided in [Reference Yang52]. Let us recall that the set of partially hyperbolic diffeomorphisms with a mostly expanding center is
![]() $C^1$
open among
$C^1$
open among
![]() $\mbox {Diff}^{1+}(M)$
.
$\mbox {Diff}^{1+}(M)$
.
3.1 Derived from Anosov diffeomorphisms
We assume A to be a linear Anosov diffeomorphism over
![]() ${\mathbb T}^3$
with three positive simple real eigenvalues
${\mathbb T}^3$
with three positive simple real eigenvalues
![]() $0<k_1<1<k_2<k_3$
.
$0<k_1<1<k_2<k_3$
.
3.1.1 Local derived from Anosov diffeomorphisms
Let us begin by recalling the construction of Mañé’s example, which is a local
![]() $C^0$
perturbation of A. The statement below is a little different from the original construction in history.
$C^0$
perturbation of A. The statement below is a little different from the original construction in history.
Example 3.1. Let p be a fixed point of A and U a small neighbourhood of p. There is a partially hyperbolic diffeomorphism
![]() $f_0$
that coincides with A on
$f_0$
that coincides with A on
![]() ${\mathbb T}^3\setminus U$
.
${\mathbb T}^3\setminus U$
.
![]() $f_0$
is topological Anosov, and
$f_0$
is topological Anosov, and
where the equality holds if and only if
![]() $x=p$
.
$x=p$
.
Because
![]() $Df_0\mid _{E^c(\cdot )}$
is expanding everywhere except at the point p, it is clear that
$Df_0\mid _{E^c(\cdot )}$
is expanding everywhere except at the point p, it is clear that
![]() $f_0$
has a mostly expanding center. Thus, by [Reference Yang52],
$f_0$
has a mostly expanding center. Thus, by [Reference Yang52],
![]() $f_0$
admits a
$f_0$
admits a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
such that every
${\mathcal U}$
such that every
![]() $C^{1+}$
diffeomorphism belonging to
$C^{1+}$
diffeomorphism belonging to
![]() ${\mathcal U}$
has a mostly expanding center.
${\mathcal U}$
has a mostly expanding center.
3.1.2 Generalised derived from Anosov diffeomorphisms
By the topological classification of partially hyperbolic diffeomorphisms that are isotopic to A ([Reference Brin, Burago and Ivanov13, Reference Hammerlindl and Potrie29, Reference Ures48]), we call such diffeomorphisms derived from Anosov A and denote this set of diffeomorphisms by
![]() ${\mathcal D}{\mathcal A}(A)$
. The following example by Shi, Viana and the author of this article [Reference Shi, Viana and Yang47] revises the fact that
${\mathcal D}{\mathcal A}(A)$
. The following example by Shi, Viana and the author of this article [Reference Shi, Viana and Yang47] revises the fact that
![]() $C^{1+}$
volume preserving derived from Anosov diffeomorphisms have a mostly expanding center whenever the volume has large metric entropy.
$C^{1+}$
volume preserving derived from Anosov diffeomorphisms have a mostly expanding center whenever the volume has large metric entropy.
Example 3.2. Let
![]() $f\in {\mathcal D}{\mathcal A}(A)$
be a
$f\in {\mathcal D}{\mathcal A}(A)$
be a
![]() $C^{1+}$
volume-preserving partially hyperbolic diffeomorphism and
$C^{1+}$
volume-preserving partially hyperbolic diffeomorphism and
![]() $h_{\operatorname {vol}}(f)>\log k_3$
; then f has a mostly expanding center.
$h_{\operatorname {vol}}(f)>\log k_3$
; then f has a mostly expanding center.
3.2 Perturbation of volume-preserving partially hyperbolic diffeomorphisms
In [Reference Dolgopyat25], Dolgopyat showed the following.
Example 3.3. Let
![]() $X_1$
be the time 1 map of a hyperbolic geodesic flow on a surface M; then for generic
$X_1$
be the time 1 map of a hyperbolic geodesic flow on a surface M; then for generic
![]() $C^\infty $
perturbation f of
$C^\infty $
perturbation f of
![]() $X_1$
, either f or its inverse
$X_1$
, either f or its inverse
![]() $f^{-1}$
has a mostly expanding center.
$f^{-1}$
has a mostly expanding center.
The following result in [Reference Yang52] allows us to obtain more examples using
![]() $C^1$
perturbation.
$C^1$
perturbation.
Proposition 3.4. Let f be a
![]() $C^{1+}$
volume-preserving partially hyperbolic diffeomorphism with a 1-dimensional center. Suppose that the center exponent of the volume measure is positive and f is accessible. Then f admits an
$C^{1+}$
volume-preserving partially hyperbolic diffeomorphism with a 1-dimensional center. Suppose that the center exponent of the volume measure is positive and f is accessible. Then f admits an
![]() $\operatorname {C}^1$
open neighbourhood, such that every
$\operatorname {C}^1$
open neighbourhood, such that every
![]() $\operatorname {C}^{1+}$
diffeomorphism in this neighbourhood (not necessarily volume preserving) has a mostly expanding center.
$\operatorname {C}^{1+}$
diffeomorphism in this neighbourhood (not necessarily volume preserving) has a mostly expanding center.
Proposition 3.4 contains an abundance of systems: by Avila [Reference Avila5],
![]() $\operatorname {C}^\infty $
volume-preserving diffeomorphisms are
$\operatorname {C}^\infty $
volume-preserving diffeomorphisms are
![]() $\operatorname {C}^1$
dense. And by Baraviera and Bonatti [Reference Baraviera and Bonatti6], the volume-preserving partially hyperbolic diffeomorphisms with a 1-dimensional center and nonvanishing center exponent are
$\operatorname {C}^1$
dense. And by Baraviera and Bonatti [Reference Baraviera and Bonatti6], the volume-preserving partially hyperbolic diffeomorphisms with a 1-dimensional center and nonvanishing center exponent are
![]() $\operatorname {C}^1$
open and dense. Moreover, the subset of accessible systems is
$\operatorname {C}^1$
open and dense. Moreover, the subset of accessible systems is
![]() $\operatorname {C}^1$
open and
$\operatorname {C}^1$
open and
![]() $\operatorname {C}^k$
dense for any
$\operatorname {C}^k$
dense for any
![]() $k\geq 1$
among all partially hyperbolic diffeomorphisms with a 1-dimensional center direction, due to the work of Burns et al. [Reference Burns, Rodriguez Hertz, Rodriguez Hertz, Talitskaya and Ures17]; see also Theorem 1.5 in Niţică and Török [Reference Niţică and Török40].
$k\geq 1$
among all partially hyperbolic diffeomorphisms with a 1-dimensional center direction, due to the work of Burns et al. [Reference Burns, Rodriguez Hertz, Rodriguez Hertz, Talitskaya and Ures17]; see also Theorem 1.5 in Niţică and Török [Reference Niţică and Török40].
Indeed, the accessibility assumption in the above proposition can be replaced by another hypothesis.
Example 3.5 (see [Reference Ures, Viana and Yang49])
Let f be a
![]() $C^{1+}$
volume-preserving partially hyperbolic diffeomorphism with a 1-dimensional center. Suppose that the center exponent of the volume measure is positive and
$C^{1+}$
volume-preserving partially hyperbolic diffeomorphism with a 1-dimensional center. Suppose that the center exponent of the volume measure is positive and
![]() $f^{-1}$
has a mostly contracting center. Then f admits an
$f^{-1}$
has a mostly contracting center. Then f admits an
![]() $\operatorname {C}^1$
open neighbourhood such that every
$\operatorname {C}^1$
open neighbourhood such that every
![]() $\operatorname {C}^{1+}$
diffeomorphism in this neighbourhood has a mostly expanding center.
$\operatorname {C}^{1+}$
diffeomorphism in this neighbourhood has a mostly expanding center.
Remark 3.6. The hypothesis that
![]() $f^{-1}$
has a mostly contracting center is equivalent to the assumption that
$f^{-1}$
has a mostly contracting center is equivalent to the assumption that
![]() ${\mathcal F}^s$
is minimal.
${\mathcal F}^s$
is minimal.
The diffeomorphisms with minimal strongly stable and unstable foliations are also quite common; they fill an open and dense subset of volume-preserving partially hyperbolic diffeomorphisms with a 1-dimensional center and have compact center leaves. This follows from a conservative version of the results in [Reference Bonatti, Díaz and Ures9].
3.3 Product of diffeomorphisms with a mostly expanding center
The following was shown by Ures, Viana and the author of this article in [Reference Ures, Viana and Yang49].
Proposition 3.7. Suppose that
![]() $f_1$
and
$f_1$
and
![]() $f_2$
are
$f_2$
are
![]() $C^{1+}$
partially hyperbolic diffeomorphisms over manifolds
$C^{1+}$
partially hyperbolic diffeomorphisms over manifolds
![]() $M_1$
and
$M_1$
and
![]() $M_2$
. Assume that both
$M_2$
. Assume that both
![]() $f_1$
and
$f_1$
and
![]() $f_2$
have a mostly expanding center. Then
$f_2$
have a mostly expanding center. Then
![]() $f_1\times f_2$
is a partially hyperbolic diffeomorphism over
$f_1\times f_2$
is a partially hyperbolic diffeomorphism over
![]() $M_1\times M_2$
with a mostly expanding center. As a result, nearby
$M_1\times M_2$
with a mostly expanding center. As a result, nearby
![]() $C^{1+}$
diffeomorphisms (which may not be products anymore) also have a mostly expanding center.
$C^{1+}$
diffeomorphisms (which may not be products anymore) also have a mostly expanding center.
4 Properties of skeletons
In this section, we introduce several basic properties for skeletons, although the existence of skeletons will be postponed to Section 6. The main tool in this section is the inclination lemma, also known as the
![]() $\lambda $
-lemma.
$\lambda $
-lemma.
To state the properties of skeletons under general situations, throughout this section we assume f to be a
![]() $C^1$
partially hyperbolic diffeomorphism with dominated splitting
$C^1$
partially hyperbolic diffeomorphism with dominated splitting
![]() $E^s\oplus E^c\oplus E^u$
, and
$E^s\oplus E^c\oplus E^u$
, and
![]() ${\mathcal S}=\{p_1,\cdots ,p_k\}$
is an index
${\mathcal S}=\{p_1,\cdots ,p_k\}$
is an index
![]() $i_{s}$
skeleton of f. In particular, we will not assume f to have a mostly expanding center. It is also worth noting that, unlike in [Reference Dolgopyat, Viana and Yang26], we will not discuss the robustness of skeletons under perturbation of f in this section. Such discussion requires f to have a mostly expanding center and is postponed to Section 7 (see Lemma 7.1).
$i_{s}$
skeleton of f. In particular, we will not assume f to have a mostly expanding center. It is also worth noting that, unlike in [Reference Dolgopyat, Viana and Yang26], we will not discuss the robustness of skeletons under perturbation of f in this section. Such discussion requires f to have a mostly expanding center and is postponed to Section 7 (see Lemma 7.1).
The first three technical lemmas provide geometrical information on the structure of skeletons. The main result in this section is Lemma 4.4, which states that every skeleton of f must have the same cardinality. The last two lemmas provide useful criteria for skeletons, which will be used multiple times in later sections.
Lemma 4.1.
-
(1) For any
 $1\leq i \leq k$
,
$1\leq i \leq k$
,
 $\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
has a nonempty interior.
$\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
has a nonempty interior. -
(2) For
 $1\leq i\neq j \leq k$
, there is no heteroclinic intersection between
$1\leq i\neq j \leq k$
, there is no heteroclinic intersection between
 $\mbox {Orb}(p_i)$
and
$\mbox {Orb}(p_i)$
and
 $\mbox {Orb}(p_j)$
; that is,
$\mbox {Orb}(p_j)$
; that is,
 ${\mathcal F}^s(\mbox { Orb}(p_i))\cap W^u(\mbox {Orb}(p_j))=\emptyset $
.
${\mathcal F}^s(\mbox { Orb}(p_i))\cap W^u(\mbox {Orb}(p_j))=\emptyset $
. -
(3)
 $\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))\cap \operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))) =\emptyset $
.
$\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))\cap \operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))) =\emptyset $
.
Proof. Because
![]() ${\mathcal S}$
is a skeleton, from (a) of the definition of a skeleton is
${\mathcal S}$
is a skeleton, from (a) of the definition of a skeleton is
 $$ \begin{align*}\bigcup_{i=1}^k \mbox{Cl}({\mathcal F}^s(\mbox{ Orb}(p_i)))=M.\end{align*} $$
$$ \begin{align*}\bigcup_{i=1}^k \mbox{Cl}({\mathcal F}^s(\mbox{ Orb}(p_i)))=M.\end{align*} $$
Suppose by contradiction that
![]() $\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
has empty interior for some
$\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
has empty interior for some
![]() $1\leq i \leq k$
; then
$1\leq i \leq k$
; then
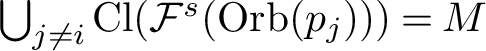 $\bigcup _{j\neq i}\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))=M$
. Thus,
$\bigcup _{j\neq i}\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))=M$
. Thus,
![]() ${\mathcal S}\setminus \{p_i\}$
also satisfies (a) of Definition 1.3, which contradicts with (b) of Definition 1.3 and the fact that
${\mathcal S}\setminus \{p_i\}$
also satisfies (a) of Definition 1.3, which contradicts with (b) of Definition 1.3 and the fact that
![]() ${\mathcal S}$
is a skeleton. This finishes the proof of (1).
${\mathcal S}$
is a skeleton. This finishes the proof of (1).
We are ready to prove (2). First, by the unstable manifold theorem,
![]() $W^u(\mbox {Orb}(p_j))$
is tangent to the bundle
$W^u(\mbox {Orb}(p_j))$
is tangent to the bundle
![]() $E^{cu}$
. Thus, if the intersection
$E^{cu}$
. Thus, if the intersection
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))\cap W^u(\mbox {Orb}(p_j))$
is not empty, it must be transversal. By the inclination lemma,
${\mathcal F}^s(\mbox {Orb}(p_i))\cap W^u(\mbox {Orb}(p_j))$
is not empty, it must be transversal. By the inclination lemma,
![]() $\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))\subset \mbox { Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
, and thus
$\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))\subset \mbox { Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
, and thus
![]() ${\mathcal S}\setminus \{p_j\}$
is a pre-skeleton, a contradiction.
${\mathcal S}\setminus \{p_j\}$
is a pre-skeleton, a contradiction.
To prove (3), we assume by contradiction that there are
![]() $1\leq i \neq j \leq k$
such that
$1\leq i \neq j \leq k$
such that
![]() $U=\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))\cap \operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))) \neq \emptyset $
. Take
$U=\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))\cap \operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j)))) \neq \emptyset $
. Take
![]() $x\in {\mathcal F}^s_R(\mbox {Orb}(p_i))\cap U$
for some
$x\in {\mathcal F}^s_R(\mbox {Orb}(p_i))\cap U$
for some
![]() $R>0$
where
$R>0$
where
![]() ${\mathcal F}^s_R(\cdot )$
is the disk in
${\mathcal F}^s_R(\cdot )$
is the disk in
![]() ${\mathcal F}^s(\cdot )$
with radius R under leaf metric; then there is
${\mathcal F}^s(\cdot )$
with radius R under leaf metric; then there is
![]() $x_n\in {\mathcal F}^s(\mbox {Orb}(p_j))\cap U$
such that
$x_n\in {\mathcal F}^s(\mbox {Orb}(p_j))\cap U$
such that
![]() $x_n\to x$
. By the continuity of stable foliation, we have
$x_n\to x$
. By the continuity of stable foliation, we have
![]() ${\mathcal F}^s_{2R}(x_n)\to {\mathcal F}^s_{2R}(x)$
and thus for n sufficiently large,
${\mathcal F}^s_{2R}(x_n)\to {\mathcal F}^s_{2R}(x)$
and thus for n sufficiently large,
![]() ${\mathcal F}^s_{2R}(x_n) \cap W^u(\mbox {Orb}(p_i))\neq \emptyset $
. Because
${\mathcal F}^s_{2R}(x_n) \cap W^u(\mbox {Orb}(p_i))\neq \emptyset $
. Because
![]() $x_n\in {\mathcal F}^s(\mbox { Orb}(p_j))$
, we have
$x_n\in {\mathcal F}^s(\mbox { Orb}(p_j))$
, we have
![]() ${\mathcal F}^s(\mbox {Orb}(p_j))\cap W^u(\mbox {Orb}(p_i))\neq \emptyset $
, which is a heteroclinic intersection between
${\mathcal F}^s(\mbox {Orb}(p_j))\cap W^u(\mbox {Orb}(p_i))\neq \emptyset $
, which is a heteroclinic intersection between
![]() $p_j$
and
$p_j$
and
![]() $p_i$
, a contradiction with item (2). □
$p_i$
, a contradiction with item (2). □
In the following, instead of using the open set
![]() $\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))$
, we are going to consider the set
$\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))$
, we are going to consider the set
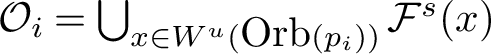 ${\mathcal O}_i=\bigcup _{x\in W^u(\mbox {Orb}(p_i))}{\mathcal F}^s(x)$
. By the transversality between
${\mathcal O}_i=\bigcup _{x\in W^u(\mbox {Orb}(p_i))}{\mathcal F}^s(x)$
. By the transversality between
![]() $E^{cu}$
and
$E^{cu}$
and
![]() $E^s$
and continuity of stable foliation, the set
$E^s$
and continuity of stable foliation, the set
![]() ${\mathcal O}_i$
is open. In the following we will reveal the relation between these two open sets.
${\mathcal O}_i$
is open. In the following we will reveal the relation between these two open sets.
For a hyperbolic saddle p, we denote by
![]() $H(p,f)$
the homoclinic class of p with respect to the map f; that is, the closure of homoclinic intersections between
$H(p,f)$
the homoclinic class of p with respect to the map f; that is, the closure of homoclinic intersections between
![]() $W^s(\mbox {Orb}(p))$
and
$W^s(\mbox {Orb}(p))$
and
![]() $W^u(\mbox {Orb}(p))$
.
$W^u(\mbox {Orb}(p))$
.
Proposition 4.2. For every
![]() $p_i\in {\mathcal S}$
,
$p_i\in {\mathcal S}$
,
-
(i)
 $\mbox {Cl}(W^u(\mbox {Orb}(p_i)))=H(p_i,f)$
.
$\mbox {Cl}(W^u(\mbox {Orb}(p_i)))=H(p_i,f)$
. -
(ii)
(4)thus, $$ \begin{align} \mbox{Cl}({\mathcal F}^s(\mbox{Orb}(p_i)))=\mbox{Cl}(\cup_{x\in W^u(\mbox{ Orb}(p_i))}{\mathcal F}^s(x)); \end{align} $$
$$ \begin{align} \mbox{Cl}({\mathcal F}^s(\mbox{Orb}(p_i)))=\mbox{Cl}(\cup_{x\in W^u(\mbox{ Orb}(p_i))}{\mathcal F}^s(x)); \end{align} $$
 ${\mathcal O}_i$
is open and dense in
${\mathcal O}_i$
is open and dense in
 $\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))$
.
$\operatorname {Int}(\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))))$
.
Proof. We first prove (i). From the definition of homoclinic class, we have
Now let us prove the other direction of the inclusion.
By the definition of skeleton,
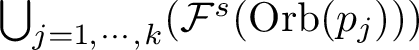 $\bigcup _{j=1,\cdots ,k} ({\mathcal F}^s(\mbox {Orb}(p_j)))$
is dense in the manifold M. Thus, for any
$\bigcup _{j=1,\cdots ,k} ({\mathcal F}^s(\mbox {Orb}(p_j)))$
is dense in the manifold M. Thus, for any
![]() $x\in W^u(\mbox {Orb}(p_i))$
, there is
$x\in W^u(\mbox {Orb}(p_i))$
, there is
![]() $p_j\in {\mathcal S}$
such that
$p_j\in {\mathcal S}$
such that
![]() $x\in \mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j))))$
. According to (2) of Lemma 4.1, there is no heteroclinic intersection between
$x\in \mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_j))))$
. According to (2) of Lemma 4.1, there is no heteroclinic intersection between
![]() ${\mathcal F}^s(\mbox {Orb}(p_j))$
and
${\mathcal F}^s(\mbox {Orb}(p_j))$
and
![]() $W^{u}(\mbox{Orb}(p_i))$
when
$W^{u}(\mbox{Orb}(p_i))$
when
![]() $i\neq j$
; thus,
$i\neq j$
; thus,
![]() $i=j$
. It then follows that
$i=j$
. It then follows that
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))$
and
${\mathcal F}^s(\mbox {Orb}(p_i))$
and
![]() $W^{u}(\mbox {Orb}(p_i))$
have nontrivial intersections arbitrarily close x, meaning that
$W^{u}(\mbox {Orb}(p_i))$
have nontrivial intersections arbitrarily close x, meaning that
![]() $x\in H(p_i,f)$
. This completes the proof of (i).
$x\in H(p_i,f)$
. This completes the proof of (i).
By the discussion above, we have shown that
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))\cap W^u(\mbox {Orb}(p_i))$
is dense inside
${\mathcal F}^s(\mbox {Orb}(p_i))\cap W^u(\mbox {Orb}(p_i))$
is dense inside
![]() $W^u(\mbox {Orb}(p_i))$
; thus,
$W^u(\mbox {Orb}(p_i))$
; thus,
 $$ \begin{align*}\mbox{Cl}({\mathcal F}^s(\mbox{Orb}(p_i)))\supset \mbox{Cl}(\cup_{x\in W^u(\mbox{Orb}(p_i))}{\mathcal F}^s(x)).\end{align*} $$
$$ \begin{align*}\mbox{Cl}({\mathcal F}^s(\mbox{Orb}(p_i)))\supset \mbox{Cl}(\cup_{x\in W^u(\mbox{Orb}(p_i))}{\mathcal F}^s(x)).\end{align*} $$
Meanwhile, because
![]() $\mbox {Orb}(p_i)\subset W^u(\mbox {Orb}(p_i))$
, the inclusion
$\mbox {Orb}(p_i)\subset W^u(\mbox {Orb}(p_i))$
, the inclusion
 $$ \begin{align*}\mbox{Cl}({\mathcal F}^s(\mbox{Orb}(p_i)))\subset \mbox{Cl}(\cup_{x\in W^u(\mbox{Orb}(p_i))}{\mathcal F}^s(x))\end{align*} $$
$$ \begin{align*}\mbox{Cl}({\mathcal F}^s(\mbox{Orb}(p_i)))\subset \mbox{Cl}(\cup_{x\in W^u(\mbox{Orb}(p_i))}{\mathcal F}^s(x))\end{align*} $$
is trivially satisfied, and the equality (4) follows immediately. □
The next two lemmas show that if one replaces
![]() $p_i\in {\mathcal S}$
by another hyperbolic periodic point
$p_i\in {\mathcal S}$
by another hyperbolic periodic point
![]() $q\in {\mathcal O}_i$
with index
$q\in {\mathcal O}_i$
with index
![]() $i_s$
, the new set
$i_s$
, the new set
![]() ${\mathcal S}' = {\mathcal S}\cup \{q\}\setminus \{p_i\}$
is still an index
${\mathcal S}' = {\mathcal S}\cup \{q\}\setminus \{p_i\}$
is still an index
![]() $i_s$
skeleton; moreover, any skeleton of f can be obtained in this way.
$i_s$
skeleton; moreover, any skeleton of f can be obtained in this way.
Lemma 4.3. Let q be an index
![]() $i_s$
hyperbolic periodic point; then
$i_s$
hyperbolic periodic point; then
![]() $q \in {\mathcal O}_i$
if and only if q and
$q \in {\mathcal O}_i$
if and only if q and
![]() $p_i$
are homoclinic related to each other. Moreover,
$p_i$
are homoclinic related to each other. Moreover,
![]() ${\mathcal S}^\prime =\{q\}\bigcup {\mathcal S}\setminus \{p_i\}$
remains an index
${\mathcal S}^\prime =\{q\}\bigcup {\mathcal S}\setminus \{p_i\}$
remains an index
![]() $i_s$
skeleton.
$i_s$
skeleton.
Proof. If q and
![]() $p_i$
are homoclinic related with each other, take
$p_i$
are homoclinic related with each other, take
![]() $a\in {\mathcal F}^s(q)\pitchfork W^u(\mbox {Orb}(p_i))$
and U a neighbourhood of a in
$a\in {\mathcal F}^s(q)\pitchfork W^u(\mbox {Orb}(p_i))$
and U a neighbourhood of a in
![]() $W^u(\mbox {Orb}(p_i))$
. By the continuity of stable foliation,
$W^u(\mbox {Orb}(p_i))$
. By the continuity of stable foliation,
![]() $\bigcup _{x\in U}{\mathcal F}^s(x)$
contains a neighbourhood of q. Then by Proposition 4.2,
$\bigcup _{x\in U}{\mathcal F}^s(x)$
contains a neighbourhood of q. Then by Proposition 4.2,
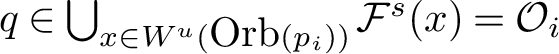 $q \in \bigcup _{x\in W^u(\mbox {Orb}(p_i))}{\mathcal F}^s(x)={\mathcal O}_i$
.
$q \in \bigcup _{x\in W^u(\mbox {Orb}(p_i))}{\mathcal F}^s(x)={\mathcal O}_i$
.
On the other hand, suppose that
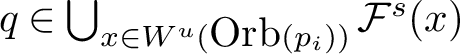 $q \in \bigcup _{x\in W^u(\mbox {Orb}(p_i))}{\mathcal F}^s(x)$
; then there exists an intersection point
$q \in \bigcup _{x\in W^u(\mbox {Orb}(p_i))}{\mathcal F}^s(x)$
; then there exists an intersection point
![]() $a\in {\mathcal F}^s(q)\pitchfork W^u(\mbox {Orb}(p_i))$
. By Proposition 4.2[(i)],
$a\in {\mathcal F}^s(q)\pitchfork W^u(\mbox {Orb}(p_i))$
. By Proposition 4.2[(i)],
![]() $a\in H(p_i,f)$
and thus can be approached by
$a\in H(p_i,f)$
and thus can be approached by
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))$
. By the continuity of stable foliation,
${\mathcal F}^s(\mbox {Orb}(p_i))$
. By the continuity of stable foliation,
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))\cap W^u(q)\neq \emptyset $
. We conclude that q and
${\mathcal F}^s(\mbox {Orb}(p_i))\cap W^u(q)\neq \emptyset $
. We conclude that q and
![]() $p_i$
are homoclinic related.
$p_i$
are homoclinic related.
Now suppose that q and
![]() $p_i$
are homoclinic related. Then by the inclination lemma, we have
$p_i$
are homoclinic related. Then by the inclination lemma, we have
![]() $\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(q)))=\mbox {Cl}({\mathcal F}^s(\mbox { Orb}(p_i)))$
, which means that
$\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(q)))=\mbox {Cl}({\mathcal F}^s(\mbox { Orb}(p_i)))$
, which means that
 $$ \begin{align*}\bigcup_{p\in {\mathcal S}^\prime}\mbox{Cl}({\mathcal F}^s(\mbox{ Orb}(p)))=M.\end{align*} $$
$$ \begin{align*}\bigcup_{p\in {\mathcal S}^\prime}\mbox{Cl}({\mathcal F}^s(\mbox{ Orb}(p)))=M.\end{align*} $$
It remains to show that
![]() ${\mathcal S}^\prime $
does not have a proper subset
${\mathcal S}^\prime $
does not have a proper subset
![]() ${\mathcal S}''$
that satisfies the above equality.
${\mathcal S}''$
that satisfies the above equality.
Assume by contradiction that
![]() ${\mathcal S}''$
is such a proper subset of
${\mathcal S}''$
is such a proper subset of
![]() ${\mathcal S}'$
. Because
${\mathcal S}'$
. Because
![]() ${\mathcal S}$
is a skeleton,
${\mathcal S}$
is a skeleton,
![]() ${{\mathcal S}}''$
has to contain q; otherwise,
${{\mathcal S}}''$
has to contain q; otherwise,
![]() ${{\mathcal S}}''$
will be a proper subset of
${{\mathcal S}}''$
will be a proper subset of
![]() ${\mathcal S}$
, which contradicts the fact that
${\mathcal S}$
, which contradicts the fact that
![]() ${\mathcal S}$
is a skeleton. By the discussion above,
${\mathcal S}$
is a skeleton. By the discussion above,
![]() $\tilde {{\mathcal S}}=\{p_i\}\bigcup {{\mathcal S}}''\setminus \{q\}$
is a pre-skeleton. However, this is impossible because
$\tilde {{\mathcal S}}=\{p_i\}\bigcup {{\mathcal S}}''\setminus \{q\}$
is a pre-skeleton. However, this is impossible because
![]() $\tilde {{\mathcal S}}$
is a proper subset of
$\tilde {{\mathcal S}}$
is a proper subset of
![]() ${\mathcal S}$
. □
${\mathcal S}$
. □
Lemma 4.4. Suppose that
![]() ${\mathcal S}^\prime =\{q_1,\cdots ,q_l\}$
is a skeleton of f; then
${\mathcal S}^\prime =\{q_1,\cdots ,q_l\}$
is a skeleton of f; then
![]() $l=k$
, and after reordering,
$l=k$
, and after reordering,
![]() $q_i$
and
$q_i$
and
![]() $p_i$
are homoclinic related for
$p_i$
are homoclinic related for
![]() $i=1,\cdots , k$
.
$i=1,\cdots , k$
.
Proof. By Definition 1.3 (a), for each
![]() $q_j\in {\mathcal S}^\prime $
there is some
$q_j\in {\mathcal S}^\prime $
there is some
![]() $p_i\in {\mathcal S}$
such that
$p_i\in {\mathcal S}$
such that
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))$
approaches
${\mathcal F}^s(\mbox {Orb}(p_i))$
approaches
![]() $p_i$
; thus,
$p_i$
; thus,
![]() $W^u(q_j)$
intersects
$W^u(q_j)$
intersects
![]() ${\mathcal F}^s(p_i)$
transversally.
${\mathcal F}^s(p_i)$
transversally.
Choose any such
![]() $p_i$
(we will see in a moment that the choice is unique). The same argument applied on
$p_i$
(we will see in a moment that the choice is unique). The same argument applied on
![]() $p_i$
shows that there exists some
$p_i$
shows that there exists some
![]() $q_k\in {\mathcal S}^\prime $
such that
$q_k\in {\mathcal S}^\prime $
such that
![]() $W^u(p_i)$
intersects
$W^u(p_i)$
intersects
![]() ${\mathcal F}^s(\mbox {Orb}(q_k))$
transversally. By the inclination lemma, there is transverse intersection between
${\mathcal F}^s(\mbox {Orb}(q_k))$
transversally. By the inclination lemma, there is transverse intersection between
![]() $W^u(\mbox {Orb}(q_j))$
and
$W^u(\mbox {Orb}(q_j))$
and
![]() ${\mathcal F}^s(\mbox { Orb}(q_k))$
. By Lemma 4.1[(2)], this can only happen if
${\mathcal F}^s(\mbox { Orb}(q_k))$
. By Lemma 4.1[(2)], this can only happen if
![]() $j=k$
. In particular,
$j=k$
. In particular,
![]() $p_i$
and
$p_i$
and
![]() $q_j$
are homoclinically related to one another.
$q_j$
are homoclinically related to one another.
Because being homoclinically related is an equivalent relation and different elements in a skeleton do not have heteroclinic intersections, it follows that the choice of
![]() $p_i$
is unique, and the map
$p_i$
is unique, and the map
![]() $q_j\mapsto p_i$
is injective. Reversing the roles of
$q_j\mapsto p_i$
is injective. Reversing the roles of
![]() ${\mathcal S}'$
and
${\mathcal S}'$
and
![]() ${\mathcal S}$
, we also get an injective map
${\mathcal S}$
, we also get an injective map
![]() $p_i \mapsto q_j$
, which, by construction, is the inverse of the previous one. Thus, both maps are bijective and, in particular,
$p_i \mapsto q_j$
, which, by construction, is the inverse of the previous one. Thus, both maps are bijective and, in particular,
![]() $\#{\mathcal S}=\#{\mathcal S}^\prime $
. Moreover, after reordering,
$\#{\mathcal S}=\#{\mathcal S}^\prime $
. Moreover, after reordering,
![]() $q_i$
and
$q_i$
and
![]() $p_i$
are homoclinic related for
$p_i$
are homoclinic related for
![]() $i=1,\cdots , k$
. □
$i=1,\cdots , k$
. □
The following lemma provides a useful criterion on the existence of skeletons, which will be used in Section 6.
Lemma 4.5. Any pre-skeleton contains a subset that forms a skeleton.
Proof. Let
![]() ${\mathcal S}^\prime =\{p_1,\cdots , p_l\}$
be a pre-skeleton. We first define a relation between the elements of
${\mathcal S}^\prime =\{p_1,\cdots , p_l\}$
be a pre-skeleton. We first define a relation between the elements of
![]() ${\mathcal S}^\prime $
: we say
${\mathcal S}^\prime $
: we say
![]() $p_i\prec p_j$
if
$p_i\prec p_j$
if
![]() $W^u(\mbox {Orb}(p_i))\pitchfork {\mathcal F}^s(p_j)\neq \emptyset $
. By the inclination lemma, it is easy to see that
$W^u(\mbox {Orb}(p_i))\pitchfork {\mathcal F}^s(p_j)\neq \emptyset $
. By the inclination lemma, it is easy to see that
![]() $\prec $
is reflexive and transitive: if
$\prec $
is reflexive and transitive: if
![]() $p_i\prec p_j$
, then
$p_i\prec p_j$
, then
Moreover, if we have
![]() $p_i\prec p_j$
and
$p_i\prec p_j$
and
![]() $p_j\prec p_i$
, then we say that they belong to the same equivalent class. Two elements belong to the same equivalent class if and only if they are homoclinic related.
$p_j\prec p_i$
, then we say that they belong to the same equivalent class. Two elements belong to the same equivalent class if and only if they are homoclinic related.
Now in the set of equivalent classes,
![]() $\prec $
induces a partial order. For every maximal equivalent class under this partial order, we pick up a representative element and then obtain a subset
$\prec $
induces a partial order. For every maximal equivalent class under this partial order, we pick up a representative element and then obtain a subset
![]() ${\mathcal S}\subset {\mathcal S}^\prime $
. By (5),
${\mathcal S}\subset {\mathcal S}^\prime $
. By (5),
![]() ${\mathcal S}$
is clearly a pre-skeleton. Moreover, from the construction, the elements of
${\mathcal S}$
is clearly a pre-skeleton. Moreover, from the construction, the elements of
![]() ${\mathcal S}$
have no heteroclinic intersection. Then this lemma is a corollary of the following result. □
${\mathcal S}$
have no heteroclinic intersection. Then this lemma is a corollary of the following result. □
Lemma 4.6. Let
![]() ${\mathcal S}=\{p_1,\cdots ,p_k\}$
be a pre-skeleton of f such that there is no heteroclinic intersection between
${\mathcal S}=\{p_1,\cdots ,p_k\}$
be a pre-skeleton of f such that there is no heteroclinic intersection between
![]() $\mbox {Orb}(p_i)$
and
$\mbox {Orb}(p_i)$
and
![]() $\mbox {Orb}(p_j)$
for
$\mbox {Orb}(p_j)$
for
![]() $1\leq i\neq j\leq k$
; then
$1\leq i\neq j\leq k$
; then
![]() ${\mathcal S}$
is a skeleton.
${\mathcal S}$
is a skeleton.
Proof. We prove by contradiction. Suppose that
![]() ${\mathcal S}$
is not a skeleton; then by Definition 1.3 (b), it contains a proper subset
${\mathcal S}$
is not a skeleton; then by Definition 1.3 (b), it contains a proper subset
![]() ${\mathcal S}''$
that forms a pre-skeleton. After reordering, we may assume
${\mathcal S}''$
that forms a pre-skeleton. After reordering, we may assume
![]() ${\mathcal S}''=\{p_1,\cdots , p_l\}$
, where
${\mathcal S}''=\{p_1,\cdots , p_l\}$
, where
![]() $l<k$
.
$l<k$
.
Then by the definition of skeleton,
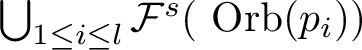 $\bigcup _{1\leq i \leq l}{\mathcal F}^s(\mbox { Orb}(p_i))$
is dense in the manifold M. As a result, there is
$\bigcup _{1\leq i \leq l}{\mathcal F}^s(\mbox { Orb}(p_i))$
is dense in the manifold M. As a result, there is
![]() $1\leq i_0\leq l$
such that
$1\leq i_0\leq l$
such that
![]() ${\mathcal F}^s(\mbox {Orb}(p_{i_0}))$
approaches
${\mathcal F}^s(\mbox {Orb}(p_{i_0}))$
approaches
![]() $p_k$
, and thus
$p_k$
, and thus
![]() ${\mathcal F}^s(\mbox {Orb}(p_{i_0}))\pitchfork W^u(p_k)\neq \emptyset $
, which contradicts the assumption that there is no heteroclinic intersection between elements of
${\mathcal F}^s(\mbox {Orb}(p_{i_0}))\pitchfork W^u(p_k)\neq \emptyset $
, which contradicts the assumption that there is no heteroclinic intersection between elements of
![]() ${\mathcal S}$
. The proof is complete. □
${\mathcal S}$
. The proof is complete. □
5 Diffeomorphisms with a mostly expanding center revisited
Throughout this section, we assume f to be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center. To make this article as self-contained as possible, we will provide a direct proof on the existence of physical measures for diffeomorphisms with a mostly expanding center. The proof is different from the original argument in [Reference Alves, Bonatti and Viana1] and is useful for the discussion in later sections.
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center. To make this article as self-contained as possible, we will provide a direct proof on the existence of physical measures for diffeomorphisms with a mostly expanding center. The proof is different from the original argument in [Reference Alves, Bonatti and Viana1] and is useful for the discussion in later sections.
One of the main difficulties in the study of diffeomorphisms with a mostly expanding center lies in the fact that the space
![]() $\mbox {Gibbs}^u(f)$
(or
$\mbox {Gibbs}^u(f)$
(or
![]() $G^u(g)$
for nearby
$G^u(g)$
for nearby
![]() $C^1$
map g; see Definition 2.10) is ‘too large’, in the sense that it contains plenty of measures that are not physical.Footnote
2
$C^1$
map g; see Definition 2.10) is ‘too large’, in the sense that it contains plenty of measures that are not physical.Footnote
2
We start solving this issue by introducing the following description for diffeomorphisms with a mostly expanding center, which turns out to be equivalent to Definition 1.2. The main advantage is that it gives a uniform estimate on the center Lyapunov exponents for measures in
![]() $\mbox {Gibbs}^u(f)$
.
$\mbox {Gibbs}^u(f)$
.
Proposition 5.1 ([Reference Yang52] [Proposition 6.1])
Suppose that f has a mostly expanding center; then there is
![]() $N_0\in \mathbb {N}$
and
$N_0\in \mathbb {N}$
and
![]() $b_0>0$
such that, for any
$b_0>0$
such that, for any
![]() $\tilde {\mu }\in \mbox {Gibbs}^u(f^{N_0})$
,
$\tilde {\mu }\in \mbox {Gibbs}^u(f^{N_0})$
,
 $$ \begin{align} \int \log \|Df^{-N_0}|_{E^{cu}(x)}\|d\tilde{\mu}(x)<-b_0. \end{align} $$
$$ \begin{align} \int \log \|Df^{-N_0}|_{E^{cu}(x)}\|d\tilde{\mu}(x)<-b_0. \end{align} $$
Remark 5.2. From now on, we assume
![]() $N_0=1$
.
$N_0=1$
.
By the upper semi-continuity of the space
![]() $\operatorname {G}^u(f)$
with respect to diffeomorphisms in
$\operatorname {G}^u(f)$
with respect to diffeomorphisms in
![]() $C^1$
topology (Proposition 2.13), we can extend this estimate to nearby
$C^1$
topology (Proposition 2.13), we can extend this estimate to nearby
![]() $C^1$
maps.
$C^1$
maps.
Lemma 5.3. There is a
![]() $C^1$
open neighbourhood
$C^1$
open neighbourhood
![]() ${\mathcal U}$
of f such that for any
${\mathcal U}$
of f such that for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
and any
$g\in {\mathcal U}$
and any
![]() $\mu \in \operatorname {G}^u(g)$
, we have
$\mu \in \operatorname {G}^u(g)$
, we have
 $$ \begin{align} \int \log \|Dg^{-1}|_{E^{cu}_g(x)}\|d\mu(x)<-b_0. \end{align} $$
$$ \begin{align} \int \log \|Dg^{-1}|_{E^{cu}_g(x)}\|d\mu(x)<-b_0. \end{align} $$
This is used in Subsection 5.1, where we show that for any
![]() $C^1$
diffeomorphism g in a small
$C^1$
diffeomorphism g in a small
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
of f, and for any
${\mathcal U}$
of f, and for any
![]() $\mu \in \operatorname {G}^u(g)$
,
$\mu \in \operatorname {G}^u(g)$
,
![]() $\mu $
typical points x have infinitely many hyperbolic times for the bundle
$\mu $
typical points x have infinitely many hyperbolic times for the bundle
![]() $E^{cu}$
in its orbit (see Lemma 5.8).
$E^{cu}$
in its orbit (see Lemma 5.8).
On the other hand, the space
![]() $\operatorname {G}^{cu}(f)$
is also ‘too large’ because it may contain measures with negative center exponents. Such measures need not be a Gibbs u-state and thus not physical due to Proposition 2.1 (4). One way to solve this issue is to take the space of intersection,
$\operatorname {G}^{cu}(f)$
is also ‘too large’ because it may contain measures with negative center exponents. Such measures need not be a Gibbs u-state and thus not physical due to Proposition 2.1 (4). One way to solve this issue is to take the space of intersection,
![]() $\operatorname {G}(f)$
, which is a much smaller space to work with. However, this creates another problem: unlike the partial entropy, which is upper semi-continuous (which makes the space
$\operatorname {G}(f)$
, which is a much smaller space to work with. However, this creates another problem: unlike the partial entropy, which is upper semi-continuous (which makes the space
![]() $\operatorname {G}^u(f)$
upper semi-continuous in f), the metric entropy
$\operatorname {G}^u(f)$
upper semi-continuous in f), the metric entropy
![]() $h_\mu $
may not have such a property. This is dealt with in Subsection 5.2, as we introduce fake foliations for partially hyperbolic diffeomorphisms and show in Lemma 5.12 that the measures in
$h_\mu $
may not have such a property. This is dealt with in Subsection 5.2, as we introduce fake foliations for partially hyperbolic diffeomorphisms and show in Lemma 5.12 that the measures in
![]() $\operatorname {G}^u(g)$
for
$\operatorname {G}^u(g)$
for
![]() $g\in {\mathcal U}$
are uniformly entropy expansive. As a consequence, in Subsection 5.3 it is shown (Corollary 5.16) that metric entropy, when restricted to measures in
$g\in {\mathcal U}$
are uniformly entropy expansive. As a consequence, in Subsection 5.3 it is shown (Corollary 5.16) that metric entropy, when restricted to measures in
![]() $\operatorname {G}^u(g)$
, varies in a upper semi-continuous fashion in weak-* topology and with respect the diffeomorphism
$\operatorname {G}^u(g)$
, varies in a upper semi-continuous fashion in weak-* topology and with respect the diffeomorphism
![]() $g\in {\mathcal U}$
in
$g\in {\mathcal U}$
in
![]() $C^1$
topology.
$C^1$
topology.
Finally, Subsection 5.4 contains the main result of this section: for any
![]() $C^{1+}$
diffeomorphism
$C^{1+}$
diffeomorphism
![]() $g\in {\mathcal U}$
, every extreme element of
$g\in {\mathcal U}$
, every extreme element of
![]() $\operatorname {G}(g)$
is an ergodic physical measure of g.
$\operatorname {G}(g)$
is an ergodic physical measure of g.
5.1 Hyperbolic times
Definition 5.4. Given
![]() $b>0$
, we say that n is a b- hyperbolic time for a point x if
$b>0$
, we say that n is a b- hyperbolic time for a point x if
 $$ \begin{align*}\frac{1}{k}\sum_{j=n-k+1}^n\log\|Df^{-1}\mid_{E^{cu}(f^j(x))}\|\leq -b \text{ for any }0<k \leq n.\end{align*} $$
$$ \begin{align*}\frac{1}{k}\sum_{j=n-k+1}^n\log\|Df^{-1}\mid_{E^{cu}(f^j(x))}\|\leq -b \text{ for any }0<k \leq n.\end{align*} $$
Let D be any
![]() $\operatorname {C}^1$
disk; we use
$\operatorname {C}^1$
disk; we use
![]() $d_D(\cdot ,\cdot )$
to denote the distance between two points in the disk. Recall that for the dominated splitting
$d_D(\cdot ,\cdot )$
to denote the distance between two points in the disk. Recall that for the dominated splitting
![]() $E^s\oplus E^{cu}$
, one can define the center unstable cone field, which is invariant under forward iteration.
$E^s\oplus E^{cu}$
, one can define the center unstable cone field, which is invariant under forward iteration.
The next lemma states that if n is a hyperbolic time for x, then on the disk
![]() $f^n(D)$
, one picks up a contraction by
$f^n(D)$
, one picks up a contraction by
![]() $e^{-b}$
for each backward iteration.
$e^{-b}$
for each backward iteration.
Lemma 5.5 ([Reference Alves, Bonatti and Viana1] Lemma 2.7)
For any
![]() $b>0$
, there is
$b>0$
, there is
![]() $r>0$
such that, given any
$r>0$
such that, given any
![]() $\operatorname {C}^1$
disk D tangent to the center-unstable cone field,
$\operatorname {C}^1$
disk D tangent to the center-unstable cone field,
![]() $x\in D$
and
$x\in D$
and
![]() $n\geq 1$
a
$n\geq 1$
a
![]() $b/2$
-hyperbolic time for x, we have
$b/2$
-hyperbolic time for x, we have
 $$ \begin{align*}d_{f^{n-k}(D)}(f^{n-k}(y),f^{n-k}(x))\leq e^{-kb/2} d_{f^n(D)}(f^n(x),f^n(y)),\end{align*} $$
$$ \begin{align*}d_{f^{n-k}(D)}(f^{n-k}(y),f^{n-k}(x))\leq e^{-kb/2} d_{f^n(D)}(f^n(x),f^n(y)),\end{align*} $$
for any point
![]() $y\in D$
with
$y\in D$
with
![]() $d_{f^n(D)}(f^n(x),f^n(y))\leq r$
and any
$d_{f^n(D)}(f^n(x),f^n(y))\leq r$
and any
![]() $1\leq k \leq n$
.
$1\leq k \leq n$
.
Remark 5.6. For fixed
![]() $b_0/2>0$
, we can take
$b_0/2>0$
, we can take
![]() $r=r_1$
to be constant for the diffeomorphisms in a
$r=r_1$
to be constant for the diffeomorphisms in a
![]() $\operatorname {C}^1$
neighbourhood of f.
$\operatorname {C}^1$
neighbourhood of f.
By Lemma 5.3 and Proposition 2.12, for any
![]() $g\in {\mathcal U}$
, there is a full-volume subset
$g\in {\mathcal U}$
, there is a full-volume subset
![]() $\Gamma _g$
such that for any
$\Gamma _g$
such that for any
![]() $x\in \Gamma _g$
, any limit of the sequence
$x\in \Gamma _g$
, any limit of the sequence
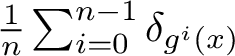 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{g^i(x)}$
belongs to
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{g^i(x)}$
belongs to
![]() $\operatorname {G}(g)$
. Thus, for any
$\operatorname {G}(g)$
. Thus, for any
![]() $x\in \Gamma _g$
,
$x\in \Gamma _g$
,
 $$ \begin{align} \begin{aligned} \limsup_{n\to \infty}\frac{1}{n}\sum_{i=0}^{n-1}\log \|Dg^{-1}\mid_{E^{cu}_g(g^i(x))}\|&=\limsup \int \log \|Dg^{-1}\mid_{E^{cu}_g(x)}\| d\frac{1}{n}\sum_{i=0}^{n-1}\delta_{g^i(x)}\\ &<-b_0<0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \limsup_{n\to \infty}\frac{1}{n}\sum_{i=0}^{n-1}\log \|Dg^{-1}\mid_{E^{cu}_g(g^i(x))}\|&=\limsup \int \log \|Dg^{-1}\mid_{E^{cu}_g(x)}\| d\frac{1}{n}\sum_{i=0}^{n-1}\delta_{g^i(x)}\\ &<-b_0<0. \end{aligned} \end{align} $$
Define
![]() $H(b_0/2,x,g)$
to be the set of
$H(b_0/2,x,g)$
to be the set of
![]() $b_0/2$
-hyperbolic times for
$b_0/2$
-hyperbolic times for
![]() $x\in \Gamma _g$
; that is, the set of times
$x\in \Gamma _g$
; that is, the set of times
![]() $m\geq 1$
such that
$m\geq 1$
such that
 $$ \begin{align} \frac{1}{k}\sum_{i=m-k+1}^{m} \log \|Dg^{-1}\mid_{E^{cu}_g(g^i(x))}\|\leq -b_0/2 \text{ for all }1\leq k \leq m. \end{align} $$
$$ \begin{align} \frac{1}{k}\sum_{i=m-k+1}^{m} \log \|Dg^{-1}\mid_{E^{cu}_g(g^i(x))}\|\leq -b_0/2 \text{ for all }1\leq k \leq m. \end{align} $$
By the Pliss lemma (see [Reference Alves, Bonatti and Viana1]), such hyperbolic times have positive density on the orbit segment from
![]() $0$
to n: there exists
$0$
to n: there exists
![]() $n_x\geq 1$
and
$n_x\geq 1$
and
![]() $\delta _1>0$
such that
$\delta _1>0$
such that
By Lemma 5.5 and Remark 5.6, there is
![]() $r_1>0$
that only depends on
$r_1>0$
that only depends on
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() $b_0/2$
, such that for any
$b_0/2$
, such that for any
![]() $x\in \Gamma _g$
and any disk D tangent to the center-unstable cone field,
$x\in \Gamma _g$
and any disk D tangent to the center-unstable cone field,
![]() $x\in D$
,
$x\in D$
,
![]() $n\in H(b_0/2,x,g)$
, we have
$n\in H(b_0/2,x,g)$
, we have
 $$ \begin{align} d_{D}(x,y)\leq e^{-nb_0/2}d_{g^n(D)}(g^n(x),f^n(y)), \end{align} $$
$$ \begin{align} d_{D}(x,y)\leq e^{-nb_0/2}d_{g^n(D)}(g^n(x),f^n(y)), \end{align} $$
for any
![]() $y\in D$
with
$y\in D$
with
![]() $d_{g^n(D)}(g^n(x),g^n(y))\leq r_1$
. (We also assume that
$d_{g^n(D)}(g^n(x),g^n(y))\leq r_1$
. (We also assume that
![]() $r_1$
satisfies the condition (15) below, which depends only on the neighbourhood
$r_1$
satisfies the condition (15) below, which depends only on the neighbourhood
![]() ${\mathcal U}$
.) In particular, for
${\mathcal U}$
.) In particular, for
![]() $x\in \Gamma _g$
and disk D tangent to the center-unstable cone field containing x,
$x\in \Gamma _g$
and disk D tangent to the center-unstable cone field containing x,
![]() $g^n(D)$
contains a smaller disk
$g^n(D)$
contains a smaller disk
![]() $D_n$
with diameter
$D_n$
with diameter
![]() $r_1$
for
$r_1$
for
![]() $n\in H(b_0/2,x,g)$
sufficiently large. Then
$n\in H(b_0/2,x,g)$
sufficiently large. Then
![]() $\cup _{z\in D_n}{\mathcal F}^s(z)$
contains an open ball with radius
$\cup _{z\in D_n}{\mathcal F}^s(z)$
contains an open ball with radius
![]() $r_1$
.
$r_1$
.
Definition 5.7. Denote by
![]() ${\mathcal H}(b_0/2,g)$
the set of points x such that for any
${\mathcal H}(b_0/2,g)$
the set of points x such that for any
![]() $k\geq 1$
,
$k\geq 1$
,
 $$ \begin{align} \frac{1}{k}\sum_{i=0}^{k-1} \log \|Dg^{-1}\mid_{E^{cu}_g(g^{-i}(x))}\|\leq -b_0/2 \text{ for all }k\geq 0. \end{align} $$
$$ \begin{align} \frac{1}{k}\sum_{i=0}^{k-1} \log \|Dg^{-1}\mid_{E^{cu}_g(g^{-i}(x))}\|\leq -b_0/2 \text{ for all }k\geq 0. \end{align} $$
In other words, for every
![]() $n>0$
, n is a hyperbolic time for the point
$n>0$
, n is a hyperbolic time for the point
![]() $f^{-n}(x)$
.
$f^{-n}(x)$
.
The next lemma shows that there are plenty of hyperbolic times on the forward orbit of x, every
![]() $\mu \in \operatorname {G}^u(g)$
and
$\mu \in \operatorname {G}^u(g)$
and
![]() $\mu $
almost every x.
$\mu $
almost every x.
Lemma 5.8. For any
![]() $g\in {\mathcal U}$
and any
$g\in {\mathcal U}$
and any
![]() $\mu \in \operatorname {G}^u(g)$
, we have
$\mu \in \operatorname {G}^u(g)$
, we have
where
![]() $\delta _1$
is given in (10).
$\delta _1$
is given in (10).
Proof. By Proposition 2.13, we may assume
![]() $\mu $
to be ergodic. By Birkhoff’s theorem, we only need to show that for
$\mu $
to be ergodic. By Birkhoff’s theorem, we only need to show that for
![]() $\mu $
almost every x,
$\mu $
almost every x,
 $\liminf \frac {1}{n}\#\{1\leq k \leq n; f^k(x)\in {\mathcal H}(b_0/2,g)\}\geq \delta _1$
. It is equivalent to show that for some fixed
$\liminf \frac {1}{n}\#\{1\leq k \leq n; f^k(x)\in {\mathcal H}(b_0/2,g)\}\geq \delta _1$
. It is equivalent to show that for some fixed
![]() $m_x$
,
$m_x$
,
 $$ \begin{align} \liminf\frac{1}{n}\#\{1\leq k \leq n; f^{k+m_x}(x)\in {\mathcal H}(b_0/2,g)\}\geq \delta_1. \end{align} $$
$$ \begin{align} \liminf\frac{1}{n}\#\{1\leq k \leq n; f^{k+m_x}(x)\in {\mathcal H}(b_0/2,g)\}\geq \delta_1. \end{align} $$
By Lemma 5.3, take x be a typical point of
![]() $\mu $
, such that
$\mu $
, such that
 $$ \begin{align*}\lim\frac{1}{n}\sum_{i=0}^{n-1} \log \|Dg^{-1}\mid_{E^{cu}_g(g^{-i}(x))}\|\leq -b_0.\end{align*} $$
$$ \begin{align*}\lim\frac{1}{n}\sum_{i=0}^{n-1} \log \|Dg^{-1}\mid_{E^{cu}_g(g^{-i}(x))}\|\leq -b_0.\end{align*} $$
We claim that there is
![]() $m>0$
such that
$m>0$
such that
![]() $g^{-m}(x)\in {\mathcal H}(b_0/2,g)$
. Otherwise, for any
$g^{-m}(x)\in {\mathcal H}(b_0/2,g)$
. Otherwise, for any
![]() $g^{-n}(x)$
, there is
$g^{-n}(x)$
, there is
![]() $i_n>0$
such that
$i_n>0$
such that
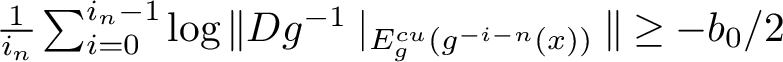 $\frac {1}{i_n}\sum _{i=0}^{i_n-1} \log \|Dg^{-1}\mid _{E^{cu}_g(g^{-i-n}(x))}\|\geq -b_0/2$
. Recursively, we obtain a sequence of points:
$\frac {1}{i_n}\sum _{i=0}^{i_n-1} \log \|Dg^{-1}\mid _{E^{cu}_g(g^{-i-n}(x))}\|\geq -b_0/2$
. Recursively, we obtain a sequence of points:
![]() $n_1=i_0$
,
$n_1=i_0$
,
![]() $n_2=n_1+i_{n_1}, \cdots $
; by induction, we have
$n_2=n_1+i_{n_1}, \cdots $
; by induction, we have
 $$ \begin{align*}\frac{1}{n_k}\sum_{i=0}^{n_k-1} \log \|Dg^{-1}\mid_{E^{cu}_g(g^{-i}(x))}\|\geq -b_0/2.\end{align*} $$
$$ \begin{align*}\frac{1}{n_k}\sum_{i=0}^{n_k-1} \log \|Dg^{-1}\mid_{E^{cu}_g(g^{-i}(x))}\|\geq -b_0/2.\end{align*} $$
This contradicts the choice of x.
Moreover, it is easy to see that for any
![]() $k\in H(b_0/2,g^{-m}(x),g)$
,
$k\in H(b_0/2,g^{-m}(x),g)$
,
![]() $g^{k-m}(x)\in {\mathcal H}(b_0/2,g)$
. Then by (10) and taking
$g^{k-m}(x)\in {\mathcal H}(b_0/2,g)$
. Then by (10) and taking
![]() $m_x=m$
in (14), we conclude the proof. □
$m_x=m$
in (14), we conclude the proof. □
5.2 Fake foliations
In order to avoid assuming dynamical coherence of f, we use locally invariant (fake) foliations, a construction that follows Burns and Wilkinson [Reference Burns and Wilkinson18] and goes back to Hirsch, Pugh and Shub [Reference Hirsch, Pugh and Shub31]. We fix
![]() ${\mathcal U}$
a small
${\mathcal U}$
a small
![]() $C^1$
neighbourhood of f provided by Lemma 5.3.
$C^1$
neighbourhood of f provided by Lemma 5.3.
Lemma 5.9. There are real numbers
![]() $\rho>r_0>0$
only depending on
$\rho>r_0>0$
only depending on
![]() ${\mathcal U}$
with the following properties. For any
${\mathcal U}$
with the following properties. For any
![]() $x\in M$
, the neighbourhood
$x\in M$
, the neighbourhood
![]() $B(x,\rho )$
admits foliations
$B(x,\rho )$
admits foliations
 $\hat {{\mathcal F}}^s_{g,x}$
and
$\hat {{\mathcal F}}^s_{g,x}$
and
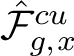 $\hat {{\mathcal F}}^{cu}_{g,x}$
such that for every
$\hat {{\mathcal F}}^{cu}_{g,x}$
such that for every
![]() $y\in B(x,r_0)$
and
$y\in B(x,r_0)$
and
![]() $*=\{s,cu\}$
:
$*=\{s,cu\}$
:
-
(1) the leaf
 $\hat {{\mathcal F}}^*_{g,x}(y)$
is
$\hat {{\mathcal F}}^*_{g,x}(y)$
is
 $C^1$
, and its tangent bundle
$C^1$
, and its tangent bundle
 $T_y(\hat {{\mathcal F}}^*_{g,x}(y))$
lies in a cone of
$T_y(\hat {{\mathcal F}}^*_{g,x}(y))$
lies in a cone of
 $E^*(x)$
;
$E^*(x)$
; -
(2)
 $g(\hat {{\mathcal F}}^s_{g,x}(y,r_0))\subset \hat {{\mathcal F}}^s_{g,g(x)}(g(y))$
and
$g(\hat {{\mathcal F}}^s_{g,x}(y,r_0))\subset \hat {{\mathcal F}}^s_{g,g(x)}(g(y))$
and
 $g^{-1}(\hat {{\mathcal F}}^{cu}_{g,x}(y,r_0))\subset \hat {{\mathcal F}}^{cu}_{g,f^{-1}(x)}(g^{-1}(y))$
;
$g^{-1}(\hat {{\mathcal F}}^{cu}_{g,x}(y,r_0))\subset \hat {{\mathcal F}}^{cu}_{g,f^{-1}(x)}(g^{-1}(y))$
; -
(3) we have product structures inside
 $B(x,r_0)$
; that is, for any
$B(x,r_0)$
; that is, for any
 $y,z\in B(x,r_0)$
, there is a unique intersection between
$y,z\in B(x,r_0)$
, there is a unique intersection between
 $\hat {{\mathcal F}}^s_{g,x}(y)$
with
$\hat {{\mathcal F}}^s_{g,x}(y)$
with
 $\hat {{\mathcal F}}^{cu}_{g,x}(z)$
, which we denote by
$\hat {{\mathcal F}}^{cu}_{g,x}(z)$
, which we denote by
 $[y,z]$
.
$[y,z]$
.
For
![]() $g\in {\mathcal U}$
and any
$g\in {\mathcal U}$
and any
![]() $x\in M$
, we consider the following three types of Bowen balls:
$x\in M$
, we consider the following three types of Bowen balls:
-
• finite Bowen ball:
 $B_n(g,x,\varepsilon )=\{y\in M: d(g^i(x),g^i(y))<\varepsilon , |i|<n\},$
$B_n(g,x,\varepsilon )=\{y\in M: d(g^i(x),g^i(y))<\varepsilon , |i|<n\},$
-
• negative Bowen ball:
 $B^-_\infty (g,x,\varepsilon )=\{y\in M: d(g^i(x),g^i(y))<\varepsilon , i<0\},$
$B^-_\infty (g,x,\varepsilon )=\{y\in M: d(g^i(x),g^i(y))<\varepsilon , i<0\},$
-
• (two sided) infinite Bowen ball:
 $$ \begin{align*}B_\infty(g,x,\varepsilon)=\{y\in M: d(g^i(x),g^i(y))<\varepsilon, i\in \mathbb{Z}\}.\end{align*} $$
$$ \begin{align*}B_\infty(g,x,\varepsilon)=\{y\in M: d(g^i(x),g^i(y))<\varepsilon, i\in \mathbb{Z}\}.\end{align*} $$
The following was shown in the proof of [Reference Liao, Viana and Yang37], [Theorem 3.1].
Lemma 5.10. For
![]() $\varepsilon <r_0/2$
and any
$\varepsilon <r_0/2$
and any
![]() $x\in M$
,
$x\in M$
,
 $B^-_\infty (g,x,\varepsilon )\subset \hat {{\mathcal F}}^{cu}_{g,x}(y,2\varepsilon )$
.
$B^-_\infty (g,x,\varepsilon )\subset \hat {{\mathcal F}}^{cu}_{g,x}(y,2\varepsilon )$
.
We may take
![]() $r_1$
in the previous section to satisfy that
$r_1$
in the previous section to satisfy that
Then as a consequence of Lemma 5.5, we show that for every point in
![]() ${\mathcal H}(b_0/2,g)$
, the unstable manifold has uniform size.
${\mathcal H}(b_0/2,g)$
, the unstable manifold has uniform size.
Lemma 5.11. For any
![]() $x\in {\mathcal H}(b_0/2,g)$
,
$x\in {\mathcal H}(b_0/2,g)$
,
 $\hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)\subset W_{\operatorname {loc}}^u(x)$
. More precisely, for any
$\hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)\subset W_{\operatorname {loc}}^u(x)$
. More precisely, for any
 $y\in \hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)$
,
$y\in \hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)$
,
 $$ \begin{align*}d_{\hat{{\mathcal F}}^{cu}_{g,g^{-n}(x)}(g^{-n}(x))}(g^{-n}(x),g^{-n}(y))\leq e^{-nb_0/2}d_{\hat{{\mathcal F}}^{cu}_{g,x}(x)}(x,y).\end{align*} $$
$$ \begin{align*}d_{\hat{{\mathcal F}}^{cu}_{g,g^{-n}(x)}(g^{-n}(x))}(g^{-n}(x),g^{-n}(y))\leq e^{-nb_0/2}d_{\hat{{\mathcal F}}^{cu}_{g,x}(x)}(x,y).\end{align*} $$
The goal of this subsection is to show that the measures in
![]() $\operatorname {G}^u(g)$
for
$\operatorname {G}^u(g)$
for
![]() $g\in {\mathcal U}$
are uniformly entropy expansiveness.
$g\in {\mathcal U}$
are uniformly entropy expansiveness.
Lemma 5.12. For any
![]() $g\in {\mathcal U}$
and any measure
$g\in {\mathcal U}$
and any measure
![]() $\mu \in \operatorname {G}^u(g)$
, for
$\mu \in \operatorname {G}^u(g)$
, for
![]() $\mu $
almost every point x,
$\mu $
almost every point x,
Proof. By Lemma 5.10 and the choice of
![]() $r_1\leq r_0/2$
, we have
$r_1\leq r_0/2$
, we have
 $$ \begin{align*}B_\infty(g,x,r_1)\subset B^-_\infty(g,x,r_1)\subset \hat{{\mathcal F}}^{cu}_{g,x}(x,r_1).\end{align*} $$
$$ \begin{align*}B_\infty(g,x,r_1)\subset B^-_\infty(g,x,r_1)\subset \hat{{\mathcal F}}^{cu}_{g,x}(x,r_1).\end{align*} $$
Let x be a
![]() $\mu $
typical point; by Lemma 5.8, we may assume that the forward orbit of x enters
$\mu $
typical point; by Lemma 5.8, we may assume that the forward orbit of x enters
![]() ${\mathcal H}(b_0/2,g)$
infinitely many times. Suppose that there is a distinct point
${\mathcal H}(b_0/2,g)$
infinitely many times. Suppose that there is a distinct point
 $y\in B_\infty (g,x,r_1/2)\subset \hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)$
, we are going to prove by contradiction that
$y\in B_\infty (g,x,r_1/2)\subset \hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)$
, we are going to prove by contradiction that
![]() $x$
and
$x$
and
![]() $y$
coincide with each other. Suppose that
$y$
coincide with each other. Suppose that
![]() $f^n(x)\in {\mathcal H}(b_0/2,g)$
, then
$f^n(x)\in {\mathcal H}(b_0/2,g)$
, then
 $f^n(y)\in B_\infty (g,g^n(x),r_1/2)\in \hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)$
. By Lemma 5.11,
$f^n(y)\in B_\infty (g,g^n(x),r_1/2)\in \hat {{\mathcal F}}^{cu}_{g,x}(x,r_1)$
. By Lemma 5.11,
 $$ \begin{align*}d_{\hat{{\mathcal F}}^{cu}_{g,x}(x)}(x,y)\leq e^{-nb_0/2}d_{\hat{{\mathcal F}}^{cu}_{g,g^n(x)}(g^n(x))}(g^n(x),g^n(y))\leq e^{-nb_0/2}r_1.\end{align*} $$
$$ \begin{align*}d_{\hat{{\mathcal F}}^{cu}_{g,x}(x)}(x,y)\leq e^{-nb_0/2}d_{\hat{{\mathcal F}}^{cu}_{g,g^n(x)}(g^n(x))}(g^n(x),g^n(y))\leq e^{-nb_0/2}r_1.\end{align*} $$
Taking
![]() $n\to \infty $
, we have
$n\to \infty $
, we have
 $d_{\hat {{\mathcal F}}^{cu}_{g,x}(x)}(x,y)=0$
. Hence,
$d_{\hat {{\mathcal F}}^{cu}_{g,x}(x)}(x,y)=0$
. Hence,
![]() $x=y$
, a contradiction with the hypothesis that x and y are distinct. The proof is complete. □
$x=y$
, a contradiction with the hypothesis that x and y are distinct. The proof is complete. □
Remark 5.13. The classical definition of entropy expansive by Bowen requires the topological entropy of
![]() $B_\infty (g,x,r_1)$
to be vanishing for every
$B_\infty (g,x,r_1)$
to be vanishing for every
![]() $x\in M$
. However, as observed in [Reference Liao, Viana and Yang37, Proposition 2.4], this is equivalent to having zero topological entropy for the infinite Bowen ball for every invariant measure
$x\in M$
. However, as observed in [Reference Liao, Viana and Yang37, Proposition 2.4], this is equivalent to having zero topological entropy for the infinite Bowen ball for every invariant measure
![]() $\mu $
and
$\mu $
and
![]() $\mu $
almost every x. The statement of the previous lemma follows this approach.
$\mu $
almost every x. The statement of the previous lemma follows this approach.
Also note that this lemma does not immediately lead to the upper semi-continuity of
![]() $h_\mu $
as in the classical case, because we only have entropy expansive on a subspace of invariant measure. However, we will see in a moment that the upper semi-continuity holds for measures in
$h_\mu $
as in the classical case, because we only have entropy expansive on a subspace of invariant measure. However, we will see in a moment that the upper semi-continuity holds for measures in
![]() $\operatorname {G}^u$
.
$\operatorname {G}^u$
.
5.3 Upper semi-continuity of metric entropy
In this section, we are going to show that the metric entropy for measures in
![]() $\operatorname {G}^u(\cdot )$
is upper semi-continuous, which is a consequence of the uniform entropy expansiveness for measures among
$\operatorname {G}^u(\cdot )$
is upper semi-continuous, which is a consequence of the uniform entropy expansiveness for measures among
![]() $\operatorname {G}^u(\cdot )$
.
$\operatorname {G}^u(\cdot )$
.
Define the
![]() $\varepsilon $
-tail entropy at x by
$\varepsilon $
-tail entropy at x by
where we use Bowen’s definition of the topological entropy [Reference Bowen12]:
 $$ \begin{align*}h_{top}(g,K) = \lim_{\varepsilon\to 0}\limsup_{n\to\infty} \frac1n\log r_n(\varepsilon,K); \end{align*} $$
$$ \begin{align*}h_{top}(g,K) = \lim_{\varepsilon\to 0}\limsup_{n\to\infty} \frac1n\log r_n(\varepsilon,K); \end{align*} $$
here
![]() $r_n(\varepsilon ,K)$
is the minimum cardinality of
$r_n(\varepsilon ,K)$
is the minimum cardinality of
![]() $(n,\varepsilon )$
-spanning sets of K. For any probability measure
$(n,\varepsilon )$
-spanning sets of K. For any probability measure
![]() $\mu $
of g, let
$\mu $
of g, let
![]() $h^*(g,\mu ,\varepsilon )=\int h^*(g,x,\varepsilon ) d\mu (x)$
.
$h^*(g,\mu ,\varepsilon )=\int h^*(g,x,\varepsilon ) d\mu (x)$
.
As a direct consequence of Lemma 5.12, we get the following.
Lemma 5.14. For any
![]() $g\in {\mathcal U}$
and any
$g\in {\mathcal U}$
and any
![]() $\mu \in \operatorname {G}^u(g)$
,
$\mu \in \operatorname {G}^u(g)$
,
![]() $h^*(g,\mu ,r_1)=0$
.
$h^*(g,\mu ,r_1)=0$
.
We also need the following lemma of [Reference Cao, Liao and You20], [Theorem 1.2].
Lemma 5.15.
![]() $h_\mu (g)-h_\mu (g,{\mathcal P})\leq h^*(g,\mu ,\rho )$
for any finite measurable partition
$h_\mu (g)-h_\mu (g,{\mathcal P})\leq h^*(g,\mu ,\rho )$
for any finite measurable partition
![]() ${\mathcal P}$
with
${\mathcal P}$
with
![]() $diam({\mathcal P})\leq \rho $
.
$diam({\mathcal P})\leq \rho $
.
By Lemma 5.14 and Lemma 5.15, we conclude that
![]() $h_\mu (g)=h_\mu (g,{\mathcal P})$
for any finite measurable partition
$h_\mu (g)=h_\mu (g,{\mathcal P})$
for any finite measurable partition
![]() ${\mathcal P}$
with
${\mathcal P}$
with
![]() $diam({\mathcal P})\leq r_1$
. In particular, by a standard argument for the upper semi-continuity of metric entropy (see, for instance, [Reference Liao, Viana and Yang37], [Lemma 2.3]), we have the following.
$diam({\mathcal P})\leq r_1$
. In particular, by a standard argument for the upper semi-continuity of metric entropy (see, for instance, [Reference Liao, Viana and Yang37], [Lemma 2.3]), we have the following.
Corollary 5.16. Let
![]() $g_n$
(
$g_n$
(
![]() $n\geq 0$
) be a sequence of
$n\geq 0$
) be a sequence of
![]() $C^1$
partially hyperbolic diffeomorphisms inside
$C^1$
partially hyperbolic diffeomorphisms inside
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() $\mu _n\in \operatorname {G}^u(g_n)$
. Suppose yjsy
$\mu _n\in \operatorname {G}^u(g_n)$
. Suppose yjsy
![]() $g_n\to g_0$
in
$g_n\to g_0$
in
![]() $C^1$
topology and
$C^1$
topology and
![]() $\mu _n \to \mu _0\in \operatorname {G}^u(g_0)$
in weak-* topology; then
$\mu _n \to \mu _0\in \operatorname {G}^u(g_0)$
in weak-* topology; then
 $$ \begin{align*}\limsup_{n\to \infty}h_{\mu_n}(g_n)\leq h_{\mu_0}(g_0).\end{align*} $$
$$ \begin{align*}\limsup_{n\to \infty}h_{\mu_n}(g_n)\leq h_{\mu_0}(g_0).\end{align*} $$
5.4 Physical measures
In this section, we will provide a uniform treatment on the existence of physical measures for all
![]() $C^{1+}$
diffeomorphisms in
$C^{1+}$
diffeomorphisms in
![]() ${\mathcal U}$
. For this purpose, let
${\mathcal U}$
. For this purpose, let
![]() $r_1>0$
be given by Lemma 5.5 and (15).
$r_1>0$
be given by Lemma 5.5 and (15).
Proposition 5.17. Let g be any
![]() $C^1$
diffeomorphism of
$C^1$
diffeomorphism of
![]() ${\mathcal U}$
. Then
${\mathcal U}$
. Then
![]() $\operatorname {G}(g)$
is compact and convex, and every extreme element of
$\operatorname {G}(g)$
is compact and convex, and every extreme element of
![]() $\operatorname {G}(g)$
is an ergodic measure. The map
$\operatorname {G}(g)$
is an ergodic measure. The map
![]() ${{\mathcal G}: g\in {\mathcal U} \mapsto \operatorname {G}(g)}$
is upper semi-continuous with respect to diffeomorphisms in
${{\mathcal G}: g\in {\mathcal U} \mapsto \operatorname {G}(g)}$
is upper semi-continuous with respect to diffeomorphisms in
![]() ${\mathcal U}$
under
${\mathcal U}$
under
![]() $C^1$
topology. Moreover, if g is
$C^1$
topology. Moreover, if g is
![]() $C^{1+}$
, then
$C^{1+}$
, then
![]() $\operatorname {G}(g)$
has finitely many extreme points, each of which is a physical measure of g and vice versa. The basin of each physical measure of g contains Lebesgue almost every point of some ball with radius
$\operatorname {G}(g)$
has finitely many extreme points, each of which is a physical measure of g and vice versa. The basin of each physical measure of g contains Lebesgue almost every point of some ball with radius
![]() $r_1$
.
$r_1$
.
Proof. Recall that
 $$ \begin{align*}\operatorname{G}^{cu}(g)=\left\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x)\right\}.\end{align*} $$
$$ \begin{align*}\operatorname{G}^{cu}(g)=\left\{\mu\in {\mathcal M}_{\mbox{inv}}(f): h_\mu(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x)\right\}.\end{align*} $$
Because the metric entropy function is affine, it follows that
![]() $\operatorname {G}^{cu}(f)$
is convex. By Proposition 2.13,
$\operatorname {G}^{cu}(f)$
is convex. By Proposition 2.13,
![]() $\operatorname {G}^u(g)$
is convex, and so is
$\operatorname {G}^u(g)$
is convex, and so is
![]() $\operatorname {G}(g)=\operatorname {G}^u(g)\bigcap \operatorname {G}^{cu}(g)$
.
$\operatorname {G}(g)=\operatorname {G}^u(g)\bigcap \operatorname {G}^{cu}(g)$
.
The compactness of
![]() $\operatorname {G}(g)$
follows from Corollary 5.16. More precisely, suppose that there is a sequence of invariant probabilities
$\operatorname {G}(g)$
follows from Corollary 5.16. More precisely, suppose that there is a sequence of invariant probabilities
![]() $\{\mu _n\}_{n=0}^\infty $
of g such that
$\{\mu _n\}_{n=0}^\infty $
of g such that
![]() $\mu _n\in \operatorname {G}(g)$
and assume
$\mu _n\in \operatorname {G}(g)$
and assume
![]() $\lim _{n\to \infty } \mu _n=\mu $
. Because
$\lim _{n\to \infty } \mu _n=\mu $
. Because
![]() $\mu _n\in \operatorname {G}^{cu}(g)$
, we have
$\mu _n\in \operatorname {G}^{cu}(g)$
, we have
 $$ \begin{align*}h_{\mu_n}(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu_n(x).\end{align*} $$
$$ \begin{align*}h_{\mu_n}(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu_n(x).\end{align*} $$
Note that
![]() $\mu _n\in \operatorname {G}^{u}(g)$
, and by Proposition 2.13,
$\mu _n\in \operatorname {G}^{u}(g)$
, and by Proposition 2.13,
![]() $\operatorname {G}^u(g)$
is compact; thus, we have
$\operatorname {G}^u(g)$
is compact; thus, we have
![]() $\mu \in \operatorname {G}^u(g)$
. It then follows from Corollary 5.16 that
$\mu \in \operatorname {G}^u(g)$
. It then follows from Corollary 5.16 that
![]() $\limsup _{n\to \infty } h_{\mu _n}(g)\leq h_\mu (g)$
, which implies
$\limsup _{n\to \infty } h_{\mu _n}(g)\leq h_\mu (g)$
, which implies
 $$ \begin{align*}h_{\mu}(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x).\end{align*} $$
$$ \begin{align*}h_{\mu}(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x).\end{align*} $$
This means that
![]() $\mu \in \operatorname {G}^{cu}(g)$
; thus,
$\mu \in \operatorname {G}^{cu}(g)$
; thus,
![]() $\mu \in \operatorname {G}^u(g)\cap \operatorname {G}^{cu}(g)=\operatorname {G}(g)$
.
$\mu \in \operatorname {G}^u(g)\cap \operatorname {G}^{cu}(g)=\operatorname {G}(g)$
.
Indeed, by Corollary 5.16 and a similar proof as above, for a sequence of
![]() $C^1$
maps
$C^1$
maps
![]() $g_n\in {\mathcal U},g_n\to g\in {\mathcal U}$
in
$g_n\in {\mathcal U},g_n\to g\in {\mathcal U}$
in
![]() $C^1$
topology and
$C^1$
topology and
![]() $\mu _n\in \operatorname {G}(g_n)$
converging to
$\mu _n\in \operatorname {G}(g_n)$
converging to
![]() $\mu $
in weak-* topology, we have
$\mu $
in weak-* topology, we have
![]() $\mu \in \operatorname {G}(g).$
Then the map
$\mu \in \operatorname {G}(g).$
Then the map
![]() ${\mathcal G}(\cdot )$
is upper semi-continuous, as claimed.
${\mathcal G}(\cdot )$
is upper semi-continuous, as claimed.
Suppose that
![]() $\mu $
is any extreme element of
$\mu $
is any extreme element of
![]() $\operatorname {G}(g)$
; then it is contained in
$\operatorname {G}(g)$
; then it is contained in
![]() $\operatorname {G}^u(g)$
. We claim the following.
$\operatorname {G}^u(g)$
. We claim the following.
Lemma 5.18.
![]() $\mu $
is ergodic.
$\mu $
is ergodic.
Proof. Let
![]() $\tilde {\mu }$
be a typical ergodic component in the ergodic decomposition of
$\tilde {\mu }$
be a typical ergodic component in the ergodic decomposition of
![]() $\mu $
. We are going to show that
$\mu $
. We are going to show that
![]() $\tilde {\mu }\in \operatorname {G}(g)$
; this implies that
$\tilde {\mu }\in \operatorname {G}(g)$
; this implies that
![]() $\tilde {\mu }$
is also an extreme element of
$\tilde {\mu }$
is also an extreme element of
![]() $\operatorname {G}(g)$
and thus it coincides with
$\operatorname {G}(g)$
and thus it coincides with
![]() $\mu $
.
$\mu $
.
By Proposition 2.13,
![]() $\tilde {\mu }\in \operatorname {G}^u(g)$
. Thus, it suffices to show that
$\tilde {\mu }\in \operatorname {G}^u(g)$
. Thus, it suffices to show that
![]() $\tilde {\mu }\in \operatorname {G}^{cu}(g)$
.
$\tilde {\mu }\in \operatorname {G}^{cu}(g)$
.
Because
![]() $g\in {\mathcal U}$
, by Lemma 5.3, any measure
$g\in {\mathcal U}$
, by Lemma 5.3, any measure
![]() $\nu \in \operatorname {G}^u(g)$
has positive center exponent. By Ruelle’s inequality,
$\nu \in \operatorname {G}^u(g)$
has positive center exponent. By Ruelle’s inequality,
 $$ \begin{align*}h_{\tilde{\mu}}(g)\leq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\tilde{\mu}(x).\end{align*} $$
$$ \begin{align*}h_{\tilde{\mu}}(g)\leq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\tilde{\mu}(x).\end{align*} $$
Because
![]() $\mu \in \operatorname {G}^{cu}(g)$
,
$\mu \in \operatorname {G}^{cu}(g)$
,
 $$ \begin{align*}h_\mu(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x).\end{align*} $$
$$ \begin{align*}h_\mu(g)\geq \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x).\end{align*} $$
Because entropy function is an affine functional with respect to invariant measures, we must have
![]() $h_{\tilde {\mu }}(g)= \int \log (\det (Dg\mid _{E^{cu}(x)}))d\tilde {\mu }(x)$
for typical ergodic components
$h_{\tilde {\mu }}(g)= \int \log (\det (Dg\mid _{E^{cu}(x)}))d\tilde {\mu }(x)$
for typical ergodic components
![]() $\tilde {\mu }$
of
$\tilde {\mu }$
of
![]() $\mu $
. Thus,
$\mu $
. Thus,
![]() $\tilde {\mu }\in \operatorname {G}^{cu}(g)$
. The proof is complete. □
$\tilde {\mu }\in \operatorname {G}^{cu}(g)$
. The proof is complete. □
We continue the proof of Proposition 5.17. Assume that
![]() $g\in {\mathcal U}$
is a
$g\in {\mathcal U}$
is a
![]() $C^{1+}$
partially hyperbolic diffeomorphism. First we suppose that
$C^{1+}$
partially hyperbolic diffeomorphism. First we suppose that
![]() $\mu $
is an extreme element of
$\mu $
is an extreme element of
![]() $\operatorname {G}(g)$
. Then by the discussion above,
$\operatorname {G}(g)$
. Then by the discussion above,
![]() $\mu $
is ergodic with positive center exponents. Moreover, by Ruelle’s inequality, we get
$\mu $
is ergodic with positive center exponents. Moreover, by Ruelle’s inequality, we get
 $$ \begin{align*}h_\mu(g)= \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x).\end{align*} $$
$$ \begin{align*}h_\mu(g)= \int \log(\det(Dg\mid_{E^{cu}(x)}))d\mu(x).\end{align*} $$
By the entropy formula of Ledrappier-Young [Reference Ledrappier and Young35], the disintegration of
![]() $\mu $
along the Pesin unstable manifold is equivalent to the Lebesgue measure on the leaves. This means, for
$\mu $
along the Pesin unstable manifold is equivalent to the Lebesgue measure on the leaves. This means, for
![]() $\mu $
almost every x, Lebesgue almost every point on the Pesin unstable manifold of x is a typical point of
$\mu $
almost every x, Lebesgue almost every point on the Pesin unstable manifold of x is a typical point of
![]() $\mu $
. Because the basin of
$\mu $
. Because the basin of
![]() $\mu $
is saturated by stable leaves (we use the fact that
$\mu $
is saturated by stable leaves (we use the fact that
![]() $E^s$
is uniformly contracting) and the stable foliation is absolutely continuous, the union of the stable leaves of the previous full Lebesgue measure subset of
$E^s$
is uniformly contracting) and the stable foliation is absolutely continuous, the union of the stable leaves of the previous full Lebesgue measure subset of
![]() $W^u(x)$
is contained in the basin of
$W^u(x)$
is contained in the basin of
![]() $\mu $
and has full volume inside a ball with center at x. Note, however, that such a ball may not have uniform radius
$\mu $
and has full volume inside a ball with center at x. Note, however, that such a ball may not have uniform radius
![]() $r_1$
.
$r_1$
.
To obtain a ball with radius
![]() $r_1$
in the basin of
$r_1$
in the basin of
![]() $\mu $
, we apply Lemma 5.8 to obtain an
$\mu $
, we apply Lemma 5.8 to obtain an
![]() $n>0$
such that
$n>0$
such that
![]() $g^n(x)\in {\mathcal H}(b_0/2,g)$
. Then by Lemma 5.11,
$g^n(x)\in {\mathcal H}(b_0/2,g)$
. Then by Lemma 5.11,
![]() $W^u(g^n(x),g)$
contains a disk with radius
$W^u(g^n(x),g)$
contains a disk with radius
![]() $r_1$
, where Lebesgue typical points in this disk are typical points of
$r_1$
, where Lebesgue typical points in this disk are typical points of
![]() $\mu $
. By the uniform transversality between the bundles
$\mu $
. By the uniform transversality between the bundles
![]() $E^s$
and
$E^s$
and
![]() $E^{cu}$
, the basin of
$E^{cu}$
, the basin of
![]() $\mu $
contains Lebesgue almost every point of a ball at
$\mu $
contains Lebesgue almost every point of a ball at
![]() $g^n(x)$
with radius
$g^n(x)$
with radius
![]() $r_1$
, which we denote by
$r_1$
, which we denote by
![]() $B_{g^n(x)}(r_1)$
. It then follows that
$B_{g^n(x)}(r_1)$
. It then follows that
To simplify notation, we write any ball obtained in the above way by
![]() $B_{\mu }$
.
$B_{\mu }$
.
Because the basins of different physical measures are disjoint,
![]() $\operatorname {G}(g)$
has only finitely many extreme elements. We denote them by
$\operatorname {G}(g)$
has only finitely many extreme elements. We denote them by
![]() $\mu _1,\cdots , \mu _k$
.
$\mu _1,\cdots , \mu _k$
.
Now we prove that every physical measure
![]() $\mu $
of g is an extreme element of
$\mu $
of g is an extreme element of
![]() $\operatorname {G}(g)$
. Because the basin of
$\operatorname {G}(g)$
. Because the basin of
![]() $\mu $
,
$\mu $
,
![]() ${\mathcal B}(\mu )$
, has positive volume, by Proposition 2.12, Lebesgue almost every point
${\mathcal B}(\mu )$
, has positive volume, by Proposition 2.12, Lebesgue almost every point
![]() $x\in {\mathcal B}(\mu )$
must satisfy
$x\in {\mathcal B}(\mu )$
must satisfy
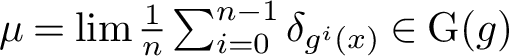 $\mu =\lim \frac {1}{n}\sum _{i=0}^{n-1}\delta _{g^i(x)}\in \operatorname {G}(g)$
. Thus, it only remains to show that
$\mu =\lim \frac {1}{n}\sum _{i=0}^{n-1}\delta _{g^i(x)}\in \operatorname {G}(g)$
. Thus, it only remains to show that
![]() $\mu $
is ergodic.
$\mu $
is ergodic.
Because
![]() $\operatorname {G}(g)$
is convex with finitely many extreme elements,
$\operatorname {G}(g)$
is convex with finitely many extreme elements,
![]() $\mu $
can be written as a combination:
$\mu $
can be written as a combination:
where
![]() $0\leq a_1,\cdots , a_k \leq 1$
and
$0\leq a_1,\cdots , a_k \leq 1$
and
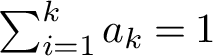 $\sum _{i=1}^k a_k=1$
. There is
$\sum _{i=1}^k a_k=1$
. There is
![]() $1\leq j\leq k$
such that
$1\leq j\leq k$
such that
![]() $a_j>0$
. Then by (16),
$a_j>0$
. Then by (16),
![]() $\mu (B_{\mu _j})=a_j \mu _j(B_{\mu _j})>0$
.
$\mu (B_{\mu _j})=a_j \mu _j(B_{\mu _j})>0$
.
Thus, for every point
![]() $x\in {\mathcal B}(\mu )$
and n sufficiently large,
$x\in {\mathcal B}(\mu )$
and n sufficiently large,
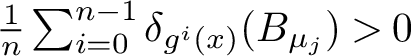 $\frac {1}{n}\sum _{i=0}^{n-1} \delta _{g^i(x)} (B_{\mu _j})>0$
. In particular, there is
$\frac {1}{n}\sum _{i=0}^{n-1} \delta _{g^i(x)} (B_{\mu _j})>0$
. In particular, there is
![]() $n_j>0$
such that
$n_j>0$
such that
![]() $g^{n_j}(x)\in B_{\mu _j}$
.
$g^{n_j}(x)\in B_{\mu _j}$
.
Because
![]() $\operatorname {vol}({\mathcal B}(\mu ))>0$
, take
$\operatorname {vol}({\mathcal B}(\mu ))>0$
, take
![]() $x\in {\mathcal B}(\mu )$
a Lebesgue density point of
$x\in {\mathcal B}(\mu )$
a Lebesgue density point of
![]() ${\mathcal B}(\mu )$
; that is, it satisfies
${\mathcal B}(\mu )$
; that is, it satisfies
 $$ \begin{align*}\lim_{r\to 0^+} \frac{\operatorname{vol}(B_x(r)\cap {\mathcal B}(\mu))}{\operatorname{vol}(B_x(r))}\to 1.\end{align*} $$
$$ \begin{align*}\lim_{r\to 0^+} \frac{\operatorname{vol}(B_x(r)\cap {\mathcal B}(\mu))}{\operatorname{vol}(B_x(r))}\to 1.\end{align*} $$
Then the above argument shows that
![]() ${\mathcal B}(\mu )\bigcap B_{\mu _j}=g^{n_j}({\mathcal B}(\mu ))\bigcap B_{\mu _j}$
has positive Lebesgue measure.
${\mathcal B}(\mu )\bigcap B_{\mu _j}=g^{n_j}({\mathcal B}(\mu ))\bigcap B_{\mu _j}$
has positive Lebesgue measure.
Recall that
![]() $B_{\mu _j}$
is in the basin of
$B_{\mu _j}$
is in the basin of
![]() $\mu _j$
. Therefore, the basin of
$\mu _j$
. Therefore, the basin of
![]() $\mu $
and
$\mu $
and
![]() $\mu _j$
has nontrivial intersection. This implies
$\mu _j$
has nontrivial intersection. This implies
![]() $\mu = \mu _j$
, and
$\mu = \mu _j$
, and
![]() $\mu $
is ergodic. The proof of Proposition 5.17 is complete. □
$\mu $
is ergodic. The proof of Proposition 5.17 is complete. □
Remark 5.19. The
![]() $C^{1+}$
regularity is used to
$C^{1+}$
regularity is used to
-
• show that the conditional measures of
 $\mu $
along unstable leaves are absolutely continuous; we need the work of Ledrappier and Young, which requires
$\mu $
along unstable leaves are absolutely continuous; we need the work of Ledrappier and Young, which requires
 $C^{1+}$
.
$C^{1+}$
. -
• show that the basin of
 $\mu $
contains Lebesgue almost every point in a ball; there we need the stable foliation to be absolutely continuous.
$\mu $
contains Lebesgue almost every point in a ball; there we need the stable foliation to be absolutely continuous.
We will see in Section 7 that such regularity condition can be bypassed for generic
![]() $C^1$
diffeomorphisms in
$C^1$
diffeomorphisms in
![]() ${\mathcal U}$
.
${\mathcal U}$
.
6 Proof of Theorem B and Corollary C
In this section, we provide the proof of Theorem B and Corollary C.
Throughout this section, we assume f to be a
![]() $C^{1+}$
diffeomorphism with a mostly expanding center and
$C^{1+}$
diffeomorphism with a mostly expanding center and
![]() ${\mathcal U}$
a sufficiently small
${\mathcal U}$
a sufficiently small
![]() $C^1$
neighbourhood of f. By Proposition 5.1, there is
$C^1$
neighbourhood of f. By Proposition 5.1, there is
![]() $b_0>0$
such that for any
$b_0>0$
such that for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
and any
$g\in {\mathcal U}$
and any
![]() $\mu \in \operatorname {G}^u(g)$
,
$\mu \in \operatorname {G}^u(g)$
,
 $$ \begin{align} \int \log \|Dg^{-1}\mid_{E^{cu}(x)}\|d\mu(x)<-b_0. \end{align} $$
$$ \begin{align} \int \log \|Dg^{-1}\mid_{E^{cu}(x)}\|d\mu(x)<-b_0. \end{align} $$
The structure of this section is as follows: In Subsection 6.1 we introduce Liao’s shadowing lemma, which will be used in Subsection 6.2 to construct skeletons. For the discussion in Section 8, we will make the construction for every
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
.
$g\in {\mathcal U}$
.
Then in Subsection 6.3, we will show that each element in
![]() ${\mathcal S}(g)$
is associated to a physical measure, assuming that f is
${\mathcal S}(g)$
is associated to a physical measure, assuming that f is
![]() $C^{1+}$
. This concludes the proof of Theorem B. Finally, in Subsection 6.4 we provide the proof of Corollary C.
$C^{1+}$
. This concludes the proof of Theorem B. Finally, in Subsection 6.4 we provide the proof of Corollary C.
6.1 Liao’s shadowing lemma
Definition 6.1. An orbit segment
![]() $(x,f(x),\cdots ,f^n(x))$
is called
$(x,f(x),\cdots ,f^n(x))$
is called
![]() $\lambda $
-quasi hyperbolic if there exists
$\lambda $
-quasi hyperbolic if there exists
![]() $0< \lambda <1$
such that for
$0< \lambda <1$
such that for
![]() $1 \leq k \leq n$
,
$1 \leq k \leq n$
,
 $$ \begin{align} \prod_{i=0}^{k-1} \|Df^{-1}\mid_{E^{cu}(f^{n-i}(x))}\|< \lambda^k, \end{align} $$
$$ \begin{align} \prod_{i=0}^{k-1} \|Df^{-1}\mid_{E^{cu}(f^{n-i}(x))}\|< \lambda^k, \end{align} $$
 $$ \begin{align} \prod_{i=0}^{k-1}\|Df|_{E^s(f^i(x))}\| \le \lambda^k \end{align} $$
$$ \begin{align} \prod_{i=0}^{k-1}\|Df|_{E^s(f^i(x))}\| \le \lambda^k \end{align} $$
and
 $$ \begin{align} \frac{\|Df|_{E^s(f^i(x))}\|}{m(Df|_{E^{cu}(f^i(x))} )}\le \lambda^2, \end{align} $$
$$ \begin{align} \frac{\|Df|_{E^s(f^i(x))}\|}{m(Df|_{E^{cu}(f^i(x))} )}\le \lambda^2, \end{align} $$
where
![]() $m(\cdot )$
is the minimum norm.
$m(\cdot )$
is the minimum norm.
Note that (19) and (20) are automatically satisfied due to the uniform contraction of
![]() $Df$
on
$Df$
on
![]() $E^s$
and the domination between
$E^s$
and the domination between
![]() $E^s$
and
$E^s$
and
![]() $E^{cu}$
. In other words,
$E^{cu}$
. In other words,
![]() $(x,f(x),\cdots ,f^n(x))$
is
$(x,f(x),\cdots ,f^n(x))$
is
![]() $\lambda $
-quasi-hyperbolic if n is a
$\lambda $
-quasi-hyperbolic if n is a
![]() $(-\log \lambda )$
-hyperbolic time for x. In this subsection we need the following shadowing lemma by Liao, which allows a quasi-hyperbolic, periodic pseudo-orbit to be shadowed by a periodic orbit with large unstable manifold.
$(-\log \lambda )$
-hyperbolic time for x. In this subsection we need the following shadowing lemma by Liao, which allows a quasi-hyperbolic, periodic pseudo-orbit to be shadowed by a periodic orbit with large unstable manifold.
Lemma 6.2 ([Reference Liao38, Reference Gan27])
For any
![]() $\lambda>0$
, there exist
$\lambda>0$
, there exist
![]() $\rho>0$
and
$\rho>0$
and
![]() $L>0$
such that for any
$L>0$
such that for any
![]() $\lambda $
-quasi-hyperbolic orbit
$\lambda $
-quasi-hyperbolic orbit
![]() $(x,f(x),\cdots ,f^n(x))$
of f with
$(x,f(x),\cdots ,f^n(x))$
of f with
![]() $d(x,f^n(x))\leq \rho $
, there exists a hyperbolic periodic point
$d(x,f^n(x))\leq \rho $
, there exists a hyperbolic periodic point
![]() $p\in M$
such that
$p\in M$
such that
-
(a) p is a hyperbolic periodic point with period n and with stable index
 $i_s$
;
$i_s$
; -
(b)
 $d(f^i(x),f^i(p))\leq L d(x,f^n(x))$
for any
$d(f^i(x),f^i(p))\leq L d(x,f^n(x))$
for any
 $0\leq i \leq n-1$
;
$0\leq i \leq n-1$
; -
(c) p has a uniformly sized unstable manifold: there is a constant
 $r>0$
depending on
$r>0$
depending on
 $\lambda $
such that the local unstable manifold of p contains a disk with radius r.
$\lambda $
such that the local unstable manifold of p contains a disk with radius r.
Remark 6.3. The parameters in the previous lemma can be made uniform for diffeomorphisms in a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal U}$
of f. Moreover, one can take
${\mathcal U}$
of f. Moreover, one can take
![]() $\delta $
sufficiently small; then
$\delta $
sufficiently small; then
![]() $d(f^i(x),f^i(p))\leq L d(x,f^n(x))$
is sufficiently small for any
$d(f^i(x),f^i(p))\leq L d(x,f^n(x))$
is sufficiently small for any
![]() $0\leq i \leq n-1$
, and then
$0\leq i \leq n-1$
, and then
 $$ \begin{align*}\prod_{i=0}^{k-1} \|Df^{-1}\mid_{E^{cu}(f^{n-i}(p))}\|\leq \lambda^k \end{align*} $$
$$ \begin{align*}\prod_{i=0}^{k-1} \|Df^{-1}\mid_{E^{cu}(f^{n-i}(p))}\|\leq \lambda^k \end{align*} $$
for any
![]() $1 \leq k \leq n$
. In particular, if one takes
$1 \leq k \leq n$
. In particular, if one takes
![]() $\lambda = e^{-b_0/2}$
, then the size of the unstable manifold of p can be chosen to be
$\lambda = e^{-b_0/2}$
, then the size of the unstable manifold of p can be chosen to be
![]() $r_1>0$
, which is the constant given by Lemma 5.11.
$r_1>0$
, which is the constant given by Lemma 5.11.
Definition 6.4. A periodic point p of
![]() $g\in {\mathcal U}$
is called a
$g\in {\mathcal U}$
is called a
![]() $\lambda $
-hyperbolic periodic point if it satisfies
$\lambda $
-hyperbolic periodic point if it satisfies
 $$ \begin{align} \prod_{i=0}^{k-1} \|Df^{-1}\mid_{E^{cu}(f^{n-i}(p))}\|\leq \lambda^k \end{align} $$
$$ \begin{align} \prod_{i=0}^{k-1} \|Df^{-1}\mid_{E^{cu}(f^{n-i}(p))}\|\leq \lambda^k \end{align} $$
for any
![]() $1 \leq k \leq \pi (p)$
.
$1 \leq k \leq \pi (p)$
.
By the previous discussion and Remark 5.6, we have shown the following.
Lemma 6.5. For any
![]() $e^{-b_0/2}$
-quasi-hyperbolic periodic point, its unstable manifold contains an
$e^{-b_0/2}$
-quasi-hyperbolic periodic point, its unstable manifold contains an
![]() $r_1$
-ball inside the
$r_1$
-ball inside the
![]() $cu$
-fake leaf
$cu$
-fake leaf
 $\hat {{\mathcal F}}^{cu}_{g,p}(p,r_1)$
$\hat {{\mathcal F}}^{cu}_{g,p}(p,r_1)$
6.2 Existence of skeleton
In this section, we will show that any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
admits a skeleton. The main result of this section is Proposition 6.8.
$g\in {\mathcal U}$
admits a skeleton. The main result of this section is Proposition 6.8.
In order to apply Liao’s shadowing lemma, we need to establish the existence of orbit segments that are quasi-hyperbolic. This follows from Proposition 2.12 and (17).
Proposition 6.6. Suppose
![]() $g\in {\mathcal U}$
. There is a full-volume subset
$g\in {\mathcal U}$
. There is a full-volume subset
![]() $\Gamma _g$
such that for Lebesgue almost every point
$\Gamma _g$
such that for Lebesgue almost every point
![]() $x\in \Gamma _g$
,
$x\in \Gamma _g$
,
 $$ \begin{align*}\limsup_{n\to \infty}\frac{1}{n}\sum_{i=0}^{n-1} \log\|Dg^{-1}\mid_{E^{cu}(g^{n-i}(x))}\|\leq -b_0.\end{align*} $$
$$ \begin{align*}\limsup_{n\to \infty}\frac{1}{n}\sum_{i=0}^{n-1} \log\|Dg^{-1}\mid_{E^{cu}(g^{n-i}(x))}\|\leq -b_0.\end{align*} $$
By the Pliss lemma (see [Reference Alves, Bonatti and Viana1]), there exists
![]() $n_x\geq 1$
and
$n_x\geq 1$
and
![]() $\delta _1>0$
such that
$\delta _1>0$
such that
where
![]() $H(b_03/4,x,g)$
is the collection of
$H(b_03/4,x,g)$
is the collection of
![]() $b_03/4$
-hyperbolic times along the forward orbit of x.
$b_03/4$
-hyperbolic times along the forward orbit of x.
Taking a sequence of integers
![]() $n_x\leq n_1< n_2 <\cdots $
such that
$n_x\leq n_1< n_2 <\cdots $
such that
![]() $n_i\in H(b_03/4,x,g))$
, we may assume that
$n_i\in H(b_03/4,x,g))$
, we may assume that
![]() $x_{n_i} = f^{n_i}(x)$
converges to a point
$x_{n_i} = f^{n_i}(x)$
converges to a point
![]() $x_0$
. For
$x_0$
. For
![]() $\lambda =e^{-\frac {3b_0}{4}}$
,
$\lambda =e^{-\frac {3b_0}{4}}$
,
![]() $\rho $
and L are obtained by Lemma 6.2. We may further assume that
$\rho $
and L are obtained by Lemma 6.2. We may further assume that
![]() $\sup _{i,j}\{d(x_{n_i},x_{n_j})\}\leq \rho _0 \leq \rho $
, where
$\sup _{i,j}\{d(x_{n_i},x_{n_j})\}\leq \rho _0 \leq \rho $
, where
![]() $\rho _0$
satisfies that for any two points
$\rho _0$
satisfies that for any two points
![]() $y,z\in M$
with
$y,z\in M$
with
![]() $d(y,z)\leq L \rho _0$
, we have
$d(y,z)\leq L \rho _0$
, we have
 $$ \begin{align} \mid \log\|Dg^{-1}\mid_{E^{cu}(y)}\|-\log\|Dg^{-1}\mid_{E^{cu}(z)}\| \mid \leq b_0/4. \end{align} $$
$$ \begin{align} \mid \log\|Dg^{-1}\mid_{E^{cu}(y)}\|-\log\|Dg^{-1}\mid_{E^{cu}(z)}\| \mid \leq b_0/4. \end{align} $$
Because for any
![]() $i<j$
, the pseudo-orbit
$i<j$
, the pseudo-orbit
![]() $\{x_{n_i},x_{n_i+1},\cdots ,x_{n_j-1}\}$
is
$\{x_{n_i},x_{n_i+1},\cdots ,x_{n_j-1}\}$
is
![]() $b_03/4$
-quasi-hyperbolic, by Lemma 6.2, this pseudo-orbit is
$b_03/4$
-quasi-hyperbolic, by Lemma 6.2, this pseudo-orbit is
![]() $L d(x_{n_i},x_{n_j})\leq L \rho _0$
shadowed by a periodic orbit
$L d(x_{n_i},x_{n_j})\leq L \rho _0$
shadowed by a periodic orbit
![]() $p_{x,i,j}$
. Because
$p_{x,i,j}$
. Because
![]() $x_{n_i}\to x_0$
as
$x_{n_i}\to x_0$
as
![]() $i\to \infty $
, all of the periodic points
$i\to \infty $
, all of the periodic points
![]() $p_{x,i,i+1}$
converge to
$p_{x,i,i+1}$
converge to
![]() $x_0$
.
$x_0$
.
Moreover, by the choice of
![]() $\rho _0$
in (23),
$\rho _0$
in (23),
![]() $p_{x,i,j}$
is a
$p_{x,i,j}$
is a
![]() $e^{-b_0/2}$
-quasi-hyperbolic periodic point. By Lemma 6.5, each periodic point
$e^{-b_0/2}$
-quasi-hyperbolic periodic point. By Lemma 6.5, each periodic point
![]() $p_{x,i,j}$
has unstable manifold with size at least
$p_{x,i,j}$
has unstable manifold with size at least
![]() $r_1$
. Their stable manifolds already have uniform size due to
$r_1$
. Their stable manifolds already have uniform size due to
![]() $E^s$
being uniformly contracting (note that all
$E^s$
being uniformly contracting (note that all
![]() $p_{x,i,j}$
s have stable index
$p_{x,i,j}$
s have stable index
![]() $i_s$
). Thus, there is
$i_s$
). Thus, there is
![]() $m_x$
such that for any
$m_x$
such that for any
![]() $i,j>m_x$
,
$i,j>m_x$
,
![]() $p_{x,i,i+1}$
and
$p_{x,i,i+1}$
and
![]() $p_{x,j,j+1}$
are homoclinic related to each other and
$p_{x,j,j+1}$
are homoclinic related to each other and
Furthermore,
![]() ${\mathcal F}^s_{\operatorname {loc}}(p_i)$
will intersect transversally with any disk center at
${\mathcal F}^s_{\operatorname {loc}}(p_i)$
will intersect transversally with any disk center at
![]() $x_j$
, tangent to the
$x_j$
, tangent to the
![]() $cu$
cone with radius at least
$cu$
cone with radius at least
![]() $r_1$
.
$r_1$
.
To simplify notation, we will write
![]() $p_{x,i,i+1}=p_{x,i}$
.
$p_{x,i,i+1}=p_{x,i}$
.
Lemma 6.7. For any
![]() $i>m_x$
,
$i>m_x$
,
![]() $x\in \mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_{x,i})))$
.
$x\in \mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_{x,i})))$
.
Proof. Let U be any small neighbourhood of x. Because for any
![]() $i>m_x$
, all of the hyperbolic periodic points
$i>m_x$
, all of the hyperbolic periodic points
![]() $p_{i}$
are homoclinic related to each other, we only need to show that there is
$p_{i}$
are homoclinic related to each other, we only need to show that there is
![]() $i>m_x$
such that
$i>m_x$
such that
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))\cap U\neq \emptyset $
; then the lemma will follow from the inclination lemma.
${\mathcal F}^s(\mbox {Orb}(p_i))\cap U\neq \emptyset $
; then the lemma will follow from the inclination lemma.
We take
![]() $\varepsilon>0$
small enough such that
$\varepsilon>0$
small enough such that
 $\hat {{\mathcal F}}^{cu}_{g,x}(x,\varepsilon )\subset U$
. By Lemma 5.5, for
$\hat {{\mathcal F}}^{cu}_{g,x}(x,\varepsilon )\subset U$
. By Lemma 5.5, for
![]() $i>m_x$
sufficiently large,
$i>m_x$
sufficiently large,
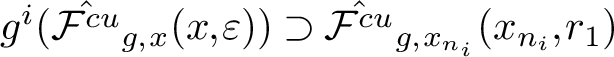 $g^{i}(\hat {{\mathcal F}^{cu}}_{g,x}(x,\varepsilon ))\supset \hat {{\mathcal F}^{cu}}_{g,x_{n_i}}(x_{n_i},r_1)$
, where the latter is a disk tangent to a
$g^{i}(\hat {{\mathcal F}^{cu}}_{g,x}(x,\varepsilon ))\supset \hat {{\mathcal F}^{cu}}_{g,x_{n_i}}(x_{n_i},r_1)$
, where the latter is a disk tangent to a
![]() $cu$
cone with uniform diameter. This means that when i is sufficiently large,
$cu$
cone with uniform diameter. This means that when i is sufficiently large,
 $$ \begin{align*}g^{n_i}(\hat{{\mathcal F}^u}_{g,x}(x,\varepsilon))\pitchfork {\mathcal F}^s_{\operatorname{loc}}(p_{i})\neq \emptyset.\end{align*} $$
$$ \begin{align*}g^{n_i}(\hat{{\mathcal F}^u}_{g,x}(x,\varepsilon))\pitchfork {\mathcal F}^s_{\operatorname{loc}}(p_{i})\neq \emptyset.\end{align*} $$
By the invariance of the stable manifold under the iteration of g, we have
![]() $U\cap {\mathcal F}^s(\mbox {Orb}(p_i))\neq \emptyset $
.
$U\cap {\mathcal F}^s(\mbox {Orb}(p_i))\neq \emptyset $
.
The proof is complete. □
Now we are ready to construct the skeleton for
![]() $g\in {\mathcal U}$
. By Proposition 6.6, for each
$g\in {\mathcal U}$
. By Proposition 6.6, for each
![]() $x\in \Gamma _g$
, we fix any one of
$x\in \Gamma _g$
, we fix any one of
![]() $p_{x,i}$
for
$p_{x,i}$
for
![]() $i>m_x$
and denote it by
$i>m_x$
and denote it by
![]() $p_x$
. Then by the previous lemma, the union
$p_x$
. Then by the previous lemma, the union
![]() $\bigcup _{x\in \Gamma }{\mathcal F}^s(\mbox {Orb}(p_x))$
is dense in the manifold M.
$\bigcup _{x\in \Gamma }{\mathcal F}^s(\mbox {Orb}(p_x))$
is dense in the manifold M.
Moreover, because each periodic point
![]() $p_x$
has stable and unstable manifold with size at least
$p_x$
has stable and unstable manifold with size at least
![]() $r_1$
, there are only finitely many of them that are not homoclinically related to each other, with number uniformly bounded from above. Take
$r_1$
, there are only finitely many of them that are not homoclinically related to each other, with number uniformly bounded from above. Take
![]() $\{p_1,\cdots ,p_k\}$
a subset of
$\{p_1,\cdots ,p_k\}$
a subset of
![]() $\{p_x\}_{x\in \Gamma }$
that are not homoclinic related and have maximal cardinality.
$\{p_x\}_{x\in \Gamma }$
that are not homoclinic related and have maximal cardinality.
We claim that
 $\bigcup _{i=1,\cdots ,k}{\mathcal F}^s(\mbox {Orb}(p_i))$
is dense in the manifold M. Assume that this is not the case; then we can take
$\bigcup _{i=1,\cdots ,k}{\mathcal F}^s(\mbox {Orb}(p_i))$
is dense in the manifold M. Assume that this is not the case; then we can take
![]() $p_x$
for
$p_x$
for
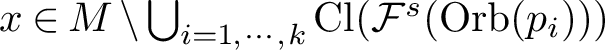 $x\in M\setminus \bigcup _{i=1,\cdots ,k}\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
. By the choice of
$x\in M\setminus \bigcup _{i=1,\cdots ,k}\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))$
. By the choice of
![]() $\{p_1,\cdots ,p_k\}$
,
$\{p_1,\cdots ,p_k\}$
,
![]() $p_x$
must be homoclinically related to some
$p_x$
must be homoclinically related to some
![]() $p_i$
. However, this means that
$p_i$
. However, this means that
![]() $\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))=\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_x)))$
by the inclination lemma. Lemma 6.7 then shows that
$\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i)))=\mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_x)))$
by the inclination lemma. Lemma 6.7 then shows that
![]() $x\in \mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))) $
, which is a contradiction.
$x\in \mbox {Cl}({\mathcal F}^s(\mbox {Orb}(p_i))) $
, which is a contradiction.
Thus,
![]() $\{p_1,\cdots ,p_k\}$
forms a pre-skeleton. By Lemma 4.5, we have shown the following.
$\{p_1,\cdots ,p_k\}$
forms a pre-skeleton. By Lemma 4.5, we have shown the following.
Proposition 6.8. Every
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
admits a skeleton
$g\in {\mathcal U}$
admits a skeleton
![]() ${\mathcal S}(g)=\{p_1,\cdots ,p_k\}$
, such that for any
${\mathcal S}(g)=\{p_1,\cdots ,p_k\}$
, such that for any
![]() $1\leq i \leq k$
,
$1\leq i \leq k$
,
![]() $W^u(p_i)$
contains a ball in the fake
$W^u(p_i)$
contains a ball in the fake
![]() $cu$
leaf with center at
$cu$
leaf with center at
![]() $p_i$
and radius
$p_i$
and radius
![]() $r_1$
.
$r_1$
.
From now on, we fix
![]() ${\mathcal S}(g)=\{p_1,\cdots ,p_k\}$
a skeleton obtained as above.
${\mathcal S}(g)=\{p_1,\cdots ,p_k\}$
a skeleton obtained as above.
6.3 Skeleton and measures
In this section we assume
![]() $g\in {\mathcal U}$
to be
$g\in {\mathcal U}$
to be
![]() $C^{1+}$
; then by Lemma 5.3, g has a mostly expanding center. We will establish a one-to-one correspondence between elements of
$C^{1+}$
; then by Lemma 5.3, g has a mostly expanding center. We will establish a one-to-one correspondence between elements of
![]() ${\mathcal S}(g)$
and the physical measures of g.
${\mathcal S}(g)$
and the physical measures of g.
By Proposition 5.17, g has only finitely many physical measures
![]() $\{\mu _1,\cdots ,\mu _l\}$
. Moreover, from Lemma 5.8 and Proposition 5.17, there is
$\{\mu _1,\cdots ,\mu _l\}$
. Moreover, from Lemma 5.8 and Proposition 5.17, there is
![]() $r_1>0$
only depending on
$r_1>0$
only depending on
![]() ${\mathcal U}$
and
${\mathcal U}$
and
![]() $b_0$
such that, for any physical measure
$b_0$
such that, for any physical measure
![]() $\mu _j$
of g, there is a
$\mu _j$
of g, there is a
![]() $\mu _j$
regular point
$\mu _j$
regular point
![]() $x_j$
such that
$x_j$
such that
-
(a)
 $x_j\in {\mathcal H}(b_0/2,g)$
and thus has Pesin unstable manifold with size larger than
$x_j\in {\mathcal H}(b_0/2,g)$
and thus has Pesin unstable manifold with size larger than
 $r_1$
;
$r_1$
; -
(b)
 $\mu $
regular points consist of Lebesgue almost every point on the Pesin unstable manifold of
$\mu $
regular points consist of Lebesgue almost every point on the Pesin unstable manifold of
 $x_j$
.
$x_j$
.
The main result of this section is the following.
Proposition 6.9. The number of physical measures and the number of elements of the skeleton of g are the same; that is,
![]() $k=l$
. Indeed, there is a bijective map
$k=l$
. Indeed, there is a bijective map
![]() $j\to i(j)$
such that for any physical measure
$j\to i(j)$
such that for any physical measure
![]() $\mu _j$
of g, there is
$\mu _j$
of g, there is
![]() $p_{i(j)}\in {\mathcal S}(g)$
such that
$p_{i(j)}\in {\mathcal S}(g)$
such that
![]() $\operatorname {supp}(\mu _j)= \mbox { Cl}(W^u(\mbox {Orb}(p_i),g))$
and Lebesgue almost every point on
$\operatorname {supp}(\mu _j)= \mbox { Cl}(W^u(\mbox {Orb}(p_i),g))$
and Lebesgue almost every point on
![]() $W^u(\mbox {Orb}(p_i),g)$
belongs to the basin of
$W^u(\mbox {Orb}(p_i),g)$
belongs to the basin of
![]() $\mu _j$
. Moreover, the closure of
$\mu _j$
. Moreover, the closure of
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of
${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of
![]() ${\mathcal B}(\mu _j)$
.
${\mathcal B}(\mu _j)$
.
Proof. Fix any physical measure
![]() $\mu _j$
of g. By (a) above, there is
$\mu _j$
of g. By (a) above, there is
![]() $p_i\in {\mathcal S}(g)$
such that
$p_i\in {\mathcal S}(g)$
such that
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))\pitchfork W^u_{r_1}(x_j,g)\neq \emptyset $
. By the inclination lemma,
${\mathcal F}^s(\mbox {Orb}(p_i))\pitchfork W^u_{r_1}(x_j,g)\neq \emptyset $
. By the inclination lemma,
![]() $g^n(W^u_{r_1}(x_j,g))$
converges to
$g^n(W^u_{r_1}(x_j,g))$
converges to
![]() $W^u(\mbox {Orb}(p_i),g)$
. Because
$W^u(\mbox {Orb}(p_i),g)$
. Because
![]() $W^u_{r_1}(x_j,g)\subset \operatorname {supp}(\mu _j)$
by (b) above, we have
$W^u_{r_1}(x_j,g)\subset \operatorname {supp}(\mu _j)$
by (b) above, we have
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i),g))\subset \operatorname {supp}(\mu _j)$
.
$\mbox {Cl}(W^u(\mbox {Orb}(p_i),g))\subset \operatorname {supp}(\mu _j)$
.
To show the reversed inclusion, note that for n large enough, by the inclination lemma,
![]() $g^n(W^u_{r_1}(x,g))$
approaches
$g^n(W^u_{r_1}(x,g))$
approaches
![]() $W^u_{\operatorname {loc}}(p)$
in the following sense: there is a stable holonomy map from
$W^u_{\operatorname {loc}}(p)$
in the following sense: there is a stable holonomy map from
![]() $W^u_{\operatorname {loc}}(p)$
to
$W^u_{\operatorname {loc}}(p)$
to
![]() $g^n(W^u_{r_1}(x,g))$
induced by the stable foliation. Because the set of
$g^n(W^u_{r_1}(x,g))$
induced by the stable foliation. Because the set of
![]() $\mu _j$
typical points is invariant under iteration, Lebesgue almost every point of
$\mu _j$
typical points is invariant under iteration, Lebesgue almost every point of
![]() $g^n(W^u_{r_1}(x,g))$
is also typical for
$g^n(W^u_{r_1}(x,g))$
is also typical for
![]() $\mu _j$
. Because stable foliation is absolutely continuous and the basin of
$\mu _j$
. Because stable foliation is absolutely continuous and the basin of
![]() $\mu _j$
is s-saturated, it follows that Lebesgue almost every point of
$\mu _j$
is s-saturated, it follows that Lebesgue almost every point of
![]() $W^u(\mbox {Orb}(p_i),g)$
belongs to the basin of
$W^u(\mbox {Orb}(p_i),g)$
belongs to the basin of
![]() $\mu _j$
.
$\mu _j$
.
Take any point
![]() $y\in W^u(p_i)\cap {\mathcal B}(\mu _j)$
. Because
$y\in W^u(p_i)\cap {\mathcal B}(\mu _j)$
. Because
![]() $g^n(y)\in W^u(\mbox { Orb}(p_i))$
for any
$g^n(y)\in W^u(\mbox { Orb}(p_i))$
for any
![]() $n\geq 0$
,
$n\geq 0$
,
 $\mu _j=\lim \frac {1}{n}\sum \delta _{g^i(y)}$
is supported on
$\mu _j=\lim \frac {1}{n}\sum \delta _{g^i(y)}$
is supported on
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i),g))$
. As a conclusion,
$\mbox {Cl}(W^u(\mbox {Orb}(p_i),g))$
. As a conclusion,
Because Lebesgue almost every point on
![]() $W^u(\mbox {Orb}(p_i),g)$
belongs to the basin of
$W^u(\mbox {Orb}(p_i),g)$
belongs to the basin of
![]() $\mu _j$
, the map
$\mu _j$
, the map
![]() $j\to i(j)$
is injective; in particular, we have
$j\to i(j)$
is injective; in particular, we have
![]() $k\geq l$
. After reordering the periodic points of
$k\geq l$
. After reordering the periodic points of
![]() ${\mathcal S}(g)$
, we may assume that
${\mathcal S}(g)$
, we may assume that
![]() $i(j)=j$
for
$i(j)=j$
for
![]() $j=1,\cdots , l$
.
$j=1,\cdots , l$
.
In order to prove
![]() $k=l$
, we only need to show that
$k=l$
, we only need to show that
![]() $\{p_1,\cdots ,p_l\}$
is a pre-skeleton; that is,
$\{p_1,\cdots ,p_l\}$
is a pre-skeleton; that is,
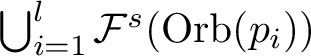 $\bigcup _{i=1}^l {\mathcal F}^s(\mbox {Orb}(p_i))$
is dense in the manifold M. By Proposition 5.17, the union of basins of physical measures has full volume; thus, it suffices to prove that for each
$\bigcup _{i=1}^l {\mathcal F}^s(\mbox {Orb}(p_i))$
is dense in the manifold M. By Proposition 5.17, the union of basins of physical measures has full volume; thus, it suffices to prove that for each
![]() $1\leq i \leq l$
, the closure of
$1\leq i \leq l$
, the closure of
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of
${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of
![]() ${\mathcal B}(\mu _i)$
.
${\mathcal B}(\mu _i)$
.
By (24) we have
![]() $p_i\in \operatorname {supp}(\mu _i)$
. Take
$p_i\in \operatorname {supp}(\mu _i)$
. Take
![]() $r>0$
sufficiently small such that
$r>0$
sufficiently small such that
![]() $\mu _i(B_r(p_i))>0$
and
$\mu _i(B_r(p_i))>0$
and
 $B_r(p_i)\subset {\mathcal O}_i=\bigcup _{y\in W^u(\mbox {Orb}(p_i),g)}{\mathcal F}^s(y)$
. For any
$B_r(p_i)\subset {\mathcal O}_i=\bigcup _{y\in W^u(\mbox {Orb}(p_i),g)}{\mathcal F}^s(y)$
. For any
![]() $x\in {\mathcal B}(\mu _i)$
, because we have
$x\in {\mathcal B}(\mu _i)$
, because we have
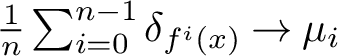 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}\to \mu _i$
, there is n sufficiently large such that
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}\to \mu _i$
, there is n sufficiently large such that
 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}(B_r(p_i))>0$
. This shows that there is
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{f^i(x)}(B_r(p_i))>0$
. This shows that there is
![]() $m>0$
such that
$m>0$
such that
![]() $f^m(x)\in B_r(p_i)\subset {\mathcal O}_i$
. By (ii) of Proposition 4.2,
$f^m(x)\in B_r(p_i)\subset {\mathcal O}_i$
. By (ii) of Proposition 4.2,
![]() $f^m(x)$
is accumulated by
$f^m(x)$
is accumulated by
![]() ${\mathcal F}^s(\mbox { Orb}(p_i))$
and so is x. Thus, we have shown that the basin of
${\mathcal F}^s(\mbox { Orb}(p_i))$
and so is x. Thus, we have shown that the basin of
![]() $\mu _i$
is contained in the closure of
$\mu _i$
is contained in the closure of
![]() ${\mathcal F}^s(\mbox {Orb}(p_i))$
, and the reversed inclusion follows immediately from the u-saturation of
${\mathcal F}^s(\mbox {Orb}(p_i))$
, and the reversed inclusion follows immediately from the u-saturation of
![]() $\operatorname {supp}(\mu _i)$
. We now conclude that
$\operatorname {supp}(\mu _i)$
. We now conclude that
![]() $k=l$
.
$k=l$
.
The proof is complete. □
Proof. Proof of Theorem B
By Proposition 6.8, f admits an index
![]() $i_s$
skeleton. Let
$i_s$
skeleton. Let
![]() ${\mathcal S}=\{p_1,\cdots ,p_k\}$
be any index
${\mathcal S}=\{p_1,\cdots ,p_k\}$
be any index
![]() $i_s$
skeleton of f. By Proposition 6.9, the number of physical measures is precisely
$i_s$
skeleton of f. By Proposition 6.9, the number of physical measures is precisely
![]() $k=\#{\mathcal S}$
, and for each
$k=\#{\mathcal S}$
, and for each
![]() $p_i\in {\mathcal S}$
there exists a distinct physical measure
$p_i\in {\mathcal S}$
there exists a distinct physical measure
![]() $\mu _i$
such that
$\mu _i$
such that
-
(1) the closure of
 $W^u(Orb(p_i))$
coincides with
$W^u(Orb(p_i))$
coincides with
 $\operatorname {supp}(\mu _i)$
and by (ii) of Proposition 4.2, they also coincide with the homoclinic class of the orbit
$\operatorname {supp}(\mu _i)$
and by (ii) of Proposition 4.2, they also coincide with the homoclinic class of the orbit
 $\mbox {Orb}(p_i)$
.
$\mbox {Orb}(p_i)$
. -
(2) the closure of
 ${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of the basin of the measure
${\mathcal F}^s(\mbox {Orb}(p_i))$
coincides with the closure of the basin of the measure
 $\mu _i$
.
$\mu _i$
.
Moreover, by (ii) of Proposition 4.2,
for
![]() $1 \leq i \neq j \leq k$
. The proof is finished. □
$1 \leq i \neq j \leq k$
. The proof is finished. □
6.4 Proof of Corollary C
We finish this section with the proof of Corollary C.
Proof. Proof of Corollary C
Let f be
![]() $C^{1+}$
. For any
$C^{1+}$
. For any
![]() $n>0$
and
$n>0$
and
![]() $\nu $
an ergodic Gibbs u-state of
$\nu $
an ergodic Gibbs u-state of
![]() $f^n$
, by Lemma 2.3,
$f^n$
, by Lemma 2.3,
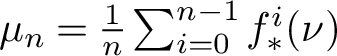 $\mu _n=\frac {1}{n}\sum _{i=0}^{n-1}f^i_*(\nu )$
is an invariant Gibbs u-state of f. It is easy to see that for
$\mu _n=\frac {1}{n}\sum _{i=0}^{n-1}f^i_*(\nu )$
is an invariant Gibbs u-state of f. It is easy to see that for
![]() $\nu $
typical point x, its center exponents with respect to
$\nu $
typical point x, its center exponents with respect to
![]() $f^n$
are n times of the corresponding exponents with respect to f. In particular, the center exponents of every Gibbs u-state of
$f^n$
are n times of the corresponding exponents with respect to f. In particular, the center exponents of every Gibbs u-state of
![]() $f^n$
are positive. Thus,
$f^n$
are positive. Thus,
![]() $f^n$
has a mostly expanding center as well.
$f^n$
has a mostly expanding center as well.
Because
![]() $\{p_1,\cdots ,p_k\}$
is an index
$\{p_1,\cdots ,p_k\}$
is an index
![]() $i_s$
skeleton of f,
$i_s$
skeleton of f,
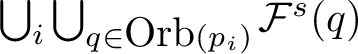 $\bigcup _i \bigcup _{q\in \mbox {Orb}(p_i)} {\mathcal F}^s(q)$
is dense in the manifold M, which means that
$\bigcup _i \bigcup _{q\in \mbox {Orb}(p_i)} {\mathcal F}^s(q)$
is dense in the manifold M, which means that
![]() ${\mathcal S} = \{q\in \mbox { Orb}(p_i),i=1,\ldots ,k\}$
is a pre-skeleton of
${\mathcal S} = \{q\in \mbox { Orb}(p_i),i=1,\ldots ,k\}$
is a pre-skeleton of
![]() $f^n$
for every
$f^n$
for every
![]() $n\ge 0$
. By Lemma 4.5, it has a subset that is a skeleton of
$n\ge 0$
. By Lemma 4.5, it has a subset that is a skeleton of
![]() $f^n$
. It follows from Theorem B that
$f^n$
. It follows from Theorem B that
![]() $f^n$
has finitely many physical measures with number bounded by
$f^n$
has finitely many physical measures with number bounded by
 $P=\prod _{i=1}^k \pi (p_i) = \# S$
.
$P=\prod _{i=1}^k \pi (p_i) = \# S$
.
Moreover, because elements of
![]() ${\mathcal S}$
are all distinct fixed points of
${\mathcal S}$
are all distinct fixed points of
![]() $f^{nP}$
for any
$f^{nP}$
for any
![]() $n>0$
, it is a skeleton for
$n>0$
, it is a skeleton for
![]() $f^{nP}$
,
$f^{nP}$
,
![]() $n>0$
. Then by Theorem B,
$n>0$
. Then by Theorem B,
![]() $f^{nP}$
have the same number of physical measures for every
$f^{nP}$
have the same number of physical measures for every
![]() $n>0$
. Let
$n>0$
. Let
![]() $\mu $
be a physical measure of
$\mu $
be a physical measure of
![]() $f^P$
. By Proposition 5.17,
$f^P$
. By Proposition 5.17,
![]() $\mu $
is ergodic, and its conditional measures along the Pesin unstable manifolds are equivalent to the Lebesgue measure on the leaves. Below we will show that
$\mu $
is ergodic, and its conditional measures along the Pesin unstable manifolds are equivalent to the Lebesgue measure on the leaves. Below we will show that
![]() $\mu $
is ergodic for
$\mu $
is ergodic for
![]() $f^{nP}$
for all
$f^{nP}$
for all
![]() $n>0$
.
$n>0$
.
To this end, let
![]() $\tilde {\mu }$
be any ergodic component of
$\tilde {\mu }$
be any ergodic component of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $f^{nP}$
; then the conditional measures of
$f^{nP}$
; then the conditional measures of
![]() $\tilde {\mu }$
along the Pesin unstable manifolds are still equivalent to the Lebesgue measure on the leaves. It then follows from the argument of Proposition 5.17 that
$\tilde {\mu }$
along the Pesin unstable manifolds are still equivalent to the Lebesgue measure on the leaves. It then follows from the argument of Proposition 5.17 that
![]() $\tilde {\mu }$
is a physical measure of
$\tilde {\mu }$
is a physical measure of
![]() $f^{nP}$
. Because the number of physical measures of
$f^{nP}$
. Because the number of physical measures of
![]() $f^{nP}$
is constant,
$f^{nP}$
is constant,
![]() $\tilde {\mu }$
must be the only ergodic component of
$\tilde {\mu }$
must be the only ergodic component of
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $f^{nP}$
. It then follows that
$f^{nP}$
. It then follows that
![]() $\mu = \tilde {\mu }$
, which is ergodic for
$\mu = \tilde {\mu }$
, which is ergodic for
![]() $f^{nP}$
.
$f^{nP}$
.
Then, by the classical work of Ornstein and Weiss [Reference Ornstein and Weiss41], every physical measure of
![]() $f^P$
is a Bernoulli measure. □
$f^P$
is a Bernoulli measure. □
7 Proof of Theorem E
In this section, we study the robustness of the skeleton and physical measures under
![]() $C^1$
topology among
$C^1$
topology among
![]() $C^{1+}$
diffeomorphisms and prove Theorem E.
$C^{1+}$
diffeomorphisms and prove Theorem E.
For this purpose, we assume that
![]() $f:M\to M$
is a
$f:M\to M$
is a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center and
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center and
![]() ${\mathcal U}$
a
${\mathcal U}$
a
![]() $C^1$
neighbourhood of f satisfying Lemma 5.3 and Proposition 5.17. Let
$C^1$
neighbourhood of f satisfying Lemma 5.3 and Proposition 5.17. Let
![]() $b_0$
be given in Lemma 5.3 and
$b_0$
be given in Lemma 5.3 and
![]() $r_1$
be given by Proposition 5.17. We take
$r_1$
be given by Proposition 5.17. We take
![]() ${\mathcal S}(f)=\{p_1,\cdots , p_k\}$
a skeleton of f. Because
${\mathcal S}(f)=\{p_1,\cdots , p_k\}$
a skeleton of f. Because
 $\bigcup _{i=1}^k{\mathcal F}^s(\mbox {Orb}(p_i(f)),f)$
is dense in the manifold M, by the continuity of stable foliation with respect to diffeomorphisms in
$\bigcup _{i=1}^k{\mathcal F}^s(\mbox {Orb}(p_i(f)),f)$
is dense in the manifold M, by the continuity of stable foliation with respect to diffeomorphisms in
![]() $C^1$
topology, we may assume that
$C^1$
topology, we may assume that
![]() ${\mathcal U}$
is sufficiently small such that for any
${\mathcal U}$
is sufficiently small such that for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $g\in {\mathcal U}$
, the continuation of
$g\in {\mathcal U}$
, the continuation of
![]() ${\mathcal S}(f)$
given by the continuation of hyperbolic saddles
${\mathcal S}(f)$
given by the continuation of hyperbolic saddles
![]() ${\mathcal S}(g) = \{p_i(g),\cdots , p_k(g)\}$
satisfies that
${\mathcal S}(g) = \{p_i(g),\cdots , p_k(g)\}$
satisfies that
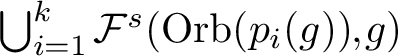 $\bigcup _{i=1}^k{\mathcal F}^s(\mbox {Orb}(p_i(g)),g)$
is
$\bigcup _{i=1}^k{\mathcal F}^s(\mbox {Orb}(p_i(g)),g)$
is
![]() $r_1$
dense; that is, for any
$r_1$
dense; that is, for any
![]() $x\in {\mathcal H}(b_0/2,g)$
,
$x\in {\mathcal H}(b_0/2,g)$
,
 $$ \begin{align*}\bigcup_{i=1}^k{\mathcal F}^s(\mbox{Orb}(p_i(g)),g)\pitchfork W^u_{r_1}(x,g)\neq \emptyset,\end{align*} $$
$$ \begin{align*}\bigcup_{i=1}^k{\mathcal F}^s(\mbox{Orb}(p_i(g)),g)\pitchfork W^u_{r_1}(x,g)\neq \emptyset,\end{align*} $$
where
![]() $W^u_{r_1}(x,g)$
is given by Lemma 5.11.
$W^u_{r_1}(x,g)$
is given by Lemma 5.11.
Note that
![]() ${\mathcal S}(g)$
may not be a skeleton. In the following, we will show the relation between skeletons of diffeomorphisms in
${\mathcal S}(g)$
may not be a skeleton. In the following, we will show the relation between skeletons of diffeomorphisms in
![]() ${\mathcal U}$
. For the discussion in the next section, we will state the following lemma for
${\mathcal U}$
. For the discussion in the next section, we will state the following lemma for
![]() $C^1$
diffeomorphisms in
$C^1$
diffeomorphisms in
![]() ${\mathcal U}$
.
${\mathcal U}$
.
Lemma 7.1. For
![]() $C^1$
diffeomorphisms in
$C^1$
diffeomorphisms in
![]() ${\mathcal U}$
, the number of elements of a skeleton varies upper semi-continuously. More precisely, for
${\mathcal U}$
, the number of elements of a skeleton varies upper semi-continuously. More precisely, for
![]() $g\in {\mathcal U}$
:
$g\in {\mathcal U}$
:
-
(1)
 ${\mathcal S}(g) = \{p_1(g),\cdots , p_k(g)\}$
is a pre-skeleton of g; thus, it contains a subset that is a skeleton of g;
${\mathcal S}(g) = \{p_1(g),\cdots , p_k(g)\}$
is a pre-skeleton of g; thus, it contains a subset that is a skeleton of g; -
(2) suppose that
 $\{q_1(g),\cdots , q_l(g)\}$
is a skeleton of g; then there is a
$\{q_1(g),\cdots , q_l(g)\}$
is a skeleton of g; then there is a
 $C^1$
neighbourhood
$C^1$
neighbourhood
 ${\mathcal V}$
of g such that for any
${\mathcal V}$
of g such that for any
 $h\in {\mathcal V}$
,
$h\in {\mathcal V}$
,
 $\{q_1(h),\cdots , q_l(h)\}$
is a pre-skeleton of h.
$\{q_1(h),\cdots , q_l(h)\}$
is a pre-skeleton of h.
Proof. By Proposition 6.8, g admits a skeleton
![]() $\{q_1(g),\cdots ,q_l(g)\}$
such that each
$\{q_1(g),\cdots ,q_l(g)\}$
such that each
![]() $q_j(g)$
(
$q_j(g)$
(
![]() $j=1,\cdots ,l$
) has unstable manifold with size
$j=1,\cdots ,l$
) has unstable manifold with size
![]() $r_1$
. Then by the previous assumption on
$r_1$
. Then by the previous assumption on
![]() ${\mathcal U}$
, for every
${\mathcal U}$
, for every
![]() $1\leq j \leq l$
, there is a
$1\leq j \leq l$
, there is a
![]() $1\leq i \leq k$
such that
$1\leq i \leq k$
such that
![]() ${\mathcal F}^s(\mbox{Orb}(p_i(g)),g)\pitchfork W^u_{r_1}(q_j(g),g)\neq \emptyset $
. Thus, by the inclination lemma,
${\mathcal F}^s(\mbox{Orb}(p_i(g)),g)\pitchfork W^u_{r_1}(q_j(g),g)\neq \emptyset $
. Thus, by the inclination lemma,
![]() ${\mathcal F}^s(\mbox {Orb}(q_j(g)),g)$
is accumulated by
${\mathcal F}^s(\mbox {Orb}(q_j(g)),g)$
is accumulated by
![]() ${\mathcal F}^s(\mbox{Orb}(p_i(g)),g)$
, which implies that
${\mathcal F}^s(\mbox{Orb}(p_i(g)),g)$
, which implies that
![]() $\cup _{i=1}^k {\mathcal F}^s(\mbox {Orb}(p_i(g)))$
is dense in the manifold M. This finishes the proof of (1).
$\cup _{i=1}^k {\mathcal F}^s(\mbox {Orb}(p_i(g)))$
is dense in the manifold M. This finishes the proof of (1).
The proof of (2) is quite similar. Take
![]() ${\mathcal V}$
sufficiently small such that for any
${\mathcal V}$
sufficiently small such that for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $h\in {\mathcal V}$
, the continuation
$h\in {\mathcal V}$
, the continuation
![]() $\{q_1(h),\cdots , q_l(h)\}$
satisfies the condition that
$\{q_1(h),\cdots , q_l(h)\}$
satisfies the condition that
![]() $\cup _{i=1}^k{\mathcal F}^s(\mbox {Orb}(q_i(h)),h)$
is
$\cup _{i=1}^k{\mathcal F}^s(\mbox {Orb}(q_i(h)),h)$
is
![]() $r_1$
dense. By Proposition 6.8, every
$r_1$
dense. By Proposition 6.8, every
![]() $h\in {\mathcal V}\subset {\mathcal U}$
admits a skeleton
$h\in {\mathcal V}\subset {\mathcal U}$
admits a skeleton
![]() $\{q^\prime _1(h),\cdots ,q^\prime _t(h)\}$
, such that each
$\{q^\prime _1(h),\cdots ,q^\prime _t(h)\}$
, such that each
![]() $q^{\prime }_i(h)$
has unstable manifold with size
$q^{\prime }_i(h)$
has unstable manifold with size
![]() $r_1$
. Then for every
$r_1$
. Then for every
![]() $1\leq j \leq t$
, there is a
$1\leq j \leq t$
, there is a
![]() $1\leq i \leq l$
such that
$1\leq i \leq l$
such that
![]() ${\mathcal F}^s(\mbox {Orb}(q_i(h)),h)\pitchfork W^u_{r_1}(q^\prime _j(h),h)\neq \emptyset $
. Thus, by the inclination lemma,
${\mathcal F}^s(\mbox {Orb}(q_i(h)),h)\pitchfork W^u_{r_1}(q^\prime _j(h),h)\neq \emptyset $
. Thus, by the inclination lemma,
![]() ${\mathcal F}^s(\mbox {Orb}(q^\prime _j(h)),h)$
is accumulated by
${\mathcal F}^s(\mbox {Orb}(q^\prime _j(h)),h)$
is accumulated by
![]() ${\mathcal F}^s(\mbox{Orb}(q_i(h)),h)$
, which implies that
${\mathcal F}^s(\mbox{Orb}(q_i(h)),h)$
, which implies that
![]() $\cup _{i=1}^k {\mathcal F}^s(\mbox {Orb}(q_i(h)),h)$
is dense in M. This finishes the proof of (2). □
$\cup _{i=1}^k {\mathcal F}^s(\mbox {Orb}(q_i(h)),h)$
is dense in M. This finishes the proof of (2). □
Thus, by Lemma 4.4, the number of elements of the skeleton of g is bounded from above by
![]() $k=\#{\mathcal S}(f)$
. It follows that, restricted to a
$k=\#{\mathcal S}(f)$
. It follows that, restricted to a
![]() $C^1$
open and dense subset
$C^1$
open and dense subset
![]() ${\mathcal U}^\circ \subset {\mathcal U}$
, the number of elements of a skeleton for diffeomorphisms of
${\mathcal U}^\circ \subset {\mathcal U}$
, the number of elements of a skeleton for diffeomorphisms of
![]() ${\mathcal U}^\circ $
is locally constant. More precisely, for any
${\mathcal U}^\circ $
is locally constant. More precisely, for any
![]() $1\leq i \leq k$
, we write
$1\leq i \leq k$
, we write
Then
![]() ${\mathcal U}_i$
is an open set, and
${\mathcal U}_i$
is an open set, and
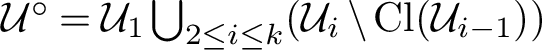 ${\mathcal U}^\circ ={\mathcal U}_1 \bigcup _{2\leq i\leq k} ({\mathcal U}_i \setminus \mbox {Cl}({\mathcal U}_{i-1}))$
satisfies our requirement.
${\mathcal U}^\circ ={\mathcal U}_1 \bigcup _{2\leq i\leq k} ({\mathcal U}_i \setminus \mbox {Cl}({\mathcal U}_{i-1}))$
satisfies our requirement.
By Theorem B, the number of physical measures for
![]() $C^{1+}$
diffeomorphisms in
$C^{1+}$
diffeomorphisms in
![]() ${\mathcal U}^\circ $
is locally constant.
${\mathcal U}^\circ $
is locally constant.
Suppose that
![]() $f_n\in {\mathcal U}^\circ $
is a sequence of
$f_n\in {\mathcal U}^\circ $
is a sequence of
![]() $C^{1+}$
diffeomorphisms such that
$C^{1+}$
diffeomorphisms such that
![]() $f_n\to f_0\in {\mathcal U}^\circ $
. We assume that all
$f_n\to f_0\in {\mathcal U}^\circ $
. We assume that all
![]() $f_n$
have
$f_n$
have
![]() $m\le k$
physical measures. By the previous argument, all diffeomorphisms
$m\le k$
physical measures. By the previous argument, all diffeomorphisms
![]() $f_n$
and
$f_n$
and
![]() $f_0$
have the same number of elements in their skeletons. In particular, by Lemma 7.1, we may take a skeleton
$f_0$
have the same number of elements in their skeletons. In particular, by Lemma 7.1, we may take a skeleton
![]() ${\mathcal S}(f_0)=\{p_1(f_0),\cdots ,p_m(f_0)\}$
of
${\mathcal S}(f_0)=\{p_1(f_0),\cdots ,p_m(f_0)\}$
of
![]() $f_0$
such that its continuation
$f_0$
such that its continuation
![]() ${\mathcal S}(f_n)=\{p_1(f_n),\cdots ,p_m(f_n)\}$
is a skeleton of
${\mathcal S}(f_n)=\{p_1(f_n),\cdots ,p_m(f_n)\}$
is a skeleton of
![]() $f_n$
. For
$f_n$
. For
![]() $f_n$
(
$f_n$
(
![]() $n\geq 0$
), denote by
$n\geq 0$
), denote by
![]() $\mu _{n,1},\cdots ,\mu _{n,m}$
the physical measures of
$\mu _{n,1},\cdots ,\mu _{n,m}$
the physical measures of
![]() $f_n$
associated with the periodic point
$f_n$
associated with the periodic point
![]() $p_j(f_n)$
as explained in Theorem B. Next we are going to show the following.
$p_j(f_n)$
as explained in Theorem B. Next we are going to show the following.
Lemma 7.2.
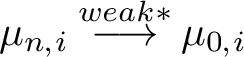 $\mu _{n,i}\overset {weak *}{\longrightarrow } \mu _{0,i}$
.
$\mu _{n,i}\overset {weak *}{\longrightarrow } \mu _{0,i}$
.
Proof. For simplicity, we will only prove it for
![]() $i=1$
. We prove by contradiction and assume (after taking subsequence if necessary) that
$i=1$
. We prove by contradiction and assume (after taking subsequence if necessary) that
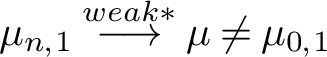 $\mu _{n,1}\overset {weak *}{\longrightarrow } \mu \neq \mu _{0,1}$
.
$\mu _{n,1}\overset {weak *}{\longrightarrow } \mu \neq \mu _{0,1}$
.
By Proposition 5.17, the space
![]() $\operatorname {G}(\cdot )$
is compact and convex; extreme elements of
$\operatorname {G}(\cdot )$
is compact and convex; extreme elements of
![]() $\operatorname {G}(\cdot )$
are precisely those physical measures, and it varies in a upper semi-continuous fashion with respect to diffeomorphisms in
$\operatorname {G}(\cdot )$
are precisely those physical measures, and it varies in a upper semi-continuous fashion with respect to diffeomorphisms in
![]() ${\mathcal U}$
under
${\mathcal U}$
under
![]() $C^1$
topology. Thus,
$C^1$
topology. Thus,
![]() $\mu _{n,1}\in \operatorname {G}(f_n)$
and
$\mu _{n,1}\in \operatorname {G}(f_n)$
and
![]() $\mu \in \operatorname {G}(f_0)$
. Moreover,
$\mu \in \operatorname {G}(f_0)$
. Moreover,
![]() $\mu $
can be written as a combination of the physical measures of
$\mu $
can be written as a combination of the physical measures of
![]() $f_0$
:
$f_0$
:
By our assumption,
![]() $a_1\neq 1$
; thus, there is
$a_1\neq 1$
; thus, there is
![]() $1< i \leq m$
such that
$1< i \leq m$
such that
![]() $a_i>0$
. We will show that this implies heteroclinic intersection between
$a_i>0$
. We will show that this implies heteroclinic intersection between
![]() $p_1(f_n)$
and
$p_1(f_n)$
and
![]() $p_i(f_n)$
, which is a contradiction.
$p_i(f_n)$
, which is a contradiction.
Take
![]() $r>0$
sufficiently small, such that
$r>0$
sufficiently small, such that
![]() $B_r(p_i(f_0))\subset \cup _{x\in W^u(p_i(f_0),f_0)} {\mathcal F}^s(x,f_0)$
. Then by the continuity of unstable manifolds of
$B_r(p_i(f_0))\subset \cup _{x\in W^u(p_i(f_0),f_0)} {\mathcal F}^s(x,f_0)$
. Then by the continuity of unstable manifolds of
![]() $p_i(\cdot )$
and the continuity of stable foliation with respect to diffeomorphisms, there is
$p_i(\cdot )$
and the continuity of stable foliation with respect to diffeomorphisms, there is
![]() $n_0$
such that for any
$n_0$
such that for any
![]() $n>n_0$
, any point
$n>n_0$
, any point
![]() $x\in B_r(p_i(f_n))$
,
$x\in B_r(p_i(f_n))$
,
By Theorem B,
![]() $p_i(f_0)\in \operatorname {supp}(\mu _{0,i})$
and
$p_i(f_0)\in \operatorname {supp}(\mu _{0,i})$
and
![]() $\mu _{0,i}(B_r(p_i(f_0)))>0$
. Because
$\mu _{0,i}(B_r(p_i(f_0)))>0$
. Because
![]() $\mu _{n,1}\to \mu $
, which also assigns positive measure to
$\mu _{n,1}\to \mu $
, which also assigns positive measure to
![]() $B_r(p_i(f_0))$
, there is
$B_r(p_i(f_0))$
, there is
![]() $n>n_0$
such that
$n>n_0$
such that
![]() $\mu _{n,1}(B_r(p_i(f_0)))>0$
. In particular, we have
$\mu _{n,1}(B_r(p_i(f_0)))>0$
. In particular, we have
![]() $\operatorname {supp}(\mu _{n,1})\cap B_r(p_i(f_0))\neq \emptyset $
. Again by Theorem B,
$\operatorname {supp}(\mu _{n,1})\cap B_r(p_i(f_0))\neq \emptyset $
. Again by Theorem B,
![]() $\operatorname {supp}(\mu _{n,1})=H(p_{1}(f_n),f_n)$
; thus,
$\operatorname {supp}(\mu _{n,1})=H(p_{1}(f_n),f_n)$
; thus,
![]() ${\mathcal F}^s(\mbox { Orb}(p_1(f_n)), f_n) \cap B_r(p_i(f_0)) \neq \emptyset $
. By (25),
${\mathcal F}^s(\mbox { Orb}(p_1(f_n)), f_n) \cap B_r(p_i(f_0)) \neq \emptyset $
. By (25),
which contradicts the fact that
![]() $\{p_{1}(f_n),\cdots , p_k(f_n)\}$
is a skeleton of
$\{p_{1}(f_n),\cdots , p_k(f_n)\}$
is a skeleton of
![]() $f_n$
and thus by Lemma 4.1[(1)] there is no heteroclinic intersection between
$f_n$
and thus by Lemma 4.1[(1)] there is no heteroclinic intersection between
![]() $p_i(f_n)$
and
$p_i(f_n)$
and
![]() $p_j(f_n)$
for
$p_j(f_n)$
for
![]() $1\leq i \neq j \leq k$
. □
$1\leq i \neq j \leq k$
. □
To prove Theorem E, it remains to show that for diffeomorphisms in
![]() $\mbox {Diff}^{1+}(M)\cap {\mathcal U}^\circ $
, the supports of corresponding physical measures and the closures of their basins vary in a lower semi-continuous fashion, both in the sense of the Hausdorff topology.
$\mbox {Diff}^{1+}(M)\cap {\mathcal U}^\circ $
, the supports of corresponding physical measures and the closures of their basins vary in a lower semi-continuous fashion, both in the sense of the Hausdorff topology.
Indeed, by the unstable manifold theorem of fixed saddle, for each
![]() $R>0$
, the local invariant manifolds
$R>0$
, the local invariant manifolds
![]() $W^u_R(\mbox {Orb}(p_i(g),g))$
vary continuously with
$W^u_R(\mbox {Orb}(p_i(g),g))$
vary continuously with
![]() $g\in {\mathcal U}$
; moreover, the stable foliation varies continuously with respect to g. Thus, the closures of
$g\in {\mathcal U}$
; moreover, the stable foliation varies continuously with respect to g. Thus, the closures of
![]() $W^u(\mbox {Orb}(p_i(g),g))$
and
$W^u(\mbox {Orb}(p_i(g),g))$
and
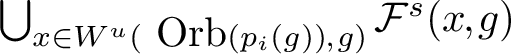 $\bigcup _{x\in W^u(\mbox { Orb}(p_i(g)),g)} {\mathcal F}^s(x,g)$
both vary in a lower semi-continuous fashion with g, relative to the Hausdorff topology. By Theorem B, this means that the supports and the closures of the basins of the physical measures vary lower semi-continuously with the dynamics. The proof of Theorem E is now complete.
$\bigcup _{x\in W^u(\mbox { Orb}(p_i(g)),g)} {\mathcal F}^s(x,g)$
both vary in a lower semi-continuous fashion with g, relative to the Hausdorff topology. By Theorem B, this means that the supports and the closures of the basins of the physical measures vary lower semi-continuously with the dynamics. The proof of Theorem E is now complete.
8 Proof of Theorem F
In this section we will generalise the result of Theorem E to
![]() $C^1$
generic diffeomorphisms in
$C^1$
generic diffeomorphisms in
![]() ${\mathcal U}$
. The proof is similar to [Reference Hua, Yang and Yang32, Theorem B]. The key observations are as follows:
${\mathcal U}$
. The proof is similar to [Reference Hua, Yang and Yang32, Theorem B]. The key observations are as follows:
-
•
 $C^{1+}$
diffeomorphisms are dense in
$C^{1+}$
diffeomorphisms are dense in
 $C^1$
topology.
$C^1$
topology. -
• Skeletons are upper semi-continuous in
 ${\mathcal U}$
.
${\mathcal U}$
. -
• The support of physical measures for
 $C^{1+} g\in {\mathcal U}$
are homoclinic classes, which are (generically) Lyapunov stable and lower semi-continuous with the dynamics.
$C^{1+} g\in {\mathcal U}$
are homoclinic classes, which are (generically) Lyapunov stable and lower semi-continuous with the dynamics. -
• The candidate space of physical measures,
 $\operatorname {G}(\cdot )$
, is upper semi-continuous.
$\operatorname {G}(\cdot )$
, is upper semi-continuous.
These properties will allow us to find a residual subset of
![]() ${\mathcal U}$
, consisting of continuity points of
${\mathcal U}$
, consisting of continuity points of
![]() $H(p_i(\cdot ),\cdot )$
and
$H(p_i(\cdot ),\cdot )$
and
![]() ${\mathcal G}(\cdot )$
. We will prove Theorem F on this residual subset of
${\mathcal G}(\cdot )$
. We will prove Theorem F on this residual subset of
![]() ${\mathcal U}$
.
${\mathcal U}$
.
Throughout this section, let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center,
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center,
![]() ${\mathcal S}(f)=\{p_1,\cdots , p_k\}$
be a skeleton of f and
${\mathcal S}(f)=\{p_1,\cdots , p_k\}$
be a skeleton of f and
![]() ${\mathcal U}$
be the
${\mathcal U}$
be the
![]() $C^1$
neighbourhood of f provided by Theorem E. Recall that by Lemma 7.1, the cardinality of skeleton varies in an upper semi-continuous way; we may choose a
$C^1$
neighbourhood of f provided by Theorem E. Recall that by Lemma 7.1, the cardinality of skeleton varies in an upper semi-continuous way; we may choose a
![]() $C^1$
open and dense subset
$C^1$
open and dense subset
![]() ${\mathcal U}^\circ \subset {\mathcal U}$
such that the cardinality of skeleton is
${\mathcal U}^\circ \subset {\mathcal U}$
such that the cardinality of skeleton is
![]() $C^1$
locally constant for diffeomorphisms in
$C^1$
locally constant for diffeomorphisms in
![]() ${\mathcal U}^\circ $
.
${\mathcal U}^\circ $
.
Take any
![]() $C^{1+}$
diffeomorphism
$C^{1+}$
diffeomorphism
![]() $g\in {\mathcal U}^\circ $
; then g has
$g\in {\mathcal U}^\circ $
; then g has
![]() $l\leq k$
physical measures due to Theorem E. Furthermore, there is a subset of the continuation
$l\leq k$
physical measures due to Theorem E. Furthermore, there is a subset of the continuation
![]() ${\mathcal S}(g) = \{p_1(g),\cdots , p_k(g)\}$
that forms a skeleton of g. After reordering, we may assume
${\mathcal S}(g) = \{p_1(g),\cdots , p_k(g)\}$
that forms a skeleton of g. After reordering, we may assume
![]() $\{p_1(g),\cdots ,p_l(g)\}$
to be a skeleton of g. Then by Lemma 7.1[(2)], there is a
$\{p_1(g),\cdots ,p_l(g)\}$
to be a skeleton of g. Then by Lemma 7.1[(2)], there is a
![]() $C^1$
neighbourhood
$C^1$
neighbourhood
![]() ${\mathcal V}\subset {\mathcal U}^\circ $
of g such that for any
${\mathcal V}\subset {\mathcal U}^\circ $
of g such that for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $h\in {\mathcal V}$
,
$h\in {\mathcal V}$
,
![]() $\{p_1(h),\cdots , p_l(h)\}$
forms a skeleton of h.
$\{p_1(h),\cdots , p_l(h)\}$
forms a skeleton of h.
Then by Lemma 4.1[(2)], for any
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $h\in {\mathcal V}$
and any
$h\in {\mathcal V}$
and any
![]() $1\leq i \neq j \leq l$
,
$1\leq i \neq j \leq l$
,
![]() $W^u(\mbox {Orb}(p_i(h)),h)\cap {\mathcal F}^s(\mbox { Orb}(p_j(h)),h)=\emptyset $
. Using Bonatti and Crovisier’s connecting lemma ([Reference Bonatti and Crovisier8]), we see that for any diffeomorphism
$W^u(\mbox {Orb}(p_i(h)),h)\cap {\mathcal F}^s(\mbox { Orb}(p_j(h)),h)=\emptyset $
. Using Bonatti and Crovisier’s connecting lemma ([Reference Bonatti and Crovisier8]), we see that for any diffeomorphism
![]() $h'\in {\mathcal V}$
and any
$h'\in {\mathcal V}$
and any
![]() $1\leq i \neq j \leq l$
,
$1\leq i \neq j \leq l$
,
because otherwise one can create a nontrivial intersection between
![]() $W^u(\mbox { Orb}(p_i(\cdot )),\cdot )$
and
$W^u(\mbox { Orb}(p_i(\cdot )),\cdot )$
and
![]() ${\mathcal F}^s(\mbox {Orb}(p_j(\cdot )),\cdot )$
.
${\mathcal F}^s(\mbox {Orb}(p_j(\cdot )),\cdot )$
.
By Proposition 4.2,
Thus, we have
We need the following generic property proved by Morales and Pacifico [17].
Proposition 8.1. For every h that belongs to a
![]() $C^1$
residual subset of diffeomorphisms
$C^1$
residual subset of diffeomorphisms
![]() ${\mathcal R}_0$
and every periodic point p of h, the set
${\mathcal R}_0$
and every periodic point p of h, the set
![]() $\mbox {Cl}(W^u(\mbox { Orb}(p),h))$
is Lyapunov stable.
$\mbox {Cl}(W^u(\mbox { Orb}(p),h))$
is Lyapunov stable.
Recall that the map
![]() ${\mathcal G}$
that maps a diffeomorphism
${\mathcal G}$
that maps a diffeomorphism
![]() $h\in {\mathcal V}$
to
$h\in {\mathcal V}$
to
![]() $\operatorname {G}(h)$
is upper semi-continuous by Proposition 5.17. Let
$\operatorname {G}(h)$
is upper semi-continuous by Proposition 5.17. Let
![]() ${\mathcal R}_1\subset {\mathcal V}$
be the residual subset of diffeomorphisms that are continuity points of the map
${\mathcal R}_1\subset {\mathcal V}$
be the residual subset of diffeomorphisms that are continuity points of the map
![]() ${\mathcal G}$
. For each
${\mathcal G}$
. For each
![]() $1\leq i \leq l$
, also consider the map
$1\leq i \leq l$
, also consider the map
![]() ${\mathcal I}_i$
from
${\mathcal I}_i$
from
![]() ${\mathcal V}$
to compact subsets of M:
${\mathcal V}$
to compact subsets of M:
Because homoclinic classes vary lower semi-continuously with respect to diffeomorphisms (because they contain hyperbolic horseshoes), there is a residual subset of diffeomorphisms
![]() ${\mathcal R}_2 \subset {\mathcal V}$
that consists of the continuity points of
${\mathcal R}_2 \subset {\mathcal V}$
that consists of the continuity points of
![]() ${\mathcal I}_i$
for every
${\mathcal I}_i$
for every
![]() $1\leq i\leq l$
. Now let us take
$1\leq i\leq l$
. Now let us take
![]() ${\mathcal R}={\mathcal R}_0\cap {\mathcal R}_1\cap {\mathcal R}_2\subset {\mathcal V}$
. We are going to show that the residual set
${\mathcal R}={\mathcal R}_0\cap {\mathcal R}_1\cap {\mathcal R}_2\subset {\mathcal V}$
. We are going to show that the residual set
![]() ${\mathcal R}$
satisfies the conditions we need.
${\mathcal R}$
satisfies the conditions we need.
Proposition 8.2. Every
![]() $C^1$
diffeomorphism
$C^1$
diffeomorphism
![]() $h\in {\mathcal R}$
has exactly l physical measures, each of which is supported on
$h\in {\mathcal R}$
has exactly l physical measures, each of which is supported on
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
for some
$\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
for some
![]() $i=1,\cdots ,k$
. Furthermore, the basin of each physical measure covers a full-volume subset within a neighbourhood of its support.
$i=1,\cdots ,k$
. Furthermore, the basin of each physical measure covers a full-volume subset within a neighbourhood of its support.
Proof. For any
![]() $C^{1+}$
diffeomorphism
$C^{1+}$
diffeomorphism
![]() $h^\prime \in {\mathcal V}$
, denote by
$h^\prime \in {\mathcal V}$
, denote by
![]() $\mu _{h^\prime ,1},\cdots , \mu _{h^\prime ,l}$
the ergodic physical measures of
$\mu _{h^\prime ,1},\cdots , \mu _{h^\prime ,l}$
the ergodic physical measures of
![]() $h^\prime $
. Then by Proposition 5.17,
$h^\prime $
. Then by Proposition 5.17,
![]() $\operatorname {G}(h^\prime )$
is the simplex generated by
$\operatorname {G}(h^\prime )$
is the simplex generated by
![]() $\{\mu _{h^\prime ,1},\cdots , \mu _{h^\prime ,l}\}$
. For any
$\{\mu _{h^\prime ,1},\cdots , \mu _{h^\prime ,l}\}$
. For any
![]() $h\in {\mathcal R}$
, by the continuity of the map
$h\in {\mathcal R}$
, by the continuity of the map
![]() ${\mathcal G}$
at h, we see that
${\mathcal G}$
at h, we see that
![]() $\operatorname {G}(h)={\mathcal G}(h)$
is a simplex of dimension
$\operatorname {G}(h)={\mathcal G}(h)$
is a simplex of dimension
![]() $m_h\leq l$
. In particular, the number of extreme elements of
$m_h\leq l$
. In particular, the number of extreme elements of
![]() $\operatorname {G}(h)$
is at most l. Below we will show that it is in fact l.
$\operatorname {G}(h)$
is at most l. Below we will show that it is in fact l.
Denote the extreme points of
![]() $\operatorname {G}(h)$
by
$\operatorname {G}(h)$
by
![]() $\mu _{h,1},\cdots , \mu _{h,m_h}$
. Let
$\mu _{h,1},\cdots , \mu _{h,m_h}$
. Let
![]() $h_n$
be a sequence of
$h_n$
be a sequence of
![]() $C^{1+}$
diffeomorphisms converging to h in
$C^{1+}$
diffeomorphisms converging to h in
![]() $C^1$
topology. By continuity of
$C^1$
topology. By continuity of
![]() ${\mathcal G}(\cdot )$
and relabelling if necessary, we may assume that
${\mathcal G}(\cdot )$
and relabelling if necessary, we may assume that
![]() $\lim \mu _{h_n,i}=\mu _{h,i}$
for
$\lim \mu _{h_n,i}=\mu _{h,i}$
for
![]() $i=1,\cdots , m_h$
. Note that
$i=1,\cdots , m_h$
. Note that
![]() $\mu _{h,i}$
is supported on
$\mu _{h,i}$
is supported on
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
. This is because by Theorem B,
$\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
. This is because by Theorem B,
![]() $\mu _{h_n,i}$
is supported on
$\mu _{h_n,i}$
is supported on
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i(h_n)),h_n))=H(p_i(h_n),h_n)$
, and h is a continuity point of the map
$\mbox {Cl}(W^u(\mbox {Orb}(p_i(h_n)),h_n))=H(p_i(h_n),h_n)$
, and h is a continuity point of the map
![]() $\Gamma _i(\cdot )$
, so we must have
$\Gamma _i(\cdot )$
, so we must have
![]() $\lim _{n} H(p_i(h_n),h_n)=H(p_i(h),h)$
.
$\lim _{n} H(p_i(h_n),h_n)=H(p_i(h),h)$
.
Next, we claim that
![]() $m_h=l$
. Assume that this is not the case. Then we take
$m_h=l$
. Assume that this is not the case. Then we take
![]() $m_h<j\leq l$
and take a weak-
$m_h<j\leq l$
and take a weak-
![]() $*$
limit
$*$
limit
![]() $\mu _{h}=\lim _n \mu _{h_n,j}$
. Note that
$\mu _{h}=\lim _n \mu _{h_n,j}$
. Note that
![]() $\mu _h\in \operatorname {G}(h)$
is supported on
$\mu _h\in \operatorname {G}(h)$
is supported on
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_j(h)),h))$
by the discussion above. Take any ergodic component
$\mbox {Cl}(W^u(\mbox {Orb}(p_j(h)),h))$
by the discussion above. Take any ergodic component
![]() $\tilde {\mu }_h$
of
$\tilde {\mu }_h$
of
![]() $\mu _h$
; then
$\mu _h$
; then
![]() $\tilde {\mu }_h\in \operatorname {G}(h)$
by Lemma 5.18 and is still supported on
$\tilde {\mu }_h\in \operatorname {G}(h)$
by Lemma 5.18 and is still supported on
![]() $\mbox {Cl}(W^u(\mbox { Orb}(p_j(h))),h)$
. Thus, by (26),
$\mbox {Cl}(W^u(\mbox { Orb}(p_j(h))),h)$
. Thus, by (26),
![]() $\tilde {\mu }_h\neq \mu _{h,i}$
for every
$\tilde {\mu }_h\neq \mu _{h,i}$
for every
![]() $i=1,\cdots , m_h$
. We have thus created a new extreme point of
$i=1,\cdots , m_h$
. We have thus created a new extreme point of
![]() $\operatorname {G}(h)$
, which is a contradiction.
$\operatorname {G}(h)$
, which is a contradiction.
To finish the proof, we have to show that each
![]() $\mu _{h,i}$
is a physical measure. Because
$\mu _{h,i}$
is a physical measure. Because
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
is Lyapunov stable, we can take
$\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
is Lyapunov stable, we can take
![]() $U_i\supset V_i$
open neighbourhoods for each
$U_i\supset V_i$
open neighbourhoods for each
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
, such that
$\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
, such that
![]() $\{U_i\}_{i=1,\cdots ,l}$
are disjoint and for each i and any
$\{U_i\}_{i=1,\cdots ,l}$
are disjoint and for each i and any
![]() $n>0$
,
$n>0$
,
![]() $h^n(V_i)\subset U_i$
. By Proposition 2.12, there is a full-volume subset
$h^n(V_i)\subset U_i$
. By Proposition 2.12, there is a full-volume subset
![]() $\Gamma _i\subset V_i$
such that for any
$\Gamma _i\subset V_i$
such that for any
![]() $x\in \Gamma _i$
, any limit
$x\in \Gamma _i$
, any limit
![]() $\mu $
of the sequence
$\mu $
of the sequence
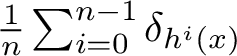 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{h^i(x)}$
belongs to
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{h^i(x)}$
belongs to
![]() $\operatorname {G}(h)$
. Note that because
$\operatorname {G}(h)$
. Note that because
![]() $x\in V_i$
, we have
$x\in V_i$
, we have
![]() $h^n(x)\in U_i$
for all
$h^n(x)\in U_i$
for all
![]() $n\geq 1$
. As a result,
$n\geq 1$
. As a result,
![]() $\mu $
is supported on
$\mu $
is supported on
![]() $U_i$
. On the other hand,
$U_i$
. On the other hand,
![]() $\mu _{h,i}$
is the only ergodic measure in
$\mu _{h,i}$
is the only ergodic measure in
![]() $\operatorname {G}(h)$
that is supported on
$\operatorname {G}(h)$
that is supported on
![]() $U_i$
. It follows that
$U_i$
. It follows that
![]() $\mu =\mu _{h,i}$
. This implies that Lebesgue almost every point of
$\mu =\mu _{h,i}$
. This implies that Lebesgue almost every point of
![]() $x\in V_i$
belongs to the basin of
$x\in V_i$
belongs to the basin of
![]() $\mu _{h,i}$
. The proof is complete. □
$\mu _{h,i}$
. The proof is complete. □
We conclude the proof of Theorem F with the following lemma.
Lemma 8.3. The basin of
![]() $\mu _{h,i}$
for
$\mu _{h,i}$
for
![]() $i=1,\cdots , l$
covers a full-volume set.
$i=1,\cdots , l$
covers a full-volume set.
Proof. Let
![]() $\Gamma $
be the full-volume subset given by Proposition 2.12. We are going to show that
$\Gamma $
be the full-volume subset given by Proposition 2.12. We are going to show that
 $\operatorname {vol}(\Gamma \setminus \bigcup _{i=1}^l {\mathcal B}(\mu _{h,i}))=0$
.
$\operatorname {vol}(\Gamma \setminus \bigcup _{i=1}^l {\mathcal B}(\mu _{h,i}))=0$
.
We prove by contradiction. Write
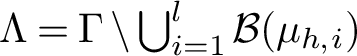 $\Lambda =\Gamma \setminus \bigcup _{i=1}^l {\mathcal B}(\mu _{h,i})$
and suppose that
$\Lambda =\Gamma \setminus \bigcup _{i=1}^l {\mathcal B}(\mu _{h,i})$
and suppose that
![]() $\operatorname {vol}(\Lambda )>0$
. Let
$\operatorname {vol}(\Lambda )>0$
. Let
![]() $x\in \Lambda $
be a Lebesgue density point of
$x\in \Lambda $
be a Lebesgue density point of
![]() $\Lambda $
, which means that for any
$\Lambda $
, which means that for any
![]() $r>0$
, we have
$r>0$
, we have
![]() $\operatorname {vol}(B_r(x)\cap \Lambda )>0$
. Let
$\operatorname {vol}(B_r(x)\cap \Lambda )>0$
. Let
![]() $\mu $
be any limit point of the sequence
$\mu $
be any limit point of the sequence
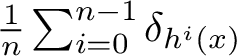 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{h^i(x)}$
. Because
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{h^i(x)}$
. Because
![]() $\mu \in \operatorname {G}(h)$
,
$\mu \in \operatorname {G}(h)$
,
![]() $\mu $
can be written as a combination of
$\mu $
can be written as a combination of
![]() $\mu _{h,i}$
:
$\mu _{h,i}$
:
where
![]() $a_1+\cdots +a_k=1$
.
$a_1+\cdots +a_k=1$
.
Suppose without loss of generality that
![]() $a_1>0$
; then
$a_1>0$
; then
![]() $\mu (V_1)>0$
, where
$\mu (V_1)>0$
, where
![]() $V_1$
is the neighbourhood of
$V_1$
is the neighbourhood of
![]() $\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
in the proof of the previous proposition. Thus, there is
$\mbox {Cl}(W^u(\mbox {Orb}(p_i(h)),h))$
in the proof of the previous proposition. Thus, there is
![]() $n>0$
such that
$n>0$
such that
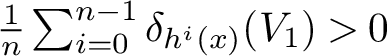 $\frac {1}{n}\sum _{i=0}^{n-1}\delta _{h^i(x)}(V_1)>0$
. In particular, there is
$\frac {1}{n}\sum _{i=0}^{n-1}\delta _{h^i(x)}(V_1)>0$
. In particular, there is
![]() $0\leq m \leq n-1$
such that
$0\leq m \leq n-1$
such that
![]() $h^m(x)\in V_1$
. Take
$h^m(x)\in V_1$
. Take
![]() $\varepsilon>0$
sufficiently small; then we have
$\varepsilon>0$
sufficiently small; then we have
![]() $h^m(B_\varepsilon (x)) \subset V_1$
. By Proposition 8.2,
$h^m(B_\varepsilon (x)) \subset V_1$
. By Proposition 8.2,
![]() $f^m(B_\varepsilon (x)\cap \Lambda )$
intersects with the basin of
$f^m(B_\varepsilon (x)\cap \Lambda )$
intersects with the basin of
![]() $\mu _{h,1}$
on a positive volume set. Because the basin of a measure is invariant under iteration of h and
$\mu _{h,1}$
on a positive volume set. Because the basin of a measure is invariant under iteration of h and
![]() $h^{-1}$
, we have
$h^{-1}$
, we have
![]() $\operatorname {vol}(\Lambda \cap {\mathcal B}(\mu _{h,1}))>0$
, which contradicts the choice of
$\operatorname {vol}(\Lambda \cap {\mathcal B}(\mu _{h,1}))>0$
, which contradicts the choice of
![]() $\Lambda $
. □
$\Lambda $
. □
9 Gibbs-Markov-Young structure
To study statistical properties of some nonuniformly hyperbolic systems, in [Reference Young53] Young constructed Markov towers, which are Markov partitions with infinitely many symbols and certain recurrence property. In particular, she used towers to study statistical properties of these nonuniformly hyperbolic systems, including the existence of physical measures, exponential decay of correlations and the validity of the central limit theorem for the physical measure. These structures have some properties which address to Gibbs states and they are nowadays commonly called as GMY structures.
In [Reference Alves and Li2], Alves and Li obtained GMY structures for partially hyperbolic attractors and they managed to prove the exponential decay of correlations: if the lack of expansion of the system at time n in the center-unstable direction is exponentially small, then the system has some GMY structure for physical measures with exponential decay of recurrence times. In this section we will show that their criterion is satisfied for any physical measures of any
![]() $C^{1+}$
diffeomorphisms with a mostly expanding center.
$C^{1+}$
diffeomorphisms with a mostly expanding center.
As before, we assume f to be a
![]() $C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center,
$C^{1+}$
partially hyperbolic diffeomorphism with a mostly expanding center,
![]() $\{p_1,\cdots ,p_k\}$
is a skeleton of f and
$\{p_1,\cdots ,p_k\}$
is a skeleton of f and
![]() $\mu _1,\cdots ,\mu _k$
are the corresponding physical measures of f in the sense of Theorem B. Recall that
$\mu _1,\cdots ,\mu _k$
are the corresponding physical measures of f in the sense of Theorem B. Recall that
 $P=\prod _{i=1}^k \pi (p_i)$
.
$P=\prod _{i=1}^k \pi (p_i)$
.
By Corollary C,
![]() $\{f^{nP}\}_{n>0}$
also have a mostly expanding center, and they share the same physical measures and skeletons. Therefore, to simply notation, we may assume that
$\{f^{nP}\}_{n>0}$
also have a mostly expanding center, and they share the same physical measures and skeletons. Therefore, to simply notation, we may assume that
![]() $\{p_i\}_{i=1}^k$
are all fixed points and
$\{p_i\}_{i=1}^k$
are all fixed points and
![]() $P=1$
. Moreover, by Proposition 5.1, we may assume that there is
$P=1$
. Moreover, by Proposition 5.1, we may assume that there is
![]() $b_0>0$
such that for any
$b_0>0$
such that for any
![]() $\mu \in \operatorname {G}^u(f)$
,
$\mu \in \operatorname {G}^u(f)$
,
 $$ \begin{align} \int \log \|Df^{-1}\mid_{E^{cu}(x)}\|d\mu(x)<-b_0. \end{align} $$
$$ \begin{align} \int \log \|Df^{-1}\mid_{E^{cu}(x)}\|d\mu(x)<-b_0. \end{align} $$
The notation below was used by Alves and Li [Reference Alves and Li2] and clearly resembles our definition of hyperbolic times.
Definition 9.1. Given
![]() $b>0$
, we say that f is b nonuniformly expanding (b-NUE) at a point x in the central-unstable direction if
$b>0$
, we say that f is b nonuniformly expanding (b-NUE) at a point x in the central-unstable direction if
 $$ \begin{align} \limsup_{n\to \infty}\frac{1}{n}\sum_{j=1}^n\log \|Df^{-1}\mid_{E^{cu}(f^{j}(x))}\|< -b. \end{align} $$
$$ \begin{align} \limsup_{n\to \infty}\frac{1}{n}\sum_{j=1}^n\log \|Df^{-1}\mid_{E^{cu}(f^{j}(x))}\|< -b. \end{align} $$
If f satisfies (b-NUE) at some point x, then the expansion time function at x,
 $$ \begin{align} {\mathcal E}_b(x)=\min\left\{ N\geq 1: \frac{1}{n}\sum^n_{i=1}\log \|Df^{-1}\mid_{E^{cu}(f^{i}(x))}\|< -b/2 \;\; \text{ for any } n\geq N\right\}, \end{align} $$
$$ \begin{align} {\mathcal E}_b(x)=\min\left\{ N\geq 1: \frac{1}{n}\sum^n_{i=1}\log \|Df^{-1}\mid_{E^{cu}(f^{i}(x))}\|< -b/2 \;\; \text{ for any } n\geq N\right\}, \end{align} $$
is defined and finite. We call
![]() $\{x:{\mathcal E}_b(x)>n\}$
the tail of
$\{x:{\mathcal E}_b(x)>n\}$
the tail of
![]() $b/2$
-hyperbolic times (at time n).
$b/2$
-hyperbolic times (at time n).
We need the following two propositions from [Reference Alves and Li2], which play a key role in the proof of decay of correlations and the central limit theorem.
Proposition 9.2 ([Reference Alves and Li2])
Assume for
![]() $b>0$
that there is a local unstable disk D of f and constants
$b>0$
that there is a local unstable disk D of f and constants
![]() $0<\tau \leq 1$
,
$0<\tau \leq 1$
,
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align*}\operatorname{vol}_D({\mathcal E}_b>n)=O(e^{-cn^\tau}).\end{align*} $$
$$ \begin{align*}\operatorname{vol}_D({\mathcal E}_b>n)=O(e^{-cn^\tau}).\end{align*} $$
Then some power
![]() $f^l$
has an physical measure
$f^l$
has an physical measure
![]() $\mu $
and there is
$\mu $
and there is
![]() $d>0$
such that
$d>0$
such that
 $$ \begin{align*}C_\mu(\phi,\psi\circ f^{ln})=O(e^{-dn^\tau})\end{align*} $$
$$ \begin{align*}C_\mu(\phi,\psi\circ f^{ln})=O(e^{-dn^\tau})\end{align*} $$
for Holder continuous
![]() $\phi :M\to \mathbb {R}$
and
$\phi :M\to \mathbb {R}$
and
![]() $\psi \in L^\infty (\mu )$
.
$\psi \in L^\infty (\mu )$
.
Proposition 9.3 ([Reference Alves and Li2])
Assume for
![]() $b>0$
that there is a local unstable disk D of f and constants
$b>0$
that there is a local unstable disk D of f and constants
![]() $0<\tau \leq 1$
,
$0<\tau \leq 1$
,
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align*}\operatorname{vol}_D({\mathcal E}_b>n)=O(e^{-cn^\tau}).\end{align*} $$
$$ \begin{align*}\operatorname{vol}_D({\mathcal E}_b>n)=O(e^{-cn^\tau}).\end{align*} $$
Then some power
![]() $f^l$
has an physical measure
$f^l$
has an physical measure
![]() $\mu $
; moreover, given any Hölder continuous function
$\mu $
; moreover, given any Hölder continuous function
![]() $\phi $
, the following limit exists:
$\phi $
, the following limit exists:
 $$ \begin{align*}\sigma^2=\lim_{n\to \infty} \frac{1}{n}\int \left(\sum_{j=0}^{n-1}\phi\circ f^{jl} -n\int \phi d\mu\right)^2d\mu.\end{align*} $$
$$ \begin{align*}\sigma^2=\lim_{n\to \infty} \frac{1}{n}\int \left(\sum_{j=0}^{n-1}\phi\circ f^{jl} -n\int \phi d\mu\right)^2d\mu.\end{align*} $$
Furthermore, if
![]() $\sigma ^2>0$
, then there is a rate function
$\sigma ^2>0$
, then there is a rate function
![]() $c(\varepsilon )>0$
such that
$c(\varepsilon )>0$
such that
 $$ \begin{align*}\lim_{n\to \infty} \frac{1}{n}\log \mu\left(\left| \sum_{j=0}^{n-1}\phi\circ f^{jl} -n\int \phi d\mu \right| \geq \varepsilon\right)=-c(\varepsilon).\end{align*} $$
$$ \begin{align*}\lim_{n\to \infty} \frac{1}{n}\log \mu\left(\left| \sum_{j=0}^{n-1}\phi\circ f^{jl} -n\int \phi d\mu \right| \geq \varepsilon\right)=-c(\varepsilon).\end{align*} $$
Remark 9.4. From the proof, the physical measure coincides with the limit of
 $$ \begin{align*}\lim_{n\to \infty}\frac1n \sum_{i=0}^{n-1}\operatorname{vol}_{f^i(\Lambda)},\end{align*} $$
$$ \begin{align*}\lim_{n\to \infty}\frac1n \sum_{i=0}^{n-1}\operatorname{vol}_{f^i(\Lambda)},\end{align*} $$
where
![]() $\Lambda \subset D$
is some subset with positive volume.
$\Lambda \subset D$
is some subset with positive volume.
With this notation, we are ready to prove Theorem G and Corollary H. It suffices for us prove only for physical measures
![]() $\mu _1$
: Take
$\mu _1$
: Take
![]() $D=W^u_r(p_1)$
. We will show in the end of this section that D satisfies the following property.
$D=W^u_r(p_1)$
. We will show in the end of this section that D satisfies the following property.
Lemma 9.5. There are constants
![]() $0<\tau \leq 1$
and
$0<\tau \leq 1$
and
![]() $c>0$
such that
$c>0$
such that
 $$ \begin{align*}\operatorname{vol}_D({\mathcal E}_{b_0}>n)=O(e^{-cn^\tau}).\end{align*} $$
$$ \begin{align*}\operatorname{vol}_D({\mathcal E}_{b_0}>n)=O(e^{-cn^\tau}).\end{align*} $$
Then we may apply Proposition 9.2 and Proposition 9.3 on some physical measure
![]() $\mu $
for some power
$\mu $
for some power
![]() $f^l$
of f. Moreover, by Proposition 6.9, Lebesgue almost every point belongs to the basin of
$f^l$
of f. Moreover, by Proposition 6.9, Lebesgue almost every point belongs to the basin of
![]() $\mu _1$
, and thus by Remark 9.4, for any subset
$\mu _1$
, and thus by Remark 9.4, for any subset
![]() $\Lambda \subset D$
with positive volume, we have
$\Lambda \subset D$
with positive volume, we have
 $$ \begin{align*}\lim_{n\to \infty} \sum_{i=0}^{n-1}\operatorname{vol}_{f^i(\Lambda)}=\mu_1.\end{align*} $$
$$ \begin{align*}\lim_{n\to \infty} \sum_{i=0}^{n-1}\operatorname{vol}_{f^i(\Lambda)}=\mu_1.\end{align*} $$
Thus, we conclude the proof of Theorem G and Corollary H.
It remains to show the proof of Lemma 9.5.
Proof. We need the following result, which generalises [Reference Dolgopyat24, Theorem 1].
Proposition 9.6 ([Reference Crovisier, Yang and Zhang23, Theorem D’])
Let
![]() ${\mathcal B}$
be any foliation box for the unstable foliation
${\mathcal B}$
be any foliation box for the unstable foliation
![]() ${\mathcal F}^u$
of f, A be any H
${\mathcal F}^u$
of f, A be any H
![]() $\ddot {o}$
lder function and
$\ddot {o}$
lder function and
 $I_A=\{\int A d\mu \}_{\mu \in \mbox { Gibbs}^u(g)}$
. Then
$I_A=\{\int A d\mu \}_{\mu \in \mbox { Gibbs}^u(g)}$
. Then
![]() $\forall \varepsilon>0$
,
$\forall \varepsilon>0$
,
![]() $\exists \delta>0$
,
$\exists \delta>0$
,
![]() $C>0$
such that for any plaque L of
$C>0$
such that for any plaque L of
![]() ${\mathcal F}^u\mid {\mathcal B}$
,
${\mathcal F}^u\mid {\mathcal B}$
,
 $$ \begin{align*}\operatorname{vol}_L\left(\left\{x:d\left(\frac{1}{n}S_n(A)(x),I_A\right)\geq \varepsilon\right\}\right)\leq C e^{-\delta n},\end{align*} $$
$$ \begin{align*}\operatorname{vol}_L\left(\left\{x:d\left(\frac{1}{n}S_n(A)(x),I_A\right)\geq \varepsilon\right\}\right)\leq C e^{-\delta n},\end{align*} $$
where
![]() $S_n(A)=\sum _{i=1}^{n}A(f^i(x))$
.
$S_n(A)=\sum _{i=1}^{n}A(f^i(x))$
.
Fix
![]() ${\mathcal B}$
to be any foliation box for the unstable foliation
${\mathcal B}$
to be any foliation box for the unstable foliation
![]() ${\mathcal F}^u$
such that
${\mathcal F}^u$
such that
![]() $D\subset {\mathcal B}$
. By (28), for
$D\subset {\mathcal B}$
. By (28), for
 $A=\log \|Df^{-1}\mid _{E^{cu}(x)}\|$
,
$A=\log \|Df^{-1}\mid _{E^{cu}(x)}\|$
,
![]() $I_A\subset (\infty , -b_0)$
. Applying the previous proposition with
$I_A\subset (\infty , -b_0)$
. Applying the previous proposition with
![]() $\varepsilon = b_0/2$
, we obtain
$\varepsilon = b_0/2$
, we obtain
![]() $C>0, \delta >0$
such that for any plaque L of
$C>0, \delta >0$
such that for any plaque L of
![]() ${\mathcal F}^u\mid {\mathcal B}$
,
${\mathcal F}^u\mid {\mathcal B}$
,
 $$ \begin{align} \operatorname{vol}_L\left(\left\{x: \frac{1}{n} \sum_{i=1}^n \log \|Df^{-1}\mid_{E^{cu}(f^i(x))}\|\geq -b_0/2\right\}\right)\leq C e^{-\delta n}. \end{align} $$
$$ \begin{align} \operatorname{vol}_L\left(\left\{x: \frac{1}{n} \sum_{i=1}^n \log \|Df^{-1}\mid_{E^{cu}(f^i(x))}\|\geq -b_0/2\right\}\right)\leq C e^{-\delta n}. \end{align} $$
Note that
 $$ \begin{align*}\{x:{\mathcal E}_{b_0}>n\}\subset \bigcup_{m\geq n} \left\{x: \frac{1}{n} \sum_{i=1}^n \log \|Df^{-1}\mid_{E^{cu}(f^i(x))}\|\geq -b_0/2\right\}.\end{align*} $$
$$ \begin{align*}\{x:{\mathcal E}_{b_0}>n\}\subset \bigcup_{m\geq n} \left\{x: \frac{1}{n} \sum_{i=1}^n \log \|Df^{-1}\mid_{E^{cu}(f^i(x))}\|\geq -b_0/2\right\}.\end{align*} $$
Thus, by (31), there are
![]() $C^\prime $
and
$C^\prime $
and
![]() $\delta ^\prime $
such that for any unstable plaque
$\delta ^\prime $
such that for any unstable plaque
![]() $L\subset {\mathcal B}$
,
$L\subset {\mathcal B}$
,
 $$ \begin{align*}\operatorname{vol}_L({\mathcal E}_{b_0}>n)\leq C^\prime e^{-\delta^\prime n}.\end{align*} $$
$$ \begin{align*}\operatorname{vol}_L({\mathcal E}_{b_0}>n)\leq C^\prime e^{-\delta^\prime n}.\end{align*} $$
Because D is the local unstable manifold at
![]() $p_1$
,
$p_1$
,
![]() ${\mathcal F}^u$
also induces a subfoliation of D (note that
${\mathcal F}^u$
also induces a subfoliation of D (note that
![]() $\dim D = \dim E^{cu}$
). It is well known that
$\dim D = \dim E^{cu}$
). It is well known that
![]() ${\mathcal F}^u$
is absolutely continuous, and so is the subfoliation of D. Then the previous inequality implies that there is
${\mathcal F}^u$
is absolutely continuous, and so is the subfoliation of D. Then the previous inequality implies that there is
![]() $C_0>0$
such that
$C_0>0$
such that
 $$ \begin{align} \operatorname{vol}_D({\mathcal E}_{b_0}>n)\leq C_0 e^{-\delta^\prime n}. \end{align} $$
$$ \begin{align} \operatorname{vol}_D({\mathcal E}_{b_0}>n)\leq C_0 e^{-\delta^\prime n}. \end{align} $$
Then Lemma 9.5 follows with
![]() $\tau =1$
. □
$\tau =1$
. □
Acknowledgement
The author thanks Fan Yang and Ali Tahzibi for reading this article carefully and giving many important suggestions. The author is also grateful to the anonymous referees for their careful reading and helpful comments, which significantly improved the presentation of the current article. J.Y. is partially supported by NNSF 11871487, CNPq, FAPERJ and PRONEX.