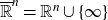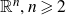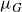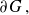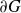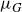1. Introduction
Conformal invariance is one of the key notions in the geometric theory of conformal and quasiconformal maps both in the plane
![]() ${\mathbb{R}}^2 = {\mathbb{C}}$
and in the Euclidean space
${\mathbb{R}}^2 = {\mathbb{C}}$
and in the Euclidean space
![]() ${\mathbb{R}}^n, n\geqslant3\,.$
Most clearly this is visible in the study of metrics: the uniformisation theorem [
Reference Beardon and Minda6
] and the hyperbolic (Poincaré) metric of the unit disk in
${\mathbb{R}}^n, n\geqslant3\,.$
Most clearly this is visible in the study of metrics: the uniformisation theorem [
Reference Beardon and Minda6
] and the hyperbolic (Poincaré) metric of the unit disk in
![]() ${\mathbb{C}}$
provide a way to define the hyperbolic metric in any plane domain G with
${\mathbb{C}}$
provide a way to define the hyperbolic metric in any plane domain G with
![]() $\mathrm{card\,}({\mathbb{C}}\setminus G)\geqslant 2.$
This method fails for
$\mathrm{card\,}({\mathbb{C}}\setminus G)\geqslant 2.$
This method fails for
![]() $n\geqslant 3 $
because by Liouville’s theorem [
Reference Gehring, Martin and Palka19, Reference Reshetnyak45
] conformal maps in dimensions
$n\geqslant 3 $
because by Liouville’s theorem [
Reference Gehring, Martin and Palka19, Reference Reshetnyak45
] conformal maps in dimensions
![]() $n\geqslant 3 $
are Möbius transformations. A widely studied natural question is whether some other methods would work and whether there are counterparts of the hyperbolic metric in subdomains G of
$n\geqslant 3 $
are Möbius transformations. A widely studied natural question is whether some other methods would work and whether there are counterparts of the hyperbolic metric in subdomains G of
![]() ${\mathbb{R}}^n$
and what sort of invariance or quasi-invariance properties, if any, such metrics might have in higher dimensions
${\mathbb{R}}^n$
and what sort of invariance or quasi-invariance properties, if any, such metrics might have in higher dimensions
![]() $n\geqslant 3.$
From the vast literature we mention A. F. Beardon [
Reference Beardon4, Reference Beardon5
], J. Ferrand [
Reference Ferrand12, Reference Ferrand13, Reference Ferrand14, Reference Ferrand, Martin and Vuorinen15, Reference Lelong–Ferrand31
], F. W. Gehring [
Reference Gehring and Hag18, Reference Gehring and Osgood20, Reference Gehring and Palka21
], D.A. Herron [
Reference Buckley and Herron11, Reference Herron24, Reference Herron, Ibragimov and Minda25, Reference Herron and Julian26, Reference Herron, Ma and Minda27
], M. Vuorinen [
Reference Hariri, Klén and Vuorinen23, Reference Vuorinen53, Reference Vuorinen55
]. The recent extensive research on metrics in geometric function theory has many faces: two examples are the monograph [
Reference Jarnicki and Pflug28
] of M. Jarnicki and P. Pflug which provides an encyclopedic treatise on invariant metrics of complex manifolds and the monograph of A. Papadopoulos which lists twelve metrics recurrent in geometric function theory [
40
, pp.42–48].
$n\geqslant 3.$
From the vast literature we mention A. F. Beardon [
Reference Beardon4, Reference Beardon5
], J. Ferrand [
Reference Ferrand12, Reference Ferrand13, Reference Ferrand14, Reference Ferrand, Martin and Vuorinen15, Reference Lelong–Ferrand31
], F. W. Gehring [
Reference Gehring and Hag18, Reference Gehring and Osgood20, Reference Gehring and Palka21
], D.A. Herron [
Reference Buckley and Herron11, Reference Herron24, Reference Herron, Ibragimov and Minda25, Reference Herron and Julian26, Reference Herron, Ma and Minda27
], M. Vuorinen [
Reference Hariri, Klén and Vuorinen23, Reference Vuorinen53, Reference Vuorinen55
]. The recent extensive research on metrics in geometric function theory has many faces: two examples are the monograph [
Reference Jarnicki and Pflug28
] of M. Jarnicki and P. Pflug which provides an encyclopedic treatise on invariant metrics of complex manifolds and the monograph of A. Papadopoulos which lists twelve metrics recurrent in geometric function theory [
40
, pp.42–48].
Our main aim is to study one of these metrics, the modulus metric of a domain
![]() $G\subset \overline{{\mathbb{R}}}^n = {\mathbb{R}}^n \cup \{\infty\}, n\geqslant 2\,,$
denoted by
$G\subset \overline{{\mathbb{R}}}^n = {\mathbb{R}}^n \cup \{\infty\}, n\geqslant 2\,,$
denoted by
![]() $\mu_G(x,y), x,y \in G\,,$
see Sections 3 and 4 for definitions. In the special case of the unit ball, the modulus metric
$\mu_G(x,y), x,y \in G\,,$
see Sections 3 and 4 for definitions. In the special case of the unit ball, the modulus metric
![]() $\mu_{{\mathbb{B}}^n}(x,y)$
has an explicit formula in terms of the hyperbolic metric of the unit ball
$\mu_{{\mathbb{B}}^n}(x,y)$
has an explicit formula in terms of the hyperbolic metric of the unit ball
![]() ${\mathbb{B}}^n$
; the case of
${\mathbb{B}}^n$
; the case of
![]() $\mu_{{\mathbb{B}}^2}(x,y)$
has already been studied by H. Grötzsch [
Reference Ahlfors1
, p.72]. The conformal invariant
$\mu_{{\mathbb{B}}^2}(x,y)$
has already been studied by H. Grötzsch [
Reference Ahlfors1
, p.72]. The conformal invariant
![]() $\mu_G(x,y)$
has found numerous applications [
Reference Hariri, Klén and Vuorinen23, Reference Vuorinen55
], but still many fundamental questions remain open. Very recently a problem due to J. Ferrand [
Reference Ferrand, Martin and Vuorinen15
], [
Reference Hariri, Klén and Vuorinen23
, pp.294–295] was solved as follows.
$\mu_G(x,y)$
has found numerous applications [
Reference Hariri, Klén and Vuorinen23, Reference Vuorinen55
], but still many fundamental questions remain open. Very recently a problem due to J. Ferrand [
Reference Ferrand, Martin and Vuorinen15
], [
Reference Hariri, Klén and Vuorinen23
, pp.294–295] was solved as follows.
Theorem A ([
Reference Betsakos and Pouliasis8, Reference Pouliasis and Yu44, Reference Zhang56
]). A homeomorphism
![]() $f\;:\;G \to G'\,,$
where G and G
′ are domains in
$f\;:\;G \to G'\,,$
where G and G
′ are domains in
![]() ${\mathbb{R}}^n, n\geqslant 2,$
is an isometry between
${\mathbb{R}}^n, n\geqslant 2,$
is an isometry between
![]() $(G,\mu_G)$
and
$(G,\mu_G)$
and
![]() $(G',\mu_{G'})$
if and only if f is conformal.
$(G',\mu_{G'})$
if and only if f is conformal.
As pointed out above,
![]() $\mu_{{\mathbb{B}}^n}(x,y)$
is closely related to the hyperbolic metric of
$\mu_{{\mathbb{B}}^n}(x,y)$
is closely related to the hyperbolic metric of
![]() ${\mathbb{B}}^n.$
We next study conditions on the domain G under which
${\mathbb{B}}^n.$
We next study conditions on the domain G under which
![]() $\mu_G$
defines an intrinsic metric of G having properties similar to the hyperbolic metric. It turns out that the geometry of this metric significantly depends on the “potential theoretic thickness” of the boundary, measured in terms of the conformal capacity. As is well known, the conformal capacity is very closely connected with the moduli of curve families [
Reference Gehring, Martin and Palka19
, theorem 5·2·3, p.164], [
Reference Hariri, Klén and Vuorinen23
, theorem 9·6, p.152].
$\mu_G$
defines an intrinsic metric of G having properties similar to the hyperbolic metric. It turns out that the geometry of this metric significantly depends on the “potential theoretic thickness” of the boundary, measured in terms of the conformal capacity. As is well known, the conformal capacity is very closely connected with the moduli of curve families [
Reference Gehring, Martin and Palka19
, theorem 5·2·3, p.164], [
Reference Hariri, Klén and Vuorinen23
, theorem 9·6, p.152].
If the boundary
![]() $\partial G$
is polar, i.e. if it has null conformal capacity
$\partial G$
is polar, i.e. if it has null conformal capacity
![]() $\mathrm{cap}\,(\partial G) = 0$
, then
$\mathrm{cap}\,(\partial G) = 0$
, then
![]() $\mu_G \equiv 0$
; otherwise
$\mu_G \equiv 0$
; otherwise
![]() $\mu_G$
is a conformally invariant metric. Even if
$\mu_G$
is a conformally invariant metric. Even if
![]() $\mathrm{cap}\,(\partial G)>0,$
the modulus metric
$\mathrm{cap}\,(\partial G)>0,$
the modulus metric
![]() $\mu_G$
might not reflect the intrinsic geometry of G very precisely. For instance, a polar compact set
$\mu_G$
might not reflect the intrinsic geometry of G very precisely. For instance, a polar compact set
![]() $N \subset G$
is invisible for the modulus metric in the sense that if
$N \subset G$
is invisible for the modulus metric in the sense that if
![]() $\mathrm{cap}\, N=0,$
then
$\mathrm{cap}\, N=0,$
then
![]() $\mu_G(x,y)=\mu_{G\setminus N}(x,y)$
for
$\mu_G(x,y)=\mu_{G\setminus N}(x,y)$
for
![]() $x,y\in G\setminus N.$
Therefore, it is meaningful to look for a condition on G so as to guarantee that
$x,y\in G\setminus N.$
Therefore, it is meaningful to look for a condition on G so as to guarantee that
![]() $\mu_G$
is a complete metric. We remark that a similar problem for the Kobayashi metric on domains in
$\mu_G$
is a complete metric. We remark that a similar problem for the Kobayashi metric on domains in
![]() ${\mathbb{C}}^n$
is rather difficult (see, e.g., [
Reference Gaussier17, Reference Pflug41
]).
${\mathbb{C}}^n$
is rather difficult (see, e.g., [
Reference Gaussier17, Reference Pflug41
]).
In connection with this completeness property, we recall another notion on metric spaces. A metric space (X, m) is called proper [
Reference Bridson and Haefliger10
] if the closed metric ball
![]() $\{x\in X\;:\; m(x,a)\leqslant r\}$
is compact whenever
$\{x\in X\;:\; m(x,a)\leqslant r\}$
is compact whenever
![]() $a\in X$
and
$a\in X$
and
![]() $r>0.$
This is equivalent to say that the open metric ball
$r>0.$
This is equivalent to say that the open metric ball
![]() $\{x\in X\;:\; m(x,a)<r\}$
is relatively compact for
$\{x\in X\;:\; m(x,a)<r\}$
is relatively compact for
![]() $a\in X$
and
$a\in X$
and
![]() $r>0.$
Note that a proper metric space is locally compact and complete. However, the converse is not true in general. (Consider, e.g.,
$r>0.$
Note that a proper metric space is locally compact and complete. However, the converse is not true in general. (Consider, e.g.,
![]() $(X,m/(1+m))$
for a locally compact but non-compact complete metric space (X, m) such as
$(X,m/(1+m))$
for a locally compact but non-compact complete metric space (X, m) such as
![]() ${\mathbb{R}}^n$
with the Euclidean metric.)
${\mathbb{R}}^n$
with the Euclidean metric.)
Our first result characterizes domains G for which the metrics
![]() $\mu_G$
are complete.
$\mu_G$
are complete.
Theorem 1·1. Let G be a domain in
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $\partial G\ne\emptyset.$
Then the following conditions are equivalent:
$\partial G\ne\emptyset.$
Then the following conditions are equivalent:
-
(i)
 $(G,\mu_G)$
is a proper metric space;
$(G,\mu_G)$
is a proper metric space; -
(ii)
 $(G,\mu_G)$
is a complete metric space;
$(G,\mu_G)$
is a complete metric space; -
(iii) G is an M-domain. That is to say, each boundary point x of G satisfies the M-condition.
The M-condition for
![]() $x\in\partial G$
was introduced by O. Martio [
Reference Martio35
]Footnote
1
in his study of potential theoretic regularity of the domain. If this condition holds for all
$x\in\partial G$
was introduced by O. Martio [
Reference Martio35
]Footnote
1
in his study of potential theoretic regularity of the domain. If this condition holds for all
![]() $x\in\partial G,$
the complement
$x\in\partial G,$
the complement
![]() ${\overline{\mathbb R}^n}\setminus G$
of G is “thick enough” at every point of
${\overline{\mathbb R}^n}\setminus G$
of G is “thick enough” at every point of
![]() $\partial G\,$
[
Reference Martio35, Reference Martio and Sarvas37
]. See Section 3 for definitions of those concepts and related properties.
$\partial G\,$
[
Reference Martio35, Reference Martio and Sarvas37
]. See Section 3 for definitions of those concepts and related properties.
Our second result refines further the case when
![]() $\mu_G$
is complete. We assume now that the boundary of a domain is uniformly perfect in the sense of Ch. Pommerenke [
Reference Pommerenke42, Reference Pommerenke43
] — in this case the M-condition is valid, see Corollary 1·5. This notion was introduced by A. F. Beardon and Ch. Pommerenke [
Reference Beardon and Pommerenke7
] for unbounded closed sets in
$\mu_G$
is complete. We assume now that the boundary of a domain is uniformly perfect in the sense of Ch. Pommerenke [
Reference Pommerenke42, Reference Pommerenke43
] — in this case the M-condition is valid, see Corollary 1·5. This notion was introduced by A. F. Beardon and Ch. Pommerenke [
Reference Beardon and Pommerenke7
] for unbounded closed sets in
![]() ${\mathbb{C}}$
, but about the same time an equivalent concept was studied by P. Tukia and J. Väisälä [
Reference Tukia and Väisälä51
] under the name “homogeneously dense sets” in the setting of general metric spaces. By definition, a compact set E in
${\mathbb{C}}$
, but about the same time an equivalent concept was studied by P. Tukia and J. Väisälä [
Reference Tukia and Väisälä51
] under the name “homogeneously dense sets” in the setting of general metric spaces. By definition, a compact set E in
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $\mathrm{card\,}(E)\geqslant 2$
is called uniformly perfect if there exists a constant
$\mathrm{card\,}(E)\geqslant 2$
is called uniformly perfect if there exists a constant
![]() $c\in(0,1)$
such that E meets the closed annulus
$c\in(0,1)$
such that E meets the closed annulus
![]() $cr\leqslant |x-a|\leqslant r$
whenever
$cr\leqslant |x-a|\leqslant r$
whenever
![]() $a\in E\setminus\{\infty\}$
and
$a\in E\setminus\{\infty\}$
and
![]() $r\in(0,\mathrm{diam}(E)),$
where
$r\in(0,\mathrm{diam}(E)),$
where
![]() $\mathrm{diam}(E)$
denotes the Euclidean diameter of E and set
$\mathrm{diam}(E)$
denotes the Euclidean diameter of E and set
![]() $\mathrm{diam}(E)=+\infty$
when
$\mathrm{diam}(E)=+\infty$
when
![]() $\infty\in E.$
In the planar case when
$\infty\in E.$
In the planar case when
![]() $G\subset{{\mathbb{R}}^2}={\mathbb{C}},$
A. F. Beardon and Ch. Pommerenke [
Reference Beardon and Pommerenke7
] gave another characterisation in terms of the hyperbolic and quasihyperbolic metrics
$G\subset{{\mathbb{R}}^2}={\mathbb{C}},$
A. F. Beardon and Ch. Pommerenke [
Reference Beardon and Pommerenke7
] gave another characterisation in terms of the hyperbolic and quasihyperbolic metrics
![]() $h_G(x,y)$
and
$h_G(x,y)$
and
![]() $k_G(x,y)\,,$
resp. (see Section 2), and proved that
$k_G(x,y)\,,$
resp. (see Section 2), and proved that
![]() $\partial G$
is uniformly perfect if and only if there is a constant
$\partial G$
is uniformly perfect if and only if there is a constant
![]() $b>0$
such that
$b>0$
such that
Here we give an alternative characterisation of uniform perfectness of
![]() $\partial G$
in terms of intrinsic metrics which is valid in higher dimensions as well and, moreover, is applicable to subsets of the Möbius space. This characterisation requires that the modulus metric be minorised by a Möbius invariant metric
$\partial G$
in terms of intrinsic metrics which is valid in higher dimensions as well and, moreover, is applicable to subsets of the Möbius space. This characterisation requires that the modulus metric be minorised by a Möbius invariant metric
![]() $\delta_G\,,$
defined in terms of the absolute ratio 2.10 for all domains
$\delta_G\,,$
defined in terms of the absolute ratio 2.10 for all domains
![]() $G \subset \overline{{\mathbb{R}}}^n$
with
$G \subset \overline{{\mathbb{R}}}^n$
with
![]() ${\textrm{ card}} (\partial G)\geqslant 2\,.$
This metric was first introduced in [
Reference Vuorinen55
, pp.115–116] and, later on, studied by P. Seittenranta in his PhD thesis [
Reference Seittenranta47
] where he also suggested the name “Möbius metric”.
${\textrm{ card}} (\partial G)\geqslant 2\,.$
This metric was first introduced in [
Reference Vuorinen55
, pp.115–116] and, later on, studied by P. Seittenranta in his PhD thesis [
Reference Seittenranta47
] where he also suggested the name “Möbius metric”.
Theorem 1·2. Let
![]() $G \subset {\overline{\mathbb R}^n}$
be a domain with
$G \subset {\overline{\mathbb R}^n}$
be a domain with
![]() $\mathrm{card\,}(\partial G)\geqslant 2.$
Then
$\mathrm{card\,}(\partial G)\geqslant 2.$
Then
![]() $\partial G$
is uniformly perfect if and only if there exists a constant
$\partial G$
is uniformly perfect if and only if there exists a constant
![]() $b>0$
such that for all
$b>0$
such that for all
![]() $x,y\in G$
the inequality
$x,y\in G$
the inequality
holds, where
![]() $\mu_G$
is the modulus metric and
$\mu_G$
is the modulus metric and
![]() $\delta_G$
is the Möbius metric.
$\delta_G$
is the Möbius metric.
For a proper subdomain G of
![]() ${{\mathbb{R}}^n},$
the lower bound 1·3 can be expressed in terms of a similarity invariant metric, the distance-ratio metric of G as follows. For
${{\mathbb{R}}^n},$
the lower bound 1·3 can be expressed in terms of a similarity invariant metric, the distance-ratio metric of G as follows. For
![]() $x,y \in G$
define
$x,y \in G$
define
which is a metric on G, where
![]() $d_G(x)$
denotes the Euclidean distance from x to the boundary
$d_G(x)$
denotes the Euclidean distance from x to the boundary
![]() $\partial G$
[
Reference Hariri, Klén and Vuorinen23
, lemma 4·6, p.59]. When
$\partial G$
[
Reference Hariri, Klén and Vuorinen23
, lemma 4·6, p.59]. When
![]() $G\subset{\mathbb{R}}^n,$
the above condition (1·3) is equivalent to the requirement that for some constant
$G\subset{\mathbb{R}}^n,$
the above condition (1·3) is equivalent to the requirement that for some constant
![]() $b'>0$
$b'>0$
for all
![]() $x,y \in G\,.$
Since
$x,y \in G\,.$
Since
![]() $(G,\delta_G)$
is a proper metric space (see Lemma 2·14 below), we have the following result as a corollary of Theorems 1·1 and 1·2.
$(G,\delta_G)$
is a proper metric space (see Lemma 2·14 below), we have the following result as a corollary of Theorems 1·1 and 1·2.
Corollary 1·5. Let
![]() $G \subset {\overline{\mathbb R}^n}$
be a domain with
$G \subset {\overline{\mathbb R}^n}$
be a domain with
![]() $\mathrm{card\,}(\partial G)\geqslant 2.$
If
$\mathrm{card\,}(\partial G)\geqslant 2.$
If
![]() $\partial G$
is uniformly perfect, then G is an M-domain.
$\partial G$
is uniformly perfect, then G is an M-domain.
The converse is not true in general. A counterexample will be given in Section 3.
The proof of Theorem 1·2 is based, in part, on a potential theoretic thickness characterisation of uniform perfectness [ Reference Järvi and Vuorinen29, Reference Vuorinen54 ]. Many authors have contributed to the research of uniformly perfect sets and related thickness conditions, see [ Reference Avkhadiev and Wirths3, Reference Bridgeman and Canary9 ], [ Reference Garnett and Marshall16 , pp.343–345], [ Reference Golberg, Sugawa and Vuorinen22, Reference Keen and Lakic30, Reference Lewis32, Reference Ma and Minda33, Reference Marden and Markovic34 ] and the survey of T. Sugawa [ Reference Sugawa48 ] on uniform perfectness.
Uniform domains play an important role in geometric function theory. See [ Reference Gehring and Osgood20 ] and the recent monograph [ Reference Gehring and Hag18 ] for details. For convenience of the reader, we will provide a brief account on this notion in the next section.
Theorem 1·6. Suppose that
![]() $G \subset {\overline{\mathbb R}^n}$
is a uniform domain. Then there exist constants
$G \subset {\overline{\mathbb R}^n}$
is a uniform domain. Then there exist constants
![]() $d_1, d_2$
depending only on n and the uniformity parameters such that
$d_1, d_2$
depending only on n and the uniformity parameters such that
Conversely, suppose that a domain G in
![]() ${\overline{\mathbb R}^2}$
with continuum as its boundary satisfies (1·7). Then G is uniform.
${\overline{\mathbb R}^2}$
with continuum as its boundary satisfies (1·7). Then G is uniform.
Note that the boundary of a domain G in
![]() ${\overline{\mathbb R}^2}={\overline{\mathbb{C}}}$
is a continuum; that is, a non-degenerate connected compact set, if and only if G is a simply connected hyperbolic domain. It is known that such a domain G is uniform precisely when G is a quasidisk, that is to say, G is the image of the unit disk
${\overline{\mathbb R}^2}={\overline{\mathbb{C}}}$
is a continuum; that is, a non-degenerate connected compact set, if and only if G is a simply connected hyperbolic domain. It is known that such a domain G is uniform precisely when G is a quasidisk, that is to say, G is the image of the unit disk
![]() $\mathbb{B}^2$
under a quasiconformal homeomorphism of
$\mathbb{B}^2$
under a quasiconformal homeomorphism of
![]() ${\overline{\mathbb{C}}}$
onto itself [
Reference Gehring and Hag18
]. Therefore, as a corollary, we have the following characterisation of quasidisks.
${\overline{\mathbb{C}}}$
onto itself [
Reference Gehring and Hag18
]. Therefore, as a corollary, we have the following characterisation of quasidisks.
Corollary 1·8. Let G be a simply connected domain in the Riemann sphere
![]() ${\overline{\mathbb{C}}}$
with
${\overline{\mathbb{C}}}$
with
![]() $\mathrm{card\,}({\overline{\mathbb{C}}}\setminus G)\geqslant 2.$
Then G is a quasidisk if and only if there are positive constants
$\mathrm{card\,}({\overline{\mathbb{C}}}\setminus G)\geqslant 2.$
Then G is a quasidisk if and only if there are positive constants
![]() $d_1$
and
$d_1$
and
![]() $d_2$
such that the inequality
$d_2$
such that the inequality
holds for all
![]() $z,w\in G.$
$z,w\in G.$
In this corollary, we may replace the modulus metric
![]() $\mu_G$
by Ferrand’s modulus metric
$\mu_G$
by Ferrand’s modulus metric
![]() $\lambda_G^{-1}$
(see Lemma 4·5 below). We remark that for
$\lambda_G^{-1}$
(see Lemma 4·5 below). We remark that for
![]() $G\subset {\mathbb{C}}$
the above condition is also equivalent to the condition
$G\subset {\mathbb{C}}$
the above condition is also equivalent to the condition
As we will see later, the constant
![]() $d_2$
in Corollary 1·8 cannot be dropped. We expect that the converse would be true for all dimensions
$d_2$
in Corollary 1·8 cannot be dropped. We expect that the converse would be true for all dimensions
![]() $n\geqslant2$
under a weaker assumption on the boundary such as uniform perfectness of the boundary. These observations lead to the following problem.
$n\geqslant2$
under a weaker assumption on the boundary such as uniform perfectness of the boundary. These observations lead to the following problem.
1·9. Open problem
Let
![]() $n\geqslant 2.$
Find a geometric condition
$n\geqslant 2.$
Find a geometric condition
![]() $(\!*\!)$
on the boundaries of domains G in
$(\!*\!)$
on the boundaries of domains G in
![]() ${\overline{\mathbb R}^n}$
with the following property: If a domain G in
${\overline{\mathbb R}^n}$
with the following property: If a domain G in
![]() ${\overline{\mathbb R}^n}$
satisfies the condition
${\overline{\mathbb R}^n}$
satisfies the condition
![]() $(\!*\!)$
and the inequality (1·7) for some constants
$(\!*\!)$
and the inequality (1·7) for some constants
![]() $d_1>0$
and
$d_1>0$
and
![]() $d_2>0,$
then G is uniform.
$d_2>0,$
then G is uniform.
Finally, we consider the hyperbolic metric
![]() $h_G$
and the Ferrand metric
$h_G$
and the Ferrand metric
![]() $\sigma_G,$
see (2·7), in planar domains G. It is well known [
Reference Beardon and Pommerenke7
] that if
$\sigma_G,$
see (2·7), in planar domains G. It is well known [
Reference Beardon and Pommerenke7
] that if
![]() $\partial G$
is uniformly perfect, then the distances in the
$\partial G$
is uniformly perfect, then the distances in the
![]() $h_G$
metric are comparable to those in the quasihyperbolic metric
$h_G$
metric are comparable to those in the quasihyperbolic metric
![]() $k_G\,.$
Furthermore, this comparison property fails to hold if the domain G has isolated boundary points. Indeed, the following asymptotic formulae hold.
$k_G\,.$
Furthermore, this comparison property fails to hold if the domain G has isolated boundary points. Indeed, the following asymptotic formulae hold.
Lemma 1·10. Let G be a hyperbolic domain in
![]() ${\overline{\mathbb{C}}}$
and suppose that G has an isolated boundary point a with
${\overline{\mathbb{C}}}$
and suppose that G has an isolated boundary point a with
![]() $a\ne\infty.$
Then, for a fixed
$a\ne\infty.$
Then, for a fixed
![]() $z_0\in G,$
as
$z_0\in G,$
as
![]() $z\to a$
$z\to a$
while
It is a challenging task, studied in [
Reference Sugawa, Vuorinen and Zhang49, Reference Sugawa and Zhang50
], to give concrete bounds for the
![]() $h_G$
distances in domains G whose boundary consists only of isolated points. Since
$h_G$
distances in domains G whose boundary consists only of isolated points. Since
![]() $\log(1+x)$
is a subadditive function on
$\log(1+x)$
is a subadditive function on
![]() $0\leqslant x<+\infty,$
we can easily see that
$0\leqslant x<+\infty,$
we can easily see that
![]() $\log(1+m(x,y))$
is a distance function on X whenever m(x, y) is a distance function on X [
Reference Anderson, Vamanamurthy and Vuorinen2
, 7·42(1)]. In view of the above behaviour of the hyperbolic distance around isolated boundary points, we are led to the introduction of the logarithmic Möbius metric
$\log(1+m(x,y))$
is a distance function on X whenever m(x, y) is a distance function on X [
Reference Anderson, Vamanamurthy and Vuorinen2
, 7·42(1)]. In view of the above behaviour of the hyperbolic distance around isolated boundary points, we are led to the introduction of the logarithmic Möbius metric
![]() $\Delta_G(x,y)$
and the logarithmic Ferrand metric
$\Delta_G(x,y)$
and the logarithmic Ferrand metric
![]() $\Sigma_G(x,y)$
for a domain
$\Sigma_G(x,y)$
for a domain
![]() $G \subset {\overline{\mathbb R}^n} $
with
$G \subset {\overline{\mathbb R}^n} $
with
![]() $\mathrm{card\,}({\overline{\mathbb R}^n} \setminus G)\geqslant 2$
as follows:
$\mathrm{card\,}({\overline{\mathbb R}^n} \setminus G)\geqslant 2$
as follows:
Because
![]() $ \delta_G$
and
$ \delta_G$
and
![]() $\sigma_G$
are Möbius invariant,
$\sigma_G$
are Möbius invariant,
![]() $\Delta_G$
and
$\Delta_G$
and
![]() $\Sigma_G$
are Möbius invariant metrics, too. We also have
$\Sigma_G$
are Möbius invariant metrics, too. We also have
![]() $\Delta_G(x,y)\leqslant \Sigma_G(x,y)$
(see Lemma 2·12 below). When the complement of G in
$\Delta_G(x,y)\leqslant \Sigma_G(x,y)$
(see Lemma 2·12 below). When the complement of G in
![]() ${\overline{\mathbb{C}}}$
is a finite set, the hyperbolic distance
${\overline{\mathbb{C}}}$
is a finite set, the hyperbolic distance
![]() $h_G$
is majorised by
$h_G$
is majorised by
![]() $\Delta_G.$
However,
$\Delta_G.$
However,
![]() $h_G$
is never minorised by it for any domain with a puncture; namely, with an isolated boundary point. In fact, we prove a slightly stronger result.
$h_G$
is never minorised by it for any domain with a puncture; namely, with an isolated boundary point. In fact, we prove a slightly stronger result.
Theorem 1·15. Let A be a finite set in
![]() ${\overline{\mathbb{C}}}$
with
${\overline{\mathbb{C}}}$
with
![]() $\mathrm{card\,}(A)\geqslant 3$
and let
$\mathrm{card\,}(A)\geqslant 3$
and let
![]() $G={\overline{\mathbb{C}}}\setminus A.$
Then there exists a positive constant
$G={\overline{\mathbb{C}}}\setminus A.$
Then there exists a positive constant
![]() $c=c(A)$
such that for all
$c=c(A)$
such that for all
![]() $z,w \in G$
,
$z,w \in G$
,
On the other hand, for an arbitrary hyperbolic domain G in
![]() ${\overline{\mathbb{C}}}$
with a puncture, there is no non-decreasing function
${\overline{\mathbb{C}}}$
with a puncture, there is no non-decreasing function
![]() $\Phi\;:\;[0,+\infty)\to[0,+\infty)$
with
$\Phi\;:\;[0,+\infty)\to[0,+\infty)$
with
![]() $\Phi(t)>0$
for
$\Phi(t)>0$
for
![]() $t>0$
such that for all
$t>0$
such that for all
![]() $z,w\in G,$
$z,w\in G,$
All the results here will be proved in the subsequent sections. More precisely, this paper is organised as follows. Section 2 is devoted to definitions and basic properties of the metrics involved, with the exception of the modulus metric, which will be defined in Section 4. In Section 3, we recall the notion of the (conformal) modulus of a curve family and its fundamental properties. We also introduce the notion of M-domains defined in terms of the continuum criterion of Martio [ Reference Martio35 ]. The modulus metric is defined and related results are established in Section 4. We give some applications of the above results to quasiconformal or quasiregular mappings in Section 5. Theorem 1·15 is proved in the last section. Two open problems are pointed out, namely 3·12 and 4·15.
2. Preliminary notation and results
We follow standard notation. See e.g. [ Reference Beardon4, Reference Väisälä52 ] for more details. We write
 \begin{eqnarray*}B^{n} (x,r)&=\{z \in {{\mathbb{R}}^n}\;:\; |z-x| < r\}, \\{\overline{B}}^{n} (x,r) &=\{z \in {{\mathbb{R}}^n}\;:\; |z-x| \leqslant r\}, \\S^{n-1} (x,r)&=\{z \in {{\mathbb{R}}^n}\;:\; |z-x| = r\},\end{eqnarray*}
\begin{eqnarray*}B^{n} (x,r)&=\{z \in {{\mathbb{R}}^n}\;:\; |z-x| < r\}, \\{\overline{B}}^{n} (x,r) &=\{z \in {{\mathbb{R}}^n}\;:\; |z-x| \leqslant r\}, \\S^{n-1} (x,r)&=\{z \in {{\mathbb{R}}^n}\;:\; |z-x| = r\},\end{eqnarray*}
for balls and spheres, respectively, and
First we recall the definition of the chordal (spherical) distance q(x, y) on
![]() ${\overline{\mathbb R}^n}$
:
${\overline{\mathbb R}^n}$
:
 \begin{eqnarray}\left\{\begin{array}{ll}\displaystyle q(x,y)=\frac{|x-y|}{\sqrt{1+|x|^2}\sqrt{1+|y|^2}}\,, &\quad \;x,y \neq \infty\,, \\[5mm]\displaystyle q(x,\infty)=q(\infty,x)=\frac{1}{\sqrt{1+|x|^2}}\,, &\quad \;x \neq \infty\,.\end{array}\right.\end{eqnarray}
\begin{eqnarray}\left\{\begin{array}{ll}\displaystyle q(x,y)=\frac{|x-y|}{\sqrt{1+|x|^2}\sqrt{1+|y|^2}}\,, &\quad \;x,y \neq \infty\,, \\[5mm]\displaystyle q(x,\infty)=q(\infty,x)=\frac{1}{\sqrt{1+|x|^2}}\,, &\quad \;x \neq \infty\,.\end{array}\right.\end{eqnarray}
For distinct points
![]() $a, b, c, d \in {\overline{\mathbb R}^n}$
, the absolute (cross) ratio is defined by
$a, b, c, d \in {\overline{\mathbb R}^n}$
, the absolute (cross) ratio is defined by
When none of the points is
![]() $\infty,$
we see that
$\infty,$
we see that
2·2. Hyperbolic metric
The hyperbolic metrics
![]() $2|dx|/(1-|x|^2)$
on
$2|dx|/(1-|x|^2)$
on
![]() ${{\mathbb{B}}^n}$
and
${{\mathbb{B}}^n}$
and
![]() $|dx|/x_n$
on
$|dx|/x_n$
on
![]() ${{\mathbb{H}}^n}$
induce the hyperbolic distances
${{\mathbb{H}}^n}$
induce the hyperbolic distances
![]() $h_{{{\mathbb{B}}^n}}(x,y)$
and
$h_{{{\mathbb{B}}^n}}(x,y)$
and
![]() $h_{{{\mathbb{H}}^n}}(x,y)$
respectively. When
$h_{{{\mathbb{H}}^n}}(x,y)$
respectively. When
![]() $n=2,$
any domain G of
$n=2,$
any domain G of
![]() $\overline{\mathbb{R}}^2={\overline{\mathbb{C}}}$
with
$\overline{\mathbb{R}}^2={\overline{\mathbb{C}}}$
with
![]() $\mathrm{card\,}(\partial G)\geqslant 3$
is known to have a holomorphic universal covering projection p of the unit disk
$\mathrm{card\,}(\partial G)\geqslant 3$
is known to have a holomorphic universal covering projection p of the unit disk
![]() $\mathbb{B}^2$
onto G. Thus the hyperbolic distance
$\mathbb{B}^2$
onto G. Thus the hyperbolic distance
![]() $h_G$
of G can be defined by
$h_G$
of G can be defined by
where
![]() $\Gamma$
is the set of all rectifiable curves joining
$\Gamma$
is the set of all rectifiable curves joining
![]() $z_1$
and
$z_1$
and
![]() $z_2$
in G and
$z_2$
in G and
![]() $\rho_G(z)$
denotes the hyperbolic density determined by the relation
$\rho_G(z)$
denotes the hyperbolic density determined by the relation
![]() $2/(1-|\zeta|^2)=\rho(p(\zeta))|p'(\zeta)|,\; \zeta\in\mathbb{B}^2$
(see [
Reference Beardon and Minda6, Reference Keen and Lakic30
] for details).
$2/(1-|\zeta|^2)=\rho(p(\zeta))|p'(\zeta)|,\; \zeta\in\mathbb{B}^2$
(see [
Reference Beardon and Minda6, Reference Keen and Lakic30
] for details).
2·3. Quasihyperbolic metric
For higher dimensions, however, we cannot define hyperbolic metric for general domains. Quasihyperbolic metrics were introduced by F.W. Gehring and B. Palka [
Reference Gehring and Palka21
] as a substitute for it. For a domain
![]() $G\subsetneq {\mathbb{R}^n}$
, the quasihyperbolic metric
$G\subsetneq {\mathbb{R}^n}$
, the quasihyperbolic metric
![]() ${k}_G$
is defined by
${k}_G$
is defined by
where
![]() $\Gamma$
is the family of all rectifiable curves in G joining x and y. Note here that the inequality
$\Gamma$
is the family of all rectifiable curves in G joining x and y. Note here that the inequality
holds for an arbitrary
![]() $G\subsetneq {\mathbb{R}^n}$
and all
$G\subsetneq {\mathbb{R}^n}$
and all
![]() $x,y \in G$
[
Reference Gehring and Palka21
, lemma 2·1].
$x,y \in G$
[
Reference Gehring and Palka21
, lemma 2·1].
2·4. Uniform domains
A proper subdomain G of
![]() ${{\mathbb{R}}^n}$
is called uniform if there exist positive constants a and b with the following property [
Reference Gehring and Osgood20, Reference Martio and Sarvas37
]: for every pair of points
${{\mathbb{R}}^n}$
is called uniform if there exist positive constants a and b with the following property [
Reference Gehring and Osgood20, Reference Martio and Sarvas37
]: for every pair of points
![]() $x_1, x_2\in G,$
there is a rectifiable curve
$x_1, x_2\in G,$
there is a rectifiable curve
![]() $\gamma$
joining
$\gamma$
joining
![]() $x_1$
and
$x_1$
and
![]() $x_2$
in G in such a way that
$x_2$
in G in such a way that
![]() $\ell(\gamma)\leqslant a|x_1-x_2|$
and that
$\ell(\gamma)\leqslant a|x_1-x_2|$
and that
![]() $\min\{\ell(\gamma_1), \ell(\gamma_2)\}\leqslant b\, d_G(x)$
for each
$\min\{\ell(\gamma_1), \ell(\gamma_2)\}\leqslant b\, d_G(x)$
for each
![]() $x\in\gamma,$
where
$x\in\gamma,$
where
![]() $\gamma_j$
is the part of
$\gamma_j$
is the part of
![]() $\gamma$
between
$\gamma$
between
![]() $x_j$
and x for each
$x_j$
and x for each
![]() $j=1,2,$
$j=1,2,$
![]() $\ell(\gamma)$
denotes the length of the curve
$\ell(\gamma)$
denotes the length of the curve
![]() $\gamma$
and
$\gamma$
and
![]() $d_G(x)$
is the Euclidean distance to the boundary of G from x. The class of uniform domains can also be defined in terms of a comparison inequality between two metrics [
Reference Gehring and Osgood20, Reference Vuorinen55
]Footnote
2
a subdomain G of
$d_G(x)$
is the Euclidean distance to the boundary of G from x. The class of uniform domains can also be defined in terms of a comparison inequality between two metrics [
Reference Gehring and Osgood20, Reference Vuorinen55
]Footnote
2
a subdomain G of
![]() ${{\mathbb{R}}^n}$
with non-empty boundary is uniform if and only if there exists a constant
${{\mathbb{R}}^n}$
with non-empty boundary is uniform if and only if there exists a constant
![]() $c\geqslant 1$
such that
$c\geqslant 1$
such that
for all
![]() $x,y \in G$
, where
$x,y \in G$
, where
![]() $k_G$
and
$k_G$
and
![]() $j_G$
are the quasihyperbolic and distance-ratio metrics, respectively. Note that
$j_G$
are the quasihyperbolic and distance-ratio metrics, respectively. Note that
![]() $j_G(x,y)\leqslant k_G(x,y)$
holds for every domain G and all
$j_G(x,y)\leqslant k_G(x,y)$
holds for every domain G and all
![]() $x,y \in G$
by [
Reference Gehring and Palka21
, lemma 2·1].
$x,y \in G$
by [
Reference Gehring and Palka21
, lemma 2·1].
2·6. Ferrand’s metric
Since the definition of the quasihyperbolic metric relies on the Euclidean metric, it is not defined for all subdomains of the Möbius space and therefore it is not Möbius invariant. To overcome this shortcoming, Ferrand [
Reference Ferrand12
] modified the definition as follows. For a subdomain G of
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $\mathrm{card\,} (\partial G) \geqslant 2,$
define a density function
$\mathrm{card\,} (\partial G) \geqslant 2,$
define a density function
and the metric
![]() $\sigma_G$
in G,
$\sigma_G$
in G,
where
![]() $\Gamma$
is the family of all rectifiable curves in G joining x and y. The following result is due to Ferrand [
Reference Ferrand12
, p.122] and
$\Gamma$
is the family of all rectifiable curves in G joining x and y. The following result is due to Ferrand [
Reference Ferrand12
, p.122] and
![]() $\sigma_G(x,y)$
is now called the Ferrand metric [
Reference Hariri, Klén and Vuorinen23
, Chapter 5].
$\sigma_G(x,y)$
is now called the Ferrand metric [
Reference Hariri, Klén and Vuorinen23
, Chapter 5].
Lemma 2·8. Let
![]() $G \subset {{\overline{\mathbb R}^n}}$
be a domain with
$G \subset {{\overline{\mathbb R}^n}}$
be a domain with
![]() $\mathrm{card\,} (\partial G) \geqslant 2$
. The Ferrand metric
$\mathrm{card\,} (\partial G) \geqslant 2$
. The Ferrand metric
![]() $\sigma_{G}$
has the following properties:
$\sigma_{G}$
has the following properties:
-
(i)
 $\sigma_{G}$
is a Möbius invariant metric;
$\sigma_{G}$
is a Möbius invariant metric; -
(ii) When G is either
 ${{\mathbb{B}}^n}$
or
${{\mathbb{B}}^n}$
or
 ${{\mathbb{H}}^n},$
${{\mathbb{H}}^n},$
 $\sigma_{G}$
coincides with the hyperbolic metric
$\sigma_{G}$
coincides with the hyperbolic metric
 $h_{G}$
;
$h_{G}$
; -
(iii)
 ${k}_G \leqslant \sigma_G \leqslant 2 {k}_G$
for every domain
${k}_G \leqslant \sigma_G \leqslant 2 {k}_G$
for every domain
 $G \subsetneq {{\mathbb{R}}^n}$
.
$G \subsetneq {{\mathbb{R}}^n}$
.
We remark that the metric
![]() $\sigma_G$
was recently studied by D. A. Herron and P. K. Julian [
Reference Herron and Julian26
].
$\sigma_G$
was recently studied by D. A. Herron and P. K. Julian [
Reference Herron and Julian26
].
2·9. Möbius metric
Let
![]() $G \subset {\overline{\mathbb R}^n}$
be an open set with
$G \subset {\overline{\mathbb R}^n}$
be an open set with
![]() $\mathrm{card\,} (\partial G) \geqslant 2$
. The Möbius metric on G is defined as follows ([
Reference Vuorinen55
, pp.115–116], Seittenranta [
Reference Seittenranta47
]):
$\mathrm{card\,} (\partial G) \geqslant 2$
. The Möbius metric on G is defined as follows ([
Reference Vuorinen55
, pp.115–116], Seittenranta [
Reference Seittenranta47
]):
Note that the Möbius metric
![]() $\delta_{G}$
coincides with the hyperbolic metric
$\delta_{G}$
coincides with the hyperbolic metric
![]() $h_{G}$
when G is either
$h_{G}$
when G is either
![]() ${{\mathbb{B}}^n}$
or
${{\mathbb{B}}^n}$
or
![]() ${{\mathbb{H}}^n}$
[
Reference Vuorinen55
, lemma 8·39]. A metric very similar to the Möbius metric is the Apollonian metric of Beardon [
Reference Beardon5
].
${{\mathbb{H}}^n}$
[
Reference Vuorinen55
, lemma 8·39]. A metric very similar to the Möbius metric is the Apollonian metric of Beardon [
Reference Beardon5
].
2·11. Chordal distance-ratio metric
For a proper subdomain G of
![]() ${\overline{\mathbb R}^n}$
we define the chordal (spherical) distance-ratio metric by
${\overline{\mathbb R}^n}$
we define the chordal (spherical) distance-ratio metric by
 \[{\,\hat{j}}_G(x, y) = \log\left(1+\frac{q(x,y)}{\min\{{\hat{d}}_G(x), {\hat{d}}_G(y)\}}\right),\]
\[{\,\hat{j}}_G(x, y) = \log\left(1+\frac{q(x,y)}{\min\{{\hat{d}}_G(x), {\hat{d}}_G(y)\}}\right),\]
where
The triangle inequality for this metric follows from [ Reference Seittenranta47 , lemma 2·2].
The following results are due to Seittenranta [ Reference Seittenranta47 ].
Lemma 2·12. Let G be an open subset of
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $\mathrm{card\,} (\partial G) \geqslant 2\,.$
Then
$\mathrm{card\,} (\partial G) \geqslant 2\,.$
Then
![]() $\delta_{G}$
is a Möbius invariant metric and the following hold:
$\delta_{G}$
is a Möbius invariant metric and the following hold:
-
(i)
 $\delta_G \leqslant \sigma_G$
;
$\delta_G \leqslant \sigma_G$
; -
(ii)
 $\delta_G \leqslant 2{\,\hat{j}}_G$
$\delta_G \leqslant 2{\,\hat{j}}_G$
-
(iii) if
 $G \subsetneq {{\mathbb{R}}^n}\,,$
then
$G \subsetneq {{\mathbb{R}}^n}\,,$
then
 $j_G \leqslant \delta_G \leqslant 2 j_G.$
$j_G \leqslant \delta_G \leqslant 2 j_G.$
Proof. The fact that
![]() $\delta_G$
satisfies the triangle inequality, assertions (i) and (iii) follow from theorems 3·3, 3·4 and 3·12 in [
Reference Seittenranta47
], respectively. In order to show assertion (ii), we introduce the auxiliary metric
$\delta_G$
satisfies the triangle inequality, assertions (i) and (iii) follow from theorems 3·3, 3·4 and 3·12 in [
Reference Seittenranta47
], respectively. In order to show assertion (ii), we introduce the auxiliary metric
 \[ j^*_G(x,y)= \log\left(1+\frac{q(x,y)}{{\hat{d}}_G(x)}\right) +\log\left(1+\frac{q(x,y)}{{\hat{d}}_G(y)}\right).\]
\[ j^*_G(x,y)= \log\left(1+\frac{q(x,y)}{{\hat{d}}_G(x)}\right) +\log\left(1+\frac{q(x,y)}{{\hat{d}}_G(y)}\right).\]
Theorem 3·6 in [
Reference Seittenranta47
] means the inequality
![]() $\delta_G(x,y)\leqslant j^*_G(x,y)$
for
$\delta_G(x,y)\leqslant j^*_G(x,y)$
for
![]() $x,y\in G.$
It is easy to verify the inequalities
$x,y\in G.$
It is easy to verify the inequalities
![]() ${\,\hat{j}}_G(x,y)\leqslant j^*_G(x,y)\leqslant 2{\,\hat{j}}_G(x,y).$
Thus assertion (ii) now follows.
${\,\hat{j}}_G(x,y)\leqslant j^*_G(x,y)\leqslant 2{\,\hat{j}}_G(x,y).$
Thus assertion (ii) now follows.
As a consequence of the previous lemma, we have the following inequality, which will be used in the proof of Theorem 1·2 later:
We note that there is no constant
![]() $c=c(n)>0$
depending only on n such that
$c=c(n)>0$
depending only on n such that
![]() $j_G(x,y)\geqslant c{\,\hat{j}}_G(x,y),\; x,y\in G,$
holds for all proper subdomains G of
$j_G(x,y)\geqslant c{\,\hat{j}}_G(x,y),\; x,y\in G,$
holds for all proper subdomains G of
![]() ${\mathbb{R}}^n.$
The following result follows also from the previous lemma.
${\mathbb{R}}^n.$
The following result follows also from the previous lemma.
Lemma 2·14. The metric space
![]() $(G,\delta_G)$
is proper for
$(G,\delta_G)$
is proper for
![]() $G\subset{\overline{\mathbb R}^n}$
with
$G\subset{\overline{\mathbb R}^n}$
with
![]() $\mathrm{card\,}(\partial G)\geqslant 2.$
$\mathrm{card\,}(\partial G)\geqslant 2.$
Proof. By the Möbius invariance, we may assume that
![]() $G\subset{\mathbb{R}}^n.$
Then
$G\subset{\mathbb{R}}^n.$
Then
![]() $j_G\leqslant \delta_G$
by Lemma 2·12 (iii). Therefore, it is enough to show that
$j_G\leqslant \delta_G$
by Lemma 2·12 (iii). Therefore, it is enough to show that
![]() $(G,j_G)$
is proper in this case. For
$(G,j_G)$
is proper in this case. For
![]() $a\in G$
and
$a\in G$
and
![]() $0<r,$
we have to show that the set
$0<r,$
we have to show that the set
![]() $B=\{x\in G\;:\; j_G(x,a)<r\}$
is relatively compact. It is enough to show that B is bounded and
$B=\{x\in G\;:\; j_G(x,a)<r\}$
is relatively compact. It is enough to show that B is bounded and
![]() $\mathrm{dist}(B, \partial G)>0.$
The inequality
$\mathrm{dist}(B, \partial G)>0.$
The inequality
![]() $\log(1+|x-a|/d_G(a))\leqslant r$
holds for
$\log(1+|x-a|/d_G(a))\leqslant r$
holds for
![]() $x\in B$
and thus
$x\in B$
and thus
![]() $|x-a|\leqslant d_G(a)(e^r-1),$
which proves that B is bounded. On the other hand, the inequality
$|x-a|\leqslant d_G(a)(e^r-1),$
which proves that B is bounded. On the other hand, the inequality
![]() $\log(1+|x-a|/d_G(x))\leqslant r$
holds for
$\log(1+|x-a|/d_G(x))\leqslant r$
holds for
![]() $x\in B.$
Note that
$x\in B.$
Note that
![]() $d_G(x)\geqslant d_G(a)/2$
if
$d_G(x)\geqslant d_G(a)/2$
if
![]() $|x-a|\leqslant d_G(a)/2.$
For
$|x-a|\leqslant d_G(a)/2.$
For
![]() $x\in B$
with
$x\in B$
with
![]() $|x-a|\geqslant d_G(a)/2,$
we thus have
$|x-a|\geqslant d_G(a)/2,$
we thus have
![]() $d_G(x)\geqslant |x-a|/(e^r-1)\geqslant d_G(a)/(e^r-1).$
Therefore, we have shown
$d_G(x)\geqslant |x-a|/(e^r-1)\geqslant d_G(a)/(e^r-1).$
Therefore, we have shown
![]() $\mathrm{dist}(B,\partial G)\geqslant \min\{d_G(a)/2, d_G(a)/(e^r-1)\}>0$
as required.
$\mathrm{dist}(B,\partial G)\geqslant \min\{d_G(a)/2, d_G(a)/(e^r-1)\}>0$
as required.
2·15. Möbius uniform domains
We now consider a Möbius invariant characterisation of uniform domains. As we saw above, uniform domains in
![]() ${\mathbb{R}}^n$
are characterised by the condition (2·5) in terms of quasihyperbolic and distance-ratio metrics. These two metrics are invariant under similarity transformations but unfortunately not under Möbius transformations. To overcome this lack of invariance we apply Ferrand’s Möbius invariant metric
${\mathbb{R}}^n$
are characterised by the condition (2·5) in terms of quasihyperbolic and distance-ratio metrics. These two metrics are invariant under similarity transformations but unfortunately not under Möbius transformations. To overcome this lack of invariance we apply Ferrand’s Möbius invariant metric
![]() $\sigma_G$
and the Möbius metric
$\sigma_G$
and the Möbius metric
![]() $\delta_G\,.$
$\delta_G\,.$
Definition 2·16 ([
Reference Seittenranta47
]). We say that a domain
![]() $G \subset {\overline{\mathbb R}^n}\,$
with
$G \subset {\overline{\mathbb R}^n}\,$
with
![]() $\mathrm{card\,}({\overline{\mathbb R}^n}\setminus G)\geqslant 2$
is Möbius uniform, if there exists a constant
$\mathrm{card\,}({\overline{\mathbb R}^n}\setminus G)\geqslant 2$
is Möbius uniform, if there exists a constant
![]() $c\geqslant1$
such that for all
$c\geqslant1$
such that for all
![]() $x,y \in G$
$x,y \in G$
Note that Definition 2·5 only applies to subdomains of
![]() ${{\mathbb{R}}^n}$
whereas Definition 2.16 applies to subdomains of
${{\mathbb{R}}^n}$
whereas Definition 2.16 applies to subdomains of
![]() $ {\overline{\mathbb R}^n} .$
Indeed, we have the following result.
$ {\overline{\mathbb R}^n} .$
Indeed, we have the following result.
Proposition 2·17. Let
![]() $G \subset {{\mathbb{R}}^n}$
be a domain with
$G \subset {{\mathbb{R}}^n}$
be a domain with
![]() $\mathrm{card\,} (\partial G) \geqslant 2$
. Then G is Möbius uniform if and only if it is uniform in the sense of (2·5).
$\mathrm{card\,} (\partial G) \geqslant 2$
. Then G is Möbius uniform if and only if it is uniform in the sense of (2·5).
Proof. From Lemmas 2·8 and 2·12 it follows that if G is Möbius uniform with a constant
![]() $c_1$
, then it is uniform in the sense of (2·5) with the constant
$c_1$
, then it is uniform in the sense of (2·5) with the constant
![]() $2 c_1\,.$
Conversely, from Lemmas 2·8 and 2·12 it follows that if G is uniform in the sense of (2·5) with a constant
$2 c_1\,.$
Conversely, from Lemmas 2·8 and 2·12 it follows that if G is uniform in the sense of (2·5) with a constant
![]() $c_2$
, then it is Möbius uniform with the the constant
$c_2$
, then it is Möbius uniform with the the constant
![]() $2 c_2\,.$
$2 c_2\,.$
Therefore, we will use the shorter term “uniform” below for both uniform domains and Möbius uniform domains unless we want to emphasise which definition is intended.
We end this section with a proof of Lemma 1·10.
Proof of Lemma 1·10. By assumption, there is a number
![]() $r>0$
such that the punctured disk
$r>0$
such that the punctured disk
![]() $0<|z-a|<r$
is contained in G. It is enough to prove the assertions for
$0<|z-a|<r$
is contained in G. It is enough to prove the assertions for
![]() $a=0$
and
$a=0$
and
![]() $r=1.$
By assumption, we can find a finite boundary point b of G so that
$r=1.$
By assumption, we can find a finite boundary point b of G so that
for
![]() $z\in G$
with
$z\in G$
with
![]() $0<|z|<|z_0|/2.$
Hence,
$0<|z|<|z_0|/2.$
Hence,
as
![]() $z\to 0.$
Next we estimate
$z\to 0.$
Next we estimate
![]() $w_G(z)$
from above for
$w_G(z)$
from above for
![]() $0<|z|\leqslant 1/4.$
For
$0<|z|\leqslant 1/4.$
For
![]() $b\in\partial G\setminus\{0\},$
we have
$b\in\partial G\setminus\{0\},$
we have
![]() $|z-b|/|b|\leqslant 1+|z|/|b|\leqslant 1+|z|$
and
$|z-b|/|b|\leqslant 1+|z|/|b|\leqslant 1+|z|$
and
![]() $|z-b|/|b|\geqslant 1-|z|/|b|\geqslant 1-|z|$
and thus
$|z-b|/|b|\geqslant 1-|z|/|b|\geqslant 1-|z|$
and thus
for
![]() $0<|z|\leqslant 1/2.$
For
$0<|z|\leqslant 1/2.$
For
![]() $b_1,b_2\in\partial G\setminus\{0\},$
we have
$b_1,b_2\in\partial G\setminus\{0\},$
we have
![]() $|z-b_j|\geqslant |b_j|-|z|\geqslant 3|b_j|/4\geqslant 3/4$
and
$|z-b_j|\geqslant |b_j|-|z|\geqslant 3|b_j|/4\geqslant 3/4$
and
as
![]() $z\to0.$
Hence, we obtain
$z\to0.$
Hence, we obtain
![]() $w_G(z)\leqslant 1/|z|+4/3$
for
$w_G(z)\leqslant 1/|z|+4/3$
for
![]() $0<|z|\leqslant 1/4.$
For a given
$0<|z|\leqslant 1/4.$
For a given
![]() $z_0,$
we take a point
$z_0,$
we take a point
![]() $z_1\in G$
so that
$z_1\in G$
so that
![]() $|z_1|\leqslant \min\{|z_0|,1/4\}.$
Then, for
$|z_1|\leqslant \min\{|z_0|,1/4\}.$
Then, for
![]() $0<|z|<|z_1|,$
we have
$0<|z|<|z_1|,$
we have
where
![]() $\gamma$
is the curve going from
$\gamma$
is the curve going from
![]() $z_1$
to the point
$z_1$
to the point
![]() $(|z_1|/|z|)z$
along the circle
$(|z_1|/|z|)z$
along the circle
![]() $|t|=|z_1|$
and then going to z radially. Since
$|t|=|z_1|$
and then going to z radially. Since
![]() $\delta_G(z,z_0)\leqslant\sigma_G(z,z_0),$
(1·11) follows.
$\delta_G(z,z_0)\leqslant\sigma_G(z,z_0),$
(1·11) follows.
Secondly, we prove (1·12). For simplicity, we further assume that
![]() $1,\infty\in\partial G.$
(For the general case, we may use a suitable Möbius transformation to reduce to this case.) Then
$1,\infty\in\partial G.$
(For the general case, we may use a suitable Möbius transformation to reduce to this case.) Then
and therefore
for
![]() $0<|z|<1.$
Since
$0<|z|<1.$
Since
where
![]() $C_0=1/\rho_{{\mathbb{C}}\setminus\{0,1\}}(-1)$
(see [
Reference Keen and Lakic30
] for instance), we have
$C_0=1/\rho_{{\mathbb{C}}\setminus\{0,1\}}(-1)$
(see [
Reference Keen and Lakic30
] for instance), we have
as
![]() $z\to0.$
Noting the fact that the real function
$z\to0.$
Noting the fact that the real function
![]() $1/[t\log^2t]$
is integrable over
$1/[t\log^2t]$
is integrable over
![]() $(0,1/2],$
we obtain the required asymptotics (1·12) as required.
$(0,1/2],$
we obtain the required asymptotics (1·12) as required.
Remark 2·18. As the above proof shows, (1·11) is valid also in dimensions
![]() $n\geqslant 2.$
$n\geqslant 2.$
3. Modulus and M-domains
We recapitulate some of the basic facts about moduli of curve families and quasiconformal maps, following [
Reference Gehring, Martin and Palka19, Reference Väisälä52
]. Let
![]() $\Gamma$
be a family of curves in
$\Gamma$
be a family of curves in
![]() ${\overline{\mathbb R}^n}$
. We say that a non-negative Borel-measurable function
${\overline{\mathbb R}^n}$
. We say that a non-negative Borel-measurable function
![]() $\rho\;:\; {{\mathbb{R}}^n}\to {\mathbb{R}} \cup \{+\infty\}$
is an admissible function for
$\rho\;:\; {{\mathbb{R}}^n}\to {\mathbb{R}} \cup \{+\infty\}$
is an admissible function for
![]() $\Gamma,$
if
$\Gamma,$
if
![]() $\int_{\gamma} \rho ds \geqslant 1$
for each locally rectifiable curve
$\int_{\gamma} \rho ds \geqslant 1$
for each locally rectifiable curve
![]() $\gamma$
in
$\gamma$
in
![]() $\Gamma$
. The (conformal) modulus of
$\Gamma$
. The (conformal) modulus of
![]() $\Gamma$
is
$\Gamma$
is
where
![]() $\mathcal{F}(\Gamma)$
is the family of admissible functions for
$\mathcal{F}(\Gamma)$
is the family of admissible functions for
![]() $\Gamma$
and m stands for the n-dimensional Lebesgue measure. We set
$\Gamma$
and m stands for the n-dimensional Lebesgue measure. We set
![]() ${\textsf{M}}(\Gamma)=\infty$
when
${\textsf{M}}(\Gamma)=\infty$
when
![]() $\mathcal{F}(\Gamma)$
is empty. The most important property of the modulus is a quasi-invariance; that is, a homeomorphism
$\mathcal{F}(\Gamma)$
is empty. The most important property of the modulus is a quasi-invariance; that is, a homeomorphism
![]() $f\;:\;G\to G'$
between domains in
$f\;:\;G\to G'$
between domains in
![]() ${\overline{\mathbb R}^n}$
is K-quasiconformal if and only if
${\overline{\mathbb R}^n}$
is K-quasiconformal if and only if
for all families of curves
![]() $\Gamma$
in G. In particular,
$\Gamma$
in G. In particular,
![]() ${\textsf{M}}(f(\Gamma))={\textsf{M}}(\Gamma)$
for a conformal homeomorphism f.
${\textsf{M}}(f(\Gamma))={\textsf{M}}(\Gamma)$
for a conformal homeomorphism f.
For two curve families
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
in
$\Gamma_2$
in
![]() ${{\overline{\mathbb R}^n}}$
, we say that
${{\overline{\mathbb R}^n}}$
, we say that
![]() $\Gamma_2$
is minorised by
$\Gamma_2$
is minorised by
![]() $\Gamma_1$
and denote
$\Gamma_1$
and denote
![]() $\Gamma_2>\Gamma_1$
if every
$\Gamma_2>\Gamma_1$
if every
![]() $\gamma \in \Gamma_2$
has a subcurve which belongs to
$\gamma \in \Gamma_2$
has a subcurve which belongs to
![]() $\Gamma_1$
. A collection of curve families
$\Gamma_1$
. A collection of curve families
![]() $\Gamma_j\;(j=1,2,\dots\!)$
is said to be disjointly supported if there are Borel sets
$\Gamma_j\;(j=1,2,\dots\!)$
is said to be disjointly supported if there are Borel sets
![]() $\Omega_j\;(j=1,2,\dots\!)$
such that all curves in
$\Omega_j\;(j=1,2,\dots\!)$
such that all curves in
![]() $\Gamma_j$
are contained in
$\Gamma_j$
are contained in
![]() $\Omega_j$
and that
$\Omega_j$
and that
![]() $m(\Omega_j\cap\Omega_{j'})=0$
for
$m(\Omega_j\cap\Omega_{j'})=0$
for
![]() $j\ne j'.$
Then the following properties of the conformal modulus are fundamental (see [
Reference Väisälä52
] or [
Reference Gehring, Martin and Palka19
]).
$j\ne j'.$
Then the following properties of the conformal modulus are fundamental (see [
Reference Väisälä52
] or [
Reference Gehring, Martin and Palka19
]).
Lemma 3·1.
-
(1) If
 $\Gamma_1 < \Gamma_2$
, then
$\Gamma_1 < \Gamma_2$
, then
 ${\textsf{M}}(\Gamma_1) \geqslant {\textsf{M}}(\Gamma_2)$
. In particular,
${\textsf{M}}(\Gamma_1) \geqslant {\textsf{M}}(\Gamma_2)$
. In particular,
 ${\textsf{M}}(\Gamma_2)\leqslant {\textsf{M}}(\Gamma_1)$
for
${\textsf{M}}(\Gamma_2)\leqslant {\textsf{M}}(\Gamma_1)$
for
 $\Gamma_2\subset\Gamma_1.$
$\Gamma_2\subset\Gamma_1.$
-
(2) For a collection of curve families
 $\Gamma_j\;(j=1,2,\dots\!),$
Moreover, equality holds if the collection is disjointly supported.
$\Gamma_j\;(j=1,2,\dots\!),$
Moreover, equality holds if the collection is disjointly supported. \[{\textsf{M}}\left(\bigcup_j \Gamma_j\right)\leqslant \sum_j{\textsf{M}}(\Gamma_j).\]
\[{\textsf{M}}\left(\bigcup_j \Gamma_j\right)\leqslant \sum_j{\textsf{M}}(\Gamma_j).\]
A pair (G, E) of a domain G in
![]() ${\overline{\mathbb R}^n}$
and a compact set E in G is called a condenser. The capacity of the condenser (G, E) is
${\overline{\mathbb R}^n}$
and a compact set E in G is called a condenser. The capacity of the condenser (G, E) is
Another equivalent definition makes use of Dirichlet integral minimisation property [
Reference Gehring, Martin and Palka19
, theorem 5·2·3]. Here and hereafter, for sets
![]() $E,F,G \subset {\overline{\mathbb R}^n}$
, let
$E,F,G \subset {\overline{\mathbb R}^n}$
, let
![]() $\Delta(E,F;\;G)$
denote the family of all curves joining the sets E and F in G, and let
$\Delta(E,F;\;G)$
denote the family of all curves joining the sets E and F in G, and let
![]() $\Delta(E,F) = \Delta(E,F;\; {\overline{\mathbb R}^n})$
. Here, a curve
$\Delta(E,F) = \Delta(E,F;\; {\overline{\mathbb R}^n})$
. Here, a curve
![]() $\gamma\;:\;[a,b]\to {\overline{\mathbb R}^n}$
is said to join E and F in G if
$\gamma\;:\;[a,b]\to {\overline{\mathbb R}^n}$
is said to join E and F in G if
![]() $\gamma(a)\in E, \gamma(b)\in F$
and if
$\gamma(a)\in E, \gamma(b)\in F$
and if
![]() $\gamma((a,b))\subset G.$
For a compact set E in
$\gamma((a,b))\subset G.$
For a compact set E in
![]() ${\overline{\mathbb R}^n}$
, we write
${\overline{\mathbb R}^n}$
, we write
![]() $\mathrm{cap}\, E =0$
$\mathrm{cap}\, E =0$
![]() $(\mathrm{cap}\, E >0)$
if
$(\mathrm{cap}\, E >0)$
if
![]() $\mathrm{cap}\,(G,E)=0$
$\mathrm{cap}\,(G,E)=0$
![]() $(\mathrm{cap}\,(G,E)>0)$
for some bounded domain G containing E cf. [
Reference Vuorinen55
, 7·12]. Note that
$(\mathrm{cap}\,(G,E)>0)$
for some bounded domain G containing E cf. [
Reference Vuorinen55
, 7·12]. Note that
![]() $\mathrm{cap}\,(G',E)=0$
for any domain G
′ containing E if
$\mathrm{cap}\,(G',E)=0$
for any domain G
′ containing E if
![]() $\mathrm{cap}\, E=0.$
It is known that E is totally disconnected and has Hausdorff dimension 0 if
$\mathrm{cap}\, E=0.$
It is known that E is totally disconnected and has Hausdorff dimension 0 if
![]() $\mathrm{cap}\, E=0\,,$
see [
Reference Reshetnyak45
, p.120, corollary 2], [
Reference Rickman46
, p.166, theorem VII·1·15].
$\mathrm{cap}\, E=0\,,$
see [
Reference Reshetnyak45
, p.120, corollary 2], [
Reference Rickman46
, p.166, theorem VII·1·15].
A domain R in
![]() ${\overline{\mathbb R}^n}$
is called a ring if the complement
${\overline{\mathbb R}^n}$
is called a ring if the complement
![]() ${\overline{\mathbb R}^n}\setminus R$
consists of exactly two connected components, say, E and F, and R is often denoted by
${\overline{\mathbb R}^n}\setminus R$
consists of exactly two connected components, say, E and F, and R is often denoted by
![]() $R(E,F).$
In particular,
$R(E,F).$
In particular,
![]() $R_{G,n}(s)\;:\!=\; R({{\overline{\mathbb{B}}^n}}, [s e_1,\infty]),\ s > 1$
, is called the Grötzsch ring and
$R_{G,n}(s)\;:\!=\; R({{\overline{\mathbb{B}}^n}}, [s e_1,\infty]),\ s > 1$
, is called the Grötzsch ring and
![]() $R_{T,n}(t)\;:\!=\; R([-e_1,0], [t e_1,\infty]),$
t > 0, is called the Teichmüller ring, where
$R_{T,n}(t)\;:\!=\; R([-e_1,0], [t e_1,\infty]),$
t > 0, is called the Teichmüller ring, where
![]() $e_1$
is the unit vector
$e_1$
is the unit vector
![]() $(1,0,\dots,0)$
in
$(1,0,\dots,0)$
in
![]() ${{\mathbb{R}}^n}.$
The capacity of the ring R(E, F) is
${{\mathbb{R}}^n}.$
The capacity of the ring R(E, F) is
![]() $\mathrm{cap}\, R(E,F) = \mathrm{cap}\,({\overline{\mathbb R}^n}\setminus F, E)$
and its modulus is
$\mathrm{cap}\, R(E,F) = \mathrm{cap}\,({\overline{\mathbb R}^n}\setminus F, E)$
and its modulus is
When
![]() $R=R(E,F)$
is the standard ring
$R=R(E,F)$
is the standard ring
![]() $\{x\in{\mathbb{R}}^n\;:\; a<|x|<b\},$
one has
$\{x\in{\mathbb{R}}^n\;:\; a<|x|<b\},$
one has
![]() ${{\textrm{mod}}\,} R=\log(b/a).$
The capacities of
${{\textrm{mod}}\,} R=\log(b/a).$
The capacities of
![]() $R_{T,n}(t)$
and
$R_{T,n}(t)$
and
![]() $R_{G,n}(s)$
are denoted by
$R_{G,n}(s)$
are denoted by
![]() $\tau_{n}(t)$
and
$\tau_{n}(t)$
and
![]() $\gamma_{n}(s)$
, respectively. By [
Reference Vuorinen55
, lemma 5·53],
$\gamma_{n}(s)$
, respectively. By [
Reference Vuorinen55
, lemma 5·53],
![]() $\tau_{n}\;:\; (0,+\infty)\rightarrow (0,+\infty)$
and
$\tau_{n}\;:\; (0,+\infty)\rightarrow (0,+\infty)$
and
![]() $\gamma_{n}\;:\; (1,+\infty)\rightarrow (0,+\infty)$
are decreasing homeomorphisms and they satisfy the functional identity
$\gamma_{n}\;:\; (1,+\infty)\rightarrow (0,+\infty)$
are decreasing homeomorphisms and they satisfy the functional identity
Here we state a couple of fundamental properties of uniformly perfect sets. Recall that a ring
![]() $R=R(E_1,E_2)$
is said to separate a set A in
$R=R(E_1,E_2)$
is said to separate a set A in
![]() ${\overline{\mathbb R}^n}$
if
${\overline{\mathbb R}^n}$
if
![]() $A\subset E_1\cup E_2$
and
$A\subset E_1\cup E_2$
and
![]() $A\cap E_j\ne\emptyset$
for
$A\cap E_j\ne\emptyset$
for
![]() $j=1,2.$
Then the following characterization of uniformly perfect sets is well known (see, for instance, [
Reference Avkhadiev and Wirths3
] for planar case and [
Reference Golberg, Sugawa and Vuorinen22
] for general case).
$j=1,2.$
Then the following characterization of uniformly perfect sets is well known (see, for instance, [
Reference Avkhadiev and Wirths3
] for planar case and [
Reference Golberg, Sugawa and Vuorinen22
] for general case).
Lemma 3·4. Let A be a compact set in
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $\mathrm{card\,}(A)\geqslant 2.$
Then A is uniformly perfect precisely when there exists a constant
$\mathrm{card\,}(A)\geqslant 2.$
Then A is uniformly perfect precisely when there exists a constant
![]() $M>0$
such that
$M>0$
such that
![]() ${{\textrm{mod}}\,} R\leqslant M$
for every ring R separating A.
${{\textrm{mod}}\,} R\leqslant M$
for every ring R separating A.
We also note the following simple fact.
Lemma 3·5. Let G be a domain in
![]() ${\overline{\mathbb R}^n}$
for which the complement
${\overline{\mathbb R}^n}$
for which the complement
![]() $C={\overline{\mathbb R}^n}\setminus G$
contains at least two points. Then
$C={\overline{\mathbb R}^n}\setminus G$
contains at least two points. Then
![]() $\partial G$
is uniformly perfect if and only if so is C.
$\partial G$
is uniformly perfect if and only if so is C.
Proof. By the previous lemma, it is enough to show that a ring R separates C if and only if R separates
![]() $\partial G.$
Indeed, if a ring
$\partial G.$
Indeed, if a ring
![]() $R=R(E_1,E_2)$
separates C then
$R=R(E_1,E_2)$
separates C then
![]() $R\subset G$
and each
$R\subset G$
and each
![]() $E_j$
meets C. Note that
$E_j$
meets C. Note that
![]() ${\overline{\mathbb R}^n}\setminus E_2=R\cup E_1$
is a domain. Choose a point a from
${\overline{\mathbb R}^n}\setminus E_2=R\cup E_1$
is a domain. Choose a point a from
![]() $E_1\cap C$
and
$E_1\cap C$
and
![]() $z_0$
from R and take a curve
$z_0$
from R and take a curve
![]() $\gamma\;:\;[0,1]\to{\overline{\mathbb R}^n}\setminus E_2$
with
$\gamma\;:\;[0,1]\to{\overline{\mathbb R}^n}\setminus E_2$
with
![]() $\gamma(0)=z_0$
and
$\gamma(0)=z_0$
and
![]() $\gamma(1)=a.$
Then there is a
$\gamma(1)=a.$
Then there is a
![]() $t\in (0,1]$
such that
$t\in (0,1]$
such that
![]() $\gamma(t)\in\partial G.$
Obviously,
$\gamma(t)\in\partial G.$
Obviously,
![]() $\gamma(t)\in E_1,$
which implies that
$\gamma(t)\in E_1,$
which implies that
![]() $E_1\cap\partial G\ne\emptyset.$
Likewise we have
$E_1\cap\partial G\ne\emptyset.$
Likewise we have
![]() $E_2\cap\partial G\ne\emptyset.$
We now conclude that R separates
$E_2\cap\partial G\ne\emptyset.$
We now conclude that R separates
![]() $\partial G.$
$\partial G.$
Conversely, suppose that a ring
![]() $R=R(E_1,E_2)$
separates
$R=R(E_1,E_2)$
separates
![]() $\partial G.$
Then
$\partial G.$
Then
![]() $R\subset G$
or
$R\subset G$
or
![]() $R\cap G=\emptyset.$
If the latter occurs, one component of
$R\cap G=\emptyset.$
If the latter occurs, one component of
![]() ${\overline{\mathbb R}^n}\setminus R,$
say
${\overline{\mathbb R}^n}\setminus R,$
say
![]() $E_1,$
contains G. Then
$E_1,$
contains G. Then
![]() $E_2\cap\partial G=\emptyset,$
which contradicts the choice of R. Hence the latter case cannot occur. Therefore, we have shown that R separates
$E_2\cap\partial G=\emptyset,$
which contradicts the choice of R. Hence the latter case cannot occur. Therefore, we have shown that R separates
![]() $C\,.$
$C\,.$
For the study of the geometry of the modulus metric below, we now introduce a new class of conformally invariant domains, M-domains. The definition of this class makes use of the continuum criterion introduced and studied by O. Martio [ Reference Martio35 ]. The continuum criterion is closely connected with the potential theoretic boundary regularity of a domain [ Reference Martio and Sarvas36 ].
3·6. Definition
We say that a closed set
![]() $C \subset {{\mathbb{R}}^n}$
satisfies the continuum criterion at
$C \subset {{\mathbb{R}}^n}$
satisfies the continuum criterion at
![]() $x \in C$
if there exists a continuum
$x \in C$
if there exists a continuum
![]() $K \subset \{x\} \cup \left({\overline{\mathbb R}^n} \setminus C\right)$
such that
$K \subset \{x\} \cup \left({\overline{\mathbb R}^n} \setminus C\right)$
such that
We write
![]() ${\textsf{M}}(x,\, C) < \infty$
if this holds, and otherwise we write
${\textsf{M}}(x,\, C) < \infty$
if this holds, and otherwise we write
![]() ${\textsf{M}}(x,\, C)=\infty.$
${\textsf{M}}(x,\, C)=\infty.$
We now recall that a continuum is a compact connected set in
![]() ${\overline{\mathbb R}^n}$
containing at least two points. We note that
${\overline{\mathbb R}^n}$
containing at least two points. We note that
![]() ${\textsf{M}}(x_0,\,C)=\infty$
if a continuum
${\textsf{M}}(x_0,\,C)=\infty$
if a continuum
![]() $C_0 \subset C$
contains
$C_0 \subset C$
contains
![]() $x_0.$
In fact, the sphere
$x_0.$
In fact, the sphere
![]() $|x-x_0|=r$
meets both K and C for all small enough
$|x-x_0|=r$
meets both K and C for all small enough
![]() $r>0$
in this case. A simple application of the following lemma implies that
$r>0$
in this case. A simple application of the following lemma implies that
for every continuum K with
![]() $x_0\in K\subset({\overline{\mathbb R}^n}\setminus C)\cup\{x_0\}.$
Here we have used the relation
$x_0\in K\subset({\overline{\mathbb R}^n}\setminus C)\cup\{x_0\}.$
Here we have used the relation
![]() $\Delta(K,C;\;{\overline{\mathbb R}^n}\setminus C)<\Delta(K,C;\;{\overline{\mathbb R}^n})$
and Lemma 3·1.
$\Delta(K,C;\;{\overline{\mathbb R}^n}\setminus C)<\Delta(K,C;\;{\overline{\mathbb R}^n})$
and Lemma 3·1.
Lemma 3·7 (Vaisala [
Reference Väisälä52
, theorem 10·12]). Let
![]() $0<a<b<+\infty.$
Let E and F be closed sets in
$0<a<b<+\infty.$
Let E and F be closed sets in
![]() ${\overline{\mathbb R}^n}$
and suppose that the sphere
${\overline{\mathbb R}^n}$
and suppose that the sphere
![]() $|x|=t$
meets both E and F for every t with
$|x|=t$
meets both E and F for every t with
![]() $a<t<b.$
Then
$a<t<b.$
Then
![]() ${\textsf{M}}(\Delta(E,F;\;{\overline{\mathbb R}^n}))\geqslant c_n\log(b/a),$
where
${\textsf{M}}(\Delta(E,F;\;{\overline{\mathbb R}^n}))\geqslant c_n\log(b/a),$
where
![]() $c_n$
is a positive constant depending only on n.
$c_n$
is a positive constant depending only on n.
We now define the notion of M-domains.
Definition 3·8. A boundary point x of a domain
![]() $G \subset {\overline{\mathbb R}^n}$
is said to satisfy the M-condition (relative to G) if
$G \subset {\overline{\mathbb R}^n}$
is said to satisfy the M-condition (relative to G) if
![]() ${\textsf{M}} (x, {\overline{\mathbb R}^n}\setminus G) =\infty;$
in other words, the complement
${\textsf{M}} (x, {\overline{\mathbb R}^n}\setminus G) =\infty;$
in other words, the complement
![]() ${\overline{\mathbb R}^n}\setminus G$
does not satisfy the continuum criterion at x. The domain G is called an M-domain if every boundary point
${\overline{\mathbb R}^n}\setminus G$
does not satisfy the continuum criterion at x. The domain G is called an M-domain if every boundary point
![]() $x \in \partial G$
satisfies the M-condition relative to G.
$x \in \partial G$
satisfies the M-condition relative to G.
By the above observation, a point
![]() $x\in \partial G$
satisfies the condition
$x\in \partial G$
satisfies the condition
![]() ${\textsf{M}}(x,{\overline{\mathbb R}^n}\setminus G)<\infty$
only if the singleton
${\textsf{M}}(x,{\overline{\mathbb R}^n}\setminus G)<\infty$
only if the singleton
![]() $\{x\}$
is a connected component of
$\{x\}$
is a connected component of
![]() $\partial G.$
On the other hand, any isolated point x of
$\partial G.$
On the other hand, any isolated point x of
![]() $\partial G$
satisfies
$\partial G$
satisfies
![]() $M(x,{\overline{\mathbb R}^n}\setminus G)<\infty.$
$M(x,{\overline{\mathbb R}^n}\setminus G)<\infty.$
We need the following result in the proof of Theorem 1·1. Our proof is similar to that of [ Reference Martio35 , lemma 3·5].
Lemma 3·9. Let G be a domain in
![]() ${\overline{\mathbb R}^n}\,.$
Suppose that a point
${\overline{\mathbb R}^n}\,.$
Suppose that a point
![]() $x_0\in\partial G\setminus\{\infty\}$
and a continuum K in
$x_0\in\partial G\setminus\{\infty\}$
and a continuum K in
![]() $G\cup\{x_0\}$
with
$G\cup\{x_0\}$
with
![]() $x_0\in K$
satisfy the condition
$x_0\in K$
satisfy the condition
![]() ${\textsf{M}}(\Delta(K,\partial G;\;G))<\infty.$
Then
${\textsf{M}}(\Delta(K,\partial G;\;G))<\infty.$
Then
Proof. If
![]() $\partial G=\{x_0\},$
the assertion trivially holds. Thus we may assume that
$\partial G=\{x_0\},$
the assertion trivially holds. Thus we may assume that
![]() $\partial G$
contains at least two points. By the conformal invariance of the capacity, we may assume that
$\partial G$
contains at least two points. By the conformal invariance of the capacity, we may assume that
![]() $\infty\in\partial G.$
For brevity, we write
$\infty\in\partial G.$
For brevity, we write
![]() ${\overline{B}}(r)=\overline{B}^n(x_0,r)$
and
${\overline{B}}(r)=\overline{B}^n(x_0,r)$
and
![]() $S(r)=\partial B(r)$
throughout the proof. Let
$S(r)=\partial B(r)$
throughout the proof. Let
![]() $M_0={\textsf{M}}(\Delta(K,\partial G;\;G))<\infty$
and choose
$M_0={\textsf{M}}(\Delta(K,\partial G;\;G))<\infty$
and choose
![]() $r_0>0$
large enough so that
$r_0>0$
large enough so that
![]() $K\subset B(r_0).$
For a decreasing sequence
$K\subset B(r_0).$
For a decreasing sequence
![]() $r_j\;(j=0,1,2,\dots\!)$
with
$r_j\;(j=0,1,2,\dots\!)$
with
![]() $r_j\to0\;(j\to\infty),$
consider the ring
$r_j\to0\;(j\to\infty),$
consider the ring
![]() $R_j=\{x\in{\mathbb{R}}^n\;:\; r_{j+1}<|x-x_0|<r_j\}.$
We can choose such a sequence so that
$R_j=\{x\in{\mathbb{R}}^n\;:\; r_{j+1}<|x-x_0|<r_j\}.$
We can choose such a sequence so that
 \[c_j\;:\!=\;\mathrm{cap}\, R_j=\left(\frac{\omega_{n-1}}{\log(r_j/r_{j+1})}\right)^{1/(n-1)}\quad {\textrm{ satisfies} } \qquad \sum_{j=0}^\infty c_j<\infty\,.\]
\[c_j\;:\!=\;\mathrm{cap}\, R_j=\left(\frac{\omega_{n-1}}{\log(r_j/r_{j+1})}\right)^{1/(n-1)}\quad {\textrm{ satisfies} } \qquad \sum_{j=0}^\infty c_j<\infty\,.\]
For instance, for
![]() $c_j=2^{-j},$
we define
$c_j=2^{-j},$
we define
![]() $r_j$
recursively by the formula
$r_j$
recursively by the formula
for
![]() $j=0,1,2,\dots.$
It is obvious that
$j=0,1,2,\dots.$
It is obvious that
![]() $r_j\to0$
as
$r_j\to0$
as
![]() $j\to\infty$
for this choice. Let
$j\to\infty$
for this choice. Let
![]() $K_j=K\cap\overline{R_j}$
and denote by
$K_j=K\cap\overline{R_j}$
and denote by
![]() $\Delta_j$
the family of curves joining
$\Delta_j$
the family of curves joining
![]() $K_j$
and
$K_j$
and
![]() $\partial G$
in the set
$\partial G$
in the set
![]() $\{x\in G\;:\; r_{j+2}<|x-x_0|<r_{j-1}\}$
for
$\{x\in G\;:\; r_{j+2}<|x-x_0|<r_{j-1}\}$
for
![]() $j=1,2,\dots.$
Then the families
$j=1,2,\dots.$
Then the families
![]() $\Delta_{N+3j}\;(j=0,1,2,\dots\!)$
are disjointly supported and contained in the family
$\Delta_{N+3j}\;(j=0,1,2,\dots\!)$
are disjointly supported and contained in the family
![]() $\Delta(K,\partial G;\; G)$
for
$\Delta(K,\partial G;\; G)$
for
![]() $N=1,2,3,\dots.$
By Lemma 3·1 (ii) we obtain
$N=1,2,3,\dots.$
By Lemma 3·1 (ii) we obtain
 \[\sum_{j=0}^\infty {\textsf{M}}(\Delta_{N+3j})\leqslant{\textsf{M}}(\Delta(K,\partial G;\; G))=M_0\quad (N=1,2,3,\dots\!)\]
\[\sum_{j=0}^\infty {\textsf{M}}(\Delta_{N+3j})\leqslant{\textsf{M}}(\Delta(K,\partial G;\; G))=M_0\quad (N=1,2,3,\dots\!)\]
and hence
 \[\sum_{j=1}^\infty {\textsf{M}}(\Delta_{j})\leqslant 3M_0.\]
\[\sum_{j=1}^\infty {\textsf{M}}(\Delta_{j})\leqslant 3M_0.\]
For a given number
![]() $\eta>0,$
take a large enough integer
$\eta>0,$
take a large enough integer
![]() $N>0$
so that
$N>0$
so that
 \[\sum_{j=N}^\infty {\textsf{M}}(\Delta_{j})<\eta\quad\textrm{and}\quad\sum_{j=N-1}^\infty c_j<\eta.\]
\[\sum_{j=N}^\infty {\textsf{M}}(\Delta_{j})<\eta\quad\textrm{and}\quad\sum_{j=N-1}^\infty c_j<\eta.\]
By construction, we easily see that the curve family
![]() $\Delta(K_j,\partial G;\; G)\setminus\Delta_j$
is minorised by the family
$\Delta(K_j,\partial G;\; G)\setminus\Delta_j$
is minorised by the family
Thus, by Lemma 3·1 (i), we obtain
 \begin{align*}{\textsf{M}}(\Delta(K_j, & \partial G;\; G)) \\& \leqslant {\textsf{M}}(\Delta_j)+{\textsf{M}}(\Delta(K_j,\partial G;\; G)\setminus\Delta_j)) \\& \leqslant {\textsf{M}}(\Delta_j)+{\textsf{M}}(\Delta(S(r_j),S(r_{j-1});\; R_{j-1}))+{\textsf{M}}(\Delta(S(r_{j+2}),S(r_{j+1});\; R_{j+1})) \\&={\textsf{M}}(\Delta_j)+\mathrm{cap}\, R_{j-1}+\mathrm{cap}\, R_{j+1}.\end{align*}
\begin{align*}{\textsf{M}}(\Delta(K_j, & \partial G;\; G)) \\& \leqslant {\textsf{M}}(\Delta_j)+{\textsf{M}}(\Delta(K_j,\partial G;\; G)\setminus\Delta_j)) \\& \leqslant {\textsf{M}}(\Delta_j)+{\textsf{M}}(\Delta(S(r_j),S(r_{j-1});\; R_{j-1}))+{\textsf{M}}(\Delta(S(r_{j+2}),S(r_{j+1});\; R_{j+1})) \\&={\textsf{M}}(\Delta_j)+\mathrm{cap}\, R_{j-1}+\mathrm{cap}\, R_{j+1}.\end{align*}
Therefore, we finally have
 \begin{eqnarray*}{\textsf{M}}(\Delta(K\cap{\overline{B}}(r_N),\partial G;\; G))&\leqslant& {\textsf{M}}(\Delta(\{x_0\},\partial G;\; G))+\sum_{j=N}^\infty \Big[{\textsf{M}}(\Delta_j)+c_{j-1}+c_{j+1}\Big] \\& <& 0+\eta+\eta+\eta=3\eta.\end{eqnarray*}
\begin{eqnarray*}{\textsf{M}}(\Delta(K\cap{\overline{B}}(r_N),\partial G;\; G))&\leqslant& {\textsf{M}}(\Delta(\{x_0\},\partial G;\; G))+\sum_{j=N}^\infty \Big[{\textsf{M}}(\Delta_j)+c_{j-1}+c_{j+1}\Big] \\& <& 0+\eta+\eta+\eta=3\eta.\end{eqnarray*}
Hence we obtain
![]() ${\textsf{M}}(\Delta(K\cap \overline{B}^n(x_0,r),\partial G;\; G))<3\eta$
for
${\textsf{M}}(\Delta(K\cap \overline{B}^n(x_0,r),\partial G;\; G))<3\eta$
for
![]() $0<r\leqslant r_N.$
$0<r\leqslant r_N.$
The next theorem due to Martio [ Reference Martio35 , theorem 3·4] will also be used in Section 4.
Lemma 3·10. Let G be a proper subdomain of
![]() ${\overline{\mathbb R}^n}$
and fix a point
${\overline{\mathbb R}^n}$
and fix a point
![]() $a\in G.$
For a boundary point
$a\in G.$
For a boundary point
![]() $x_0$
of G with
$x_0$
of G with
![]() $x_0\ne\infty,$
set
$x_0\ne\infty,$
set
where the infimum is taken over all continua K joining a and the sphere
![]() $S^{n-1}(x_0,\varepsilon)$
in G. Then
$S^{n-1}(x_0,\varepsilon)$
in G. Then
![]() ${\textsf{M}}(x_0,{\overline{\mathbb R}^n}\setminus G)=\infty$
if and only if
${\textsf{M}}(x_0,{\overline{\mathbb R}^n}\setminus G)=\infty$
if and only if
![]() $L(\varepsilon)\to \infty$
as
$L(\varepsilon)\to \infty$
as
![]() $\varepsilon\to 0^+.$
$\varepsilon\to 0^+.$
It is clear that M-domains are invariant under Möbius transformations and conformal mappings. We next give an example of an M-domain which does not have uniformly perfect boundary.
3·11. Example
Let
![]() $\{s_k\}$
and
$\{s_k\}$
and
![]() $\{r_k\}\;(k=1,2,3,\dots\!)$
be two sequences of positive numbers converging to 0 monotonically with the following property:
$\{r_k\}\;(k=1,2,3,\dots\!)$
be two sequences of positive numbers converging to 0 monotonically with the following property:
Then the closed balls
![]() ${\overline{B}}_k={\overline{B}}^n {(s_ke_1,r_k)}$
,
${\overline{B}}_k={\overline{B}}^n {(s_ke_1,r_k)}$
,
![]() $k=1,2,\ldots$
, are disjoint because
$k=1,2,\ldots$
, are disjoint because
![]() $\mathrm{dist}({\overline{B}}_k,{\overline{B}}_{k+1})=\alpha_k>0,$
where
$\mathrm{dist}({\overline{B}}_k,{\overline{B}}_{k+1})=\alpha_k>0,$
where
![]() $e_1=(1,0,\dots,0)\in{\mathbb{R}}^n.$
Let
$e_1=(1,0,\dots,0)\in{\mathbb{R}}^n.$
Let
![]() $C=\{0\}\cup\bigcup_{k=1}^\infty {\overline{B}}_k$
and
$C=\{0\}\cup\bigcup_{k=1}^\infty {\overline{B}}_k$
and
![]() $K_0=\{x=(x_1,\dots,x_n)\in{\mathbb{R}}^n\;:\; x_1\leqslant 0\}\cup\{\infty\}.$
Note that the ring
$K_0=\{x=(x_1,\dots,x_n)\in{\mathbb{R}}^n\;:\; x_1\leqslant 0\}\cup\{\infty\}.$
Note that the ring
![]() $R_k=\{x\;:\; r_k<|x-s_ke_1|<r_k'\}$
separates C, where
$R_k=\{x\;:\; r_k<|x-s_ke_1|<r_k'\}$
separates C, where
![]() $r_k'=r_k+\min\{\alpha_{k-1},\alpha_k\}.$
Observe that
$r_k'=r_k+\min\{\alpha_{k-1},\alpha_k\}.$
Observe that
![]() $\alpha_{k-1}\geqslant\alpha_{k}$
if and only if
$\alpha_{k-1}\geqslant\alpha_{k}$
if and only if
![]() $2s_k-s_{k-1}-s_{k+1}\leqslant r_{k+1}-r_{k-1}.$
This condition is fulfilled when
$2s_k-s_{k-1}-s_{k+1}\leqslant r_{k+1}-r_{k-1}.$
This condition is fulfilled when
![]() $\{s_k\}$
is convex.
$\{s_k\}$
is convex.
-
(1) The domain
 $G={\overline{\mathbb R}^n}\setminus(K_0\cup C)$
is an M-domain because every connected component of
$G={\overline{\mathbb R}^n}\setminus(K_0\cup C)$
is an M-domain because every connected component of
 $K_0\cup C$
is a continuum. However,
$K_0\cup C$
is a continuum. However,
 $\partial G$
is not uniformly perfect when
$\partial G$
is not uniformly perfect when
 $\limsup_{k\to\infty}(r_k'/r_k)=\infty.$
For instance, we can choose a convex sequence
$\limsup_{k\to\infty}(r_k'/r_k)=\infty.$
For instance, we can choose a convex sequence
 $\{s_k\}$
with
$\{s_k\}$
with
 $2s_{k+1}\leqslant s_k$
(such as
$2s_{k+1}\leqslant s_k$
(such as
 $s_k=2^{-k}$
) and let
$s_k=2^{-k}$
) and let
 $r_k=2^{-k}s_k$
for
$r_k=2^{-k}s_k$
for
 $k\geqslant 1.$
Then and thus
$k\geqslant 1.$
Then and thus \[r_{k+1}/r_k=s_{k+1}/(2s_k)\leqslant 1/4, \quad r_k'=2^{k}r_k-(2^{k+1}+1)r_{k+1}\]
as
\[r_{k+1}/r_k=s_{k+1}/(2s_k)\leqslant 1/4, \quad r_k'=2^{k}r_k-(2^{k+1}+1)r_{k+1}\]
as \[\frac{r_k'}{r_k}\geqslant 2^k-\frac14(2^{k+1}+1)=2^{k-1}-2^{-2}\to+\infty\]
\[\frac{r_k'}{r_k}\geqslant 2^k-\frac14(2^{k+1}+1)=2^{k-1}-2^{-2}\to+\infty\]
 $k\to\infty.$
$k\to\infty.$
-
(2) Let
 $G={\overline{\mathbb R}^n}\setminus C.$
Suppose that the sequence of rings
$G={\overline{\mathbb R}^n}\setminus C.$
Suppose that the sequence of rings
 $A_k=\{x\;:\; s_k-r_{k}<|x|<s_k+r_k\}$
satisfies the condition
$A_k=\{x\;:\; s_k-r_{k}<|x|<s_k+r_k\}$
satisfies the condition
 $\limsup_{k\to\infty}{{\textrm{mod}}\,} A_k=\infty.$
For instance, we can take
$\limsup_{k\to\infty}{{\textrm{mod}}\,} A_k=\infty.$
For instance, we can take
 $s_k=2^{-k^2}, r_k=s_k-2s_{k+1}.$
Then
$s_k=2^{-k^2}, r_k=s_k-2s_{k+1}.$
Then
 ${\textsf{M}}(0,C)=\infty.$
Indeed, for each k and
${\textsf{M}}(0,C)=\infty.$
Indeed, for each k and
 $t\in (s_k-r_{k}, s_k+r_k),$
the sphere
$t\in (s_k-r_{k}, s_k+r_k),$
the sphere
 $|x|=t$
intersects C by definition. Hence, for any continuum K with
$|x|=t$
intersects C by definition. Hence, for any continuum K with
 $0\in K\subset G\cup\{0\},$
Lemma 3.7 now yields for sufficiently large k. By the assumption, we have
$0\in K\subset G\cup\{0\},$
Lemma 3.7 now yields for sufficiently large k. By the assumption, we have \[{\textsf{M}}(\Delta(K, \partial G;\; G))\geqslant {\textsf{M}}(\Delta(K,C;\;{\overline{\mathbb R}^n}))\geqslant c_n\,\log\frac{s_k+r_k}{s_k-r_k}\]
\[{\textsf{M}}(\Delta(K, \partial G;\; G))\geqslant {\textsf{M}}(\Delta(K,C;\;{\overline{\mathbb R}^n}))\geqslant c_n\,\log\frac{s_k+r_k}{s_k-r_k}\]
 ${\textsf{M}}(\Delta(K,\partial G;\;G))=\infty.$
In this case, the singleton
${\textsf{M}}(\Delta(K,\partial G;\;G))=\infty.$
In this case, the singleton
 $\{0\}$
is a connected component of
$\{0\}$
is a connected component of
 $\partial G$
but the condition
$\partial G$
but the condition
 ${\textsf{M}}(0, {\overline{\mathbb R}^n}\setminus G)=\infty$
is satisfied.
${\textsf{M}}(0, {\overline{\mathbb R}^n}\setminus G)=\infty$
is satisfied.
-
(3) Let
 $G={\overline{\mathbb R}^n}\setminus C$
again. Then where
$G={\overline{\mathbb R}^n}\setminus C$
again. Then where \[\Delta(K_0,C;\; G)\subset\bigcup_{k=0}^\infty \Delta_k,\]
\[\Delta(K_0,C;\; G)\subset\bigcup_{k=0}^\infty \Delta_k,\]
 $\Delta_k=\Delta(K_0,{\overline{B}}_k;\;{\overline{\mathbb R}^n})$
for
$\Delta_k=\Delta(K_0,{\overline{B}}_k;\;{\overline{\mathbb R}^n})$
for
 $k\geqslant 1$
and
$k\geqslant 1$
and
 $\Delta_0=\Delta(K_0,\{0\};\;{\overline{\mathbb R}^n}).$
Note that
$\Delta_0=\Delta(K_0,\{0\};\;{\overline{\mathbb R}^n}).$
Note that
 $\beta_0\;:\!=\;{\textsf{M}}(\Delta_0)=0.$
Since the ring
$\beta_0\;:\!=\;{\textsf{M}}(\Delta_0)=0.$
Since the ring
 $R(K_0,{\overline{B}}_k)$
contains
$R(K_0,{\overline{B}}_k)$
contains
 $R_k$
as a subring, we have
$R_k$
as a subring, we have  \[{\textsf{M}}(\Delta_k)=\mathrm{cap}\, R(K_0,{\overline{B}}_k)\leqslant\mathrm{cap}\, R_k=\omega_{n-1}({{\textrm{mod}}\,} R_k)^{1-n}=\omega_{n-1}\left(\log\frac{r_k'}{r_k}\right)^{1-n}.\]
\[{\textsf{M}}(\Delta_k)=\mathrm{cap}\, R(K_0,{\overline{B}}_k)\leqslant\mathrm{cap}\, R_k=\omega_{n-1}({{\textrm{mod}}\,} R_k)^{1-n}=\omega_{n-1}\left(\log\frac{r_k'}{r_k}\right)^{1-n}.\]
Let
![]() $D_k=\{x\;:\; |x-s_k|<s_k\}$
for
$D_k=\{x\;:\; |x-s_k|<s_k\}$
for
![]() $k\geqslant 1$
and
$k\geqslant 1$
and
![]() $H=\{x\;:\; x_1>0\}={\overline{\mathbb R}^n}\setminus K_0.$
Then
$H=\{x\;:\; x_1>0\}={\overline{\mathbb R}^n}\setminus K_0.$
Then
for
![]() $k\geqslant 1.$
If
$k\geqslant 1.$
If
![]() $\sum_k \beta_k<+\infty,$
we have
$\sum_k \beta_k<+\infty,$
we have
 \[{\textsf{M}}(\Delta(K_0,C;\; G))\leqslant\sum_{k=0}^\infty {\textsf{M}}(\Delta_k)\leqslant\sum_{k=0}^\infty\beta_k<+\infty.\]
\[{\textsf{M}}(\Delta(K_0,C;\; G))\leqslant\sum_{k=0}^\infty {\textsf{M}}(\Delta_k)\leqslant\sum_{k=0}^\infty\beta_k<+\infty.\]
Hence
![]() ${\textsf{M}}(0,\partial G)<\infty$
in this case. For instance, if we choose
${\textsf{M}}(0,\partial G)<\infty$
in this case. For instance, if we choose
![]() $s_k$
and
$s_k$
and
![]() $r_k$
so that
$r_k$
so that
![]() $r_k=s_k e^{-k^2}$
then
$r_k=s_k e^{-k^2}$
then
![]() $\beta_k=\omega_{n-1}k^{2-2n}$
satisfies the above condition. Hence,
$\beta_k=\omega_{n-1}k^{2-2n}$
satisfies the above condition. Hence,
![]() ${\textsf{M}}(0, {\overline{\mathbb R}^n}\setminus G)<\infty.$
This gives an example of a non-isolated boundary point of a domain which does not satisfy the M-condition.
${\textsf{M}}(0, {\overline{\mathbb R}^n}\setminus G)<\infty.$
This gives an example of a non-isolated boundary point of a domain which does not satisfy the M-condition.
3·12. Open problem
It is well known that the Hausdorff dimension of the boundary of a domain with uniformly perfect boundary is positive [ Reference Järvi and Vuorinen29 ]. We do not know whether the boundary of an M-domain has positive Hausdorff dimension.
4. Modulus metric
In this section, we first give a definition of the modulus metric
![]() $\mu_G(x,y)$
and its dual quantity
$\mu_G(x,y)$
and its dual quantity
![]() $\lambda_G(x,y).$
After that, we will prove Theorems 1·1 and 1·2. For further results, we refer to [
Reference Betsakos and Pouliasis8, Reference Ferrand12-Reference Ferrand, Martin and Vuorinen15, Reference Hariri, Klén and Vuorinen23, Reference Lelong–Ferrand31, Reference Pansu38, Reference Pansu39, Reference Pouliasis and Yu44, Reference Zhang56
].
$\lambda_G(x,y).$
After that, we will prove Theorems 1·1 and 1·2. For further results, we refer to [
Reference Betsakos and Pouliasis8, Reference Ferrand12-Reference Ferrand, Martin and Vuorinen15, Reference Hariri, Klén and Vuorinen23, Reference Lelong–Ferrand31, Reference Pansu38, Reference Pansu39, Reference Pouliasis and Yu44, Reference Zhang56
].
Definition 4·1 ([
Reference Vuorinen55
, Chapter 8]). Let G be a proper subdomain of
![]() ${\overline{\mathbb R}^n}$
and
${\overline{\mathbb R}^n}$
and
![]() $x, y \in G.$
Then we define
$x, y \in G.$
Then we define
where the infimum runs over all curves
![]() $C_{xy}$
in G joining x and y. We also define
$C_{xy}$
in G joining x and y. We also define
where the infimum runs over all curves
![]() $C_x$
and
$C_x$
and
![]() $C_y$
in G joining x (respectively y) and
$C_y$
in G joining x (respectively y) and
![]() $\partial G.$
$\partial G.$
In some special cases, the extremal configurations for the curve families defining
![]() $\mu_G(x,y)$
and
$\mu_G(x,y)$
and
![]() $\lambda_G(x,y)$
are known. Indeed, for the case when
$\lambda_G(x,y)$
are known. Indeed, for the case when
![]() $G={{\mathbb{B}}^n}$
and
$G={{\mathbb{B}}^n}$
and
![]() $0\ne x\in{{\mathbb{B}}^n}, y=0,$
we have
$0\ne x\in{{\mathbb{B}}^n}, y=0,$
we have
and, by the symmetry principle [
Reference Gehring, Martin and Palka19
, theorem 4·3·5], with
![]() $e=x/|x|,$
$e=x/|x|,$
 \begin{eqnarray}\lambda_{{{\mathbb{B}}^n}}(x,0)&=&{\textsf{M}}(\Delta((-e,0], [x,e);\;{{\mathbb{B}}^n}))=2^{1-n}{\textsf{M}}(\Delta([-\infty,0], [x, e/|x|];\; {\overline{\mathbb R}^n})) \\ \nonumber&=&2^{1-n}{\textsf{M}}(\Delta([-e,0], [\frac{|x|^2}{1-|x|^2}e, +\infty];\; {\overline{\mathbb R}^n}))=2^{1-n}\tau_n(|x|^2/(1-|x|^2))\,,\end{eqnarray}
\begin{eqnarray}\lambda_{{{\mathbb{B}}^n}}(x,0)&=&{\textsf{M}}(\Delta((-e,0], [x,e);\;{{\mathbb{B}}^n}))=2^{1-n}{\textsf{M}}(\Delta([-\infty,0], [x, e/|x|];\; {\overline{\mathbb R}^n})) \\ \nonumber&=&2^{1-n}{\textsf{M}}(\Delta([-e,0], [\frac{|x|^2}{1-|x|^2}e, +\infty];\; {\overline{\mathbb R}^n}))=2^{1-n}\tau_n(|x|^2/(1-|x|^2))\,,\end{eqnarray}
see [
Reference Hariri, Klén and Vuorinen23
, theorem 10·4] for details. Here, we recall that the Grötzsch capacity function
![]() $\gamma_n(s)$
and the Teichmüller capacity function
$\gamma_n(s)$
and the Teichmüller capacity function
![]() $\tau_n(t)$
are defined by
$\tau_n(t)$
are defined by
for
![]() $0<s<1$
and
$0<s<1$
and
![]() $t>0.$
$t>0.$
Next we look at the case when
![]() $G= {\mathbb{R}}^n \setminus \{0\}.$
By the definition of
$G= {\mathbb{R}}^n \setminus \{0\}.$
By the definition of
![]() $\lambda_G(t e_1, -e_1), t >0,$
there are two natural choices to connect
$\lambda_G(t e_1, -e_1), t >0,$
there are two natural choices to connect
![]() $t e_1$
and
$t e_1$
and
![]() $ -e_1$
with the boundary
$ -e_1$
with the boundary
![]() $ \{0, \infty\}$
of the domain
$ \{0, \infty\}$
of the domain
![]() $G\,,$
either the pair
$G\,,$
either the pair
![]() $[t e_1,0), [\!-e_1,-\infty)$
or the pair
$[t e_1,0), [\!-e_1,-\infty)$
or the pair
![]() $[t e_1,\infty),[\!-e_1,0)\,.$
Therefore
$[t e_1,\infty),[\!-e_1,0)\,.$
Therefore
and, because
![]() $\tau_n\;:\; (0,\infty) \to (0,\infty)$
is a strictly decreasing homeomorphism, for
$\tau_n\;:\; (0,\infty) \to (0,\infty)$
is a strictly decreasing homeomorphism, for
![]() $t>1,$
we have
$t>1,$
we have
![]() $\tau_n(t)<\tau_n(1)<\tau_n(1/t)$
and thus
$\tau_n(t)<\tau_n(1)<\tau_n(1/t)$
and thus
See [ Reference Ahlfors1 , p.72] and [ Reference Hariri, Klén and Vuorinen23 , pp.178–181] for more details.
Suppose that
![]() $G_1$
and
$G_1$
and
![]() $G_2$
are proper subdomains of
$G_2$
are proper subdomains of
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $G_1 \subset G_2.$
Then for a continuum
$G_1 \subset G_2.$
Then for a continuum
![]() $C_{xy}$
joining x and y in
$C_{xy}$
joining x and y in
![]() $G_1$
we have
$G_1$
we have
![]() $\Delta(C_{xy},\partial G_2;\; G_2)>\Delta(C_{xy},\partial G_1;\; G_1).$
By Lemma 3·1 (i), we further obtain for all
$\Delta(C_{xy},\partial G_2;\; G_2)>\Delta(C_{xy},\partial G_1;\; G_1).$
By Lemma 3·1 (i), we further obtain for all
![]() $x,y \in G_1$
$x,y \in G_1$
Hence
![]() $\mu_{G_2} (x, y)\leqslant \mu_{G_1} (x, y)$
. By definition, the quantities
$\mu_{G_2} (x, y)\leqslant \mu_{G_1} (x, y)$
. By definition, the quantities
![]() $\mu_G(x,y)$
and
$\mu_G(x,y)$
and
![]() $\lambda_G(x,y)$
are both conformally invariant. Ferrand [
Reference Ferrand14
] proved that
$\lambda_G(x,y)$
are both conformally invariant. Ferrand [
Reference Ferrand14
] proved that
![]() $\lambda_G(x,y)^{1/(1-n)}$
is a distance function of G. Thus
$\lambda_G(x,y)^{1/(1-n)}$
is a distance function of G. Thus
![]() $\lambda_G(x,y)^{1/(1-n)}$
is often called Ferrand’s modulus metric. When
$\lambda_G(x,y)^{1/(1-n)}$
is often called Ferrand’s modulus metric. When
![]() $n=2$
and G is a simply connected domain in
$n=2$
and G is a simply connected domain in
![]() ${\overline{\mathbb R}^n}$
with
${\overline{\mathbb R}^n}$
with
![]() $\mathrm{card\,}(\partial G)\geqslant 2,$
Ferrand’s modulus metric is the same as the modulus metric (up to a constant multiple). Moreover, for
$\mathrm{card\,}(\partial G)\geqslant 2,$
Ferrand’s modulus metric is the same as the modulus metric (up to a constant multiple). Moreover, for
![]() $n\geqslant 2$
there exists [
Reference Hariri, Klén and Vuorinen23
, (9·12), theorem 10·4] a constant
$n\geqslant 2$
there exists [
Reference Hariri, Klén and Vuorinen23
, (9·12), theorem 10·4] a constant
![]() $c_n >0$
depending only on n such that for all
$c_n >0$
depending only on n such that for all
![]() $x,y \in \mathbb{B}^n$
$x,y \in \mathbb{B}^n$
Lemma 4·5. Let G be a simply connected hyperbolic domain in
![]() ${\overline{\mathbb R}^2}={\overline{\mathbb{C}}}.$
Then
${\overline{\mathbb R}^2}={\overline{\mathbb{C}}}.$
Then
![]() $\mu_G(x,y)=4\lambda_G(x,y)^{-1}.$
$\mu_G(x,y)=4\lambda_G(x,y)^{-1}.$
Proof. Fix a pair of distinct points
![]() $x,y\in G.$
The Riemann mapping theorem asserts that there is a conformal homeomorphism
$x,y\in G.$
The Riemann mapping theorem asserts that there is a conformal homeomorphism
![]() $f\;:\;G\to{{\mathbb{B}}^2}=\{z\in{\mathbb{C}}\;:\; |z|<1\}$
such that
$f\;:\;G\to{{\mathbb{B}}^2}=\{z\in{\mathbb{C}}\;:\; |z|<1\}$
such that
![]() $f(x)=0$
and
$f(x)=0$
and
![]() $f(y)=u\in(0,1).$
Since the modulus metric and Ferrand’s modulus metric are conformally invariant, we have
$f(y)=u\in(0,1).$
Since the modulus metric and Ferrand’s modulus metric are conformally invariant, we have
![]() $\mu_G(x,y)=\mu_{{\mathbb{B}}^2}(0,u)$
and
$\mu_G(x,y)=\mu_{{\mathbb{B}}^2}(0,u)$
and
![]() $\lambda_G(x,y)=\lambda_{{\mathbb{B}}^2}(0,u).$
By (4·2) and (4·3) together with (3·3), we can write
$\lambda_G(x,y)=\lambda_{{\mathbb{B}}^2}(0,u).$
By (4·2) and (4·3) together with (3·3), we can write
In view of the formula
![]() $\tau_2(t)\tau_2(1/t)=4$
[
Reference Anderson, Vamanamurthy and Vuorinen2
, 5·19 (7)], we obtain
$\tau_2(t)\tau_2(1/t)=4$
[
Reference Anderson, Vamanamurthy and Vuorinen2
, 5·19 (7)], we obtain
![]() $\mu_{{{\mathbb{B}}^2}}(0,u)\lambda_{{{\mathbb{B}}^2}}(0,u)=4$
and thus the assertion.
$\mu_{{{\mathbb{B}}^2}}(0,u)\lambda_{{{\mathbb{B}}^2}}(0,u)=4$
and thus the assertion.
We take this opportunity to state the following plausible fact with a short proof.
Lemma 4·6. Let G be a domain in
![]() ${\overline{\mathbb R}^n}$
such that the complement
${\overline{\mathbb R}^n}$
such that the complement
![]() $F={\overline{\mathbb R}^n}\setminus G$
is of positive capacity. Then there is a positive constant c(F) such that the inequality
$F={\overline{\mathbb R}^n}\setminus G$
is of positive capacity. Then there is a positive constant c(F) such that the inequality
holds for
![]() $x,y\in G,$
where
$x,y\in G,$
where
![]() $d_0>0$
is a constant depending only on n. In particular, the modulus metric
$d_0>0$
is a constant depending only on n. In particular, the modulus metric
![]() $\mu_G$
induces the same topology on G as the relative topology on G induced by
$\mu_G$
induces the same topology on G as the relative topology on G induced by
![]() ${\overline{\mathbb R}^n}$
with the spherical metric q.
${\overline{\mathbb R}^n}$
with the spherical metric q.
Proof. The inequality (4·7) follows from [
Reference Vuorinen55
, theorem 6·1] and implies the inclusion map
![]() $(G,\mu_G)\to ({\overline{\mathbb R}^n}, q)$
is continuous. In order to show the other inclusion map
$(G,\mu_G)\to ({\overline{\mathbb R}^n}, q)$
is continuous. In order to show the other inclusion map
![]() $(G, q)\to (G,\mu_G)$
is continuous, we may assume that
$(G, q)\to (G,\mu_G)$
is continuous, we may assume that
![]() $G\subset{\mathbb{R}}^n$
and replace q by the Euclidean metric. Take an arbitrary point
$G\subset{\mathbb{R}}^n$
and replace q by the Euclidean metric. Take an arbitrary point
![]() $x\in G$
and choose a small enough number
$x\in G$
and choose a small enough number
![]() $r>0$
so that
$r>0$
so that
![]() $B\;:\!=\;B^n(x,r)\subset G.$
By the domain monotonicity of the modulus metric, we obtain
$B\;:\!=\;B^n(x,r)\subset G.$
By the domain monotonicity of the modulus metric, we obtain
by (4·2). Since
![]() $\gamma(t)\to 0$
as
$\gamma(t)\to 0$
as
![]() $t\to+\infty,$
we see that
$t\to+\infty,$
we see that
![]() $\mu_G(x,y)\to 0$
as
$\mu_G(x,y)\to 0$
as
![]() $|y-x|\to 0,$
which proves the required assertion.
$|y-x|\to 0,$
which proves the required assertion.
We are now in a position to prove the first main result.
4·8. Proof of Theorem 1·1
The part (i)
![]() $\Rightarrow$
(ii) is obvious. We show now that (ii) implies (iii) by contradiction. Suppose that G is not an M-domain, namely,
$\Rightarrow$
(ii) is obvious. We show now that (ii) implies (iii) by contradiction. Suppose that G is not an M-domain, namely,
![]() ${\textsf{M}}(x_0,{\overline{\mathbb R}^n}\setminus G)<\infty$
for some
${\textsf{M}}(x_0,{\overline{\mathbb R}^n}\setminus G)<\infty$
for some
![]() $x_0\in\partial G.$
By the conformal invariance, we may assume that
$x_0\in\partial G.$
By the conformal invariance, we may assume that
![]() $x_0\ne\infty.$
We write
$x_0\ne\infty.$
We write
![]() $B(r)=B^n(x_0,r)$
and
$B(r)=B^n(x_0,r)$
and
![]() ${\overline{B}}(r)={\overline{B}}^n(x_0,r)$
for brevity. By definition, there is a continuum K with
${\overline{B}}(r)={\overline{B}}^n(x_0,r)$
for brevity. By definition, there is a continuum K with
![]() $x_0\in K\subset G\cup\{x_0\}$
such that
$x_0\in K\subset G\cup\{x_0\}$
such that
![]() $M_0\;:\!=\;{\textsf{M}}(\Delta(K,\partial G;\; G))<\infty.$
Take a point
$M_0\;:\!=\;{\textsf{M}}(\Delta(K,\partial G;\; G))<\infty.$
Take a point
![]() $x_1$
from
$x_1$
from
![]() $K\cap G$
and fix it. Let
$K\cap G$
and fix it. Let
![]() $r_1=|x_1-x_0|$
and
$r_1=|x_1-x_0|$
and
![]() $K_1=K.$
For each
$K_1=K.$
For each
![]() $x\in K\cap B(r_1)$
and
$x\in K\cap B(r_1)$
and
![]() $r\in(0,|x-x_0|),$
let
$r\in(0,|x-x_0|),$
let
![]() $K_1(x,r)$
be the connected component of
$K_1(x,r)$
be the connected component of
![]() $K_1\setminus B(r)$
containing x. Note that
$K_1\setminus B(r)$
containing x. Note that
![]() $K_1(x,r)$
is a continuum. By construction,
$K_1(x,r)$
is a continuum. By construction,
![]() $K_1(x,r)\subset K_1(x,r')$
for
$K_1(x,r)\subset K_1(x,r')$
for
![]() $0<r'<r<|x-x_0|.$
We set
$0<r'<r<|x-x_0|.$
We set
Then,
![]() $C_1$
is connected and, for
$C_1$
is connected and, for
![]() $x,y\in C_1,$
we have
$x,y\in C_1,$
we have
![]() $x,y\in K_1(x_1,r)$
for some
$x,y\in K_1(x_1,r)$
for some
![]() $0<r<r_0.$
In particular, for such a pair of points x, y and r,
$0<r<r_0.$
In particular, for such a pair of points x, y and r,
We also see that
![]() $x_0\in\overline{C_1}.$
Indeed, otherwise
$x_0\in\overline{C_1}.$
Indeed, otherwise
![]() $\overline{C_1}$
would be a continuum in
$\overline{C_1}$
would be a continuum in
![]() $K\setminus{\overline{B}}(\varepsilon)$
for small enough
$K\setminus{\overline{B}}(\varepsilon)$
for small enough
![]() $\varepsilon>0$
and thus
$\varepsilon>0$
and thus
![]() $K_1(x_1,\varepsilon)\supset\overline{C_1}\supset C_1.$
Since
$K_1(x_1,\varepsilon)\supset\overline{C_1}\supset C_1.$
Since
![]() $K_1(x_1,\varepsilon)\subset C_1,$
the set
$K_1(x_1,\varepsilon)\subset C_1,$
the set
![]() $C_1$
would be closed and have a positive distance to
$C_1$
would be closed and have a positive distance to
![]() $K\setminus C_1,$
which would violate connectedness of K.
$K\setminus C_1,$
which would violate connectedness of K.
Let
![]() $K_2$
be the connected component of the compact set
$K_2$
be the connected component of the compact set
![]() $K_1\cap{\overline{B}}(r_1/2)$
containing
$K_1\cap{\overline{B}}(r_1/2)$
containing
![]() $x_0.$
Since
$x_0.$
Since
![]() $x_0\in\overline{C_1},$
we have
$x_0\in\overline{C_1},$
we have
![]() $C_1\cap K_2\ne\emptyset.$
Take a point
$C_1\cap K_2\ne\emptyset.$
Take a point
![]() $x_2$
from
$x_2$
from
![]() $C_1\cap K_2$
and fix it. As before, set
$C_1\cap K_2$
and fix it. As before, set
![]() $C_2=C(x_2,K_2).$
Then
$C_2=C(x_2,K_2).$
Then
![]() $C_2\subset C_1\cap K_2.$
Repeating this procedure, we define sequences of points
$C_2\subset C_1\cap K_2.$
Repeating this procedure, we define sequences of points
![]() $x_j,$
continua
$x_j,$
continua
![]() $K_j$
and connected sets
$K_j$
and connected sets
![]() $C_j$
inductively with the following properties:
$C_j$
inductively with the following properties:
-
(i)
 $K_j\subset {\overline{B}}(r_1 2^{1-j});$
$K_j\subset {\overline{B}}(r_1 2^{1-j});$
-
(ii)
 $x_j\in C_j\subset C_{j-1}\cap K_j$
$x_j\in C_j\subset C_{j-1}\cap K_j$
-
(iii)
 $x_0\in \overline{C_j}\subset K_j$
and
$x_0\in \overline{C_j}\subset K_j$
and -
(iv)
 $\mu_G(x,y)\leqslant {\textsf{M}}(\Delta(K_j,\partial G;\; G))$
for all
$\mu_G(x,y)\leqslant {\textsf{M}}(\Delta(K_j,\partial G;\; G))$
for all
 $x,y\in C_j.$
$x,y\in C_j.$
In particular, we observe that
By Lemma 3·9, we have
Hence, we conclude that
![]() $\{x_j\}$
is a Cauchy sequence in
$\{x_j\}$
is a Cauchy sequence in
![]() $(G,\mu_G).$
Suppose that this sequence is convergent; that is,
$(G,\mu_G).$
Suppose that this sequence is convergent; that is,
![]() $\mu_G(x_j, x_\infty)\to 0$
as
$\mu_G(x_j, x_\infty)\to 0$
as
![]() $j\to\infty$
for some
$j\to\infty$
for some
![]() $x_\infty\in G.$
On the other hand, since
$x_\infty\in G.$
On the other hand, since
![]() $|x_j-x_0|\leqslant r_12^{1-j},$
we have
$|x_j-x_0|\leqslant r_12^{1-j},$
we have
![]() $x_j\to x_0$
in
$x_j\to x_0$
in
![]() ${\overline{\mathbb R}^n}.$
Lemma 4·6 now implies that
${\overline{\mathbb R}^n}.$
Lemma 4·6 now implies that
![]() $x_\infty=x_0\in\partial G,$
which is a contradiction. Therefore,
$x_\infty=x_0\in\partial G,$
which is a contradiction. Therefore,
![]() $(G,\mu_G)$
is not complete.
$(G,\mu_G)$
is not complete.
Finally, we prove that (iii) implies (i). If
![]() $\mathrm{cap}\,\partial G=0,$
then
$\mathrm{cap}\,\partial G=0,$
then
which is not allowed by condition (iii). Therefore,
![]() $(G,\mu_G)$
is a metric space under the assumption (iii). Suppose next that the set
$(G,\mu_G)$
is a metric space under the assumption (iii). Suppose next that the set
![]() $X=\{x\in G\;:\; \mu_G(x,a)\leqslant r_0\}$
is not compact for some
$X=\{x\in G\;:\; \mu_G(x,a)\leqslant r_0\}$
is not compact for some
![]() $a\in G$
and
$a\in G$
and
![]() $r_0>0.$
Then there is a point
$r_0>0.$
Then there is a point
![]() $x_0\in \partial X\cap(\partial G).$
We may assume that
$x_0\in \partial X\cap(\partial G).$
We may assume that
![]() $x_0\ne\infty.$
For every
$x_0\ne\infty.$
For every
![]() $\varepsilon>0,$
there exists a point
$\varepsilon>0,$
there exists a point
![]() $x\in X\cap B^n(x_0,\varepsilon).$
By definition of X,
$x\in X\cap B^n(x_0,\varepsilon).$
By definition of X,
![]() ${\textsf{M}}(\Delta(K,\partial G;\; G))\leqslant r_0$
for a continuum K in
${\textsf{M}}(\Delta(K,\partial G;\; G))\leqslant r_0$
for a continuum K in
![]() $G\cup\{x_0\}$
with
$G\cup\{x_0\}$
with
![]() $a,x\in K.$
Therefore, under the notation in Lemma 3·10, we obtain
$a,x\in K.$
Therefore, under the notation in Lemma 3·10, we obtain
![]() $L(\varepsilon)\leqslant r_0.$
However, the lemma implies that
$L(\varepsilon)\leqslant r_0.$
However, the lemma implies that
![]() ${\textsf{M}}(x_0,{\overline{\mathbb R}^n}\setminus G)<\infty.$
By contradiction, we have shown that (iii) implies (i).
${\textsf{M}}(x_0,{\overline{\mathbb R}^n}\setminus G)<\infty.$
By contradiction, we have shown that (iii) implies (i).
Next we prove our second result.
4·9. Proof of Theorem 1·2
Since the uniform perfectness is Möbius invariant (Lemma 3·4), we may assume that
![]() $\infty\in\partial G$
and thus
$\infty\in\partial G$
and thus
![]() $G\subset{{\mathbb{R}}^n}$
and
$G\subset{{\mathbb{R}}^n}$
and
![]() $\mathrm{diam}(\partial G)=+\infty.$
$\mathrm{diam}(\partial G)=+\infty.$
First suppose that the boundary
![]() $\partial G$
of G is uniformly perfect. Lemma 3·5 implies that the complement
$\partial G$
of G is uniformly perfect. Lemma 3·5 implies that the complement
![]() $E={\overline{\mathbb R}^n}\setminus G$
is also uniformly perfect. By a theorem of Järvi and Vuorinen [
Reference Järvi and Vuorinen29
], E satisfies the metric thickness condition. Vuorinen [
Reference Vuorinen54
] proved that for such a domain G there exists a constant
$E={\overline{\mathbb R}^n}\setminus G$
is also uniformly perfect. By a theorem of Järvi and Vuorinen [
Reference Järvi and Vuorinen29
], E satisfies the metric thickness condition. Vuorinen [
Reference Vuorinen54
] proved that for such a domain G there exists a constant
![]() $b_1>0$
such that for all
$b_1>0$
such that for all
![]() $x,y\in G$
$x,y\in G$
Applying (2·13), we obtain (1·3) with
![]() $b=b_1/4.$
$b=b_1/4.$
We next suppose (1·3). Then by Lemma 2·12 (iii), we have
![]() $\mu_G(x,y)\geqslant b\, j_G(x,y).$
Let
$\mu_G(x,y)\geqslant b\, j_G(x,y).$
Let
![]() $E={\overline{\mathbb R}^n}\setminus G$
and
$E={\overline{\mathbb R}^n}\setminus G$
and
 \[0<c< c_0\;:\!=\; \exp\left[-2\left(\frac{2\omega_{n-1}}{b\log 3}\right)^{1/(n-1)}\right].\]
\[0<c< c_0\;:\!=\; \exp\left[-2\left(\frac{2\omega_{n-1}}{b\log 3}\right)^{1/(n-1)}\right].\]
We prove now that
![]() $\{x\;:\; cr\leqslant |x-a|\leqslant r\}\cap E\ne \emptyset$
for every
$\{x\;:\; cr\leqslant |x-a|\leqslant r\}\cap E\ne \emptyset$
for every
![]() $a\in E\setminus\{\infty\}$
and
$a\in E\setminus\{\infty\}$
and
![]() $r>0.$
Suppose, to the contrary, that
$r>0.$
Suppose, to the contrary, that
![]() $\{x\;:\; cr\leqslant |x-a|\leqslant r\}\cap E= \emptyset$
for some
$\{x\;:\; cr\leqslant |x-a|\leqslant r\}\cap E= \emptyset$
for some
![]() $a \in E,\;a\ne\infty,$
and
$a \in E,\;a\ne\infty,$
and
![]() $r>0.$
Set
$r>0.$
Set
![]() $C_1=\{x\in{{\mathbb{R}}^n}\;:\; |x-a|\leqslant cr\}$
and
$C_1=\{x\in{{\mathbb{R}}^n}\;:\; |x-a|\leqslant cr\}$
and
![]() $C_2=\{x\in{\overline{\mathbb R}^n}\;:\; |x-a|\geqslant r\}.$
Then the assumption implies that the set E decomposes into the two non-empty sets
$C_2=\{x\in{\overline{\mathbb R}^n}\;:\; |x-a|\geqslant r\}.$
Then the assumption implies that the set E decomposes into the two non-empty sets
![]() $E_1=E\cap C_1$
and
$E_1=E\cap C_1$
and
![]() $E_2=E\cap C_2.$
Pick two points x, y from the sphere
$E_2=E\cap C_2.$
Pick two points x, y from the sphere
![]() $S=S^{n-1}(a,\rho)$
so that
$S=S^{n-1}(a,\rho)$
so that
![]() $|x-y|=2\rho,$
where
$|x-y|=2\rho,$
where
![]() $\rho=\sqrt c \, r.$
We take a curve
$\rho=\sqrt c \, r.$
We take a curve
![]() $C_{xy}^0$
joining x and y in S. Then, by the subadditivity and monotonicity of the modulus (Lemma 3·1), we obtain
$C_{xy}^0$
joining x and y in S. Then, by the subadditivity and monotonicity of the modulus (Lemma 3·1), we obtain
 \begin{eqnarray*}\mu_G(x,y) &\leqslant & {{\textsf{M}}}(\Delta(C_{xy}^0, E)) \\ &\leqslant& {{\textsf{M}}}(\Delta(C_{xy}^0, E_1))+{{\textsf{M}}}(\Delta(C_{xy}^0, E_2)) \\&\leqslant& {{\textsf{M}}}(\Delta(S, C_1;\; G_1))+{{\textsf{M}}}(\Delta(S, C_2;\;G_2)),\end{eqnarray*}
\begin{eqnarray*}\mu_G(x,y) &\leqslant & {{\textsf{M}}}(\Delta(C_{xy}^0, E)) \\ &\leqslant& {{\textsf{M}}}(\Delta(C_{xy}^0, E_1))+{{\textsf{M}}}(\Delta(C_{xy}^0, E_2)) \\&\leqslant& {{\textsf{M}}}(\Delta(S, C_1;\; G_1))+{{\textsf{M}}}(\Delta(S, C_2;\;G_2)),\end{eqnarray*}
where
![]() $G_1=\{x\;:\; |x-a|<\rho\}$
and
$G_1=\{x\;:\; |x-a|<\rho\}$
and
![]() $G_2=\{x\;:\; |x-a|>\rho\}.$
As is well known [
Reference Vuorinen55
, (5·10), (5·14)],
$G_2=\{x\;:\; |x-a|>\rho\}.$
As is well known [
Reference Vuorinen55
, (5·10), (5·14)],
we have
where
![]() $\omega_{n-1}$
is the
$\omega_{n-1}$
is the
![]() $(n -1)$
-dimensional area of
$(n -1)$
-dimensional area of
![]() $\mathbb{S}^{n-1}$
. On the other hand, since
$\mathbb{S}^{n-1}$
. On the other hand, since
![]() $d_G(x)\leqslant |x-a|=\rho$
and
$d_G(x)\leqslant |x-a|=\rho$
and
![]() $d_G(y)\leqslant |y-a|=\rho,$
we obtain
$d_G(y)\leqslant |y-a|=\rho,$
we obtain
Thus we have
![]() $b\log 3\leqslant 2\omega_{n-1}/(\!-\log\sqrt c)^{n-1},$
that is,
$b\log 3\leqslant 2\omega_{n-1}/(\!-\log\sqrt c)^{n-1},$
that is,
a contradiction.
In the case when G is either
![]() ${{\mathbb{B}}^n}$
of
${{\mathbb{B}}^n}$
of
![]() ${{\mathbb{H}}^n},$
the metric
${{\mathbb{H}}^n},$
the metric
![]() $\mu_G(x,y)$
has the explicit expression in terms of the hyperbolic metric
$\mu_G(x,y)$
has the explicit expression in terms of the hyperbolic metric
![]() $h_G$
[
Reference Vuorinen55
, theorem 8·6]
$h_G$
[
Reference Vuorinen55
, theorem 8·6]
 \begin{equation} \mu_G(x,y)= 2^{n-1}\,\tau_n \left(\frac1{\sinh^2\left(\frac12 h_{G}(x,y)\right)}\right)= \gamma_n \left(\coth^2\Big(\frac{h_{G}(x,y)}2\Big)\right).\end{equation}
\begin{equation} \mu_G(x,y)= 2^{n-1}\,\tau_n \left(\frac1{\sinh^2\left(\frac12 h_{G}(x,y)\right)}\right)= \gamma_n \left(\coth^2\Big(\frac{h_{G}(x,y)}2\Big)\right).\end{equation}
The decreasing homeomorphism
![]() $\mu\;:\; (0, 1] \Longrightarrow [0,\infty)$
is defined by
$\mu\;:\; (0, 1] \Longrightarrow [0,\infty)$
is defined by
 \begin{eqnarray*}\mu(r)=\frac{\pi}{2}\frac{{\mathcal{K}}\left(\sqrt{1-r^2}\right)}{{\mathcal{K}}(r)}\,, \quad {\mathcal{K}}(r)=\int_{0}^{\pi/2} \frac{dt}{\sqrt{1-r^2\sin^2 t}} \,,\end{eqnarray*}
\begin{eqnarray*}\mu(r)=\frac{\pi}{2}\frac{{\mathcal{K}}\left(\sqrt{1-r^2}\right)}{{\mathcal{K}}(r)}\,, \quad {\mathcal{K}}(r)=\int_{0}^{\pi/2} \frac{dt}{\sqrt{1-r^2\sin^2 t}} \,,\end{eqnarray*}
for
![]() $ r \in (0,1)\,, \, \mu(1)=0\,$
. Now the Grötzsch capacity for
$ r \in (0,1)\,, \, \mu(1)=0\,$
. Now the Grötzsch capacity for
![]() $n=2$
can be expressed as follows
$n=2$
can be expressed as follows
In conjunction with the above relations (4·10), (4·11), when G is the unit disk
![]() $\mathbb{B}^2={\mathbb{D}}$
in
$\mathbb{B}^2={\mathbb{D}}$
in
![]() ${\mathbb{C}},$
we obtain the expression
${\mathbb{C}},$
we obtain the expression
 \begin{equation} \mu_{{\mathbb{D}}}(z,w)=\gamma_2 \left(\frac{1}{\tanh \frac{1}{2}h_{{\mathbb{D}}}(z,w)}\right)=\frac{2\pi}{\mu\left({\tanh \frac{1}{2}h_{{\mathbb{D}}}(z,w)}\right)},\quad z,w \in {\mathbb{D}}.\nonumber\end{equation}
\begin{equation} \mu_{{\mathbb{D}}}(z,w)=\gamma_2 \left(\frac{1}{\tanh \frac{1}{2}h_{{\mathbb{D}}}(z,w)}\right)=\frac{2\pi}{\mu\left({\tanh \frac{1}{2}h_{{\mathbb{D}}}(z,w)}\right)},\quad z,w \in {\mathbb{D}}.\nonumber\end{equation}
The following estimate will be used later.
Lemma 4·13.
Proof. From [ Reference Anderson, Vamanamurthy and Vuorinen2 , (5·29)], we note the inequality
for
![]() $0<r<1.$
Let
$0<r<1.$
Let
![]() $v=\left(\tanh x\right)^{1/4}\in(0,1)$
for
$v=\left(\tanh x\right)^{1/4}\in(0,1)$
for
![]() $x>0.$
Since
$x>0.$
Since
![]() $0 <\tanh x=v^4<v<1,$
we obtain
$0 <\tanh x=v^4<v<1,$
we obtain
![]() $x<\,\mathrm{artanh}\, v.$
Hence,
$x<\,\mathrm{artanh}\, v.$
Hence,
We are now ready to show our third result.
4·14. Proof of Theorem 1·6
Assume that G is a Möbius uniform domain in
![]() ${\overline{\mathbb R}^n}.$
By Möbius invariance of Definition 2·16, we may assume that
${\overline{\mathbb R}^n}.$
By Möbius invariance of Definition 2·16, we may assume that
![]() $G\subset{\mathbb{R}}^n.$
By virtue of Lemmas 2·8 and 2·12, the uniformity assumption reads
$G\subset{\mathbb{R}}^n.$
By virtue of Lemmas 2·8 and 2·12, the uniformity assumption reads
for a positive constant c. By [
Reference Vuorinen55
, lemma 8·32 (ii)] (see also [
Reference Hariri, Klén and Vuorinen23
, lemma 10·7]) there are positive constants
![]() $b_1, b_2$
depending only on n such that
$b_1, b_2$
depending only on n such that
for all
![]() $x,y\in G.$
In view of Lemma 2·12, we have the required inequality with
$x,y\in G.$
In view of Lemma 2·12, we have the required inequality with
![]() $d_j=cb_j$
(j = 1, 2).
$d_j=cb_j$
(j = 1, 2).
Next we assume that the inequality (1·7) holds for a simply connected domain G in
![]() ${\overline{\mathbb{C}}}$
with non-degenerate boundary. We can also assume that
${\overline{\mathbb{C}}}$
with non-degenerate boundary. We can also assume that
![]() $G\subset{\mathbb{C}}.$
Then, as is well known, the Koebe one-quarter theorem leads to the inequality
$G\subset{\mathbb{C}}.$
Then, as is well known, the Koebe one-quarter theorem leads to the inequality
![]() $k_G(x,y)\leqslant 2h_G(x,y).$
By the Riemann mapping theorem, there is a conformal homeomorphism
$k_G(x,y)\leqslant 2h_G(x,y).$
By the Riemann mapping theorem, there is a conformal homeomorphism
![]() $f\;:\;G\to\mathbb{B}^2={\mathbb{D}}.$
Since
$f\;:\;G\to\mathbb{B}^2={\mathbb{D}}.$
Since
![]() $\mu_G$
and
$\mu_G$
and
![]() $h_G$
are conformally invariant, we obtain the formula
$h_G$
are conformally invariant, we obtain the formula
 \[\mu_G(x,y)=\mu_{\mathbb{D}}(f(x),f(y))=\frac{2\pi}{\mu\left({\tanh \frac{1}{2}h_{{\mathbb{D}}}(f(x),f(y))}\right)}=\frac{2\pi}{\mu\left({\tanh \frac{1}{2}h_{G}(x,y)}\right)}.\]
\[\mu_G(x,y)=\mu_{\mathbb{D}}(f(x),f(y))=\frac{2\pi}{\mu\left({\tanh \frac{1}{2}h_{{\mathbb{D}}}(f(x),f(y))}\right)}=\frac{2\pi}{\mu\left({\tanh \frac{1}{2}h_{G}(x,y)}\right)}.\]
We now apply Lemma 4·13 to get
Combining this with (1·7) and Lemma 2·12, we have
Now a result of Gehring and Osgood [ Reference Gehring and Osgood20 ] implies that G is uniform.
4·15. Open problem
As pointed out above, in the case of planar simply connected domains the modulus metric can be expressed as a function of the hyperbolic metric. We do not know, whether for a general hyperbolic planar domain, the hyperbolic metric has a minorant in terms of the modulus metric.
5. Application to quasimeromorphic maps
The modulus of a curve family is one of the most important conformal invariants of geometric function theory which provides a bridge connecting geometry and potential theory. The modulus is the main tool of the theory of quasiconformal, quasiregular and quasimeromorphic mappings in
![]() ${\mathbb{R}}^n$
[
Reference Anderson, Vamanamurthy and Vuorinen2, Reference Gehring, Martin and Palka19, Reference Hariri, Klén and Vuorinen23, Reference Reshetnyak45, Reference Rickman46, Reference Väisälä52
]. These mappings are the higher dimensional counterparts of the classes of conformal, analytic, and meromorphic functions of classical function theory, respectively. We will now apply our results to prove a Möbius invariant counterpart of a result of Gehring and Osgood [
Reference Gehring and Osgood20
] for quasimeromorphic mappings.
${\mathbb{R}}^n$
[
Reference Anderson, Vamanamurthy and Vuorinen2, Reference Gehring, Martin and Palka19, Reference Hariri, Klén and Vuorinen23, Reference Reshetnyak45, Reference Rickman46, Reference Väisälä52
]. These mappings are the higher dimensional counterparts of the classes of conformal, analytic, and meromorphic functions of classical function theory, respectively. We will now apply our results to prove a Möbius invariant counterpart of a result of Gehring and Osgood [
Reference Gehring and Osgood20
] for quasimeromorphic mappings.
We make use of some basic facts of the theory of quasiconformal, quasiregular, and quasimeromorphic mappings which are readily available in [ Reference Reshetnyak45, Reference Rickman46, Reference Väisälä52, Reference Vuorinen55 ]. The first result shows a Lipschitz type property of quasimeromorphic mappings with respect to the modulus metric. Note that these mappings are locally Hölder-continuous with respect to the Euclidean metric as some basic examples show [ Reference Väisälä52 , 16·2].
Theorem 5·1 [
Reference Vuorinen55
, theorem 10·18]. Let
![]() $f\;:\; G_1 \to G_2$
be a non-constant K-quasimeromorphic mapping where
$f\;:\; G_1 \to G_2$
be a non-constant K-quasimeromorphic mapping where
![]() $G_1, G_2 \subset \overline{\mathbb{R}}^n\,.$
Then for all
$G_1, G_2 \subset \overline{\mathbb{R}}^n\,.$
Then for all
![]() $x,y \in G_1$
,
$x,y \in G_1$
,
In particular,
![]() $f\;:\; (G_1, \mu_{G_1})\to (G_2, \mu_{G_2})$
is Lipschitz continuous.
$f\;:\; (G_1, \mu_{G_1})\to (G_2, \mu_{G_2})$
is Lipschitz continuous.
D. Betsakos and S. Pouliasis [ Reference Betsakos and Pouliasis8 ] have recently proved that if f is an isometric homeomorphism between the metric spaces
then f is quasiconformal and it is conformal if
![]() $n=2\,.$
This result gives a solution to a question of Ferrand– Martin– Vuorinen [
Reference Ferrand, Martin and Vuorinen15
] when
$n=2\,.$
This result gives a solution to a question of Ferrand– Martin– Vuorinen [
Reference Ferrand, Martin and Vuorinen15
] when
![]() $n=2$
. Very recently this result was strengthened by Pouliasis and Yu. Solynin [
Reference Pouliasis and Yu44
] and independently by Zhang [
Reference Zhang56
]:
$n=2$
. Very recently this result was strengthened by Pouliasis and Yu. Solynin [
Reference Pouliasis and Yu44
] and independently by Zhang [
Reference Zhang56
]:
![]() $\mu$
-isometries are conformal in all dimensions
$\mu$
-isometries are conformal in all dimensions
![]() $n \geqslant 2\,.$
$n \geqslant 2\,.$
We next prove a Harnack-type inequality.
Theorem 5·2. Let
![]() $f\;:\;G_1\to G_2$
be a K-quasiregular mapping where
$f\;:\;G_1\to G_2$
be a K-quasiregular mapping where
![]() $G_1\,, G_2$
are subdomains of
$G_1\,, G_2$
are subdomains of
![]() $ {\mathbb{R}}^n\,,n \geqslant2\,.$
If the boundary
$ {\mathbb{R}}^n\,,n \geqslant2\,.$
If the boundary
![]() $\partial G_2$
is uniformly perfect, then the function
$\partial G_2$
is uniformly perfect, then the function
satisfies the Harnack inequality, i.e. there exists a constant
![]() $D_1$
such that for all
$D_1$
such that for all
![]() $x \in G_1\,,$
and all
$x \in G_1\,,$
and all
![]() $y \in \bar{B}^n(x,d_{G_1}(x)/2)\,,$
$y \in \bar{B}^n(x,d_{G_1}(x)/2)\,,$
Moreover, there exists a constant
![]() $D_2$
such that for all
$D_2$
such that for all
![]() $x,y \in G_1$
$x,y \in G_1$
Proof. Fix
![]() $x \in G_1$
and
$x \in G_1$
and
![]() $y \in \bar{B}^n(x,d/2)\,,$
where
$y \in \bar{B}^n(x,d/2)\,,$
where
![]() $d=d_{G_1}(x).$
Then the ring
$d=d_{G_1}(x).$
Then the ring
![]() $R=\{z\;:\; d/2<|z-x|<d\}$
separates
$R=\{z\;:\; d/2<|z-x|<d\}$
separates
![]() $\{x,y\}$
from
$\{x,y\}$
from
![]() $\partial G_1$
and
$\partial G_1$
and
![]() ${{\textrm{mod}}\,} R=\log 2.$
Therefore, by the definitions of
${{\textrm{mod}}\,} R=\log 2.$
Therefore, by the definitions of
![]() $\mu_{G_1},$
$\mu_{G_1},$
where we used the relation
![]() $\Delta([x,y], G_1)>\Delta(S^{n-1}(x,d/2),S^{n-1}(x,d);\;R)$
and Lemma 3·1 (ii). (A similar estimate is found at [
Reference Vuorinen55
, 8·8].) Because
$\Delta([x,y], G_1)>\Delta(S^{n-1}(x,d/2),S^{n-1}(x,d);\;R)$
and Lemma 3·1 (ii). (A similar estimate is found at [
Reference Vuorinen55
, 8·8].) Because
![]() $\partial G_2$
is uniformly perfect, it follows from Theorem 1·2 and Lemma 2·12 that
$\partial G_2$
is uniformly perfect, it follows from Theorem 1·2 and Lemma 2·12 that
Next, by Theorem 5·1
The Harnack inequality (1) with the constant
![]() $D_1 =\exp( K M/2)$
then follows, because for all
$D_1 =\exp( K M/2)$
then follows, because for all
![]() $z \in \partial G_2$
[
Reference Vuorinen55
, (2·39)]
$z \in \partial G_2$
[
Reference Vuorinen55
, (2·39)]
The proof of (2) follows now from [ Reference Vuorinen55 , theorem 12·5].
We are next going to prove the following theorem, which extends a result of Gehring and Osgood [ Reference Gehring and Osgood20 , theorem 3] for quasiconformal mappings. This proof is based on the above Harnack inequality.
Theorem 5·3. Let
![]() $f:G_1\to G_2$
be a K-quasimeromorphic mapping where
$f:G_1\to G_2$
be a K-quasimeromorphic mapping where
![]() $G_1\,, G_2 \subset \overline{\mathbb{R}}^n\,,n \geqslant2\,.$
If the boundary
$G_1\,, G_2 \subset \overline{\mathbb{R}}^n\,,n \geqslant2\,.$
If the boundary
![]() $\partial G_2$
is uniformly perfect, then there exists a constant
$\partial G_2$
is uniformly perfect, then there exists a constant
![]() $d_3>0$
such that for all
$d_3>0$
such that for all
![]() $x,y \in G_1$
$x,y \in G_1$
We prove below in Example (5·5) that the uniform perfectness of
![]() $G_2$
cannot be dropped from Theorem 5·3 and the same example also shows that a similar remark applies to Theorem 5·2. In this example, the image domain
$G_2$
cannot be dropped from Theorem 5·3 and the same example also shows that a similar remark applies to Theorem 5·2. In this example, the image domain
![]() $G_2$
has one isolated boundary point and cannot therefore be uniformly perfect.
$G_2$
has one isolated boundary point and cannot therefore be uniformly perfect.
5·4. Proof of Theorem 5·3
Choose Möbius transformations
![]() $f_1, f_2$
such that
$f_1, f_2$
such that
![]() $0, \infty \in \partial f_1(G_1)$
and
$0, \infty \in \partial f_1(G_1)$
and
![]() $0, \infty \in \partial f_2(G_2)\,.$
Then
$0, \infty \in \partial f_2(G_2)\,.$
Then
is K-quasiregular and by Theorem 5·2 we have
Because
![]() $f_1(G_1), f_2(G_2) \subset \mathbb{R}^n\,,$
we obtain by Lemma 2·8 (iii) a similar inequality for the
$f_1(G_1), f_2(G_2) \subset \mathbb{R}^n\,,$
we obtain by Lemma 2·8 (iii) a similar inequality for the
![]() $\sigma$
metric, with a bit different constants.
$\sigma$
metric, with a bit different constants.
5·5. Example
To show that the condition
![]() $\partial G_2$
be uniformly perfect cannot be dropped from Theorem 5·3, we consider the analytic function
$\partial G_2$
be uniformly perfect cannot be dropped from Theorem 5·3, we consider the analytic function
![]() $g(z)= \exp\left(({z+1})/({z-1})\right)$
which maps the unit disk
$g(z)= \exp\left(({z+1})/({z-1})\right)$
which maps the unit disk
![]() $\mathbb{B}^2$
onto
$\mathbb{B}^2$
onto
![]() $\mathbb{B}^2\setminus \{0\}\,.$
Let
$\mathbb{B}^2\setminus \{0\}\,.$
Let
![]() $G_1=\mathbb{B}^2$
and
$G_1=\mathbb{B}^2$
and
![]() $G_2=\mathbb{B}^2\setminus \{0\}$
, and let
$G_2=\mathbb{B}^2\setminus \{0\}$
, and let
![]() $x_j=(e^j-1)/(e^j+1)$
for
$x_j=(e^j-1)/(e^j+1)$
for
![]() $j=1,2,\ldots$
. Then
$j=1,2,\ldots$
. Then
![]() $u_j=g(x_j)=\exp(-e^j).$
The standard formula for the hyperbolic distance [
Reference Beardon4
, pp.38–40], [
Reference Vuorinen55
, (2·17)] shows that
$u_j=g(x_j)=\exp(-e^j).$
The standard formula for the hyperbolic distance [
Reference Beardon4
, pp.38–40], [
Reference Vuorinen55
, (2·17)] shows that
where as
as
![]() $j \rightarrow \infty$
. Thus by (i) and (ii) of Lemma 2·8, when
$j \rightarrow \infty$
. Thus by (i) and (ii) of Lemma 2·8, when
![]() $j \rightarrow \infty$
,
$j \rightarrow \infty$
,
![]() $\sigma_{G_2}(g(x_j),g(x_{j+1}))\rightarrow +\infty$
while
$\sigma_{G_2}(g(x_j),g(x_{j+1}))\rightarrow +\infty$
while
![]() $\sigma_{G_1}(x_j,x_{j+1})=h_{G_1}(x_j,x_{j+1})=1$
. This demonstrates that uniform perfectness is needed in Theorem 5·3.
$\sigma_{G_1}(x_j,x_{j+1})=h_{G_1}(x_j,x_{j+1})=1$
. This demonstrates that uniform perfectness is needed in Theorem 5·3.
6. Logarithmic Möbius metric
In this section we study the logarithmic Möbius metric
on a planar domain G in
![]() ${\overline{\mathbb{C}}} = \overline{{\mathbb{R}}^2}$
and prove Theorem 1·15. Though the hyperbolic metric
${\overline{\mathbb{C}}} = \overline{{\mathbb{R}}^2}$
and prove Theorem 1·15. Though the hyperbolic metric
![]() $h_G(z,w)$
is majorized by twice the Möbius metric
$h_G(z,w)$
is majorized by twice the Möbius metric
![]() $2\delta_G(z,w)$
for an arbitrary hyperbolic domain
$2\delta_G(z,w)$
for an arbitrary hyperbolic domain
![]() $G\subset{\overline{\mathbb{C}}}$
(see [
Reference Seittenranta47
]), the logarithmic Möbius metric
$G\subset{\overline{\mathbb{C}}}$
(see [
Reference Seittenranta47
]), the logarithmic Möbius metric
![]() $\Delta_G(z,w)$
is not expected to majorize
$\Delta_G(z,w)$
is not expected to majorize
![]() $h_G(z,w)$
in general. Indeed,
$h_G(z,w)$
in general. Indeed,
![]() $\delta_G(z,w)$
is Lipschitz equivalent to
$\delta_G(z,w)$
is Lipschitz equivalent to
![]() $h_G(z,w)$
if
$h_G(z,w)$
if
![]() $\partial G$
is uniformly perfect as we noted in Introduction. However, the situation is different when
$\partial G$
is uniformly perfect as we noted in Introduction. However, the situation is different when
![]() $\partial G$
consists of finitely many points. We now prove the first part of Theorem 1·15. By using the results from [
Reference Sugawa and Zhang50
] or [
Reference Sugawa, Vuorinen and Zhang49
], we could obtain more explicit estimates for the bound
$\partial G$
consists of finitely many points. We now prove the first part of Theorem 1·15. By using the results from [
Reference Sugawa and Zhang50
] or [
Reference Sugawa, Vuorinen and Zhang49
], we could obtain more explicit estimates for the bound
![]() $c=c(A).$
However, for brevity, we shall be content with existence of
$c=c(A).$
However, for brevity, we shall be content with existence of
![]() $c>0$
only.
$c>0$
only.
Proof of the first part of Theorem 1·15. Let A be a finite set in
![]() ${\overline{\mathbb{C}}}$
with
${\overline{\mathbb{C}}}$
with
![]() $\mathrm{card\,}(A)\geqslant 3$
and
$\mathrm{card\,}(A)\geqslant 3$
and
![]() $G={\overline{\mathbb{C}}}\setminus A.$
Since both metrics are Möbius invariant, we may assume that
$G={\overline{\mathbb{C}}}\setminus A.$
Since both metrics are Möbius invariant, we may assume that
![]() $\infty\in A$
so that
$\infty\in A$
so that
![]() $G\subset{\mathbb{C}}.$
We now consider the function
$G\subset{\mathbb{C}}.$
We now consider the function
 \begin{eqnarray*}\nonumber\nonumber F(z,w)=\left\{\begin{array}{ll}\nonumber\displaystyle\frac{h_G(z,w)}{\Delta_G(z,w)} &\quad (z\ne w)\nonumber \\ \nonumber\nonumber& \\\nonumber\displaystyle\frac{\rho_G(z)}{w_G(z)} &\quad (z=w)\end{array}\nonumber\right.\nonumber\end{eqnarray*}
\begin{eqnarray*}\nonumber\nonumber F(z,w)=\left\{\begin{array}{ll}\nonumber\displaystyle\frac{h_G(z,w)}{\Delta_G(z,w)} &\quad (z\ne w)\nonumber \\ \nonumber\nonumber& \\\nonumber\displaystyle\frac{\rho_G(z)}{w_G(z)} &\quad (z=w)\end{array}\nonumber\right.\nonumber\end{eqnarray*}
on
![]() $G\times G.$
Here,
$G\times G.$
Here,
![]() $\rho_G(z)$
is the density of the hyperbolic metric on G and
$\rho_G(z)$
is the density of the hyperbolic metric on G and
![]() $w_G(z)$
is defined in (2·7). Our aim is to find an upper bound of
$w_G(z)$
is defined in (2·7). Our aim is to find an upper bound of
![]() $F(z,w).$
Since the hyperbolic distance is induced by the Riemannian metric
$F(z,w).$
Since the hyperbolic distance is induced by the Riemannian metric
![]() $\rho_G(z)|dz|,$
we have
$\rho_G(z)|dz|,$
we have
for
![]() $z\in G.$
On the other hand, by definition of the metric
$z\in G.$
On the other hand, by definition of the metric
![]() $\delta_G(z,w)$
and the property
$\delta_G(z,w)$
and the property
![]() $\log(1+x)=x+O(x^2)\;(x\to0),$
we have
$\log(1+x)=x+O(x^2)\;(x\to0),$
we have
 \begin{eqnarray}\lim_{w\to z}\frac{\Delta_G(z,w)}{|z-w|}&=&\lim_{w\to z}\frac{\delta_G(z,w)}{|z-w|}\nonumber \\&=&\lim_{w\to z}\frac{m_G(z,w)}{|z-w|}\nonumber \\&=&w_G(z) \nonumber\end{eqnarray}
\begin{eqnarray}\lim_{w\to z}\frac{\Delta_G(z,w)}{|z-w|}&=&\lim_{w\to z}\frac{\delta_G(z,w)}{|z-w|}\nonumber \\&=&\lim_{w\to z}\frac{m_G(z,w)}{|z-w|}\nonumber \\&=&w_G(z) \nonumber\end{eqnarray}
for
![]() $z\in G.$
Therefore, we see that the function F(z, w) is continuous on
$z\in G.$
Therefore, we see that the function F(z, w) is continuous on
![]() $G\times G.$
Since
$G\times G.$
Since
![]() ${\overline{\mathbb{C}}}\times{\overline{\mathbb{C}}}$
is compact, in order to prove that
${\overline{\mathbb{C}}}\times{\overline{\mathbb{C}}}$
is compact, in order to prove that
![]() $\sup_{(z,w)\in G\times G}F(z,w)<+\infty,$
it is enough to prove that
$\sup_{(z,w)\in G\times G}F(z,w)<+\infty,$
it is enough to prove that
for each
![]() $(\zeta,\omega)\in\partial(G\times G).$
Note that
$(\zeta,\omega)\in\partial(G\times G).$
Note that
![]() $\partial(G\times G)=(\partial G\times G)\cup(G\times\partial G)\cup(\partial G\times\partial G).$
When
$\partial(G\times G)=(\partial G\times G)\cup(G\times\partial G)\cup(\partial G\times\partial G).$
When
![]() $(a,z_0)\in \partial G\times G=A\times G,$
by Lemma 1·10, we have
$(a,z_0)\in \partial G\times G=A\times G,$
by Lemma 1·10, we have
![]() $\hat F(a,z_0)=1.$
(If
$\hat F(a,z_0)=1.$
(If
![]() $a=\infty,$
with the Möbius invariance of F(z, w) in mind, we may consider the inversion
$a=\infty,$
with the Möbius invariance of F(z, w) in mind, we may consider the inversion
![]() $1/z$
to reduce to the finite case.) Likewise, we can see that
$1/z$
to reduce to the finite case.) Likewise, we can see that
![]() $\hat F(z_0,a)=1.$
$\hat F(z_0,a)=1.$
The remaining case is when
![]() $(a,b)\in\partial G\times\partial G.$
We may further assume that
$(a,b)\in\partial G\times\partial G.$
We may further assume that
![]() $a\ne\infty\ne b.$
If
$a\ne\infty\ne b.$
If
![]() $a\ne b,$
letting
$a\ne b,$
letting
![]() $C>|a-b|^2$
be a suitable constant, we have
$C>|a-b|^2$
be a suitable constant, we have
for z, w with
![]() $|z-a|<\varepsilon$
and
$|z-a|<\varepsilon$
and
![]() $|w-b|<\varepsilon,$
where
$|w-b|<\varepsilon,$
where
![]() $\varepsilon>0$
is a small enough number. Therefore, taking a fixed point
$\varepsilon>0$
is a small enough number. Therefore, taking a fixed point
![]() $z_0\in G,$
we have for the same z, w,
$z_0\in G,$
we have for the same z, w,
 \begin{eqnarray}F(z,w)&\leqslant& \frac{h_G(z,z_0)+h_G(z_0,w)}{\Delta_G(z,w)} \nonumber\\[5pt]&\leqslant& \frac{h_G(z,z_0)}{\log\big[1+\log(1+C'/|a-z|)\big]}+\frac{h_G(z_0,w)}{\log\big[1+\log(1+C'/|b-w|)\big]},\nonumber\end{eqnarray}
\begin{eqnarray}F(z,w)&\leqslant& \frac{h_G(z,z_0)+h_G(z_0,w)}{\Delta_G(z,w)} \nonumber\\[5pt]&\leqslant& \frac{h_G(z,z_0)}{\log\big[1+\log(1+C'/|a-z|)\big]}+\frac{h_G(z_0,w)}{\log\big[1+\log(1+C'/|b-w|)\big]},\nonumber\end{eqnarray}
where
![]() $C'=C/\varepsilon.$
Taking the upper limit as
$C'=C/\varepsilon.$
Taking the upper limit as
![]() $z\to a$
and
$z\to a$
and
![]() $w\to b,$
with the help of (1·12), we finally get
$w\to b,$
with the help of (1·12), we finally get
![]() $\hat F(a,b)\leqslant 2.$
$\hat F(a,b)\leqslant 2.$
If
![]() $a=b,$
assuming
$a=b,$
assuming
![]() $a=0$
and
$a=0$
and
![]() ${\mathbb{D}}^*\subset G\subset{\mathbb{C}}\setminus\{0,1\}$
as before, we have the estimates
${\mathbb{D}}^*\subset G\subset{\mathbb{C}}\setminus\{0,1\}$
as before, we have the estimates
![]() $h_G(z,w)\leqslant h_{{\mathbb{D}}^*}(z,w)$
and
$h_G(z,w)\leqslant h_{{\mathbb{D}}^*}(z,w)$
and
![]() $m_G(z,w)\geqslant m_{{\mathbb{C}}\setminus\{0,1\}}(z,w)$
for
$m_G(z,w)\geqslant m_{{\mathbb{C}}\setminus\{0,1\}}(z,w)$
for
![]() $z,w\in{\mathbb{D}}^*.$
Hence,
$z,w\in{\mathbb{D}}^*.$
Hence,
![]() $F(z,w)\leqslant h_{{\mathbb{D}}^*}(z,w)/\Delta_{{\mathbb{C}}\setminus\{0,1\}}(z,w).$
The expected claim is now implied by (6·4), which is a consequence of the following lemma.
$F(z,w)\leqslant h_{{\mathbb{D}}^*}(z,w)/\Delta_{{\mathbb{C}}\setminus\{0,1\}}(z,w).$
The expected claim is now implied by (6·4), which is a consequence of the following lemma.
Let
![]() $E^*\;:\!=\;\{z\;:\; 0<|z|\leqslant e^{-1}\}$
. For
$E^*\;:\!=\;\{z\;:\; 0<|z|\leqslant e^{-1}\}$
. For
![]() $z_1,z_2 \in E^*$
, define
$z_1,z_2 \in E^*$
, define
 \begin{equation} D(z_1, z_2)=\frac{2\sin\!(\theta/2)}{\max\{\tau_1,\, \tau_2\}}+\left|\log\tau_2-\log\tau_1\right|,\end{equation}
\begin{equation} D(z_1, z_2)=\frac{2\sin\!(\theta/2)}{\max\{\tau_1,\, \tau_2\}}+\left|\log\tau_2-\log\tau_1\right|,\end{equation}
where
![]() $\tau_1=\log(1/|z_1|),\; \tau_2=\log(1/|z_2|),\; \theta=|\arg (z_2/z_1)| \in [0,\pi].$
It is known that
$\tau_1=\log(1/|z_1|),\; \tau_2=\log(1/|z_2|),\; \theta=|\arg (z_2/z_1)| \in [0,\pi].$
It is known that
![]() $D(z_1, z_2)$
is a distance function on
$D(z_1, z_2)$
is a distance function on
![]() $E^*$
(see [
Reference Sugawa and Zhang50
, lemma 3·1]).
$E^*$
(see [
Reference Sugawa and Zhang50
, lemma 3·1]).
Lemma 6·2. Let
![]() $\Omega={\mathbb{C}}\setminus\{0,1\}.$
$\Omega={\mathbb{C}}\setminus\{0,1\}.$
-
(i)
 $h_{{\mathbb{D}}^*}(z_1,z_2)\leqslant (\pi/4)D(z_1,z_2)$
for
$h_{{\mathbb{D}}^*}(z_1,z_2)\leqslant (\pi/4)D(z_1,z_2)$
for
 $z_1,z_2\in E^*.$
$z_1,z_2\in E^*.$
-
(ii)
 $D(z_1, z_2)\leqslant M_0{\Delta}_{\Omega}(z_1,z_2)$
for
$D(z_1, z_2)\leqslant M_0{\Delta}_{\Omega}(z_1,z_2)$
for
 $z_1,z_2\in E^*,$
where
$z_1,z_2\in E^*,$
where
 $M_0 =2/\log \left( 1+ \log3 \right) = 2.6980\ldots $
.
$M_0 =2/\log \left( 1+ \log3 \right) = 2.6980\ldots $
.
The constants
![]() $\pi/4$
and
$\pi/4$
and
![]() $M_0$
are sharp, respectively.
$M_0$
are sharp, respectively.
Proof. Part (i) is contained in theorem 3·2 of [
Reference Sugawa and Zhang50
]. The sharpness is observed for
![]() $z_1=e^{-\tau}, z_2=-e^{-\tau}$
as
$z_1=e^{-\tau}, z_2=-e^{-\tau}$
as
![]() $\tau\to+\infty.$
We prove only part (ii). Let
$\tau\to+\infty.$
We prove only part (ii). Let
![]() $z_1,z_2\in E^*.$
We may assume that
$z_1,z_2\in E^*.$
We may assume that
![]() $|z_1|\leqslant |z_2|$
by relabeling if necessary. Then
$|z_1|\leqslant |z_2|$
by relabeling if necessary. Then
![]() $|z_j|=e^{-\tau_j}\;(j=1,2)$
for some
$|z_j|=e^{-\tau_j}\;(j=1,2)$
for some
![]() $1 \leqslant \tau_2 \leqslant \tau_1 < +\infty.$
We put
$1 \leqslant \tau_2 \leqslant \tau_1 < +\infty.$
We put
![]() $\tau= \tau_2$
,
$\tau= \tau_2$
,
![]() $s=\tau_1/ \tau$
and
$s=\tau_1/ \tau$
and
![]() $\varphi=\sin (\theta/2),$
where
$\varphi=\sin (\theta/2),$
where
![]() $\theta=|\arg(z_2/z_1)|\in[0,\pi].$
Then
$\theta=|\arg(z_2/z_1)|\in[0,\pi].$
Then
![]() $s\geqslant 1$
,
$s\geqslant 1$
,
![]() $0\leqslant \varphi \leqslant 1$
. By definition, we have
$0\leqslant \varphi \leqslant 1$
. By definition, we have
Let
![]() $x\;:\!=\;e^{s-1} \geqslant 1$
. Then
$x\;:\!=\;e^{s-1} \geqslant 1$
. Then
 \begin{eqnarray}{\Delta}_{\Omega} (z_1,z_2)&\geqslant& \log\big[1+\log(1+\sqrt{(x^{\tau} -1)^2+4\varphi^2 x^{\tau}})\big]\;=\!:\;\,{f_1}(\tau,\varphi,x), \quad\textrm{and}\nonumber \\D (z_1,z_2)&=&\frac{2\varphi}{s\tau}+\log(1+\log x)\;=\!:\;\,{f_2}(\tau,\varphi,x).\nonumber\end{eqnarray}
\begin{eqnarray}{\Delta}_{\Omega} (z_1,z_2)&\geqslant& \log\big[1+\log(1+\sqrt{(x^{\tau} -1)^2+4\varphi^2 x^{\tau}})\big]\;=\!:\;\,{f_1}(\tau,\varphi,x), \quad\textrm{and}\nonumber \\D (z_1,z_2)&=&\frac{2\varphi}{s\tau}+\log(1+\log x)\;=\!:\;\,{f_2}(\tau,\varphi,x).\nonumber\end{eqnarray}
Further let
Then
![]() ${f_3}(\tau,\varphi,x)$
is decreasing in
${f_3}(\tau,\varphi,x)$
is decreasing in
![]() $1\leqslant\tau<+\infty$
, and thus
$1\leqslant\tau<+\infty$
, and thus
![]() ${f_3}(\tau,\varphi,x)\leqslant {f_3}(1,\varphi,x)$
for
${f_3}(\tau,\varphi,x)\leqslant {f_3}(1,\varphi,x)$
for
![]() $\tau\geqslant 1.$
By straightforward computations, we have
$\tau\geqslant 1.$
By straightforward computations, we have
Therefore
![]() ${f_3}(1,\varphi,x)$
is convex in
${f_3}(1,\varphi,x)$
is convex in
![]() $0\leqslant \varphi\leqslant 1$
. Since
$0\leqslant \varphi\leqslant 1$
. Since
it is easy to verify that
![]() ${f_3}(1,1,x)$
is decreasing in
${f_3}(1,1,x)$
is decreasing in
![]() $1\leqslant x$
, which leads to
$1\leqslant x$
, which leads to
![]() ${f_3}(1,1,x)\leqslant {f_3}(1,1,1)=0.$
Noting that
${f_3}(1,1,x)\leqslant {f_3}(1,1,1)=0.$
Noting that
![]() ${f_3}(1,0,x)=(1-M_0)\log(1+\log x)<0$
, we have
${f_3}(1,0,x)=(1-M_0)\log(1+\log x)<0$
, we have
![]() ${f_3}(1,\varphi,x)\hbox{$\leqslant 0$}$
from convexity, and thus
${f_3}(1,\varphi,x)\hbox{$\leqslant 0$}$
from convexity, and thus
![]() ${f_3}(\tau,\varphi,x)\leqslant {f_3}(1,\varphi,x)\leqslant 0$
. This completes the proof of the required inequality. To show its sharpness, it is enough to put
${f_3}(\tau,\varphi,x)\leqslant {f_3}(1,\varphi,x)\leqslant 0$
. This completes the proof of the required inequality. To show its sharpness, it is enough to put
![]() $z_1=e^{-1}$
and
$z_1=e^{-1}$
and
![]() $z_2=-e^{-1}$
.
$z_2=-e^{-1}$
.
Remark 6·3. As an immediate consequence of the lemma, we have the inequality
As the reader can observe in the proof, this constant
![]() $(\pi/4)M_0\approx 2.11904$
is not sharp.
$(\pi/4)M_0\approx 2.11904$
is not sharp.
We now complete the proof of Theorem 1·15.
Proof of the second part of Theorem 1·15. Let G be a hyperbolic domain in
![]() ${\overline{\mathbb{C}}}$
with a puncture at the point a. Suppose that
${\overline{\mathbb{C}}}$
with a puncture at the point a. Suppose that
![]() $\Phi(\delta_G(z,w))\leqslant h_G(z,w)$
for
$\Phi(\delta_G(z,w))\leqslant h_G(z,w)$
for
![]() $z,w\in G.$
By the Möbius invariance of
$z,w\in G.$
By the Möbius invariance of
![]() $\delta_G$
and
$\delta_G$
and
![]() $h_G,$
we may assume that
$h_G,$
we may assume that
![]() $a=0$
and that
$a=0$
and that
![]() ${\mathbb{D}}^*\subset G\subset{\mathbb{C}}.$
Then
${\mathbb{D}}^*\subset G\subset{\mathbb{C}}.$
Then
![]() $m_G(x,-x)\geqslant |0,x,\infty,-x|=2$
and thus
$m_G(x,-x)\geqslant |0,x,\infty,-x|=2$
and thus
![]() $\delta_G(x,-x)\geqslant \log 3$
for
$\delta_G(x,-x)\geqslant \log 3$
for
![]() $0<x<1.$
Therefore, we would have
$0<x<1.$
Therefore, we would have
![]() $\Phi(\log 3)\leqslant h_G(x,-x).$
On the other hand, letting
$\Phi(\log 3)\leqslant h_G(x,-x).$
On the other hand, letting
![]() $\gamma$
be the upper half of the circle
$\gamma$
be the upper half of the circle
![]() $|z|=x,$
we obtain
$|z|=x,$
we obtain
Since
![]() $\log(1/x)\to+\infty$
as
$\log(1/x)\to+\infty$
as
![]() $x\to 0^+,$
we observe that
$x\to 0^+,$
we observe that
![]() $h_G(x,-x)\to 0$
as
$h_G(x,-x)\to 0$
as
![]() $x\to 0^+,$
which contradicts the above.
$x\to 0^+,$
which contradicts the above.
Acknowledgements
The authors are indebted to the anonymous referee for valuable corrections.