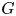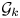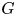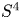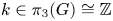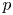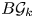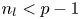1. Introduction
Let $G$![]() be a Lie group and $P\to X$
be a Lie group and $P\to X$![]() be a principal $G$
be a principal $G$![]() -bundle over a manifold $X$
-bundle over a manifold $X$![]() . Automorphisms of $P$
. Automorphisms of $P$![]() are by definition $G$
are by definition $G$![]() -equivariant self-maps of $P$
-equivariant self-maps of $P$![]() covering the identity map of $X$
covering the identity map of $X$![]() . The topological group of automorphisms of $P$
. The topological group of automorphisms of $P$![]() is called the gauge group of $P$
is called the gauge group of $P$![]() ; we denote this group by $\mathcal {G}(P)$
; we denote this group by $\mathcal {G}(P)$![]() . The classifying space of $\mathcal {G}(P)$
. The classifying space of $\mathcal {G}(P)$![]() is denoted by $B\mathcal {G}(P)$
is denoted by $B\mathcal {G}(P)$![]() .
.
Gauge groups are fundamental in modern physics and geometry. Since the classifying space $B\mathcal {G}(P)$![]() is homotopy equivalent to the moduli space of connections on $P$
is homotopy equivalent to the moduli space of connections on $P$![]() as in [Reference Atiyah and Bott1], the topology of gauge groups over $4$
as in [Reference Atiyah and Bott1], the topology of gauge groups over $4$![]() -manifolds and their classifying spaces has proved to be of immense value in studying diffeomorphism structures on $4$
-manifolds and their classifying spaces has proved to be of immense value in studying diffeomorphism structures on $4$![]() -manifolds [Reference Donaldson5], Yang–Mills theory [Reference Atiyah and Jones2], and invariants of $3$
-manifolds [Reference Donaldson5], Yang–Mills theory [Reference Atiyah and Jones2], and invariants of $3$![]() -manifolds [Reference Floer6]. Donaldson famously used the rational cohomology of $B\mathcal {G}(P)$
-manifolds [Reference Floer6]. Donaldson famously used the rational cohomology of $B\mathcal {G}(P)$![]() in the case when $G=SU(2)$
in the case when $G=SU(2)$![]() and $X$
and $X$![]() is a simply-connected $4$
is a simply-connected $4$![]() -manifold in order to construct polynomial invariants to distinguish diffeomorphism types. Ever since, an important problem has been to calculate the mod-$p$
-manifold in order to construct polynomial invariants to distinguish diffeomorphism types. Ever since, an important problem has been to calculate the mod-$p$![]() (co)-homology of $B\mathcal {G}(P)$
(co)-homology of $B\mathcal {G}(P)$![]() when $G=SU(2)$
when $G=SU(2)$![]() and $X$
and $X$![]() is a simply-connected $4$
is a simply-connected $4$![]() -manifold for a prime $p$
-manifold for a prime $p$![]() , in the hope of finding new polynomial invariants of diffeomorphism types.
, in the hope of finding new polynomial invariants of diffeomorphism types.
A certain subring of the mod-$2$![]() cohomology of $B\mathcal {G}(P)$
cohomology of $B\mathcal {G}(P)$![]() was studied by Masbaum [Reference Masbaum16] when $G=SU(2)$
was studied by Masbaum [Reference Masbaum16] when $G=SU(2)$![]() and $X$
and $X$![]() is a simply-connected closed $4$
is a simply-connected closed $4$![]() -manifold, but otherwise nothing else is known. In terms of other Lie groups, Choi [Reference Choi3] has some partial results on the mod-2 homology for $G=Sp(n)$
-manifold, but otherwise nothing else is known. In terms of other Lie groups, Choi [Reference Choi3] has some partial results on the mod-2 homology for $G=Sp(n)$![]() and $X=S^{4}$
and $X=S^{4}$![]() . In this paper we make significant progress, completely calculating the mod-$p$
. In this paper we make significant progress, completely calculating the mod-$p$![]() homology of $B\mathcal {G}(P)$
homology of $B\mathcal {G}(P)$![]() for a family of Lie groups $G$
for a family of Lie groups $G$![]() when $X=S^{4}$
when $X=S^{4}$![]() . In particular, this includes the pivotal case of $G=SU(2)$
. In particular, this includes the pivotal case of $G=SU(2)$![]() for $p\geq 5$
for $p\geq 5$![]() .
.
To state our results, we need some notation. Let $G$![]() be a compact connected simple Lie group. Principal $G$
be a compact connected simple Lie group. Principal $G$![]() -bundles over $S^{4}$
-bundles over $S^{4}$![]() are classified by $\pi _3(G)$
are classified by $\pi _3(G)$![]() , where $\pi _3(G)\cong \mathbb {Z}$
, where $\pi _3(G)\cong \mathbb {Z}$![]() since $G$
since $G$![]() is simple. Let $\mathcal {G}_k$
is simple. Let $\mathcal {G}_k$![]() denote the gauge group of a principal $G$
denote the gauge group of a principal $G$![]() -bundle over $S^{4}$
-bundle over $S^{4}$![]() corresponding to $k\in \mathbb {Z}\cong \pi _3(G)$
corresponding to $k\in \mathbb {Z}\cong \pi _3(G)$![]() . Let $\operatorname {Map}_{k}(S^{4},\,BG)$
. Let $\operatorname {Map}_{k}(S^{4},\,BG)$![]() be the component of the space of continuous (not necessarily pointed) maps from $S^{4}$
be the component of the space of continuous (not necessarily pointed) maps from $S^{4}$![]() to $BG$
to $BG$![]() which are of degree $k$
which are of degree $k$![]() , and similarly define $\operatorname {Map}^{*}_{k}(S^{4},\,BG)$
, and similarly define $\operatorname {Map}^{*}_{k}(S^{4},\,BG)$![]() with respect to pointed maps. There is a fibration
with respect to pointed maps. There is a fibration
where $ev$![]() evaluates a map at the basepoint of $S^{4}$
evaluates a map at the basepoint of $S^{4}$![]() . Let $G\langle 3\rangle$
. Let $G\langle 3\rangle$![]() be the three-connected cover of $G$
be the three-connected cover of $G$![]() . For each $k\in \mathbb {Z}$
. For each $k\in \mathbb {Z}$![]() , the space $\operatorname {Map}^{*}_{k}(S^{4},\,BG)$
, the space $\operatorname {Map}^{*}_{k}(S^{4},\,BG)$![]() is homotopy equivalent to $\Omega ^{3} G\langle 3\rangle$
is homotopy equivalent to $\Omega ^{3} G\langle 3\rangle$![]() . By [Reference Atiyah and Bott1, Reference Gottlieb7], there is a homotopy equivalence $B\mathcal {G}_k\simeq \operatorname {Map}_{k}(S^{4},\,BG)$
. By [Reference Atiyah and Bott1, Reference Gottlieb7], there is a homotopy equivalence $B\mathcal {G}_k\simeq \operatorname {Map}_{k}(S^{4},\,BG)$![]() . Thus there is a homotopy fibration
. Thus there is a homotopy fibration
The Lie group $G$![]() has type $(n_{1},\,\ldots,\,n_{l})$
has type $(n_{1},\,\ldots,\,n_{l})$![]() if the rational cohomology of $G$
if the rational cohomology of $G$![]() is generated by elements in degrees $2n_{1}-1,\,\ldots,\,2n_{l}-1$
is generated by elements in degrees $2n_{1}-1,\,\ldots,\,2n_{l}-1$![]() , where $n_{1}<\cdots < n_{l}$
, where $n_{1}<\cdots < n_{l}$![]() . Unless otherwise indicated, homology is assumed to be with mod-$p$
. Unless otherwise indicated, homology is assumed to be with mod-$p$![]() coefficients.
coefficients.
Theorem 1.1 Let $G$![]() be a compact connected simple Lie group of type $(n_{1},\,\ldots,\,n_{l})$
be a compact connected simple Lie group of type $(n_{1},\,\ldots,\,n_{l})$![]() and let $p$
and let $p$![]() be a prime. If $n_{l}< p-1$
be a prime. If $n_{l}< p-1$![]() then there is an isomorphism of $\mathbb {Z}/p\mathbb {Z}$
then there is an isomorphism of $\mathbb {Z}/p\mathbb {Z}$![]() -vector spaces
-vector spaces
Under the assumption of theorem 1.1 the Lie group $G$![]() is $p$
is $p$![]() -locally homotopy equivalent to the product $\prod _{i=1}^{l} S^{2n_i-1}$
-locally homotopy equivalent to the product $\prod _{i=1}^{l} S^{2n_i-1}$![]() , so we can also calculate the Poincaré series of $H_*(B\mathcal {G}_k)$
, so we can also calculate the Poincaré series of $H_*(B\mathcal {G}_k)$![]() by theorem 1.1 (corollary 4.5). Remarkably, theorem 1.1 implies that the mod-$p$
by theorem 1.1 (corollary 4.5). Remarkably, theorem 1.1 implies that the mod-$p$![]() homology of $B\mathcal {G}_k$
homology of $B\mathcal {G}_k$![]() is independent of $k$
is independent of $k$![]() for $p$
for $p$![]() large, whereas there is more than one $p$
large, whereas there is more than one $p$![]() -local homotopy type in the family $\{B\mathcal {G}_k\}_{k\in \mathbb {Z}}$
-local homotopy type in the family $\{B\mathcal {G}_k\}_{k\in \mathbb {Z}}$![]() for $p$
for $p$![]() large as was proved in [Reference Kishimoto and Tsutaya12]. The approach to theorem 1.1 is to consider the Serre spectral sequence applied to the fiberwise coproduct of (1.2). Control is obtained over the differentials by showing that the first nontrivial differential is a transgression on a certain element, which is not obvious, and then atomicity-style arguments (cf. [Reference Selick18]) are used to show the spectral sequence must collapse at the $E^{2}$
large as was proved in [Reference Kishimoto and Tsutaya12]. The approach to theorem 1.1 is to consider the Serre spectral sequence applied to the fiberwise coproduct of (1.2). Control is obtained over the differentials by showing that the first nontrivial differential is a transgression on a certain element, which is not obvious, and then atomicity-style arguments (cf. [Reference Selick18]) are used to show the spectral sequence must collapse at the $E^{2}$![]() -term.
-term.
Of key interest is when $G=SU(2)$![]() . Theorem 1.1 holds if $p\geq 5$
. Theorem 1.1 holds if $p\geq 5$![]() in this case. We also obtain partial results for the prime $3$
in this case. We also obtain partial results for the prime $3$![]() , which are of a different flavour than those in theorem 1.1. Let $(m,\,n)$
, which are of a different flavour than those in theorem 1.1. Let $(m,\,n)$![]() denote the gcd of integers $m$
denote the gcd of integers $m$![]() and $n$
and $n$![]() . For $(k,\,3)=1$
. For $(k,\,3)=1$![]() , it is the Serre spectral sequence for the homotopy fibration $SU(2)\to \Omega ^{3}SU(2)\langle 3\rangle \to B\mathcal {G}_k$
, it is the Serre spectral sequence for the homotopy fibration $SU(2)\to \Omega ^{3}SU(2)\langle 3\rangle \to B\mathcal {G}_k$![]() induced from (1.2) that collapses at the $E^{2}$
induced from (1.2) that collapses at the $E^{2}$![]() -term.
-term.
Theorem 1.2 Let $G=SU(2)$![]() and $p=3$
and $p=3$![]() . If $(k,\,3)=1$
. If $(k,\,3)=1$![]() then there is an isomorphism of $\mathbb {Z}/3\mathbb {Z}$
then there is an isomorphism of $\mathbb {Z}/3\mathbb {Z}$![]() -vector spaces
-vector spaces
where $x_3$![]() is a generator of $H_3(\Omega ^{3} S^{3}\langle 3\rangle )\cong \mathbb {Z}/3\mathbb {Z}$
is a generator of $H_3(\Omega ^{3} S^{3}\langle 3\rangle )\cong \mathbb {Z}/3\mathbb {Z}$![]() and $(x_{3})$
and $(x_{3})$![]() is the ideal generated by $x_{3}$
is the ideal generated by $x_{3}$![]() .
.
The case $(k,\,3)=3$![]() is still open. The difference of the mod-$p$
is still open. The difference of the mod-$p$![]() homology of $B\mathcal {G}_k$
homology of $B\mathcal {G}_k$![]() for $G=SU(2)$
for $G=SU(2)$![]() in Theorems 1.1 and 1.2 comes from the homotopy commutativity of $SU(2)$
in Theorems 1.1 and 1.2 comes from the homotopy commutativity of $SU(2)$![]() ; it is homotopy commutative if and only if $p\ge 5$
; it is homotopy commutative if and only if $p\ge 5$![]() as in [Reference McGibbon17]. This is notable because the product decomposition $\mathcal {G}_k\simeq G\times \Omega ^{4}G\langle 3\rangle$
as in [Reference McGibbon17]. This is notable because the product decomposition $\mathcal {G}_k\simeq G\times \Omega ^{4}G\langle 3\rangle$![]() as $A_n$
as $A_n$![]() -spaces is guaranteed by the higher homotopy commutativity of $G$
-spaces is guaranteed by the higher homotopy commutativity of $G$![]() as in [Reference Kishimoto and Kono11, Reference Kishimoto and Tsutaya12], whereas theorem 1.1 shows the homological product decomposition as $A_\infty$
as in [Reference Kishimoto and Kono11, Reference Kishimoto and Tsutaya12], whereas theorem 1.1 shows the homological product decomposition as $A_\infty$![]() -spaces.
-spaces.
2. Serre spectral sequence
Consider a homotopy fibration
over a path-connected base $B$![]() such that $F$
such that $F$![]() is an H-space and there is a fiberwise action of $F$
is an H-space and there is a fiberwise action of $F$![]() on $E$
on $E$![]() which restricts to the multiplication of $F$
which restricts to the multiplication of $F$![]() . We assume that $\pi _1(B)$
. We assume that $\pi _1(B)$![]() acts trivially on $H_*(F)$
acts trivially on $H_*(F)$![]() . Let $(E^{r},\,d^{r})$
. Let $(E^{r},\,d^{r})$![]() denote the associated homology Serre spectral sequence.
denote the associated homology Serre spectral sequence.
Lemma 2.1 There is a coalgebra map
having the following properties.
(1) The map
\[ \mu\colon H_p(B)\otimes H_q(F)=E^{2}_{p,0}\otimes H_q(F)\to E^{2}_{p,q} \]coincides with the canonical isomorphism;
(2) For $x\in E^{r}$
 and $y\in H_*(F),$
and $y\in H_*(F),$ \[ d^{r}(\mu(x\otimes y))=\mu(d^{r}(x)\otimes y). \]
\[ d^{r}(\mu(x\otimes y))=\mu(d^{r}(x)\otimes y). \]
Proof. Since the action of $F$![]() on $E$
on $E$![]() is fiberwise, there is a homotopy commutative diagram
is fiberwise, there is a homotopy commutative diagram

Since rows of this diagram are homotopy fibrations, there is a map between associated homology Serre spectral sequences. Since the homology Serre spectral sequences of the top row is isomorphic with $(E^{r}\otimes H_*(F),\,d^{r}\otimes 1)$![]() , we obtain the map $\mu$
, we obtain the map $\mu$![]() . By definition, $\mu$
. By definition, $\mu$![]() is a coalgebra map. The second statement holds because the differential on $H_*(F)$
is a coalgebra map. The second statement holds because the differential on $H_*(F)$![]() in $E^{r}\otimes H_*(F)$
in $E^{r}\otimes H_*(F)$![]() is trivial. Let $p\colon E\to B$
is trivial. Let $p\colon E\to B$![]() denote the projection. For each $y\in E$
denote the projection. For each $y\in E$![]() , $\pi ^{-1}(\pi (y))$
, $\pi ^{-1}(\pi (y))$![]() is homotopy equivalent to the orbit space $y\cdot F$
is homotopy equivalent to the orbit space $y\cdot F$![]() including $y$
including $y$![]() . Therefore, by the construction of the Serre spectral sequence, the first statement holds.
. Therefore, by the construction of the Serre spectral sequence, the first statement holds.
Corollary 2.2 If $d^{2}=\cdots =d^{r-1}=0$![]() , then the map $\mu \colon E^{r}_{p,0}\otimes H_q(F)\to E^{r}_{p,q}$
, then the map $\mu \colon E^{r}_{p,0}\otimes H_q(F)\to E^{r}_{p,q}$![]() coincides with the canonical isomorphism
coincides with the canonical isomorphism
Let $\overline {F}\to \overline {E}\to B$![]() be a homotopy fibration which is a homotopy retract of (2.1). Let $(\overline {E}^{r},\,\overline {d}^{r})$
be a homotopy fibration which is a homotopy retract of (2.1). Let $(\overline {E}^{r},\,\overline {d}^{r})$![]() denote the associated homology Serre spectral sequence.
denote the associated homology Serre spectral sequence.
Lemma 2.3 If $\overline {d}^{2}=\cdots =\overline {d}^{r-1}=0$![]() and $\overline {d}^{r}\ne 0,$
and $\overline {d}^{r}\ne 0,$![]() then the following statements hold:
then the following statements hold:
(1) $\overline {d}^{r}x\ne 0$
 for some $x\in H_*(B)=\overline {E}^{r}_{*,0};$
for some $x\in H_*(B)=\overline {E}^{r}_{*,0};$
(2) If $y$
 is an element of least degree in $H_*(B)=\overline {E}^{r}_{*,0}$
is an element of least degree in $H_*(B)=\overline {E}^{r}_{*,0}$ with $\overline {d}^{r}y\ne 0$
with $\overline {d}^{r}y\ne 0$ , then $y$
, then $y$ is transgressive and $\overline {d}^{r}(y)$
is transgressive and $\overline {d}^{r}(y)$ is a primitive element of $H_{*-1}(F)=\widehat {E}^{r}_{0,*-1}$
is a primitive element of $H_{*-1}(F)=\widehat {E}^{r}_{0,*-1}$ .
.
Proof. Let $i\colon \overline {E}^{2}\to E^{2}$![]() and $q\colon E^{2}\to \overline {E}^{2}$
and $q\colon E^{2}\to \overline {E}^{2}$![]() denote the inclusion and the retraction, respectively. Since
denote the inclusion and the retraction, respectively. Since
the hypothesis that $\overline {d}^{2}=0$![]() implies that $d^{2}=0$
implies that $d^{2}=0$![]() . Therefore $\overline {E}^{3}=\overline {E}^{2}$
. Therefore $\overline {E}^{3}=\overline {E}^{2}$![]() is a retract of $E^{3}=E^{2}$
is a retract of $E^{3}=E^{2}$![]() . Iterating this argument, since $\overline {d}_{3}=\cdots =\overline {d}^{r-1}=0$
. Iterating this argument, since $\overline {d}_{3}=\cdots =\overline {d}^{r-1}=0$![]() , we also obtain $d^{2}=\cdots =d^{r-1}=0$
, we also obtain $d^{2}=\cdots =d^{r-1}=0$![]() and therefore $\overline {E}^{r}$
and therefore $\overline {E}^{r}$![]() is a retract of $E^{r}$
is a retract of $E^{r}$![]() . The inclusion and retraction at the $r^{th}$
. The inclusion and retraction at the $r^{th}$![]() -stage may still be denoted by $i\colon \overline {E}^{2}\to E^{2}$
-stage may still be denoted by $i\colon \overline {E}^{2}\to E^{2}$![]() and $q\colon E^{2}\to \overline {E}^{2}$
and $q\colon E^{2}\to \overline {E}^{2}$![]() . Suppose that $\overline {d}^{r}(x)=0$
. Suppose that $\overline {d}^{r}(x)=0$![]() for all $x\in H_p(B)=\widehat {E}^{r}_{p,0}$
for all $x\in H_p(B)=\widehat {E}^{r}_{p,0}$![]() . Then
. Then
implying $d^{r}=0$![]() by lemma 2.1 and corollary 2.2. This is a contradiction, so the first statement is proved.
by lemma 2.1 and corollary 2.2. This is a contradiction, so the first statement is proved.
Let $y$![]() be an element of least degree element in $H_*(B)=\overline {E}^{r}_{*,0}$
be an element of least degree element in $H_*(B)=\overline {E}^{r}_{*,0}$![]() such that $\overline {d}^{r}y\ne 0$
such that $\overline {d}^{r}y\ne 0$![]() . Let $\Delta$
. Let $\Delta$![]() denote comultiplication, and set
denote comultiplication, and set
where $|y_i'|<|y|$![]() and $|y_i''|<|y|$
and $|y_i''|<|y|$![]() for each $i$
for each $i$![]() . Since $y$
. Since $y$![]() is an element of least degree in $H_*(B)=E^{r}_{*,0}$
is an element of least degree in $H_*(B)=E^{r}_{*,0}$![]() with $d^{r}y\ne 0$
with $d^{r}y\ne 0$![]() , we have $d^{r}y_i'=0$
, we have $d^{r}y_i'=0$![]() and $d^{r}y_i''=0$
and $d^{r}y_i''=0$![]() for each $i$
for each $i$![]() . Therefore
. Therefore

so $d^{r}(y)$![]() is primitive.
is primitive.
If $r<|y|$![]() , then by corollary 2.2, $d^{r}(y)=\mu (a\otimes b)$
, then by corollary 2.2, $d^{r}(y)=\mu (a\otimes b)$![]() for some non-trivial $a\in H_{|y|-r}(B)$
for some non-trivial $a\in H_{|y|-r}(B)$![]() and $b\in H_{r-1}(F)$
and $b\in H_{r-1}(F)$![]() . This is impossible because $\mu (a\otimes b)$
. This is impossible because $\mu (a\otimes b)$![]() is not primitive by lemma 2.1. Thus $r\ge |y|$
is not primitive by lemma 2.1. Thus $r\ge |y|$![]() . Clearly, $r\le |y|$
. Clearly, $r\le |y|$![]() since $r>|y|$
since $r>|y|$![]() implies $d^{r}(y)$
implies $d^{r}(y)$![]() lands in the second quadrant of the spectral sequence, which is zero. Therefore $r=|y|$
lands in the second quadrant of the spectral sequence, which is zero. Therefore $r=|y|$![]() , implying that $y$
, implying that $y$![]() is transgressive. Moreover, since
is transgressive. Moreover, since
and $d^{r}y$![]() is primitive, $\overline {d}^{r}y$
is primitive, $\overline {d}^{r}y$![]() is also primitive. Therefore the second statement is proved.
is also primitive. Therefore the second statement is proved.
Next, we consider a family of homotopy fibrations $F_n\to E_n\to B$![]() with a common base $B$
with a common base $B$![]() for $n\in \mathbb {Z}$
for $n\in \mathbb {Z}$![]() . Let $(E^{r}_n,\,d^{r}_n)$
. Let $(E^{r}_n,\,d^{r}_n)$![]() denote the associated homology Serre spectral sequence. We can form a homotopy fibration
denote the associated homology Serre spectral sequence. We can form a homotopy fibration
Let $(\widehat {E}^{r},\,\widehat {d}^{r})$![]() denote the associated homology spectral sequence.
denote the associated homology spectral sequence.
Lemma 2.4 If $(\widehat {E}^{r},\,\widehat {d}^{r})$![]() collapses at the second term, then so does $(E^{r}_n,\,d^{r}_n)$
collapses at the second term, then so does $(E^{r}_n,\,d^{r}_n)$![]() for each $n\in \mathbb {Z}$
for each $n\in \mathbb {Z}$![]() .
.
Proof. Since there are isomorphisms

the inclusion $E_n\to E$![]() induces an injection $E^{2}_n\to \widehat {E}^{2}$
induces an injection $E^{2}_n\to \widehat {E}^{2}$![]() . Then the statement is proved by induction on $r$
. Then the statement is proved by induction on $r$![]() .
.
3. The mod-$p$ homology of $\Omega ^{3} G\langle 3\rangle$
homology of $\Omega ^{3} G\langle 3\rangle$ when $G$
when $G$ is $p$
is $p$ -regular
-regular
Localize at an odd prime $p$![]() and take homology with mod-$p$
and take homology with mod-$p$![]() coefficients. If $G$
coefficients. If $G$![]() is $p$
is $p$![]() -regular of type $(n_{1},\,\ldots,\, n_{l})$
-regular of type $(n_{1},\,\ldots,\, n_{l})$![]() then there is a homotopy equivalence $G\simeq \prod _{i=1}^{l} S^{2n_{i}-1}$
then there is a homotopy equivalence $G\simeq \prod _{i=1}^{l} S^{2n_{i}-1}$![]() . Therefore
. Therefore

This is an equivalence of H-spaces and so induces an isomorphism of Hopf algebras in homology. In this section we record a property of $\Omega ^{3} G\langle 3\rangle$![]() which will be important later. This begins with a general definition.
which will be important later. This begins with a general definition.
In general, for a path-connected space $X$![]() of finite type, let $PH_*(X)$
of finite type, let $PH_*(X)$![]() be the subspace of primitive elements in $H_*(X)$
be the subspace of primitive elements in $H_*(X)$![]() . Let
. Let
be the dual of the Steenrod operation $\mathcal {P}^{n}$![]() . For $r\geq 1$
. For $r\geq 1$![]() , let $\beta ^{r}$
, let $\beta ^{r}$![]() be the $r^{\text{th}}$
be the $r^{\text{th}}$![]() -Bockstein. Let $MH_*(X)$
-Bockstein. Let $MH_*(X)$![]() be the subspace of $PH_*(X)$
be the subspace of $PH_*(X)$![]() defined by
defined by
Since $MH_*(X)$![]() records information about the primitive elements in $H_*(X)$
records information about the primitive elements in $H_*(X)$![]() , if $X\simeq A\times B$
, if $X\simeq A\times B$![]() then
then
Now consider $MH_*(\Omega ^{3} G\langle 3\rangle )$![]() . The product decomposition (3.1) implies that
. The product decomposition (3.1) implies that

By [Reference Cohen, Lada and May4] there is an isomorphism of Hopf algebras

such that $|a_i|=|b_i|=i$![]() . Here, the generators are primitive and many are related by the action of the dual Steenrod algebra. Selick [Reference Selick18] determined $MH_*(\Omega ^{3} S^{2n+1})$
. Here, the generators are primitive and many are related by the action of the dual Steenrod algebra. Selick [Reference Selick18] determined $MH_*(\Omega ^{3} S^{2n+1})$![]() in full, we record only the subset of elements of odd degree.
in full, we record only the subset of elements of odd degree.
Lemma 3.1 If $n>1$![]() then $MH_\text {odd}(\Omega ^{3} S^{2n+1})=\mathbb {Z}/p\mathbb {Z}\{a_{2np-3}\}$
then $MH_\text {odd}(\Omega ^{3} S^{2n+1})=\mathbb {Z}/p\mathbb {Z}\{a_{2np-3}\}$![]() .
.
In the references that follow for $\Omega ^{3} S^{3}\langle 3\rangle$![]() , the statements in [Reference Theriault19] are in terms of Anick spaces, but by [Reference Gray and Theriault8] the space $\Omega S^{3}\langle 3\rangle$
, the statements in [Reference Theriault19] are in terms of Anick spaces, but by [Reference Gray and Theriault8] the space $\Omega S^{3}\langle 3\rangle$![]() is homotopy equivalent to the Anick space $T^{2p+1}(p)$
is homotopy equivalent to the Anick space $T^{2p+1}(p)$![]() for $p\geq 3$
for $p\geq 3$![]() . By [Reference Theriault19, proposition 4.1], for $p$
. By [Reference Theriault19, proposition 4.1], for $p$![]() odd there is an isomorphism of Hopf algebras
odd there is an isomorphism of Hopf algebras
which respects the action of the dual Steenrod operations and the Bockstein operations. This can be phrased in terms of a generating set using the isomorphism of Hopf algebras

proved in [Reference Cohen, Lada and May4], where $|\bar {a}_i|=|\bar {b}_i|=i$![]() , and the $n=p$
, and the $n=p$![]() case of (3.3). Again, the generators are primitive and many are related by the action of the dual Steenrod algebra. A description of $MH_*(\Omega ^{3}\langle 3\rangle )$
case of (3.3). Again, the generators are primitive and many are related by the action of the dual Steenrod algebra. A description of $MH_*(\Omega ^{3}\langle 3\rangle )$![]() in full was given in [Reference Theriault19, lemma 4.2], but again we need to only record the subset of elements of odd degree.
in full was given in [Reference Theriault19, lemma 4.2], but again we need to only record the subset of elements of odd degree.
Lemma 3.2 $MH_\text {odd}(\Omega ^{3} S^{3}\langle 3\rangle )=\mathbb {Z}/p\mathbb {Z}\{\bar {a}_{2p-3}\}$![]() .
.
Combining (3.2), lemmas 3.1 and 3.2 we obtain the following.
Lemma 3.3 If $G$![]() is $p$
is $p$![]() -regular of type $(n_{1},\,\ldots,\,n_{l})$
-regular of type $(n_{1},\,\ldots,\,n_{l})$![]() then
then
4. The proof of theorem 1.1
We continue to localize at an odd prime $p$![]() and take homology with mod-$p$
and take homology with mod-$p$![]() coefficients. Let $G$
coefficients. Let $G$![]() be a compact connected simple Lie group of type $(n_1,\,\ldots,\,n_l)$
be a compact connected simple Lie group of type $(n_1,\,\ldots,\,n_l)$![]() . Consider the homotopy fibration sequence
. Consider the homotopy fibration sequence
First, we show properties of $\partial _k\colon G\to \Omega ^{3}G\langle 3\rangle$![]() .
.
Lemma 4.1 Suppose that $G$![]() is $p$
is $p$![]() -regular. Then $\partial _k$
-regular. Then $\partial _k$![]() are null homotopic for all $k$
are null homotopic for all $k$![]() if and only if $n_l< p-1$
if and only if $n_l< p-1$![]() .
.
Proof. Let $\epsilon _i\colon S^{2n_i-1}\to G$![]() be the inclusion for $i=1,\,\ldots,\,l$
be the inclusion for $i=1,\,\ldots,\,l$![]() , where $G\simeq \prod _{i=1}^{l} S^{2n_i-1}$
, where $G\simeq \prod _{i=1}^{l} S^{2n_i-1}$![]() . By [Reference Lang15] $\partial _k$
. By [Reference Lang15] $\partial _k$![]() corresponds to the Samelson product $\langle k\epsilon _1,\,1_G\rangle$
corresponds to the Samelson product $\langle k\epsilon _1,\,1_G\rangle$![]() through the adjoint congruence $[G,\,\Omega ^{3}G\langle 3\rangle ]\cong [S^{3}\wedge G,\,G]$
through the adjoint congruence $[G,\,\Omega ^{3}G\langle 3\rangle ]\cong [S^{3}\wedge G,\,G]$![]() , where $\Omega ^{3}G\langle 3\rangle$
, where $\Omega ^{3}G\langle 3\rangle$![]() is homotopy equivalent to the component of $\Omega ^{3}G$
is homotopy equivalent to the component of $\Omega ^{3}G$![]() containing the basepoint. By the linearity of Samelson products, $\langle k\epsilon _1,\,1_G\rangle =k\langle \epsilon _1,\,1_G\rangle$
containing the basepoint. By the linearity of Samelson products, $\langle k\epsilon _1,\,1_G\rangle =k\langle \epsilon _1,\,1_G\rangle$![]() . Thus we aim to get a condition that guarantees the triviality of $\langle \epsilon _1,\,1_G\rangle$
. Thus we aim to get a condition that guarantees the triviality of $\langle \epsilon _1,\,1_G\rangle$![]() . Arguing as in [Reference Kaji and Kishimoto10], we can see that $\langle \epsilon _1,\,1_G\rangle$
. Arguing as in [Reference Kaji and Kishimoto10], we can see that $\langle \epsilon _1,\,1_G\rangle$![]() is trivial if and only if $\langle \epsilon _1,\,\epsilon _i\rangle$
is trivial if and only if $\langle \epsilon _1,\,\epsilon _i\rangle$![]() is trivial for all $i$
is trivial for all $i$![]() . It is shown that $\langle \epsilon _1,\,\epsilon _i\rangle$
. It is shown that $\langle \epsilon _1,\,\epsilon _i\rangle$![]() is trivial for all $i$
is trivial for all $i$![]() if and only if $n_l< p-1$
if and only if $n_l< p-1$![]() in [Reference Kishimoto and Tsutaya13] when $G$
in [Reference Kishimoto and Tsutaya13] when $G$![]() is a classical group and in [Reference Hasui, Kishimoto and Ohsita9] when $G$
is a classical group and in [Reference Hasui, Kishimoto and Ohsita9] when $G$![]() is an exceptional group. Thus the proof is complete.
is an exceptional group. Thus the proof is complete.
Since $\mathcal {G}_k$![]() is homotopy equivalent to the homotopy fibre of $\partial _k$
is homotopy equivalent to the homotopy fibre of $\partial _k$![]() , the following is immediate from proposition 4.1.
, the following is immediate from proposition 4.1.
Corollary 4.2 If $n_l< p-1$![]() then there is a homotopy equivalence $\mathcal {G}_k\simeq G\times \Omega ^{4}G\langle 3\rangle$
then there is a homotopy equivalence $\mathcal {G}_k\simeq G\times \Omega ^{4}G\langle 3\rangle$![]() .
.
Next, we consider the map $g_k\colon \Omega ^{3}G\langle 3\rangle \to B\mathcal {G}_k$![]() .
.
Lemma 4.3 If $n_l< p-1$![]() then the restriction of $(g_k)_*$
then the restriction of $(g_k)_*$![]() to $MH_\text {odd}(\Omega ^{3} G\langle 3\rangle )$
to $MH_\text {odd}(\Omega ^{3} G\langle 3\rangle )$![]() is an injection.
is an injection.
Proof. First, for $n\geq 2$![]() , consider the homotopy fibration $\Omega ^{4} S^{2n+1}\to \ast \to \Omega ^{3} S^{2n+1}$
, consider the homotopy fibration $\Omega ^{4} S^{2n+1}\to \ast \to \Omega ^{3} S^{2n+1}$![]() . We claim that the element $a_{2np-3}\in H_*(\Omega ^{3} S^{2n+1})$
. We claim that the element $a_{2np-3}\in H_*(\Omega ^{3} S^{2n+1})$![]() transgresses to a nonzero element in $H_*(\Omega ^{4} S^{2n+1})$
transgresses to a nonzero element in $H_*(\Omega ^{4} S^{2n+1})$![]() . To see this, let $E^{2}\colon S^{2n-1}\to \Omega ^{2} S^{2n+1}$
. To see this, let $E^{2}\colon S^{2n-1}\to \Omega ^{2} S^{2n+1}$![]() be the double suspension. Let $W_{n}$
be the double suspension. Let $W_{n}$![]() be the homotopy fibre of $E^{2}$
be the homotopy fibre of $E^{2}$![]() . Then there is a homotopy fibration $\Omega S^{2n+1}\xrightarrow {\Omega E^{2}}\Omega ^{3} S^{2n+1}\to W_{n}$
. Then there is a homotopy fibration $\Omega S^{2n+1}\xrightarrow {\Omega E^{2}}\Omega ^{3} S^{2n+1}\to W_{n}$![]() . By [Reference Cohen, Lada and May4] this fibration induces an isomorphism of Hopf algebras
. By [Reference Cohen, Lada and May4] this fibration induces an isomorphism of Hopf algebras
In particular, since $W_{n}$![]() is $(2np-4)$
is $(2np-4)$![]() -connected, the element $a_{2np-3}\in H_*(\Omega ^{3} S^{2n+1})$
-connected, the element $a_{2np-3}\in H_*(\Omega ^{3} S^{2n+1})$![]() corresponds to an element $c\in H_{2np-3}(W_{n})$
corresponds to an element $c\in H_{2np-3}(W_{n})$![]() . On the other hand, $W_{n}$
. On the other hand, $W_{n}$![]() has a single cell in dimension $2np-3$
has a single cell in dimension $2np-3$![]() , so $c$
, so $c$![]() represents the inclusion of the bottom cell. Now consider the homotopy fibration diagram
represents the inclusion of the bottom cell. Now consider the homotopy fibration diagram

As $c$![]() represents the bottom cell in $H_{2np-3}(W_{n})$
represents the bottom cell in $H_{2np-3}(W_{n})$![]() , it transgresses nontrivially to a class $d\in H_{2np-4}(\Omega W_{n})$
, it transgresses nontrivially to a class $d\in H_{2np-4}(\Omega W_{n})$![]() . Since $a_{2np-3}$
. Since $a_{2np-3}$![]() maps to $c$
maps to $c$![]() , the naturality of the transgression implies that $a_{2np-3}$
, the naturality of the transgression implies that $a_{2np-3}$![]() must transgress to a nontrivial class in $H_{2np-4}(\Omega ^{4} S^{2n+1})$
must transgress to a nontrivial class in $H_{2np-4}(\Omega ^{4} S^{2n+1})$![]() .
.
Next, consider the homotopy fibration diagram

By corollary 4.2, the map $\Omega g_k$![]() has a left homotopy inverse. In particular, $(\Omega g_k)_{\ast }$
has a left homotopy inverse. In particular, $(\Omega g_k)_{\ast }$![]() is an injection. Since $G$
is an injection. Since $G$![]() is $p$
is $p$![]() -regular for $n_l< p$
-regular for $n_l< p$![]() , the left column in the fibration diagram is a product of the homotopy fibrations $\Omega ^{4} S^{3}\langle 3\rangle \to \ast \to \Omega ^{3} S^{3}\langle 3\rangle$
, the left column in the fibration diagram is a product of the homotopy fibrations $\Omega ^{4} S^{3}\langle 3\rangle \to \ast \to \Omega ^{3} S^{3}\langle 3\rangle$![]() and, for $2\leq i\leq n_{l}$
and, for $2\leq i\leq n_{l}$![]() , $\Omega ^{4} S^{2n_{i}-1}\to \ast \to \Omega ^{3} S^{2n_{i}-1}$
, $\Omega ^{4} S^{2n_{i}-1}\to \ast \to \Omega ^{3} S^{2n_{i}-1}$![]() . Therefore, by the argument in the first paragraph of the proof, the element $a_{2n_{i}-1}\in MH_*(\Omega ^{3} G\langle 3\rangle )$
. Therefore, by the argument in the first paragraph of the proof, the element $a_{2n_{i}-1}\in MH_*(\Omega ^{3} G\langle 3\rangle )$![]() transgresses to a nontrivial element in $H_{2n_{i}p-4}(\Omega ^{4} G\langle 3\rangle )$
transgresses to a nontrivial element in $H_{2n_{i}p-4}(\Omega ^{4} G\langle 3\rangle )$![]() . As this element injects into $H_{2n_{i}p-4}(\mathcal {G}_k)$
. As this element injects into $H_{2n_{i}p-4}(\mathcal {G}_k)$![]() , the naturality of the transgression in (4.1) implies that $(g_k)_*(a_{2n_{i}p-3})$
, the naturality of the transgression in (4.1) implies that $(g_k)_*(a_{2n_{i}p-3})$![]() must be nontrivial.
must be nontrivial.
Finally, consider the element $\bar {a}_{2p-3}\in H_*(\Omega ^{3} G\langle 3\rangle )$![]() . It comes from an element $x\in H_{2p-3}(\Omega ^{3} S^{3}\langle 3\rangle )$
. It comes from an element $x\in H_{2p-3}(\Omega ^{3} S^{3}\langle 3\rangle )$![]() . The description of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$
. The description of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$![]() in (3.4) implies that $\Omega ^{3} S^{3}\langle 3\rangle$
in (3.4) implies that $\Omega ^{3} S^{3}\langle 3\rangle$![]() is $(2p-4)$
is $(2p-4)$![]() -connected and has a single cell in dimension $2p-3$
-connected and has a single cell in dimension $2p-3$![]() . Thus $x$
. Thus $x$![]() represents the inclusion of the bottom cell. Therefore, $x$
represents the inclusion of the bottom cell. Therefore, $x$![]() transgresses to a nontrivial element in $H_{2p-4}(\Omega ^{4} S^{3}\langle 3\rangle )$
transgresses to a nontrivial element in $H_{2p-4}(\Omega ^{4} S^{3}\langle 3\rangle )$![]() , and so $\bar {a}_{2p-3}$
, and so $\bar {a}_{2p-3}$![]() transgresses to a nontrivial element in $H_{2p-4}(\Omega ^{4} G\langle 3\rangle )$
transgresses to a nontrivial element in $H_{2p-4}(\Omega ^{4} G\langle 3\rangle )$![]() . Since $(\Omega g_k)_*$
. Since $(\Omega g_k)_*$![]() is an injection, the naturality of the transgression in (4.1) implies that $(g_k)_*(a_{2p-3})$
is an injection, the naturality of the transgression in (4.1) implies that $(g_k)_*(a_{2p-3})$![]() is nontrivial.
is nontrivial.
Consider the fibration
where $ev$![]() is the evaluation map at the basepoint of $S^{4}$
is the evaluation map at the basepoint of $S^{4}$![]() . Since $G$
. Since $G$![]() is $p$
is $p$![]() -regular and we are localizing at the prime $p$
-regular and we are localizing at the prime $p$![]() , $S^{3}$
, $S^{3}$![]() is a homotopy retract of $G$
is a homotopy retract of $G$![]() . Therefore (4.2) is a homotopy retract of the fibration
. Therefore (4.2) is a homotopy retract of the fibration
We may identify $\operatorname {Map}^{*}(\Sigma G,\,BG)$![]() with $\operatorname {Map}^{*}(G,\,G)$
with $\operatorname {Map}^{*}(G,\,G)$![]() by the adjoint congruence. $\operatorname {Map}^{*}(G,\,G)$
by the adjoint congruence. $\operatorname {Map}^{*}(G,\,G)$![]() is an H-space by the composite of maps, and there is a fiberwise action of $\operatorname {Map}^{*}(G,\,G)$
is an H-space by the composite of maps, and there is a fiberwise action of $\operatorname {Map}^{*}(G,\,G)$![]() on $\operatorname {Map}(\Sigma G,\,BG)$
on $\operatorname {Map}(\Sigma G,\,BG)$![]() given by
given by
Thus lemma 2.3 applies to the fibration (4.2). The inclusion of the fibre in (4.2) may be identified with the coproduct of the maps $\operatorname {Map}^{*}_k(S^{4},\,BG)\to \operatorname {Map}_k(S^{4},\,BG)$![]() for all $k\in \mathbb {Z}$
for all $k\in \mathbb {Z}$![]() . Equivalently, this is the coproduct of the maps $g_k\colon \Omega ^{3}G\langle 3\rangle \to B\mathcal {G}_k$
. Equivalently, this is the coproduct of the maps $g_k\colon \Omega ^{3}G\langle 3\rangle \to B\mathcal {G}_k$![]() for all $k\in \mathbb {Z}$
for all $k\in \mathbb {Z}$![]() . Each $(g_{k})_{\ast }$
. Each $(g_{k})_{\ast }$![]() is injective on $MH_{odd}(\operatorname {Map}^{*}(S^{4},\,BG))$
is injective on $MH_{odd}(\operatorname {Map}^{*}(S^{4},\,BG))$![]() by lemma 4.3, so the coproduct is as well. This leads to the mod-$p$
by lemma 4.3, so the coproduct is as well. This leads to the mod-$p$![]() homology Serre spectral sequence for (4.2) collapsing at the $E^{2}$
homology Serre spectral sequence for (4.2) collapsing at the $E^{2}$![]() -term.
-term.
Proposition 4.4 Let $G$![]() be a compact connected simple Lie group of type $(n_1,\,\ldots,\,n_l)$
be a compact connected simple Lie group of type $(n_1,\,\ldots,\,n_l)$![]() , let $p$
, let $p$![]() be a prime, and suppose that $n_l< p-1$
be a prime, and suppose that $n_l< p-1$![]() . Then the mod-$p$
. Then the mod-$p$![]() homology Serre spectral sequence for (4.2) is totally nonhomologous to zero.
homology Serre spectral sequence for (4.2) is totally nonhomologous to zero.
Proof. Let $(E^{r},\,d^{r})$![]() denote the mod-$p$
denote the mod-$p$![]() homology Serre spectral sequence for (4.2). Let $z\in H_{m}(\operatorname {Map}^{*}(S^{4},\,BG))$
homology Serre spectral sequence for (4.2). Let $z\in H_{m}(\operatorname {Map}^{*}(S^{4},\,BG))$![]() be an element in the kernel of $g_*$
be an element in the kernel of $g_*$![]() of least dimension, where $g\colon \operatorname {Map}^{*}(S^{4},\,BG)\to \operatorname {Map}(S^{4},\,BG)$
of least dimension, where $g\colon \operatorname {Map}^{*}(S^{4},\,BG)\to \operatorname {Map}(S^{4},\,BG)$![]() is the fibre inclusion of (4.2). We begin by establishing some properties of $z$
is the fibre inclusion of (4.2). We begin by establishing some properties of $z$![]() .
.
Property 1: $z$![]() is primitive. If not, then $\overline {\Delta }(z)=\Sigma _{\alpha \in A} z'_{\alpha }\otimes z''_{\alpha }$
is primitive. If not, then $\overline {\Delta }(z)=\Sigma _{\alpha \in A} z'_{\alpha }\otimes z''_{\alpha }$![]() for some elements $z'_{\alpha },\,z''_{\alpha }$
for some elements $z'_{\alpha },\,z''_{\alpha }$![]() of degrees $< m$
of degrees $< m$![]() such that $\{z'_\alpha \otimes z''_\alpha \}_{\alpha \in A}$
such that $\{z'_\alpha \otimes z''_\alpha \}_{\alpha \in A}$![]() is linearly independent, where $\overline {\Delta }$
is linearly independent, where $\overline {\Delta }$![]() is the reduced diagonal. The reduced diagonal is natural for any map of spaces, so $(g_*\otimes g_*)\circ \overline {\Delta }=\overline {\Delta }\circ g_*$
is the reduced diagonal. The reduced diagonal is natural for any map of spaces, so $(g_*\otimes g_*)\circ \overline {\Delta }=\overline {\Delta }\circ g_*$![]() . Now
. Now
is a sum of linearly independent elements since $z'_{\alpha },\,z''_{\alpha }$![]() are of degrees $< m$
are of degrees $< m$![]() while the element of least degree in $\mathrm {Ker}\,g_*$
while the element of least degree in $\mathrm {Ker}\,g_*$![]() is of degree $m$
is of degree $m$![]() . On the other hand,
. On the other hand,
This contradiction implies that $\overline {\Delta }(z)$![]() must be $0$
must be $0$![]() ; that is, $z$
; that is, $z$![]() is primitive.
is primitive.
Property 2: $\mathcal {P}^{n}_*(z)=0$![]() for every $n\ge 1$
for every $n\ge 1$![]() . Suppose $\mathcal {P}^{n}_{\ast }(z)=y$
. Suppose $\mathcal {P}^{n}_{\ast }(z)=y$![]() for some $n\ge 1$
for some $n\ge 1$![]() , where $y$
, where $y$![]() is nonzero. The (dual) Steenrod operations are natural for any map of spaces, so $g_*\mathcal {P}^{n}_*=\mathcal {P}^{n}_*g_*$
is nonzero. The (dual) Steenrod operations are natural for any map of spaces, so $g_*\mathcal {P}^{n}_*=\mathcal {P}^{n}_*g_*$![]() . Now
. Now
is nonzero, since $|y|< m$![]() while the element of least degree in $\mathrm {Ker}\,g_*$
while the element of least degree in $\mathrm {Ker}\,g_*$![]() is of degree $m$
is of degree $m$![]() . On the other hand,
. On the other hand,
This contradiction implies that $\mathcal {P}^{n}_{\ast }(z)=0$![]() for every $n\ge 1$
for every $n\ge 1$![]() .
.
Property 3: $\beta ^{r}(z)=0$![]() for every $r\geq 1$
for every $r\geq 1$![]() . The reasoning is exactly as in the proof of property 2.
. The reasoning is exactly as in the proof of property 2.
Property 4: $z$![]() is in the image of the transgression for the mod- $p$
is in the image of the transgression for the mod- $p$![]() homology Serre spectral sequence for the homotopy fibration (4.2). By assumption, the first nontrivial differential $d^{r}$
homology Serre spectral sequence for the homotopy fibration (4.2). By assumption, the first nontrivial differential $d^{r}$![]() in the mod-$p$
in the mod-$p$![]() homology Serre spectral sequence for (4.2) satisfies the properties of lemma 2.3. In particular, $d^{r}$
homology Serre spectral sequence for (4.2) satisfies the properties of lemma 2.3. In particular, $d^{r}$![]() is determined by how it acts on the elements in $H_*(BG)$
is determined by how it acts on the elements in $H_*(BG)$![]() . The $E^{2}$
. The $E^{2}$![]() -term of the spectral sequence is $H_*(BG)\otimes H_*(\operatorname {Map}^{*}(S^{4},\,BG))$
-term of the spectral sequence is $H_*(BG)\otimes H_*(\operatorname {Map}^{*}(S^{4},\,BG))$![]() . Since $z$
. Since $z$![]() is an element of least degree in the kernel of $(g_k)_*$
is an element of least degree in the kernel of $(g_k)_*$![]() and is of degree $m$
and is of degree $m$![]() , the map $(g_k)_*$
, the map $(g_k)_*$![]() is an injection in degrees $< m$
is an injection in degrees $< m$![]() . Thus the spectral sequence is totally non-homologous to zero in this degree range, implying that it collapses at $E^{2}$
. Thus the spectral sequence is totally non-homologous to zero in this degree range, implying that it collapses at $E^{2}$![]() . In particular, the differential $d^{r}$
. In particular, the differential $d^{r}$![]() on an element of $H_*(BG)$
on an element of $H_*(BG)$![]() of degree $\leq m$
of degree $\leq m$![]() is zero, and so as $d^{r}$
is zero, and so as $d^{r}$![]() satisfies the properties of lemma 2.3, $d^{r}(x\otimes y)=0$
satisfies the properties of lemma 2.3, $d^{r}(x\otimes y)=0$![]() for $x\in H_t(BG)$
for $x\in H_t(BG)$![]() with $t\leq m$
with $t\leq m$![]() and $y\in H_*(\operatorname {Map}^{*}(S^{4},\,BG))$
and $y\in H_*(\operatorname {Map}^{*}(S^{4},\,BG))$![]() . Hence, for degree reasons, if $z$
. Hence, for degree reasons, if $z$![]() is in the image of $d^{r}$
is in the image of $d^{r}$![]() then the only possibility is that $z=d^{r}(x)$
then the only possibility is that $z=d^{r}(x)$![]() and $r=m+1$
and $r=m+1$![]() for some $x\in H_{m+1}(BG)$
for some $x\in H_{m+1}(BG)$![]() . That is, $z$
. That is, $z$![]() is in the image of the transgression. On the other hand, as $z\in \mathrm {Ker}\,g_*$
is in the image of the transgression. On the other hand, as $z\in \mathrm {Ker}\,g_*$![]() , it cannot survive the spectral sequence and so must be hit by some differential.
, it cannot survive the spectral sequence and so must be hit by some differential.
Property 5: $z$![]() has odd degree. By property 4, in the mod-$p$
has odd degree. By property 4, in the mod-$p$![]() homology Serre spectral sequence for (4.2), we have $z=d^{m+1}(x)$
homology Serre spectral sequence for (4.2), we have $z=d^{m+1}(x)$![]() for some $x\in H_{m+1}(BG)$
for some $x\in H_{m+1}(BG)$![]() . As $H_*(BG)$
. As $H_*(BG)$![]() is concentrated in even degrees, the degree of $z$
is concentrated in even degrees, the degree of $z$![]() must be odd.
must be odd.
Let's examine the consequences of properties 1 to 5. Collectively, Properties 1 to 3 imply that $z\in MH_*(\operatorname {Map}^{*}(S^{4},\,BG))$![]() . Property 5 then implies that $z\in MH_{odd}(\operatorname {Map}^{*}(S^{4},\,BG))$
. Property 5 then implies that $z\in MH_{odd}(\operatorname {Map}^{*}(S^{4},\,BG))$![]() . But $g_*$
. But $g_*$![]() is an injection on $MH_{odd}(\operatorname {Map}^{*}(S^{4},\,BG))$
is an injection on $MH_{odd}(\operatorname {Map}^{*}(S^{4},\,BG))$![]() as we saw above, implying in turn that $z\notin \mathrm {Ker}\,g_*$
as we saw above, implying in turn that $z\notin \mathrm {Ker}\,g_*$![]() , a contradiction. Thus $g_*$
, a contradiction. Thus $g_*$![]() is an injection, and this completes the proof.
is an injection, and this completes the proof.
We are ready to prove theorem 1.1.
Proof of theorem 1.1. By proposition 4.4, the mod-$p$![]() homology Serre spectral sequence for (4.2) collapses at the $E^{2}$
homology Serre spectral sequence for (4.2) collapses at the $E^{2}$![]() -term. Thus, as (4.2) is the fiberwise coproduct of the fibrations $\operatorname {Map}^{*}_k(S^{4},\,BG)\to \operatorname {Map}_k(S^{4},\,BG)\xrightarrow {ev} BG$
-term. Thus, as (4.2) is the fiberwise coproduct of the fibrations $\operatorname {Map}^{*}_k(S^{4},\,BG)\to \operatorname {Map}_k(S^{4},\,BG)\xrightarrow {ev} BG$![]() in (1.1) for all $k\in \mathbb {Z}$
in (1.1) for all $k\in \mathbb {Z}$![]() , it follows from lemma 2.4 that the mod-$p$
, it follows from lemma 2.4 that the mod-$p$![]() homology Serre spectral sequence for each fibration collapses at the $E^{2}$
homology Serre spectral sequence for each fibration collapses at the $E^{2}$![]() -term. Equivalently, the mod-$p$
-term. Equivalently, the mod-$p$![]() homology Serre spectral sequence for $\Omega ^{3} G\langle 3\rangle \to B\mathcal {G}_k\xrightarrow {ev} BG$
homology Serre spectral sequence for $\Omega ^{3} G\langle 3\rangle \to B\mathcal {G}_k\xrightarrow {ev} BG$![]() collapses at the $E^{2}$
collapses at the $E^{2}$![]() -term for all $k\in \mathbb {Z}$
-term for all $k\in \mathbb {Z}$![]() .
.
We calculate the Poincaré series of the mod-$p$![]() homology of $B\mathcal {G}_k$
homology of $B\mathcal {G}_k$![]() . Let $P_t(X)$
. Let $P_t(X)$![]() denote the Poincaré series of the mod-$p$
denote the Poincaré series of the mod-$p$![]() homology of a space $X$
homology of a space $X$![]() . Let
. Let

Corollary 4.5 Under the same hypothesis of theorem 1.1, the Poincaré series of the mod-$p$![]() homology of $B\mathcal {G}_k$
homology of $B\mathcal {G}_k$![]() is given by
is given by

Proof. By theorem 1.1, $P_t(B\mathcal {G}_k)=P_t(BG)P_t(\Omega ^{3}G\langle 3\rangle )$![]() . Since $n_l< p-1$
. Since $n_l< p-1$![]() , the mod-$p$
, the mod-$p$![]() cohomology of $BG$
cohomology of $BG$![]() is a polynomial algebra with generators in dimension $2n_1,\,\ldots,\,2n_l$
is a polynomial algebra with generators in dimension $2n_1,\,\ldots,\,2n_l$![]() , and so $P_t(BG)=\prod _{i=1}^{l}\frac {1}{1-t^{2n_i}}$
, and so $P_t(BG)=\prod _{i=1}^{l}\frac {1}{1-t^{2n_i}}$![]() . By (3.1), $P_t(\Omega ^{3}G\langle 3\rangle )=P_t(\Omega ^{3}S^{3}\langle 3\rangle )\prod _{i=2}^{l} P_t(\Omega ^{3}S^{2n_i-1})$
. By (3.1), $P_t(\Omega ^{3}G\langle 3\rangle )=P_t(\Omega ^{3}S^{3}\langle 3\rangle )\prod _{i=2}^{l} P_t(\Omega ^{3}S^{2n_i-1})$![]() . By (3.3), (3.4) and (3.5), $P_t(\Omega ^{3}S^{3}\langle 3\rangle )=P(t)Q_{p-1}(t)$
. By (3.3), (3.4) and (3.5), $P_t(\Omega ^{3}S^{3}\langle 3\rangle )=P(t)Q_{p-1}(t)$![]() and $P_t(\Omega ^{3}S^{2n_i-1})=P_{n_i-1}(t)$
and $P_t(\Omega ^{3}S^{2n_i-1})=P_{n_i-1}(t)$![]() , completing the proof.
, completing the proof.
5. The mod-$3$ homology of $SU(2)$
homology of $SU(2)$ -gauge groups
-gauge groups
The mod-$p$![]() homology of $B\mathcal {G}_k$
homology of $B\mathcal {G}_k$![]() for $G=SU(2)$
for $G=SU(2)$![]() and $p\geq 5$
and $p\geq 5$![]() is given by theorem 1.1. Since $SU(2)$
is given by theorem 1.1. Since $SU(2)$![]() -gauge groups are pivotal in Donaldson Theory, in this section we expand beyond the statement of theorem 1.1 by also calculating the mod-$3$
-gauge groups are pivotal in Donaldson Theory, in this section we expand beyond the statement of theorem 1.1 by also calculating the mod-$3$![]() homology.
homology.
Since there is a homeomorphism $SU(2)\cong S^{3}$![]() , we phrase what follows in terms of $S^{3}$
, we phrase what follows in terms of $S^{3}$![]() . By (1.2) there is a homotopy fibration sequence
. By (1.2) there is a homotopy fibration sequence
By [Reference Kono14] we have the following.
Lemma 5.1 The map $\partial _1\colon S^{3}\to \Omega ^{3} S^{3}\langle 3\rangle$![]() has order $12$
has order $12$![]() .
.
In the proof of lemma 4.1 it is shown that $\partial _k=k\circ \partial _1$![]() . In particular, if we localize at $p=3$
. In particular, if we localize at $p=3$![]() then $\partial _k$
then $\partial _k$![]() has order $3/(k,\,3)$
has order $3/(k,\,3)$![]() . Observe that for $p=3$
. Observe that for $p=3$![]() , the description of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$
, the description of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$![]() in (3.4) implies that $\Omega ^{3} S^{3}\langle 3\rangle$
in (3.4) implies that $\Omega ^{3} S^{3}\langle 3\rangle$![]() is $2$
is $2$![]() -connected with a single cell in dimension $3$
-connected with a single cell in dimension $3$![]() .
.
Lemma 5.2 If $p=3$![]() and $(k,\,3)=1$
and $(k,\,3)=1$![]() then the map $\partial _k\colon S^{3}\to \Omega ^{3} S^{3}\langle 3\rangle$
then the map $\partial _k\colon S^{3}\to \Omega ^{3} S^{3}\langle 3\rangle$![]() induces an injection in mod-$3$
induces an injection in mod-$3$![]() homology.
homology.
Proof. By hypothesis, $(k,\,3)=1$![]() so the above discussion implies that $\partial _{k}$
so the above discussion implies that $\partial _{k}$![]() is nontrivial. Thus it represents a nontrivial element in $\pi _{3}(\Omega ^{3} S^{3}\langle 3\rangle )\cong \pi _{6}(S^{3}\langle 3\rangle )\cong \pi _{6}(S^{3})$
is nontrivial. Thus it represents a nontrivial element in $\pi _{3}(\Omega ^{3} S^{3}\langle 3\rangle )\cong \pi _{6}(S^{3}\langle 3\rangle )\cong \pi _{6}(S^{3})$![]() . On the other hand, by [Reference Toda20], the $3$
. On the other hand, by [Reference Toda20], the $3$![]() -component of $\pi _{6}(S^{3})$
-component of $\pi _{6}(S^{3})$![]() is isomorphic to $\mathbb {Z}/3\mathbb {Z}$
is isomorphic to $\mathbb {Z}/3\mathbb {Z}$![]() . Therefore $\partial _{k}$
. Therefore $\partial _{k}$![]() represents a generator of the $3$
represents a generator of the $3$![]() -component of $\pi _{3}(\Omega ^{3} S^{3}\langle 3\rangle )$
-component of $\pi _{3}(\Omega ^{3} S^{3}\langle 3\rangle )$![]() . Next, since $\Omega ^{3}S^{3}\langle 3\rangle$
. Next, since $\Omega ^{3}S^{3}\langle 3\rangle$![]() is $2$
is $2$![]() -connected, the Hurewicz map $\pi _3(\Omega ^{3}S^{3}\langle 3\rangle )\otimes \mathbb {Z}/3\mathbb {Z}\to H_*(\Omega ^{3}S^{3}\langle 3\rangle )$
-connected, the Hurewicz map $\pi _3(\Omega ^{3}S^{3}\langle 3\rangle )\otimes \mathbb {Z}/3\mathbb {Z}\to H_*(\Omega ^{3}S^{3}\langle 3\rangle )$![]() is an isomorphism, where we take homology with mod-$3$
is an isomorphism, where we take homology with mod-$3$![]() coefficients. By the naturality of Hurewicz maps there is a commutative diagram
coefficients. By the naturality of Hurewicz maps there is a commutative diagram

where the vertical maps are the Hurewicz maps. We saw that the top and the right maps are isomorphisms. The left arrow is an isomorphism by the Hurewicz theorem. Thus the bottom arrow is an isomorphism, completing the proof.
Next, by (3.4) together with (3.3) and (3.5), $H_{3}(\Omega ^{3} S^{3}\langle 3\rangle )\cong \mathbb {Z}/3\mathbb {Z}$![]() and if $x_{3}$
and if $x_{3}$![]() is its generator, then $\Lambda (x_{3})$
is its generator, then $\Lambda (x_{3})$![]() is a tensor product factor of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$
is a tensor product factor of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$![]() .
.
Proof of theorem 1.2 Consider the homotopy fibration $S^{3}\xrightarrow {\partial _k}\Omega ^{3} S^{3}\langle 3\rangle \xrightarrow {g_k}B\mathcal {G}_k$![]() . By lemma 5.2, $(\partial _k)_*$
. By lemma 5.2, $(\partial _k)_*$![]() is an injection. Therefore the homology Serre spectral sequence for this homotopy fibration is totally non-homologous to zero, implying that it collapses at the $E^{2}$
is an injection. Therefore the homology Serre spectral sequence for this homotopy fibration is totally non-homologous to zero, implying that it collapses at the $E^{2}$![]() -term, so $H_*(\Omega ^{3} S^{3}\langle 3\rangle )\cong H_*(S^{3})\otimes H_*(B\mathcal {G}_k)$
-term, so $H_*(\Omega ^{3} S^{3}\langle 3\rangle )\cong H_*(S^{3})\otimes H_*(B\mathcal {G}_k)$![]() . Since $H_*(S^{3})\cong \Lambda (y_{3})$
. Since $H_*(S^{3})\cong \Lambda (y_{3})$![]() for $|y_3|=3$
for $|y_3|=3$![]() such that $y_3$
such that $y_3$![]() corresponds to $x_3$
corresponds to $x_3$![]() and as observed above, $\Lambda (x_{3})$
and as observed above, $\Lambda (x_{3})$![]() is a tensor product factor of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$
is a tensor product factor of $H_*(\Omega ^{3} S^{3}\langle 3\rangle )$![]() , we obtain the isomorphism asserted in the statement of the theorem.
, we obtain the isomorphism asserted in the statement of the theorem.
Acknowledgments
The authors would like to thank the referee for the helpful comments. The first author was partly supported by JSPS KAKENHI (No. 17K05248).