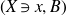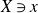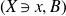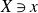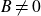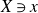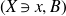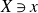1. Introduction
The minimal log discrepancy (mld) is an invariant that provides a sophisticated measure of the singularities of an algebraic variety. It not only plays an important role in the study of singularities but is also a central object in the minimal model program. Shokurov proved that the ascending chain condition (ACC) conjecture for mlds and the lower-semicontinuity (LSC) conjecture for mlds imply the termination of flips [ Reference Shokurov40 ]. For papers related to these conjectures, we refer the readers to [ Reference Ambro2 , 8 , Reference Chen, Di Cerbo, Han, Jiang and Svaldi9 , Reference Ein and Mustaţă11 , Reference Ein, Mustaţă and Yasuda12 , Reference Han, Liu and Qi14 , 15 , Reference Jiang18 , Reference Kawakita19 , Reference Kawakita20 , Reference Kawakita21 , Reference Kawakita23 , Reference Liu29 , Reference Liu and Xiao30 – 34 , Reference Shokurov38 – Reference Shokurov40 ].
Very recently, there has been studies on the mld from the perspective of K-stability theory. In particular, in [ Reference Han, Liu and Shokurov13 , Reference Han, Liu and Qi14 ], normalised volumes [ Reference Li27 ] and Kollár components (in some references, called reduced components) have played essential roles to prove some important cases of the ACC conjecture for mlds. Since the structure of the Kollár components are very well-studied [ Reference Kudryavtsev26 , 28 , Reference Prokhorov35 , Reference Shokurov38 , Reference Xu41 ], we may propose the following natural folklore question:
Question 1·1. Let
![]() $(X\ni x,B)$
be an lc germ of dimension
$(X\ni x,B)$
be an lc germ of dimension
![]() $\geq 2$
such that
$\geq 2$
such that
![]() $X\ni x$
is klt. Under what conditions will there exist a divisor E over
$X\ni x$
is klt. Under what conditions will there exist a divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
and E is a Kollár component of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
and E is a Kollár component of
![]() $X\ni x$
?
$X\ni x$
?
In the paper, we show that Question 1·1 always has a positive answer in dimension 2:
Theorem 1·2.
Let
![]() $(X\ni x,B)$
be an lc surface germ such that
$(X\ni x,B)$
be an lc surface germ such that
![]() $X\ni x$
is klt. Then there exists a divisor E over
$X\ni x$
is klt. Then there exists a divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
and E is a Kollár component of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
and E is a Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
Regrettably, Question 1·1 does not always have a positive answer in dimension
![]() $\geq 3$
even when
$\geq 3$
even when
![]() $B=0$
due to Example 6·1.
$B=0$
due to Example 6·1.
For smooth surfaces, a modified version of Question 1·1 was proved by Blum [ Reference Blum5 , theorem 1·2] and Kawakita [ Reference Kawakita22 , remark 3], who show that any divisor computing the mld is a potential lc place (see Definition 2·4 below) of the ambient variety, while Kawakita additionally shows that any such divisor is achieved by a weighted blow-up [ Reference Kawakita22 , theorem 1]. With this in mind, we may ask the following folklore question:
Question 1·3. Let
![]() $(X\ni x,B)$
be an lc germ. Under what conditions will every divisor that computes the mld be a potential lc place?
$(X\ni x,B)$
be an lc germ. Under what conditions will every divisor that computes the mld be a potential lc place?
In this paper, we also answer Question 1·3 for surfaces:
Theorem 1·4.
Let
![]() $(X\ni x,B)$
be an lc surface germ. Then every divisor E over
$(X\ni x,B)$
be an lc surface germ. Then every divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
is a potential lc place of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
is a potential lc place of
![]() $X\ni x$
if and only if
$X\ni x$
if and only if
![]() $(X\ni x,B)$
is not of the following types:
$(X\ni x,B)$
is not of the following types:
-
(i)
 $B=0$
and
$B=0$
and
 $X\ni x$
is a
$X\ni x$
is a
 $D_m$
-type Du Val singularity for some integer
$D_m$
-type Du Val singularity for some integer
 $m\geq 5$
, or
$m\geq 5$
, or -
(ii)
 $B=0$
and
$B=0$
and
 $X\ni x$
is an
$X\ni x$
is an
 $E_m$
-type Du Val singularity for some integer
$E_m$
-type Du Val singularity for some integer
 $m\in\{6,7,8\}$
.
$m\in\{6,7,8\}$
.
We say a few words about the intuition of Questions 1·1 and 1·3. Roughly speaking, a Kollár component always admits a log Fano structure that is compatible with the local singularity, and a potential lc place always admits a log Calabi–Yau structure that is compatible with the local singularity. These structures allow us to use results in global birational geometry to study the behaviour of the divisor and the local geometry of the singularity. On the other hand, we usually do not know whether a divisor calculating the mld is admits those good structures or not, and therefore, many powerful tools in global geometry are difficult to apply to the study on the mlds of a singularity.
Therefore, getting a satisfactory answer for either Question 1·1 or Question 1·3 could provide us with possibilities to apply global geometry results to tackle the ACC conjecture or the LSC conjecture for mlds. In particular, since Kollár components are well-studied in K-stability theory, with a satisfactory answer for Question 1·1, there is a strong potential for K-stability theory results to be applied to the study on mlds.
Theorem 1·2 and Theorem 1·4 follow from the following classification result on divisors computing mlds on lc surfaces:
Theorem 1·5.
Let
![]() $(X\ni x,B)$
be an lc surface germ and
$(X\ni x,B)$
be an lc surface germ and
![]() $\mathcal{C}$
the set of all prime divisors over
$\mathcal{C}$
the set of all prime divisors over
![]() $X\ni x$
which compute
$X\ni x$
which compute
![]() ${\rm{mld}}(X\ni x,B)$
.
${\rm{mld}}(X\ni x,B)$
.
-
(i) if
 $(X\ni x,B)$
is dlt, then:
$(X\ni x,B)$
is dlt, then:-
(a) if
 $X\ni x$
is smooth or an A-type singularity, then any element of
$X\ni x$
is smooth or an A-type singularity, then any element of
 $\mathcal{C}$
is a Kollár component of
$\mathcal{C}$
is a Kollár component of
 $X\ni x$
;
$X\ni x$
; -
(b) if
 $X\ni x$
is a
$X\ni x$
is a
 $D_m$
-type singularity for some integer
$D_m$
-type singularity for some integer
 $m\geq 4$
or an
$m\geq 4$
or an
 $E_m$
-type singularity for some integer
$E_m$
-type singularity for some integer
 $m\in\{6,7,8\}$
, let
$m\in\{6,7,8\}$
, let
 $f: Y\rightarrow X$
be the minimal resolution of
$f: Y\rightarrow X$
be the minimal resolution of
 $X\ni x$
and
$X\ni x$
and
 $\mathcal{D}(f)$
the dual graph of f. Then;
$\mathcal{D}(f)$
the dual graph of f. Then;-
(1) there exists a unique element
 $E\in\mathcal{C}$
that is a Kollár component of
$E\in\mathcal{C}$
that is a Kollár component of
 $X\ni x$
, and E is the unique fork of
$X\ni x$
, and E is the unique fork of
 $\mathcal{D}(f)$
;
$\mathcal{D}(f)$
; -
(2)
 $\mathcal{C}\subset{\rm{Exc}}(f)$
;
$\mathcal{C}\subset{\rm{Exc}}(f)$
; -
(3) if
 $B\not=0$
or
$B\not=0$
or
 $X\ni x$
is not Du Val, then:
$X\ni x$
is not Du Val, then:-
(A) any element of
 $\mathcal{C}$
is a potential lc place of
$\mathcal{C}$
is a potential lc place of
 $X\ni x$
;
$X\ni x$
; -
(B) if
 $X\ni x$
is an
$X\ni x$
is an
 $E_m$
-type singularity, then
$E_m$
-type singularity, then
 $\mathcal{C}$
only contains the unique fork of
$\mathcal{C}$
only contains the unique fork of
 $\mathcal{D}(f)$
.
$\mathcal{D}(f)$
.
-
-
(4) if
 $B=0$
and
$B=0$
and
 $X\ni x$
is Du Val, then:
$X\ni x$
is Du Val, then:-
(A)
 $\mathcal{C}={\rm{Exc}}(f)$
;
$\mathcal{C}={\rm{Exc}}(f)$
; -
(B) if
 $X\ni x$
is a
$X\ni x$
is a
 $D_m$
-type singularity, then an element
$D_m$
-type singularity, then an element
 $F\in\mathcal{C}$
is a potential lc place of
$F\in\mathcal{C}$
is a potential lc place of
 $X\ni x$
if and only if either F is the fork of
$X\ni x$
if and only if either F is the fork of
 $\mathcal{D}(f)$
, or the two branches which do contain F both have length 1;
$\mathcal{D}(f)$
, or the two branches which do contain F both have length 1; -
(C) if
 $X\ni x$
is an
$X\ni x$
is an
 $E_m$
-type singularity, then an element
$E_m$
-type singularity, then an element
 $F\in\mathcal{C}$
is a potential lc place of
$F\in\mathcal{C}$
is a potential lc place of
 $X\ni x$
if and only if F is the fork of
$X\ni x$
if and only if F is the fork of
 $\mathcal{D}(f)$
.
$\mathcal{D}(f)$
.
-
-
-
-
(ii) If
 $(X\ni x,B)$
is not dlt but
$(X\ni x,B)$
is not dlt but
 $X\ni x$
is klt, then:
$X\ni x$
is klt, then:-
(a) Any element of
 $\mathcal{C}$
is a potential lc place of
$\mathcal{C}$
is a potential lc place of
 $X\ni x$
;
$X\ni x$
; -
(b) There exists an element of
 $\mathcal{C}$
that is a Kollár component of
$\mathcal{C}$
that is a Kollár component of
 $X\ni x$
.
$X\ni x$
. -
(c) If
 $X\ni x$
is smooth, then any element of
$X\ni x$
is smooth, then any element of
 $\mathcal{C}$
is a Kollár component of
$\mathcal{C}$
is a Kollár component of
 ${\rm{mld}}(X\ni x,B)$
${\rm{mld}}(X\ni x,B)$
-
-
(iii) If
 $X\ni x$
is not klt, then any element of
$X\ni x$
is not klt, then any element of
 $\mathcal{C}$
is a potential lc place of
$\mathcal{C}$
is a potential lc place of
 $X\ni x$
.
$X\ni x$
.
We hope that our results could inspire people to tackle Questions 1·1 and 1·3.
Remark 1·6. Some complementary examples of our main theorems are given in Section 6.
Remark 1·7. Although the study on minimal log discrepancies was traditionally considered over
![]() $\mathbb C$
, recently there has been some studies on the structure of minimal log discrepancies over fields of arbitrary characteristics (cf. [
Reference Chen7
,
Reference Ishii17
,
Reference Shibata36
]). In this paper, the results hold over fields of arbitrary characteristics. This is because we only work on surfaces and we only care about the local behavior of surfaces. In this case, the concepts of minimal resolution, dual graphs, intersection numbers etc. will work in arbitrary characteristics. We emphasize that the key references we cite [
25
, section 4] and [
15
] also work for arbitrary characteristics.
$\mathbb C$
, recently there has been some studies on the structure of minimal log discrepancies over fields of arbitrary characteristics (cf. [
Reference Chen7
,
Reference Ishii17
,
Reference Shibata36
]). In this paper, the results hold over fields of arbitrary characteristics. This is because we only work on surfaces and we only care about the local behavior of surfaces. In this case, the concepts of minimal resolution, dual graphs, intersection numbers etc. will work in arbitrary characteristics. We emphasize that the key references we cite [
25
, section 4] and [
15
] also work for arbitrary characteristics.
2. Preliminaries
We adopt the standard notation and definitions in [ 25 ].
Definition 2·1. A pair (X,B) consists of a normal quasi-projective variety X and an
![]() $\mathbb{R}$
-divisor
$\mathbb{R}$
-divisor
![]() $B\ge0$
such that
$B\ge0$
such that
![]() $K_X+B$
is
$K_X+B$
is
![]() $\mathbb{R}$
-Cartier. If
$\mathbb{R}$
-Cartier. If
![]() $B\in [0,1]$
, then B is called a boundary.
$B\in [0,1]$
, then B is called a boundary.
Let E be a prime divisor on X and D an
![]() $\mathbb R$
-divisor on X. We define
$\mathbb R$
-divisor on X. We define
![]() ${\rm{mult}}_{E}D$
to be the multiplicity of E along D. Let
${\rm{mult}}_{E}D$
to be the multiplicity of E along D. Let
![]() $\phi:W\to X$
be any log resolution of (X,B) and let
$\phi:W\to X$
be any log resolution of (X,B) and let
The log discrepancy of a prime divisor D on W with respect to (X,B) is
![]() $1-{\rm{mult}}_{D}B_W$
and it is denoted by
$1-{\rm{mult}}_{D}B_W$
and it is denoted by
![]() $a(D,X,B).$
We say that (X,B) is lc (resp. klt) if
$a(D,X,B).$
We say that (X,B) is lc (resp. klt) if
![]() $a(D,X,B)\ge0$
(resp.
$a(D,X,B)\ge0$
(resp.
![]() $>0$
) for every log resolution
$>0$
) for every log resolution
![]() $\phi:W\to X$
as above and every prime divisor D on W. We say that (X,B) is dlt if
$\phi:W\to X$
as above and every prime divisor D on W. We say that (X,B) is dlt if
![]() $a(D,X,B)>0$
for some log resolution
$a(D,X,B)>0$
for some log resolution
![]() $\phi:W\to X$
as above and every prime divisor D on W. We say that (X,B) is plt if
$\phi:W\to X$
as above and every prime divisor D on W. We say that (X,B) is plt if
![]() $a(D,X,B)>0$
for any exceptional prime divisor D over X.
$a(D,X,B)>0$
for any exceptional prime divisor D over X.
A germ
![]() $(X\ni x,B)$
consists of a pair (X,B) and a closed point
$(X\ni x,B)$
consists of a pair (X,B) and a closed point
![]() $x\in X$
. If
$x\in X$
. If
![]() $B=0$
, the germ
$B=0$
, the germ
![]() $(X\ni x,B)$
is usually represented by
$(X\ni x,B)$
is usually represented by
![]() $X\ni x$
. We say that
$X\ni x$
. We say that
![]() $(X\ni x,B)$
is lc (resp. klt, dlt, plt) if (X,B) is lc (resp. klt, dlt, plt) near x. We say that
$(X\ni x,B)$
is lc (resp. klt, dlt, plt) if (X,B) is lc (resp. klt, dlt, plt) near x. We say that
![]() $(X\ni x,B)$
is smooth if X is smooth near x. We say that
$(X\ni x,B)$
is smooth if X is smooth near x. We say that
![]() $(X\ni x,B)$
is log smooth if X is log smooth near x. A divisor E over X is called over
$(X\ni x,B)$
is log smooth if X is log smooth near x. A divisor E over X is called over
![]() $X\ni x$
if
$X\ni x$
if
![]() ${\rm{center}}_{X}E=\bar x$
.
${\rm{center}}_{X}E=\bar x$
.
Definition 2·2. The minimal log discrepancy (mld) of an lc germ
![]() $(X\ni x,B)$
is
$(X\ni x,B)$
is
Definition 2·3 (Plt blow-ups). Let
![]() $(X\ni x,B)$
be a klt germ. A plt blow-up of
$(X\ni x,B)$
be a klt germ. A plt blow-up of
![]() $(X\ni x,B)$
is a blow-up
$(X\ni x,B)$
is a blow-up
![]() $f: Y\rightarrow X$
with the exceptional divisor E over
$f: Y\rightarrow X$
with the exceptional divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $(Y,f^{-1}_*B+E)$
is plt near E, and
$(Y,f^{-1}_*B+E)$
is plt near E, and
![]() $-E$
is ample over X. The divisor E is called a Kollár component (in some references, reduced component) of
$-E$
is ample over X. The divisor E is called a Kollár component (in some references, reduced component) of
![]() $(X\ni x,B)$
.
$(X\ni x,B)$
.
Definition 2·4 (Potential lc place). Let
![]() $(X\ni x,B)$
be an lc germ. A potential lc place of
$(X\ni x,B)$
be an lc germ. A potential lc place of
![]() $(X\ni x,B)$
is a divisor E over
$(X\ni x,B)$
is a divisor E over
![]() $X\ni x$
, such that there exists
$X\ni x$
, such that there exists
![]() $G\geq 0$
on X such that
$G\geq 0$
on X such that
![]() $(X\ni x,B+G)$
is lc and
$(X\ni x,B+G)$
is lc and
![]() $a(E,X,B+G)=0$
.
$a(E,X,B+G)=0$
.
Definition 2·5. A surface is a normal quasi-projective variety of dimension 2. A surface germ
![]() $X\ni x$
is called Du Val if
$X\ni x$
is called Du Val if
![]() ${\rm{mld}}(X\ni x,0)=1$
.
${\rm{mld}}(X\ni x,0)=1$
.
Let
![]() $X\ni x$
be a klt surface germ of type A (resp. D,E) and
$X\ni x$
be a klt surface germ of type A (resp. D,E) and
![]() $m\geq 1$
(resp.
$m\geq 1$
(resp.
![]() $m\geq 4,m\in\{6,7,8\}$
) an integer. Let f be the minimal resolution of
$m\geq 4,m\in\{6,7,8\}$
) an integer. Let f be the minimal resolution of
![]() $X\ni x$
. We say that
$X\ni x$
. We say that
![]() $X\ni x$
is an
$X\ni x$
is an
![]() $A_m$
(resp.
$A_m$
(resp.
![]() $D_m,E_m$
)-type singularity if
$D_m,E_m$
)-type singularity if
![]() ${\rm{Exc}}(f)$
contains exactly m prime divisors.
${\rm{Exc}}(f)$
contains exactly m prime divisors.
For surfaces, to check that an extraction is a plt blow-up, we only need to control the singularity as the anti-ample requirement is automatically satisfied. The following lemma is well-known and we will use it many times:
Lemma 2·6.
Let
![]() $(X\ni x,B)$
be a klt surface germ,
$(X\ni x,B)$
be a klt surface germ,
![]() $f: Y\rightarrow X$
an extraction of a prime divisor E, and
$f: Y\rightarrow X$
an extraction of a prime divisor E, and
![]() $B_Y\;:\!=\;f^{-1}_*B$
. Then:
$B_Y\;:\!=\;f^{-1}_*B$
. Then:
-
(i) if
 $(Y,B_Y+E)$
is plt near E, then E is a Kollár component of
$(Y,B_Y+E)$
is plt near E, then E is a Kollár component of
 $(X\ni x,B)$
;
$(X\ni x,B)$
; -
(ii) if
 $(Y,B_Y+E)$
is lc near E, then E is a potential lc place of
$(Y,B_Y+E)$
is lc near E, then E is a potential lc place of
 $(X\ni x,B)$
.
$(X\ni x,B)$
.
In particular, any Kollár component of
![]() $(X\ni x,B)$
is a potential lc place of
$(X\ni x,B)$
is a potential lc place of
![]() $(X\ni x,B)$
.
$(X\ni x,B)$
.
Proof. Since
![]() $(X\ni x,B)$
is a klt surface germ, X is
$(X\ni x,B)$
is a klt surface germ, X is
![]() $\mathbb{Q}$
-factorial, so there exists an f-exceptional divisor
$\mathbb{Q}$
-factorial, so there exists an f-exceptional divisor
![]() $F\geq 0$
such that
$F\geq 0$
such that
![]() $-F$
is ample over X [
Reference Birkar and Cascini4
, lemma 3·6·2(3)]. Since f only extracts E,
$-F$
is ample over X [
Reference Birkar and Cascini4
, lemma 3·6·2(3)]. Since f only extracts E,
![]() $-E$
is ample over X. This implies (ii).
$-E$
is ample over X. This implies (ii).
Since
![]() $-E$
is ample over X,
$-E$
is ample over X,
![]() $-(K_Y+B_Y+E)$
is ample over X. We may pick a general
$-(K_Y+B_Y+E)$
is ample over X. We may pick a general
![]() $G_Y\sim_{\mathbb R,X}-(K_Y+B_Y+E)$
such that
$G_Y\sim_{\mathbb R,X}-(K_Y+B_Y+E)$
such that
![]() $(Y,B_Y+E+G_Y)$
is lc near E and
$(Y,B_Y+E+G_Y)$
is lc near E and
![]() $K_Y+B_Y+E+G_Y\sim_{\mathbb R,X}0$
. Let
$K_Y+B_Y+E+G_Y\sim_{\mathbb R,X}0$
. Let
![]() $G\;:\!=\;f_*G_Y$
, then
$G\;:\!=\;f_*G_Y$
, then
![]() $(X\ni x,B+G)$
is lc and E is a potential lc place of
$(X\ni x,B+G)$
is lc and E is a potential lc place of
![]() $(X\ni x,B)$
.
$(X\ni x,B)$
.
Definition 2·7 (Dual graph). Let n be a non-negative integer, and
![]() $C=\cup_{i=1}^nC_i$
a collection of irreducible curves on a smooth surface U. We define the dual graph
$C=\cup_{i=1}^nC_i$
a collection of irreducible curves on a smooth surface U. We define the dual graph
![]() $\mathcal{D}(C)$
of C as follows.
$\mathcal{D}(C)$
of C as follows.
-
(i) The vertices
 $v_i=v_i(C_i)$
of
$v_i=v_i(C_i)$
of
 $\mathcal{D}(C)$
correspond to the curves
$\mathcal{D}(C)$
correspond to the curves
 $C_i$
.
$C_i$
. -
(ii) For
 $i\neq j$
,the vertices
$i\neq j$
,the vertices
 $v_i$
and
$v_i$
and
 $v_j$
are connected by
$v_j$
are connected by
 $C_i\cdot C_j$
edges.
$C_i\cdot C_j$
edges.
In addition,
-
(iii) if we label each
 $v_i$
by the integer
$v_i$
by the integer
 $e_i\;:\!=\;-C_i^2$
, then
$e_i\;:\!=\;-C_i^2$
, then
 $\mathcal{D}(C)$
is called the weighted dual graph of C.
$\mathcal{D}(C)$
is called the weighted dual graph of C.
A fork of a dual graph is a curve
![]() $C_i$
such that
$C_i$
such that
![]() $C_i\cdot C_j\geq 1$
for exactly three different
$C_i\cdot C_j\geq 1$
for exactly three different
![]() $j\not=i$
. A tail of a dual graph is a curve
$j\not=i$
. A tail of a dual graph is a curve
![]() $C_i$
such that
$C_i$
such that
![]() $C_i\cdot C_j\geq 1$
for at most one
$C_i\cdot C_j\geq 1$
for at most one
![]() $j\not=i$
.
$j\not=i$
.
For any birational morphism
![]() $f: Y\rightarrow X$
between surfaces, let
$f: Y\rightarrow X$
between surfaces, let
![]() $E=\cup_{i=1}^nE_i$
be the reduced exceptional divisor for some non-negative integer n. We define
$E=\cup_{i=1}^nE_i$
be the reduced exceptional divisor for some non-negative integer n. We define
![]() $\mathcal{D}(f)\;:\!=\;\mathcal{D}(E)$
.
$\mathcal{D}(f)\;:\!=\;\mathcal{D}(E)$
.
When we have a dual graph, we sometimes label
![]() $C_i$
near the vertex
$C_i$
near the vertex
![]() $v_i$
. We sometimes use black dots in the dual graph to emphasise the corresponding curves that are not exceptional.
$v_i$
. We sometimes use black dots in the dual graph to emphasise the corresponding curves that are not exceptional.
Definition 2·8. Let
![]() $\mathcal{D}$
be a dual graph. If
$\mathcal{D}$
be a dual graph. If
![]() $\mathcal{D}$
looks like the following
$\mathcal{D}$
looks like the following

for some integers
![]() $m>m_2>m_1$
, then
$m>m_2>m_1$
, then
![]() $\cup_{i=1}^{m_1}C_i$
,
$\cup_{i=1}^{m_1}C_i$
,
![]() $\cup_{i=m_1+1}^{m_2}C_i$
, and
$\cup_{i=m_1+1}^{m_2}C_i$
, and
![]() $\cup_{i=m_2+1}^{m}C_i$
will be called the branches of
$\cup_{i=m_2+1}^{m}C_i$
will be called the branches of
![]() $\mathcal{D}$
. The length of a branch is the number of irreducible curves in this branch.
$\mathcal{D}$
. The length of a branch is the number of irreducible curves in this branch.
We will use the following lemmas many times in this paper:
Lemma 2·9.
Let
![]() $X\ni x$
be a smooth germ,
$X\ni x$
be a smooth germ,
![]() $f: Y\rightarrow X$
the smooth blow-up of
$f: Y\rightarrow X$
the smooth blow-up of
![]() $X\ni x$
with exceptional divisor E, and C and D two
$X\ni x$
with exceptional divisor E, and C and D two
![]() $\mathbb{R}$
-divisors on X without common irreducible components. Then
$\mathbb{R}$
-divisors on X without common irreducible components. Then
 \begin{align*} (C\cdot D)_x&=\sum_{y\in f^{-1}(x)}(f^{-1}_*C\cdot f^{-1}_*D)_y+(f^{-1}_*C\cdot E)(f^{-1}_*D\cdot E)\\ &=\sum_{y\in f^{-1}(x)}(f^{-1}_*C\cdot f^{-1}_*D)_y+{\rm{mult}}_xC\cdot{\rm{mult}}_xD.\end{align*}
\begin{align*} (C\cdot D)_x&=\sum_{y\in f^{-1}(x)}(f^{-1}_*C\cdot f^{-1}_*D)_y+(f^{-1}_*C\cdot E)(f^{-1}_*D\cdot E)\\ &=\sum_{y\in f^{-1}(x)}(f^{-1}_*C\cdot f^{-1}_*D)_y+{\rm{mult}}_xC\cdot{\rm{mult}}_xD.\end{align*}
Proof. Possibly shrinking X to a neighbourhood of x and shrinking Y to a neighbourhood over x, we may assume that
![]() $(C\cdot D)_x=C\cdot D$
and
$(C\cdot D)_x=C\cdot D$
and
![]() $\sum_{y\in f^{-1}(x)}(f^{-1}_*C\cdot f^{-1}_*D)_y=f^{-1}_*C\cdot f^{-1}_*D$
. Thus
$\sum_{y\in f^{-1}(x)}(f^{-1}_*C\cdot f^{-1}_*D)_y=f^{-1}_*C\cdot f^{-1}_*D$
. Thus
and
By the projection formula,
Lemma 2·10
(cf. [
25
, lemma 3·41, corollary 4·2]). Let U be a smooth surface and
![]() $C=\cup_{i=1}^mC_i$
a connected proper curve on U. Assume that the intersection matrix
$C=\cup_{i=1}^mC_i$
a connected proper curve on U. Assume that the intersection matrix
![]() $\{(C_i\cdot C_j)\}_{1\leq i,j\leq m}$
is negative definite. Let
$\{(C_i\cdot C_j)\}_{1\leq i,j\leq m}$
is negative definite. Let
![]() $A=\sum_{i=1}^m a_iC_i$
and
$A=\sum_{i=1}^m a_iC_i$
and
![]() $H=\sum_{i=1}^m b_iC_i$
be
$H=\sum_{i=1}^m b_iC_i$
be
![]() $\mathbb{R}$
-linear combinations of the curves
$\mathbb{R}$
-linear combinations of the curves
![]() $C_i$
. Assume that
$C_i$
. Assume that
![]() $H\cdot C_i\leq A\cdot C_i$
for every i, then either
$H\cdot C_i\leq A\cdot C_i$
for every i, then either
![]() $a_i=b_i$
for each i or
$a_i=b_i$
for each i or
![]() $a_i<b_i$
for each i.
$a_i<b_i$
for each i.
3. Divisors computing mlds over smooth surface germs
In this section, we study the behavior of divisors computing mlds over a smooth surface germ. The following Definition-Lemma greatly simplify the notation in the rest of the paper and we will use it many times.
3·1. Definitions and lemmas
Definition-
Lemma 3·1
. Let
![]() $(X\ni x,B)$
be a smooth lc surface germ and E a divisor over
$(X\ni x,B)$
be a smooth lc surface germ and E a divisor over
![]() $X\ni x$
. By [
25
, lemma 2·45], there exists a unique positive integer
$X\ni x$
. By [
25
, lemma 2·45], there exists a unique positive integer
![]() $n=n(E)$
and a unique sequence of smooth blow-ups
$n=n(E)$
and a unique sequence of smooth blow-ups
such that E is on
![]() $X_E$
and each
$X_E$
and each
![]() $f_{i,E}$
is the smooth blow-up at
$f_{i,E}$
is the smooth blow-up at
![]() ${\rm{center}}_{X_{i-1,E}}E$
. We define
${\rm{center}}_{X_{i-1,E}}E$
. We define
![]() $f_E\;:\!=\;f_{1,E}\circ f_{2,E}\dots\circ f_{n,E}$
,
$f_E\;:\!=\;f_{1,E}\circ f_{2,E}\dots\circ f_{n,E}$
,
![]() $E^i$
the exceptional divisor of
$E^i$
the exceptional divisor of
![]() $f_{i,E}$
for each i, and
$f_{i,E}$
for each i, and
![]() $E^i_j$
the strict transform of
$E^i_j$
the strict transform of
![]() $E^i$
on
$E^i$
on
![]() $X_{j,E}$
for any
$X_{j,E}$
for any
![]() $i\leq j$
. In particular,
$i\leq j$
. In particular,
![]() $E^i_i=E^i$
for each i and
$E^i_i=E^i$
for each i and
![]() $E=E^n=E^n_n$
.
$E=E^n=E^n_n$
.
Remark 3·2. We need the following facts many times, which are elementary and we omit the proof. Let
![]() $(X\ni x,B)$
be a smooth lc surface germ, E a divisor over
$(X\ni x,B)$
be a smooth lc surface germ, E a divisor over
![]() $X\ni x$
, and
$X\ni x$
, and
![]() $n\;:\!=\;n(E)$
. Then for any
$n\;:\!=\;n(E)$
. Then for any
![]() $i\leq j$
such that
$i\leq j$
such that
![]() $i,j\in\{1,2,\dots,n\}$
,
$i,j\in\{1,2,\dots,n\}$
,
-
(i)
 $E^i_j$
is a smooth rational curve,
$E^i_j$
is a smooth rational curve, -
(ii)
 $\cup_{k=1}^iE^k_i$
is simple normal crossing,
$\cup_{k=1}^iE^k_i$
is simple normal crossing, -
(iii)
 $(E^i)^2=-1$
, and
$(E^i)^2=-1$
, and -
(iv)
 $(E^i_j)^2\leq -2$
when
$(E^i_j)^2\leq -2$
when
 $i<j$
.
$i<j$
.
Lemma 3·3.
Let
![]() $(X\ni x,B)$
be a smooth surface germ and
$(X\ni x,B)$
be a smooth surface germ and
![]() $f: Y\rightarrow X$
the smooth blow-up at x with exceptional divisor E. Then
$f: Y\rightarrow X$
the smooth blow-up at x with exceptional divisor E. Then
![]() $a(E,X,B)=2-{\rm{mult}}_xB$
. In particular,
$a(E,X,B)=2-{\rm{mult}}_xB$
. In particular,
![]() ${\rm{mld}}(X\ni x,B)\leq 2-{\rm{mult}}_xB$
.
${\rm{mld}}(X\ni x,B)\leq 2-{\rm{mult}}_xB$
.
Proof. This immediately follows from [ 25 , lemma 2·29].
Lemma 3·4.
Let
![]() $X\ni x$
be a smooth surface germ,
$X\ni x$
be a smooth surface germ,
![]() $B\geq 0$
an
$B\geq 0$
an
![]() $\mathbb{R}$
-divisor on X and C a prime divisor on X. Then
$\mathbb{R}$
-divisor on X and C a prime divisor on X. Then
![]() $(B\cdot C)_x\geq{\rm{mult}}_xB\cdot{\rm{mult}}_xC$
.
$(B\cdot C)_x\geq{\rm{mult}}_xB\cdot{\rm{mult}}_xC$
.
Proof. It immediately follows from [ Reference Hartshorne16 , excercise 5·4(a)].
Lemma 3·5.
Let
![]() $a\in [0,1]$
be a real number and
$a\in [0,1]$
be a real number and
![]() $(X\ni x,\Delta\;:\!=\;B+aC)$
a smooth surface germ, where
$(X\ni x,\Delta\;:\!=\;B+aC)$
a smooth surface germ, where
![]() $B\geq 0$
is an
$B\geq 0$
is an
![]() $\mathbb{R}$
-divisor and C is a prime divisor such that
$\mathbb{R}$
-divisor and C is a prime divisor such that
![]() $C\not\subset\operatorname{Supp} B$
and C is smooth at x. Assume that
$C\not\subset\operatorname{Supp} B$
and C is smooth at x. Assume that
![]() $(B\cdot C)_{x}<1$
, then
$(B\cdot C)_{x}<1$
, then
![]() ${\rm{mld}}(X\ni x,\Delta)>1-a$
.
${\rm{mld}}(X\ni x,\Delta)>1-a$
.
Proof. We only need to show that for any positive integer n and any sequence of smooth blow-ups
over
![]() $X\ni x$
with exceptional divisors
$X\ni x$
with exceptional divisors
![]() $E_k\;:\!=\;{\rm{Exc}}(f_k)$
for each k, we have
$E_k\;:\!=\;{\rm{Exc}}(f_k)$
for each k, we have
![]() $a(E_k,X,\Delta)>1-a$
.
$a(E_k,X,\Delta)>1-a$
.
In the following, we show that
![]() $a(E_k,X,\Delta)>1-a$
for each k by applying induction on n. When
$a(E_k,X,\Delta)>1-a$
for each k by applying induction on n. When
![]() $n=1$
, by Lemmas 3·3 and 3·4,
$n=1$
, by Lemmas 3·3 and 3·4,
Therefore, we may assume that
![]() $n\geq 2$
, and when we blow-up at most
$n\geq 2$
, and when we blow-up at most
![]() $n-1$
times, each divisor we have extracted has log discrepancy
$n-1$
times, each divisor we have extracted has log discrepancy
![]() $>1-a$
. In particular,
$>1-a$
. In particular,
![]() $a(E_k,X,\Delta)>1-a$
for any
$a(E_k,X,\Delta)>1-a$
for any
![]() $k\in\{1,2,\dots,n-1\}$
.
$k\in\{1,2,\dots,n-1\}$
.
Let
![]() $x_1\;:\!=\;{\rm{center}}_XE_n$
, and
$x_1\;:\!=\;{\rm{center}}_XE_n$
, and
![]() $B_1,C_1,\Delta_1$
the strict transforms of B,C and
$B_1,C_1,\Delta_1$
the strict transforms of B,C and
![]() $\Delta$
on
$\Delta$
on
![]() $X_1$
respectively. Then
$X_1$
respectively. Then
![]() $x_1\in E_1$
. There are three cases:
$x_1\in E_1$
. There are three cases:
Case 1.
![]() $a+{\rm{mult}}_xB-1<0$
. By Lemma 2·9,
$a+{\rm{mult}}_xB-1<0$
. By Lemma 2·9,
By induction hypothesis for the germ
![]() $(X_1\ni x_1,\Delta_1)$
and blowing-up at most
$(X_1\ni x_1,\Delta_1)$
and blowing-up at most
![]() $n-1$
times, we have
$n-1$
times, we have
and finish the proof for Case 1.
Case 2.
![]() $a+{\rm{mult}}_xB-1\geq 0$
and
$a+{\rm{mult}}_xB-1\geq 0$
and
![]() $x_1\in E_1\cap C_1$
. Let
$x_1\in E_1\cap C_1$
. Let
![]() $\tilde B_1\;:\!=\;B_1+(a+{\rm{mult}}_xB-1)E_1$
. Then
$\tilde B_1\;:\!=\;B_1+(a+{\rm{mult}}_xB-1)E_1$
. Then
We have
Since C is smooth at x,
![]() $E_1\cup C_1$
is snc at
$E_1\cup C_1$
is snc at
![]() $x_1$
, so
$x_1$
, so
![]() $(E_1\cdot C_1)_{x_1}=1$
. By Lemma 2·9,
$(E_1\cdot C_1)_{x_1}=1$
. By Lemma 2·9,
Thus
By induction hypothesis for the germ
![]() $(X_1\ni x_1,\tilde B_1+aC_1)$
and blowing-up at most
$(X_1\ni x_1,\tilde B_1+aC_1)$
and blowing-up at most
![]() $n-1$
times,
$n-1$
times,
and we finish the proof for Case 2.
Case 3.
![]() $a+{\rm{mult}}_xB-1\geq 0$
,
$a+{\rm{mult}}_xB-1\geq 0$
,
![]() $x_1\in E_1$
, but
$x_1\in E_1$
, but
![]() $x_1\not\in C_1$
. By Lemma 2·9,
$x_1\not\in C_1$
. By Lemma 2·9,
By induction hypothesis for the germ
![]() $(X_1\ni x_1,B_1+(a+{\rm{mult}}_xB-1)E_1)$
and blowing-up at most
$(X_1\ni x_1,B_1+(a+{\rm{mult}}_xB-1)E_1)$
and blowing-up at most
![]() $n-1$
times and apply Lemma 3·4,
$n-1$
times and apply Lemma 3·4,
and we finish the proof for Case 3.
Lemma 3·6.
Let
![]() $X\ni x$
be a smooth germ,
$X\ni x$
be a smooth germ,
![]() $B\geq 0$
an
$B\geq 0$
an
![]() $\mathbb{R}$
-divisor on X and C a prime divisor on X such that
$\mathbb{R}$
-divisor on X and C a prime divisor on X such that
![]() $C\not\subset\operatorname{Supp} B$
and C is smooth at x. Let
$C\not\subset\operatorname{Supp} B$
and C is smooth at x. Let
![]() $g_1: X_1\rightarrow X$
be the smooth blow-up of x with exceptional divisor
$g_1: X_1\rightarrow X$
be the smooth blow-up of x with exceptional divisor
![]() $E_1$
,
$E_1$
,
![]() $C_1\;:\!=\;(g_1^{-1})_*C$
, and
$C_1\;:\!=\;(g_1^{-1})_*C$
, and
![]() $B_1\;:\!=\;(g_1^{-1})_*B$
. Let
$B_1\;:\!=\;(g_1^{-1})_*B$
. Let
![]() $g_2: X_2\rightarrow X_1$
be the smooth blow-up at
$g_2: X_2\rightarrow X_1$
be the smooth blow-up at
![]() $x_1\;:\!=\;C_1\cap E_1$
with exceptional divisor
$x_1\;:\!=\;C_1\cap E_1$
with exceptional divisor
![]() $E_2$
and
$E_2$
and
![]() $B_2\;:\!=\;(g_2^{-1})_*B_1$
. Then
$B_2\;:\!=\;(g_2^{-1})_*B_1$
. Then
Proof. Let
![]() $C_2\;:\!=\;(g_2^{-1})_*C_1$
and
$C_2\;:\!=\;(g_2^{-1})_*C_1$
and
![]() $E_1'\;:\!=\;(g_2^{-1})_*E_1$
. By Lemma 2·9,
$E_1'\;:\!=\;(g_2^{-1})_*E_1$
. By Lemma 2·9,
and
Thus
3·2.
Dual graph of
 $f_E$
$f_E$
Roughly speaking, this subsection shows that the dual graph of
![]() $f_E$
is almost always a chain when E is a divisor which computes the mld. We remark that [
15
, lemma 3·18] shows that there exists such an E such that the dual graph of
$f_E$
is almost always a chain when E is a divisor which computes the mld. We remark that [
15
, lemma 3·18] shows that there exists such an E such that the dual graph of
![]() $f_E$
is a chain, while we show that for any such E, the dual graph of
$f_E$
is a chain, while we show that for any such E, the dual graph of
![]() $f_E$
is a chain.
$f_E$
is a chain.
We need the following result of Kawakita. Notice that the “in particular” part of the following theorem is immediate from the construction in [ Reference Kawakita22 , remark 3].
Theorem 3·7
([
Reference Kawakita22
, theorem 1, remark 3]). Let
![]() $(X\ni x,B)$
be a smooth lc surface germ and E a divisor over
$(X\ni x,B)$
be a smooth lc surface germ and E a divisor over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then there exists a weighted blow-up of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then there exists a weighted blow-up of
![]() $X\ni x$
which extracts E. In particular, E is a Kollár component of
$X\ni x$
which extracts E. In particular, E is a Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
Lemma 3·8.
Let
![]() $(X\ni x,B)$
be a smooth lc surface germ and E a divisor over
$(X\ni x,B)$
be a smooth lc surface germ and E a divisor over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then
![]() $\mathcal{D}(f_E)$
is a chain.
$\mathcal{D}(f_E)$
is a chain.
Proof. By Theorem 3·7, there exists a weighted blow-up
![]() $f: Y\rightarrow X$
which extracts E. E contains at most two singular points of Y which are cyclic quotient singularities, and locally analytically, E is one coordinate line of each cyclic quotient singularity. Let
$f: Y\rightarrow X$
which extracts E. E contains at most two singular points of Y which are cyclic quotient singularities, and locally analytically, E is one coordinate line of each cyclic quotient singularity. Let
![]() $g: W\rightarrow Y$
be the minimal resolution of Y near E, then
$g: W\rightarrow Y$
be the minimal resolution of Y near E, then
![]() $f\circ g=f_E$
and
$f\circ g=f_E$
and
![]() $\mathcal{D}(f_E)$
is a chain.
$\mathcal{D}(f_E)$
is a chain.
Lemma 3·9.
Let
![]() $a\in [0,1]$
be a real number. Assume that:
$a\in [0,1]$
be a real number. Assume that:
-
(i)
 $(X\ni x,\Delta\;:\!=\;B+aC)$
a smooth lc surface germ, where
$(X\ni x,\Delta\;:\!=\;B+aC)$
a smooth lc surface germ, where
 $B\geq 0$
is an
$B\geq 0$
is an
 $\mathbb{R}$
-divisor and C is a prime divisor;
$\mathbb{R}$
-divisor and C is a prime divisor; -
(ii)
 $C\not\subset\operatorname{Supp} B$
and C is smooth at x; and
$C\not\subset\operatorname{Supp} B$
and C is smooth at x; and -
(iii)
 $(B\cdot C)_x<2$
.
$(B\cdot C)_x<2$
.
Then any divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
satisfies the following. Let
$a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
satisfies the following. Let
![]() $C_E\;:\!=\;(f_E^{-1})_*C$
, then
$C_E\;:\!=\;(f_E^{-1})_*C$
, then
![]() $C_E\cup{\rm{Exc}}(f_E)$
is a chain and
$C_E\cup{\rm{Exc}}(f_E)$
is a chain and
![]() $C_E$
is one tail of
$C_E$
is one tail of
![]() $C_E\cup{\rm{Exc}}(f_E)$
. In particular, the dual graph of
$C_E\cup{\rm{Exc}}(f_E)$
. In particular, the dual graph of
![]() $C_E\cup{\rm{Exc}}(f_E)$
is the following:
$C_E\cup{\rm{Exc}}(f_E)$
is the following:
Here
![]() $C_E$
is denoted by the black circle.
$C_E$
is denoted by the black circle.
Proof. By the construction of
![]() $f_E$
, if
$f_E$
, if
![]() $C_E\cup{\rm{Exc}}(f_E)$
is a chain, then
$C_E\cup{\rm{Exc}}(f_E)$
is a chain, then
![]() $C_E$
is a tail of
$C_E$
is a tail of
![]() $C_E\cup{\rm{Exc}}(f_E)$
. Let
$C_E\cup{\rm{Exc}}(f_E)$
. Let
![]() $n\;:\!=\;n(E)$
and let
$n\;:\!=\;n(E)$
and let
![]() $C_i$
be the strict transform of C on
$C_i$
be the strict transform of C on
![]() $X_{i,E}$
for each
$X_{i,E}$
for each
![]() $i\in\{0,1,\dots,n\}$
. Since C is smooth at x, by the construction of
$i\in\{0,1,\dots,n\}$
. Since C is smooth at x, by the construction of
![]() $f_E$
,
$f_E$
,
![]() $C_i\cup_{k=1}^iE^k_i$
is simple normal crossing over a neighbourhood of x and its dual graph does not contain a circle for each
$C_i\cup_{k=1}^iE^k_i$
is simple normal crossing over a neighbourhood of x and its dual graph does not contain a circle for each
![]() $i\in\{0,1,\dots,n\}$
. Since
$i\in\{0,1,\dots,n\}$
. Since
![]() $a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
,
$a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
,
![]() $a(E^i,X,\Delta)\geq a(E,X,\Delta)$
for every
$a(E^i,X,\Delta)\geq a(E,X,\Delta)$
for every
![]() $i\in\{1,2,\dots,n\}$
.
$i\in\{1,2,\dots,n\}$
.
Suppose that the lemma does not hold, then there exists a positive integer
![]() $m\in\{1,2,\dots,n\}$
, such that
$m\in\{1,2,\dots,n\}$
, such that
![]() $C_i\cup_{k=1}^iE^k_i$
is a chain,
$C_i\cup_{k=1}^iE^k_i$
is a chain,
![]() $C_i$
is a tail of
$C_i$
is a tail of
![]() $C_i\cup_{k=1}^iE^k_i$
for any
$C_i\cup_{k=1}^iE^k_i$
for any
![]() $i\in\{0,1,\dots,m-1\}$
, and
$i\in\{0,1,\dots,m-1\}$
, and
![]() $C_m\cup_{k=1}^mE^k_m$
is not a chain. Since any graph without a circle that is not a chain contains at least 4 vertices,
$C_m\cup_{k=1}^mE^k_m$
is not a chain. Since any graph without a circle that is not a chain contains at least 4 vertices,
![]() $m\geq 3$
.
$m\geq 3$
.
By Lemma 2·8,
![]() $\cup_{k=1}^nE^k_n$
is a chain, hence
$\cup_{k=1}^nE^k_n$
is a chain, hence
![]() $\cup_{k=1}^mE^k_m$
is a chain. Since
$\cup_{k=1}^mE^k_m$
is a chain. Since
![]() $C_m\cup_{k=1}^mE^k_m$
is not a chain,
$C_m\cup_{k=1}^mE^k_m$
is not a chain,
![]() $x_{m-1}\;:\!=\;{\rm{center}}_{X_{m-1,E}}E^m\in E^{m-1}\backslash C_{m-1}$
, and for any integer
$x_{m-1}\;:\!=\;{\rm{center}}_{X_{m-1,E}}E^m\in E^{m-1}\backslash C_{m-1}$
, and for any integer
![]() $i\in\{1,2,\dots,m-1\}$
,
$i\in\{1,2,\dots,m-1\}$
,
![]() $f_{i,E}$
is the smooth blow-up of a point
$f_{i,E}$
is the smooth blow-up of a point
![]() $x_{i-1}\in C_{i-1}$
, and if
$x_{i-1}\in C_{i-1}$
, and if
![]() $i\in\{2,3,\dots,m-1\}$
, then
$i\in\{2,3,\dots,m-1\}$
, then
![]() $f_{i,E}$
is the smooth blow-up of
$f_{i,E}$
is the smooth blow-up of
![]() $C_{i-1}\cap E^{i-1}$
. In particular, since
$C_{i-1}\cap E^{i-1}$
. In particular, since
![]() $m\geq 3$
,
$m\geq 3$
,
![]() $x_{m-3}\in C_{m-3}$
and
$x_{m-3}\in C_{m-3}$
and
![]() $x_{m-2}\in C_{m-2}\cap E^{m-2}$
.
$x_{m-2}\in C_{m-2}\cap E^{m-2}$
.
Claim 3·10.
![]() $(B_{m-1}\cdot E^{m-1})_{x_{m-1}}\geq 1$
.
$(B_{m-1}\cdot E^{m-1})_{x_{m-1}}\geq 1$
.
Proof. Let
![]() $a_{m-1}\;:\!=\;\max\{0,1-a(E^{m-1},X,\Delta)\}$
. Since
$a_{m-1}\;:\!=\;\max\{0,1-a(E^{m-1},X,\Delta)\}$
. Since
![]() $(X\ni x,\Delta)$
is lc,
$(X\ni x,\Delta)$
is lc,
![]() $a_{m-1}\in [0,1]$
. If
$a_{m-1}\in [0,1]$
. If
![]() $(B_{m-1}\cdot E^{m-1})_{x_{m-1}}<1$
, then by Lemma 3·5,
$(B_{m-1}\cdot E^{m-1})_{x_{m-1}}<1$
, then by Lemma 3·5,
 \begin{align*} {\rm{mld}}(X\ni x,\Delta)&=a(E^n,X,\Delta)=a(E^n,X^{m-1},B_{m-1}+(1-a(E^{m-1},X,\Delta))E^{m-1})\\ &\geq a(E^n,X^{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &\geq{\rm{mld}}(X_{m-1}\ni x_{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &>1-a_{m-1}=a(E^{m-1},X,\Delta),\end{align*}
\begin{align*} {\rm{mld}}(X\ni x,\Delta)&=a(E^n,X,\Delta)=a(E^n,X^{m-1},B_{m-1}+(1-a(E^{m-1},X,\Delta))E^{m-1})\\ &\geq a(E^n,X^{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &\geq{\rm{mld}}(X_{m-1}\ni x_{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &>1-a_{m-1}=a(E^{m-1},X,\Delta),\end{align*}
a contradiction.
Proof of Lemma 2·9 continued. Since
![]() $m\geq 3$
, by Lemmas 2·9, 3·6 and Claim 3·10,
$m\geq 3$
, by Lemmas 2·9, 3·6 and Claim 3·10,
which contradicts our assumptions.
Lemma 3·11.
Let
![]() $l,r\in [0,1]$
be two real numbers. Assume that:
$l,r\in [0,1]$
be two real numbers. Assume that:
-
(i)
 $(X\ni x,\Delta\;:\!=\;B+lL+rR)$
is a smooth lc surface germ, where
$(X\ni x,\Delta\;:\!=\;B+lL+rR)$
is a smooth lc surface germ, where
 $B\geq 0$
is an
$B\geq 0$
is an
 $\mathbb{R}$
-divisor and L,R are two different prime divisors;
$\mathbb{R}$
-divisor and L,R are two different prime divisors; -
(ii)
 $L\not\subset\operatorname{Supp} B, R\not\subset\operatorname{Supp} B$
, and
$L\not\subset\operatorname{Supp} B, R\not\subset\operatorname{Supp} B$
, and
 $(X\ni x,L+R)$
is log smooth; and
$(X\ni x,L+R)$
is log smooth; and -
(iii) either
 $(B\cdot L)_x<1$
or
$(B\cdot L)_x<1$
or
 $(B\cdot R)_x<1$
.
$(B\cdot R)_x<1$
.
Then any divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
satisfies the following. Let
$a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
satisfies the following. Let
![]() $L_E\;:\!=\;(f_E^{-1})_*L$
and
$L_E\;:\!=\;(f_E^{-1})_*L$
and
![]() $R_E\;:\!=\;(f_E^{-1})_*R$
, then
$R_E\;:\!=\;(f_E^{-1})_*R$
, then
![]() $L_E\cup R_E\cup{\rm{Exc}}(f_E)$
is a chain and
$L_E\cup R_E\cup{\rm{Exc}}(f_E)$
is a chain and
![]() $L_E,R_E$
are the tails of
$L_E,R_E$
are the tails of
![]() $L_E\cup R_E\cup{\rm{Exc}}(f_E)$
. In particular, the dual graph of
$L_E\cup R_E\cup{\rm{Exc}}(f_E)$
. In particular, the dual graph of
![]() $L_E\cup R_E\cup{\rm{Exc}}(f_E)$
is the following:
$L_E\cup R_E\cup{\rm{Exc}}(f_E)$
is the following:
Here
![]() $L_E$
and
$L_E$
and
![]() $R_E$
are denoted by the left black circle and the right black circle respectively.
$R_E$
are denoted by the left black circle and the right black circle respectively.
Proof. By the construction of
![]() $f_E$
, if
$f_E$
, if
![]() $L_E\cup R_E\cup{\rm{Exc}}(f_E)$
is a chain, then
$L_E\cup R_E\cup{\rm{Exc}}(f_E)$
is a chain, then
![]() $L_E,R_E$
are the tails of
$L_E,R_E$
are the tails of
![]() $L_E\cup R_E\cup{\rm{Exc}}(f_E)$
. Let
$L_E\cup R_E\cup{\rm{Exc}}(f_E)$
. Let
![]() $n\;:\!=\;n(E)$
and let
$n\;:\!=\;n(E)$
and let
![]() $L_i,R_i$
be the strict transforms of
$L_i,R_i$
be the strict transforms of
![]() $L_i,R_i$
on
$L_i,R_i$
on
![]() $X_{i,E}$
for each
$X_{i,E}$
for each
![]() $i\in\{0,1,\dots,n\}$
. Since
$i\in\{0,1,\dots,n\}$
. Since
![]() $(X\ni x,L+R)$
is log smooth and by the construction of
$(X\ni x,L+R)$
is log smooth and by the construction of
![]() $f_E$
,
$f_E$
,
![]() $L_i\cup R_i\cup_{k=1}^iE^k_i$
is simple normal crossing over a neighbourhood of x and its dual graph does not contain a circle for each
$L_i\cup R_i\cup_{k=1}^iE^k_i$
is simple normal crossing over a neighbourhood of x and its dual graph does not contain a circle for each
![]() $i\in\{0,1,\dots,n\}$
. Since
$i\in\{0,1,\dots,n\}$
. Since
![]() $a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
,
$a(E,X,\Delta)={\rm{mld}}(X\ni x,\Delta)$
,
![]() $a(E^i,X,\Delta)\geq a(E,X,\Delta)$
for every
$a(E^i,X,\Delta)\geq a(E,X,\Delta)$
for every
![]() $i\in\{1,2,\dots,n\}$
.
$i\in\{1,2,\dots,n\}$
.
Suppose that the lemma does not hold, then there exists a positive integer
![]() $m\in\{1,2,\dots,n\}$
, such that
$m\in\{1,2,\dots,n\}$
, such that
![]() $L_i\cup R_i\cup_{k=1}^iE^k_i$
is a chain and
$L_i\cup R_i\cup_{k=1}^iE^k_i$
is a chain and
![]() $L_i,R_i$
are the tails of
$L_i,R_i$
are the tails of
![]() $L_i\cup R_i\cup_{k=1}^iE^k_i$
for any
$L_i\cup R_i\cup_{k=1}^iE^k_i$
for any
![]() $i\in\{0,1,\dots,m-1\}$
, and
$i\in\{0,1,\dots,m-1\}$
, and
![]() $L_m\cup R_m\cup_{k=1}^mE^k_m$
is not a chain. Since any graph without a circle that is not a chain contains at least 4 points,
$L_m\cup R_m\cup_{k=1}^mE^k_m$
is not a chain. Since any graph without a circle that is not a chain contains at least 4 points,
![]() $m\geq 2$
.
$m\geq 2$
.
By Theorem 3·7,
![]() $\cup_{k=1}^nE^k_n$
is a chain, hence
$\cup_{k=1}^nE^k_n$
is a chain, hence
![]() $\cup_{k=1}^mE^k_m$
is a chain. By the construction of
$\cup_{k=1}^mE^k_m$
is a chain. By the construction of
![]() $f_E$
and the choice of m,
$f_E$
and the choice of m,
![]() $x_{m-1}\;:\!=\;{\rm{center}}_{X_{m-1,E}}E^m\in E^{m-1}\backslash (L_{m-1}\cup R_{m-1})$
.
$x_{m-1}\;:\!=\;{\rm{center}}_{X_{m-1,E}}E^m\in E^{m-1}\backslash (L_{m-1}\cup R_{m-1})$
.
Claim 3·12.
![]() $(B_{m-1}\cdot E^{m-1})_{x_{m-1}}\geq 1$
.
$(B_{m-1}\cdot E^{m-1})_{x_{m-1}}\geq 1$
.
Proof. Let
![]() $a_{m-1}\;:\!=\;\max\{0,1-a(E^{m-1},X,\Delta)\}$
. Since
$a_{m-1}\;:\!=\;\max\{0,1-a(E^{m-1},X,\Delta)\}$
. Since
![]() $(X\ni x,\Delta)$
is lc,
$(X\ni x,\Delta)$
is lc,
![]() $a_{m-1}\in [0,1]$
. If
$a_{m-1}\in [0,1]$
. If
![]() $(B_{m-1}\cdot E^{m-1})_{x_{m-1}}<1$
, then by Lemma 3·5,
$(B_{m-1}\cdot E^{m-1})_{x_{m-1}}<1$
, then by Lemma 3·5,
 \begin{align*} {\rm{mld}}(X\ni x,\Delta)&=a(E^n,X,\Delta)=a(E^n,X^{m-1},B_{m-1}+(1-a(E^{m-1},X,\Delta))E^{m-1})\\ &\geq a(E^n,X^{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &\geq{\rm{mld}}(X_{m-1}\ni x_{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &>1-a_{m-1}=a(E^{m-1},X,\Delta),\end{align*}
\begin{align*} {\rm{mld}}(X\ni x,\Delta)&=a(E^n,X,\Delta)=a(E^n,X^{m-1},B_{m-1}+(1-a(E^{m-1},X,\Delta))E^{m-1})\\ &\geq a(E^n,X^{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &\geq{\rm{mld}}(X_{m-1}\ni x_{m-1},B_{m-1}+a_{m-1}E^{m-1})\\ &>1-a_{m-1}=a(E^{m-1},X,\Delta),\end{align*}
a contradiction.
Proof of Lemma 3·11 continued. Since
![]() $m\geq 2$
, by Lemma 2·9 and Claim 3·12,
$m\geq 2$
, by Lemma 2·9 and Claim 3·12,
and
which contradict our assumptions.
4. Classification of divisors computing mlds
4·1. A key lemma
The following lemma is similar to [25, theorem 4·15] and plays an important role in the proof of our main theorems.
Lemma 4·1.
Let m be a non-negative integer,
![]() $(X\ni x,B)$
a plt surface germ,
$(X\ni x,B)$
a plt surface germ,
![]() $f: Y\rightarrow X$
the minimal resolution of
$f: Y\rightarrow X$
the minimal resolution of
![]() $X\ni x$
, and
$X\ni x$
, and
![]() $B_Y\;:\!=\;f^{-1}_*B$
. Then:
$B_Y\;:\!=\;f^{-1}_*B$
. Then:
-
(i) for any prime divisor
 $F\subset{\rm{Exc}}(f)$
,
$F\subset{\rm{Exc}}(f)$
,
 $B_Y\cdot F<2$
;
$B_Y\cdot F<2$
; -
(ii) there exists at most one prime divisor
 $F\subset{\rm{Exc}}(f)$
such that
$F\subset{\rm{Exc}}(f)$
such that
 $B_Y\cdot F\geq 1$
; and
$B_Y\cdot F\geq 1$
; and -
(iii) if
 $E\subset{\rm{Exc}}(f)$
is a prime divisor such that
$E\subset{\rm{Exc}}(f)$
is a prime divisor such that
 $B_Y\cdot E\geq 1$
, then
$B_Y\cdot E\geq 1$
, then
 $X\ni x$
is an A-type singularity and E is a tail of
$X\ni x$
is an A-type singularity and E is a tail of
 $\mathcal{D}(f)$
.
$\mathcal{D}(f)$
.
.
Proof. Let
![]() $F_1,\dots,F_m$
be the prime exceptional divisors of h for some positive integer m, and let
$F_1,\dots,F_m$
be the prime exceptional divisors of h for some positive integer m, and let
![]() $v_1,\dots,v_m$
be the vertices corresponding to
$v_1,\dots,v_m$
be the vertices corresponding to
![]() $F_1,\dots,F_m$
in
$F_1,\dots,F_m$
in
![]() $\mathcal{D}(f)$
respectively. We construct an extended graph
$\mathcal{D}(f)$
respectively. We construct an extended graph
![]() $\bar{\mathcal{D}}(f)$
in the following way:
$\bar{\mathcal{D}}(f)$
in the following way:
-
(i) the vertices of
 $\bar{\mathcal{D}}(f)$
are
$\bar{\mathcal{D}}(f)$
are
 $v_0,v_1,\dots,v_m$
;
$v_0,v_1,\dots,v_m$
; -
(ii) for any
 $i,j\in\{1,2,\dots,m\}$
,
$i,j\in\{1,2,\dots,m\}$
,
 $v_i$
and
$v_i$
and
 $v_j$
are connected by a line if and only if
$v_j$
are connected by a line if and only if
 $v_i$
and
$v_i$
and
 $v_j$
are connected by a line in
$v_j$
are connected by a line in
 $\mathcal{D}(f)$
;
$\mathcal{D}(f)$
; -
(iii) for any
 $i\in\{1,2,\dots,m\}$
,
$i\in\{1,2,\dots,m\}$
,
 $v_0$
and
$v_0$
and
 $v_i$
are connected by
$v_i$
are connected by
 $\lfloor B_Y\cdot F_i\rfloor$
lines.
$\lfloor B_Y\cdot F_i\rfloor$
lines.
Moreover, we may write
where
![]() $a_i\;:\!=\;a(F_i,X,B)-1$
. Since
$a_i\;:\!=\;a(F_i,X,B)-1$
. Since
![]() $(X\ni x,B)$
is plt and f is the minimal resolution of
$(X\ni x,B)$
is plt and f is the minimal resolution of
![]() $X\ni x$
,
$X\ni x$
,
![]() $0\geq a_i>-1$
for each i. Let
$0\geq a_i>-1$
for each i. Let
![]() $A\;:\!=\;\sum_{i=1}^ma_iF_i$
.
$A\;:\!=\;\sum_{i=1}^ma_iF_i$
.
If
![]() $\bar{\mathcal{D}}(f)$
is not connected, then
$\bar{\mathcal{D}}(f)$
is not connected, then
![]() $B_Y\cdot F_i<1$
for each i and there is nothing left to prove. Therefore, we may assume that
$B_Y\cdot F_i<1$
for each i and there is nothing left to prove. Therefore, we may assume that
![]() $\bar{\mathcal{D}}(f)$
is connected.
$\bar{\mathcal{D}}(f)$
is connected.
Claim 4·2.
![]() $\bar{\mathcal{D}}(f)$
does not contain a circle.
$\bar{\mathcal{D}}(f)$
does not contain a circle.
Proof. Suppose that
![]() $\bar{\mathcal{D}}(f)$
contains a circle. We let
$\bar{\mathcal{D}}(f)$
contains a circle. We let
![]() $v_{k_0}\;:\!=\;v_0,v_{k_1},\dots,v_{k_r}$
be the vertices of this circle for some positive r such that
$v_{k_0}\;:\!=\;v_0,v_{k_1},\dots,v_{k_r}$
be the vertices of this circle for some positive r such that
![]() $\bar{\mathcal{D}}(f)$
contains one of the following sub-graphs:
$\bar{\mathcal{D}}(f)$
contains one of the following sub-graphs:

Let
![]() $H\;:\!=\;-\sum_{i=1}^rF_{k_i}$
. Then
$H\;:\!=\;-\sum_{i=1}^rF_{k_i}$
. Then
for each
![]() $i\in\{2,3,\dots,r-1\}$
,
$i\in\{2,3,\dots,r-1\}$
,
for each
![]() $i\in\{1,r\}$
when
$i\in\{1,r\}$
when
![]() $r\geq 2$
,
$r\geq 2$
,
when
![]() $r=1$
, and
$r=1$
, and
for each
![]() $i\not\in\{k_1,\dots,k_r\}$
. By Lemma 2·10,
$i\not\in\{k_1,\dots,k_r\}$
. By Lemma 2·10,
![]() $a_{k_i}\leq -1$
for each i, a contradiction.
$a_{k_i}\leq -1$
for each i, a contradiction.
Claim 4·3.
![]() $\bar{\mathcal{D}}(f)$
does not contain a fork.
$\bar{\mathcal{D}}(f)$
does not contain a fork.
Proof. Assume that
![]() $\bar{\mathcal{D}}(f)$
contains a fork. By Claim 4·2,
$\bar{\mathcal{D}}(f)$
contains a fork. By Claim 4·2,
![]() $\bar{\mathcal{D}}(f)$
does not contain a circle. Therefore,
$\bar{\mathcal{D}}(f)$
does not contain a circle. Therefore,
![]() $v_0$
is not a fork of
$v_0$
is not a fork of
![]() $\bar{\mathcal{D}}(f)$
. In particular, there exist a positive integer r and vertices
$\bar{\mathcal{D}}(f)$
. In particular, there exist a positive integer r and vertices
![]() $v_{k_0}\;:\!=\;v_0,v_{k_1},\dots,v_{k_r},v_{l_1},v_{l_2}$
such that
$v_{k_0}\;:\!=\;v_0,v_{k_1},\dots,v_{k_r},v_{l_1},v_{l_2}$
such that
![]() $\bar{\mathcal{D}}(f)$
contains the following sub-graph:
$\bar{\mathcal{D}}(f)$
contains the following sub-graph:

Let
![]() $H\;:\!=\;-\sum_{i=1}^rF_{k_i}-\frac{1}{2}F_{l_1}-\frac{1}{2}F_{l_2}$
. Then
$H\;:\!=\;-\sum_{i=1}^rF_{k_i}-\frac{1}{2}F_{l_1}-\frac{1}{2}F_{l_2}$
. Then
for each
![]() $i\in\{1,2\}$
,
$i\in\{1,2\}$
,
for each
![]() $i\in\{2,3,\dots,r-1\}$
,
$i\in\{2,3,\dots,r-1\}$
,
for
![]() $i=1$
, and
$i=1$
, and
for each
![]() $i\not\in\{k_1,\dots,k_r,l_1,l_2\}$
. By Lemma 2·10,
$i\not\in\{k_1,\dots,k_r,l_1,l_2\}$
. By Lemma 2·10,
![]() $a_{k_r}\leq -1$
, a contradiction.
$a_{k_r}\leq -1$
, a contradiction.
Proof of Lemma 4·1 continued. By Claims 4·2 and 4·3,
![]() $\bar{\mathcal{D}}(f)$
does not contain a circle or a fork. Therefore,
$\bar{\mathcal{D}}(f)$
does not contain a circle or a fork. Therefore,
![]() $\bar{\mathcal{D}}(f)$
is a chain. Since
$\bar{\mathcal{D}}(f)$
is a chain. Since
![]() $\mathcal{D}(f)$
is connected and
$\mathcal{D}(f)$
is connected and
![]() $\bar{\mathcal{D}}(f)$
has
$\bar{\mathcal{D}}(f)$
has
![]() $\mathcal{D}(f)$
as a sub-graph,
$\mathcal{D}(f)$
as a sub-graph,
![]() $\mathcal{D}(f)$
is a chain and
$\mathcal{D}(f)$
is a chain and
![]() $v_0$
is a tail of
$v_0$
is a tail of
![]() $\bar{\mathcal{D}}(f)$
. The lemma immediately follows from the structure of
$\bar{\mathcal{D}}(f)$
. The lemma immediately follows from the structure of
![]() $\bar{\mathcal{D}}(f)$
and
$\bar{\mathcal{D}}(f)$
and
![]() $\mathcal{D}(f)$
.
$\mathcal{D}(f)$
.
4·2. A-type singularities
Lemma 4·4.
Let
![]() $X\ni x$
be a surface germ of A-type, E a prime divisor on X,
$X\ni x$
be a surface germ of A-type, E a prime divisor on X,
![]() $f: Y\rightarrow X$
the minimal resolution of
$f: Y\rightarrow X$
the minimal resolution of
![]() $X\ni x$
, and
$X\ni x$
, and
![]() $E_Y\;:\!=\;f^{-1}_*E$
. Let
$E_Y\;:\!=\;f^{-1}_*E$
. Let
![]() $F_1,\dots,F_m$
be the prime exceptional divisors over
$F_1,\dots,F_m$
be the prime exceptional divisors over
![]() $X\ni x$
. Assume that
$X\ni x$
. Assume that
![]() $E_Y\cup\cup_{i=1}^mF_i$
is simple normal crossing over a neighbourhood of x and the dual graph of
$E_Y\cup\cup_{i=1}^mF_i$
is simple normal crossing over a neighbourhood of x and the dual graph of
![]() $E_Y\cup\cup_{i=1}^mF_i$
is the following:
$E_Y\cup\cup_{i=1}^mF_i$
is the following:
.
Then
![]() $(X\ni x,E)$
is plt.
$(X\ni x,E)$
is plt.
Proof. We may write
where
![]() $a_i\;:\!=\;a(F_i,X,E)-1$
. Let
$a_i\;:\!=\;a(F_i,X,E)-1$
. Let
![]() $H\;:\!=\;-\sum_{i=1}^mF_i$
and
$H\;:\!=\;-\sum_{i=1}^mF_i$
and
![]() $A\;:\!=\;\sum_{i=1}^ma_iF_i$
. Then
$A\;:\!=\;\sum_{i=1}^ma_iF_i$
. Then
if
![]() $m=1$
,
$m=1$
,
if
![]() $m\geq 2$
,
$m\geq 2$
,
if
![]() $m\geq 2$
and
$m\geq 2$
and
![]() $2\leq i\leq m-1$
, and
$2\leq i\leq m-1$
, and
if
![]() $m\geq 2$
. By Lemma 2·10,
$m\geq 2$
. By Lemma 2·10,
![]() $a_i>-1$
for each i, hence
$a_i>-1$
for each i, hence
![]() $(X\ni x,E)$
is plt.
$(X\ni x,E)$
is plt.
Theorem 4·5.
Let
![]() $(X\ni x,B)$
be a plt surface germ such that
$(X\ni x,B)$
be a plt surface germ such that
![]() $X\ni x$
is an A-type singularity. Then for any divisor E over
$X\ni x$
is an A-type singularity. Then for any divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
, E is a Kollár component of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
, E is a Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
Proof. For any model X’ of X such that
![]() ${\rm{center}}_{X'}E$
is a divisor, we let
${\rm{center}}_{X'}E$
is a divisor, we let
![]() $E_{X'}$
be the center of E on X’. Let
$E_{X'}$
be the center of E on X’. Let
![]() $h: Y\rightarrow X$
be the minimal resolution of X and
$h: Y\rightarrow X$
be the minimal resolution of X and
![]() $F_1,\dots,F_m$
the prime exceptional divisors of h with the following dual graph:
$F_1,\dots,F_m$
the prime exceptional divisors of h with the following dual graph:
Let
![]() $B_Y\;:\!=\;f^{-1}_*B$
and
$B_Y\;:\!=\;f^{-1}_*B$
and
![]() $a_i\;:\!=\;1-a(F_i,X,B)$
for each i. Then
$a_i\;:\!=\;1-a(F_i,X,B)$
for each i. Then
![]() $a_i\in [0,1)$
for each i. There are three cases:
$a_i\in [0,1)$
for each i. There are three cases:
Case 1.
E is on Y. In this case, we let
![]() $W\;:\!=\;Y$
and
$W\;:\!=\;Y$
and
![]() $g\;:\!=\;h$
. Then
$g\;:\!=\;h$
. Then
![]() $\mathcal{D}(g)$
is a chain. Moreover, by the construction of g, for any prime divisor
$\mathcal{D}(g)$
is a chain. Moreover, by the construction of g, for any prime divisor
![]() $F\not=E_W$
in
$F\not=E_W$
in
![]() ${\rm{Exc}}(g)$
,
${\rm{Exc}}(g)$
,
![]() $F^2\leq -2$
.
$F^2\leq -2$
.
Case 2.
E is not on Y,
![]() ${\rm{center}}_YE\;:\!=\;y\in F_i$
for some i, and
${\rm{center}}_YE\;:\!=\;y\in F_i$
for some i, and
![]() ${\rm{center}}_YE\not\in F_j$
for any
${\rm{center}}_YE\not\in F_j$
for any
![]() $j\not=i$
. In this case, since
$j\not=i$
. In this case, since
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
,
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
,
![]() $a(E,X,B)\leq 1-a_i$
. By Lemma 3·5,
$a(E,X,B)\leq 1-a_i$
. By Lemma 3·5,
![]() $B_Y\cdot F_i\geq 1$
. By Lemma 4·1(iii),
$B_Y\cdot F_i\geq 1$
. By Lemma 4·1(iii),
![]() $i=1$
or m. We let
$i=1$
or m. We let
![]() $f_E: W\rightarrow Y$
the sequence of smooth blow-ups as in Definition-Lemma 3·1, and
$f_E: W\rightarrow Y$
the sequence of smooth blow-ups as in Definition-Lemma 3·1, and
![]() $g\;:\!=\;h\circ f_E$
. By Lemma 4·1(i),
$g\;:\!=\;h\circ f_E$
. By Lemma 4·1(i),
![]() $B_Y\cdot F_i<2$
, hence
$B_Y\cdot F_i<2$
, hence
![]() $(B_Y\cdot F_i)_y<2$
. Since
$(B_Y\cdot F_i)_y<2$
. Since
by Lemma 3·9,
![]() $\mathcal{D}(g)$
is a chain. Moreover, by the construction of g, for any prime divisor
$\mathcal{D}(g)$
is a chain. Moreover, by the construction of g, for any prime divisor
![]() $F\not=E_W$
in
$F\not=E_W$
in
![]() ${\rm{Exc}}(g)$
,
${\rm{Exc}}(g)$
,
![]() $F^2\leq -2$
.
$F^2\leq -2$
.
Case 3.
E is not on Y and
![]() ${\rm{center}}_YE\;:\!=\;y\in F_i\cap F_{i+1}$
for some i. In this case, we let
${\rm{center}}_YE\;:\!=\;y\in F_i\cap F_{i+1}$
for some i. In this case, we let
![]() $f_E: W\rightarrow Y$
the sequence of smooth blow-ups as in Definition-Lemma 3·1, and
$f_E: W\rightarrow Y$
the sequence of smooth blow-ups as in Definition-Lemma 3·1, and
![]() $g\;:\!=\;h\circ f_E$
. By Lemma 4·1(ii), either
$g\;:\!=\;h\circ f_E$
. By Lemma 4·1(ii), either
![]() $B_Y\cdot F_i<1$
or
$B_Y\cdot F_i<1$
or
![]() $B_Y\cdot F_{i+1}<1$
, hence either
$B_Y\cdot F_{i+1}<1$
, hence either
![]() $(B_Y\cdot F_i)_y<1$
or
$(B_Y\cdot F_i)_y<1$
or
![]() $(B_Y\cdot F_{i+1})_y<1$
. Since
$(B_Y\cdot F_{i+1})_y<1$
. Since
by Lemma 3·11,
![]() $\mathcal{D}(g)$
is a chain. Moreover, by the construction of g, for any prime divisor
$\mathcal{D}(g)$
is a chain. Moreover, by the construction of g, for any prime divisor
![]() $F\not=E_W$
in
$F\not=E_W$
in
![]() ${\rm{Exc}}(g)$
,
${\rm{Exc}}(g)$
,
![]() $F^2\leq -2$
.
$F^2\leq -2$
.
By [
25
, remark 4·9(2)], there exists a contraction
![]() $\phi: W\rightarrow Z$
over X of
$\phi: W\rightarrow Z$
over X of
![]() $\operatorname{Supp}{\rm{Exc}}(g)\backslash E_W$
. Since
$\operatorname{Supp}{\rm{Exc}}(g)\backslash E_W$
. Since
![]() $\mathcal{D}(g)$
is a chain in all three cases,
$\mathcal{D}(g)$
is a chain in all three cases,
![]() ${\rm{Exc}}(g)$
is snc. By Lemma 4·4,
${\rm{Exc}}(g)$
is snc. By Lemma 4·4,
![]() $(Z\ni z,E_Z)$
is plt for any singular point z of Z in
$(Z\ni z,E_Z)$
is plt for any singular point z of Z in
![]() $E_Z$
. Thus
$E_Z$
. Thus
![]() $(Z,E_Z)$
is plt near
$(Z,E_Z)$
is plt near
![]() $E_Z$
, hence E is a Kollár component of
$E_Z$
, hence E is a Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
4·3. D-type and E-type singularities
Lemma 4·6.
Let
![]() $X\ni x$
be a surface germ of
$X\ni x$
be a surface germ of
![]() $D_m$
-type for some integer
$D_m$
-type for some integer
![]() $m\geq 3$
, E a prime divisor on X,
$m\geq 3$
, E a prime divisor on X,
![]() $f: Y\rightarrow X$
the minimal resolution of
$f: Y\rightarrow X$
the minimal resolution of
![]() $X\ni x$
, and
$X\ni x$
, and
![]() $E_Y\;:\!=\;f^{-1}_*E$
. Let
$E_Y\;:\!=\;f^{-1}_*E$
. Let
![]() $F_1,\dots,F_m$
be the prime exceptional divisors over
$F_1,\dots,F_m$
be the prime exceptional divisors over
![]() $X\ni x$
. Assume that
$X\ni x$
. Assume that
![]() $E_Y\cup\cup_{i=1}^mF_i$
is simple normal crossing over a neighbourhood of x,
$E_Y\cup\cup_{i=1}^mF_i$
is simple normal crossing over a neighbourhood of x,
![]() $F_{m-1}^2=F_m^2=-2$
, and the dual graph of
$F_{m-1}^2=F_m^2=-2$
, and the dual graph of
![]() $E_Y\cup\cup_{i=1}^mF_i$
is the following:
$E_Y\cup\cup_{i=1}^mF_i$
is the following:

Then
![]() $(X\ni x,E)$
is lc but not plt.
$(X\ni x,E)$
is lc but not plt.
Proof. By computing intersections numbers,
 \begin{align*}K_Y+E_Y+\sum_{i=1}^{m-2}F_i+\frac{1}{2}(F_{m-1}+F_m)=f^*(K_X+E).\end{align*}
\begin{align*}K_Y+E_Y+\sum_{i=1}^{m-2}F_i+\frac{1}{2}(F_{m-1}+F_m)=f^*(K_X+E).\end{align*}
Since
![]() $(Y,E_Y+\sum_{i=1}^{m-2}F_i+\frac{1}{2}(F_{m-1}+F_m))$
is log smooth over a neighbourhood of x,
$(Y,E_Y+\sum_{i=1}^{m-2}F_i+\frac{1}{2}(F_{m-1}+F_m))$
is log smooth over a neighbourhood of x,
![]() $(X\ni x,E)$
is lc but not plt.
$(X\ni x,E)$
is lc but not plt.
Lemma 4·7.
Let
![]() $0<m_1<m_2<m_3\;:\!=\;m$
be integers,
$0<m_1<m_2<m_3\;:\!=\;m$
be integers,
![]() $(X\ni x,B)$
a plt surface germ,
$(X\ni x,B)$
a plt surface germ,
![]() $f:Y\to X$
the minimal resolution of
$f:Y\to X$
the minimal resolution of
![]() $X\ni x$
with prime exceptional divisors
$X\ni x$
with prime exceptional divisors
![]() $F_0,\dots,F_{m}$
with the following dual graph
$F_0,\dots,F_{m}$
with the following dual graph
![]() $\mathcal{D}(f)$
:
$\mathcal{D}(f)$
:

Let
![]() $a_i\;:\!=\;a(F_i,X,B)-1$
for each i. Then:
$a_i\;:\!=\;a(F_i,X,B)-1$
for each i. Then:
-
(i)
 $a(F_0,X,B)\leq a(F_i,X,B)$
for any
$a(F_0,X,B)\leq a(F_i,X,B)$
for any
 $i\in\{1,2,\dots,m_1\}$
; and
$i\in\{1,2,\dots,m_1\}$
; and -
(ii) if
 $a(F_0,X,B)=a(F_l,X,B)$
for some
$a(F_0,X,B)=a(F_l,X,B)$
for some
 $l\in\{1,2,\dots,m_1\}$
, then
$l\in\{1,2,\dots,m_1\}$
, then-
(a)
 $a_i=a_0$
for every
$a_i=a_0$
for every
 $i\in\{0,1,\dots,l\}$
,
$i\in\{0,1,\dots,l\}$
, -
(b)
 $a_{m_1+1}=a_{m_2+1}=\frac{1}{2}a_0$
,
$a_{m_1+1}=a_{m_2+1}=\frac{1}{2}a_0$
, -
(c)
 $F_i^2=-2$
for any
$F_i^2=-2$
for any
 $i\in\{0,1,\dots,l-1,m_1+1,m_2+1\}$
, and
$i\in\{0,1,\dots,l-1,m_1+1,m_2+1\}$
, and -
(d) either
 $m=m_2+1=m_1+2$
, or
$m=m_2+1=m_1+2$
, or
 $B=0$
and
$B=0$
and
 $X\ni x$
Du Val.
$X\ni x$
Du Val.
-
Proof. Let
![]() $B_Y\;:\!=\;f^{-1}_*B$
. Then
$B_Y\;:\!=\;f^{-1}_*B$
. Then
Since
![]() $(X\ni x,B)$
is plt and f is the minimal resolution of
$(X\ni x,B)$
is plt and f is the minimal resolution of
![]() $X\ni x$
,
$X\ni x$
,
![]() $-1<a_i\leq 0$
for each i.
$-1<a_i\leq 0$
for each i.
If
![]() $a_0<a_i$
for any
$a_0<a_i$
for any
![]() $i\in\{1,2,\dots,m_1\}$
there is nothing to prove. Otherwise, there exists
$i\in\{1,2,\dots,m_1\}$
there is nothing to prove. Otherwise, there exists
![]() $k\in\{1,2,\dots,m_1\}$
, such that
$k\in\{1,2,\dots,m_1\}$
, such that
![]() $a_k=\min\{a_i\mid 0\leq i\leq m_1\}\leq a_0$
. We define
$a_k=\min\{a_i\mid 0\leq i\leq m_1\}\leq a_0$
. We define
 \begin{align*}A\;:\!=\;\sum_{i=0}^{k}a_iF_i+a_{m_1+1}F_{m_1+1}+a_{m_2+1}F_{m_2+1}, \text{ and } H\;:\!=\;a_k\left(\sum_{i=0}^kF_i+\frac{1}{2}F_{m_1+1}+\frac{1}{2}F_{m_2+1}\right).\end{align*}
\begin{align*}A\;:\!=\;\sum_{i=0}^{k}a_iF_i+a_{m_1+1}F_{m_1+1}+a_{m_2+1}F_{m_2+1}, \text{ and } H\;:\!=\;a_k\left(\sum_{i=0}^kF_i+\frac{1}{2}F_{m_1+1}+\frac{1}{2}F_{m_2+1}\right).\end{align*}
Then
when
![]() $0\leq i<k$
and if the equality holds then
$0\leq i<k$
and if the equality holds then
![]() $K_Y\cdot F_i=0$
,
$K_Y\cdot F_i=0$
,
and if the equality holds then
![]() $a_k=a_{k-1}$
, and
$a_k=a_{k-1}$
, and
 \begin{align*}H\cdot F_{m_i+1}&=a_k(1+\frac{1}{2}F_{m_i+1}^2)=-\frac{a_k}{2}K_Y\cdot F_{m_i+1}\leq K_Y\cdot F_{m_i+1}\\&\leq (K_Y+B_Y)\cdot F_{m_i+1}\leq A\cdot F_{m_i+1}\end{align*}
\begin{align*}H\cdot F_{m_i+1}&=a_k(1+\frac{1}{2}F_{m_i+1}^2)=-\frac{a_k}{2}K_Y\cdot F_{m_i+1}\leq K_Y\cdot F_{m_i+1}\\&\leq (K_Y+B_Y)\cdot F_{m_i+1}\leq A\cdot F_{m_i+1}\end{align*}
for
![]() $i\in\{1,2\}$
, and if the equality holds, then:
$i\in\{1,2\}$
, and if the equality holds, then:
-
(i)
 $K_Y\cdot F_{m_i+1}=0$
, and
$K_Y\cdot F_{m_i+1}=0$
, and -
(ii) either
 $m_{i+1}=m_i+1$
, or
$m_{i+1}=m_i+1$
, or
 $m_{i+1}\geq m_i+2$
and
$m_{i+1}\geq m_i+2$
and
 $a_{m_i+2}=0$
.
$a_{m_i+2}=0$
.
Thus
![]() $H\cdot F_i\leq A\cdot F_i$
for any
$H\cdot F_i\leq A\cdot F_i$
for any
![]() $i\in\{0,1,\dots,k,m_1+1,m_2+1\}$
. By Lemma 2·10,
$i\in\{0,1,\dots,k,m_1+1,m_2+1\}$
. By Lemma 2·10,
![]() $a_i\leq a_k$
for any
$a_i\leq a_k$
for any
![]() $i\in\{0,1,\dots,k\}$
and
$i\in\{0,1,\dots,k\}$
and
![]() $a_{m_1+1}=a_{m_2+1}={1}/{2}a_k$
. Since
$a_{m_1+1}=a_{m_2+1}={1}/{2}a_k$
. Since
![]() $a_k=\min\{a_i\mid 0\leq i\leq m_1\}\leq a_0$
,
$a_k=\min\{a_i\mid 0\leq i\leq m_1\}\leq a_0$
,
![]() $a_i=a_k=\min\{a_i\mid 0\leq i\leq m_1\}$
for any
$a_i=a_k=\min\{a_i\mid 0\leq i\leq m_1\}$
for any
![]() $i\in\{0,1,\dots,k\}$
. Thus for any
$i\in\{0,1,\dots,k\}$
. Thus for any
![]() $l\in\{1,2,\dots,m_1\}$
such that
$l\in\{1,2,\dots,m_1\}$
such that
![]() $a(F_0,X,B)=a(F_l,X,B)$
, we may pick
$a(F_0,X,B)=a(F_l,X,B)$
, we may pick
![]() $k=l$
, which shows (i) and (ii)(a). Moreover, we have that
$k=l$
, which shows (i) and (ii)(a). Moreover, we have that
![]() $H\cdot F_i=A\cdot F_i$
for any
$H\cdot F_i=A\cdot F_i$
for any
![]() $i\in\{0,1,\dots,l,m_1+1,m_2+1\}$
, which implies that:
$i\in\{0,1,\dots,l,m_1+1,m_2+1\}$
, which implies that:
-
(i)
 $a_{m_1+1}=a_{m_2+1}={1}/{2}a_l$
, hence (ii)(b);
$a_{m_1+1}=a_{m_2+1}={1}/{2}a_l$
, hence (ii)(b); -
(ii)
 $F_i^2=K_Y\cdot F_i=-2$
for every
$F_i^2=K_Y\cdot F_i=-2$
for every
 $i\in\{0,1,\dots,l-1,m_1+1,m_2+1\}$
, hence (ii)(c); and
$i\in\{0,1,\dots,l-1,m_1+1,m_2+1\}$
, hence (ii)(c); and -
(iii) either
 $m=m_2+1=m_1+2$
, or there exists
$m=m_2+1=m_1+2$
, or there exists
 $i\in\{1,2\}$
such that
$i\in\{1,2\}$
such that
 $m_{i+1}\geq m_i+2$
and
$m_{i+1}\geq m_i+2$
and
 $a_{m_i+2}=0$
.
$a_{m_i+2}=0$
.
If
![]() $m=m_2+1=m_1+2$
then we get (ii)(d) and the proof is completed. Otherwise, there exists
$m=m_2+1=m_1+2$
then we get (ii)(d) and the proof is completed. Otherwise, there exists
![]() $i\in\{1,2\}$
such that
$i\in\{1,2\}$
such that
![]() $m_{i+1}\geq m_i+2$
and
$m_{i+1}\geq m_i+2$
and
![]() $a_{m_i+2}=0$
. Thus
$a_{m_i+2}=0$
. Thus
which implies that
![]() $a(F_i,X,B)=a(F_i,X,0)$
, hence
$a(F_i,X,B)=a(F_i,X,0)$
, hence
![]() $B=0$
. Moreover, since f is the minimal resolution of
$B=0$
. Moreover, since f is the minimal resolution of
![]() $X\ni x$
,
$X\ni x$
,
![]() $\sum_{i=1}^ma_iF_i\sim_XK_Y$
is nef over X. By Lemma 2·10,
$\sum_{i=1}^ma_iF_i\sim_XK_Y$
is nef over X. By Lemma 2·10,
![]() $a_i=0$
for every i, and
$a_i=0$
for every i, and
![]() $X\ni x$
is Du Val.
$X\ni x$
is Du Val.
Lemma 4·8.
Let
![]() $(X\ni x,B)$
be a plt surface germ such that
$(X\ni x,B)$
be a plt surface germ such that
![]() $X\ni x$
is a
$X\ni x$
is a
![]() $D_m$
-type singularity for some integer
$D_m$
-type singularity for some integer
![]() $m\geq 4$
, or an
$m\geq 4$
, or an
![]() $E_m$
-type singularity for some integer
$E_m$
-type singularity for some integer
![]() $m\in\{6,7,8\}$
. Let
$m\in\{6,7,8\}$
. Let
![]() $f: Y\rightarrow X$
be the minimal resolution of
$f: Y\rightarrow X$
be the minimal resolution of
![]() $X\ni x$
, and E a divisor over
$X\ni x$
, and E a divisor over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then
![]() $E\subset{\rm{Exc}}(f)$
.
$E\subset{\rm{Exc}}(f)$
.
Proof. Let
![]() $F_1,\dots,F_m$
be the prime exceptional divisors of f,
$F_1,\dots,F_m$
be the prime exceptional divisors of f,
![]() $a_i\;:\!=\;1-a(F_i,X,B)$
for each i, and
$a_i\;:\!=\;1-a(F_i,X,B)$
for each i, and
![]() $B_Y\;:\!=\;f^{-1}_*B$
. Then
$B_Y\;:\!=\;f^{-1}_*B$
. Then
 \begin{align*}K_Y+B_Y+\sum_{j=1}^ma_jF_j=f^*(K_X+B).\end{align*}
\begin{align*}K_Y+B_Y+\sum_{j=1}^ma_jF_j=f^*(K_X+B).\end{align*}
Suppose that
![]() $E\not\subset{\rm{Exc}}(f)$
. Let
$E\not\subset{\rm{Exc}}(f)$
. Let
![]() $y\;:\!=\;{\rm{center}}_YE$
.
$y\;:\!=\;{\rm{center}}_YE$
.
Claim 4·9.
![]() $y=F_i\cap F_k$
for some
$y=F_i\cap F_k$
for some
![]() $i\not=k$
.
$i\not=k$
.
Proof. Then there exists an integer
![]() $i\in\{1,2,\dots,m\}$
such that
$i\in\{1,2,\dots,m\}$
such that
![]() $y\in F_i$
. Thus
$y\in F_i$
. Thus
 \begin{align*} {\rm{mld}}(Y\ni y, B_Y+\sum_{j=1}^ma_jF_j)&\leq a\left(E,Y, B_Y+\sum_{j=1}^ma_jF_j\right)\\ &=a(E,X,B)={\rm{mld}}(X\ni x,B)\leq 1-a_i.\end{align*}
\begin{align*} {\rm{mld}}(Y\ni y, B_Y+\sum_{j=1}^ma_jF_j)&\leq a\left(E,Y, B_Y+\sum_{j=1}^ma_jF_j\right)\\ &=a(E,X,B)={\rm{mld}}(X\ni x,B)\leq 1-a_i.\end{align*}
By Lemma 35,
 \begin{align*}(B+\sum_{j\not=i}a_jF_j)\cdot F_i\geq\left(\left(B+\sum_{j\not=i}a_jF_j\right)\cdot F_i\right)_y\geq 1.\end{align*}
\begin{align*}(B+\sum_{j\not=i}a_jF_j)\cdot F_i\geq\left(\left(B+\sum_{j\not=i}a_jF_j\right)\cdot F_i\right)_y\geq 1.\end{align*}
By Lemma 4·1(iii),
![]() $B\cdot F_i<1$
, which implies that there exists
$B\cdot F_i<1$
, which implies that there exists
![]() $k\not=i$
such that
$k\not=i$
such that
![]() $y\in F_k$
. In particular,
$y\in F_k$
. In particular,
![]() $y=F_i\cap F_k$
.
$y=F_i\cap F_k$
.
Proof of Lemma
4·8 continued. By Claim 4·9,
![]() $y=F_i\cap F_k$
for some
$y=F_i\cap F_k$
for some
![]() $i\not=k$
. Possibly switching i and k, we may assume that
$i\not=k$
. Possibly switching i and k, we may assume that
![]() $F_i$
is closer to the fork of
$F_i$
is closer to the fork of
![]() $\mathcal{D}(f)$
than
$\mathcal{D}(f)$
than
![]() $F_k$
. Since
$F_k$
. Since
![]() $(X\ni x,B)$
is plt and f is the minimal resolution of
$(X\ni x,B)$
is plt and f is the minimal resolution of
![]() $X\ni x$
,
$X\ni x$
,
![]() $0\leq a_k<1$
. Thus there exists an extraction
$0\leq a_k<1$
. Thus there exists an extraction
![]() $g: W\rightarrow X$
of
$g: W\rightarrow X$
of
![]() $F_k$
with induced morphism
$F_k$
with induced morphism
![]() $h: Y\rightarrow W$
. Let
$h: Y\rightarrow W$
. Let
![]() $\bar F_k$
be the center of
$\bar F_k$
be the center of
![]() $F_k$
on W and
$F_k$
on W and
![]() $w\;:\!=\;{\rm{center}}_WE$
. Then h is the minimal resolution of
$w\;:\!=\;{\rm{center}}_WE$
. Then h is the minimal resolution of
![]() $W\ni w$
. Moreover, if
$W\ni w$
. Moreover, if
![]() $F_i$
is not the fork of
$F_i$
is not the fork of
![]() $\mathcal{D}(f)$
, then
$\mathcal{D}(f)$
, then
![]() $W\ni w$
is not an A-type singularity, and if
$W\ni w$
is not an A-type singularity, and if
![]() $F_i$
is the fork of
$F_i$
is the fork of
![]() $\mathcal{D}(f)$
, then
$\mathcal{D}(f)$
, then
![]() $W\ni w$
is an A-type singularity but
$W\ni w$
is an A-type singularity but
![]() $F_i$
is not a tail of
$F_i$
is not a tail of
![]() $\mathcal{D}(h)$
. Since
$\mathcal{D}(h)$
. Since
![]() $(X\ni x,B)$
is plt,
$(X\ni x,B)$
is plt,
![]() $(W\ni w,g^{-1}_*B+a_kF_k)$
is plt. By Lemma 4·1(iii),
$(W\ni w,g^{-1}_*B+a_kF_k)$
is plt. By Lemma 4·1(iii),
 \begin{align*}\left(\left(B+\sum_{j\not=i}a_jF_j\right)\cdot F_i\right)_y=((B+a_kF_k)\cdot F_i)_y\leq (B+a_kF_k)\cdot F_i<1.\end{align*}
\begin{align*}\left(\left(B+\sum_{j\not=i}a_jF_j\right)\cdot F_i\right)_y=((B+a_kF_k)\cdot F_i)_y\leq (B+a_kF_k)\cdot F_i<1.\end{align*}
By Lemma 3·5,
 \begin{align*} {\rm{mld}}(X\ni x,B)&=a(E,X,B)=a(E,Y, B_Y+\sum_{j=1}^ma_jF_j)\\ &\geq{\rm{mld}}(Y\ni y, B_Y+\sum_{j=1}^ma_jF_j)>1-a_i\geq{\rm{mld}}(X\ni x,B),\end{align*}
\begin{align*} {\rm{mld}}(X\ni x,B)&=a(E,X,B)=a(E,Y, B_Y+\sum_{j=1}^ma_jF_j)\\ &\geq{\rm{mld}}(Y\ni y, B_Y+\sum_{j=1}^ma_jF_j)>1-a_i\geq{\rm{mld}}(X\ni x,B),\end{align*}
a contradiction.
Theorem 4·10.
Let
![]() $(X\ni x,B)$
be a plt surface germ such that
$(X\ni x,B)$
be a plt surface germ such that
![]() $X\ni x$
is a
$X\ni x$
is a
![]() $D_m$
-type singularity for some integer
$D_m$
-type singularity for some integer
![]() $m\geq 4$
or an
$m\geq 4$
or an
![]() $E_m$
-type singularity for some integer
$E_m$
-type singularity for some integer
![]() $m\in\{6,7,8\}$
. Let
$m\in\{6,7,8\}$
. Let
![]() $f: Y\rightarrow X$
be the minimal resolution of
$f: Y\rightarrow X$
be the minimal resolution of
![]() $X\ni x$
. Then there exists a unique divisor E over
$X\ni x$
. Then there exists a unique divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
, and E is a Kollár component of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
, and E is a Kollár component of
![]() $X\ni x$
. Moreover, E is the unique fork of
$X\ni x$
. Moreover, E is the unique fork of
![]() $\mathcal{D}(f)$
.
$\mathcal{D}(f)$
.
Proof. By Lemma 4·8, we may only consider divisors in
![]() ${\rm{Exc}}(f)$
. Let
${\rm{Exc}}(f)$
. Let
![]() $F_1,\dots,F_m$
be the prime exceptional divisors of f such that
$F_1,\dots,F_m$
be the prime exceptional divisors of f such that
![]() $F_1$
is the unique fork. Since
$F_1$
is the unique fork. Since
![]() $a(F_i,X,B)\leq a(F_i,X,0)\leq 1$
for each i, there exists an extraction
$a(F_i,X,B)\leq a(F_i,X,0)\leq 1$
for each i, there exists an extraction
![]() $g: Y_i\rightarrow X$
of
$g: Y_i\rightarrow X$
of
![]() $F_i$
for each i, and we let
$F_i$
for each i, and we let
![]() $\bar F_i$
be the strict transform of
$\bar F_i$
be the strict transform of
![]() $F_i$
on
$F_i$
on
![]() $Y_i$
. By Lemmas 4·4 and 4·6,
$Y_i$
. By Lemmas 4·4 and 4·6,
![]() $(Y_i,\bar F_i)$
is not plt near
$(Y_i,\bar F_i)$
is not plt near
![]() $\bar F_i$
for any
$\bar F_i$
for any
![]() $i\in\{2,3,\dots,m\}$
and
$i\in\{2,3,\dots,m\}$
and
![]() $(Y_1,\bar F_1)$
is plt near
$(Y_1,\bar F_1)$
is plt near
![]() $F_1$
. By Lemma 4·7,
$F_1$
. By Lemma 4·7,
![]() $a(F_1,X,B)={\rm{mld}}(X\ni x,B)$
. So
$a(F_1,X,B)={\rm{mld}}(X\ni x,B)$
. So
![]() $E=F_1$
is the unique divisor we want.
$E=F_1$
is the unique divisor we want.
Theorem 4·11.
Let
![]() $(X\ni x,B)$
be a plt surface germ such that
$(X\ni x,B)$
be a plt surface germ such that
![]() $X\ni x$
is a
$X\ni x$
is a
![]() $D_m$
-type singularity for some integer
$D_m$
-type singularity for some integer
![]() $m\geq 4$
or an
$m\geq 4$
or an
![]() $E_m$
-type singularity for some integer
$E_m$
-type singularity for some integer
![]() $m\in\{6,7,8\}$
. Assume that either
$m\in\{6,7,8\}$
. Assume that either
![]() $B\not=0$
or
$B\not=0$
or
![]() $X\ni x$
is not Du Val. Let E be a divisor over
$X\ni x$
is not Du Val. Let E be a divisor over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
, then E is a potential lc place of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
, then E is a potential lc place of
![]() $X\ni x$
.
$X\ni x$
.
Proof. Let
![]() $f: Y\rightarrow X$
be the minimal resolution of
$f: Y\rightarrow X$
be the minimal resolution of
![]() $X\ni x$
. By Lemma 4·8,
$X\ni x$
. By Lemma 4·8,
![]() $E\subset{\rm{Exc}}(f)$
. By Theorem 4·10, we may assume that E is not the fork of
$E\subset{\rm{Exc}}(f)$
. By Theorem 4·10, we may assume that E is not the fork of
![]() $\mathcal{D}(f)$
. Let
$\mathcal{D}(f)$
. Let
![]() $L_1,L_2,L_3$
be the three branches of
$L_1,L_2,L_3$
be the three branches of
![]() $\mathcal{D}(f)$
and assume that E belongs to
$\mathcal{D}(f)$
and assume that E belongs to
![]() $L_1$
. By Lemma 4·7(ii)(c),(ii)(d),
$L_1$
. By Lemma 4·7(ii)(c),(ii)(d),
![]() $X\ni x$
is a
$X\ni x$
is a
![]() $D_m$
-type singularity,
$D_m$
-type singularity,
![]() $L_2$
contains a unique curve
$L_2$
contains a unique curve
![]() $F_2$
and
$F_2$
and
![]() $L_3$
contains a unique curve
$L_3$
contains a unique curve
![]() $F_3$
respectively, such that
$F_3$
respectively, such that
![]() $F_2^2=F_3^2=-2$
. Since
$F_2^2=F_3^2=-2$
. Since
![]() $(X\ni x,B)$
is plt and f is the minimal resolution of
$(X\ni x,B)$
is plt and f is the minimal resolution of
![]() $X\ni x$
,
$X\ni x$
,
![]() $0<a(E,X,B)\leq 1$
, so there exists an extraction
$0<a(E,X,B)\leq 1$
, so there exists an extraction
![]() $g: W\rightarrow X$
of E with the induced morphism
$g: W\rightarrow X$
of E with the induced morphism
![]() $h: Y\rightarrow W$
. Let
$h: Y\rightarrow W$
. Let
![]() $E_W$
be the strict transform of E on W. By Lemmas 4·4 and 4·6,
$E_W$
be the strict transform of E on W. By Lemmas 4·4 and 4·6,
![]() $(W,E_W)$
is lc near
$(W,E_W)$
is lc near
![]() $E_W$
, so E is a potential lc place of
$E_W$
, so E is a potential lc place of
![]() $X\ni x$
.
$X\ni x$
.
Theorem 4·12.
Let
![]() $X\ni x$
be a Du Val singularity of
$X\ni x$
be a Du Val singularity of
![]() $D_m$
-type for some integer
$D_m$
-type for some integer
![]() $m\geq 4$
or of
$m\geq 4$
or of
![]() $E_m$
-type for some integer
$E_m$
-type for some integer
![]() $m\in\{6,7,8\}$
. Let
$m\in\{6,7,8\}$
. Let
![]() $f: Y\rightarrow X$
be the minimal resolution of
$f: Y\rightarrow X$
be the minimal resolution of
![]() $X\ni x$
, and E be a divisor over
$X\ni x$
, and E be a divisor over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,0)={\rm{mld}}(X\ni x,0)$
, then E is a potential lc place of
$a(E,X,0)={\rm{mld}}(X\ni x,0)$
, then E is a potential lc place of
![]() $X\ni x$
if and only if one of the following holds:
$X\ni x$
if and only if one of the following holds:
-
(i) E is the fork of the
 $\mathcal{D}(f)$
;
$\mathcal{D}(f)$
; -
(ii)
 $X\ni x$
is of
$X\ni x$
is of
 $D_m$
-type, the dual graph of
$D_m$
-type, the dual graph of
 $X\ni x$
looks like the following, and
$X\ni x$
looks like the following, and
 $E\in\{F_1,\dots,F_{m-2}\}$
.
$E\in\{F_1,\dots,F_{m-2}\}$
.

Proof. Since
![]() $a(E,X,0)={\rm{mld}}(X\ni x,0)$
,
$a(E,X,0)={\rm{mld}}(X\ni x,0)$
,
![]() $E\subset{\rm{Exc}}(f)$
. Since
$E\subset{\rm{Exc}}(f)$
. Since
![]() $X\ni x$
is Du Val, for any prime divisor
$X\ni x$
is Du Val, for any prime divisor
![]() $F\subset{\rm{Exc}}(f)$
,
$F\subset{\rm{Exc}}(f)$
,
![]() $F^2=-2$
. The if part follows from Lemmas 4·4 and 4·6.
$F^2=-2$
. The if part follows from Lemmas 4·4 and 4·6.
To prove the only if part, we may assume that E is not the fork of
![]() $\mathcal{D}(f)$
. Then E is a potential lc place of
$\mathcal{D}(f)$
. Then E is a potential lc place of
![]() $X\ni x$
if and only if there exists an extraction
$X\ni x$
if and only if there exists an extraction
![]() $g: W\rightarrow X$
of E such that
$g: W\rightarrow X$
of E such that
![]() $(W,E_W)$
is lc near
$(W,E_W)$
is lc near
![]() $E_W$
, where
$E_W$
, where
![]() $E_W$
is the strict transform of E on W. The theorem follows from [
25
, theorem 4·15].
$E_W$
is the strict transform of E on W. The theorem follows from [
25
, theorem 4·15].
4·4. Non-plt singularities
Definition-
Lemma 4·13 (25, theorem 4·7]). Let
![]() $X\ni x$
be an lc but not klt surface germ and
$X\ni x$
be an lc but not klt surface germ and
![]() $f: Y\rightarrow X$
the minimal resolution of
$f: Y\rightarrow X$
the minimal resolution of
![]() $X\ni x$
. Then exactly one of the following holds:
$X\ni x$
. Then exactly one of the following holds:
-
(i) (B-type)
 ${\rm{Exc}}(f)=F$
is a smooth elliptic curve.
${\rm{Exc}}(f)=F$
is a smooth elliptic curve. -
(ii) (C-type)
 ${\rm{Exc}}(f)=F$
is a nodal cubic curve;
${\rm{Exc}}(f)=F$
is a nodal cubic curve; -
(iii) (F-type)
 ${\rm{Exc}}(f)$
is a circle of smooth rational curves;
${\rm{Exc}}(f)$
is a circle of smooth rational curves; -
(iv) (H-type)
 ${\rm{Exc}}(f)$
has
${\rm{Exc}}(f)$
has
 $\geq 5$
rational curves and
$\geq 5$
rational curves and
 $\mathcal{D}(f)$
has the following weighted dual graph:
$\mathcal{D}(f)$
has the following weighted dual graph:

Let
![]() $m\geq 5$
be an integer. For an lc singularity of H
-type as above with m exceptional divisors, we call it an
$m\geq 5$
be an integer. For an lc singularity of H
-type as above with m exceptional divisors, we call it an
![]() ${{\textbf{H}}}_m$
-type singularity.
${{\textbf{H}}}_m$
-type singularity.
Although the concept of Kollár component is not defined over an lc but not klt germ, the classification of surface lc singularities tells us when there exists a divisor which “looks like a Kollár component”.
Theorem 4·14.
Let
![]() $(X\ni x,B)$
be an lc surface germ such that
$(X\ni x,B)$
be an lc surface germ such that
![]() $X\ni x$
is not klt, and E a prime divisor over X such that
$X\ni x$
is not klt, and E a prime divisor over X such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then:
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
. Then:
-
(i) E is a potential lc place of
 $(X\ni x,B)$
. In particular, there exists a divisorial contraction
$(X\ni x,B)$
. In particular, there exists a divisorial contraction
 $f: Y\rightarrow X$
which extracts E;
$f: Y\rightarrow X$
which extracts E; -
(ii)
 $K_Y+E$
is plt near E if and only if E is a B-type or an
$K_Y+E$
is plt near E if and only if E is a B-type or an
 ${{\textbf{H}}}_5$
-type singularity.
${{\textbf{H}}}_5$
-type singularity.
Proof. E is an lc place of
![]() $(X\ni x,B)$
which implies (i). Since
$(X\ni x,B)$
which implies (i). Since
![]() $(X\ni x,B)$
is lc and
$(X\ni x,B)$
is lc and
![]() $X\ni x$
is not klt,
$X\ni x$
is not klt,
![]() $B=0$
. By the connectedness of lc places,
$B=0$
. By the connectedness of lc places,
![]() $K_Y+E$
is plt near E if and only if E is the only lc place over
$K_Y+E$
is plt near E if and only if E is the only lc place over
![]() $X\ni x$
, and (ii) follows from Definition-Lemma 4·13.
$X\ni x$
, and (ii) follows from Definition-Lemma 4·13.
Now we deal with the case when
![]() $X\ni x$
is klt but
$X\ni x$
is klt but
![]() $(X\ni x,B)$
is not plt:
$(X\ni x,B)$
is not plt:
Theorem 4·15.
Let
![]() $(X\ni x,B)$
be an lc surface germ such that
$(X\ni x,B)$
be an lc surface germ such that
![]() $X\ni x$
is klt but
$X\ni x$
is klt but
![]() $(X\ni x,B)$
is not plt. Then any divisor E over
$(X\ni x,B)$
is not plt. Then any divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)$
is a potential lc place of
$a(E,X,B)={\rm{mld}}(X\ni x,B)$
is a potential lc place of
![]() $(X\ni x,B)$
.
$(X\ni x,B)$
.
Proof. Since
![]() $(X\ni x,B)$
is not plt,
$(X\ni x,B)$
is not plt,
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)=0$
, so E is an lc place of
$a(E,X,B)={\rm{mld}}(X\ni x,B)=0$
, so E is an lc place of
![]() $(X\ni x,B)$
, hence a potential lc place of
$(X\ni x,B)$
, hence a potential lc place of
![]() $(X\ni x,B)$
.
$(X\ni x,B)$
.
Theorem 4·16.
Let
![]() $(X\ni x,B)$
be an lc surface germ such that
$(X\ni x,B)$
be an lc surface germ such that
![]() $X\ni x$
is klt but
$X\ni x$
is klt but
![]() $(X\ni x,B)$
is not plt. Then there exists a divisor E over
$(X\ni x,B)$
is not plt. Then there exists a divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)=0$
and E is Kollár component of
$a(E,X,B)={\rm{mld}}(X\ni x,B)=0$
and E is Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
Proof. Let
Then there exists
![]() $\epsilon\in (0,1)$
such that
$\epsilon\in (0,1)$
such that
![]() $\delta>{\rm{mld}}(X\ni x,(1-\epsilon)B)>0$
. By Theorems 4·5 and 4·10, there exists a divisor E over
$\delta>{\rm{mld}}(X\ni x,(1-\epsilon)B)>0$
. By Theorems 4·5 and 4·10, there exists a divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,(1-\epsilon)B)={\rm{mld}}(X\ni x,(1-\epsilon)B)<\delta$
and E is a Kollár component of
$a(E,X,(1-\epsilon)B)={\rm{mld}}(X\ni x,(1-\epsilon)B)<\delta$
and E is a Kollár component of
![]() $X\ni x$
. Since
$X\ni x$
. Since
![]() $a(E,X,B)={\rm{mld}}(X\ni x,B)=0$
, so E satisfies our requirements.
$a(E,X,B)={\rm{mld}}(X\ni x,B)=0$
, so E satisfies our requirements.
Finally, recall the following result:
Theorem 4·17.
Let
![]() $(X\ni x,B)$
be a dlt surface germ that is not plt. Then
$(X\ni x,B)$
be a dlt surface germ that is not plt. Then
![]() $(X\ni x,B)$
is log smooth and
$(X\ni x,B)$
is log smooth and
![]() $B=\lfloor B\rfloor$
has exactly two irreducible components near x.
$B=\lfloor B\rfloor$
has exactly two irreducible components near x.
Proof. Since
![]() $(X\ni x,B)$
is dlt but not plt,
$(X\ni x,B)$
is dlt but not plt,
![]() $\lfloor B\rfloor$
contains at least 2 irreducible components near x. Since X is a surface,
$\lfloor B\rfloor$
contains at least 2 irreducible components near x. Since X is a surface,
![]() $B=\lfloor B\rfloor$
has exactly two irreducible components near x.
$B=\lfloor B\rfloor$
has exactly two irreducible components near x.
There exists a divisor E over
![]() $X\ni x$
such that
$X\ni x$
such that
![]() $a(E,X,B)=0$
. Since
$a(E,X,B)=0$
. Since
![]() $(X\ni x,B)$
is dlt,
$(X\ni x,B)$
is dlt,
![]() $x\;:\!=\;{\rm{center}}_XE$
belongs to the log smooth strata of (X,B), so
$x\;:\!=\;{\rm{center}}_XE$
belongs to the log smooth strata of (X,B), so
![]() $(X\ni x,B)$
is log smooth.
$(X\ni x,B)$
is log smooth.
5. Proof of the main theorems
Proof of Theorem 1·5. (i)(a) follows from Theorems 3·7, 4·5 and 4·17. For (i)(b), by Theorem 4·17,
![]() $(X\ni x,B)$
is plt. (i)(b)(1) follows from Theorem 4·10. (i)(b)(2) follows from Lemma 4·8. (i)(b)(3)(A) follows from Theorem 4·11. (i)(b)(3)(B) follows from Lemma 4·7 and (i)(b)(2). (i)(b)(4)(A) is the classification of surface Du Val singularities. (i)(b)(4)(B) and (i)(b)(4)(C) follow from Theorem 4·12. (ii)(a) follows from Theorem 4·15. (ii)(b) follows from Theorem 4·16. (ii)(c) follows from Theorem 3·7. (iii) follows from Theorem 4·14.
$(X\ni x,B)$
is plt. (i)(b)(1) follows from Theorem 4·10. (i)(b)(2) follows from Lemma 4·8. (i)(b)(3)(A) follows from Theorem 4·11. (i)(b)(3)(B) follows from Lemma 4·7 and (i)(b)(2). (i)(b)(4)(A) is the classification of surface Du Val singularities. (i)(b)(4)(B) and (i)(b)(4)(C) follow from Theorem 4·12. (ii)(a) follows from Theorem 4·15. (ii)(b) follows from Theorem 4·16. (ii)(c) follows from Theorem 3·7. (iii) follows from Theorem 4·14.
Proof of Theorem 1·2. It follows from Theorem 1·5(i)(a) (i)(b)(1), (ii)(b).
Proof of Theorem 1·4. It follows from Theorem 1·5(i)(a), (i)(b)(3)(A), (i)(b)(4)(B), (i)(b)(4)(C), (ii)(a), (iii).
6. Examples
The following example is given by Zhuang which shows that Question 1·1 does not have a general positive answer in dimension
![]() $\geq 3$
even when
$\geq 3$
even when
![]() $B=0$
. We are grateful for him sharing the example with us.
$B=0$
. We are grateful for him sharing the example with us.
Example 6·1 (c.f. [ Reference Kollár24 , excercise 41]). Consider the threefold singularity given by
This is a canonical singularity, and the only divisor E which computes the mld is attained at the ordinary blow-up. However, E is a cone over an elliptic curve, so E is lc but not klt. In particular, E is not a Kollár component of the ambient variety.
The following example of Kawakita shows that there may not exist a divisor computing
![]() ${\rm{mld}}(X\ni x,B)$
that is also a potential place of
${\rm{mld}}(X\ni x,B)$
that is also a potential place of
![]() $(X\ni x,B)$
even when X is a smooth surface. We remark that Theorem 1·2 shows that there always exists a divisor computing
$(X\ni x,B)$
even when X is a smooth surface. We remark that Theorem 1·2 shows that there always exists a divisor computing
![]() ${\rm{mld}}(X\ni x,B)$
that is a Kollár component of
${\rm{mld}}(X\ni x,B)$
that is a Kollár component of
![]() $(X\ni x,0)$
.
$(X\ni x,0)$
.
Example 6·2 (cf. [
Reference Kawakita22
, example 2]). Let
![]() $D\;:\!=\;(x_1^2+x_2^3+rx_1x_2^2=0)\subset\mathbb A^2$
for some general real number r, and
$D\;:\!=\;(x_1^2+x_2^3+rx_1x_2^2=0)\subset\mathbb A^2$
for some general real number r, and
![]() $B\;:\!=\;{2}/{3}D$
. Then there exists a unique divisor E over
$B\;:\!=\;{2}/{3}D$
. Then there exists a unique divisor E over
![]() $\mathbb A^2\ni 0$
such that
$\mathbb A^2\ni 0$
such that
![]() ${\rm{mld}}(\mathbb A^2\ni 0,B)=a(E,X,B)={2}/{3}$
. However, E is not a potential place of
${\rm{mld}}(\mathbb A^2\ni 0,B)=a(E,X,B)={2}/{3}$
. However, E is not a potential place of
![]() $(\mathbb A^2\ni 0,B)$
.
$(\mathbb A^2\ni 0,B)$
.
The following example is complementary to Theorem 4·5, which shows that the assumption “
![]() $(X\ni x,B)$
is plt” is necessary.
$(X\ni x,B)$
is plt” is necessary.
Example 6·3. Let
![]() $Z\ni z$
be a
$Z\ni z$
be a
![]() $D_4$
-type Du Val singularity with the following dual graph:
$D_4$
-type Du Val singularity with the following dual graph:

Let
![]() $g: X\rightarrow Z$
be the extraction of C. Then X has a unique singularity
$g: X\rightarrow Z$
be the extraction of C. Then X has a unique singularity
![]() $x\in C$
such that
$x\in C$
such that
![]() $X\ni x$
is an
$X\ni x$
is an
![]() $A_3$
-type Du Val singularity. Let
$A_3$
-type Du Val singularity. Let
![]() $f: Y\rightarrow X$
be the minimal resolution of
$f: Y\rightarrow X$
be the minimal resolution of
![]() $(X\ni x,C)$
and
$(X\ni x,C)$
and
![]() $C_Y\;:\!=\;f^{-1}_*C$
. Then
$C_Y\;:\!=\;f^{-1}_*C$
. Then
In particular, let
![]() $h: W\rightarrow Y$
be the smooth blow-up of
$h: W\rightarrow Y$
be the smooth blow-up of
![]() $C_Y\cap F_1$
with the exceptional divisor E. Then
$C_Y\cap F_1$
with the exceptional divisor E. Then
![]() $a(E,X,C)={\rm{mld}}(X\ni x,C)=0$
, but by [
25
, Theorem 4·15(2)], E is not a Kollár component of
$a(E,X,C)={\rm{mld}}(X\ni x,C)=0$
, but by [
25
, Theorem 4·15(2)], E is not a Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
The last example is complementary to Theorem 4·10 and 4·12, which shows that even for non-Du Val singularities of D-type and
![]() $B=0$
, it is possible that some divisor which computes the minimal log discrepancy is not a Kollár component.
$B=0$
, it is possible that some divisor which computes the minimal log discrepancy is not a Kollár component.
Example 6·4. Let
![]() $G\;:\!=\;\text{BD}_{12}(5,3)$
be a binary dihedral group in
$G\;:\!=\;\text{BD}_{12}(5,3)$
be a binary dihedral group in
![]() $\text{\rm GL}(2,\mathbb C)$
. By [
Reference Nolla de Celis10
, table 3·2], the quotient singularity
$\text{\rm GL}(2,\mathbb C)$
. By [
Reference Nolla de Celis10
, table 3·2], the quotient singularity
![]() $X\ni x\cong\mathbb C^2/G\ni 0$
is a
$X\ni x\cong\mathbb C^2/G\ni 0$
is a
![]() $D_4$
-type singularity and its minimal resolution
$D_4$
-type singularity and its minimal resolution
![]() $f: Y\rightarrow X$
has the following dual graph:
$f: Y\rightarrow X$
has the following dual graph:

where
![]() $F_1^2=-3$
and
$F_1^2=-3$
and
![]() $F_i^2=-2$
for
$F_i^2=-2$
for
![]() $i\in\{2,3,4\}$
. Thus
$i\in\{2,3,4\}$
. Thus
![]() $a(F_1,X,0)={1}/{2}={\rm{mld}}(X\ni x,0)$
, but by Theorem 4·10,
$a(F_1,X,0)={1}/{2}={\rm{mld}}(X\ni x,0)$
, but by Theorem 4·10,
![]() $F_1$
is not a Kollár component of
$F_1$
is not a Kollár component of
![]() $X\ni x$
.
$X\ni x$
.
Acknowledgements
The authors would like to thank Christopher D. Hacon for useful discussions and encouragements. The first author would like to thank Harold Blum, Jingjun Han, Yuchen Liu, Chenyang Xu, and Ziquan Zhuang for inspiration on Questions 1·1 and 1·3 and useful discussions. The authors would like to thank Jingjun Han for useful comments. Special thank to Ziquan Zhuang who kindly shares Example 6·1 after the first version of the paper was posted on arXiv. The authors were partially supported by NSF research grants no: DMS-1801851, DMS-1952522 and by a grant from the Simons Foundation; award Number: 256202.