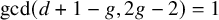1. Introduction
A classical construction from the XIX century associates with every smooth projective curve X its Jacobian (the moduli space of degree
![]() $0$
line bundles on X), a principally polarized abelian variety of dimension g. The construction carries on to smooth projective families of curves. One challenging problem arises when X ceases to be smooth. In this case, the Jacobian can still be constructed, but in general, it fails to be proper. A general problem from the mid XX century was to construct well-behaved compactifications of the Jacobian, whose boundary corresponds to degenerate line bundles of some kind.
$0$
line bundles on X), a principally polarized abelian variety of dimension g. The construction carries on to smooth projective families of curves. One challenging problem arises when X ceases to be smooth. In this case, the Jacobian can still be constructed, but in general, it fails to be proper. A general problem from the mid XX century was to construct well-behaved compactifications of the Jacobian, whose boundary corresponds to degenerate line bundles of some kind.
Many different constructions have been pursued according to the particular generality required and the initial inputs (see, for example, [Reference Igusa22], [Reference Oda and Seshadri31], [Reference Altman and Kleiman2], [Reference Caporaso12], [Reference Simpson35], [Reference Pandharipande33], [Reference Esteves16]); some of these work in the relative case of families as well.
For simplicity, here we restrict ourselves to the case where X is a nodal curve. Also, we will fix the horizon of all possible degenerations of line bundles to torsion-free coherent sheaves of rank
![]() $1$
. Since we will aim to construct proper moduli stacks of stable sheaves, without losing in generality, we will additionally assume that all sheaves are simple. In this generality, the moduli space of sheaves was constructed as an algebraic space by Altman–Kleiman [Reference Altman and Kleiman2]. Esteves [Reference Esteves16] later proved it satisfies the existence part of the valuative criterion of properness. (This moduli space is not of finite type and hence it is not proper, whenever X is reducible).
$1$
. Since we will aim to construct proper moduli stacks of stable sheaves, without losing in generality, we will additionally assume that all sheaves are simple. In this generality, the moduli space of sheaves was constructed as an algebraic space by Altman–Kleiman [Reference Altman and Kleiman2]. Esteves [Reference Esteves16] later proved it satisfies the existence part of the valuative criterion of properness. (This moduli space is not of finite type and hence it is not proper, whenever X is reducible).
Most modular constructions of fine compactified Jacobians use some set of instructions (for example, coming from GIT) to single out an open subset of the moduli space of simple sheaves choosing certain stable elements, to end up with a proper moduli stack. The construction is often followed by the observation that stability of a sheaf only depends on its multidegree and on its locally free locus in X, and then that these discrete data obey a collection of axioms (for example, the number of stable multidegrees of line bundles on a nodal curve X equals the complexity of the dual graph of X).
In this paper, we introduce an abstract notion of a fine compactified Jacobian as a connected, open subspace of the moduli space of rank
![]() $1$
torsion-free simple sheaves of some fixed degree (not necessarily zero) on X, which is furthermore proper (see Definition 3.1).Footnote 1 It was observed in [Reference Pagani and Tommasi32, Section 3] that fine compactified Jacobians can be badly behaved in the sense that they can fail to fit into a family for an infinitesimal smoothing of the curve. (This phenomenon already occurs when X has genus
$1$
torsion-free simple sheaves of some fixed degree (not necessarily zero) on X, which is furthermore proper (see Definition 3.1).Footnote 1 It was observed in [Reference Pagani and Tommasi32, Section 3] that fine compactified Jacobians can be badly behaved in the sense that they can fail to fit into a family for an infinitesimal smoothing of the curve. (This phenomenon already occurs when X has genus
![]() $1$
). Thus, we add a smoothability axiom to the objects that we aim to study. Note that our definition of smoothable fine compactified Jacobian includes the modular fine compactified Jacobians constructed in the literature (e.g., those constructed by Esteves [Reference Esteves16] and by Oda–Seshadri [Reference Oda and Seshadri31] and recently studied in [Reference Melo and Viviani29], [Reference Melo, Rapagnetta and Viviani28]) .
$1$
). Thus, we add a smoothability axiom to the objects that we aim to study. Note that our definition of smoothable fine compactified Jacobian includes the modular fine compactified Jacobians constructed in the literature (e.g., those constructed by Esteves [Reference Esteves16] and by Oda–Seshadri [Reference Oda and Seshadri31] and recently studied in [Reference Melo and Viviani29], [Reference Melo, Rapagnetta and Viviani28]) .
We then prove our first classification result, stating that smoothable fine compactified Jacobians correspond to a combinatorial datum that we call a stability assignment (for smoothable fine compactified Jacobians), which keeps track of the multidegree of the elements of the moduli space and of the locus where they are locally free:
Theorem 1.1. Let X be a nodal curve. Taking the associated assignment (see Definition 7.1) induces a bijection
 $$\begin{align*}\left\{\begin{array}{l} \textit{Smoothable fine compactified } \\ \textit{Jacobians of } X \end{array} \right\} \to \left\{\begin{array}{l} \textit{stability assignments for } X\ \textit{as}\\ \textit{introduced in Definition }4.3 \end{array} \right\} \end{align*}$$
$$\begin{align*}\left\{\begin{array}{l} \textit{Smoothable fine compactified } \\ \textit{Jacobians of } X \end{array} \right\} \to \left\{\begin{array}{l} \textit{stability assignments for } X\ \textit{as}\\ \textit{introduced in Definition }4.3 \end{array} \right\} \end{align*}$$
whose inverse is defined by taking the moduli space of sheaves that are stable with respect to a given stability assignment (Definition 6.1).
This follows by applying Corollary 7.16 to the case where S is a DVR and
![]() $\mathcal {X}/S$
is a regular smoothing of X. The most difficult part is the proof of properness of the moduli space of stable sheaves with respect to an arbitrary stability assignment (Lemma 6.5).
$\mathcal {X}/S$
is a regular smoothing of X. The most difficult part is the proof of properness of the moduli space of stable sheaves with respect to an arbitrary stability assignment (Lemma 6.5).
In fact, Corollary 7.16 is an extension of Theorem 1.1 to the case of fine compactified Jacobians of families of nodal curves whose generic element is smooth (Definition 3.7). The combinatorial notion of a stability assignment for a family is introduced in Definition 4.9 as the datum of a stability assignment for each fiber, with an additional constraint of compatibility under the degenerations that occur in the family (which induce morphisms of the corresponding dual graphs).
A natural question is whether our abstract definition of fine compactified Jacobians produces new examples. The most general procedure to construct smoothable fine compactified Jacobians that we are aware of is by means of numerical polarizations. This was introduced by Oda–Seshadri [Reference Oda and Seshadri31] for the case of a single nodal curve, and then further developed by Kass–Pagani [Reference Kass and Pagani24], [Reference Kass and Pagani25] for the case of the universal family over the moduli space of pointed stable curves (equivalent objects were constructed by Melo in [Reference Melo26] following Esteves [Reference Esteves16]). These definitions and constructions are reviewed in Section 8.
By Theorem 1.1, it is a completely combinatorial (but hard) question whether every smoothable fine compactified Jacobian is given by a numerical polarization. (Note that ‘smoothable’ here is essential, due to the aforementioned genus
![]() $1$
examples in [Reference Pagani and Tommasi32, Section 3]. Those examples are not smoothable, whereas all compactified Jacobians obtained from numerical polarizations are smoothable). The case where the genus of X equals
$1$
examples in [Reference Pagani and Tommasi32, Section 3]. Those examples are not smoothable, whereas all compactified Jacobians obtained from numerical polarizations are smoothable). The case where the genus of X equals
![]() $1$
was settled in the affirmative in [Reference Pagani and Tommasi32, Proposition 3.15], and in Example 8.7, we discuss how to extend this to the case where the first Betti number of the dual graph of X equals
$1$
was settled in the affirmative in [Reference Pagani and Tommasi32, Proposition 3.15], and in Example 8.7, we discuss how to extend this to the case where the first Betti number of the dual graph of X equals
![]() $1$
. In Example 8.8, we discuss the numerical polarization that induces integral break divisors (slightly generalizing the analogous result by Christ–Payne–Shen [Reference Christ, Payne and Shen15] for the case where X is stable).Footnote 2
$1$
. In Example 8.8, we discuss the numerical polarization that induces integral break divisors (slightly generalizing the analogous result by Christ–Payne–Shen [Reference Christ, Payne and Shen15] for the case where X is stable).Footnote 2
We resolve in the positive the similar question for the case of the universal curve over
![]() $\overline {\mathcal {M}}_g$
. Without marked points, fine compactified universal Jacobians are all given by universal numerical polarizations:
$\overline {\mathcal {M}}_g$
. Without marked points, fine compactified universal Jacobians are all given by universal numerical polarizations:
Theorem 1.2. Let
![]() $\overline {\mathcal {J}}_{g} \to \overline {\mathcal {M}}_g$
be a degree d fine compactified universal Jacobian. Then
$\overline {\mathcal {J}}_{g} \to \overline {\mathcal {M}}_g$
be a degree d fine compactified universal Jacobian. Then
![]() $\gcd (d-g+1, 2g-2)=1$
, and there exists a universal numerical polarization
$\gcd (d-g+1, 2g-2)=1$
, and there exists a universal numerical polarization
![]() $\Phi $
such that
$\Phi $
such that
![]() $\overline {\mathcal {J}}_{g}=\overline {\mathcal {J}}_{g}(\Phi )$
(as defined in Section 8).
$\overline {\mathcal {J}}_{g}=\overline {\mathcal {J}}_{g}(\Phi )$
(as defined in Section 8).
This follows from Corollary 9.8. In particular, as we observe in Remark 9.9, without marked points, there are no more fine compactified universal Jacobians than the (essentialy equivalent) ones constructed in the nineties by Caporaso [Reference Caporaso12], Pandharipande [Reference Pandharipande33] and Simpson [Reference Simpson35].
A similar result does not hold in the presence of marked points: in [Reference Pagani and Tommasi32], the authors produce examples of fine compactified universal Jacobians for
![]() $\overline {\mathcal {M}}_{1,n}$
for all
$\overline {\mathcal {M}}_{1,n}$
for all
![]() $n \geq 6$
that are not obtained from a universal numerical polarization, and hence that do not arise from the methods developed by Kass–Pagani [Reference Kass and Pagani25] or by Esteves and Melo [Reference Esteves16, Reference Melo26] (more details in Remark 8.14). An explicit combinatorial characterization of the collection
$n \geq 6$
that are not obtained from a universal numerical polarization, and hence that do not arise from the methods developed by Kass–Pagani [Reference Kass and Pagani25] or by Esteves and Melo [Reference Esteves16, Reference Melo26] (more details in Remark 8.14). An explicit combinatorial characterization of the collection
![]() $\Sigma ^d_{g,n}$
of degree d fine compactified universal Jacobians for
$\Sigma ^d_{g,n}$
of degree d fine compactified universal Jacobians for
![]() $\overline {\mathcal {M}}_{g,n}$
is available via Corollary 7.16 applied to the universal family over
$\overline {\mathcal {M}}_{g,n}$
is available via Corollary 7.16 applied to the universal family over
![]() $\overline {\mathcal {M}}_{g,n}$
(see also Definition 4.9 and Remark 4.10). It would be interesting to interpret each element of
$\overline {\mathcal {M}}_{g,n}$
(see also Definition 4.9 and Remark 4.10). It would be interesting to interpret each element of
![]() $\Sigma ^d_{g,n}$
as a (top-dimensional) chamber in some stability space, as was done in [Reference Kass and Pagani25] for the case of compactified universal Jacobians arising from numerical polarizations. We explore these questions in Section 10.
$\Sigma ^d_{g,n}$
as a (top-dimensional) chamber in some stability space, as was done in [Reference Kass and Pagani25] for the case of compactified universal Jacobians arising from numerical polarizations. We explore these questions in Section 10.
Compactified universal Jacobians have recently played a role in enumerative geometry in the theory of the (k-twisted) double ramification cycle; see [Reference Bae, Holmes, Pandharipande, Schmitt and Schwarz6]. As realized in [Reference Holmes, Kass and Pagani20], whenever a fine compactified universal Jacobian contains the locus Z of line bundles of multidegree zero, the double ramification cycle can be defined as the pullback of
![]() $[Z]$
, via some Abel–Jacobi section. This perspective plays an important role in [Reference Holmes, Molcho, Pandharipande, Pixton and Schmitt21], where an extension to a logarithmic double ramification cycle is defined as well. Because there are different fine compactified universal Jacobians containing Z, the double ramification cycle can be equivalently defined as the pullback of
$[Z]$
, via some Abel–Jacobi section. This perspective plays an important role in [Reference Holmes, Molcho, Pandharipande, Pixton and Schmitt21], where an extension to a logarithmic double ramification cycle is defined as well. Because there are different fine compactified universal Jacobians containing Z, the double ramification cycle can be equivalently defined as the pullback of
![]() $[Z]$
from different spaces, potentially leading to different formulas, and hence to relations in the cohomology of the moduli space of curves. Our classification leads to a complete description of all fine compactified universal Jacobians containing Z, whereas previously, only those obtained via Kass–Pagani’s method [Reference Kass and Pagani25] were considered.
$[Z]$
from different spaces, potentially leading to different formulas, and hence to relations in the cohomology of the moduli space of curves. Our classification leads to a complete description of all fine compactified universal Jacobians containing Z, whereas previously, only those obtained via Kass–Pagani’s method [Reference Kass and Pagani25] were considered.
The problem of studying the stability space of complexes of sheaves on a projective variety X has attracted a lot of attention in the last two decades, after Bridgeland’s breakthrough [Reference Bridgeland10] (extended to the case of families in [Reference Bayer, Lahoz, Macrì, Nuer, Perry and Stellari8]). Most of the literature has been devoted to the case where X is nonsingular. It is natural to try to explicitly describe this stability space for X singular, and one place to start is assuming that X is a nodal curve. We expect that the combinatorics developed in Theorem 1.1 should be regarded as some kind of skeleton of that stability space.
Added after peer review: After a first draft of this work had been published on the arXiv repository, Filippo Viviani shared with us his preprint [Reference Viviani37]. His work uses some of our results. Later, Alex Abreu and an anonymous referee kindly informed us of gaps in the proof of some of our results. These gaps have been fixed in this version of the paper, by also employing [Reference Viviani37, Theorem 1.20]. The latter does not use any of our results as part of its proof.
2. Notation
Throughout, we work with Noetherian schemes over a fixed algebraically closed ground field k.
A curve over an extension K of k is a
![]() $\operatorname {\mathrm {Spec}}(K)$
-scheme X that is proper over
$\operatorname {\mathrm {Spec}}(K)$
-scheme X that is proper over
![]() $\operatorname {\mathrm {Spec}}(K)$
, geometrically connected, and of pure dimension
$\operatorname {\mathrm {Spec}}(K)$
, geometrically connected, and of pure dimension
![]() $1$
. The curve X is a nodal curve if it is geometrically reduced and when passing to an algebraic closure
$1$
. The curve X is a nodal curve if it is geometrically reduced and when passing to an algebraic closure
![]() $\overline {K}$
, its local ring at every singular point is isomorphic to
$\overline {K}$
, its local ring at every singular point is isomorphic to
![]() $\overline {K}[[x,y]]/(xy)$
.
$\overline {K}[[x,y]]/(xy)$
.
A coherent sheaf on a nodal curve X has rank
![]() $\boldsymbol {1}$
if its localisation at each generic point of X has length
$\boldsymbol {1}$
if its localisation at each generic point of X has length
![]() $1$
. It is torsion-free if it has no embedded components.
$1$
. It is torsion-free if it has no embedded components.
If F is a rank
![]() $1$
torsion-free sheaf on a nodal curve X, we denote by
$1$
torsion-free sheaf on a nodal curve X, we denote by
![]() $ {\operatorname {N}}(F)$
the subset of X where F fails to be locally free. Note that
$ {\operatorname {N}}(F)$
the subset of X where F fails to be locally free. Note that
![]() $ {\operatorname {N}}(F)$
is contained in the singular locus of X. If F is a rank
$ {\operatorname {N}}(F)$
is contained in the singular locus of X. If F is a rank
![]() $1$
torsion-free sheaf on X, we say that F is simple if its automorphism group is
$1$
torsion-free sheaf on X, we say that F is simple if its automorphism group is
![]() $\mathbf {G}_m$
, or equivalently if
$\mathbf {G}_m$
, or equivalently if
![]() $X\setminus {\operatorname {N}}(F)$
is connected.
$X\setminus {\operatorname {N}}(F)$
is connected.
A family of curves over a k-scheme S is a proper, flat morphism
![]() $\mathcal {X} \to S$
whose fibers are curves. A family of curves
$\mathcal {X} \to S$
whose fibers are curves. A family of curves
![]() $\mathcal {X} \to S$
is a family of nodal curves if the fibers over all geometric points are nodal curves.
$\mathcal {X} \to S$
is a family of nodal curves if the fibers over all geometric points are nodal curves.
If X is a nodal curve over K, we denote by
![]() $\Gamma (X)$
its dual graph – that is, the labeled graph where each vertex v corresponds to an irreducible component
$\Gamma (X)$
its dual graph – that is, the labeled graph where each vertex v corresponds to an irreducible component
![]() $X_{\overline {K}}^v$
of the base change of X to (the spectrum of) an algebraic (equivalently, a separable) closure
$X_{\overline {K}}^v$
of the base change of X to (the spectrum of) an algebraic (equivalently, a separable) closure
![]() $\overline {K}$
, and edges corresponding to the nodes of
$\overline {K}$
, and edges corresponding to the nodes of
![]() $X_{\overline {K}}$
. Note that if
$X_{\overline {K}}$
. Note that if
![]() $X^v_K$
is an irreducible component defined over K, then it is also defined over any extension L of K, and the corresponding vertices of the dual graphs
$X^v_K$
is an irreducible component defined over K, then it is also defined over any extension L of K, and the corresponding vertices of the dual graphs
![]() $\Gamma (X_K)$
and
$\Gamma (X_K)$
and
![]() $\Gamma (X_L)$
are canonically identified.
$\Gamma (X_L)$
are canonically identified.
The dual graph is labeled by the geometric genus
![]() $p_g(X^v_{\overline {K}})$
. The definition of dual graph extends to the case where
$p_g(X^v_{\overline {K}})$
. The definition of dual graph extends to the case where
![]() $(X,p_1,\dots ,p_n)$
is an n-pointed curve. In this case, the dual graph
$(X,p_1,\dots ,p_n)$
is an n-pointed curve. In this case, the dual graph
![]() $\Gamma (X)$
also has n half-edges labeled from
$\Gamma (X)$
also has n half-edges labeled from
![]() $1$
to n, corresponding to the marked points
$1$
to n, corresponding to the marked points
![]() $p_1, \ldots , p_n$
. We refer to [Reference Arbarello, Cornalba and Griffiths5] and [Reference Melo, Molcho, Ulirsch and Viviani27] for a detailed definition and for the notion of graph morphisms.
$p_1, \ldots , p_n$
. We refer to [Reference Arbarello, Cornalba and Griffiths5] and [Reference Melo, Molcho, Ulirsch and Viviani27] for a detailed definition and for the notion of graph morphisms.
Recall from [Reference Cavalieri, Chan, Ulirsch and Wise14, § 7.2] that if
![]() $\mathcal {X}/S$
is a family of nodal curves and
$\mathcal {X}/S$
is a family of nodal curves and
![]() $s,t$
are geometric points of S, then every étale specialization of t to s (written as
$s,t$
are geometric points of S, then every étale specialization of t to s (written as
![]() $t \rightsquigarrow s$
) induces a morphism of dual graphs
$t \rightsquigarrow s$
) induces a morphism of dual graphs
![]() $\Gamma (X_s)\rightarrow \Gamma (X_t)$
. (For the definition of étale specialization in this context, we refer to [Reference Cavalieri, Chan, Ulirsch and Wise14, Appendix A]).
$\Gamma (X_s)\rightarrow \Gamma (X_t)$
. (For the definition of étale specialization in this context, we refer to [Reference Cavalieri, Chan, Ulirsch and Wise14, Appendix A]).
For a graph G and H a subgraph of G, we denote by
![]() $G\setminus H$
and by
$G\setminus H$
and by
![]() $G/H$
the graph obtained from G by removing the edges of H and the graph obtained from G by contracting the edges of H, respectively.
$G/H$
the graph obtained from G by removing the edges of H and the graph obtained from G by contracting the edges of H, respectively.
We denote by
![]() $c(G)$
the complexity of the graph G (i.e., the number of spanning trees in G). (In particular, if G is disconnected, then
$c(G)$
the complexity of the graph G (i.e., the number of spanning trees in G). (In particular, if G is disconnected, then
![]() $c(G)=0$
).
$c(G)=0$
).
If G is a graph and V is a subset of
![]() $\operatorname {\mathrm {Vert}}(G)$
, we denote by
$\operatorname {\mathrm {Vert}}(G)$
, we denote by
![]() $\Gamma (V)$
the induced subgraph on the vertex set V. We denote by
$\Gamma (V)$
the induced subgraph on the vertex set V. We denote by
![]() $\operatorname {\mathrm {Edges}}(V,V^c)$
the subset of
$\operatorname {\mathrm {Edges}}(V,V^c)$
the subset of
![]() $\operatorname {\mathrm {Edges}}(G)$
of the edges that connect some element of V to some element of
$\operatorname {\mathrm {Edges}}(G)$
of the edges that connect some element of V to some element of
![]() $V^c= \operatorname {\mathrm {Vert}}(G) \setminus V$
(equivalently,
$V^c= \operatorname {\mathrm {Vert}}(G) \setminus V$
(equivalently,
![]() $\operatorname {\mathrm {Edges}}(V,V^c)$
consists of the edges of G that are neither in
$\operatorname {\mathrm {Edges}}(V,V^c)$
consists of the edges of G that are neither in
![]() $\Gamma (V)$
nor in
$\Gamma (V)$
nor in
![]() $\Gamma (V^c)$
).
$\Gamma (V^c)$
).
We will denote by
![]() $\Delta $
the spectrum of a DVR with residue field K, and by
$\Delta $
the spectrum of a DVR with residue field K, and by
![]() $0$
(resp. by
$0$
(resp. by
![]() $\eta $
) its closed (resp. its generic) point. A smoothing of a nodal curve
$\eta $
) its closed (resp. its generic) point. A smoothing of a nodal curve
![]() $X/K$
over
$X/K$
over
![]() $\Delta $
is a flat family
$\Delta $
is a flat family
![]() $\mathcal {X}/\Delta $
whose generic fiber
$\mathcal {X}/\Delta $
whose generic fiber
![]() $\mathcal {X}_{\eta }/\eta $
is smooth and with an isomorphism of K-schemes
$\mathcal {X}_{\eta }/\eta $
is smooth and with an isomorphism of K-schemes
![]() $\mathcal {X}_0 \cong X$
. The smoothing is regular if so is its total space
$\mathcal {X}_0 \cong X$
. The smoothing is regular if so is its total space
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
A family of rank
![]() $\boldsymbol {1}$
torsion-free sheaves over a family of curves
$\boldsymbol {1}$
torsion-free sheaves over a family of curves
![]() $\mathcal {X} \to S$
is a coherent sheaf on
$\mathcal {X} \to S$
is a coherent sheaf on
![]() $\mathcal {X}$
, flat over S, whose fibers over the geometric points have rank
$\mathcal {X}$
, flat over S, whose fibers over the geometric points have rank
![]() $1$
and are torsion-free.
$1$
and are torsion-free.
If F is a rank
![]() $1$
torsion-free sheaf on a nodal curve X with irreducible components
$1$
torsion-free sheaf on a nodal curve X with irreducible components
![]() $X_i$
, we denote by
$X_i$
, we denote by
![]() $F_{\widetilde {X}_{i}}$
the maximal torsion-free quotient of the pullback of F to the normalization
$F_{\widetilde {X}_{i}}$
the maximal torsion-free quotient of the pullback of F to the normalization
![]() $\widetilde {X}_i$
of
$\widetilde {X}_i$
of
![]() $X_i$
, and then define the multidegree of F by
$X_i$
, and then define the multidegree of F by
We define the (total) degree of F to be
![]() $\deg _X(F):=\chi (F)-1+p_a(X)$
, where
$\deg _X(F):=\chi (F)-1+p_a(X)$
, where
![]() $p_a(X)= h^1(X, \mathcal {O}_X)$
is the arithmetic genus of X. The total degree and the multidegree of F are related by the formula
$p_a(X)= h^1(X, \mathcal {O}_X)$
is the arithmetic genus of X. The total degree and the multidegree of F are related by the formula
![]() $\deg _X(F) = \sum \deg _{X_i} F + \delta (F)$
, where
$\deg _X(F) = \sum \deg _{X_i} F + \delta (F)$
, where
![]() $\delta (F)=\# {\operatorname {N}}(F)$
denotes the number of nodes of X where F fails to be locally free.Footnote 3
$\delta (F)=\# {\operatorname {N}}(F)$
denotes the number of nodes of X where F fails to be locally free.Footnote 3
If
![]() $X' \subseteq X$
is a subcurve (by which we will always mean a union of irreducible components), then
$X' \subseteq X$
is a subcurve (by which we will always mean a union of irreducible components), then
![]() $\deg _{X'}(F)$
is defined as
$\deg _{X'}(F)$
is defined as
![]() $\deg (F_{X'})$
, where
$\deg (F_{X'})$
, where
![]() $F_{X'}$
is the maximal torsion-free quotient of
$F_{X'}$
is the maximal torsion-free quotient of
![]() $F \otimes \mathcal {O}_{X'}$
. The total degree on X is related to the degree on a subcurve by the formula
$F \otimes \mathcal {O}_{X'}$
. The total degree on X is related to the degree on a subcurve by the formula
where the overline denotes the (Zariski) closure.
From now on, we fix an integer d once and for all.
2.1. Spaces of multidegrees
Here, we define the space of multidegrees on a graph
![]() $\Gamma $
at a connected spanning subgraph as the set of all possible ways of labeling its vertices with integral weights, suitably organized by total weight (or total degree). We then define the notion of an assignment on
$\Gamma $
at a connected spanning subgraph as the set of all possible ways of labeling its vertices with integral weights, suitably organized by total weight (or total degree). We then define the notion of an assignment on
![]() $\Gamma $
.
$\Gamma $
.
Let
![]() $\Gamma $
be a graph and let
$\Gamma $
be a graph and let
![]() $G \subseteq \Gamma $
be a spanning subgraph of
$G \subseteq \Gamma $
be a spanning subgraph of
![]() $\Gamma $
. We will denote by
$\Gamma $
. We will denote by
![]() $n_\Gamma (G)$
or simply by
$n_\Gamma (G)$
or simply by
![]() $n(G)$
the number of elements in
$n(G)$
the number of elements in
![]() $\operatorname {Edges}(\Gamma ) \setminus \operatorname {Edges}(G)$
.
$\operatorname {Edges}(\Gamma ) \setminus \operatorname {Edges}(G)$
.
Define the space of multidegrees of total degree d of
![]() $\Gamma $
at G as the set
$\Gamma $
at G as the set
The elements of
![]() $S^d_{\Gamma }(\Gamma )$
are also known as degree
$S^d_{\Gamma }(\Gamma )$
are also known as degree
![]() $d-n(G)$
divisors on
$d-n(G)$
divisors on
![]() $\Gamma $
.
$\Gamma $
.
According to our convention for the multidegree, if X is a nodal curve with dual graph
![]() $\Gamma $
and F is a rank
$\Gamma $
and F is a rank
![]() $1$
torsion-free sheaf on X, then the subgraph
$1$
torsion-free sheaf on X, then the subgraph
![]() $G(F)$
obtained from
$G(F)$
obtained from
![]() $\Gamma $
by removing the edges
$\Gamma $
by removing the edges
![]() $ {\operatorname {N}}(F)$
is a spanning subgraph of
$ {\operatorname {N}}(F)$
is a spanning subgraph of
![]() $\Gamma $
, and we have
$\Gamma $
, and we have
We are now ready for the definition of an assignment on a graph
![]() $\Gamma $
, which will play a role in the definition of a stability assignment (Definition 4.3).
$\Gamma $
, which will play a role in the definition of a stability assignment (Definition 4.3).
Definition 2.1.
A degree
![]() $\boldsymbol {d}$
assignment for the graph
$\boldsymbol {d}$
assignment for the graph
![]() $\boldsymbol {\Gamma }$
is a subset
$\boldsymbol {\Gamma }$
is a subset
If
![]() $\sigma $
is a degree d assignment for the graph
$\sigma $
is a degree d assignment for the graph
![]() $\Gamma $
and
$\Gamma $
and
![]() $G \subseteq \Gamma $
is a subgraph, we define
$G \subseteq \Gamma $
is a subgraph, we define
(and the latter is empty unless G is connected and spanning).
3. Fine compactified Jacobians
In this section, we introduce the notion of a (smoothable) fine compactified Jacobian for a nodal curve (Definition 3.1) and for a flat family of nodal curves (Definition 3.7).
Let
![]() $\mathcal {X}/S$
be a flat family of nodal curves over a k-scheme S. Then there is an algebraic space
$\mathcal {X}/S$
be a flat family of nodal curves over a k-scheme S. Then there is an algebraic space
![]() $\operatorname {Pic}^d(\mathcal {X}/S)$
parameterizing line bundles on
$\operatorname {Pic}^d(\mathcal {X}/S)$
parameterizing line bundles on
![]() $\mathcal {X}/S$
of relative degree d (see [Reference Bosch, Lütkebohmert and Raynaud9, Chapter 8.3]). By [Reference Altman and Kleiman2] and [Reference Esteves16], the space
$\mathcal {X}/S$
of relative degree d (see [Reference Bosch, Lütkebohmert and Raynaud9, Chapter 8.3]). By [Reference Altman and Kleiman2] and [Reference Esteves16], the space
![]() $\operatorname {Pic}^d(\mathcal {X}/S)$
embeds in an algebraic space
$\operatorname {Pic}^d(\mathcal {X}/S)$
embeds in an algebraic space
![]() $ {\operatorname {Simp}}^{d}(\mathcal {X}/S)$
parameterizing flat families of degree d rank
$ {\operatorname {Simp}}^{d}(\mathcal {X}/S)$
parameterizing flat families of degree d rank
![]() $1$
torsion-free simple sheaves on
$1$
torsion-free simple sheaves on
![]() $\mathcal {X}/S$
. The latter is locally of finite type over S and satisfies the existence part of the valuative criterion of properness. However, it can fail to be of finite type and separated. In the special case of
$\mathcal {X}/S$
. The latter is locally of finite type over S and satisfies the existence part of the valuative criterion of properness. However, it can fail to be of finite type and separated. In the special case of
![]() $S= {\operatorname {Spec}}(K)$
and
$S= {\operatorname {Spec}}(K)$
and
![]() $X=\mathcal {X}/S$
, we will simply write
$X=\mathcal {X}/S$
, we will simply write
![]() $ \operatorname {Pic}^d(X)$
(resp.
$ \operatorname {Pic}^d(X)$
(resp.
![]() $ {\operatorname {Simp}}^d(X)$
) for
$ {\operatorname {Simp}}^d(X)$
) for
![]() $\operatorname {Pic}^d(\mathcal {X}/S)$
(resp. for
$\operatorname {Pic}^d(\mathcal {X}/S)$
(resp. for
![]() $ {\operatorname {Simp}}^d(\mathcal {X}/S)$
).
$ {\operatorname {Simp}}^d(\mathcal {X}/S)$
).
Let X be a nodal curve over some field extension K of k. The main point of this paper is to describe well-behaved subspaces of
![]() $ {\operatorname {Simp}}^{d}(X)$
, generalizing existing notions of compactified Jacobians in the literature. Specifically, we study the following subschemes.
$ {\operatorname {Simp}}^{d}(X)$
, generalizing existing notions of compactified Jacobians in the literature. Specifically, we study the following subschemes.
Definition 3.1. A degree
![]() $\boldsymbol {d}$
fine compactified Jacobian is a geometrically connected open subscheme
$\boldsymbol {d}$
fine compactified Jacobian is a geometrically connected open subscheme
![]() $\overline {J}\subseteq {\operatorname {Simp}}^{d}(X)$
that is proper over
$\overline {J}\subseteq {\operatorname {Simp}}^{d}(X)$
that is proper over
![]() $\operatorname {\mathrm {Spec}}(K)$
.
$\operatorname {\mathrm {Spec}}(K)$
.
We say that the fine compactified Jacobian
![]() $\overline {J}$
is smoothable if there exists a regular smoothing
$\overline {J}$
is smoothable if there exists a regular smoothing
![]() $\mathcal X\to \Delta $
of X, where
$\mathcal X\to \Delta $
of X, where
![]() $\Delta $
is the spectrum of a DVR with residue field K, such that
$\Delta $
is the spectrum of a DVR with residue field K, such that
![]() $\overline {J}$
is the fiber over
$\overline {J}$
is the fiber over
![]() $0\in \Delta $
of an open and
$0\in \Delta $
of an open and
![]() $\Delta $
-proper subscheme of
$\Delta $
-proper subscheme of
![]() $ {\operatorname {Simp}}^{d}(\mathcal {X}/\Delta )$
.
$ {\operatorname {Simp}}^{d}(\mathcal {X}/\Delta )$
.
Note that the fiber over the generic point
![]() $\eta $
of a nonempty, open and
$\eta $
of a nonempty, open and
![]() $\Delta $
-proper subscheme of
$\Delta $
-proper subscheme of
![]() $ {\operatorname {Simp}}^{d}(\mathcal {X}/\Delta )$
is necessarily the moduli space of degree d line bundles
$ {\operatorname {Simp}}^{d}(\mathcal {X}/\Delta )$
is necessarily the moduli space of degree d line bundles
![]() $\operatorname {Pic}^d(\mathcal {X}_{\eta }/{\eta })$
. As openness and properness are stable under base change, the fiber over
$\operatorname {Pic}^d(\mathcal {X}_{\eta }/{\eta })$
. As openness and properness are stable under base change, the fiber over
![]() $0 \in \Delta $
is open in
$0 \in \Delta $
is open in
![]() $ {\operatorname {Simp}}^d(X)$
and K-proper. The axiom ‘geometrically connected’ is redundant in the smoothable case because the moduli space of degree d line bundles on the generic point is geometrically connected and dense in
$ {\operatorname {Simp}}^d(X)$
and K-proper. The axiom ‘geometrically connected’ is redundant in the smoothable case because the moduli space of degree d line bundles on the generic point is geometrically connected and dense in
![]() $ {\operatorname {Simp}}^{d}(\mathcal {X}/\Delta )$
.
$ {\operatorname {Simp}}^{d}(\mathcal {X}/\Delta )$
.
Remark 3.2. It follows from Lemma 6.5 (combined with Proposition 7.2) that requiring the subscheme
![]() $\overline {J} \subseteq {\operatorname {Simp}}^d(X)$
to extend to some regular smoothing of the curve is equivalent to requiring that it extends to all smoothings.
$\overline {J} \subseteq {\operatorname {Simp}}^d(X)$
to extend to some regular smoothing of the curve is equivalent to requiring that it extends to all smoothings.
In this paper, we will focus on smoothable fine compactified Jacobians, since they are better behaved and occur more often in applications.
Remark 3.3. When
![]() $K=k$
is algebraically closed and
$K=k$
is algebraically closed and
![]() $\operatorname {char}(k)=0$
, Definition 3.1 coincides with [Reference Pagani and Tommasi32, Definitions 2.1, 2.4] (by passing to the completion of the DVR).
$\operatorname {char}(k)=0$
, Definition 3.1 coincides with [Reference Pagani and Tommasi32, Definitions 2.1, 2.4] (by passing to the completion of the DVR).
In [Reference Pagani and Tommasi32, Section 3], the authors give a complete classification of fine compactified Jacobians of curves of genus
![]() $1$
, showing in particular the existence of nonsmoothable examples.
$1$
, showing in particular the existence of nonsmoothable examples.
Example 3.4. If X is a geometrically irreducible curve over K, then
![]() $ {\operatorname {Simp}}^d(X)$
is proper over K, so the only degree d fine compactified Jacobian is
$ {\operatorname {Simp}}^d(X)$
is proper over K, so the only degree d fine compactified Jacobian is
![]() $ {\operatorname {Simp}}^d(X)$
itself. These Jacobians are always smoothable. (See Examples 4.5 and 8.5 for the corresponding unique stability assignment).
$ {\operatorname {Simp}}^d(X)$
itself. These Jacobians are always smoothable. (See Examples 4.5 and 8.5 for the corresponding unique stability assignment).
Example 3.5. In the case of curves with two geometrically irreducible components, fine compactified Jacobians are no longer irreducible. Assume for simplicity that X is a vine curve of type
![]() $\boldsymbol {t}$
– that is, the union of two nonsingular curves intersecting transversely at t nodes. We will later see in Example 7.5 that every fine compactified Jacobian of X is smoothable, and that it consists of t irreducible components whose generic points correspond to line bundles of consecutive bidegrees.
$\boldsymbol {t}$
– that is, the union of two nonsingular curves intersecting transversely at t nodes. We will later see in Example 7.5 that every fine compactified Jacobian of X is smoothable, and that it consists of t irreducible components whose generic points correspond to line bundles of consecutive bidegrees.
Remark 3.6. The moduli space
![]() $ {\operatorname {Simp}}^d(X)$
of a nodal curve X admits a natural stratification (see, for example, [Reference Melo and Viviani29]) into locally closed subsets
$ {\operatorname {Simp}}^d(X)$
of a nodal curve X admits a natural stratification (see, for example, [Reference Melo and Viviani29]) into locally closed subsets
 $$ \begin{align} {\operatorname{Simp}}^d(X) = \bigsqcup_{(\Gamma_{0},\underline{\mathbf d})}\mathcal J_{(\Gamma_{0},\underline{\mathbf d}),}\end{align} $$
$$ \begin{align} {\operatorname{Simp}}^d(X) = \bigsqcup_{(\Gamma_{0},\underline{\mathbf d})}\mathcal J_{(\Gamma_{0},\underline{\mathbf d}),}\end{align} $$
where the union runs over all connected spanning subgraphs
![]() $\Gamma _{0}\subseteq \Gamma (X)$
and all multidegrees
$\Gamma _{0}\subseteq \Gamma (X)$
and all multidegrees
![]() $\underline {\mathbf d}\in S^d_{\Gamma (X)}(G)$
. Each subspace
$\underline {\mathbf d}\in S^d_{\Gamma (X)}(G)$
. Each subspace
![]() $\mathcal J_{(\Gamma _{0},\underline {\mathbf d})}\subset {\operatorname {Simp}}^d(X)$
is defined as the locus whose points are sheaves F that fail to be locally free on
$\mathcal J_{(\Gamma _{0},\underline {\mathbf d})}\subset {\operatorname {Simp}}^d(X)$
is defined as the locus whose points are sheaves F that fail to be locally free on
![]() $ {\operatorname {N}}(F)=\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(\Gamma _{0})$
, and whose multidegree
$ {\operatorname {N}}(F)=\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(\Gamma _{0})$
, and whose multidegree
![]() $\underline {\deg }(F)$
equals
$\underline {\deg }(F)$
equals
![]() $ \underline {\mathbf {d}}$
.
$ \underline {\mathbf {d}}$
.
We now extend the notion of a fine compactified Jacobian to the case of a family of nodal curves
![]() $\mathcal {X}/S$
. Recall that the moduli space
$\mathcal {X}/S$
. Recall that the moduli space
![]() $ {\operatorname {Simp}}^d(\mathcal {X}/S)$
is also defined in [Reference Melo26] when
$ {\operatorname {Simp}}^d(\mathcal {X}/S)$
is also defined in [Reference Melo26] when
![]() $\mathcal {X}/S$
is the universal curve
$\mathcal {X}/S$
is the universal curve
![]() $\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n}$
over the moduli stack of stable n-pointed curves of arithmetic genus g. In this case,
$\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n}$
over the moduli stack of stable n-pointed curves of arithmetic genus g. In this case,
![]() $ {\operatorname {Simp}}^d(\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n})$
is a Deligne–Mumford stack representable (by algebraic spaces) and flat over
$ {\operatorname {Simp}}^d(\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n})$
is a Deligne–Mumford stack representable (by algebraic spaces) and flat over
![]() $\overline {\mathcal {M}}_{g,n}$
.
$\overline {\mathcal {M}}_{g,n}$
.
Definition 3.7. Assume that S is irreducible with generic point
![]() $\theta $
, and assume that the generic fiber
$\theta $
, and assume that the generic fiber
![]() $\mathcal {X}_\theta /\theta $
is smooth.
$\mathcal {X}_\theta /\theta $
is smooth.
A family of degree
![]() $\boldsymbol {d}$
fine compactified Jacobians for the family
$\boldsymbol {d}$
fine compactified Jacobians for the family
![]() $\mathcal {X}/S$
is an open algebraic subspace
$\mathcal {X}/S$
is an open algebraic subspace
![]() $\overline {\mathcal J} \subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
that is proper over S.
$\overline {\mathcal J} \subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
that is proper over S.
We say that a degree d fine compactified Jacobian
![]() $\overline {\mathcal J}_{{{g,n}}} \subset {\operatorname {Simp}}^d(\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n})$
is a degree
$\overline {\mathcal J}_{{{g,n}}} \subset {\operatorname {Simp}}^d(\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n})$
is a degree
![]() $\boldsymbol {d}$
fine compactified universal Jacobian for the universal curve over
$\boldsymbol {d}$
fine compactified universal Jacobian for the universal curve over
![]() $\overline {\mathcal {\boldsymbol {M}}}_{\boldsymbol {g},\boldsymbol {n}}$
. (We will often omit to specify ‘for the universal curve over
$\overline {\mathcal {\boldsymbol {M}}}_{\boldsymbol {g},\boldsymbol {n}}$
. (We will often omit to specify ‘for the universal curve over
![]() $\overline {\mathcal {M}}_{g,n}$
’, when clear from the context).
$\overline {\mathcal {M}}_{g,n}$
’, when clear from the context).
Note that the assumption that the generic fiber is smooth implies that all fibers over S of a degree d fine compactified Jacobian are smoothable.
4. Stability assignments for smoothable fine compactified Jacobians
Here, we define the combinatorial data identifying smoothable fine compactified Jacobians. We first do so for a single nodal curve – that is, for a fixed dual graph (Definition 4.3) – and then we generalize the definition to families (Definition 4.9).
If X is a nodal curve over an algebraically closed field, a sheaf
![]() $F\in {\operatorname {Simp}}^d(X)$
has two natural combinatorial invariants, given by its multidegree and by the subset
$F\in {\operatorname {Simp}}^d(X)$
has two natural combinatorial invariants, given by its multidegree and by the subset
![]() $ {\operatorname {N}}(F)\subseteq \operatorname {Sing}(X)=\operatorname {\mathrm {Edges}}(\Gamma (X))$
of points of the curve where F fails to be locally free. Hence, it makes sense to study a fine compactified Jacobian
$ {\operatorname {N}}(F)\subseteq \operatorname {Sing}(X)=\operatorname {\mathrm {Edges}}(\Gamma (X))$
of points of the curve where F fails to be locally free. Hence, it makes sense to study a fine compactified Jacobian
![]() $\overline {J}$
on X by looking at all pairs
$\overline {J}$
on X by looking at all pairs
![]() $\left (G(F)= \Gamma (X) \setminus {\operatorname {N}}(F),\underline {\deg }(F)\right )$
with
$\left (G(F)= \Gamma (X) \setminus {\operatorname {N}}(F),\underline {\deg }(F)\right )$
with
![]() $F\in \overline {J}$
. Recall that, with the notation introduced in Equation 2.2, we can regard
$F\in \overline {J}$
. Recall that, with the notation introduced in Equation 2.2, we can regard
![]() $\underline {\deg }(F)$
as an element of the space of multidegrees
$\underline {\deg }(F)$
as an element of the space of multidegrees
![]() $S_{\Gamma (X)}^d(G(F))$
.
$S_{\Gamma (X)}^d(G(F))$
.
For a single curve X, we identify, in Definition 4.3, the two properties characterizing the set of such pairs. One is related to properness, combined with the smoothability of the Jacobian, and it requires that the set of stable multidegrees should be a minimal complete set of representatives for the natural chip-firing action on the dual graph (see Definition 4.1). The other corresponds to openness. In combinatorial terms, this means that if we add an edge e to G, the set of stable multidegrees on
![]() $\Gamma \cup \{e\}$
should contain all multidegrees obtained by ‘adding a chip’ to either endpoints of e.
$\Gamma \cup \{e\}$
should contain all multidegrees obtained by ‘adding a chip’ to either endpoints of e.
For a family of curves, we further require compatibility with all contractions of the dual graphs involved.
4.1. Stability assignments for a single curve
We start by introducing the twister group of a graph, which will play a role in characterizing smoothable compactified Jacobians.
Definition 4.1. Let G be a graph. For each
![]() $v \in \operatorname {\mathrm {Vert}}(G)$
, define the twister of G at v to be the element of
$v \in \operatorname {\mathrm {Vert}}(G)$
, define the twister of G at v to be the element of
![]() $\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
defined by
$\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
defined by
 $$\begin{align*}\operatorname{\mathrm{Tw}}_{G, v} (w) = \begin{cases} \text{ # of edges of } G \text{ having } v \text{ and } w \text{ as endpoints }& \text{when } w \neq v, \\ - \text{ # of nonloop edges of } G \text{ having } v \text{ as an endpoint} & \text{when } w =v.\end{cases} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Tw}}_{G, v} (w) = \begin{cases} \text{ # of edges of } G \text{ having } v \text{ and } w \text{ as endpoints }& \text{when } w \neq v, \\ - \text{ # of nonloop edges of } G \text{ having } v \text{ as an endpoint} & \text{when } w =v.\end{cases} \end{align*}$$
The twister group (or chip-firing group)
![]() $\operatorname {\mathrm {Tw}}(G)$
is the subgroup of
$\operatorname {\mathrm {Tw}}(G)$
is the subgroup of
![]() $\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
generated by the set
$\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
generated by the set
![]() $\{\operatorname {\mathrm {Tw}}_{G, v}\}_{ v \in \operatorname {\mathrm {Vert}}(G)}$
.
$\{\operatorname {\mathrm {Tw}}_{G, v}\}_{ v \in \operatorname {\mathrm {Vert}}(G)}$
.
Recall from Equation (2.2) the definition of the space of multidegrees
![]() $S^d_{G}(G)$
of total degree equal to d. The twister group of G is contained in the sum zero submodule
$S^d_{G}(G)$
of total degree equal to d. The twister group of G is contained in the sum zero submodule
![]() $S^0_{G}(G)$
of
$S^0_{G}(G)$
of
![]() $\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
. Hence, the group structure on
$\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
. Hence, the group structure on
![]() $\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
restricts to an action of
$\mathbf {Z}^{\operatorname {\mathrm {Vert}}(G)}$
restricts to an action of
![]() $\operatorname {\mathrm {Tw}}(G)$
on
$\operatorname {\mathrm {Tw}}(G)$
on
![]() $S^d_{G}(G)$
. The quotient group
$S^d_{G}(G)$
. The quotient group
is then a torsor over
![]() $J^0(G)$
, which is a finite abelian group. The latter is also known as the Jacobian of the graph G, and it has a number of element equal to the complexity
$J^0(G)$
, which is a finite abelian group. The latter is also known as the Jacobian of the graph G, and it has a number of element equal to the complexity
![]() $c(G)$
of the graph G. (It is also known by other names in the literature, such as the degree class group, or the sandpile group, or the critical group of the graph G).
$c(G)$
of the graph G. (It is also known by other names in the literature, such as the degree class group, or the sandpile group, or the critical group of the graph G).
Remark 4.2. Let
![]() $\mathcal {X}$
be a regular smoothing of X over some discrete valuation ring
$\mathcal {X}$
be a regular smoothing of X over some discrete valuation ring
![]() $\Delta $
with generic point
$\Delta $
with generic point
![]() $\eta $
. Let T be the image under the restriction map
$\eta $
. Let T be the image under the restriction map
![]() $\operatorname {\mathrm {Pic}}(\mathcal X)\rightarrow \operatorname {\mathrm {Pic}}(X)$
of the kernel of the surjection
$\operatorname {\mathrm {Pic}}(\mathcal X)\rightarrow \operatorname {\mathrm {Pic}}(X)$
of the kernel of the surjection
![]() $\operatorname {\mathrm {Pic}}(\mathcal X)\rightarrow \operatorname {\mathrm {Pic}}(\mathcal X_\eta )$
(the restriction to the generic point). We claim that the restriction to T of the multidegree homomorphism
$\operatorname {\mathrm {Pic}}(\mathcal X)\rightarrow \operatorname {\mathrm {Pic}}(\mathcal X_\eta )$
(the restriction to the generic point). We claim that the restriction to T of the multidegree homomorphism
![]() $\operatorname {\mathrm {Pic}}(X) \to \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
defines an isomorphism
$\operatorname {\mathrm {Pic}}(X) \to \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
defines an isomorphism
![]() $T \to \operatorname {\mathrm {Tw}}(\Gamma )$
.
$T \to \operatorname {\mathrm {Tw}}(\Gamma )$
.
Since
![]() $\mathcal X$
is regular, the irreducible components
$\mathcal X$
is regular, the irreducible components
![]() $\{X_v\}_{v\in \operatorname {\mathrm {Vert}}(\Gamma )}$
of X are Cartier divisors on
$\{X_v\}_{v\in \operatorname {\mathrm {Vert}}(\Gamma )}$
of X are Cartier divisors on
![]() $\mathcal X$
, and it is easy to check that the elements of T are of the form
$\mathcal X$
, and it is easy to check that the elements of T are of the form
 $$\begin{align*}\mathcal O_{\mathcal X}\left(\sum_{v\in\operatorname{\mathrm{Vert}}(\Gamma)}{d_vX_v}\right)\otimes \mathcal O_X \end{align*}$$
$$\begin{align*}\mathcal O_{\mathcal X}\left(\sum_{v\in\operatorname{\mathrm{Vert}}(\Gamma)}{d_vX_v}\right)\otimes \mathcal O_X \end{align*}$$
with
![]() $\underline {\mathbf d}\in \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
. One can explicitly compute that the restriction to T of the multidegree map
$\underline {\mathbf d}\in \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
. One can explicitly compute that the restriction to T of the multidegree map
![]() $\operatorname {\mathrm {Pic}}(X)\rightarrow \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
is given by
$\operatorname {\mathrm {Pic}}(X)\rightarrow \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
is given by
This homomorphism is injective by [Reference Raynaud34, (5.2)], and its image is
![]() $\operatorname {\mathrm {Tw}}(\Gamma )$
(by definition). This proves that
$\operatorname {\mathrm {Tw}}(\Gamma )$
(by definition). This proves that
![]() $T \to \operatorname {\mathrm {Tw}}(\Gamma )$
is an isomorphism. In particular, T as an abstract group is independent of the choice of the regular smoothing (though one could see that the embedding
$T \to \operatorname {\mathrm {Tw}}(\Gamma )$
is an isomorphism. In particular, T as an abstract group is independent of the choice of the regular smoothing (though one could see that the embedding
![]() $T \subset \operatorname {Pic}(X)$
is not independent of the smoothing).
$T \subset \operatorname {Pic}(X)$
is not independent of the smoothing).
We are now ready to define our notion of a stability assignment.
Definition 4.3. A degree
![]() $\boldsymbol {d}$
smoothable fine compactified Jacobian stability assignment, or shortly, a degree
$\boldsymbol {d}$
smoothable fine compactified Jacobian stability assignment, or shortly, a degree
![]() $\boldsymbol {d}$
stability assignment for the graph
$\boldsymbol {d}$
stability assignment for the graph
![]() $\Gamma $
, is a degree d assignment for
$\Gamma $
, is a degree d assignment for
![]() $\Gamma $
(as in Definition 2.1) that satisfies the following conditions:
$\Gamma $
(as in Definition 2.1) that satisfies the following conditions:
-
1. For all edges e of
 $\operatorname {\mathrm {Edges}}(\Gamma )\setminus \operatorname {\mathrm {Edges}}(G)$
with endpoints
$\operatorname {\mathrm {Edges}}(\Gamma )\setminus \operatorname {\mathrm {Edges}}(G)$
with endpoints
 $v_1$
and
$v_1$
and
 $v_2$
, we have where
$v_2$
, we have where $$\begin{align*}(G,\underline{\mathbf d})\in\sigma \Rightarrow (G\cup\{e\},\underline{\mathbf d}+\underline{\mathbf e}_{v_1}),(G\cup\{e\},\underline{\mathbf d}+\underline{\mathbf e}_{v_2})\in\sigma, \end{align*}$$
$$\begin{align*}(G,\underline{\mathbf d})\in\sigma \Rightarrow (G\cup\{e\},\underline{\mathbf d}+\underline{\mathbf e}_{v_1}),(G\cup\{e\},\underline{\mathbf d}+\underline{\mathbf e}_{v_2})\in\sigma, \end{align*}$$
 $\underline {\mathbf e}_{v_i}$
denotes the vector in the standard basis of
$\underline {\mathbf e}_{v_i}$
denotes the vector in the standard basis of
 $\mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
corresponding to
$\mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
corresponding to
 $v_i$
.
$v_i$
.
-
2. For every connected spanning subgraph G, the subset
is a minimal complete set of representatives for the action of the twister group $$\begin{align*}\sigma(G) := \{\underline{\mathbf d}:\;(G,\underline{\mathbf d})\in\sigma\} \subset S^d_{\Gamma}(G)\end{align*}$$
$$\begin{align*}\sigma(G) := \{\underline{\mathbf d}:\;(G,\underline{\mathbf d})\in\sigma\} \subset S^d_{\Gamma}(G)\end{align*}$$
 $\operatorname {\mathrm {Tw}}(G)$
on
$\operatorname {\mathrm {Tw}}(G)$
on
 $S^d_{\Gamma }(G)$
.
$S^d_{\Gamma }(G)$
.
If X is a nodal curve, a degree d stability assignment on X is a degree d stability assignment on its dual graph
![]() $\Gamma (X)$
.
$\Gamma (X)$
.
Note that the genus of each of the components of X does not play any role in the above definition.
Remark 4.4. With the notation as above, the number of elements of
![]() $\sigma (G)$
equals the number of elements of the Jacobian
$\sigma (G)$
equals the number of elements of the Jacobian
![]() $J^0(G)$
. By the Kirchoff–Trent theorem, this number equals the complexity
$J^0(G)$
. By the Kirchoff–Trent theorem, this number equals the complexity
![]() $c(G)$
of the graph G. In particular, it is finite.
$c(G)$
of the graph G. In particular, it is finite.
It is, in general, hard to classify all stability assignments on a given stable graph. However, the task is within reach when the number of vertices is small.
Example 4.5. If
![]() $\Gamma $
only has
$\Gamma $
only has
![]() $1$
vertex (i.e., it is the dual graph of an irreducible curve), there is exactly
$1$
vertex (i.e., it is the dual graph of an irreducible curve), there is exactly
![]() $1$
stability assignment on
$1$
stability assignment on
![]() $\Gamma $
. If there are t edges, the unique degree d stability assignment is
$\Gamma $
. If there are t edges, the unique degree d stability assignment is
 $$\begin{align*}\sigma=\bigcup_{0 \leq i \leq t} \bigcup_{E \subseteq \operatorname{\mathrm{Edges}}(\Gamma), |E|=i} \{(\Gamma \setminus E,d-i)\}.\end{align*}$$
$$\begin{align*}\sigma=\bigcup_{0 \leq i \leq t} \bigcup_{E \subseteq \operatorname{\mathrm{Edges}}(\Gamma), |E|=i} \{(\Gamma \setminus E,d-i)\}.\end{align*}$$
Example 4.6. If instead
![]() $\Gamma $
consists of
$\Gamma $
consists of
![]() $2$
vertices
$2$
vertices
![]() $v_1, v_2$
connected by t edges, and no other edges (i.e.,
$v_1, v_2$
connected by t edges, and no other edges (i.e.,
![]() $\Gamma $
is the dual graph of a vine curve of type t; see Example 3.5), let
$\Gamma $
is the dual graph of a vine curve of type t; see Example 3.5), let
![]() $\Gamma _1, \ldots , \Gamma _t$
be the spanning trees. Then it follows from the definition that for every stability assignment
$\Gamma _1, \ldots , \Gamma _t$
be the spanning trees. Then it follows from the definition that for every stability assignment
![]() $\sigma $
, there exists a unique integer
$\sigma $
, there exists a unique integer
![]() $\lambda $
such that
$\lambda $
such that
-
1.
 $\sigma (\Gamma _i)=\{(\lambda ,d+1-\lambda -t)\}$
for all
$\sigma (\Gamma _i)=\{(\lambda ,d+1-\lambda -t)\}$
for all
 $i=1, \ldots , t$
;
$i=1, \ldots , t$
; -
2.
 $\sigma (\Gamma )=\{(\lambda , d-\lambda ) ,(\lambda +1, d-\lambda -1), \ldots , (\lambda +t-1, d+1-\lambda -t)\}$
.
$\sigma (\Gamma )=\{(\lambda , d-\lambda ) ,(\lambda +1, d-\lambda -1), \ldots , (\lambda +t-1, d+1-\lambda -t)\}$
.
The following result will be used later as a tool to prove that certain collections are stability assignments. It was first proved by Barmak [Reference Barmak7]. A first publicly available proof of part of this result, based upon Barmak’s argument, appeared in Yuen’s Phd thesis, [Reference Yuen38, Theorem 3.5.1].
Proposition 4.7 [Reference Viviani37, Theorem 1.17 Part (1) and (2.a)]
Let
![]() $\sigma $
be a degree d assignment on the graph
$\sigma $
be a degree d assignment on the graph
![]() $\Gamma $
(see Definition 2.1), and assume that
$\Gamma $
(see Definition 2.1), and assume that
![]() $\sigma $
satisfies Part (1) of Definition 4.3, and that
$\sigma $
satisfies Part (1) of Definition 4.3, and that
![]() $\sigma (T)$
is nonempty for every spanning tree
$\sigma (T)$
is nonempty for every spanning tree
![]() $T \subseteq \Gamma $
.
$T \subseteq \Gamma $
.
Then for all spanning subgraphs
![]() $G \subseteq \Gamma $
, we have
$G \subseteq \Gamma $
, we have
![]() $|\sigma (G)| \geq c(G)$
(the complexity of G). Moreover, if
$|\sigma (G)| \geq c(G)$
(the complexity of G). Moreover, if
![]() $|\sigma (\Gamma )|=c(\Gamma )$
, then
$|\sigma (\Gamma )|=c(\Gamma )$
, then
![]() $|\sigma (G)|= c(G)$
for each spanning subgraph
$|\sigma (G)|= c(G)$
for each spanning subgraph
![]() $G \subseteq \Gamma $
.
$G \subseteq \Gamma $
.
4.2. Stability assignments for families
So far, we have discussed the notion of a stability assignment for a curve in isolation. The flatness condition for families of sheaves imposes an additional compatibility constraint.
Definition 4.8. Let
![]() $f\colon \Gamma \to \Gamma '$
be a morphism of graphs and let
$f\colon \Gamma \to \Gamma '$
be a morphism of graphs and let
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
be degree d stability assignments on
$\sigma '$
be degree d stability assignments on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '$
, respectively. We say that
$\Gamma '$
, respectively. We say that
![]() $\sigma $
is f-compatible with
$\sigma $
is f-compatible with
![]() $\sigma '$
if for every connected spanning subgraph G of
$\sigma '$
if for every connected spanning subgraph G of
![]() $\Gamma $
, we have
$\Gamma $
, we have
where
![]() $G'$
is the image of G under f (and therefore, it is a connected spanning subgraph of
$G'$
is the image of G under f (and therefore, it is a connected spanning subgraph of
![]() $\Gamma '$
), and
$\Gamma '$
), and
![]() $\underline {\mathbf d'}$
is defined by
$\underline {\mathbf d'}$
is defined by
 $$ \begin{align} \underline{\mathbf d'}(w) = \sum_{f(v)=w} \underline{\mathbf d}(v) + \# \left\{\textrm{edges of } \Gamma\setminus G \textrm{ that are contracted to } w \textrm{ by } f\right\}. \end{align} $$
$$ \begin{align} \underline{\mathbf d'}(w) = \sum_{f(v)=w} \underline{\mathbf d}(v) + \# \left\{\textrm{edges of } \Gamma\setminus G \textrm{ that are contracted to } w \textrm{ by } f\right\}. \end{align} $$
Note that the notion of f-compatibility only depends upon the map that f induces on the set of vertices of the two graphs. We are now ready for the definition of the compatibility constraint.
Definition 4.9. Let
![]() $\mathcal {X}/S$
be a family of nodal curves. A family of degree
$\mathcal {X}/S$
be a family of nodal curves. A family of degree
![]() $\boldsymbol {d}$
stability assignments (for fine compactified Jacobians) for
$\boldsymbol {d}$
stability assignments (for fine compactified Jacobians) for
![]() $\mathcal X/S$
consists of associating a degree d stability assignment
$\mathcal X/S$
consists of associating a degree d stability assignment
![]() $\sigma _s$
on
$\sigma _s$
on
![]() $\Gamma (X_s)$
(as in Definition 4.3) with every geometric point s in S, in a way that is compatible with all morphisms
$\Gamma (X_s)$
(as in Definition 4.3) with every geometric point s in S, in a way that is compatible with all morphisms
![]() $\Gamma (X_s) \to \Gamma (X_t)$
arising from any étale specialization
$\Gamma (X_s) \to \Gamma (X_t)$
arising from any étale specialization
![]() $t \rightsquigarrow s$
occurring on S.
$t \rightsquigarrow s$
occurring on S.
We will say that a family of degree d stability assignments for the universal family
![]() $\overline {\mathcal {C}}_{g,n}$
over
$\overline {\mathcal {C}}_{g,n}$
over
![]() $\overline {\mathcal {M}}_{g,n}$
is a degree
$\overline {\mathcal {M}}_{g,n}$
is a degree
![]() $\boldsymbol {d}$
universal stability assignment of type
$\boldsymbol {d}$
universal stability assignment of type
![]() $\mathbf {(g,n)}$
(and often omit ‘of type
$\mathbf {(g,n)}$
(and often omit ‘of type
![]() $(g,n)$
’ when clear from the context). These stability assignments will be studied in Section 9.
$(g,n)$
’ when clear from the context). These stability assignments will be studied in Section 9.
Universal stability assignments can be defined purely in terms of the category
![]() $G_{g,n}$
of stable graphs:
$G_{g,n}$
of stable graphs:
Remark 4.10. In the case of universal stability assignments, the étale specializations of points of
![]() $\overline {\mathcal {M}}_{g,n}$
induce all morphisms in the category
$\overline {\mathcal {M}}_{g,n}$
induce all morphisms in the category
![]() $G_{g,n}$
of stable graphs of genus g with n marked half-edges.
$G_{g,n}$
of stable graphs of genus g with n marked half-edges.
In particular, if
![]() $\sigma $
is a degree d universal stability assignment of type
$\sigma $
is a degree d universal stability assignment of type
![]() $(g,n)$
and
$(g,n)$
and
![]() $\alpha \colon \Gamma (X_1) \to \Gamma (X_2)$
is an isomorphism of the dual graphs of two pointed curves
$\alpha \colon \Gamma (X_1) \to \Gamma (X_2)$
is an isomorphism of the dual graphs of two pointed curves
![]() $[X_1],[X_2]\in \overline {\mathcal {M}}_{g,n}$
, then
$[X_1],[X_2]\in \overline {\mathcal {M}}_{g,n}$
, then
![]() $\alpha $
identifies
$\alpha $
identifies
![]() $\sigma _{[X_1]}$
with
$\sigma _{[X_1]}$
with
![]() $\sigma _{[X_2]}$
.
$\sigma _{[X_2]}$
.
We conclude that a degree d universal stability assignment of type
![]() $(g,n)$
is a collection
$(g,n)$
is a collection
![]() $\{\sigma _\Gamma \}_{\Gamma \in G_{g,n}}$
such that
$\{\sigma _\Gamma \}_{\Gamma \in G_{g,n}}$
such that
![]() $\sigma _\Gamma $
is a degree d stability assignment on
$\sigma _\Gamma $
is a degree d stability assignment on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\sigma _{\Gamma }$
is f-compatible with
$\sigma _{\Gamma }$
is f-compatible with
![]() $\sigma _{\Gamma '}$
for any morphism
$\sigma _{\Gamma '}$
for any morphism
![]() $f:\;\Gamma \rightarrow \Gamma '$
in
$f:\;\Gamma \rightarrow \Gamma '$
in
![]() $G_{g,n}$
.
$G_{g,n}$
.
5. Combinatorial preparation: Perturbations and lifts
This section contains combinatorial results that will be used in later proofs. First, we introduce the notion of a perturbation for the multidegree of a sheaf that fails to be locally free at some nodes. This corresponds to deforming a simple sheaf into a line bundle (Lemma 5.2). Then we investigate the relationship between the chip-firing action on a graph
![]() $\Gamma $
and the chip-firing action on the graph obtained from
$\Gamma $
and the chip-firing action on the graph obtained from
![]() $\Gamma $
by subdividing each of its edges a certain number of times. In terms of dual graphs, this construction corresponds to blowing up a certain number of times the nodes of our curve. Our main techincal result here is Proposition 5.4.
$\Gamma $
by subdividing each of its edges a certain number of times. In terms of dual graphs, this construction corresponds to blowing up a certain number of times the nodes of our curve. Our main techincal result here is Proposition 5.4.
Definition 5.1. Let
![]() $G \subseteq \Gamma $
be a connected spanning subgraph. A G-perturbation is an element in
$G \subseteq \Gamma $
be a connected spanning subgraph. A G-perturbation is an element in
![]() $S^{n(G)}_{G}(G)$
(for
$S^{n(G)}_{G}(G)$
(for
![]() $n(G)=|\operatorname {Edges}(\Gamma ) \setminus \operatorname {Edges}(G)|$
) of the form
$n(G)=|\operatorname {Edges}(\Gamma ) \setminus \operatorname {Edges}(G)|$
) of the form
 $$\begin{align*}\sum_{e \in \operatorname{\mathrm{Edges}}(\Gamma) \setminus \operatorname{\mathrm{Edges}}(G)} {\underline{\mathbf e}}_{t(e),} \end{align*}$$
$$\begin{align*}\sum_{e \in \operatorname{\mathrm{Edges}}(\Gamma) \setminus \operatorname{\mathrm{Edges}}(G)} {\underline{\mathbf e}}_{t(e),} \end{align*}$$
where t is some choice of an orientation on
![]() $\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(G)$
.
$\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(G)$
.
(If D is a G-perturbation for some G, then D is also known in the literature as a semibreak divisor; see [Reference Gross, Shokrieh and Tóthmérész19, Definition 3.1]).
By the description in Remark 3.6 of the stratification of
![]() $ {\operatorname {Simp}}^d(X)$
, and by Lemma 5.2, if G is a connected spanning subgraph of
$ {\operatorname {Simp}}^d(X)$
, and by Lemma 5.2, if G is a connected spanning subgraph of
![]() $\Gamma $
, a G-perturbation is the same as the multidegree of a line bundle on X that specializes to a sheaf F with
$\Gamma $
, a G-perturbation is the same as the multidegree of a line bundle on X that specializes to a sheaf F with
![]() $G(F)=G$
,
$G(F)=G$
,
![]() $\underline {\deg }(F)=\underline {\mathbf 0}$
. We are now ready for the following technical lemma.
$\underline {\deg }(F)=\underline {\mathbf 0}$
. We are now ready for the following technical lemma.
Lemma 5.2. Let
![]() $\mathcal X$
be a family of nodal curves over the spectrum
$\mathcal X$
be a family of nodal curves over the spectrum
![]() $\Delta $
of a DVR with algebraically closed residue field
$\Delta $
of a DVR with algebraically closed residue field
![]() $\overline {K}$
, and consider a section
$\overline {K}$
, and consider a section
![]() $\sigma :\;\Delta \rightarrow {\operatorname {Simp}}^d(\mathcal X/\Delta )$
. Let us fix a geometric point
$\sigma :\;\Delta \rightarrow {\operatorname {Simp}}^d(\mathcal X/\Delta )$
. Let us fix a geometric point
![]() $\overline \eta $
lying over the generic point of
$\overline \eta $
lying over the generic point of
![]() $\Delta $
and denote by
$\Delta $
and denote by
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '$
the dual graphs of the geometric fibers
$\Gamma '$
the dual graphs of the geometric fibers
![]() $X_0$
and
$X_0$
and
![]() $X_{\overline \eta }$
of
$X_{\overline \eta }$
of
![]() $\mathcal X$
, respectively, and by
$\mathcal X$
, respectively, and by
![]() $f:\;\Gamma \rightarrow \Gamma '$
the morphism of graphs induced by the specialization of
$f:\;\Gamma \rightarrow \Gamma '$
the morphism of graphs induced by the specialization of
![]() $\overline \eta $
to
$\overline \eta $
to
![]() $0$
. Write
$0$
. Write
![]() $F_0$
and
$F_0$
and
![]() $F_{\overline {\eta }}$
for
$F_{\overline {\eta }}$
for
![]() $\sigma (0)$
and
$\sigma (0)$
and
![]() $\sigma (\overline \eta )$
, respectively, and set
$\sigma (\overline \eta )$
, respectively, and set
![]() $G=G(F_0)\subseteq \Gamma $
and
$G=G(F_0)\subseteq \Gamma $
and
![]() $G'=G(F_{\overline {\eta }})\subseteq \Gamma '$
for the connected subgraphs where the corresponding sheaf is locally free. Then there exists a
$G'=G(F_{\overline {\eta }})\subseteq \Gamma '$
for the connected subgraphs where the corresponding sheaf is locally free. Then there exists a
![]() $G\subseteq f^{-1}(G')$
-perturbation T such that the multidegrees
$G\subseteq f^{-1}(G')$
-perturbation T such that the multidegrees
![]() $\underline {\mathbf d}=\underline {\deg }(F_0)$
and
$\underline {\mathbf d}=\underline {\deg }(F_0)$
and
![]() $\underline {\mathbf d}' = \underline {\deg }(F_{\overline \eta })$
satisfy the relation
$\underline {\mathbf d}' = \underline {\deg }(F_{\overline \eta })$
satisfy the relation
Note that if
![]() $G'\subseteq \Gamma '$
is connected and spanning, then so is
$G'\subseteq \Gamma '$
is connected and spanning, then so is
![]() $f^{-1}(G') \subseteq \Gamma $
.
$f^{-1}(G') \subseteq \Gamma $
.
Proof. The section
![]() $\sigma $
defines a rank
$\sigma $
defines a rank
![]() $1$
sheaf
$1$
sheaf
![]() $\mathcal F$
over
$\mathcal F$
over
![]() $\mathcal X/\Delta $
. By [Reference Esteves and Pacini17, Proposition 5.5], the projectivization
$\mathcal X/\Delta $
. By [Reference Esteves and Pacini17, Proposition 5.5], the projectivization
![]() $\mathcal Y=\mathbf P_{\mathcal X}(\mathcal F)$
is a family of curves over
$\mathcal Y=\mathbf P_{\mathcal X}(\mathcal F)$
is a family of curves over
![]() $\Delta $
, and there exists a line bundle
$\Delta $
, and there exists a line bundle
![]() $\mathcal L$
over
$\mathcal L$
over
![]() $\mathcal Y/\Delta $
such that
$\mathcal Y/\Delta $
such that
![]() $\mathcal F = \psi _*\mathcal L$
holds for the natural map
$\mathcal F = \psi _*\mathcal L$
holds for the natural map
![]() $\psi :\;\mathcal Y\rightarrow \mathcal X$
. Geometrically, the restriction of
$\psi :\;\mathcal Y\rightarrow \mathcal X$
. Geometrically, the restriction of
![]() $\psi $
to
$\psi $
to
![]() $Y_{\overline \eta }\rightarrow X_{\overline \eta }$
is the blow-up that corresponds to adding a genus
$Y_{\overline \eta }\rightarrow X_{\overline \eta }$
is the blow-up that corresponds to adding a genus
![]() $0$
vertex on all edges of
$0$
vertex on all edges of
![]() $\Gamma '$
that do not belong to
$\Gamma '$
that do not belong to
![]() $G'$
. The description of
$G'$
. The description of
![]() $\psi _0:\;Y_0\rightarrow X_0$
in terms of
$\psi _0:\;Y_0\rightarrow X_0$
in terms of
![]() $\Gamma $
and G is completely analogous. Moreover, the multidegrees of
$\Gamma $
and G is completely analogous. Moreover, the multidegrees of
![]() $L_{\overline \eta }$
and
$L_{\overline \eta }$
and
![]() $L_{0}$
can be obtained from the multidegrees of
$L_{0}$
can be obtained from the multidegrees of
![]() $F_{\overline \eta }$
and
$F_{\overline \eta }$
and
![]() $F_{0}$
, respectively, by taking
$F_{0}$
, respectively, by taking
![]() $\underline {\mathbf d}'$
(resp.
$\underline {\mathbf d}'$
(resp.
![]() $\underline {\mathbf d}$
) and assigning degree
$\underline {\mathbf d}$
) and assigning degree
![]() $1$
to the additional vertices. Then the claim follows from the fact that
$1$
to the additional vertices. Then the claim follows from the fact that
![]() $L_0$
is a specialization of the line bundle
$L_0$
is a specialization of the line bundle
![]() $L_{\overline \eta }$
.
$L_{\overline \eta }$
.
We will now prove some combinatorial ingredients that relate the chip-firing on a graph with the chip-firing on its blow-up. We fix a graph
![]() $\Gamma $
and a function
$\Gamma $
and a function
![]() $m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
and let
$m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
and let
![]() ${{\widetilde {\Gamma }}}_m$
be the graph obtained by subdividing each edge e of
${{\widetilde {\Gamma }}}_m$
be the graph obtained by subdividing each edge e of
![]() $\Gamma $
into
$\Gamma $
into
![]() $m(e)+1$
edges (called an exceptional chain) by adding
$m(e)+1$
edges (called an exceptional chain) by adding
![]() $m(e)$
vertices (called exceptional vertices) in the middle.
$m(e)$
vertices (called exceptional vertices) in the middle.
We start by relating the complexities of
![]() $\Gamma $
and
$\Gamma $
and
![]() ${\widetilde {\Gamma }}$
.
${\widetilde {\Gamma }}$
.
Lemma 5.3 [Reference Busonero, Melo and Stoppino11, Theorem 3.4]
The following formula relates the number of spanning trees (i.e., the complexity) of
![]() ${{\widetilde {\Gamma }}}_m$
with the complexity of the spanning subgraphs of
${{\widetilde {\Gamma }}}_m$
with the complexity of the spanning subgraphs of
![]() $\Gamma $
:
$\Gamma $
:
 $$ \begin{align} c({{\widetilde{\Gamma}}}_m)= \sum_{\substack{G \subseteq \Gamma \text{ connected}\\ \text{ spanning subgraph}}} \left( \prod_{e \in \operatorname{\mathrm{Edges}}(\Gamma) \setminus \operatorname{\mathrm{Edges}}(G)} m(e)\right) \cdot c(G). \end{align} $$
$$ \begin{align} c({{\widetilde{\Gamma}}}_m)= \sum_{\substack{G \subseteq \Gamma \text{ connected}\\ \text{ spanning subgraph}}} \left( \prod_{e \in \operatorname{\mathrm{Edges}}(\Gamma) \setminus \operatorname{\mathrm{Edges}}(G)} m(e)\right) \cdot c(G). \end{align} $$
In order to state and then prove Proposition 5.4, we first need to define the lift of an assignment to
![]() $\widetilde {\Gamma }$
.
$\widetilde {\Gamma }$
.
Let
![]() $\sigma $
be a degree d assignment for
$\sigma $
be a degree d assignment for
![]() $\Gamma $
(see Definition 2.1). For each
$\Gamma $
(see Definition 2.1). For each
![]() $m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
, let
$m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
, let
![]() $\widetilde {\sigma }_m$
, and then define the lift
$\widetilde {\sigma }_m$
, and then define the lift
![]() $\widetilde {\sigma }_m \subset S^d_{\widetilde {\Gamma }}(\widetilde {\Gamma })$
of
$\widetilde {\sigma }_m \subset S^d_{\widetilde {\Gamma }}(\widetilde {\Gamma })$
of
![]() $\sigma $
as follows. First of all, for every element
$\sigma $
as follows. First of all, for every element
![]() $(\Gamma ,\underline {\mathbf d}) \in \sigma $
, we can naturally identify
$(\Gamma ,\underline {\mathbf d}) \in \sigma $
, we can naturally identify
![]() $\underline {\mathbf d}$
with the element of
$\underline {\mathbf d}$
with the element of
![]() $\mathbf {Z}^{\operatorname {\mathrm {Vert}}(\widetilde {\Gamma })}$
obtained by extending
$\mathbf {Z}^{\operatorname {\mathrm {Vert}}(\widetilde {\Gamma })}$
obtained by extending
![]() $\underline {\mathbf {d}}$
to zero on all exceptional vertices. Then a lift of
$\underline {\mathbf {d}}$
to zero on all exceptional vertices. Then a lift of
![]() $(G,\underline {\mathbf d})$
is any element
$(G,\underline {\mathbf d})$
is any element
![]() $\widetilde {\underline {\mathbf d}}\in S^d_{\widetilde {\Gamma }}(\widetilde {\Gamma })$
of the form
$\widetilde {\underline {\mathbf d}}\in S^d_{\widetilde {\Gamma }}(\widetilde {\Gamma })$
of the form
 $$ \begin{align}\widetilde{\underline{\mathbf d}} = \underline{\mathbf d}+\sum_{e\in \operatorname{\mathrm{Edges}}(\Gamma)\setminus\operatorname{\mathrm{Edges}}(G)}\underline{\mathbf e}_{v(e)}, \end{align} $$
$$ \begin{align}\widetilde{\underline{\mathbf d}} = \underline{\mathbf d}+\sum_{e\in \operatorname{\mathrm{Edges}}(\Gamma)\setminus\operatorname{\mathrm{Edges}}(G)}\underline{\mathbf e}_{v(e)}, \end{align} $$
for any choice of a function
![]() $v\colon \operatorname {\mathrm {Edges}}(\Gamma )\setminus \operatorname {\mathrm {Edges}}(G) \to \operatorname {\mathrm {Vert}}(\widetilde {\Gamma })$
such that each vertex
$v\colon \operatorname {\mathrm {Edges}}(\Gamma )\setminus \operatorname {\mathrm {Edges}}(G) \to \operatorname {\mathrm {Vert}}(\widetilde {\Gamma })$
such that each vertex
![]() $v(e)$
is one of the
$v(e)$
is one of the
![]() $m(e)$
interior vertices of the exceptional chain in
$m(e)$
interior vertices of the exceptional chain in
![]() $\widetilde {\Gamma }$
that corresponds to the edge e.
$\widetilde {\Gamma }$
that corresponds to the edge e.
Then we have the following:
Proposition 5.4. Let
![]() $\sigma $
be a degree d assignment on
$\sigma $
be a degree d assignment on
![]() $\Gamma $
that satisfies Part (1) of Definition 4.3. Then,
$\Gamma $
that satisfies Part (1) of Definition 4.3. Then,
-
1. Let
 $m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
be the constant function equal to
$m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
be the constant function equal to
 $1$
, and let
$1$
, and let
 $\widetilde {\Gamma }=\widetilde {\Gamma }_m$
and
$\widetilde {\Gamma }=\widetilde {\Gamma }_m$
and
 $\tilde {\sigma }=\tilde {\sigma }_m$
be as defined above. Assume that
$\tilde {\sigma }=\tilde {\sigma }_m$
be as defined above. Assume that
 $|\sigma (G)| \geq c(G)$
for all connected spanning subgraphs G of
$|\sigma (G)| \geq c(G)$
for all connected spanning subgraphs G of
 $\Gamma $
. If
$\Gamma $
. If
 $\widetilde {\sigma }\subset S^d({{\widetilde {\Gamma }}})$
is a minimal complete set of representatives for the action of
$\widetilde {\sigma }\subset S^d({{\widetilde {\Gamma }}})$
is a minimal complete set of representatives for the action of
 $\operatorname {\mathrm {Tw}}({{\widetilde {\Gamma }}})$
, then the assignment
$\operatorname {\mathrm {Tw}}({{\widetilde {\Gamma }}})$
, then the assignment
 $\sigma $
is a degree d stability assignment for
$\sigma $
is a degree d stability assignment for
 $\Gamma $
.
$\Gamma $
. -
2. If the assignment
 $\sigma $
also satisfies Part (2) of Definition 4.3, then for all
$\sigma $
also satisfies Part (2) of Definition 4.3, then for all
 $m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
, the lift
$m \colon \operatorname {\mathrm {Edges}}(\Gamma ) \to \mathbf {N}$
, the lift
 $\widetilde {\sigma }_m\subset S^d({{\widetilde {\Gamma }}}_m)$
(defined above) is a minimal complete set of representatives for the action of
$\widetilde {\sigma }_m\subset S^d({{\widetilde {\Gamma }}}_m)$
(defined above) is a minimal complete set of representatives for the action of
 $\operatorname {\mathrm {Tw}}({{\widetilde {\Gamma }}}_m)$
.
$\operatorname {\mathrm {Tw}}({{\widetilde {\Gamma }}}_m)$
.
Proof. We first prove (1) (i.e., we assume m is constant and equal to
![]() $1$
and prove that
$1$
and prove that
![]() $\sigma $
also satisfies Part (2) of Definition 4.3). By [Reference Viviani37, Theorem 1.20, (c)
$\sigma $
also satisfies Part (2) of Definition 4.3). By [Reference Viviani37, Theorem 1.20, (c)
![]() $\kern2.00em \Rightarrow \kern2.00em$
(b)], it suffices to prove that
$\kern2.00em \Rightarrow \kern2.00em$
(b)], it suffices to prove that
![]() $|\sigma (G)|=c(G)$
for all
$|\sigma (G)|=c(G)$
for all
![]() $G \subseteq \Gamma $
. By Proposition 4.7, it suffices to prove the inequality
$G \subseteq \Gamma $
. By Proposition 4.7, it suffices to prove the inequality
![]() $|\sigma (\Gamma )|\leq c(\Gamma )$
. Arguing by contradiction, it is enough to show that if any two different elements
$|\sigma (\Gamma )|\leq c(\Gamma )$
. Arguing by contradiction, it is enough to show that if any two different elements
![]() $\mathbf {\underline {e}}$
and
$\mathbf {\underline {e}}$
and
![]() $\mathbf {\underline {e}}'$
of
$\mathbf {\underline {e}}'$
of
![]() $\sigma (\Gamma )$
are in the same orbit for the action of
$\sigma (\Gamma )$
are in the same orbit for the action of
![]() $\operatorname {\mathrm {Tw}}(\Gamma )$
, then the corresponding lifts
$\operatorname {\mathrm {Tw}}(\Gamma )$
, then the corresponding lifts
![]() $\mathbf { \underline {\tilde {e}}}$
and
$\mathbf { \underline {\tilde {e}}}$
and
![]() $\mathbf {\underline {\tilde {e}}}'$
to
$\mathbf {\underline {\tilde {e}}}'$
to
![]() $\widetilde {\sigma }$
via Equation 5.2 are different and in the same
$\widetilde {\sigma }$
via Equation 5.2 are different and in the same
![]() $\operatorname {\mathrm {Tw}}(\widetilde {\Gamma })$
-orbit.
$\operatorname {\mathrm {Tw}}(\widetilde {\Gamma })$
-orbit.
Therefore, we assume that there exists
![]() $f \colon \operatorname {\mathrm {Vert}}(\Gamma) \to \mathbf {Z}$
such that
$f \colon \operatorname {\mathrm {Vert}}(\Gamma) \to \mathbf {Z}$
such that
We now defineFootnote 4 a lift
![]() $g \colon \operatorname {\mathrm {Vert}}({{\widetilde {\Gamma }}}) \to \mathbf {Z}$
of f as follows:
$g \colon \operatorname {\mathrm {Vert}}({{\widetilde {\Gamma }}}) \to \mathbf {Z}$
of f as follows:
 $$\begin{align*}g(v)= \begin{cases} 2 f(v') & \textrm{ when } v \textrm{ is not exceptional and corresponds to }v' \in \operatorname{\mathrm{Vert}}(\Gamma), \\ f(w)+f(w') &\textrm{ when } v \textrm{ is exceptional and lies between } w,w' \in \operatorname{\mathrm{Vert}}(\Gamma).\end{cases} \end{align*}$$
$$\begin{align*}g(v)= \begin{cases} 2 f(v') & \textrm{ when } v \textrm{ is not exceptional and corresponds to }v' \in \operatorname{\mathrm{Vert}}(\Gamma), \\ f(w)+f(w') &\textrm{ when } v \textrm{ is exceptional and lies between } w,w' \in \operatorname{\mathrm{Vert}}(\Gamma).\end{cases} \end{align*}$$
With this definition, we have
 $$\begin{align*}\mathbf{\tilde{\underline{e}}}- \mathbf{\tilde{\underline{e}}}' = \sum_{v \in \operatorname{\mathrm{Vert}}({{\widetilde{\Gamma}}})} g(v) \operatorname{\mathrm{Tw}}_{{{\widetilde{\Gamma}}},v}. \end{align*}$$
$$\begin{align*}\mathbf{\tilde{\underline{e}}}- \mathbf{\tilde{\underline{e}}}' = \sum_{v \in \operatorname{\mathrm{Vert}}({{\widetilde{\Gamma}}})} g(v) \operatorname{\mathrm{Tw}}_{{{\widetilde{\Gamma}}},v}. \end{align*}$$
This proves that the lifts
![]() $\mathbf {\tilde {\underline {e}}}$
and
$\mathbf {\tilde {\underline {e}}}$
and
![]() $ \mathbf {\tilde {\underline {e}}}'$
, which are different elements of
$ \mathbf {\tilde {\underline {e}}}'$
, which are different elements of
![]() $\widetilde {\sigma }$
, are in the same
$\widetilde {\sigma }$
, are in the same
![]() $\operatorname {\mathrm {Tw}}({{\widetilde {\Gamma }}})$
-orbit. This completes our proof of (1).
$\operatorname {\mathrm {Tw}}({{\widetilde {\Gamma }}})$
-orbit. This completes our proof of (1).
To prove (2), we begin by observing that if
![]() $\sigma $
is a stability assignment (as in Definition 4.3), then the number of elements of
$\sigma $
is a stability assignment (as in Definition 4.3), then the number of elements of
![]() $\widetilde {\sigma }_m$
equals the right-hand side of (5.1), which equals the complexity of
$\widetilde {\sigma }_m$
equals the right-hand side of (5.1), which equals the complexity of
![]() ${{\widetilde {\Gamma }}}_m$
by Lemma (5.3). Thus, it suffices to prove that any two different elements
${{\widetilde {\Gamma }}}_m$
by Lemma (5.3). Thus, it suffices to prove that any two different elements
![]() $\mathbf {\underline {\tilde {e}}}$
and
$\mathbf {\underline {\tilde {e}}}$
and
![]() $\mathbf { \underline {\tilde {e}}}'$
of
$\mathbf { \underline {\tilde {e}}}'$
of
![]() $\widetilde {\sigma }_m$
belong to different
$\widetilde {\sigma }_m$
belong to different
![]() $\operatorname {\mathrm {Tw}}(\widetilde {\Gamma }_m)$
-orbits. By Lemma 5.5 below, it suffices to prove the inequality
$\operatorname {\mathrm {Tw}}(\widetilde {\Gamma }_m)$
-orbits. By Lemma 5.5 below, it suffices to prove the inequality
 $$ \begin{align} \left| \sum_{v \in \widetilde{V}} \mathbf{\underline{\tilde{e}}}(v)-\mathbf{\underline{\tilde{e}}}'(v) \right|< \left|\operatorname{\mathrm{Edges}}(\widetilde{V},\widetilde{V}^c)\right| \end{align} $$
$$ \begin{align} \left| \sum_{v \in \widetilde{V}} \mathbf{\underline{\tilde{e}}}(v)-\mathbf{\underline{\tilde{e}}}'(v) \right|< \left|\operatorname{\mathrm{Edges}}(\widetilde{V},\widetilde{V}^c)\right| \end{align} $$
for all
![]() $\widetilde {V} \subset \operatorname {\mathrm {Vert}}(\widetilde {\Gamma }_m)$
such that the induced subgraph
$\widetilde {V} \subset \operatorname {\mathrm {Vert}}(\widetilde {\Gamma }_m)$
such that the induced subgraph
![]() $\Gamma (\widetilde {V})$
is connected.
$\Gamma (\widetilde {V})$
is connected.
Let
![]() $j \colon \operatorname {\mathrm {Vert}}(\Gamma ) \to \operatorname {\mathrm {Vert}}(\widetilde {\Gamma })$
be the inclusion of the nonexceptional vertices. If
$j \colon \operatorname {\mathrm {Vert}}(\Gamma ) \to \operatorname {\mathrm {Vert}}(\widetilde {\Gamma })$
be the inclusion of the nonexceptional vertices. If
![]() $\widetilde {V}$
is not in the image of j, then
$\widetilde {V}$
is not in the image of j, then
![]() $\widetilde {V}$
is a subset of an exceptional chain, so the right-hand side of (5.3) equals
$\widetilde {V}$
is a subset of an exceptional chain, so the right-hand side of (5.3) equals
![]() $2$
and by the definition of a lift, we have that the left-hand side of (5.3) equals
$2$
and by the definition of a lift, we have that the left-hand side of (5.3) equals
![]() $0$
or
$0$
or
![]() $1$
. From now on, we will assume that
$1$
. From now on, we will assume that
![]() $\widetilde {V}$
contains some nonexceptional vertices.
$\widetilde {V}$
contains some nonexceptional vertices.
We now prove (5.3) under the additional assumption that
![]() $\mathbf {\underline {\tilde {e}}}$
and
$\mathbf {\underline {\tilde {e}}}$
and
![]() $\mathbf {\underline {\tilde {e}}}'$
are zero on all exceptional vertices – namely, that they are lifts of elements
$\mathbf {\underline {\tilde {e}}}'$
are zero on all exceptional vertices – namely, that they are lifts of elements
![]() $\mathbf { \underline {{e}}}$
and
$\mathbf { \underline {{e}}}$
and
![]() $\mathbf {\underline {{e}}}'$
that belong to
$\mathbf {\underline {{e}}}'$
that belong to
![]() $\sigma (\Gamma )$
. Because
$\sigma (\Gamma )$
. Because
![]() $\sigma $
is a degree d stability assignment for
$\sigma $
is a degree d stability assignment for
![]() $\Gamma $
, by [Reference Viviani37, Theorem 1.20, (b)
$\Gamma $
, by [Reference Viviani37, Theorem 1.20, (b)
![]() $\Rightarrow $
(a)], it is also a ‘V-stability condition’ in the sense of [Reference Viviani37]. By [Reference Viviani37, Remark 1.10]), this means that, for all
$\Rightarrow $
(a)], it is also a ‘V-stability condition’ in the sense of [Reference Viviani37]. By [Reference Viviani37, Remark 1.10]), this means that, for all
![]() $V \subseteq \operatorname {\mathrm {Vert}}(\Gamma )$
such that
$V \subseteq \operatorname {\mathrm {Vert}}(\Gamma )$
such that
![]() $\Gamma (V)$
is connected, there exist integers
$\Gamma (V)$
is connected, there exist integers
![]() $n_{\mathbf {\vec {e}}}(V)$
and
$n_{\mathbf {\vec {e}}}(V)$
and
![]() $n_{\mathbf {\vec {e}'}}(V)$
such that the inequalities
$n_{\mathbf {\vec {e}'}}(V)$
such that the inequalities
and
hold. The combination of these two inequalities applied to
![]() $V:=j^{-1}(\widetilde {V})$
implies Inequality (5.3).
$V:=j^{-1}(\widetilde {V})$
implies Inequality (5.3).
If
![]() $\mathbf {\underline {\tilde {e}}}$
and
$\mathbf {\underline {\tilde {e}}}$
and
![]() $\mathbf {\underline {\tilde {e}}}'$
are not zero on all of the exceptional vertices of
$\mathbf {\underline {\tilde {e}}}'$
are not zero on all of the exceptional vertices of
![]() $\widetilde {\Gamma }$
, we first replace them by elements of
$\widetilde {\Gamma }$
, we first replace them by elements of
![]() $\widetilde {\sigma }_m$
that satisfy this additional hypothesis. This can be achieved by replacing each
$\widetilde {\sigma }_m$
that satisfy this additional hypothesis. This can be achieved by replacing each
![]() $1$
on each exceptional vertex in
$1$
on each exceptional vertex in
![]() $\tilde {V}$
(resp. in
$\tilde {V}$
(resp. in
![]() $\tilde {V}^c$
) with a
$\tilde {V}^c$
) with a
![]() $0$
, and for each such replacement by adding
$0$
, and for each such replacement by adding
![]() $+1$
on (one of) the closest nonexceptional vertex in
$+1$
on (one of) the closest nonexceptional vertex in
![]() $\Gamma (\tilde {V})$
(resp. in
$\Gamma (\tilde {V})$
(resp. in
![]() $\Gamma (\tilde {V}^c)$
). This replacement does not change the left-hand side of (5.3). That these replacements are also elements of
$\Gamma (\tilde {V}^c)$
). This replacement does not change the left-hand side of (5.3). That these replacements are also elements of
![]() $\widetilde {\sigma }_m$
follows from the fact that
$\widetilde {\sigma }_m$
follows from the fact that
![]() $\sigma $
satisfies Part (1) of Definition 4.3. This concludes our proof.
$\sigma $
satisfies Part (1) of Definition 4.3. This concludes our proof.
We conclude by proving the following, which was used in the proof of the above.
Lemma 5.5. Let
![]() $\mathbf {\underline {\tilde {e}}}$
and
$\mathbf {\underline {\tilde {e}}}$
and
![]() $\mathbf {\underline {\tilde {e}}}'$
be elements of
$\mathbf {\underline {\tilde {e}}}'$
be elements of
![]() $\tilde {\sigma }_m$
. If the inequality
$\tilde {\sigma }_m$
. If the inequality
 $$ \begin{align} \left| \sum_{v \in W} \mathbf{\underline{\tilde{e}}}(v)-\mathbf{\underline{\tilde{e}}}'(v) \right|< \left|\operatorname{\mathrm{Edges}}(W,W^c)\right| \end{align} $$
$$ \begin{align} \left| \sum_{v \in W} \mathbf{\underline{\tilde{e}}}(v)-\mathbf{\underline{\tilde{e}}}'(v) \right|< \left|\operatorname{\mathrm{Edges}}(W,W^c)\right| \end{align} $$
holds for all
![]() $W \subset \operatorname {\mathrm {Vert}}(\widetilde {\Gamma }_m)$
such that the induced subgraph
$W \subset \operatorname {\mathrm {Vert}}(\widetilde {\Gamma }_m)$
such that the induced subgraph
![]() $\Gamma (W)$
is connected, then
$\Gamma (W)$
is connected, then
![]() $\mathbf {\underline {\tilde {e}}}$
and
$\mathbf {\underline {\tilde {e}}}$
and
![]() $\mathbf {\underline {\tilde {e}}}'$
belong to different
$\mathbf {\underline {\tilde {e}}}'$
belong to different
![]() $\operatorname {\mathrm {Tw}}(\widetilde {\Gamma }_m)$
-orbits.
$\operatorname {\mathrm {Tw}}(\widetilde {\Gamma }_m)$
-orbits.
Proof. Assume for a contradiction that there exists
![]() $f \colon \operatorname {\mathrm {Vert}}(\widetilde {\Gamma }_m) \to \mathbf {Z}$
such that
$f \colon \operatorname {\mathrm {Vert}}(\widetilde {\Gamma }_m) \to \mathbf {Z}$
such that
 $$\begin{align*}\mathbf{\underline{\tilde{e}}'}= \mathbf{\underline{\tilde{e}}}+ \sum_{v \in \operatorname{\mathrm{Vert}}(\widetilde{\Gamma}_m)} f(v) \operatorname{\mathrm{Tw}}_{\widetilde{\Gamma}_m, v}. \end{align*}$$
$$\begin{align*}\mathbf{\underline{\tilde{e}}'}= \mathbf{\underline{\tilde{e}}}+ \sum_{v \in \operatorname{\mathrm{Vert}}(\widetilde{\Gamma}_m)} f(v) \operatorname{\mathrm{Tw}}_{\widetilde{\Gamma}_m, v}. \end{align*}$$
Defining W to be a subset of
![]() $\{w: \ f(w)=\min _{v\in \operatorname {\mathrm {Vert}}(\Gamma )}(f)\}$
such that both induced subgraph
$\{w: \ f(w)=\min _{v\in \operatorname {\mathrm {Vert}}(\Gamma )}(f)\}$
such that both induced subgraph
![]() $\Gamma (W)$
is connected (one such W subset always exists), we then deduce
$\Gamma (W)$
is connected (one such W subset always exists), we then deduce
This contradicts (5.4), thus concluding our proof.
6. From stability assignments to smoothable fine compactified Jacobians
In this section, we show how to construct a fine compactified Jacobian from a given stability assignment. We define a sheaf to be stable if its multidegree is as prescribed by the stability assignment, both in the case of a single nodal curve and for families. Then we show that the moduli space of stable sheaves thus defined is a fine compactified Jacobian as introduced in Definitions 3.1 and 3.7. The case of a curve in isolation is Corollary 6.4, and the more general case of families with smooth generic element is Theorem 6.3. The most difficult part is the proof of properness (Lemma 6.5).
Throughout this section, let X be a nodal curve over some field extension K of k, and let
![]() $\Gamma $
be its dual graph.
$\Gamma $
be its dual graph.
Definition 6.1. Let
![]() $\sigma $
be a degree d stability assignment for
$\sigma $
be a degree d stability assignment for
![]() $\Gamma $
(see Definition 4.3). We say that
$\Gamma $
(see Definition 4.3). We say that
![]() $[F] \in {\operatorname {Simp}}^d(X)$
is stable with respect to
$[F] \in {\operatorname {Simp}}^d(X)$
is stable with respect to
![]() $\boldsymbol {\sigma }$
if
$\boldsymbol {\sigma }$
if
![]() $(G(F),\underline {\deg }(F))$
is in
$(G(F),\underline {\deg }(F))$
is in
![]() $\sigma $
, where
$\sigma $
, where
![]() $G(F)=\Gamma \setminus {\operatorname {N}}(F)$
is the (necessarily connected and spanning) subgraph of
$G(F)=\Gamma \setminus {\operatorname {N}}(F)$
is the (necessarily connected and spanning) subgraph of
![]() $\Gamma $
that is dual to the normalization of X at the points (necessarily nodes) where F fails to be locally free.
$\Gamma $
that is dual to the normalization of X at the points (necessarily nodes) where F fails to be locally free.
We define
![]() $\overline {J}_\sigma \subseteq {\operatorname {Simp}}^d(X)$
as the subscheme of sheaves that are stable with respect to
$\overline {J}_\sigma \subseteq {\operatorname {Simp}}^d(X)$
as the subscheme of sheaves that are stable with respect to
![]() $\sigma $
.
$\sigma $
.
Let now
![]() $\mathcal {X}/S$
be a family of nodal curves over a k-scheme S. For every geometric point s of S, denote by
$\mathcal {X}/S$
be a family of nodal curves over a k-scheme S. For every geometric point s of S, denote by
![]() $\Gamma _s$
the dual graph of the fiber
$\Gamma _s$
the dual graph of the fiber
![]() $\mathcal {X}_s$
.
$\mathcal {X}_s$
.
Definition 6.2. Let
![]() $\mathfrak {S}=\{\sigma _s\}_{s \in S}$
be a family of degree d stability assignments for
$\mathfrak {S}=\{\sigma _s\}_{s \in S}$
be a family of degree d stability assignments for
![]() $\mathcal {X}/S$
as in Definition 4.9.
$\mathcal {X}/S$
as in Definition 4.9.
If F is a geometric point of
![]() $ {\operatorname {Simp}}^d(\mathcal {X}/S)$
lying over
$ {\operatorname {Simp}}^d(\mathcal {X}/S)$
lying over
![]() $s\in S$
, we say that F is stable with respect to
$s\in S$
, we say that F is stable with respect to
![]() $\mathfrak {\boldsymbol {S}}$
if F is stable with respect to
$\mathfrak {\boldsymbol {S}}$
if F is stable with respect to
![]() $\sigma _s$
(see Definition 6.1).
$\sigma _s$
(see Definition 6.1).
We define
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}\subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
as the algebraic subspace whose geometric points are sheaves that are stable with respect to
$\overline {\mathcal {J}}^d_{\mathfrak {S}}\subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
as the algebraic subspace whose geometric points are sheaves that are stable with respect to
![]() $\mathfrak {S}$
.
$\mathfrak {S}$
.
The main result of this section is the following:
Theorem 6.3. Assume that S is irreducible with generic point
![]() $\theta $
and that the generic element of the family
$\theta $
and that the generic element of the family
![]() $\mathcal {X}_\theta /\theta $
is smooth. Let
$\mathcal {X}_\theta /\theta $
is smooth. Let
![]() $\mathfrak {S}$
be a family of degree d stability assignments for
$\mathfrak {S}$
be a family of degree d stability assignments for
![]() $\mathcal {X}/S$
. Then
$\mathcal {X}/S$
. Then
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}\subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
is a degree d fine compactified Jacobian for the family
$\overline {\mathcal {J}}^d_{\mathfrak {S}}\subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
is a degree d fine compactified Jacobian for the family
![]() $\mathcal {X}/S$
.
$\mathcal {X}/S$
.
We immediately deduce the following:
Corollary 6.4. The moduli space
![]() $\overline {J}_\sigma \subseteq {\operatorname {Simp}}^d(X)$
of
$\overline {J}_\sigma \subseteq {\operatorname {Simp}}^d(X)$
of
![]() $\sigma $
-stable sheaves is a smoothable degree d fine compactified Jacobian for X.
$\sigma $
-stable sheaves is a smoothable degree d fine compactified Jacobian for X.
Proof. Apply Theorem 6.3 to a regular smoothing
![]() $\mathcal {X}/\Delta $
of X.
$\mathcal {X}/\Delta $
of X.
The most delicate part of the proof of Theorem 6.3 is the following result, which builds on the combinatorial preparation of the previous section.
Lemma 6.5. With the same assumptions as in Theorem 6.3, the moduli space
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is proper over S.
$\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is proper over S.
Proof. By Definitions 4.3 and 6.1, the scheme
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is the union of finitely many locally closed strata and hence of finite type and quasi-separated over S. To prove properness, we apply the refined valuative criterion [36, Lemma 70.22.3].
$\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is the union of finitely many locally closed strata and hence of finite type and quasi-separated over S. To prove properness, we apply the refined valuative criterion [36, Lemma 70.22.3].
Given the spectrum
![]() $\Delta $
of a DVR and a commutative diagram (of solid arrows)
$\Delta $
of a DVR and a commutative diagram (of solid arrows)

we need to prove that there exists exactly one dotted arrow that keeps the diagram commutative. (Note that
![]() $\operatorname {Pic}^d(\mathcal {X}_{\theta })$
is open and dense in
$\operatorname {Pic}^d(\mathcal {X}_{\theta })$
is open and dense in
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}$
).
$\overline {\mathcal {J}}^d_{\mathfrak {S}}$
).
Let us recall that morphisms to moduli spaces of sheaves (line bundles, simple sheaves) correspond to sheaves on the corresponding family of curves, but this correspondence is a bijection only after identifying two such sheaves whenever they differ by the pullback of a line bundle from the base. In the remainder of this proof, we will slightly abuse the notation and assume this identification.
Let us denote by
![]() $\mathcal X_{\Delta }/\Delta $
the base change of
$\mathcal X_{\Delta }/\Delta $
the base change of
![]() $\mathcal X/S$
under
$\mathcal X/S$
under
![]() $\Delta \rightarrow S$
and by
$\Delta \rightarrow S$
and by
![]() $\overline {\mathcal {J}}^d_{\Delta }\subseteq {\operatorname {Simp}}^d(\mathcal X/\Delta )$
the base change of
$\overline {\mathcal {J}}^d_{\Delta }\subseteq {\operatorname {Simp}}^d(\mathcal X/\Delta )$
the base change of
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}$
. Let s be the image of
$\overline {\mathcal {J}}^d_{\mathfrak {S}}$
. Let s be the image of
![]() $0 \in \Delta $
under
$0 \in \Delta $
under
![]() $\Delta \to S$
. Denoting by
$\Delta \to S$
. Denoting by
![]() $X= \mathcal {X}_s=\mathcal {X}_{\Delta ,0}$
the fiber over
$X= \mathcal {X}_s=\mathcal {X}_{\Delta ,0}$
the fiber over
![]() $0 \in \Delta $
of the family
$0 \in \Delta $
of the family
![]() $\mathcal {X}_{\Delta }/\Delta $
, by the hypothesis that
$\mathcal {X}_{\Delta }/\Delta $
, by the hypothesis that
![]() $\mathcal {X}_{\theta }/\theta $
is smooth, we deduce that
$\mathcal {X}_{\theta }/\theta $
is smooth, we deduce that
![]() $\mathcal {X}_{\Delta }/\Delta $
is a smoothing of X. Moreover, we have that
$\mathcal {X}_{\Delta }/\Delta $
is a smoothing of X. Moreover, we have that
![]() $\overline {\mathcal {J}}^d_{\Delta }$
is the disjoint union of
$\overline {\mathcal {J}}^d_{\Delta }$
is the disjoint union of
![]() $\operatorname {Pic}^d(\mathcal {X}_{\Delta , \eta })= {\operatorname {Simp}}^d(\mathcal {X}_{\Delta , \eta })$
and of
$\operatorname {Pic}^d(\mathcal {X}_{\Delta , \eta })= {\operatorname {Simp}}^d(\mathcal {X}_{\Delta , \eta })$
and of
![]() $\overline {J}_\sigma \subseteq {\operatorname {Simp}}^d(X)$
, where
$\overline {J}_\sigma \subseteq {\operatorname {Simp}}^d(X)$
, where
![]() $\sigma $
is the stability assignment for
$\sigma $
is the stability assignment for
![]() $\mathcal {X}_s$
.
$\mathcal {X}_s$
.
The morphism
![]() $f\colon \Delta \setminus \{0\}\rightarrow \operatorname {Pic}^d(\mathcal {X}_\theta )$
corresponds to a line bundle
$f\colon \Delta \setminus \{0\}\rightarrow \operatorname {Pic}^d(\mathcal {X}_\theta )$
corresponds to a line bundle
![]() $\mathcal [\mathcal {L}_{\eta }] \in \operatorname {Pic}^d(\mathcal {X}_{\Delta , \eta }/\eta )$
. We know from [Reference Esteves16] that
$\mathcal [\mathcal {L}_{\eta }] \in \operatorname {Pic}^d(\mathcal {X}_{\Delta , \eta }/\eta )$
. We know from [Reference Esteves16] that
![]() $ {\operatorname {Simp}}^d(\mathcal X_\Delta /\Delta )$
satisfies the existence part of the valuative criterion of properness; hence,
$ {\operatorname {Simp}}^d(\mathcal X_\Delta /\Delta )$
satisfies the existence part of the valuative criterion of properness; hence,
![]() $\mathcal L_{\eta }$
extends (possibly nonuniquely) to an element
$\mathcal L_{\eta }$
extends (possibly nonuniquely) to an element
![]() $[\mathcal L'] \in {\operatorname {Simp}}^d(\mathcal {X}_\Delta /\Delta )$
. Our proof is concluded if we can show that
$[\mathcal L'] \in {\operatorname {Simp}}^d(\mathcal {X}_\Delta /\Delta )$
. Our proof is concluded if we can show that
![]() $\mathcal L_{\eta }$
extends to a unique
$\mathcal L_{\eta }$
extends to a unique
![]() $[\mathcal L] \in \overline {\mathcal {J}}^d_{ \Delta }$
. When the total space
$[\mathcal L] \in \overline {\mathcal {J}}^d_{ \Delta }$
. When the total space
![]() $\mathcal {X}_{\Delta }$
of the smoothing
$\mathcal {X}_{\Delta }$
of the smoothing
![]() $\mathcal {X}_\Delta /\Delta $
is regular, this follows immediately from Remark 4.2.
$\mathcal {X}_\Delta /\Delta $
is regular, this follows immediately from Remark 4.2.
In general, each node e of the central fiber
![]() $X \subset \mathcal {X}_\Delta $
is a singularity of type
$X \subset \mathcal {X}_\Delta $
is a singularity of type
![]() $A_{m(e)}$
of the total space
$A_{m(e)}$
of the total space
![]() $\mathcal X_\Delta $
, for some
$\mathcal X_\Delta $
, for some
![]() $m(e) \in \mathbf {N}$
. Let
$m(e) \in \mathbf {N}$
. Let
![]() $g \colon \widetilde {\mathcal {X}} \to \mathcal {X}_\Delta $
be the resolution of singularities obtained by blowing up
$g \colon \widetilde {\mathcal {X}} \to \mathcal {X}_\Delta $
be the resolution of singularities obtained by blowing up
![]() $m(e)$
times each singularity e of
$m(e)$
times each singularity e of
![]() $\mathcal X_\Delta $
. The central fiber
$\mathcal X_\Delta $
. The central fiber
![]() $\widetilde {X} \subset \widetilde {\mathcal {X}}$
is therefore obtained by replacing each node e of the central fiber X of
$\widetilde {X} \subset \widetilde {\mathcal {X}}$
is therefore obtained by replacing each node e of the central fiber X of
![]() $\mathcal {X}_\Delta $
with a rational bridge of length
$\mathcal {X}_\Delta $
with a rational bridge of length
![]() $m(e)$
. In other words, the dual graph
$m(e)$
. In other words, the dual graph
![]() $\widetilde {\Gamma }$
of
$\widetilde {\Gamma }$
of
![]() $\widetilde {X}$
is obtained by subdividing
$\widetilde {X}$
is obtained by subdividing
![]() $m(e)$
times each edge of
$m(e)$
times each edge of
![]() $\Gamma =\Gamma (X)$
by adding
$\Gamma =\Gamma (X)$
by adding
![]() $m(e)$
additional genus
$m(e)$
additional genus
![]() $0$
vertices.
$0$
vertices.
We have now achieved that
![]() $\widetilde {\mathcal {X}}$
is regular. Moreover, by [Reference Esteves and Pacini17, Proposition 5.5], for each
$\widetilde {\mathcal {X}}$
is regular. Moreover, by [Reference Esteves and Pacini17, Proposition 5.5], for each
![]() $[F] \in {\operatorname {Simp}}^d(X)$
, there exists
$[F] \in {\operatorname {Simp}}^d(X)$
, there exists
![]() $[L] \in \operatorname {Pic}^d(\widetilde {X})$
such that
$[L] \in \operatorname {Pic}^d(\widetilde {X})$
such that
![]() $g_*(L)=F$
, and the multidegree
$g_*(L)=F$
, and the multidegree
![]() $\mathbf {d}$
of F and the multidegree
$\mathbf {d}$
of F and the multidegree
![]() $\widetilde {\mathbf {d}}$
of any such L are related by Equation (5.2), where
$\widetilde {\mathbf {d}}$
of any such L are related by Equation (5.2), where
![]() $G:=G(F)$
is the spanning subgraph consisting of all nodes where F is locally free.
$G:=G(F)$
is the spanning subgraph consisting of all nodes where F is locally free.
In order to prove the existence and uniqueness of an extension of
![]() $\mathcal L_{\eta }$
to
$\mathcal L_{\eta }$
to
![]() $\mathcal {X}_\Delta /\Delta $
with a sheaf in
$\mathcal {X}_\Delta /\Delta $
with a sheaf in
![]() $\overline {\mathcal {J}}^d_{\Delta }$
, we prove that
$\overline {\mathcal {J}}^d_{\Delta }$
, we prove that
![]() $g^*(\mathcal L_{\eta })$
extends uniquely on
$g^*(\mathcal L_{\eta })$
extends uniquely on
![]() $\widetilde {\mathcal {X}}/\Delta $
to a line bundle whose restriction to
$\widetilde {\mathcal {X}}/\Delta $
to a line bundle whose restriction to
![]() $\widetilde {X}$
has multidegree in
$\widetilde {X}$
has multidegree in
![]() $\widetilde {\sigma }$
, where the elements of
$\widetilde {\sigma }$
, where the elements of
![]() $\widetilde {\sigma }$
are defined by lifting elements of
$\widetilde {\sigma }$
are defined by lifting elements of
![]() $\sigma $
to
$\sigma $
to
![]() $\widetilde {\Gamma }$
as in Equation (5.2). Note that taking the direct image via g maps line bundles on
$\widetilde {\Gamma }$
as in Equation (5.2). Note that taking the direct image via g maps line bundles on
![]() $\widetilde {X}$
whose multidegree is in
$\widetilde {X}$
whose multidegree is in
![]() $\widetilde {\sigma }$
to rank
$\widetilde {\sigma }$
to rank
![]() $1$
, torsion free, simple sheaves on X whose multidegree is in
$1$
, torsion free, simple sheaves on X whose multidegree is in
![]() $\sigma (G)$
for
$\sigma (G)$
for
![]() $G \subseteq \Gamma $
the spanning subgraph whose edges correspond to the exceptional rational bridges in
$G \subseteq \Gamma $
the spanning subgraph whose edges correspond to the exceptional rational bridges in
![]() $\widetilde {\Gamma }$
where the multidegree of the line bundle is equal to zero on all vertices.
$\widetilde {\Gamma }$
where the multidegree of the line bundle is equal to zero on all vertices.
By Part (2) of Proposition 5.4, we deduce that
![]() $\widetilde {\sigma }$
is a minimal complete set of representatives for the action of the twister group
$\widetilde {\sigma }$
is a minimal complete set of representatives for the action of the twister group
![]() $\operatorname {\mathrm {Tw}}(\widetilde {\Gamma })$
on
$\operatorname {\mathrm {Tw}}(\widetilde {\Gamma })$
on
![]() $S^d(\widetilde {\Gamma })$
.
$S^d(\widetilde {\Gamma })$
.
We conclude, as in the regular case, that
![]() $g^*(\mathcal L_{\eta })$
extends to a unique line bundle
$g^*(\mathcal L_{\eta })$
extends to a unique line bundle
![]() $\widetilde {\mathcal L}$
on
$\widetilde {\mathcal L}$
on
![]() $\widetilde {\mathcal {X}}/\Delta $
whose multidegree on the central fiber
$\widetilde {\mathcal {X}}/\Delta $
whose multidegree on the central fiber
![]() $\widetilde {X}$
is an element of
$\widetilde {X}$
is an element of
![]() $\widetilde {\sigma }$
. Therefore,
$\widetilde {\sigma }$
. Therefore,
![]() $g_*{\widetilde {\mathcal {L}}}$
is the unique extension of
$g_*{\widetilde {\mathcal {L}}}$
is the unique extension of
![]() $\mathcal L_{\eta }$
whose multidegree on X is an element of
$\mathcal L_{\eta }$
whose multidegree on X is an element of
![]() $\sigma $
. This completes the proof.
$\sigma $
. This completes the proof.
We are now ready to complete the proof of Theorem 6.3.
Proof of Theorem 6.3
As
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is by definition constructible, openness is shown by proving that
$\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is by definition constructible, openness is shown by proving that
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}} \subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
is stable under generalization ([36, Lemma 5.19.10]). That
$\overline {\mathcal {J}}^d_{\mathfrak {S}} \subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
is stable under generalization ([36, Lemma 5.19.10]). That
![]() $\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is stable under generalization follows from the first requirement of Definition 4.3 and from the requirement that the family of stability assignments is compatible for graph morphisms arising from étale specializations (as specified in Definition 4.9).
$\overline {\mathcal {J}}^d_{\mathfrak {S}}$
is stable under generalization follows from the first requirement of Definition 4.3 and from the requirement that the family of stability assignments is compatible for graph morphisms arising from étale specializations (as specified in Definition 4.9).
Properness is Lemma 6.5.
7. From smoothable fine compactified Jacobians to stability assignments
In this section, we show that a smoothable fine compactified Jacobian defines a stability assignment in a natural way.
We start by considering the case of a curve in isolation and prove that the stability assignment associated with a (not necessarily smoothable) fine compactified Jacobian satisfies the first condition of Definition 4.3. This enables us to describe in Section 7.2 all fine compactified Jacobians for two classes of examples: vine curves and curves whose dual graph has topological genus
![]() $1$
. As an application, we prove in Lemma 7.8 that the stability assignment of a fine compactified Jacobian of an arbitrary nodal curve is nonempty for every connected spanning subgraph of the dual graph
$1$
. As an application, we prove in Lemma 7.8 that the stability assignment of a fine compactified Jacobian of an arbitrary nodal curve is nonempty for every connected spanning subgraph of the dual graph
![]() $\Gamma $
of the curve (a result needed in the proof of our main results, Corollaries 7.13 and 7.16).
$\Gamma $
of the curve (a result needed in the proof of our main results, Corollaries 7.13 and 7.16).
Then we restrict ourselves to the case where the fine compactified Jacobian is smoothable and proceed to prove the second condition of Definition 4.3 for the associated stability assignment (Corollary 7.13). Finally, we consider the case of families (Proposition 7.14), and we conclude by proving our main result, Corollary 7.16, which establishes that the operations described in this section and in the previous one are inverse to each other.
Throughout this section, we will consider a fixed nodal curve X over a field extension K of k, with dual graph
![]() $\Gamma $
, and denote by
$\Gamma $
, and denote by
![]() $\overline {J} \subset \operatorname {Simp}^{d}(X)$
a degree d fine compactified Jacobian of X.
$\overline {J} \subset \operatorname {Simp}^{d}(X)$
a degree d fine compactified Jacobian of X.
7.1. Definition and first properties
Definition 7.1. We define the associated assignment
![]() $\sigma _{\overline {J}}$
of
$\sigma _{\overline {J}}$
of
![]() ${\overline {J}}$
as
${\overline {J}}$
as
where
![]() $G(F)=\Gamma \setminus {\operatorname {N}}(F)$
is the connected spanning subgraph of
$G(F)=\Gamma \setminus {\operatorname {N}}(F)$
is the connected spanning subgraph of
![]() $\Gamma $
obtained by removing the edges corresponding to the nodes where F fails to be locally free.
$\Gamma $
obtained by removing the edges corresponding to the nodes where F fails to be locally free.
A key point is that if a sheaf is an element of a given fine compactified Jacobian, then so are all other sheaves that fail to be locally free on the same set of nodes and that have the same multidegree:
Lemma 7.2. Let
![]() $\overline {J} \subset {\operatorname {Simp}}^d(X)$
be a degree d fine compactified Jacobian, and assume that
$\overline {J} \subset {\operatorname {Simp}}^d(X)$
be a degree d fine compactified Jacobian, and assume that
![]() $(G,\underline {\mathbf d}) \in \sigma _{\overline {J}}$
. Then
$(G,\underline {\mathbf d}) \in \sigma _{\overline {J}}$
. Then
![]() $\overline {J}$
contains all sheaves
$\overline {J}$
contains all sheaves
![]() $[F]\in {\operatorname {Simp}}^d(X)$
with
$[F]\in {\operatorname {Simp}}^d(X)$
with
![]() $ {\operatorname {N}}(F) =\Gamma \setminus G$
and
$ {\operatorname {N}}(F) =\Gamma \setminus G$
and
![]() $\underline {\deg }(F)=\underline {\mathbf d}$
.
$\underline {\deg }(F)=\underline {\mathbf d}$
.
Proof. By possibly passing to the partial normalization of X at the nodes in
![]() $\Gamma \setminus G$
, we may assume that
$\Gamma \setminus G$
, we may assume that
![]() $G=\Gamma $
. Thus, we aim to prove that if
$G=\Gamma $
. Thus, we aim to prove that if
![]() $\mathcal {J}^{\underline {\mathbf d}}(X)\cap \overline {J} \neq \emptyset $
, then
$\mathcal {J}^{\underline {\mathbf d}}(X)\cap \overline {J} \neq \emptyset $
, then
![]() $\mathcal {J}^{\underline {\mathbf d}}(X) \subset \overline {J}$
.
$\mathcal {J}^{\underline {\mathbf d}}(X) \subset \overline {J}$
.
The moduli space of line bundles
![]() $\mathcal {J}^{\underline {\mathbf d}}(X)$
of multidegree
$\mathcal {J}^{\underline {\mathbf d}}(X)$
of multidegree
![]() $\underline {\mathbf d}$
is irreducible and
$\underline {\mathbf d}$
is irreducible and
![]() $\overline {J}$
is open, so
$\overline {J}$
is open, so
![]() $\mathcal {J}^{\underline {\mathbf d}}(X) \cap \overline {J} \neq \emptyset $
implies that
$\mathcal {J}^{\underline {\mathbf d}}(X) \cap \overline {J} \neq \emptyset $
implies that
![]() $\mathcal {J}^{\underline {\mathbf d}}(X)\cap \overline {J}$
is dense in
$\mathcal {J}^{\underline {\mathbf d}}(X)\cap \overline {J}$
is dense in
![]() $\mathcal {J}^{\underline {\mathbf d}}(X)$
. For
$\mathcal {J}^{\underline {\mathbf d}}(X)$
. For
![]() $[F]$
in
$[F]$
in
![]() $\mathcal {J}^{\underline {\mathbf d}}(X)$
, we can then find a line bundle L on
$\mathcal {J}^{\underline {\mathbf d}}(X)$
, we can then find a line bundle L on
![]() $X \times \Delta $
, for some
$X \times \Delta $
, for some
![]() $\Delta $
, spectrum of a DVR, whose generic element
$\Delta $
, spectrum of a DVR, whose generic element
![]() $L_{\eta }$
is in
$L_{\eta }$
is in
![]() $\mathcal {J}^{\underline {\mathbf d}}(X) \cap \overline {J}$
and whose special fiber
$\mathcal {J}^{\underline {\mathbf d}}(X) \cap \overline {J}$
and whose special fiber
![]() $L_0$
equals F.
$L_0$
equals F.
By properness of
![]() $\overline {J}$
, there exists a sheaf
$\overline {J}$
, there exists a sheaf
![]() $L'$
on
$L'$
on
![]() $X\times \Delta $
with the property that
$X\times \Delta $
with the property that
![]() $L^{\prime }_{X \times \eta }=L_{X \times \eta }$
(here,
$L^{\prime }_{X \times \eta }=L_{X \times \eta }$
(here,
![]() $\eta $
is the generic point of
$\eta $
is the generic point of
![]() $\Delta $
) and whose special fiber
$\Delta $
) and whose special fiber
![]() $L^{\prime }_0$
is in
$L^{\prime }_0$
is in
![]() $\overline {J}$
. Then
$\overline {J}$
. Then
![]() $L' \otimes L^{-1}$
defines a morphism
$L' \otimes L^{-1}$
defines a morphism
![]() $\Delta \to {\operatorname {Simp}}^0(X)$
that maps the generic point
$\Delta \to {\operatorname {Simp}}^0(X)$
that maps the generic point
![]() $\eta $
to a closed point; hence, it must be the constant morphism. We conclude, in particular, that
$\eta $
to a closed point; hence, it must be the constant morphism. We conclude, in particular, that
![]() $[F]=[L_0']$
and so
$[F]=[L_0']$
and so
![]() $[F] \in \overline {J}$
.
$[F] \in \overline {J}$
.
As a consequence of Lemma 5.2, the associated assignment to a fine compactified Jacobian satisfies the first condition of Definition 4.3:
Corollary 7.3. The associated assignment
![]() $\sigma _{\overline {J}}$
satisfies
$\sigma _{\overline {J}}$
satisfies
for all spanning subgraphs
![]() $G\subseteq \Gamma $
and all edges e of
$G\subseteq \Gamma $
and all edges e of
![]() $\operatorname {\mathrm {Edges}}(\Gamma )\setminus \operatorname {\mathrm {Edges}}(G)$
with endpoints
$\operatorname {\mathrm {Edges}}(\Gamma )\setminus \operatorname {\mathrm {Edges}}(G)$
with endpoints
![]() $v_1$
and
$v_1$
and
![]() $v_2$
.
$v_2$
.
Note that the above statement remains valid (with the same proof) for an arbitrary open subscheme of
![]() $ {\operatorname {Simp}}^d(X)$
; properness does not play any role here.
$ {\operatorname {Simp}}^d(X)$
; properness does not play any role here.
For every connected spanning subgraph G of
![]() $\Gamma $
, the pairs
$\Gamma $
, the pairs
![]() $(G,\underline {\mathbf d})\in \sigma $
with
$(G,\underline {\mathbf d})\in \sigma $
with
![]() $G\subset G$
define a fine compactified Jacobian on a partial normalization of the curves X.
$G\subset G$
define a fine compactified Jacobian on a partial normalization of the curves X.
Lemma 7.4. Let
![]() $f \colon X' \to X$
be a partial normalization of X at some nodes
$f \colon X' \to X$
be a partial normalization of X at some nodes
![]() $e_1, \ldots , e_k \in \operatorname {\mathrm {Edges}}(\Gamma )$
and let
$e_1, \ldots , e_k \in \operatorname {\mathrm {Edges}}(\Gamma )$
and let
![]() $j_f \colon {\operatorname {Simp}}^{d-k}(X') \to {\operatorname {Simp}}^d(X)$
be the morphism induced by taking the pushforward along f. If
$j_f \colon {\operatorname {Simp}}^{d-k}(X') \to {\operatorname {Simp}}^d(X)$
be the morphism induced by taking the pushforward along f. If
![]() $\overline {J}$
is a fine compactified Jacobian of X, then any geometrically connected component of
$\overline {J}$
is a fine compactified Jacobian of X, then any geometrically connected component of
![]() $j_f^{-1} (\overline {J})$
is a fine compactified Jacobian of
$j_f^{-1} (\overline {J})$
is a fine compactified Jacobian of
![]() $X'$
. Moreover, for every
$X'$
. Moreover, for every
![]() $G \subseteq \Gamma (X')$
, we have
$G \subseteq \Gamma (X')$
, we have
 $$ \begin{align} \bigcup_{J'\subset j_f^{-1}(\overline{J})}\sigma_{J'}(G)=\sigma_{\overline{J}}(G),\end{align} $$
$$ \begin{align} \bigcup_{J'\subset j_f^{-1}(\overline{J})}\sigma_{J'}(G)=\sigma_{\overline{J}}(G),\end{align} $$
where the union is over all geometrically connected components
![]() $J'$
of
$J'$
of
![]() $j_f^{-1}(\overline {J})$
.
$j_f^{-1}(\overline {J})$
.
Note that Lemma 7.4 does not exclude the possibility that
![]() $j_f^{-1} (\overline {J})= \emptyset $
. This possibility will be excluded later, in Lemma 7.8. Moreover, we observe that the pullback
$j_f^{-1} (\overline {J})= \emptyset $
. This possibility will be excluded later, in Lemma 7.8. Moreover, we observe that the pullback
![]() $j_f^{-1} (\overline {J})$
is not necessarily connected: an example is given by nonsmoothable fine compactified Jacobians of curves of arithmetic genus
$j_f^{-1} (\overline {J})$
is not necessarily connected: an example is given by nonsmoothable fine compactified Jacobians of curves of arithmetic genus
![]() $1$
; see the
$1$
; see the
![]() $\rho \geq 2$
case of [Reference Pagani and Tommasi32, Lemma 3.7].
$\rho \geq 2$
case of [Reference Pagani and Tommasi32, Lemma 3.7].
Proof. The fact that
![]() $j_f^{-1} (\overline {J})$
is open in
$j_f^{-1} (\overline {J})$
is open in
![]() $ {\operatorname {Simp}}^{d-k}(X')$
follows from the fact that openness is stable under base change.
$ {\operatorname {Simp}}^{d-k}(X')$
follows from the fact that openness is stable under base change.
Moreover,
![]() $j_f^{-1} (\overline {J})$
is separated and of finite type because
$j_f^{-1} (\overline {J})$
is separated and of finite type because
![]() $\overline {J}$
is. To complete the first part of the statement, it remains to show that
$\overline {J}$
is. To complete the first part of the statement, it remains to show that
![]() $j_f^{-1} (\overline {J})$
satisfies the existence part of the valuative criterion of properness.
$j_f^{-1} (\overline {J})$
satisfies the existence part of the valuative criterion of properness.
Let
![]() $\Delta \setminus \{0 \} \to j_f^{-1} (\overline {J})$
be a morphism out of a DVR without its closed point, which corresponds to an element
$\Delta \setminus \{0 \} \to j_f^{-1} (\overline {J})$
be a morphism out of a DVR without its closed point, which corresponds to an element
![]() $\mathcal {F'}$
in
$\mathcal {F'}$
in
![]() $ {\operatorname {Simp}}^{d-k}( X'\times \eta /\eta )$
. Because
$ {\operatorname {Simp}}^{d-k}( X'\times \eta /\eta )$
. Because
![]() $\overline {J}$
satisfies the existence part of the valuative criterion of properness, there exists a family of sheaves
$\overline {J}$
satisfies the existence part of the valuative criterion of properness, there exists a family of sheaves
![]() $\tilde {\mathcal {F}}$
in
$\tilde {\mathcal {F}}$
in
![]() $ {\operatorname {Simp}}^{d-k}(X \times \Delta /\Delta )$
whose restriction to
$ {\operatorname {Simp}}^{d-k}(X \times \Delta /\Delta )$
whose restriction to
![]() $\eta $
equals
$\eta $
equals
![]() $f_* (\mathcal {F})$
. Then the family
$f_* (\mathcal {F})$
. Then the family
![]() $f^*(\tilde {\mathcal {F}})/\text {torsion}$
is an extension of the original family
$f^*(\tilde {\mathcal {F}})/\text {torsion}$
is an extension of the original family
![]() $\mathcal {F}'$
, and with central fiber belonging to
$\mathcal {F}'$
, and with central fiber belonging to
![]() $j_f^{-1} (\overline {J})$
(because
$j_f^{-1} (\overline {J})$
(because
![]() $f^*(f_*(\tilde {\mathcal {F}}))/\text {torsion}=\tilde {\mathcal {F}}$
– see [Reference Alexeev1, Lemma 1.5]). This concludes the first part.
$f^*(f_*(\tilde {\mathcal {F}}))/\text {torsion}=\tilde {\mathcal {F}}$
– see [Reference Alexeev1, Lemma 1.5]). This concludes the first part.
The second part, or Equation (7.2), follows immediately from the definition of an associated assignment.
7.2. Examples
In this subsection, we consider fine compactified Jacobians for two classes of curves: vine curves (defined in Example 3.5) and curves whose dual graph
![]() $\Gamma $
has first Betti number
$\Gamma $
has first Betti number
![]() $1$
.
$1$
.
In the case of vine curves, Corollary 7.3 allows us to describe explicitly all fine compactified Jacobians and conclude that they are automatically smoothable.
Example 7.5. Let X be a vine curve of type t (as defined in Example 3.5) over some algebraically closed field K. We claim that any fine compactified Jacobian
![]() $\overline {J}$
of X is of the form
$\overline {J}$
of X is of the form
![]() $\overline {J} = \overline {J}_\sigma (X)$
for some stability assignment
$\overline {J} = \overline {J}_\sigma (X)$
for some stability assignment
![]() $\sigma $
as in Example 4.6. In particular, by Corollary 6.4,
$\sigma $
as in Example 4.6. In particular, by Corollary 6.4,
![]() $\overline {J}$
is smoothable.
$\overline {J}$
is smoothable.
This is clear when
![]() $t=1$
, as in that case each geometrically connected component of
$t=1$
, as in that case each geometrically connected component of
![]() $ {\operatorname {Simp}}^d(X)=\operatorname {Pic}^d(X)$
is proper.
$ {\operatorname {Simp}}^d(X)=\operatorname {Pic}^d(X)$
is proper.
For the case of arbitrary
![]() $t>1$
, we work by induction on t, using only Part (1) of Definition 4.3 and the claim of Lemma 7.2 (neither of which relies on the hypothesis of smoothability).
$t>1$
, we work by induction on t, using only Part (1) of Definition 4.3 and the claim of Lemma 7.2 (neither of which relies on the hypothesis of smoothability).
For
![]() $e \in \operatorname {\mathrm {Edges}}(\Gamma (X))$
, we let
$e \in \operatorname {\mathrm {Edges}}(\Gamma (X))$
, we let
![]() $X_e$
be the partial normalization of X at the node e only. In view of
$X_e$
be the partial normalization of X at the node e only. In view of
![]() $t>1$
, we have that
$t>1$
, we have that
![]() $X_e$
is connected and therefore
$X_e$
is connected and therefore
![]() $ {\operatorname {Simp}}^{d-1}(X_e) \neq \emptyset $
. Let
$ {\operatorname {Simp}}^{d-1}(X_e) \neq \emptyset $
. Let
![]() $j_e \colon {\operatorname {Simp}}^{d-1}(X_e) \to {\operatorname {Simp}}^{d}(X)$
be the morphism obtained by taking the pushforward along the partial normalization
$j_e \colon {\operatorname {Simp}}^{d-1}(X_e) \to {\operatorname {Simp}}^{d}(X)$
be the morphism obtained by taking the pushforward along the partial normalization
![]() $X_e \to X$
.
$X_e \to X$
.
We observe that there exists an
![]() $e \in \operatorname {\mathrm {Edges}}(\Gamma (X))$
such that
$e \in \operatorname {\mathrm {Edges}}(\Gamma (X))$
such that
![]() $j_e^{-1}\left (\overline {J}\right ) \neq \emptyset $
, for otherwise we would have that
$j_e^{-1}\left (\overline {J}\right ) \neq \emptyset $
, for otherwise we would have that
![]() $\overline {J}$
is contained in
$\overline {J}$
is contained in
![]() $\operatorname {Pic}^d(X)$
, so
$\operatorname {Pic}^d(X)$
, so
![]() $\overline {J}$
could not be proper. Fix one such edge e and let
$\overline {J}$
could not be proper. Fix one such edge e and let
![]() $\overline {J}_e \subseteq j_e^{-1}\left (\overline {J}\right )$
be a connected component. Then
$\overline {J}_e \subseteq j_e^{-1}\left (\overline {J}\right )$
be a connected component. Then
![]() $\overline {J}_e$
is a degree
$\overline {J}_e$
is a degree
![]() $d-1$
fine compactified Jacobian of
$d-1$
fine compactified Jacobian of
![]() $X_e$
, and
$X_e$
, and
![]() $X_e$
is a vine curve of type
$X_e$
is a vine curve of type
![]() $t-1$
. We apply the induction hypothesis to deduce that there exists some degree
$t-1$
. We apply the induction hypothesis to deduce that there exists some degree
![]() $d-1$
stability assignment
$d-1$
stability assignment
![]() $\sigma _e$
as described in Example 4.6 such that
$\sigma _e$
as described in Example 4.6 such that
![]() $\overline {J}_e=\overline {J}_{\sigma _e}(X_e)$
.
$\overline {J}_e=\overline {J}_{\sigma _e}(X_e)$
.
Let
![]() $\sigma $
be the stability assignment on X of the type studied in Example 4.6 that is minimal among those that respect Condition (1) of Definition 4.3 and whose restriction to
$\sigma $
be the stability assignment on X of the type studied in Example 4.6 that is minimal among those that respect Condition (1) of Definition 4.3 and whose restriction to
![]() $X_e$
equals
$X_e$
equals
![]() $\sigma _e$
. By Corollary 7.3, we have that
$\sigma _e$
. By Corollary 7.3, we have that
![]() $\overline {J}_e=\overline {J}_\sigma (X)$
is contained in
$\overline {J}_e=\overline {J}_\sigma (X)$
is contained in
![]() $\overline {J}$
. By Corollary 6.4,
$\overline {J}$
. By Corollary 6.4,
![]() $\overline {J}_\sigma (X)$
is open in
$\overline {J}_\sigma (X)$
is open in
![]() $ {\operatorname {Simp}}^d(X)$
, and it is proper and geometrically connected. As
$ {\operatorname {Simp}}^d(X)$
, and it is proper and geometrically connected. As
![]() $\overline {J}$
also enjoys these three properties, we conclude that
$\overline {J}$
also enjoys these three properties, we conclude that
![]() $\overline {J}=\overline {J}_\sigma (X)$
.
$\overline {J}=\overline {J}_\sigma (X)$
.
Next, we discuss curves whose unlabeled dual graph has genus
![]() $1$
, and we prove that the combinatorial description of the strata of fine compactified Jacobians of nodal curves of arithmetic genus
$1$
, and we prove that the combinatorial description of the strata of fine compactified Jacobians of nodal curves of arithmetic genus
![]() $1$
given in [Reference Pagani and Tommasi32, Section 3] generalizes to the fine compactified Jacobians of an arbitrary nodal curve X with dual graph
$1$
given in [Reference Pagani and Tommasi32, Section 3] generalizes to the fine compactified Jacobians of an arbitrary nodal curve X with dual graph
![]() $\Gamma $
with
$\Gamma $
with
![]() $b_1(\Gamma )=1$
.
$b_1(\Gamma )=1$
.
Lemma 7.6. If
![]() $\overline {J}$
is a fine compactified Jacobian of a curve X with
$\overline {J}$
is a fine compactified Jacobian of a curve X with
![]() $b_1(\Gamma )=1$
, then
$b_1(\Gamma )=1$
, then
![]() $\sigma _{\overline {J}}(G) \neq \emptyset $
holds for all connected spanning subgraphs
$\sigma _{\overline {J}}(G) \neq \emptyset $
holds for all connected spanning subgraphs
![]() $G \subseteq \Gamma $
.
$G \subseteq \Gamma $
.
Proof. We can assume that
![]() $\Gamma $
has no separating edges. Indeed, by [Reference Pagani and Tommasi32, Lemma 2.7], the fine compactified Jacobian of a curve with a separating node is the product of fine compactified Jacobians of the two curves obtained by normalizing that node.
$\Gamma $
has no separating edges. Indeed, by [Reference Pagani and Tommasi32, Lemma 2.7], the fine compactified Jacobian of a curve with a separating node is the product of fine compactified Jacobians of the two curves obtained by normalizing that node.
We may also assume that
![]() $\Gamma $
does not contain any loops based at one vertex, as the claim is trivial in that case. Let us assume that
$\Gamma $
does not contain any loops based at one vertex, as the claim is trivial in that case. Let us assume that
![]() $|\operatorname {\mathrm {Vert}}(\Gamma )|=n\geq 2$
. Because
$|\operatorname {\mathrm {Vert}}(\Gamma )|=n\geq 2$
. Because
![]() $b_1(\Gamma )=1$
, we can imagine
$b_1(\Gamma )=1$
, we can imagine
![]() $\Gamma $
as a ‘necklace’of n vertices each connected to the next by one edge, each carrying its own genus weighting. The only possible connected spanning subgraphs of
$\Gamma $
as a ‘necklace’of n vertices each connected to the next by one edge, each carrying its own genus weighting. The only possible connected spanning subgraphs of
![]() $\Gamma $
in this case are
$\Gamma $
in this case are
![]() $\Gamma $
itself, and all graphs obtained by removing any one edge from
$\Gamma $
itself, and all graphs obtained by removing any one edge from
![]() $\Gamma $
.
$\Gamma $
.
The generalized Jacobian
![]() $\mathcal {J}^{\mathbf 0}(X)$
of X is a semi-abelian variety which is a
$\mathcal {J}^{\mathbf 0}(X)$
of X is a semi-abelian variety which is a
![]() $\mathbf G_m$
-bundle over the product of the Jacobians of the irreducible components of X. As a consequence, the strata
$\mathbf G_m$
-bundle over the product of the Jacobians of the irreducible components of X. As a consequence, the strata
![]() $\mathcal {J}^d_{(G,\underline {\mathbf d})}$
of
$\mathcal {J}^d_{(G,\underline {\mathbf d})}$
of
![]() $ {\operatorname {Simp}}^d(X)$
are either open (when
$ {\operatorname {Simp}}^d(X)$
are either open (when
![]() $G=\Gamma $
) or closed (when G is obtained by removing one edge e from
$G=\Gamma $
) or closed (when G is obtained by removing one edge e from
![]() $\Gamma $
). The open strata are all isomorphic to
$\Gamma $
). The open strata are all isomorphic to
![]() $\mathcal {J}^{\mathbf 0}(X)$
, while the closed ones are isomorphic to the abelian variety given by the product of the degree
$\mathcal {J}^{\mathbf 0}(X)$
, while the closed ones are isomorphic to the abelian variety given by the product of the degree
![]() $0$
Jacobians of the components of X.
$0$
Jacobians of the components of X.
Let
![]() $\overline {J}$
be a fine compactified Jacobian of X. By openness, there exists some
$\overline {J}$
be a fine compactified Jacobian of X. By openness, there exists some
![]() $\underline {\mathbf {d}}$
such that
$\underline {\mathbf {d}}$
such that
![]() $\overline {J}$
contains the open stratum
$\overline {J}$
contains the open stratum
![]() $\mathcal {J}^d_{(\Gamma ,\underline {\mathbf d)}}$
.
$\mathcal {J}^d_{(\Gamma ,\underline {\mathbf d)}}$
.
We have that
![]() $\overline {J}$
satisfies the valuative criterion for properness; thus, the present situation is similar to [Reference Pagani and Tommasi32, Section 3]. Consider any morphism
$\overline {J}$
satisfies the valuative criterion for properness; thus, the present situation is similar to [Reference Pagani and Tommasi32, Section 3]. Consider any morphism
![]() $\Delta \setminus \{0 \} \to \mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
(where
$\Delta \setminus \{0 \} \to \mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
(where
![]() $\Delta $
is the spectrum of a DVR), which is not the restriction of a morphism
$\Delta $
is the spectrum of a DVR), which is not the restriction of a morphism
![]() $\Delta \to \mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
. Then the argument in loc. cit. can be adapted to show that
$\Delta \to \mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
. Then the argument in loc. cit. can be adapted to show that
![]() $f\colon \Delta \setminus \{0 \} \to \mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
extends to a morphism
$f\colon \Delta \setminus \{0 \} \to \mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
extends to a morphism
![]() $\Delta \to {\operatorname {Simp}}^d(X)$
in n different ways, each one of them hitting a different closed stratum
$\Delta \to {\operatorname {Simp}}^d(X)$
in n different ways, each one of them hitting a different closed stratum
![]() $\mathcal J^d_{(\Gamma \setminus \{e\},\underline {\mathbf {d}'})}$
for some
$\mathcal J^d_{(\Gamma \setminus \{e\},\underline {\mathbf {d}'})}$
for some
![]() $\underline {\mathbf {d}'}$
.
$\underline {\mathbf {d}'}$
.
This implies that the closure of
![]() $\mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
inside
$\mathcal J^d_{(\Gamma ,\underline {\mathbf {d}})}$
inside
![]() $ {\operatorname {Simp}}^d(X)$
looks like a compactification of the semi-abelian variety which is made non-separated by the fact that the divisors over both the
$ {\operatorname {Simp}}^d(X)$
looks like a compactification of the semi-abelian variety which is made non-separated by the fact that the divisors over both the
![]() $0$
-section and the
$0$
-section and the
![]() $\infty $
-section of the extension of the
$\infty $
-section of the extension of the
![]() $\mathbf G_m$
-bundle
$\mathbf G_m$
-bundle
![]() $\mathcal {J}^{\mathbf 0}(X)$
to a
$\mathcal {J}^{\mathbf 0}(X)$
to a
![]() $\mathbf P^1$
-bundle are present in n copies.
$\mathbf P^1$
-bundle are present in n copies.
Moreover, the poset associated with the stratification of
![]() $ {\operatorname {Simp}}^d(X)$
is isomorphic to the poset associated with the stratification of
$ {\operatorname {Simp}}^d(X)$
is isomorphic to the poset associated with the stratification of
![]() $ {\operatorname {Simp}}^d(X')$
, where
$ {\operatorname {Simp}}^d(X')$
, where
![]() $\Gamma (X)$
and
$\Gamma (X)$
and
![]() $\Gamma (X')$
have the same underlying graph, but possibly a different genus weighting on each vertex. Hence, the combinatorial characterization of the neighborhoods of the points of
$\Gamma (X')$
have the same underlying graph, but possibly a different genus weighting on each vertex. Hence, the combinatorial characterization of the neighborhoods of the points of
![]() $\mathcal J^d_{(\Gamma \setminus \{e\},\underline {\mathbf {d}})}$
is the same as in the genus
$\mathcal J^d_{(\Gamma \setminus \{e\},\underline {\mathbf {d}})}$
is the same as in the genus
![]() $1$
case. This allows us to conclude that the geometrical considerations applied to the description of the fine compactified Jacobians of
$1$
case. This allows us to conclude that the geometrical considerations applied to the description of the fine compactified Jacobians of
![]() $X'$
in [Reference Pagani and Tommasi32, Section 3] apply in the same way to the fine compactified Jacobians of X. This establishes, in particular, that
$X'$
in [Reference Pagani and Tommasi32, Section 3] apply in the same way to the fine compactified Jacobians of X. This establishes, in particular, that
![]() $\sigma _{\overline {J}}(\Gamma \setminus \{e\})$
is nonempty for every edge e.
$\sigma _{\overline {J}}(\Gamma \setminus \{e\})$
is nonempty for every edge e.
Remark 7.7. The proof of Lemma 7.6 above actually shows that if
![]() $X'$
is an arbitrary curve whose dual graph
$X'$
is an arbitrary curve whose dual graph
![]() $\Gamma '$
is isomorphic to
$\Gamma '$
is isomorphic to
![]() $\Gamma $
, with possibly a different choice of the genera labeling the vertices, then the assignment
$\Gamma $
, with possibly a different choice of the genera labeling the vertices, then the assignment
![]() $\sigma _{\overline {J}}$
associated with
$\sigma _{\overline {J}}$
associated with
![]() $\overline {J}$
also describes a fine compactified Jacobian on
$\overline {J}$
also describes a fine compactified Jacobian on
![]() $X'$
. We can deduce from this that the combinatorial description of fine compactified Jacobians of nodal curves of arithmetic genus
$X'$
. We can deduce from this that the combinatorial description of fine compactified Jacobians of nodal curves of arithmetic genus
![]() $1$
given in [Reference Pagani and Tommasi32, Section 3] generalizes to fine compactified Jacobians of arbitrary nodal curves with dual graph
$1$
given in [Reference Pagani and Tommasi32, Section 3] generalizes to fine compactified Jacobians of arbitrary nodal curves with dual graph
![]() $\Gamma $
with
$\Gamma $
with
![]() $b_1(\Gamma )=1$
.
$b_1(\Gamma )=1$
.
In preparation of our main results later (Corollaries 7.13, 7.16), we now prove the following.
Lemma 7.8.
Footnote 5 Let
![]() $\overline {J} \subset {\operatorname {Simp}}^d(X)$
be a degree d fine compactified Jacobian. Then
$\overline {J} \subset {\operatorname {Simp}}^d(X)$
be a degree d fine compactified Jacobian. Then
![]() $\sigma _{\overline {J}}(G) \neq \emptyset $
holds for all connected spanning subgraphs
$\sigma _{\overline {J}}(G) \neq \emptyset $
holds for all connected spanning subgraphs
![]() $G \subseteq \Gamma $
.
$G \subseteq \Gamma $
.
In the course of the proof, we will use the following
Lemma 7.9. Let
![]() $\overline {J} \subset {\operatorname {Simp}}^d(X)$
be a degree d fine compactified Jacobian. Then there exists a spanning tree T of
$\overline {J} \subset {\operatorname {Simp}}^d(X)$
be a degree d fine compactified Jacobian. Then there exists a spanning tree T of
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\sigma (T)\neq \emptyset $
.
$\sigma (T)\neq \emptyset $
.
Proof. By Lemma 7.2, we have that
![]() $\overline {J}$
is a union of strata of
$\overline {J}$
is a union of strata of
![]() $ {\operatorname {Simp}}^d(X)$
. The strata of
$ {\operatorname {Simp}}^d(X)$
. The strata of
![]() $ {\operatorname {Simp}}^d(X)$
in (3.1) that are universally closed are the minimal strata (i.e., those that correspond to the case where G in (3.1) is a spanning tree of
$ {\operatorname {Simp}}^d(X)$
in (3.1) that are universally closed are the minimal strata (i.e., those that correspond to the case where G in (3.1) is a spanning tree of
![]() $\Gamma $
). Because
$\Gamma $
). Because
![]() $\overline {J}$
is universally closed, it must contain at least one minimal stratum of
$\overline {J}$
is universally closed, it must contain at least one minimal stratum of
![]() $ {\operatorname {Simp}}^d(X)$
.
$ {\operatorname {Simp}}^d(X)$
.
Proof of Lemma 7.8
Let us recall from Lemma 7.9 that there exists a spanning tree
![]() $T \subseteq \Gamma $
such that
$T \subseteq \Gamma $
such that
![]() $\sigma _{\overline {J}}(T) \neq \emptyset $
. If
$\sigma _{\overline {J}}(T) \neq \emptyset $
. If
![]() $b_1(\Gamma )=0$
, then
$b_1(\Gamma )=0$
, then
![]() $\Gamma =T$
, and the proof is concluded. If
$\Gamma =T$
, and the proof is concluded. If
![]() $b_1(\Gamma )=1$
, then the result follows from Lemma 7.6. From now on, we assume
$b_1(\Gamma )=1$
, then the result follows from Lemma 7.6. From now on, we assume
![]() $b_1(\Gamma ) \geq 2$
.
$b_1(\Gamma ) \geq 2$
.
Let us assume by contradiction that there exists a connected spanning subgraph G such that
![]() $\sigma _{\overline {J}}(G) = \emptyset $
. Let us choose G maximal for this property; note that G is always different from
$\sigma _{\overline {J}}(G) = \emptyset $
. Let us choose G maximal for this property; note that G is always different from
![]() $\Gamma $
as a consequence of the fact that
$\Gamma $
as a consequence of the fact that
![]() $\overline {J}$
is open in
$\overline {J}$
is open in
![]() $ {\operatorname {Simp}}^d(X)$
. After possibly replacing
$ {\operatorname {Simp}}^d(X)$
. After possibly replacing
![]() $\Gamma $
with a subgraph containing G and X with the partial normalization corresponding to this subgraph, and by Lemma 7.4, we may assume that G is obtained from
$\Gamma $
with a subgraph containing G and X with the partial normalization corresponding to this subgraph, and by Lemma 7.4, we may assume that G is obtained from
![]() $\Gamma $
by removing a single edge e.
$\Gamma $
by removing a single edge e.
If
![]() $T \subseteq G$
, then a contradiction arises immediately from Corollary 7.3. We can therefore assume
$T \subseteq G$
, then a contradiction arises immediately from Corollary 7.3. We can therefore assume
![]() $T \not \subset G$
– in other words, that
$T \not \subset G$
– in other words, that
![]() $e \in \operatorname {\mathrm {Edges}}(T) \setminus \operatorname {\mathrm {Edges}}(G)$
.
$e \in \operatorname {\mathrm {Edges}}(T) \setminus \operatorname {\mathrm {Edges}}(G)$
.
There exists
![]() $e' \in \operatorname {\mathrm {Edges}}(G) \setminus \operatorname {\mathrm {Edges}}(T)$
such that the graph
$e' \in \operatorname {\mathrm {Edges}}(G) \setminus \operatorname {\mathrm {Edges}}(T)$
such that the graph
![]() $T'$
, obtained from T by adding the edge
$T'$
, obtained from T by adding the edge
![]() $e'$
and removing the edge e, is connected (hence a spanning tree) and contained in G. We set
$e'$
and removing the edge e, is connected (hence a spanning tree) and contained in G. We set
![]() $\Gamma '$
to be the graph obtained by adding
$\Gamma '$
to be the graph obtained by adding
![]() $e'$
to the edge set of T (or equivalently, by adding e to the edge set of
$e'$
to the edge set of T (or equivalently, by adding e to the edge set of
![]() $T'$
). Then we have that
$T'$
). Then we have that
![]() $b_1(\Gamma ')=1$
.
$b_1(\Gamma ')=1$
.
Let
![]() $X' \subset X$
be the subcurve whose dual graph equals
$X' \subset X$
be the subcurve whose dual graph equals
![]() $\Gamma '$
, let
$\Gamma '$
, let
![]() $k:=\left |\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(\Gamma ')\right |$
, and let
$k:=\left |\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(\Gamma ')\right |$
, and let
![]() $j \colon {\operatorname {Simp}}^{d-k}(X') \to {\operatorname {Simp}}^{d}(X)$
be the morphism obtained by taking the pushforward along the partial normalization
$j \colon {\operatorname {Simp}}^{d-k}(X') \to {\operatorname {Simp}}^{d}(X)$
be the morphism obtained by taking the pushforward along the partial normalization
![]() $X' \to X$
. Because
$X' \to X$
. Because
![]() $\sigma _{\overline {J}}(T) \neq \emptyset $
, and by Lemma 7.4, there exists some geometrically connected component
$\sigma _{\overline {J}}(T) \neq \emptyset $
, and by Lemma 7.4, there exists some geometrically connected component
![]() $J'$
of
$J'$
of
![]() $j^*(\overline {J})$
that is a degree
$j^*(\overline {J})$
that is a degree
![]() $d-k$
fine compactified Jacobian of
$d-k$
fine compactified Jacobian of
![]() $X'$
.
$X'$
.
Because
![]() $b_1(\Gamma ')=1$
, from the last paragraph, we can then conclude by Lemma 7.6 that
$b_1(\Gamma ')=1$
, from the last paragraph, we can then conclude by Lemma 7.6 that
![]() $\sigma (T') \neq \emptyset $
for all spanning trees
$\sigma (T') \neq \emptyset $
for all spanning trees
![]() $T' \subseteq \Gamma '$
. In particular, there exists a
$T' \subseteq \Gamma '$
. In particular, there exists a
![]() $T' \subseteq G$
such that
$T' \subseteq G$
such that
![]() $\sigma (T') \neq \emptyset $
; thus, by Equation (7.2) combined with Corollary 7.3, we conclude that
$\sigma (T') \neq \emptyset $
; thus, by Equation (7.2) combined with Corollary 7.3, we conclude that
![]() $\sigma _{\overline {J}}(G) \neq \emptyset $
, which contradicts the assumption
$\sigma _{\overline {J}}(G) \neq \emptyset $
, which contradicts the assumption
![]() $\sigma _{\overline {J}}(G) = \emptyset $
made at the beginning.
$\sigma _{\overline {J}}(G) = \emptyset $
made at the beginning.
7.3. Stability assignments of smoothable fine compactified Jacobians
We now go back to our main line of reasoning and show that the assignment associated to a smoothable fine compactified Jacobian also satisfies the second condition of Definition 4.3.
Proposition 7.10. If
![]() $\overline {J} \subseteq {\operatorname {Simp}}^d(X)$
is also smoothable, then for all spanning subgraphs
$\overline {J} \subseteq {\operatorname {Simp}}^d(X)$
is also smoothable, then for all spanning subgraphs
![]() $G \subseteq \Gamma $
, the subset
$G \subseteq \Gamma $
, the subset
![]() $\sigma _{\overline {J}}(G)\subset S^d_{\Gamma }(G)$
is a minimal complete set of representatives for the action of the twister group
$\sigma _{\overline {J}}(G)\subset S^d_{\Gamma }(G)$
is a minimal complete set of representatives for the action of the twister group
![]() $\operatorname {\mathrm {Tw}}(G)$
on
$\operatorname {\mathrm {Tw}}(G)$
on
![]() $S^d_{\Gamma }(G)$
.
$S^d_{\Gamma }(G)$
.
Proof. We first fix some notation for our proof. Let
![]() $\mathcal {X}/\Delta $
be a regular smoothing of X such that there exists an open
$\mathcal {X}/\Delta $
be a regular smoothing of X such that there exists an open
![]() $\overline {\mathcal J}_{\mathcal {X}/\Delta } \subseteq {\operatorname {Simp}}^d(\mathcal {X}/\Delta )$
and
$\overline {\mathcal J}_{\mathcal {X}/\Delta } \subseteq {\operatorname {Simp}}^d(\mathcal {X}/\Delta )$
and
![]() $\Delta $
-proper subscheme, whose special fiber equals
$\Delta $
-proper subscheme, whose special fiber equals
![]() $\overline {J}$
. Then consider the degree
$\overline {J}$
. Then consider the degree
![]() $2$
base change
$2$
base change
![]() $\Delta \to \Delta $
of
$\Delta \to \Delta $
of
![]() $\mathcal {X}/\Delta $
, giving a nonregular smoothing
$\mathcal {X}/\Delta $
, giving a nonregular smoothing
![]() $\mathcal {X}'/ \Delta $
with
$\mathcal {X}'/ \Delta $
with
![]() $A_1$
singularities at all nodes of the special fiber X. By functoriality of the Picard functor, and by stability under base change of openness and properness, we have that the base change
$A_1$
singularities at all nodes of the special fiber X. By functoriality of the Picard functor, and by stability under base change of openness and properness, we have that the base change
![]() $\overline {\mathcal J}^{\prime }_{\mathcal {X}'/\Delta }$
is also an open and
$\overline {\mathcal J}^{\prime }_{\mathcal {X}'/\Delta }$
is also an open and
![]() $\Delta $
-proper subscheme of
$\Delta $
-proper subscheme of
![]() $ {\operatorname {Simp}}^d(\mathcal {X}'/\Delta )$
. Finally, let
$ {\operatorname {Simp}}^d(\mathcal {X}'/\Delta )$
. Finally, let
![]() $f \colon \widetilde {\mathcal {X}} \to \mathcal {X}' $
be the blow-up at all singularities. The family
$f \colon \widetilde {\mathcal {X}} \to \mathcal {X}' $
be the blow-up at all singularities. The family
![]() $\widetilde {\mathcal {X}}$
is then a regular smoothing of the special fiber
$\widetilde {\mathcal {X}}$
is then a regular smoothing of the special fiber
![]() $\widetilde {X}$
, the curve obtained from X by replacing each node with an irreducible rational bridge.
$\widetilde {X}$
, the curve obtained from X by replacing each node with an irreducible rational bridge.
We are now ready for the proof. First, observe that, by Corollary 7.3 and by Lemma 7.8 combined with Proposition 4.7, the set
![]() $\sigma _{\overline {J}}$
satisfies the hypothesis of Proposition 5.4 Part (1). By applying loc. cit., it is enough to prove that the collection
$\sigma _{\overline {J}}$
satisfies the hypothesis of Proposition 5.4 Part (1). By applying loc. cit., it is enough to prove that the collection
![]() $\widetilde {\sigma }_{\overline {J}}$
obtained by lifting every element of
$\widetilde {\sigma }_{\overline {J}}$
obtained by lifting every element of
![]() $\sigma _{\overline {J}}$
via Equation 5.2 is a minimal complete set of representatives for the action of
$\sigma _{\overline {J}}$
via Equation 5.2 is a minimal complete set of representatives for the action of
![]() $\operatorname {\mathrm {Tw}}({\Gamma (\widetilde {X}}))$
.
$\operatorname {\mathrm {Tw}}({\Gamma (\widetilde {X}}))$
.
Let
![]() $\mathbf {\vec {d}}$
be the lift via (5.2) of some
$\mathbf {\vec {d}}$
be the lift via (5.2) of some
![]() ${\mathbf d} \in S^d_\Gamma (G)$
for some
${\mathbf d} \in S^d_\Gamma (G)$
for some
![]() $G \subseteq \Gamma $
. There exists
$G \subseteq \Gamma $
. There exists
![]() $[L] \in \operatorname {\mathrm {Pic}}^d(\widetilde {X})$
such that
$[L] \in \operatorname {\mathrm {Pic}}^d(\widetilde {X})$
such that
![]() $\underline {\deg }(f_*(L)) \in S^{\mathbf{d}}_{\Gamma }(G)$
. By Hensel’s lemma, L extends to a family
$\underline {\deg }(f_*(L)) \in S^{\mathbf{d}}_{\Gamma }(G)$
. By Hensel’s lemma, L extends to a family
![]() $[\mathcal {L}] \in \operatorname {Pic}^d(\widetilde {\mathcal {X}}/\Delta )$
. Since
$[\mathcal {L}] \in \operatorname {Pic}^d(\widetilde {\mathcal {X}}/\Delta )$
. Since
![]() $\overline {J}_{\mathcal {X}'/\Delta }$
is universally closed over
$\overline {J}_{\mathcal {X}'/\Delta }$
is universally closed over
![]() $\Delta $
, there exists
$\Delta $
, there exists
![]() $\mathcal {F}'\in {\operatorname {Simp}}^d(\mathcal {X}'/\Delta )$
such that
$\mathcal {F}'\in {\operatorname {Simp}}^d(\mathcal {X}'/\Delta )$
such that
![]() $\mathcal {F}'|_{\mathcal {X}^{\prime }_\eta }= f_* \mathcal {L}_{\mathcal {X}^{\prime }_\eta }$
and
$\mathcal {F}'|_{\mathcal {X}^{\prime }_\eta }= f_* \mathcal {L}_{\mathcal {X}^{\prime }_\eta }$
and
![]() $[\mathcal {F}'|_X] \in \overline {J}_{X'}$
. We take
$[\mathcal {F}'|_X] \in \overline {J}_{X'}$
. We take
![]() $[\mathcal {L}'] \in \operatorname {Pic}^d(\widetilde {\mathcal {X}}/\Delta )$
such that
$[\mathcal {L}'] \in \operatorname {Pic}^d(\widetilde {\mathcal {X}}/\Delta )$
such that
![]() $f_*(\mathcal {L}')= \mathcal {F}'$
. Thus, we have that
$f_*(\mathcal {L}')= \mathcal {F}'$
. Thus, we have that
![]() $\left (\mathcal {L}'\otimes \mathcal {L}^{-1}\right )_{\widetilde {\mathcal {X}}_{\eta }}=\mathcal {O}_{\mathcal {X}_{\eta }}$
. We let then
$\left (\mathcal {L}'\otimes \mathcal {L}^{-1}\right )_{\widetilde {\mathcal {X}}_{\eta }}=\mathcal {O}_{\mathcal {X}_{\eta }}$
. We let then
![]() $\mathbf {\vec {t}}= \underline {\deg }(\mathcal {L}'\otimes \mathcal {L}^{-1}|_{\widetilde {X}})$
, and so
$\mathbf {\vec {t}}= \underline {\deg }(\mathcal {L}'\otimes \mathcal {L}^{-1}|_{\widetilde {X}})$
, and so
![]() $\mathbf {\vec {d}}+\mathbf {\vec {t}}= \underline {\deg } (\mathcal {L}'|_{\widetilde {X}})$
is in
$\mathbf {\vec {d}}+\mathbf {\vec {t}}= \underline {\deg } (\mathcal {L}'|_{\widetilde {X}})$
is in
![]() $\widetilde {\sigma }_{\overline {J}}$
. This proves that
$\widetilde {\sigma }_{\overline {J}}$
. This proves that
![]() $\widetilde {\sigma }_{\overline {J}}$
is a complete set of representatives.
$\widetilde {\sigma }_{\overline {J}}$
is a complete set of representatives.
To prove minimality, assume that there exist lifts
![]() $\mathbf {\vec {d}_1}, \mathbf {\vec {d}_2} \in \widetilde {\sigma }_{\overline {J}}$
such that
$\mathbf {\vec {d}_1}, \mathbf {\vec {d}_2} \in \widetilde {\sigma }_{\overline {J}}$
such that
![]() $\mathbf {\vec {d}_2}=\mathbf {\vec {d}_1}+ \mathbf {\vec {t}}$
for some
$\mathbf {\vec {d}_2}=\mathbf {\vec {d}_1}+ \mathbf {\vec {t}}$
for some
![]() $\mathbf {\vec {t}} \in \operatorname {\mathrm {Tw}}(\Gamma (\widetilde {X}))$
. By Hensel’s lemma and by Lemma 7.2, there exist
$\mathbf {\vec {t}} \in \operatorname {\mathrm {Tw}}(\Gamma (\widetilde {X}))$
. By Hensel’s lemma and by Lemma 7.2, there exist
![]() $[\mathcal {L}_1], [\mathcal {L}_2] \in \operatorname {\mathrm {Pic}}^d(\widetilde {\mathcal {X}}/\Delta )$
, coinciding on the generic fiber, and whose multidegrees on
$[\mathcal {L}_1], [\mathcal {L}_2] \in \operatorname {\mathrm {Pic}}^d(\widetilde {\mathcal {X}}/\Delta )$
, coinciding on the generic fiber, and whose multidegrees on
![]() $\widetilde {X}$
equal
$\widetilde {X}$
equal
![]() $\mathbf {\vec {d}_1}, \mathbf {\vec {d}_2}$
. The pushforwards
$\mathbf {\vec {d}_1}, \mathbf {\vec {d}_2}$
. The pushforwards
![]() $f_*(\mathcal {L}_1)$
and
$f_*(\mathcal {L}_1)$
and
![]() $f_*(\mathcal {L}_2)$
coincide on
$f_*(\mathcal {L}_2)$
coincide on
![]() $\mathcal {X}^{\prime }_{\eta }$
, and because
$\mathcal {X}^{\prime }_{\eta }$
, and because
![]() $\overline {J}_{\mathcal {X}'/\Delta }$
is separated over
$\overline {J}_{\mathcal {X}'/\Delta }$
is separated over
![]() $\Delta $
, their central fibers must coincide, which implies that
$\Delta $
, their central fibers must coincide, which implies that
![]() $\mathbf {\vec {t}}=0$
. This proves minimality.
$\mathbf {\vec {t}}=0$
. This proves minimality.
Remark 7.11. In [Reference Caporaso13], Caporaso introduced the notion of ‘being of Néron type’ for a degree d compactified Jacobian of a nodal curve X. In our notation, this can be restated as the property that
![]() $\sigma _{\overline {J}}(\Gamma (X))$
is a minimal complete set of representatives for the action of
$\sigma _{\overline {J}}(\Gamma (X))$
is a minimal complete set of representatives for the action of
![]() $\operatorname {\mathrm {Tw}}(\Gamma (X))$
on
$\operatorname {\mathrm {Tw}}(\Gamma (X))$
on
![]() $S^d_{\Gamma (X)}(\Gamma (X))$
.
$S^d_{\Gamma (X)}(\Gamma (X))$
.
Proposition 7.10 proves, in particular, that all smoothable fine compactified Jacobians are of Néron type. Similar results were obtained in [Reference Kass23] and [Reference Melo and Viviani29] for fine compactified Jacobians obtained from some numerical polarizations (see Section 8 for the notion of a numerical polarization).
We refer the reader to [Reference Kass23] for the definition of a Néron model and its relations with compactified Jacobians.
Remark 7.12. The smoothability assumption in the statement of Proposition 7.10 is crucial. In [Reference Pagani and Tommasi32], the authors give an example, for X a nodal curve of genus
![]() $1$
, of degree
$1$
, of degree
![]() $0$
fine compactified Jacobians
$0$
fine compactified Jacobians
![]() $\overline {J} \subset {\operatorname {Simp}}^0(X)$
whose collection of line bundle multidegrees contain an arbitrary number
$\overline {J} \subset {\operatorname {Simp}}^0(X)$
whose collection of line bundle multidegrees contain an arbitrary number
![]() $r\geq 2$
of elements for each orbit of the action of
$r\geq 2$
of elements for each orbit of the action of
![]() $\operatorname {\mathrm {Tw}}(\Gamma )$
on
$\operatorname {\mathrm {Tw}}(\Gamma )$
on
![]() $S^0_{\Gamma }(\Gamma )$
. Such compactified Jacobians can always be extended to a universally closed family over a regular smoothing, but such extensions are separated if and only if r equals
$S^0_{\Gamma }(\Gamma )$
. Such compactified Jacobians can always be extended to a universally closed family over a regular smoothing, but such extensions are separated if and only if r equals
![]() $1$
.
$1$
.
We conclude with the main result:
Corollary 7.13. The associated assignment (Definition 7.1) to a smoothable degree d fine compactified Jacobian of X is a degree d stability assignment for the dual graph
![]() $\Gamma (X)$
(as in Definition 4.3).
$\Gamma (X)$
(as in Definition 4.3).
We conclude by observing that the same result holds for families.
Proposition 7.14. Let
![]() $\mathcal {X}/S$
be a family of nodal curves over a base scheme (or Deligne–Mumford stack) S, and let
$\mathcal {X}/S$
be a family of nodal curves over a base scheme (or Deligne–Mumford stack) S, and let
![]() $\overline {\mathcal J}=\overline {\mathcal J}_{\mathcal {X}/S}$
be a degree d fine compactified Jacobian for the family. Assume that for each geometric point s of S, the fine compactified Jacobian
$\overline {\mathcal J}=\overline {\mathcal J}_{\mathcal {X}/S}$
be a degree d fine compactified Jacobian for the family. Assume that for each geometric point s of S, the fine compactified Jacobian
![]() $\overline {J}_s$
of the fiber
$\overline {J}_s$
of the fiber
![]() $X_s$
over
$X_s$
over
![]() $s \in S$
is smoothable.
$s \in S$
is smoothable.
Then the collection
![]() $\{\sigma _{\overline {J}_s}\}$
of associated assignments of
$\{\sigma _{\overline {J}_s}\}$
of associated assignments of
![]() $\overline {J}_s$
for all geometric points s of S is a family of degree d stability assignments (as in Definition 4.9).
$\overline {J}_s$
for all geometric points s of S is a family of degree d stability assignments (as in Definition 4.9).
Proof. The case where S is a single geometric point is Corollary 7.13.
To complete our proof, we will show that the assignment of
![]() $\sigma _{\overline {J}_s}$
is compatible with all morphisms
$\sigma _{\overline {J}_s}$
is compatible with all morphisms
![]() $f \colon \Gamma (\mathcal {X}_{s}) \to \Gamma (\mathcal {X}_t)$
arising from étale specializations
$f \colon \Gamma (\mathcal {X}_{s}) \to \Gamma (\mathcal {X}_t)$
arising from étale specializations
![]() $t \rightsquigarrow s$
.
$t \rightsquigarrow s$
.
Assume that
![]() $F_{t}$
is a simple sheaf on the nodal curve
$F_{t}$
is a simple sheaf on the nodal curve
![]() $\mathcal {X}_{t}$
that specializes to
$\mathcal {X}_{t}$
that specializes to
![]() $F_s$
on
$F_s$
on
![]() $\mathcal {X}_s$
. Suppose that the subcurve
$\mathcal {X}_s$
. Suppose that the subcurve
![]() $\mathcal {X}_{t, 0} \subseteq \mathcal {X}_{t}$
generalizes the subcurve
$\mathcal {X}_{t, 0} \subseteq \mathcal {X}_{t}$
generalizes the subcurve
![]() $\mathcal {X}_{s, 0} \subseteq \mathcal {X}_s$
. By flatness and by continuity of the Euler characteristic, and because we are passing to the torsion-free quotients, the degrees are related by
$\mathcal {X}_{s, 0} \subseteq \mathcal {X}_s$
. By flatness and by continuity of the Euler characteristic, and because we are passing to the torsion-free quotients, the degrees are related by
where
![]() $n(F_s,f)$
is the number of nodes of
$n(F_s,f)$
is the number of nodes of
![]() $\mathcal {X}_{s,0}$
that are smoothened in t and where
$\mathcal {X}_{s,0}$
that are smoothened in t and where
![]() $F_s$
fails to be locally free. (See Equation (2.1)). Formula (7.3) is precisely the condition of Equation (4.2).
$F_s$
fails to be locally free. (See Equation (2.1)). Formula (7.3) is precisely the condition of Equation (4.2).
Remark 7.15. Assume that the dual graph of the fibers of
![]() $\mathcal {X}/S$
is constant in S, and let S be irreducible with
$\mathcal {X}/S$
is constant in S, and let S be irreducible with
![]() $\eta \in S$
its generic point. Then the family
$\eta \in S$
its generic point. Then the family
![]() $\mathcal X/S$
induces a group homomorphism from the group of étale specializations of
$\mathcal X/S$
induces a group homomorphism from the group of étale specializations of
![]() $\eta $
to itself, which equals the Galois group
$\eta $
to itself, which equals the Galois group
![]() $\operatorname {Gal}(k(\eta )^{\operatorname {sep}}, k(\eta )))$
, to the automorphism group
$\operatorname {Gal}(k(\eta )^{\operatorname {sep}}, k(\eta )))$
, to the automorphism group
![]() $\operatorname {Aut}(\Gamma (X_{k(\eta )^{\operatorname {sep}}}))$
of the dual graph of the generic fiber. Let G be the image of this group homomorphism. In this case, Proposition 7.14 implies that the associated assignment
$\operatorname {Aut}(\Gamma (X_{k(\eta )^{\operatorname {sep}}}))$
of the dual graph of the generic fiber. Let G be the image of this group homomorphism. In this case, Proposition 7.14 implies that the associated assignment
![]() $\sigma _{\overline {J}_{k(\eta )}}$
, which is defined as a collection of discrete data on the dual graph
$\sigma _{\overline {J}_{k(\eta )}}$
, which is defined as a collection of discrete data on the dual graph
![]() $\Gamma (X_{k(\eta )^{\operatorname {sep}}})=\Gamma (X_{\overline {k(\eta )}})$
, is invariant under the action of G.
$\Gamma (X_{k(\eta )^{\operatorname {sep}}})=\Gamma (X_{\overline {k(\eta )}})$
, is invariant under the action of G.
In the particular case where S is a stratum of
![]() $\overline {\mathcal {M}}_{g,n}$
(i.e., S is the Deligne–Mumford moduli stack of curves whose dual graph is isomorphic to a fixed graph
$\overline {\mathcal {M}}_{g,n}$
(i.e., S is the Deligne–Mumford moduli stack of curves whose dual graph is isomorphic to a fixed graph
![]() $\Gamma \in G_{g,n}$
), we have
$\Gamma \in G_{g,n}$
), we have
![]() $G=\operatorname {Aut}(\Gamma )$
.
$G=\operatorname {Aut}(\Gamma )$
.
By combining Theorem 6.3/Corollary 6.4 with Proposition 7.14 and Lemma 7.2, we immediately obtain that the two operations of (1) taking the associated assignment to a fine compactified Jacobian, and (2) constructing the moduli space of stable sheaves associated with a given stability assignment, are inverses of each other.
Corollary 7.16. Let
![]() $\mathcal {X}/S$
be a family of nodal curves over an irreducible scheme (or Deligne–Mumford stack) S, and assume that
$\mathcal {X}/S$
be a family of nodal curves over an irreducible scheme (or Deligne–Mumford stack) S, and assume that
![]() $\mathcal {X}_{\theta }/\theta $
is smooth for
$\mathcal {X}_{\theta }/\theta $
is smooth for
![]() $\theta $
the generic point of S.
$\theta $
the generic point of S.
If
![]() $\overline {\mathcal J} \subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
is a degree d fine compactified Jacobian and
$\overline {\mathcal J} \subseteq {\operatorname {Simp}}^d(\mathcal {X}/S)$
is a degree d fine compactified Jacobian and
![]() $\sigma _{\overline {\mathcal J}}$
is its associated assignment (Definition 7.1), then the moduli space
$\sigma _{\overline {\mathcal J}}$
is its associated assignment (Definition 7.1), then the moduli space
![]() $\overline {\mathcal {J}}_{\sigma _{\overline {\mathcal J}}}$
of
$\overline {\mathcal {J}}_{\sigma _{\overline {\mathcal J}}}$
of
![]() $\sigma _{\overline {\mathcal J}}$
-stable sheaves (Definitions 6.1 and 6.2) equals
$\sigma _{\overline {\mathcal J}}$
-stable sheaves (Definitions 6.1 and 6.2) equals
![]() $\overline {\mathcal J}$
.
$\overline {\mathcal J}$
.
Conversely, if
![]() $\tau $
is a family of degree d stability assignments, and
$\tau $
is a family of degree d stability assignments, and
![]() $\overline {\mathcal J}_\tau $
is the moduli space of
$\overline {\mathcal J}_\tau $
is the moduli space of
![]() $\tau $
-stable sheaves, then the associated assignment
$\tau $
-stable sheaves, then the associated assignment
![]() $\sigma _{\overline {\mathcal J}_\tau }$
equals
$\sigma _{\overline {\mathcal J}_\tau }$
equals
![]() $\tau $
.
$\tau $
.
8. Numerical polarizations
An example of a (smoothable fine compactified Jacobian) stability assignment on a nodal curve
![]() $X/K$
(as in Definition 4.3) comes from numerical polarizations, introduced by Oda–Seshadri in [Reference Oda and Seshadri31]. (In fact, the Oda–Seshadri formalism permits to also construct compactified Jacobians that are not necessarily fine in the sense of Definition 3.1).
$X/K$
(as in Definition 4.3) comes from numerical polarizations, introduced by Oda–Seshadri in [Reference Oda and Seshadri31]. (In fact, the Oda–Seshadri formalism permits to also construct compactified Jacobians that are not necessarily fine in the sense of Definition 3.1).
In this section, we review the notion of numerical stability for a single curve (Definition 8.1) and extend it to families (Definition 8.10) following [Reference Kass and Pagani25].
We let
![]() $\Gamma $
be the dual graph of X.
$\Gamma $
be the dual graph of X.
Definition 8.1. Let
![]() $V^d(\Gamma ) \subset \mathbf {R}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
be the sum-d affine subspace. Let
$V^d(\Gamma ) \subset \mathbf {R}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
be the sum-d affine subspace. Let
![]() ${\phi } \in V^d(\Gamma )$
, and let G be a (not necessarily connected) spanning subgraph of
${\phi } \in V^d(\Gamma )$
, and let G be a (not necessarily connected) spanning subgraph of
![]() $\Gamma $
, with
$\Gamma $
, with
![]() $E_0:= \operatorname {\mathrm {Edges}}(G)$
and
$E_0:= \operatorname {\mathrm {Edges}}(G)$
and
![]() $E_0^c:= \operatorname {\mathrm {Edges}}(\Gamma ) \setminus E_0$
. We say that
$E_0^c:= \operatorname {\mathrm {Edges}}(\Gamma ) \setminus E_0$
. We say that
![]() $\underline {\mathbf d} \in S^d_{\Gamma }(G)$
is
$\underline {\mathbf d} \in S^d_{\Gamma }(G)$
is
![]() ${\boldsymbol {\phi }}$
-semistable (resp.
${\boldsymbol {\phi }}$
-semistable (resp.
![]() ${\boldsymbol {\phi }}$
-stable) on G when the inequality
${\boldsymbol {\phi }}$
-stable) on G when the inequality
 $$ \begin{align} \left|\sum_{v \in V}( \underline{\mathbf{d}}(v) -\phi(v)) + \left|E_0^c \cap E(\Gamma(V)) \right|+\frac{\left|E_0^c \cap \operatorname{E}(V,V^c)\right|}{2}\right|\leq \frac{\left|E_0 \cap \operatorname{E}(V,V^c) \right|}{2} \end{align} $$
$$ \begin{align} \left|\sum_{v \in V}( \underline{\mathbf{d}}(v) -\phi(v)) + \left|E_0^c \cap E(\Gamma(V)) \right|+\frac{\left|E_0^c \cap \operatorname{E}(V,V^c)\right|}{2}\right|\leq \frac{\left|E_0 \cap \operatorname{E}(V,V^c) \right|}{2} \end{align} $$
(resp.
![]() $<$
) is satisfied for all
$<$
) is satisfied for all
![]() $\emptyset \neq V \subsetneq \operatorname {\mathrm {Vert}}(\Gamma )$
. (To keep the notation compact, in the inequality, we have denoted the edge sets by
$\emptyset \neq V \subsetneq \operatorname {\mathrm {Vert}}(\Gamma )$
. (To keep the notation compact, in the inequality, we have denoted the edge sets by
![]() $\operatorname {E}$
instead of
$\operatorname {E}$
instead of
![]() $\operatorname {\mathrm {Edges}}$
).
$\operatorname {\mathrm {Edges}}$
).
For
![]() $\phi \in V^d(\Gamma )$
, we define the (numerical, Oda–Seshadri) assignment associated with
$\phi \in V^d(\Gamma )$
, we define the (numerical, Oda–Seshadri) assignment associated with
![]() $\phi $
, denoted
$\phi $
, denoted
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , \phi }$
, by setting
$\operatorname {\mathrm {\sigma }}_{\Gamma , \phi }$
, by setting
for all spanning subgraphs
![]() $G \subseteq \Gamma $
.
$G \subseteq \Gamma $
.
We define
![]() ${\phi } \in V^d(\Gamma )$
to be nondegenerate when for every spanning subgraph
${\phi } \in V^d(\Gamma )$
to be nondegenerate when for every spanning subgraph
![]() $G\subseteq \Gamma $
, all elements of
$G\subseteq \Gamma $
, all elements of
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}(G)$
are
$\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}(G)$
are
![]() ${\phi }$
-stable.
${\phi }$
-stable.
Elements of
![]() $V^d(\Gamma )$
are called numerical polarizations.
$V^d(\Gamma )$
are called numerical polarizations.
Remark 8.2. If the spanning subgraph
![]() $G \subseteq \Gamma $
is not connected, then
$G \subseteq \Gamma $
is not connected, then
![]() $\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(G)$
is a collection of edges that disconnects
$\operatorname {\mathrm {Edges}}(\Gamma ) \setminus \operatorname {\mathrm {Edges}}(G)$
is a collection of edges that disconnects
![]() $\Gamma $
. If we take for V a subset of
$\Gamma $
. If we take for V a subset of
![]() $\operatorname {\mathrm {Vert}}(\Gamma )$
such that the induced subgraph
$\operatorname {\mathrm {Vert}}(\Gamma )$
such that the induced subgraph
![]() $\Gamma (V)$
is a connected component of G, the right-hand side of Inequality (8.1) equals zero. Therefore, if
$\Gamma (V)$
is a connected component of G, the right-hand side of Inequality (8.1) equals zero. Therefore, if
![]() ${\phi }$
is nondegenerate, we always have
${\phi }$
is nondegenerate, we always have
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }} (G) = \emptyset $
whenever G is not connected.
$\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }} (G) = \emptyset $
whenever G is not connected.
We conclude that, for nondegenerate
![]() ${\phi }$
’s, the disconnected spanning subgraphs G of
${\phi }$
’s, the disconnected spanning subgraphs G of
![]() $\Gamma $
do not carry any additional information and they can be disregarded, as we have done in Definition 4.3.
$\Gamma $
do not carry any additional information and they can be disregarded, as we have done in Definition 4.3.
Every nondegenerate numerical polarization gives a stability assignment:
Proposition 8.3. Let X be a nodal curve and let
![]() ${\phi } \in V^d(\Gamma (X))$
be nondegenerate. Then the numerical assignment
${\phi } \in V^d(\Gamma (X))$
be nondegenerate. Then the numerical assignment
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
defined in 8.1 is a degree d stability assignment (as in 4.3), and the moduli space
$\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
defined in 8.1 is a degree d stability assignment (as in 4.3), and the moduli space
![]() $\overline {J}_{\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}}(X)$
of sheaves that are stable with respect to
$\overline {J}_{\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}}(X)$
of sheaves that are stable with respect to
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
(as defined in 6.1) is a degree d smoothable fine compactified Jacobian.
$\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
(as defined in 6.1) is a degree d smoothable fine compactified Jacobian.
Proof. The fact that the moduli space is a smoothable fine compactified Jacobian is [Reference Pagani and Tommasi32, Proposition 2.9]. Thus,
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
defines a stability assignment by Corollary 7.13.
$\operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
defines a stability assignment by Corollary 7.13.
This leads to the following natural question:
Question 8.4. Let
![]() $\sigma _\Gamma $
be a degree d stability assignment. Does there exist a
$\sigma _\Gamma $
be a degree d stability assignment. Does there exist a
![]() ${\phi } \in V^d(\Gamma )$
such that
${\phi } \in V^d(\Gamma )$
such that
![]() $\sigma _{\Gamma } = \operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
? (If one such
$\sigma _{\Gamma } = \operatorname {\mathrm {\sigma }}_{\Gamma , {\phi }}$
? (If one such
![]() ${\phi }$
exists, it is necessarily nondegenerate).
${\phi }$
exists, it is necessarily nondegenerate).
Below, we give three classes of examples where we can answer Question 8.4 in the positive.Footnote 6
Example 8.5 (Irreducible curves)
If X is irreducible, then there is a unique stability assignment
![]() $\sigma $
(see Example 4.5), and we have
$\sigma $
(see Example 4.5), and we have
![]() $\sigma =\sigma _{\phi }$
for
$\sigma =\sigma _{\phi }$
for
![]() $\phi $
the only element of
$\phi $
the only element of
![]() $V^d(X)=\{d\}$
.
$V^d(X)=\{d\}$
.
Example 8.6 (Vine curves of type t)
Let
![]() $\Gamma $
consist of
$\Gamma $
consist of
![]() $2$
vertices
$2$
vertices
![]() $v_1, v_2$
connected by t edges (and no loops). The complexity of
$v_1, v_2$
connected by t edges (and no loops). The complexity of
![]() $\Gamma $
equals t. With the notation as in Example 4.6, it is straightforward to check that a stability assignment
$\Gamma $
equals t. With the notation as in Example 4.6, it is straightforward to check that a stability assignment
![]() $\sigma _{\Gamma }$
determined by some
$\sigma _{\Gamma }$
determined by some
![]() $\lambda \in \mathbf {Z}$
as described in loc. cit. equals
$\lambda \in \mathbf {Z}$
as described in loc. cit. equals
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma , \phi _\Gamma }$
for
$\operatorname {\mathrm {\sigma }}_{\Gamma , \phi _\Gamma }$
for
 $$\begin{align*}\phi_\Gamma(v_1, v_2):= \left(\lambda- \frac{t-1}{2}, d -\lambda + \frac{t-1}{2} \right),\end{align*}$$
$$\begin{align*}\phi_\Gamma(v_1, v_2):= \left(\lambda- \frac{t-1}{2}, d -\lambda + \frac{t-1}{2} \right),\end{align*}$$
and that
![]() $\phi _\Gamma \in V^d(\Gamma )$
is nondegenerate.
$\phi _\Gamma \in V^d(\Gamma )$
is nondegenerate.
Example 8.7 (Curves whose dual graph has genus
 $1$
)
$1$
)
Let X be such that
![]() $b_1(\Gamma (X))=1$
. A degree d stability assignment
$b_1(\Gamma (X))=1$
. A degree d stability assignment
![]() $\sigma $
on
$\sigma $
on
![]() $\Gamma (X)$
is the same datum as a stability assignment on
$\Gamma (X)$
is the same datum as a stability assignment on
![]() $\Gamma '$
, where
$\Gamma '$
, where
![]() $\Gamma '$
is obtained from
$\Gamma '$
is obtained from
![]() $\Gamma (X)$
by setting the genus of each vertex to
$\Gamma (X)$
by setting the genus of each vertex to
![]() $0$
. Let
$0$
. Let
![]() $X'$
be a curve whose dual graph is
$X'$
be a curve whose dual graph is
![]() $\Gamma '$
. Then by Corollary 6.4, the scheme
$\Gamma '$
. Then by Corollary 6.4, the scheme
![]() $\overline {J}_{\sigma }(X')$
is a smoothable fine compactified Jacobian. Smoothable fine compactified Jacobians on
$\overline {J}_{\sigma }(X')$
is a smoothable fine compactified Jacobian. Smoothable fine compactified Jacobians on
![]() $X'$
have been classified in [Reference Pagani and Tommasi32]: they all arise as
$X'$
have been classified in [Reference Pagani and Tommasi32]: they all arise as
![]() $\overline {J}_{\sigma _\phi }(X')$
for some
$\overline {J}_{\sigma _\phi }(X')$
for some
![]() $\phi \in V^d(\Gamma ')=V^d(\Gamma (X))$
. Thus, by Corollary 7.13, we have that
$\phi \in V^d(\Gamma ')=V^d(\Gamma (X))$
. Thus, by Corollary 7.13, we have that
![]() $\sigma $
is also of that form.
$\sigma $
is also of that form.
Example 8.8 (Integral Break Divisors)
Let
![]() $\Gamma $
be a (not necessarily stable) graph and assume
$\Gamma $
be a (not necessarily stable) graph and assume
![]() $d=g(\Gamma )$
. Define the stability assignment
$d=g(\Gamma )$
. Define the stability assignment
![]() $\sigma _{\operatorname {IBD}}$
by
$\sigma _{\operatorname {IBD}}$
by
for all connected spanning subgraphs
![]() $G \subseteq \Gamma $
. Recall that
$G \subseteq \Gamma $
. Recall that
![]() $\underline {\mathbf {d}} \in S^{g(\Gamma )}_{\Gamma }(G)$
is an integral break divisor for G if and only if it is of the form
$\underline {\mathbf {d}} \in S^{g(\Gamma )}_{\Gamma }(G)$
is an integral break divisor for G if and only if it is of the form
 $$\begin{align*}\underline{\mathbf{d}} (v) =g(v) + \sum_{e \in \operatorname{\mathrm{Edges}}(G) \setminus \operatorname{\mathrm{Edges}}(T)} \underline{\mathbf{e}}_{t(e)}(v) \end{align*}$$
$$\begin{align*}\underline{\mathbf{d}} (v) =g(v) + \sum_{e \in \operatorname{\mathrm{Edges}}(G) \setminus \operatorname{\mathrm{Edges}}(T)} \underline{\mathbf{e}}_{t(e)}(v) \end{align*}$$
for some choice of a spanning tree
![]() $T \subseteq G$
and of an orientation
$T \subseteq G$
and of an orientation
![]() $t \colon \operatorname {\mathrm {Edges}}(G) \setminus \operatorname {\mathrm {Edges}}(T) \to \operatorname {\mathrm {Vert}}(G)$
(for
$t \colon \operatorname {\mathrm {Edges}}(G) \setminus \operatorname {\mathrm {Edges}}(T) \to \operatorname {\mathrm {Vert}}(G)$
(for
![]() $w \in \operatorname {\mathrm {Vert}}(G)$
, we denote by
$w \in \operatorname {\mathrm {Vert}}(G)$
, we denote by
![]() $\underline {\mathbf {e}}_w$
the function that is
$\underline {\mathbf {e}}_w$
the function that is
![]() $1$
on the vertex w and
$1$
on the vertex w and
![]() $0$
elsewhere).
$0$
elsewhere).
We claim that
![]() $\sigma _{\operatorname {IBD}}$
is indeed a degree
$\sigma _{\operatorname {IBD}}$
is indeed a degree
![]() $d=g(\Gamma )$
stability assignment. Condition (1) of Definition 4.3 follows directly from the definition of an integral break divisor. The second axiom follows immediately from [Reference An, Baker, Kuperberg and Shokrieh4, Theorem 1.3] (earlier proved in [Reference Mikhalkin and Zharkov30]).
$d=g(\Gamma )$
stability assignment. Condition (1) of Definition 4.3 follows directly from the definition of an integral break divisor. The second axiom follows immediately from [Reference An, Baker, Kuperberg and Shokrieh4, Theorem 1.3] (earlier proved in [Reference Mikhalkin and Zharkov30]).
When
![]() $\Gamma $
is stable, it follows from [Reference Christ, Payne and Shen15, Lemma 5.1.5] that
$\Gamma $
is stable, it follows from [Reference Christ, Payne and Shen15, Lemma 5.1.5] that
![]() $\sigma _{\operatorname {IBD}}= \sigma _{\Gamma , \phi _{\operatorname {can}}^{\Gamma }}$
, for
$\sigma _{\operatorname {IBD}}= \sigma _{\Gamma , \phi _{\operatorname {can}}^{\Gamma }}$
, for
where
![]() $\operatorname {val}_{\Gamma }(v)$
is the valence of the vertex v in
$\operatorname {val}_{\Gamma }(v)$
is the valence of the vertex v in
![]() $\Gamma $
. (This follows from loc. cit. as
$\Gamma $
. (This follows from loc. cit. as
![]() $\phi ^{\Gamma }_{\operatorname {can}}$
is induced from the canonical divisor, which is ample when
$\phi ^{\Gamma }_{\operatorname {can}}$
is induced from the canonical divisor, which is ample when
![]() $\Gamma $
is stable).
$\Gamma $
is stable).
When
![]() $\Gamma $
is not necessarily stable, we define
$\Gamma $
is not necessarily stable, we define
We claim that
![]() $\sigma _{\operatorname {IBD}}= \sigma _{\Gamma , \phi _{\operatorname {IBD}}}$
.
$\sigma _{\operatorname {IBD}}= \sigma _{\Gamma , \phi _{\operatorname {IBD}}}$
.
Let
![]() $\Gamma '$
be the graph obtained from
$\Gamma '$
be the graph obtained from
![]() $\Gamma $
by increasing the genus of each vertex by
$\Gamma $
by increasing the genus of each vertex by
![]() $1$
. Then the integral break divisors of
$1$
. Then the integral break divisors of
![]() $\Gamma '$
are the integral break divisors on
$\Gamma '$
are the integral break divisors on
![]() $\Gamma $
increased by
$\Gamma $
increased by
![]() $1$
on each vertex and
$1$
on each vertex and
![]() $\Gamma '$
is stable. Therefore, the integral break divisors on
$\Gamma '$
is stable. Therefore, the integral break divisors on
![]() $\Gamma $
are stable for the stability assignment
$\Gamma $
are stable for the stability assignment
![]() $\phi _{\operatorname {can}}^{\Gamma '}-1$
, which equals
$\phi _{\operatorname {can}}^{\Gamma '}-1$
, which equals
![]() $\phi _{\operatorname {IBD}}$
. This proves our claim.
$\phi _{\operatorname {IBD}}$
. This proves our claim.
We are now ready to define families of numerical polarizations, similarly to what was done in Definition 4.9 for families of stability assignments. We shall see that there are two ways of doing so, and that they are not equivalent.
Definition 8.9. Let
![]() $f \colon \Gamma \to \Gamma '$
be a morphism of stable graphs. We say that
$f \colon \Gamma \to \Gamma '$
be a morphism of stable graphs. We say that
![]() $\phi \in V^d(\Gamma )$
is f-compatible with
$\phi \in V^d(\Gamma )$
is f-compatible with
![]() $\phi ' \in V^d(\Gamma ')$
if
$\phi ' \in V^d(\Gamma ')$
if
 $$\begin{align*}\phi'(w)= \sum_{f(v)=w} \phi(v). \end{align*}$$
$$\begin{align*}\phi'(w)= \sum_{f(v)=w} \phi(v). \end{align*}$$
Definition 8.10. Let
![]() $\mathcal {X}/S$
be a family of nodal curves, and let
$\mathcal {X}/S$
be a family of nodal curves, and let
![]() $\Phi =(\phi _s \in V^d(\Gamma (\mathcal {X}_s)) )_{s \in S}$
be a collection of numerical polarizations, one for each geometric point of S. Assume also that
$\Phi =(\phi _s \in V^d(\Gamma (\mathcal {X}_s)) )_{s \in S}$
be a collection of numerical polarizations, one for each geometric point of S. Assume also that
![]() $\Phi $
is nondegenerate, by which we mean that so is each of its coordinates
$\Phi $
is nondegenerate, by which we mean that so is each of its coordinates
![]() $\phi _s$
for
$\phi _s$
for
![]() $s \in S$
(as per Definition 8.1).
$s \in S$
(as per Definition 8.1).
The collection
![]() $\Phi $
is weakly compatible if the collection
$\Phi $
is weakly compatible if the collection
![]() $\sigma _{\Phi }:=(\sigma _{\Gamma (X_s), \Phi (\Gamma (X_s))})_{s \in S}$
of degree d stability assignments defined via Proposition 8.3 is a family of degree d stability assignments as prescribed by Definition 4.9.
$\sigma _{\Phi }:=(\sigma _{\Gamma (X_s), \Phi (\Gamma (X_s))})_{s \in S}$
of degree d stability assignments defined via Proposition 8.3 is a family of degree d stability assignments as prescribed by Definition 4.9.
The collection
![]() $\Phi $
is strongly compatible if it is f-compatible for all morphisms
$\Phi $
is strongly compatible if it is f-compatible for all morphisms
![]() $f \colon \Gamma (\mathcal {X}_{s}) \to \Gamma (\mathcal {X}_t)$
that arise from some étale specialization
$f \colon \Gamma (\mathcal {X}_{s}) \to \Gamma (\mathcal {X}_t)$
that arise from some étale specialization
![]() $t \rightsquigarrow s$
occurring on S.
$t \rightsquigarrow s$
occurring on S.
For a strongly compatible collection, one can define the notion of a
![]() $\Phi $
-stable sheaf for all fibers as in Definition 8.1. We shall not do that, as this would be a repetition of our Definition 6.2. Instead, we observe the following:
$\Phi $
-stable sheaf for all fibers as in Definition 8.1. We shall not do that, as this would be a repetition of our Definition 6.2. Instead, we observe the following:
Corollary 8.11. Let
![]() $\mathcal {X}/S$
be a family of nodal curves over an irreducible scheme S with generic point
$\mathcal {X}/S$
be a family of nodal curves over an irreducible scheme S with generic point
![]() $\theta $
, and assume that the generic element
$\theta $
, and assume that the generic element
![]() $\mathcal {X}_\theta /\theta $
is smooth. If
$\mathcal {X}_\theta /\theta $
is smooth. If
![]() $\Phi $
is a nondegenerate and weakly compatible family of numerical polarizations, the moduli space
$\Phi $
is a nondegenerate and weakly compatible family of numerical polarizations, the moduli space
![]() $\overline {\mathcal {J}}_{\sigma _{\Phi }}$
of sheaves that are stable with respect to
$\overline {\mathcal {J}}_{\sigma _{\Phi }}$
of sheaves that are stable with respect to
![]() $\sigma _{\Phi }$
is a family of degree d fine compactified Jacobians.
$\sigma _{\Phi }$
is a family of degree d fine compactified Jacobians.
Proof. By combining Proposition 8.3 with the fact that
![]() $\Phi $
is nondegenerate and weakly compatible, we deduce that
$\Phi $
is nondegenerate and weakly compatible, we deduce that
![]() $\sigma _{\Phi }$
is a family of stability assignments for
$\sigma _{\Phi }$
is a family of stability assignments for
![]() $\mathcal {X}/S$
. The result follows then from Theorem 6.3.
$\mathcal {X}/S$
. The result follows then from Theorem 6.3.
In [Reference Kass and Pagani25], the authors studied the theory of universal Oda–Seshadri stability assignments for compactified Jacobians. In loc. cit., they defined, for fixed
![]() $(g,n)$
such that
$(g,n)$
such that
![]() $2g-2+n>0$
, the space
$2g-2+n>0$
, the space
![]() $V_{g,n}^d$
of universal numerical polarizations – that is, elements
$V_{g,n}^d$
of universal numerical polarizations – that is, elements
![]() $\Phi =(\phi _s)_{s \in \overline {\mathcal {M}}_{g,n}}$
that are strongly compatible for morphisms
$\Phi =(\phi _s)_{s \in \overline {\mathcal {M}}_{g,n}}$
that are strongly compatible for morphisms
![]() $f \colon \Gamma _1 \to \Gamma _2$
between any two elements of
$f \colon \Gamma _1 \to \Gamma _2$
between any two elements of
![]() ${G}_{g,n}$
(a skeleton of the category of stable n-pointed graphs of genus g).
${G}_{g,n}$
(a skeleton of the category of stable n-pointed graphs of genus g).
In loc. cit., the authors also constructed, for each such nondegenerate
![]() $\Phi \in V_{g,n}^d$
, a compactified Jacobian
$\Phi \in V_{g,n}^d$
, a compactified Jacobian
![]() $\overline {\mathcal {J}}_{g,n}(\Phi )$
. In the language of this paper, this can be rephrased as follows.
$\overline {\mathcal {J}}_{g,n}(\Phi )$
. In the language of this paper, this can be rephrased as follows.
Corollary 8.12. If
![]() $\Phi \in V_{g,n}^d$
is a nondegenerate universal numerical stability condition, then
$\Phi \in V_{g,n}^d$
is a nondegenerate universal numerical stability condition, then
![]() $\overline {\mathcal {J}}_{g,n}(\Phi ) \subset {\operatorname {Simp}}^d(\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n})$
is a fine compactified universal Jacobian.
$\overline {\mathcal {J}}_{g,n}(\Phi ) \subset {\operatorname {Simp}}^d(\overline {\mathcal {C}}_{g,n}/\overline {\mathcal {M}}_{g,n})$
is a fine compactified universal Jacobian.
Remark 8.13. The space
![]() $V^d_{g,n}$
is never empty, as it always contains the universal canonical polarization, defined as
$V^d_{g,n}$
is never empty, as it always contains the universal canonical polarization, defined as
![]() $\Phi _{\operatorname {can}}^d := \frac {d}{2g-2}\; \underline {\deg }(\omega _{\pi }) \in V^d_{g,n}$
. (When
$\Phi _{\operatorname {can}}^d := \frac {d}{2g-2}\; \underline {\deg }(\omega _{\pi }) \in V^d_{g,n}$
. (When
![]() $d=g$
, this coincides with the polarization defined in Equation (8.3)). It was observed in [Reference Kass and Pagani25, Remark 5.13] that
$d=g$
, this coincides with the polarization defined in Equation (8.3)). It was observed in [Reference Kass and Pagani25, Remark 5.13] that
![]() $\Phi _{\operatorname {can}}^d$
is nondegenerate precisely when
$\Phi _{\operatorname {can}}^d$
is nondegenerate precisely when
![]() $d-g+1$
and
$d-g+1$
and
![]() $2g-2$
are coprime. (In the
$2g-2$
are coprime. (In the
![]() $n=0$
case, this is already in [Reference Caporaso12, p. 594]).
$n=0$
case, this is already in [Reference Caporaso12, p. 594]).
A natural question that we will address next is whether every fine compactified universal Jacobian arises as in Corollary 8.12, or if one can construct fine compactified universal Jacobian from nondegenerate weakly compatible numerical stability conditions that are not strongly compatible.
Remark 8.14. It is clear that a strongly compatible nondegenerate family of numerical polarizations is also weakly compatible. The converse is not true. Even more: on some families
![]() $\mathcal {X}/S$
there exist nondegenerate families of numerical polarizations
$\mathcal {X}/S$
there exist nondegenerate families of numerical polarizations
![]() $\Phi =\left (\phi _s \in V(\Gamma _s)\right )$
that are weakly compatible, and such that there exists no nondegenerate
$\Phi =\left (\phi _s \in V(\Gamma _s)\right )$
that are weakly compatible, and such that there exists no nondegenerate
![]() $\Phi '=(\phi ^{\prime }_s)_{s \in S}$
that is strongly compatible and satisfies
$\Phi '=(\phi ^{\prime }_s)_{s \in S}$
that is strongly compatible and satisfies
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma _s, \phi ^{\prime }_s}=\operatorname {\mathrm {\sigma }}_{\Gamma _s, \phi _s}$
for all
$\operatorname {\mathrm {\sigma }}_{\Gamma _s, \phi ^{\prime }_s}=\operatorname {\mathrm {\sigma }}_{\Gamma _s, \phi _s}$
for all
![]() $s \in S$
.
$s \in S$
.
Such examples are shown to exist in [Reference Pagani and Tommasi32, Section 6], when
![]() $\mathcal {X}/S$
is the universal family
$\mathcal {X}/S$
is the universal family
![]() $\overline {\mathcal {C}}_{1,n}/ \overline {\mathcal {M}}_{1,n}$
and
$\overline {\mathcal {C}}_{1,n}/ \overline {\mathcal {M}}_{1,n}$
and
![]() $n \geq 6$
. In other words, for all
$n \geq 6$
. In other words, for all
![]() $n\geq 6$
, there are fine compactified universal Jacobians
$n\geq 6$
, there are fine compactified universal Jacobians
![]() $\overline {\mathcal {J}}_{1,n}$
that are not of the form
$\overline {\mathcal {J}}_{1,n}$
that are not of the form
![]() $\overline {\mathcal {J}}_{1,n}(\Phi )$
for any
$\overline {\mathcal {J}}_{1,n}(\Phi )$
for any
![]() $\Phi \in V^d_{1,n}$
.
$\Phi \in V^d_{1,n}$
.
Our main result in the next section, Theorem 9.7, settles in the affirmative the analogous question for the case of the universal family
![]() $\overline {\mathcal {C}}_{g}/ \overline {\mathcal {M}}_{g}$
for all
$\overline {\mathcal {C}}_{g}/ \overline {\mathcal {M}}_{g}$
for all
![]() $g \geq 2$
. More explicitly, when
$g \geq 2$
. More explicitly, when
![]() $n=0$
, every fine compactified universal Jacobian
$n=0$
, every fine compactified universal Jacobian
![]() $\overline {\mathcal {J}}_{g}$
arises as in Corollary 8.12 (i.e., it is of the form
$\overline {\mathcal {J}}_{g}$
arises as in Corollary 8.12 (i.e., it is of the form
![]() $\overline {\mathcal {J}}_{g}(\Phi )$
for some
$\overline {\mathcal {J}}_{g}(\Phi )$
for some
![]() $\Phi \in V_g^d=V_{g,0}^d$
).
$\Phi \in V_g^d=V_{g,0}^d$
).
9. Classification of universal stability assignments
The main result in this section is a classification of universal stability assignments – that is, the case where the family
![]() $\mathcal {X}/S$
is the universal family over
$\mathcal {X}/S$
is the universal family over
![]() $S= \overline {\mathcal {M}}_g$
, the moduli stack of stable curves of genus g (and no marked points). As an intermediate step, we will also produce results that are valid for the case of the universal family over
$S= \overline {\mathcal {M}}_g$
, the moduli stack of stable curves of genus g (and no marked points). As an intermediate step, we will also produce results that are valid for the case of the universal family over
![]() $S= \overline {\mathcal {M}}_{g,n}$
for arbitrary n.
$S= \overline {\mathcal {M}}_{g,n}$
for arbitrary n.
One way to generate universal stability assignments is by means of strongly compatible (universal) numerical polarizations; see Definition 8.10 and Corollary 8.12. Our main result here is Theorem 9.7, where we classify all universal stability assignments with
![]() $n=0$
and for every genus, by proving that they all arise from strongly compatible numerical polarizations (i.e., they all are of the form
$n=0$
and for every genus, by proving that they all arise from strongly compatible numerical polarizations (i.e., they all are of the form
![]() $\operatorname {\mathrm {\sigma }}_{\Phi }$
for some
$\operatorname {\mathrm {\sigma }}_{\Phi }$
for some
![]() $\Phi \in V_g^d$
(see Corollary 8.11 and Corollary 8.12)). Combining with the fact, shown in Proposition 7.14, that universal stability assignments classify fine compactified universal Jacobians, we deduce in Corollary 9.8 that, in the absence of marked points, there are no fine compactified universal Jacobians other than the classical ones constructed in the nineties by Caporaso, Pandharipande and Simpson.
$\Phi \in V_g^d$
(see Corollary 8.11 and Corollary 8.12)). Combining with the fact, shown in Proposition 7.14, that universal stability assignments classify fine compactified universal Jacobians, we deduce in Corollary 9.8 that, in the absence of marked points, there are no fine compactified universal Jacobians other than the classical ones constructed in the nineties by Caporaso, Pandharipande and Simpson.
As discussed in Remark 8.14, an analogous result does not hold, in general, when
![]() $n>0$
.
$n>0$
.
Recall from Example 3.5 that for
![]() $t \in \mathbf {N}$
, a vine curve of type
$t \in \mathbf {N}$
, a vine curve of type
![]() $\boldsymbol {t}$
is a curve with
$\boldsymbol {t}$
is a curve with
![]() $2$
nonsingular irreducible components joined by t nodes. These curves and their dual graphs will play an important role in this section.
$2$
nonsingular irreducible components joined by t nodes. These curves and their dual graphs will play an important role in this section.
We will break down our argument in
![]() $3$
parts.
$3$
parts.
9.1. First part: Universal stability assignments are uniquely determined by their restrictions to vine curves
The main result of this subsection, summarized in the title, is Corollary 9.3 below. The result is obtained as a combination of Lemma 9.1 and Lemma 9.2. The first establishes that a stability assignment for a given curve is uniquely determined by its restriction to the spanning trees of the dual graph of that curve. The second one shows that an assignment of integers on all spanning trees of all elements of
![]() $G_{g,n}$
that is compatible with graph morphisms is uniquely determined by its values over the dual graphs of all vine curves.
$G_{g,n}$
that is compatible with graph morphisms is uniquely determined by its values over the dual graphs of all vine curves.
Let us fix a degree d universal stability assignment
![]() $\sigma $
of type
$\sigma $
of type
![]() $(g,n)$
. Recall from Definition 4.9 (and Remark 4.10) that this is the datum of a collection
$(g,n)$
. Recall from Definition 4.9 (and Remark 4.10) that this is the datum of a collection
that is compatible with all graph morphisms in
![]() $G_{g,n}$
.
$G_{g,n}$
.
By Condition (1) of Definition 4.3, if
![]() $T \subseteq \Gamma $
is a spanning tree, then
$T \subseteq \Gamma $
is a spanning tree, then
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma }(T)= \{\underline {\mathbf d}_{T}\}$
contains a unique multidegree
$\operatorname {\mathrm {\sigma }}_{\Gamma }(T)= \{\underline {\mathbf d}_{T}\}$
contains a unique multidegree
![]() $\underline {\mathbf d}_{T} \in S^d_\Gamma (T)$
. The following lemma shows that a stability assignment is ‘overdetermined’ by the collection of data obtained by extracting this unique value from all spanning trees.
$\underline {\mathbf d}_{T} \in S^d_\Gamma (T)$
. The following lemma shows that a stability assignment is ‘overdetermined’ by the collection of data obtained by extracting this unique value from all spanning trees.
Lemma 9.1. Let
![]() $\Gamma $
be a stable graph and let us fix, for all spanning trees T of
$\Gamma $
be a stable graph and let us fix, for all spanning trees T of
![]() $\Gamma $
, a multidegree
$\Gamma $
, a multidegree
![]() $\underline {\mathbf d}_{T} \in S^d_\Gamma (T)$
. Then there exists at most one degree d stability assignment
$\underline {\mathbf d}_{T} \in S^d_\Gamma (T)$
. Then there exists at most one degree d stability assignment
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma }$
whose value
$\operatorname {\mathrm {\sigma }}_{\Gamma }$
whose value
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma }(T)$
equals
$\operatorname {\mathrm {\sigma }}_{\Gamma }(T)$
equals
![]() $\{\underline {\mathbf d}_{T}\}$
for all spanning trees T.
$\{\underline {\mathbf d}_{T}\}$
for all spanning trees T.
Proof. Let
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma }$
be a degree d stability assignment that satisfies the hypothesis. Inductively define another collection
$\operatorname {\mathrm {\sigma }}_{\Gamma }$
be a degree d stability assignment that satisfies the hypothesis. Inductively define another collection
![]() $M_{\Gamma }$
by defining
$M_{\Gamma }$
by defining
![]() $M_{\Gamma }(G) \subset S_{\Gamma }^d(G)$
for all spanning subgraphs G of
$M_{\Gamma }(G) \subset S_{\Gamma }^d(G)$
for all spanning subgraphs G of
![]() $\Gamma $
. Starting from the assignments
$\Gamma $
. Starting from the assignments
![]() $M_{\Gamma }(T):=\{d_{T}\}$
for all spanning trees
$M_{\Gamma }(T):=\{d_{T}\}$
for all spanning trees
![]() $T \subseteq G$
, let
$T \subseteq G$
, let
![]() $M_{\Gamma }$
be the minimal assignment that satisfies Condition (1) of Definition 4.3.
$M_{\Gamma }$
be the minimal assignment that satisfies Condition (1) of Definition 4.3.
Because
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma }$
satisfies Condition (1) of Definition 4.3, for all spanning subgraphs
$\operatorname {\mathrm {\sigma }}_{\Gamma }$
satisfies Condition (1) of Definition 4.3, for all spanning subgraphs
![]() $G \subseteq \Gamma $
, we have the inclusion
$G \subseteq \Gamma $
, we have the inclusion
![]() $M_{\Gamma }(G) \subseteq \operatorname {\mathrm {\sigma }}_{\Gamma }(G)$
. The inequality
$M_{\Gamma }(G) \subseteq \operatorname {\mathrm {\sigma }}_{\Gamma }(G)$
. The inequality
![]() $|M_{\Gamma }(G)|\geq c(G)$
follows from Proposition 4.7. By Condition (2) of Definition 4.3, we also have the equality
$|M_{\Gamma }(G)|\geq c(G)$
follows from Proposition 4.7. By Condition (2) of Definition 4.3, we also have the equality
![]() $|\operatorname {\mathrm {\sigma }}_{\Gamma }(G)| = c(G)$
. From this, we conclude that
$|\operatorname {\mathrm {\sigma }}_{\Gamma }(G)| = c(G)$
. From this, we conclude that
![]() $M_{\Gamma }(G)$
and
$M_{\Gamma }(G)$
and
![]() $\operatorname {\mathrm {\sigma }}_{\Gamma }(G)$
must coincide.
$\operatorname {\mathrm {\sigma }}_{\Gamma }(G)$
must coincide.
By applying the same idea as in [Reference Kass and Pagani24, Lemma 3.8] and [Reference Kass and Pagani25, Lemma 3.9], we now see how compatibility with graph morphisms propagates an assignment of multidegrees on all strata of vine curves (with the exception of the vine curves whose graph admits a symmetry that swaps the two vertices) to an assignment on all vertices of all spanning trees of all graphs
![]() $\Gamma \in G_{g,n}$
. The reason for excluding the symmetric graphs is that compatibility under automorphisms forces all universal degree d stability assignments to have the same value on those graphs.
$\Gamma \in G_{g,n}$
. The reason for excluding the symmetric graphs is that compatibility under automorphisms forces all universal degree d stability assignments to have the same value on those graphs.
Let
![]() $T_{g,n} \subseteq G_{g,n}$
be the collection of loopless graphs with
$T_{g,n} \subseteq G_{g,n}$
be the collection of loopless graphs with
![]() $2$
vertices, and let
$2$
vertices, and let
![]() $T^{\prime }_{g,n} \subseteq T_{g,n}$
be the subset of graphs such that each automorphism fixes the two vertices. For each element
$T^{\prime }_{g,n} \subseteq T_{g,n}$
be the subset of graphs such that each automorphism fixes the two vertices. For each element
![]() $G \in T_{g,n}$
, fix an ordering of its two vertices (i.e.,
$G \in T_{g,n}$
, fix an ordering of its two vertices (i.e.,
![]() $\operatorname {\mathrm {Vert}}(G)=\{v_1^G, v_2^G\}$
). Let
$\operatorname {\mathrm {Vert}}(G)=\{v_1^G, v_2^G\}$
). Let
![]() $C_{g,n} \subseteq T_{g,n}$
and be the subset of graphs with exactly
$C_{g,n} \subseteq T_{g,n}$
and be the subset of graphs with exactly
![]() $1$
edge (equivalently, the dual graphs of vine curves with no separating nodes, equivalently, the dual graphs of vine curves whose strata have codimension
$1$
edge (equivalently, the dual graphs of vine curves with no separating nodes, equivalently, the dual graphs of vine curves whose strata have codimension
![]() $1$
in
$1$
in
![]() $\overline {\mathcal {M}}_{g,n}$
), and let
$\overline {\mathcal {M}}_{g,n}$
), and let
![]() $G_{g,n}^{\operatorname {NS}} \subseteq G_{g,n}$
be the subset of graphs without separating edges.
$G_{g,n}^{\operatorname {NS}} \subseteq G_{g,n}$
be the subset of graphs without separating edges.
Lemma 9.2. For each function
![]() $\alpha \colon T^{\prime }_{g,n} \to \mathbf {Z}$
, there exists a unique collection of assignments
$\alpha \colon T^{\prime }_{g,n} \to \mathbf {Z}$
, there exists a unique collection of assignments
![]() $\underline {\mathbf d}_{\Gamma , T} \in S^d_{\Gamma }(T)$
for each spanning tree
$\underline {\mathbf d}_{\Gamma , T} \in S^d_{\Gamma }(T)$
for each spanning tree
![]() $T \subseteq \Gamma $
of each element
$T \subseteq \Gamma $
of each element
![]() $\Gamma \in G_{g,n}$
such that we have
$\Gamma \in G_{g,n}$
such that we have
 $$ \begin{align} \sum_{v \in \operatorname{\mathrm{Vert}}(\Gamma) : f(v) = v_1^G} \underline{\mathbf d}_{\Gamma, T}(v) = \alpha(G) \end{align} $$
$$ \begin{align} \sum_{v \in \operatorname{\mathrm{Vert}}(\Gamma) : f(v) = v_1^G} \underline{\mathbf d}_{\Gamma, T}(v) = \alpha(G) \end{align} $$
for all morphisms
![]() $f \colon \Gamma \to G$
where G is in
$f \colon \Gamma \to G$
where G is in
![]() $T_{g,n}$
.
$T_{g,n}$
.
Similarly, for each function
![]() $\beta \colon T^{\prime }_{g,n}\setminus C_{g,n} \to \mathbf {Z}$
, there exists a unique collection of assignments
$\beta \colon T^{\prime }_{g,n}\setminus C_{g,n} \to \mathbf {Z}$
, there exists a unique collection of assignments
![]() $\underline {\mathbf d}_{\Gamma , T} \in S^d_{\Gamma }(T)$
for each spanning tree
$\underline {\mathbf d}_{\Gamma , T} \in S^d_{\Gamma }(T)$
for each spanning tree
![]() $T \subseteq \Gamma $
of each element
$T \subseteq \Gamma $
of each element
![]() $\Gamma \in G_{g,n}^{\operatorname {NS}}$
such that (9.1) is satisfied for all morphisms
$\Gamma \in G_{g,n}^{\operatorname {NS}}$
such that (9.1) is satisfied for all morphisms
![]() $f \colon \Gamma \to G$
where G is in
$f \colon \Gamma \to G$
where G is in
![]() $T_{g,n}$
.
$T_{g,n}$
.
Note that Equation (9.1) is the same as compatibility for graph morphisms defined in Definition 4.8, Equation (4.2).
Proof. We only prove the first statement and leave the second to the reader.
The statement is an extension of the proof given in [Reference Kass and Pagani24, Lemma 3.8]. The main point of the proof is that for a fixed spanning tree
![]() $T \subseteq \Gamma $
, contracting all but one edge of T induces a bijection from
$T \subseteq \Gamma $
, contracting all but one edge of T induces a bijection from
![]() $\operatorname {\mathrm {Edges}}(T)$
to the set of morphisms from
$\operatorname {\mathrm {Edges}}(T)$
to the set of morphisms from
![]() $\Gamma $
to some graph G isomorphic to an element of
$\Gamma $
to some graph G isomorphic to an element of
![]() $T_{g,n}$
. The isomorphism is unique when
$T_{g,n}$
. The isomorphism is unique when
![]() $G \in T^{\prime }_{g,n}$
, and there are two isomorphisms when
$G \in T^{\prime }_{g,n}$
, and there are two isomorphisms when
![]() $G \in T_{g,n} \setminus T^{\prime }_{g,n}$
.
$G \in T_{g,n} \setminus T^{\prime }_{g,n}$
.
Each
![]() $e \in \operatorname {\mathrm {Edges}}(T)$
induces a morphism
$e \in \operatorname {\mathrm {Edges}}(T)$
induces a morphism
![]() $\Gamma \to \Gamma _e$
obtained by contracting all edges
$\Gamma \to \Gamma _e$
obtained by contracting all edges
![]() $\operatorname {\mathrm {Edges}}(T) \setminus \{ e\}$
. There are two cases, depending on how each automorphism of
$\operatorname {\mathrm {Edges}}(T) \setminus \{ e\}$
. There are two cases, depending on how each automorphism of
![]() $\Gamma _e$
acts on
$\Gamma _e$
acts on
![]() $\operatorname {\mathrm {Vert}}(\Gamma _e)$
: (1) If each acts trivially, then there exists a unique isomorphism from
$\operatorname {\mathrm {Vert}}(\Gamma _e)$
: (1) If each acts trivially, then there exists a unique isomorphism from
![]() $\Gamma _e$
to an element of
$\Gamma _e$
to an element of
![]() $T^{\prime }_{g,n}$
. (2) If some act nontrivially, there are two isomorphisms from
$T^{\prime }_{g,n}$
. (2) If some act nontrivially, there are two isomorphisms from
![]() $\Gamma _e$
to an element of
$\Gamma _e$
to an element of
![]() $T_{g,n} \setminus T^{\prime }_{g,n}$
.
$T_{g,n} \setminus T^{\prime }_{g,n}$
.
Now we view
![]() $\underline {\mathbf {d}}_{\Gamma , T}$
as a vector with
$\underline {\mathbf {d}}_{\Gamma , T}$
as a vector with
![]() $|\operatorname {\mathrm {Vert}}{T}|=|\operatorname {\mathrm {Vert}}{\Gamma }|$
unknown entries. In Case (1), we obtain an affine linear constraint among these unknowns by Equation (9.1). In Case (2), a linear constraint is given by compatibility for the extra automorphism, which imposes that the sum of the values of
$|\operatorname {\mathrm {Vert}}{T}|=|\operatorname {\mathrm {Vert}}{\Gamma }|$
unknown entries. In Case (1), we obtain an affine linear constraint among these unknowns by Equation (9.1). In Case (2), a linear constraint is given by compatibility for the extra automorphism, which imposes that the sum of the values of
![]() $\underline {\mathbf {d}}_{\Gamma , T}$
on the vertices on one side of e equals the sum of the values on the vertices on the other side of e. Altogether, this gives
$\underline {\mathbf {d}}_{\Gamma , T}$
on the vertices on one side of e equals the sum of the values on the vertices on the other side of e. Altogether, this gives
![]() $\left |\operatorname {\mathrm {Edges}}(T)\right |=\left |\operatorname {\mathrm {Vert}}(\Gamma )\right |-1$
affine linear constraints on the
$\left |\operatorname {\mathrm {Edges}}(T)\right |=\left |\operatorname {\mathrm {Vert}}(\Gamma )\right |-1$
affine linear constraints on the
![]() $\left |\operatorname {\mathrm {Vert}}(\Gamma )\right |$
different entries of
$\left |\operatorname {\mathrm {Vert}}(\Gamma )\right |$
different entries of
![]() $\underline {\mathbf d}_{\Gamma , T}$
. One more affine linear constraint is given by the fact that
$\underline {\mathbf d}_{\Gamma , T}$
. One more affine linear constraint is given by the fact that
![]() $\underline {\mathbf {d}}_{\Gamma , T} \in S^d_{\Gamma }(T) \subset \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
. All in all, we obtain an affine linear system of
$\underline {\mathbf {d}}_{\Gamma , T} \in S^d_{\Gamma }(T) \subset \mathbf {Z}^{\operatorname {\mathrm {Vert}}(\Gamma )}$
. All in all, we obtain an affine linear system of
![]() $|\operatorname {Vert}(T)|$
equations in
$|\operatorname {Vert}(T)|$
equations in
![]() $|\operatorname {Vert}(T)|$
unknowns, which one can check has invertible determinant over
$|\operatorname {Vert}(T)|$
unknowns, which one can check has invertible determinant over
![]() $\mathbf {Z}$
– hence a unique solution for
$\mathbf {Z}$
– hence a unique solution for
![]() $\underline {\mathbf d}_{\Gamma , T}$
.
$\underline {\mathbf d}_{\Gamma , T}$
.
Lemmas 9.1 and 9.2 allow us to regard every degree d universal stability assignment of type
![]() $(g,n)$
as an element of
$(g,n)$
as an element of
![]() $\mathbf {Z}^{T^{\prime }_{g,n}}$
. However, not all elements of
$\mathbf {Z}^{T^{\prime }_{g,n}}$
. However, not all elements of
![]() $\mathbf {Z}^{T^{\prime }_{g,n}}$
give rise to a universal stability assignment. For
$\mathbf {Z}^{T^{\prime }_{g,n}}$
give rise to a universal stability assignment. For
![]() $\Gamma \in G_{g,n}$
, it can happen that the collection on all spanning trees
$\Gamma \in G_{g,n}$
, it can happen that the collection on all spanning trees
![]() $\{\underline {\mathbf {d}}_{\Gamma ,T}\}_{T}$
obtained from some
$\{\underline {\mathbf {d}}_{\Gamma ,T}\}_{T}$
obtained from some
![]() $\alpha \in \mathbf {Z}^{T^{\prime }_{g,n}}$
as in Lemma 9.2 is not the restriction of any stability assignment on the graph
$\alpha \in \mathbf {Z}^{T^{\prime }_{g,n}}$
as in Lemma 9.2 is not the restriction of any stability assignment on the graph
![]() $\Gamma $
(see Lemma 9.1).
$\Gamma $
(see Lemma 9.1).
Corollary 9.3. Let
![]() $\sigma , \tau $
be degree d universal stability assignments of type
$\sigma , \tau $
be degree d universal stability assignments of type
![]() $(g,n)$
. If
$(g,n)$
. If
![]() $\sigma _G=\tau _G$
for all
$\sigma _G=\tau _G$
for all
![]() $G \in T^{\prime }_{g,n}$
, then
$G \in T^{\prime }_{g,n}$
, then
![]() $\sigma =\tau $
. If
$\sigma =\tau $
. If
![]() $\sigma _G = \tau _G$
for all
$\sigma _G = \tau _G$
for all
![]() $G \in T^{\prime }_{g,n} \setminus C_{g,n}$
, then
$G \in T^{\prime }_{g,n} \setminus C_{g,n}$
, then
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
coincide on all curves that have no separating nodes.
$\tau $
coincide on all curves that have no separating nodes.
9.2. Second part: When
 $n=0$
, over each vine curve with at least
$n=0$
, over each vine curve with at least
 $2$
nodes there is at most
$2$
nodes there is at most
 $1$
stability assignment that extends to a universal stability
$1$
stability assignment that extends to a universal stability
In this subsection, we fix
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $n=0$
. The main result here is Corollary 9.5.
$n=0$
. The main result here is Corollary 9.5.
We first need some combinatorial preparation. Let
![]() $\operatorname {GSym}_g$
be the trivalent graph with
$\operatorname {GSym}_g$
be the trivalent graph with
![]() $2g-2$
vertices
$2g-2$
vertices
![]() $v_1, \ldots , v_{2g-2}$
of genus
$v_1, \ldots , v_{2g-2}$
of genus
![]() $0$
, where each vertex
$0$
, where each vertex
![]() $v_i$
is connected to
$v_i$
is connected to
![]() $v_{i-1}$
,
$v_{i-1}$
,
![]() $v_{i+1}$
and
$v_{i+1}$
and
![]() $v_{i+g-1}$
(indices should be considered modulo
$v_{i+g-1}$
(indices should be considered modulo
![]() $2g-2$
). For
$2g-2$
). For
![]() $i\in \mathbf {Z}/(2g-2)\mathbf {Z}$
and
$i\in \mathbf {Z}/(2g-2)\mathbf {Z}$
and
![]() $j=1,\dots ,g-1$
, we shall denote by
$j=1,\dots ,g-1$
, we shall denote by
![]() $e_i$
the edge joining
$e_i$
the edge joining
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
and by
$v_{i+1}$
and by
![]() $e_j'$
the edge joining
$e_j'$
the edge joining
![]() $v_j$
and
$v_j$
and
![]() $v_{j+g-1}$
. (See Picture 1).
$v_{j+g-1}$
. (See Picture 1).

Figure 1 A picture of the graph
![]() $\operatorname {GSym}_g$
.
$\operatorname {GSym}_g$
.
Let
![]() $\Gamma _g \subset \operatorname {GSym}_g$
be the maximal
$\Gamma _g \subset \operatorname {GSym}_g$
be the maximal
![]() $1$
-cycle consisting of all edges of the form
$1$
-cycle consisting of all edges of the form
![]() $e_i$
.
$e_i$
.
Lemma 9.4. For every
![]() $d \in \mathbf {Z}$
, there is [12pc]at most one assignment
$d \in \mathbf {Z}$
, there is [12pc]at most one assignment
that satisfies the two conditions of Definition 4.3 and that extends to a degree d universal stability assignment of type
![]() $(g,0)$
. When such an assignment exists, the integers
$(g,0)$
. When such an assignment exists, the integers
![]() $d-g+1$
and
$d-g+1$
and
![]() $2g-2$
are necessarily coprime.
$2g-2$
are necessarily coprime.
Proof. Assume that
![]() $\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}$
is the restriction to
$\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}$
is the restriction to
![]() $\operatorname {GSym}_g$
of some universal stability
$\operatorname {GSym}_g$
of some universal stability
![]() $\operatorname {\mathrm {\sigma }}$
. Since
$\operatorname {\mathrm {\sigma }}$
. Since
![]() $\Gamma _g$
is a graph of genus
$\Gamma _g$
is a graph of genus
![]() $1$
, we can apply the results from [Reference Pagani and Tommasi32, Section 3] to describe the assignment
$1$
, we can apply the results from [Reference Pagani and Tommasi32, Section 3] to describe the assignment
![]() $\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}(\Gamma _g)$
. Namely, in genus
$\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}(\Gamma _g)$
. Namely, in genus
![]() $1$
, it is known that all such assignments are induced by a polarization
$1$
, it is known that all such assignments are induced by a polarization
![]() $\phi $
whose value
$\phi $
whose value
![]() $\phi (v_i)$
at each vertex
$\phi (v_i)$
at each vertex
![]() $v_i$
is given by the average of the
$v_i$
is given by the average of the
![]() $2g-2$
admissible multidegrees in
$2g-2$
admissible multidegrees in
![]() $\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}(\Gamma _g)$
. In particular, the polarization
$\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}(\Gamma _g)$
. In particular, the polarization
![]() $\phi $
should be invariant under the automorphisms of
$\phi $
should be invariant under the automorphisms of
![]() $\operatorname {GSym}_g$
preserving
$\operatorname {GSym}_g$
preserving
![]() $\Gamma _g$
, such as the cyclic automorphism mapping
$\Gamma _g$
, such as the cyclic automorphism mapping
![]() $e_i$
to
$e_i$
to
![]() $e_{i+1}$
for all i. From this, we deduce that all
$e_{i+1}$
for all i. From this, we deduce that all
![]() $\phi (v_i)$
are equal, and since we have obtained
$\phi (v_i)$
are equal, and since we have obtained
![]() $\Gamma _g$
from
$\Gamma _g$
from
![]() $\operatorname {GSym}_g$
by removing the
$\operatorname {GSym}_g$
by removing the
![]() $g-1$
edges
$g-1$
edges
![]() $e_i'$
, we have
$e_i'$
, we have
![]() $\sum _{i\in \mathbf {Z}/(2g-2)\mathbf {Z}}\phi _i=d-g+1$
. It follows that there exists at most
$\sum _{i\in \mathbf {Z}/(2g-2)\mathbf {Z}}\phi _i=d-g+1$
. It follows that there exists at most
![]() $1$
assignment, and that this assignment should be the one induced by
$1$
assignment, and that this assignment should be the one induced by
![]() $\phi (v_i)=\frac {d-g+1}{2g-2}$
for all
$\phi (v_i)=\frac {d-g+1}{2g-2}$
for all
![]() $i=1, \ldots , 2g-2$
. Then the claim follows from the fact that this polarization is nondegenerate if and only if
$i=1, \ldots , 2g-2$
. Then the claim follows from the fact that this polarization is nondegenerate if and only if
![]() $d-g+1$
and
$d-g+1$
and
![]() $2g-2$
are coprime.
$2g-2$
are coprime.
We can now prove the following.
Corollary 9.5. If
![]() $G\in T_{g,0} \setminus C_{g,0} \subseteq G_{g,0}$
is a loopless graph with
$G\in T_{g,0} \setminus C_{g,0} \subseteq G_{g,0}$
is a loopless graph with
![]() $2$
vertices and at least
$2$
vertices and at least
![]() $2$
edges, there exists at most one degree d stability assignment for the graph G that extends to a degree d universal stability assignment.
$2$
edges, there exists at most one degree d stability assignment for the graph G that extends to a degree d universal stability assignment.
In the proof, we will denote by
![]() $\Gamma (t,i,j)$
the object of
$\Gamma (t,i,j)$
the object of
![]() $G_{g}$
that consists of two vertices of genus i and j connected by t edges. (Note that
$G_{g}$
that consists of two vertices of genus i and j connected by t edges. (Note that
![]() $g=i+j+t-1$
).
$g=i+j+t-1$
).
Proof. The claim is obtained by proving that the value of an assignment on vine curves of type
![]() $t \geq 2$
can be obtained, using compatibility with graph morphisms (Definition 4.8), from the assignment calculated on
$t \geq 2$
can be obtained, using compatibility with graph morphisms (Definition 4.8), from the assignment calculated on
![]() $\Gamma _g \subset \operatorname {GSym}_g$
(described in Lemma 9.4). Recall that a degree d stability assignment over a graph with
$\Gamma _g \subset \operatorname {GSym}_g$
(described in Lemma 9.4). Recall that a degree d stability assignment over a graph with
![]() $2$
vertices has the same value on all spanning trees and is uniquely determined by this value (Example 4.6).
$2$
vertices has the same value on all spanning trees and is uniquely determined by this value (Example 4.6).
First, we prove the claim when
![]() $G = \Gamma (t, i,0)$
has one vertex of genus zero. Apply Lemma 9.4 to deduce the uniqueness of an assignment
$G = \Gamma (t, i,0)$
has one vertex of genus zero. Apply Lemma 9.4 to deduce the uniqueness of an assignment
![]() $\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}(\Gamma _g)$
that satisfies the two conditions of Definition 4.3 and automorphism-invariance. Then apply to
$\operatorname {\mathrm {\sigma }}_{\operatorname {GSym}_g}(\Gamma _g)$
that satisfies the two conditions of Definition 4.3 and automorphism-invariance. Then apply to
![]() $\Gamma _g$
the first composition of contractions defined in [Reference Kass and Pagani25, Lemma 3.9].
$\Gamma _g$
the first composition of contractions defined in [Reference Kass and Pagani25, Lemma 3.9].
The statement for an arbitrary graph
![]() $G= \Gamma (t, i, j)$
is obtained by applying the second set of contractions used in the proof of [Reference Kass and Pagani25, Lemma 3.9] to deduce the value of
$G= \Gamma (t, i, j)$
is obtained by applying the second set of contractions used in the proof of [Reference Kass and Pagani25, Lemma 3.9] to deduce the value of
![]() $\operatorname {\mathrm {\sigma }}$
on
$\operatorname {\mathrm {\sigma }}$
on
![]() $\Gamma (t, i, j)$
from the value of
$\Gamma (t, i, j)$
from the value of
![]() $\operatorname {\mathrm {\sigma }}$
on
$\operatorname {\mathrm {\sigma }}$
on
![]() $G=\Gamma ( i-j+2, t+2j-2, 0)$
. More precisely, consider the graph
$G=\Gamma ( i-j+2, t+2j-2, 0)$
. More precisely, consider the graph
![]() $G'$
with
$G'$
with
![]() $4$
vertices
$4$
vertices
![]() $w_1,w_2,w_3,w_4$
defined in the proof of [Reference Kass and Pagani25, Lemma 3.9] and its spanning subgraph
$w_1,w_2,w_3,w_4$
defined in the proof of [Reference Kass and Pagani25, Lemma 3.9] and its spanning subgraph
![]() ${G}_0':=w_1-w_2-w_4-w_3-w_1$
. Let
${G}_0':=w_1-w_2-w_4-w_3-w_1$
. Let
![]() $\alpha \in \mathbf {Z}$
be defined by the condition
$\alpha \in \mathbf {Z}$
be defined by the condition
for
![]() ${G}_0$
a spanning tree of
${G}_0$
a spanning tree of
![]() $\Gamma ( i-j+2, t+2j-2, 0)$
. By combining the axioms of a degree d stability with compatibility with graph morphisms (Definition 4.8), we find out
$\Gamma ( i-j+2, t+2j-2, 0)$
. By combining the axioms of a degree d stability with compatibility with graph morphisms (Definition 4.8), we find out
for the unique
![]() $\beta \in \mathbf {Z}$
such that
$\beta \in \mathbf {Z}$
such that
![]() $2\alpha + 2 \beta = d+1 - t - i + j$
(observe that
$2\alpha + 2 \beta = d+1 - t - i + j$
(observe that
![]() $d+1-t - i + j$
must be even since so is
$d+1-t - i + j$
must be even since so is
![]() $d-g+1$
, because by Lemma 9.4, it is coprime with
$d-g+1$
, because by Lemma 9.4, it is coprime with
![]() $2g-2$
, and by using
$2g-2$
, and by using
![]() $g=t + i + j -1$
). From Condition (1) of Definition 4.3, we deduce that the unique assignment on the spanning tree
$g=t + i + j -1$
). From Condition (1) of Definition 4.3, we deduce that the unique assignment on the spanning tree
![]() ${G}_0" \subset {G}_0'$
defined by
${G}_0" \subset {G}_0'$
defined by
![]() $w_2- w_1 -w_3 - w_4$
equals
$w_2- w_1 -w_3 - w_4$
equals
and applying the second set of contractions used in the proof of [Reference Kass and Pagani25, Lemma 3.9], we deduce the value of
![]() $\operatorname {\mathrm {\sigma }}$
on the graph
$\operatorname {\mathrm {\sigma }}$
on the graph
![]() $G= \Gamma (t, i, j)$
.
$G= \Gamma (t, i, j)$
.
9.3. Third part: Conclusion
In this subsection, we fix
![]() $g \geq 2$
and
$g \geq 2$
and
![]() $n=0$
.
$n=0$
.
Note that if
![]() $\gcd (d-g+1,2g-2)=1$
, the universal canonical numerical polarization
$\gcd (d-g+1,2g-2)=1$
, the universal canonical numerical polarization
![]() $\Phi _{\operatorname {can}}^d$
defined in Remark 8.13 is nondegenerate, and so there is a canonical universal stability assignment
$\Phi _{\operatorname {can}}^d$
defined in Remark 8.13 is nondegenerate, and so there is a canonical universal stability assignment
![]() $\operatorname {\mathrm {\sigma }}_{\Phi ^d_{\operatorname {can}}}$
of type
$\operatorname {\mathrm {\sigma }}_{\Phi ^d_{\operatorname {can}}}$
of type
![]() $(g,0)$
defined via Definition 8.10. More stability assignments can be obtained by modifying the stable bidegrees over the boundary divisors of
$(g,0)$
defined via Definition 8.10. More stability assignments can be obtained by modifying the stable bidegrees over the boundary divisors of
![]() $\overline {\mathcal {M}}_g$
having two components (the vine curves whose dual graph, borrowing from the notation of the previous subsection, has the form
$\overline {\mathcal {M}}_g$
having two components (the vine curves whose dual graph, borrowing from the notation of the previous subsection, has the form
![]() $G=\Gamma (1,i,g-i)$
for
$G=\Gamma (1,i,g-i)$
for
![]() $1 \leq i<g/2$
, the first vertex having genus i and the second having genus
$1 \leq i<g/2$
, the first vertex having genus i and the second having genus
![]() $g-i$
).
$g-i$
).
Proposition 9.6. Assume
![]() $\gcd (d-g+1,2g-2)=1$
and fix an integer
$\gcd (d-g+1,2g-2)=1$
and fix an integer
![]() $\alpha _i$
for each
$\alpha _i$
for each
![]() $1 \leq i <\lfloor \frac {g-1}{2} \rfloor $
. Then there exists a stability assignment of the form
$1 \leq i <\lfloor \frac {g-1}{2} \rfloor $
. Then there exists a stability assignment of the form
![]() $\operatorname {\mathrm {\sigma }}_{\Phi }$
for
$\operatorname {\mathrm {\sigma }}_{\Phi }$
for
![]() $\Phi $
a nondegenerate element of
$\Phi $
a nondegenerate element of
![]() $V_g^d$
(as in Definition 8.10) such that
$V_g^d$
(as in Definition 8.10) such that
![]() $\Phi (G(1,i,g-i))=(\alpha _i, d-\alpha _i)$
for all i.
$\Phi (G(1,i,g-i))=(\alpha _i, d-\alpha _i)$
for all i.
Proof. The existence of a nondegenerate universal stability assignment
![]() $\Phi $
that satisfies the given constraints follows immediately from [Reference Kass and Pagani25, Corollary 3.6, and Theorem 2, in the
$\Phi $
that satisfies the given constraints follows immediately from [Reference Kass and Pagani25, Corollary 3.6, and Theorem 2, in the
![]() $n=0$
case]. By Corollary 8.12, the assignment
$n=0$
case]. By Corollary 8.12, the assignment
![]() $\operatorname {\mathrm {\sigma }}_{\Phi }$
defines a degree d universal stability assignment.
$\operatorname {\mathrm {\sigma }}_{\Phi }$
defines a degree d universal stability assignment.
We are now in a position to conclude.
Theorem 9.7. If a degree d universal stability assignment of type
![]() $(g,0)$
(Definition 4.9 and Remark 4.10) exists, then
$(g,0)$
(Definition 4.9 and Remark 4.10) exists, then
![]() $\gcd (d-g+1, 2g-2)=1$
. Assuming the latter equality holds, let
$\gcd (d-g+1, 2g-2)=1$
. Assuming the latter equality holds, let
![]() $\tau $
be one such stability assignment. Then there exists a unique stability assignment of the form
$\tau $
be one such stability assignment. Then there exists a unique stability assignment of the form
![]() $\sigma _{\Phi }$
for
$\sigma _{\Phi }$
for
![]() $\Phi \in V_{g}^d$
nondegenerate such that
$\Phi \in V_{g}^d$
nondegenerate such that
![]() $\tau $
equals
$\tau $
equals
![]() $\operatorname {\mathrm {\sigma }}_{\Phi }$
. This stability assignment coincides with the canonical stability assignment
$\operatorname {\mathrm {\sigma }}_{\Phi }$
. This stability assignment coincides with the canonical stability assignment
![]() $\operatorname {\mathrm {\sigma }}_{\Phi ^d_{\operatorname {can}}}$
(see Remark 8.13) on all curves
$\operatorname {\mathrm {\sigma }}_{\Phi ^d_{\operatorname {can}}}$
(see Remark 8.13) on all curves
![]() $[C] \in \overline {\mathcal {M}}_g$
with no separating nodes.
$[C] \in \overline {\mathcal {M}}_g$
with no separating nodes.
Proof. By Lemma 9.4, if
![]() $\gcd (d-g+1, 2g-2) \neq 1$
, there exists no universal stability assignment. From now on, we will assume
$\gcd (d-g+1, 2g-2) \neq 1$
, there exists no universal stability assignment. From now on, we will assume
![]() $\gcd (d-g+1, 2g-2) = 1$
.
$\gcd (d-g+1, 2g-2) = 1$
.
We now prove the second statement. By the first part of Corollary 9.3, proving the equality
![]() $\tau = \operatorname {\mathrm {\sigma }}_{\Phi }$
for some nondegenerate
$\tau = \operatorname {\mathrm {\sigma }}_{\Phi }$
for some nondegenerate
![]() $\Phi \in V_g^d$
is equivalent to proving the equality of the restrictions
$\Phi \in V_g^d$
is equivalent to proving the equality of the restrictions
By Proposition 9.6, there exists a stability assignment of the form
![]() $\operatorname {\mathrm {\sigma }}_{\Phi }$
that coincides with
$\operatorname {\mathrm {\sigma }}_{\Phi }$
that coincides with
![]() $\tau $
when restricted to all loopless graphs G with
$\tau $
when restricted to all loopless graphs G with
![]() $2$
vertices and
$2$
vertices and
![]() $1$
edge. By the uniqueness statement in Corollary 9.5, we conclude that Condition (9.2) holds, and hence that
$1$
edge. By the uniqueness statement in Corollary 9.5, we conclude that Condition (9.2) holds, and hence that
![]() $\tau = \operatorname {\mathrm {\sigma }}_{\Phi }$
.
$\tau = \operatorname {\mathrm {\sigma }}_{\Phi }$
.
Our last statement follows from the second part of Corollary 9.3.
By combining Theorem 9.7 and Proposition 7.14 (with
![]() $\mathcal {X}/S$
the universal family over
$\mathcal {X}/S$
the universal family over
![]() $S=\overline {\mathcal {M}}_g$
), we immediately deduce the following classification result.
$S=\overline {\mathcal {M}}_g$
), we immediately deduce the following classification result.
Corollary 9.8. If
![]() $\overline {\mathcal {J}}_g$
is a degree d fine compactified universal Jacobian for
$\overline {\mathcal {J}}_g$
is a degree d fine compactified universal Jacobian for
![]() $\overline {\mathcal {M}}_g$
, then d satisfies
$\overline {\mathcal {M}}_g$
, then d satisfies
![]() $\gcd (d-g+1, 2g-2)=1$
, and there exists
$\gcd (d-g+1, 2g-2)=1$
, and there exists
![]() $\Phi \in V_{g}^d$
such that
$\Phi \in V_{g}^d$
such that
![]() $\overline {\mathcal {J}}_g = \overline {\mathcal {J}}_{g} (\Phi )$
.
$\overline {\mathcal {J}}_g = \overline {\mathcal {J}}_{g} (\Phi )$
.
We conclude by relating this result to the compactified universal Jacobians constructed in the nineties by Caporaso [Reference Caporaso12], Pandharipande [Reference Pandharipande33] and Simpson [Reference Simpson35]. By earlier work, this amounts to relating
![]() $\overline {\mathcal {J}}(\Phi )$
, for any
$\overline {\mathcal {J}}(\Phi )$
, for any
![]() $\Phi \in V_g^d$
, to the canonical fine compactified universal Jacobian
$\Phi \in V_g^d$
, to the canonical fine compactified universal Jacobian
![]() $\overline {\mathcal {J}}(\Phi ^d_{\text {can}})$
.
$\overline {\mathcal {J}}(\Phi ^d_{\text {can}})$
.
Remark 9.9. Let
![]() $\Phi \in V_g^d$
and assume
$\Phi \in V_g^d$
and assume
![]() $\gcd (d-g+1,2g-2)=1$
. Then we claim that there exists a line bundle
$\gcd (d-g+1,2g-2)=1$
. Then we claim that there exists a line bundle
![]() $M \in \operatorname {Pic}^0(\overline {\mathcal {C}}_g)$
such that
$M \in \operatorname {Pic}^0(\overline {\mathcal {C}}_g)$
such that
![]() $\Phi =\Phi ^d_{\operatorname {can}} + \underline {\deg }(M)$
. In particular, translation by M induces an isomorphism
$\Phi =\Phi ^d_{\operatorname {can}} + \underline {\deg }(M)$
. In particular, translation by M induces an isomorphism
![]() $ \overline {\mathcal {J}}_g(\Phi ^d_{\operatorname {can}}) \to \overline {\mathcal {J}}_g(\Phi )$
that commutes with the forgetful maps to
$ \overline {\mathcal {J}}_g(\Phi ^d_{\operatorname {can}}) \to \overline {\mathcal {J}}_g(\Phi )$
that commutes with the forgetful maps to
![]() $\overline {\mathcal {M}}_g$
.
$\overline {\mathcal {M}}_g$
.
The claim follows from [Reference Kass and Pagani25, Section 6]. In loc. cit., the authors study the natural translation action of
![]() $\operatorname {Pic}^0(\overline {\mathcal {C}}_{g,n})$
on
$\operatorname {Pic}^0(\overline {\mathcal {C}}_{g,n})$
on
![]() $V^d_{g,n}$
. This action induces an action on the collection of connected components of the nondegenerate locus, and by [Reference Kass and Pagani25, Lemma 6.15 (2)], this action is transitive when n equals zero.
$V^d_{g,n}$
. This action induces an action on the collection of connected components of the nondegenerate locus, and by [Reference Kass and Pagani25, Lemma 6.15 (2)], this action is transitive when n equals zero.
The relation between
![]() $\overline {\mathcal {J}}_g(\Phi ^d_{\operatorname {can}})$
and the compactified Jacobians of Caporaso [Reference Caporaso12], Pandharipande [Reference Pandharipande33] is discussed in [Reference Kass and Pagani25, Remark 5.14]. The relation with Simpson’s stability with respect to an ample line bundle is established in [Reference Kass and Pagani25, Corollary 4.3] (see also [Reference Kass and Pagani24, Section 3]).
$\overline {\mathcal {J}}_g(\Phi ^d_{\operatorname {can}})$
and the compactified Jacobians of Caporaso [Reference Caporaso12], Pandharipande [Reference Pandharipande33] is discussed in [Reference Kass and Pagani25, Remark 5.14]. The relation with Simpson’s stability with respect to an ample line bundle is established in [Reference Kass and Pagani25, Corollary 4.3] (see also [Reference Kass and Pagani24, Section 3]).
10. Final remarks and open questions
In Definitions 4.3 and 4.9, we introduced the notion of families of degree d stability assignments for a single curve X and for the universal family
![]() $\overline {\mathcal {C}}_{g,n}\to \overline {\mathcal {M}}_{g,n}$
.
$\overline {\mathcal {C}}_{g,n}\to \overline {\mathcal {M}}_{g,n}$
.
For X a nodal curve with dual graph
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $\Sigma ^d(\Gamma )$
be the set of all degree d stability assignments. In Section 8, we defined, following Oda–Seshadri [Reference Oda and Seshadri31], a stability space
$\Sigma ^d(\Gamma )$
be the set of all degree d stability assignments. In Section 8, we defined, following Oda–Seshadri [Reference Oda and Seshadri31], a stability space
![]() $V^d(\Gamma )$
with a subspace of degenerate elements (a union of hyperplanes). We define
$V^d(\Gamma )$
with a subspace of degenerate elements (a union of hyperplanes). We define
![]() $\mathcal {P}^d(\Gamma )$
to be the set whose elements are the connected components (maximal dimensional polytopes) of the nondegenerate locus in
$\mathcal {P}^d(\Gamma )$
to be the set whose elements are the connected components (maximal dimensional polytopes) of the nondegenerate locus in
![]() $V^d(\Gamma )$
. By Corollary 7.16 and Proposition 8.3, there is an injection
$V^d(\Gamma )$
. By Corollary 7.16 and Proposition 8.3, there is an injection
![]() $\mathcal {P}^d(\Gamma ) \to \Sigma ^d(\Gamma )$
, and it is natural to ask when this map is surjective. This is the same as Question 8.4, the case where
$\mathcal {P}^d(\Gamma ) \to \Sigma ^d(\Gamma )$
, and it is natural to ask when this map is surjective. This is the same as Question 8.4, the case where
![]() $g(X)=1$
(or even
$g(X)=1$
(or even
![]() $b_1(\Gamma (X))=1$
) was settled in the affirmative in [Reference Pagani and Tommasi32]; see Example 8.7.
$b_1(\Gamma (X))=1$
) was settled in the affirmative in [Reference Pagani and Tommasi32]; see Example 8.7.
Then let
![]() $\Sigma ^d_{g,n}$
be the set of all degree d stability assignments of type
$\Sigma ^d_{g,n}$
be the set of all degree d stability assignments of type
![]() $(g,n)$
. The latter can be described as the inverse limit
$(g,n)$
. The latter can be described as the inverse limit
where
![]() $G_{g,n}$
is the category of stable n-pointed dual graphs of genus g.
$G_{g,n}$
is the category of stable n-pointed dual graphs of genus g.
Similarly, for universal (and strongly compatible) numerical polarizations (see Section 8), in [Reference Kass and Pagani25], the authors defined the affine space
(where morphisms are as in Definition 8.9). The latter is always nonempty, as it contains the canonical stability assignment.
Let
![]() $\mathcal {P}^d_{g,n}$
be the set whose elements are the connected components of the complement of the degenerate stability assignments in
$\mathcal {P}^d_{g,n}$
be the set whose elements are the connected components of the complement of the degenerate stability assignments in
![]() $V_{g,n}^d$
(see Definition 8.10). By Corollary 7.16 and Corollary 8.3, we have a natural injection
$V_{g,n}^d$
(see Definition 8.10). By Corollary 7.16 and Corollary 8.3, we have a natural injection
![]() $\mathcal {P}^d_{g,n} \to \Sigma ^d_{g,n}$
, and one can ask under which assumptions the latter is surjective.Footnote 7 The genus
$\mathcal {P}^d_{g,n} \to \Sigma ^d_{g,n}$
, and one can ask under which assumptions the latter is surjective.Footnote 7 The genus
![]() $1$
case was settled in [Reference Pagani and Tommasi32]: the map
$1$
case was settled in [Reference Pagani and Tommasi32]: the map
![]() $\mathcal {P}^d_{1,n} \to \Sigma ^d_{1,n}$
is a bijection if and only if
$\mathcal {P}^d_{1,n} \to \Sigma ^d_{1,n}$
is a bijection if and only if
![]() $n \leq 5$
(see Remark 8.14). The case without marked points is solved by Corollary 9.8: the map
$n \leq 5$
(see Remark 8.14). The case without marked points is solved by Corollary 9.8: the map
![]() $\mathcal {P}^d_g \to \Sigma ^d_g$
is a bijection for all g.
$\mathcal {P}^d_g \to \Sigma ^d_g$
is a bijection for all g.
Here are some natural future problems to address.
-
1. What is the analogue of Theorem 1.1 for the case of smoothable compactified Jacobians (not necessarily fine)? By this, we mean a smoothable open substack of the moduli space of rank
 $1$
torsion-free sheaves (not just the simple ones) that have a proper good moduli space.
$1$
torsion-free sheaves (not just the simple ones) that have a proper good moduli space. -
2. Is there a natural stability space with walls, containing
 $V^d_{g,n}$
, and a natural bijection from the set of its maximal-dimensional chambers to
$V^d_{g,n}$
, and a natural bijection from the set of its maximal-dimensional chambers to
 $\Sigma ^d_{g,n}$
?
$\Sigma ^d_{g,n}$
?
Acknowledgements
Many of the initial ideas of this project are owed to Jesse Kass. It is with great pleasure that we acknowledge his intellectual contribution to this work.
We are grateful to Jonathan Barmak for sharing with us [Reference Barmak7] a solution to the combinatorial problem that appears in the proof of Lemma 9.1.
NP is very thankful to Alex Abreu and Filippo Viviani for several important contributions that came after an early version of the preprint was shared with them. In particular, Filippo Viviani pointed out a gap in the proof of the earlier version of Proposition 7.10, and Alex Abreu suggested the numerical polarization of Example 8.8. NP also wants to thank Marco Fava for several helpful discussions.
We are very grateful to the anonymous referees for the careful reading of the previous version of this paper. Their kind comments have helped us improve the contents and the exposition.
Competing interests
The authors have no competing interest to declare.
Funding statement
NP acknowledges support from EPSRC grant EP/P004881 during the early stages of this project. OT is a member of INdAM-GNSAGA and was partially supported during the preparation of this paper by the PRIN2020 research grant Curves, Ricci flat Varieties and their Interactions.