1 Introduction
1.1 Motivation
In the pioneering work [Reference Furstenberg17], Furstenberg applied the countable Furstenberg–Zimmer structure theory, developed by him in the same article and by Zimmer in [Reference Zimmer47, Reference Zimmer48] around the same time, to prove multiple recurrence for
![]() $\mathbb {Z}$
-actions and show that this multiple recurrence theorem is equivalent to Szemerédi’s theorem [Reference Szemerédi43]. (Here countable refers to systems of countable measure-theoretic complexity such as measure-preserving
$\mathbb {Z}$
-actions and show that this multiple recurrence theorem is equivalent to Szemerédi’s theorem [Reference Szemerédi43]. (Here countable refers to systems of countable measure-theoretic complexity such as measure-preserving
![]() $\mathbb {Z}$
-actions on standard Borel probability spaces. The precise meaning of countable measure-theoretic complexity is given later in the introduction.) The Furstenberg–Zimmer structure theory is significantly refined in the Host–Kra–Ziegler structure theory [Reference Host and Kra26, Reference Ziegler46] which establishes a description of the characteristic factors governing multiple recurrence for
$\mathbb {Z}$
-actions on standard Borel probability spaces. The precise meaning of countable measure-theoretic complexity is given later in the introduction.) The Furstenberg–Zimmer structure theory is significantly refined in the Host–Kra–Ziegler structure theory [Reference Host and Kra26, Reference Ziegler46] which establishes a description of the characteristic factors governing multiple recurrence for
![]() $\mathbb {Z}$
-actions as inverse limits of rotations on nilmanifolds. The finitary counterpart of the Host–Kra–Ziegler structure theorem is known as the inverse theorem for the Gowers uniformity norms by Green, Tao, and Ziegler [Reference Green, Tao and Ziegler23]—a foundational result in the area of higher-order Fourier analysis initiated by Gower’s seminal work [Reference Gowers21, Reference Gowers22] on Szemerédi’s theorem.
$\mathbb {Z}$
-actions as inverse limits of rotations on nilmanifolds. The finitary counterpart of the Host–Kra–Ziegler structure theorem is known as the inverse theorem for the Gowers uniformity norms by Green, Tao, and Ziegler [Reference Green, Tao and Ziegler23]—a foundational result in the area of higher-order Fourier analysis initiated by Gower’s seminal work [Reference Gowers21, Reference Gowers22] on Szemerédi’s theorem.
Beyond the natural (intrinsic) motivation of generalizing ergodic theory to uncountable systems, we hope that an uncountable Host–Kra–Ziegler structure theory (such as for the action of hyperfinite abelian groups on Loeb probability spaces) may help to clarify the relationship between the ergodic-theoretical and analytic (higher-order Fourier analysis) approaches to Szemerédi’s theorem. See [Reference Jamneshan, Shalom and Tao29, Reference Jamneshan and Tao30] for some recent progress.
By proving an uncountable Moore–Schmidt theorem [Reference Jamneshan and Tao33] and an uncountable Mackey–Zimmer theorem [Reference Jamneshan and Tao32] (and clarifying in [Reference Jamneshan and Tao31] some foundational aspects of uncountable measure theory), first basic results in ergodic structure theory were successfully extended to uncountable settings. The present paper aims to establish another part by developing an uncountable Furstenberg–Zimmer structure theory.
The uncountable Furstenberg–Zimmer structure theory of this paper was applied in the joint work [Reference Durcik, Greenfeld, Iseli, Jamneshan and Madrid10] by the author and others to obtain an uncountable and uniform extension of the double recurrence theorem for amenable groups by Bergelson, McCutcheon, and Zhang [Reference Bergelson, McCutcheon and Zhang4].
1.2 Main results
Let
![]() $\Gamma $
be a group and X be a
$\Gamma $
be a group and X be a
![]() $\sigma $
-complete Boolean algebra equipped with a countably additive measure
$\sigma $
-complete Boolean algebra equipped with a countably additive measure
![]() $\mu $
of total mass
$\mu $
of total mass
![]() $1$
. Suppose that
$1$
. Suppose that
![]() $\Gamma $
acts on the probability algebra
$\Gamma $
acts on the probability algebra
![]() $(X,\mu )$
by a group homomorphism (this definition is equivalent to that given in Definition 2.1, where by reversing the arrows in the category of probability algebras, we can work with an action of
$(X,\mu )$
by a group homomorphism (this definition is equivalent to that given in Definition 2.1, where by reversing the arrows in the category of probability algebras, we can work with an action of
![]() $\Gamma $
instead of its opposite)
$\Gamma $
instead of its opposite)
![]() $T:\Gamma ^{\operatorname {op}}\to \operatorname {Aut}(X,\mu )$
, where
$T:\Gamma ^{\operatorname {op}}\to \operatorname {Aut}(X,\mu )$
, where
![]() $\operatorname {Aut}(X,\mu )$
denotes the automorphism group of
$\operatorname {Aut}(X,\mu )$
denotes the automorphism group of
![]() $(X,\mu )$
and
$(X,\mu )$
and
![]() $\Gamma ^{\operatorname {op}}$
the opposite group. The automorphisms of
$\Gamma ^{\operatorname {op}}$
the opposite group. The automorphisms of
![]() $(X,\mu )$
are measure-preserving bijective Boolean homomorphisms of X. (In the ergodic theory literature, it is common to call the pair
$(X,\mu )$
are measure-preserving bijective Boolean homomorphisms of X. (In the ergodic theory literature, it is common to call the pair
![]() $(X,\mu )$
, where X is a
$(X,\mu )$
, where X is a
![]() $\sigma $
-complete Boolean algebra and
$\sigma $
-complete Boolean algebra and
![]() $\mu $
is a countably additive probability measure on X, a measure algebra, e.g., see [Reference Glasner19, Reference Kerr and Li36]. We follow the conventions of Fremlin [Reference Fremlin16] to call
$\mu $
is a countably additive probability measure on X, a measure algebra, e.g., see [Reference Glasner19, Reference Kerr and Li36]. We follow the conventions of Fremlin [Reference Fremlin16] to call
![]() $(X,\mu )$
a probability algebra and reserve the name measure algebra for abstract measures of arbitrary total mass.) We call
$(X,\mu )$
a probability algebra and reserve the name measure algebra for abstract measures of arbitrary total mass.) We call
![]() $\mathcal {X}=(X,\mu ,T)$
a probability algebra
$\mathcal {X}=(X,\mu ,T)$
a probability algebra
![]() $\Gamma $
-dynamical system. The category of such dynamical systems and some basic tools to study them are collected in the preliminaries in §2. A main goal of this paper is to establish the following.
$\Gamma $
-dynamical system. The category of such dynamical systems and some basic tools to study them are collected in the preliminaries in §2. A main goal of this paper is to establish the following.
Theorem 1.1. (Uncountable Furstenberg–Zimmer structure theorem)
Let
![]() $\Gamma $
be a group. For any probability algebra
$\Gamma $
be a group. For any probability algebra
![]() $\Gamma $
-dynamical system
$\Gamma $
-dynamical system
![]() $\mathcal {X}=(X,\mu ,T)$
, there exists an ordinal
$\mathcal {X}=(X,\mu ,T)$
, there exists an ordinal
![]() $\beta $
and for each ordinal
$\beta $
and for each ordinal
![]() $\alpha \leq \beta $
, a factor
$\alpha \leq \beta $
, a factor
![]() $\mathcal {X}\to \mathcal {Y}_\alpha =(Y_\alpha ,\nu _\alpha ,S_\alpha )$
satisfying the following properties:
$\mathcal {X}\to \mathcal {Y}_\alpha =(Y_\alpha ,\nu _\alpha ,S_\alpha )$
satisfying the following properties:
-
(i)
 $\mathcal {Y}_0$
is trivial;
$\mathcal {Y}_0$
is trivial; -
(ii)
 $\mathcal {Y}_{\alpha +1}\to \mathcal {Y}_{\alpha }$
is a relatively compact extension for every successor ordinal
$\mathcal {Y}_{\alpha +1}\to \mathcal {Y}_{\alpha }$
is a relatively compact extension for every successor ordinal
 $\alpha +1\leq \beta $
;
$\alpha +1\leq \beta $
; -
(iii)
 $\mathcal {Y}_\alpha $
is the inverse limit of the systems
$\mathcal {Y}_\alpha $
is the inverse limit of the systems
 $\mathcal {Y}_{\eta }$
,
$\mathcal {Y}_{\eta }$
,
 $\eta <\alpha $
for every limit ordinal
$\eta <\alpha $
for every limit ordinal
 $\alpha \leq \beta $
, in the sense that
$\alpha \leq \beta $
, in the sense that
 $Y_\alpha $
is generated by
$Y_\alpha $
is generated by
 $\bigcup _{\eta <\alpha } Y_\eta $
as a
$\bigcup _{\eta <\alpha } Y_\eta $
as a
 $\sigma $
-complete Boolean algebra;
$\sigma $
-complete Boolean algebra; -
(iv)
 $\mathcal {X}\to \mathcal {Y}_\beta $
is a relatively weakly mixing extension.
$\mathcal {X}\to \mathcal {Y}_\beta $
is a relatively weakly mixing extension.
Theorem 1.1 follows from the following relative dichotomy between relatively weakly mixing and relatively compact extensions of probability algebra
![]() $\Gamma $
-dynamical systems by transfinite induction.
$\Gamma $
-dynamical systems by transfinite induction.
Theorem 1.2. (Uncountable relative dichotomy)
Let
![]() $\mathcal {X}=(X,\mu ,T)$
and
$\mathcal {X}=(X,\mu ,T)$
and
![]() $\mathcal {Y}=(Y,\nu ,S)$
be probability algebra
$\mathcal {Y}=(Y,\nu ,S)$
be probability algebra
![]() $\Gamma $
-dynamical systems and
$\Gamma $
-dynamical systems and
![]() $\pi : \mathcal {X}\to \mathcal {Y}$
an extension. Exactly one of the following statements is true:
$\pi : \mathcal {X}\to \mathcal {Y}$
an extension. Exactly one of the following statements is true:
-
(i)
 $\pi : \mathcal {X}\to \mathcal {Y}$
is a relatively weakly mixing extension;
$\pi : \mathcal {X}\to \mathcal {Y}$
is a relatively weakly mixing extension; -
(ii) there exist a probability algebra
 $\Gamma $
-dynamical system
$\Gamma $
-dynamical system
 $\mathcal {Z}=(Z,\unicode{x3bb} ,R)$
and extensions
$\mathcal {Z}=(Z,\unicode{x3bb} ,R)$
and extensions
 $\phi :\mathcal {X}\to \mathcal {Z}$
and
$\phi :\mathcal {X}\to \mathcal {Z}$
and
 $\psi :\mathcal {Z}\to \mathcal {Y}$
such that
$\psi :\mathcal {Z}\to \mathcal {Y}$
such that
 $\psi $
is a non-trivial relatively compact extension.
$\psi $
is a non-trivial relatively compact extension.
We prove Theorems 1.1 and 1.2 in §6. Compact and weakly mixing extensions of probability algebra systems are defined in §§4 and 6 respectively. Moreover, we establish various characterizations of relatively compact extensions in terms of (a) certain invariant finitely generated modules, (b) non-trivial invariant conditional Hilbert–Schmidt operators, and (c) conditionally almost periodic orbits. We establish the equivalence of (a)–(c) in smaller conditional
![]() $L^\infty $
-modules similarly to the classical theory and also in larger conditional
$L^\infty $
-modules similarly to the classical theory and also in larger conditional
![]() $L^0$
-modules (where
$L^0$
-modules (where
![]() $L^0$
denotes the ring of equivalence classes of complex measurable functions), and we show that these descriptions in the larger and the smaller modules are equivalent. In the case of ergodic systems, we prove in §5 that relatively compact extensions are isomorphic to isometric extensions (that is, probability algebra homogeneous skew-product systems as introduced in [Reference Jamneshan and Tao32]).
$L^0$
denotes the ring of equivalence classes of complex measurable functions), and we show that these descriptions in the larger and the smaller modules are equivalent. In the case of ergodic systems, we prove in §5 that relatively compact extensions are isomorphic to isometric extensions (that is, probability algebra homogeneous skew-product systems as introduced in [Reference Jamneshan and Tao32]).
These results are well understood for systems of countable measure-theoretic complexity, see [Reference Furstenberg17, Reference Zimmer47, Reference Zimmer48] for the original papers and [Reference Einsiedler and Ward12, Reference Furstenberg18, Reference Glasner19, Reference Kerr and Li36, Reference Tao44] for some textbook expositions. The aim of this paper is to extend them to systems of uncountable measure-theoretic complexity. We say that a probability algebra
![]() $\Gamma $
-dynamical system
$\Gamma $
-dynamical system
![]() $(X,\mu ,T)$
has countable measure-theoretic complexity if
$(X,\mu ,T)$
has countable measure-theoretic complexity if
![]() $\Gamma $
is countable and
$\Gamma $
is countable and
![]() $(X,\mu )$
is separable (we have a metric structure on X defined by
$(X,\mu )$
is separable (we have a metric structure on X defined by
![]() $d(E,F)=\mu (E\Delta F))$
, and has uncountable measure-theoretic complexity otherwise. In Table 1, we compare some features of systems of countable and uncountable complexity.
$d(E,F)=\mu (E\Delta F))$
, and has uncountable measure-theoretic complexity otherwise. In Table 1, we compare some features of systems of countable and uncountable complexity.
Table 1 The group-theoretic, measure-theoretic, topological, and methodological differences of systems of countable and uncountable complexity (with a view towards their Furstenberg–Zimmer structure theory).

We establish a Furstenberg–Zimmer structure theory for not necessarily countable groups and not necessarily separable probability algebras. To achieve such generality, we have to introduce novel tools to study the structure of probability algebra systems relative to some factor since many classical tools, such as disintegration of measures, measurable selection lemmas, and the theory of measurable Hilbert bundles, rely on such countability and separability hypotheses. Instead, we apply tools from topos theory as suggested in [Reference Tao45] by Tao. We will not use topos theory directly nor define a sheaf anywhere in this paper. Instead, we use the closely related conditional analysis as developed in [Reference Cheridito, Kupper and Vogelpoth6, Reference Drapeau, Jamneshan, Karliczek and Kupper9, Reference Filipović, Kupper and Vogelpoth15, Reference Jamneshan, Kupper and Streckfuß28]. A main advantage of conditional analysis is that it can be setup without much cost and understood with basic knowledge in measure theory and functional analysis. The ergodic theoretic results of this paper are organized in a self-contained presentation and no familiarity with topos theory is required for the reader purely interested in the ergodic theoretic content. In fact, the use of conditional analysis and the greater generality lead to significant simplifications of the proofs of several results in Furstenberg–Zimmer structure theory.
For the readers familiar with topos theory and interested in the connection between ergodic theory and topos theory, we include several remarks relating the conditional analysis of this paper to the internal discourse in Boolean Grothendieck sheaf topoi. To the best knowledge of the author, these remarks comprise novel insight into the semantics of such topoi.
We would like to point out that in recent work [Reference Edeko, Haase and Kreidler11], a slightly different proof of Theorem 1.1 is provided which is based on a functional analytic decomposition theorem for group representations on Kaplansky–Hilbert modules.
1.3 Technical innovations
A priori probability algebras are not
![]() $\sigma $
-algebras of subsets of an underlying set. We view probability algebras as abstract pointfree probability spaces as opposed to concrete point-set probability spaces defined on
$\sigma $
-algebras of subsets of an underlying set. We view probability algebras as abstract pointfree probability spaces as opposed to concrete point-set probability spaces defined on
![]() $\sigma $
-algebras of sets. In countable ergodic theory, the starting points are concrete countably generated probability spaces on which a measure-preserving action by a countable or second-countable group on the underlying set is defined. In the countable theory, a distinction is made between an action which is defined everywhere on the underlying set and a near-action which is only defined almost everywhere, e.g., see [Reference Zimmer48]. This distinction is non-trivial, since there are natural examples of systems of countable complexity for Polish group near-actions that cannot be realized by a pointwise action, e.g., see [Reference Glasner, Tsirelson and Weiss20, Reference Moore and Solecki39].
$\sigma $
-algebras of sets. In countable ergodic theory, the starting points are concrete countably generated probability spaces on which a measure-preserving action by a countable or second-countable group on the underlying set is defined. In the countable theory, a distinction is made between an action which is defined everywhere on the underlying set and a near-action which is only defined almost everywhere, e.g., see [Reference Zimmer48]. This distinction is non-trivial, since there are natural examples of systems of countable complexity for Polish group near-actions that cannot be realized by a pointwise action, e.g., see [Reference Glasner, Tsirelson and Weiss20, Reference Moore and Solecki39].
In uncountable ergodic theory, the starting points are arbitrary (not necessarily countably generated or separable) probability algebras on which an arbitrary (not necessarily countable or second-countable) group acts by measure-preserving Boolean isomorphisms. A major advantage of working with pointfree probability algebras is that one systematically avoids to have to deal with null set issues. In this regard, the abstract pointfree perspective, which has been already implemented in our previous works [Reference Jamneshan and Tao32, Reference Jamneshan and Tao33] and systematically developed in the foundational paper [Reference Jamneshan and Tao31], seems to be more natural in uncountable ergodic theory.
Furthermore, the category of probability algebra dynamical systems is dually equivalent to the dynamical category of commutative tracial von Neumann algebras (see Figure 1) such that all structural results established in this paper for probability algebra dynamical systems have natural analogs in the dynamical category of commutative tracial von Neumann algebras, see [Reference Kerr and Li36, §3.2] for this correspondence for systems of countable complexity. See [Reference Popa41, §2] for a proof of a non-commutative Furstenberg–Zimmer-type dichotomy of relatively weakly mixing and relatively compact extensions for countable group actions on separable von Neumann algebras. In fact, the analogies extend also to the other two dynamical categories of commutative tracial
![]() $C^*$
-algebras and topological dynamical systems preserving a Baire–Radon probability measure in Figure 1 by restricting to the image of the
$C^*$
-algebras and topological dynamical systems preserving a Baire–Radon probability measure in Figure 1 by restricting to the image of the
![]() $\mathtt {Conc}$
and
$\mathtt {Conc}$
and
![]() $\mathtt {Inc}$
functors, see §2 for the definition of these functors.
$\mathtt {Inc}$
functors, see §2 for the definition of these functors.

Figure 1 Adjacent auxiliary dynamical categories. Tailed arrows are faithful functors, while arrows with two heads are full functors. The diagram commutes up to natural isomorphisms.
However, by quotienting out the null ideal, to any concrete countable complexity system we can associate an abstract probability algebra system. In this regard, the abstract perspective is implicitly present in the countable theory, e.g., see [Reference Furstenberg18, §5], [Reference Glasner19, §2], the preliminaries of [Reference Zimmer47, Reference Zimmer48], and the expositions in [Reference Kerr and Li36, Reference Tao44].
To study the Furstenberg–Zimmer structure theory of abstract pointfree systems, analogs of some basic and more advanced tools from measure theory and functional analysis are required. These are the basic Hilbert theory of
![]() $L^2$
-spaces, disintegration of measures, and the theory of measurable Hilbert bundles. However, classical disintegration of measures and the theory of measurable Hilbert bundles are, in general, only applicable for systems of countable measure-theoretic complexity. Therefore, the main technical difficulty in extending the Furstenberg–Zimmer structure theory is to find viable alternatives which work for abstract systems of uncountable measure-theoretic complexity as well. We divide the above tools into two sets. The first set are basic tools from measure theory and the second one consists of tools needed for the analysis relative to some factor.
$L^2$
-spaces, disintegration of measures, and the theory of measurable Hilbert bundles. However, classical disintegration of measures and the theory of measurable Hilbert bundles are, in general, only applicable for systems of countable measure-theoretic complexity. Therefore, the main technical difficulty in extending the Furstenberg–Zimmer structure theory is to find viable alternatives which work for abstract systems of uncountable measure-theoretic complexity as well. We divide the above tools into two sets. The first set are basic tools from measure theory and the second one consists of tools needed for the analysis relative to some factor.
For the first group, we have two options. We can either use the abstract measure theory for measure algebras, as systematically developed in [Reference Fremlin16], or we can use concrete measure theory after passing to a canonical model. The canonical model, which is introduced in §2 (see also [Reference Eisner, Farkas, Haase and Nagel13] and the references given in Remark 2.5), is a functor associating to any probability algebra dynamical system a unique compact Hausdorff probability measure-preserving dynamical system where the underlying group acts by homeomorphisms. The canonical model comes with some favorable properties, for example, a canonical disintegration of measures, see §2.4.
We replace the second set of tools by conditional analysis which permits performing analysis in relative situations without any countability or separability assumptions. More precisely, we introduce a conditional Hilbert space and its conditional tensor product representing conditional Hilbert–Schmidt operators, and we study a conditional Gram–Schmidt process and a conditional version of the spectral theorem for these conditional Hilbert–Schmidt operators in §3 and Appendix A.
We found it convenient to explicitly use the language of category theory in this paper. It helps to clearly separate the concrete from the abstract probability spaces, and clarifies the relationships between these categories by way of functorial relations. These functors work particularly well with dynamics. This allows to safely pass back and forth between these categories, and thus take advantage of tools available in both the concrete and abstract settings. Functors establishing dualities of categories, such as the useful Gelfand duality, permit to efficiently translate into functional analytic categories to a similar effect. Practically, these categorical relations help with a basic housekeeping, avoiding making unnecessary mistakes. An illustrating example may be the clarification of category-dependent notions of measurability and various product constructions whose relations to each other can be worked out by functorial relations, cf. [Reference Jamneshan and Tao31, Reference Jamneshan and Tao32]. In fact, once these categorical relations are explicitly established and well understood, certain frequently used constructions and arguments automatize and simplify.
2 Preliminaries
2.1 The categories
Throughout this paper, we fix an arbitrary group
![]() $\Gamma $
. We define the category
$\Gamma $
. We define the category
![]() ${\mathbf {PrbAlg}_\Gamma }$
of probability algebra
${\mathbf {PrbAlg}_\Gamma }$
of probability algebra
![]() $\Gamma $
-dynamical systems to be the opposite of a category of Boolean algebras equipped with a probability measure-preserving dynamical structure.
$\Gamma $
-dynamical systems to be the opposite of a category of Boolean algebras equipped with a probability measure-preserving dynamical structure.
A thorough discussion of some categorical aspects of ergodic theory and adjacent areas in measure theory and functional analysis, such as the auxiliary categories depicted in Figure 1, together with useful references to basic category theory can be found in the accompanying paper [Reference Jamneshan and Tao31], to the relevant parts of which we will provide exact referencing as we proceed. The interested reader is also referred to [Reference Jamneshan and Tao31] for our categorical notation and conventions.
Definition 2.1. (The category
 ${\mathbf {PrbAlg}_\Gamma }$
)
${\mathbf {PrbAlg}_\Gamma }$
)
-
(i) A
 ${\mathbf {Bool}_\sigma }$
-object is a
${\mathbf {Bool}_\sigma }$
-object is a
 $\sigma $
-complete Boolean algebra
$\sigma $
-complete Boolean algebra
 $X=(X,\vee ,\wedge , \bar \cdot , 0,1)$
and a
$X=(X,\vee ,\wedge , \bar \cdot , 0,1)$
and a
 ${\mathbf {Bool}_\sigma }$
-morphism from a
${\mathbf {Bool}_\sigma }$
-morphism from a
 ${\mathbf {Bool}_\sigma }$
-algebra X to another
${\mathbf {Bool}_\sigma }$
-algebra X to another
 ${\mathbf {Bool}_\sigma }$
-algebra Y is a
${\mathbf {Bool}_\sigma }$
-algebra Y is a
 $\sigma $
-complete Boolean homomorphism
$\sigma $
-complete Boolean homomorphism
 $f:X\to Y$
.
$f:X\to Y$
. -
(ii) The category
 $\mathbf {AbsMbl}$
of abstract measurable spaces is the opposite category of
$\mathbf {AbsMbl}$
of abstract measurable spaces is the opposite category of
 ${\mathbf {Bool}_\sigma }$
.
${\mathbf {Bool}_\sigma }$
. -
(iii) The objects of
 ${\mathbf {PrbAlg}}$
are probability algebras
${\mathbf {PrbAlg}}$
are probability algebras
 $(X,\mu )$
, where X is a
$(X,\mu )$
, where X is a
 ${\mathbf {Bool}_\sigma }$
-algebra and
${\mathbf {Bool}_\sigma }$
-algebra and
 $\mu :X\to [0,1]$
is a countably additive probability measure, that is (a)
$\mu :X\to [0,1]$
is a countably additive probability measure, that is (a)
 $\mu (\bigvee _n E_n)=\sum _n \mu (E_n)$
for any sequence
$\mu (\bigvee _n E_n)=\sum _n \mu (E_n)$
for any sequence
 $(E_n)$
of pairwise disjoint elements in X, (b)
$(E_n)$
of pairwise disjoint elements in X, (b)
 $\mu (X)=1$
, and (c)
$\mu (X)=1$
, and (c)
 $\mu (E)=0$
if and only if
$\mu (E)=0$
if and only if
 $E=0$
. A
$E=0$
. A
 ${\mathbf {PrbAlg}}$
-morphism from a
${\mathbf {PrbAlg}}$
-morphism from a
 ${\mathbf {PrbAlg}}$
-algebra
${\mathbf {PrbAlg}}$
-algebra
 $(X,\mu )$
to another
$(X,\mu )$
to another
 ${\mathbf {PrbAlg}}$
-algebra
${\mathbf {PrbAlg}}$
-algebra
 $(Y,\nu )$
is a Boolean algebra homomorphism
$(Y,\nu )$
is a Boolean algebra homomorphism
 $\pi :Y\to X$
such that
$\pi :Y\to X$
such that
 $\mu _*\pi (E)=\nu (E)$
for all
$\mu _*\pi (E)=\nu (E)$
for all
 $E\in Y$
(notice the opposite direction of the arrow. We implicitly work with an opposite category here to keep certain functors covariant), where we denote by
$E\in Y$
(notice the opposite direction of the arrow. We implicitly work with an opposite category here to keep certain functors covariant), where we denote by
 $\mu _*\pi $
the pullback probability measure on Y defined by
$\mu _*\pi $
the pullback probability measure on Y defined by
 $\mu _*\pi (E):= \mu (\pi (E))$
. The
$\mu _*\pi (E):= \mu (\pi (E))$
. The
 ${\mathbf {Bool}_\sigma }$
-algebra X of a
${\mathbf {Bool}_\sigma }$
-algebra X of a
 ${\mathbf {PrbAlg}}$
-object automatically upgrades to a complete Boolean algebra (that is, a Boolean algebra in which arbitrary joins and meets exist) and the underlying Boolean algebra homomorphism of a
${\mathbf {PrbAlg}}$
-object automatically upgrades to a complete Boolean algebra (that is, a Boolean algebra in which arbitrary joins and meets exist) and the underlying Boolean algebra homomorphism of a
 ${\mathbf {PrbAlg}}$
-morphism automatically upgrades to a complete Boolean algebra homomorphism (that is, one that preserves arbitrary joins and meets), see Remark 2.2. Let
${\mathbf {PrbAlg}}$
-morphism automatically upgrades to a complete Boolean algebra homomorphism (that is, one that preserves arbitrary joins and meets), see Remark 2.2. Let
 $\operatorname {Aut}(X,\mu )$
denote the automorphism group of a
$\operatorname {Aut}(X,\mu )$
denote the automorphism group of a
 ${\mathbf {PrbAlg}}$
-algebra
${\mathbf {PrbAlg}}$
-algebra
 $(X,\mu )$
in the category
$(X,\mu )$
in the category
 ${\mathbf {PrbAlg}}$
.
${\mathbf {PrbAlg}}$
. -
(iv) A
 ${\mathbf {PrbAlg}_\Gamma }$
-system is a tuple
${\mathbf {PrbAlg}_\Gamma }$
-system is a tuple
 $(X,\mu ,T)$
where
$(X,\mu ,T)$
where
 $(X,\mu )$
is a
$(X,\mu )$
is a
 ${\mathbf {PrbAlg}}$
-algebra and
${\mathbf {PrbAlg}}$
-algebra and
 $T:\Gamma \to \operatorname {Aut}(X,\mu )$
is a group homomorphism
$T:\Gamma \to \operatorname {Aut}(X,\mu )$
is a group homomorphism
 $\gamma \mapsto T_{\gamma }$
. A
$\gamma \mapsto T_{\gamma }$
. A
 ${\mathbf {PrbAlg}_\Gamma }$
-morphism from a
${\mathbf {PrbAlg}_\Gamma }$
-morphism from a
 ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
 $(X,\mu ,T)$
to another
$(X,\mu ,T)$
to another
 ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
 $(Y,\nu ,S)$
is a
$(Y,\nu ,S)$
is a
 ${\mathbf {PrbAlg}}$
-morphism
${\mathbf {PrbAlg}}$
-morphism
 $\pi :(X,\mu )\to (Y,\nu )$
such that
$\pi :(X,\mu )\to (Y,\nu )$
such that
 $\pi \circ T_{\gamma }=S_{\gamma }\circ \pi $
for all
$\pi \circ T_{\gamma }=S_{\gamma }\circ \pi $
for all
 $\gamma \in \Gamma $
. We call
$\gamma \in \Gamma $
. We call
 ${\mathbf {PrbAlg}_\Gamma }$
the category of probability algebra
${\mathbf {PrbAlg}_\Gamma }$
the category of probability algebra
 $\Gamma $
-dynamical systems. We denote a
$\Gamma $
-dynamical systems. We denote a
 ${\mathbf {PrbAlg}_\Gamma }$
-system by
${\mathbf {PrbAlg}_\Gamma }$
-system by
 $\mathcal {X}=(X,\mu ,T)$
. If
$\mathcal {X}=(X,\mu ,T)$
. If
 $\pi :\mathcal {X}\to \mathcal {Y}$
is a
$\pi :\mathcal {X}\to \mathcal {Y}$
is a
 ${\mathbf {PrbAlg}_\Gamma }$
-morphism, we call
${\mathbf {PrbAlg}_\Gamma }$
-morphism, we call
 $\mathcal {X}$
a
$\mathcal {X}$
a
 ${\mathbf {PrbAlg}_\Gamma }$
-extension of
${\mathbf {PrbAlg}_\Gamma }$
-extension of
 $\mathcal {Y}$
and
$\mathcal {Y}$
and
 $\mathcal {Y}$
a
$\mathcal {Y}$
a
 ${\mathbf {PrbAlg}_\Gamma }$
-factor of
${\mathbf {PrbAlg}_\Gamma }$
-factor of
 $\mathcal {X}$
. We sometimes also refer to the
$\mathcal {X}$
. We sometimes also refer to the
 ${\mathbf {PrbAlg}_\Gamma }$
-morphism
${\mathbf {PrbAlg}_\Gamma }$
-morphism
 $\pi $
itself as a
$\pi $
itself as a
 ${\mathbf {PrbAlg}_\Gamma }$
-extension or a
${\mathbf {PrbAlg}_\Gamma }$
-extension or a
 ${\mathbf {PrbAlg}_\Gamma }$
-factor.
${\mathbf {PrbAlg}_\Gamma }$
-factor.
An extensive discussion of the previously introduced categories can be found in [Reference Jamneshan and Tao31, §6].
Remark 2.2. It is well known that the
![]() ${\mathbf {Bool}_\sigma }$
-algebra X of a
${\mathbf {Bool}_\sigma }$
-algebra X of a
![]() ${\mathbf {PrbAlg}}$
-algebra
${\mathbf {PrbAlg}}$
-algebra
![]() $(X,\mu )$
is automatically a complete Boolean algebra. We provide the short proof for the convenience of the reader. Let
$(X,\mu )$
is automatically a complete Boolean algebra. We provide the short proof for the convenience of the reader. Let
![]() $(E_i)_{i\in I}$
be an arbitrary family in X. Well order I by
$(E_i)_{i\in I}$
be an arbitrary family in X. Well order I by
![]() $<$
and let
$<$
and let
![]() $F_i=E_i\wedge \overline {\bigvee _{j<i} E_j}$
for each
$F_i=E_i\wedge \overline {\bigvee _{j<i} E_j}$
for each
![]() $i\in I$
. By construction,
$i\in I$
. By construction,
![]() $(F_i)_{i\in I}$
is a family of pairwise disjoint elements of X. Since
$(F_i)_{i\in I}$
is a family of pairwise disjoint elements of X. Since
![]() $\mu $
is a finite measure, only countably many of the
$\mu $
is a finite measure, only countably many of the
![]() $F_i$
are non-zero (this property is also called the countable chain condition). Thus
$F_i$
are non-zero (this property is also called the countable chain condition). Thus
![]() $\bigvee _{i\in I} E_i=\bigvee _{i\in I, F_i> 0} F_i$
, and by
$\bigvee _{i\in I} E_i=\bigvee _{i\in I, F_i> 0} F_i$
, and by
![]() $\sigma $
-completeness of X,
$\sigma $
-completeness of X,
![]() $\bigvee _{i\in I, F_i\neq 0} F_i\in X$
. Moreover, if
$\bigvee _{i\in I, F_i\neq 0} F_i\in X$
. Moreover, if
![]() $\pi :(Y,\nu )\to (X,\mu )$
is a
$\pi :(Y,\nu )\to (X,\mu )$
is a
![]() ${\mathbf {PrbAlg}}$
-morphism (the underlying
${\mathbf {PrbAlg}}$
-morphism (the underlying
![]() ${\mathbf {Bool}_\sigma }$
-morphism of which does not necessarily preserve countable joins and meets by definition), then
${\mathbf {Bool}_\sigma }$
-morphism of which does not necessarily preserve countable joins and meets by definition), then
![]() $\pi $
automatically upgrades to a complete Boolean homomorphism due to the automatic injectivity of
$\pi $
automatically upgrades to a complete Boolean homomorphism due to the automatic injectivity of
![]() $\pi $
and the countable chain condition, cf. [Reference Jamneshan and Tao32, Remark 1.2].
$\pi $
and the countable chain condition, cf. [Reference Jamneshan and Tao32, Remark 1.2].
Next we introduce some basic tools to study the structure of
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems. We obtain these tools by relating the category
${\mathbf {PrbAlg}_\Gamma }$
-systems. We obtain these tools by relating the category
![]() ${\mathbf {PrbAlg}_\Gamma }$
to some adjacent auxiliary dynamical categories of algebras and spaces, as illustrated in Figure 1. The symbol
${\mathbf {PrbAlg}_\Gamma }$
to some adjacent auxiliary dynamical categories of algebras and spaces, as illustrated in Figure 1. The symbol
![]() ${\operatorname {op}}$
on a category indicates the use of opposite category, while
${\operatorname {op}}$
on a category indicates the use of opposite category, while
![]() $\Gamma ^{\operatorname {op}}$
for a group
$\Gamma ^{\operatorname {op}}$
for a group
![]() $\Gamma $
means the use of the opposite group.
$\Gamma $
means the use of the opposite group.
Definition 2.3. (Adjacent dynamical categories)
First we introduce the remaining categories in Figure 1 without a dynamical structure. Then we apply a universal procedure to turn these categories into corresponding dynamical categories.
-
(i) A
 ${\mathbf {CHPrb}}$
-space is a tuple
${\mathbf {CHPrb}}$
-space is a tuple
 $(X,\mathcal {B}a(X),\mu )$
, where X is a compact Hausdorff space,
$(X,\mathcal {B}a(X),\mu )$
, where X is a compact Hausdorff space,
 $\mathcal {B}a(X)$
is the Baire
$\mathcal {B}a(X)$
is the Baire
 $\sigma $
-algebra of X (that is, the smallest
$\sigma $
-algebra of X (that is, the smallest
 $\sigma $
-algebra on X rendering continuous functions measurable), and
$\sigma $
-algebra on X rendering continuous functions measurable), and
 $\mu $
is a Baire-Radon probability measure on the measurable space
$\mu $
is a Baire-Radon probability measure on the measurable space
 $(X,\mathcal {B}a(X))$
. A
$(X,\mathcal {B}a(X))$
. A
 ${\mathbf {CHPrb}}$
-morphism
${\mathbf {CHPrb}}$
-morphism
 $\pi :(X,\mathcal {B}a(X),\mu )\to (Y,\mathcal {B}a(Y),\nu )$
between compact Hausdorff probability spaces is a continuous function
$\pi :(X,\mathcal {B}a(X),\mu )\to (Y,\mathcal {B}a(Y),\nu )$
between compact Hausdorff probability spaces is a continuous function
 $\pi :X\to Y$
such that
$\pi :X\to Y$
such that
 $\pi _\ast \mu =\nu $
, where
$\pi _\ast \mu =\nu $
, where
 $\pi _\ast \mu $
denotes pushforward measure (a continuous function between compact Hausdorff spaces is always Baire-measurable since its pullback preservers compact
$\pi _\ast \mu $
denotes pushforward measure (a continuous function between compact Hausdorff spaces is always Baire-measurable since its pullback preservers compact
 $G_\delta $
sets).
$G_\delta $
sets). -
(ii) A
 ${\mathbf {CC^*Alg}^\tau }$
-algebra
${\mathbf {CC^*Alg}^\tau }$
-algebra
 $(\mathcal {A},\tau )$
is a unital commutative
$(\mathcal {A},\tau )$
is a unital commutative
 $C^*$
-algebra equipped with a state
$C^*$
-algebra equipped with a state
 $\tau :\mathcal {A}\to \mathbb {C}$
that is a bounded linear functional which is non-negative (it maps non-negative elements to non-negative reals) and is of operator norm
$\tau :\mathcal {A}\to \mathbb {C}$
that is a bounded linear functional which is non-negative (it maps non-negative elements to non-negative reals) and is of operator norm
 $1$
. A
$1$
. A
 ${\mathbf {CC^*Alg}^\tau }$
-morphism
${\mathbf {CC^*Alg}^\tau }$
-morphism
 $\Phi :(\mathcal {A},\tau _{\mathcal {A}})\to (\mathcal {B},\tau _{\mathcal {B}})$
between
$\Phi :(\mathcal {A},\tau _{\mathcal {A}})\to (\mathcal {B},\tau _{\mathcal {B}})$
between
 ${\mathbf {CC^*Alg}^\tau }$
-algebras is a unital
${\mathbf {CC^*Alg}^\tau }$
-algebras is a unital
 $*$
-homomorphism
$*$
-homomorphism
 $\Phi :\mathcal {A}\to \mathcal {B}$
such that
$\Phi :\mathcal {A}\to \mathcal {B}$
such that
 $\tau _{\mathcal {B}}\circ \Phi =\tau _{\mathcal {A}}$
.
$\tau _{\mathcal {B}}\circ \Phi =\tau _{\mathcal {A}}$
. -
(iii) A
 ${\mathbf {CvNAlg}^\tau }$
-algebra
${\mathbf {CvNAlg}^\tau }$
-algebra
 $(\mathcal {A},\tau _{\mathcal {A}})$
is a commutative von Neumann algebra
$(\mathcal {A},\tau _{\mathcal {A}})$
is a commutative von Neumann algebra
 $\mathcal {A}$
equipped with a faithful trace
$\mathcal {A}$
equipped with a faithful trace
 $\tau _{\mathcal {A}}$
, that is to say a
$\tau _{\mathcal {A}}$
, that is to say a
 $*$
-linear functional
$*$
-linear functional
 $\tau _{\mathcal {A}}: \mathcal {A}\to \mathbb {C}$
with
$\tau _{\mathcal {A}}: \mathcal {A}\to \mathbb {C}$
with
 $\tau _{\mathcal {A}}(1) = 1$
, and
$\tau _{\mathcal {A}}(1) = 1$
, and
 $\tau _{\mathcal {A}}(aa^*)\geq 0$
for any
$\tau _{\mathcal {A}}(aa^*)\geq 0$
for any
 $a \in \mathcal {A}$
, with equality if and only if
$a \in \mathcal {A}$
, with equality if and only if
 $a = 0$
. A
$a = 0$
. A
 ${\mathbf {CvNAlg}^\tau }$
-morphism
${\mathbf {CvNAlg}^\tau }$
-morphism
 $\Phi :(\mathcal {A},\tau _{\mathcal {A}})\to (\mathcal {B},\tau _{\mathcal {B}})$
between
$\Phi :(\mathcal {A},\tau _{\mathcal {A}})\to (\mathcal {B},\tau _{\mathcal {B}})$
between
 ${\mathbf {CvNAlg}^\tau }$
-algebras is a von Neumann algebra homomorphism
${\mathbf {CvNAlg}^\tau }$
-algebras is a von Neumann algebra homomorphism
 $\Phi :\mathcal {A}\to \mathcal {B}$
such that
$\Phi :\mathcal {A}\to \mathcal {B}$
such that
 $\tau _{\mathcal {A}}=\tau _{\mathcal {B}}\circ \Phi $
.
$\tau _{\mathcal {A}}=\tau _{\mathcal {B}}\circ \Phi $
.
Let
![]() $\mathcal {C}$
be one of the categories
$\mathcal {C}$
be one of the categories
![]() ${\mathbf {CHPrb}},{\mathbf {CC^*Alg}^\tau }$
, or
${\mathbf {CHPrb}},{\mathbf {CC^*Alg}^\tau }$
, or
![]() ${\mathbf {CvNAlg}^\tau }$
. For a
${\mathbf {CvNAlg}^\tau }$
. For a
![]() $\mathcal {C}$
-object X, let
$\mathcal {C}$
-object X, let
![]() $\operatorname {Aut}_{\mathcal {C}}(X)$
be the automorphism group of X in
$\operatorname {Aut}_{\mathcal {C}}(X)$
be the automorphism group of X in
![]() $\mathcal {C}$
. We define a
$\mathcal {C}$
. We define a
![]() $\mathcal {C}_\Gamma $
-object (respectively a
$\mathcal {C}_\Gamma $
-object (respectively a
![]() $\mathcal {C}_{\Gamma ^{\operatorname {op}}}$
-object) to be a tuple
$\mathcal {C}_{\Gamma ^{\operatorname {op}}}$
-object) to be a tuple
![]() $(X,T)$
, where X is a
$(X,T)$
, where X is a
![]() $\mathcal {C}$
-object and
$\mathcal {C}$
-object and
![]() $T:\Gamma \to \operatorname {Aut}_{\mathcal {C}}(X)$
is a homomorphism
$T:\Gamma \to \operatorname {Aut}_{\mathcal {C}}(X)$
is a homomorphism
![]() $\gamma \mapsto T^\gamma $
of groups (respectively
$\gamma \mapsto T^\gamma $
of groups (respectively
![]() $T:\Gamma ^{\operatorname {op}}\to \operatorname {Aut}_{\mathcal {C}}(X)$
is a homomorphism
$T:\Gamma ^{\operatorname {op}}\to \operatorname {Aut}_{\mathcal {C}}(X)$
is a homomorphism
![]() $\gamma ^{\operatorname {op}}\mapsto T^{\gamma ^{\operatorname {op}}}$
of groups). A
$\gamma ^{\operatorname {op}}\mapsto T^{\gamma ^{\operatorname {op}}}$
of groups). A
![]() $\mathcal {C}_\Gamma $
-morphism
$\mathcal {C}_\Gamma $
-morphism
![]() $\pi :(X,T)\to (Y,S)$
(respectively
$\pi :(X,T)\to (Y,S)$
(respectively
![]() $\mathcal {C}_{\Gamma ^{\operatorname {op}}}$
-morphism
$\mathcal {C}_{\Gamma ^{\operatorname {op}}}$
-morphism
![]() $\pi :(Y,S)\to (X,T)$
) between
$\pi :(Y,S)\to (X,T)$
) between
![]() $\mathcal {C}_\Gamma $
-objects (respectively
$\mathcal {C}_\Gamma $
-objects (respectively
![]() $\mathcal {C}_{\Gamma ^{\operatorname {op}}}$
-objects) is a
$\mathcal {C}_{\Gamma ^{\operatorname {op}}}$
-objects) is a
![]() $\mathcal {C}$
-morphism
$\mathcal {C}$
-morphism
![]() $\pi :X\to Y$
(respectively a
$\pi :X\to Y$
(respectively a
![]() $\mathcal {C}$
-morphism
$\mathcal {C}$
-morphism
![]() $\pi :Y\to X$
) obeying the intertwining property
$\pi :Y\to X$
) obeying the intertwining property
![]() $\pi \circ T^\gamma =S^\gamma \circ \pi $
for all
$\pi \circ T^\gamma =S^\gamma \circ \pi $
for all
![]() $\gamma \in \Gamma $
(respectively
$\gamma \in \Gamma $
(respectively
![]() $\pi \circ S^{\gamma ^{\operatorname {op}}}=T^{\gamma ^{\operatorname {op}}}\circ \pi $
for all
$\pi \circ S^{\gamma ^{\operatorname {op}}}=T^{\gamma ^{\operatorname {op}}}\circ \pi $
for all
![]() $\gamma ^{\operatorname {op}}\in \Gamma ^{\operatorname {op}}$
).
$\gamma ^{\operatorname {op}}\in \Gamma ^{\operatorname {op}}$
).
2.2 The functors
The functors in Figure 1, in particular
![]() $L^\infty $
, C,
$L^\infty $
, C,
![]() $\mathtt {Proj}$
,
$\mathtt {Proj}$
,
![]() $\mathtt {Riesz}$
, and
$\mathtt {Riesz}$
, and
![]() $\mathtt {Conc}$
, are the means by which we represent the objects and morphisms in the dynamical category
$\mathtt {Conc}$
, are the means by which we represent the objects and morphisms in the dynamical category
![]() ${\mathbf {PrbAlg}_\Gamma }$
by objects and morphisms in the adjacent dynamical categories
${\mathbf {PrbAlg}_\Gamma }$
by objects and morphisms in the adjacent dynamical categories
![]() ${\mathbf {CHPrb}_\Gamma },{\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}},{\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
to use the tools available in the latter categories to study structural properties of systems in the former, while the canonical model functor
${\mathbf {CHPrb}_\Gamma },{\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}},{\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
to use the tools available in the latter categories to study structural properties of systems in the former, while the canonical model functor
![]() $\mathtt {Conc}$
is our main player. We start by describing the two Gelfand-type dualities in Figure 2 which yield the dualities of the dynamical categories in Figure 1 from which we then derive the canonical model functor
$\mathtt {Conc}$
is our main player. We start by describing the two Gelfand-type dualities in Figure 2 which yield the dualities of the dynamical categories in Figure 1 from which we then derive the canonical model functor
![]() $\mathtt {Conc}$
in the same figure.
$\mathtt {Conc}$
in the same figure.

Figure 2 Gelfand-type dualities between opposite probability algebras and tracial commutative von Neumann algebra and between compact Hausdorff probability spaces and tracial commutative unital
![]() $C^*$
-algebras.
$C^*$
-algebras.
Gelfand duality (cf. Figure 3) establishes a well-known equivalence between the category
![]() $\mathbf {CH}$
of compact Hausdorff spaces and the category
$\mathbf {CH}$
of compact Hausdorff spaces and the category
![]() ${\mathbf {CC^*Alg}}$
of unital commutative
${\mathbf {CC^*Alg}}$
of unital commutative
![]() $C^*$
-algebras. The functor
$C^*$
-algebras. The functor
![]() $\mathtt {Spec}$
associates to each unital commutative
$\mathtt {Spec}$
associates to each unital commutative
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $\mathcal {A}$
its spectrum
$\mathcal {A}$
its spectrum
![]() $\mathtt {Spec}(\mathcal {A})$
(the set of
$\mathtt {Spec}(\mathcal {A})$
(the set of
![]() ${\mathbf {CC^*Alg}}$
-morphisms from
${\mathbf {CC^*Alg}}$
-morphisms from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathbb {C}$
) which is a compact Hausdorff space by the Banach–Alaoglu theorem and to each unital
$\mathbb {C}$
) which is a compact Hausdorff space by the Banach–Alaoglu theorem and to each unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\Phi :\mathcal {A}\to \mathcal {B}$
the continuous function
$\Phi :\mathcal {A}\to \mathcal {B}$
the continuous function
![]() $\mathtt {Spec}(\Phi ):\mathtt {Spec}(\mathcal {B})\to \mathtt {Spec}(\mathcal {A})$
,
$\mathtt {Spec}(\Phi ):\mathtt {Spec}(\mathcal {B})\to \mathtt {Spec}(\mathcal {A})$
,
![]() $\mathtt {Spec}(\Phi )(f):=f\circ \Phi $
. The functor C associates with each compact Hausdorff space X the unital commutative
$\mathtt {Spec}(\Phi )(f):=f\circ \Phi $
. The functor C associates with each compact Hausdorff space X the unital commutative
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C(X)$
of continuous functions
$C(X)$
of continuous functions
![]() $f:X\to \mathbb {C}$
and with each continuous function
$f:X\to \mathbb {C}$
and with each continuous function
![]() $\pi :X\to Y$
between
$\pi :X\to Y$
between
![]() $\mathbf {CH}$
-spaces the Koopmann operator
$\mathbf {CH}$
-spaces the Koopmann operator
![]() $C(\pi ):C(Y)\to C(X)$
,
$C(\pi ):C(Y)\to C(X)$
,
![]() $C(\pi )(f):=f\circ \pi $
. See [Reference Jamneshan and Tao31, §2] for a more detailed exposition.
$C(\pi )(f):=f\circ \pi $
. See [Reference Jamneshan and Tao31, §2] for a more detailed exposition.

Figure 3 Gelfand duality between the category of compact Hausdorff spaces and commutative unital
![]() $C^*$
-algebras.
$C^*$
-algebras.
The Gelfand duality in Figure 3 extends to a ‘Riesz duality’ between
![]() ${\mathbf {CHPrb}}$
and
${\mathbf {CHPrb}}$
and
![]() ${\mathbf {CC^*Alg}^\tau }$
as follows. A
${\mathbf {CC^*Alg}^\tau }$
as follows. A
![]() ${\mathbf {CHPrb}}$
-space
${\mathbf {CHPrb}}$
-space
![]() $(X,\mathcal {B}a(X),\mu )$
is mapped via the C-functor to the
$(X,\mathcal {B}a(X),\mu )$
is mapped via the C-functor to the
![]() ${\mathbf {CC^*Alg}^\tau }$
-algebra
${\mathbf {CC^*Alg}^\tau }$
-algebra
![]() $(C(X),\tau _\mu )$
, where the state
$(C(X),\tau _\mu )$
, where the state
![]() $\tau _\mu :C(X)\to \mathbb {C}$
is defined by integration
$\tau _\mu :C(X)\to \mathbb {C}$
is defined by integration
![]() $\tau _\mu (f):=\int _X f\,d\mu $
. If
$\tau _\mu (f):=\int _X f\,d\mu $
. If
![]() $\pi :(X,\mathcal {B}a(X),\mu )\to (Y,\mathcal {B}a(Y),\nu )$
is a
$\pi :(X,\mathcal {B}a(X),\mu )\to (Y,\mathcal {B}a(Y),\nu )$
is a
![]() ${\mathbf {CHPrb}}$
-morphism, then the Koopman operator
${\mathbf {CHPrb}}$
-morphism, then the Koopman operator
![]() $C(\pi ):C(Y)\to C(X)$
satisfies
$C(\pi ):C(Y)\to C(X)$
satisfies
![]() $\tau _\nu =\tau _\mu \circ C(\pi )$
. Conversely, using Gelfand duality and the Riesz representation theorem, we can associate to each
$\tau _\nu =\tau _\mu \circ C(\pi )$
. Conversely, using Gelfand duality and the Riesz representation theorem, we can associate to each
![]() ${\mathbf {CC^*Alg}^\tau }$
-algebra
${\mathbf {CC^*Alg}^\tau }$
-algebra
![]() $(\mathcal {A},\tau _{\mathcal {A}})$
a unique
$(\mathcal {A},\tau _{\mathcal {A}})$
a unique
![]() ${\mathbf {CHPrb}}$
-space
${\mathbf {CHPrb}}$
-space
![]() $\mathtt {Riesz}(\mathcal {A},\tau _{\mathcal {A}}):= (\mathtt {Spec}(\mathcal {A}),\mathcal {B}a(\mathtt {Spec}(\mathcal {A})),\mu _{\tau _{\mathcal {A}}})$
. Uniqueness in the Riesz representation theorem also yields that if
$\mathtt {Riesz}(\mathcal {A},\tau _{\mathcal {A}}):= (\mathtt {Spec}(\mathcal {A}),\mathcal {B}a(\mathtt {Spec}(\mathcal {A})),\mu _{\tau _{\mathcal {A}}})$
. Uniqueness in the Riesz representation theorem also yields that if
![]() $\Phi :(\mathcal {A},\tau _{\mathcal {A}})\to (\mathcal {B},\tau _{\mathcal {B}})$
is a
$\Phi :(\mathcal {A},\tau _{\mathcal {A}})\to (\mathcal {B},\tau _{\mathcal {B}})$
is a
![]() ${\mathbf {CC^*Alg}^\tau }$
-morphism, then the continuous function
${\mathbf {CC^*Alg}^\tau }$
-morphism, then the continuous function
![]() $\mathtt {Spec}(\Phi ):\mathtt {Spec}(\mathcal {B})\to \mathtt {Spec}(\mathcal {A})$
pushes forward
$\mathtt {Spec}(\Phi ):\mathtt {Spec}(\mathcal {B})\to \mathtt {Spec}(\mathcal {A})$
pushes forward
![]() $\nu _{\tau _{\mathcal {B}}}$
to
$\nu _{\tau _{\mathcal {B}}}$
to
![]() $\mu _{\tau _{\mathcal {A}}}$
. This ‘Riesz duality’ between
$\mu _{\tau _{\mathcal {A}}}$
. This ‘Riesz duality’ between
![]() ${\mathbf {CHPrb}}$
and
${\mathbf {CHPrb}}$
and
![]() ${\mathbf {CC^*Alg}^\tau }$
can be promoted in the obvious way to a duality between the corresponding dynamical categories
${\mathbf {CC^*Alg}^\tau }$
can be promoted in the obvious way to a duality between the corresponding dynamical categories
![]() ${\mathbf {CHPrb}_\Gamma }$
and
${\mathbf {CHPrb}_\Gamma }$
and
![]() ${\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
. This establishes the duality on the right-hand side of Figure 2. See [Reference Jamneshan and Tao31, §5] for a more detailed exposition.
${\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
. This establishes the duality on the right-hand side of Figure 2. See [Reference Jamneshan and Tao31, §5] for a more detailed exposition.
As for the duality on the left-hand side of Figure 2, let
![]() $(X,\mu )$
be a
$(X,\mu )$
be a
![]() ${\mathbf {PrbAlg}}$
-space. We define
${\mathbf {PrbAlg}}$
-space. We define
![]() $L^\infty (X)$
to be the set of
$L^\infty (X)$
to be the set of
![]() $\mathbf {AbsMbl}$
-morphisms
$\mathbf {AbsMbl}$
-morphisms
![]() $f:X\to \mathcal {B}o(\mathbb {C})$
, where
$f:X\to \mathcal {B}o(\mathbb {C})$
, where
![]() $\mathcal {B}o(\mathbb {C})$
denotes the Borel
$\mathcal {B}o(\mathbb {C})$
denotes the Borel
![]() $\sigma $
-algebra of the complex numbers
$\sigma $
-algebra of the complex numbers
![]() $\mathbb {C}$
, which are bounded in the sense that there exists a real number
$\mathbb {C}$
, which are bounded in the sense that there exists a real number
![]() $M\geq 0$
such that
$M\geq 0$
such that
![]() $f( \{ z \in \mathbb {C}: |z| \leq M \} ) = 1$
, with
$f( \{ z \in \mathbb {C}: |z| \leq M \} ) = 1$
, with
![]() $\|f\|_{L^\infty (X)}$
defined to equal the infimum of all such M. We can equip
$\|f\|_{L^\infty (X)}$
defined to equal the infimum of all such M. We can equip
![]() $L^\infty (X)$
with the structure of a commutative
$L^\infty (X)$
with the structure of a commutative
![]() $*$
-algebra by lifting all
$*$
-algebra by lifting all
![]() $*$
-algebra operations from
$*$
-algebra operations from
![]() $\mathbb {C}$
to the set of all
$\mathbb {C}$
to the set of all
![]() $\mathbf {AbsMbl}$
-morphisms
$\mathbf {AbsMbl}$
-morphisms
![]() $f:X\to \mathcal {B}o(\mathbb {C})$
. Every element E of X generates an idempotent element
$f:X\to \mathcal {B}o(\mathbb {C})$
. Every element E of X generates an idempotent element
![]() $1_E$
of
$1_E$
of
![]() $L^\infty (X)$
. The set of finite linear combinations of idempotents form a dense subspace of
$L^\infty (X)$
. The set of finite linear combinations of idempotents form a dense subspace of
![]() $L^\infty (X)$
. One can then define a trace
$L^\infty (X)$
. One can then define a trace
![]() $\tau $
on this algebra by defining
$\tau $
on this algebra by defining
![]() $\tau ( \sum _{n=1}^N c_n 1_{E_n} ) := \sum _{n=1}^N c_n \mu (E_n)$
for any finite sequence of complex numbers
$\tau ( \sum _{n=1}^N c_n 1_{E_n} ) := \sum _{n=1}^N c_n \mu (E_n)$
for any finite sequence of complex numbers
![]() $c_n$
and
$c_n$
and
![]() $E_n \in X$
, and then extending by density. Thus,
$E_n \in X$
, and then extending by density. Thus,
![]() $L^\infty (X)$
can be viewed as an element of
$L^\infty (X)$
can be viewed as an element of
![]() ${\mathbf {CvNAlg}^\tau }$
. If
${\mathbf {CvNAlg}^\tau }$
. If
![]() $\pi \colon X \to Y$
is a
$\pi \colon X \to Y$
is a
![]() ${\mathbf {PrbAlg}}$
-morphism, one can define the
${\mathbf {PrbAlg}}$
-morphism, one can define the
![]() ${\mathbf {CvNAlg}^\tau }$
-morphism
${\mathbf {CvNAlg}^\tau }$
-morphism
![]() $L^\infty (\pi ) \colon L^\infty (Y) \to L^\infty (X)$
by the Koopman operator
$L^\infty (\pi ) \colon L^\infty (Y) \to L^\infty (X)$
by the Koopman operator
![]() $L^\infty (\pi )(f) := f \circ \pi $
. See [Reference Jamneshan and Tao31, §§6 and 7] for details of these constructions.
$L^\infty (\pi )(f) := f \circ \pi $
. See [Reference Jamneshan and Tao31, §§6 and 7] for details of these constructions.
Conversely, suppose that
![]() $({\mathcal A},\tau _{\mathcal A})$
is a
$({\mathcal A},\tau _{\mathcal A})$
is a
![]() ${\mathbf {CvNAlg}^\tau }$
-algebra. We can form the collection
${\mathbf {CvNAlg}^\tau }$
-algebra. We can form the collection
![]() ${\mathcal P}_{\mathcal A}$
of real projections in
${\mathcal P}_{\mathcal A}$
of real projections in
![]() ${\mathcal A}$
. As is well-known, these projections have the structure of a complete Boolean algebra. The trace
${\mathcal A}$
. As is well-known, these projections have the structure of a complete Boolean algebra. The trace
![]() $\tau _{\mathcal A}$
then becomes a countably additive probability measure on
$\tau _{\mathcal A}$
then becomes a countably additive probability measure on
![]() ${\mathcal P}_{\mathcal A}$
, and we write
${\mathcal P}_{\mathcal A}$
, and we write
![]() $\mathtt {Proj}({\mathcal A},\tau _{\mathcal A})$
for the opposite probability algebra of
$\mathtt {Proj}({\mathcal A},\tau _{\mathcal A})$
for the opposite probability algebra of
![]() $( {\mathcal P}_{\mathcal A}, \tau _{\mathcal A})$
. If
$( {\mathcal P}_{\mathcal A}, \tau _{\mathcal A})$
. If
![]() $\Phi \colon ({\mathcal A},\tau _{\mathcal A}) \to ({\mathcal B},\tau _{\mathcal B})$
is a
$\Phi \colon ({\mathcal A},\tau _{\mathcal A}) \to ({\mathcal B},\tau _{\mathcal B})$
is a
![]() ${\mathbf {CvNAlg}^\tau }$
-morphism, we observe that the associated von Neumann algebra homomorphism
${\mathbf {CvNAlg}^\tau }$
-morphism, we observe that the associated von Neumann algebra homomorphism
![]() $\Phi \colon {\mathcal A} \to {\mathcal B}$
maps projections in
$\Phi \colon {\mathcal A} \to {\mathcal B}$
maps projections in
![]() ${\mathcal P}_{\mathcal A}$
to projections in
${\mathcal P}_{\mathcal A}$
to projections in
![]() ${\mathcal P}_{\mathcal B}$
, in a manner that preserves the trace as well as being a
${\mathcal P}_{\mathcal B}$
, in a manner that preserves the trace as well as being a
![]() ${\mathbf {Bool}_\sigma }$
-morphism. We then define
${\mathbf {Bool}_\sigma }$
-morphism. We then define
![]() $\mathtt {Proj}(\Phi ) \colon \mathtt {Proj}({\mathcal B},\tau _{\mathcal B}) \to \mathtt {Proj}({\mathcal A},\tau _{\mathcal A})$
to be the
$\mathtt {Proj}(\Phi ) \colon \mathtt {Proj}({\mathcal B},\tau _{\mathcal B}) \to \mathtt {Proj}({\mathcal A},\tau _{\mathcal A})$
to be the
![]() ${\mathbf {PrbAlg}}$
-morphism associated with this
${\mathbf {PrbAlg}}$
-morphism associated with this
![]() ${\mathbf {Bool}_\sigma }$
-morphism. See [Reference Jamneshan and Tao31, §7] for a proof that
${\mathbf {Bool}_\sigma }$
-morphism. See [Reference Jamneshan and Tao31, §7] for a proof that
![]() $\mathtt {Proj}$
and
$\mathtt {Proj}$
and
![]() $L^\infty $
establish a duality of categories between
$L^\infty $
establish a duality of categories between
![]() ${\mathbf {CvNAlg}^\tau }$
and
${\mathbf {CvNAlg}^\tau }$
and
![]() ${\mathbf {PrbAlg}}$
. This duality then extends naturally to the dynamical categories
${\mathbf {PrbAlg}}$
. This duality then extends naturally to the dynamical categories
![]() ${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
and
${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
and
![]() ${\mathbf {PrbAlg}_\Gamma }$
.
${\mathbf {PrbAlg}_\Gamma }$
.
Every von Neumann algebra is also a unital
![]() $C^*$
-algebra, and a faithful trace on a commutative von Neumann algebra becomes a state on the corresponding
$C^*$
-algebra, and a faithful trace on a commutative von Neumann algebra becomes a state on the corresponding
![]() $C^*$
-algebra. From this, it is easy to see that there is a forgetful inclusion functor
$C^*$
-algebra. From this, it is easy to see that there is a forgetful inclusion functor
![]() $\mathtt {Inc}$
from
$\mathtt {Inc}$
from
![]() ${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
to
${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
to
![]() ${\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
.
${\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
.
Finally, we define the canonical model functor by
Remark 2.4. There is a more direct way to define the canonical model functor using the Stone and Loomis–Sikorski representation theorems where the underlying compact Hausdorff space is the Stonean space associated to a complete Boolean algebra by Stone’s representation theorem, e.g., see [Reference Jamneshan and Tao31, §9].
Remark 2.5. The canonical model has been implicitly introduced in the literature at several occasions, e.g., see [Reference Derndinger, Palm and Nagel7, Reference Dieudonné8, Reference Eisner, Farkas, Haase and Nagel13, Reference Ellis14, Reference Fremlin16, Reference Halmos24, Reference Kakutani34, Reference Segal42], where such models are also referred to as ‘Stone’ or ‘Kakutani models’.
For a countable group
![]() $\Gamma $
, let us denote by
$\Gamma $
, let us denote by
![]() $\mathbf {PrbAlg}^\sigma _\Gamma $
the subcategory of
$\mathbf {PrbAlg}^\sigma _\Gamma $
the subcategory of
![]() ${\mathbf {PrbAlg}_\Gamma }$
whose systems consist of separable probability algebras. In [Reference Glasner19, §2], a ‘Cantor model’ is associated to each
${\mathbf {PrbAlg}_\Gamma }$
whose systems consist of separable probability algebras. In [Reference Glasner19, §2], a ‘Cantor model’ is associated to each
![]() $\mathbf {PrbAlg}^\sigma _\Gamma $
-system which satisfies some functoriality properties, (such Cantor models are formed on closed subspaces of the classical Cantor set). These Cantor models are not canonical, but amenable to classical disintegration of measures. Furstenberg [Reference Furstenberg18, §§5–6] works with ‘separable systems’ which are concrete probability spaces on which a countable group acts measure-preservingly (modulo null sets) such that the associated
$\mathbf {PrbAlg}^\sigma _\Gamma $
-system which satisfies some functoriality properties, (such Cantor models are formed on closed subspaces of the classical Cantor set). These Cantor models are not canonical, but amenable to classical disintegration of measures. Furstenberg [Reference Furstenberg18, §§5–6] works with ‘separable systems’ which are concrete probability spaces on which a countable group acts measure-preservingly (modulo null sets) such that the associated
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems (with the help of the
${\mathbf {PrbAlg}_\Gamma }$
-systems (with the help of the
![]() $\mathtt {AlgAbs}$
-functor which is described below) are in the subcategory
$\mathtt {AlgAbs}$
-functor which is described below) are in the subcategory
![]() $\mathbf {PrbAlg}^\sigma _\Gamma $
.
$\mathbf {PrbAlg}^\sigma _\Gamma $
.
The categories
![]() ${\mathbf {PrbAlg}_\Gamma }$
and
${\mathbf {PrbAlg}_\Gamma }$
and
![]() ${\mathbf {CHPrb}_\Gamma }$
are not dual to each other (similarly, as the categories
${\mathbf {CHPrb}_\Gamma }$
are not dual to each other (similarly, as the categories
![]() ${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
and
${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
and
![]() ${\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
are not so). However, we have a functor
${\mathbf {CC^*Alg}^\tau _{\Gamma ^{\operatorname {op}}}}$
are not so). However, we have a functor
![]() $\mathtt {AlgAbs}$
(cf. Figure 4) that associates with every
$\mathtt {AlgAbs}$
(cf. Figure 4) that associates with every
![]() ${\mathbf {CHPrb}_\Gamma }$
-system a
${\mathbf {CHPrb}_\Gamma }$
-system a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system such that
${\mathbf {PrbAlg}_\Gamma }$
-system such that
![]() $\mathtt {AlgAbs}\circ \mathtt {Conc}$
is naturally isomorphic to the identity functor on
$\mathtt {AlgAbs}\circ \mathtt {Conc}$
is naturally isomorphic to the identity functor on
![]() ${\mathbf {PrbAlg}_\Gamma }$
.
${\mathbf {PrbAlg}_\Gamma }$
.
Figure 4 The
![]() $\mathtt {AlgAbs}$
functor first abstracts away from the set structure of a
$\mathtt {AlgAbs}$
functor first abstracts away from the set structure of a
![]() ${\mathbf {CHPrb}_\Gamma }$
-system and then deletes the null ideal of this abstract system to obtain a
${\mathbf {CHPrb}_\Gamma }$
-system and then deletes the null ideal of this abstract system to obtain a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system.
${\mathbf {PrbAlg}_\Gamma }$
-system.
Next we define the functor
![]() $\mathtt {AlgAbs}$
. Let
$\mathtt {AlgAbs}$
. Let
![]() $(X,\mathcal {B}a(X),\mu )$
be a
$(X,\mathcal {B}a(X),\mu )$
be a
![]() ${\mathbf {CHPrb}}$
-space. Denote by
${\mathbf {CHPrb}}$
-space. Denote by
![]() $\mathcal {N}_\mu $
the
$\mathcal {N}_\mu $
the
![]() $\mu $
-null ideal of
$\mu $
-null ideal of
![]() $\mathcal {B}a(X)$
, that is, the collection of
$\mathcal {B}a(X)$
, that is, the collection of
![]() $E\in \mathcal {B}a(X)$
such that
$E\in \mathcal {B}a(X)$
such that
![]() $\mu (E)=0$
. We can form the quotient Boolean
$\mu (E)=0$
. We can form the quotient Boolean
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $X_\mu =\mathcal {B}a(X)/\mathcal {N}_\mu $
by identifying
$X_\mu =\mathcal {B}a(X)/\mathcal {N}_\mu $
by identifying
![]() $E,F\in \mathcal {B}a(X)$
if
$E,F\in \mathcal {B}a(X)$
if
![]() $E\Delta F\in \mathcal {N}_\mu $
. Let
$E\Delta F\in \mathcal {N}_\mu $
. Let
![]() $\pi _X:\mathcal {B}a(X)\to X_\mu $
be the canonical
$\pi _X:\mathcal {B}a(X)\to X_\mu $
be the canonical
![]() ${\mathbf {Bool}_\sigma }$
-epimorphism. We define a probability measure
${\mathbf {Bool}_\sigma }$
-epimorphism. We define a probability measure
![]() $\hat \mu :X_\mu \to [0,1]$
by
$\hat \mu :X_\mu \to [0,1]$
by
![]() $\hat \mu (\pi (E)):= \mu (E)$
. We obtain a
$\hat \mu (\pi (E)):= \mu (E)$
. We obtain a
![]() ${\mathbf {PrbAlg}}$
-algebra
${\mathbf {PrbAlg}}$
-algebra
![]() $(X_\mu , \hat \mu )$
, applying the opposite functor to
$(X_\mu , \hat \mu )$
, applying the opposite functor to
![]() $(X_\mu , \hat \mu )$
associates with
$(X_\mu , \hat \mu )$
associates with
![]() $(X,\mathcal {B}a(X),\mu )$
a
$(X,\mathcal {B}a(X),\mu )$
a
![]() ${\mathbf {PrbAlg}}$
-space. If
${\mathbf {PrbAlg}}$
-space. If
![]() $f:(X,\mathcal {B}a(X),\mu )\to (Y,\mathcal {B}a(Y),\nu )$
is a
$f:(X,\mathcal {B}a(X),\mu )\to (Y,\mathcal {B}a(Y),\nu )$
is a
![]() ${\mathbf {CHPrb}}$
-morphism, then the pullback map
${\mathbf {CHPrb}}$
-morphism, then the pullback map
![]() $f^*:\mathcal {B}a(Y)\to \mathcal {B}a(X)$
defined by
$f^*:\mathcal {B}a(Y)\to \mathcal {B}a(X)$
defined by
![]() $E\mapsto f^*(E):= f^{-1}(E)$
is a
$E\mapsto f^*(E):= f^{-1}(E)$
is a
![]() ${\mathbf {Bool}_\sigma }$
-morphism. We define the
${\mathbf {Bool}_\sigma }$
-morphism. We define the
![]() ${\mathbf {PrbAlg}}$
-morphism
${\mathbf {PrbAlg}}$
-morphism
![]() $\mathtt {AlgAbs}(f): (X_\mu , \hat \mu )\to (Y_\nu , \hat \nu )$
by
$\mathtt {AlgAbs}(f): (X_\mu , \hat \mu )\to (Y_\nu , \hat \nu )$
by
![]() $\pi _Y(E)\mapsto \mathtt {AlgAbs}(f)(\pi _Y(E)):= \pi _X(f^*(E))$
. The functor
$\pi _Y(E)\mapsto \mathtt {AlgAbs}(f)(\pi _Y(E)):= \pi _X(f^*(E))$
. The functor
![]() $\mathtt {AlgAbs}$
promotes to a functor from
$\mathtt {AlgAbs}$
promotes to a functor from
![]() ${\mathbf {CHPrb}_\Gamma }$
to
${\mathbf {CHPrb}_\Gamma }$
to
![]() ${\mathbf {PrbAlg}_\Gamma }$
. The functor
${\mathbf {PrbAlg}_\Gamma }$
. The functor
![]() $\mathtt {AlgAbs}$
is not injective on objects since a
$\mathtt {AlgAbs}$
is not injective on objects since a
![]() ${\mathbf {CHPrb}}$
-space and its measure-theoretic completion are mapped to the same
${\mathbf {CHPrb}}$
-space and its measure-theoretic completion are mapped to the same
![]() ${\mathbf {PrbAlg}}$
-space. Moreover,
${\mathbf {PrbAlg}}$
-space. Moreover,
![]() $\mathtt {Conc}(\mathtt {AlgAbs}(X,\mathcal {B}a(X),\mu ))$
is typically much larger than
$\mathtt {Conc}(\mathtt {AlgAbs}(X,\mathcal {B}a(X),\mu ))$
is typically much larger than
![]() $(X,\mathcal {B}a(X),\mu )$
.
$(X,\mathcal {B}a(X),\mu )$
.
2.3 Abstract Lebesgue spaces
The following notation will be used throughout the remainder of this paper.
Let
![]() $\mathcal {X}=(X,\mu ,T)$
be a
$\mathcal {X}=(X,\mu ,T)$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system. We denote the canonical model
${\mathbf {PrbAlg}_\Gamma }$
-system. We denote the canonical model
![]() $\mathtt {Conc}(\mathcal {X})$
by
$\mathtt {Conc}(\mathcal {X})$
by
![]() $\tilde {\mathcal {X}}$
, its underlying Stonean space by
$\tilde {\mathcal {X}}$
, its underlying Stonean space by
![]() $\tilde {X}$
(cf. Remark 2.4), its Baire–Radon measure by
$\tilde {X}$
(cf. Remark 2.4), its Baire–Radon measure by
![]() $\tilde {\mu }$
, and its
$\tilde {\mu }$
, and its
![]() $\Gamma $
-action by
$\Gamma $
-action by
![]() $\tilde {T}$
, so that
$\tilde {T}$
, so that
If
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
is a
$\pi :\mathcal {X}\to \mathcal {Y}$
is a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor, then we denote its canonical representation
${\mathbf {PrbAlg}_\Gamma }$
-factor, then we denote its canonical representation
![]() $\mathtt {Conc}(\pi )$
by
$\mathtt {Conc}(\pi )$
by
![]() $\tilde {\pi }$
.
$\tilde {\pi }$
.
We can use the canonical model to define integration and Lebesgue spaces for probability algebras (in [Reference Fremlin16, §§363–366], a direct construction for integration and Lebesgue spaces for measure algebras is provided which is equivalent to our construction via canonical models). For any
![]() $0\leq p\leq \infty $
, we define the complex vector space
$0\leq p\leq \infty $
, we define the complex vector space
For any
![]() $f\in L^1(X)$
, we define
$f\in L^1(X)$
, we define
Let
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
be a
$\pi :\mathcal {X}\to \mathcal {Y}$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor with canonical representation
${\mathbf {PrbAlg}_\Gamma }$
-factor with canonical representation
![]() $\tilde {\pi }$
. Then
$\tilde {\pi }$
. Then
![]() $\tilde {\pi }$
gives rise to a Koopman operator
$\tilde {\pi }$
gives rise to a Koopman operator
![]() $\tilde {\pi }^*:L^p(Y)\to L^p(X)$
defined by pullback as
$\tilde {\pi }^*:L^p(Y)\to L^p(X)$
defined by pullback as
In particular, we can use the Koopman operator to identify
![]() $L^p(Y)$
with a (closed) subspace of
$L^p(Y)$
with a (closed) subspace of
![]() $L^p(X)$
. Henceforth, we will make use of these identifications without further notice.
$L^p(X)$
. Henceforth, we will make use of these identifications without further notice.
2.4 Canonical disintegration and relatively independent products
A main advantage of the canonical model is that it yields a canonical disintegration of measures from which, in turn, several key basic measure-theoretic concepts can be defined. Canonical disintegration of measures relies on an important property which we coined the strong Lusin property in [Reference Jamneshan and Tao31] (a property well known in the literature, though under a different guise). It implies that we have a
![]() ${\mathbf {CC^*Alg}}$
-isomorphism
${\mathbf {CC^*Alg}}$
-isomorphism
for any
![]() ${\mathbf {PrbAlg}}$
-algebra
${\mathbf {PrbAlg}}$
-algebra
![]() $(X,\mu )$
with Stone space
$(X,\mu )$
with Stone space
![]() $\tilde {X}$
. The strong Lusin property implies the following disintegration result.
$\tilde {X}$
. The strong Lusin property implies the following disintegration result.
Theorem 2.6. (Canonical disintegration) [Reference Jamneshan and Tao31, §8]
Let
![]() $\mathcal {X}=(X,\mu ,T)$
and
$\mathcal {X}=(X,\mu ,T)$
and
![]() $\mathcal {Y}=(Y,\nu ,S)$
be
$\mathcal {Y}=(Y,\nu ,S)$
be
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems and
${\mathbf {PrbAlg}_\Gamma }$
-systems and
![]() $\pi \colon \mathcal {X}\to \mathcal {Y}$
be a
$\pi \colon \mathcal {X}\to \mathcal {Y}$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor. Then there is a unique Radon probability measure
${\mathbf {PrbAlg}_\Gamma }$
-factor. Then there is a unique Radon probability measure
![]() $\mu _y$
on
$\mu _y$
on
![]() $\tilde {X}$
for each
$\tilde {X}$
for each
![]() $y \in \tilde {Y}$
which depends continuously on y in the vague topology in the sense that
$y \in \tilde {Y}$
which depends continuously on y in the vague topology in the sense that
![]() $y \mapsto \int _{\tilde {X}} f \,d\mu _y$
is continuous for every
$y \mapsto \int _{\tilde {X}} f \,d\mu _y$
is continuous for every
![]() $f\in C(\tilde {X})$
, and such that
$f\in C(\tilde {X})$
, and such that
 $$ \begin{align} \int_{\tilde X} f \tilde{\pi}^*g \,d\tilde\mu = \int_{\tilde{Y}} \bigg(\int_{\tilde{X}} f \,d\mu_y\bigg) g \,d\tilde{\nu}\end{align} $$
$$ \begin{align} \int_{\tilde X} f \tilde{\pi}^*g \,d\tilde\mu = \int_{\tilde{Y}} \bigg(\int_{\tilde{X}} f \,d\mu_y\bigg) g \,d\tilde{\nu}\end{align} $$
for all
![]() $f \in C(\tilde {X})$
,
$f \in C(\tilde {X})$
,
![]() $g \in C(\tilde {Y})$
. Furthermore, for each
$g \in C(\tilde {Y})$
. Furthermore, for each
![]() $y \in \tilde {Y}$
,
$y \in \tilde {Y}$
,
![]() $\mu _y$
is supported on the compact set
$\mu _y$
is supported on the compact set
![]() $\tilde {\pi }^{-1}(\{y\})$
, in the sense that
$\tilde {\pi }^{-1}(\{y\})$
, in the sense that
![]() $\mu _y(E)=0$
whenever E is a measurable set disjoint from
$\mu _y(E)=0$
whenever E is a measurable set disjoint from
![]() $\tilde {\pi }^{-1}(\{y\})$
(this conclusion does not require the fibers
$\tilde {\pi }^{-1}(\{y\})$
(this conclusion does not require the fibers
![]() $\tilde {\pi }^{-1}(\{y\})$
to be measurable). Moreover, we have
$\tilde {\pi }^{-1}(\{y\})$
to be measurable). Moreover, we have
for all
![]() $y\in \tilde {Y}$
and
$y\in \tilde {Y}$
and
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
We can apply the canonical disintegration to construct relatively independent products in the dynamical category
![]() ${\mathbf {PrbAlg}_\Gamma }$
(cf. [Reference Ellis14, §2]).
${\mathbf {PrbAlg}_\Gamma }$
(cf. [Reference Ellis14, §2]).
Theorem 2.7. (Relative products in
 ${\mathbf {PrbAlg}_\Gamma }$
) [Reference Jamneshan and Tao31, §8]
${\mathbf {PrbAlg}_\Gamma }$
) [Reference Jamneshan and Tao31, §8]
Let
![]() $\mathcal {X}_1=(X_1,\mu _1,T_1)$
,
$\mathcal {X}_1=(X_1,\mu _1,T_1)$
,
![]() $\mathcal {X}_2=(X_2,\mu _2,T_2)$
, and
$\mathcal {X}_2=(X_2,\mu _2,T_2)$
, and
![]() $\mathcal {Y}=(Y,\nu ,S)$
be
$\mathcal {Y}=(Y,\nu ,S)$
be
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems. Suppose that one has
${\mathbf {PrbAlg}_\Gamma }$
-systems. Suppose that one has
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factors
${\mathbf {PrbAlg}_\Gamma }$
-factors
![]() $\pi _1 \colon \mathcal {X}_1 \to \mathcal {Y}$
,
$\pi _1 \colon \mathcal {X}_1 \to \mathcal {Y}$
,
![]() $\pi _2 \colon \mathcal {X}_2 \to \mathcal {Y}$
. Then there exists a
$\pi _2 \colon \mathcal {X}_2 \to \mathcal {Y}$
. Then there exists a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-commutative diagram
${\mathbf {PrbAlg}_\Gamma }$
-commutative diagram

for some
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
![]() $\mathcal {X}_1 \times _{\mathcal {Y}} \mathcal {X}_2=(X_1\times _Y X_2,\mu \times _Y\mu , T\times T)$
and
$\mathcal {X}_1 \times _{\mathcal {Y}} \mathcal {X}_2=(X_1\times _Y X_2,\mu \times _Y\mu , T\times T)$
and
![]() ${\mathbf {PrbAlg}_\Gamma }$
-morphisms
${\mathbf {PrbAlg}_\Gamma }$
-morphisms
![]() $\Pi _1 \colon \mathcal {X}_1 \times _{\mathcal {Y}} \mathcal {X}_2 \to \mathcal {X}_1$
,
$\Pi _1 \colon \mathcal {X}_1 \times _{\mathcal {Y}} \mathcal {X}_2 \to \mathcal {X}_1$
,
![]() $\Pi _2 \colon \mathcal {X}_1 \times _{\mathcal {Y}} \mathcal {X}_2 \to \mathcal {X}_2$
such that one has
$\Pi _2 \colon \mathcal {X}_1 \times _{\mathcal {Y}} \mathcal {X}_2 \to \mathcal {X}_2$
such that one has
 $$ \begin{align} \int_{X_1 \times_Y X_2} f_1 f_2 \,d\mu\times_Y\mu= \int_Y \mathbb{E}(f_1|Y) \mathbb{E}(f_2|Y) \,d\nu \end{align} $$
$$ \begin{align} \int_{X_1 \times_Y X_2} f_1 f_2 \,d\mu\times_Y\mu= \int_Y \mathbb{E}(f_1|Y) \mathbb{E}(f_2|Y) \,d\nu \end{align} $$
for all
![]() $f_1 \in L^\infty (X_1)$
,
$f_1 \in L^\infty (X_1)$
,
![]() $f_2 \in L^\infty (X_2)$
, where we embed
$f_2 \in L^\infty (X_2)$
, where we embed
![]() $L^\infty (Y)$
into
$L^\infty (Y)$
into
![]() $L^\infty (X_1), L^\infty (X_2)$
, and embed these algebras in turn into
$L^\infty (X_1), L^\infty (X_2)$
, and embed these algebras in turn into
![]() $L^\infty (X_1 \times _Y X_2)$
. Furthermore, the
$L^\infty (X_1 \times _Y X_2)$
. Furthermore, the
![]() ${\mathbf {Bool}_\sigma }$
-algebra of
${\mathbf {Bool}_\sigma }$
-algebra of
![]() $X_1\times _Y X_2$
is generated by the
$X_1\times _Y X_2$
is generated by the
![]() ${\mathbf {Bool}_\sigma }$
-algebras
${\mathbf {Bool}_\sigma }$
-algebras
![]() $X_1$
,
$X_1$
,
![]() $X_2$
(where we identify the latter with
$X_2$
(where we identify the latter with
![]() $\sigma $
-complete subalgebras of the former in the obvious way).
$\sigma $
-complete subalgebras of the former in the obvious way).
2.5 The invariant factor functor and the Alaoglu–Birkhoff ergodic theorem
Since we assume no structure on
![]() $\Gamma $
other than it being a group, the only ergodic theorem available to us is the Alaoglu–Birkhoff ergodic theorem. We first introduce the functor
$\Gamma $
other than it being a group, the only ergodic theorem available to us is the Alaoglu–Birkhoff ergodic theorem. We first introduce the functor
![]() $\mathtt {Inv}_\Gamma $
from
$\mathtt {Inv}_\Gamma $
from
![]() ${\mathbf {PrbAlg}_\Gamma }$
into itself.
${\mathbf {PrbAlg}_\Gamma }$
into itself.
Definition 2.8. (Invariant factor functor)
-
(i) If
 $\mathcal {X} = (X,\mu ,T)$
is a
$\mathcal {X} = (X,\mu ,T)$
is a
 ${\mathbf {PrbAlg}_\Gamma }$
-system, we define to be the
${\mathbf {PrbAlg}_\Gamma }$
-system, we define to be the $$ \begin{align*}\mathtt{Inv}_\Gamma(\mathcal{X})=(\mathtt{Inv}_\Gamma(X),\mu_{\mathtt{Inv}_\Gamma(X)},T_{\mathtt{Inv}_\Gamma(X)})\end{align*} $$
$$ \begin{align*}\mathtt{Inv}_\Gamma(\mathcal{X})=(\mathtt{Inv}_\Gamma(X),\mu_{\mathtt{Inv}_\Gamma(X)},T_{\mathtt{Inv}_\Gamma(X)})\end{align*} $$
 ${\mathbf {PrbAlg}_\Gamma }$
-system with
${\mathbf {PrbAlg}_\Gamma }$
-system with
 $\mathbf {AbsMbl}$
-space measure
$\mathbf {AbsMbl}$
-space measure $$ \begin{align*}\mathtt{Inv}_\Gamma(X):= \{ E \in X: T^\gamma(E) = E \text{ for all } \gamma \in \Gamma \},\end{align*} $$
for all
$$ \begin{align*}\mathtt{Inv}_\Gamma(X):= \{ E \in X: T^\gamma(E) = E \text{ for all } \gamma \in \Gamma \},\end{align*} $$
for all $$ \begin{align*} \mu_{\mathtt{Inv}_\Gamma(X)}(E) := \mu(E)\end{align*} $$
$$ \begin{align*} \mu_{\mathtt{Inv}_\Gamma(X)}(E) := \mu(E)\end{align*} $$
 $E \in X$
, and action defined by for all
$E \in X$
, and action defined by for all $$ \begin{align*} T_{\mathtt{Inv}_\Gamma(X)}^\gamma(E) := T^\gamma(E)\end{align*} $$
$$ \begin{align*} T_{\mathtt{Inv}_\Gamma(X)}^\gamma(E) := T^\gamma(E)\end{align*} $$
 $E \in \mathtt {Inv}_\Gamma (X)$
and
$E \in \mathtt {Inv}_\Gamma (X)$
and
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
-
(ii) If
 $f \colon \mathcal {X} \to \mathcal {Y}$
is a
$f \colon \mathcal {X} \to \mathcal {Y}$
is a
 ${\mathbf {PrbAlg}_\Gamma }$
-factor, we define
${\mathbf {PrbAlg}_\Gamma }$
-factor, we define
 $\mathtt {Inv}_\Gamma (f) \colon \mathtt {Inv}_\Gamma (\mathcal {X}) \to \mathtt {Inv}_\Gamma (\mathcal {Y})$
by whenever
$\mathtt {Inv}_\Gamma (f) \colon \mathtt {Inv}_\Gamma (\mathcal {X}) \to \mathtt {Inv}_\Gamma (\mathcal {Y})$
by whenever $$ \begin{align*}\mathtt{Inv}_\Gamma(f)(E) := f(E)\end{align*} $$
$$ \begin{align*}\mathtt{Inv}_\Gamma(f)(E) := f(E)\end{align*} $$
 $E \in \mathtt {Inv}_\Gamma (Y)$
.
$E \in \mathtt {Inv}_\Gamma (Y)$
.
-
(iii) A
 ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
 $\mathcal {X}$
is said to be ergodic if
$\mathcal {X}$
is said to be ergodic if
 $\mathtt {Inv}_\Gamma (X)$
is the trivial algebra
$\mathtt {Inv}_\Gamma (X)$
is the trivial algebra
 $\{0,1\}$
.
$\{0,1\}$
.
There is a natural epimorphism from the identity functor on
![]() ${\mathbf {PrbAlg}_\Gamma }$
to
${\mathbf {PrbAlg}_\Gamma }$
to
![]() $\mathtt {Inv}_\Gamma $
that gives a
$\mathtt {Inv}_\Gamma $
that gives a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor
${\mathbf {PrbAlg}_\Gamma }$
-factor
![]() $\pi \colon \mathcal {X} \to \mathtt {Inv}_\Gamma (\mathcal {X})$
defined by inclusion. Using this factor, one can view
$\pi \colon \mathcal {X} \to \mathtt {Inv}_\Gamma (\mathcal {X})$
defined by inclusion. Using this factor, one can view
![]() $L^2(\mathtt {Inv}_\Gamma (X))$
as a subspace of
$L^2(\mathtt {Inv}_\Gamma (X))$
as a subspace of
![]() $L^2(X)$
. Each shift
$L^2(X)$
. Each shift
![]() $T^\gamma \colon X \to X$
induces a unitary Koopman operator
$T^\gamma \colon X \to X$
induces a unitary Koopman operator
![]() $(T^\gamma )^* \colon L^2(X) \to L^2(X)$
. For any
$(T^\gamma )^* \colon L^2(X) \to L^2(X)$
. For any
![]() $f\in L^0(X)$
, we denote by
$f\in L^0(X)$
, we denote by
![]() $\mathtt {Orb}_\Gamma (f)$
the orbit
$\mathtt {Orb}_\Gamma (f)$
the orbit
![]() $\{(T^\gamma )^* f \colon \gamma \in \Gamma \}$
of f.
$\{(T^\gamma )^* f \colon \gamma \in \Gamma \}$
of f.
Theorem 2.9. ((Alaoglu–Birkhoff abstract ergodic theorem) [Reference Alaoglu and Birkhoff1])
Let
![]() $\mathcal {X} = (X,\mu , T)$
be a
$\mathcal {X} = (X,\mu , T)$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system and
${\mathbf {PrbAlg}_\Gamma }$
-system and
![]() $\mathbb {E}(\cdot |\mathtt {Inv}_\Gamma (X)) \colon L^2(X) \to L^2(\mathtt {Inv}_\Gamma (X))$
be the orthogonal projection. Then for any
$\mathbb {E}(\cdot |\mathtt {Inv}_\Gamma (X)) \colon L^2(X) \to L^2(\mathtt {Inv}_\Gamma (X))$
be the orthogonal projection. Then for any
![]() $f \in L^2(X)$
,
$f \in L^2(X)$
,
![]() $\mathbb {E}(f|\mathtt {Inv}_\Gamma (X))$
is the unique element of minimal norm in the closed convex hull of
$\mathbb {E}(f|\mathtt {Inv}_\Gamma (X))$
is the unique element of minimal norm in the closed convex hull of
![]() $\mathtt {Orb}_\Gamma (f)$
.
$\mathtt {Orb}_\Gamma (f)$
.
3 Conditional Hilbert spaces and Hilbert–Schmidt operators
In this section, we develop some conditional analysis which is used in §4 to study relatively compact extensions. Specifically, we introduce a conditional Hilbert space and its conditional tensor product and establish some useful properties of them. We do not aim to give the most general and systematic treatment of conditional Hilbert space theory, but present, in a self-contained manner, the minimal amount of that theory needed, directed towards its application to the study of extensions of
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems. In several remarks, we discuss and provide references on how to interpret the results in Boolean sheaf topoi, which are addressed to the reader with familiarity to topos theory and categorical logic. The ergodic-theoretically inclined reader can view the theory of conditional Hilbert spaces as a natural extension of the theory of measurable Hilbert bundles (e.g., see [Reference Glasner19, §9] and [Reference Furstenberg18, §6]) in situations where separability and countability hypotheses are not satisfied.
${\mathbf {PrbAlg}_\Gamma }$
-systems. In several remarks, we discuss and provide references on how to interpret the results in Boolean sheaf topoi, which are addressed to the reader with familiarity to topos theory and categorical logic. The ergodic-theoretically inclined reader can view the theory of conditional Hilbert spaces as a natural extension of the theory of measurable Hilbert bundles (e.g., see [Reference Glasner19, §9] and [Reference Furstenberg18, §6]) in situations where separability and countability hypotheses are not satisfied.
We do not assume any dynamical structure in this section and fix a
![]() ${\mathbf {PrbAlg}}$
-morphism
${\mathbf {PrbAlg}}$
-morphism
![]() $\pi :(X,\mu )\to (Y,\nu )$
throughout. Recall that we have corresponding embeddings
$\pi :(X,\mu )\to (Y,\nu )$
throughout. Recall that we have corresponding embeddings
![]() $\pi ^*:L^0(Y)\to L^0(X)$
and
$\pi ^*:L^0(Y)\to L^0(X)$
and
![]() $\pi ^*:L^2(Y)\to L^2(X)$
defined by
$\pi ^*:L^2(Y)\to L^2(X)$
defined by
![]() $\pi ^*(f)=f\circ \tilde \pi $
, where
$\pi ^*(f)=f\circ \tilde \pi $
, where
![]() $\tilde {\pi }:\tilde X\to \tilde Y$
is the canonical representation. We identify
$\tilde {\pi }:\tilde X\to \tilde Y$
is the canonical representation. We identify
![]() $L^0(Y)$
with the closed subspace
$L^0(Y)$
with the closed subspace
![]() $\pi ^*(L^0(Y))$
of
$\pi ^*(L^0(Y))$
of
![]() $L^0(X)$
(with respect to convergence in probability) and
$L^0(X)$
(with respect to convergence in probability) and
![]() $L^2(Y)$
with the closed subspace
$L^2(Y)$
with the closed subspace
![]() $\pi ^*(L^2(Y))$
of
$\pi ^*(L^2(Y))$
of
![]() $L^2(X)$
. We also identify
$L^2(X)$
. We also identify
![]() $\mathcal {B}a(\tilde {Y})$
with the sub-
$\mathcal {B}a(\tilde {Y})$
with the sub-
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\tilde \pi ^*(\mathcal {B}a(\tilde {Y}))$
of
$\tilde \pi ^*(\mathcal {B}a(\tilde {Y}))$
of
![]() $\mathcal {B}a(\tilde {X})$
. Throughout, all equalities, inequalities, and inclusions between measurable functions and measurable sets are understood in the almost sure sense. We have the canonical disintegration
$\mathcal {B}a(\tilde {X})$
. Throughout, all equalities, inequalities, and inclusions between measurable functions and measurable sets are understood in the almost sure sense. We have the canonical disintegration
![]() $(\mu _y)_{y\in \tilde {Y}}$
of
$(\mu _y)_{y\in \tilde {Y}}$
of
![]() $\mu $
over Y. This leads to the relatively independent product
$\mu $
over Y. This leads to the relatively independent product
![]() $(X\times _Y X, \mu \times _Y \mu )$
. We can use the canonical
$(X\times _Y X, \mu \times _Y \mu )$
. We can use the canonical
![]() ${\mathbf {PrbAlg}}$
-morphism
${\mathbf {PrbAlg}}$
-morphism
![]() $\psi :(X\times _Y X, \mu \times _Y \mu )\to (Y,\nu )$
to identify
$\psi :(X\times _Y X, \mu \times _Y \mu )\to (Y,\nu )$
to identify
![]() $L^0(Y)$
with a subspace of
$L^0(Y)$
with a subspace of
![]() $L^0(X\times _Y X)$
, and similarly for the respective
$L^0(X\times _Y X)$
, and similarly for the respective
![]() $L^2$
spaces.
$L^2$
spaces.
A partition
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $\tilde {X}$
is called a Y-partition if its elements are measurable sets in
$\tilde {X}$
is called a Y-partition if its elements are measurable sets in
![]() $\mathcal {B}a(\tilde Y)$
. For technical reasons, we allow the empty set to be an element of a partition. Let
$\mathcal {B}a(\tilde Y)$
. For technical reasons, we allow the empty set to be an element of a partition. Let
![]() $\mathcal {P}$
be a Y-partition and
$\mathcal {P}$
be a Y-partition and
![]() $f_E\in L^0(X)$
for each
$f_E\in L^0(X)$
for each
![]() $E\in \mathcal {P}$
. Then there is a unique
$E\in \mathcal {P}$
. Then there is a unique
![]() $f\in L^0(X)$
such that
$f\in L^0(X)$
such that
![]() $f1_E=f_E1_E$
for all
$f1_E=f_E1_E$
for all
![]() $E\in \mathcal {P}$
. We denote this unique element f by
$E\in \mathcal {P}$
. We denote this unique element f by
![]() $\sum _{E\in \mathcal {P}} f_E 1_E$
and call it a Y-countable concatenation in
$\sum _{E\in \mathcal {P}} f_E 1_E$
and call it a Y-countable concatenation in
![]() $L^0(X)$
. Similarly, we define Y-countable concatenations in
$L^0(X)$
. Similarly, we define Y-countable concatenations in
![]() $L^0(X\times _Y X)$
. We will be interested in subspaces of
$L^0(X\times _Y X)$
. We will be interested in subspaces of
![]() $L^0(X)$
and
$L^0(X)$
and
![]() $L^0(X\times _Y X)$
which are closed under Y-countable concatenations. More specifically, these subspaces are a conditional version of the classical
$L^0(X\times _Y X)$
which are closed under Y-countable concatenations. More specifically, these subspaces are a conditional version of the classical
![]() $L^2$
space and its conditional Hilbert space tensor product which are defined as follows.
$L^2$
space and its conditional Hilbert space tensor product which are defined as follows.
Definition 3.1. We define the conditional Hilbert space
 $$ \begin{align*} \mathtt{L^2(X|Y)}:=\bigg\{f\in L^0(X): \mathbb{E}(|f|^2|Y)=\int_{\tilde{X}} |f|^2 \,d\mu_y<\infty\bigg\} \end{align*} $$
$$ \begin{align*} \mathtt{L^2(X|Y)}:=\bigg\{f\in L^0(X): \mathbb{E}(|f|^2|Y)=\int_{\tilde{X}} |f|^2 \,d\mu_y<\infty\bigg\} \end{align*} $$
and the conditional Hilbert-Schmidt space
 $$ \begin{align*} \mathtt{HS(X|Y)}:=\bigg\{K\in L^0(X\times_Y X): \mathbb{E}(|K|^2|Y)=\int_{\tilde{X}\times\tilde{X}} |K|^2 \,d\mu_y\times \mu_y<\infty\bigg\}. \end{align*} $$
$$ \begin{align*} \mathtt{HS(X|Y)}:=\bigg\{K\in L^0(X\times_Y X): \mathbb{E}(|K|^2|Y)=\int_{\tilde{X}\times\tilde{X}} |K|^2 \,d\mu_y\times \mu_y<\infty\bigg\}. \end{align*} $$
One easily verifies that
 $$ \begin{align*} \mathtt{L^2(X|Y)}&=\{f\in L^0(X): \text{there exist } g\in L^0(Y), h\in L^2(X)\ \text{such that }f=g h\}, \\\mathtt{HS(X|Y)}&=\{f\in L^0(X\times_Y X): \text{there exist } g\in L^0(Y), h\in L^2(X\times_Y X) \text{ such that }f=g h\}. \end{align*} $$
$$ \begin{align*} \mathtt{L^2(X|Y)}&=\{f\in L^0(X): \text{there exist } g\in L^0(Y), h\in L^2(X)\ \text{such that }f=g h\}, \\\mathtt{HS(X|Y)}&=\{f\in L^0(X\times_Y X): \text{there exist } g\in L^0(Y), h\in L^2(X\times_Y X) \text{ such that }f=g h\}. \end{align*} $$
In particular, both
![]() $\mathtt {L^2(X|Y)}$
and
$\mathtt {L^2(X|Y)}$
and
![]() $\mathtt {HS(X|Y)}$
are modules over the ring
$\mathtt {HS(X|Y)}$
are modules over the ring
![]() $L^0(Y)$
closed under Y-countable concatenations.
$L^0(Y)$
closed under Y-countable concatenations.
Remark 3.2. In [Reference Tao44, §2.13], the same notation
![]() $\mathtt {L^2(X|Y)}$
is used for the smaller
$\mathtt {L^2(X|Y)}$
is used for the smaller
![]() $L^\infty (Y)$
-module
$L^\infty (Y)$
-module
The crucial difference between the smaller conditional Hilbert space in [Reference Tao44] and our larger conditional Hilbert space
![]() $\mathtt {L^2(X|Y)}$
is that the latter is closed under Y-countable concatenations. It is exactly this property that makes
$\mathtt {L^2(X|Y)}$
is that the latter is closed under Y-countable concatenations. It is exactly this property that makes
![]() $\mathtt {L^2(X|Y)}$
amenable to topos-theoretic tools, see the following Remark 3.5.
$\mathtt {L^2(X|Y)}$
amenable to topos-theoretic tools, see the following Remark 3.5.
We define a conditional version of inner product and norm.
Definition 3.3. For
![]() $f,g\in \mathtt {L^2(X|Y)}$
, we define their conditional inner product as
$f,g\in \mathtt {L^2(X|Y)}$
, we define their conditional inner product as
For
![]() $f\in \mathtt {L^2(X|Y)}$
, we define its conditional norm as
$f\in \mathtt {L^2(X|Y)}$
, we define its conditional norm as
The conditional norm
![]() $\|\cdot \|_{L^2(X|Y)}$
induces a probabilistic metric on
$\|\cdot \|_{L^2(X|Y)}$
induces a probabilistic metric on
![]() $\mathtt {L^2(X|Y)}$
by
$\mathtt {L^2(X|Y)}$
by
Similarly, we define
![]() $\langle \cdot ,\cdot \rangle _{\mathtt {HS(X|Y)}}$
,
$\langle \cdot ,\cdot \rangle _{\mathtt {HS(X|Y)}}$
,
![]() $\|\cdot \|_{\mathtt {HS}(X|Y)}$
, and
$\|\cdot \|_{\mathtt {HS}(X|Y)}$
, and
![]() $\mathtt {d}_{\mathtt {HS(X|Y)}}$
.
$\mathtt {d}_{\mathtt {HS(X|Y)}}$
.
We verify some basic properties.
Proposition 3.4.
-
(i) The conditional inner product
 $\langle \cdot ,\cdot \rangle _{L^2(X|Y)}$
satisfies the following properties.
$\langle \cdot ,\cdot \rangle _{L^2(X|Y)}$
satisfies the following properties.-
(a) For all Y-partitions
 $\mathcal {P},\mathcal {P}'$
and families
$\mathcal {P},\mathcal {P}'$
and families
 $(f_E)_{E\in \mathcal {P}},(f_{E'})_{E'\in \mathcal {P}'}$
in
$(f_E)_{E\in \mathcal {P}},(f_{E'})_{E'\in \mathcal {P}'}$
in
 $\mathtt {L^2(X|Y)}$
, we have where
$\mathtt {L^2(X|Y)}$
, we have where $$ \begin{align*}\bigg\langle \sum_{E\in \mathcal{P}}f_E 1_E,\sum_{E'\in \mathcal{P}'}f_{E'}1_{E'}\bigg\rangle_{L^2(X|Y)}=\sum_{E\cap E'\in \mathcal{P}\cap \mathcal{P}'}\langle f_E,f_{E'}\rangle_{L^2(X|Y)}1_{E\cap E'},\end{align*} $$
$$ \begin{align*}\bigg\langle \sum_{E\in \mathcal{P}}f_E 1_E,\sum_{E'\in \mathcal{P}'}f_{E'}1_{E'}\bigg\rangle_{L^2(X|Y)}=\sum_{E\cap E'\in \mathcal{P}\cap \mathcal{P}'}\langle f_E,f_{E'}\rangle_{L^2(X|Y)}1_{E\cap E'},\end{align*} $$
 $\mathcal {P}\cap \mathcal {P}':= \{E\cap E'\colon E\in \mathcal {P}, \ E'\in \mathcal {P}'\}$
.
$\mathcal {P}\cap \mathcal {P}':= \{E\cap E'\colon E\in \mathcal {P}, \ E'\in \mathcal {P}'\}$
.
-
(b) For all
 $f,g\in \mathtt {L^2(X|Y)}$
, it holds that
$f,g\in \mathtt {L^2(X|Y)}$
, it holds that
 $\langle f,g\rangle _{L^2(X|Y)} = \overline {\langle g,f\rangle _{L^2(X|Y)}}$
.
$\langle f,g\rangle _{L^2(X|Y)} = \overline {\langle g,f\rangle _{L^2(X|Y)}}$
. -
(c) For all
 $f,g,h\in \mathtt {L^2(X|Y)}$
and
$f,g,h\in \mathtt {L^2(X|Y)}$
and
 $a\in L^0(Y)$
, it holds that
$a\in L^0(Y)$
, it holds that  $$ \begin{align*}\langle a f + g,h\rangle_{L^2(X|Y)}=a \langle f,h\rangle_{L^2(X|Y)} + \langle g,h\rangle_{L^2(X|Y)}.\end{align*} $$
$$ \begin{align*}\langle a f + g,h\rangle_{L^2(X|Y)}=a \langle f,h\rangle_{L^2(X|Y)} + \langle g,h\rangle_{L^2(X|Y)}.\end{align*} $$
-
(d) For all
 $f\in \mathtt {L^2(X|Y)}$
, it holds that
$f\in \mathtt {L^2(X|Y)}$
, it holds that
 $\langle f,f\rangle _{L^2(X|Y)}\geq 0$
.
$\langle f,f\rangle _{L^2(X|Y)}\geq 0$
.
Similarly, for
 $\langle \cdot ,\cdot \rangle _{\mathtt {HS(X|Y)}}$
.
$\langle \cdot ,\cdot \rangle _{\mathtt {HS(X|Y)}}$
. -
-
(ii) The conditional norm
 $\|\cdot \|_{L^2(X|Y)}$
satisfies the following properties.
$\|\cdot \|_{L^2(X|Y)}$
satisfies the following properties.-
(a) For all Y-partitions and families
 $(f_E)_{E\in \mathcal {P}}$
in
$(f_E)_{E\in \mathcal {P}}$
in
 $\mathtt {L^2(X|Y)}$
, we have
$\mathtt {L^2(X|Y)}$
, we have  $$ \begin{align*} \bigg\|\sum_{E\in\mathcal{P}} f_E1_E\bigg\|_{L^2(X|Y)}=\sum_{E\in\mathcal{P}} \|f_E\|_{L^2(X|Y)}1_E. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{E\in\mathcal{P}} f_E1_E\bigg\|_{L^2(X|Y)}=\sum_{E\in\mathcal{P}} \|f_E\|_{L^2(X|Y)}1_E. \end{align*} $$
-
(b)
 $\|f\|_{L^2(X|Y)}=0$
if and only if
$\|f\|_{L^2(X|Y)}=0$
if and only if
 $f=0$
.
$f=0$
. -
(c) For every
 $a\in L^0(Y)$
and
$a\in L^0(Y)$
and
 $f\in \mathtt {L^2(X|Y)}$
, we have
$f\in \mathtt {L^2(X|Y)}$
, we have
 $\|af\|_{L^2(X|Y)}=|a|\|f\|_{L^2(X|Y)}$
.
$\|af\|_{L^2(X|Y)}=|a|\|f\|_{L^2(X|Y)}$
. -
(d) For all
 $f,g\in \mathtt {L^2(X|Y)}$
, we have
$f,g\in \mathtt {L^2(X|Y)}$
, we have
 $\|f+g\|_{L^2(X|Y)} \leq \|f\|_{L^2(X|Y)}+\|g\|_{L^2(X|Y)}$
.
$\|f+g\|_{L^2(X|Y)} \leq \|f\|_{L^2(X|Y)}+\|g\|_{L^2(X|Y)}$
.
Similarly, for
 $\|\cdot \|_{\mathtt {HS}(X|Y)}$
.
$\|\cdot \|_{\mathtt {HS}(X|Y)}$
. -
-
(iii) (Conditional Cauchy–Schwarz inequality) For all
 $f,g\in \mathtt {L^2(X|Y)}$
, it holds that (7)Similarly, for
$f,g\in \mathtt {L^2(X|Y)}$
, it holds that (7)Similarly, for $$ \begin{align} |\langle f,g\rangle_{L^2(X|Y)}|\leq \|f\|_{L^2(X|Y)} \|g\|_{L^2(X|Y)}. \end{align} $$
$$ \begin{align} |\langle f,g\rangle_{L^2(X|Y)}|\leq \|f\|_{L^2(X|Y)} \|g\|_{L^2(X|Y)}. \end{align} $$
 $\mathtt {HS(X|Y)}$
.
$\mathtt {HS(X|Y)}$
.
-
(iv) The space
where $$ \begin{align*} \mathcal{D}=\bigg\{\sum_{i=1}^n c_i f_i\otimes g_i{\colon\kern-2pt}n\in \mathbb{N}, c_i\in \mathbb{C}, f_i,g_i\in \mathtt{L^2(X|Y)}\bigg\}, \end{align*} $$
$$ \begin{align*} \mathcal{D}=\bigg\{\sum_{i=1}^n c_i f_i\otimes g_i{\colon\kern-2pt}n\in \mathbb{N}, c_i\in \mathbb{C}, f_i,g_i\in \mathtt{L^2(X|Y)}\bigg\}, \end{align*} $$
 $f\otimes g(x,x'):= f(x)g(x')$
, is dense in
$f\otimes g(x,x'):= f(x)g(x')$
, is dense in
 $\mathtt {HS(X|Y)}$
with respect to the metric
$\mathtt {HS(X|Y)}$
with respect to the metric
 $\mathtt {d}_{\mathtt {HS(X|Y)}}$
.
$\mathtt {d}_{\mathtt {HS(X|Y)}}$
.
-
(v) For any
 $K\in \mathtt {HS(X|Y)}$
and
$K\in \mathtt {HS(X|Y)}$
and
 $f\in \mathtt {L^2(X|Y)}$
, define The mapping
$f\in \mathtt {L^2(X|Y)}$
, define The mapping $$ \begin{align*} K\ast_Y f(x):= \langle K(x,\cdot),\bar{f}\rangle_{L^2(X|Y)}(\tilde{\pi}(x)). \end{align*} $$
$$ \begin{align*} K\ast_Y f(x):= \langle K(x,\cdot),\bar{f}\rangle_{L^2(X|Y)}(\tilde{\pi}(x)). \end{align*} $$
 $f\mapsto K\ast _Y f$
is well defined from
$f\mapsto K\ast _Y f$
is well defined from
 $\mathtt {L^2(X|Y)}$
to
$\mathtt {L^2(X|Y)}$
to
 $\mathtt {L^2(X|Y)}$
. Moreover, it holds (8)for all
$\mathtt {L^2(X|Y)}$
. Moreover, it holds (8)for all $$ \begin{align} \|K\ast_Y f\|_{L^2(X|Y)}\leq \|K\|_{\mathtt{HS}(X|Y)} \|f\|_{L^2(X|Y)} \end{align} $$
$$ \begin{align} \|K\ast_Y f\|_{L^2(X|Y)}\leq \|K\|_{\mathtt{HS}(X|Y)} \|f\|_{L^2(X|Y)} \end{align} $$
 $K\in \mathtt {HS(X|Y)}$
and
$K\in \mathtt {HS(X|Y)}$
and
 $f\in \mathtt {L^2(X|Y)}$
. In particular,
$f\in \mathtt {L^2(X|Y)}$
. In particular,
 $f\mapsto K\ast _Y f$
from
$f\mapsto K\ast _Y f$
from
 $\mathtt {L^2(X|Y)}$
to
$\mathtt {L^2(X|Y)}$
to
 $\mathtt {L^2(X|Y)}$
is continuous with respect to the metric
$\mathtt {L^2(X|Y)}$
is continuous with respect to the metric
 $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
-
(vi) Convergence with respect to
 $L^2$
-metric is equivalent to convergence with respect to the metric
$L^2$
-metric is equivalent to convergence with respect to the metric
 $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
on
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
on
 $L^2(X)$
. Similarly for
$L^2(X)$
. Similarly for
 $\mathtt {d}_{\mathtt {HS(X|Y)}}$
on
$\mathtt {d}_{\mathtt {HS(X|Y)}}$
on
 $L^2(X\times _YX)$
.
$L^2(X\times _YX)$
. -
(vii) The space
 $L^\infty (X)$
(respectively
$L^\infty (X)$
(respectively
 $L^\infty (X\times _Y X)$
) is dense in
$L^\infty (X\times _Y X)$
) is dense in
 $\mathtt {L^2(X|Y)}$
(respectively
$\mathtt {L^2(X|Y)}$
(respectively
 $\mathtt {HS(X|Y)}$
) with respect to the topology induced by the metric
$\mathtt {HS(X|Y)}$
) with respect to the topology induced by the metric
 $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
(respectively
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
(respectively
 $\mathtt {d}_{\mathtt {HS(X|Y)}}$
).
$\mathtt {d}_{\mathtt {HS(X|Y)}}$
).
Proof. The assertions in (i) and (ii) follow by standard properties of conditional expectations.
As for (iii), we follow the proof of the classical Cauchy–Schwarz inequality with some necessary modifications. First suppose that
![]() $f,g\in \mathtt {L^2(X|Y)}$
satisfy
$f,g\in \mathtt {L^2(X|Y)}$
satisfy
![]() $\|f\|_{L^2(X|Y)}, \|g\|_{L^2(X|Y)},\|f-ag\|_{L^2(X|Y)}>0$
for all
$\|f\|_{L^2(X|Y)}, \|g\|_{L^2(X|Y)},\|f-ag\|_{L^2(X|Y)}>0$
for all
![]() $a\in L^0(Y)$
. Then we have
$a\in L^0(Y)$
. Then we have
for all
![]() $a\in L^0(Y)$
. Setting
$a\in L^0(Y)$
. Setting
 $$ \begin{align*}a=\frac{|\langle f,g\rangle_{L^2(X|Y)}|^2}{\|f'\|_{L^2(X|Y)}^2\langle f,f'\rangle_{L^2(X|Y)}}\end{align*} $$
$$ \begin{align*}a=\frac{|\langle f,g\rangle_{L^2(X|Y)}|^2}{\|f'\|_{L^2(X|Y)}^2\langle f,f'\rangle_{L^2(X|Y)}}\end{align*} $$
and after some elementary algebraic manipulations, we obtain equation (7) in this case.
Second suppose that
![]() $f,g\in \mathtt {L^2(X|Y)}$
satisfy only
$f,g\in \mathtt {L^2(X|Y)}$
satisfy only
![]() $\|f\|_{L^2(X|Y)},\|g\|_{L^2(X|Y)}>0$
. Let
$\|f\|_{L^2(X|Y)},\|g\|_{L^2(X|Y)}>0$
. Let
By completeness of Y (see Remark 2.2), there exists a least upper bound
![]() $E_{\max }$
for
$E_{\max }$
for
![]() $\mathcal {E}$
(with respect to almost sure inclusion). By the countable chain condition, there is
$\mathcal {E}$
(with respect to almost sure inclusion). By the countable chain condition, there is
![]() $\mathcal {E}'\subset \mathcal {E}$
countable such that
$\mathcal {E}'\subset \mathcal {E}$
countable such that
![]() $E_{\max }=\bigcup \mathcal {E}'$
. We can assume that
$E_{\max }=\bigcup \mathcal {E}'$
. We can assume that
![]() $\mathcal {E}'$
is a Y-partition of
$\mathcal {E}'$
is a Y-partition of
![]() $E_{\max }$
. Choose
$E_{\max }$
. Choose
![]() $a\in L^0(Y)$
such that
$a\in L^0(Y)$
such that
![]() $a=a_E$
on E with
$a=a_E$
on E with
![]() $a_E$
such that
$a_E$
such that
![]() $f=a_E g$
for all
$f=a_E g$
for all
![]() $E\in \mathcal {E}'$
. Then
$E\in \mathcal {E}'$
. Then
![]() $f=ag$
on
$f=ag$
on
![]() $E_{\max }$
. It holds that
$E_{\max }$
. It holds that
![]() $\|f\|_{L^2(X|Y)},\|g\|_{L^2(X|Y)},\|f-ag\|_{L^2(X|Y)}>0$
on
$\|f\|_{L^2(X|Y)},\|g\|_{L^2(X|Y)},\|f-ag\|_{L^2(X|Y)}>0$
on
![]() $E_{\max }^c$
for all
$E_{\max }^c$
for all
![]() $a\in L^0(Y)$
. Thus, equation (7) is satisfied on
$a\in L^0(Y)$
. Thus, equation (7) is satisfied on
![]() $E_{\max }^c$
by repeating the first step on
$E_{\max }^c$
by repeating the first step on
![]() $E_{\max }^c$
. Since equation (7) is also trivially satisfied on
$E_{\max }^c$
. Since equation (7) is also trivially satisfied on
![]() $E_{\max }$
, we obtain equation (7) also in this case.
$E_{\max }$
, we obtain equation (7) also in this case.
Finally, suppose that
![]() $\|f\|_{L^2(X|Y)}$
or
$\|f\|_{L^2(X|Y)}$
or
![]() $\|g\|_{L^2(X|Y)}$
are equal to
$\|g\|_{L^2(X|Y)}$
are equal to
![]() $0$
on a set of positive measure. Let
$0$
on a set of positive measure. Let
![]() $E=\{\|f\|_{L^2(X|Y)}=0\}\cup \{ \|g\|_{L^2(X|Y)}=0\}$
. Then equation (7) is satisfied on
$E=\{\|f\|_{L^2(X|Y)}=0\}\cup \{ \|g\|_{L^2(X|Y)}=0\}$
. Then equation (7) is satisfied on
![]() $E^c$
by repeating the second step on
$E^c$
by repeating the second step on
![]() $E^c$
. Since equation (7) is also trivially satisfied on E, we obtain equation (7) also in this case, and this completes the proof of (iii).
$E^c$
. Since equation (7) is also trivially satisfied on E, we obtain equation (7) also in this case, and this completes the proof of (iii).
It is enough to prove (iv) for
![]() $K\in \mathtt {HS(X|Y)}$
with
$K\in \mathtt {HS(X|Y)}$
with
![]() $K\geq 0$
. By the Stone–Weierstraß theorem, the algebra of finite disjoint unions of rectangles
$K\geq 0$
. By the Stone–Weierstraß theorem, the algebra of finite disjoint unions of rectangles
![]() $E\times F$
with
$E\times F$
with
![]() $E,F\in \mathcal {B}a(\tilde {X})$
generates
$E,F\in \mathcal {B}a(\tilde {X})$
generates
![]() $\mathcal {B}a(\tilde {X}\times \tilde {X})$
. Hence there is a sequence
$\mathcal {B}a(\tilde {X}\times \tilde {X})$
. Hence there is a sequence
![]() $(K_n)$
in
$(K_n)$
in
![]() $\mathcal {D}$
such that
$\mathcal {D}$
such that
![]() $K_n\uparrow K \tilde \mu \times _{\tilde Y}\tilde \mu $
-almost surely as
$K_n\uparrow K \tilde \mu \times _{\tilde Y}\tilde \mu $
-almost surely as
![]() $n\to \infty $
. By monotone convergence,
$n\to \infty $
. By monotone convergence,
![]() $\|K_n- K\|_{\mathtt {HS}(X|Y)}\to 0\ \tilde \nu $
-almost surely. Hence
$\|K_n- K\|_{\mathtt {HS}(X|Y)}\to 0\ \tilde \nu $
-almost surely. Hence
![]() $\|K_n-K\|_{\mathtt {HS}(X|Y)}\to 0$
in convergence in
$\|K_n-K\|_{\mathtt {HS}(X|Y)}\to 0$
in convergence in
![]() $\tilde \nu $
-measure, and this proves (iv).
$\tilde \nu $
-measure, and this proves (iv).
As for (v), let
![]() $K\in \mathtt {HS(X|Y)}$
and
$K\in \mathtt {HS(X|Y)}$
and
![]() $f\in \mathtt {L^2(X|Y)}$
. By the conditional Cauchy–Schwarz inequality and the Fubini–Tonelli theorem, one obtains
$f\in \mathtt {L^2(X|Y)}$
. By the conditional Cauchy–Schwarz inequality and the Fubini–Tonelli theorem, one obtains
 $$ \begin{align*} \int_{\tilde{X}}| K\ast_Y f |^2(x) \,d\mu_y(x) &= \int_{\tilde{X}}|\langle K(x,\cdot),\bar{f}\rangle_{L^2(X|Y)}(\tilde{\pi}(x)) |^2 \,d\mu_y(x) \\ &\leq \|f\|_{L^2(X|Y)}^2\int_{\tilde{X}} \|K(x,\cdot)\|_{L^2(X|Y)}^2(\tilde{\pi}(x)) \,d\mu_y(x) \\ &=\|K\|_{\mathtt{HS}(X|Y)}^2 \|f\|_{L^2(X|Y)}^2 <\infty. \end{align*} $$
$$ \begin{align*} \int_{\tilde{X}}| K\ast_Y f |^2(x) \,d\mu_y(x) &= \int_{\tilde{X}}|\langle K(x,\cdot),\bar{f}\rangle_{L^2(X|Y)}(\tilde{\pi}(x)) |^2 \,d\mu_y(x) \\ &\leq \|f\|_{L^2(X|Y)}^2\int_{\tilde{X}} \|K(x,\cdot)\|_{L^2(X|Y)}^2(\tilde{\pi}(x)) \,d\mu_y(x) \\ &=\|K\|_{\mathtt{HS}(X|Y)}^2 \|f\|_{L^2(X|Y)}^2 <\infty. \end{align*} $$
This shows that
![]() $K\ast _Y f\in \mathtt {L^2(X|Y)}$
, equation (8), and continuity.
$K\ast _Y f\in \mathtt {L^2(X|Y)}$
, equation (8), and continuity.
As for (vi), we only prove the claim for
![]() $\mathtt {L^2(X|Y)}$
(the arguments for
$\mathtt {L^2(X|Y)}$
(the arguments for
![]() $\mathtt {HS(X|Y)}$
are identical). For
$\mathtt {HS(X|Y)}$
are identical). For
![]() $f\in L^2(X)$
, it holds
$f\in L^2(X)$
, it holds
In particular, we have
The assertion follows from the fact that convergence in
![]() $L^2$
is equivalent to convergence in measure.
$L^2$
is equivalent to convergence in measure.
Finally, as for (vii), let
![]() $f\in \mathtt {L^2(X|Y)}$
. Define
$f\in \mathtt {L^2(X|Y)}$
. Define
![]() $f_m=f 1_{\|f\|_{L^2(X|Y)}\leq m}$
for
$f_m=f 1_{\|f\|_{L^2(X|Y)}\leq m}$
for
![]() $m\geq 1$
. Then
$m\geq 1$
. Then
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}(f,f_m)\to 0$
as
$\mathtt {d}_{\mathtt {L^2(X|Y)}}(f,f_m)\to 0$
as
![]() $m\to \infty $
. By (ii) and equation (9),
$m\to \infty $
. By (ii) and equation (9),
![]() $f_m\in L^2(X)$
. As
$f_m\in L^2(X)$
. As
![]() $L^\infty (X)$
is dense in
$L^\infty (X)$
is dense in
![]() $L^2(X)$
in
$L^2(X)$
in
![]() $L^2$
-topology, we can approximate each
$L^2$
-topology, we can approximate each
![]() $f_m$
by a sequence
$f_m$
by a sequence
![]() $(f_{m,n})$
in
$(f_{m,n})$
in
![]() $L^\infty (X)$
in
$L^\infty (X)$
in
![]() $L^2$
-metric. The claim now follows from equation (9), (vi), and triangle inequality.
$L^2$
-metric. The claim now follows from equation (9), (vi), and triangle inequality.
Remark 3.5. Let
![]() $\mathtt {Sh}(Y)$
be the Grothendieck topos of sheaves on the site
$\mathtt {Sh}(Y)$
be the Grothendieck topos of sheaves on the site
![]() $(Y,J)$
, where J is the Grothendieck sup-topology on the complete Boolean algebra Y. We refer the interested reader to [Reference MacLane and Moerdijk38] for an introduction to Grothendieck sheaf topoi. By the countable chain condition (see Remark 2.2), a Grothendieck basis of the sup-topology J is given by the sets of countable partitions of elements of Y. Since the spaces
$(Y,J)$
, where J is the Grothendieck sup-topology on the complete Boolean algebra Y. We refer the interested reader to [Reference MacLane and Moerdijk38] for an introduction to Grothendieck sheaf topoi. By the countable chain condition (see Remark 2.2), a Grothendieck basis of the sup-topology J is given by the sets of countable partitions of elements of Y. Since the spaces
![]() $L^0(Y), \mathtt {L^2(X|Y)}, \mathtt {HS(X|Y)}$
are closed under countable Y-concatenations, they can be given the structure of a sheaf on the site
$L^0(Y), \mathtt {L^2(X|Y)}, \mathtt {HS(X|Y)}$
are closed under countable Y-concatenations, they can be given the structure of a sheaf on the site
![]() $(Y,J)$
. Since Y is a complete Boolean algebra, the topos
$(Y,J)$
. Since Y is a complete Boolean algebra, the topos
![]() $\mathtt {Sh}(Y)$
is Boolean and satisfies the axiom of choice. Thus its internal logic is strong enough to permit an internal mathematical discourse sufficient for the bulk of classical mathematics, see [Reference MacLane and Moerdijk38, Ch. IV]. In particular, we can interpret the external space
$\mathtt {Sh}(Y)$
is Boolean and satisfies the axiom of choice. Thus its internal logic is strong enough to permit an internal mathematical discourse sufficient for the bulk of classical mathematics, see [Reference MacLane and Moerdijk38, Ch. IV]. In particular, we can interpret the external space
![]() $L^0(Y)$
as the internal complex numbers of
$L^0(Y)$
as the internal complex numbers of
![]() $\mathtt {Sh}(Y)$
. Now Proposition 3.4 shows that the external space
$\mathtt {Sh}(Y)$
. Now Proposition 3.4 shows that the external space
![]() $\mathtt {L^2(X|Y)}$
can be interpreted as an internal complex Hilbert space, and the external space
$\mathtt {L^2(X|Y)}$
can be interpreted as an internal complex Hilbert space, and the external space
![]() $\mathtt {HS(X|Y)}$
as its internal Hilbert space tensor product whose elements represent the internal Hilbert–Schmidt operators. Externally,
$\mathtt {HS(X|Y)}$
as its internal Hilbert space tensor product whose elements represent the internal Hilbert–Schmidt operators. Externally,
![]() $L^0(Y)$
is a commutative ring and
$L^0(Y)$
is a commutative ring and
![]() $\mathtt {L^2(X|Y)}$
and
$\mathtt {L^2(X|Y)}$
and
![]() $\mathtt {HS(X|Y)}$
are topological modules over
$\mathtt {HS(X|Y)}$
are topological modules over
![]() $L^0(Y)$
(given the topology induced by
$L^0(Y)$
(given the topology induced by
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
,
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
,
![]() $\mathtt {d}_{\mathtt {HS(X|Y)}}$
, and convergence in probability).
$\mathtt {d}_{\mathtt {HS(X|Y)}}$
, and convergence in probability).
The conditional analysis of this section is an external interpretation and significant simplification of some results in the internal Hilbert space theory of
![]() $\mathtt {Sh}(Y)$
. For example, Proposition 3.4(iv) and (v) essentially describe the
$\mathtt {Sh}(Y)$
. For example, Proposition 3.4(iv) and (v) essentially describe the
![]() $\mathtt {Sh}(Y)$
-spectral theorem of
$\mathtt {Sh}(Y)$
-spectral theorem of
![]() $\mathtt {Sh}(Y)$
-Hilbert–Schmidt operators. This interpretation is enabled by conditional set theory (the connection of conditional set theory to Boolean Grothendieck topoi is established in [Reference Jamneshan27], see also [Reference Carl and Jamneshan5] for a relation to the akin theory of Boolean-valued models) and conditional analysis as developed in [Reference Cheridito, Kupper and Vogelpoth6, Reference Drapeau, Jamneshan, Karliczek and Kupper9, Reference Filipović, Kupper and Vogelpoth15], which, initially, were developed independently of topos theory and can be viewed in retrospect as an exploration of the semantics of the internal discourse of Boolean Grothendieck topoi.
$\mathtt {Sh}(Y)$
-Hilbert–Schmidt operators. This interpretation is enabled by conditional set theory (the connection of conditional set theory to Boolean Grothendieck topoi is established in [Reference Jamneshan27], see also [Reference Carl and Jamneshan5] for a relation to the akin theory of Boolean-valued models) and conditional analysis as developed in [Reference Cheridito, Kupper and Vogelpoth6, Reference Drapeau, Jamneshan, Karliczek and Kupper9, Reference Filipović, Kupper and Vogelpoth15], which, initially, were developed independently of topos theory and can be viewed in retrospect as an exploration of the semantics of the internal discourse of Boolean Grothendieck topoi.
We continue to develop some basic conditional analysis of the conditional Hilbert space
![]() $\mathtt {L^2(X|Y)}$
.
$\mathtt {L^2(X|Y)}$
.
Definition 3.6. An
![]() $L^0(Y)$
-linear combination in
$L^0(Y)$
-linear combination in
![]() $\mathtt {L^2(X|Y)}$
is an expression of the form
$\mathtt {L^2(X|Y)}$
is an expression of the form
![]() $\sum _{f\in \mathcal {F}} a_f f$
for some finite set
$\sum _{f\in \mathcal {F}} a_f f$
for some finite set
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathtt {L^2(X|Y)}$
and
$\mathtt {L^2(X|Y)}$
and
![]() $a_f\in L^0(Y), f\in \mathcal {F}$
. A subset
$a_f\in L^0(Y), f\in \mathcal {F}$
. A subset
![]() $\mathcal {M}\subset \mathtt {L^2(X|Y)}$
is called a finitely generated
$\mathcal {M}\subset \mathtt {L^2(X|Y)}$
is called a finitely generated
![]() $L^0(Y)$
-submodule if there is a finite collection
$L^0(Y)$
-submodule if there is a finite collection
![]() $\mathcal {F}$
in
$\mathcal {F}$
in
![]() $\mathtt {L^2(X|Y)}$
such that each
$\mathtt {L^2(X|Y)}$
such that each
![]() $f\in \mathcal {M}$
can be expressed as
$f\in \mathcal {M}$
can be expressed as
![]() $\sum _{f\in \mathcal {F}} a_f f$
for some
$\sum _{f\in \mathcal {F}} a_f f$
for some
![]() $(a_f)_{f\in \mathcal {F}}$
in
$(a_f)_{f\in \mathcal {F}}$
in
![]() $L^0(Y)$
.
$L^0(Y)$
.
Proposition 3.7. (Conditional Gram–Schmidt process)
Let
![]() $\mathcal {M}$
be a finitely generated
$\mathcal {M}$
be a finitely generated
![]() $L^0(Y)$
-submodule of
$L^0(Y)$
-submodule of
![]() $\mathtt {L^2(X|Y)}$
. Then there is a finite Y-partition
$\mathtt {L^2(X|Y)}$
. Then there is a finite Y-partition
![]() $\mathcal {P}$
and for each
$\mathcal {P}$
and for each
![]() $E\in \mathcal {P}$
, there is a finite set
$E\in \mathcal {P}$
, there is a finite set
![]() $\mathcal {F}_E$
in
$\mathcal {F}_E$
in
![]() $\mathtt {L^2(X|Y)}$
satisfying the following properties.
$\mathtt {L^2(X|Y)}$
satisfying the following properties.
-
(i) There is
 $E_0\in \mathcal {P}$
such that
$E_0\in \mathcal {P}$
such that
 $\mathcal {F}_{E_0}=\{0\}$
.
$\mathcal {F}_{E_0}=\{0\}$
. -
(ii)
 $\|f\|_{L^2(X|Y)}=1$
on E for all
$\|f\|_{L^2(X|Y)}=1$
on E for all
 $f\in \mathcal {F}_E$
and
$f\in \mathcal {F}_E$
and
 $E\in \mathcal {P}\backslash \{E_0\}$
.
$E\in \mathcal {P}\backslash \{E_0\}$
. -
(iii)
 $\langle f,g\rangle _{L^2(X|Y)}=0$
on E for all distinct
$\langle f,g\rangle _{L^2(X|Y)}=0$
on E for all distinct
 $f,g\in \mathcal {F}_E$
and
$f,g\in \mathcal {F}_E$
and
 $E\in \mathcal {P}$
.
$E\in \mathcal {P}$
. -
(iv) It holds that
 $$ \begin{align*}\mathcal{M}&=\bigg\{\sum_{E\in\mathcal{P}} f_E 1_E \colon\text{for all } E\in\mathcal{P} \text{ there exists } (a^E_f)_{f\in\mathcal{F}_E}\\ &\quad\subset L^0(Y) \text{ such that } f_E=\sum_{f\in \mathcal{F}_E} a^E_f f\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal{M}&=\bigg\{\sum_{E\in\mathcal{P}} f_E 1_E \colon\text{for all } E\in\mathcal{P} \text{ there exists } (a^E_f)_{f\in\mathcal{F}_E}\\ &\quad\subset L^0(Y) \text{ such that } f_E=\sum_{f\in \mathcal{F}_E} a^E_f f\bigg\}.\end{align*} $$
We call
![]() $\mathtt {cdim}(\mathcal {M})=\sum _{E\in \mathcal {P}} \#(\mathcal {F}_E)|E$
the conditional dimension of
$\mathtt {cdim}(\mathcal {M})=\sum _{E\in \mathcal {P}} \#(\mathcal {F}_E)|E$
the conditional dimension of
![]() $\mathcal {M}$
, where
$\mathcal {M}$
, where
![]() $\#$
denotes cardinality (note that
$\#$
denotes cardinality (note that
![]() $\mathtt {cdim}(\mathcal {M})$
is a
$\mathtt {cdim}(\mathcal {M})$
is a
![]() $\mathcal {B}a(\tilde {Y})$
-measurable random variable).
$\mathcal {B}a(\tilde {Y})$
-measurable random variable).
Proof. Let
![]() $f_1,\ldots ,f_n\in \mathtt {L^2(X|Y)}$
be a collection of generators of
$f_1,\ldots ,f_n\in \mathtt {L^2(X|Y)}$
be a collection of generators of
![]() $\mathcal {M}$
. Define
$\mathcal {M}$
. Define
 $$ \begin{align*}h_1=\frac{f_1}{\|f_1\|_{L^2(X|Y)}} 1_{\|f_1\|_{L^2(X|Y)}>0}.\end{align*} $$
$$ \begin{align*}h_1=\frac{f_1}{\|f_1\|_{L^2(X|Y)}} 1_{\|f_1\|_{L^2(X|Y)}>0}.\end{align*} $$
Next suppose we defined
![]() $h_1,\ldots ,h_k$
with
$h_1,\ldots ,h_k$
with
![]() $k\leq n-1$
. Set
$k\leq n-1$
. Set
 $$ \begin{align*}g_{k+1}=f_{k+1}-\sum_{i=1}^k \langle f_{k+1},h_i\rangle_{L^2(X|Y)} h_i\end{align*} $$
$$ \begin{align*}g_{k+1}=f_{k+1}-\sum_{i=1}^k \langle f_{k+1},h_i\rangle_{L^2(X|Y)} h_i\end{align*} $$
and define
Denote by
![]() $F_i=\{ \|g_{i}\|_{L^2(X|Y)}>0\}$
and
$F_i=\{ \|g_{i}\|_{L^2(X|Y)}>0\}$
and
![]() $F_{i+n}=F_i^c$
for all
$F_{i+n}=F_i^c$
for all
![]() $i=1,\ldots , n$
. Form all finite intersections
$i=1,\ldots , n$
. Form all finite intersections
![]() $F_{i_1}\cap F_{i_2}\cap \cdots \cap F_{i_k}$
with
$F_{i_1}\cap F_{i_2}\cap \cdots \cap F_{i_k}$
with
![]() $1\kern-1pt\leq i_1\kern-1pt<i_2<\cdots <i_k\kern-1pt\leq 2n$
for some
$1\kern-1pt\leq i_1\kern-1pt<i_2<\cdots <i_k\kern-1pt\leq 2n$
for some
![]() $1\kern-1pt\leq k\kern-1pt\leq 2n$
. Let
$1\kern-1pt\leq k\kern-1pt\leq 2n$
. Let
![]() $\mathcal {P}_0$
denote the set of all such finite intersections whose measure is positive. Then
$\mathcal {P}_0$
denote the set of all such finite intersections whose measure is positive. Then
![]() $\mathcal {P}_0$
forms a Y-partition. For
$\mathcal {P}_0$
forms a Y-partition. For
![]() $E=F_{i_1}\cap F_{i_2}\cap \cdots \cap F_{i_k}\in \mathcal {P}_0$
, let
$E=F_{i_1}\cap F_{i_2}\cap \cdots \cap F_{i_k}\in \mathcal {P}_0$
, let
![]() $\mathcal {F}_{E}=\{h_{i_j}: i_j\leq n, j=1,\ldots ,k\}$
. Let
$\mathcal {F}_{E}=\{h_{i_j}: i_j\leq n, j=1,\ldots ,k\}$
. Let
![]() $\mathcal {P}$
consist of those
$\mathcal {P}$
consist of those
![]() $E\in \mathcal {P}_0$
such that
$E\in \mathcal {P}_0$
such that
![]() $\mathcal {F}_E$
is not empty. Set
$\mathcal {F}_E$
is not empty. Set
![]() $E_0=(\bigcup _{E\in \mathcal {P}} E)^c$
. By construction,
$E_0=(\bigcup _{E\in \mathcal {P}} E)^c$
. By construction,
![]() $\mathcal {P}$
,
$\mathcal {P}$
,
![]() $(\mathcal {F}_E)_{E\in \mathcal {P}}$
, and
$(\mathcal {F}_E)_{E\in \mathcal {P}}$
, and
![]() $E_0$
satisfy properties (i)–(iv).
$E_0$
satisfy properties (i)–(iv).
Lemma 3.8. Let
![]() $\mathcal {M}$
be a finitely generated
$\mathcal {M}$
be a finitely generated
![]() $L^0(Y)$
-submodule of
$L^0(Y)$
-submodule of
![]() $\mathtt {L^2(X|Y)}$
. Then
$\mathtt {L^2(X|Y)}$
. Then
![]() $\mathcal {M}$
is closed with respect to the metric
$\mathcal {M}$
is closed with respect to the metric
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
Proof. Let
![]() $\mathcal {P}$
and
$\mathcal {P}$
and
![]() $(\mathcal {F}_E)_{E\in \mathcal {P}}$
satisfy properties (i)–(iv) in Lemma 3.7 for
$(\mathcal {F}_E)_{E\in \mathcal {P}}$
satisfy properties (i)–(iv) in Lemma 3.7 for
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $(f_n)$
be a sequence in
$(f_n)$
be a sequence in
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}(f_n,f)\to 0$
as
$\mathtt {d}_{\mathtt {L^2(X|Y)}}(f_n,f)\to 0$
as
![]() $n\to \infty $
for some
$n\to \infty $
for some
![]() $f\in \mathtt {L^2(X|Y)}$
. Each
$f\in \mathtt {L^2(X|Y)}$
. Each
![]() $f_n$
is of the form
$f_n$
is of the form
 $$ \begin{align*}f_n=\sum_{E\in \mathcal{P}}\bigg(\sum_{f_E\in \mathcal{F}_E}a_{f_E}^n f_E \bigg)|E\end{align*} $$
$$ \begin{align*}f_n=\sum_{E\in \mathcal{P}}\bigg(\sum_{f_E\in \mathcal{F}_E}a_{f_E}^n f_E \bigg)|E\end{align*} $$
for some
![]() $(a_{f_E}^n)_{f\in \mathcal {F}_E}$
for each
$(a_{f_E}^n)_{f\in \mathcal {F}_E}$
for each
![]() $E\in \mathcal {P}$
. For arbitrary
$E\in \mathcal {P}$
. For arbitrary
![]() $n,m$
, by Proposition 3.4(ii) and Proposition 3.7(ii) and (iii),
$n,m$
, by Proposition 3.4(ii) and Proposition 3.7(ii) and (iii),
 $$ \begin{align} \|f_n-f_m\|_{L^2(X|Y)}=\sum_{E\in \mathcal{P}}\bigg(\sum_{f_E\in \mathcal{F}_E}|a_{f_E}^n-a_{f_E}^m|\bigg)|E. \end{align} $$
$$ \begin{align} \|f_n-f_m\|_{L^2(X|Y)}=\sum_{E\in \mathcal{P}}\bigg(\sum_{f_E\in \mathcal{F}_E}|a_{f_E}^n-a_{f_E}^m|\bigg)|E. \end{align} $$
Since
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}(f_n,f_m)\to 0$
as
$\mathtt {d}_{\mathtt {L^2(X|Y)}}(f_n,f_m)\to 0$
as
![]() $n,m\to \infty $
by hypothesis, the claim follows by applying [Reference Kallenberg35, Lemma 4.6] to (11).
$n,m\to \infty $
by hypothesis, the claim follows by applying [Reference Kallenberg35, Lemma 4.6] to (11).
4 Relatively compact extensions
In this section, we establish various characterizations of relatively compact extensions of
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems which are collected in the following.
${\mathbf {PrbAlg}_\Gamma }$
-systems which are collected in the following.
Theorem 4.1. Let
![]() $\mathcal {X}=(X,\mu ,T)$
and
$\mathcal {X}=(X,\mu ,T)$
and
![]() $\mathcal {Y}= (Y,\nu ,S)$
be
$\mathcal {Y}= (Y,\nu ,S)$
be
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems, and
${\mathbf {PrbAlg}_\Gamma }$
-systems, and
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
be a
$\pi :\mathcal {X}\to \mathcal {Y}$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension. Then the following are equivalent.
${\mathbf {PrbAlg}_\Gamma }$
-extension. Then the following are equivalent.
-
(i) The conditional Hilbert space
 $\mathtt {L^2(X|Y)}$
is the
$\mathtt {L^2(X|Y)}$
is the
 $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
-closure of
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
-closure of  $$ \begin{align*} \{K\ast_Y f:K\in \mathtt{HS(X|Y)}\ \Gamma\text{-invariant, } f\in \mathtt{L^2(X|Y)} \}. \end{align*} $$
$$ \begin{align*} \{K\ast_Y f:K\in \mathtt{HS(X|Y)}\ \Gamma\text{-invariant, } f\in \mathtt{L^2(X|Y)} \}. \end{align*} $$
-
(ii) The conditional Hilbert space
 $\mathtt {L^2(X|Y)}$
is the
$\mathtt {L^2(X|Y)}$
is the
 $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
-closure of the union of all its finitely generated and
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
-closure of the union of all its finitely generated and
 $\Gamma $
-invariant
$\Gamma $
-invariant
 $L^0(Y)$
-submodules.
$L^0(Y)$
-submodules. -
(iii) There exists a dense set
 $\mathcal {G}$
with respect to the metric
$\mathcal {G}$
with respect to the metric
 $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
such that for all
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
such that for all
 $f\in \mathcal {G}$
and every
$f\in \mathcal {G}$
and every
 $\varepsilon>0$
, there is a finite set
$\varepsilon>0$
, there is a finite set
 $\mathcal {F}$
in
$\mathcal {F}$
in
 $\mathtt {L^2(X|Y)}$
such that for all
$\mathtt {L^2(X|Y)}$
such that for all
 $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,  $$ \begin{align*} \min_{g\in\mathcal{F}} \|(T^\gamma)^*f - g\|_{L^2(X|Y)}<\varepsilon. \end{align*} $$
$$ \begin{align*} \min_{g\in\mathcal{F}} \|(T^\gamma)^*f - g\|_{L^2(X|Y)}<\varepsilon. \end{align*} $$
-
(i)′ The classical Hilbert space
 $L^2(X)$
is the
$L^2(X)$
is the
 $L^2$
-closure of
$L^2$
-closure of  $$ \begin{align*} \{K\ast_Y f: K\in L^\infty(X\times_Y X)\ \Gamma\text{-invariant, } f\in L^2(X) \}. \end{align*} $$
$$ \begin{align*} \{K\ast_Y f: K\in L^\infty(X\times_Y X)\ \Gamma\text{-invariant, } f\in L^2(X) \}. \end{align*} $$
-
(ii)′ The classical Hilbert space
 $L^2(X)$
is the
$L^2(X)$
is the
 $L^2$
-closure of the union of all its closed,
$L^2$
-closure of the union of all its closed,
 $\Gamma $
-invariant, and finitely generated
$\Gamma $
-invariant, and finitely generated
 $L^\infty (Y)$
-submodules.
$L^\infty (Y)$
-submodules. -
(iii)′ There exists a dense set
 $\mathcal {H}$
in
$\mathcal {H}$
in
 $L^2(X)$
such that for all
$L^2(X)$
such that for all
 $f\in \mathcal {H}$
and every
$f\in \mathcal {H}$
and every
 $\varepsilon>0$
, there is a finite set
$\varepsilon>0$
, there is a finite set
 $\mathcal {F}$
in
$\mathcal {F}$
in
 $L^2(X)$
such that for all
$L^2(X)$
such that for all
 $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,  $$ \begin{align*} \min_{g\in\mathcal{F}} \|(T^\gamma)^*f - g\|_{L^2(X|Y)}<\varepsilon. \end{align*} $$
$$ \begin{align*} \min_{g\in\mathcal{F}} \|(T^\gamma)^*f - g\|_{L^2(X|Y)}<\varepsilon. \end{align*} $$
A
![]() ${\mathbf {PrbAlg}_\Gamma }$
-morphism
${\mathbf {PrbAlg}_\Gamma }$
-morphism
![]() $\pi $
fulfilling one (and therefore all) of the above six properties is called a relatively compact
$\pi $
fulfilling one (and therefore all) of the above six properties is called a relatively compact
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension.
${\mathbf {PrbAlg}_\Gamma }$
-extension.
Remark 4.2. Property (ii)′ is used by Zimmer in [Reference Zimmer47, Reference Zimmer48] under the name of ‘relatively discrete spectrum’. Ellis [Reference Ellis14] used a variant of property (ii)′ to generalize some parts of Zimmer’s work, see §5. Properties (i)′ and (iii)′ appear in Furstenberg [Reference Furstenberg18, §6]. We prove that (i)′, (ii)′, and (iii)′ are equivalent and relate them to their analogs in the larger conditional Hilbert spaces
![]() $\mathtt {L^2(X|Y)}$
and
$\mathtt {L^2(X|Y)}$
and
![]() $\mathtt {HS(X|Y)}$
. Our proof of Theorem 4.1 combines ideas from the countable theory as in [Reference Furstenberg18, §6] with the conditional analysis developed in §3 and Appendix A.
$\mathtt {HS(X|Y)}$
. Our proof of Theorem 4.1 combines ideas from the countable theory as in [Reference Furstenberg18, §6] with the conditional analysis developed in §3 and Appendix A.
Remark 4.3. Using conditional integration theory as developed in [Reference Jamneshan, Kupper and Streckfuß28] (in particular, a conditional version of the Carathéodory extension theorem and the results in [Reference Jamneshan, Kupper and Streckfuß28, §4]), one can construct, in a slightly tedious process, an internal
![]() $\mathtt {Sh}(Y)$
-system from an external extension
$\mathtt {Sh}(Y)$
-system from an external extension
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
. Then the properties (i)–(iii) in Theorem 4.1 characterizing relatively compact extensions or systems of relative discrete spectrum can be viewed as an external interpretation of characterizations of internal compact systems or internal systems of discrete spectrum.
$\pi :\mathcal {X}\to \mathcal {Y}$
. Then the properties (i)–(iii) in Theorem 4.1 characterizing relatively compact extensions or systems of relative discrete spectrum can be viewed as an external interpretation of characterizations of internal compact systems or internal systems of discrete spectrum.
Lemma 4.4. Assertion (i)′ implies assertion (ii)′ in Theorem 4.1.
Proof. To prove (ii)′ from (i)′, it suffices to show that the union of the closed and finitely generated
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^\infty (Y)$
-submodules of the range of
$L^\infty (Y)$
-submodules of the range of
![]() $K\ast _Y\colon L^2(X)\to L^2(X)$
is dense in the range of
$K\ast _Y\colon L^2(X)\to L^2(X)$
is dense in the range of
![]() $K\ast _Y$
for any
$K\ast _Y$
for any
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $K\in L^\infty (X\times _Y X)$
. (We thank the anonymous referee for pointing out a gap in a previous version of this argument. The current arguments are borrowed from a forthcoming work joint with Pieter Spaas, where we establish a non-commutative analog of several results in (uncountable) Furstenberg–Zimmer structure theory.) By splitting into real and imaginary parts and then further into positive and negative parts, we can assume that
$K\in L^\infty (X\times _Y X)$
. (We thank the anonymous referee for pointing out a gap in a previous version of this argument. The current arguments are borrowed from a forthcoming work joint with Pieter Spaas, where we establish a non-commutative analog of several results in (uncountable) Furstenberg–Zimmer structure theory.) By splitting into real and imaginary parts and then further into positive and negative parts, we can assume that
![]() $K\in L^\infty (X\times _Y X)$
is non-negative. Note that
$K\in L^\infty (X\times _Y X)$
is non-negative. Note that
![]() $K\ast _Y\colon L^2(X)\to L^2(X)$
is then a bounded and positive operator (cf. Lemma A.5) and thus its spectrum is compact and contained in
$K\ast _Y\colon L^2(X)\to L^2(X)$
is then a bounded and positive operator (cf. Lemma A.5) and thus its spectrum is compact and contained in
![]() $[0,+\infty )$
. For
$[0,+\infty )$
. For
![]() $\varepsilon>0$
, consider the spectral projection
$\varepsilon>0$
, consider the spectral projection
![]() $P_\varepsilon := 1_{[\varepsilon , \|K\|_{L^\infty (X\times _YX)}]}(K\ast _Y)$
, where we apply Borel functional calculus to
$P_\varepsilon := 1_{[\varepsilon , \|K\|_{L^\infty (X\times _YX)}]}(K\ast _Y)$
, where we apply Borel functional calculus to
![]() $K\ast _Y$
as an operator from
$K\ast _Y$
as an operator from
![]() $L^2(X)$
to
$L^2(X)$
to
![]() $L^2(X)$
to define
$L^2(X)$
to define
![]() $P_\varepsilon $
. Since
$P_\varepsilon $
. Since
![]() $P_\varepsilon $
arises as a limit of polynomials in
$P_\varepsilon $
arises as a limit of polynomials in
![]() $K\ast _Y$
in the strong operator topology,
$K\ast _Y$
in the strong operator topology,
![]() $P_\varepsilon $
is
$P_\varepsilon $
is
![]() $\Gamma $
-invariant. Thus its range
$\Gamma $
-invariant. Thus its range
![]() $\mathcal {H}_\varepsilon := P_\varepsilon (L^2(X))$
is a
$\mathcal {H}_\varepsilon := P_\varepsilon (L^2(X))$
is a
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $L^2(X)$
(this follows from that
$L^2(X)$
(this follows from that
![]() $L^\infty (Y)$
-linearity is preserved when passing to strong operator limits as well). By standard properties of the Borel functional calculus,
$L^\infty (Y)$
-linearity is preserved when passing to strong operator limits as well). By standard properties of the Borel functional calculus,
![]() $P_\varepsilon \circ K = K\circ P_\varepsilon = K\vert _{\mathcal {H}_\varepsilon } \geq \varepsilon \mathrm {Id}_{\mathcal {H}_\varepsilon }$
(where the inequality is understood in the sense of operators on the Hilbert space
$P_\varepsilon \circ K = K\circ P_\varepsilon = K\vert _{\mathcal {H}_\varepsilon } \geq \varepsilon \mathrm {Id}_{\mathcal {H}_\varepsilon }$
(where the inequality is understood in the sense of operators on the Hilbert space
![]() $\mathcal {H}_\varepsilon $
). Now we can apply Proposition A.6 and obtain that
$\mathcal {H}_\varepsilon $
). Now we can apply Proposition A.6 and obtain that
![]() $\mathcal {H}_\varepsilon $
is necessarily finitely generated as an
$\mathcal {H}_\varepsilon $
is necessarily finitely generated as an
![]() $L^\infty (Y)$
-module. Letting
$L^\infty (Y)$
-module. Letting
![]() $\varepsilon \to 0$
, we get that the increasing union of the finitely generated
$\varepsilon \to 0$
, we get that the increasing union of the finitely generated
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^\infty (Y)$
-submodules of the range of K is dense in the range of K. This concludes the proof of (i)′
$L^\infty (Y)$
-submodules of the range of K is dense in the range of K. This concludes the proof of (i)′
![]() $\Rightarrow $
(ii)′.
$\Rightarrow $
(ii)′.
Remark 4.5. An alternative proof of the implication (i)′
![]() $\Rightarrow $
(ii)′, or better to say of (i)
$\Rightarrow $
(ii)′, or better to say of (i)
![]() $\Rightarrow $
(ii) (from which then (i)′
$\Rightarrow $
(ii) (from which then (i)′
![]() $\Rightarrow $
(ii)′ could be easily deduced), would be to invoke a conditional spectral theorem for the conditional Hilbert–Schmidt operator
$\Rightarrow $
(ii)′ could be easily deduced), would be to invoke a conditional spectral theorem for the conditional Hilbert–Schmidt operator
![]() $K\ast _Y \colon \mathtt {L^2(X|Y)} \to \mathtt {L^2(X|Y)}$
for any
$K\ast _Y \colon \mathtt {L^2(X|Y)} \to \mathtt {L^2(X|Y)}$
for any
![]() $K\in \mathtt {HS(X|Y)}$
. The internal logic of
$K\in \mathtt {HS(X|Y)}$
. The internal logic of
![]() $\mathtt {Sh}(Y)$
admits such a
$\mathtt {Sh}(Y)$
admits such a
![]() $\mathtt {Sh}(Y)$
-spectral theorem, whose proof one could then interpret externally by hand for the conditional Hilbert–Schmidt operator
$\mathtt {Sh}(Y)$
-spectral theorem, whose proof one could then interpret externally by hand for the conditional Hilbert–Schmidt operator
![]() $K\ast _Y \colon \mathtt {L^2(X|Y)} \to \mathtt {L^2(X|Y)}$
(in some sense, this is carried out in a topological setting in [Reference Edeko, Haase and Kreidler11, Part I, §4], see the comments at the end of this part). We can also compare with the relative spectral theorem for measurable Hilbert bundles proved in [Reference Glasner19, Ch. 9, §3] in the countable complexity setting. We manage to avoid using explicitly a relative/conditional spectral theorem by combining Borel functional calculus with a mix of conditional analysis and classical arguments as needed in the proof of Proposition A.6 in Appendix A.
$K\ast _Y \colon \mathtt {L^2(X|Y)} \to \mathtt {L^2(X|Y)}$
(in some sense, this is carried out in a topological setting in [Reference Edeko, Haase and Kreidler11, Part I, §4], see the comments at the end of this part). We can also compare with the relative spectral theorem for measurable Hilbert bundles proved in [Reference Glasner19, Ch. 9, §3] in the countable complexity setting. We manage to avoid using explicitly a relative/conditional spectral theorem by combining Borel functional calculus with a mix of conditional analysis and classical arguments as needed in the proof of Proposition A.6 in Appendix A.
Lemma 4.6. Assertion (ii) implies assertion (iii) in Theorem 4.1.
Proof. Let
![]() $\mathfrak {A}$
be the union of finitely generated and
$\mathfrak {A}$
be the union of finitely generated and
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^0(Y)$
-submodules and let
$L^0(Y)$
-submodules and let
![]() $\mathcal {G}=\{f\in \mathfrak {A}: \text {there exists } M>0 \text {such that} \|f\|_{L^2(X|Y)}< M\}$
. By assumption and Lemma 3.8,
$\mathcal {G}=\{f\in \mathfrak {A}: \text {there exists } M>0 \text {such that} \|f\|_{L^2(X|Y)}< M\}$
. By assumption and Lemma 3.8,
![]() $\mathcal {G}$
is dense in
$\mathcal {G}$
is dense in
![]() $\mathtt {L^2(X|Y)}$
with respect to the metric
$\mathtt {L^2(X|Y)}$
with respect to the metric
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
Fix
![]() $f\in \mathcal {G}$
and
$f\in \mathcal {G}$
and
![]() $\varepsilon>0$
. Then there is a finitely generated and
$\varepsilon>0$
. Then there is a finitely generated and
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^0(Y)$
-submodule
$L^0(Y)$
-submodule
![]() $\mathcal {M}$
such that
$\mathcal {M}$
such that
![]() $f\in \mathcal {M}$
. By Proposition 3.7, there are a finite Y-partition
$f\in \mathcal {M}$
. By Proposition 3.7, there are a finite Y-partition
![]() $\mathcal {P}$
and for each
$\mathcal {P}$
and for each
![]() $E\in \mathcal {P}$
, a finite family
$E\in \mathcal {P}$
, a finite family
![]() $\mathcal {F}_E$
such that for all
$\mathcal {F}_E$
such that for all
![]() $f\in \mathcal {M}$
, we have the representation
$f\in \mathcal {M}$
, we have the representation
![]() $f=\sum _{E\in \mathcal {P}} f_E1_E$
, where
$f=\sum _{E\in \mathcal {P}} f_E1_E$
, where
![]() $f_E=\sum _{g\in \mathcal {F}_E} a_{g} g$
is an
$f_E=\sum _{g\in \mathcal {F}_E} a_{g} g$
is an
![]() $L^0(Y)$
-linear combination for each
$L^0(Y)$
-linear combination for each
![]() $E\in \mathcal {P}$
. Since
$E\in \mathcal {P}$
. Since
![]() $\|(T^\gamma )^*f\|_{L^2(X|Y)}=(T^\gamma )^*\|f\|_{L^2(X|Y)} <M$
for all
$\|(T^\gamma )^*f\|_{L^2(X|Y)}=(T^\gamma )^*\|f\|_{L^2(X|Y)} <M$
for all
![]() $\gamma \in \Gamma $
, the orbit
$\gamma \in \Gamma $
, the orbit
![]() $\mathtt {Orb}_\Gamma (f)$
is bounded with respect to the conditional norm
$\mathtt {Orb}_\Gamma (f)$
is bounded with respect to the conditional norm
![]() $\|\cdot \|_{L^2(X|Y)}$
. It follows from Proposition 3.4(ii) and Proposition 3.7 that for all
$\|\cdot \|_{L^2(X|Y)}$
. It follows from Proposition 3.4(ii) and Proposition 3.7 that for all
![]() $h\in \mathtt {Orb}_\Gamma (f)$
,
$h\in \mathtt {Orb}_\Gamma (f)$
,
 $$ \begin{align*} \|h\|_{L^2(X|Y)}&=\bigg\|\sum_{E\in\mathcal{P}} h_E 1_E\bigg\|_{L^2(X|Y)}=\sum_{E\in\mathcal{P}}\|h_E\|_{L^2(X|Y)} 1_E\\ &=\sum_{E\in\mathcal{P}} \bigg(\sum_{g\in\mathcal{F}_E} |a^h_{g}|^{2}\bigg)^{1/2} 1_E <M. \end{align*} $$
$$ \begin{align*} \|h\|_{L^2(X|Y)}&=\bigg\|\sum_{E\in\mathcal{P}} h_E 1_E\bigg\|_{L^2(X|Y)}=\sum_{E\in\mathcal{P}}\|h_E\|_{L^2(X|Y)} 1_E\\ &=\sum_{E\in\mathcal{P}} \bigg(\sum_{g\in\mathcal{F}_E} |a^h_{g}|^{2}\bigg)^{1/2} 1_E <M. \end{align*} $$
For each
![]() $E\in \mathcal {P}$
, choose
$E\in \mathcal {P}$
, choose
![]() $c_1^E,\ldots , c_{j_E}^E\in \mathbb {C}^{\#(\mathcal {F}_{E})}$
such that the closed ball in
$c_1^E,\ldots , c_{j_E}^E\in \mathbb {C}^{\#(\mathcal {F}_{E})}$
such that the closed ball in
![]() $\mathbb {C}^{\#(\mathcal {F}_{E})}$
with radius M and center the origin is covered by the union of the open balls of radius
$\mathbb {C}^{\#(\mathcal {F}_{E})}$
with radius M and center the origin is covered by the union of the open balls of radius
![]() $\varepsilon $
and center
$\varepsilon $
and center
![]() $c_k^E$
,
$c_k^E$
,
![]() $k=1,\ldots , j_E$
. Denote by
$k=1,\ldots , j_E$
. Denote by
![]() $C_k^E$
the constant measurable vector in
$C_k^E$
the constant measurable vector in
![]() $L^0(Y)^{\#(\mathcal {F}_{E})}$
with value
$L^0(Y)^{\#(\mathcal {F}_{E})}$
with value
![]() $c_k^E$
. For
$c_k^E$
. For
![]() $f\in \mathcal {F}_{E}$
, let
$f\in \mathcal {F}_{E}$
, let
![]() $C_k^E(f)$
denote a component of the vector
$C_k^E(f)$
denote a component of the vector
![]() $C_k^E$
. Put
$C_k^E$
. Put
 $$ \begin{align*} \mathcal{L}_E=\bigg\{\sum_{f\in\mathcal{F}_{E}} C_k^E(f) f: k=1,\ldots, j_E\bigg\} \end{align*} $$
$$ \begin{align*} \mathcal{L}_E=\bigg\{\sum_{f\in\mathcal{F}_{E}} C_k^E(f) f: k=1,\ldots, j_E\bigg\} \end{align*} $$
and define
 $$ \begin{align*} \mathcal{L}= \bigg\{\sum_{E\in\mathcal{P}} g_E|E: g_E\in\mathcal{L}_E \text{ for each } E\in\mathcal{P} \bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}= \bigg\{\sum_{E\in\mathcal{P}} g_E|E: g_E\in\mathcal{L}_E \text{ for each } E\in\mathcal{P} \bigg\}. \end{align*} $$
Clearly,
![]() $\mathcal {L}$
is finite and by construction, it holds that
$\mathcal {L}$
is finite and by construction, it holds that
Remark 4.7. The idea of the previous proof is a conditional version of the Heine–Borel theorem (see [Reference Drapeau, Jamneshan, Karliczek and Kupper9, Theorem 4.6]) or the internal Heine–Borel theorem of
![]() $\mathtt {Sh}(Y)$
.
$\mathtt {Sh}(Y)$
.
Lemma 4.8. Assertion (i) is equivalent to assertion (i)′ in Theorem 4.1.
Proof. The equivalence is a consequence of Proposition 3.4(v)–(vii).
Lemma 4.9. Assertion (ii) is equivalent to assertion (ii)′ in Theorem 4.1.
Proof. We first show that (ii) implies (ii)′. Let
![]() $\mathcal {M}$
be an finitely generated and
$\mathcal {M}$
be an finitely generated and
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^0(Y)$
-submodule of
$L^0(Y)$
-submodule of
![]() $\mathtt {L^2(X|Y)}$
. For
$\mathtt {L^2(X|Y)}$
. For
![]() $\mathcal {M}$
, choose a finite Y-partition
$\mathcal {M}$
, choose a finite Y-partition
![]() $\mathcal {P}$
and for each
$\mathcal {P}$
and for each
![]() $E\in \mathcal {P}$
, a finite set
$E\in \mathcal {P}$
, a finite set
![]() $\mathcal {F}_E$
satisfying the properties in Proposition 3.7. Let
$\mathcal {F}_E$
satisfying the properties in Proposition 3.7. Let
 $$ \begin{align*} \mathcal{L}=\bigg\{\sum_{E\in\mathcal{P}} g_E|E: g_E\in \mathcal{F}_E \text{ each } E\in\mathcal{P}\bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}=\bigg\{\sum_{E\in\mathcal{P}} g_E|E: g_E\in \mathcal{F}_E \text{ each } E\in\mathcal{P}\bigg\}. \end{align*} $$
By property (ii) in Proposition 3.7,
![]() $\|g\|_{L^2(X|Y)}\leq 1$
for each
$\|g\|_{L^2(X|Y)}\leq 1$
for each
![]() $g\in \mathcal {L}$
. Thus by equation (10),
$g\in \mathcal {L}$
. Thus by equation (10),
![]() $\|g\|_{L^2(X)}\leq 1$
for all
$\|g\|_{L^2(X)}\leq 1$
for all
![]() $g\in \mathcal {L}$
. Let
$g\in \mathcal {L}$
. Let
![]() $\mathcal {M}'$
be the
$\mathcal {M}'$
be the
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $L^2(X)$
generated by
$L^2(X)$
generated by
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $\mathcal {M}'$
is
$\mathcal {M}'$
is
![]() $\Gamma $
-invariant since
$\Gamma $
-invariant since
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\Gamma $
-invariant, and by Proposition 3.4(vi),
$\Gamma $
-invariant, and by Proposition 3.4(vi),
![]() $\mathcal {M}'$
is also
$\mathcal {M}'$
is also
![]() $L^2$
-closed. It remains to show that the union of all
$L^2$
-closed. It remains to show that the union of all
![]() $\mathcal {M}'$
, where
$\mathcal {M}'$
, where
![]() $\mathcal {M}$
is a finitely generated and
$\mathcal {M}$
is a finitely generated and
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^0(Y)$
-submodule of
$L^0(Y)$
-submodule of
![]() $\mathtt {L^2(X|Y)}$
, is dense in
$\mathtt {L^2(X|Y)}$
, is dense in
![]() $L^2(X)$
. However, this follows from Proposition 3.4(v) and (vii).
$L^2(X)$
. However, this follows from Proposition 3.4(v) and (vii).
Let us show that (ii)′ implies (ii). Let
![]() $\mathcal {M}'$
be an
$\mathcal {M}'$
be an
![]() $L^\infty (Y)$
-finitely generated,
$L^\infty (Y)$
-finitely generated,
![]() $\Gamma $
-invariant, and closed submodule of
$\Gamma $
-invariant, and closed submodule of
![]() $L^2(X)$
. Let
$L^2(X)$
. Let
![]() $\mathcal {L}$
be a finite set of generators of
$\mathcal {L}$
be a finite set of generators of
![]() $\mathcal {M}'$
. Let
$\mathcal {M}'$
. Let
![]() $\mathcal {M}=\{\sum _{g\in \mathcal {L}} a_g g: a_g\in L^0(Y) \text { for all } g \in \mathcal {L}\}$
. By construction and Proposition 3.4(ii),
$\mathcal {M}=\{\sum _{g\in \mathcal {L}} a_g g: a_g\in L^0(Y) \text { for all } g \in \mathcal {L}\}$
. By construction and Proposition 3.4(ii),
![]() $\mathcal {M}$
is a finitely generated and
$\mathcal {M}$
is a finitely generated and
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $L^0(Y)$
-submodule of
$L^0(Y)$
-submodule of
![]() $\mathtt {L^2(X|Y)}$
. By Proposition 3.4(vii), the union of all such
$\mathtt {L^2(X|Y)}$
. By Proposition 3.4(vii), the union of all such
![]() $\mathcal {M}$
is dense in
$\mathcal {M}$
is dense in
![]() $\mathtt {L^2(X|Y)}$
with respect to
$\mathtt {L^2(X|Y)}$
with respect to
![]() $\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
$\mathtt {d}_{\mathtt {L^2(X|Y)}}$
.
Lemma 4.10. Assertion (iii) is equivalent to assertion (iii)′ in Theorem 4.1.
Proof. Let
![]() $\mathcal {G}$
be a dense set in
$\mathcal {G}$
be a dense set in
![]() $\mathtt {L^2(X|Y)}$
satisfying the property in (iii). Let
$\mathtt {L^2(X|Y)}$
satisfying the property in (iii). Let
![]() $f\in \mathcal {G}$
and
$f\in \mathcal {G}$
and
![]() $M>0$
. By Proposition 3.4(ii),
$M>0$
. By Proposition 3.4(ii),
![]() $f 1_{\|f\|_{L^2(X|Y)}\leq M}$
is also an element of
$f 1_{\|f\|_{L^2(X|Y)}\leq M}$
is also an element of
![]() $\mathcal {G}$
. Then
$\mathcal {G}$
. Then
![]() $\mathcal {R}=\{f 1_{\|f\|_{L^2(X|Y)}\leq M}: f\in \mathcal {S}, M>0\}$
is a subset of
$\mathcal {R}=\{f 1_{\|f\|_{L^2(X|Y)}\leq M}: f\in \mathcal {S}, M>0\}$
is a subset of
![]() $L^2(X)$
by Proposition 3.4(v) and dense in
$L^2(X)$
by Proposition 3.4(v) and dense in
![]() $\mathtt {L^2(X|Y)}$
. Now (iii)′ follows from Proposition 3.4(vi). The converse direction is an immediate consequence of Proposition 3.4(vii).
$\mathtt {L^2(X|Y)}$
. Now (iii)′ follows from Proposition 3.4(vi). The converse direction is an immediate consequence of Proposition 3.4(vii).
We conclude the proof of Theorem 4.1 by establishing the following.
Lemma 4.11. Assertion (iii)′ implies assertion (i)′ in Theorem 4.1.
Proof. We show that if
![]() $f\in \mathcal {H}$
is orthogonal to all functions of the form
$f\in \mathcal {H}$
is orthogonal to all functions of the form
![]() $K\ast _Y g$
, where K ranges over
$K\ast _Y g$
, where K ranges over
![]() $\Gamma $
-invariant functions in
$\Gamma $
-invariant functions in
![]() $L^\infty (X\times _Y X)$
and g ranges over
$L^\infty (X\times _Y X)$
and g ranges over
![]() $L^2(X)$
, then
$L^2(X)$
, then
![]() $f=0$
. Let K be the unique element of minimal norm in the closed convex hull of
$f=0$
. Let K be the unique element of minimal norm in the closed convex hull of
![]() $\mathtt {Orb}_\Gamma (f\otimes \bar f)$
in
$\mathtt {Orb}_\Gamma (f\otimes \bar f)$
in
![]() $L^2(X\times _Y X)$
, which is
$L^2(X\times _Y X)$
, which is
![]() $\Gamma $
-invariant by Theorem 2.9. Set
$\Gamma $
-invariant by Theorem 2.9. Set
![]() $K_M=K1_{|K|\leq M}$
for
$K_M=K1_{|K|\leq M}$
for
![]() $M\geq 0$
. By hypothesis, f is orthogonal to
$M\geq 0$
. By hypothesis, f is orthogonal to
![]() $K_M\ast _Y \bar f$
. We can rewrite this, using the disintegration
$K_M\ast _Y \bar f$
. We can rewrite this, using the disintegration
![]() $(\mu _y)_{y\in \tilde {Y}}$
of
$(\mu _y)_{y\in \tilde {Y}}$
of
![]() $\tilde {\mu }$
, as
$\tilde {\mu }$
, as
 $$ \begin{align*} 0&=\int_{\tilde{X}} f(x) \bigg(\int_{\tilde{X}} K_M(x,x') \bar f(x') \,d\mu_{\tilde{\pi}(x)}(x')\bigg) \,d\tilde{\mu}(x) \\[3pt] &= \int_{\tilde{Y}} \int_{\tilde{X}} f(x) \bigg(\int_{\tilde{X}} K_M(x,x') \bar f(x') \,d\mu_y(x')\bigg) \,d\mu_y(x) \,d\tilde{\nu}(y) \\[3pt] &= \int_{\tilde{X}\times\tilde{X}} f\otimes \bar f K_M \,d\tilde\mu\times_{\tilde{Y}} \tilde\mu. \end{align*} $$
$$ \begin{align*} 0&=\int_{\tilde{X}} f(x) \bigg(\int_{\tilde{X}} K_M(x,x') \bar f(x') \,d\mu_{\tilde{\pi}(x)}(x')\bigg) \,d\tilde{\mu}(x) \\[3pt] &= \int_{\tilde{Y}} \int_{\tilde{X}} f(x) \bigg(\int_{\tilde{X}} K_M(x,x') \bar f(x') \,d\mu_y(x')\bigg) \,d\mu_y(x) \,d\tilde{\nu}(y) \\[3pt] &= \int_{\tilde{X}\times\tilde{X}} f\otimes \bar f K_M \,d\tilde\mu\times_{\tilde{Y}} \tilde\mu. \end{align*} $$
Thus
![]() $ f\otimes \bar f$
is orthogonal to
$ f\otimes \bar f$
is orthogonal to
![]() $K_M$
in
$K_M$
in
![]() $L^2(X\times _Y X)$
. As
$L^2(X\times _Y X)$
. As
![]() $K_M$
is
$K_M$
is
![]() $\Gamma $
-invariant,
$\Gamma $
-invariant,
![]() $(T^\gamma \times T^\gamma )^* f\otimes \bar f$
is orthogonal to
$(T^\gamma \times T^\gamma )^* f\otimes \bar f$
is orthogonal to
![]() $K_M$
for all
$K_M$
for all
![]() $\gamma \in \Gamma $
as well. Thus K must be orthogonal to all
$\gamma \in \Gamma $
as well. Thus K must be orthogonal to all
![]() $K_M$
which implies that
$K_M$
which implies that
![]() $K_M=0$
for all
$K_M=0$
for all
![]() $M\geq 0$
, and therefore also
$M\geq 0$
, and therefore also
![]() $K=0$
.
$K=0$
.
Now choose a finite set
![]() $\mathcal {F}$
such that the property in (iii)′ is satisfied for f and an arbitrary
$\mathcal {F}$
such that the property in (iii)′ is satisfied for f and an arbitrary
![]() $\varepsilon>0$
. Let
$\varepsilon>0$
. Let
![]() $(K_n)$
be a sequence in the convex hull of
$(K_n)$
be a sequence in the convex hull of
![]() $\mathtt {Orb}_\Gamma (f\otimes \bar f)$
such that
$\mathtt {Orb}_\Gamma (f\otimes \bar f)$
such that
![]() $\lim \|K_n\|_{L^2(X\times _Y X)}\to 0$
. By Cauchy–Schwarz, we also have
$\lim \|K_n\|_{L^2(X\times _Y X)}\to 0$
. By Cauchy–Schwarz, we also have
![]() $\langle K_n, g\otimes \bar g\rangle _{L^2(X\times _Y X)}\to 0$
for all
$\langle K_n, g\otimes \bar g\rangle _{L^2(X\times _Y X)}\to 0$
for all
![]() $g\in \mathcal {F}$
. Expanding the inner product and choosing n large enough, we can always obtain a
$g\in \mathcal {F}$
. Expanding the inner product and choosing n large enough, we can always obtain a
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
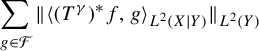 $$ \begin{align*} \sum_{g\in\mathcal{F}} \|\langle (T^{\gamma})^*f,g\rangle_{L^2(X|Y)}\|_{L^2(Y)} \end{align*} $$
$$ \begin{align*} \sum_{g\in\mathcal{F}} \|\langle (T^{\gamma})^*f,g\rangle_{L^2(X|Y)}\|_{L^2(Y)} \end{align*} $$
is arbitrarily small. Thus for any
![]() $\delta>0$
, we can find a set
$\delta>0$
, we can find a set
![]() $E\in \mathcal {B}a(\tilde {Y})$
with
$E\in \mathcal {B}a(\tilde {Y})$
with
![]() $\tilde \nu (E^c)<\delta $
such that
$\tilde \nu (E^c)<\delta $
such that
for all
![]() $g\in \mathcal {F}$
for some
$g\in \mathcal {F}$
for some
![]() $\gamma $
. By (iii)′, we also have for all
$\gamma $
. By (iii)′, we also have for all
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
By triangle inequality,
for some
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\varepsilon ,\delta $
were chosen arbitrarily, it follows that
$\varepsilon ,\delta $
were chosen arbitrarily, it follows that
![]() $f=0$
, and this finishes the proof of Theorem 4.1.
$f=0$
, and this finishes the proof of Theorem 4.1.
5 The uncountable Mackey–Zimmer theorem and isometric extensions
Under the hypothesis of ergodicity, relatively compact extensions are isomorphic to homogeneous skew-product extensions. This characterization is a relative version of the Halmos–von Neumann theorem (proved for
![]() $\mathbb {Z}$
-actions by Halmos and von Neumann [Reference Halmos and von Neumann25], then generalized by Mackey [Reference Mackey37] to second-countable locally compact group actions, see [Reference Eisner, Farkas, Haase and Nagel13, Theorem 17.5] for an uncountable Halmos–von Neumann theorem for ergodic Markov semi-group actions). The relative version of the Halmos–von Neumann theorem was obtained by Zimmer [Reference Zimmer47] for actions of second-countable locally compact groups on standard Borel spaces. In this section, we extend Zimmer’s theorem to systems of uncountable complexity. The key ingredient in the proof is the Mackey–Zimmer theorem classifying ergodic homogeneous extensions. We use the uncountable Mackey–Zimmer theorem [Reference Jamneshan and Tao32] established by Tao and the author. We point out that similar results to those in this section were obtained by Ellis [Reference Ellis14, §5], though with different methods. In short, the methods of [Reference Ellis14] rely on topological dynamics and the theory of Banach bundles of spaces of continuous functions which is akin to the methods used in [Reference Edeko, Haase and Kreidler11], whereas our methods are ergodic-theoretic and based off measure theory and topos theory.
$\mathbb {Z}$
-actions by Halmos and von Neumann [Reference Halmos and von Neumann25], then generalized by Mackey [Reference Mackey37] to second-countable locally compact group actions, see [Reference Eisner, Farkas, Haase and Nagel13, Theorem 17.5] for an uncountable Halmos–von Neumann theorem for ergodic Markov semi-group actions). The relative version of the Halmos–von Neumann theorem was obtained by Zimmer [Reference Zimmer47] for actions of second-countable locally compact groups on standard Borel spaces. In this section, we extend Zimmer’s theorem to systems of uncountable complexity. The key ingredient in the proof is the Mackey–Zimmer theorem classifying ergodic homogeneous extensions. We use the uncountable Mackey–Zimmer theorem [Reference Jamneshan and Tao32] established by Tao and the author. We point out that similar results to those in this section were obtained by Ellis [Reference Ellis14, §5], though with different methods. In short, the methods of [Reference Ellis14] rely on topological dynamics and the theory of Banach bundles of spaces of continuous functions which is akin to the methods used in [Reference Edeko, Haase and Kreidler11], whereas our methods are ergodic-theoretic and based off measure theory and topos theory.
We start by recalling the uncountable Mackey–Zimmer theorem [Reference Jamneshan and Tao32]. Let K be a compact Hausdorff group and
![]() $(Y,\nu )$
a
$(Y,\nu )$
a
![]() ${\mathbf {PrbAlg}}$
-space. We denote by
${\mathbf {PrbAlg}}$
-space. We denote by
![]() $\mathtt {Cond}_Y(K)$
the set of all
$\mathtt {Cond}_Y(K)$
the set of all
![]() $\mathbf {AbsMbl}$
-morphisms from Y to
$\mathbf {AbsMbl}$
-morphisms from Y to
![]() $\mathcal {B}a(K)$
. Let
$\mathcal {B}a(K)$
. Let
![]() ${\widetilde {\mathtt {Cond}}}_Y(K)$
denote the set of continuous functions from
${\widetilde {\mathtt {Cond}}}_Y(K)$
denote the set of continuous functions from
![]() $\tilde {Y}$
to K. It is a remarkable property of the canonical model that we have the isomorphism
$\tilde {Y}$
to K. It is a remarkable property of the canonical model that we have the isomorphism
see [Reference Jamneshan and Tao31, Proposition 7.9] for a proof (here, isomorphism is understood in the sense of sets, that is, there is a bijection between the sets
![]() $\mathtt {Cond}_Y(K)$
and
$\mathtt {Cond}_Y(K)$
and
![]() ${\widetilde {\mathtt {Cond}}}_Y(K)$
). The set
${\widetilde {\mathtt {Cond}}}_Y(K)$
). The set
![]() ${\widetilde {\mathtt {Cond}}}_T(K)$
has the structure of a group defining the group law in a pointwise way. Therefore, also
${\widetilde {\mathtt {Cond}}}_T(K)$
has the structure of a group defining the group law in a pointwise way. Therefore, also
![]() $\mathtt {Cond}_Y(K)$
has a group structure. We introduce
$\mathtt {Cond}_Y(K)$
has a group structure. We introduce
![]() ${\mathbf {PrbAlg}_\Gamma }$
-cocycles, homogeneous skew-products, and extensions.
${\mathbf {PrbAlg}_\Gamma }$
-cocycles, homogeneous skew-products, and extensions.
Definition 5.1. Let
![]() $\mathcal {Y}=(Y,\nu ,S)$
be a
$\mathcal {Y}=(Y,\nu ,S)$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system, K a compact Hausdorff group, and
${\mathbf {PrbAlg}_\Gamma }$
-system, K a compact Hausdorff group, and
![]() $L\leq K$
a closed subgroup.
$L\leq K$
a closed subgroup.
-
(i) A K-valued
 ${\mathbf {PrbAlg}_\Gamma }$
-cocycle is a family
${\mathbf {PrbAlg}_\Gamma }$
-cocycle is a family
 $\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
of elements
$\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
of elements
 $\rho _\gamma \in \mathtt {Cond}_Y(K)$
satisfying the
$\rho _\gamma \in \mathtt {Cond}_Y(K)$
satisfying the
 ${\mathbf {PrbAlg}_\Gamma }$
-cocycle property for all
${\mathbf {PrbAlg}_\Gamma }$
-cocycle property for all $$ \begin{align*}\rho_{\gamma\gamma'}=(\rho_\gamma\circ S^{\gamma'})\rho_{\gamma'}\end{align*} $$
$$ \begin{align*}\rho_{\gamma\gamma'}=(\rho_\gamma\circ S^{\gamma'})\rho_{\gamma'}\end{align*} $$
 $\gamma ,\gamma '\in \Gamma $
. Any K-valued
$\gamma ,\gamma '\in \Gamma $
. Any K-valued
 ${\mathbf {PrbAlg}_\Gamma }$
-cocycle
${\mathbf {PrbAlg}_\Gamma }$
-cocycle
 $\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
has a canonical representation
$\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
has a canonical representation
 $\tilde {\rho }=(\tilde {\rho }_\gamma )_{\gamma \in \Gamma }$
, where
$\tilde {\rho }=(\tilde {\rho }_\gamma )_{\gamma \in \Gamma }$
, where
 $\tilde {\rho }_\gamma \in {\widetilde {\mathtt {Cond}}}_Y(K)$
is defined by the isomorphism in equation (12) such that
$\tilde {\rho }_\gamma \in {\widetilde {\mathtt {Cond}}}_Y(K)$
is defined by the isomorphism in equation (12) such that
 $\tilde {\rho }=(\tilde {\rho }_\gamma )_{\gamma \in \Gamma }$
is a
$\tilde {\rho }=(\tilde {\rho }_\gamma )_{\gamma \in \Gamma }$
is a
 ${\mathbf {CHPrb}_\Gamma }$
-cocycle on
${\mathbf {CHPrb}_\Gamma }$
-cocycle on
 $\tilde {Y}$
.
$\tilde {Y}$
.
-
(ii) Let
 $\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
be a
$\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
be a
 ${\mathbf {PrbAlg}_\Gamma }$
-cocycle with canonical representation
${\mathbf {PrbAlg}_\Gamma }$
-cocycle with canonical representation
 $\tilde {\rho }=(\tilde {\rho }_\gamma )_{\gamma \in \Gamma }$
. We denote by
$\tilde {\rho }=(\tilde {\rho }_\gamma )_{\gamma \in \Gamma }$
. We denote by
 $\tilde {Y}\rtimes _{\tilde {\rho }} K/L$
the
$\tilde {Y}\rtimes _{\tilde {\rho }} K/L$
the
 ${\mathbf {CHPrb}_\Gamma }$
-homogeneous skew-product defined by the following data:
${\mathbf {CHPrb}_\Gamma }$
-homogeneous skew-product defined by the following data:-
• the homogeneous space
 $K/L$
is equipped with Baire
$K/L$
is equipped with Baire
 $\sigma $
-algebra and Haar measure;
$\sigma $
-algebra and Haar measure; -
• we equip
 $\tilde {Y}\times K/L$
with the product Baire probability measure;
$\tilde {Y}\times K/L$
with the product Baire probability measure; -
• the
 ${\mathbf {CHPrb}_\Gamma }$
-action
${\mathbf {CHPrb}_\Gamma }$
-action
 $T:\Gamma \to \operatorname {Aut}(\tilde {Y}\times K/L)$
is defined by for all
$T:\Gamma \to \operatorname {Aut}(\tilde {Y}\times K/L)$
is defined by for all $$ \begin{align*}T^\gamma(y,kL)=(S^\gamma y,\tilde{\rho}_\gamma(y) kL)\end{align*} $$
$$ \begin{align*}T^\gamma(y,kL)=(S^\gamma y,\tilde{\rho}_\gamma(y) kL)\end{align*} $$
 $(y,kL)\in \tilde {Y}\times K/L$
and
$(y,kL)\in \tilde {Y}\times K/L$
and
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
We define the
 ${\mathbf {PrbAlg}_\Gamma }$
-homogeneous skew-product
${\mathbf {PrbAlg}_\Gamma }$
-homogeneous skew-product
 $\mathcal {Y}\rtimes _\rho K/L$
to be the
$\mathcal {Y}\rtimes _\rho K/L$
to be the
 ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system  $$ \begin{align*}\mathtt{AlgAbs}(\tilde{Y}\rtimes_{\tilde{\rho}} K/L).\end{align*} $$
$$ \begin{align*}\mathtt{AlgAbs}(\tilde{Y}\rtimes_{\tilde{\rho}} K/L).\end{align*} $$
-
-
(iii) A
 ${\mathbf {PrbAlg}_\Gamma }$
-homogeneous extension of
${\mathbf {PrbAlg}_\Gamma }$
-homogeneous extension of
 $\mathcal {Y}$
by
$\mathcal {Y}$
by
 $K/L$
is a tuple
$K/L$
is a tuple
 $(\mathcal {X},\pi ,\theta ,\rho )$
, where
$(\mathcal {X},\pi ,\theta ,\rho )$
, where
 $\mathcal {X}=(X,\mu ,T)$
is a
$\mathcal {X}=(X,\mu ,T)$
is a
 ${\mathbf {PrbAlg}_\Gamma }$
-system,
${\mathbf {PrbAlg}_\Gamma }$
-system,
 $\pi :(X,\mu ,T)\to (Y,\nu ,S)$
is a
$\pi :(X,\mu ,T)\to (Y,\nu ,S)$
is a
 ${\mathbf {PrbAlg}_\Gamma }$
-extension,
${\mathbf {PrbAlg}_\Gamma }$
-extension,
 $\theta \in \mathtt {Cond}_X(K/L)$
is a vertical coordinate such that
$\theta \in \mathtt {Cond}_X(K/L)$
is a vertical coordinate such that
 $\pi ,\theta $
jointly generate the
$\pi ,\theta $
jointly generate the
 ${\mathbf {Bool}_\sigma }$
-algebra X, and
${\mathbf {Bool}_\sigma }$
-algebra X, and
 $\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
is a
$\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
is a
 ${\mathbf {PrbAlg}_\Gamma }$
-cocycle such that for all
${\mathbf {PrbAlg}_\Gamma }$
-cocycle such that for all $$ \begin{align*}\theta\circ T^\gamma = (\rho_\gamma\circ \pi)\theta\end{align*} $$
$$ \begin{align*}\theta\circ T^\gamma = (\rho_\gamma\circ \pi)\theta\end{align*} $$
 $\gamma \in \Gamma $
using the natural action of
$\gamma \in \Gamma $
using the natural action of
 $\mathtt {Cond}_X(K)$
on
$\mathtt {Cond}_X(K)$
on
 $\mathtt {Cond}_X(K/L)$
.
$\mathtt {Cond}_X(K/L)$
.
Theorem 5.2. (Uncountable Mackey–Zimmer [Reference Jamneshan and Tao32])
Let
![]() $\mathcal {Y}=(Y,\nu ,S)$
be an ergodic
$\mathcal {Y}=(Y,\nu ,S)$
be an ergodic
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system and K be a compact Hausdorff group. Every ergodic
${\mathbf {PrbAlg}_\Gamma }$
-system and K be a compact Hausdorff group. Every ergodic
![]() ${\mathbf {PrbAlg}_\Gamma }$
- homogeneous extension
${\mathbf {PrbAlg}_\Gamma }$
- homogeneous extension
![]() $\mathcal {X}$
of
$\mathcal {X}$
of
![]() $\mathcal {Y}$
by
$\mathcal {Y}$
by
![]() $K/L$
for some compact subgroup L of K is isomorphic in
$K/L$
for some compact subgroup L of K is isomorphic in
![]() ${\mathbf {PrbAlg}_\Gamma }$
to a
${\mathbf {PrbAlg}_\Gamma }$
to a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-homogeneous skew-product
${\mathbf {PrbAlg}_\Gamma }$
-homogeneous skew-product
![]() $\mathcal {Y} \rtimes _\rho H/M$
for some compact subgroup H of K, some compact subgroup M of H, and some H-valued
$\mathcal {Y} \rtimes _\rho H/M$
for some compact subgroup H of K, some compact subgroup M of H, and some H-valued
![]() ${\mathbf {PrbAlg}_\Gamma }$
-cocycle
${\mathbf {PrbAlg}_\Gamma }$
-cocycle
![]() $\rho $
.
$\rho $
.
We apply the uncountable Mackey–Zimmer theorem to establish a geometric characterization of relatively compact extensions.
Theorem 5.3. If
![]() $\pi :(X,\mu ,T)\to (Y,\nu ,S)$
is an ergodic relatively compact
$\pi :(X,\mu ,T)\to (Y,\nu ,S)$
is an ergodic relatively compact
![]() ${\mathbf {PrbAlg}_\Gamma }$
- extension, then
${\mathbf {PrbAlg}_\Gamma }$
- extension, then
![]() $(X,\mu ,T)$
is
$(X,\mu ,T)$
is
![]() ${\mathbf {PrbAlg}_\Gamma }$
-isomorphic to a homogeneous skew-product extension
${\mathbf {PrbAlg}_\Gamma }$
-isomorphic to a homogeneous skew-product extension
![]() $\mathcal {Y}\rtimes _\rho H/M$
for a compact Hausdorff group H, a closed subgroup M of H, and an H-valued
$\mathcal {Y}\rtimes _\rho H/M$
for a compact Hausdorff group H, a closed subgroup M of H, and an H-valued
![]() ${\mathbf {PrbAlg}_\Gamma }$
-cocycle
${\mathbf {PrbAlg}_\Gamma }$
-cocycle
![]() $\rho $
.
$\rho $
.
In the proof, we need some properties about cocycles with values in quotient and product spaces which are recorded in the following lemma.
Lemma 5.4. Let A be an index set and for every
![]() $\alpha \in A$
, let
$\alpha \in A$
, let
![]() $K_\alpha $
be a compact Hausdorff group and
$K_\alpha $
be a compact Hausdorff group and
![]() $L_\alpha $
a closed subgroup of
$L_\alpha $
a closed subgroup of
![]() $K_\alpha $
. Let
$K_\alpha $
. Let
![]() $(Y,\nu )$
be a
$(Y,\nu )$
be a
![]() ${\mathbf {PrbAlg}}$
-space. Then the following identities hold:
${\mathbf {PrbAlg}}$
-space. Then the following identities hold:
 $$ \begin{align*} \mathtt{Cond}_Y\bigg(\prod_{\alpha\in A} K_\alpha\bigg)&=\prod_{\alpha\in A} \mathtt{Cond}_Y(K_\alpha)\\ \mathtt{Cond}_Y\bigg(\prod_{\alpha\in A} (K_\alpha/L_\alpha)\bigg)&=\mathtt{Cond}_Y\bigg(\prod_{\alpha\in A} K_\alpha/\prod_{\alpha\in A} L_\alpha\bigg). \end{align*} $$
$$ \begin{align*} \mathtt{Cond}_Y\bigg(\prod_{\alpha\in A} K_\alpha\bigg)&=\prod_{\alpha\in A} \mathtt{Cond}_Y(K_\alpha)\\ \mathtt{Cond}_Y\bigg(\prod_{\alpha\in A} (K_\alpha/L_\alpha)\bigg)&=\mathtt{Cond}_Y\bigg(\prod_{\alpha\in A} K_\alpha/\prod_{\alpha\in A} L_\alpha\bigg). \end{align*} $$
Proof. The first identity is proved in [Reference Jamneshan and Tao33, Corollary 3.5]. Routine verification shows that
is a
![]() $\mathbf {CH}$
-isomorphism. This proves the second identity.
$\mathbf {CH}$
-isomorphism. This proves the second identity.
Proof of Theorem 5.3
Let
![]() $\pi :(X,\mu ,T)\to (Y,\nu ,S)$
be a relatively compact
$\pi :(X,\mu ,T)\to (Y,\nu ,S)$
be a relatively compact
![]() ${\mathbf {PrbAlg}_\Gamma }$
- extension of ergodic systems. Let
${\mathbf {PrbAlg}_\Gamma }$
- extension of ergodic systems. Let
![]() $(\mathcal {M}_\alpha )_{\alpha \in A}$
be the family of all
$(\mathcal {M}_\alpha )_{\alpha \in A}$
be the family of all
![]() $\Gamma $
-invariant closed finitely generated
$\Gamma $
-invariant closed finitely generated
![]() $L^\infty (Y)$
-submodules of
$L^\infty (Y)$
-submodules of
![]() $L^2(X)$
. By Theorem 4.1(ii)′,
$L^2(X)$
. By Theorem 4.1(ii)′,
![]() $L^2(X)$
is the
$L^2(X)$
is the
![]() $L^2$
closure of
$L^2$
closure of
![]() $\bigcup _{\alpha \in A} \mathcal {M}_\alpha $
. Fix
$\bigcup _{\alpha \in A} \mathcal {M}_\alpha $
. Fix
![]() $\alpha \in A$
. Since
$\alpha \in A$
. Since
![]() $\mathcal {M}_\alpha $
is
$\mathcal {M}_\alpha $
is
![]() $\Gamma $
-invariant, the map
$\Gamma $
-invariant, the map
![]() $\mathtt {cdim}(\mathcal {M}_\alpha )$
is also
$\mathtt {cdim}(\mathcal {M}_\alpha )$
is also
![]() $\Gamma $
-invariant and by ergodicity,
$\Gamma $
-invariant and by ergodicity,
![]() $\mathtt {cdim}(\mathcal {M}_\alpha )\equiv d_\alpha $
for some integer
$\mathtt {cdim}(\mathcal {M}_\alpha )\equiv d_\alpha $
for some integer
![]() $d_\alpha \geq 1$
. By Proposition 3.7, we find
$d_\alpha \geq 1$
. By Proposition 3.7, we find
![]() $f^\alpha _1,\ldots ,f^\alpha _{d_\alpha }\in \mathcal {M}_\alpha $
such that
$f^\alpha _1,\ldots ,f^\alpha _{d_\alpha }\in \mathcal {M}_\alpha $
such that
![]() $\|f^\alpha _i\|_{L^2(X|Y)}=1$
for all
$\|f^\alpha _i\|_{L^2(X|Y)}=1$
for all
![]() $i=1,\ldots ,d_\alpha $
and
$i=1,\ldots ,d_\alpha $
and
![]() $\langle f^\alpha _i,f^\alpha _j\rangle _{L^2(X|Y)}=0$
whenever
$\langle f^\alpha _i,f^\alpha _j\rangle _{L^2(X|Y)}=0$
whenever
![]() $i\neq j$
. In fact, we can choose
$i\neq j$
. In fact, we can choose
![]() $f^\alpha _1,\ldots ,f^\alpha _{d_\alpha }$
such that all
$f^\alpha _1,\ldots ,f^\alpha _{d_\alpha }$
such that all
![]() $f^\alpha _i$
take values in the unit circle
$f^\alpha _i$
take values in the unit circle
![]() $\mathbb {S}$
. For any
$\mathbb {S}$
. For any
![]() $\gamma \in \Gamma $
, then
$\gamma \in \Gamma $
, then
![]() $(\tilde T^\gamma )^*f^\alpha _1,\ldots , (\tilde T^\gamma )^*f^\alpha _{d_\alpha }$
also satisfies
$(\tilde T^\gamma )^*f^\alpha _1,\ldots , (\tilde T^\gamma )^*f^\alpha _{d_\alpha }$
also satisfies
![]() $\|(\tilde T^\gamma )^*f^\alpha _i\|_{L^2(X|Y)}=1$
for all
$\|(\tilde T^\gamma )^*f^\alpha _i\|_{L^2(X|Y)}=1$
for all
![]() $i=1,\ldots ,d_\alpha $
and
$i=1,\ldots ,d_\alpha $
and
![]() $\langle (\tilde T^\gamma )^*f^\alpha _i,(\tilde T^\gamma )^*f^\alpha _j\rangle _{L^2(X|Y)}=0$
whenever
$\langle (\tilde T^\gamma )^*f^\alpha _i,(\tilde T^\gamma )^*f^\alpha _j\rangle _{L^2(X|Y)}=0$
whenever
![]() $i\neq j$
. Let
$i\neq j$
. Let
 $$ \begin{align*}\Lambda_\gamma^\alpha= \begin{bmatrix} a_{11}^\gamma & \cdots & a_{1d_{\alpha}}^\gamma \\ \vdots & \ddots & \vdots \\ a_{d_{\alpha}1}^\gamma & \cdots & a_{d_{\alpha}d_{\alpha}}^\gamma \end{bmatrix} \end{align*} $$
$$ \begin{align*}\Lambda_\gamma^\alpha= \begin{bmatrix} a_{11}^\gamma & \cdots & a_{1d_{\alpha}}^\gamma \\ \vdots & \ddots & \vdots \\ a_{d_{\alpha}1}^\gamma & \cdots & a_{d_{\alpha}d_{\alpha}}^\gamma \end{bmatrix} \end{align*} $$
where
![]() $a^\gamma _{ij}\in L^\infty (Y)$
is such that
$a^\gamma _{ij}\in L^\infty (Y)$
is such that
![]() $f^\alpha _i=\sum _{j=1}^{d_\alpha } a_{ij}^\gamma (\tilde T^\gamma )^*f^\alpha _j$
for all
$f^\alpha _i=\sum _{j=1}^{d_\alpha } a_{ij}^\gamma (\tilde T^\gamma )^*f^\alpha _j$
for all
![]() $i=1,\ldots ,d_\alpha $
. We can identify
$i=1,\ldots ,d_\alpha $
. We can identify
![]() $\Lambda _\gamma ^\alpha $
with an element of the function space
$\Lambda _\gamma ^\alpha $
with an element of the function space
![]() $L^0(Y\to \mathbb {U}(d_{\alpha }))$
of equivalence classes of
$L^0(Y\to \mathbb {U}(d_{\alpha }))$
of equivalence classes of
![]() $\mathbb {U}(d_{\alpha })$
-valued random variables on
$\mathbb {U}(d_{\alpha })$
-valued random variables on
![]() $\tilde {Y}$
, where
$\tilde {Y}$
, where
![]() $\mathbb {U}(d_{\alpha })$
is the group of
$\mathbb {U}(d_{\alpha })$
is the group of
![]() $d_{\alpha }\times d_{\alpha }$
unitary matrices. We obtain the identity
$d_{\alpha }\times d_{\alpha }$
unitary matrices. We obtain the identity
![]() $F^{\alpha }=\Lambda _\gamma ^\alpha F^{\alpha }_\gamma $
, where
$F^{\alpha }=\Lambda _\gamma ^\alpha F^{\alpha }_\gamma $
, where
![]() $F^{\alpha }=(f^{\alpha }_1,\ldots ,f^{\alpha }_{d_{\alpha }})$
and
$F^{\alpha }=(f^{\alpha }_1,\ldots ,f^{\alpha }_{d_{\alpha }})$
and
![]() $F^{\alpha }_\gamma =((\tilde T^\gamma )^*f^{\alpha }_1,\ldots , (\tilde T^\gamma )^*f^{\alpha }_{d_{\alpha }})$
. Let
$F^{\alpha }_\gamma =((\tilde T^\gamma )^*f^{\alpha }_1,\ldots , (\tilde T^\gamma )^*f^{\alpha }_{d_{\alpha }})$
. Let
![]() $\rho ^\alpha _\gamma := ((\Lambda _\gamma ^\alpha )^*)^{\operatorname {op}}$
, which is an element of
$\rho ^\alpha _\gamma := ((\Lambda _\gamma ^\alpha )^*)^{\operatorname {op}}$
, which is an element of
![]() $\mathtt {Cond}_Y(\mathbb {U}(d_{\alpha }))$
. We thus obtain a
$\mathtt {Cond}_Y(\mathbb {U}(d_{\alpha }))$
. We thus obtain a
![]() $\mathbb {U}(d_{\alpha })$
-valued
$\mathbb {U}(d_{\alpha })$
-valued
![]() ${\mathbf {PrbAlg}_\Gamma }$
-cocycle
${\mathbf {PrbAlg}_\Gamma }$
-cocycle
![]() $\rho ^\alpha =(\rho ^\alpha _\gamma )_{\gamma \in \Gamma }$
on
$\rho ^\alpha =(\rho ^\alpha _\gamma )_{\gamma \in \Gamma }$
on
![]() $(Y,\nu ,S)$
. Define the
$(Y,\nu ,S)$
. Define the
![]() $\mathbf {AbsMbl}$
-morphism
$\mathbf {AbsMbl}$
-morphism
![]() $\theta _\alpha :Y\to \mathcal {B}a(\mathbb {S}^{2d_{\alpha }-1})$
by
$\theta _\alpha :Y\to \mathcal {B}a(\mathbb {S}^{2d_{\alpha }-1})$
by
![]() $\theta _\alpha := ((({1}/{\sqrt {d_{\alpha }}}) F^\alpha )^*)^{\operatorname {op}}$
.
$\theta _\alpha := ((({1}/{\sqrt {d_{\alpha }}}) F^\alpha )^*)^{\operatorname {op}}$
.
Now define
![]() $\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
by
$\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
by
![]() $\rho _\gamma =(\rho _\gamma ^\alpha )_{\alpha \in A}$
,
$\rho _\gamma =(\rho _\gamma ^\alpha )_{\alpha \in A}$
,
![]() $\theta =(\theta _\alpha )_{\alpha \in A}$
,
$\theta =(\theta _\alpha )_{\alpha \in A}$
,
![]() $K=\prod _{\alpha \in A} \mathbb {U}(d_\alpha )$
, and
$K=\prod _{\alpha \in A} \mathbb {U}(d_\alpha )$
, and
![]() $L=\prod _{\alpha \in A} \mathbb {U}(d_\alpha -1)$
. By Lemma 5.4,
$L=\prod _{\alpha \in A} \mathbb {U}(d_\alpha -1)$
. By Lemma 5.4,
![]() $\theta \in \mathtt {Cond}_Y(K/L)$
is a vertical coordinate such that
$\theta \in \mathtt {Cond}_Y(K/L)$
is a vertical coordinate such that
![]() $\pi ,\theta $
jointly generate the
$\pi ,\theta $
jointly generate the
![]() ${\mathbf {Bool}_\sigma }$
-algebra X, and
${\mathbf {Bool}_\sigma }$
-algebra X, and
![]() $\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
is a
$\rho =(\rho _\gamma )_{\gamma \in \Gamma }$
is a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-cocycle such that
${\mathbf {PrbAlg}_\Gamma }$
-cocycle such that
![]() $\theta \circ T^\gamma = (\rho _\gamma \circ \pi )\theta $
. The claim follows from Theorem 5.2.
$\theta \circ T^\gamma = (\rho _\gamma \circ \pi )\theta $
. The claim follows from Theorem 5.2.
Remark 5.5. Conversely, every (not necessarily ergodic)
![]() ${\mathbf {PrbAlg}_\Gamma }$
-homogeneous skew-product
${\mathbf {PrbAlg}_\Gamma }$
-homogeneous skew-product
![]() $\mathcal {Y}\rtimes _\rho K/L$
is a relatively compact
$\mathcal {Y}\rtimes _\rho K/L$
is a relatively compact
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension of
${\mathbf {PrbAlg}_\Gamma }$
-extension of
![]() $\mathcal {Y}$
. It is sufficient to show this for
$\mathcal {Y}$
. It is sufficient to show this for
![]() ${\mathbf {PrbAlg}_\Gamma }$
-group skew-products
${\mathbf {PrbAlg}_\Gamma }$
-group skew-products
![]() $\mathcal {Y}\rtimes _\rho K$
. Indeed, if
$\mathcal {Y}\rtimes _\rho K$
. Indeed, if
![]() $\mathcal {Y}\rtimes _\rho K\to \mathcal {Y}$
is a relatively compact
$\mathcal {Y}\rtimes _\rho K\to \mathcal {Y}$
is a relatively compact
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension, then so is
${\mathbf {PrbAlg}_\Gamma }$
-extension, then so is
![]() $\mathcal {Y}\rtimes _\rho K/L\to \mathcal {Y}$
since we have a
$\mathcal {Y}\rtimes _\rho K/L\to \mathcal {Y}$
since we have a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension
${\mathbf {PrbAlg}_\Gamma }$
-extension
![]() $\mathcal {Y}\rtimes _\rho K\to \mathcal {Y}\rtimes _\rho K/L$
.
$\mathcal {Y}\rtimes _\rho K\to \mathcal {Y}\rtimes _\rho K/L$
.
Now
![]() $L^2(Y\rtimes _\rho K)$
is the Hilbert space tensor product of
$L^2(Y\rtimes _\rho K)$
is the Hilbert space tensor product of
![]() $L^2(Y)$
and
$L^2(Y)$
and
![]() $L^2(K)$
. By the Peter–Weyl theorem,
$L^2(K)$
. By the Peter–Weyl theorem,
![]() $L^2(K)$
is the closure of the union of finite-dimensional K-invariant subspaces. For any g in a finite-dimensional K-invariant subspace of
$L^2(K)$
is the closure of the union of finite-dimensional K-invariant subspaces. For any g in a finite-dimensional K-invariant subspace of
![]() $L^2(K)$
and
$L^2(K)$
and
![]() $f\in L^\infty (Y)$
, the tensor
$f\in L^\infty (Y)$
, the tensor
![]() $f\otimes g$
lies in a
$f\otimes g$
lies in a
![]() $\Gamma $
-invariant finitely generated
$\Gamma $
-invariant finitely generated
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $L^2(Y\rtimes _\rho K)$
. The claim follows from Theorem 4.1.
$L^2(Y\rtimes _\rho K)$
. The claim follows from Theorem 4.1.
Remark 5.6. We call
![]() $(\mathcal {Y}_\alpha )_{\alpha \leq \beta }$
in Theorem 1.1 the Furstenberg tower associated to the
$(\mathcal {Y}_\alpha )_{\alpha \leq \beta }$
in Theorem 1.1 the Furstenberg tower associated to the
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
![]() $\mathcal {X}$
and call
$\mathcal {X}$
and call
![]() $\beta $
the length of this tower. If
$\beta $
the length of this tower. If
![]() $\mathcal {X}$
is a
$\mathcal {X}$
is a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system of countable complexity, then the length of the Furstenberg tower of
${\mathbf {PrbAlg}_\Gamma }$
-system of countable complexity, then the length of the Furstenberg tower of
![]() $\mathcal {X}$
must be a countable ordinal since
$\mathcal {X}$
must be a countable ordinal since
![]() $L^2(X)$
is separable. Beleznay and Foreman [Reference Beleznay and Foreman3] proved that any countable ordinal can be realized as the length of the Furstenberg tower of a
$L^2(X)$
is separable. Beleznay and Foreman [Reference Beleznay and Foreman3] proved that any countable ordinal can be realized as the length of the Furstenberg tower of a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system of countable complexity. By a transfinite recursion, we can build out of
${\mathbf {PrbAlg}_\Gamma }$
-system of countable complexity. By a transfinite recursion, we can build out of
![]() ${\mathbf {PrbAlg}_\Gamma }$
-group skew-products
${\mathbf {PrbAlg}_\Gamma }$
-group skew-products
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems of Furstenberg tower of arbitrary length (cf. Remark 5.5). We leave the details to the interested reader.
${\mathbf {PrbAlg}_\Gamma }$
-systems of Furstenberg tower of arbitrary length (cf. Remark 5.5). We leave the details to the interested reader.
Remark 5.7. Austin establishes a relatively ergodic version of Theorem 5.3 for systems of countable complexity in [Reference Austin2, §4]. We think that a significantly heavier application of the topos-theoretic machinery will prove a generalization of Austin’s result to systems of arbitrary (not necessarily countable) complexity. We hope to work out the details of this in future work.
6 Dichotomy
Given any
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system X, it is well known that
${\mathbf {PrbAlg}_\Gamma }$
-system X, it is well known that
![]() $L^2(X)$
is the orthogonal sum of the compact and weakly mixing factors of X, e.g., see Ch. 1.7 of the lecture notes [Reference Peterson40] by Peterson. This is an ergodic theoretic manifestation of the dichotomy between structure and randomness. In this section, we establish a relative or conditional version of this dichotomy for
$L^2(X)$
is the orthogonal sum of the compact and weakly mixing factors of X, e.g., see Ch. 1.7 of the lecture notes [Reference Peterson40] by Peterson. This is an ergodic theoretic manifestation of the dichotomy between structure and randomness. In this section, we establish a relative or conditional version of this dichotomy for
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extensions. Let us first define relatively weakly mixing functions and extensions.
${\mathbf {PrbAlg}_\Gamma }$
-extensions. Let us first define relatively weakly mixing functions and extensions.
Definition 6.1. Let
![]() $\mathcal {X}=(X,\mu ,T)$
and
$\mathcal {X}=(X,\mu ,T)$
and
![]() $\mathcal {Y}=(Y,\nu ,S)$
be
$\mathcal {Y}=(Y,\nu ,S)$
be
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems. Let
${\mathbf {PrbAlg}_\Gamma }$
-systems. Let
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
be a
$\pi :\mathcal {X}\to \mathcal {Y}$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension. A function
${\mathbf {PrbAlg}_\Gamma }$
-extension. A function
![]() $f\in L^2(X)$
with
$f\in L^2(X)$
with
![]() $\mathbb {E}(f|Y)=0$
is said to be relatively weakly mixing if for all
$\mathbb {E}(f|Y)=0$
is said to be relatively weakly mixing if for all
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
Moreover, we say that
![]() $\mathcal {X}$
is a relatively weakly mixing
$\mathcal {X}$
is a relatively weakly mixing
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension of
${\mathbf {PrbAlg}_\Gamma }$
-extension of
![]() $\mathcal {Y}$
if all
$\mathcal {Y}$
if all
![]() $f\in L^2(X)$
with
$f\in L^2(X)$
with
![]() $\mathbb {E}(f|Y)=0$
are relatively weakly mixing. Finally, we denote by
$\mathbb {E}(f|Y)=0$
are relatively weakly mixing. Finally, we denote by
![]() $\mathtt {WM}_{X|Y}$
the subspace of all relatively mixing functions in
$\mathtt {WM}_{X|Y}$
the subspace of all relatively mixing functions in
![]() $L^2(X)$
.
$L^2(X)$
.
We denote by
![]() $\mathtt {AP}_{X|Y}$
the
$\mathtt {AP}_{X|Y}$
the
![]() $L^2$
closure of all
$L^2$
closure of all
![]() $\Gamma $
-invariant finitely generated
$\Gamma $
-invariant finitely generated
![]() $L^\infty (Y)$
-submodules of
$L^\infty (Y)$
-submodules of
![]() $L^2(X)$
. The relative or conditional version of the classical dichotomy between the compact and weakly mixing parts of a system is
$L^2(X)$
. The relative or conditional version of the classical dichotomy between the compact and weakly mixing parts of a system is
where the sum is in the sense of the Hilbert space
![]() $L^2(X)$
. This relative dichotomy is well understood for systems of countable measure-theoretic complexity, e.g., see [Reference Tao44, §2.14] for an exposition in the case of
$L^2(X)$
. This relative dichotomy is well understood for systems of countable measure-theoretic complexity, e.g., see [Reference Tao44, §2.14] for an exposition in the case of
![]() $\mathbb {Z}$
-actions. Theorem 1.2 extends this relative dichotomy to systems of uncountable complexity which we restate next for the convenience of the reader.
$\mathbb {Z}$
-actions. Theorem 1.2 extends this relative dichotomy to systems of uncountable complexity which we restate next for the convenience of the reader.
Theorem 6.2. (Uncountable relative dichotomy)
Let
![]() $\mathcal {X}=(X,\mu ,T)$
and
$\mathcal {X}=(X,\mu ,T)$
and
![]() $\mathcal {Y}=(Y,\nu ,S)$
be
$\mathcal {Y}=(Y,\nu ,S)$
be
![]() ${\mathbf {PrbAlg}_\Gamma }$
-systems and
${\mathbf {PrbAlg}_\Gamma }$
-systems and
![]() $\pi : \mathcal {X}\to \mathcal {Y}$
be a
$\pi : \mathcal {X}\to \mathcal {Y}$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension. Exactly one of the following statements is true.
${\mathbf {PrbAlg}_\Gamma }$
-extension. Exactly one of the following statements is true.
-
(i)
 $\pi : \mathcal {X}\to \mathcal {Y}$
is a relatively weakly mixing
$\pi : \mathcal {X}\to \mathcal {Y}$
is a relatively weakly mixing
 ${\mathbf {PrbAlg}_\Gamma }$
-extension.
${\mathbf {PrbAlg}_\Gamma }$
-extension. -
(ii) There exist a
 ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
 $\mathcal {Z}=(Z,\unicode{x3bb} ,R)$
and
$\mathcal {Z}=(Z,\unicode{x3bb} ,R)$
and
 ${\mathbf {PrbAlg}_\Gamma }$
-extensions
${\mathbf {PrbAlg}_\Gamma }$
-extensions
 $\phi :\mathcal {X}\to \mathcal {Z}$
and
$\phi :\mathcal {X}\to \mathcal {Z}$
and
 $\psi :\mathcal {Z}\to \mathcal {Y}$
such that
$\psi :\mathcal {Z}\to \mathcal {Y}$
such that
 $\psi $
is a non-trivial relatively compact
$\psi $
is a non-trivial relatively compact
 ${\mathbf {PrbAlg}_\Gamma }$
-extension.
${\mathbf {PrbAlg}_\Gamma }$
-extension.
Proof. If (i) is false, there are
![]() $f\in L^2(X)$
with
$f\in L^2(X)$
with
![]() $\mathbb {E}(f|Y)=0$
and
$\mathbb {E}(f|Y)=0$
and
![]() $\varepsilon>0$
such that for all
$\varepsilon>0$
such that for all
![]() $\gamma \in \Gamma $
,
$\gamma \in \Gamma $
,
Let K be the unique element of minimal norm in the closed convex hull of
![]() $\mathtt {Orb}_\Gamma (f\otimes \bar f)$
. By Theorem 2.9, K is
$\mathtt {Orb}_\Gamma (f\otimes \bar f)$
. By Theorem 2.9, K is
![]() $\Gamma $
-invariant, and by equation (14), K is non-trivial. Since
$\Gamma $
-invariant, and by equation (14), K is non-trivial. Since
![]() $\mathbb {E}(f|Y)=0$
, there must exist
$\mathbb {E}(f|Y)=0$
, there must exist
![]() $g\in L^2(X)$
such that
$g\in L^2(X)$
such that
![]() $K\ast _Y g\in L^2(X)\backslash L^2(Y)$
. Let
$K\ast _Y g\in L^2(X)\backslash L^2(Y)$
. Let
![]() $\mathcal {A}=\{K\ast _Y g\in L^\infty (X): g\in L^2(X)\}$
. By Theorem 4.1, every
$\mathcal {A}=\{K\ast _Y g\in L^\infty (X): g\in L^2(X)\}$
. By Theorem 4.1, every
![]() $K\ast _Y g\in \mathcal {A}$
is contained in a closed
$K\ast _Y g\in \mathcal {A}$
is contained in a closed
![]() $\Gamma $
-invariant finitely generated
$\Gamma $
-invariant finitely generated
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $L^2(X)$
. It is not difficult to check that
$L^2(X)$
. It is not difficult to check that
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $\Gamma $
-invariant vector subspace of
$\Gamma $
-invariant vector subspace of
![]() $L^\infty (X)$
closed under complex conjugation and multiplication. Thus
$L^\infty (X)$
closed under complex conjugation and multiplication. Thus
![]() $\mathcal {A}$
has the structure of a
$\mathcal {A}$
has the structure of a
![]() ${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
-system such that
${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
-system such that
![]() $\Phi :\mathcal {A}\to L^\infty (X,\mu ,T)$
and
$\Phi :\mathcal {A}\to L^\infty (X,\mu ,T)$
and
![]() $\Psi :L^\infty (Y,\nu ,S)\to \mathcal {A}$
are
$\Psi :L^\infty (Y,\nu ,S)\to \mathcal {A}$
are
![]() ${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
-factors with
${\mathbf {CvNAlg}^\tau _{\Gamma ^{\operatorname {op}}}}$
-factors with
![]() $\Psi $
non-trivial. Then
$\Psi $
non-trivial. Then
![]() $(Z,\unicode{x3bb} , R):= \mathtt {Proj}(\mathcal {A})$
,
$(Z,\unicode{x3bb} , R):= \mathtt {Proj}(\mathcal {A})$
,
![]() $\phi := \mathtt {Proj}(\Phi )$
, and
$\phi := \mathtt {Proj}(\Phi )$
, and
![]() $\psi := \mathtt {Proj}(\Psi )$
satisfy (ii).
$\psi := \mathtt {Proj}(\Psi )$
satisfy (ii).
Now let f be relatively weakly mixing and
![]() $g\in \mathtt {AP}_{X|Y}$
. Without loss of generality, we may assume that f is bounded and g is an element of an invariant finitely generated
$g\in \mathtt {AP}_{X|Y}$
. Without loss of generality, we may assume that f is bounded and g is an element of an invariant finitely generated
![]() $L^\infty (Y)$
-submodule
$L^\infty (Y)$
-submodule
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $L^2(X)$
. For any
$L^2(X)$
. For any
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $h\in \mathcal {M}$
, we have
$h\in \mathcal {M}$
, we have
 $$ \begin{align*} &\|\langle f,g\rangle_{L^2(X|Y)}\|_{L^2(Y)}\\[3pt] &\quad=\|\langle (T^\gamma)^*f,(T^\gamma)^*g\rangle_{L^2(X|Y)}\|_{L^2(Y)}\\[3pt] &\quad\leq \|\langle (T^\gamma)^*f,(T^\gamma)^*g - h\rangle_{L^2(X|Y)}\|_{L^2(Y)}+\|\langle (T^\gamma)^*f,h\rangle_{L^2(X|Y)}\|_{L^2(Y)} \\[3pt] &\quad\leq \|\|(T^\gamma)^*f\|_{L^2(X|Y)}\|(T^\gamma)^*g - h\|_{L^2(X|Y)}\|_{L^2(Y)} +\|\langle (T^\gamma)^*f,h\rangle_{L^2(X|Y)}\|_{L^2(Y)} \\[3pt] &\quad\leq \|f\|_{L^\infty(X)}\|\|(T^\gamma)^*g - h\|_{L^2(X|Y)}\|_{L^2(Y)} + \|\langle (T^\gamma)^*f,h\rangle_{L^2(X|Y)}\|_{L^2(Y)}, \end{align*} $$
$$ \begin{align*} &\|\langle f,g\rangle_{L^2(X|Y)}\|_{L^2(Y)}\\[3pt] &\quad=\|\langle (T^\gamma)^*f,(T^\gamma)^*g\rangle_{L^2(X|Y)}\|_{L^2(Y)}\\[3pt] &\quad\leq \|\langle (T^\gamma)^*f,(T^\gamma)^*g - h\rangle_{L^2(X|Y)}\|_{L^2(Y)}+\|\langle (T^\gamma)^*f,h\rangle_{L^2(X|Y)}\|_{L^2(Y)} \\[3pt] &\quad\leq \|\|(T^\gamma)^*f\|_{L^2(X|Y)}\|(T^\gamma)^*g - h\|_{L^2(X|Y)}\|_{L^2(Y)} +\|\langle (T^\gamma)^*f,h\rangle_{L^2(X|Y)}\|_{L^2(Y)} \\[3pt] &\quad\leq \|f\|_{L^\infty(X)}\|\|(T^\gamma)^*g - h\|_{L^2(X|Y)}\|_{L^2(Y)} + \|\langle (T^\gamma)^*f,h\rangle_{L^2(X|Y)}\|_{L^2(Y)}, \end{align*} $$
where the second inequality follows from the conditional Cauchy–Schwarz inequality. For any
![]() $\delta>0$
, we can first choose h and then
$\delta>0$
, we can first choose h and then
![]() $\gamma $
such that the last term is
$\gamma $
such that the last term is
![]() $<\delta $
uniformly in
$<\delta $
uniformly in
![]() $\gamma $
. Hence
$\gamma $
. Hence
![]() $\|\langle f,g\rangle _{L^2(X|Y)}\|_{L^2(Y)}=0$
, and thus
$\|\langle f,g\rangle _{L^2(X|Y)}\|_{L^2(Y)}=0$
, and thus
![]() $\langle f,g\rangle _{L^2(X)}=0$
. It remains to show that if
$\langle f,g\rangle _{L^2(X)}=0$
. It remains to show that if
![]() $f\not \in \mathtt {WM}_{X|Y}$
, then f must correlate with some
$f\not \in \mathtt {WM}_{X|Y}$
, then f must correlate with some
![]() $g\in \mathtt {AP}_{X|Y}$
, but this follows by a similar argument as in the first part of the proof.
$g\in \mathtt {AP}_{X|Y}$
, but this follows by a similar argument as in the first part of the proof.
Remark 6.3. A
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension
${\mathbf {PrbAlg}_\Gamma }$
-extension
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
is said to be relatively ergodic if
$\pi :\mathcal {X}\to \mathcal {Y}$
is said to be relatively ergodic if
![]() $\mathtt {Inv}_\Gamma (\mathcal {X})=\mathtt {Inv}_\Gamma (\mathcal {Y})$
(after identifying
$\mathtt {Inv}_\Gamma (\mathcal {X})=\mathtt {Inv}_\Gamma (\mathcal {Y})$
(after identifying
![]() $\mathtt {Inv}_\Gamma (\mathcal {Y})$
with a subalgebra of
$\mathtt {Inv}_\Gamma (\mathcal {Y})$
with a subalgebra of
![]() $\mathcal {X}$
). Using the relative dichotomy in equation (13), it is not difficult to show that a
$\mathcal {X}$
). Using the relative dichotomy in equation (13), it is not difficult to show that a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension
${\mathbf {PrbAlg}_\Gamma }$
-extension
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
is relatively weakly mixing if and only if
$\pi :\mathcal {X}\to \mathcal {Y}$
is relatively weakly mixing if and only if
![]() $\mathcal {X}\times _{\mathcal {Y}} \mathcal {X}$
is a relatively ergodic extension of
$\mathcal {X}\times _{\mathcal {Y}} \mathcal {X}$
is a relatively ergodic extension of
![]() $\mathcal {Y}$
.
$\mathcal {Y}$
.
Remark 6.4. The relative dichotomy in equation (13) can be extended to a conditional Halmos–von Neumann-type decomposition of the conditional Hilbert space
![]() $\mathtt {L^2(X|Y)}$
, which is the external interpretation of the internal Halmos–von Neumann theorem of the topos
$\mathtt {L^2(X|Y)}$
, which is the external interpretation of the internal Halmos–von Neumann theorem of the topos
![]() $\mathtt {Sh}(Y)$
. In fact, this provides an alternative route to the proof of Theorem 6.2. To be more precise, construct from a
$\mathtt {Sh}(Y)$
. In fact, this provides an alternative route to the proof of Theorem 6.2. To be more precise, construct from a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension
${\mathbf {PrbAlg}_\Gamma }$
-extension
![]() $\pi :\mathcal {X}\to \mathcal {Y}$
an internal measure-preserving dynamical system in
$\pi :\mathcal {X}\to \mathcal {Y}$
an internal measure-preserving dynamical system in
![]() $\mathtt {Sh}(Y)$
(see Remark 4.3), apply to that internal system the internal Halmos–von Neumann theorem, and then externally interpret the resulting internal orthogonal decomposition. This reasoning, which basically reduces to a translation process between the external and internal universes, is enabled by a logical Boolean transfer principle powerful enough to yield a Halmos–von Neumann theorem in the internal logic of the topos
$\mathtt {Sh}(Y)$
(see Remark 4.3), apply to that internal system the internal Halmos–von Neumann theorem, and then externally interpret the resulting internal orthogonal decomposition. This reasoning, which basically reduces to a translation process between the external and internal universes, is enabled by a logical Boolean transfer principle powerful enough to yield a Halmos–von Neumann theorem in the internal logic of the topos
![]() $\mathtt {Sh}(Y)$
. In fact, the above proof of Theorem 6.2 is a reflection and validation of this transfer principle.
$\mathtt {Sh}(Y)$
. In fact, the above proof of Theorem 6.2 is a reflection and validation of this transfer principle.
We can use Theorem 6.2 to prove our main result, Theorem 1.1, which we now restate.
Theorem 6.5. Let
![]() $\mathcal {X}=(X,\mu ,T)$
be a
$\mathcal {X}=(X,\mu ,T)$
be a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system. Then there is an ordinal number
${\mathbf {PrbAlg}_\Gamma }$
-system. Then there is an ordinal number
![]() $\beta $
such that for each ordinal number
$\beta $
such that for each ordinal number
![]() $\alpha \leq \beta $
, there are a
$\alpha \leq \beta $
, there are a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
![]() $\mathcal {Y}_\alpha =(Y_\alpha ,\nu _\alpha ,S_\alpha )$
and a
$\mathcal {Y}_\alpha =(Y_\alpha ,\nu _\alpha ,S_\alpha )$
and a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor
${\mathbf {PrbAlg}_\Gamma }$
-factor
![]() $\pi _\alpha \colon \mathcal {X}\to \mathcal {Y}_\alpha $
, and for every successor ordinal number
$\pi _\alpha \colon \mathcal {X}\to \mathcal {Y}_\alpha $
, and for every successor ordinal number
![]() $\alpha +1\leq \beta $
, there is a
$\alpha +1\leq \beta $
, there is a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor
${\mathbf {PrbAlg}_\Gamma }$
-factor
![]() $\pi _{\alpha +1,\alpha } \colon \mathcal {Y}_{\alpha +1}\to \mathcal {Y}_{\alpha }$
with the following properties:
$\pi _{\alpha +1,\alpha } \colon \mathcal {Y}_{\alpha +1}\to \mathcal {Y}_{\alpha }$
with the following properties:
-
(i)
 $Y_0$
is the trivial algebra;
$Y_0$
is the trivial algebra; -
(ii)
 $\pi _{\alpha +1,\alpha } \colon \mathcal {Y}_{\alpha +1}\to \mathcal {Y}_{\alpha }$
is a non-trivial relatively compact
$\pi _{\alpha +1,\alpha } \colon \mathcal {Y}_{\alpha +1}\to \mathcal {Y}_{\alpha }$
is a non-trivial relatively compact
 ${\mathbf {PrbAlg}_\Gamma }$
-extension;
${\mathbf {PrbAlg}_\Gamma }$
-extension; -
(iii)
 $\mathcal {Y}_\alpha $
is the inverse limit of the systems
$\mathcal {Y}_\alpha $
is the inverse limit of the systems
 $\mathcal {Y}_{\eta }$
,
$\mathcal {Y}_{\eta }$
,
 $\eta <\alpha $
for every limit ordinal number
$\eta <\alpha $
for every limit ordinal number
 $\alpha \leq \beta $
, in the sense that
$\alpha \leq \beta $
, in the sense that
 $Y_\alpha $
is generated by
$Y_\alpha $
is generated by
 $\bigcup _{\eta <\alpha } Y_\eta $
as a
$\bigcup _{\eta <\alpha } Y_\eta $
as a
 $\sigma $
-complete Boolean algebra;
$\sigma $
-complete Boolean algebra; -
(iv)
 $\pi _{\beta } \colon \mathcal {X}\to \mathcal {Y}_\beta $
is a relatively weakly mixing
$\pi _{\beta } \colon \mathcal {X}\to \mathcal {Y}_\beta $
is a relatively weakly mixing
 ${\mathbf {PrbAlg}_\Gamma }$
-extension.
${\mathbf {PrbAlg}_\Gamma }$
-extension.
Proof. Let
![]() $\mathcal {Y}_0$
be the trivial
$\mathcal {Y}_0$
be the trivial
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system, and let
${\mathbf {PrbAlg}_\Gamma }$
-system, and let
![]() $\pi _0\colon \mathcal {X}\to \mathcal {Y}_0$
be the corresponding
$\pi _0\colon \mathcal {X}\to \mathcal {Y}_0$
be the corresponding
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factor map. By Theorem 6.2,
${\mathbf {PrbAlg}_\Gamma }$
-factor map. By Theorem 6.2,
![]() $\pi _0\colon \mathcal {X}\to \mathcal {Y}_0$
is either a relatively weakly mixing
$\pi _0\colon \mathcal {X}\to \mathcal {Y}_0$
is either a relatively weakly mixing
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension, in which case we set
${\mathbf {PrbAlg}_\Gamma }$
-extension, in which case we set
![]() $\beta =0$
, or there are a
$\beta =0$
, or there are a
![]() ${\mathbf {PrbAlg}_\Gamma }$
-system
${\mathbf {PrbAlg}_\Gamma }$
-system
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extensions
${\mathbf {PrbAlg}_\Gamma }$
-extensions
![]() $\phi \colon \mathcal {X}\to \mathcal {Z}$
and
$\phi \colon \mathcal {X}\to \mathcal {Z}$
and
![]() $\psi \colon \mathcal {Z}\to \mathcal {Y}_0$
such that
$\psi \colon \mathcal {Z}\to \mathcal {Y}_0$
such that
![]() $\psi \colon \mathcal {Z} \to \mathcal {Y}_0$
is a non-trivial relatively compact
$\psi \colon \mathcal {Z} \to \mathcal {Y}_0$
is a non-trivial relatively compact
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension of
${\mathbf {PrbAlg}_\Gamma }$
-extension of
![]() $\mathcal {Y}_0$
. Then set
$\mathcal {Y}_0$
. Then set
![]() $\mathcal {Y}_1:= \mathtt {AP_{X|Y_0}}$
, let
$\mathcal {Y}_1:= \mathtt {AP_{X|Y_0}}$
, let
![]() $\pi _1\colon \mathcal {X}\to \mathcal {Y}_1$
and
$\pi _1\colon \mathcal {X}\to \mathcal {Y}_1$
and
![]() $\pi _{1,0}\colon \mathcal {Y}_1\to \mathcal {Y}_0$
be the corresponding
$\pi _{1,0}\colon \mathcal {Y}_1\to \mathcal {Y}_0$
be the corresponding
![]() ${\mathbf {PrbAlg}_\Gamma }$
-factors, and repeat the previous step with
${\mathbf {PrbAlg}_\Gamma }$
-factors, and repeat the previous step with
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}_1$
instead of
$\mathcal {Y}_1$
instead of
![]() $\mathcal {Y}_0$
using Theorem 6.2. This process may end here if
$\mathcal {Y}_0$
using Theorem 6.2. This process may end here if
![]() $\pi _1\colon \mathcal {X}\to \mathcal {Y}_1$
is a relatively weakly mixing
$\pi _1\colon \mathcal {X}\to \mathcal {Y}_1$
is a relatively weakly mixing
![]() ${\mathbf {PrbAlg}_\Gamma }$
-extension and we set
${\mathbf {PrbAlg}_\Gamma }$
-extension and we set
![]() $\beta =1$
, or we may need to continue and repeat the previous step again. Now repeating the previous steps in a transfinite recursion, while passing to inverse limits at limit ordinals, this process will eventually terminate at an ordinal number
$\beta =1$
, or we may need to continue and repeat the previous step again. Now repeating the previous steps in a transfinite recursion, while passing to inverse limits at limit ordinals, this process will eventually terminate at an ordinal number
![]() $\beta $
.
$\beta $
.
Acknowledgements
A.J. was supported by DFG-research fellowship JA 2512/3-1. A.J. offers his thanks to Terence Tao for suggesting this project, many helpful discussions, and his encouragement and support. He is grateful to Pieter Spaas for several helpful discussions. A.J. thanks Markus Haase for organizing an online workshop on structural ergodic theory where the results of this paper and the parallel work [Reference Edeko, Haase and Kreidler11] could be discussed, and Nikolai Edeko, Markus Haase, and Henrik Kreidler for helpful comments on an early version of the manuscript. A.J. is indebted to the anonymous referee for several useful suggestions and corrections.
A Appendix. A conditional spectral analysis
In this appendix, we collect some auxiliary results needed in the proof of Lemma 4.4. The notation is the same as in §3.
Definition A.1. (Conditional orthonormal sets)
A set M in
![]() $\mathtt {L^2(X|Y)}$
is said to be conditional orthonormal if and only if
$\mathtt {L^2(X|Y)}$
is said to be conditional orthonormal if and only if
![]() $\langle f,g\rangle _{L^2(X|Y)}=0$
for all
$\langle f,g\rangle _{L^2(X|Y)}=0$
for all
![]() $f,g\in M$
and
$f,g\in M$
and
![]() $\langle f,f\rangle _{L^2(X|Y)}=1_E$
for some
$\langle f,f\rangle _{L^2(X|Y)}=1_E$
for some
![]() $E\in Y$
for all
$E\in Y$
for all
![]() $f\in M$
(where E may depend on f).
$f\in M$
(where E may depend on f).
Lemma A.2. Let
![]() $K\in L^\infty (X\times _Y X)$
, and let M be a countable conditional orthonormal set. Then
$K\in L^\infty (X\times _Y X)$
, and let M be a countable conditional orthonormal set. Then
![]() $\sum _{f\in M} \|K\ast _Y f\|^2_{L^2(X)}<\infty $
.
$\sum _{f\in M} \|K\ast _Y f\|^2_{L^2(X)}<\infty $
.
Proof. Applying Bessel’s inequality pointwise almost everywhere, we have
 $$ \begin{align*}\sum_{f\in M} |(K\ast_Y f)(x)|^2\leq \|K(x,\cdot)\|_{L^2(X|Y)}^2(\tilde{\pi}(x))<C,\end{align*} $$
$$ \begin{align*}\sum_{f\in M} |(K\ast_Y f)(x)|^2\leq \|K(x,\cdot)\|_{L^2(X|Y)}^2(\tilde{\pi}(x))<C,\end{align*} $$
where
![]() $|K|^2$
is bounded by the constant
$|K|^2$
is bounded by the constant
![]() $C>0$
. The claim follows from the monotone convergence theorem.
$C>0$
. The claim follows from the monotone convergence theorem.
Remark A.3. The assumption that M has countable cardinality, which guarantees measurability when applying a pointwise argument, can be removed from Lemma A.2 as follows. Instead of using Bessel’s inequality pointwise, we could apply a conditional version of Bessel’s inequality for arbitrary conditional orthonormal sets. This conditional version of Bessel’s inequality is an interpretation of the internal
![]() $\mathtt {Sh}(Y)$
-Bessel’s inequality. However, we do not need this stronger version of the conditional Bessel’s inequality here.
$\mathtt {Sh}(Y)$
-Bessel’s inequality. However, we do not need this stronger version of the conditional Bessel’s inequality here.
We need a slight modification of some results in [Reference Kerr and Li36, Appendix C].
Lemma A.4. (Cf. [Reference Kerr and Li36, Lemma C.10])
Let
![]() $f\in L^2(X)$
be non-zero. Then for every
$f\in L^2(X)$
be non-zero. Then for every
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $g\in L^\infty (Y) f$
such that
$g\in L^\infty (Y) f$
such that
![]() $\langle g,g\rangle _{L^2(X|Y)}=1_E$
for some non-zero
$\langle g,g\rangle _{L^2(X|Y)}=1_E$
for some non-zero
![]() $E\in Y$
and
$E\in Y$
and
![]() $\|f-\langle f,g\rangle _{L^2(X|Y)}g\|_{L^2(X)}<\varepsilon $
.
$\|f-\langle f,g\rangle _{L^2(X|Y)}g\|_{L^2(X)}<\varepsilon $
.
Proof. Let
![]() $E_N=\{y\in \tilde {Y}\colon 0<\|f\|_{L^2(X|Y)}(y)\leq N\}$
for an integer
$E_N=\{y\in \tilde {Y}\colon 0<\|f\|_{L^2(X|Y)}(y)\leq N\}$
for an integer
![]() $N\geq 1$
. Next, choose N large enough such that
$N\geq 1$
. Next, choose N large enough such that
![]() $\|f 1_{E_N^c}\|_{L^2(X)}=\|\|f\|_{L^2(X|Y)}1_{E_N^c}\|_{L^2(Y)}<\varepsilon $
. Put
$\|f 1_{E_N^c}\|_{L^2(X)}=\|\|f\|_{L^2(X|Y)}1_{E_N^c}\|_{L^2(Y)}<\varepsilon $
. Put
![]() $E=E_N$
and define
$E=E_N$
and define
![]() $h\in L^\infty (Y)$
by
$h\in L^\infty (Y)$
by
![]() $1_E h^2 \langle f,f\rangle _{L^2(X|Y)}=1_E$
. Then
$1_E h^2 \langle f,f\rangle _{L^2(X|Y)}=1_E$
. Then
![]() $g:= 1_E hf$
has the desired properties.
$g:= 1_E hf$
has the desired properties.
Lemma A.5. (Cf. [Reference Kerr and Li36, Lemma C.14])
Let
![]() $K\in L^\infty (X\times _Y X)$
, and let
$K\in L^\infty (X\times _Y X)$
, and let
![]() $\mathcal {H}$
be a closed
$\mathcal {H}$
be a closed
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $L^2(X)$
. Then
$L^2(X)$
. Then
![]() $K\ast _Y\colon \mathcal {H}\to \mathcal {H}$
is a bounded
$K\ast _Y\colon \mathcal {H}\to \mathcal {H}$
is a bounded
![]() $L^\infty (Y)$
-linear operator. Moreover, its classical operator norm can be computed as
$L^\infty (Y)$
-linear operator. Moreover, its classical operator norm can be computed as
 $$ \begin{align*} \|K\ast_Y \| := &\sup\{\|K\ast_Y f\|_{L^2(X)} \mid f\in \mathcal{H}, \ \|f\|_{L^2(X)} \leq 1\}\\ = &\sup\{\|K\ast_Y f\|_{L^2(X)} \mid f\in \mathcal{H},\ \langle f,f\rangle_{L^2(X|Y)}=1_E \text{ for some } E\in Y\}. \end{align*} $$
$$ \begin{align*} \|K\ast_Y \| := &\sup\{\|K\ast_Y f\|_{L^2(X)} \mid f\in \mathcal{H}, \ \|f\|_{L^2(X)} \leq 1\}\\ = &\sup\{\|K\ast_Y f\|_{L^2(X)} \mid f\in \mathcal{H},\ \langle f,f\rangle_{L^2(X|Y)}=1_E \text{ for some } E\in Y\}. \end{align*} $$
Proof. By definition,
![]() $K\ast _Y$
is
$K\ast _Y$
is
![]() $L^\infty (Y)$
-linear (meaning that
$L^\infty (Y)$
-linear (meaning that
![]() $K\ast _Y(gf)=gK_\ast (f)$
for all
$K\ast _Y(gf)=gK_\ast (f)$
for all
![]() $f\in \mathcal {H}, g\in L^\infty (Y)$
). By equation (8), the operator norm
$f\in \mathcal {H}, g\in L^\infty (Y)$
). By equation (8), the operator norm
![]() $\|K\ast _Y \|\leq \|K\|_{L^\infty (X\times _Y X)}$
, and thus
$\|K\ast _Y \|\leq \|K\|_{L^\infty (X\times _Y X)}$
, and thus
![]() $K\ast _Y\colon \mathcal {H}\to \mathcal {H}$
is a bounded operator.
$K\ast _Y\colon \mathcal {H}\to \mathcal {H}$
is a bounded operator.
Now fix
![]() $\varepsilon>0$
. Then there is a non-zero
$\varepsilon>0$
. Then there is a non-zero
![]() $f\in \mathcal {H}$
with
$f\in \mathcal {H}$
with
![]() $\|f\|_{L^2(X)} \leq 1$
such that
$\|f\|_{L^2(X)} \leq 1$
such that
![]() $\|K\ast _Y f\|_{L^2(X)} \geq \|K\ast _Y \|-{\varepsilon }/{2}$
. For any
$\|K\ast _Y f\|_{L^2(X)} \geq \|K\ast _Y \|-{\varepsilon }/{2}$
. For any
![]() $\delta>0$
, using Lemma A.2, we can find
$\delta>0$
, using Lemma A.2, we can find
![]() $g\in L^\infty (Y)f$
such that
$g\in L^\infty (Y)f$
such that
![]() $\langle g,g\rangle _{L^2(X|Y)}=1_E$
for some non-zero
$\langle g,g\rangle _{L^2(X|Y)}=1_E$
for some non-zero
![]() $E\in Y$
and
$E\in Y$
and
![]() $\|f\kern-2pt -\kern-2pt \langle f,g\rangle _{L^2(X|Y)}g\|_{L^2(X)}\!<\delta $
. We obtain
$\|f\kern-2pt -\kern-2pt \langle f,g\rangle _{L^2(X|Y)}g\|_{L^2(X)}\!<\delta $
. We obtain
Upon taking
![]() $\delta $
small enough, we can thus ensure that
$\delta $
small enough, we can thus ensure that
Meanwhile, we obtain from the conditional Cauchy–Schwarz inequality (7):
 $$ \begin{align*} \|\langle f,g\rangle_{L^2(X|Y)}\|^2_{L^2(Y)} &= \int_{Y} |\langle f,g\rangle_{L^2(X|Y)}|^2 \,d\nu \\ &\leq \int_Y \|f\|_{L^2(X|Y)}^2 \|g\|_{L^2(X|Y)}^2 \,d\nu \\ &\leq 1. \end{align*} $$
$$ \begin{align*} \|\langle f,g\rangle_{L^2(X|Y)}\|^2_{L^2(Y)} &= \int_{Y} |\langle f,g\rangle_{L^2(X|Y)}|^2 \,d\nu \\ &\leq \int_Y \|f\|_{L^2(X|Y)}^2 \|g\|_{L^2(X|Y)}^2 \,d\nu \\ &\leq 1. \end{align*} $$
Putting things together, we get
 $$ \begin{align*} \|K\ast_Y g\|_{L^2(X)} &\geq \|\langle f,g\rangle_{L^2(X|Y)}\|_{L^2(Y)} \|K\ast_Y g\|_{L^2(X)}\\ &\geq \|K\ast_Y(\langle f,g\rangle_{L^2(X|Y)} g)\|_{L^2(X)} \geq \|K\ast_Y \|-\varepsilon,\end{align*} $$
$$ \begin{align*} \|K\ast_Y g\|_{L^2(X)} &\geq \|\langle f,g\rangle_{L^2(X|Y)}\|_{L^2(Y)} \|K\ast_Y g\|_{L^2(X)}\\ &\geq \|K\ast_Y(\langle f,g\rangle_{L^2(X|Y)} g)\|_{L^2(X)} \geq \|K\ast_Y \|-\varepsilon,\end{align*} $$
which finishes the proof of the lemma.
The following proposition will serve us as a substitute of a conditional version of the spectral theorem (when combined with spectral projections).
Proposition A.6. (Cf. [Reference Kerr and Li36, Proposition C.15])
Let
![]() $K\in L^\infty (X\times _Y X)$
, let
$K\in L^\infty (X\times _Y X)$
, let
![]() $\mathcal {H}_0$
be a closed
$\mathcal {H}_0$
be a closed
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $L^2(X)$
, and let
$L^2(X)$
, and let
![]() $\varepsilon>0$
be arbitrary. Then there is a finite conditional orthonormal set
$\varepsilon>0$
be arbitrary. Then there is a finite conditional orthonormal set
![]() $M\subset \mathcal {H}_0$
such that
$M\subset \mathcal {H}_0$
such that
![]() $\|K\ast _Y f\|_{L^2(X)} \leq \varepsilon \|f\|_{L^2(X)}$
for every
$\|K\ast _Y f\|_{L^2(X)} \leq \varepsilon \|f\|_{L^2(X)}$
for every
![]() $f\in \mathcal {H}_0$
which is conditionally orthogonal to M.
$f\in \mathcal {H}_0$
which is conditionally orthogonal to M.
Proof. For notational convenience, we denote
![]() $U:= K\ast _Y$
. Note that
$U:= K\ast _Y$
. Note that
![]() $U:\mathcal {H}_0\to \mathcal {H}_0$
is a bounded and
$U:\mathcal {H}_0\to \mathcal {H}_0$
is a bounded and
![]() $L^\infty (Y)$
-linear operator. Fix
$L^\infty (Y)$
-linear operator. Fix
![]() $\varepsilon>0$
. By the previous Lemma A.5, we can find
$\varepsilon>0$
. By the previous Lemma A.5, we can find
![]() $f_1\in \mathcal {H}_0$
such that
$f_1\in \mathcal {H}_0$
such that
![]() $\|U(f_1)\|_{L^2(X)} \geq \|U\|-{\varepsilon }/{2}$
and
$\|U(f_1)\|_{L^2(X)} \geq \|U\|-{\varepsilon }/{2}$
and
![]() $\langle f_1,f_1\rangle _{L^2(X|Y)}=1_{E_1}$
for some non-zero
$\langle f_1,f_1\rangle _{L^2(X|Y)}=1_{E_1}$
for some non-zero
![]() $E_1\in Y$
. Let
$E_1\in Y$
. Let
![]() $\mathcal {H}_1=\{g\in \mathcal {H}_0\colon \langle f_1,g\rangle _{L^2(X|Y)}=0\}$
, and note that
$\mathcal {H}_1=\{g\in \mathcal {H}_0\colon \langle f_1,g\rangle _{L^2(X|Y)}=0\}$
, and note that
![]() $\mathcal {H}_1$
is a closed
$\mathcal {H}_1$
is a closed
![]() $L^\infty (Y)$
-submodule of
$L^\infty (Y)$
-submodule of
![]() $\mathcal {H}_0$
. We consider the restriction
$\mathcal {H}_0$
. We consider the restriction
![]() $U_1$
of U to
$U_1$
of U to
![]() $\mathcal {H}_1$
. We can apply again Lemma A.5 now to
$\mathcal {H}_1$
. We can apply again Lemma A.5 now to
![]() $U_1\colon \mathcal {H}_1\to \mathcal {H}_1$
to find
$U_1\colon \mathcal {H}_1\to \mathcal {H}_1$
to find
![]() $f_2\in \mathcal {H}_1$
such that
$f_2\in \mathcal {H}_1$
such that
![]() $\|U_1(f_2)\|_{L^2(X)} \geq \|U_1\|-{\varepsilon }/{2}$
and
$\|U_1(f_2)\|_{L^2(X)} \geq \|U_1\|-{\varepsilon }/{2}$
and
![]() $\langle f_2,f_2\rangle _{L^2(X|Y)}=1_{E_2}$
for some non-zero
$\langle f_2,f_2\rangle _{L^2(X|Y)}=1_{E_2}$
for some non-zero
![]() $E_2\in Y$
. Continuing in this way, we can construct a conditional orthonormal sequence
$E_2\in Y$
. Continuing in this way, we can construct a conditional orthonormal sequence
![]() $\{f_n\}_{n\in \mathbb {N}}$
such that
$\{f_n\}_{n\in \mathbb {N}}$
such that
![]() $\|U_n(f_{n+1})\|_{L^2(X)} \geq \|U_n\|-{\varepsilon }/{2}$
, where
$\|U_n(f_{n+1})\|_{L^2(X)} \geq \|U_n\|-{\varepsilon }/{2}$
, where
![]() $\mathcal {H}_n = \{g\in \mathcal {H}_{0}\colon \langle f_k,g\rangle _{L^2(X|Y)}=0, \text {for all } k=1,\ldots , n\}$
and
$\mathcal {H}_n = \{g\in \mathcal {H}_{0}\colon \langle f_k,g\rangle _{L^2(X|Y)}=0, \text {for all } k=1,\ldots , n\}$
and
![]() $f_{n+1}\in \mathcal {H}_n$
. By Lemma A.2, we can take n large enough so that
$f_{n+1}\in \mathcal {H}_n$
. By Lemma A.2, we can take n large enough so that
![]() $\|U(f_n)\|_{L^2(X)}\leq {\varepsilon }/{2}$
, and thus
$\|U(f_n)\|_{L^2(X)}\leq {\varepsilon }/{2}$
, and thus
![]() $\|U_n\|\leq \varepsilon $
. Then
$\|U_n\|\leq \varepsilon $
. Then
![]() $M= \{f_1, \ldots , f_n\}$
satisfies the desired proof.
$M= \{f_1, \ldots , f_n\}$
satisfies the desired proof.

















