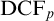1 Introduction
In this paper we investigate model-theoretically the so-called derivations of the Frobenius map building on results by Kowalski in [Reference Kowalski4]. Let K be a field of characteristic
![]() $p>0$
and let n be a natural number. A derivation of the n-th power of Frobenius map on K is an additive map
$p>0$
and let n be a natural number. A derivation of the n-th power of Frobenius map on K is an additive map
![]() $\partial \colon K\to K$
satisfying the following twisted Leibniz rule
$\partial \colon K\to K$
satisfying the following twisted Leibniz rule
for
![]() $x,y\in K$
. In [Reference Kowalski4] they are also called n-derivations for short, but we choose a more expressive name
$x,y\in K$
. In [Reference Kowalski4] they are also called n-derivations for short, but we choose a more expressive name
![]() $\operatorname {\mathrm {Fr}}^n$
-derivation. If
$\operatorname {\mathrm {Fr}}^n$
-derivation. If
![]() $D\colon K\to K$
is a derivation in the usual sense, then
$D\colon K\to K$
is a derivation in the usual sense, then
![]() $\operatorname {\mathrm {Fr}}^n\circ D$
is a
$\operatorname {\mathrm {Fr}}^n\circ D$
is a
![]() $\operatorname {\mathrm {Fr}}^n$
-derivation, but most
$\operatorname {\mathrm {Fr}}^n$
-derivation, but most
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations do not come from usual derivations.
$\operatorname {\mathrm {Fr}}^n$
-derivations do not come from usual derivations.
Derivations of the Frobenius map have some reasonable model theory, which was explored in [Reference Kowalski4]. In particular, the theory of fields with a
![]() $\operatorname {\mathrm {Fr}}^n$
-derivation (or
$\operatorname {\mathrm {Fr}}^n$
-derivation (or
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields for short) has a model companion, this model companion is strictly stable and eliminates quantifiers in a natural language (details below). In this paper we establish some further algebraic and model-theoretic properties of
$\operatorname {\mathrm {Fr}}^n$
-differential fields for short) has a model companion, this model companion is strictly stable and eliminates quantifiers in a natural language (details below). In this paper we establish some further algebraic and model-theoretic properties of
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations and answer the six questions stated in [Reference Kowalski4].
$\operatorname {\mathrm {Fr}}^n$
-derivations and answer the six questions stated in [Reference Kowalski4].
We now recall some definitions and facts from [Reference Kowalski4]. Fix a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field
$\operatorname {\mathrm {Fr}}^n$
-differential field
![]() $\left ( K, \partial \right )$
of characteristic
$\left ( K, \partial \right )$
of characteristic
![]() $p>0$
. The kernel of
$p>0$
. The kernel of
![]() $\partial $
, called the constants of
$\partial $
, called the constants of
![]() $\left ( K, \partial \right )$
, is denoted by
$\left ( K, \partial \right )$
, is denoted by
![]() $K^\partial $
and it is a field extension of
$K^\partial $
and it is a field extension of
![]() $K^p$
. We call
$K^p$
. We call
![]() $\left ( K, \partial \right )$
strict if
$\left ( K, \partial \right )$
strict if
![]() $K^\partial = K^p$
. There is an obvious notion of
$K^\partial = K^p$
. There is an obvious notion of
![]() $\operatorname {\mathrm {Fr}}^n$
-differential extensions and any
$\operatorname {\mathrm {Fr}}^n$
-differential extensions and any
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field has a strict
$\operatorname {\mathrm {Fr}}^n$
-differential field has a strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential extension (Lemma 1.9 in [Reference Kowalski4]). Moreover, derivations of the Frobenius map extend to separable field extensions and for algebraic extensions this extension is unique. We call a
$\operatorname {\mathrm {Fr}}^n$
-differential extension (Lemma 1.9 in [Reference Kowalski4]). Moreover, derivations of the Frobenius map extend to separable field extensions and for algebraic extensions this extension is unique. We call a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field differentially perfect, if any of its
$\operatorname {\mathrm {Fr}}^n$
-differential field differentially perfect, if any of its
![]() $\operatorname {\mathrm {Fr}}^n$
-differential extension is separable. Since there is always a strict extension, we have that any differentially perfect field is strict. Lemma 2.1 says that the converse also holds.
$\operatorname {\mathrm {Fr}}^n$
-differential extension is separable. Since there is always a strict extension, we have that any differentially perfect field is strict. Lemma 2.1 says that the converse also holds.
An important property of derivations of the Frobenius, which we will use a few times, is the following: for
![]() $m, n>0$
, the composition of an
$m, n>0$
, the composition of an
![]() $\operatorname {\mathrm {Fr}}^m$
-derivation and an
$\operatorname {\mathrm {Fr}}^m$
-derivation and an
![]() $\operatorname {\mathrm {Fr}}^n$
-derivation is an
$\operatorname {\mathrm {Fr}}^n$
-derivation is an
![]() $\operatorname {\mathrm {Fr}}^{m+n}$
-derivation. This does not hold for usual derivations, as compositions of derivations produces “operators of higher order” (a Hasse-Schmidt derivation).
$\operatorname {\mathrm {Fr}}^{m+n}$
-derivation. This does not hold for usual derivations, as compositions of derivations produces “operators of higher order” (a Hasse-Schmidt derivation).
Let
![]() $L^\partial $
be the language of fields together with one unary function symbol
$L^\partial $
be the language of fields together with one unary function symbol
![]() $\partial $
. Clearly, there is an
$\partial $
. Clearly, there is an
![]() $L^\partial $
-theory
$L^\partial $
-theory
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
(called
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
(called
![]() $\operatorname {DF}_{p,n}$
in [Reference Kowalski4]), whose models are precisely
$\operatorname {DF}_{p,n}$
in [Reference Kowalski4]), whose models are precisely
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field of characteristic p. We can and will also consider this theory in the languages
$\operatorname {\mathrm {Fr}}^n$
-differential field of characteristic p. We can and will also consider this theory in the languages
![]() $L^\partial _\lambda $
and
$L^\partial _\lambda $
and
![]() $L^\partial _{\lambda _0}$
, where we add the function symbols for the
$L^\partial _{\lambda _0}$
, where we add the function symbols for the
![]() $\lambda $
-functions and only
$\lambda $
-functions and only
![]() $\lambda _0$
respectively (see [Reference Chatzidakis2, Section 1.8] for the definition of
$\lambda _0$
respectively (see [Reference Chatzidakis2, Section 1.8] for the definition of
![]() $\lambda $
-functions). Recall that
$\lambda $
-functions). Recall that
![]() $\lambda _0$
is interpreted in a field K as a function, which is the inverse of the Frobenius on
$\lambda _0$
is interpreted in a field K as a function, which is the inverse of the Frobenius on
![]() $K^p$
and zero everywhere else. The theory
$K^p$
and zero everywhere else. The theory
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
has a model companion in the language
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
has a model companion in the language
![]() $L^\partial $
, which we call
$L^\partial $
, which we call
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. The axioms of this theory are geometric (see the beginning of Section 2 in [Reference Kowalski4]), of a similar form as the geometric axioms for
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. The axioms of this theory are geometric (see the beginning of Section 2 in [Reference Kowalski4]), of a similar form as the geometric axioms for
![]() $\operatorname {\mathrm {DCF}}_0$
(see [Reference Pierce and Pillay7]). Unfortunately, there is an unnaturally looking assumption in the geometric axioms of
$\operatorname {\mathrm {DCF}}_0$
(see [Reference Pierce and Pillay7]). Unfortunately, there is an unnaturally looking assumption in the geometric axioms of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
about the density of a certain equalizer. The results of this paper provide a more elegant geometric axiomatization of
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
about the density of a certain equalizer. The results of this paper provide a more elegant geometric axiomatization of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. A possibility for such an axiomatization was also the content of Question 4 in [Reference Kowalski4]. Since we will only use the fact that
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. A possibility for such an axiomatization was also the content of Question 4 in [Reference Kowalski4]. Since we will only use the fact that
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
has a model companion and not the specific axiomatization of it, we will not recall the original geometric axioms and instead just present the nicer version following from our work (see Remark 3.14).
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
has a model companion and not the specific axiomatization of it, we will not recall the original geometric axioms and instead just present the nicer version following from our work (see Remark 3.14).
The theory
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
eliminates quantifiers in the language
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
eliminates quantifiers in the language
![]() $L^\partial _\lambda $
(see Theorem 2.2(v) in [Reference Kowalski4]). In [Reference Kowalski4] it is wrongly claimed that
$L^\partial _\lambda $
(see Theorem 2.2(v) in [Reference Kowalski4]). In [Reference Kowalski4] it is wrongly claimed that
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
is also a model companion of
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
is also a model companion of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
in the language
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}_p$
in the language
![]() $L^\partial _\lambda $
, but this can be easily fixed (see the discussion above Remark 3.5). In Section 2 we prove that
$L^\partial _\lambda $
, but this can be easily fixed (see the discussion above Remark 3.5). In Section 2 we prove that
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
eliminates quantifiers already in the language
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
eliminates quantifiers already in the language
![]() $L^\partial _{\lambda _0}$
, answering Question 3 from [Reference Kowalski4]. Actually, in Lemmas 2.1 and 2.2 we provide an easy proof of a surprisingly general fact, which implies quantifier elimination results for a very general class of theories of fields with operators. More precisely (see Section 2.1), we give a new and shorter proof of quantifier elimination in the framework of B-operators (introduced in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]) and a stronger quantifier elimination result in the setting of
$L^\partial _{\lambda _0}$
, answering Question 3 from [Reference Kowalski4]. Actually, in Lemmas 2.1 and 2.2 we provide an easy proof of a surprisingly general fact, which implies quantifier elimination results for a very general class of theories of fields with operators. More precisely (see Section 2.1), we give a new and shorter proof of quantifier elimination in the framework of B-operators (introduced in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]) and a stronger quantifier elimination result in the setting of
![]() $\mathcal {B}$
-operators (introduced in [Reference Gogolok and Kowalski3]).
$\mathcal {B}$
-operators (introduced in [Reference Gogolok and Kowalski3]).
In Section 3 we prove that
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
can be axiomatized by the same axioms (Theorem 3.13), which were used by Wood to axiomatize
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
can be axiomatized by the same axioms (Theorem 3.13), which were used by Wood to axiomatize
![]() $\operatorname {\mathrm {DCF}}_p$
(see [Reference Wood10]). This result answers Questions 4 and 5 from [Reference Kowalski4]. To formulate Wood’s axioms we need the concept of differential polynomials, but this works just as in the (
$\operatorname {\mathrm {DCF}}_p$
(see [Reference Wood10]). This result answers Questions 4 and 5 from [Reference Kowalski4]. To formulate Wood’s axioms we need the concept of differential polynomials, but this works just as in the (
![]() $\operatorname {\mathrm {Fr}}^0$
-)differential case. Namely, for a
$\operatorname {\mathrm {Fr}}^0$
-)differential case. Namely, for a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field
$\operatorname {\mathrm {Fr}}^n$
-differential field
![]() $\left ( K, \partial \right )$
we consider the polynomial ring
$\left ( K, \partial \right )$
we consider the polynomial ring
![]() $K\left \{ X \right \} = K \left [ X, X',\dotsc , X^{\left ( i \right )}, \dotsc \right ]$
in countably many variables, and consider it with the unique
$K\left \{ X \right \} = K \left [ X, X',\dotsc , X^{\left ( i \right )}, \dotsc \right ]$
in countably many variables, and consider it with the unique
![]() $\operatorname {\mathrm {Fr}}^n$
-derivation
$\operatorname {\mathrm {Fr}}^n$
-derivation
![]() $\partial '$
on
$\partial '$
on
![]() $K\left \{ X \right \}$
, which extends
$K\left \{ X \right \}$
, which extends
![]() $\partial \colon K \to K$
and has the property that
$\partial \colon K \to K$
and has the property that
![]() $\partial \left ( X^{\left ( i \right )}\right ) = X^{\left ( i+1 \right )}$
. By the usual abuse of notation, we write
$\partial \left ( X^{\left ( i \right )}\right ) = X^{\left ( i+1 \right )}$
. By the usual abuse of notation, we write
![]() $\partial $
instead of
$\partial $
instead of
![]() $\partial '$
. We call elements of
$\partial '$
. We call elements of
![]() $K\left \{ X \right \}$
differential polynomials with coefficients in K. For
$K\left \{ X \right \}$
differential polynomials with coefficients in K. For
![]() $f\in K\left \{ X \right \}$
and
$f\in K\left \{ X \right \}$
and
![]() $a\in K$
, we may evaluate f at a in an obvious manner, and we write
$a\in K$
, we may evaluate f at a in an obvious manner, and we write
![]() $f\left ( a \right )$
for this evaluation. The order of
$f\left ( a \right )$
for this evaluation. The order of
![]() $f\in K\left \{ X \right \}\setminus \left \{ 0 \right \}$
is the biggest i such that
$f\in K\left \{ X \right \}\setminus \left \{ 0 \right \}$
is the biggest i such that
![]() $X^{\left ( i \right )}$
appears in f, if f is not constant, and
$X^{\left ( i \right )}$
appears in f, if f is not constant, and
![]() ${-}1$
if f is a non-zero constant. Let us denote by
${-}1$
if f is a non-zero constant. Let us denote by
![]() $T_{\operatorname {Wood}}$
the following scheme of axioms: a
$T_{\operatorname {Wood}}$
the following scheme of axioms: a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field
$\operatorname {\mathrm {Fr}}^n$
-differential field
![]() $\left ( K,\partial \right )$
satisfies T if and only if
$\left ( K,\partial \right )$
satisfies T if and only if
-
(1) K is strict and
-
(2) for any non-zero differential polynomials
 $f, g\in K\left \{ X \right \}$
, where the order of f is equal m and the order of g is smaller than m, if
$f, g\in K\left \{ X \right \}$
, where the order of f is equal m and the order of g is smaller than m, if
 $\frac {\partial f}{\partial X^{\left ( m \right )}}\neq 0$
, then there is some
$\frac {\partial f}{\partial X^{\left ( m \right )}}\neq 0$
, then there is some
 $a\in K$
such that
$a\in K$
such that
 $f\left ( a \right ) = 0$
and
$f\left ( a \right ) = 0$
and
 $g\left ( a \right )\neq 0$
.
$g\left ( a \right )\neq 0$
.
It is clear that the axioms above are expressible in
![]() $L^\partial $
. Moreover, the sentences expressing these axioms are verbatim the same as the Wood axioms for
$L^\partial $
. Moreover, the sentences expressing these axioms are verbatim the same as the Wood axioms for
![]() $\operatorname {\mathrm {DCF}}_p$
in [Reference Wood10] (i.e., they do not depend on n).
$\operatorname {\mathrm {DCF}}_p$
in [Reference Wood10] (i.e., they do not depend on n).
The proofs in Section 3 are in the spirit of the proof from [Reference Wood10] that the Wood axioms work for
![]() $\operatorname {\mathrm {DCF}}_p$
, although we had to overcome some obstacles. For example, for usual derivations, the ring of differential polynomial has nice division properties, which is not the case for
$\operatorname {\mathrm {DCF}}_p$
, although we had to overcome some obstacles. For example, for usual derivations, the ring of differential polynomial has nice division properties, which is not the case for
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations for
$\operatorname {\mathrm {Fr}}^n$
-derivations for
![]() $n>0$
, since e.g., for
$n>0$
, since e.g., for
![]() $a\in K$
we have
$a\in K$
we have
so applying
![]() $\partial $
increases the degree in lower-order variables, which complicates possible division algorithms. Because of this lack of division, we can not use “constrained ideals” as in [Reference Wood10], but we still can reason using some “choosing polynomials of minimal order/degree” type of reasoning, which is somewhat reminiscent of a division algorithm.
$\partial $
increases the degree in lower-order variables, which complicates possible division algorithms. Because of this lack of division, we can not use “constrained ideals” as in [Reference Wood10], but we still can reason using some “choosing polynomials of minimal order/degree” type of reasoning, which is somewhat reminiscent of a division algorithm.
In what follows n is always a positive natural number (i.e., we do not speak about usual derivations, when considering
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations), all fields are of characteristic
$\operatorname {\mathrm {Fr}}^n$
-derivations), all fields are of characteristic
![]() $p>0$
and we set
$p>0$
and we set
![]() $q=p^n$
, so that an
$q=p^n$
, so that an
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field
$\operatorname {\mathrm {Fr}}^n$
-differential field
![]() $\left ( K, \partial \right )$
obeys
$\left ( K, \partial \right )$
obeys
for all
![]() $x,y\in K$
.
$x,y\in K$
.
2 Quantifier elimination
Let
![]() $\left ( K, \partial \right )$
be a field of characteristic p with some operators, i.e., a tuple (possibly infinite) of unary functions
$\left ( K, \partial \right )$
be a field of characteristic p with some operators, i.e., a tuple (possibly infinite) of unary functions
![]() $\partial = \left ( \partial _i\colon K\to K \right )_{i \in I}$
. We define the constants of
$\partial = \left ( \partial _i\colon K\to K \right )_{i \in I}$
. We define the constants of
![]() $\left ( K, \partial \right )$
as the set of common zeroes of all
$\left ( K, \partial \right )$
as the set of common zeroes of all
![]() $\partial _i$
and denote it by
$\partial _i$
and denote it by
![]() $K^\partial $
. We assume that
$K^\partial $
. We assume that
![]() $K^\partial $
is a field. We also assume that every
$K^\partial $
is a field. We also assume that every
![]() $\partial _i$
is additive and “
$\partial _i$
is additive and “
![]() $\operatorname {\mathrm {Fr}}^m$
-linear over the constants”, i.e., there is some natural number
$\operatorname {\mathrm {Fr}}^m$
-linear over the constants”, i.e., there is some natural number
![]() $m_i$
such that for any
$m_i$
such that for any
![]() $a\in K^\partial ,\ x \in K$
we have
$a\in K^\partial ,\ x \in K$
we have
![]() $\partial \left ( ax \right ) = a^{p^{m_i}} \partial \left ( x \right )$
. Examples of such operators include derivations, difference operators, Hasse–Schmidt derivations and derivations of the Frobenius map (see also Section 2.1).
$\partial \left ( ax \right ) = a^{p^{m_i}} \partial \left ( x \right )$
. Examples of such operators include derivations, difference operators, Hasse–Schmidt derivations and derivations of the Frobenius map (see also Section 2.1).
Let
![]() $\left ( K, \partial \right ) \subseteq \left ( L, \partial ' \right )$
be an extension of fields with operators in the above sense, that is,
$\left ( K, \partial \right ) \subseteq \left ( L, \partial ' \right )$
be an extension of fields with operators in the above sense, that is,
![]() $\partial '|_K = \partial $
and the numbers
$\partial '|_K = \partial $
and the numbers
![]() $m_i$
mentioned above are the same for K and L. By abuse of notation, we will use the same symbol
$m_i$
mentioned above are the same for K and L. By abuse of notation, we will use the same symbol
![]() $\partial $
for the operators on K and on L.
$\partial $
for the operators on K and on L.
Lemma 2.1. Let
![]() $\left ( K, \partial \right ) \subseteq \left ( L, \partial \right )$
be as above. Assume that
$\left ( K, \partial \right ) \subseteq \left ( L, \partial \right )$
be as above. Assume that
![]() $L^p\subseteq L^\partial $
and that K is strict, i.e.,
$L^p\subseteq L^\partial $
and that K is strict, i.e.,
![]() $K^\partial = K^p$
. Then
$K^\partial = K^p$
. Then
![]() $L^\partial $
and K are linearly disjoint over
$L^\partial $
and K are linearly disjoint over
![]() $K^\partial $
.
$K^\partial $
.
Proof. Assume the conclusion is not true and take the minimal
![]() $n>1$
such that there are some
$n>1$
such that there are some
![]() $x_1,\dotsc , x_n\in L^\partial $
linearly dependent over K, but linearly independent over
$x_1,\dotsc , x_n\in L^\partial $
linearly dependent over K, but linearly independent over
![]() $K^\partial $
. By the minimality assumption, there are
$K^\partial $
. By the minimality assumption, there are
![]() $a_1, \dotsc , a_n\in K\setminus \left \{ 0 \right \}$
such that:
$a_1, \dotsc , a_n\in K\setminus \left \{ 0 \right \}$
such that:
Then for any
![]() $i\in I$
:
$i\in I$
:
 $$ \begin{align*}0=\partial_i\left( \frac{a_1}{a_n}x_1+\cdots + \frac{a_{n-1}}{a_n}x_{n-1} +x_n\right)= \partial_i\left(\frac{a_1}{a_n}\right)x_1^{p^{m_i}}+\cdots + \partial_i\left(\frac{a_{n-1}}{a_n}\right)x_{n-1}^{p^{m_i}}.\end{align*} $$
$$ \begin{align*}0=\partial_i\left( \frac{a_1}{a_n}x_1+\cdots + \frac{a_{n-1}}{a_n}x_{n-1} +x_n\right)= \partial_i\left(\frac{a_1}{a_n}\right)x_1^{p^{m_i}}+\cdots + \partial_i\left(\frac{a_{n-1}}{a_n}\right)x_{n-1}^{p^{m_i}}.\end{align*} $$
If some
![]() $\partial _i \left ( \frac {a_j}{a_n} \right )$
is nonzero, then
$\partial _i \left ( \frac {a_j}{a_n} \right )$
is nonzero, then
![]() $x_1^{p^{m_i}},\dotsc , x_{n-1}^{p^{m_i}}\in L^p\subseteq L^\partial $
are linearly dependent over K, so by the minimality assumption on m we get that
$x_1^{p^{m_i}},\dotsc , x_{n-1}^{p^{m_i}}\in L^p\subseteq L^\partial $
are linearly dependent over K, so by the minimality assumption on m we get that
![]() $x_1^{p^{m_i}},\dotsc , x_{n-1}^{p^{m_i}}$
are linearly dependent over
$x_1^{p^{m_i}},\dotsc , x_{n-1}^{p^{m_i}}$
are linearly dependent over
![]() $K^\partial =K^p$
, hence
$K^\partial =K^p$
, hence
![]() $x_1^{p^{m_i-1}}, \dotsc , x_{n-1}^{p^{m_i-1}}$
are linearly dependent over K. Repeating this reasoning yields that
$x_1^{p^{m_i-1}}, \dotsc , x_{n-1}^{p^{m_i-1}}$
are linearly dependent over K. Repeating this reasoning yields that
![]() $x_1,\dotsc , x_{n-1}$
are linearly dependent over
$x_1,\dotsc , x_{n-1}$
are linearly dependent over
![]() $K^p$
, contrary to the assumption, that they are independent over
$K^p$
, contrary to the assumption, that they are independent over
![]() $K^\partial =K^p$
.
$K^\partial =K^p$
.
Therefore for any i we have
![]() $\partial _i\left ( \frac {a_1}{a_n} \right ) = \cdots = \partial _i\left (\frac {a_{n-1}}{a_n}\right )=0$
, hence
$\partial _i\left ( \frac {a_1}{a_n} \right ) = \cdots = \partial _i\left (\frac {a_{n-1}}{a_n}\right )=0$
, hence
![]() $\frac {a_1}{a_n},\dotsc , \frac {a_{n-1}}{a_n}\in K^\partial $
. By the strictness assumption we get that for some
$\frac {a_1}{a_n},\dotsc , \frac {a_{n-1}}{a_n}\in K^\partial $
. By the strictness assumption we get that for some
![]() $b_1,\dotsc , b_{n-1}\in K\setminus \left \{ 0 \right \}\hspace{-2.5pt}:$
$b_1,\dotsc , b_{n-1}\in K\setminus \left \{ 0 \right \}\hspace{-2.5pt}:$
thus
hence
![]() $x_1, \dotsc , x_n$
are linearly dependent over
$x_1, \dotsc , x_n$
are linearly dependent over
![]() $K^p=K^\partial $
, contrary to the assumption.⊣
$K^p=K^\partial $
, contrary to the assumption.⊣
From the proof it is clear that in the linear case (i.e., for every i we have
![]() $m_i=0$
) we have the following
$m_i=0$
) we have the following
Lemma 2.2. Let
![]() $\left ( K, \partial \right ) \subseteq \left ( L, \partial \right )$
be an extension of fields with operators linear over the constants. Then
$\left ( K, \partial \right ) \subseteq \left ( L, \partial \right )$
be an extension of fields with operators linear over the constants. Then
![]() $L^\partial $
and K are linearly disjoint over
$L^\partial $
and K are linearly disjoint over
![]() $K^\partial $
.
$K^\partial $
.
The strictness assumption in Lemma 2.1 is necessary (which gives a negative answer to Question 1 in [Reference Kowalski4]), as shown by the example below.
Example 2.3. Take
![]() $K=\mathbb {F}_p\left ( X, Y, \lambda , \mu \right ), L=\mathbb {F}_p\left ( X^{1/p}, Y^{1/p}, \lambda , \mu \right )$
and define a derivation of the Frobenius map on L by setting
$K=\mathbb {F}_p\left ( X, Y, \lambda , \mu \right ), L=\mathbb {F}_p\left ( X^{1/p}, Y^{1/p}, \lambda , \mu \right )$
and define a derivation of the Frobenius map on L by setting
We will show that
![]() $L^\partial $
and K are not linearly disjoint over
$L^\partial $
and K are not linearly disjoint over
![]() $K^\partial $
. Note that
$K^\partial $
. Note that
Thus,
![]() $X^{1/p}, Y^{1/p}, \lambda X^{1/p} + \mu Y^{1/p}$
are elements of
$X^{1/p}, Y^{1/p}, \lambda X^{1/p} + \mu Y^{1/p}$
are elements of
![]() $L^\partial $
, linearly dependent over K. However, they are independent over
$L^\partial $
, linearly dependent over K. However, they are independent over
![]() $K^\partial $
:
$K^\partial $
:
Indeed, for any
![]() $a, b, c \in K^\partial $
, if
$a, b, c \in K^\partial $
, if
then
but
![]() $X^{1/p}$
and
$X^{1/p}$
and
![]() $Y^{1/p}$
are linearly independent over K, so
$Y^{1/p}$
are linearly independent over K, so
![]() $a+c\lambda = b+c\mu = 0.$
If
$a+c\lambda = b+c\mu = 0.$
If
![]() $c\neq 0$
, then
$c\neq 0$
, then
![]() $\lambda = {-\frac {a}{c}}\in K^\partial $
, which is not the case. Thus
$\lambda = {-\frac {a}{c}}\in K^\partial $
, which is not the case. Thus
![]() $c=0$
and therefore
$c=0$
and therefore
![]() $a=b=0$
, hence
$a=b=0$
, hence
![]() $X^{1/p}, Y^{1/p}, \lambda X^{1/p} + \mu Y^{1/p}$
are linearly independent over
$X^{1/p}, Y^{1/p}, \lambda X^{1/p} + \mu Y^{1/p}$
are linearly independent over
![]() $K^\partial $
.
$K^\partial $
.
Lemma 2.1 answers Question 2 from [Reference Kowalski4], which asks whether strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields are differentially perfect. As explained there, it also implies a positive answer to Question 3, i.e.,
$\operatorname {\mathrm {Fr}}^n$
-differential fields are differentially perfect. As explained there, it also implies a positive answer to Question 3, i.e.,
Theorem 2.4. The theory
![]() $\operatorname {\mathrm {Fr}}^{n}-\operatorname {\mathrm {DCF}}_p$
eliminates quantifiers in the language
$\operatorname {\mathrm {Fr}}^{n}-\operatorname {\mathrm {DCF}}_p$
eliminates quantifiers in the language
![]() $L_{\lambda _0}^{\partial }$
.
$L_{\lambda _0}^{\partial }$
.
2.1 Quantifier elimination for more general operators
Lemmas 2.1 and 2.2 are very general and actually provide quantifier elimination in more general frameworks, which we will now briefly discuss.
We begin with the setting of B-operators. They were introduced by Moosa and Scanlon (under the name
![]() $\mathcal {D}$
-ring structures) in [Reference Moosa and Scanlon5] and investigated further in [Reference Moosa and Scanlon6], but we are mostly interested in the positive characteristic case considered by Beyarslan et al. in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]. Let k be a field, let B be a finite k-algebra together with a k-algebra homomorphism
$\mathcal {D}$
-ring structures) in [Reference Moosa and Scanlon5] and investigated further in [Reference Moosa and Scanlon6], but we are mostly interested in the positive characteristic case considered by Beyarslan et al. in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]. Let k be a field, let B be a finite k-algebra together with a k-algebra homomorphism
![]() $\pi \colon B\to k$
. A B-operator on a k-algebra R is then a k-algebra homomorphism
$\pi \colon B\to k$
. A B-operator on a k-algebra R is then a k-algebra homomorphism
![]() $\partial \colon R\to R\otimes _k B$
such that the following diagram commutes
$\partial \colon R\to R\otimes _k B$
such that the following diagram commutes

Fix a basis
![]() $b_0,\dotsc , b_d$
of B over k such that
$b_0,\dotsc , b_d$
of B over k such that
![]() $\pi \left ( b_0 \right ) = 1$
and
$\pi \left ( b_0 \right ) = 1$
and
![]() $\pi \left ( b_i \right ) = 0$
for
$\pi \left ( b_i \right ) = 0$
for
![]() $i>0$
. A B-operator is then the same as a d-tuple of maps
$i>0$
. A B-operator is then the same as a d-tuple of maps
![]() $\partial _1,\dotsc , \partial _d\colon R\to R$
such that the map
$\partial _1,\dotsc , \partial _d\colon R\to R$
such that the map
is a homomorphism of k-algebras.
Example 2.5. If
![]() $B=k\times k$
and
$B=k\times k$
and
![]() $b_0=\left ( 1, 0 \right ), b_1=\left ( 0, 1 \right )$
, then
$b_0=\left ( 1, 0 \right ), b_1=\left ( 0, 1 \right )$
, then
![]() $\partial _1\colon R\to R$
is a B-operator if and only if
$\partial _1\colon R\to R$
is a B-operator if and only if
![]() $\partial _1$
is and k-algebra endomorphism.
$\partial _1$
is and k-algebra endomorphism.
The ring of constants of a B-operator
![]() $\partial $
on R is defined as
$\partial $
on R is defined as
Note that in general this is not the same as the constants in our sense, i.e., the intersection of the kernels of
![]() $\partial _1,\dotsc , \partial _d$
. For example, consider a k-algebra automorphism
$\partial _1,\dotsc , \partial _d$
. For example, consider a k-algebra automorphism
![]() $\partial _1$
of R, which is a B-operator as in Example 2.5. Then the ring of constants in our sense is
$\partial _1$
of R, which is a B-operator as in Example 2.5. Then the ring of constants in our sense is
![]() $\left \{ 0 \right \}$
, but the ring of constants defined above is the fixed field of
$\left \{ 0 \right \}$
, but the ring of constants defined above is the fixed field of
![]() $\partial _1$
.
$\partial _1$
.
However, if we take the basis
![]() $b_0,\dotsc , b_d$
of B over k so that
$b_0,\dotsc , b_d$
of B over k so that
![]() $b_0=1$
, then both notions of constants agree. Moreover, it is then easy to calculate that such operators are linear over the constants, so they fit into our considerations. Therefore, we may apply Lemma 2.2, which is in this instance the same as Corollary 4.5 in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1], namely
$b_0=1$
, then both notions of constants agree. Moreover, it is then easy to calculate that such operators are linear over the constants, so they fit into our considerations. Therefore, we may apply Lemma 2.2, which is in this instance the same as Corollary 4.5 in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1], namely
Corollary 2.6. Let
![]() $\left ( K, \partial \right ) \subseteq \left ( L, \partial \right )$
be an extension of B-fields (i.e., fields with B-operators). Then
$\left ( K, \partial \right ) \subseteq \left ( L, \partial \right )$
be an extension of B-fields (i.e., fields with B-operators). Then
![]() $L^\partial $
and K are linearly disjoint over
$L^\partial $
and K are linearly disjoint over
![]() $K^\partial $
.
$K^\partial $
.
Our proof is easier than the proof in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]. This corollary is then applied as follows. The main result of [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1] is a complete classification for which B the theory of B-fields has a model companion
![]() $B-\operatorname {\mathrm {DCF}}$
(see Corollary 3.9 there for details). This happens in essentially two cases, one of which is when B is local and the nilradical of B coincides with the kernel of the Frobenius homomorphisms on B (e.g., the case of derivations). Corollary 2.6 is used to prove the following (Theorem 4.11 in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]):
$B-\operatorname {\mathrm {DCF}}$
(see Corollary 3.9 there for details). This happens in essentially two cases, one of which is when B is local and the nilradical of B coincides with the kernel of the Frobenius homomorphisms on B (e.g., the case of derivations). Corollary 2.6 is used to prove the following (Theorem 4.11 in [Reference Beyarslan, Hoffmann, Kamensky and Kowalski1]):
Theorem 2.7. Assume that B is local and the nilradical of B coincides with the kernel of the Frobenius homomorphisms on B. Then the theory
![]() $B-\operatorname {\mathrm {DCF}}$
has quantifier elimination in the language
$B-\operatorname {\mathrm {DCF}}$
has quantifier elimination in the language
![]() $L_{\lambda _0}^\partial $
(the language of fields with d unary symbols
$L_{\lambda _0}^\partial $
(the language of fields with d unary symbols
![]() $\partial _1, \dotsc , \partial _d$
and an unary symbol for the
$\partial _1, \dotsc , \partial _d$
and an unary symbol for the
![]() $\lambda _0$
-function).
$\lambda _0$
-function).
Even more generally, we can get a quantifier-elimination result for so-called
![]() $\mathcal {B}$
-operators considered in [Reference Gogolok and Kowalski3]. We will not recall the precise definition of a
$\mathcal {B}$
-operators considered in [Reference Gogolok and Kowalski3]. We will not recall the precise definition of a
![]() $\mathcal {B}$
-operator, as it is a bit involved, but the rough idea is to replace the functor
$\mathcal {B}$
-operator, as it is a bit involved, but the rough idea is to replace the functor
![]() $-\hspace{-2.6pt}{\otimes _k} B$
in the context of B-operators by an appropriate functor
$-\hspace{-2.6pt}{\otimes _k} B$
in the context of B-operators by an appropriate functor
![]() $\mathcal {B}$
and the map
$\mathcal {B}$
and the map
![]() $\pi $
by a natural transformation
$\pi $
by a natural transformation
![]() $\mathcal {B}\longrightarrow \operatorname {id}$
.
$\mathcal {B}\longrightarrow \operatorname {id}$
.
Theorem 2.19 in [Reference Gogolok and Kowalski3] says, that we can replace
![]() $\mathcal {B}$
by an isomorphic
$\mathcal {B}$
by an isomorphic
![]() $\mathcal {B}'$
in a somewhat “normal form.” This normal form has the property that there is some k-algebra B such that B-operators “twisted” by an appropriate sequence of Frobenius maps are
$\mathcal {B}'$
in a somewhat “normal form.” This normal form has the property that there is some k-algebra B such that B-operators “twisted” by an appropriate sequence of Frobenius maps are
![]() $\mathcal {B}$
-operators. In other words, Theorem 2.19 in [Reference Gogolok and Kowalski3] says that general
$\mathcal {B}$
-operators. In other words, Theorem 2.19 in [Reference Gogolok and Kowalski3] says that general
![]() $\mathcal {B}$
-operators are related to B-operators in the same way as derivations of the Frobenius map are related to derivations. Now, in order to speak about
$\mathcal {B}$
-operators are related to B-operators in the same way as derivations of the Frobenius map are related to derivations. Now, in order to speak about
![]() $\mathcal {B}$
-operators as tuples of maps
$\mathcal {B}$
-operators as tuples of maps
![]() $\partial _1, \dotsc , \partial _d \colon R\to R$
(as opposed to a k-algebra homomorphism
$\partial _1, \dotsc , \partial _d \colon R\to R$
(as opposed to a k-algebra homomorphism
![]() $\partial \colon R\to \mathcal {B}\left ( R \right )$
) it is enough to fix a basis
$\partial \colon R\to \mathcal {B}\left ( R \right )$
) it is enough to fix a basis
![]() $b_0,\dotsc , b_d$
of this algebra B over k. If we choose it so that
$b_0,\dotsc , b_d$
of this algebra B over k. If we choose it so that
![]() $b_0=1$
, then the tuple
$b_0=1$
, then the tuple
![]() $\partial _1,\dotsc , \partial _d$
is “
$\partial _1,\dotsc , \partial _d$
is “
![]() $\operatorname {\mathrm {Fr}}^n$
-linear over the constants” (see the proof of Lemma 4.16 in [Reference Gogolok and Kowalski3] for details), so they fall under the class of operators considered in Lemma 2.1.
$\operatorname {\mathrm {Fr}}^n$
-linear over the constants” (see the proof of Lemma 4.16 in [Reference Gogolok and Kowalski3] for details), so they fall under the class of operators considered in Lemma 2.1.
One of the main results of [Reference Gogolok and Kowalski3] says that the theory of
![]() $\mathcal {B}$
-fields has a model companion
$\mathcal {B}$
-fields has a model companion
![]() $\mathcal {B}-\operatorname {\mathrm {DCF}}$
, provided that the theory of B-field is companionable, where
$\mathcal {B}-\operatorname {\mathrm {DCF}}$
, provided that the theory of B-field is companionable, where
![]() $B:=\mathcal {B}\left ( k^{\operatorname {\mathrm {alg}}}\right )$
. If B satisfies the assumptions of Theorem 2.7, then we can use our Lemma 2.1 to show the following
$B:=\mathcal {B}\left ( k^{\operatorname {\mathrm {alg}}}\right )$
. If B satisfies the assumptions of Theorem 2.7, then we can use our Lemma 2.1 to show the following
Theorem 2.8. Assume that
![]() $B:=\mathcal {B}\left ( k^{\operatorname {\mathrm {alg}}}\right )$
satisfies the assumptions of Theorem 2.7. Then, the theory
$B:=\mathcal {B}\left ( k^{\operatorname {\mathrm {alg}}}\right )$
satisfies the assumptions of Theorem 2.7. Then, the theory
![]() $\mathcal {B}-\operatorname {\mathrm {DCF}}$
eliminates quantifiers in the language
$\mathcal {B}-\operatorname {\mathrm {DCF}}$
eliminates quantifiers in the language
![]() $L^\partial _{\lambda _0}$
.
$L^\partial _{\lambda _0}$
.
The proof is completely analogous to the proofs of Theorems 2.4 and 2.7. Theorem 2.8 is new and strengthens Theorem 4.14 from [Reference Gogolok and Kowalski3], which states that
![]() $\mathcal {B}-\operatorname {\mathrm {DCF}}$
eliminates quantifiers in the language
$\mathcal {B}-\operatorname {\mathrm {DCF}}$
eliminates quantifiers in the language
![]() $L_{\lambda }^\partial $
. This theorem is also a vast generalization of Theorem 2.4.
$L_{\lambda }^\partial $
. This theorem is also a vast generalization of Theorem 2.4.
3 Wood axioms for
 $\operatorname {Fr}^n-\operatorname {DCF}_p$
$\operatorname {Fr}^n-\operatorname {DCF}_p$
We are now going to prove, that the Wood axioms
![]() $T_{\operatorname {Wood}}$
described in the Introduction do axiomatize
$T_{\operatorname {Wood}}$
described in the Introduction do axiomatize
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. The proof consists of two steps. First we prove some sort of primitive element theorem for
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. The proof consists of two steps. First we prove some sort of primitive element theorem for
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations (Proposition 3.2), which implies that for
$\operatorname {\mathrm {Fr}}^n$
-derivations (Proposition 3.2), which implies that for
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields 1-existential closedness is equivalent to existential closedness (Corollary 3.7). In the second step, we show that Wood axioms, as expected, axiomatize 1-existentially closed
$\operatorname {\mathrm {Fr}}^n$
-differential fields 1-existential closedness is equivalent to existential closedness (Corollary 3.7). In the second step, we show that Wood axioms, as expected, axiomatize 1-existentially closed
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields (Theorem 3.13).
$\operatorname {\mathrm {Fr}}^n$
-differential fields (Theorem 3.13).
For an extension of (
![]() $\operatorname {\mathrm {Fr}}^n$
-)differential fields
$\operatorname {\mathrm {Fr}}^n$
-)differential fields
![]() $K\subseteq L$
and a tuple
$K\subseteq L$
and a tuple
![]() $\bar {a}\in L$
, denote by
$\bar {a}\in L$
, denote by
![]() $K\left \langle \bar {a} \right \rangle $
the (
$K\left \langle \bar {a} \right \rangle $
the (
![]() $\operatorname {\mathrm {Fr}}^n$
-)differential field generated by K and
$\operatorname {\mathrm {Fr}}^n$
-)differential field generated by K and
![]() $\bar {a}$
. The proof in [Reference Wood10] that
$\bar {a}$
. The proof in [Reference Wood10] that
![]() $\operatorname {\mathrm {DCF}}_p$
can be axiomatized by the Wood axioms relays on the following primitive element theorem (Theorem 1 in [Reference Seidenberg9]):
$\operatorname {\mathrm {DCF}}_p$
can be axiomatized by the Wood axioms relays on the following primitive element theorem (Theorem 1 in [Reference Seidenberg9]):
Theorem 3.1. Let
![]() $\left ( K, \partial \right )$
be a differentially perfect differential field which has infinite dimension over its constants (equivalenty: every non-zero differential polynomial assumes a non-zero value). Let
$\left ( K, \partial \right )$
be a differentially perfect differential field which has infinite dimension over its constants (equivalenty: every non-zero differential polynomial assumes a non-zero value). Let
![]() $K\subseteq L$
be an extension of differential fields and let
$K\subseteq L$
be an extension of differential fields and let
![]() $a_1,\dotsc , a_m\in L$
be differential-algebraic over K. Then there is some
$a_1,\dotsc , a_m\in L$
be differential-algebraic over K. Then there is some
![]() $c\in L$
such that
$c\in L$
such that
![]() $K\left \langle a_1, \dotsc , a_m \right \rangle = K\left \langle c \right \rangle $
. Moreover, c can be taken from
$K\left \langle a_1, \dotsc , a_m \right \rangle = K\left \langle c \right \rangle $
. Moreover, c can be taken from
![]() $Ka_1+\cdots + K a_m$
.
$Ka_1+\cdots + K a_m$
.
It seems that the above fact does not hold for
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations, but in any case, we have the following weaker version, which suffices for our purposes. The proof is similar to the proof of Theorem 3.1 given in [Reference Seidenberg9], although additional steps are needed.
$\operatorname {\mathrm {Fr}}^n$
-derivations, but in any case, we have the following weaker version, which suffices for our purposes. The proof is similar to the proof of Theorem 3.1 given in [Reference Seidenberg9], although additional steps are needed.
Proposition 3.2. Let
![]() $n>0$
and let
$n>0$
and let
![]() $\left ( K, \partial \right )$
be a differentially perfect
$\left ( K, \partial \right )$
be a differentially perfect
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field such that every non-zero differential polynomial assumes a non-zero value. Let
$\operatorname {\mathrm {Fr}}^n$
-differential field such that every non-zero differential polynomial assumes a non-zero value. Let
![]() $K\subseteq L$
be an extension of
$K\subseteq L$
be an extension of
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields and let
$\operatorname {\mathrm {Fr}}^n$
-differential fields and let
![]() $a_1,\dotsc , a_m\in L$
be differential-algebraic over K. Then there is some
$a_1,\dotsc , a_m\in L$
be differential-algebraic over K. Then there is some
![]() $c\in L$
and some
$c\in L$
and some
![]() $i>0$
such that
$i>0$
such that
![]() $a_1^{q^i}, \dotsc , a_m^{q^i} \in K\left \langle c \right \rangle $
. Moreover, c can be taken from
$a_1^{q^i}, \dotsc , a_m^{q^i} \in K\left \langle c \right \rangle $
. Moreover, c can be taken from
![]() $Ka_1+\cdots + K a_m$
.
$Ka_1+\cdots + K a_m$
.
Remark 3.3.
-
(1) For derivations, the assumption “every non-zero differential polynomial assumes a non-zero value” is equivalent to “the dimension of K over
 $K^\partial $
is infinite,” which can be proven using Wronskians (see [Reference Seidenberg9] for details). For
$K^\partial $
is infinite,” which can be proven using Wronskians (see [Reference Seidenberg9] for details). For
 $\operatorname {\mathrm {Fr}}^n$
-derivations with
$\operatorname {\mathrm {Fr}}^n$
-derivations with
 $n>0$
this is no longer true. To see that, let
$n>0$
this is no longer true. To see that, let
 $(K, \partial _0)$
be a differential field with infinite dimension over its constant. For
$(K, \partial _0)$
be a differential field with infinite dimension over its constant. For
 $n>0$
define
$n>0$
define
 $\partial _n =\operatorname {\mathrm {Fr}}^n\circ \partial _0$
. Since
$\partial _n =\operatorname {\mathrm {Fr}}^n\circ \partial _0$
. Since
 $K^{\partial _0}=K^{\partial _n}$
we have that
$K^{\partial _0}=K^{\partial _n}$
we have that
 $(K, \partial _n)$
is a
$(K, \partial _n)$
is a
 $\operatorname {\mathrm {Fr}}^n$
-differential field with infinite dimension over its constants, but the differential polynomial
$\operatorname {\mathrm {Fr}}^n$
-differential field with infinite dimension over its constants, but the differential polynomial
 $X''$
is zero when evaluated on K.
$X''$
is zero when evaluated on K. -
(2) In our work, we will use Proposition 3.2 only in the case when K is 1-existentially closed. For such K the assumption about differential polynomials is satisfied, which can be seen e.g., by considering the field of “differential-rational functions” over K.
Proof of Proposition 3.2. It is enough to prove the proposition for
![]() $m=2$
. Let
$m=2$
. Let
![]() $u, v\in L$
be differentially algebraic over K. Let
$u, v\in L$
be differentially algebraic over K. Let
![]() $\Lambda $
be a differentially transcendental indeterminate. The elements
$\Lambda $
be a differentially transcendental indeterminate. The elements
![]() $u, v, \Lambda \in L\left \langle \Lambda \right \rangle $
are differentially algebraic over
$u, v, \Lambda \in L\left \langle \Lambda \right \rangle $
are differentially algebraic over
![]() $K\left \langle \Lambda \right \rangle $
, hence so is
$K\left \langle \Lambda \right \rangle $
, hence so is
![]() $u+\Lambda v$
, thus there is some non-zero polynomial
$u+\Lambda v$
, thus there is some non-zero polynomial
![]() $G\in K\left [ X_0, \dotsc , X_t, Y_0, \dotsc , Y_s\right ]$
such that
$G\in K\left [ X_0, \dotsc , X_t, Y_0, \dotsc , Y_s\right ]$
such that
Without out loss of generality assume that the total degree of G is minimal.
Fix
![]() $i\in \left \{ 0, \dotsc , s \right \}$
. To simplify the notation, we set
$i\in \left \{ 0, \dotsc , s \right \}$
. To simplify the notation, we set
Let
![]() $\frac {\partial }{\partial \Lambda ^{\left ( i \right )}}$
denote the obvious partial derivation on the field
$\frac {\partial }{\partial \Lambda ^{\left ( i \right )}}$
denote the obvious partial derivation on the field
![]() $L \left \langle \Lambda \right \rangle $
. Using the chain rule, we may differentiate the equality
$L \left \langle \Lambda \right \rangle $
. Using the chain rule, we may differentiate the equality
![]() $\left ( \ast \right )$
with respect to
$\left ( \ast \right )$
with respect to
![]() $\Lambda ^{\left ( i \right )}$
$\Lambda ^{\left ( i \right )}$
 $$ \begin{align*} 0&=\frac{\partial}{\partial \Lambda^{\left( i \right)}}G\left( \Lambda, \dotsc, \Lambda^{\left( t \right)},u+\Lambda v, \dotsc , \left( u+\Lambda v\right)^{\left( s \right)} \right) \\ &=\sum_{k=0}^t \frac{\partial G}{\partial X_k}\left( \bar{\Lambda} \right) \cdot \frac{\partial \Lambda^{\left( k \right)}}{\partial \Lambda^{\left( i \right)}} + \sum_{k=0}^s \frac{\partial G}{\partial Y_k}\left( \bar{\Lambda} \right) \cdot \frac{\partial \left( u+\Lambda v\right)^{\left( k \right)} }{\partial \Lambda^{\left( i \right)}} \\ &= \frac{\partial G}{\partial X_i}\left( \bar{\Lambda} \right) + \frac{\partial G}{\partial Y_i}\left( \bar{\Lambda} \right) \cdot v^{q^i}, \end{align*} $$
$$ \begin{align*} 0&=\frac{\partial}{\partial \Lambda^{\left( i \right)}}G\left( \Lambda, \dotsc, \Lambda^{\left( t \right)},u+\Lambda v, \dotsc , \left( u+\Lambda v\right)^{\left( s \right)} \right) \\ &=\sum_{k=0}^t \frac{\partial G}{\partial X_k}\left( \bar{\Lambda} \right) \cdot \frac{\partial \Lambda^{\left( k \right)}}{\partial \Lambda^{\left( i \right)}} + \sum_{k=0}^s \frac{\partial G}{\partial Y_k}\left( \bar{\Lambda} \right) \cdot \frac{\partial \left( u+\Lambda v\right)^{\left( k \right)} }{\partial \Lambda^{\left( i \right)}} \\ &= \frac{\partial G}{\partial X_i}\left( \bar{\Lambda} \right) + \frac{\partial G}{\partial Y_i}\left( \bar{\Lambda} \right) \cdot v^{q^i}, \end{align*} $$
since for
![]() $i>0$
we have
$i>0$
we have
and for
![]() $i=0$
$i=0$
where
![]() $\delta _{ik}$
is the Kronecker delta.
$\delta _{ik}$
is the Kronecker delta.
Claim 1. There is some
![]() $i\in \left \{ 0, \dotsc , s \right \}$
such that
$i\in \left \{ 0, \dotsc , s \right \}$
such that
![]() $\frac {\partial G}{\partial Y_i}$
is not the zero polynomial.
$\frac {\partial G}{\partial Y_i}$
is not the zero polynomial.
Proof of Claim 1: Assume this is not the case. Then also each
![]() $\frac {\partial G}{\partial X_i}$
is the zero polynomial—otherwise,
$\frac {\partial G}{\partial X_i}$
is the zero polynomial—otherwise,
![]() $\frac {\partial G}{\partial X_i}\left ( \bar {\Lambda } \right ) = 0$
by the formula above, which would contradict the minimality assumptions on G. Thus G is a polynomial in
$\frac {\partial G}{\partial X_i}\left ( \bar {\Lambda } \right ) = 0$
by the formula above, which would contradict the minimality assumptions on G. Thus G is a polynomial in
![]() $X_0^p,\dotsc , X_t^p, Y_0^p, \dotsc Y_s^p$
. Therefore
$X_0^p,\dotsc , X_t^p, Y_0^p, \dotsc Y_s^p$
. Therefore
![]() $( \ast )$
expresses the linear dependence over K of pth powers of some monomials in
$( \ast )$
expresses the linear dependence over K of pth powers of some monomials in
![]() $\Lambda , \dotsc , \Lambda ^{\left ( t \right )},u+\Lambda v, \dotsc , \left ( u+\Lambda v\right )^{\left ( s \right )}$
. Lemma 2.1 implies that the pth powers of these monomials are already linearly dependent over
$\Lambda , \dotsc , \Lambda ^{\left ( t \right )},u+\Lambda v, \dotsc , \left ( u+\Lambda v\right )^{\left ( s \right )}$
. Lemma 2.1 implies that the pth powers of these monomials are already linearly dependent over
![]() $K^p$
, hence the monomials are linearly dependent over K. Since
$K^p$
, hence the monomials are linearly dependent over K. Since
![]() $\Lambda , \dotsc , \Lambda ^{\left ( t \right )}$
are algebraically independent over K, some
$\Lambda , \dotsc , \Lambda ^{\left ( t \right )}$
are algebraically independent over K, some
![]() $\left ( u+\Lambda v\right )^{\left ( i\right )}$
must appear in this dependence relation, thus we get a relation of the form
$\left ( u+\Lambda v\right )^{\left ( i\right )}$
must appear in this dependence relation, thus we get a relation of the form
where F is a multivariate polynomial over K with lower total degree than G, contrary to the minimality assumption.⊣
Thus, for some
![]() $i\in \left \{ 0, \dotsc , s \right \}$
we have the following equality:
$i\in \left \{ 0, \dotsc , s \right \}$
we have the following equality:
 $$ \begin{align*}v^{q^i} = - \frac{\frac{\partial G}{\partial X_i} \left( \bar{\Lambda} \right) }{ \frac{\partial G}{\partial Y_i}\left( \bar{\Lambda} \right) }.\end{align*} $$
$$ \begin{align*}v^{q^i} = - \frac{\frac{\partial G}{\partial X_i} \left( \bar{\Lambda} \right) }{ \frac{\partial G}{\partial Y_i}\left( \bar{\Lambda} \right) }.\end{align*} $$
Claim 2. There is some
![]() $\lambda \in K$
such that
$\lambda \in K$
such that
Proof of Claim 2: Here
![]() $\frac {\partial G}{\partial Y_i}$
is a non-zero differential polynomial, but not over K, so we cannot use the assumption about K directly. However, expanding
$\frac {\partial G}{\partial Y_i}$
is a non-zero differential polynomial, but not over K, so we cannot use the assumption about K directly. However, expanding
![]() $u, v$
according to some transcendence basis of L over K, we may rewrite the above (desired) inequality as a conjunction of polynomial inequalities over K of the form
$u, v$
according to some transcendence basis of L over K, we may rewrite the above (desired) inequality as a conjunction of polynomial inequalities over K of the form
 $$ \begin{align*}\bigwedge_{k=0}^N f_k\left( \lambda \right) \neq 0,\end{align*} $$
$$ \begin{align*}\bigwedge_{k=0}^N f_k\left( \lambda \right) \neq 0,\end{align*} $$
for some
![]() $f_0,\dotsc , f_N\in K\left \{ X \right \}$
. But this conjunction is equivalent to the single inequality
$f_0,\dotsc , f_N\in K\left \{ X \right \}$
. But this conjunction is equivalent to the single inequality
![]() $\prod _{k=0}^N f_k\left ( \lambda \right ) \neq 0$
, to which the assumption about K applies, yielding the desired
$\prod _{k=0}^N f_k\left ( \lambda \right ) \neq 0$
, to which the assumption about K applies, yielding the desired
![]() $\lambda $
.⊣
$\lambda $
.⊣
For this
![]() $\lambda $
from Claim 2 one has therefore
$\lambda $
from Claim 2 one has therefore
![]() $v^{q^i}\in K\left \langle u+\lambda v \right \rangle $
and it follows that
$v^{q^i}\in K\left \langle u+\lambda v \right \rangle $
and it follows that
![]() $u^{q^i}\in K\left \langle u+\lambda v \right \rangle $
, which finishes the proof.⊣
$u^{q^i}\in K\left \langle u+\lambda v \right \rangle $
, which finishes the proof.⊣
Remark 3.4. Theorem 2.2(v) in [Reference Kowalski4] states (in our notation) that
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
is a model companion of
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
is a model companion of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
in
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
in
![]() $L^\partial _\lambda $
. This is not true however, as proved by the following example. Let K be a model of
$L^\partial _\lambda $
. This is not true however, as proved by the following example. Let K be a model of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
which is not strict (e.g., any imperfect field with the zero
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
which is not strict (e.g., any imperfect field with the zero
![]() $\operatorname {\mathrm {Fr}}^n$
-derivation) and
$\operatorname {\mathrm {Fr}}^n$
-derivation) and
![]() $K\subseteq L$
be an
$K\subseteq L$
be an
![]() $L^\partial $
-extension of K such that L is a model of
$L^\partial $
-extension of K such that L is a model of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. Since L is strict and K is not, this extension is not separable (as L contains p-roots not present in K), thus
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
. Since L is strict and K is not, this extension is not separable (as L contains p-roots not present in K), thus
![]() $K\subseteq L$
is not an
$K\subseteq L$
is not an
![]() $L^\partial _{\lambda }$
-extension. Hence
$L^\partial _{\lambda }$
-extension. Hence
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
is not a model companion of
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
is not a model companion of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
in
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
in
![]() $L^\partial _\lambda $
.
$L^\partial _\lambda $
.
It can be easily fixed by replacing
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
by
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF}$
by
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {DF} + \mbox { “strictness” }$
and the proof from [Reference Kowalski4] goes through.
$\operatorname {\mathrm {Fr}}^n-\operatorname {DF} + \mbox { “strictness” }$
and the proof from [Reference Kowalski4] goes through.
For the above reasons, in the following few auxiliary facts about existential closedness, the strictness assumption is present.
Lemma 3.5. Let K be a strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field and let
$\operatorname {\mathrm {Fr}}^n$
-differential field and let
![]() $\phi \left ( x \right )$
be a quantifier-free
$\phi \left ( x \right )$
be a quantifier-free
![]() $L^\partial _{\lambda _0}$
-formula with parameters from K, which has a solution in some
$L^\partial _{\lambda _0}$
-formula with parameters from K, which has a solution in some
![]() $L^\partial _{\lambda _0}$
-extension
$L^\partial _{\lambda _0}$
-extension
![]() $L\supseteq K$
. Then there exists a quantifier free
$L\supseteq K$
. Then there exists a quantifier free
![]() $L^\partial $
-formula
$L^\partial $
-formula
![]() $\psi \left ( x \right )$
with parameters from K, satisfiable in some
$\psi \left ( x \right )$
with parameters from K, satisfiable in some
![]() $L^\partial _{\lambda _0}$
-extension of K, which has the following property: in any
$L^\partial _{\lambda _0}$
-extension of K, which has the following property: in any
![]() $L^\partial _{\lambda _0}$
-extension
$L^\partial _{\lambda _0}$
-extension
![]() $L\supseteq K$
(equivalenty:
$L\supseteq K$
(equivalenty:
![]() $L^\partial $
-extension) we have
$L^\partial $
-extension) we have
![]() $L\models \psi \left ( x \right ) \rightarrow \phi \left ( x \right )$
.
$L\models \psi \left ( x \right ) \rightarrow \phi \left ( x \right )$
.
Proof. When plugging a solution a into
![]() $\phi \left ( x \right )$
, any instance of
$\phi \left ( x \right )$
, any instance of
![]() $\lambda _0\left ( b \right )$
becomes either zero or
$\lambda _0\left ( b \right )$
becomes either zero or
![]() $b^{1/p}$
. Applying a high enough power of the Frobenius automorphisms to every equality and adding some formulas of the form
$b^{1/p}$
. Applying a high enough power of the Frobenius automorphisms to every equality and adding some formulas of the form
![]() $\partial \left ( t\left ( x \right ) \right ) =0$
for some
$\partial \left ( t\left ( x \right ) \right ) =0$
for some
![]() $L^\partial $
-terms t (this formulas keep track whether
$L^\partial $
-terms t (this formulas keep track whether
![]() $a\models \lambda _0\left ( t\left ( x \right ) \right ) = 0$
), we get a quantifier free
$a\models \lambda _0\left ( t\left ( x \right ) \right ) = 0$
), we get a quantifier free
![]() $L^\partial $
-formula
$L^\partial $
-formula
![]() $\psi \left ( x \right )$
with the following property: in any
$\psi \left ( x \right )$
with the following property: in any
![]() $L^\partial _{\lambda _0}$
-extension
$L^\partial _{\lambda _0}$
-extension
![]() $L\supseteq K$
(equivalenty:
$L\supseteq K$
(equivalenty:
![]() $L^\partial $
-extension) we have
$L^\partial $
-extension) we have
![]() $L\models \psi \left ( x \right ) \rightarrow \phi \left ( x \right )$
, as desired.⊣
$L\models \psi \left ( x \right ) \rightarrow \phi \left ( x \right )$
, as desired.⊣
Proposition 3.6. In the language
![]() $L^\partial _{\lambda _0}$
, strict 1-existentially closed
$L^\partial _{\lambda _0}$
, strict 1-existentially closed
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields are existentially closed.
$\operatorname {\mathrm {Fr}}^n$
-differential fields are existentially closed.
Proof. Let K be a strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field, which is 1-existentially closed in
$\operatorname {\mathrm {Fr}}^n$
-differential field, which is 1-existentially closed in
![]() $L^\partial _{\lambda _0}$
. Let
$L^\partial _{\lambda _0}$
. Let
![]() $\phi $
be an existential
$\phi $
be an existential
![]() $L^\partial _{\lambda _0}$
-sentence with parameters from K and let
$L^\partial _{\lambda _0}$
-sentence with parameters from K and let
![]() $K\subseteq L$
be an extension of
$K\subseteq L$
be an extension of
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields such that L satisfies
$\operatorname {\mathrm {Fr}}^n$
-differential fields such that L satisfies
![]() $\phi $
. By Remark 3.5 we may assume, that
$\phi $
. By Remark 3.5 we may assume, that
![]() $\phi $
is an
$\phi $
is an
![]() $L^\partial $
-sentence and by the standard tricks we may assume that
$L^\partial $
-sentence and by the standard tricks we may assume that
![]() $\phi $
is of the form
$\phi $
is of the form
![]() $\left ( \exists x \right ) \left ( \bigwedge _{i=1}^k f_i\left ( x \right ) = 0 \right )$
where x is a tuple of variables and
$\left ( \exists x \right ) \left ( \bigwedge _{i=1}^k f_i\left ( x \right ) = 0 \right )$
where x is a tuple of variables and
![]() $f_1,\dotsc , f_k$
are multivariate differential polynomials with coefficients from K.
$f_1,\dotsc , f_k$
are multivariate differential polynomials with coefficients from K.
Take a tuple
![]() $a = \left ( a_1,\dotsc a_m \right )$
from L such that
$a = \left ( a_1,\dotsc a_m \right )$
from L such that
![]() $f_1\left ( a \right ) = \cdots = f_k\left ( a \right ) = 0$
. We may assume that every element of a is differentially algebraic over K.Footnote
1
Then, by Lemma 3.2 there is some single element
$f_1\left ( a \right ) = \cdots = f_k\left ( a \right ) = 0$
. We may assume that every element of a is differentially algebraic over K.Footnote
1
Then, by Lemma 3.2 there is some single element
![]() $c\in L$
such that for each i we have
$c\in L$
such that for each i we have
![]() $a_i^{q^N}\in K\left \langle c \right \rangle $
for some natural number N. Thus there are univariate differential polynomials
$a_i^{q^N}\in K\left \langle c \right \rangle $
for some natural number N. Thus there are univariate differential polynomials
![]() $g_1, h_1, \dotsc , g_m, h_m$
over K, such that
$g_1, h_1, \dotsc , g_m, h_m$
over K, such that
 $$ \begin{align*}a_1^{q^N}=\frac{g_1\left( c \right)}{h_1\left( c \right)}, \dotsc , a_m^{q^N}=\frac{g_m\left( c \right)}{h_m\left( c \right)},\end{align*} $$
$$ \begin{align*}a_1^{q^N}=\frac{g_1\left( c \right)}{h_1\left( c \right)}, \dotsc , a_m^{q^N}=\frac{g_m\left( c \right)}{h_m\left( c \right)},\end{align*} $$
or in other words
 $$ \begin{align*}a_1=\lambda_0^{nN}\left( \frac{g_1\left( c \right)}{h_1\left( c \right)} \right) , \dotsc , a_m=\lambda_0^{nN}\left( \frac{g_m\left( c \right)}{h_m\left( c \right)} \right),\end{align*} $$
$$ \begin{align*}a_1=\lambda_0^{nN}\left( \frac{g_1\left( c \right)}{h_1\left( c \right)} \right) , \dotsc , a_m=\lambda_0^{nN}\left( \frac{g_m\left( c \right)}{h_m\left( c \right)} \right),\end{align*} $$
since
![]() $q=p^n$
. Consider the following formula:
$q=p^n$
. Consider the following formula:
 $$ \begin{align*}\psi\left( y \right) \colon \ \bigwedge_{i=1}^k h_i\left( y \right)\neq 0 \wedge\bigwedge_{i=1}^k f_i\left( \lambda_0^N\left( \frac{g_1\left( y \right)}{h_1\left( y \right)} \right), \dotsc , \lambda_0^N\left( \frac{g_m\left( y \right)}{h_m\left( y \right)} \right) \right) = 0.\end{align*} $$
$$ \begin{align*}\psi\left( y \right) \colon \ \bigwedge_{i=1}^k h_i\left( y \right)\neq 0 \wedge\bigwedge_{i=1}^k f_i\left( \lambda_0^N\left( \frac{g_1\left( y \right)}{h_1\left( y \right)} \right), \dotsc , \lambda_0^N\left( \frac{g_m\left( y \right)}{h_m\left( y \right)} \right) \right) = 0.\end{align*} $$
Then
![]() $L\models \psi \left ( c \right )$
, therefore by
$L\models \psi \left ( c \right )$
, therefore by
![]() $1$
-existential closedness of K in
$1$
-existential closedness of K in
![]() $L^\partial _{\lambda _0}$
there is some
$L^\partial _{\lambda _0}$
there is some
![]() $b\in K$
such that
$b\in K$
such that
![]() $L\models \psi \left ( b \right )$
. Then the tuple
$L\models \psi \left ( b \right )$
. Then the tuple
![]() $ \left ( \lambda _0^N\left ( \frac {g_1\left ( b \right )}{h_1\left ( b \right )} \right ), \dotsc , \lambda _0^N\left ( \frac {g_m\left ( b \right )}{h_m\left ( b \right )} \right )\right )$
witnesses the satisfiability of
$ \left ( \lambda _0^N\left ( \frac {g_1\left ( b \right )}{h_1\left ( b \right )} \right ), \dotsc , \lambda _0^N\left ( \frac {g_m\left ( b \right )}{h_m\left ( b \right )} \right )\right )$
witnesses the satisfiability of
![]() $\phi $
in K, as desired.⊣
$\phi $
in K, as desired.⊣
Corollary 3.7. For a strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field
$\operatorname {\mathrm {Fr}}^n$
-differential field
![]() $\left ( K, \partial \right )$
, the following conditions are equivalent:
$\left ( K, \partial \right )$
, the following conditions are equivalent:
-
(1) K is a
 $1$
-existentially closed
$1$
-existentially closed
 $\operatorname {\mathrm {Fr}}^n$
-differential field in the language
$\operatorname {\mathrm {Fr}}^n$
-differential field in the language
 $L^\partial $
.
$L^\partial $
. -
(2) K is a existentially closed
 $\operatorname {\mathrm {Fr}}^n$
-differential field in the language
$\operatorname {\mathrm {Fr}}^n$
-differential field in the language
 $L^\partial $
.
$L^\partial $
. -
(3) K is a
 $1$
-existentially closed
$1$
-existentially closed
 $\operatorname {\mathrm {Fr}}^n$
-differential field in the language
$\operatorname {\mathrm {Fr}}^n$
-differential field in the language
 $L^\partial _{\lambda _0}$
.
$L^\partial _{\lambda _0}$
. -
(4) K is a existentially closed
 $\operatorname {\mathrm {Fr}}^n$
-differential field in the language
$\operatorname {\mathrm {Fr}}^n$
-differential field in the language
 $L^\partial _{\lambda _0}$
.
$L^\partial _{\lambda _0}$
.
Proof. The implications
![]() $(2)\Longrightarrow (1)$
and
$(2)\Longrightarrow (1)$
and
![]() $(4)\Longrightarrow (3)$
are obvious. Corollary 3.6 gives the implication
$(4)\Longrightarrow (3)$
are obvious. Corollary 3.6 gives the implication
![]() $(3)\Longrightarrow (4)$
. It is now enough to prove
$(3)\Longrightarrow (4)$
. It is now enough to prove
![]() $(1)\Longleftrightarrow (3)$
and
$(1)\Longleftrightarrow (3)$
and
![]() $(2)\Longleftrightarrow (4)$
.
$(2)\Longleftrightarrow (4)$
.
By Lemma 2.1, K has the same extensions in the languages
![]() $L^\partial $
and
$L^\partial $
and
![]() $L^\partial _{\lambda _0}$
, hence
$L^\partial _{\lambda _0}$
, hence
![]() $(3)\Longrightarrow (1)$
and
$(3)\Longrightarrow (1)$
and
![]() $(4)\Longrightarrow (2)$
. Moreover, by this and by Lemma 3.5, if K is (1-)existentially closed in
$(4)\Longrightarrow (2)$
. Moreover, by this and by Lemma 3.5, if K is (1-)existentially closed in
![]() $L^\partial $
, it is also (1-)existentially closed in
$L^\partial $
, it is also (1-)existentially closed in
![]() $L^\partial _{\lambda _0}$
, therefore
$L^\partial _{\lambda _0}$
, therefore
![]() $(1)\Longrightarrow (3)$
and
$(1)\Longrightarrow (3)$
and
![]() $(2)\Longrightarrow (4)$
, which finishes the proof.⊣
$(2)\Longrightarrow (4)$
, which finishes the proof.⊣
Remark 3.8. Corollary 3.7 is the key ingredient of the proof of our main result, Theorem 3.13 (i.e., that
![]() $T_{\operatorname {Wood}}$
axiomatizes
$T_{\operatorname {Wood}}$
axiomatizes
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}$
). Using this Corollary, we are basically just left to prove, that models of
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}$
). Using this Corollary, we are basically just left to prove, that models of
![]() $T_{\operatorname {Wood}}$
are
$T_{\operatorname {Wood}}$
are
![]() $1$
-existentially closed
$1$
-existentially closed
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields, a statement which seems natural.
$\operatorname {\mathrm {Fr}}^n$
-differential fields, a statement which seems natural.
It seems that idea of the proof of Theorem 3.13 can be applied in a more general context. Whenever we have a theory
![]() $T'$
of fields with some operators satisfying some primitive element theorem (e.g., as in [Reference Pogudin8]), then
$T'$
of fields with some operators satisfying some primitive element theorem (e.g., as in [Reference Pogudin8]), then
![]() $1$
-existential closedness is equivalent to existential closedness. On the other hand, if a theory of fields
$1$
-existential closedness is equivalent to existential closedness. On the other hand, if a theory of fields
![]() $T'$
has a model companion which eliminates quantifiers (in some reasonable language L), then it is easy to see that the class of
$T'$
has a model companion which eliminates quantifiers (in some reasonable language L), then it is easy to see that the class of
![]() $1$
-existentially closed models of
$1$
-existentially closed models of
![]() $T'$
in the language L is elementary. A more explicit axiomatization of
$T'$
in the language L is elementary. A more explicit axiomatization of
![]() $1$
-existentially closedness models, so “Wood axioms for
$1$
-existentially closedness models, so “Wood axioms for
![]() $T'$
,” should come from a division algorithm for the analogue of the ring of differential polynomials for
$T'$
,” should come from a division algorithm for the analogue of the ring of differential polynomials for
![]() $T'$
. Thus, we find it appropriate to ask the following.
$T'$
. Thus, we find it appropriate to ask the following.
Question 3.9. Can the above strategy be carried out in some interesting case, for example in the case of B-operators?
Remark 3.10. It is worth noting, that the idea in Remark 3.8 does not apply to
![]() $\operatorname {ACFA}$
. Recall that
$\operatorname {ACFA}$
. Recall that
![]() $\operatorname {ACFA}$
has quantifier eliminations only up to a single existential quantifier. Moreover, the fixed field of a model of
$\operatorname {ACFA}$
has quantifier eliminations only up to a single existential quantifier. Moreover, the fixed field of a model of
![]() $\operatorname {ACFA}$
is pseudofinite, a condition which is not axiomatizable by formulas in one variable, hence it seems unlikely that
$\operatorname {ACFA}$
is pseudofinite, a condition which is not axiomatizable by formulas in one variable, hence it seems unlikely that
![]() $\operatorname {ACFA}$
can be axiomatized so.
$\operatorname {ACFA}$
can be axiomatized so.
In what follows, we will use the following notation: if K is a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field,
$\operatorname {\mathrm {Fr}}^n$
-differential field,
![]() $a\in K$
and
$a\in K$
and
![]() $m>0$
, then
$m>0$
, then
![]() $\partial ^{<m}\left ( a \right )$
denotes the tuple
$\partial ^{<m}\left ( a \right )$
denotes the tuple
![]() $\left ( a, \partial \left ( a \right ), \dotsc , \partial ^{m-1}\left ( a \right ) \right )$
and analogously for
$\left ( a, \partial \left ( a \right ), \dotsc , \partial ^{m-1}\left ( a \right ) \right )$
and analogously for
![]() $\partial ^{\le m} \left ( a \right )$
. The following Lemma is well-known in the case of derivations (see [Reference Wood10, p. 333]) and we prove a generalization of it to the
$\partial ^{\le m} \left ( a \right )$
. The following Lemma is well-known in the case of derivations (see [Reference Wood10, p. 333]) and we prove a generalization of it to the
![]() $\operatorname {\mathrm {Fr}}^n$
-differential case.
$\operatorname {\mathrm {Fr}}^n$
-differential case.
Lemma 3.11. Let K be a strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field,
$\operatorname {\mathrm {Fr}}^n$
-differential field,
![]() $K\subseteq L$
an
$K\subseteq L$
an
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field extension and
$\operatorname {\mathrm {Fr}}^n$
-differential field extension and
![]() $a\in L$
. For any
$a\in L$
. For any
![]() $m>0$
, if
$m>0$
, if
![]() $\partial ^m \left ( a \right )$
is algebraic over
$\partial ^m \left ( a \right )$
is algebraic over
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right )$
, then
$K\left ( \partial ^{<m} \left ( a \right ) \right )$
, then
![]() $\partial ^m \left ( a \right )$
is separably algebraic over
$\partial ^m \left ( a \right )$
is separably algebraic over
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right )$
.
$K\left ( \partial ^{<m} \left ( a \right ) \right )$
.
Proof. Note that if
![]() $\partial ^m \left ( a \right )$
is separably algebraic over
$\partial ^m \left ( a \right )$
is separably algebraic over
![]() $K\left ( \partial ^{ m} \left ( a \right ) \right )$
, then for any
$K\left ( \partial ^{ m} \left ( a \right ) \right )$
, then for any
![]() $k>m$
we have
$k>m$
we have
![]() $\partial ^{k}\left ( a \right ) \in K\left ( \partial ^{\le m} \left ( a \right ) \right )$
. Indeed, if f is the (separable) minimal polynomial of
$\partial ^{k}\left ( a \right ) \in K\left ( \partial ^{\le m} \left ( a \right ) \right )$
. Indeed, if f is the (separable) minimal polynomial of
![]() $\partial ^m \left ( a \right )$
over
$\partial ^m \left ( a \right )$
over
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right )$
, then
$K\left ( \partial ^{<m} \left ( a \right ) \right )$
, then
and since
![]() $f'\left ( \partial ^m \left ( a \right ) \right )\neq 0$
, the claim follows. Here
$f'\left ( \partial ^m \left ( a \right ) \right )\neq 0$
, the claim follows. Here
![]() $f^\partial $
denotes the polynomial obtained by applying
$f^\partial $
denotes the polynomial obtained by applying
![]() $\partial $
to the coefficients of f.
$\partial $
to the coefficients of f.
We may therefore assume that the tuple
![]() $\bar {a}=\partial ^{<m} \left ( a \right )$
is algebraically independent over K. Let
$\bar {a}=\partial ^{<m} \left ( a \right )$
is algebraically independent over K. Let
![]() $f\left ( X \right ) = \sum _{i=0}^N f_i\left ( \bar {a} \right ) X^i$
be the minimal polynomial of
$f\left ( X \right ) = \sum _{i=0}^N f_i\left ( \bar {a} \right ) X^i$
be the minimal polynomial of
![]() $b=\partial ^{m} \left ( a \right )$
over
$b=\partial ^{m} \left ( a \right )$
over
![]() $K\left [ \bar {a}\right ]$
- by this we mean that
$K\left [ \bar {a}\right ]$
- by this we mean that
![]() $f\in K\left [ \bar {a}\right ] \left [ X \right ]$
is a minimal-degree (
$f\in K\left [ \bar {a}\right ] \left [ X \right ]$
is a minimal-degree (
![]() $=N$
) polynomial vanishing on b and the coefficients
$=N$
) polynomial vanishing on b and the coefficients
![]() $f_i$
have minimal total degree. Since the tuple
$f_i$
have minimal total degree. Since the tuple
![]() $\bar {a}$
is algebraically independent over K, the ring
$\bar {a}$
is algebraically independent over K, the ring
![]() $K\left [ \bar {a}\right ] \left [ X\right ]$
is UFD, the polynomials
$K\left [ \bar {a}\right ] \left [ X\right ]$
is UFD, the polynomials
![]() $f_0,\dotsc , f_N$
are uniquely determined and saying that they have minimal degree is the same as saying that they are coprime.
$f_0,\dotsc , f_N$
are uniquely determined and saying that they have minimal degree is the same as saying that they are coprime.
Assume that the claim of the Lemma does not hold, i.e., that
![]() $f'=0$
. Using this and the chain rule we can do the following calculations:
$f'=0$
. Using this and the chain rule we can do the following calculations:
 $$ \begin{align*} 0 &= \partial \left( f \left( b \right) \right) = \partial \left( \sum_{i=0}^N f_i\left( \bar{a}\right) b^i \right) = \sum_{i=0}^N \partial \left( f_i\left( \bar{a} \right) \right) b^{qi} \\ &= \sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-1} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) b^{qi} \\ &= \sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-2} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) b^{qi} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q \partial^{m} \left( a \right) b^{qi} \\ &=\sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-2} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) b^{qi} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q b^{qi+1}. \end{align*} $$
$$ \begin{align*} 0 &= \partial \left( f \left( b \right) \right) = \partial \left( \sum_{i=0}^N f_i\left( \bar{a}\right) b^i \right) = \sum_{i=0}^N \partial \left( f_i\left( \bar{a} \right) \right) b^{qi} \\ &= \sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-1} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) b^{qi} \\ &= \sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-2} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) b^{qi} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q \partial^{m} \left( a \right) b^{qi} \\ &=\sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-2} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) b^{qi} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q b^{qi+1}. \end{align*} $$
Let us define
![]() $g\in K\left [ \bar {a}\right ] \left [ X \right ]$
by the following formula:
$g\in K\left [ \bar {a}\right ] \left [ X \right ]$
by the following formula:
 $$ \begin{align*}g\left( X \right) = \sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-2} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) X^{qi} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q X^{qi+1}.\end{align*} $$
$$ \begin{align*}g\left( X \right) = \sum_{i=0}^N \left( f_i^\partial\left( \bar{a}^q \right) + \sum_{j=0}^{m-2} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^q \partial^{j+1} \left( a \right)\right) X^{qi} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q X^{qi+1}.\end{align*} $$
Since the polynomial g vanishes at b we have that, using Gauss Lemma, g is divisible by f in the ring
![]() $K\left [ \bar {a}\right ] \left [ X \right ]$
(here we used the fact that the coefficients of f are coprime). Therefore, since
$K\left [ \bar {a}\right ] \left [ X \right ]$
(here we used the fact that the coefficients of f are coprime). Therefore, since
![]() $f'=0$
, also
$f'=0$
, also
![]() $g'$
is divisible by f, hence
$g'$
is divisible by f, hence
![]() $g'\left ( b \right ) = 0$
. A direct calculation shows that
$g'\left ( b \right ) = 0$
. A direct calculation shows that
 $$ \begin{align*}g'\left( X \right) = \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q X^{qi} = \left( \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right) X^{i}\right)^q,\end{align*} $$
$$ \begin{align*}g'\left( X \right) = \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right)^q X^{qi} = \left( \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-1}} \left( \bar{a}\right) X^{i}\right)^q,\end{align*} $$
thus
![]() $\sum _{i=0}^N\frac {\partial f_i}{\partial X_{m-1}} \left ( \bar {a}\right ) b^{i} = 0$
. By the minimality assumption on f, for any i we have
$\sum _{i=0}^N\frac {\partial f_i}{\partial X_{m-1}} \left ( \bar {a}\right ) b^{i} = 0$
. By the minimality assumption on f, for any i we have
![]() $\frac {\partial f_i}{\partial X_{m-1}} \left ( \bar {a}\right ) = 0 $
and, since
$\frac {\partial f_i}{\partial X_{m-1}} \left ( \bar {a}\right ) = 0 $
and, since
![]() $\bar {a}$
is algebraically independent over K, also
$\bar {a}$
is algebraically independent over K, also
![]() $\frac {\partial f_i}{\partial X_{m-1}} = 0$
.
$\frac {\partial f_i}{\partial X_{m-1}} = 0$
.
By repeating analogous calculations we may also show that
![]() $\frac {\partial f_i}{\partial X_{j}} = 0$
for any
$\frac {\partial f_i}{\partial X_{j}} = 0$
for any
![]() $i, j$
—as an example, we will prove this for
$i, j$
—as an example, we will prove this for
![]() $j=m-2$
. Recall that
$j=m-2$
. Recall that
![]() $\partial ^2=\partial \circ \partial $
is a derivation of
$\partial ^2=\partial \circ \partial $
is a derivation of
![]() $x\mapsto x^{q^2}$
. Using the fact
$x\mapsto x^{q^2}$
. Using the fact
![]() $\frac {\partial f_i}{\partial X_{m-1}} = 0$
and the same identities as previously, we arrive at
$\frac {\partial f_i}{\partial X_{m-1}} = 0$
and the same identities as previously, we arrive at
 $$ \begin{align*}0&=\partial^2\left( f \left( b\right) \right) \\&= \sum_{i=0}^N \left( f_i^{\partial^2}\left( \bar{a}^{q^2} \right) + \sum_{j=0}^{m-3} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^{q^2} \partial^{j+2} \left( a \right)\right) b^{q^2i} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-2}} \left( \bar{a}\right)^{q^2} b^{q^2i+1}.\end{align*} $$
$$ \begin{align*}0&=\partial^2\left( f \left( b\right) \right) \\&= \sum_{i=0}^N \left( f_i^{\partial^2}\left( \bar{a}^{q^2} \right) + \sum_{j=0}^{m-3} \frac{\partial f_i}{\partial X_j} \left( \bar{a}\right)^{q^2} \partial^{j+2} \left( a \right)\right) b^{q^2i} + \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-2}} \left( \bar{a}\right)^{q^2} b^{q^2i+1}.\end{align*} $$
Let
![]() $h\in K\left [ \bar {a}\right ] \left [ X \right ]$
play the role of g above. As previously,
$h\in K\left [ \bar {a}\right ] \left [ X \right ]$
play the role of g above. As previously,
![]() $h'\left ( b \right )=0$
and direct calculations show that
$h'\left ( b \right )=0$
and direct calculations show that
 $$ \begin{align*}h'\left( X \right) = \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-2}} \left( \bar{a}\right)^{q^2} X^{q^2i} = \left(\sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-2}} \left( \bar{a}\right) X^{i} \right)^{q^2},\end{align*} $$
$$ \begin{align*}h'\left( X \right) = \sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-2}} \left( \bar{a}\right)^{q^2} X^{q^2i} = \left(\sum_{i=0}^N \frac{\partial f_i}{\partial X_{m-2}} \left( \bar{a}\right) X^{i} \right)^{q^2},\end{align*} $$
hence
![]() $\sum _{i=0}^N \frac {\partial f_i}{\partial X_{m-2}} \left ( \bar {a}\right ) b^{i} = 0$
, thus by the minimality assumptions on f and the independence of
$\sum _{i=0}^N \frac {\partial f_i}{\partial X_{m-2}} \left ( \bar {a}\right ) b^{i} = 0$
, thus by the minimality assumptions on f and the independence of
![]() $\bar {a}$
we get that
$\bar {a}$
we get that
![]() $\frac {\partial f_i}{\partial X_{m-2}}=0$
for any i.
$\frac {\partial f_i}{\partial X_{m-2}}=0$
for any i.
Since
![]() $\frac {\partial f_i}{\partial X_{j}} = 0$
for any
$\frac {\partial f_i}{\partial X_{j}} = 0$
for any
![]() $i, j$
, we get that every
$i, j$
, we get that every
![]() $f_i$
is a polynomial in
$f_i$
is a polynomial in
![]() $X_0^p,\dotsc , X_{m-1}^p$
. Consider the equality
$X_0^p,\dotsc , X_{m-1}^p$
. Consider the equality
 $$ \begin{align*}\sum_{i=0}^N f_i\left( \bar{a} \right) b^i = 0.\end{align*} $$
$$ \begin{align*}\sum_{i=0}^N f_i\left( \bar{a} \right) b^i = 0.\end{align*} $$
Since
![]() $f_i=0$
if i is not divisible by p and every
$f_i=0$
if i is not divisible by p and every
![]() $f_i$
is a polynomial in
$f_i$
is a polynomial in
![]() $X_0^p,\dotsc , X_{m-1}^p$
, this equality expresses the linear dependence over K of pth powers of some elements of L, namely some monomials in
$X_0^p,\dotsc , X_{m-1}^p$
, this equality expresses the linear dependence over K of pth powers of some elements of L, namely some monomials in
![]() $\bar {a}$
and b whose degree in b is not greater than
$\bar {a}$
and b whose degree in b is not greater than
![]() $N/p$
. Since
$N/p$
. Since
![]() $K\subseteq L$
is an separable extension, already this monomials must be linearly dependent over K. Because of the algebraic independence of
$K\subseteq L$
is an separable extension, already this monomials must be linearly dependent over K. Because of the algebraic independence of
![]() $\bar {a}$
over K, this dependence relation must contain b. Thus we get that b satisfies some algebraic relation over
$\bar {a}$
over K, this dependence relation must contain b. Thus we get that b satisfies some algebraic relation over
![]() $K\left [ \bar {a}\right ]$
of degree smaller than N, contrary to the minimality of N.⊣
$K\left [ \bar {a}\right ]$
of degree smaller than N, contrary to the minimality of N.⊣
Lemma 3.12. A strict
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field K is 1-existentially closed in the language
$\operatorname {\mathrm {Fr}}^n$
-differential field K is 1-existentially closed in the language
![]() $L^\partial $
if and only if the following condition holds: if
$L^\partial $
if and only if the following condition holds: if
![]() $f, g \in K\{ X\}$
and there is some
$f, g \in K\{ X\}$
and there is some
![]() $\operatorname {\mathrm {Fr}}^n$
-differential extension
$\operatorname {\mathrm {Fr}}^n$
-differential extension
![]() $K\subseteq L$
such that
$K\subseteq L$
such that
![]() $L \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
, then
$L \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
, then
![]() $K \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
.
$K \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
.
Proof. The implication
![]() $\left ( \Longrightarrow \right )$
is immediate. For
$\left ( \Longrightarrow \right )$
is immediate. For
![]() $\left ( \Longleftarrow \right )$
assume that K satisfies the condition from the statement of the Lemma. Let
$\left ( \Longleftarrow \right )$
assume that K satisfies the condition from the statement of the Lemma. Let
![]() $\phi \left ( x \right )$
be a quantifier free
$\phi \left ( x \right )$
be a quantifier free
![]() $L^\partial $
-formula (in one variable, with parameters from K) for which there is some extension
$L^\partial $
-formula (in one variable, with parameters from K) for which there is some extension
![]() $K\subseteq L$
such that
$K\subseteq L$
such that
![]() $L\models \left (\exists x\right ) \phi \left ( x \right )$
. We may assume that this formula is of the form
$L\models \left (\exists x\right ) \phi \left ( x \right )$
. We may assume that this formula is of the form
for some differential polynomials
![]() $f_1,\dotsc , f_m, g \in K\{ X\}$
. Take N such that
$f_1,\dotsc , f_m, g \in K\{ X\}$
. Take N such that
![]() $m<p^N$
and pick some
$m<p^N$
and pick some
![]() $t\in K \setminus K^p$
. By Lemma 2.1, for any extension
$t\in K \setminus K^p$
. By Lemma 2.1, for any extension
![]() $K\subseteq L$
in the language
$K\subseteq L$
in the language
![]() $L^\partial $
we have
$L^\partial $
we have
![]() $t\in L\setminus L^p$
, thus we have
$t\in L\setminus L^p$
, thus we have
 $$ \begin{align*}&L\models \left(\exists x\right)\left( f_1\left( x \right) = 0 \wedge \cdots \wedge f_m\left( x \right) = 0 \wedge g\left( x \right) \neq 0\right) \\&\qquad\Longleftrightarrow L \models \left(\exists x\right) \left( f\left( x \right) = 0 \wedge g\left( x \right)\neq 0\right),\end{align*} $$
$$ \begin{align*}&L\models \left(\exists x\right)\left( f_1\left( x \right) = 0 \wedge \cdots \wedge f_m\left( x \right) = 0 \wedge g\left( x \right) \neq 0\right) \\&\qquad\Longleftrightarrow L \models \left(\exists x\right) \left( f\left( x \right) = 0 \wedge g\left( x \right)\neq 0\right),\end{align*} $$
where
![]() $f\left ( x \right ) = f_1\left ( x \right )^{p^N}+t f_2\left ( x \right )^{p^N}+\cdots +t^{m-1}f_m\left ( x \right )^{p^N}$
. Since
$f\left ( x \right ) = f_1\left ( x \right )^{p^N}+t f_2\left ( x \right )^{p^N}+\cdots +t^{m-1}f_m\left ( x \right )^{p^N}$
. Since
![]() $L\models \left (\exists x\right ) \phi \left ( x \right )$
, we have that
$L\models \left (\exists x\right ) \phi \left ( x \right )$
, we have that
![]() $L \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0\wedge g\left ( x \right )\neq 0\right )$
, thus
$L \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0\wedge g\left ( x \right )\neq 0\right )$
, thus
![]() $K \models \left (\exists x\right ) \big( f\left ( x \right ) = 0\wedge g\left ( x \right )\neq 0\big )$
, hence also
$K \models \left (\exists x\right ) \big( f\left ( x \right ) = 0\wedge g\left ( x \right )\neq 0\big )$
, hence also
![]() $K\models \left (\exists x\right ) \phi \left ( x \right )$
. Therefore, K is 1-existentially closed.⊣
$K\models \left (\exists x\right ) \phi \left ( x \right )$
. Therefore, K is 1-existentially closed.⊣
We are now ready to prove our main theorem. Recall that the theory
![]() $T_{\operatorname {Wood}}$
was defined in the Introduction.
$T_{\operatorname {Wood}}$
was defined in the Introduction.
Theorem 3.13. The theory
![]() $T_{\operatorname {Wood}}$
has the same models as
$T_{\operatorname {Wood}}$
has the same models as
![]() $\operatorname {\mathrm {Fr}}^n - \operatorname {\mathrm {DCF}}_p$
.
$\operatorname {\mathrm {Fr}}^n - \operatorname {\mathrm {DCF}}_p$
.
Proof. Since the theory
![]() $\operatorname {\mathrm {Fr}}^n - \operatorname {\mathrm {DCF}}_p$
contains
$\operatorname {\mathrm {Fr}}^n - \operatorname {\mathrm {DCF}}_p$
contains
![]() $T_{\operatorname {Wood}}$
(see [Reference Kowalski4], after Question 3), every model of
$T_{\operatorname {Wood}}$
(see [Reference Kowalski4], after Question 3), every model of
![]() $\operatorname {\mathrm {Fr}}^n - \operatorname {\mathrm {DCF}}_p$
is a model of
$\operatorname {\mathrm {Fr}}^n - \operatorname {\mathrm {DCF}}_p$
is a model of
![]() $T_{\operatorname {Wood}}$
.
$T_{\operatorname {Wood}}$
.
For the other direction, note that by Corollary 3.7 it is enough to prove that models of
![]() $T_{\operatorname {Wood}}$
are 1-existentially closed
$T_{\operatorname {Wood}}$
are 1-existentially closed
![]() $\operatorname {\mathrm {Fr}}^n$
-differential fields in the language
$\operatorname {\mathrm {Fr}}^n$
-differential fields in the language
![]() $L^\partial $
. In order to prove this, we will verify the condition from Lemma 3.12. Assume that this condition is not verified, i.e., there are
$L^\partial $
. In order to prove this, we will verify the condition from Lemma 3.12. Assume that this condition is not verified, i.e., there are
![]() $f, g \in K\{ X\}$
and some
$f, g \in K\{ X\}$
and some
![]() $\operatorname {\mathrm {Fr}}^n$
-differential extension
$\operatorname {\mathrm {Fr}}^n$
-differential extension
![]() $K\subseteq L$
such that
$K\subseteq L$
such that
![]() $L \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
, but
$L \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
, but
![]() $K \not \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
. Among all such
$K \not \models \left (\exists x\right ) \left ( f\left ( x \right ) = 0, g\left ( x \right )\neq 0\right )$
. Among all such
![]() $f, g$
pick a pair which is minimal in the following sense: f has minimal order, minimal degree in the highest variable and g has (for this f) minimal order. Note that
$f, g$
pick a pair which is minimal in the following sense: f has minimal order, minimal degree in the highest variable and g has (for this f) minimal order. Note that
![]() $f\neq 0$
, since
$f\neq 0$
, since
![]() $T_{\operatorname {Wood}}$
proves that for any non-zero
$T_{\operatorname {Wood}}$
proves that for any non-zero
![]() $g\in K\{ X\}$
there is some
$g\in K\{ X\}$
there is some
![]() $a\in K$
such that
$a\in K$
such that
![]() $g\left ( a \right ) \neq 0$
.
$g\left ( a \right ) \neq 0$
.
Let L be an
![]() $\operatorname {\mathrm {Fr}}^n$
-extension of K and let
$\operatorname {\mathrm {Fr}}^n$
-extension of K and let
![]() $a\in L$
be such that
$a\in L$
be such that
![]() $f\left ( a \right ) = 0, g\left ( a \right )\neq 0$
. Let m be the maximal numbers such that the tuple
$f\left ( a \right ) = 0, g\left ( a \right )\neq 0$
. Let m be the maximal numbers such that the tuple
![]() $\partial ^{<m}\left ( a \right )$
is algebraically independent over K. Let
$\partial ^{<m}\left ( a \right )$
is algebraically independent over K. Let
![]() $\tilde {F}\left ( X \right )$
be the minimal polynomial of
$\tilde {F}\left ( X \right )$
be the minimal polynomial of
![]() $\partial ^m \left ( a \right )$
over
$\partial ^m \left ( a \right )$
over
![]() $K\left [ \partial ^{<m}\left ( a \right )\right ]$
, in the same sense as in the proof of Lemma 3.11. Let
$K\left [ \partial ^{<m}\left ( a \right )\right ]$
, in the same sense as in the proof of Lemma 3.11. Let
![]() $\tilde {f}$
be the differential polynomial obtained from
$\tilde {f}$
be the differential polynomial obtained from
![]() $\tilde {F}\left ( X \right )$
by replacing the appearances of
$\tilde {F}\left ( X \right )$
by replacing the appearances of
![]() $\partial ^{<m} \left ( a \right )$
in
$\partial ^{<m} \left ( a \right )$
in
![]() $\tilde {F}$
by
$\tilde {F}$
by
![]() $\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
. By Lemma 3.11
$\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
. By Lemma 3.11
![]() $f'\neq 0$
and, as in the proof of this Lemma, for any
$f'\neq 0$
and, as in the proof of this Lemma, for any
![]() $k>m$
we have
$k>m$
we have
![]() $\partial ^{k} \left ( a \right )\in K\left ( \partial ^{\le m } \left ( a \right ) \right )$
and actually there is a polynomial
$\partial ^{k} \left ( a \right )\in K\left ( \partial ^{\le m } \left ( a \right ) \right )$
and actually there is a polynomial
![]() $P_k\in K\left [ X_0,\dotsc , X_m \right ]$
, depending only on
$P_k\in K\left [ X_0,\dotsc , X_m \right ]$
, depending only on
![]() $\tilde {f}$
, such that
$\tilde {f}$
, such that
 $$\begin{align} \partial^{k} \left( a \right)=\frac{P_k\left( \partial^{\le m } \left( a \right)\right) }{\tilde{f}'\left( \partial^m \left( a \right) \right)^{q^{k-m}}}. \end{align}$$
$$\begin{align} \partial^{k} \left( a \right)=\frac{P_k\left( \partial^{\le m } \left( a \right)\right) }{\tilde{f}'\left( \partial^m \left( a \right) \right)^{q^{k-m}}}. \end{align}$$
Let
![]() $f_0$
be the differential rational function obtained from the differential polynomial f by replacing
$f_0$
be the differential rational function obtained from the differential polynomial f by replacing
![]() $X^{\left ( k \right )}$
by
$X^{\left ( k \right )}$
by
 $$ \begin{align*}\frac{P_k\left( X, X', \dotsc, X^{\left( m \right)} \right)}{\tilde{f}'\left( X^{\left( m \right)} \right)^{q^{k-m}}},\end{align*} $$
$$ \begin{align*}\frac{P_k\left( X, X', \dotsc, X^{\left( m \right)} \right)}{\tilde{f}'\left( X^{\left( m \right)} \right)^{q^{k-m}}},\end{align*} $$
for
![]() $k>m$
. We see that
$k>m$
. We see that
 $$ \begin{align*}f_0 = \frac{f_1}{\tilde{f}'\left( X^{\left( m \right)} \right)^{N}},\end{align*} $$
$$ \begin{align*}f_0 = \frac{f_1}{\tilde{f}'\left( X^{\left( m \right)} \right)^{N}},\end{align*} $$
for some
![]() $N>0$
and some differential polynomial
$N>0$
and some differential polynomial
![]() $f_1\in K\left \{ X \right \}$
of order at most m. By the equality (*) we have that
$f_1\in K\left \{ X \right \}$
of order at most m. By the equality (*) we have that
![]() $f_0\left ( a \right ) = f\left ( a \right ) = 0$
. Thus
$f_0\left ( a \right ) = f\left ( a \right ) = 0$
. Thus
![]() $f_1 = f_2 \cdot \tilde {f}$
for some
$f_1 = f_2 \cdot \tilde {f}$
for some
![]() $f_2\in K \left \{ X \right \}$
.
$f_2\in K \left \{ X \right \}$
.
Claim 1. If
![]() $b\in L$
is a solution of the system
$b\in L$
is a solution of the system
![]() $\tilde {f} \left ( x \right ) = 0, \ \tilde {f}'\left ( x \right ) \cdot g\left ( x \right ) \neq 0$
, then it is also a solution of
$\tilde {f} \left ( x \right ) = 0, \ \tilde {f}'\left ( x \right ) \cdot g\left ( x \right ) \neq 0$
, then it is also a solution of
![]() $f\left ( x \right ) = 0, \ g\left ( x \right ) \neq 0$
.
$f\left ( x \right ) = 0, \ g\left ( x \right ) \neq 0$
.
Proof of Claim 1. Let
![]() $b\in L$
be a solution of the system
$b\in L$
be a solution of the system
![]() $\tilde {f} \left ( x \right ) = 0, \ \tilde {f}'\left ( x \right ) \cdot g\left ( x \right ) \neq 0$
. Surely
$\tilde {f} \left ( x \right ) = 0, \ \tilde {f}'\left ( x \right ) \cdot g\left ( x \right ) \neq 0$
. Surely
![]() $g\left ( b \right ) \neq 0$
, so we need only to show that
$g\left ( b \right ) \neq 0$
, so we need only to show that
![]() $f\left ( b \right ) = 0$
. Since
$f\left ( b \right ) = 0$
. Since
![]() $\partial ^{<m}\left ( a \right )$
is algebraically independent over K, by the formula (*) we have that
$\partial ^{<m}\left ( a \right )$
is algebraically independent over K, by the formula (*) we have that
 $$ \begin{align*}\partial^{k} \left( b \right)=\frac{P_k\left( \partial^{\le m } \left( b \right)\right) }{\tilde{f}'\left( \partial^m \left( b \right) \right)^{q^{k-m}}},\end{align*} $$
$$ \begin{align*}\partial^{k} \left( b \right)=\frac{P_k\left( \partial^{\le m } \left( b \right)\right) }{\tilde{f}'\left( \partial^m \left( b \right) \right)^{q^{k-m}}},\end{align*} $$
for
![]() $k>m$
. Thus, by the definition of
$k>m$
. Thus, by the definition of
![]() $f_0$
we have
$f_0$
we have
![]() $f_0\left ( b \right ) = f \left ( b \right )$
. On the other hand
$f_0\left ( b \right ) = f \left ( b \right )$
. On the other hand
 $$ \begin{align*}f_0\left( b\right) = \frac{f_1\left( b\right) }{\tilde{f}'\left( \partial^m\left( b \right) \right)^N} = \frac{f_2 \left( b\right ) \cdot \tilde{f}\left( b\right ) }{\tilde{f}'\left( \partial^m\left( b \right) \right)^N} = 0,\end{align*} $$
$$ \begin{align*}f_0\left( b\right) = \frac{f_1\left( b\right) }{\tilde{f}'\left( \partial^m\left( b \right) \right)^N} = \frac{f_2 \left( b\right ) \cdot \tilde{f}\left( b\right ) }{\tilde{f}'\left( \partial^m\left( b \right) \right)^N} = 0,\end{align*} $$
since
![]() $\tilde {f} \left ( b\right ) = 0$
. Thus
$\tilde {f} \left ( b\right ) = 0$
. Thus
![]() $f\left ( b \right ) = f_0\left ( b \right ) = 0$
, as desired.⊣
$f\left ( b \right ) = f_0\left ( b \right ) = 0$
, as desired.⊣
Therefore, by the minimality assumptions on f and g, we have that the order of the original f is m, f is separable as a polynomial in the variable
![]() $X^{(m)}$
. Reasoning as in Claim 1. we may assume that the order of g is at most m. If g would have order strictly smaller than m, then
$X^{(m)}$
. Reasoning as in Claim 1. we may assume that the order of g is at most m. If g would have order strictly smaller than m, then
![]() $K\models \left ( \exists x \right ) \left ( f\left ( x\right ) = 0 , g\left ( x\right ) \neq 0 \right )$
, as K satisfies the Wood axioms, contrary to the assumptions. Thus g has order precisely m.
$K\models \left ( \exists x \right ) \left ( f\left ( x\right ) = 0 , g\left ( x\right ) \neq 0 \right )$
, as K satisfies the Wood axioms, contrary to the assumptions. Thus g has order precisely m.
Denote by
![]() $F, G\in K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
the polynomials obtained from
$F, G\in K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
the polynomials obtained from
![]() $f, g$
by replacing
$f, g$
by replacing
![]() $\partial ^{<m} \left ( a \right )$
by
$\partial ^{<m} \left ( a \right )$
by
![]() $\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
.
$\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
.
Claim 2. The elements F and G of
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
are coprime.
$K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
are coprime.
Proof of Claim 2. Denote the greatest common divisor of F and G in
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
by
$K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
by
![]() $\tilde {G}$
and assume it is not invertible, i.e., not an element of
$\tilde {G}$
and assume it is not invertible, i.e., not an element of
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right )$
. By multiplying
$K\left ( \partial ^{<m} \left ( a \right ) \right )$
. By multiplying
![]() $\tilde {G}$
by some non-zero element of
$\tilde {G}$
by some non-zero element of
![]() $K\left [ \partial ^{<m} \left ( a \right ) \right ]$
we may assume that
$K\left [ \partial ^{<m} \left ( a \right ) \right ]$
we may assume that
![]() $\tilde {G}\in K\left [ \partial ^{<m} \left ( a \right ) \right ] \big [ X^{(m)} \big ]$
. By replacing the appearances of
$\tilde {G}\in K\left [ \partial ^{<m} \left ( a \right ) \right ] \big [ X^{(m)} \big ]$
. By replacing the appearances of
![]() $\partial ^{<m} \left ( a \right )$
in
$\partial ^{<m} \left ( a \right )$
in
![]() $\tilde {G}$
by
$\tilde {G}$
by
![]() $\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
we obtain a differential polynomial
$\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
we obtain a differential polynomial
![]() $\tilde {g}\in K\left \{ X \right \}$
. Since
$\tilde {g}\in K\left \{ X \right \}$
. Since
![]() $\tilde {G}$
divides
$\tilde {G}$
divides
![]() $F, G$
and the tuple
$F, G$
and the tuple
![]() $\partial ^{<m} \left ( a \right )$
is algebraically independent over K, we get that
$\partial ^{<m} \left ( a \right )$
is algebraically independent over K, we get that
![]() $\tilde {g}$
divides f and g in the ring
$\tilde {g}$
divides f and g in the ring
![]() $K\left \{ X \right \}$
. Let
$K\left \{ X \right \}$
. Let
![]() $\tilde {f}$
be the quotient of f by
$\tilde {f}$
be the quotient of f by
![]() $\tilde {g}$
. Then
$\tilde {g}$
. Then
but
![]() $\tilde {f}$
has smaller degree in
$\tilde {f}$
has smaller degree in
![]() $X^{\left ( m \right )}$
than f, which contradicts the minimality assumptions on f and g.⊣
$X^{\left ( m \right )}$
than f, which contradicts the minimality assumptions on f and g.⊣
Using Claim 2 and Euclidean division in the ring
![]() $K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
we can find some
$K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
we can find some
![]() $P_0, Q_0 \in K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
such that
$P_0, Q_0 \in K\left ( \partial ^{<m} \left ( a \right ) \right ) \big [ X^{(m)} \big ]$
such that
By multiplying this equality by some non-zero element of
![]() $K\left [ \partial ^{<m} \left ( a \right ) \right ]$
we get that there are some non-zero
$K\left [ \partial ^{<m} \left ( a \right ) \right ]$
we get that there are some non-zero
![]() $P, Q \in K\left [ \partial ^{<m} \left ( a \right ) \right ] \big [ X^{(m)} \big ]$
such that
$P, Q \in K\left [ \partial ^{<m} \left ( a \right ) \right ] \big [ X^{(m)} \big ]$
such that
![]() $\tilde {G}:=PF+QG\in K\left [ \partial ^{<m} \left ( a \right ) \right ]\setminus \left \{ 0 \right \}$
. We again replace all appearances of
$\tilde {G}:=PF+QG\in K\left [ \partial ^{<m} \left ( a \right ) \right ]\setminus \left \{ 0 \right \}$
. We again replace all appearances of
![]() $\partial ^{<m} \left ( a \right )$
in
$\partial ^{<m} \left ( a \right )$
in
![]() $\tilde {G}$
by
$\tilde {G}$
by
![]() $\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
and obtain that there are non-zero differential polynomials
$\left ( X, \dotsc , X^{\left ( m-1 \right )}\right )$
and obtain that there are non-zero differential polynomials
![]() $p, q\in K\left \{ X \right \}$
such that
$p, q\in K\left \{ X \right \}$
such that
![]() $\tilde {g}\left ( X \right ) := p\left ( X \right )f\left ( X \right )+q\left ( X \right )g\left ( X \right )$
is non-zero and of order smaller than m.
$\tilde {g}\left ( X \right ) := p\left ( X \right )f\left ( X \right )+q\left ( X \right )g\left ( X \right )$
is non-zero and of order smaller than m.
The differential polynomial f has order m and is separable in
![]() $X^{\left ( m \right )}$
, and g is non-zero, of order smaller that m. Thus, the system
$X^{\left ( m \right )}$
, and g is non-zero, of order smaller that m. Thus, the system
has a solution in K, by the Wood axioms. But, since
![]() $\tilde {g}\left ( X \right ) = p\left ( X \right )f\left ( X \right )+q\left ( X \right )g\left ( X \right )$
, any solution of this system is also a solution of the original system
$\tilde {g}\left ( X \right ) = p\left ( X \right )f\left ( X \right )+q\left ( X \right )g\left ( X \right )$
, any solution of this system is also a solution of the original system
which had no solution in K - a contradiction.⊣
Remark 3.14. Using Theorem 3.13 we can now give a positive answer to Question 4 from [Reference Kowalski4]. We also slightly improve on the form of the geometric axioms suggested there. Let
![]() $\left ( K, \partial \right )$
be a
$\left ( K, \partial \right )$
be a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field. We work in some big ambient algebraically closed field
$\operatorname {\mathrm {Fr}}^n$
-differential field. We work in some big ambient algebraically closed field
![]() $\Omega $
containing K. For a K-variety V we recall the definition of the “twisted Frobenius tangent bundle of V” (denoted
$\Omega $
containing K. For a K-variety V we recall the definition of the “twisted Frobenius tangent bundle of V” (denoted
![]() $V^{\left ( 1 \right )}$
) from [Reference Kowalski4]. Suppose V is given as the zero locus of an ideal
$V^{\left ( 1 \right )}$
) from [Reference Kowalski4]. Suppose V is given as the zero locus of an ideal
![]() $I\trianglelefteq K\left [ \bar {X} \right ]$
, where
$I\trianglelefteq K\left [ \bar {X} \right ]$
, where
![]() $\bar {X}=\left ( X_1,\dotsc , X_m \right )$
is a tuple of variables. Let
$\bar {X}=\left ( X_1,\dotsc , X_m \right )$
is a tuple of variables. Let
![]() $\bar {X}'=\left ( X^{\prime }_1,\dotsc , X^{\prime }_m \right )$
be a new tuple of variables. For
$\bar {X}'=\left ( X^{\prime }_1,\dotsc , X^{\prime }_m \right )$
be a new tuple of variables. For
![]() $f\in K\left [ \bar {X} \right ]$
we set
$f\in K\left [ \bar {X} \right ]$
we set
 $$ \begin{align*}\partial\left( f \right) \left( \bar{X}, \bar{X}' \right) = f^\partial\left( \bar{X}^q \right) + \sum_{i=1}^m \frac{\partial f}{\partial X_i}\left( \bar{X} \right)^q X_i'.\end{align*} $$
$$ \begin{align*}\partial\left( f \right) \left( \bar{X}, \bar{X}' \right) = f^\partial\left( \bar{X}^q \right) + \sum_{i=1}^m \frac{\partial f}{\partial X_i}\left( \bar{X} \right)^q X_i'.\end{align*} $$
We define
![]() $V^{\left ( 1 \right )}$
as the set of zeroes of the ideal
$V^{\left ( 1 \right )}$
as the set of zeroes of the ideal
![]() $\left ( I, \partial \left ( I \right ) \right ) \trianglelefteq K\left [ \bar {X}, \bar {X}' \right ]$
. If we took in the above formulas
$\left ( I, \partial \left ( I \right ) \right ) \trianglelefteq K\left [ \bar {X}, \bar {X}' \right ]$
. If we took in the above formulas
![]() $\partial = 0, q= 1$
, then the resulting
$\partial = 0, q= 1$
, then the resulting
![]() $V^{\left ( 1 \right )}$
would be the usual tangent bundle of V. Note that for any
$V^{\left ( 1 \right )}$
would be the usual tangent bundle of V. Note that for any
![]() $a\in V\left ( K \right )$
we have
$a\in V\left ( K \right )$
we have
![]() $\left ( a, \partial \left ( a \right ) \right )\in V^{\left ( 1 \right )}\left ( K \right )$
. Also, since I is contained in
$\left ( a, \partial \left ( a \right ) \right )\in V^{\left ( 1 \right )}\left ( K \right )$
. Also, since I is contained in
![]() $\left ( I, \partial \left ( I \right ) \right )$
, we have a projection map
$\left ( I, \partial \left ( I \right ) \right )$
, we have a projection map
![]() $V^{\left ( 1 \right )}\to V$
.
$V^{\left ( 1 \right )}\to V$
.
We are now able to state the new geometric axioms for
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
:
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
:
Suppose
![]() $V, W$
are K-irreducible K-varieties and
$V, W$
are K-irreducible K-varieties and
![]() $W\subseteq V^ {\left ( 1 \right )}$
. If the projection map
$W\subseteq V^ {\left ( 1 \right )}$
. If the projection map
![]() $W\to V$
is separable, then there is some
$W\to V$
is separable, then there is some
![]() $a\in V\left ( K \right )$
such that
$a\in V\left ( K \right )$
such that
![]() $\left ( a, \partial \left ( a \right ) \right )\in W$
.
$\left ( a, \partial \left ( a \right ) \right )\in W$
.
It is standard, that this is expressible by a scheme of first-order conditions, as explained in [Reference Kowalski4]. This looks a bit different than what is suggested in Question 4 from [Reference Kowalski4], so we explain the changes. Literally, Question 4 suggests the following axioms
Assume K is strict. Suppose
![]() $V, W$
are K-irreducible K-varieties and
$V, W$
are K-irreducible K-varieties and
![]() $W\subseteq V^{\left ( 1 \right )}$
. If the projection map
$W\subseteq V^{\left ( 1 \right )}$
. If the projection map
![]() $W\to V$
is dominant and separable, then there is some
$W\to V$
is dominant and separable, then there is some
![]() $a\in V\left ( K \right )$
such that
$a\in V\left ( K \right )$
such that
![]() ${\left ( a, \partial \left ( a \right ) \right )\in W\setminus X}$
.
${\left ( a, \partial \left ( a \right ) \right )\in W\setminus X}$
.
The word “dominant” is redundant, as separable morphisms are by definition dominant. The variety X can be removed by replacing W and V by some higher dimensional variety. Finally, strictness of K follows from the latter part of the axioms, as follows. Assume K is a
![]() $\operatorname {\mathrm {Fr}}^n$
-differential field satisfying the above axioms, but without the sentence “K is strict.” We will prove that K is strict. Assume that is not the case and let
$\operatorname {\mathrm {Fr}}^n$
-differential field satisfying the above axioms, but without the sentence “K is strict.” We will prove that K is strict. Assume that is not the case and let
![]() $c\in K^\partial \setminus K^p $
be a constant, which is not a p-th power. Define
$c\in K^\partial \setminus K^p $
be a constant, which is not a p-th power. Define
![]() $V:=\left \{ c^{1/p} \right \}$
, i.e., V is the zero locus of the irreducible polynomial
$V:=\left \{ c^{1/p} \right \}$
, i.e., V is the zero locus of the irreducible polynomial
![]() $f\left ( X \right ) = X^p-c$
. Thus, the twisted tangent bundle
$f\left ( X \right ) = X^p-c$
. Thus, the twisted tangent bundle
![]() $V^{(1)}$
is the zero locus of the polynomial
$V^{(1)}$
is the zero locus of the polynomial
i.e.,
![]() $V^{(1)} = \left \{ c^{1/p} \right \}\times \mathbb {A}^1$
. Set
$V^{(1)} = \left \{ c^{1/p} \right \}\times \mathbb {A}^1$
. Set
![]() $W:=\left \{ \left ( c^{1/p}, 0 \right ) \right \}$
. Clearly
$W:=\left \{ \left ( c^{1/p}, 0 \right ) \right \}$
. Clearly
![]() $W\subseteq V^{(1)}$
and the projection map
$W\subseteq V^{(1)}$
and the projection map
![]() $W\to V$
is separable, therefore by the geometric axioms there exists some
$W\to V$
is separable, therefore by the geometric axioms there exists some
![]() $a\in V\left ( K \right )$
such that
$a\in V\left ( K \right )$
such that
![]() $\left ( a, \partial \left ( a \right )\right ) \in W\left ( K \right )$
. But
$\left ( a, \partial \left ( a \right )\right ) \in W\left ( K \right )$
. But
![]() $a\in V\left ( K \right )$
means that
$a\in V\left ( K \right )$
means that
![]() $a\in K$
and
$a\in K$
and
![]() $a^p=c$
, contrary to the assumption that
$a^p=c$
, contrary to the assumption that
![]() $c\not \in K^p$
.
$c\not \in K^p$
.
Since the axioms described above are contained in the original axioms of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
and they contain the Wood axioms (as explained in [Reference Kowalski4] above Question 4), we get a new geometric axiomatization of
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
and they contain the Wood axioms (as explained in [Reference Kowalski4] above Question 4), we get a new geometric axiomatization of
![]() $\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
.
$\operatorname {\mathrm {Fr}}^n-\operatorname {\mathrm {DCF}}_p$
.
Question 3.15. Is
![]() $\mathcal {B}-\operatorname {\mathrm {DCF}}$
also axiomatizable by simpler geometric axioms, analogous to the above? Is there a direct proof (i.e., not using “one-dimensional” axiomatizations) of that, even in the case of
$\mathcal {B}-\operatorname {\mathrm {DCF}}$
also axiomatizable by simpler geometric axioms, analogous to the above? Is there a direct proof (i.e., not using “one-dimensional” axiomatizations) of that, even in the case of
![]() $\operatorname {\mathrm {Fr}}^n$
-derivations?
$\operatorname {\mathrm {Fr}}^n$
-derivations?
Remark 3.16. For the sake of completeness we point out, that Question 6 from [Reference Kowalski4] has an obvious negative answer. It asks whether
![]() $\left ( K, \partial ^2 \right )$
is a model of
$\left ( K, \partial ^2 \right )$
is a model of
![]() $\operatorname {\mathrm {Fr}}^{2n}-\operatorname {\mathrm {DCF}}_p$
, provided that
$\operatorname {\mathrm {Fr}}^{2n}-\operatorname {\mathrm {DCF}}_p$
, provided that
![]() $\left ( K, \partial \right )$
is a model of
$\left ( K, \partial \right )$
is a model of
![]() $\operatorname {\mathrm {Fr}}^{n}-\operatorname {\mathrm {DCF}}_p$
. The answer is negative, since the constants of
$\operatorname {\mathrm {Fr}}^{n}-\operatorname {\mathrm {DCF}}_p$
. The answer is negative, since the constants of
![]() $\left ( K, \partial ^2 \right )$
are strictly bigger than
$\left ( K, \partial ^2 \right )$
are strictly bigger than
![]() $K^p=K^\partial $
, so
$K^p=K^\partial $
, so
![]() $\left ( K, \partial ^2 \right )$
is not even strict.
$\left ( K, \partial ^2 \right )$
is not even strict.
Acknowledgment
I would like to thank Piotr Kowalski for his careful reading of this paper and many valuable comments. I would also like to thank the anonymous referee for suggesting improvements. This research was supported by the Narodowe Centrum Nauki grant no. 2018/31/B/ST1/00357.