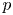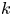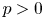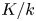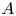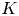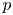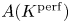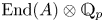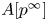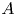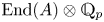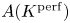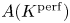1. Introduction
Let 
$p$ be a prime number and 
$k$ a finite field of characteristic 
$p>0$. Let 
$K/k$ be a finitely generated extension of fields (e.g. 
$\mathbb {F}_p(t)/\mathbb {F}_p$), fix an algebraic closure 
$K\subseteq \overline {K}$ and write 
$K\subseteq K^{\mathrm {perf}}$ for the perfect closure of 
$K$, i.e. the smallest perfect field containing 
$K$ (or, equivalently, the field obtained adding to 
$K$ all the 
$p^{n}$-roots of its elements). Let 
$A$ be a 
$K$-abelian variety. Motivated by applications to the ‘full’ Mordell–Lang conjecture, in this paper we study the structure of 
$A(K^{\mathrm {perf}})$ using 
$p$-adic cohomology. The main novelty of our approach is the use of ‘mixed’ 
$p$-divisible groups and overconvergent 
$F$-isocrystals associated to elements in 
$A(K^{\mathrm {perf}})$.
1.1 Motivation
In recent years there has been a remarkable interest in the study of the group 
$A(K^{\mathrm {perf}})$, see, e.g., [Reference Ambrosi and D'AddezioAD22, Reference Bragg and LieblichBL22, Reference D'AddezioD'A23, Reference Ghioca and MoosaGM06, Reference GhiocaGhi10, Reference RösslerRös15, Reference RösslerRös20, Reference XinyiXin21].
This interest is mainly motivated by its relation with the ‘full’ Mordell–Lang conjecture (see, e.g., [Reference Ghioca and MoosaGM06, Conjecture 1.2]). Roughly, this conjecture states that if 
$\Gamma \subseteq A(\overline K)$ is a finite rank subgroup and 
$X\subseteq A_{\overline K}$ is an irreducible 
$\overline K$-subvariety, then 
$X(\overline K) \cap \Gamma$ is not Zariski dense, unless 
$X$ is a ‘special’ (e.g. the translate of an abelian subvariety of 
$A$).
The characteristic zero version of the Mordell–Lang conjecture 
$\mathrm {ML}$ is a celebrated theorem of Faltings [Reference FaltingsFal91] for finitely generated subgroups, extended to the finite rank ones by Hindry [Reference HindryHin88]. In our positive characteristic setting, the conjecture has been proved in [Reference HrushovskiHru96] under the extra assumption that 
$\Gamma \otimes \mathbb {Z}_p$ is a finitely generated 
$\mathbb {Z}_p$-module. However, the case of arbitrary subgroups of finite rank has proven to be more elusive and few results are known.
In [Reference Ghioca and MoosaGM06], Ghioca and Moosa reduced the ‘full’ conjecture to the case in which the subgroup 
$\Gamma$ is included 
$A(L^{\mathrm {perf}})$, for 
$K\subseteq L$ a finite field extension. Combining this with the fact that the conjecture is known when 
$\Gamma$ is finitely generated, the following question arises naturally.
Question 1.1.1 When is 
$A(K^{\mathrm {perf}})$ finitely generated? What is the structure of 
$A(K^{\mathrm {perf}})$?
Our main result (Theorem 1.3.1.2) roughly states that whether 
$A(K^{\mathrm {perf}})$ is finitely generated or not depends only on the action of 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$ on the 
$p$-divisible group of 
$A$ and on the 
$p$-rank of the isogeny factors of 
$A$. As a corollary of our result, one gets the Mordell–Lang conjecture for a sufficiently generic abelian variety with Newton polygon of positive 
$p$-rank. To simplify the exposition, we assume for the rest of the introduction that 
$A$ is simple and we refer the reader to main text (and, in particular, to Theorem 3.1.1) for the general case.
1.2 Perfect points
Let us recall that, while 
$A(K)$ is finitely generated by the Lang–Néron theorem [Reference Lang and NéronLN59], it is well known that 
$A(K^{\mathrm {perf}})$ is not always finitely generated. For example, if 
$A(K)$ contains a non-torsion element and 
$A$ is defined up to isogeny over 
$k$ or 
$A$ is of 
$p$-rank 
$0$, then 
$A(K^{\mathrm {perf}})$ is not finitely generated. Even worst, Helm constructed in [Reference HelmHel22] an ordinary abelian variety without isotrivial isogeny factors such that 
$A(K^{\mathrm {perf}})$ is not finitely generated. Thus, to have finite generation, one has to impose further conditions.
On the positive side, it is well known that the torsion subgroup 
$A(K^{\mathrm {perf}})_{\mathrm {tors}}\subseteq A(K^{\mathrm {perf}})$ is finite (see, for example, [Reference Ghioca and MoosaGM06, p. 7]), so that the interesting part to study is its torsion free quotient 
$A(K^{\mathrm {perf}})_{\mathrm {tf}}:=A(K^{\mathrm {perf}})/A(K^{\mathrm {perf}})_{\mathrm {tors}}$. Since the 
$i$th-power Frobenius 
$F^i:A\rightarrow A^{(p^i)}$ and the Verschiebung 
$V^i:A^{(p^i)}\rightarrow A$ induce a factorization
where the union is taken along the injections 
$F^i:A(K)\hookrightarrow A^{(p^i)}(K)$, one has that
\begin{equation} A(K)[1/p]=A(K^{\mathrm{perf}})[1/p]. \end{equation}
Hence, to study 
$A(K^{\mathrm {perf}})$, one is reduced to understand how much the non-torsion elements of 
$A(K)$ become 
$p^n$-divisible in 
$A(K^{\mathrm {perf}})$. There are essentially two phenomena that can make 
$A(K^{\mathrm {perf}})$ not finitely generated:
(a) there might be a sequence
$\{x_n\}_{n\in \mathbb {N}}$ of non-torsion elements $x_n\in A(K)$ such that $x_n$ becomes $p^n$-divisible but not $p^{n+1}$-divisible; or(b) there might be a non-torsion element
$x\in A(K)$ that becomes infinitely $p$-divisible in $A(K^{\mathrm {perf}})$.
Both cases can happen and our main result says that the occurring of phenomenon (a) depends only on the action of 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$ on the 
$p$-divisible group of 
$A$ and the occurring of phenomenon (b) only on the 
$p$-rank of 
$A$.
1.3 Main results
1.3.1 Finite generation of perfect points
To state our main result, recall that the 
$p$-divisible group 
$A[p^{\infty }]$ of 
$A$ fits into a canonical connected-étale exact sequence
\begin{equation} 0\rightarrow A[p^{\infty}]^0\rightarrow A[p^{\infty}]\rightarrow A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}\rightarrow 0 \end{equation}
with 
$A[p^{\infty }]^0$ (respectively, 
$A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$) a connected (respectively, étale) 
$p$-divisible group. Then we prove the following.
Theorem 1.3.1.2 Assume that 
$A(K)\otimes \mathbb {Q}\neq 0$ (and recall that 
$A$ is assumed to be simple). Then:
(i)
$A(K^{\mathrm {perf}})$ is not finitely generated if and only if and there exists an idempotent $0\neq e\in \mathrm {End}(A)\otimes \mathbb {Q}_p$ (i.e. $e^2=e$) that acts as $0$ on (the isogeny class of) $A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$;(ii) every infinitely
$p$-divisible point is torsion if and only if $A$ is of positive $p$-rank.
Remark 1.3.1.3 Let us recall that, since 
$A$ is simple, 
$\mathrm {End}(A)\otimes \mathbb {Q}$ is a division algebra, hence the idempotent appearing in Theorem 1.3.1.2(i) has to live in 
$\mathrm {End}(A)\otimes \mathbb {Q}_{p}\setminus \mathrm {End}(A)\otimes \mathbb {Q}$. As often happens, it is much easier to construct 
$\mathbb {Q}_p$-linear combination of endomorphisms of 
$A$ (i.e. elements in 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$) than actual endomorphisms of 
$A$ (i.e. elements in 
$\mathrm {End}(A)$). This kind of phenomena appears, for example, in the proof of the Tate conjecture for endomorphism of abelian varieties over finite fields [Reference TateTat66].
Beyond the ordinary case, these seem to be the first general results towards the understanding of the torsion free part of 
$A(K^{\mathrm {perf}})$. Coming back to phenomena (a) and (b) of § 1.2, Theorem 1.3.1.2 says that case (a) happens if and only if there exists an idempotent as in Theorem 1.3.1.2(i) and case (b) happens if and only if the 
$p$-rank of 
$A$ is 
$0$. As an immediate corollary we get the following.
Corollary 1.3.1.4 If 
$A$ has positive 
$p$-rank and 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$ is a simple algebra, then 
$A(K^{\mathrm {perf}})$ is finitely generated.
Since for every Newton stratum of positive 
$p$-rank of the moduli space of abelian varieties of fixed dimension the generic member has 
$\mathrm {End}(A_{\overline K})\simeq \mathbb {Z}$, Corollary 1.3.1.4, together with the main results of [Reference HrushovskiHru96] and [Reference Ghioca and MoosaGM06], implies the Mordell–Lang conjecture for such a generic abelian variety.
1.3.2 Comparison with previous results
We compare Theorem 1.3.1.2 with some of the previously known results, assuming that (
$A$ is simple and) 
$A(K)\otimes \mathbb {Q}\neq 0$.
As already mentioned, if 
$A$ is isogenous to an abelian variety defined over 
$k$, 
$A(K^{\mathrm {perf}})$ is not finitely generated. This is coherent with Theorem 1.3.1.2(i), since in this case the sequence (1.3.1.1) splits canonically up to isogeny and this splitting is induced, by the 
$p$-adic Tate conjecture for abelian varieties, from an idempotent 
$e\in \mathrm {End}(A)\otimes \mathbb {Q}_p$. Similarly, the fact that if 
$A$ is of 
$p$-rank 
$0$ then 
$A(K^{\mathrm {perf}})$ is not finitely generated, is coherent with Theorem 1.3.1.2(i), taking 
$e={\rm Id}_A$.
When 
$A$ is ordinary, Theorem 1.3.1.2 was essentially already known, since part (ii) follows from [Reference RösslerRös20, Theorem 1.4] and part (i) follows from combining [Reference RösslerRös20, Theorem 1.1]) with [Reference D'AddezioD'A23, Theorem 1.1.3] (and their proofs). Always in the ordinary case, if 
$\textrm {Dim}(A)\leq 2$, then 
$A(K^{\mathrm {perf}})$ is always finitely generated: this can be either deduced from [Reference RösslerRös20, Theorem 1.2(g)]) or from Theorem 1.3.1.2(ii).
Remark 1.3.2.1 Most of the results recalled in this section also holds replacing 
$k$ with 
$\overline k$, assuming that 
$A_{\overline K}$ is not isogenous to an abelian variety defined over 
$\overline k$. In addition, our Theorem 1.3.1.2 holds replacing 
$k$ with 
$\overline k$, as we show in Theorem 3.4.1, by elaborating the arguments used in the proof of Theorem 1.3.1.2.
1.4 Strategy
Our proof is mostly cohomological, in the sense that we work with 
$p$-divisible group and crystals. To lift our cohomological results to 
$\mathrm {End}(A)$ and 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$, we use the assumption that 
$K$ is finitely generated over a finite field, to be able to apply the 
$p$-adic Tate conjecture for abelian varieties.
1.4.1 $p$-adic Abel–Jacobi maps
To prove Theorem 1.3.1.2, we start, in § 2, considering various Abel–Jacobi maps. By using the short exact sequence 
$0\rightarrow A[p^n]\rightarrow A\xrightarrow {p^n} A\rightarrow 0$ one constructs a Abel–Jacobi map
\[ \mathrm{AJ}:A(K)\otimes \mathbb{Q}\rightarrow \mathrm{Ext}^1(\mathbb{Q}_p/\mathbb{Z}_p,A[p^{\infty}])\otimes \mathbb{Q}_p. \]
Composing with the quotient map 
$A[p^{\infty }]\rightarrow A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$, we get a morphism
\[ \mathrm{AJ}^{ \unicode{x00E9}{\textrm{t}}}:A(K)\otimes \mathbb{Q}\rightarrow \mathrm{Ext}^1(\mathbb{Q}_p/\mathbb{Z}_p,A[p^{\infty}])\otimes \mathbb{Q}_p\rightarrow \mathrm{Ext}^1(\mathbb{Q}_p/\mathbb{Z}_p,A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb{Q}_p, \]
which we call the étale Abel–Jacobi map, and we consider its 
$\mathbb {Q}_p$-linearization
\[ \mathrm{AJ}^{ \unicode{x00E9}{\textrm{t}}}_p:A(K)\otimes \mathbb{Q}_{p}\rightarrow \mathrm{Ext}^1(\mathbb{Q}_p/\mathbb{Z}_p,A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb{Q}_p, \]
which we call the 
$p$-adic étale Abel–Jacobi map. In Proposition 2.1.2.1 we prove that every infinitely 
$p$-divisible element is torsion if and only if 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}$ is injective and that 
$A(K^{\mathrm {perf}})$ is finitely generated if and only if 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}_p$ is injective. Hence, we can translate the two statements of Theorem 1.3.1.2 into two statements on ‘mixed’ 
$p$-divisible groups associated to elements in 
$A(K)\otimes \mathbb {Q}_p$ and 
$A(K)\otimes \mathbb {Q}$.
Remark 1.4.1.1 Since the two properties of having a non torsion infinitely 
$p$-divisible point and having a finitely generated group of perfect points are codified by two different maps (one 
$\mathbb {Q}_p$-linear and the other 
$\mathbb {Q}$-linear), it is natural to consider two different statements in Theorem 1.3.1.2. This is slightly different from what one could aspects from apparently similar motivic conjectures (see, e.g., the Jansen injectivity conjecture [Reference JannsenJan94, Conjecture 9.15]). Roughly, this shows that the behavior of 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}_p$ is not motivic, since 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}_p$ might not be injective even when 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}$ is.
1.4.2 $p$-divisible groups and crystals
For 
$x\in A(K)\otimes \mathbb {Q}_p$, let
\begin{equation} 0\rightarrow A[p^{\infty}]\rightarrow M_x[p^{\infty}]\rightarrow \mathbb{Q}_p/ \mathbb{Z}_p\rightarrow 0 \quad \text{and}\quad 0\rightarrow A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}\rightarrow M_x[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}\rightarrow \mathbb{Q}_p/\mathbb{Z}_p\rightarrow 0 \end{equation}
be the exact sequences of 
$p$-divisible groups representing 
$\mathrm {AJ}_p(x)$ and 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}_p(x)$. By the finite generation of 
$A(K)$, we know that first does not split and we want to understand when and why second splits. To do this, we spread out 
$A\rightarrow K$ to an abelian scheme 
$\mathcal {A}\rightarrow X$ over some smooth connected 
$k$-variety 
$X$ with function field 
$K$ and we consider the category 
$\mathbf {F\textrm {-}Isoc}(X)$ of 
$F$-isocrystals and the fully faithful contravariant Dieudonné functor [Reference Berthelot, Breen and MessingBBM82]
\[ \mathbb{D}:\mathbf{pDiv}(X)_{\mathbb{Q}}\rightarrow \mathbf{F\textrm{-}Isoc}(X). \]
By fully faithfulness, we translate the splitting properties of (1.4.2.1) into analogous splitting properties of an exact sequence of 
$F$-isocrystals. As in [Reference Ambrosi and D'AddezioAD22], the advantage of doing this is that we can prove in Proposition 3.3.3.1 that the image via 
$\mathbb {D}:\mathbf {pDiv}(X)_{\mathbb {Q}}\rightarrow \mathbf {F\textrm {-}Isoc}(X),$ of the first sequence in (1.4.2.1) lies inside the much better behaved subcategory 
$\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\subseteq \mathbf {F\textrm {-}Isoc}(X)$ of overconvergent 
$F$-isocrystals.
Since 
$\mathbb {D}(A[p^{\infty }])$ is semisimple in 
$\mathbf {F\textrm {-}Isoc}^{\dagger}(X)$, we can apply recent advances in 
$p$-adic cohomology (see [Reference TsuzukiTsu23] and its improvement done in [Reference D'AddezioD'A23]) to construct, from the splitting of 
$\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}_p$, an idempotent in 
$\mathrm {End}(A[p^{\infty }])\otimes \mathbb {Q}_p$ with the desired properties, which, since 
$K$ is finitely generated over a finite field, lifts to 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$, by the 
$p$-adic Tate conjecture for abelian varieties.
This is enough to conclude the proof of Theorem 1.3.1.2(i), but to complete the proof of Theorem 1.3.1.2(ii) one needs to show that such a splitting cannot exist if the sequence (1.4.2.1) comes from an 
$x\in A(K)\otimes \mathbb {Q}$ and not from a random 
$x\in A(K)\otimes \mathbb {Q}_p$. This follows from Lemma 2.2.3.2 which shows that even if 
$\mathrm {End}(A[p^{\infty }])$ can be big and with lots of idempotency, one always has that 
$\mathrm {End}(M_x[p^{\infty }])\otimes \mathbb {Q}_p\simeq \mathbb {Q}_p$ if 
$x\in A(K)\otimes \mathbb {Q}$. This is essentially due to the geometric origin of 
$M_x[p^{\infty }]$, which makes 
$M_x[p^{\infty }]$ much more rigid for a 
$x\in A(K)\otimes \mathbb {Q}$ than for a random 
$x\in A(K)\otimes \mathbb {Q}_p$. This extra rigidity is the reason for difference between the two different parts of Theorem 1.3.1.2.
1.5 Organization of the paper
In § 2 we study various 
$p$-adic Kummer and Abel–Jacobi maps, their relation with the group of perfect points and with the extensions of 
$p$-divisible groups. In § 3 we use this to prove Theorem 1.3.1.2 assuming the overconvergence result Proposition 4.1.2. Finally, in § 4 we prove this overconvergence result.
2. Abel–Jacobi and étale Abel–Jacobi maps
Let 
$S$ be a noetherian 
$\mathbb {F}_p$-scheme and let 
$A\rightarrow S$ be an abelian scheme. We write 
$\mathbf {SH}_{\mathrm {fppf}}(S)$ for the category of fppf sheaves in abelian groups on 
$S$. Write 
$A(S)_{\mathrm {tors}}\subseteq A(S)$ for the torsion subgroup of 
$A(S)$, 
$A(S)_{\mathrm {tf}}:=A(S)/A(S)_{\mathrm {tors}}$ for its torsion free quotient and
\[ A(S)_{p^{\infty}}:=\{x\in A(S) \text{ such that for every }n\in \mathbb{N} \text{ there exists a } y_n\in A(S)\text{ with }p^ny_n=x\} \]
for its subgroup of infinitely 
$p$-divisible elements.
2.1 Kummer maps
2.1.1 Kummer map
For every 
$n\in \mathbb {N}$, the exact sequence
\[ 0\rightarrow A[p^n]\rightarrow A\xrightarrow{p^n} A\rightarrow 0 \]
in 
$\mathbf {SH}_{\mathrm {fppf}}(S)$, induces an injective morphism
\[ \mathrm{Kum}_n:A(S)/p^n\hookrightarrow H^1_{\mathrm{fl}}(S,A[p^n]) \]
and taking the projective limit and tensoring with 
$\mathbb {Q}$, we get the following commutative diagram.
We call 
$\mathrm {Kum}$: 
$A(S)\otimes \mathbb {Q}\rightarrow (\varprojlim _n H^1_{\mathrm {fl}}(S,A[p^n]))\otimes \mathbb {Q}$ the Kummer map and 
$\mathrm {Kum}_p$: 
$A(S)\otimes \mathbb {Q}_p\rightarrow (\varprojlim _n H^1_{\mathrm {fl}}(S,A[p^n]))\otimes \mathbb {Q}$ the 
$p$-adic Kummer map. By construction, one has the following lemma, which we state for further reference.
Lemma 2.1.1.1
(i) The Kummer map
$\mathrm {Kum}$ is injective if and only if $A(S)_{p^{\infty }}\subseteq A(S)_{\mathrm {tors}}$;(ii) If
$A(S)_{\mathrm {tf}}$ is finitely generated, then $\mathrm {Kum}_p$ is injective.
Proof. Statement (i) follows by tensoring with 
$\mathbb {Q}$ the short exact sequence
\[ 0\rightarrow A(S)_{p^{\infty}}\rightarrow A(S)\rightarrow \varprojlim_n H^1_{\mathrm{fl}}(S,A[p^n]). \]
For statement (ii), one uses that if 
$A(S)_{\mathrm {tf}}$ is finitely generated, then the kernel of 
$A(S)\otimes \mathbb {Z}_p\rightarrow \varprojlim _n A(S)/p^n$ is torsion, so that the map 
$A(S)\otimes \mathbb {Q}_p\rightarrow (\varprojlim _n A(S)/p^n)\otimes \mathbb {Q}$ is injective.
2.1.2 Étale Kummer maps
Assume now that 
$S=\mathrm {Spec}(K)$ is the spectrum of a field and write 
$K^{\mathrm {perf}}$ for the perfection of 
$K$. Then, the quotient maps 
$A[p^n]\rightarrow A[p^n]^{ \unicode{x00E9}{\textrm{t}}}$ induce a commutative diagram
where 
$T_p(A):=\varprojlim _n A(\overline K)[p^n]$ is the 
$p$-adic étale module of 
$A$ and 
$H^1_{ \unicode{x00E9}{\textrm{t}}}(K,T_p(A))$ is its first continuous étale cohomology group. We call 
$\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}$: 
$A(K)\otimes \mathbb {Q}\rightarrow H^1_{ \unicode{x00E9}{\textrm{t}}}(K,T_p(A))\otimes \mathbb {Q}$ the étale Kummer map and 
$\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}_p$: 
$A(K)\otimes \mathbb {Q}_p\rightarrow H^1_{ \unicode{x00E9}{\textrm{t}}}(K,T_p(A))\otimes \mathbb {Q}$ the 
$p$-adic étale Kummer map. The following proposition links the properties of 
$\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}$ and 
$\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}_p$ with the study of 
$A(K^{\mathrm {perf}})$.
Proposition 2.1.2.1 We have:
(i)
$A(K^{\mathrm {perf}})_{p^{\infty }}\subseteq A(K^{\mathrm {perf}})_{\mathrm {tors}}$ if and only if $\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}$ is injective;(ii)
$A(K^{\mathrm {perf}})_{\mathrm {tf}}$ is finitely generated if and only if $A(K)_{\mathrm {tf}}$ is finitely generated and $\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}_p$ is injective.
Proof. Let us recall that:
(a) since
$K\subseteq K^{\mathrm {perf}}$ is purely inseparable, for every finite étale group scheme $G$ the natural map $H^1(K,G)\rightarrow H^1(K^{\mathrm {perf}},G)$ is an isomorphism (see, e.g., [Sta20, Tag 04DZ]);(b) if
$L$ is a perfect field, then $H^1_{\mathrm {fl}}(L,H)\rightarrow H^1_{\mathrm {fl}}(L,H^{ \unicode{x00E9}{\textrm{t}}})$ is injective for every finite group scheme $H$ over $L$, since $H^1_{\mathrm {fl}}(L,G)=0$ for every finite connected group scheme $G$ (see, e.g., [Reference Česnavic〶iusČes15, Lemma 2.7(a)]).
Hence, part (i) and the only if part of item (ii) follow from Lemma 2.1.1.1 and the commutative diagram for 
$?\in \{\emptyset, p\}$:
where the left vertical isomorphism follows from (1.2.1), the right vertical isomorphism from part (a) and the bottom right injection from part (b).
Thus, we are left to prove that if 
$A(K)_{\mathrm {tf}}$ is finitely generated and 
$\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}_p$ is injective, then 
$A(K^{\mathrm {perf}})_{\mathrm {tf}}$ is finitely generated. Since 
$A(K)_{\mathrm {tf}}[1/p]=A(K^{\mathrm {perf}})_{\mathrm {tf}}[1/p]$ is a finitely generated 
$\mathbb {Z}[1/p]$-module, it is enough to show that 
$A(K^{\mathrm {perf}})_{\mathrm {tf}}\otimes \mathbb {Z}_p$ is a finitely generated 
$\mathbb {Z}_p$-module. Since the kernel of 
$\mathrm {Kum}_p^{ \unicode{x00E9}{\textrm{t}}}$ is a torsion group by assumption and 
$A(K)\otimes \mathbb {Q}=A(K^{\mathrm {perf}})\otimes \mathbb {Q}$, the group 
$A(K^{\mathrm {perf}})_{\mathrm {tf}}\otimes \mathbb {Z}_p$ injects in the torsion free quotient of the image of 
$\mathrm {Kum}_p^{ \unicode{x00E9}{\textrm{t}}}$. Hence, it is enough to show that the image of 
$A(K^{\mathrm {perf}})\otimes \mathbb {Z}_p$ in 
$H^1(K^{\mathrm {perf}},T_p(A))\simeq H^1(K,T_p(A))$ lies in a finitely generated sub-
$\mathbb {Z}_p$-module.
Since 
$A(K)_{\mathrm {tf}}$ is finitely generated, we can choose a set 
$x_1,\ldots x_r\in A(K)$ which generates 
$A(K)_{\mathrm {tf}}$ and write 
$T_p(M_{x_i})$ for the 
$\mathbb {Z}_p$-linear 
$\pi _1(K)$-representation corresponding to the exact sequence 
$\mathrm {Kum}^{ \unicode{x00E9}{\textrm{t}}}(x_i)$
\begin{equation} 0\rightarrow T_p(A)\rightarrow T_p(M_{x_i})\rightarrow \mathbb{Z}_p\rightarrow 0 \quad \text{ in } \quad H^1(K,T_p(A))\simeq \mathrm{Ext}^1_K(\mathbb{Z}_p,T_p(A)). \end{equation}Let
\[ \Pi\subseteq \mathrm{GL}(T_p(M_{x_1}))\times \cdots \times \mathrm{GL}(T_p(M_{x_r})) \]
be the image of 
$\pi _1(K^{\mathrm {perf}})$ acting on 
$T_p(M_{x_1})\times \cdots \times T_p(M_{x_r})$ and write 
$K^{\mathrm {perf}}\subseteq L$ for the Galois extension corresponding to the closed subgroup 
$\mathrm {Ker}(\pi _1(K^{\mathrm {perf}})\twoheadrightarrow \Pi )$.
Since 
$\Pi$ is a closed subgroup of 
$\mathrm {GL}(T_p(A))$, it is a compact 
$p$-adic Lie group by [Reference Dixon, du Sautoy, Mann and SegalDdSMS91, Corollary 9.36]. In particular, by [Reference SerreSer64, Prop. 9], 
$H^1(\Pi,T_p(A))\subseteq H^1(K^{\mathrm {perf}},T_p(A))$ is a finitely generated 
$\mathbb {Z}_p$-module. We are left to show that the image of 
$A(K^{\mathrm {perf}})\otimes \mathbb {Z}_p$ in 
$H^1(K^{\mathrm {perf}},T_p(A))$ lies in 
$H^1(\Pi,T_p(A))$. Since 
$H^1(\Pi,T_p(A))$ is a sub-
$\mathbb {Z}_p$-module of 
$H^1(K^{\mathrm {perf}},T_p(A))$, it is enough to show that the image of 
$A(K^{\mathrm {perf}})$ lies in 
$H^1(\Pi,T_p(A))$.
The inflation–restriction exact sequence
reduces us to show that the composition
\[ \phi:A(K^{\mathrm{perf}})\rightarrow H^1(\pi_1(K^{\mathrm{perf}}),T_p(A))\rightarrow H^1(\pi_1(L),T_p(A)) \]
is the zero map. Since 
$\pi _1(L)$ acts trivially on 
$T_p(M_{x_i})$, it acts trivially 
$T_p(A)$, so that
\[ H^1(\pi_1(L),T_p(A))=\mathrm{Hom}(\pi_1(L),\mathbb{Z}_p^{p(A)}) \]
is torsion free, hence it is enough to show that for every non-torsion 
$x\in A(K^{\mathrm {perf}})$, there exists an 
$n$ such that 
$\phi (p^nx)=0$. Since, by (1.2.1), for every 
$x\in A(K^{\mathrm {perf}})$, there exists an 
$n$ such that 
$p^nx\in A(K)$, it is enough to show that the map
\[ \phi':A(K)_{\mathrm{tf}}\rightarrow H^1(\pi_1(L),T_p(A)) \]
is zero.
Since 
$A(K)_{\mathrm {tf}}$ is generated by 
$x_1,\ldots, x_r$, it is enough to show that 
$\phi '(x_i)=0$ for every 
$1\leq i\leq r$. However, the exact sequence corresponding to 
$\phi '(x_i)$ is the restriction of the exact sequence (2.1.2.2) to 
$\pi _1(L)$. By construction, this sequence is an exact sequence of trivial 
$\pi _1(L)$-representations, hence it splits as a 
$\pi _1(L)$-module for all the 
$x_i\in A(K)$. Hence, 
$\phi '(x_i)=0$ and this concludes the proof.
2.2 Interpretation in terms of Abel–Jacobi maps
In this section, we compare the Kummer map with an Abel–Jacobi map constructed via 
$p$-divisible groups and 1-motives.
Write 
$\mathbf {pDiv}(S)$ for the category of 
$p$-divisible group over 
$S$ and 
$\mathbf {pDiv}(S)\otimes \mathbb {Q}$ for its isogeny category.
2.2.1 $p$-divisible group associate to a point
Let 
$s\in A(S)$ be a section. Since 
$s:S\rightarrow A$ corresponds to a morphism of fppf 
$S$-groups schemes 
$s:\mathbb {Z}\rightarrow A$, we can consider the 1-motive 
$[s:\mathbb {Z}\rightarrow A]$. We now recall how to associate to 
$[s:\mathbb {Z}\rightarrow A]$ a 
$p$-divisible group 
$M_s[p^{\infty }]$ over 
$S$ (see, for example, [Reference Andreatta and Barbieri-VialeAB05, § 1.3] for more details). Define
\[ M_s[p^n]:=\frac{\mathrm{Ker}(s+p^n:\mathbb{Z}\times_S A\rightarrow A)}{\mathrm{Im}((p^n,-s):\mathbb{Z}\rightarrow \mathbb{Z}\times_S A)}, \]
so that there is an exact sequence
\begin{equation} 0\rightarrow A[p^n]\rightarrow M_s[p^n]\rightarrow \mathbb{Z}/p^n\mathbb{Z}_{S}\rightarrow 0 \end{equation}
of finite flat 
$S$-group schemes. Define
\[ M_{s}[p^{\infty}]=\varinjlim_n M_s[p^n] \]
so that 
$M_{s}[p^{\infty }]$ is a 
$p$-divisible group fitting into an exact sequence
\begin{equation} 0\rightarrow A[p^{\infty}]\rightarrow M_s[p^{\infty}]\rightarrow (\mathbb{Q}_p/\mathbb{Z}_p)_S\rightarrow 0. \end{equation}
We let 
$[M_s[p^{\infty }]]$ be the corresponding class in 
$\mathrm {Ext}^1(\mathbb {Q}_p/\mathbb {Z}_p, A[p^\infty ])$.
2.2.2 Comparison with the Kummer class
Since 
$H^1_{\mathrm {fl}}(S,A[p^n])\simeq \mathrm {Ext}^1(\mathbb {Z}/p^{n}\mathbb {Z}, A[p^n])$, where the latter is the group of extension 
$A[p^n]$ by 
$\mathbb {Z}/p^n\mathbb {Z}$ as 
$\mathbb {Z}/p^n\mathbb {Z}$-sheaf, the Kummer map can be interpreted as a morphism
\[ \mathrm{Kum}: A(S)\rightarrow \varprojlim_n \mathrm{Ext}^1(\mathbb{Z}/p^{n}\mathbb{Z}, A[p^n]). \]
On the other hand, since 
$\mathrm {Hom}(\mathbb {Z}/p^{n}\mathbb {Z}, A[p^n])$ is finite, taking 
$p^n$-torsion we get a natural injective morphism
\[ \varphi:\mathrm{Ext}^1(\mathbb{Q}_p/\mathbb{Z}_p, A[p^\infty])\hookrightarrow \varprojlim_n \mathrm{Ext}^1(\mathbb{Z}/p^{n}\mathbb{Z}, A[p^n]). \]
In the next lemma, which follows essentially from the constructions involved, we prove that 
$\varphi ([M_s[p^{\infty }])$ and 
$\mathrm {Kum}(s)$ represent the same class.
Lemma 2.2.2.1 There is an equality 
$\mathrm {Kum}(s)=\varphi ([M_s[p^{\infty }]])$.
Proof. It is enough to show that, for every 
$n$, the sequence (2.2.1.1) identifies with the class of 
$\mathrm {Kum}(s)\in H^1_{\mathrm {fl}}(S,A[p^n])\simeq \mathrm {Ext}^1(\mathbb {Z}/p^{n}\mathbb {Z}, A[p^n])$. By definition, the 
$A[p^n]$-torsor 
$\mathrm {Kum}(s)\in H^1_{\mathrm {fl}}(S,A[p^n])$ is the pullback of the inclusion of 
$s\hookrightarrow A$ along the multiplication by 
$p^n:A\rightarrow A$.
Let 
$\mathbb {Z}/p^n\mathbb {Z}[\mathrm {Kum}(s)]$ be the free 
$\mathbb {Z}/p^n\mathbb {Z}$-sheaf on 
$[\mathrm {Kum}(s)]$, let 
$\deg :\mathbb {Z}/p^n\mathbb {Z}[\mathrm {Kum}(s)]\rightarrow \mathbb {Z}/p^n\mathbb {Z}$ be the ‘degree’ map sending 
$\sum n_iz_i$ to 
$\sum n_i$ and write 
$B:=\mathrm {Ker}(\deg )$.
By construction (see, e.g., [Sta20, 03AJ]), the sequence
\begin{equation} 0\rightarrow A[p^n]\rightarrow \widetilde{\mathrm{Kum}(s)}\rightarrow \mathbb{Z}/p^n\mathbb{Z}\rightarrow 0, \end{equation}
in 
$\mathrm {Ext}^1(\mathbb {Z}/p^{n}\mathbb {Z}, A[p^n])$ corresponding to 
$\mathrm {Kum}(s)$, is obtained by pushing out the exact sequence
\[ 0\rightarrow B\rightarrow \mathbb{Z}/p^n\mathbb{Z}[\mathrm{Kum}(s)]\rightarrow \mathbb{Z}/p^n\mathbb{Z}\rightarrow 0, \]
along the map 
$B\rightarrow A[p^n]$ sending the generators of the form 
$x-x'$ to the unique 
$a$ such that 
$x+a=x'$. The isomorphism of the sequence (2.2.2.2) with the sequence (2.2.1.1) is then induced by the map 
$\widetilde {\mathrm {Kum}(s)}\rightarrow M_x[p^n]$ obtained by the universal property of pushout using the natural inclusion 
$A[p^n]\subseteq \{0\}\times A\subseteq \mathbb {Z}\times A$ and the map 
$\mathbb {Z}[\mathrm {Kum}(s)]\rightarrow A$ sending 
$s\in \mathrm {Kum}(s)$ to 
$(1,-s)\in \mathbb {Z}\times A$.
Hence, from now on, if 
$S=\mathrm {Spec}(K)$ is the spectrum of a field, we interpret, for 
$?\in \{\emptyset, p\}$ and 
$\Delta \in \{\emptyset, { \unicode{x00E9}{\textrm{t}}}\}$ the Kummer maps as (
$p$-adic, étale) Abel–Jacobi maps
\[ \mathrm{AJ}_?^{\Delta}: A(K)\otimes \mathbb{Q}_?\rightarrow \mathrm{Ext}^1(\mathbb{Q}_p/\mathbb{Z}_p, A[p^{\infty}]^{\Delta})\otimes \mathbb{Q}. \]
We can then rephrase the work done in this section in the following corollary, which is a direct consequence of Proposition 2.1.2.1 and Lemma 2.2.2.1.
Corollary 2.2.2.3 We have:
(i)
$A(K^{\mathrm {perf}})_{\mathrm {tf}}$ is finitely generated if and only if $A(K)_{\mathrm {tf}}$ is finitely generated and $\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}_{p}$ is injective;(ii)
$A(K^{\mathrm {perf}})_{p^{\infty }}\subseteq A(K^{\mathrm {perf}})_{\mathrm {tors}}$ if and only if $\mathrm {AJ}^{ \unicode{x00E9}{\textrm{t}}}$ is injective.
2.2.3 Rigidity of the Abel–Jacobi extension
Suppose that 
$S=Spec(K)$ for a finitely generated field 
$K$ over 
$\mathbb {F}_p$. We give a first application of the interpretation of 
$\mathrm {Kum}$ in terms of 
$p$-divisible groups, proving that the extensions in the image of 
$\mathrm {AJ}$ are more rigid than a general extension in the image of 
$\mathrm {AJ}_p$. This sets an important difference between the maps 
$\mathrm {AJ}$ and 
$\mathrm {AJ}_p$ and it is the reason why one has to consider two different statements in Theorem 1.3.1.2.
We begin with an easy but important lemma, which is the only place in which some assumption on the geometry of 
$A$ is used.
Lemma 2.2.3.1 Assume that 
$A$ is simple and 
$x\in A(K)$ is a non-torsion point. Then the map
\[ \psi_x:\mathrm{End}(A)\rightarrow A(K) \]
sending 
$f$ to 
$f(x)$ is injective.
Proof. Take any morphism 
$f:A\rightarrow A$ such that 
$f(x)=0$. If 
$f:A\rightarrow A$ is not the zero map, then, since 
$A$ is simple, 
$\mathrm {Ker}(f)$ is finite. On the other hand, 
$x$ is in 
$\mathrm {Ker}(f)$ which is a contradiction with the fact that 
$x$ is not torsion.
Then one has the following result, which is a consequence of the Tate conjecture for abelian varieties and a concrete incarnation of the Tate conjecture for 1-motives.
Lemma 2.2.3.2 If 
$A$ is simple and 
$x\in A(K)$ is not torsion, then 
$\mathrm {End}_{\mathbf {pDiv}(K)}(M_{x}[p^{\infty }])\simeq \mathbb {Z}_p$.
Proof. Applying the functor 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(M_x[p^{\infty }],-)$ to the exact sequence (2.2.1.2) we get an exact sequence
\[ 0\rightarrow \mathrm{Hom}_{\mathbf{pDiv}(K)}(M_x[p^{\infty}],A[p^{\infty}])\rightarrow \mathrm{End}_{\mathbf{pDiv}(K)}(M_x[p^{\infty}])\rightarrow \mathrm{Hom}_{\mathbf{pDiv}(K)}(M_x[p^{\infty}],\mathbb{Q}_p/\mathbb{Z}_p). \]
Since 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(A[p^{\infty }],\mathbb {Q}_p/\mathbb {Z}_p)=0$, applying the functor 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(-,\mathbb {Q}_p/\mathbb {Z}_p)$ to (2.2.1.2) one sees that 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(M_x[p^{\infty }],\mathbb {Q}_p/\mathbb {Z}_p)\simeq \mathrm {End}_{\mathbf {pDiv}(K)}(\mathbb {Q}_p/\mathbb {Z}_p)\simeq \mathbb {Z}_p$. Hence, it is then enough to prove that
\[ \mathrm{Hom}_{\mathbf{pDiv}(K)}(M_x[p^{\infty}],A[p^{\infty}])=0. \]
Since 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(\mathbb {Q}_p/\mathbb {Z}_p,A[p^{\infty }])=0$, applying the functor 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(-,A[p^{\infty }])$ to the exact sequence (2.2.1.2) we get an exact sequence
\[ 0\rightarrow \mathrm{Hom}_{\mathbf{pDiv}(K)}(M[p^{\infty}],A[p^{\infty}])\rightarrow \mathrm{End}_{\mathbf{pDiv}(K)}(A[p^{\infty}])\rightarrow \mathrm{Ext}_{\mathbf{pDiv}(K)}^{1}(\mathbb{Q}_p/\mathbb{Z}_p,A[p^{\infty}]). \]
Since 
$\mathrm {Hom}_{\mathbf {pDiv}(K)}(M[p^{\infty }],A[p^{\infty }])$ is torsion free, we are left to show that the natural map
\[ \mathrm{End}_{\mathbf{pDiv}(K)}(A[p^{\infty}])\otimes \mathbb{Q}\rightarrow \mathrm{Ext}_{\mathbf{pDiv}(K)}^{1}(\mathbb{Q}_p/\mathbb{Z}_p,A[p^{\infty}])\otimes \mathbb{Q} \]
is injective.
Consider the commutative diagram
where 
$\psi _x\otimes \text {Id}$ is induced by the map 
$\psi _x:\mathrm {End}(A)\rightarrow A(K)$ sending a morphism 
$f$ to 
$f(x)$. Since 
$K$ if finitely generated, 
$A(K)$ is a finitely generated group, hence by Lemma 2.1.1.1 
$\mathrm {AJ}_p$ is injective. By the 
$p$-adic Tate conjecture for abelian varieties proved in [Reference de JongdJ98, Theorem 2.6], the left vertical map is an isomorphism. Thus, since 
$A$ is simple, we conclude by using Lemma 2.2.3.1.
2.2.4 Kummer class and semiabelian schemes
Let 
$s\in A(S)$. As a second application of the interpretation of 
$\mathrm {Kum}$ in terms of 
$p$-divisible groups we give a geometric interpretation of the Cartier dual of the class of 
$[M_x[p^{\infty }]]$. This will be important to prove Proposition 3.3.3.1. The dual of the 1-motive 
$[\mathbb {Z}\rightarrow A]$ is a semiabelian scheme
\[ 0\rightarrow \mathbb{G}_{m,S}\rightarrow G_s\rightarrow A^{\vee}\rightarrow 0, \]
where 
$A^{\vee }$ is the dual abelian variety, and the 
$p$-divisible group 
$G_s[p^{\infty }]$ of 
$G_s$ is the Cartier dual 
$M_{s}[p^{\infty }]^{\vee }$ of 
$M_{s}[p^{\infty }]$ (see, for example, [Reference Andreatta and Barbieri-VialeAB05, § 1.3]). Hence, the class of the dual of the extension (2.2.1.2) in 
$\mathrm {Ext}^1(A^{\vee }[p^{\infty }],\mu _{p^{\infty }})$ is the extension
\[ 0\rightarrow \mathbb{G}_{m}[p^{\infty}]\rightarrow G_s[p^{\infty}]\rightarrow A^{\vee}[p^{\infty}]\rightarrow 0, \]
associated to the 
$p$-divisible group of a semi-abelian 
$S$-scheme 
$G_s\rightarrow S$.
3. On the injectivity of the étale Abel–Jacobi map
In this section, we prove the main theorem of the paper (Theorem 3.1.1) and its geometric variant (Theorem 3.4.1) assuming an overconvergence result (Proposition 4.1.2) which will be proved in the next § 4 (since it relies on different techniques).
3.1 Notation and statements
We assume that 
$k$ is a finite field, 
$K/k$ is a finitely generated field extension and 
$A$ a 
$K$-abelian variety. Write 
$p(A)$ (respectively, 
$r(A)$) for the 
$p$-rank of 
$A$ (respectively, the rank of 
$A(K)$, which is finite by the Lang–Néron theorem) and if 
$A_1,\ldots, A_n$ are the simple isogeny factors of 
$A$, set 
$p(A)^{\mathrm {min}}$ (respectively, 
$r(A)^{\mathrm {min}}$) as the minimum of 
$p(A_i)$ (respectively, of 
$r(A_i)$). If 
$e\in \mathrm {End}(A)\otimes \mathbb {Q}_p$, we write 
$e[p^{\infty }]\in \mathrm {End}(A[p^{\infty }])\otimes \mathbb {Q}_p$ (respectively, 
$e[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}\in \mathrm {End}(A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb {Q}$) for the induced morphism. Finally, set
\[ A(S)_{p^{\infty}}:=\{x\in A(S) \text{ such that for every }n\in \mathbb{N} \text{ there exists a } y_n\in A(S)\text{ with }p^ny_n=x\}. \]
In this section, we prove the following.
Theorem 3.1.1 Assume that 
$r(A)^{\mathrm {min}}>0$. Then:
(i)
$A(K^{\mathrm {perf}})$ is not finitely generated if and only if and there exists an idempotent $0\neq e\in \mathrm {End}(A)\otimes \mathbb {Q}_p$ (i.e. $e^2=e$) such that $0=e[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}\in \mathrm {End}(A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb {Q}_p$;(ii)
$A(K^{\mathrm {perf}})_{p^{\infty }}\subseteq A(K^{\mathrm {perf}})_{\mathrm {tors}}$ if and only if $p(A)^{\mathrm {min}}>0$.
Since 
$A(K^{\mathrm {perf}})_{\mathrm {tors}}$ is finite by [Reference Ghioca and MoosaGM06, p. 7], thanks to Corollary 2.2.2.3, Theorem 1.3.1.2 is equivalent to the following.
Theorem 3.1.2 Assume that 
$r(A)^{\mathrm {min}}>0$. Then:
(i) the morphism
is not injective if and only there exists an idempotent\[ \mathrm{AJ}^{ \unicode{x00E9}{\textrm{t}}}_p: A(K)\otimes \mathbb{Q}_p\rightarrow \mathrm{Ext}^1_{\mathbf{pDiv}(K)}(\mathbb{Q}_p/\mathbb{Z}_p, A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}})\otimes\mathbb{Q} \]
$0\neq e\in \mathrm {End}(A)\otimes \mathbb {Q}_p$ such that $0=e[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}\in \mathrm {End}(A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb {Q}$;(ii) the morphism
is not injective if and only if\[ \mathrm{AJ}^{ \unicode{x00E9}{\textrm{t}}}: A(K)\otimes \mathbb{Q}\rightarrow \mathrm{Ext}^1_{\mathbf{pDiv}(K)}(\mathbb{Q}_p/\mathbb{Z}_p, A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb{Q} \]
$p(A)^{\mathrm {min}}=0$.
3.2 Preliminaries and the first implication
3.2.1 Reduction to $A$ simple
Since the assumptions and the conclusions are stable under products and isogenies of abelian varieties, we can assume that 
$A$ is simple (that will be used to apply Lemmas 2.2.3.1 and 2.2.3.2) and 
$r(A)>0$. Since the statements with 
$p(A)=0$ are trivial, we can assume that 
$p(A)>0$.
3.2.2 First implication
We first prove the if part of Theorem 3.1.2(i). Assume that there exists an idempotent 
$0\neq e\in \mathrm {End}(A)\otimes \mathbb {Q}_p$ such that 
$e[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}=0$ in 
$\mathrm {End}(A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb {Q}_p$. Choose an 
$n$ such that 
$p^ne=:u\in \mathrm {End}(A)\otimes \mathbb {Z}_p$. Since 
$e[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}=0$ and 
$\mathrm {End}(A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})$ is torsion free, also 
$u[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}=0$. Take a non-torsion 
$x\in A(K)$ (which exists by assumption). Since 
$A$ is simple, by Lemma 2.2.3.1, the map
\[ \psi_x\otimes \text{Id}_{\mathbb{Q}_p}:\mathrm{End}(A)\otimes \mathbb{Q}_p\rightarrow A(K)\otimes \mathbb{Q}_p \]
is injective, where 
$\psi _x:\mathrm {End}(A)\rightarrow A(K)$ is the map sending 
$f$ to 
$f(x)$. Hence, 
$e(x)\neq 0$, therefore 
$u(x)\neq 0$. The commutative diagram
shows that 
$u(x)$ goes to zero in 
$\mathrm {Ext}_{\mathbf {pDiv}(K)}^{1}(\mathbb {Q}_p/\mathbb {Z}_p,A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb {Q}$. This concludes the proof of the if part of Theorem 3.1.2(i).
3.2.3 Reduction to Proposition 3.2.3.1
We are left to prove the only if part of Theorem 3.1.2(i) and 3.1.2(ii). We first show that the following Proposition 3.2.3.1 implies Theorem 3.1.2.
Proposition 3.2.3.1 Let 
$x\in A(K)\otimes \mathbb {Q}_p$ be such that 
$\mathrm {AJ}_p(x)=0$. Then there exists an idempotent 
$0\neq e\in \mathrm {End}(M_x[p^{\infty }])\otimes \mathbb {Q}_p$ which preserves the sub-
$p$-divisible group 
$A[p^{\infty }]\subseteq M_x[p^{\infty }]$ and it induces a non-zero idempotent 
$e[p^{\infty }]\in \mathrm {End}(A[p^{\infty }])\otimes \mathbb {Q}_p$ acting as 
$0$ on 
$A_x[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$.
Assume that Proposition 3.2.3.1 holds. Then Theorem 3.1.2(ii) follows from it and Lemma 2.2.3.1. To deduce Theorem 3.1.2(i), we use that, by the 
$p$-adic Tate conjecture for abelian varieties proved in [Reference de JongdJ98, Theorem 2.6], the natural map
\[ \mathrm{End}(A)\otimes \mathbb{Q}_p \xrightarrow{\simeq} \mathrm{End}_{\mathbf{pDiv}(K)}(A[p^{\infty}])\otimes \mathbb{Q}_p \]
is an isomorphism, so that 
$e[p^{\infty }]$ is induced by a non-zero idempotent in 
$\mathrm {End}(A)\otimes \mathbb {Q}_p$ acting as 
$0$ on 
$A_x[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$. Hence, we are left to prove Proposition 3.2.3.1.
3.3 Proof of Proposition 3.2.3.1
3.3.1 Spreading out
Let 
$x\in A(K)\otimes \mathbb {Q}_p$ be such that 
$\mathrm {AJ}_p(x)=0$. To prove Proposition 3.2.3.1 we can replace 
$x$ with 
$p^nx$, hence we may and do assume that 
$x\in A(K)\otimes \mathbb {Z}_p$ is not torsion. Let
\begin{equation} 0\rightarrow A[p^{\infty}]\rightarrow M_{x}[p^{\infty}]\rightarrow \mathbb{Q}_p/\mathbb{Z}_p\rightarrow 0 \end{equation}and
\begin{equation} 0\rightarrow A[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}\rightarrow M_{x}[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}\rightarrow \mathbb{Q}_p/\mathbb{Z}_p\rightarrow 0 \end{equation}
be the extensions associated to 
$\mathrm {AJ}_p(x)$ and 
$AJ^{ \unicode{x00E9}{\textrm{t}}}_p(x)$, respectively. Since 
$AJ^{ \unicode{x00E9}{\textrm{t}}}_p(x)=0$, the exact sequence (3.3.1.2) splits. Replacing 
$k$ with a finite field extension, we can assume that 
$k$ is algebraically closed in 
$K$ and take an affine smooth geometrically connected 
$k$-variety 
$X$ with function field 
$K$. Replacing 
$X$ with a dense open subset, we can assume that 
$A$ extends to an abelian scheme 
$\mathcal {A}\rightarrow X$ with constant Newton polygon and that, since 
$A(K)$ is finitely generated, the natural map 
$\mathcal {A}(X)\otimes \mathbb {Z}_p\rightarrow A(K)\otimes \mathbb {Z}_p$ is an isomorphism. In particular, 
$x$ extends to a non-torsion element 
$\mathfrak t\in \mathcal {A}(X)\otimes \mathbb {Z}_p$. By [Reference de JongdJ95], the natural functor
\[ \mathbf{pDiv}(X)\otimes \mathbb{Q}\rightarrow \mathbf{pDiv}(K)\otimes \mathbb{Q} \]
is fully faithful, so that our assumption is equivalent to the fact that the sequence
\begin{equation} 0\rightarrow \mathcal{A}[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}_{X}\rightarrow \mathcal{M}_{\mathfrak t}[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}_{X}\rightarrow \mathbb{Q}_p/\mathbb{Z}_p\rightarrow 0 \end{equation}
splits in 
$\mathbf {pDiv}(X)\otimes \mathbb {Q}$ and we know (by Lemma 2.1.1.1) that the exact sequence
\begin{equation} 0\rightarrow \mathcal{A}[p^{\infty}]_{X}\rightarrow \mathcal{M}_{\mathfrak t}[p^{\infty}]_{X}\rightarrow \mathbb{Q}_p/\mathbb{Z}_p\rightarrow 0 \end{equation}does not split.
3.3.2 $F$-isocrystals
Let 
$\mathbf {F\textrm {-}Isoc}(X)$ be the category of 
$F$-isocrystals over 
$X$ (as defined for example in [Reference MorrowMor19, § A.1]). By [Reference KedlayaKed22, Corollary 4.2], every 
$F$-isocrystal 
$\mathcal {E}$ with constant Newton polygon admits a slope filtration
\[ 0=\mathcal{E}_s\subseteq \mathcal{E}_{s+1}\cdots \subseteq \mathcal{E}_{r-1}\subseteq \mathcal{E}_{r}=\mathcal{E} \]
such that 
$\mathcal {E}_i/\mathcal {E}_{i-1}$ is isoclinic of some slope 
$s_i\in \mathbb {Q}$ with 
$s_i< s_{i+1}$. By [Reference Berthelot, Breen and MessingBBM82], there is a fully faithful contravariant functor 
$\mathbb {D}: \mathbf {pDiv}(X)\otimes \mathbb {Q}\rightarrow \mathbf {F\textrm {-}Isoc}(X)$. Write
\[ \mathcal{E}:=\mathbb{D}(\mathcal{A}[p^{\infty}]);\quad \mathcal{O}^{\mathrm{crys}}_X:=\mathbb{D}(\mathbb{Q}_p/\mathbb{Z}_p); \quad \mathcal{E}_{\mathfrak t}:=\mathbb{D}(\mathcal{M}_{\mathfrak t}[p^{\infty}]_{X}), \]
so that 
$\mathcal {E}$ and 
$\mathcal {E}_{\mathfrak t}$ have constant Newton polygon by the preliminary reduction. Recall that the slopes appearing in an 
$F$-isocrystal associated to a 
$p$-divisible group are between 
$0$ and 
$1$ and that a 
$p$-divisible group is étale if and only after applying 
$\mathbb {D}$ has constant slope 
$0$. Hence,
\[ \mathcal{E}_{1}:=\mathbb{D}(\mathcal{A}[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}_X) \quad \text{and}\quad \mathcal{E}_{\mathfrak t,1}:=\mathbb{D}(\mathcal{M}_{\mathfrak t}[p^{\infty}]^{ \unicode{x00E9}{\textrm{t}}}_X) \]
are the sub-
$F$-isocrystals of minimal slope of 
$\mathcal {E}$ and 
$\mathcal {E}_{\mathfrak t}$, respectively. Then the sequences (3.3.1.3) and (3.3.1.4) are sent to exact sequences
\begin{equation} 0\rightarrow \mathcal{O}^{\mathrm{crys}}_{X}\rightarrow \mathcal{E}_t \rightarrow \mathcal{E}\rightarrow 0 \end{equation}and
\begin{equation} 0\rightarrow \mathcal{O}^{\mathrm{crys}}_{X}\rightarrow \mathcal{E}_{t,1} \rightarrow \mathcal{E}_1\rightarrow 0. \end{equation}
By fully faithfulness of 
$\mathbb {D}:\mathbf {pDiv}(X)\otimes \mathbb {Q}\rightarrow \mathbf {F\textrm {-}Isoc}(X)$ and the assumption, the sequence (3.3.2.2) splits and (3.3.2.1) does not split.
3.3.3 Overconvergence
Let 
$\mathbf {F\textrm {-}Isoc}^{\dagger}(X)$ be the category of overconvergent 
$F$-isocrystals over 
$X$ (see, for example, [Reference BerthelotBer96, Definition 2.3.6]). By [Reference BerthelotBer96, Theorem 2.4.2], every 
$F$-isocrystals is convergent, hence there is a natural functor 
$\Phi :\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\rightarrow \mathbf {F\textrm {-}Isoc}(X)$.
Recall that, by [Reference KedlayaKed04], the functor 
$\Phi :\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\rightarrow \mathbf {F\textrm {-}Isoc}(X)$ is fully faithful, so that we can identify 
$\mathbf {F\textrm {-}Isoc}^{\dagger}(X)$ with a full subcategory of 
$\mathbf {F\textrm {-}Isoc}(X)$. If 
$\mathcal {G}$ in 
$\mathbf {F\textrm {-}Isoc}(X)$ is in the essential image of 
$\Phi :\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\rightarrow \mathbf {F\textrm {-}Isoc}(X)$ we say that it is overconvergent and we write 
$\mathcal {G}^{{\dagger} }$ for its (unique) overconvergent extension. By [Reference ÉtesseÉte02], 
$\mathcal {E}$ is overconvergent. As a consequence of Proposition 4.1.2, that will be proved in § 4, and the geometric interpretation of 
$\mathcal {E}_{\mathfrak t}$ given in § 2.2.4, we can show that 
$\mathcal {E}_{\mathfrak t}$ is also overconvergent.
Proposition 3.3.3.1 The 
$F$-isocrystal 
$\mathcal {E}_{\mathfrak t}$ is overconvergent.
Proof. Since inside 
$\mathrm {Ext}^1_{\mathbf {F\textrm {-}Isoc}(X)}(\mathcal {E}, \mathcal {O}^{\mathrm {crys}}_X)$ the class of 
$\mathcal {E}_{\mathfrak t}$ is a 
$\mathbb {Q}_p$-linear combination of classes 
$\mathcal {E}_{\mathfrak v}$ with 
$\mathfrak v\in \mathcal {A}(X)$ and the morphism 
$\mathrm {Ext}^1_{\mathbf {F\textrm {-}Isoc}^{\dagger}(X)}(\mathcal {E}^{{\dagger} }, \mathcal {O}^{{\dagger} }_X)\rightarrow \mathrm {Ext}^1_{\mathbf {F\textrm {-}Isoc}(X)}(\mathcal {E}, \mathcal {O}^{\mathrm {crys}}_X)$ is 
$\mathbb {Q}_p$-linear, we can assume that 
$\mathfrak t\in \mathcal {A}(X)$. It is then enough to show that 
$\mathcal {E}^{\vee }_{\mathfrak t}(1)$ (where 
$(-)^{\vee }$ is the dual 
$F$-isocrystals and 
$(-)(1)$ is the Tate twist) is overconvergent. By § 2.2.4 and the compatibility of the functor 
$\mathbb {D}$ with dualities ([Reference Berthelot, Breen and MessingBBM82, (5.3.3.1)]), one has that 
$\mathcal {E}^{\vee }_{\mathfrak t}(1)$ identifies with 
$\mathbb {D}(G[p^{\infty }])$, where 
$G[p^{\infty }]$ is the 
$p$-divisible group of an algebraic group 
$G$ which is an extension
\[ 0\rightarrow \mathbb{G}_m\rightarrow G\rightarrow A\rightarrow 0 \]
of an abelian variety and a 
$\mathbb {G}_m$. Then the overconvergence of 
$\mathcal {E}^{\vee }_{\mathfrak t}(1)$ follows from Proposition 4.1.2, that we will prove in § 4.
Since 
$\mathcal {E}$ and 
$\mathcal {E}_{\mathfrak t}$ are overconvergent and the functor 
$\Phi :\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\rightarrow \mathbf {F\textrm {-}Isoc}(X)$ is fully faithful, the non-split exact sequence (3.3.2.1) lifts to a non-split exact sequence
\begin{equation} 0\rightarrow \mathcal{O}^{{\dagger}}_X\rightarrow \mathcal{E}^{{\dagger}}_{\mathfrak t}\xrightarrow{\pi} \mathcal{E}^{{\dagger}}\rightarrow 0. \end{equation}
On the other hand, by construction, the exact sequence (3.3.2.2) is obtained by applying 
$\Phi :\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\rightarrow \mathbf {F\textrm {-}Isoc}(X)$ to (3.3.3.2) and then base changing it along 
$\mathcal {E}_1\rightarrow \mathcal {E}$.
3.3.4 Minimal slope conjecture
Chose a splitting 
$s:\mathcal {E}_1\rightarrow \mathcal {E}_{\mathfrak t,1}$ of the sequence (3.3.2.2). Consider the smallest overconvergent object 
$\widetilde {\mathcal {E}}^{{\dagger} }$ contained in 
$\mathcal {E}^{{\dagger} }_{\mathfrak t}$ and containing 
$s(\mathcal {E}_1)$.
Since 
$p(A)>0$, we have 
$\widetilde {\mathcal {E}}^{{\dagger} }\neq 0$. By the recent work [Reference TsuzukiTsu23] and its improvement done in [Reference D'AddezioD'A23, Theorem 4.1.3], one has 
$s(\mathcal {E}_1)=\widetilde {\mathcal {E}}_1$ so that 
$\widetilde {\mathcal {E}}^{{\dagger} }\cap \mathcal {O}^{\mathrm {crys}}_{X}=0$. Hence, the natural composite map
\[ \widetilde{\mathcal{E}}^{{\dagger}}\hookrightarrow \mathcal{E}^{{\dagger}}_{\mathfrak t}\xrightarrow{\pi} \mathcal{E}^{{\dagger}} \]
is injective and it induces an isomorphism 
$\pi : \widetilde {\mathcal {E}}^{{\dagger} }\xrightarrow {\simeq } \pi (\widetilde {\mathcal {E}}^{{\dagger} })$. By construction, the sequence (3.3.3.2) splits after base change along 
$\pi (\widetilde {\mathcal {E}}^{{\dagger} })\subseteq \mathcal {E}^{{\dagger} }$.
Since the sequence (3.3.3.2) does not split, 
$\pi (\widetilde {\mathcal {E}}^{{\dagger} })\neq \mathcal {E}^{{\dagger} }$. By a result of Pál [Reference PálPál22, Theorem 1.2], the overconvergent 
$F$-isocrystal 
$\mathcal {E}^{{\dagger} }$ is semisimple, hence there is a projection 
$\widetilde e:\mathcal {E}^{{\dagger} }\rightarrow \mathcal {E}^{{\dagger} }$ onto 
$\pi (\widetilde {\mathcal {E}}^{{\dagger} })$. Since 
$\widetilde {\mathcal {E}}$ contains 
$s(\mathcal {E}_1)$, the non-zero idempotent 
$1-\widetilde e$ acts as zero on 
$\mathcal {E}_1$. By the faithfulness of the composite functor 
$\mathbf {F\textrm {-}Isoc}^{\dagger}(X)\xrightarrow {\Phi } \mathbf {F\textrm {-}Isoc}(X)\xrightarrow {\mathbb {D}} \mathbf {pDiv}(X)\otimes \mathbb {Q}$, we get a non-zero idempotent 
$e[p^{\infty }]$ in 
$\mathrm {End}(A[p^{\infty }])\otimes \mathbb {Q}_p$ acting as zero on 
$A[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$. Observe that the composite map
\[ \mathcal{E}_{\mathfrak t}^{{\dagger}}\xrightarrow{\pi} \mathcal{E}^{{\dagger}}\xrightarrow{\widetilde e}\pi(\widetilde{\mathcal{E}}^{{\dagger}})\xrightarrow{\pi^{-1}}\widetilde{\mathcal{E}}^{{\dagger}}\subseteq \mathcal{E}_{\mathfrak t}^{{\dagger}} \]
is a projection onto 
$\widetilde {\mathcal {E}}^{{\dagger} }$. Hence, there exists a non-zero idempotent 
$e\in \mathrm {End}(\mathcal {E}_{\mathfrak t}^{{\dagger} })\simeq \mathrm {End}_{\mathbf {pDiv}(K)}(M_x[p^{\infty }])\otimes \mathbb {Q}_p$ which induces the non-zero idempotent in 
$e[p^{\infty }]\in \mathrm {End}(A[p^{\infty }])\otimes \mathbb {Q}_p$ acting as 
$0$ on 
$A_x[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}$. This concludes the proof of Proposition 3.2.3.1.
3.4 Geometric variant
Write 
$L:=\overline kK\subseteq \overline K$ for the field generated by 
$\overline k$ and 
$K$ in 
$\overline K$. Let 
$\mathrm {Tr}_{\overline K/\overline k}(A)$ be the 
$(\overline K/\overline k)$-trace of 
$A_{\overline K}$ (i.e. the biggest 
$\overline k$-isotrivial quotient 
$A_{\overline K}\rightarrow \mathrm {Tr}_{\overline K/\overline k}(A)$ of 
$A_{\overline K}$). A modification of the previous arguments gives us the following geometric variant.
Theorem 3.4.1 Assume that 
$r(A)^{\mathrm {min}}>0$. Then:
(i) if
$\mathrm {Tr}_{\overline K/\overline k}(A)=0$, then $A(L^{\mathrm {perf}})$ is not finitely generated if and only if there exists an idempotent $0\neq e\in \mathrm {End}(A_{L})\otimes \mathbb {Q}_p$ such that $0=e[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}}\in \mathrm {End}(A_L[p^{\infty }]^{ \unicode{x00E9}{\textrm{t}}})\otimes \mathbb {Q}_p$;(ii)
$A(L^{\mathrm {perf}})_{p^{\infty }}\subseteq A(L^{\mathrm {perf}})_{\mathrm {tors}}$ if and only if $p(A)^{\mathrm {min}}>0$.
Proof. Since 
$A(L)_{\mathrm {tf}}$ is finitely generated by the Lang–Néron theorem and the action of 
$\pi _1(K)$ on 
$\mathrm {End}(A)$ factors through a finite quotient, there exists a finite extension 
$K\subseteq K'\subseteq L$ such that 
$A(K')\otimes \mathbb {Q}=A(L)\otimes \mathbb {Q}$ and 
$\mathrm {End}(A_{K'})=\mathrm {End}(A_L)$. For 
$?\in \{\emptyset, p\}$ we consider the following commutative diagrams.
Moreover, if 
$\mathrm {Tr}(A)=0$ then 
$A(L^{\mathrm {perf}})_{\mathrm {tors}}$ is finite by [Reference Ambrosi and D'AddezioAD22]. Since 
$A(L)_{\mathrm {tf}}$ is finitely generated, by Corollary 2.2.2.3 and Theorem 3.1.2 it is enough to show that 
$\phi$ is injective. Since 
$\pi _1(L)\subseteq \pi _1(K')$ is an normal subgroup, the Hochschild–Serre spectral sequence gives us an exact sequence
\[ 0\rightarrow H^1(\pi_1(K')/\pi_1(L),T_p(A)^{\pi_1(L)})\otimes \mathbb{Q}\rightarrow H^1(\pi_1(K'),T_p(A))\otimes \mathbb{Q} \rightarrow H^1(\pi_1(L),T_p(A))\otimes \mathbb{Q}. \]
Since 
$\pi _1(K')/\pi _1(L)$ is pro-cyclic, one has
\[ H^1(\pi_1(K')/\pi_1(L),T_p(A)^{\pi_1(L)})\otimes \mathbb{Q} \simeq (T_p(A)^{\pi_1(L)}\otimes \mathbb{Q})_{\pi_1(K')/\pi_1(L)}, \]
where the last terms are the coinvariants. However, since 
$A(K^{\mathrm {perf}})[p^{\infty }]$ is finite, one has
\[ (T_p(A)^{\pi_1(L)}\otimes \mathbb{Q})^{\pi_1(K')/\pi_1(L)}=(T_p(A)\otimes \mathbb{Q})^{\pi_1(K')}=0=(T_p(A)^{\pi_1(L)}\otimes \mathbb{Q})_{\pi_1(K')/\pi_1(L)}, \]
and this concludes the proof.
4. Overconvergence
4.1 Statement
Let 
$X$ be a smooth geometrically connected variety over a finite field 
$k$ of characteristic 
$p$ and let
\begin{equation} 0\rightarrow W\rightarrow G\rightarrow A\rightarrow 0 \end{equation}
be an extension of an abelian 
$X$-scheme 
$A$ by a torus 
$W$ over 
$X$. By applying the Dieudonné functor 
$\mathbb {D}:\mathbf {pDiv}(X)\otimes \mathbb {Q}\rightarrow \mathbf {F\textrm {-}Isoc}(X)$ to the exact sequence 
$0\rightarrow W[p^{\infty }]\rightarrow G[p^{\infty }]\rightarrow A[p^{\infty }]\rightarrow 0$, we get an exact sequence
\[ 0\rightarrow \mathbb{D}(A[p^{\infty}])\rightarrow \mathbb{D}(G[p^{\infty}])\rightarrow \mathbb{D}(W[p^{\infty}])\rightarrow 0. \]
The main result of this section is the following.
Proposition 4.1.2 The 
$F$-isocrystal 
$\mathbb {D}(G[p^{\infty }])$ is overconvergent.
To prove Proposition 4.1.2, we reduce to the case in which 
$X$ is a curve and the abelian scheme has everywhere semistable reduction. Then, in § 4.3, we use a result of Trihan [Reference TrihanTri08] to reduce to prove a semistability result for 
$G[p^{\infty }]$. We conclude the proof in §§ 4.4 and 4.5, proving this semistability.
4.2 Preliminary reductions
By [Reference Grub, Kedlaya and UptonGKU21, Lemma 4.2], to prove overconvergence, we can freely replace 
$X$ with a smooth variety 
$Y$ admitting a dominant morphism 
$Y\rightarrow X$. Thus, we can assume that 
$W\simeq \mathbb {G}_{m,X}^m$ and that 
$A(X)[n]\simeq (\mathbb {Z}/n\mathbb {Z})^{2g}$ for some fixed 
$n\geq 3$ coprime with 
$p$. By [Reference Deligne and KatzDK73, Proposition 4.7, Exposé IX, p. 48], this last condition implies that, for every smooth curve 
$C$ and every morphism 
$C\rightarrow X$, the abelian scheme 
$A\times _X C$ has everywhere semistable reduction. Moreover, by de Jong's alteration theorem [Reference de JongdJ98], we can assume that 
$X$ admits a compactification whose complementary is a normal crossing divisor. In this situation, by [Reference de JongdJ98, 2.5] and [Reference TrihanTri08, Corollary 3.14], for every smooth curve 
$C$ and every morphism 
$f:C\rightarrow X$, the 
$F$-isocrystals 
$f^*\mathbb {D}(A[p^{\infty }])\simeq \mathbb {D}(A\times _XC[p^{\infty }])$ has everywhere semistable reduction. Therefore, we can apply the cut by curve criterion for overconvergence proved in [Reference Grub, Kedlaya and UptonGKU21, Lemma 6.7] to reduce to the case in which 
$X$ is a curve. Thus, from now we assume that 
$X$ is a curve with smooth compactification 
$\overline X$ and 
$A$ has every everywhere semistable reduction.
4.3 Passing to $p$-divisible groups
For every 
$x\in \overline X-X$ we let 
$S_x$ be the spectrum of the completion of 
$\overline X$ in 
$x$ and 
$\eta _x$ the generic point of 
$S_x$. Write 
$A_{\eta _x}$ and 
$G_{\eta _x}$ for the base change of 
$A\rightarrow X$ and 
$G \rightarrow X$ trough 
$\eta _x \rightarrow X$. By [Reference TrihanTri08, Theorem 4.5], to prove Proposition 4.1.2, it is enough to show that for every 
$x\in \overline X-X$, the 
$p$-divisible group 
$G_{\eta _x}[p^{\infty }]$ is semistable, i.e. that there exists a filtration
\[ G_{\eta_x}[p^{\infty}]^{\mathrm{t}}\subseteq G_{\eta_x}[p^{\infty}]^{\mathrm{f}}\subseteq G_{\eta_x}[p^{\infty}] \]
such that:
(i)
$G_{\eta _x}[p^{\infty }]^{\mathrm {f}}$ and $G_{\eta _x}[p^{\infty }]/G_{\eta _x}[p^{\infty }]^{\mathrm {t}}$ extend to $p$-divisible groups $G[p^{\infty }]_{x,1}$ and $G[p^{\infty }]_{x,2}$ over $S_x$; in this case, by [Reference de JongdJ98], the natural map $G_{\eta _x}[p^{\infty }]^{\mathrm {f}}\rightarrow G_{\eta _x}[p^{\infty }]/G_{\eta _x}[p^{\infty }]^{\mathrm {t}}$ extends to a map $G[p^{\infty }]_{x,1}\rightarrow G[p^{\infty }]_{x,2}$;(ii)
$\mathrm {Ker}(G[p^{\infty }]_{x,1}\rightarrow G[p^{\infty }]_{x,2})$ is a multiplicative $p$-divisible group and $\mathrm {Coker}(G[p^{\infty }]_{x,1}\rightarrow G[p^{\infty }]_{x,2})$ is an étale $p$-divisible group.
Since the situation is now entirely local, we drop the subscript 
$x$ from the notation.
4.4 Construction of the filtration
By [Reference Bosch, Lutkebohmert and RaynaudBLR90, Proposition 7, p. 292] and its proof, there exists an exact sequence of smooth group 
$S$-schemes with connected fibers
\[ 0\rightarrow W\rightarrow \mathcal{G}^0\rightarrow \mathcal{A}^0\rightarrow 0, \]
where 
$\mathcal {A}\rightarrow S$ is the Néron model of 
$A_\eta$ and 
$\mathcal {A}^0\rightarrow S$ is its connected component of the identity, having as a generic fiber the sequence
\[ 0\rightarrow W_\eta\rightarrow G_\eta\rightarrow A_\eta\rightarrow 0. \]
Since 
$A_{\eta }$ has semistable reduction, the special fiber 
$\mathcal {A}^0_s$ fits into an exact sequence
\[ 0\rightarrow T\rightarrow \mathcal{A}_s^0\rightarrow B\rightarrow 0 \]
with 
$T$ a 
$k$-torus and 
$B$ a 
$k$-abelian variety. Let 
$\mathcal {A}^0[p^n]^{\mathrm {f}}\subseteq \mathcal {A}^0[p^n]$ be the maximal subgroup which is finite over 
$S$ and 
$\mathcal {A}^0[p^n]^{\mathrm {t}}\subseteq \mathcal {A}^0[p^n]^{\mathrm {f}}$ be the unique lifting of the finite subgroup 
$T[p^n]\subseteq \mathcal {A}^0_{s}[p^n]$ to 
$\mathcal {A}^0[p^n]^{\mathrm {f}}$. For 
$?\in \{\mathrm {t},\mathrm {f}\}$, we define 
$\mathcal {G}^0[p^n]^{?}\subseteq \mathcal {G}^0[p^n]$ via the following cartesian diagram with exact rows.
Taking the direct limit with 
$n$ and applying [Reference Deligne and KatzDK73, Proposition 5.6, Exposé IX, p. 180] and [Reference MessingMes72, (2.4.3)], we get a filtration 
$\mathcal {G}^0[p^{\infty }]^{\mathrm {t}}\subseteq \mathcal {G}^0[p^{\infty }]^{\mathrm {f}}\subseteq \mathcal {G}^0[p^{\infty }],$ of 
$p$-divisible groups. Set
\[ G[p^{\infty}]_{\eta}^{\mathrm{t}}:=\mathcal{G}^0[p^{\infty}]^{\mathrm{t}}_{\eta};\quad G[p^{\infty}]_{\eta}^{\mathrm{f}}:= \mathcal{G}^0[p^{\infty}]^{\mathrm{f}}_{\eta};\quad A[p^{\infty}]_{\eta}^{\mathrm{t}}:=\mathcal{A}^0[p^{\infty}]^{\mathrm{t}}_{\eta};\quad A[p^{\infty}]_{\eta}^{\mathrm{f}}:= \mathcal{A}^0[p^{\infty}]^{\mathrm{f}}_{\eta}; \]
so that there are filtrations
\[ G[p^{\infty}]_{\eta}^{\mathrm{t}}\subseteq G[p^{\infty}]_{\eta}^{\mathrm{f}}\subseteq G_{\eta}[p^{\infty}]\quad \text{and}\quad A[p^{\infty}]_{\eta}^{\mathrm{t}}\subseteq A[p^{\infty}]_{\eta}^{\mathrm{f}}\subseteq A_{\eta}[p^{\infty}]. \]
4.5 End of the proof
By [Reference Deligne and KatzDK73, Exposé IX], the inclusions 
$A[p^{\infty }]_{\eta }^{\mathrm {t}}\subseteq A[p^{\infty }]_{\eta }^{\mathrm {f}}\subseteq A_{\eta }[p^{\infty }]$ produce a filtration of 
$A[p^{\infty }]_{\eta }$ giving semistable reduction for 
$A_{\eta }[p^{\infty }]$, in the sense that:
(i)
$A[p^{\infty }]_{\eta }^{\mathrm {f}}$ and $A_{\eta }[p^{\infty }]/A[p^{\infty }]^{\mathrm {t}}_{\eta }$ extend to $p$-divisible groups $A[p^{\infty }]_{1}$ and $A[p^{\infty }]_{2}$ over $S$ (see [Reference Deligne and KatzDK73, Proposition 5.6, p. 380, Exposé IX]);(ii) if
$f_A:A[p^{\infty }]_{1}\rightarrow A[p^{\infty }]_{2}$ denotes the natural induced map, then $\mathrm {Ker}(f_A)$ is a multiplicative $p$-divisible group and $\mathrm {Coker}(f_A)$ is an étale $p$-divisible group (this follows from the orthogonality theorem [Reference Deligne and KatzDK73, Proposition 5.2, p. 372, Exposé IX], which implies that $\mathrm {Ker}(f_A)\simeq \mathcal {A}^0[p^{\infty }]^{\mathrm {t}}$ and $\mathrm {Coker}(f_A)\simeq (\mathcal (\mathcal {A}^{\vee })^0[p^{\infty }]^{\mathrm {t}})^{\vee }$, where $\mathcal {A}^{\vee }$ is Néron-model of the dual abelian $A_\eta ^\vee$ and $(\mathcal {A}^{\vee }[p^{\infty }]^{\mathrm {t}})^{\vee }$ is the Cartier dual of $\mathcal {A}^{\vee }[p^{\infty }]^{\mathrm {t}}$).
To conclude the proof we now deduce for (i) and (ii) above that the same properties holds for the filtration 
$G[p^{\infty }]_{\eta }^{\mathrm {t}}\subseteq G[p^{\infty }]_{\eta }^{\mathrm {f}}\subseteq G_{\eta }[p^{\infty }]$.
(i) By construction,
$G[p^{\infty }]_{\eta }^{\mathrm {f}}$ extends over $S$ to the $p$-divisible group $G[p^{\infty }]_1:=\mathcal {G}^0[p^{\infty }]^{\mathrm {f}}$. On the other hand, the diagram (4.4.1) shows that $G_{\eta }[p^{\infty }]/G[p^{\infty }]_{\eta }^{\mathrm {t}}\simeq A_{\eta }[p^{\infty }]/A[p^{\infty }]_{\eta }^{\mathrm {t}}$, so that we can set $G[p^{\infty }]_2:=A[p^{\infty }]_2$.(ii) Let
$f:G[p^{\infty }]_1\rightarrow G[p^{\infty }]_2$ be the induced morphism. We are left to prove that $\mathrm {Ker}(f)$ and $\mathrm {Coker}(f)$ are $p$-divisible groups and $\mathrm {Ker}(f)$ is multiplicative and $\mathrm {Coker}(f)$ is étale. This can be deduced from the analogues properties for $A[p^{\infty }]_1$ and $A[p^{\infty }]_2$, thanks to the following commutative diagram with exact rows and columns.
Conflicts of Interest
None.
