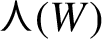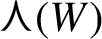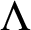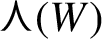1 Introduction
The Nobel Prize discovery of quasicrystals [Reference Shechtman, Blech, Gratias and Cahn19] sparked many questions regarding the nature of solids with long-range aperiodic order. This discovery led to establishment of a new area of mathematics, the area of aperiodic order. The goal of this new field is to study objects that show long-range order, but are not necessarily periodic.
The best mathematical models for point sets that show long-range order and are typically aperiodic were discovered in the earlier pioneering work of Meyer [Reference Meyer13] and have been popularized in the field by Moody [Reference Moody and Moody14, Reference Moody, Axel, Dénoyer and Gazeau15] and Lagarias [Reference Lagarias9, Reference Lagarias, Baake and Moody10]. Called model sets, they are constructed via a cut-and-project scheme, a mechanism that starts with a lattice
${\mathcal L}$
in a higher dimensional space that sits at an ‘irrational slope’ with respect to the real space
${\mathbb R}^d$
, cuts a strip around the real space
${\mathbb R}^d$
of bounded width W (called the ‘window’) and projects it on the real space
${\mathbb R}^d$
(see Definition 2.13 for the exact definition). Under various weak conditions, the high order present in the lattice
${\mathcal L}$
shows in the resulting model set, typically via a clear diffraction diagram; for example, see [Reference Baake and Moody5, Reference Lenz, Spindeler and Strungaru11, Reference Richard17, Reference Schlottmann, Baake and Moody18] just to name a few.
Meyer sets are relatively dense subsets of model sets. As subsets of model sets they inherit part of the high order present in the former, which is evident in their characterization via discrete geometry, harmonic analysis and algebraic properties [Reference Lagarias9, Reference Meyer13, Reference Moody and Moody14]. While they typically have positive entropy and hence are usually not pure point diffractive (see [Reference Baake, Lenz and Richard4]; compare [Reference Baake and Grimm2] for a discussion), they still show a highly ordered diffraction diagram [Reference Strungaru21, Reference Strungaru, Baake and Grimm23–Reference Strungaru25] with a relatively dense supported pure point spectrum [Reference Strungaru20–Reference Strungaru22, Reference Strungaru25].
In [Reference Klick, Strungaru and Tcaciuc8], we showed a different type of order in Meyer sets in the form of the existence of arbitrarily long arithmetic progressions. More precisely, we proved that given a Meyer set
$\Lambda \subseteq {\mathbb R}^d$
, for all
$N \in \mathbb N$
there exists some
$R>0$
such that the set
$\Lambda \cap B_R(x)$
contains an arithmetic progression of length N for all
$x \in {\mathbb R}^d$
. Moreover, we showed that van der Waerden-type theorems hold in Meyer sets. More recently, related results have been investigated in [Reference Aedo, Grimm, Nagai and Staynova1, Reference Nagai, Akiyama and Lee16].
Consider now a Meyer set
$\Lambda \subseteq {\mathbb R}^d$
. While
$\Lambda $
spreads relatively densely in all directions of
${\mathbb R}^d$
, any arithmetic progression is one-dimensional and hence only gives partial information about the structure of Meyer sets. This suggests that one should look for higher dimensional arithmetic progressions, which is the goal of this paper. By an m-dimensional arithmetic progression we understand a set of the form
$$ \begin{align*} A=\{ s+c_1r_1+\cdots+c_mr_m : 0 \leq c_j \leq N_j \text{ for all } 1 \leq j \leq m \} \end{align*} $$
for some fixed
$s,r_1,\ldots ,r_m \in {\mathbb R}^d$
and
$N_1,\ldots ,N_m \in \mathbb N$
. The elements
$r_1,\ldots ,r_m$
are called the ratios and
$\vec {N}=(N_1,\ldots ,N_m)$
is the vector length of the progression. The arithmetic progression is proper if all the elements
$s+c_1r_1+\cdots +c_mr_m$
are distinct.
By a standard application of the Chinese remainder theorem, we show in Proposition 3.3 that for all
$n \in \mathbb N$
and
$\vec {N} \in \mathbb N^m$
, every Meyer set contains a proper n-dimensional arithmetic progression of length
$\vec {N}$
. While the arithmetic progression is proper, every pair of ratios is linearly dependent over
${\mathbb Z}$
and hence the arithmetic progression is a subset of a one-dimensional affine
${\mathbb Q}$
-space.
To make the question more interesting and meaningful, we add the extra condition that the ratios are linearly independent over
${\mathbb Z}$
(or equivalently over
${\mathbb Q}$
). Given a fully Euclidean model set
in a cut-and-project scheme (or simply a CPS)
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
, we show in Theorem 4.3 that
has n-dimensional arithmetic progressions of arbitrary length with linearly independent ratios if and only if
$n \leq d+m$
.
Next, for any Meyer set
$\Lambda $
, it is well known that there exist some fully Euclidean model set
in some CPS
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
and a finite set
$F \subseteq {\mathbb R}^d$
such that
We show in Theorem 5.2 that
$\Lambda $
has n-dimensional arithmetic progressions of arbitrary length with linearly independent ratios if and only if
$n \leq d+m$
. This implies that, while in general there exist multiple fully Euclidean model sets
and finite sets F such that (1-1) holds, m must be the same for all these model sets.
We complete the paper by answering the following question.
Question 1.1. Which Meyer sets
$\Lambda \subseteq {\mathbb R}^d$
are subsets of fully Euclidean model sets?
To our knowledge, no characterization for these sets (that we call fully Euclidean Meyer sets) is known so far. We show in Theorem 6.1 that a Meyer set
$\Lambda \subseteq {\mathbb R}^d$
is a subset of a fully Euclidean model set if and only if it has n-dimensional arithmetic progressions of arbitrary length with linearly independent ratios, where n is the rank of the
${\mathbb Z}$
-module generated by
$\Lambda $
. The characterization is of number theory/combinatorics origin, emphasizing once again the nice order present in Meyer sets and model sets.
The paper is structured in the following way. In Section 2.1, we give basic definitions and prove a higher dimensional version of van der Waerden’s theorem [Reference van der Waerden26]. We prove, in Section 3, that Meyer sets
$\Lambda \subset {\mathbb R}^d$
contain arithmetic progression of arbitrary length and dimension, albeit with linearly dependent ratios. In Section 4, we establish both the existence of arithmetic progressions with linearly independent ratios and a higher-dimensional van der Waerden-type result for fully Euclidean model sets. In Section 5, we extend these results to arbitrary Meyer sets in
${\mathbb R}^d$
. We complete the paper by characterizing the fully Euclidean Meyer sets.
2 Preliminaries
In this section, we review the basic definitions and results needed in the paper.
2.1 Finitely generated free
${\mathbb Z}$
-modules
We start by recalling a few basic results about finitely generated free
${\mathbb Z}$
-modules. First recall [Reference Grillet7, Theorem VIII.4.12] that if M is a free
${\mathbb Z}$
-module, then all the bases of M have the same cardinality. The common cardinality of these bases is called the rank of M and is denoted by
$\mathrm {rank}(M)$
. Also, a finitely generated
${\mathbb Z}$
-module is free if and only if it is torsion free [Reference Dummit and Foote6, Theorem 12.5].
Next let us recall the following two results that we use a few times in the paper.
Lemma 2.1 [Reference Grillet7, Theorem VIII.6.1]
Let M be a free
${\mathbb Z}$
-module of rank k. If N is a submodule of M, then N is free and
$$ \begin{align*} \mathrm{rank}(N) \leq \mathrm{rank}(M). \end{align*} $$
In particular, Lemma 2.1 implies the following result.
Corollary 2.2. Let M be a free
${\mathbb Z}$
-module of rank k. If
$v_1,\ldots ,v_m \in M$
are linearly independent over
${\mathbb Z}$
, then
$m \leq k$
.
Proof.
$v_1,\ldots ,v_m$
are a basis for the submodule of M generated by
$\{ v_1,\ldots ,v_m \}$
. The claim follows from Lemma 2.1.
Next let us recall the following result about
${\mathbb Z}$
-submodules of the same rank as the full module.
Lemma 2.3. Let M be a finitely generated free
${\mathbb Z}$
-module and let N be a submodule of M. If
$$ \begin{align*} \mathrm{rank}(M)= \mathrm{rank}(N), \end{align*} $$
then there exists some positive integer n such that
$$ \begin{align*} \{ nv :v \in M \}=: n\cdot M \subseteq N. \end{align*} $$
Proof. This follows from [Reference Grillet7, Theorem VIII.6.1].
We complete the section by proving the following simple result. This result is surely known, but we could not find a good reference for it.
Lemma 2.4. Let M be a finitely generated free
${\mathbb Z}$
-module with
$k=\mathrm {rank}(M)$
and let S be a generating set for M. Then there exist k linearly independent elements
$v_1,\ldots ,v_k \in ~S$
.
Proof. By a standard application of Zorn’s lemma, there exists some
$S'=\{ v_1,\ldots , v_m\} \subseteq S$
that is a maximal linearly independent subset. Let N be the submodule of M generated by
$S'$
. Then
$\mathrm {rank}(N)=m$
. To complete the proof, we show that
$m=k$
. By [Reference Dummit and Foote6, Theorem 12.4], there exist a basis
$y_1,\ldots , y_k$
of M and
$n_1,\ldots , n_m \in {\mathbb Z}$
such that
$n_1y_1,\ldots ,n_my_m$
is a basis for N.
Now assume by contradiction that
$m <k$
. Since S spans M, there exist elements
$x_1,\ldots , x_l \in S$
and
$k_1,\ldots ,k_l \in {\mathbb Z}$
such that
$$ \begin{align*} y_k =k_1x_1+\cdots+k_lx_l. \end{align*} $$
Next note that for each
$1 \leq j \leq l$
, we either have
$x_j \in S'$
or
$S' \cup x_j$
is linearly dependent. In both cases, there exists some nonzero
$f_j \in {\mathbb Z}$
such that
$f_j x_j \in N$
. Let
$f = f_1 \cdots f_l$
. Then f is a nonzero integer and
$$ \begin{align*} fy_k \in N. \end{align*} $$
Since
$n_1y_1,\ldots ,n_my_m$
is a basis for N,
$fy_k$
can be written as a linear combination of
$n_1y_1,\ldots ,n_my_m$
. As
$f \neq 0$
, this gives that
$y_1,\ldots ,y_m,y_k$
are linearly dependent over
${\mathbb Z}$
, which is a contradiction. Thus,
$m=k$
.
Note that one can alternatively prove the above lemma by embedding M into a
${\mathbb Q}$
-vector space and looking at the subspace generated by
$S'$
.
2.2 Higher dimensional arithmetic progressions
In this section, we look at higher dimensional arithmetic progressions. Let us start with the following definition.
Definition 2.5. A higher dimensional arithmetic progression is a set of the form
$$ \begin{align*} A := \{s+ c_1r_1 + c_2r_2+\cdots+c_nr_n : 0\leq c_1 \leq N_1, 0 \leq c_2 \leq N_2,\ldots, 0 \leq c_n \leq N_n\} \, \end{align*} $$
for some fixed vectors
$s, r_1,\ldots ,r_n \in {\mathbb R}^d$
and some arbitrarily fixed natural numbers
$N_1,\ldots ,N_n \in \mathbb {N}$
. If the elements in A are distinct, then the progression is called proper. We call n the dimension of the projection and
$\vec {N}=(N_1,\ldots ,N_n)$
the vector length of the progression. The rank of the projection is the rank of the
${\mathbb Z}$
-module generated by the ratios
$\{ r_1,\ldots ,r_n \}$
. We say that the arithmetic progression is a li-arithmetic progression if the ratios
$r_1,\ldots ,r_n$
are linearly independent over
${\mathbb Z}$
.
In the remainder of the paper, we simply refer to a higher dimensional arithmetic progression simply as an ‘arithmetic progression’.
Remark 2.6. The rank of a generalized arithmetic progression is simply the largest cardinality of any
${\mathbb Z}$
-linearly independent subset of
$\{r_1,\ldots ,r_n\}$
. It is obvious that the rank of any arithmetic progression is at most its dimension, with equality if and only if the arithmetic progression is a li-arithmetic progression.
Next let us note here that since our goal is to study the existence of arithmetic progressions of arbitrary length,
$\vec {N}=(N_1,\ldots , N_n)$
, it is sufficient to restrict to the case
$N_1=N_2=\ldots =N_n=:N$
. In this case, we say that the length of the progression is
$N \in \mathbb N$
.
Next let us review some standard notation. As usual, for
$N \in \mathbb N$
with
$N \geq 1$
, we denote by
$[N]$
the set
$$ \begin{align*} [N] :=\{0,1,2,\ldots, N\} = \mathbb N \cap [0,N]. \end{align*} $$
Also,
$[N]^d$
denotes the Cartesian product of d copies of
$[N]$
, that is,
$$ \begin{align*} [N]^d=\{ (k_1,\ldots, k_d) : k_j \in [N]\ \text{for all } 1 \leq j \leq d \}. \end{align*} $$
We also need the following definition.
Definition 2.7. A d-dimensional grid of depth n is a set of the form
$$ \begin{align*}[k_1,\ldots,k_d;l_1,\ldots,l_d;n]:=\{ (l_1+m_1k_1,l_2+ m_2k_2,\ldots,l_d+m_dk_d) : m_1,\ldots, m_d \in [n] \} \end{align*} $$
for some fixed positive integers
$k_1,\ldots , k_d$
and fixed
$l_1, \ldots , l_d$
.
Note that a d-dimensional grid of depth n is simply an arithmetic progression inside
${\mathbb Z}^d$
of dimension d with the ratios
$$ \begin{align*} r_j= k_j e_j \, \end{align*} $$
for some
$k_j \in \mathbb N$
, where
$e_j=(0,0,\ldots , 1, 0,\ldots ,0)$
is the canonical basis.
We now prove the following higher dimensional version of van der Waerden’s theorem. For the analogous statement of the one-dimensional version of this theorem, we refer the reader to [Reference Klick, Strungaru and Tcaciuc8, Reference van der Waerden26]. Note that there are already higher dimensional generalizations of van der Waerdens’s theorem, such as the Gallai–Witt theorem; see [Reference Maddux12] for a brief discussion and references therein.
Theorem 2.8 (van der Waerden in
${\mathbb Z}^d$
)
Given any natural numbers
$k,r,d$
, there exists a number
$W(r, k,d)$
such that, no matter how we colour
${\mathbb Z}^d$
with r colours, for each
$N \geq W(r,k,d)$
, we can find a monochromatic d-dimensional grid
$[k_1,\ldots ,k_d; l_1, \ldots , l_d;k] \subseteq [N]^d$
of depth k.
Proof. We prove the claim via induction on d.
$P(1)$
: This is the standard van der Waerden theorem [Reference van der Waerden26].
$P(d) \Rightarrow P(d+1)$
: Let r and k be given. Let A be the set of all d-dimensional grids of depth k that are subsets of
$[W(r,k,d)]^d$
. Now set
$$ \begin{align*} W(r,k,d+1)=W(|A|\cdot r, k, 1). \end{align*} $$
We show that this choice works. Note first that the van der Waerden theorem is equivalent to the fact that given a set X with
$|A| \cdot r$
elements, for any function
$v: \mathbb N \to X$
and any
$N \geq W(|A|\cdot r, k, 1)$
, there exists an element
$x \in X$
such that
$$ \begin{align*} v^{-1}(x) \cap [N] \end{align*} $$
contains an arithmetic progression of length k.
Now consider any colouring of
${\mathbb Z}^{d+1}$
with r colours
$c_1,\ldots ,c_r$
. Let
$N \geq W(r,k,d+1)$
. Next, for each
$1 \leq j \leq N$
, consider the colouring of
${\mathbb Z}^d \times \{ j \} \subseteq {\mathbb Z}^{d+1}$
. By
$P(d)$
, the set
$[W(r,k,d)]^d \times \{ j \}$
contains a monochromatic grid
$M_j$
of depth k. Let
$c(\hspace{1.5pt}j)$
be the colour of this grid. We can now define a function
$$ \begin{align*} v&: [N] \to A \times \{c_1,\ldots, c_r\} \\ v(j)&=(M_j, c(j)). \end{align*} $$
Then there exists some
$(M,c_l) \in A \times \{c_1,\ldots , c_r\}$
such that
$$ \begin{align*} v^{-1}(M, c_l) \cap [N] \end{align*} $$
contains an arithmetic progression of length k. Let
$l_{d+1}, k_{d+1}$
be so that
$l_{d+1}+m k_{d+1} \in v^{-1}(M, c_l) \cap [N]$
for all
$m \in [k]$
. Next, since M is a monochromatic grid of depth k, there exists some
$k_1,\ldots ,k_d;l_1,\ldots ,l_d$
such that
$$ \begin{align*} M=[k_1,\ldots,k_d;l_1,\ldots,l_d;k] \subseteq [W(r,k,d)]^d. \end{align*} $$
Then, by construction, the grid
$$ \begin{align*} [k_1,\ldots,k_d, k_{d+1};l_1,\ldots,l_d,l_{d+1};k] \subseteq [W(r,k,d)]^d \times [N] \subseteq [N]^{d+1} \end{align*} $$
is monochromatic of colour
$c_l$
. This proves the claim.
Remark 2.9. If we denote by
$W(r, k,d)$
the smallest value that satisfies Theorem 2.8, then it is obvious that
$W(r,k, 1)=W(r,k)$
. Moreover, the proof above yields the very poor upper bound
$$ \begin{align*} W(r,k,d+1) \leq W(l, k, 1), \end{align*} $$
where
$l=|A|\cdot r$
. Note that
$$ \begin{align*} |A|= \bigg( \sum_{j=0}^{W(n,k,d)} \bigg\lfloor \frac{ W(n,k,d)-j }{d} \bigg\rfloor \bigg)^d, \end{align*} $$
which can be seen by observing that, for each
$1 \leq i \leq d$
and for every particular choice
$1 \leq j \leq W(n,k,d)$
,
$$ \begin{align*} 1 \leq l_j \leq \frac{ W(n,k,d)-j }{d}. \end{align*} $$
2.3 Meyer sets and model sets
In this subsection, we review the notion of model sets and Meyer sets in
${\mathbb R}^d$
. For a more detailed review of these definitions and properties, we refer the reader to the monograph [Reference Baake and Grimm3] and to [Reference Moody and Moody14, Reference Moody, Axel, Dénoyer and Gazeau15].
We start by reviewing some of the basic definitions for point sets.
Definition 2.10. Let
$\Lambda \subseteq {\mathbb R}^d$
be a point set. We say that
$\Lambda $
is:
-
• relatively dense if there exists some
$R>0$
such that for all
$x \in {\mathbb R}^d$
, the set
$\Lambda \cap B_{R}(x)$
contains at least one point; -
• uniformly discrete if there exists some
$r>0$
such that for all
$x \in {\mathbb R}^d$
, the set
$\Lambda \cap B_{r}(x)$
contains at most a point; -
• Delone if
$\Lambda $
is relatively dense and uniformly discrete; -
• locally finite if for all
$R>0$
and
$x \in {\mathbb R}^d$
, the set
$\Lambda \cap B_{R}(x)$
is finite.
Relatively denseness and uniform discreteness are usually defined in arbitrary locally compact Abelian groups (LCAGs) G, using compact sets and open sets, respectively. It is easy to see that in the case of
$G={\mathbb R}^d$
, the usual definitions are equivalent to Definition 2.10.
Next, in the spirit of [Reference Moody and Moody14], we introduce the following definition.
Definition 2.11. We say that two Delone sets
$\Lambda _1,\Lambda _2$
are equivalent by finite translations if there exist finite sets
$F_1,F_2$
such that
$$ \begin{align*} \Lambda_1 &\subseteq \Lambda_2+F_2, \\ \Lambda_2 &\subseteq \Lambda_1+F_1. \end{align*} $$
Remark 2.12.
-
(a) It is easy to see that being equivalent by finite translations is an equivalence relation on the set of Delone subsets of
${\mathbb R}^d$
. -
(b) By replacing
$F_1,F_2$
by
$F=F_1 \cup F_2$
, one can assume without loss of generality that
$F_1=F_2$
.
Next we review the notion of cut-and-project schemes and model sets.
Definition 2.13. By a cut-and-project scheme, or simply CPS, we understand a triple
$({\mathbb R}^d, H, {\mathcal L})$
consisting of
${\mathbb R}^d$
, a LCAG H, together with a lattice (that is, a discrete co-compact subgroup)
${\mathcal L} \subset {\mathbb R}^d \times H$
with the following two properties:
-
• the restriction
$\pi ^{{\mathbb R}^d}|_{{\mathcal L}}$
of the canonical projection
$\pi ^{{\mathbb R}^d}:{\mathbb R}^d \times H \to {\mathbb R}^d$
to
${\mathcal L}$
is a one-to-one function; -
• the image
$\pi ^H({\mathcal L})$
of
${\mathcal L}$
under the canonical projection
$\pi ^H: {\mathbb R}^d \times H \to H$
is dense in H.
In the special case where
$H = {\mathbb R}^m$
, then we refer to
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
as a fully Euclidean CPS.
Next we define, in the usual way,
$L:= \pi ^{{\mathbb R}^d}({\mathcal L})$
and
$\star : L \to H$
, known as the
$\star $
-mapping, by
$$ \begin{align*} \star= \pi^H \circ ( \pi^{{\mathbb R}^d}|_{{\mathcal L}})^{-1}. \end{align*} $$
This allows us rewrite
$$ \begin{align*}{\mathcal L}= \{ (x,x^\star) : x \in L \}.\end{align*} $$
Note that the range of the
$\star $
-mapping is
$$ \begin{align*}\star(L)=:L^\star= \pi^H({\mathcal L}).\end{align*} $$
We can summarize the CPS in the diagram below.
We can now review the definition of model sets.
Definition 2.14. Given a CPS
$({\mathbb R}^d,H,{\mathcal L})$
and some subset
$W \subseteq H$
, we denote by
its preimage under the
$\star $
-mapping, that is,
When W is precompact and has nonempty interior, the set
is called a model set. If furthermore
$H={\mathbb R}^m$
for some m, then
is called a fully Euclidean model set.
We want to emphasize here that the condition that W has nonempty interior is essential later in the paper in the proof of Theorem 4.3.
Next let us recall the following result.
Proposition 2.15 [Reference Moody and Moody14, Proposition 2.6] and [Reference Baake and Grimm3, Proposition 7.5]
Let
$({\mathbb R}^d, H, {\mathcal L})$
be a CPS and
$W \subseteq H$
.
-
(a) If
$W \subseteq H$
is precompact, then
is uniformly discrete. -
(b) If
$W \subseteq H$
has nonempty interior, then
is relatively dense.
In particular, every model set is a Delone set.
Next we review the concept of Meyer sets. We start by recalling the following theorem.
Theorem 2.16 [Reference Lagarias9, Reference Meyer13, Reference Moody and Moody14]
Let
$\Lambda \subseteq {\mathbb R}^d$
be relatively dense. Then the following are equivalent.
-
(i)
$\Lambda $
is a subset of a model set. -
(ii) There exist a fully Euclidean model set
and a finite set F such that -
(iii)
$\Lambda - \Lambda $
is uniformly discrete. -
(iv)
$\Lambda $
is locally finite and there exists a finite set
$F_1$
such that
$$ \begin{align*} \Lambda - \Lambda \subseteq \Lambda +F_1. \end{align*} $$
Proof. The equivalence (i)
$\Leftrightarrow $
(iii)
$\Leftrightarrow $
(iv) can be found in [Reference Moody and Moody14], while (ii)
$\Leftrightarrow $
(iv) is [Reference Meyer13, Theorem IV].
The above theorem gives the concept of a Meyer set. More precisely, we have the following definition.
Definition 2.17. A relatively dense set
$\Lambda \subset {\mathbb R}^n$
is called a Meyer set if it satisfies one (and hence all) of the equivalent conditions of Theorem 2.16.
A relatively dense set
$\Lambda $
is called a fully Euclidean Meyer set if there exists some fully Euclidean model set
such that
One of the goals of this paper is to characterize fully Euclidean Meyer sets.
Next let us recall the following result from [Reference Moody and Moody14].
Lemma 2.18. Let
$\Lambda \subseteq {\mathbb R}^d$
be a Meyer set. Then the group
$\langle \Lambda \rangle $
generated by
$\Lambda $
is finitely generated. In particular,
$\langle \Lambda \rangle $
is a free
${\mathbb Z}$
-module of finite rank.
Proof. By [Reference Moody and Moody14, Theorem 9.1],
$\langle \Lambda \rangle $
is finitely generated. It is therefore a finitely generated
${\mathbb Z}$
-module. Moreover, since
${\mathbb R}$
is torsion free as a
${\mathbb Z}$
-module, so is
$\langle \Lambda \rangle $
. Therefore,
$\langle \Lambda \rangle $
is a free
${\mathbb Z}$
-module by [Reference Dummit and Foote6, Theorem 12.5].
This allows us introduce the following definition.
Definition 2.19. Let
$\Lambda \subseteq {\mathbb R}^d$
be any Meyer set. We define the rank of
$\Lambda $
to be
$$ \begin{align*} \mathrm{rank}(\Lambda):= \mathrm{rank}_{{\mathbb Z}} (\langle \Lambda \rangle). \end{align*} $$
We complete the section by showing that each Meyer set is equivalent by finitely many translates with a fully Euclidean model set.
Lemma 2.20. Let
$\Lambda $
be a Meyer set, F finite and
a fully Euclidean model set such that
Then
$\Lambda $
and
are equivalent by finite translations.
Proof. Since
is a Meyer set and F is finite,
is also a Meyer set [Reference Meyer13, Reference Moody and Moody14]. The claim follows now from [Reference Strungaru, Baake and Grimm23, Lemma 5.5.1].
3 Higher dimensional arithmetic progressions in Meyer sets
In this section we show that Meyer sets contain arithmetic progressions of arbitrary dimensions and length. The proofs show that the existence of arithmetic progressions of arbitrary length in Meyer sets is interesting only in the case of li-arithmetic progressions. We study these in the subsequent sections.
We start by recalling the following well-known theorem.
Lemma 3.1 (Chinese remainder theorem [Reference Dummit and Foote6, Corollary 7.18])
If
$k_1,\ldots , k_n$
are pairwise coprime and
$a_1,\ldots ,a_n$
are integers, then there exists
$x \in \mathbb {Z}^+$
such that
$$ \begin{align*} \left\{ \begin{array}{@{}ll} x &\equiv a_1 \mod k_1,\\ x &\equiv a_2 \mod k_2,\\ & \hspace{0.95cm} \vdots \\ x & \equiv a_n \mod k_n. \end{array} \right. \end{align*} $$
Moreover, any two solutions are congruent modulo
$k_1,k_2, \ldots , k_n$
.
As an immediate consequence, we get the following result.
Corollary 3.2. For each
$n,N \in \mathbb {N}$
, there exist
$m_1,\ldots ,m_n \in \mathbb {N}$
such that
$\sum ^{n}_{i=1}c_im_i$
are distinct for all
$0 \leq c_i \leq N$
.
Proof. Let
$p_1,\ldots ,p_n$
be distinct primes such that for all
$1 \leq i \leq n$
, we have
$p_i> N$
. By the Chinese remainder theorem, there exist
$m_1,\ldots ,m_n$
such that for each
$1 \leq i \leq n$
,
$$ \begin{align*} \left\{ \begin{array}{@{}ll} m_i &\equiv 1\ \mathrm{mod}\ p_i\\ m_i &\equiv 0\ \mathrm{mod}\ p_j \quad \text{for all } j \neq i. \end{array} \right. \end{align*} $$
Now, if
$ \sum ^{n}_{i=1}c_im_i =\sum ^{n}_{i=1}c^{\prime }_im_i $
, then, for all
$1 \leq k \leq n$
,
$$ \begin{align*} \sum^{n}_{i=1}c_im_i \equiv \sum^{n}_{i=1}c^{\prime}_im_i\ \mathrm{mod}\ p_k \end{align*} $$
and hence
$c^{}_k \equiv c^{\prime }_{k}\ \mathrm {mod}\ p^{}_{k} $
. Since
$$ \begin{align*}0 \leq c_{k}, c^{\prime}_{k} \leq N < p_k,\end{align*} $$
we get
$c_k=c^{\prime }_k$
for all
$1 \leq k \leq n$
.
We can now prove the following result.
Proposition 3.3. Let
$n,N \in \mathbb {N}$
and let
$\Lambda \in {\mathbb R}^d$
be a Meyer set. Then there exists some
$R>0$
such that
$\Lambda \cap B_R(x)$
contains a nontrivial and proper n-dimensional arithmetic progression of length N for all
$x \in \mathbb {R}^d$
.
Proof. Let
$n, N \in \mathbb {N}$
be given. We show that, for some
$R>0$
, there exist
$$ \begin{align*} s, r_1, r_2, \ldots , r_n \in \Lambda \end{align*} $$
such that
$$ \begin{align*} s + \sum^{n}_{i=1}c_ir_i \in \Lambda \cap B_R(x) \quad \text{for all } 0\leq c_i\leq N \end{align*} $$
and that the elements
$s + \sum ^{n}_{i=1}c_ir_i $
are distinct. Let
$m_1,\ldots , m_n$
be as in Corollary 3.2 and set
$N'= Nm_1+\cdots +Nm_n$
. By [Reference Klick, Strungaru and Tcaciuc8, Lemma 4.3], there exist an
$R>0$
and some nonzero
$s, r \in \Lambda $
such that
$$ \begin{align*} s, s+r, \ldots , s+N'r \in \Lambda \cap B_R(x). \end{align*} $$
Now define
$r_j:= m_jr$
. It follows that, for
$0 \leq \sum ^{n}_{i=1}c_im_i \leq N'$
,
$$ \begin{align*} s + \sum^{n}_{i=1}c_ir_i = s+ \sum^{n}_{i=1}c_im_ir \in \Lambda \cap B_R(x). \end{align*} $$
Moreover, by Corollary 3.2, the progression is proper.
Note here in passing that, by construction, the arithmetic progression in Proposition 3.3 has rank one.
It becomes natural to ask if one can construct arithmetic progressions of higher rank. It is easy to see that one can focus on li-arithmetic progressions. Indeed, exactly as in Proposition 3.3, one can prove the following result.
Lemma 3.4. Let
$\Lambda \subseteq {\mathbb R}^d$
be any Meyer set and
$k \in \mathbb N$
. Then
$\Lambda $
contains li-arithmetic progressions of rank k and arbitrary length if and only if for each
$d \geq k$
,
$\Lambda $
contains arithmetic progressions of rank k, dimension d and arbitrary length.
Since the proof is similar to that of Proposition 3.3, we skip it.
4 Higher dimensional arithmetic progressions with linearly independent ratios
In this section, we discuss the existence of li-arithmetic progressions in fully Euclidean model sets. We show that the maximal rank of any such progression is the rank of the lattice in the CPS and that for this rank, we can find li-arithmetic progressions of arbitrary length.
We start by proving the following result (compare [Reference Moody and Moody14, Proposition 2.6]).
Lemma 4.1. Let
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
be a fully Euclidean CPS and let
$W \subseteq {\mathbb R}^m$
be any set with nonempty interior. Then
generates
$L=\pi _{{\mathbb R}^d}({\mathcal L})$
. In particular,
In particular, there exist vectors
that are linearly independent over
${\mathbb Z}$
.
Proof. It suffices to show that
generates L. Note that
$0$
is an interior point in
$W-W$
and hence we can find some
$r>0$
such that
$B_r(0) \subseteq W-W$
.
Now let
$x \in L$
be arbitrary. Pick some n such that
$d(x,0) < nr$
. Then
$({x}/{n}) \in B_r(0)$
. Note here that
$({x}/{n}) \in B_r(0) \cap B_{{x}/{n}}({x}/{n})$
. Since this set is open, by the density of
$\pi _{{\mathbb R}^m}({\mathcal L})$
in
${\mathbb R}^m$
, there exist some
$(z,z^\star ) \in {\mathcal L}$
such that
$z^\star \in B_r(0) \cap B_{{x}/{n}}({x}/{n})$
. Then
and
$d(x^\star , nz^\star )<r$
and thus
$x^\star -nz^\star \in B_r(0) \subseteq W-W$
. Therefore,
This gives
. The last claim now follows from Lemma 2.4.
Next we prove the following generalization of [Reference Klick, Strungaru and Tcaciuc8, Proposition 4.2].
Proposition 4.2. Let
$({\mathbb R}^d,H, {\mathcal L})$
be any CPS and let
$W \subseteq H$
be any set with nonempty interior. Then, for all
$M \in \mathbb N$
, we can find open sets
$U_M, V_M \subset H$
such that
$0 \in V_M$
and
Proof. As W has nonempty interior, there exist nonempty open sets
$U_M \subseteq H$
and
$0 \in V_M \subseteq H$
such that
$$ \begin{align*} U_M + \underbrace{V_M+V_M+\cdots+V_M}_{M~\mathrm{ times }}\subseteq W. \end{align*} $$
Then
This completes the proof.
By combining Proposition 4.2 with Corollary 2.2, we get the following result.
Theorem 4.3. Let
be a model set in a fully Euclidean CPS
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
. Then:
-
(a) any arithmetic progression of length N in
has rank at most
$d+m$
; -
(b) for each N, there exists some
$R>0$
such that the set
contains a li-arithmetic progression of length N and rank
$d+m$
for all
$y \in {\mathbb R}^d$
.
Proof.
-
(a) For any arithmetic progression of rank k in
, the set
$\{r_1^{},\ldots ,r_k^{} \} $
, with
$r_i^{}$
the ratios of the progression, is
$\mathbb {Z}$
-linearly independent in L. Therefore, by Corollary 2.2, we have
$k \leq m+d$
. This proves (a). -
(b) Let N be given. We show that there exists some
$R>0$
such that, for all
$y \in {\mathbb R}^d$
, there exist some
and
$\mathbb {Z}$
-linearly independent
$r_1^{},\ldots ,r_{m+d}^{}$
with
for all
$0 \leq c_j^{} \leq N.$
Set
$M:= N\cdot (m+d).$
By Proposition 4.2, there exist open sets
$U_M, V_M \subseteq {\mathbb R}^m$
such that
$0 \in V_M$
and
As
$U_M^{}$
has nonempty interior, by Proposition 2.15, there exists
$R'> 0$
such that
. Next, by Lemma 2.4, there exist
${\mathbb Z}$
-linearly independent vectors
. Define
$$ \begin{align*} R:= N\cdot(\|r_1^{}\|+\cdots+\|r_{m+d}^{}\|)+R'. \end{align*} $$
Let
$y \in \mathbb {R}^d$
be arbitrary. By the definition of
$R'$
, there exists some
Then, for all
$ 0 \leq c_i \leq N$
, as
,
Moreover, for all
$ 0 \leq c_i \leq N$
,
$$ \begin{align*} d\bigg(s+\sum_{i=1}^{m+d}c_i^{}r_i,y\bigg)& = \bigg\| y- \bigg(s+\sum_{i=1}^{m+d}c_i^{}r_i \bigg) \bigg\| \leq \| y- s \| + \bigg\| \sum_{i=1}^{m+d}c_i^{}r_i \bigg\| \\ &\leq R' +\sum_{i=1}^{m+d} \| c_i^{}r_i \| = R' +\sum_{i=1}^{m+d}c_i^{} \| r_i \| \leq R' +\sum_{i=1}^{m+d}N \| r_i \|= R. \end{align*} $$
This implies that, for each
$0 \leq c_i^{} \leq N$
,
establishing the claim.
Theorem 4.3 suggests the following definition.
Definition 4.4. Let
$\Lambda \subseteq {\mathbb R}^d$
be a Meyer set.
The ap-rank of
$\Lambda $
, denoted by
$\mbox {ap-rank}(\Lambda )$
, is the largest
$k \in \mathbb N$
with the property that, for all
$N \in \mathbb N$
, there exists a li-arithmetic progression of length N and rank k in
$\Lambda $
.
Note here in passing that by Lemma 3.4, the ap-rank of
$\Lambda $
is the largest positive integer k such that for all
$N \in \mathbb N$
, the set
$\Lambda $
contains an arithmetic progression of length N and rank k.
The next result tells us that the definition of ap-rank makes sense.
Lemma 4.5. Let
$\Lambda \subseteq {\mathbb R}^d$
be any Meyer set. Then
$$ \begin{align*} 1 \leq \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) \leq \mathrm{rank}(\Lambda). \end{align*} $$
Proof. The lower bound follows immediately from [Reference Klick, Strungaru and Tcaciuc8]. Note here that any nontrivial one-dimensional arithmetic progression in
${\mathbb R}^d$
has rank one.
Next consider any arithmetic progression of length
$N \geq 2$
and rank k in
$\Lambda $
and let
$r_1,\ldots ,r_k$
be the linearly independent ratios. Then
$r_1,\ldots ,r_k$
are linearly independent vectors in
$\langle \Lambda \rangle $
. The claim follows from Corollary 2.2.
Remark 4.6.
-
(a) Theorem 4.3 says that for a fully Euclidean model set
in the CPS
$({\mathbb R}^d,{\mathbb R}^m,{\mathcal L})$
, -
(b) Since the ap-rank does not change under translates, but the rank changes for translates outside the
${\mathbb Z}$
-module generated by the set, it is easy to construct examples of translates of fully Euclidean model sets such thatIn Example 5.5, for each
$n \in \mathbb N$
, we construct a Meyer set
$\Lambda $
such that
$$ \begin{align*} \mathrm{rank}(\Lambda) = \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) +n. \end{align*} $$
-
(c) If
$\Lambda \subseteq {\mathbb R}^d$
is a Meyer set, we show in Corollary 5.4 that
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) \geq d. \end{align*} $$
We complete the section by providing a colouring version of Theorem 4.3.
Theorem 4.7. Let
be a model set in a fully Euclidean CPS
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
. Then, for each
$r,k$
, there exists some R such that, no matter how we colour
with r colours, the set
contains a monochromatic li-arithmetic progression of length k and rank
$d+m$
for all
$y \in {\mathbb R}^d$
.
Proof. Let N be such that van der Waerden’s theorem (Theorem 2.8) holds for
$r,k$
applied to
$[N]^{d+m}.$
By Theorem 4.3, there exists some
$R>0$
such that, for all
$y \in \mathbb {R}$
, the set
contains a nontrivial li-arithmetic progression length N. We show that this R works.
Arbitrarily colour
with r colours and let
$y \in \mathbb {R}^d$
be given. By Theorem 4.3, there exist
$s, r_1^{},\ldots ,r_{m+d}^{}$
such that
$r_1^{},\ldots ,r_{m+d}^{}$
are
${\mathbb Z}$
-linearly independent and, for all
$0 \leq c_i \leq N$
,
Colour the set
$[N]^{m+d}$
by colouring
$(c_1,\ldots ,c_{m+d})$
with the colour of
$s+\sum _{i=1}^{m+d}c_ir_i^{}$
. By the choice of N, there exists a monochromatic grid
$$ \begin{align*} [k_1,\ldots,k_{d+m};l_1,\ldots,l_{d+m};k]\in [N]^{d+m} \end{align*} $$
of length k and dimension
$d+m$
. Then, for all
$1 \leq m_j \leq k$
, the set
is monochromatic. Now set
$s':=s+\sum _{j=1}^{m+d} l_jr_j$
and
$r^{\prime }_j:=k_jr_j$
. Then, for all
$(m_1,\ldots , m_{m+d}) \in [k]^{m+d}$
,
is a monochromatic li-arithmetic progression of length k and rank
$m+d.$
5 ap-rank of Meyer sets
In this section, we calculate the ap-rank of a Meyer set
$\Lambda $
. We know that
$\Lambda $
is equivalent by finite translates to a fully Euclidean model set
and we use this to show that
We start by proving the following result.
Lemma 5.1. Let
$\Lambda , \Gamma \subseteq {\mathbb R}^d$
be Meyer sets that are equivalent by finite translates. Then
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda)= \mathrm{ap}\text{-}\mathrm{rank}(\Gamma). \end{align*} $$
Proof. By symmetry, it suffices to show that
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) \leq \mathrm{ap}\text{-}\mathrm{rank}(\Gamma). \end{align*} $$
Let
$F = \{f_1, \ldots , f_r\}$
be such that
$$ \begin{align*} \Lambda \subseteq \Gamma+F \end{align*} $$
and let
$k=\mbox {ap-rank}(\Lambda )$
. We show that
$\Gamma $
contains arithmetic progressions of length N and rank k.
First, colour F with r colours such that no two points of F have the same colour. Next let
$N \in \mathbb N$
be arbitrary and let
$N'=W(|F|,N,d)$
be given by Theorem 2.8. Since
$k=\mbox {ap-rank}(\Lambda )$
, by definition, there exists a li-arithmetic progression
$$ \begin{align*} \{ s+ c_1r_2+\cdots+c_kr_k : 0 \leq c_j \leq N' \} \end{align*} $$
of length
$N'$
and rank k in
$\Lambda $
. Now, for each
$(c_1,\ldots ,c_k) \in [0,N']^k$
, there exists some
$f_j \in F$
so that
$$ \begin{align*} x:= s+ c_1r_2+\cdots+c_kr_k \in \bigcup^{r}_{j=1} \Gamma +f_j. \end{align*} $$
Pick the smallest j such that
$x = y+f_j$
for some
$y \in \Gamma .$
Colour
$(c_1,\ldots ,c_k)$
with the colour of this
$f_j \in F$
. Then, by Theorem 2.8, there exists a monochromatic grid
$[c^{\prime }_1d_1,\ldots ,c^{\prime }_kd_k;k] \subseteq [N']^k$
of depth N. Define
$$ \begin{align*} s'&=s-f_j,\\ r_j'&=d_jr_j. \end{align*} $$
Then, for all
$0 \leq c^{\prime }_j \leq N$
,
$$ \begin{align*} x = s'+ c^{\prime}_1r_1'+\cdots+c^{\prime}_kr^{\prime}_k \in \Gamma \end{align*} $$
is a li-arithmetic progression of length N and rank k. Since
$N \in \mathbb N$
is arbitrary,
$k \leq \mbox {ap-rank}(\Gamma )$
.
Now, by combining all results so far, we get the following theorem, which is the first main result in the paper.
Theorem 5.2. Let
$\Lambda \subseteq {\mathbb R}^d$
be a Meyer set, let
be any fully Euclidean model set in
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
and
$F \subseteq {\mathbb R}^d$
be finite such that
Then
Moreover, for each N, there exists some
$R>0$
such that the set
$\Lambda \cap B_{R}(y)$
contains a li-arithmetic progression of length N and rank
$d+m$
for all
$y \in {\mathbb R}^d$
.
Proof. By Lemma 2.20,
$\Lambda $
and
are equivalent by finite translates. Therefore, by Lemma 5.1,
Moreover, by Theorem 4.3,
Next, since
$\Lambda $
and
are equivalent by finite translates, there exists some finite set
$F= \{t_1^{},\ldots ,t_r^{} \}$
such that
Colour F with r colours so that each point of F has a different colour. Let
$R'$
be the constant given by Theorem 4.7 for
with r colours and length N. Define
$$ \begin{align*} R := \max\{R' + \|t_j^{}\| : 1 \leq j \leq r \}. \end{align*} $$
Colour
the following way: for each
, there exists some minimal j such that
$x \in t_j^{} + \Lambda $
. Colour each x by the colour of
$t_j^{} $
for this minimal j. This gives an r-colouring of
. Note here that any choice of
$t_j$
works, but one needs to make a choice in case some
belongs to
$t_j^{} + \Lambda $
for more than one j.
Now let
$y \in \mathbb {R}^d$
be arbitrary. By Theorem 4.7, there exists a monochromatic li-arithmetic progression
of rank
$m+d$
for all
${0 \leq c_i^{} \leq N}$
.
Since the arithmetic progression is monochromatic, there exists some j such that, for all
$0 \leq c_i \leq N$
,
$$ \begin{align*} s+\sum_{i=1}^{m+d}c_i^{}r_i^{} \in t_j^{} + \Lambda. \end{align*} $$
Thus, for all
$0 \leq c_i^{} \leq N$
,
$$ \begin{align*} s-t_j^{}+\sum_{i=1}^{m+d}c_i^{}r_i \in \Lambda, \end{align*} $$
which is a li-arithmetic progression of length N and rank
$m+d$
. Moreover, for each
$0 \leq c_i^{} \leq N$
,
$$ \begin{align*} d\bigg(s-t_j^{} +\sum_{i=1}^{m+d}c_i^{}r_i, y\bigg) =\bigg\|s+\sum_{i=1}^{m+d}c_i^{}r_i - t_j^{} -y\bigg\| \leq \bigg\|s+\sum_{i=1}^{m+d}c_i^{}r_i -y\bigg\| + \|t_j^{}\| \leq R. \end{align*} $$
This proves the last claim.
We start by listing some consequences of this result.
As a first immediate consequence, we get that if
$\Lambda $
is a Meyer set,
a fully Euclidean model set in
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
and F a finite set such that
then m is invariant for
$\Lambda $
.
Corollary 5.3. Let
$\Lambda \subseteq {\mathbb R}^d$
be any Meyer set. If
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
and
$({\mathbb R}^d, {\mathbb R}^n, {\mathcal L})$
are two different CPSs,
$W \subseteq {\mathbb R}^m, W' \subseteq {\mathbb R}^n$
are precompact windows with nonempty interior and
$F,F'$
are finite sets such that
then
$m=n$
.
Proof. By Theorem 5.2,
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) &=d+m, \\ \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) &=d+n. \end{align*} $$
Therefore,
$d+m=d+n$
and hence
$m=n$
.
As an immediate consequence, we get the following improvement on the lower bound from Lemma 4.5.
Corollary 5.4. Let
$\Lambda \subseteq {\mathbb R}^d$
be any Meyer set. Then
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda)\geq d. \end{align*} $$
Next we show that in general there is no upper bound for
$\mbox {ap-rank}(\Lambda )$
in terms of
$\mbox {rank}(\Lambda )$
.
Example 5.5. Let
be any fully Euclidean model set and let
$r_1,\ldots ,r_k$
be such that
Let
$s_1,\ldots ,s_n$
be such that
$r_1,\ldots ,r_k, s_1,\ldots ,s_n$
are linearly independent over
${\mathbb Z}$
and let
$F= \{s_1,\ldots ,s_n\}$
. Then
is a Meyer set and
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda)&=k, \\ \mathrm{rank}(\Lambda)&=k+n. \end{align*} $$
Remark 5.6. If
is a fully Euclidean model set with
$k=\mbox {ap-rank}(\Lambda )$
, then, by Theorem 4.3, every li-arithmetic progression in
has rank at most k. The same is not true in Meyer sets.
Indeed, let
$k \leq d$
and N be any positive integers. Let A be any li-arithmetic progression of rank d and length N, and let
be any fully Euclidean model set of rank k such that
. Then
is a Meyer set, with
$\mbox {ap-rank}(\Lambda )=k$
, which contains the li-arithmetic progression A of rank d and length N.
Note that
$\mbox {ap-rank}(\Lambda )=k$
means that for all
$d>k$
, if
$\Lambda $
contains li-arithmetic progressions of rank d, then they are bounded in length. We see later in Corollary 6.3 that for fully Euclidean Meyer sets, the rank of every li-arithmetic progression is also bounded by the ap-rank.
We complete the section by extending, as usual, Theorem 5.2 to colourings of
$\Lambda $
.
Theorem 5.7. Let
$\Lambda \subset {\mathbb R}^d$
be a Meyer set and let
$k=\mathrm{ap}\mbox{-}\mathrm{rank}(\Lambda )$
. Then, for each
$r,N$
, there exists some R such that, no matter how we colour
$\Lambda $
with r colours, the set
$\Lambda \cap B_{R}(y)$
contains a monochromatic li-arithmetic progression of length N and rank k for all
$y \in {\mathbb R}^d$
.
Proof. Pick
$N'$
such that van der Waerden’s theorem holds for
$r,k$
applied to
$[N']^{d+m}$
. By Theorem 5.2, there exists
$R>0$
such that for all
$y \in \mathbb {R}^d$
, the set
$\Lambda \cap B_R^{}(y)$
contains an arithmetic progression of length N and dimension k. The rest of the proof is identical to that of Theorem 4.7.
6 A characterization of fully Euclidean Meyer sets
We complete the paper by characterizing fully Euclidean Meyer sets. To our knowledge, this is the first result in this direction.
Theorem 6.1. Let
$\Lambda \subseteq {\mathbb R}^d$
be a Meyer set. Then
$\Lambda $
is a fully Euclidean Meyer set if and only if
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda)=\mathrm{rank}(\Lambda). \end{align*} $$
Proof.
$\Longrightarrow $
:
Let
be a fully Euclidean model set such that
Then
. Therefore, by Lemma 4.5 and Theorem 5.2,
This gives
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) = \mathrm{rank}(\Lambda). \end{align*} $$
$\Longleftarrow $
:
Let
$k:= \mbox {ap-rank}(\Lambda )=\mbox {rank}(\Lambda ).$
By Theorem 2.16, there exist a CPS
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L})$
, a window
$W \subseteq {\mathbb R}^m$
and a finite set
$F=\{ f_1,\ldots , f_l \}$
such that
Moreover, without loss of generality, we can assume that no proper subset
$F'$
of F satisfies (6-1). We start by showing that there exists some n so that
$n \Lambda \subseteq L=\pi _{{\mathbb R}^d}({\mathcal L})$
.
First, note that by Theorem 5.2,
By (6-1), we can partition
$\Lambda $
as
Note that for all
$1 \leq j \leq l$
,
and hence
We claim that
$\Gamma := \bigcup _{j=1}^l (\Lambda _j -\Lambda _j)$
is relatively dense. Indeed, set
$$ \begin{align*} J:= \{ j : 1 \leq j \leq l, \Lambda_j \neq \emptyset \}. \end{align*} $$
Then
$$ \begin{align*} \Gamma= \bigcup_{j \in J} ( \Lambda_j - \Lambda_j ). \end{align*} $$
Now, for each
$j \in J$
, fix some
$x_j \in \Lambda _j$
, that exists by the definition of J. Let
$$ \begin{align*} F'= \{ x_j : j \in J \}. \end{align*} $$
Then
$$ \begin{align*} \Lambda &= \bigcup_{j \in J} \Lambda_j= \bigcup_{j \in J} (\Lambda_j -x_j+x_j) \subseteq \bigcup_{j \in J} (\Lambda_j -x_j+F')\\ &=\bigg(\bigcup_{j \in J} (\Lambda_j -x_j)\bigg)+F' \subseteq \bigg(\bigcup_{j \in J} (\Lambda_j -\Lambda_j)\bigg)+F'= \Gamma+F'. \end{align*} $$
Since
$\Lambda $
is relatively dense, it follows immediately that
$\Gamma $
is relatively dense. In particular,
$\Gamma $
is a Meyer set. Now, by Theorem 5.2,
Since
,
and hence
$\mbox {rank}(\Gamma )= k.$
Next let
$L_1 = \langle \Lambda \rangle $
and
$L_2 = \langle \Gamma \rangle $
be the
${\mathbb Z}$
-modules generated by
$\Lambda $
and
$\Gamma $
, respectively. Since, for each
$1 \leq j \leq l$
, we have
$\Lambda _j \subseteq \Lambda $
and hence
$\Lambda _j -\Lambda _j \subseteq \Lambda -\Lambda \subseteq L_1$
, we get that
$L_2$
is a
${\mathbb Z}$
-submodule of
$L_1$
.
Now recall that by Lemma 4.1,
Since
, we have
$\Gamma \subseteq L$
and hence
$L_2$
is a submodule of L. Moreover, by the above,
$$ \begin{align*} \mathrm{rank}(L_1)=\mathrm{rank}(L_2)=k \end{align*} $$
and by Lemma 2.3 there exists some positive integer n such that
$nL_1 \subseteq L_2$
. Therefore,
$$ \begin{align*} n \Lambda \subseteq n L_1 \subseteq L_2 \subseteq L, \end{align*} $$
as claimed. Next let
$v_1,\ldots , v_{d+m}$
be the vectors such that
$$ \begin{align*} {\mathcal L}= {\mathbb Z} v_1 \oplus \cdots \oplus {\mathbb Z} v_{m+d}. \end{align*} $$
Now, by enlarging the lattice
${\mathcal L}$
, we can make sure that
$\Lambda $
is inside the projection of the lattice on
${\mathbb R}^d$
. Indeed, for each
$1 \leq j \leq m+d$
, let
$$ \begin{align*} w_j= \frac{1}{n} v_j \end{align*} $$
and set
$$ \begin{align*} {\mathcal L}':= {\mathbb Z} w_1 \oplus \cdots \oplus {\mathbb Z} w_{m+d}. \end{align*} $$
Then it is obvious that
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L}')$
is a CPS and that
$$ \begin{align*} L'=\pi_{{\mathbb R}^d}({\mathcal L}')= \frac{1}{m} \pi_{{\mathbb R}^d}({\mathcal L})= \frac{1}{n} L. \end{align*} $$
Moreover, by construction,
${\mathcal L} \subseteq {\mathcal L}'$
. This gives
$$ \begin{align*} \Lambda \subseteq \frac{1}{n} L=L'. \end{align*} $$
We complete the proof by showing that
$F \subseteq L'$
. The result follows from this.
Let
$f \in F$
be arbitrary. By the minimality of F,
Therefore, there exists some
$x \in \Lambda $
such that
. However, as
,
Thus, there exists some
such that
$x=y+f$
. It follows that
as claimed. Therefore, for all
$1 \leq j \leq l$
, there exists some
$g_j \in {\mathbb R}^m$
such that
$(f_j,g_j) \in {\mathcal L}'$
. Define
$$ \begin{align*} W'= \bigcup_{j=1}^l g_j +W \subseteq {\mathbb R}^m. \end{align*} $$
Then
$W'$
is precompact and has nonempty interior.
We show that
which, as
is a fully Euclidean model set in the CPS
$({\mathbb R}^d, {\mathbb R}^m, {\mathcal L}')$
, completes the proof.
Let
$x \in \Lambda $
be arbitrary. Then, as
, there exist some
and
$1 \leq j \leq l$
such that
$$ \begin{align*} x=y+f_j. \end{align*} $$
Since
, there exists some
$z \in W$
such that
$(y,z) \in L \subseteq L'$
. Then
$$ \begin{align*} (x,z+g_j) &=(y,z)+(f_j,g_j) \in {\mathcal L}+{\mathcal L}' \subseteq {\mathcal L}'+{\mathcal L}'={\mathcal L}', \\ z+g_j &\in g_j+W \subseteq W' \end{align*} $$
and hence
.
Remark 6.2. Theorem 6.1 can be equivalently stated as follows.
Let
$\Lambda \subseteq {\mathbb R}^d$
be a Meyer set. Then
$\Lambda $
is a fully Euclidean Meyer set if and only if for
$k = \mbox {rank}(\Lambda )$
, for each
$N \in {\mathbb N}$
, there exist some
$s, r_1,\ldots ,r_k \in {\mathbb R}^d$
such that
$r_1,\ldots ,r_k$
are linearly independent over
${\mathbb Z}$
and, for all
$0 \leq C_j \leq N$
,
$$ \begin{align*} s+C_1r_1+\cdots+C_kr_k \in \Lambda. \end{align*} $$
Note here that if A is a li-arithmetic progression of length
$N \geq 1$
in a fully Euclidean Meyer set
, with ratios
$r_1,r_2,\ldots ,r_k$
, then
$r_1,r_2,\ldots ,r_k \in \langle \Lambda \rangle $
, which gives
. Therefore, we get the following.
Corollary 6.3. Let
$\Lambda \subseteq {\mathbb R}^d$
be a fully Euclidean Meyer set with
$\mathrm {rank}(\Lambda )=k$
. Then:
-
(a) every li-arithmetic progression in
$\Lambda $
of length
$N \geq 1$
has rank at most k; -
(b) for each
$N \in \mathbb N$
, there exists a li-arithmetic progression in
$\Lambda $
of rank k and length N.
We complete the paper by giving an explicit example of a Meyer set
$\Lambda $
that is not fully Euclidean and we explicitly construct a CPS that produces it as a not fully Euclidean Meyer set. In fact,
$\Lambda $
is a regular model in this CPS.
Example 6.4. Let
$\textit {Fib}$
denote the well-known Fibonacci model set with its corresponding CPS
$({\mathbb R}, {\mathbb R}, {\mathcal L})$
, where
${\mathcal L}= {\mathbb Z}(1,1) \oplus {\mathbb Z}(\tau , \tau ')$
. We refer the reader to [Reference Baake and Grimm3] for a full description. Note that
$\textit {Fib}$
is a fully Euclidean regular model set within a two-dimensional CPS.
Now take
$\Lambda = \pi + \textit {Fib}$
; it follows that
$\Lambda $
is still relatively dense and thus a Meyer set. As the ap-rank is invariant under translates,
$$ \begin{align*} \mathrm{ap}\text{-}\mathrm{rank}(\Lambda) = \mathrm{ap}\text{-}\mathrm{rank}(\textit{Fib}) =2. \end{align*} $$
Now, since
$\tau $
is an algebraic integer and
$\pi $
is transcendental,
$1, \tau , \pi $
are linearly independent over
${\mathbb Z}$
. It is easy to see that
$$ \begin{align*}1, \tau, \pi \subseteq \langle \pi+ \textit{Fib} \rangle \subseteq {\mathbb Z}+ {\mathbb Z} \tau +{\mathbb Z} \pi.\end{align*} $$
This immediately implies that
$\langle \pi + \textit {Fib} \rangle = {\mathbb Z}+ {\mathbb Z} \tau +{\mathbb Z} \pi $
and hence
$$ \begin{align*} \mathrm{rank}(\Lambda) = 3 .\end{align*} $$
Therefore, by Theorem 6.1,
$\Lambda $
is a Meyer set that is not fully Euclidean.
In fact,
$\Lambda $
is a regular model set. Indeed, consider
$$ \begin{align*}{\mathcal L}:= \{ m+n \tau +k \pi : m,n,k \in {\mathbb Z} \} \subseteq {\mathbb R} \times ( {\mathbb R} \times ({\mathbb Z} \pi) ). \end{align*} $$
Then it is easy to see that
$({\mathbb R}, {\mathbb R} \times ({\mathbb Z} \pi ), {\mathcal L})$
is a CPS and
Remark 6.5. Suppose that we are given a CPS
$(G, H, {\mathcal L})$
, a window W and some
$a \in G$
. As usual, let us denote
$L=\pi _G({\mathcal L})$
.
If
$a \in L$
, then
is a model set in the same CPS.
Otherwise, it is shown implicitly in [Reference Strungaru, Baake and Grimm23, Proposition 5.6.19] that one can make
into a model set in the following way.
Let
$H_0$
be the cyclic subgroup of
$G/L$
generated by
$a+L$
. Define
$$ \begin{align*}{\mathcal L}':= \{ (x+na, na+L, x^\star) : (x,x^\star) \in {\mathcal L} , n \in {\mathbb Z} \}. \end{align*} $$
Then
$(G, H \times H_0, {\mathcal L}')$
is a CPS and
Let us note here in passing that
$H_0$
is a cyclic group of order at least two, so it is isomorphic either to some
${\mathbb Z}/n{\mathbb Z}$
or to
${\mathbb Z}$
.
Remark 6.6. Let
$\Lambda \subseteq {\mathbb R}^d$
be a Meyer set. Then, by [Reference Strungaru, Baake and Grimm23, Corollary 5.9.20] and the structure theorem for compactly generated LCAGs, there exist a cut-and-project scheme
${({\mathbb R}^d, {\mathbb R}^m \times {\mathbb Z}^n \times \mathbb K, {\mathcal L})}$
, with
$\mathbb K$
a compact Abelian group, and some compact
${W \subseteq {\mathbb R}^m \times {\mathbb Z}^n \times \mathbb K}$
such that
Now let
$\pi: {\mathbb R}^m \times {\mathbb Z}^n \times \mathbb K \to {\mathbb R}^m \times {\mathbb Z}^n $
be the canonical projection and let
$$ \begin{align*}{\mathcal L}':= \{ (x, \pi(x^\star)) : (x,x^\star) \in {\mathcal L} \}. \end{align*} $$
Then
$({\mathbb R}^d, {\mathbb R}^m \times {\mathbb Z}^n, {\mathcal L}')$
is a CPS and
This shows that every Meyer set
$\Lambda \subseteq {\mathbb R}^d$
is a subset of a model set in a CPS of the form
$({\mathbb R}^d, {\mathbb R}^m \times {\mathbb Z}^n, {\mathcal L})$
for some
$n \geq 0$
. If the Meyer set is not fully Euclidean, then every such CPS must have
$n>0$
. We suspect that the smallest possible value n can take among all the CPSs of this form is exactly
$$ \begin{align*} n=\mathrm{rank}(\Lambda)-\mathrm{ap}\text{-}\mathrm{rank}(\Lambda). \end{align*} $$
Acknowledgment
We would like to thank the anonymous reviewer for many helpful suggestions that improved the quality of the paper.
