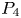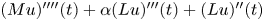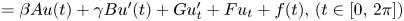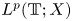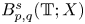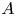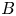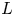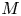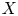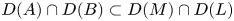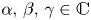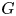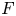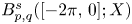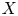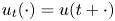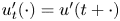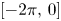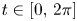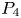1. Introduction
The characterizations of the well-posedness for abstract degenerate differential equations with periodic initial conditions have been studied extensively in the last years. See e.g. [Reference Arendt and Bu5–Reference Conejero, Lizama, Murillo-Arcila and Seoane-Sepulveda11], [Reference Kaltenbacher, Lasiecka and Pospieszalska14–Reference Ponce20] and the references therein. For examples, Lizama and Ponce [Reference Lizama and Ponce16] considered the first-order degenerate equation:
they gave necessary and sufficient conditions to guarantee the well-posedness of (1.1) in Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$![]() , periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$
, periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$![]() and periodic Triebel–Lizorkin spaces $F_{p,q}^s(\mathbb {T}; X)$
and periodic Triebel–Lizorkin spaces $F_{p,q}^s(\mathbb {T}; X)$![]() under some appropriate assumptions on the modified resolvent operator determined by (1.1). Moreover, they also investigated the first-order degenerate equation with infinite delay [Reference Lizama and Ponce17]:
under some appropriate assumptions on the modified resolvent operator determined by (1.1). Moreover, they also investigated the first-order degenerate equation with infinite delay [Reference Lizama and Ponce17]:
where $A$![]() and $M$
and $M$![]() are closed linear operators defined on a Banach space $X$
are closed linear operators defined on a Banach space $X$![]() with $D(A)\subseteq D(M)$
with $D(A)\subseteq D(M)$![]() , $a\in L^1(\mathbb {R}_+)$
, $a\in L^1(\mathbb {R}_+)$![]() is a scalar-valued kernel, $\alpha \in \mathbb {R}\backslash \left \{0\right \}$
is a scalar-valued kernel, $\alpha \in \mathbb {R}\backslash \left \{0\right \}$![]() and $f$
and $f$![]() an $X$
an $X$![]() -valued function defined on $\mathbb {T}$
-valued function defined on $\mathbb {T}$![]() .
.
Bu [Reference Bu9] considered a new second-order degenerate equation and gave necessary or sufficient conditions for this equation to be $L^p$![]() -well-posed (respectively $B_{p,q}^s$
-well-posed (respectively $B_{p,q}^s$![]() -well-posed and $F_{p,q}^s$
-well-posed and $F_{p,q}^s$![]() -well-posed), which recover some known results presented in [Reference Arendt and Bu5, Reference Arendt and Bu6, Reference Bu and Kim10] in the simpler case $M=I_X$
-well-posed), which recover some known results presented in [Reference Arendt and Bu5, Reference Arendt and Bu6, Reference Bu and Kim10] in the simpler case $M=I_X$![]() . We notice that third-order differential equations also describe some kinds of models arising from natural phenomena, such as flexible space structures with internal damping, the well-posedness of third-order differential equations has been investigated extensively by many authors. See [Reference Aparicio and Keyantuo1–Reference Aparicio and Keyantuo3, Reference Bose and Gorain7, Reference Bose and Gorain8, Reference Gorain13, Reference Kaltenbacher, Lasiecka and Pospieszalska14, Reference Poblete and Pozo19] for more information and references therein. For example, Poblete and Pozo [Reference Poblete and Pozo19] studied the well-posedness for the abstract third-order equation:
. We notice that third-order differential equations also describe some kinds of models arising from natural phenomena, such as flexible space structures with internal damping, the well-posedness of third-order differential equations has been investigated extensively by many authors. See [Reference Aparicio and Keyantuo1–Reference Aparicio and Keyantuo3, Reference Bose and Gorain7, Reference Bose and Gorain8, Reference Gorain13, Reference Kaltenbacher, Lasiecka and Pospieszalska14, Reference Poblete and Pozo19] for more information and references therein. For example, Poblete and Pozo [Reference Poblete and Pozo19] studied the well-posedness for the abstract third-order equation:
where $A$![]() and $B$
and $B$![]() are closed linear operators defined on a Banach space $X$
are closed linear operators defined on a Banach space $X$![]() with $D(A)\cap D(B)\neq \emptyset$
with $D(A)\cap D(B)\neq \emptyset$![]() , the constants $\alpha,\,\beta,\,\gamma \in \mathbb {R}^+$
, the constants $\alpha,\,\beta,\,\gamma \in \mathbb {R}^+$![]() and $f$
and $f$![]() belong to either the Lebesgue–Bochner spaces, or periodic Besov spaces, or periodic Triebel–Lizorkin spaces. They give necessary and sufficient conditions for (1.3) to be $L^p$
belong to either the Lebesgue–Bochner spaces, or periodic Besov spaces, or periodic Triebel–Lizorkin spaces. They give necessary and sufficient conditions for (1.3) to be $L^p$![]() -well-posed (respectively $B_{p,q}^s$
-well-posed (respectively $B_{p,q}^s$![]() -well-posed and $F_{p,q}^s$
-well-posed and $F_{p,q}^s$![]() -well-posed) by using vector-valued Fourier theorems in the vector-valued function spaces.
-well-posed) by using vector-valued Fourier theorems in the vector-valued function spaces.
In this paper, we study the following four-order degenerate differential equation:
where $A$![]() , $B$
, $B$![]() , $L$
, $L$![]() and $M$
and $M$![]() are closed linear operators on a Banach space $X$
are closed linear operators on a Banach space $X$![]() such that $D(A)\cap D(B)\subset D(M)\cap D(L)$
such that $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() and $\alpha,\,\beta,\,\gamma \in \mathbb {C}$
and $\alpha,\,\beta,\,\gamma \in \mathbb {C}$![]() , $G$
, $G$![]() and $F$
and $F$![]() are bounded linear operators from $L^p([-2\pi,\,0];X)$
are bounded linear operators from $L^p([-2\pi,\,0];X)$![]() (respectively $B_{p,q}^s([-2\pi,\,0];X)$
(respectively $B_{p,q}^s([-2\pi,\,0];X)$![]() ) into $X$
) into $X$![]() , $u_t(\cdot ) = u(t+\cdot )$
, $u_t(\cdot ) = u(t+\cdot )$![]() and $u'_t(\cdot ) = u'(\cdot +t)$
and $u'_t(\cdot ) = u'(\cdot +t)$![]() are defined on $[-2\pi,\,0]$
are defined on $[-2\pi,\,0]$![]() for $t\in [0,\, 2\pi ]$
for $t\in [0,\, 2\pi ]$![]() .
.
Let $f\in L^p(\mathbb {T}; X)$![]() be given, a function $u\in W_{\text {per}}^{1,p}(\mathbb {T}; X)\cap L^p(\mathbb {T}; D(A))$
be given, a function $u\in W_{\text {per}}^{1,p}(\mathbb {T}; X)\cap L^p(\mathbb {T}; D(A))$![]() is called a strong $L^p$
is called a strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ), if $Mu\in W_{\text {per}}^{4,p}(\mathbb {T}; X),\,Lu\in W_{\text {per}}^{3,p}(\mathbb {T}; X),\,\ u'\in L^p(\mathbb {T}; D(B))$
), if $Mu\in W_{\text {per}}^{4,p}(\mathbb {T}; X),\,Lu\in W_{\text {per}}^{3,p}(\mathbb {T}; X),\,\ u'\in L^p(\mathbb {T}; D(B))$![]() and ($P_4$
and ($P_4$![]() ) is satisfied a.e. on $\mathbb {T}$
) is satisfied a.e. on $\mathbb {T}$![]() , here we consider $D(A)$
, here we consider $D(A)$![]() and $D(B)$
and $D(B)$![]() as Banach spaces equipped with the graph norms. We say that ($P_4$
as Banach spaces equipped with the graph norms. We say that ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed, if for each $f\in L^p(\mathbb {T}; X)$
-well-posed, if for each $f\in L^p(\mathbb {T}; X)$![]() , there exists a unique strong $L^p$
, there exists a unique strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ). We introduce similarly the $B_{p,q}^s$
). We introduce similarly the $B_{p,q}^s$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ).
).
The main purpose of this paper is to give some characterizations of the well-posedness of ($P_4$![]() ) in Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$
) in Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$![]() and periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$
and periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$![]() . The characterizations of the well-posedness of ($P_4$
. The characterizations of the well-posedness of ($P_4$![]() ) involve the Rademacher boundedness (or norm boundedness) of the $M$
) involve the Rademacher boundedness (or norm boundedness) of the $M$![]() -resolvent of $A$
-resolvent of $A$![]() , $B$
, $B$![]() and $L$
and $L$![]() defined by ($P_4$
defined by ($P_4$![]() ). More precisely, we show that when $X$
). More precisely, we show that when $X$![]() is a UMD Banach space and $1 < p < \infty$
is a UMD Banach space and $1 < p < \infty$![]() , if $\{k(G_{k+1}-G_{k}):\ k\in \mathbb {Z}\}$
, if $\{k(G_{k+1}-G_{k}):\ k\in \mathbb {Z}\}$![]() is Rademacher-bounded, then ($P_4$
is Rademacher-bounded, then ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed if and only if $\rho _{M}(A,\,B,\,L) = \mathbb {Z}$
-well-posed if and only if $\rho _{M}(A,\,B,\,L) = \mathbb {Z}$![]() (the $M$
(the $M$![]() -resolvent set of $A$
-resolvent set of $A$![]() , $B$
, $B$![]() and $L$
and $L$![]() defined by ($P_4$
defined by ($P_4$![]() )) and the sets
)) and the sets
are Rademacher-bounded, where
$G_k,\, F_k,\,H_k \in \mathcal {L} (X)$![]() are defined by $G_k x = G(e_kx)$
are defined by $G_k x = G(e_kx)$![]() , $F_k x = F(e_kx)$
, $F_k x = F(e_kx)$![]() , $x\in X$
, $x\in X$![]() . Since this characterization of the $L^p$
. Since this characterization of the $L^p$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ) does not depend on the space parameter $1 < p < \infty$
) does not depend on the space parameter $1 < p < \infty$![]() , we deduce that when $X$
, we deduce that when $X$![]() is a UMD Banach space and the set $\{k(G_{k+1}-G_{k}):\ k\in \mathbb {Z}\}$
is a UMD Banach space and the set $\{k(G_{k+1}-G_{k}):\ k\in \mathbb {Z}\}$![]() is Rademacher-bounded, then ($P_4$
is Rademacher-bounded, then ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed for some $1 < p < \infty$
-well-posed for some $1 < p < \infty$![]() if and only if it is $L^p$
if and only if it is $L^p$![]() -well-posed for all $1 < p < \infty$
-well-posed for all $1 < p < \infty$![]() .
.
We also give a similar characterization for the $B_{p,q}^s$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ): let $X$
): let $X$![]() be a Banach space, $1\leq p,\,q\leq \infty,\,\ s>0$
be a Banach space, $1\leq p,\,q\leq \infty,\,\ s>0$![]() , assume that the sets $\{k(F_{k+2}-2F_{k+1}+F_k):\ k\in \mathbb {Z}\}$
, assume that the sets $\{k(F_{k+2}-2F_{k+1}+F_k):\ k\in \mathbb {Z}\}$![]() , $\{k(G_{k+1}-G_{k}):\ k\in \mathbb {Z}\}$
, $\{k(G_{k+1}-G_{k}):\ k\in \mathbb {Z}\}$![]() and $\{k^2(G_{k+2}-2G_{k+1}+G_k):\ k\in \mathbb {Z}\}$
and $\{k^2(G_{k+2}-2G_{k+1}+G_k):\ k\in \mathbb {Z}\}$![]() are norm-bounded, then the problem ($P_4$
are norm-bounded, then the problem ($P_4$![]() ) is $B_{p,q}^s$
) is $B_{p,q}^s$![]() -well-posed if and only if $\subset \rho _{M}(A,\,B,\,L) = \mathbb {Z}$
-well-posed if and only if $\subset \rho _{M}(A,\,B,\,L) = \mathbb {Z}$![]() and the sets
and the sets
are norm-bounded, where $N_k,\, \ F_k,\,\ G_k$![]() and $H_k$
and $H_k$![]() are defined as in the $L^p$
are defined as in the $L^p$![]() -well-posedness case. Since this characterization of the $B_{p,q}^s$
-well-posedness case. Since this characterization of the $B_{p,q}^s$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ) does not depend on the parameters $1\leq p,\,q\leq \infty,\,\ s>0$
) does not depend on the parameters $1\leq p,\,q\leq \infty,\,\ s>0$![]() , we deduce that when the sets $\{k(F_{k+2}-2F_{k+1}+F_k):\ k\in \mathbb {Z}\}$
, we deduce that when the sets $\{k(F_{k+2}-2F_{k+1}+F_k):\ k\in \mathbb {Z}\}$![]() , $\{k(G_{k+1}-G_{k}): k\in \mathbb {Z}\}$
, $\{k(G_{k+1}-G_{k}): k\in \mathbb {Z}\}$![]() and $\{k^2(G_{k+2}-2G_{k+1}+G_k):\ k\in \mathbb {Z}\}$
and $\{k^2(G_{k+2}-2G_{k+1}+G_k):\ k\in \mathbb {Z}\}$![]() are norm-bounded, then ($P_4$
are norm-bounded, then ($P_4$![]() ) is $B_{p,q}^s$
) is $B_{p,q}^s$![]() -well-posed for some $1\leq p,\,q\leq \infty,\,\ s>0$
-well-posed for some $1\leq p,\,q\leq \infty,\,\ s>0$![]() if and only if it is $B_{p,q}^s$
if and only if it is $B_{p,q}^s$![]() -well-posed for all $1\leq p,\,q\leq \infty,\,\ s>0$
-well-posed for all $1\leq p,\,q\leq \infty,\,\ s>0$![]() .
.
Our main tools in the investigation of the well-posedness of ($P_4$![]() ) are the operator-valued Fourier multiplier theorems obtained by Arendt and Bu [Reference Arendt and Bu5, Reference Arendt and Bu6] on $L^p(\mathbb {T}; X)$
) are the operator-valued Fourier multiplier theorems obtained by Arendt and Bu [Reference Arendt and Bu5, Reference Arendt and Bu6] on $L^p(\mathbb {T}; X)$![]() and $B_{p,q}^s(\mathbb {T}; X)$
and $B_{p,q}^s(\mathbb {T}; X)$![]() . In fact, our main idea is to transform the well-posedness of ($P_4$
. In fact, our main idea is to transform the well-posedness of ($P_4$![]() ) to an operator-valued Fourier multiplier problem in the corresponding vector-valued function space.
) to an operator-valued Fourier multiplier problem in the corresponding vector-valued function space.
This work is organized as follows: in § $2$![]() , we study the well-posedness of ($P_4$
, we study the well-posedness of ($P_4$![]() ) in vector-valued Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$
) in vector-valued Lebesgue–Bochner spaces $L^p(\mathbb {T}; X)$![]() . In § $3$
. In § $3$![]() , we consider the well-posedness of ($P_4$
, we consider the well-posedness of ($P_4$![]() ) in periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$
) in periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$![]() . In the last section, we give some examples of degenerate differential equations with finite delay to which our abstract results may be applied.
. In the last section, we give some examples of degenerate differential equations with finite delay to which our abstract results may be applied.
2. Well-posedness of ($P_4$ ) in Lebesgue–Bochner spaces
) in Lebesgue–Bochner spaces
Let $X$![]() and $Y$
and $Y$![]() be complex Banach spaces and let $\mathbb {T}:=[0,\,2\pi ]$
be complex Banach spaces and let $\mathbb {T}:=[0,\,2\pi ]$![]() . We denote by $\mathcal {L}(X,\,Y)$
. We denote by $\mathcal {L}(X,\,Y)$![]() the space of all bounded linear operators from $X$
the space of all bounded linear operators from $X$![]() to $Y$
to $Y$![]() . If $X=Y$
. If $X=Y$![]() , we will simply denote it by $\mathcal {L}(X)$
, we will simply denote it by $\mathcal {L}(X)$![]() . For $1\leq p<\infty$
. For $1\leq p<\infty$![]() , we denote by $L^p(\mathbb {T}; X)$
, we denote by $L^p(\mathbb {T}; X)$![]() the space of all equivalent class of $X$
the space of all equivalent class of $X$![]() -valued measurable functions $f$
-valued measurable functions $f$![]() defined on $\mathbb {T}$
defined on $\mathbb {T}$![]() satisfying
satisfying

For $f\in L^1(\mathbb {T}; X)$![]() , the $k$
, the $k$![]() -th Fourier coefficient of $f$
-th Fourier coefficient of $f$![]() is defined by
is defined by
where $k\in \mathbb {Z}$![]() and $e_k(t)=e^{ikt}$
and $e_k(t)=e^{ikt}$![]() when $t\in \mathbb {T}$
when $t\in \mathbb {T}$![]() .
.
Definition 2.1 Let $X$![]() and $Y$
and $Y$![]() be complex Banach spaces and $1\leq p<\infty$
be complex Banach spaces and $1\leq p<\infty$![]() , we say that $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$
, we say that $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() is an $L^p$
is an $L^p$![]() -Fourier multiplier, if for each $f\in L^p(\mathbb {T}; X)$
-Fourier multiplier, if for each $f\in L^p(\mathbb {T}; X)$![]() , there exists a unique $u\in L^p(\mathbb {T}; Y)$
, there exists a unique $u\in L^p(\mathbb {T}; Y)$![]() such that $\hat {u}(k)=M_k\hat {f}(k)$
such that $\hat {u}(k)=M_k\hat {f}(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() .
.
From the closed graph theorem, if $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() is an $L^p$
is an $L^p$![]() -Fourier multiplier, then there exists a unique bounded linear operator $T\in \mathcal {L}(L^p(\mathbb {T}; X),\, L^p(\mathbb {T}; Y))$
-Fourier multiplier, then there exists a unique bounded linear operator $T\in \mathcal {L}(L^p(\mathbb {T}; X),\, L^p(\mathbb {T}; Y))$![]() satisfying $(Tf)^\wedge (k) = M_k\hat f(k)$
satisfying $(Tf)^\wedge (k) = M_k\hat f(k)$![]() when $f\in L^p(\mathbb {T}; X)$
when $f\in L^p(\mathbb {T}; X)$![]() and $k\in \mathbb {Z}$
and $k\in \mathbb {Z}$![]() . The operator-valued Fourier multiplier theorem on $L^p(\mathbb {T}; X)$
. The operator-valued Fourier multiplier theorem on $L^p(\mathbb {T}; X)$![]() obtained in [Reference Arendt and Bu5] involves the Rademacher boundedness for sets of bounded linear operators. Let $\gamma _j$
obtained in [Reference Arendt and Bu5] involves the Rademacher boundedness for sets of bounded linear operators. Let $\gamma _j$![]() be the $j$
be the $j$![]() -th Rademacher function on $[0,\,1]$
-th Rademacher function on $[0,\,1]$![]() defined by $\gamma _j(t)=\rm {sgn}(\sin (2^{j-1}t))$
defined by $\gamma _j(t)=\rm {sgn}(\sin (2^{j-1}t))$![]() when $j\geq 1$
when $j\geq 1$![]() . For $x\in X$
. For $x\in X$![]() , we denote by $\gamma _j\otimes x$
, we denote by $\gamma _j\otimes x$![]() the vector-valued function $t\rightarrow r_j(t)x$
the vector-valued function $t\rightarrow r_j(t)x$![]() on $[0,\,1]$
on $[0,\,1]$![]() .
.
Definition 2.2 Let $X$![]() and $Y$
and $Y$![]() be Banach spaces. A set ${\bf {T}}\subset \mathcal {L}(X,\,Y)$
be Banach spaces. A set ${\bf {T}}\subset \mathcal {L}(X,\,Y)$![]() is said to be Rademacher-bounded (R-bounded, in short), if there exists $C>0$
is said to be Rademacher-bounded (R-bounded, in short), if there exists $C>0$![]() such that
such that

for all $T_1,\,\ldots,\,T_n\in {\bf {T}},\,x_1,\,\ldots,\,x_n\in X$![]() and $n\in \mathbb {N}$
and $n\in \mathbb {N}$![]() .
.
Remark 2.3
(i) Let ${\bf {S}},\,{\bf {T}}\subset \mathcal {L}(X)$
 be $R$
be $R$ -bounded sets. Then it can be shown easily from the definition that ${\bf {ST}}:=\left \{ST:S\in {\bf {S}},\, T\in {\bf {T}}\right \}$
-bounded sets. Then it can be shown easily from the definition that ${\bf {ST}}:=\left \{ST:S\in {\bf {S}},\, T\in {\bf {T}}\right \}$ and ${\bf {S}}+{\bf {T}}:=\left \{S+T:S\in {\bf {S}},\, T\in {\bf {T}}\right \}$
and ${\bf {S}}+{\bf {T}}:=\left \{S+T:S\in {\bf {S}},\, T\in {\bf {T}}\right \}$ are still $R$
are still $R$ -bounded.
-bounded.(ii) Let $X$
 be a $\rm {UMD}$
be a $\rm {UMD}$ Banach space and let $M_k=m_kI_X$
Banach space and let $M_k=m_kI_X$ with $m_k\in \mathbb {C}$
with $m_k\in \mathbb {C}$ , where $I_X$
, where $I_X$ is the identity operator on $X$
is the identity operator on $X$ , if $\sup _{k\in \mathbb {Z}}\left \vert m_k\right \vert < \infty$
, if $\sup _{k\in \mathbb {Z}}\left \vert m_k\right \vert < \infty$ and $\sup _{k\in \mathbb {Z}}\left \vert k(m_{k+1}-m_k)\right \vert <\infty$
and $\sup _{k\in \mathbb {Z}}\left \vert k(m_{k+1}-m_k)\right \vert <\infty$ , then $(M_k)_{k\in \mathbb {Z}}$
, then $(M_k)_{k\in \mathbb {Z}}$ is an $L^p$
is an $L^p$ -Fourier multiplier whenever $1 < p < \infty$
-Fourier multiplier whenever $1 < p < \infty$ [Reference Arendt and Bu5].
[Reference Arendt and Bu5].
The main tool in our study of $L^p$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ) is the $L^p$
) is the $L^p$![]() -Fourier multiplier theorem established in [Reference Arendt and Bu5]. The following results will be very important in the proof of our main result of this section. For the concept of UMD Banach spaces, we refer the readers to [Reference Arendt and Bu5] and references therein.
-Fourier multiplier theorem established in [Reference Arendt and Bu5]. The following results will be very important in the proof of our main result of this section. For the concept of UMD Banach spaces, we refer the readers to [Reference Arendt and Bu5] and references therein.
Theorem 2.4 [Reference Arendt and Bu5, Theorem 1.3]
Let $X,\,Y$![]() be UMD Banach spaces and $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$
be UMD Banach spaces and $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() . If the sets $\{M_k:\ k\in \mathbb {Z}\}$
. If the sets $\{M_k:\ k\in \mathbb {Z}\}$![]() and $\{k(M_{k+1}-M_k): \ k\in \mathbb {Z}\}$
and $\{k(M_{k+1}-M_k): \ k\in \mathbb {Z}\}$![]() are $R$
are $R$![]() -bounded, then $(M_k)_{k\in \mathbb {Z}}$
-bounded, then $(M_k)_{k\in \mathbb {Z}}$![]() defines an $L^p$
defines an $L^p$![]() -Fourier multiplier whenever $1< p<\infty$
-Fourier multiplier whenever $1< p<\infty$![]() .
.
Proposition 2.5 [Reference Arendt and Bu5, Proposition 1.11]
Let $X,\,\ Y$![]() be Banach spaces, $1\leq p < \infty$
be Banach spaces, $1\leq p < \infty$![]() , and let $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$
, and let $(M_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() be an $L^p$
be an $L^p$![]() -Fourier multiplier, then the set $\{M_k:\ k\in \mathbb {Z}\}$
-Fourier multiplier, then the set $\{M_k:\ k\in \mathbb {Z}\}$![]() is $R$
is $R$![]() -bounded.
-bounded.
Now we consider the following four-order degenerate differential equations with finite delays:
where $A,\, B,\, M$![]() and $L$
and $L$![]() are closed linear operators on a Banach space $X$
are closed linear operators on a Banach space $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() , $\alpha,\,\beta,\,\gamma \in \mathbb {C}$
, $\alpha,\,\beta,\,\gamma \in \mathbb {C}$![]() are given and $F,\,G:L^p([-2\pi,\,0];X)\rightarrow X$
are given and $F,\,G:L^p([-2\pi,\,0];X)\rightarrow X$![]() are bounded linear operators ($F$
are bounded linear operators ($F$![]() and $G$
and $G$![]() are known as the delay operators). Moreover, for fixed $t\in \mathbb {T}$
are known as the delay operators). Moreover, for fixed $t\in \mathbb {T}$![]() , the functions $u_t$
, the functions $u_t$![]() and $u'_t$
and $u'_t$![]() are elements in $L^p([-2\pi,\,0];X)$
are elements in $L^p([-2\pi,\,0];X)$![]() defined by $u_t(s)=u(t+s),\, \ u'_t(s) = u'(t+s)$
defined by $u_t(s)=u(t+s),\, \ u'_t(s) = u'(t+s)$![]() for $-2\pi \leq s\leq 0$
for $-2\pi \leq s\leq 0$![]() , here we identify a function $u$
, here we identify a function $u$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() with its natural $2\pi$
with its natural $2\pi$![]() -periodic extension on $\mathbb {R}$
-periodic extension on $\mathbb {R}$![]() .
.
Let $F,\,G\in \mathcal {L}((L^p[-2\pi,\,0];X),\,X)$![]() and $k\in \mathbb {Z}$
and $k\in \mathbb {Z}$![]() . We define the linear operators $F_k,\,G_k\in \mathcal {L}(X)$
. We define the linear operators $F_k,\,G_k\in \mathcal {L}(X)$![]() by
by
for $x\in X$![]() , where $e_k(t) = e^{ikt}$
, where $e_k(t) = e^{ikt}$![]() when $t\in \mathbb {T}$
when $t\in \mathbb {T}$![]() . It is clear that $\left \Vert F_k\right \Vert \leq \left \Vert F\right \Vert$
. It is clear that $\left \Vert F_k\right \Vert \leq \left \Vert F\right \Vert$![]() and $\left \Vert G_k\right \Vert \leq \left \Vert G\right \Vert$
and $\left \Vert G_k\right \Vert \leq \left \Vert G\right \Vert$![]() as $\left \Vert e_k\right \Vert _p = 1$
as $\left \Vert e_k\right \Vert _p = 1$![]() . It is easy to see that when $u\in L^p(\mathbb {T}; X)$
. It is easy to see that when $u\in L^p(\mathbb {T}; X)$![]() , then
, then
for $k\in \mathbb {Z}$![]() . This implies that $(F_k)_{k\in \mathbb {Z}}$
. This implies that $(F_k)_{k\in \mathbb {Z}}$![]() and $(G_k)_{k\in \mathbb {Z}}$
and $(G_k)_{k\in \mathbb {Z}}$![]() are $L^p$
are $L^p$![]() -Fourier multipliers as
-Fourier multipliers as
and
for $t\in \mathbb {T}$![]() so that $Fu_\cdot,\,\ Gu_\cdot,\,\ Hu_\cdot \in L^p(\mathbb {T}; X)$
so that $Fu_\cdot,\,\ Gu_\cdot,\,\ Hu_\cdot \in L^p(\mathbb {T}; X)$![]() .
.
Now we define the resolvent set of ($P_4$![]() ) by
) by

For the sake of simplicity, when $k\in \rho _{M}(A,\,B,\,L)$![]() , we will use the following notation:
, we will use the following notation:
where
If $k\in \rho _{M}(A,\,B,\,L)$![]() , then $MN_k,\,\ LN_k,\,\ AN_k$
, then $MN_k,\,\ LN_k,\,\ AN_k$![]() and $BN_k$
and $BN_k$![]() make sense as $D(A)\cap D(B)\subset D(M)\cap D(L)$
make sense as $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() by assumption, and they belong to $\mathcal {L}(X)$
by assumption, and they belong to $\mathcal {L}(X)$![]() by the closed graph theorem and the closedness of $A,\,\ B,\,\ M$
by the closed graph theorem and the closedness of $A,\,\ B,\,\ M$![]() and $L$
and $L$![]() .
.
Let $(L_k)_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() be a given sequence of operators. We define
be a given sequence of operators. We define
and for $n=2,\,3,\,\ldots,$![]() set
set
Definition 2.6 A sequence $(d_k)_{k\in \mathbb {Z}}\subseteq \mathbb {C}\backslash \left \{0\right \}$![]() is called $1$
is called $1$![]() -regular if the sequence $(k\frac {\triangle ^1d_k}{d_k})_{k\in \mathbb {Z}}$
-regular if the sequence $(k\frac {\triangle ^1d_k}{d_k})_{k\in \mathbb {Z}}$![]() is bounded; it is called $2$
is bounded; it is called $2$![]() -regular if it is $1$
-regular if it is $1$![]() -regular and the sequence $(k^2\frac {\triangle ^2d_k}{d_k})_{k\in \mathbb {Z}}$
-regular and the sequence $(k^2\frac {\triangle ^2d_k}{d_k})_{k\in \mathbb {Z}}$![]() is bounded; it is called $3$
is bounded; it is called $3$![]() -regular if it is $2$
-regular if it is $2$![]() -regular and the sequence $(k^3\frac {\triangle ^3d_k}{d_k})_{k\in \mathbb {Z}}$
-regular and the sequence $(k^3\frac {\triangle ^3d_k}{d_k})_{k\in \mathbb {Z}}$![]() is bounded.
is bounded.
Remark 2.7 It is easy to see that $(a_k)_{k\in \mathbb {N}}$![]() , $(b_k)_{k\in \mathbb {N}}$
, $(b_k)_{k\in \mathbb {N}}$![]() and $(c_k)_{k\in \mathbb {N}}$
and $(c_k)_{k\in \mathbb {N}}$![]() are $3$
are $3$![]() -regular.
-regular.
Definition 2.8 Let $1\leq p<\infty$![]() , $n\geq 1$
, $n\geq 1$![]() be an integer and let $X$
be an integer and let $X$![]() be a Banach space, we define the the following vector-valued function spaces:
be a Banach space, we define the the following vector-valued function spaces:

$W_{\text {per}}^{n,p}(\mathbb {T}; X)$![]() is the $n$
is the $n$![]() -th $X$
-th $X$![]() -valued periodic Sobolev space.
-valued periodic Sobolev space.
Remark 2.9 We have the following two useful properties concerning these spaces:
(i) Let $m,\,n\in \mathbb {N}$
 . If $n\leq m$
. If $n\leq m$ , then $W_{\text {per}}^{m,p}(\mathbb {T}; X)\subseteq W_{\text {per}}^{n,p}(\mathbb {T}; X)$
, then $W_{\text {per}}^{m,p}(\mathbb {T}; X)\subseteq W_{\text {per}}^{n,p}(\mathbb {T}; X)$ .
.(ii) If $u\in W_{\text {per}}^{n,p}(\mathbb {T}; X)$
 , then for any $0\leq k\leq n-1$
, then for any $0\leq k\leq n-1$ , we have $u^{(k)}(0)=u^{(k)}(2\pi )$
, we have $u^{(k)}(0)=u^{(k)}(2\pi )$ .
.
Let $1\leq p<\infty$![]() , we define the solution space of the $L^p$
, we define the solution space of the $L^p$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ) by
) by

here we consider $D(A)$![]() and $D(B)$
and $D(B)$![]() as Banach spaces equipped with their graph norms. The space $S_p(A,\,B,\,M,\,L)$
as Banach spaces equipped with their graph norms. The space $S_p(A,\,B,\,M,\,L)$![]() is complete equipped with the norm
is complete equipped with the norm

If $u\in S_p(A,\,B,\,M,\,L)$![]() , then $Mu$
, then $Mu$![]() , $(Mu)'$
, $(Mu)'$![]() , $(Mu)''$
, $(Mu)''$![]() and $(Mu)'''$
and $(Mu)'''$![]() are $X$
are $X$![]() -valued continuous functions on $\mathbb {T}$
-valued continuous functions on $\mathbb {T}$![]() , and $Mu(0)=Mu(2\pi )$
, and $Mu(0)=Mu(2\pi )$![]() , $(Mu)'(0)=(Mu)'(2\pi )$
, $(Mu)'(0)=(Mu)'(2\pi )$![]() , $(Mu)''(0)=(Mu)''(2\pi )$
, $(Mu)''(0)=(Mu)''(2\pi )$![]() , $(Mu)'''(0)=(Mu)'''(2\pi )$
, $(Mu)'''(0)=(Mu)'''(2\pi )$![]() by [Reference Arendt and Bu5, Lemma 2.1].
by [Reference Arendt and Bu5, Lemma 2.1].
Definition 2.10 Let $1\leq p<\infty$![]() and $f\in L^p(\mathbb {T}; X)$
and $f\in L^p(\mathbb {T}; X)$![]() , $u\in S_p(A,\,B,\,M,\,L)$
, $u\in S_p(A,\,B,\,M,\,L)$![]() is called a strong $L^p$
is called a strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ), if ($P_4$
), if ($P_4$![]() ) is satisfied a.e. on $\mathbb {T}$
) is satisfied a.e. on $\mathbb {T}$![]() . We say that ($P_4$
. We say that ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed, if for each $f\in L^p(\mathbb {T}; X)$
-well-posed, if for each $f\in L^p(\mathbb {T}; X)$![]() , there exists a unique strong $L^p$
, there exists a unique strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ).
).
If ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed, then there exists a constant $C>0$
-well-posed, then there exists a constant $C>0$![]() , such that for each $f\in L^p(\mathbb {T}; X)$
, such that for each $f\in L^p(\mathbb {T}; X)$![]() , if $u\in S_p(A,\,B,\,M,\,L)$
, if $u\in S_p(A,\,B,\,M,\,L)$![]() is the unique strong $L^p$
is the unique strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ), we have
), we have
This follows easily from the closed graph theorem.
In order to prove our main result of this section, we need the following preparations.
Proposition 2.11 Let $A$![]() , $B$
, $B$![]() , $M$
, $M$![]() and $L$
and $L$![]() be closed linear operators defined on a UMD Banach space $X$
be closed linear operators defined on a UMD Banach space $X$![]() such that $D(A)\cap D(B)\subset D(M)\cap D(L)$
such that $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() , $1 < p < \infty$
, $1 < p < \infty$![]() and $\alpha,\,\ \beta,\, \gamma \in \mathbb {C}$
and $\alpha,\,\ \beta,\, \gamma \in \mathbb {C}$![]() . Let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$
. Let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$![]() . Assume that $\rho _{M}(A,\,B,\,L) = \mathbb {Z}$
. Assume that $\rho _{M}(A,\,B,\,L) = \mathbb {Z}$![]() and the sets $\left \{a_kMN_k:k\in \mathbb {Z}\right \}$
and the sets $\left \{a_kMN_k:k\in \mathbb {Z}\right \}$![]() , $\left \{b_kLN_k:k\in \mathbb {Z}\right \}$
, $\left \{b_kLN_k:k\in \mathbb {Z}\right \}$![]() , $\left \{c_kBN_k:k\in \mathbb {Z}\right \}$
, $\left \{c_kBN_k:k\in \mathbb {Z}\right \}$![]() , $\{k\triangle G_k: k\in \mathbb {Z}\}$
, $\{k\triangle G_k: k\in \mathbb {Z}\}$![]() and $\left \{kN_k:k\in \mathbb {Z}\right \}$
and $\left \{kN_k:k\in \mathbb {Z}\right \}$![]() are $R$
are $R$![]() -bounded, then $\left (a_kMN_k\right )_{k\in \mathbb {Z}}$
-bounded, then $\left (a_kMN_k\right )_{k\in \mathbb {Z}}$![]() , $\left (b_kLN_k\right )_{k\in \mathbb {Z}}$
, $\left (b_kLN_k\right )_{k\in \mathbb {Z}}$![]() , $\left (c_kBN_k\right )_{k\in \mathbb {Z}}$
, $\left (c_kBN_k\right )_{k\in \mathbb {Z}}$![]() and $\left (kN_k\right )_{k\in \mathbb {Z}}$
and $\left (kN_k\right )_{k\in \mathbb {Z}}$![]() are $L^p$
are $L^p$![]() -Fourier multipliers.
-Fourier multipliers.
Proof. We only need to show that the set $\{k(N_k^{-1} - N_{k+1}^{-1})N_k: k\in \mathbb {Z}\}$![]() is $R$
is $R$![]() -bounded by [Reference Conejero, Lizama, Murillo-Arcila and Seoane-Sepulveda11, Theorem 1.1] and theorem 2.4, here we have used the facts that $(a_k)_{k\in \mathbb {N}}$
-bounded by [Reference Conejero, Lizama, Murillo-Arcila and Seoane-Sepulveda11, Theorem 1.1] and theorem 2.4, here we have used the facts that $(a_k)_{k\in \mathbb {N}}$![]() , $(b_k)_{k\in \mathbb {N}}$
, $(b_k)_{k\in \mathbb {N}}$![]() and $(c_k)_{k\in \mathbb {N}}$
and $(c_k)_{k\in \mathbb {N}}$![]() are $1$
are $1$![]() -regular sequences. It follows from the definition of $N_k$
-regular sequences. It follows from the definition of $N_k$![]() that
that

which implies

when $k\neq 0$![]() . It follows from remark 2.3 that the products and sums of $R$
. It follows from remark 2.3 that the products and sums of $R$![]() -bounded sets are still $R$
-bounded sets are still $R$![]() -bounded. Thus, the set $\{k(N_k^{-1} - N_{k+1}^{-1})N_k: k\in \mathbb {Z}\}$
-bounded. Thus, the set $\{k(N_k^{-1} - N_{k+1}^{-1})N_k: k\in \mathbb {Z}\}$![]() is $R$
is $R$![]() -bounded. This completes the proof.
-bounded. This completes the proof.
The following statement is the main result of this section which gives a necessary and sufficient condition for the $L^p$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ).
).
Theorem 2.12 Let $X$![]() be a UMD Banach space, $1< p<\infty$
be a UMD Banach space, $1< p<\infty$![]() and let $A,\, B,\, L$
and let $A,\, B,\, L$![]() and $M$
and $M$![]() be closed linear operators on $X$
be closed linear operators on $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() and $\alpha,\,\ \beta,\, \gamma \in \mathbb {C}$
and $\alpha,\,\ \beta,\, \gamma \in \mathbb {C}$![]() . Let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$
. Let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$![]() be such that the set $\{k\Delta G_k:\ k\in \mathbb {Z}\}$
be such that the set $\{k\Delta G_k:\ k\in \mathbb {Z}\}$![]() is $R$
is $R$![]() -bounded. Then the following assertions are equivalent:
-bounded. Then the following assertions are equivalent:
(i) ($P_4$
 ) is $L^p$
) is $L^p$ -well-posed;
-well-posed;(ii) $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$
 , the sets $\{k^4MN_k:k\in \mathbb {Z}\},\, \{k^3LN_k:k\in \mathbb {Z}\}$
, the sets $\{k^4MN_k:k\in \mathbb {Z}\},\, \{k^3LN_k:k\in \mathbb {Z}\}$ , $\{kBN_k:k\in \mathbb {Z}\}$
, $\{kBN_k:k\in \mathbb {Z}\}$ and $\{kN_k:k\in \mathbb {Z}\}$
and $\{kN_k:k\in \mathbb {Z}\}$ are $R$
are $R$ -bounded, where $N_k$
-bounded, where $N_k$ is defined by (2.3), the operators $F_k$
is defined by (2.3), the operators $F_k$ and $G_k$
and $G_k$ are defined by (2.1).
are defined by (2.1).
Proof. First we show that the implication $(i)\Rightarrow (ii)$![]() holds true. We assume that ($P_4$
holds true. We assume that ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed and let $k\in \mathbb {Z}$
-well-posed and let $k\in \mathbb {Z}$![]() and $y\in X$
and $y\in X$![]() be fixed, we consider the function $f$
be fixed, we consider the function $f$![]() defined by $f(t)=e^{ikt}y$
defined by $f(t)=e^{ikt}y$![]() when $t\in \mathbb {T}$
when $t\in \mathbb {T}$![]() . Then it is clear that $f\in L^p(\mathbb {T};X),\, \hat {f}(k)=y$
. Then it is clear that $f\in L^p(\mathbb {T};X),\, \hat {f}(k)=y$![]() and $\hat {f}(n)=0$
and $\hat {f}(n)=0$![]() when $n\neq k$
when $n\neq k$![]() . Since ($P_4$
. Since ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed, there exists a unique $u\in S_p(A,\,B,\,L,\,M)$
-well-posed, there exists a unique $u\in S_p(A,\,B,\,L,\,M)$![]() satisfying
satisfying
a.e. on $\mathbb {T}$![]() . We have $\hat {u}(n)\in D(A)\cap D(B)$
. We have $\hat {u}(n)\in D(A)\cap D(B)$![]() when $n\in \mathbb {Z}$
when $n\in \mathbb {Z}$![]() by [Reference Arendt and Bu5, Lemma 3.1] as $u\in L^p (\mathbb {T}; D(A))\cap L^p(\mathbb {T}; D(B))$
by [Reference Arendt and Bu5, Lemma 3.1] as $u\in L^p (\mathbb {T}; D(A))\cap L^p(\mathbb {T}; D(B))$![]() . Taking Fourier transforms on both sides of (2.8), we obtain
. Taking Fourier transforms on both sides of (2.8), we obtain
and $[n^4M - (\alpha in^3+n^2)L - \beta A - i\gamma nB - inG_n - F_n]\hat {u}(n)=0$![]() when $n\neq k$
when $n\neq k$![]() . This implies that the operator $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$
. This implies that the operator $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$![]() defined on $D(A)\cap D(B)$
defined on $D(A)\cap D(B)$![]() with values in $X$
with values in $X$![]() is surjective. To show that it is also injective, we let $x\in D(A)\cap D(B)$
is surjective. To show that it is also injective, we let $x\in D(A)\cap D(B)$![]() be such that
be such that
Let $u$![]() be the function given by $u(t)=e^{ikt}x$
be the function given by $u(t)=e^{ikt}x$![]() when $t\in \mathbb {T}$
when $t\in \mathbb {T}$![]() , then it is clear that $u\in S_p(A,\,B,\,M,\,L)$
, then it is clear that $u\in S_p(A,\,B,\,M,\,L)$![]() and ($P_4$
and ($P_4$![]() ) is satisfied a.e. on $\mathbb {T}$
) is satisfied a.e. on $\mathbb {T}$![]() when $f=0$
when $f=0$![]() . Thus, $u$
. Thus, $u$![]() is a strong $L^p$
is a strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ) when taking $f=0$
) when taking $f=0$![]() . We obtain $x=0$
. We obtain $x=0$![]() by the uniqueness assumption. We have shown that the operator $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$
by the uniqueness assumption. We have shown that the operator $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$![]() from $D(A)\cap D(B)$
from $D(A)\cap D(B)$![]() into $X$
into $X$![]() is injective. Therefore, $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$
is injective. Therefore, $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$![]() is bijective from $D(A)\cap D(B)$
is bijective from $D(A)\cap D(B)$![]() onto $X$
onto $X$![]() .
.
Next we show that $[k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k]^{-1}\in \mathcal {L}(X)$![]() . For $f(t)=e^{ikt}y$
. For $f(t)=e^{ikt}y$![]() , we let $u\in S_p(A,\,B,\,M,\,L)$
, we let $u\in S_p(A,\,B,\,M,\,L)$![]() be the unique strong $L^p$
be the unique strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ). Then
). Then

by (2.9). This implies that $u$![]() is given by
is given by
when $t\in \mathbb {T}$![]() . By (2.5), there exists a constant $C>0$
. By (2.5), there exists a constant $C>0$![]() independent from $y$
independent from $y$![]() and $k$
and $k$![]() , such that $\left \Vert u\right \Vert _{L^p}\leq C\left \Vert f\right \Vert _{L^p}$
, such that $\left \Vert u\right \Vert _{L^p}\leq C\left \Vert f\right \Vert _{L^p}$![]() . This implies that
. This implies that
when $y\in X$![]() , or equivalently
, or equivalently
We have shown that $k\in \rho _{M}(A,\,B,\,L)$![]() for all $k\in \mathbb {Z}$
for all $k\in \mathbb {Z}$![]() . Thus, $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$
. Thus, $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$![]() .
.
Finally, we show that $(k^4MN_k)_{k\in \mathbb {Z}},\,\ (k^3LN_k)_{k\in \mathbb {Z}}$![]() , $(kN_k)_{k\in \mathbb {Z}}$
, $(kN_k)_{k\in \mathbb {Z}}$![]() and $(kBN_k)_{k\in \mathbb {Z}}$
and $(kBN_k)_{k\in \mathbb {Z}}$![]() define $L^p$
define $L^p$![]() -Fourier multipliers. Let $f\in L^p(\mathbb {T};X)$
-Fourier multipliers. Let $f\in L^p(\mathbb {T};X)$![]() , then there exists $u\in S_p(A,\,B,\,M,\,L)$
, then there exists $u\in S_p(A,\,B,\,M,\,L)$![]() , a strong $L^p$
, a strong $L^p$![]() -solution of ($P_4$
-solution of ($P_4$![]() ) by assumption. Taking Fourier transforms on both sides of ($P_4$
) by assumption. Taking Fourier transforms on both sides of ($P_4$![]() ), we get that $\hat {u}(k)\in D(A)\cap D(B)$
), we get that $\hat {u}(k)\in D(A)\cap D(B)$![]() by [Reference Arendt and Bu5, Lemma 3.1] and
by [Reference Arendt and Bu5, Lemma 3.1] and
for $k\in \mathbb {Z}$![]() . Since $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$
. Since $k^4M - (\alpha ik^3+k^2)L - \beta A - i\gamma kB - ikG_k - F_k$![]() is invertible, we have
is invertible, we have
when $k\in \mathbb {Z}$![]() . It follows from $u\in S_p(A,\,B,\,M,\,L)$
. It follows from $u\in S_p(A,\,B,\,M,\,L)$![]() that $u\in L^{p}(\mathbb {T}; D(A))\cap W_{\text {per}}^{1,p}(\mathbb {T};X)$
that $u\in L^{p}(\mathbb {T}; D(A))\cap W_{\text {per}}^{1,p}(\mathbb {T};X)$![]() , $Mu\in W_{\text {per}}^{4,p}(\mathbb {T};X)$
, $Mu\in W_{\text {per}}^{4,p}(\mathbb {T};X)$![]() , $Lu \in W_{\text {per}}^{3,p}(\mathbb {T};X)$
, $Lu \in W_{\text {per}}^{3,p}(\mathbb {T};X)$![]() and $u'\in L^p(\mathbb {T}; D(B))$
and $u'\in L^p(\mathbb {T}; D(B))$![]() . We have
. We have

when $k\in \mathbb {Z}$![]() . We conclude that $(k^4MN_k)_{k\in \mathbb {Z}},\, (k^3LN_k)_{k\in \mathbb {Z}}$
. We conclude that $(k^4MN_k)_{k\in \mathbb {Z}},\, (k^3LN_k)_{k\in \mathbb {Z}}$![]() , $(kBN_k)_{k\in \mathbb {Z}}$
, $(kBN_k)_{k\in \mathbb {Z}}$![]() and $(kN_k)_{k\in \mathbb {Z}}$
and $(kN_k)_{k\in \mathbb {Z}}$![]() define $L^p$
define $L^p$![]() -Fourier multipliers as $(Mu)'''',\,\ (Lu)''',\,\ Bu',\,\ u'\in L^p(\mathbb {T};X)$
-Fourier multipliers as $(Mu)'''',\,\ (Lu)''',\,\ Bu',\,\ u'\in L^p(\mathbb {T};X)$![]() . It follows from proposition 2.5 that the sets $\{k^4MN_k:k\in \mathbb {Z}\},\, \{k^3LN_k:k\in \mathbb {Z}\}$
. It follows from proposition 2.5 that the sets $\{k^4MN_k:k\in \mathbb {Z}\},\, \{k^3LN_k:k\in \mathbb {Z}\}$![]() , $\{kBN_k:k\in \mathbb {Z}\}$
, $\{kBN_k:k\in \mathbb {Z}\}$![]() and $\{kN_k:k\in \mathbb {Z}\}$
and $\{kN_k:k\in \mathbb {Z}\}$![]() are $R$
are $R$![]() -bounded. We have shown that the implication $(i)\Rightarrow (ii)$
-bounded. We have shown that the implication $(i)\Rightarrow (ii)$![]() is true.
is true.
Next we show that the implication $(ii)\Rightarrow (i)$![]() is valid. Assume that $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$
is valid. Assume that $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$![]() and the sets $\{k^4MN_k:k\in \mathbb {Z}\},\, \{k^3LN_k:k\in \mathbb {Z}\}$
and the sets $\{k^4MN_k:k\in \mathbb {Z}\},\, \{k^3LN_k:k\in \mathbb {Z}\}$![]() , $\{kN_k:k\in \mathbb {Z}\}$
, $\{kN_k:k\in \mathbb {Z}\}$![]() and $\{kBN_k:k\in \mathbb {Z}\}$
and $\{kBN_k:k\in \mathbb {Z}\}$![]() are $R$
are $R$![]() -bounded. It follows from proposition 2.11 that $(k^4MN_k)_{k\in \mathbb {Z}}$
-bounded. It follows from proposition 2.11 that $(k^4MN_k)_{k\in \mathbb {Z}}$![]() , $(k^3LN_k)_{k\in \mathbb {Z}}$
, $(k^3LN_k)_{k\in \mathbb {Z}}$![]() , $(kBN_k)_{k\in \mathbb {Z}}$
, $(kBN_k)_{k\in \mathbb {Z}}$![]() and $(kN_k)_{k\in \mathbb {Z}}$
and $(kN_k)_{k\in \mathbb {Z}}$![]() are $L^p$
are $L^p$![]() -Fourier multipliers. This implies that the sequences $(N_k)_{k\in \mathbb {Z}}$
-Fourier multipliers. This implies that the sequences $(N_k)_{k\in \mathbb {Z}}$![]() , $(BN_k)_{k\in \mathbb {Z}}$
, $(BN_k)_{k\in \mathbb {Z}}$![]() , $(k^2LN_k)_{k\in \mathbb {Z}}$
, $(k^2LN_k)_{k\in \mathbb {Z}}$![]() , $(MN_k)_{k\in \mathbb {Z}}$
, $(MN_k)_{k\in \mathbb {Z}}$![]() , $(LN_k)_{k\in \mathbb {Z}}$
, $(LN_k)_{k\in \mathbb {Z}}$![]() are $L^p$
are $L^p$![]() -Fourier multiplier. Here we have used the easy fact that $(d_k)_{k\in \mathbb {Z}}$
-Fourier multiplier. Here we have used the easy fact that $(d_k)_{k\in \mathbb {Z}}$![]() is an $L^p$
is an $L^p$![]() -Fourier multiplier and the fact that the product of two $L^p$
-Fourier multiplier and the fact that the product of two $L^p$![]() -Fourier multipliers is still an $L^p$
-Fourier multipliers is still an $L^p$![]() -Fourier multiplier, where $d_k$
-Fourier multiplier, where $d_k$![]() is defined by $d_k = 1/k$
is defined by $d_k = 1/k$![]() when $k\not = 0$
when $k\not = 0$![]() and $d_0 =0$
and $d_0 =0$![]() . In particular, considering $N_k\in \mathcal {L}(X,\, D(B))$
. In particular, considering $N_k\in \mathcal {L}(X,\, D(B))$![]() , the sequence $(N_k)_{k\in \mathbb {Z}}$
, the sequence $(N_k)_{k\in \mathbb {Z}}$![]() is an $L^p$
is an $L^p$![]() -Fourier multiplier. Then for all $f\in L^p(\mathbb {T};X)$
-Fourier multiplier. Then for all $f\in L^p(\mathbb {T};X)$![]() , there exist $u_i\in L^p(\mathbb {T};X)$
, there exist $u_i\in L^p(\mathbb {T};X)$![]() ($1\leq i\leq 7$
($1\leq i\leq 7$![]() ) and $u\in L^p(\mathbb {T}; D(B))$
) and $u\in L^p(\mathbb {T}; D(B))$![]() satisfying
satisfying


for $k\in \mathbb {Z}$![]() . Hence, $\hat u_2(k) = ik\hat u(k)$
. Hence, $\hat u_2(k) = ik\hat u(k)$![]() for $k\in \mathbb {Z}$
for $k\in \mathbb {Z}$![]() by (2.10). This implies that $u\in W_{\text {per}}^{1,p}(\mathbb {T};X)$
by (2.10). This implies that $u\in W_{\text {per}}^{1,p}(\mathbb {T};X)$![]() . It follows from (2.11) that $\widehat {u'}(k) = ik\hat u(k) = ikN_k\hat f(k)$
. It follows from (2.11) that $\widehat {u'}(k) = ik\hat u(k) = ikN_k\hat f(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() . This together with $\hat u_5(k) =ikBN_k\hat f(k)$
. This together with $\hat u_5(k) =ikBN_k\hat f(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() implies that $u'\in L^p(\mathbb {T}; D(B))$
implies that $u'\in L^p(\mathbb {T}; D(B))$![]() [Reference Arendt and Bu5, Lemma 3.1]. By (2.10) and (2.11), we have $\hat u_3(k)= M\hat u(k)$
[Reference Arendt and Bu5, Lemma 3.1]. By (2.10) and (2.11), we have $\hat u_3(k)= M\hat u(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() . Hence, $u\in L^p(\mathbb {T}; D(M))$
. Hence, $u\in L^p(\mathbb {T}; D(M))$![]() and $Mu = u_3$
and $Mu = u_3$![]() . Similarly, by using (2.10) and (2.11), we have $\hat u_4(k) = L\hat u(k)$
. Similarly, by using (2.10) and (2.11), we have $\hat u_4(k) = L\hat u(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() . Thus, $u\in L^p(\mathbb {T}; D(L))$
. Thus, $u\in L^p(\mathbb {T}; D(L))$![]() and $Lu = u_4$
and $Lu = u_4$![]() [Reference Arendt and Bu5, Lemma 3.1]. By (2.10) and the fact that $Mu = u_3$
[Reference Arendt and Bu5, Lemma 3.1]. By (2.10) and the fact that $Mu = u_3$![]() , we deduce $\hat u_1(k) = (ik)^4\widehat {Mu}(k) = (ik)^4\hat u_3(k)$
, we deduce $\hat u_1(k) = (ik)^4\widehat {Mu}(k) = (ik)^4\hat u_3(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() . Thus, $Mu \in W_{\text {per}}^{4,p}(\mathbb {T}; X)$
. Thus, $Mu \in W_{\text {per}}^{4,p}(\mathbb {T}; X)$![]() . Similarly, using (2.11) and the fact hat $Lu = u_4$
. Similarly, using (2.11) and the fact hat $Lu = u_4$![]() , we deduce that $Lu \in W_{\text {per}}^{3,p}(\mathbb {T}; X)$
, we deduce that $Lu \in W_{\text {per}}^{3,p}(\mathbb {T}; X)$![]() .
.
We note that $(G_k)_{k\in \mathbb {Z}}$![]() and $(F_k)_{k\in \mathbb {Z}}$
and $(F_k)_{k\in \mathbb {Z}}$![]() are $L^p$
are $L^p$![]() -Fourier multipliers by (2.2), where $G_k,\, \ F_k$
-Fourier multipliers by (2.2), where $G_k,\, \ F_k$![]() and $H_k$
and $H_k$![]() are defined by (2.1). Thus, $(ikG_kN_k)_{k\in \mathbb {Z}}$
are defined by (2.1). Thus, $(ikG_kN_k)_{k\in \mathbb {Z}}$![]() and $(F_kD_k)_{k\in \mathbb {Z}}$
and $(F_kD_k)_{k\in \mathbb {Z}}$![]() are $L^p$
are $L^p$![]() -Fourier multipliers as the product of two $L^p$
-Fourier multipliers as the product of two $L^p$![]() -Fourier multipliers is still an $L^p$
-Fourier multipliers is still an $L^p$![]() -Fourier multiplier. We have
-Fourier multiplier. We have
for $k\in \mathbb {Z}$![]() . It follows that $\left (AN_k\right )_{k\in \mathbb {Z}}$
. It follows that $\left (AN_k\right )_{k\in \mathbb {Z}}$![]() is also an $L^p$
is also an $L^p$![]() -Fourier multiplier as the sum of $L^p$
-Fourier multiplier as the sum of $L^p$![]() -Fourier multipliers is an $L^p$
-Fourier multipliers is an $L^p$![]() -Fourier multiplier. We deduce from (2.11) and [Reference Arendt and Bu5, Lemma 3.1] that $u\in L^p(\mathbb {T};D(A))$
-Fourier multiplier. We deduce from (2.11) and [Reference Arendt and Bu5, Lemma 3.1] that $u\in L^p(\mathbb {T};D(A))$![]() . We have shown that $u\in S_p(A,\,B,\,M,\,L)$
. We have shown that $u\in S_p(A,\,B,\,M,\,L)$![]() . This shows the existence of strong $L^p$
. This shows the existence of strong $L^p$![]() -solution.
-solution.
To show uniqueness of strong $L^p$![]() -solution, we let $u\in S_p(A,\,B,\,M,\,L)$
-solution, we let $u\in S_p(A,\,B,\,M,\,L)$![]() be such that
be such that
a.e. on $\mathbb {T}$![]() . Taking the Fourier transforms on both sides, we deduce that
. Taking the Fourier transforms on both sides, we deduce that
when $k\in \mathbb {Z}$![]() . Since $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$
. Since $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$![]() , this implies that $\hat {u}(k)=0$
, this implies that $\hat {u}(k)=0$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() and thus $u=0$
and thus $u=0$![]() . This shows that the solution is unique. This completes the proof.
. This shows that the solution is unique. This completes the proof.
We notice that the assumption that the underlying Banach space $X$![]() is a UMD space in theorem 2.12 was only used in the implication $(ii)\Rightarrow (i)$
is a UMD space in theorem 2.12 was only used in the implication $(ii)\Rightarrow (i)$![]() . Since the second statement of theorem 2.12 does not depend on the space parameter $1 < p < \infty$
. Since the second statement of theorem 2.12 does not depend on the space parameter $1 < p < \infty$![]() , theorem 2.12 has the following immediate consequence.
, theorem 2.12 has the following immediate consequence.
Corollary 2.13 Let $X$![]() be a $\rm {UMD}$
be a $\rm {UMD}$![]() Banach space, let $A,\,B,\,L$
Banach space, let $A,\,B,\,L$![]() and $M$
and $M$![]() be closed linear operators on $X$
be closed linear operators on $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() , and $\alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$
, and $\alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$![]() . Then if ($P_4$
. Then if ($P_4$![]() ) is $L^p$
) is $L^p$![]() -well-posed for some $1 < p < \infty$
-well-posed for some $1 < p < \infty$![]() , then it is $L^p$
, then it is $L^p$![]() -well-posed for all $1 < p < \infty$
-well-posed for all $1 < p < \infty$![]() .
.
3. Well-posedness of ($P_4$ ) in Besov spaces
) in Besov spaces
In this section, we consider the well-posedness of ($P_4$![]() ) in periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$
) in periodic Besov spaces $B_{p,q}^s(\mathbb {T}; X)$![]() . Firstly, we briefly recall the definition of periodic Besov spaces in the vector-valued case introduced in [Reference Arendt and Bu6]. Let $\mathcal {S}(\mathbb {R})$
. Firstly, we briefly recall the definition of periodic Besov spaces in the vector-valued case introduced in [Reference Arendt and Bu6]. Let $\mathcal {S}(\mathbb {R})$![]() be the Schwartz space of all rapidly decreasing smooth functions on $\mathbb {R}$
be the Schwartz space of all rapidly decreasing smooth functions on $\mathbb {R}$![]() . Let $\mathcal {D}(\mathbb {T})$
. Let $\mathcal {D}(\mathbb {T})$![]() be the space of all infinitely differentiable functions on $\mathbb {T}$
be the space of all infinitely differentiable functions on $\mathbb {T}$![]() equipped with the locally convex topology given by the seminorms $\left \Vert f\right \Vert _{\alpha }=\sup _{x\in \mathbb {T}}\left \vert f^{(\alpha )}(x)\right \vert$
equipped with the locally convex topology given by the seminorms $\left \Vert f\right \Vert _{\alpha }=\sup _{x\in \mathbb {T}}\left \vert f^{(\alpha )}(x)\right \vert$![]() for $\alpha \in \mathbb {N}_0:=\mathbb {N}\cup \left \{0\right \}$
for $\alpha \in \mathbb {N}_0:=\mathbb {N}\cup \left \{0\right \}$![]() . Let $\mathcal {D}'(\mathbb {T}; X):=\mathcal {L}(\mathcal {D}(\mathbb {T}),\,X)$
. Let $\mathcal {D}'(\mathbb {T}; X):=\mathcal {L}(\mathcal {D}(\mathbb {T}),\,X)$![]() be the space of all continuous linear operator from $\mathcal {D}(\mathbb {T})$
be the space of all continuous linear operator from $\mathcal {D}(\mathbb {T})$![]() to $X$
to $X$![]() . We consider the dyadic-like subsets of $\mathbb {R}$
. We consider the dyadic-like subsets of $\mathbb {R}$![]() :
:
for $k\in \mathbb {N}$![]() . Let $\phi (\mathbb {R})$
. Let $\phi (\mathbb {R})$![]() be the set of all systems $\phi =(\phi _k)_{k\in \mathbb {N}_0}\subset \mathcal {S}(\mathbb {R})$
be the set of all systems $\phi =(\phi _k)_{k\in \mathbb {N}_0}\subset \mathcal {S}(\mathbb {R})$![]() satisfying $\text {supp}(\phi _k)\subset \bar {I}_k$
satisfying $\text {supp}(\phi _k)\subset \bar {I}_k$![]() for each $k\in \mathbb {N}_0$
for each $k\in \mathbb {N}_0$![]() , $\sum _{k\in \mathbb {N}_0}\phi _k(x)=1$
, $\sum _{k\in \mathbb {N}_0}\phi _k(x)=1$![]() for $x\in \mathbb {R}$
for $x\in \mathbb {R}$![]() , and for each $\alpha \in \mathbb {N}_0$
, and for each $\alpha \in \mathbb {N}_0$![]() , $\sup _{ x\in \mathbb {R},\, k\in \mathbb {N}_0 }2^{k\alpha }\vert \phi _k^{(\alpha )}(x)\vert <\infty$
, $\sup _{ x\in \mathbb {R},\, k\in \mathbb {N}_0 }2^{k\alpha }\vert \phi _k^{(\alpha )}(x)\vert <\infty$![]() . Let $\phi =(\phi _k)_{k\in \mathbb {N}_0}\subset \phi (\mathbb {R})$
. Let $\phi =(\phi _k)_{k\in \mathbb {N}_0}\subset \phi (\mathbb {R})$![]() be fixed. For $1\leq p, q\leq \infty, \,s\in \mathbb {R}$
be fixed. For $1\leq p, q\leq \infty, \,s\in \mathbb {R}$![]() , the $X$
, the $X$![]() -valued periodic Besov space is defined by
-valued periodic Besov space is defined by

with the usual modification if $q=\infty$![]() . The space $B_{p,q}^s(\mathbb {T}; X)$
. The space $B_{p,q}^s(\mathbb {T}; X)$![]() is independent from the choice of $\phi$
is independent from the choice of $\phi$![]() and different choices of $\phi$
and different choices of $\phi$![]() lead to equivalent norms on $B_{p,q}^s(\mathbb {T}; X)$
lead to equivalent norms on $B_{p,q}^s(\mathbb {T}; X)$![]() . $B_{p,q}^s(\mathbb {T}; X)$
. $B_{p,q}^s(\mathbb {T}; X)$![]() equipped with the norm $\left \Vert \cdot \right \Vert _{B_{p,q}^s}$
equipped with the norm $\left \Vert \cdot \right \Vert _{B_{p,q}^s}$![]() is a Banach space. See [Reference Arendt and Bu6, Section 2] for more information about the space $B_{p,q}^s(\mathbb {T}; X)$
is a Banach space. See [Reference Arendt and Bu6, Section 2] for more information about the space $B_{p,q}^s(\mathbb {T}; X)$![]() . It is well known that if $s_1\leq s_2$
. It is well known that if $s_1\leq s_2$![]() , then $B_{p,q}^{s_1}(\mathbb {T}; X)\subset B_{p,q}^{s_2}(\mathbb {T}; X)$
, then $B_{p,q}^{s_1}(\mathbb {T}; X)\subset B_{p,q}^{s_2}(\mathbb {T}; X)$![]() and the embedding is continuous [Reference Arendt and Bu6, Theorem 2.3]. When $s>0$
and the embedding is continuous [Reference Arendt and Bu6, Theorem 2.3]. When $s>0$![]() , it is shown in [Reference Arendt and Bu6, Theorem 2.3] that $B_{p,q}^s(\mathbb {T}; X)\subset L^p(\mathbb {T}; X)$
, it is shown in [Reference Arendt and Bu6, Theorem 2.3] that $B_{p,q}^s(\mathbb {T}; X)\subset L^p(\mathbb {T}; X)$![]() , $f\in B_{p,q}^{s+1}(\mathbb {T}; X)$
, $f\in B_{p,q}^{s+1}(\mathbb {T}; X)$![]() if and only if $f$
if and only if $f$![]() is differentiable a.e. on $\mathbb {T}$
is differentiable a.e. on $\mathbb {T}$![]() and $f'\in B_{p,q}^s(\mathbb {T}; X)$
and $f'\in B_{p,q}^s(\mathbb {T}; X)$![]() . This implies that if $u\in B_{p,q}^s(\mathbb {T}; X)$
. This implies that if $u\in B_{p,q}^s(\mathbb {T}; X)$![]() is such that there exists $v\in B_{p,q}^s(\mathbb {T}; X)$
is such that there exists $v\in B_{p,q}^s(\mathbb {T}; X)$![]() satisfying $\hat {v}(k)=ik\hat {u}(k)$
satisfying $\hat {v}(k)=ik\hat {u}(k)$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() , then $u\in B_{p,q}^{s+1}(\mathbb {T}; X)$
, then $u\in B_{p,q}^{s+1}(\mathbb {T}; X)$![]() and $u'=v$
and $u'=v$![]() .
.
Let $1\leq p,\,q\leq \infty,\, s>0$![]() be fixed. We consider the following four-order degenerate differential equations with finite delay:
be fixed. We consider the following four-order degenerate differential equations with finite delay:
where $A,\, B,\, M$![]() and $L$
and $L$![]() are closed linear operators on a Banach space $X$
are closed linear operators on a Banach space $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() and $\alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$
and $\alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$![]() , $f\in B_{p,q}^s(\mathbb {T};X)$
, $f\in B_{p,q}^s(\mathbb {T};X)$![]() is given, and $F,\,G:B_{p,q}^s([-2\pi,\,0];X)\rightarrow X$
is given, and $F,\,G:B_{p,q}^s([-2\pi,\,0];X)\rightarrow X$![]() are bounded linear operators. Moreover, for fixed $t\in \mathbb {T}$
are bounded linear operators. Moreover, for fixed $t\in \mathbb {T}$![]() , $u_t\in B_{p,q}^s([-2\pi,\,0];X)$
, $u_t\in B_{p,q}^s([-2\pi,\,0];X)$![]() is defined by $u_t(s)=u(t+s)$
is defined by $u_t(s)=u(t+s)$![]() for $-2\pi \leq s\leq 0$
for $-2\pi \leq s\leq 0$![]() , here we identify a function $u$
, here we identify a function $u$![]() on $\mathbb {T}$
on $\mathbb {T}$![]() with its natural $2\pi$
with its natural $2\pi$![]() -periodic extension on $\mathbb {R}$
-periodic extension on $\mathbb {R}$![]() .
.
Let $F,\,G\in \mathcal {L}(B_{p,q}^s[-2\pi,\,0];X),\,X)$![]() and $k\in \mathbb {Z}$
and $k\in \mathbb {Z}$![]() . We define the linear operators $F_k,\,\ G_k$
. We define the linear operators $F_k,\,\ G_k$![]() by
by
when $x\in X$![]() . It is clear that there exists a constant $C>0$
. It is clear that there exists a constant $C>0$![]() such that $\left \Vert e_k\otimes x\right \Vert _{B_{p,q}^s(\mathbb {T}; X)}\leq C\left \Vert x\right \Vert$
such that $\left \Vert e_k\otimes x\right \Vert _{B_{p,q}^s(\mathbb {T}; X)}\leq C\left \Vert x\right \Vert$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() . Thus,
. Thus,
whenever $k\in \mathbb {Z}$![]() . It can be seen easily that when $u\in B_{p,q}^s(\mathbb {T}; X)$
. It can be seen easily that when $u\in B_{p,q}^s(\mathbb {T}; X)$![]() , then
, then
for $k\in \mathbb {Z}$![]() . The resolvent set of ($P_4$
. The resolvent set of ($P_4$![]() ) in the $B_{p,q}^s$
) in the $B_{p,q}^s$![]() -well-posedness setting is defined by
-well-posedness setting is defined by

For the sake of simplicity, when $k\in \rho _{M}(A,\,B,\,L)$![]() , we will use the following notation:
, we will use the following notation:
If $k\in \rho _{M}(A,\,B,\,L)$![]() , then $MN_k,\,\ LN_k,\,\ AN_k$
, then $MN_k,\,\ LN_k,\,\ AN_k$![]() and $BN_k$
and $BN_k$![]() make sense as $D(A)\cap D(B)\subset D(M)\cap D(L)$
make sense as $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() by assumption, and they belong to $\mathcal {L}(X)$
by assumption, and they belong to $\mathcal {L}(X)$![]() by the closed graph theorem and the closedness of $A,\,\ B,\,\ M$
by the closed graph theorem and the closedness of $A,\,\ B,\,\ M$![]() and $L$
and $L$![]() .
.
Let $1\leq p,\,q\leq \infty,\,s>0$![]() . It is noted that that the functions $Gu_.$
. It is noted that that the functions $Gu_.$![]() and $Fu'_.$
and $Fu'_.$![]() are uniformly bounded on $\mathbb {T}$
are uniformly bounded on $\mathbb {T}$![]() , but they are not necessarily in $B_{p,q}^s(\mathbb {T};X)$
, but they are not necessarily in $B_{p,q}^s(\mathbb {T};X)$![]() . We define the solution space of $B_{p,q}^s$
. We define the solution space of $B_{p,q}^s$![]() -well-posedness for ($P_4$
-well-posedness for ($P_4$![]() ) by
) by

Here again we consider $D(A)$![]() and $D(B)$
and $D(B)$![]() as Banach spaces equipped with their graph norms. $S_{p,q,s}(A,\, B,\, M,\, L)$
as Banach spaces equipped with their graph norms. $S_{p,q,s}(A,\, B,\, M,\, L)$![]() is a Banach space with the norm
is a Banach space with the norm

If $u\in S_{p,q,s}(A,\, B,\, M,\, L)$![]() , then $Mu$
, then $Mu$![]() , $(Mu)'$
, $(Mu)'$![]() , $(Mu)''$
, $(Mu)''$![]() and $(Mu)'''$
and $(Mu)'''$![]() are $X$
are $X$![]() -valued continuous function on $\mathbb {T}$
-valued continuous function on $\mathbb {T}$![]() , and $Mu(0)=Mu(2\pi )$
, and $Mu(0)=Mu(2\pi )$![]() ,$(Mu)'(0)=(Mu)'(2\pi )$
,$(Mu)'(0)=(Mu)'(2\pi )$![]() , $(Mu)''(0)=(Mu)''(2\pi )$
, $(Mu)''(0)=(Mu)''(2\pi )$![]() and $(Mu)'''(0)=(Mu)'''(2\pi )$
and $(Mu)'''(0)=(Mu)'''(2\pi )$![]() by [Reference Arendt and Bu5, Lemma 2.1].
by [Reference Arendt and Bu5, Lemma 2.1].
Now we give the definition of the $B_{p,q}^s$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ).
).
Definition 3.1 Let $1\leq p,\,q\leq \infty,\,s>0$![]() and $f\in B_{p,q}^s(\mathbb {T}; X)$
and $f\in B_{p,q}^s(\mathbb {T}; X)$![]() , $u\in S_{p,q,s}(A,\,B, M,\,L)$
, $u\in S_{p,q,s}(A,\,B, M,\,L)$![]() is called a strong $B_{p,q}^s$
is called a strong $B_{p,q}^s$![]() -solution of ($P_4$
-solution of ($P_4$![]() ), if ($P_4$
), if ($P_4$![]() ) is satisfied a.e. on $\mathbb {T}$
) is satisfied a.e. on $\mathbb {T}$![]() . We say that ($P_4$
. We say that ($P_4$![]() ) is $B_{p,q}^s$
) is $B_{p,q}^s$![]() -well-posed, if for each $f\in B_{p,q}^s(\mathbb {T}; X)$
-well-posed, if for each $f\in B_{p,q}^s(\mathbb {T}; X)$![]() , there exists a unique strong $B_{p,q}^s$
, there exists a unique strong $B_{p,q}^s$![]() -solution of ($P_4$
-solution of ($P_4$![]() ).
).
If ($P_4$![]() ) is $B_{p,q}^s$
) is $B_{p,q}^s$![]() -well-posed and $u\in S_{p,q,s}(A,\,B,\,M,\,L)$
-well-posed and $u\in S_{p,q,s}(A,\,B,\,M,\,L)$![]() is the unique strong $B_{p,q}^s$
is the unique strong $B_{p,q}^s$![]() -solution of ($P_4$
-solution of ($P_4$![]() ), there exists a constant $C>0$
), there exists a constant $C>0$![]() such that for each $f\in B_{p,q}^s(\mathbb {T}; X)$
such that for each $f\in B_{p,q}^s(\mathbb {T}; X)$![]() , we have
, we have
This is an easy result that can be obtained by the closedness of the operators $A$![]() , $B$
, $B$![]() , $M$
, $M$![]() and $L$
and $L$![]() and the closed graph theorem.
and the closed graph theorem.
Next we give the definition of operator-valued Fourier multipliers in the context of periodic Besov spaces, which is important in the proof of our main result of this section.
Definition 3.2 Let $X,\,Y$![]() be Banach spaces, $1\leq p,\,q\leq \infty,\,s\in \mathbb {R}$
be Banach spaces, $1\leq p,\,q\leq \infty,\,s\in \mathbb {R}$![]() and let $\left (M_k\right )_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$
and let $\left (M_k\right )_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() . We say that $\left (M_k\right )_{k\in \mathbb {Z}}$
. We say that $\left (M_k\right )_{k\in \mathbb {Z}}$![]() is a $B_{p,q}^s$
is a $B_{p,q}^s$![]() -Fourier multiplier, if for each $f\in B_{p,q}^s(\mathbb {T}; X)$
-Fourier multiplier, if for each $f\in B_{p,q}^s(\mathbb {T}; X)$![]() , there exists $u\in B_{p,q}^s(\mathbb {T}; Y)$
, there exists $u\in B_{p,q}^s(\mathbb {T}; Y)$![]() , such that $\hat {u}(k)=M_k\hat {f}(k)$
, such that $\hat {u}(k)=M_k\hat {f}(k)$![]() for all $k\in \mathbb {Z}$
for all $k\in \mathbb {Z}$![]() .
.
The following result has been obtained in [Reference Arendt and Bu6, Theorem 4.5] which gives a sufficient condition for an operator-valued sequence to be a $B_{p,q}^s$![]() -Fourier multiplier. For the notions of $B$
-Fourier multiplier. For the notions of $B$![]() -convex Banach spaces, we refer the readers to [Reference Arendt and Bu6] and references therein.
-convex Banach spaces, we refer the readers to [Reference Arendt and Bu6] and references therein.
Theorem 3.3 Let $X,\,Y$![]() be Banach spaces and let $\left (M_k\right )_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$
be Banach spaces and let $\left (M_k\right )_{k\in \mathbb {Z}}\subset \mathcal {L}(X,\,Y)$![]() . We assume that
. We assume that
Then for $1\leq p,\,q\leq \infty,\,s\in \mathbb {R}$![]() , $\left (M_k\right )_{k\in \mathbb {Z}}$
, $\left (M_k\right )_{k\in \mathbb {Z}}$![]() is an $B_{p,q}^s$
is an $B_{p,q}^s$![]() -multiplier. If $X$
-multiplier. If $X$![]() is $B$
is $B$![]() -convex, then the first-order condition (3.5) is already sufficient for $\left (M_k\right )_{k\in \mathbb {Z}}$
-convex, then the first-order condition (3.5) is already sufficient for $\left (M_k\right )_{k\in \mathbb {Z}}$![]() to be a $B_{p,q}^s$
to be a $B_{p,q}^s$![]() -multiplier.
-multiplier.
Remark 3.4
(i) If $\left (M_k\right )_{k\in \mathbb {Z}}$
 is a $B_{p,q}^s$
is a $B_{p,q}^s$ -Fourier multiplier, then there exists a bounded linear operator $T$
-Fourier multiplier, then there exists a bounded linear operator $T$ from $B_{p,q}^s(\mathbb {T}; X)$
from $B_{p,q}^s(\mathbb {T}; X)$ to $B_{p,q}^s(\mathbb {T}; Y)$
to $B_{p,q}^s(\mathbb {T}; Y)$ satisfying $\widehat {Tf}(k) = M_k\hat f(k)$
satisfying $\widehat {Tf}(k) = M_k\hat f(k)$ when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$ . This implies in particular that $\left (M_k\right )_{k\in \mathbb {Z}}$
. This implies in particular that $\left (M_k\right )_{k\in \mathbb {Z}}$ must be bounded.
must be bounded.(ii) If $\left (M_k\right )_{k\in \mathbb {Z}}$
 and $\left (N_k\right )_{k\in \mathbb {Z}}$
and $\left (N_k\right )_{k\in \mathbb {Z}}$ are $B_{p,q}^s$
are $B_{p,q}^s$ -Fourier multipliers, it can be seen easily that the product sequence $\left (M_kN_k\right )_{k\in \mathbb {Z}}$
-Fourier multipliers, it can be seen easily that the product sequence $\left (M_kN_k\right )_{k\in \mathbb {Z}}$ and the sum sequence $\left (M_k+N_k\right )_{k\in \mathbb {Z}}$
and the sum sequence $\left (M_k+N_k\right )_{k\in \mathbb {Z}}$ are still $B_{p,q}^s$
are still $B_{p,q}^s$ -Fourier multipliers.
-Fourier multipliers.(iii) Let $c_k=\frac {1}{k}$
 when $k\neq 0$
when $k\neq 0$ and $c_0=1$
and $c_0=1$ , then it is easy to see that the sequence $\left (c_kI_X\right )_{k\in \mathbb {Z}}$
, then it is easy to see that the sequence $\left (c_kI_X\right )_{k\in \mathbb {Z}}$ satisfies the conditions (3.2) and (3.3). Thus, the sequence $\left (c_kI_X\right )_{k\in \mathbb {Z}}$
satisfies the conditions (3.2) and (3.3). Thus, the sequence $\left (c_kI_X\right )_{k\in \mathbb {Z}}$ is a $B_{p,q}^s$
is a $B_{p,q}^s$ -Fourier multiplier by theorem 3.3.
-Fourier multiplier by theorem 3.3.
In order to prove our main result, we need the following facts.
Proposition 3.5 Let $A,\, B,\, M$![]() and $L$
and $L$![]() be closed linear operators defined on a Banach space $X$
be closed linear operators defined on a Banach space $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L),\,\ \alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L),\,\ \alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$![]() and let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$
and let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$![]() , where $1\leq p,\,q\leq \infty$
, where $1\leq p,\,q\leq \infty$![]() and $s>0$
and $s>0$![]() . Assume that $\rho _M(A,\,B,\,L)=\mathbb {Z}$
. Assume that $\rho _M(A,\,B,\,L)=\mathbb {Z}$![]() and the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$
and the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$![]() , $\{k\Delta G_{k}:\ k\in \mathbb {Z}\},\,\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}, \left \{k^4MN_k:\ k\in \mathbb {Z}\right \},\,\ \{k^3LN_k:k\in \mathbb {Z}\},\,\ \{kBN_k:k\in \mathbb {Z}\}$
, $\{k\Delta G_{k}:\ k\in \mathbb {Z}\},\,\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}, \left \{k^4MN_k:\ k\in \mathbb {Z}\right \},\,\ \{k^3LN_k:k\in \mathbb {Z}\},\,\ \{kBN_k:k\in \mathbb {Z}\}$![]() and $\left \{kN_k:\ k\in \mathbb {Z}\right \}$
and $\left \{kN_k:\ k\in \mathbb {Z}\right \}$![]() are norm-bounded, where $N_k$
are norm-bounded, where $N_k$![]() is defined by (3.3), the operators $F_k,\,\ G_k,\,\ H_k$
is defined by (3.3), the operators $F_k,\,\ G_k,\,\ H_k$![]() are defined by (3.1). Then $(k^4MN_k)_{k\in \mathbb {Z}}$
are defined by (3.1). Then $(k^4MN_k)_{k\in \mathbb {Z}}$![]() , $(k^3LN_k)_{k\in \mathbb {Z}}$
, $(k^3LN_k)_{k\in \mathbb {Z}}$![]() , $(kBN_k)_{k\in \mathbb {Z}}$
, $(kBN_k)_{k\in \mathbb {Z}}$![]() , $(N_k)_{k\in \mathbb {Z}}$
, $(N_k)_{k\in \mathbb {Z}}$![]() , $(kN_k)_{k\in \mathbb {Z}}$
, $(kN_k)_{k\in \mathbb {Z}}$![]() , $(F_kN_k)_{k\in \mathbb {Z}}$
, $(F_kN_k)_{k\in \mathbb {Z}}$![]() and $(kG_kN_k)_{k\in \mathbb {Z}}$
and $(kG_kN_k)_{k\in \mathbb {Z}}$![]() are $B_{p,q}^s$
are $B_{p,q}^s$![]() -Fourier multipliers.
-Fourier multipliers.
Proof. It follows immediately from the norm boundedness of the set $\{kN_k:k\in \mathbb {Z}\}$![]() that the set $\{N_k:k\in \mathbb {Z}\}$
that the set $\{N_k:k\in \mathbb {Z}\}$![]() is norm-bounded. Let $L_k =(N_k^{-1} - N_{k+1}^{-1})N_k$
is norm-bounded. Let $L_k =(N_k^{-1} - N_{k+1}^{-1})N_k$![]() when $k\in \mathbb {Z}$
when $k\in \mathbb {Z}$![]() . Then the set $\{kL_k: k\in \mathbb {Z}\}$
. Then the set $\{kL_k: k\in \mathbb {Z}\}$![]() is norm-bounded by the proof of proposition 2.11. Since remark 2.7 and the sequence $(k^j)_{k\in \mathbb {Z}}$
is norm-bounded by the proof of proposition 2.11. Since remark 2.7 and the sequence $(k^j)_{k\in \mathbb {Z}}$![]() is $2$
is $2$![]() -regular when $0\leq j\leq 3$
-regular when $0\leq j\leq 3$![]() , to show that $(k^4MN_k)_{k\in \mathbb {Z}}$
, to show that $(k^4MN_k)_{k\in \mathbb {Z}}$![]() , $(k^3LN_k)_{k\in \mathbb {Z}}$
, $(k^3LN_k)_{k\in \mathbb {Z}}$![]() , $(kBN_k)_{k\in \mathbb {Z}}$
, $(kBN_k)_{k\in \mathbb {Z}}$![]() , $(N_k)_{k\in \mathbb {Z}}$
, $(N_k)_{k\in \mathbb {Z}}$![]() and $(kN_k)_{k\in \mathbb {Z}}$
and $(kN_k)_{k\in \mathbb {Z}}$![]() are $B_{p,q}^s$
are $B_{p,q}^s$![]() -Fourier multipliers, we only need to show that the set $\{k^2\Delta L_k: k\in \mathbb {Z}\}$
-Fourier multipliers, we only need to show that the set $\{k^2\Delta L_k: k\in \mathbb {Z}\}$![]() is norm-bounded by [Reference Conejero, Lizama, Murillo-Arcila and Seoane-Sepulveda11, Theorem 1.1] and theorem 3.3. We have
is norm-bounded by [Reference Conejero, Lizama, Murillo-Arcila and Seoane-Sepulveda11, Theorem 1.1] and theorem 3.3. We have
where

when $k\in \mathbb {Z}$![]() by (2.6). We observe that
by (2.6). We observe that

and

when $k\in \mathbb {Z}$![]() . It follows from (3.7) and (3.8) that the sets$\{k^2\Delta L_k^{(1)}: k\in \mathbb {Z}\}$
. It follows from (3.7) and (3.8) that the sets$\{k^2\Delta L_k^{(1)}: k\in \mathbb {Z}\}$![]() and $\{k^2\Delta L_k^{(2)}: k\in \mathbb {Z}\}$
and $\{k^2\Delta L_k^{(2)}: k\in \mathbb {Z}\}$![]() are norm-bounded by the norm boundedness of the sets $\{kL_k: k\in \mathbb {Z}\}$
are norm-bounded by the norm boundedness of the sets $\{kL_k: k\in \mathbb {Z}\}$![]() and the assumptions that the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$
and the assumptions that the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$![]() , $\{k\Delta G_{k}: k\in \mathbb {Z}\},\,\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\},\, \left \{k^4MN_k:\ k\in \mathbb {Z}\right \},\,\{k^3LN_k:k\in \mathbb {Z}\},\,\{kBN_k:k\in \mathbb {Z}\}$
, $\{k\Delta G_{k}: k\in \mathbb {Z}\},\,\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\},\, \left \{k^4MN_k:\ k\in \mathbb {Z}\right \},\,\{k^3LN_k:k\in \mathbb {Z}\},\,\{kBN_k:k\in \mathbb {Z}\}$ and $\left \{kN_k:\ k\in \mathbb {Z}\right \}$
and $\left \{kN_k:\ k\in \mathbb {Z}\right \}$![]() are norm-bounded.
are norm-bounded.
It remains to show that the sequences $(F_kN_k)_{ k\in \mathbb {Z}}$![]() and $(kG_kN_k)_{ k\in \mathbb {Z}}$
and $(kG_kN_k)_{ k\in \mathbb {Z}}$![]() satisfy (3.5) and (3.6). This follows easily from the norm boundedness of the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$
satisfy (3.5) and (3.6). This follows easily from the norm boundedness of the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$![]() , $\{k\Delta G_{k}: k\in \mathbb {Z}\}$
, $\{k\Delta G_{k}: k\in \mathbb {Z}\}$![]() and $\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}$
and $\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}$![]() . We omit the details. The proof is completed.
. We omit the details. The proof is completed.
Next we give a necessary and sufficient condition for $B_{p,q}^s$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ). Its proof is just an easy adaptation of the proof of theorem 2.12 by using proposition 3.5. We omit the detail.
). Its proof is just an easy adaptation of the proof of theorem 2.12 by using proposition 3.5. We omit the detail.
Theorem 3.6 Let $X$![]() be a Banach space, $1\leq p,\,q\leq \infty,\, s>0$
be a Banach space, $1\leq p,\,q\leq \infty,\, s>0$![]() , let $A,\, B,\, M$
, let $A,\, B,\, M$![]() and $L$
and $L$![]() be closed linear operators on $X$
be closed linear operators on $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() and $\alpha,\, \beta,\,\ \gamma \in \mathbb {C}$
and $\alpha,\, \beta,\,\ \gamma \in \mathbb {C}$![]() . Let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$
. Let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$![]() . We assume that the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$
. We assume that the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$![]() , $\{k\Delta G_{k}: k\in \mathbb {Z}\}$
, $\{k\Delta G_{k}: k\in \mathbb {Z}\}$![]() and $\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}$
and $\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}$![]() are norm-bounded. Then the following assertions are equivalent:
are norm-bounded. Then the following assertions are equivalent:
(i) ($P_4$
 ) is $B_{p,q}^s$
) is $B_{p,q}^s$ -well-posed.
-well-posed.(ii) $\rho _{M}(A,\,B,\,L)=\mathbb {Z}$
 and the sets $\left \{k^4MN_k: k\in \mathbb {Z}\right \},\,\ \{k^3LN_k:k\in \mathbb {Z}\},\,\ \{kBN_k:k\in \mathbb {Z}\}$
and the sets $\left \{k^4MN_k: k\in \mathbb {Z}\right \},\,\ \{k^3LN_k:k\in \mathbb {Z}\},\,\ \{kBN_k:k\in \mathbb {Z}\}$ and $\left \{kN_k:\ k\in \mathbb {Z}\right \}$
and $\left \{kN_k:\ k\in \mathbb {Z}\right \}$ are norm-bounded, where $N_k$
are norm-bounded, where $N_k$ is defined by (3.3).
is defined by (3.3).
When the underlying Banach space $X$![]() is $B$
is $B$![]() -convex, the first-order Marcinkiewicz-type condition (3.5) is already sufficient for an operator-valued sequence to be a $B_{p,q}^s$
-convex, the first-order Marcinkiewicz-type condition (3.5) is already sufficient for an operator-valued sequence to be a $B_{p,q}^s$![]() -Fourier multiplier. This remark together with the proof of theorem 2.12 gives immediately the following result which gives an characterization of the $B_{p,q}^s$
-Fourier multiplier. This remark together with the proof of theorem 2.12 gives immediately the following result which gives an characterization of the $B_{p,q}^s$![]() -well-posedness of ($P_4$
-well-posedness of ($P_4$![]() ) under a weaker condition on the sequence $(G_k)_{k\in \mathbb {Z}}$
) under a weaker condition on the sequence $(G_k)_{k\in \mathbb {Z}}$![]() when the underlying Banach space is $B$
when the underlying Banach space is $B$![]() -convex.
-convex.
Theorem 3.7 Let $X$![]() be a $B$
be a $B$![]() -convex Banach space, $1\leq p,\,q\leq \infty,\, s>0$
-convex Banach space, $1\leq p,\,q\leq \infty,\, s>0$![]() , let $A,\, B,\, M$
, let $A,\, B,\, M$![]() and $L$
and $L$![]() be closed linear operators on $X$
be closed linear operators on $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() and $\alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$
and $\alpha,\,\ \beta,\,\ \gamma \in \mathbb {C}$![]() . Let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$
. Let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$![]() . We assume that $\left \{k\Delta G_{k}:k\in \mathbb {Z}\right \}$
. We assume that $\left \{k\Delta G_{k}:k\in \mathbb {Z}\right \}$![]() is norm-bounded. Then the following assertions are equivalent:
is norm-bounded. Then the following assertions are equivalent:
(i) ($P_4$
 ) is $B_{p,q}^s$
) is $B_{p,q}^s$ -well-posed.
-well-posed.(ii) $\rho _M(A,\,B,\,L)=\mathbb {Z}$
 and the sets $\left \{k^4MN_k:\ k\in \mathbb {Z}\right \},\, \{k^3LN_k:k\in \mathbb {Z}\},\,\ \{kBN_k:k\in \mathbb {Z}\}$
and the sets $\left \{k^4MN_k:\ k\in \mathbb {Z}\right \},\, \{k^3LN_k:k\in \mathbb {Z}\},\,\ \{kBN_k:k\in \mathbb {Z}\}$ and $\left \{kN_k: k\in \mathbb {Z}\right \}$
and $\left \{kN_k: k\in \mathbb {Z}\right \}$ are norm-bounded, where $N_k$
are norm-bounded, where $N_k$ is defined by (3.3).
is defined by (3.3).
Since the second statement of theorem 3.6 does not depend on the parameters $1\leq p,\,q\leq \infty,\, s>0$![]() , theorem 3.6 has the following immediate consequence.
, theorem 3.6 has the following immediate consequence.
Corollary 3.8 Let $X$![]() be a Banach space, $1\leq p,\,q\leq \infty,\, s>0$
be a Banach space, $1\leq p,\,q\leq \infty,\, s>0$![]() , let $A,\, B,\, M$
, let $A,\, B,\, M$![]() and $L$
and $L$![]() be closed linear operators on $X$
be closed linear operators on $X$![]() satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$
satisfying $D(A)\cap D(B)\subset D(M)\cap D(L)$![]() and $\alpha,\, \beta,\,\ \gamma \in \mathbb {C}$
and $\alpha,\, \beta,\,\ \gamma \in \mathbb {C}$![]() . Let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$
. Let $F,\,G\in \mathcal {L}(B_{p,q}^s([-2\pi,\,0];X),\,X)$![]() . We assume that the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$
. We assume that the sets $\{k\Delta ^2F_k:\ k\in \mathbb {Z}\}$![]() , $\{k\Delta G_{k}: k\in \mathbb {Z}\}$
, $\{k\Delta G_{k}: k\in \mathbb {Z}\}$![]() and $\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}$
and $\{k^2\Delta ^2G_k:\ k\in \mathbb {Z}\}$![]() are norm-bounded. Then if ($P_4$
are norm-bounded. Then if ($P_4$![]() ) is $B_{p,q}^s$
) is $B_{p,q}^s$![]() -well-posed for some $1\leq p,\,q\leq \infty,\, s>0$
-well-posed for some $1\leq p,\,q\leq \infty,\, s>0$![]() , then it is $B_{p,q}^s$
, then it is $B_{p,q}^s$![]() -well-posed for all $1\leq p,\,q\leq \infty,\, s>0$
-well-posed for all $1\leq p,\,q\leq \infty,\, s>0$![]() .
.
4. Applications
Example 4.1 Let $\Omega$![]() be a bounded domain in $\mathbb {R}^k$
be a bounded domain in $\mathbb {R}^k$![]() with smooth boundary, $m$
with smooth boundary, $m$![]() be a given non-negative-bounded measurable function on $\Omega$
be a given non-negative-bounded measurable function on $\Omega$![]() and let $\alpha,\, \gamma \in \mathbb {C},\,\ \beta >0$
and let $\alpha,\, \gamma \in \mathbb {C},\,\ \beta >0$![]() be given. We let $X$
be given. We let $X$![]() be the Hilbert space $H^{-1}(\Omega )$
be the Hilbert space $H^{-1}(\Omega )$![]() , and let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$
, and let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$![]() for some $1 < p< \infty$
for some $1 < p< \infty$![]() . We consider the problem
. We consider the problem

where $f$![]() is defined on $\mathbb {T}\times \Omega$
is defined on $\mathbb {T}\times \Omega$![]() and the Laplacian $\Delta$
and the Laplacian $\Delta$![]() only acts on the space variable $x\in \Omega$
only acts on the space variable $x\in \Omega$![]() , $u_t'$
, $u_t'$![]() and $u_t$
and $u_t$![]() are defined by $u_t' (s,\, x) = u'(t+s,\, x)$
are defined by $u_t' (s,\, x) = u'(t+s,\, x)$![]() and $u_t' (s,\, x) = u(t+s,\, x)$
and $u_t' (s,\, x) = u(t+s,\, x)$![]() when $t\in \mathbb {T},\, \ s\in [-2\pi,\, 0]$
when $t\in \mathbb {T},\, \ s\in [-2\pi,\, 0]$![]() and $x\in \Omega$
and $x\in \Omega$![]() .
.
Let $M$![]() be the multiplication operator on $X$
be the multiplication operator on $X$![]() by $m$
by $m$![]() , then there exist constants $C >0,\, \beta > 0$
, then there exist constants $C >0,\, \beta > 0$![]() , such that
, such that
whenever $Re (z)\leq \beta ( 1 + \vert Im (z)\vert )$![]() by [Reference Favini and Yagi12, Section 3.7], where $\Delta$
by [Reference Favini and Yagi12, Section 3.7], where $\Delta$![]() is the Laplacian on $H^{-1}(\Omega )$
is the Laplacian on $H^{-1}(\Omega )$![]() with Dirichlet boundary condition. Let $A = \Delta$
with Dirichlet boundary condition. Let $A = \Delta$![]() and we assume that $D(A)\subset D(M)$
and we assume that $D(A)\subset D(M)$![]() . Then the above equation may be rewritten in the form
. Then the above equation may be rewritten in the form
a differential equation on $\mathbb {T}$![]() with values in $X$
with values in $X$![]() , where $f\in L^p(\mathbb {T}; X)$
, where $f\in L^p(\mathbb {T}; X)$![]() and the solution $u\in W_{\text {per}}^{1,p}(\mathbb {T}; D(A))$
and the solution $u\in W_{\text {per}}^{1,p}(\mathbb {T}; D(A))$![]() satisfies $\ Mu\in W_{\text {per}}^{4,p}(\mathbb {T}; X)$
satisfies $\ Mu\in W_{\text {per}}^{4,p}(\mathbb {T}; X)$![]() .
.
We assume that $\rho _{M}(A,\,A,\,M)=\mathbb {Z}$![]() and the set $\left \{k\Delta G_{k}:k\in \mathbb {Z}\right \}$
and the set $\left \{k\Delta G_{k}:k\in \mathbb {Z}\right \}$![]() is norm-bounded. Furthermore, we assume that $m > 0$
is norm-bounded. Furthermore, we assume that $m > 0$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() and $m$
and $m$![]() is regular enough so that the multiplication operator by $m^{-1}$
is regular enough so that the multiplication operator by $m^{-1}$![]() is bounded on $H^{-1}(\Omega )$
is bounded on $H^{-1}(\Omega )$![]() , then
, then
whenever $Re z\leq \beta ( 1 + \vert Im z\vert )$![]() by (4.1). We claim that ($P_1$
by (4.1). We claim that ($P_1$![]() ) is $L^p$
) is $L^p$![]() -well-posed. Indeed, the operator $(k^4 - \alpha ik^3 - k^2)M - (\beta +ik) A - ikG_k - F_k: D(A) \to X$
-well-posed. Indeed, the operator $(k^4 - \alpha ik^3 - k^2)M - (\beta +ik) A - ikG_k - F_k: D(A) \to X$![]() is bijective and $[(k^4 - \alpha ik^3 - k^2)M - (\beta +ik) A - ikG_k - F_k]^{-1} \in \mathcal {L} (X)$
is bijective and $[(k^4 - \alpha ik^3 - k^2)M - (\beta +ik) A - ikG_k - F_k]^{-1} \in \mathcal {L} (X)$![]() whenever $k\in \mathbb {Z}$
whenever $k\in \mathbb {Z}$![]() by the assumption $\rho _{M}(A,\,A,\,M)=\mathbb {Z}$
by the assumption $\rho _{M}(A,\,A,\,M)=\mathbb {Z}$![]() . It follows that the sets
. It follows that the sets
are norm-bounded by (4.1) and (4.2), where $N_k = [(k^4 - \alpha ik^3 - k^2)M - (\beta +ik) A - ikG_k - F_k]^{-1}$![]() . Here we have used the uniform boundedness of the sequences $(F_k)_{k\in \mathbb {Z}}$
. Here we have used the uniform boundedness of the sequences $(F_k)_{k\in \mathbb {Z}}$![]() and $(G_k)_{k\in \mathbb {Z}}$
and $(G_k)_{k\in \mathbb {Z}}$![]() . Thus, the problem ($P_1$
. Thus, the problem ($P_1$![]() ) is $L^p$
) is $L^p$![]() -well-posed by theorem 2.12. Here we have used the fact that $H^{-1} (\Omega )$
-well-posed by theorem 2.12. Here we have used the fact that $H^{-1} (\Omega )$![]() is a Hilbert space and the fact that every norm-bounded subset of $\mathcal {L}(X)$
is a Hilbert space and the fact that every norm-bounded subset of $\mathcal {L}(X)$![]() is $R$
is $R$![]() -bounded when $X$
-bounded when $X$![]() is isomorphic to a Hilbert space [Reference Arendt and Bu5].
is isomorphic to a Hilbert space [Reference Arendt and Bu5].
Under the same assumptions, we obtain the $B_{p,q}^s$![]() -well-posedness of ($P_1$
-well-posedness of ($P_1$![]() ) when $1\leq p,\, q\leq \infty$
) when $1\leq p,\, q\leq \infty$![]() by corollary 3.8.
by corollary 3.8.
Example 4.2 Let $H$![]() be a Hilbert space, $P$
be a Hilbert space, $P$![]() be a densely defined positive self-adjoint operator on $H$
be a densely defined positive self-adjoint operator on $H$![]() with $P\geq \delta > 0$
with $P\geq \delta > 0$![]() . Let $M = P- \epsilon$
. Let $M = P- \epsilon$![]() with $\epsilon < \delta$
with $\epsilon < \delta$![]() , and let $A = \sum _{i=0}^k a_iP^i$
, and let $A = \sum _{i=0}^k a_iP^i$![]() with $a_i\geq 0,\,\ a_k > 0$
with $a_i\geq 0,\,\ a_k > 0$![]() , where $k$
, where $k$![]() is an integer $\geq 2$
is an integer $\geq 2$![]() . Then there exists $C > 0$
. Then there exists $C > 0$![]() and $\beta >0$
and $\beta >0$![]() such that
such that
whenever $Re z\geq -\beta ( 1 + \vert Im z\vert )$![]() by [Reference Favini and Yagi12, page 73]. If $M$
by [Reference Favini and Yagi12, page 73]. If $M$![]() is regular enough so that $0\in \rho (M)$
is regular enough so that $0\in \rho (M)$![]() , then
, then
whenever $Re z\geq -\beta ( 1 + \vert Im z\vert )$![]() by (4.3).
by (4.3).
Let $\Omega = (0,\, 1)$![]() and let $H = L^2(\Omega )$
and let $H = L^2(\Omega )$![]() . It is clear that the operator $\frac {{\rm d}^2}{{\rm d}x^2}$
. It is clear that the operator $\frac {{\rm d}^2}{{\rm d}x^2}$![]() with domain $H^2(\Omega )\cap H_0^1(\Omega )$
with domain $H^2(\Omega )\cap H_0^1(\Omega )$![]() generates a contraction semigroup on $H$
generates a contraction semigroup on $H$![]() and $P = - \frac {{\rm d}^2}{{\rm d}x^2}$
and $P = - \frac {{\rm d}^2}{{\rm d}x^2}$![]() is positive and self-adjoint in $H$
is positive and self-adjoint in $H$![]() [Reference Arendt, Batty, Hieber and Neubrander4, Example 3.4.7]. Hence, $1\in \rho (\frac {{\rm d}^2}{{\rm d}x^2})$
[Reference Arendt, Batty, Hieber and Neubrander4, Example 3.4.7]. Hence, $1\in \rho (\frac {{\rm d}^2}{{\rm d}x^2})$![]() , or equivalently $M = I_X+ P$
, or equivalently $M = I_X+ P$![]() has a bounded inverse. Let $\alpha,\, \gamma \in \mathbb {C}$
has a bounded inverse. Let $\alpha,\, \gamma \in \mathbb {C}$![]() and $\beta < 0$
and $\beta < 0$![]() be fixed and let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$
be fixed and let $F,\,G\in \mathcal {L}(L^p([-2\pi,\,0];X),\,X)$![]() for some $1 < p< \infty$
for some $1 < p< \infty$![]() , we consider the following equations:
, we consider the following equations:

This equation can be rewritten in the compact form:
a differential equation on $\mathbb {T}$![]() with values in $H$
with values in $H$![]() , where $f\in L^p(\mathbb {T}; H)$
, where $f\in L^p(\mathbb {T}; H)$![]() and the solution $u$
and the solution $u$![]() is in $u\in W_{\text {per}}^{1,p}(\mathbb {T}; D(A))$
is in $u\in W_{\text {per}}^{1,p}(\mathbb {T}; D(A))$![]() , satisfies $Mu\in W_{\text {per}}^{4,p}(\mathbb {T}; H)$
, satisfies $Mu\in W_{\text {per}}^{4,p}(\mathbb {T}; H)$![]() , where $M = 1- \frac {\partial ^2}{\partial x^2}$
, where $M = 1- \frac {\partial ^2}{\partial x^2}$![]() and $A= \Delta ^2$
and $A= \Delta ^2$![]() , here we consider $\Delta$
, here we consider $\Delta$![]() as the Laplacian on $L^2(\Omega )$
as the Laplacian on $L^2(\Omega )$![]() with Dirichlet boundary condition. If $\rho _{M}(A,\,A,\,M)=\mathbb {Z}$
with Dirichlet boundary condition. If $\rho _{M}(A,\,A,\,M)=\mathbb {Z}$![]() , one can obtain the $L^p$
, one can obtain the $L^p$![]() -well-posedness of ($P_2$
-well-posedness of ($P_2$![]() ) by using (4.3), (4.4) and theorem 2.12 under suitable assumption on the delay operator $G$
) by using (4.3), (4.4) and theorem 2.12 under suitable assumption on the delay operator $G$![]() . Here again we have used the fact that $L^2 (\Omega )$
. Here again we have used the fact that $L^2 (\Omega )$![]() is a Hilbert space and the fact that every norm-bounded subset of $\mathcal {L}(X)$
is a Hilbert space and the fact that every norm-bounded subset of $\mathcal {L}(X)$![]() is $R$
is $R$![]() -bounded when $X$
-bounded when $X$![]() is isomorphic to a Hilbert space [Reference Arendt and Bu5]. One can also obtain the $B_{p,q}^s$
is isomorphic to a Hilbert space [Reference Arendt and Bu5]. One can also obtain the $B_{p,q}^s$![]() -well-posedness pf ($P_2$
-well-posedness pf ($P_2$![]() ) when $1\leq p,\, q\leq \infty$
) when $1\leq p,\, q\leq \infty$![]() by using theorem 3.6 or corollary 3.8.
by using theorem 3.6 or corollary 3.8.
Acknowledgements
This work was supported by the NSF of China (grant No. 12171266, 12171062) and the Natural Science Foundation of Chongqing (grant No. CSTB2022NSCQ-JQX0004).