Introduction
The mechanical properties of metallic materials are usually controlled by their microstructure. During processing, varying parameters allow for changing the grain size distribution as well as the volume, size, and morphology of secondary phases. The composition and structure of interphase interfaces as well as grain boundaries also evolve and have a tremendous influence on physical properties. Knowledge of the precise composition and structure of interfaces has progressively been established via careful microscopy and microanalysis, whenever possible at near-atomic resolution. Yet, there are still aspects of the true, detailed atomic structure and composition of an interface or gain boundary that remains unresolved. Field-ion microscopy and later atom probe tomography (APT) analyses have significantly complemented extensive transmission electron microscopy (TEM) investigations. The strength of the combination of these techniques was further demonstrated by the development of direct correlative approaches (Krakauer et al., Reference Krakauer, Hu, Kuo, Mallick, Seki, Seidman, Baker and Loyd1990; Felfer et al., Reference Felfer, Alam, Ringer and Cairney2012a; Herbig et al., Reference Herbig, Raabe, Li, Choi, Zaefferer and Goto2014; Stoffers et al., Reference Stoffers, Barthel, Liebscher, Gault, Cojocaru-Mirédin, Scheu and Raabe2017) including at high resolution (Liebscher et al., Reference Liebscher, Stoffers, Alam, Lymperakis, Cojocaru-Mirédin, Gault, Neugebauer, Dehm, Scheu and Raabe2018a, Reference Liebscher, Yao, Dey, Lipińska-Chwalek, Berkels, Gault, Hickel, Herbig, Mayer, Neugebauer, Raabe, Dehm and Scheu2018b).
APT has risen in prominence as a microanalytical technique over the past two decades, in particular, due to its unique combination of compositional sensitivity and capacity for three-dimensional analytical imaging at the sub-nanometer scale (Blavette et al., Reference Blavette, Deconihout, Bostel, Sarrau, Bouet and Menand1993; Kelly & Miller, Reference Kelly and Miller2007; Marquis et al., Reference Marquis, Bachhav, Chen, Dong, Gordon and McFarland2013). Hence, APT would appear perfectly suited for the analysis of interfaces. Yet, APT is primarily a mass spectrometry technique (Müller et al., Reference Müller, Panitz and McLane1968), albeit with a very high spatial resolution (Vurpillot et al., Reference Vurpillot, Bostel, Cadel and Blavette2000b, Reference Vurpillot, Da Costa, Menand and Blavette2001; Gault et al., Reference Gault, Moody, De Geuser, Haley, Stephenson and Ringer2009, Reference Gault, Moody, De Geuser, La Fontaine, Stephenson, Haley and Ringer2010). The spatial resolution in APT results from a complex interplay between the field evaporation process that dictates the order in which ions are removed from the surface (Vurpillot et al., Reference Vurpillot, Bostel, Cadel and Blavette2000b; Marquis & Vurpillot, Reference Marquis and Vurpillot2008; Gault et al., Reference Gault, Moody, De Geuser, La Fontaine, Stephenson, Haley and Ringer2010; De Geuser & Gault, Reference De Geuser and Gault2020) and the shape of the specimen up to the level of the atomic arrangements at the specimen's surface. Combined, these factors determine the nature of the projection of the ions from the apex of the specimen onto the position-sensitive ion detector (Rolland et al., Reference Rolland, Larson, Geiser, Duguay, Vurpillot and Blavette2015; De Geuser & Gault, Reference De Geuser and Gault2017). The simple approach implemented in the commonly used reconstruction protocol (Bas et al., Reference Bas, Bostel, Deconihout and Blavette1995; Geiser et al., Reference Geiser, Larson, Oltman, Gerstl, Reinhard, Kelly and Prosa2009; Gault et al., Reference Gault, Haley, de Geuser, Moody, Marquis, Larson and Geiser2011b), which generates the 3D atom-by-atom image of the original specimen, completely ignores such complexities. In turn, this strongly limits the accuracy and precision of the analysis of interfaces.
Inaccuracies in the reconstruction associated with trajectory aberrations coming from a specific field evaporation behavior of the interface or grain boundary region can often be identified by fluctuations in the atomic density, i.e. the point density in the reconstructed data (Vurpillot et al., Reference Vurpillot, Bostel and Blavette2000a; Blavette et al., Reference Blavette, Vurpillot, Pareige and Menand2001; Oberdorfer et al., Reference Oberdorfer, Eich and Schmitz2013). These fluctuations can sometimes be used to trace the location of features of interest (Tang et al., Reference Tang, Gault, Ringer, Martin, Bendavid and Cairney2010) but most often simply lead to an uncontrolled degradation of the spatial performance of APT. These effects have led to a strong debate regarding the accuracy of APT for the characterization of interfaces, particularly in comparison to other microscopy techniques such as high-resolution (scanning) TEM [HR-(S)TEM] and associated microanalytical techniques such as energy-dispersive X-ray spectroscopy (EDS). HR-(S)TEM often reveals near-atomically sharp interfaces at grain boundaries in metals (Mills, Reference Mills1993; Harmer, Reference Harmer2011; Medlin et al., Reference Medlin, Hattar, Zimmerman, Abdeljawad and Foiles2017) or interphase interfaces. In contrast, measured APT composition profiles are rarely below several nanometers in width. Such concentration profiles provide integral values over a given area of an interface, and there is evidence that the spatial resolution has a wide impact on the measured profiles (Felfer et al., Reference Felfer, Gault, Sha, Stephenson, Ringer and Cairney2012b).
It is also common for researchers, on the basis of APT analysis, to report a single value of the composition of the interface, or more recently, the trend is to report the relative excess of solutes (Felfer et al., Reference Felfer, Scherrer, Demeulemeester, Vandervorst and Cairney2015), following the early work by Krakauer & Seidman (Reference Krakauer and Seidman1993). However, variations in the local composition across the plane of an interface may be revealing of actual physical phenomena pertaining to, for example, segregation or phase transformation (Kwiatkowski da Silva et al., Reference Kwiatkowski da Silva, Ponge, Peng, Inden, Lu, Breen, Gault and Raabe2018). Therefore, the tendency to only report a single value leads to those being overlooked when, for example, correlating the nature of interfaces to resulting material properties.
Here, in the analysis of several exemplar and simulated materials systems, we aim to provide some perspective on how the processing of the data itself can cause issues beyond the intrinsic limitations of the technique, in particular when it comes to reporting on the width of a segregation, how the excess might not be devoid of issues, and how those utilizing the APT technique can learn from practices in other communities.
Materials and Methods
In the section “Compositional Width of an Interface”, the material investigated was a ternary Fe–0.12 wt%C–2 wt%Mn, prepared in a vacuum induction furnace. The ingot was hot-rolled and subsequently cold-rolled. Samples were reaustenitized at 1,250°C for 48 h under Ar atmosphere in order to remove any Mn microsegregation and prevent any decarburization and finally cold-rolled to a 1 mm thickness. The sample of interest here was heated at 10°C/s to 1,100°C for 1 min, cooled down rapidly to 680°C, within the dilatometer, and maintained at this temperature for 3 h (10,800 s). A transformation interface was targeted by using scanning electron microscopy and electron backscattered diffraction (EBSD) to prepare specimens for atom probe by focused-ion beam milling. A bar of the material containing the interface of interest was lifted out, mounted on a support, and milled into a sharp needle with suitable dimensions for APT analysis (Prosa & Larson, Reference Prosa and Larson2017). All the details of the preparation can be found in Danoix et al. (Reference Danoix, Sauvage, Huin, Germain and Gouné2016). APT data were acquired on a Cameca LEAP 4000 HR, at a base temperature of 80 K, in a high-voltage pulsing mode with a pulse fraction of 20% and at a repetition rate of 200 kHz. Data reconstruction and processing were performed with Cameca IVAS® 3.6.8.
The material investigated in the section “Grain Boundary Analysis by APT” was a forged ASME SA508 Grade 4N bainitic steel in the quenched and tempered conditions. The composition of the bainitic steel is shown in Table 1.
Table 1. Nominal Composition (wt%) of the ASME SA508 Grade 4N Bainitic Steel.

A specimen, containing a grain boundary, was prepared for APT analysis using focused-ion beam milling on a Zeiss NVision 40 dual-beam scanning electron microscope/focused ion beam (SEM/FIB). Standard FIB procedures were followed (Miller et al., Reference Miller, Russell and Thompson2005; Thompson et al., Reference Thompson, Lawrence, Larson, Olson, Kelly and Gorman2007). The APT analysis was conducted using a Cameca LEAP 5000 XR, with a base temperature of 50 K, a pulse frequency of 200 kHz, and a pulse fraction of 25%. Data reconstruction was performed in Cameca IVAS® 3.6.8.
Compositional Width of an Interface
Background
In steels, the allotropic transformation from the high-temperature face-centered cubic (fcc) phase to the low-temperature body-centered cubic (bcc) is one of the degrees of freedom that can be used to adjust the alloy's properties. The partitioning of solutes between the bcc-ferrite and fcc-austenite and their interactions with migrating α–γ interfaces during the growth of ferrite has been a topic of intense research for decades, as recently reviewed thoroughly (Purdy et al., Reference Purdy, Ågren, Borgenstam, Bréchet, Enomoto, Furuhara, Gamsjager, Gouné, Hillert, Hutchinson, Militzer and Zurob2011; Gouné et al., Reference Gouné, Danoix, Ågren, Bréchet, Hutchinson, Militzer, Purdy, van der Zwaag and Zurob2015). Modeling the growth of ferrite in low alloyed steels has been extensively investigated because of its great importance for the design of new steel grades (Guo & Enomoto, Reference Guo and Enomoto2007). Precise measurements of the local composition of solutes at and in the vicinity of the moving interface are sparse (Fletcher et al., Reference Fletcher, Garratt-Reed, Aaronson, Purdy, Reynolds and Smith2001; Thuillier et al., Reference Thuillier, Danoix, Gouné and Blavette2006; Danoix et al., Reference Danoix, Sauvage, Huin, Germain and Gouné2016; Van Landeghem et al., Reference Van Landeghem, Langelier, Panahi, Purdy, Hutchinson, Botton and Zurob2016, Reference Van Landeghem, Langelier, Gault, Panahi, Korinek, Purdy and Zurob2017). Here, we explore how the measured width of the profile is dependent on the local fluctuations of the depth resolution of the technique and that, by selecting the appropriate region, the width of the profile can be in the range of 4–5 atomic (011) planes (<1 nm).
Experimental Results
Figure 1a shows a tomographic reconstruction containing an α–γ interface, which was selected due to its close adherence to the Kurdjumov–Sachs (K–S) orientation relationship (OR) (Danoix et al., Reference Danoix, Sauvage, Huin, Germain and Gouné2016). The application of the filtering technique introduced by Yao (Reference Yao2016) reveals a clear crystallographic pole in the detector hit maps on both sides of the interface, as shown in Figures 1b and 1c. The likelihood of observing a pole in the desorption pattern formed on the detector is directly proportional to the interplanar spacing in this direction. Hence, when only a single pole is observed, it likely represents a low index direction. Here, we made use of the information from the correlative EBSD analysis to guide the identification of the pole as being a (011) in the bcc-ferrite. Upon cooling, γ has transformed into martensite and is hence body-centered tetragonal (bct). Assuming that the K–S OR also applied to the austenite–martensite transformation, then the (011)martensite originates from the (111) (Yardley & Payton, Reference Yardley and Payton2014). This would explain the shape of the pole seen in the bottom grain, which can hence be identified as also being (011) in the martensite. Superimposed poles have previously been considered as an indication of a specific OR (Chang et al., Reference Chang, Breen, Tarzimoghadam, Kürnsteiner, Gardner, Ackerman, Radecka, Bagot, Lu, Li, Jägle, Herbig, Stephenson, Moody, Rugg, Dye, Ponge, Raabe and Gault2018). For this particular interface, the relationship between (011)martensite //(011)α has been previously reported (Zhang & Kelly, Reference Zhang and Kelly2002). With only a single pole visible in each grain, the full analysis of the misorientation cannot be performed from the APT data (Moody et al., Reference Moody, Tang, Gault, Ringer and Cairney2011; Breen et al., Reference Breen, Babinsky, Day, Eder, Oakman, Trimby, Primig, Cairney and Ringer2017). However, assuming that the angular field of view is 55°, the change in the pole position would translate into approx. 2° difference in the orientation between the two grains.

Fig. 1. (a) Reconstructed APT map showing the distribution of Mn, C, and Fe in the dataset containing the interface. For clarity, only 5% of the Fe ions are displayed. (b,c) Detector hit maps calculated for a slice of 0.5 million ions at different depths indicated by the arrow of the corresponding color in (a). In (b), a pole is indicated with a red arrow and the position of the α–γ interface is marked by a pink dashed line.
Figure 2 shows a carbon composition profile calculated within a cylindrical region of interest that crosses the entire interface, aligned manually as close as possible to normal to the interface. The full-width at half-maximum (FWHM) of the carbon peak across the interface is approx. 2.3 nm and is consistent with previous reports (Danoix et al., Reference Danoix, Sauvage, Huin, Germain and Gouné2016; Van Landeghem et al., Reference Van Landeghem, Langelier, Gault, Panahi, Korinek, Purdy and Zurob2017). It is worth noting that carbon can be notoriously difficult to quantify by APT partly because of overlaps between atomic and molecular ions, but also its tendency to be detected as part of multiple hits and lost because of pile-up at the detector (Sha et al., Reference Sha, Chang, Smith, Liu and Mittemeijer1992; Thuvander et al., Reference Thuvander, Weidow, Angseryd, Falk, Liu, Sonestedt, Stiller and Andrén2011; Peng et al., Reference Peng, Vurpillot, Choi, Li, Raabe and Gault2018). Carbon-containing molecular ions can also dissociate, with an exchange of kinetic energy that can lead to additional trajectory aberrations that will tend to further broaden the peak in the composition profile (Peng et al., Reference Peng, Zanuttini, Gervais, Jacquet, Blum, Choi, Raabe, Vurpillot and Gault2019b).

Fig. 2. Carbon and manganese composition profiles, red and blue, respectively, along a cylinder encompassing the entire interface within the dataset positioned perpendicular to the interface and with a step size of 0.2 nm.
Here, the locations of the crystallographic pole in the top and bottom grains indicate where the spatial resolution of this measurement will be maximized. Hence, composition profiles were calculated along a series of 4-nm-diameter cylinders positioned at systematically increasing distances from the pole along the interface, as indicated in Figure 3a. Each profile was then fitted with a Gaussian function to derive the local width and amplitude of the peak. In Figure 3b, the cumulative number of carbon atoms detected is plotted as a function of the cumulative number of all atoms detected along each of the cylinders.

Fig. 3. (a) A 5-nm-thick slice through the data that show the interface edge-on and contain the trace of the two (011) poles and corresponding sets of (011) planes. Two normal axes are defined at the crossing between the interface and the poles. A succession of profiles is calculated within a 4-nm-diameter cylinder, and each profile is fitted with a Gaussian function, as shown in inset. (b) Integral profile for each of the corresponding profiles, the color reported in the legend indicates the distance to the pole. (c) FWHM of the fitted Gaussian function for the C (red) and Mn (blue).
This analysis is known as an integral profile and can provide a measure of the solute excess (Krakauer & Seidman, Reference Krakauer and Seidman1993). The thick purple line is the profile obtained at the pole, and it clearly shows the sharpest transition, which contrasts with the transition observed further away from the pole, e.g. 25 nm. Figure 3c reports the change in the FWHM of the composition peak obtained from the fitted Gaussian function. At or near the pole, the FWHM of the peak is in the range of 1 nm for both C and Mn. Similar observations of an erroneous widening of the thin interfacial layer in the reconstructed APT data as a function of the distance of a pole have previously been reported (Araullo-Peters et al., Reference Araullo-Peters, Gault, de Geuser, Deschamps and Cairney2014).
In-Plane Solute Distribution
These significant changes in the local excess motivated a more detailed investigation of the distribution of solutes at the interface. Figure 4a shows a plane view image of the interface, within a 5-nm-thick slice. An iso-composition surface encompasses regions of the APT point cloud where the Mn composition is higher than 6 at% was added. Interestingly, this surface reveals two elongated regions with a high composition of Mn. These appear similar to Mn-decorated dislocations as recently reported (Kuzmina et al., Reference Kuzmina, Herbig, Ponge, Sandlobes and Raabe2015; Kwiatkowski da Silva et al., Reference Kwiatkowski da Silva, Leyson, Kuzmina, Ponge, Herbig, Sandlöbes, Gault, Neugebauer and Raabe2017). These dislocations likely sit at the interface to accommodate the slight misorientation. The distance between the dislocations is approx. 18 nm, which, according to Frank's equation and for typical Burgers vectors of dislocations on the  $\langle 110 \rangle$ planes, would correspond to less than approx. 1° misorientation. In Figure 4b, three 5-nm-diameter cylindrical regions of interest are indicated within the atom map and colored pink, brown, and light blue, respectively. The corresponding composition profiles of Mn and C are plotted in Figures 4c and 4e, respectively. These profiles indicate that there are significant fluctuations of the local composition at the interface; indeed, the peak Mn composition at the dislocations is in the range of 10 at%, while that of carbon is in the range of 8–10 at%. These segregations also explain the fluctuations of the excess revealed in Figure 3b.
$\langle 110 \rangle$ planes, would correspond to less than approx. 1° misorientation. In Figure 4b, three 5-nm-diameter cylindrical regions of interest are indicated within the atom map and colored pink, brown, and light blue, respectively. The corresponding composition profiles of Mn and C are plotted in Figures 4c and 4e, respectively. These profiles indicate that there are significant fluctuations of the local composition at the interface; indeed, the peak Mn composition at the dislocations is in the range of 10 at%, while that of carbon is in the range of 8–10 at%. These segregations also explain the fluctuations of the excess revealed in Figure 3b.

Fig. 4. Distribution of the atoms in the plane of the interface, with an added iso-composition surface viewed (a) from the top and (b) tilted to show the three cylindrical regions of interest used to calculate the composition profiles in (c–e), each profile bounded by a rectangle of the corresponding color.
The Mn segregation at the interface originated from the ferrite growth at 680°C and not at lower temperatures (i.e. during the quench or at room temperature), as the diffusivity of Mn in austenite is already only approx. 10−19 m2/s at 680°C (Gouné et al., Reference Gouné, Danoix, Ågren, Bréchet, Hutchinson, Militzer, Purdy, van der Zwaag and Zurob2015). Regarding C, it has been shown to diffuse even at room temperature, and C segregation could happen during quenching or specimen storage at room temperature (Van Landeghem et al., Reference Van Landeghem, Langelier, Gault, Panahi, Korinek, Purdy and Zurob2017). However, the observed dislocations could carry Mn within the interface and assist the diffusion of C, enhancing the likelihood of carbon diffusing within the interface during the ferritic transformation. Finally, on the basis of thermodynamic arguments, it has previously been shown that the presence of Mn at austenite grain boundaries induces the co-segregation of C (Enomoto et al., Reference Enomoto, White and Aaronson1988). The case of an α/γ interface is likely more complex because of the different phases and associated different thermodynamic interactions on either side of the interface and the uncertainty associated with the properties of the interface itself. We can, however, conclude that C segregation to the α/γ interface is likely, provided that Mn segregation occurs concomitantly during the transformation, strengthening the likelihood of a coupled solute drag mechanism as suggested in Danoix et al. (Reference Danoix, Sauvage, Huin, Germain and Gouné2016).
Grain Boundary Analysis by APT
Background
It is desirable to be able to quantitatively measure the segregation behavior of elements present at grain boundaries in a reliable and reproducible way. Satisfying both of these criteria is required if multiple measurements of grain boundary segregation are to be used comparatively. This is a necessity if a thorough understanding of how the chemical nature of a grain boundary varies as a result of the dissimilar grain boundary physical structure or due to exposure to different environments.
In the case of the ASME SA508 Grade 4N bainitic steel, exposure to the elevated temperature for long periods of time was observed to lead to nonhardening embrittlement. Understanding why this nonhardening embrittlement arose is key if models that accurately predict the safe operational lifetime of the component are to be created. It is also of interest to understand grain boundary embrittlement phenomena for the development of new alloys with longer operational lifetimes. Therefore, prior to determining what had caused the embrittlement of the grain boundaries, a reliable, quantitative measurement of the grain boundary chemistry in its as-received state was required. The following section highlights some of the difficulties that arise when attempting to make quantitative measurements from APT data using the most popular and currently implemented analysis method.
Quantitative measures of solute segregation present at interfaces, commonly calculated using the methods proposed by Krakauer & Seidman (Reference Krakauer and Seidman1993), often reduce the characterization to a single value, i.e. the Gibbsian interfacial excess. However, the previous section highlights some critical challenges when characterizing interfaces using APT, namely chemical inhomogeneity across this surface, the introduction of subjectivity by requisite user-inputs defining where the interface is sampled and the manner in which the analysis is applied, and inaccuracies originating from reconstruction artifacts. While it is not possible to overcome or account for all of these phenomena, it is important that those interpreting such analyses are aware of them and the potential impact they may have on results. Hence, in the subsequent sections, we address some key issues as they relate to the Gibbsian interfacial excess characterization of the chemical nature of a grain boundary using APT.
APT Evaporation Artifacts/Density Changes
A key artifact that has potential to impact the calculation of Gibbsian interfacial excess is the apparent change in atomic density throughout reconstructed APT datasets. This can arise due to the presence of crystallographic poles or due to the different evaporation behavior exhibited by compositionally dissimilar regions.
The measured point density inside the dataset (the number of atoms per unit volume) can sometimes be higher at interfaces than in the surrounding matrix on either side of the interface, as it is the case in Figure 5. As the grain boundary is likely to have a different composition to the surrounding matrix, the unphysically high measured atomic density at the grain boundary is the result of the local magnification effect (Miller & Hetherington, Reference Miller and Hetherington1991). The amplitude of the local magnification effect at interfaces has been shown to be minimized when the interface is perpendicular to the analysis direction during field evaporation (Maruyama et al., Reference Maruyama, Smith and Cerezo2003). Furthermore, the variation in atomic density between a grain boundary and the surrounding matrix has previously been shown to arise in grain boundaries which undergo simulated field evaporation (Oberdorfer et al., Reference Oberdorfer, Eich and Schmitz2013). The authors observed that the change in atomic density at the grain boundary occurred even in simulated materials with homogeneous evaporation fields, indicating that the measured atomic density within APT reconstruction is affected by the structural defect of a grain boundary as well as by the varying evaporation fields of the elements present at the boundary (Oberdorfer et al., Reference Oberdorfer, Eich and Schmitz2013). This was also observed in the analysis of a coherent boundary in a pure Al bicrystal (Wei et al., Reference Wei, Peng, Kühbach, Breen, Legros, Larranaga, Mompiou and Gault2019).

Fig. 5. (a) Distribution of Mn and Ni atoms within the specimen. (b) Atomic density (atoms/nm3) measured throughout the APT tip and (c) variation in the number of atoms detected in per 0.1 nm bin along the region of interest in (a).
Both of the above effects lead to more atoms of each species being erroneously reconstructed at the boundary. Therefore, an apparent excess of all atoms would be observed at the boundary, even in a homogeneous material. If one was to simply measure the number of atoms of element i within a series of sampling bins (of fixed width) across the interface versus distance, it may appear that there is an excess of i atoms when, in reality, i shows no segregation to the interface. To avoid the above phenomenon, it is important to calculate the Gibbsian interfacial excess by carefully applying the equations outlined in Krakauer & Seidman (Reference Krakauer and Seidman1993). The aforementioned aberration effects will also lead to the apparent composition of the interface region being different to the true composition. If one is to report composition, it is, therefore, important to correct for this (Blavette et al., Reference Blavette, Vurpillot, Pareige and Menand2001).
Repeatability of Measurements
A factor that greatly affects the reproducibility of Gibbsian interfacial excess calculations is the large number of parameters that must be selected by the user performing the analysis. These parameters include defining the extents of Grain A and Grain B, the position of the Gibbs dividing surface, the area of the interface that is analyzed, the location the measurement is performed on the interface, and the bin size selected. Varying either of these can have a large effect on the calculated excess values, and it is important that users report the parameters that were used, why they were selected, and how sensitive their results are to changes in the parameters.
Another issue that researchers often fail to account for is the consequence of the region of interest not being perpendicular to the interface. If the analysis direction is not perpendicular to the interface, the calculated Gibbsian interfacial excess value (Γi) will underestimate the true value. This underestimation in Γi arises as, due to the contribution of some of the matrix at all distances along the region of interest, the measured peak composition of segregating species will be lower than if the analysis is performed perpendicularly to the interface.
The positions where Grain A ends and the interface begins and where the interface ends and Grain B begins, respectively, are almost always not clearly defined in experimental data with the interfacial region often taking the form of a tanh function (Fig. 6). Whether this shape is the reflective of the true solute distribution, or arises due to aberrations, cannot be determined. The user performing the analysis must make a subjective decision as to where to define the positions of these boundaries.

Fig. 6. Simulated cumulative plot of the number of P atoms versus the cumulative number of all atoms, showing where two users could define the interface region as beginning and ending.
The selection of the positions defining the extents of the grain boundary can significantly impact the calculation of Γi. Figure 6 demonstrates the way in which two independent users may define the position of the grain boundary encountered in Figure 6.
The effect this has on the calculated Γi, using the method outlined in Equation (1) in the original paper (Krakauer & Seidman, Reference Krakauer and Seidman1993), is not trivial. This is demonstrated by the resulting measurements presented in Table 2. Reducing the sensitivity of the calculated Γi with respect to user input is therefore critical to make such measurements meaningful and robust. The fitting refinement procedure used in Peng et al. (Reference Peng, Lu, Hatzoglou, Kwiatkowski da Silva, Vurpillot, Ponge, Raabe and Gault2019a) removes the requirement for user input in defining the start and end of the interface region. Other statistical approaches may also be implemented.
Table 2. Effect of the Selected Interface Start and End Values Can Have on the Calculated Gibbsian Interfacial Excess Values (Fig. 6 and Assuming Area = 100 nm2 and η = 0.37).
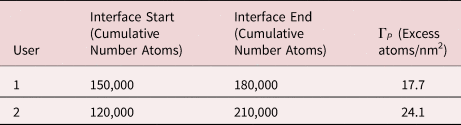
The location of the Gibbs dividing surface within the interface region will also affect the calculated Γi. However, lower and upper bounds can be determined by placing the surface at the very start or end of the interface region.
Loosely Defined Variables
Another issue which influences the reproducibility of results is that the definitions provided in the original paper (Krakauer & Seidman, Reference Krakauer and Seidman1993) are not strict, particularly in the case of more complex material systems. For example, the authors define  $C_i^\alpha$ and
$C_i^\alpha$ and  $C_i^\beta$ as “the atomic compositions of element i in the homogeneous regions of phases α and β, i.e., the bulk regions of the two phases.” However, the segregation of solutes to interfaces can lead to a denuded zone around the interface (Zhao et al., Reference Zhao, De Geuser, Kwiatkowski da Silva, Szczepaniak, Gault, Ponge and Raabe2018), meaning that phases α and β are not homogeneous. Furthermore, precipitate or cluster formation occurs in many material systems and means that individual grains/phases are often not homogeneous.
$C_i^\beta$ as “the atomic compositions of element i in the homogeneous regions of phases α and β, i.e., the bulk regions of the two phases.” However, the segregation of solutes to interfaces can lead to a denuded zone around the interface (Zhao et al., Reference Zhao, De Geuser, Kwiatkowski da Silva, Szczepaniak, Gault, Ponge and Raabe2018), meaning that phases α and β are not homogeneous. Furthermore, precipitate or cluster formation occurs in many material systems and means that individual grains/phases are often not homogeneous.
If this occurs, then what is precisely meant by the definition of the “homogeneous regions of phases α and β” is no longer rigid. Figure 7 demonstrates four different regions in the same material which may be considered “homogeneous” by a user who is calculating Gibssian interfacial excess values. The selection of either of these regions has the potential to greatly affect the calculated Γi values and, therefore, the reproducibility of results.

Fig. 7. Schematic diagram demonstrating the presence of a precipitate free zone adjacent to an interface, and the four different regions that independent users could decide best reflect the “homogeneous” regions of phase α.
In Figure 7, Region 1 may be considered “homogeneous”, as this is the area adjacent to the interface and contains no other phases. However, the choice of Region 2 may also be justified since this region is representative of phase α before the precipitate free zone formed. Region 3 could be selected, as it samples both the region adjacent to the interface and phase α away from the interface, offering a compromise between Region 1 and Region 2. Region 4 selects the matrix of phase α away from the interface but does not incorporate the precipitates in the matrix. This choice could be justified since the precipitates may be a different phase to the α matrix. There is no widely accepted protocol on how to proceed in this circumstance, and a user could reasonably select any of the regions to describe the homogeneous region of phase α. It is, therefore, important that one justifies why and accurately describes how measurements have been made.
Inhomogeneous Interfaces
In the cases of interfaces where solutes are not homogeneously distributed across the interface, the reporting of a single value to describe the segregation leads to a loss of information. Some studies have applied a mesh to the interface to be analyzed and reported a map that shows the variation of Γi across the boundary (Felfer et al., Reference Felfer, Scherrer, Demeulemeester, Vandervorst and Cairney2015; Peng et al., Reference Peng, Lu, Hatzoglou, Kwiatkowski da Silva, Vurpillot, Ponge, Raabe and Gault2019a). This is an improvement, but Γi will still vary for each region depending on the size of the mesh, and these approaches introduce another variable which must be defined by the operator. The maps also provide a qualitative, not quantitative description of segregation; this presents an issue in developing mathematical models which simulate grain boundary segregation.
Discussion
Targeted Specimen Preparation
It is now routine to combine APT with electron microscopy techniques, in particular EBSD or electron channeling contrast imaging (Zaefferer & Elhami, Reference Zaefferer and Elhami2014; Kontis et al., Reference Kontis, Li, Collins, Cormier, Raabe and Gault2018) prior to FIB milling in order to select a specific orientation. There are also possibilities to use such techniques during preparation with, for example, transmission Kikuchi diffraction (Babinsky et al., Reference Babinsky, De Kloe, Clemens and Primig2014; Schwarz et al., Reference Schwarz, Stechmann, Gault, Cojocaru-Mirédin, Wuerz and Raabe2017). The preparation of specimens along particular orientations should, when possible, help maximize the spatial resolution, with the optimal configuration being when the interface is strictly perpendicular to the specimen's main axis to limit distortions associated with the tomographic reconstruction. These aspects have been discussed previously but are not commonly taken into account (Stoffers et al., Reference Stoffers, Barthel, Liebscher, Gault, Cojocaru-Mirédin, Scheu and Raabe2017).
In the analysis of complex interfaces by TEM-based techniques, the challenge is often to find a suitable orientation to visualize the interface edge-on. This has often led to the use of specific bicrystals or model interfaces, which may not have relevance to microstructures encountered in engineering materials. Analyzing interfaces and grain boundaries with the near-atomic resolution by TEM-based techniques, in particular STEM, requires the two grains to have a common zone axis direction that is close to the normal of the sample surface so as to observe the interface edge-on. The possible broadening of the electron beam traveling through the specimen and the possibility that the interface is not straight, which is likely for transformation interfaces such as the one investigated herein, imposes the use of very thin specimens, in the range of 10–30 nm. The width of this same interface measured by EDS in an aberration-corrected STEM is also in the range of several nanometers (Danoix et al., Reference Danoix, Sauvage, Huin, Germain and Gouné2016) and so was that measured by electron-energy loss spectroscopy on model interfaces (Fletcher et al., Reference Fletcher, Garratt-Reed, Aaronson, Purdy, Reynolds and Smith2001). We demonstrated above once again the importance of maximizing the spatial resolution, which can be done by ensuring that a set of low index atomic planes is close to the center of the field of view.
Issues Inherent to Data Processing
The analyses in “Compositional Width of an Interface” also point to a number of shortcomings of the typical approaches used to extract information from the APT reconstruction. The use of composition profiles as a function to the distance to a selected iso-composition surface (i.e., proximity histogram) has now become widespread (Hellman et al., Reference Hellman, Vandenbroucke, Rüsing, Isheim and Seidman2000). Although the concept of such calculations is interesting, its implementation is not without idiosyncrasies. In particular, this approach requires an isosurface, which is calculated on a grid, which is usually smoothed by a Gaussian blurring function, in a process coined delocalization (Hellman et al., Reference Hellman, du Rivage and Seidman2003). This can lead to a strong smoothing of the compositional field and a widening of the actual interface, which is often noticed in the analysis of large populations of precipitates of varying sizes (Martin et al., Reference Martin, Radecka, Sun, Simm, Dye, Perkins, Gault, Moody and Bagot2016). Alternative approaches have been proposed that may alleviate these concerns (Felfer et al., Reference Felfer, Scherrer, Demeulemeester, Vandervorst and Cairney2015; Kwiatkowski da Silva et al., Reference Kwiatkowski da Silva, Ponge, Peng, Inden, Lu, Breen, Gault and Raabe2018; Peng et al., Reference Peng, Lu, Hatzoglou, Kwiatkowski da Silva, Vurpillot, Ponge, Raabe and Gault2019a), but they are not accessible to most, and they systematically require input parameters. Albeit more labor-intensive, using simpler means of data extraction, e.g. composition profiles, often leads to a better understanding of the underlying assumptions made to obtain information. Here, similarly, scientists using APT must understand the limitations of the technique and also potentially accept not to do what is easy, but limit their analysis to regions in the point cloud that are highly resolved, which may require finding a suitable orientation and location to analyze the data more deeply. A first step would already be for the authors to include in their report of APT results, the voxel size and delocalization parameters used in the software they use for processing the data. There have been efforts in some parts of the community to standardize the information reported when discussing APT datasets and, as a community, we should likely build on this preliminary work by Blum et al. (Reference Blum, Darling, Kelly, Larson, Moser, Perez-Huerta, Prosa, Reddy, Reinhard, Saxey, Ulfig, Valley, Moser, Corfu, Darling, Reddy and Tait2017).
The results in Figures 3 and 4 point to the importance of performing two-dimensional mapping of the distribution of solutes at interfaces. This has been discussed in several studies recently (Felfer et al., Reference Felfer, Ceguerra, Ringer and Cairney2013, Reference Felfer, Scherrer, Demeulemeester, Vandervorst and Cairney2015; Felfer & Cairney, Reference Felfer and Cairney2018; Kwiatkowski da Silva et al., Reference Kwiatkowski da Silva, Ponge, Peng, Inden, Lu, Breen, Gault and Raabe2018; Peng et al., Reference Peng, Lu, Hatzoglou, Kwiatkowski da Silva, Vurpillot, Ponge, Raabe and Gault2019a), and tools are becoming more easily available. These tools usually allow for compositional mapping but do not yet include means to see if the observed fluctuations are beyond what would be expected in a random distribution of solutes confined to an interfacial region. These tests are commonly applied in the analysis of APT data (Moody et al., Reference Moody, Stephenson, Ceguerra and Ringer2008) but have so far not been applied in a two-dimensional case.
Although the information from APT is primarily compositional, often structural information is buried in the data (Gault et al., Reference Gault, Moody, Cairney and Ringer2012). This has been known since the inception of APT, with early reports of atomic planes and segregation to crystalline defects (Blavette et al., Reference Blavette, Cadel, Fraczkeiwicz and Menand1999). Through appropriate processing, this information was exploited to push the analysis further. In the investigation of the ternary Fe–0.12 wt%C–2 wt%Mn in “Compositional Width of an Interface”, this was complemented by electron microscopy (Mills, Reference Mills1993). Ignoring this information can lead to misinterpretation of the data, whereas it could be crucial to understand microstructural evolution. The values of the composition of Mn and C at the dislocations imaged herein are 20–30% higher than the peak value reported in Figure 2. Solutes are known to pin dislocations, and the presence of such high concentrations of Mn and C at these will affect their mobility. The interface analyzed here is a moving interface, and to accommodate the progressive displacement of the interface, these dislocations likely need to move. The presence of such high compositions needs to be accounted for in models developed to explain the mobility of these transformation interfaces.
Finally, there have been preliminary reports of trying to correct composition for changes in the atomic density (Sauvage et al., Reference Sauvage, Renaud, Deconihout, Blavette, Ping and Hono2001; Gault et al., Reference Gault, de Geuser, Bourgeois, Gabble, Ringer and Muddle2011a), but these are not widely used and do not correct according to the respective field evaporation behavior of different features. An approach using input from field evaporation simulations was also proposed for precipitates (Blavette et al., Reference Blavette, Vurpillot, Pareige and Menand2001) but has not been used for interfaces.
Is the Gibbs Excess Measurement Fit for Purpose?
In addition to the issues arising when trying to calculate the Gibbsian interfacial excess from APT data, the validity of using the Gibbsian interfacial excess to correlate changes in properties with the evolution of the grain boundary nature in real material systems is debatable. The quantity Γi is a measure of the composition of the interface with respect to the composition of two phases either side of it (i.e., segregation strength). Therefore, in order to compare measurements between different datasets and material systems, it is also necessary to report the composition of the two phases on either side of the interface. Consider a simplistic scenario where two batches of the material are produced. One batch may have a higher overall impurity (C i) level than the other (Table 3), but the segregation behavior of this impurity element to grain boundaries may be different in each system. If grain boundaries from each of these materials were then analyzed, the composition profiles shown in Figure 8 may be collected.

Fig. 8. Cartoon composition profiles across the same type of the interface in two respective batches of the same material with different impurity levels.
Table 3. Variation in Composition of Different Regions in Two Batches of a Material, as well as Calculated Γi Values (Assuming η = 1, A = 1,000 nm2, N = 100,000 atoms, and ξ = 0.5).

It is clear that there is a higher composition of the impurity element, i, at the interface in the “bad batch” material. However, Table 3 shows that the calculated value of Γi is actually higher for the “good batch”.
This raises the question as to what is more important in determining macroscale material properties, the composition of the interface, or the composition of the interface with respect to the matrix. If it is the composition of the interface that is of most importance, then the validity of applying Γi to relate the character of microstructural interfaces to material properties is questionable. Reporting the Gibbsian interfacial excess of each element, together with the composition of phases α and β would provide a more holistic description of the interface.
A key assumption made by Gibbs in his model was that the interface is a 2D plane (Gibbs, Reference Gibbs1948). This is probably not strictly true for many real interfaces. Guggenheim treated the interface as an interphase with a finite thickness (Guggenheim, Reference Guggenheim1950). Since it is known that most grain boundaries do not take the form of idealized 2D features, assuming all segregation is confined to a single plane is likely naive. If this assumption is made, interfacial excess values higher than those permitted by the atomic density of the material are possible. This may be evidence for more than one monolayer of coverage at the interface; however, there is no way to confirm the lattice site location of the excess atoms in the enriched region.
The estimated width of the interface is also extremely important because it determines the transformation kinetics derived from models, e.g. coupled solute drag, reviewed for instance in Gouné et al. (Reference Gouné, Danoix, Ågren, Bréchet, Hutchinson, Militzer, Purdy, van der Zwaag and Zurob2015). It is also related to the binding energy for solute at a moving interface, which is usually derived from such profiles (Danoix et al., Reference Danoix, Sauvage, Huin, Germain and Gouné2016; Van Landeghem et al., Reference Van Landeghem, Langelier, Gault, Panahi, Korinek, Purdy and Zurob2017). An overestimation of the interface's width leads to an underestimation of the solutes’ segregation energy at the interface. Here, by going further into the processing of the data and targeting regions from within the data where the resolution is optimal, the width of the interface can finally be accurately measured and reported.
The use of the Gibbsian interfacial excess values to calculate thermodynamic quantities relies on the assumption that the system is at thermodynamic equilibrium. However, many materials subject to APT are not at thermodynamic equilibrium at the time of analysis. Therefore, Γi should not be used to calculate thermodynamic quantities. In the case of nonequilibrium segregation, the segregation will be a zone of “considerably greater width around the appropriate interface than occurred with the equilibrium mechanism … ” (Hondros et al., Reference Hondros, Seah, Hofmann, Lejček, Cahn and Haasen1996). The authors state that this zone may vary in thickness from the nanometer to micrometer scale (Hondros et al., Reference Hondros, Seah, Hofmann, Lejček, Cahn and Haasen1996). Therefore, assuming all of the segregation is confined to a single plane does not accurately reflect what is physically present in the system and thereby will lead to an overestimation of the interfacial excess.
Conclusion
To conclude, we wanted to provide some perspective on the analysis of transformation interfaces and grain boundaries by APT. Although it is known that the spatial resolution of APT varies across the field of view within a single dataset, we have shown that this resolution affects the width of composition profiles. This allowed us to reveal the segregation of Mn and C within only less than 0.5–0.6 nm, i.e. 2–3 (110) interplanar spacing, specifically around the pole, where the depth resolution is the highest. When analyzed appropriately, the data reveal that the transformation interface is only semi-coherent and contains dislocations that lead to a complex segregation behavior with stronger segregation at the dislocations than at the interface. These details had not been revealed before. While other microscopy techniques tend to optimize the specimen preparation strategy to ensure that the desired observation can be performed, it is not always common practice for this to be achieved during APT sample preparation. We also discussed in detail how the sometimes blind use of the interfacial excess in lieu of the interfacial composition can lead to details of the analysis being lost. In line with other recent work, we challenged the belief that the excess is not affected by trajectory aberrations but also provided some discussion points regarding whether the interfacial excess is always an appropriate metric in the case of complex interfaces where phase transformation has occurred. We expect that these points will help start a discussion within the community.
Funding
B.M.J. and M.P.M. would like to acknowledge financial support from EPSRC EP/P005640/1 and EP/M022803/1. B.M.J. and M.P.M. would also like to thank Rolls-Royce Plc. for financial support and for providing the ASME SA508 Grade 4N bainitic steel.













