No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let 1 ≤ p < ∞, let 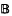 be the open unit ball of lp and let Δ be the open unit disc in ℂ. We prove that there is a holomorphic map
be the open unit ball of lp and let Δ be the open unit disc in ℂ. We prove that there is a holomorphic map 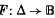 such that F(Δ) is dense in
such that F(Δ) is dense in 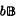 and such that
and such that 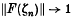 whenever
whenever 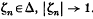 .
.