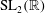Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T13:54:22.528Z Has data issue: false hasContentIssue false
  • English
  • Français

The constructive membership problem for discrete free subgroups of rank 2 of $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathrm{SL}_2(\mathbb{R})$

Part of: Other groups of matrices

Published online by Cambridge University Press:  01 August 2014

B. Eick ,
M. Kirschmer  and
C. Leedham-Green
B. Eick
Affiliation:
Institut Computational Mathematics, TU Braunschweig, Pockelsstrasse 14, 38106 Braunschweig, Germany email [email protected]
M. Kirschmer
Affiliation:
Lehrstuhl D für Mathematik, RWTH Aachen University, Templergraben 64, 52062 Aachen, Germany email [email protected]
C. Leedham-Green
Affiliation:
School of Mathematical Sciences, Queen Mary College University of London, Mile End Road, London E1 4NS, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We exhibit a practical algorithm for solving the constructive membership problem for discrete free subgroups of rank 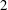$2$ in 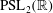$\mathrm{PSL}_2(\mathbb{R})$ or 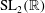$\mathrm{SL}_2(\mathbb{R})$. This algorithm, together with methods for checking whether a two-generator subgroup of 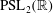$\mathrm{PSL}_2(\mathbb{R})$ or 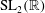$\mathrm{SL}_2(\mathbb{R})$ is discrete and free, have been implemented in Magma for groups defined over real algebraic number fields.

Supplementary materials are available with this article.

MSC classification

Secondary: 20H10: Fuchsian groups and their generalizations
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 17 , Issue 1 , 2014 , pp. 345 - 359
Copyright
© The Author(s) 2014 

References

Assmann, B. and Eick, B., ‘Computing polycyclic presentations of polycyclic matrix groups’, J. Symbolic Comput. 40 (2005) 1269–1284.Google Scholar
Beals, R., ‘Improved algorithms for the Tits alternative’, Groups and computation III , Ohio State University Mathematical Research Institute Publications 8 (eds Kantor, W. M. and Seress, A.; de Gruyter, New York, 2001) 63–77.Google Scholar
Beardon, A. F., The geometry of discrete groups , Graduate Texts in Mathematics 91 (Springer, New York, 1983).Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997) no. 3–4, 235–265.Google Scholar
Cohen, H., A course in computational algebraic number theory (Springer, 1993).Google Scholar
Detinko, A. S., Eick, B. and Flannery, D. L., ‘Computing with matrix groups over infinite fields’, Groups St Andrews 2009 in Bath Volume 1 , London Mathematical Society Lecture Note Series 387 (Cambridge University Press, Cambridge, 2010) 256–269.Google Scholar
Detinko, A. S., Flannery, D. L. and O’Brien, E. A., ‘Algorithms for the Tits alternative and related problems’, J. Algebra 344 (2011) 397–406.Google Scholar
Fricke, R. and Klein, F., Vorlesungen über die Theorie der Automorphen Functionen (Teubner, 1897).Google Scholar
Katok, S., Fuchsian groups , Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 1992).Google Scholar
Kern-Isberner, G. and Rosenberger, G., ‘Über Diskretheitsbedingungen und die Diophantische Gleichung a x 2 + b y 2 + c z 2 = d x y z ’, Arch. Math. (Basel) 34 (1980) no. 6, 481–493.Google Scholar
Lyndon, R. C. and Schupp, P. E., Combinatorial group theory (Springer, 1977).Google Scholar
Miller, C. F., On group-theoretic decision problems and their classification (Princeton University Press, Princeton, 1971).Google Scholar
Ostheimer, G., ‘Practical algorithms for polycyclic matrix groups’, J. Symbolic Comput. 28 (1999) no. 3, 361–379.Google Scholar
Purzitsky, N., ‘Two-generator discrete free products’, Math. Z. 126 (1972) 209–223.Google Scholar
Purzitsky, N., ‘Real two-dimensional representations of two-generator free groups’, Math. Z. 127 (1972) 95–104.CrossRefGoogle Scholar
Purzitsky, N., ‘A cutting and pasting of noncompact polygons with applications to Fuchsian groups’, Acta Math. 143 (1979) 233–250.Google Scholar
Rosenberger, G., ‘Fuchssche Gruppen, die freies Produkt zweier zyklischer Gruppen sind, und die Gleichung x 2 + y 2 + z 2 = x y z ’, Math. Ann. 199 (1972) 213–227.Google Scholar
Supplementary material: File

Eick Supplementary Material

Supplementary Material

Download Eick Supplementary Material(File)
File 7.7 KB