In Chapter X of The Structure of appearance the concept of linear array is given in terms of a two-place predicate “M” for matching. Also given in terms of “M” is the two-place predicate “B” for besideness. It is unnecessary to discuss here the formal definitions, since Goodman has proved that they are adequate to describe our presystematic ideas of linear array and besideness. Thus, we shall be concerned with a finite collection of elements with an assigned order satisfying:

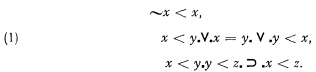
This order is not uniquely defined by the relation M; either of the two end points may be taken as the ‘first.’ We shall represent the order in diagrams by the convention that x is to the left of y if x < y. For x ≠ y, we shall define S(x, y), the distance between x and y, as one more than the number of elements strictly between them, in the order <; also, S(x, x) = 0. Thus S(x, y) = 1 if and only if x is beside y. The order is connected with the reflexive and symmetric matching relation M by the conditions

(2) Bx, y ⊃ Mx, y,

(3) Mx, y▪x ≤; u ≤ ν ≤ y▪ ⊃ ▪Mu, ν.

Condition (3) is what Goodman calls the weak mapping rule. All arrays considered here must satisfy (3). To avoid trivial cases, we shall assume that not all elements match. There is a strong mapping rule,

(4) Mx, y▪ ∼Mu, ν▪ ▪ ▪S(x, y) < S(u, ν),

which it is desirable, but not necessary, for arrays to satisfy. An array which does satisfy (4) is called regular.

In this paper we consider certain formal properties of deductive systems which, in special cases, reduce to the property of ω-consistency; and we then seek to understand the significance of these properties by relating them to the use of models in providing interpretations of the deductive systems.

The notion of ω-consistency arises in connection with deductive systems of arithmetic. For definiteness, let us suppose that the system is a functional calculus whose domain of individuals is construed as the set of natural numbers, and that the system possesses individual constants ν0, ν1, ν2, … such that νi functions as a name for the number i. Such a system is called ω-consistent, if there is no well-formed formula A(x) (in which x is the only free variable) such that A(ν0), A(ν1), A(ν2), … and ∼(x)A(x) are all formal theorems of the system, where A(νi) is the formula resulting from A(x) by substituting the constant νi for each free occurrence of the individual variable x.

Now consider an arbitrary applied functional calculus F, and let Γ be any non-empty set of its individual constants. In imitation of the definition of ω-consistency, we may say that the system F is Γ-consistent, if it contains no formula A(x) (in which x is the only free variable) such that ⊦ A (α) for every constant α in Γ, and also ⊦ ∼(x)A(x) (where an occurrence of “⊦” indicates that the formula which it precedes is a formal theorem). We easily see that the condition of Γ-consistency is equivalent to the condition that the system F contain no formula B(x) such that ⊦ ∼ B(α) for each α in Γ, and also ⊦ (∃x)B(x).

1. In this paper we construct a model for part of the system NF of [4]. Specifically, we define a relation R of natural numbers such that the R-relativiseds of all the axioms except P9 of Hailperin's finitization [2] of NF become theorems of say Zermelo set theory. We start with an informal explanation of the model.

2. Scrutiny of P1-P8 of [2] suggests that a model for these axioms might be constructed by so to speak starting with a universe that contained a “universe set” and a “cardinal 1”, and passing to its closure under the operations implicit in P1-P7, viz., the Boolean, the domain, the direct product, the converse, and the mixtures of product and inverse operations represented by P3 and P4. To obtain such closure we must find a way of representing the operations that involve ordered pairs and triples.

We take as universe of the model the set of natural numbers ω; we let 0 represent the “universe set” and 1 represent “cardinal 1”. Then, in order to be able to refer in the model to the unordered pair of two sets, we determine all representatives of unordered pairs in advance by assigning them the even numbers in unique fashion (see d3 and d25); we can now define the operations that involve ordered pairs and triples, and obtain closure under them using the odd numbers. It remains to weed out, as in d26, the unnecessary sets so as to satisfy the axiom of extensionality.

In previous papers, Post, Webb, Götlind and the present author have described some Sheffer functions (in Swift's terminology, “independent binary generators”) in m-valued logic. Professor J. Dean Swift has recently isolated the symmetric Sheffer functions of 3-valued logic. In the present paper, we will prove some properties of Sheffer functions in m-valued logic and isolate all of the Sheffer functions of 3-valued logic.

Before we proceed we will define some terms which we will find convenient. A set of functions in m-valued logic is functionally complete, if the set of the functions which can be defined explicitly from the functions of the set is exactly the set of all functions of m-valued logic. A function is functionally complete, if its unit set is functionally complete. A Sheffer function is a two-place functionally complete function. If i and j are truth values (1 i, j ≤ m), we will say i ~ j (D), if D is a decomposition of the truth values 1, …, m into 2 or more disjoint non-empty classes and i and j are elements of the same class. A binary function f(p, q) satisfies the substitution law for a decomposition D, if for any truth values h, i, j, k, whenever h ~ j (D) and i~k(D), then f(h, i) ~ f(j, k) (D). The function f(p,q) satisfies the co-substitution law for D, if for any truth values h, i, j, k, whenever f(h, i) ~ f(j, k) (D), then h ~ j (D) or i ~ k (D). We will say f(p, q) has the proper substitution property, if there is a decomposition of the truth values into less than m classes for which it satisfies the substitution law.

The decision procedures to be described in this paper constitute simplifications of methods previously developed by G. H. von Wright. The decision problems for both the systems under consideration have already been solved, but the known solutions are hopelessly impractical. Our methods for S4 and M, while not “practical” in the sense that they can be applied quickly and easily to any formula, do constitute a vast improvement over any other known methods. It appears, for example, that our methods (with the aid of very little ingenuity) will yield decisions readily when applied to modal functions of degree two (or less) with three (or fewer) distinct propositional variables.