The characterization of classes of r.e. sets by their index sets has proved valuable in producing new results about the r.e. sets and degrees. The classic example is Yates' proof [5, Theorem 7] of Sacks' density theorem for r.e. degrees using his classification of {e: We ≤TD) as Σ3(D) whenever D is r.e. Theorem 1 of this paper is a refinement of this index set theorem of Yates which has already proved to have interesting consequences about the r.e. degrees. This theorem was originally announced by Kallibekov [1, Theorem 1]. Kallibekov there proposed a new and ingenious method for doing priority arguments which has also since been used by Kinber [2]. Unfortunately his proof to this particular theorem contains an error. We have a totally different proof using standard techniques which is of independent interest.

The proof to Theorem 1 is an infinite injury priority argument. In §1 therefore we give a short summary of the infinite injury priority method. We draw heavily on the exposition of Soare [4] where a complete description of the method is given along with many examples. In §2 we prove the main theorem and also give what we think are the most interesting corollaries to this theorem announced by Kallibekov. In §3 we prove a theorem about Σ3 sets of indices of r.e. sets. This theorem is a strengthening of a theorem of Kinber [2, Theorem 1] which was proved using a modification of Kallibekov's technique. As application, we use our theorem to show that an r.e. set A has supersets of every r.e. degree iff A is not simple.

Let T be a countable complete theory and C(T) the category whose objects are the models of T and morphisms are the elementary maps. The main object of this paper will be the study of C(T). The idea that a better understanding of the category may give us model theoretic information about T is quite natural: The (semi) group of automorphisms (endomorphisms) of a given structure is often a powerful tool for studying this structure. But certainly, one of the very first questions to be answered is: “to what extent does this category C(T) determine T?”

There is some obvious limitation: for example let T0 be the theory of infinite sets (in a language containing only =) and T1 the theory, in the language ( =, U(ν0),f(ν0)) stating that:

(1) U is infinite.

(2)f is a bijective map from U onto its complement.

It is quite easy to see that C(T0) is equivalent to C(T1). But, in this case, T0 andT1 can be “interpreted” each in the other. To make this notion of interpretation precise, we shall associate with each theory T a category, loosely denoted by T, defined as follows:

(1) The objects are the formulas in the given language.

(2) The morphisms from into are the formulas such that

(i.e. f defines a map from ϕ into ϕ; two morphisms defining the same map in all models of T should be identified).

The category of enumerations over P1 is investigated. Objects are the enumerations of the set of partial recursive functions in one variable φ: N → P1 where φ is a total effective function from the natural numbers N onto P1.

To each a ∈ P1 we call φ−1(a) the set of all indices for a, the fibre over a.

Morphisms from one enumeration φ to another one ψ are (partial) recursive functions f, for which φ(n) = ψ(f(n)) holds for all n where f is denned, i.e. f is fibrepreserving. They are also called translators if f is total. The existence of a translator induces a partial ordering on the enumerations:

Let φ ≤ ψ, iff there exists a translator f with φ = ψ·f; φ ≡ ψ iff φ ≤ ψ and ψ ≤ φ. Two enumerations are called incomparable iff φ ≰,ψ and ψ ≰ φ.

Given a recursively enumerable family of enumerations {φi}i∈ω then their direct sum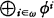 = π is defined by a bijective recursive pairing function g(i, n) (e.g. g(i, n) = (i + n)(i + n + 1)/2 + i) summing up the φi by φi(n) = 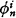= πg(i, n) into π. We also say π decomposes into .

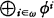Direct sums satisfy the universal property of sums in categories.

We want to operate decompositiontheory on special kinds of objects in our category, the Gödelnumberings and the Friedbergnumberings.

A Gödelnumbering φ is defined by (a) enumeration theorem (i.e. φ is object of our category) and (b) 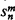-theorem, which means that each m + n-place p.r. function can be effectively replaced by an enumeration of n-place p.r. functions given by means of the total 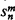-function (see Rogers [3]).

Let κB be the least cardinal for which the Baire category theorem fails for the real line R. Thus κB is the least κ such that the real line can be covered by κ many nowhere dense sets. It is shown that κB cannot have countable cofinality. On the other hand it is consistent that the corresponding cardinal for 2ω1 be ℵω. Similar questions are considered for the ideal of measure zero sets, other ω1, saturated ideals, and the ideal of zero-dimensional subsets of Rω1.

Frege's conception of reference has been interpreted as calling for a completely extensional language, on the grounds that according to it the reference of a complex expression is a function of the references of its parts. To meet this demand and still allow for oblique contexts, one uses Frege's idea that in an oblique context an expression has as reference what is ordinarily its sense.

A purely extensional formalized intensional logic was constructed in the 1940s by Alonzo Church: his logic of sense and denotation [2], [3]. The ambiguity of the “direct” and “oblique” reference of an expression is avoided. For each denoting expression A there is an expression A denoting its sense, which then replaces A in “oblique” contexts. A consequence of this approach is that for each natural number n, in a context with n-fold embedding of intensional operators A is paraphrased by the result of iterating the operation à n times, so that A is treated as if it were infinitely ambiguous. Church's underlying logic is a simple theory of types, in fact just an expansion of the extensional typed λ-calculus so as to contain ωth-order predicate logic.

In this paper we study a variant of Church's logic that admits a possible-worlds semantics, i.e. a version of Church's Alternative (2) [3, pp. 4–5], [4]. This type of logic has been perspicuously formulated by David Kaplan [11], [12], and we follow his version.

In §1 we formulate Kaplan's logic L-Church-O with two alterations: the typed λ-calculus is replaced by combinators, and unlike Kaplan (but like Church) we allow concepts (that is, senses) that are not concepts of anything.

Jockusch and Posner [4] showed that every minimal ω-degree is GL2. This is achieved by exhibiting a function f recursive in 0′ which dominates every function of minimal ω-degree. The function f has the peculiar property that for every s, f(s) is defined after a search (using 0′) over the power set of Ls (Gödel's constructible hierarchy at the level s). It can be seen that a function defined in a similar manner over an infinite successor cardinal k will not be a total function, since for example if k = ρ+, then f(ρ) will not be defined until after all the subsets of ρ have been examined, and this will take at least k steps. The following questions then naturally arise: (i) For successor cardinals k, is there a function dominating every set of minimal k-degree? (ii) For arbitrary cardinals k, is every minimal k-degree GL2 (i.e. b″ = (b ∨ 0′) for b of minimal k-degree)? In this paper we answer (i) in the negative and provide a positive answer to (ii), assuming V = L. We show in fact that if k is a successor cardinal and h ≤k 0′, then there is a function of minimal k-degree below 0′ not dominated by h (Theorem 1). This implies that any refinement of the function f described above will not be able to remove the difficulties encountered. On the other hand, we introduce the notion of ‘strong domination’ to provide a positive answer to (ii) (Theorem 2 and Corollary 1). We end this paper by indicating that for limit cardinals k, there is a function below 0′ dominating every function of minimal k-degree.

The following problem is studied: How large and how small can the Löwenheim and Hanf numbers of unbounded logics be in relation to the most common large cardinals? The main result is that the Löwenheim number of the logic with the Härtig-quantifier can be consistently put in between any two of the first weakly inaccessible, the first weakly Mahlo, the first weakly compact, the first Ramsey, the first measurable and the first supercompact cardinals.

The structure (D, ≤) of the Turing degrees under Turing reducibility is quite complicated. This is true even if we restrict our attention to the substructure (R, ≤) of r.e. degrees. However, the theorems which imply that these structures are complicated all involve ad hoc constructions of sets having the desired reducibility relations. The complexity disappears when we turn to degrees occurring in nature. Of the degrees in R, only 0 and 0′ seem natural. In D, only 0, 0′, 0″, …, 0ω, 0ω+1, … (and on into the transfinite) seem natural. Thus the natural degrees appear to be wellordered, with successors given by Turing jump.

If this is true, one would like to prove it. Of course the first problem is to make the concept of naturalness more precise. The following requirements seem plausible: a natural degree should be definable, its definition should relativise to an arbitrary degree, and this relativisation should preserve reducibility relations among natural degrees. Thus to each natural degree c is associated a definable fc: D → D so that fc(0) = c and ∀d(d ≤ fc(d)). Moreover, b ≤ c iff ∀d(fb(d) ≤, fc(d)). To be specific, let us take the definability of fc to mean that fc ∈ L(R).

If P is a property of degrees, we say P holds almost everywhere (a.e.) iff ∃c∀d ≥: c P(d). For f, g: D → D, let f ≤mgiff f(d) ≤ g(d) a.e. Define f′ by f′(d) = f{d)′, and let M = {f: D → D/f ∈ L(R) ∧ d ≤ f(d) a.e.}. The following conjecture is due to D. A. Martin:

Conjecture. M is prewellordered by ≤m. If f ∈ M has rank α in ≤m, then f′ has rank α + 1.

We distinguish between two kinds of mathematical assertions: objective and constructive. An objective assertion describes the universe of mathematical objects; a constructive one describes the (idealized) mathematician's ability to find mathematical objects with various properties. The familiar formalizations of classical mathematics are based on formal languages designed for expressing objective assertions only. The constructivist program stresses, on the contrary, the importance of constructive assertions; moreover, intuitionism claims that constructive activities of the mind constitute the very subject matter of mathematics, and thus questions the semantic status of objective assertions.

The purpose of this paper is to show that classical mathematics can be extended to include constructive sentences, so that both objective and constructive properties can be discussed in the framework of the same theory. To achieve this goal, we introduce a new property of mathematical objects, calculability.

The word “calculable” may be applied to objects of various types: natural numbers, integers, rational or real numbers, polynomials with rational or real coefficients, etc. In each case it has a different meaning, so that actually we define not one, but many new properties.

A recent result of J.P. Burgess [1] states:

Theorem 0. Let F be a multifunction from an analytic subset T of a Polish space to a Polish space X. If F is Borel measurable, Graph(F) is coanalytic in T × X and F(t) is nonmeager in its closure for each t Є T, then F admits a Borel measurable selector.

The above result unifies and significantly extends earlier results of H. Sarbadhikari [8], S.M. Srivastava [9] and G. Debs (unpublished). The reader is referred to [1] for details.

The aim of this article is to give an effective version of Theorem 0. We do this by proving a basis theorem for Π11 sets which are nonmeager in their closure and satisfy a local version of the measurability condition in Theorem 0. Our basis theorem generalizes a well-known result of P.G. Hinman [4] and S.K. Thomason [10] (see also [5] and [7, 4F.20]). Our methods are similar to those used by A. Louveau to prove that a , σ-compact set is contained in a , σ-compact set (see [7, 4F.18]).

The paper is organized as follows. §2 is devoted to preliminaries. In §3, we prove the basis theorem and deduce as a consequence an effective version of Theorem 0. We show in §4 how our methods can be used to give alternative proofs of some known results.

Discussions with R. Barua, B.V. Rao and V.V. Srivatsa are gratefully acknowledged. I am indebted to J.P. Burgess for drawing my attention to an error in an earlier draft of this paper.

It is known that every < ε0-recursive function is also a primitive recursive functional. Kreisel has proved this by means of Gödel's functional-interpretation, using that every < ε0-recursive function is provably recursive in Heyting's arithmetic [2, §3.4]. Parsons obtained a refinement of Kreisel's result by a further examination of Gödel's interpretation with regard to type levels [3, Theorem 5], [4, §4]. A quite different proof is provided by the research into extensions of the Grzegorczyk hierarchy as done by Schwichtenberg and Wainer: this yields another characterization of the < ε0-recursive functions from which easily appears that these are primitive recursive functionals (see [5] in combination with [6, Chapter II]).

However, these proofs are indirect and do not show how, in general, given a definition tree of an ordinal recursive functional, transfinite recursions can be replaced (in a straightforward way) by recursions over wellorderings of lower order types. The argument given by Tait in [9, pp. 189–191] seems to be an improvement in this respect, but the crucial step in it is (at least in my opinion) not very clear.

Let P0 be the subsystem of Peano arithmetic obtained by restricting induction to bounded quantifier formulas. Let M be a countable, nonstandard model of P0 whose domain we suppose to be the standard integers. Let T be a recursively enumerable extension of Peano arithmetic all of whose existential consequences are satisfied in the standard model. Then there is an initial segment M′ of M which is a model of T such that the complete diagram of M′ is Turing reducible to the atomic diagram of M. Moreover, neither the addition nor the multiplication of M is recursive.

Flipping properties were introduced in set theory by Abramson, Harrington, Kleinberg and Zwicker [1]. Here we consider them in the context of arithmetic and link them with combinatorial properties of initial segments of nonstandard models studied in [3]. As a corollary we obtain independence resutls involving flipping properties.

We follow the notation of the author and Paris in [3] and [2], and assume some knowledge of [3]. M will denote a countable nonstandard model of P (Peano arithmetic) and I will be a proper initial segment of M. We denote by N the standard model or the standard part of M. X ↑ I will mean that X is unbounded in I. If X ⊆ M is coded in M and M ≺ K, let X(K) be the subset of K coded in K by the element which codes X in M. So X(K) ⋂ M = X.

Recall that M ≺IK (K is an I-extension of M) if M ≺ K and for some c∈K,

In [3] regular and strong initial segments are defined, and among other things it is shown that I is regular if and only if there exists an I-extension of M.

The purpose of this paper is to study a formal system PA(Q2) of first order Peano arithmetic, PA, augmented by a Ramsey quantifier Q2 which binds two free variables. The intended meaning of Q2xx′φ(x, x′) is that there exists an infinite set X of natural numbers such that φ(a, a′) holds for all a, a′ Є X such that a ≠ a′. Such an X is called a witness set for Q2xx′φ(x, x′). Our results would not be affected by the addition of further Ramsey quantifiers Q3, Q4, …, Here of course the intended meaning of Qkx1 … xkφ(x1,…xk) is that there exists an infinite set X such that φ(a1…, ak) holds for all k-element subsets {a1, … ak} of X.

Ramsey quantifiers were first introduced in a general model theoretic setting by Magidor and Malitz [13]. The system PA{Q2), or rather, a system essentially equivalent to it, was first defined and studied by Macintyre [12]. Some of Macintyre's results were obtained independently by Morgenstern [15]. The present paper is essentially self-contained, but all of our results have been directly inspired by those of Macintyre [12].

After some preliminaries in §1, we begin in §2 by giving a new completeness proof for PA(Q2). A by-product of our proof is that for every regular uncountable cardinal k, every consistent extension of PA(Q2) has a k-like model in which all classes are definable. (By a class we mean a subset of the universe of the model, every initial segment of which is finite in the sense of the model.)