Published online by Cambridge University Press: 12 March 2014
We discuss the existence of universal spaces (either in the sense of embeddings or continuous images) for some classes of scattered Eberlein compacta. Given a cardinal κ, we consider the class δκof all scattered Eberlein compact spaces K of weight ≤ κ and such that the second Cantor-Bendixson derivative of K is a singleton. We prove that if κ is an uncountable cardinal such that κ = 2≤κ, then there exists a space X in δκ such that every member of δκ is homeomorphic to a retract of X. We show that it is consistent that there does not exist a universal space (either by embeddings or by mappings onto) in 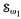 . Assuming that
. Assuming that 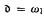 = ω1, we prove that there exists a space X ∈
= ω1, we prove that there exists a space X ∈ 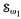 which is universal in the sense of embeddings. We also show that it is consistent that there exists a space X bΕ
which is universal in the sense of embeddings. We also show that it is consistent that there exists a space X bΕ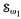 , universal in the sense of embeddings, but δω1 does not contain an universal element in the sense of mappings onto.
, universal in the sense of embeddings, but δω1 does not contain an universal element in the sense of mappings onto.