Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T17:06:08.115Z Has data issue: false hasContentIssue false
  • English
  • Français

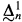sets of reals

Published online by Cambridge University Press:  12 March 2014

Joan Bagaria  and
W. Hugh Woodin
Joan Bagaria
Affiliation:
Departament de Lògica, Història I Filosofia de la Ciència, Universitat de Barcelona, Baldiri i Reixach, s/n, 08028 Barcelona, Spain E-mail: [email protected]
W. Hugh Woodin
Affiliation:
Department of Mathematics, University of California, Berkeley, Berkeley, CA 94720, USA E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Some of the most striking results in modern set theory have emerged from the study of simply-definable sets of real numbers. Indeed, simple questions like: what are the posible cardinalities?, are they measurable?, do they have the property of Baire?, etc., cannot be answered in ZFC.

When one restricts the attention to the analytic sets, i.e., the continuous images of Borel sets, then ZFC does provide an answer to these questions. But this is no longer true for the projective sets, i.e., all the sets of reals that can be obtained from the Borel sets by taking continuous images and complements. In this paper we shall concentrate on particular projective classes, the 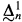, and using forcing constructions we will produce models of ZFC where, for some n, all 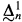, sets have some specified property. For the definition and basic facts about the projective classes 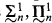, and 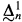, as well as the Kleene (or lightface) classes 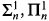, and 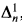, we refer the reader to Moschovakis [19].

The first part of the paper is about measure and category. Early in this century, Luzin [16] and Luzin-Sierpiński [17] showed that all analytic (i.e., 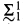) sets of reals are Lebesgue measurable and have the property of Baire.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 4 , December 1997 , pp. 1379 - 1428
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bagaria, J., Definable forcing and regularity properties of projective sets of reals, Ph.D. thesis, Berkeley, 1991.Google Scholar
[2]Bagaria, J., The preservation of forcing axioms under forcing with measure algebras, unpublished, 1992.Google Scholar
[3]Bagaria, J., Fragments of Martin's axiom and sets of reals, Annals of Pure and Applied Logic, vol. 69 (1994), pp. 1–25.CrossRefGoogle Scholar
[4]Bartoszyński, T., Additivity of measure implies additivity of category, Transactions of the American Mathematical Society, vol. 281 (1984), no. 1, pp. 209–213.CrossRefGoogle Scholar
[5]David, R., reals, Annals of Mathematical Logic, vol. 23 (1982), pp. 121–125.CrossRefGoogle Scholar
[6]Fremlin, D., Measure algebras, Handbook of Boolean algebras (Monk, J. Donald with Bonnet, Robert, editor), Elsevier Science Publishers B.V., 1989.Google Scholar
[7]Gödel, K., The consistency of the axiom of choice and of the generalized continuum hypothesis, Proceedings of the National Academy of Sciences of the United States of America, vol. 24 (1938), pp. 556–557.CrossRefGoogle ScholarPubMed
[8]Halmos, P. R., Measure theory, van Nostrand-Reinhold, Princeton, New Jersey, 1950.CrossRefGoogle Scholar
[9]Harrington, L., Long projective well-orderings, Annals of Mathematical Logic, vol. 12 (1977), pp. 1–24.CrossRefGoogle Scholar
[10]Harrington, L. and Shelah, S., Some exact equiconsistency results in set theory, Notre Dame Journal of Formal Logic, vol. 26 (1985), no. 2, pp. 178–188.CrossRefGoogle Scholar
[11]Jech, T., Set theory, Academic Press, 1978.Google Scholar
[12]Judah, H. and Shelah, S., sets of reals, Annals of Pure and Applied Logic, vol. 42 (1989), no. 3, pp. 207–223.Google Scholar
[13]Judah, H. and Shelah, S., sets of reals, this Journal, vol. 58 (1993), no. 1, pp. 72–80.Google Scholar
[14]Koppelberg, S., General theory of Boolean algebras, Handbook of Boolean algebras (by Monk, J. Donald with Bonnet, Robert, editor), Elsevier Science Publishers B.V., 1989.Google Scholar
[15]Kunen, K., (κ, λ*)-gaps under MA, handwritten notes, 1976.Google Scholar
[16]Luzin, N. N., Sur la classification de M. Baire, Comptes Rendus de l'Académie des Sciences Paris, vol. 164 (1917), pp. 91–94.Google Scholar
[17]Luzin, N. N. and Sierpiński, W., Sur un ensemble non measurable B, Journal de Mathématiques. Neuviéme Série, vol. 2 (1923), pp. 53–72.Google Scholar
[18]Martin, D. and Solovay, R., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[19]Moschovakis, Y. N., Descriptive set theory, North-Holland, 1980.Google Scholar
[20]Oxtoby, J. C., Measure and category, Springer-Verlag, 1971.CrossRefGoogle Scholar
[21]Raisonnier, J. and Stern, J., The strength of measurability hypotheses, Israel Journal of Mathematics, vol. 50 (1985), no. 4, pp. 337–349.CrossRefGoogle Scholar
[22]Roitman, J., Adding a random or a Cohen real: topological consequences and the effect on Martin's axiom, Fundamenta Mathematicae, vol. CIII (1979), pp. 47–60.CrossRefGoogle Scholar
[23]Shelah, S., Can you take Solovay's inaccessible away?, Israel Journal of Mathematics, vol. 48 (1984), no. 1, pp. 1–47.CrossRefGoogle Scholar
[24]Solovay, R., A model of set-theory in which every set of reals is Lebesgue measurable, Annals of Mathematics (1970), pp. 1–56.Google Scholar
[25]Solovay, R. and Tennenbaum, S., Iterated Cohen extensions and Souslin's problem, Annals of Mathematics, vol. 94 (1971), pp. 201–245.CrossRefGoogle Scholar
[26]Truss, J., Sets having calibre ℵ1, Logic colloquium '76, North-Holland, Oxford, pp. 595–612.Google Scholar
[27]Woodin, W. H., On the strength of projective uniformization, Logic colloquium '81 (Stern, J., editor), pp. 365–383.Google Scholar
[28]Woodin, W. H., Discontinuous homomorphisms of C (Ω) and set theory, Ph.D. dissertation, University of California, Berkeley, 1984.Google Scholar