Hostname: page-component-7479d7b7d-k7p5g Total loading time: 0 Render date: 2024-07-15T21:05:40.989Z Has data issue: false hasContentIssue false
  • English
  • Français

Filter Logics on ω

Published online by Cambridge University Press:  12 March 2014

Matt Kaufmann
Matt Kaufmann*
Affiliation:
Purdue University, West Lafayette, Indiana 47907
Get access Rights & Permissions [Opens in a new window]

Abstract

Logics LF(M) are considered, in which M (“most”) is a new first-order quantifier whose interpretation depends on a given filter F of subsets of ω. It is proved that countable compactness and axiomatizability are each equivalent to the assertion that F is not of the form {(⋂F) ∪ X: ∣ω − X∣ < ω} with ∣ω − ⋂F∣ = ω. Moreover the set of validities of LF (M) and even of 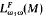depends only on a few basic properties of F. Similar characterizations are given of the class of filters F for which LF (M) has the interpolation or Robinson properties. An omitting types theorem is also proved. These results sharpen the corresponding known theorems on weak models (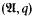, where the collection q is allowed to vary. In addition they provide extensions of first-order logic which possess some nice properties, thus escaping from contradicting Lindström's Theorem [1969] only because satisfaction is not isomorphism-invariant (as it is tied to the filter F). However, Lindström's argument is applied to characterize the invariant sentences as just those of first-order logic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 1 , March 1984 , pp. 241 - 256
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bruce, K. [1978a], Ideal models and some not so ideal problems in the model theory of L(Q), this Journal, vol. 43, pp. 304–321.Google Scholar
Bruce, K. [1978b], Model-theoretic forcing in logic with a generalized quantifier, Annals of Mathematical Logic, vol. 13, pp. 225–265.CrossRefGoogle Scholar
Buechler, S. [1980], Ideal models and uniform validity (preprint).Google Scholar
Ebbinghaus, H.-D. [1984], Abstract model theory and stronger logics: an introductory vademecum, Chapter II in Higher model theory: Logics of mathematical concepts (Barwise, J. and Feferman, S., editors), Springer-Verlag, Berlin (to appear).Google Scholar
Ebbinghaus, H.-D. and Ziegler, M. [198?], Interpolation in Logiken monotoner Systeme, Archiv für Mathematische Logik und Grundlagenforschung (to appear).Google Scholar
Flum, J. [1984], Characterizing logics, Chapter III in Higher model theory: Logics of mathematical concepts (Barwise, J. and Feferman, S., editors), Springer-Verlag, Berlin (to appear).Google Scholar
Guichard, D. [1980], A many-sorted interpolation theorem for L(Q), Proceedings of the American Mathematical Society, vol. 80, pp. 469–474.Google Scholar
Kaufmann, M. [1981a], Filter logics, this Journal, vol. 46, p. 192.Google Scholar
Kaufmann, M. [1981b], Filter logics: filters on ω1, Annals of Mathematical Logic, vol. 20, pp. 155–200.CrossRefGoogle Scholar
Kaufmann, M. [1984], The quantifier “there exist uncountably many” and some of its relatives, Chapter IV in Higher model theory: Logics of mathematical concepts (Barwise, J. and Feferman, S., editors), Springer-Verlag, Berlin (to appear).Google Scholar
Keisler, H. J. [1970], Logic with the quantifier “there exist uncountably many”, Annals of Mathematical Logic, vol. 1, pp. 1–93.CrossRefGoogle Scholar
Keisler, H. J. [1971], Model theory for infinitary logic, North-Holland, Amsterdam.Google Scholar
Lindström, P. [1969], On extensions of elementary logic, Theoria, vol. 35, pp. 1–11.CrossRefGoogle Scholar
Makowsky, J. and Mundici, D. [1984]. Abstract equivalence relations, Chapter XIX in Higher model thtory: Logics of mathematical concepts (Barwise, J. and Feferman, S., editors), Springer-Verlag, Berlin (to appear).Google Scholar
Sun, X. [1981], Model theory in Lω1ω(Q). Part I: Consistency property and its applications(preprint).Google Scholar