Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-19T06:37:21.558Z Has data issue: false hasContentIssue false
  • English
  • Français

Dual weak pigeonhole principle, pseudo-surjective functions, and provability of circuit lower bounds

Published online by Cambridge University Press:  12 March 2014

Jan Krajíček
Jan Krajíček*
Affiliation:
Mathematical Institute, Academy of Sciences, Žitná 25, Prague 1, CZ-115 67, The Czech Republic, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This article is a continuation of our search for tautologies that are hard even for strong propositional proof systems like EF. cf. [14, 15]. The particular tautologies we study, the τ-formulas. are obtained from any 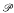/poly map g; they express that a string is outside of the range of g, Maps g considered here are particular pseudorandom generators. The ultimate goal is to deduce the hardness of the τ-formulas for at least EF from some general, plausible computational hardness hypothesis.

In this paper we introduce the notions of pseudo-surjective and iterable functions (related to free functions of [15]). These two properties imply the hardness of the τ-formulas from the function but unlike the hardness they are preserved under composition and iteration. We link the existence of maps with these two properties to the provability of circuit lower bounds, and we characterize maps g yielding hard τ-formulas in terms of a hitting set type property (all relative to a propositional proof system). We show that a proof system containing EF admits a pseudo-surjective function unless it simulates a proof system WF introduced by Jeřábek [11]. an extension of EF.

We propose a concrete map g as a candidate function possibly pseudo-surjective or free for strong proof systems. The map is defined as a Nisan-Wigderson generator based on a random function and on a random sparse matrix. We prove that it is iterable in a particular way in resolution, yielding the output/input ratio n3 −ε (that improves upon a direct construction of Alekhnovich et al. [2]).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 1 , March 2004 , pp. 265 - 286
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ajtai, M., The complexity of the pigeonhole principle, Proceedings of the IEEE 29th Annual Symposium on Foundation of Computer Science, 1988, pp. 346–355.Google Scholar
[2]Alekhnovich, M., Ben-Sasson, E., Razborov, A. A., and Wigderson, A., Pseudorandom generators in propositional proof complexity, Electronic Colloquium on Computational Complexity, vol. 23, 2000. abstract in Proceedings of the 41st Annual Symposium on Foundation of Computer Science, 2000, pp. 43–53.Google Scholar
[3]Atserias, A. and Bonet, M. L., On the automatizability of resolution and related propositional proof systems, 11th Annual Conference of the European Association for Computer Science Logic (CSL), Lecture Notes in Computer Science, vol. 2471, Springer-Verlag, 2002, pp. 569–583.Google Scholar
[4]Ben-Sasson, E. and Wigderson, A., Short proofs are narrow—resolution made simple, Proceedings of the 31st ACM Symposium on Theory of Computation, 1999, pp. 517–526.Google Scholar
[5]Buss, S. R., Impagliazzo, R., Krajíček, J., Pudlák, P., Razborov, A. A., and Sgall, J., Proof complexity in algebraic systems and bounded depth Frege systems with modular counting, Computational Complexity, vol. 6 (1996/1997), no. 3, pp. 256–298.CrossRefGoogle Scholar
[6]Cook, S. A., Feasibly constructive proofs and the propositional calculus, Proceedings of the 7th Annual ACM Symposium on Theory of Computing, ACM Press, 1975, pp. 83–97.Google Scholar
[7]Cook, S. A. and Reckhow, A. R., The relative efficiency of propositional proof systems, this Journal, vol. 44 (1979), no. 1, pp. 36–50.Google Scholar
[8]Goldreich, O., Candidate one-way functions based on expander graphs, Electronic Colloquium on Computational Complexity, vol. 90 (2000).Google Scholar
[9]Goldreich, O., Goldwasser, S., and Micali, S., HOW to construct random functions, Journal of the ACM, vol. 33 (1986), no. 4, pp. 792–807.Google Scholar
[10]Impagliazzo, R. and Wigderson, A., P = BPP unless E has sub-exponential circuits: derandomizing the XOR lemma, Proceedings of the 29th Annual ACM Symposium on Theory of Computing, 1997, pp. 220–229.Google Scholar
[11]Jeřábek, E., Dual weak pigeonhole principle, Boolean complexity, and derandomization, Annals of Pure and Applied Logic, to appear.Google Scholar
[12]Krajíček, J., NO counter-example interpretation and interactive computation, Logic from Computer Science, Proceedings of a Workshop held November 13–17, 1989, in Berkeley (Moschovakis, Y. N., editor), Mathematical Sciences Research Institute Publication, vol. 21, Springer-Verlag, 1992, pp. 287–293.Google Scholar
[13]Krajíček, J., Bounded arithmetic, propositional logic, and complexity theory, Encyclopedia of Mathematics and its Applications, vol. 60, Cambridge University Press, 1995.CrossRefGoogle Scholar
[14]Krajíček, J., On the weak pigeonhole principle, Fundamenta Mathematicae, vol. 170 (2001). no. 1-3, pp. 123–140.Google Scholar
[15]Krajíček, J., Tautologies from pseudo-random generators, The Bulletin of Symbolic Logic, vol. 7 (2001), no. 2, pp. 197–212.Google Scholar
[16]Krajíček, J., Hardness assumptions in the foundations of theoretical computer science, preprint in ITI series: http://iti.mff.cuni.cz/series/index.html, 01 2003.Google Scholar
[17]Krajíček, J. and Pudlák, P., Propositional proof systems, the consistency of first order theories and the complexity of computations, this Journal, vol. 54 (1989), no. 3, pp. 1063–1079.Google Scholar
[18]Krajíček, J. and Pudlák, P., Propositional provability in models of weak arithmetic, Computer Science Logic (Kaiserlautern, October '89) (Boerger, E., Kleine-Bunning, H., and Richter, M. M., editors). Lecture Notes in Computer Science, vol. 440, Springer-Verlag, 1990, pp. 193–210.Google Scholar
[19]Krajíček, J. and Pudlák, P., Some consequences of cryptographical conjectures for and EF, Information and Computation, vol. 140 (1998), no. 1, pp. 82–94.CrossRefGoogle Scholar
[20]Krajíček, J., Pudlák, P., and Sgall, J., Interactive computations of optimal solutions, Mathematical Foundations of Computer Science (B. Bystrica, August '90) (Rovan, B., editor). Lecture Notes in Computer Science, vol. 452, Springer-Verlag, 1990, pp. 48–60.Google Scholar
[21]Nisan, N. and Wigderson, A., Hardness versus randomness, Journal of Computer and System Sciences, vol. 49 (1994), pp. 149–167.Google Scholar
[22]Paris, J. B. and Wilkie, A. J., Counting problems in bounded arithmetic, Methods in Mathematical Logic, Lecture Notes in Mathematics, vol. 1130, Springer-Verlag, 1985, pp. 317–340.Google Scholar
[23]Paris, J. B., Wilkie, A. J., and Woods, A. R., Provability of the pigeonhole principle and the existence of infinitely many primes, this Journal, vol. 53 (1988), pp. 1235–1244.Google Scholar
[24]Pudlák, P., Some relations between subsystems of arithmetic and the complexity of computations, Logic from Computer Science, Proceedings of a Workshop held November 13–17, 1989, in Berkeley (Moschovakis, Y. N., editor). Mathematical Sciences Research Institute Publication, vol. 21, Springer-Verlag, 1992, pp. 499–519.Google Scholar
[25]Pudlák, P., The lengths of proofs, Handbook of proof theory (Buss, S. R., editor), Elsevier, 1998. pp. 547–637.CrossRefGoogle Scholar
[26]Razborov, A. A., Pseudorandom generators hard for k-DNF resolution and polynomial calculus resolution, preprint, 05 2003.Google Scholar
[27]Razborov, A. A., Unprovability of lower bounds on the circuit size in certain fragments of bounded arithmetic, Rossiĭskaya Akademiya Nauk, Seriya Matematicheskaya, vol. 59 (1995), no. 1, pp. 201–224.Google Scholar
[28]Razborov, A. A., Resolution lower bounds for perfect matching principles, Proceedings of the 17th IEEE Conference on Computational Complexity, 2002, pp. 29–38.Google Scholar
[29]Rudich, S., Super-bits, demi-bits, and ÑP/q poly-natural proofs, Proceedings of the 1st International Symposium on Randomization and Approximation Techniques in Computer Science, Lecture Notes in Computer Science, vol. 1269, Springer-Verlag, 1997, pp. 85–93.Google Scholar